{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "# Warning\n",
    "\n",
    "This tutorial is a work in progress, it does not cover all the functionalities yet. However, it will give you a good overview how you can generate tumor segmentations with BraTS Toolkit.\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "# Glioma segmentation with BraTS Toolkit\n",
    "\n",
    "In this Notebook, we will demonstrate how to preprocess brain MR images with the [BrainLes preprocessing package](https://github.com/BrainLesion/preprocessing/tree/main/brainles_preprocessing). Following we will generate glioma segmentations with multiple algorithms from [BraTS Toolkit](https://github.com/neuronflow/BraTS-Toolkit) and fuse them together.\n",
    "\n",
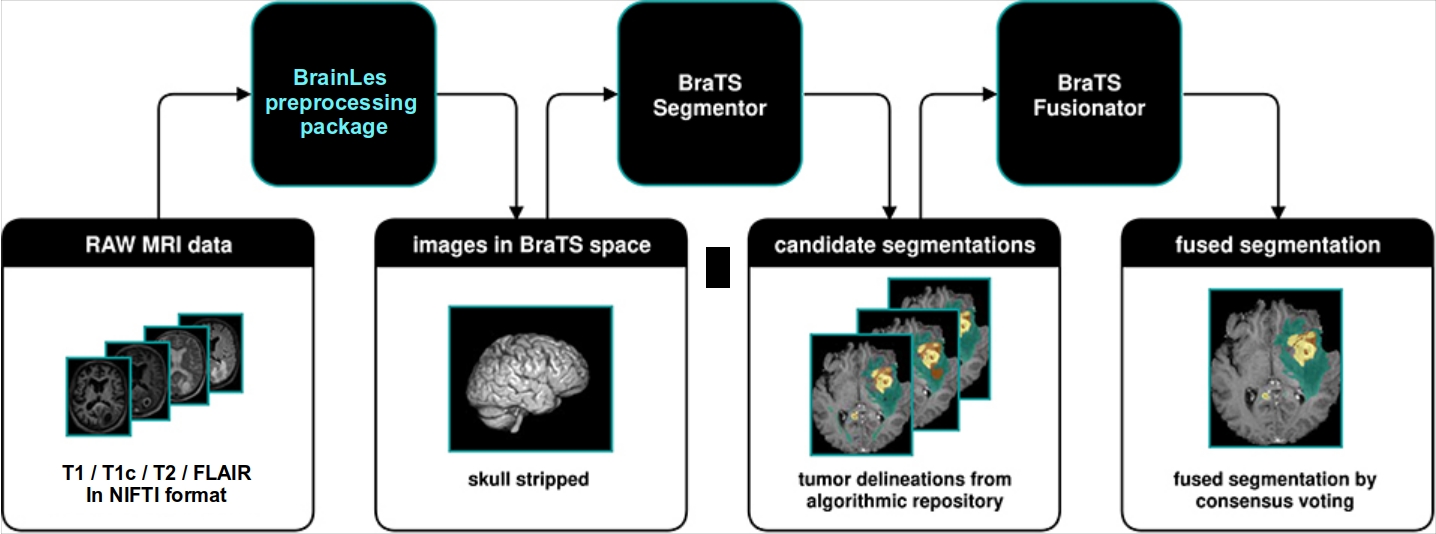    "![Pipeline Overview](Pipeline_overview.jpg)\n",
    "\n",
    "---   \n",
    "### Agenda: \n",
    "\n",
    "1. Getting started (requirements, installations)\n",
    "  \n",
    "         \n",
    "2. **Import** of raw data (cMRI)\n",
    "    \n",
    "        \n",
    "3. **Preprocessing via BrainLes preprocessig package** instead of vanilla preprocessing pipeline from BraTS Toolkit. BraTS challenge algorithms expect preprocessed files (co-registered, skullstripped in SRI-24 space)\n",
    "     \n",
    "          \n",
    "4. **Segmentation with BraTS Toolkit** \n",
    "      \n",
    "            \n",
    "5. **Fusion** of generated segementations \n",
    "\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## 1. Getting Started\n",
    "\n",
    "### Requirements\n",
    "\n",
    "This tutorial requires:\n",
    "\n",
    "- Python 3.10+ environment\n",
    "- Docker (we recommended the most recent version)\n",
    "<!-- TODO specify version -->\n",
    "\n",
    "optional (but recommended):\n",
    "\n",
    "- CUDA drivers\n",
    "- a GPU that is supported (each algorithms supports different set of GPUs)\n",
    "<!-- TODO specify -->\n",
    "\n",
    "Run the subsequent cell to check CUDA availability, your python and docker version.  "
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 1,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Python 3.10.12 (main, Nov 20 2023, 15:14:05) [GCC 11.4.0]\n",
      "CUDA is available with 1 device(s): NVIDIA GeForce GTX 1660 SUPER\n",
      "Docker version 24.0.5, build 24.0.5-0ubuntu1~22.04.1\n"
     ]
    }
   ],
   "source": [
    "# Your python version (in this notebook) is:\n",
    "import sys\n",
    "\n",
    "print(f\"Python {sys.version}\")\n",
    "\n",
    "# Check if CUDA is available\n",
    "import torch\n",
    "\n",
    "if torch.cuda.is_available():\n",
    "    # Get the number of available CUDA devices\n",
    "    num_cuda_devices = torch.cuda.device_count()\n",
    "    print(\n",
    "        f\"CUDA is available with {num_cuda_devices} device(s): {torch.cuda.get_device_name()}\"\n",
    "    )\n",
    "else:\n",
    "    print(\"CUDA is not available on this system.\")\n",
    "\n",
    "\n",
    "# Print docker version\n",
    "import subprocess\n",
    "\n",
    "try:\n",
    "    result = subprocess.run([\"docker\", \"--version\"])\n",
    "except FileNotFoundError as e:\n",
    "    print(\n",
    "        \"'docker' seems not to be installed. For installation guide see https://docs.docker.com/get-docker/\"\n",
    "    )"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Installation of dependencies\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 2,
   "metadata": {},
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Note: you may need to restart the kernel to use updated packages.\n",
      "Note: you may need to restart the kernel to use updated packages.\n"
     ]
    }
   ],
   "source": [
    "%pip install -U brainles_preprocessing brats_toolkit auxiliary > /dev/null\n",
    "%pip install -U matplotlib > /dev/null\n",
    "\n",
    "%load_ext autoreload\n",
    "%autoreload 2\n",
    "\n",
    "# package installation may take a while"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## Setup Colab environment (optional)\n",
    "\n",
    "If you installed the packages and requirements on your own machine, you can skip this section and start from the import section. Otherwise you can follow and execute the tutorial on your browser. In order to start working on the notebook, click on the following button, this will open this page in the Colab environment and you will be able to execute the code on your own (*Google account required*).\n",
    "\n",
    "<a target=\"_blank\" href=\"https://colab.research.google.com/github/BrainLesion/tutorials/blob/main/BraTS-Toolkit/glioma_segmentation_with_BraTS_Toolkit.ipynb\">\n",
    "  <img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open In Colab\"/>\n",
    "</a>\n",
    "\n",
    "(EVA VERSION):\n",
    "<a target=\"_blank\" href=\"https://colab.research.google.com/github/evamariie/tutorials/blob/main/BraTS-Toolkit/glioma_segmentation_with_BraTS_Toolkit.ipynb\">\n",
    "  <img src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"\"/>\n",
    "</a>\n",
    "\n",
    "Now that you are visualizing the notebook in Colab, run the next cell to install the packages we will use. There are few things you should follow in order to properly set the notebook up:\n",
    "\n",
    "- Warning: This notebook was not authored by Google. Click on 'Run anyway'.\n",
    "- When the installation commands are done, there might be \"Restart runtime\" button at the end of the output. Please, click it.\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "If you run the next cell in a Google Colab environment, it will **clone the 'tutorials' repository** in your google drive. This will create a **new folder** called \"tutorials\" in **your Google Drive**.\n",
    "All generated file will be created/uploaded to your Google Drive respectively.\n",
    "\n",
    "After the first execution of the next cell, you might receive some warnings and notifications, please follow these instructions:\n",
    "   - 'Permit this notebook to access your Google Drive files?' Click on 'Yes', and select your account.\n",
    "   - Google Drive for desktop wants to access your Google Account. Click on 'Allow'.\n",
    "\n",
    "This will create the \"tutorials\" folder. You can navigate it through the lefthand panel in Colab. You might also have received an email that informs you about the access on your Google Drive."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 3,
   "metadata": {},
   "outputs": [],
   "source": [
    "import sys\n",
    "\n",
    "# Check if we are in google colab currently\n",
    "try:\n",
    "    import google.colab\n",
    "\n",
    "    colabFlag = True\n",
    "except ImportError as r:\n",
    "    colabFlag = False\n",
    "\n",
    "# Execute certain steps only if we are in a colab environment\n",
    "if colabFlag:\n",
    "    # Create a folder in your Google Drive\n",
    "    from google.colab import drive\n",
    "\n",
    "    drive.mount(\"/content/drive\")\n",
    "    # clone repository and set path\n",
    "    !git clone https://github.com/BrainLesion/tutorials.git /content/drive/MyDrive/tutorials\n",
    "    BASE_PATH = \"/content/drive/MyDrive/tutorials/BraTS-Toolkit/\"\n",
    "    sys.path.insert(0, BASE_PATH)\n",
    "\n",
    "else:  # normal jupyter notebook environment\n",
    "    BASE_PATH = \"./\"  # current working directory would be BraTs-Toolkit anyways if you are not in colab"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## 2. Import raw input data\n",
    "\n",
    "Raw imput data require\n",
    "- exam with skull and 4 sequences (T1, T1c, T2, T2-FLAIR), only one file each (in total 4 files) \n",
    "    - file names must end with \"*t1.nii.gz\", \"*t1c.nii.gz\", \"*t2.nii.gz\" and \"*fla.nii.gz\"\n",
    "    - [Nifti \".nii.gz\"](https://brainder.org/2012/09/23/the-nifti-file-format/) file type \n",
    "- each exam (4 files) needs to be places in an individual folder within the data folder \n",
    "```<this repository>/BraTS-Toolkit/data/```. \n",
    "\n",
    "The structure is shown using two example exams:\n",
    "```\n",
    "BraTS-Toolkit\n",
    "├── data\n",
    "│   ├── TCGA-DU-7294\n",
    "│   │   ├── *_t1c.nii.gz\n",
    "│   │   ├── *_t1.nii.gz\n",
    "│   │   ├── *_t2.nii.gz\n",
    "│   │   ├── *_fla.nii.gz\n",
    "│   ├── OtherEXampleFromTCIA\n",
    "│   │   ├── *_t1c.nii.gz\n",
    "│   │   ├── *_t1.nii.gz\n",
    "│   │   ├── *_t2.nii.gz\n",
    "│   │   ├── *_fla.nii.gz\n",
    "```\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### Example Data\n",
    "Two examples of cMRI from TCIA/TCGA with T1, T1c, T2, T2-FLAIR with skull are provided.\n",
    "\n",
    "Run the subsequent cell for visualizing one example sample.\n",
    " "
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 4,
   "metadata": {
    "scrolled": false
   },
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "/home/eva/.local/lib/python3.10/site-packages/matplotlib/projections/__init__.py:63: UserWarning: Unable to import Axes3D. This may be due to multiple versions of Matplotlib being installed (e.g. as a system package and as a pip package). As a result, the 3D projection is not available.\n",
      "  warnings.warn(\"Unable to import Axes3D. This may be due to multiple versions of \"\n"
     ]
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAqwAAADRCAYAAAAJ4eAGAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/H5lhTAAAACXBIWXMAAAsTAAALEwEAmpwYAAEAAElEQVR4nOz9WaxkWXoein07hhPzPJ15zOlkZY3s6mY3iy3yQqAs0YJE8EWCYfgC1pPhp2tAsP3iC/veFwPSNaF7bcAyYAuCYECAL0i1IDab7IFNNtnF7uqasjIr5zOPEXFink5EbD+c+lb+sXLtHZHF7jyndOMHDk7Ejr3XXsO//vX9w/qXZds2pjSlKU1pSlOa0pSmNKWrSp7LrsCUpjSlKU1pSlOa0pSm5EZTwDqlKU1pSlOa0pSmNKUrTVPAOqUpTWlKU5rSlKY0pStNU8A6pSlNaUpTmtKUpjSlK01TwDqlKU1pSlOa0pSmNKUrTVPAOqUpTWlKU5rSlKY0pStNU8A6pSlNaUpTmtKUpvQlyLKsm5ZlfWRZVt2yrLJlWf/NhM/9sWVZ/6tfdf3+cyLfZVdgSlOa0pSmNKUpTekrSv8cwA9t237Lsqz/z6QP2bb99391VfrPk6YW1ilNaUpTmtKUpjSlL0crAD77ZRZoWdbUmGigKWCd0pSmNKUpTWlKU3pJsizrBwB+G8B/b1lWA8CM+C1lWdZ/tCzr1LKssy8+L4rff2RZ1j/74vN/aVnWTyzL+u8syyoB+K9fcVO+EjQFrFOa0pSmNKUpTWlKL0m2bf8XAP4CwP/Wtu0ogJ742QPg/40LC+wygDaA/96luG8AeAqgAOC//ZVU+CtOU7PzlKY0pSlNaUpTmtIvkWzbLgH4//G7ZVn/LYAfujxyYNv2v/ric/9XWbevKk0B65SmNKUpTWlKU5rSL5EsywoD+O8A/M8ApL64HLMsy2vb9sDwyO4rq9xXlKYhAVOa0pSmNKUpTWlKv1z63wG4CeAbtm3HAXz7i+uWw/32K6nVV5imgHVKU5rSlKZ0JcmyrC3Lsv7uF59vWJb1R19sYilblvUnlmXdvOw6TmlKDhTDRdxqxbKsNID/0yXX5ytPU8A6pSlNaUpT+ipQEsB/wIXVqgDgbwD80WVWaEpTcqH/G4AQgCKAnwL47qXW5j8Dsmx7aoWe0pSmNKUpXS2yLOvfAvhfAOgCGAD4P9u2/X8Vv6cBlABkv9jgMqUpTek/Y5oC1ilNaUpTmtKVJMuytgD8M9u2/8zw2z8G8P+wbXvuVddrSlOa0qunaUjAlKY0pSlN6StFXyRg/x8A/FeXXZcpTWlKr4amgHVKU5rSlKb0lSHLsnIAvgfg/27b9v/3suszpSlN6dXQFLBOaUpTmtKUriqNxKxZlpXCBVj9D7ZtT08DmtKU/idEU8A6pSlNaUpTuqp0DGAdACzLigP4EwA/sW37f3+ptZrSlKb0ymm66WpKU5rSlKZ0JcmyrH8E4F8BiOPi1KD/GkALo5bX27Zt77z62k1JkmVZtmW9mBNfxxjyHo/Hg+FwqO4zPc9nbNuGx+NR5enf5X3yvbJMftbrpN/LusjrlmVhOBw61t+p3iyH9/F5Wb68LsvT26c/xzqZ3su6yjL4LNunf9fJDR/q9dev6//135zKHw6HTgcrTAHrlKY0pSlNaUpT+tuRDlh1sCLuG/md1wicdJAmwZXpOQkExwFP+ZsJTPLdOuAi+JPPAlDXndqoAzO9LfJ3E8A2AWtTe5y+O4FQE1iV3031cAOZpveaxsKNxFg4AtZpSMCUpjSlKU1pSlP6pZIODCVQk9f1Z3TwZQJwOpAELsCmCYjpAFe+ZzAYOFr/nK7pdXGj4XDoep8EiPyuW5z19hHUm/rPqWz9Pr7HCfjrJPtVb7upHibgKn/Tx0Mv04l8Y++Y0pSmNKUpTWlKUxpDTm7iceRkjdPBHACji9sJcLlZIk1WUd2NbrLq8jvDAfQ6ezyekTKd2sT3yftJLFe3HpvKk232eDwYDAZGAKkDeb5XPquHF0iLt+l98h6nfnKy+I6zBJtoClinNKUpTWlKU5rSL41s24bX6zVa+dxCBEwuav0+CeJMYMpUtv5dB1Wsqw4MdUAqr0ugJssyAVM91MEp/EGvrymGdTgcwuv1qnfL/pBgVXfxyz7T+8QpFlXW1VQ3p5AI2X59/MeFNLjRNCRgSlOa0pSmNKUp/a1JghvdHW4Cqk5AyRRCoP+ugz+TVdb0u9s9Tt/1e2Ud9HaaYlR1a6KTi93Jfe4Ua6pvAjMBdN0qK5/XQywkSWurW3v097lZYk2/vYxFfrrpakpTmtKUrhBZYvOKm+WDpMeE6W44UzyZKTbPybL1skSrkL6YmtrxMpYWU10luVnyTNYs+U59s40OEsaBFzdyG0unMdA/m8Z1XH3cNq/8KshyyBIwCbiZhBecyjbx2aTlSjAnN1Y5gSvdTS//65ZIJ3e3bsnVwxDcrJlO1l8Tz4wLkdD70amOer859fU4a7dOTvJmmiVgSlOa0pS+IsSF32nR1e594bube27cYqqXO+69k4Io/V3jgJ4TYDEt6DqYM/Wd2zNO9ZkEYLpdN71Tluv2flM7TORWb9u2rwRglfGNwIvAUDzvOObyfifeexked+ILPqfHyUqgKst2UoIYm2qqow5WTTGspvk3TnFyajvbMy79ldO73YC0qY9l35qeMQF8OcaDwWCaJWBKU5rSlL4qpFsHdUuK/nkS4Oj27LjPbnXU73OyYDkBQDdQ7FRPvVwdzOjPuIFRuVg61dMJpDot2PK/7CeT1c7JkqcDJjeaxBr5KsgJ+OjuZdlO/bP808vR+9LEezpQ0suTpANT/qc1k3/yu1OdTCAceNG1bgLfet/pbXNTXp341QTmTaT3td63en869b2pTqZxNj3L39xy2gJTC+uUpjSlKV0psizL/uL/yHUTKDUBHP1+/fNL1OMFy9A4K5fp3ZNcn7QepmtOYFRalUz3m0CAXpa0lL1sneU73Nr0ZfrEjYT17pVbWHVrqg7ITEnx3RQNh/e8wIOyPNO9slydj53AoH6vvGayPprqJl35sj9MSpYp/6wTb+h1YporCawt68UwA1O/6e92UiydwLV8xgS69T4cp1hP87BOaUpTmtJXiJwWKf27CfS4Wf2cyGmRcnpet8BMUqZ+v5OFUpKpzXrZJsulG8h0s16Z3vFlwaob6fUd1w9fVXJTCiSYkffyHifLqH7NZI3V308yud9JulXV9B69zHEbk2TcKZ81nexlskCa5o+TNVWPZ3Xqky8DVk1joM9/AmZZhpsi5qR4j6MpYH0Jsixry7Ksvyu+/z8ty3pgWdbQsqz/8hKrNqUpvUBTfv3Ph5yAm5tFQyc3N57TM/r73MrQF0EuStIaNQ4E6GUPh8OxbkL9/aZ3ync5tVMCBRPQcgIQ8t5J+slE4yyy+judfpNlXQaZlBC9nySQ0S2COm/ov+lWQvleySv6WOpWPt3qaVkWvF6vsUwTMHNTHnWFyfQb/8u68hADnXf19jqBXqa08ng8LwBzJ+uzPkdNSoIJWLIvTOMk62Wyrup9Kd8xjnengPVvRx8D+N8A+MVlV2RKU5qApvz6FSUnq6D+mxvwGQdK3SwiTtYQp89OIE6vj6mOpjImuV9/hwlwSADgpAQ4veNllIZxZTrRuPt1AMB3XhUyKQ3yOmC2sJoUC30zkARFpn6WYyrBlA6Oed20GUwvS9bJCXSbAJ+sp2yTqb6TAGCn1FnyXXp4guR/0zt0QO9WZ/k+AmK9L9zmlv5OkgTe8r8TTQHrhGRZ1r8FsAzgO5ZlNSzL+ue2bf8Ptm1/H0Dnkqs3pSmN0Mvyq2VZXsuy/o+WZT2xLKtuWdYHlmUtvfKKT2kiGmeZ0BeuSS13uqVkHJksMyYgNwkQ1hctt4XPBNxITsnYXxZQ633oRk51cSvTjcbdN65vLwvEjht7HSSynbol3ckyLvvZaXe9aSxMypIEdG7WUP1EKPkeva6mMmWbfD7fyIEKbLdeB92roIN6vQ91QK3Hbg8Gg5F7TYcHSMCpt1fvS/kHYMQ6rD/vNC90gDwJz05PupqQbNv+X1qW9ZsA/plt23922fWZ0pTc6Evw638F4J8C+AcAHgJ4A0DrV1jFKY0h3fLBa5LcgKXTwuFmqTS9R1/EdZCp1xF48ZhHJwChP/NlwLLejknLcLIkOV13u8dpsdX7y6RYOAFp/TmnvLa6hcv0nqtCTn3hBFokEJP36+mgnMbcxMc6mHSzbspynMbcdF1X3HiNwM7tffI52U7TsbFu/OPULzKtGO8xHQEry+GRr3qZ+r0sy0nmOCmK4+YRaQpYpzSlKQHAPwPwz23bfvDF948vszJTmsxlri8WL1PeJIBYJycriqlMUz3d2mZ6l25lnbTNTmBW/246O90EINxAulufjQNgJougExBx6utJLWOvgsaB0HHWTxMwdXqPXq4JFOll6/XU66v3qUkRk9dNuVad6mJK5K8/b9ujOWClRVovk+VJ4E7rrd5Ovc0m3neyduqg04m/3BQ9pzGR9ZlE0ZyGBExpSlMCgCUATy67ElNyJjfQN87yalowJgWRJkuSGzAxbWgxWaic3jOuDU7fec1UTyfrm2mDiuk+J2urbq1zq7+ss9vCPE5pkOWPUwwukyQgJ42zuMn4SAkKJUkw5wQOTf9lvSTP6vyqWxz1Nshr+n3yfdLSqHsb+A5985RuyTTF4urtl9fclCh5zSlswWm8nOKJ9Wflb/JPkikcYZJ5AUwtrC9LlxMYNKUpfTl6GX7dBbAB4O6vqC5T+pJksiiOs/LpVhyn9DuTHJ8q36eDT1P93ECEm6VFJ5MFWJbhdL+sF9tnAnNOeUDd6mU6ftJkJTWVY6qfG+CV5NRfTlbEywKuuqVXb5/JUih/IzkpRG5KgH7NacxNz4xTqkzzTILNfr8/kfXYifR5I8t1Cn3QLa1O/er0/knmvZOyYeonJ5kk5Y8+LpMAbUlTwPpydAxgnV8sy5rBhZXaAuC3LCsIoGfb9mR5WKY0pV8tvQy//r8A/F8sy7oH4DGA1wHs27ZdevXVntI4YKdf53cTOHWKJR0H1CYFB+Pq5va7DiadQIvpebZVB8pssw6e9MXUDQjpQN303CQg17S4m95v6gtJ4/pTL+cyaZK6yu8mPmY5OnAyAUb5rM4T8n7pftcVB/nZCRBOwvu0enq9Xvh8vpE2DIdD9Pt9VZZtv5jFwo3/TTxsUmZlPUyAUALJceB23BxkuU6KHNvoZJ3VU3uN493pSVcvQZZl/SMA/wpAHMB/A+B/DuDvaLf9tm3bP3rFVZvSlF6gl+FXy7K8AP4PAP7XALIAPgfwe7Zt773CKk8JgPXFSVdffH7hdx3gmT67lD1SzgR1meg+0zMmsKYnOJf1dgLMTiBbAleTpdKprfpzkiatA38ztVUvb1IAOem9ep86vd+27VeKXC3Lsp2szU6WOhJd4U7td1LanO51sgLqz7spcG75fz0eD/x+P0KhkNr9HwgE4PV6EQgE4Pf7MTMzg1gsBp/Ph3a7jeFwiF6vh16vh/Pzc3S7XbTbbbTbbXXdLTuAVMRYX5lxQG+rSek1gV2ne/V66DTunU79auINqUj0+31Hvp0C1ilNaUpTukIkAesX313BjG7tIL0MWJLl6DTJu90WP5N1RQedTpYjExhzepduydHBk2lRdnqv3n5Tu53qp7/DicaNjwlQ6XU2tU/c/8oBq1OqKd3SyOskNyVMliM/c8yB0VANKiMkfde65D1TSIwOGr1eL7xerwKgiUQCyWQSiUQCMzMziMfjiMfjCAaDCAQCCIVCGA6HODk5QalUgt/vRyqVQigUQigUwmAwQKfTQb1eR7vdRqVSQblcRrVaRaVSQb1eR7PZVNZYWQ857uPCeUwyYZzCauJJk4JmutdNkXKa1/pzX1hkp4B1SlOa0pS+CkRL1csAwb/Fu760BdXtO+vrZiU1WcFM5TpYD40LqxOYM5VveofTIvqy/SPrJMsx1c1EboB0XP+KMl45YJUWP9af9ZNWbQm4+FmGs5gS04v3jLyXlkbd+shy5Pv5PjkeJAlUfT4fwuEwYrEYstks0uk0CoUCUqkUkskkMpkMvF6vAqmsl3T7p1IpDIdD7O3t4eTkBOVyGcFgEJlMBqlUCn6/X1laG40GisUiyuUy9vf3US6XUSwWUa1W0ev1RsZ+XOy1bKMJfOshDnraLPmbNr7Geaj3sSnzgT7P5Fjr5U4B65SmNKUpfUWIgBV4OTexk9XS5T0T3Tfpe1+27ElAm36f02I4rj6mhdQNxOrXncZgEmCrg6NxVrFJFRE3S+QX77sUwDrJRj5Tv5ksyvpY6e01pZWSO+1NfKi/Q9ZrZmYGmUwG8/PzWFlZwcLCAnK5HJLJJAKBgHp/s9lUQLJer6Pb7Y649Pv9PobDIdLpNGZnZ+H3+7G7u4u7d+/i/Pwcfr8fhUIB8/PzylJLqtVqODg4wNHREXZ3d3F4eIjT01NVPkEr6+80ByRg1ZUHp37XwavbWI5ToJ3mjwSsJqVsClinNKUpTekrQibAOgnYcbO86ZYQE7lZLZ1+dyrDZPkxWcpM5TtYC13f+zJkAvamd5jqMmld5X16jO3LWsadwLn+TsO1SwkJcOpHp/7S2ySBlpM1UX9WT4bPZ6WF0WnzYSAQQDweR6FQwPXr13H9+nXMzs4iFouh3W7D6/Wi3W7j7OwMxWIRpVIJtVoNtVoNnU5nJD2VKdWW1+tFOp3GysoKLMtSbv9qtQqPx4N0Oo1cLqcsr6lUCl6vF91uF4eHh9jd3cXW1ha2t7dxenqKTqcz8i7ZJtlPbL8ORnmv/rs+L2Q/6cDSSQlzs/rKPnfjk8FgMAWsU5rSlKb0VSDrixhW0wLxsmAHcLc6msDCy6wJEqBKi4y+ucoEWNzA4suQbn1z2yyj10c+Z7LU6S5NvQxTX5je4wTaf5XkZqn6VZAErG59Z+on+dnBWgzADLq+sMqN8KE+NrS4ynKDwSBWVlawurqKzc1N3LhxA7lcDoPBQMWVVioVHBwc4Pj4GJVKBZ1OR22WknXx+Xzqv9frhWVZIxbZTCaDarUKACqEoNvtotPpqLoy/CCfz6vQg2g0ik6ng4ODA+zt7eHJkyfY29vD2dkZzs/PVZ/owF0nj8ejwgEGg8ELYF4fCxOYdEsR51SGCdDK+/R5+AX4nwLWKU1pSlP6KpC0sEpyAkT653GWOJO1RAcG8h18znTNqQ4m4AE4pyKSz+h14GLr8/ng8/kQi8WQTqcRjUYRDofh9XoxGAzQ7/dxfn6u/vd6PbTbbQUyut0uzs/PlUXM6ZhM2TY9llK/dxxoHXddluV2pKXpupul/Iv/rxyw6qDRpJToQN4EMnUgKt7xwnPA80T4+jzQ+8jn8yGZTOLWrVv42te+huvXr2NpaQnRaFS54Hd2drC3t4fT01PUajUVk+rz+VRGgHg8DgAIhUJqA1UwGIRt2+h2uwiHwyprAMMMjo6OMBgM4Pf7VZnHx8col8sIh8OYmZnBzMwMwuEwIpGICkXI5XIIBoNot9sol8v4/PPPsbW1hYODA7RaLVWW1+sd6WcCevaJDNfgPfp3w5g6zhH5Lp30uW9y/+u8wOe+NGC1DOlVxmmZ+qTUGVJnVL2B4ya76Tm38kz1cnvXuHJNdZj0N7d3yXrKPjMl/B7XBqfFy0l7chIqsqxx/e42nq9a0//ivX8rTWySSTxugXZbyE0T1cRnfEbe4wQeTPUzlT2Op03lO1031cmpXi/zu9Mzr1rBftWLPjBZDKvTPJW/v4wckvLG9G5Tv4/jDf26rDM3tCQSCYRCIQSDQfWfwMCyLIRCIcTjcQVS5+bmEAgEMBgMVCog27YVYOXnwWCgQCstY61WC+VyGaVSCYPBAKenp2g2m2g0GiMbW/Q+GUeUj6Z4StM4OMlJCbBMzzjNNaexvgwLq+wzk/yS5JQH1NRW9q++aUj2PYlAV1IgEEAul8P6+jp+4zd+A2+//TZSqRSi0SharRZ+/vOfKyB4eHgI27YVL4ZCIYTDYSQSCQQCASQSCbVJLB6Po1Qq4eTkBMViEZ1OB71eDwAQDofh8XjUu+v1Ovr9PrxeL1KpFFqtForFIqLRKEKhELrdLo6Pj1U7LctCPB5HKpXC8vIywuEwwuEw6vU6tra28Pnnn+Pw8BClUgndbveFtV6CVPY3AKXgAXAEkrIvTWuWaXxM4yjL0cdXv0eM3d8OsDotpKYKmhZyncaBHf0+p+/j7nV6v37/ywDYcb9/WcA6boFye2bcQj5O2OlljAMzpnud+vMLgfKVA6wTvgPA+Png9JsJIMhy9bK/DDCU7xqnqJjGlf9NqWj059wAvKkNTvNl3HO/TBpX7mXy7jhFZxK5Jcocq1yZZO0kckV+14GX/N3n8yEajaoNLblcDvF4HNlsVgFXCWTD4TB8Ph+GwyG63S5KpRL29/dxdHSEcrmM8/NzZT21rItk7X6/H8FgEJFIRFmtCByY5/P4+BhHR0dIJpM4OjrC6empSkFUqVTU4k8yHQ2qy95x/TWpEjCur93msf7bZQJWyWsmMK7XWYJONz6Vv+tlAaPHAhMsLiws4Nq1a3jttdewubmJQqGA4XCIdruN3d1dfPrpp3j48CGKxaICk5lMBrFYDLFYDNFoVLn3Z2ZmkEwmUavV0Gq1cHZ2hmfPnuHs7Az9fh/lchm9Xg+DwUBtpJLeAcashsNhBINB5HI5BSB7vR4ajYbKDNDv99Hr9eD1epHJZJDP5zE3N4d8Po9+v4+9vT3s7OxgZ2cHBwcHqg6y37nGyL6VsavjvBt6Hw+HQ5VeS7fOjuN/J4ygX/vSMaxugPVlQIsbuSFzp0VQnxROgM+tfqZ3Two09YFxA9ymcr/se93eNY5M/TVOKxr3zknALvDqBecX9fiVWVhN97ktKG6T1Y2cAKUTr7uNnVtMmbzXqc6mMp3aqZNbWaa6jwPlvyrw6lC3S7Owusm4L+4bV47rgj+uX8ctMvoCp+fCJDFXZTgcRjwex2/+5m8ik8kgEAggHA5jMBig1WqpmL5er4dms6nc941GA91uV210oQWVx1bq7mACi3A4jGg0qnJgRiIRxGIxvP3229ja2sLZ2RmWl5fRarVQq9VwcnKC3d1d7O7u4vj4GM1m84XNNLIfTOQmC5zWzC9Dk/DAZcawfvFd/dev6THOukIs22Vab02nnEmwGgqFUCgUcO3aNdy5cwcbGxtYWVkBAJyenmJ/fx9PnjzBgwcPUC6X0e/3kc1msbS0hNnZWSSTSZX03+/3w7ZtpRx1Oh0Ui0Xs7e1hd3cXlUoFgUAAmUxGHQrAAwFs21bAk3xZKBQQiURgWRYikQji8Tjy+TxmZmYU2GUu1kajgUajgX6/j2AwiHg8jrW1NeRyOfj9ftRqNZTLZezs7CjrMN9LuS9BpkkR0y2w7GMd6PK/LFeCXtOJVnL83HCQvOeXBlgnmYzjFlCnxrjRuLLJrE7A2q0ObkJdzxU2SVuc6u5UL1NbTIuU/qxss6n+ckHRmWgSYemmpEzyXz7zVQGsbguMfh/gbv009fnLAExTvdyAxqRt0q+byp5kTJ3a78RbTjzo1H43MPw/FcA65h4AkwEeNxkjP+sgwHS/fDfL1uM8+TkYDCKbzWJ1dVXlsOz3+1heXkan08HZ2ZnaLd1sNtFqtdDr9ZTFlHWKxWKwLEttaJHvZhwqQaxt2yrFEK1TdMP6fD7MzMwgGo0q0BoOh5HP5xGJRBCNRtHv93F2dobt7W1sbW1hd3cXjUZDuVDlLnAu6m5jNKm8dStDf9YkB0z8ctkhAZJ0ZUdf50zznSCL36UypMstycOJRAIbGxvY3NzEa6+9huXlZczMzKBYLGJ/fx+PHz/GkydPUCwWcX5+Do/Hg/X1dczOzmJxcVGBwX6/j3a7jfPzc5W6qtlsolar4ejoCEdHR2g0GggEAggEAiPgzrIstNttpSg1Gg20Wi00m014vV7EYjEVsxoMBhEOh7G+vo5QKAS/3w/gIjUWDxM4OztTG7SYKisWiyEcDiOXy6FWq+Hx48d4/Pgxnj17hlqtpvpDn+86rvF4POj3+2Nlty4n9Lkv265/d+JZE578WwFWt0XVSag5IeovW4apE7R6jgWGbnWQZbp9N/1mAg365HQb0Enr6wZO9L40pa+Rv+lA1g2UjavjuDH6KgHWlygbgJkPx4E4t7lhAgX6xJa/Oy2W4/jObe45LbJObXCa80786jTPTG1wm1uviq4CYDUtDIZnXpjXY96hyjaV48YrvI/38L9cxFKpFNbX17G5uYl8Po9QKISzszNlyex0OqhWq6jVahgOhwpM8ojLYDCIer2OXq+Ha9euIZlMIhQKqRABLrKmv06ng36/j1qthna7jZmZGfUbwwiAi8Tu9Xpd5cKMx+OYm5tDPB5XMa6PHj3C48ePsbe3p55jm/V4SrcxchufcePqdo9TeZchdy1x0pU+f02b7QzPvyBb9NRLgHn9te2LeM1CoYCbN2/inXfewebmJpLJJCqVCvb39/Hs2TNsb29jd3cXHo8H0WgUlmWNhKnMzMyoLAGMfSawbbVaaLVa6HQ6KJfLsKyLTAN+vx/hcBj9fh+NRgPtdlsd20oly+fzKZ7s9XoIBAKYmZlRG7Msy1KnZdEzkMlkEI1G0ev1VOw1gTO9BZlMBtevX8fi4qIKmfnss8/wwQcfoFqtqr70+/1K6dLXFP4R3Jri2N0MgiYZwfL0cZLP6WUBF+ET5+fnv1zAaqqwrJhpMdQrNk4LcwJRTu80lTkJOPwyzzqV51Qf0wLgVifTfZOCbxNzkJzKc1Ma3NqpPyuf14TJlQGsbrwFvBwgGgdQncozgTopPIAXcwiaAKWp7+XnSTbQuCkf45Qatz4wlW+qx8sA0y8zRn9bugze9Xg89rjxNsmDSYD9ONk5bswlkNAXPNu2EQgEMDc3h5s3b+L69etIpVJoNBrY2tqC1+tVKXq63a6KOaVFiSEC2WxWWcR8Ph/S6bQ6QYhuWlpafT4fer0ePB4POp2OqhPBRaPRgMfjwczMDDweD3q9HkqlEhqNBjqdjkoN5PV61caaubk5zM7OIpVKwbZtHBwc4PPPP8fTp09xfHysnpGgXadJ5K7TNSeZ6kQSLMt7LxOwmur4xT0jMs4JxJuOWjX1AWUkweo777yDd955B0tLS/B4PDg+PsbOzg6ePXuGw8NDNBoNxONxzM7Oqryng8FAxZiWSiXs7u7i7OwMlUpFbchjVgkCWsa60o1Pt79t2yoGmvxNYNrr9eDz+ZRC5ff71QYr27bV0a8AkEgksLy8DNu21cEClUoFR0dHqFarI2EwCwsLuHXrFvL5PGzbxvHxMX7yk5/gk08+QaVSUf3DNUH2t5MMkGOgr03yPicZIcMJdB6Q95me7ff7vzrAqr/c7ZoTAJoEGOn3OwE0l7Y43uc0YHr5ToJ+EgAhf3ObqG4LyJcht/51W6Sc6uXULhPAEYx+ZQCrds/I90lBkhPIk7+beMEBzBvrIst2AytOoGYSnnHitZcFrE71Mt03KZAy1XOScr4MjZENl25hFXXR73uZMl8oQ2+3DAkw3SvrIePWeF80GsXq6iquXbuG1dVVBAIBVCoV7O3toVqtwufzqY0tiURCgUTukvb5fAoMNJtN1Ot1eL1exONx2LaNZrOJmZkZhEIhVRe/30+rjAIPTOjOdEP9fh+RSATJZFK9j0diEpjQcjYcDpWblcA1Ho+jWq1id3cXn332GXZ3d5XLlf3mtqjLvp5EwXP67lSmkyy/rJAAnUypwfRYVycQJWWgBFzAc7A6MzOD5eVl3L59G2+//TYymQyGwyGOj4/x5MkTPH36FK1WS2WcWFhYQDKZRCQSURbURqOB4+Nj7O7uqlRozFfKTVGBQADZbBbn5+dIJBLIZDI4Pj7GwcEBbNtWIJSueipilUoFw+FQ8aht2+j1ekgkEiPuf/IecBFOk0qlEIlE1H2xWAzn5+c4PT1Vm7vOzs4wHA6Ry+Vw/fp1rKysIJVK4fDwED/96U/xwQcf4OzsTPU5yYnH9Ovj+NiJN03XxsmrSRStL7XpSn+B6Z5xC6gTs5rKNXWOSesaB+7cfjdNEqfnTfV1AjFOAuhlwLt+j15ft4k+CY3hgRfKc2qXU9lXFbCKewG4W5Tcrr3s/HAbQzcQOa7ObrzF36XQn0TZG3eP0xzne9zaZSpnkr58WXKai5PQVQCsLzOXXwbQm+a2fKd+r4nXKIdTqRQ2NjZU8nUAKJVKODw8xMnJCaLRqLJkcde1zLVJ8MENWNxoBUD9PhwOVYwrAGW9Yrqf4XCoYgy5acu2bWUZi8Vi6qjNaDSKSCSCmZkZteO7UqmoMILhcKisxQsLC5idnVUWuwcPHuDevXsolUqOidrd5vskysOkwNVpTfqi3y4NsEpZo9fLqb46ANfBuN5u4EJJWllZwbvvvou1tTVks1llIX327JmyiPMEqXw+j2w2C8uycHZ2hp2dHezv76sYU6Y/CwaDyipvWRb6/T6SyST8fj/K5TIWFxcxHA6xs7OjwlAKhQIWFhZUCAzTW+3s7OD4+FiFpdBbEI/HEYlE4PP5VCxtJBJRbSS4zWazSKVS8Pv9iEajSnnjiVkMWYjFYtjY2MDq6iry+TzOzs7wgx/8AJ988ok6tMAtEwPHS46H7HNTSjGnsXTCC/oaYXq3G9/6nH6QhcpK6L85LQI6k5kaM4mGJd/rdN1UV/ke/V6nDpba3CQ0rkwyuzxlYxzY1dtjesc4IORWtlM/O43TJPXSy5VlTtqXr5LG8dGk95uEqttzbuDO6RnTPSbljdfd+ntcufI+0/yU97v12aSA3Gn+uPHklyHZP181GqesmBb5ScthGfpnE2/K+6SHyOPxIJvN4rXXXsPq6iqy2axy+x8fH6tNKT6fT1mPAKj4OlpCuWCHw2ElN6LRKHw+H2zbVqDA4/GgXC7Dtm3limU8IAEBgQJ3YAeDQbUJ69mzZzg4OEAikUAikVC5OJPJJLLZLOr1utrk0u12VTaBarWKubk5ZDIZvP322wgGg/jkk09wfHz8wo53CdRMC7c+diYyyVfTOJrA3JdRzH5ZpPOjtMSbskjo8ovEe2Sye97L74lEAteuXcPbb7+N5eVlxONxdDodHB0dqY1HHo8Hs7OzWFhYQCwWQ7lcxsHBAXq9Hg4PD3F0dKQAH133wMWpU4FAAI1GYyRTwMzMDNrttlKKut0uhsMhZmdn8dZbbyn+jcViKqn/8vIyLMtCsVhEu93GYDBAMBhUllufz4dut4tKpYLBYIBCoQDLspQ3gaA7EAig0+kgGAyq0JhgMIjBYIBarYZisagyaVy7dg1LS0v4+te/DgC4d+8eyuWyshqz700y1rTrX46rPtZufMDPpt8nKUensYB1HMAxNcKpHP0eU6WdOki/rv83/SbrP8mO/3Edpwsl/T2mCWfqF6c6OoFPJyA9TpnQn5fXTXUbB56dyAloXDWA8GUEudsEdVK4TGPhxAumMTQpGePOgXcaQ/37JIvoJEBxknk+TilwAsVO75tk7H5Z5VwVMo0fr8v/JsAin9PPWjfJK52cyiRo8Hg8mJ+fx5tvvolbt24hHA6j0Whge3sb29vbyo2aTqfVZirgIq0QAJUNgNajUCiEUCiEaDSKWCymXKK0PNXrdbz//vuIRqNYW1tDtVrFvXv3cHJyouYI0xm99dZbuHPnjtrx3Wg0cHJygqOjIxwcHKBcLquz4SORCNLpNDKZDPx+v0qD1W63cXR0hMPDQzSbTZRKJaysrCCbzeL27dvw+/348MMP1QlGTvLBbU46yXQnGTKOd53KfRXkxF9sr4kH+VnmyZXlSYuf5LtIJIKVlRXcvn0b165dAwC02218+OGHymLKLBW5XA6BQAClUglnZ2cKcBKMxuNxtXvf5/ONvJeWeNu2FRhMJpMqN/BgMFBxz/LENf4RVOZyOfh8PhwdHaHb7arMAszVyqwErVYL+/v7KqOGx+NBMBhEq9WCZV1YhZlhIJlMqo1ZJycn8Pv9ODo6wqeffopqtYpOp4N8Po+1tTUV302vgB7Sw3GRSgX7XHpCnOSRHCMpK/i7U6iR/D4Jz44FrKaCnWjcC02Nk9edJrXTxB8HeGVZTmDMSVB7PB74/X4V4M9YFnkKhQSt8khA/sl4m3ELtv5dH3SdAeR9JkZwAqmTAE/9s+lZUzlXHag6jcWXAU6mhWZSxc1Uhonf5fhJoaGXP05ouNVHPqOT03nT+nvcdvLy3U5CStIkAm0cb32Z905aj1dJ8t3jMgQALy7u44CQSbbI6/q7ee9gMFB5HQuFAt59913cvHlTuUq5o96yLCSTSQX+5IYobmJhKMH8/DxyuRxisZiKSQ0Gg1hcXEQymYRlXeSrPD4+xv7+Pr797W+jUCgAAP76r/8a/+k//Sd1tnswGMR7772Hr3/962rHNYHyxsYGGo2Giqt98uQJzs7OUC6XcXR0pOIKZ2ZmlNs2kUhgZWUFpVIJ5XIZwAXQXllZwcbGhtpAc3p6OrIoj1MwnZRQfSxk//PaJIaBywCsrJteH33DD9tFHmA6MvKH3mbgOaAFoHKerq6uYn19HcFgEIeHhzg4OMCTJ09wfn6OUCiETCaDbDYLj8ejUlB1Oh1lHQWgrOvMxUovADdh8cAAn8+HQqGAZ8+ewbZtZfn0er3IZrPw+Xyo1WqIRCJqc2Gr1VI8zgMt5ufnVaw141qZX5WJ/32+C1g2HA6VV4H9wiNaW60WbPsixVU6nUYkEkEoFILX68Xp6Sl2dnYwHA7x2muvIRaL4ebNm6r/JWg1xRLzsxxT9r+si76mErDr/CzHVueXSbEJaeKQAP2lJsAkr7uVoZdnAmn68+MWM10Ay9/HaafUrOSOvkAgoLQr7mQNBoMq5Qp3+JF4UkW73VZupXq9jrOzM+U60MnUFieQ4QaITEJM7z8T4HRjEt0NY/pvasMkZb9qehng4XSv28Juekbvq0nSEunfeVJLMBhUAp6JqXkMpUkYuCkTlmWpDQEsUx7rRyGqt1Gf+7pA0/lDvtMNjMtr43jfSfA5AdlJFA+3Mi6Tf039Y1Jc+bup7/Tn5D0yx6X+HtN42fZzC4vH40GhUMDXvvY1vPnmm+h2uyqJ+t7eHmzbRqFQUNafer2OVqulQOXc3Bz8fj+GwyH8fj8sy0K321Wbrvx+P3q9Hp4+fap268fjcSQSCfzO7/wOotGoStPzd/7O38GTJ0/wl3/5l8jn8/jmN7+Jb33rWwqIBAIBVW+eopVMJrG0tIRbt25hb28P29vb2NvbU0nYeURsKpVCoVBAs9lUG3FKpRKazSYGgwFWVlawsrIC27Zx9+5dFItFY3y40/omlU99XuhzR7eEOfGKfN9lkOndupWU/6kA6c/p/cYUZrZtK8vi2toaNjc3kU6nUalU8PjxY+zs7CgAyPRktm1je3tbbeBrtVqK7whKQ6EQ0uk0ACiwqJ9ONRwOMTMzg9nZWezu7sK2bWWNJUBlnlbGcFvWRexrvV5X34fDIfL5PFqtlsodzFzBoVAI/X5fZSLg8cKsE+t+fn6OwWCgMgqk02kEg0EsLy/D6/ViZmYGh4eHqj9u3ryJ+fl5ABdhMnfv3kW5XDbGq+rrPsdvnGxwwhimzzoW08fbjVwBq+mFbkLcbRF3ArVuCxm/UxMAXuw8Ux0k6RYCliVBKtOp8EhACkiv14vd3V1cv35dme4tyxoBDCxXBmgDUDnZms0mjo+P1eYDnlrhNDjjtG4n0vvXJARNz5BJnchNK5LlOCkJlw1anQCUJCcA5NZvk4AySbrQlkJBfxd3T/O0FW4modLj8XjU4s4gfpalJ6/m/X6/H7Ozs9jc3FRWJAAqLyW9A91uVyW4pkWi2+2qBNomt51JYTKBQScQZpItpkXeSemcRMkYN+YmAXrVyEnujesjva/d+tBpDIDncYiZTAZvvvkm3nrrLQwGA+zu7mJrawvFYhEA1NGWyWRSnfozGAxU7shcLodIJILFxUV1AtbMzAwajQYODw9VkvThcIinT5/Csix11CqVtuFwiLm5Ody6dQsLCws4Pz/HW2+9hV//9V/H4uIibNtWG7ukYYFApdfrYWZmRsn7bDaL4+NjlEolZXjgBrBwOIx0Oo3z83M0m030ej1sb2/D7/cjnU5jdXUVAPDxxx+r+FqdnPrdSXbqY2EaP5P8cHrPqyBZPzmvndYD2Q65mYfPyvZRtoXDYSwsLODmzZvI5XI4Pz/H7u6ucrWHQiHMzc1hdXVVKReUXZRlPEhCKm2hUAjn5+fKwi9jPfl+Zrc4OzsbAZKUwQTW5XIZmUwGtm0rQxaPCwYuLPTM28psBMPhEIVCAYuLi/B6verwC+Yqjsfj8Hg8KtQBgIrVnpmZgd/vV3OK2Ob4+BjHx8cK+M7MzGBubk6FCzSbzZGxkbJ90rXbTW6awgBM2I+f/9aA1anS4xrjBEidnjGhd4JLmXOPpzGYJrnpeWo/BJS6FZVpLvgXDodVkHez2USn00G73cbPfvYztTlAMph0ZdB9EAqFkEgkVAqVYDCIGzduYH19HeVyGXt7e9jf31dpKZz6TZJJSDn9LvtcX8DGLUomkOH0eRIF5iqBVWByIDIO3MjrOlB1A6JOz+r3BINBlSidig8FrRwHavgEkrIOBKncRZ3P5/HWW2/h+vXriEajKBQKCAaD+PDDD5HP51W+Srqhut2uWqAZ83V4eKhSqjSbTXVutVP/mdo3KYh04t2XIRPfvwyY+CqQrLtT216GTGBD8moul8Prr7+Od955B36/Hw8ePMCjR49UvkfuxAYuYgp5pGShUEA8HkcymcT8/Dyi0SgWFhYQDoextbWFcrmM2dlZ3Lp1Cw8fPsTp6SkODg7Q6XRUuAHlP/Op7u/vIxgMIp1Oqw0my8vLCAaDSvZTZgNQm1hmZmZU6ixmAmDdisWiShrfarUAXKw76XQagUAAh4eH6ijXJ0+eIBwOw+fzYX19HYPBAJ9++ukLoFUfAzelfxJZ6yTvZdmXwc98pymNlR4uYbIu63k79bhgxiffvn0b6+vrOD8/x97eHh4/fox6vY5oNIq5uTkkEgkEAgGVAqrdbiuruPRSDYdDBINBxRP0nNq2rWQqs0Uw/VQ0GkU0GkWpVEIkEkGv11NeAmIVxpjyUAwC02AwqMBms9lU8dJ8D8EycGEJ7Xa7iMfjqFQqKBaLSKfTKrzG5/OplGztdhvpdBq9Xk/hD57y5vF4sLe3h4ODA7z33nuYm5tT68qDBw9UJg2Zmk32uZ7lQec1PUWnlNtyPPX4ZTn2L6NsTRTDqgMd/UU6KHDaDahX1LSgmSazTGuiWxCcrAUy1pTaFC2pZFLGNhWLRWxtbSkrFv8Y9CyP9SNTUijKd56fn6PRaGB3d1dpa8FgEIlEAvl8HrlcDrdv38by8jIODw+xtbWFUqmkmMbU15J0Ycb7TQniTWPj1M9Oi5qTsmG6bqrbZdOvQnibwI8bCDKNl/xuem44HKJeryvLAIUn3Uf0Ctj2xe5pCjwZl0QepburUCigUCjgzTffxPz8PEqlEtLpNLa3t2HbF6lTOEf4LJU2j8eD8/NznJ2dodFooFwuY2trC0+ePFHJuOXcNC3Qsn2m36RwkxYXN0XqZemXAeheFU0qyCWPv+ycdlKoTGDV4/EgmUzi5s2buHPnDoLBIHZ3d/H06VMcHBwoPiMfESRw0xXd61SW4vE4QqEQqtUqfvSjH6FSqSCdTuPmzZtYW1vDYDBAqVRCq9VSLlWGAZDfmWYqGAxibW0Ns7OzarE+OzvD8fGxysnKZ2ZmZvDWW28hm80qGU9vhWVdWHKZ+7JSqeD4+BitVgvValXVneCZsn5paUnVvdfr4f79+wrAO1mRnP7L+8bd40aXydeSt+R65MbH+qlI0mtk2zb8fj+y2Sxu3ryJ27dvI5vN4uOPP8aTJ0/QbDYRCoWQz+eRSqVgWRa2t7cV/zA3L2VbJpNRCfzpSWIaKxkOxVy7BJLM55vL5XB6eqqOVpUGK2IEAkbyqWVZI5uoCGTlKVgAVEgAZTAPzvB4PDg7O0MwGIRt2+rEK3o4zs7OEA6HlWeY3mLyQbFYxOeff64suXfu3MHZ2ZnKITtOFrBPOFZOxhZ97PXxl/foz+nvM9FEgNUp/s6t0m4vnwSUcdHiQOpWG1mGz+dDLBZDMBgcEVBkEH7mmcBcXCnEACggwGBtlidPoyBQkHEtAEYsrYwJbLfbKj0K8xEyWHxubg6Li4tYWlrCzs4OHj9+7OhKMvW3SYGQv8v+0q+bvuv36+9wAqNOgPYqkVOfmoSnybphutdJ8Jr6Xt5P69C4cZZpfii4GMMn41mZi08CC46XHhzf7Xbx+PFjbG9v4/T0VLk2ASghy7yAyWQS6XQa/X5fbYaJxWLq5JXz83O88cYbqFarePLkCT788EPcv38fzWZzJGTHrQ/1vjGFpZg0frcy3Hja6Rk3HrjKRFljmo9uc1EqAvpJNqbFiRSNRrG+vo533nkHmUwG+/v7ePToEXZ2dlQOytnZWXi9XtRqNeXmj0ajyOfzmJubU4naqSxZloVWq4VisYh+v49isaiMBxsbG4jH4yoVj0ywzkWdO6tt28bc3BzS6TTa7TY+/vhjZZ2lbKbngO//7d/+bWSzWQyHQ9RqNRwfH+Pk5ASBQEDl0zw4OAAAHB8fo1qtjmQ9YJqsg4MDVZ+FhQXVJgAKtDr1qek3need+NFJvl8lWazX22RlA0bTKPE5uYGHytLm5iZee+01pFIpHB8fY3t7G8fHx/D5fEilUpidnUUgEMDBwYHKrcvQEoLIubk5LC8vKxlK9/vJyQnOz89VKqx6vY5gMIjZ2Vklcy3LQq/XQywWQzqdxunpqTrBSmIFaVggfxIIs72hUAjdblfJeHoDOC8BqDDDcDiM5eVlVKtVVCoVxONxhY3kRm8C8Gg0ilarhWg0qmKx+/0+Tk5OYFkXx8ky0wazJejWbdM46uGKpjh44OU9m5Mo5qSJLaxOgo2/myaJmxB0AkEmy4IOnvTfhsMhMpkM3n33XSwsLODf/tt/q/LjyYWQLiVuouKJFAyyp7mf7gHgIl8g40O4SPR6PaW5yTgQxrRws8zi4iIWFhaUxezk5ASnp6coFos4OjrC6uoqbt26hbW1Ndy/fx9PnjxBo9Ew9pWTpi7vHWctMZUl+9ykwetKib5QuvEDhc1VpEkWAcAMApwUB/m8ycsg+9JpYvIeHv23vr6OhYUFFR4jz58ul8tqwwiD6KmIMXaq1WqhVCphb28P0WhUuT6ZsJp5K2u1Gg4ODpSrjIswc/7Nzs5ibm5Ogdm5uTnkcjksLCzgzp07uHfvHv76r/8ajx49UjtwTf1p0qxN/afLmkmUCRP/SppEIF4VsKpbJCQ58Z3eF26KpxP/63F7tm0jGAxifX0d3/rWtxCLxXB0dIStrS21+SSRSAC4CGWpVqvKUh+Px7G0tITV1VXMz8+jUqng448/RrvdRqPRwK/92q8hk8lgcXFRbXry+XzKOra4uIhcLqdyufr9fhwcHMCynm/WCYVCKJVKyGQy8Hq9uHv3Lh49eqTCaGT7e70eBoMBqtUq7t69i/feew+BQADVahWHh4colUrqJKSNjQ2EQqERCxXTIAEXAJ7tODo6gmVdnAV/8+ZNlEoldQ59u91+YZe87G/TemaaE26GCKe19FWTBFuAs4fLFM/P53mvvCcSiWB9fR03b95EPp9Ht9vF06dPcXh4qJQlWrlrtRosy0Kj0UC73Uav11PjxvGXMaDMg7q4uIjz83O138Tj8eDGjRvw+XwqtAW4AGn0JjBm27IsdfoaN0XR4iq9Y8wVTC+YTKFFYxjHk3Xj+6iwdbtddDod1aZCoaAMcrZtK4txIBDA2dkZUqmUwjaMEWfmi2AwiEwmo8K/OA5c3/U8rPqY6Wmu3PCd03qpK82/NMBq+q83ho1wKsNJoE660JgWQO4aJDj9R//oH6FcLuPf/Jt/A9u21Y5Sxq/STe/z+RCJRNQubJrmAShAQCale4taDL8ztYSsF4UT4we5WzWfz2NhYQGlUglbW1s4PDxUsSnXrl1TmwXu3r2Lw8PDF+JbTeOhf3YjN0HmBIZNjKYDVDcg/VWxVrnRJBYLJ6DP7/J3J7DPvg4EAsjn8ygUCgocJhIJbG5uIpvNot1uo1gs4vj4GO12G+VyGbVaTW3I4qJBgcg47fn5eWxubuLatWsqTooxVsAFwKYLjBuvDg8PUS6X0Wg08NFHH+GDDz7AzMwMMpkMFhYWsLy8jEQigaWlJXzzm9/EnTt38Nd//df48Y9/rCxPkyisbtecFCITjev7SefNVeFbnT+AF2PKSCbZql/XdwWbytflstfrxeLiIl5//XWsr68rYPfs2TP0ej1ks1msr6/Dtm1Uq1Xl8uRRq41GAw8fPkSpVEIwGMTJyQlarZayAL3++uu4ceMGisUiOp2O2lA1HA5RKpVw69YtFTpwfHys6koZGwwGUalUcPPmTRWqwowEPNud5dEi5PV6VXorn8+Hhw8fqo0odLmGQiGsrKyoE7KePn2KSqWiwAh3Zh8dHeHk5ATb29soFArweC4OUvjt3/5t/Nmf/Rn29vZG8l6a+p4k3eLyXskP+v0moHrZ/Cvbx3roMZKAGbBIPrfti534mUwGa2trKv5ye3sbjx49QrVaVSF+6XQaMzMzyqJKayPr02g00Ov1cHx8jOvXryMQCIzkSmU9w+Ewut0ulpaWVFgUiaCR/EEL6GAwUNZSxsB2Oh21L4YhLZx/ErTyszwBq9frwbIs5aVg/TudjlKUer0elpeXkclklIX0/Pxc8TwND/V6HZFIBHNzcwgEAtje3sbBwQEymQwAqCwYxWLRUT7KMdGtrLRUOxmtTPxgks9uG78lTQRYTYzmtIiY7pkExLhNTNN7AChNJ5lM4u2338bm5ib+4i/+Avfv30e/30c2m8XGxoZy35BJPB6Pij8hOGUKCzJ7vV7H0dGREqLUQmTbOHhyUxiTYdNK1mg0VPwTLVK5XA6Hh4d4+PAhHj16hFqthvX1dQVK3n//fTx79kyBELf+chJ+biDKLUegCZy6aT/jxu0qLPwmmkSouylUTjw9ju9lf8q+8/v96hhI5q5cWFhQp+s0Gg08fvwYW1tbuHfvHnZ2dnB2dqbcpXT/AM9TsnDzFhOd83Qfy7pII8SzqQGoHbaVSkVZV5eWllAoFNBut2FZFxsXed72p59+inv37iGVSmF1dRUbGxvY2NjAe++9h5s3b+L73/8+PvjgA+WBkH2n96XsH9096MTfpC8DSPU6OAHcyyKTVUP/TSdTH7vNV5nXkiBO8jA/82SnxcVF1Ot1HB4e4qOPPkKj0UAikUChUMD8/Lw6i53xd7RKkXf29vaUhWkwGKDZbGJ7e1u5aLe2tlCv10fqxTjAbreLjz/+WLn06cHy+/3odDrKCnVycqLkNV2yXMS5S5oxiLlcDu12G8+ePVPWUAKXSCSCwWCAdruNRCKhwHYwGFSg9vz8HOFwWCmRp6enePz4MU5PT/H7v//7SKVSuHfvHk5PT9HpdF7gTdM4jRtDp4XfiRdeNbFO+vtpxJEnPrINnOcEQ3oZ8Xgca2truHXrFiKRCE5OTvD555+jWCzC4/GoDc7FYhHNZhNHR0c4OztTrv14PI5sNqv4k8rW9evXEQ6H1eZRmU2CSgc3VtN4xE1MBNLcbHV2dgYASCQSqt4+nw+tVksZroghGDpAPMLfaBwj+KNxDbgILXn69Km6p9FoYHV1VVmFmUmGoQU+nw/1eh22fRHr2mg08Oabb2J5eRmBQAD37t3D9vY2bt++jUgkMuJlYzslgJSgVIZ16B5sPTer5Av+57OSF/Tn3WjigwPctD5WQn7XP+tluU04k3VA3uvxeBCNRpFIJJDJZPCNb3wDq6ur2NnZwZ/+6Z/i2bNn6txo27YVOKWLlEKH4NSyLo4BDIVC8Hg86kxpGQdLRuAkky4Cpgji7lXWl893u10FXOv1OpaWlrCxsYHZ2Vk8e/YMT58+xd27dzEYDDA7O4tkMonr16/j3r17Iwu3iUzCzwkUOVlp9Gf0/nZ7v7xXjrvOF1eNvqyFTbccyLJMQFW/x2QlIejLZrOIRCJYXl7G66+/jkwmg3a7jXv37uFP/uRPsL29rZJRZ7NZZcVirJTsa6/Xq46m5ClB3HDQaDRwenqKvb095TalwK7X64q3yc/D4VBZHmKxGO7cuQOfz4dms4nd3V18+OGHePbsGR49eoSVlRXMz8/j93//97G0tIQf/OAHKrWKU/9T+OmkuxdN5Nbn8h4TP+syyGmMXjVJ4O60ALjJA31ThA5yZPw9MLrQyL6KRCK4ffs2Njc30el08Pnnn+ODDz5ApVJBNBpVp0M1Gg21qQWAiv/jKVVM0dNut1WqKS6Qh4eHKl8mAJVOiDLetm0VRiB5lRulqGgxRAbAyLGXtVptxKWbSCRU6Nfe3h5OTk7UXga6aKPRqFpUmc+Sabm4BjSbTcTjcczMzCiLLl3Ez549w9nZGVZWVrC7u4uDg4ORDZF6X0/Cw/J3kwwCro7CBbyIA7ipTVcQTWsOr9GSvbKygmQyiVarNXLkL096oixi3nN6QblnhHnV6Vo/OjpSeYKZm9Xv96u0acwmQf7imk+jFnmUAJahVe12Gz6fD9lsVm0Q5F4EGrg6nY7y7JKnafCidbbVailcITMT0QCWSCSwvLw8kq1IrulU0AaDgVLwtra2kMvlkMlkkM/ncXBwgFwuh/n5eZU+i9lh9JANnd+cFGEnzCB5wYRHxuFFSRMdzSor5KT9mawUUpvXGz3OQquXT2LuPOYce/fddxEIBPC9730PP//5z9HpdLCwsIAbN24oN+fJyYmykMoUQHzfYDDA6enpiEuG2g2tsFKj4POMf+HEo4VWggdpiW21Wtjb20On08Ha2po6gzsej+PBgwe4d+8earUalpeXkUwm0Wg01IkVkwLTcQM+qYVGF46m+5zGUr/3qtGkgn0SkPOy75Xk9/uxtLSEtbU1Fcj/ta99DRsbGzg4OMCPfvQj/Pmf/zm2trbg9XqxsLCAZDKJTqej0qYwnolxUlzQQ6GQWihoeUokErh9+7ZaPLm7VMa+Ai9ugmCojG3bKoQmGo3C6/VifX0dw+FQuX739vawtraG5eVlvP322ygUCvjud7+Lzz///IV5wTKdFuBJFQGTgmsqZ9y1q0R6u9wWel7jd2kFkRYrp0VHyhLygtfrxerqKu7cuaMWvIcPHyqwypjmaDSKYrGoZGSr1VL8wZRPfr8f1WpVuT1pdQKAg4MDdQa6bqFJJpPY399HpVIZOXhFxv61Wi0VL2jbtgr3sm17xENFtys3WNG1ykWdfcbNXLz/4OBAJWznRlzOmVKphHw+r+Iqu90ujo6O8Nlnn+H27dvY2NjA0dGRSpFFKxjHSx9Lnc/HyWJ9/C6bp3XgIfnKxMMkp5RX9DKtra0hHA7j6OhIubQ9Hg8WFxcRDocVQKMhqtPpIBwOq3zAlvU8U9Di4iL29/dxfHyMVCqFQCCgjFgEkrFYTFn6me1Hr3e/31fZCRKJhNojMDc3h1gspn6nhda2bRV+0Gw21UEFNBAw9pX7aizLUlkEEokE3nzzTZRKJXzyyScq/pRhAsxcJEMT6JmgV+Ps7Axer1elgCsWi3jy5AkSiQQWFhbUs/v7+yNtlWuBnslBGqTkhjnZT+xH3i9D0Hi/CUc60UQnXU1ivSCj6UBKVsKkSellSdLfyx2a4XAYm5ubeP3119HpdPA//o//I549e4ZoNIo33ngD+Xxe7dZnzjxT0nMOrBTUvCY1eTKsHCC6YvXypFWIz1MQk3mPj49V/Ew+n1e7FnlaB7X83/zN38SPf/xj7O7uvgBaTZqKSVC4Lfom8Ok21pNaAJze96rJDcC4Lfj8znudypa/u/W1aZHx+/1YX1/H2tqailF95513AAA//OEP8Z3vfAc7OzuIRCK4ceMGlpaWMBwOcXh4qDJQ0NUo0/yQfwEoYcZYq8PDQxwdHSGXyyGbzaok6VJ4eL1e5aLiDlW6QBnu4vF4VAo4j+cikfzGxgbm5+dx79493L9/H7VaDfV6Hbdu3cI//af/FN/5znfw4YcfjsRmuynDOggdZ026Cgv2L5tM/GOSmaa+MPWbaY7zPplGCLhwxW5ubiKTyWB3dxePHz/G0dGROp89m80iGo0qqyYVdh6lSkBKnorH4yOnCwFQ8pNufLn4EXQeHh4qZUzyNnmWO7Qpp5m/klk0dHnZ6XRwenqqUmDZ9kX6on6/D7/frzYkMq0W9yvQWMGd6A8fPkSr1VKWO1qaaZElMFheXsbOzo4yPMg+1xdxfZy5Bo0z5owzUrwq0tdIygqneSn5Tj5n289jV1dXVzE3N4dms4n9/X0cHh4qL2Uul1NAC4DK8pPP51UssrSI+v1+JBIJpaC0222VAcC2L6zmiURCbaim8iINVFQ6YrGYChvhgQA8kIVWU5kuLRwOq+cJZhl72+12Ua/X0el0EIvFRjIksE99Ph9yuRyWlpZUnWjVJcDudrsqLpuZXxgy0+l0VCYiHpm8v7+vUtItLS2h1WopT7DuhZUhQzJ8Q5LuPWCfyfVW4iPdkvtLCQnQQZD+33TfuDL0CWu6Xyea94PBoIpXLRaL+MM//EOVdHp5eRnRaFTFoJbLZVSrVRXTxHN+KXyo2fB91FQ4WIyDAp4HjcucadIUz4Hg/dx1J4PN2bZ+v68SULdaLczOziKTyaDf76v8lsPhEG+++SZ+67d+Cz/4wQ/UkYcmUKQLZZPWzutu4zNuDPTx16+5veMyyA1s6r+ZgKf87vTMJO3V+V0eJuH3+/Gbv/mbuHPnDu7evYt//+//PT766CPMzMxgc3MTS0tLiMViOD09VbFZdD1R2HIhp4uKWq0M9vf5fNjc3MTR0RHq9bo6wjAajY7wKJNcczGm25Onu52dnaFarap4Wdu2lbt3dXUV3/zmN/HkyRN1pne328WdO3fwT/7JP0EikcBf/dVfvRDX6sRr+q7qScZOv2Yq1+33q0imvtKtHfrnccqTLpfkZ7/fj5WVFaytraFcLuP+/fvY399HIBBQMfihUEiFWAEXu+aXl5cxPz+vrF5MUwVALaJMz0bekO0g31IGV6tV5RmTYAEYzc0NQJ2AdHJyonIYh8NhtUufC3e/31cxge+++66ymrbbbQAXYRASxLKfaCUjGJ2dncXR0RGq1apqP71iPCo0Ho8jlUphcXFRbY50Su0kx0h+1hUJkpMMvmy+lsBDB6Q6SJeAVpe5wWAQ8/PzWFtbUymZaK2mws7wKLn+UJEiv9i2rQ6OIK/lcjmllHONZ87pcDiMaDSKWq2GdDqt6mbbtpKZ/X5fHXyxv78P4ELBk5kIZmZm1DNsG0Gfz+dTShVlsM/nw+7urrL0mjJKtNttLC0tIRKJKG8xAOURqNfrKgUh5TXnItNf0UAXCoUwHA5xdHSEVCqFlZUVbG5uKq9du91+4f0m+Sp5zhRqKMlprJ1woIkmsrDK/zqZwKisrKycjqCdJq1exszMjLKsvvbaa3jjjTfw9OlT/Mf/+B/RbDZx7do1ddwfk0YzDQk1HLqNpLUTeH6sGvA8fkp1zhfWUQIBfUAs63nwsGVZymIgtWa2h4CCu/6YjPrBgwdoNBpYWlpSO/nu3buHra0tAMA3vvENvPfee/j+97+Pk5OTF/rNZNnT+52ka/Juioe++JlAsT6OToL1qpGbUHfjT9PCMO5+nfx+P1577TXlSv/d3/1d5HI5/Lt/9+/wve99D/V6HYuLi0ilUiph9P7+Pk5OTmDbttKcCUzlSXC8Lt9VqVRUXBbnAjdp0YpFHmagPy0L3KgiY6x4SADdqfy9XC6jXq9jY2MDr7/+Ovx+Px4+fKgC+t9991383u/9HrLZLL773e+qjQqm/pdt0PteHyc3AOtU/leByGfSJecGaHhNXxScQKxciE2u+KWlJZyfnyvrIACVmD0ajSpXKuP9bNtWp/fxmOtCoYBsNouTkxPUajVldW82m0gmk4qHyZ9s43A4VDGuelukS5FWMypk8/PzajHmszQKyB3j9HIdHR0hHA4rBY2bsCzr4gABv9+vNmcR0AQCAXXKEY0jg8FAuYbb7Tba7TaOjo5weHiIxcVFzM3NYW9vT7mI9TE20TiQ6ibzLxO4SjBqAuZO9WWdGWZXKBTUqXy9Xg+lUgn7+/vodrtqczIT51PJsG1bxVEzTrrVailgxzAPyr1Go6E8SF6vV+Vpp3WWGSEkz1FJ6vV6iMfjOD4+VrzIDYXSkBUIBJTSpY8JvU3cPFatVpUxgFkM+D7bttWRrpZlqc2ExBWlUgmJRALpdFp5fxkCQyPbcDjE6empmi/cREtcwiNvW60Wnj17NhIiZlI8nKz/ThhBz1ICvLi5dhxNvOkKcF6cnbQ7k9VuHKJ2AquRSAQ3b97Em2++iQcPHuCP//iPcX5+jps3b6JQKGA4HOLs7AwnJyfqJBLguVteLvQUinyftDqQCFIl6UewkckJJKR1VloOWBbdBAQAZMLt7W10u11sbGyo1Cgff/wxtra24PP58I1vfAPf+ta38Gd/9mdoNBovgPq/DSh02tmnj4cck3FAl/eY0l1cFo1bAEzktAA4PeOmhQIXgPL27dtYW1tDKBTC3/27fxehUAh/8Ad/gL/5m79RuYQZ/7e7u4u9vT2lKVM71t/FmD66YSnk6FHgzn/uAqXrSsYCSj4g73KTCRUzeaqL3EjAOdbpdPDw4UP4/X5lvfr444/h9/vxs5/9DH/v7/09/MN/+A/RaDTwp3/6p8ryoZMuHE1j8ssgvfyrYKEi6YrvJH0hFxNJJmVbXpfEY0YzmQzq9brKq8uMEfRy0ULEhRq48CqVy2UVLwdAbY6NRCJqc1aj0UCxWFTWTQnKWcd+v692OuuhXJwHdK1Go1FEIhEVk8iy4/E4LMtCu91Wbl5aWRuNBj7//HOsrKwoQGDbNiqVCnZ2dlTYQzwex9zcnFLICHZo3WO7B4OB2ojG3KzPnj1T4RALCwvKyqov6E6b3vRx1uWJk9y+TB6Wa4BUsnSwo98vreXBYFCllYrH46hWq9ja2lK5R9fW1nDt2jV1jC7jQhlf7/F4VOwpgJFTAlk3WjHlaVPSaillnbTmy3WOqbQYN8vMERJcUvnnus0/PeaUWYSePHmCWq2mQDTrKE8zPD8/VwYDHtXK+FS5x4a4hH0hc3MDz0/wYuaFeDyO9fV1nJ2d4fT0FNVqdWS8THzpJKd0HtefdbLGjsMLLwVYTRXVXygrbZqAutXObXLxBItwOIzr16/j7bffxqNHj/C9730PvV4P6+vrmJubQ7vdxsnJCc7OztRgsH5MYs04PoJM3QKq108KUVpe5SBwsBmnwkWcsVhcDBhbxfYwfkvuMGRsYr/fx+bmJlKpFG7evInPPvsMz549QygUwttvv4033ngD77///khciOxDHczobTMpEJJMFkS3PnJ79m8LpH9Z5DRhXoYmfdbJmkAQuLq6itXVVViWhd/5nd9BMBjEH/zBH+CTTz7B/Py8OsXl/Pwc6XQaDx8+RKPRQDabVd4B4PlCwGTRw+FwxHtAvqfASqVS6sQgnWTYC3mdGrqMyeZ98pS3QCCg8hz3+30EAgE0m008efIE+Xxe5Xzd2trC0dERisUifD4flpeXcefOHfziF78YEa7sMyfF2K3fJc+5yRXdSmWyWl1FcgIx+t4BqWQ7ARq22WTxCIfDuHHjBizLUrvoaS3NZDIIhUIqFRAX0vPzcySTyRFwyQ12BHrhcFjVl2CUm2T8fr9agIHnrlMaA7gg0khABSqTyaj4QY/Hg2KxiMePH2Nvbw+NRkMZEeg5oEWLz0trE3mY3gPm8ZyZmUE+n8fR0ZGy1nHx5yl0Jycn6Pf7SCaTCigTlIfDYRUznsvl1EmLOrBz4/NJFWY3fnkVRP6TmR50wCOVJ/Kf5EOPx6PWv83NTcTjcXzwwQfY29tDr9fD7Oyscon7/X4UCgVl6Zf5VOXJUcQAHF8ZOkU+5boMQAE71p+glsS5Qytnq9VSp7hxMxWtsABGQq8ajYbCHxzzTqeDWq2mPBvHx8cjMpwAnC59tpVgmd4Dbjxj39BbNhgMRkAqDQWxWAyRSASVSkWFHP79v//38frrr6ujXPWUbDruY3/IzzqGksYrnZf1kI5x5ApYnRZgvXI6mtbvcQM7OqCQjaXGvLa2hl/7tV/D9vY2vve976HdbuPatWtYWFhAvV5XAkrGP7EMprSiZVMyG+/nMxS2tBzIestcbRwI3iOPZGObeA+BhPwjKJBlUIDato0bN25gbm4O/X4fn332GR49eoRwOIyvfe1r2N/fx/b29gt9qC/CLNtNA5cg08ky6gQenADtVVv0x9XnZaxqTlZa/V1yYvL3+fl5tUP/vffeQyqVwr/8l/8S9+/fVzlMM5kMms0mnj59+kLOSfKvPKqYwl/Gr8o4P2kxpeACoEAGf6MVlfxCAQk8zzHMNtG9FAgEkEwmFYCgYOfu1c8//xxvvfUWNjY2MDMzg/v37+Mv/uIvEA6H8Y1vfAM+nw8PHjxAtVo1yo9JAOfL3Od0/1XjV5ITcHdrr+kZKU85tvK/BPsez8XO642NDfziF7/AgwcP1EajlZUVZUW3bVsd7SsPYNHjLWXWikajoRL9M16UO+vJU7Ztj4SpSIuUlKmy/GvXrqFSqaBareKHP/whKpWKkq/yBCDyM4EALa8MC6ActixLbVA5OztDPB7HrVu3sLy8rOK3LctSB9YwVO34+FhttmFu1qOjI7WJdnZ2FouLizg4OFDtl7JWX/9eFqCa+OFVE9dWXWlyqovput/vRyaTwcrKCuLxOD7//HM8efJEucppwJIbmwgOCcT8fv+IG57KkrSWSuWHeIGKO+tNhUyXo17vxfHDZ2dnKoNFPp9XBivZB8wBPxwOVRouehlkn9F6H4/H1V4BGtmoAFYqFRUSQB6k5ZUhXATpEgMxLzJPbut0Oirbx8LCAnw+H/b391EsFnHv3j18/etfxxtvvKG8DSxLrivyv84Dcp7K7/KaCUuawLBOroDVqWDAHKcwiUVPCl63iUghmM/n8c4776BUKuGHP/whms2mslTxOEnmLZMAzbZtpWXQsknrKjUc5gkkWOXvFI56SIA+GU0dLF2kLEtaVSlEGcSvg8ezszPcv38f165dw+LiItrtNp4+fYoHDx4gnU7j3XffxenpqTplSx+HSRZ9SZOMnw6GxykmJvB8FUguDOOscIB7/zmBV9PCk06ncefOHQBQOYP/9b/+1/jwww+xsrKCjY0NxGIxxc+dTkcttIynki54CjkKKlqpKNjIz9I9pAMBAl8JQFlf27aVy1eGxkjejsVi6p3yLGvurj04OEAwGMTrr7+OQqGAer2Ora0tzM7OYmtrC9evX8frr7+On/70p0pR1GULadyYSeXAaUyuqkLlRLpgd6q3EwCX4UmyPMmX/EwLbTgcxu3bt+H1elGtVtXRjhsbGwpodjodtYs4Go0ilUopi6N06zK+VMpRyk+585pHTdKIwLpLXiUf2rY9opjRmuXz+XB0dKROfOPGF5YnXb0AlExm2dJCxxhHZsRoNBpqNzfds+FwGOl0Gl//+tdV7Cv/M+4xkUigXq+PnNXOPJh7e3sjdeF/Ew+78e8kMuxVk+Rb/ue6B4ymP9LbZVkXscMrKytIpVKo1WrY3t7G0dERBoOBOvCB1tJ6va5inbn5jblELetiZz55kDKUdZFhAsyVKq2oMlSAVli+Vx53zRhqtq9UKo3s9GfsMwCVm5cxt81mc8TS22g0YFkWksmk2vEfj8cBPE+hSQuqBILSkEDDmoy9JbAlKOY7I5EIZmdnVbmtVguPHj3C7OwsXn/9dRWPzRPm5B4fqeiasIec81IOOWEmyRtu9KVCAki6Nc7JWioralqUdGDDI03D4TDeeust2LaNv/iLv8DJyQny+TzW1tZwfn6uzp+mEJQLOQeRQJWgkfXgxgEAIwmppeCVYFMX+CQKUpZLLYyglHFTMs0LNTc+L116tn2xQ/Xhw4dqpy4PHLh79y6+/vWv49atW/joo49eiBHS+1Pv10m1GNOz+vjqwlUf+6sCVJ3aYrpPf0YnHTg5ASv5WygUwrVr11Ts1Z07d/Af/sN/wF/91V8hlUqp400rlQoODw8xHA7VoRYyBZScYxSQzBRACylJBuvLDQcyJIYuUBnXJ60OBAx8jos168d5wd2odKHF43EFGHZ2duD1ejE/P49UKoVqtYrT01OEQiEkk0n8g3/wD7C3t6c8BtK9bepnp4XbCayaxkQvy03puGzSLYrjeFnep8sUSbIced/8/DyuX7+O09NTbG1tYTgcYnl5GQsLCyOgjErY7Ows0um0StpuWZZSPuiK19cG8hTloFNubMoYad2hizMYDCKXy2FtbU3J/WazqeQ9jQEEClTo+J2KoHQT070rXdaU5WdnZypuMBKJIJ1O47333kMikcDx8fFI6iC6h9PptEo9d3h4iFQqhYWFBSwsLKiDBPQFX46hPl4mPnCjy+BhHZySdHewVGr4O5URpgOzLEudSlUqlVRoRjweV0pTqVRScaBMaUYZRM8mrYtyhzwAJd94EhvrIJV027ZHEv9TPvI5pkBj1ha5ucm2L3b1c9MTv+/t7WFhYUEdikFXPfmWp73xwANiEmZl8Xg8Cq+wXGZFaLfb8HgujkaWPOXz+bCxsYFKpYJSqYRWqwXLeu5hiEQi2NjYwNnZGQ4PD/Hpp59iaWkJ77zzzkhmGpPC62S8Yv+SL3id/3XZxraNA60vbsd1oXFC36kRLwsWqBmtrq5ifn4eH3zwgTq9anV1VaWAqFarakFmHJJ0j1LoyPLJ2BRiwOhizvZRu+fvUuvX3TgsX3f9EwhIrVIu7hTAPGZQgt52u43t7W0Ui0UsLS3B5/MpE/2dO3eQz+fH9qcbOHUC4E5CUWdW/V2Tav6vmkwWJXnd7bvOl6YydZL3eb1ezM7OIp/Pw+fz4etf/zo+++wz/PCHP1QpfmKxGHq9Hk5PT+H3+9WpLHQ9yYMpWD4nO60HUhBLsMD5wIWXIHM4HKrchTKon21iGIK03BIAMNsGn2VdmIMzkUgglUop4f306VO1+WR5eRnARbL4R48eIZ/P43d/93cRjUZf6HPd8qTPNZ3Hx1ma9HKcxu+qkBTobnzotGBIkvIJMFsy/H4/rl+/jmw2i0ePHqFcLiOVSmF9fR0ez8UBLMxLKnmQqQO5iEr+YxJ27sSWctSyLAVYGRsqY7MpZ4Hnh7fE43Hk83lsbGzgjTfewO3btxEMBlXieMpdKlR0BTOMgfsN6OWSRxrToCA9bOT/eDw+Es/6ta99DZ1OB3/yJ3+iQgq4Sev8/ByVSgXARVaFUCiE8/NznJ6eotfrIZvNjqSEk+Ojj7OTa93JqnUVSCpC/E7i+Mr4VinbGGbBtFO7u7s4OjpS8cGMoablEoCyEubzeWXx5wZVyr5QKKTGknhA8hoNS1ScdHnIeFF5khs3E8ZiMSQSCbWm08pJvpbAtVqt4uTkBO12W8l/lknrLlN2DQYDxONxVfdQKKRyvzIMgTw6GAyUMsbyAKjr9KYxfdXa2hpSqRRarRb29/dVjPn8/Lw6Xeuzzz7DzMwMvvGNb2B5eXlk7SBJbKXHopJ/dS81f6MslnLul2JhddPonSxsJvCiTzCTFZCabzgcRjwex2uvvaZODrFtWx3RVq1W0Wg0Rkz1etC00wYTKQhkCgoJXiUwpYtI7u536icSQSrrJMMRWJ4E1XLi0hVM7Wtrawvz8/PI5XLqHPf5+Xm8/fbb+PGPf6wmrkn46Qu9G6h8GU1ff8akQbmVc1VJt8Y5tcOpL3V+jkajyrr6zjvvoN/v44/+6I8Qi8UQCASUdYBxcRSopgB12de6oiXHheCUwlhaR7lZAYCyOADPwwUoQKTiZFmWSh9DniYoke4sAlwuBgSstDDF43EsLy9jfX0dd+/eRSgUwsOHD/Huu+/io48+UqEBpvGQJJXFSRZrN568SoqVTqY4cie+NPGjk9FAKqoyhCqVSuH27duo1Wp4+vQpBoMBNjY2kM1m0el0cHx8jFarhWw2C9u+CBk5PDxUz/OkK6mwU2niMZRycaJrU+aslDwv5fTMzIzKArC2toaNjQ3Mzc2pDWC02nJHNAEzLUmNRkNZ4RjfKI9qJcjkPOGpc3T993o9NJtNZLNZbG5uotvt4gc/+IFS4HK5HNLpNJaXl9FsNvHgwQPMzMygUCiozDWcf2wLwYzuYjXJWDl+JsXLZDS4THIzaJnkGom51rlJlHGVwWAQs7OzKr5zOLw4Kpox9PomNuC5Is768PAT6UUi6GPeUZPBSg/FIrClpZVertPTU7TbbRWvSvlHRa7VaiEUCmFlZWXkWRm/DUBZhGnppYGN9QkEAiiXy0in0yo7AecS72f8bjgcHpljDAcIh8NYXFzEzMwMDg8PUS6Xsbi4iGAwiGQyiUqlgl6vh4cPH+LmzZv4+te/rg5u0I2SrLe0mvOzVFwkX8jn9Awg42S6q4VVZwJ9sjgtAm7Ax0kzJHNwUl+/fh2JRAIff/wxKpUKcrkcCoUC+v0+yuWyOsVEInwygASwJtQumRIY3b2vx7PymoxTYX31icnvMohbuk95TVrR+G6ZKsuynqcOotme7Wq1Wtjd3VWakgwUZx1MC7ETuNTb4tQ2fp5UKF5lMDAJOfGzCQiY+tTj8WB+fl7FLL322mv48Y9/jKdPn2I4HCKfz2NpaWkECALPN0T1+/0RIUOQKIWqCZgQhFLTZ5nUtJm0n1ZN3suYVdluCWhoTWV96B2gNZbnuVPZ470zMzNot9s4ODhQ8V2pVAqVSgVPnjxBr9fDt7/9bXV+u2yTDsSdFCN9UTeNzTi6aos+4GxdHQdenOapfh/llM/nw8rKCgqFAnZ2dlAsFhGPx7GysoJ+v4+dnR3UajWEQiGVIF9ubtUVc2B0hzCVLBk/xzrSC0AwSaWHFhcCgnw+r06Gs20bT58+xWeffYZisaj4TcpWWqRCodDIufAEArSqdbtdlf5NbjAMBoMqfZff70c+n8eNGzfQ6XTwk5/8BI1GQ8UnFotFlSP0xo0bCIVC2NvbQ7fbVcB3b28PlUoFsVgMuVxuBLzLPzlOJpntpKjp8spk2XoVJJUhKT+k3JLtkOsEM5owhprhFul0Gul0WlnZo9Goyv0rQaV067NM8hx5U/KhlLmsj8zew/aQv6Rc42ZBKkrMtzocDpWs5fxoNpsIh8PY2NhAIpFQbaaXi31FY0AgEFD16Ha7KuSA1tN4PK5ALME2jXeWZSEWi8G2bWXM8ng86qAOme6TFuKjoyPs7e1hOBxifn5ehVBwL8L6+jquX78+4hlwwj4SiAJm4w7/63HDk5ArV8uJY1oUTIu66Zr+jKkBwIWGRc3pxo0b2N7exuPHj+H1epFMJnF+fo5isTiSokdfYJkVQOZgc9JSZcorktTKpAWWk0DfXCAtUSQKWgph1pOLO929UnuTli3ZR9wUwPgp9sH5+TnefPNNFAqFF8bMzbQ+qWLhpGiYrr0MkH2VNA7AOIE+SXrbTN9lHCDLikQiyOVyGA6H+I3f+A189tln+PM//3N4PB4sLS1hY2MDyWRyREunMGUSdW4ekIKUYQIyVECCA8bjUZBxYeY7ACh3UywWU22g8JPzhURBT9cu5wXrw5AW27ZVLKAEM8FgUMWjeb1erKysoNvtolwu48MPP8S1a9ewubnpCMAmVX5MPOwkaySx/EnB7aukccCTZDIs8F6T9VJSPB7HzZs3MRgM8OzZMzQaDXV06enpKcrlskptRZnDsXaSw1S8uHjLWGi5aYRAUfI160zPF3loMBjg+PgYT58+xc9//nN897vfRSgUGjEIyHCEdDqNubk55HI5xOPxkcwsMm6Vspoyv91uo1qtolwuo1wuo9VqYXNzEwDw/vvvo9FooNVqqfRHPFigVCrB6/UqYHt4eKjCzwaDAXZ3d2HbNgqFwojr1kRu66k+3jpfjFsDflWk85y0fNIIZALm5JlwOKzyip6enuLg4EDlJ00mk4jH4yMgz7ZtBdZYDmUZFQ45tlSG5DXWgTJMZhWSm/6kAs/3ybaGQiEFUskfPHLVtm0Vt8p5QRlJayjrQ/6V4QWNRkOFESQSCWQyGXWaJ8EsFUi5Z4Zzj1ZYbkhrt9sKcNNSy/0TqVRK7T+IRqNKKXvnnXewvr4+AuTZ5/K/lDd6rDKJPCEVC1mGG71USIBTJU3POFWC5ZnK4pm4a2tr8Hg8+OSTT0byqjIdg893kZ+VWkqv11MuKWktpTneJOAptGScqcw5psfgkHmkcJUufVku329y10rrAUkHwHIwLetiF3atVkMmk4HP50Or1cL29jZef/113L59GycnJ2qjgQRhk4JIJ+Bq0o7k+EnecBrTqwJkdY1QB51Oz4xT1EzPezweZLNZJBIJdLtdzM7O4vvf/z6KxSLW19fVpoJKpaKSYUsLpm3bSghxYWe5sm/1Hfxy8wLwPE0LnwmHw2rxZ6JteTKMbJ/+HnkwBuO+qJBRuErrMIW6tBSfnJyoVCoLCws4OjrC1tYWbty4gW9+85v45JNPVMofJxmigy7TfU6AzknTvyo86kQmq5TTfHN6HnD2pMzPz2Nubg6Hh4fY2tpSqQSHw6HaIfzaa69hY2NDxQvyOhdcyl+Zo5QLvkynRqsm8NwyS76lTJX15pxot9sol8s4Pj5WLv58Pq9cmMwJ3O12EYvFRlzCmUwGANSiLTfPUCmkFZbHWJ6dnSEYDKr4xNPTU9y/f1/lZ6XLVSqJ7XYbxWIRs7OzmJubQ6lUQjKZVBazo6MjnJycoFAoIJlMqnhgXdllmSZDj0npkHxw2bxsqpest3QZs00cewLMXq+Ho6MjtNttLCwsIJPJqHHgGi0PggCeG5ok4JPeRxlKpO9BkXJ0OByquGNmr5DjIcEqU7nJo98HgwFOTk5ULHS328Xy8jKSyeRIRoHBYKAAMmUmrdDSY8A+k6dWAVAbWwm+pXLHtjCTAseFIFyGlEUiEXWoBzNtrK6uolQq4d69e/i1X/s17O7uIplM4o033kC1WsX+/r7CTjqe4fhzPdN5W/KDjp90njfRxEez8rPOhOOe0SeTk2ZIjSgWi2FlZQVbW1vKfUoXPzV1uWGKmoQ85kwKQmnt0d9JsEqNZzAYIBAIqHgQmauV9ZbxJjogBTCSkUDvJxN4Z5lSG5XhB3wHj5GLRqNot9s4PT3F6ekpXnvtNTx48EDttNaBmNM79QXbjVFMoM30WS9jEo3pV0njQKkTKDItAKY+kM/KsmZmZrC8vIzBYIA7d+6gXq/jZz/7GUKhEAqFAqLRqNr0wQVd7k6ltYHxSKa20MIqravk58FgoBZTClgmag+Hw4hEImqjjFwoZCYN2TaWze+0AEurmbQ2mYAKMx/s7u4CuDjPu1gsotfr4cGDB7h9+zbm5+fx5MkTYz/rgs/03Wmc5f1u95mUmcsikzJoqptpIdDns5sCS4t3LBbDw4cPUSqVMDc3h3w+r45U5UlNt2/fRiKRwMnJCX79138dn3zyidoJzwNTpJyU9ZLKDmW5BLW0tkoZKMe21+shnU4jlUohFouh0+nA7/ejXq/D6/WqDSk8fciyLHUIR71eR71eV3VlnzDkq9VqKeVSxsHSSlapVFAulxVYZeo22V7OYYLQpaUlnJycKCtvo9FQdVhcXEQmk8HJyclI1gSTUj1u/XVTti+DCEBNIQmyPRIgAlCAj2EYR0dHyuLHHfPMRCFTRck5osebSrkFYASAUo7V63Ulh03PUC5T5po2UDOUxbZtZV2l1XRxcVHFfUtDlwSl5HfpFZb9IuvMsAPdeimNB7VaDefn50gkEir8henjeFgHlTtujGQKsZs3b+Lb3/42vv/97+OnP/0p1tfX8c1vflPFtS8uLqrNl2yDDkhNfKwb9XSDl3zOjb6UhVX/XVZEJ90S4CSImdcxl8vB6/Xi/v37qNVqmJ2dxcLCAjwej+p4uVmEu0HJPCyXwJW7TyVolXWWuwKl+57/pfuTxAWaAFrvaDIlF3U3oaO7YKmty3qQISqVChYWFtDv99Fut/H48WMsLS3hzp07avehqY0605gEnRu45TNO4ynrKJn0MtxSkkx86wSq3QCM/G4qQ7+Wy+VUWrYbN27gD//wD1GtVrG8vKx2XDKwnkCORKEoQ0YIBri5SVom5E594LnCRqHIMnmqic/nw7Nnz+Dz+VQ+QPKyBAyy/bIfZCgA5xljYJvN5ohyR0DC+RWNRtFoNLC/v49kMolsNquOAWy1Wrhz5w62t7eVUqjXw2mc9PHheJh4fBxdBbAKjO66NYEUE2/q80/GEDr1RSwWw9LSEobDIfb29nB+fo75+XnUajUcHx9jMBhgdnZWuQd5DOr6+rqyku/u7uLhw4fKvc56SfetlAlSUZeKhz5mBA/dbhcLCwuYn5+HbT8/BCCRSKBWq2FmZkbtIE8mkwiFQvjoo49w584dxONx7O7uwuv14vDwEK1Wa8STRr5lrmAaMAAoayvXFh50QG+D1+tVseAy3nY4HCIejyMcDuPu3buYm5tDJBJRC30wGMT8/Lw6blQfE5OCMo6fJQgwjferIsoy3VomgaqUX1wnLctSOUc/++wzVKtVlTWAp6i1Wi0VOywVYqlAyPhUHY/QAimVbYbZ2fbzmFLKuEAgoHhFpjyTVlwAKiyKm/CSySROTk6wuLiIa9euwbKex3B3u11lzadixGfJ79JrxnGURizpfSXQZX/Ik64Y6shsGMQWMlMR8ZPP50OpVFJ7C1jXv/qrv0KxWFRhmsPhEI8fP1aKmS5rTAYFJ7nsZHxwo4nzsJoWDZOQdNIO9QbIinu9XoX6A4EAHj58iJ2dHfh8PmSzWSwsLCj3qSnfKmNXZUJqulblkXuy01gndjbN6hx4CiSZDki2hbvb6LqVZcqNB5Lp+DvrrsfB0tJLBmfdGVDNI9yy2SwODg5QLpfx9OlTXLt2DQ8ePMCTJ09chZqTFmS6l/c4CUAJYPUxNoHfy6JxgtvNQmECqE6LCu/x+/2Yn5+H1+vF9evXUavV8NOf/hTJZBLr6+tIJpMqtogbTqhoybAALuaMqZI8LN8pLZ/Ac8ArM2WQf6noeDwedaQq0wHxGansmcJUZCotaZmg50N3BXMhJx8Hg0H0+31sbW0hmUyqXbdHR0fqIAEemWkSZOOUZqdxMo2r03hfJTL1gQnIm/pIV4T1ezyei3yP3M3OIyH9fr86UpWxq9xlXS6XlaVc5p/0+/1oNpsqD6lU5nVrEJUYYPQEQf4m603eIb9a1kUObSZDr1armJ+fx+LioqpvOBzGu+++i6OjI2xvb+NnP/uZSl0VCoVGFECeAAQAKysr2NvbU9Zb27ZRr9fRarWU1Yoxs/SC8EAB+UfwlMvlVCYFZkKgJy+VSilXrNN6KkmX16a1+KrwL9c809on4035n/fyaNL3338f1WoVfr8f6XQa8XhcnSTGzUMAVFy93EhEGSozRxBk8p5WqzUCAGmoosylnKO1HYDyvlqWpWQo30cZTYAYjUbh8/nw7rvvjsRzc+yloUFaKdlXpvnAe2WqQwJeGgy4R4E4iOEuwPOwB/I638k+YHq4x48fI5/Po1AoIJ/P48GDB+j3+/jWt76Ft99+G36/H7/4xS+UHKD1Wfa/k7GB31kffX2RvzvRRIDVDdTwhXrlTALWiRgMHYlEcOPGDfzoRz9Co9FAIpFANptV7oJWqzXCnCxXN/Nz8Dm4ZBC6o3SSmhgXbclIkqFkW6TrwATo3LRiqVlKKxUFocwLKMF5uVxWufx6vR6ePHmCbDaLO3fu4PDwUO0MNPW5k7DT663/prdF54dJwO9lkclKYVoM3ICr/tmp/QBU+p3BYIDr16/j/fffR6lUwtLSEnK5nFrA6UblJivpQpVp0ehRIEAkCNQVJMlL0oolLQ0EuNyUIrV5XakDXnTbEajyTwpRKbA512RMIMunAnh2dqYWnHq9jnK5rPJr/vmf/7kCFU7jIZXjlwGbTve5WbIug9zqMAlA1/vOZLH1+XxYXV1FMplUx+SGw2GVC9K2L46JTqfTCmxQvtRqNRXewd3HTMkjQ0tkmItUfAgYpBwnoGNZrGMymcTDhw+VZa1ararE7fl8XgFAuYmw1+sp4MNd2ixbxvv1+xcnFx0cHOCdd95BPB5Hu91GOp1Gu93GRx99NHJEMvB8PjCWVSqEXq9X7eKenZ3Fzs6OOi2LYMm2bbXb/eTkZISPnRQsN0PEVTMQ6AYsKZ94jwQ7lCvARe7at956C3fv3kUqlUIymYTH40G9XkexWFTvoVWQsaJyfee7uHYyvI/vAp6HNpFXKG9lzCrrzdhPhjZR2SEfsa3cpOjz+XDr1i3EYjFUq1VltZdAVW5e5TskdmJ8KhVIWXd9jwCVRvIflUDKUBoRZHorGheCwSDK5TJs+yIss1KpYHt7G4lEAqurq6hUKjg7O1PrFPO1Hh8fo9lsjuAxnQ9MvOHE46bPJpo494UJiE5yv9NvssKM/5ibm0On01FH1+XzeZVYnTvbALygfQDPtTf+SUag9VQ1WnSuBJ1SG+F9UtDKzyxXT8ugawtu1iEuIgSrXq9XgVWWy3Zw4vd6Pezv72NmZkbt+Hv48CHm5uawsrLiCMZ0S42TxdRkVTSBBL0Mk3XgKiz8knRLBvDlAYredpaZSqWUKyscDuMXv/gFAoEAlpaWkM1mlVWT2q/kU/KbjMOm8KTAkRkCgFH3kLRokUe5KEQiEQAXgp5glVYE6eKiUJXarwTMrJtuEeB8kNZXaf2lAJUaNt25tm0rAP/Nb34TqVTKdVzcFC2d/3Uw8FUnU/vcrpsWEv4Wj8extLSkTuChu/vs7AzlchmJRAKzs7PKbRqPx5WSwv0BxWJRgVgSdy9zQ6yUy1y89bAPAOp+zgUChkQigfX1dQyHQ9RqNfT7fXUiUqvVgt/vR6PRUB6oTz/9FD/4wQ9wcHCgYv6YLUPmJiZvc0/A3/zN3+D09FSFq0gwI+cmXavcmNNsNlVsa6/XU7GviURCnWJHYMrTsJgezCmMTh8r0/jrMuwq8Le0mAKjeTml/KVcYt8yj7NMvcfUZDzetlarqQMcaDkFXkxLyTpwDwr/M8aY4X+UV/yjcsV66vsHuLlKbtQmKGa4FveZUM4TOMu6sUzptpdjKQ1wusJiGmO5r4b3yncRWHPvD+W/13txOlupVFIA3ufz4eDgAEdHR0phqFar2N3dxaNHjxAMBrG0tDQio6Vhg7Jex0U6j+hYRP650USAdZKJME4DdKzAF2Z7r/fiVCCevBCJRNSueAIzmd+MzKqnmeLiLhvPDpSDKd9PJiVzs82mesv0Kxwop47WBYkEviS+0+fzIRQKKaaRwEFauLjRgNpTt9tFqVRSJ9XQ5O9kDXUbCyeLlrTYOYFx2Z9uk+tV0jirqT4uJmXDNJmcnvd6vchms+j3+9jc3MTZ2RmePXumTsEBLvqHqVikAkQrldTGuSDSbU7eprDhuOhWKmld4FwgOOZmBek+YxyVTJUFYGTcAaj3SpIWV30BpQVNz9zB9CoU2lTYarUa7ty5g+Xl5ZFTaeS4OQEzE79/Gf67akqWSajzmnQdyr6RHiHKEV2RtCwLs7OzyOVyKJfLKBaLsCxLbWyam5vD2toaCoUCwuEwhsOL9HrpdFqdOsQ0Z4wtZOjS+fk5ms3mC5ZUjjN5k/WhV0vytwQS0m2ZSCRULLZlXZyKGIvF4PP58PDhQ3znO9/BH//xH+PZs2cAoOokASvDxzhnAShAtLW1hd3dXRwcHKgThwCM5MzmWkJDirSecd7y2sLCAhqNhooZJLhl2i3KaxNIlWMrf5NAxmSEuEy5y/ro6c5MgER+Z4J8276IVaVXlfxkWZba/CY3XEu+IXCkQkSSfAhgBEDyv/Q28RrrR1kpPV/S2i5jSwmkucFJhgwyZRrjP2nRlXKcZVmWpfZBUBbK/TT8k2BV1ocWUeYhDgaDKpUh+6/VauHhw4cjcdThcBitVgt7e3vo9XpYWlpCv9/H48ePUSqVAACrq6vKy0s5L3mSY6vLa/4u26zLbZMCJ2miLAE6ONErppMTmDFdJ/BjZ/I0BekO6Ha7ODk5UQzAhsmFUdaFAoWmcAkMnOolBROvkbFJLEcHq+wTU7mm/tSDpzlZpOWM76NWxEBpgtmzszMAUO6qk5MTrK2tYXl5GQ8ePHhhfNzGzAkEyN+dxlQHb26Ky2WRrnxMOmZO4EcHDbyPFgGv14tbt27hu9/9Lvr9PjKZDLLZLDweD87OzkbCNriwUcgAz2OQCOi4qMpYLOmWl+NKHqUbjHzKrADSkirbIMsmj1Pou/GLSQlijKKu5XMxkUccMt0LBXy/38dbb72Fx48fq9OH9DFk/Z34VB8/qXyYyO23q0I62DT1gd4OXaGSNDMzg1wuh1AohP39fZXGienYzs/PkcvlFDiMx+MIBoOo1Wrwer1YXV2Fx3ORenA4fJ57UipMtEhRlnIx1TMIAM9DUiSvEyRKjwTBCN3rtM796Ec/UmmnyL8yfEZfHCXvA1AbITlH0+n0iLuVfzJEi/NTGiG4NjC8K5FIIBgM4uzsTAHn09NTXLt2Del0Wm1E1OW0ScGQ/eUGVC+bl01KP78DozKTxI2hw+FQHQoUj8eVYlAqldSGq1QqpTYfU3ZS0QEueEeeusexIrCSdTHVjfwp75eGMd6rr9e2bas862dnZ4hGo0in00oWU5bRHS/7Ro4n29JoNEbAsjRksZ5sI9tOSyoNa9JTK+Nx2+02dnZ2VIYMAEgmk+j3+yoPbjQaVfGsu7u72N/fRzweR6FQwMrKCg4ODtBut0cUYxmSRpCtYxr+ZlqHx/HuSx/N6gTCTAzgdF0+w0FPpVIYDoc4OjpCIBBQZwITqEkNiGVI4CetpuwQ2Rly8GS9WY7c9SzL0q2x0vUgtYFJ+kmWIy1fuqWE98jf6MKg9indEYFAAFtbW1heXsbNmzeVlVpfvPUJYhLgsg5ubdPvcSrvMrV91sXtN124mvrIre2yX2OxGGZmZpQG+pOf/ERtzGAIB2OaKHw40aXW7vV6lYWKShctMVJgykwCJvACjIaUsL5ykZXWewJdqfCR9Hkh2882cOGQKdkkSOHmMrql6vU6qtUqQqEQPB4PGo0Gnj59ilu3biGfz6NSqTgu2rLf5edfBjC9Sgu/iS/dZLD+jL6IkGKxGGZnZxEIBNSxkul0Gpubm2pBy+fzyupFK3yj0cDBwYECiwsLC+pgCJlikLvqpbwkn+j1lG2Q91Mm0wUrLa+Mj/b7/djZ2cGnn3464p5lm3VgKb0TnIO0dNGSx3PfvV6vOmGJbn4eU0ximwCMeAU4b5k6iLw/GAwU31M2nJ6eGtNbSWWNpCsqkjdMcvlVkz6uUonmuJAkP/LIWlonASjAenh4iGq1qk5f4i51HnOqy1Mq/+QTqXxz7KRVUPazPveZaxXAC7GuMkaWz9HN3+l00Gg0EIlEVHpCy7LU5j++Q5exrBvXfPKn3Kwm5TD5TJZBIwfjs6VFudVq4eTkBM1mU1leB4PBiLU/k8mojAHz8/OYnZ3FwcGB2pA1NzeHpaUlbG1t4ezsbMRjIvlQKtbyN84ZJ3nuRhNnCZDkZJHTF3v9GR1AAVCLdKFQwOnpKWq1GsLhMFKp1Ej6H8uy1FGQ+rs5gDIuhoJKxkM5TWYyu9SUqb3wunSHsj5ysZf1kWBNBxJyMFknGbMiXbW8LndsyzbLTWVMD7S+vo7Hjx/j/v37LwAM0ziZxsp0v942/ftlL+4vS5MAGydAS5KTzOPxIJVKIRgM4vr163j06BG63a5KA9Tr9VQMlknBouBgnCetB1yUpTVJ8pu+gOnAVF6Tbi1+B54fm8i5oo8pBb+MVdL/y3vJ06w/rciMV2W2gFAohEajoU4hqlQqmJmZwRtvvIGNjQ08evToBQGtj4MTb0461rKdTt8vg5xkrH5tHECRsYRSSY7H48jn8+j1esr1vbKygnq9ju3tbbz11lsjIVmDwQBnZ2dKKeMJWExlxo13JG6SbbVaI7uXdQOADN+SwEF6xWg1ouJDue71elEqlRAOh9XiL3Nt6nxPK6mbPGYM6s7ODuLxOIrFIhqNhjHExrKskXAGj+diF7aMF6Symc/n0e/3FdhnXeLxuLIGs090ucOyneS2LqcnVcx+VSTrYZIlutfEsix1JLvcfOzxeBTwoxxkGdz0s7S0NJJ+KhwOq5AMhjlx/KWlU5ehXNu5855GLI63BKkSHLNd/J1xrPQO8SALKRd50BGBJecYQyNlX9m2reKwCVylNZ995ff7VQaLfv/iwAA+R+DKsBS5Aev8/BzJZBKxWEzF4SaTSRUi0+l0VFq23d1dHB8fq9zCy8vLODw8VFldZN3lf5Mhj2sm6yNDNt1o4iwB44CKCaTp2p8kXucimUql8PDhQ5yfnyMajaozd8kwunVUmvmBFzdKyd/lwq0LeMmstEZJ66asr9RkSNTWTZqjFMS6BZXWAk5eE9CVAJzuVP1d2WwW9Xodw+EQT548wW/8xm9gc3MT+/v7qFQqI+809b8TAJPPkbnks/rvuqXkKmj7Opkmjryuj4HTs6ZrXq9XuVYymYzK+Tg3N6fGUW4c5EInd0MzCwZ/o2VGTmYZwyr5VoJJ3i/nHp/TE26T//Xn9X7RlSY+K5UrqWTRBUUXbTQaVXOFoIBWZ3ouWq0WKpUK+v0+bty4gZ/85Ceo1WrGMTN9l+NiAiVXAYhOSiblUlfWpVvNBNIk8OO4Mp1aNptFJpNBtVpFtVqFz+dDoVBQeUq9Xi/m5+fVqVJ0l8sjegGoVFcyvk7OIY63Xm/WXQJWqfxJA0I4HFYLG+U6rW2W9TzNEJU0GcoleY7uS7mzX7eyARfhM71eD2dnZyMKlz7fOW8om7nOzM7OIpvNKsDLAzvoaq1Wq2g0GlhZWUEul1PJ8vXFnvXT+WEcn1yW3HVaO0h6nDt/Z7zqzMyMGifguXxpNpvweDxIp9Mj77NtG+VyWWVckKCfx0xLPuWYk8fkhizKTOnFldjCFFpAJZ9Am/WNxWIIhULK2MZyZZtpcZUWf+aTJQ9T7pKkJZl1t21bgWSfz6dSy3Gd8Xq9KuXV4uIi/H6/2lTJsJtUKqXqZVmWOiL37OwMxWIRm5ubmJ2dxbNnz7C3t4f5+XkVFvDo0SNUKhVlfdbnvo4FpIFF92RPIp/HbroyaUluv7sxrEkDpFZK7dPjuYhnJRNQW5KLMhtLASbrIYEhO4EgwCQQdODLa6YypFuLmr5JYOht1hcaSRJ8UJDzGb5L1oHXLMtS8avs15OTE5ycnGB1dRWrq6sKeOjaoE4mpUO3Ypmel9dMZU+iMb1qGsejTp/15/UxDoVCandooVAYyb9IYVosFtWGK6eUJnLSAxg5clhq/jKdigQlwCgIpYVKar/yyEJ9s4HOqzqY10EreVX+0VJMQZlIJFR2AunyBaBipniCW6fTQbVaxdramtqopve1Poa6IjJu4XZb0K+KkmXiTcoBfc6ZFgNJ+nOBQACzs7NqA2elUlE72judjkoZlUgkVG5svoMW1Vwuh0KhoFyerE+73VbpniSfAqOp02gtlXJX8hJlImMRpStePsu4cRLnXCaTwdzcHFKplLJm6V43qRzKzbRU7GjZk33H+SkTx3Ne0OVaKpXQ6/UwPz+Pa9euqQ1qlnWRm5XWK558R+OMiQecZJCTYq3zz2UQ+0uu12yHjIvnH4+I9nguNqUx1j4ej6vsD9FoFNFoFLFYTG2yY5gcZQo9sNIQ0Gw2VdYKKjIej0cpIiQZysRMDjr/Uq5Jo5GUq5RlMzMzSKfTysIpgac8npX4RtYXGE1FyHfI2Gjmcx0Oh2qzGoEoY6UjkQji8TiGwyGi0SiWlpbUaaJzc3OIx+PIZrNYXFxUG8VoaOABHF6vF6enpwCgDu3Y3t7G/v4+PB6POmac/CsVT8kLOm9IfKEbusbRWMAqGctpYXB6jpUwgR9+ljuUme+Lu88YbK9r6Hq9gNFckW6N14W3jHWSmwHke7iDW4IM/maynuoAXgJR0wBJsCLrov/JtEC8v9/vK8seE/8Gg0HcunXrBY3UNDZ6fU33OY21qS36fVcFAADu7SPpAM3UB/o4Ahen7vh8PmQyGfj9fjx8+BAAVPqPTqejTqmSG08k8OTCSteqLhxlPB5BhOR7lqOHrOhuSxmjKp/hO8jn+nyn0ihBrpzfUvOny4mbdqRFmO3i92KxiGq1qqwipVIJoVAI165dG8lcYPpzGj85huP43PTbVeDbcXUwgXVd4SDPSH5IJBIoFAro9y/OJ6/X62pzSLlchmVZKpSFWQM4jgBUYv2FhQVsbGxgeXkZ6XQawWBQhXjpQFSGP0kZKvmWgFWGcQ0GA+XO1K0w3NgVj8fVGmHbF+mQuGBzpznduTJGG3gOONiX0uXKOU/ZT3Ah+5oWL/ZlrVbD4eEh3n//ffzJn/yJAi1bW1sIBAJYXl7GcDhUoDaXyyGfz7/gEtUtU/KarJvkEzkPL4PkmgqM7v9g3aQRRV6LxWIIBoNKaaUS1G63MTMzo2QjeVC6v6X84klP/CMwZfyxDLWS6S+B58YjaVmlnKRnQfIvFZzh8HncLddvKlpyozR/5xgxYwb7B3h+uhq9GdLgRZkpjVoMQeGm2nw+r+YycyLncjkVdsJ65nI5dXQrwyWkoYxWa1psc7mcOsHr4OAA1WoVwWAQy8vLyOfzI5ZgXW6Z8IPEQ04A1kQvndZKL9yk7euATf4uy6NgonbVaDSU5kRmo6AydYTUfGRaCxORkZzaZnLr84/aNnPt8boeW6eDHJbvBvgo7Fg/tpsAld/pMpJ1HA6HqNfr6mQNADg6OsLx8TFWVlZw/fr1kbgyk9Jg6gu3MZPt5XWTkuAGDq4iyXrqC4XbvcBFW9PpNHw+HxYXF9FqtbC/v49gMIhkMgkA2N/fV65TWgboCgKg0u14vV6l4YbD4ZEFmy4jj8fzwrjyz+RqlfxHrZv3UwADo3NEDwFh2RI0mBYmziMuMlKQ8Tnpjo3H4+h0Ojg8PFSCs9PpoF6v49q1a+q4Rqe+l3V0skaNU65lGePe86rIaX6a5pWUO24WDOBizJLJJFKpFM7Pz9WmiVQqhW63i3q9jkQioTwDPGkwm80qDwJwAQwqlYraVMTdxJlMRh1LKmP+qcSwvvxMhUQCR+lZk9kjCCjYLipVBBWUj91uF5VKBQcHByiVSkoRYgy1BKty4SRIlsnQCRyk9ZXtYj5QWggJCuhFOTg4wIMHD5DJZNT7stksAoEAKpUKarUakskkZmdnRzbisM/08dR5QF9nL5tndTIBacoKCeIIBhmLSl5pNBojmR5kajESgZ+ML5Wpx6QcY0op8hPjZaVyJTMO6GNBC6r0chH0kmf5vmAwCJ/PN3IAigwf0XOncg7I+FjW0WS0YJ154htPWGRYhW1feBq4cY3tZp+Q9wlgpYGCYVw8ifDk5ATJZBIbGxsYDAY4PDxUoVvz8/NYWFhQeb5NfKjzgS7DpII4jiYCrLpwnIRMoNZUUcuyVIwSYzS4kDOVhbRo6h0iASeFHAda/k6SZUnSzfDSIkGBxclBAOHUV6bFUwfv+ncJUCWIlek0ZL3J4NVqFYPBQJ1p3el08PTpU3g8HmxubmJ+ft4RbOr9I7V6p3boz+vtkGM8icb0qyR9gpjqYhon/jcpYyZiHJA8BaRarSIajWJ2dhalUgn1el25lBgXSF6VwJUW1lgshsXFRczPzyOZTCIQCCCTySASicDj8ajdnxRcJmACvOhR8Pl8SmDLfIWmeSGtARxPGXctwa10kcl4cmnBoAsrGo0iHo8rSwJ3ztKdzDPd19bWjF4CJ0WY33WedgvJ4T1XccGXpMtOk2Jsulfvp5mZGczOziKVSqFareL09HRko0Wr1cLs7Kw6JCAQCCAajSogKt2S/X4flUoF9XpdxRkGg0FlLeOiyIVYtw4BGAGEUiGSVlFmHiDg4X2MG5VAgYBD5jTmdWkR5cIdiUSUu96yLlz9sVhMpfGS84h/EjBzowoBivRaWJalLNYsh3O73+/j9PQUoVAIs7OzI2ENTuBUH0sTz45Ttn+VZDJ4yM+6YsvvVI68Xq/K58u1lnmb5alNAJQBJxAI4Pz8XIVvUJ4RUDKXKS2eMr4TeB5GQ1nYarVUfaUcs217RFmjQYChIXwv/9NTzLhp8jh5lsY1YhY9XAUYDVOQngfyqb7XgBiC1l/OQWkIY91lX0qLsqwLc8Cenp4quZBOp3F8fIz9/f0RwEqrLsmEGckPcuzl50n49qWyBLhZoXQBqi/ychLzd2pKsVhsZHMV0znQTWjaTc8/mYtNdooJLMn3y9+kNsay9A1W1O7kc1Lbc7JwAKMWKB0IknHZfmnB0q1ZcsDJtO12G7VaDalUSoH7w8NDHB0doVAo4NatWyiXy6jVasb2mwCKaTz1PnO7Jut7meT0fhMvmsC6XpYOEPidJ4dEIhFks1m8//77AC7OlK5UKmpXMPmMGrFc+Cj0gsGg2oBAlw8FD09D83g8qNVqarykNUDWT/4nD/LoTW4EYay4FH4EoCYFUQerJAIPGWfL+/Q5yznD3aw8Q/zTTz9V7ulOp4N8Po+lpSU8e/ZsJGvHuPF1u8dJmbyKJPlRCn1TbKDpOal083osFsP8/Dx8Ph+KxaLaxe/xeEbi1c7Pz/HTn/4UrVYLyWRSbSIhSNva2kKz2VRuRrl7XoITyQtyQZObTaigy30KMiMM1wU99pBly+M5gee8SIWfYFeuEewfaVHlb9Kt7EQsm3OPG8CoRLIPWq2W8mqwfXRn0xobi8WQSqVwfHzsygskJ0OCPv6vmlgnqYCbjFR6aIfP51NxkFSm2T80DjHlEvs8FAqNpDFj/8o8z1SWvV4votEoPB6Pcp0zpIp9ORgMFAjmWFLmkE+Gw4ssAPJ5zgdiFnkaIC3ptPyyXOYrlsYC3YoqLdEyOwA/837pSZPHeLPvCcYJYsmTnB+MX9X3R3AN8Pl8Ks1bPB7HwsIC7t69i62tLWxsbODGjRtYW1vDo0ePcHJyoqziEv/IfTbkhUmwhYkmBqx6gbrGZ/rd9JsUoASA3HDBxYym9n6/j0ajoVze0rojFz59EZVMpsfb6Yu7Di5JslNpGeLzXNRZfzctVweo+m8SrOrAgBNbWskksGZbqtWq2m1Ki8T9+/cRj8dx7do17Ozs4PPPPx+xXjgBUr2++ljr48t26NdeRmv6VZGst5OFgr+RnMCq24TjBOfGlUePHilwwPGiy49jIHMLy7rpGwzJc9JlyE0BwHMQIBdjvc6sQyAQQK1WQz6fV0dqnp+fK6sthaDefgle5Rzkb3oogZxnMtxArxetb8zJSiuAz+fD4eGhArLBYFApY05zVY6jaVzl9atOeht1Pp7kWX28uCilUimk02nlcm00GkgkEhgOhygWiwgGg8jn82g2m3j27BkODw/h9/vVMa3pdBrxeBzXr1/HyckJTk9PUSqVFDiQyhfw3MouYxellVPyta7Ec8c0Xe7SAsaFlql9CDCoDMq26zzNutA6J3N06rzN+vC7x+NRAISZCti/tLTKvJf8TB5maE84HMbs7KxKFUYLoJTzuvJsMjLoY0+6DF6X854yQ8516d6XBijKAQI5jlmn08HZ2RlardaIAiT7l8YC8hLX6cFgoHiGigRBn9yAzXvlrnoag1gXxtRy/GU/k98lH8jfe70eqtUqkskkZmZmEA6HldzlPCFIZJukDGefyXVCerTIg/xOSzTxAfvq/PxcZaqQmRHo/ZBxuTKsy+/3o1wu4/j4GLOzs5ibm8POzg6ePXuGg4MDzM/PY3l5Gbdv38bR0RGePXs2El7AeuveOraP/024w0QTx7C6gVMTmQSsLogJ+CKRiDo/mBNXxprIPHgy/oJl8E/GuEj3DN8tQYCsh8llyDbLuBVel+/X+4XlSouD7AfZlzoQlfEpMjZGAk1uKKAWOTMzg0qloixmZLwHDx7g+9//PgaDAQqFwsjOcNZX/o0jvR36mDpdvwo0bsGXv+mTynSvXEjoVrRtG+l0Gs1mE48fP1ZavdRgqYzJjR+0APHdg8FA5WuV4SHNZlMt2Lp1VfcI6KEtrOtwOFT5C5l7D4AqW7ZRttPJqup0jXWQSqOM/5OeDMafnZ6eKiWU9bEsC3Nzc8r6ogu0cSBOX/zH0VXhVxONAy1OfCsXQO5eTqVSaLfbI/ktj4+PcXp6imQyiXQ6jWw2q3a8n56eYm9vDx9//DE+/PBDPHz4ELVaTaUfZB5dxpvKP8ps/pFfpTKuk20/d7/SAnp6eorj42Nl5eXzNG6wrQzZqtVqKj5RtzLLuUurF98lAYluDeRn8jHbQhDK9YoLPfmea9POzg6KxaKKM4zFYjg9PVWua31DkhxXyf9OsnhSWf4qSF/XpAVRjjv7SMoE/m82m/D5fIhGo7AsS/WrLIMhcXJNZlgV/1N+SiMBw1oIkumyl3KZ/SvHkt/lcdmU0XTxE8QylIFpn2h4MMkZ1ktiFB0gUz5KjzPfy/hcuQlNegBYd+4XkiECPCqbeINGA4L+4XCo8gen02nkcjnU63U8ffoUp6ensG0b6+vrWF9fV2uKNFDIz4A5ZpXtHSeDX8rCOk7wOy0o8rsOIC3r4vQHnsxEjZumZU5ixoKQueWi7AQ4uWACo+6oSRYmMmggEFDWCMaJSq1B1+LZZvk+U/9IZtN31Opt4Dsp+KTLy7Yvzl4+PT3F3NwcgAsQn0qlkMvl1E7tUCiktEgdXDu9m/fqwMBp0TTxx2UKUF2Tc9LgTP0wiYLGxYsegEKhgL29PXUuO2OYpLCW2i8ns9TuuQhWq1Wl6Q+HF7tO6c7hPJDxcqyP1NqB55ZXWnUikYha4HnWtOwfuXhIjd6p73QrFMvRgYiUH9J7wmTWtPTKOdbtdjE7O4tEIoHDw8MX+t7JomS67jTubvLqssitHiYwo1/X5yw/h8NhFAoFzMzMYH9/Xy1S4XAYwEVGC/6eTCaV/KSrlIs8YwvT6TQSiQRardYLB2Lo4EsHAZLPpAVTtoPKmx7nJj1wwGiqJJbBcBNp2ZPWXlqTmCKIQIlWOCnHdVkvAa70IHBfA3/n4RjcGBMIBPAbv/Eb+Mf/+B/jX/yLfwGPx4N8Po96va4MNfJ5yQv6eJrmo1RaLlP5kuuxaf7p9aaXhcqqjPFMpVI4PDxEp9NRoSsEfVyj5Ql6tGpb1sUOfWYckrxMxYnvpsWfa6IEigSynAN6tgiCU4kBuEZXq1V4PB5UKhX4fD5sbGyod5N3KA+l9Z58asI1cu1geAIPldF5QgJAWltlKICuMMoYWRrqmIWoVqupMID5+Xk8e/YM+/v7OD4+Ri6XQyqVwvXr17G1taXikHVrs046n0v54Mhbrr86vEDX5OR1CYTcrIu8j1YnnptL5mEKEm7IkFqBzOcnLa26Js+BlYw4ruPkfRIkUpNWHaeBZr1fnP479aP8Ly0AUpunFkawwqBon8+HcrkM27YVeBoOh0gmkyomkgmU3cbRSUPXAarJsmUCwZctOEluVinT4qDzsBMwp2YejUbVOex7e3tqEaNbSZYpF1WP5yKejUoRNXSWT4DKLBUyebuMp5YKj7Rc8Z28jxtsYrGYmnvkb6YkkgqSHG9ZnoyTkv2r10FaWCQgoHBqNBrKhdfv9xGJRDA3N6f6pd1uo1AoYH5+fiQsYRIy3WtS0q4q6WOne4dMYNtpDpLXCEiZ65ZH4qZSKaysrCCRSKhDBZrNJkql0ojSxEWsUqmgWCwqq0ssFkOhUFCbW6S1So6bDma5+MuNJQQjXLSbzaY6cEPGMXs8F4nkdUWI1iKZtoi8xzWFCp8EMuxbglmpDEowwvAEzgHmtmR50kUcjUZRKBQQCoVUHZ4+fYrvfe97aLVauHv3LtrtNg4PD40AheOrXzcZFuT9l8XnUl6w36WiIflThoXITc0SVKXTaayvr6twFRlCIGVSLBZTMpRy1OPxqDSC5ElueAuFQkq+SoutlHmsr35ohL6xiPdLXuY1ehiYBYU5jGVebJYtQw4BjGSBMW1msqznex+IE6RiR1lLnpfXyct8Vnpw+X8wGKgczdxDcXx8rGLa0+k0Tk5OsLu7i0ajgXA4jOvXr6uTx+S7+FlfV78Mn04MWHWQor/QtDjI/6brujZCRqZwJJiVLn7+xpgUDppcgOUAO4FUU9v0euqAUcbOSDep1G7cYjclc0tmlaELwOgpKlLbk2Ca7aUG32630Wq1EI1GFUAol8vweDwqH6GshxuYNIFs2Sapyeu/yeeuAkBwer9sgy6knKwaepmWZSmFgAmti8UivF6v2mkttUa5cHNxpRCTR65S8BK40bIgXevSkiTdlqY+J99Y1sU56bQKy1AFKaxZVz2eT4IPea8EzDrIlbkO2S5a6LiBgEd4DodDLC8vK+FNJZbXJOnuI73dpu+sl5PMukpk6mf9N1MbdYWXNDMzg0KhgHw+j8FggPv376sd7tKdSiX3/v37SkECRhV05mZstVqo1+sjPEXwJhdE3RtgcreShyRwM8lSyrxr167h9u3bKrUUQSLwPA6cfEbQQeDCesmd51yk9VAuzk2ZuorgR8bY8uAQzlfmul1dXVXgqdvtqphMj8eDX/ziF6hUKvj2t7/9gjVKzlnJC7q84n+T0ngZxD5kv0qZIQGRBONc82X4yGAwwMLCgurPw8NDHBwcqP6m0kEZwjHv9Xqo1+sqPrtcLqs+53jzyFzWF3huLSd2kLlQ2Q56pPhe9jHDmoCLfud+nEwmo9bkTCYD27ZH0mixnSSCaCfsxGdYX7npW443+19iB31OEYzzu37oQr1ex8nJieqLUCiEWq2GUqmEYDCo8jg/fvwYe3t7qFQqyGQyuHbtGnK5nNHz5oQX+H0SrPbSm650Iaq7D/UFQQc58juZgBuFbNtW3/V369omBRsFIAePGgPBrRS0TiBNr6+8nxNK5lNzeh54nnHAJFRkG2TaLdt+nkJDbp6RfxKoSmag4GQqILr3PB4P6vU6er0eotEoksmk6hu9zk594VR/N6Cr9/FVAAVOi77TdycFhv/l7zwSL51OIxQK4ejoCF6vV8UNM/5ZWgWk4sKdsBQ8ko/5nffqgJoCTvc2SCHM+2hJZe7NfD4/IiB1C5hJgOhWCFPYi7SuAC9uiJS5BRmfKH8jCKA8GA6HWFlZUeEV8j2m+ezGe/piaRpP/ftlEUGILmuBF+UqydQ+UjgcVieHffTRR8pSynCharUK4OKo552dHezs7Ci+ZRgJrZ9UQJhySIIHpii0bVsBA9ZRHt/IZ8iDUiGSm3NkfzAGMBqN4rd+67fQaDSws7ODZDKpUqKRl+i2pVWWYFXOIypR7DvKR76XIWGcO9KIoANwPuf3+5FMJrG8vIy1tTW1x4D5hDnXCXhu3bqFlZUVlTJMtleXt/r8M/HMOBn9qySdZ02hcvwuZRaBIfuVuCASiaBcLo/sapeJ9akMSznI8aBrXc95zdhMGqCYmQV4btXkWFJGkVcp13gNeG58kkYtGiLW19cRCoXQ6XSwsLAAv9+vwK1U0mRf6W58/kZgDowaEzyei6OLCdglANUVHKlAsI0ydIfW2FqthvPzcywuLqLdbqNYLKr0cYeHh+oUub29PRweHuL4+FilX+QmLMab63yh48iXxQoTAVY3oOf2EpMwlUTtlXEnciDkYJJR5M42qVXKgQCeTwo5+E4AxdQuab0wuWBJbsHEZEB9EaHAd9J6pNYlN3rp1gkyNy3RHo9HHQvHmJtWq4VyuYyFhQWkUqkXXAMmzdw0Vk73uoF/UzlfFXLqE/13uRDyJCC6ucPhMOr1uhK2HFdpwZHWAT0fKwC1wOpAxbafB/nrwIXCUwopuuG5s1kX9FKR0a0huptM3sNnpVdEtpECVAfUEujKeS7zLdq2rQ4QSCQSiMViqFQqxvFwu6aPpZuiIr9fJt/qMkuvo0no62PIe3iNoSD9fh9vv/02BoMBfvKTn2B9fV3JSfLt06dPVaw0E4vH43EFqrxeL05OThCNRtWO+UgkosAEc0DqGS847jKtGT+z3pTxfI6ynTxNUPBHf/RHsO2LhOiM1SexTlLxkh4y9qHulpXyl20IBAJIp9NK4Wc/E1TRIs0+DIVCyGaziMfjytLHjWkejwdnZ2dKcfB4PCiVSrh3757KMCDzgMp+keNpMipcBb5l/8n1Srew6SCKcpDWUSqsTNHEMpLJJDqdDkqlkvK2yPUVwAsKkjy4RPafzCahx69KRZvPkneku5/t4e/kcXqKuFlsdXUVW1tbiidlRgrdOMbrAEbmBQC1z0FaQckLJjzBtUECbemV03EU+Y7PxuNxFZ8eCoVQLBZh2zZqtRqOj4+xuLiIVCqFYrGIzz//HPPz85idncXCwgIWFhbw6NEjBVilbNLj1fX5N45/XyoPqwklT0KmirBzyWTcfCEXPaf3y9gN4MVBltbISdtDQSXrKhlAggC9DdLyRQYwWZ+c6iA/y0VeAhjWTbaRApx9wSDpcDisMiuUy2UsLy8jm82OpFxxsizJsXVioklB7lUhJ8XKiT+cAII+znSDer1eLC4uqtPQLOvizPBut6vy1+nChMJCWlR1NzeFi4wtlVq0aWMLiYsq683yuSD4fD60Wi2VxUC2VfK/BEP63JD8KushiVYs+Q4p4CX4puv0yZMnuHXrFlqtFiqVCnK53EhiddOYmhRD01iOI1nGZfOwVBichDmv6xZJfW6Hw2FsbGzg937v9/D+++/jO9/5DobDocr5a9sXadhKpZI6xYZylov7wsKCSqEXCARQLpcVH/V6PRQKBXg8HmXtbDabCvByV7UEfOQ1Kn7MuS3BKg0FBAydTgehUAgffPABbt68iVqtpo6mlpkupJLG53WAQ/7Vra4+n0/F5S4tLQGASqsWCoUQi8WQyWSQzWYVL8diMZU2iMfdMj61XC6rE7GoCMzMzKDVaqFYLCr+jkajai+Ck6KlrxdOQPWyeZekK76muSXDfWihBy5kjNxsOjMzg6OjI6UgMFaSsdiMSbUsS+2cpyJDHtbTmLHfqMzL9ZVymrJJbpSSawB5W8popsKKx+MqHp8yTPYJ600lSRrKKHN1Oa97jvW5LxVEaVSQni3J64wPZ+o1KmuMBfd6vUin02o/xfHxMebm5rCysoLd3V0cHBzg8PAQc3NzWF5exuzsLAqFAorFouoX0/rEvpBtG0djAatJgOuT3skiJwGcPrF4TSYEJqPRJM2yaIHlQLJMPU6HAGCSdpiEuyxTt1pQuMlJR9ID5k3asAQ7el/yXmmdYqyUnFwSQMh20O1Rr9fR6XQQi8VU/EmxWESv10MqlVJav94nprGTpI+nG/i7KoKSNA7AjGuTCbxyHOmi9PkuEl9zI1G73cbp6Sny+bxaYKnRSjco8DyEhMKSwoULIV2vdInpllDZDgpBOS90wcCgfwIJ4HkslS70JI/qc0fWXwIF4LniKC0QugLH+c3FKhKJoFqtYm9vD8lkEq1WC4FAALu7u1hZWVExYLpMcQKYOmDTrzmN71UAq7ri6DZHneawvMasId1uFz//+c/xi1/8Ap1OR7n7JWis1Wpqs4heB54CxSMfy+UygOf8c3h4iFwuh3w+j0QioRSthw8f4vPPP1eGBRlaIC2qkigPCQq4DjAH8erqKkKhEAqFAkqlkgLNtPbrsZScG5IXJSCnIQSAmtcAcHJygnq9rjZYpdNpZDIZVCoVfPbZZzg+Pka/38fm5ibee+89ddIXf3/w4IECVjQY0ONyfn6usogkEgm1GUiSzufjwKwTgH0VpPMgAaT0FOrgCngOJhniJj1PXAtt+yLfuDRYcZNfu91WQJVKOcuhsizlIo0E7E9upiZAlCCXdSLPSEVdyj1T2fQ4BAIBVKtV1R+MHZXWRhowZDiCBLTcwCuBLj0UHHPWTcdObAfXHrmnwOPxKOstlbxgMKjCKhiGIffKdDodnJ6eqrys29vbag8ST3fM5/N48uSJGkPWR/Ko7gGfROa+lIWV5LZYSAuN6RlZWQAqfkRquMy1p2+ekgNMcCotVbIDdHc73yH/y/eyDW4TnZNF1ktasvS6ykVf/51WJZbJzxSwMpZHtkNap2R7/H4/ms2mCgEgg1cqFTSbTSQSCaRSKezv778wLrLtulDUhaAJvOoKxFUDr6b6mBQWp3v1+3gPXajBYFCdGkWXdjqdVrvvefoK+VtfhOWpV+QdadHXlRlpgdD5W/Ky1NDJjwQH1OhZhuwPLvQUbnJOsQ6m91IQ8p3cSCbnvcxrTAsGLSRnZ2fY2dnB/Pw8KpUKstksfD4fdnd3MT8/rzausE8mVTRMC7rTGF8V0nlSlylyrpmAuKRAIIBUKqUsKLVaTZ1wxRhsvpMKreQR4CKt4P7+vvIclEol1Go1ABdjQavX/v4+Tk9PEQ6HkUgkkM/n1THC0sWvt0XytVyE6ZEARhUrylBahPkOukKljOR8k2mPgOfAme9hvbhI85hgxt5yJ/rh4SF2d3cVL3PNsm0bS0tLqFQq+Pzzz7G7u4tut6vCBhKJhDqcgZY5pnaLx+OIxWIj81FXFHVZqytul016HaWVUCoMrL9u0KFsorWz2WyqtFR+v18dehGJRFSeXZnnWuZhp0JAcMd4ZMo06WnUY/5l6CGfZd3lEcEExJLYLtt+nhElFArh7OwMzWYT0WgUnU7nBYOYVND0NZegmfeQ5Hojx4D/Zduk5ZltlKnhWL5cm+Q8obW7VCqpAx14sMvh4SEePXqEa9euYXl5WZ1QeP/+fTSbzZH+kfhQ8vCkmGEsYHUqwKTN6SjZpC3yPhnPJDs5HA6r0yFkbJBMPyHrxoGRblYJnvS2uAEV3cIky+BiLOOuyHQm64eMV5ECRtZBxnzplmF9IKWZX75HCgHbtnF2doa5uTlEo1F1DN3h4SE2NzdVrBcnnRwTHXzKsdSZyQRadbpKoHUcUDUpXjrpPG5ZFyluuGM4EAjg5ORELT48DCMSiaBUKgF4foSrSUmQAfZcmOW9pk1XTvXTeVm3npIXJU9JQajXRfaXBEu6S0p39bNdLFtusOICRkFK19PR0ZE6eYm5Ppk6KRqNjpwD7sTDTgrWVeDFlyUJ5PgdGFXw9fHWeZmLfSwWU8ddM96dR1ZyU5XchCRDk/r9/oiF6+joSG0gkfUbDodKcT44OMCjR49UaipgdGe0BDZybHRlSl98JT9zXPVE7gQULFs3ZshwMvK7jHFlLCLlPk8U4sYumSiePNxut3H37l3s7e2hVqspfmd7KAsIhvr9vspiMDMzg1QqpVy07B/TmJs+y2s6P7xKknVxckcDz41OHH8an2j5B6AAa7/fRzQaVetaOBxGLBYbOT5XV3BoFSUPE6DRui2NBbQCk69kPLS0Ysq2yf+UcQSobJtc32dmZtSJV8w7Ly2lrLu+aZvWX1oqpcJGHmc9pWyWip7EWKyr9IwRyDO8hpvMJaYiYLUsC91uV3listksstksyuUy9vf3VQgX/05PT1Woj1wb9H6cVD5PZGF1Yn6nxV9+5zVdm5LubQkwqQkdHh4qN6lpAposqKpRhg1Set1MZTrFnUorgGQu3RrGjpeLv8miw//UXOTklYwlB9nUFlkvAgYm8Y5EImqTSrFYBADMzs6qzRGyP0z9I99hYiQdrJqUgasGEEyKxbg6uj0j+SUcDqNWq40ILMYGdTod5bZizKvcxUmXGADl0iRv0Z3I95vAi1N9Td8lwNDH2+Qp0PmM1zmf5UYEaU3lnJbAh7HqBDpMWTMYDNQGl8FgoDYMdrtdFItFFUtIwToJf8rxkvdOomhdJb7VZafeJn7W75H/4/E40uk0otEoDg4O1E7mdDqt+p9J1klcAOX7mA+V/6W7VY9VI8iTViMunNKtCrwYkuLxeFRCf9u2R3b8E0zo48r66OMnLbrS+g+MehJ4jSCHc5f38XQjHgNLgDMYDNTRqkdHRyrdl+6KPj8/V+Fvtv181zlzi6dSKZUWS7ZFelP09kn+12XxZfCwaY2W9ZO8LK+zjzi25JN2u634gJ4YGXPJd8ix5XvY/3ynNDLRwimNYAS+0ovEdZ37a6iYABgxJnDeyI1OfC/d6eFwWGGaSCSCs7MzJftZf+myl+BOAmzZx1LBkrwhPRjymsRZ+nys1+sqywdDayKRiJo/PATj+PhYeQbq9TqSySTm5uZwcHCAnZ0dlMtlFAoFlauVWRJ0fMi2yTpNQhPFsOpkerkb6WBGli0HmAs5N4VIYKVbMqWLXGoVvF+3WJoWL70NpkWBRIaQnUuwqt+rg3X9OwClAerxflJoO4FV3k+trtlsjgSV81QuTjjmoWMwdKVScQWhTu0wCUWTgnLZWr4TyT42jYsOaOQzsgw+L3MEezweNBoNdT8tBtwten5+rgQt4wap3cvNKKyLFFgmkOU2FpK4EBOASKEqAbBUunSLGYAXhKZuFZOLpL7JikdXyoWGuSu5QDAOmHlZydcejwcLCwtoNBqIxWI4Ojp6QUlyarvT+Jmu679fFeBq4kddlpH0eWfbtrLcpVIpdTQo+TQajcLv96sjHWU5Oi8QFNKyyD9pHJDKPAGEvqFQyjUqZ5J0ZZ/1kKnepOzX40+5jjCVEa/JMDIZgkBFSgcI+n4F6cKW1+UZ8AwLkMYXqVDQ0ib3IzAzBtNhSQVV8oDToq6Dv6sgc03gVLbBtM7I9T0UCmE4HKLRaCCbzSrLqDy4R8pMGneYlokbBnW3PvmAigOtvqFQSB3uQO8j66J7gCXPSNlPZZtKGkPyuIeBm8kI6AjkyAuUzTqfyzAu4EUPK69ZljUSHkCDiLTAcmyk8YFlNxoNrKysAIDaM0FiP3LjGI9jrVQqWFtbQy6XQyQSweHhIQ4PD7G0tIREIqE2epvWVlqWpbx1wzuksXeYtDXTxHACOnoZ+oLAAWOnsPNDoZAKSmcCaNPpJaohnufHrZlIFzROk1syghS0fK+eJkMKKFN7pZDWwTHdydxgxQkghbxsG6+x36id27atwA8AtSBRY63X62g2m4jFYlhaWhpxeegg3QTg9UVQ/mbqXzdeeNXkpJA4gS1JelvYD7zGGM1QKAS/368sK9zZSpcTk4gvLS2p03kGg4HK10chyEVWnqMux4W8JoEn/yS/0DoghZt0YzIuTC7CujIohZpTf5DvKehpSZLnVJfLZZRKJVSrVeWylalWAKg5EAqF1MZBCkgKvHg8ro5t1XnQNMam319mMb8qfGsCSXobOfbS3cp7A4EAEokEPB4PstmsSg/k8VxsuGJcZ6fTUQDWBJCpdFBJllYrLtJU0LhARyIRBAIBpZyzHfIwCSk/JTjkd+kulptfgOdgUSp7rIOUobqyJ79z/dEtUpIkr7I/JBjo9Xqo1Wpq7wXbTpmtg1bWk4CVbaGFVfKrbjmUpPODE4+8SpIWbdZJyijgxUM/gNFYUmZVYVwyxz8YDKrQDz20iu2WoFYqzjJJPutEecux05VwGepEvqKMAzBigZeZBMhX9BYRVBOk6rG1kjgfiAnYN+w3+Z+fpbLG+sj+1pVeWou5IaxcLiMSiagsF7IPJKZoNpsIh8OqT3hwSDKZRDabRaVSUflXeapYIpEYCdWU46XztNM6LOlLbbrSSV9UTVqfDlql1iU1IGD0TFu5qMqGU6uR2rcJGEpyuu4Esvgen8+HZDKpNCAZ16Evhrr1QwdGJs1Sr5vU+HX3mQSr0oIhwUyj0UA8HofP51MMWKlUMD8/j4WFBcTjcaUlmepo6jPTPXpbTKD1MjV+Ux2kRR4wj4kTL5AogBhjTUthvV5X48QUY4PBYCTpuASKBJ10h0mXj9SyJZ/IOkprp3SpmuYiyxoMBip9DkGyE7DTLVp8J60Z1JI5hwlqGAYBQG02sSxLpVqj4ietYPzfbrcV4JCxZ/F4XFkpJJg2Ldo66WM6jkyg5VWSm/zSx1W3YgGjYVIzMzNIJBJqASmVSqqP2adHR0eqj7vdrsowwrL0LBDAi3kigecLuLzfKeSJSpUEZLrVR64PnDMkKuQEKLohRJdBcu2Q84EAQ8pb/i4VSfkM1wQZssB4VJ6G5DSnaH2jssvcowzJ4IYsHYQ4hYXo7ZQg9zJIGpL0OclxkWuelDH9fl/1Ay3/Xq9XHTcuc0jz5DHpFpdlc51kHCbDLAhMA4GAkr88+jqXy6n3sG7yaFNprSUfyLaR12np5Bj2ej2Ew2G1aVTyNMeL7SZ/0KrMerK/eF16M0iSX6mIsh+kTKc1mAeGdDodXLt2TcVkS6VK5sOV7+W7S6USNjY2kM1msbu7i62tLbRaLeRyOYTDYcTj8ZH5zHY4rbO/NMAqC9I1fF2zc1og9EnGAZBmb4Iw6daRi7W0KEjtXDejO2mlJtLbI+tIl4C0Srp1qklzlKQLZ13zkG3h7zpY5ITgxJF9yAD3RqOhLGkErACQyWSQyWRUImCTdVivt5NlxySYLhOgmkivo8ktNQnANi2APIZSbhyiYGPScAooWlwo2KRlh+MHjJ50Rl6X1inZJjeel5Yg3uv1epHJZFRKIgoz04Y/yacsW3eb8jMTfVuWNeIxIP+x32Kx2As7e0lUrgjwGavGeFYeHiA3C8j6muqvz7VJF/HLBKt8v0lumD7r8kMfO2aqSKVSGAwGagOUz+dT49NsNnF+fq4sg6VSSSnEMg6VY65v0uP79U2Ckj85Z6Rsk8BKV8CkR0tf3Nk+aTgARjfy0Cqm11PGr0rAYVJIeZ38zndx3gDPXcYyFpFzgfWkoiUzvjBDAeU4vQkyjngcb5iUtMvkXQlI5We5xlAGSgBO63y320WlUkE+n0ckEkG321WeANlWjjfDBKTckzwkre3yWdu21Wa3SCSCeDyulGMdTxCkEbQSJOuKnLR0Svc912t6M6jIE+Ow7ewv6cGVMd5sPzGRHsLD+hGo8nq321UyWhpL2Nfn5+dYXV2FZVlqDwbrRk+ZxEG0MOuGA27WqlQqqNVqmJubU4eVyPaZFNeXwQ/jgwYcSAepbv/15+R/MhhRPwOcufhFIhFEo1FEo1FEIpGR86A5qNQMpItJfn7ZSazfT8FIISYnoA6K+d0JqEpBpoNRU59JUGnbtlrUpaCWbjoykjwHHADOzs5UjtbZ2dkRsOBUF1MbnZQAUz9cNpkEueRbJ0GvKxOmBUIKEWYJ4CLf6XSUdknhoCsHXLy5sEpLmf6Zi7fU4p3mmL6wy/YGg0Fks1kFCCWIN/GhBAdyTslr/M8FmRYmWkWo7XOhIACRWjz5VN+RS4FJisfjKsbPxK9uAu+yQejLkpNsdQLhTsojY4MTiQSq1apaJD0eD6LRqAKxlnWRQ/HWrVtIJBJKGZNyRio/kjckSQsbAQDlpww/kfNKWtw47iZ5Ky39wOgxxgQMEijrm2doBaX8lC57KQ85J2V75RyQAFwHX5yrMuyBrld6BBmzSgse5bK0vMr+NvHBJL9fBskxlfGfsn4yHAR4HsYBAPv7+yiXywoP0JXO/pJlyVhR3VMrc4hKxYfjxr0ycqwo26RhQYI0lkUDhY4DSFTI2Uau2eFweEQWU5YxNFAqYsDzfQeSt8jH7C/yMo0e0gLM0ALmAWeIQrVaVenVeHwswSsPOwAuQgnl+HFfAd81HA5xcHCA4+NjlTaPJ2HxoBGGGQEvrsF6KNAkNBFgdQIouoaqo2V9weR9umbImAoAKsZDPqfHeJJ5ddch/6SA0xdjCeJGOsLz4iYnp3rr/WLqcB0wuAkSJyHEcvifcbxciKTFg4zM+2VaiuFwqPIvxuNxpFKpkaBq+V4TYDaNo+leU3mXTXrfSiuMTm51liCBvC+tq7RE8ThAWlV44on+Hvl+3Zoj75Gg1aQkSouDzq/SjcqF4uDgQKU1krtZ+T4JhvW6yH4jMJBCkguPvFdapiiMpaCXu6n5WS70Mq59dnbWGH+tj5Gb4vUy1y+b3OSNBAa6AizbHwgEEI/HlRXc7/ejVqspAMVYY6a+unPnDjY2NlRMG/O0ynfzGEeOqwlYyjrKsBYJUuSaIflPziu3PvF6vYhEIop/gOeAUd6vy2HKSn0fBPtQj1nVQTYBhtxXIPmUn2dmZlQfMjc23dAAVCJ26SEjuDC9V5dBer1NStyrJvYzgSDrJ5VwXgNGN6OVSiVks1l1EMT5+bmyOutHk5qUaJbNMvVsAnKfDK9L5YpgVbrUCVCJP6hg6J5JuRdH9gVJKimHh4cjijzrzP9cS1guMKqcsf3sNxoLJHCXIQz1eh2VSkWFbAWDQSwsLKBQKACACtVi2kUCWypPMoMNAHVKW7VaRaVSwdnZGaLRKAqFAprNJorFImq1GmZnZ5FKpUbyHUu5YMKB42hiC6vT4uB0zUnYkngfzct0hfR6PRW8ToaUpnG5MMrFUC7a+gKvg1iWpbunnCyn0srAd5isO3p79UVeXpf3S2FqEtIy558+KVgmGV1aARgfxZhX5n7L5XJqp6Ssu5vAkwqKLuTdhORVEKCAWbnQx1UunHKhM42lDEu5du0a6vW6ShnEBTcSiSjNU7cCUTO2bVsJHcmrkh91K5qsr97/TkqUFIzSbSYFua4B63wmx14CUBNQNc0f6TLWBb6sP8tstVrqQAwAKk2KrMs4UDOO/9xk1mWSSbHndXlN9qPOu5Srkv9KpRK63a6yoDLWOhqNIh6PIxgM4t1338Xrr7+OTCajjg2VMaASUElwR5DGjVaSKJf5n5ZzLq46P+gpeySgJeCIxWLKiyHXAtk/fJ+0pnLxlwu/7DfpluUcYP8RZMhMCTQOyGT0oVAI8Xgc2WwWGxsb2NzcHAEVkucYOsRDSEwKrpsixjK/jDfxl0lSMWXfyT4EXkw5SXm3u7sLv9+P119/XVmeaRmNxWJqfaN1kdZJuRFK5kFlKJb8neNjSmZPQwNlMNda1pHGIGldB57LUwI9AlfZfo4PLcYPHjxQgFDiEbnPAXjOw9J7qoe/SGu1SV4w5jUWi6nwB2YQkvUlniJeoBeO76Li2+l0MDs7qw4IsCwLR0dHaDabyOVyGA6HypsLYCTzhVRanZTvcaB14rRW4wCa/ptJ+OtaNwAV98d4Kh79RdCpCzLdasRy9cBiAC9oV5OSqe6yM6md67v4TNqDE+kDJ5/X+9y2n8et8s8NQFuWpYRpPB5XR90y8Xc6nR45WlF/v9N3J5Ah75X/rxKZQJ+sr7wGmPNaynvY//l8HnNzc9jZ2UGlUlF9VKvVYFkWUqmUEpAsk5YuqVDQPSXjkhkeIy0vshwdsHLxl+2RFlPyHGPsZFohChO2T5bL3/Sy3UifB7LPGGdNoiDnbwBU3JrX60WlUlGLObMGsF4mWWMCoG6L/bh7LpN0vnWypuvzj/cSPPr9fjQaDTXn6QEgH8zOzipFNhQKYXFxUR0q4Pf7sbOzg08//VSBMwmO5IIsFRO5WUnep/OnHvIir0saDofKrX5+fo5YLKY8BdLbpMtjPTWR5Hnew/kowx34TtZFgmvTQmtZltpkyHC25eVlvPbaawgGg8oqK086kqCXqd5Mh+SYxlmnq6B8mdZ4GTqk79a37Ys46cXFRXz729/GH/7hH+JnP/sZACjQk06nsb29rcqVqcSA54YsCQrlCVl6Sj8dGOohHwBUSIJc84fD4YhHTYa60CtMICjbLI0VnU4H+Xx+ZAOTtLBL0A889556PB51uArXDLZPejDYLspYn2/0EADdKCH5WbafdeF8owJ648YNdVoX44xrtRoajYZao8rlMlqtFjKZjNrLIOeV9IhInplkfflSaa1M95Ak4OJ3/R5Zptw1xwkcjUYRi8UAYMT6JC2H1KjkO7nQt9ttNBoN9Sc7QjfBT9Iu3Rr1ZbVZCQhMC61umWK/yBgf0ySjwCVT8D8tKUwGzOPsIpEIksnkC/VjvUxAwEkJMfWXBN5XyWql0zjLhbxH/25Zlsot+uTJE5WBQR6zyvghOVlpOZALoBQkFLaxWAzZbFYpFyYLpl4/t8VM8gtjlfg+afVxcpPqShIwmnid7+Azsm8lUKEgpKeE80p6ReQCUCqVFPBJJpOIx+PG+SP7QQJut7GdVLm8LNI9Puwnkgmk6go9LX3D4RCVSkWlvEskEioVWyQSQSgUQqlUwsnJCeLxOHq9Hh4+fIgf/vCH+Mu//Ev4fD689957CsRyXwEBlozFZqyflLt0tUpekuND/pbhMbSEyjASJo/PZrPwer1YWVlBPp8fiQEknwOjYFIPvZF8Qn7T4xmB5x4uPYxAWn55TPPS0hKWl5eRy+WQSqUQCoWQTqfRbDaV8iA3CvV6PbRaLWXh4385xvpnHZSa+PcylS+2TVdy5X+OhW1fHAdMC2ipVFIbVLmGRaP///betEmOI7sSPVlr7ntl7QuAAlHYARIgm021utWtaWkkk2xk83V+w/yT+RVj82lmZDY20phppThs8pEACWLfCrVvWbkvVVl75vtQfW7ddHhEZrHZLPR7ec1gqIyMjPBw97h+7rmLB9HX1/eWK94EXLpaA78jIUbCh+ujZvCB5u3UOS6aWeUY876cv/xex8WaJAEZ366uLikt6ff7BfQCzRsRAc0JWx6Pp2kHMM5V4GTLVb0+AM2x5NrINY0e6mCer40Js78Yh8vn9fl8iEajaDQaUoqwu/u4HKEu18h3WM8BraP0e9gKl32vslbmYqEnprlwmIufvgY7Vk+Ko6PjnUPorjIBHMGqXkDZUbyHmfXM2AytxDjRzbAA87N+Rv1MtOb0vU6z8NnAqu4Xs01kCcjO8RkYSuHxnGyZxt8w7icYDGJ7exvlchk7OzuSyOYEbtzaZzIQbm0/S6UJ2OefG6gzf+v0XMBJbFGlUkGxWMT09HQTY8mFh2Onw1JorWoXIz8TNPK+PIefbS+0Zuv5Gx3HR2VuipNy0O+304Kplbap6EwwYL5rpn7g3OU1KWQH+O7SZW22zTbv9P212Ob1Wc9TJzHbqsdFj7nONNZCV2B3dze2t7exu7uLWq2Gnp4exONx1OvHse1cmF69eoX19XXMzMzg8PAQuVxOauiWy2UMDQ3hk08+QSaTwc7ODg4ODhAOh5vch9lsFk+fPpV5rAGj7fl05jRw4r1iCSDKwcEBotEoYrEYhoaGkEql8OrVKxSLRdmZR8fys494TR3GYL4rNJb0+sV+pehMZzM5kEA0kUggFArJ3vHr6+uYn59HrVbDnTt3MDo6Cq/X21RblJUweD9u9+w0T01D1QTfeq782GK+d6aOAJo3i6CeOjw8xMrKCmZnZyVp0+fzyRyjd4X1PTUo05sEUF8AzdtAa3wANHt7Go2TXcfYPrMCBM/TBroG5by/jsHnM+tE8r6+PkSjUWxtbckx3kvXFCabCkBqz2pCg0CTep331mNAhlWvIRrc8zgNMb6j5ljpCjacowTf3d3HJcf6+/tRrVYxODiI7u5uCXHRdXR1e5zmSzvSNmDVF7UpUrdzTYCrj3u9XiwtLWF1dVUmHwGp3tZLW2falaWzRPVLDDRnIAPNW01qJarbb1pwur36Pmbn63uY12kVl2HrFyeQVK/Xm7Z01S8GX3YmRVBxRyIRKejLxCu/398UfG6z1s1xc5pUNgPlXQEBTkaE2xzW3zn9Xluw3OGGC1e9flyInYu5eQ8qJzNWTc8d07Wp55A5b/WcJkAkyDMrSjCmyfZeaqvXDDswn8HNONPPocGqfg4T6FLps4YrFSxjAzn3dWmrVgax2XYt78r8bCXmO2UCAi5epmEPHLORgUAAPT3HdaTr9TpqtZqwrswX4AK5vLyMrq4urK+v4/LlyxgYGEChUJCtGBcXFxGNRvGf/tN/wubmJubn55sMd7/fj7t37yIej+Orr76SOaRDQbhIk2XTC60Glt3d3U0lhPgeMcuZuv27776TOpomM6nnl+2d5jyn6LAyri+mkaBdvfyezx4KhYQcKZVK2NjYQF9fH16+fAm/34/h4WGphev3+8UtTGawv7+/CQjpMeYzmc/iNkd+bNHzT7fV9BTYDCxuX01XvNfrlax0bgtaqVTkO01C6dAT8x2gcL3XLKbO+DeTQTXA1YCU35lhTBoE8jhJAoK2w8PjrYV1zV7+Xt+XHibtSjfjgE0AzetSZ7IvnP7xuQA0VVoguNegm/qbCZr8DT0CDL+gIbe3t4dsNovz588LcaPXLNvaq9cvNzl1HVYn4Go2yImh0Z3GxdPr9eL69evI5/NiNdH1o+NEOKBsg66xZmadAvZ6pjouxewc7R41v9dAGUCTotZKmd/pF6Od8AM34QRmuSQzoYH9qdvD563X6xJbsre3h62trSbmg783+8lJ3IwTJ/Bw1mID3q3mq23eAifPpWOQdnd3hSXhOHBes+/1XtXmfNHH+eI6GTlOBiDwtpuF4MBcMGg1a4bJ7AvdH5rJ0X3i1D4ATda9dvvre9E43d/fx/b2tjB1uq8Y0tPf349gMChK3K0N5vi69eO7LO08nzlO+hgz1L1eLwqFguwayEQIbhfMYvV7e3tSgufVq1e4dOkSarUaFhYWJHRrcXERr169wvz8PFZWVqTiRKVSQTQalWQtr9eLWq3WtOABb2/HqrO1eR635qTxB0Di/3Z3d1EqlbC7uytsJcvv6HlLQMt3j++knn/aYKc+1++dOd95js7gZshPX18fgsEgYrEYVlZWZAthsmCbm5tIJBIIBoPIZDJNZAq9hjpOXQN7/Q5qF7ttHpyl3tUAR4+F/p9GCT83Gsdew52dHQDHtZrZn0dHx4X+6/U6gsEgVlZWAEAy2m3EDu9FgKgTSgmotKua+loDTXq9CNp0zD3BHNdgHqebXhs6BKoej0feNSY8sQasBsLAya6BmmAw2U9d0YDPb1tPeB+9/rCNxAp095PJZV/orWUJ6PVxnb8TCASaiBECcl3ZyVxXNamhMVUrcq8twKoXSScrrx02Tl+H/w4ODhCJRASJM0CY7iwier3I6wVZM1Hmefqe+jvdMTbr1AxxsF2fCTMaNNvurwGB7bOTcHFnnCQXFp3hx8lr9rcGIuy/QCAgVqxpselnNw0T2/M7GSz6N++COAE7N6XeCphRUfj9flng+TuyA3oOMMaPiVem+14rcz1uev6Zv9Pnms+qLVW9aPAauuyPvobTQmg+u60PTRbIXLTMeaGNKcbwUXlq4KQBBeerWYfVad45gTpb+99lMd81J6Bt9q3H45Fdrvx+P0qlEmq1Gg4PD5v292a9YJa4YhwhgRljqbmZQKFQwP/8n/9TEjk1QKxUKkin0wBOtsg0Fyr9P+eh1ofUTVxITfc4f8MyQWTzNDDhAh8IBISx1wktQHNSF9ukAa0GNWSt9BwjoOZ7H4/HMTU1hbW1Nbx48QK1Wk3qEns8Hln4uVbouD4Ctmg02uQ502JbW/X7bRqlZyG8r7n+muGC+n3UYREE85y7XV1dUpqKwJFeQh0zqo0NAl09tgSuZrsIRNlGtsc0SigcL31Ob2+vFRTyPA0s+T1/39V1nBTJOshODC9xkvYss5/Zr6aeZNs1KOc/9i9wsq0yCRdddo3Go9Ynug91RSd6F/v6+prCANgm/d7Z9HC72KHtKgF6IGxgtZ3f6sVF08y0mPx+PyqVStNe18ViUQZaM0gmC8XB4wTT9+a9eI4NiPI35kLn9PKz3Xpg9LNpMUGyG2glk8qJxAkfjUbFAufk1sH77GO+CLw+wwNCoZDsB8w6gk7jaC6KWuno780x1dcwr3lWYhojtmezLQ4mwKKwb2u1GkZHR2UzC5YJoiKgtapfVs2eaLCorXwdf6cNKKf+BZpdmdoC1zFVdDXxufQ81WwOr2GLOTXdq2yzDo/gc5muf3OxIpAAIO5RxkbRdUbQcnR0hHK53LTjjW6HbZxs81Cf7zTX3zXhnNV9z/Zrw5rCMe7pOd7JiiBoa2sL1WoVAIRRLZVK6O3txdTUFOr1OiqVCoDj/iGLSRKB8fKHh4fIZDKiP6hTvV4v4vE4uru7sby83ARmdbs1aOQc0xUCtOHC+UEgwuNM8iKY1fqM+jEcDmN0dBQbGxtSf1Ibf/zfxurwnaXBb64Vup39/f1IJBK4ceMG8vk87t+/L+XYuIEGwzKA480v2DearYpGo02hOuYc0Pe2GdQ23fZji/mO67AG7XLXRgX1E6VYLMp86u4+3jGQ4RL0xPAe0Wi0qUIEwRYBHo0NrXd5ns4r0J5TfR7HyAwhMJ+JOoufbYQYgTQNLSaQ+Xw+YV/5LmgQroG5uZaxDTxGNpbPx3bokl+8llmBiX3GPuT7xHWMSW/EJxy7Wq0mGEPv4sXtibXu123X4oTHbNISsJoLfasXygZSbY3iNbhA0+VXLBaxs7MDj8cj++9q9yJwwgZp96pefHl9Uxm5saZmp/Ja2r2vX0jGbugXRjMGnDw6xla3w9bPBwcHwjYxxlRbVBRdE067zvhC6Oc4ODjAzs4OSqUSGo2TrENb8ooeP5tSNMUJ0J+VhW+Knqt63G1z1Hxe23zVCpgLDcdZu4QoVIpcaHXYCstYAc1WvOk6d2L7dZttwEWDTI47vRicE9rlqhcZHZ9nfqevr987p/feVFRUyjr0R7uXeF8qc3oFtra2EIvFmkJe3Fhhm2HiNN7vmriRBCYbaZ5H6enpkbqLJAbodg0GgwAg8azvvfeeuPu5mBK0av1rGt16jgwMDCAajWJlZUVKunF+kKXRc5vX4cJKcKxd+fRiBAKBpufiTjw6fq7RaEh1jXg8Lkll2WxWALeeX3o9IdjQDJlevNleAmXOv/7+foyNjeHDDz9EJpPBv/zLvwigajQaMnfJCPp8PmGiuBWrx+ORUA3NAtsMZqf335SznttaV7LfqYeAtxOYu7q6UKvVUKlUMDIygvv37wsrzo0VGBbA0mA62Zj6lGsbx0obWzoBloaNXq81EUTQR5DI8zl3Tb3CeaXfE9N1zn4hIN3e3hadHAgEJFZbx3vqNmrAy+/4fCbG4N+c00xeZDgV20l2mMBdzynGxOrKGJpAI/m1vb2NarWKsbExAbcMQyJo1R4Kcy47YQgnORXD2uo720Jvfmd+1vE7HFy9qwUz3JsarShxmzixl9qasi1wwElik63N7Fxa1noic0ABSF09v9/fsl0m20CXv9kuDXbYNs0a033aaBy7+TjZmKnX19eHSqUiL7+OBdT3sgE8m2VHcerHd0F0e822tzK8zGtoUKgBHC1TjrVZO5IuWK/X28REarc876FZToqOY7MllWhjis9ARaUtcFrNdLHxnaLio2uO9zCNPQ0QNRjWgf+67fr3bJ/+LRW3dvHzNwTYVJb1+knhb7edrnTfmOfYQLT597sk7TAOGrzo3wFoYu0ASH1rLmRc/IaHh9HT04OpqSl88803yOVyqNfrMj+4cOsFURvkHs8Jw1kqlWRHnXq9LjvlMIlOZxxTF/Jc7f1i+0OhELa3twWE0tiKx+N4/fp10+LKGFLqvkKhgN3dXWSz2ab5p71tfH8Ikk0wG4vFMDo6imQyKQYmwQg3BYhGo3jw4AE+/fRT2YSB/QagyVgg0DKTUHRyjiZIOLamceY279+1+Uz9o9uvdRo/Hx0dYWtrS8ZwdXUVPT3He9PTaIlEIjKPOX/pjQGOARl1kvYAcNyo27RrHICMLT9rHW5j37W+NokKXov6mkCaz8+1Ynd3F9999x2uXbsmBlmhUGgi47im07jnO2LmzbAvTXyj54IGuExu47wjcDUNYFYBIPjWXr/BwUFsbm5ieXkZPp9P4rljsRi2trak0hOBPN9B3WZzPTG9BzY5dVkrJ6tPgxrzuNOi0Wic1L2jC4svMM+lRaUnlMlYajHpeP7TncXvbG3Ubki+CBxIglOdGKLdopxYtJZ5PZvbySYakGilpeN0TQtbf9allAiaWV5CB4lrcO0kNnDqxGDZLP93RXHaAKr5t/7ficUwz9fGQjgclrJByWQSACQuiwCRc4OKjoujNkTM7FPNCnHcdCwTf2vGzYZCIYkFowKlUtrf30c0GhWDxmwDhc9JBkwbcZzz2ko2+0lfR5+rWQKGuGg3ti7hRSCyvb0t76OZXWyOtRvIc5uTNgPmrMSml8z3Sus0k10HjseNjBTjV5kExYWdkslk8MEHH+AnP/kJHjx4gPX1dTQajaa5q1krhm9wEe3qOt5Bi0YZvQk6+9gsBQXgrXbzXM7JoaEhXLp0SRLGVlZWmpJHPZ4TdpI7oBGUd3V1CaPM/jKFc1P3IXV5f38/JicnEQwGsbW1BQAStsaksNnZWczPz2N+fl6y/Ulm6K03/X4/EokE9vf3Ja5Wkx66L4HmRDQeM7PYW8lZEAdaF2gwqllpve7oeb6zs4OdnR2MjY1hcHAQz58/R09PD2q1GorFIiKRiBjinEdkvGng6jboPq7VaqJ3uIGDbodeH/U80Ouv6d3Vv9cxtgDEELd53ghmSUwxOYlbJbOtGmsQW9BYYkgJQSivy3VfM60mmUbXPsMseNyMfS2Xy7ITly7Bpef1xMQEgsFg085dlUqlqY9JNnBstP4yAXc7+rftkACKzZrXx93YN/29dmmTkqeLZG9vTxA7B4Uda7rHeS2nY7pTdFttAJb/ezyet1wJGoAy+JuAm5YQlRbjRChmgpMZakAFr0VPJBNQ29qsXbkEPj09PU1Wv14oWK/VTUyQZruv02/eRXFqrw3A2p5Dn6ddHFQI8XhcvAN0aW1vbzdZ7ASgtvlnKkMN9nQsFUXPcf6uXj/eGg9AE3ggYCajmUqlkM1mRcmZ1wSaKyHYwmt4b7Nv+Z1mfglGGE/IuFVeQ7ulGNbCmD7qAjIaTjpF/62VoM0AMeVdmrfmwm9rt81Y5DGCRY6Dz+dDuVxuSj7hPGRd5lKphMuXLyMYDGJubg7Ly8tIp9NSAYALKPUK2XouyMViEYlEAtFotEnnmEaNBl7aCCIbQz1IoFwul7G8vIylpSX09PQglUqJ/hoeHgZwEnpDsKp1q26H7k/dD5x7uj2Hh4dYWlp6q9IB30fqe7J8AKQyCDcM8Pv98lw0Evi+6FrM3d3dMud1UiTbZ7KrNgPFXGvPej7rcddMmg534HdHR0eo1WpSbD4ajSIQCKBWq2Frawu7u7uIxWIIBALIZrMCgA4PDzEwMNB0Hw326vV6k5FrAjcCXdZ71fobsJc508BYx8AyQbCr6yTxq1arNRlBHHu+ByMjI4hGo+IFJdYxw350rW6d7MXEb03MkUzTupf9wXeVc08TI9S3DBNj2JgOm9DEHI1X1h0GIEYxx4/zWicm83/b/PxBAKsbEDUnpPkb/TuzkRq40u1kVgrQrhq9t6/Tg2pARiEgtJ3vBMiokNnRnNycwJrtIoPFf7pygLaSOEmp/HQGoW2x10BV31Nnw+q6a7ynm+ua/7MMkxNgNQGc0xi6WfFuwO8sxGnht31ne17b7zgfmGTBsks7OztNQf3cEpMKRVvs2jLWcct6bPiZ489juo3ahaiLSTOui8/AgHkzO1Y/I5Wa3onFZgVrFtAEBEdHR8J+6Xiqw8NDRKPRpmQBCgEA+8bn80ltYc51rfS1mDrHpmts7/u7Mj+dxDZndb9TzHM4/o1GA4FAQMAA/zF+eH9/H+l0GoFAQJjBixcvIh6P49GjR1hfXxcgwOsSCJCFZbm9QqEgOoaADjipN2yGvFDX83g8Hm/SZZubm8jn8ygUCpKEw/CCmzdv4u7du/j8889lZx3qbRplOkHLDNWxsT0a9HCh5VziYq3fNepxzaSOjY3h3LlzEurG94+1rzUg0p6N/v5+IUH0u2x7N216180Y+zHFjQAww0o4p/b29rC9vS3rKfuqv78fpVIJOzs7AtCoL8lEcotQlmXSTCDXaAJKTYaRkGLbgsGgrKlsp3aFA5Br0fDWoJux3pwjOqlKe4Wo95jAxOuzPXxOjVkIgGlosc38m+8k5xp1N/teE34asGowTIDv8ZwkA2rjSd+XoJ3tZr8wqdPv9yMSiWB/fx+lUqmJjTaNcT1HzL9t0hbDavt8GuBim7x6oWR8WjgcFpfJzs4OgsGgBA1rCxho3iOdnQu8zcCarkuebyoD/QwEyXwJOFEIDjnR+NJxQjMuVC+qtvvY6pI5WcyciASsrPtHJcuFXFuVGqSbLmcNgE1Q5ATObGDFFN2H+u9WE/DHFhuQbgVkbb8HTlhWlgvieHB+0G3JeEJzTFlijJ4F1iLlIgugaTzNeWW2icqan6m4TFCq26lrDFLJHRwcyLabul80O6YXHrN/Dg8PZbcTPhvBBBWmVpAEN2QB6S5jzWFt+Ol+MPvCCUzrc83xdZKzBgD6ndMsje290vOKn4GT8KZ6vS5hKxpEstQdQwAIRAOBAAqFQlPNZp2QRKY+Ho8jEAggl8uhVqvJnDVrXbIt+pnMeDXqTrLqmj1ibU7qv2AwiGw2i0wmg9HRUTGMqNN4n6Oj4yLzu7u7TckqZt9p1pT6W4d8UWfq988kQhi/x3AbHXfo8/kwPDwMr9criWwEVXw3CNR1GAN1to591+Nt6lub/v0xhX1EfWMzqtlvek4TsHIHqFAohFAoJPHUNIrYN9VqVTa/WF9fRyqVki2D9VpIAknfWwNNGkZ0c2vjXrPcHEsAb7Go2vNLfd7VdZyLYgu/6+7ulhAExuNyUwTN3vKa1I9kjrVO1/kGegzoBWGbtceqr69PQi9LpRKq1arEm9brdezs7EgyGBPbNG7gO8p+SKfT4oljaSwC1nK5LFUe9PqjiQdTd7fSud9ra1bdOfomGj3r700mRjdcx1iwoHW5XJatGoFja6Rarb61WGkrSFvqGlx5vd6msiJme5yei1YR47X0PdkOXRiYk4DP5gR03O6tmVH2CYEFJyHbwMmjmSudpcgXnS8k3WVerxe9vb3yclFsRoWTJc/vncb9XRKzXU7A1HYuv3MaOxtzTkW5u7sr9YUZ26etVW6MwaQBXqtWq2F3d1eSSDjPCBw0UDTZT/7N63J+6PeC2ZvFYlFYVg1wu7qOy8mZ8UVm32kXqQ5l4Dyka09n2ppziwbg1tbWWxsrUMLhsFQ04Nw1x9dprG1A1vbZadzPSjiX9GfNkNiMFdv5ZP80i69/Q+Zqd3dXACrHlKEA3F2Iol2Lg4ODGBwcxP3797GxsfGW8aLJAraJxzTDxrnAzHmOs9Z/jMmNRCJSD/bNmzfwer2IRCLY2tpqctPTuCEg1fclCNFrAt8TtkdX8dDPpT1jfK8IKAlGNKDw+XxIJpMYHh7GkydP8PDhQzEWarWatE17Vkx9xGcwPWf8rN9VPU9+bNFt1e0zxfYctVpNtg5PJpOIRCISRkFDq16vo1qtwuPxYHh4GH6/v6lsG9dlxnnyN36/XwxxXXqQ489+52f2nWbS6QUGTkAs/weak7XpDdDPR3e/Jpg8Ho8wxDTOuIbokB4yrmSG6Y5nuzSjyr7V84geam62QWLE4/Fga2sLpVJJGGZKtVoVTyGxFWO3Oa/z+TwWFhZkrDhH/X6/sK+1Wk3wE3WB9h7rtaEdQ+vUgNVm2TuBMxvTps/l4LCkSTQahdfrRS6XE9ZVxyAxRogPx4LLZKk4MQlgeQ2dBOUGovV3+nxm2+t6f7QMaRmbz00FTQXpZEmYiw/bQ6uKE5HuOh2jql0VnFTaGt/f3xe2iookFovJi2Jjx2x/28a11ThTzhrEtgKr7HOTFdDn28CMyfhHIhEEg0FRDoxl5sJs9o+OI9TfcQcXM6ua35ugkcf14kWFqBdl7W6qVqui2HUsnRbNHunFXrffBEkEMpxr+hqayTIVVXd3tyxEfL9pwVNBJxIJYW3NsbAB01ag1AmI2849C7E9k9MzmO8x9YeOX2aCD9n7Uqkk8+/g4ACVSkV2FSMTRZIgkUg0jR29TyyHxUQkjpnWf1yYqcc1KNTPw3VAM/h6Aef3Ou66VCrJ+TTWNbPL+W4aeeY7pZNCKLYYXB7ndww1YD/zWgTNlHPnzsHv92NkZAR/9md/hn/+538WQNBoNCTshQyVHk9tbOrx1X3IY+a7dRZi01Hm2qsNVs4XGkg7OzuypTWBP8kWzuuJiQmkUilhRI+Ojje46O3tRbVaxd7eHvx+vwA8M5afc5jrpXbzcz3XgJPEjwaoFF6PXlkATedxrmkvlg5d2draQiKRgN/vl7AAtlkDPP0eaaNLG/68vzZMafTx3ec6wDWGTDDDtPRz8/40YFlibHd3F+VyWWpj6x0K9/f3EY/Hm/CZrkCg1w2nuesmbQNWJ6BqLhi2m2pLUf+GCxypce4TDkAmIxUCXaWaYeGiTkuADBEXVg4gqW2nZ7K93Npq1dnMBBj9/f2SdMBzyZJpK9dkdlv1MRdpxgAy1ky7ifVCxZfRvD8Vtc4i7OnpQSKRAHBS5NdsmzlGTorSxmS59fFZidt8tAFwJ2Wv5xUVJ/t4a2sLlUoFoVAIiUQChUJBFCENKSoj7erXDCXbQYtZZ8uzTdpIIbOu3fS8rp6DVGRUdJwjPT09TVmiJrOp31lzDtjcfsDJe3Z4eFw2i5mjplfE7G8WWa/VamKd9/f3S/gLS6uwcLjJQtnGutXcdVOQZw1WdRtMcO92jvkdYzABSIhHPp/H7u4u4vG4gCvtcaFe2N3dRX9/P8LhMKamphCJRMRt6/f78eGHH+K9997Db37zG9FbOsREA05zDmnRgJNznK5fusz53EdHR5LIRC8G9V9XV5fMHQ0uNeDTelOHLbAdbDvBghk2xbmrk1NYM1yX/tLVQfb397G0tCShFozD1WsSPYAaDOvxpbQzX9td+H+fosdbG7jse5uuoc6gbqLh6vF4pDA9114CI5JRnMONRkNiqRuNhnXd1/OS99bAj2Novmt6ndVzikaLLSSReo9zg2sw122/349yuSzvlNbVnFd6IxrqRb3xBPuOz2Ey9TxG1hc4MQ6pn0li6fAxPj/fE9ZW1YQEACEa9vb2pP5yOByGx3PM3jJxy5yXph7mvGmFF7731qy2G7TDYujrcJCJ3rmbEwDJsIvH4yiXy1IXkJOE12fHaUaHHcHO1q5Um7iBFP3C6ZfNtHz081BMS828jqkMzf7jIs2FwDynp6dHWGU9AbSblcB9f38f4XAYqVSqKR6I/Wj+7QTetDKygT7T+j/rxd9UnGb7bec6faf7glYtLclqtSoLEgBhixhDRWUNnLgVTWZMu4O0mPfVLikNZglezTEjgNDzTgNHXleLZqWcxEm5dHV1IRQKoVQqiZI1+1/3p36HGSpxcHCA7e3tJpa2Vqu9FcTPa5rtsh0zzz3ruekm2iigOAFt2zvbaDSEsRocHEQoFEIgEMDa2pqU96nVajJH9ViS0fL7/RgaGsLQ0JCEkFy8eBE3btyAx+PB3/7t3+L169dSFUC3z2RKgWY2yjTqte7i/Ozr65NqEhpgNBonyTSMpx0YGBAATs+WTrYy5zPZNr2Y8rf8p3cyJEhlaAK9bjp0jaQC28XYwc8++wx9fX0YGxtDpVIRIKFDHQh0dWgXdaiTHjXnNJ/xXZjXbDfBmSaA+Dx6jh8dHddhZWxooVCQ9ZPgiuWSXr9+jWAwiGQyid3dXezu7kp4BZO1GEqgvQta9+s5ovUJjXiThSdYZp/T06NjW3VZMz0XdfKqXhN8Ph98Ph8KhYKEYWkmlVn2FO09owdPhyJo4bUajZPdrahTGW9OQKzfX96X9zo6OhKDipiH/QdAEje9Xi82NzfFCw5AKjzod8ycI6fFC21VCXC6iG3BMhcmJ9aGg8L4FVq4rGPJgH+/349gMCg7NWl3DDtQTy52so4N1C+yja0wASXwtiuGilYzXDoWwxR+r0GFXpj1efoeZlYemSc+q7bs9PX5fFT2BD3d3d3yciWTSYTDYayurorVyt/pRY/HbHIaEOrGrPzYYmOj2mXYzN8AJ7F8tErr9ToCgYDsxsS463g8DuCEQdIvvGlImSBS30+LyVLoOCpew2RuTaVGEEugawNAWvT1TGPLBBP8vbk5hQb52tjjOcPDw5JAwwLrBwcHCIVCODw8RD6fR7FYfOt+prR77F0Wm6FlstP833x/CQB0/Bi9UGRTG42GJHxQX9A1DhzrnUgkgnq9jocPH0ocHZMHHz9+jJcvXzaFZZEd0rqK46vnjvmMNuOdIQlsEw257u5ulMtluTaZuYGBAUxPT8uc2dnZkc0D2AYCCv7NftL9SQBwcHAgW9sy+Q8AotEoIpEI1tfXZWtbLsi9vb2ygQjnMcHB/v4+8vm8jGN393HJO72tM39DkGIaJzay6F0hBtgmk6Ez339z/Lnm8XflchmXL1/Ghx9+iPX1dXg8HgGlfX19CIVCWFlZwbNnz/Dxxx8jFAqh0TgpT1Uul2WuUB/SAKNhpNumMYGtpBTP03HK+hwCPnokNNuqw8a0h00bYKFQSDxyxEN6/Hkevck00IDmzSn0GsDf8vPR0cnuWjSw6vW6hAtqXUyvDKu7AJBNL3QlBOZh8F0CjgkF7jYHQDzQZsgNDRm9hrU7f9tmWFuJGyAwG8XjnKRE/r29vYjFYhK/wh0uGCfB35qKUDNW+jgpdq2MWDqDg2QqSn0Pc6HXsapm0LUJxjWboEW/JPp+WswXq16vS8mIQCDwlhuX/aoBCl8w7WoYGBhoyk60iY2hM8VkctyMknbmzu9TTGXuBFadWDkbq8VnovXIuB4AEscKHMcrlctliT3WAJ4uHtNtRUZBJz7pcdXlsjj++jztujLFBhxM5kGPlxO7qo+b46wXV4bo8PpUxvX6SWUEKtSenuOtRDc2NpBIJJoyqUOhELxeL8rlclPcom2sWh07jZzl3LUZwk7PZ76HBFwETOxvAiPOW/Z7MplEJpNpMu4ZM5/JZGTR6e/vRzabxcrKimTxEwhzMediRJ2j2RX+0zqTrDrBJxkautx5Ha0zCQJ1mNTa2hqq1aqEoPD8QCAgYIbVZsy5SsaKbSdjFAqFpJD9xsYGarUa0uk05ufn5V1jxjffLbJeBO8E+mb4DQ2GcDiMcDgsbuB8Pt/EqrGfzPE3gayNkT8r0WuwJou0rtFrl8YCtVpNqgDQUGA9VhoLrEzx8OFDXL9+HdFoFJVKRUC/ds+bAFSH9XGNNskorRt13CuP6XHkNbUuJrgGTggp6m4AAgYbjZOqP2wzmWKdq6Pfa4/npIKGBtFsGw02nsf5TG8s42Y1MGbIAhOEGXbFRDEd5sDnIOhm/hExRSqVQigUwsHBgZQk02NgM2R4vB2C61RlrTSQa2eBcAMzHABOVMZCJBIJKSe1vb2NeDwuAcoEiRpsaveJdtfX63UZGL2do26LE1jV55iLP8GgZmL5t1bQwEmAPuMF9XV1GzjxTfDBkj600Mvlslj+vI8NGDIkgC887zE0NCSKVrMptjEyj5tjamN4bL87awXqdH+3drk9txbW9OM84tjw3/7+PgYHB1GpVJqyjnVSBhUCjR9mxlar1SbFSteM2W7TqNLz2nwXNQtGBW3G6WlpFbZiLv6m+880AOkm00qf/RGJRFAsFkXZHxwcoFaryVaNZqF6Nz1kjlmr85zkrOcuxTb3eNzpGJNC6WYmEbC/vy/7gMdiMRweHooX6/DwUEAfcGKY6Jh4ug9HR0extLQkc1mfqwkC4MQbxpg7c876/X7cvHlTzgkGg3j69KnsMkWQSm8G8xt4Pkvx0PVK9z3jXUOhkMTTUUyWXr8LBKAej0e2sUwmk3j9+jXS6TQajYbMY16DRgKf1+v1IhwOC0hmjXGuSbVaDTs7O0ilUlL5IJ/PCwur11oT4Ol2u+nesxD2hQbTQLOucCI6uKkI8zboiq5Wq9ja2kI4HEaj0cDQ0BDGxsZQr9fx6NEjDA0NYXx8XAwzZsRrt78WAjrNnFJ3Ac3ElF7r6vW6eCy0ntUGFecjExaJIXgv7dGigUaPAhlMYhuCWs5t3W86TFD3pQ6p0ccILLu7uxEIBMQzkk6ncXh4iHg8joGBAYTDYQln0xhLx3yzf+j5Zbm2vb09hEIh2UK3Wq1KWAzFnBennbvfi2F1Uv5OL49upGkZagDFZIBgMIjNzU0prgtA6ulpK57KS4NYDgoD8Dl4/KcXSpNl0s+h42E1ANCA0ryenox8aXkdKjjzJdCLu3b5aYtPAxngJH6GLwlZPg2ePJ7j4Oeenh5UKhUEAgEpM6R3sGhH9HjqMTWBqU0RvWtia6MNBNrEPM6F/OjoCOvr6xgfH0c0GkUikUC1WpWtHaks9ELEbfjoltVGV1fXcaIRgR3ZW1PxmmBSGz/m//r5AUjMrf6t/t6cnyYbot8rKnJ9zDY3OEe114OLzP7+PtbW1iQxkGze4OCgGJzMOLUpQCexGdXt/E6fe1ZiAhLTMAWaSQRNBpDBKxaLsnVpJBJBV9dxge9qtYrR0VGUSiX4/X6cP38eL1++FD2TTCal1A2NHLo+G40GEokEhoaGBFAS5BWLxaZ8A4JK6k4Nvsg+9vb24sKFC4hGo2IEBgIBlMtlrK2tCaPKBbRUKjXF3nGNoMuf68De3p4k7Hm9XmxtbTX1k2bP+vr6msJkOEd3dnawuroqoWoApOoMz2ffDg4OSh1WJhKyLBjfNV6b9SkHBgYQCoVQLpexsrLStFmBHl9zzPX/el36vsbZDyFsqw4x0jrBZkDyb+q5Wq0m4C0SicjcI/NYr5+EXnV3d6NSqSCfz+PZs2cYGhpCOByW9uicEs1AayCn13Pt+TGBlWZTdSgg5wHHgGw6CTedCKjnP4EoE6pLpRJGR0dFx9MNbxJz2nDRFYR0v+pQBP6exj7P7+7ulmz+hYUFMVgJMLWuB048gnosGZ5AnULDmF5dbgahdRT71MQR7YLWU+10ZSpH00Ky/e324mjASuuKcVIbGxvY3d2VzEHuEqJjUTiAOrRA7zRFIKAXbF1A2nSP2p7Zdlwv5tqi0YqG52nQyc/moNhcv1zg+c/j8cjk1+Uz+BtOUrqWgGOQT4WeSCQke8+MA3Qbn+/zWc+Ns170TXEzqtoBM3wH2Nd8yQmmhoaG4Pf7xVXa3d2NYDAorhjgZAcezumdnZ2mShRmW23bsppzVrvf+Fn/z+vphBIzRMAGBNlX2sDRBpn+ji5a3Zd6XuowFPYhwc7a2hoODw+RTCbR3d0tRhWZKhoGehHS42V7V52M6nblLBZ9U5x0qX4+G3tFxq9araJWqyGVSiGVSkloBcGbx3Mct3b37l0kk0nZRIC7Na2srODly5cST0oWiUw6AW4oFEK9Xm/a3Ux7HvjeUGcSGHJRXllZwVdffYVSqQTgOLYvHo8jmUyiq6sLa2tryGazTQmkZKMYf8u5SN1JPRgOhyXEQe/wp41Iv98vYRSaGeauS41GAwMDA6hUKgBOwFC9XpewFW61SXd2V9dxItXq6iq6urqwuLiITCYji7nX60UqlUJfXx9WV1dRKpWa6onrf7Y5rueCyRifld61AQ9be9hODWR3dnawsrIi4ScMBSIjzXnO72nYc3vTfD6PSqUi480x1+Ux+ftG4yQZiXOS4691MRlFznuTZaQBwnto4oFGGfNJ2H72Eb0fDIXiRjN60wxdhUIzwxps00Ai8Of7T6OJ4FjnW9CTsbu7K6SACegJzkkY6Lwej8cjoQG1Wg2FQgG9vb2YmJiA3+/HxsZGU/wqRferniftGllthQToycZOtylSJ/bNqUEaTJJNDQQCCIVCoki54xVj/fgbdpgGdgS+unNoBekFlwsnAQXbZ3vJtYufk0UrPOCkdBD/1oOg2SjtMrWFILCdtF64QOvC8QTjOq6E/cLn58Qma+DxeGRSbm1tIZfLNQVnm5PG/N8U2/cm2DtLS99JbIDUBGZOv9PPpVkBjhOBZygUQjgcloWJ4RycC2R2NBOhwa1NCD70+6KBpjaMzDlqnsP55cSwaytdt8dkYRn3x0VHu3t1P9O6p6JiaTqeS3eSjkv0er0SRhGJRMR1zZgoc+ycxsl2vB15l+atkxGlCQSepxdLgsdSqYRcLoehoSEkk0nEYjFsbGygWCyiVquhp6cHhUIBhUIB586dw9WrV9FoNPD//D//Dx49eoRSqSSZxcx+Xl1dlbACHW/X3d0te7739vaiXC7LbkVctHVYDPWg3+9vcrcDQD6fx9zcHLq7uxGJRACc1MOs1+v45S9/CeA4dpU7WXEvcwIBZogzlIahJtrtenR0vBtSpVIRFyers3BeJpNJ3LlzRxJkAAi7e3R0hGq1iuXlZayvr0vWfyqVwrlz53D+/Hl89NFHWF5extzcnLhg9/f3EYvFkEgkcHR0hFwuh0ql0lRnWOtQ7WbXc8PUxWcJVtkmDa41kWO+VyaGODw8lIpABPN0RetdA3UMP68djUYRjUaF2WQIAeeL9sxQ7xKMMa+FYJFxydTJXJe1TjXXT75zZP7JkDIXQXsTtKGpkxTZHoJTDVZ1P7FP+A7pOdLV1SXEHcOoOE+YEEiSjTiI7yETuxhO4fF4BPxzBzK2nUCU7Pf29jbC4TDGxsYk9EXfi89oI0hOY2S1FRJgAyFOgFS/RKbYGkTLhzEPw8PDSCQSknxyeHi8VWOlUpFBAk5qsulFleCQGXvACWjVC65OdDHbqxcIMlHcaYPFdXVWo94Ji99pd6wuh8EXR++Yoa0utpP3JojXBY15Tf3yaBBDCz0ej0vdxXA4jEQiAZ/PJ0yFmSymx1mPeytQajt+lgrTFPP52pmfrRhWnsP5wUSW7e1t2XlFGxpMuiJg5HjxHF0CRcc7cb4QGG9vb0vZNz3+tPydnksz99p9ry1ms690P5jsLq+j96Q2mSCeQ0ZXG2pcMLq6upDP56X8lc/nkzjrWq0mYJUlU2wJKea42I63Y5SYz/cugVYbUDGPm8/I+VkoFLC9vY3d3V1JWllbW0Mul8Pu7i78fj+q1Srm5+fRaBxnB798+RJLS0tS6WJ3d1d0VrVaxdLSEra3t2WnrP7+fqRSKXR1dSGXywE4zqafm5tDsVgUHWy6aEk0ZDIZAJAtOHUsaFdXl7iDyXg2Gg1sbm5iY2NDgEpXV5cUNM/lclLWr9FoyMYG2rtFcAJA2DuCJm2MMgwimUzi5z//OcrlMp4/f95UconZ6SQJ/H4/crkcFhYW8PjxY/zJn/wJ8vk85ufnmzazGR8fRzgclo0bdDs0y2WOux5zG8FwVqBV39tc15yAKnCybrM8IAHrwcEBUqkU1tbWZCczXcuW6zGz3xmWEo1GRfeYOl+PP/NiyKoyKZEeM7KT1GVcy7m2U1+z/R6PRzxtrGjA6/P52SZ6gPXazTWZMdkej0cqrRDnaPKL3gxuNsPn0p6PlZUVIVFIajBkptFooFgsolQq4eLFi01hhzyXNXFLpRI2NjYwMDAgz8E1gAmJ7733HgYHBwVssxqJnhPaG6SJH46P6Tk0pe2yVq1eBidQ0Iql00qDwb6Dg4MIBAICFBlEr61PglUOEEEcY2DoNtIMKgCxMvR1NFMBoAkYE7ByIPlSACcJV9pVyWeiO4KWE9DsttUWhtmnjIMhAKbiJIOg22iGO5CljsViODo6LsJ9+fJledGz2Syy2azjYmwLbdD953TctJZPYzX9vsRtnrZ73GSw9LkcF70IdXV1IRKJwOPxiKUPHFcPCAQCKBaL8pIS8JKd1XFuXLiY3UnrloklnPc6nEQH61P091SeekcibUzp8dJxaLZ+Mt8X/VsCDmZREzyZoS+s08d3nPF8tPZjsRgikQj6+vok7pLXthlXrca1lSHS7rk/ppjvkl4wKea7RyErXS6Xsb+/j0gkgpGREczOzspmFww3yWazUuS+0WhIfx8eHkrWPl3cZDXpciSjyNCB3t5eFItFmfu6bwlCyTgdHBxga2urKcyJupRMKFlQzu/d3V18+eWXMpeB5ndGgyXei+FRdN9qzxeAJv1OIoL92dPTI4z0T37yE3R1dWFlZQWNRgPb29soFAoSwsLENV3Y/p/+6Z/Q09ODhYUFAJDkFMa8Li8vY2trC7VarclDp/vORgq8a4YVYG+fGerGZ9F6g7qJwOjatWtinDNprlKpCINPzysrTJTLZWFGdTlLhnhw7Mn204DiXGGyJw1nMqFczzVoJLOpPa1afxIQmgmJ7BvqbepkGj/lcllArK6NbObTNBoN9Pf3CxPK73QyF0Egc1c0buH4HB0dYXh4uMn7xd0x+dwkU5LJJMrlMh4/foyjoyNEIhGMj4+LJ6K7uxuTk5OIRqNNHkcbE20jjjRL7Can2jjAnIi6Ie0sBjZwwwGldXVwcIBkMolAIIB8Pi8Tios5A5n58MCJhUbLiEqWCzsHvR0Ao12rekIxZkZ3KJUZFwNOcoIH7ebVYQz6HqYi0swsJ1Kj0WhKPGHymd6qlvX7uru7kUwm0dPTg3K5jJ6eHly4cEHqsK2srEiJLLM/nNgom4Vs9pu2nN4VhtUNhLoZUfpvGzPA7whYG40Gtra2UK1WMTY2hvHxcdy/f18YqmAwKDXv6IIimKOrlTGA2qDRLhS2wwwFMZ/XBJomQ8MQBTNm1cbe6OPaG8Dj2pPAd1CH5VBZ0Vvg9/ubvCAE+H19fQgGg4jH47LIkK0aHByUzPZisfhWiI6pf77vAt5qfp+l2IC0/t/JMGSlBcb2+f1+jI2NIRQKSUIWdQXZPbKxdKdzv/Z4PC4MN7fRpF4cGBhAtVpFoVBoyuYnADMNK+BkwaQxw3eCcct6Ew4dZxiPxyWUYW9vT0gN0+iibubc1EmpfDbqTR2zGggEpJB/V1eXxEIODg6iUCigUqlgcHAQU1NTKJfL4rbNZrOYn5+X+uGHh4cCqHkO16Wuri4kk0lMTEygu7tb5raOXzXHWYu52DvNjbMUrRNsBhX1jzYuaLzMzc3hgw8+wPvvv4979+4JM53NZhGJRBAKhWQr4WAwiL6+PkQiEQFJ7EcCSZOQAiCxpXShc+3e39+XqiRsH0Eb60PrKj16rmkArGNMtTHm8ZxUy+Aazncim81KTDOF81x7jTm/eA/qAJ0AxndCh1eagJqs9MTEBKrVKhYWFtDT04Ph4WEEAgFZ30i8XbhwAQMDA1hfX5fQrmq1inK5jHA4jPHxcan2wmRPM/fBpqdspJCTfK+tWZ0WN5vYrENeg0qLQcalUkmypgcHB5HJZIRR5E4tlUql6cWnMmLNy6OjIySTSfj9/rfCBYC3dxnSi562QPTLxDgo4MSS1xQ+ABlAtkkDZB7TStSprzipzRhDDbz50pC91QkABEeMxRkaGkI8HkcgEMDu7i6Wl5etdf6cFKMeQ9v/+nvbsXdBeVJMEOrGqpnPah4DTurj0lAoFosAgEQigVQqJVmSNDiCwaBka+7v78tc5gLJNvFebu5AJ9G/49zQv2UMGJl4xjGZz6pdQ9pQ03/Tkta7eXEuajDLdjCkge8QY6OCwSCGh4fFOueud2NjY1IaaHNzs8kz4GRs2UD4aebguzZnzfmn54nN2NYAluOTz+eRzWYxPT2NsbExJJNJLCwsoFQqCQDjIkoPFA30eDyOP/7jP0axWMT9+/clw53lonp6ejA0NIQHDx5ge3u7KSmJIJTt1XNLj5/2nNXrx1ngQ0NDuHDhguhRMusjIyMSdkDvli6dY1ag0Ewu3w2WH/T5fAIyGNoTCoVw4cIF+P1+xONxAQusP8vQtGAwiLGxMWGv7t69iz/+4z/Gmzdv8OrVK6lfy3JWmUxGKt1kMhlcvnwZo6OjUlu4Uqk0gQq3ecDP+n/TaDtr0cBUv5uaWeTY8ju6krPZLObm5nDp0iXcuXNHQliKxWJTQvH29ra41ukW1xUt6vV6k5tbV5MgeURmkcw/jWkaKzSoOZ+p00gqAWhaq7XhxLlmEmecowwnYUUkxvByoxQa+gCkFj1ZT12Mn+yxSVQQHOuwBI1z+Dw0BAHg5cuXog+Ic7jjII0DvTVxJpPBzs4OLl26hLGxMYk3psdAt9NcX/V8bcWsUk6ddKWPOSn2dhU+z+PeyoVCAeVyGSMjI5iYmMDs7Cyq1Sr29vYQjUZlEwGddESFVSqVpOOZoanZTd6PlpHJaGrAZSpUZsN1d3eLAtMWOxUnQaR5TeBEYZvuWj1Q+m9trQEncS2Mh+SLwKDnSqUiFRYYQwUAU1NTSCQS6OvrwzfffIOVlRXXyeHGpNvOM0GOG5t+VmI+gw3c6HNtLBbF/A2zsBnsXy6XEY/HMTY2hu+++w6VSgWpVEoyiXd3d4WNpULl7lhmIHq7ol1G/OzxeGQh17F7VLQsqK6Vnbkg6s/mXOU5zOjnZw1Yufc0AQmVpk6G6O7uFuOyq6tLEteSySQGBwfR09ODXC6H+fl5ySB30z2t2KlW8i6AVZMc0LpJ6y3zN1wo9ef9/X1sbm7Klrajo6OYmJiQrPRisYhEIoGenh709fXh6tWrskiOjIxgcnISy8vLuHfvnlRsIevo9XoxNDSEvr4+bG5uNlVgAewLuZ6rWm9ooE2mi1UBOM+6u7uliDxj8tgWfQ3NMgFoAhq6f2g8aqOqVCqhUChgbGwM169fRzabxebmJpaWlpDL5VAul9Hd3Y1qtYp0Oo3e3l6Ew2GEQiFcu3YN09PTOH/+PHK5HNbX1yWUjVnga2trSKVSuHr1Kvx+PxYWFiTRSMf4so1ORrTbeWclpv7Q3hd+b/7juQSs9AjkcjlMTExgeHgYFy5cwOvXr2UOk22nR5UgFTiJufT7/eI1INuq13ftmiao465oZFCpPwludVK0fh6Cbw3KOc+1R0wnQvH+NP7oeUun0xLucHBwICEPnJ+8v8570B4MXWFCzxcCb80k6yTtQCCAZDIpGzVEIhGJ/db3p37mJheFQgFerxcDAwOIxWIAIKEdLG+n+4ptMjGWOX+cpG2G1XZh80VxYqTM35rKaWdnB5FIBNvb21LPcmRkBJFIRPbDTqVSGB0dlSQATb3TRc5/WjHSgrC5rLWV5NReXWFAT1a+GF1dXVLQ33xODrS+tgat/JsvlWZK+UIyA5b0v2ZWj46OsL29jWKxiK6uLiQSCQwPDwvTMTAwgGvXrklixdzcnCz6bmNqiuk+1ueZltK7KG7gxvy+XcaC31HBxmIx1Go1lMtlnDt3DmNjYxLTd3h4KPtGh0IhbG5u4vDwsGmvdPOd0syUGRbAvz0ej7iJtELg9+ZOJhrUdHcfb62nC2FTdLyp7iuTadXHtfFGBa8NOZZQoaeCoUDsg2AwKCESgUAAIyMjmJqawsHBATY2NiQz3cmgso31u7KQn1a0ruBn4GSMbGBV/62fe29vD5VKBZubm9jZ2UEymcTMzAxev36NcrmMdDqNsbExNBoNVCoVVKtVXLx4EcPDwwCAr7/+Gk+fPpVMYB3TOjAwgMuXL2N1dVWMFsb/UWdxsWQ8IsGw1v9kchqNhrwLzB3QsaAErIeHh0ilUk0uYuAkD4JhUwQh1FF6sWT7tDeMu/MsLCxImZ6LFy+it7cX6XRa3JxsDwkE6oBMJoPz58/jvffek+L2Ozs7+Oqrr1AoFKSc4PT0NEZHR5HJZCRcg8aATdeac8OcJ7bzz2Le29Z+/Uwca36v2UoAwublcjkB+LFYDOPj44jFYsKyDg8Pi3teF68nO0pvJxO36D6nca4rVRDIaqOec5HeKeYNMA6a84X/CAI1gAUg3xEbaCOd8d2M0e/qOi7dVqlUkEgkpP2cqzyfxpmZmEidzbWDYVX0LhwdHckujPy7v79fEtZqtRoSiQRCoRDW1taQTCYRCoUEzDNck14wANjY2JB4bHpvaPTl83kxGDi+5nz9Prr6ewFWihMrYypc8zfm31QA29vb4h7hC//dd98hm81iaGhIdg1aXl4WcMe4J25VxvACoHm/dwbtm8DRBq61JaVZAloZTIjiQPh8PoldoiXG62nrTrtHbP1jhhnQKtLfMzicLgrS9bFYDBMTE/B6vRLcT3YVOGYCV1dXm4B1K0BmLpg2hWSOv9M1zlJsTIX+v5WY81r/f3h4iFwuh7GxMWxtbWFzcxPj4+OYmJhAMBhEuVzG+vo6RkdHxTKNx+MoFotvKXOK3k+cc0yHt9BQo0LURpFm4Mg8MEaL81LHeJljrBWh2QdsDwEG28JFx1RAGoTTzaW3x6Q7jxnmTNhhfJ/P50OxWMTCwgLm5+eb9tg222UCNXPc/tDECYibTIX5GzOMhKzVxsYG8vk8BgYGMDY2hqtXr+I3v/kNtre38fr1a0SjUUxOTiKZTGJnZwf37t2Tsk7MlAcgHq7p6WncunUL9Xodq6ur4ibUbeUC39/fj7GxMezt7WFhYaGpGobJCgOQXf10PKyuVNDT04P3338fKysrEpLC771eL3w+H3Z3dyUHwqa3GCpAbxXfh4ODAxQKBRwcHODv//7v8dOf/hQ3btzAJ598glQqhd/85jfI5/MCILibGGPDnz59ijdv3mBoaAg3btzA0tISPvvsM+RyOdRqNYRCIczMzEjpH6/Xi5WVFQH37AcNsHWf2uaI01z4scW2NpjPocfcnNMAJI51fX0d+XweFy9exNDQkMRO5nI5jI+PA4CEdDBGmDpLb2JCvcfx5nykDtX3Z3vJrJIMoIFP9tLGZmpgpgGv1qcEkiQrNDnh8/mQSCSwvb0tRj1Dx4gLtHt/Z2enaUtgEnU6WYvXJmlAEmFzcxNdXV0YHh5GT0+PsKF+vx9TU1N48OABXrx4gcHBwSaSjhsP8flYhu3KlSuYnp4GcOwJpqdcx2Sb86Qd49sm7jUEYEe+tpfJXKzMc92kXj/ZRnVzcxPlchlerxcXL15EIBDA0tISCoUCuru7MTQ0JNSzWauMC7QGJLQ0CCRJ15uLtV5cNbjUWX5ktFgBgOwswTInFv/W8VHasjQXHR2Azt+TAQBO4l4YIL6/v98UmhAKhTAxMYF4PC41FePxOM6fPy8xgrTSnJhS29hqZsJ2Ls/X/zudd5ZiA1K2NtrAtwm8zO/r9brEoe3s7CCXywkwuHr1qpTtoeJkaaHR0VEkEglxbxEEHhycbCtIDwDnB0NTaNFrUKkNJB3Dyvmu5w23qWQsF59FF33nuJOZMJ+fwnabAJZKXC9UXV1d4h1hjVXGqdLgGxoawrVr1zA4OIjd3V2srKxgYWEBmUymJfNkvsfm2LeSd2neOrFm5rtovqM8xu+pS/L5PNLpNLa2tpBKpXD79m1MTU1JrDvnCuPP6vXjsjlMwurq6kIoFEIikcCVK1dw6dIllEolvHjxQlyI4XBY2NdwOIxkMolwOIxYLIbr1683Jd1p9k0npzYaDZmr3FeeeQx6bmcyGWxsbCCTyWB9fV2K7gMQN6aeEzaXLRftmZkZDA4OSsF/4PhdKBaL+Oqrr/D8+XPE43G8//77Er5Dt3M0GpUQFxoHtVpN9rrf29uD3++XePbp6WmcO3dOwPejR49QKBSaamo6Gdha9Fxtpct+bNH31uyaZtJNwMJjBKDpdBq5XA4ez3EN8ZGREfT29iKbzQrQp8ucc0brKQ3WADR5s7RHk/9rIofJd11dxxUmGKesjSs+D/GB9tbyO4/HI97fRqMh3gFtNNVqNQGhxBa6LiwTGxmmwEQmDaYpmlTQ40A9vrOzg66uLsRiMWQyGeRyOam0UK/XUalU0NfXh/Hxcal2wWPRaBT9/f2oVqvI5/NYXV1FrVaDz+fD9PQ0BgcHARwTY5lMBqVSSfpUkxn6f9NAa2fOthXDquX7vBxOlqC+NmM0S6US1tbWEI/HJZb15cuXWF1dlb1uBwcHZVIznEDXJtUTlbQ/hRaJCVBNYXyU3+9v2q5MW3KmZbW/v/9WjVQ+J4GGrb84MQkOdO1NTnbNzurSXX6/HyMjIxgcHES5XJZMv+npacmopUGgY6TcxszJSDF/p8/RIOddYbTafQ79nRNL5/TbRuN4C8xcLodkMikLfjgcxvXr1/Hs2TNkMhmk02mMjo4iEAhgYGBAAug3NjYkUQU4fuE5X7iwUnmZ8c9m2wlie3t7BRhSydLS1TGAOp6byhuAKFV+5h7XOtuV1+bvdEUDtts0FNhmFgWPRCKy8xIV9vnz5zExMYHe3l7kcjnMzs7i6dOn2N7edpyzNnDaip2yialAz1qcQKtunzkXbUBmb28PxWIRs7OziMVimJqaQjKZxOXLl8VVTWOXY0iGnsaRLgVFkFiv18V4D4VCknzHpI3l5WXs7u5iamoK6XRaSmYBzXpZGzmm54yMqcdz7PZ9//338eWXX2J5eVmK8LOGpt/vh9/vl4WV85qx1Dq8q9E4ToS8c+cOBgYGsLq6ivn5edlalutRpVKR5EgmAZNl5v9cD8hE8zm4tezc3JxsQHDlyhX4fD6Uy2V89913WF5efisuUsdYOs3JVvPzLOavJmOAk2fRxolJ1mgQSGEM5ObmJvb29hCPxzE1NYVoNIpcLodMJoPx8fGmWFEmapply3SYEokfzmfdbh6jp4AZ8Nxql0YbRW8Go+Nq+d7wHP6vQWRPT48QbZw/vDdjb5mlr3eNY/iWZnJ1ErfGJRQ+uyYnSGa9ePGiKSGbnm5ujc1wBpZVpAHLEmONxnGN44mJCUxNTUly58LCQhPp0orM0uSPua6ZcqqyVqbValvgdaNs7JvJXPHz0dFRk4tkamoKPp8Pk5OTokxGR0elbBB3cQFOtoTkTg2VSqVpgPTiqSexW+fQncBtIZ36RFuM2qXPF5Tf6aBvfq9fbLZfl6ygwtUsFRkTMqfj4+OYmppCvV7H/Pw8arUarly5grGxMXg8Hpw/f176ikyFkzgpObPdJug3x/X7gIXfh7Ri5LQ4gVIbADdfwMPDQ+Tzeezs7MgCl0qlEI1GMT09jWw2i+XlZfh8PoyOjiISici5zCSmscb4Ip/P91aGqRaylVSOOku0UChIVjLDSghAdYkdveuPNpQ0yx8IBGTBp3DO811iXJ8GBubc0JUJwuGwsBZke/1+P8bHxzE6Oiou3XQ6jUePHmF5ednVEHJayL8vAD1rsOpmTDmdo9kV83lZoWF5eRmxWAzRaFTi3YeGhvD69Wvk83mpxEK3KWv/0n2tQwPIKPl8PgQCASENhoeHMTIygrm5OTQaDYRCIczNzWFlZUWK+dNtSSNdGzjUL3TRJ5NJjI6ONpWXYlwuPQb7+/uoVquSOKJj9TTDR53PRJ14PC6xkSxWPzExgb29PaTTaZRKJemnra0tiUUlqC6Xy6KfE4kExsbGpMg6N2bIZDICnq9fv47JyUkkEgmZ13wOjqmZpNRqrTV17bvgJTDXBpPAAeyYgmPEEpcsk5ZIJHDhwgWJWy4UChgYGBC9OT8/j/7+fkQiEdkgQidF61hqbYjrWqv8jgCNXqCenh4xWEgi0EDX4Jc7W+m1mnOa4SrEHeZ5NFh6eo53SWMCua7vyt/oBFce08ltes0gcOdzUqdXq1UkEgkEg0EsLCzg6tWr8Hq94s1gFaLDw0OEw2EJQaSbn8A1kUjg6tWryOfzWFhYQDAYxNramrTfLX7VnAeAc+1vLW1tHEBxu5kb8+r2Oy3c3iubzSKTyWBmZgbhcBijo6N48uQJ5ubmRNmOjIzI6W66XgAAUQVJREFUNqN68EjDk2onla7ZBgDCdupgbJNBooLTwFZ3vGaYOHH4fHoisbSJ2U866JsKnElVuvAwlSLbcnR0JIkptDRfvXqFQqGAyclJKcD+3nvvwe/3Y35+Hq9evUK5XH7rOdzEHF/bpHMCfu+KOM01p+fQCtTpN7a+YMFrr9eL2dlZSdYYHh6W+KtIJCLZlyxl1d3djXw+D4/HIwqYe1lzTmvrXCtbzl2ym/yedQnpztUKkuwBAIkx4t98N1jihwwbF37NvnHR1obM4eGhxF/pfqzX6xKfyt2rWHd2c3MTADA0NISLFy9KAhBjrslO2cCn20L+hy7mM+kFzoxTtRmInA88f39/H8ViEc+ePUNXVxeuXbsmoQG5XA4rKyvCGPb390tyBWOLgRNdSZCpgeXAwADee+89BINB/N//+38xOzsrizUTO3QpIwIE7hTI69HVy1i/UqnU9NvFxUXZmIXvCAFKPp9HuVyWMkFkO3WOA9vv8/lw/vx5lEolSUYlyx+LxXDp0iUEg0FcvXoV8Xgcn3/+Oebm5iQRlvOaujuXy+Hw8BDT09NS0m5tbQ2bm5uo1Wq4ePEiZmZmMDY2hs3NTTESdAKxHj/9t0ly2D7rPj0r0eyqBiqmaIDK3+nzG43jRGzGrMbjcam8wu1tJycn4ff7Ze4NDQ0hlUpJjV666jlOvLaeu2TcNctLY4qEFwEiXfDaq8CkQA0IdcUVnfSlvU9cz7UHlXPT5/NJNQqv19vkmWVIANcIXo/6uL+/v6lUG0En+4Dnsqbr+Pg4Hj9+jMnJSUQiEWFFWTmDNd4BSLwqvYJdXV24evUq/vN//s+oVqt48OABRkZGBPSSGLERQHquaALMNHRs8r3qsJ7mO/M8EwzoB2HAdV9fH169eoXJyUlcunQJ6+vr8Hq9WFxclLioSCSCoaEhscYYeKxjVJlhXywWEQwGBURy4wEOHgsQMzBZuxHYoebCoJOjAHvZHx2fRWCq42eAE9DKl0gDW042XV6DSWXJZBJjY2Po7+/HysoKVlZWZKHxer24du0aIpEIFhYW8PTpU7x69arJpeDEGpoGimm9m+c5jb2bIfNjihsr58RYUNyMMHM+HB4eYnV1FalUSmL7Pv74Y5w/fx7z8/PIZDKSnHLhwgVhAra3twWoMhNV1yfUbdBzjuwWA/A1IwtAdoniFnlM1qPi5bZ52n2mDbbu7m5RzJz/7B9dtYIKrru7W5Ju2HZdcm5vbw8DAwNSJ9jj8QjjNjk5iatXr+LChQuIRCLIZDJYWFjAN998g9XV1ab3ym1Bd5J2FnEbQDyrxV+Pu/nOaaOY/+tzbKEiACSplRnvXq8XH374Ia5cuYJ8Po9PP/0UKysrskjSYJmcnEQoFMLr168BQMKRNJvj9XqRTCbRaDTwD//wD5ibm2sq/UdWVpf94/zQ9R4bjYbE6zGGlslXOl6bZXSYnKUrDxwcHCCfz8u81u+ULvPGDQLW19ebduXiNbkhAnMDyIZub28LMGEogtbTi4uL6O3txdrammx7yfCgVCqFYDCIL7/8UkqN6Rq0fAaOv7nIm/rA1MH6vFau1d+H6LY7sar833xGU9/V63UpKTYzM4OJiQlcuHABT58+xerqKhYWFnD37l0cHh7iwoULwgLSANC7U+nwAI/HI653klvcbEgzqHwegkrmj/D3h4eHwkbyfE2aaWCsAS2P6fBFPV4kuFgNwe/3i/HGe+hYWRp7bCMNNTLFPAZAQsvozWbZqqWlJdy4cQOhUEhCr0xigyzy6uoqjo6OcPXqVUxOTqK3txd/9md/hp6eHnz66adYW1uTZMl2yQVT37lJ24DVCYCYgKYdsbG2fJCtrS2EQiHk83m8fv0af/Inf4Lbt29jbm4Oy8vLePr0qSQZJRIJAaW6k2h5s+wFy5V4vV6JtQJOEhJ0bCcXZ7O0Dy0lXp+DqbfyM8tX6OvxM+NSdHkMugM46cy4FCpzuo4Y0xMKhZBOp7GwsID+/n7cvXsXd+/excTEBJLJJDY3N/Hy5Us8evQIGxsbTf1sA6N6PMzxcRpvbSGdNTg1xfbC2L5rR2wvHo/zWLVaxcbGBgKBABYWFjA4OIhLly7h9u3bUpopk8mI25ulnGjEkDniPNPKW5dK0QwB3fl6TPW8ZUwfGSoAAjI1YwtALGpeV89DbcmTjaURRrCqY7R5HuNTWR+Y/2ezWQmduHz5Mi5duoRoNCol2V69eoUXL15IoqDbWJrj4sSO63F0Gl+nzz+2nAaM63PM5DcNHLi7FeMm4/E4rl69ilu3biGbzeLp06dYXl6WIuys3hCPxzEzM4P9/X0kk0kAkG1ZGb/6+vVr/N3f/Z0kH1LH0cBm2EBvb6+UASRBwcWcAJbEAcEg9R/d/Eyg0YxSrVaT7HD2C8GCLu1DYMJyVKxKAxxnQYdCIaysrKBUKqFer+P+/fuYmJgQYM8SPyQHWHqN4LNWq4krO51Oo9FoSJmr8+fPY2lpCa9evcLa2pqAapvedJvDtvVTA0DNKp6FaD3E59NxuWbIg/6Nfm6WYrx27RpGR0dx584dMf43Njawvr6OiYmJJkO5r68POzs7Te5+7YrXgI/6inNRf9auem0s0ZjLZDLCxtNzqeOOdU6KTijkNTin9fPqGNqjoyOp2631Ls8hU8t3hziBuIXJW3wW7Q3RVYaSySTW19eF0WUf6XZub2+Lx6tWq+HcuXO4fPkyrly5IqTI+++/jydPnuCLL75AtVoVr7MO9aHY1mL+32retp105YSMTbbOCeC4iT6HSqy3txeLi4tYWlrCe++9h//wH/4D/ut//a/Y2trCixcvEAgEEI/HkUqlUK/XpQwGB5QThoowGAxKzTO6DKjogJPYVio0LTxOcMGsOrpM6/W6vCjaJcJr6pAEtsd8cbXbVrdle3tbrlGv1yWrNZFIYG1tDW/evAEAfPTRR/izP/szyfBbXV3F06dP8Zvf/AYvXrxocuGa1ruTxesUp6o/m0BBX8P2mx9TnOalE3tlKs3TGGHA8dxdW1tDLBZDf38/Hj9+jHg8jhs3bqBWq+Fv//ZvsbKygmAwKGxiIBBoAqEskaOTAur1epNSZS0+ze5qi57H6Z7iwq2fnwqPYJNGF3+vExWAkwxtndCoPRr8m6wE5y4ACeNJpVLw+/2SoRqNRnHjxg3MzMwgGo1Krc/Xr1/j4cOH1oQUcyzbldOO5VmLG/tvfmeCFZ5jeoHoUszn8+jp6cHz588RjUYxPDyMW7duYXNzE4VCASsrKxgeHobP55P44YODA9lgIBgMAkATA7q2tiZMPkkE6koa2KzPyjAYMkQ6+5+/01uz8jm6urowNTWF5eVlycjf2dlpMui4ePMf2TbqVF5Hx22zz1KpFC5cuCCu+mq1ilwuh8XFRYyPj0tSJd+nYDCI8+fP4/Lly3j48CHW1takMkA6ncb29jYmJiZw48YNTE9Po7e3F/fv38fi4qL0kRtR4DRfW62xZ+kd4P01eNOkjda9+hwATedzXBYWFrCxsSExwh988AGeP3+OxcVFLCwsiFHFGHqdzc9xJ3ildwk4IaC47hLEmvH5XDf5256eHgm1ikQiout0dr828gkOgWN9qbedZrgVgSTvTyzB65DdpDeWz8N+NNusWV2uHX6/vylHAUBTaM3GxgampqaavMk8v1QqIZvNSkz3rVu3cOfOHVy6dAm7u7v49ttvpYYzy+A5Me0aM5r6rJ0521YMqxu7ak44E6y4gVl9TX0NbuGYyWSEUb169Sp+/etf4//8n/+D9fV1vH79Gjdv3kQkEgEAWcjT6bS4ozRYpPumq6tLwCoTCaLRqFgg2iWgg4ZpxbFQP0MIqPz4ouhwAttg6QBwinZX8G+WSOJz0Bq6dOkSIpGIxPcdHh7i/fffxy9/+UtMTk6iUChgYWEBr1+/xoMHD/D06VOJwzHHRn+2uWTMc23KVc8Nc368ayDBBKNazOPm3LY9h63/KpUKFhcXEQqFkMvl8OTJEwFmR0dH+O///b/j0aNHODg4wOXLlxEKhYRt9Xg8YnTp2KOjoyNUKhUcHR0hGo023ZfMPOP1NOupF3r+z/nEuUbXrwbNmh3Riocxr2Qd6GLSYBU42cP+4OBAdq0aGBiA3++XsmvBYBDvv/8+Ll26hHA4LO7T5eVl/Ou//iu+++47CVtwGzen8WtnzN9VafXOODHJTu+lfg+Pjo43G8lkMujpOd6KNBqNYmZmBtVqFf/2b/8mbAvLNTG+leCQMabpdFr01ezsrGwvSubQ5/NhaGgIf/mXf4lsNovZ2VmpHxmJRCRpVv9GM5gjIyMoFovi3h0dHcXMzIxk65N1Ys4CAHH30sulcww4b3VIgu6bnZ0dBAIBJBIJyYTe3t7G6uoqPv74Y6RSKayurgoDDQD5fB4vXrxAsVjExsYGisUi0uk08vk8hoaG8Ktf/QoXL15EIpHAP/3TP+H58+eS/U4j0yZmDKjWR7Y1U39/1iQBdYFJilDcjmt9w8oMNBgSiQSuXbuGn/zkJ8jlclJ54vLly2K8RKNRuRYNdg0GtaeI+lAnaBFEMjZVb+rCuqe1Wk3wBuedBr86LpXCOUjii+3ToJhhK8Qae3t7UvGFOpmgnM9DEKuZXOp3M5aXAJqbVJDECAQCSKfT6Ovrw+joqPQZwymr1Sqy2SyCwSCuX78uHjHG287Pz+PBgweYm5tDLpdzDeEyx/s07CrwA2wcoMUGaM3Gmi+dTXZ3d1Eul9HT04O5uTnEYjEEg0H86le/QqVSwaefforXr19L4C9LmqRSKRwdHSGbzUpZEna+pswZw1EsFmUfYt1OglbGh3DTAcYddncf71Sxt7fXlJGqQYLH42mqpaaZJx0vA5zUqNT9yQBn9lckEsGVK1cQj8exvr6OhYUFHBwc4P3338df/MVfYHJyUuL+Xrx4gTdv3mBjY8Na4UCPjbmgtTOu5nd/KEDAbd45PYetX8w+MxVtOp1GMBiE3+/H7OwsUqkUrl+/jgsXLuBv/uZv8Pd///d4/fo1uru7MTMzg1AoJC5GZqXScNObaujYa84d7TqlwcV5qJMBuVizndo9qhNhqNA1s0nlS6Wu47L5/Oa7VavVEI/HMTw8jEQiIUpxY2MDPp8Pt27dwu3btzE5OYnZ2Vk8e/YMS0tL+O677/Dq1SvpA93vp51nrYDfuzp3nRhTfgc0Z2LbYtKdmDuO1fb2NtLpNPr7+4U1uXbtGnZ2dvDZZ58hk8m8lc1MkDUwMIDd3V1ks1mJASwWi+IFACC7m/3sZz/DwMAAPv30U9mRb3BwUBL7gJMEQj4XQxd6e3sxMDAgQDmRSGBzcxONRkP0O5nQRqOBYDCIcDgMv98vwFc/P+9Tr9clfICG18HBgWSDX7x4EWtrawCO16KlpSX86le/kkLrXDMCgQDW1taEXX769KlksYfDYXzyySeIx+NIJBL45ptv8ODBA6yurspmA27z06arnJgoNyPtxxYnYK2NYJ7H7/RvTcN3a2sL33zzDaampmRsb9y4gWfPnuHp06dYWlqSTXOWl5exuroKv9/flNBEt7gGRNoDyvVZr9E6H0DHjNJzFIlEBNhqg18/j06w4lwjy8par5x/jUZDdo0CjmsJV6tVKRHH7esZ3629yATSOq+A55Ot5XfEJTs7O7IGkLSYm5sTzwEJinK5LBsOzczM4MqVK7h69SoAYHl5GbOzs3j48CGePHkidVtta2MrQ0vPCTdpKyRAL8i2mzg1wPxeN8q8nnkuk1G6u7vx9OlTBAIB3Lp1C3/913+Nvr4+/OM//iNevXolQdcsPUIlS6TPhZRB9WRWt7e30dfXh1Ao1MQ+aGBL5cvvmYhCEMwC0fytx+NpKpary1Lwejo8QF+bIIJ9o+MYGbSfSCSwvLyMxcVF1Ot13L59G//+3/97TE1NYXZ2Fv/4j/+I+/fvS5asORGcWBn9vf7f/N5cSG3zwfz9uyImqDTFTcG3YmNNOTw8xOLiIuLxOPr6+vDtt9+i0Wjg2rVrAI7nxj/8wz9IzdyRkRGEw2EpZ0XgyBg7jqUTG6NLrPAcHSPF+UeQo5VUo9EQZcrf0R2nGVczuco0sjhnqRxZuiqVSgE4LvROEHTz5k3cuXMHkUgEKysr+Prrr/HFF1/g+fPnKBaLAl5aLbxuusVtfMxxfBfFFttoe1a3PtLvq8nAEdCtr6/j2bNnCAaDuHbtGq5fv45KpSLgiowR2Z9AICDF27kZCbds5ULKGLrx8XFcu3YNi4uLUt+U9YfpTqVh7vV6BURy8wyGLpAU0IssvWMMOwmHwxgaGpKakgTS7COGbtGwozHIRZ3XzefzuHTpEu7duyeVZgqFAtbX13H79m2sr68jk8nIJgOVSgXFYhFPnjzBxsaGVLr56KOPMDIyguvXr+PJkyf4/PPPsbS0hGq1KqxXK+PZZKeczjPHuhUh9GNJO++jqZP1OYxFXVtbwzfffINkMonBwUFMTk7i5s2bePPmDUqlElZWVjAwMICpqSm8fv0a2WwW3d3dwrTrHdK08a13odLsKHUj12/qv66uLpRKJSGvmDCnSTFuemHqRs2Y08sLHOcYsA9IcHk8HgQCAamLrMOu2Fe8Dz9z3HW8LFliglzqaMZc8/lYvSUej4vXgs+6vr6OWq2G8fFx3Lx5Ex999BF8Ph/m5+exuLiI+/fvSyUXzm3t8rfNcyfd1Y4+bjskwHw5zBs7/dYUJybABHH1eh2lUkke/sGDB+jq6sLt27fx61//GgcHB/jiiy9kG1ImdLDQdCAQwObmpuz/TNaHLwaTBXRiCQGutgI5Kdg+s/RUIBCQuoCcJKarRydaAW/vRAEcM6q0BrlbCssiccevubk5LC0toaenBx999BH+/M//HNPT01hZWcFnn32Gzz77DNls1tVgaDVGblZPOwuoeexdUJxAMzPlJE7Gl9Oz2V42nru7u4tXr14hHo/D6/Xi+fPnCIfDOHfuHI6OjvDzn/8c9+7dw9LSEnZ2djAyMiL7otOtVa1WhV1ipiefwbY46eB6Kgs+LzNogeOFgJU2uEUsRYOIYDAo32lGV4Nb3keDVb/fj3g8jomJCTQaDWxsbIii//jjj3HlyhVEo1Hs7e3h5cuX+M1vfoNvv/1Wylc56Qg9LuZ4tDOmf0ji9K45PU8r5c8Fl9fl3CgWi1hcXBT9OTExgdu3b2NnZwdPnjwR/erxeBCJRJBOp4WVZ7krj8cjcdDAsevU6/Xigw8+QCwWky1gGa/KawDHTGwgEJAKBtSdXJBpsNG7QFKAbCgA2cuc3ie68/me+Hw+KXzO5+buX9FoVHT50dER8vk8wuEwEomE1EjlWjQzM4Nf//rXmJ2dRalUwvz8PNbW1rC8vIzNzU3s7OwgFArh448/xsWLF3H79m28efMG//zP/4zV1VUUi0UB3Vpa5Qo4jbWeE+/aPCcw1PMNwFt6Sz8DwRl1CgDJWv/2228RDAbxySefIBaL4aOPPsKjR4/w9OlTrKysIJFI4OLFi5iYmEAul2sqzM+5xrJNbA9D+thOreN0fKleO7i9rvbA8nk1KNQJXHp3QuINbVB5vV65Buu5cr4zPpZGHb/ntcn+sg/ZZh36oI1Obbytrq5iaGhIkg11BZnNzU2k02mUy2VcvHgRH3zwAX76058iHA5jdnYW9+/fx+PHjyUEU4NV4O0NmjSI1UbKacmuU20cYP7tROXaPtsWIhs7p6/LOnyNRgMrKysAjqny69ev4y//8i/h8Xhw7949KblC92osFpMwgXA4LMWbOZCNRkOUqt7TV8efsh20hPTEAE4Cqsk6ARAlyVpwunSVBkp6oDjJqaD5UkUiEUxPT2N4eBiNRgOvX78Wd8dPf/pT/Omf/inGxsaQy+Xw9ddf4ze/+U0TWHVSDKY4GR+txrmVkfIuKc92xWkeuokbiC+VSnjy5AmuX7+Orq4uPH78GAMDA7hw4YJYvp9//jlWVlaws7ODc+fOoavruOQOy+oAx3OPzKN+6bVip1ICTlhSgkiKLvvC3Ux0DBQVHssImeBeJzXo2EC6WHktbrnaaDSQTqeF8bh27Rpu3ryJkZER2R3s9evXePPmjcRV2eatyRi1wyi+KyzT7yJuutH83tTPNp2rAQHl4OBA4kvD4bDoVy6wjx49wps3b9Df3y/MKe/Df3pjiZ6eHkSjUdy5cwd37txBNpvF8+fPhbVvNBoCQo6OjuD3+2VzChpU2hPABVozYnTx7u3tIRAIYGhoCDMzM3j69Cmq1aoUOKeXy+/3IxKJoL+/X+IBCUJJcPBd4hbBiUQC6+vrAjJyuRz+9V//VbYIzmazUvkjm82iWCwimUziJz/5Cc6dO4epqSncv38fX3zxBZaWliS+V4M4p/WzlbgxlXpunIVwfpkx8PqZbWuEE6HAMJNyuYyvv/4a4XAYt2/fxvDwMH71q19hc3MT2WwWS0tLsg0wGXkm+TE+mjqOmfJcdw8ODhAOh5vaQXc/va08RuZVVxFiDD89VTpBls9OMgE4TuDyeI5rvBIrkHXV27z39fWhWq3Khh7sD+IOhjOQgeUc1pn+psHAGO9UKoV0Og2fz9eUjL63tydgtVKpYHh4GNevX8f777+PVCqFjY0NfP3113j48KFUw6hWq01Jv608mDrGuV3dTjl1HVbzRq0YkVbX4HFbw8lwkgXq6urC559/jq6uLty4cQN//dd/jUQigX/7t3/D3Nwctra2cOnSJSSTSfh8PtmnnG4s7j5ie4m0i5OTgRYPgKZSEpoh1awAJ87Ozo4oeE5eE7TyPnt7e5Ik1t3djXg8jvHxcYyNjcHn8yGbzWJubg6bm5sYGBjAL3/5S/z0pz9FPB7H2toaHjx4IBa8rQ/NZzX71+2Yjf3W48XfmGNrXvMPXdrpKy1aSayurooL6ejoCF988QXu3r2LkZERcXd+8cUXePPmDZ49e4bx8XFMTExITCsAiSsqFotNbIAJXsz4MM5LJgYwCYqu0GAwKPFMvCYtZYJl3qO7uxvBYBCxWAw+nw8HBwfY3NzE5uZmU1z2yMgIhoeHcXh4iHQ6jXQ6jUgkgsuXL+P27dsYHR1FuVxGoVDAgwcP8OWXX8rmH04Lrls/OxnBf8iGE+D+zunvnfrGBAO6P/Rnso2bm5t4/PixgLzp6WlZOB8/foyXL1/i6OgIU1NTErMXDofR39+PZDKJ8fFx2SBlYGAAAwMDWFlZwd/93d8hnU4L4NSJLzTugZNyQQSI1I8EmB6PB8FgUBKsuKAHg0F8+OGHmJubQz6fR7VaFeDb19eHcDgsQDwQCAiAod4tlUqyoxffKW6jSiaqt7cX+Xy+aUvKXC6H9fV1rKysYHt7Wxb28+fPY3BwEEtLS3jw4IGwVDs7OwK4te60EQS2sbYZbraxtY3/jyl6jbOt5ybz5vY8mmXt6upCOp3G559/Dr/fj3PnzuHatWv4xS9+gb//+7/HxsYG/H4/Ll++LAwlQ5e6u7sldIRglS5vepIYrkeQqdd9Xc2BFYIoNLq018sGwPR4dHd3S3m/crksu7Qx7IaGFbEP62czSZHgVntxaQByUwHOZYbaaIzD9YShApxflUoFm5ubWF1dRaFQQCwWw8WLF3Hnzh1cvnwZm5ub+PTTT/Ho0SPk83lJSiRI1muQbpc5391w4A/CsNoa4DbhbA3R3+vG6uvajgPHC2+hUJDakZ9++ikajYZM2P7+fnz++efY2NjAw4cPMT09jXPnzkmcEd2sDBOoVCrCItEaY0fTomKcFNkjHeOiy/lwsdZg4eDgALlcTiwpXUuQwsBoltwaHR3F+Pg4BgcHEQgEcHR0hOXlZbx580aA+K9+9SvcuXNHAqS//fbbt8pWnWYczUVMj5FN2ZhjaBs3t3E8C7GBGrfjp7mG23W10l1aWkK9XsetW7ewtLSE3t5ezMzMYHJyUhipb7/9Ft999x3m5+exvb2NqakpYZ6GhoZkYWeGqY6Vtr2TuvwJA/17e3sxNjaGwcFBLC8vI5lMYnd3F4uLi+L6qtVqCAaDwpZqFpVxi4FAQLZYZfJiNBrFwMAAUqkUdnZ2JNRhcHAQN2/exI0bN6Ru8sLCAh48eCAhPfRiuLGHtrlkM57N7/5QpRWzajvHFKc+1O8pXaI7OztIp9N4/vw5QqEQ7ty5g2vXrqFer0tC0YsXL9BoNDAxMSE7tRUKBYknHRkZwXvvvYf+/n48e/YMn332GTY2NuDxeGQXKSYIMlmFc04ntHKB5qYAJAAIMpn0dHh4iFu3bknpKdaLpIEYDocRj8fh9/tF1wPH4Vf0WDDvQXvQWNZqYGBA3L4MZ9ja2kI6ncby8jLW1tZQrVYxOjqKGzdu4I/+6I8wOTmJp0+f4uHDh1haWsL6+rqsEea4cByc1kwnUkDPCdtcOOt5byOwzGd2A+gEVxTGWwcCASwvL+PLL79Ef38/Ll++jDt37uDFixd49OgRlpaWEAqFMDg4KDtB6WL5vBdLq7HqCdd4zgGdkKeNDO191e8P9SR3kOL5+jeNRkMSpOr1OsrlMoLBIJLJJHK5nOhnGn09PcdbB7NeNTdCCoVCMhfNWvB8RpY9rFQqMucbjZOqAEwyJNYgs7q2tiYbaYTDYXz44Yf4q7/6K8zMzCCdTuOzzz7D48ePpcSVruJiI0xMYT84heW1sx6fauMAp0VDN8YEoRoMOS0wbouNXvi5d/Ph4SH+6Z/+CblcDnfu3MHHH3+M3t5eKa3w9OlTlEolqZ3n8/kwMjIiW7xtbGxIJQFtIZBF5eSiNcLB54TRYQQcKJ7PDFxdSF27FWjdHx0db686OTnZtJ0qWS7Gq3Z1deGTTz7BH//xH+PKlSsAgIcPH0rc3+LiomOSipvF4jY5TstOmQrINo5nJU7PYAM57QJT23m2uc7j9XodKysrODg4wJUrV7C/v49CoYBMJoPLly/j/Pnz6Ovrw9jYGO7du4fZ2Vns7u5KKRcA4rrxer3ittTuF/Pd0uLz+eDxeMSCZj1NljHZ398XT8S9e/eaylcxDEHv285jPT09iMViGBsbQywWw/7+vrhIfT4fZmZmpM4qy9TNzs7i3r17ePz4MZaWlsT6N+ecEwh1Ghu3hd5NTmO4/JjCdplMugY3bm23VQ6w9RGvQ1CwuroqISKffPIJLl26JIvoo0eP8Pr1a2xvb2NychLRaFRi/TY2NmTP9EAggCdPnshCTEA6ODiIwcFBzM/PvwVgdGZ2T08PUqkUfD4f1tfXpVoKdWtPTw/+5m/+BuFwGPfu3cOLFy+kNiZBcSKRkHAq/ezxeFw8CoyDLRaLsl0ycxsASNIJN6YpFouyXSgTCC9duoQPP/wQH3zwAbxeL77++ms8ePBAFn8CiVbz2AZG3eaFHjvbPDkLcVpvnOarkx6laDaWoUoejwezs7Pwer2IRqO4ffs2fD4f/st/+S9YWFjAmzdvxMjgJheNRkPIo3K5LO5zZt3TY8D7cx4yHlR7UBuNhlQNYpgLDb69vT2JR9UAjs9PjyvxQzqdxtjYGJLJpGw+oJNludPg1taWVFrp6elpIivItjKuHDjxrPG94rPQK2HWgt3Z2cHi4iJWV1dRrVYRiUTw0Ucf4S/+4i8wMTGBtbU13Lt3Dw8fPpQd2hhaZib58nltlY9sxrPW8z8oYLWxobZznKxBt0ab57u93NyjmfXMCoUC7t69i1u3biEajWJyclKAXD6fF/d6PB5HKBTC+Pi4xDRtbm4KO8BSIwSpjA3R1gOTALxeryhGWmxkS5mFx4kPnMRkMWbF4/Hg/PnzOHfuHAYGBhAOh9HVdbxNJ0MACoUCkskkPvnkE/zyl7/E6Ogodnd38eDBA/zLv/wLvvnmG4mn0v1nGgROVrnNsHAT81r6s3YrtAMyfmxxA6L6xWkXxLfDbOl7AMd9tLGxITuFMNZue3sbt27dQiqVEqOlp6cHCwsLMg8Yb0pvQCAQkLqDdB2ZZdUYx9rd3Y1kMinbT3IHHrrMyODSnUQmt6+vT7KtGbLCMAL+jolbTN4hm5RMJnH9+nWpBMBM3ydPnuDbb7/FN998Ix4T25xxGh+3sTT7u51zzfPfJdF60sk4Mt95/bcbONWgFzgBBmQQV1ZWJLn02rVrmJiYwM9+9jMcHh5K0fbDw0OMjo7KZhCcA69evUI4HMbu7i56enpklzXg2B179+5dHBwcyFwx28NFMBAIwOfzSaY0mf6enh7k83lks1mEQiG8efNGDKje3l5Eo1FcuHABFy5cwNLS0lsZ+b29vUgmk8KM6a1WgePNA3QIGbOpt7a2ZHel7e1tBAIBjI+P486dO7h69SoajYaw0EtLSygUCgJmzFCwdsdef3aby+2+G79voVGh22LDAXr9MdcKzazqGFgAsuYDwOPHj6U28M2bN/Ef/+N/xH/7b/8Nm5ubTWUo4/G4FLPP5XLweDySNM0KQQz1Y1y+Jp9oSJH95986qYpVJ3SGvt4di3OLsdcMQwEgiU8DAwMol8sSOkNmmLVOBwYGmuJSzV26yMoyt2Z3d1eSu9h3xCtsU3d3N8rlstSz3dvbw9jYGD766CPJkSmXy/jqq6/w9ddfY3l5WXapI8nHMbMlDjrFszrhxHbIrbYAayvg48aKODXUdg+ne5odsbu7i7W1NVlMC4UCbt++jenpaSSTSUxMTOCrr77Cq1ev8Pr1a+TzeUxMTGB4eBjBYFCsd5YlYWkWncGpXUSMt6Jrn/tps22sCciJzInC3XyY1XpwcCA7yzBTmtvHZjIZLC8vY319Hb29vbh69Sp+8Ytf4O7duwiFQshkMrh//z7+5V/+BU+ePJHtBNthUJ0Uh9PvnBZCt+u5GSBnLe0CHCdpl4k1F18bcC+VSnj+/DkKhQJu3LiB/f197OzsYHx8HOPj47h48SL8fj9evHiBJ0+eYHl5GZlMBkNDQ1KHMBAIIJlMolKpyE5DNLz0OPT19SGZTKKnpweFQgEAZJOBRCIhRhjraq6urko4QHd3txTzp+sqFoshGo1KSaJG43gr5UwmI5tpXL16VWL5uBtbLpfD7OwsPv/8c8zOzjaVrtJ9YwOnum9/KDnrhf00YhqfGoya/7uxyzZGw/Z+000+Pz8v1SmuX7+OK1euyFaoz549w8rKihhdg4ODCIfD6Ovrk0SMrq4uidMLBAIol8sol8tYWFjA1atXUa/XUa1WraFYXOhSqRQWFxcBHLs5+/v7xeVPjwXZt3A4jIGBAUxPT2NsbAwbGxuir1mTEoAAVHqzCDToYYjFYvjyyy/x5s0bVKtV8SqsrKwgm80CABKJBCYmJnD37l1cuHABAPDmzRu8evUKc3NzstnB3t6etFEnmpiJV/pvM1lJj40be/muiW2OmvpRJyLxHCfwrUkjEkkvXrxAKBRCKpXCT3/6U6ysrOB//+//jUKhIOyh1+sVoonxqibgbDQaTYaNLhHI0ALgZIc01oflWJGIGhwcfKsyAktzMg6W4QbcHIml/UKhEMbGxiRGmy5/FvCvVCqIxWLi/dBMK8MMuK0r+8vj8aBarUq8KvuTu3Llcjlks1msra2hXq9jamoKP/vZz/Dxxx9jbGwMW1tb+Prrr/HVV19haWlJPNza4NBMsm0OtMuk2gwYm7S9NauN7XACreZvdYPMv92Ome3Q9zo8PEQ2m23atWpzcxMzMzOYmprCyMgIHj9+jK+//lrclKlUChMTE0ilUpJ5t729jXK5LKCVpUy065PPoUtY8J6NRqPJrRkKhcRty10larUaEokEzp07h2g0KiC7UCigXC6jVCohn8/j8PAQIyMj+NnPfoYPP/wQ09PTqNVq+PbbbyVedXFxUeq/uY2XWz+3AghOxkI74/eHAgS02F4qLa0+69+an20KeG9vTwqIz8zMCOtZLBYxNTUloSzj4+N4+PAhXrx4gcXFRdk5iKCRcXncq52eAgJXzj+WlIpGo/D5fDLni8Uiuru7MT4+Lm2oVqvCKB0eHuLcuXOSBAacxD8VCgUBtD09Pbh8+TKuXbuGqakppFIp7O3tYWNjA8+fP8eTJ0/w7NkzLCwsSD1kpz63KblWfe8k7Y7nuy5OIBR4G6Ta5p2tD8zf6XJCLK23vLws7NPNmzcxMTGBP/mTP4HX68Xjx48FnDL8KhKJSHIh2VW/3y8LKbc6HRwcxMjIiLjbCRr0NsFdXV2IxWK4fPkyCoUCuru7kc1msbi4iIGBAeTzeSkmT2Zsd3dXisfrSi1sDxd6erRCoVATEVGv1/HFF1/IDoNMeikUClJicWxsDNPT07h586ZsgDA/P483b97IPvd8D83tldsxnH8XAGqyXGclboYnP3Ou2UCMLdTJ4znZQYoen7W1NXz77bfweDz49a9/jb/6q79CPp/HF198IUxgd3e3eDKpu/QmKDTgycjqXQN1WwiSuf0o8wMIFmmwkcgya11r9pnXoit/bGxMPFBjY2NSEYDvHr0KR0dHGB0dledguSwATawn5/PBwQF8Pp+cx/seHBwgk8lgZWUFhUIBXV3HGzC9//77+PnPf45EIoFisYgvv/wS33zzjTCr7DOb3rAZ1TRKCOJtGNLpuOPccjvB4/E0nJg0N9DjZN3r35t/m411YvdsbfF6vYjH44jFYpiamsL09LQsnJlMBt999x2ePXuGzc1NAEAsFsPIyAgGBgZkIwCWUGHNVmZ2aherjlWlkIKntcjg6GKx2LRd5sDAgBRSL5VKspsPJ2Q8Hsf169fxy1/+EjMzM1JK5cWLF/jmm2/w8OFDZDKZloHN5li02+c21qXVfcxxcJJ6vf6ja1GPx9M2KvkhGLdWrKt5jP+Hw2GMjo6KITU4OIipqSmMjY3J/s/z8/N4/fo1Xr58iWq1Klme0WhUyrEAJ4CFXgMATUaXjik6PDxELBZDMpmURJj79+8jnU4jlUpJIfaBgQEJyi+VSiiVSshkMtja2kJ/fz+GhoZw5coVXL9+HePj41KV4PXr11hbW8P9+/fx7NkzFAqFt2L5zD5ql8n+MaXRaJzJ3HUC9O14Nk4L6p3iH30+n1RbmZmZwbVr1zA8PIzt7W08ePAAX3/9tdRhZKmcoaEhRCIR0YV07dOwD4fDGB4eRiQSQbValVAVMu7UpWNjY7hy5YqUzLl3755UQ6G37Be/+AW6urokJ4HC8Bhei8CFG7/QwNNlE5mIRY8H908nqxSPx3H+/HlcvXoV09PTiEajqFarsg323NycJKIwvu+0i7EeX5P4aZfQ4TV+C5B+1Lnr8XgaOsnIzeDU5I9us9ln/E6DcV67r68P8Xgco6Oj+MUvfoGf/vSn2NzcxP/4H/8D9+7dkzJs09PTmJiYQDgclrHmnGAY1OHhIXw+Hw4PD1GpVCTsj9gAOMmjASCMJRO2meikz9e7qOnauwwNYD8wxIohgaFQCPF4XAw8AOIlYNgYDTx6AHQYAI/rdzAajcpmGQw7rFQq6O/vx5UrV/Cnf/qn+OCDDxAKhVAsFvHVV1/hyy+/bKofbCZ267HSoN70ENiwoUmI6eu4zdu2AOtp0LDT+W4gyA2YOjFX5jl9fX1S/DqVSmFkZAS3bt3CyMgIfD4fVlZW8OLFCzx//hxra2tS6zSRSCASiQgToGl+fibbqq0+Dg6DnXVZB8a0lMtlqbHJwfb7/TKZ/H4/kskkhoaG8P777+PWrVtIJpMoFAqy5dnjx4+ldIpT/5l972RMmL9tBUydGKp2xkr//a4AVrfF/IdgiNsx3sxzadCEQiGcO3cOQ0NDSCaTGBsbw8WLFzE0NASfzydz6cWLF5ifnxfvAktjMSA/FApJGZdAIPBWbTzGG5Id29rakvImDx8+hMfjwfXr1zE6OirsQC6XQy6XQz6fl4SVRCKBGzduSChOIBBApVKR0JaHDx9idnYWi4uLUiLG9p63q0+cdInt3HbHqp1zzxKwtvPetTLq9XkmoNHXtAEMj8cjenV4eBjT09O4ceMGRkdH0dfXJwl0S0tL2NzclIon8Xhc4kQBiHuWNSBjsRgajeOY03A4LN+xJmooFBJ9/ODBA7x48QKbm5t48uQJ8vk8fD6fJPP9/Oc/x+PHj+HxeKRKAJ+jr69PcgrIPDUaJ2UL9Tk7OzvY2dlBpVJBpVKRSgGBQAATExO4evUq3nvvPUxNTaGrqwuLi4t48+YN5ubmJFmFYNVpXp2GPf0+xpp5/bMArGRDndrvtJ63A1Q1yNX6LBAI4OLFi/j444/x4YcfolQq4X/9r/+Fp0+fIpfLwe/3Y2pqChMTE0gmk2g0GhJjzLJPLDtW/21tUxo9jDnt7u6WcwkE9Vqr3eJkFQHItbRoHHF0dCRufMag7u3tIZfLoVgsytbE5XJZNmThZhdkisnkMl41HA7j6OhISmsyvDGfz6NQKGBxcRHVahXDw8O4ceMG/t2/+3eSDLy6uoqnT5/iiy++QCaTESOMIFQ/GzGQXl90eS8NXM010ZaQ1Y6h1RKwWo413biVuFlN/N68vrZObfc2r6+FSjAWiyGVSuHSpUs4f/48JicnAQDZbBYvXrzAixcvkE6npcYbS6kwmcrn80lgst7ajVY7B4XWNCl4xtXWajXk83nk8/mmCdrb24tYLIbx8XFcvXoVqVQK586dw9jYGPb397G+vo7vvvsO3377rVhB7QBQN2DvZuma/ep0HTeGx9a2s1Scv73/j07NtQKsTv3K4729vRgaGsK5c+eQSqWQSqUwOjqK6elppFIp2V0onU5jdXUVCwsLsouUuYMOF3zW92Psli7hxu0v8/k8MpkM9vf3EY1GEQwGZYHn9pf1+vHOMIODgxgfH8etW7dw8eLFpnm7uLiI+fl5PH36FHNzcyiXy9Z3+YcGn7/Lb1rJu8CwGt85Egg833xHT2uoaWBAPcf4zomJCczMzMgcrdVqMuYLCwvI5XJSCzIWi0lpNupQkgu6qDpj9ViNgAtxb2+vbGfq8XiwsbGBTCYDALh58yauXbsm27ceHh4ikUhI7CiApvhB7uCmn5neAIY1sNYqXbxDQ0O4evUqZmZmMDo6iq6uLmSz2Sb3f6FQkNJbzL62jZvuW9MV7gbwbONnfnZaY8+KYdUsqmbO2Hazzfpc/g2c7M6mXelaeA1uEDQ9PY2f//znuHr1KnK5HD7//HM8fvwYCwsL6O/vx9jYmNS57u3txebmpsQvV6tVbG1tSZgfE5x6enokX+bixYvwer2yyQ/Hj3HKel5x/jKMgc+m/9ahWzSqGo2G1AtmtZXV1VWUSiWJIWflIyZSsQwmwxr4TnETAu5ExXyIvb09TE5O4oMPPsDPfvYzTE9Po1QqYXFxEV999RVevnwpWymz5rFut+57Anfz2dxIGwJWoDlhm8cODw8d5+2p67Dqmzp9Nl8e/RBOLxv/tj2w7T62FxSAxNdxB4bNzU0sLi5iamoKMzMzGB4eFstiZWUFKysrsj/0zs7OW8XZyZ7SitHtZHwUFSJjPJg84PF4BACTWRgfH8f09DSuXr2KWCwmZbOWl5fx4sULPH78GM+fP0cul2sCIDawr8WmKLUy5GetGNphZWzHnPrerS3vivw+QI2TOM1ttsOUg4MDrK6uolwuY3h4GIlEArlcDhsbGxgeHpbyUVNTU7h48SJ+8pOfIJfLYXNzE9VqFbOzs8hmszL/WbJH79bGxZ3zl6XdAAhIpYuWc4fG34ULFySpZWhoCPV6Xcr3PHr0CM+fP0c6nRZ2qhWjZHuX3RbmVkD3XZxvv4s4zRc3A9Lpczt9ZmNa+Zk1F5kAwrjVkZERXLp0CcPDw5ifn8fCwgKWlpaQTqexsbEhbvhAICDx1jqrmfflAk99yOQaEgY0uLxeryze2WwWq6urUv6HCyvrrpIxI1DlJi8HBwfY2dmRpDEmLgLH7NTIyAguXryICxcuYGpqCn19fcjlclhbW5PtWEulUlOlDoIWs2/NY5q8AJq3rGxnHtjENFjMYz+WaOBtMGZN764Zn2q2u9U5GvTTG9rd3Y25uTkhlD744AP8+Z//OUKhEHp7e5u8PUdHRxgeHkYymZTY5KGhIan1SiNEGyCMaY7H47LNMNvEslisDcznoJ4l20lWlH3BOFgyoQSYTPZizVUywCTCEokEstksjo6OMDExIV60SCQibWWyGT29S0tLyGQy8Hg8uHTpEj7++GPcunULMzMzor+//fZbzM/Py7tBZtUcW34GTnbP4zvMMTH1is1g0WPb7rr8vUMC2l2MHK7r2Ein69qOmwDM9p3P50MwGEQikcDo6Ki4BoaGhiRzdGdnB4VCAel0GqVSSZKhGMfKuqma4mY8HgeLz8MMRIYnMMFgcnJSChp7PB6p67e5uYm1tTW8efMGb968QT6fbwrWb9VXwNs1F50WunbGzq3/zeu1e6/GGbFUv+frvzUeTi9dq3Nt/d3T0wOfz4eBgQEMDw9jYGAAg4ODsotQMBjEyMgI/H6/sPy0iLe2tpDL5eR/LrAsa8U4bJYu0htceL1eJJNJ9Pf3IxwOy1arjGdldjUD9lkvmCCF2ban6UfAnUk8zbV+aNB6VnPXBtaNdrnqYzeA6kYC6N/ra5B16uvrE/Z0bGwMk5OTUjqwr68P5XIZm5ubmJ+flx36WCGF4JWMKw15erOAk3I7XNy7u7tRKBTg8XikVBaTAre2tmRTgVgshuHh4aZ92cl+sVQQs7m5Qw+rFPD3ExMTkv8Qj8clUWxlZQVzc3NvAVWGemkdrfuz1ViY/ev2e6dxchvDs2BYyRIax62Mm9NzaFbSNFA1a8t1mG581tKdmprCH/3RH+Hu3bsAgAcPHuD+/fv49ttvsb29jVgsJl5NhlCR5T84OJCKQcxnOTg4QLFYRH9/P86fP99UuhJAUxkqHb9sAmuCaQ1kWQXg4OAAkUhEtrgmmeDz+TA/Py9JV8FgELdv30atVsPm5iampqbQaDSkzjHJM8Znb2xsSDJtMBjE5cuX8atf/QpTU1OYmprC2toavv76a3z33XdIp9PY2tqS3Q5b4Ttz3lOckv9s89gGgH+wkAC3F88mrRgl89xWIKoVSDavw/sz/iQSiSAWiyGRSGBoaAiDg4MSE8Ki7AAkKJsZ18xK5MvEoGkdp8KELAAS1B+JRBAKheDz+bC3tyfWzubmpuyUwkLUOvFA99nvsgib/aVfdCcLx+w/2+/Ne/D3Tp//vwhY22wDAOfYTIqbAmescyKRQCqVQiKRkGSroaEhpFIp2YKyt7dXdgHSbD8XWQbxs25wIBCQeoAej0eC9wOBAPr6+qQSQSgUEqMuk8lgc3MTr1+/llI/LNpuskduz2/73g2UnZWc5dy1KXTbe2qe63ZMSyu96kRW0JiKRCJIJpNIJBLibk0kErKZQD6fFx23trYmc4UsEg1+xskyLMDn8zUZUtrQIuPEeL2DgwPxAMRiMXg8HqlNqc/d3t6Wecqdjrg72/j4uFSWoUFWq9WQzWYxPz8vxhm9EUx0Oe14uIy3K3HjppPdfvNjz12PCgmwGVzm+qO/06LBqY1ptQEkrs0kqCYnJ3H37l18+OGH8Hq9ePbsGe7duyfJ1319fRgZGZHdJcPh8Fs7nnGnNf5bX1/H0NAQgsFgkxdWx0RrMKsrBdDY4m+095TeWVa8YJITM/zT6TRyuZzEh3u9XgkVZNiN3oKeoV7FYlGqDyUSCdy+fRu3bt3ClStXEA6HkU6n8fXXX+PZs2cS9sDdDJ1iTPWYuI0j3wl9XL8r5u/13z8IYHVSiGZDTEDk9DD6WDuWo+2+7Yq+Pouf00VFEMuMabJIjGll4hUDsKlkeT0CWQASe8UYF8Y2FYtF2c4sm83KP+1acHq2dhVfuwsbzzWVq2bFTOXYjqFgXlv/5v8vMay/va/1JXQ7z+0Yhe5Qbos6NjYmhpbP50MikRCwmkwmJQmLLKrH42naF5vbBJKFoguJyp/ehcPDQwnWX11dxfLysux2wh23tDgxf2cJOn8XOSvA2o5ubFfa0QE2neB2Hlkpxg8ys3lkZARDQ0MYHR2VXdoYQrC+vi7F9wuFggBIgk/qVp1LwIRA6lUCThr3h4eHTSCXIS9aB3NjDQDitZicnMTExIS0V9frzOVyWF1dFZBNNlUn5jgBMv5t06nmZ7cxaBek6t+a43YWgJXPbrbLOO+t/nMLjdDnuoFhfsdNVpLJpGyZm0qlkM/n8fz5c9y/fx+zs7MCClmZZWBgQEpKcX7XajXxsLIiBo0y7rrGOcc8FsZw6wQkfq+3iAXQtLkGqxBks9mmCjAMeyBrurW1BY/nOGGQGyExMYueB1bX6Ovrw+TkJO7cuYNbt27hwoULaDQaePnypfRDLpcT74MOBbONhxup4ITf3NY6m547Ojr6/oDV6cVyegC3h3FboG1sgtP92rl/qwWSE4XAVANYMk+RSAR9fX1NsVa0wlh/jVYJJyRZALpmC4UCKpWKTAjN1jqJ0wRodcxmhZovug3IuhkWtvFzU7am0m40fvzyKr+9/5kiJFvfmt+3A+psY8tQF7KqwWAQoVAIoVAI4XAY4XAYXq9XXFCsDUx3q17YuYc2g+v39/clto+LdT6fRy6Xk1g/PX/dns/te6f+aNVX7V7zhwLJZw1Yf9uGtgGr+dxOOoPn2s5rBWYpZEe5BzrDoLgF9ujoKIaHh6VGJdmora0tycQvFApNu0qRXdI7WzGxQwNPHYr1Wx0j5wOQ39NDwHJa4+PjmJycRDKZlORCeg/IBHMnLYIV/tM7c7mNh9Pca2cd/V1JAuP4OwdYaZS4YQKnc23X4zET1Pb19UnpvwsXLuCDDz7AzZs3ARxv8vDNN98I23pwcIBQKCThe8wt4SYqnEflchm5XE7Wf25EoHFAuVyG1+tFLBYT97+u+8pQLL1pAokE1rUOBAJSN5YlB3d2dsSA4qZBrCns8/kkPIbsP7+7fv06PvzwQ7z33nsIh8OoVCr47rvv8PLlSywuLgqLzM0K9Pi5ES+tDGo3AKvPN4Hxb/vsdwOsthu5gRzzIVuBWrdz3BbxH+qaHs9J7CmtdWasarBqvjhUlASqjUZDgrOp5Bjr2moxNj/rtrstvraFxk3ZtVIUbkDUzeK3AVbVT/+/AaxOL3srQKZ/045olp8LNfdB1+5VKj0aWsxc1a4dzldufVgqlSSOiUmFtkxRJ+PRac7YnrtV3zj95seSswasrd7HVv3hNgZuuqLV+67Po+5kqIDf72/aundgYEA8WHRh6iLwu7u7qFQqUjpteXkZGxsbKBaLMi8ZRkCSgfOaYVzclQqAVMeIRCJIpVJIJpOIRqMYGhqSmEXWWy0Wi5Iglk6nm7Y7ZlgBdXs7epH96tSf7fZru+I2vmcFWNt9Lqd+83jerrvqBKT4WYNbABLXSmMlFovh7t27uHHjBsbHx7Gzs4NvvvkGX3zxBRYXF8XFTk8BQ7BYI5UJUgCE6WeiH/9mWb/e3l4MDAyIkaWZdepitp0kwfb2tuwwmEgkmrZ2BYCNjQ1Uq1Vsb28jk8mIF4HeX16Lz3DhwgVcv34d169fRzwex97eHtbX1/Hy5UvMz88jl8u9VYpN6xLNeNuIKN5Pj6Wpk/i3GSqmx84cz99iqt89JMBslL6RnihuANNpEXea3KbVZD4ojzuB49MoGVN06SrgZHD0gNisx9MsvPp3bt879YPt+czfOxka7VhNtrbwezfryfzt/1cZVqc+dANnTtehtANqnYAe56aet7TkzfisRqPRlLFKZUc2wDa3f9fndBInQ+ddkLM0tto1HN2Akvl7/u12fjt6k7/X40T2iICSSVpkXxl+xbArlrwiMcANKo6OjqR8Wzqdlg1W6AljjDUzr3lvJkMxDptbGdOzsL29Lewu2dxyuSy7FwEQA+3g4MDRE2abq61Af6tjWloBYXP9cdIfZwVYjWNvnaeBkO19t+k389lt1zTvRUYzEAgI+z89PY1bt27h6tWrsuX506dPcf/+fSmbxk0EwuGwxLfG43H4/X65Nnepou4kMO3v70elUoHH45Gkqu7ubsEPNNRYlorueCYk8h+Zf3okuNsaQSYAiYltNBqSozM2Nob33nsP7733HgYGBrC/v498Po/FxUXMzc1JYrkZAtDKsNXA0wSzTv2vr2v7rXmeGrffjWFtBfTc0Lj5MO0AVUqrF9Joq6syaOd7fd73XTCdBs12zAk8OoFup5faPM/2bPqerUCBrT3tKF8biPrt8XcasH4fkPV9pB2DwM3AMH/rdswmHB8zmcF2PadF44fsp9Ncz00HOM3XH0LOau62AvGnBZtOn52uwXu46Wuna3k8nqbMa/4zASyBRDAYRDAYhN/vl/AVnufxeIRhZSY278vQKx3+cnR0JFtls44wXa2M7yuVSk3JtDqci14Ft2dzM9QaDefKNU595nQ9fb7bGuwC4s4MsNrWG3WedV7q701xW+ucztf/k3UPhUIYGxvD5cuXcf36dWFRl5aW8PLlS6ysrODNmzeyPW9/f7+wtIlEQupb+3w+2VSIALPRaLw1f+jVYvyqDmXZ2tpCOp1Go9GQOsUEy4ynZkULxmM3GiebJCUSCQkHGxoawsjICM6dO4dgMAiPx4NcLof5+XksLi5ifX0dxWJRwhJ1iItT35n9a8NKJhNujq/TOU4Gy2/nzPcDrB3pSEc60pEfV5wAK+U0Bg+PtQIBtt+fhs1yEzKvBK2a9deufYYSMCSLnxmeBZy4UPl7r9crhdHJdh0cHMjCzBg9uvcJKFgrW8cYtiBvbIa4Yz+1IlvaMSxt13EiYGznnSVgNdtoe3aTgWtFZNmAu9OY2M5vNBqSuBoMBjE6OoqZmRlMTk5idHQUPp8PxWIRCwsLmJ2dxatXr5DJZIR9Z7ggS7EFg8Gm3AAATYw/EwV5XBtfu7u7KJVK8r2ussKQA85lMsXcmjWVSmFychJTU1OysyfLY/G6i4uLWF1dRTqdbgKqTFikYcW+N/vO9pnHzHF063/z2q2MlQ5g7UhHOtKRPyAxAetvj8nfNuZbf2dc663fmee5gSongOQkrc4hw683ZCGANcNX6CbVLC1ZK95HZ19rZpVsqY69pptfb/Kia2u3I6dlrFsZHW5A1MYq2sbHaa6c1U5XbK/ZTv3ZzRhyqiveal7Z7mcBQ+jp6UEgEJDSbCxvdf78eczMzKCvrw/ZbBZra2sCXNfW1qQqCuewx+ORpGzNpuptU/X8VOMi85Dt0/O00TjZacvj8SAUCkk9bpZgGx4elvCBer0u1TdyuZwkD3IXN+Yo8H3QgFKDed1P7fSnk06y6RMzFMCmhyjfOySgIx3pSEc68uOKx2VLbDc3sBsrS3FbjPT1bddwA8ouz9KSZdNg1ePxCBvFf/o7fS4ZVV6XAIHHzX8aEDite7bF2WTsnPrSlNMwqrbzbMfdxtw89ywAq+05ncCp/l6zca2Om+cAzQyeyeyZ1+K5ZPb7+vqQSCQQj8cxPj4uO2IyzpTgdWFhQUqyscyULrEGQOYf/2lwSyDKY9w+lZtxMLmrr68PwHEJtpGREUlc5IYxrFiwvb2NfD6P1dVV2WKbx1kBxizF5jYmTsaYG6vt9G5ocO50Dyfj+XuXtepIRzrSkY78uGICVqdFwwZincSm583F3jzfDfTa7ncaptLtdyZI1c9r1sQGIAwWS16Z4NT23G6LsNvzuC3aTue5saWt2mC7R6vfvUsMq63dJstnft+K5TfuaWVvzSQf83ydBEWQyLAU7oo5MjIilS18Pp8wluVyGevr65JhT/DKslLcOIA7tWlwHAwGpRoRkwf5HcNfuAGCrobh8Rx7EzKZjJSD49+VSkVKazJpkW1y6zsN8vmu2OKvtQHH880xsG29qj/bALM5HsoI7QDWjnSkIx35QxBPG/Wv1bmOi3grMNDqfP29FpMlaWcNOQ2YdQIpbuDMBuBPe/922Gnzvq3kNOC+FQBth101rnfmDOv3nXNO57Y71/md+dlk/vgdawoTJDJGNR6PI5VKSY1W1mnn7/WmEowR3d3dhcdzvIEBcByTGgwGpT42y79ptpXhLAcHB9IOXd91e3tb4lG3traQz+ebtgnWbC89Cra+s8053Zduxps5nuY1NfhsRz/otuhNFjoMa0c60pGO/IGIx9ia1Ym1aJc1bcWgui1kbuxhO8dNsNAOm6ifpRVAbQdEft972X6vGbx2QYAb2+j0fOa13Fhap2c5C8BqtgNoL665FVh1up7tO5MJ1ADK3LRAs4tkGAle9UYrZF6j0ajU9NWVLng/glAmU3m9Xtn+en9/X3YaZDw1E6t2dnaaKlUQiHJr4UKhIMlTlUpFmNSDgwOJxzb7WTOftnFxY0Z13zuVotLixN7q+9iMGdvvOwxrRzrSkY78gYi58BvfvQVW3ACs/p7ntMM0OoHLVozWaZhUfU2nBc2JUXNyT7YCxE5A/TSAtdVx83sbuHJijVsxyk5tsJ17loDVNufMsTN+29b85WezLjrvo/93uhZBmFluSQOzRqPRVJqNyVRM/mPFAG7zTtd+IBBAb2+vbFvs8XgEhDYaDUl+YrUKAk4mapGpZck1lm47ODgQBlZXuNAx3OY765ToZPZRKwOS37F0l208be+S7f2wjZU5vh3A2pGOdKQjfyBiMqwtznVl6dwYODeWqhWDYt6rHabTqc1OAAZodhW2WlTd7tuKZTaP/RAMdCugYIobQDc/twPwzjrpyjbOGiiaz2KypIyH5TGX+57qPN0O3c5W461Ls7EygMfjEUbW3J1K35cgW9dh1eXUGo2G1GnlM+gdNA8ODgT0atZUA1N9v9MYtTa22Qn8uhlY+vq2Sg9uhrO+TgewdqQjHenIH4iYDKuToncCN7ZFRUs77J7bMae22e6hz7GBE9vv3ArvO7XHBg5b9ZPtGjbQ4gZOnX5rnu80bm5AolV7W51/FgyryVw6ML+O4NAGZHjc4Z5N35vsn3mu2/3cwJxNmPynn1XXGTbFBt61YUYwSqCqj9uet5Xhon9jstK2MbAxo07nO7XF9sxO77xT2zuAtSMd6UhH/kDEBKzquOMiZbIp7bKupwVD5vXcGBynBcypXeZxJ+bX7f9W0opJs5172vNaLd7mMafnPo3Y+uEsAKtbP5kMntt5lO8Djpzu63T9Vu1ya6utFJftngAExOoyV7wG7+/WBifwbz57q/eulf4w57FNt2gQbN7bqY1OgNVsWwewdqQjHenIH4i4AVagvSSiFtdvySzZ7tcKLJ4GrJmLmAkavi9wM9vtdh3zezfWl2IyiG7P1k673NrnBtqd7vUuAFYnIKKlFTg0wZN24fO8Vgaa7Xsng6Gda+j22K7X7nwyn98NTLfTNi3aO2H+3gZq3e5httPpXq2ucVrpANaOdKQjHfkDEROwugGwVguP0yLyQwBCW5vcAIF53G1Bb3XvViDU6bftMHStQKLtd99XbPdo93qtxvAsAKsNMP32u7fOt80Ntz53A/Zk+04zfu28J1psiVpOxoPtvbS1We+A5QTWna6t79uqf08zR52MRycj001Oa3D99pjjvO1p+yk60pGOdKQjP4qYi4GT283J/Wa7Rqt7mMfbYSdtf9uuZ7bPjY1t53624+a99PetwBPwdskjN1a4XcbL7fsfipFq514/htiYcTfg1u585jGnRB59jm2euM1lfW4rZtRprjnNS9s9TACo2WOTQbbdt9V7b+t/23x2MggI/J2ubYoT+NTPat6/lZHrJm9HBnekIx3pSEfOVGyLnw3w6P/5tw0kuLkC9fdu97N97wRU3VhOt4Xe9kxO57oB3u+zGJrP5cQk2a5ta4sbk+TEiLmxiE7SLhP5+xYn4Gg7j2ICTtt5TvPTPG62wzaO+nf63k7joxOjzO9tAN1NnIArqwfoc3Tf6ASudgw987lMVti8jwkmze/1eeZnPd7tjpfTO96OdEICOtKRjnTkHRKPKmsFuLvVbee1cf222MB2FuNWbNRpgGMrkOPGDrV7PX62bRXpxnD9kGKCjtNe3xwfWz//FkCcSQzr9xmrdkUDOP5tA1z6vm7z0NZ/Tn1ri6PV88ZpzrgBW5M9trGh5vX0dfmd0/Pa2tLOmDi11+xjt2uyb9p5p/VntxjWDsPakY50pCN/IGJjg8xjbgxGO8dsbJPb79wY2VbnmKDRSczznJivVvd2Y/N4TTfW74cGX073cLuP2ZcmODlLEsoJDLVi691Ez2ezXJTOUtf31vPDqX+c5qIJ/EzA2Q4Qbpdd1sf18+k54GaY8jyn94HHzcoEbv3u9o7Y7q3/dgPZrd79dt6tDmDtSEc60pF3UGxMSzusnG1ROs1CwvPdFnQbK2U7V59vHm/1HG5i1qe03dsGMJyk1TO0au9pXJ2tntnJAGlXfkhQ/X3FNncBd5Di1i+aVXUD5TYXtdN5eh6b42+bp2RSTRbXidG0gTBzMwT9uV6vy0YC/Gyeo9um22QKz3HbmtVJTPDpBMpNsY2NW/+Yv3X6TksHsHakIx3pyDsoprL/vuyZk6vU6VyeRzHv6wRUndjUdhcrWztMt6c+5tZe8/qtQGA7jJKtfbbfn3aMfleA+7ue/0OKyRDqf7Y55cawm8DMjc10AjxOY+70Gw0WzevYxtyJsbU9qwa4FHOTBdv/JlC29avZDrN/zb6zbWygv29XX9iMPPOdNZ/byehudS+gA1g70pGOdOSdFSclfhoWzc2l6HRuO9c022YumjbGsdWzOIFd06VpezYn8GADTa2es10X5e9L3gWW9PuI2a/Mfm8HjLjNUycm1mmOOYE/fQ2Pp7kUlpuhpV3u3MlKs7NubLzJ4roBTP1bt/4wWWGn98ppnrsZWGb/uXkObIaIk0Fpu4/T75ykk3TVkY50pCMd6UhHfifxGMmCFJPpO21ohgaFNgPFDfi4ASoNJPX3OrnK1h7b/ZzAKeBezL/dPrCdo6/XDhPqNga2fqDYtkq2PXc77bb93mxLJ+mqIx3pSEc60pGO/OjSKoRDi+24W9iHLTzABKRObSEo1VujknW1XdtsiwZp7YaI2H5vttutD3Tbna6r72t6KMw22phPfU23cAWnZ26LKf0e7CrQ2TigIx3pSEc60pGO/EBiAikbILF9bhWq0g4r+EOHfdieRX9nc+Wb92iHdXRjXtsJCTKf24xR1YDcFktqAl4nttWJebb1vZPhYAujaJeZ7TCsHelIRzrSkY505AcRt5hk83i759liIdsBmybgNNvm5NJ2Apq2Z3OLX7X9rlXb2ZZ2AZ1mUZ1ivd3AuXm+032dDA/btW1MtvmdU4UDN+kA1o50pCMd6UhHOvKDSDuJN61CA8zftiNOYMoWP9oKEDoxjW5AVF/X3J3Kdm2TlXQSt+95Lyf3vhv4bGUkOI2jmzixwW4xsO2yq0AnJKAjHelIRzrSkY78QOIW2+jGkLolELnFipqJTk4gq52wA1s7bW04TXKRKSaINJOabGDOCSw6gU7bM7j1i/m3E8A87bO5hYQ4hXS4SYdh7UhHOtKRjnSkIz+oaMaxlUvcBpDcEpdMINcK0Nnu0W7bzes7XbMVgGvVLts99O5rbi59k9E1mV43xtgWU2qy4q3CDNxCJZxAsC0UoSXjfppB7EhHOtKRjnSkIx3pSEd+bOkwrB3pSEc60pGOdKQjHXmnpQNYO9KRjnSkIx3pSEc68k5LB7B2pCMd6UhHOtKRjnTknZYOYO1IRzrSkY50pCMd6cg7LR3A2pGOdKQjHelIRzrSkXdaOoC1Ix3pSEc60pGOdKQj77T8v6VdU82b4vNGAAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 864x720 with 4 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "from utils import visualize_data, visualize_data2\n",
    "from pathlib import Path\n",
    "\n",
    "# paths to example files\n",
    "t1c_path = Path(\n",
    "    f\"{BASE_PATH}/data/OtherEXampleFromTCIA/MRHR_T1_AX_POST_GAD_OtherEXampleTCIA_TCGA-FG-6692_Si_TCGA-FG-6692_MRHR_T1_AX_POST_GAD_SE_13_se2d1r_t1c.nii.gz\"\n",
    ")\n",
    "t1_path = Path(\n",
    "    f\"{BASE_PATH}/data/OtherEXampleFromTCIA/T1_AX_OtherEXampleTCIA_TCGA-FG-6692_Si_TCGA-FG-6692_T1_AX_SE_10_se2d1_t1.nii.gz\"\n",
    ")\n",
    "t2_path = Path(\n",
    "    f\"{BASE_PATH}/data/OtherEXampleFromTCIA/MRHR_T2_AX_OtherEXampleTCIA_TCGA-FG-6692_Si_TCGA-FG-6692_MRHR_T2_AX_SE_2_tse2d1_11_t2.nii.gz\"\n",
    ")\n",
    "flair_path = Path(\n",
    "    f\"{BASE_PATH}/data/OtherEXampleFromTCIA/MRHR_FLAIR_AX_OtherEXampleTCIA_TCGA-FG-6692_Si_TCGA-FG-6692_MRHR_FLAIR_AX_SE_IR_5_tir2d1_21_fla.nii.gz\"\n",
    ")\n",
    "\n",
    "# visualize example images\n",
    "visualize_data2(t1c_path, t1_path, t2_path, flair_path, height_p=0.75)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## 3. Preprocessing\n",
    "\n",
    "BraTS challenge algorithms expect co-registered, skullstripped files in SRI-24 space, to achieve this preprocessing is required.\n",
    "Instead of using the vanilla preprocessing pipeline from BraTS Toolkit, we recommend using the new [BrainLes preprocessing package](https://github.com/BrainLesion/preprocessing/tree/main/brainles_preprocessing).\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "#### First, we define a function that processes an exam."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 5,
   "metadata": {},
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "/home/eva/.local/lib/python3.10/site-packages/brainles_preprocessing/registration/__init__.py:6: UserWarning: ANTS package not found. If you want to use it, please install it using 'pip install brainles_preprocessing[ants]'\n",
      "  warnings.warn(\n"
     ]
    }
   ],
   "source": [
    "from auxiliary.normalization.percentile_normalizer import PercentileNormalizer\n",
    "from auxiliary.turbopath import turbopath\n",
    "from tqdm import tqdm\n",
    "\n",
    "from brainles_preprocessing.brain_extraction import HDBetExtractor\n",
    "from brainles_preprocessing.modality import Modality\n",
    "from brainles_preprocessing.preprocessor import Preprocessor\n",
    "from brainles_preprocessing.registration import NiftyRegRegistrator  # for linux\n",
    "\n",
    "# from brainles_preprocessing.registration import ANTsRegistrator # for windows\n",
    "\n",
    "\n",
    "def preprocess_exam_in_brats_style(inputDir: str) -> None:\n",
    "    \"\"\"\n",
    "    Perform BRATS (Brain Tumor Segmentation) style preprocessing on MRI exam data.\n",
    "\n",
    "    Args:\n",
    "        inputDir (str): Path to the directory containing raw MRI files for an exam.\n",
    "        File names must end with \"t1.nii.gz\", \"t1c.nii.gz\" \"t2.nii.gz\" or \"fla.nii.gz\" to be found!\n",
    "\n",
    "    Raises:\n",
    "        Exception: If any error occurs during the preprocessing.\n",
    "\n",
    "    Example:\n",
    "        brat_style_preprocess_exam(\"/path/to/exam_directory\")\n",
    "\n",
    "    This function preprocesses MRI exam data following the BRATS style, which includes the following steps:\n",
    "    1. Normalization using a percentile normalizer.\n",
    "    2. Registration and correction using NiftyReg.\n",
    "    3. Brain extraction using HDBet.\n",
    "\n",
    "    The processed data is saved in a structured directory within the input directory.\n",
    "\n",
    "    Args:\n",
    "        inputDir (str): Path to the directory containing raw MRI files for an exam.\n",
    "\n",
    "    Returns:\n",
    "        None\n",
    "    \"\"\"\n",
    "    inputDir = turbopath(inputDir)\n",
    "    print(\"*** start ***\")\n",
    "    brainles_dir = turbopath(inputDir) + \"/\" + inputDir.name + \"_brainles\"\n",
    "    norm_bet_dir = brainles_dir / \"normalized_bet\"\n",
    "    raw_bet_dir = brainles_dir / \"raw_bet\"\n",
    "\n",
    "    t1_file = inputDir.files(\"*t1.nii.gz\")\n",
    "    t1c_file = inputDir.files(\"*t1c.nii.gz\")\n",
    "    t2_file = inputDir.files(\"*t2.nii.gz\")\n",
    "    flair_file = inputDir.files(\"*fla.nii.gz\")\n",
    "\n",
    "    # we check that we have only one file of each type\n",
    "    if len(t1_file) == len(t1c_file) == len(t2_file) == len(flair_file) == 1:\n",
    "        t1File = t1_file[0]\n",
    "        t1cFile = t1c_file[0]\n",
    "        t2File = t2_file[0]\n",
    "        flaFile = flair_file[0]\n",
    "\n",
    "        # normalizer\n",
    "        percentile_normalizer = PercentileNormalizer(\n",
    "            lower_percentile=0.1,\n",
    "            upper_percentile=99.9,\n",
    "            lower_limit=0,\n",
    "            upper_limit=1,\n",
    "        )\n",
    "        # define modalities\n",
    "        center = Modality(\n",
    "            modality_name=\"t1c\",\n",
    "            input_path=t1cFile,\n",
    "            raw_bet_output_path=raw_bet_dir / inputDir.name + \"_t1c_bet.nii.gz\",\n",
    "            atlas_correction=True,\n",
    "            normalizer=percentile_normalizer,\n",
    "        )\n",
    "        moving_modalities = [\n",
    "            Modality(\n",
    "                modality_name=\"t1\",\n",
    "                input_path=t1File,\n",
    "                raw_bet_output_path=raw_bet_dir / inputDir.name + \"_t1_bet.nii.gz\",\n",
    "                atlas_correction=True,\n",
    "                normalizer=percentile_normalizer,\n",
    "            ),\n",
    "            Modality(\n",
    "                modality_name=\"t2\",\n",
    "                input_path=t2File,\n",
    "                raw_bet_output_path=raw_bet_dir / inputDir.name + \"_t2_bet.nii.gz\",\n",
    "                atlas_correction=True,\n",
    "                normalizer=percentile_normalizer,\n",
    "            ),\n",
    "            Modality(\n",
    "                modality_name=\"flair\",\n",
    "                input_path=flaFile,\n",
    "                raw_bet_output_path=raw_bet_dir / inputDir.name + \"_fla_bet.nii.gz\",\n",
    "                atlas_correction=True,\n",
    "                normalizer=percentile_normalizer,\n",
    "            ),\n",
    "        ]\n",
    "        preprocessor = Preprocessor(\n",
    "            center_modality=center,\n",
    "            moving_modalities=moving_modalities,\n",
    "            registrator=NiftyRegRegistrator(),  # Use this line if you are on linux\n",
    "            # registrator=ANTsRegistrator(), #Use this line if you are on windows\n",
    "            brain_extractor=HDBetExtractor(),\n",
    "            temp_folder=\"temporary_directory\",\n",
    "            limit_cuda_visible_devices=\"0\",\n",
    "        )\n",
    "        preprocessor.run()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "#### Now we loop through the exams to preprocess the data:\n",
    "(This may take more than 10 minutes)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 6,
   "metadata": {
    "scrolled": true
   },
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "\r",
      "  0%|                                                                                                                            | 0/2 [00:00<?, ?it/s]"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "processing: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294\n",
      "*** start ***\n",
      "File: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/temporary_directory/atlas-space/atlas__t1c.nii.gz\n",
      "preprocessing...\n",
      "image shape after preprocessing:  (103, 160, 160)\n",
      "prediction (CNN id)...\n",
      "0\n",
      "1\n",
      "2\n",
      "3\n",
      "4\n",
      "exporting segmentation...\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "\r",
      " 50%|█████████████████████████████████████████████████████████▌                                                         | 1/2 [06:20<06:20, 380.56s/it]"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "processing: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA\n",
      "*** start ***\n",
      "File: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/temporary_directory/atlas-space/atlas__t1c.nii.gz\n",
      "preprocessing...\n",
      "image shape after preprocessing:  (103, 160, 160)\n",
      "prediction (CNN id)...\n",
      "0\n",
      "1\n",
      "2\n",
      "3\n",
      "4\n",
      "exporting segmentation...\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 2/2 [10:11<00:00, 305.98s/it]\n"
     ]
    }
   ],
   "source": [
    "EXAMPLE_DATA_DIR = turbopath(f\"{BASE_PATH}/data\")\n",
    "\n",
    "exams = EXAMPLE_DATA_DIR.dirs()\n",
    "\n",
    "for exam in tqdm(exams):\n",
    "    print(\"processing:\", exam)\n",
    "    preprocess_exam_in_brats_style(exam)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "#### Storage of preprocessed data \n",
    "\n",
    "The preprocessed data is saved in a newly created folder \"raw_bet\": \n",
    "\n",
    "```data/<datasetName>/<datasetName>_brainles/raw_bet```\n",
    "\n",
    "Run the subsequent cell for visualizing one preprocessed example sample."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 7,
   "metadata": {
    "scrolled": true
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAqwAAACvCAYAAAA4yYy3AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/H5lhTAAAACXBIWXMAAAsTAAALEwEAmpwYAACbh0lEQVR4nO39eYym93UeCj7vt+97fbV1VfVKNtlic5Uo0jQRRZatKLZsw3AMI4mvEwmIHcw/M3PhBBcDzAVuLgLMH76T5HoCb7EnTmzAyTiQNfJItH0thSJNUeKubrL36tqXb9/3d/4oPec771tFaiG76qvq3wM0urvqW96q77znd85znnOOZds2DAwMDAwMDAwMDCYVnqO+AAMDAwMDAwMDA4MPgglYDQwMDAwMDAwMJhomYDUwMDAwMDAwMJhomIDVwMDAwMDAwMBgomECVgMDAwMDAwMDg4mGCVgNDAwMDAwMDAwmGiZgNTAwMDAwMDD4EWBZ1oOWZb1pWVbdsqySZVn/6gd83v/Psqz/4V5f30mCCVh/CFiWtWxZ1k+o//+OZVnXLMsaWZb1q0d4aQYG+2Ds1eC4Q9uwZVkPWJb1Jcuydr8XGHzNsqwHj/oaDe57/AaAv7FtOw7gz3/QJ9m2/fds2/5/37vLOnkwAeuHw1sA/jmA14/6QgwMfgAYezU4zkhhLyB4EMA0gFcBfOkoL8jAAMASgCsf5QtaluX7KF/vpMAErD8gLMv6IwCLAL5sWVbDsqzfsG37t2zb/msAnSO+PAMDB35Ye7Usy2tZ1v9kWdat75W2XrMsa+HQL9zA4Htw2zCAv2Pb9u/btl2ybbsP4H8D8KBlWdkjvVCD+xaWZf0fAD4F4H//no0G1PfSlmX9f79XESh/79+n1Pe/blnWF7/371+1LOsly7L+N8uyigD+50P+UY4FTMD6A8K27X8MYAXAz9i2HbNt+/9x1NdkYPB++BHs9f8C4JcBfA5AAsA/BdC6t1dpYPD++AFs+HkAW7ZtFw//6gwMANu2/y6AFwH8n2zbjgHoqW97APwB9hjYRQBtAP/7B7zc0wBuY6968L/ekws+5jC0s4GBAQB8EcBv2LZ97Xv/f+soL8bA4IPwPabqt7CXaBkYTBy+l0j9f/h/y7L+VwB/8wFP2bBt+99979+De3ltxxUmYDUwMACABQC3jvoiDAy+HyzLmgLwAoD/l23bf3LU12NgcBAsy4pgT7byWQDp7305blmW17bt4QFPWT20izumMJKAHw72UV+AgcEPgR/GXlcBnLtXF2Jg8CPCYcOWZaWxF6z+uW3bpmxqMMn4v2KvQfBp27YT2JOwAID1Po838cX3gQlYfzhsAzjL/1iWFbAsK4Q9A/RblhWyLMv8Tg0mBT+Mvf4egP/FsqwL1h4um2YWgwmA2LBlWQkAXwPwkm3b//JIr8rA4Psjjj3dasWyrAyA//sRX8+xhwmufjj8awD/N8uyKpZl/Y/Yy/TbAJ4F8Dvf+/fzH/B8A4PDxA9jr78J4E+/95gagN8HED70KzYwcEJsGMD/GcDHAfyT702+4J/FI71CA4OD8f/Eng8tAHgFwFeP9GpOACzbNiy0gYGBgYGBgYHB5MIwrAYGBgYGBgYGBhMNE7AaGBgYGBgYGBhMNEzAamBgYGBgYGBgMNEwAauBgYGBgYGBgcFE4wMXB1iWZTqyDD40bNt+v7lz9wzGdg0+ChyF7Xo8HmO7Bh8ao9HoUG3X7/cbuzX40Oj3++9rt4ZhNTAwMDAwMDAwmGiYgNXAwMDAwMDAwGCiYQJWAwMDAwMDAwODiYYJWA0MDAwMDAwMDCYaJmA1MDAwMDAwMDCYaJiA1cDAwMDAwMDAYKJhAlYDAwMDAwMDA4OJhglYDQwMDAwMDAwMJhomYDUwMDAwMDAwMJhomIDVwMDAwMDAwMBgomECVgMDAwMDAwMDg4mGCVgNDAwMDAwMDAwmGiZgNTAwMDAwMDAwmGiYgNXAwMDAwMDAwGCiYQJWAwMDAwMDAwODiYYJWA0MDAwMDAwMDCYaJmA1MDAwMDAwMDCYaJiA1cDAwMDAwMDAYKLhO+oLmBR4PM7Y3bbtD/y/gcGkwLIs+VvbqbFZg0mH2+/SloE9+x2NRod9SQYGHwjLsuDxeBy2Cjj97XA4POzLui9w3wesoVAIZ8+exfPPP49ut4ter4dOp4NCoYDd3V0Mh0MMh0Osrq6i2+0e9eUaGAiCwSBOnTqFRx55BD6fD16vF7Zto16vo1wuo9VqodfrYW1tDc1m0wSwBhODQCCAqakpXLhwAbFYDIFAAACwuLiIVCqFcrmMYrGIv/3bv8XKygr6/f4RX7GBARCJRPDII4/gp3/6pxGJRODz+eDz+VAqlbC8vIxut4tut4tvfvOb2N3dxWAwOOpLPlGwPugQsyzrRJ9w4XAYTz75JM6fPw+v1wuPxyMZf6PRQKVSQavVQrPZRK1WQ6FQQK1Wg2VZ6PV6EgBYloVQKATbtiXrGo1G+9iB+9Xp2rZtff9HfbS4H2z34Ycfxvnz5xEMBhEKheD1euX7g8EAvV4PtVoN29vb8sfj8aDZbAoD4PP5kEwmMRgM4PV6MRqNMBgMMBwOYdu2sFzGdg8PHo/nxNquZVlIJBL41Kc+hVgsJl+jL11cXMTMzAy8Xi+8Xi+63S5effVVfOUrX0G73Xb4XY/Hg0AggOFwCL/fLz58OBxiNBqJL79fk7XRaHSotuv3+0/sL9nj8SCVSuEXfuEX8Nxzz6Hf76PT6YhddbtdlMtldDodFItFrK+v4+rVqygWi/D5fGi32+JzPR6PxAs+n09iBl1tsG0btVrtvrTbfr//vnZ7Xwasjz32GDqdDqanp2HbNrLZLDKZDCKRCDweD3q9HgaDATweD2zbRr/fR7PZRLFYRLvdRjAYxJ07dzAYDFAqlZBMJvHYY49hNBohHo8D2HOSfJ1+v49WqyUZV7/fR7fbRbvdvi9KXiZg/ehw+fJl+Hw+LC0todPpIJVKCUPl8/nEwdm2LbbWbDbR7/fh8/kwPT2NXq+HXq8Hn88nAcLt27cRjUYxHA7R7Xbx3nvvYTAYoFqtCtvFYLbb7aJer98XZS8TsH40sCwLDz/8MBYWFvDMM89gMBhge3tbEiMm+IlEApFIBLFYDIlEAolEArFYDLu7u/jGN76Bv/mbv0GpVMJwOEQ6ncbDDz8M27Zx+fJlTE9PS3Ws1+vJc1944QV0Oh34/X4Mh0Pcvn0b7Xb7qH8l9xwmYP3wsCwLP/mTP4lYLIZPfvKTQko1Gg30+334/X4AewQBk/5arYbhcIirV69iNBohn89jeXkZt2/fRqvVQiKRwCc+8QmEw2FMT0/D7/cjHA7D7/djMBgIIfbGG2+I/KDVauHNN99EvV4/4t/IvYcJWL+HbDaL2dlZzMzMoFQqIZ1OY3Z2FrFYTAxmOByi1+sB2DPWfr8vBzUDzUqlgmq1ikqlglKphLNnzyKVSiGdTkvQEAwG4ff7EQgEUKvVUK/XEQ6HJQjY3t7G5uYmyuWyGPtJhQlYPzwymQxmZ2fxwAMPIBAIoNPpIB6PC7tqWZYjYLUsC8PhEIPBQAKCbreLWq2Gn/iJn8BP/dRPIZFIoNVq4b/+1/+KO3fuoN/vI5VKIRKJYHl5GT6fD81mE41GA8FgEB6PB5lMBjMzM3jhhRdw5coVtFqtE82+moD1w2NqagqPPvooPvWpT+HcuXPY2dnB7du35dCnnXo8Hjm8GWwGAgFht+LxOP7oj/4Ir7zyCkajEbLZLB5//HHkcjlMTU3B4/Fgc3NT7oHZ2VnMz8/jnXfeQa1WQygUEunM17/+dWxvb2NnZ+eIfzv3DiZg/XA4deoUnnnmGTz33HPY2tqCbdtIJpNoNBrodrsYjUYSUAIQVr9eryOZTKJSqaBer6NarSISiWBlZQXFYhHRaBRPPfUU5ubm4PF40O/3EY1GUa/X0ev1pNKVTqfR6XSQTCZh2zbeeOMNvPzyy+h0Otje3j7i3869wwcFrCdew2pZFi5duoRkMgmfzyflo9nZWcTjcWQyGSmn0tGxzOSm8CORCHq9HtrtNkKhkLBb0WgUqVQK2WwWfr9fWNNQKIRgMAiv1wvLspDNZhEOh9HtdnH27FlsbGxgY2MDxWIRhUIB1Wr1viwBGBwM2i7tzLIsjEYjtFotRKNRhMNhBAIBWJYlZVU+hs7T7/dLwMrvvfXWW3jooYdw4cIFvPDCC1hZWZGEqVKpoNPpiM0yUA0EAggEAohGo4hGo/iJn/gJLC0tYWtrC+vr67h169Z9wbga/GCwLAvnz5/HxYsX8eCDDyKRSMC2bfR6PYRCIQyHQ7TbbUmoer0ehsMhvF4v2u02Op0Out2uBLPxeBwPPvggnn32WaytraFarWJpaQnT09Not9tiw8PhUIJS/l/LtHq9Hi5evIh/+S//Jd588028+uqrePnll0900mXwg8Pr9eK5557DpUuXMDc3h3Q6jVKphO3tbUQiEcTjcSGkut2unNcs+9u2LVXaSCSCaDQqMqz5+XnYto2FhQWcOnVK5AC2bYtMKxgMAgCq1SpyuZwQDZFIBOfOncP09DT6/T7W1tbw1a9+9b7rqzmxAavH48EnP/lJ9Ho9nDp1CuVyGQBw/vx5pFIpjEYj1Ot1WJYl2j/btkU7xQOcB7fX6xVtVDAYxGAwQCKRkEM9n88jkUgAAHq9HjweD4LBIHw+nxihz+dDPB5HOp1Gr9fD1NQUpqamUK/X0Wg0sLq6ikKhIGUtg/sTHo8HTzzxBDqdDs6ePQuPxyPsPctFXq9XglUGimxcYcZP58lKAQPbdruNF154AW+//TbeffddYQmoWQUAv98Pn88nJapQKCSJ3MbGhrzf9PQ0ZmZmkMvlsLGxgVardaJZK4MPhmVZOHv2LBKJBH7qp34KZ86cQbVaxe3bt8Wvzc3Nwev1io2NRiMhCPjvTqeDTqeDfr8Pj8eDwWCA5eVlLC4uYnFxEaurq1hcXBSJynA4lMSKAepgMJDXq9VqElBUKhVcvnwZS0tL8Hq9iMViWF5exmAwwPXr1w1pcJ+B/o9Vp+effx7tdluasAeDAebn59FsNkUKRc00ddOj0Qg+nw/9fh+BQMBhQ7lcDs1mE5FIBLlcDouLi4jFYvJaOrGij+12u0I49Pt9YWlt20apVMKjjz6KqakprK6uotVq4aWXXrov5IUnMmD92Mc+hp/+6Z9Gq9XC1tYWhsMhTp06Bb/fLywnM3se6sDeQU86HhgHqwBEZD0YDJBMJjEajVAqlRAIBJBIJBAOh+WAp8H5fD5EIhEMBgMEAgExasoP+v0+vF4vQqEQZmZmcObMGdRqNezu7mJ7exs3b968b7SCBnt44IEH8OlPfxr9fh+7u7sIhUJIJBKIRqMAIE6NYEBKO6bz5N/AuAGLttZut7G9vY1QKCSMP22XAQJfm3bL//N1GVz0+31EIhFcuHABS0tLqFQqKBaLuHXrFqrV6omWuhg4MTMzg8ceewzT09NYWlpCLpfD9vY2NjY2UC6XxY+x8qRtl2QBm6aGwyH6/T6CwaAk+Lu7u6JxTaVSyGQyok2Nx+OIx+OwLAvlclkaZRuNhlQlKPVis0wwGEQwGMTp06dx6tQpBINBPPXUU3j11Vexvr6OVqt1lL9Og0PCk08+iX/2z/4ZkskklpeXUS6X4fP50Ol0AECkVqFQCN1uV3ymbtLW0hafzwe/349Op4NYLIZIJIJ6vY5arYZIJIJQKCS2T8Kh3+8jkUhIbwHfy7ZttNttCY4bjQZarRYajQbm5+dx9uxZDIdDPPXUU/jLv/xL3LlzB81m8yh/nfcUJypg9fv9WFpawmc/+1nU63XU63UEAgGk02kxkEAgAK/XK2xVp9NxzFWjEVqWJYctjYa6QTZnlUolABANIUuylmWJYfM9w+GwBMA00k6ng1KpJMLtRCIhTjQcDovupVAo3LedrvcL/H4/5ubm8OlPf1oSJx7CHo/H0U0K7M35YzZO9h8YswUMWhmsskrAakK/38fW1paDXdV2z4CCNkw2jNfQ6XTQbrfl65TCZLNZpFIpzM/P486dO7hz58592+16v8Dn8yGXy+HHf/zHkU6nkc/nsbCwgI2NDWxvb6NSqaDZbMLj8aDdbmN3dxe2bYv0hNDVLR7c8/PzYs/dbhelUgnxeBylUgmhUAitVkvs37Is5PN56RlotVoIhULyekyuEokEFhYWZAqBZVlIp9PIZDJIJBIi1/rOd76Dd999VwJdg5OFYDCIRx55BP/iX/wLAMDa2ho2NzeRy+Ucun/6LrLxACSRp5aVf7Py1el0xIcCQD6fx2g0QqFQgNfrlaZs9si0Wi3EYjEh0ljF7ff7QngBe5ItsrulUkkasubm5vAP/sE/wPLyMl5//XW8++67J1IucGIC1ueeew7nz59HNBoVZocZOgCHFo8Bpt/vl2wHgBzwzJQAiHFRSB2NRiUwDQaDkll1u10JhP1+vxz83W4XgUAA8XhctFW9Xk8c6nA4RCQSAbAXRDQaDXg8Hly4cAHT09OYmprCzZs3sb6+jlKpdF/Q/vcbHn30UTzyyCPiDGk3wFimoqUrTIJYMtKslNZUjUYjcbzM2hmY2rYttglAGlJ8Pp+wsQxQR6OR2LQe5h6PxyVYYOmMjBinb8zPz+PGjRvS1GVwsjA/P48LFy5gYWEB6XQaqVQKCwsLormmNpXl+cFgIKV52iXtjLbGAHF+fh65XA6lUknK/mQ9c7kcUqkUut0u1tbW0Gq1UC6XxY4ZBGxubordhkIhZDIZaXbZ3NxEo9GA1+tFMpkEANTrdQSDQZw5cwYPPPAANjY28Md//MfY3d09st+xwUePT3ziE/jZn/1ZPP7442g0Grh58yY2NzfR6XSQzWYlUKRN0reyD4aJPhumOYXF7/eLzQMQv+z1eiWZCgaD6HQ6CAQCjnGCzWYT0WjUofPu9/tyBgwGA2kQp9+mvjsajaLZbGJ6eho///M/j6effhr/5b/8FyHVTgqOfcC6tLSExx9/HJ/85CfF4JjpcCRVr9eTrn33AU5jojOlw6QGlUFkMplEOp2GZVnCGLG8H4vFZIyQ3+9HJBJBp9MRI/d6vYhGow5HSo0WmVQaervdRjqdlkYw6l6uXbuG9957Dzs7OyZoPSHI5XK4dOkSnn32WVlYwUBVN/0B4w5UJj084OlQNbNKG9dlVSZlmlElGwBAkjCtg2WAHA6HpWyrdYH8P+UETAC9Xi/6/T5CoZAEMlNTU3jttdekzGZwvBGNRjE3N4fLly8jHo9LAOnz+RCLxcTXslHP6/WKb2bwqSdZ+Hx7RxFtnslOsVhEsVgU+2q1WiLL2traQr/fRzwel4ra+vq6+FNWsHi/zMzMIBqNIhQKoVQqOSZcRKNRrK2tiVSGzVvZbBa//Mu/jP/0n/7TiTv870dkMhk8+eST+OIXv4hEIoGtrS2sra1hZ2cHtVoN0WgUgUBAmHcGjMCeD9YyASb1TOhJBnQ6HUxNTYlchTY2Go2QyWQQDofR6/UwGo0QCoXQ6XSQSCRkZKYOZumXWeXNZrOo1Wriu3u9HjKZjMQxvKazZ8/iV37lV/BHf/RHKBaLR/b7/qhxrAPWixcv4jd/8zfx1ltvYW1tTUajxONxjEYjGdbLw5W6Ox7+DGKB8QHNAz0YDMKyLNTrdXg8HiSTSQkqtdg6lUoJ69rr9YTB5cggGhsZMc5kpZOOxWLyWgwGvF6vjCuiw4/FYkgmk3j11Vexvb1tgtZjjoWFBfzar/0aer2elIfowJhs6UHSWp5C0T9ZT11Wpf2Q+WfTnx69wq+xgZBdrXS8BANi/b5kU+lIGfzyvdzSAd47ly5dAgB85zvfOZGlqvsJqVRKyv+RSATJZBLBYFCa7WKxmDSgsJqlGfyVlRXR2dEf64ks0WgUi4uLqFQqoiUNBoPiRykn4FSVbDaLdDotwS19OatZo9EIkUgE2WxWbH17exvdbhfValXKtY1GQ6pp9OXsQ/j85z+PL33pS9K8a3D8MDs7iy984Qu4fPmyjO5bXl7GaDRCNBqVnhI2XJHEAvYaqePxuJz/ZGDph/UZTrZey7TYZJXL5aSXoNFoSKJGn6kXF9GGdexC6OuKxWIy+5WVM2BvCccv//Iv44//+I9PTLJ1bAPWixcv4l/9q3+FV155Bdvb2wiHwwiFQo5BvsxkKKCmZoqHLOf9udknBgJkvDjvUjNKgUDAwSiR3aImRTer8HV52DNrY0MWGTKWB/j6DC6YTZGN/du//VvcvXvX6AKPKebm5vCFL3xBlkfQUZJBBSBjpIAx+0l7IkvFx+qgkTpUv98vNkvbY6Zv27bYOJ+vA1U6Sf192qiuGlDvzQCCjtvn80lyph936dIlWJaF73znO4ZpPaZIJpP48R//cSwsLDj8FMdKhUIhFItFNBoNtNtthy6aTNLp06dx9epVxzY1ABLQxuNxdDodrK6uolqtSuJO/whAJChc3hKPx9FsNtHpdFCv1yV5ov1zvJBt28I4ce42bZX+mxU23hPdbheJRAKf//zn8ed//ucmaD2GmJ2dxa//+q9jbm4OoVBImgGZpEciEam0cgyVJgLor6gzZYme01dYDQX25FWFQmHftBY2BXa7XXQ6HdFX62kslGlp2QEAkRzq6nC9XpdKL6cesaGcAe7i4iJ+5Vd+Bf/5P//nEyFrOZYB6wMPPIB//a//Nb773e9ia2tLOv/pbMggMSPiwc5sW4v4yQjpQ5mZEkv2sVhMMnNgHIBqBozjVMgWMODQ7AFfE4A4QxopS2NkEOjE6dSpg7148SKi0Si++c1v4ubNm6YL+5iBWT43UPFgZVBJJxmJRIQt5ddpx2TzdcLiHs/G4JLPYRCqg1/aMR2etmktq9GZPf/Ne4ZJHINkzcjqTlgGro888ghCoRBeeuml+2Lb0ElCMpnE888/LzKPzc1NR7nTsizZ6MeAlZ89/RQPUfYa6MRIa7N3dnZQqVQcSRoZL70gg0wXCYBeryfNVmSogsEgkskk+v0+6vX6PmIgFArJNjjaO/29XuoSDofxuc99Dl/5yldQqVQO+bdv8KNiZmYG//yf/3Pk83kAezNOC4WCQ14FwDF+MplMit/tdrtIpVJSMWV8wCoCCSX2w7CHJpFIOM5v3g8AHLEEWV1KEFjdJShTZFBt2zZisZhIFdnQ2Gq15DooSfR6vVhaWsIXv/hF/N7v/d6xD1qPXcBqWRb+6T/9p7h58ybW1taQTCYRj8eFYqch8aDmh8/OOy2GprOj7k8710ajISwsMx4amT74mcnoOZUE/08tLWl7nbkR/X4f/X4fyWRSAgrS+wwKQqEQQqEQ5ufn8dxzzwEAbty4YcZeHRNYloXPfOYzooPmLEodlDLj1w1U7MDXQSDtWk+10E1RtHfaMzNzggEAD/VQKLTvWnk/MBjRFQoGqLQ9Bt5ktfgeuuTFYPjBBx+Ebdt46aWXDNN6TGBZlsx+jEaj2N3dRalUEt1dOByWZQB6DSqTK13abDQaCIfDqFQqDpbesiyphlWrVVl9qV+L9wltkDIV+kdgzL4Ce/4/l8shGAyiXq87EjXeT7FYDIVCQXwtAxB2e/f7fZRKJQSDQUSjUXz605/GCy+8cF+syTzu8Hg8+Nmf/VmcP39eJu1wdS9XoWpSicwmg0yCo9iAcXJG38rtbJa1t7KVjXtM5IE9H06NLANT3ifuiUS8D3g9vA5er64eJJNJadKl/WuygTFHLpfDF7/4RfzO7/zOsda0HruA9Vd/9VeRy+Xw3e9+VzZP0Ji0Bo+GosuquhlFH6bUWlEDSwcYDofFEN3lKwahzMo7nY5jvI8uhfI9NLRRcRKB1sRoA2YWSKlBLBbD/Pw8PvGJT6DRaGBtbe3e/+INPjR+8id/Eg899BB2dnak5OgeV8VkhskVnaMu2QNjplMnT9TukQHga1FzxeeRXdI2poNh9791Mud2qLRLahX5NZaqNPSygzNnzuDu3bu4efPmR/1rNrgHuHjxIhYWFhAIBNBqtaRxlFo/BqV65i9lU9qnspua9krbpu/1+Xzy+gAcz9fsFBMugg1d9NVazsKpBOxB0JNguI3ozp07MrOVyVW325WfTy82iEajOH/+PN54443D/yAMfmBYloVPf/rTeP755wGMSap2u+2QYlHHr78GQJh7gokT/Zu70sr5qHwsiSZtSyTAIpGIrHonwcagmQw/JQb0x16vV1hU+ng2iHGMljsIZxOYz+fD4uIiLly4gFKpdGzlhMcqYP35n/95/MN/+A/xV3/1V2g2m8hms5Kt6I46lo7czBM/QAa3ND5dYqJxRCIRmZ3KspAOIPSGCt4Afr9fBlvz9fQ1RCIR6UzlTUFpgu4+ZGmBZQI9w5WHAxsZzp07h1qthlqtdjQfisEPhKeeego/93M/Jw0n4XBYnA4w1okSlIa4pwFoe6It0r61TemRVDrZ4teYaFG/p5klt2SAr0lWVzcnUsNFuKsH7ukF/Hnn5ubwMz/zM/jyl79sgtYJx9LSEj7+8Y8jk8kgn89Lk2Aul3Ow95xPXSgUxC64brLX60mFqlqtSlMpn0ufXavVZCwQZ1ID+xsAk8kkAoEAZmdnAQArKyuo1Wr77JdTXgaDAdLptATUwN5kACaCnCtMO/f5fKjX6+KX4/G4LHyJRqP4u3/376LX6+Hdd981DbATiieffBKf+9zn0Gw2RX7ChJ5D+hkk6pFVlFJxwQQw3l7p1v3zPNZTVEgIkCRgLwFtkWvhWeYvFAqi0XbLXRir0Jbps0luUQrA+4VsLeORSCQiI+Y2NjYwPz+P2dlZbG5uHsug9VgFrDMzM/j2t7+Nq1evyuwxnWnrphN25mkmiYctD3P9dd0gxUyFpVo98oo0P7M1Dv7Xz+dyAhoa/6ZEgI+lwbGcpUdl8Pq63a6j67ZcLqPT6aBcLmN7exvD4RD5fF7YAYPJxPz8PEqlksyF1N3OenQJWVc6SAAOR8sESydoAByMJ7NxN+OkA1aWajUrqtlVOk4dFPO6dZDB6+F9o9kJVgTYrc3Gx3q9js3NTSSTSVy4cAErKytmOPsEI5/P4/Tp05ifn5fkmmOt9OIKHta2baNcLsOyLGl20gwoEyY9Oo3+jnZNfelBM4gty8K5c+fE/1mWhWQyKZpolvsJBiYMTlqtlti43+9HtVpFs9mUxhZdHePjZmdn8eijjyKbzSKTyQAAnn76afzar/3aienAPkmwLAvT09Oo1+u4deuW9KJoVpRl/8FgIMyl3++XLVadTgeRSERGXLGCS9ukz221WmJ7nEXNs1if51wWxIoux1LpOIQTYABIIMzNWroRy+fzYWZmRiQ4mnBjHBGJRGBZFgqFAhqNBm7cuCHa2t3d3WM5F/vYBKxPPfUULl++jG9961sSrHY6HTSbTbRaLaHVdfDHobo8oIGxHtCdyWhmSJc/gfEICa13pWFMTU0hHo9L8KmDV60v5Nd0U5W7FEDdIUtg1LCSaW00Gtje3sbW1pZs3Zqfn0coFJKVrscxazrpOH36NC5fvoy1tTVH6bxeryMWi0mFgEGgbgzUtkPZiv4+7VgzsO4kzh14srTFxEwneZpFAOCYoKGlLgAcmls6ct1goxmx0WhvMDbXGYdCIfT7faRSKVy8eBFXr141DYQTiPn5eTzxxBMYDAZYWVmRcWk8yDn+CYBjtA6D2E6ng1QqhWQyiW63K1UpYOxn9f91ZQoYa/p0BWI0GuHq1atotVqiIyX7pMun+rm2bQuDyuC61WrBtm1cv35dAg5t37wXotEozpw5g2g0itXVVbz++utoNpvw+/34+3//7+PP/uzPTvQ6zOOIS5cu4fOf/zx6vR7C4bCsN7VtG1tbWzKAfzTaG3kWDAZlHBSTJLLxgUBA7IvsK+2EmzI1cUCWnzZLIs3j8ch8Vrfd8n21b6XdcvoFYxQtTymXy+L3A4GA6GT1uEJe46OPPopgMIhGo4GZmRn87d/+7bEbMXgsAtaLFy/iN37jN7C9vY2pqSnJRPSsNK374Afb6XQcBy7Z0Xg8DmDsFAE4ml7oOFmu7/V68jefRyNkVsZyEaHZTl4vwaCFj6GuhY6elL7uGOx2uzK/lSsEGSgkEgkJesrlsglaJwjz8/P4x//4HyOXyzmyaX72tEk9Dkp35uuDut1uOxhOYH91gH/0/GHdsMXXZ8KnA1QGumwEcAeufK7O5vX4Nr4G5TgaZI+npqYQiUQkUeN92+12cePGDVMlmCAkk0k8++yz8Pl82N7eFv1pIpEQSRIAGdXHpiXN6Pd6PdRqNWSzWfR6PZTLZccoID5eS1YAyFg2+jhgPFqIpADvHV2lIGtEnR8wnpDB4IC2PRgMZDQQfS3HIzIwB/Zsf3V1Fbdu3UKxWBR2mKXlz33uc/jyl79sGggnBKdOncKv/uqvIpFIoNFooNvtShMUG0x5flPGQvkJmVb6OGpSOSKTRJOOAWhn1ERzoyAnFJG193r3VrtSRkCmPxaLodvtot/vv6/dMrFjpZWz2KlPZRxCVpX3F+fEA3vnA+e2Pvfcc/D5fPjGN75xrJjWiQ9YPR4Pfv7nfx4ejwfr6+vwer0yLoKsDQPUUCgk44BYbuWhTAMjtZ5IJBwD1Wmg+vBmZ78OjNnZTUOq1WqwLEt2WvP71GjxtbWOVgcb+gagIbOZgUwUpQR+vx/5fF7GdlEzE4lEcObMGTQaDXQ6HWlYMDhaWJaFH/uxH0Mmk8HW1paj85QBHBuiOHtSM/u6k58JlbtpRQe2+sAHxk0GOhDl13lgazaf4LXxvtEVCv1e/J6+h3h/8R7RTYjU7fI6mJxNTU3h4YcfRrlcluHzBkcLy7KwtLSETCYjwWitVsNgMEClUkEkEkEikQAANJtNR9MoNfc6uel0OpienpYJLPSl7mSLVaZ0Oo1kMim6agaliUQCtm3j/PnzqFar2N7elu5vslHUwfLw14mclsboZkJqcLnuldfIUVhMABmUs1LR6XSQz+fxyU9+El//+teP6uMy+B48Hg+eeeYZGWHF8YEs1VuWhUwmI8wnG/goP+FmKvrqaDSKer0utqTjBPeYy0QigXg87mguZExAO19fX0c8Hkc8HkcqlRJZ1nA4xO7urqNazIqbHr1Ff804IhwOy/vQ77JPhgkd4wQtK5iamsLzzz+PcrmM11577Qg+qR8NEx+wzs3N4TOf+QyuXLmCTqcja//cq/9oIAwImDXQIfFwHA6HqNfrDkYLgDA+usmk3W5LAKnnqQGQjSgsc/r9fsTjcSkH0OnSqbsZLl3+ZDbGUhW1VLqTnD8DGTPdDOb3+5FMJnHx4kU0Gg3cvn37WGVNJxWZTAZPPPGE2BAZIzoRju1hRk8NKJMjrRMlk0rtlA4UdUMebYvOin/cz6Hd0q5o1yz3AuMJG4CzGsEAWE8icJe2dBMYX582rVlUBhQzMzO4ePEi6vW6mc86AQiHwzh//rxjiDkPeU4IqFar4s/0vGsyRUzQeSjTJ+qmP8BZRSBzyyUwtF8m/7Ozs1hbW8Pi4iJ2dnYwPz+PTqcjYwh7vR5u3bqFtbU1OdTdFQtdyeDPxYUFlDEwQObPX61WHZIZvm673Ua5XMbHPvYx3LlzB3fv3j2CT8uAyOVyePbZZ9HpdNDr9aS3YzQaSTBIP+j1elGv18VeeXZrSRP9c7vdRiqVckxW0Y1VZGnp93SzK0v39Lc+nw+lUgmWZUkC5vf7MT8/L2c3ZVv0z5rwYmUXgDQu8n30uU9CjT8LCQwmgNlsFj/3cz+H3d1drKysHObH9CNj4gPWn/mZn0EwGMTGxobs2OUMSx6AFM8DzhVnNCIetsxA9EYsd2mWxsyDn46WWQ0dGgdjnz59GqlUSsZlaCfI7VQ6SNFgiViXxfRIFp0d8efltbqZWJZbH3roIdTrdWxsbBzK52Pw/njmmWcwMzODjY0NKZ2znAjAEdAB48Ypfk3bMZ2Stg19yBM6CNABpdZEswEmkUjIddGh6UYYfp2vx9fhdQFwOGz3WBb3pAGyADqA4NeDwSDOnj2LjY0NMzVgAjA7O4vFxUX5TKmLo/1QIqVtkiwW1w3TJhgwsCta70nXtsEkjdq7SqUiJdxwOIxcLoelpSW8++67+OY3v4lisQi/349sNotQKCRJP6+Vdu7e6qYrbjpYZaDK84TNj6xEMBGjTycTC+xNEXjmmWckUDY4Gjz77LNIJBKo1WrCvOsxUEygAMgkAH6u1HOyBE+yi2V8bm7TiTxw8IQByhRp96VSCcViET/+4z/umKvNiTH0/ZFIRDSneumLTpboVzUBMBqNhAnWs7B5LzHQpm13u13U63XMzc3h05/+NP7jf/yPx8JuJz5gTSaTWF1dxdramnzIulOPDk0Hp7pxhVkPHRPHRumMm4eoW8sHjDdS0cmRGaBxJxIJyZK0jktruBhUuwNiHWjwptHlVZ0x8bF0yiz9W5Yl0gFgL8NcXFxEqVQymqojBnesA5BkBoAw5nQsmrFxB4jug5ZO0d3Q506GtA3z+XRatCmyBwxWdeOh1qm6A1j9c7gnEGg2WEMzF1rywAqBz+dDKpXC6dOnsb6+bljWI0YoFEIqlZLPstFoiM6TDVcM8LTek+wQfRftV88zJdyNrvrfui+B866pdQbGcpdKpSLsJw9jBhW6mZYHPG2O7897UY8WpL/WJVRd8eJr0u+zKjYzM4OzZ8/ixo0b9+pjMfg+8Pv9KBQK2NnZEXkKMCZ/6Of4f12dck+kYKWKsjyt62fyrf30cDgUMiwcDsv7UabIhlPbtlGv1yV54zXpCQM6RtC+3x036PnajB/4fQbWlJJRMqnPjWaziTNnzmBhYQHLy8uH8hl9GEx0wErn+M4776Ddboug2C2gZ1YcjUZFYAyMB0xrPQgDPAaEmrmiUWiD0CyW1mTRMNlwwMOfDAGdHo2fjk2zZXSCuumAWT+DYjpJHgB0ogzcWZbic3w+nzAOJmA9OpDJ39zcxM7Ozr6AkJ8hs2jtlIBxwuIevq//Tzt1OzHdiMj/a/vR0hKyWpoJZfDM63WX8Qmt6XL/7WaH9c/lvnaWX71er6xZNgHr0UE3kly4cEHIAr0pKhgMSqJcqVQc7DqrS2SXtG2QWWWwqH2wBgNQ6vTi8TgSiYRjCgzZXF5Tu91GrVYTX6pHwQHj6hsZJ31f6MexgqWbbPiz0f+S9MhkMpJs6XvO4PDBBuTl5WVsbm5iZmZGGqsYHJJd5cB9Skk0WaUDUSb6ZNh5HvP5jD/I5HIlMADHuClWCdg4S2ki/WOtVpP7joww7xGeHa1WS+Q1tHE+n9JIJnIAHBVbytE0caa151ryNcmY6IB1fn4ezzzzDL70pS85tKXUlrgbpHQGwg+fASWHQbtZJJ2Z6BKm7vzj65MxYBeg1svSwOho6VT16wBwMAzuRgDttN2Mgc70GVDwZhqNRhKc0mHqn9Pg8JHNZvHII49gd3dXGgNZCgXGgRsZRs340yaZmOkyPeBkC3RTCQCHDfP1+cfj8SCZTMLj8cjECb1liK+j7Z/XepDsQN837gNfByT659L27tZ0s2Ts3uplcLgIBoM4c+YMMpkM1tfXAYyH7DcaDRnhRN+k/Zw+SNmlTXJB+1+3fbltimV3PX6oUqnIe+vlKe77hfao30NXCfj+miDQdtzpdMSvkvmijQIQu3YHBKlU6l59JAY/ALLZLM6fP4+VlRUsLCyg0+lgd3cXAJBKpZBIJMQGw+GwxAy6KYoBoj5jaY/8PxlL+lVgLwZIp9MO/Sqw1ytAyQnZXr6Pfj6DWx3waq01Yw89BlNXMGiLepawDryZwPE+oZ/vdrtoNpvHJtGa6ICVNDp1SpoZoniYHyqDRE31k8ancdEB6cOZBqYzKv6tg2QtfubzKUHQjCownqHmzlrcLII2HP5c7oCU16evlwGsDmTIBrwfY2FwuODnxcUPeiwJ7ZiBmTvD14c6P9P3K6US7mRHSwJ0U5WuTmhJAu8BXSHgaxE66NSyF/23vsfoHPXPx//rDV/8umY/DI4OlmUhlUrh1q1bMpw/EAjIdinq9Vm6b7fbDpaGnzErZGQ12RirD0d3wk6dITu6y+Uydnd35evhcFh2sNNHutl7LTn5IIKC78kGF94zTJ70PanlM7onYTQaSfCTTqcRi8UO5TMy2A/6mUceeQQAJCnnLHNuf6LfpQ1rVlUnL7QNzXjqXhaCr0EJip5NHI/Hxa/q16FUkdetfwbdYE3QNml/OlgdDAZCWLnlW/r+0Ju9GGfEYjGp0B4HTGzAGgwG8Yu/+Iuo1+vSPc0Mxa3P44GsD2VdFqJjdWtA3AGjWz9IbSwPee2UWa7VTJZeHsDgldfA63Ubp3aeB10fbybNQuigQP8eeHjo0VkGh49AIIDPfvaz+8pI2unoxMc9+kQ7Fe1I3UynTmJoKwTfj9oqft+t3SJoy+7XB7Dv3tDzKd1Jkr5e93xNd3bvtl3qsk3AenTw+/04ffo0/H4/isWilMY5i5r2pKtO7okUlAL0ej2EQiHRcQN7h6aWSRG0CT32iraibY9BMBvA+L12uy3lemA8V5s2p7+ur5XvTfkBr4H3JAMWjgvixBhqWcPhMNLpNPL5PM6ePYvTp0/j7bffNoTBISMSieCzn/0skskkIpEIdnd3ZTg/AzMm6hzcz1GULJPznNekkK5wanvUOlD6d67ytW0bjUZD7Ie2osdcMh7haDQdT7ibtHUiCEASJ95HlDrQv/NnpjzATYbw56DP3dnZcYzAmmRMbFRz6dIlPPTQQ1hdXZUPn4Gpu4FJM0jAWMOnAzx3CdJd4tQZMw3SPQRYj7dyP58HsM6OtAPXekJ3IKCNRJeo9M/D/2uWl2M12IRVr9dRKpXQaDSQz+fN5qsjAg8uavt0iVvP1juoPAqM7UIzR9pR8jPV0gCdENHhAmMn5WYG3GV8Pu6g++Kg7FvbrTsA0AEy/9bBO+8VVj3oOJvNJvr9PhYXF3Hnzp1jk/WfJExPTyOfzyOZTEqpkIyOlrNw1iQTFNqCPpQ1A+oe46cPT8BZ0aK2DoBDXsW+AW3zmogA4HhN/X78o+2cduiuYEWjUQmsmfgxGOE9xPuMowzD4TAsy8I/+kf/CF/96leP3Qah447Lly/j/PnzKBQKSCQS4ju63S6q1aoEnsD+5SZ6bBv9lG2PN1G6SQZts7piy2CYyRLHA/Ks1q/JTn3AOfeaiSAfw/fU1WIGt3wuqxl6wQDvN35dSwqodw0EAtjZ2YHH40E+n5dZ4ZOMiQ1Y/X4/2u02bt++LZtSaBjMWvT/NQulHZlmg7QmRLM9BwWNOgDlYzS1ro1WH9ZurZQOCLRha7pel195OOibSP9O9A3C8jL/HY/HEQqFhKFIp9Nmz/URgR3M/X5fNjvRMenPUNuLZiw1Y8pkzF2m1/ajkzN+z22DwH7WnmAA7U6UNNysKAMSt427AxLdWMbrIaPMw0CzZsViURyoweGi3W7D5/Ph0qVLqFarKJVKKJfL6HQ6aLfbaLVaDsmRPtB5yLL06fF4ZJa1bjp0V8joD1kqDQaDjqY7yq9YuaLNMdHRM6x1JYqP4XMZaOt7xOPxSBDA57lnWFNrqDdqkc3t9XqoVqvY3NzE9evXcf78eVnXanB4GI1G2Nraws7ODs6fP49kMinjzShj4Rmutf+Ug2j2Ukv7GEtQw6pti0kTG6Jo4wwa6R/5eNoxJSdkYjW5xp+FSRnvC5JTDF4Z1OrlBe7YQPff6ASP1+7z+bC4uIi5uTmkUikUCgWsra0d5sf2Q2NiA9Z4PI5ut4tCoSCMKkXFNAaOtXJn0G56HBgfyO6Su5vl1HoUPobBpQ4mtUhbZ00689FDq9+PqXIHrW5JAQDHfEKtW7Esy6GLoYGSIVhbWzsWNP9JAydVFItFx8g1ivV5UOrPxs2aamenZSW6/O9uGHD/TejKAl9Xs75ac6rfw12yPSgA1lM19P2lnS7vAz5ea8V0MMv7iDNZd3d3j8VswJMCHnqxWAy5XA7pdBqtVktK+qw0kW112wf1m5yawsdrWwawL1jVzJaWDzC44HQLPfqN9sUyrp6uoh/DrYMcF8QxXO7gg+eLDkr1dfAe1AklfxfU9DL4mJqaQiwWkxmtBvcWDNBKpRJqtRq2t7dlRTtZcM4G1p89P2cGfvTReuwl4wz6MvopnRzpJihW1CzLEo0s/S/Pak6p4Kg32iqlKLpqwFFUZPs1cabliPo6+DX9t5a7MIlst9sIh8PIZDK4ePEiNjc3USgUJnq60EQGrD6fD4899hj6/b6sYQWcpXGtGXUHZfxg+G/NHOkA8qDSPA1a77sGIAevHnGiS7sMWPn6ejEBM306b7Js7qxKXwswDgzYgKAzJB1geDx7XYxkAtrtNqLRKHK5nOhTDA4HPp9PRP9cvUdoZhGAI4jk56sPSrdWCnAe8G4mVtuTtiM+Xuv33FIFnQyRidKvpVk0/X4MRvQhoGU3+r57v8SJlQKyZOFwGEtLS3j99ddNwHqI8Hq9uHDhAvr9Pt566y34/X6USiXRo7J7XpMDusza7XaRSCRE76p1qDpJ0bbA16HPpA3q4eckEDgrVbNY7koBME76dPLPoIFJo74GLc15P/mLW5et/T+vgyXb6elphMNhE7AeEgKBAD7zmc/g7t27uHTpkqznZZAXi8WEDQecJBEJBM2qa1keq1sMJrUcj7bi9lH8eq/Xk4RJJzxMwnRSr/2kruCShGIQzdd2N4Bre9aSSFat9PYuPrbdbktwGo/HMT8/L1uwJhUTGbACY+aS8+2i0agcmJzNp5tSdIZBR6WDO2D/DEh+zZ1R02BorG4GVgfBDBJ5bTrI1UanJxUQNDbeIHTS2pm7A3EdsGvHrG8k/vyJREIyNoPDAW0pmUzKgaVL+rq5A3A2NrnZdq2ndgedbg0gH8/30c/l69MuaXPUPGkmFBg7YP4sDCT5unycu1LBr7mrFfq1tG7Qbdv8Ph39QdMQDO4d9OfYbDbRaDTQaDSEedQ6Vl1KpR20Wi35HtkmdyKvbQkYJ2268qDtnK/n1hvqVZqsqOnX02cFy7xuXak+/Pkc9z2l2S7aPpleXfHjWTQajRzbFQ0OB6PRCFNTU4hEIojH4xJQMgBrNBqOs5l+itVLBpVsVqL98LX5NT6HdqenS2gCQH9d2yTnCAMQdp72pM8ALQfo9XqIRqOOgFXLwDTBxefxdbjISMsoOTWBTZHdbhfRaBThcHji7XYiA1bLsoQxBCCbJnjgu2ewuhkfTcO7GSp3Gfag7+nn82vuMRbA2NHREdIR60ydzphZjg5KtK5VG6CbpXIzb61WS1YfUoejD3heg/49GRwOLMuSUT4sL7kZHvdnr6EPax246r8BOByvLlUeZOeaHeJzefi6G1Dcz9PaQPd16MTMbb/669p+2ZQAjFkLLVGgU9cVEIPDw3A4RCwWE80cV7CSNeWhDjjHq/EzZscz/88SP325TlR0eZXfA8YLX2g/+rFaI8t1rAxg3eynz7e3TCaZTMr16HFVOiGjvenAmMEqHx+LxbC0tIRoNIpWq4V6vY5yuSxruqlzdTcvGtxb2PZesxOTXdpvr9eTz4mz2OlntP4UgCQatJ1MJiPMvj7/eR7zvTRrq8v7Ojkjy6+rWu4xm5p4433Gr5Os42PJBmuZIO2N9qpli5FIRH4ONlyNRiPRpicSiX2Vj0nFxAasuotOH/YMwpid6KBMH950rO4A1a3Dcwe8AA48xAE4Dm4dTLKDlXAHq9y9fVCg4s7cNMOgobu8i8UiNjY2JAukDoUbPXQmaXD4iMVi4uSYeZOZYUDGz9rdCAiMN00RuvzvZqd0WUonSzphA5wNUrQtBgvUaLmbYmi/tFV9XbR9XdJyVy70dVnWXqMKu3bZvBMKhZBIJESnxWuedMd5EkEbiUajYqM89MmYcmMQ/aBmFgke4mRh+doEP2M9Q5t+Vq951YkbfS+D0H6/j3q9Lok7kzBei2VZiEajmJqaQiqVciwwcFc1NCOlfw7Njg0GAyQSCeTzeZw5c0Y6wK9du4a3334bpVIJ3W5XgnyDwwWbW/UyCxI7Pp8PyWRSfBXXZLslIJop1eetPqt1Pw1tNRwOC5tJm9E9KLQrJlStVgvVahWAc2rMcDiU5KfVaslUjGg0KoGqvl7d28Lr54irYDCIVqsFn8+HRCKBarWKcrmMra0tBAIBmWSzvr6OZrOJ2dlZhwxnUjGRAavWedDBaBaSThRwbpniHx2kaoPTgaYOOJmh0XAovtaBpD7EdRbPrEnLEjStz0OaXa8Hjb06yEj0tRI0Wp/Ph1wuh1arhUajgXK5jHq9jvn5eXkP901jcDhgskXW6KBRToRmPQEnM6k/dx2UuqdQsMRDm9Qsri6/69cHIJooJnxubRQfr+9DMlz6Gnk/6GYDt23rygcZaJ/Ph3a7LVk+y3m6emFYqsMHZ44y0W61Wmi1WvB49sb8cd0lB7GTONB+lskPfSehkx36c76XfrxbR8r/85qA8RQZyxpvu9Lav3A4jHw+j1OnTom9NRqNfRUwXbblNep7BhjLr7rdLu7evYvNzU1Eo1EsLS3hscceQyqVwje+8Q1ZC6t16waHA50AcZRTq9VCLBYTRpETMJLJpGOyhJZ9MIEhE6+TJQaquvTPJAuAkGy6f2Y4HKJSqUiMQCZes/m0/U6nI/dcs9mUpqhkMikBqC7Z62SQwTLfl/cBY5q5uTkkEgl0u11sb2/j5ZdfxuOPP46FhQWsrq5KxWLSMZERDR0fHRCDAADyQerhzjzEqdd0H5aagdUMq9YDaj0JmQQd8Ll1d7oRjIEpgwWyYHoYerPZxHA4RDwelyDAzVi52Vu3RoWOlZrIUCiEWCyGVquF3d1drK+vYzQaIZFIOMppBocLOkhqh5iV63V+Wm7ibgoEsC9Yc7OZByVIfJ47UHCXiOgs9T3C92aiBezdf/V6He12Ww4Ear1oq9qpa7htmY+jnjAcDiMajSIajaLZbKJUKsl9Tts19nu4YMUGGAeH/OxzuRyWlpYQiURQLBaFKCB0cqSrOzrJ4uMIBqokCCgX0Xpp3WClD+RoNIp0Oo1+vy8Ehra1bDaLhYUFTE9PIxgMYjgcYnV1VQIHEhS6WqGDbneVislms9mUMnOxWMTa2hqefPJJPPXUU3jrrbdkdu2kM1UnDfS5/Px7vR4SiQSSySTa7TYqlYoEr2Q5W62Wo3oEjP2utm8dQ9A2GdDqJkQtI9TxAb9P5lb3vQDje6fT6aBWq6Fer0vSoxtRaefabnl9/D/JBb4uABn9xurEww8/jEwmgytXriAcDiOXy8lK10nHRAaszDZ0Sci292aWcXsFvzYajSRY5L5efQDr0qxms3SZFYAYDADRXVE7ooNVnXnrRioGCXqqAEedVCoVyY50FqMbp/i3ljHogFv/TF7v3qIEOnQyX9vb29jd3T1Q82hweGACpLNojlWhw6MOD3Bu36HTdZfZ3ckXbZGsAm2UNqGdoT48daOifj8+R5dma7WadIl7vXuDsHn9dOhaP+W+79yJI+AMxL3evU1BgUAAlUoFpVJJ9FQ6eDA4fOhRUnNzc3jooYdg27YMGo/FYrLdp9VqydYptz24P0MdIPBz5upiJj60Wfo2XfYkKcDpMZx1rMmHdDqNc+fOYWFhAZlMBh6PRypyvE73tA4mavr+c+toOYoIgEwb2NjYQLvdxjPPPIPBYIDbt2/Lz2NwuNDypmAwiGg0ikqlgkaj4bAD3Uegu/+B/VJBnrO2bTuWFlFnzeCT36ddMfnTlSsuw+DYSQCyvbNarUrZnjNd+dxkMilVNF2BYkxDqQB1vNquWXmg36ddLiwsIBgM4pVXXsGzzz4Lv9+PnZ2dfVLEScNEBqzAuOOUTqhWq4kOSetA6VAYZGoWSbNAbmZUl1D1warL/zxQ+XhmO/weMx6K+nVwQGa1Wq2iVqvJHmM+XwclmqFyZ+YHaa5ofHTkLCnk83ns7OzAtm2Ew2FhHQwOF/V6XZwXP+dms+n4urZT7STdOlD350871c5HVyT4nrrbWQe+fF8On9bOjdcyHA5la1qtVkO325Uym74OzWjohj/dQACMday0W36NAb3X60Umk0GxWMTOzg5CoRCmp6dNwHoE4GfLSQ1TU1P42Mc+hnA4jGq1ikwmI+NwOIeUfsmdXAPOAFWXSnUi49bpaR0rpwEwQOAfzlbl61NaEAwGMT8/j7m5OWQyGfHNgUBAAk72Qrg1jJqQcJdVeTZoAoX3T7FYxOuvv44nn3wSDzzwgLHbQ4Zt22g2m0LkhEIhDAYDlEolbGxsSICo56JTqqc/Y2DPjqgBpZ3SdunzeGZzzBowljDpwJekhWZE19fXcenSJcfkC01scaMa75V4PI5sNot6ve6oNPM+4Osz0dNnCwCZjsEGW061sCwLs7OzOHfuHF5++WUkEgmsra1NfLwwsQErM4bRaCQ7nGu1GjqdjhhlOBxGKBQScbJuuHIHqW42S+v6aGjUgVDPwq+ze5Bf5+vSCPRwXhoF9aVsDKBAWpcGNPtLaKepGWIdULNMpplfGnMsFkO1WpWynXGehw+yOExEBoMBarWaOEDaKp2WDhZ10KoPTV2G1wctWXktawkGg44RVQw2NXPFzFsHjTrw1cyZHtHC9+K1aGbWzay6dWHubmxt96PRXgNWv99HtVrF+fPnHVoxg3sP+pd4PI5qtYp8Po+LFy/i/PnzWF9fl73jtVoNrVZLuqT1tAg3w0p7ZqKumVL6VJb4tR3X63UZSUWNKn2nZVlIp9OSWNFegT02amZmRppQafu2bTsGudMu9X1EewUOnovNe4Z+XjPCpVIJKysruHDhAmKxmKluHSJs20axWEQikZDPZn19Hbdu3cLZs2eRSqXks+N4Nk1k6WZnYJz4U56k/TFtmZ+/nlmqx21SWsjAVydr9Xpdki6ScYVCAZVKRXSsfHwgEEAsFkOpVNpXHQsEAvv8s5YxkNDSs+W1brbdbiObzaJQKGB9fR2bm5sTb7cTGbCORiMpPXErRKPRkGYjllxYCnezSjxID3JGND4dxGqGaDgcynvygNXsp3ZoLFe5RdbdblfmGFJvq6HfS3f6uQ2b76Of4y7x8rr4N3UqWuJgcHgYjUYolUqYnZ2VzTftdhvBYBCpVMqxmhWAwx61HISfM+1Zj2HR2lG33fLfwHiWMRkIrgV0l+d1eZ+PZTWDj6N98lp0SYr3F99LsxF8Pq9JO1TeLzrpSiQS8Pv9uHPnjum2PmTw4J+fn8e5c+eQTCaRSqXw8ssvy4pszbIz+SG0vAkYd0fTv3o87z9qjwPWAUggTFaVdswAgKtbLcuSVdTD4RChUAj5fB65XE7kXLx/mHwBzs1vuomRAYH28+7Svr53tGQhFouhXq/j2rVrWFpaMg2vhwjbtrG8vAyv14utrS1MTU2h3+/jqaeegt/vR7ValapAt9tFJBIRX0bfpjvkdbINQNa7Mr6gtK/VagkhAYwbqsPhsBBdfD0+LhKJoNFoyDlQr9eletxoNByrj23bxszMjFR5te/m+wHOigV/HwAchAEAxwav4XAokq/Z2VmcPXsWf/EXf4HV1dV7+ll9WEzkXTUcDvH222/j8uXLWF1dRTAYxPT0NLLZLEKhkIMN0v/WRsYRI8xE9GOA/fpOOp5ms+kIUilN0JpDPl+zYoTeCsPAFxgbFTWszIj4b95AWpurg9aD9GAMePVqQuq7QqGQMNQGh4fhcIgrV65gYWEBOzs7GI1GmJmZkb3WOuFwf5783LVT0janEyTanZ4I4U5SyFrxcKXDY3CpbYzQY4x0eZQaVl3i0g6c13+Qzkozqm4GVieDnCfs9/vNWtYjgG3bKBQKaDab+Dt/5+/g7t27+PKXv4ytrS00Gg0JHrUkCYDj39qvackKg8SDtJ0kBngwc9A7S7e9Xk/sh4GD9vW0QZZP9Yg0297r2q9Wq47GRPfYIU1a6KCcr6OlL2w+1A2EqVRKEj2doBncewyHQ9y8eRMf+9jHcPXqVTzyyCN44oknMBgMsLW15QgoGQvoz5/reLVEBRgnUXrsGkv9gUAAmUwGq6urUq7X1TLaBu3U3ZPDDVSsVLA6xvtnONwbl/X44487KsaMd/TUIc5Z5XnvlmRpppgML2OjwWCAbDaLVCqFS5cu4dq1a46tX5OGiQxYgbGT8/l8WFxcRCqVEgE0f9m6vKi1fezO52w2d+bhLvvwwOXra30gG7r0QU0jdG97YfBIJ0uJAQORQCAgTWHasQPO8VtudlUfALrcxsYuHYTzJvP7/Ugmk0YScASg+D8cDiOdTktGrztD9aB82o8+5NzSAAaH7oSLj6NTbTQaDjaL2j0e9LTRSCQijpo6QV1ipa2T/WdXP4NkVgZ0V7e7O1xXKNx6W/68buaVBwnLZQaHi3a7jbfffhsXL17E3/zN32B1dVU24nBChFsvRxv2+/2Ow1/75YOSc/6f9pFMJhEOh6VCxYYSvhaDZfpW3XASCoUQj8dFBsBzAQAajQaKxaJjQYFmq3RTlZ6V7D4neC3RaBShUAipVEpmf3a7XRQKBYem0ODwQL+WTCbx8Y9/XEijVColjDxjAk0aDYdD0a3qaUPAmInnGa6nCLGcnkgksLm5KQsC+KfX6yEcDssCDr4+/TLHslFLq4kGxhSLi4v42Mc+hmvXrsl16QqcvlZKVdh4pe87+mEmlmwYtCwL8XhcSMBz587J72pSMbEBK7BHYXNlGEurdCQej0c2WmitZ7/fR6PRkI0XumSqM2w3Q+rxeORQ57w2YDznUmdQ/DrLW3wPygiYMekJAsDeQPmDSvoMAgCn7MCtX9RlZL4/BeZ6BRs7JUOh0D4GzeDeg6zLmTNnJLPm3D+3NkonWhzxQz1eKBRy2Iq2DcCZwFAPy/tjMBhIRyxX7rHcxGsIhUKSyQPj6gNLXUyqAoEATp06JRpTwLkFSzOm2r7dTVZuaB2gDkrI5BnbPXxYloWtrS184xvfwO7uLrxeL06dOoXFxUU0m00UCgWxTx2UcbMQoW1HJ166gsTHab2eZe2tNWbfAjumORWA7D+DVh7QkUgE0WhUFhvoe0tfM99T33+8Vp4D+kzQowfp36vVqlTSotEoYrGYYyyiCVYPH0ympqamkM/nUa1WEYlEUKvVpDqq5UvA2Pa0DIQ+KRaLAdi/TAgY23owGMTc3By++93vSgLFM5iD/0lWeL1eKclTrsLFHPSpenqB1+vFpUuXhIXVcixNbjHw1E2KPGt08kRmOBaLScxAn9tsNh336SRjogNWOh+WB9lwFQ6HJYhlVgzAQYszW9faDnejB0EHSpG/1l7RyXJmoM70ybDSCTNgpjPVM9FYJtAHur4ezerqG4rGqNlgOlq9dYOzBnlz6OYYg8OHz+dDqVRCIBBAPB4Xhocbctz6ItraYDAQh0LmSZfadfasy7DU0dExs4xKm+NhTo01D1c+t9/vCwuhkzGtCed783q1blU7SH04uP9NaN0YmTpqwPSoGIPDh9/vx2OPPYY7d+6IFrBcLuPKlSsO+dFBGmW3z6Gv1BUD/q0lKiQF2ETL+Zk8cHlo8w/ZKTJbwWBQ5mzqUVjsf9BVA/pa2jO/ZlmWsMnhcFjuEQYoWlZGJrnb7aJSqcjPzz32x+HwP0nw+/3IZrPodrtYX19Ho9HAtWvXMDMzsy/41GcumU+9cRAY+yeeqbQRJumj0d4igtOnTyMQCEhlS0tYWq0WAoGASKko0/P7/Wg2mxIruANpxgr5fF4CWib/urLMa9OJm06y3FKd4XAoyzN04zZ7GI5DRWtiA9bRaIRwOIxTp06hWCwCAFKplOhQ6EiAcXmcpUu9ok0bAw99/cFox2JZ4z3wuhGFHy4fSzbTzSAxyya7qo2QzCev1/3e+mfQ0Nl9r9eTTTT8Hg96PY9TX5s59A8fLEf5fD7RF1FkT3tgtq03tTEh4+epD0h94AP7F19wuDRtgK/LcWqdTkcOYjpEYjjcG7vFQFaL/pkM8XW1LovP1cyZZoH1fcYsXztQQssJdCnZ4PDBz/natWtSpnz11Vexs7MjKy31Zh+tQwYgrD11folEAgBkhaoGg14GwZxQQDuNx+NyGLsrC2tra4jH47CsveYWzbAySKYfZ+DrbgDT1wDs2V4kEhEtOOUynEbDUq/WI+pqGku9hig4fFiWhampKQQCAWlyffLJJ5FKpdBut0VioicCsBIZCAQQjUaFJaXdBoNB1Go1+Tzphxnk1ut1LCwsYGpqCjs7O+h0OiJpcSdBtEsGq2yw0j0ovD7btkVORn+qK1nAODHU8hZeH+MjShIp+dJVDa1TJcvM82OSMbEB62AwEC0mwQOfDod/88Mm60RnpTV0mkbXcgDdJEI6nx2AgHOoNA9cHqhkZJm90Hh00MprpjPT0E6N16C7rwneYK1WC5VKRZwona8Wc2vWYNKN76SCQRzn5wGQAFGzpMB+1l+zlJpZdTOtbg23boRhhs/AodPpyH3AZI7NKMCebpEHr1tHy+ew45UBpU663NelmwN05YIj3nSFQjcU8DXp2A0OH0yUbt68ieFwb6j/YLC34Ul/5jqZ1/YaCARkhzl1pXrDG7C/OQ+AsKU6eIhGo+KHdVDMZBDYKwWTpGBQwD8MWLkxkQc87dStC+c9wp+NP/dwOEQymcSpU6ckaNU/Q7/fx+7urqzIpozB4PDg8XiQz+cRi8VQLBZldrTuJdFnImeiM5jTUo5oNIpkMumoaukkhI9lsrO4uIirV69KDMD3JhHAqgHjmWazKYkP7wvNojJ4ZEVMxwkMQLUEwV25AMbNWM1mE7VazUGAMABmsyClNsdh4cXEBqx0CqPRSET0zF4BODIS3cChG1T0B0hDPYjdJDSjxKyFzo8sK69JU+9au8qDX5fzAQhLpa/hoOtxB6v8eRkw+Hw+GZeljUsH6vF43KHjMjhc8OCmFlqX77VmFXAuunCXpbQsxV0O0rpnlq+APWfbaDTkWtiAyJIUg1lqvrTdusv4OojQ+irtvHWAra+TB79mr5jcUZfFQwOAJIr8t65oGBweeNCxsQQYd1GTmWcXvh68zuScBy8fTx/t1gq6ExXaIKsS1ADGYjG5V/Rz9CxULRPTow4p5dLSLK2f5f/1327mn6VfMrVTU1OIRCKIxWKIx+OIRqMIBAJoNpv49re/jY2NDZmzaXB48Pl8ss2KgaOOAXSwykScA/Xph+irLcsSrbR71Sl9Iv3bYDDA7OwsgsGgrOWlT2UPAbDnl7mWvVKpoNlsOqb48F6h/w2Hw9J4qkkzvqfbvnR8QR/NxmtKarT8hk2CnU4HU1NT+xjcScXEBqzaUEhf0xDJHNGRaW0TDUkzQVob6nZQboNmIMpDlw5YZ+1kFWhMWgyt9XcMZjUr+36lIgYnvG6+toYeo9JqtaTURU0Vg1jbtpFMJo0k4IjAw5clJ72Bik4QgOOz5qgcrYnW+lY3C6kZLp00UdKi9aW0ST2Hkn/rcSo6GNZVC62b1swvoR2l/rl0sE17DofDwlIxKSUTMRwOkU6nHc1dBocLfvb8fFkZsm1bmCL6RfrEfr/v2ExIpoiHIgMEbc98Hx6+lDwBe+sqY7GYo4ta25B72gY1rPyjEz++Ln8eXalwEwe6QUVLcCgR6HQ6qFariMViog1PpVI4ffo0Hn74YQDASy+9ZCQBRwD6MgZqWrbB858BojtpoX/WrCh9pSYGtD/jGe/1eiWJoWRG2xIAmXqRzWZlRTflNrxOzf57PB7p3Kf2mjEHcPBEIU6D0aSaljZyrTZJi36/j3K5jFu3bgEAcrkcwuHwxCdaExuw6qy8UCiIAfHDoqPS+k3+W+s5AOcsS7cUwF0q0IZAIbMusxJaM6qDaM0kEHwNBrx8X7dxaPZWP1dnX7wBWdrl4UHHXywWhRVoNBrGcR4BdMLS6XSknEqboWPUTBNZUvc6P629OwhaWE+HRaZLM5V8nNYv8T5xVyO0LfPeYNCiA1tg/0YgBivaybqvnYcDKyYejweNRgNra2sA9rYVMYA1OHyMRiOkUinE43EsLCxIs4ieK03mnjNTeZBzsgUJBa3R1mCAoQNJBpb0b9QDMmBlpYD3kZaWsLTr9/uFNdONUXztg1gkdwDLhIssLe2e90StVpN7q9FoYGdnB71eD4899hg6nQ5WV1cnnqk6aSCLyFXotCM2XDEwBOD4bJkA6dGDZEhpY+7YQPcUBINBmWO6s7PjIBY44pKNpLqaQHvmPaVjB92oRbkWK2i8RsBZLdBf05U4Qld8mXwuLi4CAJaXl9HtdlEqlSZ+WcvEBqz8QGu1Gu7evYtgMIh0Oi0MDQ9mYFy60c0f+sNyOw+t5dAjqdzvr9kprVMltJFoLYou99LYtcPWQaQOng8qS+mAgP9ngKMdN3Wyo9EI9XodHo8HGxsbhqk6AnC96HA4xMbGBrrdLmKxmHTxcxagHl5NGQpw8GetS0eaIdWBo7Zzjl2h5on2xQBYJ1pkHWjHWoPNMr2b/ef7uysWmgHm47TmS0PrbxOJBBYWFlCpVODxeLC+vj7xzvOkotPpYG5uDhcuXBAdab1el9K4HnTe7/dl9TRtSDNGOvk+6PNncqYbSVlt4D1CDTQZWM346+oXzwT32aBlWhr6nnKzbu5GWy2V0RUNy9prqvnOd76DWCyGBx54AK+99powzgaHh3q9jp2dHZTLZczOziIajSIajcp5TEJAf65M8nl+t9vtfbJCJuGU5TF5pxwlFAohkUiILXAdMJMw9i/QFsngUnZA5pf3kF7drf2mW8rCoJjf05KsSCQiEhv6en3e8Oe/dOkSBoMBCoWCrFyeZExswMoPNplMYnp6GrlczrFajHAHhO6GFkIHAXyMZjndhy9LogAcZSutcyFGo5FkSrpjj3/rEUE6Y+dztWjaXV7Vgm8dBOiv0bl6PB7Mz89ja2sLlUpFMk2DwwVH3aRSKcRiMczMzAiryoOVpUoetgc1Brh1qprd1Nk4n0PmMhaLSdmJh72eqAGMm/sYIOggQ8tdeB3awetDXP/b/TVeNwPxg5gt/s0mgG63i1qtJlvCDA4XPHS3trZg23tretvtNqrVqkO/rJN3zebohiPakz783VIsnbTQhzLBIWOqZVc6ENbVCbfPp7QGGHdB85r4vvpM0KVinbzpBR9aEuPWordaLbz55pvI5XLY3t52zKQ1OBzQhs6cOSM6a/orBqmUabF6ys+Z8hPagva7BDXbujrLAJPjCmnDtHnaAV+Tywt0oEn2XjO3DJJZJdVyGGBMAvBnJpPrtv9AIOCYnU1/D+wlppFIBBcuXMDXv/513LlzZ+KrWhMdsHJshM/nE30mDU/rjPRByA/jIOE14BxmTuPTGhUaMOB0fu4sRzti7eT4ugSdms5udJmW70toZ8xsyR3camepSxsMQkKhEMrl8sRnSycVZJ3OnDmDeDwuYnzAOUBfy1d0KUc7LcBZQdCspf4eEQ6H0Wg0ZK6lTo4YvPJ1yU4dpBHXr8mAgM5fO2z9GG3P7tfg/eF+nJY/eL1e+X3pQe8Ghwd+DoVCAeVyWRgq3XgFOPeV0//QRtxJ8kG+UftMHuxkoyhB0UyqDpLpFzkzW99T/B5fw930pZsX+Xj367pZYs3YalKB5wTtt9VqYXl5WaQtBocHJv/hcBgzMzNoNBpS2udnSp2n9kv8PGm3Ojmir3RXjXg+6ykrrExZliW+l7JF2oauhun7RcsIdZM2ZQ60M/dYTE2SAeO5sgxUSZTp53Y6HUdzJDdy+f1+lMvle/oZfRSY2LlHo9FIAi6WurWzAJzZD6G76QCnJhUYl3a0MyTch7D+t7vU735NnbEfBM2saraAX9d/tAPWj9dNCu7Hu99bB0kGhwt+XuxcBpzMvw5OdfDIx+jH8vX4Gu7vUWfq9XrlsKegX9sIsF9OwGRN2xOvHRjv0uaIFzc7pR2wvq/0Qe+Gvle01koH6mQ7DA4fWoJC38LDXNuP+7PTtq2ZV83W66RFM6xs0NJlV82KaQaUZVDqUvXILP04Bgya3WepFRj3FbjvSX0/8ZoZ/BLcYKSnZ3i9exvldnZ2sLOzcwiflIEGZ59Sv6xntTMxd7OibnKLOmhOJWKQq/2bTtb7/T5qtZpUMzUxxffj/UAWNBQKOUZhAuP7RMsSotGoNDYC4yqU3mSpfbht2w4JDTCe+KGrx1o6w6CWEzCOQ1VgYhnW0WivgYjd8DrjJXTA6i43ftDj+OG7g1/dJAA4tan6ucxOdBDtDlr19TKQOCiAdB/gvBa3voqP5XuORqN9g4F5Ld1uV35nBoePfr+Pra0tlEolx2gSd4KlD0Q6Hh0wAM5mpoOgD/9IJIJGo7FPlO8Ofpl5UwrAawTGDVea0Q2Hw/sqFYS+Xh0M6+DbnQRqBlaXWoE9BmB7e9tor48IXIlq27aMCeLnxANON0CRndINpTpx0UGvntYC7F+KwvdgKZeP0Qk+X59Brp5J6ZYNMCjhczh9QlcUeG/RRsmI6ffS9y1/llOnTmE4HKJUKklAH4/HsbW1ZSpbRwCOemQCk0wmUS6XpapEOyQDqf0bK5XAWFrIz1836+mqJ4NEspLUces/JM50TMB5wWzE5TlOqcBwOBQtKVfTczwWH6urwgymg8GgY8ybO9kcjUYiWyDLSpa4Wq2iXC47rnVSMbEM62AwwI0bN8QQaWwMxuiktM7O3TGvy08HafK0Q9XZudap6qyM7wE4S5zMWjQLxfcB4Nic4c6s+FpuTZWGfpx2oKT0ObCaw4ipXzQB69Gg0+ngu9/9LorFosyy1LIOOj3+311m1YwqnRAPYq1XZpZMBsHv90t5yq1JPagkS2E/naFm6inWb7fbKJVKjqxds6i0SfdraAZNH/i8R7xeL5rNpkMbSSnF5uamYViPCJVKBe+99x6q1apsd/J6vYhGo8hkMrISG3AyU1rypG2DdqkrWjpB0+SAtm9+jbbMoFZPi9FnQqfTcWgQ+f6xWEyuR481op0ySNBfc98/tm1LQMHpCJVKBfl8HvPz80in00gmk4jFYrhx44bxu0eAarWKL3/5y/B4PLh165bM5NXTeYAxm0nfyVFoTLx0rEASSCdatFlOObFtG61WSwJJHYNwCgZfjw1ZqVRKyvA6uadNcxEFfSJHEvJ819UF/kxMInUFxOv1olaridyGQSubtRkr1Gq1Y9PvMrEMKwDRsnHobTwelwNer4vUjovMkc44ADgCT/3BaIqfFLputtLvAYyDCF0K07urdalXa5y48YLPP0i/6mawdAmWf/PnYYmK3bN6LmulUjEM1RGDthuJRBzlRgAORhMYj3CjveryFeC0OcCZ4JDt93g8+z5zHrra5vUsYS0/YNDLxi3dBEa70tprHXDrZBDAvioFn6t1YmS8Go0GarWajE6q1+siaTA4GvBzaLVauHjxopQ7AUgTFrBnx9FoVNZfNhoNh3SKBzz9o/aHulzKx2oZCckBHraauWJwCUACC67fbLfbSCQS8nyWYKkt1OOB9DYsd5LlljnQZhk8VyoVbG9vI5vNymtFIhHUarXD+IgMDkC1WkUikcC3vvUtnDt3TtZiB4NBlMtl1Go1eL1epNNpAOPRlAz2uBRAS0qoqafN6+qQu5qq4w8Go8C4kkabzefzKBaLEjCzAsvHDod7ywUoSWDzLGMekmPsKRiNRnKmuO1YJ5KNRsOxntuyLJGwHAc5ADDhAWuv10OpVEI6ncbm5qYEfNTWMfNttVqyq1rvSNeHsLscxQ/MXep0B4daBwM4B7YD4zEs+rEMEMhS9Xo9YYnfj3bXTJvWrRI6eNWNVhyrQUfKOXTuMV0Ghwt2Ws/MzDicoN54RQfJQJOORAd8/Ftrohic6uz8oPK/Tqz4WPdz9GYgNgmwEYuP/aCRQHSw7jKvbhjU0hneEyxjMdOnDqxSqaBard7DT8bg+2E0Gok0YH5+HrZtY2dnR+ZcWpaFWCyGXC6HBx54APV6HRsbG8II8Y9OYugXdccyMJ5WoYNGPk4zVbRBtyyKjCeTw2QyKRvm3HbG99UsrLZjHcxqcoDP4TlCpmt3d1caBRcWFlAqlVAsFg/tczJwgjrMer2Ou3fv4vLly3L21ut1+P1+5HI5RKNRkWuRedQNTW5f5m5w1YQUdamUD2jpCYf/Mw6hXYdCIWSzWZk13W63pSJKlpT2pu8TJoAkP7T9er1eqYjQz1Kqo6tXemxXIpFAsVhErVaTgHzSMdEB62AwwObmJtLptJRkSGnbto12u41Wq4VyuSyBG/V5bqPTgSYDSs0OuQNNd/e9O1AkdOmLh7/unNXZFQ3OrUfU5VoatXbOwFg7pcscvBGi0agYPFmJg/SyBoeHXq+HnZ0dDAYDlMtlhMNhRKNRB4PEMqVt24hGowCcHdU6udGJlWaX+D2+ZjAYRCQSQb1eP1D3qpMtvh410P1+X7J9OkhuDnI3AjLQ4H2ly1+6rKrZV/2+2vGTHYjFYqhWq8cm2z+p6Pf7qFQqcsjT17JsmEwmMTs7i0uXLmF3dxcbGxvodDrSEKIZctqmXjrg1lTrr/F1WDHT664PKs/S13MMYqPRQDKZFOmCW1+rG2d11YBsFYe269nBZMIoteIyg3a7jUKhINd/9+5dw7AeISqVCm7fvg2/349SqSS20mq1EAgEkM/nEY1Gsba2JhvbtNaUTXqUpvR6PTQaDbEVMvV8TT42mUxK8MvznaumfT4fUqkUksmkVD9ZuY1Go3IG8P7ga4TDYdGcAhBfzEkaOpgFsC941RVojgP1+/0yrYCPmZqawjvvvHNsfO5EB6wAUCwWxdHRIXo8HjSbTbRaLWxubsqAYGqp9OgSfmiaoXTr+QDnmBUdVPLwJvPk3rKim0f4OD06Q1P4WltFzYxmefX1kDmgU2Ugy0YDveXLHUybYHUyUK1WhQUPh8OOsqJmibRUBBhn9ICzMYUMLZ0mHZ97aLqeXwmMO6TdkhXa5HA4lHuLA9uZlfM9mZTp0T86uGYAy9cjc8Dvk3VwB6/8t2VZou0yOHrYti0BGsekUZaVy+XwyU9+Equrq1heXpZNV+xIZuJj2+OtPrQlnazw3z6fT2yODSZkg7RWT2unGQzwaxzAXq/XRX7FDYW0f2C/7EpLrOj7I5EI8vk8AIgGkMPhOSeYjTFcu8kg3+BoQVKr1WohGAzKOMxMJgOfz4e1tTXxd81mE4BzOhDtl19rtVoYjUaOUVU8rxn0JZNJ8X9kOkOhEGKxGBKJhKwaZmLFAJVnQzweF0KOUiyuqHb7bl3Z5d9er1eqEfx5o9EoEomENHHF43FJ5PjzJxIJLC8vy+/hOGDiA9ZyuexgkDiCoV6vY2trS0TMenOQLunwsCX0IatlAfwe/6YjZealt2vpg5/XxYOdxsCMhu/Dv3U5VmuldNCqZQ10wJphY5cfpRG6zExGwuDoUalUkMlk0Gq15GBkImLbe13YPNw1i681czqLBvY35AHORRf8N1+LSZxOnDTbpMuvZK2CwaAwXZZlyagh9/g0zajqQID3XDQaRaVSQavVksNc735nAsgAfnNzE5ubmx/1x2DwI4CHNKUBo9EIiUQCp06dwqVLl7C+vo7V1VU50Kl1BiBSF74OP189FxIY2y0bZCifAiCNtfq1dKmUmj7eKwyOW60WWq2WjJ1iwMqzAIDcBwD26b673a50TJ85cwYLCwtoNpsy55OViEajIYwufy+GXT16rKysIJPJOBo3eeayEhAKhVCtVtFsNiVJ55nNBIm2SkaTlVPakm3b0sVP5jIQCCAaje6rIJA5HQ6HaDabDm20be+N2EqlUo5qVSaTcRAZujpFn637bwDIWuRyuYzd3V1HQ+3u7i7C4bD8vACwvb2Nd999F41G4zA/og+FiQ9Yq9Uq3nvvPaRSKVQqFUSjURH4h8NhJBIJKWnqw92tQwLgOFz5Nxkvfp8GA2Bf+V13Z/PxgHP3NGUB7sNcl3PpnGlMwNgQ+dp6w4ttjzsRNXvL7Ivsb61Ww8bGxrEYAHw/oFgs4utf/zoefPBBydCp1yRTqkvwhE6yaDvusUDarjTzpG2OyZa2My0z0Jos2i1n/bFZTDdY8Xp00KzvJ94HwHiaQDqdllW1ZOn488ZiMQkAKpUKVldXcfXq1Xv7oRj8QOj3+6Jvy+VysG0bCwsLePLJJ5FMJlGtVmULD3sJAGelys1c6WYrLTHRVSKOy9KSAD12iP/mYa59JMv0jUYDsVhMgm7eA3oEFu1US8c0eVEoFGDbNpaWlpBIJITxYqlXBzeJRAIvvvgiXnrppUP7fAwOxq1bt1Cv1xGPx/Hee+8hl8tJub1UKiESiQhpwCSGrCp9nZ7mMxgMJMCjjTHxYcAKQBhd+ko2+9GXMh7hvFiOt6JGm3adyWTQ6/WQTqclAGZPgWZYddWB1z0YDBCPx+H3+2VCDbcubm5uitSA90OtVsPKygo2NjYO+2P6kTHxASuwxygmEgmsrKwgnU7D7/cjk8nIh6nHQ+imEncTCqEDzYP+zSyfwSoNj1kXg1dd6tIZPF/P3RVLo9QHPh2uFviz1GtZlmRNNFqyHizXaXbL4/HI3DiDo4dt29je3sbHPvYxcRg+nw/5fF7sCRgHdzqY1GyrZu21zIWPY4DADJ72ou8LJjW0M63Lor1ziDSfy2Y+APvWVB5UtdDBtdZP5fN5JJNJ9Ho9KafqbVZ8LqcRGEwGms0mCoUCfvqnfxq7u7vweDy4fv06Njc3paypR0np3gA3aONMWGhDuhLl9XplxaQOWHXCT1tJJBKo1WoyhF1rwuv1ugQTDBB47+nqk+4P0PcYg+RisYhmsynBRTqdRj6fF+kK2bR4PI5CoWBGsU0A9Ll769YtxONxqeJwtCTHS3G+tO79IIGgV6cCY1aeJBGZWk6G6Pf7CIfDIgVgQkVWk7bHxipOB9CrU8ma8nU8Ho9ItOhTtWxRVy+Y7DExy2azEmCz+kxWuVarybUdNwnhsQhYo9EostksNjY2kEwmEY/HHWOrNEOlP1R9iLqDRDpLXZLXBz9LtCxdkkrXbKt2dG6JAEtWgLMpRl+HO1h2ByyAc3wVA+REIuEY+UKD7/V60gRgMBng4VqtViXB0ttQtMSEjwfGw/fd7D8fwy5VbTd0tAxQ9dgUvViCtttqtRAOhx1JFINUlkD1vaGDZK3F1n+TveJ1saLA51G+w7KWDnbW19cP74Mx+L4gyxoIBLC9vY3bt2+jUqk4mqpoE/y8deKtv++2Hzd0Mk/9M4exH1Q9iMVi2NnZcczGpL2xAYsH9vcjLrRUS2sEqaFtt9uoVCrY2trCzZs3JZljOTgSiRgpywSBPlc3G/HMZkLCqgD9HDAmfLSeeTgcOsah6dFqrJDt7OwIaxqLxRCPx0XHqjdu8XU5aouyguFwb6FAp9NxzJx3nwnuGIbkAP/Pn0nHJD6fD5lMRrYVdrtdGYXIhG5lZeUwP54PhWMRsA4GA0SjUSSTScdcPToYfeBr56QDQe1AtWhaG4F+Da2TCoVCEqzS6PSQab23V5fC+P56LJAeneK+Xl6zO+vhtfDm0w5cN7loraTBZKDb7SKRSCCbzTrmUtL+tK3yb37WB5Xx+TwdyFIuoJMtapwZrGpGl7apu7bJvpJ11TargwV3QOJmWrXtMnjlvcJgQAcFPBA4a9BgslAoFPDtb38b29vbqNVqomd1251O2IGxjQH7+wb015hkMelmiZTaWbJfbDrs9/uIxWKIRqOOe0Azt51OB51OR84J+kv3pAsNt+yF0A2S+mfQzZRzc3OmqjVB8Pv9iEajyOfzkrBrLSkDNvpaLQ+hz9IbLhlkAhD7p7yEw/cZcDKRIavJngBqYFm+py9mD4N7PCU10nx/+ny+Dq/XXaHl11lJIKmhA1sGq5FI5MBEbpJxLE6It99+Gw899BBGo5F0wdEgGBzqoeTA/t3tunTudjxurRUZKk3Ja50snZh7qxYzLvfAdh7Ebj3XQaB0wP0abk2sFmG7gwiDycGVK1ekE5O2BMCR+OjESQejhHZI7s9erxg+KNHioUpJgGZB+V5a06pHsuj7iVouzbjyGgjatU6iyGbor+vEjo9zN3QZHD0GgwHq9bqUGJvNpuiQeejSXuhHmYBon0U5idblA2P9KEukZL9qtRoajYZoD1utljBhHNDvDni1rrvRaMjZQN0psD+50rbrTvj4HMA5EtHNIvv9foTDYcTj8Xv+eRj8YNja2kI4HMbMzAzm5+fl3KR8L5PJOEae0c5ou8B4jjQwDhj5f9p3q9VCvV6XoJMzXqPRqIyVCofDMl+b+upkMoloNOqIHzjiirIWSqd0sAk4pQnaj+vGLL4u/aomzyKRiFTnuEX0OOFYBKykzjkQOhaLSRDIobsA9m2Y0NAaQbez4v91YwCzIh72ulOQ7BQnFvAgZ7Dgbo7RBsfg+KCg1R2Y6NmW2uh0sKBZXN6QBpMD27YxPT2Nq1evOiYB8LDjZ8fPVAejupzK7/HfwWDQsZqPts1DmqOC3M0p2lbYgKJfm41XZCV4HZpl0jKag35ed1KnE0odmPK19HYkg8nCcDjE7OwsSqUSVldXhekkc+XurtYsO30R/bKuQumAls/lIcptZ/1+X4JXHrack8rxUww2aNNktLhIBoC8rz4X3KSF9q1kT2OxmASu/Bn0aEP+LNycZDAZsG0bMzMzaLfbwoT2ej2xH11ZYuygbZU2wT/RaBS2bQtpxSCVozUHg4E0+VGKQO0qm8IZ3DabTczNzSEWi4l8iwldOByWpq7RaIRqterQfgOQGetaruUOei3LktfivchqiK7CulcqHwccm6ttNBqIRqNIp9MilmbzBoelUzMKYN8BywNUf18HB1ovwpIopQD8YHVwyCyo0WggHo/vkydo+l4zWe/HSLmDbGZOdNwsFWg9rM72dSZlMFlgwsXNJzz8Wq2WOC1+j2ATnz743balJwAwsGSgSiaK70unxQCSq3zJKlATDoynFGhb07otQt9jOhHUDt/n80lzIG2UdnqQPtdg8nDnzh3s7u6iVCqJfcXjcXg8Hlnhyg5kJmWaPQLg2DZFu2IjKbX5mvXhH7K6JBBCoRByuZxUEJh0MShhwEo7pNxF+2cN7T9pwzqJ41B4fQ7os4SMnGm4mixks1lZHUwpHVlONtFRw88khOwm9aNM4GOxmCMR9/v9MmO62WxiNBohl8tJFYq2yoSHfnAwGKBWqyGRSDgkCYxfeA3NZlOapDidQjO/APYRANTesjLGM4ekhpY7AOPRc+9X6Z1UHJuAtdfrIZVKSScpB1pHo1FHJqy1TPy/dkDAfv0SH8/nsGyrJwRYluUYgs15fTQy3Ymq2TEAjmkCvHn0dbgPaxoVbyQdsPK13GU56r5ardZH90s3+EjAcSPAuFuaMxt5CPLrWjcKjBMX2oienaqTLNowdVB6R7UuDbEsz2HoLJ8SPOCBsZSGpTPt8GjzejahDjwZSPPrtEsydLwmvg+7uw0mC6PRCNvb2xgMBgiHw3K4jkYjlMtlDAYDRCIRxxY33XHPRhYADv/IMiu3WpH9ASC6wEajIeOHKG1JpVJSZQuFQnIfsfualQveM5R18VzQdgmMp7Jo1p/LAehj0+m0oyLCa9GyhLt37x72R2PwAQgGg+K3GMS1221Eo1FZTsKmOdpCv98Xxp5+jP0zeiEQG+10PMAgVfe60AYZFFcqFVk00G63JY4AIL6a780gWfc6aHkhk0JgnPCz0ZCTELTkhj8bWeLhcIhqtYqdnZ1D/Vw+LI5NwNrtdpFKpcRBMQjg2AqdHetSKj80TfHrw1ZrQvSkARogAwoGjWSb2NE3PT3tCI7pJHVwrDv++DV344m+Ns380rjcB73u5Gb21mg0zPDqCQQnO3D+Koet62RIB6ZkXZkwAeMOVtofnTEAx8grbhjSJUy9JpUHeyQSERuinhYYB6xkF3RDFrBf+0ccJBmgVorOmE00vAbtVFOplOm0nkDQf3GbDw/uWq0mByu7ooHxaB4dFDIQ1ZpXAOJDgb3kXLOlzWbTcQBzhJDH48GpU6ccchYmVUx8dALF7+lzgeVR+n4tT+BzOGKNfyKRCNrttjR8AUA8HpdVn2+99dbhfSgG3xecydvpdBCPx1Gv12UbJuebat0oCSk267FfhpuzdCWLMgO3PTOxou/l18iWrq2t4cEHH0QsFpMJGKx40T7pKzlRhlUw+lJdZdM+m9dWr9clhtBJG1+/XC7L12q12rHzuccmYC2Xy3jwwQexsbEBn8+HRCIhDkx3wrmboLQmlcGALmPqDxcYC6zJBjAo4EFLOQApda1p0h3RmiXlNbpLUjp4dnf56Y5q7sVmk43WBerARWtlDSYHV69exXPPPYdyuSzDnDkDj/ZISQAF/b1eT6oH7XbbsZpVl4F06YqlLtqSzswBiN0Eg0Fsb2+LTk/LZoDxPQCMA1jN5vIx/Fvbu763AIgkQEsKyFJwg1AwGES1WjVylglEq9VCoVDA0tKSVHL0KtZIJCLDyun/eMiS5dLBIW3X5/NJub1SqYhv4/52ymWoWWXiDgBnzpzBm2++6bArJleDwUACXq0z1Yy+rkjw/+6eBgat2iZ1gws7wvWSD4PJAROflZUVPPzwwzI3dzgcIplMIhKJIBwOOxquaAcMWCkxZFDLszYajUqFl3IuvfIUgEiyvN69mcKbm5vY3t7Gpz71KczOzmJ7e1uCZCZrlHRpm+doNWC8NhYYV5K1RpX/bjabwiRTpkB9t2VZUomtVqtH8+F8CBybgPXdd9/FE088Ib90jiwhS6PHUNAxuZkhvarNXWYFxo6LzlcHsTRaDu5n+ZIOk4GyDnZZRtIsrw4E6OgOCmJ1+dXj8UjgokdakD1jEL28vHwPfvMGHxZ/9Vd/hdOnT4v4nmwUPzsentQxMWCkTXu9XtFVs5uajShMnNwaVu3ANLvEa9ja2kI+n0cikdinUdX6UwYBOqnSjTWAcyKHu8LBYIK2TmYVAJLJJGq1GorFIm7cuHF4H4jBD4zNzU2Ew2E89dRTCIVCcsBySxlZfN1BrzWsAKRTX8uayLxHo1GZRqADVtoNg1rKEUKhEJLJJFKplAS09KXcz86xVu4qlk6udLOVlrNweQaZYrK89Lvso2BgUi6X8Vu/9VvHTgt40vHNb34TZ8+exfLyMi5evIhMJiO+kV37rALpKRMAxDap6x8Oh6LTpm8mMdBqtcQm6JOZ5DPgLRaLuH37Nra2trCysoLLly9LgkUijX0GfG2+vmb5gfGMd/ps+lv9+H6/L/EJteZer9fBvq6vr+PGjRvHLtk6NgFrvV7HnTt3kMvlZD4ZD3TtYIAxK6SDUmo4aHA0Vr0NyE2l87k0GL13mvPYmM0AkHKsLotqTaAu97odHJ+jx1FonarO2NhIw1ltHJRt9KuTiUqlgrfffhs/9mM/hna77WAzASAcDktjEiUA1Knato35+XlEIhEUCgW0Wi2HLsrr9aJUKol9A+MAUjtgOjgAeOSRRzA/P4933nlHVsbqe8edQGn7dZejNHPG8rEeCUPHzMAikUggHA6j2WyiWq3KqtrjmO3fDxgMBtjc3MTGxgZmZ2cBQEb1cAIFE3r6Y63ZJ5ulWU5q6sgYhUIhCTJZBdD6U908WCgU8Ju/+Zs4ffo0FhcXsbm5KYe4x+MRQoENNFqawsqb1lrrgJWrvskSd7tdaeaq1+uO5rAzZ84gFovhjTfewLvvvnuUH5HBAajVaigUCshkMuh2u2KDXIfKKpeezaoTmkgkIiV/N4EAjLX4AEQ6qHtSYrGYXEsgEEC1WkW/38fVq1cxNzcnZzr9vZ4uxHuF0wg0CaDnsJNkiEaj0vhNyU6j0ZBeHwCylW13dxf1eh2VSkXiqOOEYxOwAnuTAh588EEHSwNgH4OkA06WWUm56wYs3RWtO7T1XEF36dN9oPO1yXa69Sh6UgAw1k/pzm7dDEBnyS1WzL6oveFr6rVwpVLJjAWacIxGI+TzeTSbTYegn1k6HaBmNv1+P6ampqSkw0CvXq8LS0D2vVgs7tNkMwHSB3W/38fq6ioKhQJSqZTMwATGSRMDADpqBqhM6NwBLp+jqxD8men0mRRSG06Giqs4DSYXw+EQW1tbmJ2dddgoE3SWX3XFYDQaIR6PIxaLifyFgWetVsPu7q74cX5PJzua6dczsSORCB599FFcu3ZNgg6eBfSf1HTzUG+1Wg7ttZZ56YDA5/PJBAI2AVIHyWstFouivWXQYTCZSKVSAPbILt2pzzFSLOszudH6Vj21xev1ytxUJi48x8PhMGq1mgS+wLiiwCA2Fothbm4OU1NTsCwL29vbOH36tGP1dTgclmUZOplibKJlCwDkXmEcQ+KBldfp6WkMh0PUajV5D1ZFSHAdRxyru219fR1PPfWUNK7o7k92AupOVAAyK9Ud0LGExMxa60vdjSVu1pQjK6hxotNz61D5Gjpz0h3eOlDm/zWLa9s2Go0GyuUyQqGQ7ELWJVte+3Hr9rvfsLy8LCVMMk3sVmX3pg4Eg8Eg0uk0bNvG3bt3EY1GkUgkkEwmheUhY6/H7TDR0k1QWtPd7/dRrVZx/fp1PPzww4hEIsJqaeZfB78A9gWVOuHSXwP2kkYe6qVSSZhVPW4IgAQyx2k14P2Ifr+PQqEgnzntislGq9VCo9EAAGF4QqEQMpkMstmsJCelUgmlUgnZbBazs7MoFosAIMGCZvIJ7Zf7/T7i8ThyuRwsy8JXvvIVCSx4qPNe0jModUCrfbm2Ydp3qVRCIpFAJpPBuXPn4PF4UKlUUCwW0Wg0HE2vHo8Hv//7v384H4LBD41Go4FYLIZSqYROp4NUKiWBJsdRkV3VbCntiSRStVpFq9VCPB6HbdsyY5U2T9vhuCsGtFrjPDMzg6mpKbTbbZElaOkfZS8MOHl/6aqwrsICkOSQ/6aE4e7du7h79y7m5+dx6tQpITeCwSASiQSuX79+bJuzj1XAevfuXTE0ZhTauLQAng0AFFXTKdExUutEp0t5gD6YtW6E78WDPRaLOUpgdIZa3KyDVl6Tmz0AxtuteM00Lj6mXq9ja2sL6+vriMVisqLW4/Gg3W47siiDycStW7dkDzl1gPwMgbG98t9c1UenRbF8tVoVm8vn82J31N4B+9cTa3kBbSsWi6HX6yEWi4mURNs7X5cBgz7omSTq/+tAhg6Y9ru9vY3d3V3H/nVgzBIY251s9Pt9LC8vw+PxIJ/PyxiqwWAg23tarZYkP3zc7OwsfD4fGo0GdnZ2ZGbrzs4OTp8+jampKUfQQJsDxqQBWVBgryLRbDZx9+5dLC4uOhgw3kcc6aO1qnw92rVujnUnXGzkojzhzJkzeOaZZwDsSXtarRa63S5isRhOnz5tZFgTjLt37yKZTOL27dvIZDK4ePGiNEyxGlCr1aRaQDaf0wN4lnOiCll2Mv0MTvl6euoEYw9qYWOxGE6dOoXbt29LWV/r+kkQkJ2ljTIu4GvqsXCMd/QEIdu2cfr0afT7fbz55pt4/fXXMTs7KwsMPB4Pbty4cWx97rEKWG3bxo0bN7C0tIRGoyGOTDOjwHhbRbfbFfaTQ4S5uYoOjVpUPQKCgakWJGs9Kd+TywMIlng1za/HUOigmQarr5nOlNfG4JpMaqFQQKlUwu7u7r7ylsFkw7ZtvPXWW/j0pz+Nu3fvirSD2iJm5Qw24/G4lFmr1aowRrTRTqeD27dvY2pqal+nv2ZJ3QncaDSShRhkuxqNhgTBvA8046plAG67fb+fVTcvLiwsoFgsolgsolwuS+Dg8/lkxqXBZGNnZwff+ta38IUvfAHVahXb29sy9geA4/Ccnp7GwsIC/H4/dnZ2sLKyAr/fj0wmg0wmg3K5jNu3b+Pxxx8XxojBgLY7+kHaJu+Hzc1NnD17VkbFcRqB1iACkK5unVzpBFF3V/M9tBZ2Y2NDtNaPP/44zp8/D4/HIwkkG7IMJhfVahWVSgWVSsUx2ooMJjX2AIT5BMaj2BYXF5HNZuH1enHr1i28+uqrSCaTktxwwQXtltMISEbQVnSzHmem67GE/DoJKzbm6v4AMrI6+QLG1VzLslCr1RAKhfDAAw9gbm4O3/nOd3Dr1i0hSdwN58cNxy7aeemll6Rkw7ESDDB1iYfa0eFwKKNXqJ8DxoPP9So2zdJqxoiGorMSZkOVSsWRVTHzoWPUjVx8HgMLXXbVHbYAJLuj3IHvl0gkUKvVHPMO3eNXDCYTL730Ek6dOoVz587JnmhWAHQVgKx6q9WS8jptVXfgUzutD2E3a+S2CzJg0WgUW1tbch9Q06RZXy1X0RIDd9CqKwU6aOY9BextnqEGl9egS14Gk43BYIBXXnkFjzzyCB566CHRb3L0Gu3Vsizk83lEo1FsbGzg+vXrsG0b8XjcMcWFg/k5PJ22oKsMelwgv9btdrG7uyuMbrFYFB9On8p7SftU2pibUdUyLFYUWMpl88qtW7dQKBSQy+UQi8UcGnQt4TKYLNi2jZWVFXi9Xjz33HOYnZ1FJBIRRlQzq7ZtIxaLCZtKuR4lL+FwWOR5tDPd7ExCgdpVPcWo3+/L69HeqtWqdPZb1nhCDOUrHEfFKqrX65XEDIBMN+A4QwatrEJ0u10EAgE8++yzePDBB2XJx2AwwPb29rGdKHTsAlb+0hOJxL4d5LpUqZ0fR6Iwk+YHSzG+eyyLfj39t85o3DIBHrzM2EKhkHxfH+xaR6VZXd1hyPfQszd5balUSqYS2PberEDOdDOYbNCZMNHRM4G1bVHcz3ISoRtaOp0OstksIpGIDFGnw+PhTdAGGRBztNZoNJLd0pz/yvdjKUrbrJazaG2se5SVluyw8YDsA8dyAXuSgEqlcki/fYMPi06ng1deeQWnTp2ScVTU9LGTngeo3+9HsViUpItaZjapMIDlimAdsGoGiCOGdCMiABnREw6HpWFLNy4C40TLzeC7/Tp9ODBuAuRYIpaGd3d3US6X5f5gw4yZfT3ZoK+8evUqnnnmGbEhTmvhTF0Gmtp3tlotLC8vy7zq9fV1ScA7nQ5arRaazaYQRnwut7RxMgHtsNVqSaWAr2FZe5M03PJGMqI62NUb4yhh5P/5s9KmeYZEIhGREPr9fkdieRxx7AJWAHj55ZfxiU98QvRTABwHqVsiQKejm0SoX6WhHtTxqUtMuluahsktLRyTwcxcN9Dog1+/ptZW8fr5N6+TTQR8TQaudJq6jHVcDfB+w3//7/8dn//851Gv14VlBcYlVV2uGgwGMuyaCRHtiTMq2cHMZAzYPycVgCN5ajQaSKVSEmjQKfJeAOAIGnRTCgNSrcdmkKGTMbJPrVZL7i3eA/xZuWXL2O7xQK/Xw8rKCu7cuYNLly5JCXJjY0P8q24KAeDQC7JDGQDOnz+PZrOJSqUiAatuIgHGfptJmF6JubOzA5/Ph1QqJXMyKW1hhY1VKJIRmhw4iHEFxuuwSTrouax6qoH2/waTje3tbdy8eRObm5sybkon3ZTpcbJPuVyWyTtsjiVb+vjjjyMYDGJzcxOtVguVSkXWW/Ocp21wYgXtaXNzE9VqFbu7u0gmk8jlckilUjLfmPpY2jBHHY5GI0medJWC5wElNcD+vgDdVKbncx/XqtaxDFjJrM7MzGB1dVWyYh3sAeNMpF6vOxYMaLaIzS98rNuhAc51lTQUspt8LW6m0IezHriug1R+TweaulFGM7gAZLQKx1tR7tBut1GpVHD37l1Tmjom6HQ6WF1dxeLiIm7evCmHsW4GoR12u12USiX4fD6Uy2UR8VPiQifF7JvOTAeruizPQ1vrUhlosiTllh4c1HR10P2h/09duJbTkLXia5KFffPNN4VxMJh81Ot1vPfeezh79qyjSYnVJY/Hg2q1il6vh/PnzwtrT911q9XC0tISQqEQrl+/LowPGX4Glfxbzz6l7+OSgUQigVKpJPpENuRquYo72QIgDWPAmCggY8XAgPYfiUTkcdy+RXt/+eWX5R40mFzQjr75zW9iamoKiUTC4SMpC+B5nUqlsL29jeFwKKPZAGBubg6BQAA7OzuoVqtie1oGSHsi4RCPx2VmcTQaxc7ODuLxOC5duiRNsxyfppMh9t3omEZLH+nX+RideLHSxooDE69Wq4XNzU288847xzZeOJbdDq1WC3/wB3+AUCgkY1PopHRpUgejdKzAmI2lEemd7u7sW2td3UwRG7j0/mCyrLrUq7V/Gjpw1oGBlgcwQKEjZUmh0Whgd3cXhUIBu7u7h/WrN/iQaLVa+N3f/V0AkBmr/OzdA/pZvh8Oh5iamsL09DQymQxCoZBo/8j+6ADTrWGlvbO0xNFauVxOGFXqrnRHqg46yVS5kzYGK3wvAJKkka1iIKMXGFQqFaytrWF5efnYZvv3G0ajvRE/t2/fxvr6OoAxE6+ZpHK5jK2tLYTDYTz88MNIpVJYWFjAuXPncPnyZaTTaayvr2NnZ0c0gLqUDzhXANPeBoMByuUy1tbWRA7AxRPU9bPiFAwGHb4a2L/R0C3/YgCgNwnVajVZjcyANh6Po9Fo4J133tnH0BpMHnq9Hq5fv44bN27g1q1bUlHSZzoJKE6AePTRR/Hggw9icXERMzMzmJ+fRywWQ6PRkDFnxWJRmrn1hCLOAeZITY9nb6rQ2bNnMT09LRMmeK+Uy2XZpMXqLDCWgPEeI8kFjGcO897TkgLaPwNVYM/2d3Z2cPfuXayurh5buz2WDCuwN5O12+0im83Ctm0UCoV9eiJdCuLBygCSm1PYoefW+QHOzmoewro5KxgMikGyk5+ZG1kjBs7ubVd0nvxbb7A4qKGFpQKW1zj0eHNz897/sg0+UqytraFcLiOfz0tmzYxXa6lpMyyfAxBdqy7J65FVtCd32V7/ISvEEi1tjfePlinoCQGUoDCIAMb2S7vX94vWlGubtm0bpVIJb7/99j3/XRt8tODnf/XqVXz84x+XQx+AJELdbhc3btxAvV6XlZi0uXa7jY2NDWxtbUn3Nv2xbprSg9tZKqVc5tSpU2g0GgiFQjLIn68Ri8UQDAZRr9eFtQWc+j5gPEmGDC4PfDKqhA6ceT+ur6/jz/7sz+7tL9rgI0W73cbc3ByuX7+OfD6PfD4vgR6DVVay2LAUjUYlBmBiVCwWUSgUsLW1heFwKP0kPJdJQLApiqPfQqGQjGLjOuxyuYx2uy02R42/HpXJxloGwPT/PDN0Eqa1t4xR2LQF7M0Cv3bt2rEmCI5twAoAX/nKV/CLv/iLiEajjgwbGGtUWM4nk8SAlEGq3sSjaXKyq3R6dKY669GsEZ2ybkRxX4cGgxC9Xo2BrVvvqoMB6qgajQaKxaIppx5T/Omf/il+7dd+DblcDjs7O1K+0ZMqaEM62dGlJ9qsPpR1w4k7MdJOjX9zCwwAR8LH96Bmlq/J9+K9QCetN8wdNH6F9wmnHqyurpoZlscUu7u7mJqawu7urkxfoS+ldq/b7WJ5eRlbW1vi18g4tdtt1Ot1GeieTCYlMNC+0t1c0u/3RfdHnSqwl+zH43Gk02nZUsWNcnqOJe2RQXYmk0GxWESpVJJpK51OB1NTUzIlwLIsGeoOAOVyGe+88w4KhcLR/PINfmS89tpreP7557G8vCzTHjgJQgeZ5XLZwVjati0a6WKxiLW1NXS7XZltynFslK24t/m1222ZP82NWZVKBT6fD5lMRiRT1LHSr/Pc59cAyPxXzuimxlsHyHp9LNlk3o/HXXd9rAPWt99+G6PRCL/0S78kK//o9HSjkw4EgLEj1F/TndAES5f6INZsER0hGU/+m46OcgF3yZTvR00UDSwejwtTy8yMQYIe/0Jm1Wy3Or5488038e///b/Hr//6r0vzE5sAgXGXvh4tBThnDruTFT2PT4v2+XitYWXZinMsyY6xqc/N9mv5Ct+LOmpeJ0uqACSBZPBKG2+323j33Xdx586de/wbNrhXqFQquH79Oubm5mSsVTAYlF4CndQ0Gg2xHdu2JZjkLnNq/7V2j6OlOIKIASaf32g0sLS0hFQqhTNnzsiIK478Gw6HjvFsvC901YHBAoMRBqubm5sIBALI5XIi7+LP12q18O1vfxuvvvrqUf76DX4E2LaNa9euCUsZCoWwsLAghBSrozyPmZAzRqhWq9I0Va1WxSa4dZOSEcvam/8ejUYlOG2321hfX5clBZwWw6ZqNm3Ztu3oJdDSrFQqJdKZTqcjuljKGHidvH8AiJzMtm2899572NjYOOJP4cPjWAesAHDjxg3UajXEYjGsra2hWq2Kk9Hz+OgE6aw4UoXGq+UC2qlZloVqtSoZE5krPWWg0+mgWCw6ml7chqfB99asqe7g46FP49fdso1GAxsbG9je3j7W1L4B8O677+LWrVvI5XKO2X9kHslKeb1eydA1yw5AbFeXLqnHG41GaDabwoAxW6/X6/L4TCYjOkLdxa+ZXK3B5vszidJDrYFxcsiRLrqZZjQa4ebNmzKb0+D4olwuY3V1FWfOnEEmkxGbYCULGLPw9HONRkPWZbKRhdUv+mpgnFzl83m0Wi3UajWxqUwmg2AwiH6/j2KxiFQqhXQ6LWPaKDVgz4J7WguDUMCpFWeljY0pPp9PZgdHIhF4vV587Wtfw1/+5V86RsYZHC+sra1hZWUFm5ubmJ6exvnz5zE7O4tAIOAgjwBIgsRKZjgcltghHo87pvkAEFlKqVRCs9lENptFMplEIBDA1atXpZK2tbWFGzduyDa1YDCIfD4vRAEXEWjWFtiT3LRaLVllDIz7aBiLcKKMlgfcvn0b169fP7a6VY1jH7B2u1387u/+Ln7pl34JqVQKW1tb8sEDkIYP3QzF7UE6eNXQGtZoNCrrT/l4AHLIMzOiRsvn8yESiUgzF0ulwFhn0uv15PEMULmDm/S+3+9HOByWsmuv15Pd7IVCwRz4JwC9Xg+//du/jX/yT/4J8vk8ut2usOa0KyYvlJ9wuxA1de4yPsGubZ/PJ9Ms+BqUvujRPFzVSrvSts7Xo+1yfjGbAMh+8bUYhOgOatu2Ua1WcefOHWO7JwDD4RBvvvkm8vk8stksstmsdEHz+yxxkhUdjUaYm5tDLBbD1tbWPvvRiVG320Wr1cLMzAxyuZywULOzs/D7/dje3sapU6dgWRZKpRJqtZpoYrmB0K1hDQQCyGQyDl9br9cxHA4Ri8VkAgGHupNlDQaD2NjYwDe+8Q0TrB5z9Ho9/PVf/zUeeughbGxsyOjATCYjowb7/T4ikQiazab0xuTzeSSTSWm0isfjwl6SDKAeNZfL4ebNmyiVSkgmk7Ld7a233kI8Hpf50yQGEokEYrGYVBm4hIBgpUE3ZuvG8eFwKAFsKBRCq9USP72xsYE7d+6ciGAVOKZTAtyoVCr42te+hkcffRRTU1PwePbWmiYSCcTjcRm2TzrdveqSh7gug9J5BgIBhMNh0TBxtiTL+XqcEMv5DI51tyrg3GdNo2J5lsEHr4+BKzM/jrDa3Nw0w6pPEGq1Gr70pS/h1KlT6Ha7jqCPjScM/qrVKhqNhoxMAcZaa5bd6Zio1aMkhQdxtVpFvV4X57y9vS3OjropBru6g5YYDAao1+vSMMBkjLOIOQuTzpRBcr1ex9tvv210qycI3W4XL730Em7cuCHJFfezb29vY319HRsbG9jZ2YFt23jggQeQy+Uk+WFyT5ZIa6QZdLZaLWQyGeRyOUxPTyORSIimdGZmBhsbG6hUKqIx5LxM2iEAR2CRSqVw+vRpTE9Pw7IsSeZCoRBmZ2eRyWRkNFe/30cymcRgMMAf/MEfGAnWCQFZx0wmg9XVVdy6dQu7u7toNBqoVqsol8tYWVnB1taWkEfUgfZ6PRlVZVmWaLgpZ6GEMJ/Py71w584dNJtNR8MU57um02kkEgmJORiH6BFZDEp3d3cxGAyk/E9CjOwqK7vxeFzuwVu3bp2oPpdjz7ASq6urePHFF/HJT34S165dAwAZN2XbNprNpmT81N3pUhEPfQAymJ2HfjqdFlE0AwSOpADGZVgAji5B/lt/n+Bat2QyKYJpXgcHwXNHfKfTQaFQELG3wcnC6uoq/uzP/gxPP/20MD90QPz8yVSxaZAlUD0Chcst9Fw+OjuySoPBAKVSSWQulmXJtind7c0gls7TDW7sYuJH/Ve9XpcmQt5ftVoN3/3ud1EqlQ7ht2lwmKhUKnjxxRcxNTWFbDYrLCcTE05jWVpaQjKZRLlcFraIrGcqlQIACTJpxzz8G42GoyyazWYdfpKsUiAQkHmsbFTRJAS3EF26dAmJRAKFQgGpVArlclk0szMzMyK34TSOf/fv/h2uXr16JL9fg3uDarWKW7duYX5+XmICVpUYNHL9O+cHa0aU0qhMJoNIJCK22uv1UCqVHDEDewQKhYJUsdjlz0kEvB/0XGPtg5PJJK5evSqBbKfTEba20+nIzNhUKoVGo4E7d+5gfX1dFiudFJyYgHU4HOIrX/kKvF4vHnjgAayurgoDRL2dHs3DQ10zUu6ZqaTo/X4/UqmUbBXq9/uyP5s6qeFwiEQiIdo/zuwDxswq/21Ze4sGtre3hZVtNpsSMHg8HilVMVhdX183Q6pPKIbDIb785S/Dsiw8/fTT2NnZkaRK66R0YgM4GXuyq+6ykWXtrcNkJt5qtZBIJEQbFQgEUKlUHM0veokGr083MzII7nQ6ou/T0wGq1aq8f61WM13VJxij0Qg3btzAX//1X+Pv/b2/JyuzyQBFo1Ekk0mk02nU63XR/7OylEgkkEgkZCOaHkXIZhaOx6LPZbLGqQGNRkNKoHpVJgNVJlS2bcsWo4WFBfR6PSwsLCAejwOAMGnT09OIRCJYWlrCv/23/xbf/va3j/i3bPBRYzQa4fr16xgOhxK0ejx766Oj0agM9K9UKshmsxI/sPLERj89IYVSKybtnETAmcFMxIDxjHUm/myg0otjWCluNpuYmppCPB7H1atX8fDDD8vaYy4JYBIYDofx9ttvY21t7USuvT4xASuwZ4QvvviiY0+1HrmiG0XYGUiwQYCddnp6AA9irV/Scy0BSFcgDZoMmab2WQpgCYpz33TnNQ//4XCIra0tbG1tYX19/dhupjD4wTAajfDyyy9jdnZWRqQx8SFbr9ew6rFXlAPoiRR8TT3Tjwkb2VbOr6RjBOBotmKSpdf7ccxPNBpFsVh0bF+jE65Wq6hUKuj3+/jud797Ih2nwRjswL548SIuX74sQaueMkHWktMwAAgRwKUo9H29Xg+hUEimpdDmyWxRwkW2ipuyarUaSqWSJHu8P7j+kuzV+vo6lpaWMD8/L88Fxs2yXHTwW7/1W3jxxReP5pdqcM9h23vz2zc3N3HlyhXMzc1Jwu73+1GtVoXc0gtZKM+LRqOOiUOMH9hAzXmu1WpVFgL0+33E43EZzwaM+2zY7c++FvbckKk9c+YMrly5gtu3b+P06dMiUaBdN5tNvPbaa/j2t7994phV4kRoWDWKxSJeeOEF6S6t1Wri2GgwetA6MD7YeTCzW1A3AJBZdYuXOeSaI6moWyW7SiaAule9cYubWuhk+foMWNvtNnZ2dkywep9gZ2cHX/rSl2QUULfblUSKYnzAOQSdQShlA5oN5ffp1DhxgtIYACI9ob6K2b4e2k7Nq9ZrUxNeqVTktVhViEajGA6HuHLliglW7xPUajX8xV/8Bd544w3EYjEkEglZgaoHrGvpE/sMaG9MztiMlU6nkclkkEgkZGwVpSYcQ8XVrq1WS/woMJ4pnEwmce7cOZEkeL1esedcLodsNiu+ms1X6XQa/+bf/BsTrN4HqFQq+Na3voUXX3wRr7/+Ora2tlAsFmXDGeMHsq9erxftdhvNZhPNZhPAeH1vr9eTfpd0Og3LstBsNsU3c657Op1GLpeT+INjDbmmm41+jF9Y+Zqensb09DSuXLmCnZ0dCWY9Hg9arRbu3r2LN954Q86Pk4gTxbAS29vb+MpXvoLz58+LpoPjUJhRM5un0VAKQE0eg08yWZph0iCzpXdR6+5qlk5ZzmfAS4dKjSK3UwDjrUErKyumSeU+w8bGBv7wD/8QTz/9NJaWltDtdhEKhQCMbYnZPkv2THI4moqlKz5Oz6DkCCF3GYnMgH6eDoT1uDctm2FSxTWvtOFr166Jxtvg/kCxWMSf/MmfoFAo4Gd/9mextLQka6OnpqbQbDYd2wNZgqcN1ut1OYBHoxGSySSy2azIBQCIBIWzU1n94tQW2rvf75cVmKlUCoPBQJjfRCKBdDoNn8+Hubk5tNttqXS1Wi383u/9Ht54442j/FUaHCLq9TquXLkiE3jm5+cxMzOD4XCIer2Ora0tnD17VuRTuqGPjGkkEpEtWZQEhMNhh9aajdaUBvR6PUSjUQSDQRSLRYkfYrEYyuWyQ2JAv9poNNBqtXDt2jX4/X7k83mEw2E0Gg3cuHHjxPvcExmwEjdv3pQB0TMzM4jH41JKIkMEjLWAPIQ5rFo7V/ecSzKnAPYFqKTwKUHgoa+7/in0JpvAwJTzK69cuXLijc/gYNi2jVdeeQVvvfUWHnroISwuLsKyLHGULL8DzmUBzP713FN2R1P3x9fXw6Y5Woj/5/PIyOoVrfye3sBSq9UwGAyQSqXg8Xjw8ssvY3t7+yh/hQZHBNu28Zd/+Zd49dVX8Qu/8Av4zGc+g2AwiGw2C7/fj42NDVk3ye5qMq2lUkn8bqvVwtbWFqLRqIwQYtWL/pU+kxM0RqORSMA4wiqfzwOAVCei0ShOnTqFZDIpm4JOnTqFaDSKQqGAP/zDPzQNVvchbNvG5uYmdnd3MT8/j4ceeggej0fmnp85cwa2bUvACuwFq4VCAbFYDNPT09jd3RU5SrVaRbvdloUErVZLJFQ8/wEgkUg4JFkkD5rNpmNkZrlcxmAwQLlclubCd955B7Ozs0gmk3jttdckOTzJONEBK7DHZO7s7KBcLkvDCEtBABxaK71tpdlsOg5wBqfMmDgai3Q9D3O9Ho0BAh3jaDSSxiyWcgGgVCqhXq8DGM/SPO4r1Aw+PNrtNl5//XWZepHJZDA9PY1UKuUYyk470pIW3WWqta6j0UhGY7HZhAEtta06KWOgoIMF2niv10OhUMDu7q58D4CUygzuT/Bg/w//4T/gq1/9KrxeL5555hl84QtfQDweF1vjjGCy+6yGMRnrdDrY2tpCOp2WcYHUaXPDD8usnEzBMYS2bSObzYpOkCPh9KKNL33pS/hv/+2/ScWg1+vdF4e+wcEgwXT37l1JuCORCKanp6UCSr8YiUREjgIA+XwemUwGpVJJmqpZ7fJ4PNjY2JCGV93lz1FwHO3m9XpFm8rRV7y2er0uDCtndi8vLzuIipOOEx+wEgw4aQwcY8KMHhh38PP/zIKAsRa11+uhVqvJ8H52XnO1JR+r92JTn9Lr9RAIBGRcFVe/mnE/Bh8EBoDNZhP1el0aUPQKVSZHZELZAABANLDAXnlpY2NDHCWDWAakfLxu7GKCxnnGDBJ2dnawvr5+XzhKgx8etm1jfX0dALCysoK1tTVcunQJ2Wx2X2Lu9XqltMqJEkyuGNBSY72+vo7t7W088MADaLfbyGQykqxxritZ21QqJdvcisWiVCT+4i/+Ar/zO7/j8PEGBgAkIQIgWukbN27g4YcfBrA37iyTyaBarWJra0uCybm5ORmNpZe6FAoFXL16FbZtSzWK81fZmN3r9cRfkyC4ffs2HnzwQZnpyjna9zMhcN8ErBrtdhtXr17F5uYmHn74YRFNE1pHReOhDpVGymwH2FtTyK4/GiA1gwx0m82mjLogS1AoFEywavBDoVKp4Dvf+Q5WVlbwzDPPOPSttm1LZyln82lWoF6v4/bt21hbWxMmaX5+HnNzc1hcXHTMW9UsFxur2Jg1Go3kdQwMflC89NJL+Na3voWlpSX84i/+ovhKNonoVdUAHNWrSCSCarWKF198EX/+538uCdrjjz+O6elpBINBKZdynWosFpNNXKwEdLtd/NVf/RW+9rWvmQUsBj8Qms0m/uRP/gRnz57F5z73OZFCDYdDGS3FPhT6YBIHxWIRr732Gu7evSs2G4lE0Gg08MQTTyAajSISicgSC24z3NjYQLlcxt27dxGPxzEajfDee+/d9z0t1gexI5ZlnXjqJBQKYXp6Gslkch9LpQeoj0YjlEollMtlFAqFfSv6vF6vdJi6R2Ix4K3X6w5Gt9lsnpiVaR8E27at7/+ojxb3g+2yqSSRSMhYIJblg8GglKWAvUB3d3cXN27c2Ld8IhAIYHZ2FvPz8+JsgT37bTabqFQqsvWFAXCtVrsv1lQehe16PJ4Tb7v5fB5PPPEE5ufnJUhtt9vSwe/z+RCLxaQJJZvN4k//9E/3leyz2SweffRR/NiP/RiazaY0XHE8FQD89m//tgyA5yzW+2Hyymg0OlTb9fv9J95uM5kMTp8+jYsXL6JYLDqSpGw2Kww/N1NduXIFN2/ePHD9+/T0NM6cOSPLB3q9HsrlMsrlMu7cuSOVLm7Voo71pKPf77+v3d73AesHIRwOY2pqSg5uCvsNfjiYgPXwEY/HMT8/D2BPv7ezs3NfBJgfNUzAeviIx+N4/PHH4ff7sby8jNXVVVO6/xFgAtbDxdTUFJ5++mkAwHvvvYeVlRVjtz8CTMD6IaCnAxj8aDAB69GA0wNMkvWjwwSsRwOOsbofmNB7BROwHi6oXwXg6Akw+OHwQQHrfalh/WFgjM7guILd/gYGxw0mUDU4buCUAYN7hxO36crAwMDAwMDAwOBkwQSsBgYGBgYGBgYGEw0TsBoYGBgYGBgYGEw0TMBqYGBgYGBgYGAw0TABq4GBgYGBgYGBwUTDBKwGBgYGBgYGBgYTDROwGhgYGBgYGBgYTDRMwGpgYGBgYGBgYDDRMAGrgYGBgYGBgYHBRMMErAYGBgYGBgYGBhMNE7AaGBgYGBgYGBhMNEzAamBgYGBgYGBgMNEwAauBgYGBgYGBgcFEwwSsBgYGBgYGBgYGEw0TsBoYGBgYGBgYGEw0TMBqYGBgYGBgYGAw0TABq4GBgYGBgYGBwUTDBKwGBgYGBgYGBgYTDROwGhgYGBgYGBgYTDRMwGpgYGBgYGBgYDDRMAGrgYGBgYGBgYHBRMMErAYGBgYGBgYGBhMNE7AaGBgYGBgYGBhMNEzAamBgYGBgYGBgMNEwAauBgYGBgYGBgcFEwwSsBgYGBgYGBgYGEw3Ltu2jvgYDAwMDAwMDAwOD94VhWA0MDAwMDAwMDCYaJmA1MDAwMDAwMDCYaJiA1cDAwMDAwMDAYKJhAlYDAwMDAwMDA4OJhglYDQwMDAwMDAwMJhomYDUwMDAwMDAwMJho/P8B+VQaqC/yHZMAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 864x720 with 4 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "from utils import visualize_data2\n",
    "from pathlib import Path\n",
    "\n",
    "# paths to example files\n",
    "t1c_path = Path(\n",
    "    f\"{BASE_PATH}/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/raw_bet/OtherEXampleFromTCIA_t1c_bet.nii.gz\"\n",
    ")\n",
    "t1_path = Path(\n",
    "    f\"{BASE_PATH}/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/raw_bet/OtherEXampleFromTCIA_t1_bet.nii.gz\"\n",
    ")\n",
    "t2_path = Path(\n",
    "    f\"{BASE_PATH}/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/raw_bet/OtherEXampleFromTCIA_t2_bet.nii.gz\"\n",
    ")\n",
    "flair_path = Path(\n",
    "    f\"{BASE_PATH}/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/raw_bet/OtherEXampleFromTCIA_fla_bet.nii.gz\"\n",
    ")\n",
    "# visualize example images\n",
    "visualize_data2(t1c_path, t1_path, t2_path, flair_path, height_p=0.60)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "---"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## 4. Segmentation with BraTS Toolkit\n",
    "\n",
    "Now that we have preprocessed the data, we can start segmenting the data with BraTS Toolkit.\n",
    "\n",
    "#### Therefore, we again define a function to segment our files:"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 8,
   "metadata": {},
   "outputs": [],
   "source": [
    "from brats_toolkit.segmentor import Segmentor\n",
    "import os\n",
    "from auxiliary.turbopath import turbopath\n",
    "from tqdm import tqdm\n",
    "\n",
    "\n",
    "def segment_exam(\n",
    "    t1_file: str,\n",
    "    t1c_file: str,\n",
    "    t2_file: str,\n",
    "    fla_file: str,\n",
    "    segmentation_file: str,\n",
    "    cid: str,\n",
    "    cuda_device=\"0\",\n",
    ") -> None:\n",
    "    \"\"\"\n",
    "    segment_exam - Segments MRI images using a specified algorithm from the BRATS toolkit.\n",
    "\n",
    "    Parameters:\n",
    "        t1_file (str): Path to the T1-weighted MRI image file.\n",
    "        t1c_file (str): Path to the T1-weighted contrast-enhanced MRI image file.\n",
    "        t2_file (str): Path to the T2-weighted MRI image file.\n",
    "        fla_file (str): Path to the Fluid-attenuated inversion recovery (FLAIR) MRI image file.\n",
    "        segmentation_file (str): Path to the output file where the segmented image will be saved.\n",
    "        cid (str): Algorithm identifier for segmentation.\n",
    "        cuda_device (str, optional): CUDA device ID for GPU acceleration. Default is \"0\".\n",
    "\n",
    "    Returns:\n",
    "        None\n",
    "\n",
    "    Example:\n",
    "        segment_exam(\n",
    "            t1_file='/path/to/t1.nii.gz',\n",
    "            t1c_file='/path/to/t1c.nii.gz',\n",
    "            t2_file='/path/to/t2.nii.gz',\n",
    "            fla_file='/path/to/fla.nii.gz',\n",
    "            segmentation_file='/path/to/segmentation_result.nii.gz',\n",
    "            cid=\"mic-dkfz\"\n",
    "        )\n",
    "\n",
    "    This function segments MRI images using the specified algorithm from the BRATS toolkit. It accepts paths to T1-weighted,\n",
    "    T1-weighted contrast-enhanced, T2-weighted, and FLAIR MRI images, and performs segmentation using the specified algorithm.\n",
    "    The segmented image is saved in the specified output file.\n",
    "\n",
    "    Note:\n",
    "        - The function uses the BRATS toolkit's Segmentor for segmentation.\n",
    "        - The 'cid' parameter specifies the algorithm to use.\n",
    "        - Segmentation results are saved with a file name corresponding to the algorithm identifier (cid).\n",
    "        - Errors during segmentation are caught, and an error message is printed.\n",
    "    \"\"\"\n",
    "\n",
    "    # instantiate\n",
    "    seg = Segmentor(\n",
    "        verbose=True,\n",
    "        gpu=cuda_device,\n",
    "    )\n",
    "\n",
    "    # algorithms we want to select for segmentation\n",
    "\n",
    "    # execute it\n",
    "    if not os.path.exists(segmentation_file):\n",
    "        seg.segment(\n",
    "            t1=t1_file,\n",
    "            t2=t2_file,\n",
    "            t1c=t1c_file,\n",
    "            fla=fla_file,\n",
    "            cid=cid,\n",
    "            outputPath=segmentation_file,\n",
    "        )\n",
    "    else:\n",
    "        print(segmentation_file, \"already exists\")"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "#### Now we again loop through our exams:\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 9,
   "metadata": {
    "scrolled": true
   },
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "Exams:   0%|                                                                                                                     | 0/2 [00:00<?, ?it/s]\n",
      "Algorithms:   0%|                                                                                                                | 0/5 [00:00<?, ?it/s]\u001b[A"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "segmenting: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294 with algorithm: isen-20\n"
     ]
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">──────────────────────────────────────── </span>Thank you for using <span style=\"font-weight: bold\">BraTS Toolkit</span><span style=\"color: #00ff00; text-decoration-color: #00ff00\"> ────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m──────────────────────────────────────── \u001b[0mThank you for using \u001b[1mBraTS Toolkit\u001b[0m\u001b[92m ────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n",
       "</pre>\n"
      ],
      "text/plain": [
       "   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">                        <span style=\"color: #0000ff; text-decoration-color: #0000ff; text-decoration: underline\">https://github.com/neuronflow/BraTS-Toolkit#citation</span> -- Thank you!                         \n",
       "</pre>\n"
      ],
      "text/plain": [
       "                        \u001b[4;94mhttps://github.com/neuronflow/BraTS-Toolkit#citation\u001b[0m -- Thank you!                         \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">───────────────────────────────────────────────────────────────────────────────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m───────────────────────────────────────────────────────────────────────────────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "/home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/isen-20.nii.gz already exists\n",
      "segmenting: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294 with algorithm: hnfnetv1-20\n"
     ]
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">──────────────────────────────────────── </span>Thank you for using <span style=\"font-weight: bold\">BraTS Toolkit</span><span style=\"color: #00ff00; text-decoration-color: #00ff00\"> ────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m──────────────────────────────────────── \u001b[0mThank you for using \u001b[1mBraTS Toolkit\u001b[0m\u001b[92m ────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n",
       "</pre>\n"
      ],
      "text/plain": [
       "   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">                        <span style=\"color: #0000ff; text-decoration-color: #0000ff; text-decoration: underline\">https://github.com/neuronflow/BraTS-Toolkit#citation</span> -- Thank you!                         \n",
       "</pre>\n"
      ],
      "text/plain": [
       "                        \u001b[4;94mhttps://github.com/neuronflow/BraTS-Toolkit#citation\u001b[0m -- Thank you!                         \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">───────────────────────────────────────────────────────────────────────────────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m───────────────────────────────────────────────────────────────────────────────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "/home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/hnfnetv1-20.nii.gz already exists\n",
      "segmenting: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294 with algorithm: yixinmpl-20\n"
     ]
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">──────────────────────────────────────── </span>Thank you for using <span style=\"font-weight: bold\">BraTS Toolkit</span><span style=\"color: #00ff00; text-decoration-color: #00ff00\"> ────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m──────────────────────────────────────── \u001b[0mThank you for using \u001b[1mBraTS Toolkit\u001b[0m\u001b[92m ────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n",
       "</pre>\n"
      ],
      "text/plain": [
       "   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">                        <span style=\"color: #0000ff; text-decoration-color: #0000ff; text-decoration: underline\">https://github.com/neuronflow/BraTS-Toolkit#citation</span> -- Thank you!                         \n",
       "</pre>\n"
      ],
      "text/plain": [
       "                        \u001b[4;94mhttps://github.com/neuronflow/BraTS-Toolkit#citation\u001b[0m -- Thank you!                         \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">───────────────────────────────────────────────────────────────────────────────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m───────────────────────────────────────────────────────────────────────────────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "/home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/yixinmpl-20.nii.gz already exists\n",
      "segmenting: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294 with algorithm: sanet0-20\n"
     ]
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">──────────────────────────────────────── </span>Thank you for using <span style=\"font-weight: bold\">BraTS Toolkit</span><span style=\"color: #00ff00; text-decoration-color: #00ff00\"> ────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m──────────────────────────────────────── \u001b[0mThank you for using \u001b[1mBraTS Toolkit\u001b[0m\u001b[92m ────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n",
       "</pre>\n"
      ],
      "text/plain": [
       "   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">                        <span style=\"color: #0000ff; text-decoration-color: #0000ff; text-decoration: underline\">https://github.com/neuronflow/BraTS-Toolkit#citation</span> -- Thank you!                         \n",
       "</pre>\n"
      ],
      "text/plain": [
       "                        \u001b[4;94mhttps://github.com/neuronflow/BraTS-Toolkit#citation\u001b[0m -- Thank you!                         \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">───────────────────────────────────────────────────────────────────────────────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m───────────────────────────────────────────────────────────────────────────────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "/home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/sanet0-20.nii.gz already exists\n",
      "segmenting: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294 with algorithm: scan-20\n"
     ]
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">──────────────────────────────────────── </span>Thank you for using <span style=\"font-weight: bold\">BraTS Toolkit</span><span style=\"color: #00ff00; text-decoration-color: #00ff00\"> ────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m──────────────────────────────────────── \u001b[0mThank you for using \u001b[1mBraTS Toolkit\u001b[0m\u001b[92m ────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n",
       "</pre>\n"
      ],
      "text/plain": [
       "   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">                        <span style=\"color: #0000ff; text-decoration-color: #0000ff; text-decoration: underline\">https://github.com/neuronflow/BraTS-Toolkit#citation</span> -- Thank you!                         \n",
       "</pre>\n"
      ],
      "text/plain": [
       "                        \u001b[4;94mhttps://github.com/neuronflow/BraTS-Toolkit#citation\u001b[0m -- Thank you!                         \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">───────────────────────────────────────────────────────────────────────────────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m───────────────────────────────────────────────────────────────────────────────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "\n",
      "                                                                                                                                                       \u001b[A"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "/home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/scan-20.nii.gz already exists\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "\n",
      "Algorithms:   0%|                                                                                                                | 0/5 [00:00<?, ?it/s]\u001b[A"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "segmenting: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA with algorithm: isen-20\n"
     ]
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">──────────────────────────────────────── </span>Thank you for using <span style=\"font-weight: bold\">BraTS Toolkit</span><span style=\"color: #00ff00; text-decoration-color: #00ff00\"> ────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m──────────────────────────────────────── \u001b[0mThank you for using \u001b[1mBraTS Toolkit\u001b[0m\u001b[92m ────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n",
       "</pre>\n"
      ],
      "text/plain": [
       "   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">                        <span style=\"color: #0000ff; text-decoration-color: #0000ff; text-decoration: underline\">https://github.com/neuronflow/BraTS-Toolkit#citation</span> -- Thank you!                         \n",
       "</pre>\n"
      ],
      "text/plain": [
       "                        \u001b[4;94mhttps://github.com/neuronflow/BraTS-Toolkit#citation\u001b[0m -- Thank you!                         \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">───────────────────────────────────────────────────────────────────────────────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m───────────────────────────────────────────────────────────────────────────────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "/home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/isen-20.nii.gz already exists\n",
      "segmenting: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA with algorithm: hnfnetv1-20\n"
     ]
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">──────────────────────────────────────── </span>Thank you for using <span style=\"font-weight: bold\">BraTS Toolkit</span><span style=\"color: #00ff00; text-decoration-color: #00ff00\"> ────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m──────────────────────────────────────── \u001b[0mThank you for using \u001b[1mBraTS Toolkit\u001b[0m\u001b[92m ────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n",
       "</pre>\n"
      ],
      "text/plain": [
       "   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">                        <span style=\"color: #0000ff; text-decoration-color: #0000ff; text-decoration: underline\">https://github.com/neuronflow/BraTS-Toolkit#citation</span> -- Thank you!                         \n",
       "</pre>\n"
      ],
      "text/plain": [
       "                        \u001b[4;94mhttps://github.com/neuronflow/BraTS-Toolkit#citation\u001b[0m -- Thank you!                         \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">───────────────────────────────────────────────────────────────────────────────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m───────────────────────────────────────────────────────────────────────────────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "/home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/hnfnetv1-20.nii.gz already exists\n",
      "segmenting: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA with algorithm: yixinmpl-20\n"
     ]
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">──────────────────────────────────────── </span>Thank you for using <span style=\"font-weight: bold\">BraTS Toolkit</span><span style=\"color: #00ff00; text-decoration-color: #00ff00\"> ────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m──────────────────────────────────────── \u001b[0mThank you for using \u001b[1mBraTS Toolkit\u001b[0m\u001b[92m ────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n",
       "</pre>\n"
      ],
      "text/plain": [
       "   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">                        <span style=\"color: #0000ff; text-decoration-color: #0000ff; text-decoration: underline\">https://github.com/neuronflow/BraTS-Toolkit#citation</span> -- Thank you!                         \n",
       "</pre>\n"
      ],
      "text/plain": [
       "                        \u001b[4;94mhttps://github.com/neuronflow/BraTS-Toolkit#citation\u001b[0m -- Thank you!                         \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">───────────────────────────────────────────────────────────────────────────────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m───────────────────────────────────────────────────────────────────────────────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "/home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/yixinmpl-20.nii.gz already exists\n",
      "segmenting: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA with algorithm: sanet0-20\n"
     ]
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">──────────────────────────────────────── </span>Thank you for using <span style=\"font-weight: bold\">BraTS Toolkit</span><span style=\"color: #00ff00; text-decoration-color: #00ff00\"> ────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m──────────────────────────────────────── \u001b[0mThank you for using \u001b[1mBraTS Toolkit\u001b[0m\u001b[92m ────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n",
       "</pre>\n"
      ],
      "text/plain": [
       "   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">                        <span style=\"color: #0000ff; text-decoration-color: #0000ff; text-decoration: underline\">https://github.com/neuronflow/BraTS-Toolkit#citation</span> -- Thank you!                         \n",
       "</pre>\n"
      ],
      "text/plain": [
       "                        \u001b[4;94mhttps://github.com/neuronflow/BraTS-Toolkit#citation\u001b[0m -- Thank you!                         \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">───────────────────────────────────────────────────────────────────────────────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m───────────────────────────────────────────────────────────────────────────────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "/home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/sanet0-20.nii.gz already exists\n",
      "segmenting: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA with algorithm: scan-20\n"
     ]
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">──────────────────────────────────────── </span>Thank you for using <span style=\"font-weight: bold\">BraTS Toolkit</span><span style=\"color: #00ff00; text-decoration-color: #00ff00\"> ────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m──────────────────────────────────────── \u001b[0mThank you for using \u001b[1mBraTS Toolkit\u001b[0m\u001b[92m ────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n",
       "</pre>\n"
      ],
      "text/plain": [
       "   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">                        <span style=\"color: #0000ff; text-decoration-color: #0000ff; text-decoration: underline\">https://github.com/neuronflow/BraTS-Toolkit#citation</span> -- Thank you!                         \n",
       "</pre>\n"
      ],
      "text/plain": [
       "                        \u001b[4;94mhttps://github.com/neuronflow/BraTS-Toolkit#citation\u001b[0m -- Thank you!                         \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">───────────────────────────────────────────────────────────────────────────────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m───────────────────────────────────────────────────────────────────────────────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "\n",
      "Exams: 100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████| 2/2 [00:00<00:00, 29.71it/s]\u001b[A"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "/home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/scan-20.nii.gz already exists\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "\n"
     ]
    }
   ],
   "source": [
    "EXAMPLE_DATA_DIR = turbopath(f\"{BASE_PATH}/data\")\n",
    "\n",
    "exams = EXAMPLE_DATA_DIR.dirs()\n",
    "# we use these five algorithms to segment the images\n",
    "# 2019 algorithms\n",
    "# cids = [\"mic-dkfz\", \"scan\", \"xfeng\", \"lfb_rwth\", \"zyx_2019\", \"scan_2019\"]\n",
    "\n",
    "# 2020 algorithms\n",
    "cids = [\"isen-20\", \"hnfnetv1-20\", \"yixinmpl-20\", \"sanet0-20\", \"scan-20\"]\n",
    "\n",
    "\n",
    "for exam in tqdm(exams, desc=\"Exams\"):\n",
    "    for cid in tqdm(cids, desc=\"Algorithms\", leave=False):\n",
    "        print(\"segmenting:\", exam, \"with algorithm:\", cid)\n",
    "        brainles_folder = exam / exam.name + \"_brainles\"\n",
    "        preprocessed_folder = brainles_folder / \"raw_bet\"\n",
    "        segmentation_folder = brainles_folder / \"segmentation\"\n",
    "\n",
    "        segmentation_file = segmentation_folder / cid + \".nii.gz\"\n",
    "\n",
    "        segment_exam(\n",
    "            t1_file=preprocessed_folder / exam.name + \"_t1_bet.nii.gz\",\n",
    "            t1c_file=preprocessed_folder / exam.name + \"_t1c_bet.nii.gz\",\n",
    "            t2_file=preprocessed_folder / exam.name + \"_t2_bet.nii.gz\",\n",
    "            fla_file=preprocessed_folder / exam.name + \"_fla_bet.nii.gz\",\n",
    "            segmentation_file=segmentation_file,\n",
    "            cid=cid,\n",
    "            cuda_device=\"0\",\n",
    "        ),"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "#### The segementations are stored in folder \"segmentation\" \n",
    "```data/<datasetName>/<datasetName>_brainles```\n",
    "\n",
    "Segmentation results are saved with a file name corresponding to the algorithm identifier (cid).\n",
    "\n",
    "Algorithms used in this notebook:\n",
    "- yixinmpl-20\n",
    "- isen-20\n",
    "- hnfnetv1-20\n",
    "- scan-20\n",
    "- sanet0-20\n",
    " \n",
    "For more details on the algorithms (docker images) see the [publication table of the BraTS toolkit](https://github.com/neuronflow/BraTS-Toolkit/tree/main?tab=readme-ov-file#citation)\n",
    "\n",
    "---"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "## 5. Fusion\n",
    "\n",
    "#### Now we can fuse the generated segmentations together. Therefore we again define a function to process our exams:\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 10,
   "metadata": {},
   "outputs": [],
   "source": [
    "from brats_toolkit.fusionator import Fusionator\n",
    "\n",
    "\n",
    "def fuse_segmentation_exam(\n",
    "    segmentation_folder: str,\n",
    "    fusion_folder: str,\n",
    "):\n",
    "    \"\"\"\n",
    "    Fuse multiple segmentations using different methods and save the results.\n",
    "\n",
    "    Parameters:\n",
    "    - segmentation_folder (str): Path to the folder containing segmentation files in NIfTI format (*.nii.gz).\n",
    "    - fusion_folder (str): Path to the folder where fused segmentation results will be saved.\n",
    "\n",
    "    Returns:\n",
    "    None\n",
    "\n",
    "    Example:\n",
    "    ```python\n",
    "    fuse_segmentation_exam(\"/path/to/segmentations\", \"/path/to/fusion_results\")\n",
    "    ```\n",
    "\n",
    "    This function uses the Fusionator class from the brats_toolkit to fuse segmentations using two different methods:\n",
    "    1. Multimodal Average (MAV) method.\n",
    "    2. Simple fusion method.\n",
    "\n",
    "    The fused segmentations are saved in the specified `fusion_folder` with file names \"mav.nii.gz\" and \"simple.nii.gz\".\n",
    "\n",
    "    Note:\n",
    "    - The Fusionator class must be available and correctly imported from the brats_toolkit.\n",
    "    - The segmentation files in the `segmentation_folder` should be in NIfTI format (*.nii.gz).\n",
    "\n",
    "    Args:\n",
    "    - segmentation_folder (str): Path to the folder containing segmentation files in NIfTI format (*.nii.gz).\n",
    "    - fusion_folder (str): Path to the folder where fused segmentation results will be saved.\n",
    "    \"\"\"\n",
    "    # instantiate\n",
    "    fus = Fusionator(verbose=True)\n",
    "\n",
    "    # segmentation file paths\n",
    "    segmentations = segmentation_folder.files(\"*.nii.gz\")\n",
    "\n",
    "    # execution\n",
    "    # mav\n",
    "    mavPath = fusion_folder / \"mav.nii.gz\"\n",
    "    fus.fuse(\n",
    "        segmentations=segmentations,\n",
    "        outputPath=mavPath,\n",
    "        method=\"mav\",\n",
    "        weights=None,\n",
    "    )\n",
    "\n",
    "    # simple\n",
    "    simplePath = fusion_folder / \"simple.nii.gz\"\n",
    "    fus.fuse(\n",
    "        segmentations=segmentations,\n",
    "        outputPath=simplePath,\n",
    "        method=\"simple\",\n",
    "        weights=None,\n",
    "    )"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "####Now we can again loop through our exams:\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 11,
   "metadata": {},
   "outputs": [
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "\r",
      "  0%|                                                                                                                            | 0/2 [00:00<?, ?it/s]"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "segmenting: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294\n"
     ]
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">──────────────────────────────────────── </span>Thank you for using <span style=\"font-weight: bold\">BraTS Toolkit</span><span style=\"color: #00ff00; text-decoration-color: #00ff00\"> ────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m──────────────────────────────────────── \u001b[0mThank you for using \u001b[1mBraTS Toolkit\u001b[0m\u001b[92m ────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n",
       "</pre>\n"
      ],
      "text/plain": [
       "   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">                        <span style=\"color: #0000ff; text-decoration-color: #0000ff; text-decoration: underline\">https://github.com/neuronflow/BraTS-Toolkit#citation</span> -- Thank you!                         \n",
       "</pre>\n"
      ],
      "text/plain": [
       "                        \u001b[4;94mhttps://github.com/neuronflow/BraTS-Toolkit#citation\u001b[0m -- Thank you!                         \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">───────────────────────────────────────────────────────────────────────────────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m───────────────────────────────────────────────────────────────────────────────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/yixinmpl-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/isen-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/hnfnetv1-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/scan-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/sanet0-20.nii.gz\n",
      "Orchestra: Now fusing all passed .nii.gz files using MAJORITY VOTING. For more output, set the -v or --verbose flag or instantiate the fusionator class with verbose=true\n",
      "Number of segmentations to be fused using compound majority vote is:  5\n",
      "Labels of current candidate: [0 1 2], dtype: uint8\n",
      "Labels of current candidate: [0 1 2], dtype: uint8\n",
      "Labels of current candidate: [0 1 2 4], dtype: uint8\n",
      "Labels of current candidate: [0 1 2], dtype: uint8\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "WARNING:root:No labels passed, choosing those labels automatically: [0 1 2 4]\n"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Labels of current candidate: [0 1 2 4], dtype: uint8\n",
      "Labels: [1 2 4]\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "5\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "5\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "5\n",
      "Shape of result: (155, 240, 240)\n",
      "Labels and datatype of result: 2.0 0.0 float64\n",
      "Converting float64 to uint8 np.ndarray\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/yixinmpl-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/isen-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/hnfnetv1-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/scan-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/TCGA-DU-7294/TCGA-DU-7294_brainles/segmentation/sanet0-20.nii.gz\n",
      "Orchestra: Now fusing all passed .nii.gz files in using SIMPLE. For more output, set the -v or --verbose flag or instantiate the fusionator class with verbose=true\n",
      "Number of segmentations to be fused using SIMPLE is:  5\n",
      "Labels of current candidate: [0 1 2], dtype: uint8\n",
      "Labels of current candidate: [0 1 2], dtype: uint8\n",
      "Labels of current candidate: [0 1 2 4], dtype: uint8\n",
      "Labels of current candidate: [0 1 2], dtype: uint8\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "WARNING:root:No labels passed, choosing those labels automatically: [0 1 2 4]\n"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Labels of current candidate: [0 1 2 4], dtype: uint8\n",
      "Currently fusing label 1\n",
      "(155, 240, 240)\n",
      "Number of segmentations to be fused using compound majority vote is:  5\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 9122\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 9180\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 10541\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 9115\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 9608\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "Shape of result: (155, 240, 240)\n",
      "Shape of current input array: (155, 240, 240)\n",
      "Labels and datatype of current output: 1.0 0.0 float64\n",
      "Number of segmentations to be fused using compound majority vote is:  5\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 9122\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 9180\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 10541\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 9115\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 9608\n",
      "weight is: 3.740271506862001\n",
      "weight is: 3.8240892486370663\n",
      "weight is: 3.637696953801965\n",
      "weight is: 3.69218021577528\n",
      "weight is: 3.8234751640007185\n",
      "Shape of result: (155, 240, 240)\n",
      "Shape of current input array: (155, 240, 240)\n",
      "Labels and datatype of current output: 1.0 0.0 float64\n",
      "Convergence for label 1 after 0 iterations reached.\n",
      "Currently fusing label 2\n",
      "(155, 240, 240)\n",
      "Number of segmentations to be fused using compound majority vote is:  5\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 14547\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 14527\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 14450\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 15764\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 14593\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "Shape of result: (155, 240, 240)\n",
      "Shape of current input array: (155, 240, 240)\n",
      "Labels and datatype of current output: 1.0 0.0 float64\n",
      "Number of segmentations to be fused using compound majority vote is:  5\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 14547\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 14527\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 14450\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 15764\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 14593\n",
      "weight is: 3.752705851139802\n",
      "weight is: 3.7886928242593774\n",
      "weight is: 3.6542352407582173\n",
      "weight is: 3.7032811775246737\n",
      "weight is: 3.849843061189314\n",
      "Shape of result: (155, 240, 240)\n",
      "Shape of current input array: (155, 240, 240)\n",
      "Labels and datatype of current output: 1.0 0.0 float64\n",
      "Convergence for label 2 after 0 iterations reached.\n",
      "Currently fusing label 4\n",
      "(155, 240, 240)\n",
      "Number of segmentations to be fused using compound majority vote is:  5\n",
      "Candidate with shape (155, 240, 240) and values [0] and sum 0\n",
      "Candidate with shape (155, 240, 240) and values [0] and sum 0\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 352\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "WARNING:root:The passed segmentation contains labels other than 1 and 0.\n",
      "WARNING:root:The passed segmentation contains labels other than 1 and 0.\n",
      "WARNING:root:The passed segmentation contains labels other than 1 and 0.\n",
      "ERROR:root:Majority Voting in SIMPLE returned an empty array\n"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Candidate with shape (155, 240, 240) and values [0] and sum 0\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 279\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "Shape of result: (155, 240, 240)\n",
      "Shape of current input array: (155, 240, 240)\n",
      "Labels and datatype of current output: 0.0 0.0 float64\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "/home/eva/.local/lib/python3.10/site-packages/brats_toolkit/fusionator.py:556: RuntimeWarning: invalid value encountered in scalar divide\n",
      "  FNR = FN / (FN + TP)\n",
      "/home/eva/.local/lib/python3.10/site-packages/brats_toolkit/fusionator.py:557: RuntimeWarning: invalid value encountered in scalar divide\n",
      "  TPR = TP / (TP + FN)\n",
      "/home/eva/.local/lib/python3.10/site-packages/brats_toolkit/fusionator.py:565: RuntimeWarning: invalid value encountered in scalar divide\n",
      "  score = 2 * TP / (2 * TP + FP + FN)\n"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Number of segmentations to be fused using compound majority vote is:  5\n",
      "Candidate with shape (155, 240, 240) and values [0] and sum 0\n",
      "Candidate with shape (155, 240, 240) and values [0] and sum 0\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "WARNING:root:The passed segmentation contains labels other than 1 and 0.\n",
      "WARNING:root:The passed segmentation contains labels other than 1 and 0.\n"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 352\n",
      "Candidate with shape (155, 240, 240) and values [0] and sum 0\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 279\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1.0\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "WARNING:root:The passed segmentation contains labels other than 1 and 0.\n",
      " 50%|██████████████████████████████████████████████████████████                                                          | 1/2 [00:06<00:06,  6.36s/it]"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "weight is: 1\n",
      "weight is: 1.0\n",
      "Shape of result: (155, 240, 240)\n",
      "Shape of current input array: (155, 240, 240)\n",
      "Labels and datatype of current output: 0.0 0.0 float64\n",
      "Convergence for label 4 after 0 iterations reached.\n",
      "Shape of result: (155, 240, 240)\n",
      "Shape of current input array: (155, 240, 240)\n",
      "Labels and datatype of current output: 2.0 0.0 float64\n",
      "Converting float64 to uint8 np.ndarray\n",
      "segmenting: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA\n"
     ]
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">──────────────────────────────────────── </span>Thank you for using <span style=\"font-weight: bold\">BraTS Toolkit</span><span style=\"color: #00ff00; text-decoration-color: #00ff00\"> ────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m──────────────────────────────────────── \u001b[0mThank you for using \u001b[1mBraTS Toolkit\u001b[0m\u001b[92m ────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n",
       "</pre>\n"
      ],
      "text/plain": [
       "   Please support our development by citing BraTS Toolkit and the papers of the segmentation algorithms you use:   \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">                        <span style=\"color: #0000ff; text-decoration-color: #0000ff; text-decoration: underline\">https://github.com/neuronflow/BraTS-Toolkit#citation</span> -- Thank you!                         \n",
       "</pre>\n"
      ],
      "text/plain": [
       "                        \u001b[4;94mhttps://github.com/neuronflow/BraTS-Toolkit#citation\u001b[0m -- Thank you!                         \n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\"><span style=\"color: #00ff00; text-decoration-color: #00ff00\">───────────────────────────────────────────────────────────────────────────────────────────────────────────────────</span>\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\u001b[92m───────────────────────────────────────────────────────────────────────────────────────────────────────────────────\u001b[0m\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "data": {
      "text/html": [
       "<pre style=\"white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace\">\n",
       "</pre>\n"
      ],
      "text/plain": [
       "\n"
      ]
     },
     "metadata": {},
     "output_type": "display_data"
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/yixinmpl-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/isen-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/hnfnetv1-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/scan-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/sanet0-20.nii.gz\n",
      "Orchestra: Now fusing all passed .nii.gz files using MAJORITY VOTING. For more output, set the -v or --verbose flag or instantiate the fusionator class with verbose=true\n",
      "Number of segmentations to be fused using compound majority vote is:  5\n",
      "Labels of current candidate: [0 1 2 4], dtype: uint8\n",
      "Labels of current candidate: [0 1 2 4], dtype: uint8\n",
      "Labels of current candidate: [0 1 2 4], dtype: uint8\n",
      "Labels of current candidate: [0 1 2 4], dtype: uint8\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "WARNING:root:No labels passed, choosing those labels automatically: [0 1 2 4]\n"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Labels of current candidate: [0 1 2 4], dtype: uint8\n",
      "Labels: [1 2 4]\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "5\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "5\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "5\n",
      "Shape of result: (155, 240, 240)\n",
      "Labels and datatype of result: 4.0 0.0 float64\n",
      "Converting float64 to uint8 np.ndarray\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/yixinmpl-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/isen-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/hnfnetv1-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/scan-20.nii.gz\n",
      "Loaded: /home/eva/Schreibtisch/GitHub_repos/tutorials_branch/BraTS-Toolkit/data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/segmentation/sanet0-20.nii.gz\n",
      "Orchestra: Now fusing all passed .nii.gz files in using SIMPLE. For more output, set the -v or --verbose flag or instantiate the fusionator class with verbose=true\n",
      "Number of segmentations to be fused using SIMPLE is:  5\n",
      "Labels of current candidate: [0 1 2 4], dtype: uint8\n",
      "Labels of current candidate: [0 1 2 4], dtype: uint8\n",
      "Labels of current candidate: [0 1 2 4], dtype: uint8\n",
      "Labels of current candidate: [0 1 2 4], dtype: uint8\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "WARNING:root:No labels passed, choosing those labels automatically: [0 1 2 4]\n"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Labels of current candidate: [0 1 2 4], dtype: uint8\n",
      "Currently fusing label 1\n",
      "(155, 240, 240)\n",
      "Number of segmentations to be fused using compound majority vote is:  5\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 1886\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 2155\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 3410\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 2867\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 3005\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "Shape of result: (155, 240, 240)\n",
      "Shape of current input array: (155, 240, 240)\n",
      "Labels and datatype of current output: 1.0 0.0 float64\n",
      "Number of segmentations to be fused using compound majority vote is:  5\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 1886\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 2155\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 3410\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 2867\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 3005\n",
      "weight is: 3.1511742446548916\n",
      "weight is: 3.343718586032138\n",
      "weight is: 3.258616779885049\n",
      "weight is: 3.0533377014683207\n",
      "weight is: 3.5990560996214467\n",
      "Shape of result: (155, 240, 240)\n",
      "Shape of current input array: (155, 240, 240)\n",
      "Labels and datatype of current output: 1.0 0.0 float64\n",
      "Convergence for label 1 after 0 iterations reached.\n",
      "Currently fusing label 2\n",
      "(155, 240, 240)\n",
      "Number of segmentations to be fused using compound majority vote is:  5\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 24365\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 26045\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 19746\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 16958\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 19935\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "Shape of result: (155, 240, 240)\n",
      "Shape of current input array: (155, 240, 240)\n",
      "Labels and datatype of current output: 1.0 0.0 float64\n",
      "Number of segmentations to be fused using compound majority vote is:  5\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 24365\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 26045\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 19746\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 16958\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 19935\n",
      "weight is: 3.6451807045381535\n",
      "weight is: 3.5102207691555116\n",
      "weight is: 3.806188837471846\n",
      "weight is: 3.4225978325341364\n",
      "weight is: 3.861889228137042\n",
      "Shape of result: (155, 240, 240)\n",
      "Shape of current input array: (155, 240, 240)\n",
      "Labels and datatype of current output: 1.0 0.0 float64\n",
      "Convergence for label 2 after 0 iterations reached.\n",
      "Currently fusing label 4\n",
      "(155, 240, 240)\n",
      "Number of segmentations to be fused using compound majority vote is:  5\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 7628\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 7605\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 6569\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 5909\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 6808\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "weight is: 1\n",
      "Shape of result: (155, 240, 240)\n",
      "Shape of current input array: (155, 240, 240)\n",
      "Labels and datatype of current output: 1.0 0.0 float64\n",
      "Number of segmentations to be fused using compound majority vote is:  5\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 7628\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 7605\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 6569\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 5909\n",
      "Candidate with shape (155, 240, 240) and values [0 1] and sum 6808\n",
      "weight is: 3.776505044184724\n",
      "weight is: 3.7866546517920887\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 2/2 [00:12<00:00,  6.31s/it]"
     ]
    },
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "weight is: 3.895390628501695\n",
      "weight is: 3.7132313583169902\n",
      "weight is: 3.9573242849181356\n",
      "Shape of result: (155, 240, 240)\n",
      "Shape of current input array: (155, 240, 240)\n",
      "Labels and datatype of current output: 1.0 0.0 float64\n",
      "Convergence for label 4 after 0 iterations reached.\n",
      "Shape of result: (155, 240, 240)\n",
      "Shape of current input array: (155, 240, 240)\n",
      "Labels and datatype of current output: 4.0 0.0 float64\n",
      "Converting float64 to uint8 np.ndarray\n"
     ]
    },
    {
     "name": "stderr",
     "output_type": "stream",
     "text": [
      "\n"
     ]
    }
   ],
   "source": [
    "EXAMPLE_DATA_DIR = turbopath(\"data\")\n",
    "\n",
    "exams = EXAMPLE_DATA_DIR.dirs()\n",
    "\n",
    "for exam in tqdm(exams):\n",
    "    print(\"segmenting:\", exam)\n",
    "    brainles_folder = exam / exam.name + \"_brainles\"\n",
    "    segmentation_folder = brainles_folder / \"segmentation\"\n",
    "    fusion_folder = brainles_folder / \"fusion\"\n",
    "\n",
    "    fuse_segmentation_exam(\n",
    "        segmentation_folder=segmentation_folder,\n",
    "        fusion_folder=fusion_folder,\n",
    "    )"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<!-- ## Viz TODO add such visualizations## Data\n",
    "\n",
    "AURORA expects _preprocessed_ input data as NIfTI file or NumPy Array (_preprocessed_ meaning the files should be co-registerend, skullstripped and in SRI-24 space).\n",
    "\n",
    "In this example we provide sample data from the [ASNR-MICCAI BraTS Brain Metastasis Challenge](https://www.synapse.org/#!Synapse:syn51156910/wiki/622553), which is already preprocessed in the `AURORA/data` folder in the form of 4 modalities of the same brain (T1, T1C, T2, FLAIR). To get an intuition of the data, one example slice of the 3D scans is visualized below.\n",
    "\n",
    "For your own data:\n",
    "If the data is _not_ preprocessed yet, consider using our [BrainLes preprocessing](https://github.com/BrainLesion/preprocessing) package (or its predecessor [BraTS-Toolkit](https://github.com/neuronflow/BraTS-Toolkit)). -->\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "### The fused segementation is saved in the folder \"fusion\"\n",
    "```BraTS-Toolkit/data/<datasetName>/<datasetName>_brainles/fusion```\n",
    "\n",
    "Run the subsequent cell for visualizing one example sample (T1c with segementation).\n",
    "\n",
    "**The BraTS-Toolkit segementation comprise the GD-enhancing tumor (label 4), the peritumoral edematous tissue (label 2), and the necrotic tumor core (label 1).**\n",
    "\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 12,
   "metadata": {},
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAjMAAAEYCAYAAACp0XeqAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/H5lhTAAAACXBIWXMAAAsTAAALEwEAmpwYAADN0UlEQVR4nOz9W7AlR3YdCC73iPO8j7yZiQQSQBUKVQCLYteDIIoURRVZUjcpdlOvlrqbGvWwx6zbJI1J1n8ya/VPd8+P5m/mg7L50Zds5kvWjxmZZlocGxOHlIaUiqIokSWRQrEK9QBQeGbmzfs6zwj3+QhfO1b4PQkkgKwqZKUvs2v33nPi4RHnhPvytdfe7mKMKCgoKCgoKCh4WOG/3w0oKCgoKCgoKPgwKGSmoKCgoKCg4KFGITMFBQUFBQUFDzUKmSkoKCgoKCh4qFHITEFBQUFBQcFDjfrd3nTOlVSngoKC90SM0X2Y/cf1z5a+pqCg4D2xaX51Z19TlJmCgoKCgoKChxqFzBQUFBQUFBQ81ChkpqCgoKCgoOChRiEzBQUFBQUFBQ81CpkpKCgoKCgoeKhRyExBQUFBQUHBQ41CZgoKCgoKCgoeahQyU1BQUFBQUPBQo5CZgoKCgoKCgocahcwUFBQUFBQUPNQoZKagoKCgoKDgoUYhMwUFBQUFBQUPNQqZKSgoKCgoKHioUchMQUFBQUFBwUONQmYKCgoKCgoKHmoUMlNQUFBQUFDwUKOQmYKCgoKCgoKHGoXMFBQUFBQUFDzUKGSmoKCgoKCg4KFGITMFBQUFBQUFDzUKmSkoKCgoKCh4qFHITEFBQUFBQcFDjUJmCgoKCgoKCh5qFDJTUFBQUFBQ8FCjkJmCgoKCgoKChxqFzBQUFBQUFBQ81ChkpqCgoKCgoOChRiEzBQUFBQUFBQ81CpkpKCgoKCgoeKhRyExBQUFBQUHBQ41CZgoKCgoKCgoeahQyU1BQUFBQUPBQo5CZgoKCgoKCgocahcwUFBQUFBQUPNQoZKagoKCgoKDgoUYhMwUFBQUFBQUPNQqZKSgoKCgoKHioUchMQUFBQUFBwUONQmYKCgoKCgoKHmoUMlNQUFBQUFDwUKOQmYKCgoKCgoKHGoXMFBQUFBQUFDzUKGSmoKCgoKCg4KFGITMFBQUFBQUFDzUKmSkoKCgoKCh4qFHITEFBQUFBQcFDjUJmCgoKCgoKCh5qFDJTUFBQUFBQ8FCjkJmCgoKCgoKChxqFzBQUFBQUFBQ81ChkpqCgoKCgoOChRiEzBQUFBQUFBQ816u93Awq+d6iqCh/72MdQVRW896jrGt57hBDQNA1OTk7wzjvvPLDzXbt2DZ/+9KftHF/+8pcf2LELCgo+uvDO4/DKIbxzcM7Bew/nHGKMCCFgtV7j4uLigZ1vPpvh+vXrdo5XX3vtgR274OFAITOPAObzOa5evQrnHK5fv479/X1Mp1M45wAAbduiaRpcuXIFVVXhzTff/MDneuqppzCfz1FVFa5evYpnnnkG3ns0TYPnnnsOALDdbvHmm29is9k8kOsrKCj4aGA0GmE2m8GhIxjj8Rh1XQOpr4khIISAyWYD7xzOzs8/8LkODw4wGo3gvMdsOsWVK1fgnEMIAdeuXQMAhLbF2fk52rZ9EJdX8BFGITM/gDg8PBz8f+XKFTz55JNwaZa0t7eH6XSKuq7RNA3atkXbtphMJhiNRthut7h9+/b7OufTTz+N9XqNT37ykzg8PMRkMoFzDtvtFgDQNA2ef/55xBixWq3QNA0WiwVWqxVWq9UDu/aCgoLvHaaTyeD/yXSKg/19wDk4AKNEZqjOxhAQYkRV16i8RxsCFovF+zrn4eEh2qbB0dWrmEwmqKsKcA5tCADQk5kY0TQNQgjYbrfYNg2apnlQl17wEUMhMw85vPeYpA6FEuszzzxj75HAAMBkMsFsNsN0OkVVVZhOp/awUyU5PDzED//wD+N3f/d34Zy7pxRcVRX29/cRY4RzDl/4whdw9+7drnOp667jitHa0aSOJISAqqrw8Y9/HG3b4tatW3j77bdtW7b3QUrQBQUFHx7OuU5lEVy5csXeI4EBgLqqUI9GHZFJ+7FPoEoymUzw2PXreGO7hXPunkqtdx7jyRiIEXAOTz35JFarFapEkmKMg/4jJPUnxgjnPQ6vXEFMpOk861fe7bwFDxccvwQ733Tu3m8WfN/hnMOVK1fw3HPPWUez3W4HJKKuayMY0+kU165duxTDXq1WWK/X2G63WK1WWCwWCCFgPB7jy1/+MmKa4ehxb9y4gZ/8yZ9EjBHee7z11luo6xpHR0eYzWY2E+NP0zRYrVZwzllYi7+1g6vrGnVd47d/+7dNMXq372jBRwMxRvfeW90b4/pny4f8EYaDw3Q6wdVr1+DQ9QFtCB3BAKxPIcGo69rCTSQ6VEqatkVIzz77q6qqOp9L7JSViP64e3t7+NjTTyOm/y/Oz+G979Tl0cj6Mf6wv3EAQvqf4a2ILtSFdA3ee3zn9dfTNtHOW/DRxab51Z19TSEzDyGotDzxxBN4/vnnLTTEcE1VVXDOYTKZWMyaIaS6rjEejzEajVBVFTabDdq2xToZ8i4uLrDZbDAajdA0jZmFf+d3fgdnZ2cAgOeeew4/9VM/hddffx11XSPGiPV6jRs3bmA+nw9ICMmMc87UGW6vag0A+z2ZTBBjxGazwR/8wR/g9PT0+3CXC94PCpn5wQS1lv39PVy7dg2+qoyIAIDzHg7owkZMLKgq+PR3VVWovIfzvusTQkDTtthuNthst2jbFlWa+Lg0wXrj9dexXndqybVrV/Gxj38cZ2dn8N53hKhtsTefYzQaIcSISJKSyIwDenUGQJv6GFWL+buqayBNpt555x2s1uvv8R0ueL8oZOYHCF/4whfw2GOPGVnYbrcYjUZGEoDO9EtFhsRFf4/HY7Rta0rMcrnEarUyybWqKusAvPfYbDZm6p3NZlgul1gul9aBXLt2zUgSVZntdovNZoMYo5EokhQlM23bdjHt7dZmSyRmnGW9+eabeP31179v97zg3VHIzA8maOhHes7bEFB5byQB6Ey/VGRIXPR3VVUISZXZbrdotlt77oGOEBkRScqtdw7T2Qyjuu68Ltttp5nEiNls1hGnNGmLMSJwAgUYiSJJadq2JzMhoA0BoW0tpE1ixv70/Pwcp2niVvDRw73ITPHMPCT4G3/jb2AymWC73eLk5ARnZ2dYr9f2QJKETKdTjEYjTKdTU2WqqkJVVRbC8b4vL8QHWGPOfA3owj6qtJyfn2O5XGK73WI6nWKz2eAgZRVUVWXH5SxtOp1aSAsA1uu1mYPZubVta9vTMMzYfAgBbdvi2rVrnRT96qvf/ZtdUPAI4yd+4idQVxXaELBerbDebDri4hyqRDaA7hn1qV/h8+udg0sTEn3uARghMtaaQk8avo4MCaU+rdlu0YbQeW7aFpPxuCMx0od55+BS32YhLXRkq0qZVCERmOA9XAhonUNI18H+MMaIkMiS8x4nJyff3Rtd8EBRyMxHHFVV4Wd+5mfwjW98w0hD27bw3mM8HlvMmQY7emMYUqIyQ7LB2Q9nQOv1Guv12hQUn+RgZjoBsJg2s5Oo/uzt7WE8HmM2mxkh0vo13BeAKTzj8dji6/TQ0BSs16zn5zGrqsJ4PMbLL7/8vfwICgoeCXjn8YlPPIPj42MjDTGFiKtEbpCecX3WKyEvlfddiMm5zuMCAM4hJoWkTYoM/S88DidPEX3oKrQtWhKd0QhIpuIYI5DMvQPCJCEkthmivjgAPkYEIVg+9UU8v/kJk7pz586d78WtL3gAKGTmI4bPf/7z+OQnP4n1et3JnaenprrQDEflpWkaOOewXq8HsyWGkVSVAWAdB9CRC6ZFkxA55waqDlWT8XiMi4sLU1DG47H5akiiKO2yY+HxSGzY6TC0xHYSPDeJjHZINA8zw4mG5/F4jBACXn75ZVN0CgoK7g83n3gCR1evom0aC/2yH9mgS6uuEmEJIQAkF6KkMIxEAkDFhGQFgCUQNE1jhIgmYpf6qNC2Xcp2VWG72SCkvopKkK8qeAlFkfCkEwCS1EB1RsPklfdoASCETmFKKpJPITOHjkQxrL3d0LPTGZ45Ebxz5xhtKDVrPoooZOYjgp//+Z+H9x5HR0fY29vDYrEYSLRUV1T50HARt6XUyh+SAxIHKihN0wwUGfpdeA6bjaV4c9u25puhwqLn0xRJ7psTHAADBYbkaptSMxnKUiWGahCPr21gB/OJT3wCTdPg9u3bZlIuKCjYjefTZGA6nWKUJi2QZ9SLHyUv7wAA0PAMwzrOGTmoRJWNSL63FKpGIiyexmASD+c6M2+MiCm07aUP4/ksOypGROfgATMOewkxAZ3qAvaR6XratE2kcpTazH3ppaHfxqeQuEvm46OjKwghYLFcmkJd8NFAITMfAfyxP/bH8JnPfAYAzFi72WzQNM2AwFBtsdgwem8JB3tur4bfKuuYSBpyJWY8HttxgKGSkxvFlcCwDXn2Et+nnMyOadAxClTBIWEJInOPx2NMp1MsFgtTZZxzuHnzpqk98/ncCND7LfxXUPCDjo9/7GO48fjjAIAmFZLjhEUJjHlgEmHxISCmvoCDvW2flA4npIDbQJSYSpQY6wdSv9LECMc+Jk9KScejuReAmYEt5KRhraTUOO/h75HgEjnhQ0+GIhUemQRut1ubNME57O/vm9ozGo3ggA9U+K/gwaOQme8DRqMRPvGJT9hg/aUvfcmyeVh7hSEkKipUKlQJAXqlhQRBQzW6PaFhIU3XVp9L0zTw3pvBmCoMO70YI7bbLeq6xnq9Hpyf2+n59D36Y/LQFLfx0mGqOZnEiiEuVaZ4zY8//jiuX78OoDMahxBwfHz8AD+5goKHC5WvcHR0xZ6nT3ziE5bNE3TyAZiiQqWCRMYlhcMLSQBg3hiGmEypSfDeo+UkJpmFc2MwJyRUe6jCBCEq7CvapukJS0KIET4EBPTKDRFj7Lw7JC5CtoBezXaApXYjqUmqTA/6p2Q+3tvbw2w+B9AZjWOMWC6XD+pjK/gAKGTme4zRaISPf/zj+It/8S8asSCBWa/XWIp8OZvNBh4TgjMbHehJcEhKnDywJCus6UISMZ/PB/vmigk7FraTpIZZSHVdW6x9ImXNeQ6Gs/RYeWVgJWvcjx0c49ckURo2o6+GPp7pdAoAlnk1n8+xv7+P3/u93wOAEn4qeORQ+QpXrhzij/zIj/RhYBaxbNsuUyg9n/VoNPCYEMxO0oEeeZ8hpIBkRSdZjs85yZBzyLVZ75wRklhVqKT2VEsy45xlKHH/mMJNjhmYJCzos5OARE44AcwVY24LIVFumJXFYnveOfi6BkYjW5ohjkZ4fDzGm2+9BQAl/PR9QiEz30NUVYVPfvKT+PN//s9bmjUJxnq9xtnZGRaLhSkbzE6apQXbNHzErCM11qpiQ2jKNd8jGeJDp0RJyRXJBn0tTdNgnopVsUowAKsePJ/PL3l5NINK20RyohkNGloyI2IKt6mhmAQoxoj5fG5ZVSQyii996UsIIeDXfu3XyhpQBY8MvPO4evUIP/zDP2xp1racQNNgk55ZDvZ8BkfiVdvHGME7tL4byF1dA5xYAJcmPwzo6Hs+hW2aLA2a53TSF9TpvCGdYzQaoUp9D/uxpm3RpvcGXh7v4buD9j4Z9IqLZVWl9nnpe0Iiapw0qUHZ0+OXQvij8bjr0xKRUXziE59AjBHf/OY3yxpQ3wf4996k4EHAOYfPfe5z+NN/+k/ba977QVrzbDbD1atXcXR0hOl0irZtcXp6Cuf6ar5UR+ghUQVGZ0Q8viouVHGY+TOZTDCfz40o0eRLMkPSQ/UF6OrYTKdTW8+J6dWqMvF1Hos/XmY6bCsJUVVVFvZiJ7NcLq1TYLhKO4npdIqjoyMcHh4OwmXj8diuiwW2fvqnfxqz2ey7+REXFHwk4ODwxBOP44d+6If615zDKKmZEZ0SM03rtNV1jZgmVEikoqoq/LmbDs+GA/OQODt+HwaGTJYGigsJAutViYfPOdcVr0sVgVn91yc/H4lPrsBaerWoTLo0SkjEJMpESSdM1i9K2AvJt7OVSuQMl/F/tmU6nWIymQxT0bUYaVqH6hPPPDPI1Cz43qAoM98j/Kk/9afwwgsvDEJKTHlumsbICmcHrBVzcnKC8/Pz7iGSAZ9hm9lshrqusVwubTajaco6e2HHoMbdEMIgtMX3SFhYqZemYf60bYvFYnFpsUq2Tc2/eaE+tovXwDby2nUdqDydnO2o6xr7+/sWKuO5eH90TSh2OPcyHhcU/CDhuec+hZs3b5onpkmh2M1226m9VYWY1AU+S5X3WKXsxlqK0lW+/7tOA/g2PZ+V91Z4DuhrygCw0EyVyJOFnbdbIys07RphSf0IlydgWCumauL5YpU0HdNIbOne2XPuugYN2shr55IHSOcbTPykrg6zPSOSAuVcdz+S8swwlVM1p+B7iqLMfI/AsM6dO3fAtEjWT6EpdjqdYn9/H3t7e5jP57hy5Qoef/xxc9BfklYTmJGkadNqvOU+WhiK9Vu0AJ/33sI6FxcXOD8/x3a7tRozSqI2mw1OTk6w2WzwsY99DIeHh0Y62KGQ4FBN0ZkPvS+5ckTys9lsTNkhuB/vk5U1T+3XbC9mPimJ+dKXvmQG4YKCH1Q479G0bWdIFdWUk4RfvDHCD7mr3QA9HuOH/DX80tN7Fq4lUXEO+KlP3sKLzVU7Niv+atq0Gm+NLDAEk8JMJCma0cjJy5bPevo78PypP2nbFuvVCm3b4vDw0CqId4d35nmxMBGG4fVBcT32NWxbUqSp7Ng9TPvZWnZ1bcSJirWqMySEvA/PfuIT3TIQBd8zFGXme4C/8Tf+Bp577jkzoTZNg7t371omEAALq1B9GafYLB9C1mKhqVYVEDXjLZdL88Dog0domjQAU4pIHqjQKGmZTqd46qmncOPGDcQY8e1vf9s6DapJ+/v7lkGUe3eoFJEw5dlLKufqUgqazaWqDF+3Yl7AJfLG7bkA53q9hvceL7zwAr761a/itddeezAfbkHBRwg/8RM/gWtXr2G96Z7jEALccov/+LG1KRDj6RlevLHAj6HG628/hn81OsOv351iNAqWatwREgCuAdBXDWeIyQHYJl8dADPM6jIDzBJiKIdKEcmD+WikL6rrGgezGeZ7e0CMuHtyYn0kvSrj8dgyiHLvTmhbNOgX21W1yEJjhBqEgWF9nKTKwDnLwtLwvZ2RIaxkVOaq4CwZcfvWLZyUhXK/Jyhk5ruMv/7X/zp+5Ed+ZEA0dE0lM96JqZdhptlsZotFLhaLvrZBGqx1lkNFQ2vKkDgMyntjuB4TfTsaetLje+9xfn5u5lmSKM1uunPnDvb39wfLK/DYqgppyIjG4FYkZ/7mbIezRCo8qmDp7IjH47XpD6+DC3FWVYXnn38e4/EY3/jGN753X4SCgu8yfuLHfxw3HrsBOMA3Hs/gED96sIL3EdP5etAPjEYRMWzwzFO38eTmEJvtBL+ybM3s/2f39rC3fw4Hh+duHsO/eQ3/enzSkZb0HHslNyQOkgmE9L/WgqnpiQMwTt4UJSWq5NqyCOm5Bbo6XJzotRIiMtVFvDyWQp7OFzlJQk+ynOvrytAsbJMmZoeSqHECpupO7LO8mAXFhTi9c7am3J1SIuK7jkJmvst47rnnsLe3h5OTE6tkO5lMbBaiVW9ns5nVmrFYtpATDUmp+qGEQUNRuQGY0HoySopms5kpP5SleV6SmaOjIwDdukzXrl3DjRs3cHJyMliiQNUiYlctGkt7TB2eZj6R0GiYidI0ADuPSr18j4oMy7Pz2Lxvk8kEBwcHD/iTLij4/uLqtWsYjUdYr9b4xHYPnz5c4tpj54ghog0eMUTEpLKM6hHa0GLqt9jbP4HDFD/3nev4VdyGcw7fPpvg6GiBahYw21vhyjQAIREBTsJoCna90RZZX8NnPqDPKnIpa4rVgXXS0TQNzhOZYbmFUTLy783nWCX113s/qCA86OMSqSBC7JUlvq9rRzGkBPXPuG49KQBWHND6VddVK3ZJ2WlD6JQiZkL5bhkGOIdJXWNcsii/Jyhk5ruIf//f//cHoRV6O6g0ALBBWFWKKnt4ckMr0M8gNMREUqJSau5HUYKhikluyGVYC4Cdc7lcdivKpjYxxs4wlfp26IdRhQbAgIwN4trZ/yQo7OhUhRnUiJBQFIkYZWwWItTlEKhgDeTmgoKHHJ/85CftufpUOMSzBxe4/tgZYqzRokGFCtFFhBiAiO43AOc7RaUetXjm47fxR19+DL9VvYOXJmfY+851PPf0CebztdVf0dCNR5+OjfQagEE9GXsLsGwjC0ml19uU6g30vrpt06BuW1M6xqIIcyJI3471L5wwZX2eKUYQTw/QVRxWgkLVKSM+3N+5vlaNXg9DTPxRlch7f7miccF3BYXMfJfw4z/+4/hLf+kvGWEgkaHxljVkmG3DlOm8KJymLu/t7ZnPhuTGHuws3VlJTK6KAH3lzfx1oDfaasG72WyG/f197O/vG5FZLpfYbrc4Pz83okG1iQoIj6VkhOdQIqV1c5SckWTxPU3vBIaVOnk/tJig3icSSN6vg4ODUkyv4KHH0089hc985jNwcPhYu4c/cmWJK1dOEGKf/QMPhNDCRdeRmTbAeQfvKxtwnWvwmefexPHXr+MbozP8a3+G8VvXcHVvjeOVQxjFbi0kTj4AW7gRQD9oZ32KFaHb0XYlEkAXmqnTQrnjtNDlaDzull1YLLDZbPpwj++qEteuSydnwTwNCfEcTEnXtPKBmkSFx+6Fs2q/dj3pfWZC2e907RbeDgHUk9mXTSaTUkzvu4xCZh4wnHN45pln8N//9/89Tk5OLESzXC7Rtq15YFjkDhhm8ehDqNV/p9MpnHPmS6E3JVc5VIFge7RaMEkUz6vnpPLDQV8rER8cHFgW0dWrV7FcLvGtb30Ly+USBwcHmM/nAyVFi+5RnVGiQsLDdqjawuvQlGySQQCDRTH5Gs+ry0FophaVGr6/v7+P5557Dn/4h39Y1lUpeCjh4HDl6Aq+9Cf+BNarroTCZ/dW2N9/B22IqKsKIU0aBvVfqGbIsbT675d++BjNN65j7Rv8QbXExXqDOF6hct7MvMDQp5JeuFQt2CYw9MvJM6/FMbUS8SRlJY7HY1TTGbYpYaLZbjFOpRfMB8PjJNUkJnKkPp5AdQXDwn7qt8n7YqrUVdUtiOklkcLOK5OlIPtRqYkhoEnewmtXr+LW7duDshkFDxaFzDxAeO9x48YN/PIv/7KV/D87O7NsGn7x+aAul8ud2TwkFEpKSAyYxTOZTIygqIJCdYf7qGKj9V9Ye4XkwTIMkmpEsnFwcGCqCWdLd+/exde//nVst1scHR1ZrRudfVBpolGYoSc1GKspODfujkajS2nZbC+9REAfRlMCo6SG+7LD4ucSY8Th4SFefPFF/NZv/VbpZAoeKjjnsLe3h1/4j34hlfxvUa1bbOoG28nQhF9VFRpmQ8ox6Flp2waULWp0z+fPPncHAPAvvv44vlWdo0GLFfrUZ+9cF1LJfHumekjoxzuHWFVGghiaMQU1qTuTVAQ0iMdttVrhzp07CG3bFfjjwrtVZdlQiBGB3jj0YWojbOxX0nskWjTvVklt0XtbJYXGS4aWhsKsHo5ci92HRNqC66oZR3QFSp968km89tp30IZhlfKCB4NSZ+YB4umnn8bf+3t/D/v7++aD0bRn/n1+fg6gM9FqaGi9XmOxWJhx1Tlnxevu3LmD27dv4/z83IgROyoO1lr7gAZZoFc2SCI4cKtxliSGD6UaiRna0TTn7XZrWVCsp6AKD0mFKkIsFmjly2WBS607A/Q+HR5X28LKx1RoSGyovmw2G1xcXJghWWvPaP0ZGqZ/7ud+bme4raDgo4rDw0P8hb/wFzCejBFDhI/An7mxxcGV4wGhp8o6Ss9MjAExdobV7XaTjKuxIzJ1N1lYLpdYppDOi8++jv/s2TN8cXSA2onhVn16EtZRn0qMfQVgDvJUM0i2AAyMxMxgCqzs2zQIbWtZUFZZVxUemQSRuASackWJsklNlhihk0n6eNgWVj6uqsraBqD3ybQtNsmTl1cG1vozNEx/6rlPYXfAreDDopCZB4iqqnBwcGCD+OnpKdasqpkGVD44JDccbFkqmynZe3t7RmTG47EViSP50SwohlpIEKhgsEgWHyx2clpILvfX8Djj8Rh7e3vWNqolNP3yeg4PDxFjVzGYniC+B8CunwRKPT2cQeXmZ90X6JdQIBnJqwxrejf/1+2V5GlHw89hs9ngl37pl767X46CggcIn5QMDuL/yY0L1OOLS1mCQL/afTfYVqjrEaq6Rl2PUKf1hkhkWBLBUqgTWfj402/jz16Z9oooYAM4FR6qMMz2iUn1GBhyU/s13FNVFUai3kZ0BGc8Gj67k8kEEGXWC0kBulBV27ZWldjC10BvSKYSBPQrfQOXllBgH5FXGbbCenIs3X4Q4iLpY/uS+v35z3/uu/CNKChhpgeEH/3RH8V/+9/+t2iaxpYpuH37tvlk+GCRCMQYcX5+bq+TnKjhdzQaWZVgoFdSAFhIhR4cLlzpnDOTHLfNa9LosRh2AWDF+ujTUVLB/bmyN8NlMUYzA7PdGtLRGRjJC0NN+jq3Y5hMSZqmoDPUpgZqzvRIvHh8hsc0W4yql2aWsYjhL/7iL+If/IN/UEJOBR9p3Lx5Ez/9xZ/uJiZVhT/3xAKnp2eIMaCqawujUClAjF3YGhGISMsF6FpFnSckhBZNk4VLkNKnEXDl6AS/ON7D//ROp7j49Ew5SO0VKiHipaHJt0lqBgBbUoGqsRISHq9pG1s6wSfSNB6P0aTn0/m0uGRSnG2pAfRGX/PpZCQESTXSSsZsKwD4RMS4XIEmLDD8ZEoyw2vJO0PS0zbN0EuT+vfVaoXPfOYzeOnfvVRCTg8Qhcw8IIxGI8znc6xWK1xcXODOnTuDuif8IusAy7CPkhjN8GHIRL0lGp6hsZchGSoqGi4iNKsKGKZqq9rDbauqsorE169fH6hLe3t7ODg4sLLiVHs4e2KbtU4OiYpmcClJYZtIVNQ0zPuiJEXfAzDojLQCMgCrOaPZUCRPanaezWb4+Z//efyTf/JPLBRYUPBRQ5W+x03ToNlssanPEVOqNdc1MkM9B1jngFRnhiP+nduHuHs6tX5F10Tjs/P0zTPM97eJ2ARMZxf4T6/P8D+9EwbrEikcuroy9nTGPgVa1R5u653rqgk7h9l8PlCXxqMRxpNJt15Uui7WfamlrIX33ghURJfuzX5Ns5uo0phXRrw02g8pSdH3gESiQoDTDE3ngKrqwmMkeFXVpX+nc7B/bVLY7Lnnn8O3v/UtrFMfVPDhUMjMA8DP/uzP4pd+6ZdQVRUWiwXeeecdKyTHGK/NPITIUEFhtk0rUqdmAanDPicvJBO68jVVG3YcGmbi8ZTsULFQDw1nHSEEzOdzHB4e2qKYvB6qJLzGqupW2GblXl3xmh1e3lkqmNatsx5uT5WG7eW2qmTxuHq92tmy3gzJHrObSOTW6zWOjo4GJKmg4KOET33qU/j85z4P5x2qTcTPVG1fSC5TF2IIaGOAQyo26YC333oCbdvVmdlsPZpYoYJHDEAbPUJgNmHXd7z59gFGx8CVgy2uXrsAXMB8bwt/p+pNvEzPFj8K2P8AA7ITQ7By/wxHkUxxMjOZTLo1msRv45Nnxeq8eI8WQIXeyNy1W+q6CGHK4ZN/h+EyhpEAwFX98i8xkSKafYGOfIV0HpIxKjLwHjVg9WbY/4S2HRiG26axDNWCB4NCZh4AHnvsMTzzzDM4PT3F3bt3cXx8PFh3SUmHDsBAH6P1vl9WAOi8HMvlcrDqc+590TTmtm2N7FCdUJMbt9MUaG0fCQcJFBUL55wZk1dpsbeLiwvblwqLkgqelyErJSX5LEehytAuBWkwO0ozSf7N68u33fUZ6AKWvJ80D4cQ8MILL+ArX/kK7t69+36+BgUF33XM53NcObqC9WqNzarB7MabWK62iJRbXJ+OHCLroHTvHt96DJ/9o1+Hc+3gGTm7NcO//FdPp77Do6o8nPPw3mEbIjbriBBqLJZzXGxG+PSn3sZ/UF3Hr8Zjq+hLYzBBIsMUaK2sS8JBRcSyFp3rjMlpIlTHiM12aySDISElFZGKjfR9g5DSPfoa9b4M+iMqMfI/w1jg9aT3GcqCc/AhdGnhso/ZB8Sj42grSP33zZs38dZbb2FZqgR/aBQy8yHx+c9/Hp/85Cdx+/Zt3L17FxcXFzg7O7OQClUQPoQc3PnaZDIxVYFmVYaXOMhqhVvOXLTSrS4kSf+M1nHJSQyAwd9sJ/0n2r4QAs7OzrBYLOzhpKKkKdVsH/cdZA8k4qHtBN69cJ8afHPwdVVQ9DhsN6+RbR2NRuaHyckcw2BN0+DjH/84Xn755UJmCj5SuPnEE7h6dGQTi9E6Yr3ZILShJwiiSgyfAeDZ597G6KdvIdTBzKr1Kx4nb+8hhIgQIuq6t+hWvsYPf+oWZvtnOL51gLfePsJzz9zC48++gcoDP/HyTfyr6jY2sRn4Y6hYIEZEEgqZeNFTMuiTnANCwJrJAlQwUhVgU3l4M9K+/M11okg8fNanqBE4h3eua+eOvsZImRI1SLhK289wGrpQIP1BuZcnoFsQM4SAwytXcOf4uJCZB4BCZj4kvvjFL+KFF17A8fGx+WRWq5UN3iqV5r4YZubwfyouDH+o4Zev0+TKjCQSEIZ21LjL8+bxYIaecsVEQ0NUVTjIr1YrOz4JFH0y6sXRY6n/J1dNdJtcdcnDa5rKqeRQyaKSntwvpPvuCnORQGoqa36MgoLvNz7+zDO4efNJrJYrxOUGN7dzNM02+ULSoJoUAp1gOERcvXmO6X/0joVDYgio36hx6198HL/3b56Gcw287/uINhGkq08cY/5j38HRG1Nc/cZ1zP/cK3DtCLd+50fwuR96G//u61NsY69aqCeFtVzMDCxqiIaGrJ9M7Wqaxky2MRETpn+zTzCkY5nSg14tMYWF7dlFaOR4pljL8UhQlCxGOcalyRbvL//mPWFzfbcGVIh9FuauCVvB+0chMx8CV69eNcMtvSOnp6dWlI0DtQ64ukwAw0okClq4jsSGf89mMwuRbLdbU2hoBOSDwUwjXV07V09UlVHkNV5oulVCxuwnZhbx+nN1Rf9XT5DWwdFMI26v90yPpaSI18H7Sak6JzZqmqYpWe8VDcW8nwDs/pcOpuCjhNlsZsZ1X3kcuhlefOY1bDZ9ZlJ0aThP2UrepYlGHTD5D9/uQkivhc7a4SJe+6fP4ve/ehMxMtsvIISI0ai2/ug3f+NZ/Pgq4uhLr+Pgc68hBABtxFdPahxd6yZSVdWvfs3BHIARgV1Pkj7v3aZJaeUkIvVdbfLjsOYLCUnMlBKCFXh1cckq+WNojjbtSdQdaVhPYLhduhYudQAxWeu1Otd5hgZ9kXh5HDovDX0/MYRuGYfS1zwQFDLzIfBf/pf/JT7/+c9bMTwWvOMgqys2a+0HmlTn87mRE375uVQBK+4CwMXFBWaz2WDBSdZH2dvbs4F4NBrZ8WiS5QOtGUuqGOUEQNOmQwhYLpeD7CAeiynhOrvSh1gzj0h2aHijP4XtVqOwLkPAcwLD9GwlGmrg1e1y4kKDL4kYFSaqXVRkeO94rKLQFHwU8MILL+CJJ56w7/p2G9G0jZGWGDqPjPMcxLkMpANQ2+ThN//eT2PddO93z06DGAO8r5JCuUlZiDQDB/zWbz2Dz56O8cR/8i34eYUwi/gL/4f/H47/x+e7CVNSX7SeS0yhJF2MMicAHOD5epMM+gAGx6pzFZmGXMiEBdI3pH3oHUIiEMH7Abkg2bCJl3O2+CTbEIHuNcAMvJaJJYpTSO8jnbNtmp6IpXtEs3Objt8y0wyX+7WC949CZj4EuKTA2dkZbt26hTfffNP8JFRONLSiagLfOz8/t8F7tVqZCZXhoslkAgBYrVZWoI4D82q1MqKk9VeAoTFXDcNKVvjwkCCpapKrOfP53Lw8NAIDPQHZbDbWEel6T0pGNENKCRK312UZ1BOj3ho1PfPalDRRgckN12oW5vVyOxIZrTr8hS98AS+99BJefvnlB/69KSh4v6jTM7Far7BYXCCeBayWK8ABla9Q1X19JweGeSLadoQ33rqBj+HbXa2ZEBFjV8Mlhj6tmaZfAGjbJtXGAmIMaJoW/+YPHsfifB/P/u+/YplFR7/4Nez/H38Kq0qSCqgEY0hWIH0JJ3RUMgbvo5uUsbpuk2q1AJefecg5gF5xyftcJUjc3tRmZiVp2CgRsyjHI4lR0mSqMq+LZEfNwiQ66bjsN3WS9ORTT+HWrVu4c+fOh/2aPNIoZOZDgNV6F4sFFosFLi4uAMBWlubgqLUQmHbNMBAftPV6bdVvuQglycVsNrtEhvb39y3k00m9lZEV4LIhludRpYQF/jStUUM6fPDon6Gi5JyzGjQkF/p37pPh8gNsC5UhfaC993aevC6PhqxsRiXv67E0VKYqCzsfnp+fC5Uw/rCejvd+QG4KCr6fqOsao3ok39NuPaZuZWlRWlMtGT5/V64t8PG/8k8B1z+D3eTJIZryqMuF1ABc4hYRznmMx+l5ZT+W1AjvPf7jP3KMf/SHN/CWW3Y5U4kIcHVt9b1Z4bj0HgmDR59dVFM1dr2plzVoTNHR0BXJR1JJuPwAgAHxsOwlwLajMhMBgAqNhq/EQ6Ph+dx3x3tj5+D5XO/bYegrtG2nyEjYXf2UBR8cpaDGh8DFxQVOT09NIZnP5zYgsxQ/OwldE0gfcpqAqdTwAeHCiSQvrIzLQnQ6M2CYiiqHhmR0eQGmcAOwfUiAmEmlqdUkRlpld7lc4uzsbPAgKlnTa1bVRTsCDbWp+qILS+oaTPoDDIkJ96X6kqe9q9qk6zjxM6IaxmUXePycRBUUfD+xSd/RpmngfF/8MYSApk2qI1yn1FRpyQJfdVEQwJYN+Mm/+Rt4/KiF2HVlMtCRlxA6stM9Ox3liDHg1TeP8LX/y0+aAdZ7j2v/8dfx5/+9N/F8OOwqCftuyQSGn4Auc4deGiY1eOcGKd3aDzAUtW0arDebPhTkXO97kdAQ5Bi5AZnX7rP+QxeWrJho4fqUayM13Fb3jZeTDjSxgfVwvPRPDb2QIdiyC2D7XFmt6UGgkJkPiP/6v/6vcXh4iOPjYywWi0sqAx9OpvvydRIEzlT29vZsPRSuJ8RtmBUFdPUldE0hVT64vQ7WMUZTOVTt4INIhUXTpdluPS4zllTipYpCUpUXrNNryQ3QPI8SErZfM7iYms7/OXtRhUtVGb3n2sno+kwkklRkNpuNLW/AkB4JVNM0+OxnP4sXX3zxgX1nCgo+CP7oH/2jmEwmWK6WNgkhlOS3oa9hlZvlne+q6YZZxI/+776MT37sYjCZ6PqIYGEe5/qwE5WbJx87x7/3l/8FANiaRWHUwtctvvDkMf6zxyJ+qjns6tt0J7Zzw/XLI2i7OZB77y1jSUNWpgYzHKQhI5msWaXxdL2DEBEwKJAH/u96w67+D9ebmXfZBPSeq3lX12fyiRxFUWGaVHPGe4+KbUY3Fjz++ON46sknP/R35VFGCTN9APwX/8V/geeffx7b7daq/XLhSJpjOajTx6JSIjuRpmksTAX02UJ1XRsJCqFby4PKDQdx9dYoCcpDRED/ABOaQURiAwwXgdT9SIg0pMX1plSV0dCYdqrasebhIM1w4vYkMGoq1n1U8tXMKO0IdS0UtlNT31erla15pUscsI0sDsjPpqDg+4Ef/fznce3aNYQ24GJxgXXyq+2102617Mp31YCrCpVP32HXezWc68MY9WiEertFeAL44f/wD/D8eYXbX30Cv/uVj5ky0zYNXF0B6AfxvpREQLhZ9YZcwAbs0WSNEYBnng6o3ryKf4pjgIZb8ZV453oPiSgezjnAd9lMbfrh9lxvimnlRo7keQeGpmGgn9SYgiuel8H2SUWxKr6yDcNYJDbMjLKMKPR1akiALHMqdsXxqLIDsJW3zRSdtt2k8GHBB0chMx8AL774ImazGU5PT3F2doazs7PBIK1eFK1qS/AhpGLCGjF8j2QhhIB1KlWee0wAXAoPUQnRCr25b4bH0BTofFu+xlkgSQXVktFoZCtpqz8mX0BSSQr/33UdPDdJh2Z+EbtmRfdKCdesMQBGwtbrtREUqjFctZzqEM+zWq2w2Wxw5coVPPvss/jWt751H9+MgoIHiyeffAqjeoTz9Tk263UXdkmDZBtaVKHCqBolXwiNp/0zsTjbw/n/9QU8/Vf+LSJ9KwC2n2oRwxaPH72GL93oCmJu18CXf/OPpGdg+Iw+c/Mcn/qJb9qq2FRCtpvNoB7LZLrBtStLuJOs1o2Efro2wgrVRXShKCMGNO7Hbv0krqSt/hgLKUnflfex2rcp6NXR9G3dylKxuwP11yBtTifpM57SviR+TdtimzJLmcXkJas1HRQRsmjwdIqrR0c4LsU6PxAKmfkAODg4wGq1Mr8MMHyY1uu1DexMhaaCQMTYLXKoUi+PA/SrZtPLQSVBTakcjHWfvOqw/uSdixoCNVVbFQrdhucmAeBMQn0xPIYeS1WZPDSkISrNBMihpEzvIYlLnkbNNmjtntVqheVyiRgjptOpeZh435xzl2R8hp0KmSn4fmA86T14H9vMsd/MAUTMU5fRtJ0aDNeZf51nbZXOR7LZjPC7bxzhZtuab8RUBe/RPBMxevYYlfeYrCN+fPkmmqbBV77y1OB5uvrYGcKL5/Cu68O4BpOGdZz9yDMK9L4WUSzsPfY16JWSIP0ACUCQcgm92wfIqYr2QXloyKoCsy07iA7k2JC+BjF2yhGPiy5lW8mNmXyTGrNtGkT0S9YwNMdraJNqRTDsVMjMB0MhM+8Tzz//PNq2NSJDE68ShO12i/Pzc+zv7w8GaNY4UeVDPSn8G+hX4QZgywmcnp5a6jfVGyozHMxJfnSxyFydUfWCRCbPEKJZmAoRs5noQWG4RmcaWh8GGK4ArmoKkc+kdL+c4CkhIsnS0JRCyZimkzdNl3I6mUwwnU6NSOVmX5I0tns6neLatWsldbLge4rr164hhoj1eo0nNhN85nCN64/dMSnAoUYb2n5xVxdtdG9Di8o51HWD5/a3qP/tBOHz2z7sm5QVoF+FGzOg/svfwXa7xacv5livYFlFR48ve+MuVdSmgfsXB9gsZYFLC+H0xEl9K5YEgOGkylQjTsSAQaG8NgyXPqGqQpjHJYWg7LUE7SE07Tpmx8nDVFRkNDQ1oEAycRukk4eAuqpQMflCJ2O874AteUAiV9c15rMZFsvlfXxDChSFzLwPOOfw1/7aX8Pt27dxfHxs/hj6OkgguHo2SYeCvhoOoBxgq6rC1atXLUOBXhiGkjj4XlxcwHuP+XxuRevopdlsNpZpxE5ByYl6dpxzg+wdoA8L8SFumgbz+dweztlsZgRLKw3nBIbnUAKiBIr38l5Qr4ySFv0cVG3KyRJJFH1Hy+XSwnlqTM7vR5DOSCsWHxwc4MUXX8Q//sf/+AN8awoK3j8cHF78whewWC6wWi7xH1ytceXKGUKsgNiteu1955fZbreAA7wbPichtKiqLR577C5+6//5x/DHb/wGwlPdPrPptKvxEoeG+qqqsKlrfPyvfA0bqfTdPbsjM9G2bYvNeo3/+R99ET/2+Cn2DtbDZzGN+i6pEFRW1JjL0BNIYEYjhJTBWafsQwBoGO7OJh3Wb+1Qhe3Y3T/3vM8Dr0wWquo+B9mf2wgZIzHjWktNCitdMiZLW8EJLWDp4fThjCcTPPnkk3j5G9+4vy9KgaGQmfcBmnCZig1cHrzbtsV0OsXe3p7VhNBQEAu7EVQ86NmYz+fmu+GAy2329/eNTCgBoVrCkJeafxWa1aSqhFbyJYnRdGfvPQ4PDzGdTuG9x9nZGZbL5c4l7EnE1KDL69D0xXz2o1V3SQLzAlMalsrJmnqC1OwbY8RsNru0REFuMtb2sgggqwPr/S4o+F6gqis4dJOdmRvBuz4847xDFSuE2D1r49EYbWg7NcZXFubpnqsGVQV8/GNv4tf+7hfxpb/1m3CH3TOkS55omNcBlrwADAkIn5mmaVAtPP7Ep19Hs62QJ8ZqDZdcGbZnKUa0otawHawu7pzDZr3GNiVF5KTEQtgM++ya4GhYLZ0zr+Dr0YW5eExrK4kHhioNjxnTvbPQWSJhIQsf8VisXMwwl06gAlXt5GkqeP8oZOY+MZvN8Lf+1t/C8fGx+V2895hOpwD6B5Uhir29PSyXS5yfn6PLBBjvHKhVIaFP5urVq9jf38d2u8XFxYURIHYw6l8Zj8eYzWZYr9dYLpfmCdGOhzMrVscF+hCQhohIDNTnw2t8+umnsdls8Oqrr1q4CxguM8Df6rXR8/Ge5aZgtpVtUiOwhpyUcHFfNSrzPd2PpIV/s6NULw3Qh5ZYe4YG4PF4bPsUFHwvMBqN8MUvfhHL1RKIEX/2RovJdAnE9B106Tlru+dhNB7DpXAqIr0XztQa1lR57pNvokELtw1YpVDTbDqFH48R2hab9BzZ81+ldY5kwlaPRmibBs12i//T//nz+E+fXGE0bntjsPfw1bBEgtV74QRGws8xBKs345xDPRrh+sEh2rbFyemJlU6A7K+eFiMYGIaONLux39xZSjeVEZIbJUE8hnp6SHwGPhfuJ+E0nbAx64vZTdYXputh7RlOMqsUlsqV6IL7Q+mh7wPXrl3Df/6f/+dWnVcXYsxDSXwYFosFvPdWqZeKCAdSyrdaU4ZgFg1DR1R7WFl4s9lY6ISZN+fn57h79y4Wi4UZznSmEmMcpIkTOhNRjwhVCe+7ZRZ+7/d+D3t7e1a46/z83JQaeoM0lRPAwNwL9IZloCdPPCf/zhUaDQfl4Sx6dubzuZElDWmpxKvZW1p/hySHhmaSN6baE/P5HH/yT/5J/Pqv//qH/ToVFNwT89kMn/3c53qjvJB0Bwfn1d/R/dpuOx8dvWwhBji4bqFJ/p0G1tv/9z+Cb37rcXzxL/4OFi9cdH3LZGKTmBD7Ipo+TboYOmHmDT1ov/ix065QnvNm8u0IACxNfKCl5GGfpEi3oq42TYM333oT49EITeojWJWb16iF5mLsUtDNkwLYUgpc0JFeHaoqMYWLVDkavAcJg7P/kD6bZCm27YDEUHGJ7HcB+wy1r6OhmYq8JmAAHZn95LPP4psl6eB9oZCZ+wCXD2AI5eLiYmB+5YNIsmKx1DRwAsOlAngcvkZVYLFY2IOyWq0GRtu9vT3EGE19Wa1WNkBvt1szCRM0FGvFW/WSaGaVKiK7PDbb7RbHx8c4Pz/HfD7HdDrFxcWFkbvFYmErgAMYXD+hMx4lGkpmSGTymi+amcTjeO8tfMQQUq7C6P3R8zF8xnaFEAb3HgAODw9xcHBgoazVaoXZbPbAvlMFBbvgUtiY3+ftZoO2HdZscnDdApPeAxHdMgJR1htyXJ+pe48ZTl0GTcTHnn4b/+pXPofPHb+M8CdPupARzbdti1EiDM12i608X50a1GK7aHDrf3wuNTiFn1KmDjCs4tuG0BWQS+DrSORIJ1xAp1qslktsNhub7PnU17IvHNV1X4CPx3L9IpGq1LgURmJWlQMGi0LmNV/U0EvSRcXIykowjOU9XIydh0bCRgxPGdkSky/7Xw13TSYTTNJnzjGjlv654P5QyMx9gOZchklYQVaziPLMIR1guT2ZOCvcauYSv8SsK7Nery1TiQTq9PR0oAqpUfXs7MyOT7WIi1Tq+kT02Oj6Tzwet+FDyxnDfD7HY489hnfeeQfb7RZHR0f41Kc+hXfeeceujfuyeJ/6WdSkrAZjQlUdXo8SGqAnQzwWj69hKB6HpKRpGguxqQqj7VLFjDPA6XRqRQLpnblXynhBwYOEdw6z6Qxt2/RpylQxK5dMtQ4ePq2FlMhDWo8pxIDQJjUmGYS7SYAHklrhPXD16il+69d/BM+/8g4e+99+1arskkCxHwL6PmH8co2v/r9/DEePfQdNk5Y9QUfAqqQwv/nGEb58vrX2MHxsCgbQrRothCbGPmWbWZwXiwVCUqSvXr2KxcWF3YstuoGL/a/1J6K6WF/McFGCKjG2krUQGgCDbCgqPeaZIVGJEa6qjJSEEFA7h1ZUZudcp95wEpuumWOC+hVZJZjFAgvePwqZuQ9QBTg/P7eCcavVyr7guxQahnTU4MvVrinjqhcmD4twEOXsRMMyQL9IYh7SUXVCs6w0yydvq3pn1HvC9tEz4r3H+fk5vPe4ceMGrl+/js1mY+EdXRpA13gi9CEHhmqN/taHXbfj3xrb3vW/Ep9dBIvQVFD6abgf2zGZTDAajbBYLHB2dvZhv0oFBe+KTgWosdms4dNE5suvz/ATT6xw5WiFt99+DKfLCf7I828bIfBVv2SIi8lkG2JXgyb69D0PncJTMVwT8Pj1C2y3Ndb/nycxmm3hf+ZW7/GQENHoD2a4ePUKTpYjVNUS6+U8RZVcn6odAl597Qb+zWqD225lnhM14qoaA+8H3hP2U7X0GyxDMa9rzOZzm+jE2KWFc2kA89zIfRyYdUVlMRVG7vcgzVv7GlgWvP0PVWzS9h6wejOXCFYCCROPV0siA9tR1TV81a3Dt0lr+xXcPwqZuU/wy04vyXQ6tcFSQyHq1t+VvaNGW5VOlYRwe27LNOh7hWV4Lhp+tWBf3j4N0+hAnoeaeB6Gp0ho6NFhRldVVeYx4b5axZfnyYkLoYZf4HKIade2OdQPo6SGhDI/hqaNs81U0nZ9liQ1m80Gn/70p/GHf/iH9/mtKSh4/+CwzAyX1yZL7L1ziP1bR7hTtVjUS9TfeALPf+ot2z667ndA6EbLCt0K2gyJOI8Yg3k1nPfYP+jKR5zeOoL3W1z7Zw0aecb4LN25dYDzky7EOp6uehLj+wJwr7z6GF5aN3jTLUAtxEiAEAmGWlSVSczInj0zwSa1ukmrZnvn4NLEjgQoxIgqRiM0Sj4i0BEZ+V/DO5dCTIpM0YFsl5McpDCb9VtyDOc9Kk7WMAw7RTmH9lt1VaGtazx2/Tpu3b69oxUFu1DIzH2gbVucnJyYv4UmWfWh6GCcKw9q/OLx2MkwBJIbxJTQMLTUd0y9wZXHUyNr7tvJB2m2aSCdymt6fPpFqG6o6sGlDUhociKgiopek0Lj5Xq/c/KTqzP3OobeI34emg2hBIsEJt9X9+P7zAp75plnMBqN8NJLL90zBb6g4IMixIjVetUN7m1rJtmv+XMbSB08vhIjxq/eAAA887F3OrHAe/hEapxzQNXVo0nRKCCtiO2is4HcvDRtjbdffrwfaNErDx156dunfZD3Hm++cQ2/v27whr/onyd9piWs5LLXTN1IzzD9O2aoRcpOSt4bEho9R67K8P9hL9ErLQpdEdvanKkzw4O4gbrD85jpV/wxcA6V643AkDbTw4PYr1dl9yiFA69cuQJfVbj1zi1bqqLg3ihk5j5AMkNvC5UAGmCVzChpIZTgALBCewAG5IHH4eDM19RBT1KgISlVdPLwkXpgiJwMsI18T9vhnMPZ2ZmRFbYZgPlRGEZT6PkZdtq1+rXeM1WH8tCXxaAz4qMELPfhqCGSYAiLBJK+Iw0t8byqsuln8tM//dP4+te/XshMwQNHDAHr1apLiwYAyc7jgBhDwF2/wv+36cIwf/7OFRxdOwUQ+8yihNrXpkR05KEvVhfsNVgoyIsPxEhBUl8iuqq19rpzuHt8iN9eNrjtV53hOFNPL/c0sMGbJAAhdL8BrJNvzSYY3Id9aCIIg3um23lvqhFVIAttSZv4OtWaXD0yAqYQApb7cOyaZT+GsAYKfqaS20QytYNGZrb5mWeewZ07dxCaQmbeC4XM3AdIHrQYGzsXfZ1hGfpLiF3qAgnIer2+tD6TDsIkDJpZxPdURVAyw2Ots7grB30+XHnYSsmPGoNDCLh79+4gfVwzICzenVW85ODP+6HkQDs9noOdGD1CvE4lJoQahneRH1V3NHOJXiQ9vpJJHjvvcHhPWJxwV7iroOBDw/XF1cy7QiKdSABXouZ38h+erfCfjWfwvrFj1HWL0ThlUqbvcNO2WK9ng7WT6lHAeNLa8gE2QUJfD0W9Jx1JcFitpvDO4x+fBCx8YzVvDFEMubEPJe0KMzmXjMGxX+RVyyJYhhD/R09aSB4sc0kVYCFxfbOkr+CEkX0Lj7VjwkTDsJ4LSERG1J0gx2IxPCvSB1hNmkF4KR3T7k9qfyWT5YL3RiEz9wGuxcQCeQAwnU7N8ErVQT0jfGB0sNSQFB9ipkjT7EvPCwd2NZSt12urQkyox8V7f2nxSnYKbJ8qGQCMkDGEpA8PB3wanvOFJTW0pl4XHp/HBXryoUZczZiKMZofifvmpEqR+4BycqREhp8Ra2SwHXmYidek6hePwTWv9J4WFDxoxGSkV6Wzrmu0TWOZN6wSG5NKA+fwP9/qlQHnHF7YPobPPPs2VDv0foT/1ztjXISNpVK/EG7ghU/dQSereFR1R5SatkVV1wNlJUSHtnGIscL/9LZDGxp4d7lApoWwIOEUDFVopAkCiQYHfD6X+cKSIUZ4dCqRJ1GR314UcVOOZLLFe0UiRT+S604y6BNz8jBQm5R8cFu5fhYBZN/m0jV0GWfoVRvI+lKur0IcQkCb+iy9pwXvjUJm7gNt2+LOnTu4evUqZrOZzRxYxI5pvBwklTDooKupxHyPxIPZTTS8KRkg4eHvXSoFyQDPxeJ2JER8IJmiPB6PBwtfApdDZG3bWqaStk9JFxUaXjfVGW67Xq/tWhji4bWrIqL3goZoduh5FpSG3Pi/XgPVMt5Ldiw0KSthU3VNVSb92Ww2OD8/t3o/pYMp+G4hxK6W1Gw6RZ36Fj5/HrA0XlCFAEwpUB/Jv6ru4HdeqWxgj0Ba26gvexBDwL/CLfzrb3QkYc/V+MvPdWqu91VXzSZG0Oly984h/uFZp87G2CYi0a3cTWLivLfwTQwsKtotiDlQJFKbQQIik7yqqhCTeV9Xmu6ytSKQrpuZTDaJbBojNlQ8TAmiCp3awG1a6YeA3uBrobp0n5z+n9rLczGUZH196jcQu+Ua+JlE3h8hNjHGvkJwugebzQahbTFO9oKC+0MhM/eBEAIuLi6wWq3w5JNPmuF1tVoN0pA1NhpCGAysSmLUsEvSwfRsDqhaHZjKAvcjUWJ6NhUN/jC8pP4X/k+FIi8ap9txwA+hqzFzfn5u18n2VlWFo6Mj2473KS9gx/ATfT9KPPTvXMUitJ3cB+iWccizufQ69TPgcfLZF99nCjrbvUsR4vpXo1LMquC7iBgjtqn69MH+Ppx488wPIgbYgH4A1oFyEBqRMBPJu4Y3qtQXLdHi//bNEbzz+N88tcVo3CIC+P2Xn8Dv+DsI7QW2YZip2LTp+YSEXHxff6Z7DtNzKoRLfTzsf1jdnNfZhoBtUjryBAN7ftO1MgTnk3nWyEJ/Y4ehHYa9NHyl4aa0D9ApzwPfkXMW6ouiCvMemOIk99jeJ2nD0O/Ha+L5uJxEwf2jkJn7REwzprOzMyMaZt6Sh4LKw/7+PpbL5WAblUGV4KixWNUKVsHMPToaVtFQFBUiDSnx/JoKPijJnREK7TBIpkajEVarFQ4ODjAajXBycoLlcombN2+irmucnZ3ZYK+qEoBL7WWblPTl5EEzvHjv+ZuhMN6L/LcqKyRX/K0LarJtvAdUqvIlH7gvP6fpdGrVggsKvhuIANrtFuvNxoiGZgHxbw6Qo/EYTaoqC4jq4Rw8wyvptSp5RaJsF5EmTN6jBRBdxP/j1bEtSbDxJ51qgGiKBhUil44HIQX6jNNQrGoEt4lCMPj8V+nZH08m8FWF9WqFZrtFvb/fhdHXa8Q02IcQ4GMqepdCNab+kMTJvdI+yO5fpp6bipKOZf5CTiLlN0kZw1c6mVXfHTBcnbuqKrRJdaJqFAD4RE75OXGJlbLy5P2hkJn7hIaCOAjq4MltuBCkEhF6TYxxez9QLnS9IhIKDsZ5aImhJC0gpQyfvzmbY8fCsEtuksuNvrkqootgaoiGoaaqqnB+fm7qkoaGAFj4S8+jfqI800oNzIRupz4cEkfeBx5fPUskVdwnV35IcNpUbZRhtTz0xvAXa+wUFHy3wMmAhiVAEhJkyYKqWwiybdsu+yl2KcwA4MNwAUceh7N9XVwxhi6biGsZxRhx4RogNsMBG33WjYW30HlTqJIgqRZB3qMK4vk+Qy8kQNLnAeiJQjpnlVKyfVVhk4Xn2V6gV0VqVTpi70vRTCK7h0LCIO0b+HvQm3yNlKH3LJn5WNQhoCeLhJf7zSSHGCMgipD112I5KLg/FDLzHnj22WfxZ/7Mn8Hh4SFee+01q957L2UmVx+A3jDLHw3LcLBXw58uXKkzCULjs3punRloe/TB5Hn0Ick7Bc4I9GHWwbxpGkwmE+zv7+Pk5MT+3yWZapt5XaoK8f7xtRCGBfo0lKT3Ts9DAqjvUcHR+7lLGdLQXYz9sgY8PskT26G+pIKCB4mrR0f4oU9/GpPJBKenp0bGteaKqg0D9UHUVSfbqeIQAVvUkbCMIPTkRGGKBt/TfgU9YeD+JDr5RIlweq5E1kLbDgZ+HcxDCKirCuPxBKv1yv5XMpQ/jSSBTHEO0kZLgY5diIgVh0narJ167yTsZOE5eY8KDu+n1YxJBIfbq+EXsV/WgMf3AKKECkPy3RTcH8pa4++B+XyOmzdv2oDN9ZKAy4XhlLBo6GZXqCX3jewylXIwp7IzMJkBl86tZEJDLTqI63l0QLeH0fdLHfB3flymNo/HY0wmEzsHiYWG03hMJXDq0clJiBKYgUwrbclJi7Zdt9Fr0LRxVaU0HKaqkd5/JYf5PSwoeFAYjUb9grZUceV7p6Ecqh15mu+ldGWgHxDToL6LjNPvEuTZ0zDQgOS4rNJuCINMoUtEKp2bA7r2X7wuenxIhnhcpjZXVYWaxuXUXp3IcZ9dfSvkvAOCIgRG74gpOcgIjRxb28twn4X2kjHZiCb7G7aV4SWdqOq9EeJaJk73j6LMvAc2mw3eeecdvPnmm+aZmE6nl9QQDd3kBMDlD4HrPSWXZE6Bqg8aPsnfZ3hI23AvcqSDvCo52r5d6odW0gUwIAGaPq7EglAfTP5w6nnVLL2LCOWy8C5ykxOgPOspv3f5vaA/BhgSNy2ul4fBCgoeBNq2xeLiolv/TEo0qBqiioQpJdkAOFAh9Jl5t74m/eYAruEU3VcnRhZWugc5goS6zJArKslgX1VskqpCKAnQTKVdkzrzoNCEO2hUfy6r2SPkadBPcxe51zm5yQnQYI2njAgOjkPFSL15MRpxCySH2WS54N1RyMx7oGkanJ6e4q233sLBwQG22y2m06n5Z4D+AeegOB6PLx1nIO0mRUC9JHxdCREHeFUvqBaoKqSD+a7Bn/vo8fSc91Jr+L96fDh7PDg4AAAr+seqxur7AfqCfryG0Wh0qU0qSTO8lBM5bQdJhV6L+ofyzo375IX4dKbGjoXhNQCWKcbVszXDq6DgQSOErsbM+cUFJuMxQko0yGs4QZ5rDUkTquJQEWhl4OTrGo7iAD9QLyQ0okZaoPeD5OEWxL72jXdDomMkRIgLiRP/t/7AdR6ZsXMYpwVg26bpsruYXZSuiUoNVSleQ8XwXKYY6UTJXqfiI4rJvdR0ntvUMblfWvCQ98XOL5+hAyzFHunvNvSrZ2uGV8H9oZCZ90DbtlgsFpbNc3JygrZt8fjjj1sRPQ3BxBitcN16vcZoNLKBXh/sPFNHkasbqnpwezW5ssNjOCr3ohBMBSehyBUk/s3jLRaLwfVVVYX9/X3UdY2joyMzO+fKiB6PRmmSFCU6SnLysBZ9K6omcf+8g1Q1JfcN0Qidn4/3T8kQjdtaJZjbkggxHb+g4EEjxM4/1zQNJuMxVus1QozY29vrv3N8tpJy0ratkRWfQjHqERmoH9rXyDPKkBEzaah6mNGVht70jHrn0MZhWX/9G2nbJmVIkUTEdF4n56TaYpXNuX9KuPC+S8v2lR+GqNCTH15bAGwpAxKSvC+8FAoDEFJ9GlN7hAgOzLnoqhRbGCrGwT75RNImTOmzMkIa+poybSIxlhEl5E77tYL3RumV3wXqd5lMJmZMXSwW+OY3v4mDgwPs7e1hOp0OKugCndeG6g0reuYqC3B53SYOsJrtw2My80bVBx6PX3yGfdSbwmPyPaonnNXlbQohdB2I75cgaNvWTL9AN6jfvXsXy+US+/v72G63gweZyzDk5IadtV6rkqVBHNy5wT1gZ5AveKnbMpylnQnPofeD+zJja71eY7VaWVVnqjDqH2J2wXq9Lp1MwQOF+l3qqupWjg5dJuTd42OMJxOMk1JDQzC/+8wsjLGr3EvPxiXfi5cUb/TKCJWXS2FihmAkTKvPk/MelbzO0EqM3XIITEdWNUSfP/p0NEGCyk6VEi2AblBfpRTt8XjcDf5CanxVXUoRj+jMztavCelw6FUcBwBVNQiZWYiKirEQSJ4T0jfZ8Xk/ISFBUWNsYpT6kaZtO2IjvkY9bggBTdvCeSdLcRfcC+7dDEbOuUfaffRzP/dz+OIXv4iXXnoJ4/EYN2/eRAjBBvLbt29juVyirmvM53Pz0ozHY8xmM+zv71txN03f5mC/Wq0GBAPoB2UOoJpSrCqCKg9adl8HX+188kURVS1RxYfHB/p1oLgW0eOPPw7vPU5PT9E0DY6OjnDr1i0jPlYXQY7vXLceEv+m4qEEjvsya4gPspqGgaHSQ6LFAoG5p4fXwXtDhY2+mNVqheVyie12a7/5uTCcNhqNzPAdY7ecBFdP39/fx6//+q/j7Ozsg3/BfoAQY/xQwf1x/bOPdF/z3Kc+hY8/8wxu3bplCujgu7pYYCv1juq01EBVVaj1eyohDpIUnwplUrXQtYgGBlVJKdaQCgdoM7ZCqnKn86gnJmRjCpca0DAOwW1pPG6aBhHA3t4enHNYr9c2uVosFtaP+JQFBcAqBDv05S3gnHlQ9Itp6pL3A1PwIIyXroXLR7A/btiHJ5Km4DIG/Hu73ZovpmkaNNttl6GVfvNzYTit4sQ5kbKmbbFedaunj8djfOtb37q01t6jik3zqzv7mqLM3AP/1X/1X+Hzn/883njjDUynU8xmM6tOSaKyt7eH73znOxiNRnjmmWcwn8/x0ksvYblc2s/+/j5ms5lV3qXCoVV/FSqLqi+GAzmhplaSBSpB/F/TmxlfV2JA4qFhrLz+TYzR1oMajUZYLBZdufXZzPYjiVLvEAALFY3HY1MzeI58/Sq2SVPG1SdjaZoyi2uaxiqDLpdLrNdr24dhN+ectfXi4gJ37941JYYFBqk4jcdjzOdzu5ckaWzzer3GdDrF22+/bRWDCwo+LH7sx34MTzzxBM7Pzrpq2YnUO+cwqmuMDw8xHo1wenaGyntcuXIFo9EIt27dwrZpUKXBcjweox6NusGWPrOk5g4UYPY5om4MfDHAME1Z1I4gqi77Fs1gZIjLMnbQqyQ8lipCJAYsrsf1oCpfYbvddAXzUlgcquRSZXF9iJ/krkn3zrwuIQz8OHYtokYzLAW9d75Pc2ffE2NEs912xIaqFolV+rycc9ikMhZUYtrQLZZJxYkTJt7LfBmcNhX5vLi4sKURCt4dhczcA/SVMAWZ5EA9FN57PP3003jqqadw/fp1vPzyy1itVmba4pd5sVhgPp9jNpuZz4S/OdtQBYGDp3piiJzU8DXuS/LA7TTcpA+vqiOqBNGkS1JBAsaBnWoQl03gtai/h+A1sI4OzbTsGNjJktzwb3YabCePpb4Z3jemhtOkqx0ryQpr4ZydnRmR4ex3NpsBgF0fzb2cUZEAkvhNJhM89thjmM/n+Lmf+zn883/+z/HWW299uC9bwSONyncrUTMFWcO7IUYgPauHBwc4ODjAbD7H8Z073SRCVNkQI6pUxboejboKs8lLE0MwZYfZQboqtwfg0rlt2rtDZbGwSTLAVlrhV8Nasp+uKu2AQUjHe2++FGbxVAwji4piC20Cg36LIMFhHR0aatVnZ9WLUxjMJl4xdpWPNWTNa/D9WnFVanObxgDnHCqSqURWVklJ2qS+kablWSKaQB8m5zhhE0mGudK9q6sK8/kco9EIn/rUp/Dqa6/h/Pz8g33JHgEUMnMPUI1QlQPoQyIhBBsIz87OLH3bOYe9vT2Tgjkj4oBImZjHUlMq1RPNUOCgqg9wnvasg7yGl3QmoufR7CSdXbnUOdHXogZcAEYYqKpoJVyelwZZXjsJlR6TBEmXcWBbSBY1vKbXwuPR2EtiomE6TaleLpc4Pz83wrW/v4/r169jPB5bW/TzZT0hJZAkngDMIDydTnH16lVMUqZFQcEHRVXXgMMllUPDxRwI15sNLhaLblBzDuPRqAtXkKTwmeVgK8fis8TFD50QG0A8bHxB1Bq+D6oiVFRJXnic2Btv9bnlStqaHeWc630totgAQBtSVk9qa9MOi2dCFGFeO1OtA5MSqLKQ0KX3tZBdDFJqIb1uakw6N/tOEhP1zoQYEZsGMQRsUgKBT33+eDxGnVR5tmWgYoVUADCfAIqdgH3hdDbrti24JwqZuQc0TLPdbk0BIKtWIsDB/uDgwGb4HBB1UB4YxtAvfki1QtWYnHyokTb3m2inB8BIkRKZfEFIbqdmMzUF8xoZHqMsOplMrOQ/1RT+zX3YmakpmCAZosLDdrCdVGm07bvSrvWzAboY+2KxGLSNHp2maeyzoU9pPp+jqiqsVqvBtatKpQOA/nAV7SeeeAIvvvginHP49re//eG/dAWPJGyASwMxUt9ClcTCH+LtmEgV8lrUHAB9po6oIzS1Uq0wNYbPlJAPZhpdgpAQhnkiemMxM57Ug6feG7ghyTEi5Xrzc0jek8p3mVmWdZhICAkI96GC0sq9IdpksI2uW6MqNcjCU1RpLNzG40MUJPRm6DYEVOjWwkKaLLFgIISYjVPfT5/SaDSC832dLSfXa21J9wExWgVhZqttNhvs7+3hySefBJzD3bt3398X7BFBITM78JM/+ZN49tlnL61krd6OXaGZ/f19tG1roSYtKKfgA0oyQMVmV4aMemjy/5XUWEeUtVUHZC3vr1lR1uEIyck9MEriVFHRdaVI8NSnw5mFpSEK6SFUdSHU4a8/bJ9mQVFdIZFkhlLTNPa5TCYTS6VXw99kMsFqtRqcQ2fGvDZt+3Q6tY7pscces5o7BQXvFx/72MdwdHTUTwKAYXVd/i0EpfIebjxGoDqRjKQsUKdgTZSQlBiEcKnvMLBvkXNDzn2pTVR42NfI65YV5YbF5SxMBdigrQTKnj+HRGp647CuK+WlfTQVB6ooUVKclTSlazHVJdvfyEV2rVSkXOx9hewPQwhokZZrSZ9LXfXrx5GUOHRho6ZpBp+nfQ5OQn/8vNBnsEZ0GbKTHTXMCjoUMrMDL7zwAp5++mlcXFwM1vXJXe95p6D+DzW25kRFfS91XZs/ZxdydUYVGKCfTfBv3U8H/9w/ky/UpoRHlR5urypKrhoxzKOhHqD3u/C+abhMj51fq4aneP9ypUZTshlW4v3Uc5Js8XMkEeM9oR9KlRi9hph1egxVnZ2d2TpVZTG4gg+Kmzdv4vDgEJvtxrJhOOAP1I+0vaZZVzH2VWKzyYsh9h4Mn8gB7tHXWP+WFAKSDAMVGf4t+/F/hpL0WFbaXwZ2tkuzoUgqvNyHXDWiYdgytlIbgt4zkilpkxGW7Fp5PL4/uJd6T9I1xxD6xTz184oRjiq871cAtywv8QcOlBi5Bm0f2zIej7FZr01Zz5Xugh6FzGRgHRUOvPRWAD1x4CAO9F9oLYqnPgodDDVWqoOnLWfvh5k9uj1f19owevw81s732F59GJhJxVCPEjP9u6oqy9pRVUPDSXqdeZiJ0HujxIa+GpI5JVdKWvIOmudRAqVeHt5H+p5y+VnvvfdddhoJCclOTmY0DDUej23RTWZFFRS8X3CW3flU0rPDN0kkMpXVo1c0gOS3IbJJDoBByMQBlmVkAyq3UdWZx0hKToypaq9Mmi5NvmJfZ0XrOTUpNOOQ/CByfaqG+DQpiZAJSdpO22rX6SRUoxOi2NfVYZtCSEsDeN+F1nh+ufaBAiOncuhTsdXLohlScM6ysPKcI7tX6Xc9GlnfTbJziahSZQNQuS7FvGkay4oq2I1CZjJ8/vOfx9WrV7FcLs0MSvMoFQnn+uJ4/LLmBe1IHvKQiHYEDImocZfbaBlrNQXzuDpI64DLcI+qI3xfC+sx80dJCN9T9s8aD+PxGJvNxs5DBYVp5tyf58hnELwPJB8MP/GHkq1CryMnXHqvNpuNhfXUX8O2kuAoWdJ2WcGxdB16n3PwOkmALHWyoOB94oknnsBsOsW22ZoZlOZRm1gAQxXC9csEmFGVCicVjPR6TlYGEwNRG2gSBqSCLiTUCwzCQ0jHY20VO4+oHzwXSYqGkkBSkanMVIBzQ3+MsV/GgOfk9WD4PKcDIQr5CPL8eypT2bNtRfd4rYmA0EPDe9W2XVXj6IZ+G7aVv51znbFXrw+45A1ycp9z8DpJgLabTV8jqOASCpnJwFk3a4nkJf0BDAZvgjN2Dtr5+xqC2qb0SYLGYouPZioGj28dhO+r8vLYuwiW+lJY1RboQ1t51pSqIVRu2LbNZmPF83gP2D4SGhKk/Bp0pqZmZ7Y1z8LifrzPvPf59XM7elj4nob5mInkpQPMKzGPRiPMZjNbtoIqlJIZEkr1CrG9TBEvRa0K3g+qqkIbghFiU/ikr9HBm3CA1WVhqCTq+2l7hkSUrBixT99lHcDpY/FCikh8LFSVSJKFgFN7vfNAaC3FWUPEle+L7bENUSYlIyEOfH6bphkQI7avkvIYNqETomX/x6HZmfdNlRJpkKVWm2KTXT9VMvbRJIt2/EQKNVurjX29HZtwpiKHTEzIkyD4+VX8TGJaYyq1gX6dEtq+jEJmMhweHsL7ro6JFa5KzJhF6bTUPTA02Wr4Qv0lHGzrusbe3p6RBg62HOi5D7/kOhDT28Hj5WoDB1vWV1FoCCbGrpotDc56DJ6DJmZWMD49PbVt2FGxjavV6tJ1ss0kJeys+TeJHzCsIcP/VeHJCY/JtFmoiQRFQ3L8nEhiqDCRjK1TPJqfB9PtlRjpjFaJFe8Bqz8XMlPwfsAw6Ha77eu2pO+4Eud8QB6EaPgahmFwhnXGo5F5QiztN3ZZU1RsKqoFMhA7eSaD9GtArzBE9PVVguQuWOG81M6mba2ui5EytidNwjwnCyH0z5GSgNRH5SUjjHCQdIVgJI5/sxYO75FDvzqAk+vWiaORGCFxWotGPUF8P8pxNBRumWTSvhj7dHvzDXESSFXNJdNxaqv3ffXnQmYuo5AZwQsvvIDr16/j2rVrmM1muLi4wMXFhS0cmVenpXLAL29u0nWuz9DRAVsLxAGXTb5a7VZTwDXkoplDqqCQCFHR4GDN/agKaThJ/SBapVgVkPPz80tmWRbD22VOVpOunpv3kteg16d+GhKr3BukHQZnsrmvhsfWqprcjtfrvbeaMSEEqx0zmUwGHhglZmPxOAAwcpSrXAUF74Unb97EjIU06xE22w02XOojD9NGKarG11xv0u3+dZeKvtGMq8pNlMHWBn+qNU5qwcRoYRI7bxpoY3rPA91v12UftRKapVeFqowSBQ21hBhRU31N27CPULNsGwJqKlTSfgADP4udm4VNnaSPp+sh2WIbjViJSsXj8D622g/J/UVSXyx8lcgHFSL2S20IiFmGZ1XXtiQDP1OSGE08QdvCpz6dmWsFl1HIjODw8NDWVwJ67wprkfBHC+mRgeceFk25dju+fFZVMqv4yQGeUivr23DAztUHdkSTycTIALdh2WwqHSzvn/tqBhKnc3YsVTxyw7P6eOq6tgJ6JEnaDio23J/ETInKQIoVkqf+GyUy3nfVes/Pz7Ferwekg9dFGVfrO+g5qNKQ+IQQcH5+bjVolGTyOHwtDwHu+owLCu4F1qGis8WhU2UaCb/wGSTRgNthek2DKYvk7foetuJfUdWBikZIz2otoVNIO9R749E94zH9jxDQumjrClkf1bZ2bBqA2V4L8TiH2ns7Tvf25XpazvuOXKFXbfk6SYPeM810ZGq69c3yY+fIVBVuR8LCcWCz2XRLJch+vBbtq3RfnqOqKrQQI3SM5vXzeq9dX+7DPosoi4Wm+1ZwGWXpX4GuucTBWmfdJDFcETtPXwb6hzE36fI9oI97EmoWJkg2mB6uRCbP+iFB4f9qaNX/eW6XPTwq2wLDzAYqL+PxeLCsgyI3MCuBUyJCtYbG4clkcikrisfSoni72hljHGQr5R15brpmnJ2/tZJwXde21ITeF5IcLSQI9Etd6PILRZkpeD/g4pCj8QjOOzjvBrNukhj2P4Owhwy4ppSoagMMwirq3bNBUjalD2az3VoatT4HPJeSH1MdqHZQHfV+cG6ah83864aVfiHHZ7+h9bm07XZMIXN2Dj1mUl9iUpXqqivA52VbPZbnNbStkS2SEd6rmplmJGPS12i4iffO0tMlrGR9W6raDH6WiWgaaeW9AiyV3ktbizKzG0WZEdy4cQNHR0fY29uzzB0OfkpSgOGAzQefD56GlnQGz22VkAAYkAM9rg66OjDrwK5hKyVQ+QxtF2Fxrk/NplrCWUHuB1IVidejSwAAsFBcrl7oPeDfqmblMyoqU0oQdhGa9XqN+Xxuyo/ObJRgaQYYr0llXP7PeLQuZsnt88+UCpOGtAoK7hd7yWc1HnWetC22NgiSKAyUv7SfzvZdjIPQkoWCCJKIbLIAPUb6WxUMUySQKQEkOKKIDJSW/sDWFqaR+9iHrSxUk/dViSSoisTrUbUWgIXiVL3g9dodiJ3R2Aga35P+yLs+K4vqkBIakpOmHS6/ArkG65eQZYCl/ZXUmbomfZT5Y3i+7DO1EGKUkFbBJZQeWHDt2jVcvXoVs9nMsm508FdFhK8R/JIrIdD3dm0LDImPvk+oN0Z9NYNYuWyfD/hUDtRMC/QhmPxatJ15thMHcb0n9yJrev36N4mBLmuQEy9VqfLr09d4DfP5HOu0wBvvP9/P7yfPlYcGKSXzs9ilqplcLNWOtTMrKLhfzGYzzKYz1KMabWiHz5F+n3YoAap0XPqeAgP1gdsCkuKtfZFsSlXFlJNMJYCQC3tdlBYN9dqA7vo1iYxc6P4J+RpREcPqwepRGVzbjv6nb2DK6Ep1YZweJzvXruuzY0hfOhqN0HByi55wBCVCejxemx7bOatmTKIzaFNqp60o7hwCiZ4ct2CIQmYEWvJeZ/vGoGUgzJUZ/mYYhSoO38tf+yCDX06mgGHHlCsJ2i7N6CHy41CR0PPloSNVPXh/iJzM8QHPjbchhMGilVo0LyeCu65TDcu8pul0Oqj3omZtJRu6/lJ+/Jwo6j3a9XmpFF7ITMH7QSXhWp3t23eTz7KYYIGh6hDQD5Q6KDt57dLgfJ9QMkXzsAP6FHD5bRlSaXsjWBkBk4P3hlk530B1Qv/cOne5poupO+jVXntd9o3ozcAkBpDj5xOlwbWlbfQeO+9Ri3oCDCdrkM9KzwW5d0qCcuKJ/DUeVvyApafZjUJmBPRohBDM9Av0D3Y++OtDxAGNKzmrJMnBF+izfPhaPnDncmpuvM0fPp0RMVykD/Z2ux2kamssnNeVZ0Cxffd6H+h8I3mBvPy4SuY0BMbjkNDQqHwv4pCTC6oouv4T28mwoHN99pEuo8DjaRtzT5F+TrnyomoSlZpCZgreN2LsFJlNHEwKnLyvyshAlUihiRhCV2HX+4E6wpou9Go44FKBOuByv3ZJnc37GvQDMWK00BTfi23b12vh9pmyZJMWJQgc9FXd8d7M0ZWoynYNGsrBUGExVUjISxv6hXGpeAzuN+9xTsCSisKKv4MQEO+B68PWIYQh2VDykcgQsvu9KyUbgC33wNct9Fb6mp0oZEYwn8+xWq2wXC5NNQBwyd8BYKBM8D1db0lJAxWPvNz+LhWAAy+Nf2oO1s5H28b25KEtggPveDzGer0eGJCVuOTqCI/BujAkaFod12UPcq5GaRYW1ZL1ej2owcB7oT4dXkN+XXosJXpMKSdJ1FCQkjD93JRk6nnZrp2ztgT6ZLz3RhgLCu4XnAw02wZt2/SDJIkKMPBlWPn89Lqut8RtXfrfoS/rb4NfNvjzGA4w47F6UFQJYtuY4m3pzlRtdoSeqqpC2zRwdd3VsUEiGTpA89pEdYkhwFUVKl8hIlu/jX1UCGhzNSqRBF47+4yG6dkMC6drsn5XiRd2hKni5QruTCmnamPp75CQkmzL8w0mPBmRGdzPDDQHu0TKBuncBYZCZgRUVljgbb1eW00AkhFuB8DSppWk6MydZEQH/11LE/B1ri4NDLOAmEXFbTSEwvaRlGhb8mvhcVTl0YFeDb5OHmQd+Fer1aAqshI3FhWkeVrbqIREs61UgVJymKtibC/bQkJHwkTjrr6ubeQ5cvN1HiIkeCxtn557vV5juVxitVpdur6CgveEDYpdgbe2aazsPgdkoFcOKj5nMjjaQo2AGWJDCDYg7lqaAOhSWL33do4YU20UDIt0aqoxIDVrpH+wsFIa4Hkt+WK7iBGuqgY+Eg21UFmygd87tE1fFZlEDTEipL5VJ3WQNiohsdo5mQ/Pwlai9gy8K0oG03130gdw1e4oShQ/B57jkp2A97v7QPo2irLGfU2Zi535OKZxJIZ3n2Q9yihkRkDicH5+jrt37w7WZ9rb28N0OrWHQkkDSYTWGhiNRtjb24P3HmdnZ4NBlGGfUSprTVhNCfGVOOcwnU4vhYBUTVHioWEqHZA17BJjl3LNJQtIsPJwFdDPLvJVrKuqX4SS16BkQRUPkjotQb7LRJyHanJ1hG1VBSbfNidYDCNppeBd6Z6534bqkZqJqUyx2B6JHVO7CwruG+kZ4/eoSeHtqq4xTll1HNxDjHAS8tTnhX3QKD3Lm/V68CyFVISv8n6wSKFW9Y0xWl2Yuq4vhYBYIdhCIDrQo1dQNVxiz2aMVt3XQiXJL3MpzJX+jhnx4PpOSGSJr1uI3bm+Sm76mxWVY3781KaB/4fnzVQZy3QSUmjkJ12nKmMxpkyvROzYTj2mEVV+PqlvVXIXQr8EBcNjrBPG1O6CyyhkRkB1QLOAQghYLBbYbDaYp4qdWogu72A4KF5cXGC5XOLatWu4cuWKHYODMAdIDfewDTwmFSF+kXPzKgdwDUnl5EMVHp6bRIokKQ8TkdQoudLBPicdvE+5+qKp5Zc6ix3H0dovu7xDJHgkGPqjZI/n1WJ4vDd5zR4lgRpCVOLK11arFZxzWC6XuHv3LrbbLRaLhZHDgoL7hYUgOCCn7982VQEejUYY1fWlRRWVTDD8s9lusW0azGYzTKZTO4b1FTGa6gNkJlm2JxEMC6F4P/BvIAQEwCr6ar/CisEDP0siA85360DV6VrMTxO78v704Ci5CtJP5EEXffZtG++BlLFEomF+nf6GD46jSzwYqZLPhgSPBANyXCV7gfdWPsOQiNTAnJ32t6UT5FyWVSqfS9M0gHNotttO/U19X8TlyVhBh9IDCyaTCfb3960652KxsDARSc46zXzuNYDpYLndbnHnzh1cv359YCzNCQT308Ugc4VDPS2qAvF/zQra5e9Rbw3Q+26YjqwDvSoYum4RHzwuAaBkhMchAVLipqqPEq08W4zVeNkenis39nIAyNebUqWKBmEuOaFqjRKzvN5MPlsk6eQPl7i4uLiw78BoNMJjjz0G5xy+/vWvf9CvX8EjhCopo3XV+65IsElymrYFmuaeA9hgUG1bLJdLzGez/jucQiMuIzH0eeTGfTuDcwOSoc9GiBFoWyvmhqQa6UDMhRI1xBRiRM3/SXQwTBcPIRWYS+Zf7715Y5SMULUI0g/wvC52pmTrA2XCot4VqiFAHx7S/kWVHWunEBElepXcT9aBiRj6jZDOAfU+yf1B2l6/A9tNt8TFdrOx70Dlu8rnDsDtO3fe+4v2CKGQGQFXT6YKQoIBYLA0PWf5q9VqkM2SD+jsLPiQqN+FoRkdTJWgqOqgBIRt05CO7qPkiJ2QmmV5nRzgrZMKvalWw1W7MpmUzOm2OstU0zT35zWzU6W/hiEcVZ5U5clVK1VjrKMSUmPyePY+Pwd9XcNpSs6apsFqtbIKxNoOJXZsK5WugoL7QeUrjOoRQtt5LrSmCrN9jHDwGeZ31Dkb0BkGYcjETL3S/9AwaqQGGXmn6qBkHmlCJYRpENYGzPdhxuAoZtl0Lio59AIZ+QqXC3yy7+jOaQ21gVy31cwqCzNxYiTqjmY4WQVy32dTmelXJi9si6pgvEYNMUH+5ufH0CDJ0OB1hsjSfSDY97ZCCnUyBdeH+mL67IsSfBnljqD74v7sz/4sJpPJwITKh4trFXnfFU2aTCZmrCV0xp8bSfOquAAGBdo0tLOrRg2PmcvEatTTQZ4EJPe5KPkZjUaD4+XH0HWl1OTMB48DuBqPVdUhaWDWhpIFPS+PR4KWfy4awsr9AiRI+es5udLrBy7XoCGoRJmPQT43/QwODg7McMw2MB3/hRdewO/+7u/e93ev4NGCg8OnPvVJVHVawwxpYEzPR11VpiB4AKiqjtSo0TXGgXkX0h8MQrocaEXtjDEOSAAHSEhfk5MG7uvkN5UHC5GFgFaIgPahlc+MwHIMKAFyfegGse8fYux8NzwmCZuFo5Iq4wEjf3B9qreREk4Ys4kLj6FrJCmRoXIT2/ZyphnvGSQkpuRSxgIlMNqvasaqkhjnHCZp2RySNBqsfVXhyZs38cabb97rq/bIoZCZhB/6oR8yqTfPWlJiwwFWVQYNy2jtGA135KnU3F6RkxVVa1QZ4WsaUuLrPA6JRh5q4nsa6tJzsmPJw2AMp2gasipENNoSSs401MNMp1y9GXSglHOlA1JYTFtCXUr8FEoCdf9d0DAS26jhQe43Ho8tFAkAq9XKfDb7+/uFzBS8K65dv47QpsEr9ObU7o8hafBV1Rt3hcQ4GXy5X+WH5lOfDZ4KJReAGGOF5HQv9eTDBng5b0dWKjRCqngMl4iUemUG5yQhyJ5h7z185dGGtjf8Zn2CXk+u0NC/MlBdqQwlggK9fiEueT+Skxdtf468XdDzZNAwkrWR9yH0tWqqqkIlHkJODJnAUchMj0Jm0H2R5vO5PSjqEwF6nwu3BfpsIQCW5aLGYKAnAMz6UfVDC9kBu4vi6SCshEpfUzWG+yrx4Xa5sVjbQigpU5ICwBaapI+I7Xg3VUTVICWB71Y5V0NMOjNTYsn7r8ZdvS96TTkhGhj+Yr/0ghIZZrCR8Oksk6btvb092288Htv3JsaIJ598Em+88QYKCi7Bpf4CES6KT4QDfPJddNsOs4WAtDJwjANjMEACUFnWjyoSQY+px9Vm6XOo5EX3EaXC1CDnBy5dI2LJU2PPW6b+KCnTPgToy1dwcmnPPoRYkJywvUkN4bm8H64kbm0YfhSWBWVERkkLf4vfZvB+dg81pGXXlh2ffQ6JTAihWwST3qaYKim7PnN1lPoXmzCyXwwBBwcHODs7Q0EhM4Zr167h+vXrWK1WODk5Mb+EhjeA7gvKQV9X1FbjFgDzgei+quJwH76ugyyVER2EOYgqg+e+BAd2NbLlqg4xmAlIJ6KKB8+Zt1mrDHM/VU+UeKkJmPdErzm/hvx6eL/zWU9eLDBXdfT+sk27yFOMXar1crnEyckJYoyYzWZWJJDnoYF4PB7bCtsMRZGo0VD94osv4n/9X/9XFBTswmw2w3w273xZ65X5JRgC0hAGB316T7q3h2sS0QeiJEM9Ldwn/QGX0qQBXPJ18HheyQKPwV2QJjEAQgwdIyDh996K5EG3BwbhLD2nk3PGrM30nhDeObSZKkMSQ3XGFBpJD8/DZvnfJB703gxCQjpxg3C3e/RbJIKXNJnUNzfbLVbrNRAjaqrk8vn6RJ6qqsKoruGrvniqQ18jqPIeTz75ZCEzCYXMJLRti/39fZyentr/XLyQ3g+GSdS0S+Rplnx48pL7HCA5CLNeS8geYh2gdXVqVQqAYSgsxt6Uu16vB0oMSYhmF+1Kt1Y/DeO5WhywrmtMU/on1Yj8fqhKxXvDcJvOJhl64j3R+0SCtEs5yosOqnFY7z8JFEkew2PT6RSTyQTr9Rrn5+eWRj+fzwckZle7eN/oKeIK6+oLUk9OQUGOGIJV4wY6wtLSq+e7jBWPFNoU067N8pOCkA+arPrLzBsOkDaxkYmBPVV8xuT5714OfaXftKkSIIga3KY0YioiJCEWXnLDtYzsXECvMKU+r07PWwzi/UvGWKaMp5tg98U71xXkS/fGVxV8uj+8NoaeaP41k27af3BP5L286OBgvaXst/bZzJ6q6xp1VaFpW2zaFtvNBltJeOBnZGQmSigxfZZUmMapDyWpgRsmSjzqKGQm4bHHHsNyubR6MG3bYrFYYLVaYW9vD+Px2IgMFZjlcjnICgK6zoChGNYqocKRpyhzkORDC/QKzzgZv7RmhGZXaRYVw2IALhEGVXc42Gp4Rh8GDR2FEHD16lUsl0sjAlxHaTqd4uLiwpQXtj1PeVYipWSCD6QqHzwvr1ENcby/bC89SOpRyskg39MMMvqI2rbFyckJFouFDShXrlzpantIqroqR/ys1B+UK1shBCuoV1BwL8zne9g2W3u2Y+jKODRNg9F4jColGLDibIwRzXY7zApC9x1lsT0tkOmFRJgynMIXl77XgBl02xS64OCfh4I4YFt2lBIGYOg5cX2mkMvfi32Ks0/EaDadYdtsu3ZmdaI2y6W1YeR9T9jkPlCxsGt1DiGFmkhCBh4ioMu4Yj+T2sj7a2GhMFy6wFSxdB2qSGmSQSWkbpXqhLWpH5pOJl0hQQknDpSjRGjMQkBCyPfRq/x5BeRHGYXMJGw2G0ynU0ynU3z729/GO++8g8lkgmvXrqFtW1xcXNjgm1f/1VBOVVU2QG42G8xmM5u5s0gdFQVWjaWplgsuUlkBYN6N1WoFADawqyGM4Q2bdUnb8hCOc86WNSBpUsmaqKoKs9kMIQS89dZbmE6nuHr1qi1ZwJDMeDy2jodqhZrvgOGilG3b2n1gGE7JSV55OM8mIpT88bxAryzx3lAl4j3Zbre4uLgwNWwymWA2mw0GAiWauTqk4TEOIFSp8gKIBQW7QIWzrmvcPbmLxcUFqlRFOsSI7WbTFZpLYRf6NTSUQsLRtK2pOLXva1DVdd1l96Rne8QJRyIjps7GVM8GQF1VcOyf0A/sA59aUnyo/mjbBj1IUkTYLpcUE+6jcN6jHnXP0vnFeaf+zqb23DIkU9W1FahrQ18RWYmNLkqJ9Ex6lzK60rZmJuZz6lxPakRdJpT88bxI181QVkjqka0RldrYkLCm9o/qepAaT/I1IElyD3WSbCQHuz2WjzoKmUlwzuHf/bt/hzt37uDOnTuIMeLo6Ag3btzA8fExXn/9ddR1jccff3xgOtWMHKowk8kEm83GlAA13PJnLKYukgH1o3Awv7i46IpricKhBmNdk4gG3f39/UGIDBgqNPP53EzJzMQheD1asp84OTnB6ekp3nrrLYQQMJ1OEWM0BUr9KCpXA7D09vF4PEh5JqlhG9Xvw+NwW/X5MNQzHo8xn88HhCcvTEhFiMSHbSaZ0vTukHdWch3aZi53oN8flqcvs6WCd4UDbr3zDpbLZad8ogt97s3nWK5WODs7sxDm4LtItQMAQkCDjoC0gKUuWz/T7QSH5IVDrzRQ8bFCcOm9jZjzOci28hx6369JVKWJwXg8HoTIANjgjBj7SRbQLTypfYTrC9h1Ie2+1MV6tcZ6vcJ5Kk7p6trIiXmLeDszhbROpKmKfQIBFY5K2hjiUFlSI7IaoGPo1s9iX6WEJw+nafZVSGbsuq6tyCCXjTBSx883u46W7UiEdSR9tAPQpr5yEL57xFHqIqMbqP6H/+F/sMHs8PAQV69exWazwXe+8x2cnp5if38f3nucnp6aoqGDMGfoSjQ060dDQZxxqOeD2wDdl5oenclkMqjnkhdxsy+8KDQMa+XSs/5Pj8d0OrVlGphuzIf6+Ph4QGa4FhEXV/S+q0YJXK5jkysrmj3F6+O1acE5qhtqIOb/BK+fKpFWEmbWlX62uUdIO2y2R8Nleg30TpGk8Bp0uYa8vfxeFBTkiDHi137t14xcTCYTzKZTtG2L07MzrNdrWzON1cbprQD6MEQrimVugqeCAvRhHOsrskkGkrrgvUedzsNnIi/ixsGXmTRV9swje554jfR40B83Sj4S7/sqwqu0Dh7BJVy4uCL7jK4JWRE/9H0wX2dYhtdXV1V3nSl0xfsGSAaWEAv5wAAMkyOomOwqb3GpsjH7PR7L9b4+6HmTatSkPsWMz+mYkSHAdE2m0sn5H3UUZSaBGUycrQOXi7vx4Voul9hut5jP5wNlZtcglhMaKjX5rJ5QVYaeE5b0Z5tUraCSkw/g+XpJquqQaOUkSs+tBQBV4RiNRrhy5QpijJaeDMA6YW0fHzgNP43HY/ufHcR6vbZiddqm/B6pukSioSQqV4fy5Q64nX6muYdAVSEz/UksPMZoxIYhQBqlNbOpoOBeYBacryqMRHkBYISAZGWbMp1Go1Ff/yXGXmEQXDKgxr4irkH/ToNrTL8Z5lU1SNUKDrD2XApBGoRo0o8+l4NwjJwbQrzMHwKgDS18VWE6mSACGIsi0kiYTL03DhiEn6qq6tOzE9lqmwYhXaeXe3UpdV2uB65fcJL3ioqW3XuqXM4Nwki5X2jgjXFuQBZ1f6T/GxLHFC6jUTqkz8Lv+B48qii9bgbWENlsNuZb4YA3Go0sTNK2LVarlSk0NhuRh4D/5xkx6mtR6EBM5J4NvpaHt3g+Pa/OVHQ7NRirZKqdl2ZA0eei5yYh4/7aHg2z5GRATcya9UXSR5WJr3E7dqAkDhrmU+TrPXnvzR+js0a9t3rtStxIXnlMfh+IxWJhs2g9XslmKrgfeO8tQ4W+FQsN+d7cHkNfJZvhCnpCOPDxfxvw2GfE4TIFhh19DQdUfc8Ihg7wWSiWAy8zn3TwZv/ndOCGpGtD+itgsIYTiRIzfdgLDgyx0jfSv2P9r+sr8VL9AIT0OTfoE7kdj2/LSbB/8MN09ZD7mRJJ0vuoyhH0dUimVNsaeeX5mnYYqg5caDj7rIo/r0chMwIabff29qzGDND5PQCYcZYDpBbWU+mTg6kZv0TapNeDJkBVBTgwamgmn20p9EFWP05OUHQ7JVga+uH2uW8kB9umhQIZ3lLCoGQqL0CYt18lXv0stJ4Nj6veIr3nekxux/bpvcvvh6pgmjLPti6XS6xWKzCMWFWVfU4aulLlpnhmCt4L3jlsmqYjMzJhqYW0W6gTsAUYAQxq0UCfN/TVb6l4tCF05luZOIDPhTynA9UBO4yl+r8QA5IlJTJOnmsSLCMTUbKbeJ579DVsW0VTbTJE0x+k94CkTgsQqjHY2u8u13/RBSDBa0C2HhPJmPY1sp0Zk+Xe2eck9y2m63d53xs6s3CTFhYNKZvNCExShwZEMe1X0KGQGYH3HhcXFwPDLpUIVSF03SMlEQzhAL2aQ8VBfTIMG2lYxXuP2Wx2yRfDY5HcWDw7yxZShYLtUrLA/dRIrAoGSYxmRGm4jZ1rTkBUDdLQjypBen/1ninhUVKnXpl85qTvcXsNhelxSCz0GnkvdxGp3GwMYGDq1deAjuTyczcJPC1QWVDwbnDOdVlLvjfsUokYLDqZBrGWg7AoChY+cn3adFQFIYWo7LkUlaJOajJTlzlIWztk8M6zhXicgTIiA7gpL36YTemBLh2aqoIqS3JfQhyuxM1rds51lX95vcjCc0I0lJyZaTr2oRy238lxTTmiyqTv8RgSktLjUFUaTMzYhh1ESvs/U4w48eP9SJ9nRLfKuilJJGtJsSvoUMiMgLPvW7du4eDgYEA+mFHE7ahEaAhHZ/kqr6oHhcSDgybNtFy8UAkFs3J09p8PvHloRgdxbqcPmJIUdnL6nqZWk6zka1YB3aDNJSCUtOXVevN7RXLB8+dtVc+MqizA5RBTHsIi+JArgeEionpdPE9e40dDWEw918+AZNT7bhFS/Sw2mw1u3779ob6HBT/4iOj8HYvFApPxuPeYtC1QyaKrMSJyIiUqhJGOdCyfSIwNkOgynJxMGJqmQYjRFi+MSihCGJAPHhsYToY0NGPqiqieDB+x7XYMwNKiua9NapL/g3+zXQSVYBIR62NDv6gkz2eqTQrPWZgJPeHw6MNJAX1aNVxfiyYPMVkIK/8cpe/n9dbs33n9MjHLJ1s8PlWYmNLPuQ37K9e2qJic4XpVeLFc3se37dFAITMJ+/v7lmFzcnJigxw9Mupc599qwqUBVwdLHXQ1dMTBk0oMH1atEcEOhCRFiYsO4By42V4OwqqC5OSBCg0AC3kpickr6gL9g0WyQjMzB3CmabJ6MLfRkNx0OrWaO+r7UbVFCQu3UaKmayHlBl1Vi/KwHzNDeM94PzQcpeE8Hpfn0nsF9GrVYrEYqHghBLz88svfle9owQ8GJuMxKt9lD61SCQU+t1RcbPbvfVdvJg1+rPPCsIMpFjLoqrLK52okfYqvKiMN3vdF4jRUSuKSh6G1HyMhYCjGQZQSUXZsAKfq4Pr6MNzfVKfuRP2CmfKccwBnnRwvXpyg78fO82fhOZ4TQyVWCYuqtpD7UbE2jhAPI3rsI9P2VGLalJLNezYgSjGacpZ/VjwXACtg2KJXq0IqIeFkvzt37jzQ7+bDjEJm0A1Mf+fv/B3cunXLBk9m7gB9obrpdArnnIWHWGfFHmBgsB6T1jshEVBVZL1eW40WDU3owwsMF45U2VZ9NZqFxXOp4qBEJfeRqH+Gr7PNujq4ZmPVdY3FYmFKExUKZvToQ8oHlbVt1PfCTlz/Bjp/Uh6Kcs6ZUsJj5mEr/V8VFd4nnl//J7kjKVRyxIwlVjzWDCwS0MViAQA4PDzEU0899WC+lAU/kHDO4Rd+4U9jsVjAMazZtpbt471HC3QmWNeHh+pUZwXS1/jkp+Cg6LxHBfRVa/uTokn9gU6QgOFgC3TkybOPkdd1YkAyBaSifJniQNVEV8u2sK6EiXx63UzLTJAABmSL6rCV/k/9cQjh8qrWzlkRQaRjtyQ76Z5oRV+kflFVLx6rSqSPRETDVkaA0v3V1GlTcEhcuK+Qu0E4O11HXVWdlyqRFp/qA7Up8y2GgK2EuA8ODj7Yl/AHFIXMJGy3W1y5csXqlLC2CIBBPRmaP3OvBoCBIqDhHxIIJT3EcrnEaDSydGUNq+hMaFfxOyUr6jsBMCAIfJ2DP9uqoTHdVv0nvHYqQEoItOqwqj/8rX4aDb+t12t7jyEsFtVjxpB2jjwew4C6+KWmQaui1UrnraoMjctac0ZrSPDYtrBbIkYapiLx4Xv8/86dO1gW2bfgPdCGFpPpBNV5muhoDSp+71O/YYO1eDWAPqRj4Ro+Y2nAN0IiaLZbeElXNrUgU3SMgIgqMwiPoC9QFtERlNwvYoX50IfEqFxEea5MgUJaGDL1J+ZrS9uw6rCTULuGsCD9T5T3GvW6se9KxLAR8pEujjfXFCGfzhvlHtj9EFXIJ89NI6oMKx5rzRmqM6baS2ibREnDVN57BCo5QoSWyyWabV9ksKCQGYP3HtPpFNeuXcNisbDBmwOohhHon+HsH8AloqIlyzUMoSET9YIoEVKvDI/LQVzJCDAMP5kULYpDTl7U18L25L4UXo/G3zmwz+dzG7y1wJeuiJ2HjfTe8LpViclVE55Pf+vnpGZoVadyaZ3t1wKGOttTEsbPhWqOemT0npB01XWN7XaL9XrddSxNg8Vigd/93d99H9+6gkcRJMCz2az7Dkm4o01KAL+7VZqtW1ipOwAA9Nk3YViskvvbs5MUAqTBk9sgkQ2ajCGDfm727w4zrJ2i4Ree09qX+VqsPW7oS0GMQ3WF5wFQp5B1CKGvLYN+lXC2TcNGdiz0XiJVYgaqcTZhUtWbxzaFXNRhhvsg56aqoxM3pO0rEiy2k6GsRFjMHxSCVVyGc6i9R0NCk9L3uRbXdrvFG2++eT9ft0cGhcyg+5IdHByYoZPqDAd7KjQcaDl719AMf6u6wodDU5O5DV/nvtw2Tz3WwVvj1dxPTcnqGWGbc7WCShHDOLm5Ng85cT+GkM7Pz+0+UW3SFHNgaKTVv7WzoGrCcyj5UlKyy+CrPhruo+QyXy5BO+VcDtfXdXs1/pJ8KRnVsBm/P7qsQkHBLjg4TMZdFlxd1ZeUQQuLSn8yICAQRSIRCydeC4Z9INtcIkKiFOQDsw7Yg2ckbQ+gN/amgXqQbIDeaEs1iSX8ra6KvMf2udjXmaFHhH1UXVXmM/Hem4m4a0q/ppH1MXG4xhFVE6S2OSVfcu1O+grbl32S670qvE56bgaKFu8t+jFBlSK+TjLl2OeE0BFLfoaiHDHlm20dp8rpeVsfdRQyk8DBTMMmk8nEwiA6iOXqioad7nXsXYO9KhYkFUqEuJ22bzADw+6UZXpL8vDPaDTCer3Ger0eVCHWwV7Jkg7wXHNqPp+jbVsL3Whb8nbpPVHClisp3H5XOCw/rrZX75vWpNHX+fcu8sJjKdlU8zE/CxIadlpUYy4uLrDdbjGdTnHjxo2dn31BQY5+dt9ny9RVhVb7kTRo299IoZ00y0d6PQLwGXnJnxWGMGwbCe0wLKOTDSU1JEw81qVzONf5dCAhZnThsqZtEZIiqunc3C9/Js0/E0JHYEajrv5K21oGErQN2i6dLGXbkezo9kYu/DB9XI87aG/a1gFGPAhmRdk2onLBuUFILsSh2g35fDxwmdAkNWaz3SIktX8vLSFTMMQjXwt5MpngL/2lv4TtdovVamWp0pwx5SnZnPkzQ0eL6ym0XouGf/IMIwXJlM50eF6LqybknU9uEmYIh3L23t6eZRo558wTpB2KtkPbq2oHSRAJgLZDCUUe+srbbR2lzAiBnsioEsX99F7o/dJt3q1TzongrpkN75sqVEoIeUz93Lm+1d7eHj7zmc9cOmZBAdCpkZ/57GfQhn75C2b0MDXX+oWksNgEK4RBcT0FPR0WqpHnQBUCBRWZIM+KnZeKBbdFP6g79BV4uT1DON57jOoRxqNxn2nkXL/eEIC8JTFrr6odPvl/rBCetIsF5KztJDB6f6jQkKA4NwhDkcjk/ZSGqQbqsd7/rD3mX+JPTgQvfQK910mLCipJ5DUNiipyfavxGI8//viOoz66eOSVmdFohJ/5mZ8xtUFL6OdqjSow/D/PqFHooKmEJzcDVzvkTYIeF1VyctVCiUPuk2EHyeJvDKHotWm4SR9eTb8GMFBj6AfiYE+ipwRF7wH/Zvv0t26r5lpeg16vtm8XWdH7reSD90g/Ew1rKVnUsFMO3pcYoy0GSsUrxojHH38cv//7v7/zsyx4tFF5j0888wnEENG0zUC1rJx4MdJM3QbTmIy0HHy7nQbH1kFzl9LAV7QgX45BeInHy4+lxEEmIR2hSd7AGCybSJVr1n3JVZqIyxmcDcmPTEI42FPhMJOzEgC9H9pOeY1hJvO3oFeWBoRG/layYuRI77fcZyMxSvjQf5ZKFrWdlz6X2HupKu8RvYevKjMZ7+3t3eOTfDTxyJMZDclwDR++zkFes2c48GkxO53BayiIx8mJCh/ae22Th6TyWDb30WvQ4+YhrO12a6tdk4js7e1huVxeOq8SDVYi5n3g/eEaVTmRUlKmhl69Z845I2e54sHjcTHKvKovP5u88F1+H/S+5UZf3VYVJT3+vaR6hhvX6zWc61P1AeDs7Azb7bZkMxXcG+k5iojDsKjr1+rxopZw4OsIQoQP4fLSAflsPu9rMPRv5NtcCt8KAUDMyIL8bW3IyFUbWlvTzDmHGt0ikdumuXxeIUQhDdBUK3h/uEZVTqQsK8g5W4qARC3GvpZLkHsICBmR/j20fXVkuz72Y/dSt3g8Ek29plx1l3upBfHsPb3Xsff/0PgM14Uhec7Neo02hJLNlOGRJjPee+zv79vAltckca5fdp4F03QAVDVDZcrcnJUrHxzIdYkDmmhVDcjNsDkpUiLB9uYqEtOJWS/GOWcVbJmZo8XwlDjwfCQ1DDHltXR2KSM8BgmKeoJydUVxL9Mu22adXLZNDiVO2t48JKWhspzEKElkaHG9XltdHV2sU9s1Ho/NgF1QAPSTJrKQGIahUDjXr4QdwiCMwqq1NoOXgbRKtUjsPJDvLXqCwoGez2Q+gTK1gM9A1teY2hClAnHoK+d2KkI7qBfj0E886tROrYGjzxfP1qZj0mfj0yAeeV/SfdBrtPazHxJi4tifsp2CmEiRhtBykoVEjHSbHJptltf+4blVZRuEvvobbO9ZaD+RLC+lPXgP2S6dVD/qeKTJzMHBAb70pS9ZR6M1VYBhmIZqxfn5ub02m80G/hGGSYhcVdGQB2f5Gs7KO5ldSocaUwkenx0Hr0OXRaD/ZDweo6oqS/XWNvGYec0bXXuI5+P9IcFQskIConVwmKpOEqXp4Wy/ZiRxn/w6ed7cV5SrWaqO8fPUAoZ5KErboUQuhGCmaR7n4OAAk5RRwGvcbDY4OzvDeDzGxz/+8VIFuGCAyWSCT3ziE3BIC5pWl+soaXZP9F1GIo2v9WhkacZUQ1zeB2AYCqHSEWOXGaN90M7wU0Yu7Dyq3qTjk5Cw2J8tgqiTg5RWzlRvVZNIOLh2lAMsdXxAo4SkmEIFWHYR96tt877uC0kUQ3e8Loe+TgzvJ4v8qULCzyX3FV26H2yb3Dsv7VVSCVGS9F7z77ZpuhBbOud4MumK6Ymfqm1bbNKk6sqVK6UKcMIjTWaAft2PyWSC6XQ6mG0DQyUlxoiDg4MBSaFqYQ+PmIWVoACX1xtisbw8g4j7K0nhe2yHDtD6v6pHWs2W23L/vBooCQLbxm3oBVFCQyMxt+OsIVdAVP3gNrzW3FRNAsT20IuiqhcVJFV7NJWd4D1kqrkqVXn2V55tpZlrDLWpKXs6neLg4MAIcH7c5XJZQk0FOxFjhK88qroylXOggnCwTa9NuJRG+r+lUuAcIGSdA7XO9um1oCrjvDcjqQ7KRmhiXx3X3qNaoIO5DL62ICQuL25rNV3Qp0a3cUgQHPrQkPfevCDW9kSGSH5IEkzFkvbxGqi2mEfFucF9UlVI+wJTX4R8WH0aoF8ANA7XjeK9DCFYG3NlRklkesHaqkpxm1QrptHXdY3JeGzhyfy4zXZbQk2CR5rMnJyc4B/9o3+EL3zhC3jiiScAwNQD9chwoOYArJVwgX7GzwdECUH+ReZrOmgzFMRBn9D9cj9HXj+GBEG9KipBjkajPoMinYcmXj0+20gSQ+LivbclF1SR4bHZDrZRZxEALMxFfxILEfLceSiN16nZStphaqes2U+EkgtdXylXmHi/tJ36ufE+OedMjdH6OrxGfkdIcAoKFKvVCl/72tfw1JNPYW+/M26aEpu24UBIsyfQK7IW5kiDqg3W6TWXjKwcKPV4Omjb8UQdQb4fj5ter6goCBmwZzVGaxMHeV/169aRXKhSOngG0ZXrj+m6Q3rutI6UqiM+kQ4tuEdSFrqDd6EqpPIMJAyiOvG4g9CRc4NsJapSRt5iNOVlZ4gOwFYmT7w22cjuF8kKQ2pUbHxS5Fxdo6prW77BlKTuC2GKWCU+moJHnMwA3Zd6Op2irmscHx9b+IXvaVyXgynXZOIDy4FNycSAcQsxAnoyRFAlyVUC4PKyBEpggGF9GV1zRSvZauiJ7wG4VAyQbeT2i8XCQk5UfLSIoBIIVVB4Dt4fLUTHda1UsXLSgSmRoOGY2+k+IQQjnpp1pdvquXkfeHxVd0hCNQynyhKXMlCypR6n3BNUYtgFu+DQf29Wy1VnPPVS8yVtpyEerslkz5Z8d1WRsP3UI4Kh9w3oyUCuEgAdKYJmJKZjGnGQ/nAw+VFFgaoJiUt6zSY6Eg6260lhby2Yp96RrplCIPR60/+8PzQGW78p19J/EG6gXLF9RmDS+ZQAqdVAw3Q8np5bKxFbmC6REm7LCSfVnth9OKjQT9p4ndrvMxxp55XP4VHHI09mONAdHR3h9u3bAHDJMKuDPTDMXtL3NBxF6MOoP8rwNRVZSYqqD3kYJW+TPuwkBko0eA6+pn4dbqNhLSVMusQAj6U1MUhQ8o6TJI8PJ+8pSZYujqmKFuvaKLHRWaWGpJSkqYJDApgrPTlxU8LFtaZyNS2vOaOqDFU1/lZvTUGBoiMGAdPpFMtFF4qMIZhhlrNz3Z4F2AaDGPpJB+R5G1T5db2nhBV+SRA4SCtJocphx0mkx2VtsuMLGRo896KEqKqsRIhqB03ESsLoW6GKwfAN/UFt2/bbaJPSviRIVGd4jbo4JkkLa9ioygN99mPv1wmhX0KBxyApZIVmIy87PkslXBayks/CiEu6ViNBrle5Qwj9Wk4hdIpW1LvwaKOQmRhxfn6OGLvUbBbN42DPwZIVcDWtWAc3VSKAYUl/3Zbv6WCu5thdIQqVLnOlhuB+zIzSyrh8nyGte2VM2ewmdQoamuLr2n4qNpptlId7iDwEpfv6rJPIzbz6O78/Gobi/gAGRCY39OZhP7ZZvTt57R/9zPmjfhr9rEsHU7AL7GOAfvkQFonL+wcaV2M2yJKcqAqqReVU7eQ5Q4yoZN+dakWCdw6B6mZSSXhuwgGIaYD3adBmCCadvJ98KDmT6zH1KREjDU3pdbD9LpEO55wtNjl4jruN7X6wHRqmspCUEC+7p37ok+T+Cq3ey/15ry1USKKmhI3vcVtRsUgWtccYKD/pd0siw88+O29BITPWiWhqrQ54ujYPVYY8S8ZlD6wOnjr40VxKX4aqG2rSHXQcouIAQ4Xm0oxH9tFwhxIdJQpsr4a48vuiA70O6Bp2ywf9PJ7MbXMV617LKeR/vxvya9T7lRuPd90rJVW7jNh6P/T4+eu8JmY1FRTk0H4gIg6UBFMnqBYwjOTEH5ORA8jAlk5gg5+pjqn4nJfvvj5vgwGb321VbuxU71KsL1NqAAmVCNR7ku9PokHyMhjQldRJ+0w9yY5P9UPbbiqJtNPug9yTd0O+0Kddt3P9WlPSxpwsuqTGmIojfYpuO/g8Y5+Kr/eZY9N6vX7Pdj8qeOTJTIydGfX8/HzgBeF7+lCqb0Q7Bp2x3wvMjKEyQrKhaoySJ/5PqJlXM5h2qRo6w9AZTNu2A08IoQTAYvEZGePfg3i9kKxdKpG2Kyd8eahNSR/v13tBTch67Pze5dembdRrVWKZf54M3ennkHeA3J5G6YICRYxdDRYuhQLIs0JSomoL0neR/RGGYYx3O08ryjAVGRf7UBJJha4bRAzMvCRaHKA5uPLZlePZAE41SDwhBu4LURaEVNhm6PseemMGfhY9Hv/kPcwIH8niwMeS3a/3Qj6JsWPr73R8U7Ky6zKPD7L+J29zIrxcowkZadNjqk/yUccjT2aapsFXvvIVPPHEE4PKlXnKMgcx59xgRWoOhlq2W/0dAEyRIRnSDKJdCoUqBaou5GqBQsnFrgGaygrDUGpwVSMsr1fDZOoR2RUC0to6eRvZ/pycqBqk6eZ6DbuOpfsDw05Gw3z3Ii+6rx4zNzLn16KEUD9b/U1TckHBLoQQ8NZbb2Fvfx+Btakgqixn7t5bWKSVZ8QGNT+s2WJECKIMh774HF9XxYKhkAAM+gymPt+bKmHgedFz2wAd+iQI7z1iUodIgKgIuaRoaH0WpOc24PIzG/Eekya5H7vay32ivDa4j4NdsnASVSx53lXZGZxX273jmHbs1AZWELbrSu9Z6C4nTdJvF/R45O/GZrPBP/yH/9CWm9dZUyuzKJIREhISGoZg8hL93ntbpFKJBr0x6rXR1GwdKDUTh++FMMyWArIHy/U+Hg0H8TevJ1dEtAYNj6PH05CTqlW5krOLUOj1sr3aTkJJ3y6vTO5H2RXS0vtkmSJppnMvfw1f08+XbcmNvfo90GM1TYOLiwucnp7e71ev4BFD27Z46atf7fqX9OxbeXt+P4WMcFauSiCzhlTt1OfXCE/WD1Cd4bHtmRUFhopK1B9kKieGYRD1diDbp23b3uQqhMCKA2bKhaoxSrAGioy0eReh0Otle5G9ZvdSPCh8TY81UFxydSS7T9aPsd1Z34TsHPr5ar/FVcKVlOZenRACNtttCTFlKNPIBA5ix8fHmM1mAHpVoa5rK/2/Xq+7suTolzRQ82geKqE/Rmcq3IcdEL+UrA0DDEkJZ/w08AIYDNRUhtS4TOKUV+8Fuloq4/F4UByOxOBeVXc5kKuKw9dZx8W5rpCcDvJqDtYUalUylOSwkKAqRloIUJcp4PWraqZZYEqs2FY9F9uSm5aV5PEcvG+8Z/wO8J6tVivcvn0bf/AHf3Bf37eCRxcxdIPYarlEnRIMqJp47630f5vCmt0+wTw2XGRRw00MYZFsMCzEMA8JRMv6LSmjJu1sRIPPnT4T9hykYzMMZeFYSJmGrK9pqcyiDwORGNCMbPeF2+ixsywkn+6Nw+UFej2PkZ59hD7FOaZrVpJTeW+1XrRWjqk4aXvrGdL9NFO03LucHJraItesJG1wzdyWn2fsw4RAn00a0/egaRosFwu8/c47KOhRyAy6L9rXv/51PPvss7hx4wbeeustW3/Hua7mChWN8XhsYaDlcmnF9PgAqUGWISuahwmGci4uLowA6EyfAzIHaJISDV8p8dGHn8SC5EP/5rZMPZ/P54MCgBrmItj2zWaDzWaD0Wh0qZNTDxDDWNw39/WoEqTEgiDJ4/1T8PpJMPk+lRKSoDx8p8TkXqGrQfqj3AcqMd57q9ZcVRVWq5Vd22q1wsnJCc7Pz+/vC1fw6CICd+7cxtHRVcz39nBxft6tsVPXVjCPCk2VMpqcc11BNmb+cfCUATUkBSTueN5imlQhPXcxBMS2BaqqK4jHZ9/1WUg26MpAb5cQZSkDIR+Dv1O7YuzCJew3eEw+8QOTcSJsfJ61eKDLzh1jRHCyHlwKV13y0yQCYoRIP4pEppiZpVDlWokdlbFWrlfDdwM/0z1CV865rg6Pkh9RYpxzVq3Zu2H9raZpsFqvy9pvO+DyWfvgTefe2xn1A4Rf/uVfxt27d/HGG28gxm7pgtFohNPTU1MHOHMheSGBUDWDKdzAMMTBL6TKmiQuVGk0RJIXl+P7JE98XTOxeHzWdFGiouQghGAVbdWUDGCQbcVKwBzIWeWW7eHaTYPy7BgqJsSuziGveKxt1O303iv4oJM4sSNk23hc9TnxM6ESxDZr2nt+XobomqaxFch5X1arFV599VX84R/+4f1/2X7AEGN8V5vFe2Fc/+wj1df8wi/8AlarFc7PzhABTMZjeD5vIQw8JiQvVCM0U8fWHgL6QZ6DpIRK1E9ClUZDJJbtJM+v9XXdC91xQr9CtaoIQK+4RFz2t3F9IfPFpfdUGWEl4JD6M19lSrVOGEVlGSgm/UktvMT+Nq94rG0cKCZUcjIyQsKm6zkFuX88rtYK42dCJYj3ke3ddV7tz0wNTve5aRqcnpzgVqqJ9ihi0/zqzr6mKDOC8/NzHB4eIoSAk5MTIwTz+RzrxIZ1MNUaKbnRVtce4m9VNLaypobOhtTzQfIQYzTTLjA0reZ+FK3qq+nkrOSr6kY+aCuRILHQh01DUKoeceHK7XY7KPev5INhJn3QVQXJFRJ9jdfD15Rg6D3Qe71er03V4jYhBCwWCwBdmEhVLL2uXDHSUBm3Oz8/x/HxMQAMPpuCgvvBZrPpQ9erlRGC0WiEls/JDkWTfwMwX4Y9M0pq+h37onxCYmyQ5Y/rKvfqBAvoB2IqBuo9sWc5Dczmn8sKT/qMVCD26zRZG0MYkC9mX9n1JoWHa0whhEG5fyUfNlkJYXDNPKMpTpnaZM0REqIEw0JF6RpIONu2ReuGIW6dUFJFj4ClcNtnys8qu1YlSJvNBqu03lvuGyzoUciMYDab4bHHHsN6vcbp6ampEgw5ccBn+EcJCAmHxWsxrOKrgzdDVwyV6AKNOmMi2FnlSgcwNNyqQrSLJLC9quxwMFdTq3acfN97j+l0aiEgqjcMkRH3Ihm8Z0pKCFWeSIz0eAAuKVu8l3r9fJ9kKi/2R1M2jb1AT0TUN8Rr5PG4L83c0+kUN2/exGw2w+npqS27UFBwvxjVI8znc7RNi7Vbd16WpFBUdW3qBg20RkC877N6SBBCX7uEXg4OxHDOVlwOiQCQNND0q0Ojfd9zpQNDwy3TrgEMSQJkQIb4VHguKhucyAg5gjxzdV33puSkBjFEZptn+6g/Bq6vmDwgKuiJD1f0lgvsr1O2NVIj16/noGKkBIn9kPZPNh60bRc+S5835Hzc1/suo62ua+zv72OUFv1V/2DBEIXMCEhIuFYT0C+QWNe1mVstpps6Ca24yy+uEgYNqehsH4BVGM6zjEgWZrOZldnnfrn/Q0lCPrNS9eVeWUWEzbxUmpUYNuF9XxmZfhwSMn2Y85kkoT4a/k2ikLdZO0j90c9AiY7NgoSU5GRH/Uskpxoi42eu/iedqfLaZ7OZhZwKmSl4P4iI9r03VTcEVEC3Rg8JNXovCQc5L89vAFAngmIkBjAvCNA/fyzHn2cZMdRTj0amzoR0voExFTCC0l3DMOtH+w17/vnsx2HYS49nhluSFxIx71ElMmbXK4TMBn/gUjvtPksfR/JkWV9Zm2N+PN7TFE4ygkeilq6PYTcjPnK9udLMz9LznFpvKCOXFpoCUKfEiF0JHQUdHvnUbMX/8r/8L1itVphOp5jP55cGbBpPOWDq4JmrC4PZgOvXF9Ltc+KSm1AHUq/OejAc5Pm+1kDZ5U3hT358Qo+pGUesWqxLIeiMQ8mKzhzyc+RmYH09T0/ftT+Pr5WM1ZukP3qv+bd+dhoi1DZwiQL9W5Ub3u+maWymdHx8bOt6FRTcD/7dH/yBec1GiUQAooSm77CTUAqXDjAi4C6XwudAzPe4wjZJg3lUtB/JBlAd1JH9b2pI6M28PJ/1H9Lu/PgGITWmqFBp3VHLyY4thzDSI+3qDz+cqOnrIYRBCrq1J+8P5Zm386U2648Thcbue/rfS590qQ2Sit9mbTIlDqn8R1r6YrlaYZFCTgVDFDIj+Gf/7J/h7OwMdV1jNpsN0m/5wwGR3pC8VoqmXusDSeTqBwduZuOQeVdVZWGjPOyj+/H1PPyU78O2aXgmV1x0ew0RKanhPjrIqz9ISVVeOycnSzly8hKzh/te9zQ/lt4ffV9JTP65KWHJ74WeX4kMK/0ul8uyhEHB+8Irr76Kzbrz4I3q0SD9loM/B0TzhqjSAdggas9NPmOXAVdVgxClQjA68sGwkaocJDb2vOWDupxHQ0Vs2yA8w5CZti1tb/0hr53PGgd46T8G/qA4NOMO7oOQn12kJidYRuLi0COT39NLx8r6LFOjqWzxZ7BLRqTkXug9UCLDsHhT6svcEyXMlOHi4sJCO1qpl4OYDog5+ydZIEGgEmFMW2ZUPB6xTV9SEiU10t5r8Fd/Cx/0PGw0SCvMiAU7jTxMpcfltTJrifeA7WNojPvyOpUkMYSUv77L7JuHhPi3XpNeS06klJBouCknbQyf8f9d4TVVypScbbdbLJdLxBgxmUxK1d+CD4TNdoN6VMNX2er1gKkzOtDrgGiKLJ+X7sXL/gv0s3sitC2atu2Ug6oysqRKQw4qBbnnRBo0XFRRBmQdpOH6hSmNCMTeO2MEjapICitpfRfIMR16cuXRh3vg3IA85cqI/qa6REJjC1Fm/ZoSqQHhkfPatcl98YBdr12n3Ktdk1Wroty22KYsr7qqdo4DBR1KL5zhzTffxJUrVzAejzGdTrFYLEwxYfYLkXtPSByY9cQw1S5Combb9XptkrPJzhIWygmK7stzO+csm0gJBomKppYzTJMP1qqsMEWZx5lOp6ZEqG9F08X5P+8Jr5PXrg9tbkxW8qLhqNyDQzKhRmTdXxUUtos+GU195/3jZ8r7kl8/r4HnATrCu9lsMJvNLiliBQX3i/Pzc0wn0z4Eut2aYmLZLwkD5UOItz1fLHEgpMB24fMBoJHaT957IzJ5CIvn1JW7WdfGIfl7fL/sArd3rveVIJsYdc3vCUxMxwezn9JxtIYUvSuaxnxpIknFKf1tx8omQ6oW6XvWxwiJcelYbSKVSMSCBM3ITzoes5lI1jT8z/tXsS4PpJ4V1TFRvXgeANikUPeori8rYgUDFJqX4Zd/+Zfx+uuvYzabYX9/H5PJZFCwjhlOwOUQBEkJ36PaokpNHiph+MZ7j9lshul0itFoNPB8KIHK3exUDHgMJSE6MHPbzWYz8IKwGB5VF/piVqsV7t69i1u3buHs7Ayr1cpMyhp2Ysr6+fm5pWfnvpntdmvnzUNOzDAiqSChA/p6NzyOZhspkdKw1i7w/uQmXVWevPeYTCaYTCZGIHmNm80G6/Ua6/Xa7sV8PsfVq1cvqU0FBfeLL3/5yzg7O8WoHmE8nqBKmXX27KYZOSAhH8DeMxUTndrSNk2v1GgoI3uGnHMYpefMU/2lOqN9i+xr+8sxSDAYxgrpfW7btm03MIcw6IvyfrBpGqxWKywWC6xTX0STcpR2M2V9s9l0pE+2SSft7kPbWtE5yDVwYkdSMZjQte3gOCQteT0Ykrt7EYsYdofCSUD5U1cVatYMkklYm1Szpm3tXoxGI0xns4EKVXAZRZnZAeecEQrnHGazmYWfGDLZ9YVVHwoL0qlqA/RF3ngeEqC9vb1BCrGadXlOdgQ62MYY7Tx8T6vwEtrWvOaLVpjk+1R4SFC4HTO6VPUAumwstpcxXR6H5+Z1aN2WGOOATGknp2pOTsy0Y8i9QGzrxcUFDg8PrZ1s466MLufc4J7wfLx+Hn86nWJ/fx/Xrl3D6ekpzs7OSjXOgg8O5+CrPnNoVNfYbLcYJSXRwhnZbgxFhNgVpHNpgNYwUQj98gKqyoylUCTDRU6fSYia44c1VyrvEamQuL6IXdY4uTw3aIf9rcpxCis1MQ4mXpASCd73RfLaFCKLMaKR/qBKbSdRQYxWadcldYXKVwgBlZCWgZpD0sLJDxUrhtJEWWJbN9stJpOJtZNtHPic+PmkfYyYkCRmJIwZtLPZrJtMybqBBZdRKgDvgHMOf/kv/2W8+OKLOD8/x507d0ytoDEX6GcMGrZgSGpvb8++3JPJBECvEChxYOhmOp0O2kBCw4FXM5XYRr7HGYaGbojc8EulIT+XSs+LxQLed2tGscItQ2ZVVQ3UI7aL92S73Q4607Ztsbe3Z/VoclNzHnrTdat4bqow2k6V0XXGF2NXMG+5XMI5h8lkgtlsNlBzNKNJ7xnvD49J5YrETQvrtW2Lu3fv4jd+4zfwxhtvfIBv2Q8WYqkA/IHg4PDZz30WTz75JDabjXmxmqbpzL9iDM7DFhyYx6NRtxxCmvEDfXl8JQ5aW2nQBgmN0GuiBMrCVjKB0H6IsEFeFJxdiQl5aNy5bs0oVrhlZpfzqexFet6pilgZjLYd+lpCwCj1L5GTPpIgIXkABmtdsd5Mk5QtvcYBGUn72cKPiUw1aamIuqpQj0YDNYdEMb9nVHD4WXHyROJGPxKve7Va4ZVXXimJBigVgN8XYozY39/H0dGRPfivvPIKQgi2ThO34xeybbuVlWkI5QPHwZkDN+PBWtAtjwFzsGbVXmDoMeFxct9I27ZGinJvj6o+AIywEFQgtA1cu2kymSCErnquzpxIcHiPdl0Xi9JNJhPrqNWgq4ZfVWVIHA8PD02G5vEZisp9NnocVYe4ermamZUI8t7RW6P/835yXyV45+fnl9aPKih4P4iI5s/j83hyctIN2smH1m0nxtXQraxMQyjrvlCt4MCtHjEIgciVERIjVSvtPdenGTOcFdNgbOZ7vaB0PA90ahGGExykY7Qh9F4bJhSE0C2yyT6N155MysBwDbUgfhO2MyalaksyxnCRtpOkMIWWmuSLYT+nCrERC7ln9jmkvwfqUAhAWmfLwnei+pB0QdqLRE55P82TKASvFOZ8bxQycw/Qg7K/v48YI5599ll84xvf6Ex70+nAF6LhHk2p1sGT26m6ooX3gD60AWAQZqKiMJlMzHuyWq2swJ8O0LrkQP7lJ8kgEeKAzc6GYTTNVKI6wXbxN03OWuiPSoj6fGiyJXnS99QcmJMvqjdcxHG9XluWF4kViUpOZHgsbssQkp5zV4hQFSOdvfK+6f1s2xb/+l//a9y5c+f9frUKCgZQMzoi4I4cjo+PsdlsOnIdh76XCJhx11Kq+SN9ifplWPRNTbOWBSRhJioTJFKhbdGgr4DNc8SkGPhsgCdIMkgGaBQOaSBnGM2n9g/UCVEsgD6JIIZuGQMSC/Oc8Nyp32B/pjV4rD/CkHw59OtMNU2D9WqFpu0WufRCrNgn2XVm95fFBuHcoD8yEqP3JlN8BmG6GC/1TzEEvPnGG1guSn2Zd0MhM/cAjawcxJxzePLJJ/HWW2+ZKUu/5ABMMeBq25pBYwYy+VvDHQQVBz7YucJDf4kSAzWhqrKyK+zE/2ls5vH5OjsgNfqSNI3HYyM2VFss60Bmevqbf9ODozF2k8xzWRc9sVPjMY+lVVNXq5Xtq6oPqzhzW14n1aQ8XEcSxLbkSxqwPfQAHB8f4/z8vMSwCz40OiNr/z1zAA7293F+cdE9L1VlIRXO8k35rCqb5ev+Ntg6ByTlwWrVJAyWM0hhF1CFib1Hj8SAJGLgJYFkCaEPR/nQ12uq6houtYHQsBXJmim6MtkiyamrCoH73+s3YKt5B3l2AQyL6rlhqjs9Qmo8btN2GtJummZYODD2XkB+HnavUjuQndc511X9pYLG+8ftqIDJvV6mPjDEosy8GwqZuQf+5b/8lzg6OsLnPvc5GyRHoxFu3LiB09NT204lTg6UBL/c6qvJ39+1SGEeV6aplwQrH/A5UOvr2mnpcVVFys9D6MAO9MZfmnlJDvL9uC+AQZu0s8v9LibZZmqNZj2RlGh7eO/0PlC1AjoyM51OB4QuJ1h5m/Vz0JmRSs8xRpydneGll14yv1NBwYfB66+/jul0isefeAIRaVCvKuylBW4BAFU18H5U2QTFZvohIOCyUqJhmOyNSwNrCF1F2iihIA6wXvdLr+80MPCZj51p2Om2+fNP0hX7JAafUtNdIln5frYvZDVs12dWDe4JABfjIMxk+0s7ESXDyfXhaw3TI6lXzJgCMAh75+fVe6VtVlUnV21MXY4Rm/Uat27dwraEs98ThczcAy+99JKpJs8//7ylDo5GI8xmM6xWK1NgNMUPuNyRALjkrVAmr1/wXNmguXW1WiHGLr6uJIIPmxpa+VoO7cyUZFgHkoVSuJ0SsTwMo8X2eCy9H9oR5CqUXqcqIHofqero4pFUjUjs+EPlCujIDGPguWqlUIN0TrI0HMjrX61WeP311/Gd73yn+GUKHgjeuXXLVJNr166j8Q3a9Ro+GUqbpunXX8onEDv6ml3PMBUd9XuYZ4X7pYG6SSnhlRAooA9xqaHVlKAMTlUfDu47lNjBPhg+dw5A1P5Drpl+Fb0fZlQGhiG1dBwn++fhJraTYS9wQpXCWraWFQlT7C0BdV2b1ydI23OQoJhill0PgH6ZCHRjxtnZGU5PT4tf5j5QyMy74Pd///cxmUzwoz/6o5bqe35+PvCo5CRCF4UcpBlm0BoyGs7I0bYtLpLczPWiSBg4wOugC/TKzrupEbq+kcm7mbmO7eSDqwQMGK5DxTbtCm2pSqM+mbxtGmvWTk3NzvTI6MrXuk4WCQ+zypjWqOEtgtelPiVV0zRsxdDb7du38e1vf7uElwoeKN5++23UVYUnbt5ECAHbVP+JYQt6VZREVN5btdkYArBLeQGsKF4EBuGMHDF0Kcbm/5PEBEvRBmzxxe7gbpjabCd1XcgKuDRR0GdfvT3OeyDLKNKsHl3M0bsstJWgKg1JgwMutU29L/aDfgkJkrmYmahtyYd0P0Lo15KqR6Ou/bv68tin0gPJIK1KkpI414WXFssl7p6cIIbLn2nBZRQycx/w3mM6neLg4ACr1QoXFxcDRULVFGXVMcZLnhJCTbpKKjT1WD0y8/nc0ptVrcgNraoUKSFQQsUQEwmKbkMlg8RsPB7j4uLCBm9tq16LEgmVtLUNmrV1LxXGe2+hIh5byQ+JF6XdvFAfr40ZAEwh18+S16qp2LsGAYLHu3v3Lr75zW/iO9/5zj23LSj4MKDqOU5+tO1m05ERYBD20XAKTbXIvCyEmnQtBKITKFEa+NwzvVnVClMU+KzopETVBSUHydMTQ+hW8RYVOsa+bL9PfcgWfTjL1KT8WkQ5yT0n3JbZS6YsaV/DtgMWKuKxnbxH0mdlIVgHhsQmXZslaVSXq7XzWi1VPp0/pDZeUtZc56lZrVa4e3w8sDQUvDsKmXkPNE2D8/NzzOdzeO+xt7cH55yFfTi4Aj1hYDVbDrB5dk8ezlAyRJLBc6/X6wE5YbbUrjCOEgeSKR5fi/3llXX5uoao6P/ZbDZ2PlVP7uXTUW+LEig1Gut5laho2Ebvya7QFL1GDCexrcu0oizvGcNOebFDEhmtK0MjnxKnGLtshpOTE3zrW9/CW2+99e5fmIKCDwhOXkjIR+MxkJ6LS4pK8sawmi1NtJrdc8lnovvzGU37hdCleys5YbbUTnWXhMX1RfFIHrzvi/1dqqyLofJKwy7QZ3cqwQJgGVpss55HQ0eRivEuVUTuBxUVuajeN5TtSxWG3j32Ym3bwm23aHC53+b18x4F6V95z733cBrGS9u2IWCdqq+fX1yg4P5RiubdB27evIm/+Tf/Jo6Pj1HXNVarFZbLpRENDnwkAVaxMS0cqWm+6h/RAZzH0dL8VByokPA47Oxy7Br0taKttpOm4rzirZIrEhsqIAzXaDiGISAlK0oE2K5cfdIQWx7K0eUZNBNJQzs5gdTOabPZGNnkZ0KvEe877y+Xc1iv13DOGTnS8Nr5+TleffVVvPzyy6VA3j0QS9G8B4KD/X381E/9cSxXS3jfVeputtueaEAG86rCqK7RtN1SBi7z7ql/xEgHesVDV5ym4kCFxPopMcMqdg36WtFWCQIrBecVb5VcGbHxHm3oli6IiVCxvd7360hJQwaKzGCySMKUCB6JFLdj2EdD3zy2LhugEzb9DfSFUHktFfsrHiudpw19dfi2aYDUd2p6eYhdNfTTkxPcOT4uBfLugXsVzStk5j6xt7eH/+6/++9w69Ytm92vVisLiXDApHpCoqNLDQC4RH5UMSDUE8JaKrqStta4IahgkCjca+BXX4t6VPigqa+FBf5UudElFZQYxRgHhb/YnrzT2xV243F4X7VKck7QdI0lTdHO791isTDCOZlMcHh4OKj/oyE8Gu2WyyXm8zlms5m1b7lc4q233sLLL7+M11577f6+LI8gCpl5cBiPx/jSl76ExWJhIZsmFVADYANmREdUSHRYzn+gAgM7FRNCn20+y6yxYitV7wiFWMiX29hbuw396lGxpQLYD0IWnMXlEJSpTa73zagCbMbfrK8x8iavmecn9gs+3kuVsawiXM6G1Hu33W6NcNZV1a/vJn29rkm1Wa+xTeU9RnVt7W62W5xfXOD4zh2clPDSPXEvMlMWmrxPXFxc4G//7b+Nw8NDxBitEizQe0ZYBbhpGiust1qtrHqthlQ4COcmYe7DInGs70JVZtfaRAo+fHlYZ5eCoQoMCVLuaSHJocK0Wq1wnGK5JBZaSC8nK0qA8pCcpl8r2WNHxWuh+qMp40zFZq2cnESRAOYqSw5uP5vNAHQrGZ+dneH8/BwnJyd455138J3vfKf4ZAq+Z9hsNvin//SfduHT2FWYJZFhvZgQ+8Um67q2LCQ+k2Z6lT4iZMTCaqukJQT4nNkzSgJCorAjfMM2DV++rGA4ec8Wh4zDonIkOT49k03TYJn6QjPkxz7ZwfoyIVCWDSQKs5GjdM7cX2gqEsQAzGOk+2Q1suR+kkQxlZwqC68lB7evJYS/pjK8WuFiscDZ6SlOT4si80FQPDPvA8vlEo899pjVF6EKoJ4Pyo5cv4gF9rg91REqOHydIZbFYmH7z+fzwYOXKy6q0NBDwkE7TxcnGPtV/whDOXkGj2ZLse1VVWE2mw2UIh6XUJKlv9VjpESG+6tSpOG4/Pi6VIEajrXz8t7bIpNvv/32JVWG90HbePPmTSu2d3p6iuPjY9y5cwff/va3LylhBQXfTWy3W1tOBJDnQzwfIUa4RGZ8en5Zf0YnJlRw+DpDLFwGhVW/7RvO0JAqOCQg6JdN4KC9a1KVTtarQel/l8gYPSIkDT75R1SZcd53lYITWbBrkFNoppIDLAVbz6f+Fcg5+BpVnV3Ht6UK0j1vkalAsa987r235BCSHru+lHnmUxv29/dNWV6v11gtl1gul7h79wSXlxUtuB8UZeZ9IISAv/t3/y6uX7+OK1eu4ODgALPZbJARpIOlqhB8QOnVUFkXgHlSuB7R4eHhpQFdQz6afsz/gcuLyPH8hPpycgKS+2aoPLGjYtiLBekGUm8iFLuWbtBzKlT5IfJlIgazTemQeW7dX1Pl2UmcnJwMUufzNFEaqknOmDUWQsArr7yCb3zjG4PsqoKC7wVijPidf/kvMZ/NMZlOMRmPMaJimbZxQioGvg4hGrYKs/pB2rYLTfmuEjjrZQE96TFTb+pvWnmeVUXd1W6D65cp0FAVM4UC1RLn+qwiOT9D3RZOzhQRJWh2H9B7gQbtSq/fi6DphI2hr/SGGY01tZqkzMy/aSkEnbQNjpPuLcN4VbIgUDU+OTnB8fEx2lBKPnxQFDLzPvGVr3wFv/Irv4IYI/b29mx1bCUw9H+QWOignheO0wGdg+l8PrcvuSoOeSZO3rns8t7s+j8P7wxi7DLQs0PR0BMJg5IGladzAyL/1zCQkpV7Ie7okAimb19cXFy6BiUrbdvi7Ozs0v3R+6ZkjDV8jo+P8dJLL+Gb3/xmMeEVfN/w5ltv4Wtf/xoQI0bjMUbjsRVnMwJD74oqMoCtOTTwpqEfkDmYjkYjC42o4sDjRHleNESD7PnMn1cd0EmuLNQDmMKk21u4J7WDhEHXnqIJ+JIatEMN1vDRuyqrGdlSOOcQ2rarv5Ndg7UZHVFabza90owhydJt4Zyt+7RaLnHr1i0c373bV3su+EAoYaYPgF/91V/FeDzG5z73uYHpdbFYXAqxqOGWr/G3DqpVVQ0WUlSlR0MxqvAwPMXsppwoaAejxl4NcWm7GOrS7eh54QxJZW9dNyonXjxmfh16LZoGrZV9+b5W+FXQYH1ycmJenpzIAZ1KRSVMiYwSLr7GWdLdu3fxyiuv4Gtf+xqOj4/v9ytRUPBdwTe+8Q1UVYUnHn98oIRut9sBIaBakSsjLg2iSkZ8Gkyr7Jl0OvgDPQlRdYfp0PfYlm2hKqGq0aBd6Ad8J/uHGFFjuLachsloAM4NvzzG4DqEeNEMDddX9o2ALXNgC3Fm9995j2a7xXq1gk8qfE7kkNobQ5cur+QtT3SIiUg6720R3Tu3b1tJiYIPjkJmPiB+5Vd+BQDw2c9+FvP53FztXHxSB+O80FyepcOBnsfgtlRyOKCrqqDmY4XKnDyOPlT5Q5h7ZXQ//a3rIOkx1G+T17vRayC0LbmHhcSJJKcRgyPvA+8VzciLxcLWYOJ+/M0Q0mKxwHq9tvRs/VyUEJ6dneHVV1/FN7/5TSwWi/f7lSgo+K7ga1/7GgDg8ccft+zINgRbfBIxIqA3/AKwgVoVi+7tvoquhXZIVJzrPSeiqmgW1QA7SIP2LrnWoV6bgcJhO/QTHyR/0MAf43q/jV1TpnyoGZkKFc+tHpYYY+/3QT/5owHYlCH03rztdmsTJ723VMG4YnfDejnSLlW4fVVhs17j9OQEd4+PsSlh7AeCEmb6EPiVX/kVfPWrXzUvy+HhoakkJCaafcSBn4Y7NdDm4ScNlXBQ5zG5knSuMuQeFyUVqkzsCi3xQZ5MJrZKNk1t0+nUzLQkG1pgjiCBo5dHM6S0no6qMuv1elBhGBhmV90rNMaMpdVqNdhW759zDgcHB3DOWZq2FhNUQ/PZ2ZlV933llVfKIpIFHyl87Wtfw+1UFgIxds8mq+vGrjidrgtkIZrkz6AaAFwOP2moZPCcpb4nrz8FdL4b3VdNvoMQixIcqinpWHXq8+q67lbWdp1Hhv0OyYYpuHpDYl8fh2ZoU3dCX09HVZwmhYsGvpnY17y5V2iME6OmacznkytgcA7jyaQ7z3ZrmWZ2T5LyM6prbNZrHN+9i9OzM9w9OSlrvD0gFGXmQ2I+n+Pw8BAXFxeDDASGajR1maEkYCi98jV6ZzQ0Q3LBmjYxRktVZKl+VSJ0VW2eR1Wd8Xhs+6tZmIM7SQoNycQyue3ZNl3biVlbSqaUjKm6xAeXHQ4JXwjB0tlzTwszlgiGtUajERaLhc2YBnH1tP14PMbR0ZGtqM320Pg4Go1w+/ZtvPbaa1gul3jppZfKuksFH0mw1MB2s0Gbnv+BmprCJ0AXHrGCdwxtx2jVdqMQACBlS6Znv2kaq9zbsIq5+lQ4AUrqCWFp1gynVBXapkEb42DSZSSB/sJkSAa6xSS3TdOtEh0v++BGSQVuhUyxBSHtr+EkoE+TDm1ryyrUdY2QJjYaNgoh9BWH0Rcc9El1CVwCBhiGr9D1S+zD2nR/fQioUnG8ynsslsuurMV2i1vv3EKIZQHJB4VCZj4k/v7f//t47bXX8Gf/7J+Fcw6LxQIXFxddjYTlcmAI1oURdfbQygyIygcVHtao4XFYfZj1Z9SDw1kEf6s6xGNuNptBirfOPBh2IZEh2eGSACwEyPMBvQSrigffz/0sVKZIenS5hxC6InYkUgwlachO1Ze2bTGdTnF+fo7VamWF7jSEx2vZ29vD0dGR3X/6nBaLBd544w2cnZ1hs9ngN37jN76L35SCgg+Hf/Nv/y1OT0/x6U//MEaumwhsNxs0IaBJ4W0jE+k5qcVzZxk5aaDlgo5UeHQS5gCrPmxh3tQOS31mmClTh5zrCvi1KWPKFqXMwlmm/qT+CUh1tDabrqIx+zaeVyZlJBOI3TIGrE1DYsLQD0Nk5pFJ98MKhCbSZhlLSOnm6NWXkPoi1rWqRyMjUc65bkHNFI4bj0bwKewN9MX9ttstzs/OsN5s0LYtvv3KKw/8+/Goo5CZB4Df/M3fxN27d/FX/+pfxcHBAV5//XU0TYODgwMjBkowNpuNfcnVA0PSwBnXer22QRvoSMVisRgoKDwuf1rpGACYdMsHmKRof38fG3Hfq+GXSpEaggmSsty8y1CShoB4fVSPVP3hMRiWYselKddAn46u/iG2TVPBt9vtQJFR1ck5h2vXriHGrlz4xcUFzs7OcHZ2Ziuh/+Zv/uaD/2IUFDxgvPLKq1itVnjxxS9gMp7gLJx2iutk0iscQjDsmQcsRMLS+gDMBNymEIoW5+Skgs+VeVDSQE4yBPTkxieCo36UUVogV308FnqpKtRIREVDUujVYuc6I7OjKVjCYSROvF5TjdAnGZiyk8gTpA8BFSbASJIDbFVsoFeaNbWd5wBD/fQFOtcV4Ez3frPdYrNeY73Z2Eror7zy6oP9UhQAQFnO4EGBEuNsNsN/89/8N7h79y7u3r1rFYAZ2tBFIgGY94UPJ0kKScBkMrH1g6qqwu3btzGZTHB0dIS9vT3raEiA1KeiBELTk1nPRskAO7E8DMTVp6mCALDUce7Pyser1cqynhgeG2RKQGY7mWpEAsP2k/CpkqOLW9JsfXZ2Bu89jo6OMJvN7P5qKIqk6uLiYuCdWa/XOD4+xm/8xm+UuPWHRCzLGXzP4J1HPaoxqmv88S9+cVBlvGmazowqpnlC+wYoSSEpSJ64tm3hncNiuUSd+rVRmpw4wNKKB5V8hUDYmBK76sWWWp2VadA+if8zc1Indrp/DN2CmLp2G703mk0F9MbiXDUyYpfab0VGRckxI3FSb9rQLUPgXLd+W538jiQ5ERiQqu1mg22qrhxSm1fLJb79yivvWpKi4L1RljP4LqNtW1xcXOD27dv45V/+ZRwcHODKlSvY29vDdDpFjBGLxaJbDTWFRkgAOAPSirsATJ3xvlutmyoNa9vkKcZAr7BoyIjH1zANPTB5QTiSKTXqsnouVSXuQ6NvbvAdjUY7103KVR52tBoD13NqdhP31xkjz6eF+rR9LJx39+5dHB8f4+Liwu77er3G7du38du//duFyBQ8VAgxJJV2id/68pcxGU8wnUwwTs9dBAaJAlyygF4YJJUDzg0GfIZ2xqORqTSj8djMuZBtAQzMvEYYqAwJqaEHxkzDCaru8jj///bOrbeNuuviaw6e8SE2TtM0oqVvGwoUUfWuqgQXHCrEHdwgPgMXfAw+C/dcICQEElcgpEYInhd4H9qUps0TNzQnx3Z8GHtm3gv/9997JkFPBT1k2vWTIkIS2+NEM12z99prS3quVJXkMTa0D9lrnac8g9nfUW58Wt1M2bUO8hxGnInYkccnaXbrtxZk+eNznKnBeDgcYjgYIDLXxomplg36fWy0WhQyjxCKmYdMmqZotVr47LPP0Gg0UK/XbVrueDy2nhpZhCiVAl2VAbILKQHYCSjxyug2Sz6E76hqiLSHpB0TBIEVIkA2YE+H4snzSIVGxJE25w4GA1t90qmW+sTNp/xqU7R+fXmcrIPQX9ebxOV3lL+rk7tM2XEVmR61bNKWVtiff/6JX375BQcHBw/zz0/IYyNFik63i3/9778QhmUEphrqui4Sc66M5ZxV27etR0T57bSwkQkoHYkgFYiMaEhzk0qYmXsTM2kkYsH6XJC9Rrm555UxaREKkmAsX58YkeAaISOBf1q4HEr5zVVbMhNL5rqbydwxVZvMhFhO+KXJbEFlYm7mYmMwzoeaHvR6uH//vq02kUcDxcwj4tdff8XXX38N13VRrVbt5AwAWy3odDoYDAbTuyHVfhKRokXFeDyG53m2KqMvMtokK48X8aJNwfr7ciwiTqRqIiclkM3DkQuU/KwICylxS6tLjjdzoTToCkveKKyFk1xUwjBEtVrNZNxo5Fjl/WqTsJTcRYSNRiP7342NDayurmJ3d/dh/skJeSLcv38ft/64Zc9B3+wyAmCrBSOzqdkBMu0nqTZoURGbiZ5AnsuZBc5Zv0uuEqz9JmKile9LPo1UblJ106KXWTo5QRQbISJrGeR8llaXTQI2vwddm9EVFi24MoLMmeXkeOZm0V7vcr9jCdqz7zdNM8JNPmJTiYnjGPFkgm6ng93dXfQZivfIoQH4EfLtt9+iVqshTVPMz8+jXq/D930MBoNMCJOedsobW3WlQfwoR2W8yF2AeFh01UXQI9xi9BUxo/08emxb/l8jrzUYDGyFRvYb5QWWNvNq8h6avJlZFnTKcwoiyqR8Li0ufbenPxfTtBixt7a2cPv2bezs7Pyjvy0hx4nbt28jMMsiK2aXk+tO02sjU2WwhtdUGWvF2OrMDL6JafXq2AfkzsEUsxA8XXURrL/G/IznulPjcZJMx5SlpQ5kgvBSx6QWq9dCmmIirWVntt/IwcyQbE3PR7Rx8h4aaWuZ/5n6E9VzTgAgjqcTV0lyqMU1SVPYGFAlluzePSNo+gcH2Gu3GcD5mKCYecR88cUXAIArV67gpZdeQhAEWFxcRLVatbk0chKISViEjK5WiJlWixhddQFmJl5preTbPbrCId+XTd3D4RDVahW1Ws1WWLTAknKslEplAktC9fJCJm861pNbWqhpwWUvrub1xJOjjcBy9zMcDq3ok+pW/vcpgnE0GqHT6eDg4AC3bt3iviXyVPL7jRsAgDOnT+PEiRPwPA/VWg0llUsj7RNHjLO6QjP9BD5mfhIrYdLZFBKgqqyTybRiocai9fftqLPrwlHndKlUmo4xm6pQ6szWrcjjrY8OsC2rklSdRGCpSq5UWeRrSNPsJuwjPDR6yikx1x7XcZBg5q+RnCvXmQbiwXHgye/TiLTE/F4nZhhiHEXY3dvjvqXHCMXMY2JlZQUrKys4d+4cPvjgA4RhiHPnztkQu8lkYvNpjvoHXmfTCHmfibSj5OTTk0lywsvX9Xh0mqYYDodI09SaffVaBsH3fQRBAJk2iuMYYRiiXC5nhEj+2PLPo6s9ukwtryEXNXk/YpIWz8vc3BwajYZ9n7ITK45jm+2jy7/7+/v48ccfab4jzwQbrRY2Wi00m01cvHgRnu/jubk5G2KXJMk0CVdVVPTItQgTjZ5eStMUvmlHJUli/SzyczAeF/m6a/7BF+EwMYF4nmkVxeY5kLtGeJ5np43SJIFvDM72OI/wwGjBBSBz7ZEWWL4aLC2uJI4RGaOyeF6CILCLhGPMdmKlySzbR09xjYZDtO7dO1QVJ48ejmY/IYIgwMcff2zHixuNRiYED5heCLQHRVpNwOE2jRiMO52ONfjq58mbf7XAiaIInU4HURSh0WhgYWEhkybsuq71+OiEYd/30Wg0UKvV7M+JUJHnF3RVSUSIVGv0xFLezCy+mNFoZE3TpVIJzWYTg8HAjq23zdZZ6avL8fm+j5WVlUfxJySKlKPZxxbP83DlyhUkcYxRFM08d+pnUqmeOE6m1QQcbtOIwXhkRpXzu9fy5l9rqgXsuSw3QtVKZRasZ64J4vHRCcMSUxFIYJ1qZVsho47Tvg95XswqLUf5+aA8PLG5Vo4nE3im8jxWoabD4dCKQhFxcu3baLUe1p+N/AV/NZpNMfOE+eSTT7C9vW1zVSRmPwiCzJi0GHa1cVZORrmLEHSKrjxGT/qk6oQGYE/Qfr+POI7tigbx0MiqhslkgnK5bBdrSstJqjn56lF+wkjaZXJ8eiRbV2u0oBH/j0wjyTh5rVZDkiR2Iuznn39Gu91+2H8e8oBQzBx/rl69as9xyWeRPBo9Ji2G3XzVBsChmxSpaNivpLNdR9rLYr+tbqySNLUrGsRDI6saxLdnF2uq6UfXcWyS7+xlZ5UjOV55T4kMBqhrZ37iU47NmnjVOHnJVKMnRuD8ubmJAXe3PTEoZo4pUur86KOPUK/XM+PRpVIJgUnPlLscObn1nYm+QwCmnhnxsOhKiTyPzoQBkBEL0nqSCSw52e/du2dXHDSbTSwsLNiQPDEA66A93UbSd2i6F57PnQFmbab8jinJ8Tk4OLDveW9vDz/88ENmOoo8GShmjj/TNg9w6dJrCMJw1m5xpisNPM+z1RD5mogR3aLR51ocxzYsTldK5Hn0dQBARixIO1kmsET09Lpdu+KgXC6jWqnMdsHpag+y4sqKGDEWK0PwodwZzK69+R1TqWnDjaPIvufhYID1//wHaZIiPWR3Jo8TipljThiGeO+993Dy5MlM+qX4UUQ0CLL3SNpPumetU3X1xUenDGsDr4gdETTyGBEWURShUqng0qVLaDQauHPnDn777Te780hPPgj6WLUxuFQqZaat9Di44zg28XgymdhR9HK5jOFwiJ2dHWxtbWFvbw+9Xg+///77odA/8mSgmCkOvu/jwoUL1iwPwObK2IqG+nnZvm2Tc+XfDNW2EbEj7R478WT8N9J2kmuLXAOgfk6+XvJ9LJ46hTAMsd9uY2trC6UgyHjzMtcX/eaUkdlzXbsJXMzJ0kpyAJt4nCTJdKO1qYZPJhMM+n0c9PvTALwowvb2DuKEC2iPAxQzBaDRaOCtt97ChQsXsL+/j36/j9FoZPNWyuUywjAEMNskq30qADLiBMiWVOVxMk0gnhSdkzCZTNDpdNDv920VJo5jLC8v480338Srr76K3d1dfPPNN/jpp59QrVanu0iAIwWUHIN8iGjRuTba4yKtrKWlJczPz6NUKqHdbmN9fR13797FxsYGbty4gSRJMGSp99hAMVMsymGIc+fP48T8PIaj0TQ/ajKxeSu+2fQMIGOSzbdo9LluBY1BxINngu20T0++NzKvLVWYNEnQnJ/H+XPncPLkSQwGA9z64w9sbm5Ooxq0Z9C0sfRraiOziJZEC5ncddL3fczVaihXKvBcD8PhEPudfezv76Pb6WB7Z8deJ8nx4K/EDKeZjhGdTgfXr1/HjRs30Gw2cfXqVbRaLfR6PTtCHQQBKpWK9ajoSSbgsE9Fo1s3+qKiKySSvlsul6ejndUqAOD06dNoNpsIwxBnz57FtWvX0G63sba2Zh8jPhh5bel566/Ja+tjkNwYMTi//PLLuHz5Mvr9PlZXV3Hz5k2sra2h1Wphc3OTuQ2E/EOGoxFaGxvY2dlBuVzGmTNn7Pb4NElsVETJ922oHhyTA6OvIcqnkuZaNdK6sRUbMQKnaaZK7Pv+tDJifIGSmu75PhrPPYcXl5cxHA7RbrdnlWVpLxmhJanFdmpTjsMeUGrD/mKT7Ou6LhZOLODU0imMx2Ps7u5id2cH7XYb3W4XvV6Pld8CQTFzzNjc3MTm5iaazSZ830e328Xly5fRbrfthNJ4PEZgyq5a1MgE0lGmWmC2UkCqGjpyW6cG12o11Go1dDrTjbyLi4tYWlqC7/vo9XqoVCo4ffo03n77bXz++efY3d3FZDJBs9nEnIyAmqwXufOSu6CjfDryIUF+UolZW1vD9evXsb6+jk6ng16vRyFDyEOi2+uh2+uhUi7DdV1EoxFOLS3Z1STANLXXtrSVqJEJJJ3gC23+V8JFX2eghhCSJEFQKqFk4inSNEW1VsNcbW56PFGEku+jXq9j+fx5/N+//22DOu1aF8exO5Qmav2BzuPSPh35SNNpkN9wOEBnv4N2ew8brRY6+/vT3W1qxxspBmwzHXM8z8O7776Lzc1NvPLKK/B9396hVCoV6ykRE66uysh0kXyIkJBxZr26QO9hqdfrCMMQW1tbCIIAURThhRdewNzcnE36lXyZbreL7777DuPxGGfOnMHS0hJKpRKiKEKv10O327XrDnQ6sSzb1LuqANjXr1QqaLVauHPnDttJBYBtpuLjOi5evPAier0eFhYW4Lru9NxLU/gm5E58NWIWlqqMo6oiugorN1eyDgAw7WjjwQnCEL7n4aDft9cHmaScJv168PypmIpGEe6u30USx6g3Gpir1eCax0RRhMhEM4gJWPwycq3Tu6oAAI6DMAjgl0rodrtot9tsJxUAtpkKShzH+OqrrwAAzz//vK2qSLZKpVJBvV634U7ioxGzrQ7SE3/NeDxGFEWZllQcx7aFlSQJ7t27h52dHdTrdXz55ZdHJlnW63V8+umn6Ha7CMMQ29vb9nPJvRHR4nme3Y0kVRaptPT7ffR6vcf9qyWEKJI0werqKgCgPjeXyXnCcAi/VEIoIsP3Z8F1xmzrOCpIz5kF0ck1RsRPkk7XAZTMIEK318Og30cQhrh58+aRgiIMQ1x75xqi0Qie76Pf79vPJfdGRItjJibjycTuZNNLckdc+PhUwspMAXnjjTcQhiH29vbsfqdKpYIgCGz+SpqmmVZUfpWAvmOSHBuZcCqVStjY2MD333//wMf0/vvv2zbS4uIigiDA1tYW7ty5g06nYwWMHgvv9/vcJPuUwMrM08n/nD0Lz/cxHAwQy7XCVHElfwXmuiKtKNtOkrwa046yFWMxBMcxXM9Dt9PB3fX1Bz6mixcv2hu2WrUKz1R29k1wpggYPQQRmQW5pPhwmukp5cSJE3j99ddtgFy/37cVGPGhyBoCafVoY7CMRA4GA9sWunv37t8+nnfeeQdpmqLVamF7exsHBwfcT/IMQDHz9FOtVPDC2bOzADkT5y/ZVeJV8UxmjPhrBFlnMDZ+uWg0Qnt//28fz/LyMpCm6Ha70xsjU4EmTzcUM88QH374IRzHsXcoUirO94/jOMbq6io9KeQfQzHzbPLaa69NN03nvDHSupbVBmmSYMcMChDyT6CYeYawG2sfIBWXybnkYUAx82xiq7wP8Ndjci55GNAA/AzB7dCEkMcBb4bIccH97z9CCCGEEHJ8oZghhBBCSKGhmCGEEEJIoaGYIYQQQkihoZghhBBCSKGhmCGEEEJIoaGYIYQQQkihoZghhBBCSKGhmCGEEEJIoaGYIYQQQkihoZghhBBCSKGhmCGEEEJIoaGYIYQQQkihoZghhBBCSKGhmCGEEEJIoaGYIYQQQkihoZghhBBCSKGhmCGEEEJIoaGYIYQQQkihoZghhBBCSKGhmCGEEEJIoaGYIYQQQkihoZghhBBCSKGhmCGEEEJIoaGYIYQQQkihoZghhBBCSKGhmCGEEEJIoaGYIYQQQkihoZghhBBCSKGhmCGEEEJIoaGYIYQQQkihoZghhBBCSKGhmCGEEEJIoaGYIYQQQkihoZghhBBCSKGhmCGEEEJIoaGYIYQQQkihcdI0fdLHQAghhBDyt2FlhhBCCCGFhmKGEEIIIYWGYoYQQgghhYZihhBCCCGFhmKGEEIIIYWGYoYQQgghheb/AdwaFY+l5cbgAAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 576x288 with 2 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "from utils import visualize_segmentation\n",
    "\n",
    "visualize_segmentation(\n",
    "    modality_file=\"data//OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/raw_bet/OtherEXampleFromTCIA_t1c_bet.nii.gz\",\n",
    "    segmentation_file=\"data/OtherEXampleFromTCIA/OtherEXampleFromTCIA_brainles/fusion/simple.nii.gz\",\n",
    "    slice_p=0.63,  # default is 0.5\n",
    ")"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": []
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3 (ipykernel)",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.10.12"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 4
}