Appendix B¶
This section describes a complete database for a sample test case. The test case is compressible turbulent flow past a flat plat at zero incidence. The domain is divided into two zones as shown in the figure below. The interface between the two zones is 1-to-1.
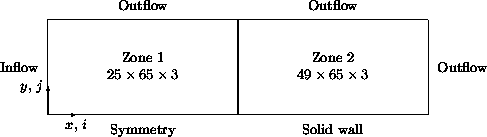
Two-Zone Flat Plate Test Case¶
The database description includes the following:
range of indices within each zone
grid coordinates of vertices
flowfield solution at cell centers including a row of ghost-cells along each boundary; the flowfield includes the conservation variables and a turbulent transport variable
multizone interface connectivity information
boundary condition information
reference state
description of the compressible Navier-Stokes equations including one-equation turbulence model
Each of these items is described in separate sections to make the information more readable. The same database is presented in each section, but only that information needed for the particular focus is included. The overall layout of the database is presented in the following section.
All data for this test case is nondimensional and is normalized consistently by the following (dimensional) quantities: plate length \(L\), freestream static density \(\rho_\infty\), freestream static speed of sound \(c_\infty\), and freestream static temperature \(T_\infty\). The fact that the database is completely nondimensional is reflected in the value of the globally set data class.
B.1 Overall Layout¶
This section describes the overall layout of the database. Included are the cell dimension and physical dimension of the grid, the globally set data class, the global reference state and flow-equations description, and data pertaining to each zone.
Each zone contains the grid size, grid coordinates, flow solution, multizone interfaces and boundary conditions. All entities given by {{*}} are expanded in subsequent sections. Note that because this example contains structured zones, IndexDimension = CellDimension = 3 in each zone.
CGNSBase_t TwoZoneCase =
{{
int CellDimension = 3 ;
int PhysicalDimension = 3 ;
DataClass_t DataClass = NormalizedByUnknownDimensional ;
ReferenceState_t ReferenceState = {{*}} ;
FlowEquationSet_t<3> FlowEquationSet = {{*}} ;
! CellDimension = 3, PhysicalDimension = 3
Zone_t<3,3> Zone1 =
{{
int VertexSize = [25,65,3] ;
int CellSize = [24,64,2] ;
int VertexSizeBoundary = [0,0,0];
ZoneType_t ZoneType = Structured;
! IndexDimension = 3
GridCoordinates_t<3,VertexSize> GridCoordinates = {{*}} ;
FlowSolution_t<3,VertexSize,CellSize> FlowSolution = {{*}} ;
ZoneGridConnectivity_t<3,3> ZoneGridConnectivity = {{*}} ;
ZoneBC_t<3,3> ZoneBC = {{*}} ;
}} ; ! end Zone1
! CellDimension = 3, PhysicalDimension = 3
Zone_t<3,3> Zone2 =
{{
int VertexSize = [49,65,3] ;
int CellSize = [48,64,2] ;
int VertexSizeBoundary = [0,0,0];
ZoneType_t ZoneType = Structured;
! IndexDimension = 3
GridCoordinates_t<3,VertexSize> GridCoordinates = {{*}} ;
FlowSolution_t<3,VertexSize,CellSize> FlowSolution = {{*}} ;
ZoneGridConnectivity_t<3,3> ZoneGridConnectivity = {{*}} ;
ZoneBC_t<3,3> ZoneBC = {{*}} ;
}} ; ! end Zone2
}} ; ! end TwoZoneCase
B.2 Grid Coordinates¶
This section describes the grid-coordinate entities for each zone.
Since the coordinates are all nondimensional, the individual DataArray_t entities do not include a data-class qualifier; instead, this information is derived from the globally set data class. The grid-coordinate entities for zone 2 are abbreviated.
CGNSBase_t TwoZoneCase =
{{
int CellDimension = 3 ;
int PhysicalDimension = 3 ;
DataClass_t DataClass = NormalizedByUnknownDimensional ;
! CellDimension = 3, PhysicalDimension = 3
Zone_t<3,3> Zone1 =
{{
int VertexSize = [25,65,3] ;
int CellSize = [24,64,2] ;
int VertexSizeBoundary = [0,0,0];
ZoneType_t ZoneType = Structured;
! IndexDimension = 3
! VertexSize = [25,65,3]
GridCoordinates_t<3, [25,65,3]> GridCoordinates =
{{
DataArray_t<real, 3, [25,65,3]> CoordinateX =
{{
Data(real, 3, [25,65,3]) = (((x(i,j,k), i=1,25), j=1,65), k=1,3) ;
}} ;
DataArray_t<real, 3, [25,65,3]> CoordinateY =
{{
Data(real, 3, [25,65,3]) = (((y(i,j,k), i=1,25), j=1,65), k=1,3) ;
}} ;
DataArray_t<real, 3, [25,65,3]> CoordinateZ =
{{
Data(real, 3, [25,65,3]) = (((z(i,j,k), i=1,25), j=1,65), k=1,3) ;
}} ;
}} ; ! end Zone1/GridCoordinates
}} ; ! end Zone1
! CellDimension = 3, PhysicalDimension = 3
Zone_t<3,3> Zone2 =
{{
int VertexSize = [49,65,3] ;
int CellSize = [48,64,2] ;
int VertexSizeBoundary = [0,0,0];
ZoneType_t ZoneType = Structured;
! IndexDimension = 3
! VertexSize = [49,65,3]
GridCoordinates_t<3, [49,65,3]> GridCoordinates =
{{
DataArray_t<real, 3, [49,65,3]> CoordinateX = {{*}} ;
DataArray_t<real, 3, [49,65,3]> CoordinateY = {{*}} ;
DataArray_t<real, 3, [49,65,3]> CoordinateZ = {{*}} ;
}} ; ! end Zone2/GridCoordinates
}} ; ! end Zone2
}} ; ! end TwoZoneCase
B.3 Flowfield Solution¶
This section provides a description of the flowfield solution including the conservation variables and the Spalart-Allmaras turbulent-transport quantity (\(\nu_{SA}\)). The flowfield solution is given at cell centers with a single row of ghost-cell values along each boundary.
As with the case for grid coordinates, the flow solution is nondimensional, and this fact is derived from the globally set data class. The normalizations for each flow variable are,
where primed quantities are nondimensional and all others are dimensional.
Only the Density entity for zone 1 is fully described in the following. The momentum, energy and turbulence solution are abbreviated. The entire flow-solution data for zone 2 is also abbreviated.
CGNSBase_t TwoZoneCase =
{{
int CellDimension = 3 ;
int PhysicalDimension = 3 ;
DataClass_t DataClass = NormalizedByUnknownDimensional ;
! CellDimension = 3, PhysicalDimension = 3
Zone_t<3,3> Zone1 =
{{
int VertexSize = [25,65,3] ;
int CellSize = [24,64,2] ;
int VertexSizeBoundary = [0,0,0];
ZoneType_t ZoneType = Structured;
! IndexDimension = 3
! VertexSize = [25,65,3]
! CellSize = [24,64,2]
FlowSolution_t<3, [25,65,3], [24,64,2]> FlowSolution =
{{
GridLocation_t GridLocation = CellCenter ;
! IndexDimension = 3
Rind_t<3> Rind =
{{
int[6] RindPlanes = [1,1,1,1,1,1] ;
}} ;
! IndexDimension = 3
! DataSize = CellSize + [2,2,2] = [26,66,4]
DataArray_t<real, 3, [26,66,4]> Density =
{{
Data(real, 3, [26,66,4]) = (((rho(i,j,k), i=0,25), j=0,65), k=0,3) ;
}} ;
DataArray_t<real, 3, [26,66,4]> MomentumX = {{*}} ;
DataArray_t<real, 3, [26,66,4]> MomentumY = {{*}} ;
DataArray_t<real, 3, [26,66,4]> MomentumZ = {{*}} ;
DataArray_t<real, 3, [26,66,4]> EnergyStagnationDensity = {{*}} ;
DataArray_t<real, 3, [26,66,4]> TurbulentSANutilde = {{*}} ;
}} ; ! end Zone1/FlowSolution
}} ; ! end Zone1
Zone_t<3,3> Zone2 = {{*}} ;
}} ; ! end TwoZoneCase
B.4 Interface Connectivity¶
This section describes the interface connectivity between zones 1 and 2; it also includes the k-plane periodicity for each zone (which is essentially an interface connectivity of a zone onto itself).
Each interface entity is repeated with the receiver and donor-zone roles reversed; this includes the periodic k-plane interfaces.
Since each interface is a complete zone face, the GridConnectivity1to1_t entities are named after the face.
Because of the orientation of the zones, the index transformation matrices (Transform) for all interfaces are diagonal.
This means that each matrix is its own inverse, and the value of Transform is the same for every pair of interface entities.
CGNSBase_t TwoZoneCase =
{{
int CellDimension = 3 ;
int PhysicalDimension = 3 ;
! ----- ZONE 1 Interfaces ------
! CellDimension = 3, PhysicalDimension = 3
Zone_t<3,3> Zone1 =
{{
int VertexSize = [25,65,3] ;
int CellSize = [24,64,2] ;
int VertexSizeBoundary = [0,0,0];
ZoneType_t ZoneType = Structured;
! IndexDimension = 3, CellDimension = 3
ZoneGridConnectivity_t<3,3> ZoneGridConnectivity =
{{
! IndexDimension = 3
GridConnectivity1to1_t<3> IMax = ! ZONE 1 IMax
{{
int[3] Transform = [1,2,3] ;
IndexRange_t<3> PointRange =
{{
int[3] Begin = [25,1 ,1] ;
int[3] End = [25,65,3] ;
}} ;
IndexRange_t<3> PointRangeDonor =
{{
int[3] Begin = [1,1 ,1] ;
int[3] End = [1,65,3] ;
}} ;
Identifier(Zone_t) ZoneDonorName = Zone2 ;
}} ;
GridConnectivity1to1_t<3> KMin = ! ZONE 1 KMin
{{
int[3] Transform = [1,2,-3] ;
IndexRange_t<3> PointRange =
{{
int[3] Begin = [1 ,1 ,1] ;
int[3] End = [25,65,1] ;
}} ;
IndexRange_t<3> PointRangeDonor =
{{
int[3] Begin = [1 ,1 ,3] ;
int[3] End = [25,65,3] ;
}} ;
Identifier(Zone_t) ZoneDonorName = Zone1 ;
}} ;
GridConnectivity1to1_t<3> KMax = ! ZONE 1 KMax
{{
int[3] Transform = [1,2,-3] ;
IndexRange_t<3> PointRange =
{{
int[3] Begin = [1 ,1 ,3] ;
int[3] End = [25,65,3] ;
}} ;
IndexRange_t<3> PointRangeDonor =
{{
int[3] Begin = [1 ,1 ,1] ;
int[3] End = [25,65,1] ;
}} ;
Identifier(Zone_t) ZoneDonorName = Zone1 ;
}} ;
}} ; ! end Zone1/ZoneGridConnectivity
}} ; ! end Zone1
! ----- ZONE 2 Interfaces ------
! CellDimension = 3, PhysicalDimension = 3
Zone_t<3,3> Zone2 =
{{
int VertexSize = [49,65,3] ;
int CellSize = [48,64,2] ;
int VertexSizeBoundary = [0,0,0];
ZoneType_t ZoneType = Structured;
! IndexDimension = 3, CellDimension = 3
ZoneGridConnectivity_t<3,3> ZoneGridConnectivity =
{{
! IndexDimension = 3
GridConnectivity1to1_t<3> IMin = ! ZONE 2 IMin
{{
int[3] Transform = [1,2,3] ;
IndexRange_t<3> PointRange =
{{
int[3] Begin = [1,1 ,1] ;
int[3] End = [1,65,3] ;
}} ;
IndexRange_t<3> PointRangeDonor =
{{
int[3] Begin = [25,1 ,1] ;
int[3] End = [25,65,3] ;
}} ;
Identifier(Zone_t) ZoneDonorName = Zone1 ;
}} ;
GridConnectivity1to1_t<3> KMin = ! ZONE 2 KMin
{{
int[3] Transform = [1,2,-3] ;
IndexRange_t<3> PointRange =
{{
int[3] Begin = [1 ,1 ,1] ;
int[3] End = [49,65,1] ;
}} ;
IndexRange_t<3> PointRangeDonor =
{{
int[3] Begin = [1 ,1 ,3] ;
int[3] End = [49,65,3] ;
}} ;
Identifier(Zone_t) ZoneDonorName = Zone2 ;
}} ;
GridConnectivity1to1_t<3> KMax = ! ZONE 2 KMax
{{
int[3] Transform = [1,2,-3] ;
IndexRange_t<3> PointRange =
{{
int[3] Begin = [1 ,1 ,3] ;
int[3] End = [49,65,3] ;
}} ;
IndexRange_t<3> PointRangeDonor =
{{
int[3] Begin = [1 ,1 ,1] ;
int[3] End = [49,65,1] ;
}} ;
Identifier(Zone_t) ZoneDonorName = Zone2 ;
}} ;
}} ; ! end Zone2/ZoneGridConnectivity
}} ; ! end Zone2
}} ; ! end TwoZoneCase
B.5 Boundary Conditions¶
Boundary conditions for the flat plate case are described in this section.
The minimal information necessary is included in each boundary condition; this includes the boundary-condition type and BC-patch specification.
The lone exception is the viscous wall, which is isothermal and has an imposed temperature profile (given by the array temperatureprofile()).
For all other boundary conditions a flow solver is free to impose appropriate BC-data since none is provided in the following.
The imposed BC-data for all cases should be evaluated at the globally set reference state, since no other reference states have been specified.
No boundary condition descriptions are provided for the multizone interface or for the k-plane periodicity in each zone.
All relevant information is provided for these interfaces in the GridConnectivity1to1_t entities of the previous section.
The practice of naming BC_t entities after the face is followed.
CGNSBase_t TwoZoneCase =
{{
int CellDimension = 3 ;
int PhysicalDimension = 3 ;
DataClass_t DataClass = NormalizedByUnknownDimensional ;
! ----- ZONE 1 BC's ------
! CellDimension = 3, PhysicalDimension = 3
Zone_t<3,3> Zone1 =
{{
int VertexSize = [25,65,3] ;
int CellSize = [24,64,2] ;
int VertexSizeBoundary = [0,0,0];
ZoneType_t ZoneType = Structured;
! IndexDimension = 3, PhysicalDimension = 3
ZoneBC_t<3,3> ZoneBC =
{{
! IndexDimension = 3, PhysicalDimension = 3
BC_t<3,3> IMin = ! ZONE 1 IMin
{{
BCType_t BCType = BCInflowSubsonic ;
IndexRange_t<3> PointRange =
{{
int[3] Begin = [1,1 ,1] ;
int[3] End = [1,65,3] ;
}} ;
}} ;
BC_t<3,3> JMin = ! ZONE 1 JMin
{{
BCType_t BCType = BCSymmetryPlane ;
IndexRange_t<3> PointRange =
{{
int[3] Begin = [1 ,1,1] ;
int[3] End = [25,1,3] ;
}} ;
}} ;
BC_t<3,3> JMax = ! ZONE 1 JMax
{{
BCType_t BCType = BCOutFlowSubsonic ;
IndexRange_t<3> PointRange =
{{
int[3] Begin = [1 ,65,1] ;
int[3] End = [25,65,3] ;
}} ;
}} ;
}} ; ! end Zone1/ZoneBC
}} ; ! end Zone1
! ----- ZONE 2 BC's ------
! CellDimension = 3, PhysicalDimension = 3
Zone_t<3,3> Zone2 =
{{
int VertexSize = [49,65,3] ;
int CellSize = [48,64,2] ;
int VertexSizeBoundary = [0,0,0];
ZoneType_t ZoneType = Structured;
! IndexDimension = 3, PhysicalDimension = 3
ZoneBC_t<3,3> ZoneBC =
{{
! IndexDimension = 3, PhysicalDimension = 3
BC_t<3,3> IMax = ! ZONE 2 IMax
{{
BCType_t BCType = BCOutflowSubsonic ;
IndexRange_t<3> PointRange =
{{
int[3] Begin = [49,1 ,1] ;
int[3] End = [49,65,3] ;
}} ;
}} ; ! end Zone2/ZoneBC/IMax
BC_t<3,3> JMin = ! ZONE 2 JMin
{{
BCType_t BCType = BCWallViscous ;
IndexRange_t<3> PointRange =
{{
int[3] Begin = [1 ,1,1] ;
int[3] End = [49,1,3] ;
}} ;
! ListLength = 49*3 = 147
BCDataSet<147> BCDataSet =
{{
BCTypeSimple_t BCTypeSimple = BCWallViscousIsothermal ;
! Data array length = ListLength = 147
BCData_t<147> DirichletData =
{{
DataArray_t<real, 1, 147> Temperature =
{{
Data(real, 1, 147) = (temperatureprofile(n), n=1,147) ;
}} ;
}} ;
}} ;
}} ; ! end Zone2/ZoneBC/JMin
BC_t<3,3> JMax = ! ZONE 2 JMax
{{
BCType_t BCType = BCOutFlowSubsonic ;
IndexRange_t<3> PointRange =
{{
int[3] Begin = [1 ,65,1] ;
int[3] End = [49,65,3] ;
}} ;
}} ; ! end Zone2/ZoneBC/JMax
}} ; ! end Zone2/ZoneBC
}} ; ! end Zone2
}} ; ! end TwoZoneCase
B.6 Global Reference State¶
This section provides a description of the freestream reference state. As previously stated, all data is nondimensional including all reference state quantities. The dimensional plate length \(L\) and freestream scales \(\rho_\infty\), \(c_\infty\) and \(T_\infty\) are used for normalization.
The freestream Mach number is 0.5 and the Reynolds number is \(10^6\) based on freestream velocity and kinematic viscosity and the plate length. These are the only nondimensional parameters included in the reference state. The defining scales for each parameter are also included; these defining scales are nondimensional.
Using consistent normalization, the following nondimensional freestream quantities are defined:
where \(\Gamma ≡ 1 + (\gamma−1) M_\infty^{2} / 2\) based on \(M_\infty = 0.5\) and \(\gamma = 1.4\).
Except for the nondimensional parameters Mach number and Reynolds number, all DataArray_t entities are abbreviated.
CGNSBase_t TwoZoneCase =
{{
DataClass_t DataClass = NormalizedByUnknownDimensional ;
ReferenceState_t ReferenceState =
{{
Descriptor_t ReferenceStateDescription =
{{
Data(char, 1, 10) = "Freestream" ;
}} ;
DataArray_t<real, 1, 1> Mach =
{{
Data(real, 1, 1) = 0.5 ;
DataClass_t DataClass = NondimensionalParameter ;
}} ;
DataArray_t<real, 1, 1> Mach_Velocity = {{ 0.5 }} ;
DataArray_t<real, 1, 1> Mach_VelocitySound = {{ 1 }} ;
DataArray_t<real, 1, 1> Reynolds =
{{
Data(real, 1, 1) = 1.0e+06 ;
DataClass_t DataClass = NondimensionalParameter ;
}} ;
DataArray_t<real, 1, 1> Reynolds_Velocity = {{ 0.5 }} ;
DataArray_t<real, 1, 1> Reynolds_Length = {{ 1. }} ;
DataArray_t<real, 1, 1> Reynolds_ViscosityKinematic = {{ 5.0E-07 }} ;
DataArray_t<real, 1, 1> Density = {{ 1. }} ;
DataArray_t<real, 1, 1> LengthReference = {{ 1. }} ;
DataArray_t<real, 1, 1> VelocitySound = {{ 1. }} ;
DataArray_t<real, 1, 1> VelocityX = {{ 0.5 }} ;
DataArray_t<real, 1, 1> VelocityY = {{ 0 }};
DataArray_t<real, 1, 1> VelocityZ = {{ 0 }} ;
DataArray_t<real, 1, 1> Pressure = {{ 0.714286 }} ;
DataArray_t<real, 1, 1> Temperature = {{ 1. }} ;
DataArray_t<real, 1, 1> EnergyInternal = {{ 1.785714 }} ;
DataArray_t<real, 1, 1> Enthalpy = {{ 2.5 }} ;
DataArray_t<real, 1, 1> EntropyApprox = {{ 0.714286 }} ;
DataArray_t<real, 1, 1> DensityStagnation = {{ 1.129726 }} ;
DataArray_t<real, 1, 1> PressureStagnation = {{ 0.847295 }} ;
DataArray_t<real, 1, 1> EnergyStagnation = {{ 1.875 }} ;
DataArray_t<real, 1, 1> EnthalpyStagnation = {{ 2.625 }} ;
DataArray_t<real, 1, 1> TemperatureStagnation = {{ 1.05 }} ;
DataArray_t<real, 1, 1> VelocitySoundStagnation = {{ 1.024695 }} ;
DataArray_t<real, 1, 1> ViscosityKinematic = {{ 5.0E-07 }} ;
}} ;
}} ; ! end TwoZoneCase
B.7 Equation Description¶
This section provides a description of the flow equations used to solve the problem. The flow equation set is turbulent, compressible 3-D Navier-Stokes with the Spalart-Allmaras (S-A) one-equation turbulence model. The thin-layer Navier-Stokes diffusion terms are modeled; only diffusion in the j-coordinate direction is included.
A perfect gas assumption is made with \(\gamma = 1.4\); based on the normalization used in this database, the nondimensional scales defining \(\gamma\) are \((c_{p})′ = 1 / (\gamma−1)\) and \((c_{v})′ = 1 / \gamma(\gamma−1)\). The molecular viscosity is obtained from Sutherland’s Law. In order to nondimensionalize the viscosity formula, standard atmospheric conditions are assumed (i.e., \(T_\infty = 288.15\ \text{K}\)). A constant Prandtl number assumption is made for the thermal conductivity coefficient; \(Pr = 0.72\). The defining scales of \(Pr\) are evaluated at freestream conditions; the nondimensional thermal conductivity is \(k′_{\infty} = μ′_{\infty}(c_{p})′ / Pr\).
The Navier-Stokes equations are closed with an eddy viscosity assumption using the S-A model. A turbulent Prandtl number of \(Pr_{t} = 0.9\) is prescribed. All parameters not provided are defaulted.
Except for the nondimensional parameters \(\gamma\) and \(Pr\), all DataArray_t entities are abbreviated.
CGNSBase_t TwoZoneCase =
{{
int CellDimension = 3 ;
int PhysicalDimension = 3 ;
DataClass_t DataClass = NormalizedByUnknownDimensional ;
! CellDimension = 3
FlowEquationSet_t<3> FlowEquationSet =
{{
int EquationDimension = 3
! CellDimension = 3 ;
GoverningEquations_t<3> GoverningEquations =
{{
GoverningEquationsType_t GoverningEquationsType = NSTurbulent ;
int[6] DiffusionModel = [0,1,0,0,0,0] ;
}} ;
GasModel_t GasModel =
{{
GasModelType_t GasModelType = CaloricallyPerfect ;
DataArray_t<real, 1, 1> SpecificHeatRatio =
{{
Data(real, 1, 1) = 1.4 ;
DataClass_t DataClass = NondimensionalParameter ;
}} ;
DataArray_t<real, 1, 1> SpecificHeatRatio_Pressure = {{ 2.5 }} ;
DataArray_t<real, 1, 1> SpecificHeatRatio_Volume = {{ 1.785714 }} ;
}} ;
ViscosityModel_t ViscosityModel =
{{
ViscosityModelType_t ViscosityModelType = SutherLandLaw ;
DataArray_t<real, 1, 1> SutherLandLawConstant = {{ 0.38383 }} ;
DataArray_t<real, 1, 1> TemperatureReference = {{ 1.05491 }} ;
DataArray_t<real, 1, 1> ViscosityMolecularReference = {{ 5.0E-07 }} ;
}} ;
ThermalConductivityModel_t ThermalConductivityModel =
{{
ThermalConductivityModelType_t ThermalConductivityModelType =
ConstantPrandtl ;
DataArray_t<real, 1, 1> Prandtl =
{{
Data(real, 1, 1) = 0.72 ;
DataClass_t DataClass = NondimensionalParameter ;
}} ;
DataArray_t<real, 1, 1> Prandtl_ThermalConductivity = {{ 1.73611E-0.6 }} ;
DataArray_t<real, 1, 1> Prandtl_ViscosityMolecular = {{ 5.0E-0.7 }} ;
DataArray_t<real, 1, 1> Prandtl_SpecificHeatPressure = {{ 2.5 }} ;
}} ;
TurbulenceClosure_t TurbulenceClosure =
{{
TurbulenceClosureType_t TurbulenceClosureType = EddyViscosity ;
DataArray<real, 1, 1> PrandtlTurbulent = {{ 0.90 }} ;
}} ;
TurbulenceModel_t<3> TurbulenceModel =
{{
TurbulenceModelType_t TurbulenceModelType =
OneEquation_SpalartAllmaras ;
int[6] DiffusionModel = [0,1,0,0,0,0] ;
}} ;
}} ; ! end FlowEquationSet
}} ; ! TwoZoneCase