9. Boundary Conditions

This section is an attempt to unify boundary-condition specifications within Navier-Stokes codes. The structures and conventions developed are a compromise between simplicity and generality. It is imperative that they be easy to use initially, but that they are general enough to provide future flexibility and extensibility.

This section may be somewhat daunting initially. It is suggested that the reader refer to the Boundary Condition Examples during study of the following sections to help resolve any questions and confusions that might arise.

The difficulty with boundary conditions is that there is such a wide variety used, and even a single boundary-condition equation is often implemented differently in different codes. Some boundary conditions, such as a symmetry plane, are fairly well defined. Other boundary conditions are much looser in their definition and implementation. An inflow boundary is a good example. It is generally accepted how many solution quantities should be specified at an inflow boundary (from mathematical well-posedness arguments), but what those quantities are will change with the class of flow problems (e.g., internal flows vs. external flows), and they will also change from code to code.

An additional difficulty for CFD analysis is that in some situations different boundary-condition equations are applied depending on local flow conditions. Any boundary where the flow can change from inflow to outflow or supersonic to subsonic is a candidate for flow-dependent boundary-condition equations.

These difficulties have molded the design of our boundary-condition specification structures and conventions. We define boundary-condition types that establish the equations to be enforced. However, for those more loosely defined boundary conditions, such as inflow/outflow, the boundary-condition type merely establishes general guidelines on the equations to be imposed. Augmenting (and superseding) the information provided by the boundary-condition type is precisely defined boundary-condition solution data. We rely on our conventions for data-name identifiers to identify the exact quantities involved in the boundary conditions.

One flexibility that is provided by this approach is that boundary-condition information can easily be built during the course of an analysis. For example, during grid-generation phases minimal information (e.g., the boundary-condition type) may be given. Then prior to running of the flow solver, more specific boundary-condition information, such as Dirichlet or Neumann data, may be added to the database.

An additional flexibility provided by the structures of this section is that both uniform and non-uniform boundary-condition data can be described within the same framework.

We realize that most current codes allow little or no flexibility in choosing solution quantities to specify for a given boundary-condition type. We also realize the coding effort involved with checking for consistency between I/O specifications and internal boundary-condition routines. To make these boundary-condition structures more palatable initially, we adopt the convention that if no solution quantities are specified for a given boundary-condition type, then the code is free to enforce any appropriate boundary condition (see Boundary Condition Specification Data).

Note that there are no boundary-condition structures defined for abutting or overset interfaces, unless they involve cases of symmetry or degeneracy. In other words, it is a CGNS design intent that a given zone boundary segment or location should at most be defined (or covered) by either a boundary condition or a multizone interface connectivity, but not by both. There is also no separate boundary-condition structure for periodic boundary conditions (i.e., when a zone interfaces with itself). Both of these situations are addressed by interface connectivity data structures.

In the sections to follow, the definitions of boundary-condition structures are presented in the first six sections. Boundary-condition types are then discussed in detail, including a description of the boundary-condition equations to be enforced for each type; this section also describes the distinction between boundary-condition types that impose a set of equations regardless of local flow conditions and those that impose different sets of boundary-condition equations depending on the local flow solution. The rules for matching boundary-condition types and the appropriate sets of boundary-condition equations are next discussed. Details of specifying data to be imposed in boundary-condition equations are provided next. Finally, several examples of boundary conditions are presented.

9.1. Boundary Condition Structures Overview

Prior to presenting the detailed boundary condition structures, we give a brief overview of the hierarchy used to describe boundary conditions.

Boundary conditions are classified as either fixed or flow-dependent. Fixed boundary conditions enforce a given set of boundary-condition equations regardless of flow conditions; whereas, flow-dependent boundary conditions enforce different sets of boundary-condition equations depending on local flow conditions. We incorporate both fixed and flow-dependent boundary conditions into a uniform framework. This allows all boundary conditions to be described in a similar manner. We consider this functionally superior to separately treating fixed and flow-dependent boundary conditions, even though the latter allows a simpler description mechanism for fixed boundary conditions. The current organization also makes sense considering the fact that flow-dependent boundary conditions are composed of multiple sets of fixed boundary conditions.

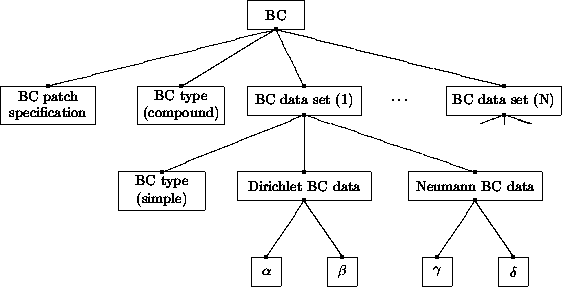
Hierarchy for Boundary Condition Structures

The above figure depicts the hierarchy used for prescribing a single boundary condition. Each boundary condition includes a type that describes the general equations to enforce, a patch specification, and a collection of data sets. The minimum required information for any boundary condition is the patch specification and the boundary-condition type (indicated by “BC type (compound)” in the figure). This minimum information is similar to that used in many existing flow solvers.

Generality in prescribing equations to enforce and their associated boundary-condition data is provided in the optional data sets. Each data set contains all boundary condition data required for a given fixed or simple boundary condition. Each data set is also tagged with a boundary-condition type. For fixed boundary conditions, the hierarchical tree contains a single data set, and the two boundary-condition types shown in the above figure are identical. Flow-dependent or compound boundary conditions contain multiple data sets, each to be applied separately depending on local flow conditions. The compound boundary-condition type describes the general flow-dependent boundary conditions, and each data set contains associated simple boundary-condition types. For example, a farfield boundary condition would contain four data sets, where each applies to the different combinations of subsonic and supersonic inflow and outflow. See the sections Boundary Condition Type Structure Definition: BCType_t and Matching Boundary Condition Data Sets for more details.

Within a single data set, boundary condition data is grouped by equation type into Dirichlet and Neumann data. The lower leaves of the above figure show data for generic flow-solution quantities \(\alpha\) and \(\beta\) to be applied in Dirichlet conditions, and data for \(\gamma\) and \(\delta\) to be applied in Neumann boundary conditions. DataArray_t entities are employed to store these data and to identify the specific flow variables they are associated with.

In situations where the data sets (or any information contained therein) are absent from a given boundary-condition hierarchy, flow solvers are free to impose any appropriate boundary conditions. Although not pictured in the above figure, it is also possible to specify the reference state from which the flow solver should extract the boundary-condition data.

9.2. Zonal Boundary Condition Structure Definition: ZoneBC_t

All boundary-condition information pertaining to a given zone is contained in the ZoneBC_t structure.

ZoneBC_t< int CellDimension, int IndexDimension, int PhysicalDimension > :=
  {
  List( Descriptor_t Descriptor1 ... DescriptorN ) ;                 (o)

  List( BC_t<CellDimension, IndexDimension, int PhysicalDimension>
        BC1 ... BCN ) ;                                              (o)

  ReferenceState_t ReferenceState ;                                  (o)

  DataClass_t DataClass ;                                            (o)

  DimensionalUnits_t DimensionalUnits ;                              (o)

  List( UserDefinedData_t UserDefinedData1 ... UserDefinedDataN ) ;  (o)
  } ;

Note

1. Default names for the Descriptor_t, BC_t, and UserDefinedData_t lists are as shown; users may choose other legitimate names. Legitimate names must be unique within a given instance of ZoneBC_t and shall not include the names DataClass, DimensionalUnits, or ReferenceState.

2. All lists within a ZoneBC_t structure entity may be empty.

ZoneBC_t requires three structure parameters, CellDimension, IndexDimension and PhysicalDimension, which are passed onto all BC_t substructures.

Boundary-condition information for a single patch is contained in the BC_t structure. All boundary-condition information pertaining to a given zone is contained in the list of BC_t structure entities. If a zone contains N boundary-condition patches, then N (and only N) separate instances of BC_t must be provided in the ZoneBC_t entity for the zone. That is, each boundary-condition patch must be represented by a single BC_t entity.

Reference data applicable to all boundary conditions of a zone is contained in the ReferenceState structure. DataClass defines the zonal default for the class of data contained in the boundary conditions of a zone. If the boundary conditions contain dimensional data, DimensionalUnits may be used to describe the system of dimensional units employed. If present, these three entities take precedence over all corresponding entities at higher levels of the hierarchy, following the standard precedence rules.

Reference-state data is useful for situations where boundary-condition data is not provided, and flow solvers are free to enforce any appropriate boundary condition equations. The presense of ReferenceState at this level or below specifies the appropriate flow conditions from which the flow solver should extract its boundary-condition data. For example, when computing an external flowfield around an airplane, an engine nozzle exit is often simulated by imposing a stagnation pressure boundary condition (or some other stagnation quantity) different from freestream. The nozzle-exit stagnation quantities could be specified in an instance of ReferenceState at this level or below in lieu of providing explicit Dirichlet or Neumann data. (See Boundary Condition Specification Data.)

The UserDefinedData_t data structure allows arbitrary user-defined data to be stored in Descriptor_t and DataArray_t children without the restrictions or implicit meanings imposed on these node types at other node locations.

9.3. Boundary Condition Structure Definition: BC_t

BC_t contains boundary-condition information for a single BC surface patch of a zone. A BC patch is the subrange of the face of a zone where a given boundary condition is applied.

The structure contains a boundary-condition type, as well as one or more sets of boundary-condition data that are used to define the boundary-condition equations to be enforced on the BC patch. For most boundary conditions, a single data set is all that is needed. The structure also contains information describing the normal vector to the BC surface patch.

BC_t< int CellDimension, int IndexDimension, int PhysicalDimension > :=
  {
  List( Descriptor_t Descriptor1 ... DescriptorN ) ;                 (o)

  BCType_t BCType ;                                                  (r)

  GridLocation_t GridLocation ;                                      (o/d)

  IndexRange_t<IndexDimension> PointRange ;                          (r:o)
  IndexArray_t<IndexDimension, ListLength[], int> PointList ;        (o:r)

  int[IndexDimension] InwardNormalIndex ;                            (o)

  IndexArray_t<PhysicalDimension, ListLength[], real>
     InwardNormalList ;                                              (o)

  List( BCDataSet_t<CellDimension, IndexDimension, ListLength[], GridLocation>
        BCDataSet1 ... BCDataSetN ) ;                                (o)

  BCProperty_t BCProperty ;                                          (o)

  FamilyName_t FamilyName ;                                          (o)

  List( AdditionalFamilyName_t AddFamilyName1 ... AddFamilyNameN ) ; (o)

  ReferenceState_t ReferenceState ;                                  (o)

  DataClass_t DataClass ;                                            (o)

  DimensionalUnits_t DimensionalUnits ;                              (o)

  List( UserDefinedData_t UserDefinedData1 ... UserDefinedDataN ) ;  (o)

  int Ordinal ;                                                      (o)
  } ;

Note

1. Default names for the Descriptor_t, BCDataSet_t, and UserDefinedData_t lists are as shown; users may choose other legitimate names. Legitimate names must be unique within a given instance of BC_t and shall not include the names BCProperty, BCType, DataClass, DimensionalUnits, FamilyName, GridLocation, InwardNormalIndex, InwardNormalList, Ordinal, PointList, PointRange, or ReferenceState.

2. GridLocation is optional; if absent its default value is Vertex. For other allowble values, see the table below.

3. One of PointRange or PointList must be specified but not both. They must define a subrange of the zone.

4. InwardNormalIndex is only an option for structured grids. For unstructured grid boundaries, it should not be used. InwardNormalIndex may have only one nonzero element, whose sign indicates the computational-coordinate direction of the BC patch normal; this normal points into the interior of the zone.

5. InwardNormalList contains a list of vectors normal to the BC patch pointing into the interior of the zone. It is a function of PhysicalDimension and ListLength[]. The vectors are located at the vertices of the BC patch when GridLocation is set to Vertex. Otherwise, they are located at edge/face midpoints. The vectors are not required to have unit magnitude.

6. If PointRange and InwardNormalList are specified, an ordering convention is needed for indices on the BC patch. An ordering convention is also needed if a range is specified and local data is present in the BCDataSet_t substructures. FORTRAN multidimensional array ordering is used.

BCType specifies the boundary-condition type, which gives general information on the boundary-condition equations to be enforced.

The BC patch may be specified by PointRange if it constitutes a logically rectangular region. In all other cases, PointList should be used to list the vertices or cell edges/faces making up the BC patch. When GridLocation is set to Vertex, then PointList or PointRange refer to vertex indices, for both structured and unstructured grids. When GridLocation is set to EdgeCenter, then PointRange/List refer to edge elements. For 3-D grids, when GridLocation is set to FaceCenter, IFaceCenter, etc., then PointRange/List refer to face elements. The interpretation of PointRange/List is summarized in the table below:

CellDimension	GridLocation
	Vertex	EdgeCenter	*FaceCenter	CellCenter
1	vertices	-	-	cells (line elements)
2	vertices	edges	-	cells (area elements)
3	vertices	edges	faces	cells (volume elements)

Note: In the table, *FaceCenter stands for the possible types: IFaceCenter, JFaceCenter, KFaceCenter, or FaceCenter.

For structured grids, face centers are indexed using the minimum of the connecting vertex indices, as described in Structured Grid Notation and Indexing Conventions. For unstructured grids, edge and face elements are indexed using their element numbering as defined in the Elements_t data structures.

The BC patch defined by PointRange/List is a surface region over which the particular set of boundary conditions is applied. However, in the current standard there is no mechanism to specify whether boundary conditions are enforced in the weak or strong form. If boundary conditions are imposed using collocation (i.e., strong form), there is also no requirement that they be imposed at the same locations used to define the BC patch (via PointRange/List). In the case when BC patches are defined in terms of vertices (or edges in 3-D), then the bounding vertices will be located on multiple BC patches. If boundary conditions are imposed using collocation at vertices, then for this case there is no mechanism to determine which BC patch takes precedence for any of these bounding vertices.

Some boundary conditions require a normal direction to be specified in order to be properly imposed. For structured zones a computational-coordinate normal can be derived from the BC patch specification by examining redundant index components. Alternatively, for structured zones this information can be provided directly by InwardNormalIndex. From Note 4, this vector points into the zone and can have only one non-zero element. For exterior faces of a zone in 3-D, InwardNormalIndex should take the following values:

Face	InwardNormalIndex	Face	InwardNormalIndex
i-min	[+1,0,0]	i-max	[−1,0,0]
j-min	[0,+1,0]	j-max	[0,−1,0]
k-min	[0,0,+1]	k-max	[0,0,−1]

The physical-space normal vectors of the BC patch may be described by InwardNormalList; these are located at vertices or cell faces, consistent with the BC patch specification. InwardNormalList is listed as an optional field because it is not always needed to enforce boundary conditions, and the physical-space normals of a BC patch can usually be constructed from the grid. However, there are some situations, such as grid-coordinate singularity lines, where InwardNormalList becomes a required field, because it cannot be generated from other information.

The BC_t structure provides for a list of boundary-condition data sets, described in the next section. In general, the proper BCDataSet_t instance to impose on the BC patch is determined by the BCType association table. The mechanics of determining the proper data set to impose is described in the section Matching Boundary Condition Data Sets.

For a few boundary conditions, such as a symmetry plane or polar singularity, the value of BCType completely describes the equations to impose, and no instances of BCDataSet_t are needed. For “simple” boundary conditions, where a single set of Dirichlet and/or Neumann data is applied, a single BCDataSet_t will likely appear (although this is not a requirement). For “compound” boundary conditions, where the equations to impose are dependent on local flow conditions, several instances of BCDataSet_t will likely appear; the procedure for choosing the proper data set is more complex as described in the section Matching Boundary Condition Data Sets.

A BCProperty_t data structure may be used to record special properties associated with particular boundary condition patches, such as wall functions or bleed regions.

FamilyName identifies the family to which the boundary belongs. Family names link the mesh boundaries to the CAD surfaces. (See the section on Family Data Structure Definition for more details.) Boundary conditions may also be defined directly on families. In this case, the BCType must be FamilySpecified. If, under a BC_t structure, both FamilyName_t and BCType_t are present, and the BCType is not FamilySpecified, then the BCType that is specified takes precedence over any BCType that might be stored in a FamilyBC_t structure under the specified Family_t. The actual name of the referred-to Family_t can be in the same base or another base, as detailed in Base Level Families.

Reference data applicable to the boundary conditions of a BC patch is contained in the ReferenceState structure. DataClass defines the default for the class of data contained in the boundary conditions. If the boundary conditions contain dimensional data, DimensionalUnits may be used to describe the system of dimensional units employed. If present, these three entities take precedence over all corresponding entities at higher levels of the hierarchy, following the standard precedence rules.

The UserDefinedData_t data structure allows arbitrary user-defined data to be stored in Descriptor_t and DataArray_t children without the restrictions or implicit meanings imposed on these node types at other node locations.

Ordinal is user-defined and has no restrictions on the values that it can contain. It is included for backward compatibility to assist implementation of the CGNS system into applications whose I/O depends heavily on the numbering of BC patches. Since there are no restrictions on the values contained in Ordinal (or that Ordinal is even provided), there is no guarantee that the BC patches for a given zone in an existing CGNS database will have sequential values from 1 to N without holes or repetitions. Use of Ordinal is discouraged and is on a user-beware basis.

FUNCTION ListLength()

Return value

int

Dependencies

PointRange, PointList

BC_t requires the structure function ListLength, which is used to specify the number of vertices or edge/face elements making up the BC patch. If PointRange is specified, then ListLength is obtained from the number of points (inclusive) between the beginning and ending indices of PointRange. If PointList is specified, then ListLength is the number of indices in the list of points. In this situation, ListLength becomes a user input along with the indices of the list PointList. By user we mean the application code that is generating the CGNS database.

ListLength is also the number of elements in the list InwardNormalList. Note that syntactically PointList and InwardNormalList must have the same number of elements.

If neither PointRange or PointList is specified in a particular BCDataSet_t substructure, ListLength must be passed into it to determine the length of BC data arrays.

9.4. Boundary Condition Data Set Structure Definition: BCDataSet_t

BCDataSet_t contains Dirichlet and Neumann data for a single set of boundary-condition equations. Its intended use is for simple boundary-condition types, where the equations imposed do not depend on local flow conditions.

BCDataSet_t< int CellDimension, int IndexDimension,
  int ListLengthParameter, GridLocation_t GridLocationParameter > :=
  {
  List( Descriptor_t Descriptor1 ... DescriptorN ) ;                 (o)

  BCTypeSimple_t BCTypeSimple ;                                      (r)

  BCData_t<ListLengthBCData[]> DirichletData ;                       (o)
  BCData_t<ListLengthBCData[]> NeumannData ;                         (o)

  GridLocation_t GridLocation ;                                      (o/d)

  IndexRange_t<IndexDimension> PointRange ;                          (o)
  IndexArray_t<IndexDimension, ListLength, int> PointList ;          (o)

  ReferenceState_t ReferenceState ;                                  (o)

  DataClass_t DataClass ;                                            (o)

  DimensionalUnits_t DimensionalUnits ;                              (o)

  List( UserDefinedData_t UserDefinedData1 ... UserDefinedDataN ) ;  (o)
  } ;

Note

1. Default names for the Descriptor_t and UserDefinedData_t lists are as shown; users may choose other legitimate names. Legitimate names must be unique within a given instance of BCDataSet_t and shall not include the names BCTypeSimple, DataClass, DimensionalUnits, DirichletData, GridLocation, NeumannData, PointList, PointRange, or ReferenceState.

2. BCTypeSimple is the only required field. All other fields are optional and the Descriptor_t list may be empty.

3. GridLocation is optional; if absent its default value is GridLocationParameter. For 2-D grids (CellDimension = 2), GridLocation may take the values of Vertex or EdgeCenter. For 3-D grids (CellDimension = 3), GridLocation may take the values of Vertex, EdgeCenter, FaceCenter, IFaceCenter, JFaceCenter or KFaceCenter.

4. PointRange and PointList are both optional; only one of them may be specified. They must define a face subrange of the zone.

BCDataSet_t requires the structure parameters CellDimension, IndexDimension, ListLengthParameter, and GridLocationParameter. These are all used to control the grid location and length of data arrays in the Dirichlet and Neumann substructures. They are inputs for the structure functions ListLength[] and ListLengthBCData[] defined below.

BCTypeSimple specifies the boundary-condition type, which gives general information on the boundary-condition equations to be enforced. BCTypeSimple is also used for matching boundary condition data sets.

Boundary-condition data is separated by equation type into Dirichlet and Neumann conditions. Dirichlet boundary conditions impose the value of the given variables, whereas Neumann boundary conditions impose the normal derivative of the given variables. The mechanics of specifying Dirichlet and Neumann data for boundary conditions is covered in the section Boundary Condition Specification Data.

The substructures DirichletData and NeumannData contain boundary-condition data that may be constant over the BC patch, or defined locally at each vertex or edge/face of the patch. Locally defined data may be specified in one of two ways. If GridLocation, PointRange and PointList are all absent, then the data is defined consistent with the BC patch specification of the parent BC_t structure. In this case, the location of the locally defined data is given by GridLocationParameter and the length of the data arrays are given by ListLengthParameter. If GridLocation and one of PointRange or PointList is present, then the length of the data arrays is given by ListLength[].

Reference quantities applicable to the set of boundary-condition data are contained in the ReferenceState structure. DataClass defines the default for the class of data contained in the boundary-condition data. If the boundary conditions contain dimensional data, DimensionalUnits may be used to describe the system of dimensional units employed. If present, these three entities take precedence over all corresponding entities at higher levels of the hierarchy, following the standard precedence rules.

The UserDefinedData_t data structure allows arbitrary user-defined data to be stored in Descriptor_t and DataArray_t children without the restrictions or implicit meanings imposed on these node types at other node locations.

FUNCTION ListLength()

Return value

int

Dependencies

PointRange, PointList

BCDataSet_t requires the structure function ListLength, which is used to specify the length of locally defined Dirichlet and Neumann data arrays when the grid location of these quantities differs from that of the BC patch definition. If PointRange is specified, then ListLength is obtained from the number of points (inclusive) between the beginning and ending indices of PointRange. If PointList is specified, then ListLength is the number of indices in the list of points. In this situation, ListLength becomes a user input along with the indices of the list PointList. By user we mean the application code that is generating the CGNS database.

If neither PointRange or PointList is specified in a particular BCDataSet_t substructure, ListLength must be passed into it to determine the length of BC data arrays.

FUNCTION ListLengthBCData()

Return value

int

Dependencies

ListLengthParameter, PointRange, PointList

BCDataSet_t also requires the structure function ListLengthBCData. If PointRange or PointList is present, then ListLengthBCData takes the value of ListLength. If both are absent, then it takes the value ListLengthParameter.

9.5. Boundary Condition Data Structure Definition: BCData_t

BCData_t contains a list of variables and associated data for boundary-condition specification. Each variable may be given as global data (i.e., a scalar) or local data defined at each grid point or cell face of the BC patch. By convention all data specified in a given instance of BCData_t is to be used in the same type of boundary-condition equation. For example, the use of separate BCData_t substructures for Dirichlet and Neumann equations in the BCDataSet_t structure of the previous section.

BCData_t< int ListLength > :=
  {
  List( Descriptor_t  Descriptor1 ... DescriptorN ) ;                (o)

  List( DataArray_t<DataType, 1, 1>
        DataGlobal1 ... DataGlobalN ) ;                              (o)

  List( DataArray_t<DataType, 1, ListLength>
        DataLocal1 ... DataLocalN ) ;                                (o)

  DataClass_t DataClass ;                                            (o)

  DimensionalUnits_t DimensionalUnits ;                              (o)

  List( UserDefinedData_t UserDefinedData1 ... UserDefinedDataN ) ;  (o)
  } ;

Note

1. Default names for the Descriptor_t, DataArray_t, and UserDefinedData_t lists are as shown; users may choose other legitimate names. Legitimate names must be unique within a given instance of BCData_t and shall not include the names DataClass or DimensionalUnits.

2. There are no required elements; all three lists may be empty.

This structure definition shows separate lists for global verses local data. The global data is essentially scalars, while the local data variables have size determined by the structure parameter ListLength. For DataArray_t entities with standardized data-name identifiers, DataType is determined by convention. For user-defined variables, DataType is a user input.

Two important points need to be mentioned regarding this structure definition. First, this definition allows a given instance of BCData_t to have a mixture of global and local data. For example, if a user specifies Dirichlet data that has a uniform stagnation pressure but has a non-uniform velocity profile, this structure allows the user to describe the stagnation pressure by a scalar in the DataGlobal list and the velocity by an array in the DataLocal list. Second, the only distinction between the lists (aside from default names, which will be seldom used) is the parameters passed into the DataArray_t structure. Therefore, in actual implementation of this BCData_t structure it may not be possible to distinguish between members of the global and local lists without querying inside the DataArray_t substructures. Straightforward mapping onto the ADF or HDF database will not provide any distinctions between the members of the two lists. This hopefully will not cause any problems.

DataClass defines the default for the class of data contained in the boundary-condition data. If the boundary-condition data is dimensional, DimensionalUnits may be used to describe the system of dimensional units employed. If present, these two entities take precedence over all corresponding entities at higher levels of the hierarchy, following the standard precedence rules.

The UserDefinedData_t data structure allows arbitrary user-defined data to be stored in Descriptor_t and DataArray_t children without the restrictions or implicit meanings imposed on these node types at other node locations.

9.6. Boundary Condition Property Structure Definition: BCProperty_t

BCProperty_t allows the recording of special properties associated with particular boundary condition patches. At the current time, only two properties (WallFunction_t and Area_t) are included, but extensions involving boundary conditions may be implemented as additional nodes under BCProperty_t in the future.

BCProperty_t :=
  {
  List( Descriptor_t  Descriptor1 ... DescriptorN ) ;                (o)

  WallFunction_t WallFunction ;                                      (o)

  Area_t Area ;                                                      (o)

  List( UserDefinedData_t UserDefinedData1 ... UserDefinedDataN ) ;  (o)
  } ;

Note

Default names for the Descriptor_t and UserDefinedData_t lists are as shown; users may choose other legitimate names. Legitimate names must be unique within a given instance of BCProperty_t and shall not include the names WallFunction or Area.

The WallFunction_t and Area_t data structures may be used to record properties associated with the use of wall functions, or area-related boundary conditions such as bleed, respectively.

The UserDefinedData_t data structure allows arbitrary user-defined data to be stored in Descriptor_t and DataArray_t children without the restrictions or implicit meanings imposed on these node types at other node locations.

9.6.1. Wall Function Structure Definition: WallFunction_t

The WallFunction_t data structure allows data associated with the use of wall function boundary conditions to be recorded.

WallFunction_t :=
  {
  List( Descriptor_t  Descriptor1 ... DescriptorN ) ;                (o)

  WallFunctionType_t WallFunctionType ;                              (r)

  List( UserDefinedData_t UserDefinedData1 ... UserDefinedDataN ) ;  (o)
  } ;

Note

Default names for the Descriptor_t and UserDefinedData_t lists are as shown; users may choose other legitimate names. Legitimate names must be unique within a given instance of WallFunction_t and shall not include the name WallFunctionType.

WallFunctionType_t is a required enumeration data structure that is used to define the type of wall functions being used.

WallFunctionType_t := Enumeration(
  WallFunctionTypeNull,
  WallFunctionTypeUserDefined,
  Generic ) ;

Because there is such a wide array of methods for employing wall functions (few of which are well-documented), the type Generic is used to simply indicate that a wall function is employed, without specifying details.

9.6.2. Area Structure Definition: Area_t

The Area_t data structure allows data associated with area-related boundary conditions such as bleed to be recorded.

Area_t :=
  {
  List( Descriptor_t  Descriptor1 ... DescriptorN ) ;                (o)

  AreaType_t AreaType ;                                              (r)
  DataArray_t<real, 1, 1>  SurfaceArea ;                             (r)
  DataArray_t<real, 1, 32> RegionName ;                              (r)

  List( UserDefinedData_t UserDefinedData1 ... UserDefinedDataN ) ;  (o)
  } ;

Note

Default names for the Descriptor_t and UserDefinedData_t lists are as shown; users may choose other legitimate names. Legitimate names must be unique within a given instance of Area_t and shall not include the names AreaType, RegionName, or SurfaceArea.

AreaType_t is a required enumeration data structure that is used to define the type of area being defined.

AreaType_t := Enumeration(
  AreaTypeNull,
  AreaTypeUserDefined,
  BleedArea,
  CaptureArea ) ;

If AreaType is set to BleedArea, the value of SurfaceArea is the size of the current bleed surface. Note that bleed is commonly used with wall boundary conditions. The bleed area is the surface area of the boundary condition patch.

If AreaType is set to CaptureArea, then SurfaceArea represents the size of the current capture surface. For inlet flows, for example, the capture area is the area of a fictitious surface in front of the inlet in which mass is pulled into the inlet. This is used to calculate the mass flow for the boundary condition patch based on the formula:

\[\text{mass flow} = \mathit{MFR}\ \rho_\infty U_\infty A_{cap}\]

where \(\mathit{MFR}\) is the desired mass flow ratio and \(A_{cap}\) is the capture area. Another interpretation is the far-upstream cross-sectional area of the stream tube that feeds the inlet. Note that the capture area is usually defined with an outflow boundary condition, which is commonly used at an engine face.

The RegionName is character identifier, and is needed so that a specific region can span multiple surfaces over multiple zones.

9.7. Boundary Condition Type Structure Definition: BCType_t

BCType_t is an enumeration type that identifies the boundary-condition equations to be enforced at a given boundary location.

BCType_t := Enumeration(
  BCTypeNull, BCTypeUserDefined, BCAxisymmetricWedge, BCDegenerateLine.
  BCDegeneratePoint, BCDirichlet, BCExtrapolate, BCFarfield, BCGeneral,
  BCInflow, BCInflowSubsonic, BCInflowSupersonic, BCNeumann,
  BCOutflow, BCOutflowSubsonic, BCOutflowSupersonic, BCSymmetryPlane,
  BCSymmetryPolar, BCTunnelInflow, BCTunnelOutflow, BCWall,
  BCWallInviscid, BCWallViscous, BCWallViscousHeatFlux,
  BCWallViscousIsothermal, FamilySpecified ) ;

The boundary-condition type is further defined as simple, BCTypeSimple_t, or compound, BCTypeCompound_t, which are subsets of the enumeration type BCType_t.

BCTypeSimple_t := Enumeration(
  BCTypeNull, BCTypeUserDefined, BCAxisymmetricWedge, BCDegenerateLine.
  BCDegeneratePoint, BCDirichlet, BCExtrapolate, BCGeneral,
  BCInflowSubsonic, BCInflowSupersonic, BCNeumann,
  BCOutflowSubsonic, BCOutflowSupersonic, BCSymmetryPlane,
  BCSymmetryPolar, BCTunnelInflow, BCTunnelOutflow, BCWall,
  BCWallInviscid, BCWallViscous, BCWallViscousHeatFlux,
  BCWallViscousIsothermal, FamilySpecified ) ;

BCTypeCompound_t := Enumeration(
  BCTypeNull, BCTypeUserDefined, BCInflow, BCOutflow,
  BCFarfield ) ;

The members of BCTypeSimple_t completely identify the equations to impose, while those of BCTypeCompound_t give a general description of the class of boundary-condition equations to impose. The specific boundary-condition equations to enforce for each value of BCType_t are listed in separate tables for Simple Boundary Condition Types and Compound Boundary Condition Types.

The subdivision of BCType_t is based on function. For simple boundary conditions, the equations and data imposed are fixed; whereas, for compound boundary conditions different sets of equations are imposed depending on local flow conditions at the boundary. This distinction requires additional rules for dealing with simple and compound boundary-condition types.

For the inflow/outflow boundary-condition descriptions, 3-D inviscid compressible flow is assumed; the 2-D equivalent should be obvious. These same boundary conditions are typically used for viscous cases also. This “3-D Euler” assumption will be noted wherever used.

In the following tables, \(Q\) is the solution vector, \(\mathbf{q}\) is the velocity vector whose magnitude is \(q\), the unit normal to the boundary is \(\mathbf{n}\), and \(\partial () / \partial n =\mathbf{n} \cdot \nabla\) is differentiation normal to the boundary.

Simple Boundary Condition Types

BCType_t or BCTypeSimple_t Identifier	Boundary Condition Description
BCGeneral	Arbitrary conditions on \(Q\) or \(\partial Q / \partial n\)
BCDirichlet	Dirichlet condition on \(Q\) vector
BCNeumann	Neumann condition on \(\partial Q / \partial n\)
BCExtrapolate	Extrapolate \(Q\) from interior
BCWallInviscid	Inviscid (slip) wall normal velocity specified (default: \(\mathbf{q} \cdot \mathbf{n} = 0\))
BCWallViscousHeatFlux	Viscous no-slip wall with heat flux velocity Dirichlet (default: \(q = 0\)) temperature Neumann (default: adiabatic, \(\partial T / \partial n = 0\))
BCWallViscousIsothermal	Viscous no-slip, isothermal wall velocity Dirichlet (default: \(q = 0\)) temperature Dirichlet
BCWallViscous	Viscous no-slip wall; special cases are BCWallViscousHeatFlux and BCWallViscousIsothermal velocity Dirichlet (default: \(q = 0\)) Dirichlet or Neumann on temperature
BCWall	General wall condition; special cases are BCWallInviscid, BCWallViscous, BCWallViscousHeatFlux, and BCWallViscousIsothermal
BCInflowSubsonic	Inflow with subsonic normal velocity specify 4; extrapolate 1 (3-D Euler)
BCInflowSupersonic	Inflow with supersonic normal velocity specify 5; extrapolate 0 (3-D Euler) Same as BCDirichlet
BCOutflowSubsonic	Outflow with subsonic normal velocity specify 1; extrapolate 4 (3-D Euler)
BCOutflowSupersonic	Outflow with supersonic normal velocity specify 0; extrapolate 5 (3-D Euler) Same as BCExtrapolate
BCTunnelInflow	Tunnel inlet (subsonic normal velocity) specify cross-flow velocity, stagnation enthalpy, entropy extrapolate 1 (3-D Euler)
BCTunnelOutflow	Tunnel exit (subsonic normal velocity) specify static pressure extrapolate 4 (3-D Euler)
BCDegenerateLine	Face degenerated to a line
BCDegeneratePoint	Face degenerated to a point
BCSymmetryPlane	Symmetry plane; face should be coplanar density, pressure: \(\partial () / \partial n = \mathbf{n} \cdot \nabla = 0\) tangential velocity: \(\partial (\mathbf{q} \times \mathbf{n}) / \partial n = 0\) normal velocity: \(\mathbf{q} \cdot \mathbf{n} = 0\)
BCSymmetryPolar	Polar-coordinate singularity line; special case of BCDegenerateLine where degenerate face is a straight line and flowfield has polar symmetry; \(\mathbf{s}\) is singularity line tangential unit vector normal velocity: \(\mathbf{q} \times \mathbf{s} = 0\) all others: \(\partial () / \partial n = \mathbf{n} \cdot \nabla = 0\), \(\mathbf{n}\) normal to \(\mathbf{s}\)
BCAxisymmetricWedge	Axisymmetric wedge; special case of BCDegenerateLine where degenerate face is a straight line
FamilySpecified	A boundary condition type is being specified for the family to which the current boundary belongs. A FamilyName_t specification must exist under BC_t, corresponding to a Family_t structure under CGNSBase_t. Under the Family_t structure there must be a FamilyBC_t structure specifying a valid BCType (other than FamilySpecified!). If any of these are absent, the boundary condition type is undefined.

Compound Boundary Condition Types

BCType_t or BCTypeCompound_t Identifier	Boundary Condition Description
BCInflow	Inflow, arbitrary normal Mach; test on normal Mach, then perform one of: BCInflowSubsonic, BCInflowSupersonic
BCOutflow	Outflow, arbitrary normal Mach; test on normal Mach, then perform one of: BCOutflowSubsonic, BCOutflowSupersonic
BCFarfield	Farfield inflow/outflow, arbitrary normal Mach; test on normal velocity and normal Mach, then perform one of: BCInflowSubsonic, BCInflowSupersonic, BCOutflowSubsonic, BCOutflowSupersonic

9.8. Matching Boundary Condition Data Sets

The BC_t structure allows for a arbitrary list of boundary-condition data sets, described by the BCDataSet_t structure. For simple boundary conditions, a single data set must be chosen from a list that may contain more than one element. Likewise, for a compound boundary condition, a limited number of data sets must be chosen and applied appropriately. The mechanism for the proper choice of data sets is controlled by the BCType field of the BC_t structure, the BCTypeSimple field of the BCDataSet_t structure, and the boundary-condition type association table. In the following discussion, we will use the “/” notation for fields or elements of a structure type.

BC_t is used for both simple and compound boundary conditions; hence, the field BC_t/BCType is of type BCType. Conversely, the substructure BCDataSet_t is intended to enforce a single set of boundary-condition equations independent of local flow conditions (i.e., it is appropriate only for simple boundary conditions). This is why the field BCDataSet_t/BCTypeSimple is of type BCTypeSimple_t and not BCType_t. The appropriate choice of data sets is determined by matching the field BC_t/BCType with the field BCDataSet_t/BCTypeSimple as specified in the boundary-condition type association table.

For simple boundary conditions, a single match from the list of BCDataSet_t instances is required. For all BCTypeSimple_t identifiers, except BCInflowSupersonic and BCOutflowSupersonic, an exact match is necessary. BCInflowSupersonic will match itself or BCDirichlet; BCOutflowSupersonic will match itself or BCExtrapolate.

For compound boundary conditions, the association table specifies which simple boundary-condition types are appropriate. Since compound boundary conditions enforce different boundary-condition equation sets depending on local flow conditions, several instances of BCDataSet_t will be matched for each BCTypeCompound_t identifier. The accompanying rule determines which of the matching data sets to apply at a given location on the BC patch.

This provides a general procedure applicable to both BCTypeSimple_t and BCTypeCompound_t situations. For a given BC_t/BCType use those instances of BCDataSet_t whose field BCDataSet_t/BCTypeSimple matches according to the following table. Apply the matching data set or sets as prescribed by the appropriate usage rule.

Associated Boundary Condition Types and Usage Rules

BCType_t Identifier	Associated BCTypeSimple_t Identifiers and Usage Rules
BCInflow	BCInflowSupersonic BCInflowSubsonic Usage Rule: if supersonic normal Mach, choose BCInflowSupersonic; else, choose BCInflowSubsonic
BCOutflow	BCOutflowSupersonic BCOutflowSubsonic Usage Rule: if supersonic normal Mach, choose BCOutflowSupersonic; else, choose BCOutflowSubsonic
BCFarfield	BCInflowSupersonic BCInflowSubsonic BCOutflowSupersonic BCOutflowSubsonic Usage Rule: if inflow and supersonic normal Mach, choose BCInflowSupersonic; else if inflow, choose BCInflowSubsonic; else if outflow and supersonic normal Mach, choose BCOutflowSupersonic; else, choose BCOutflowSubsonic
BCInflowSupersonic	BCInflowSupersonic BCDirichlet Usage Rule: choose either; BCInflowSupersonic takes precedence
BCOutflowSupersonic	BCOutflowSupersonic BCExtrapolate Usage Rule: choose either; BCOutflowSupersonic takes precedence
All others	Self-matching

Although we present a strict division between the two categories of boundary-condition types, we realize that some overlap may exist. For example, some of the more general simple boundary-condition types, such as BCWall, may include a situation of inflow/outflow (say if the wall is porous). These complications require further guidelines on appropriate definition and use of boundary-condition types. The real distinctions between BCTypeSimple_t and BCTypeCompound_t are as follows:

• BCTypeSimple_t identifiers always match themselves; BCTypeCompound_t identifiers never match themselves.

• BCTypeSimple_t identifiers always produce a single match; BCTypeCompound_t will produce multiple matches.

• The usage rule for BCTypeSimple_t identifiers is always trivial - apply the single matching data set regardless of local flow conditions.

Therefore, any boundary condition that involves application of different data sets depending on local flow conditions should be classified BCTypeCompound_t. If a type that we have classified BCTypeSimple_t is used as a compound type (BCWall for a porous wall is an example), then it should somehow be reclassified. One option is to define a new BCTypeCompound_t identifier and provide associated BCTypeSimple_t types and a usage rule. Another option may be to allow some identifiers to be both BCTypeSimple_t and BCTypeCompound_t and let their appropriate use be based on context. This is still undetermined.

9.9. Boundary Condition Specification Data

For a given simple boundary condition (i.e., one that is not dependent on local flow conditions), the database provides a set of boundary-condition equations to be enforced through the structure definitions for BCDataSet_t and BCData_t. Apart from the boundary-condition type, the precise equations to be enforced are described by boundary-condition solution data. These specified solution data are arranged by “equation type”:

Dirichlet

\(Q = Q_{specified}\)

Neumann

\(\partial Q / \partial n = (\partial Q / \partial n)_{specified}\)

The DirichletData and NeumannData entities of BCData_t list both the solution variables involved in the equations (through the data-name identifier conventions) and the specified solution data.

Two issues need to be addressed for specifying Dirichlet or Neumann boundary-condition data. The first is whether the data is global or local:

Global BC data

Data applied globally to the BC patch; for example, specifying a uniform total pressure at an inflow boundary

Local BC data

Data applied locally at each vertex or cell face of the BC patch; an example of this is varying total pressure specified at each grid point at an inflow boundary

The second issue is describing the actual solution quantities that are to be specified. Both of these issues are addressed by use of the DataArray_t structure.

For some types of boundary conditions, many different combinations of solution quantities could be specified. For example, BCInflowSubsonic requires 4 solution quantities to be specified in 3-D, but what those 4 quantities are varies with applications (e.g., internal verses external flows) and codes. We propose the convention that the actual data being specified for any BCType is given by the list of DataArray_t entities included in DirichletData and NeumannData structures (actually by the identifier attached to each instance of DataArray_t). This frees us from having to define many versions of a given BCType (e.g., BCInflowSubsonic1, BCInflowSubsonic2, etc.), where each has a precisely defined set of Dirichlet data. We are left with the easier task of defining how many Dirichlet or Neumann quantities must be provided for each BCType.

An example of using DataArray_t-identifier conventions to describe BC specification data is the following: subsonic inflow with uniform stagnation pressure, mass flow and cross-flow angle specified; the Dirichlet data are stagnation pressure = 2.56, mass flow = 1.34, and cross-flow angle has a y-component of 0.043 and a z-component of 0.02 (ignore dimensional-units or normalization for the present). The specified solution variables and associated data are described as shown:

BCData_t<ListLength=?> DirichletData =
  {{
  DataArray_t<real, 1, 1> PressureStagnation = {{ Data(real, 1, 1) = 2.56  }} ;
  DataArray_t<real, 1, 1> MassFlow           = {{ Data(real, 1, 1) = 1.34  }} ;
  DataArray_t<real, 1, 1> VelocityAngleY     = {{ Data(real, 1, 1) = 0.043 }} ;
  DataArray_t<real, 1, 1> VelocityAngleZ     = {{ Data(real, 1, 1) = 0.02  }} ;
  }} ;

Basically, this states that DirichletData contains four instances of DataArray_t with identifiers or names PressureStagnation, MassFlow, VelocityAngleY and VelocityAngleZ. Each DataArray_t structure entity contains a single floating-point value; these are the Dirichlet data for the BC. Note that Data(real, 1, 1) means a single floating-point value.

The global verses local data issue can be easily handled by storing either a scalar, as shown above, for the global BC data case; or storing an array for the local BC data case. Storing an array of local BC data allows the capability for specifying non-constant solution profiles, such as “analytic” boundary-layer profiles or profiles derived from experimental data. For the above example, if the stagnation pressure is instead specified at every vertex of the boundary-condition patch the following results:

BCData_t<ListLength=99> DirichletData =
  {{
  DataArray_t<real, 1, 99> PressureStagnation =
    {{ Data(real, 1, 99) = (PTOT(n), n=1,99) }} ;
  DataArray_t<real, 1, 1> MassFlow           = {{ Data(real, 1, 1) = 1.34  }} ;
  DataArray_t<real, 1, 1> VelocityAngleY     = {{ Data(real, 1, 1) = 0.043 }} ;
  DataArray_t<real, 1, 1> VelocityAngleZ     = {{ Data(real, 1, 1) = 0.02  }} ;
  }} ;

where, say, the boundary face is logically rectangular and contains \(11 \times 9\) vertices and the stagnation pressure at the vertices is given by the array PTOT().

To facilitate implementation of boundary conditions into existing flow solvers, we adopt the convention that if no boundary-condition data is specified, then flow solvers are free to enforce any appropriate boundary-condition equations. This includes situations where entities of BCDataSet_t, BCData_t or DataArray_t are absent within the boundary-condition hierarchy. By convention, if no BCDataSet entities are present, then application codes are free to enforce appropriate BCs for the given value of BCType. Furthermore, if the entities DirichletData and NeumannData are not present in an instance of BCDataSet_t, or if insufficient data is present in DirichletData or NeumannData (e.g., if only one Dirichlet variable is present for a subsonic inflow condition), then application codes are free to fill out the boundary-condition data as appropriate for the BCTypeSimple identifier.

The various levels of BC implementation allowed are shown in the following figure, from the lowest level in which the application codes interpret the BCType, to the fully SIDS-compliant BC implementation that completely defines the BC within the CGNS file.

Boundary Condition Implementation Levels

Lowest-level allowed (application code interprets meaning of BCType )

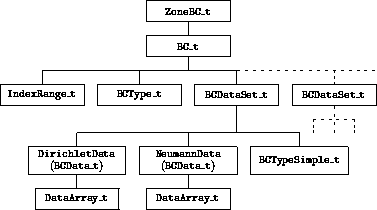
Fully SIDS-compliant

An alternative approach to the present design could be to list all the solution variables and data (as DataArray_t-like structures) for the boundary condition, and contain descriptive tags in each one to indicate if they are Dirichlet or Neumann data. We have not taken this approach. We think grouping boundary-condition data by “equation type” as we have done better allows for future extension to other types of boundary conditions (e.g., 2nd-order non-reflecting BC’s that result in partial differential equations to be solved at the boundary).

9.10. Boundary Condition Examples

This section contains boundary-condition examples with increasing complexity. Included is the most simple BC_t entity and one of the most complex. The examples show situations of local and global boundary-condition data, simple and compound boundary-condition types, and multiple boundary-condition data sets that must be matched with the appropriate boundary-condition type.

9.10.1. Example - Symmetry Plane

Symmetry plane for a patch on the i-min face of a 3-D structured zone.

!  CellDimension = 3, IndexDimension = 3
BC_t<3,3,3> BC1 =
  {{
  BCType_t BCType = BCSymmetryPlane ;

  IndexRange_t<3> PointRange =
    {{
    int[3] Begin = [1,1,1 ] ;
    int[3] End   = [1,9,17] ;
    }} ;
  }} ;

Since the boundary-condition equations to be enforced are completely defined by the boundary-condition type BCSymmetryPlane, no other information needs to be provided, except for the extent of the BC patch. The BC patch is specified by PointRange with a beginning index of (1,1,1) and an ending index of (1,9,17). By default, these refer to vertices.

9.10.2. Example - Viscous Solid Wall I

A viscous solid wall for a 3-D structured zone, where a Dirichlet condition is enforced for temperature; the wall temperature for the entire wall is specified to be 273 K. The BC patch is on the j-min face and is bounded by the indices (1,1,1) and (33,1,9).

!  CellDimension = 3, IndexDimension = 3
BC_t<3,3,3> BC2 =
  {{
  BCType_t BCType = BCWallViscousIsothermal ;

  IndexRange_t<3> PointRange =
    {{
    int[3] Begin = [1 ,1,1] ;
    int[3] End   = [33,1,9] ;
    }} ;

  !  ListLength = 33*9 = 297
  BCDataSet_t<297> BCDataSet1 =
    {{
    BCTypeSimple_t BCTypeSimple = BCWallViscousIsothermal ;

    !  Data array length = ListLength = 297
    BCData_t<297> DirichletData =
      {{
      DataArray_t<real, 1, 1> Temperature =
        {{
        Data(real, 1, 1) = 273. ;

        DataClass_t DataClass = Dimensional ;

        DimensionalUnits_t DimensionalUnits =
          {{
          MassUnits        = MassUnitsNull ;
          LengthUnits      = LengthUnitsNull ;
          TimeUnits        = TimeUnitsNull ;
          TemperatureUnits = Kelvin ;
          AngleUnits       = AngleUnitsNull ;
          }} ;
        }} ;
      }} ;
    }} ;
  }} ;

This is an example of a simple boundary-condition type, BCWallViscousIsothermal. By default there is a zero Dirichlet condition on the velocity, and BCDataSet1 states there is a Dirichlet condition on temperature with a global value of 273 K. The data set contains a single BCData_t entity, called DirichletData, meaning a (possibly empty) collection of Dirichlet conditions should be enforced. Within DirichletData, there is a single DataArray_t entity; this narrows the specification to a single Dirichlet condition. This lone entity has the identifier Temperature, which by the data-name identifier conventions is the identifier for static temperature. The data contained in Temperature is a floating-point scalar with a value of 273. The qualifiers DataClass and DimensionalUnits specify that the temperature is dimensional with units of Kelvin.

Since BCWallViscousIsothermal is a simple boundary-condition type, the appropriate data set contains a BCTypeSimple entity whose value is BCWallViscousIsothermal. For this example, only a single data set is provided, and this data set has the correct boundary-condition type. This is an example of a trivial data-set match.

Apart from velocity and temperature, additional “numerical” boundary conditions are typically required by Navier-Stokes flow solvers, but none are given here; therefore, a code is free to implement other additional boundary conditions as desired.

Although the boundary-condition data is global, we include in this example structure parameters that are the lengths of potential local-data arrays. Comments are added to the example with the “!” notation to document the structure parameters. The BC_t structure function ListLength is evaluated based on PointRange. Since GridLocation is not specified in BC2, any local data is at vertices by default. The entity Temperature contains global data, so the value of ListLength is unused in DirichletData.

This example raises the question of whether unused structure parameters are required in structure entities. The answer is no. We included them here for completeness. The purpose of structure parameters is to mimic the need to define elements of a entity based on information contained elsewhere (at a higher level) in the CGNS database. When this need is not present in a given instance of a structure entity, the structure parameters are superfluous. In some of the following examples, structure parameters that are superfluous or otherwise not needed are denoted by “?”.

9.10.3. Example - Subsonic Inflow

Subsonic inflow for a 2-D structured zone: The BC patch is on the i-min face and includes \(j \in [2, 7]\). As prescribed by the boundary-condition type, three quantities must be specified. Uniform entropy and stagnation enthalpy are specified with values of 0.94 and 2.85, respectively. A velocity profile is specified at face midpoints, given by the array v_inflow(j). No dimensional or nondimensional information is provided.

!  CellDimension = 2, IndexDimension = 2
BC_t<2,2,?> BC3 =
  {{
  BCType_t BCType = BCInflowSubsonic ;

  GridLocation_t GridLocation = FaceCenter ;

  IndexRange_t<2> PointRange =
    {{
    int[2] Begin = [1,2] ;
    int[2] End   = [1,6] ;
    }} ;

  !  ListLength = 5
  BCDataSet_t<5> BCDataSet1 =
    {{
    BCTypeSimple_t BCTypeSimple = BCInflowSubsonic ;

    !  Data array length = ListLength = 5
    BCData_t<5> DirichletData =
      {{
      DataArray_t<real, 1, 1> EntropyApprox =
        {{
        Data(real, 1, 1) = 0.94 ;
        }} ;

      DataArray_t<real, 1, 1> EnthalpyStagnation =
        {{
        Data(real, 1, 1) = 2.85 ;
        }} ;

      DataArray_t<real, 1, 5> VelocityY =
        {{
        Data(real, 1, 5) = (v_inflow(j), j=3,7) ;
        }} ;
      }} ;
    }} ;
  }} ;

This is another example of a simple boundary-condition type. The primary additional complexity included in this example is multiple Dirichlet conditions with one containing local data. DirichletData contains three DataArray_t entities named EntropyApprox, EnthalpyStagnation and VelocityY. This specifies three Dirichlet boundary conditions to be enforced, and the names identify the solution quantities to set. Since both EntropyApprox and EnthalpyStagnation have an array-length structure parameter of one, they identify global data, and the values are provided. VelocityY is an array of data values and contains the values in v_inflow(). The length of the array is given by ListLength, which represents the number of cell faces because BC3 is specified using the value of FaceCenter for GridLocation. Note that the beginning and ending indices on the array v_inflow() are unimportant (they are user inputs); there just needs to be five values provided.

9.10.4. Example - Outflow

Outflow boundary condition with unspecified normal Mach number for an i-max face of a 3-D structured zone: For subsonic outflow, a uniform pressure is specified; for supersonic outflow, no boundary-condition equations are specified.

!  CellDimension = 3, IndexDimension = 3
BC_t<3,3,3> BC4 =
  {{
  BCType_t BCType = BCOutflow ;

  IndexRange_t<3> PointRange = {{ }} ;

  BCDataSet_t<?> BCDataSetSubsonic =
    {{
    BCTypeSimple_t BCTypeSimple = BCOutflowSubsonic ;

    BCData_t<?> DirichletData =
      {{
      DataArray_t<real, 1, 1> Pressure = {{ }} ;
      }} ;
    }} ;

  BCDataSet_t<?> BCDataSetSupersonic =
    {{
    BCTypeSimple_t BCTypeSimple = BCOutflowSupersonic ;
    }} ;
  }} ;

This is an example of a complex boundary-condition type; the equation set to be enforced depends on the local flow conditions, namely the Mach number normal to the boundary. Two data sets are provided, BCDataSetSubsonic and BCDataSetSupersonic; recall the names are unimportant and are user defined. The first data set has a boundary-condition type of BCOutflowSubsonic and prescribes a global Dirichlet condition on static pressure. Any additional boundary conditions needed may be applied by a flow solver. The second data set has a boundary-condition type of BCOutflowSupersonic with no additional boundary-condition equation specification. Typically, all solution quantities are extrapolated from the interior for supersonic outflow. From the boundary-condition type association table, BCOutflow requires two data sets with boundary-condition types BCOutflowSubsonic and BCOutflowSupersonic. The accompanying usage rule states that the data set for BCOutflowSubsonic should be used for a subsonic normal Mach number; otherwise, the data set for BCOutflowSupersonic should be enforced.

Any additional data sets with boundary-condition types other than BCOutflowSubsonic or BCOutflowSupersonic could be provided (the definition of BC_t allows an arbitrary list of BCDataSet_t entities); however, they should be ignored by any code processing the boundary-condition information. Another caveat is that providing two data sets with the same simple boundary-condition type would cause indeterminate results - which one is the correct data set to apply?

The actual global data value for static pressure is not provided; an abbreviated form of the Pressure entity is shown. This example also uses the “?” notation for unused data-array-length structure parameters.

9.10.5. Example - Farfield

Farfield boundary condition with arbitrary flow conditions for a j-max face of a 2-D structured zone: If subsonic inflow, specify entropy, vorticity and incoming acoustic characteristics; if supersonic inflow specify entire flow state; if subsonic outflow, specify incoming acoustic characteristic; and if supersonic outflow, extrapolate all flow quantities. None of the extrapolated quantities for the different boundary condition possibilities need be stated.

!  CellDimension = 2, IndexDimension = 2
BC_t<2,2,2> BC5 =
  {{
  BCType_t BCType = BCFarfield ;

  IndexRange_t<2> PointRange = {{ }} ;

  int[2] InwardNormalIndex = [0,-1] ;

  BCDataSet_t<?> BCDataSetInflowSupersonic =
    {{
    BCTypeSimple_t BCTypeSimple = BCInflowSupersonic ;
    }} ;

  BCDataSet_t<?> BCDataSetInflowSubsonic =
    {{
    BCTypeSimple_t BCTypeSimple = BCInflowSubsonic ;

    BCData<?> DirichletData =
      {{
      DataArray_t<real, 1, 1> CharacteristicEntropy      = {{ }} ;
      DataArray_t<real, 1, 1> CharacteristicVorticity1   = {{ }} ;
      DataArray_t<real, 1, 1> CharacteristicAcousticPlus = {{ }} ;
      }} ;
    }} ;

  BCDataSet_t<?> BCDataSetOutflowSupersonic =
    {{
    BCTypeSimple_t BCTypeSimple = BCOutflowSupersonic ;
    }} ;

  BCDataSet_t<?> BCDataSetOutflowSubsonic =
    {{
    BCTypeSimple_t BCTypeSimple = BCOutflowSubsonic ;

    BCData<?> DirichletData =
      {{
      DataArray_t<real, 1, 1> CharacteristicAcousticMinus = {{ }} ;
      }} ;
    }} ;
  }} ;

The farfield boundary-condition type is the most complex of the compound boundary-condition types. BCFarfield requires four data sets; these data sets must contain the simple boundary-condition types BCInflowSupersonic, BCInflowSubsonic, BCOutflowSupersonic and BCOutflowSubsonic. This example provides four appropriate data sets. The usage rule given for BCFarfield states which set of boundary-condition equations to be enforced based on the normal velocity and normal Mach number.

The data set for supersonic-inflow provides no information other than the boundary-condition type. A flow solver is free to apply any conditions that are appropriate; typically all solution quantities are set to freestream reference state values. The data set for subsonic-inflow states that three Dirichlet conditions should be enforced; the three data identifiers provided are from the standard data-name identifier conventions. The data set for supersonic-outflow only provides the boundary-condition type, and the data set for subsonic-outflow provides one Dirichlet condition on the incoming acoustic characteristic, CharacteristicAcousticMinus.

Also provided in the example is the inward-pointing computational-coordinate normal; the normal points in the \(-j\) direction, meaning the BC patch is a j-max face. This information could also be obtained from the BC patch description given in IndexRange.

Note that this example shows only the overall layout of the boundary-condition entity. IndexRange and all DataArray_t entities are abbreviated, and all unused structure functions are not evaluated.

9.10.6. Example - Viscous Solid Wall II

There are circumstances when a user may wish to define a BC patch using vertices (under BC_t), but store the BC data at face centers (under BCDataSet_t). The following example is similar to the Viscous Solid Wall example given previously, with the exception that the Dirichlet data for temperature is stored at face centers rather than at vertices.

As before, the example is a viscous solid wall in a 3-D structured zone, where a Dirichlet condition is enforced for temperature; the wall temperature for the entire wall is specified to be 273 K. The BC patch is on the j-min face and is bounded by the indices (1,1,1) and (33,1,9).

!  CellDimension = 3, IndexDimension = 3
BC_t<3,3,3> BC2 =
  {{
  BCType_t BCType = BCWallViscousIsothermal ;

  !  Grid location is Vertex by default
  IndexRange_t<3> PointRange =
    {{
    int[3] Begin = [1 ,1,1] ;
    int[3] End   = [33,1,9] ;
    }} ;

  !  ListLength = 33*9 = 297
  BCDataSet_t<297> BCDataSet1 =
    {{
    BCTypeSimple_t BCTypeSimple = BCWallViscousIsothermal ;

    GridLocation_t GridLocation = FaceCenter ;
    IndexRange_t<3> PointRange =
      {{
      int[3] Begin = [1 ,1,1] ;
      int[3] End   = [32,1,8] ;
      }} ;

    !  ListLength = 32*8 = 256
    BCData_t<256> DirichletData =
      {{
      DataArray_t<real, 1, 1> Temperature =
        {{
        Data(real, 1, 1) = 273. ;

        DataClass_t DataClass = Dimensional ;

        DimensionalUnits_t DimensionalUnits =
          {{
          MassUnits        = MassUnitsNull ;
          LengthUnits      = LengthUnitsNull ;
          TimeUnits        = TimeUnitsNull ;
          TemperatureUnits = Kelvin ;
          AngleUnits       = AngleUnitsNull ;
          }} ;
        }} ;
      }} ;
    }} ;
  }} ;

As in the previous Viscous Solid Wall example, although the boundary-condition data is global, we include in this example structure parameters that are the lengths of potential local-data arrays. In BC_t, GridLocation is not specified, and thus is Vertex by default. The structure function ListLength is 297, based on the specification of PointRange, and that value is passed to BCDataSet_t.

In this example PointRange is specified in BCDataSet_t, so the ListLength passed into it from BC_t is not used. In BCDataSet_t, GridLocation is specified as FaceCenter, and PointRange is set accordingly. The corresponding value of ListLength is 256, which is passed into BCData_t.

As before, in BCData_t the entity Temperature contains global data, so the value of ListLength is unused.