@[toc]

原论文

$\mathbf{\text{1. }}$$\textbf{1. }$热带几何$\mathbf{\text{\&}}$$\textbf{\&}$热带代数

$\mathbf{\text{1.1. }}$$\textbf{1.1. }$热带半环

1️⃣基本概念：集合$+$${+}$集合上的运算$\text{+}$$\text{+}$单位元，即$(K,\oplus ,\otimes ,\mathbb{0},\mathbb{1})=(\mathbb{R}\cup \{-\mathrm{\infty }\},max,+,-\mathrm{\infty },0)$$({K,\oplus,\otimes,\mathbb{0},\mathbb{1}}){=}({\mathbb{R}{\cup}\{{-}{\infty} \},\max,{+},{-}{\infty},0})$

1. 集合：所有实数加一个特殊元素(负无穷$-\mathrm{\infty }$${-}\infty$)，即$\mathbb{R}\cup \{-\mathrm{\infty }\}$$\mathbb{R}{\cup}\{{-}\infty\}$

2. 运算：对$x,y\in \mathbb{R}\cup \{-\mathrm{\infty }\}$$x,y{\in}{\mathbb{R}{\cup}\{{-}\infty \}}$，热带加法$x\oplus y=max\{x,y\}$$x{\oplus}y{=}\max\{x,y\}$，热带乘法$x\otimes y=x+y$$x{\otimes}y{=}x{+}y$

3. 单位元：$-\mathrm{\infty }$${-}\infty$是热带加的单位元$max\{x,-\mathrm{\infty }\}=x$$\max\{x,{-}\infty\}{=}x$，$0$$0$是热带乘的单位元$x+0=x$$x{+}0{=}x$

2️⃣基本性质：环❌$/$$/$半环✅$/$$/$半域✅

1. 为何是半环：满足以下运算定律

   运算律	对热带加法	对热带乘法
   交换律	$max\{a,b\}=max\{b,a\}$$\max\{a,b\}{=}\max\{b,a\}$	$a+b=b+a$$a{+}b{=}b{+}a$
   结合律	$max\{max\{a,b\},c\}=max\{a,max\{b,c\}\}$$\max\{\max\{a,b\},c\}{=}\max\{a,\max\{b,c\}\}$	$a+(b+c)=(b+a)+c$$a{+}(b{+}c){=}(b{+}a){+}c$

   • 分配律：$a+max\{b,c\}=max\{a+b,a+c\}$$a{+}\max\{b,c\}{=}\max\{a{+}b,a{+}c\}$

2. 关于逆元：对热带半环，加法逆元❌$/$$/$乘法逆元✅

   逆元类型	定义	对热带半环
   加法逆元	若$x\oplus y=\mathbb{0}$$x{\oplus}y{=}\mathbb{0}$则$y$$y$为$x$$x$加法逆元，记$y=-x$$y{=}{-}x$	不存在$max\{x,y\}=-\mathrm{\infty }$$\max\{x,y\}{=}{-}{\infty}$故不为环
   乘法逆元	若$x\otimes y=\mathbb{1}$$x{\otimes}y{=}\mathbb{1}$则$y$$y$为$x$$x$乘法逆元，记$y=x^{-1}$$y{=}x^{{-}1}$	存在$x+(-x)=0$$x{+}(-x){=}0$故为半域，故可进行除法

   • 所谓环：在半环的基础上，所有元素都必须有其对应的加法逆元

   • 所谓半域：在半环的基础上，除了加法单位元以外的所有元素，都必须有其对应的乘法逆元

3️⃣热带函数：有理函数(热带多项式的热带商)$\stackrel{}{\leftarrow }$${\xleftarrow{}}$多项式$\stackrel{}{\leftarrow }$${\xleftarrow{}}$扩展运算

1. 运算扩展：热带幂和热带商

   运算	半环中	热带半环中	特殊的
   热带幂	$x^{\otimes a}=x\otimes \cdots \otimes x$$x^{{\otimes}a}{=}x{\otimes}{\cdots}{\otimes}x$	$x^{\otimes a}=ax$$x^{{\otimes}a}{=}ax$	$(-\mathrm{\infty }{)}^{\otimes a}=-\mathrm{\infty }$$({-}{\infty})^{{\otimes}a}{=}{-}{\infty}$及$(-\mathrm{\infty }{)}^{\otimes 0}=0$$({-}{\infty})^{{\otimes}0}{=}0$
   热带商	$a\oslash b=a\otimes b^{\otimes (-1)}$$a{\oslash}b{=}a{\otimes}b^{{\otimes}({-}1)}$	$a\oslash b=a-b$$a{\oslash}b{=}a{-}b$	$\text{N/A}$$\text{N/A}$

2. 热带多项式$\mathrm{\&}$$\&$有理函数：令$\mathbf{x}=⟨x_1,...,x_d⟩$$\mathbf{x}{=}\langle{x_1,...,x_d}\rangle$

   • 热带多项式：相当于多个线性函数(更精确地说，仿射函数)取最大值

     算式	结构	转换回常规运算	性质
     热带单项式	$L_i(\mathbf{x})=c_i\otimes x_1^{\otimes a_1}\otimes \cdots \otimes x_d^{\otimes a_d}$$L_i(\mathbf{x}){=}c_i{\otimes}x_{1}^{{\otimes}a_{1}}{\otimes}{\cdots}{\otimes}x_{d}^{{\otimes}a_{d}}$	$c_i+a_{i1}{x}_1+\cdots +a_{id}{x}_d$$c_i{+}a_{i1}x_{1}{+}{\cdots}{+}a_{id}x_{d}$	线性函数
     热带多项式	$f(\mathbf{x})=L_1\oplus L_2\oplus \cdots \oplus L_r$$f(\mathbf{x}){=}L_1{\oplus}L_2{\oplus}{\cdots}{\oplus}L_r$	$max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$$\max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$	凸函数

   • 热带有理函数：热带多项式的热带商，且定义$f(\mathbf{x})\oslash g(\mathbf{x})=f(\mathbf{x})-g(\mathbf{x})$$f(\mathbf{x}){\oslash}g(\mathbf{x}){=}f(\mathbf{x}){-}g(\mathbf{x})$

     符号	定义	转换回常规运算	性质
     $h(\mathbf{x})$$h(\mathbf{x})$	$f(\mathbf{x})\oslash g(\mathbf{x})$$f(\mathbf{x}){\oslash}g(\mathbf{x})$	$max\{L_1,...,L_r\}-max\{L_1^{\prime },...,L_s^{\prime }\}$$\max\{L_1,...,L_r\}{-}\max\{L_1',...,L_s'\}$	两凸函数差($\text{DC}$$\text{DC}$函数)

   • 补充：对$\mathbf{x}=⟨x_1,...,x_d⟩$$\mathbf{x}{=}\langle{x_1,...,x_d}\rangle$及${\mathit{\alpha }}_{\mathit{i}}=⟨a_{i1},...,a_{id}⟩$$\boldsymbol{\alpha_i}{=}\langle{a_{i1},...,a_{id}}\rangle$，多项式$c_i\otimes x_1^{\otimes a_{i1}}\otimes \cdots \otimes x_d^{\otimes a_{id}}$$c_i{\otimes}x_{1}^{{\otimes}a_{i1}}{\otimes}{\cdots}{\otimes}x_{d}^{{\otimes}a_{id}}$可简写为$c_i{\mathbf{x}}^{{\mathit{\alpha }}_{\mathit{i}}}$$c_i\mathbf{x}^{\boldsymbol{\alpha_i}}$

3. 一些推广：函数集代数结构与向量值函数

   • 函数集的代数结构：注意，热带多项式可看作热带有理函数分母为$\mathbb{1}=0$$\mathbb{1}{=}0$时

     集合	半环结构	半域
     $x_1,...,x_d$$x_1,...,x_d$构成的所有热带多项式集	$(\mathbb{T}[x_1,...,x_d],max,+,-\mathrm{\infty },0)$$(\mathbb{T}[x_1,...,x_d],\max,{+},{-}{\infty},{0})$	❌
     $x_1,...,x_d$$x_1,...,x_d$构成的所有热带有理函数集	$(\mathbb{T}(x_1,...,x_d),max,+,-\mathrm{\infty },0)$$(\mathbb{T}(x_1,...,x_d),\max,{+},{-}{\infty},{0})$	✅

   • 向量值函数：将不同的函数$/$$/$多项式一次拼接

     向量函数类型	函数${\mathbb{R}}^{\mathit{d}}\mathbf{\to }{\mathbb{R}}^{\mathit{p}}$$\boldsymbol{\mathbb{R}^d{\to}\mathbb{R}^{p}}$的定义	补充
     热带多项式	$F_f:F(\mathbf{x})=(f_1(\mathbf{x}),...,f_p(\mathbf{x}))$$F_f{:\,}F(\mathbf{x}){=}(f_1(\mathbf{x}),...,f_p(\mathbf{x}))$	$\text{Pol}(d,p)$$\text{Pol}(d,p)$为所有$F_f:{\mathbb{R}}^d\to {\mathbb{R}}^p$$F_f{:\,}\mathbb{R}^d{\to}\mathbb{R}^{p}$函数集
     热带有理函数	$F_h:F(\mathbf{x})=(h_1(\mathbf{x}),...,h_p(\mathbf{x}))$$F_h{:\,}F(\mathbf{x}){=}(h_1(\mathbf{x}),...,h_p(\mathbf{x}))$	$\text{Rat}(d,p)$$\text{Rat}(d,p)$为所有$F_h:{\mathbb{R}}^d\to {\mathbb{R}}^p$$F_h{:\,}\mathbb{R}^d{\to}\mathbb{R}^{p}$函数集

$\mathbf{\text{1.2. }}$$\textbf{1.2. }$热带超曲面与牛顿对偶

1️⃣热带超曲面

1. 定义：考虑热带多项式$f(\mathbf{x})=max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$$f(\mathbf{x}){=}\max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$

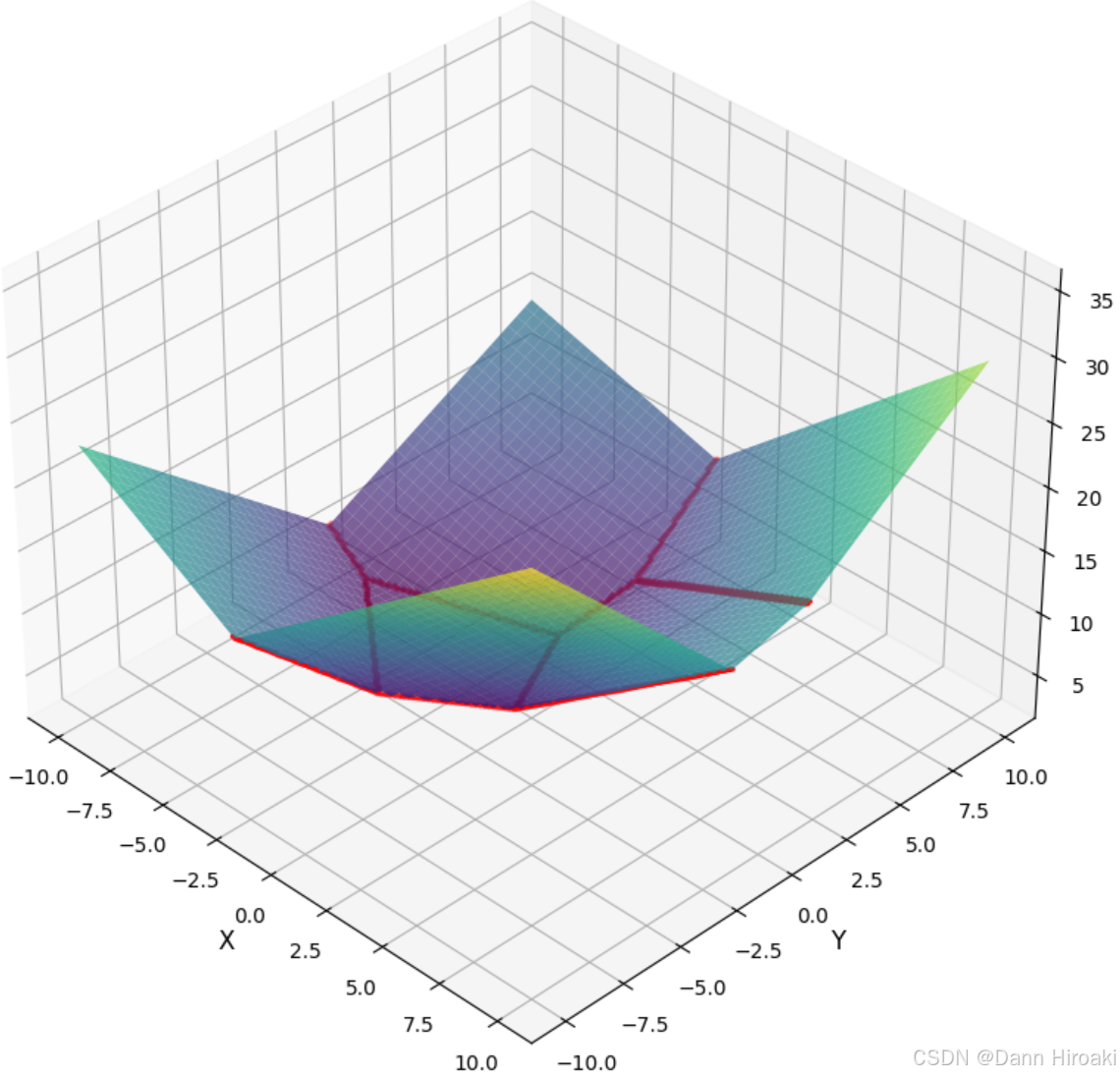
   • 形式定义：$\mathcal{T}(f)=\{\mathbf{x}\in {\mathbb{R}}^d\mid c_i{\mathbf{x}}^{{\mathit{\alpha }}_{\mathit{i}}}=c_j{\mathbf{x}}^{{\mathit{\alpha }}_{\mathit{j}}}=f(\mathbf{x}),i\ne j\}$$\mathcal{T}(f){=}\{\mathbf{x}{\in}\mathbb{R}^d\mid{}c_i\mathbf{x}^{\boldsymbol{\alpha_i}}{=}c_j\mathbf{x}^{\boldsymbol{\alpha_j}}{=}f(\mathbf{x}),i{\neq}j\}$，当$d=2$$d{=}2$时从热带超曲面退化为热带曲线

   • 直观理解：多项式由最高平面$max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$$\max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$拼接成，热带超曲面即两最高平面连接处

   • 基本含义：在某点$\mathbf{x}$$\mathbf{x}$至少两单项式同时取得最大值，即$L_i(\mathbf{x})=L_j(\mathbf{x})=max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$$L_i(\mathbf{x}){=}L_j(\mathbf{x}){=}\max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$

2. 本质：将$f(\mathbf{x})=max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$$f(\mathbf{x}){=}\max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$划分为多个凸胞腔

   • 直观理解：每个凸胞腔都是一个单项式“称霸”的区域，即每个凸胞腔内$f(\mathbf{x})$$f(\mathbf{x})$可用一单项式精确描述

   • 形式定义：单项式$c_j{\mathbf{x}}^{{\alpha }_j}$$c_j\mathbf{x}^{\alpha_j}$取得最大值的胞腔是$\{\mathbf{x}\in {\mathbb{R}}^d\mid c_j+{{\mathit{\alpha }}_{\mathit{j}}}^T\mathbf{x}\ge c_i+{{\mathit{\alpha }}_{\mathit{i}}}^T\mathbf{x},\mathrm{\forall }i\ne j\}$$\{\mathbf{x}{\in}\mathbb{R}^d\mid{}c_j{+}{\boldsymbol{\alpha_j}}^{T}\mathbf{x}{\geq}c_i{+}{\boldsymbol{\alpha_i}}^{T}\mathbf{x},\forall{i{\neq}j}\}$

2️⃣牛顿多边形及牛顿对偶

1. 第一步：以$f(x_1,x_2)=(1\otimes x_1^2)\oplus (1\otimes x_2^2)\oplus (2\otimes x_1\otimes x_2)\oplus (2\otimes x_1)\oplus (2\otimes x_2)\oplus (2)$$f(x_1,x_2){=}(1{\otimes}x_1^2){\oplus}(1{\otimes}x_2^2){\oplus}(2{\otimes}x_1{\otimes}x_2){\oplus}(2{\otimes}x_1){\oplus}(2{\otimes}x_2){\oplus}(2)$为例，提取因子

   单项式	${\mathit{x}}_{\mathbf{1}}$$\boldsymbol{x_1}$次方	${\mathit{x}}_{\mathbf{2}}$$\boldsymbol{x_2}$次方	常数项	指数点$\mathit{\alpha }$$\boldsymbol{\alpha}$	$\mathit{c}$$\boldsymbol{c}$
   $1\otimes x_1^2$$1{\otimes}x_1^2$	$2$$2$	$0$$0$	$1$$1$	${\alpha }_1=(2,0)$$\alpha_1{=}(2,0)$	$c_1=1$$c_1{=}1$
   $1\otimes x_2^2$$1{\otimes}x_2^2$	$0$$0$	$2$$2$	$1$$1$	${\alpha }_2=(0,2)$$\alpha_2{=}(0,2)$	$c_2=1$$c_2{=}1$
   $2\otimes x_1\otimes x_2$$2{\otimes}x_1{\otimes}x_2$	$1$$1$	$1$$1$	$2$$2$	${\alpha }_3=(1,1)$$\alpha_3{=}(1,1)$	$c_3=2$$c_3{=}2$
   $2\otimes x_1$$2{\otimes}x_1$	$1$$1$	$0$$0$	$2$$2$	${\alpha }_4=(1,0)$$\alpha_4{=}(1,0)$	$c_4=2$$c_4{=}2$
   $2\otimes x_2$$2{\otimes}x_2$	$0$$0$	$1$$1$	$2$$2$	${\alpha }_5=(0,1)$$\alpha_5{=}(0,1)$	$c_5=2$$c_5{=}2$
   $2$$2$	$0$$0$	$0$$0$	$2$$2$	${\alpha }_6=(0,0)$$\alpha_6{=}(0,0)$	$c_6=2$$c_6{=}2$

2. 之后步：(注意所谓上表面，即表面法向量与$d$$d$维中从最后一维$/$$/$高度维夹角为锐角)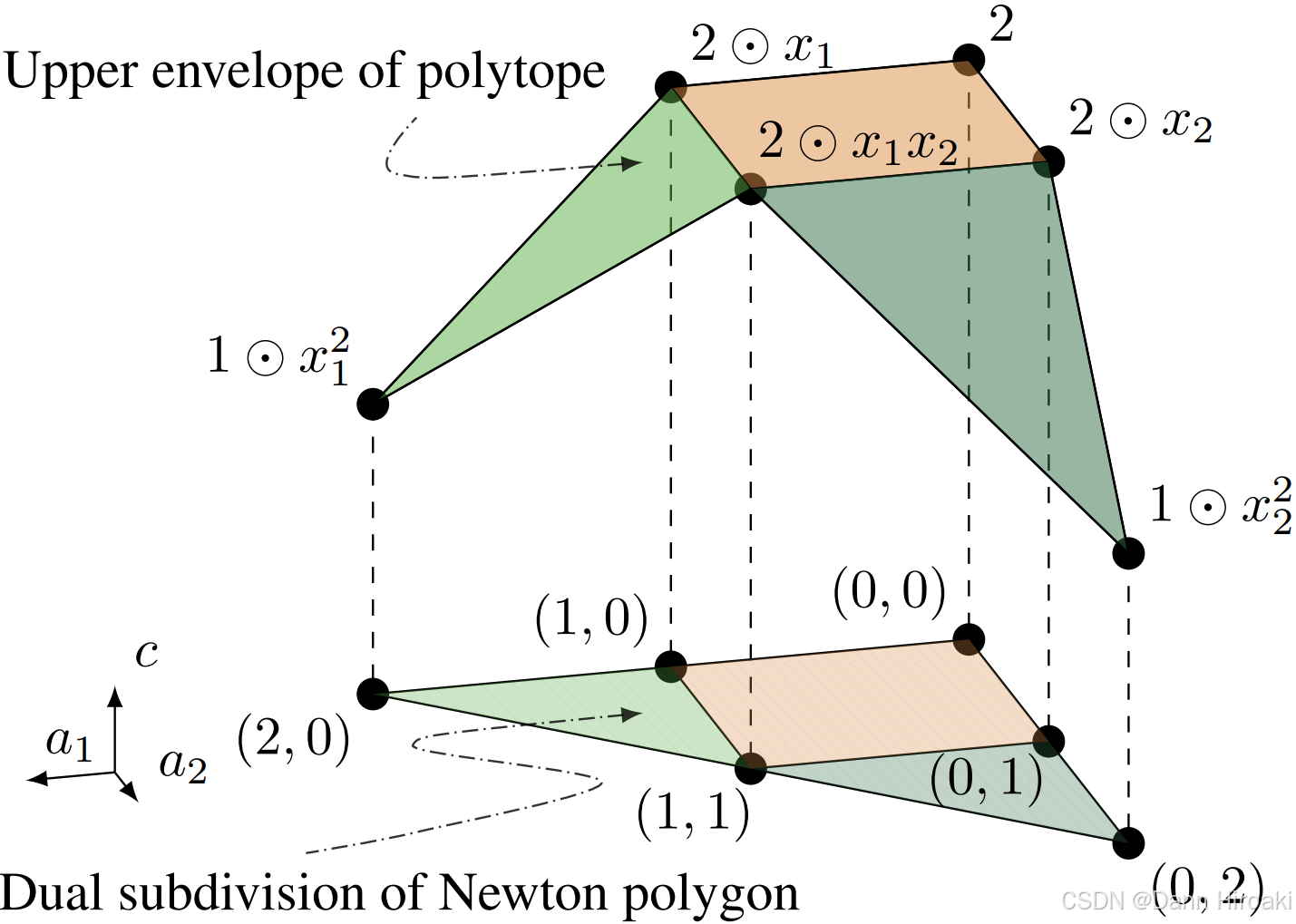

   操作	描述
   牛顿多边形$\mathrm{\Delta }(f)$$\Delta(f)$	取所有指数点$\alpha$${\alpha}$的凸包(相当于用橡皮筋围住最外围点)
   多面体$\mathcal{P}(f)$$\mathcal{P}(f)$	基于牛顿多边形，在$\alpha$${\alpha}$基础上增加一个值为$c$$c$的维度，成为$({\mathit{\alpha }}_{\mathit{i}},c_i)$$(\boldsymbol{\alpha_i},c_i)$
   对偶细分$\delta (f)$$\delta(f)$	将多面体$\mathcal{P}(f)$$\mathcal{P}(f)$上表面的边和顶点，垂直投影回到底部牛顿多边形$\mathrm{\Delta }(f)$$\Delta(f)$

3. 最后步：对牛顿多边形$\mathrm{\Delta }(f)$$\Delta(f)$上的对偶细分$\delta (f)$$\delta(f)$，建立对偶细分$\delta (f)$$\delta(f)$和热带超曲面$\mathcal{T}(f)$$\mathcal{T}(f)$的联系

   偶细分$\mathit{\delta }\mathbf{(}\mathit{f}\mathbf{)}$$\boldsymbol{\delta(f)}$	对应超曲面$\mathcal{T}\mathbf{(}\mathit{f}\mathbf{)}$$\boldsymbol{\mathcal{T}(f)}$	含义	$\mathit{\delta }\mathbf{(}\mathit{f}\mathbf{)}$$\boldsymbol{\delta(f)}$示例	对应$\mathcal{T}\mathbf{(}\mathit{f}\mathbf{)}$$\boldsymbol{\mathcal{T}(f)}$示例
   $k$$k$维面	$(d-k)$$(d{-}k)$维面	$k+1$$k{+}1$个$L_i$$L_i$打平	$\text{N/A}$$\text{N/A}$	$\text{N/A}$$\text{N/A}$
   边$(k=1)$$(k{=}1)$	折痕$(k=1/d=2)$$(k{=}1/d{=}2)$	两$L_i$$L_i$打平	线$(1,0)\to (0,0)$$(1,0){\to}(0,0)$	折痕($2\otimes x_1=2$$2{\otimes}x_1{=}2$)
   顶点$(k=0)$$(k{=}0)$	线性区$(k=0/d=2)$$(k{=}0/d{=}2)$	一$L_i$$L_i$主导	点$(1,0)$$(1,0)$	线性区($2\otimes x_1$$2{\otimes}x_1$主导)

   • 对偶定理：$\mathcal{T}(f)$${\mathcal{T}(f)}$线性区域数$=\mathcal{P}(f)$${=}\mathcal{P}(f)$上表面顶点数$\le \mathcal{P}(f)$${\leq}\mathcal{P}(f)$总顶点数

3️⃣线性区域：

1. 含义：$F$$F$定义域中保持其线性的最大的连通子集，即同一线性区域内不同的两点都线性可达

2. 性质：当$F$$F$为热带多项式(凸函数)时其线性区域为凸，当$F$$F$为热带有理函数($\text{DC}$$\text{DC}$函数)时其线性区域非凸

3. 意义：$F$$F$线性区域数量记为$\mathcal{N}(F)$$\mathcal{N}(F)$，一个神经网络能划分出更多线性区域，去拟合能力更强

$\mathbf{\text{1.3. }}$$\textbf{1.3. }$热带多项式的几何学描述

0️⃣闵可夫斯基和：形式定义与一些延申

1. 形式定义：对两集合$P_1/P_2$$P_1/P_2$而言，其$\text{Minkowski}$$\text{Minkowski}$和为$P_1+P_2\text{:=}\{x_1+x_2\mid x_1\in P_1,x_2\in P_2\}$$P_1{+}P_2 \mathrel{\text{:=}}\{x_1{+}x_2 \mid x_1{\in}P_1,x_2{\in}P_2\}$

2. 直观理解：将形状$P_2$$P_2$的原点，在形状$P_1$$P_1$每个点上移动，移动过程中$P_2$$P_2$扫描的区域即$\text{Minkowski}$$\text{Minkowski}$和

3. 对多面体：多面体$\mathcal{P}(f)$$\mathcal{P}(f)$合$\mathcal{P}(g)$$\mathcal{P}(g)$的$\text{Minko.}$$\text{Minko.}$和，即顶点集$\mathcal{V}(\mathcal{P}(f))$$\mathcal{V}(\mathcal{P}(f))$和$\mathcal{V}(\mathcal{P}(g))$$\mathcal{V}(\mathcal{P}(g))$的$\text{Minko.}$$\text{Minko.}$和，再求凸包

4. 一些扩展：两个(或多个)线段的$\text{Minkowski}$$\text{Minkowski}$和(一线段每个点与另一线段每个点相加)，为带状多面体

1️⃣构建与变换：热带多项式的几何学

1. 单项式与顶点：

   • 结构上：$f$$f$一单项式$L_i=c_i+a_{i1}{x}_1+\cdots +a_{id}{x}_d\stackrel{\text{对}\text{应}}{\iff }\mathcal{P}(f)$$L_i{=}c_i{+}a_{i1}x_{1}{+}{\cdots}{+}a_{id}x_{d}{\xLeftrightarrow{对应}}\mathcal{P}(f)$一生成顶点$({\mathit{\alpha }}_{\mathit{i}},c_i)=(a_{i1},...,a_{id},c_i)$$(\boldsymbol{\alpha_i},c_i){=}(a_{i1},...,a_{id},c_i)$

   • 运算上：$f$$f$单项式的热带运算$\stackrel{\text{等}\text{价}}{\iff }$${\xLeftrightarrow{等价}}$对$\mathcal{P}(f)$$\mathcal{P}(f)$顶点的几何变换，具体如下

     单项式的热带运算	转为常规运算	相当于对多面体中....
     $L_1\otimes \cdots \otimes L_n$$L_1{\otimes}{\cdots}{\otimes}L_n$	$L_1+\cdots +L_n$$L_1{+}{\cdots}{+}L_n$	将$({\mathit{\alpha }}_{\mathit{i}},c_i)$$(\boldsymbol{\alpha_i},c_i)$求和变成求$({\mathit{\alpha }}_{\mathbf{1}}\mathbf{+}\mathbf{\cdots }\mathbf{+}{\mathit{\alpha }}_{\mathit{n}},c_1+\cdots +c_n)$$(\boldsymbol{\alpha_1{+}{\cdots}{+}\alpha_n},c_1{+}{\cdots}{+}{c_n})$
     $L_i^{\otimes a}$$L_i^{{\otimes}a}$	$a{L}_i$$aL_i$	放缩$({\mathit{\alpha }}_{\mathit{i}},c_i)$$(\boldsymbol{\alpha_i},c_i)$成$(a{\mathit{\alpha }}_{\mathit{i}},a{c}_i)$$(a\boldsymbol{\alpha_i},ac_i)$

2. 单项式到多项式

   • 结构上：多个单项式热带相加$\stackrel{\text{等}\text{价}}{\iff }$${\xLeftrightarrow{等价}}$多个顶点求凸包以生成成多面体

   • 运算上：$f=L_1\oplus \cdots \oplus L_n$$f{=}L_1{\oplus}{\cdots}{\oplus}L_n$可转化为$f=max\{L_1,...,L_n\}$$f{=}\max\{L_1,...,L_n\}$，即求$\{({\mathit{\alpha }}_{\mathbf{1}},c_1),...,({\mathit{\alpha }}_{\mathit{n}},c_n)\}$$\{(\boldsymbol{\alpha_1},c_1),...,(\boldsymbol{\alpha_n},c_n)\}$凸包

3. 多项式与多面体：

   • 热带幂$f^{\otimes a}$$f^{{\otimes}a}$：相当于缩放，即$\mathcal{P}(f^{\otimes a})=a\mathcal{P}(f)$$\mathcal{P}(f^{{\otimes}a}){=}a\mathcal{P}(f)$

     领域	操作	解释
     热带运算	热带幂$f^{\otimes a}$$f^{{\otimes}a}$	相当于$a\times f$$a{\times}f$，即每个单项式系数$c_i$$c_i$和指数${\mathit{\alpha }}_{\mathit{i}}=\{a_{i1},..,a_{id}\}$$\boldsymbol{\alpha_i}{=}\{a_{i1},..,a_{id}\}$乘上$a$$a$
     几何变换	缩放	每个顶点$({\mathit{\alpha }}_{\mathit{i}},c_i)$$(\boldsymbol{\alpha_i},c_i)$变为$(a{\mathit{\alpha }}_{\mathit{i}},a{c}_i)$$(a\boldsymbol{\alpha_i},ac_i)$，即每个顶点都相对原点拉伸$a$$a$倍

   • 热带积$f\otimes g$$f{\otimes}g$：相当于闵可夫斯基和，即$\mathcal{P}(f\otimes g)=\mathcal{P}(f)+\mathcal{P}(g)$$\mathcal{P}(f{\otimes}g){=}\mathcal{P}(f){+}\mathcal{P}(g)$

     领域	操作	解释
     热带运算	热带积$f\otimes g$$f{\otimes}g$	$f$$f$每个单项式与$g$$g$每个单项式热带乘(相加)再热带加(求$max$$\max$)
     几何变换	多面体$\text{Minko.}$$\text{Minko.}$和	$\mathcal{P}(f)$$\mathcal{P}(f)$每个顶点与$\mathcal{P}(g)$$\mathcal{P}(g)$每个顶点坐标依次相加，再求凸包

   • 热带和$f\oplus g$$f{\oplus}g$：相当于顶点联合的凸包，即$\mathcal{P}(f\oplus g)=\text{Conv}(\mathcal{V}(\mathcal{P}(f))\cup \mathcal{V}(\mathcal{P}(g)))$$\mathcal{P}(f{\oplus}g){=}\text{Conv}(\mathcal{V}(\mathcal{P}(f)){\cup}\mathcal{V}(\mathcal{P}(g)))$

     领域	操作	解释
     热带运算	热带积$f\oplus g$$f{\oplus}g$	$f$$f$和$g$$g$各自的多项式合在一起，再求合一起后的最大值
     几何变换	顶点联合的凸包	$\mathcal{P}(f)$$\mathcal{P}(f)$与$\mathcal{P}(g)$$\mathcal{P}(g)$中所有顶点合在一起，对合一起后的点集求凸包

2️⃣理论保证：如何界定新生成多面体的顶点数

1. $\text{Gritzmann-Sturmfels}$$\text{Gritzmann-Sturmfels}$定理：生成多面体最多多少个顶点

   • 参数说明：$d+1$$d{+}1$表示多面体$P_1,...,P_k$$P_1,...,P_k$所处空间的维度，$m$$m$为收集所有$P_i$$P_i$棱后非平行棱的总数

   • 定理内容：令多面体$P_1,...,P_k$$P_1,...,P_k$进行$\text{Minkowski}$$\text{Minkowski}$和后新多面体顶点数为$N$$N$，则$N\le 2{\displaystyle \sum _{j=0}^d{\mathbf{C}}_{m-1}^j}$$N{\leq}2\displaystyle{\sum_{j=0}^{d}\mathbf{C}_{m{-}1}^j}$

   • 取等条件：每个多面体$P_i$$P_i$都为带状多面体，且构成每个$P_i$$P_i$的线段都处于一般位置

2. 定理的关键推论：新生成多面体上表面有多少顶点，即多项式有多少线性区域数

   • 条件改变：$P_1,...,P_k$$P_1,...,P_k$从任意形状的多面体限定为了带状多面体，

   • 结论改变：$P_1,...,P_k$$P_1,...,P_k$进行$\text{Minkowski}$$\text{Minkowski}$和后新多面体上表面顶点数为$N^{\prime }$$N'$，则$N^{\prime }\le {\displaystyle \sum _{j=0}^d{\mathbf{C}}_m^j}$$N'{\leq}\displaystyle{\sum_{j=0}^{d}\mathbf{C}_{m}^j}$

   • 取等条件：$P_i$$P_i$所有$m$$m$条线段都处于一般位置，新多面体($d+1$$d{+}1$维)顶点投影回$d$$d$维后都处于一般位置

3. (补充)关于一般位置：即任意$k$$k$个点不会被维度$\le k-2$${\leq}k{-}2$的空间容纳，例如四点不共面，三点不共线

$\mathbf{\text{2. }}$$\textbf{2. }$神经网络的热带几何$\mathbf{\text{\&}}$$\textbf{\&}$代数

$\mathbf{\text{2.1. }}$$\textbf{2.1. }$神经网络及其假设

1️⃣神经网络的数学模型：定义一个共$L^{(n)}$$L^{(n)}$层全连接的前馈网络$$$%以下内容我对原文的符号体系做了一些改变，力求符合我自己的符号体系，在审查时请忽略符号体系的改变$

1. 对于每一层$L^{(i)}$$L^{(i)}$：

   • 结构：输入$d_{i-1}$$d_{i-1}$维的${\mathbf{\text{x}}}^{(i-1)}$$\textbf{x}^{(i-1)}$后输出$d_i$$d_i$维的${\mathbf{\text{x}}}^{(i)}$$\textbf{x}^{(i)}$，每层可学习参数有权重矩阵${\mathbf{A}}_{d_i\times d_{i-1}}$$\mathbf{A}_{d_i{\times}d_{i-1}}$及偏置向量${\mathbf{b}}_{d_i}$$\mathbf{b}_{d_i}$

   • 运算：先将${\mathbf{\text{x}}}^{(i-1)}$$\textbf{x}^{(i-1)}$输入仿射变换${\rho }_i\left({\mathbf{\text{x}}}^{(i-1)}\right)={\mathbf{A}}_{d_i\times d_{i-1}}{\mathbf{\text{x}}}^{(i-1)}+{\mathbf{b}}_{d_i}$$\rho_i{\left(\textbf{x}^{(i-1)}\right)}{=}\mathbf{A}_{d_i{\times}d_{i-1}}\textbf{x}^{(i-1)}{+}\mathbf{b}_{d_i}$再激活${\mathbf{\text{x}}}_i={\sigma }_i\left({\rho }_i\left({\mathbf{\text{x}}}^{(i-1)}\right)\right)$$\textbf{x}_{i}{=}\sigma_i\left(\rho_i{\left(\textbf{x}^{(i-1)}\right)}\right)$

   • 补充：本文${\sigma }_i$$\sigma_i$采用广义$\text{ReLU}$$\text{ReLU}$(详见下)，因为其为最典型的激活函数，也方便用热带代数描述

2. 对于所有$L^{(n)}$$L^{(n)}$层：

   • 结构：$\nu =({\sigma }_n\circ {\rho }_n)\circ ({\sigma }_{n-1}\circ {\rho }_{n-1})\circ \cdots \circ ({\sigma }_1\circ {\rho }_1)$$\nu{=}(\sigma_n{\circ}\rho_n){\circ}(\sigma_{n-1}{\circ}\rho_{n-1}){\circ}{\cdots}{\circ}(\sigma_1{\circ}\rho_1)$即$\nu \left({\mathbf{\text{x}}}^{(0)}\right)={\mathbf{\text{x}}}^{(n)}$$\nu\left(\textbf{x}^{(0)}\right){=}\textbf{x}^{(n)}$，但不会$\text{Softmax}\left({\mathbf{\text{x}}}^{(n)}\right)$$\text{Softmax}\left(\textbf{x}^{(n)}\right)$一下

   • 运算：${\mathbf{\text{x}}}^{(0)}\stackrel{{\sigma }_1\left({\rho }_1\left({\mathbf{\text{x}}}^{(0)}\right)\right)}{\to }{\mathbf{\text{x}}}^{(1)}\stackrel{{\sigma }_2\left({\rho }_2\left({\mathbf{\text{x}}}^{(1)}\right)\right)}{\to }{\mathbf{\text{x}}}^{(2)}\to \cdots \to {\mathbf{\text{x}}}^{(n-1)}\stackrel{{\sigma }_n\left({\rho }_n\left({\mathbf{\text{x}}}^{(n-1)}\right)\right)}{\to }{\mathbf{\text{x}}}^{(n)}$$\textbf{x}^{(0)} {\xrightarrow[]{\sigma_1\left(\rho_1{\left(\textbf{x}^{(0)}\right)}\right)}} \textbf{x}^{(1)} {\xrightarrow[]{\sigma_2\left(\rho_2{\left(\textbf{x}^{(1)}\right)}\right)}} \textbf{x}^{(2)} {\to}{\cdots}{\to} \textbf{x}^{(n-1)} {\xrightarrow[]{\sigma_n\left(\rho_n{\left(\textbf{x}^{(n-1)}\right)}\right)}} \textbf{x}^{(n)}$

2️⃣三条较温和的假设：使神经网络行为能严格对应热带运算

1. 对权重矩阵：${\mathbf{A}}_{d_i\times d_{i-1}}$$\mathbf{A}_{d_i{\times}d_{i-1}}$每个权重都是整数，这种假设是温和的(见下例)，对应了热带单项式的指数 $\left[\begin{array}{cc}0.5& 1.2\\ 2.5& \sqrt{2}\end{array}\right](\text{实}\text{数})\stackrel{\text{用}\text{有}\text{理}\text{数}\text{估}\text{计}\text{无}\text{理}\text{数}}{\to }\left[\begin{array}{cc}0.5& 1.2\\ 2.5& 1.4\end{array}\right](\text{有}\text{理}\text{数})\stackrel{\text{通}\text{分}\text{以}\text{去}\text{除}\text{小}\text{数}\text{点}}{\to }\left[\begin{array}{cc}5& 12\\ 25& 14\end{array}\right](\text{整}\text{数})$$\begin{bmatrix} 0.5 & 1.2 \\ 2.5 & \sqrt{2} \end{bmatrix}(实数){\xrightarrow{用有理数估计无理数}}\begin{bmatrix} 0.5 & 1.2 \\ 2.5 & 1.4 \end{bmatrix}(有理数){\xrightarrow{通分以去除小数点}}\begin{bmatrix} 5 & 12 \\ 25 & 14 \end{bmatrix}(整数)$

2. 对偏置向量：${\mathbf{b}}_{d_i}$$\mathbf{b}_{d_i}$的每个值都是实数，对应热带单项式的系数$c$$c$

3. 广义$\text{ReLU}$$\text{ReLU}$：即$\sigma (x_j)=max\{x_j,t_j\}=x_j\oplus t_j$$\sigma{(x_j)}{=}\max\{x_j,t_j\}{=}x_j{\oplus}t_j$(逐个应用在$\mathbf{x}$$\mathbf{x}$每维)，非线性激活可用热带运算表述

   • 可退化为其它的激活函数：当$t=0$$t{=}0$时退化为普通$\text{ReLU}$$\text{ReLU}$函数，当$t=-\mathrm{\infty }$$t{=}{-}{\infty}$时$\sigma (x)=x$$\sigma{(x)}{=}x$

   • 不可退化为平滑激活函数：如$\text{sigmoid/tanh}$$\text{sigmoid/tanh}$等

$\mathbf{\text{2.2. }}$$\textbf{2.2. }$神经网络的热带代数

1️⃣从神经网络到热带有理函数：写在前面

1. 灵感所在：热带多项式为凸$\stackrel{\text{两}\text{凸}\text{之}\text{差}\text{非}\text{凸}}{\to }$${\xrightarrow{两凸之差非凸}}$热带有理函数非凸；神经网络也非凸，是否等于热带有理函数

2. 计算要素：$\mathbf{A}\mathbf{\text{x}}+\mathbf{b}$$\mathbf{A}\textbf{x}{+}\mathbf{b}$过程中，神经网络中的参数最终会到热带多项式的哪里

   $\mathbf{A}\mathbf{\text{x}}+\mathbf{b}$$\mathbf{A}\textbf{x}{+}\mathbf{b}$过程	热带代数中	备注
   $\mathbf{A}\mathbf{\text{x}}$$\mathbf{A}\textbf{x}$中的$a_{kj}{x}_j$$a_{kj}x_j$	$(x_j{)}^{\otimes a_{kj}}$$(x_j)^{\otimes a_{kj}}$	权重参数$\stackrel{\text{变}\text{为}}{\to }$${\xrightarrow{变为}}$热带多项式中的幂，幂必为整数故权重只能为整数
   $+\mathbf{b}$${+}\mathbf{b}$中的$+b_k$${+}b_k$	$\otimes b_k$$\otimes{b_k}$	偏置参数$\stackrel{\text{变}\text{为}}{\to }$${\xrightarrow{变为}}$热带多项式的系数

2️⃣从神经网络到热带有理函数：递归证明(全文最核心部分)

1. 基础步骤：原始输入${\mathbf{x}}^{(0)}$$\mathbf{x}^{(0)}$，经过第$1$$1$层$L^{(1)}$$L^{(1)}$的输出${\mathbf{x}}^{(1)}$$\mathbf{x}^{(1)}$是怎么样的

   • 每层输出：得到${\mathbf{x}}^{(1)}=max\{\left({\mathbf{A}}_{d_1\times d_0}{\mathbf{\text{x}}}^{(0)}+{\mathbf{b}}_{d_1}\right),{\mathbf{t}}_{d_1}\}$$\mathbf{x}^{(1)}{=}\max\left\{\left(\mathbf{A}_{d_1{\times}d_0}\textbf{x}^{(0)}{+}\mathbf{b}_{d_1}\right),\mathbf{t}_{d_1 }\right\}$

   • 权重分解：提取${\mathbf{A}}_{d_1\times d_0}$$\mathbf{A}_{d_1{\times}d_0}$绝对值以分解为${\mathbf{A}}_{d_1\times d_0}^{(+)}$$\mathbf{A}_{d_1{\times}d_0}^{(+)}$和${\mathbf{A}}_{d_1\times d_0}^{(-)}$$\mathbf{A}_{d_1{\times}d_0}^{(-)}$，且${\mathbf{A}}_{d_1\times d_0}={\mathbf{A}}_{d_1\times d_0}^{(+)}-{\mathbf{A}}_{d_1\times d_0}^{(-)}$$\mathbf{A}_{d_1{\times}d_0}{=}\mathbf{A}_{d_1{\times}d_0}^{(+)}{-}\mathbf{A}_{d_1{\times}d_0}^{(-)}$

   • 恒等变换：得到${\mathbf{x}}^{(1)}=max\{\left({\mathbf{A}}_{d_1\times d_0}^{(+)}{\mathbf{\text{x}}}^{(0)}+{\mathbf{b}}_{d_1}\right),\left({\mathbf{A}}_{d_1\times d_0}^{(-)}{\mathbf{\text{x}}}^{(0)}+{\mathbf{t}}_{d_1}\right)\}-{\mathbf{A}}_{d_1\times d_0}^{(-)}{\mathbf{\text{x}}}^{(0)}$$\mathbf{x}^{(1)}{=}\max\left\{\left(\mathbf{A}_{d_1{\times}d_0}^{(+)}\textbf{x}^{(0)}{+}\mathbf{b}_{d_1}\right),\left(\mathbf{A}_{d_1{\times}d_0}^{(-)}\textbf{x}^{(0)}{+}\mathbf{t}_{d_1}\right)\right\}{-}\mathbf{A}_{d_1{\times}d_0}^{(-)}\textbf{x}^{(0)}$

   • 热带表示：设置${\mathbf{x}}^{(1)}=F^{(1)}\left({\mathbf{\text{x}}}^{(0)}\right)-G^{(1)}\left({\mathbf{\text{x}}}^{(0)}\right)$$\mathbf{x}^{(1)}{=}F^{(1)}\left(\textbf{x}^{(0)}\right){-}G^{(1)}\left(\textbf{x}^{(0)}\right)$，(如下表)${\mathbf{x}}^{(1)}$$\mathbf{x}^{(1)}$每一维都是热带有理函数

     项(共${\mathit{d}}_{\mathit{i}}$$\boldsymbol{d_i}$维)	热带算式	热带多项式
     $F^{(1)}$$F^{(1)}$第$k$$k$维	${\displaystyle \left[b_k\otimes \left(\underset{j}{⨂}{\left(x_j^{(0)}\right)}^{\otimes a_{kj}^{(+)}}\right)\right]\oplus \left[t_k\otimes \left(\underset{j}{⨂}{\left(x_j^{(0)}\right)}^{\otimes a_{kj}^{(-)}}\right)\right]}$$\displaystyle\left[ b_k{\otimes}\left(\bigotimes_{j}\left(x_j^{(0)}\right)^{\otimes a_{kj}^{(+)}} \right)\right]{\oplus}\left[t_k{\otimes}\left(\bigotimes_{j}\left(x_j^{(0)}\right)^{\otimes a_{kj}^{(-)}} \right) \right]$	✅
     $G^{(1)}$$G^{(1)}$第$k$$k$维	${\displaystyle \left(\underset{j}{⨂}{\left(x_j^{(0)}\right)}^{\otimes a_{kj}^{(-)}}\right)}$$\displaystyle\left(\bigotimes_{j}\left(x_j^{(0)}\right)^{\otimes a_{kj}^{(-)}} \right)$	✅

   • 最终结论：输出${\mathbf{x}}^{(1)}$$\mathbf{x}^{(1)}$每一维严格满足热带有理函数定义，即${\mathbf{x}}^{(1)}$$\mathbf{x}^{(1)}$每一维都是热带有理函数

2. 归纳步骤：第$i$$i$层$L^{(i)}$$L^{(i)}$的输出${\mathbf{x}}^{(i)}$$\mathbf{x}^{(i)}$，经过第$i+1$$i{+}1$层$L^{(i+1)}$$L^{(i+1)}$的输出${\mathbf{x}}^{(i+1)}$$\mathbf{x}^{(i+1)}$是怎么样的

   符号	值	每维依然是热带多项式
   $H^{(i+1)}$$H^{(i+1)}$	$\left({\mathbf{A}}_{d_{i+1}\times d_i}^{(+)}{F}^{(i)}+{\mathbf{A}}_{d_{i+1}\times d_i}^{(-)}{G}^{(i)}+{\mathbf{b}}_{d_{i+1}}\right)$$\left(\mathbf{A}_{d_{i+1}{\times}d_i}^{(+)}F^{(i)}{+}\mathbf{A}_{d_{i+1}{\times}d_i}^{(-)}G^{(i)}{+}\mathbf{b}_{d_{i+1}}\right)$	✅
   $G^{(i+1)}$$G^{(i+1)}$	$\left({\mathbf{A}}_{d_{i+1}\times d_i}^{(-)}{F}^{(i)}+{\mathbf{A}}_{d_{i+1}\times d_i}^{(+)}{G}^{(i)}\right)$$\left(\mathbf{A}_{d_{i+1}{\times}d_i}^{(-)}F^{(i)}{+}\mathbf{A}_{d_{i+1}{\times}d_i}^{(+)}G^{(i)}\right)$	✅
   $F^{(i+1)}$$F^{(i+1)}$	$max\{H^{(i+1)},\left(G^{(i+1)}+{\mathbf{t}}_{d_{i+1}}\right)\}$$\max\left\{H^{(i+1)},\left(G^{(i+1)}{+}\mathbf{t}_{d_{i+1}}\right)\right\}$	✅

   • 仿射：${\rho }^{(i+1)}={\mathbf{A}}_{d_{i+1}\times d_i}{\mathbf{x}}^{(i)}+{\mathbf{b}}_{d_{i+1}}=H^{(i+1)}-G^{(i+1)}$$\rho^{(i+1)}{=}\mathbf{A}_{d_{i+1}{\times}d_i}\mathbf{x}^{(i)}{+}\mathbf{b}_{d_{i+1}}{=}H^{(i+1)}{-}G^{(i+1)}$

   • 激活：${\mathbf{x}}^{(i+1)}=max\{H^{(i+1)},\left(G^{(i+1)}+{\mathbf{t}}_{d_{i+1}}\right)\}-G^{(i+1)}=F^{(i+1)}-G^{(i+1)}$$\mathbf{x}^{(i+1)}{=}\max\left\{H^{(i+1)},\left(G^{(i+1)}{+}\mathbf{t}_{d_{i+1}}\right)\right\}{-}G^{(i+1)}{=}F^{(i+1)}{-}G^{(i+1)}$，为一个热带有理函数

   • 结论：每一层的输出${\mathbf{x}}^{(i)}$$\mathbf{x}^{(i)}$的每一维都是一个热带有理函数

3. 最终结论：函数$\nu$$\nu$满足三条假设的神经网络$\stackrel{\text{等}\text{价}\text{于}}{\iff }\nu$${\xLeftrightarrow{等价于}}\nu$可以被看作一个热带有理函数

3️⃣从神经网络到热带有理函数：结论扩展

1. 引入上界：视热带函数$f\oslash g$$f{\oslash}g$为$n$$n$层神经网络，则$n\le max\{\lceil {\log }_2{r}_f\rceil ,\lceil {\log }_2{r}_g\rceil \}+2$$n{\leq}\max\left\{\lceil\log_{2}{r_f}\rceil,\lceil\log_{2}{r_g}\rceil\right\}{+}2$($r$$r$为单项式数量)

2. 新的等价：现引入并考虑连续分段线性函数，则以下三者任意二者互相等价

   • 整数系数连续分段线性函数$f-g$$f{-}g$

   • 热带有理函数$f\oslash g$$f{\oslash}g$

   • 满足三条假设的神经网络

3. 更强等价：去除权重为整数的限制的神经网络$\stackrel{\text{可}\text{视}\text{作}}{\Rightarrow }$${\xRightarrow{可视作}}$热带有理符号映射

   • 热带符号函数：即${\displaystyle \phi \left(x\right)=\underset{k=1}{\overset{m}{⨁}}\left(b_k\otimes \left(\underset{j=1}{\overset{n}{⨂}}{x}_j^{a_{kj}}\right)\right)}$$\displaystyle\varphi\left(x\right){=}\bigoplus_{k = 1}^{m}\left({b}_{k}{\otimes}\left(\bigotimes_{j = 1}^{n}{x}_{j}^{{a}_{kj}}\right)\right)$，$a_{kj}$$a_{kj}$为实数(多项式中只能是整数)

   • 热带有理符号映射：类似于热带有理函数，被定义为连哥哥热带符号函数的热带商${\phi }_1\oslash {\phi }_2$$\varphi_1{\oslash}\varphi_2$

   • 一些讨论：本文非要使用热带符号函数的“退化”热带多项式，因为只有后者才属于热带几何范畴

$\mathbf{\text{2.3. }}$$\textbf{2.3. }$神经网络的热带几何

$\mathbf{\text{2.3.1. }}$$\textbf{2.3.1. }$决策边界的热带几何性质

1️⃣决策边界的概念

1. 评分函数：变换神经网络输出${\mathbf{\text{x}}}^{(n)}$$\textbf{x}^{(n)}$以得到评分$s\left({\mathbf{\text{x}}}^{(n)}\right)$$s\left(\textbf{x}^{(n)}\right)$，如$\text{Softmax}\left({\mathbf{\text{x}}}^{(n)}\right)/\text{Sigmiod}\left({\mathbf{\text{x}}}^{(n)}\right)$$\text{Softmax}\left(\textbf{x}^{(n)}\right)/\text{Sigmiod}\left(\textbf{x}^{(n)}\right)$

2. 决策规则：用于分类，比如二元分类中$s\left({\mathbf{\text{x}}}^{(n)}\right)$$s\left(\textbf{x}^{(n)}\right)$大于阈值$c$$c$就归为一类，小于阈值$c$$c$就归为另一类

3. 决策边界：使评分等于决策阈值的神经网络输入集$\mathcal{B}:=\{{\mathbf{\text{x}}}^{(0)}\in {\mathbb{R}}^{d_0}|s\left(\nu \left({\mathbf{\text{x}}}^{(0)}\right)\right)=s\left({\mathbf{\text{x}}}^{(n)}\right)=c\}$$\mathcal{B}{:=}\left\{\textbf{x}^{(0)}{\in}\mathbb{R}^{d_0}|s\left(\nu\left(\textbf{x}^{(0)}\right)\right){=}s\left(\textbf{x}^{(n)}\right){=}c\right\}$

2️⃣决策边界的热带几何性

0. 前提条件：所有研究是神经网络$\nu$$\nu$是怎么样的

   • $\nu$$\nu$满足前面所提到的三个假设，即权重为整数$/$$/$偏置量为实数$/$$/$激活函数为广义$\text{ReLU}$$\text{ReLU}$

   • $\nu$$\nu$最后一层$L^{(n)}$$L^{(n)}$只进行仿射变换不激活，即令${\mathbf{t}}_{d_n}=-\mathbf{\infty }$$\mathbf{t}_{d_n}{=}{-}\boldsymbol{{\infty}}$使$\sigma \left({\mathbf{\text{x}}}^{(n)}\right)=max\{{\mathbf{\text{x}}}^{(n)},-\mathbf{\infty }\}={\mathbf{\text{x}}}^{(n)}$$\sigma{\left(\textbf{x}^{(n)}\right)}{=}\max\left\{\textbf{x}^{(n)},{-}\boldsymbol{{\infty}}\right\}{=}\textbf{x}^{(n)}$

   • $\nu$$\nu$可写为两热带多项式$f\left({\mathbf{\text{x}}}^{(0)}\right)$$f\left(\textbf{x}^{(0)}\right)$和$g\left({\mathbf{\text{x}}}^{(0)}\right)$$g\left(\textbf{x}^{(0)}\right)$的热带商，即$\nu \left({\mathbf{\text{x}}}^{(0)}\right)=f\left({\mathbf{\text{x}}}^{(0)}\right)\oslash g\left({\mathbf{\text{x}}}^{(0)}\right)$$\nu\left(\textbf{x}^{(0)}\right){=}f\left(\textbf{x}^{(0)}\right){\oslash}g\left(\textbf{x}^{(0)}\right)$

1. 结论一：决策边界划分出来的正区域的数量，存在一个天然的上界$\mathcal{N}(f)$$\mathcal{N}(f)$

   • 正区：即评分大于阈值$s\left(\nu \left({\mathbf{\text{x}}}^{(0)}\right)\right)\ge c$$s\left(\nu\left(\textbf{x}^{(0)}\right)\right){\geq}c$，即$f\left({\mathbf{\text{x}}}^{(0)}\right)\ge g\left({\mathbf{\text{x}}}^{(0)}\right)+s^{-1}(c)$$f\left(\textbf{x}^{(0)}\right){\geq}g\left(\textbf{x}^{(0)}\right){+}s^{-1}(c)$的区域，含义如下

     结构	如何理解
     $f\left({\mathbf{\text{x}}}^{(0)}\right)$$f\left(\textbf{x}^{(0)}\right)$	好比一个"地表"(多项式)，由$\mathcal{N}(f)$$\mathcal{N}(f)$个平坦"斜面"(某个单项式)拼接而成
     $g\left({\mathbf{\text{x}}}^{(0)}\right)+s^{-1}(c)$$g\left(\textbf{x}^{(0)}\right){+}s^{-1}(c)$	好比一个"水面"(多项式)，由$\mathcal{N}(g)$$\mathcal{N}(g)$个平坦"斜面"(某个单项式)拼接而成
     正区	"地表"没有被"水面"淹没的地方，即好比"孤岛"

   • 结论：对$f\left({\mathbf{\text{x}}}^{(0)}\right)$$f\left(\textbf{x}^{(0)}\right)$每块"斜面"，或被淹没$/$$/$与其他"斜面"一起构成"孤岛"，故"孤岛"定少于"斜面"

2. 结论二：神经网络的决策边界$\mathcal{B}$$\mathcal{B}$，被一个更完整的热带超曲面包含

   • 上表面：即$h\left({\mathbf{\text{x}}}^{(0)}\right)=max\{f\left({\mathbf{\text{x}}}^{(0)}\right),(g\left({\mathbf{\text{x}}}^{(0)}\right)+s^{-1}(c))\}$$h\left(\textbf{x}^{(0)}\right){=}\max\left\{f\left(\textbf{x}^{(0)}\right),\left(g\left(\textbf{x}^{(0)}\right){+}s^{-1}(c)\right)\right\}$，好比“可见地貌”("水面"$+$$+$"孤岛")

   • 超曲面：即$\mathcal{T}\left(h\left({\mathbf{\text{x}}}^{(0)}\right)\right)$$\mathcal{T}\left(h\left(\textbf{x}^{(0)}\right)\right)$，表示“可见地貌”上的所有"斜面"的"棱线"，这些"棱线"分为三类

     类型	如何理解
     “海岸线”	即决策边界$\mathcal{B}$$\mathcal{B}$，也就是$f\left({\mathbf{\text{x}}}^{(0)}\right)=g\left({\mathbf{\text{x}}}^{(0)}\right)+s^{-1}(c)$$f\left(\textbf{x}^{(0)}\right){=}g\left(\textbf{x}^{(0)}\right){+}s^{-1}(c)$"地表"和"水面"等高的地方
     “陆地线”	$\mathcal{T}\left(f\left({\mathbf{\text{x}}}^{(0)}\right)\right)$$\mathcal{T}\left(f\left(\textbf{x}^{(0)}\right)\right)$的被“海岸线”(决策边界)截去的上半部分
     “海洋线”	$\mathcal{T}(g\left({\mathbf{\text{x}}}^{(0)}\right)+s^{-1}(c))$$\mathcal{T}\left(g\left(\textbf{x}^{(0)}\right){+}s^{-1}(c)\right)$的被“海岸线”(决策边界)截去的下半部分

   • 结论：神经网络的决策边界$\mathcal{B}$$\mathcal{B}$被热带超曲面$\mathcal{T}(h)$$\mathcal{T}(h)$容纳，即$\mathcal{B}\subseteq \mathcal{T}(h)$$\mathcal{B}{\subseteq}\mathcal{T}(h)$

$\mathbf{\text{2.3.2. }}$$\textbf{2.3.2. }$神经网络的热带几何演化

1️⃣知识回顾：递推公式与几何变换

1. 逐层递推：设神经网络$L^{(i)}$$L^{(i)}$层输出为两热带多项式的热带商${\mathbf{x}}^{(i)}=F^{(i)}\left({\mathbf{\text{x}}}^{(i-1)}\right)-G^{(i)}\left({\mathbf{\text{x}}}^{(i-1)}\right)$$\mathbf{x}^{(i)}{=}F^{(i)}\left(\textbf{x}^{(i-1)}\right){-}G^{(i)}\left(\textbf{x}^{(i-1)}\right)$，则 $\{\begin{array}{l}{G}^{(i+1)}=\left({\mathbf{A}}_{d_{i+1}\times d_i}^{(-)}{F}^{(i)}+{\mathbf{A}}_{d_{i+1}\times d_i}^{(+)}{G}^{(i)}\right)\\ \\ F^{(i+1)}=max\{\left({\mathbf{A}}_{d_{i+1}\times d_i}^{(+)}{F}^{(i)}+{\mathbf{A}}_{d_{i+1}\times d_i}^{(-)}{G}^{(i)}+{\mathbf{b}}_{d_{i+1}}\right),\left({\mathbf{A}}_{d_{i+1}\times d_i}^{(-)}{F}^{(i)}+{\mathbf{A}}_{d_{i+1}\times d_i}^{(+)}{G}^{(i)}+{\mathbf{t}}_{d_{i+1}}\right)\}\end{array}$$\begin{cases} G^{(i+1)}{=}\left(\mathbf{A}_{d_{i+1}{\times}d_i}^{(-)}F^{(i)}{+}\mathbf{A}_{d_{i+1}{\times}d_i}^{(+)}G^{(i)}\right) \\\\ F^{(i+1)}{=}\max\left\{\left(\mathbf{A}_{d_{i+1}{\times}d_i}^{(+)}F^{(i)}{+}\mathbf{A}_{d_{i+1}{\times}d_i}^{(-)}G^{(i)}{+}\mathbf{b}_{d_{i+1}}\right),\left(\mathbf{A}_{d_{i+1}{\times}d_i}^{(-)}F^{(i)}{+}\mathbf{A}_{d_{i+1}{\times}d_i}^{(+)}G^{(i)}{+}\mathbf{t}_{d_{i+1}}\right)\right\} \end{cases}$

2. 几何变换：多项式$f$$f$的运算$\stackrel{\text{等}\text{价}\text{地}\text{体}\text{现}}{\iff }$${\xLeftrightarrow{等价地体现}}$多项式的多面体$\mathcal{P}(f)$$\mathcal{P}(f)$的几何变换

   多项式中	多项式的多面体中	解释
   热带幂$f^{\otimes a}$$f^{{\otimes}a}$	$\mathcal{P}(f^{\otimes a})=a\mathcal{P}(f)$$\mathcal{P}(f^{{\otimes}a}){=}a\mathcal{P}(f)$	相当于缩放
   热带积$f\otimes g$$f{\otimes}g$	$\mathcal{P}(f\otimes g)=\mathcal{P}(f)+\mathcal{P}(g)$$\mathcal{P}(f{\otimes}g){=}\mathcal{P}(f){+}\mathcal{P}(g)$	相当于闵可夫斯基和
   热带和$f\oplus g$$f{\oplus}g$	$\mathcal{P}(f\oplus g)=\text{Conv}(\mathcal{V}(\mathcal{P}(f))\cup \mathcal{V}(\mathcal{P}(g)))$$\mathcal{P}(f{\oplus}g){=}\text{Conv}(\mathcal{V}(\mathcal{P}(f)){\cup}\mathcal{V}(\mathcal{P}(g)))$	相当于顶点联合的凸包

2️⃣逐层递归：一个几何结构变换的视角，从点$\to$${\to}$线段$\to$${\to}$带状多面体$\to$${\to}$复杂多面体

0. 第$0$$0$层：拆解${\mathbf{\text{x}}}^{(0)}={\mathbf{\text{x}}}^{(0)}-\mathbf{\text{0}}$$\textbf{x}^{(0)}{=}\textbf{x}^{(0)}{-}\textbf{0}$

   结构	视角	解读
   $F^{(0)}$$F^{(0)}$第$k$$k$维	代数	$x_k^{(0)}$$x_k^{(0)}$
   $G^{(0)}$$G^{(0)}$第$k$$k$维	代数	$0$$0$
   $\mathcal{P}\left(F^{(0)}\text{第}k\text{维}\right)$${\mathcal{P}\left(F^{(0)}第k维\right)}$	几何	点$(\underset{1\text{在第}k\text{位}}{\underbrace{0,\dots ,1,\dots ,0}},0)$$(\underbrace{0,{\ldots},1,{\ldots},0}_{1\text{在第}k\text{位}},0)$
   $\mathcal{P}\left(G^{(0)}\text{第}k\text{维}\right)$${\mathcal{P}\left(G^{(0)}第k维\right)}$	几何	点$(\underset{d_0\text{个}0}{\underbrace{0,\dots ,0,\dots ,0}},0)$$(\underbrace{0,{\ldots},0,{\ldots},0}_{d_0\text{个}0},0)$

1. 第$1$$1$层：代入递归，注$b_k^{(1)}/t_k^{(1)}$$b_k^{(1)}/t_k^{(1)}$为${\mathbf{b}}_{d_1}/{\mathbf{t}}_{d_1}$$\mathbf{b}_{d_{1}}/\mathbf{t}_{d_{1}}$第$k$$k$维，$a_{kj}^{(1)(+)}/a_{kj}^{(1)(-)}$$a_{kj}^{(1)(+)}/a_{kj}^{(1)(-)}$为${\mathbf{A}}_{d_{i+1}\times d_i}^{(+)}/{\mathbf{A}}_{d_{i+1}\times d_i}^{(-)}$$\mathbf{A}_{d_{i+1}{\times}d_i}^{(+)}/\mathbf{A}_{d_{i+1}{\times}d_i}^{(-)}$第$k$$k$行$j$$j$列

   结构	视角	解读
   $F^{(1)}$$F^{(1)}$第$k$$k$维	代数	${\displaystyle \left[\left(\underset{j=1}{\overset{d_0}{⨂}}{\left(x_j^{(0)}\right)}^{\otimes a_{kj}^{(1)(+)}}\right)\otimes b_k^{(1)}\right]\oplus \left[\left(\underset{j=1}{\overset{d_0}{⨂}}{\left(x_j^{(0)}\right)}^{\otimes a_{kj}^{(1)(-)}}\right)\otimes t_k^{(1)}\right]}$$\displaystyle\left[\left(\bigotimes_{j=1}^{d_0}\left(x_j^{(0)}\right)^{\otimes a_{kj}^{(1)(+)}}\right){\otimes}b_k^{(1)}\right] {\oplus}\left[\left(\bigotimes_{j=1}^{d_0}\left(x_j^{(0)}\right)^{\otimes a_{kj}^{(1)(-)}}\right){\otimes}t_k^{(1)}\right]$
   $G^{(1)}$$G^{(1)}$第$k$$k$维	代数	$\left({\displaystyle \underset{j=1}{\overset{d_0}{⨂}}{\left(x_j^{(0)}\right)}^{\otimes a_{kj}^{(1)(-)}}}\right)$$\left(\displaystyle\bigotimes_{j=1}^{d_0}\left(x_j^{(0)}\right)^{\otimes a_{kj}^{(1)(-)}}\right)$
   $\mathcal{P}\left(F^{(1)}\text{第}k\text{维}\right)$${\mathcal{P}\left(F^{(1)}第k维\right)}$	几何	线段$(a_{k1}^{(1)(+)},\dots ,a_{k,d_0}^{(1)(+)},b_k^{(1)})\stackrel{\text{连}\text{线}}{\leftrightarrow }(a_{k1}^{(1)(-)},\dots ,a_{k,d_0}^{(1)(-)},t_k^{(1)})$$\left(a_{k 1}^{(1)(+)}, \ldots, a_{k, d_0}^{(1)(+)},b_k^{(1)}\right){\xleftrightarrow{连线}}\left(a_{k 1}^{(1)(-)}, \ldots, a_{k, d_0}^{(1)(-)},t_k^{(1)}\right)$
   $\mathcal{P}\left(G^{(1)}\text{第}k\text{维}\right)$${\mathcal{P}\left(G^{(1)}第k维\right)}$	几何	单点$(a_{k1}^{(1)(-)},\dots ,a_{k,d_0}^{(1)(-)},0)$$\left(a_{k 1}^{(1)(-)},\ldots, a_{k, d_0}^{(1)(-)},0\right)$

2. 第$2$$2$层：再代入递归，向量$/$$/$矩阵的元素符号与上类似

   结构	视角	解读
   $F^{(2)}$$F^{(2)}$第$k$$k$维	代数	形式上为两个复杂多项式的$\oplus$${\oplus}$
   $G^{(2)}$$G^{(2)}$第$k$$k$维	代数	形式上为两个复杂多项式的$\otimes$${\otimes}$
   $\mathcal{P}\left(F^{(2)}\text{第}k\text{维}\right)$${\mathcal{P}\left(F^{(2)}第k维\right)}$	几何	多项式的$\oplus \to$${\oplus}{\to}$多个线段$/$$/$多面体的端点合并后求凸包$\to$${\to}$复杂多面体
   $\mathcal{P}\left(G^{(2)}\text{第}k\text{维}\right)$${\mathcal{P}\left(G^{(2)}第k维\right)}$	几何	多项式的$\otimes \to$${\otimes}{\to}$多个线段求闵可夫斯基和$\to$${\to}$带状多面体(简单多面体)

3. 第$n$$n$层：不断递归，已经是多面体了再递归$\mathcal{P}\left(F^{(n)}\text{第}k\text{维}\right)/\mathcal{P}\left(F^{(n)}\text{第}k\text{维}\right)$${\mathcal{P}\left(F^{(n)}第k维\right)}/{\mathcal{P}\left(F^{(n)}第k维\right)}$只会生成更复杂多面体

$\mathbf{\text{2.3.3. }}$$\textbf{2.3.3. }$神经网络的几何复杂度

1️⃣基本思路

1. 度量：神经网络可等价为热带多项式，而热带多项式的线性区域数目越多，神经网络就越强

2. 目标：利用前面建立的热带几何框架，推导出这个线性区域数量的上限

2️⃣主定理$$$%符号体系做了"本土化"$

1. 内容：对深度为$n$$n$宽度为$d_{i,max}$$d_{i,\max}$的神经网络，输入维度为$d_0$$d_0$时线性区域数量为$\mathcal{O}((d_{i,max}{)}^{d_0(n-1)})$$\mathcal{O}\left((d_{i,\max})^{d_0(n{-}1)}\right)$

2. 证明：思路是转化为证明热带几何中多面体顶点数的上界，具体过程在笔记中略

3. 洞见：增加深度(指数级增加)，是比增加宽度(多项式级增长)更有效提升网络表达能力的手段