@[toc] [原论文](https://doi.org/10.48550/arXiv.1805.07091) # $\textbf{1. }$热带几何$\textbf{\&}$热带代数 > ## $\textbf{1.1. }$热带半环 > > > :one:基本概念：集合${+}$集合上的运算$\text{+}$单位元，即$({K,\oplus,\otimes,\mathbb{0},\mathbb{1}}){=}({\mathbb{R}{\cup}\{{-}{\infty} \},\max,{+},{-}{\infty},0})$ > > > > 1. 集合：所有实数加一个特殊元素(负无穷${-}\infty$)，即$\mathbb{R}{\cup}\{{-}\infty\}$ > > 2. 运算：对$x,y{\in}{\mathbb{R}{\cup}\{{-}\infty \}}$，热带加法$x{\oplus}y{=}\max\{x,y\}$，热带乘法$x{\otimes}y{=}x{+}y$ > > 3. 单位元：${-}\infty$是热带加的单位元$\max\{x,{-}\infty\}{=}x$，$0$是热带乘的单位元$x{+}0{=}x$ > > > > :two:基本性质：环❌$/$半环✅$/$半域✅ > > > > 1. 为何是半环：满足以下运算定律 > > | 运算律 | 对热带加法 | 对热带乘法 | > > | :----: | :---------------------------------------------- | :-------------------------- | > > | 交换律 | $\max\{a,b\}{=}\max\{b,a\}$ | $a{+}b{=}b{+}a$ | > > | 结合律 | $\max\{\max\{a,b\},c\}{=}\max\{a,\max\{b,c\}\}$ | $a{+}(b{+}c){=}(b{+}a){+}c$ | > > - 分配律：$a{+}\max\{b,c\}{=}\max\{a{+}b,a{+}c\}$ > > 2. 关于逆元：对热带半环，加法逆元❌$/$乘法逆元✅ > > | 逆元类型 | 定义 | 对热带半环 | > > | :------: | :----------------------------------------------------------- | :---------------------------------------- | > > | 加法逆元 | 若$x{\oplus}y{=}\mathbb{0}$则$y$为$x$加法逆元，记$y{=}{-}x$ | 不存在$\max\{x,y\}{=}{-}{\infty}$故不为环 | > > | 乘法逆元 | 若$x{\otimes}y{=}\mathbb{1}$则$y$为$x$乘法逆元，记$y{=}x^{{-}1}$ | 存在$x{+}(-x){=}0$故为半域，故可进行除法 | > > - 所谓环：在半环的基础上，所有元素都必须有其对应的加法逆元 > > - 所谓半域：在半环的基础上，除了加法单位元以外的所有元素，都必须有其对应的乘法逆元 > > > > :three:热带函数：有理函数(热带多项式的热带商)${\xleftarrow{}}$多项式${\xleftarrow{}}$扩展运算 > > > > 1. 运算扩展：热带幂和热带商 > > | 运算 | 半环中 | 热带半环中 | 特殊的 | > > | :----: | :---------------------------------------------: | :-------------------: | :----------------------------------------------------------- | > > | 热带幂 | $x^{{\otimes}a}{=}x{\otimes}{\cdots}{\otimes}x$ | $x^{{\otimes}a}{=}ax$ | $({-}{\infty})^{{\otimes}a}{=}{-}{\infty}$及$({-}{\infty})^{{\otimes}0}{=}0$ | > > | 热带商 | $a{\oslash}b{=}a{\otimes}b^{{\otimes}({-}1)}$ | $a{\oslash}b{=}a{-}b$ | $\text{N/A}$ | > > 2. 热带多项式$\&$有理函数：令$\mathbf{x}{=}\langle{x_1,...,x_d}\rangle$ > > - 热带多项式：相当于多个线性函数(更精确地说，仿射函数)取最大值 > > | 算式 | 结构 | 转换回常规运算 | 性质 | > > | :--------: | ------------------------------------------------------------ | --------------------------------------------- | :------: | > > | 热带单项式 | $L_i(\mathbf{x}){=}c_i{\otimes}x_{1}^{{\otimes}a_{1}}{\otimes}{\cdots}{\otimes}x_{d}^{{\otimes}a_{d}}$ | $c_i{+}a_{i1}x_{1}{+}{\cdots}{+}a_{id}x_{d}$ | 线性函数 | > > | 热带多项式 | $f(\mathbf{x}){=}L_1{\oplus}L_2{\oplus}{\cdots}{\oplus}L_r$ | $\max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$ | 凸函数 | > > - 热带有理函数：热带多项式的热带商，且定义$f(\mathbf{x}){\oslash}g(\mathbf{x}){=}f(\mathbf{x}){-}g(\mathbf{x})$ > > | 符号 | 定义 | 转换回常规运算 | 性质 | > > | :-------------: | :-----------------------------------: | --------------------------------------------- | --------------------------- | > > | $h(\mathbf{x})$ | $f(\mathbf{x}){\oslash}g(\mathbf{x})$ | $\max\{L_1,...,L_r\}{-}\max\{L_1',...,L_s'\}$ | 两凸函数差($\text{DC}$函数) | > > - 补充：对$\mathbf{x}{=}\langle{x_1,...,x_d}\rangle$及$\boldsymbol{\alpha_i}{=}\langle{a_{i1},...,a_{id}}\rangle$，多项式$c_i{\otimes}x_{1}^{{\otimes}a_{i1}}{\otimes}{\cdots}{\otimes}x_{d}^{{\otimes}a_{id}}$可简写为$c_i\mathbf{x}^{\boldsymbol{\alpha_i}}$ > > 3. 一些推广：函数集代数结构与向量值函数 > > - 函数集的代数结构：注意，**热带多项式**可看作**热带有理函数**分母为$\mathbb{1}{=}0$时 > > | 集合 | 半环结构 | 半域 | > > | :------------------------------------------------: | :--------------------------------------------------: | :--: | > > | $x_1,...,x_d$构成的所有热带多项式集 | $(\mathbb{T}[x_1,...,x_d],\max,{+},{-}{\infty},{0})$ | ❌ | > > | $x_1,...,x_d$构成的所有热带有理函数集 | $(\mathbb{T}(x_1,...,x_d),\max,{+},{-}{\infty},{0})$ | ✅ | > > - 向量值函数：将不同的函数$/$多项式一次拼接 > > | 向量函数类型 | 函数$\boldsymbol{\mathbb{R}^d{\to}\mathbb{R}^{p}}$的定义 | 补充 | > > | :----------: | :----------------------------------------------------------- | :----------------------------------------------------------- | > > | 热带多项式 | $F_f{:\,}F(\mathbf{x}){=}(f_1(\mathbf{x}),...,f_p(\mathbf{x}))$ | $\text{Pol}(d,p)$为所有$F_f{:\,}\mathbb{R}^d{\to}\mathbb{R}^{p}$函数集 | > > | 热带有理函数 | $F_h{:\,}F(\mathbf{x}){=}(h_1(\mathbf{x}),...,h_p(\mathbf{x}))$ | $\text{Rat}(d,p)$为所有$F_h{:\,}\mathbb{R}^d{\to}\mathbb{R}^{p}$函数集 | > > ## $\textbf{1.2. }$热带超曲面与牛顿对偶 > > > :one:热带超曲面 > > > > 1. 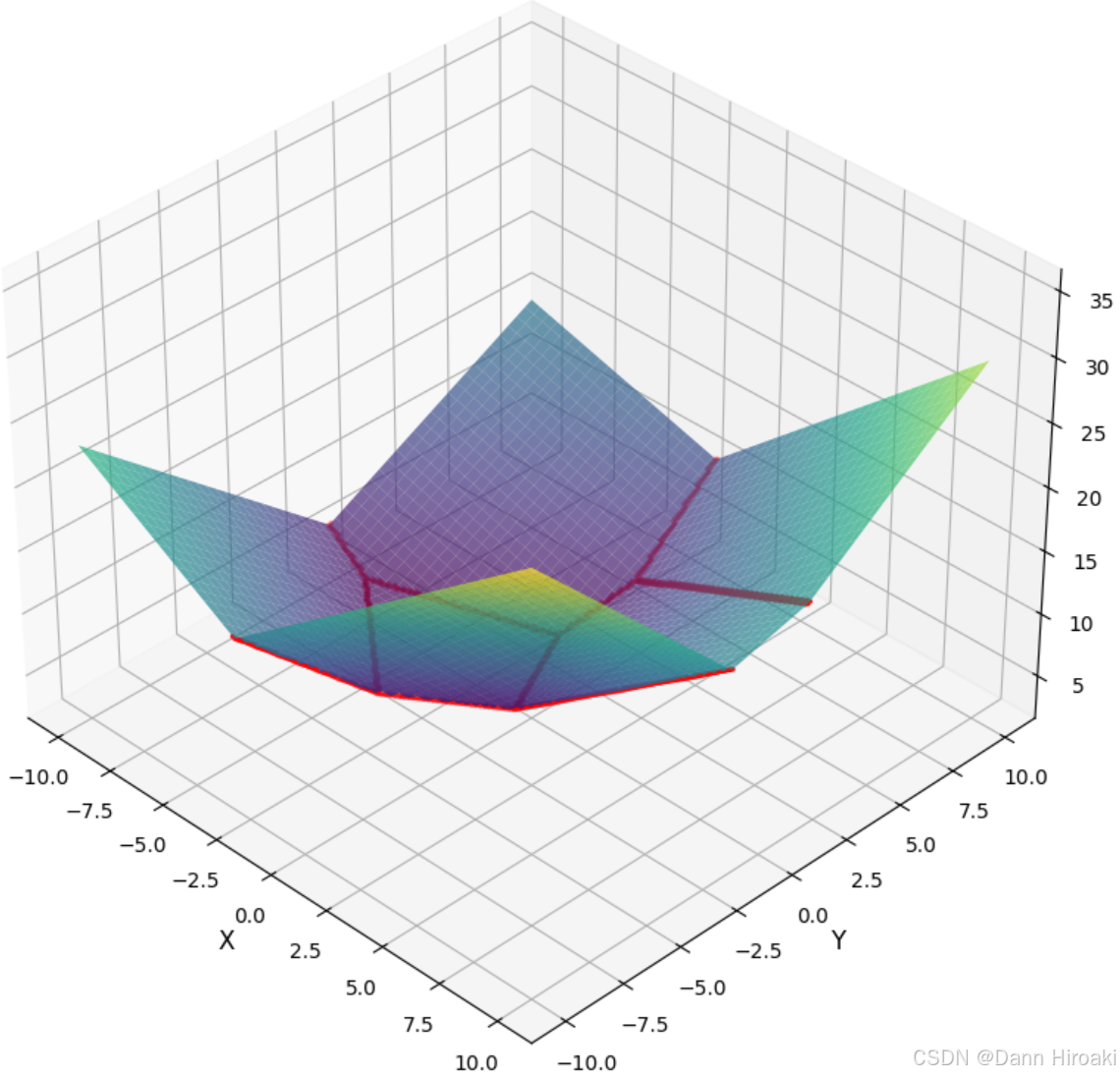定义：考虑热带多项式$f(\mathbf{x}){=}\max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$ > > image-20250706010940441 > > - 形式定义：$\mathcal{T}(f){=}\{\mathbf{x}{\in}\mathbb{R}^d\mid{}c_i\mathbf{x}^{\boldsymbol{\alpha_i}}{=}c_j\mathbf{x}^{\boldsymbol{\alpha_j}}{=}f(\mathbf{x}),i{\neq}j\}$，当$d{=}2$时从热带超曲面退化为热带曲线 > > - 直观理解：多项式由最高平面$\max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$拼接成，热带超曲面即两最高平面连接处 > > - 基本含义：在某点$\mathbf{x}$至少两单项式同时取得最大值，即$L_i(\mathbf{x}){=}L_j(\mathbf{x}){=}\max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$ > > 2. 本质：将$f(\mathbf{x}){=}\max\{L_1(\mathbf{x}),...,L_r(\mathbf{x})\}$划分为多个**凸胞腔** > > - 直观理解：每个凸胞腔都是一个单项式“称霸”的区域，即每个凸胞腔内$f(\mathbf{x})$可用一单项式精确描述 > > - 形式定义：单项式$c_j\mathbf{x}^{\alpha_j}$取得最大值的胞腔是$\{\mathbf{x}{\in}\mathbb{R}^d\mid{}c_j{+}{\boldsymbol{\alpha_j}}^{T}\mathbf{x}{\geq}c_i{+}{\boldsymbol{\alpha_i}}^{T}\mathbf{x},\forall{i{\neq}j}\}$ > > > > :two:牛顿多边形及牛顿对偶 > > > > 1. 第一步：以$f(x_1,x_2){=}(1{\otimes}x_1^2){\oplus}(1{\otimes}x_2^2){\oplus}(2{\otimes}x_1{\otimes}x_2){\oplus}(2{\otimes}x_1){\oplus}(2{\otimes}x_2){\oplus}(2)$为例，提取因子 > > | 单项式 | $\boldsymbol{x_1}$次方 | $\boldsymbol{x_2}$次方 | 常数项 | 指数点$\boldsymbol{\alpha}$ | $\boldsymbol{c}$ | > > | :-------------------------: | :--------------------: | :--------------------: | :----: | :-------------------------: | :--------------: | > > | $1{\otimes}x_1^2$ | $2$ | $0$ | $1$ | $\alpha_1{=}(2,0)$ | $c_1{=}1$ | > > | $1{\otimes}x_2^2$ | $0$ | $2$ | $1$ | $\alpha_2{=}(0,2)$ | $c_2{=}1$ | > > | $2{\otimes}x_1{\otimes}x_2$ | $1$ | $1$ | $2$ | $\alpha_3{=}(1,1)$ | $c_3{=}2$ | > > | $2{\otimes}x_1$ | $1$ | $0$ | $2$ | $\alpha_4{=}(1,0)$ | $c_4{=}2$ | > > | $2{\otimes}x_2$ | $0$ | $1$ | $2$ | $\alpha_5{=}(0,1)$ | $c_5{=}2$ | > > | $2$ | $0$ | $0$ | $2$ | $\alpha_6{=}(0,0)$ | $c_6{=}2$ | > > 2. 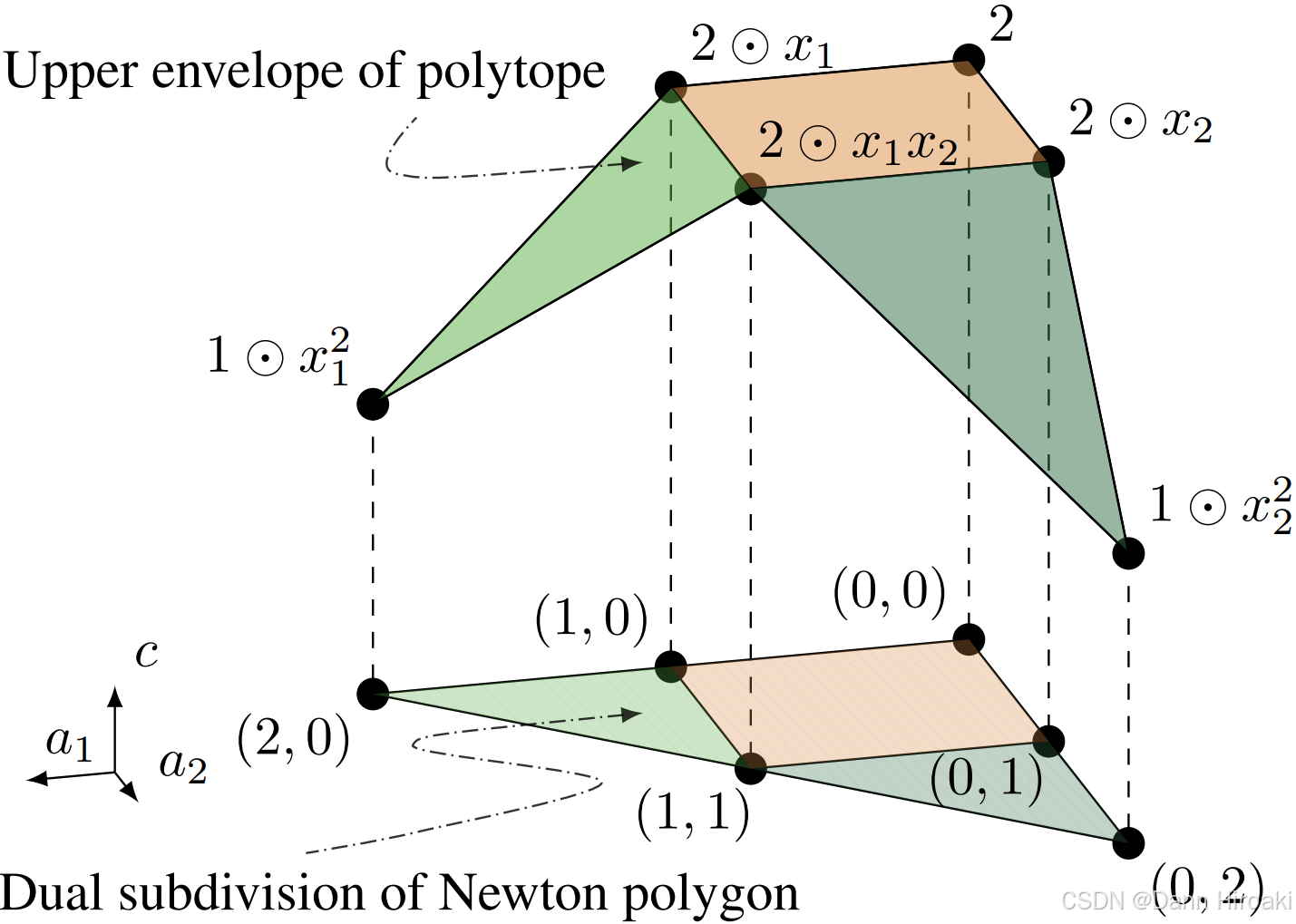之后步：(注意所谓上表面，即表面法向量与$d$维中从最后一维$/$高度维夹角为锐角) > > image-20250706020701704 > > | 操作 | 描述 | > > | :--------------------: | :----------------------------------------------------------- | > > | 牛顿多边形$\Delta(f)$ | 取所有指数点${\alpha}$的凸包(相当于用橡皮筋围住最外围点) | > > | 多面体$\mathcal{P}(f)$ | 基于牛顿多边形，在${\alpha}$基础上增加一个值为$c$的维度，成为$(\boldsymbol{\alpha_i},c_i)$ | > > | 对偶细分$\delta(f)$ | 将多面体$\mathcal{P}(f)$上表面的边和顶点，垂直投影回到底部牛顿多边形$\Delta(f)$ | > > 3. 最后步：对牛顿多边形$\Delta(f)$上的对偶细分$\delta(f)$，建立对偶细分$\delta(f)$和热带超曲面$\mathcal{T}(f)$的联系 > > | 偶细分$\boldsymbol{\delta(f)}$ | 对应超曲面$\boldsymbol{\mathcal{T}(f)}$ | 含义 | $\boldsymbol{\delta(f)}$示例 | 对应$\boldsymbol{\mathcal{T}(f)}$示例 | > > | :----------------------------: | --------------------------------------- | ------------------ | ---------------------------- | ------------------------------------- | > > | $k$维面 | $(d{-}k)$维面 | $k{+}1$个$L_i$打平 | $\text{N/A}$ | $\text{N/A}$ | > > | 边$(k{=}1)$ | 折痕$(k{=}1/d{=}2)$ | 两$L_i$打平 | 线$(1,0){\to}(0,0)$ | 折痕($2{\otimes}x_1{=}2$) | > > | 顶点$(k{=}0)$ | 线性区$(k{=}0/d{=}2)$ | 一$L_i$主导 | 点$(1,0)$ | 线性区($2{\otimes}x_1$主导) | > > - 对偶定理：${\mathcal{T}(f)}$线性区域数${=}\mathcal{P}(f)$上表面顶点数${\leq}\mathcal{P}(f)$总顶点数 > > > > :three:线性区域： > > > > 1. 含义：$F$定义域中保持其线性的最大的连通子集，即同一线性区域内不同的两点都线性可达 > > 2. 性质：当$F$为热带多项式(凸函数)时其线性区域为凸，当$F$为热带有理函数($\text{DC}$函数)时其线性区域非凸 > > 3. 意义：$F$线性区域数量记为$\mathcal{N}(F)$，一个神经网络能划分出更多线性区域，去拟合能力更强 > > ## $\textbf{1.3. }$热带多项式的几何学描述 > > > :zero:闵可夫斯基和：形式定义与一些延申 > > > > 1. 形式定义：对两集合$P_1/P_2$而言，其$\text{Minkowski}$和为$P_1{+}P_2 \mathrel{\text{:=}}\{x_1{+}x_2 \mid x_1{\in}P_1,x_2{\in}P_2\}$ > > 2. 直观理解：将形状$P_2$的原点，在形状$P_1$每个点上移动，移动过程中$P_2$扫描的区域即$\text{Minkowski}$和 > > 3. 对多面体：多面体$\mathcal{P}(f)$合$\mathcal{P}(g)$的$\text{Minko.}$和，即顶点集$\mathcal{V}(\mathcal{P}(f))$和$\mathcal{V}(\mathcal{P}(g))$的$\text{Minko.}$和，再求凸包 > > 4. 一些扩展：两个(或多个)线段的$\text{Minkowski}$和(一线段每个点与另一线段每个点相加)，为带状多面体 > > image-20250707023657057 > > > > :one:构建与变换：热带多项式的几何学 > > > > 1. 单项式与顶点： > > - 结构上：$f$一单项式$L_i{=}c_i{+}a_{i1}x_{1}{+}{\cdots}{+}a_{id}x_{d}{\xLeftrightarrow{对应}}\mathcal{P}(f)$一生成顶点$(\boldsymbol{\alpha_i},c_i){=}(a_{i1},...,a_{id},c_i)$ > > - 运算上：$f$单项式的热带运算${\xLeftrightarrow{等价}}$对$\mathcal{P}(f)$顶点的几何变换，具体如下 > > | 单项式的热带运算 | 转为常规运算 | 相当于对多面体中.... | > > | :--------------------------------: | :--------------------: | :----------------------------------------------------------- | > > | $L_1{\otimes}{\cdots}{\otimes}L_n$ | $L_1{+}{\cdots}{+}L_n$ | 将$(\boldsymbol{\alpha_i},c_i)$求和变成求$(\boldsymbol{\alpha_1{+}{\cdots}{+}\alpha_n},c_1{+}{\cdots}{+}{c_n})$ | > > | $L_i^{{\otimes}a}$ | $aL_i$ | 放缩$(\boldsymbol{\alpha_i},c_i)$成$(a\boldsymbol{\alpha_i},ac_i)$ | > > 2. 单项式到多项式 > > - 结构上：多个单项式热带相加${\xLeftrightarrow{等价}}$多个顶点求凸包以生成成多面体 > > - 运算上：$f{=}L_1{\oplus}{\cdots}{\oplus}L_n$可转化为$f{=}\max\{L_1,...,L_n\}$，即求$\{(\boldsymbol{\alpha_1},c_1),...,(\boldsymbol{\alpha_n},c_n)\}$凸包 > > 3. 多项式与多面体： > > - 热带幂$f^{{\otimes}a}$：相当于缩放，即$\mathcal{P}(f^{{\otimes}a}){=}a\mathcal{P}(f)$ > > | 领域 | 操作 | 解释 | > > | :------: | :--------------------: | :----------------------------------------------------------- | > > | 热带运算 | 热带幂$f^{{\otimes}a}$ | 相当于$a{\times}f$，即每个单项式系数$c_i$和指数$\boldsymbol{\alpha_i}{=}\{a_{i1},..,a_{id}\}$乘上$a$ | > > | 几何变换 | 缩放 | 每个顶点$(\boldsymbol{\alpha_i},c_i)$变为$(a\boldsymbol{\alpha_i},ac_i)$，即每个顶点都相对原点拉伸$a$倍 | > > - 热带积$f{\otimes}g$：相当于闵可夫斯基和，即$\mathcal{P}(f{\otimes}g){=}\mathcal{P}(f){+}\mathcal{P}(g)$ > > | 领域 | 操作 | 解释 | > > | :------: | ----------------------- | :----------------------------------------------------------- | > > | 热带运算 | 热带积$f{\otimes}g$ | $f$每个单项式与$g$每个单项式热带乘(相加)再热带加(求$\max$) | > > | 几何变换 | 多面体$\text{Minko.}$和 | $\mathcal{P}(f)$每个顶点与$\mathcal{P}(g)$每个顶点坐标依次相加，再求凸包 | > > - 热带和$f{\oplus}g$：相当于顶点联合的凸包，即$\mathcal{P}(f{\oplus}g){=}\text{Conv}(\mathcal{V}(\mathcal{P}(f)){\cup}\mathcal{V}(\mathcal{P}(g)))$ > > | 领域 | 操作 | 解释 | > > | :------: | ------------------ | :----------------------------------------------------------- | > > | 热带运算 | 热带积$f{\oplus}g$ | $f$和$g$各自的多项式合在一起，再求合一起后的最大值 | > > | 几何变换 | 顶点联合的凸包 | $\mathcal{P}(f)$与$\mathcal{P}(g)$中所有顶点合在一起，对合一起后的点集求凸包 | > > > > :two:理论保证：如何界定新生成多面体的顶点数 > > > > 1. $\text{Gritzmann-Sturmfels}$定理：生成多面体最多多少个顶点 > > - 参数说明：$d{+}1$表示多面体$P_1,...,P_k$所处空间的维度，$m$为收集所有$P_i$棱后非平行棱的总数 > > - 定理内容：令多面体$P_1,...,P_k$进行$\text{Minkowski}$和后新多面体顶点数为$N$，则$N{\leq}2\displaystyle{\sum_{j=0}^{d}\mathbf{C}_{m{-}1}^j}$ > > - 取等条件：每个多面体$P_i$都为带状多面体，且构成每个$P_i$的线段都处于一般位置 > > 2. 定理的关键推论：新生成多面体上表面有多少顶点，即多项式有多少线性区域数 > > - 条件改变：$P_1,...,P_k$从**任意形状的多面体**限定为了**带状多面体**， > > - 结论改变：$P_1,...,P_k$进行$\text{Minkowski}$和后新多面体上表面顶点数为$N'$，则$N'{\leq}\displaystyle{\sum_{j=0}^{d}\mathbf{C}_{m}^j}$ > > - 取等条件：$P_i$所有$m$条线段都处于一般位置，新多面体($d{+}1$维)顶点投影回$d$维后都处于一般位置 > > 3. (补充)关于一般位置：即任意$k$个点不会被维度${\leq}k{-}2$的空间容纳，例如四点不共面，三点不共线 > > # $\textbf{2. }$神经网络的热带几何$\textbf{\&}$代数 > ## $\textbf{2.1. }$神经网络及其假设 > > > :one:神经网络的数学模型：定义一个共$L^{(n)}$层全连接的前馈网络$%以下内容我对原文的符号体系做了一些改变，力求符合我自己的符号体系，在审查时请忽略符号体系的改变$ > > > > 1. 对于每一层$L^{(i)}$： > > - 结构：输入$d_{i-1}$维的$\textbf{x}^{(i-1)}$后输出$d_i$维的$\textbf{x}^{(i)}$，每层可学习参数有权重矩阵$\mathbf{A}_{d_i{\times}d_{i-1}}$及偏置向量$\mathbf{b}_{d_i}$ > > - 运算：先将$\textbf{x}^{(i-1)}$输入仿射变换$\rho_i{\left(\textbf{x}^{(i-1)}\right)}{=}\mathbf{A}_{d_i{\times}d_{i-1}}\textbf{x}^{(i-1)}{+}\mathbf{b}_{d_i}$再激活$\textbf{x}_{i}{=}\sigma_i\left(\rho_i{\left(\textbf{x}^{(i-1)}\right)}\right)$ > > - 补充：本文$\sigma_i$采用广义$\text{ReLU}$(详见下)，因为其为最典型的激活函数，也方便用热带代数描述 > > 2. 对于所有$L^{(n)}$层： > > - 结构：$\nu{=}(\sigma_n{\circ}\rho_n){\circ}(\sigma_{n-1}{\circ}\rho_{n-1}){\circ}{\cdots}{\circ}(\sigma_1{\circ}\rho_1)$即$\nu\left(\textbf{x}^{(0)}\right){=}\textbf{x}^{(n)}$，但不会$\text{Softmax}\left(\textbf{x}^{(n)}\right)$一下 > > - 运算：$\textbf{x}^{(0)} > > {\xrightarrow[]{\sigma_1\left(\rho_1{\left(\textbf{x}^{(0)}\right)}\right)}} > > \textbf{x}^{(1)} > > {\xrightarrow[]{\sigma_2\left(\rho_2{\left(\textbf{x}^{(1)}\right)}\right)}} > > \textbf{x}^{(2)} > > {\to}{\cdots}{\to} > > \textbf{x}^{(n-1)} > > {\xrightarrow[]{\sigma_n\left(\rho_n{\left(\textbf{x}^{(n-1)}\right)}\right)}} > > \textbf{x}^{(n)}$ > > > > :two:三条较温和的假设：使神经网络行为能严格对应热带运算 > > > > 1. 对权重矩阵：$\mathbf{A}_{d_i{\times}d_{i-1}}$每个权重都是整数，这种假设是温和的(见下例)，对应了热带单项式的指数 > > $\begin{bmatrix} 0.5 & 1.2 \\ 2.5 & \sqrt{2} \end{bmatrix}(实数){\xrightarrow{用有理数估计无理数}}\begin{bmatrix} 0.5 & 1.2 \\ 2.5 & 1.4 \end{bmatrix}(有理数){\xrightarrow{通分以去除小数点}}\begin{bmatrix} 5 & 12 \\ 25 & 14 \end{bmatrix}(整数)$ > > 2. 对偏置向量：$\mathbf{b}_{d_i}$的每个值都是实数，对应热带单项式的系数$c$ > > 3. 广义$\text{ReLU}$：即$\sigma{(x_j)}{=}\max\{x_j,t_j\}{=}x_j{\oplus}t_j$(逐个应用在$\mathbf{x}$每维)，非线性激活可用热带运算表述 > > - 可退化为其它的激活函数：当$t{=}0$时退化为普通$\text{ReLU}$函数，当$t{=}{-}{\infty}$时$\sigma{(x)}{=}x$ > > - 不可退化为平滑激活函数：如$\text{sigmoid/tanh}$等 > > ## $\textbf{2.2. }$神经网络的热带代数 > > > :one:从神经网络到热带有理函数：写在前面 > > > > 1. 灵感所在：热带多项式为凸${\xrightarrow{两凸之差非凸}}$热带有理函数非凸；神经网络也非凸，是否等于热带有理函数 > > 2. 计算要素：$\mathbf{A}\textbf{x}{+}\mathbf{b}$过程中，神经网络中的参数最终会到热带多项式的哪里 > > | $\mathbf{A}\textbf{x}{+}\mathbf{b}$过程 | 热带代数中 | 备注 | > > | :-------------------------------------: | :----------------------: | :----------------------------------------------------------- | > > | $\mathbf{A}\textbf{x}$中的$a_{kj}x_j$ | $(x_j)^{\otimes a_{kj}}$ | 权重参数${\xrightarrow{变为}}$热带多项式中的幂，幂必为整数故权重只能为整数 | > > | ${+}\mathbf{b}$中的${+}b_k$ | $\otimes{b_k}$ | 偏置参数${\xrightarrow{变为}}$热带多项式的系数 | > > > > :two:从神经网络到热带有理函数：递归证明**(全文最核心部分)** > > > > 1. 基础步骤：原始输入$\mathbf{x}^{(0)}$，经过第$1$层$L^{(1)}$的输出$\mathbf{x}^{(1)}$是怎么样的 > > - 每层输出：得到$\mathbf{x}^{(1)}{=}\max\left\{\left(\mathbf{A}_{d_1{\times}d_0}\textbf{x}^{(0)}{+}\mathbf{b}_{d_1}\right),\mathbf{t}_{d_1 }\right\}$ > > - 权重分解：提取$\mathbf{A}_{d_1{\times}d_0}$绝对值以分解为$\mathbf{A}_{d_1{\times}d_0}^{(+)}$和$\mathbf{A}_{d_1{\times}d_0}^{(-)}$，且$\mathbf{A}_{d_1{\times}d_0}{=}\mathbf{A}_{d_1{\times}d_0}^{(+)}{-}\mathbf{A}_{d_1{\times}d_0}^{(-)}$ > > - 恒等变换：得到$\mathbf{x}^{(1)}{=}\max\left\{\left(\mathbf{A}_{d_1{\times}d_0}^{(+)}\textbf{x}^{(0)}{+}\mathbf{b}_{d_1}\right),\left(\mathbf{A}_{d_1{\times}d_0}^{(-)}\textbf{x}^{(0)}{+}\mathbf{t}_{d_1}\right)\right\}{-}\mathbf{A}_{d_1{\times}d_0}^{(-)}\textbf{x}^{(0)}$ > > - 热带表示：设置$\mathbf{x}^{(1)}{=}F^{(1)}\left(\textbf{x}^{(0)}\right){-}G^{(1)}\left(\textbf{x}^{(0)}\right)$，(如下表)$\mathbf{x}^{(1)}$每一维都是热带有理函数 > > | 项(共$\boldsymbol{d_i}$维) | 热带算式 | 热带多项式 | > > | :------------------------: | :----------------------------------------------------------- | :--------: | > > | $F^{(1)}$第$k$维 | $\displaystyle\left[ b_k{\otimes}\left(\bigotimes_{j}\left(x_j^{(0)}\right)^{\otimes a_{kj}^{(+)}} \right)\right]{\oplus}\left[t_k{\otimes}\left(\bigotimes_{j}\left(x_j^{(0)}\right)^{\otimes a_{kj}^{(-)}} \right) \right]$ | ✅ | > > | $G^{(1)}$第$k$维 | $\displaystyle\left(\bigotimes_{j}\left(x_j^{(0)}\right)^{\otimes a_{kj}^{(-)}} \right)$ | ✅ | > > - 最终结论：输出$\mathbf{x}^{(1)}$每一维严格满足热带有理函数定义，即$\mathbf{x}^{(1)}$每一维都是热带有理函数 > > 2. 归纳步骤：第$i$层$L^{(i)}$的输出$\mathbf{x}^{(i)}$，经过第$i{+}1$层$L^{(i+1)}$的输出$\mathbf{x}^{(i+1)}$是怎么样的 > > | 符号 | 值 | 每维依然是热带多项式 | > > | :---------: | :----------------------------------------------------------- | :------------------: | > > | $H^{(i+1)}$ | $\left(\mathbf{A}_{d_{i+1}{\times}d_i}^{(+)}F^{(i)}{+}\mathbf{A}_{d_{i+1}{\times}d_i}^{(-)}G^{(i)}{+}\mathbf{b}_{d_{i+1}}\right)$ | ✅ | > > | $G^{(i+1)}$ | $\left(\mathbf{A}_{d_{i+1}{\times}d_i}^{(-)}F^{(i)}{+}\mathbf{A}_{d_{i+1}{\times}d_i}^{(+)}G^{(i)}\right)$ | ✅ | > > | $F^{(i+1)}$ | $\max\left\{H^{(i+1)},\left(G^{(i+1)}{+}\mathbf{t}_{d_{i+1}}\right)\right\}$ | ✅ | > > - 仿射：$\rho^{(i+1)}{=}\mathbf{A}_{d_{i+1}{\times}d_i}\mathbf{x}^{(i)}{+}\mathbf{b}_{d_{i+1}}{=}H^{(i+1)}{-}G^{(i+1)}$ > > - 激活：$\mathbf{x}^{(i+1)}{=}\max\left\{H^{(i+1)},\left(G^{(i+1)}{+}\mathbf{t}_{d_{i+1}}\right)\right\}{-}G^{(i+1)}{=}F^{(i+1)}{-}G^{(i+1)}$，为一个热带有理函数 > > - 结论：每一层的输出$\mathbf{x}^{(i)}$的每一维都是一个热带有理函数 > > 3. 最终结论：函数$\nu$满足三条假设的神经网络${\xLeftrightarrow{等价于}}\nu$可以被看作一个热带有理函数 > > > > :three:从神经网络到热带有理函数：结论扩展 > > > > 1. 引入上界：视热带函数$f{\oslash}g$为$n$层神经网络，则$n{\leq}\max\left\{\lceil\log_{2}{r_f}\rceil,\lceil\log_{2}{r_g}\rceil\right\}{+}2$($r$为单项式数量) > > 2. 新的等价：现引入并考虑连续分段线性函数，则以下三者任意二者互相等价 > > - 整数系数连续分段线性函数$f{-}g$ > > - 热带有理函数$f{\oslash}g$ > > - 满足三条假设的神经网络 > > 3. 更强等价：去除权重为整数的限制的神经网络${\xRightarrow{可视作}}$热带有理符号映射 > > - 热带符号函数：即$\displaystyle\varphi\left(x\right){=}\bigoplus_{k = 1}^{m}\left({b}_{k}{\otimes}\left(\bigotimes_{j = 1}^{n}{x}_{j}^{{a}_{kj}}\right)\right)$，$a_{kj}$为实数(多项式中只能是整数) > > - 热带有理符号映射：类似于热带有理函数，被定义为连哥哥热带符号函数的热带商$\varphi_1{\oslash}\varphi_2$ > > - 一些讨论：本文非要使用热带符号函数的“退化”热带多项式，因为只有后者才属于热带几何范畴 > > ## $\textbf{2.3. }$神经网络的热带几何 > > > ### $\textbf{2.3.1. }$决策边界的热带几何性质 > > > > > :one:决策边界的概念 > > > > > > 1. 评分函数：变换神经网络输出$\textbf{x}^{(n)}$以得到评分$s\left(\textbf{x}^{(n)}\right)$，如$\text{Softmax}\left(\textbf{x}^{(n)}\right)/\text{Sigmiod}\left(\textbf{x}^{(n)}\right)$ > > > 2. 决策规则：用于分类，比如二元分类中$s\left(\textbf{x}^{(n)}\right)$大于阈值$c$就归为一类，小于阈值$c$就归为另一类 > > > 3. 决策边界：使评分等于决策阈值的神经网络输入集$\mathcal{B}{:=}\left\{\textbf{x}^{(0)}{\in}\mathbb{R}^{d_0}|s\left(\nu\left(\textbf{x}^{(0)}\right)\right){=}s\left(\textbf{x}^{(n)}\right){=}c\right\}$ > > > > > > :two:决策边界的热带几何性 > > > > > > 0. 前提条件：所有研究是神经网络$\nu$是怎么样的 > > > - $\nu$满足前面所提到的三个假设，即权重为整数$/$偏置量为实数$/$激活函数为广义$\text{ReLU}$ > > > - $\nu$最后一层$L^{(n)}$只进行仿射变换不激活，即令$\mathbf{t}_{d_n}{=}{-}\boldsymbol{{\infty}}$使$\sigma{\left(\textbf{x}^{(n)}\right)}{=}\max\left\{\textbf{x}^{(n)},{-}\boldsymbol{{\infty}}\right\}{=}\textbf{x}^{(n)}$ > > > - $\nu$可写为两热带多项式$f\left(\textbf{x}^{(0)}\right)$和$g\left(\textbf{x}^{(0)}\right)$的热带商，即$\nu\left(\textbf{x}^{(0)}\right){=}f\left(\textbf{x}^{(0)}\right){\oslash}g\left(\textbf{x}^{(0)}\right)$ > > > 1. 结论一：决策边界划分出来的正区域的数量，存在一个天然的上界$\mathcal{N}(f)$ > > > - 正区：即评分大于阈值$s\left(\nu\left(\textbf{x}^{(0)}\right)\right){\geq}c$，即$f\left(\textbf{x}^{(0)}\right){\geq}g\left(\textbf{x}^{(0)}\right){+}s^{-1}(c)$的区域，含义如下 > > > | 结构 | 如何理解 | > > > | :------------------------------------------: | :----------------------------------------------------------- | > > > | $f\left(\textbf{x}^{(0)}\right)$ | 好比一个"地表"(多项式)，由$\mathcal{N}(f)$个平坦"斜面"(某个单项式)拼接而成 | > > > | $g\left(\textbf{x}^{(0)}\right){+}s^{-1}(c)$ | 好比一个"水面"(多项式)，由$\mathcal{N}(g)$个平坦"斜面"(某个单项式)拼接而成 | > > > | 正区 | "地表"没有被"水面"淹没的地方，即好比"孤岛" | > > > - 结论：对$f\left(\textbf{x}^{(0)}\right)$每块"斜面"，或被淹没$/$与其他"斜面"一起构成"孤岛"，故"孤岛"定少于"斜面" > > > 2. 结论二：神经网络的决策边界$\mathcal{B}$，被一个更完整的热带超曲面包含 > > > - 上表面：即$h\left(\textbf{x}^{(0)}\right){=}\max\left\{f\left(\textbf{x}^{(0)}\right),\left(g\left(\textbf{x}^{(0)}\right){+}s^{-1}(c)\right)\right\}$，好比“可见地貌”("水面"$+$"孤岛") > > > - 超曲面：即$\mathcal{T}\left(h\left(\textbf{x}^{(0)}\right)\right)$，表示“可见地貌”上的所有"斜面"的"棱线"，这些"棱线"分为三类 > > > | 类型 | 如何理解 | > > > | :------: | :----------------------------------------------------------- | > > > | “海岸线” | 即决策边界$\mathcal{B}$，也就是$f\left(\textbf{x}^{(0)}\right){=}g\left(\textbf{x}^{(0)}\right){+}s^{-1}(c)$"地表"和"水面"等高的地方 | > > > | “陆地线” | $\mathcal{T}\left(f\left(\textbf{x}^{(0)}\right)\right)$的被“海岸线”(决策边界)截去的上半部分 | > > > | “海洋线” | $\mathcal{T}\left(g\left(\textbf{x}^{(0)}\right){+}s^{-1}(c)\right)$的被“海岸线”(决策边界)截去的下半部分 | > > > - 结论：神经网络的决策边界$\mathcal{B}$被热带超曲面$\mathcal{T}(h)$容纳，即$\mathcal{B}{\subseteq}\mathcal{T}(h)$ > > > > > ### $\textbf{2.3.2. }$神经网络的热带几何演化 > > > > > :one:知识回顾：递推公式与几何变换 > > > > > > 1. 逐层递推：设神经网络$L^{(i)}$层输出为两热带多项式的热带商$\mathbf{x}^{(i)}{=}F^{(i)}\left(\textbf{x}^{(i-1)}\right){-}G^{(i)}\left(\textbf{x}^{(i-1)}\right)$，则 > > > $\begin{cases} > > > G^{(i+1)}{=}\left(\mathbf{A}_{d_{i+1}{\times}d_i}^{(-)}F^{(i)}{+}\mathbf{A}_{d_{i+1}{\times}d_i}^{(+)}G^{(i)}\right) > > > \\\\ > > > F^{(i+1)}{=}\max\left\{\left(\mathbf{A}_{d_{i+1}{\times}d_i}^{(+)}F^{(i)}{+}\mathbf{A}_{d_{i+1}{\times}d_i}^{(-)}G^{(i)}{+}\mathbf{b}_{d_{i+1}}\right),\left(\mathbf{A}_{d_{i+1}{\times}d_i}^{(-)}F^{(i)}{+}\mathbf{A}_{d_{i+1}{\times}d_i}^{(+)}G^{(i)}{+}\mathbf{t}_{d_{i+1}}\right)\right\} > > > \end{cases}$ > > > 2. 几何变换：多项式$f$的运算${\xLeftrightarrow{等价地体现}}$多项式的多面体$\mathcal{P}(f)$的几何变换 > > > | 多项式中 | 多项式的多面体中 | 解释 | > > > | :--------------------: | :----------------------------------------------------------- | :------------------- | > > > | 热带幂$f^{{\otimes}a}$ | $\mathcal{P}(f^{{\otimes}a}){=}a\mathcal{P}(f)$ | 相当于缩放 | > > > | 热带积$f{\otimes}g$ | $\mathcal{P}(f{\otimes}g){=}\mathcal{P}(f){+}\mathcal{P}(g)$ | 相当于闵可夫斯基和 | > > > | 热带和$f{\oplus}g$ | $\mathcal{P}(f{\oplus}g){=}\text{Conv}(\mathcal{V}(\mathcal{P}(f)){\cup}\mathcal{V}(\mathcal{P}(g)))$ | 相当于顶点联合的凸包 | > > > > > > :two:逐层递归：一个几何结构变换的视角，从点${\to}$线段${\to}$带状多面体${\to}$复杂多面体 > > > > > > 0. 第$0$层：拆解$\textbf{x}^{(0)}{=}\textbf{x}^{(0)}{-}\textbf{0}$ > > > | 结构 | 视角 | 解读 | > > > | :--------------------------------------: | :--: | :----------------------------------------------------------- | > > > | $F^{(0)}$第$k$维 | 代数 | $x_k^{(0)}$ | > > > | $G^{(0)}$第$k$维 | 代数 | $0$ | > > > | ${\mathcal{P}\left(F^{(0)}第k维\right)}$ | 几何 | 点$(\underbrace{0,{\ldots},1,{\ldots},0}_{1\text{在第}k\text{位}},0)$ | > > > | ${\mathcal{P}\left(G^{(0)}第k维\right)}$ | 几何 | 点$(\underbrace{0,{\ldots},0,{\ldots},0}_{d_0\text{个}0},0)$ | > > > 1. 第$1$层：代入递归，注$b_k^{(1)}/t_k^{(1)}$为$\mathbf{b}_{d_{1}}/\mathbf{t}_{d_{1}}$第$k$维，$a_{kj}^{(1)(+)}/a_{kj}^{(1)(-)}$为$\mathbf{A}_{d_{i+1}{\times}d_i}^{(+)}/\mathbf{A}_{d_{i+1}{\times}d_i}^{(-)}$第$k$行$j$列 > > > | 结构 | 视角 | 解读 | > > > | :--------------------------------------: | :--: | :----------------------------------------------------------- | > > > | $F^{(1)}$第$k$维 | 代数 | $\displaystyle\left[\left(\bigotimes_{j=1}^{d_0}\left(x_j^{(0)}\right)^{\otimes a_{kj}^{(1)(+)}}\right){\otimes}b_k^{(1)}\right] {\oplus}\left[\left(\bigotimes_{j=1}^{d_0}\left(x_j^{(0)}\right)^{\otimes a_{kj}^{(1)(-)}}\right){\otimes}t_k^{(1)}\right]$ | > > > | $G^{(1)}$第$k$维 | 代数 | $\left(\displaystyle\bigotimes_{j=1}^{d_0}\left(x_j^{(0)}\right)^{\otimes a_{kj}^{(1)(-)}}\right)$ | > > > | ${\mathcal{P}\left(F^{(1)}第k维\right)}$ | 几何 | 线段$\left(a_{k 1}^{(1)(+)}, \ldots, a_{k, d_0}^{(1)(+)},b_k^{(1)}\right){\xleftrightarrow{连线}}\left(a_{k 1}^{(1)(-)}, \ldots, a_{k, d_0}^{(1)(-)},t_k^{(1)}\right)$ | > > > | ${\mathcal{P}\left(G^{(1)}第k维\right)}$ | 几何 | 单点$\left(a_{k 1}^{(1)(-)},\ldots, a_{k, d_0}^{(1)(-)},0\right)$ | > > > 2. 第$2$层：再代入递归，向量$/$矩阵的元素符号与上类似 > > > | 结构 | 视角 | 解读 | > > > | :--------------------------------------: | :--: | :----------------------------------------------------------- | > > > | $F^{(2)}$第$k$维 | 代数 | 形式上为两个复杂多项式的${\oplus}$ | > > > | $G^{(2)}$第$k$维 | 代数 | 形式上为两个复杂多项式的${\otimes}$ | > > > | ${\mathcal{P}\left(F^{(2)}第k维\right)}$ | 几何 | 多项式的${\oplus}{\to}$多个线段$/$多面体的端点合并后求凸包${\to}$复杂多面体 | > > > | ${\mathcal{P}\left(G^{(2)}第k维\right)}$ | 几何 | 多项式的${\otimes}{\to}$多个线段求闵可夫斯基和${\to}$带状多面体(简单多面体) | > > > 3. 第$n$层：不断递归，已经是多面体了再递归${\mathcal{P}\left(F^{(n)}第k维\right)}/{\mathcal{P}\left(F^{(n)}第k维\right)}$只会生成更复杂多面体 > > > > > ### $\textbf{2.3.3. }$神经网络的几何复杂度 > > > > > :one:基本思路 > > > > > > 1. 度量：神经网络可等价为热带多项式，而热带多项式的线性区域数目越多，神经网络就越强 > > > 2. 目标：利用前面建立的热带几何框架，推导出这个线性区域数量的上限 > > > > > > :two:主定理$%符号体系做了"本土化"$ > > > > > > 1. 内容：对深度为$n$宽度为$d_{i,\max}$的神经网络，输入维度为$d_0$时线性区域数量为$\mathcal{O}\left((d_{i,\max})^{d_0(n{-}1)}\right)$ > > > 2. 证明：思路是转化为证明热带几何中多面体顶点数的上界，具体过程在笔记中略 > > > 3. 洞见：增加深度(指数级增加)，是比增加宽度(多项式级增长)更有效提升网络表达能力的手段