Table of Contents
- Author(s) of this documentation:
- Pierre Gueth
Introduction
The DEC package allows the embedding of a discrete manifold contained in an higher dimension Euclidean space. For example, one could use the DEC package to represent a curved surface embedded in a three dimensional Euclidean space. Throughout this documentation \(n\) stands for in embedded manifold dimension, \(m\) stands for this ambient space dimension and \(k\) is used to characterize the dimension of cells inside the DEC structure.
\[ 0 \le k \le n \le m \]
Only lower dimensions k-cells can be inserted into a DEC structure ( \(k \le n\)). Those embedded and ambient dimensions are enforced as the first and second template parameters of DiscreteExteriorCalculus. Dual and primal operators are defined with respect the the embedding dimension.
DEC factory
DiscreteExteriorCalculusFactory is a helper class to easily create DEC structures from digital sets or combinatorial structures such as digital surfaces (DigitalSurface).
As usual, one can fill the DEC structure manually using DiscreteExteriorCalculus.insertSCell. Every k-cells should then be inserted manually with their correct primal and dual sizes. Primal and dual sizes default to 1 when not specified. On the other hand, one could create automatically a DEC structure from a range of n-cells using DiscreteExteriorCalculusFactory::createFromNSCells. Incident lower dimension cells are then inserted and weighted automatically. The first template parameter of DiscreteExteriorCalculusFactory::createFromNSCells represents the embedded dimension of the generated manifold.
- Note
- By definition 0-cell must have a primal size equals to 1 and n-cell must have dual size equals to 1.
When the ambient space has the same dimension as the embedded manifold, one could use DiscreteExteriorCalculusFactory::createFromDigitalSet. Similarly to DiscreteExteriorCalculusFactory::createFromNSCells, incident lower dimension cells are automatically inserted with proper primal and dual sizes. Each point of the set is inserted in the DEC structure as a primal n-cell.
- Note
- DiscreteExteriorCalculusFactory::createFromNSCells is compatible with iterators over DigitalSurface.
To define a DEC factory, one must pass the linear algebra backend as the first template parameter. Here is a snippet that define a factory using EigenLinearAlgebraBackend.
Border definition
When using a DEC factory to generate DEC structures, one could specify if borders are inserted in the generated structure using the second parameter add_border. Cell belonging to the border are (n-1)-cells incident with to one n-cell, along with their lower incident k-cells counterparts. When passing add_border=false to DEC factory static functions, cells belonging to the border are not inserted.
- Note
- Choosing to add borders or not changes boundary condition of the DEC problems generated with the structure. add_border=true enforces Neumann boundary condition on primal operators. add_border=false enforces Dirichlet boudary condition on primal operators. See 1D Poisson resolution for an example.
| add_border | boundary condition of primal operators | boundary condition of dual operators |
|---|---|---|
| true | Neumann \(\nabla f(x) \cdot n(x)=0~\forall x \in \partial M\) | Dirichlet \(f(x)=0~\forall x \in \partial M\) |
| false | Dirichlet \(f(x)=0~\forall x \in \partial M\) | Neumann \(\nabla f(x) \cdot n(x)=0~\forall x \in \partial M\) |
1D examples
In this example, we show how to embed linear structure into different ambient spaces. See testEmbedding.cpp for details. First, let's start be defining types of DEC structures used in this example.
Calculus1D represents a 1D discrete manifold embedded in 1D Euclidean space, Calculus2D represents a 1D discrete manifold embedded in 2D Euclidean space and Calculus3D represents a 1D discrete manifold embedded in 3D Euclidean space.
After defining and filling the input forward traversal containers (std::set, std::list, std::vector, ...), DEC structures are generated by calling DiscreteExteriorCalculusFactory::createFromNSCells.

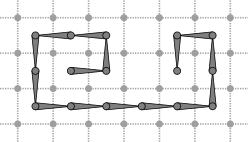
Operators generated from these structures are all identical.
2D examples
In this example, we show how to discrete curved surface into different ambient spaces. See testEmbedding.cpp for details. First, let's start be defining types of DEC structures used in this example.
Calculus2D represents a 2D discrete manifold embedded in 2D Euclidean space and Calculus3D represents a 2D discrete manifold embedded in 3D Euclidean space.
After defining and filling the input forward traversal containers (std::set, std::list, std::vector, ...), DEC structures are generated by calling DiscreteExteriorCalculusFactory::createFromNSCells.
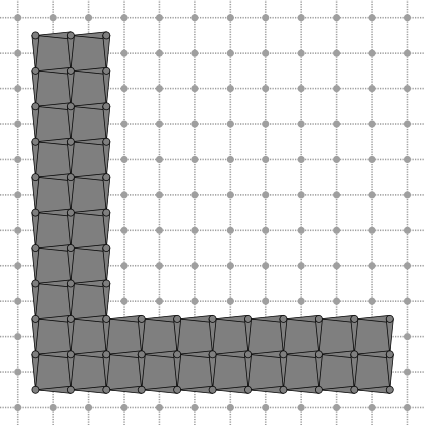
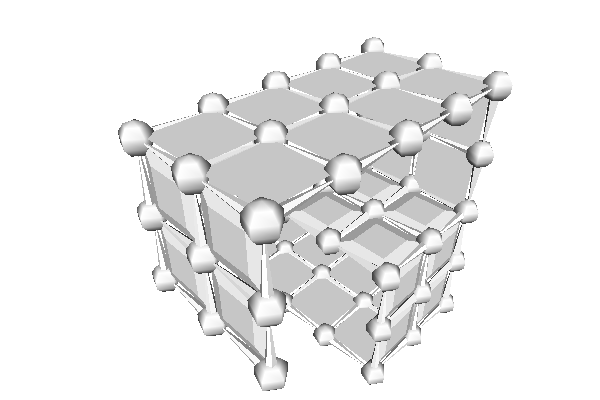
Borderless DEC structures are generated by calling DiscreteExteriorCalculusFactory::createFromNSCells with third parameter equals to false.
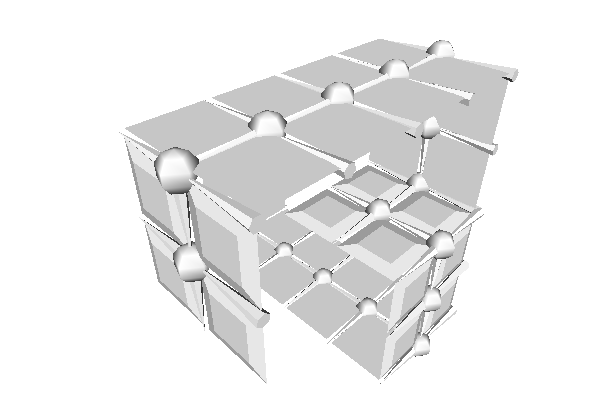
Embedding structure in higher dimension ambient space does not affect generated operators.
Digital surface examples
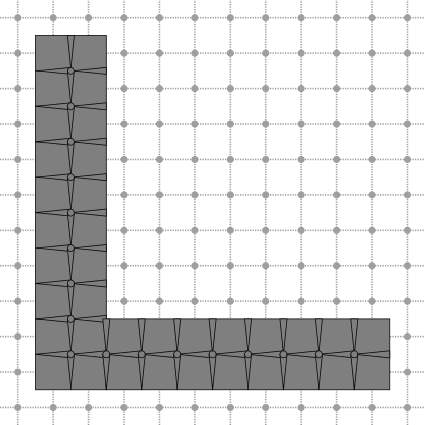
In this example, we show how to import a DigitalSurface into a DEC structure. See exampleDECSurface.cpp for details. First, let's define the input set whose boundary will be used to define the digital surface.

Let's then define the digital surface as the boundary of the input set, oriented positive inward.
The DEC structure is created by calling DiscreteExteriorCalculusFactory::createFromNSCells with iterators DigitalSurface.begin() and DigitalSurface.end(). Incident lower cells are added automatically as well as Hodge weights.