- Author(s) of this documentation:
- Pierre Gueth
Helmoltz decomposition
Helmoltz decomposition states that any 1-form \(\omega\) can be uniquely expressed as the sum of three terms.
\[ \omega = d\alpha + \delta\beta + \gamma \]
where \(d\) is the exterior derivative from 0-form to 1-form and \(\delta = \star d \star \) is the exterior antiderivative from 2-form to 1-form. \(\alpha\) is a 0-form scalar potential and \(d\alpha\) is the curl free term.
\[ \nabla \wedge (d \alpha) = ( \star d d \alpha )^\sharp = 0 \]
\(\beta\) is a 2-form vector potential and \(\delta\beta\) is the divergence free term.
\[ \nabla \cdot (\delta \beta) = \star d \star \delta \beta = \delta \delta \beta = 0 \]
The remaining part \(\gamma\) is the 1-form harmonic part. \(\gamma\) has null antiderivative and null derivative since if they were not null, they would be part of \(d\alpha\) and \(\delta\beta\).
\[ \delta \gamma = d \gamma = 0 \]
By differentiating \(\omega\), one can isolate DEC solvable expressions for \(\alpha\) and \(\beta\).
\[ d \delta \beta = d \omega \]
\[ \delta \omega = \delta d \alpha \]
The harmonic component \(\gamma\) is computed by subtracting \(d\alpha\) and \(\delta\beta\) from \(\omega\). The interest of the Helmoltz decomposition is that \(\gamma\) has a strong connection with the topology of the structure.
2D Helmoltz decomposition
In this example, we compute primal and dual Helmoltz decomposition of an arbitrary vector field on a 2D double ring shape. Snippets are taken from exampleDiscreteExteriorCalculusSolve.cpp.
Here is the definition of objects used during the primal decomposition.
Calculus::PrimalVectorField input_vector_field(
calculus);
for (Calculus::Index ii=0; ii<input_vector_field.length(); ii++)
{
input_vector_field.myCoordinates(ii, 0) = cos(-.5*cell_center[0]+ .3*cell_center[1]);
input_vector_field.myCoordinates(ii, 1) = cos(.4*cell_center[0]+ .8*cell_center[1]);
}
const Calculus::PrimalForm1 input_one_form =
calculus.flat(input_vector_field);
const Calculus::PrimalForm0 input_one_form_anti_derivated = ad1 * input_one_form;
const Calculus::PrimalForm2 input_one_form_derivated = d1 * input_one_form;
Space::RealPoint RealPoint
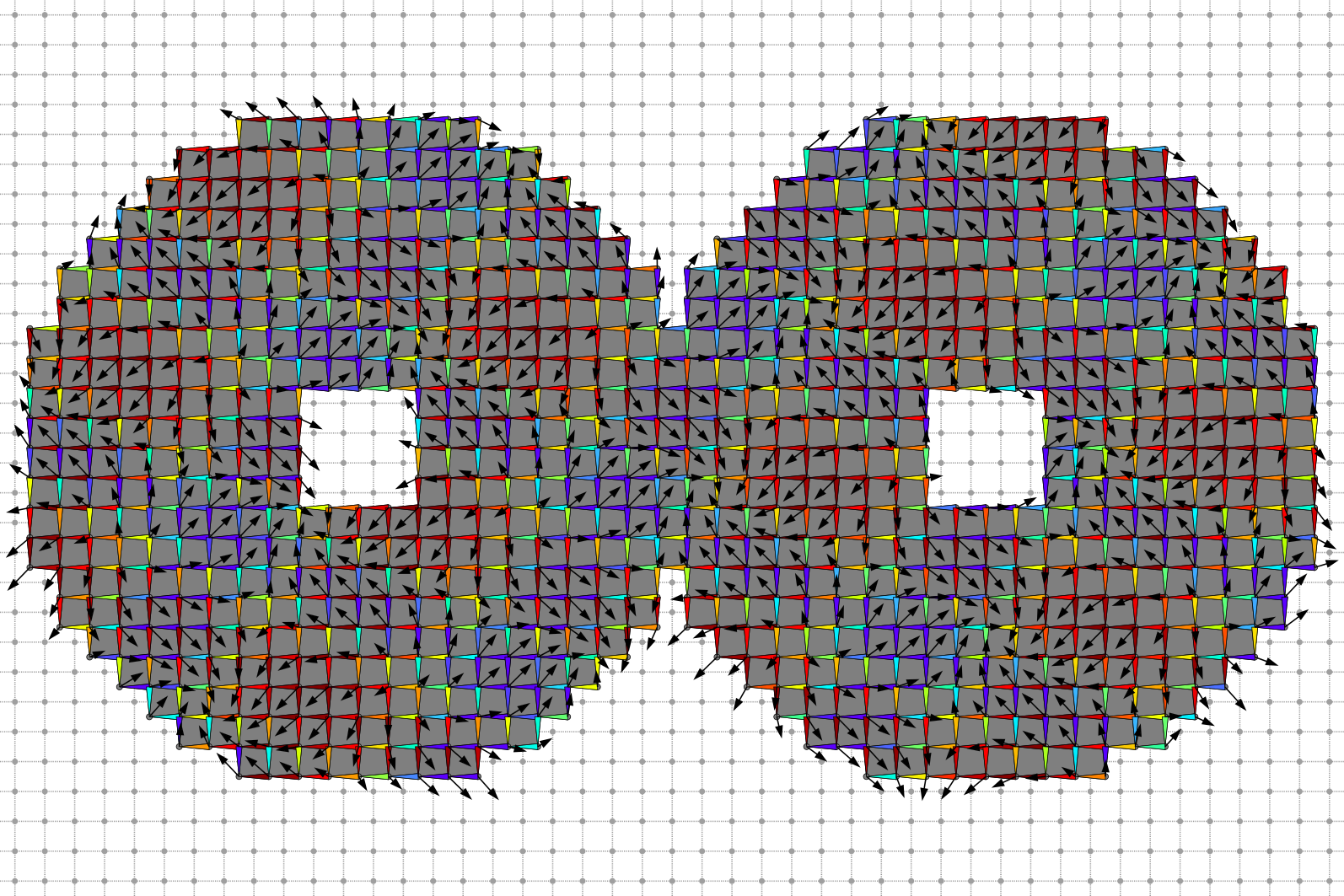
Primal Helmoltz decomposition. Primal input vector field and 1-form.
And here are very similar objects used during the dual decomposition.
Calculus::DualVectorField input_vector_field(
calculus);
for (Calculus::Index ii=0; ii<input_vector_field.length(); ii++)
{
input_vector_field.myCoordinates(ii, 0) = cos(-.5*cell_center[0]+ .3*cell_center[1]);
input_vector_field.myCoordinates(ii, 1) = cos(.4*cell_center[0]+ .8*cell_center[1]);
}
const Calculus::DualForm1 input_one_form =
calculus.flat(input_vector_field);
const Calculus::DualForm0 input_one_form_anti_derivated = ad1 * input_one_form;
const Calculus::DualForm2 input_one_form_derivated = d1 * input_one_form;
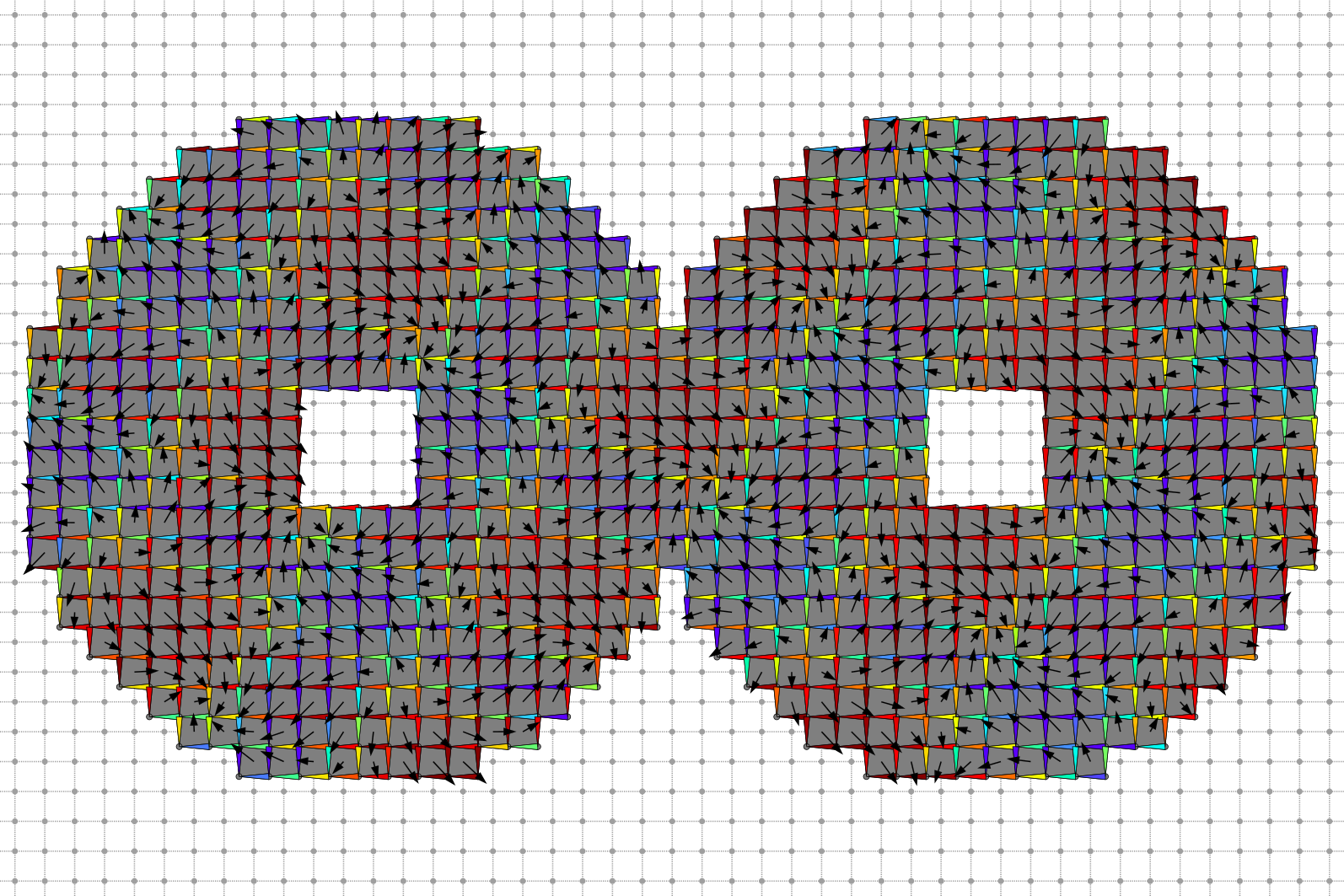
Dual Helmoltz decomposition. Dual input vector field and 1-form.
Definition of useful operators for primal decomposition.
const Calculus::PrimalDerivative0 d0 =
calculus.derivative<0,
PRIMAL>();
const Calculus::PrimalDerivative1 d1 =
calculus.derivative<1,
PRIMAL>();
const Calculus::DualDerivative0 d0p =
calculus.derivative<0,
DUAL>();
const Calculus::DualDerivative1 d1p =
calculus.derivative<1,
DUAL>();
const LinearOperator<Calculus, 1, PRIMAL, 0, PRIMAL> ad1 = h2p * d1p * h1;
const LinearOperator<Calculus, 2, PRIMAL, 1, PRIMAL> ad2 = h1p * d0p * h2;
Definition of useful operators for dual decomposition.
const Calculus::DualDerivative0 d0 =
calculus.derivative<0,
DUAL>();
const Calculus::DualDerivative1 d1 =
calculus.derivative<1,
DUAL>();
const Calculus::PrimalDerivative0 d0p =
calculus.derivative<0,
PRIMAL>();
const Calculus::PrimalDerivative1 d1p =
calculus.derivative<1,
PRIMAL>();
const LinearOperator<Calculus, 1, DUAL, 0, DUAL> ad1 = h2p * d1p * h1;
const LinearOperator<Calculus, 2, DUAL, 1, DUAL> ad2 = h1p * d0p * h2;
Resolution of the curl-free component \(d\alpha\) for primal decomposition.
typedef DiscreteExteriorCalculusSolver<Calculus, LinearAlgebraSolver, 0, PRIMAL, 0, PRIMAL> Solver;
Solver solver;
solver.compute(ad1 * d0);
solution_curl_free = solver.solve(input_one_form_anti_derivated);
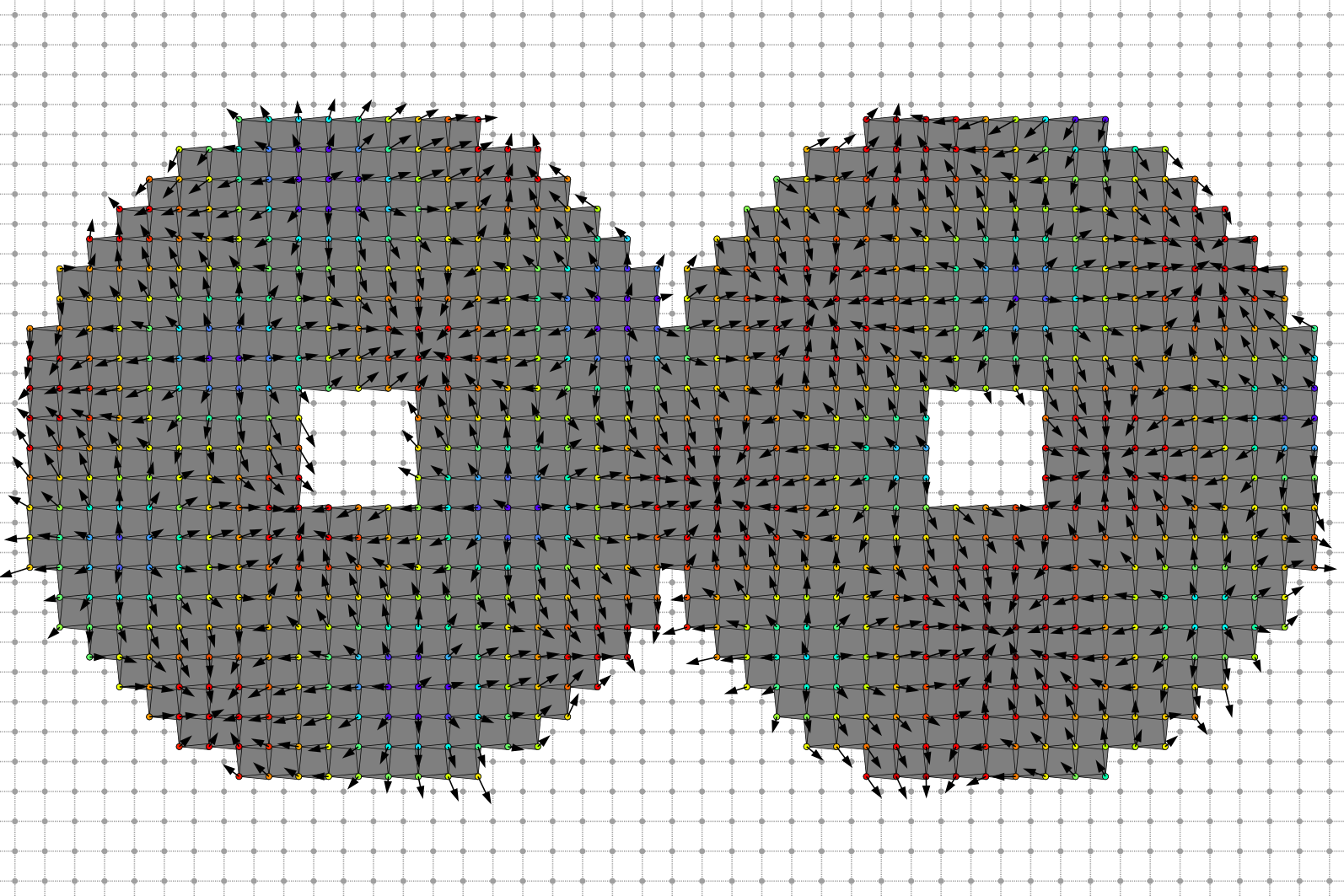
Primal Helmoltz decomposition curl-free component and scalar potential field.
Resolution of the curl-free component \(d\alpha\) for dual decomposition.
typedef DiscreteExteriorCalculusSolver<Calculus, LinearAlgebraSolver, 0, DUAL, 0, DUAL> Solver;
Solver solver;
solver.compute(ad1 * d0);
solution_curl_free = solver.solve(input_one_form_anti_derivated);
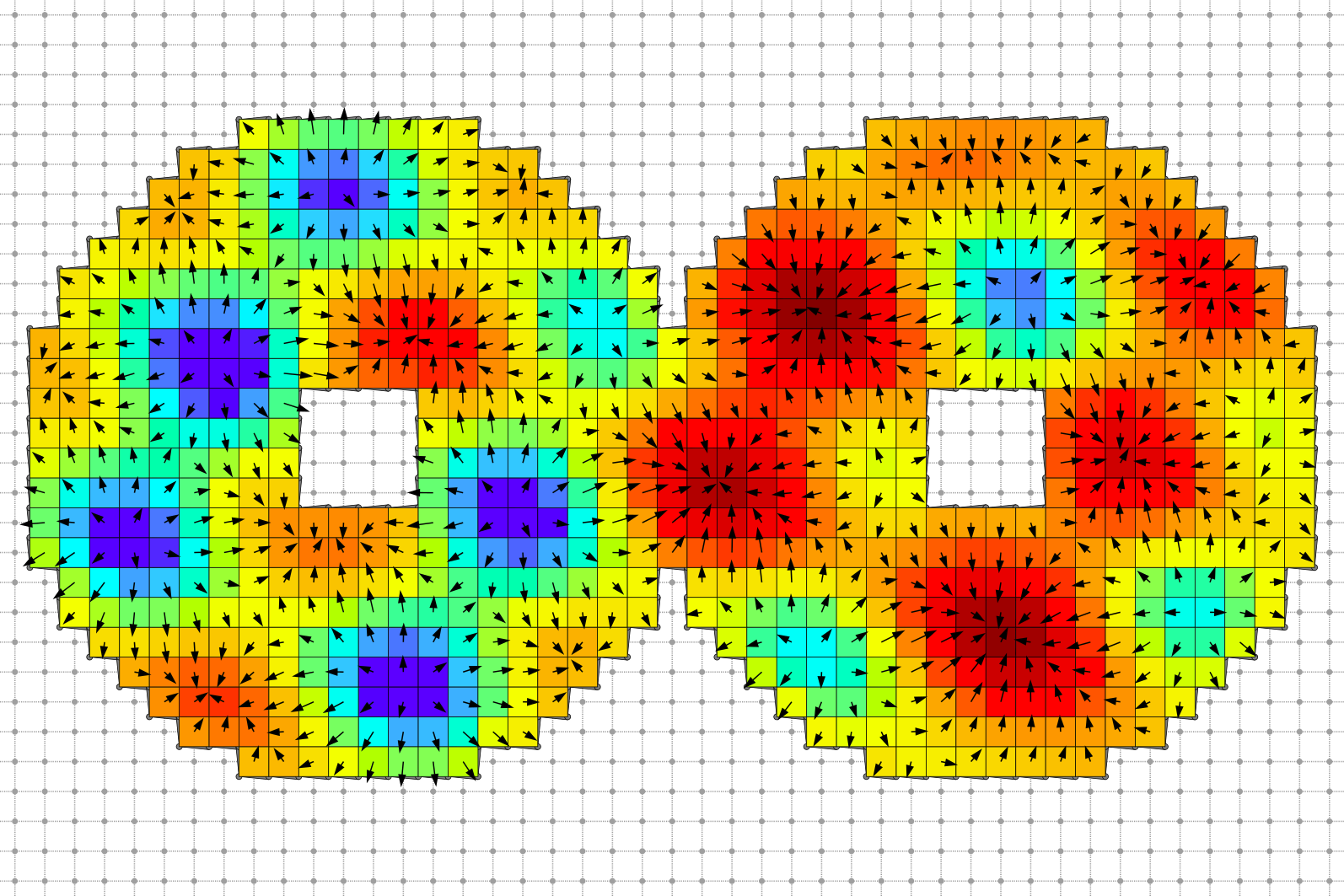
Dual Helmoltz decomposition curl-free component and scalar potential field.
Resolution of the div-free component \(\delta\beta\) for primal decomposition.
typedef DiscreteExteriorCalculusSolver<Calculus, LinearAlgebraSolver, 2, PRIMAL, 2, PRIMAL> Solver;
Solver solver;
solver.compute(d1 * ad2);
solution_div_free = solver.solve(input_one_form_derivated);
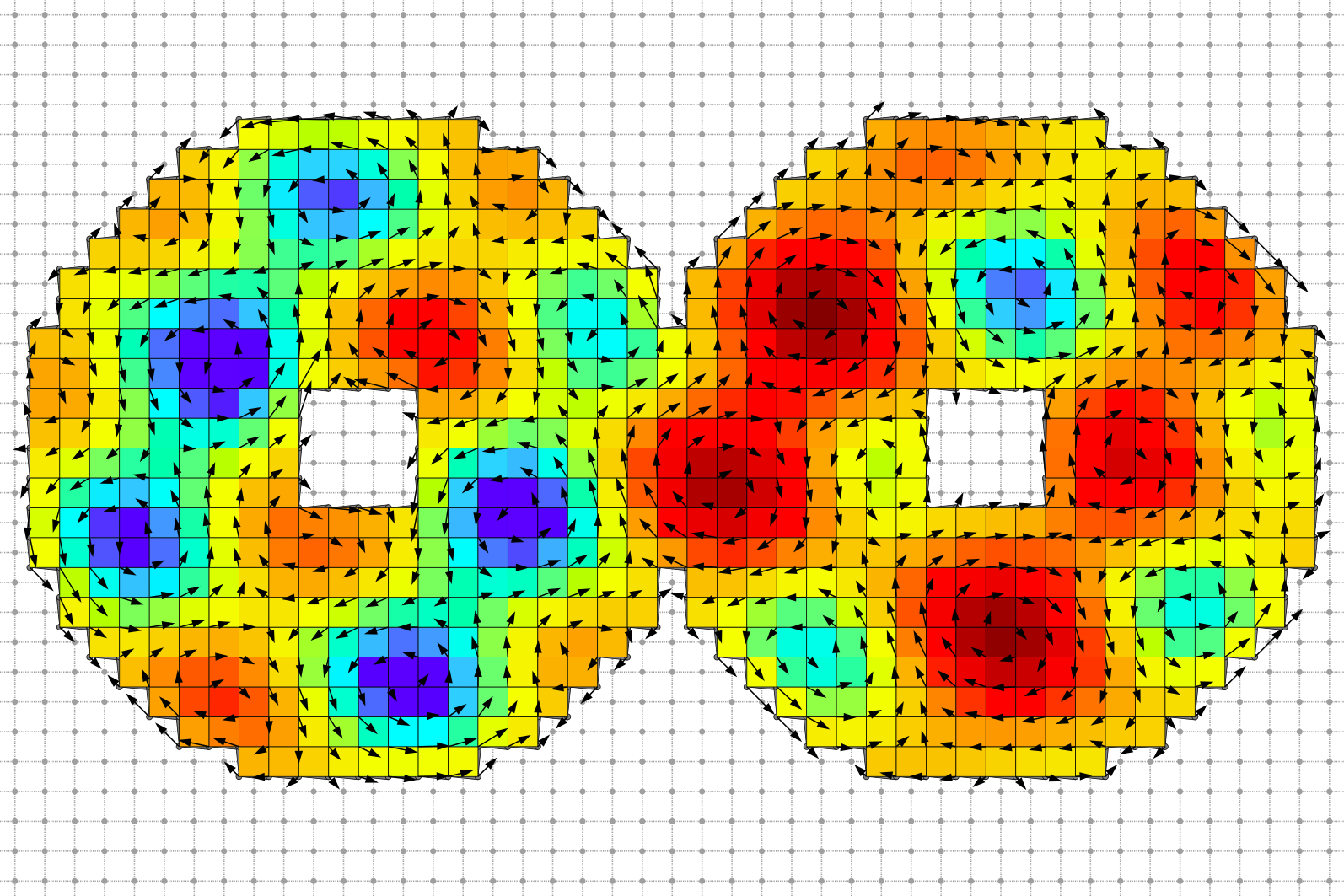
Primal Helmoltz decomposition divergence-free component and vector potential field.
Resolution of the div-free component \(\delta\beta\) for dual decomposition.
typedef DiscreteExteriorCalculusSolver<Calculus, LinearAlgebraSolver, 2, DUAL, 2, DUAL> Solver;
Solver solver;
solver.compute(d1 * ad2);
solution_div_free = solver.solve(input_one_form_derivated);
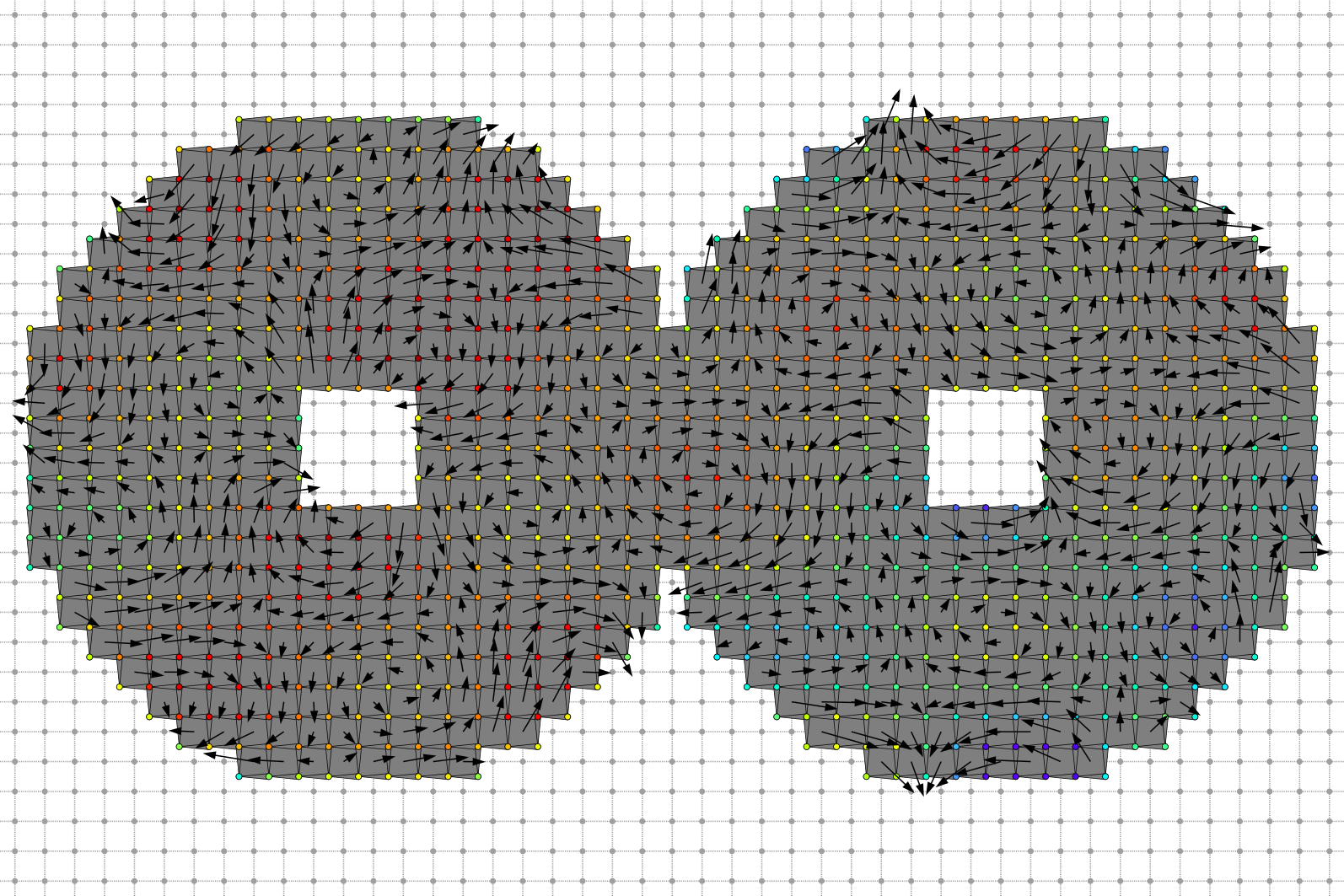
Dual Helmoltz decomposition divergence-free component and vector potential field.
Computation of the primal harmonic component \(\omega\).
const Calculus::PrimalForm1 solution_harmonic = input_one_form - d0*solution_curl_free - ad2*solution_div_free;
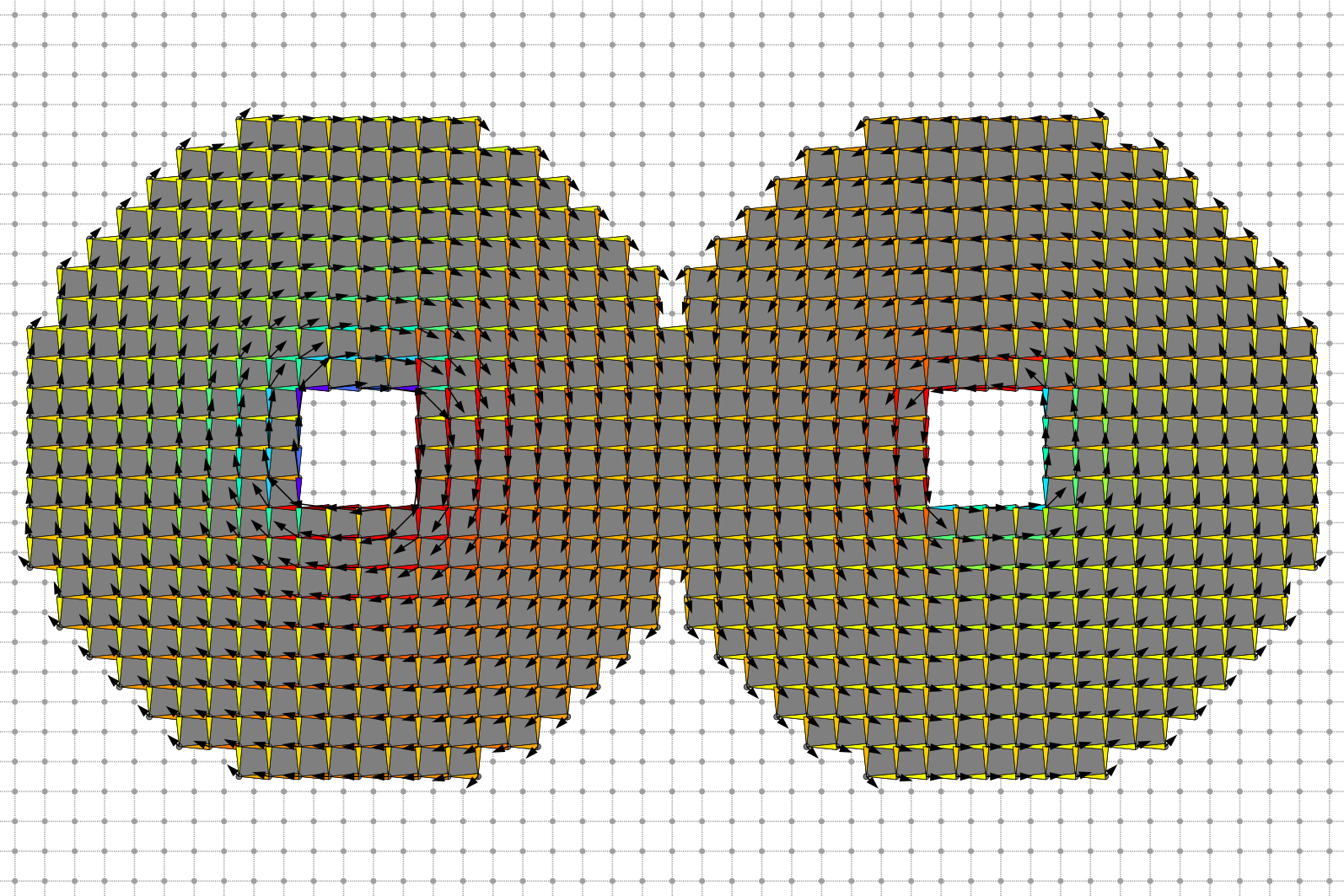
Primal Helmoltz decomposition harmonic component.
Computation of the dual harmonic component \(\omega\).
const Calculus::DualForm1 solution_harmonic = input_one_form - d0*solution_curl_free - ad2*solution_div_free;
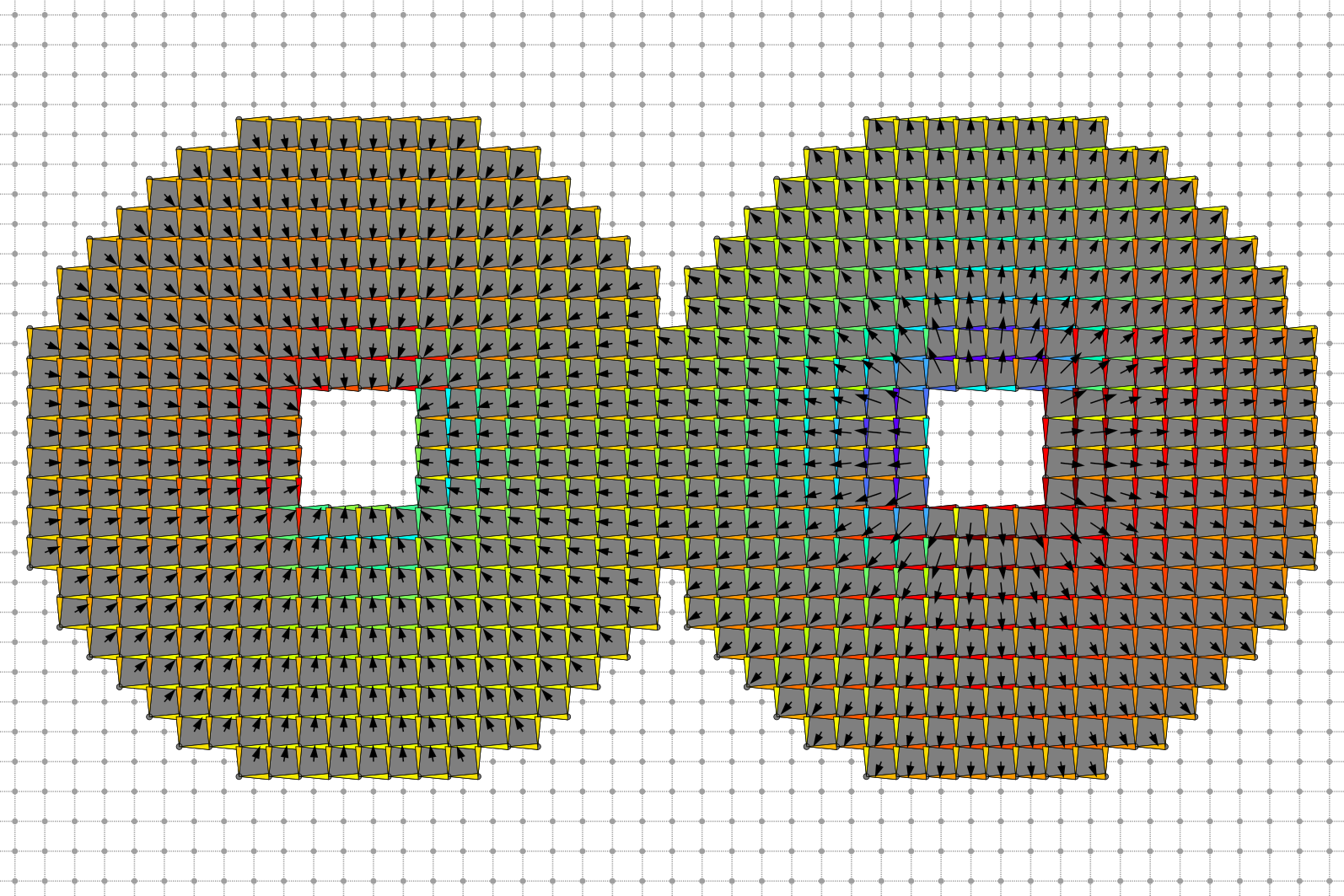
Dual Helmoltz decomposition harmonic component.
3D Helmoltz decomposition
In this example, we show how to compute the Helmoltz decomposition of a primal vector field defined on a 2D toroidal surface embedded in 3D. Snippets are taken from exampleDiscreteExteriorCalculusSolve.cpp.
First the calculus structure is filled manually with 0-, 1- and 2-cells to create a torus structure.
typedef DiscreteExteriorCalculus<3, 3, EigenLinearAlgebraBackend> Calculus;
for (int kk=2; kk<=18; kk++)
for (int ll=4; ll<=36; ll++)
{
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::NEG;
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::POS;
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = ( *
calculus.myKSpace.uDirs(cell) == 2 ? Calculus::KSpace::NEG : Calculus::KSpace::POS );
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = ( *
calculus.myKSpace.uDirs(cell) == 2 ? Calculus::KSpace::POS : Calculus::KSpace::NEG );
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
}
for (int kk=2; kk<=18; kk++)
for (int ll=16; ll<=24; ll++)
{
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = ( *
calculus.myKSpace.uDirs(cell) == 0 ? Calculus::KSpace::NEG : Calculus::KSpace::POS );
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = ( *
calculus.myKSpace.uDirs(cell) == 0 ? Calculus::KSpace::POS : Calculus::KSpace::NEG );
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::POS;
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::NEG;
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
}
for (int kk=4; kk<=36; kk++)
for (int ll=0; ll<=12; ll++)
{
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::POS;
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::NEG;
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::POS;
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::NEG;
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
}
for (int kk=0; kk<=12; kk++)
for (int ll=16; ll<=24; ll++)
{
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::POS;
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::NEG;
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::POS;
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
{
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::NEG;
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
}
HyperRectDomain< Space > Domain
DGtal::uint32_t Dimension
The primal input vector field is then filled and the associated input 1-form is computed using DiscreteExteriorCalculus.flat.
Calculus::PrimalVectorField input_vector_field(
calculus);
for (Calculus::Index ii=0; ii<input_vector_field.length(); ii++)
{
input_vector_field.myCoordinates(ii, 0) = -cos(-.3*cell_center[0] + .6*cell_center[1] + .8*cell_center[2]);
input_vector_field.myCoordinates(ii, 1) = sin(.8*cell_center[0] + .3*cell_center[1] - .4*cell_center[2]);
input_vector_field.myCoordinates(ii, 2) = -cos(cell_center[2]*.5);
}
const Calculus::PrimalForm1 input_one_form =
calculus.flat(input_vector_field);
Space::RealPoint RealPoint
Harmonic vector fields are aligned with natural map direction on the structure.
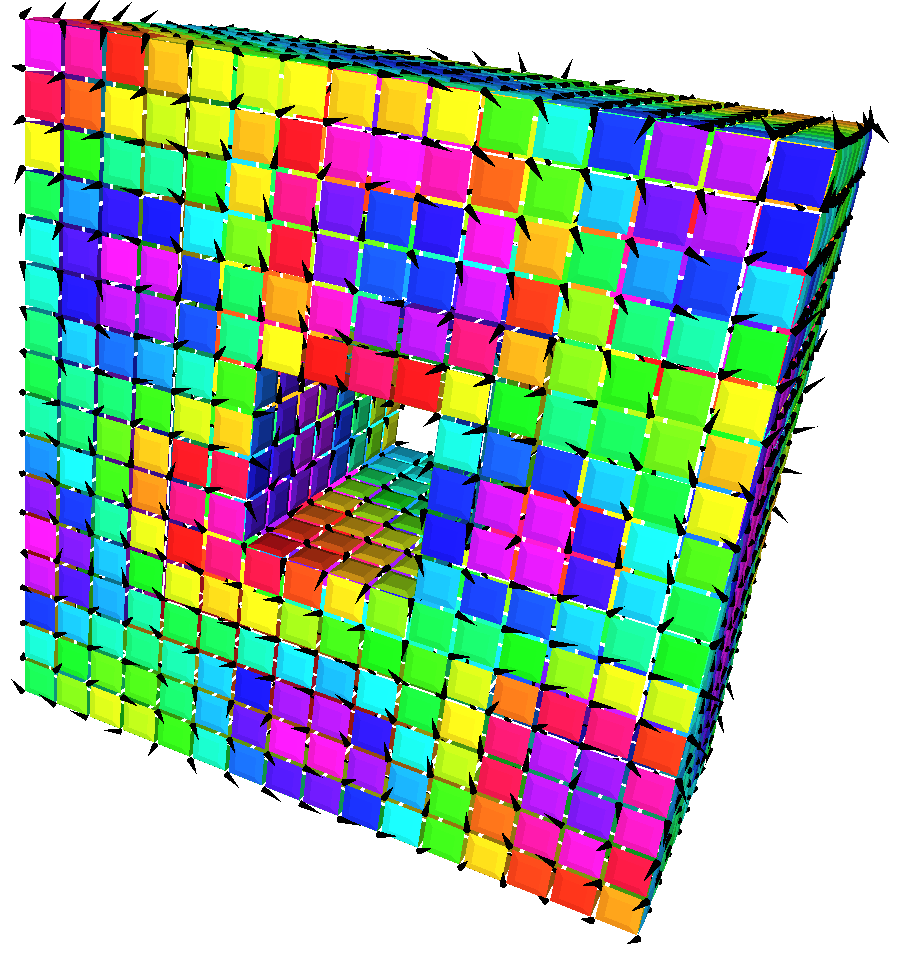
Manually created tore structure and input vector field.
Linear operators are then defined. Note the expression of antiderivative computed from Hodge operators and dual exterior derivative.
const Calculus::PrimalDerivative0 d0 =
calculus.derivative<0,
PRIMAL>();
const Calculus::PrimalDerivative1 d1 =
calculus.derivative<1,
PRIMAL>();
const Calculus::DualDerivative1 d1p =
calculus.derivative<1,
DUAL>();
const Calculus::DualDerivative2 d2p =
calculus.derivative<2,
DUAL>();
const LinearOperator<Calculus, 1, PRIMAL, 0, PRIMAL> ad1 = h3p * d2p * h1;
const LinearOperator<Calculus, 2, PRIMAL, 1, PRIMAL> ad2 = h2p * d1p * h2;
Values of \(\alpha\) are computed from previous expression using DiscreteExteriorCalculusSolver.solve.
typedef DiscreteExteriorCalculusSolver<Calculus, LinearAlgebraSolver, 0, PRIMAL, 0, PRIMAL> Solver;
Solver solver;
solver.compute(ad1 * d0);
solution_curl_free = solver.solve(input_one_form_anti_derivated);
Values of \(\beta\) are computed from previous expression using DiscreteExteriorCalculusSolver.solve.
typedef DiscreteExteriorCalculusSolver<Calculus, LinearAlgebraSolver, 2, PRIMAL, 2, PRIMAL> Solver;
Solver solver;
solver.compute(d1 * ad2);
solution_div_free = solver.solve(input_one_form_derivated);
Values of \(\gamma\) are computed by subtraction.
const Calculus::PrimalForm1 solution_harmonic = input_one_form - d0*solution_curl_free - ad2*solution_div_free;
\(\gamma\) has a strong connection with the structure topology and can be used to create local maps of the structure.
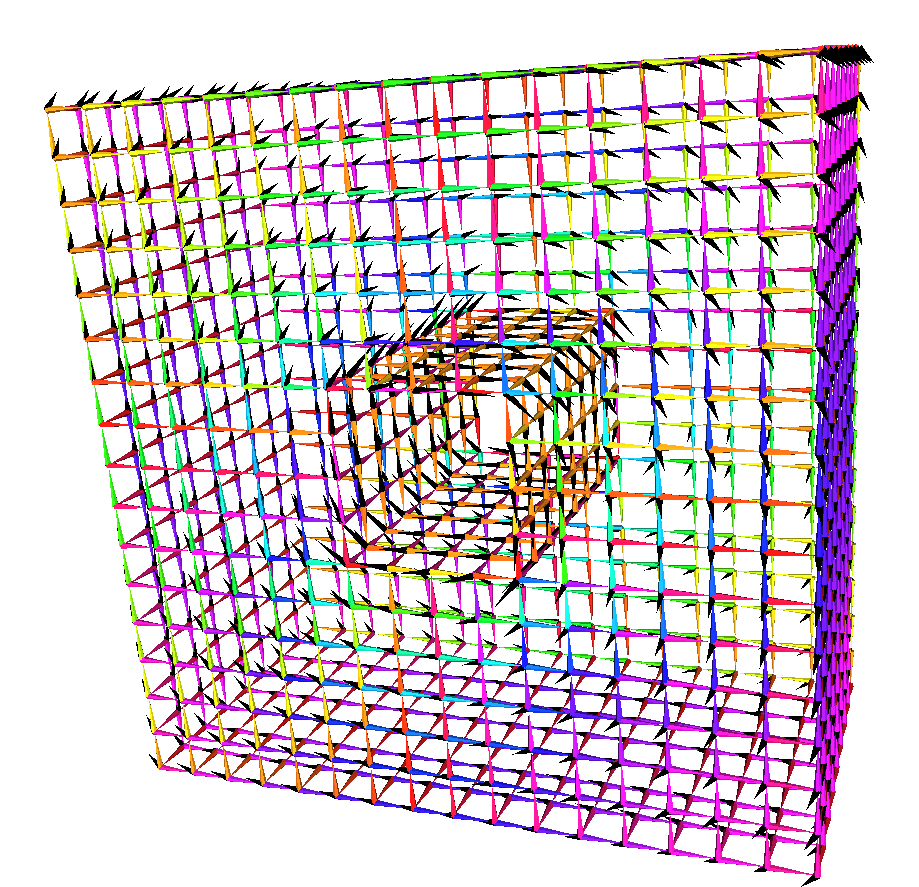
Harmonic component of the input vector field.

Harmonic component of the input vector field. Zoom on inner hole.

Harmonic component of the input vector field. Zoom on outer shell.











