Table of Contents
- Author(s) of this documentation:
- Kacper Pluta
- Date
- 2014/07/17
Overview
This module gather classes which represent geometric transformations.
Rigid transformations
Rigid transformations in \(\mathbb{R}^n\) are isometries which preserve in particular the distance and angles between every pair and triples of points respectively. The set of rigid transformations includes rotations, translations and reflections(excluded from the image processing applications from practical reasons), or combinations of those. Also an inverse of rigid transformation is rigid transformation therefore rigid transformation are bijective.
In general rigid transformation can be written like:
\[ \begin{array}{l l} \mathcal{U}: \mathbb{R}^n & \to \mathbb{R}^n \\ \mathbf{x} & \mapsto \mathbf{R . x} + \mathbf{t} \end{array} \]
where \(\textbf{R}\) denotes rotation matrix and \(\textbf{t}\) translation vector. Where discrete rigid transformations can be defined as follows:
\[ U = \mathcal{D} \circ \mathcal{U}_{| \mathbb{Z}^n} \]
\[ T = \mathcal{D} \circ \mathcal{T}_{| \mathbb{Z}^n} = \mathcal{D} \circ (\mathcal{U}^{-1})_{| \mathbb{Z}^n} \]
where \(\mathcal{D}\) is a standard rounding function (another interpolation method are for this moment not implemented in DGtal). Unfortunately discrete rigid transformations are in general nighter isometries nor bijective. From above difficulties we can consider two models of discrete rigid transformations: forward - Lagrangian and backward - Eulerian. First of them consists of computing \(U\) and second \(T\) but from the perspective of transformed space therefore all its points have defined value, which is not always true for the forward model.
Rigid transformations in 2D discrete space
DGtal contains both models, and below snippets of code present how to apply them for a 2D image. In order to illustrate how to use discrete rigid transformation we are going to:
a) add those includes:
b) define these types:
where DomainRigidTransformation2D is a helper functor which returns lower and upper bounds of transformed domain.
c) create transformation by providing information about origin, angle in radians, and translation:
d) if needed create a transformed domain eg:
e1) apply rigid transformation to image with forward model:
e2) or with backward which can be used with ConstImageAdapter or ImageAdapter:
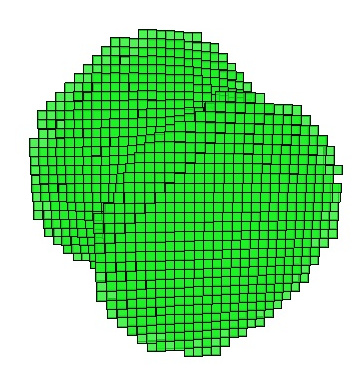
Below image presents result for forward model and image "Church.pgm"

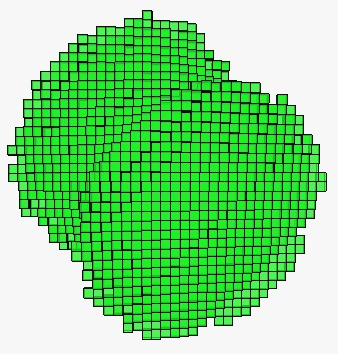
and for backward as well:

Rigid transformations in 3D discrete space
Discrete rigid transformations in 3D were implemented thanks to Rodrigues' rotation formula [12] which allow defining rotation around any arbitrary axis with exception for \((0,0,0)\). Usage is analogous to the 2D implementation and can be illustrated in the following steps:
a) add those includes:
b) define these types:
where DomainRigidTransformation3D is a helper functor which returns lower and upper bounds of transformed domain.
c) create transformation by providing information about origin, rotation axis (not need to be normalize), angle in radians, and translation:
d) if needed create a transformed domain eg:
e1) apply rigid transformation to image with forward model:
e2) or with backward which can be used with ConstImageAdapter or ImageAdapter:
Below image presents result for forward model and image "cat10.vol"
and for backward as well: