Loading...
Searching...
No Matches
topology/cubical-complex-illustrations.cpp
Source of examples used to generate illustrations of Cubical Complex module documentation.
- See also
- Cubical Complex
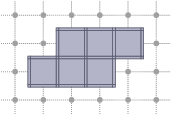 One of the generated illustration: displaying a 2D cubical complex on a Board.
One of the generated illustration: displaying a 2D cubical complex on a Board.
#include <iostream>
#include <map>
#include "DGtal/base/Common.h"
#include "DGtal/helpers/StdDefs.h"
#include "DGtal/topology/KhalimskySpaceND.h"
#include "DGtal/topology/CubicalComplex.h"
#include "DGtal/io/boards/Board2D.h"
using namespace std;
using namespace DGtal;
{
using namespace DGtal::Z2i;
X.close();
trace.endBlock();
trace.beginBlock( "Displays Cubical Complex" );
Board2D board;
board << domain;
board << CustomStyle( X.className(),
<< X;
trace.endBlock();
board << CustomStyle( X.className(),
<< S;
board.saveTikZ( "cubical-complex-illustrations-S.tikz" );
board.clear();
board << domain;
board << CustomStyle( X.className(),
<< X;
board << CustomStyle( X.className(),
<< X.closure( S );
board.saveTikZ( "cubical-complex-illustrations-closure.tikz" );
board.clear();
board << domain;
board << CustomStyle( X.className(),
<< X;
board << CustomStyle( X.className(),
<< X.star( S );
board.saveTikZ( "cubical-complex-illustrations-star.tikz" );
board.clear();
board << domain;
board << CustomStyle( X.className(),
<< X;
board << CustomStyle( X.className(),
<< X.link( S );
board.saveTikZ( "cubical-complex-illustrations-link.tikz" );
board.clear();
board << domain;
board << CustomStyle( X.className(),
<< X;
board << CustomStyle( X.className(),
<< X.boundary();
board.saveTikZ( "cubical-complex-illustrations-bd.tikz" );
board.clear();
board << domain;
board << CustomStyle( X.className(),
<< X;
board << CustomStyle( X.className(),
<< X.interior();
board.saveTikZ( "cubical-complex-illustrations-int.tikz" );
board.clear();
board << domain;
board << CustomStyle( X.className(),
<< X;
X[ p1 ] = CC::FIXED;
X[ p2 ] = CC::FIXED;
CC::DefaultCellMapIteratorPriority P;
functions::collapse( X, X.begin(), X.end(), P, true, true, true );
board << CustomStyle( X.className(),
<< X
<< p1 << p2;
board.saveTikZ( "cubical-complex-illustrations-collapse.tikz" );
board.clear();
return 0;
}
Aim: This class specializes a 'Board' class so as to display DGtal objects more naturally (with <<)....
Definition Board2D.h:71
Aim: This class represents an arbitrary cubical complex living in some Khalimsky space....
Definition CubicalComplex.h:176
void beginBlock(const std::string &keyword="")
double endBlock()
void saveTikZ(const char *filename, PageSize size=Board::BoundingBox, double margin=10.0) const
Definition Board.cpp:1218
void clear(const DGtal::Color &color=DGtal::Color::None)
Definition Board.cpp:151
Definition testClone2.cpp:346
Z2i this namespace gathers the standard of types for 2D imagery.
DGtal is the top-level namespace which contains all DGtal functions and types.
Definition ClosedIntegerHalfPlane.h:49
STL namespace.
Custom style class redefining the pen color and the fill color. You may use Board2D::Color::None for ...
Definition Board2D.h:279
Definition Board2D.h:217
std::string className() const
Return the style name used for drawing this object.