A Maze is given as N*N binary matrix of blocks where source block is the upper left most block i.e., maze[0][0] and destination block is lower rightmost block i.e., maze[N-1][N-1]. A rat starts from source and has to reach the destination. The rat can move only in two directions: forward and down. In the maze matrix, 0 means the block is a dead end and 1 means the block can be used in the path from source to destination. Note that this is a simple version of the typical Maze problem. For example, a more complex version can be that the rat can move in 4 directions and a more complex version can be with a limited number of moves.
Following is an example maze.
Gray blocks are dead ends (value = 0).
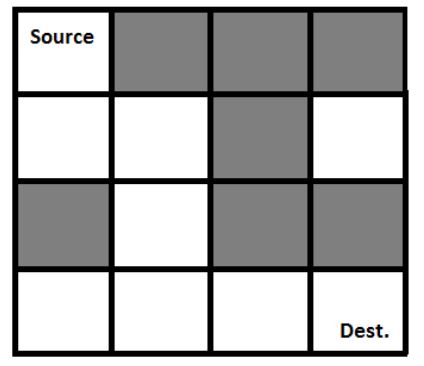
Following is a binary matrix representation of the above maze.
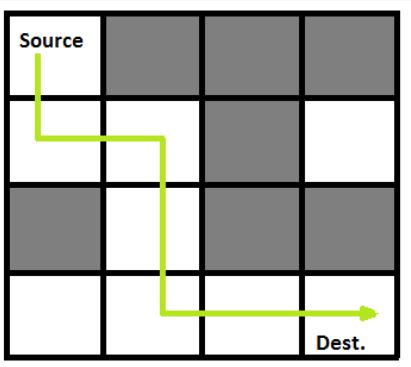
Following is the solution matrix (output of program) for the above input matrix.
{1, 0, 0, 0}
{1, 1, 0, 0}
{0, 1, 0, 0}
{0, 1, 1, 1}
All entries in solution path are marked as 1.
Algorithm:
1. Create a solution matrix, initially filled with 0’s.
2. Create a recursive function, which takes initial matrix, output matrix and position of rat (i, j).
3. if the position is out of the matrix or the position is not valid then return.
4. Mark the position output[i][j] as 1 and check if the current position is destination or not. If destination is reached print the output matrix and return.
5. Recursively call for position (i+1, j) and (i, j+1).
6. Unmark position (i, j), i.e output[i][j] = 0.
/* C++ program to solve Rat in
a Maze problem using backtracking */
#include < stdio.h >
// Maze size
#define N 4
bool solveMazeUtil(
int maze[N][N], int x,
int y, int sol[N][N]);
/* A utility function to print
solution matrix sol[N][N] */
void printSolution(int sol[N][N])
{
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++)
printf(" %d ", sol[i][j]);
printf("\n");
}
}
/* A utility function to check if x,
y is valid index for N*N maze */
bool isSafe(int maze[N][N], int x, int y)
{
// if (x, y outside maze) return false
if (
x >= 0 && x < N && y >= 0
&& y < N && maze[x][y] == 1)
return true;
return false;
}
/* This function solves the Maze problem
using Backtracking. It mainly uses
solveMazeUtil() to solve the problem.
It returns false if no path is possible,
otherwise return true and prints the path
in the form of 1s. Please note that there
may be more than one solutions, this
function prints one of the feasible
solutions.*/
bool solveMaze(int maze[N][N])
{
int sol[N][N] = { { 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 } };
if (solveMazeUtil(
maze, 0, 0, sol)
== false) {
printf("Solution doesn't exist");
return false;
}
printSolution(sol);
return true;
}
/* A recursive utility function
to solve Maze problem */
bool solveMazeUtil(
int maze[N][N], int x,
int y, int sol[N][N])
{
// if (x, y is goal) return true
if (
x == N - 1 && y == N - 1
&& maze[x][y] == 1) {
sol[x][y] = 1;
return true;
}
// Check if maze[x][y] is valid
if (isSafe(maze, x, y) == true) {
// Check if the current block is already part of solution path.
if (sol[x][y] == 1)
return false;
// mark x, y as part of solution path
sol[x][y] = 1;
/* Move forward in x direction */
if (solveMazeUtil(
maze, x + 1, y, sol)
== true)
return true;
/* If moving in x direction
doesn't give solution then
Move down in y direction */
if (solveMazeUtil(
maze, x, y + 1, sol)
== true)
return true;
/* If none of the above movements
work then BACKTRACK: unmark
x, y as part of solution path */
sol[x][y] = 0;
return false;
}
return false;
}
// driver program to test above function
int main()
{
int maze[N][N] = { { 1, 0, 0, 0 },
{ 1, 1, 0, 1 },
{ 0, 1, 0, 0 },
{ 1, 1, 1, 1 } };
solveMaze(maze);
return 0;
}
Output:
The 1 values show the path for rat
1 0 0 0
1 1 0 0
0 1 0 0
0 1 1 1