Document

Representing Sets

Every subset of a set {0,1,2,...,n‒1} can be represented as an n bit integer whose one bits indicate which elements belong to the subset. This is an efficient way to represent sets, because every element requires only one bit of memory, and set operations can be implemented as bit operations.
For example, since int is a 32-bit type, an int number can represent any subset of the set {0,1,2,...,31}. The bit representation of the set {1,3,4,8} is

00000000000000000000000100011010

which corresponds to the number 28 + 24 + 23 + 21 = 282.

Set implementation

The following code declares an int variable x that can contain a subset of {0,1,2,...,31}. After this, the code adds the elements 1, 3, 4 and 8 to the set and prints the size of the set.

int x = 0;
x |= (1<<1);
x |= (1<<3);
x |= (1<<4);
x |= (1<<8);
cout << x << __builtin_popcount(x) << "\n" ; // 4

Then, the following code prints all elements that belong to the set:

for(int i = 0; i < 32; i++) {
if (x&(1<<i)) cout << i << " ";
}
// output: 1 3 4 8

Set operations

Set operations can be implemented as follows as bit operations: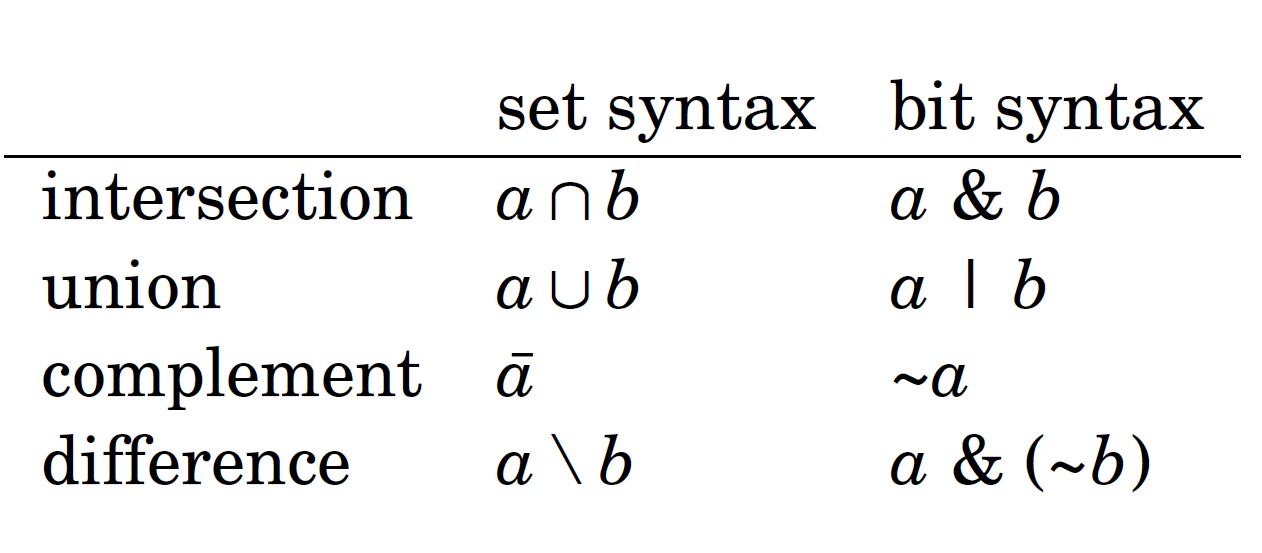

For example, the following code first constructs the sets x = {1,3,4,8} and y = {3,6,8,9}, and then constructs the set z = x∪y = {1,3,4,6,8,9}:

int x = (1<<1) + (1<<3) + (1<<4) + (1<<8);
int y = (1<<3) + (1<<6) + (1<<8) + (1<<9);
int z = x|y;
cout << __builtin_popcount(z) << "\n" ; // 6

Iterating through subsets

The following code goes through the subsets of {0,1,...,n‒1}:

for(int b = 0; b < (1<<n); b++) {
// process subset b
}

The following code goes through the subsets with exactly k elements:

for(int b = 0; b < (1<<n); b++) {
if(__builtin_popcount(b) == k) {
// process subset b
}
}

The following code goes through the subsets of a set x:

int b = 0;
do {
// process subset b
} while (b=(b-x)&x);