Combinatorics is the branch of Mathematics dealing with the study of finite or countable discrete structures. It includes the enumeration or counting of objects having certain properties. Counting helps us solve several types of problems such as counting the number of available IPv4 or IPv6 addresses.

There are two basic counting principles, sum rule and product rule.
Sum Rule – If a task can be done in one of n1 ways or one of n2 ways, where none of the set of n1 ways is the same as any of the set of n2 ways, then there are n1 + n2 ways to do the task.
Product Rule – If a task can be broken down into a sequence of k subtasks, where each subtask can be performed in n1, n2,.. nk respectively, then the total number of ways the task can be performed is n1* n2 * ... * nk .

• Example 1 – In how many ways can 3 winning prizes be given to the top 3 players in a game played by 12 players?


• Solution – We have to distribute 3 prizes among 12 players. This task can be divided into 3 subtasks of assigning a single prize to a certain player. Giving out the first prize can be done in 12 different ways. After giving out the first prize, two prizes remain and 11 players remain. Similarly, the second prize and third prize can be given in 11 ways and 10 ways. The total number of ways by the product rule is 12 * 11 * 10 = 1320.


• Example 2 – In how many ways can a person choose a project from three lists of projects of sizes 10, 15, and 19 respectively?


• Solution – The person has a choice of choosing a project from either of the three lists. So the person can choose from either 10 projects or 15 projects or 19 projects. Since choosing from one list is not the same as choosing another list, the total number of ways of choosing a project by the sum-rule is 10 + 15 + 19 = 44.


• Example 3 – How many distinct license plates are possible in the given format- Two alphabets in uppercase, followed by two digits then a hyphen and finally four digits. Sample- AB12-3456.


• Solution – There are 26 possibilities for the each of the two letters and 10 possibilities for each of the digits. Therefore the total number of possibilities is – 26 * 26 * 10 * 10 * 10 * 10 * 10 * 10 = 676000000.


• Example 4 – How many variable names of length upto 3 exist if the variable names are alphanumeric and case sensitive with the restriction that the first character has to be an alphabet?


• Solution – Let N1, N2, and N3 denote the number of possible variable names of length 1, 2, and 3. Therefore, total number of variable names is N1 + N2 + N3 . For N1 there are only 52 possibilities since the first character has to be an alphabet. For N2 , there are 52 * 62 = 3224 possibilities For N1 , there are 52 * 62 * 62 = 199888 possibilities Therefore, total number of variable names = 52 + 3224 + 199888 = 203164

The sum-rule mentioned above states that if there are multiple sets of ways of doing a task, there shouldn’t be any way that is common between two sets of ways because if there is, it would be counted twice and the enumeration would be wrong.
The principle of inclusion-exclusion says that in order to count only unique ways of doing a task, we must add the number of ways to do it in one way and the number of ways to do it in another and then subtract the number of ways to do the task that are common to both sets of ways.
The principle of inclusion-exclusion is also known as the subtraction principle. For two sets of ways A1 and A2 , the enumeration would like-

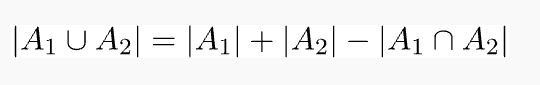
• Example 1 – How many binary strings of length 8 either start with a ‘1’ bit or end with two bits ’00’?


• Solution – If the string starts with one, there are 7 characters left which can be filled in 27 = 128 ways. If the string ends with ’00’ then 6 characters can be filled in 26 = 64 ways. Now if we add the above sets of ways and conclude that it is the final answer, then it would be wrong. This is because there are strings with start with ‘1’ and end with ’00’ both, and since they satisfy both criteria they are counted twice. So we need to subtract such strings to get a correct count. Strings that start with ‘1’ and end with ’00’ have five characters that can be filled in 27 = 32 ways. So by the inclusion-exclusion principle we get- Total strings = 128 + 64 – 32 = 160


• Example 2 – How many numbers between 1 and 1000, including both, are divisible by 3 or 4?


• Solution – Number of numbers divisible by 3 = |A1| =[1000/3] = 333 .
  Number of numbers divisible by 4 = |A2| = [1000/4] = 250 .
  Number of numbers divisible by 3 and 4 = |A1 ∪ A2| = [1000/12] = 83 .
  Therefore, number of numbers divisible by 3 or 4 = |A1 ∪ A2| = 333 + 250 – 83 = 500