Given a sorted array arr[] of n elements, write a function to search a given element x in arr[].
A simple approach is to do a linear search. The time complexity of the above algorithm is O(n).
Another approach to perform the same task is using Binary Search.
Binary Search: Search a sorted array by repeatedly dividing the search interval in
half. Begin with
an interval covering the whole array. If the value of the search key is less than the item in the
middle of the interval, narrow the interval to the lower half. Otherwise, narrow it to the upper
half. Repeatedly check until the value is found or the interval is empty.
Example :
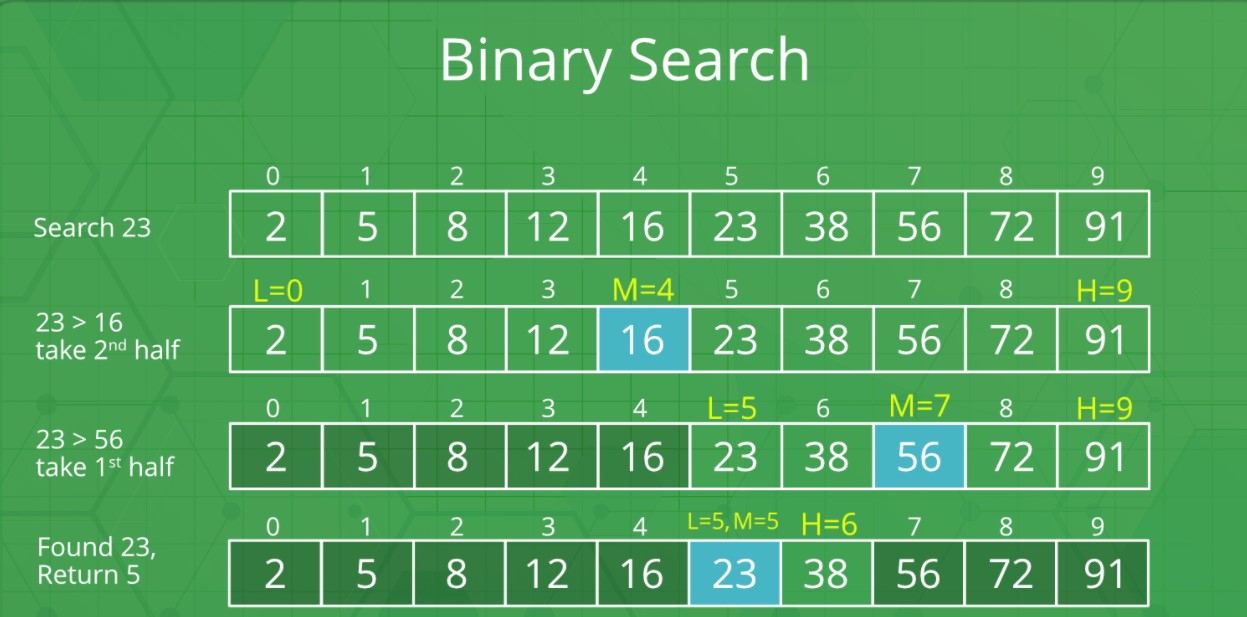
The idea of binary search is to use the information that the array is sorted and reduce the time complexity to O(Log n).
We basically ignore half of the elements just after one comparison.
- Compare x with the middle element.
- If x matches with the middle element, we return the mid index.
- Else If x is greater than the mid element, then x can only lie in the right half subarray after the mid element. So we recur for the right half.
- Else (x is smaller) recur for the left half.
using namespace std;
/* A iterative binary search function. It returns location of x in given array arr[l..r] if present, otherwise -1 */
int binarySearch(int arr[], int l, int r, int x)
{
while (l <= r) {
int m = l + (r - l) / 2;
/* Check if x is present at mid */
if(arr[m] == x)
return m;
/* If x greater, ignore left half */
if(arr[m] < x)
l = m + 1;
/* If x is smaller, ignore right half */
else
r = m - 1;
}
/* if we reach here, then element was not present */
return -1;
}
int main(void)
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
int n = sizeof(arr) / sizeof(arr[0]);
int result = binarySearch(arr, 0, n - 1, x);
(result == -1)
? cout << "Element is not present in array"
: cout << "Element is present at index " << result;
return 0;
}