{
"cells": [
{
"cell_type": "markdown",
"source": [
"# Post processing and visualization\n",
"\n",
"\n",
"\n",
"*Figure 1*: Heat flux computed from the solution to the heat equation on\n",
"the unit square, see previous example: Heat equation."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"## Introduction\n",
"\n",
"After running a simulation, we usually want to postprocess and visualize the results in\n",
"different ways. Ferrite provides several tools to facilitate these tasks:\n",
"\n",
" - L2 projection of (discrete) data onto FE interpolations using the `L2Projector`\n",
" - Evalutation of fields (solutions, projections, etc) at arbitrary, user-defined, points\n",
" using the `PointEvalHandler`\n",
" - Builtin functionality for exporting data (solutions, cell data, projections, etc) to\n",
" the VTK format\n",
" - [Makie.jl](https://docs.makie.org/) based plotting using\n",
" [FerriteViz.jl](https://ferrite-fem.github.io/FerriteViz.jl/)\n",
"\n",
"This how-to demonstrates the VTK export, the `L2Projector` for projecting discrete\n",
"quadrature point data onto a continuous FE interpolation, and the `PointEvalHandler` for\n",
"evaluating the FE solution, and the projection, along a user-defined cut line through the\n",
"domain."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"> **Custom visualization**\n",
">\n",
"> A common assumption is that the numbering of degrees of freedom matche the numbering\n",
"> of the nodes in the grid. This is *NOT* the case in Ferrite. If the available tools\n",
"> don't suit your needs and you decide to \"roll your own\" visualization you need to be\n",
"> aware of this and take it into account. For the specific case of evaluating the\n",
"> solution at the grid nodes you can use `evaluate_at_grid_nodes`.\n",
"\n",
"This example continues from the Heat equation example, where the temperature field was\n",
"determined on a square domain. In this example, we first compute the heat flux in each\n",
"integration point (based on the solved temperature field) and then we do an L2-projection\n",
"of the fluxes to the nodes of the mesh. By doing this, we can more easily visualize\n",
"integration points quantities. Finally, we visualize the temperature field and the heat fluxes along a cut-line.\n",
"\n",
"The L2-projection is defined as follows: Find projection $q(\\boldsymbol{x}) \\in U_h(\\Omega)$ such that\n",
"$$\n",
"\\int v q \\ \\mathrm{d}\\Omega = \\int v d \\ \\mathrm{d}\\Omega \\quad \\forall v \\in U_h(\\Omega),\n",
"$$\n",
"where $d$ is the quadrature data to project. Since the flux is a vector the projection function\n",
"will be solved with multiple right hand sides, e.g. with $d = q_x$ and $d = q_y$ for this 2D problem.\n",
"In this example, we use standard Lagrange interpolations, and the finite element space $U_h$ is then\n",
"a subset of the $H^1$ space (continuous functions).\n",
"\n",
"Ferrite has functionality for doing much of this automatically, as displayed in the code below.\n",
"In particular `L2Projector` for assembling the left hand side, and\n",
"`project` for assembling the right hand sides and solving for the projection."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"## Implementation\n",
"\n",
"Start by simply running the Heat equation example to solve the problem"
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"include(\"../tutorials/heat_equation.jl\");"
],
"metadata": {},
"execution_count": 1
},
{
"cell_type": "markdown",
"source": [
"Next we define a function that computes the heat flux for each integration point in the domain.\n",
"Fourier's law is adopted, where the conductivity tensor is assumed to be isotropic with unit\n",
"conductivity $\\lambda = 1 ⇒ q = - \\nabla u$, where $u$ is the temperature."
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "compute_heat_fluxes (generic function with 1 method)"
},
"metadata": {},
"execution_count": 2
}
],
"cell_type": "code",
"source": [
"function compute_heat_fluxes(cellvalues::CellValues, dh::DofHandler, a::AbstractVector{T}) where {T}\n",
"\n",
" n = getnbasefunctions(cellvalues)\n",
" cell_dofs = zeros(Int, n)\n",
" nqp = getnquadpoints(cellvalues)\n",
"\n",
" # Allocate storage for the fluxes to store\n",
" q = [Vec{2, T}[] for _ in 1:getncells(dh.grid)]\n",
"\n",
" for (cell_num, cell) in enumerate(CellIterator(dh))\n",
" q_cell = q[cell_num]\n",
" celldofs!(cell_dofs, dh, cell_num)\n",
" aᵉ = a[cell_dofs]\n",
" reinit!(cellvalues, cell)\n",
"\n",
" for q_point in 1:nqp\n",
" q_qp = - function_gradient(cellvalues, q_point, aᵉ)\n",
" push!(q_cell, q_qp)\n",
" end\n",
" end\n",
" return q\n",
"end"
],
"metadata": {},
"execution_count": 2
},
{
"cell_type": "markdown",
"source": [
"Now call the function to get all the fluxes."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"q_gp = compute_heat_fluxes(cellvalues, dh, u);"
],
"metadata": {},
"execution_count": 3
},
{
"cell_type": "markdown",
"source": [
"Next, create an `L2Projector` using the same interpolation as was used to approximate the\n",
"temperature field. On instantiation, the projector assembles the coefficient matrix `M` and\n",
"computes the Cholesky factorization of it. By doing so, the projector can be reused without\n",
"having to invert `M` every time."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"projector = L2Projector(ip, grid);"
],
"metadata": {},
"execution_count": 4
},
{
"cell_type": "markdown",
"source": [
"Project the integration point values to the nodal values"
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"q_projected = project(projector, q_gp, qr);"
],
"metadata": {},
"execution_count": 5
},
{
"cell_type": "markdown",
"source": [
"## Exporting to VTK\n",
"To visualize the heat flux, we export the projected field `q_projected`\n",
"to a VTK-file, which can be viewed in e.g. [ParaView](https://www.paraview.org/).\n",
"The result is also visualized in *Figure 1*."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"VTKGridFile(\"heat_equation_flux\", grid) do vtk\n",
" write_projection(vtk, projector, q_projected, \"q\")\n",
"end;"
],
"metadata": {},
"execution_count": 6
},
{
"cell_type": "markdown",
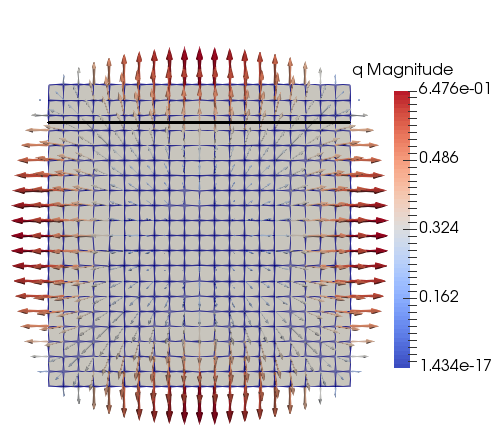
"source": [
"## Point evaluation\n",
"\n",
"\n",
"*Figure 2*: Visualization of the cut line where we want to compute\n",
"the temperature and heat flux."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"Consider a cut-line through the domain like the black line in *Figure 2* above.\n",
"We will evaluate the temperature and the heat flux distribution along a horizontal line."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"points = [Vec((x, 0.75)) for x in range(-1.0, 1.0, length = 101)];"
],
"metadata": {},
"execution_count": 7
},
{
"cell_type": "markdown",
"source": [
"First, we need to generate a `PointEvalHandler`. This will find and store the cells\n",
"containing the input points."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"ph = PointEvalHandler(grid, points);"
],
"metadata": {},
"execution_count": 8
},
{
"cell_type": "markdown",
"source": [
"After the L2-Projection, the heat fluxes `q_projected` are stored in the DoF-ordering\n",
"determined by the projector's internal DoFHandler, so to evaluate the flux `q` at our points\n",
"we give the `PointEvalHandler`, the `L2Projector` and the values `q_projected`."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"q_points = evaluate_at_points(ph, projector, q_projected);"
],
"metadata": {},
"execution_count": 9
},
{
"cell_type": "markdown",
"source": [
"We can also extract the field values, here the temperature, right away from the result\n",
"vector of the simulation, that is stored in `u`. These values are stored in the order of\n",
"our initial DofHandler so the input is not the `PointEvalHandler`, the original `DofHandler`,\n",
"the dof-vector `u`, and (optionally for single-field problems) the name of the field.\n",
"From the `L2Projection`, the values are stored in the order of the degrees of freedom."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"u_points = evaluate_at_points(ph, dh, u, :u);"
],
"metadata": {},
"execution_count": 10
},
{
"cell_type": "markdown",
"source": [
"Now, we can plot the temperature and flux values with the help of any plotting library, e.g. Plots.jl.\n",
"To do this, we need to import the package:"
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"import Plots"
],
"metadata": {},
"execution_count": 11
},
{
"cell_type": "markdown",
"source": [
"Firstly, we are going to plot the temperature values along the given line."
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "Plot{Plots.GRBackend() n=1}",
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlgAAAGQCAIAAAD9V4nPAAAABmJLR0QA/wD/AP+gvaeTAAAgAElEQVR4nOzdeUAU5f8H8GdmlmO5QeQ+5PZERUXNE/IEUREzz9IsNa/6amn1VSurb2Z2aZm3+bMyTU1FUFG8EEnxQDw4FJBDbrmXBXZn5vfHFhEuCrj3vl9/scOzy4dhed77zDzzDMXzPAEAANBXtLoLAAAAUCcEIQAA6DUEIQAA6DUEIQAA6DUEIQAA6DUEIQAA6DUEIQAA6DUEIQAA6DUEIQAA6DUEIQAA6DVdC8KDBw9evny5lY1ZllVqMdAUx3HqLkGP8DyPHa5K6ExUSeF7W9eC8OLFi9evX29l49raWqUWA02JxWJ0zSojlUobGhrUXYUeQWeiSgrf27oWhAAAAG2CIAQAAL2GIAQAAL2GIAQAAL2GIAQAAL2GIAQAAL2GIAQAAL2GIAQAAL0mUHcBANBOYikpEPMFtaRIzOfXkmIxnycixWI+v5YUignH0fYmUmdTYmdMOZkQBxPKQUgcTSh7IXE2pUzxrw/wN/w3AGiukjpSJOYLakmhmC+sJfm1fLGY5In44jqSL+IlPHEUUo4mxF5IOZkQOyE12IHYC2lHIbE1lPIcX8kxj0SkuI7PryUZVXx8Ecmv5YrEJF/EE0KcTSk7IXEyoRyExMGEcjIhdsaUsymxE1L2QkKp+3cHUBkEIYBGEEnJmUdcbD7/sPqfEZ6lIbEXUo4mxEFIOZgQdzOqX0fibELbCYmzKWVh0OKrSSSEZXl3Y8rfhhB5oSaSkkcivkhMCmr5QjEprOXPVZDiOu6RiBSJ+bJ60tGYcjAhjkLiYkoFOVGjnGlrI+X99gDqhCAEUKcHVXx0Lh+VwyUU84EdqbGu9AgnYi+kZSMzQ6WdxDcVEF9LyteSyI1JKUeK6/iCWlJQSx7W8D8/4ObFsb06UCGudIgr1cMGw0XQKQhCAFWrZ0lcIR+dy0Xl8jUSMtaVmt+FPjiCNm95hKdiApo4mVBOJrJH1OKutFhKLhTyx3O4iac5KU9CXKkQV+pFJ9oEXQhoP7yLAVTkkYiPzuWjc/lzBVxXKyrUjf4tmO7VgdKK4ZVQQMa4UGNcGEJIagUflct/e4ebcY59wZ4KdaVDXCkvC634PQDkQBACKBHLkz+L+agc7kQen1vDj3ahX/Kkdgw16KDN59s6W1GdrajlPegqCTmdx53I4z+/xVoYUCGuVIgrPdRRiUd0AZQBQQigeKV15GQeF53Lx+RxbmbUWFfqhxeY/nYUo1ujJgsDEuFBR3gQnjA3S/noXH7NdfZeBR/sRIe4UmNdKGdT3fqFQUchCAEUgydEFgZRuVzK32Gwob/AyUT3w4AiJMCWCrClVvWmS+vIqTwuKpd/7yrrakaFuFKhrrTufQgAXYIgBHheCcX8zjQuOpczN6BCXalP+jD6fHjQ1pjM8KZneBOWZ2SHhRddZmWHhV/1pUc5Iw9B4yAIAdovvohfe4NNryJLu9Hv9xRgwkhTDEUG2VOD7Jn/9SN5Ij4ql1/2J2tmQNb0ZkJcsaNAgyAIAdojvohfd4u9XUb+050+1oU2YtRdkGZzMaXmd6be8KOjcrnV19kPEsl/e9OTPWjkIWgCBCFA21wo4D++weaIyH970YdH0Ab6egi0HWiKhLnRoa70Hw+5T25yX9zi1vSmw9wRh6BmCEKA1rpUyH90g82sJu/1pF/zpQWIwHahKRLhQU/yoI/ncGtvcKuuc+/0oGd608hDUBcEIcCznX7Er73JlojJf3vT071oTIB8fhQhYW70ODc6Mptbe5P76ja3pjcd3glxCGqAIAR4mlN5/NqbbHk9+W8veioiUNEoQsa702HudFQOv/Ym+/FNblUverIH4hBUCkEIIF90Lv/JTbZaQlb1oqd4omtWIoqQcW7UODdBdC6/9ia79iaHfQ6qhCAEaC4ql//4BlvHEoxOVCzElQpxFchG4Wtvcqt60y97YhQOSocgBPjHmUf8f6+xtVLyrj89wxtdsHqMdqFGuwguFfIf3mBXX+NWYmoSKBmCEIDwhBzL5tbe5FiOfBhAT+yEQaD6DXagYkMEsfn8xzfYr25z/+1FT/dCHIJSIAhBr/GEyK5poymyujc9Ade0aZgXnagXnQTnCvi1N9hPbnL/7UXP9EYcgoIhCEF/HcvmVl/nDGmytg89zg0RqLmCHKmgUMHFQv7jG+wnN7k1AfQrPvh7gcIgCEEf1UjIkgT2chH/9QAmFOteaomhDlRsiOBSIb/sCnswi9s1VNDRWN01gU7AIQbQO9dK+YAjUpYj1ycKkIJaZ7ADdTlM0MeW6nlYEpXLq7sc0AUIQtAjPCHf3eFCTko/DqD/bzhjZqDugqBdBDT5KID5NUjw5iX2rQS2nlV3QaDlEISgL/JE/ItR0iPZ3PVwwTQvvPO13nBHKmmSIE9EBhyTplRgaAjth+4A9MIfD7m+R6RDHakzIQJXUxwO1RE2RuTQCOY/3emhx6Xf3eEQhtA+mCwDOk4sJe8lssdy+EMjBIPsEYE66BUfur8dNf0ce76A3zGU6WCk7oJA2yhxRFhXV3f58uW0tLSntCkvL8/JyWm6heO4lJSUhISE8vLyxo21tbWZTdTW1iqraNAtNx/zAUekFQ0keRJSUJf5WVIJ4wXeFqTXYenZfIwMoW2UFYSpqak+Pj7vv//+6NGjZ82axfPN35pnz5719vbu0KHD0KFDGzdmZGQ4OzuHh4evXLmyU6dOW7ZskW2PjY3t1q3byL9dvXpVSWWDzuAJ+eo2N+akdE1ves8wxhzzYnSdIU2+7M/sGsq8coF9L5GVcOouCLSHsoJw9erV06ZNu3DhQnJy8sWLF2NjY5s18PLy+u23344cOdJ0o7m5+cmTJ1NTUy9evHj48OElS5ZUVVXJvtWnT5+Mvw0fPlxJZYNuKBaTcaekv2dxl8MwL0a/jHSmksIFKRVk4DFpeiWGhtAqSukjGhoajh49OmfOHEKIhYVFeHj4wYMHm7Vxd3fv27evoaFh0412dnY9e/aUfd2nTx+pVFpRUSF7yHFcRkZGWVmZMgoGXXIqj+9zRNrDhoobJ/CywOFQvWNrTI6OZJZ2owdFSr+7g4EhPJtSJssUFhZKJJJOnTrJHnbq1On06dNtfZHNmzcHBga6ubnJHt65c2f8+PG5ubmBgYH79u3r2LGj3GfV1NSkpqY2/jiGYYYOHUrT8vOe4ziOw/+Jiqhgb4ul5N1E7mQe2TecesGeIkR//7zc39RdiNrM9CK9beiZF7hLhdyWQbS1kmfQ6PneVrE27e2W+v+mlBKEtbW1FEU1jvaMjY1FIlGbXiEyMvK77747f/687OGwYcNKSkqMjIxqamomT578zjvv7NmzR+4T8/PzMzMzU1JSZA+FQmGXLl3Mzc3lNhaLxQzDtKkwaDexWMzzfGvelO1zp4J6LcGghxV/aZTUwoDX8wlVEomEZVk975o9jEjsi2TNLUHAEWbbAMmgjkrcG+hMVKlNe9vY2FggeEbSKSUIHR0deZ4vKyuTjdtKS0sdHR1b//SYmJjXX389MjKyS5cusi0WFhayL8zMzBYtWvTWW2+19FxfX9/Q0NAlS5a05gfxPG9mZtb6wuB5UBQlFAqVEYQ8IdtTuTXX2bV9mHmdaUIwff6vIDQ21ve1OM0I2TyUnHnEz75IRXSiNvRnDJTzSQydiSopfG8r5U1haWnp5+d38eJF2cO4uLjAwMBWPvfSpUuzZs36/fffW3pKdnZ2hw4dFFMoaL8iMQk9Jd2VzsWHCeZ1xrwYkGOEM3V9ouB+FT/0uDSzGjNooDllXVC/bNmyd955hxBy9+7dmzdv7tu3jxCSnp4eGBiYnZ1taWlZVFT0008/paenV1ZWfvHFF46Ojq+88sr9+/fHjBkTHByckJCQkJBACJkxY4aLi8vnn39uYmLi7u6ekpKybt26zZs3K6ls0C4ncvnX49g5vtRHAQzuUQdPYS8kUaMFG+9wA45KvxrAzPLG2wX+oawgnDdvnqmp6aFDh6ysrOLi4mxsbAgh1tbWCxYsMDIyIoSwLFteXt6xY8f58+eXl5fLxrkMwyxevJgQ0ng1vVQqJYT07dv3jz/+iI+Pt7e3j4qKGjx4sJLKBm1Rz5IPb7C/ZfC/BjHDHDE1FJ6NIuSt7vRIF2raWfZYNr9tMKPsGTSgLagnL3XXakuXLvXx8WnlOcLq6uqW5tGAwolEIkWdI0yp4KefYz3Nqe1DGBv0ZfLgHOFT1LFk5VX2aDa/dzgzxEExn6LQmaiSwvc2jg+AlvnjITfsuHRJN/rQCKQgtIcxQ74byGx6gZ4SK/0xRa8n1oIMFt0GbbIvg1t+hT01VtC7Aw6HwnMJc6MTxlMvRrNiKVnWA0MCvYY/P2iNXx5w717lTo1BCoJidDKn4scLdqVz7yXi3r56DUEI2mFbKvffa9y5EKaHDVIQFMZBSM6GCE7k8shCfYYgBC3wwz3u81tcbAjjY4kUBAWzE5LzoYJz+fyiy6xOTR2EVkMQgqb7XxK38S4XN47BCtqgJNZG5NRYwfVSflE8slAfIQhBo310g/35AXculHExRQqCElkZktgQQVolP/McK8VMUj2DIAQNxROy/Ap7LJu/ME7gZIIUBKUzFZDIUYLSOn7medzXV78gCEET8YS8ncBeKOBPhwg64qJwUBUTAYkcLahnyaQz0jrMntEbCELQOCxP5l5kbz7mz4UKOuCSeVAtQ5rsf5ExYqgIZKHeQBCCZpFyZNZ5NlfEnxgjMDdQdzWglwxp8lsQY2VIjTslFUnVXQ0oH4IQNEgDR6aeYysa+GMjBaZY9QjUR0CTvcOZTubUmJPSKom6qwElQxCCpqhnyZRYtoElf4wQCJGCoG40RbYPYfrYUsFR0sf16q4GlAlBCBqhVkrCYqTGDDk0gjFi1F0NACGEEIqQbwcwY12pEdHSkjp1VwNKgyAE9auWkDEnpS6m1C9BjAHekqBhPunDjHOjgqKkhWJ1lwLKgV4H1KyigYw8Ie1uTe0cyjC4XBA00id9mBne9LDj0lwRVp7RQQhCUKfyejLqhLSvLfXDIIQgaLT3e9JvdaOHHmczqpCFugZBCGpTJCbDoqTBTtT3LyAFQQss7Eq/35Meepy9V4Es1CmYnAfqUVBLRkRLp3jSHwbg0xhojXmdaTMDMuoEe2I07gimOxCEoAZZ1fyIaHZRVxp3BgetM92LpgkZfVIaNRr3iNYR6IZA1dIr+eFR7FvdkYKgraZ60dsGC8aelCYU4xipLkBPBCqVWsGPiGY/DKCXdsN7D7TYODfqp2GC8THSs/nIQq2HzghUJ+kxHxQl/bQv/Zov3nig9ca4UAdfFEw/Jz39CFmo3dAfgYpce0yFxHCbBzGv+OBdBzpimCN18EXBzPPSmAKsh6TF0CWBKmTX8FPjBDuGMOGd8JYDnTLYgYocJVhwRXDzMcaF2gq9EihdHUsmn2H/04ULcVF3KQBKENiR+q6vZNIZFuuRaikEISjdwnjWz4pa5IebnILOCnPhpnpSU89KpZy6S4G2QxCCcn1zh7v5mN82GGdQQMd91pcRMmTFVXzg0z4IQlCis/n8F7fYwyMYE6zcALqOpsje4YLIHH53OkaFWgZBCMqSU8PPPC/dFyzwMMfqG6AXrI1I5CjmvUT2WikmzmgTBCEohVhKws+wK/yZIEekIOiRzlbU5heYl2LZUkyc0R4IQlCKhZfZLlbU293xBgO9E+FBT/eipsRi4ozWQD8Fivf1bS4JE2RAj33ShzERYOKM1kAQgoKdzee/SMYEGdBrmDijXRCEoEiyCTK/YYIM6D1MnNEiCEJQmDqWRJxhV2KCDAAhhJDOVtTWwcxkrDij8RCEoDCvx7FdrKi3MEEG4G8T3enpXlhxRtOhzwLF+Po2d7ec34IJMgD/9ilWnNF4CEJQgLP5/HpMkAGQBxNnNB+CEJ5XNlaQAXgqTJzRcAhCeC5iKYk4w77XExNkAJ4GE2c0GYIQnotsBZml3fBGAniGie70DG9q0hmpBIdINQz6L2i/r29zt8uwggxAa33ShzE3wMQZjYMghHaKzefXJ7O/v8gIMUEGoHVoivwWLDiVh4kzmgVBCO2RXcPPwgoyAG1nYUAOj2DeS2QTSzBxRlMgCKHNGifIDMcEGYC262xFbRvMvBTLFovVXQoQQhCE0A6YIAPwnCa40zO9qYhYaQMOkWoA9GXQNl/d5pIe81sxQQbg+aztw1hi4oxmUFYQ5uXlRUREeHl5jR07Ni0t7ckG8fHx7777bkhIyPr165tuT05OHjFihJeX1/Tp04uLi2UbeZ7//PPPu3bt2rNnz507dyqpZnim2Hz+q9vs0ZFYQQbgedEU+TlIEJ3L732AUaGaKSsIZ8yY4eTkdPHixYEDB06YMIHjmv+lb926ZWhoyDDMvXv3GjdKJJLQ0NCxY8devHjR2Nh47ty5su179+7duXPn77//vnXr1vfee+/ixYtKKhueQjZB5pcggZsZTg0CKICVITk2knnnCibOqJlSgvDevXuJiYnr1q1zdnZetWpVZWXl+fPnm7VZuHDhZ5991qNHj6Ybo6KijIyMli9f7uzsvH79+lOnTuXm5hJCtmzZsmLFim7dug0YMGDevHlbt25VRtnwFFhBBkAZMHFGEygrCP38/ExNTQkhNE337t37zp07rXni3bt3+/TpI/va1tbW1dVVNl68e/duQECAbHtAQMDdu3eVUTY8BSbIACgJJs6onVJO9ZSWllpYWDQ+tLKyKikpafcTGxoaqqqqGrc//dWSkpJ27NixZs0a2UNTU9MrV65YWlrKbSwSiSgK45tn25jK3ChhTr/YUFPT/hepra1lWZamEaWqIJFIWJaVSqXqLkRfPGdnssKPXCsSLIuXruuNP9mztWlvGxsbCwTPSDqlBKGVlZVIJGp8WFVVZWNj08onFhUVNXuioaGhqalp4wtWV1c/5dX8/f1DQ0PnzZsne8gwTNNkbYbneTMzs9YUps9i8/mNadKE8QI7c8PneR2KooRCIYJQNWRBaGxsrO5C9MXzdyYHRpEBR6W/5xvO8cX/yDMovOtWyh739PR88OCBRCKRPUxNTfXy8mrlE1NSUmRfi0SivLw8T09P2fbU1NTGV5NtlIumaRMTE+u/PSUFoTXya/mZ57CCDIDSWRiQ319k3ktk75Rj4oyqKSUI+/Xr5+TkJJvScvjw4erq6jFjxhBC4uPjv/zyS1mb+vr68vJysVjc+AUhZOLEiZmZmTExMYSQjRs3+vv7d+7cmRDyyiuvbNq0SSwWP378eOfOnbNmzVJG2fCktxK4eZ1prCADoALdrKnP+jLz4lgOUahaSglCiqL27t27adMmW1vbt99+e9++fYaGhoSQjIwMWcgRQnbv3u3l5bVnz55Tp055eXl98cUXhBBzc/Nffvll9uzZtra2+/bt2717t6zxkiVLPD09HR0dvby8wsLCIiIilFE2NHMil08u49/vhWvnAVRkrh8tFJCtqZg2o1IUzyvxs4dIJJLNHVXIE+vr6xmGefppz6VLl/r4+CxZsqQ1P6W6utrc3Lwd5emDWinpfki6YwgT7KSY4aBIJMI5QpXBOUIVU2Bnkl7JDzkuvTFR4GyKIzHyKbzrVm6v1L4UbOmJRkZGz5z8A4ry32tskCOlqBQEgFbytaQWdKbf/hODQtV5WhA2NDTk5+cXFxc/uS4M6LZbZfxvGdwXgTgoCqAGH/Ri7pbzx7LR8aqInCC8du3a0qVLu3XrZmRk5OzsbG9vb2RkNHDgwA8//PDhw4cqrxBUjeXJ3Ivshv6MLY6rAaiDEUO2DGaWJnA1EnWXoh/+daQxLi5uxYoVf/75p7Oz88CBAydNmmRjYyOVSouLi+/cubNx48ZPP/00PDx83bp13t7e6qoYlO27O5yFAZnujZN5AGoz1IEKdqLWXGe/HoADM0r3TxAePXp06tSps2fP/uabbwYMGPBkU4lEEhMTs3379u7du6enp7u5uamwTlCR7Bp+3S02YbwA5wYB1OvL/kyPQ5IZ3nQfW/w7Ktc/Qejn53f//n0XF5eWmhoYGISGhoaGht68eRMLsuiqpQncsh6MlwX+8QDUrIMRWR/IvHaRvTZRYIADNMr0z97t3LnzU1Kwqd69e7dyyTTQLr9ncZlV/PIe+J8D0AgzvWl7Idl0F7NmlOtpXV5lZWViYmJ0dLTKqgE1qpKQ5X9yWwcz+OwJoDm2DWbW3WKzqrHYjBLJ7/MaGhoWLlzYsWPHwMDAxgWsFyxYMHXqVBXWBiq18iob5k69YI+DogAapJM59Z8ezKLLrLoL0WXyg3DFihV79+793//+t3nz5saN4eHhx44dq6urU1VtoDpXivnIHP6zvpifBqBx3u1BF9SS37NwgFRZ5ARhQ0PD9u3bv/rqq3feeadr166N23v06CEWi2W3jAddIuXI/EvsdwNoq+e6zxIAKIWAJlsHM28ncOX16i5FR8kJwpKSktra2iFDhjTbLpspWlFRoYq6QIXWJ3NOpiTCA+cGATRUYEdqgjv1wTUcIFUKOX2flZUVwzBPLiJz48YNQkgrZ5aCtnhQxX97h90yCAdFATTa5/2Y4zn85SLMmlE8OUFoamo6YsSI1atXl5SUUNRfUycKCgqWL18+YMAAR0dH1VYIyrUwnn2/F+NmhjkyABrN0pB8M4Ced4ltwLlCRZN/M4eNGzcOGTLE19fXz8+voqJi3LhxcXFxhJDz58+rtDpQsr0PuGIxWdIVB0UBtMBkD3rvA35DMvdBL/zPKpL8venr65uUlPTqq69WV1cbGhreu3cvIiLi+vXrvXv3VnF9oDxl9WTlVXbnUEaA/ykALbFpIP31bTatEgdIFUnOiFAkEn3yySdTpkz59ttvVV8QqMzyK+w0LyxjCKBN3Myo//ZmFlxiz4ZiQWCFkTMWqK6u/uKLLyQS3P9Dl10o4M/l8x8HYI4MgJZZ2o2ulpCfH+BUocLICUI7Ozt7e/vMzEzVVwOqUc+SN+PZjQNpMwN1lwIAbcRQZOdQ5t0rbAlWN1EQOUFI0/T69etXr159584d1RcEKvBZEtvdmhrvjnODAFqppw013YtecRWXFSqG/Fmjx48fr66u7tmzp4eHh6urq0DwT7PTp0+rqjZQinsV/NZULikcg0EALba2D9P9kPRcAR/kiHOFz0t+EBJC/P39VVkHqAZPyOJ49uMAxtFE3aUAwHMwMyA/DmLmX2KTJwmMca7/+cgPwgMHDqi4DlCN7alcLUvmdcZBUQCtN9aV2pVO/S+JXdsHSfhc0CHqkSIxWXWN3TqYoXEoBUAnbHqB2ZrK3avAZYXPRf6IMDIysqXbLb300kvKrAeU6K0E9o3OdE8bxCCAjnAQko8CmPmX2IvjcFlh+8kPwjfeeKOoqEjut3geHz200sk8/nopv3toi2eFAUAbze9M//KA25HKvYFTHu0lv1u8cuUKy/4zMbeqqurChQtfffXVpk2bVFUYKFKtlCyKZ7cMZoTIQQDdQlNky2AmKEoa6kY5mWBY2B7y+0V3d/dmW3r16mVjY/Puu++GhYXRND53aJmPbrCD7KmRzvgnAdBB3a2peZ3p5Ve4fUGYNdMebYi0kSNH3r9/PyUlRXnVgDIkPeb/7z731QD8hwDorFW9mGsl/IlcnLpqjzYEYVpaGiHEyMhIacWA4nE8WRjPruvHdDRWdykAoDRCAdk+hFl4ma3BKtFt16pZo1KpNCMjY/PmzZ06dfL09FRVbaAA39/jDBnyqi+OZgPouOGO1GB7au1Ndn0gDv+0TWtnjdI0HRwc/O233+IEoRYpqCWfJbHncbsWAP3w7UCm+0HJNC+6dwf807dBq2aNCgQCBwcHQ0NDVVUFirEwnl3clelihX8JAL3QwYj8rx8z/xKbMF7A4P++1eQHoZWVlampadO1tgkhUqm0urra2tpaJYXB84rK5VMq+N+CcZAEQI/M9qV/ecBtvsct6Yajd60lf0/5+fldvXq12cbExEQbGxvllwQKUC0hb15ifxzMGCEHAfQJRciPg5hPbrJ5Iswgba02fGSQSqUGBrh3j3ZYe4Md7ULh/iwAesjHklrcjVl+Bbewb61/Hfysq6sTi8WEEI7jqqury8vLG78lEokOHTrk7Oys6gKh7YrEZFc6lzwJq8gA6KkV/rT3AWlyGe+PtYVb4V995Y8//rhs2TLZ12PGjHmy9RdffKGKouD5rE9mZ/nQzqb4BwDQU8YM+U93+tOb3IEXcXbk2f4VhCNGjNi6dSsh5N13312wYIGXl1fjt8zNzbt3796jRw9VFwhtVFpH9qRztzAcBNBvb3ahNyRLbpfRPTAofJZ/dZc9evSQRV1DQ0N4eDgOhGqjdbfY6d4YDgLoOxMBWdaD+SyJw9TxZ5I/bli8eLGK6wCFKK0je+5zN8MxHAQAsrAr7bUfg8Jna7HHzM3NPXbsWGZmZk1NTdPtsmOnoJnWJ7NTPWkXDAcBgBBTAflPd+Z/t3BXimeQH4SxsbETJkyQSqWGhoYMw3AcV1VVJRQKHR0dVVwftF5pHdmdjuEgAPxjcTfaa7/kTjnd3Rqfj1sk/zrCt99+u3///qWlpREREYsWLaqsrIyLi3N2dl61apWK64PW+zKZnYLhIAA0YSogb3VnPk/CNYVPIycI6+vrU1JS1qxZY2ZmRgiRSqWEkMGDB2/btu2tt96SXWgImuZxPdmRxq3wx6JKAPAvS7rSZ/O51AosNNMiOf1mRUUFy7Kyo6BWVlaNl9UPGDCgurpadldC0DQbktkpnrS7GYaDAPAvZgZkSTfmUwwKWyYnCDt27GhkZPTo0SNCiIeHx8WLF2V3okhKSiKEyIaJoFEe15PtqdxKDAcBQJ6l3egzj7i0SgwK5ZPTddI0PXTo0OjoaELI1KlTs7OzBw8ePH/+/PHjx/v7++PGvBro69vsZA+6kzmGgwAgh5kBWdyV+ewmBoXyyZ9h+MMPP0rym1IAACAASURBVMiOiNrZ2R07duzzzz8/ffr00KFDN2zY0Pob816/fj06OtrW1nb69OmWlpZPNiguLv71119ra2vDw8O7dOlCCKmsrNy/f3/TNoMHD+7atWt2dvapU6caN44dO9bV1bWVZei8snqyNYVLnIjJogDQoqXdae/9krRK2s8Sn5ibk5NqPM/b2tp27dpV9nDEiBGxsbGZmZmHDh3y8PBo5etGRUWNHDmS47hz584NHDjwySk2paWlAQEBycnJtbW1AwcOlN31qa6u7vrfLl++PH/+/IKCAkJIcnLyhx9+2PitysrK9v/GOufr2+wkD9oDw0EAaJmFAVncDdNH5ZMzjCgoKHB2do6JiRk5cmS7X/fTTz9dt27dvHnzeJ4PDAw8cODAq6++2rTB9u3be/XqtWvXLkKIkZHRunXrDh8+bG9v33jB/oEDBy5cuBAUFCR76OXlhWv5n1TRQLalclcmYDgIAM/wdnfaa78kvZL2xaDw3+SMCK2trQUCAcO0fyUCkUj0559/hoSEEEIoiho7duyZM2eatYmNjR07dqzs67Fjx8bGxjZrsHPnzjlz5jQeiS0vL9++ffvvv//++PHjdheme76+zY53x3AQAJ7NwoAs7sqsu4VBYXNyRhJCoXDKlCk//fRTcHBw+15UdjzTzs5O9tDBweHy5ctPtrG3t29sUFVVVVNT0zglNS8v79y5c9u2bZM9NDIycnd3T05OTk1NffPNN2NiYgICAuT+6Ly8vLt37+bk5Pz16wkEK1asMDExkdu4vr7e0NCwfb+jJqhsIJvvURfG8PX1UnXX8mz19fU0Tbf+HDM8D4lEwrIsReETkopoS2fypg/peoS6WyL1tlB3Kc+hTXu7NeM6+YfUQkNDly9fPnTo0PHjxzs7OwsE/zR76aWXnvmDZZ0dz/81VZdl2SfroGma4/76YCL7ommbnTt3BgUFubu7yx6OGjVq1KhRsq+XL1++cuXK06dPy/3RhoaGJiYm1tbWsocmJiaGhoYtdb7a3i9/n0bGuRJfK+3o7Oi/qbsQvUDTNM/z2Nsqoy3vbWtj8mZnsuEutW2Qukt5Dm3a2635OCg/CJctW1ZUVFRYWBgXF9fsW43x9hSOjo4URRUUFHTq1IkQUlBQ8OQipU5OToWFhbKvCwoKrK2thUJh44/Yu3fvZ599JvfFR4wYcfDgwZZ+tJ2dnY+Pz5IlS55ZJCHEwMDAwMCgNS01UGUD+TFVEh8mMDDQjiCU7W2t6Cx0A03T2vv21jpa1Jm805P4HJDk1gk8tfaUisL3tvxe6cqVKxktaM2LCoXC4cOHHzlyhBAilUqPHz8uO18omxQquzx/7NixR48elcXqkSNHGs8XEkJiY2PLy8snTJjQuEX2FJkzZ874+fm153fVLd/d5UJdcdIbANrG0pAs6EL/D9NHm5A/Imw8JtluH374YXh4+P3791NTU01MTCZOnEgIycrK6tu3b3l5uZWV1Zw5c7Zs2TJhwgR7e/vDhw9fuHCh8bm7du2aOXOmsbFx45Y5c+ZUVla6ubmlpKQkJyc3vaZQP1VJyPd32UthmCwKAG22rAfje0CS1Qvz7P5CtXSok2XZc+fO3blzp7a29oMPPiCEpKSkmJmZtf5K9qysrNjYWGtr63HjxhkZGRFCRCJRfHx8cHCw7KRjTU3N8ePHa2trx44d2/TYaVxcnJ+fX+NcG0JIQUFBfHz848eP7e3tg4ODLSxaPM+7dOnS1h8ara6uNjc3b+Wvo1E+uck9qOL3DNOme4yJRCKhUIhDo6ohmyzT9NMkKJXWdSarrrHFdWTbYG3qQxopfG/LD8KioqKQkJAbN24IBAJ7e/u8vDxCyH/+85/ExMRLly4p8McrnD4EYZWEeO+XxIUJtGuFCAShKiEIVUzrOpOyeuJ7QJI4UaCNg0KF7235vdIbb7xRXl5++fLlmJiYxo0vv/xyQkJCVVWVAn88tMOmu9wYF6yTBADtZ2NE5nehv8A1hYQQuUEoEomio6O/++67gQMHNv387uPjw3Fcbm6uCsuD5mokZNNd9r+9Ma4CgOeyrAdzMIt7WI1bUsgLwsrKSpZlvb29m22XXe1XX1+virqgBRvvciOcMRwEgOfVwYi80Zn+IhmDQnlBaGtra2Jicu3atWbbY2NjGYbx8vJSSWEgh0hKNt1lV/XCcBAAFOAdf+ZAJpddo++DQjldqqGh4dSpU1euXHnhwoXGa/JPnz69bNmy8PBwuTdUAtXYdJcLdqI7a8lSMgCg4WSDwvV6PyiUfyHaN998k5aWNnz4cFNT04aGhg4dOpSVlXXv3v2HH35QcX3QqEZCvr3DngvFtYMAoDDLezBdfpe835N2MdXfT9jye1ULC4vz588fPnw4JiamsLDQ2tp62LBhzS5yBxXbnMINd6S7YDgIAIrT0Zi85kevu8V9/4JWXlOoEC0OLwQCwZQpU6ZMmaLKaqAlIin5+jZ7eiyGgwCgYCv8mc6/S97T40Hh0zrWlJSUW7duPXr0yN7evnv37r169VJZWdDM5nvcMEe6h42evk0BQHlsjclsX3p9MrdxoJ4OCuUHYXV19ezZsw8fPtx0Y1BQ0L59+xpvIggqUyslX99mT2E4CADK8a4/0/WgZKU/7ayXg0L5E/Hnzp0bHR396aef3rt3r6ysLD09/bvvvktKSoqIiFBxfUAI+TGFG+JA+2M4CADKYS8kr/rQX97W0+mjcgYZ1dXVhw8f3rx587x582RbrK2tfXx8PD09w8LCHjx48OS19qA8dSz55g4XPVpPD1kAgGqs6Ml0OyhZ4U87mejdZ245I0KxWMyy7LBhw5ptHz58OCGkurpaBWVBo833uAF2FIaDAKBUDkIyy4feoJfXFMoJwo4dO3p7eyckJDTbnpCQYGlp2blzZ5UUBoQQUseSr+9wq7GyKAAo33s9mT33ufxavVtoRs6hUYqidu3aNWPGjOrq6vDwcEdHx+Li4pMnT65du/ann34SCoWqr1JvbUnhAjtSPTEcBADlcxCSmd7017e5Df3161yM/KHGSy+9lJubu3TpUldXV4FA4OTk9Nprrz18+DA8PJz6244dO1Rcq74RS8mXydwaDAcBQFVW9qR3p3NFYnXXoVryZ+SvWrVKJBI9/ZmBgYFKqAf+sT2N69eR6tUBw0EAUBEnE2q6F70hmf1SnwaF8oNw8eLFKq4DmqlnyZfJ3B8j9ei9CACa4INeTI9Dknf9GTu9OQ+Gw24aalsqF2BL9bXFcBAAVMrRhLzsRX91m1V3IarT4mIliYmJx44dy87Orqura7r9wIEDyq9K39WzZH0yd3gEhoMAoAbv9aR7HZYu76Evg0L5Qfjll1+uWLHC1NTUzc3NxMRExTXBjjSuVwfSryOGgwCgBq6m1Mue9Dd32M/76cXHcTlBKJVKP/zww9dee+3777/HxRKq18CRL5O5Ay/qxfsPADTT+73oXoely3owHfXg5ntyzhGWlZWJxeKFCxciBdViZxrXzZoEYjgIAOrjakq95EF/e0cvzhTKX1nG3d09MzNT9dWAhCPrk7k1vTEcBAA1+6AXvSWFK6l7dkttJycIKYravHnz6tWrr1y5ovqC9NyudK6zJelvh+EgAKiZmxkV4UF/pweDQvmTZYKDg/v16zdgwAALCwtbW9um38rIyFBJYfpIypF1t7h9QRgOAoBG+KAn3feI9B1/xspQ3aUok/wgnDNnzv79+4cOHert7S0Q4H6wKnIij3M2IQMwHAQAzdDJnBrpQv/ygFvUVZcvOpcTclVVVfv379+wYcOyZctUX5A+25HGz/XT5XcbAGidub708iusbgehnN9NIpHwPC+7+yCoTKGYxBVyL3no8rsNALTOi86USEqul+ryvZnkdLsdOnQIDAyMj49XfTX6bFcaN8WDNjNQdx0AAE1QhMz2oXem6fINe+Wf//vss8/mzp3b0NAwatQoU1PTpt/y9PRUSWH6hSdkdzr3K6bJAIDmmeNL+R9mN/RnTHR0xoj8X2vmzJlFRUXvvPPOk9/ieV0eIKvLuXxeKMCaagCgiZxNqRfsqd+zuFd9dPPcjfwg3L59e7O1tkGpdqZxb2CaDABoqrl+9Ne39SwIw8LCVFyHPqtoICfzuE0v4PQgAGioca70ongupYLvYqWDB66eFu81NTU3b96Mi4tTWTX6ae99bqwrbWOk7joAAFogoMkrPtRP6bo5ZUZ+EEokkrfeeqtDhw4BAQHTpk2TbZw3b9706dNVWJu+2JXO4fJBANBwb3Sm/+8+J9HFKJTf/65cuXLnzp0fffTRpk2bGjdOmjTpyJEjOHeoWIklfGUDGeagg0cbAECXeJpTflZUZI4OJqGcIGxoaNi2bduXX375/vvv9+jRo3G7v7+/WCzOzc1VYXm6b2ca97ofTSMHAUDjzfXTzQsK5QRhaWmpSCR6cmUZMzMzQkhFRYUKytITIin5PYub7YsYBAAtMLkTfaWYzxXp2kV0coLQ0tKSYZicnJxm25OSkgghzs7OqqhLPxzI5AY70E4mCEIA0AJCAZnqRe9O14MgNDU1DQ4OXr169ePHjynqrz5adn19YGCgk5OTaivUZTvTuLkYDgKA9pjXmd6RyrG6FYXyryPcuHHjkCFDfH19u3TpUlFRER4efv78eZZlz507p+L6dFhaJZ9ZzY91xXxRANAa/jaUnZCczedHOuvOh3j5vXDnzp2TkpKmTZtWVFRkYGBw/fr1sLCwxMTEPn36qLg+HbY9lZvjSxsgBwFAq+jelJkWl1B1dnb+/vvvVVmKXmngyM8PuEthOrqELQDorule9AeJkpI6pqOxuktREPnjkSlTpty7d6/Zxnv37o0cOVL5JemFY9lcN2vK20J3ji0AgJ6wNCTj3emfH+jOoFB+EF68ePHJyyQqKipiY2OVX5Je2JmG1WQAQFvN9aO3pep6EMqVnZ1ta2urvFL0R56ITyzhw90RhACglYY6UBQhfxbryOTRf52jOnTo0JYtWwgh5eXlb7/9tqWlZeO36urqrl+/HhIS0vqXlkgkubm5Tk5OxsYtHkjOy8szMTGxsbFpzQvm5+cbGBh07Nix9TVoph1p3HRvWojzgwCgtWb70jvTuAF2unA78dYOSqytrZctWyaLydY4d+6cm5tbaGioi4vL4cOHn2xQWlrav3//wYMH+/r6Ll68WHa/36KiIqqJjz76SNa4pqZmxIgRgYGB3bt3nzFjhlQqbWUZGojjyU/p/Gu+GA4CgBZ71Yc+9JCrlqi7DkX416gkIiIiIiKCEDJq1KgNGzb4+/u370U5jps7d+6GDRtmzJhx9uzZyZMnjxkzxsTEpGmbTz75xN3d/c8//ywvLw8ICBg3btyYMWMIIQYGBg0NDc1e8JtvvqEoKjs7u76+vn///vv27Zs1a1b7alO7mEe8nZD06oBpMgCgxeyFZLgjvT+Te137pzvI/wViYmLanYKEkISEhKqqqqlTpxJCgoODHRwcoqOjm7X59ddfFy1aRFGUjY3NtGnT9u3b1/it+vr6ZmO+X3/9dcGCBQzDmJiYzJkzp2ljrYNpMgCgG173o3foxAWF//TIDx8+bOWC2llZWZWVlU9p8PDhQ09PT4b569ixj4/Pw4cPmzaoqakpLS318fGRPfT29s7KypJ9LZFIHBwczM3NR44cmZmZKduYnZ3t7e39ZOMnNTQ05ObmXv9bSkpKa34jlSmpI7H53DQvBCEAaL3RLlS+iNwp1/opM/8cGr1y5cqbb765ePHi2bNne3p6ym199erV7du37927NyUlpelUmmaqq6uFQmHjQxMTk6qqqqYNZA8b25iamsq2WFpa3r9/39vbu6amZuHChVOnTr169apEIhGLxU82luv+/fvp6emnT5/+69cTCP7444+WSq2pqWnpdZRke5og1Imi6uqq9e+ujrW1tVKplKbxIUAVJBIJy7ISiU6cwNEGqu9MNMT0ToIfb0vW9VbpvI027W1jY2MDA4Ont/knCF9++WUDA4P33nvv008/7dmz58CBA/38/GxsbKRSaUlJyZ07d+Lj4zMzM4cNG3bp0iUPD4+nvKi9vX15eXnjw/Lycnt7+6YNOnbsSNN0RUWFtbU1IaSsrEzWwNjYWDbyMzMzW7dunbOzc1lZmY2NjbW1deNotbGxXN26dZs4ceKSJUue/ms3Mjc3b2VLhfjloXTbEMbcXFfWY2gLmqaFQiGCUDVkQfiUCdugcCruTDTEgu58v6PSrwYJjVU7e1Sxe/tfk2UmTZo0ceLEkydP7tmz59ChQ8XFxY3f8vLyGjly5BtvvNGa5Ub9/f3T09MrKystLS1Zlr127drq1aubNjAwMOjateuVK1dkgXrlypVevXo1e5GysjKGYWQDwZ49e165ciUwMLClxlohvohnefKCPabJAICO6GRO9e5AHc3mXvbU4s+4za9lo2k6JCQkJCSE5/nCwsKSkhKBQODg4NDKS/1kvLy8goODFy5c+O677+7atcvd3X3QoEGEkAMHDhw4cODgwYOEkMWLF69Zs8bd3T0rK+vIkSPXr18nhERFRRUXF3fp0qWkpGT16tXTpk2TBeGSJUuWLFnSo0ePqqqqnTt3xsTEKGwHqNDONO71zrgXPQDoFNka3DoVhI0oinJ0dHR0dGzf6/7888+rVq168803u3TpcuzYMdnGDh06+Pn5yb6eN29eXV3dypUrzc3Njxw5IjsiamNjs3fv3u3bt1tZWb3yyisLFy6UNZ40aVJFRcXHH39saGi4Z8+efv36ta8qNaqRkKPZ3Lp+zzhUDQCgXcI70UsT2Iwq3ktrF0+mZFey64ylS5f6+Pi08hxhdXW1yg7rb03lzjzif39RF1ZhaB+RSIRzhCqDc4QqpsrORAMt+5M1MyBr+6iof1P43kavpCK4fBAAdNW8zvTudF57b1uPrlkVbpfxhbVEl27oDADQqLMV5WJKTuZpaxIiCFVhRxr3mh/FIAcBQEdp9W3rEYRKV8+S3zK5OVhlGwB011RP+nwBV1Cr7jraBb2z0h16yPXuQLmbYTwIADrLzIBEdKL/775WDgrlXz4xZcqUpkvDNNW4ehm00s40bkEXfOAAAB33uh/9ygV2RU/tu1q6VR10ZWVlQkLC1atXlV2N7smq5m+X8ePdEIQAoOP621FChsQVat+UGfkjwgMHDjTbUlJSMnny5FGjRim/JJ2yI417xYc20t+rBwFAj8huWz/UQcu6vNaOVDp27Pj111+vWbPm6TdggqakHNlzn38Nlw8CgH6Y5UMfy+bK69VdRxu1oY92cnKqq6vLyMhQXjU65kQe18mMdLXSugPmAADt0cGIjHah92Vo2ZSZ1gYhz/Pbt28nhHTq1EmJ5eiWnWk8VpMBAL0y14/emqplQdiqWaNSqTQrKys7O3vmzJltug2FPisUk4uF3M/Dsco2AOiREc6USEpulPIBtlpzMKzFu080ZWRk9OKLL44ZMyYiIkLZBemM3encSx60GXIQAPQJRcirPvTOdC7AVmumzLR21ii0CU/I7nTu5+Fa8z4AAFCU13wp/8Psl4GMSauGWuqHM1hKcb6AN2ZIYEetOTIAAKAozqbUADvq0EOtOVOIIFSKnWnc65gmAwD6SrvW4EZnrXgVDSQqh5vuhX0LAHpqvBudXsmnVmjHKjPorBXv5wfcWFfaFvcGBwB9JaDJLG96d7p2DAoRhIqH46IAAHP96P+7z0m0IQrRXyvYtVK+soEMd8Q0GQDQa76WlK8lFZWrBUmIIFQw2XBQ+25DAgCgaNoyZQZBqEhiKTmYxc32RQwCAJCXPOiEIj5XpOlTZhCEirQ/kxtoRzuZIAgBAIhQQKZ40nvSEYT6ZGc6N9cPKQgA8Je5fvSudI7T7ChEECpMWiX/oJIPccUuBQD4Sx9bysqQnM3X6CREr60wO1K5Ob60AfYoAEATc/3onZp9QSG6bcWQcuSXDG6OL/YnAMC/zPSmT+ZypXXqrqNl6LgV42g219mS8rHECUIAgH+xNCRhbvQvDzR3UIggVIyd6RxuRg8AINdcP3qHBl9QiL5bAfJE/JViPrwTdiYAgBzDHCkpT64Ua+iUGfTdCrD3AT/Vi9aWW1ACAKjeqz70nvsaOihEECrA0Wxusgf2JABAi17yoI5m85o5JET3/byKxCS9kh9sj2kyAAAt8rKgLAzJjVJNjEIE4fOKzOHGuuDyQQCAZxjvRkXmaOLRUfTfzysyhw9zw3AQAOAZwtzoY9kYEeocsZRcKODGYFk1AIBnecGeyq/ls2s0LgvRgz+XM/lcX1vKylDddQAAaDyaImNc6KgcBKFuiczhw9ywDwEAWiVMI08TohNvP56Q6Fw+FCcIAQBaZ7QLfbmIr5aou45/QxC2X2IJb21IvC0QhAAArWJmQF6wp2LyNGtQiCBsv8gcbrw7UhAAoA3C3OhIDTtNiCBsv2PZOEEIANA2E9ypqFyO1aQoRD/eTjk1fKGYD+yIESEAQBs4m1JuZlRCkQYlIYKwnY5m82FuNI0cBABoI02bO4ogbKfIHA4LygAAtEOYG31Mk04TIgjbo0pCrpbwI5yx9wAA2izAlqqRkPRKTclCdOXtcSqPG2RPmeIGhAAAbUcRMs6N0py5owjC9jiWzU9wx64DAGin8W605pwmVNaghuO4b775JjIy0tbWdsWKFYGBgU+2OXPmzMaNG0Ui0bRp015//XVCSE1NzY4dOy5cuFBZWdm7d+8VK1bY29sTQpKTk3/44YfGJy5ZsqR79+5KqvyZWJ6czOM+74fxIABAOwU7UdPP8Y/rSQcjdZeivCD89ttvd+/evWXLljt37owePTolJcXBwaFpg5SUlEmTJv34449OTk6vvvqqqanptGnTsrKyEhISZsyYYWdnt3HjxpEjRyYlJdE0nZ2dfeHChU8++UT23A4dOiip7Na4VMh7mFMuppgpAwDQTkYMCXKiT+RyM73Vf3RNWUG4cePG77//fvDgwYMHD46Ojv7pp5/ee++9pg1+/PHHqVOnzpgxgxDy4Ycfbty4cdq0aT169Ni/f7+sQa9evSwtLR8+fOjp6UkIsbW1femll5RUbZtE5nC4jh4A4DmFuVGROfxMb3XXoaRzhOXl5dnZ2QMHDpQ9HDhw4M2bN5u1SUpKGjBgQGODpKQknv/XidOUlBShUNg4jszKypo6deqCBQvOnj2rjJpbD3fiBQB4fuPc6NOPuAYNOFGolBFhYWEhRVFWVlayhzY2NoWFhc3aFBUVWVtby762trauq6urrKxsfEpNTc0bb7zx8ccfm5iYEEKcnZ2XLVvm5eWVmpoaHh6+efNm2VDySXfv3v3jjz92794te8gwzJEjRywtLeU2FolEFNW2SEuvosRSQy8jUU1Nm54HpLa2lmVZmsZgWhUkEgnLslKpVN2F6It2dCYgJMTX3OBkZm2wQ9vCsE1729jYWCB4RtIpJQgtLCx4nq+rqzM1NSWEiESiJ6PI3NxcLBbLvq6traVpWtaYECIWi8PCwvr37//OO+/ItgQEBAQEBMi+NjMz+/bbb1sKQm9v7z59+rz88suyhwYGBs7Ozi3VyfO8mZlZm361M5ncBHfevI3PAkIIRVFCoRBBqBqyIDQ2NlZ3IfqiHZ0JEEImenBnSgTjvZk2PUvhe1spQWhvb29sbJyRkeHv708IycjIcHNza9bGzc0tIyND9nVGRoaTk5OBgQEhpK6ubuLEia6urlu3bpWb+e7u7o8fP27pRxsZGbm6uvbp00dhv8y/ReZwq3u37W8GAAByjXenxp7kNg5UcxlK+XguEAgmT578448/EkKKi4sPHz48bdo0QkhZWdn69evr6+sJIdOmTfvll19qamp4nt+6dausQUNDw5QpUywsLHbt2tV06JCamio7yFNTU/PDDz8MGTJEGWU/0+N6cqeMH+aAAyAAAArQ1YoyYkhymZqvrFfWcarPPvvs4sWLXbt27dat2/Tp0wcNGkQIKSoqWrlypeyI6KRJkwIDA729vX19ffPz82VzSi9fvhwZGXnw4EEDAwOKoiiKunTpEiFk48aNHTp06Nq1q6OjI0VRGzZsUFLZT3c8hxvpTBthQAgAoCDjXKlj2WoOQqrZXE0F4nk+IyPDysrK1ta2cSPLsgzzT5IUFRWJRCLZBRJPV1ZWVlpa6uDgYGFh8ZRmS5cu9fHxWbJkSWsqrK6uNjc3b01Lmcmx7AR3apYGXPWijUQiEc4RqgzOEapYWzsTaHSugH/vKntlQhvO0yl8bytxeRSKory9m18h0jQFCSGyhWNaw8bGxsbGRjGVtUs9S2IfcVsGGaixBgAAHTPUgcqs5h+JeGf1rVKCj+etda6A97ehbPEJGwBAcRiKjHKmT+Sp8+gogrC1InO4MCy0DQCgaGHqvhMFevbWisrhx2NBGQAARRvrSl8o4GrVt/wDgrBVkh7zRgzxtUQQAgAomKUh6WtLxearbbE1BGGrHM3mJ7gjBQEAlCLMjVbj0VEEYavgjhMAAMozsRN1LJvj1BSF6NyfLb+Wf1jND7TDiBAAQCnczaiOxlRiiXqSEEH4bMey+VA3WoBdBQCgNOPdqcgc9ZwmRO/+bJE5HG5ACACgVGo8TYggfAaRlMQX8aNdsKMAAJQosCNVLOazqtWQhejfnyEmjxtgR5ljYTUAAGWiKRLqRh9Xx6AQQfgMkTk85osCAKhAmJt6ThOii38ajifRuVyoK04QAgAo3Shn+moJX9Gg6p+LIHyaP4t5RxOqkzmCEABA6YQCMsSBislT9aAQQfg0kTkc1hcFAFAZtcwdRRA+zbFsHnecAABQmTA3+kQuJ1XtmBC9fIsyqviKBtLHFiNCAAAVcTQhnhbUpSKVDgoRhC06lsOHuVGIQQAAVQpzo1U8dxRB2KLIbNyJFwBA1ca7U0ezMSLUABUN5MZjPtgRA0IAAJXqaUNJOZJSobosTJToewAAGCpJREFURBDKF53LBTnSQoG66wAA0D9hbpQq544iCOWLzOHDcCdeAAB1CHNX6WlCBKEcEo7E5HEhrtg5AABqEORI3S3ni8Qq+nHo6+W4WMj7WVIOQnXXAQCglwxoMsKJPpGrokEhglCOyBzMFwUAUKcwd9WdJkR3L0dUDo878QIAqFGoK302n6tjVfGzEITN3SnnpTzpbo0gBABQGxsj4m9DnctXxaAQQdjcsWx+AuaLAgCom8rmjiIIm4vM4XAnXgAAtZvoTh3L4VUwJESP/y/FYpJWyQ9xwIgQAEDNvC0oMwG5War0KEQQ/ktkDjfahTbEXgEA0ADj3aljyj86ii7/XyIxXxQAQGOo5j69CMJ/iKXkfAE31gX7BABAI7xgT+XW8Hki5WYhOv1/xObzAR0oayN11wEAAIQQQhiKjHVV+qAQQfgPLCgDAKBpwtwoZV9EgX7/LzwhUbk4QQgAoFlGu9DxhXyNRIk/AkH4l+ulvIUB8bZAEAIAaBBzAzLQnop5pMRBIYLwL8eyOSwoAwCggZQ9dxRB+Jdj2TwWlAEA0EDj3anoXI5VWhSi6yeEkJwavkDM97fDiBAAQOO4mlJOJtSfxcpKQgQhIYQcy+FDXWkGOQgAoJHGK3PuKIKQEEIisznMFwUA0Fhh7nRkNkaESlMjIVdK+BHO2BUAABqqjy1VJSH3K5WShej9yYk8bpA9ZW6g7joAAKAFFCGhrtTxXAShckRivigAgMYLc6cjs5VymlDfA4Dlyck8bhxOEAIAaLYRTtTNx/zjesW/sr4HYXwR725GuZgiCAEANJoRQ4Y70qfyFD8oFCj8FRtdv379xo0bXbp0GTx4sNwG+fn5p0+fNjMzCwkJEQqFjdvPnj2bmZkZGBjo7+/fuLG0tPTkyZMGBgYhISHm5uaKKjIyGwttAwBohzB3KjKHD7NT8MsqKwO+/vrrCRMm3Lp1a/bs2StXrnyyQVJSUvfu3S9cuLBly5ZBgwaJxWLZ9gULFixatCgpKWn06NE7duyQbczIyOjWrdvJkyd//fXXgICAsrIyRdV5DHfiBQDQEuNc6VN5XIPCx4S8EtTU1FhaWiYmJvI8n52dbWxs/OjRo2ZtIiIiVq1axfM8y7L9+/ffsWMHz/P37983MTEpKirief7s2bMODg719fU8z8+fP3/BggWyJ44dO/bzzz9v6UcvWbJk48aNrazz+qNq518lXJt/P2iPmpoalmXVXYW+aGhoEIvF6q5Cj1RVVam7BH0x8Kjk2P0axb6mUkaEly5dsrKy6tu3LyHEzc2tV69eMTExzdI3KioqIiKCEELT9MSJE6Oioggh0dHRgwYNsrOzI4QMHz5cIpFcv36dEBIVFTVp0iTZcyMiImSNn1/0I2aCO4XxIACAtghzp0/kKzi5lHKOMD8/39nZufGhs7Pzo0ePmjYoKyurq6trbOPk5JSfn9/siRRFOTo6Pnr0iOO4wsLCJxvLVVJSkpWVVV1dLXtoYmLyxhtvGBoaym184hH1fi9OIlHuLR9BRiKRCAQCmsYZWVWQSCQsyzIMo+5C9IVEIpFIlHnHPPhbiBOZcI9p/d5mGOaZ3Y5SgpBlWarJQIumaZZlmzUghDS2YRhGKpW29ESO4ziOe7KxXPX19bW1tY0nEauqqurr61vqDsKdG4baGf67NFAWlmVlh0bVXYheYP+m7kL0Bfa2yviZk/meDSwrf3jzpNZ8+FZKEDo6OhYXFzc+LCoqGjVqVNMGtra2BgYGxcXFtra2sgZOTk6yJ6akpDR9opOTk0AgsLOzKy4u7tKlCyGksLBQ1lguFxeXoKCgJUuWtKbO+Z0l5ibGbfzloJ1YljU2NsaIUDUYhpHtcHUXoi8kEgn2tsos7qrgva2UXmngwIF5eXkPHjwghJSXlycmJg4fPpwQIhaLZWM1mqaHDx9+8uRJWfuTJ08GBwcTQoKCguLi4kQiESEkKSmprq4uICBAtv3UqVOyxqdOnZI1BgAAeH5KGRHa2NgsXLgwPDx89uzZBw8enDRpkre3NyHkp59+2rp1a1JSEiHk/fffDw8PF4lE2dnZaWlp+/fvJ4T07t172LBhoaGhYWFh27ZtW758uampKSHk3XffHT58OMMwVVVVp0+fvnHjhjLKBgAAPaSs41RffvnlRx99VFZWtnjx4j179sg2BgcHr127VvZ1UFDQ+fPnOY7r2rVrYmKitbW1bPvBgwdnz55dVla2YcOG1atXyzb27t37ypUrRkZGTk5ON27ccHFxUUiRMTExHIeZMipy9erV0tJSdVehL7Kzs+/evavuKvRFbW3thQsX1F2FHmk8mqgolI5NXli6dKmPj08rzxE6ODgkJSU5ODgouyoghEycOHHWrFmya2ZA2b766qvs7OyNGzequxC9cPXq1YULF167dk3dhegLQ0NDkUhkYKCwewZh5gKojo596tJk2NUArYcgBAAAvYYgBAAAvaZr5whDQkIyMzNdXV1b0zguLq5///4trTsDipWcnOzg4CBbPw+ULScnp66uztfXV92F6IWqqqrU1NTAwEB1F6Ivzp49GxQURLVufczw8PCFCxc+vY2uBWFiYmJeXl4r79OUlZXl4eGh7JJAJj8/38bGBhcdq0ZVVVVDQ4NswQpQNpZlHz165Obmpu5C9EWbum4PDw8vL6+nt9G1IAQAAGgTnCMEAAC9hiAEAAC9hiAEAAC9hiAEAAC9ppRFtzVfUVFRSkqKp6dnSxO9KioqTp48yTDMmDFjWjkHFVpSXV198uRJjuPGjBljaWnZ7LsikSghIaHxoZ+fXyuvfoFGcXFxDx486NevX/fu3eU2yMjIiIuLc3Z2fvHFF3EnrOeUk5Nz7tw5e3v7ESNGCATNu9Dc3Ny0tLTGhwMHDpTdOQDaJz8/PzU1tXPnzi3dfa+0tDQmJsbY2HjMmDEmJibt/DG8/hk1apRQKDQ1Nf3mm2/kNsjNzXV2do6IiBg/frynp2dxcbGKK9QlRUVFHh4e48ePj4iIcHFxyc3NbdYgJSXF0NBwxN8OHz6sljq116JFi3x8fObPn29vb79z584nGxw/frxDhw6vv/567969J06cqPoKdcnZs2dtbGzmzp0bGBg4atQo2b2mm9q0aZODg0Pj+/nhw4dqqVM3BAYGmpmZCYXC3bt3y22Qnp5uZ2c3ffr00aNHd+vWrbKysn0/SB+DMCsrSyKRjBkzpqUgXLZs2axZs2Rfh4eHf/TRRyqsTtesWbMmPDxc9vWsWbOWL1/erEFKSoqdnZ3K69IRGRkZQqGwoKCA5/nY2FgHB4eGhoZmbXr27PnTTz/xPF9dXe3o6BgXF6eGQnXFoEGDvv/+e57nxWKxp6fniRMnmjXYtGnT9OnT1VGaDsrMzJRKpQMGDGgpCF977bUlS5bwPM9xXFBQUEtd+jPp40GSTp06PXlAo6njx49PnjxZ9nVERMTx48dVUpduas3OZFk2NjY2Pj5edk9maL3o6OgXXnhBdgeVoKAgiUSSmJjYtEFOTk5ycrLsph9mZmajR4/G+7ndysrK4uPjZTvT2Ng4NDRU7s4sLy8/ceLEzZs3cZe35+Th4cEwzFMaHD9+XPbn+P/27j4oqqoNAPjZD5bvBZZguYCAS8sI8aVAQFhQYg3GgIGpxFROYsUIjGnaFOCAkWEwKoOZlTISSuQSKkQpaIpCTATxDYFIAUIssLvsALuwy+6+f5zpzg4siCLwAs/vr3ufc+69Z8/u3Gf33rP3UCiU+ZyrV2MifKi+vj4rKyu8bGVl1dvbu7TtWdZ6e3sf2plMJjMjIyMmJobL5arfLwQP1dvbS07PSaFQCIKY0sN9fX3GxsYGBgZ4FT7P89HX10en09lsNl7V2JkUCoXP53/11Vdbt2718fERCASL3szVQi6XDw0NkZ//+Xy2V+ZgmV27dtXV1U0Jbtmy5ejRo3PZfHJyknyKHY1Gm5ycfMLtW1kuXbqksWPxW6BQKMjRGRo7k8vldnZ24uXk5OQ9e/Y0NTUtZHtXFIVCof7ERTqdPqWHp1SAz/N84A/z7CeH999/f+/evQghmUwWFBR05MiRjIyMxW7o6qBQKJRK5RM5V6/MRHj48GGJRDIlaGxsPMfNCYIYHBzEy3w+f6bRSgALDAx0cnKaqZQgiIGBAbyssTPVL31EREQkJydPTExoa2svRFNXHoIg1Gein97DFhYWw8PDMpkMP1yez+cTBLHYrVwp8C3Y4eFhfDLR2Jnk55nBYGzbti0vL2+xW7lq6OjomJiYDA4OcjgcNL9z9cq8NMrhcJynIX9BaySXy0UiEV4OCAi4fv06Xi4pKQkICFjoBi9rLBZrem+T4/hn6kyRSCSXy6fs6s8//zQ3N4csOHcBAQHl5eX4a19DQ8PY2JiHhwdCSCKRjI6OIoTWrl1rY2Nz48YN9N+92BdffHFp27x8sdlsJyenkpIShJBKpSotLcWdqVAoNF4Crampgf8CPXH4uwheflLn6pX5i3B258+fr6ysbG5uFovFra2tUVFRXl5eJSUlb775plAoRAjt37/fz89PX19fJpPl5+dPGX0AHklcXJyXl5eJiQmDwcjKyqqoqMBxDoeTm5sbFBSUnp7e1tbm4ODQ29ublZV14sSJpW3w8rJ+/frnn38+ODg4JCTkm2++2bdvH74dmJCQ8ODBg0uXLlGp1I8//vjdd9/dv39/eXk5k8ncsmXLUrd6GYuPj4+Li+vu7q6pqZHJZGFhYQihuro6T09PmUympaUVGRlpaWnJZrOrqqpKSkrKy8uXusnL2OnTp+vr6zs7O7OzsysrK2NjY52dnfPz8xMSEvD9lEOHDr3yyisUCkUgEJSVlZ08efLxDkRLSkp6kg1fDoaHh7W1tV944QV3d3dLS8tnnnmGxWLp6uo6Ojq6ubkhhMzNzcPCwlpbW3V0dDIzMx86hQeYBYvF2r59e1tbG5VKzcjIcHR0xHFLS0sfHx8mk0kQxMjISH9/P5vNPnr0aFBQ0NI2eNkJDw9XKpUPHjx46623oqOjcdDIyMjV1RVfMvLw8HB1dW1paXFxcTl58iTMhDUfLi4uzz77bHNzM5fLPXXqFP7awWAwuFyup6cnhUKxtLQcHBwUiUSurq5nzpyBid7mQygU6unpvfTSSy4uLpaWls7OzkZGRnp6ek5OTviak7W19auvvtrS0mJkZPTll1+S4/IeFUzDBAAAYFVbmfcIAQAAgDmCRAgAAGBVg0QIAABgVYNECAAAYFWDRAgAAGBVg0QIAABgVYNECMCCEwqFPB5PJpMtdUNQQUHBzZs38XJXV1d2djZ+AM0iE4lEPB5vYmJi8Q8NwHSQCAFYcPHx8d9++y1+2ufSSklJOXv2LF7+448/du3axefz57/b6urqrKysuddnMpmJiYmnTp2a/6EBmD9IhAAsrPb29rNnzyYmJi51Q6Zydnb+9NNPTU1N57+rwsLC2NjYuden0WiHDh1KSUkRi8XzPzoA8wSJEICFdebMGVtb240bN06JKxQKPp+vcS5iqVTa398/06XU2UvJCuRDo8bHx/l8/vRJYtetW5eQkDB9VpbJyUly9pUplErlwMDAI012I5PJ+vv7pVLplPiOHTsmJycvXLgw910BsEAgEQLwaGJjY62trTs6OvDq5OTkpk2bNmzYoPFmm1KpzMnJee2119QnBRwfHz9w4ICZmZmFhYWBgYG9vT2eHQIhxOfzw8PDjYyMCIIwMTGJjo5Wn1Csr68vNDQUP6CVxWLFxsaOj4/jor///pvFYuXk5EREROAKQqFQoVB8+OGHLBbLwsLCysrq+++/V29bcXExQRBdXV141dPTMy4u7vjx42ZmZubm5iwWKzMzk6xcVVUVEBCgo6PDZrP19fX9/Pzq6+tx0cGDB9PS0qRSKYvFwsfCcbFYHBUVZWJiQhAEk8kMDw9Xz6/6+vqbN2/Ozs5+nPcAgCdLBQB4FKOjo46Ojq6urlKpVKVSffTRR3Q6vaKiQmPl2tpahFBBQYF6MDg4mMFgJCcnV1dXV1VVZWRkXLlyRaVSTUxMuLm5GRsbZ2dn19fXp6ena2lphYWF4a2kUqmTkxOLxbp48WJ9fX1qaiqdTn/jjTdw6b179xBC5ubmb7/99o0bN37++WeJRHL48GEKhZKYmNjY2HjlyhUbGxtjY+OdO3fiTXg8HkKoo6MDr3K5XAsLi40bN167du23334LDQ2l0WgtLS24tKioKCEh4fbt262trcXFxe7u7hYWFqOjoyqVqrW1NTIyUltbu7S0tLS09ObNmyqVSi6X+/r6EgSRnZ3d3Nx8+fJlW1tbb29vhUJB9sMXX3xBo9FEItGTeWMAeFyQCAF4ZI2Njbq6unFxcb/88guVSk1LS5up5nfffYcQampqIiN40GZ6evr0yjgz5ebmkpGEhASEUH19vUqlysnJQQj9+OOPZOnBgwcpFEpbW5vqv0QYGBhIlkqlUkNDw4iICDKCf3fOkgjNzc3FYjFeFQqFWlpaqampGl8XPlxRURFeTUxM1NPTU6+Qm5uLELp79y4ZKSsrQwjdunWLjFy9ehUhVF5ervEQACya1TgfIQDz5OzsfOLEiejo6PPnzwcFBR04cGCmmvhiIIvFIiOlpaUIod27d0+vXFdXR6PRtm3bRkZ27tyZkpJy584dV1fXuro6bW3trVu3kqU7duxIS0u7c+eOg4MDjoSEhJCl9+/fHxkZCQ8PJyObNm2afkdQnZ+fH5PJxMsmJiYWFhY9PT1kaU9PD4/H6+7uxjf8qFQqeX14uuvXrxsaGo6Pj5NXfRUKBY1Ga2pqImdPxeN0BgYGZmkSAIsAEiEAjyMyMvKTTz4RCoVJSUnq9/+moNPpCCH10SVDQ0P6+voaE1J3d/dTTz2lpaVFRiwtLRFCePbz7u5uNptNpVI1lmLk/TmEUG9v75QIQoggiFlelHrCRghpa2uTQ3IuXLjwzjvvODo6ent7m5iYUCgUKpU6y5hPPp8vkUi2b9+uHmQymSKRiFyVy+UIIfXXC8CSgEQIwOOIiYmRy+V2dnYxMTF3796d6WzOZrMRQgKBYM2aNThibGw8NjY2OjqK53RVp6+vLxQKlUolme3wD0ojIyNcOjQ0pF5fvRRTT8nm5uYIIY2bPIYjR44EBwcXFBTgVbFYfOzYsVnqGxkZmZqazv4nRZzCcRcBsIRg1CgAjywvLy87O/v06dM8Hq+2tjY+Pn6mml5eXgihxsZGMuLv748QwvfnpvD29pbL5SUlJWSkqKgIIeTr64sQ8vHxkUgkt27d0lg6HZfL1dHRuXbtGhmprq6ekhfnSKVS/fPPPxs2bCAjxcXF6hUMDAwmJibU/6Hh7+8/MDBw+/btWXbb0NCgo6Pj4uLyGE0C4Ela6puUACwz7e3thoaGUVFRePX48eMUCuXq1asz1edwOO+99x65qlAofH198dDQoaGhwcHBwsLCX3/9VaVSjY6O2tnZ2dnZlZWVicXi/Px8JpPp7++PNxSLxdbW1vb29hUVFcPDw3l5eQYGBi+//DIuxaNXeDye+qH37t3LYDDOnTs3MjJSW1vr4uKip6c3y2CZ3bt3q2/+9NNP79mzBy97eHhwudympiaJRFJYWGhra0uj0ZKSknDpTz/9hBBKTU2trKysqalRqVRjY2OOjo5WVlY8Hk8gEAiFwt9///2DDz5ob28n9x8YGLh58+ZH6HoAFgYkQgAegVQqdXd3d3JyGhsbwxGlUhkaGspisbq6ujRu8tlnn5mZmclkMjIiEAjCwsLI65+GhoaXL1/GRX/99ZeHhwf5PTUoKGhgYIDcsKmpyc3NDRdRKJSQkBCBQICLNCZCiUTy+uuv4/oMBuPYsWPr169/vERYXV1tZ2eHd2VqalpYWKirq0smQqVSuW/fPoIgKBQKg8HAQfyvR/JlUqnU5557rqenB5fy+Xw6nf7DDz/Mue8BWCgU1X+PnwAALITBwUF7e/tz586ROQkbGhrq7Ow0MDDgcDg6OjrqRffv3xcIBNbW1ng4zBQdHR1CoXDNmjWzj3whdXd39/f3Ozg4TB+hg0dyzvGFyOXytrY2pVK5bt26uT83VSQS3bt3T09Pz9raWr0BqampX3/9dVtb2//DI1jBKgeJEIAF9/nnn1+8eLGhoUF9zOdqNjY2xuFwMjMzpwwrBWBJQCIEYMHJ5fKenh4bGxv8bwoglUr//ffftWvXzvLPEwAWDSRCAAAAqxpcqAEAALCqQSIEAACwqkEiBAAAsKpBIgQAALCq/Q+q9CxlurG6fAAAAABJRU5ErkJggg==",
"text/html": [
"<?xml version=\"1.0\" encoding=\"utf-8\"?>\n",
"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" width=\"600\" height=\"400\" viewBox=\"0 0 2400 1600\">\n",
"<defs>\n",
" <clipPath id=\"clip170\">\n",
" <rect x=\"0\" y=\"0\" width=\"2400\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<path clip-path=\"url(#clip170)\" d=\"M0 1600 L2400 1600 L2400 0 L0 0 Z\" fill=\"#ffffff\" fill-rule=\"evenodd\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip171\">\n",
" <rect x=\"480\" y=\"0\" width=\"1681\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<path clip-path=\"url(#clip170)\" d=\"M279.704 1423.18 L2352.76 1423.18 L2352.76 47.2441 L279.704 47.2441 Z\" fill=\"#ffffff\" fill-rule=\"evenodd\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip172\">\n",
" <rect x=\"279\" y=\"47\" width=\"2074\" height=\"1377\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polyline clip-path=\"url(#clip172)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"338.375,1423.18 338.375,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip172)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"827.303,1423.18 827.303,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip172)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"1316.23,1423.18 1316.23,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip172)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"1805.16,1423.18 1805.16,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip172)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"2294.08,1423.18 2294.08,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip172)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"279.704,1384.24 2352.76,1384.24 \"/>\n",
"<polyline clip-path=\"url(#clip172)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"279.704,1150.76 2352.76,1150.76 \"/>\n",
"<polyline clip-path=\"url(#clip172)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"279.704,917.284 2352.76,917.284 \"/>\n",
"<polyline clip-path=\"url(#clip172)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"279.704,683.806 2352.76,683.806 \"/>\n",
"<polyline clip-path=\"url(#clip172)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"279.704,450.329 2352.76,450.329 \"/>\n",
"<polyline clip-path=\"url(#clip172)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"279.704,216.852 2352.76,216.852 \"/>\n",
"<polyline clip-path=\"url(#clip170)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,1423.18 2352.76,1423.18 \"/>\n",
"<polyline clip-path=\"url(#clip170)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"338.375,1423.18 338.375,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip170)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"827.303,1423.18 827.303,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip170)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"1316.23,1423.18 1316.23,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip170)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"1805.16,1423.18 1805.16,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip170)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"2294.08,1423.18 2294.08,1404.28 \"/>\n",
"<path clip-path=\"url(#clip170)\" d=\"M284.903 1468.75 L314.579 1468.75 L314.579 1472.69 L284.903 1472.69 L284.903 1468.75 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M325.482 1481.64 L333.121 1481.64 L333.121 1455.28 L324.81 1456.95 L324.81 1452.69 L333.074 1451.02 L337.75 1451.02 L337.75 1481.64 L345.389 1481.64 L345.389 1485.58 L325.482 1485.58 L325.482 1481.64 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M354.833 1479.7 L359.718 1479.7 L359.718 1485.58 L354.833 1485.58 L354.833 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M379.903 1454.1 Q376.292 1454.1 374.463 1457.66 Q372.657 1461.2 372.657 1468.33 Q372.657 1475.44 374.463 1479.01 Q376.292 1482.55 379.903 1482.55 Q383.537 1482.55 385.343 1479.01 Q387.171 1475.44 387.171 1468.33 Q387.171 1461.2 385.343 1457.66 Q383.537 1454.1 379.903 1454.1 M379.903 1450.39 Q385.713 1450.39 388.768 1455 Q391.847 1459.58 391.847 1468.33 Q391.847 1477.06 388.768 1481.67 Q385.713 1486.25 379.903 1486.25 Q374.093 1486.25 371.014 1481.67 Q367.958 1477.06 367.958 1468.33 Q367.958 1459.58 371.014 1455 Q374.093 1450.39 379.903 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M774.328 1468.75 L804.004 1468.75 L804.004 1472.69 L774.328 1472.69 L774.328 1468.75 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M824.097 1454.1 Q820.485 1454.1 818.657 1457.66 Q816.851 1461.2 816.851 1468.33 Q816.851 1475.44 818.657 1479.01 Q820.485 1482.55 824.097 1482.55 Q827.731 1482.55 829.536 1479.01 Q831.365 1475.44 831.365 1468.33 Q831.365 1461.2 829.536 1457.66 Q827.731 1454.1 824.097 1454.1 M824.097 1450.39 Q829.907 1450.39 832.962 1455 Q836.041 1459.58 836.041 1468.33 Q836.041 1477.06 832.962 1481.67 Q829.907 1486.25 824.097 1486.25 Q818.286 1486.25 815.208 1481.67 Q812.152 1477.06 812.152 1468.33 Q812.152 1459.58 815.208 1455 Q818.286 1450.39 824.097 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M844.258 1479.7 L849.143 1479.7 L849.143 1485.58 L844.258 1485.58 L844.258 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M859.374 1451.02 L877.731 1451.02 L877.731 1454.96 L863.657 1454.96 L863.657 1463.43 Q864.675 1463.08 865.694 1462.92 Q866.712 1462.73 867.731 1462.73 Q873.518 1462.73 876.897 1465.9 Q880.277 1469.08 880.277 1474.49 Q880.277 1480.07 876.805 1483.17 Q873.332 1486.25 867.013 1486.25 Q864.837 1486.25 862.569 1485.88 Q860.323 1485.51 857.916 1484.77 L857.916 1480.07 Q859.999 1481.2 862.221 1481.76 Q864.444 1482.32 866.92 1482.32 Q870.925 1482.32 873.263 1480.21 Q875.601 1478.1 875.601 1474.49 Q875.601 1470.88 873.263 1468.77 Q870.925 1466.67 866.92 1466.67 Q865.045 1466.67 863.17 1467.08 Q861.319 1467.5 859.374 1468.38 L859.374 1451.02 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1293.61 1454.1 Q1290 1454.1 1288.17 1457.66 Q1286.37 1461.2 1286.37 1468.33 Q1286.37 1475.44 1288.17 1479.01 Q1290 1482.55 1293.61 1482.55 Q1297.25 1482.55 1299.05 1479.01 Q1300.88 1475.44 1300.88 1468.33 Q1300.88 1461.2 1299.05 1457.66 Q1297.25 1454.1 1293.61 1454.1 M1293.61 1450.39 Q1299.42 1450.39 1302.48 1455 Q1305.56 1459.58 1305.56 1468.33 Q1305.56 1477.06 1302.48 1481.67 Q1299.42 1486.25 1293.61 1486.25 Q1287.8 1486.25 1284.73 1481.67 Q1281.67 1477.06 1281.67 1468.33 Q1281.67 1459.58 1284.73 1455 Q1287.8 1450.39 1293.61 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1313.78 1479.7 L1318.66 1479.7 L1318.66 1485.58 L1313.78 1485.58 L1313.78 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1338.85 1454.1 Q1335.23 1454.1 1333.41 1457.66 Q1331.6 1461.2 1331.6 1468.33 Q1331.6 1475.44 1333.41 1479.01 Q1335.23 1482.55 1338.85 1482.55 Q1342.48 1482.55 1344.29 1479.01 Q1346.11 1475.44 1346.11 1468.33 Q1346.11 1461.2 1344.29 1457.66 Q1342.48 1454.1 1338.85 1454.1 M1338.85 1450.39 Q1344.66 1450.39 1347.71 1455 Q1350.79 1459.58 1350.79 1468.33 Q1350.79 1477.06 1347.71 1481.67 Q1344.66 1486.25 1338.85 1486.25 Q1333.04 1486.25 1329.96 1481.67 Q1326.9 1477.06 1326.9 1468.33 Q1326.9 1459.58 1329.96 1455 Q1333.04 1450.39 1338.85 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1783.04 1454.1 Q1779.43 1454.1 1777.6 1457.66 Q1775.79 1461.2 1775.79 1468.33 Q1775.79 1475.44 1777.6 1479.01 Q1779.43 1482.55 1783.04 1482.55 Q1786.67 1482.55 1788.48 1479.01 Q1790.31 1475.44 1790.31 1468.33 Q1790.31 1461.2 1788.48 1457.66 Q1786.67 1454.1 1783.04 1454.1 M1783.04 1450.39 Q1788.85 1450.39 1791.91 1455 Q1794.98 1459.58 1794.98 1468.33 Q1794.98 1477.06 1791.91 1481.67 Q1788.85 1486.25 1783.04 1486.25 Q1777.23 1486.25 1774.15 1481.67 Q1771.09 1477.06 1771.09 1468.33 Q1771.09 1459.58 1774.15 1455 Q1777.23 1450.39 1783.04 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1803.2 1479.7 L1808.09 1479.7 L1808.09 1485.58 L1803.2 1485.58 L1803.2 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1818.32 1451.02 L1836.67 1451.02 L1836.67 1454.96 L1822.6 1454.96 L1822.6 1463.43 Q1823.62 1463.08 1824.64 1462.92 Q1825.65 1462.73 1826.67 1462.73 Q1832.46 1462.73 1835.84 1465.9 Q1839.22 1469.08 1839.22 1474.49 Q1839.22 1480.07 1835.75 1483.17 Q1832.28 1486.25 1825.96 1486.25 Q1823.78 1486.25 1821.51 1485.88 Q1819.27 1485.51 1816.86 1484.77 L1816.86 1480.07 Q1818.94 1481.2 1821.16 1481.76 Q1823.39 1482.32 1825.86 1482.32 Q1829.87 1482.32 1832.21 1480.21 Q1834.54 1478.1 1834.54 1474.49 Q1834.54 1470.88 1832.21 1468.77 Q1829.87 1466.67 1825.86 1466.67 Q1823.99 1466.67 1822.11 1467.08 Q1820.26 1467.5 1818.32 1468.38 L1818.32 1451.02 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M2261.24 1481.64 L2268.88 1481.64 L2268.88 1455.28 L2260.57 1456.95 L2260.57 1452.69 L2268.83 1451.02 L2273.51 1451.02 L2273.51 1481.64 L2281.14 1481.64 L2281.14 1485.58 L2261.24 1485.58 L2261.24 1481.64 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M2290.59 1479.7 L2295.47 1479.7 L2295.47 1485.58 L2290.59 1485.58 L2290.59 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M2315.66 1454.1 Q2312.05 1454.1 2310.22 1457.66 Q2308.41 1461.2 2308.41 1468.33 Q2308.41 1475.44 2310.22 1479.01 Q2312.05 1482.55 2315.66 1482.55 Q2319.29 1482.55 2321.1 1479.01 Q2322.93 1475.44 2322.93 1468.33 Q2322.93 1461.2 2321.1 1457.66 Q2319.29 1454.1 2315.66 1454.1 M2315.66 1450.39 Q2321.47 1450.39 2324.52 1455 Q2327.6 1459.58 2327.6 1468.33 Q2327.6 1477.06 2324.52 1481.67 Q2321.47 1486.25 2315.66 1486.25 Q2309.85 1486.25 2306.77 1481.67 Q2303.71 1477.06 2303.71 1468.33 Q2303.71 1459.58 2306.77 1455 Q2309.85 1450.39 2315.66 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1124.96 1532.4 L1112.07 1549.74 L1125.62 1568.04 L1118.72 1568.04 L1108.34 1554.04 L1097.97 1568.04 L1091.06 1568.04 L1104.9 1549.39 L1092.24 1532.4 L1099.14 1532.4 L1108.6 1545.1 L1118.05 1532.4 L1124.96 1532.4 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1168.69 1518.58 Q1164.42 1525.9 1162.35 1533.06 Q1160.29 1540.23 1160.29 1547.58 Q1160.29 1554.93 1162.35 1562.16 Q1164.46 1569.35 1168.69 1576.64 L1163.6 1576.64 Q1158.82 1569.16 1156.43 1561.93 Q1154.08 1554.71 1154.08 1547.58 Q1154.08 1540.48 1156.43 1533.29 Q1158.79 1526.09 1163.6 1518.58 L1168.69 1518.58 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1205.71 1533.76 L1205.71 1539.24 Q1203.22 1537.87 1200.71 1537.2 Q1198.23 1536.5 1195.68 1536.5 Q1189.98 1536.5 1186.83 1540.13 Q1183.68 1543.73 1183.68 1550.25 Q1183.68 1556.78 1186.83 1560.4 Q1189.98 1564 1195.68 1564 Q1198.23 1564 1200.71 1563.33 Q1203.22 1562.63 1205.71 1561.26 L1205.71 1566.68 Q1203.25 1567.82 1200.61 1568.39 Q1198 1568.97 1195.04 1568.97 Q1186.99 1568.97 1182.25 1563.91 Q1177.51 1558.85 1177.51 1550.25 Q1177.51 1541.53 1182.28 1536.53 Q1187.09 1531.54 1195.42 1531.54 Q1198.13 1531.54 1200.71 1532.11 Q1203.29 1532.65 1205.71 1533.76 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1229.7 1536.5 Q1224.99 1536.5 1222.26 1540.19 Q1219.52 1543.85 1219.52 1550.25 Q1219.52 1556.65 1222.22 1560.34 Q1224.96 1564 1229.7 1564 Q1234.38 1564 1237.12 1560.31 Q1239.86 1556.62 1239.86 1550.25 Q1239.86 1543.92 1237.12 1540.23 Q1234.38 1536.5 1229.7 1536.5 M1229.7 1531.54 Q1237.34 1531.54 1241.7 1536.5 Q1246.06 1541.47 1246.06 1550.25 Q1246.06 1559 1241.7 1564 Q1237.34 1568.97 1229.7 1568.97 Q1222.03 1568.97 1217.67 1564 Q1213.34 1559 1213.34 1550.25 Q1213.34 1541.47 1217.67 1536.5 Q1222.03 1531.54 1229.7 1531.54 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1269.59 1536.5 Q1264.87 1536.5 1262.14 1540.19 Q1259.4 1543.85 1259.4 1550.25 Q1259.4 1556.65 1262.11 1560.34 Q1264.84 1564 1269.59 1564 Q1274.26 1564 1277 1560.31 Q1279.74 1556.62 1279.74 1550.25 Q1279.74 1543.92 1277 1540.23 Q1274.26 1536.5 1269.59 1536.5 M1269.59 1531.54 Q1277.22 1531.54 1281.58 1536.5 Q1285.95 1541.47 1285.95 1550.25 Q1285.95 1559 1281.58 1564 Q1277.22 1568.97 1269.59 1568.97 Q1261.91 1568.97 1257.55 1564 Q1253.23 1559 1253.23 1550.25 Q1253.23 1541.47 1257.55 1536.5 Q1261.91 1531.54 1269.59 1531.54 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1316.31 1537.87 Q1315.32 1537.3 1314.15 1537.04 Q1313 1536.76 1311.6 1536.76 Q1306.63 1536.76 1303.96 1540 Q1301.32 1543.22 1301.32 1549.27 L1301.32 1568.04 L1295.43 1568.04 L1295.43 1532.4 L1301.32 1532.4 L1301.32 1537.93 Q1303.16 1534.69 1306.12 1533.13 Q1309.08 1531.54 1313.32 1531.54 Q1313.92 1531.54 1314.65 1531.63 Q1315.39 1531.7 1316.28 1531.85 L1316.31 1537.87 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1344.76 1537.81 L1344.76 1518.52 L1350.62 1518.52 L1350.62 1568.04 L1344.76 1568.04 L1344.76 1562.7 Q1342.92 1565.88 1340.09 1567.44 Q1337.28 1568.97 1333.34 1568.97 Q1326.88 1568.97 1322.8 1563.81 Q1318.76 1558.65 1318.76 1550.25 Q1318.76 1541.85 1322.8 1536.69 Q1326.88 1531.54 1333.34 1531.54 Q1337.28 1531.54 1340.09 1533.1 Q1342.92 1534.62 1344.76 1537.81 M1324.81 1550.25 Q1324.81 1556.71 1327.45 1560.4 Q1330.12 1564.07 1334.77 1564.07 Q1339.42 1564.07 1342.09 1560.4 Q1344.76 1556.71 1344.76 1550.25 Q1344.76 1543.79 1342.09 1540.13 Q1339.42 1536.44 1334.77 1536.44 Q1330.12 1536.44 1327.45 1540.13 Q1324.81 1543.79 1324.81 1550.25 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1362.68 1532.4 L1368.54 1532.4 L1368.54 1568.04 L1362.68 1568.04 L1362.68 1532.4 M1362.68 1518.52 L1368.54 1518.52 L1368.54 1525.93 L1362.68 1525.93 L1362.68 1518.52 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1410.43 1546.53 L1410.43 1568.04 L1404.57 1568.04 L1404.57 1546.72 Q1404.57 1541.66 1402.6 1539.14 Q1400.62 1536.63 1396.68 1536.63 Q1391.93 1536.63 1389.2 1539.65 Q1386.46 1542.68 1386.46 1547.9 L1386.46 1568.04 L1380.57 1568.04 L1380.57 1532.4 L1386.46 1532.4 L1386.46 1537.93 Q1388.56 1534.72 1391.39 1533.13 Q1394.26 1531.54 1397.98 1531.54 Q1404.12 1531.54 1407.28 1535.36 Q1410.43 1539.14 1410.43 1546.53 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1438.31 1550.12 Q1431.21 1550.12 1428.47 1551.75 Q1425.74 1553.37 1425.74 1557.29 Q1425.74 1560.4 1427.77 1562.25 Q1429.84 1564.07 1433.37 1564.07 Q1438.24 1564.07 1441.17 1560.63 Q1444.13 1557.16 1444.13 1551.43 L1444.13 1550.12 L1438.31 1550.12 M1449.99 1547.71 L1449.99 1568.04 L1444.13 1568.04 L1444.13 1562.63 Q1442.13 1565.88 1439.14 1567.44 Q1436.14 1568.97 1431.82 1568.97 Q1426.34 1568.97 1423.09 1565.91 Q1419.88 1562.82 1419.88 1557.67 Q1419.88 1551.65 1423.89 1548.6 Q1427.93 1545.54 1435.92 1545.54 L1444.13 1545.54 L1444.13 1544.97 Q1444.13 1540.93 1441.46 1538.73 Q1438.82 1536.5 1434.01 1536.5 Q1430.96 1536.5 1428.06 1537.23 Q1425.16 1537.97 1422.49 1539.43 L1422.49 1534.02 Q1425.7 1532.78 1428.73 1532.17 Q1431.75 1531.54 1434.62 1531.54 Q1442.35 1531.54 1446.17 1535.55 Q1449.99 1539.56 1449.99 1547.71 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1467.85 1522.27 L1467.85 1532.4 L1479.91 1532.4 L1479.91 1536.95 L1467.85 1536.95 L1467.85 1556.3 Q1467.85 1560.66 1469.02 1561.9 Q1470.23 1563.14 1473.89 1563.14 L1479.91 1563.14 L1479.91 1568.04 L1473.89 1568.04 Q1467.11 1568.04 1464.53 1565.53 Q1461.96 1562.98 1461.96 1556.3 L1461.96 1536.95 L1457.66 1536.95 L1457.66 1532.4 L1461.96 1532.4 L1461.96 1522.27 L1467.85 1522.27 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1518.1 1548.76 L1518.1 1551.62 L1491.18 1551.62 Q1491.56 1557.67 1494.8 1560.85 Q1498.08 1564 1503.91 1564 Q1507.28 1564 1510.43 1563.17 Q1513.61 1562.35 1516.73 1560.69 L1516.73 1566.23 Q1513.58 1567.57 1510.27 1568.27 Q1506.96 1568.97 1503.56 1568.97 Q1495.03 1568.97 1490.03 1564 Q1485.06 1559.04 1485.06 1550.57 Q1485.06 1541.82 1489.77 1536.69 Q1494.52 1531.54 1502.54 1531.54 Q1509.73 1531.54 1513.9 1536.18 Q1518.1 1540.8 1518.1 1548.76 M1512.25 1547.04 Q1512.18 1542.23 1509.54 1539.37 Q1506.93 1536.5 1502.6 1536.5 Q1497.7 1536.5 1494.74 1539.27 Q1491.81 1542.04 1491.37 1547.07 L1512.25 1547.04 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M1526.79 1518.58 L1531.88 1518.58 Q1536.66 1526.09 1539.01 1533.29 Q1541.4 1540.48 1541.4 1547.58 Q1541.4 1554.71 1539.01 1561.93 Q1536.66 1569.16 1531.88 1576.64 L1526.79 1576.64 Q1531.02 1569.35 1533.09 1562.16 Q1535.19 1554.93 1535.19 1547.58 Q1535.19 1540.23 1533.09 1533.06 Q1531.02 1525.9 1526.79 1518.58 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><polyline clip-path=\"url(#clip170)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,1423.18 279.704,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip170)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,1384.24 298.602,1384.24 \"/>\n",
"<polyline clip-path=\"url(#clip170)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,1150.76 298.602,1150.76 \"/>\n",
"<polyline clip-path=\"url(#clip170)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,917.284 298.602,917.284 \"/>\n",
"<polyline clip-path=\"url(#clip170)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,683.806 298.602,683.806 \"/>\n",
"<polyline clip-path=\"url(#clip170)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,450.329 298.602,450.329 \"/>\n",
"<polyline clip-path=\"url(#clip170)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,216.852 298.602,216.852 \"/>\n",
"<path clip-path=\"url(#clip170)\" d=\"M126.205 1370.04 Q122.593 1370.04 120.765 1373.6 Q118.959 1377.14 118.959 1384.27 Q118.959 1391.38 120.765 1394.94 Q122.593 1398.49 126.205 1398.49 Q129.839 1398.49 131.644 1394.94 Q133.473 1391.38 133.473 1384.27 Q133.473 1377.14 131.644 1373.6 Q129.839 1370.04 126.205 1370.04 M126.205 1366.33 Q132.015 1366.33 135.07 1370.94 Q138.149 1375.52 138.149 1384.27 Q138.149 1393 135.07 1397.61 Q132.015 1402.19 126.205 1402.19 Q120.394 1402.19 117.316 1397.61 Q114.26 1393 114.26 1384.27 Q114.26 1375.52 117.316 1370.94 Q120.394 1366.33 126.205 1366.33 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M146.366 1395.64 L151.251 1395.64 L151.251 1401.52 L146.366 1401.52 L146.366 1395.64 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M171.436 1370.04 Q167.825 1370.04 165.996 1373.6 Q164.19 1377.14 164.19 1384.27 Q164.19 1391.38 165.996 1394.94 Q167.825 1398.49 171.436 1398.49 Q175.07 1398.49 176.876 1394.94 Q178.704 1391.38 178.704 1384.27 Q178.704 1377.14 176.876 1373.6 Q175.07 1370.04 171.436 1370.04 M171.436 1366.33 Q177.246 1366.33 180.301 1370.94 Q183.38 1375.52 183.38 1384.27 Q183.38 1393 180.301 1397.61 Q177.246 1402.19 171.436 1402.19 Q165.626 1402.19 162.547 1397.61 Q159.491 1393 159.491 1384.27 Q159.491 1375.52 162.547 1370.94 Q165.626 1366.33 171.436 1366.33 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M201.598 1370.04 Q197.987 1370.04 196.158 1373.6 Q194.352 1377.14 194.352 1384.27 Q194.352 1391.38 196.158 1394.94 Q197.987 1398.49 201.598 1398.49 Q205.232 1398.49 207.037 1394.94 Q208.866 1391.38 208.866 1384.27 Q208.866 1377.14 207.037 1373.6 Q205.232 1370.04 201.598 1370.04 M201.598 1366.33 Q207.408 1366.33 210.463 1370.94 Q213.542 1375.52 213.542 1384.27 Q213.542 1393 210.463 1397.61 Q207.408 1402.19 201.598 1402.19 Q195.787 1402.19 192.709 1397.61 Q189.653 1393 189.653 1384.27 Q189.653 1375.52 192.709 1370.94 Q195.787 1366.33 201.598 1366.33 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M231.76 1370.04 Q228.148 1370.04 226.32 1373.6 Q224.514 1377.14 224.514 1384.27 Q224.514 1391.38 226.32 1394.94 Q228.148 1398.49 231.76 1398.49 Q235.394 1398.49 237.199 1394.94 Q239.028 1391.38 239.028 1384.27 Q239.028 1377.14 237.199 1373.6 Q235.394 1370.04 231.76 1370.04 M231.76 1366.33 Q237.57 1366.33 240.625 1370.94 Q243.704 1375.52 243.704 1384.27 Q243.704 1393 240.625 1397.61 Q237.57 1402.19 231.76 1402.19 Q225.949 1402.19 222.871 1397.61 Q219.815 1393 219.815 1384.27 Q219.815 1375.52 222.871 1370.94 Q225.949 1366.33 231.76 1366.33 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M127.2 1136.56 Q123.589 1136.56 121.76 1140.12 Q119.955 1143.67 119.955 1150.8 Q119.955 1157.9 121.76 1161.47 Q123.589 1165.01 127.2 1165.01 Q130.834 1165.01 132.64 1161.47 Q134.468 1157.9 134.468 1150.8 Q134.468 1143.67 132.64 1140.12 Q130.834 1136.56 127.2 1136.56 M127.2 1132.86 Q133.01 1132.86 136.066 1137.46 Q139.144 1142.05 139.144 1150.8 Q139.144 1159.52 136.066 1164.13 Q133.01 1168.71 127.2 1168.71 Q121.39 1168.71 118.311 1164.13 Q115.256 1159.52 115.256 1150.8 Q115.256 1142.05 118.311 1137.46 Q121.39 1132.86 127.2 1132.86 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M147.362 1162.16 L152.246 1162.16 L152.246 1168.04 L147.362 1168.04 L147.362 1162.16 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M172.431 1136.56 Q168.82 1136.56 166.991 1140.12 Q165.186 1143.67 165.186 1150.8 Q165.186 1157.9 166.991 1161.47 Q168.82 1165.01 172.431 1165.01 Q176.065 1165.01 177.871 1161.47 Q179.7 1157.9 179.7 1150.8 Q179.7 1143.67 177.871 1140.12 Q176.065 1136.56 172.431 1136.56 M172.431 1132.86 Q178.241 1132.86 181.297 1137.46 Q184.376 1142.05 184.376 1150.8 Q184.376 1159.52 181.297 1164.13 Q178.241 1168.71 172.431 1168.71 Q166.621 1168.71 163.542 1164.13 Q160.487 1159.52 160.487 1150.8 Q160.487 1142.05 163.542 1137.46 Q166.621 1132.86 172.431 1132.86 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M196.621 1164.11 L212.94 1164.11 L212.94 1168.04 L190.996 1168.04 L190.996 1164.11 Q193.658 1161.35 198.241 1156.72 Q202.848 1152.07 204.028 1150.73 Q206.274 1148.2 207.153 1146.47 Q208.056 1144.71 208.056 1143.02 Q208.056 1140.26 206.112 1138.53 Q204.19 1136.79 201.088 1136.79 Q198.889 1136.79 196.436 1137.55 Q194.005 1138.32 191.227 1139.87 L191.227 1135.15 Q194.051 1134.01 196.505 1133.43 Q198.959 1132.86 200.996 1132.86 Q206.366 1132.86 209.561 1135.54 Q212.755 1138.23 212.755 1142.72 Q212.755 1144.85 211.945 1146.77 Q211.158 1148.67 209.051 1151.26 Q208.473 1151.93 205.371 1155.15 Q202.269 1158.34 196.621 1164.11 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M222.801 1133.48 L241.158 1133.48 L241.158 1137.42 L227.084 1137.42 L227.084 1145.89 Q228.102 1145.54 229.121 1145.38 Q230.139 1145.19 231.158 1145.19 Q236.945 1145.19 240.324 1148.37 Q243.704 1151.54 243.704 1156.95 Q243.704 1162.53 240.232 1165.63 Q236.76 1168.71 230.44 1168.71 Q228.264 1168.71 225.996 1168.34 Q223.75 1167.97 221.343 1167.23 L221.343 1162.53 Q223.426 1163.67 225.648 1164.22 Q227.871 1164.78 230.347 1164.78 Q234.352 1164.78 236.69 1162.67 Q239.028 1160.56 239.028 1156.95 Q239.028 1153.34 236.69 1151.24 Q234.352 1149.13 230.347 1149.13 Q228.473 1149.13 226.598 1149.55 Q224.746 1149.96 222.801 1150.84 L222.801 1133.48 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M126.205 903.082 Q122.593 903.082 120.765 906.647 Q118.959 910.189 118.959 917.318 Q118.959 924.425 120.765 927.99 Q122.593 931.531 126.205 931.531 Q129.839 931.531 131.644 927.99 Q133.473 924.425 133.473 917.318 Q133.473 910.189 131.644 906.647 Q129.839 903.082 126.205 903.082 M126.205 899.379 Q132.015 899.379 135.07 903.985 Q138.149 908.568 138.149 917.318 Q138.149 926.045 135.07 930.652 Q132.015 935.235 126.205 935.235 Q120.394 935.235 117.316 930.652 Q114.26 926.045 114.26 917.318 Q114.26 908.568 117.316 903.985 Q120.394 899.379 126.205 899.379 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M146.366 928.684 L151.251 928.684 L151.251 934.564 L146.366 934.564 L146.366 928.684 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M171.436 903.082 Q167.825 903.082 165.996 906.647 Q164.19 910.189 164.19 917.318 Q164.19 924.425 165.996 927.99 Q167.825 931.531 171.436 931.531 Q175.07 931.531 176.876 927.99 Q178.704 924.425 178.704 917.318 Q178.704 910.189 176.876 906.647 Q175.07 903.082 171.436 903.082 M171.436 899.379 Q177.246 899.379 180.301 903.985 Q183.38 908.568 183.38 917.318 Q183.38 926.045 180.301 930.652 Q177.246 935.235 171.436 935.235 Q165.626 935.235 162.547 930.652 Q159.491 926.045 159.491 917.318 Q159.491 908.568 162.547 903.985 Q165.626 899.379 171.436 899.379 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M191.644 900.004 L210 900.004 L210 903.939 L195.926 903.939 L195.926 912.411 Q196.945 912.064 197.963 911.902 Q198.982 911.716 200 911.716 Q205.787 911.716 209.167 914.888 Q212.547 918.059 212.547 923.476 Q212.547 929.054 209.074 932.156 Q205.602 935.235 199.283 935.235 Q197.107 935.235 194.838 934.865 Q192.593 934.494 190.186 933.753 L190.186 929.054 Q192.269 930.189 194.491 930.744 Q196.713 931.3 199.19 931.3 Q203.195 931.3 205.533 929.193 Q207.871 927.087 207.871 923.476 Q207.871 919.865 205.533 917.758 Q203.195 915.652 199.19 915.652 Q197.315 915.652 195.44 916.068 Q193.588 916.485 191.644 917.365 L191.644 900.004 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M231.76 903.082 Q228.148 903.082 226.32 906.647 Q224.514 910.189 224.514 917.318 Q224.514 924.425 226.32 927.99 Q228.148 931.531 231.76 931.531 Q235.394 931.531 237.199 927.99 Q239.028 924.425 239.028 917.318 Q239.028 910.189 237.199 906.647 Q235.394 903.082 231.76 903.082 M231.76 899.379 Q237.57 899.379 240.625 903.985 Q243.704 908.568 243.704 917.318 Q243.704 926.045 240.625 930.652 Q237.57 935.235 231.76 935.235 Q225.949 935.235 222.871 930.652 Q219.815 926.045 219.815 917.318 Q219.815 908.568 222.871 903.985 Q225.949 899.379 231.76 899.379 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M127.2 669.605 Q123.589 669.605 121.76 673.17 Q119.955 676.711 119.955 683.841 Q119.955 690.947 121.76 694.512 Q123.589 698.054 127.2 698.054 Q130.834 698.054 132.64 694.512 Q134.468 690.947 134.468 683.841 Q134.468 676.711 132.64 673.17 Q130.834 669.605 127.2 669.605 M127.2 665.901 Q133.01 665.901 136.066 670.508 Q139.144 675.091 139.144 683.841 Q139.144 692.568 136.066 697.174 Q133.01 701.758 127.2 701.758 Q121.39 701.758 118.311 697.174 Q115.256 692.568 115.256 683.841 Q115.256 675.091 118.311 670.508 Q121.39 665.901 127.2 665.901 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M147.362 695.207 L152.246 695.207 L152.246 701.086 L147.362 701.086 L147.362 695.207 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M172.431 669.605 Q168.82 669.605 166.991 673.17 Q165.186 676.711 165.186 683.841 Q165.186 690.947 166.991 694.512 Q168.82 698.054 172.431 698.054 Q176.065 698.054 177.871 694.512 Q179.7 690.947 179.7 683.841 Q179.7 676.711 177.871 673.17 Q176.065 669.605 172.431 669.605 M172.431 665.901 Q178.241 665.901 181.297 670.508 Q184.376 675.091 184.376 683.841 Q184.376 692.568 181.297 697.174 Q178.241 701.758 172.431 701.758 Q166.621 701.758 163.542 697.174 Q160.487 692.568 160.487 683.841 Q160.487 675.091 163.542 670.508 Q166.621 665.901 172.431 665.901 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M191.413 666.526 L213.635 666.526 L213.635 668.517 L201.088 701.086 L196.204 701.086 L208.01 670.461 L191.413 670.461 L191.413 666.526 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M222.801 666.526 L241.158 666.526 L241.158 670.461 L227.084 670.461 L227.084 678.934 Q228.102 678.586 229.121 678.424 Q230.139 678.239 231.158 678.239 Q236.945 678.239 240.324 681.41 Q243.704 684.582 243.704 689.998 Q243.704 695.577 240.232 698.679 Q236.76 701.758 230.44 701.758 Q228.264 701.758 225.996 701.387 Q223.75 701.017 221.343 700.276 L221.343 695.577 Q223.426 696.711 225.648 697.267 Q227.871 697.822 230.347 697.822 Q234.352 697.822 236.69 695.716 Q239.028 693.609 239.028 689.998 Q239.028 686.387 236.69 684.281 Q234.352 682.174 230.347 682.174 Q228.473 682.174 226.598 682.591 Q224.746 683.008 222.801 683.887 L222.801 666.526 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M126.205 436.128 Q122.593 436.128 120.765 439.692 Q118.959 443.234 118.959 450.364 Q118.959 457.47 120.765 461.035 Q122.593 464.577 126.205 464.577 Q129.839 464.577 131.644 461.035 Q133.473 457.47 133.473 450.364 Q133.473 443.234 131.644 439.692 Q129.839 436.128 126.205 436.128 M126.205 432.424 Q132.015 432.424 135.07 437.03 Q138.149 441.614 138.149 450.364 Q138.149 459.09 135.07 463.697 Q132.015 468.28 126.205 468.28 Q120.394 468.28 117.316 463.697 Q114.26 459.09 114.26 450.364 Q114.26 441.614 117.316 437.03 Q120.394 432.424 126.205 432.424 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M146.366 461.729 L151.251 461.729 L151.251 467.609 L146.366 467.609 L146.366 461.729 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M162.246 463.674 L169.885 463.674 L169.885 437.308 L161.575 438.975 L161.575 434.716 L169.839 433.049 L174.514 433.049 L174.514 463.674 L182.153 463.674 L182.153 467.609 L162.246 467.609 L162.246 463.674 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M201.598 436.128 Q197.987 436.128 196.158 439.692 Q194.352 443.234 194.352 450.364 Q194.352 457.47 196.158 461.035 Q197.987 464.577 201.598 464.577 Q205.232 464.577 207.037 461.035 Q208.866 457.47 208.866 450.364 Q208.866 443.234 207.037 439.692 Q205.232 436.128 201.598 436.128 M201.598 432.424 Q207.408 432.424 210.463 437.03 Q213.542 441.614 213.542 450.364 Q213.542 459.09 210.463 463.697 Q207.408 468.28 201.598 468.28 Q195.787 468.28 192.709 463.697 Q189.653 459.09 189.653 450.364 Q189.653 441.614 192.709 437.03 Q195.787 432.424 201.598 432.424 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M231.76 436.128 Q228.148 436.128 226.32 439.692 Q224.514 443.234 224.514 450.364 Q224.514 457.47 226.32 461.035 Q228.148 464.577 231.76 464.577 Q235.394 464.577 237.199 461.035 Q239.028 457.47 239.028 450.364 Q239.028 443.234 237.199 439.692 Q235.394 436.128 231.76 436.128 M231.76 432.424 Q237.57 432.424 240.625 437.03 Q243.704 441.614 243.704 450.364 Q243.704 459.09 240.625 463.697 Q237.57 468.28 231.76 468.28 Q225.949 468.28 222.871 463.697 Q219.815 459.09 219.815 450.364 Q219.815 441.614 222.871 437.03 Q225.949 432.424 231.76 432.424 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M127.2 202.65 Q123.589 202.65 121.76 206.215 Q119.955 209.757 119.955 216.886 Q119.955 223.993 121.76 227.558 Q123.589 231.099 127.2 231.099 Q130.834 231.099 132.64 227.558 Q134.468 223.993 134.468 216.886 Q134.468 209.757 132.64 206.215 Q130.834 202.65 127.2 202.65 M127.2 198.947 Q133.01 198.947 136.066 203.553 Q139.144 208.136 139.144 216.886 Q139.144 225.613 136.066 230.22 Q133.01 234.803 127.2 234.803 Q121.39 234.803 118.311 230.22 Q115.256 225.613 115.256 216.886 Q115.256 208.136 118.311 203.553 Q121.39 198.947 127.2 198.947 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M147.362 228.252 L152.246 228.252 L152.246 234.132 L147.362 234.132 L147.362 228.252 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M163.241 230.196 L170.88 230.196 L170.88 203.831 L162.57 205.497 L162.57 201.238 L170.834 199.572 L175.51 199.572 L175.51 230.196 L183.149 230.196 L183.149 234.132 L163.241 234.132 L163.241 230.196 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M196.621 230.196 L212.94 230.196 L212.94 234.132 L190.996 234.132 L190.996 230.196 Q193.658 227.442 198.241 222.812 Q202.848 218.159 204.028 216.817 Q206.274 214.294 207.153 212.558 Q208.056 210.798 208.056 209.109 Q208.056 206.354 206.112 204.618 Q204.19 202.882 201.088 202.882 Q198.889 202.882 196.436 203.646 Q194.005 204.41 191.227 205.96 L191.227 201.238 Q194.051 200.104 196.505 199.525 Q198.959 198.947 200.996 198.947 Q206.366 198.947 209.561 201.632 Q212.755 204.317 212.755 208.808 Q212.755 210.937 211.945 212.859 Q211.158 214.757 209.051 217.349 Q208.473 218.021 205.371 221.238 Q202.269 224.433 196.621 230.196 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M222.801 199.572 L241.158 199.572 L241.158 203.507 L227.084 203.507 L227.084 211.979 Q228.102 211.632 229.121 211.47 Q230.139 211.284 231.158 211.284 Q236.945 211.284 240.324 214.456 Q243.704 217.627 243.704 223.044 Q243.704 228.622 240.232 231.724 Q236.76 234.803 230.44 234.803 Q228.264 234.803 225.996 234.433 Q223.75 234.062 221.343 233.321 L221.343 228.622 Q223.426 229.757 225.648 230.312 Q227.871 230.868 230.347 230.868 Q234.352 230.868 236.69 228.761 Q239.028 226.655 239.028 223.044 Q239.028 219.433 236.69 217.326 Q234.352 215.22 230.347 215.22 Q228.473 215.22 226.598 215.636 Q224.746 216.053 222.801 216.933 L222.801 199.572 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M49.9359 990.954 L28.3562 990.954 L28.3562 985.098 L49.7131 985.098 Q54.7739 985.098 57.3202 983.124 Q59.8346 981.151 59.8346 977.204 Q59.8346 972.462 56.8109 969.725 Q53.7872 966.956 48.5673 966.956 L28.3562 966.956 L28.3562 961.099 L64.0042 961.099 L64.0042 966.956 L58.5296 966.956 Q61.7762 969.088 63.3676 971.921 Q64.9272 974.722 64.9272 978.446 Q64.9272 984.589 61.1078 987.771 Q57.2883 990.954 49.9359 990.954 M27.4968 976.218 L27.4968 976.218 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M14.5426 914.247 Q21.8632 918.512 29.0246 920.581 Q36.186 922.65 43.5384 922.65 Q50.8908 922.65 58.1159 920.581 Q65.3091 918.481 72.5979 914.247 L72.5979 919.34 Q65.1182 924.114 57.8931 926.501 Q50.668 928.857 43.5384 928.857 Q36.4406 928.857 29.2474 926.501 Q22.0542 924.146 14.5426 919.34 L14.5426 914.247 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M18.2347 897.092 L28.3562 897.092 L28.3562 885.029 L32.9077 885.029 L32.9077 897.092 L52.2594 897.092 Q56.6199 897.092 57.8613 895.914 Q59.1026 894.705 59.1026 891.044 L59.1026 885.029 L64.0042 885.029 L64.0042 891.044 Q64.0042 897.824 61.4897 900.402 Q58.9434 902.98 52.2594 902.98 L32.9077 902.98 L32.9077 907.277 L28.3562 907.277 L28.3562 902.98 L18.2347 902.98 L18.2347 897.092 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M44.7161 846.835 L47.5806 846.835 L47.5806 873.762 Q53.6281 873.38 56.8109 870.133 Q59.9619 866.855 59.9619 861.03 Q59.9619 857.656 59.1344 854.505 Q58.3069 851.322 56.6518 848.203 L62.1899 848.203 Q63.5267 851.354 64.227 854.664 Q64.9272 857.975 64.9272 861.38 Q64.9272 869.91 59.9619 874.907 Q54.9967 879.873 46.5303 879.873 Q37.7774 879.873 32.6531 875.162 Q27.4968 870.42 27.4968 862.399 Q27.4968 855.206 32.1438 851.036 Q36.7589 846.835 44.7161 846.835 M42.9973 852.691 Q38.1912 852.755 35.3266 855.397 Q32.4621 858.006 32.4621 862.335 Q32.4621 867.237 35.2312 870.197 Q38.0002 873.125 43.0292 873.571 L42.9973 852.691 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M35.1993 809.468 Q31.2526 807.272 29.3747 804.216 Q27.4968 801.161 27.4968 797.023 Q27.4968 791.453 31.4117 788.429 Q35.2948 785.406 42.4881 785.406 L64.0042 785.406 L64.0042 791.294 L42.679 791.294 Q37.5546 791.294 35.072 793.108 Q32.5894 794.922 32.5894 798.646 Q32.5894 803.198 35.6131 805.839 Q38.6368 808.481 43.8567 808.481 L64.0042 808.481 L64.0042 814.37 L42.679 814.37 Q37.5228 814.37 35.072 816.184 Q32.5894 817.998 32.5894 821.786 Q32.5894 826.273 35.6449 828.915 Q38.6686 831.557 43.8567 831.557 L64.0042 831.557 L64.0042 837.445 L28.3562 837.445 L28.3562 831.557 L33.8944 831.557 Q30.616 829.552 29.0564 826.751 Q27.4968 823.95 27.4968 820.099 Q27.4968 816.216 29.4702 813.51 Q31.4436 810.773 35.1993 809.468 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M58.657 768.059 L77.5631 768.059 L77.5631 773.947 L28.3562 773.947 L28.3562 768.059 L33.7671 768.059 Q30.5842 766.213 29.0564 763.412 Q27.4968 760.579 27.4968 756.664 Q27.4968 750.171 32.6531 746.129 Q37.8093 742.055 46.212 742.055 Q54.6147 742.055 59.771 746.129 Q64.9272 750.171 64.9272 756.664 Q64.9272 760.579 63.3994 763.412 Q61.8398 766.213 58.657 768.059 M46.212 748.134 Q39.7508 748.134 36.0905 750.808 Q32.3984 753.45 32.3984 758.097 Q32.3984 762.744 36.0905 765.417 Q39.7508 768.059 46.212 768.059 Q52.6732 768.059 56.3653 765.417 Q60.0256 762.744 60.0256 758.097 Q60.0256 753.45 56.3653 750.808 Q52.6732 748.134 46.212 748.134 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M44.7161 701.856 L47.5806 701.856 L47.5806 728.783 Q53.6281 728.401 56.8109 725.154 Q59.9619 721.876 59.9619 716.051 Q59.9619 712.677 59.1344 709.526 Q58.3069 706.343 56.6518 703.224 L62.1899 703.224 Q63.5267 706.375 64.227 709.685 Q64.9272 712.996 64.9272 716.401 Q64.9272 724.931 59.9619 729.928 Q54.9967 734.894 46.5303 734.894 Q37.7774 734.894 32.6531 730.183 Q27.4968 725.441 27.4968 717.42 Q27.4968 710.227 32.1438 706.057 Q36.7589 701.856 44.7161 701.856 M42.9973 707.712 Q38.1912 707.776 35.3266 710.418 Q32.4621 713.027 32.4621 717.356 Q32.4621 722.258 35.2312 725.218 Q38.0002 728.146 43.0292 728.592 L42.9973 707.712 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M33.8307 671.587 Q33.2578 672.573 33.0032 673.751 Q32.7167 674.897 32.7167 676.297 Q32.7167 681.263 35.9632 683.936 Q39.1779 686.578 45.2253 686.578 L64.0042 686.578 L64.0042 692.466 L28.3562 692.466 L28.3562 686.578 L33.8944 686.578 Q30.6479 684.732 29.0883 681.772 Q27.4968 678.812 27.4968 674.579 Q27.4968 673.974 27.5923 673.242 Q27.656 672.51 27.8151 671.619 L33.8307 671.587 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M46.0847 649.243 Q46.0847 656.341 47.7079 659.078 Q49.3312 661.815 53.2461 661.815 Q56.3653 661.815 58.2114 659.778 Q60.0256 657.709 60.0256 654.177 Q60.0256 649.307 56.5881 646.379 Q53.1188 643.418 47.3897 643.418 L46.0847 643.418 L46.0847 649.243 M43.6657 637.562 L64.0042 637.562 L64.0042 643.418 L58.5933 643.418 Q61.8398 645.424 63.3994 648.416 Q64.9272 651.407 64.9272 655.736 Q64.9272 661.211 61.8716 664.457 Q58.7843 667.672 53.6281 667.672 Q47.6125 667.672 44.5569 663.661 Q41.5014 659.619 41.5014 651.63 L41.5014 643.418 L40.9285 643.418 Q36.8862 643.418 34.6901 646.092 Q32.4621 648.734 32.4621 653.54 Q32.4621 656.595 33.1941 659.492 Q33.9262 662.388 35.3903 665.062 L29.9795 665.062 Q28.7381 661.847 28.1334 658.823 Q27.4968 655.8 27.4968 652.935 Q27.4968 645.201 31.5072 641.381 Q35.5176 637.562 43.6657 637.562 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M18.2347 619.706 L28.3562 619.706 L28.3562 607.643 L32.9077 607.643 L32.9077 619.706 L52.2594 619.706 Q56.6199 619.706 57.8613 618.529 Q59.1026 617.319 59.1026 613.659 L59.1026 607.643 L64.0042 607.643 L64.0042 613.659 Q64.0042 620.438 61.4897 623.016 Q58.9434 625.595 52.2594 625.595 L32.9077 625.595 L32.9077 629.891 L28.3562 629.891 L28.3562 625.595 L18.2347 625.595 L18.2347 619.706 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M49.9359 600.545 L28.3562 600.545 L28.3562 594.689 L49.7131 594.689 Q54.7739 594.689 57.3202 592.716 Q59.8346 590.742 59.8346 586.796 Q59.8346 582.053 56.8109 579.316 Q53.7872 576.547 48.5673 576.547 L28.3562 576.547 L28.3562 570.69 L64.0042 570.69 L64.0042 576.547 L58.5296 576.547 Q61.7762 578.679 63.3676 581.512 Q64.9272 584.313 64.9272 588.037 Q64.9272 594.18 61.1078 597.363 Q57.2883 600.545 49.9359 600.545 M27.4968 585.809 L27.4968 585.809 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M33.8307 537.971 Q33.2578 538.957 33.0032 540.135 Q32.7167 541.281 32.7167 542.681 Q32.7167 547.646 35.9632 550.32 Q39.1779 552.962 45.2253 552.962 L64.0042 552.962 L64.0042 558.85 L28.3562 558.85 L28.3562 552.962 L33.8944 552.962 Q30.6479 551.116 29.0883 548.156 Q27.4968 545.196 27.4968 540.962 Q27.4968 540.358 27.5923 539.626 Q27.656 538.894 27.8151 538.002 L33.8307 537.971 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M44.7161 502.768 L47.5806 502.768 L47.5806 529.695 Q53.6281 529.313 56.8109 526.067 Q59.9619 522.788 59.9619 516.964 Q59.9619 513.59 59.1344 510.439 Q58.3069 507.256 56.6518 504.137 L62.1899 504.137 Q63.5267 507.288 64.227 510.598 Q64.9272 513.908 64.9272 517.314 Q64.9272 525.844 59.9619 530.841 Q54.9967 535.806 46.5303 535.806 Q37.7774 535.806 32.6531 531.096 Q27.4968 526.353 27.4968 518.332 Q27.4968 511.139 32.1438 506.97 Q36.7589 502.768 44.7161 502.768 M42.9973 508.625 Q38.1912 508.688 35.3266 511.33 Q32.4621 513.94 32.4621 518.269 Q32.4621 523.17 35.2312 526.13 Q38.0002 529.059 43.0292 529.504 L42.9973 508.625 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip170)\" d=\"M14.5426 494.079 L14.5426 488.986 Q22.0542 484.212 29.2474 481.857 Q36.4406 479.47 43.5384 479.47 Q50.668 479.47 57.8931 481.857 Q65.1182 484.212 72.5979 488.986 L72.5979 494.079 Q65.3091 489.846 58.1159 487.777 Q50.8908 485.676 43.5384 485.676 Q36.186 485.676 29.0246 487.777 Q21.8632 489.846 14.5426 494.079 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><polyline clip-path=\"url(#clip172)\" style=\"stroke:#009af9; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"338.375,1384.24 357.932,1319.8 377.489,1255.35 397.046,1190.91 416.604,1126.47 436.161,1062.03 455.718,1011.9 475.275,961.77 494.832,911.642 514.389,861.515 533.946,811.387 553.503,772.017 573.06,732.648 592.617,693.279 612.175,653.909 631.732,614.54 651.289,583.444 670.846,552.349 690.403,521.254 709.96,490.158 729.517,459.063 749.074,434.627 768.631,410.192 788.188,385.756 807.745,361.32 827.303,336.885 846.86,318.026 866.417,299.168 885.974,280.31 905.531,261.452 925.088,242.594 944.645,228.572 964.202,214.55 983.759,200.528 1003.32,186.505 1022.87,172.483 1042.43,162.792 1061.99,153.1 1081.54,143.408 1101.1,133.717 1120.66,124.025 1140.22,118.334 1159.77,112.643 1179.33,106.952 1198.89,101.261 1218.44,95.5699 1238,93.693 1257.56,91.8162 1277.12,89.9394 1296.67,88.0625 1316.23,86.1857 1335.79,88.0625 1355.34,89.9394 1374.9,91.8162 1394.46,93.693 1414.02,95.5699 1433.57,101.261 1453.13,106.952 1472.69,112.643 1492.24,118.334 1511.8,124.025 1531.36,133.717 1550.92,143.408 1570.47,153.1 1590.03,162.792 1609.59,172.483 1629.14,186.505 1648.7,200.528 1668.26,214.55 1687.81,228.572 1707.37,242.594 1726.93,261.452 1746.49,280.31 1766.04,299.168 1785.6,318.026 1805.16,336.885 1824.71,361.32 1844.27,385.756 1863.83,410.192 1883.39,434.627 1902.94,459.063 1922.5,490.158 1942.06,521.254 1961.61,552.349 1981.17,583.444 2000.73,614.54 2020.29,653.909 2039.84,693.279 2059.4,732.648 2078.96,772.017 2098.51,811.387 2118.07,861.515 2137.63,911.642 2157.18,961.77 2176.74,1011.9 2196.3,1062.03 2215.86,1126.47 2235.41,1190.91 2254.97,1255.35 2274.53,1319.8 2294.08,1384.24 \"/>\n",
"</svg>\n"
],
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\"?>\n",
"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" width=\"600\" height=\"400\" viewBox=\"0 0 2400 1600\">\n",
"<defs>\n",
" <clipPath id=\"clip140\">\n",
" <rect x=\"0\" y=\"0\" width=\"2400\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<path clip-path=\"url(#clip140)\" d=\"M0 1600 L2400 1600 L2400 0 L0 0 Z\" fill=\"#ffffff\" fill-rule=\"evenodd\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip141\">\n",
" <rect x=\"480\" y=\"0\" width=\"1681\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<path clip-path=\"url(#clip140)\" d=\"M279.704 1423.18 L2352.76 1423.18 L2352.76 47.2441 L279.704 47.2441 Z\" fill=\"#ffffff\" fill-rule=\"evenodd\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip142\">\n",
" <rect x=\"279\" y=\"47\" width=\"2074\" height=\"1377\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polyline clip-path=\"url(#clip142)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"338.375,1423.18 338.375,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip142)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"827.303,1423.18 827.303,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip142)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"1316.23,1423.18 1316.23,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip142)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"1805.16,1423.18 1805.16,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip142)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"2294.08,1423.18 2294.08,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip142)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"279.704,1384.24 2352.76,1384.24 \"/>\n",
"<polyline clip-path=\"url(#clip142)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"279.704,1150.76 2352.76,1150.76 \"/>\n",
"<polyline clip-path=\"url(#clip142)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"279.704,917.284 2352.76,917.284 \"/>\n",
"<polyline clip-path=\"url(#clip142)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"279.704,683.806 2352.76,683.806 \"/>\n",
"<polyline clip-path=\"url(#clip142)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"279.704,450.329 2352.76,450.329 \"/>\n",
"<polyline clip-path=\"url(#clip142)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"279.704,216.852 2352.76,216.852 \"/>\n",
"<polyline clip-path=\"url(#clip140)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,1423.18 2352.76,1423.18 \"/>\n",
"<polyline clip-path=\"url(#clip140)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"338.375,1423.18 338.375,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip140)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"827.303,1423.18 827.303,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip140)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"1316.23,1423.18 1316.23,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip140)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"1805.16,1423.18 1805.16,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip140)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"2294.08,1423.18 2294.08,1404.28 \"/>\n",
"<path clip-path=\"url(#clip140)\" d=\"M284.903 1468.75 L314.579 1468.75 L314.579 1472.69 L284.903 1472.69 L284.903 1468.75 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M325.482 1481.64 L333.121 1481.64 L333.121 1455.28 L324.81 1456.95 L324.81 1452.69 L333.074 1451.02 L337.75 1451.02 L337.75 1481.64 L345.389 1481.64 L345.389 1485.58 L325.482 1485.58 L325.482 1481.64 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M354.833 1479.7 L359.718 1479.7 L359.718 1485.58 L354.833 1485.58 L354.833 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M379.903 1454.1 Q376.292 1454.1 374.463 1457.66 Q372.657 1461.2 372.657 1468.33 Q372.657 1475.44 374.463 1479.01 Q376.292 1482.55 379.903 1482.55 Q383.537 1482.55 385.343 1479.01 Q387.171 1475.44 387.171 1468.33 Q387.171 1461.2 385.343 1457.66 Q383.537 1454.1 379.903 1454.1 M379.903 1450.39 Q385.713 1450.39 388.768 1455 Q391.847 1459.58 391.847 1468.33 Q391.847 1477.06 388.768 1481.67 Q385.713 1486.25 379.903 1486.25 Q374.093 1486.25 371.014 1481.67 Q367.958 1477.06 367.958 1468.33 Q367.958 1459.58 371.014 1455 Q374.093 1450.39 379.903 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M774.328 1468.75 L804.004 1468.75 L804.004 1472.69 L774.328 1472.69 L774.328 1468.75 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M824.097 1454.1 Q820.485 1454.1 818.657 1457.66 Q816.851 1461.2 816.851 1468.33 Q816.851 1475.44 818.657 1479.01 Q820.485 1482.55 824.097 1482.55 Q827.731 1482.55 829.536 1479.01 Q831.365 1475.44 831.365 1468.33 Q831.365 1461.2 829.536 1457.66 Q827.731 1454.1 824.097 1454.1 M824.097 1450.39 Q829.907 1450.39 832.962 1455 Q836.041 1459.58 836.041 1468.33 Q836.041 1477.06 832.962 1481.67 Q829.907 1486.25 824.097 1486.25 Q818.286 1486.25 815.208 1481.67 Q812.152 1477.06 812.152 1468.33 Q812.152 1459.58 815.208 1455 Q818.286 1450.39 824.097 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M844.258 1479.7 L849.143 1479.7 L849.143 1485.58 L844.258 1485.58 L844.258 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M859.374 1451.02 L877.731 1451.02 L877.731 1454.96 L863.657 1454.96 L863.657 1463.43 Q864.675 1463.08 865.694 1462.92 Q866.712 1462.73 867.731 1462.73 Q873.518 1462.73 876.897 1465.9 Q880.277 1469.08 880.277 1474.49 Q880.277 1480.07 876.805 1483.17 Q873.332 1486.25 867.013 1486.25 Q864.837 1486.25 862.569 1485.88 Q860.323 1485.51 857.916 1484.77 L857.916 1480.07 Q859.999 1481.2 862.221 1481.76 Q864.444 1482.32 866.92 1482.32 Q870.925 1482.32 873.263 1480.21 Q875.601 1478.1 875.601 1474.49 Q875.601 1470.88 873.263 1468.77 Q870.925 1466.67 866.92 1466.67 Q865.045 1466.67 863.17 1467.08 Q861.319 1467.5 859.374 1468.38 L859.374 1451.02 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1293.61 1454.1 Q1290 1454.1 1288.17 1457.66 Q1286.37 1461.2 1286.37 1468.33 Q1286.37 1475.44 1288.17 1479.01 Q1290 1482.55 1293.61 1482.55 Q1297.25 1482.55 1299.05 1479.01 Q1300.88 1475.44 1300.88 1468.33 Q1300.88 1461.2 1299.05 1457.66 Q1297.25 1454.1 1293.61 1454.1 M1293.61 1450.39 Q1299.42 1450.39 1302.48 1455 Q1305.56 1459.58 1305.56 1468.33 Q1305.56 1477.06 1302.48 1481.67 Q1299.42 1486.25 1293.61 1486.25 Q1287.8 1486.25 1284.73 1481.67 Q1281.67 1477.06 1281.67 1468.33 Q1281.67 1459.58 1284.73 1455 Q1287.8 1450.39 1293.61 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1313.78 1479.7 L1318.66 1479.7 L1318.66 1485.58 L1313.78 1485.58 L1313.78 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1338.85 1454.1 Q1335.23 1454.1 1333.41 1457.66 Q1331.6 1461.2 1331.6 1468.33 Q1331.6 1475.44 1333.41 1479.01 Q1335.23 1482.55 1338.85 1482.55 Q1342.48 1482.55 1344.29 1479.01 Q1346.11 1475.44 1346.11 1468.33 Q1346.11 1461.2 1344.29 1457.66 Q1342.48 1454.1 1338.85 1454.1 M1338.85 1450.39 Q1344.66 1450.39 1347.71 1455 Q1350.79 1459.58 1350.79 1468.33 Q1350.79 1477.06 1347.71 1481.67 Q1344.66 1486.25 1338.85 1486.25 Q1333.04 1486.25 1329.96 1481.67 Q1326.9 1477.06 1326.9 1468.33 Q1326.9 1459.58 1329.96 1455 Q1333.04 1450.39 1338.85 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1783.04 1454.1 Q1779.43 1454.1 1777.6 1457.66 Q1775.79 1461.2 1775.79 1468.33 Q1775.79 1475.44 1777.6 1479.01 Q1779.43 1482.55 1783.04 1482.55 Q1786.67 1482.55 1788.48 1479.01 Q1790.31 1475.44 1790.31 1468.33 Q1790.31 1461.2 1788.48 1457.66 Q1786.67 1454.1 1783.04 1454.1 M1783.04 1450.39 Q1788.85 1450.39 1791.91 1455 Q1794.98 1459.58 1794.98 1468.33 Q1794.98 1477.06 1791.91 1481.67 Q1788.85 1486.25 1783.04 1486.25 Q1777.23 1486.25 1774.15 1481.67 Q1771.09 1477.06 1771.09 1468.33 Q1771.09 1459.58 1774.15 1455 Q1777.23 1450.39 1783.04 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1803.2 1479.7 L1808.09 1479.7 L1808.09 1485.58 L1803.2 1485.58 L1803.2 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1818.32 1451.02 L1836.67 1451.02 L1836.67 1454.96 L1822.6 1454.96 L1822.6 1463.43 Q1823.62 1463.08 1824.64 1462.92 Q1825.65 1462.73 1826.67 1462.73 Q1832.46 1462.73 1835.84 1465.9 Q1839.22 1469.08 1839.22 1474.49 Q1839.22 1480.07 1835.75 1483.17 Q1832.28 1486.25 1825.96 1486.25 Q1823.78 1486.25 1821.51 1485.88 Q1819.27 1485.51 1816.86 1484.77 L1816.86 1480.07 Q1818.94 1481.2 1821.16 1481.76 Q1823.39 1482.32 1825.86 1482.32 Q1829.87 1482.32 1832.21 1480.21 Q1834.54 1478.1 1834.54 1474.49 Q1834.54 1470.88 1832.21 1468.77 Q1829.87 1466.67 1825.86 1466.67 Q1823.99 1466.67 1822.11 1467.08 Q1820.26 1467.5 1818.32 1468.38 L1818.32 1451.02 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M2261.24 1481.64 L2268.88 1481.64 L2268.88 1455.28 L2260.57 1456.95 L2260.57 1452.69 L2268.83 1451.02 L2273.51 1451.02 L2273.51 1481.64 L2281.14 1481.64 L2281.14 1485.58 L2261.24 1485.58 L2261.24 1481.64 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M2290.59 1479.7 L2295.47 1479.7 L2295.47 1485.58 L2290.59 1485.58 L2290.59 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M2315.66 1454.1 Q2312.05 1454.1 2310.22 1457.66 Q2308.41 1461.2 2308.41 1468.33 Q2308.41 1475.44 2310.22 1479.01 Q2312.05 1482.55 2315.66 1482.55 Q2319.29 1482.55 2321.1 1479.01 Q2322.93 1475.44 2322.93 1468.33 Q2322.93 1461.2 2321.1 1457.66 Q2319.29 1454.1 2315.66 1454.1 M2315.66 1450.39 Q2321.47 1450.39 2324.52 1455 Q2327.6 1459.58 2327.6 1468.33 Q2327.6 1477.06 2324.52 1481.67 Q2321.47 1486.25 2315.66 1486.25 Q2309.85 1486.25 2306.77 1481.67 Q2303.71 1477.06 2303.71 1468.33 Q2303.71 1459.58 2306.77 1455 Q2309.85 1450.39 2315.66 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1124.96 1532.4 L1112.07 1549.74 L1125.62 1568.04 L1118.72 1568.04 L1108.34 1554.04 L1097.97 1568.04 L1091.06 1568.04 L1104.9 1549.39 L1092.24 1532.4 L1099.14 1532.4 L1108.6 1545.1 L1118.05 1532.4 L1124.96 1532.4 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1168.69 1518.58 Q1164.42 1525.9 1162.35 1533.06 Q1160.29 1540.23 1160.29 1547.58 Q1160.29 1554.93 1162.35 1562.16 Q1164.46 1569.35 1168.69 1576.64 L1163.6 1576.64 Q1158.82 1569.16 1156.43 1561.93 Q1154.08 1554.71 1154.08 1547.58 Q1154.08 1540.48 1156.43 1533.29 Q1158.79 1526.09 1163.6 1518.58 L1168.69 1518.58 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1205.71 1533.76 L1205.71 1539.24 Q1203.22 1537.87 1200.71 1537.2 Q1198.23 1536.5 1195.68 1536.5 Q1189.98 1536.5 1186.83 1540.13 Q1183.68 1543.73 1183.68 1550.25 Q1183.68 1556.78 1186.83 1560.4 Q1189.98 1564 1195.68 1564 Q1198.23 1564 1200.71 1563.33 Q1203.22 1562.63 1205.71 1561.26 L1205.71 1566.68 Q1203.25 1567.82 1200.61 1568.39 Q1198 1568.97 1195.04 1568.97 Q1186.99 1568.97 1182.25 1563.91 Q1177.51 1558.85 1177.51 1550.25 Q1177.51 1541.53 1182.28 1536.53 Q1187.09 1531.54 1195.42 1531.54 Q1198.13 1531.54 1200.71 1532.11 Q1203.29 1532.65 1205.71 1533.76 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1229.7 1536.5 Q1224.99 1536.5 1222.26 1540.19 Q1219.52 1543.85 1219.52 1550.25 Q1219.52 1556.65 1222.22 1560.34 Q1224.96 1564 1229.7 1564 Q1234.38 1564 1237.12 1560.31 Q1239.86 1556.62 1239.86 1550.25 Q1239.86 1543.92 1237.12 1540.23 Q1234.38 1536.5 1229.7 1536.5 M1229.7 1531.54 Q1237.34 1531.54 1241.7 1536.5 Q1246.06 1541.47 1246.06 1550.25 Q1246.06 1559 1241.7 1564 Q1237.34 1568.97 1229.7 1568.97 Q1222.03 1568.97 1217.67 1564 Q1213.34 1559 1213.34 1550.25 Q1213.34 1541.47 1217.67 1536.5 Q1222.03 1531.54 1229.7 1531.54 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1269.59 1536.5 Q1264.87 1536.5 1262.14 1540.19 Q1259.4 1543.85 1259.4 1550.25 Q1259.4 1556.65 1262.11 1560.34 Q1264.84 1564 1269.59 1564 Q1274.26 1564 1277 1560.31 Q1279.74 1556.62 1279.74 1550.25 Q1279.74 1543.92 1277 1540.23 Q1274.26 1536.5 1269.59 1536.5 M1269.59 1531.54 Q1277.22 1531.54 1281.58 1536.5 Q1285.95 1541.47 1285.95 1550.25 Q1285.95 1559 1281.58 1564 Q1277.22 1568.97 1269.59 1568.97 Q1261.91 1568.97 1257.55 1564 Q1253.23 1559 1253.23 1550.25 Q1253.23 1541.47 1257.55 1536.5 Q1261.91 1531.54 1269.59 1531.54 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1316.31 1537.87 Q1315.32 1537.3 1314.15 1537.04 Q1313 1536.76 1311.6 1536.76 Q1306.63 1536.76 1303.96 1540 Q1301.32 1543.22 1301.32 1549.27 L1301.32 1568.04 L1295.43 1568.04 L1295.43 1532.4 L1301.32 1532.4 L1301.32 1537.93 Q1303.16 1534.69 1306.12 1533.13 Q1309.08 1531.54 1313.32 1531.54 Q1313.92 1531.54 1314.65 1531.63 Q1315.39 1531.7 1316.28 1531.85 L1316.31 1537.87 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1344.76 1537.81 L1344.76 1518.52 L1350.62 1518.52 L1350.62 1568.04 L1344.76 1568.04 L1344.76 1562.7 Q1342.92 1565.88 1340.09 1567.44 Q1337.28 1568.97 1333.34 1568.97 Q1326.88 1568.97 1322.8 1563.81 Q1318.76 1558.65 1318.76 1550.25 Q1318.76 1541.85 1322.8 1536.69 Q1326.88 1531.54 1333.34 1531.54 Q1337.28 1531.54 1340.09 1533.1 Q1342.92 1534.62 1344.76 1537.81 M1324.81 1550.25 Q1324.81 1556.71 1327.45 1560.4 Q1330.12 1564.07 1334.77 1564.07 Q1339.42 1564.07 1342.09 1560.4 Q1344.76 1556.71 1344.76 1550.25 Q1344.76 1543.79 1342.09 1540.13 Q1339.42 1536.44 1334.77 1536.44 Q1330.12 1536.44 1327.45 1540.13 Q1324.81 1543.79 1324.81 1550.25 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1362.68 1532.4 L1368.54 1532.4 L1368.54 1568.04 L1362.68 1568.04 L1362.68 1532.4 M1362.68 1518.52 L1368.54 1518.52 L1368.54 1525.93 L1362.68 1525.93 L1362.68 1518.52 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1410.43 1546.53 L1410.43 1568.04 L1404.57 1568.04 L1404.57 1546.72 Q1404.57 1541.66 1402.6 1539.14 Q1400.62 1536.63 1396.68 1536.63 Q1391.93 1536.63 1389.2 1539.65 Q1386.46 1542.68 1386.46 1547.9 L1386.46 1568.04 L1380.57 1568.04 L1380.57 1532.4 L1386.46 1532.4 L1386.46 1537.93 Q1388.56 1534.72 1391.39 1533.13 Q1394.26 1531.54 1397.98 1531.54 Q1404.12 1531.54 1407.28 1535.36 Q1410.43 1539.14 1410.43 1546.53 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1438.31 1550.12 Q1431.21 1550.12 1428.47 1551.75 Q1425.74 1553.37 1425.74 1557.29 Q1425.74 1560.4 1427.77 1562.25 Q1429.84 1564.07 1433.37 1564.07 Q1438.24 1564.07 1441.17 1560.63 Q1444.13 1557.16 1444.13 1551.43 L1444.13 1550.12 L1438.31 1550.12 M1449.99 1547.71 L1449.99 1568.04 L1444.13 1568.04 L1444.13 1562.63 Q1442.13 1565.88 1439.14 1567.44 Q1436.14 1568.97 1431.82 1568.97 Q1426.34 1568.97 1423.09 1565.91 Q1419.88 1562.82 1419.88 1557.67 Q1419.88 1551.65 1423.89 1548.6 Q1427.93 1545.54 1435.92 1545.54 L1444.13 1545.54 L1444.13 1544.97 Q1444.13 1540.93 1441.46 1538.73 Q1438.82 1536.5 1434.01 1536.5 Q1430.96 1536.5 1428.06 1537.23 Q1425.16 1537.97 1422.49 1539.43 L1422.49 1534.02 Q1425.7 1532.78 1428.73 1532.17 Q1431.75 1531.54 1434.62 1531.54 Q1442.35 1531.54 1446.17 1535.55 Q1449.99 1539.56 1449.99 1547.71 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1467.85 1522.27 L1467.85 1532.4 L1479.91 1532.4 L1479.91 1536.95 L1467.85 1536.95 L1467.85 1556.3 Q1467.85 1560.66 1469.02 1561.9 Q1470.23 1563.14 1473.89 1563.14 L1479.91 1563.14 L1479.91 1568.04 L1473.89 1568.04 Q1467.11 1568.04 1464.53 1565.53 Q1461.96 1562.98 1461.96 1556.3 L1461.96 1536.95 L1457.66 1536.95 L1457.66 1532.4 L1461.96 1532.4 L1461.96 1522.27 L1467.85 1522.27 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1518.1 1548.76 L1518.1 1551.62 L1491.18 1551.62 Q1491.56 1557.67 1494.8 1560.85 Q1498.08 1564 1503.91 1564 Q1507.28 1564 1510.43 1563.17 Q1513.61 1562.35 1516.73 1560.69 L1516.73 1566.23 Q1513.58 1567.57 1510.27 1568.27 Q1506.96 1568.97 1503.56 1568.97 Q1495.03 1568.97 1490.03 1564 Q1485.06 1559.04 1485.06 1550.57 Q1485.06 1541.82 1489.77 1536.69 Q1494.52 1531.54 1502.54 1531.54 Q1509.73 1531.54 1513.9 1536.18 Q1518.1 1540.8 1518.1 1548.76 M1512.25 1547.04 Q1512.18 1542.23 1509.54 1539.37 Q1506.93 1536.5 1502.6 1536.5 Q1497.7 1536.5 1494.74 1539.27 Q1491.81 1542.04 1491.37 1547.07 L1512.25 1547.04 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M1526.79 1518.58 L1531.88 1518.58 Q1536.66 1526.09 1539.01 1533.29 Q1541.4 1540.48 1541.4 1547.58 Q1541.4 1554.71 1539.01 1561.93 Q1536.66 1569.16 1531.88 1576.64 L1526.79 1576.64 Q1531.02 1569.35 1533.09 1562.16 Q1535.19 1554.93 1535.19 1547.58 Q1535.19 1540.23 1533.09 1533.06 Q1531.02 1525.9 1526.79 1518.58 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><polyline clip-path=\"url(#clip140)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,1423.18 279.704,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip140)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,1384.24 298.602,1384.24 \"/>\n",
"<polyline clip-path=\"url(#clip140)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,1150.76 298.602,1150.76 \"/>\n",
"<polyline clip-path=\"url(#clip140)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,917.284 298.602,917.284 \"/>\n",
"<polyline clip-path=\"url(#clip140)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,683.806 298.602,683.806 \"/>\n",
"<polyline clip-path=\"url(#clip140)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,450.329 298.602,450.329 \"/>\n",
"<polyline clip-path=\"url(#clip140)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"279.704,216.852 298.602,216.852 \"/>\n",
"<path clip-path=\"url(#clip140)\" d=\"M126.205 1370.04 Q122.593 1370.04 120.765 1373.6 Q118.959 1377.14 118.959 1384.27 Q118.959 1391.38 120.765 1394.94 Q122.593 1398.49 126.205 1398.49 Q129.839 1398.49 131.644 1394.94 Q133.473 1391.38 133.473 1384.27 Q133.473 1377.14 131.644 1373.6 Q129.839 1370.04 126.205 1370.04 M126.205 1366.33 Q132.015 1366.33 135.07 1370.94 Q138.149 1375.52 138.149 1384.27 Q138.149 1393 135.07 1397.61 Q132.015 1402.19 126.205 1402.19 Q120.394 1402.19 117.316 1397.61 Q114.26 1393 114.26 1384.27 Q114.26 1375.52 117.316 1370.94 Q120.394 1366.33 126.205 1366.33 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M146.366 1395.64 L151.251 1395.64 L151.251 1401.52 L146.366 1401.52 L146.366 1395.64 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M171.436 1370.04 Q167.825 1370.04 165.996 1373.6 Q164.19 1377.14 164.19 1384.27 Q164.19 1391.38 165.996 1394.94 Q167.825 1398.49 171.436 1398.49 Q175.07 1398.49 176.876 1394.94 Q178.704 1391.38 178.704 1384.27 Q178.704 1377.14 176.876 1373.6 Q175.07 1370.04 171.436 1370.04 M171.436 1366.33 Q177.246 1366.33 180.301 1370.94 Q183.38 1375.52 183.38 1384.27 Q183.38 1393 180.301 1397.61 Q177.246 1402.19 171.436 1402.19 Q165.626 1402.19 162.547 1397.61 Q159.491 1393 159.491 1384.27 Q159.491 1375.52 162.547 1370.94 Q165.626 1366.33 171.436 1366.33 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M201.598 1370.04 Q197.987 1370.04 196.158 1373.6 Q194.352 1377.14 194.352 1384.27 Q194.352 1391.38 196.158 1394.94 Q197.987 1398.49 201.598 1398.49 Q205.232 1398.49 207.037 1394.94 Q208.866 1391.38 208.866 1384.27 Q208.866 1377.14 207.037 1373.6 Q205.232 1370.04 201.598 1370.04 M201.598 1366.33 Q207.408 1366.33 210.463 1370.94 Q213.542 1375.52 213.542 1384.27 Q213.542 1393 210.463 1397.61 Q207.408 1402.19 201.598 1402.19 Q195.787 1402.19 192.709 1397.61 Q189.653 1393 189.653 1384.27 Q189.653 1375.52 192.709 1370.94 Q195.787 1366.33 201.598 1366.33 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M231.76 1370.04 Q228.148 1370.04 226.32 1373.6 Q224.514 1377.14 224.514 1384.27 Q224.514 1391.38 226.32 1394.94 Q228.148 1398.49 231.76 1398.49 Q235.394 1398.49 237.199 1394.94 Q239.028 1391.38 239.028 1384.27 Q239.028 1377.14 237.199 1373.6 Q235.394 1370.04 231.76 1370.04 M231.76 1366.33 Q237.57 1366.33 240.625 1370.94 Q243.704 1375.52 243.704 1384.27 Q243.704 1393 240.625 1397.61 Q237.57 1402.19 231.76 1402.19 Q225.949 1402.19 222.871 1397.61 Q219.815 1393 219.815 1384.27 Q219.815 1375.52 222.871 1370.94 Q225.949 1366.33 231.76 1366.33 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M127.2 1136.56 Q123.589 1136.56 121.76 1140.12 Q119.955 1143.67 119.955 1150.8 Q119.955 1157.9 121.76 1161.47 Q123.589 1165.01 127.2 1165.01 Q130.834 1165.01 132.64 1161.47 Q134.468 1157.9 134.468 1150.8 Q134.468 1143.67 132.64 1140.12 Q130.834 1136.56 127.2 1136.56 M127.2 1132.86 Q133.01 1132.86 136.066 1137.46 Q139.144 1142.05 139.144 1150.8 Q139.144 1159.52 136.066 1164.13 Q133.01 1168.71 127.2 1168.71 Q121.39 1168.71 118.311 1164.13 Q115.256 1159.52 115.256 1150.8 Q115.256 1142.05 118.311 1137.46 Q121.39 1132.86 127.2 1132.86 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M147.362 1162.16 L152.246 1162.16 L152.246 1168.04 L147.362 1168.04 L147.362 1162.16 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M172.431 1136.56 Q168.82 1136.56 166.991 1140.12 Q165.186 1143.67 165.186 1150.8 Q165.186 1157.9 166.991 1161.47 Q168.82 1165.01 172.431 1165.01 Q176.065 1165.01 177.871 1161.47 Q179.7 1157.9 179.7 1150.8 Q179.7 1143.67 177.871 1140.12 Q176.065 1136.56 172.431 1136.56 M172.431 1132.86 Q178.241 1132.86 181.297 1137.46 Q184.376 1142.05 184.376 1150.8 Q184.376 1159.52 181.297 1164.13 Q178.241 1168.71 172.431 1168.71 Q166.621 1168.71 163.542 1164.13 Q160.487 1159.52 160.487 1150.8 Q160.487 1142.05 163.542 1137.46 Q166.621 1132.86 172.431 1132.86 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M196.621 1164.11 L212.94 1164.11 L212.94 1168.04 L190.996 1168.04 L190.996 1164.11 Q193.658 1161.35 198.241 1156.72 Q202.848 1152.07 204.028 1150.73 Q206.274 1148.2 207.153 1146.47 Q208.056 1144.71 208.056 1143.02 Q208.056 1140.26 206.112 1138.53 Q204.19 1136.79 201.088 1136.79 Q198.889 1136.79 196.436 1137.55 Q194.005 1138.32 191.227 1139.87 L191.227 1135.15 Q194.051 1134.01 196.505 1133.43 Q198.959 1132.86 200.996 1132.86 Q206.366 1132.86 209.561 1135.54 Q212.755 1138.23 212.755 1142.72 Q212.755 1144.85 211.945 1146.77 Q211.158 1148.67 209.051 1151.26 Q208.473 1151.93 205.371 1155.15 Q202.269 1158.34 196.621 1164.11 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M222.801 1133.48 L241.158 1133.48 L241.158 1137.42 L227.084 1137.42 L227.084 1145.89 Q228.102 1145.54 229.121 1145.38 Q230.139 1145.19 231.158 1145.19 Q236.945 1145.19 240.324 1148.37 Q243.704 1151.54 243.704 1156.95 Q243.704 1162.53 240.232 1165.63 Q236.76 1168.71 230.44 1168.71 Q228.264 1168.71 225.996 1168.34 Q223.75 1167.97 221.343 1167.23 L221.343 1162.53 Q223.426 1163.67 225.648 1164.22 Q227.871 1164.78 230.347 1164.78 Q234.352 1164.78 236.69 1162.67 Q239.028 1160.56 239.028 1156.95 Q239.028 1153.34 236.69 1151.24 Q234.352 1149.13 230.347 1149.13 Q228.473 1149.13 226.598 1149.55 Q224.746 1149.96 222.801 1150.84 L222.801 1133.48 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M126.205 903.082 Q122.593 903.082 120.765 906.647 Q118.959 910.189 118.959 917.318 Q118.959 924.425 120.765 927.99 Q122.593 931.531 126.205 931.531 Q129.839 931.531 131.644 927.99 Q133.473 924.425 133.473 917.318 Q133.473 910.189 131.644 906.647 Q129.839 903.082 126.205 903.082 M126.205 899.379 Q132.015 899.379 135.07 903.985 Q138.149 908.568 138.149 917.318 Q138.149 926.045 135.07 930.652 Q132.015 935.235 126.205 935.235 Q120.394 935.235 117.316 930.652 Q114.26 926.045 114.26 917.318 Q114.26 908.568 117.316 903.985 Q120.394 899.379 126.205 899.379 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M146.366 928.684 L151.251 928.684 L151.251 934.564 L146.366 934.564 L146.366 928.684 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M171.436 903.082 Q167.825 903.082 165.996 906.647 Q164.19 910.189 164.19 917.318 Q164.19 924.425 165.996 927.99 Q167.825 931.531 171.436 931.531 Q175.07 931.531 176.876 927.99 Q178.704 924.425 178.704 917.318 Q178.704 910.189 176.876 906.647 Q175.07 903.082 171.436 903.082 M171.436 899.379 Q177.246 899.379 180.301 903.985 Q183.38 908.568 183.38 917.318 Q183.38 926.045 180.301 930.652 Q177.246 935.235 171.436 935.235 Q165.626 935.235 162.547 930.652 Q159.491 926.045 159.491 917.318 Q159.491 908.568 162.547 903.985 Q165.626 899.379 171.436 899.379 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M191.644 900.004 L210 900.004 L210 903.939 L195.926 903.939 L195.926 912.411 Q196.945 912.064 197.963 911.902 Q198.982 911.716 200 911.716 Q205.787 911.716 209.167 914.888 Q212.547 918.059 212.547 923.476 Q212.547 929.054 209.074 932.156 Q205.602 935.235 199.283 935.235 Q197.107 935.235 194.838 934.865 Q192.593 934.494 190.186 933.753 L190.186 929.054 Q192.269 930.189 194.491 930.744 Q196.713 931.3 199.19 931.3 Q203.195 931.3 205.533 929.193 Q207.871 927.087 207.871 923.476 Q207.871 919.865 205.533 917.758 Q203.195 915.652 199.19 915.652 Q197.315 915.652 195.44 916.068 Q193.588 916.485 191.644 917.365 L191.644 900.004 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M231.76 903.082 Q228.148 903.082 226.32 906.647 Q224.514 910.189 224.514 917.318 Q224.514 924.425 226.32 927.99 Q228.148 931.531 231.76 931.531 Q235.394 931.531 237.199 927.99 Q239.028 924.425 239.028 917.318 Q239.028 910.189 237.199 906.647 Q235.394 903.082 231.76 903.082 M231.76 899.379 Q237.57 899.379 240.625 903.985 Q243.704 908.568 243.704 917.318 Q243.704 926.045 240.625 930.652 Q237.57 935.235 231.76 935.235 Q225.949 935.235 222.871 930.652 Q219.815 926.045 219.815 917.318 Q219.815 908.568 222.871 903.985 Q225.949 899.379 231.76 899.379 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M127.2 669.605 Q123.589 669.605 121.76 673.17 Q119.955 676.711 119.955 683.841 Q119.955 690.947 121.76 694.512 Q123.589 698.054 127.2 698.054 Q130.834 698.054 132.64 694.512 Q134.468 690.947 134.468 683.841 Q134.468 676.711 132.64 673.17 Q130.834 669.605 127.2 669.605 M127.2 665.901 Q133.01 665.901 136.066 670.508 Q139.144 675.091 139.144 683.841 Q139.144 692.568 136.066 697.174 Q133.01 701.758 127.2 701.758 Q121.39 701.758 118.311 697.174 Q115.256 692.568 115.256 683.841 Q115.256 675.091 118.311 670.508 Q121.39 665.901 127.2 665.901 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M147.362 695.207 L152.246 695.207 L152.246 701.086 L147.362 701.086 L147.362 695.207 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M172.431 669.605 Q168.82 669.605 166.991 673.17 Q165.186 676.711 165.186 683.841 Q165.186 690.947 166.991 694.512 Q168.82 698.054 172.431 698.054 Q176.065 698.054 177.871 694.512 Q179.7 690.947 179.7 683.841 Q179.7 676.711 177.871 673.17 Q176.065 669.605 172.431 669.605 M172.431 665.901 Q178.241 665.901 181.297 670.508 Q184.376 675.091 184.376 683.841 Q184.376 692.568 181.297 697.174 Q178.241 701.758 172.431 701.758 Q166.621 701.758 163.542 697.174 Q160.487 692.568 160.487 683.841 Q160.487 675.091 163.542 670.508 Q166.621 665.901 172.431 665.901 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M191.413 666.526 L213.635 666.526 L213.635 668.517 L201.088 701.086 L196.204 701.086 L208.01 670.461 L191.413 670.461 L191.413 666.526 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M222.801 666.526 L241.158 666.526 L241.158 670.461 L227.084 670.461 L227.084 678.934 Q228.102 678.586 229.121 678.424 Q230.139 678.239 231.158 678.239 Q236.945 678.239 240.324 681.41 Q243.704 684.582 243.704 689.998 Q243.704 695.577 240.232 698.679 Q236.76 701.758 230.44 701.758 Q228.264 701.758 225.996 701.387 Q223.75 701.017 221.343 700.276 L221.343 695.577 Q223.426 696.711 225.648 697.267 Q227.871 697.822 230.347 697.822 Q234.352 697.822 236.69 695.716 Q239.028 693.609 239.028 689.998 Q239.028 686.387 236.69 684.281 Q234.352 682.174 230.347 682.174 Q228.473 682.174 226.598 682.591 Q224.746 683.008 222.801 683.887 L222.801 666.526 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M126.205 436.128 Q122.593 436.128 120.765 439.692 Q118.959 443.234 118.959 450.364 Q118.959 457.47 120.765 461.035 Q122.593 464.577 126.205 464.577 Q129.839 464.577 131.644 461.035 Q133.473 457.47 133.473 450.364 Q133.473 443.234 131.644 439.692 Q129.839 436.128 126.205 436.128 M126.205 432.424 Q132.015 432.424 135.07 437.03 Q138.149 441.614 138.149 450.364 Q138.149 459.09 135.07 463.697 Q132.015 468.28 126.205 468.28 Q120.394 468.28 117.316 463.697 Q114.26 459.09 114.26 450.364 Q114.26 441.614 117.316 437.03 Q120.394 432.424 126.205 432.424 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M146.366 461.729 L151.251 461.729 L151.251 467.609 L146.366 467.609 L146.366 461.729 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M162.246 463.674 L169.885 463.674 L169.885 437.308 L161.575 438.975 L161.575 434.716 L169.839 433.049 L174.514 433.049 L174.514 463.674 L182.153 463.674 L182.153 467.609 L162.246 467.609 L162.246 463.674 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M201.598 436.128 Q197.987 436.128 196.158 439.692 Q194.352 443.234 194.352 450.364 Q194.352 457.47 196.158 461.035 Q197.987 464.577 201.598 464.577 Q205.232 464.577 207.037 461.035 Q208.866 457.47 208.866 450.364 Q208.866 443.234 207.037 439.692 Q205.232 436.128 201.598 436.128 M201.598 432.424 Q207.408 432.424 210.463 437.03 Q213.542 441.614 213.542 450.364 Q213.542 459.09 210.463 463.697 Q207.408 468.28 201.598 468.28 Q195.787 468.28 192.709 463.697 Q189.653 459.09 189.653 450.364 Q189.653 441.614 192.709 437.03 Q195.787 432.424 201.598 432.424 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M231.76 436.128 Q228.148 436.128 226.32 439.692 Q224.514 443.234 224.514 450.364 Q224.514 457.47 226.32 461.035 Q228.148 464.577 231.76 464.577 Q235.394 464.577 237.199 461.035 Q239.028 457.47 239.028 450.364 Q239.028 443.234 237.199 439.692 Q235.394 436.128 231.76 436.128 M231.76 432.424 Q237.57 432.424 240.625 437.03 Q243.704 441.614 243.704 450.364 Q243.704 459.09 240.625 463.697 Q237.57 468.28 231.76 468.28 Q225.949 468.28 222.871 463.697 Q219.815 459.09 219.815 450.364 Q219.815 441.614 222.871 437.03 Q225.949 432.424 231.76 432.424 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M127.2 202.65 Q123.589 202.65 121.76 206.215 Q119.955 209.757 119.955 216.886 Q119.955 223.993 121.76 227.558 Q123.589 231.099 127.2 231.099 Q130.834 231.099 132.64 227.558 Q134.468 223.993 134.468 216.886 Q134.468 209.757 132.64 206.215 Q130.834 202.65 127.2 202.65 M127.2 198.947 Q133.01 198.947 136.066 203.553 Q139.144 208.136 139.144 216.886 Q139.144 225.613 136.066 230.22 Q133.01 234.803 127.2 234.803 Q121.39 234.803 118.311 230.22 Q115.256 225.613 115.256 216.886 Q115.256 208.136 118.311 203.553 Q121.39 198.947 127.2 198.947 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M147.362 228.252 L152.246 228.252 L152.246 234.132 L147.362 234.132 L147.362 228.252 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M163.241 230.196 L170.88 230.196 L170.88 203.831 L162.57 205.497 L162.57 201.238 L170.834 199.572 L175.51 199.572 L175.51 230.196 L183.149 230.196 L183.149 234.132 L163.241 234.132 L163.241 230.196 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M196.621 230.196 L212.94 230.196 L212.94 234.132 L190.996 234.132 L190.996 230.196 Q193.658 227.442 198.241 222.812 Q202.848 218.159 204.028 216.817 Q206.274 214.294 207.153 212.558 Q208.056 210.798 208.056 209.109 Q208.056 206.354 206.112 204.618 Q204.19 202.882 201.088 202.882 Q198.889 202.882 196.436 203.646 Q194.005 204.41 191.227 205.96 L191.227 201.238 Q194.051 200.104 196.505 199.525 Q198.959 198.947 200.996 198.947 Q206.366 198.947 209.561 201.632 Q212.755 204.317 212.755 208.808 Q212.755 210.937 211.945 212.859 Q211.158 214.757 209.051 217.349 Q208.473 218.021 205.371 221.238 Q202.269 224.433 196.621 230.196 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M222.801 199.572 L241.158 199.572 L241.158 203.507 L227.084 203.507 L227.084 211.979 Q228.102 211.632 229.121 211.47 Q230.139 211.284 231.158 211.284 Q236.945 211.284 240.324 214.456 Q243.704 217.627 243.704 223.044 Q243.704 228.622 240.232 231.724 Q236.76 234.803 230.44 234.803 Q228.264 234.803 225.996 234.433 Q223.75 234.062 221.343 233.321 L221.343 228.622 Q223.426 229.757 225.648 230.312 Q227.871 230.868 230.347 230.868 Q234.352 230.868 236.69 228.761 Q239.028 226.655 239.028 223.044 Q239.028 219.433 236.69 217.326 Q234.352 215.22 230.347 215.22 Q228.473 215.22 226.598 215.636 Q224.746 216.053 222.801 216.933 L222.801 199.572 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M49.9359 990.954 L28.3562 990.954 L28.3562 985.098 L49.7131 985.098 Q54.7739 985.098 57.3202 983.124 Q59.8346 981.151 59.8346 977.204 Q59.8346 972.462 56.8109 969.725 Q53.7872 966.956 48.5673 966.956 L28.3562 966.956 L28.3562 961.099 L64.0042 961.099 L64.0042 966.956 L58.5296 966.956 Q61.7762 969.088 63.3676 971.921 Q64.9272 974.722 64.9272 978.446 Q64.9272 984.589 61.1078 987.771 Q57.2883 990.954 49.9359 990.954 M27.4968 976.218 L27.4968 976.218 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M14.5426 914.247 Q21.8632 918.512 29.0246 920.581 Q36.186 922.65 43.5384 922.65 Q50.8908 922.65 58.1159 920.581 Q65.3091 918.481 72.5979 914.247 L72.5979 919.34 Q65.1182 924.114 57.8931 926.501 Q50.668 928.857 43.5384 928.857 Q36.4406 928.857 29.2474 926.501 Q22.0542 924.146 14.5426 919.34 L14.5426 914.247 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M18.2347 897.092 L28.3562 897.092 L28.3562 885.029 L32.9077 885.029 L32.9077 897.092 L52.2594 897.092 Q56.6199 897.092 57.8613 895.914 Q59.1026 894.705 59.1026 891.044 L59.1026 885.029 L64.0042 885.029 L64.0042 891.044 Q64.0042 897.824 61.4897 900.402 Q58.9434 902.98 52.2594 902.98 L32.9077 902.98 L32.9077 907.277 L28.3562 907.277 L28.3562 902.98 L18.2347 902.98 L18.2347 897.092 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M44.7161 846.835 L47.5806 846.835 L47.5806 873.762 Q53.6281 873.38 56.8109 870.133 Q59.9619 866.855 59.9619 861.03 Q59.9619 857.656 59.1344 854.505 Q58.3069 851.322 56.6518 848.203 L62.1899 848.203 Q63.5267 851.354 64.227 854.664 Q64.9272 857.975 64.9272 861.38 Q64.9272 869.91 59.9619 874.907 Q54.9967 879.873 46.5303 879.873 Q37.7774 879.873 32.6531 875.162 Q27.4968 870.42 27.4968 862.399 Q27.4968 855.206 32.1438 851.036 Q36.7589 846.835 44.7161 846.835 M42.9973 852.691 Q38.1912 852.755 35.3266 855.397 Q32.4621 858.006 32.4621 862.335 Q32.4621 867.237 35.2312 870.197 Q38.0002 873.125 43.0292 873.571 L42.9973 852.691 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M35.1993 809.468 Q31.2526 807.272 29.3747 804.216 Q27.4968 801.161 27.4968 797.023 Q27.4968 791.453 31.4117 788.429 Q35.2948 785.406 42.4881 785.406 L64.0042 785.406 L64.0042 791.294 L42.679 791.294 Q37.5546 791.294 35.072 793.108 Q32.5894 794.922 32.5894 798.646 Q32.5894 803.198 35.6131 805.839 Q38.6368 808.481 43.8567 808.481 L64.0042 808.481 L64.0042 814.37 L42.679 814.37 Q37.5228 814.37 35.072 816.184 Q32.5894 817.998 32.5894 821.786 Q32.5894 826.273 35.6449 828.915 Q38.6686 831.557 43.8567 831.557 L64.0042 831.557 L64.0042 837.445 L28.3562 837.445 L28.3562 831.557 L33.8944 831.557 Q30.616 829.552 29.0564 826.751 Q27.4968 823.95 27.4968 820.099 Q27.4968 816.216 29.4702 813.51 Q31.4436 810.773 35.1993 809.468 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M58.657 768.059 L77.5631 768.059 L77.5631 773.947 L28.3562 773.947 L28.3562 768.059 L33.7671 768.059 Q30.5842 766.213 29.0564 763.412 Q27.4968 760.579 27.4968 756.664 Q27.4968 750.171 32.6531 746.129 Q37.8093 742.055 46.212 742.055 Q54.6147 742.055 59.771 746.129 Q64.9272 750.171 64.9272 756.664 Q64.9272 760.579 63.3994 763.412 Q61.8398 766.213 58.657 768.059 M46.212 748.134 Q39.7508 748.134 36.0905 750.808 Q32.3984 753.45 32.3984 758.097 Q32.3984 762.744 36.0905 765.417 Q39.7508 768.059 46.212 768.059 Q52.6732 768.059 56.3653 765.417 Q60.0256 762.744 60.0256 758.097 Q60.0256 753.45 56.3653 750.808 Q52.6732 748.134 46.212 748.134 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M44.7161 701.856 L47.5806 701.856 L47.5806 728.783 Q53.6281 728.401 56.8109 725.154 Q59.9619 721.876 59.9619 716.051 Q59.9619 712.677 59.1344 709.526 Q58.3069 706.343 56.6518 703.224 L62.1899 703.224 Q63.5267 706.375 64.227 709.685 Q64.9272 712.996 64.9272 716.401 Q64.9272 724.931 59.9619 729.928 Q54.9967 734.894 46.5303 734.894 Q37.7774 734.894 32.6531 730.183 Q27.4968 725.441 27.4968 717.42 Q27.4968 710.227 32.1438 706.057 Q36.7589 701.856 44.7161 701.856 M42.9973 707.712 Q38.1912 707.776 35.3266 710.418 Q32.4621 713.027 32.4621 717.356 Q32.4621 722.258 35.2312 725.218 Q38.0002 728.146 43.0292 728.592 L42.9973 707.712 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M33.8307 671.587 Q33.2578 672.573 33.0032 673.751 Q32.7167 674.897 32.7167 676.297 Q32.7167 681.263 35.9632 683.936 Q39.1779 686.578 45.2253 686.578 L64.0042 686.578 L64.0042 692.466 L28.3562 692.466 L28.3562 686.578 L33.8944 686.578 Q30.6479 684.732 29.0883 681.772 Q27.4968 678.812 27.4968 674.579 Q27.4968 673.974 27.5923 673.242 Q27.656 672.51 27.8151 671.619 L33.8307 671.587 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M46.0847 649.243 Q46.0847 656.341 47.7079 659.078 Q49.3312 661.815 53.2461 661.815 Q56.3653 661.815 58.2114 659.778 Q60.0256 657.709 60.0256 654.177 Q60.0256 649.307 56.5881 646.379 Q53.1188 643.418 47.3897 643.418 L46.0847 643.418 L46.0847 649.243 M43.6657 637.562 L64.0042 637.562 L64.0042 643.418 L58.5933 643.418 Q61.8398 645.424 63.3994 648.416 Q64.9272 651.407 64.9272 655.736 Q64.9272 661.211 61.8716 664.457 Q58.7843 667.672 53.6281 667.672 Q47.6125 667.672 44.5569 663.661 Q41.5014 659.619 41.5014 651.63 L41.5014 643.418 L40.9285 643.418 Q36.8862 643.418 34.6901 646.092 Q32.4621 648.734 32.4621 653.54 Q32.4621 656.595 33.1941 659.492 Q33.9262 662.388 35.3903 665.062 L29.9795 665.062 Q28.7381 661.847 28.1334 658.823 Q27.4968 655.8 27.4968 652.935 Q27.4968 645.201 31.5072 641.381 Q35.5176 637.562 43.6657 637.562 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M18.2347 619.706 L28.3562 619.706 L28.3562 607.643 L32.9077 607.643 L32.9077 619.706 L52.2594 619.706 Q56.6199 619.706 57.8613 618.529 Q59.1026 617.319 59.1026 613.659 L59.1026 607.643 L64.0042 607.643 L64.0042 613.659 Q64.0042 620.438 61.4897 623.016 Q58.9434 625.595 52.2594 625.595 L32.9077 625.595 L32.9077 629.891 L28.3562 629.891 L28.3562 625.595 L18.2347 625.595 L18.2347 619.706 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M49.9359 600.545 L28.3562 600.545 L28.3562 594.689 L49.7131 594.689 Q54.7739 594.689 57.3202 592.716 Q59.8346 590.742 59.8346 586.796 Q59.8346 582.053 56.8109 579.316 Q53.7872 576.547 48.5673 576.547 L28.3562 576.547 L28.3562 570.69 L64.0042 570.69 L64.0042 576.547 L58.5296 576.547 Q61.7762 578.679 63.3676 581.512 Q64.9272 584.313 64.9272 588.037 Q64.9272 594.18 61.1078 597.363 Q57.2883 600.545 49.9359 600.545 M27.4968 585.809 L27.4968 585.809 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M33.8307 537.971 Q33.2578 538.957 33.0032 540.135 Q32.7167 541.281 32.7167 542.681 Q32.7167 547.646 35.9632 550.32 Q39.1779 552.962 45.2253 552.962 L64.0042 552.962 L64.0042 558.85 L28.3562 558.85 L28.3562 552.962 L33.8944 552.962 Q30.6479 551.116 29.0883 548.156 Q27.4968 545.196 27.4968 540.962 Q27.4968 540.358 27.5923 539.626 Q27.656 538.894 27.8151 538.002 L33.8307 537.971 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M44.7161 502.768 L47.5806 502.768 L47.5806 529.695 Q53.6281 529.313 56.8109 526.067 Q59.9619 522.788 59.9619 516.964 Q59.9619 513.59 59.1344 510.439 Q58.3069 507.256 56.6518 504.137 L62.1899 504.137 Q63.5267 507.288 64.227 510.598 Q64.9272 513.908 64.9272 517.314 Q64.9272 525.844 59.9619 530.841 Q54.9967 535.806 46.5303 535.806 Q37.7774 535.806 32.6531 531.096 Q27.4968 526.353 27.4968 518.332 Q27.4968 511.139 32.1438 506.97 Q36.7589 502.768 44.7161 502.768 M42.9973 508.625 Q38.1912 508.688 35.3266 511.33 Q32.4621 513.94 32.4621 518.269 Q32.4621 523.17 35.2312 526.13 Q38.0002 529.059 43.0292 529.504 L42.9973 508.625 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip140)\" d=\"M14.5426 494.079 L14.5426 488.986 Q22.0542 484.212 29.2474 481.857 Q36.4406 479.47 43.5384 479.47 Q50.668 479.47 57.8931 481.857 Q65.1182 484.212 72.5979 488.986 L72.5979 494.079 Q65.3091 489.846 58.1159 487.777 Q50.8908 485.676 43.5384 485.676 Q36.186 485.676 29.0246 487.777 Q21.8632 489.846 14.5426 494.079 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><polyline clip-path=\"url(#clip142)\" style=\"stroke:#009af9; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"338.375,1384.24 357.932,1319.8 377.489,1255.35 397.046,1190.91 416.604,1126.47 436.161,1062.03 455.718,1011.9 475.275,961.77 494.832,911.642 514.389,861.515 533.946,811.387 553.503,772.017 573.06,732.648 592.617,693.279 612.175,653.909 631.732,614.54 651.289,583.444 670.846,552.349 690.403,521.254 709.96,490.158 729.517,459.063 749.074,434.627 768.631,410.192 788.188,385.756 807.745,361.32 827.303,336.885 846.86,318.026 866.417,299.168 885.974,280.31 905.531,261.452 925.088,242.594 944.645,228.572 964.202,214.55 983.759,200.528 1003.32,186.505 1022.87,172.483 1042.43,162.792 1061.99,153.1 1081.54,143.408 1101.1,133.717 1120.66,124.025 1140.22,118.334 1159.77,112.643 1179.33,106.952 1198.89,101.261 1218.44,95.5699 1238,93.693 1257.56,91.8162 1277.12,89.9394 1296.67,88.0625 1316.23,86.1857 1335.79,88.0625 1355.34,89.9394 1374.9,91.8162 1394.46,93.693 1414.02,95.5699 1433.57,101.261 1453.13,106.952 1472.69,112.643 1492.24,118.334 1511.8,124.025 1531.36,133.717 1550.92,143.408 1570.47,153.1 1590.03,162.792 1609.59,172.483 1629.14,186.505 1648.7,200.528 1668.26,214.55 1687.81,228.572 1707.37,242.594 1726.93,261.452 1746.49,280.31 1766.04,299.168 1785.6,318.026 1805.16,336.885 1824.71,361.32 1844.27,385.756 1863.83,410.192 1883.39,434.627 1902.94,459.063 1922.5,490.158 1942.06,521.254 1961.61,552.349 1981.17,583.444 2000.73,614.54 2020.29,653.909 2039.84,693.279 2059.4,732.648 2078.96,772.017 2098.51,811.387 2118.07,861.515 2137.63,911.642 2157.18,961.77 2176.74,1011.9 2196.3,1062.03 2215.86,1126.47 2235.41,1190.91 2254.97,1255.35 2274.53,1319.8 2294.08,1384.24 \"/>\n",
"</svg>\n"
]
},
"metadata": {},
"execution_count": 12
}
],
"cell_type": "code",
"source": [
"Plots.plot(getindex.(points, 1), u_points, xlabel = \"x (coordinate)\", ylabel = \"u (temperature)\", label = nothing)"
],
"metadata": {},
"execution_count": 12
},
{
"cell_type": "markdown",
"source": [
"*Figure 3*: Temperature along the cut line from *Figure 2*."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"Secondly, the horizontal heat flux (i.e. the first component of the heat flux vector) is plotted."
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "Plot{Plots.GRBackend() n=1}",
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlgAAAGQCAIAAAD9V4nPAAAABmJLR0QA/wD/AP+gvaeTAAAgAElEQVR4nOzdeXxMV/8H8DP3zmTf98WaIEEoUhoiCGLfIqhdG081bZ8+WqVapeqptbRFq4q2llDUvstCRO0iREJIJEEE2SP7ZOae8/tjnt/QZEJkmcnMfN5/eM3cOZn7zWTMZ865554rYowRAAAAfcVpugAAAABNQhACAIBeQxACAIBeQxACAIBeQxACAIBeQxACAIBeQxACAIBeQxACAIBeQxACAIBeQxACAIBe0+4gjIuL27p1aw0bM8awnpyaCYKg6RL0DqVU0yXoF7zg6lfvHyzaHYTx8fGRkZE1bFxRUSGXyxu0HqiktLRU0yXoF0ppeXm5pqvQL3iTq1+9v+baHYQAAAB1hCAEAAC9hiAEAAC9hiAEAAC9hiAEAAC9hiAEAAC9hiAEAAC9hiAEAAC9hiAEAACtsTOFTjxnUL/PKa7fpwMAAGggvybSb6/TvX4yQgzr8WkRhAAAoAVWxNENd2j0MN5RVM+rRiMIAQCgUWOEzL0iHHvI/h7Gu5qKiorq+fkRhAAA0HgJjMz4W0gsYOeGi63rc0D0OQQhAAA0UlKBTDojFFWwiCFi0wbLK8waBQCAxqhETkZGyOWUHBrQgClIEIQAANAI5UvJgBNyR2PR3n68Ed+w+0IQAgBA4/K0jPQ5Jn/TTrSlNy9u+JhCEAIAQCOSUsh8D8snunNruvMitewRk2UAAKCxiM9jg8OErztzMzzV109DEAIAQKNwNZuNjJCv9uHHual1tBJBCAAAmhf1hE04Ld/SWzyoiXoGRJ9DEAIAgIYdekBDzgn7+ot9HdWdggRBCAAAmvXbXfpNLD05WPyGjQZSkCAIAQBAg9beoqsTaNQQvrWlZlKQIAgBAEBTVsTRrcn07DC+ianGUpAgCAEAQP0oIx+eF67lsLPDxHZGGi4GQQgAAGpVQcnUM0JmGTs1VGwh0XQ1CEIAAFCnUjkZc0ouFolODBI39CKiNYQl1gAAQE0KKsjAk3JbQ9H+/g2+lHbNIQgBAEAdMsuI/zF5JxvRVrUspV1zjakWAADQUQ+Kmd9R+cAmop968Jwmp4iqoLFjhCUlJYQQU1PT6hoUFxfzPG9sbKzGogAAoP7lSUmfY8KcDtyH7Rpj70sDNcnl8mnTprm6ujZp0mTq1KkymaxSg0uXLrm4uDRr1szR0bFLly5xcXHqLxIAAOrLh+eF0S1EjTMFiUaCcPPmzXFxcRkZGRkZGbdu3frjjz8qNXB3d7969WpeXl5+fr6/v/+MGTPUXyQAANSL9Yk0uZAtfbPRzI2pQgNBGBoa+v7775uampqYmISEhISGhlZqYG9v7+rqSgjhed7f3z87O1v9RQIAQN3dLmALrwk7+vCGjTcHNXGMMCUlxdPTU3Hbw8MjNTW1apuKiootW7bk5+fv2rVr2bJl1T0VY6y4uFj5DBKJxNXVleMaae8bAECvlAtk4mlhRTfe06qRTY/5Jw0EYWFhoXKOjJmZWUFBQdU2jLHU1NRHjx6VlZWJRNW+gvfu3YuMjOzXr59yy6ZNm3x8fFQ2lkqlHMdJJI1gGQO9UVJS8pI/H9Q7Sml5eTmlVNOF6BHFvD9QadY1sZupaKxLeXFxfT7ta32wmJiYvLJ3pIEgtLe3V4ZfQUGBg4ND1TaGhobLly8nhJw7d27QoEHDhw9XOX20devWo0aNqjq4qpJEIkEQqhljzMzMTNNV6BFKqVgsNjEx0XQh+gVvcpWOp7PwJ8L1QLGZoWH9PnO9f7BoYBTRy8srJiZGcTsmJsbLy+sljd3d3UtKSkpLS9VSGgAA1INHJSz4rHxXX966nkOwQWigR/jBBx8EBwf37dtXJBKtXr1606ZNiu0BAQFLly7t2rXrgQMHxGJxmzZt8vLylixZ4u/vb2trq/46AQCgFigj06KF/7TnfRy048iIBoJw8ODBixYt+vjjjxlj33zzzdChQxXbra2tFeOWxsbGP/30U1pamrW1tZ+f3+eff67+IgEAoHaW3KACI3Pf0Jp5iyLGmKZrqL3t27eHhYXV8BghJsuoX1FRkbm5uaar0COKyTI4RqhOxcXFOEb4oivZbHi4/OpIcTOzhuoO1vsHi9YkNgAANHIFFWT8aWFjT77hUrAhIAgBAKB+fHheGN5MNLK5liULLswLAAD14Le79HY+uzRS+2JF+yoGAIDGJrGAzbsqRA9rLBedfy1a1oEFAIDGRiqQiVHC0q5828a9lFp1EIQAAFAnc64I7haif3loa6BgaBQAAGrvRDo79IBdD9TiNNHi0gEAQLMyy8h754TdfXkbbVhKrTra2pMFAADNooxMPiN/35PzddTKQ4NKCEIAAKiNFTepjJJ5nbQ+RzA0CgAAr+1SFluTIMSMEvPa3RskBD1CAAB4XcUyMjVa+LUn38RU+2MQQQgAAK8r5LwQ4CoapW1LqVUHQ6MAAPAaNifRG7nsqhYupVYd3flNAACgod0rZHOvCJFDxMY6lB460rEFAICGJqNkUpTwX2++o40uHBpUQhACAECNfHFVcDUVhbTVteDQoc4tAAA0mBPpbG+adi+lVh0d/JUAAKB+ZZWRf/0thPbR7qXUqqNrPVwAAKhfjJDgs/L3PEV9XXTq0KASghAAAF5m5U36TEbmd9LCS+7WDIZGAQCgWtdy2PfxwuURYrHu9pt09zcDAIC6KZaRSVHCGh++hbluDooqIAgBAECFEjl5+7S8t7NovLuOJ4WO/3oAAFALT0pJ76NyJ2PRzz109tCgEoIQAAD+IT6PdT8sH9ZM9HsvXqIHKYHJMgAA8Fx4BptyRr7ah5+g6yOiSghCAAD4n/WJdPF1eihA7OOgy7NjKkEQAgAAoYzMuSKcSGfnhvMtdXqOaFUIQgAAfVcukHeihexydmGE2MpA09Wonb4MAQMAgEpPy0ivo3JjMTkxSB9TkCAIAQD02a181v2wfEhT0eZevIG+BgKGRgEA9FRkBpt0Rv7DW/ykVvqagYQQBCEAgH76I4l+dVXY00/cy0m/psZUpbEgTEhIyMnJ8fb2Njc3r/qoVCqNj48vKyvz8vKytrZWf3kAALqKEbIoVthxj50ZJvaw1PcUJC8JQrlcnpaWlp2dLRaLnZ2dmzZtWo97nTZt2tmzZ9u0aRMXF3fixInOnTu/+OilS5eGDBnSsmVLMzOzuLi49evXT5gwoR73DgCgt8rkZGq0kF3OLo8U6+RVdmuhchDKZLKDBw9u27YtOjq6qKhIud3JySkgIGD69Om9e/eu4y7//vvviIiI27dvW1lZLV269Msvvzx58uSLDVxcXGJjY1u0aEEI2b179/vvv//2229znF4PYQMA1F1WGRkRIW9jIQofLNbbqTFVPQ9CSumOHTvmzZv35MkTHx+f999/39PT09raWi6X5+TkxMfHnzt3rk+fPt7e3t9//31d4nDfvn3Dhw+3srIihEydOnXBggWFhYUWFhbKBs2aNVPe7tixY3FxsVQqNTY2rvUeAQAg+RkbFi5McBct7MJjPPRFz4Nw9+7dc+bMmTVr1uTJk11cXFS2vnXr1m+//TZ48OD4+Hh3d/fa7TI9Pd3b21tx29XVleO4jIyMF4PwRWvWrBkxYkR1KVhWVvbw4cO//vrrf7+MWNy3b9/qnopSqvwX1INSihdcnej/03QhekRbXvDTT8jkM8J33bjJ7iJGKdN0PXXxWq95TUYTnwehn59fSkqKqanpS1q3b9/+xx9//Pzzz1/e7OXKy8slEonitkgkkkgkZWVlKltu2LAhLCzswoUL1T1VTk5OWlrarl27lFtcXFy8vLxUNpZKpRzHKXcNalBWVsbzun8Nl8aDUlpeXq7pKvRLWVlZ4z9wsyON/zqO39pD3tOBlpZqupo6e60PFhMTk1f+gZ4HYZMmTWr4vM7OzjVsqZKTk1Nubq7idklJSVlZmcon3Lp16+LFi6Oiol6yu6ZNm/bu3Ts0NLQm+5VIJAhCNWOMmZmZaboKPUIpFYvFJiYmmi5EvzTmNzkjZH6MsCeN/T2cb2OpI8vG1PsHiwa+yPj4+Jw9e1ZxOzo6umXLlo6OjpXa7NmzZ968eWFhYa1atVJ7gQAAukAqkClnhKjH7PxwcRucJlE91UFYWlq6fPlyHx8fFxcXm3+q+y4nTJjw8OHD2bNn//XXXzNnzpw1a5ai3xoYGLh48WJCyIULFyZMmNC/f/8jR46sWLFixYoV+fn5dd8vAID+yJWSASfkFQI5NURsb6Tpaho31ecRTpky5cCBA/369Rs3bpyRUT2/hGZmZufPn1+7du2RI0cWLVo0ceJExfagoCDFJB1TU9PZs2cTQpT5pxXHogEAGol7hWxomDCoiehHH55DV/BVRIxVnj1UUVFhZma2dOlSRRo1Ztu3bw8LC6vhMUJMllG/oqIilSsHQQNRTJbBMUJ1Ki4ubmzHCE+ks+Cz8uXd+GmtG/ssntqp9w8WFT3CgoICmUzWr1+/etwNAAA0tApKvrwq7E1jf/UT++n9CqI1p+L7gr29fZs2beLj49VfDQAA1E5aEet9VJ5aSGIDkYKvR0UQikSiP/74Y+nSpREREXK5XP01AQDAa9mWTLsdko934/YH8LZYQfQ1qZ4sExwc/ODBgwEDBkgkkkrD33l5eWopDAAAXq1QRkLOCfF5LGqo2MsaHcHaqHbWaHFxsZpLAQCA13I1m02MEro7iC6PFJvg8rK1pfqVmz9/vprrAACAmmOErE2gS24IP/Xg33bTzdmhavPqrxCNcHIwAIA+e1JKppyRyyi5Fihuaorh0Lqq9nvEqVOn/P39ra2tzc3NLSwsevTosX//fnVWBgAAVR1LZ94HZb2cudNDkYL1Q3WP8ODBg0FBQQ4ODuPHj3dycsrJyTl27FhQUND69etDQkLUXCIAABBCpAJZGCvsSmG7++IEifqkOghnz57dv3//Q4cOKddX+/HHH4ODg7/88svg4GADAx1ZwhwAQFvcfcYmnBZamItiA8U2OEGiXqkYGs3Ozk5JSVm4cOGLq4yKxeJvv/22oKAgMTFRjeUBAAD5/S71OyIPacvt788jBetdtZNlRKLK/e6qWwAAoEEVysgH54QbuezUEHEHG3wINwjVS6y5ubktXry4oqJCuZFS+t///tfS0tLT01ON5QEA6K8r2azLATkvIldHIQUbkOoe4XfffTd27Fh3d/dRo0a5uLhkZWUdP348KSnpp59+MjREtxwAoGFRRpbF0Z9vCRt68iOa4zTBhqU6CIOCgk6cOPHtt9/++uuvcrmc47jOnTvv3r173Lhxaq4PAEDfZJSwKWcEQkjMKLErTpBoeNUeIxw4cODAgQOlUmlpaamRkZGxsbE6ywIA0E+HH9AZ54SQttyCzjyPEFSLV6wsY2hoiLFQAAA1KBfI3CvCoQdsbz9xT5wmqEbPg/DmzZtHjx719/fv3r37mjVrSkpKVP7AvHnz1FUbAIC+OJ/JPjgvtLMSxY0WW+JUbfV6HoTXr19fsGDB0qVLu3fvvmLFiszMTJU/gCAEAKhHGSVs7lUa/YSt7MaNd8e8GA14HoTTpk2bNm2a4vbjx481VA8AgL6QUfLLbfrtdWFSK+72GLG5RNMF6SvVxwifPXtmamoqFv/jUblcXlRUZG1trZbCAAB02aEH9LPLtIO16MoosZs5jghqkupuuIeHx5UrVyptvHr1qo2NTcOXBACgyxIL2MAT8nlX6Xpf/kAAjxTUuNe4pLFcLpdI0HUHAKilYhlZFS+sT6SzvPhPO3AGOCDYOPwjCMvLy8vKygghlNKioqL8/HzlQ6Wlpfv27XN1dVV3gQAA2o8ysjmJzo8RhjXj4kdLHHBidmPyjyBcv379rFmzFLcHDRpUtfXy5cvVURQAgA65ms1mXhTkjBwIEPs4YCC00flHEPbv33/Dhg2EkDlz5oSEhLi7uysfMjMz69ChQ4cOHdRdIACA1npSSr6JFY6nsyVvclNac8jAxukfQaiMuoqKisDAQAyEAgDUjlQgqxPoqnjhPQ8ucYzYDPMrGjHVk2WCg4MFQai0sbi4WCQSmZqaNnxVAABaLDKD/eei4G5BLo0Qu1ugH9jYqZ60NHDgwK+//rrSxl9//fWNN95o+JIAALTVnQI26KT8PxeFNd35IwOQgtpBRRBWVFRcuHBh1KhRlbYHBgampKQ8fPhQLYUBAGiTZxXks8tCr6PyQU24uNHiAFdEoNZQEYQ5OTmUUkdHx0rbHRwcCCHVrUEKAKCfGCHbkmnbvbLsMhIfJPnEi5PgBEGtouIYoZWVlVgsTkhI8PT0fHF7fHw8IcTW1lZNpQEANHqXc7gvIuUGPDkyQOxth16gVlLxvcXExKRv375z5869f/++cmNWVtbMmTPbtWvn5uamvuoAABqrK9lsSJg8+KJkphd3bjhSUIupnjX6448/9uzZ09PTs2/fvq6urk+fPj1z5gylNDw8XM31AQA0NnF5bMl1ejmbzfLitvmU2lmaaboiqBPVQdiuXbvY2NilS5dGREScP3/e0tIyMDDwyy+/bNu2bb3stbCwcM+ePUVFRUOHDm3dunXVBlKpNC4u7sGDB/7+/nZ2dvWyUwCAOrqZxxYrI7APb8ST4mJN1wR1Vu2i2y1atNi4cWND7LK4uLhbt27t2rVr2bJl165dT5w40b179xcbMMYsLCyaN29+//79qKgoBCEAaFzVCASd8bKrT1RUVKSmpmZnZ/v5+dXjLkNDQ+3s7Pbt2ycSiezt7ZcsWXL06NEXG4hEoqysLEtLS0zMAQCNu5bDvokVbuaRL97gtvvzuGSE7lH9JxUEYe7cuVZWVm3btp0wYYJi4/Tp0ydPnlz3XYaHhw8bNkwkEhFChg8fHhERQSmt1MbS0rLuOwIAqIvYHDYiXAiMEAY34ZLGij9oiwsn6SbVPcKvvvpq7dq1c+fOtbCw+OGHHxQbR48e/fbbb0ulUkNDw7rsMiMjw9nZWXHbxcWloqIiJydHcZLi68rNzb1+/fqcOXMUd3menz59erNmzVQ2lkqlHMdVDV1oOFKp1MDAQNNV6BFKqVQq5XkM29VVQj5ZFs+dy2QftyWhPZkRLxA5kcpVtJRKpbhQq5q91geLgYGBot/1EiqCUCaTrVu37rvvvvv444+jo6OV2zt16lRSUpKent6qVauaV1yVSCRijCluK268ssqXkEgkVlZWLz55XWoDAD13I48sucnF5pLZXuwPX2aILxV6QEUQZmdnFxcX9+vXr9J2CwsLQsiLV+utHRcXF+XyNE+fPjUwMKj1sUBbW1svL6+vvvqqhu05jsN3N3WqqKio4/gBvBZKKWMMr3nt3Mhli2JpTA77vCP3V3+uhtNhZDIZXnA1q/cPFhUD3hYWFhzHZWRkVNp+8+ZNQoiLi0sddzlgwICjR48q+oJHjhwJCAjgOI4Qcv/+/YKCgjo+OQDA64rLY6MjhWHhQl8XUfI48cfta5qCoBtUBKGZmVnv3r2/+eabZ8+eKUca8/Ly5syZ4+3tXfeLFE6ePDk7O3vMmDGzZ89evny5sj8XGBj4559/Km7PmjVr3LhxxcXFCxYsGDdu3NOnT+u4UwCAqm7msaBIYWiY0MdZdA8RqK9UT5ZZu3atn5+fh4dHu3btCgsLJ06cGBERUVpaeurUqbrv0tzc/MqVK3v37i0qKrp69aryiOMPP/zQokULxe2BAwcWFhaOHTtWcdfMDAs3AEB9upXPVsTRiAz6iRe/vQ9v/LJTyUDHqf7je3l5xcbGLl68WJl//v7+X3/9tZeXV73s1cLCIjg4uNJGf39/5e2BAwfWy44AACqJesJWJ9CYbDanI7ehpwQRCCreAmVlZWvXrh06dOjvv/+u/oIAABqCVCC7UunqBFohkJle3C5/9ALhf1S8EQoKCr744os+ffqovRgAgPqXXU5+TaTrE4WONqLlXfkBTXCWFfyDiskyDg4OdnZ2uBI9AGi7W/nsvb8Fjz2y9BIWOUR8cpB4IFIQqlDRI+R5fvHixV9//bW3tzeuPggAWocREvaI/RgvxOezD9vySWMldkaargkaMdVj5KdOncrKyvL09Gzfvn2liz9ERESopTAAgNdWJieh9+iaBGrAk0+9uPHuWB0UXq3ag8VdunRRZx0AAHXxpJT8kihsvEN9HLiffXl/Z4yAQk2pDsK//vpLzXUAANTO9Vy2OoEefUgnuHPnholbWyIC4fVg+jAAaCXKyJGHdHUCTSkk/27PrfaRWGPJT6iV50GYlZWVnJzcokULV1fXq1evVlRUqPwBX19fddUGAKBCsYxsTqJrb1FbI/KpFxfUghPjQCDUwfMgPHbsWHBw8NKlS7/88sthw4ZlZWWp/AHlFZQAANTsSSnZcEdYd5v6OIjW+/L9XTEKCvXgeRAOHTr077//Vqz2eeTIkep6hAAAakYZCXvENt6hfz+l77ThYkaJm5shAqHePA9CBwcH5WXiu3XrpqF6AACee1pGtibRDXeojSGZ4cmF9pGY4YqiUN8wWQYAGh3KSEQG23iHRj2h41pye/vxXezQBYSG8jwIw8LCVq1a9cofwAn1ANBwMsvIliS68Q414snU1txvfpgLCg2u2h5hTEzMs2fPPD09XVxcsrKyEhMTJRIJpowCQENghJzKYBvu0FOPaVALbnc//k10AUFdngfhwIEDlVcBXLNmzaNHj86dO9e+fXvFlvv370+cOLFz584aqBEAdFe+lOxJo2sSKCNkWmtuQ0+JDbqAoF4qeoQymeybb77Zu3evMgUJIS1atPj99987duz4+eefV1p9FADgdTFCoh6zDXdoRAYNbM790Yt/ywFdQNAMFUGYk5NTUFDg5ORUabuTk5NcLr9//z6CEABqraCC/JVKf7pF5Yy805pb74suIGiYivUYbGxszMzMNm7cWGn7pk2bOI5r1qyZWgoDAJ3CCDnzhE2MElrukl3IZBv9+MQx4rlvcEhB0DgVPUJDQ8Mvvvhi/vz5CQkJgYGBTk5OOTk5J06cOHr06AcffKA81xAAoCYUXcCfb9MKgbzbhvuph8QW4QeNiepZo1999ZWtre2yZcs+/vhjxRZHR8fFixd//vnnaqwNALSYwEjYI7YliUZk0BHNufW+vK8jjgJCY1Tt6RMhISEhISF5eXmPHj1ycnJCRxAAaiixgG1NpqHJrJkZeacNt9FPYmWg6ZoAqveKlWWsrKxkMpmNjY16qgEA7fWsguxKpVuS6MNiMqW16NQQ3tMKXUDQAq8IwkePHjVv3jw2NhZnEAKASpSRU4/ZliR6PJ0GuHILOvMDm4h4JCBoD6w1CgC1lPyMbU2m25KZgzF5pw33Uw+cCAFaCUEIAK+nSEb2pNHNSTT5GZvUijs2kO9ggw4gaDEEIQDUCGUk+inbkkQPP6B9nLk5HbjBTTkJLg0P2u8VQejs7BwTE+Pp6ameagCgEUorYluT6dZkZikh77bhVr0lsTfSdE0A9Ud1EBYUFFhZWRFCJBKJt7e3cvvdu3c9PDzUVBoAaFSJnOxLo5uT6K18NsGd29+f72yLIVDQQarHNfz8/E6ePFlp4969e996662GLwkANIkycuYJCz4rNN0p25vGPm7PPZooWdMdKQg6S3UQtmrVaujQoQsWLBAEgRBSWloaHBw8duzYwMBA9ZYHAOqTWMC+ihFa7pZ/eknoYCO6PUZyeAA/ugVngAOBoNNUD43u27fvu+++W7BgwdmzZ+fPnz9z5sz09PRt27ZNmTJFzfUBQEPLLie7UmjoPfq4lEx0Fx0byHtZo/MHekR1EHIc98UXX/j5+Q0ePHjAgAEeHh4xMTE4OgigS6QCOfKQht5jZ5/Q4c24JW/y/VxEHBIQ9E+1s0aLiorWr19fVFTUtGnTBw8enD59GkEIoAMYIeefstB7dF8a7WwnmtKK29FHYibRdFkAmqN67P/27dvdu3c/cuTIzp07U1JSZs6c+dFHHwUGBubn59fLXg8ePDht2rSPP/74zp07KhskJiZ+/PHH06ZNO3z4cL3sEQDuFbJvYoVWu+Uh5wV3C9GN0eKIweKprTmkIOg51UE4YMAAIyOj2NjY8ePHSySS5cuX79+/Pzo6+sVTKWrtr7/+CgkJGTBggJ2dXc+ePTMzMys1ePr0ac+ePe3t7QcMGDBjxoy9e/fWfacAeitPSn5NpL5H5H5H5M8qyN7+fEKQ+POOXBNTDIMCEFLd0GhISMicOXMMDZ+vGzhq1KjOnTtPmDCh7rtcuXLlsmXLJk2aRAiJjY39/fff582b92KD3377zc/P7+uvvyaESKXSlStXjhkzpu77BdArFZScSKfbktnpx3RQU+6rTvwAV5EY8z8BqlAdhPPnz6+6sXnz5tHR0XXcn0wmi42N7d27t+Junz59oqKiKrW5dOlS//79Fbd79+793nvvyeVysRirwQHUyOUsFnqP/pVK21mLprbmNveWWGDwE6B6r5cuEkld/z9lZWVRSm1tbRV37e3tnzx5UqnN06dPlQ3s7OwopZmZma6urlWfLT09PTo6evTo0cotc+bM6dChg8pdS6VSjuPq/itAzZWUlIhEGH9Tk4clZGcav+s+LxLJJrSkZwLkzUwJIYRISbFUw7XpsJKSEk2XoHde64PFxMSE414xEqLubpaxsTEhpKKiQnG3vLzcxMSkahtlA6lUSgip2kbBzs6uZcuW48ePV9zleb5t27bVNeZ5HkGoZoIgVPfngPryrILsu89C77HEAja2BdnUXdarqWIlUFwVXh0opXiTq9lrfbC8MgWJ+oPQ2traxMTk4cOH9vb2hJCHDx9W7eq5uro+fPhQcfvhw4empqaKhU+rMjY2btas2bhx42qya+7/1aF8eD14wRuOnJKwDBaaTMMe0X6u3GcduEFNOTGh5eUyvObqhDe5+tX7a67uv59IJBo9enRoaCghpKysbM+ePUFBQYSQ0tLSnTt3lpWVEUKCgoL27NmjuB0aGhoUFDePT40AACAASURBVIThNQClaznsk0tCk52yZTcEfxdR6tuSvf34Ec2xEBpALWlgBsrChQv79u178+bNx48ft2nTZuTIkYSQ3NzciRMnPnr0yNXVNTAwcOvWrV26dHF2dk5JSTl9+rT6iwRobB6VsO33WGgylVIypRV3frjY3QJfEAHqgQaCsFWrVnfv3o2JiTE3N+/UqZNio4uLy/37952cnAghYrH4yJEjcXFxRUVFXbt2NTLCpc9AfxXJyP77dFsyjctlY924jX58D0eMkADUJ9VBSCndtWvXoUOH0tPTlfNWFGJiYuq+V2NjYz8/vxe38DzfvHlz5V2RSKTMSAA9JDASmcFC79FjD2lvZ+6jdtzQppwhr+myAHSR6iD84IMPNm7c2KZNm7Zt2xoYYO4ZgPrczGOhyfTPFNbUjExuxa3pLrE1fPVPAUCtqQhCuVy+bdu2OXPmrFixArNUANTjSSnZmUK3JdOCCjK5lej0UN7DEv/7ANRBRRDm5uaWl5ePHz8eKQjQ0MoFcuA+3ZZMr2SzUc25Nd35Xs74jwegViqC0N7e3tXVNS0trUuXLuovCEBPXM5iW5LpX6m0q71oWmtuf3/OGMsIAmiCiv95HMetW7du3rx5bdu2bdeunfprAtBhT0pJ6D26JYkKjExrzcWNFuMqEACapfor6Lp1654+fdqhQ4dmzZopl/1UqJdZowD6RiqQww/p1iR6IYsFteA2+fG+jsg/gEZBdRA2b968ulXNAOC1XMthW5LorlT6ho3onTbcX/04EwyBAjQmqv9Hbtq0Sc11AOiYrDKyI4VuTqIlMjKtDRczStzcDF1AgMYIX00B6pOMkuPpdHMSO/uUjmjG/YRZoACN3vMgfPDgwdWrVzt06ODh4XH06NHy8nKVP4CLxQOodDOPbU6if6ZQT0vRO2247X0kZrjkF4A2eB6Ep0+fDg4OXrp06Zdffjl9+vSsrCyVP8AYU1dtAFogV0r+vEc3J9FcKZnWWnQBa2EDaJvnQThmzJhevXop5oheuXJFLpdrriqAxk5g5OQjtjmJnsqgw5pxK9/i/Z1FHBIQQAs9D0Jzc3Nzc3PF7RfXvwaAF2WUsN+T2G93qIspmd6G+91PYonleAG0GSbLANQIZeTkI7bxDv37KR3vzh0ZyL9hgw4ggC5AEAK8wuNS9sdd9ttd6mhMZnhyO/wlpvh/A6BD8B8aQDXKSEQG23CHRj+h49y4AwF8Z1t0AQF0EIIQoLKnZeSPu/S3u9TGkMzw5Lb1xokQALoMQQjwP5SRU4/Zhjv09GM6piW3px/vbYcuIIDuUx2Eqampbm5uVbdHRUX5+/s3cEkA6pZZRrYk0U13qYWEzPDkNveSmKMLCKA3OJVb+/btu2bNmhe3UEpXrFgREBCglqoA1IERcuoxe/u00HavLLmQ/enPxwaKQ9pySEEAvaK6Rzhq1KhPPvnk0qVLGzZssLCwePz48aRJk86dO7do0SI11wfQELLL/9cFNObJ+57cxp44FxBAf6kOwtWrV/fs2fNf//qXt7f3rFmzFi5caGhoePr0aT8/PzXXB1C/zj1lvyTSE+l0VAtuW2/exwFHAQH0XbWTZcaMGdOxY8c333zzww8/7Nix46lTp+zs7NRZGUA9klGyJ43+GE8LZeTf7bhffCVW6AICACGkumOEhJD09PTg4GCpVOrr6xsfH79s2bKKigp1VgZQL3KlZFkcbblb/sddurALnzhG/HF7DikIAEqqg/DIkSOdO3dOT0+Pioo6d+7cli1b1q9f36NHj5SUFDXXB1Brd5+xD84Lrf+SJT9jxwfykUPEw5phXWwAqEx1EL733nu9evWKi4vr0aMHIWTq1Knnzp179uyZt7e3essDqI1zT9m4U0Kfo3JLAxI/WvxHL74j1gUFgGqoPka4atWqSZMmiV64sHaXLl2uXbv2/vvvq6swgNdWLpA/U+jqBEoImdme29ZHYsRruiYAaPRUB+HkyZOrbrSwsNi5c2cD1wNQG1llZHMS/fk29bQiS97khjXDCCgA1BSWWAPtdjOPrU6gBx/Qt924iMG8pxUSEABej+ogdHJyyszMVPkQY6wh6wGoEcrIiUfsx3jhzjPyUTsueZzE1lDTNQGAdlIdhPPnzy8pKVHeLS8vj46Ovnr16qeffqquwgBUK5GTbcl0TQI1k5BPvbhxbpyk2pOAAABeTXUQ/vvf/6668bPPPouPj2/gegCq9aiErbtNf7tLezlxm/x4PyeMggJAPXiNY4QfffSRu7t7enp606ZNG64ggKri89iyOBr2iE5tzV0eKXYzRwQCQL15jSCklBJC8vLyEISgNgn5bFEsPZ9JP+vA/9pTYoHrQgBAfavR0ZXy8vK4uLgPP/zQ2NjYw8Oj7ns9fPiwr69vhw4dFi1apMjXSjZt2hQSEhIQEHDr1q267w600e0CNvWMEHBc/qad6N44yWcdOKQgADSE15g1ampq+vPPPxsZGdVxl3fu3Jk8efKOHTtatWo1fvx4KyurmTNnvtiAMRYeHu7t7b1jx46CgoI67g60zq189u11Gv2EzunI/9pTYoJzfACgIdVo1qiRkVHz5s19fX3t7e3rvstNmzYFBQUNHz6cELJw4cJ58+ZVCkKRSLRnzx5CyMqVK+u+O9AiiQVs2Q0ankFD2nIb/TAQCgDq8BqzRutLQkLCiBEjFLfffPPNpKQkqVRqaIizwPTaixGY5IsIBAD1aZBRp5ycnGvXrlXd3qtXL2Nj46ysLCsrK8UWa2trxlh2dnaTJk1qsaOkpKSDBw+2bNlSuWXjxo0+Pj4qG0ulUo7jJBJ8xKpPcXHxK9vcLRR9f1t8OpOb3kqIHSKYixkpJ0XlaqhOB1FKpVKpIAiaLkSPlJSUYJkRNavJB4uSiYkJz79i0eHnQXj27NkNGza88kl37Njxyjb3799fu3Zt1e2dOnUyNja2srJS/hpFRUWEEGUuvq7WrVv379//+++/V9zleb5p06Ycp3oGkIGBAYJQ/czNzat7KLWIrYijhx7QkLbchj48eoF1RymVSCQmJiaaLkSPiEQiMzMzTVehd17ywVILz4MwPz8/ISGhXp70zTffPHbsWHWPurm5JSUlKW4nJSU5ODjU+m2keAu6ubnV7sdBU+4+Y99ep5EZdFYH/t44iRkiEAA053kQjhw5cuTIkWrY5eTJkydNmjR79mxHR8c1a9ZMmTJFsX3NmjXdunXr3r07IaSwsFAQBMZYUVFRfn6+paVldf080C5pRWz5//cC1/WQWOJK8QCgac/T5c8//1SEECFk8eLFDx48aKBd+vv7BwcHt23b1sHBobS0dP78+YrtBw4cSExMVNweOHCgu7s7IWTixInu7u4NVwyoTdIzNvWM4HNY3sJcdG+c5JsuPFIQABqD5z1CxlheXp7i9s8//9y3b9/mzZs30F4XL168YMECmUz24qDomTNnlLcvXrzYQLsG9Ut+xr69TsMy6Mz2/DpfiTkGQgGgMXkehG5ubmlpaXv37u3YsaMgCI8fP05NTa36A/V1QM7Q0BCnTOi8lCLRj7HCyUf0P4hAAGisngehj4/P0KFDx44dq7irvFEJJgpDTRRUkG9ihR3JBp90EP3UA+cFAkDj9TwIRSLRgQMH4uPjU1NTp02bNnv27HpZVhT0DWVk+z0694oQ4MpdHlThZo8jgQDQqFU+ob5Dhw4dOnQYMGDA6NGj27Vrp5GaQHudz2T/uSiYiMnxQeLOtqKiIowfAEBjp3plmb/++kvNdYC2yyhhc6/S6CdsRTdugjuHCwYCgLZ4fvrEjRs3anhCfVhYWFZWVoOVBFpGRsmaBPrGfrmtIbk9RjwRKQgAWuV5EGZmZnp7ewcFBR09elQul1dtWlRUtGXLlu7du48bN04mk6mxSGi8Dj2gbffKzzxhV0aJ13TnMS8UALTO86HRgQMHxsbGfvnllyNHjjQxMfH29m7Tpo2NjY1cLs/Ly7t58+bNmzd5nn/33XcPHTrk4OCgwaKhMUgsYJ9cFB6VkPW+fIArOoEAoK3+cYywffv2hw8fTk1NDQ0NjYqK2rdvX15eHs/z9vb2Xbt2nTp16uTJk21sbDRVKzQSBRVkeZywJYl+6sV/2oEzwOJ3AKDNVEyWcXNzW7hw4cKFCwkhMplMLBaLRPi+D4QQQhn5I4kuiBFGNOfigyT2RpouCACgzl5xPUJctAiUzmeymRcFI/5/p0ZouhwAgPrRIBfmBR3zuJR9cYWefsKWvslNaY1JoQCgU3B4B15GKpBlcbTjPnlTM3J3rHgqUhAAdA56hFCtww/orMvUy1p0eaTY3QIJCAC6CUEIKiQ9Y59eEu4VkrXd+SFNEYEAoMswNAr/UEHJl1eFnkfk/V25hCAxUhAAdJ7qIDxy5EjVjZTSFStWNHA9oEn3CpnvYfntApIQJPnUi5PgaxIA6AHVH3Xvvffeu+++W1JSotySlZU1ZMiQefPmqaswULc9abTnEfnkVtzBAN7BWNPVAACoi+og/P777/fu3du1a1fFMtxRUVGdOnWKi4sLCwtTb3mgDkUyMvWM8PU1enKQeKYX5oUCgH5RHYSTJk2KiYkxMDDo1q3blClTAgIC2rdvf+PGjf79+6u5PmhoV7NZlwNyYzG5NkrcCafJA4D+qfYokIeHx4EDB8Ri8fbt2728vI4dO+bo6KjOyqChMULWJNChYfJvvbkNPXkTzCAGAL1UbRCGh4f7+PhYWlrOnj379u3b/fr1e/TokTorgwaVVUaGhsl3ptJLI8Xj3TErBgD0l+pPwIULFw4ePLhr167Xr19fuXLl2bNn09PTO3XqdPToUTXXBw3hRDrrdEDW1U50bpjYzRzDoQCg11QH4R9//LFixYojR47Y2dkRQnx8fK5fv+7n5zdixAj1lgf1rIKSzy4LIeeFXX3Fi7x5MbqCAKD3VB8XOnHihJeX14tbrK2t9+/fv3btWrVUBQ0i6RmbECU0MxXFBoptDTVdDQBA46C6R1ApBRVEItHMmTMVt0+fPu3v79+AdUF925ZMfY/Ip7biDgTwSEEAAKVazhQsKyt78uRJ/ZYCDaRQRkLOCfF57MxQcXtrHBEEAPgHHCPScVezmfcBuVhELo9ECgIAqIBzx3QWI2RtAl1yQ/ipB/+2G77xAACohiDUTY9L2dQzgoySa4HipqboCAIAVAsdBR10LJ15H5D3cuZOD0UKAgC8AnqEOkUqkIWxwq4U9lc/sZ8TIhAA4NUQhLrjTgGbGCW0MBfFBoptcIIEAEDN1HJotEWLFpMnT67fUqAudqXQXkflH7Tl9vfnkYIAADWnukf47NkzSulLfszFxWXOnDl13Hd5ebmRkVF1jzLGZDKZgYFBHfeiD5bcoL/dpaeHir1wggQAwGtS3SP08PCweZXQ0NBa7/XXX3+1tbV1cnLq169fVlZWpUfv3r3br18/U1NTGxubt9566/r167Xekc6TUxJyTjj0gF4cgRQEAKgN1T3CVatWffbZZ66urqNHj3Z0dMzNzT1+/HhcXNzixYudnJwUbd58883a7TIpKenzzz+/cOFC27Ztp0+fPnfu3M2bN7/YoLy8/L333jt8+LCxsfH8+fPHjBmTkpJSu33ptnwpCYqUWxmKzgwV42qCAAC1I2KMVd06duxYc3PzP/7448WNCxYsiIyMvHjxYh13OX/+/Hv37u3atYsQcuvWra5du+bl5VU3Rnrv3r3WrVsXFxebmppWfXT79u1hYWE17JtKpVKO4yQSSV2KbzxSi9iwMGFIU9F33XiusXYFi4qKzM3NNV2FHqGUlpeXm5iYaLoQPVJcXGxmZqbpKvRLvX+wqBgaLS4u3r9//yeffFJp+8yZMy9dunTv3r067jIlJaVt27aK256enlKpNCMjo7rGhw4d8vb2VpmChBDGWEVFRf4LVOa67rmUxXoekf+nPbfqrcabggAAWkHFgFpxcTGl9NmzZ5W2K7YUFha+8kkzMzMrjXYqTJ061cXFpaCgQPkFiud5Y2Pj/Px8lc9z4cKFJUuWREREVLej5OTkgwcPhoeH/++XEYv//PPP7t27q2ysMz3CQ+ncp9fEv3QTBrlIi4s1Xc1LlZSUiEQIavVR9AhfPtMN6ldJSYmmS9A7r/XBYmJiwnGvOD9CRRA6Ojq2adPmk08+OXjwYNOmTRUbc3JyPvjgA1tb23bt2r1yx4IgFKv6hBYEgRBiZ2enTFOZTFZaWurg4FC18bVr1wIDA//8809vb+/qdtSmTZtx48bVcGhUIpHoQBCuSaCr4mnYYL6zrRbMp2WMYdRInSilYrEYQ6Nqhje5mtX7B4uKIBSJRL///vuQIUPc3d27du3q7OyclZUVExNDKd29e/dLTnhQcnFxWbx4cXWPtmvX7sKFC4rb169ft7KycnZ2rtQmLi5u2LBhmzZtGjRo0Ov8OrpMRslHF4RrOezySN7FBN0sAID6obrD2LNnz1u3bs2aNcvMzCwxMdHAwOD999+Pi4sbOXJk3Xc5bdq06OjoAwcOZGRkzJ8//91331X00r766qtt27YRQpKSkvr37x8YGGhiYhIZGRkZGVlaWlr3/Wq1ZxVkaJj8aSmJHipGCgIA1KNqJ903bdp0+fLlDbFLFxeXvXv3LliwICcnZ9CgQcq+I6VUMdUlIyOjU6dOycnJK1asUDy0detWfR7tyShhw8KFbvaidT14MZZJBwCoV6pPn9AW+nD6xJVsFhghzH2D+0977ctAnD6hZjh9Qv1w+oT61fsHC07DbtQO3Kch54Xf/PjhzbQvBQEAtAKCsPFaFU/XJtCTg8SdbXFQEACgoSAIGyOBkZkXhbNP2bnhfDMzpCAAQANCEDY6xTIy/rRcRsm54WILLTugCQCgfXDkqXHJKGG9jspdTEXHBiIFAQDUAUHYiFzLYT6HhamtuY09cZoEAICaYGi0sTj8gL53TtjYkx/ZHBkIAKA+CMJGYU0CXRlPjw0Uv2mHqTEAAGqFINQwgZFPLwlRj9n54XxzTBAFAFA7BKEmSQUSFCmXM3J+BKbGAABoBoJQk764Kog50cF+mBoDAKAxCEKNOfmI7Utj10eLkYIAABqEINSMzDIy/ayw3Z+3NdR0KQAA+g2dEQ2gjEw5I5/hyfk7Y3YMAICGIQg1YOVNWiaQ+Z3x4gMAaB6GRtUtJof9kCBcGSnm0RsEAGgE0ClRq0IZGX9aWO+LUwYBABoLBKFafXhe6O8iGt0CLzsAQGOBoVH12ZZMr+ewq6PwmgMANCL4UFaTlEI2+7IQMURsgpccAKAxwRidOsgomXRGWNiFf8MGhwYBABoXBKE6zLsq2BqSD9vh1QYAaHQwTtfgwjPY7lQWGyhGZxAAoBFCEDaszDLybrSww5+3M9J0KQAAoAoG6xoQI+Rff8uDPUR9sJQaAEBjhSBsQD/E06wy8nVnXtOFAABAtTA02lBic9h3N4VLI8QSfNkAAGjE8CHdIErkZGKUsNqHb2mOQVEAgEYNQdggPjov+DmJJrjj5QUAaOwwNFr/9qTRC1nsGpZSAwDQBviwrmepReyj80LYYLG5RNOlAABADWDsrj7JKZkcJXzVie9si0ODAADaAUFYnxZcE6wMyX+88KoCAGgNDI3Wm+gnbGsyvR4oQWcQAECLaCYIGWM3b95kjHXs2JHjVPSfnj17lpyczPO8h4eHiYmJ+it8XdnlZPIZYVtvsaOxpksBAIDXoYEgLCoqGjBgQHFxsUgkMjExCQ8Pt7CweLHBqVOnxo4d6+npWV5enp6evn379oEDB6q/zppjhPzrb2FKK1F/V/QGAQC0jAaOZq1fv97Y2DguLu7GjRvm5ua//PJLpQY9evTIzs6+cOFCbGzsvHnzZs2apf4iX8vaBPq4hH3jjaXUAAC0jwaCcM+ePdOmTeM4juO4adOm7dmzp1IDY2Njnv9fqLi4uIhEjbqbdSOXLY0TdvfjDTBFBgBAC2lgaPThw4ctW7ZU3G7ZsmV6enrVNlKpdOHChVlZWTdv3tywYUN1TyWVSp88eRIZGanc4uPjY2ZmVu81V0exlNoPb/FuWEoNAEA7NUgQnjhxYsuWLZU28jz/559/EkLKysoMDAwUG42MjEpKSqo+g0gkcnNzMzMzO3/+/Pnz5319fVXu6OnTpwkJCUuXLlVu+fbbb9944w2VjaVSKcdxEkl9nuj+0RVxF2sy0kleXFyPz6o7SkpKGnmHXsdQSsvLyymlmi5Ej6j8BIMG9VofLCYmJiqnZL6oQYKwTZs248aNq7RRWYqTk1NeXp7idm5urrOzc9VnMDAwmDFjBiEkMDCwU6dOISEhlSbUKDRv3jwgICA0NLQmVUkkkvoNwn1p9EIOjQ0Um2ERmWowxtTZQQdKqVgs1oqJ1roEb3I1q/cPlgYJQnd3d3d39+oe7dq167lz54YMGUII+fvvv7t27fqSpzI2Nm6cX2/TS9hHF4RDAVhKDQBAu2ngGOF//vOfAQMGeHh4cBz3008/nTx5UrG9RYsWW7du7d2794YNG4qKijw9PbOzs9euXfv222+r7A5qkJySCaeFOR35txww7gcAoN00EIRvvfXWgQMHfv/9d0LIvn37fHx8FNsnTZrk4uJCCOnatev27dvPnz9vaWk5c+bMSZMmqb/Il/v6mmAuIbM6YJ4oAIDW08zKMn379u3bt2+ljUuWLFHc6NKlS5cuXdReVE0tvCbsv8+ih4nRGQQA0AFYa/Q1MEI+uyREP2Vnh4kdsJQaAIBOQBDWlMDIe38LKYXs9BCxpYGmqwEAgHqCIKwRqUAmRglSgZ0cJDbGawYAoEMw3ePVimVkWLjciCcHApCCAAC6BkH4CnlS0v+EvLWFKLQPL8GrBQCgc/DR/jKPS1nvo/I+zqJffHkOk0QBAHQRgrBaqUWs11HhnTbc8q64vhIAgM7CIS/VYnPYsHD5sq78tNb4rgAAoMsQhCqcfcrGnpJv6MmPao4UBADQcQjCyo6ls3ej5Tv8xQGuOCoIAKD7EIT/sDOFfnJJODRA3B2raQMA6AcE4XPrE+mSGzRysLiDDVIQAEBfIAj/Z/F1ujWZnhvGtzBHCgIA6BEE4f+W0j79mP09XOyEpbQBAPSMvgehwMj754T4PHZqqNjWUNPVAACA2ul1EFZQMilKyJOyU0PEZhJNVwMAAJqgv+fJlcjJ8DC5nJLjA5GCAAD6S0+DMF9KAo7LnU1Ee/rxhlhADQBAj+ljED4tI32OyXs5izb35sX6+AIAAMBzepcDaUXM74h8UitueVce50kAAIB+TZa5XUCGRwoLOnPveerdNwAAAFBJj4LwWi4ZHUV+7sGNaYkUBACA/9GjIKygoh29SL+mSEEAAHhOj4Kwuz3jcJl5AAD4J3SPAABAryEIAQBAr+lREN65cyc1NVXTVeiXsLAwxpimq9Aj2dnZV69e1XQV+uX8+fOFhYWarkKPyGSyU6dO1e9z6lEQ7tixY9++fZquQr+89957BQUFmq5Cj0RHR//000+arkK/LF++HF8+1On+/fuzZ8+u3+fUoyAkhKB3AroN73CAWtCvIAQAAKgEQQgAAHpNu88jfPTo0enTpwMCAmrSODk5WSKRnDlzpoGLgudKSkpGjx4tFmv320yLZGZmZmVl1fB/BNSLuLi4uXPnWltba7oQfVFWVvbkyZOav8kDAwM//PDDl7cRafVBhSdPnpw+fdrR0bEmjfPy8niet7S0bOiqQCktLa1ly5aarkKPlJeX5+fnOzs7a7oQPfLo0SNHR0eJBBc1VRPG2IMHD1q0aFHD9i1btnR3d395G+0OQgAAgDrCMUIAANBrCEIAANBrCEIAANBrCEIAANBrejGvvby8/ObNm4yxt956S2UDxlh0dHRaWlqPHj08PDzUXJ5OevjwYVRUlIODQ0BAQNXTJx49enTnzh3lXR8fHzMzM/UWqAtiYmLi4+O9vLy6du2qssHjx49PnTplbW09YMAAAwMDNZene+RyeURERFZWVt++fZs2bVq1QVRUlCAIittOTk5eXl7qLVAHpaSkpKWldevWzcLCQmWDBw8enDlzxtHRMSAggOf5Wu6G6bqtW7caGBjY2tp26tSpujZTp05t167djBkz7O3td+3apc7ydFJUVJSNjU1wcHC3bt0CAgIEQajUYN26dY6Ojv3/X2pqqkbq1GrLli1r2rRpSEhIs2bNvv3226oNLl++bGNj8+677/r6+vr6+kqlUvUXqUvkcnnfvn3feuut4OBgGxub6Ojoqm3Mzc179uypeFcvW7ZM/UXqkoqKCmtra2tra57nL1++rLJNZGSkjY3N9OnTu3btOmjQoKofNTWk+0GYlZVVUFCwc+fO6oLw5s2blpaWubm5jLGDBw+6ubnV+tUEhZ49e65du5YxVlZW5ubmdvz48UoN1q1bN378eE2UpiPy8/NNTU0TEhIYY3fu3DExMcnLy6vUZvDgwUuWLGGMVVRUdOjQAd/w6ujIkSPu7u7l5eWMsTVr1vTq1atqG3Nz8/v376u9NN0kCEJKSgpjzMLCorog7N69+y+//MIYKy0tbdGiheJyN7Wg+8cI7e3tX34S/dGjR/39/W1sbAghQ4YMefLkya1bt9RVnQ4qKCg4d+7cmDFjCCFGRkbDhg07evSoymYnTpy4fv06pVTtNWq9qKiopk2btm/fnhDi4eHh7u4eGRn5YgOZTBYeHh4UFEQIkUgkI0eOVPlXgJo7evTo8OHDDQ0NCSFjxow5e/asyqsvXb169dSpUzk5OWovUNdwHOfm5vaSBjk5ORcvXlS8yY2NjYcMGVLrN7nuB+ErZWRkNGnSRHFbIpE4ODhkZGRotiSt9vjxY7FY7OTkpLjr6upa9fUUiURZWVnr168fNWqUj49Pbm6u2svUbi++aYmqF/np06eCICjbqPwrwGvJyMhwdXVV3HZycuJ5vupLamtru3nz5v/+978tW7bcQHXtZAAADVxJREFUunWr2mvUL48fP1Z8Yivu1uVNrguTZfbv3//f//636vaYmJiarHIpCMKLyyOJxWK5XF6f9emi2bNnV+qCEEK6deu2ceNGQRBEIpFyI8/zVV/PGTNmfPDBB4SQioqKoUOHLlq0aO3atQ1dsy6p9CJXfdMqpmwo26j8K8BrEQSB4/7XcxCJRBzHVX1J7927p5ivcfz48aCgoOHDhyuGmqAhvPgXIXV7k+tCEPr7+7dp06bq9hrOIHJ2dr59+7biNqU0KyvLxcWlPuvTRTNnznznnXcqbVTM/HRycpLJZPn5+YqPgMzMzKpLXyr/NAYGBkFBQTt27GjwinWLs7NzVlaW8m5mZmalN62iR56dnd28eXOVDeB1vfia5+XlyWSyqi+p8o09ZMgQQ0PDxMREX19ftVapT5ycnKRSaWFhoWJCqcqPmhrShaFRa2trL1Ve/MpcVX5+vkwmI4T06dPnzJkzFRUVhJCLFy8aGRkpDr3ASzRt2rTqC65YBtfe3t7Lyys8PJwQwhiLiIjw9/cnhAiCoHIINDY2VuVMdHiJnj173rlz58mTJ4SQrKys+Ph4Pz8/Qkh5ebniwJWRkZGPj4/ir0AICQ8P79Onj+bq1QV9+vQJDw9njBFCwsPDO3bsaGtrSwgpKioqKyur1PjevXuFhYV4YzeEsrKyoqIiQoiTk5Onp6fiTU4pjYyMVHzU1EYtJ/Rojzt37syYMaNfv362trYzZsxYvXq1Yru9vf2hQ4cUt3v16jVo0KAffvjB3d195cqVmitWR/z5558ODg4rV64cP35827ZtFRPtrl27RghR3J44ceLs2bNXrlw5btw4S0tLxVme8FpmzJjh7e29evXqbt26TZ8+XbFx1apV3bt3V9w+fPiwjY3NihUr3nnnnZYtWxYWFmquWF1QVlbm4eExYcKElStXOjg47N69W7E9ICBg0aJFjLHjx4+PHTt26dKl8+fPd3V1/eCDDzRary6YP3/+jBkzDAwMRo0aNWPGjJycHMbYV199NXToUEWD0NBQJyenVatWjRs3rn379rU+R0j3rz7x+PHjF6cSNWnSZMiQIYSQ7du39+rVq1mzZoSQsrKyLVu2pKen+/r6Dh06VGO16pCzZ8+Gh4fb2tq+++67VlZWhJDc3Nz9+/dPnz6d47hLly5FR0cXFBQ0adJk7NixysPdUHOU0p07dypOqJ8wYYJiUC4+Pj4tLW3EiBGKNpcuXTp27JilpeU777xjZ2en0Xp1QX5+/ubNm/Py8gYNGtSzZ0/FxhMnTjg5OXXu3DkvL+/gwYOpqalGRkbdu3fv16+fZqvVAbt373727Jny7sSJE83MzGJiYnJzcwcOHKjYeObMmYiICHt7+3fffbfWV9nT/SAEAAB4CV04RggAAFBrCEIAANBrCEIAANBrCEIAANBrCEIAANBrCEIAANBrCEKAhlJWVrZnz54XT4TSlJMnTx4+fFhxOzs7e+vWrZmZmeovo7y8fM+ePQUFBerfNcBLIAgBGsr333+/aNEic3NzTRdC1q1bt2rVKsXte/fuvfPOO3fv3q370yYmJm7cuFEqldawvZGR0bp161QukQ+gQQhCgAaRm5v73XffzZ8//8UF8hsDxRXtFQvD1tHZs2fff//90tLSmv/IvHnz1q1bd//+/brvHaC+NK7/ogA6Y/PmzSKRaOTIkZW2M8aysrJUXtNVKpU+ffq0vLxc5RMqHn1J90vRQHEBJkJIRUVFZmZm1QvTuLq6zp8/X7G44IsEQcjOzq5uqamsrCzFwvQ1JJfLnz59WlJSUml7//79HR0dN23aVPOnAmhoCEKAGlm6dKm9vf2VK1cUdxlj48ePb9WqVXUH27Zt2zZ06FBjY2PlFkEQvv32WycnJ0dHR0tLyyZNmuzatUvxUGFh4TvvvGNlZeXs7GxlZTVhwoS8vDzlDxYUFEyePNnS0lLx6JQpU5SH2crLy21sbNasWRMSEqJooLim2PLly+3s7JycnBwcHCpd6/HatWvOzs6XL19W3B0+fPiYMWNCQ0NdXV0dHBwsLCwWLFigbJycnDxw4EBjY2NHR0dTU9POnTtHR0crHvrxxx9nzZpFCHFzc7OxsbGxsVFcll0qlc6aNcvOzs7Z2dnCwiIgIODF/h/HcSNHjsRFa6FxqY8lwgF0n0wm8/X1bdasWW5uLmNs7dq1IpHowIEDKhtnZWWJRKK1a9e+uHHGjBkcx82aNevSpUuxsbEbN27csmWL4qGAgAAjI6Off/755s2bGzduNDU17dGjhyAIjDFKaa9evUxMTNavX3/z5s1ffvnF2Ni4d+/elFLGmGJY0sHBYfjw4SdPnoyMjMzOzt64cSMh5MMPP7xx40Z4eLinp6etra2fn59iXxcuXCCEREdHK+726dPHwcHhjTfeOHTo0OXLl4ODgwkhp06dUjx68eLFWbNmRUZGJiYmRkZG9u7d28zMLCMjgzGWlpb2ySefEEIOHDgQERERERGhWPt/1KhRVlZWv/zyS0JCwsmTJ728vFq1alVaWqp8HRSXn7xz5069/W0A6gZBCFBT6enptra2w4cPv3HjhpGR0aefflpdy8jISELIyZMnlVsSExNFIpHKH1Ek04vX//r1118JIcePH2eMRUVFEUJezNTVq1crs0oRhO3atVOkpkKLFi169eqlvHvr1i2RSPSSIDQ2Nk5PT1fclUql9vb2//73v1X+Xs+ePTMwMFi/fv2Ldebl5SkbKPqLO3fuVG5JSkoSiUTbt29XbomJiSGEKC9jBKBxunCFegD1aNKkyebNm0eOHBkdHd2hQ4fly5dX11IxSGhjY6Pcosit6dOnV21848YNQsjbb7+t3PL222+HhIScPXt28ODBVR8dP378J598cvbs2b59+yq2DB8+XDklp6Cg4P79+59++qmyfbt27dq1a/eS38vLy6tJkyaK2wYGBq1atUpPT1c+mp2dvXv37tTUVMUBP0NDw3v37lX3VGFhYSKRyNTUVPFVQMHGxiYhIUF5V3E9W+XV3gE0DkEI8BoGDx7cqlWr5OTkr776ysDAoLpmYrGYEPLiRBVFNCrz5kUPHz4UiUTOzs7KLVZWViYmJrm5uYpHxWKxvb298lEHh/9r7/5e2fvjOIC/t9mHHcJkP9BEKPNzkkTb/ChpUeIPsAsWV4rIhQtXI0pKKSUSd5QSk6aoFaWE5mplNltrOyxmfmbnOJ+Ld9/TifH19f36zDevx9Xp/XqfH9suntvO65wjjYqKwlVMJpOxyx6PByEkl8u5u0hJSXmny4Yb2Aih6Ohoti/GbDY3NzenpaVptdqkpCQ+ny8QCMJ2+mAkSfJ4PL1e/2KcezElfluEQuFbGwHgD4MgBOAfGBwcdDqdubm5fX19tbW1b10jiJOJm1X46cQkSb5+dihBEAzD+P1+Nr3u7u7u7+/xzNjYWIqiAoGAWCzG1cvLS4qiuNvh8XjsMn7KMc5d1sXFRXx8/Cde7/DwcHFxscViwdHOMMzk5OQ78xMSEvh8vsfj4XYJvYCP7UVUAxBB0DUKwEdtb2+PjIwYjUaTyXR+ft7e3v7WTJVKJRQKj4+P2RGtVosQWlxcfD25oqICIbS2tsaOrK6usuPl5eUIIZPJFLb6mkQikclkGxsb7IjL5cKtpJ/gcDhUKhVOQYSQxWK5vb1lq/h7wMPDAztSVVVFUdTy8vI727RarQihsrKyzx0SAP+9CJ+jBOB/wufzpaSk6HQ63K65tLSEEJqenn5rvkajaWxs5I60tLSIRKKJiQmv13t1dbW5ubmyssIwDE3TpaWlycnJJpMpGAyazWa5XK5UKp+enhiGCYVChYWFONuCweD6+rpEIikqKqIoivmrWWZ8fJy7o6GhIT6fPzo6GggEbDabWq0mCOKdZpn6+nru6tXV1TqdDi83NTVJpdK9vb3Hx8etra2srCyRSGQwGHD18PAQIdTb27uzs7O/vx8KhWiaVqvVYrF4ZmaGJMlgMHhwcDAwMLC7u8tuX6/X5+XlfeIjAOCLQBAC8Pdomq6rq5PJZD6fjx3s6OiIiYk5OjoKu8rc3NyvX7/8fj87cnd319bWxv66EolEU1NTuOTxeGpqativp5WVlQ6Hg13R5XJpNBq2qtVqXS4XLoUNQoqiOjs7cfuMQCDo7u5uaGj4XBCenJzk5+fj/cbFxc3OzmZnZ7NByDCM0WhUKBQCgQAhdH5+zjBMIBBobW1lXyZCqKSkxGq14vkPDw+JiYljY2Mfet8B+CN4zBs3kgAA/BuPj485OTk9PT3cBk6E0PX1tc1mIwgiIyMjLi6OW3K73V6vVyqVhr3/2dnZGUmScrn89U1hwvJ6vW63OzMzk9tog9E0jaPrI2iattvtt7e3SqXynTN/L9zc3NhstqioKIVCgdtEsYWFha6urtPTU/aUJwARB0EIwFeZn5/v7++32+0EQUT6WL4FmqYLCgoMBgO+JQ0A3wQEIQBf5fn52el0pqamxsTERPpYvoVQKOR2u9PT07l/nAIQcRCEAAAAfjS4fAIAAMCPBkEIAADgR4MgBAAA8KNBEAIAAPjRfgOlTdPWogMVFgAAAABJRU5ErkJggg==",
"text/html": [
"<?xml version=\"1.0\" encoding=\"utf-8\"?>\n",
"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" width=\"600\" height=\"400\" viewBox=\"0 0 2400 1600\">\n",
"<defs>\n",
" <clipPath id=\"clip230\">\n",
" <rect x=\"0\" y=\"0\" width=\"2400\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<path clip-path=\"url(#clip230)\" d=\"M0 1600 L2400 1600 L2400 0 L0 0 Z\" fill=\"#ffffff\" fill-rule=\"evenodd\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip231\">\n",
" <rect x=\"480\" y=\"0\" width=\"1681\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<path clip-path=\"url(#clip230)\" d=\"M256.556 1423.18 L2352.76 1423.18 L2352.76 47.2441 L256.556 47.2441 Z\" fill=\"#ffffff\" fill-rule=\"evenodd\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip232\">\n",
" <rect x=\"256\" y=\"47\" width=\"2097\" height=\"1377\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polyline clip-path=\"url(#clip232)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"315.882,1423.18 315.882,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip232)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"810.269,1423.18 810.269,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip232)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"1304.66,1423.18 1304.66,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip232)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"1799.04,1423.18 1799.04,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip232)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"2293.43,1423.18 2293.43,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip232)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"256.556,1272.91 2352.76,1272.91 \"/>\n",
"<polyline clip-path=\"url(#clip232)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"256.556,1093.67 2352.76,1093.67 \"/>\n",
"<polyline clip-path=\"url(#clip232)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"256.556,914.443 2352.76,914.443 \"/>\n",
"<polyline clip-path=\"url(#clip232)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"256.556,735.212 2352.76,735.212 \"/>\n",
"<polyline clip-path=\"url(#clip232)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"256.556,555.981 2352.76,555.981 \"/>\n",
"<polyline clip-path=\"url(#clip232)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"256.556,376.749 2352.76,376.749 \"/>\n",
"<polyline clip-path=\"url(#clip232)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"256.556,197.518 2352.76,197.518 \"/>\n",
"<polyline clip-path=\"url(#clip230)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,1423.18 2352.76,1423.18 \"/>\n",
"<polyline clip-path=\"url(#clip230)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"315.882,1423.18 315.882,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip230)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"810.269,1423.18 810.269,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip230)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"1304.66,1423.18 1304.66,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip230)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"1799.04,1423.18 1799.04,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip230)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"2293.43,1423.18 2293.43,1404.28 \"/>\n",
"<path clip-path=\"url(#clip230)\" d=\"M262.41 1468.75 L292.086 1468.75 L292.086 1472.69 L262.41 1472.69 L262.41 1468.75 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M302.989 1481.64 L310.628 1481.64 L310.628 1455.28 L302.318 1456.95 L302.318 1452.69 L310.581 1451.02 L315.257 1451.02 L315.257 1481.64 L322.896 1481.64 L322.896 1485.58 L302.989 1485.58 L302.989 1481.64 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M332.341 1479.7 L337.225 1479.7 L337.225 1485.58 L332.341 1485.58 L332.341 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M357.41 1454.1 Q353.799 1454.1 351.97 1457.66 Q350.165 1461.2 350.165 1468.33 Q350.165 1475.44 351.97 1479.01 Q353.799 1482.55 357.41 1482.55 Q361.044 1482.55 362.85 1479.01 Q364.678 1475.44 364.678 1468.33 Q364.678 1461.2 362.85 1457.66 Q361.044 1454.1 357.41 1454.1 M357.41 1450.39 Q363.22 1450.39 366.276 1455 Q369.354 1459.58 369.354 1468.33 Q369.354 1477.06 366.276 1481.67 Q363.22 1486.25 357.41 1486.25 Q351.6 1486.25 348.521 1481.67 Q345.465 1477.06 345.465 1468.33 Q345.465 1459.58 348.521 1455 Q351.6 1450.39 357.41 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M757.295 1468.75 L786.971 1468.75 L786.971 1472.69 L757.295 1472.69 L757.295 1468.75 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M807.063 1454.1 Q803.452 1454.1 801.623 1457.66 Q799.818 1461.2 799.818 1468.33 Q799.818 1475.44 801.623 1479.01 Q803.452 1482.55 807.063 1482.55 Q810.697 1482.55 812.503 1479.01 Q814.332 1475.44 814.332 1468.33 Q814.332 1461.2 812.503 1457.66 Q810.697 1454.1 807.063 1454.1 M807.063 1450.39 Q812.873 1450.39 815.929 1455 Q819.007 1459.58 819.007 1468.33 Q819.007 1477.06 815.929 1481.67 Q812.873 1486.25 807.063 1486.25 Q801.253 1486.25 798.174 1481.67 Q795.119 1477.06 795.119 1468.33 Q795.119 1459.58 798.174 1455 Q801.253 1450.39 807.063 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M827.225 1479.7 L832.109 1479.7 L832.109 1485.58 L827.225 1485.58 L827.225 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M842.341 1451.02 L860.697 1451.02 L860.697 1454.96 L846.623 1454.96 L846.623 1463.43 Q847.642 1463.08 848.66 1462.92 Q849.679 1462.73 850.697 1462.73 Q856.484 1462.73 859.864 1465.9 Q863.243 1469.08 863.243 1474.49 Q863.243 1480.07 859.771 1483.17 Q856.299 1486.25 849.98 1486.25 Q847.804 1486.25 845.535 1485.88 Q843.29 1485.51 840.882 1484.77 L840.882 1480.07 Q842.966 1481.2 845.188 1481.76 Q847.41 1482.32 849.887 1482.32 Q853.892 1482.32 856.229 1480.21 Q858.567 1478.1 858.567 1474.49 Q858.567 1470.88 856.229 1468.77 Q853.892 1466.67 849.887 1466.67 Q848.012 1466.67 846.137 1467.08 Q844.285 1467.5 842.341 1468.38 L842.341 1451.02 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1282.04 1454.1 Q1278.43 1454.1 1276.6 1457.66 Q1274.79 1461.2 1274.79 1468.33 Q1274.79 1475.44 1276.6 1479.01 Q1278.43 1482.55 1282.04 1482.55 Q1285.67 1482.55 1287.48 1479.01 Q1289.31 1475.44 1289.31 1468.33 Q1289.31 1461.2 1287.48 1457.66 Q1285.67 1454.1 1282.04 1454.1 M1282.04 1450.39 Q1287.85 1450.39 1290.91 1455 Q1293.98 1459.58 1293.98 1468.33 Q1293.98 1477.06 1290.91 1481.67 Q1287.85 1486.25 1282.04 1486.25 Q1276.23 1486.25 1273.15 1481.67 Q1270.1 1477.06 1270.1 1468.33 Q1270.1 1459.58 1273.15 1455 Q1276.23 1450.39 1282.04 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1302.2 1479.7 L1307.09 1479.7 L1307.09 1485.58 L1302.2 1485.58 L1302.2 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1327.27 1454.1 Q1323.66 1454.1 1321.83 1457.66 Q1320.03 1461.2 1320.03 1468.33 Q1320.03 1475.44 1321.83 1479.01 Q1323.66 1482.55 1327.27 1482.55 Q1330.91 1482.55 1332.71 1479.01 Q1334.54 1475.44 1334.54 1468.33 Q1334.54 1461.2 1332.71 1457.66 Q1330.91 1454.1 1327.27 1454.1 M1327.27 1450.39 Q1333.08 1450.39 1336.14 1455 Q1339.22 1459.58 1339.22 1468.33 Q1339.22 1477.06 1336.14 1481.67 Q1333.08 1486.25 1327.27 1486.25 Q1321.46 1486.25 1318.38 1481.67 Q1315.33 1477.06 1315.33 1468.33 Q1315.33 1459.58 1318.38 1455 Q1321.46 1450.39 1327.27 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1776.92 1454.1 Q1773.31 1454.1 1771.48 1457.66 Q1769.68 1461.2 1769.68 1468.33 Q1769.68 1475.44 1771.48 1479.01 Q1773.31 1482.55 1776.92 1482.55 Q1780.56 1482.55 1782.36 1479.01 Q1784.19 1475.44 1784.19 1468.33 Q1784.19 1461.2 1782.36 1457.66 Q1780.56 1454.1 1776.92 1454.1 M1776.92 1450.39 Q1782.73 1450.39 1785.79 1455 Q1788.87 1459.58 1788.87 1468.33 Q1788.87 1477.06 1785.79 1481.67 Q1782.73 1486.25 1776.92 1486.25 Q1771.11 1486.25 1768.04 1481.67 Q1764.98 1477.06 1764.98 1468.33 Q1764.98 1459.58 1768.04 1455 Q1771.11 1450.39 1776.92 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1797.09 1479.7 L1801.97 1479.7 L1801.97 1485.58 L1797.09 1485.58 L1797.09 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1812.2 1451.02 L1830.56 1451.02 L1830.56 1454.96 L1816.48 1454.96 L1816.48 1463.43 Q1817.5 1463.08 1818.52 1462.92 Q1819.54 1462.73 1820.56 1462.73 Q1826.35 1462.73 1829.73 1465.9 Q1833.11 1469.08 1833.11 1474.49 Q1833.11 1480.07 1829.63 1483.17 Q1826.16 1486.25 1819.84 1486.25 Q1817.67 1486.25 1815.4 1485.88 Q1813.15 1485.51 1810.74 1484.77 L1810.74 1480.07 Q1812.83 1481.2 1815.05 1481.76 Q1817.27 1482.32 1819.75 1482.32 Q1823.75 1482.32 1826.09 1480.21 Q1828.43 1478.1 1828.43 1474.49 Q1828.43 1470.88 1826.09 1468.77 Q1823.75 1466.67 1819.75 1466.67 Q1817.87 1466.67 1816 1467.08 Q1814.15 1467.5 1812.2 1468.38 L1812.2 1451.02 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M2260.58 1481.64 L2268.22 1481.64 L2268.22 1455.28 L2259.91 1456.95 L2259.91 1452.69 L2268.17 1451.02 L2272.85 1451.02 L2272.85 1481.64 L2280.49 1481.64 L2280.49 1485.58 L2260.58 1485.58 L2260.58 1481.64 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M2289.93 1479.7 L2294.82 1479.7 L2294.82 1485.58 L2289.93 1485.58 L2289.93 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M2315 1454.1 Q2311.39 1454.1 2309.56 1457.66 Q2307.76 1461.2 2307.76 1468.33 Q2307.76 1475.44 2309.56 1479.01 Q2311.39 1482.55 2315 1482.55 Q2318.64 1482.55 2320.44 1479.01 Q2322.27 1475.44 2322.27 1468.33 Q2322.27 1461.2 2320.44 1457.66 Q2318.64 1454.1 2315 1454.1 M2315 1450.39 Q2320.81 1450.39 2323.87 1455 Q2326.95 1459.58 2326.95 1468.33 Q2326.95 1477.06 2323.87 1481.67 Q2320.81 1486.25 2315 1486.25 Q2309.19 1486.25 2306.11 1481.67 Q2303.06 1477.06 2303.06 1468.33 Q2303.06 1459.58 2306.11 1455 Q2309.19 1450.39 2315 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1113.38 1532.4 L1100.49 1549.74 L1114.05 1568.04 L1107.14 1568.04 L1096.77 1554.04 L1086.39 1568.04 L1079.48 1568.04 L1093.33 1549.39 L1080.66 1532.4 L1087.57 1532.4 L1097.02 1545.1 L1106.48 1532.4 L1113.38 1532.4 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1157.11 1518.58 Q1152.85 1525.9 1150.78 1533.06 Q1148.71 1540.23 1148.71 1547.58 Q1148.71 1554.93 1150.78 1562.16 Q1152.88 1569.35 1157.11 1576.64 L1152.02 1576.64 Q1147.25 1569.16 1144.86 1561.93 Q1142.51 1554.71 1142.51 1547.58 Q1142.51 1540.48 1144.86 1533.29 Q1147.22 1526.09 1152.02 1518.58 L1157.11 1518.58 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1194.13 1533.76 L1194.13 1539.24 Q1191.65 1537.87 1189.13 1537.2 Q1186.65 1536.5 1184.11 1536.5 Q1178.41 1536.5 1175.26 1540.13 Q1172.11 1543.73 1172.11 1550.25 Q1172.11 1556.78 1175.26 1560.4 Q1178.41 1564 1184.11 1564 Q1186.65 1564 1189.13 1563.33 Q1191.65 1562.63 1194.13 1561.26 L1194.13 1566.68 Q1191.68 1567.82 1189.04 1568.39 Q1186.43 1568.97 1183.47 1568.97 Q1175.42 1568.97 1170.67 1563.91 Q1165.93 1558.85 1165.93 1550.25 Q1165.93 1541.53 1170.71 1536.53 Q1175.51 1531.54 1183.85 1531.54 Q1186.56 1531.54 1189.13 1532.11 Q1191.71 1532.65 1194.13 1533.76 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1218.13 1536.5 Q1213.42 1536.5 1210.68 1540.19 Q1207.94 1543.85 1207.94 1550.25 Q1207.94 1556.65 1210.65 1560.34 Q1213.39 1564 1218.13 1564 Q1222.81 1564 1225.55 1560.31 Q1228.28 1556.62 1228.28 1550.25 Q1228.28 1543.92 1225.55 1540.23 Q1222.81 1536.5 1218.13 1536.5 M1218.13 1531.54 Q1225.77 1531.54 1230.13 1536.5 Q1234.49 1541.47 1234.49 1550.25 Q1234.49 1559 1230.13 1564 Q1225.77 1568.97 1218.13 1568.97 Q1210.46 1568.97 1206.1 1564 Q1201.77 1559 1201.77 1550.25 Q1201.77 1541.47 1206.1 1536.5 Q1210.46 1531.54 1218.13 1531.54 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1258.01 1536.5 Q1253.3 1536.5 1250.56 1540.19 Q1247.83 1543.85 1247.83 1550.25 Q1247.83 1556.65 1250.53 1560.34 Q1253.27 1564 1258.01 1564 Q1262.69 1564 1265.43 1560.31 Q1268.16 1556.62 1268.16 1550.25 Q1268.16 1543.92 1265.43 1540.23 Q1262.69 1536.5 1258.01 1536.5 M1258.01 1531.54 Q1265.65 1531.54 1270.01 1536.5 Q1274.37 1541.47 1274.37 1550.25 Q1274.37 1559 1270.01 1564 Q1265.65 1568.97 1258.01 1568.97 Q1250.34 1568.97 1245.98 1564 Q1241.65 1559 1241.65 1550.25 Q1241.65 1541.47 1245.98 1536.5 Q1250.34 1531.54 1258.01 1531.54 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1304.74 1537.87 Q1303.75 1537.3 1302.57 1537.04 Q1301.43 1536.76 1300.02 1536.76 Q1295.06 1536.76 1292.39 1540 Q1289.74 1543.22 1289.74 1549.27 L1289.74 1568.04 L1283.86 1568.04 L1283.86 1532.4 L1289.74 1532.4 L1289.74 1537.93 Q1291.59 1534.69 1294.55 1533.13 Q1297.51 1531.54 1301.74 1531.54 Q1302.35 1531.54 1303.08 1531.63 Q1303.81 1531.7 1304.7 1531.85 L1304.74 1537.87 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1333.19 1537.81 L1333.19 1518.52 L1339.05 1518.52 L1339.05 1568.04 L1333.19 1568.04 L1333.19 1562.7 Q1331.34 1565.88 1328.51 1567.44 Q1325.71 1568.97 1321.76 1568.97 Q1315.3 1568.97 1311.23 1563.81 Q1307.19 1558.65 1307.19 1550.25 Q1307.19 1541.85 1311.23 1536.69 Q1315.3 1531.54 1321.76 1531.54 Q1325.71 1531.54 1328.51 1533.1 Q1331.34 1534.62 1333.19 1537.81 M1313.23 1550.25 Q1313.23 1556.71 1315.88 1560.4 Q1318.55 1564.07 1323.2 1564.07 Q1327.84 1564.07 1330.52 1560.4 Q1333.19 1556.71 1333.19 1550.25 Q1333.19 1543.79 1330.52 1540.13 Q1327.84 1536.44 1323.2 1536.44 Q1318.55 1536.44 1315.88 1540.13 Q1313.23 1543.79 1313.23 1550.25 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1351.11 1532.4 L1356.97 1532.4 L1356.97 1568.04 L1351.11 1568.04 L1351.11 1532.4 M1351.11 1518.52 L1356.97 1518.52 L1356.97 1525.93 L1351.11 1525.93 L1351.11 1518.52 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1398.85 1546.53 L1398.85 1568.04 L1393 1568.04 L1393 1546.72 Q1393 1541.66 1391.02 1539.14 Q1389.05 1536.63 1385.1 1536.63 Q1380.36 1536.63 1377.62 1539.65 Q1374.89 1542.68 1374.89 1547.9 L1374.89 1568.04 L1369 1568.04 L1369 1532.4 L1374.89 1532.4 L1374.89 1537.93 Q1376.99 1534.72 1379.82 1533.13 Q1382.68 1531.54 1386.41 1531.54 Q1392.55 1531.54 1395.7 1535.36 Q1398.85 1539.14 1398.85 1546.53 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1426.73 1550.12 Q1419.64 1550.12 1416.9 1551.75 Q1414.16 1553.37 1414.16 1557.29 Q1414.16 1560.4 1416.2 1562.25 Q1418.27 1564.07 1421.8 1564.07 Q1426.67 1564.07 1429.6 1560.63 Q1432.56 1557.16 1432.56 1551.43 L1432.56 1550.12 L1426.73 1550.12 M1438.42 1547.71 L1438.42 1568.04 L1432.56 1568.04 L1432.56 1562.63 Q1430.55 1565.88 1427.56 1567.44 Q1424.57 1568.97 1420.24 1568.97 Q1414.77 1568.97 1411.52 1565.91 Q1408.31 1562.82 1408.31 1557.67 Q1408.31 1551.65 1412.32 1548.6 Q1416.36 1545.54 1424.35 1545.54 L1432.56 1545.54 L1432.56 1544.97 Q1432.56 1540.93 1429.89 1538.73 Q1427.24 1536.5 1422.44 1536.5 Q1419.38 1536.5 1416.49 1537.23 Q1413.59 1537.97 1410.92 1539.43 L1410.92 1534.02 Q1414.13 1532.78 1417.15 1532.17 Q1420.18 1531.54 1423.04 1531.54 Q1430.78 1531.54 1434.6 1535.55 Q1438.42 1539.56 1438.42 1547.71 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1456.27 1522.27 L1456.27 1532.4 L1468.33 1532.4 L1468.33 1536.95 L1456.27 1536.95 L1456.27 1556.3 Q1456.27 1560.66 1457.45 1561.9 Q1458.66 1563.14 1462.32 1563.14 L1468.33 1563.14 L1468.33 1568.04 L1462.32 1568.04 Q1455.54 1568.04 1452.96 1565.53 Q1450.38 1562.98 1450.38 1556.3 L1450.38 1536.95 L1446.09 1536.95 L1446.09 1532.4 L1450.38 1532.4 L1450.38 1522.27 L1456.27 1522.27 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1506.53 1548.76 L1506.53 1551.62 L1479.6 1551.62 Q1479.98 1557.67 1483.23 1560.85 Q1486.51 1564 1492.33 1564 Q1495.71 1564 1498.86 1563.17 Q1502.04 1562.35 1505.16 1560.69 L1505.16 1566.23 Q1502.01 1567.57 1498.7 1568.27 Q1495.39 1568.97 1491.98 1568.97 Q1483.45 1568.97 1478.46 1564 Q1473.49 1559.04 1473.49 1550.57 Q1473.49 1541.82 1478.2 1536.69 Q1482.94 1531.54 1490.96 1531.54 Q1498.16 1531.54 1502.33 1536.18 Q1506.53 1540.8 1506.53 1548.76 M1500.67 1547.04 Q1500.61 1542.23 1497.97 1539.37 Q1495.36 1536.5 1491.03 1536.5 Q1486.13 1536.5 1483.17 1539.27 Q1480.24 1542.04 1479.79 1547.07 L1500.67 1547.04 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M1515.22 1518.58 L1520.31 1518.58 Q1525.08 1526.09 1527.44 1533.29 Q1529.83 1540.48 1529.83 1547.58 Q1529.83 1554.71 1527.44 1561.93 Q1525.08 1569.16 1520.31 1576.64 L1515.22 1576.64 Q1519.45 1569.35 1521.52 1562.16 Q1523.62 1554.93 1523.62 1547.58 Q1523.62 1540.23 1521.52 1533.06 Q1519.45 1525.9 1515.22 1518.58 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><polyline clip-path=\"url(#clip230)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,1423.18 256.556,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip230)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,1272.91 275.454,1272.91 \"/>\n",
"<polyline clip-path=\"url(#clip230)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,1093.67 275.454,1093.67 \"/>\n",
"<polyline clip-path=\"url(#clip230)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,914.443 275.454,914.443 \"/>\n",
"<polyline clip-path=\"url(#clip230)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,735.212 275.454,735.212 \"/>\n",
"<polyline clip-path=\"url(#clip230)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,555.981 275.454,555.981 \"/>\n",
"<polyline clip-path=\"url(#clip230)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,376.749 275.454,376.749 \"/>\n",
"<polyline clip-path=\"url(#clip230)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,197.518 275.454,197.518 \"/>\n",
"<path clip-path=\"url(#clip230)\" d=\"M114.26 1273.36 L143.936 1273.36 L143.936 1277.29 L114.26 1277.29 L114.26 1273.36 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M164.028 1258.7 Q160.417 1258.7 158.589 1262.27 Q156.783 1265.81 156.783 1272.94 Q156.783 1280.05 158.589 1283.61 Q160.417 1287.15 164.028 1287.15 Q167.663 1287.15 169.468 1283.61 Q171.297 1280.05 171.297 1272.94 Q171.297 1265.81 169.468 1262.27 Q167.663 1258.7 164.028 1258.7 M164.028 1255 Q169.839 1255 172.894 1259.61 Q175.973 1264.19 175.973 1272.94 Q175.973 1281.67 172.894 1286.27 Q169.839 1290.86 164.028 1290.86 Q158.218 1290.86 155.14 1286.27 Q152.084 1281.67 152.084 1272.94 Q152.084 1264.19 155.14 1259.61 Q158.218 1255 164.028 1255 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M184.19 1284.31 L189.075 1284.31 L189.075 1290.19 L184.19 1290.19 L184.19 1284.31 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M213.426 1271.55 Q216.783 1272.27 218.658 1274.54 Q220.556 1276.81 220.556 1280.14 Q220.556 1285.26 217.037 1288.06 Q213.519 1290.86 207.037 1290.86 Q204.862 1290.86 202.547 1290.42 Q200.255 1290 197.801 1289.14 L197.801 1284.63 Q199.746 1285.76 202.061 1286.34 Q204.375 1286.92 206.899 1286.92 Q211.297 1286.92 213.588 1285.19 Q215.903 1283.45 215.903 1280.14 Q215.903 1277.08 213.75 1275.37 Q211.621 1273.64 207.801 1273.64 L203.774 1273.64 L203.774 1269.79 L207.987 1269.79 Q211.436 1269.79 213.264 1268.43 Q215.093 1267.04 215.093 1264.45 Q215.093 1261.78 213.195 1260.37 Q211.32 1258.94 207.801 1258.94 Q205.88 1258.94 203.681 1259.35 Q201.482 1259.77 198.843 1260.65 L198.843 1256.48 Q201.505 1255.74 203.82 1255.37 Q206.158 1255 208.218 1255 Q213.542 1255 216.644 1257.43 Q219.746 1259.84 219.746 1263.96 Q219.746 1266.83 218.102 1268.82 Q216.459 1270.79 213.426 1271.55 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M115.209 1094.13 L144.885 1094.13 L144.885 1098.06 L115.209 1098.06 L115.209 1094.13 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M164.977 1079.47 Q161.366 1079.47 159.538 1083.04 Q157.732 1086.58 157.732 1093.71 Q157.732 1100.82 159.538 1104.38 Q161.366 1107.92 164.977 1107.92 Q168.612 1107.92 170.417 1104.38 Q172.246 1100.82 172.246 1093.71 Q172.246 1086.58 170.417 1083.04 Q168.612 1079.47 164.977 1079.47 M164.977 1075.77 Q170.788 1075.77 173.843 1080.38 Q176.922 1084.96 176.922 1093.71 Q176.922 1102.44 173.843 1107.04 Q170.788 1111.63 164.977 1111.63 Q159.167 1111.63 156.089 1107.04 Q153.033 1102.44 153.033 1093.71 Q153.033 1084.96 156.089 1080.38 Q159.167 1075.77 164.977 1075.77 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M185.139 1105.07 L190.024 1105.07 L190.024 1110.95 L185.139 1110.95 L185.139 1105.07 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M204.237 1107.02 L220.556 1107.02 L220.556 1110.95 L198.612 1110.95 L198.612 1107.02 Q201.274 1104.26 205.857 1099.64 Q210.463 1094.98 211.644 1093.64 Q213.889 1091.12 214.769 1089.38 Q215.672 1087.62 215.672 1085.93 Q215.672 1083.18 213.727 1081.44 Q211.806 1079.7 208.704 1079.7 Q206.505 1079.7 204.051 1080.47 Q201.621 1081.23 198.843 1082.78 L198.843 1078.06 Q201.667 1076.93 204.121 1076.35 Q206.574 1075.77 208.612 1075.77 Q213.982 1075.77 217.176 1078.45 Q220.371 1081.14 220.371 1085.63 Q220.371 1087.76 219.561 1089.68 Q218.773 1091.58 216.667 1094.17 Q216.088 1094.84 212.986 1098.06 Q209.885 1101.26 204.237 1107.02 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M114.839 914.895 L144.515 914.895 L144.515 918.83 L114.839 918.83 L114.839 914.895 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M164.607 900.242 Q160.996 900.242 159.167 903.807 Q157.362 907.348 157.362 914.478 Q157.362 921.584 159.167 925.149 Q160.996 928.691 164.607 928.691 Q168.241 928.691 170.047 925.149 Q171.876 921.584 171.876 914.478 Q171.876 907.348 170.047 903.807 Q168.241 900.242 164.607 900.242 M164.607 896.538 Q170.417 896.538 173.473 901.145 Q176.551 905.728 176.551 914.478 Q176.551 923.205 173.473 927.811 Q170.417 932.395 164.607 932.395 Q158.797 932.395 155.718 927.811 Q152.663 923.205 152.663 914.478 Q152.663 905.728 155.718 901.145 Q158.797 896.538 164.607 896.538 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M184.769 925.844 L189.653 925.844 L189.653 931.723 L184.769 931.723 L184.769 925.844 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M200.649 927.788 L208.287 927.788 L208.287 901.422 L199.977 903.089 L199.977 898.83 L208.241 897.163 L212.917 897.163 L212.917 927.788 L220.556 927.788 L220.556 931.723 L200.649 931.723 L200.649 927.788 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M163.38 721.011 Q159.769 721.011 157.94 724.575 Q156.135 728.117 156.135 735.247 Q156.135 742.353 157.94 745.918 Q159.769 749.46 163.38 749.46 Q167.015 749.46 168.82 745.918 Q170.649 742.353 170.649 735.247 Q170.649 728.117 168.82 724.575 Q167.015 721.011 163.38 721.011 M163.38 717.307 Q169.19 717.307 172.246 721.913 Q175.325 726.497 175.325 735.247 Q175.325 743.973 172.246 748.58 Q169.19 753.163 163.38 753.163 Q157.57 753.163 154.491 748.58 Q151.436 743.973 151.436 735.247 Q151.436 726.497 154.491 721.913 Q157.57 717.307 163.38 717.307 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M183.542 746.612 L188.426 746.612 L188.426 752.492 L183.542 752.492 L183.542 746.612 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M208.612 721.011 Q205 721.011 203.172 724.575 Q201.366 728.117 201.366 735.247 Q201.366 742.353 203.172 745.918 Q205 749.46 208.612 749.46 Q212.246 749.46 214.051 745.918 Q215.88 742.353 215.88 735.247 Q215.88 728.117 214.051 724.575 Q212.246 721.011 208.612 721.011 M208.612 717.307 Q214.422 717.307 217.477 721.913 Q220.556 726.497 220.556 735.247 Q220.556 743.973 217.477 748.58 Q214.422 753.163 208.612 753.163 Q202.801 753.163 199.723 748.58 Q196.667 743.973 196.667 735.247 Q196.667 726.497 199.723 721.913 Q202.801 717.307 208.612 717.307 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M164.607 541.779 Q160.996 541.779 159.167 545.344 Q157.362 548.886 157.362 556.015 Q157.362 563.122 159.167 566.687 Q160.996 570.228 164.607 570.228 Q168.241 570.228 170.047 566.687 Q171.876 563.122 171.876 556.015 Q171.876 548.886 170.047 545.344 Q168.241 541.779 164.607 541.779 M164.607 538.076 Q170.417 538.076 173.473 542.682 Q176.551 547.265 176.551 556.015 Q176.551 564.742 173.473 569.349 Q170.417 573.932 164.607 573.932 Q158.797 573.932 155.718 569.349 Q152.663 564.742 152.663 556.015 Q152.663 547.265 155.718 542.682 Q158.797 538.076 164.607 538.076 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M184.769 567.381 L189.653 567.381 L189.653 573.261 L184.769 573.261 L184.769 567.381 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M200.649 569.326 L208.287 569.326 L208.287 542.96 L199.977 544.627 L199.977 540.367 L208.241 538.701 L212.917 538.701 L212.917 569.326 L220.556 569.326 L220.556 573.261 L200.649 573.261 L200.649 569.326 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M164.977 362.548 Q161.366 362.548 159.538 366.113 Q157.732 369.655 157.732 376.784 Q157.732 383.891 159.538 387.455 Q161.366 390.997 164.977 390.997 Q168.612 390.997 170.417 387.455 Q172.246 383.891 172.246 376.784 Q172.246 369.655 170.417 366.113 Q168.612 362.548 164.977 362.548 M164.977 358.844 Q170.788 358.844 173.843 363.451 Q176.922 368.034 176.922 376.784 Q176.922 385.511 173.843 390.117 Q170.788 394.701 164.977 394.701 Q159.167 394.701 156.089 390.117 Q153.033 385.511 153.033 376.784 Q153.033 368.034 156.089 363.451 Q159.167 358.844 164.977 358.844 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M185.139 388.15 L190.024 388.15 L190.024 394.029 L185.139 394.029 L185.139 388.15 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M204.237 390.094 L220.556 390.094 L220.556 394.029 L198.612 394.029 L198.612 390.094 Q201.274 387.34 205.857 382.71 Q210.463 378.057 211.644 376.715 Q213.889 374.192 214.769 372.455 Q215.672 370.696 215.672 369.006 Q215.672 366.252 213.727 364.516 Q211.806 362.78 208.704 362.78 Q206.505 362.78 204.051 363.543 Q201.621 364.307 198.843 365.858 L198.843 361.136 Q201.667 360.002 204.121 359.423 Q206.574 358.844 208.612 358.844 Q213.982 358.844 217.176 361.53 Q220.371 364.215 220.371 368.705 Q220.371 370.835 219.561 372.756 Q218.773 374.654 216.667 377.247 Q216.088 377.918 212.986 381.136 Q209.885 384.33 204.237 390.094 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M164.028 183.317 Q160.417 183.317 158.589 186.882 Q156.783 190.423 156.783 197.553 Q156.783 204.659 158.589 208.224 Q160.417 211.766 164.028 211.766 Q167.663 211.766 169.468 208.224 Q171.297 204.659 171.297 197.553 Q171.297 190.423 169.468 186.882 Q167.663 183.317 164.028 183.317 M164.028 179.613 Q169.839 179.613 172.894 184.22 Q175.973 188.803 175.973 197.553 Q175.973 206.28 172.894 210.886 Q169.839 215.469 164.028 215.469 Q158.218 215.469 155.14 210.886 Q152.084 206.28 152.084 197.553 Q152.084 188.803 155.14 184.22 Q158.218 179.613 164.028 179.613 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M184.19 208.918 L189.075 208.918 L189.075 214.798 L184.19 214.798 L184.19 208.918 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M213.426 196.164 Q216.783 196.882 218.658 199.15 Q220.556 201.419 220.556 204.752 Q220.556 209.868 217.037 212.668 Q213.519 215.469 207.037 215.469 Q204.862 215.469 202.547 215.03 Q200.255 214.613 197.801 213.756 L197.801 209.243 Q199.746 210.377 202.061 210.956 Q204.375 211.534 206.899 211.534 Q211.297 211.534 213.588 209.798 Q215.903 208.062 215.903 204.752 Q215.903 201.696 213.75 199.983 Q211.621 198.247 207.801 198.247 L203.774 198.247 L203.774 194.405 L207.987 194.405 Q211.436 194.405 213.264 193.039 Q215.093 191.65 215.093 189.057 Q215.093 186.395 213.195 184.983 Q211.32 183.548 207.801 183.548 Q205.88 183.548 203.681 183.965 Q201.482 184.382 198.843 185.261 L198.843 181.095 Q201.505 180.354 203.82 179.983 Q206.158 179.613 208.218 179.613 Q213.542 179.613 216.644 182.044 Q219.746 184.451 219.746 188.571 Q219.746 191.442 218.102 193.432 Q216.459 195.4 213.426 196.164 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M46.212 1101.42 Q52.6732 1101.42 56.3653 1098.77 Q60.0256 1096.1 60.0256 1091.45 Q60.0256 1086.81 56.3653 1084.13 Q52.6732 1081.46 46.212 1081.46 Q39.7508 1081.46 36.0905 1084.13 Q32.3984 1086.81 32.3984 1091.45 Q32.3984 1096.1 36.0905 1098.77 Q39.7508 1101.42 46.212 1101.42 M58.657 1081.46 Q61.8398 1083.3 63.3994 1086.14 Q64.9272 1088.94 64.9272 1092.89 Q64.9272 1099.35 59.771 1103.42 Q54.6147 1107.46 46.212 1107.46 Q37.8093 1107.46 32.6531 1103.42 Q27.4968 1099.35 27.4968 1092.89 Q27.4968 1088.94 29.0564 1086.14 Q30.5842 1083.3 33.7671 1081.46 L28.3562 1081.46 L28.3562 1075.6 L77.5631 1075.6 L77.5631 1081.46 L58.657 1081.46 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M74.8259 1036.45 L79.3773 1036.45 L79.3773 1070.32 L74.8259 1070.32 L74.8259 1036.45 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M28.3562 1001.31 L45.7028 1014.2 L64.0042 1000.65 L64.0042 1007.55 L49.9996 1017.93 L64.0042 1028.31 L64.0042 1035.21 L45.3526 1021.37 L28.3562 1034.03 L28.3562 1027.13 L41.0558 1017.67 L28.3562 1008.22 L28.3562 1001.31 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M14.5426 957.582 Q21.8632 961.847 29.0246 963.916 Q36.186 965.985 43.5384 965.985 Q50.8908 965.985 58.1159 963.916 Q65.3091 961.815 72.5979 957.582 L72.5979 962.675 Q65.1182 967.449 57.8931 969.836 Q50.668 972.191 43.5384 972.191 Q36.4406 972.191 29.2474 969.836 Q22.0542 967.481 14.5426 962.675 L14.5426 957.582 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M14.479 928.172 L19.3487 928.172 L19.3487 933.774 Q19.3487 936.925 20.6219 938.167 Q21.895 939.376 25.2052 939.376 L28.3562 939.376 L28.3562 929.732 L32.9077 929.732 L32.9077 939.376 L64.0042 939.376 L64.0042 945.264 L32.9077 945.264 L32.9077 950.866 L28.3562 950.866 L28.3562 945.264 L25.8736 945.264 Q19.9216 945.264 17.2162 942.495 Q14.479 939.726 14.479 933.711 L14.479 928.172 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M14.479 923.271 L14.479 917.414 L64.0042 917.414 L64.0042 923.271 L14.479 923.271 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M49.9359 905.765 L28.3562 905.765 L28.3562 899.909 L49.7131 899.909 Q54.7739 899.909 57.3202 897.935 Q59.8346 895.962 59.8346 892.015 Q59.8346 887.273 56.8109 884.536 Q53.7872 881.766 48.5673 881.766 L28.3562 881.766 L28.3562 875.91 L64.0042 875.91 L64.0042 881.766 L58.5296 881.766 Q61.7762 883.899 63.3676 886.732 Q64.9272 889.533 64.9272 893.257 Q64.9272 899.399 61.1078 902.582 Q57.2883 905.765 49.9359 905.765 M27.4968 891.029 L27.4968 891.029 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M28.3562 834.215 L45.7028 847.105 L64.0042 833.546 L64.0042 840.453 L49.9996 850.829 L64.0042 861.205 L64.0042 868.112 L45.3526 854.267 L28.3562 866.934 L28.3562 860.028 L41.0558 850.574 L28.3562 841.121 L28.3562 834.215 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M28.3562 804.55 L28.3562 798.694 L64.0042 798.694 L64.0042 804.55 L28.3562 804.55 M14.479 804.55 L14.479 798.694 L21.895 798.694 L21.895 804.55 L14.479 804.55 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M42.4881 756.808 L64.0042 756.808 L64.0042 762.664 L42.679 762.664 Q37.6183 762.664 35.1038 764.637 Q32.5894 766.611 32.5894 770.558 Q32.5894 775.3 35.6131 778.037 Q38.6368 780.775 43.8567 780.775 L64.0042 780.775 L64.0042 786.663 L28.3562 786.663 L28.3562 780.775 L33.8944 780.775 Q30.6797 778.674 29.0883 775.841 Q27.4968 772.977 27.4968 769.253 Q27.4968 763.11 31.3163 759.959 Q35.1038 756.808 42.4881 756.808 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M28.3562 694.774 L45.7028 707.664 L64.0042 694.105 L64.0042 701.012 L49.9996 711.388 L64.0042 721.764 L64.0042 728.671 L45.3526 714.826 L28.3562 727.494 L28.3562 720.587 L41.0558 711.134 L28.3562 701.681 L28.3562 694.774 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M43.5384 688.79 L43.5384 671.634 L48.7583 671.634 L48.7583 688.79 L43.5384 688.79 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M33.7671 638.851 L14.479 638.851 L14.479 632.995 L64.0042 632.995 L64.0042 638.851 L58.657 638.851 Q61.8398 640.697 63.3994 643.53 Q64.9272 646.331 64.9272 650.278 Q64.9272 656.739 59.771 660.813 Q54.6147 664.855 46.212 664.855 Q37.8093 664.855 32.6531 660.813 Q27.4968 656.739 27.4968 650.278 Q27.4968 646.331 29.0564 643.53 Q30.5842 640.697 33.7671 638.851 M46.212 658.808 Q52.6732 658.808 56.3653 656.166 Q60.0256 653.492 60.0256 648.845 Q60.0256 644.198 56.3653 641.525 Q52.6732 638.851 46.212 638.851 Q39.7508 638.851 36.0905 641.525 Q32.3984 644.198 32.3984 648.845 Q32.3984 653.492 36.0905 656.166 Q39.7508 658.808 46.212 658.808 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M28.3562 620.932 L28.3562 615.075 L64.0042 615.075 L64.0042 620.932 L28.3562 620.932 M14.479 620.932 L14.479 615.075 L21.895 615.075 L21.895 620.932 L14.479 620.932 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M33.8307 582.164 Q33.2578 583.151 33.0032 584.329 Q32.7167 585.475 32.7167 586.875 Q32.7167 591.84 35.9632 594.514 Q39.1779 597.156 45.2253 597.156 L64.0042 597.156 L64.0042 603.044 L28.3562 603.044 L28.3562 597.156 L33.8944 597.156 Q30.6479 595.31 29.0883 592.35 Q27.4968 589.39 27.4968 585.156 Q27.4968 584.552 27.5923 583.82 Q27.656 583.087 27.8151 582.196 L33.8307 582.164 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M44.7161 546.962 L47.5806 546.962 L47.5806 573.889 Q53.6281 573.507 56.8109 570.261 Q59.9619 566.982 59.9619 561.158 Q59.9619 557.784 59.1344 554.633 Q58.3069 551.45 56.6518 548.331 L62.1899 548.331 Q63.5267 551.482 64.227 554.792 Q64.9272 558.102 64.9272 561.508 Q64.9272 570.038 59.9619 575.035 Q54.9967 580 46.5303 580 Q37.7774 580 32.6531 575.29 Q27.4968 570.547 27.4968 562.526 Q27.4968 555.333 32.1438 551.163 Q36.7589 546.962 44.7161 546.962 M42.9973 552.819 Q38.1912 552.882 35.3266 555.524 Q32.4621 558.134 32.4621 562.463 Q32.4621 567.364 35.2312 570.324 Q38.0002 573.252 43.0292 573.698 L42.9973 552.819 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M29.7248 511.696 L35.1993 511.696 Q33.8307 514.179 33.1623 516.693 Q32.4621 519.176 32.4621 521.722 Q32.4621 527.419 36.0905 530.57 Q39.6872 533.721 46.212 533.721 Q52.7369 533.721 56.3653 530.57 Q59.9619 527.419 59.9619 521.722 Q59.9619 519.176 59.2935 516.693 Q58.5933 514.179 57.2247 511.696 L62.6355 511.696 Q63.7814 514.147 64.3543 516.789 Q64.9272 519.399 64.9272 522.359 Q64.9272 530.411 59.8664 535.154 Q54.8057 539.896 46.212 539.896 Q37.491 539.896 32.4939 535.122 Q27.4968 530.316 27.4968 521.977 Q27.4968 519.271 28.0697 516.693 Q28.6108 514.115 29.7248 511.696 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M18.2347 495.718 L28.3562 495.718 L28.3562 483.655 L32.9077 483.655 L32.9077 495.718 L52.2594 495.718 Q56.6199 495.718 57.8613 494.541 Q59.1026 493.331 59.1026 489.671 L59.1026 483.655 L64.0042 483.655 L64.0042 489.671 Q64.0042 496.45 61.4897 499.028 Q58.9434 501.606 52.2594 501.606 L32.9077 501.606 L32.9077 505.903 L28.3562 505.903 L28.3562 501.606 L18.2347 501.606 L18.2347 495.718 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M28.3562 475.953 L28.3562 470.096 L64.0042 470.096 L64.0042 475.953 L28.3562 475.953 M14.479 475.953 L14.479 470.096 L21.895 470.096 L21.895 475.953 L14.479 475.953 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M32.4621 444.029 Q32.4621 448.739 36.1542 451.477 Q39.8145 454.214 46.212 454.214 Q52.6095 454.214 56.3017 451.508 Q59.9619 448.771 59.9619 444.029 Q59.9619 439.35 56.2698 436.613 Q52.5777 433.875 46.212 433.875 Q39.8781 433.875 36.186 436.613 Q32.4621 439.35 32.4621 444.029 M27.4968 444.029 Q27.4968 436.39 32.4621 432.029 Q37.4273 427.669 46.212 427.669 Q54.9649 427.669 59.9619 432.029 Q64.9272 436.39 64.9272 444.029 Q64.9272 451.699 59.9619 456.06 Q54.9649 460.388 46.212 460.388 Q37.4273 460.388 32.4621 456.06 Q27.4968 451.699 27.4968 444.029 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M42.4881 388.329 L64.0042 388.329 L64.0042 394.185 L42.679 394.185 Q37.6183 394.185 35.1038 396.159 Q32.5894 398.132 32.5894 402.079 Q32.5894 406.821 35.6131 409.558 Q38.6368 412.296 43.8567 412.296 L64.0042 412.296 L64.0042 418.184 L28.3562 418.184 L28.3562 412.296 L33.8944 412.296 Q30.6797 410.195 29.0883 407.362 Q27.4968 404.498 27.4968 400.774 Q27.4968 394.631 31.3163 391.48 Q35.1038 388.329 42.4881 388.329 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip230)\" d=\"M14.5426 377.571 L14.5426 372.478 Q22.0542 367.704 29.2474 365.348 Q36.4406 362.961 43.5384 362.961 Q50.668 362.961 57.8931 365.348 Q65.1182 367.704 72.5979 372.478 L72.5979 377.571 Q65.3091 373.337 58.1159 371.269 Q50.8908 369.168 43.5384 369.168 Q36.186 369.168 29.0246 371.269 Q21.8632 373.337 14.5426 377.571 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><polyline clip-path=\"url(#clip232)\" style=\"stroke:#009af9; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"315.882,1384.24 335.658,1365.85 355.433,1347.46 375.209,1329.06 394.984,1310.67 414.76,1292.28 434.535,1265.04 454.311,1237.8 474.086,1210.55 493.862,1183.31 513.637,1156.07 533.412,1139.07 553.188,1122.08 572.963,1105.09 592.739,1088.09 612.514,1071.1 632.29,1056.74 652.065,1042.38 671.841,1028.02 691.616,1013.66 711.392,999.295 731.167,987.752 750.943,976.208 770.718,964.665 790.494,953.122 810.269,941.579 830.045,931.658 849.82,921.736 869.596,911.815 889.371,901.893 909.146,891.972 928.922,883.245 948.697,874.518 968.473,865.791 988.248,857.064 1008.02,848.336 1027.8,840.391 1047.57,832.445 1067.35,824.5 1087.13,816.554 1106.9,808.609 1126.68,801.152 1146.45,793.696 1166.23,786.24 1186,778.783 1205.78,771.327 1225.55,764.104 1245.33,756.881 1265.1,749.658 1284.88,742.435 1304.66,735.212 1324.43,727.989 1344.21,720.766 1363.98,713.543 1383.76,706.32 1403.53,699.097 1423.31,691.641 1443.08,684.184 1462.86,676.728 1482.64,669.272 1502.41,661.815 1522.19,653.87 1541.96,645.924 1561.74,637.979 1581.51,630.033 1601.29,622.088 1621.06,613.36 1640.84,604.633 1660.61,595.906 1680.39,587.179 1700.17,578.452 1719.94,568.53 1739.72,558.609 1759.49,548.688 1779.27,538.766 1799.04,528.845 1818.82,517.302 1838.59,505.759 1858.37,494.215 1878.14,482.672 1897.92,471.129 1917.7,456.768 1937.47,442.407 1957.25,428.046 1977.02,413.685 1996.8,399.324 2016.57,382.331 2036.35,365.337 2056.12,348.344 2075.9,331.35 2095.67,314.357 2115.45,287.114 2135.23,259.871 2155,232.627 2174.78,205.384 2194.55,178.141 2214.33,159.75 2234.1,141.359 2253.88,122.968 2273.65,104.577 2293.43,86.1857 \"/>\n",
"</svg>\n"
],
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\"?>\n",
"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" width=\"600\" height=\"400\" viewBox=\"0 0 2400 1600\">\n",
"<defs>\n",
" <clipPath id=\"clip200\">\n",
" <rect x=\"0\" y=\"0\" width=\"2400\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<path clip-path=\"url(#clip200)\" d=\"M0 1600 L2400 1600 L2400 0 L0 0 Z\" fill=\"#ffffff\" fill-rule=\"evenodd\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip201\">\n",
" <rect x=\"480\" y=\"0\" width=\"1681\" height=\"1600\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<path clip-path=\"url(#clip200)\" d=\"M256.556 1423.18 L2352.76 1423.18 L2352.76 47.2441 L256.556 47.2441 Z\" fill=\"#ffffff\" fill-rule=\"evenodd\" fill-opacity=\"1\"/>\n",
"<defs>\n",
" <clipPath id=\"clip202\">\n",
" <rect x=\"256\" y=\"47\" width=\"2097\" height=\"1377\"/>\n",
" </clipPath>\n",
"</defs>\n",
"<polyline clip-path=\"url(#clip202)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"315.882,1423.18 315.882,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip202)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"810.269,1423.18 810.269,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip202)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"1304.66,1423.18 1304.66,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip202)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"1799.04,1423.18 1799.04,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip202)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"2293.43,1423.18 2293.43,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip202)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"256.556,1272.91 2352.76,1272.91 \"/>\n",
"<polyline clip-path=\"url(#clip202)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"256.556,1093.67 2352.76,1093.67 \"/>\n",
"<polyline clip-path=\"url(#clip202)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"256.556,914.443 2352.76,914.443 \"/>\n",
"<polyline clip-path=\"url(#clip202)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"256.556,735.212 2352.76,735.212 \"/>\n",
"<polyline clip-path=\"url(#clip202)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"256.556,555.981 2352.76,555.981 \"/>\n",
"<polyline clip-path=\"url(#clip202)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"256.556,376.749 2352.76,376.749 \"/>\n",
"<polyline clip-path=\"url(#clip202)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:2; stroke-opacity:0.1; fill:none\" points=\"256.556,197.518 2352.76,197.518 \"/>\n",
"<polyline clip-path=\"url(#clip200)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,1423.18 2352.76,1423.18 \"/>\n",
"<polyline clip-path=\"url(#clip200)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"315.882,1423.18 315.882,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip200)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"810.269,1423.18 810.269,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip200)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"1304.66,1423.18 1304.66,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip200)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"1799.04,1423.18 1799.04,1404.28 \"/>\n",
"<polyline clip-path=\"url(#clip200)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"2293.43,1423.18 2293.43,1404.28 \"/>\n",
"<path clip-path=\"url(#clip200)\" d=\"M262.41 1468.75 L292.086 1468.75 L292.086 1472.69 L262.41 1472.69 L262.41 1468.75 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M302.989 1481.64 L310.628 1481.64 L310.628 1455.28 L302.318 1456.95 L302.318 1452.69 L310.581 1451.02 L315.257 1451.02 L315.257 1481.64 L322.896 1481.64 L322.896 1485.58 L302.989 1485.58 L302.989 1481.64 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M332.341 1479.7 L337.225 1479.7 L337.225 1485.58 L332.341 1485.58 L332.341 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M357.41 1454.1 Q353.799 1454.1 351.97 1457.66 Q350.165 1461.2 350.165 1468.33 Q350.165 1475.44 351.97 1479.01 Q353.799 1482.55 357.41 1482.55 Q361.044 1482.55 362.85 1479.01 Q364.678 1475.44 364.678 1468.33 Q364.678 1461.2 362.85 1457.66 Q361.044 1454.1 357.41 1454.1 M357.41 1450.39 Q363.22 1450.39 366.276 1455 Q369.354 1459.58 369.354 1468.33 Q369.354 1477.06 366.276 1481.67 Q363.22 1486.25 357.41 1486.25 Q351.6 1486.25 348.521 1481.67 Q345.465 1477.06 345.465 1468.33 Q345.465 1459.58 348.521 1455 Q351.6 1450.39 357.41 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M757.295 1468.75 L786.971 1468.75 L786.971 1472.69 L757.295 1472.69 L757.295 1468.75 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M807.063 1454.1 Q803.452 1454.1 801.623 1457.66 Q799.818 1461.2 799.818 1468.33 Q799.818 1475.44 801.623 1479.01 Q803.452 1482.55 807.063 1482.55 Q810.697 1482.55 812.503 1479.01 Q814.332 1475.44 814.332 1468.33 Q814.332 1461.2 812.503 1457.66 Q810.697 1454.1 807.063 1454.1 M807.063 1450.39 Q812.873 1450.39 815.929 1455 Q819.007 1459.58 819.007 1468.33 Q819.007 1477.06 815.929 1481.67 Q812.873 1486.25 807.063 1486.25 Q801.253 1486.25 798.174 1481.67 Q795.119 1477.06 795.119 1468.33 Q795.119 1459.58 798.174 1455 Q801.253 1450.39 807.063 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M827.225 1479.7 L832.109 1479.7 L832.109 1485.58 L827.225 1485.58 L827.225 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M842.341 1451.02 L860.697 1451.02 L860.697 1454.96 L846.623 1454.96 L846.623 1463.43 Q847.642 1463.08 848.66 1462.92 Q849.679 1462.73 850.697 1462.73 Q856.484 1462.73 859.864 1465.9 Q863.243 1469.08 863.243 1474.49 Q863.243 1480.07 859.771 1483.17 Q856.299 1486.25 849.98 1486.25 Q847.804 1486.25 845.535 1485.88 Q843.29 1485.51 840.882 1484.77 L840.882 1480.07 Q842.966 1481.2 845.188 1481.76 Q847.41 1482.32 849.887 1482.32 Q853.892 1482.32 856.229 1480.21 Q858.567 1478.1 858.567 1474.49 Q858.567 1470.88 856.229 1468.77 Q853.892 1466.67 849.887 1466.67 Q848.012 1466.67 846.137 1467.08 Q844.285 1467.5 842.341 1468.38 L842.341 1451.02 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1282.04 1454.1 Q1278.43 1454.1 1276.6 1457.66 Q1274.79 1461.2 1274.79 1468.33 Q1274.79 1475.44 1276.6 1479.01 Q1278.43 1482.55 1282.04 1482.55 Q1285.67 1482.55 1287.48 1479.01 Q1289.31 1475.44 1289.31 1468.33 Q1289.31 1461.2 1287.48 1457.66 Q1285.67 1454.1 1282.04 1454.1 M1282.04 1450.39 Q1287.85 1450.39 1290.91 1455 Q1293.98 1459.58 1293.98 1468.33 Q1293.98 1477.06 1290.91 1481.67 Q1287.85 1486.25 1282.04 1486.25 Q1276.23 1486.25 1273.15 1481.67 Q1270.1 1477.06 1270.1 1468.33 Q1270.1 1459.58 1273.15 1455 Q1276.23 1450.39 1282.04 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1302.2 1479.7 L1307.09 1479.7 L1307.09 1485.58 L1302.2 1485.58 L1302.2 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1327.27 1454.1 Q1323.66 1454.1 1321.83 1457.66 Q1320.03 1461.2 1320.03 1468.33 Q1320.03 1475.44 1321.83 1479.01 Q1323.66 1482.55 1327.27 1482.55 Q1330.91 1482.55 1332.71 1479.01 Q1334.54 1475.44 1334.54 1468.33 Q1334.54 1461.2 1332.71 1457.66 Q1330.91 1454.1 1327.27 1454.1 M1327.27 1450.39 Q1333.08 1450.39 1336.14 1455 Q1339.22 1459.58 1339.22 1468.33 Q1339.22 1477.06 1336.14 1481.67 Q1333.08 1486.25 1327.27 1486.25 Q1321.46 1486.25 1318.38 1481.67 Q1315.33 1477.06 1315.33 1468.33 Q1315.33 1459.58 1318.38 1455 Q1321.46 1450.39 1327.27 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1776.92 1454.1 Q1773.31 1454.1 1771.48 1457.66 Q1769.68 1461.2 1769.68 1468.33 Q1769.68 1475.44 1771.48 1479.01 Q1773.31 1482.55 1776.92 1482.55 Q1780.56 1482.55 1782.36 1479.01 Q1784.19 1475.44 1784.19 1468.33 Q1784.19 1461.2 1782.36 1457.66 Q1780.56 1454.1 1776.92 1454.1 M1776.92 1450.39 Q1782.73 1450.39 1785.79 1455 Q1788.87 1459.58 1788.87 1468.33 Q1788.87 1477.06 1785.79 1481.67 Q1782.73 1486.25 1776.92 1486.25 Q1771.11 1486.25 1768.04 1481.67 Q1764.98 1477.06 1764.98 1468.33 Q1764.98 1459.58 1768.04 1455 Q1771.11 1450.39 1776.92 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1797.09 1479.7 L1801.97 1479.7 L1801.97 1485.58 L1797.09 1485.58 L1797.09 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1812.2 1451.02 L1830.56 1451.02 L1830.56 1454.96 L1816.48 1454.96 L1816.48 1463.43 Q1817.5 1463.08 1818.52 1462.92 Q1819.54 1462.73 1820.56 1462.73 Q1826.35 1462.73 1829.73 1465.9 Q1833.11 1469.08 1833.11 1474.49 Q1833.11 1480.07 1829.63 1483.17 Q1826.16 1486.25 1819.84 1486.25 Q1817.67 1486.25 1815.4 1485.88 Q1813.15 1485.51 1810.74 1484.77 L1810.74 1480.07 Q1812.83 1481.2 1815.05 1481.76 Q1817.27 1482.32 1819.75 1482.32 Q1823.75 1482.32 1826.09 1480.21 Q1828.43 1478.1 1828.43 1474.49 Q1828.43 1470.88 1826.09 1468.77 Q1823.75 1466.67 1819.75 1466.67 Q1817.87 1466.67 1816 1467.08 Q1814.15 1467.5 1812.2 1468.38 L1812.2 1451.02 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M2260.58 1481.64 L2268.22 1481.64 L2268.22 1455.28 L2259.91 1456.95 L2259.91 1452.69 L2268.17 1451.02 L2272.85 1451.02 L2272.85 1481.64 L2280.49 1481.64 L2280.49 1485.58 L2260.58 1485.58 L2260.58 1481.64 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M2289.93 1479.7 L2294.82 1479.7 L2294.82 1485.58 L2289.93 1485.58 L2289.93 1479.7 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M2315 1454.1 Q2311.39 1454.1 2309.56 1457.66 Q2307.76 1461.2 2307.76 1468.33 Q2307.76 1475.44 2309.56 1479.01 Q2311.39 1482.55 2315 1482.55 Q2318.64 1482.55 2320.44 1479.01 Q2322.27 1475.44 2322.27 1468.33 Q2322.27 1461.2 2320.44 1457.66 Q2318.64 1454.1 2315 1454.1 M2315 1450.39 Q2320.81 1450.39 2323.87 1455 Q2326.95 1459.58 2326.95 1468.33 Q2326.95 1477.06 2323.87 1481.67 Q2320.81 1486.25 2315 1486.25 Q2309.19 1486.25 2306.11 1481.67 Q2303.06 1477.06 2303.06 1468.33 Q2303.06 1459.58 2306.11 1455 Q2309.19 1450.39 2315 1450.39 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1113.38 1532.4 L1100.49 1549.74 L1114.05 1568.04 L1107.14 1568.04 L1096.77 1554.04 L1086.39 1568.04 L1079.48 1568.04 L1093.33 1549.39 L1080.66 1532.4 L1087.57 1532.4 L1097.02 1545.1 L1106.48 1532.4 L1113.38 1532.4 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1157.11 1518.58 Q1152.85 1525.9 1150.78 1533.06 Q1148.71 1540.23 1148.71 1547.58 Q1148.71 1554.93 1150.78 1562.16 Q1152.88 1569.35 1157.11 1576.64 L1152.02 1576.64 Q1147.25 1569.16 1144.86 1561.93 Q1142.51 1554.71 1142.51 1547.58 Q1142.51 1540.48 1144.86 1533.29 Q1147.22 1526.09 1152.02 1518.58 L1157.11 1518.58 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1194.13 1533.76 L1194.13 1539.24 Q1191.65 1537.87 1189.13 1537.2 Q1186.65 1536.5 1184.11 1536.5 Q1178.41 1536.5 1175.26 1540.13 Q1172.11 1543.73 1172.11 1550.25 Q1172.11 1556.78 1175.26 1560.4 Q1178.41 1564 1184.11 1564 Q1186.65 1564 1189.13 1563.33 Q1191.65 1562.63 1194.13 1561.26 L1194.13 1566.68 Q1191.68 1567.82 1189.04 1568.39 Q1186.43 1568.97 1183.47 1568.97 Q1175.42 1568.97 1170.67 1563.91 Q1165.93 1558.85 1165.93 1550.25 Q1165.93 1541.53 1170.71 1536.53 Q1175.51 1531.54 1183.85 1531.54 Q1186.56 1531.54 1189.13 1532.11 Q1191.71 1532.65 1194.13 1533.76 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1218.13 1536.5 Q1213.42 1536.5 1210.68 1540.19 Q1207.94 1543.85 1207.94 1550.25 Q1207.94 1556.65 1210.65 1560.34 Q1213.39 1564 1218.13 1564 Q1222.81 1564 1225.55 1560.31 Q1228.28 1556.62 1228.28 1550.25 Q1228.28 1543.92 1225.55 1540.23 Q1222.81 1536.5 1218.13 1536.5 M1218.13 1531.54 Q1225.77 1531.54 1230.13 1536.5 Q1234.49 1541.47 1234.49 1550.25 Q1234.49 1559 1230.13 1564 Q1225.77 1568.97 1218.13 1568.97 Q1210.46 1568.97 1206.1 1564 Q1201.77 1559 1201.77 1550.25 Q1201.77 1541.47 1206.1 1536.5 Q1210.46 1531.54 1218.13 1531.54 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1258.01 1536.5 Q1253.3 1536.5 1250.56 1540.19 Q1247.83 1543.85 1247.83 1550.25 Q1247.83 1556.65 1250.53 1560.34 Q1253.27 1564 1258.01 1564 Q1262.69 1564 1265.43 1560.31 Q1268.16 1556.62 1268.16 1550.25 Q1268.16 1543.92 1265.43 1540.23 Q1262.69 1536.5 1258.01 1536.5 M1258.01 1531.54 Q1265.65 1531.54 1270.01 1536.5 Q1274.37 1541.47 1274.37 1550.25 Q1274.37 1559 1270.01 1564 Q1265.65 1568.97 1258.01 1568.97 Q1250.34 1568.97 1245.98 1564 Q1241.65 1559 1241.65 1550.25 Q1241.65 1541.47 1245.98 1536.5 Q1250.34 1531.54 1258.01 1531.54 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1304.74 1537.87 Q1303.75 1537.3 1302.57 1537.04 Q1301.43 1536.76 1300.02 1536.76 Q1295.06 1536.76 1292.39 1540 Q1289.74 1543.22 1289.74 1549.27 L1289.74 1568.04 L1283.86 1568.04 L1283.86 1532.4 L1289.74 1532.4 L1289.74 1537.93 Q1291.59 1534.69 1294.55 1533.13 Q1297.51 1531.54 1301.74 1531.54 Q1302.35 1531.54 1303.08 1531.63 Q1303.81 1531.7 1304.7 1531.85 L1304.74 1537.87 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1333.19 1537.81 L1333.19 1518.52 L1339.05 1518.52 L1339.05 1568.04 L1333.19 1568.04 L1333.19 1562.7 Q1331.34 1565.88 1328.51 1567.44 Q1325.71 1568.97 1321.76 1568.97 Q1315.3 1568.97 1311.23 1563.81 Q1307.19 1558.65 1307.19 1550.25 Q1307.19 1541.85 1311.23 1536.69 Q1315.3 1531.54 1321.76 1531.54 Q1325.71 1531.54 1328.51 1533.1 Q1331.34 1534.62 1333.19 1537.81 M1313.23 1550.25 Q1313.23 1556.71 1315.88 1560.4 Q1318.55 1564.07 1323.2 1564.07 Q1327.84 1564.07 1330.52 1560.4 Q1333.19 1556.71 1333.19 1550.25 Q1333.19 1543.79 1330.52 1540.13 Q1327.84 1536.44 1323.2 1536.44 Q1318.55 1536.44 1315.88 1540.13 Q1313.23 1543.79 1313.23 1550.25 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1351.11 1532.4 L1356.97 1532.4 L1356.97 1568.04 L1351.11 1568.04 L1351.11 1532.4 M1351.11 1518.52 L1356.97 1518.52 L1356.97 1525.93 L1351.11 1525.93 L1351.11 1518.52 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1398.85 1546.53 L1398.85 1568.04 L1393 1568.04 L1393 1546.72 Q1393 1541.66 1391.02 1539.14 Q1389.05 1536.63 1385.1 1536.63 Q1380.36 1536.63 1377.62 1539.65 Q1374.89 1542.68 1374.89 1547.9 L1374.89 1568.04 L1369 1568.04 L1369 1532.4 L1374.89 1532.4 L1374.89 1537.93 Q1376.99 1534.72 1379.82 1533.13 Q1382.68 1531.54 1386.41 1531.54 Q1392.55 1531.54 1395.7 1535.36 Q1398.85 1539.14 1398.85 1546.53 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1426.73 1550.12 Q1419.64 1550.12 1416.9 1551.75 Q1414.16 1553.37 1414.16 1557.29 Q1414.16 1560.4 1416.2 1562.25 Q1418.27 1564.07 1421.8 1564.07 Q1426.67 1564.07 1429.6 1560.63 Q1432.56 1557.16 1432.56 1551.43 L1432.56 1550.12 L1426.73 1550.12 M1438.42 1547.71 L1438.42 1568.04 L1432.56 1568.04 L1432.56 1562.63 Q1430.55 1565.88 1427.56 1567.44 Q1424.57 1568.97 1420.24 1568.97 Q1414.77 1568.97 1411.52 1565.91 Q1408.31 1562.82 1408.31 1557.67 Q1408.31 1551.65 1412.32 1548.6 Q1416.36 1545.54 1424.35 1545.54 L1432.56 1545.54 L1432.56 1544.97 Q1432.56 1540.93 1429.89 1538.73 Q1427.24 1536.5 1422.44 1536.5 Q1419.38 1536.5 1416.49 1537.23 Q1413.59 1537.97 1410.92 1539.43 L1410.92 1534.02 Q1414.13 1532.78 1417.15 1532.17 Q1420.18 1531.54 1423.04 1531.54 Q1430.78 1531.54 1434.6 1535.55 Q1438.42 1539.56 1438.42 1547.71 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1456.27 1522.27 L1456.27 1532.4 L1468.33 1532.4 L1468.33 1536.95 L1456.27 1536.95 L1456.27 1556.3 Q1456.27 1560.66 1457.45 1561.9 Q1458.66 1563.14 1462.32 1563.14 L1468.33 1563.14 L1468.33 1568.04 L1462.32 1568.04 Q1455.54 1568.04 1452.96 1565.53 Q1450.38 1562.98 1450.38 1556.3 L1450.38 1536.95 L1446.09 1536.95 L1446.09 1532.4 L1450.38 1532.4 L1450.38 1522.27 L1456.27 1522.27 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1506.53 1548.76 L1506.53 1551.62 L1479.6 1551.62 Q1479.98 1557.67 1483.23 1560.85 Q1486.51 1564 1492.33 1564 Q1495.71 1564 1498.86 1563.17 Q1502.04 1562.35 1505.16 1560.69 L1505.16 1566.23 Q1502.01 1567.57 1498.7 1568.27 Q1495.39 1568.97 1491.98 1568.97 Q1483.45 1568.97 1478.46 1564 Q1473.49 1559.04 1473.49 1550.57 Q1473.49 1541.82 1478.2 1536.69 Q1482.94 1531.54 1490.96 1531.54 Q1498.16 1531.54 1502.33 1536.18 Q1506.53 1540.8 1506.53 1548.76 M1500.67 1547.04 Q1500.61 1542.23 1497.97 1539.37 Q1495.36 1536.5 1491.03 1536.5 Q1486.13 1536.5 1483.17 1539.27 Q1480.24 1542.04 1479.79 1547.07 L1500.67 1547.04 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M1515.22 1518.58 L1520.31 1518.58 Q1525.08 1526.09 1527.44 1533.29 Q1529.83 1540.48 1529.83 1547.58 Q1529.83 1554.71 1527.44 1561.93 Q1525.08 1569.16 1520.31 1576.64 L1515.22 1576.64 Q1519.45 1569.35 1521.52 1562.16 Q1523.62 1554.93 1523.62 1547.58 Q1523.62 1540.23 1521.52 1533.06 Q1519.45 1525.9 1515.22 1518.58 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><polyline clip-path=\"url(#clip200)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,1423.18 256.556,47.2441 \"/>\n",
"<polyline clip-path=\"url(#clip200)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,1272.91 275.454,1272.91 \"/>\n",
"<polyline clip-path=\"url(#clip200)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,1093.67 275.454,1093.67 \"/>\n",
"<polyline clip-path=\"url(#clip200)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,914.443 275.454,914.443 \"/>\n",
"<polyline clip-path=\"url(#clip200)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,735.212 275.454,735.212 \"/>\n",
"<polyline clip-path=\"url(#clip200)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,555.981 275.454,555.981 \"/>\n",
"<polyline clip-path=\"url(#clip200)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,376.749 275.454,376.749 \"/>\n",
"<polyline clip-path=\"url(#clip200)\" style=\"stroke:#000000; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"256.556,197.518 275.454,197.518 \"/>\n",
"<path clip-path=\"url(#clip200)\" d=\"M114.26 1273.36 L143.936 1273.36 L143.936 1277.29 L114.26 1277.29 L114.26 1273.36 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M164.028 1258.7 Q160.417 1258.7 158.589 1262.27 Q156.783 1265.81 156.783 1272.94 Q156.783 1280.05 158.589 1283.61 Q160.417 1287.15 164.028 1287.15 Q167.663 1287.15 169.468 1283.61 Q171.297 1280.05 171.297 1272.94 Q171.297 1265.81 169.468 1262.27 Q167.663 1258.7 164.028 1258.7 M164.028 1255 Q169.839 1255 172.894 1259.61 Q175.973 1264.19 175.973 1272.94 Q175.973 1281.67 172.894 1286.27 Q169.839 1290.86 164.028 1290.86 Q158.218 1290.86 155.14 1286.27 Q152.084 1281.67 152.084 1272.94 Q152.084 1264.19 155.14 1259.61 Q158.218 1255 164.028 1255 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M184.19 1284.31 L189.075 1284.31 L189.075 1290.19 L184.19 1290.19 L184.19 1284.31 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M213.426 1271.55 Q216.783 1272.27 218.658 1274.54 Q220.556 1276.81 220.556 1280.14 Q220.556 1285.26 217.037 1288.06 Q213.519 1290.86 207.037 1290.86 Q204.862 1290.86 202.547 1290.42 Q200.255 1290 197.801 1289.14 L197.801 1284.63 Q199.746 1285.76 202.061 1286.34 Q204.375 1286.92 206.899 1286.92 Q211.297 1286.92 213.588 1285.19 Q215.903 1283.45 215.903 1280.14 Q215.903 1277.08 213.75 1275.37 Q211.621 1273.64 207.801 1273.64 L203.774 1273.64 L203.774 1269.79 L207.987 1269.79 Q211.436 1269.79 213.264 1268.43 Q215.093 1267.04 215.093 1264.45 Q215.093 1261.78 213.195 1260.37 Q211.32 1258.94 207.801 1258.94 Q205.88 1258.94 203.681 1259.35 Q201.482 1259.77 198.843 1260.65 L198.843 1256.48 Q201.505 1255.74 203.82 1255.37 Q206.158 1255 208.218 1255 Q213.542 1255 216.644 1257.43 Q219.746 1259.84 219.746 1263.96 Q219.746 1266.83 218.102 1268.82 Q216.459 1270.79 213.426 1271.55 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M115.209 1094.13 L144.885 1094.13 L144.885 1098.06 L115.209 1098.06 L115.209 1094.13 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M164.977 1079.47 Q161.366 1079.47 159.538 1083.04 Q157.732 1086.58 157.732 1093.71 Q157.732 1100.82 159.538 1104.38 Q161.366 1107.92 164.977 1107.92 Q168.612 1107.92 170.417 1104.38 Q172.246 1100.82 172.246 1093.71 Q172.246 1086.58 170.417 1083.04 Q168.612 1079.47 164.977 1079.47 M164.977 1075.77 Q170.788 1075.77 173.843 1080.38 Q176.922 1084.96 176.922 1093.71 Q176.922 1102.44 173.843 1107.04 Q170.788 1111.63 164.977 1111.63 Q159.167 1111.63 156.089 1107.04 Q153.033 1102.44 153.033 1093.71 Q153.033 1084.96 156.089 1080.38 Q159.167 1075.77 164.977 1075.77 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M185.139 1105.07 L190.024 1105.07 L190.024 1110.95 L185.139 1110.95 L185.139 1105.07 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M204.237 1107.02 L220.556 1107.02 L220.556 1110.95 L198.612 1110.95 L198.612 1107.02 Q201.274 1104.26 205.857 1099.64 Q210.463 1094.98 211.644 1093.64 Q213.889 1091.12 214.769 1089.38 Q215.672 1087.62 215.672 1085.93 Q215.672 1083.18 213.727 1081.44 Q211.806 1079.7 208.704 1079.7 Q206.505 1079.7 204.051 1080.47 Q201.621 1081.23 198.843 1082.78 L198.843 1078.06 Q201.667 1076.93 204.121 1076.35 Q206.574 1075.77 208.612 1075.77 Q213.982 1075.77 217.176 1078.45 Q220.371 1081.14 220.371 1085.63 Q220.371 1087.76 219.561 1089.68 Q218.773 1091.58 216.667 1094.17 Q216.088 1094.84 212.986 1098.06 Q209.885 1101.26 204.237 1107.02 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M114.839 914.895 L144.515 914.895 L144.515 918.83 L114.839 918.83 L114.839 914.895 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M164.607 900.242 Q160.996 900.242 159.167 903.807 Q157.362 907.348 157.362 914.478 Q157.362 921.584 159.167 925.149 Q160.996 928.691 164.607 928.691 Q168.241 928.691 170.047 925.149 Q171.876 921.584 171.876 914.478 Q171.876 907.348 170.047 903.807 Q168.241 900.242 164.607 900.242 M164.607 896.538 Q170.417 896.538 173.473 901.145 Q176.551 905.728 176.551 914.478 Q176.551 923.205 173.473 927.811 Q170.417 932.395 164.607 932.395 Q158.797 932.395 155.718 927.811 Q152.663 923.205 152.663 914.478 Q152.663 905.728 155.718 901.145 Q158.797 896.538 164.607 896.538 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M184.769 925.844 L189.653 925.844 L189.653 931.723 L184.769 931.723 L184.769 925.844 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M200.649 927.788 L208.287 927.788 L208.287 901.422 L199.977 903.089 L199.977 898.83 L208.241 897.163 L212.917 897.163 L212.917 927.788 L220.556 927.788 L220.556 931.723 L200.649 931.723 L200.649 927.788 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M163.38 721.011 Q159.769 721.011 157.94 724.575 Q156.135 728.117 156.135 735.247 Q156.135 742.353 157.94 745.918 Q159.769 749.46 163.38 749.46 Q167.015 749.46 168.82 745.918 Q170.649 742.353 170.649 735.247 Q170.649 728.117 168.82 724.575 Q167.015 721.011 163.38 721.011 M163.38 717.307 Q169.19 717.307 172.246 721.913 Q175.325 726.497 175.325 735.247 Q175.325 743.973 172.246 748.58 Q169.19 753.163 163.38 753.163 Q157.57 753.163 154.491 748.58 Q151.436 743.973 151.436 735.247 Q151.436 726.497 154.491 721.913 Q157.57 717.307 163.38 717.307 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M183.542 746.612 L188.426 746.612 L188.426 752.492 L183.542 752.492 L183.542 746.612 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M208.612 721.011 Q205 721.011 203.172 724.575 Q201.366 728.117 201.366 735.247 Q201.366 742.353 203.172 745.918 Q205 749.46 208.612 749.46 Q212.246 749.46 214.051 745.918 Q215.88 742.353 215.88 735.247 Q215.88 728.117 214.051 724.575 Q212.246 721.011 208.612 721.011 M208.612 717.307 Q214.422 717.307 217.477 721.913 Q220.556 726.497 220.556 735.247 Q220.556 743.973 217.477 748.58 Q214.422 753.163 208.612 753.163 Q202.801 753.163 199.723 748.58 Q196.667 743.973 196.667 735.247 Q196.667 726.497 199.723 721.913 Q202.801 717.307 208.612 717.307 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M164.607 541.779 Q160.996 541.779 159.167 545.344 Q157.362 548.886 157.362 556.015 Q157.362 563.122 159.167 566.687 Q160.996 570.228 164.607 570.228 Q168.241 570.228 170.047 566.687 Q171.876 563.122 171.876 556.015 Q171.876 548.886 170.047 545.344 Q168.241 541.779 164.607 541.779 M164.607 538.076 Q170.417 538.076 173.473 542.682 Q176.551 547.265 176.551 556.015 Q176.551 564.742 173.473 569.349 Q170.417 573.932 164.607 573.932 Q158.797 573.932 155.718 569.349 Q152.663 564.742 152.663 556.015 Q152.663 547.265 155.718 542.682 Q158.797 538.076 164.607 538.076 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M184.769 567.381 L189.653 567.381 L189.653 573.261 L184.769 573.261 L184.769 567.381 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M200.649 569.326 L208.287 569.326 L208.287 542.96 L199.977 544.627 L199.977 540.367 L208.241 538.701 L212.917 538.701 L212.917 569.326 L220.556 569.326 L220.556 573.261 L200.649 573.261 L200.649 569.326 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M164.977 362.548 Q161.366 362.548 159.538 366.113 Q157.732 369.655 157.732 376.784 Q157.732 383.891 159.538 387.455 Q161.366 390.997 164.977 390.997 Q168.612 390.997 170.417 387.455 Q172.246 383.891 172.246 376.784 Q172.246 369.655 170.417 366.113 Q168.612 362.548 164.977 362.548 M164.977 358.844 Q170.788 358.844 173.843 363.451 Q176.922 368.034 176.922 376.784 Q176.922 385.511 173.843 390.117 Q170.788 394.701 164.977 394.701 Q159.167 394.701 156.089 390.117 Q153.033 385.511 153.033 376.784 Q153.033 368.034 156.089 363.451 Q159.167 358.844 164.977 358.844 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M185.139 388.15 L190.024 388.15 L190.024 394.029 L185.139 394.029 L185.139 388.15 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M204.237 390.094 L220.556 390.094 L220.556 394.029 L198.612 394.029 L198.612 390.094 Q201.274 387.34 205.857 382.71 Q210.463 378.057 211.644 376.715 Q213.889 374.192 214.769 372.455 Q215.672 370.696 215.672 369.006 Q215.672 366.252 213.727 364.516 Q211.806 362.78 208.704 362.78 Q206.505 362.78 204.051 363.543 Q201.621 364.307 198.843 365.858 L198.843 361.136 Q201.667 360.002 204.121 359.423 Q206.574 358.844 208.612 358.844 Q213.982 358.844 217.176 361.53 Q220.371 364.215 220.371 368.705 Q220.371 370.835 219.561 372.756 Q218.773 374.654 216.667 377.247 Q216.088 377.918 212.986 381.136 Q209.885 384.33 204.237 390.094 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M164.028 183.317 Q160.417 183.317 158.589 186.882 Q156.783 190.423 156.783 197.553 Q156.783 204.659 158.589 208.224 Q160.417 211.766 164.028 211.766 Q167.663 211.766 169.468 208.224 Q171.297 204.659 171.297 197.553 Q171.297 190.423 169.468 186.882 Q167.663 183.317 164.028 183.317 M164.028 179.613 Q169.839 179.613 172.894 184.22 Q175.973 188.803 175.973 197.553 Q175.973 206.28 172.894 210.886 Q169.839 215.469 164.028 215.469 Q158.218 215.469 155.14 210.886 Q152.084 206.28 152.084 197.553 Q152.084 188.803 155.14 184.22 Q158.218 179.613 164.028 179.613 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M184.19 208.918 L189.075 208.918 L189.075 214.798 L184.19 214.798 L184.19 208.918 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M213.426 196.164 Q216.783 196.882 218.658 199.15 Q220.556 201.419 220.556 204.752 Q220.556 209.868 217.037 212.668 Q213.519 215.469 207.037 215.469 Q204.862 215.469 202.547 215.03 Q200.255 214.613 197.801 213.756 L197.801 209.243 Q199.746 210.377 202.061 210.956 Q204.375 211.534 206.899 211.534 Q211.297 211.534 213.588 209.798 Q215.903 208.062 215.903 204.752 Q215.903 201.696 213.75 199.983 Q211.621 198.247 207.801 198.247 L203.774 198.247 L203.774 194.405 L207.987 194.405 Q211.436 194.405 213.264 193.039 Q215.093 191.65 215.093 189.057 Q215.093 186.395 213.195 184.983 Q211.32 183.548 207.801 183.548 Q205.88 183.548 203.681 183.965 Q201.482 184.382 198.843 185.261 L198.843 181.095 Q201.505 180.354 203.82 179.983 Q206.158 179.613 208.218 179.613 Q213.542 179.613 216.644 182.044 Q219.746 184.451 219.746 188.571 Q219.746 191.442 218.102 193.432 Q216.459 195.4 213.426 196.164 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M46.212 1101.42 Q52.6732 1101.42 56.3653 1098.77 Q60.0256 1096.1 60.0256 1091.45 Q60.0256 1086.81 56.3653 1084.13 Q52.6732 1081.46 46.212 1081.46 Q39.7508 1081.46 36.0905 1084.13 Q32.3984 1086.81 32.3984 1091.45 Q32.3984 1096.1 36.0905 1098.77 Q39.7508 1101.42 46.212 1101.42 M58.657 1081.46 Q61.8398 1083.3 63.3994 1086.14 Q64.9272 1088.94 64.9272 1092.89 Q64.9272 1099.35 59.771 1103.42 Q54.6147 1107.46 46.212 1107.46 Q37.8093 1107.46 32.6531 1103.42 Q27.4968 1099.35 27.4968 1092.89 Q27.4968 1088.94 29.0564 1086.14 Q30.5842 1083.3 33.7671 1081.46 L28.3562 1081.46 L28.3562 1075.6 L77.5631 1075.6 L77.5631 1081.46 L58.657 1081.46 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M74.8259 1036.45 L79.3773 1036.45 L79.3773 1070.32 L74.8259 1070.32 L74.8259 1036.45 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M28.3562 1001.31 L45.7028 1014.2 L64.0042 1000.65 L64.0042 1007.55 L49.9996 1017.93 L64.0042 1028.31 L64.0042 1035.21 L45.3526 1021.37 L28.3562 1034.03 L28.3562 1027.13 L41.0558 1017.67 L28.3562 1008.22 L28.3562 1001.31 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M14.5426 957.582 Q21.8632 961.847 29.0246 963.916 Q36.186 965.985 43.5384 965.985 Q50.8908 965.985 58.1159 963.916 Q65.3091 961.815 72.5979 957.582 L72.5979 962.675 Q65.1182 967.449 57.8931 969.836 Q50.668 972.191 43.5384 972.191 Q36.4406 972.191 29.2474 969.836 Q22.0542 967.481 14.5426 962.675 L14.5426 957.582 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M14.479 928.172 L19.3487 928.172 L19.3487 933.774 Q19.3487 936.925 20.6219 938.167 Q21.895 939.376 25.2052 939.376 L28.3562 939.376 L28.3562 929.732 L32.9077 929.732 L32.9077 939.376 L64.0042 939.376 L64.0042 945.264 L32.9077 945.264 L32.9077 950.866 L28.3562 950.866 L28.3562 945.264 L25.8736 945.264 Q19.9216 945.264 17.2162 942.495 Q14.479 939.726 14.479 933.711 L14.479 928.172 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M14.479 923.271 L14.479 917.414 L64.0042 917.414 L64.0042 923.271 L14.479 923.271 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M49.9359 905.765 L28.3562 905.765 L28.3562 899.909 L49.7131 899.909 Q54.7739 899.909 57.3202 897.935 Q59.8346 895.962 59.8346 892.015 Q59.8346 887.273 56.8109 884.536 Q53.7872 881.766 48.5673 881.766 L28.3562 881.766 L28.3562 875.91 L64.0042 875.91 L64.0042 881.766 L58.5296 881.766 Q61.7762 883.899 63.3676 886.732 Q64.9272 889.533 64.9272 893.257 Q64.9272 899.399 61.1078 902.582 Q57.2883 905.765 49.9359 905.765 M27.4968 891.029 L27.4968 891.029 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M28.3562 834.215 L45.7028 847.105 L64.0042 833.546 L64.0042 840.453 L49.9996 850.829 L64.0042 861.205 L64.0042 868.112 L45.3526 854.267 L28.3562 866.934 L28.3562 860.028 L41.0558 850.574 L28.3562 841.121 L28.3562 834.215 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M28.3562 804.55 L28.3562 798.694 L64.0042 798.694 L64.0042 804.55 L28.3562 804.55 M14.479 804.55 L14.479 798.694 L21.895 798.694 L21.895 804.55 L14.479 804.55 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M42.4881 756.808 L64.0042 756.808 L64.0042 762.664 L42.679 762.664 Q37.6183 762.664 35.1038 764.637 Q32.5894 766.611 32.5894 770.558 Q32.5894 775.3 35.6131 778.037 Q38.6368 780.775 43.8567 780.775 L64.0042 780.775 L64.0042 786.663 L28.3562 786.663 L28.3562 780.775 L33.8944 780.775 Q30.6797 778.674 29.0883 775.841 Q27.4968 772.977 27.4968 769.253 Q27.4968 763.11 31.3163 759.959 Q35.1038 756.808 42.4881 756.808 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M28.3562 694.774 L45.7028 707.664 L64.0042 694.105 L64.0042 701.012 L49.9996 711.388 L64.0042 721.764 L64.0042 728.671 L45.3526 714.826 L28.3562 727.494 L28.3562 720.587 L41.0558 711.134 L28.3562 701.681 L28.3562 694.774 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M43.5384 688.79 L43.5384 671.634 L48.7583 671.634 L48.7583 688.79 L43.5384 688.79 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M33.7671 638.851 L14.479 638.851 L14.479 632.995 L64.0042 632.995 L64.0042 638.851 L58.657 638.851 Q61.8398 640.697 63.3994 643.53 Q64.9272 646.331 64.9272 650.278 Q64.9272 656.739 59.771 660.813 Q54.6147 664.855 46.212 664.855 Q37.8093 664.855 32.6531 660.813 Q27.4968 656.739 27.4968 650.278 Q27.4968 646.331 29.0564 643.53 Q30.5842 640.697 33.7671 638.851 M46.212 658.808 Q52.6732 658.808 56.3653 656.166 Q60.0256 653.492 60.0256 648.845 Q60.0256 644.198 56.3653 641.525 Q52.6732 638.851 46.212 638.851 Q39.7508 638.851 36.0905 641.525 Q32.3984 644.198 32.3984 648.845 Q32.3984 653.492 36.0905 656.166 Q39.7508 658.808 46.212 658.808 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M28.3562 620.932 L28.3562 615.075 L64.0042 615.075 L64.0042 620.932 L28.3562 620.932 M14.479 620.932 L14.479 615.075 L21.895 615.075 L21.895 620.932 L14.479 620.932 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M33.8307 582.164 Q33.2578 583.151 33.0032 584.329 Q32.7167 585.475 32.7167 586.875 Q32.7167 591.84 35.9632 594.514 Q39.1779 597.156 45.2253 597.156 L64.0042 597.156 L64.0042 603.044 L28.3562 603.044 L28.3562 597.156 L33.8944 597.156 Q30.6479 595.31 29.0883 592.35 Q27.4968 589.39 27.4968 585.156 Q27.4968 584.552 27.5923 583.82 Q27.656 583.087 27.8151 582.196 L33.8307 582.164 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M44.7161 546.962 L47.5806 546.962 L47.5806 573.889 Q53.6281 573.507 56.8109 570.261 Q59.9619 566.982 59.9619 561.158 Q59.9619 557.784 59.1344 554.633 Q58.3069 551.45 56.6518 548.331 L62.1899 548.331 Q63.5267 551.482 64.227 554.792 Q64.9272 558.102 64.9272 561.508 Q64.9272 570.038 59.9619 575.035 Q54.9967 580 46.5303 580 Q37.7774 580 32.6531 575.29 Q27.4968 570.547 27.4968 562.526 Q27.4968 555.333 32.1438 551.163 Q36.7589 546.962 44.7161 546.962 M42.9973 552.819 Q38.1912 552.882 35.3266 555.524 Q32.4621 558.134 32.4621 562.463 Q32.4621 567.364 35.2312 570.324 Q38.0002 573.252 43.0292 573.698 L42.9973 552.819 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M29.7248 511.696 L35.1993 511.696 Q33.8307 514.179 33.1623 516.693 Q32.4621 519.176 32.4621 521.722 Q32.4621 527.419 36.0905 530.57 Q39.6872 533.721 46.212 533.721 Q52.7369 533.721 56.3653 530.57 Q59.9619 527.419 59.9619 521.722 Q59.9619 519.176 59.2935 516.693 Q58.5933 514.179 57.2247 511.696 L62.6355 511.696 Q63.7814 514.147 64.3543 516.789 Q64.9272 519.399 64.9272 522.359 Q64.9272 530.411 59.8664 535.154 Q54.8057 539.896 46.212 539.896 Q37.491 539.896 32.4939 535.122 Q27.4968 530.316 27.4968 521.977 Q27.4968 519.271 28.0697 516.693 Q28.6108 514.115 29.7248 511.696 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M18.2347 495.718 L28.3562 495.718 L28.3562 483.655 L32.9077 483.655 L32.9077 495.718 L52.2594 495.718 Q56.6199 495.718 57.8613 494.541 Q59.1026 493.331 59.1026 489.671 L59.1026 483.655 L64.0042 483.655 L64.0042 489.671 Q64.0042 496.45 61.4897 499.028 Q58.9434 501.606 52.2594 501.606 L32.9077 501.606 L32.9077 505.903 L28.3562 505.903 L28.3562 501.606 L18.2347 501.606 L18.2347 495.718 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M28.3562 475.953 L28.3562 470.096 L64.0042 470.096 L64.0042 475.953 L28.3562 475.953 M14.479 475.953 L14.479 470.096 L21.895 470.096 L21.895 475.953 L14.479 475.953 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M32.4621 444.029 Q32.4621 448.739 36.1542 451.477 Q39.8145 454.214 46.212 454.214 Q52.6095 454.214 56.3017 451.508 Q59.9619 448.771 59.9619 444.029 Q59.9619 439.35 56.2698 436.613 Q52.5777 433.875 46.212 433.875 Q39.8781 433.875 36.186 436.613 Q32.4621 439.35 32.4621 444.029 M27.4968 444.029 Q27.4968 436.39 32.4621 432.029 Q37.4273 427.669 46.212 427.669 Q54.9649 427.669 59.9619 432.029 Q64.9272 436.39 64.9272 444.029 Q64.9272 451.699 59.9619 456.06 Q54.9649 460.388 46.212 460.388 Q37.4273 460.388 32.4621 456.06 Q27.4968 451.699 27.4968 444.029 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M42.4881 388.329 L64.0042 388.329 L64.0042 394.185 L42.679 394.185 Q37.6183 394.185 35.1038 396.159 Q32.5894 398.132 32.5894 402.079 Q32.5894 406.821 35.6131 409.558 Q38.6368 412.296 43.8567 412.296 L64.0042 412.296 L64.0042 418.184 L28.3562 418.184 L28.3562 412.296 L33.8944 412.296 Q30.6797 410.195 29.0883 407.362 Q27.4968 404.498 27.4968 400.774 Q27.4968 394.631 31.3163 391.48 Q35.1038 388.329 42.4881 388.329 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><path clip-path=\"url(#clip200)\" d=\"M14.5426 377.571 L14.5426 372.478 Q22.0542 367.704 29.2474 365.348 Q36.4406 362.961 43.5384 362.961 Q50.668 362.961 57.8931 365.348 Q65.1182 367.704 72.5979 372.478 L72.5979 377.571 Q65.3091 373.337 58.1159 371.269 Q50.8908 369.168 43.5384 369.168 Q36.186 369.168 29.0246 371.269 Q21.8632 373.337 14.5426 377.571 Z\" fill=\"#000000\" fill-rule=\"nonzero\" fill-opacity=\"1\" /><polyline clip-path=\"url(#clip202)\" style=\"stroke:#009af9; stroke-linecap:round; stroke-linejoin:round; stroke-width:4; stroke-opacity:1; fill:none\" points=\"315.882,1384.24 335.658,1365.85 355.433,1347.46 375.209,1329.06 394.984,1310.67 414.76,1292.28 434.535,1265.04 454.311,1237.8 474.086,1210.55 493.862,1183.31 513.637,1156.07 533.412,1139.07 553.188,1122.08 572.963,1105.09 592.739,1088.09 612.514,1071.1 632.29,1056.74 652.065,1042.38 671.841,1028.02 691.616,1013.66 711.392,999.295 731.167,987.752 750.943,976.208 770.718,964.665 790.494,953.122 810.269,941.579 830.045,931.658 849.82,921.736 869.596,911.815 889.371,901.893 909.146,891.972 928.922,883.245 948.697,874.518 968.473,865.791 988.248,857.064 1008.02,848.336 1027.8,840.391 1047.57,832.445 1067.35,824.5 1087.13,816.554 1106.9,808.609 1126.68,801.152 1146.45,793.696 1166.23,786.24 1186,778.783 1205.78,771.327 1225.55,764.104 1245.33,756.881 1265.1,749.658 1284.88,742.435 1304.66,735.212 1324.43,727.989 1344.21,720.766 1363.98,713.543 1383.76,706.32 1403.53,699.097 1423.31,691.641 1443.08,684.184 1462.86,676.728 1482.64,669.272 1502.41,661.815 1522.19,653.87 1541.96,645.924 1561.74,637.979 1581.51,630.033 1601.29,622.088 1621.06,613.36 1640.84,604.633 1660.61,595.906 1680.39,587.179 1700.17,578.452 1719.94,568.53 1739.72,558.609 1759.49,548.688 1779.27,538.766 1799.04,528.845 1818.82,517.302 1838.59,505.759 1858.37,494.215 1878.14,482.672 1897.92,471.129 1917.7,456.768 1937.47,442.407 1957.25,428.046 1977.02,413.685 1996.8,399.324 2016.57,382.331 2036.35,365.337 2056.12,348.344 2075.9,331.35 2095.67,314.357 2115.45,287.114 2135.23,259.871 2155,232.627 2174.78,205.384 2194.55,178.141 2214.33,159.75 2234.1,141.359 2253.88,122.968 2273.65,104.577 2293.43,86.1857 \"/>\n",
"</svg>\n"
]
},
"metadata": {},
"execution_count": 13
}
],
"cell_type": "code",
"source": [
"Plots.plot(getindex.(points, 1), getindex.(q_points, 1), xlabel = \"x (coordinate)\", ylabel = \"q_x (flux in x-direction)\", label = nothing)"
],
"metadata": {},
"execution_count": 13
},
{
"cell_type": "markdown",
"source": [
"*Figure 4*: $x$-component of the flux along the cut line from *Figure 2*."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"---\n",
"\n",
"*This notebook was generated using [Literate.jl](https://github.com/fredrikekre/Literate.jl).*"
],
"metadata": {}
}
],
"nbformat_minor": 3,
"metadata": {
"language_info": {
"file_extension": ".jl",
"mimetype": "application/julia",
"name": "julia",
"version": "1.11.3"
},
"kernelspec": {
"name": "julia-1.11",
"display_name": "Julia 1.11.3",
"language": "julia"
}
},
"nbformat": 4
}