{
"cells": [
{
"cell_type": "markdown",
"source": [
"# Heat equation\n",
"\n",
"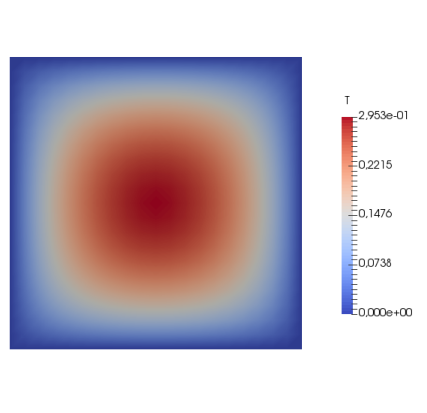\n",
"\n",
"*Figure 1*: Temperature field on the unit square with an internal uniform heat source\n",
"solved with homogeneous Dirichlet boundary conditions on the boundary."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"## Introduction\n",
"\n",
"The heat equation is the \"Hello, world!\" equation of finite elements.\n",
"Here we solve the equation on a unit square, with a uniform internal source.\n",
"The strong form of the (linear) heat equation is given by\n",
"\n",
"$$\n",
" -\\nabla \\cdot (k \\nabla u) = f \\quad \\textbf{x} \\in \\Omega,\n",
"$$\n",
"\n",
"where $u$ is the unknown temperature field, $k$ the heat conductivity,\n",
"$f$ the heat source and $\\Omega$ the domain. For simplicity we set $f = 1$\n",
"and $k = 1$. We will consider homogeneous Dirichlet boundary conditions such that\n",
"$$\n",
"u(\\textbf{x}) = 0 \\quad \\textbf{x} \\in \\partial \\Omega,\n",
"$$\n",
"where $\\partial \\Omega$ denotes the boundary of $\\Omega$.\n",
"The resulting weak form is given as follows: Find $u \\in \\mathbb{U}$ such that\n",
"$$\n",
"\\int_{\\Omega} \\nabla \\delta u \\cdot \\nabla u \\ d\\Omega = \\int_{\\Omega} \\delta u \\ d\\Omega \\quad \\forall \\delta u \\in \\mathbb{T},\n",
"$$\n",
"where $\\delta u$ is a test function, and where $\\mathbb{U}$ and $\\mathbb{T}$ are suitable\n",
"trial and test function sets, respectively."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"## Commented Program\n",
"\n",
"Now we solve the problem in Ferrite. What follows is a program spliced with comments.\n",
"\n",
"First we load Ferrite, and some other packages we need"
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"using Ferrite, SparseArrays"
],
"metadata": {},
"execution_count": 1
},
{
"cell_type": "markdown",
"source": [
"We start by generating a simple grid with 20x20 quadrilateral elements\n",
"using `generate_grid`. The generator defaults to the unit square,\n",
"so we don't need to specify the corners of the domain."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"grid = generate_grid(Quadrilateral, (20, 20));"
],
"metadata": {},
"execution_count": 2
},
{
"cell_type": "markdown",
"source": [
"### Trial and test functions\n",
"A `CellValues` facilitates the process of evaluating values and gradients of\n",
"test and trial functions (among other things). To define\n",
"this we need to specify an interpolation space for the shape functions.\n",
"We use Lagrange functions\n",
"based on the two-dimensional reference quadrilateral. We also define a quadrature rule based on\n",
"the same reference element. We combine the interpolation and the quadrature rule\n",
"to a `CellValues` object."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"ip = Lagrange{RefQuadrilateral, 1}()\n",
"qr = QuadratureRule{RefQuadrilateral}(2)\n",
"cellvalues = CellValues(qr, ip);"
],
"metadata": {},
"execution_count": 3
},
{
"cell_type": "markdown",
"source": [
"### Degrees of freedom\n",
"Next we need to define a `DofHandler`, which will take care of numbering\n",
"and distribution of degrees of freedom for our approximated fields.\n",
"We create the `DofHandler` and then add a single scalar field called `:u` based on\n",
"our interpolation `ip` defined above.\n",
"Lastly we `close!` the `DofHandler`, it is now that the dofs are distributed\n",
"for all the elements."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"dh = DofHandler(grid)\n",
"add!(dh, :u, ip)\n",
"close!(dh);"
],
"metadata": {},
"execution_count": 4
},
{
"cell_type": "markdown",
"source": [
"> **Numbering of degrees of freedom**\n",
">\n",
"> A common assumption is that the numbering of degrees of freedom follows the global\n",
"> numbering of the nodes in the grid. This is *NOT* the case in Ferrite. For more\n",
"> details, see the Ferrite numbering rules."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"Now that we have distributed all our dofs we can create our tangent matrix,\n",
"using `allocate_matrix`. This function returns a sparse matrix\n",
"with the correct entries stored."
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "441×441 SparseMatrixCSC{Float64, Int64} with 3721 stored entries:\n⎡⠻⣦⡀⠀⢧⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⎤\n⎢⠀⠈⠻⣦⠈⢧⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⎥\n⎢⠉⠓⠦⣄⡻⣮⡳⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠙⢮⡻⣮⡳⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠙⢮⡻⣮⡳⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠀⠀⠙⢮⡻⢎⡳⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⢮⡻⣮⡳⣤⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⣮⡻⣮⡳⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⢮⡻⣮⡳⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⢮⡻⣮⡳⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⢮⡻⣮⡳⣆⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠹⢮⡻⣮⡳⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⢮⡻⣮⡳⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⢮⡻⣮⡳⣄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⢮⡱⣮⡳⣄⠀⠀⠀⠀⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⢮⡻⣮⡳⣄⠀⠀⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⢮⡻⣮⡳⣄⠀⠀⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⢮⡻⣮⠳⣄⠀⠀⎥\n⎢⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⢦⡻⣮⡳⣄⎥\n⎣⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠙⢮⠻⣦⎦"
},
"metadata": {},
"execution_count": 5
}
],
"cell_type": "code",
"source": [
"K = allocate_matrix(dh)"
],
"metadata": {},
"execution_count": 5
},
{
"cell_type": "markdown",
"source": [
"### Boundary conditions\n",
"In Ferrite constraints like Dirichlet boundary conditions\n",
"are handled by a `ConstraintHandler`."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"ch = ConstraintHandler(dh);"
],
"metadata": {},
"execution_count": 6
},
{
"cell_type": "markdown",
"source": [
"Next we need to add constraints to `ch`. For this problem we define\n",
"homogeneous Dirichlet boundary conditions on the whole boundary, i.e.\n",
"the `union` of all the facet sets on the boundary."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"∂Ω = union(\n",
" getfacetset(grid, \"left\"),\n",
" getfacetset(grid, \"right\"),\n",
" getfacetset(grid, \"top\"),\n",
" getfacetset(grid, \"bottom\"),\n",
");"
],
"metadata": {},
"execution_count": 7
},
{
"cell_type": "markdown",
"source": [
"Now we are set up to define our constraint. We specify which field\n",
"the condition is for, and our combined facet set `∂Ω`. The last\n",
"argument is a function of the form $f(\\textbf{x})$ or $f(\\textbf{x}, t)$,\n",
"where $\\textbf{x}$ is the spatial coordinate and\n",
"$t$ the current time, and returns the prescribed value. Since the boundary condition in\n",
"this case do not depend on time we define our function as $f(\\textbf{x}) = 0$, i.e.\n",
"no matter what $\\textbf{x}$ we return $0$. When we have\n",
"specified our constraint we `add!` it to `ch`."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"dbc = Dirichlet(:u, ∂Ω, (x, t) -> 0)\n",
"add!(ch, dbc);"
],
"metadata": {},
"execution_count": 8
},
{
"cell_type": "markdown",
"source": [
"Finally we also need to `close!` our constraint handler. When we call `close!`\n",
"the dofs corresponding to our constraints are calculated and stored\n",
"in our `ch` object."
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "ConstraintHandler:\n BCs:\n Field: u, Components: [1]"
},
"metadata": {},
"execution_count": 9
}
],
"cell_type": "code",
"source": [
"close!(ch)"
],
"metadata": {},
"execution_count": 9
},
{
"cell_type": "markdown",
"source": [
"Note that if one or more of the constraints are time dependent we would use\n",
"`update!` to recompute prescribed values in each new timestep."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"### Assembling the linear system\n",
"\n",
"Now we have all the pieces needed to assemble the linear system, $K u = f$.\n",
"Assembling of the global system is done by looping over all the elements in order to\n",
"compute the element contributions $K_e$ and $f_e$, which are then assembled to the\n",
"appropriate place in the global $K$ and $f$.\n",
"\n",
"#### Element assembly\n",
"We define the function `assemble_element!` (see below) which computes the contribution for\n",
"an element. The function takes pre-allocated `Ke` and `fe` (they are allocated once and\n",
"then reused for all elements) so we first need to make sure that they are all zeroes at\n",
"the start of the function by using `fill!`. Then we loop over all the quadrature points,\n",
"and for each quadrature point we loop over all the (local) shape functions. We need the\n",
"value and gradient of the test function, `δu` and also the gradient of the trial function\n",
"`u`. We get all of these from `cellvalues`.\n",
"\n",
"> **Notation**\n",
">\n",
"> Comparing with the brief finite element introduction in Introduction to FEM,\n",
"> the variables `δu`, `∇δu` and `∇u` are actually $\\phi_i(\\textbf{x}_q)$, $\\nabla\n",
"> \\phi_i(\\textbf{x}_q)$ and $\\nabla \\phi_j(\\textbf{x}_q)$, i.e. the evaluation of the\n",
"> trial and test functions in the quadrature point $\\textbf{x}_q$. However, to\n",
"> underline the strong parallel between the weak form and the implementation, this\n",
"> example uses the symbols appearing in the weak form."
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "assemble_element! (generic function with 1 method)"
},
"metadata": {},
"execution_count": 10
}
],
"cell_type": "code",
"source": [
"function assemble_element!(Ke::Matrix, fe::Vector, cellvalues::CellValues)\n",
" n_basefuncs = getnbasefunctions(cellvalues)\n",
" # Reset to 0\n",
" fill!(Ke, 0)\n",
" fill!(fe, 0)\n",
" # Loop over quadrature points\n",
" for q_point in 1:getnquadpoints(cellvalues)\n",
" # Get the quadrature weight\n",
" dΩ = getdetJdV(cellvalues, q_point)\n",
" # Loop over test shape functions\n",
" for i in 1:n_basefuncs\n",
" δu = shape_value(cellvalues, q_point, i)\n",
" ∇δu = shape_gradient(cellvalues, q_point, i)\n",
" # Add contribution to fe\n",
" fe[i] += δu * dΩ\n",
" # Loop over trial shape functions\n",
" for j in 1:n_basefuncs\n",
" ∇u = shape_gradient(cellvalues, q_point, j)\n",
" # Add contribution to Ke\n",
" Ke[i, j] += (∇δu ⋅ ∇u) * dΩ\n",
" end\n",
" end\n",
" end\n",
" return Ke, fe\n",
"end"
],
"metadata": {},
"execution_count": 10
},
{
"cell_type": "markdown",
"source": [
"#### Global assembly\n",
"We define the function `assemble_global` to loop over the elements and do the global\n",
"assembly. The function takes our `cellvalues`, the sparse matrix `K`, and our DofHandler\n",
"as input arguments and returns the assembled global stiffness matrix, and the assembled\n",
"global force vector. We start by allocating `Ke`, `fe`, and the global force vector `f`.\n",
"We also create an assembler by using `start_assemble`. The assembler lets us assemble into\n",
"`K` and `f` efficiently. We then start the loop over all the elements. In each loop\n",
"iteration we reinitialize `cellvalues` (to update derivatives of shape functions etc.),\n",
"compute the element contribution with `assemble_element!`, and then assemble into the\n",
"global `K` and `f` with `assemble!`.\n",
"\n",
"> **Notation**\n",
">\n",
"> Comparing again with Introduction to FEM, `f` and `u` correspond to\n",
"> $\\underline{\\hat{f}}$ and $\\underline{\\hat{u}}$, since they represent the discretized\n",
"> versions. However, through the code we use `f` and `u` instead to reflect the strong\n",
"> connection between the weak form and the Ferrite implementation."
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "assemble_global (generic function with 1 method)"
},
"metadata": {},
"execution_count": 11
}
],
"cell_type": "code",
"source": [
"function assemble_global(cellvalues::CellValues, K::SparseMatrixCSC, dh::DofHandler)\n",
" # Allocate the element stiffness matrix and element force vector\n",
" n_basefuncs = getnbasefunctions(cellvalues)\n",
" Ke = zeros(n_basefuncs, n_basefuncs)\n",
" fe = zeros(n_basefuncs)\n",
" # Allocate global force vector f\n",
" f = zeros(ndofs(dh))\n",
" # Create an assembler\n",
" assembler = start_assemble(K, f)\n",
" # Loop over all cels\n",
" for cell in CellIterator(dh)\n",
" # Reinitialize cellvalues for this cell\n",
" reinit!(cellvalues, cell)\n",
" # Compute element contribution\n",
" assemble_element!(Ke, fe, cellvalues)\n",
" # Assemble Ke and fe into K and f\n",
" assemble!(assembler, celldofs(cell), Ke, fe)\n",
" end\n",
" return K, f\n",
"end"
],
"metadata": {},
"execution_count": 11
},
{
"cell_type": "markdown",
"source": [
"### Solution of the system\n",
"The last step is to solve the system. First we call `assemble_global`\n",
"to obtain the global stiffness matrix `K` and force vector `f`."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"K, f = assemble_global(cellvalues, K, dh);"
],
"metadata": {},
"execution_count": 12
},
{
"cell_type": "markdown",
"source": [
"To account for the boundary conditions we use the `apply!` function.\n",
"This modifies elements in `K` and `f` respectively, such that\n",
"we can get the correct solution vector `u` by using `\\`."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"apply!(K, f, ch)\n",
"u = K \\ f;"
],
"metadata": {},
"execution_count": 13
},
{
"cell_type": "markdown",
"source": [
"> **Numbering of degrees of freedom**\n",
">\n",
"> Once again, recall that numbering of degrees of freedom does *NOT* follow the global\n",
"> numbering of the nodes in the grid. Specifically, `u[i]` is *NOT* the temperature at\n",
"> node `i`."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"### Exporting to VTK\n",
"To visualize the result we export the grid and our field `u`\n",
"to a VTK-file, which can be viewed in e.g. [ParaView](https://www.paraview.org/)."
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "VTKGridFile for the closed file \"heat_equation.vtu\"."
},
"metadata": {},
"execution_count": 14
}
],
"cell_type": "code",
"source": [
"VTKGridFile(\"heat_equation\", dh) do vtk\n",
" write_solution(vtk, dh, u)\n",
"end"
],
"metadata": {},
"execution_count": 14
},
{
"cell_type": "markdown",
"source": [
"---\n",
"\n",
"*This notebook was generated using [Literate.jl](https://github.com/fredrikekre/Literate.jl).*"
],
"metadata": {}
}
],
"nbformat_minor": 3,
"metadata": {
"language_info": {
"file_extension": ".jl",
"mimetype": "application/julia",
"name": "julia",
"version": "1.11.3"
},
"kernelspec": {
"name": "julia-1.11",
"display_name": "Julia 1.11.3",
"language": "julia"
}
},
"nbformat": 4
}