{
"cells": [
{
"cell_type": "markdown",
"source": [
"# Von Mises plasticity\n",
"\n",
"\n",
"\n",
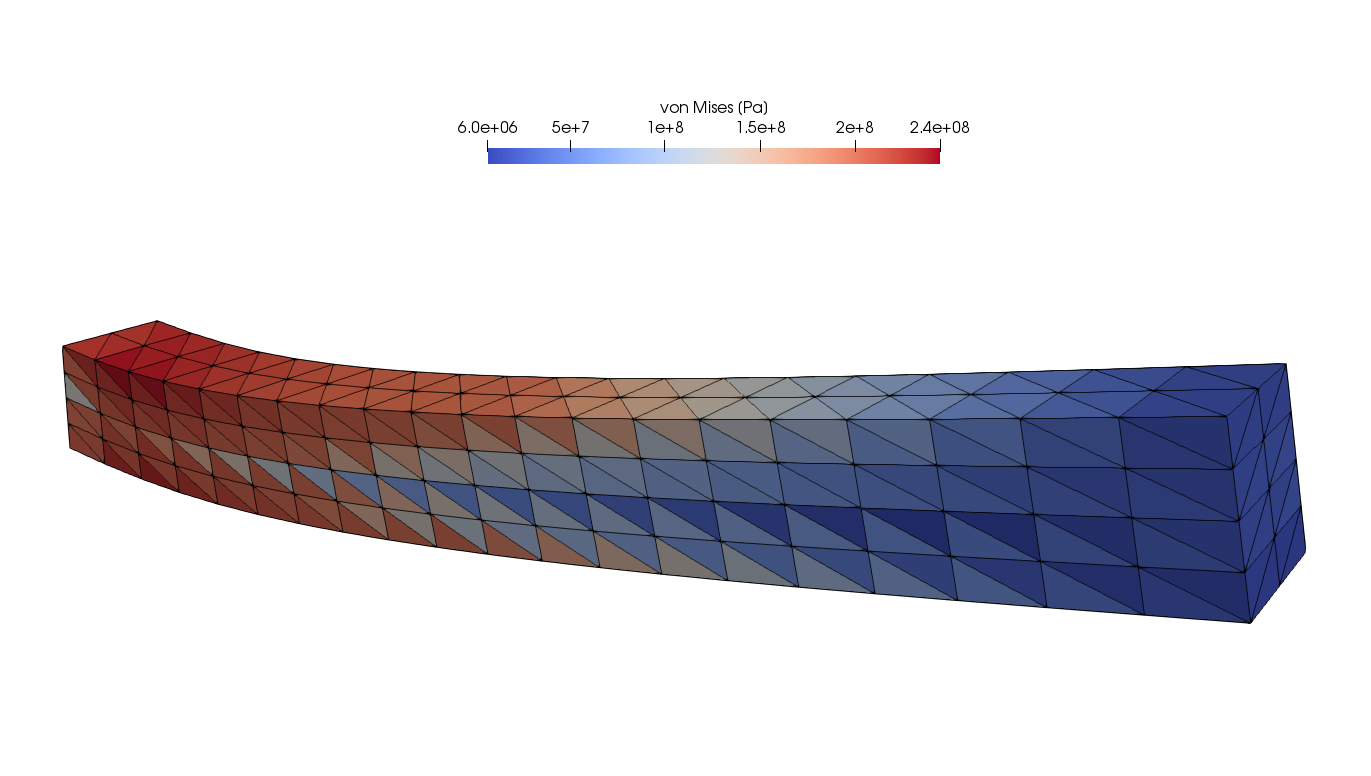
"*Figure 1.* A coarse mesh solution of a cantilever beam subjected to a load\n",
"causing plastic deformations. The initial yield limit is 200 MPa but due to\n",
"hardening it increases up to approximately 240 MPa."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"## Introduction\n",
"\n",
"This example illustrates the use of a nonlinear material model in Ferrite.\n",
"The particular model is von Mises plasticity (also know as J₂-plasticity) with\n",
"isotropic hardening. The model is fully 3D, meaning that no assumptions like *plane stress*\n",
"or *plane strain* are introduced.\n",
"\n",
"Also note that the theory of the model is not described here, instead one is\n",
"referred to standard textbooks on material modeling.\n",
"\n",
"To illustrate the use of the plasticity model, we setup and solve a FE-problem\n",
"consisting of a cantilever beam loaded at its free end. But first, we shortly\n",
"describe the parts of the implementation dealing with the material modeling."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"## Material modeling\n",
"This section describes the `struct`s and methods used to implement the material\n",
"model"
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"### Material parameters and state variables\n",
"\n",
"Start by loading some necessary packages"
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"using Ferrite, Tensors, SparseArrays, LinearAlgebra, Printf"
],
"metadata": {},
"execution_count": 1
},
{
"cell_type": "markdown",
"source": [
"We define a J₂-plasticity-material, containing material parameters and the elastic\n",
"stiffness Dᵉ (since it is constant)"
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"struct J2Plasticity{T, S <: SymmetricTensor{4, 3, T}}\n",
" G::T # Shear modulus\n",
" K::T # Bulk modulus\n",
" σ₀::T # Initial yield limit\n",
" H::T # Hardening modulus\n",
" Dᵉ::S # Elastic stiffness tensor\n",
"end;"
],
"metadata": {},
"execution_count": 2
},
{
"cell_type": "markdown",
"source": [
"Next, we define a constructor for the material instance."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"function J2Plasticity(E, ν, σ₀, H)\n",
" δ(i, j) = i == j ? 1.0 : 0.0 # helper function\n",
" G = E / 2(1 + ν)\n",
" K = E / 3(1 - 2ν)\n",
"\n",
" Isymdev(i, j, k, l) = 0.5 * (δ(i, k) * δ(j, l) + δ(i, l) * δ(j, k)) - 1.0 / 3.0 * δ(i, j) * δ(k, l)\n",
" temp(i, j, k, l) = 2.0G * (0.5 * (δ(i, k) * δ(j, l) + δ(i, l) * δ(j, k)) + ν / (1.0 - 2.0ν) * δ(i, j) * δ(k, l))\n",
" Dᵉ = SymmetricTensor{4, 3}(temp)\n",
" return J2Plasticity(G, K, σ₀, H, Dᵉ)\n",
"end;"
],
"metadata": {},
"execution_count": 3
},
{
"cell_type": "markdown",
"source": [
"Define a `struct` to store the material state for a Gauss point."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"struct MaterialState{T, S <: SecondOrderTensor{3, T}}\n",
" # Store \"converged\" values\n",
" ϵᵖ::S # plastic strain\n",
" σ::S # stress\n",
" k::T # hardening variable\n",
"end"
],
"metadata": {},
"execution_count": 4
},
{
"cell_type": "markdown",
"source": [
"Constructor for initializing a material state. Every quantity is set to zero."
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "Main.var\"##325\".MaterialState"
},
"metadata": {},
"execution_count": 5
}
],
"cell_type": "code",
"source": [
"function MaterialState()\n",
" return MaterialState(\n",
" zero(SymmetricTensor{2, 3}),\n",
" zero(SymmetricTensor{2, 3}),\n",
" 0.0\n",
" )\n",
"end"
],
"metadata": {},
"execution_count": 5
},
{
"cell_type": "markdown",
"source": [
"For later use, during the post-processing step, we define a function to\n",
"compute the von Mises effective stress."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"function vonMises(σ)\n",
" s = dev(σ)\n",
" return sqrt(3.0 / 2.0 * s ⊡ s)\n",
"end;"
],
"metadata": {},
"execution_count": 6
},
{
"cell_type": "markdown",
"source": [
"## Constitutive driver\n",
"\n",
"This is the actual method which computes the stress and material tangent\n",
"stiffness in a given integration point.\n",
"Input is the current strain and the material state from the previous timestep."
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "compute_stress_tangent (generic function with 1 method)"
},
"metadata": {},
"execution_count": 7
}
],
"cell_type": "code",
"source": [
"function compute_stress_tangent(ϵ::SymmetricTensor{2, 3}, material::J2Plasticity, state::MaterialState)\n",
" # unpack some material parameters\n",
" G = material.G\n",
" H = material.H\n",
"\n",
" # We use (•)ᵗ to denote *trial*-values\n",
" σᵗ = material.Dᵉ ⊡ (ϵ - state.ϵᵖ) # trial-stress\n",
" sᵗ = dev(σᵗ) # deviatoric part of trial-stress\n",
" J₂ = 0.5 * sᵗ ⊡ sᵗ # second invariant of sᵗ\n",
" σᵗₑ = sqrt(3.0 * J₂) # effective trial-stress (von Mises stress)\n",
" σʸ = material.σ₀ + H * state.k # Previous yield limit\n",
"\n",
" φᵗ = σᵗₑ - σʸ # Trial-value of the yield surface\n",
"\n",
" if φᵗ < 0.0 # elastic loading\n",
" return σᵗ, material.Dᵉ, MaterialState(state.ϵᵖ, σᵗ, state.k)\n",
" else # plastic loading\n",
" h = H + 3G\n",
" μ = φᵗ / h # plastic multiplier\n",
"\n",
" c1 = 1 - 3G * μ / σᵗₑ\n",
" s = c1 * sᵗ # updated deviatoric stress\n",
" σ = s + vol(σᵗ) # updated stress\n",
"\n",
" # Compute algorithmic tangent stiffness $D = \\frac{\\Delta \\sigma }{\\Delta \\epsilon}$\n",
" κ = H * (state.k + μ) # drag stress\n",
" σₑ = material.σ₀ + κ # updated yield surface\n",
"\n",
" δ(i, j) = i == j ? 1.0 : 0.0\n",
" Isymdev(i, j, k, l) = 0.5 * (δ(i, k) * δ(j, l) + δ(i, l) * δ(j, k)) - 1.0 / 3.0 * δ(i, j) * δ(k, l)\n",
" Q(i, j, k, l) = Isymdev(i, j, k, l) - 3.0 / (2.0 * σₑ^2) * s[i, j] * s[k, l]\n",
" b = (3G * μ / σₑ) / (1.0 + 3G * μ / σₑ)\n",
"\n",
" Dtemp(i, j, k, l) = -2G * b * Q(i, j, k, l) - 9G^2 / (h * σₑ^2) * s[i, j] * s[k, l]\n",
" D = material.Dᵉ + SymmetricTensor{4, 3}(Dtemp)\n",
"\n",
" # Return new state\n",
" Δϵᵖ = 3 / 2 * μ / σₑ * s # plastic strain\n",
" ϵᵖ = state.ϵᵖ + Δϵᵖ # plastic strain\n",
" k = state.k + μ # hardening variable\n",
" return σ, D, MaterialState(ϵᵖ, σ, k)\n",
" end\n",
"end"
],
"metadata": {},
"execution_count": 7
},
{
"cell_type": "markdown",
"source": [
"## FE-problem\n",
"What follows are methods for assembling and and solving the FE-problem."
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"function create_values(interpolation)\n",
" # setup quadrature rules\n",
" qr = QuadratureRule{RefTetrahedron}(2)\n",
" facet_qr = FacetQuadratureRule{RefTetrahedron}(3)\n",
"\n",
" # cell and facetvalues for u\n",
" cellvalues_u = CellValues(qr, interpolation)\n",
" facetvalues_u = FacetValues(facet_qr, interpolation)\n",
"\n",
" return cellvalues_u, facetvalues_u\n",
"end;"
],
"metadata": {},
"execution_count": 8
},
{
"cell_type": "markdown",
"source": [
"### Add degrees of freedom"
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "create_dofhandler (generic function with 1 method)"
},
"metadata": {},
"execution_count": 9
}
],
"cell_type": "code",
"source": [
"function create_dofhandler(grid, interpolation)\n",
" dh = DofHandler(grid)\n",
" add!(dh, :u, interpolation) # add a displacement field with 3 components\n",
" close!(dh)\n",
" return dh\n",
"end"
],
"metadata": {},
"execution_count": 9
},
{
"cell_type": "markdown",
"source": [
"### Boundary conditions"
],
"metadata": {}
},
{
"outputs": [],
"cell_type": "code",
"source": [
"function create_bc(dh, grid)\n",
" dbcs = ConstraintHandler(dh)\n",
" # Clamped on the left side\n",
" dofs = [1, 2, 3]\n",
" dbc = Dirichlet(:u, getfacetset(grid, \"left\"), (x, t) -> [0.0, 0.0, 0.0], dofs)\n",
" add!(dbcs, dbc)\n",
" close!(dbcs)\n",
" return dbcs\n",
"end;"
],
"metadata": {},
"execution_count": 10
},
{
"cell_type": "markdown",
"source": [
"### Assembling of element contributions\n",
"\n",
"* Residual vector `r`\n",
"* Tangent stiffness `K`"
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "doassemble! (generic function with 1 method)"
},
"metadata": {},
"execution_count": 11
}
],
"cell_type": "code",
"source": [
"function doassemble!(\n",
" K::SparseMatrixCSC, r::Vector, cellvalues::CellValues, dh::DofHandler,\n",
" material::J2Plasticity, u, states, states_old\n",
" )\n",
" assembler = start_assemble(K, r)\n",
" nu = getnbasefunctions(cellvalues)\n",
" re = zeros(nu) # element residual vector\n",
" ke = zeros(nu, nu) # element tangent matrix\n",
"\n",
" for (i, cell) in enumerate(CellIterator(dh))\n",
" fill!(ke, 0)\n",
" fill!(re, 0)\n",
" eldofs = celldofs(cell)\n",
" ue = u[eldofs]\n",
" state = @view states[:, i]\n",
" state_old = @view states_old[:, i]\n",
" assemble_cell!(ke, re, cell, cellvalues, material, ue, state, state_old)\n",
" assemble!(assembler, eldofs, ke, re)\n",
" end\n",
" return K, r\n",
"end"
],
"metadata": {},
"execution_count": 11
},
{
"cell_type": "markdown",
"source": [
"Compute element contribution to the residual and the tangent."
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "assemble_cell! (generic function with 1 method)"
},
"metadata": {},
"execution_count": 12
}
],
"cell_type": "code",
"source": [
"function assemble_cell!(Ke, re, cell, cellvalues, material, ue, state, state_old)\n",
" n_basefuncs = getnbasefunctions(cellvalues)\n",
" reinit!(cellvalues, cell)\n",
"\n",
" for q_point in 1:getnquadpoints(cellvalues)\n",
" # For each integration point, compute stress and material stiffness\n",
" ϵ = function_symmetric_gradient(cellvalues, q_point, ue) # Total strain\n",
" σ, D, state[q_point] = compute_stress_tangent(ϵ, material, state_old[q_point])\n",
"\n",
" dΩ = getdetJdV(cellvalues, q_point)\n",
" for i in 1:n_basefuncs\n",
" δϵ = shape_symmetric_gradient(cellvalues, q_point, i)\n",
" re[i] += (δϵ ⊡ σ) * dΩ # add internal force to residual\n",
" for j in 1:i # loop only over lower half\n",
" Δϵ = shape_symmetric_gradient(cellvalues, q_point, j)\n",
" Ke[i, j] += δϵ ⊡ D ⊡ Δϵ * dΩ\n",
" end\n",
" end\n",
" end\n",
" symmetrize_lower!(Ke)\n",
" return\n",
"end"
],
"metadata": {},
"execution_count": 12
},
{
"cell_type": "markdown",
"source": [
"Helper function to symmetrize the material tangent"
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "doassemble_neumann! (generic function with 1 method)"
},
"metadata": {},
"execution_count": 13
}
],
"cell_type": "code",
"source": [
"function symmetrize_lower!(K)\n",
" for i in 1:size(K, 1)\n",
" for j in (i + 1):size(K, 1)\n",
" K[i, j] = K[j, i]\n",
" end\n",
" end\n",
" return\n",
"end;\n",
"\n",
"function doassemble_neumann!(r, dh, facetset, facetvalues, t)\n",
" n_basefuncs = getnbasefunctions(facetvalues)\n",
" re = zeros(n_basefuncs) # element residual vector\n",
" for fc in FacetIterator(dh, facetset)\n",
" # Add traction as a negative contribution to the element residual `re`:\n",
" reinit!(facetvalues, fc)\n",
" fill!(re, 0)\n",
" for q_point in 1:getnquadpoints(facetvalues)\n",
" dΓ = getdetJdV(facetvalues, q_point)\n",
" for i in 1:n_basefuncs\n",
" δu = shape_value(facetvalues, q_point, i)\n",
" re[i] -= (δu ⋅ t) * dΓ\n",
" end\n",
" end\n",
" assemble!(r, celldofs(fc), re)\n",
" end\n",
" return r\n",
"end"
],
"metadata": {},
"execution_count": 13
},
{
"cell_type": "markdown",
"source": [
"Define a function which solves the FE-problem."
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "solve (generic function with 1 method)"
},
"metadata": {},
"execution_count": 14
}
],
"cell_type": "code",
"source": [
"function solve()\n",
" # Define material parameters\n",
" E = 200.0e9 # [Pa]\n",
" H = E / 20 # [Pa]\n",
" ν = 0.3 # [-]\n",
" σ₀ = 200.0e6 # [Pa]\n",
" material = J2Plasticity(E, ν, σ₀, H)\n",
"\n",
" L = 10.0 # beam length [m]\n",
" w = 1.0 # beam width [m]\n",
" h = 1.0 # beam height[m]\n",
" n_timesteps = 10\n",
" u_max = zeros(n_timesteps)\n",
" traction_magnitude = 1.0e7 * range(0.5, 1.0, length = n_timesteps)\n",
"\n",
" # Create geometry, dofs and boundary conditions\n",
" n = 2\n",
" nels = (10n, n, 2n) # number of elements in each spatial direction\n",
" P1 = Vec((0.0, 0.0, 0.0)) # start point for geometry\n",
" P2 = Vec((L, w, h)) # end point for geometry\n",
" grid = generate_grid(Tetrahedron, nels, P1, P2)\n",
" interpolation = Lagrange{RefTetrahedron, 1}()^3\n",
"\n",
" dh = create_dofhandler(grid, interpolation) # JuaFEM helper function\n",
" dbcs = create_bc(dh, grid) # create Dirichlet boundary-conditions\n",
"\n",
" cellvalues, facetvalues = create_values(interpolation)\n",
"\n",
" # Pre-allocate solution vectors, etc.\n",
" n_dofs = ndofs(dh) # total number of dofs\n",
" u = zeros(n_dofs) # solution vector\n",
" Δu = zeros(n_dofs) # displacement correction\n",
" r = zeros(n_dofs) # residual\n",
" K = allocate_matrix(dh) # tangent stiffness matrix\n",
"\n",
" # Create material states. One array for each cell, where each element is an array of material-\n",
" # states - one for each integration point\n",
" nqp = getnquadpoints(cellvalues)\n",
" states = [MaterialState() for _ in 1:nqp, _ in 1:getncells(grid)]\n",
" states_old = [MaterialState() for _ in 1:nqp, _ in 1:getncells(grid)]\n",
"\n",
" # Newton-Raphson loop\n",
" NEWTON_TOL = 1 # 1 N\n",
" print(\"\\n Starting Netwon iterations:\\n\")\n",
"\n",
" for timestep in 1:n_timesteps\n",
" t = timestep # actual time (used for evaluating d-bndc)\n",
" traction = Vec((0.0, 0.0, traction_magnitude[timestep]))\n",
" newton_itr = -1\n",
" print(\"\\n Time step @time = $timestep:\\n\")\n",
" update!(dbcs, t) # evaluates the D-bndc at time t\n",
" apply!(u, dbcs) # set the prescribed values in the solution vector\n",
"\n",
" while true\n",
" newton_itr += 1\n",
" if newton_itr > 8\n",
" error(\"Reached maximum Newton iterations, aborting\")\n",
" break\n",
" end\n",
" # Tangent and residual contribution from the cells (volume integral)\n",
" doassemble!(K, r, cellvalues, dh, material, u, states, states_old)\n",
" # Residual contribution from the Neumann boundary (surface integral)\n",
" doassemble_neumann!(r, dh, getfacetset(grid, \"right\"), facetvalues, traction)\n",
" norm_r = norm(r[Ferrite.free_dofs(dbcs)])\n",
"\n",
" print(\"Iteration: $newton_itr \\tresidual: $(@sprintf(\"%.8f\", norm_r))\\n\")\n",
" if norm_r < NEWTON_TOL\n",
" break\n",
" end\n",
"\n",
" apply_zero!(K, r, dbcs)\n",
" Δu = Symmetric(K) \\ r\n",
" u -= Δu\n",
" end\n",
"\n",
" # Update the old states with the converged values for next timestep\n",
" states_old .= states\n",
"\n",
" u_max[timestep] = maximum(abs, u) # maximum displacement in current timestep\n",
" end\n",
"\n",
" # ## Postprocessing\n",
" # Only a vtu-file corresponding to the last time-step is exported.\n",
" #\n",
" # The following is a quick (and dirty) way of extracting average cell data for export.\n",
" mises_values = zeros(getncells(grid))\n",
" κ_values = zeros(getncells(grid))\n",
" for (el, cell_states) in enumerate(eachcol(states))\n",
" for state in cell_states\n",
" mises_values[el] += vonMises(state.σ)\n",
" κ_values[el] += state.k * material.H\n",
" end\n",
" mises_values[el] /= length(cell_states) # average von Mises stress\n",
" κ_values[el] /= length(cell_states) # average drag stress\n",
" end\n",
" VTKGridFile(\"plasticity\", dh) do vtk\n",
" write_solution(vtk, dh, u) # displacement field\n",
" write_cell_data(vtk, mises_values, \"von Mises [Pa]\")\n",
" write_cell_data(vtk, κ_values, \"Drag stress [Pa]\")\n",
" end\n",
"\n",
" return u_max, traction_magnitude\n",
"end"
],
"metadata": {},
"execution_count": 14
},
{
"cell_type": "markdown",
"source": [
"Solve the FE-problem and for each time-step extract maximum displacement and\n",
"the corresponding traction load. Also compute the limit-traction-load"
],
"metadata": {}
},
{
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
" Starting Netwon iterations:\n",
"\n",
" Time step @time = 1:\n",
"Iteration: 0 \tresidual: 1435838.41167605\n",
"Iteration: 1 \tresidual: 118655.22430368\n",
"Iteration: 2 \tresidual: 59.50456058\n",
"Iteration: 3 \tresidual: 0.00002560\n",
"\n",
" Time step @time = 2:\n",
"Iteration: 0 \tresidual: 159537.60129725\n",
"Iteration: 1 \tresidual: 1706974.26597926\n",
"Iteration: 2 \tresidual: 97346.48157049\n",
"Iteration: 3 \tresidual: 37.17532011\n",
"Iteration: 4 \tresidual: 0.00001524\n",
"\n",
" Time step @time = 3:\n",
"Iteration: 0 \tresidual: 159537.60129701\n",
"Iteration: 1 \tresidual: 3033614.51718249\n",
"Iteration: 2 \tresidual: 183762.82986491\n",
"Iteration: 3 \tresidual: 187.23777242\n",
"Iteration: 4 \tresidual: 0.00023135\n",
"\n",
" Time step @time = 4:\n",
"Iteration: 0 \tresidual: 159537.60129742\n",
"Iteration: 1 \tresidual: 3668226.41190261\n",
"Iteration: 2 \tresidual: 85645.15221552\n",
"Iteration: 3 \tresidual: 33.39133787\n",
"Iteration: 4 \tresidual: 0.00002312\n",
"\n",
" Time step @time = 5:\n",
"Iteration: 0 \tresidual: 159537.60129764\n",
"Iteration: 1 \tresidual: 4942707.09611024\n",
"Iteration: 2 \tresidual: 822244.81049667\n",
"Iteration: 3 \tresidual: 2806.49948363\n",
"Iteration: 4 \tresidual: 0.04196782\n",
"\n",
" Time step @time = 6:\n",
"Iteration: 0 \tresidual: 159537.60129723\n",
"Iteration: 1 \tresidual: 6350622.82330476\n",
"Iteration: 2 \tresidual: 1433617.64531907\n",
"Iteration: 3 \tresidual: 11917.22662334\n",
"Iteration: 4 \tresidual: 0.96519065\n",
"\n",
" Time step @time = 7:\n",
"Iteration: 0 \tresidual: 159537.60130042\n",
"Iteration: 1 \tresidual: 7442093.81842929\n",
"Iteration: 2 \tresidual: 2293366.32653456\n",
"Iteration: 3 \tresidual: 27806.00144416\n",
"Iteration: 4 \tresidual: 4.78936691\n",
"Iteration: 5 \tresidual: 0.00002337\n",
"\n",
" Time step @time = 8:\n",
"Iteration: 0 \tresidual: 159537.60129787\n",
"Iteration: 1 \tresidual: 7898429.46749798\n",
"Iteration: 2 \tresidual: 2166408.36902476\n",
"Iteration: 3 \tresidual: 19078.14976325\n",
"Iteration: 4 \tresidual: 2.12913739\n",
"Iteration: 5 \tresidual: 0.00003700\n",
"\n",
" Time step @time = 9:\n",
"Iteration: 0 \tresidual: 159537.60129718\n",
"Iteration: 1 \tresidual: 9113096.78354406\n",
"Iteration: 2 \tresidual: 1942261.17847130\n",
"Iteration: 3 \tresidual: 14972.09948485\n",
"Iteration: 4 \tresidual: 1.53213288\n",
"Iteration: 5 \tresidual: 0.00003588\n",
"\n",
" Time step @time = 10:\n",
"Iteration: 0 \tresidual: 159537.60129681\n",
"Iteration: 1 \tresidual: 9810716.23843057\n",
"Iteration: 2 \tresidual: 1947382.98912119\n",
"Iteration: 3 \tresidual: 34190.85171497\n",
"Iteration: 4 \tresidual: 4.44141634\n",
"Iteration: 5 \tresidual: 0.00005322\n"
]
}
],
"cell_type": "code",
"source": [
"u_max, traction_magnitude = solve();"
],
"metadata": {},
"execution_count": 15
},
{
"cell_type": "markdown",
"source": [
"Finally we plot the load-displacement curve."
],
"metadata": {}
},
{
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": "Plot{Plots.GRBackend() n=1}",
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAlgAAAGQCAIAAAD9V4nPAAAABmJLR0QA/wD/AP+gvaeTAAAgAElEQVR4nOzdd3gU1foH8HdmN72HkCoJEAgBadI7kQRCt4EgIEpRQH5SvAKCICiCBfTiFQVpKoJUxVADJPTeO5iQhPTeSN3dmTm/PwaWJQlJgGx2N/l+nvvcJ3v27OzZMcw3M3POuxxjjAAAAGor3tADAAAAMCQEIcBzmT9//rhx49RqtaEHQjdv3pwwYcKmTZu0LX/++ee4ceNu3LhR5e81d+7ccePGiaJY5VsGqH4IQjB2p06dMq+EmTNn6nUYq1ev/vPPP0u3//333+vWrRMEQa/vXhnx8fGrVq06efKktuXUqVPr1q2Lj4+v8vfavn37unXrJEmq8i2blry8vFWrVu3evdvQA4HnojT0AAAqYG9v37VrV92WM2fOFBcXt2vXztbWVtvYoEEDvQ5j0qRJnp6eI0aMKNHeoUMHFxcXhUKh13d/Nn5+fgEBAXXq1DH0QGqsjIyMCRMm9OrVa+DAgYYeCzw7BCEYu+bNmx8+fFi3pWHDhjExMatXr27durWhRqW1du1aQw/hiaZMmTJlyhRDjwLA2CEIoSaIjo7Ozs5u2rSplZXViRMnrly5wvP85MmT5Wfj4+MvXLgQHx/PGGvUqFFgYKClpWWZ27l169aZM2cyMzPd3NxatmwpB21WVlZMTAxjTK1WX7x4Ue5pb2/fuHFj+SVFRUVt2rThOE53U9euXTtz5sz9+/e9vLyCgoLq1q2r+2xqampCQkK9evVcXV1v3bp19OhRlUrVqlWrgICAEtspx+3btw8fPiwIQuvWrbt37166Q3x8fFpaWuPGje3t7bWNCQkJ586di4+PVyqVbm5uHTt2rFevnvyUIAhXr161sbHx9/dPS0vbv39/WlpagwYN+vXrZ2VlVeF44uLiLl68KO/nxo0b9+rV60n7+ebNm2fPns3MzHR3d2/ZsmWrVq1KdMjMzAwPD09ISLCysurYsWObNm10n71//35kZGTdunW9vb1jYmLCw8MLCgrat2/fpUsXuUNRUdGePXtiY2O9vLwGDBhgZ2dXegzp6enh4eGJiYk2NjadO3cuMYacnJyoqCg3N7cXXnghNjb24MGD9+/fb9KkSXBwsFL54LCZnJws33/Ny8vT/mLIo6pwX4FxYQCmRr4KevnyZW3L0KFDiWj37t2dO3eWf7EtLS3lpzp16lTid97Nze3gwYMlthkfH9+rV68SPfv27csY27BhQ+l/OMHBwfILmzdvTkQFBQXaTWVlZfXv31+3s5WV1ZIlS3Tf7rvvviOi//73vx988IFuz6CgoMLCwgr3gCiKU6ZM0Y3MHj16yLcwJ0+erO0m/ymwd+9ebctnn31W+iruunXr5GfT0tKIqH379hs2bNBNvvr16+vubcZYkyZNiEitVmtb2rdvX2Kz7u7u4eHhJUYeFxcXEBBQoueAAQO0HSRJWrhwYYncDQ4OzsrK0vbZt28fEU2cOPHLL7/k+UcTHUaMGCEIwokTJ9zc3LSN9erVu3v3bom9N3fuXAsLC923GDRoUG5urrbP33//TUTTp09ftGiR7h5r3bp1Wlqa3GfBggVUiu7+B1OBIATT86Qg9Pb27tChw++//37q1Kk//vhDfuqll15avHjxoUOH/v3337Nnz86bN8/S0tLW1jYuLk778szMzPr16xPRq6++Gh4eHhUVdfz48W+//Xb48OGMseTk5IMHD/I8X7du3YMPXbp0SX5tiSAUBKFHjx5EFBgYeOzYscjIyPXr17u6uhLR8uXLte8oB2GDBg28vLzWrl174cKFHTt2+Pn5EdGCBQsq3AOLFi0iIj8/v71798bFxYWHh7dq1crT07P8IDxw4AARNWnS5J9//omOjo6IiAgLC5s2bdqWLVvkDnIQuri4WFpafv7555GRkbdv3/7Pf/4jp1pmZqZ2y6WDsFWrVl999ZV2P8tJY29vn5CQoO2Tnp7u4+NDRK+99tqhQ4fk/fzNN9+MGDFC22fOnDlE5O/vv2nTplu3bh0/fnzYsGFE1KtXL0mS5D5yEPr4+Dg4OCxfvvz8+fM7duyQ/wt+8cUXTk5OEyZMOHTo0MmTJ4cMGUJEffr00d1706dPJ6LmzZtv3bpVPh1/7bXXiKh///7aPnIQNmjQwMHBYdmyZefOnQsNDZX/qHrnnXfkPlFRUX/88YecjtpfjNu3b1f4nw+MDYIQTE85Qah7ZvYky5YtK5E306ZNI6JRo0ZpD7WlKRSKevXqlW4vEYTbt2+Xw6a4uFjb58SJE0Tk5OSUn58vt8hBaG1tHRsbq+125coVjuOaN29e/vhzc3NtbGzMzMyioqK0jampqfLUoXKC8JNPPiGiHTt2PGnLchAS0cyZM3Xb3333XSKaN2+etqV0EJYmf8aFCxdqWz788EM5SJ60n//991+e5729vXNycnTbBwwYQEShoaHyQzkIOY47ceKEts/+/fvlwU+dOlXbqFKp3N3dOY7TbvDq1ascxzVq1CgvL0/3LeTrAUePHpUfykHI8/yZM2e0fVJTU62srGxtbbXjj46OlkO6nP0Axg/LJ6DmmDJlirW1dYXdXnnlFSI6d+6c/JAxJq+9W7RoUeXvzz2JfAD96KOPdK+8de3atUePHtnZ2YcOHdLtPGzYMN37Sa1atXJzc4uJiSn/LQ4cOFBQUPDqq682bNhQ2+jq6jp69OjyX+jk5ERE8pG9nG48z8vnTFrySaH80SrvGfbzxo0bJUn68MMPHRwcdNsnTZpERHv37tVt7Nixo+504h49esib1R28ubl5p06dGGP37t2TWzZs2MAYmz59uu6U4ye9RY8ePTp27Kh96Orq2rp16/z8/PT09MrsATAVmCwDNUezZs1KNyYnJ3/zzTeHDx9OTEzMzMzUtmdkZMg/pKSkpKam1qlTp0rmONy6dYuIXnrppRLtbdu2PXbs2M2bNwcNGqRtlK+F6nJzc0tJScnLy7Ozs8vJydm5c6fus4GBgV5eXvJblJ5gUuEc2jfffHPhwoXffPNNSEhI//79AwICAgMDS//p4Obm5u7urtvSrFkzc3Pz27dvS5Kke09OV1JS0tdff33kyJHExMSsrCxtu3Y/JyYmZmRkuLq6enl5PWmEly9fJqLz58/LJ68lNqINM1mJvWdpaWlnZ6dWq0v8d5SnKWlPduW3OHnyZFxcnG63lJSU0m8hn/jqku8+pqamype7oWZAEELNUWJmJhElJCR06NAhJSWlQ4cO7777rpOTk1KpLCoq+vzzz7VVUe7fv09EHh4eVTKG/Px8Iip9lJQPoHl5ebqNpUNIjhn5jC0hIeGdd97RfXbPnj1eXl7yW5T+sBUemuvXr3/27NnPPvts375933///ffff29lZTVhwoQvv/zSxsZG2630lnmed3FxSUpKKigoKHMGZlxcXMeOHVNTUzt27DhmzBhnZ2eFQlFYWPjFF1881X7Ozs4motDQ0NIzepycnEo0lrn3rKysSpxuyrtUu/Y/JyeHiPbs2VM60Sv5Frpbg5oBQQg12dKlS5OTkxcuXDh37lxt4507dz7//HPtQ/kqXFJSUpW8o5wTqamp8qwQLfmEQ3cZQ4Xq169fomSJPDNTfgvtKY5Wampqhdts1qzZ9u3bi4qKzp49e/DgwbVr1y5btiw/P3/16tXaPqW3LElSenq6QqHQzUtdS5YsSUlJWbx48ezZs7WNN2/e/OKLL7QPK7Of5Y+2ZcuWvn37VvhZno18RTQkJKRnz556egswObhHCDXZ1atXiWj48OG6jZcuXdJ96O7u7uHhIS8WLGdTZmZmlamjJs+duXDhQon28+fPE1GLFi0qN3AiIltb2wGPk8/V5LeQL/HpKvG5ymFlZRUQELBo0aKLFy8qlcq//vpL99nU1NTExETdluvXr2s0mmbNmj3pumhl9rOnp6ebm1t6enqJa5K65EvKulXiqlzVvoWZmRkRGUOBPXgeCEKoyeTkiI2N1baoVCp57YEueZrJ7Nmzy5lF4uXllZmZWVRUVP47yvP1ly1bVlxcrG08evToyZMnXVxcXn755af/ECX17t3bzs5u586dkZGR2saUlBR5Kn855GuqulxcXMzNzVUqle4HZ4x9//33ut2WLl1KDz9amcrcz4sXL9btw3Hc22+/TUSffPLJk/bz6NGjFQrFypUrdTclkySpsLDwyR+ust59912O43788cfS56aiKD7tW7i7uysUioSEhOcfGBgQghBqMjl43n///b///jsiIiI0NDQwMFA3omRz5szx8/PbsmVLv3799uzZc/PmzUOHDi1evPiNN97Q9mnXrp1arX7ttdf++9//rlq1qsT0Qq2BAwcGBQVFRkYGBwcfOHDg5s2bq1atkrfz1VdfVaY+S4VsbW3nz58vCEJwcPBff/0VGRm5a9euXr16ubi4lP/CiRMnBgUFrVmz5vjx45GRkYcOHXrjjTcKCwuHDh2qe1/N1dV1xYoVs2fPvnbt2qVLlyZPnrxhw4YXXnhh6tSpT9qyvJ/Hjx+/Y8eOiIiIffv29erVq/Q3csydO7dRo0abNm0aMGDA3r17b968GR4evmjRInn1CxE1adLk888/z8jI6Nix49KlS48cOXLt2rVdu3YtWLDA19e3xJzbZ9OyZcs5c+akpKS0b9/+v//979GjR69duxYSEjJv3rwGDRqcPn36qbamVCpbt24dHR09cuTI//3vfyWKnoPJMNS6DYBn9qR1hOfPny/RUxCEkSNH6v7Ct27dWr6o2LZtW92eycnJ8mI1XW+88Ya2Q3x8fGBgoLa8VjmVZe7fv689ssvs7Ox++ukn3beT19j98MMPJQYsX7jTLXFSJkmSPvnkE90LlUFBQVu2bKFy1xHOnj1bvpSnxXHcsGHDtCvqtJVltm3bpns70M/P7+bNm7oDKLGOUKPRvPXWW7pbbtOmjVx1rEOHDrovTEpK6tevX4n9/Oabb+r2WbVqVemJP61atbpy5YrcQVtZpsRucXR0dHJyKtE4YcIE0lmDKPvxxx9L1yJv06bNrVu35A7ayjIltvb6668TkXYkjLErV660bdtW+5cEKsuYIo7hG+rB1Ny7d0+j0fj4+Jibm8stqampBQUFXl5eJepmyW7evHn16tWioiJ/f3+5Btu9e/csLCxKz+O/e/fu2bNn8/Pz69at26JFC7maqC5RFFNSUlQqlZWVlTwBMi4uTqVSNWrUqMRkxaioqNOnT+fn53t6evbs2bPEwrjc3NzMzMw6deqUaE9MTFSpVPXr13/S3ThdMTExx44dEwShefPmHTt2LCwsTElJsbe3154apqen5+TkeHl5aWc/FhQUXLx4MS4urrCw0NPTs1WrVtpCo3J/V1fX9u3bnzt3Ljs7OywsLCsrq0GDBgEBAdpdLYuNjVWr1SX2z40bN65evapSqfz9/eXVe7GxsWXu58jIyHPnzsn7uWXLlo0aNSrRobi4+MyZM9HR0ZIkeXh4vPjii3LhGFnpTyqTFz/o9iSijIyM+/fve3h4lDgdLyoqOn36tHxjWC55qrsrCgoKUlNTHRwcSuSl/Jv2wgsvlNgharU6NTVVo9GUHhUYPwQhADygG4SGHgtA9cE9QgAAqNUQhAAAUKthQT0APGBjY/P1119XVZEdAFOBe4QAAFCr4dIoAADUaghCAACo1RCEAABQqyEIAQCgVkMQAgBArYYgBACAWg1BWNKdO3c2b95cyc5YfFIa9klp2CclyJWODT0K44J9Ulq17RMEYUlXrlwJCQmpTE/GWJV8QVpNIopihd/YV9sIglD6i59qOUEQVCqVoUdhXDQajUajMfQojItara6eLz2uRUG4b9++dg/5+vqmpKQYekQAAGB4tSgI+/Xrd+HChQsXLqxYscLV1dXd3d3QIwIAAMOrRUGotXbt2rFjxxp6FAAAYBRqXRAWFRXt3r172LBhhh4IAAAYhVoXhNu3b+/du7e9vb2hBwIAAM+i/T+C8x+aqPtVNqFUX0F46dKlb7/9dtSoUb/99tuT+oSGhvbr1y8gIGDlypXaxoKCghkzZnTp0mXEiBGRkZGVea/U1NTVq1dPmDBh0qRJuu2FhYWzZs2SNxURESE34rooAIBJu6+hbBWJVbewQl/fR7hjx47U1NSoqCgXF5cyO9y4cePNN99cs2aNu7v76NGjbW1tR40aRURTp05NSEj48ccfd+7c2bt378jISDMzMyJijHEcp7sFbcuVK1cOHjxoZWV1+PBh3Q7Tp0+PiYn58ccfd+/eHRQUdPfu3cTExJSUlG7duunpUwMAgMnR7/cRfvDBB+bm5suWLSv91IcffqjRaORzwbVr165evfrMmTPZ2dmenp43btzw9fUloqZNmy5atOj1118noiFDhowYMUL+mYjmzJnj4OAwa9Ys7QYPHjw4bty4uLg4+WFOTo6np+eVK1f8/PyIqHnz5vPnz+/Xr19hYaGrq2s5Y/7ll19WrFjx5ptvyg95nn/rrbc8PT1L95TXEdrY2Dz9jqmxRFFUqVTW1taGHogREQRBo9FYWVkZeiBGRKPRiKJoaWlp6IEYEbVaTUTm5uaGHogRUalUPM/L50JE1G4nReWTIJFKImJkb0YKnojo9ABqaPfEjSiVyhInUWX0qbIhP6UrV66MGzdO/rlTp06TJ09mjN25c8fW1lZOQSLq2LHj5cuX5fD78ssve/furVarhw8fPm/evNDQ0LCwsHK2HxERYWlpKaegdlNDhw61tbUtf2AqlUqlUmVlZWlbcnNz3dzcSvdkjImiKIpipT90zSc+ZOiBGBHsk9KwT0qT9wb2iS5RFCPv07ls6WQadyqNi8p77Nn7D8sPqIXydptCoTDeIExLS3N0dJR/dnZ2VqlUOTk5qampTk5O2j7Ozs6pqanyz/7+/nv37g0ODt62bVtsbGx4eLhuz9LK2VT5XF1dW7duvXTp0gp7MsYkScJftbpEUeQ4DvtElyAICoUC+0SXQqHAGWEJPM8TzgiJREZXM9nxFHYilR1P5lOLH2WYnRl1qMt1cuV/i5QSC9j5V5S+9hwR2ZubKSpIugoYLAjt7Oy09ckKCgp4nrezs7O3t9ctWlZQUODg4KB92KJFi/79+69du3bdunXlpyARlb8pAAAwEhqJrmWxsER2IlU6mcqyH1Xf49ysqH1drpsb39WN6+jKmfFERNtiJCKyNycni6oZgMGC0MfHJyoqSv757t27Xl5eSqXSx8cnLS0tLy/Pzs6OiKKiol599VXtS+bNm3fp0qWTJ08OGzbMyspq+PDh5W8/IyMjNzdXzr+oqKj+/fvr8wMBAEBl5WnobNqD5DuRwop1rm16WFM3Nz7Ii2vvpHnRmTc303tOVWsQZmZmrlq16qOPPrKwsHjrrbfmzJkzbdo0W1vblStXjhgxgoh8fX3btGmzevXqjz766MaNG2fOnNmwYYP82rlz54aGhspXRPft2xccHGxpaakbkyXUr1+/Q4cOq1atmjFjxs2bN0+ePPnrr79W0+cEAIBSUorofLp0MpWFJbLLmUx6OFNTwVEzR66bO9fVjevpwfnYPrjQqVJRmZc8z7+qFCWyr8KryEw/5s+fr/suixYtYozdvn2biHJzcxljgiCMGTOmbt26Pj4+3bp1y8rKkl944cIFb2/vpk2bOjk5rVy5UrvBbdu2afswxq5fv3769Gn556tXr+q+V7t27eT2S5cu+fj4yJv6+eefKznyTZs2DR8+vDI9JUnKz8+v5GZrCUEQCgoKDD0K46LRaAoLCw09CuOiVquLiooMPQrjIk/TM/Qoql7Ufen3CPH940KzbRpardb+T7lW3XaHZsopYWu0mFlc9muLi4vVanU1DFK/yycqlJGRoVKpvLy8dBtFUYyLi3N1dX3+lQmiKMbHx7u4uFQ4WVRr8+bNISEhmzZtqrAnw/KJUrB8ojQsnygNyydKqzHLJ0RGd3KYfMHzSDKLL3gUMbZm1MmV6+rGdXPju7lzlooKNlVi+YT+GOweoazM5fYKhaJBgwZVsn2FQlG/fv0q2RQAAJSpUKBLGexkKjuRKp1IYTnqR0+5W1G7UrNdjI2BgxAAAEyR7myX4ylMpTPbpaEd19XtwT2/Zk4VLeIzAghCAAColORCks/5TqY+cbbLy55cPRvjz77HIAgBAOCJovOYnHwnUtitnEc3/Mx4eqkOF+T14J5fVS3pMwgEIQAAPKKd7RKWyI4kS+nFj56yM6OOTzPbxVQgCAEAajvd2S7HU1iuzmwXD2tq68LJK9xfqsPxJnbVs1IQhAAANdNXV6Ul18TZrRQzWpYxWfO+hs6lsbAk6UQKu5DxxNkuLzrVxOh7HIIQAKBmKhZYtoqKdBIuqfDB3b4nzXYJ8uICPPi6tWyFJ4IQAKAmy1ax9ZHSyVR2MJHF5D2a7WKtpJfqPDjt6+7OO5r8Uv5nhyAEAKhRvroqfXNV1EgkX+1cdkPSPlXHgrq6893duW5uXFsXI13eXv0QhAAANUF6MYUnSuFJbHuMpDvbRWtyM/7HLs/5zX01E4IQAMBUFQp0PIWFJUphSexq5qPK0S4W1N2dLxJZaAL7pJViZkueiKyUZX+ZAyAIAQBMicjoSiYLS3ww4VP7TX5WSurqxgV5PlrnMP+iGJrArJRV9gW2NRWCEADABETnsbBEFpbIwpOkrIff4c5z1NaFC/Ligjxr1Ar3aoYgBAAwUunFdCRZCktkBxLZPZ0Jnw3tuCAvLsiLC/TknZ98tvdJK8W05gorHOYrgj0EAGBEigQ6mcrCkqQSX+PuYkkve/BBXlwfL66+XaVu9lkpCSlYGdhJAAAGJjK6lEmHkrnDqUL5t/1AHxCEAACG8fhtPznlmAK3/aodghAAoPo86bZfA1sK9KQ+9RTl3/YDfUAQAgDoV6FAp8q67VfXkgIe3vbztNAQkbk5ar0YAIIQAKDq6a72O57y6LsdrJXUpazbfuqyasFA9UAQAgBUGe1tv7AkKfvhaj/d237d3TkL3PYzMghCAIDnor3ttz+BxeaXsdovyJNHbRdjhiAEACjbrxHSl5elMX783JdK3rrTve13KeNRkU/tbb/gFzgfWyx3MA0IQgCAsuWqKTqPZaoexFxlbvu1ceGQfiYHQQgAUJ5cNa26I+G2Xw2GIAQAeMyvEdLCy1KRQDlqJj/8NeLBU/6OXJAnF+TFBXjwDrX4K91rGAQhAMADWSraEy/9cEOK0VnqrjW+Cb+6O079aiAEIQDUdtF5LCSW7YyVjqcw8WECvujM1bGgY8lsjB839yUFETmY4/ZfzYQgBIBa6mY22xYj7Y5jFzMepJ+Co65u3CBv/vX6XGMHbtkN6Viy6GDONazctz2AiUIQAkAtUizSiRS2K0766x5LLHiQfzZKetmTG9qAH+zDO+LOX+2DIASAmi9LReFJ0q5YFhIr3dc8aPS25fq+wA305oJf4Mus8TnGjx/sw+GKaI2HIASAGuteHjuQyHbFSfsTmEZ60NjMkRvkww2sx3d1r2DNn4M57gvWCghCAKhpnnTzb2gD/vUGXD0bZBs8BkEIADUBbv7BM0MQAoAJe7abfwC6EIQAYHpi8tjOWLY7Xjqa/Cw3/wB0IQgBwGTg5h/oA4IQAIxa+Tf/XvFBzU94XghCADBGZd7887HlgnHzD6oaghAADGDIEcXtXGFnH8WLTo9dz8TNP6h+CEIAMIDEQhadR9rvtsXNPzAgBCEAGMzZNPZ75GM3/5wsKMiTH+jN4eYfVBsEIQBUn8EHxJvZrFCgtGKOiD449eCU0MuGe6M+N9iH7+nOKXHzD6oXghAAqklCAbuQwZILy/jO2529FW1ccP0TDANBCAD6pZZoV6y0NkI6kPDga2+9bEgtUnoxaSfLeFkjBcFgEIQAoC//5rJfI6RfI6S0IiIiCwW97s2/3Zjr7S523s3Sizkva3znLRgeghAAqliRQLvjpVV3pPBEJl8GberIvdOYH9uEr2tJRKTRiOVuAKBaIQgBoMpczGCr7kiboqQ8DRGRvRm94sOPbswHeZU87fsrQCIzC1wRBWOAIASA55Wtom0x0s+3pKtZDybCtHXh3vfnR/jytmZlv8TTmiwtkYJgFBCEAPCMJEaHktiqO1JIrKSWiIjcrejNhvz4JnwLZ4QcmAwEIQA8tYQCtvEuW3lHupfHiIjnKMiLe9+ff9WHN8MqQDA1CEIAqCyVSDvjpPWR0r74BwshGjtwI3y5MX68jy1OAcFUIQgBoGK3ctj6SGntv1JGMRGRpYJe9+bf9+cDvVAFG0weghAAnui+hjZHSesjpZOpD2bBNHPkRjfmx/vzdSwMOzSAKoMgBIAyyAshNt6VCgQiIgdzGtaQn+DPoxAa1DwIQgB4JLmQ1kdKa/6V7t5/MAumqxs3ujE/qhFvjaMF1FD41QaodSaeEC9ksJXdFO0ent6JjA4nsVV3pH9iJfnrcD2tubcbc+814X3tcQoINRyCEKDWichlFzOYXPwlIpf9GSX9GsHi8hkRKR4uhHjNh8fXIUEtgSAEqKWOJrPFV0RtOdAmDtwYP36MH+9qZeCBAVQzBCFAbSFfERUZ3cpmRPT5JZGIeI4Ge/OzWvGdXXEJFGqp2hWEkiSdPXs2ISGhXbt2DRo0MPRwAKrVnRx2MaPkl+JKjKY2RwpCrVaLglCSpDfeeMPBwaFJkyb37t2bMWOGoUcEUE0kRn9GSZH3Hzy0N6P7GtJOlvFzQApCrVaLgnDr1q116tRZs2aNoQcCUK3Ck9jMc+KlDEZETR25z9vyK25Jh5OZnwPXFosCAYhq0bSwo0ePmpmZBQcH9+7d++TJk4YeDoDe3cphb4aLQXuFSxnMy4b7pZvi+hvKoQ1q0b96gMqoRWeE2dnZmZmZe/fujY6O7tOnT1RUlFJZiz4+1CoJBWzhZWntv5LIyNaM/tOCn9VSYfXw931lN0WeBldEAR4wxiTIzc3NzMz08fFRKBRVuCl3d/c2bdqYmVZEF3MAACAASURBVJk1adLEzs4uKSnJ29u7SgYMYDzyNbT0uvjtNalIIDOexjXhF7ZVlFgRgQgE0KWXiyTbtm3jHnf9+vUSffr37699tmHDhtr27777rn79+gMHDmzcuPHNmzcr83ZLly5t3ry5Uqn8z3/+o9u+bNkyeVONGjW6fv36q6++evToUVEU7927l5eX5+Hh8fyfFMB4aCRadUfy3ar5/JJULNDQBvztIcpfupVMQQAoQS9BOHToUPbQ2rVr/f39W7RoUbrbhg0b5D7R0dFyS0xMzPz588+ePXvr1q0xY8ZMnTpV2/nKlSu6r7127ZokSfLPLVu2XLly5fDhw3U7xMbGzp079/Tp07du3XrvvfemTJkSEBAQGBgYGBg4ZsyY9evXm5mZVfHHBjAQRrQtRmq6XZhwQkwros6u3PFByq2BClRHA6gMvV8aXbt27fjx48t8SpKk/Px8W1tbbcuWLVt69erl5+dHRJMmTVqwYEFKSoq7u3t6evqgQYOWLFkip11YWNjbb7999OhRuWefPn2IaP369bob37p1a8+ePf39/Ylo4sSJn332WVJS0kcfffTRRx+VP+CYmJj9+/e3adNG2/Ltt9926tSpdE/GWFFREWMlF2bVZqIoqlQq7d8oQESCIGg0GlEU9bT9sxn8p1cUZzN4IvKzZ3NbCK/Vk4goP19Pb1gF5B0iCIKhB2JE1Go1EZmbmxt6IEZEpVLxPP+cJy3W1tY8X8Epn36DMCIi4vz583/99VeZz06aNGnixIl16tT5+uuvR4wYQUT37t1r3Lix/KyLi4uDg0NsbKy7u3vdunXDw8ODgoIEQfD29n7nnXd27Nghp+CT6G7K2dnZycnp3r17np6eFY7Z29u7ffv2ixcv1rY0b97cwqKM715jjPE8b2NjU+E2aw9RFM3MzKytrQ09ECMiB6GVVdVfoLydw+ZflLbFSETkac3Nb8OP9eOVvAkcSeUgtLS0NPRAjAiCsDQzM7PnD8LK0G8QrlmzZtCgQe7u7qWfWrZsma+vr0Kh2Llz57Bhw1588cVWrVrl5+fXqVNH28fa2jovL0/+2c/Pb//+/YGBgYIghISElHmKpis/P1/3LqDupsqnUCicnZ3btm1bmc4ABpFYwL54OCnURkn/9yL/aWuFHS72AzwTPa4oEgRhw4YNY8eOLfNZPz8/eVLo4MGDu3fvfujQISJydXXNycnR9snOznZzc9M+TEpKYoxZWFjExcVV+O7lbwrAROVr6JurUtPtwqo7Es/R+/581DCzr9sjBQGenR7PCHfv3s0YCw4OrrBnZmamfKewdevWP/zwg9x47do1pVLp6+srPzx27Njo0aN37Njh7OwcFBSk0WhGjRpVzjZbt269ZMkS+eebN28yxho1avRcnwfAoDQS/RohfXZRTC0iIhrozX3fUdEYCyEAnpsezwjXrVs3duxY3UXrP//8szxxJjc3d+7cuWFhYceOHZs4cWJ8fPwrr7xCREOGDElKSlq8ePH58+enTp06duxY+W5TWlraiBEj/v77706dOvn5+R04cGD27Nl37tyRN3vjxo1t27ZFR0dHRERs27ZNbn/99dfT0tK+/PLL8+fPT5kyZcyYMbqzcgCMXL9Qod0/Qnrxg4e74qRm24UJJ8TUIurkyh0bqNzVR4kUBKgS+joj1Gg09erVKzFf1MvLq7CwkIjMzc3z8/O/+uorURSbN29+9uxZV1dXIrK2tg4PD1+4cOHevXt79er16aefyi90dXW9du2as7Oz/NDf3//q1avah1FRUWFhYfK5Y1hYmL29vb+/v5WV1aFDh7744ovQ0NCAgIC5c+fq6ZMC6MO1LEoqZBqJnUmjGefEEymMiJo4cAvb8UMa8AhAgCrEYfZ/CZs3bw4JCdm0aVOFPRljhYWFmDWqS14+gVmjup5t1qjXn0JSIRvoze2OY0TkYklzWysmN6sh3xqPWaOlYdZoaVWyfKIyjLHEGkCt1S9USC8miVFKESOi3XGM58jdijs1WOmDS/sA+oEgBDAi8hVR3RaJUVIhM+MZES6IAugFghDAWDCikY24H24wtUQKjhMZ29dXUdeSIyL5/wFAHxCEAEYhrYjGHhP2xDMiersRH5bEkguppTPnaY0IBNCvGnHnHcDEHUxkrXdo9sQzF0sK6a1YH6BA+gFUG5wRAhhSsUgLLolLrkkSo0BP7veeCi8bjoj29VVoJFwRBagOCEIAg7mdw0YcFq9kMjOe5r3Ef/aSQrtCsKUzIhCgmiAIAQxjfaQ06aRYKFATB+7PlxVtXJB8AIaBIASobunFNO6YuCtOIqK3G/E/d1XYomQ2gOEgCAGqVVgie+eomFTIHMxpZVfFcF9MWAMwMAQhQDXRSLToirjwsiQxetmDWx+geMEGl0MBDA9BCFAd7uSwEYfFy5lMydO8l/h5LymwQgLASCAIAfRuYzQ37bxQIFB9O25jgKKLGzIQwIggCAH0KEdNE47T1hgFYV4MgLHCjXqAqvTlZan3PuFoMiOiQ0ms+V/C1hhmb8Y2BCjWByAFAYwRghCgKl3PZmGJLKmQLbgk9t4nJBawjnXpdH9xZCP8WwMwUrg0ClD1FlwUI+6TPC9mdgsmCYYeEAA8GYIQoAp8eVk6miIR0fl0RkQR98lKSc2duJc9eAUnSoYeHgCUA0EIUAXkK6K6LUUCnU9nqUXsSS8BACPxKAjDw8P/97//VfJlK1as8PT01M+QAEzPxy34lEI6liJxHDFGc1srenpwRNTCmSPCCSGAUXsUhHFxcYcPH27WrFmFrzl79uySJUv0OSoAU5JcSJNPiefTmZ0Zta7DH0+RWjhTkNeDxYICbhACGLfHLo22bt362LFjFb5GoVDobTwAJuZaFht0QIzLZw3tuF3Bis8v4fwPwMQ8CkIfH58ePXpU5jWvvfaanZ2d3oYEYDL2xbPhh4T7Gurixu0IUrpa0dzW/HtN+Bb4NkEA0/EoCHv16tWrV6/KvGb79u16Gw+AyfjhhvTRWVFiNNyX/7WHwlJBRNTCmWth6IEBwFPBrFGApyZINOW0uOK2xBHNb8MvaIObBQAmrLwgzMnJiY6OzsrK0m0MCgrS85AAjFqWioaECYeTmY2S/ghQvFYfJWMATFvZQZienj569OjQ0NDSTzGGdVFQe929zwbuF//NZZ7WXEgfRTsX3AsEMHllB+GECRMuXbr066+/bt++3c3N7dVXX92zZ8/WrVt/+umnah4fgPEIS2RDw4UcNbVy5nb2UXjbIgUBaoIyruowxvbv37906dJ33323bt267u7ugwYNWrly5dy5c7/66qvqHyKAMVjzr9R/v5Cjptfr86cGK5GCADVGGUGYlpZWWFjYvn17IrKwsMjLy5Pb33nnnevXr0dGRlbrAAEMTWT0yXnxveOiRqIpL/LbAhXWmGQGUIOU8Q/awcGB4zg5/7y8vI4fPy63q1QqIiooKKjO8QEYVr6GRhwWd8VJ5jyt6q54pzGmxgDUNGX8q7a0tGzatOmFCxeIKDg4+PDhw8uWLTt27NiECRPs7Oz8/PyqfZAA1WrUEbH3PiG1iBIKWI/dwq44qY4FHeinRAoC1EhlX+KZM2dOZmYmEXXo0OG9996bPn06EVlZWa1evdra2rpaBwhQ7U6msnt57FSqNOmkmFpEjR243X0Ufg64KQhQM5UdhCNHjtT+/PPPP8+bNy8mJqZp06ZOTk7VNTAAAxtxWCwWqbcXtzVQ6Whu6NEAgN6UDMK9e/f+8MMPERERrq6u/fv3nzNnjpmZmYeHh4eHh0HGB1BtRh0R5a8PTChgRFQsUj1bkhipREOPDAD06bEgPHbs2KBBg8zNzf38/KKjoxcsWJCenr58+XJDDQ6gOslXRHVb4vMpPp8VCYwI10UBaqzHbv6vWLHCzc3tzp07V69eTUxMHDZs2Jo1a9RqtaEGB1Cdfu+hGOjNEz1IvQ09FQf7KQ/2U7pZIQUBarLHgjAyMnL06NE+Pj5EZG5u/sknn6hUqtjYWAONDaD6iIx+i5R2x0kWCnK15IioqzsX5MUFeXFWWDUIUKM9FoQZGRlubm7ah+7u7kSUnp5e3YMCqF6CRO8eFX+NkGyUtLuPEuvlAWoV/IuH2k4t0fBD4o57koM57Q1WdnHj/uipKBYJV0QBaomSQbho0SLt7BhRFIlo6NChlpaW2g5RUVHVNjgAfSsU6LWDwoFE5mRBoX2VHepyRNTNHREIUIs8FoTdunVLTU3VbWncuHH1jgeg+hQINPiAcCiJuVnRgX7Kls7IP4Da6LEg3LBhg6HGAVDNctTUP1Q4ncY8rCmsv7KZI1IQoJbCPUKojbJU1DdUOJ/OfGy58P4KX3ukIEDt9WjWqFqt1n7jUvmys7MlSdLbkAD0K7WIAvYI59NZEwfuxCCkIEBt9ygIN27cOGDAgMq8xsXF5e7du3obEoAexeWz7ruF61msmSN3aIDiBRukIEBt99il0aKiotu3bxtqKAD6di+PBe4Vo/NYGxduf1+li2XFLwGAGu+xILxw4UKzZs0MNRQAvbqTw4L2iYkFrH1dLrSv0tnC0AMCAOPwKAiDgoJCQkIq+TIvLy/9jAegKq24LR1OYpOa8a6W1HufkFxIPT24XX2UdmaGHhkAGI1HQVivXr169eoZcCgAVe5COtsWIzV1op9uSpkq6leP+ytQidqhAKALhwSo+ZZck4oEGuTNbwtUWCgMPRoAMDIIQqiB5CuiRHQ8hRFRkUDeNpwFT6fS2MsemCYKAI9BEEINJF8R1W2JK2BxBayfN4cgBIASEIRQA01qxnd05eZeENOLiYgmNuV7eXJE1M4FKQgAJSEIoQbyd+DePy6mF5ObFaUWUfu63NAGfMUvA4BaCUcHqGlERiOPiJczma89F+iJ33AAqMATzwj37dsXEhISHx+vVqt12w8ePKj/UQE8u6mnxZ2xkosl7QtW5Gro1focrogCQDnKDsIZM2YsXbrU3d3dz8/P3Ny8mscE8My+uSr9dEuyUlJIb2VjB9wXBICKlRGEoij+/PPPEydO/PHHH5VK3EQEk7EtRppzQeQ52hCg6OKG/AOASikj5zIyMgoLC8ePH48UBBNyIoWNPiJKjL7vpHi9Pm4NAkBllXG8cHFxcXNzS0pKqv7RADybqPvs9TChWKQJ/vz05khBAHgKZRwyFArFd999N2/evPj4+OofkF5FRUVNnjx50KBBa9euNfRYoMpkFFO//WJ6MQ2ox/3UFSXUAODplH3xMyQkJCkpyc/Pr1mzZs7OzrpPme6s0YyMjMGDB//444/+/v7JycmGHg5UjSKBXjkoROayti7clkClAncGAeApPfEuYKtWrapzHNVg9erVb7/9dv369TUaTdu2bQ09HKgCEqO3j4qnUll9O253sNIGN7UB4OmVfeTYunVrNY+jGty6devOnTsxMTERERFdunRZtGiRoUcEz+vjs+JfMZKDOe3srXC3MvRoAMA01aI/oXme79q167JlyzQajbe396xZs+zt7Q09KHhqe+PZbxFS/3qcSqL/3pDMePorSNnCGZdEAeAZPTEI7927t2zZsqtXryYkJLi7u7do0eL//u//mjVrVpmNSpK0Zs0a7cPmzZt36dKldLezZ8/u27fP1dV11KhR2kwqKirauHFjfHz8yy+/HBAQUJm3U6vVN27cuHbtWpMmTTp37qxt124qICDg5Zdfbty4McdxRGRmZmZvb19QUIAgNEWRuWxbjKSS+D1xEke0prsi0BMpCADPruyJ5hcuXGjVqtXy5cuLi4tbtGjBGFu3bl2bNm32799fmY0KgjBhwoQzZ85cvHjx4sWLZc4+/fvvvwcMGKBUKg8dOtS1a1eVSkVEjLGgoKDt27dbWlqOGjVq9erVlXm74cOHDx06dN68edu3b9c2MsaCg4O3bt1qaWk5evToX3755d133922bdvevXuXLFni7u7u4eFRmY2DcdoXL4mMFrZTjG6MxRIA8HxYWTp06NC0adO7d+9qWxITE7t27ert7S2KYpkv0SWnWl5eXjl9Wrdu/fvvvzPGRFFs1arVn3/+yRg7cOBAvXr1VCoVY2zv3r0+Pj6CIDDGsrKyZs6cqVar5ddKkvTZZ5/FxcXJD4uLixlj77333kcffaTdfnh4uJeXl7yp/fv316tXTxCEyMjIxYsX//TTTwUFBU8a2IYNG4KDgy88dOnSJe37liBJUn5+foV7o1YRBKGcffs89sRJQ8OEoWFCs20aWq2m1eoGmzRDw4Rf/634F9KwNBpNYWGhoUdhXNRqdVFRkaFHYVxUKpV8vAKt4uLiJx1+q1YZl0ZzcnLOnTu3f/9+X19fbaOnp+cvv/zSvHnzf//9t2nTppWJ2I0bN5qZmXXt2rVJkyYlnsrMzLxy5Uq/fv2IiOf54ODg8PDwt95669ChQ0FBQXJ106CgoKSkpKioKD8/P3t7+/j4+OHDh2/evFmpVH744YdXr16dMWOGvDULC4vS737o0KHAwEB5U7169UpLS4uIiGjatOns2bPLH/a9e/fOnTs3fvx4bcvXX39d5qVdxlhRUZEkSaWfqrVEUVSr1aIoVvmWb6Qpt8U89usak89i8pmLmfCGh1Dlb1eFBEHQaDSCYNSDrGYajUYURY1GY+iBGBH56w1Q21mXSqXied7MzOx5NmJtba1QVLC8uIwgLCoqIqK6deuWaHd1dSWiwsLCyrx3hw4dbt68mZ2dPXXq1K+//nry5Mm6z6akpCgUChcXF/mhu7v79evXiSg5Odnd3V1uNDMzq1OnjrycUaFQ/P7778OHDx8+fLirq+utW7dCQ0NtbGzKGUBycrI8YCJSKpUuLi5JSUmViXBfX9/g4OBNmzZV2JMxplAoyh9GbSOKokqlsra2rvItv9aI1Xdmy25Ip1MZEfV+gXuvCU9Eje2VdnZGfY9QDkIrK8xqfUQOQktLS0MPxIggCEszNzd//iCsjDKC0NXV1cXFZe3atcuXL9dtX7t2rbm5eePGjSvcqLm5+dmzZ+WfDxw4MHjw4DFjxugeHHmel09I5dkroijKdU3ldm03URS1SW5mZrZp06YmTZrk5OTExMRUGD/lbApMUWMHbmOUdDqVWfJULFEzR3zXLgBUjTKCUKFQzJw5c+bMmZGRkcOGDfPw8EhPT9+1a9fff/89derUp51p+fLLL6vV6tjYWN2zMQ8PD0mSUlNT5RkrycnJnp6eROTp6RkbGyv3KS4uzs7OltuJiDE2bdq0+vXr16lTZ9y4cZs3by7/zwRPT8/IyEj5Z5VKlZWVpd0UmKId96SFlyUFR6P9+FV3cDkaAKpM2csnPv74YyL66quvDhw4ILfY2trOmjXriy++qMxGBUHQfnNFeHi4hYVF/fr1iSgpKSk/P9/Pz8/R0bFr1647duz44IMPNBrNnj17vvnmGyLq16/fG2+8UVBQYGNjs3v37kaNGjVs2JCIGGNTpky5fv36vn37rKys3n77bfl+YTlZ2K9fvxUrVuTn59va2srzbipzLgvG6VYOe/fog2+WGFiPC/LiGtsb9eVQADAhZQchx3EzZsyYNm3a9evXs7KyHBwcmjdvXvmbHOvXr1+zZk3Lli2zs7P37t37ww8/yK9dvXr1yZMn5XD9/PPPhw4deuPGjevXr7u5uQ0cOJCIunbt2rFjx549e3bu3Hnz5s0rV66Ur51mZmbm5uZq7wv+/vvvkydPjouLk6fz/Pbbbxs3brx9+7ZCobh27dr48eOHDRvWqVOnbt269ezZs0uXLlu2bFm+fLm8KTA5mSoafEC8r6G3Gz34Zgn5G3cBAKoEp3sjraoUFhaeOnXq3r17tra2nTp1kk8HiSgmJiY3N7d169byw+jo6CNHjjg7Ow8YMEB7bieK4v79+5OSkrp16+bv71+Zt4uKioqJidE+bNSokfyOkiSFhoYmJSV17dq1kjNdiWjz5s0hISGVnCxTWFiIyTK6qnyyjEai4H3C4WTW1oU7PlBpZYKlkDBZpjRMlikNk2VKq5JZo5XxKAgTEhKuXbvm7+/fsGHD8PBweS1gaf3799f3mAwLQfg8qjwIJ50UV96WPKzp/CtKLxuTPBFEEJaGICwNQVhatQXhoz+wDx48OHbs2MWLF8+ePXvEiBFpaWllvkAfZ5AAZVoXIa28LVkq6J/eppqCAGD8HgXhq6++2q5dO3kZ39GjR7HWFQzrRAqbdEIkop+7KjrURQoCgL48CkInJycnJyf550renAPQk9h89ka4oJZoZkt+jB/WCwKAHpV9iOnYseOlS5dKNF6+fFm36BqAnhQJ9EaYmFZEwS9wi9ujDAIA6FfZQRgbG1tcXFyisbCw8N69e3ofEdRujOjdY+LFDNbEgdvcS6nANVEA0LOnuOh06dIlNzc3/Q0FgIg+vyRujZbszejv3gpHTKADAP17bFnWunXrFi1aREQZGRlDhw7Vndycl5eXnp7+/vvvV/cAoTb5J1ZaeFniOdrUS9nMESeDAFAdHgtCb2/voKAgIvrjjz/at2+ve/7n4ODQokWL4cOHV/cAoda4lcPeOSJKjL7rqOhfDykIANXksSAMCgqSg1CSpI8//rj09wgC6IluHbWPWmCaKABUn7IrVq1evbqaxwG1mUaioWFC1H3W1oX7pRumiQJAtSr7T+8xY8Z88sknJRqXLVsml8YGqFpTT4uHk5mHNYX0VphiNVEAMGllBKEoips2berZs2eJ9sDAwL179z6p9BrAs/k1QlqBOmoAYDhlBGFaWppKpWrQoEGJ9gYNGjDGEhISqmVgUCucSGETT4hE9BPqqAGAgZQRhDY2NhzHab8pXkteTY8i+lBVdOuojUUdNQAwkDKOPvb29i+99NIXX3yhW1xGFMX58+e7u7v7+flV4/CgxtLWUevjhTpqAGBIZc9M+Pbbb4ODg/39/d96660XXnghJSXlr7/+un379saNGxUKHLPgeTGiMQ/rqG0JRB01ADCksoMwMDDwwIEDn3zyyTfffCN/AWGLFi3++eefV155pXqHBzXTF5ekLaijBgDG4Ylz1Xv16nXu3LmcnJysrCwHB4c6depU57CgBvsnVvrisshz9CfqqAGAEahg0Zajo6Ojo2P1DAVqA906agNQRw0AjMATg7C4uPj48ePR0dE5OTm67bNmzdL/qKBmykIdNQAwPmUH4Y0bN/r161fmkkEEITwbjURDUEcNAIxP2X+VT5gwwcnJ6caNG6NHj/7000+Tk5NXr17t7e194MCBah4f1BioowYAxqmMA5IgCOfPn//nn39efPFFnudFUXR3dx8/fryjo+Po0aPj4+OVShzG4Olo66jtCEIdNQAwLmWcEWZkZGg0mkaNGhGRra1tbm6u3N63b9+UlJQ7d+5U6wDB9J1MfVRHraMrUhAAjEsZQeji4qJUKuXi2vXq1btw4YLcHhcXR0Q8jzkO8BRi89nrYYJaohmoowYARqmMA5NSqezQocORI0eIaMiQIZcuXRo1atT3338/dOhQb2/vxo0bV/cYwWTp1lH7CnXUAMAolf0X+pIlS1q2bElEDRs2XLFixZEjR/7zn//wPL9lyxYzM7PqHSGYKtRRAwCTUPa0ly5dumh/fu+999577z2VSmVhYVFdo4KaAHXUAMAklHFGmJqa6uzsXGKlBFIQngrqqAGAqSjjjNDa2jonJ8fa2rr6RwM1w+2HddSWoo4aABi9Ms4I7ezsgoKCQkJCqn80UANkq7lBD+uo/Qd11ADA6JV9j3DatGnjxo3Lzs4ePHiwh4eH7pKJtm3bVtfYwPQIEo04xkfdZ21QRw0ATMRjQTh+/Pi+ffsOGTJk7Nixqampa9euXbt2bYkXyF9PCFCm6efYsTQeddQAwIQ8dqw6ePCgr68vEW3dulWtVhtoSGCqfo2QVtxmch21F1BHDQBMRNl/tPfo0aOaxwGmTltH7b/txY6uWGwKACYDcxmgCmjrqH3cghvdUDL0cAAAnkLJM8IjR45IUnkHsk8//VSf4wHTo1tHbVFbTsA1dQAwKSWD8MCBA+V/6SCCEHSVqqMmCoYeEgDAUykZhB9//PHEiRMNMhQwRQsvP1ZHTRQNPSAAgKdUMgidnZ3liaMAFfonVvr8EuqoAYBpw1IveEaoowYANQNmjcKzyFKRXEdtFOqoAYCJe+yM8H//+1+jRo0MNRQwFYJEQ8MF1FEDgJrhsSB85ZVXDDUOMCFTz4iHkpi7FYX0Vljj4joAmDhc1IKn82uE9PMtyVJB//RGHTUAqAkQhPAUtHXUfuqq6OiKFASAmgBBCJUV96iOGj/WD785AFBD4HAGlaJbR+3rDpggAwA1B4IQKibXUbuQwfwe1FEz9IAAAKoOghAq9qiOWpDC0dzQowEAqFIIQqhAiE4dtRedcDIIADUNVoFBeW7nsNFHRInREtRRA4AaCmeE8ERZKhr8sI7ax6ijBgA1FI5uUDa5jtpd1FEDgJoOQQhlm4Y6agBQOyAIoQy/RUg/oY4aANQOCEIo6VQqm3hSJKLlXVBHDQBqPgQhPCYun70WJqhE+rgFP64Jfj0AoObDkQ4e0dZR6406agBQayAI4QFGNPb4gzpqW1FHDQBqjVoXhJIk5eTkGHoUxujLy9LmKMkOddQAoJapXUH4448/tmnT5o033pg8ebKhx2JcQmKlBXIdtZdRRw0AapdatEDs7Nmz27dvP3funLk5znceo62j9m0HxUBvpCAA1C61KAi3bNnSr1+/RYsWmZmZTZo0qU6dOoYekVHQraM2o2XtukIAAEC16tJoYmLihg0bgoKC6tat26dPH8aYoUdkeKijBgBQi4LQyclp5MiR3bt3nzBhQkFBQXJysqFHZHioowYAoJcgjIyMHD9+fIsWLV588cVJkyZlZGSU7jNnzpzeD7399tva9hMnTnTr1q1Ro0bjxo27f/9+Zd7u4MGD06ZN69u378qVH1UWlgAAIABJREFUK3XbT5061b1790aNGo0ZMyY3N7dr166JiYlEpFKpcnNz7e3tn+9TmjxtHbUdqKMGALWYXoIwIiKicePGGzZs+Ouvv+7du/fOO++U7nPlypX27dvPmjVr1qxZEydOlBtzc3MHDx48fvz4I0eOZGdnT58+XdtfpVLpvlz34ZUrVxwdHVUqVWRkpLYxLy9v0KBBY8aMOXLkSF5e3tSpU9988824uLjhw4cHBATMmDHD1ta2ij+2SdGto9YJddQAoBbj9H2r7OTJk3379s3LyyvR3r9//5EjR44cOVK38Zdfflm/fv3JkyeJKCIionXr1ikpKfb29unp6Z07d969e7e/vz8RJSYmBgUF7dixQ34oe//99+3s7L777jv54Zo1a9asWXPmzBkiioqKevHFF1NSUhwdHZOSkqytrR0dHZ804OXLl//0008DBw7UtowZM8bX17d0T8ZYYWGhjY3N0+4Tg4svoC57ufRibloz9nXbqvwFEEVRpVJZW1tX4TZNnSAIGo3GysrK0AMxIhqNRhRFS0tLQw/EiKjVaiLCnHZdKpWK53kzM7Pn2Yi5uTnHVfC3vt7vC505c6ZFixZlPvXNN98sX77c399/9uzZfn5+RHTr1q22bdvKz/r5+SkUiujo6NatW9etW/frr78OCgrav39/nTp1+vTpM2nSJN0ULE13U76+vpaWllFRUW3btvX09Cx/wEql0tzc3MnJSdtiZWXF82WcOjPGeJ4v8yljViTQ8KOUXkxBnrS4LcfzVXk6aKL7RK/4hww9ECPC87z8q2LogRgReW9gn+iqtn87+g3Cq1evfvnll6GhoaWfeuedd9zc3CwsLDZt2tSlS5cbN264u7tnZGQ0aNBA28fR0TE9PV3+eciQIYIg9O3b18rKavLkyVOmTCn/rTMyMry8vMrcVPkcHR2bNWs2Z86cCnsyxszMzJ7zr5VqxogmnBAvZkp+Dty2IKVVVf/1yfO8JEmmtU/0Tf5rFPukhOf/S7+GkS/OYZ/okiSpen5P9BiEt2/f7tev36pVqzp27Fj62WHDhsk/dO7c+dSpUzt37nz//fcdHR0LCgq0fe7fv+/s7Kx92L17d47jsrKygoODK3z38jdVa6GOGgBACfo65YyIiOjTp8+33347dOjQCjs7OTkVFhYSka+v7+3bt+XGpKSkwsJCHx8f+WFKSkqfPn0+/vjjlStXBgUF3bx5s/xt6m4qJSUlLy+vfv36z/xxagbUUQMAKE0vQRgdHR0YGDht2rQBAwZkZ2dnZ2fLZ/2hoaE///wzERUWFh45ckQQBMbYX3/9deLEicDAQCJ66623Tpw4ce7cOcbYkiVL+vXr5+LiQkQZGRk9e/acOHHilClThgwZ8v333/ft2zcmJkZ+u6KiouzsbJVKVVxcnJ2dXVxcTETDhw8/ffr0mTNnGGNLly4NDg52dXXVx4c1Fbdz2DtHRYnR1+1RRw0A4BG9XBo9duyYubn5zz//LMceEV27ds3GxubWrVvnz5//4IMPNBrN5MmTIyMjzczM6tWrt379enlCjYeHxy+//DJw4EBBEJo0abJlyxb55c7OzsuXL+/du7f88M0336xbt6522suKFSt++ukn+efQ0NCZM2dOmDDBzc1t9erVgwcPFgTBz89v8+bN+vikpkKuo5arRh01AICS9L58ohyiKAqCYGFhUfqpwsLCqpqC/7Sb2rx5c0hIyKZNmyrsaSrLJwSJgkOFQ0msjQt3fKBSrxVksHyiNCyfKA3LJ0rD8onSqmT5RGUYsqyWQqFQKMqub1mFR1IclKejjhoAwJPhKlkN91uEtBx11AAAngxBWJOhjhoAQIUQhDVWXD57PUxQifSfFvy4JvgPDQBQNhwfa6Yigd4IE1OLqLcX93V7fNEgAMATIQhrIEY09rh4IYP5OXBbeimV+I8MAPBkOEbWQIt06qg5lbE4BQAAHkEQ1jQhsdJ81FEDAKg0LCurUbR11L7pgDpqAACVgjPCmkNbR21kI34m6qgBAFQODpc1hCDRm+HC3fusjQu3qhumiQIAVBaCsIaYfkYMRx01AICnhyCsCeQ6ahaoowYA8PQQhCYPddQAAJ4HgtC0aeuofdSCH486agAATw+HThNWJNCQ8Ad11L5BHTUAgGeCIDRVch218+msgR23CXXUAACeFQ6fpkpbR21XH0Ud1FEDAHhWCEKTtC+eLUAdNQCAqoAVZ6bnTg5767Agoo4aAEBVwBmhiclS0aADYq6ahjbgZ6COGgDAc8OR1JSIjEYeFu7eZy/V4X7rqcDJIADA80MQmpLpZ8TQBOZuRTv7oI4aAEDVQBCajN8jpR9vSuY8bQ1EHTUAgCqDIDQNp1LZhBMiEf3UVdHdHSkIAFBlEIQmIKmQDQ0XUUcNAEAfcFQ1dkUCvXpQTCpkqKMGAKAPCEKjxojGPayj9ufLqKMGAFD1cGQ1aouvSJse1lFzsTT0aAAAaiIEofEKTWDzL6KOGgCAfmExmpG6k8OGHxJERl+3Rx01AAA9whmhMdLWURvSgJ/ZCv+NAAD0CAdZoyMyGnXkQR2131FHDQBAzxCERmf6GXFfPOqoAQBUEwShcZHrqJmhjhoAQHVBEBoRbR21n1FHDQCguiAIjYW2jtr05qijBgBQfXDANQq6ddS+7YA6agAA1QdBaHioowYAYEA46Boe6qgBABgQgtDAUEcNAMCwsE7NkFBHDQDA4HBGaDCoowYAYAxw/DUM1FEDADASCELD+OhhHbUQ1FEDADAoBKEB/B4p/e9hHbV6qKMGAGBQCMLqdjoNddQAAIwIgrBaJRWyIWGoowYAYERwLK4+2jpqQaijBgBgNBCE1US3jtom1FEDADAaOB5Xk69QRw0AwCghCKtDaAL77KLIc7TxZQXqqAEAGBUsYdM7bR21r9orBnnjLw8AAOOC47J+ZevUUZuFOmoAAMYHh2Y9EhmNRB01AADjhiDUI7mOmhvqqAEAGDEEob6sRx01AABTgCDUi9Np7P0TIhH91EXRA3XUAACMGIKw6mnrqE1rzr/njz0MAGDUcJiuYrp11JagjhoAgNFDEFYl1FEDADA5OFRXJW0dtZ2oowYAYCIQhFVGt45ac9RRAwAwEVjdVjVQRw0AwEThkF0FslU0+CDqqAEAmKRadNTetWtX586dmzVr9umnnwqC8Pwb/PuetO4un1pEI48IkbmoowYAYJJqy6XRyMjIkSNHbty4sUmTJiNGjHBwcJg5c+ZzbnPxVXYpQ3k6C3XUAABMWG05I1y7du0rr7wyaNAgPz+/BQsWrFy5sqq2vCkKddQAAExYbTmFuXHjRu/eveWf27VrFxMTU1BQYGNj8wyb+vuelFFMRJRY8KDlLV/+Tg5r5shhyQQAgMmpLUGYnp7u4OAg/+zo6EhEaWlpDRo0KN3z7t27f//9t5OTk/yQ5/k//vije/fu2g5fXDS/mv3YmfT6SGl9JDWzLmrlJOnrA5gIURTVarUoioYeiBERBEGj0VTJbekaQ6PRiKKo0WgMPRAjolaricjc3NzQAzEiKpWK53kzM7Pn2Yi1tbVCUUGRr9oShI6Ojvn5+fLPeXl5RKSNuhJ8fX0HDhy4Zs0abYuDw/+3d+dRTVz7A8BvWMIiBMhCSBAQoRFQFBSwigR4IHEBWdT6RBHcoKXV1tfqO10sjx5P1QpqcX/2PHGpClWRKsgmCgKKIqAWkEWUJUgkRGRNgGR+f9z35peTBERZTe7nr8ydO5dvbiZ8MzN35hqoqf1/5ltpJZnbiQEAEmolb3pBoIUaTQcAAMzJuvp6qn52VCwWi0QiXV3d8Q5kAoGJUEdHZ7wDmUBgItTWRqdQ/h9KhPKIROLwE+FQqEoinDp1amVlJXxdWVlJJpPhcaE8AoFAJBIHSpMAgO8d/psUi/hYMR/7wVFtNlXV8x+CIMiHS1UGy6xduzYhIaGhoUEikRw4cCAkJGS8I0IQBEEmBFVJhK6urlu2bLG3t6fRaJ2dnVFRUcNvc5GxcKn+SzRARhqPx3v48OF4RzGxNDY2Pn78eLyjmFhevHhRVlY23lFMLDU1NVVVVeMdxcRSUVHx/PnzMfhDqpIIAQA7d+5saWmpr69PT08f5Mzn0M3lZ4OzkeYqf11Q2q1btw4fPjzeUUws6enp//73v8c7ioklOTn5zJkz4x3FxJKYmHjx4sXxjmJiOXfu3JUrV8bgD6nKNUJIU1NzBK+7Yhg2Uk0pDdQn8lCfyEN9Ig/1iUJj0y0qdESIIAiCIPJQIkQQBEFUGgEdj8uIjY2NiYmZMWPGW2vy+fzGxkYHB4cxiOpD0dzczOfzh9J7qoPL5ba3t9va2o53IBNIfX29UChksVjjHcgEUltbi2GYlZXVeAcygVRXVxOJRAsLi+E0EhgYGBkZOXgd1bpGOBRr166l0+kmJiZvrSkSiVpbW5lM5hhE9aHo6el58+bNUHpPdXR2dvb09NBotPEOZAJpb2/v6+ujUCjjHcgE0tbWhmHYiIzjUxoCgUBdXR1/KNj7UfgEMRnoiBBBEARRaegaIYIgCKLSUCJEEARBVBpKhAiCIIhKQ4kQQRAEUWlo1OhgGhoasrOzjY2NFy5cqKGhoK+6u7vT0tKEQiGHw5EeAldeXl5YWGhlZcVms8cw3rHQ3NyclZVFIpE4HI6WlpZ8BZFIlJ6e3t7e7u3tjQ8fvX//fnt7O3xNIpFcXFzGLuLRV11dnZ+fb25u7unpSSAoeORed3f348ePNTQ0nJycpMuLi4sfPXo0ffp0JesQAEBdXd3t27fpdLq3t7fC745QKHzy5El/f/+8efPwwry8PKFQCF9TqVQluzfpyZMnRUVFLBbL1dVVfq1IJMrLy+NyuRYWFmw2W3pHKigoqKysnDNnzsyZM8cw3rFQWVlZUFAwZcoUDw8P+e9OX19fQUFBXV0dk8n09PTEpxXMzs6WSP47+aupqekI3JuEIQO4ffu2kZHRhg0b5s6d6+Xl1d/fL1Ohra3N1taWw+GsXr2aTqdXV1fD8vj4eBqNFhERYWNjExERMeaBj6KSkhIymRwaGuru7u7s7NzT0yNToaenx9nZmc1mh4aGUiiUkpISWO7i4uLo6Ojt7e3t7R0ZGTnmgY+iy5cvUyiUzZs329vbr169Wr7CoUOHiEQimUxms9nS5b/88oupqWlERISFhUVUVNQYhTsmbt68SSaTN27c6Ozs7OPjIxaLZSqcP3+eSCRSKJTp06dLl5ubm8+dOxfuJz/88MMYhjzqjh8/TqfTIyIirK2tv/rqK/kKTCZzwYIFYWFh06ZN8/T0FIlEsPzrr7+2srKKiIhgMBhHjx4d26hHV2JiIpVKDQ8PnzFjRkhIiHyFGTNmzJ07NywsbObMmXPmzOno6IDlRCKRzWbD/SQ2Nnb4kaBEOCA2m33w4EEMw4RCobW19fXr12UqxMTEeHl5SSQSDMM+//zzzZs3YxjW19dnamp648YNDMNevXqlp6dXVVU15rGPlqCgoJ07d2IY1t/f7+TkFB8fL1MhPj5+9uzZ8EdDVFRUYGAgLHdxcYF9omQkEsm0adMuXryIYVhbWxuFQikqKpKp09zc3N7efvz4celE2N7erq+vD38oVFdX6+jotLS0jGXko2r+/PlHjhzBMKynp8fS0jItLU2mQktLS1tb26VLl+QTIf7jSZkIhUIajZaTk4NhGJfL1dHRqaurk6lTU1MDX3R1dTGZzMuXL2MY1tDQoK2tXV9fj2FYfn4+hUKR//X5gRKLxVZWVvBtvn792sjIqLS0VKYO3ie9vb02NjYnTpyAi0Qi8eXLlyMYDLpGqNibN29yc3NXrFgBANDS0vL19b1+/bpMnevXry9fvhwezq9YsQJWKCkp6ezsXLhwIQCARqO5ubmlpKSMefijAsOwlJQU2Cfq6uoBAQEK+yQgIACewVixYkVqaip+BqOioiIjI6OxsXGMwx5VVVVVtbW1/v7+AAADA4OFCxfK9wmdTtfX15cphKcN4ak/a2trGxubzMzMsYl5tLW2thYUFCxfvhwAoK2tvXTpUvk+oVKpA90l/ejRo8zMTB6PN+qBjqHCwkICgeDm5gYAYDKZc+fOTU1NlamDP1NGV1eXRCLBCevT0tKcnJzMzMwAAPPnz9fS0rp79+7Yxj5aKioqGhsbfX19AQCGhoZeXl7y+wneJ5qamlQqFfYJVFhYmJ2d3draOiLBoESoWFNTk5qaGoPBgIumpqZcLlemDpfLNTU1xSvweLz+/n4ul8tgMPBz2Qo3/EDx+XyRSCT9lt/aJyKRiM/nAwAmTZqUmpoaGxtra2s7IpNBThBNTU1UKlVb+7+TUg794+ZyuZMnT8YXlWk/aWpq0tTUNDY2hovv9NYMDQ0vXLiwZ88eKyurQ4cOjVqMYw1+L/BrYKampk1NTQNVTkxMbG9vX7x4MQCgsbFRej9hMpnKtJ8YGxsTiUS4OPh+kpWVVV5eDn9dAQBoNNrJkyf/9a9/WVpanj9/fvjBoMEyionFYgKBgO+46urq/f398nXU1NTwCvBgH26I11G44QdKLBYDAN6pTwAAsE5mZiZcLC8vd3JyWrZs2Zw5c8Ys8tHz3h+3zIYaGhrKtJ+89bszkOLiYrif5Ofn/+1vf/P39zc3Nx+tQMfQ0PeTe/fuffHFF4mJifCIWen3E3xxkD4pKysLCQn5z3/+gx+Z1NXVwf3kypUr69at8/Pzkz/p8k7QEaFiJiYmYrEYP+7m8Xj4Z4BjMBivXr3CK1AoFC0tLQaD0dLSgtdRuOEHikajqaur4++Ox+PJP2dVpk/U1dXpdDr4X1IEANjZ2c2cObO0tHSsoh5dDAZDIBDAnwjgXT5u6Y4CA3TmB8rExKS3t/fNmzdw8Z2+Avh+4urqymAwnjx5Miohjjn5j1thnxQXFwcEBMTHx3t4eMASJpOprPsJg8FobW3FL50M1CdVVVUcDic2NhZegIDw/SQwMFAsFldVVQ0zGJQIFaNSqfb29hkZGQAADMMyMzM9PT0BANLZ0dPTE1YAAGRkZMB918HBob+//+HDhwAAoVCYm5sLN1QC6urqbDZb/i1LJBJ8h/bw8MArpKenu7m54bss1N7e/uzZM+X4mQ8AYLFYZDI5JycHANDX13fr1i34cff19b1+/XqQDV1dXWtqahoaGgAAra2tJSUlSnOnDZ1Ot7W1Hfy781ZNTU3Nzc3w2pgScHJyamtrKy8vBwB0dXUVFBTAPhGJRG1tbbDO48ePly5deuLEiSVLluAburu737t3D956VFVVxePxlOZOG1tbWz09vby8PDDwd6empsbLyysqKio4OFhhI+Xl5SKRaAT2kxEceKNkLl68aGxsvG/fvuDgYBsbGzhYq6SkBADQ3d2NYVhjYyOVSv3qq6+io6NJJFJhYSHc8KeffmKxWAcOHFi4cCGHwxnP9zDSMjIyDA0Nd+/eHR4ebmZmJhAIMAyD/80bGhowDBMIBGZmZps2bdq9e7eRkVF6ejqGYZWVlRwOJzo6eteuXdOnT/fy8pIfT//h+vXXXy0sLPbv3+/r6ztv3jw4ivjGjRskEglWKCkpCQ8Pd3NzYzAY4eHh+Mi3yMhIR0fHgwcPfvzxx6GhoeMV/2g4d+4cnU6PiYlZtWqVnZ0dvBPgwYMH8N8chmHV1dXh4eELFy40MjIKDw+HI+Dz8vL8/f137doFr/0ovBflw/Xtt9/a2dkdOHDAw8MjICAAFp46dYrFYmEYJpFIqFSqjY1N+P+kpKTAOkFBQW5ubgcPHpwxY8aOHTvG7Q2MgtjYWEtLy/379y9ZssTNzQ1+d65du0ahUGCFadOmTZkyBe+TxMREDMOSkpJWrVq1e/fu7777zsTEZNu2bcOPBM0+MZg7d+6kp6dTKJSwsDA4PYpAILh8+fKGDRvggU59ff25c+d6e3tXrFghPQlfcnLyvXv3LC0tQ0NDFd51/uEqKipKTk7W19cPDQ2Fpz27urrOnz8fHBw8adIkAACPxzt9+nRHR4e/vz+8f1woFCYlJVVUVBAIhFmzZgUEBODXEZVDWlpabm6uqalpWFgY7ITGxsabN2+GhoYCAF68eIEfJQMApk6d6u3tDQCQSCQJCQmPHj2ys7Nbs2aNzKHzhy4nJyczM5NKpYaFhRkaGgIA+Hx+UlLSpk2bCARCc3Pzn3/+iVdmMpm+vr7t7e1Xr16trq7W1NR0cnJavHixwqcTfKAwDLty5UpRUZG1tXVISAgcJFJdXV1aWrpy5UoMw06ePCld39nZ2dHREQDQ19d39uzZqqoqJycnfJi60khNTc3Ly5s8efL69et1dHQAAA0NDbdv3w4JCQEAnD59WiQS4ZXt7e3nzZvH5/OTk5Nra2t1dXXnz58/IqfcUCJEEARBVJpS/TBHEARBkHeFEiGCIAii0lAiRBAEQVQaSoQIgiCISkOJEEEQBFFpKBEiCIIgKg09axRB3kdGRoaamhq8I3CC6+npOXv2rIeHB4vFGkp9DMMKCwvh/Jrr1q27evWqsbHx/PnzRzywCxcu2NjYwLvlRpBIJLp48SJ87eXlJf3Q6qHLzc19/vw5AGDy5MleXl4jGR8yAQ3/nnwEmVCuXLkyderUqVOnlpWVSZcLBAIWizV16lQ4zeQweXp6+vj4DL+dMdDc3AwAkJ88UiGJRLJkyRINDQ1LS8vZs2djGMZisdavXz/MGKqqqk6cOIFPrArp6+t/9913w2xZHpzwxNra2tXVNT8///0a+fHHH11dXUkk0qJFi0Y2PGQCQqdGEWXT0dFRW1vb1NQUHx8vXX7x4sX6+vra2trBnwI6RBs2bAgLCxt+OxPNgwcPUlNTr1y5UltbCx+ZOyIKCwsjIiJken7nzp1w5s7R8M9//jMvL++9D2Sjo6Pz8vJmzZo1slEhExNKhIhyCggIOHPmjPTELvHx8YGBgQorv3r1SnrOz6FYu3bt6tWr5cs7OjrwiRcggUDw3lPn9PT0wOMb6fa7u7uHsu2bN28EAsEgFdra2uTnv62rqwMASD8vUKHu7u7m5ua+vj6Fa4VC4SBrcdu3b8enWcAJBALp+Vvk8fn8t7Y8CAzDXr16Jd1Cf3//SM3vinygUCJElFNoaGhrayv+kM/y8vL79+/LHMPBGV50dHTodPqkSZNmz56dm5sLV/X19bm7uzs7O+NZp7m52crKCn8K/sqVK/HXt2/fJpPJqampPj4+BgYGhoaG8MmZd+/etbOzo1Ao+DlAWD8mJkZmxpl9+/bhJW1tbWQy+dixYxs3bjQwMKDRaLNmzaqpqamvr/fy8iKRSCQS6ZNPPunq6hrovfN4vMWLFxsZGVEolDlz5vz1118yFZKTk+3s7IyMjExMTMzNzfErasuWLVu/fj0AwNHRkUwmR0dHyzdeVVW1aNEiEonEYDDIZPL27dul03xNTY2fnx9cq62t7ebmJhAITpw48emnnwIA7O3tyWQymUyG6ZbFYu3ZswffNiUlxcbGhkKhGBsbW1lZ/fHHH/iqPXv2MBiMoqIie3t7Go02adKkwMDAzs7OgXpA3qeffjpv3rw///zTzMyMTqcbGRn9+uuvGIb9/PPPZDKZSqWam5vfuXNn6A0iygQlQkQ50el0Hx+f06dPw8X4+Hg7OztnZ2fpOq2trTNmzLh+/XpFRUVaWpq+vr6vr+/Lly8BAJqamr/99ltlZeXWrVsBABKJZN26dV1dXfv378e3xQ8j4MQxERER7u7uhYWFx48fz8zM3LRpU2ho6I4dOx48eBAZGbl79+4bN27A+j09PTInCaVLMAx7/fp1dHS0mpra7du3r169yuPxQkJCgoKCfHx87t+/HxcXl5SUhEciQyKRBAYGFhYWnjt37q+//goODl67dq10hatXrwYFBbm4uNy9e7e4uNjPzy84ODg9PR0AEBUV9eWXXwIAjhw5kpiYuGbNGpnGuVyum5sbn8+/du1aWVnZ3r17jx079s0338C1TU1NCxYsePTo0alTp8rKym7evOns7Nzb27tkyZItW7YAAI4dO5aYmJiYmAjnr29ubu7o6IDb5ubm+vv7m5qa5ubm5ufn29rarlq1KjU1Fa4VCoV8Pn/t2rVffvllUVHR3r17r127tm/fvsH3AWnd3d1Pnz799ttv4+LiCgsL/fz8tm3bFh4enp2dnZSUlJOTQ6VSV69eLf2IZ0SFjO8lSgQZcTD5FRcXJyQkEIlEeCaNwWD88ssv8FRhVFSUwg3b2tqIRCI+TRKGYRcuXAAAnDlzBqalrKwsfJX0YBl43Pn111/ja5cvXw4ASEpKgotisZjJZG7evBku/vTTT1paWtJ/Ojo6Gi+BQXp4eOBrd+/eDQD4/vvv8RJfX19HR0eF7yIrKwvGjJfARAUHy0gkEisrK5lhPmw229vbG74+f/48AOD58+f4WunBMlu2bDEyMmppacHX7tmzh0gkwlEwW7du1dDQqKiokI/q7NmzAID6+nrpQunBMhwOh0ajdXV1wcXe3l5zc3MXFxe4GBUVBQC4fPkyvu2yZcvs7e0V9gA8mXzy5EnpwpCQEAKBUFpaChfb2to0NDRMTEw6OzthCfwpcOfOHemt3Nzc0GAZVYBun0CUVkBAgL6+fkJCgrm5eUtLi8yBEdTS0pKQkFBbWwvPNGppadXU1OBr//73v2dkZHz22WdCofDHH38cfBg9h8PBX7NYLAKBgI8EUVNT++ijj+DEjUPk4+Mj3Zp8yb179xRuCKfMDAoKwkuWL18eExMDXz979uzZs2eLFy+G+RKaPHnyzZs3hxJVRkbGRx99VFpaipfo6Oj09vZWVlbOmTMnKytr/vz5NjY2Q2lKRmlpqZ+fn66uLlzU1NQMCgqKi4vr7u6GhQQCYdGiRXh9Ozs7/Dz2EJmYmOCDXwwMDExMTD7++GM4bRYAYNq0aQCAd/qMEKWBEiGitIhE4qpVq06fPm1mZsbVzMOfAAAEyUlEQVThcBgMhswJyfT09MDAQDMzMzc3NzKZrKampq6uDmcDx23ZsuXUqVMkEgk/ATgQOGMl/qeJRCL+TxaWvNN4HJnWZEq0tLQGao3L5err60v/aSaTib+Go2Pi4+N///13mQ0lEslb54nk8XgvXrz45JNPZEKFB2F8Pt/BwWHwFhQSiUQ8Hk/muimTyZRIJK9fv4aJUEtLC0+TYNAeGIh0BwIAiESifCe/a5uIckCJEFFmYWFhR48eLS4uhmf8ZPz888+Ojo65ublwUlwMw44cOSJdQSgUbtiwwdramsvlbt++/ejRoyMSlYaGhlgsxjAMn2QVv1Q2fMbGxp2dnUKhUFtbG5a8evUKX2tgYAAAiI2NDQ8Pf4/GSSQSm81OTk5WuNbQ0FB+GOpQaGpqwpPY0oUtLS0EAoFEIr1HgwjyTtBgGUSZOTs7BwcH+/j4LFu2TH7t8+fPHRwc8Knhc3JyZAYi/uMf/3j69OmlS5cOHjx47NgxeMlw+ExNTfv7++HISQAAhmE5OTkj0jIAAF45w4fLAgDS0tLw17a2tsbGxtIDMt+Ju7t7bm7uQNnO3d29oKCAy+XKr9LX1wcA9PT0KNxQTU3NxcUlPT0dH4CKYVhKSsr06dPhhggyqlAiRJTc77//npKSoqWlJb/KwcHh0qVLDx48EIlEt27d2rRpk46ODr720qVLx44di4uLmzVrVnh4+Jo1az777LPa2trhh+Th4UEkErdt21ZXV1dbW/vFF188ffp0+M1CHA7HxsZm69at+fn5XV1dly9fPnz4ML5WXV19165dWVlZGzdurKys7Onpqa2tPXPmzN69e4fS+Pfffy8Wi/38/O7cudPV1fXy5cuMjIxNmzbBtTt27FBXV/fz84N/ur6+/tChQ/A4z9bWlkAgxMXF5efnP3z4UH5w5vbt21+8eLFx48aGhoampqbIyMjy8vIdO3aMUK8gyGBQIkRU1/79+2k0mouLi7a2tr+//w8//IBfTquvr4+IiFi5cuXmzZthyfHjx01MTFatWjX8y0jm5uaHDx++cePGlClTrK2tW1tb4d0FI0JTUzM5OVlPT2/BggV6enqff/55XFycdIXNmzf/9ttvqampNjY2urq6VlZW33zzDbxC9lbTpk3Lzs6WSCRsNltPT4/JZPr7++O37VtbW2dmZvb29sI/bWFhgd/jwWKxYmNjr1+/7uHh4eTk1NTUJNPysmXLjh8/npycbG5ubmpqeu7cudjY2JCQkGH3B4K8HQH7302+CKKCxGLxs2fPOjs7bW1tpQ8H30oikQAA3jq6ZBCdnZ3V1dVUKtXMzOy9GxkIhmFlZWV9fX3Tp09XmOQkEkllZWVHRwedTp88eTJ+flhhTQKBgF/OhBoaGl6+fKmvr29paYlfjMTV1NQIBAIqlWppaSmz4eAti0Si8vJyiURiZ2f3Th+HtNbWViqVevLkSfxQ9b2x2exJkybhN4AiygolQgRBlApMhOrq6mpqaklJSUuXLn2PRtasWfPHH3/09/dzOByUCJUeSoQIgigVsVhcVVUFX5uZmenp6b1HI1wuF95Io6enNxqH7MiEghIhgiAIotLQYBkEQRBEpaFEiCAIgqg0lAgRBEEQlYYSIYIgCKLS/g/9YaWJRzHqkAAAAABJRU5ErkJggg==",
"text/html": [
"\n",
"\n"
],
"image/svg+xml": [
"\n",
"\n"
]
},
"metadata": {},
"execution_count": 16
}
],
"cell_type": "code",
"source": [
"using Plots\n",
"plot(\n",
" vcat(0.0, u_max), # add the origin as a point\n",
" vcat(0.0, traction_magnitude),\n",
" linewidth = 2,\n",
" title = \"Traction-displacement\",\n",
" label = nothing,\n",
" markershape = :auto\n",
")\n",
"ylabel!(\"Traction [Pa]\")\n",
"xlabel!(\"Maximum deflection [m]\")"
],
"metadata": {},
"execution_count": 16
},
{
"cell_type": "markdown",
"source": [
"*Figure 2.* Load-displacement-curve for the beam, showing a clear decrease\n",
"in stiffness as more material starts to yield."
],
"metadata": {}
},
{
"cell_type": "markdown",
"source": [
"---\n",
"\n",
"*This notebook was generated using [Literate.jl](https://github.com/fredrikekre/Literate.jl).*"
],
"metadata": {}
}
],
"nbformat_minor": 3,
"metadata": {
"language_info": {
"file_extension": ".jl",
"mimetype": "application/julia",
"name": "julia",
"version": "1.11.6"
},
"kernelspec": {
"name": "julia-1.11",
"display_name": "Julia 1.11.6",
"language": "julia"
}
},
"nbformat": 4
}