1.索引
1.1 创建索引的方式
索引就是用来帮助表快速检索目标数据的
那么,索引有哪几种创建方式:
● CREATE
CREATE INDEX indexName ON tableName (columnName(length) [ASC|DESC]);
indexName:当前创建的索引,创建成功后索引的名字;
tableName:要在哪张表上创建一个索引,这里指定表名;
columnName:要为表中的哪个字段创建索引,这里指定字段名;
length:如果字段存储的值过长,选用值的前多少个字符创建索引;
ASC|DESC:指定索引的排序方式,ASC是升序,DESC是降序,默认ASC
● ALTER
ALTER TABLE tableName ADD INDEX indexName(columnName(length) [ASC|DESC]);
● DDL (建表时创建索引)适合已经确定了索引项的情况下建立
CREATE TABLE tableName(
columnName1 INT(8) NOT NULL,
columnName2 ....,
.....,
INDEX [indexName] (columnName(length))
);
不同的索引有不同的创建方式:(后面会具体介绍各类索引)
● 唯一索引
-- 方式①
CREATE UNIQUE INDEX indexName ON tableName (columnName(length));
-- 方式②
ALTER TABLE tableName ADD UNIQUE INDEX indexName(columnName);
-- 方式③
CREATE TABLE tableName(
columnName1 INT(8) NOT NULL,
columnName2 ....,
.....,
UNIQUE INDEX [indexName] (columnName(length))
);
● 主键索引
-- 方式①
ALTER TABLE tableName ADD PRIMARY KEY indexName(columnName);
-- 方式②
CREATE TABLE tableName(
columnName1 INT(8) NOT NULL,
columnName2 ....,
.....,
PRIMARY KEY [indexName] (columnName(length))
);
● 全文索引——不常用
-- 方式①
ALTER TABLE tableName ADD FULLTEXT INDEX indexName(columnName);
-- 方式②
CREATE FULLTEXT INDEX indexName ON tableName(columnName);
注意点:
○ 5.6版本的MySQL中,存储引擎必须为MyISAM才能创建。
○ 创建全文索引的字段,其类型必须要为CHAR、VARCHAR、TEXT等文本类型。
○ 如果想要创建出的全文索引支持中文,需要在最后指定解析器:with parser ngram。
○ 优化器无法自动选择全文索引,他有自己的语法
● 空间索引(仅有MyISAM支持空间索引)—— 不常用
ALTER TABLE tableName ADD SPATIAL KEY indexName(columnName);
注意:空间索引必须要建立在类型为GEOMETRY、POINT、LINESTRING、POLYGON的字段上
● 联合索引
○ 联合索引的意思是可以使用多个字段建立索引。那该如何创建联合索引呢,不需要特殊的关键字,方法如下:
CREATE INDEX indexName ON tableName (column1(length),column2...);
ALTER TABLE tableName ADD INDEX indexName(column1(length),column2...);
注意:
● 使用联合索引时,SELECT语句的查询条件中,必须包含组成联合索引的第一个字段,此时才会触发联合索引,否则是无法使用联合索引的。
● 创建主键索引时,必须要将索引字段先设为主键,否则会抛1068错误码。
● 这里也不能使用CREATE(指方式①)语句创建索引,否则会提示1064语法错误。不过:一般主键索引都会在建表的DDL语句中创建,不会在表已经建立后再创建
● 同时创建索引时,关键字要换成KEY,并非INDEX,否则也会提示语法错误。
1.2 操作索引
● 查看索引
SHOW INDEX FROM tableName
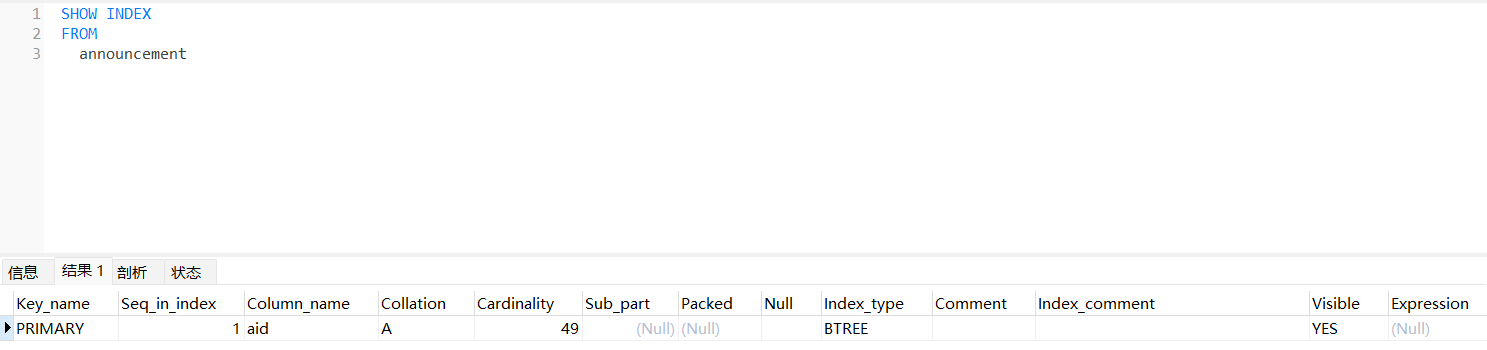 每个字段的含义:
每个字段的含义:
● ①Table:当前索引属于那张表。
● ②Non_unique:目前索引是否属于唯一索引,0代表是的,1代表不是。
● ③Key_name:当前索引的名字。
● ④Seq_in_index:如果当前是联合索引,目前字段在联合索引中排第几个。
● ⑤Column_name:当前索引是位于哪个字段上建立的。
● ⑥Collation:字段值以什么方式存储在索引中,A表示有序存储,NULL表无序。
● ⑦Cardinality:当前索引的散列程度,也就是索引中存储了多少个不同的值。
● ⑧Sub_part:当前索引使用了字段值的多少个字符建立,NULL表示全部。
● ⑨Packed:表示索引在存储字段值时,以什么方式压缩,NULL表示未压缩,
● ⑩Null:当前作为索引字段的值中,是否存在NULL值,YES表示存在。
● ⑪Index_type:当前索引的结构(BTREE, FULLTEXT, HASH, RTREE)。
● ⑫Comment:创建索引时,是否对索引有备注信息。
后续排除问题、性能调优时,可以通过分析其中的Cardinality字段值,如果该值少于数据的实际行数,那目前索引有可能失效
● 如果新建错了索引,只能删除再重新创建
DROP INDEX indexName ON tableName;
● 指定索引
SELECT * FROM table_name FORCE INDEX(index_name) WHERE .....;
这个关键字的用法是:当一条查询语句在有多个索引可以检索数据时,显式指定一个索引,减少优化器选择索引的耗时。但是如果对业务系统不熟悉,还是得让优化器自己来选择。
1.3 索引的本质
数据库是基于磁盘工作的,所有数据都再磁盘上面存储,索引也是数据的一种,同样存储在磁盘上,但是索引最终会以哪种方式进行存储,这是由索引的数据结构来决定的,同时索引机制又是由存储引擎实现的,不同的存储引擎下的索引文件,保存在本地的格式是不同的。
当数据量越少时,创建索引越好 ,因为创建索引时,会基于原有的数据重新在本地创建索引文件,并同时做好排序并与表数据产生映射的关系。
1.4索引的分类
● 数据结构层次划分
○ B+Tree类型:MySQL中最常用的索引结构,大部分引擎支持,有序
○ Hash类型:大部分存储引擎都支持,字段值不重复的情况下查询最快,无序
○ R-Tree类型:MyISAM引擎支持,也就是空间索引的默认结构类型
○ T-Tree类型:NDB-Cluster引擎支持,主要用于MySQL-Cluster服务中
B+树和哈希索引是最常见的索引结构,B+Tree是有序的,哈希是无序的。在MySQL中创建索引时,其默认的数据结构就为B+Tree,可以在建表时使用using字段改变索引的数据结构。
CREATE INDEX indexName ON tableName (columnName(length) [ASC|DESC]) USING HASH;
● 字段数量的层次划分
○ 单列索引
■ 主键索引
■ 唯一索引
■ 普通索引
○ 多列索引
■ 联合索引、组合索引、复合索引 、多值索引...很多种叫法,本质即由多个字段组成的索引
使用多列索引的注意事项:当建立多列索引后,一条SELECT语句,只有当查询条件中了包含了多列索引的第一个字段时,才能使用多列索引
● 使用一个字段值中的前N个字符创建出的索引,就可以被称为前缀索引 (length指定长度)
前缀索引能够在很大程度上,节省索引文件的存储空间,也能很大程度上提升索引的性能
● 功能逻辑层次划分
○ 普通索引、唯一索引、主键索引、全文索引、空间索引
● 存储方式划分
○ 聚簇索引:也被称为聚集索引、簇类索引
■ 逻辑上连续且物理空间上的连续
○ 非聚簇索引:也叫非聚集索引、非簇类索引、二级索引、辅助索引、次级索引
■ 逻辑上的连续,物理空间上不连续
注意:
1.一张表中只能存在一个聚簇索引,一般都会选用主键作为聚簇索引,其他字段上建立的索引都属于非聚簇索引,或者称之为辅助索引、次级索引。
2.误区:虽然MySQL默认会使用主键上建立的索引作为聚簇索引,但也可以指定其他字段上的索引为聚簇索引,一般聚簇索引要求索引必须是非空唯一索引才行。
3.如果表中就算没有定义主键,InnoDB中会选择一个唯一的非空索引作为聚簇索引,但如果非空唯一索引也不存在,InnoDB隐式定义一个主键来作为聚簇索引(一般适合采用带有自增性的顺序值)。
]]>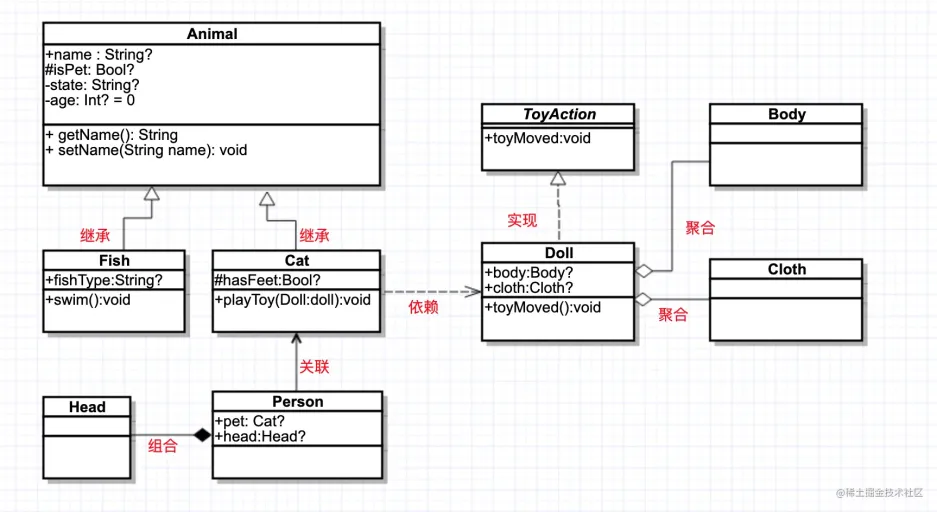

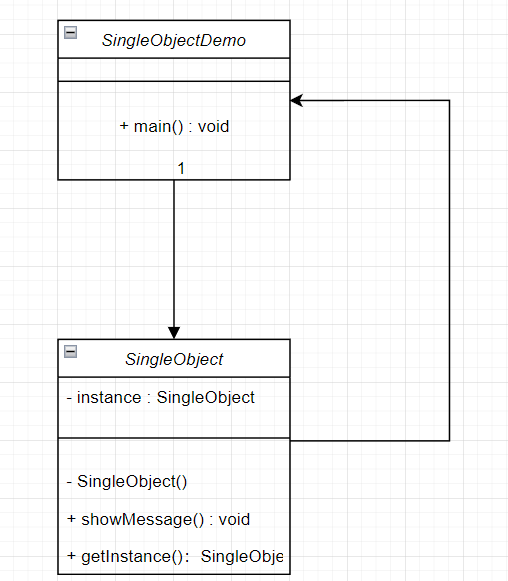
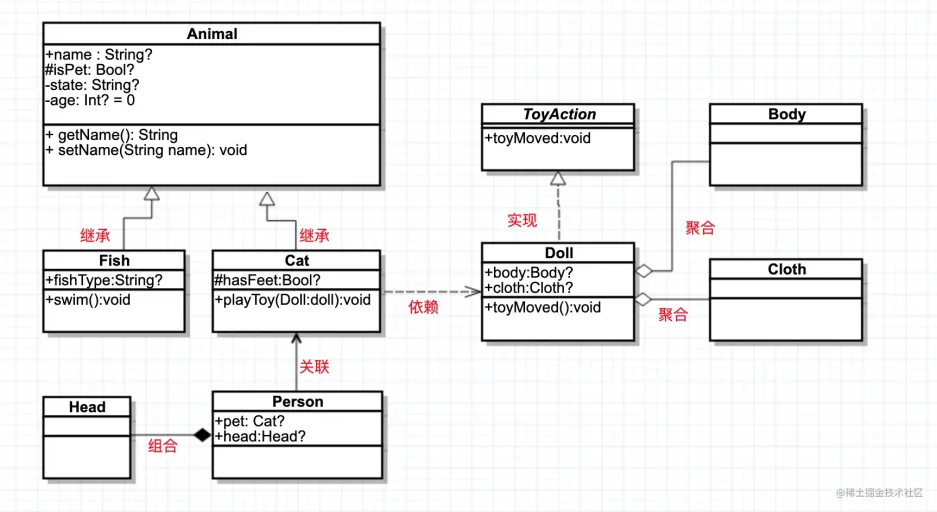 类与类之间的关系:
泛化(继承)、实现、依赖、关联、聚合、组合
类与类之间的关系:
泛化(继承)、实现、依赖、关联、聚合、组合
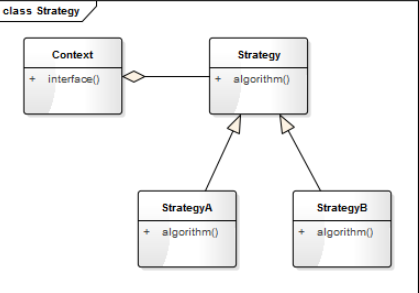 定义一系列算法,将每个算法都封装起来,并且使他们之间可以相互替换。策略模式使算法可以独立于使用它的用户而变化(聚合)
策略模式的结构:
● 环境(Context)角色: 持有一个Strategy的引用;
● 抽象策略(Strategy)角色: 这是一个抽象角色,通常由一个接口或抽象类实现。此角色给出所有的具体策略类所需的接口;(关系是:实现或继承)
● 具体策略(ConcreteStrategy)角色: 包装了相关的算法或行为
使用步骤:(举例)
● 定义Strategy接口,包含抽象方法
定义一系列算法,将每个算法都封装起来,并且使他们之间可以相互替换。策略模式使算法可以独立于使用它的用户而变化(聚合)
策略模式的结构:
● 环境(Context)角色: 持有一个Strategy的引用;
● 抽象策略(Strategy)角色: 这是一个抽象角色,通常由一个接口或抽象类实现。此角色给出所有的具体策略类所需的接口;(关系是:实现或继承)
● 具体策略(ConcreteStrategy)角色: 包装了相关的算法或行为
使用步骤:(举例)
● 定义Strategy接口,包含抽象方法
 每个字段的含义:
每个字段的含义: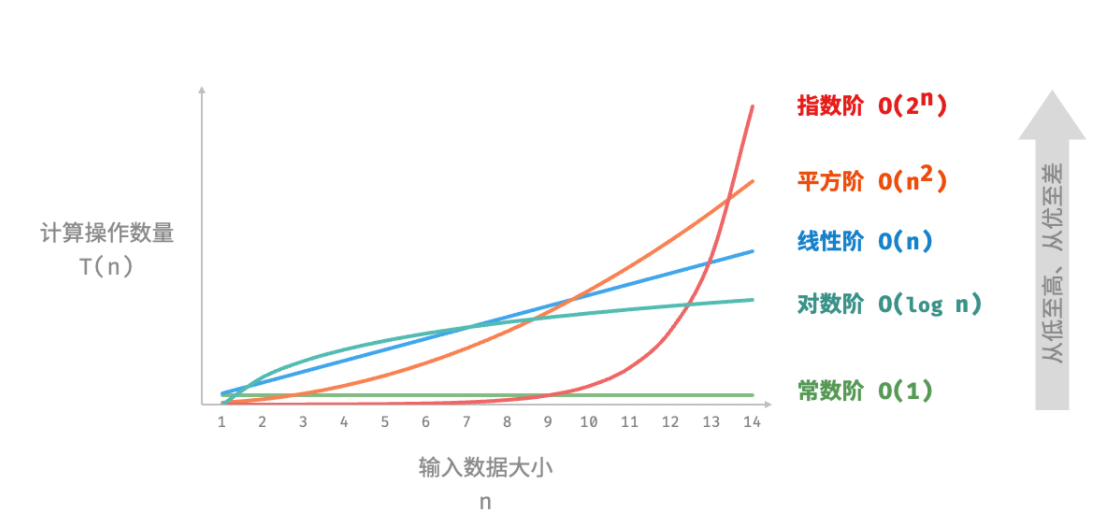 (图来源不明,侵删,抱歉)
(图来源不明,侵删,抱歉)

 ]]>
]]>




