"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"# Importar librerias basicas\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import sympy as sym\n",
"\n",
"%matplotlib inline\n",
"plt.style.use('bmh') # estilo de las graficas\n",
"from IPython.display import Latex # para visualizar ecuaciones en jupyter"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Función de Transferencia\n",
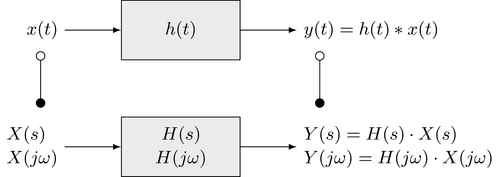
"En el dominio del tiempo se utilizan diferentes representaciones para caracterizar los sistemas lineales invariantes en el tiempo (LTI). Por ejemplo, los coeficientes constantes de ecuaciones diferenciales parciales ordinarias (EDO), la respuesta al impulso y la respuesta a paso. La Funcion de transferencia denota el factor complejo $H(s)$, sobre la función propia $e^{s t}$ en la entrada de un sistema LTI y se pondera cuando pasa por el sistema. Dado que la transformada de Laplace descompone señales con respecto a estas funciones propias, la función de transferencia constituye una representación de un sistema LTI en el dominio espectral (Laplace o Fourier). Los enlaces entre la función de transferencia y las representaciones en el dominio del tiempo de los sistemas LTI se analizan en este capitulo.\n",
"\n",
"## Relación con la respuesta al impulso y las señales de entrada / salida\n",
"\n",
"Ya se describió en el contexto del teorema de convolución de Fourier y la transformada de Laplace, que un sistema LTI puede representarse de manera equivalente en el dominio del tiempo y en el dominio de la frecuencia (espectro). En el dominio del tiempo, la salida $y(t)$ de un sistema LTI se da al convolucionar la señal de entrada $x(t)$ con la respuesta de impulso $h(t)$ de sistema\n",
"\n",
"$$\n",
"y(t) = x(t) * h(t)\n",
"$$\n",
"\n",
"Aplicando el teorema de convolución de la transformada de Laplace produce\n",
"\n",
"$$\n",
"Y(s) = X(s) \\cdot H(s)\n",
"$$\n",
"\n",
"donde $X(s) = \\mathcal{L} \\{ x(t) \\}$ y $Y(s) = \\mathcal{L} \\{ y(t) \\}$ son las transformadas de Laplace de la señal de entrada y salida, respectivamente. La función de transferencia $H(s)$ se da como la transformada de Laplace de la respuesta al impulso $h(t)$\n",
"\n",
"$$\n",
"H(s) = \\mathcal{L} \\{ h(t) \\}\n",
"$$\n",
"\n",
"Esto también se puede concluir a partir de la relacion entre la respuesta al impulso y la funcion de transferencia. Los resultados derivados muestran que un sistema LTI se puede caracterizar completamente en el dominio del tiempo y de la frecuencia por su respuesta al impulso $h(t)$ o la función de transferencia $H(s)$ o la respuesta en frecuencia $H(j \\omega)$, respectivamente.\n",
"\n",
"\n",
"\n",
"Además, se puede concluir que la función de transferencia se da como el cociente entre la salida $Y(s)$ y la señal de entrada $X(s)$ en el dominio de Laplace\n",
"\n",
"$$\n",
"H(s) = \\frac{Y(s)}{X(s)}\n",
"$$\n",
"\n",
"para $X(s) \\neq 0$. Las mismas relaciones se mantienen en el dominio de Fourier si la región de convergencia (ROC) de la respuesta al impulso incluye el eje imaginario $\\Re \\{ s \\} = 0$. En general, la función de transferencia puede derivarse mediante la división de los espectros de la señal de salida y entrada. Esto se puede utilizar para medir la función de transferencia de un sistema mediante señales de entrada específicas que cumplen con $X(s) \\neq 0$ con $X(s) \\approx$ constante.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Ejemplo**\n",
"\n",
"La función de transferencia $H(s)$ de un filtro pasa bajos de segundo orden es:\n",
"\n",
"$$\n",
"H(s) = \\frac{1}{C L s^2 + C R s + 1}\n",
"$$\n",
"\n",
"la respuesta al impulso $h(t)$ del paso bajo está dada por la transformada inversa de Laplace de la función de transferencia $H(s)$. Primero, la función de transferencia se define en `SymPy`"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAJkAAAAtCAYAAAC9B8nZAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAF4klEQVR4Ae2di3EURxCGdSoFICsEOQNhR2ApA1FkABlAOQJKzgDIwFIGQATGzgAyMCgD+ftWO/Ls3j5Op5njTnRXjXbn1Tv97z89vbPLsbi5udkLCQRqIrBfU/lj1L1YLM5J30iHj9G+GjYd1FD62HS2hHqHXV9JR6Qg2D1ucniyFcAipLgmPSW9oPlfK3SJJhkCQbIMjDitg0CQrA6uoTVDIEiWgRGndRAIktXBNbRmCATJMjDitA4CQbI6uIbWDIEgWQZGnNZBIEhWB9fQmiEQJMvAiNM6CCziBflqwPJq6Q0tfaV0SvK10j+kL6T3YPiWY8gIAkGyEWCiuBwCsVyWwzI0jSAQJBsBJorLIRAkK4dlaBpBIEg2AkwUl0MgSFYOy9A0gkCQbASYKC6HQJCsHJahaQSBINkIMFFcDoEFquLfxJXDMzQNIBA7/gOgRFFZBGK5LItnaBtAYKf+3SUvqS+wwZfTxyRfTr/i5fQ1x5AtRmBnlsuWYG8gleTaI3/J4Zj8ky3GN4YGAru0XJ737thr8ieQTa8WssUIjC6X3DyXpeekM1K+JDXfT7U39wWe5FXfPupSv0SMUt9epWXSS6Yx5WX9oWwkXxirq3bQ4p/kEpx395s1Br/XT1j2kvSN9HygTuL4Ad9gfd6eNm6PfM7LSp2j13Go/7CUznX0cP2SWDmBO/cD/U4i7ZRonbptyzNG74m86NyTzqCtJL0nfe43zA2iTpJpuDFRR0fKU+cXpLa5SGUlj+h1jC/X1UlfAXlI/5JYnTAWsRocD+XGn9afrGvvVD/0ro0FfcXB8cmJNM4OyfapyOUjGcnxhEFd5xW9c5X5IyRNEN6rS1mXWUXSFhWWJ58yP3D9P4oqvp+ykliJufLh9rD0VxIqU/fktsWG/8oT0uSP0dyRjBsnEzXGDnPG+BNKf87Y0wCHrjHgZroPV7fxnjPFX9j5LlIBqybuxSZj145wLb2MS6aTampSd/ptU+bAwWCIRhisf8GQFHhaNSYaqzeZEgm7BNpUB8ahzn/bNhL9Uw489RL3Z8oagrX5r3mbtm+1QyWstGsJd64lwfxdtCtsfDpkFG0mMRvqs+myhmRcNHkFvdmsYLAEGPV27c1Xz8pejD5/097N1aYPeZdZ98ASoSStgL6mTvAV6wbBb2rr/CmNVVoKnew+RCh6NonnE+VvY5NoDjP6bodggAMxiC4WWKJLMqjvVP1ziXZ6Upr935a84N8FkJz71KLOTsr73OccPWsFu/QrjZXE0qY7W7UDcWVx4nXKk42Uz2KW2s4d0bUWFn296Bm0JXmyIxooK635zCANH/Vk6HEWyppRT9bTYYznTJZIxno+rnf6kv/JNvcVdEr4Zjy9vofkj6h/1is3a9gw5iFLY5XisQ6eXP8tY3Nl+Z20tBdJ2SxmtOlIBSw6+kczGGNdMzs9n0u0lfWTj9LUq3Rpzyfpps5Z2tn+IC8RXCLtO9k/6XnIkWusNXvpVwOrpT0wrtN4Ko5Ldclu6opghp61sEjjSEf0DHqyfSqUFAdp2JycoXQ0oGe2JK8xtXXhFknjNWl/TDon79OTs1qP5cw9tW5uMN+hviRWKR4bwirVNR4rt3PXMEskc0lRUlB7m+v9xTjbDbnuvKVEUTrL3W1RsyTKdmONJO65vUsZiHZNava/OK60fKe+GzqWxCpNyE8DY/+1LdNzNgL+LvHKTmF24Ii9mRhgDHLJ0ddAnfdklOlOJc8qn9bYVp1L3g493iBJlsdXztRO/EM728yRmSabl8JYPdOCIawoviOXbcBEz6Znd6tjpzBrSMagNfQKQ7z5Fxx13ykQ1SDjglEvR3tnmN5IEJoljjJnWxLLkvt3zyfptl69/gcMnluurlX36+yzcXkIVg4WWw3ofyE1mLRYdX64hWsY+LuFc9Zi4z1Kbzi2CrPWniPGmjzzR8pchW4/pmDgnP94Agh6XB8+0o378UBoLa6Nxc58tFiaAQCrxzyCZNsY95U2d1JfbSz+A0fuz7q8eXDZAAAAAElFTkSuQmCC\n",
"text/latex": [
"$\\displaystyle \\frac{1}{C L s^{2} + C R s + 1}$"
],
"text/plain": [
" 1 \n",
"──────────────────\n",
" 2 \n",
"C⋅L⋅s + C⋅R⋅s + 1"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import sympy as sym\n",
"%matplotlib inline\n",
"sym.init_printing()\n",
"\n",
"R, L, C = sym.symbols('R L C', positive=True)\n",
"s = sym.symbols('s', complex=True)\n",
"\n",
"H = 1/(C*L*s**2 + C*R*s + 1)\n",
"H"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Luego, la transformada inversa de Laplace se calcula para los valores normalizados específicos $L = .5$, $R = 1$, $C = .4$ de los elementos del circuito."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAJEAAAAuCAYAAAAoRPuDAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAHx0lEQVR4Ae2cjVEcNxTHfQwFYErAHUDSAe7AnlQQ6MAeKsjgDuxUEOwOTCog0IHpwOE6IP+frLfsaqX90N2Zy9zTjNBK70N/PT09aXdvWTw+Pr7YprRYLG6F53fhutsmXI6lbIHFNjmRHOhAUB+UXwrXsgzbKdtkgb1tAiMsp8r37kBbNisjcLbCiRSBjpQ/Cuul8pJr5eMR7M9KjpjP1glCOs/QO0en+A+i3Cws9IPclL6i/jIutrO4pXEWead8EOtMIhP7xng2XaovMKzcn3SAnW3x3SYwSy8G/Zrqju3YjPw15uOUb6gumc/KR0M8RhMfkZt+OAa8Uf5otKFSfFn8IzJFXMGBEFbC6Fy08+WQ4nXTYt+TDDjUt/TgRIxjI/ilF2fv4FSdifzcxqU6kRUcp+12rpXg/6ac03Ob8qd1ydlCCYs+6kRxU09lrC6eHv4WbTau5mCtkIXia2W89Eb5ixTfq5ydpItVcT5B8K36WMInGVYVk/BygtyzsRDa1fmJcHbGp3ZWKneVYTwGUO0sThZrZ1xqx0aMd2G8VoqG830X7YO1paV4cEAWySejqQ0nwqZfrC0txZPFb3yiz8elDm0766wia/9ZpQbBVhowqGQ1dFboz8Ix1o9w9aIHMko4y7dUXm04FwydbU11trxsxFE7439IdVldNByhR1cb/ZwZX64UPYvfeEWfjWtPQtuSXgkIEZB0oUFVRUGEtZo4NB6Tqa8roRddBWzgpV8cYEoi8hL5e0n6iWb30gVPLr1X41Wb0Brrv+329vUIfmOdjWvfJCnViZ3WMQSTykGt99BPfNAvlL8rk+AltFZPvORZsefSTUT6S7mYxINzMFj6O1QGz2/q/0Q0JprVBJ2w/laZsSHzpzJ0JsB4dPniV+UbyRe3D5iUCPWliT8JHP0/5sjmFGyD4AUHjs64c33TD9g7/YmfcSGLXDvRTlr+KLJ/s/ijznpcMpxtZ+GU36oDlPDYORRSV+6ERNXh3cgh1vBYqX6YgNydUWcrEQ9nvN4WrTawM9bmzk3XNtbBLTTKDW4XhpNSCVtx0bGN6kymWH7YPleKzoLubXdqw3nQSdnO4cYop8vaxM+4i/hFq8IVHMg6ScvYaTM5qmNswDa34bpmUlnVnT0/1bWuuvphYsDQuQtRvXEK+lLCYDknon2V80Qz9rExqR8cNocBe/UcpK1PdCa0sb3RaMvJqo1Bj+lEtohftCpc+xIcSmwXpwp3rFCuuWsgHaqNbYdE+Hwv+lAYDYzr+KN+rtU3+/6DSkI9TsGd5NhW1O6+tO2yIIYSW+ekcQobE3ItXJ27uKichVC8g4o8YGTRpom2zljVl22Zf6TMSX0MfxWu4EQCQVjEUdJ93QwGcAbF6mDCmttK1Z8jgfNCmUHj2Jcaw6fChIncS8XDZ4+zokFYwgLL4RENR8WeOP+sFGWRuUkEcdSl+htzzETsqboKrr2ohsnIJVuZ/7SIpVXcYtncpQbLBLANE/14XsNzFozIK4PSOBBZR8L5zCZZfcLAQnslXE0EArPhFu0XBEVvDsyi5XQSNUq2XqKjlTg/jUUh2IfwV+MyJ7piQlqg7JJJuRPNQFtp9KaUIWx7a9o2dEHotrvI0IXwERlZhcHBQuNm/jCpTG42yQZgey08jQNFRhzL0mtd3FlFMtByuGnr2DvOQ6dN8kRiXlp3tjjTn5RD+KtxmROxHbCHN0l1JgqDhVvkSMDbO6tdfLwARLY6lEbdc4oL+k0EqDerO9JSnkRkdpXJzy228GxKNI4FvEDGnsGmKmk71yRbVAFTuI5j4BjROJVolugnHQ+0K2Wc1fpknnCAKamIX8L1uDSAcIcmJXg+zoBnM3CuO3dA8CoRcaBRMoDiLaPpXmep/nBiMNK3YaAeHkWoxMDgByyZawyUa6eNSMD5BF7u+np3U4ZfNPru3TFFu/BIwfpMy0ZGPNiZ/gZtJzr6ene8amMsZv/sHBnetJTcEP5qXM27M3XgaYIFFD24TWbLssgyQWoei/oIE6o+eIi71rQK/hKuvbUi3A1lRD1eO2wycaYiymwirYI/i8sjUcU0aUWyHbXPORVa8iLSzXb1t6JQ9uyVl5rXWoN/CJdHonn2N+7sijTiiiVnuPbNzIrqsuI1+Iu4PBJlbTzeqJXJuYXD/NoevEonh22ecm/svGUjm4N/DJc7kVnVy2oL+HZWbToXNAu4E5klvKy2AO+deDDmyS1QbQE/E1WbzgXNAr6dmSW8rLaAO1G16VzQLOBOZJbwstoC7kTVpnNBs8C+XXj5ZIH4NNdesh5FCr+kzP3u50lwR6/ciZKJlwPxApRPfJr3V2rjzfetSn4CkvuhWKJlt6p+i5/MtxyFF42Tv6lPxHey6mei/rTz6z9+VZgmIhA/BQ4/TU2Ju1x3J+rPPm/Q53xT39ewYy2+nU2ccEUgfhbLIdv/n2RiM49EiUFyVTkQWxwO9EEH62WOZ5fbPBJNmP0Yhfj+rrljmyC2MyzuRCNTLQcKP5iXA/GTUk8ZC/h2ljGKNcmBwle97kBmkXzpTpS3C1+X8lHj0Df1Bcnda3Ynysy5HIhnQWPf1Gckd7PJz0TJvMuBuAvju7L2/xbgVcihMp81r/2rVOn9Xyd3omT65EThG/ik2ar89w13IrNGLP8DOxvevD28BPYAAAAASUVORK5CYII=\n",
"text/latex": [
"$\\displaystyle \\frac{5 e^{- t} \\sin{\\left(2 t \\right)} \\theta\\left(t\\right)}{2}$"
],
"text/plain": [
" -t \n",
"5⋅ℯ ⋅sin(2⋅t)⋅Heaviside(t)\n",
"───────────────────────────\n",
" 2 "
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"t = sym.symbols('t', real=True)\n",
"RLC = {R: 1, L: sym.Rational('.5'), C: sym.Rational('.4')}\n",
"\n",
"h = sym.inverse_laplace_transform(H.subs(RLC), s, t)\n",
"h"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Se grafican los resultados"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZAAAADyCAYAAABj9JMpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nO29eZRcV32o++2auqqn6upB3ZolbMm2JE/YsbEVBgPGYrK5wiSGYBwWBnJj4XcXIfcZSIBrcglJXgj3LSA2ARIgN4AB5+LwLHwBD3jAwlzAsmVbg221xuqu7i5Vd1VXdU37/VHDLrWqx1PDqaPft5ZWd9U5tc8+32nV7+yzf3tvpbVGEARBEJaKq9kVEARBEFoTCSCCIAjCspAAIgiCICwLCSCCIAjCspAAIgiCICwLCSCCIAjCspAAIgiCICwLCSCCIAjCspAAIgiCICwLCSCCIAjCsvAsZiel1CDwJuBioAc4BTwN/FRrHa5f9QRBEAS7Mm8LRCl1gVLqB8BzwM2AFwgXf94M7FNK/UAptaXuNRUEQRBshZpvMkWl1B7g74D/0FrPVNnuA24APqq1vqputRQEQRBsx7wBRBAEQRDmYtGd6EqpH83x/r21q44gCILQKiy6BaKUmtRad1d5f0Jr3VvzmgmCIAi2ZsEsLKXUncVffRW/l3gFMFzzWlng5Zdf1j09Pc2uhi04deoU4qKAuDCIC4O4MIRCIbXUzywmjXdt8aer4ncADRwFPrPUg9aTQCDQ7CrYBnFhEBcGcWEQF9ZYMIBord8PoJR6Qmv9T/WvkjXC4TDr169vdjVsgbgwiAuDuDCIC2ssNA5kRen3+YJHcaChLfB6vc2ugm0QFwZxYRAXBnFhjYWysB5SSn1FKXWVUuq0fZVSLqXUq5RSXwF+Xr8qLo1gMNjsKtgGcWEQFwZxYRAX1lgogFxKYRT6V4EppdQzSqknlFLPAHHgLuBZ4JX1rebiGRsba3YVbIO4MIgLg7gwiAtrzNsHorVOA18CvqSUWgdsozAXVhTYq7U+Xv8qLg25ozCIC4O4MIgLg7iwxqImUywSBnYAlwCdwLuVKmR9aa3fV/uqLY90Ot3sKtgGcWEQFwZxYRAX1lhKAPkmhdl4/wMYqU91rJNMJptdBdsgLgziwiAuDOLCGksZiR4FNmqtT9W3StYIh8O6ra1t2Z9PZnL85vgUL40n2djn5/fWdNPmcdewho1jZmYGKy6chLgwiAuDuDAsZyDhUhaUOgLY3vSBAweW/dl0Ns/X9pzgf+0bZc/RU9z//BjfeOoEqWy+hjVsHOGwLNVSQlwYxIVBXFhj3kdYSqnXV7z8FvAjpdT/YNYjLK31g3WoW8O577lRXhhL0OZWXLqqk5cmZtgfmebfnx3l3ZcMNbt6S8bn8zW7CrZBXBjEhUFcWGOhPpCvV3nvc7NeawpzYtkCl2t5q/ROTKd58MVTeF3w/stWceGqLg6NTfOVXx7jsZdP8ap1QTb2tta0B11dXc2ugm0QFwZxYRAX1pj321ZrvXER/2wTPACy2eyyPvfIS6eYmM5wTn87F64q/FGd29/OhUOdpLJ5frJ/vJbVbAjj461X53ohLgziwiAurLG823Ub4/EsJbGsQF5rnj45RcDr4jUbTp+Z820X9HNicoanT04xGm+tlL9QKNTsKtgGcWEQFwZxYQ3HBZB8fukd3i+MJojP5Gj3urhwZedp2wY6fbxpcx8vTaRarhUiKYoGcWEQFwZxYQ0JIMDek3FGExkuWtmFu0ofyms39rC5P8CBsWlaaQngVCrV7CrYBnFhEBcGcWENxwWQ5cyu+bNDUcJTaa5cV31ag0tWdzE+neVXRyd5ITJttYoNY2io9TLH6oW4MIgLg7iwhm0CiFLqG0qpUaXUs3Ns/yOl1N7ivyeUUhdX2y+TySzpuJFEGo3m0lWdbBvqrLqPSyl2nNfL1sEOfnV0cknlNxPJcTeIC4O4MIgLa9gmgAD/QmGurbl4GXit1voi4LMUZgg+g6Wm8T4/mmA8kcHnduFxzT0Q89JVXewbSfDIS9Elld9M/H5/s6tgG8SFQVwYxIU1bBNAtNa/ACbm2f6E1rr07f0ksKbafksNIL89PsV0Js8lq6q3PkpsHexkRaeXrjY3x2Kt8dxUlus0iAuDuDCIC2ssPefVHnwA2F1tQyQSYfv27Xg8HnK5HDt37uS2224jHA7T0dGB2+1mcnKSgYEBJiYmePpYYWqvYG6K8fGCjng8zuDgIJFIBKUUvb29RCIRzu3x8sSxaX66d5j3XLGBcDiM1+slGAwyNjZGMBgknU6TTCYZGhoiHA7j8/no6upifHycUChEMpkklUqVt/v9fgKBANFolL6+Pqampkin0+XtgUAAn89HLBajv7+fWCxGJpMpb692TlprBgYGOHz4MKtXr573nLq7u8nlciQSiXKZdj6nkZEROjs7l3xOU1NTbNy40VHntNzrlMvliEajjjqn5V6nI0eO0NXV5ahzWu51Wk5K86InU2wESqkNwI+11tvm2eca4CvA72utz8irfeyxx/TWrVsXdbzETJYb//UZlFL8+/suos0zf+vlJ/vH+cKjR7hqfZD/dq2txk9WJR6Pl/84znbEhUFcGMSFod6TKTYdpdRFwNeAG6oFD1haGu+h8SQ+t+LKtd0LBg+AV64ujFB/+sQUubx9Au9cTE1NNbsKtkFcGMSFQVxYo2UCSHFFxHuBm7XWc065u5QAcnA8STKrCQUWl/q7otPH6u42pjN5DozZP51XFssxiAuDuDCIC2vYpg9EKfUd4HVAv1LqGPBpwAugtb4L+BTQB3yluBJiVmt9+exyljIO5FAxCJzbv/iOtEtWdZLK5tg/Os0FKzoW/blmIDnuBnFhEBcGcWEN27RAtNbv1lqv1Fp7tdZrtNZf11rfVQweaK1v1VqHtNaXFP+dETxgaeNAMrk82wY7OLdv8QHk4pWFQYV7jsYW/ZlmITnuBnFhEBcGcWEN27RAasVi03jTuTyPDxeCwPrQ4gPIhcXBhs+PJsjlNe55xo40G0lRNIgLg7gwiAtr2KYFUiuKj7cW5OipFHkNq7rbFtWBXqKvw8tQl4/pTJ7DUXtPxCaL5RjEhUFcGMSFNRwXQHK53KL2OxwtDAbcsITWR4mtg4W+j30jiSV/tpHEYvZ/zNYoxIVBXBjEhTUcF0AWux5IJJ5m62AHF6xoX/Ixtg4WHmPZPYD09/c3uwq2QVwYxIVBXFjDcQFksS2Q/ZFp9o0k6O9YehN2y4oOtgx2MJ6wdwqg3F0ZxIVBXBjEhTUc14m+2JH1R2MzAKwNti35GOtDfl4cm2Ymp5lMZen221PjUmcmdjLiwiAuDOLCGo5rgSxmHEgurzkxWQggq5cRQNwuxTl9hUdfB208oFBy3A3iwiAuDOLCGo4LIIu5ozg5OUM2rxno8BLwupd1nE39hQBi5xHpkuNuEBcGcWEQF9ZwXABxuxcOCMcnUwT97vKYjuWwqTh6/eCYfVN5OzrsPVK+kYgLg7gwiAtrOC6ALIYTk2liqRzty2x9gGmB2PkR1mKC6dmCuDCIC4O4sIbjAshisrBOThWyp1Z2L38Q0boeP20eFyPxNJOp7LLLqSeTk62z/G69ERcGcWEQF9ZwXABZTCd6qQN9ZffSO9BLuF2Kc3oLj7Hs2g8yMDDQ7CrYBnFhEBcGcWENxwWQbHbh1kA5A8tCAAH7P8aamJhzheCzDnFhEBcGcWENew5gqCN5rQkFCqc91GVtHpzNA6WOdHsGEDutNtlsxIVBXBjEhTUc1wJZaCqT6HSWZ8IJpmZyy07hLWFaIPbMxJLmuUFcGMSFQVxYw3EBZKFxIKPF6UdWdC5+4am5WBs0HekxG3akj4yMNLsKtkFcGMSFQVxYwzYBRCn1DaXUqFLq2Tm2K6XU/6uUOqSU2quUemW1/RZKyxspZmANdlqfxtntUuXFqOz4GKuzc/njXJyGuDCIC4O4sIZtAgjwL8COeba/GdhU/Pch4B+Xc5BSC2SgBgEEClO7nz/QXu6YFwRBOFuwTQDRWv8CmC8l4gbgW7rAk0CPUmrl7J0WGgcSiRcfYS1jFt5qrAn6eaE4s6/diMfjza6CbRAXBnFhEBfWsE0AWQSrgaMVr48V3zuNhcaBjMYLfSQratQC2RDyA3B4wn4d6YODg82ugm0QFwZxYRAX1milNN5qa9WekYM3OjrKBz/4QTweD7lcjp07d3LbbbcRDofp6OjgZKzwRd/tyXHs2DG01gwMDDAyMlJ+HhqPxxkcHCQSiaCUore3l0gkQnd3N7lcjkQiwdDQEOFwGJ8q9LkcOZVibCJKPpshmUya7T4fXV1djI+PEwqFSCaTpFKp8na/308gECAajdLX18fU1BTpdLq8PRAI4PP5iMVi9Pf3E4vFyGQy5e0dHR243W4mJycZGBhgYmKifE4HDx5k1apVSz4nr9dLMBhkbGyMYDBIOp22zTkt9zrF43E2bNjgqHNa7nXK5/O4XC5HndNyr9Phw4fp7Ox01Dkt9zqFQqGlfynbKQ9aKbUB+LHWeluVbXcDD2utv1N8vR94ndb6ZOV+jzzyiL7ooovmPMY7v72XqZkc3/ujbYQC1jOxAN73vX2Ep9L80zvPZ/0ylsitF8eOHWPNmjXNroYtEBcGcWEQF4ZQKFTtJn1eWukR1n3A+4rZWK8CYrODB8w/DiSZyTE1k8PrVvTUcBGo8mOs4jrrdqG3t7fZVbAN4sIgLgziwhq2CSBKqe8AvwTOU0odU0p9QCn1J0qpPynucj/wEnAI+CfgT6uVM984kNGKDnSllhxs52RDsdVhtwASiUSaXQXbIC4M4sIgLqxhmz4QrfW7F9iugdsWKme+cSCmA702j65K2LUjvbu7u9lVsA3iwiAuDOLCGrZpgTQCMwq9NhlYJezaAlnM1PZnC+LCIC4M4sIajgsg8/1BxJJZPC5V8wCypqcNlyrM8juTzde0bCskEvYbm9IsxIVBXBjEhTUcF0DmGwdyvLgWel97bR9h+dwu1gT9aArpvHZhaGio2VWwDeLCIC4M4sIajgsg83WiT0wXttU6gEBlJpZ9+kHC4XCzq2AbxIVBXBjEhTUcF0Dmy64qBZDeOgaQYRv1gyxmdcazBXFhEBcGcWENxwWQ+bKwJpKFKdfrE0Ds15EeDAabXQXbIC4M4sIgLqzhuAAy15K2mVyeWCqLS1HTQYQlNvTa7xHW2NhYs6tgG8SFQVwYxIU1HBdA5mqBRIutj56AB7erdoMIS6zsasPrVozGMyTS9kgNlLsrg7gwiAuDuLCG4wLIXHN7lfs/ajT/1WzcLsX6Hnv1g6TT6WZXwTaIC4O4MIgLazgugOTz1cdhTCTrl4FVwm6ZWMmkPephB8SFQVwYxIU1HBdA5sqqmJiuXwd6Cbt1pEuOu0FcGMSFQVxYw3EBZK5xIPVM4S1ht450yXE3iAuDuDCIC2s4LoC4XNVPabzcB1K/+SPLLZAJe7RAfL7aTtnSyogLg7gwiAtrnDUBpBEtkIEOL+1eF6dSWaLJuUfEN4qurq5mV8E2iAuDuDCIC2s4LoDMNQ6k1IlezwCilCq3QuyQiTU+Pt7sKtgGcWEQFwZxYQ3HBZC5ViQsdaLXMwsLYL2NVidczhrHTkVcGMSFQVxYw3EBpFoaby6vy4+UQnXsAwF7pfJKiqJBXBjEhUFcWMM2AUQptUMptV8pdUgpdUeV7euUUg8ppX6rlNqrlHpLtXKqBZBYKkteQ9Dvweuu7ylv6LVPR3oq1fw62AVxYRAXBnFhDVssaauUcgNfBq4FjgFPKaXu01o/V7HbXwD3aK3/USm1hcIa6Rtml1VtHMipZIaLhjrorsMcWLNZ39NGd5sbRWFUfC3XXl8qkuNuEBcGcWEQF9awSwvkCuCQ1volrXUa+C5ww6x9NFBawDgInKhWULVxIKdSWfaGE0zN1H+OqlDAiwb2jSbKqcPNQnLcDeLCIC4M4sIatmiBAKuBoxWvjwFXztrnM8D/Vkp9BOgA3litoGg0yvbt2/F4PORyOXbu3MmFb3kvAG0qRzQaZXJykoGBASYmJtBaMzAwwMjICJ2dnQDE43EGBweJRCIopejt7SUSidDd3U0ulyORSDA0NEQ4HMbr9RIMBhkbGyMYDJJOpxkMKKZm4Kn9R7hkZQddXV2Mj48TCoVIJpOkUqny5/1+P4FAgGg0Sl9fH1NTU6TT6fL2QCCAz+cjFovR399PLBYjk8mUt3d0dOB2u6ueUyKRKGeZWD2nZDJZ3u7z+Zp2Tsu9TqlUikQi4ahzWu518ng8DA8PO+qclnudUqkUw8PDjjqn5V6n5SQUqLkmH2wkSql3AddprW8tvr4ZuEJr/ZGKfT5Kob5/r5S6Cvg6sE1rfVqnx2OPPaa3bt16Wvn3PRfhS08c423n93P776+t9+nwD48eYff+cf70qjW8Y+tA3Y83F5OTk3R3dy+841mAuDCIC4O4MIRCoSU/b7fLI6xjQOU3+xrOfET1AeAeAK31LwE/0D+7oGrjQGKpwntd/rkXm6ola4uz8jZ7ffRoNNrU49sJcWEQFwZxYQ27BJCngE1KqY1KKR9wE3DfrH2OAG8AUEpdQCGARGYXVG0cyGSq0PcRbEAnOsC6njYAjjY5gPT19TX1+HZCXBjEhUFcWMMWAURrnQV2AQ8Az1PIttqnlLpTKXV9cbc/Az6olHoa+A7wx7rK87dqabyTM4UWSHdbowKIPVogU1NTTT2+nRAXBnFhEBfWsEsnOlrr+ymk5la+96mK358Dti9UTtUAUnyE1d2gR1grOn20eVxEk1mmZrJ0NShwzUYWyzGIC4O4MIgLa9iiBVJLqo0DaXQLxKUUa4OFx1jNbIVIjrtBXBjEhUFcWMNxAaTaOJBSH0gjBhKWMB3pMw075mwkx90gLgziwiAurOG4AFJtOvdSC6RRnehg+kGa2ZEeCASadmy7IS4M4sIgLqzhuAAye+qQdC5PMpPHraDd27jTtUNHuiyWYxAXBnFhEBfWcFwAyeVOn65kquLxVSPnpSql8jYzgMRisaYd226IC4O4MIgLazgugMweB1IaRNioDvQSq7rbcCkYmUozkz0zM6wR9PefMc7yrEVcGMSFQVxYw3EBZHYLpJyB1cD+DwCv28Wq7jY0cCzWnFaI3F0ZxIVBXBjEhTUcF0Bmjy0sjwFpa8wYkErWNTkTq1pG2tmKuDCIC4O4sIbjAsjscSCTM41P4S3R7EwsyXE3iAuDuDCIC2s4LoDMvqMo94E0MYA0qyNdctwN4sIgLgziwhqOCyBu9+mPqspjQJr6CKs5AaSjo6Mpx7Uj4sIgLgziwhqOCyCzmWpiC2RtMZX3eGyGXL7x667MDqZnM+LCIC4M4sIajgsgs7OwYsVxIM2Y0DDgdTPQ4SWT14SnGt+RPjk52fBj2hVxYRAXBnFhDccFkDM70Rs/jUklzczEGhho3mqIdkNcGMSFQVxYw3EBZPaKhI2eyn02zewHmZiYaPgx7Yq4MIgLg7iwhuMCyGzKabxNWpOjmcvb2mG9e7sgLgziwiAurGGbAKKU2qGU2q+UOqSUumOOff5AKfWcUmqfUurfqu1TOZVJNq9JpHO4FHQ2IQsLmtsCkea5QVwYxIVBXFjDFgFEKeUGvgy8GdgCvFsptWXWPpuAjwPbtdZbgf9SrazKcSClDKyuNg+uBk6kWEnl+uiNvtsZGRlp6PHsjLgwiAuDuLCGLQIIcAVwSGv9ktY6DXwXuGHWPh8Evqy1jgJorUerFVSZlhebKQWQ5qXq9QS8dLe5mc7kGZ9u7LQJnZ2dDT2enREXBnFhEBfWsEsAWQ0crXh9rPheJZuBzUqpx5VSTyqldixUaGklwmZlYJVo9oBCQRCEetDcb1ZDtedLs5/3eIBNwOuANcCjSqltWutTlTuNjY2xffv2Ql/I6m20vf5WOr2K4eFhOjo6cLvdTE5OMjAwwMTEBFprBgYGGBkZKd+NxONxBgcHiUQiKKXo7e0lEonQ3d1NLpcjkUgwNDREOBzG6/USDAYZGxsjGAySTqdJJpPl7T6fj5Udbp4FDoRjrPYkSaVS5e1+v59AIEA0GqWvr4+pqSnS6XR5eyAQwOfzEYvF6O/vJxaLkclkytvnO6fjx4+XvdT6nLq6uhgfHycUCpFMNu6clnudpqam8Pv9jjqn5V6nXC5HPB531Dkt9zqdPHmSeDzuqHNa7nUKhUJL/+K2QxaCUuoq4DNa6+uKrz8OoLX+64p97gKe1Fr/S/H1z4E7tNZPVZb1+OOP6y1bCt0n978wxhcfO8p1m3v5s9esb8i5VOOHz4xy957jvO2Cfm7fvrZhx02lUvj9/oYdz86IC4O4MIgLQygUWnJHsV0eYT0FbFJKbVRK+YCbgPtm7fO/gGsAlFL9FB5pvTS7oMpxIOW1QJqUwluiWbPyRiKRhh7PzogLg7gwiAtr2CKAaK2zwC7gAeB54B6t9T6l1J1KqeuLuz0AjCulngMeAv5caz0+X7mTqeZN5V5Js/pAGrmEr90RFwZxYRAX1rBLHwha6/uB+2e996mK3zXw0eK/OakcBzLZxIkUKxno9NLmcRFNZpmayTZsXq7e3t6GHKcVEBcGcWEQF9awRQukllSOA4k1cTXCSlxKsS7YRl+7l6MNnBNLmucGcWEQFwZxYQ3HBZDKcSBTM/ZI4wXY0BtgfDrD4WiyYcfs7u5u2LHsjrgwiAuDuLCG4wJIJaYF0vwAUlobZDjauH6Q2VPbn82IC4O4MIgLazgugFT+QZSzsJo0E28l63sCABxuYABJJBINO5bdERcGcWEQF9ZwXAAprQeSy2viM81bTGo2G0KFTKzhU417hDU0NNSwY9kdcWEQFwZxYQ3HBZBSJ3o8nUNTmAfL7Wp+qt5gl482j4uJ6UImViMIh8MNOU4rIC4M4sIgLqzhuABSyuuOVczEawdcSpVn5m1UP8js1RnPZsSFQVwYxIU1HBdASllYpancgzbo/yixPtTYfpBgMNiQ47QC4sIgLgziwhqOCyClqUxiNpnGpJJyP0iDUnnHxsYacpxWQFwYxIVBXFjDcQGk1AIpTWPSZYMxICVKAURaII1HXBjEhUFcWMNxAaQ0u3AphTfY5FHolZRSeRvVB5JOpxtynFZAXBjEhUFcWMNxASSfzwP2mQerkhWdXgJeF6dS2XInfz1JJhuXMmx3xIVBXBjEhTUcF0BKWRV2mYm3EqVUeWbeRvSDSI67QVwYxIVBXFjDcQGkNA7Ejp3o0Nh+EMlxN4gLg7gwiAtrOC6AuFyFU+ryudk21EGPjVog0NhUXp/PV/djtAriwiAuDOLCGvb6dq0BpQBycGyal6Mp2n32ipEmlbf+AaSrq6vux2gVxIVBXBjEhTXs9e1aA0rjQBKZQh9Iu88+WVgA6yvGgtR7Pfrx8XkXbDyrEBcGcWEQF9awTQBRSu1QSu1XSh1SSt0xz343KqW0UuryattLKxJOpwvZWB1eewWQ/nYv7V4XkzM5TiXrm4kVCoXqWn4rIS4M4sIgLqxhiwCilHIDXwbeDGwB3q2U2lJlvy7gdmDPXGXl83m01kwXWyAdNmuBKKXYUOoHqfMa6ZKiaBAXBnFhEBfWsEUAAa4ADmmtX9Jap4HvAjdU2e+zwN8Cc37z5vN5kpk8eQ1+j8sWM/HOpvQY6/BEff94U6nGrT1id8SFQVwYxIU17NKJvho4WvH6GHBl5Q5KqUuBtVrrHyulPjZXQbFYjDe99Xra//CvmI5N8IUvfIHbbruNcDhMR0cHbrebyclJBgYGmJiYQGvNwMAAIyMjdHZ2AhCPxxkcHCQSiaCUore3l0gkQnd3N7lcjkQiwdDQEOFwGK/XSzAYZGxsjGAwSDqdJplMlrf7fD66uroYHx8nFAqRTCbpphA49h0d4+oBTSAQIBqN0tfXx9TUFOl0uvz5QCCAz+cjFovR399PLBYjk8mUt893TrlcrvyMt97nlEqlytv9fn/dzmm510kpRSKRcNQ5Lfc69fb2Mjw87KhzWu51UkoxPDzsqHNa7nVazuM8Ve+O3EVVQql3AddprW8tvr4ZuEJr/ZHiaxfwIPDHWuvDSqmHgY9prX89u6yHH35YB9dt5kM/fIF1PX6+duMFjTuRRfKb45PcsftFtg528A9v31y34wwPD7N+/fq6ld9KiAuDuDCIC0MoFFry4xq7PMI6BqyteL0GOFHxugvYBjyslDoMvAq4r1pHusvlIpEu9X/Y5fROpzQWZDiaqmsmlt/vr1vZrYa4MIgLg7iwhl2+YZ8CNimlNiqlfMBNwH2ljVrrmNa6X2u9QWu9AXgSuL5aC+T0AGKvDvQSvQEPXW1u4ukcE9P1y8QKBAJ1K7vVEBcGcWEQF9awRQDRWmeBXcADwPPAPVrrfUqpO5VS1y+lrGw2S6KYwttusxTeEkop1veUpjSpX0d6NBqtW9mthrgwiAuDuLCGXTrR0VrfD9w/671PzbHv6+Yqx+Px2L4FAoVMrGdHEhyOprhsTXddjtHX11eXclsRcWEQFwZxYQ1btEBqST6fZ7oFAsiGUP3XBpmamqpb2a2GuDCIC4O4sIYjA0ipBWK3aUwqKU9pcqp+j7BksRyDuDCIC4O4sIbjAojX6y3Pg9Xhte/pra+YVLFemViy1oFBXBjEhUFcWMO+37DLJJPJtEQfSCjgJej3MJ3JE0lk6nIMWevAIC4M4sIgLqzhuADSCmm8Jdb31Hdqd0lRNIgLg7gwiAtrOC6AKKXKaby2DyCh+qbyymI5BnFhEBcGcWENxwWQXC7XMi2Qei8uFYvF6lJuKyIuDOLCIC6s4bgA0irjQKBiSpM6Teve399fl3JbEXFhEBcGcWENxwWQXC5n27VAZrM+1MZFKzvxuhS5fO0zseTuyiAuDOLCIC6s4bgAorVumRZI0O/l5OQMz44kOD45U/PyM5n6ZHe1IuLCIC4M4sIajgsgbo+XvIY2t8Jjw8WkZnNufzsAh8ama1625LgbxIVBXBjEhTUcF0DSxTsKu7c+SmwqBZDx2mdiSY67QVwYxIVBXFjDcQEEVTglO09jUsmmvkJH+sE6tEA6OjpqXmarIi4M4sIgLnqTnMoAABvgSURBVKzhuABS6otulRbIuRUtkFpPaeJ2t4aDRiAuDOLCIC6s4bgAks21Rgd6ib52L72BQurxyanaTuw2OTlZ0/JaGXFhEBcGcWENxwUQ5SoEjlYJIFC/jvSBgYGaltfKiAuDuDCIC2vYJoAopXYopfYrpQ4ppe6osv2jSqnnlFJ7lVI/V0qtr1ZOuQVi09UIq3FuqR+kxh3pExMTNS2vlREXBnFhEBfWsEUAUUq5gS8Dbwa2AO9WSm2Ztdtvgcu11hcBPwD+tlpZpg/EFqe2KOrVAqnXNPGtiLgwiAuDuLCGXb5lrwAOaa1f0lqnge8CN1TuoLV+SGtd+oZ9ElhTtaQWy8IC2FynjnRpnhvEhUFcGMSFNeyyJvpq4GjF62PAlfPs/wFgd7UNiekE4Oef7/5H7t73IDt37uS2224jHA7T0dGB2+1mcnKSgYEBJiYm0FozMDDAyMgInZ2dAMTjcQYHB4lEIiil6O3tJRKJ0N3dXZisMZFgaGiIcDiM1+slGAwyNjZGMBgknU6TTCbL230+H11dXYyPjxMKhUgmk6RSqfJ2v9+P3++n06uIpbLse/k4Xe5ceXsgEMDn8xGLxejv7ycWi5HJZMrb5zunAwcOsHr16qacUyAQIBqN0tfXx9TUFOl0uibntNzrNDU1xcaNGx11Tsu9TrlcDrfb7ahzWu51evnll+nq6nLUOS33OoVCoSV/cSs7NOGUUu8CrtNa31p8fTNwhdb6I1X2fS+wC3it1vqM+T9++JOH9Oef0fzZa9Zx3ea+ele9Ztyx+xC/OT7Fp9+4ke0bempS5vj4OH19reOgnogLg7gwiAtDKBRa8tQddnmEdQxYW/F6DXBi9k5KqTcCnwSurxY8oKIPpIU60cEMKKzHiHRBEIR6YJcA8hSwSSm1USnlA24C7qvcQSl1KXA3heAxOldB+WKLqpXSeKE+HenxeLxmZbU64sIgLgziwhq2CCBa6yyFx1IPAM8D92it9yml7lRKXV/c7e+ATuD7SqnfKaXuq1pW8WfLBZC+QgA5OF67ADI4OFizslodcWEQFwZxYQ27dKKjtb4fuH/We5+q+P2NiymnsK6Gaqk0XoCV3T7avS4mprOMT2foa/daLjMSibB27dqFdzwLEBcGcWEQF9ZorW/ZRVDqA2mlNF4Al1LlVkitHmMpZf/p7BuFuDCIC4O4sIbjAkirPsIC2NRf2xHpvb29NSnHCYgLg7gwiAtrOC+AaPC6FT53651arTvSI5FITcpxAuLCIC4M4sIarfctuwhaLYW3xKbSI6wadaR3d3fXpBwnIC4M4sIgLqzhzADSgo+vAFYH22jzuBiNZ4ilspbLyxUnlhTERSXiwiAurCEBxEa4XYpzeosDCmvwGCuRSFguwymIC4O4MIgLazg0gLTuaZmOdOsBZGhoyHIZTkFcGMSFQVxYo3W/aeehVVsgANuGOtjcH+DliZTlssLhcA1q5AzEhUFcGMSFNWwzkLCWtHIAOaevnQNjSSKJDFprS3nqXq/1wYhOQVwYxIVBXFjDkS2QVhtEWMnq7jaCfg/RZJawxTXSg8FgjWrV+ogLg7gwiAtrODKAtGoaLxRGxm5Z0QHAvhFrHXxjY2O1qJIjEBcGcWEQF9ZwZgBp4RYIwNbBQgB5zmIAcerdVXwmy2g8TXQ6w9RMlmQmRy6v513N0akuloO4MIgLa0gfiA3ZMlhqgVibajqdtvYIrNlk85pD49M8ezLO0dgMR0+lOBqbod3r4mSVx3ub+9vJa83aHj9rgm2sCfo5p9fP6qC/5V3UEnFhEBfWcGQAaW/hNF4ofBF6XIrD0RSJdG7ZATGZbM3FqQ5Hk/zvAxP8/NAEq7vbeHZWSyybd9Hf4SWT02TzmmwuTzqnORxNks7p0xblumBFO8PRFBu6XVy+PsfWwU7OH2gn0OI3GVZo1b+LeiAurOHIANLKfSAAPo+LTf0Bnh+d5vnRBJevWd50C62U457O5Xni8Cl+8EyEAxWDKLvb3Fy/pZ91PX7WBv2s7Wmjr91bNTttMpXlWGyGY7FUubUyEk8zncnz3Hie58YLKZuDnT4GOr28clUXl67u4ryBDjyus2dW1lb6u6g34sIazgwgDri73DrYyfOj0zw3svwAEg6HWb9+fY1rVnueCcf54qNH6Al4ODA2TYfPzete0cObNvdx/kD7olOZu/0etvg95UeAJcYTGR7ed5jRXICXJ5LsDccZiad5NpzgW78J0+518ap1Qc4baOey1d2s7Wlz9DTfrfJ30QjEhTUkgNiULSs66PS5CE9VXfp9Ufh8vhrWqPZMzWT52q9OsHv/OAA5rfmz16zjda8I0eap3WPIvg4vV6/tZOXKlUChE/7pk3F+e2KK3xyfIpXJ8+CLUR58MQocp7/dyyWrOrl0dRcXDnUy1NVWs7rYAbv/XTQScWEN23QWKKV2KKX2K6UOKaXuqLK9TSn1veL2PUqpDXOV5YQAsm2og+lMnkdfPkU6l19WGffdV3XV36ajtebhF6Pc+oPn2b1/HI9L8UeXDvHVnRdw3ea+mgaPEpUuOts8bN/Qw66r1/KNd23hi9dv5mOvWcfrzwkRCngYm86wNxzn7x45wvu+9xzv/e6z/O3Dh3ngwBiHo8niqpeti13/LpqBuDAopT605M/Ml/rYKJRSbuAAcC1wDHgKeLfW+rmKff4UuEhr/SdKqZuA/6S1/sPZZX3zvp/r6666pC5fQo3mQz98nsPRFH//tk1cONS55M9v376dxx9/vA41Wz6ZXJ5/+fVJ7t8/TiKdY9tgB//X769lfShQ1+Mu1oXWmsPRFM+PxnnyyCTPhhPE04UZW7cNdvDsSAK/x8W5/QE297ezqS/Axt4Aa4J+fC3yNzeXC601M9lCQkI6l2cmW/iZyeXJ5DSZvCaTK6RLp/OaXOmf1iggky+UkdegMIu7AbR5FDPZwjtKgUuBQhV+Fn93u8DjcqHRuFC4XIWVOl2Ay6Vwq8L+hd8LY6bcSpXLcymF26VQFMsv7a9K76nisYrHVIq3vPnN/OQnu4vvFR5blrZXQxe3z0flV6rWulxY6btWQ9lRZbmlffSsN3XxqNXfP/3zs49/RsXmODGvW3HO6sH/o7W+fK7zqoZdHmFdARzSWr8EoJT6LnAD8FzFPjcAnyn+/gPgS0oppWdHQJ3D53bG8+uLV3ZxOJridyemlhVAPB67XN4CyUyOO3/2Mv/n+BSb+wO85fx+dpzXh6sB/Q2LdaGUYmNvISi85fwBcvlCdtfek3HCU2kiiUy5/+TZcIJOn4t4Oo8CVnT6WNvTxupuP+t72gi1e+lt99LX7qUn4KnLIme5vCaZyTGdyZNM50hk8kxnckyncySKr3P5PNFklul0nmQmR+BNt/Hx3YeIJrOksjlSmTzJbJ5UJs+2oQ6eCZ+e9bY22MbRmHmUet5AO/sjp0/2uT7kZzhq5m/zuRXpnPmveeGscmdvL3FOX4AXZ63I2eF1kcic3gpf0eFlNJE54/NbVrTz3OiZE5FuWdHBc6Onn9fGXj8df/S3vPPbz5z2/ub+AAfGqmdnlW4iZjP7/BZ6/6KhDvZWeb/asas5meucAM4faOeFyJkO5juvi5bx/QL2aYHcCOzQWt9afH0zcKXWelfFPs8W9zlWfP1icZ/ThpLef//9emRkBKUUWmtCoRADAwNkMhnc7sKjrVwuh9frJZstrLnh8XiWtT2TyRTugtxustksbre7cAeWz5e3u1wuXC4X2WwWj8dDPp9f9PZYMk1kOo/foxhsd+HxeMjlcmity5+fr86nTp0qL5jT7HPK5vJEkppUNo/bBSs7vbjJL/mclnudEokEwWCwJuek3G6S6RwzWY1WikQ6R1Zz2m1g5R13CZ9bkde6fCfsUaCVguKcZ4rCfaZWLvL5whem26XI5CrvXDUahVdBKqdPu9v0uCBb5WlntfeLhz0Dv0eRzutiXYp39er0O1yfx0U2ly/XWWuN1+0iW6yzy+VC5/PlO3qtNR63m2xx7Q2lXOR1cbsunJPLVThnl1Ll8yzaoNQuyFdUWAH5ohRN4c5aa43XpcotodJ3QKnOMxUStC5cj5msqWfldZrJ6TNaUQB+tyJVJfD5PS5SsyQr5g6UbW7FTF6bAxQP5vMUr3dFU6dwTlXKmHVOhWIUXhfFa1jpDzwuRTZvWi6V29s8LpKRY/tuvvnmbWccaB7scota7RZ0trHF7EN7ezvveMc7alKpZjM1k+XGbz+D26W4930X4l/iI5Lh4WFbZJiMxtN84icvcuRUisHONv76zeewJuhvaB3q7SKTyxOeSpfTiE9lchycTDKRzDAxnSWazNDX7iVScde8JtjGsfKdfeFPefbd/sou76xBk4X/BhcOdfJMOI4CAl4X7V43/Z1e0IW54Nq9bjp8Ltp9boJtHnweF+1eFwGvm0R0jHWrh8qv/V43fo8Lv8eF+yxKZwb7/B+xA6HQNUsKHmCfAHIMWFvxeg1wYo59jimlPEAQmJhdkJNm1+xq83Buf4CDY0meG4nzytVLS+e1Q477kVMpPr77EJFEhg0hP3+941z6Ohp/jertwut2sbbHz9oeP4U/zdPJ5TXxdJZkJs90Ok8ikyNd7G/I6UJfQjavcbsKd8eu4vN9r0vhcinaPC7aPAqfu/BF3+ZxEfAWfl9qyvHMTDttbc7KLFsudvg/0srYJYA8BWxSSm0EjgM3Ae+Ztc99wC3AL4EbgQfP6P8AMpkzn4u2Mhev7OLgWJLfnVh6AGl2jvv+SIJP/uRFJmdybFnRwWevewVdbc35k2u2C7dLEfR7aXDDqyrNdmEnxIU1bJE2orXOAruAB4DngXu01vuUUncqpa4v7vZ1oE8pdQj4KHBaqm8pDfjFF1/ki1/8YiOrX1cuXdXJOX1+RhY5HuTYsWNcf/31XHnlldx4443cddddda5hdV4cn+ZffxNmcibHFWu7+fxbzm1a8MjlcrznPe/hpptuasrx7UIsFuOWW25h586dXHnllfzqV79qdpWaxle+8hWuuuoq3vWud3HrrbeSSllfwK2V2LVrF5s3b+bqq68uv6eU6lVK/VQpdbD4M7RQObYIIABa6/u11pu11udorf978b1Paa3vK/6e0lq/S2t9rtb6ilLGFpTTgL8MvHnz5s388Ic/5IUXXmjOidSYbUOdHDk1w8MvnSKaXLh15fF4+OxnP8uePXv40Y9+xNe//vWGuxiNp/mLB15iz9FJ3nJeH5+59hVL7r+pJXfddRebNm1q2vHtwsc//nHe8IY38NBDD/Hoo49y3nnnNbtKTeHEiRN89atf5cEHH+RnP/sZuVyOe++9t9nVaijvec97+P73vz/77TuAn2utNwE/Z9ZNejVsE0AsUk4DzuVy7Ny5k927dze7TjUh4HVz8cpONPDU0ckF9x8aGuLiiy8GCo/zNm/ezMmTJ+tcS0N8JssnH3iR8ekMFw118qdXr2nqPFPHjx/npz/9KW9961ubVgc7MDk5yRNPPMHNN99MNBrF5/Od1VOZZ7NZUqkUkUiEZDJ51vWFXH311YRCZzQwbgC+Wfz9m8CC2UhOCSCrgaNQuANftWpVQ780682Vawv/0X+1iABSyfT0NHv37uWyyy6rR7XOIJPL899+9jLD0RTrevx8+tqNdRn7sBQ+8YlP8JnPfIaenp6m1qPZDA8P09/fz65du3jve9/L7bffTiJhbb2ZVmXVqlXs2rWLiy66iOuuu47u7m5e//rXN7tadmBQa30SoPhzxUIfcEoAKd/ilvLnnTQZ3hXrCp3nvz42SXaR02jE43E++MEP8rnPfa48FqSeaK35wqNHePpknN6Ah/9+3TlN6/Mo8cADDzAwMMAll1zC9PSZA6vOJrLZLE8//TTvf//7ueeee2hvb3dUX+FSOHXqFLt37+a3v/0tDz74INPT09xzzz3NrlZL4pQAUk4DzufznDhxwlFN0pVdbazr8TOdybMvvPAiU5lMhltuuYUdO3bw9re/vQE1hO/tHWE0nsbvcXHndecw2NX8Ser27NnD7t27ufjii/nYxz7Go48+yoc//OFmV6sprFq1ilWrVnH55ZeTTqe54YYb2Lt3b7Or1RQefvhh1q1bR39/P1pr3va2t53VCQUVjCilVgIUf44u9AGnBJByGrDH4+Hee+9lx44dza5TTblibaEVsWeBx1haa26//XY2b97Mn//5nzeiajx1dJJ/fuokz4QTfOKa9Wzub2/IcRfiU5/6FPv27ePpp5/mq1/9Kq9+9au5++67m12tpjA4OMjq1as5ePAgQ0NDPPLII2dtJ/qaNWv49a9/zfT0NIODg/ziF79g8+bNza6WHSgNlaD480cLfcAu40AsobXOKqV2AQ+88MILvOMd7+CCCy5odrVqylXrghwYS/BCJFGepqEae/bs4Xvf+x5btmzhta99LT6fj7/8y7/k2muvrUu9TkzO8NcPHUYD77tsJa9ab8++homJM8acnnX8zd/8DR/+8IdJJBJs2rSJL33pS82uUlO4/PLLuf7667nmmmvI5/Ncdtll3HLLLQt/0EHceuutPP7444yPj7N161buuOMOgM8D9yilPgAcAd61UDm2mAurlvziF7/QF154YbOrUXNyec1N//YssVSWu3eez8behWevHR0dZcWKBfvBlk0yk+O/3HeAl6MprloX5NPXbmzIxIjLod4uWglxYRAXhlAotOT/vE55hFXGSZ3nlbhdiqvXF7KxHn351KI+U8/FcrTW/MOjR3g5mmJNsI3/+rr1tg0eIAsHVSIuDOLCGo4LILnijJ9O5NUbe1jV7eNwNMliWo6xWKxudfn3fRFGptKEAh4+88ZX2H4Rr3q6aDXEhUFcWMNxAcRua2DUkktWdpJI53nscIxDVdYHmE1/f39d6rEvHOef9hzn+cg0u65ew7qQDSZ4WoB6uWhFxIVBXFjDcQHEyS0Qj9vF615RGD3680MLdwrX4+4qmszwVw8eJqfhndsGePXGBafLsQVyp2kQFwZxYQ3HBRCnJQXM5g3nFr6wD0SmF1ybu9YzE+fyms8/dJjx6QzbBjv4wBWra1p+PXHaLM1WEBcGcWENxwUQJ60HUo3zBtq5ZFUnz44kePLI/HdPtR5M+a3fnOS3J+L0+D188vUbmzrH1VJx0sBSq4gLg7iwhuMCiNPvKJRS5bmx7n9hfN59w+FwzY6750iM7/xuBJeCT7x+Q1MWhbJCLV20OuLCIC6s4bgAUloP28lcu6kXr6vQH3F8cu51Qjo6OmpyvBOxFP/jsaMA3HLZSi5Z1VWTchtJrVw4AXFhEBfWcFwAORvo9nt4y/n9HBpP8qN9kTn3q0UwTaRzfPpnL+NxwZs29fKHFw9aLrMZnA03FotFXBjEhUEp9aBSakkDY5oeQBazCpZS6hKl1C+VUvuUUnuVUn84V3lOzsKqZMd5fQD8ZP84k6ls1X0mJ5c2/ftsSp3mw9EUXreL/3zVGlsPFpwPqy6chLgwiIsCJ06cgMLMJOmlfK7pAYTFrYI1DbxPa70V2AF8USlVddIlp3eilzinr51Xru6iN+DhgQPV+0IGBgYsHeOff32CPUcn6Wpzc+ebzrH9YMH5sOrCSYgLg7iAhx56iE9+8pMAYaXU+5byWTsEkAVXwdJaH9BaHyz+foLCNMNVr3w2W/1u3IncfOkQJ6bS/NvvRpiaOfO8rUwg+NOD49yzdxS3gr98w0ZWB9usVLXpyGSKBnFhEBdwzTXXlB7lfUFr/a2lfNYOw7ZPWwVLKTXvzGZKqSsAH/Bite0TExNs374dj8dDaXnb2267jXA4TEdHB263m8nJSQYGBpiYmEBrzcDAACMjI3R2dgKFxZgGBweJRCIopejt7SUSidDd3U0ulyORSDA0NEQ4HMbr9RIMBhkbGyMYDJJOp8tLZIbDYXw+H11dXYyPjxMKhUgmk6RSqfJ2v99PIBAgGo3S19fH1NQU6XS6vD0QCODz+YjFYvT39xOLxchkMgwNDdE5M87W/jZeOjXDt584xB9fue60c4pGowQCgSWf03Bc8w97CvNtvf+SPlZ5kgwPTzTknOp1neLxOKFQqCnXyW5/e/l8nuHhYUedk5XrlMvlHHdOS71OxUf/v1nql3dDZuNVSv0MqJZw/Ungm1rrnop9o1rrqsObi4ucPAzcorV+sto+jz/+uN6yZYv1SrcIh8amuWP3IZKZPF995/msDpppRVKpFH7/0qYZOR5L8fePHuHZcILrt/Sz6+q1ta5yU1iOC6ciLgziAp5//nk+97nP8eMf/1gppW7QWi+4DkiJhjzC0lq/UWu9rcq/H7HIVbCUUt3A/wf8xVzBA5w/DmQ25/a386p1QQa7fHzjqZPkK24IRkZGllRWeGqG/3r/IZ4LJ3j7Bf3851etqXV1m8ZSXTgZcWEQFxAKheju7kYp9R7giaV81g59IAuuglVMLft34Fta6+/PV9jZmJb3oStXkczkefTwKe591qT1lprbi+H4ZIr/+/5DRBIZLhjs4NYrVuFuoZHmC7EUF05HXBjERWE0/pe//GW01v+mtZ57XEAV7BBAPg9cq5Q6CFxbfI1S6nKl1NeK+/wB8Brgj5VSvyv+u6Q51bUf3X4vH9m+hs39Ab6/d4S9J6eW9Pn9kQQf/Y+DhNo9XLCinb+67hwC3rMvEAuCsDSaHkC01uNa6zdorTcVf04U3/+11vrW4u//qrX2aq0vqfj3u2rlnS3jQGZz9foeLlrZSSqT4+49x3l+NEE8Hl/wcz8/NMHHfnyQaDKLz+3iczvObel03blYjIuzBXFhEBfWsEMWVk05W8aBVOMDv7eaXL6w2NP/88gwf7Ctj/Vz7BuJz/CPTx7n6ZNxAl4315wT5PbfX9tSEyQuhcHB1hxBXw/EhUFcWMNxAeRsGgcyG7dL8aErV6NUYdnbb/8mzAOHYly3uY/zV7TjUnBwLMljh09xcirNi+NJAl4Xu7av4XXnhBy7HDBAJBJh7VpnZJRZRVwYxIU1HBdAznbcLsWHr1zN2h4/u/eFyWnN//xtmIlkhnROEwp4iCazeF3wjq393HjhICs6nb8utJOD41IRFwZxYQ3HBZC2ttYeMV0LlFK89fx+fm+ojb2RDIfGpzk0lmQknubVG4P0d/h4zcYe+jucHzhK9Pb2NrsKtkFcGMSFNRwXQM72QUGVJGMTvHHTet64Sf6TRCIR1q+fq0fo7EJcGMSFNZqehVVruru7m10F2yAuDOLCIC4M4sIajgsgZ2sabzXEhUFcGMSFQVxYw3EBJJFINLsKtkFcGMSFQVwYxIU1GjKZYiMJh8NaOtILzMzMSFJBEXFhEBcGcWEIhUJLTklzXAskHA43uwq2QVwYxIVBXBjEhTUcF0DO5pHosxEXBnFhEBcGcWENxwWQYDDY7CrYBnFhEBcGcWEQF9ZwXAAZGxtrdhVsg7gwiAuDuDCIC2s4rhNdEARBaAyOa4EIgiAIjUECiCAIgrAsJIAIgiAIy0ICiCAIgrAsJIAIgiAIy0ICiCAIgrAs/n+uFBexh4OABgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"sym.plot(h, (t, 0, 10), xlabel='$t$', ylabel='h(t)');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Relacion con las Ecuaciones Diferenciales de Coeficientes Constantes\n",
"\n",
"Como se habia encontrado anteriormente la función de transferencia $H(s)$ del sistema como\n",
"\n",
"$$\n",
"H(s) = \\frac{Y(s)}{X(s)} = \\frac{\\sum_{m=0}^{M} \\beta_m s^m}{\\sum_{n=0}^{N} \\alpha_n s^n}\n",
"$$\n",
"\n",
"La función de transferencia de un sistema LTI cuya relación de entrada y salida puede caracterizarse por una ecuacion diferencial de coeficientes constantes se da como función racional en $s$. Los coeficientes de su polinomio numerador y denominador están dados por los coeficientes $\\beta_m$ y $\\alpha_n$ de la ecuacion diferencial. La conversión entre ambas representaciones de un sistema LTI es, por lo tanto, sencilla."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Ejemplo**\n",
"\n",
"Los coeficientes para el filtro pasa bajos de segundo orden se pueden determinar a partir de la ecuaicon diferencial de coeficientes constantes o desde la función de transferencia anterior como\n",
"\n",
"$$\n",
"\\begin{align}\n",
"\\beta_0 &= 1 & \\alpha_0 &= 1 \\\\\n",
"& & \\alpha_1 &= C R \\\\\n",
"& & \\alpha_2 &= C L\n",
"\\end{align}\n",
"$$\n",
"\n",
"A partir de estos coeficientes, la función de transferencia $H(s)$ se construye en `SymPy`"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAJkAAAAtCAYAAAC9B8nZAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAF4klEQVR4Ae2di3EURxCGdSoFICsEOQNhR2ApA1FkABlAOQJKzgDIwFIGQATGzgAyMCgD+ftWO/Ls3j5Op5njTnRXjXbn1Tv97z89vbPLsbi5udkLCQRqIrBfU/lj1L1YLM5J30iHj9G+GjYd1FD62HS2hHqHXV9JR6Qg2D1ucniyFcAipLgmPSW9oPlfK3SJJhkCQbIMjDitg0CQrA6uoTVDIEiWgRGndRAIktXBNbRmCATJMjDitA4CQbI6uIbWDIEgWQZGnNZBIEhWB9fQmiEQJMvAiNM6CCziBflqwPJq6Q0tfaV0SvK10j+kL6T3YPiWY8gIAkGyEWCiuBwCsVyWwzI0jSAQJBsBJorLIRAkK4dlaBpBIEg2AkwUl0MgSFYOy9A0gkCQbASYKC6HQJCsHJahaQSBINkIMFFcDoEFquLfxJXDMzQNIBA7/gOgRFFZBGK5LItnaBtAYKf+3SUvqS+wwZfTxyRfTr/i5fQ1x5AtRmBnlsuWYG8gleTaI3/J4Zj8ky3GN4YGAru0XJ737thr8ieQTa8WssUIjC6X3DyXpeekM1K+JDXfT7U39wWe5FXfPupSv0SMUt9epWXSS6Yx5WX9oWwkXxirq3bQ4p/kEpx395s1Br/XT1j2kvSN9HygTuL4Ad9gfd6eNm6PfM7LSp2j13Go/7CUznX0cP2SWDmBO/cD/U4i7ZRonbptyzNG74m86NyTzqCtJL0nfe43zA2iTpJpuDFRR0fKU+cXpLa5SGUlj+h1jC/X1UlfAXlI/5JYnTAWsRocD+XGn9afrGvvVD/0ro0FfcXB8cmJNM4OyfapyOUjGcnxhEFd5xW9c5X5IyRNEN6rS1mXWUXSFhWWJ58yP3D9P4oqvp+ykliJufLh9rD0VxIqU/fktsWG/8oT0uSP0dyRjBsnEzXGDnPG+BNKf87Y0wCHrjHgZroPV7fxnjPFX9j5LlIBqybuxSZj145wLb2MS6aTampSd/ptU+bAwWCIRhisf8GQFHhaNSYaqzeZEgm7BNpUB8ahzn/bNhL9Uw489RL3Z8oagrX5r3mbtm+1QyWstGsJd64lwfxdtCtsfDpkFG0mMRvqs+myhmRcNHkFvdmsYLAEGPV27c1Xz8pejD5/097N1aYPeZdZ98ASoSStgL6mTvAV6wbBb2rr/CmNVVoKnew+RCh6NonnE+VvY5NoDjP6bodggAMxiC4WWKJLMqjvVP1ziXZ6Upr935a84N8FkJz71KLOTsr73OccPWsFu/QrjZXE0qY7W7UDcWVx4nXKk42Uz2KW2s4d0bUWFn296Bm0JXmyIxooK635zCANH/Vk6HEWyppRT9bTYYznTJZIxno+rnf6kv/JNvcVdEr4Zjy9vofkj6h/1is3a9gw5iFLY5XisQ6eXP8tY3Nl+Z20tBdJ2SxmtOlIBSw6+kczGGNdMzs9n0u0lfWTj9LUq3Rpzyfpps5Z2tn+IC8RXCLtO9k/6XnIkWusNXvpVwOrpT0wrtN4Ko5Ldclu6opghp61sEjjSEf0DHqyfSqUFAdp2JycoXQ0oGe2JK8xtXXhFknjNWl/TDon79OTs1qP5cw9tW5uMN+hviRWKR4bwirVNR4rt3PXMEskc0lRUlB7m+v9xTjbDbnuvKVEUTrL3W1RsyTKdmONJO65vUsZiHZNava/OK60fKe+GzqWxCpNyE8DY/+1LdNzNgL+LvHKTmF24Ii9mRhgDHLJ0ddAnfdklOlOJc8qn9bYVp1L3g493iBJlsdXztRO/EM728yRmSabl8JYPdOCIawoviOXbcBEz6Znd6tjpzBrSMagNfQKQ7z5Fxx13ykQ1SDjglEvR3tnmN5IEJoljjJnWxLLkvt3zyfptl69/gcMnluurlX36+yzcXkIVg4WWw3ofyE1mLRYdX64hWsY+LuFc9Zi4z1Kbzi2CrPWniPGmjzzR8pchW4/pmDgnP94Agh6XB8+0o378UBoLa6Nxc58tFiaAQCrxzyCZNsY95U2d1JfbSz+A0fuz7q8eXDZAAAAAElFTkSuQmCC\n",
"text/latex": [
"$\\displaystyle \\frac{1}{C L s^{2} + C R s + 1}$"
],
"text/plain": [
" 1 \n",
"──────────────────\n",
" 2 \n",
"C⋅L⋅s + C⋅R⋅s + 1"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"R, L, C = sym.symbols('R L C', positive=True)\n",
"beta = 1\n",
"alpha = L*C, R*C, 1\n",
"\n",
"H = sym.Poly(beta, s) / sym.Poly(alpha, s)\n",
"H"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Muchos paquetes de software para procesamiento de señales tienen la funcionalidad para el cálculo de la función de transferencia desde los coeficientes $\\beta_m$ y $\\alpha_n$ de un sistema. Por ejemplo, la caja de herramientas de procesamiento de señal de Python [`scipy.signal`](http://docs.scipy.org/doc/scipy/reference/signal.html) proporciona una función para evaluar numéricamente la función de transferencia $H(j \\omega)$ en un número de frecuencias angulares $\\omega_i$ para un conjunto dado de coeficientes. Esto se ilustra a continuación para los valores normalizados $R$, $L$ y $C$ utilizados anteriormente."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"from scipy import signal\n",
"\n",
"R = 1\n",
"L = 0.5\n",
"C = 0.4\n",
"beta = 1\n",
"alpha = L*C, R*C, 1\n",
"\n",
"w, H = signal.freqresp((beta, alpha))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Esto da como resultado el vector `w` de frecuencias angulares discretas $\\omega_i$ y el vector `H` con los valores de $H(j \\omega)$ en estas frecuencias."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYYAAAEICAYAAABbOlNNAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nO3deZhcVZ3/8fe3q3rft2ydrbMT1rAT9gRlEVnEBVQiis7ogPuMy+hPGdQZZBwdRVxGxeg4Ayqjsq8JKIQAYQuQhCxk7WydTu/79v39UZWmO3SS7qS6blfV5/U89XTdWzf3fusJ5NPnnHvPMXdHRERkn7SgCxARkdFFwSAiIgMoGEREZAAFg4iIDKBgEBGRARQMIiIyQDjoAo7Uk08+6ZmZmUGXISKSUFpbW2sWLlxYPthnCR8MmZmZzJkzJ+gyREQSyksvvbTlQJ+pK0lERAZQMIiIyAAKBhERGUDBICIiAygYRERkAAWDiIgMkPC3q6a67l6ntrWLkBklOWHMLOiSRCTBKRgSUE+vs/TNWh5dV8vq3S109UbW1MjLCHHm1EKuOnYMU4uzA65SRBKVgiHBvLyjiR8v28a2ho6+faU56XT19NLY0cMj62p5bH0tHzh+LItOHE8oTS0IERkeBUOC6Ol1fvPiTn6/cjcOTCjI4APHjeXsyiLyMsO4O1UNHfz59T088EYNd76ym8217Xxt4VQyQhpKEpGh078YCaC9u5ebHtvIXSt3YwbXnjiOX1x1FBfPKSMvM5LtZsakoiw+c9YkbrlkBvmZIZZvbeCWJzbT06vlW0Vk6BQMo1xzRzdffWgDz21rJD8zxK2XzODaE8eTfpBWwLwJ+dx6yQxyM0I8vbmB37y4M44Vi0iiCywYzOwOM6s2s9cP8PmHzOzV6OsZMzs+3jUGra2rh68/spFVu1soz03nB5fO4rjx+UP6s9NLc7jpgkrSDO5auZvntzWMcLUikiyCbDEsBi46yOebgHPd/TjgW8B/xaOo0aKzp5ebHtvE6uoWxuSl84N3z2JycdawznH8hHw+ctJ4AH7w1DZaOntGolQRSTKBBYO7/w2oPcjnz7h7XXTzWWBiXAobBXrdueWJLby8o4ni7DDfvXgGY/IyDutc7z9uLHPKc9jb2sUdK3bEuFIRSUaJMsZwPfBQ0EXEy29e2MnTm+vJzQjxrxdNp6JweC2F/kJpxufOmkzI4P41Nby5tzWGlYpIMhr1wWBm5xMJhi8P9nlNTQ0LFizoey1evDiu9cXakg213LlyN2kGX18wlemlOUd8zmml2Vx2dDkO/EqtBhE5hFH9HIOZHQf8ErjY3fcOdkxZWRlLly6Nb2EjZE11C99/aisAnzp9IidNLIjZuT94wjgeWbuXF6qaeGVHEydMGNogtoiknlHbYjCzycCfgGvdfV3Q9Yy06uZObnpsI109zqVzyrhsbllMz1+YFeZ9x40F0O2rInJQQd6ueiewHJhtZlVmdr2ZfdLMPhk95BtAKfATM3vFzF4IqtaR1tHdy788vpG6tm5OmJDHP8yfOCKT4V15dDl5GSFW7W5h1a7mmJ9fRJJDYF1J7n7NIT7/OPDxOJUTGHfntmXbWF/Txrj8DL6+oJLwCM1vlJMR4t1zy7jzld38/tXd3Dwub0SuIyKJbdR2JaWK+9bU8Oj6WjJDxjcvqKQga2Sz+oqjy8kIGc9ubWRTbduIXktEEpOCIUCrdjXz0+VVAHzhnMkxuQPpUIqz07lwVikA96zeM+LXE5HEo2AIyN6WLr61ZBM9Du85ppzzp5fE7dqXzy0HYOmGOj0NLSJvo2AIQFdPL99asonatm6OH5/HJ06tiOv1Jxdncfz4PNq7e3l8/QEfPheRFKVgCMBPl29ndXVkYrx/XjA1kMV03n1U5HbY+9bU4K5puUXkLQqGOHt47V7uf6OG9JDxzQumUZydHkgd86cWUZIdZmt9O6/p1lUR6UfBEEerdjdz27JtAHzmzEnMKh/5weYDCacZF86ODEI/sk7dSSLyFgVDnOxq6uCmxzbR1etcNres786gIL1zZmTA+6lN9bR1aRBaRCIUDHHQ0tnDNx7dSEN7NydV5POp00fHDOIVhVnMHZNLe3cvT2+uD7ocERklFAwjrKfXueWJzWyua2dSYSZfC2iw+UDeMSvSanhMdyeJSJSCYQS5Oz9/bnvfes03v3M6eZmja0LbcyuLSA8ZK3c0U93cGXQ5IjIKKBhG0F0rd/OXVXsIp0Wmu6gozAy6pLfJywwzf0ohDnqmQUQABcOIeeiNGn79wk4M+PJ5Uzhu/Ohd/+Ad0UHoJzbWHeJIEUkFCoYRsGxzPT+M3pZ6w/yJnDutOOCKDu7EigLyM0NsqWtnc50m1hNJdQqGGFu+pYHvLN1Mr8OH543jsui8RKNZOM04a2oRAH/dqLuTRFKdgiGGntlSz7eWbKK717nymHKuPXFc0CUN2bnT9gVDnabIEElxCoYYeWpTPd96PBIKVx1TzidPqxiRVdhGyvHj8ynMClPV0MFGrdMgktIUDDFwz6o9fDs6hfZ7jx3D3yVYKACE0oyzKyOthiff1CC0SCpTMByBXnd+tWIHty+vwoFFJ43nE6dOSLhQ2Oe8aHfSkxvr1Z0kksJG19NWCaSls4db/7qF5VsaSDP4/NmTR8X8R0fi6LF5lOSE2d3cydo9rcwZkxt0SSISALUYDsOm2jZu/Mtalm9pIC8jxLcvnJ7woQCR7qRzKiO31mruJJHUpWAYhp5e5+7Xqvn0PWvZ3tjBtJJsfnzFbE6eWBB0aTFz1tRCAJ7e3KDuJJEUpa6kIdpa185/LtvK67taALhwVgk3zJ9EVji5svXosXkUZoXZ0djB5rp2Kkuygy5JROJMwXAIje3d/O7lXdy7eg+9DiXZYT539mROn1wYdGkjIpRmzJ9SyENr9/L05noFg0gKCuzXXTO7w8yqzez1A3xuZvYjM9tgZq+a2YnxrK+utYtfPb+dRb9fxV9W7QHgXXNK+a+rjkraUNjnzGh30jKNM4ikpCBbDIuBHwO/PcDnFwMzo6/TgJ9Gf46Yrp5eXtrexGPra1m+pYGu3kgf+7wJ+fz9aRVMK02N355PmJBPTnoaG2vb2dHYwYSC0TcrrIiMnMCCwd3/ZmZTD3LI5cBvPTIC+qyZFZnZeHffGaPrU9vWzabaNjbVtvHarmZW7mymrasXAAPmTynk6uPHptxtmxmhNE6bXMgTb9axbHM97ztubNAliUgcjeYxhgpgW7/tqui+mATDY+tr+d7ftr5t/5TiLBZML+aCmSWU52bE4lIJ6cyp+4KhQcEgkmJGczAM9vjw2+6frKmpYcGCBX3bixYt4rrrrjvkyScXZZGbEaKyJIvK4mxmledwYkV+SodBf6dMLCAjZKyubmFvSxeluelBlyQicTKag6EKmNRveyKwY/+DysrKWLp06bBPPqs8hz9de2zCTl8x0rLTQ5w0sYDlWxpYtqU+IaYPF5HYGM034d8LLIrenXQ60BCr8QWANDOFwiGcpbuTRFJSYC0GM7sTOA8oM7Mq4JtAOoC7/wx4ELgE2AC0Ah8NptLUddqkQtIMVu5sprG9m4Ks0dzAFJFYCfKupGsO8bkDN8SpHBlEQVaY48fn8/KOJp7d2sA7k2A+KBE5tNHclSSjwFvdSQ0BVyIi8aJgkIOaPyWyRsOL2xtp6+oJuBoRiQcFgxxUaW46c8fk0tnjrKhqDLocEYkDBYMc0pnqThJJKQoGOaQzp0a6k57b2kBnT2/A1YjISFMwyCFNKMhkWkkWrV29vLKjKehyRGSEKRhkSPa1GtSdJJL8FAwyJGdG7056ZksDPb1a8lMkmSkYZEgqS7KYUJBBQ3s3q3a3BF2OiIwgBYMMiZn1PdOwbIvmThJJZgoGGbKz+sYZ6onMWCIiyUjBIEM2Z0wOJTlhqpu7WL+3LehyRGSEKBhkyNL6dydpKm6RpKVgkGHRpHoiyU/BIMNy3Ph88jNDbK1vZ2t9e9DliMgIUDDIsITTjNMma2U3kWSmYJBhU3eSSHJTMMiwnVRRQGY4jXU1rVQ3dwZdjojEmIJBhi0znMYpEwsAdSeJJCMFgxyWfd1Jz2xRd5JIslEwyGE5bXIh4TTjtV3N1Ld1BV2OiMSQgkEOS25GiBMm5NHrsHyrlvwUSSYKBjls++ZOekbjDCJJRcEgh+2MyYUY8NL2Jlo6e4IuR0RiJNBgMLOLzGytmW0ws68M8vlkM3vCzF42s1fN7JIg6pTBFeekc8y4PLp6neUahBZJGoEFg5mFgNuBi4G5wDVmNne/w74O/MHd5wFXAz+Jb5VyKOdNi3Qn/XVjXcCViEisBNliOBXY4O4b3b0TuAu4fL9jHCiIvi8EdsSxPhmCsyqLSDN4oaqRxvbuoMsRkRgIMhgqgG39tqui+/q7CfiwmVUBDwKfjk9pMlTF2emcMCGfHodl6k4SSQpBBoMNsm//ZcGuARa7+0TgEuC/zWxAzTU1NSxYsKDvtXjx4pGpVg7ovGnFADz5prqTRJJBOMBrVwGT+m1P5O1dRdcDFwG4+3IzywLKgOp9B5SVlbF06dIRLlUO5syphfxombFyZxN1bV0UZ6cHXZKIHIEgWwwrgJlmVmlmGUQGl+/d75itwEIAMzsKyAL2xLVKOaT8zDAnVeTT6/DUJj3TIJLoAgsGd+8GbgQeAdYQuftolZndbGaXRQ/7IvAJM1sJ3Alc51qFflQ6b3q0O0l3J4kkvCC7knD3B4kMKvff941+71cDZ8a7Lhm+MyYXkhEyVu1qYU9LJ+W5GUGXJCKHSU8+S0zkZIQ4dVIhDvxto7qTRBKZgkFi5rzpkYfd1J0kktiG1JVkZl8iMvA7pMOBVnf/98OuShLSaZMKyUlPY+2eVrbWtzO5aKj/yYjIaDKkYHD3W0e6EEl8meE0zqks5uF1e1myvpaPnjIh6JJE5DCoK0li6oKZJQA8vqGWXt1AJpKQhn1XkpnlAfOBmUTmMWoBdgHPuHtVbMuTRHPMuFzG5mWwu7mTV3c2c8KE/KBLEpFhGnKLwczmmtlPgP8EZhMJg+eBjUTGHz5nZr80sw+MSKWSENLM+loNj62vDbgaETkcQx18/gCQA3ze3TsOcewp0cHq29y9LQY1SoK5YEYx//PyLp7aVM+N8yeSnR4KuiQRGYahthiWu/uvDxUKAO6+AvgPItNkSwqqKMxi7phc2rt7WbZZM66KJJohBYO7b91/n5mNM7MxBzi+x913HWlxkrj6D0KLSGI5kruS/gR8zMyuM7NLY1WQJIdzpxWRnma8vL2JPS2dQZcjIsNw2MHg7vPd/RZ3XwxkmdlnY1eWJLr8zDBnTIlMkfHIOrUaRBJJTJ5jcPe70epqsp9L5pQC8PDaGnp69UyDSKI4omAws5PM7Pdm9ivgbzGqSZLECRPyGZ+fQXVzFy9ubwy6HBEZoiMKBnd/0d0/ANwF7I5NSZIs0sy4aHak1fDgG3sDrkZEhuqwg8HMLtn33t0fA66MSUWSVC6cVUrI4NmtDext7Qq6HBEZgiNpMSwzsyvN7D1mdiuRVoPIACU56ZwxpZBeh0fXqdUgkgiGFQxm9tN+m1OAZuBBd/+Su98Uy8IkeVw8uwyIdCdpYj2R0W+4LYZf93v/UeBy4Hkze9jMPm9mlbErTZLFiRX5fRPrvVjVFHQ5InIIwwoGd3++3+bz7n6jux8HfApoA36uSfRkf6E067t19d7VewKuRkQO5UjGGO4zswUA7r7J3X/m7u8ENM+yvM3Fs0tJDxnPbWtke0N70OWIyEEcyZPPze6+tP8+M7uISBeTyABF2eksmF4MwL2rawKuRkQO5pDBYGaVZnb1UE7m7g8D15jZ3x9xZZJ0Lp9bDsAj6/bS2tkTcDUiciCHDAZ33wQ8Z2bfNbMbzexoM7P+x5hZrpmdb2bfAd4L/GKE6pUENqMsh2PG5dLa1atFfERGsaFOu73J3b9MZNqLK4A/m9kjZva4mT0E/ASoBL7n7t93996hnNfMLjKztWa2wcy+coBj3m9mq81slZn979C+loxWVxwdaTXcs3qPbl0VGaWGu+Zzprt/JxYXNrMQcDvwDqAKWGFm97r76n7HzAS+Cpzp7nUHWv9BEseZU4ooy02nqqGDF6oaOXWS1nMSGW2GO/h8rZllxOjapwIb3H2ju3cSeXL68v2O+QRwu7vXAbh7dYyuLQEJpRlXRMca/viq/jpFRqPhBsMHgVozW2pm/8/MzjKzdAAzmz/Mc1UA2/ptV0X39TcLmGVmy8zs2ehdT5Lg3nVUGTnpaazc2cya6pagyxGR/Qw3GD4HTCYyuPxO4HdAnZk9Cnx7mOeyQfbt3+kcBmYC5wHXAL80s6L+B9TU1LBgwYK+1+LFi4dZhsRbbkaIdx8VmSbjDys1Ka/IaDOsMQZ3/1307Z1mluHuvzGzCuAc4IZhXrsKmNRveyKwY5BjnnX3LmCTma0lEhQr9h1QVlbG0qVLkcRyxTFj+NOqPTyzpYGt9e1MLsoKuiQRiRruJHof7LfpAO6+3d3vBG4b5rVXADOjz0lkAFcD9+53zF+A86PXLiPStbRxmNeRUag0J513zCzBgT++qlaDyGgy3K6kfzCzy80sb/8P3P33wzmRu3cDNwKPAGuAP7j7KjO72cwuix72CLDXzFYDTwD/5O6auzlJvO/YsaQZLNlQR01LZ9DliEjUcG9XbQY+RmSMYa+ZTQeWAc8CV7r7b4ZzMnd/EHhwv33f6PfegS9EX5JkKgozOXtqEX/dVM8fXq3mH86YGHRJIsLwWwzfdPfLgXHAtUAL8Hkidxf9MMa1SQq45oRxADzwRo1aDSKjxHCn3X4u+rPX3V9w91vd/WKgDPjVSBQoyW1aaTbnVBbR1ePcpTuUREaFI5l2u0/0rqHfHfJAkUF8+MRxGPDQG3upblarQSRoMQkGAHd/OVbnktQytTib86YX09Xr3PnKrqDLEUl5Qxp8NrMvAUO90dyAVnf/98OuSlLOh+aN468b63h47V7ef/xYxudnBl2SSMoaUjC4+60jXYiktslFWZw/vZglG+r47Ys7+fJ5U4MuSSRlxawrSeRILTppPOlpxpINdayvaQ26HJGUpWCQUWN8fiaXzY3MofSL57fjWq9BJBAKBhlVrjlhHPmZIV7Z0cyKqsagyxFJSQoGGVUKssJ9D7394rkd9PSq1SASbwoGGXUum1vGuPwMttS389BaTY0lEm8KBhl1MkJpfPzUCQD8+oUdNLR3B1yRSGpRMMiodPbUIuZNyKepo4c7Vuy/TIeIjCQFg4xKZsYN8ycSTjMeWrtXS4CKxJGCQUatyUVZXHXsGABuW7ZNA9EicaJgkFHtgyeMpTw3nQ1727hvTU3Q5YikBAWDjGrZ6aG+BXzuWLGDXU0dAVckkvwUDDLqnTm1iHMqi2jv7uUHT23TE9EiI0zBIAnhhjMmUpAZ4uUdTTy8rjbockSSmoJBEkJxTnpfl9LPn63SMqAiI0jBIAnj/OnFnD65gNauXv7jb1vpVZeSyIhQMEjCMDM+e+ZkCjJDvLi9iT+/vifokkSSkoJBEkppbjpfOGcyELlL6c29WrdBJNYUDJJw5k8p4tI5ZXT1Ov/2xBbau3uDLkkkqQQaDGZ2kZmtNbMNZvaVgxz3XjNzMzs5nvXJ6PV3p1cwuSiLrfXt/HR5VdDliCSVwILBzELA7cDFwFzgGjObO8hx+cBngOfiW6GMZlnhNL56/hTSQ5G5lB5dp+m5RWIlyBbDqcAGd9/o7p3AXcDlgxz3LeBWoD2excnoN700hxvnTwLgR8u2sUHrRIvERJDBUAFs67ddFd3Xx8zmAZPc/f54FiaJ4+LZpVw8u5TOHufmJZto1NoNIkcsyGCwQfb13ZhuZmnAD4AvHuwkNTU1LFiwoO+1ePHi2FYpo94NZ0xkVlkOu5o6ueXJzZqFVeQIhQO8dhUwqd/2RKD/iiz5wDHAk2YGMA6418wuc/cX9h1UVlbG0qVL41CujFYZ4TT+38JKbrxnLS9UNfGzZ6u4Yf6kQ/9BERlUkC2GFcBMM6s0swzgauDefR+6e4O7l7n7VHefCjwLDAgFkX3G5mfwzQsqSU8z7lldw59frw66JJGEFVgwuHs3cCPwCLAG+IO7rzKzm83ssqDqksR1zLg8vhh9+O3nz23n2a0NAVckkpgCfY7B3R9091nuPt3dvxPd9w13v3eQY89Ta0EOZcGMEhadOI5eh39dupk3tCSoyLDpyWdJOh+aN44LZpbQ3t3L1x55k811bUGXJJJQFAySdMyML5w9mdMmFdDU0cNXH3qTnVr5TWTIFAySlMJpxtcXVnLcuDz2tnbxlQc3sLe1K+iyRBKCgkGSVmY4jX955zRmlmWzs6mTf3pgPXtbFA4ih6JgkKSWmxHiXy+awbSSLKoaOvjiA+upbtbqbyIHo2CQpFeYFebWS2YyozSbHY0d/OMD69mlMQeRA1IwSEooyArz3UtmMLs8MnXGF+9fz9Z6zcsoMhgFg6SM/Mwwt1w8g7ljctnT0sXn71vHqt3NQZclMuooGCSl5GaEuOWSGX23sn75wQ0s36InpEX6UzBIyskKp3HTO6b1Tdf9L49v5N7Ve4IuS2TUUDBISgqlGZ87a1Lf9Bk/fqaKHz69la4erR8tomCQlGVmfPjE8Xzp3MgSoQ+8sZcvP7iBujY96yCpTcEgKe+CmSV8/9KZlOWk8/ruFm78y1rW7tHke5K6FAwiwOzyXG67Yna/O5bW83+vVeOu1eAk9SgYRKJKc9K59V0zuHxuOd29zs+f2843H9uodaQl5SgYRPrJCKVxw/yJfOOCSvIyQjy7tZFP/vkNVu5oCro0kbhRMIgM4qypRfz0yjkcNSaHmpYu/unBDdz+TBVtXT1BlyYy4hQMIgcwNj+D/7h0FotOHEfI4J7Ve/jUn9/gtV16WlqSm4JB5CDCaZFbWn98xWymlWSxo7GTf7x/PT9+ZhvNHRp7kOSkYBAZgumlOdx2+Ww+NG8cZnDv6hquv3sNSzbU6s4lSToKBpEhSg+l8ZGTxvOTK+Ywd0wudW3dfPfJLXzpwQ1srdNMrZI8FAwiwzStNJvvv3smXzxnMgWZIVbubObv/rSG25Zt01PTkhQUDCKHIc2MC2eVcsf75vKuOaUA3Lemho/+YTV3vrKL9m7NuSSJS8EgcgQKssJ89qzJ/Ow9czh1UgGtXb38+oWdfOyPq3ngjRpNyicJKdBgMLOLzGytmW0ws68M8vkXzGy1mb1qZkvMbEoQdYocytTibL594XS+e/EMppdmU9PSxQ+f3sZHFRCSgAILBjMLAbcDFwNzgWvMbO5+h70MnOzuxwF3A7fGt0qR4ZlXkc/tV8zmq+dPZUpRFtXNbwXE/Wtq6FQXkySAIFsMpwIb3H2ju3cCdwGX9z/A3Z9w99bo5rPAxDjXKDJsaWacP72Yn181h68teCsgfrRsGx++axW/e3kXDZp/SUaxcIDXrgC29duuAk47yPHXAw+NaEUiMZRmxrnTijm7soinNtVz18rdvLm3jd++uJPfv7KLd8wq5apjyqkozAq6VJEBggwGG2TfoE8KmdmHgZOBc/f/rKamhgULFvRtL1q0iOuuuy5GJYocuX0BcU5lEa/sbObuV6tZUdXI/WtqeGBNDSdPLOBdR5Vy2qRCQmmD/W8hEl9BBkMVMKnf9kRgx/4HmdkFwNeAc929Y//Py8rKWLp06YgVKRIrZsa8CfnMm5DPlro2/u+1PSx5s5YVVY2sqGqkLCedi2aXcvGcUspzM4IuV1JYkMGwAphpZpXAduBq4IP9DzCzecDPgYvcvTr+JYqMjCnF2XzhnMl8/NQJPLq+lgffqKGqoYPfvbyL/31lF6dMLGDhjBLOmFJIZlh3lUt8BRYM7t5tZjcCjwAh4A53X2VmNwMvuPu9wL8DecAfzQxgq7tfFlTNIrFWkBXmvceO4apjylm5s5kH1tSwbEsDz21r5LltjeSkp3F2ZREXzCjh2PF5pJm6mmTkWaJPALZ8+XKfM2dO0GWIxExdWxdPvlnHkg11rKtp7dtfnpveN5g9uzxHISFH5KWXXnpx4cKFJw/2WZBdSSIyiOLsdK48ZgxXHjOGrfXtLFlfy5I3a6lu7uLu16q5+7VqynLSOXNqEWdXFnL02DwNWktMKRhERrHJRVl89JQJfOTk8aza3cJTm+p5enM9NS1d3LN6D/es3kNRVpgzphRyyqQCTpyQT05GKOiyJcEpGEQSQJoZx47L49hxeXzq9ArW7mnl6c2RkNjR2MlDa/fy0Nq9hNOMo8fmcuqkAk6dVMDkoixMXU4yTAoGkQRjZswZk8ucMblcf8oENtW289y2BlZsa2R1dQsrdzazcmczv3h+B2PzMpg3IZ/jJ+Rxwvh8SnPTgy5fEoCCQSSBmRnTSrOZVprNNSeMo7G9m5e2N/F8VSMrtjWyu7mTh9ft5eF1ewGYWJjJCRPyOWF8HseNz6MoW0Ehb6dgEEkiBVlhzptezHnTi+l1Z0NNG6/sbOKVHU28vquFqoYOqho6uH9NDQBTirKYOzY38hqTy8TCTHU9iYJBJFmlmTGrPIdZ5Tm8/7ixdPc6a/e0sHJHM6/sbGL17ha21Lezpb6dh9ZGWhT5mSHmjnkrKGaW5WgwOwUpGERSRGRgOo+jx+bxwXnj6Ozp5c29baza3cLq3S2srm6mtrW77+E6iExoVlGYycyyHGaWZjOzLIcZZTnkKiySmoJBJEVlhNI4akwuR43JhWPB3alu7mJ1dXM0KFrYXNve1/30xJt1fX+2oiCTGWXZzCjNobIki6nF2ZTnpqsbKkkoGEQEiAxkj83PYGx+CedPLwGgq6eXzXXtrK9pZUNNG+v3trKxto3tjR1sb+zgrxvr+/58TnoaU4uz+4Ji38+CLP0zk2j0NyYiB5QeSot0I5Xl9O3r7nW21LWxrqaNTbWR1+a6dhrau1ldHWlp9FecHWZSYRYVhZlMKsykojCLSUWZjMvPJKwntkclBYOIDEs4zZhemsP00pwB++vauthc287mujY2RX9urmunrq2burZmXt3VPOD4kMH4gkwmFmYyMRoc4/MzGJ+fSXlehtiu0r8AAAhcSURBVEIjQAoGEYmJ4ux0iivSmVeR37ev1509zV1UNewbq3hrzKK6ubPvPTQOOFeaQXluBuPy970iobHvZ1F2WOMZI0jBICIjJq1v3CKDk/Zbsb2ju5cdjR1sa2hnezQgdjV1squpg5qWLnY3d7K7uZOVO99+3syQUZ6XQXluOmW5b/0ck5dOeW4GZbnp5GWEFB6HScEgIoHIDKdRWZJNZUn22z7r7OllT3MnO5s6+8JiZ/TnrqZOmjp6+rU2BpcVTqMsNxIU5bnplOamU5KdTnFOmNLsdIpz0inODpOdrltv96dgEJFRJyOURkVhFhWFWYN+3tLZw56WTmpautjT3Mmelq63tqPv27p6DxkeELmbqniQwCjNSac4O53C7DCFmWEKs8NkpchqegoGEUk4uRkhcjOymVr89tYGRJ7JaO3qpbp5X1h0UtvaRW1bN7WtXdS1dVHb2k1tWxetXb20dkVuvz2UzJBRmB2mIDNMUXaYwqwwBVlhiqI/C/d75WWEEnKtDAWDiCQdMyM3I3TArqp93J2Wzp63B8a+923dNLS/9eroiTwEWN3cNeRacjNC5GWEyM8MkZcZIj8zPGA7LyNMfua+7TD5GZH9uRmhwFbpUzCISMoyM/Iyw+RlhplcNHi31T7uTltXLw0d3TS0ddPY0U19WzeN0dCob++msb1nQJA0d/bQEn3tbj7o6d9eG9FQiYZEbnr0Z0Za9GfkdelRZTEfJ1EwiIgMgZmRkxEiJyPE+PzMIf2Znt5Ii6S5s4emjm6aOnpo7nhru//7puj75o7IdmtXb2S7s+eg17hodmksvt4ACgYRkRESSjMKouMPMLQw2WdfqDR19NDS9VbLo7VfK6Sls4ecEbirSsEgIjIKDQyV+EqNe69ERGTIFAwiIjJAoMFgZheZ2Voz22BmXxnk80wz+3308+fMbGr8qxQRSS2BBYOZhYDbgYuBucA1ZjZ3v8OuB+rcfQbwA+C78a1SRCT1BNliOBXY4O4b3b0TuAu4fL9jLgd+E31/N7DQYjAr1uLFi4/0FAknFb8zpOb3TsXvDKn5vUfqOwcZDBXAtn7bVdF9gx7j7t1AA3DEN+3+9re/PdJTJJxU/M6Qmt87Fb8zpOb3HqnvHOTtqoP95u/DPaampoYFCxb0bS9atIjrrrvuiIsTEUlV5r7/v8VxurDZGcBN7n5hdPurAO7+b/2OeSR6zHIzCwO7gHLvV/SSJUv2AFuGc+3a2tqykpKSmhh8jYSRit8ZUvN7p+J3htT83kf4nacsXLiwfLAPggyGMLAOWAhsB1YAH3T3Vf2OuQE41t0/aWZXA+9x9/cHUrCISIoIrCvJ3bvN7EbgESAE3OHuq8zsZuAFd78X+BXw32a2AagFrg6qXhGRVBFYi0FEREanlHry+VAP1CUjM5tkZk+Y2RozW2Vmnw26pngxs5CZvWxm9wddS7yYWZGZ3W1mb0T/zs8IuqaRZmafj/63/bqZ3WlmB58/O0GZ2R1mVm1mr/fbV2Jmj5nZ+ujP4lhcK2WCYYgP1CWjbuCL7n4UcDpwQ4p8b4DPAmuCLiLOfgg87O5zgONJ8u9vZhXAZ4CT3f0YIt3SydrlvBi4aL99XwGWuPtMYEl0+4ilTDAwtAfqko6773T3l6Lvm4j8Q7H/8yJJx8wmAu8Cfhl0LfFiZgXAOUTG5nD3TnevD7aquAgD2dEbWnKAHQHXMyLc/W9Exlr76/8Q8G+AK2JxrVQKhqE8UJfUonNNzQOeC7aSuPhP4EtAb9CFxNE0YA/w62gX2i/NLDfookaSu28HvgdsBXYCDe7+aLBVxdVYd98JkV8CgTGxOGkqBcNQHqhLWmaWB/wf8Dl3bwy6npFkZpcC1e7+YtC1xFkYOBH4qbvPA1qIUdfCaBXtU78cqAQmALlm9uFgq0p8qRQMVcCkftsTSdIm5/7MLJ1IKPyPu/8p6Hri4EzgMjPbTKTLcIGZ/S7YkuKiCqhy930twruJBEUyuwDY5O573L0L+BMwP+Ca4mm3mY0HiP6sjsVJUykYVgAzzazSzDKIDFDdG3BNIy466eCvgDXu/v2g64kHd/+qu09096lE/p6XunvS/xbp7ruAbWY2O7prIbA6wJLiYStwupnlRP9bX0iSD7jv517gI9H3HwHuicVJU2ZpzwM9UBdwWfFwJnAt8JqZvRLd98/u/mCANcnI+TTwP9FffjYCHw24nhHl7s+Z2d3AS0TuwHsZ+K9gqxoZZnYncB5QZmZVwDeBW4A/mNn1RELyfTG5lh5wExGR/lKpK0lERIZAwSAiIgMoGEREZAAFg4iIDKBgEBGRARQMIiIygIJB5DBFp3o+Lw7XKTKzq8zsn0f6WiKQQg+4icSaux8dp+vUm9mLwLHxuJ6IWgwiIjKAWgwihyk6Sd/H3f3x6PsfA4uAKcDDwEfcvX0Y5xsDLNhvd427Px6bikWGRsEgEjvvJ7LCVjuwDLgO+NlQ/7C7VxOZDVYkUOpKEomKDvJeOsj+5WY2YQin+JG773D3WuA+4ISDXKvAzD5tZu8ysy8eoq584L3AyWamcQYZcQoGkbcsBB4EMLOT++2/j6GtBLer3/tWIO8gx15JZH2QZUTWID8gd29y9++5+6Xu/toQ6hA5IgoGkX7cfV8AfKnf7l3RtQ5i6SGgDHgdSLWV5mSUUzCIvOV0ADN7B5FlMTGz9wE1sbyImZ0K3OTuH4te8/RYnl/kSCkYRN7SambriCwXaWa2EZjo7rFe6a8GeNXMLicyYP21GJ9f5IhooR4RERlALQYRERlAwSAiIgMoGEREZAAFg4iIDKBgEBGRARQMIiIygIJBREQGUDCIiMgACgYRERlAwSAiIgP8fwDZcqJKO2iqAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"import matplotlib.pyplot as plt\n",
"\n",
"plt.plot(w, abs(H))\n",
"plt.xlabel('$\\omega$ in $s^{-1}$')\n",
"plt.ylabel('$|H(j \\omega)|$')\n",
"plt.grid();"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Diagramas de BODE\n",
"\n",
"La función de la respuesta en freuencia Fourier $H(j \\omega)$ caracteriza las propiedades de transmisión de un sistema (LTI) con respecto a una señal exponencial armónica $e^{j \\omega t}$ con frecuencia angular $\\omega = 2 \\pi f$. Para ilustrar las características de un sistema LTI, a menudo la magnitud $| H(j \\omega) |$ y la fase $\\varphi_H(j \\omega)$ de la función de transferencia se consideran por separado. Descomponiendo la señal de salida $Y(j \\omega) = X(j \\omega) \\cdot H(j \\omega)$ en su magnitud $| Y(j \\omega) |$ y la grafica de fase $\\varphi_Y(j \\omega)$\n",
"\n",
"\\begin{align}\n",
"| Y(j \\omega) | &= | X(j \\omega) | \\cdot | H(j \\omega) | \\\\\n",
"\\varphi_Y(j \\omega) &= \\varphi_X(j \\omega) + \\varphi_H(j \\omega)\n",
"\\end{align}\n",
"\n",
"donde $X(j \\omega)$ denota la señal de entrada, y $| X(j \\omega) |$ y $\\varphi_X(j \\omega)$ su magnitud y fase, respectivamente. Se puede concluir de las ecuaciones anteriores, que la magnitud $| H(j \\omega) |$ proporciona la atenuación dependiente de la frecuencia de la magnitud $| X(j \\omega) |$ de la señal de entrada por el sistema, mientras que $\\varphi_H(j \\omega)$ proporciona el cambio de fase introducido.\n",
"\n",
"Una ilustración gráfica de uso común de las propiedades del sistema en términos de magnitud y fase de la función de transferencia son los diagramas de Bode. Aquí la magnitud logarítmica de la función de transferencia $20 \\log_{10} | H(j \\omega) |$ en decibelios se grafica contra el logaritmo de la frecuencia $\\omega$ o $f$. La fase $\\varphi_H(j \\omega)$ se grafica linealmente contra el logaritmo de la frecuencia. "
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAALgAAAAtCAYAAAAdmKE3AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAGfElEQVR4Ae2djXEUORCFvZQD8G0IkIHhIjjIAO4iADIwRQRXkIEhArAzMETg4zIwIYAzMO+T1VMazXh2GUu2PG5VyTv6a7VeP7V6ZodldXFxsePJEVgqAg+WurAW17VarZ4r/1Tea1G/Jeq0u8RFtbSmSOaP0umH8lrZyX2DBnIPXhlshYDnyi+UX2uq08rTufgMASd4BogXl4WAE3xZ9vTVZAg4wTNAvLgsBJzgy7KnryZDwAmeAeLFZSHgBF+WPX01GQJO8AwQLy4LASf4suzpq8kQcIJngHhxWQis/GWr+gbV1/WHmoWv6Z8q81X9/8rflU+E/wd9eqqEgBO8ErAutg0EPERpww6uRSUEnOCVgHWxbSDgBG/DDq5FJQSc4JWAdbFtIOAEb8MOrkUlBJzglYB1sW0g4ARvww6uRSUEnOCVgHWxbSCwkhr+uxFt2MK1qICAf5NZAVQX2Q4CHqK0YwvXpAIC9/p3UfQS1DthystPD5V5+emNXn4616enhSBwb0OUSO5DERpi76h8pI+HKj9eiG19GULgPocozzMG/KvyvoiON/e0EASqhSgiCkf/K+VnyumxH96BjkR6LY/5JsdSbTbOSFjr/WkLTVDBdEzrctWqlrVuTpE9YQJmo6kwrsdxEmxl6UjzL+cddS1mp3QWUgfKP5Vf5bJVB2n5BwCj7Wl/9eER5llaV+ta86AX80Gw4phsI1NzQ/ABZjZWbSVxxdH01in5bG4wgOS9ttbL0hn7wame/YouAuHKJ8pn+UQpQGqD4ABJzDuqg9r41y/0eXdVn5L1mgedD+bK1FgAnj1+al7JLYnrvuSB66iuqmeT0b4/pVOpNs0zGzeNBRf0hU+md4/gD9RQMn2VMIj5WACcTwhGmXP1CTd4V/SzY5oNUzXp2Odpyhfp877qRPOFl8QV+5C+XH4M/rIBSFP2u+xxy3/hmPLkD5sWI7hIwi4CHCbcBA4/Jfx5Az7BEJJ1lSE2DN+uWXoT77Pr+fXX5lIFXMM9kdbLfU0vaS68KWEKm33K+fTGtVwoQnABAygQ5buAsRuXqXUDHl5zKrFZBkYYG6D5J708+inzw/PmvYKYWH5k5KasbB5sbKridZpvT/lA+ZDPdAKVa+AKBgOnobkgN79jfiw87PQM6qhtFr5h8C3/KUJwrcG8H158YxKAk+GJADUiDgyRC1dfNtamzcKJQbzWkVfjuGbcqa75nxcwME90btpzvRUehEaEbW+V01Qa13T9bCryiTIxN6T+S7q8SBVQ2yx8Uxm3eb1baHLIQdpIyMtuG/+aB5n0HFEK8f7kYy02lAwFiVLyEtdCeojVJfp2hcoX0gkPfRqngVipflSXxtUcx8tkne8jidlMg0e2qpuLL/rfegoE1wIxtBl8G6UgASBZCLGOg3IDjcpivgTgsT7BEOpz5YaJOj/R4B5BEaa2bxqbfyN5pibTlyc3f9D3d5Nk4/WNKOlwMFyr/Z+0Ml4TuvU8Y6z/oXoL6fCUOcFK42rxd28TS4cP0pvTlxOk00F1rHMWvhrXS4Vx68meLGhxo4/pfqdeE0AeDdksS/3wSpOPoJClPHhOa/LVBhnwfoNHXarjGOYr+N66VFf1caPks66BPrkeY+U4ljWz8Tu9Va6B6+AZt+YBS+bvtak8WI/qiuIrebNxy7Di/mWAYakYPHha7VKA2pSeSbHOk+ado9egeio84djktHiUj1cZr9Mbu6VeI6JurArPyc0doRQngaWSuEJMUg+by6ru3oR7lTTdeXxLEdxu8uymKAWpu5bx6NcdgV1D/8Li79HwRDLYqd/iEJ6OmOEITbhmDpMRu4VjliO4uSSdITR6f4rKQXZLJXG1sOo/E558/hmvOTFCinrdeXx3bUHX+cSbChBizCN98tV676ZPdRxDkG6b11HpyzE98PKSg8EhuMXP9PmqeuaDKH8rmx5rXePlQ2yLjrpuMT1BKel3rHVwAnYkQ2fV2Xqui2u4NxjDNZ0TXTQnGw5d7j6+WnAX8133WoBAMjwlxyA3J2TKT6dkq51x9MUzE0eFeDDWDepNltoZx1z0Z2yI7fXJJuC9BPIgjrTxJT81z+xYUmNZIxtx9D0U1c/ClfUpgX+O62Ce2A8swS5gps/q+GqO2bgl6wM/bG08CHjSfm/fBxcYRZO8Hobi3ZpWv+4vut5Swmrj5gQvZCkZCm+3FsFbDYUKrbSsmNq4/QIKys06ux6nMAAAAABJRU5ErkJggg==\n",
"text/latex": [
"$\\displaystyle \\frac{1}{- C L \\omega^{2} + i C R \\omega + 1}$"
],
"text/plain": [
" 1 \n",
"──────────────────────\n",
" 2 \n",
"- C⋅L⋅ω + ⅈ⋅C⋅R⋅ω + 1"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"%matplotlib inline\n",
"sym.init_printing()\n",
"\n",
"\n",
"s = sym.symbols('s')\n",
"w = sym.symbols('omega', real=True)\n",
"R, L, C = sym.symbols('R L C', positive=True)\n",
"\n",
"H = 1/(C*L*s**2 + C*R*s + 1)\n",
"H = H.subs(s, sym.I * w)\n",
"H"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"El diagrama de bode se genera para los valores normalizados $R = 1$, $L = 0.5$ y $C = 0.4$"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZAAAAFBCAYAAABZ3flGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nO29eZxdV3Xn+1v33rp1a56rNFm2bMuyBsvygDGE0CAbbBzjCRsb6BgH0gkdeGnIe4HQkJBP58OHPHj9EjqE0A0hshk8YAYbYzA2ooEYbINkSZYlS9ZgWVPNpZrHe1f/ca/kUunW3fucvc+ufa7W95OKVHV+e6215R9aOufufTYxMwRBEAQhKImFLkAQBEGIJ9JABEEQhFBIAxEEQRBCIQ1EEARBCIU0EEEQBCEU0kAEQRCEUEgDEQRBEEIhDUQQBEEIhVEDIaJ2IrqNiFbbKkgQBEGIB9oNhIiWEtH3iOglIvo3IloLYDeArwDYTkR3RValIAiC4B1B7kC+AmAAwMcAEIAnAPwxM7cDuAPAf7VfniAIguArpPsuLCLqA7CYmaeIqBrAIIA0FwIQ0SAzN0RXqiAIguATQe5AKph5CgCYeQzAMJ/efchqZYIgCILXpIJoieiteK1RzP0+abUyQRAEwWuCPMJ6BUBJMTOvsFCTIAiCEAO0G4ggCIIgzEY2EgqCIAih0PoMhIj+m46Omf/GrBxBEAQhLuh+iH7OrN9nALwLwG8BHAKwHMBVAL5rtzRBEATBZwJ/BkJEDwD4DjN/d9bPbgNwBzO/x3J9giAIgqeEaSCDAJqZOTvrZ0kA/bKRUBAE4ewhzIfo+wB8eM7P/gzAfvNyBEEQhLgQ5g7kMgDfR/7zk6MAlgKYAXAbM2+1XqEgCILgJaH2gRBRBYCrASwBcBzAb5h52nJtgiAIgsfIRkJBEAQhFLKRUBAEQQiFNBBBEAQhFNJABEEQhFAEeZ07AICI0gDuAbABQO3sa8x8t52yBEEQBN8J3EAA3AvgUgA/BNBltxxBEAQhLoTZBzIAYAUzn4imJEEQBCEOhPkM5FUAlbYLEQRBEOJFmEdY9wF4hIi+iDmPsJh5s5WqBEEQBO8J8wjr4DyXmJnPNy9JEARBiAOyE10QBEEIhe6JhG9m5l8Wfr9xPp08whIEQTh70LoDIaKdzLyu8Ht5hCUIgiDIIyxBEAQhHPIqE0EQBCEU0kAEQRCEUEgDEQRBEEIhDUQQBEEIhTQQQRAEIRS6+0A+DiCjGZMAjDHzF0JXJQiCIHiPLOMVBEEQQiGPsARBEIRQhDmRsBbAGwGsBFAPYBRAJ4BfM/MRu+UJgiAIvqL9CIuI1gD4CIA0gO0AjgE4AaAKQDOA9QAaATzJzA9GUq0gCILgDbrvwroTQDWAbzPzpEL7OgBvBfBPzDxupUpBEATBO3QbyHJmflU7KFESQBszd5oUJwiCIPhL6FVYRLQIQI6Zu+2WJAiCIMQBkwbyawCPIv8Bei8zP2azMEEQBMFvrOwDIaLbASxl5i+alyQIgiDEAWsbCYloHzNfaCWYIAiC4D2B94HMhoiuAPBxACMAfmmlIkEQBCEWGO1EZ+YtzHwngAcAdNkpSRAEQYgDoRsIEd1w8vfM/CSAW61UJAiCIMQCk1VYDQA2Iv/23auRfwPv39orTRAEQfCZQA2EiP6Fmf9z4ffrAXQA+BUzT0RUnyAIguApQRvIVcz8XOH3/wCgAsCbkX8v1hMAfsDMB6MoVBAEQfALk0dY72Hm+wu/XwHgOgC3AfhXeZmiIAhC+WPSQGoBXMXMm+f8/I+Z+Ws2ijPh4MGD3NjYOO/1EydOoNT1OOJqTjbzmMQKOlZXr6NTacRf/uQKGysqf+loF8pfTU1NFEQfehUWM48UaR7XA/ijsDFtUlVVZXQ9jriak808JrGCjtXV6+jEX/HJFTZWVP7S0cbFX8oGQkQriOgunWDM/BMA7yGiPzWuzJDOztIvAlZdjyOu5mQzj0msoGN19To68Vd8coWNFZW/dLRx8ZdyJzozHyQiENH/C+AwgJ8D2MWznn0RUQ2AqwBcC6APwD9GVK82FRUVRtfjiKs52cxjEivoWF29jk78FZ9cYWNF5S8dbVz8pfUqk8LKqk8Ulu7eAuCzRFQFIAlgGkA3gF8A+P+YeSCqYoPQ0NBgdD2OuJqTzTwmsYKO1dXr6MRf8ckVNlZU/tLRxsVfQT8DqWTmzzLzLcx8HTNfy8zvYOb3M/PXfWkeANDb22t0PY64mpPNPCaxgo7V1evoxF/xyRU2VlT+0tHGxV9BG8gfElE6kkosE5cObhO5A7GjlzuQ4sgdiD392XoH8l4A/US0mYj+mojeREQVAEBEb7RfXnimpqaMrscRV3OymcckVtCxunodnfgrPrnCxorKXzrauPgr6OvcPwrgceQ3Df4ZgA8CaC2cTphC/t1YXjA+Pm50PY64mpPNPCaxgo7V1evoysFf2VwOEzM5MAPJBKEySUgk5v83pcs5+eCxqPylo42Lv0w2Er6fme8loqXIv87kw8z8JqvVGdDZ2cmVlZXzXp+cnESp63HE1Zxs5jGJFXSsrl5Hp9L44K8cM7qGp3BkcAJHhyYxMDaNgYkZDE1kkc0xmBmJBCGbY+QYSCUI1RUJZFJJtNVW4LymDNZ21KKpusL5nHzwWFT+0tEulL8i3UhIRO+d9S0DADMfLbzS5J+CxIqavXv3lrzuyzpqm8g+EDv6uO4D6Rmdwm8OncDXnjuKjz/+Mj70vZfw/od24dvbuvDLAyewo3MUR05MYmBsCuPTWWQZAANJIuSYMZ3LYWgyi8NDE3j+2DDu39aFTz+xH3/xw734+f5+HDp63NlcfPCY7ANRE/QR1p8R0SiAn829ELf3X6XTsVgLEAhXc7KZxyRW0LG6eh2dShP1f4tsjrG/bxwvdo3g5d4xbDs+gt7RaVzcXo2XusdO6RbXpdFeW4FzGjLoqE2juTqFtpo06iqTqM+kkJz1yGpiOou+sWkcH57Eof4JvHJiAscGJ9E1MoXP/fwQNrSn8YaxbtxwcSsqU0Zn0SnxwWNR+UtHu9D+0iVoAxkB8AEAXwXQR0QXAHgawDMAbmXmey3XF5pSz3IBoK6uzlEl7nA1J5t5TGIFHaur19GpNLb/W4xOZbG7exS7ukaxs2sEL3WPYWImBwC4oLkKvaPTqEkn0VaTxpWX1WNlazUuaqtGS7X+hrNMRRJLG5JY2pDBlcsaTuV95tAgHnupF7t7xzBNJ/C9nT348BuX4erl0a0E8sFjUflLR+vaX2EJ2kA+w8zPElECwOXIf2j+MQBvRP6RljcNZGZmpuT1vr4+1NbWOqrGDa7mZDOPSaygY3X1OjqVxmRezIxjQ1PY23uyYYziYP84cnM+rlxSX4m1HTXYsKQOK1ursLwxgwQFeoStpCadxDUrm7Hxwib8aOs+PHZoBl0jU3hoexe2HBnCn169DKmE3ZyAHx6Lyl862ij9ZZNADYSZny38mgPwu8LX5wtLef/efnnhSaVKT62pqclRJe5wNSebeUxiBR2rq9fRqTRBahsYm8ZLPWPY0zOKvb1j2NMzhuHJLAhAZSqBiZkckgSsaqvGuo4arO2oxdqOmlMfbruAiPDmlR14x2V1+N7Objy0oxs7u0bx6olJfPqa81BXGfTfoqXxwWNR+UtHa9NfUWLlvzozTxPRN23EskUulyt5fXx8HPX19Y6qcYOrOdnMYxIr6FhdvY5OpSl2nZkxMD6DgwPj2N87jpd6xrC3dxTdI9NnjG+qSmFVWzU2LK7DBS1VWNVeg0zEnzuoODmnO9Z3YG1HLf72yQN4/tgw/suje/F3bz8fSxsy1nMtZKyo/KWjNb3uCmv/bGDm523FsoGqgUxMlN8pvK7mZDOPSaygY3X1OrpSGmZG9+AYjmWHcWhgAocGxvO/npjA8GQWCQCJBGGm8EyqqiKBi1qrsaqtGqvaarCqrRptNRUgy4+jTJk95zUdNfinm1fhM0/ux4H+Cfz5o3vx19eswIYldp7N++CxqPylozW97gqtfSBE9HEAuv+8IABjzPwFk8JMefrpp3nNmjXzXvdhnb5tZB+IHb3uPhBKVaBnZBpdI/m9Fq8MTJxqGEOT2aLjatNJnNuUwbpFtVjWUIlVbdU4pyGDZASfI9im2J/L2FQWf/+/X8Gzrw7hsqV1eO+GRVi/2PzZvA8ek30ganTfxvv5cOUsHNPTZz4WmE1nZyfOPfdcR9W4wdWcbOYxiRV0rK7+pG5iJofukSl0DU+hayT/dfL7Y4NjGJxkMIDmqhT6x09ftFGVIqxorsa5TZn8V2MG5zVVobk65d2dhS7F/vyq00l85trz8b+ePYrvv9iDl3vH8A/vvAjLG80eZ/ngsaj8paM1ve4Ku598eYRqGW8mY+95rS+4mpPNPCaxgo7NZDJgZkzM5DA4PoOBiRn0j01jYPzkr9PoH5/B1OQk9v/qBZyYKL2SL0FAW00FFtWmcfXyBixrzOC8QsPIDvdj0aJFoefmI/P9eScThD95/VJ0Dk/hN68O4tNP7McX33mR0Yf8PngsjL9saU2vu8KogRDRFQD+AsDJJQGDAP4HM//GtDBF3usBfBH580i+xsxnrABTNRBfjoS0ydlypO3JJjDGFXh1YAKj01mMTmUxNpX/dSbH6B2dxtDkDAYnshienMHQxAwGJ6YxPHUc01nG0vpKHB2aLBp/VUslTkzMIJUgtNdWoL02jY6TX3X5X6sxhfM6muddwjqUrQ48L98p9d8qmSD81VvPxV/+aB/29o7hb548gC/8wcrQH/wvtMfCjDsbj7Q1vQO5BMD7mXkGAIioEsDdACJrIESUBPDPAN4G4AiA3xLRo8y8a7ZOtQ9kYGDAi1UMNnE1p2J5sjnGTOFrOpvDTI4xlWXMZBlT2RymsvmfT536PofJGUZnTy9q6scxmWVMzeSQThJ6RqcxMZPD+HQWEzM5TEznMD6TQ3VFAodPTGJsOnvGnojZXNhShX19879sLp0kdNSlUVuZRFNVCk1VFWiqSqG5ugJNVRWYGe7DJW+/EM3VFfPuqzh06BBSiZZAf0ZxRzWnqook/u7t5+PPH92LPT1j+NzPX8HfXLMi1Oc7Nv/8wsYKOi6IXqU1ve4K0wbSAeByIjoOIAugHUCjcVWluQrAPmY+AABE9ACAmwGc1kBU+0BaWor/j390Kosdx0fAYDCffOFX/lr+1UF8+venvi38f37t50B+RUGWX1PkChd59viT358am/8+k0xgbCaX/56BXKGmXGFMjk/GZFQkCENjjFTnUeQK1077NZevvb4yhd6xaeSYkc2h8Gtel531+0V1abx6YgIzOT7VHLKzGkTulzuworkKu7tHMVMYM5eO2jS6Roq/djqdJExlTw567dUblyyqwQudo0XHLG+sxMhU/sPpylQCVSlCbWUKNekkqiuSqEknUZNOoLW6Am88rxH1lUnUV6ZQn8n/mspOYlFLg/JfxSMjKdTWlH5VxHz+0b0eR3Tm1FRdgc9edwE++sM9GJ/K4sHtXXjvZcEf5dn88wsbK+i4IHpT//jiL9MG8iUA7wewGvkXM74E4OumRSlYivzZ7Cc5AuD1c0WqZbzDw8NFd3J2DU/hM08eMCzxNeoqkxieZ0WOiksW1eKFzhEtbUdtBbqK7CeYy7qOGuzsKv4X9OnUYE/PWEnFdJZPNQECUJEkpBKEimQCqQShrbYC6SQhnUqgIkFIJxOoSOZ/rU4nkCBCdnIcTfW1qEwlUJlKoCGTwsYLm1GVSiBTkUAmlUBVRTL/ayqB6nQS1ekkUgnC8ePHsXjxYo255Dl+fBCZlHoD1nzeCKLRiRE3dOe0vCmDv3rrefj0Ewewo3MEly2tw+r2mkhyRRkr6LggelP/+OIvowbCzKMAvmypFl2K3Q+f8e/f/v5+bNz42vEkd999N+65555T3893IEt1OoGrl9cXEhEK/3cqaf6JBuHkk41T12i2hk5dSycTmMnlACIkTo3PxybKf0+FMYST3+evNVSmsLK1ConCtQQVdIQzflaRAPoHTqC5uenUPoMEERIF7clfM6kEbri4FckEIUl5XZIIyUT++snfJ4mQSOQbQpIKvxa+7zx2FOcuX4bEyaZQuBaGQ4cO4dxzl4UaKwdKuSXInK46pwG3X9KOh1/oxt///BV8+daLUZNORpIrqlhyoJSa0OeBzBuQaC0zv2g16Onx3wDgb5n5usL3nwQAZv7cbJ3sA4lHnjjvA/H9PBDbBJ3TVDaH//LoXuzvG8fbVjbjL/+D/rJTHzwm+0DUGL0bgYg+SUR/M+vrMwA+pxxoxm8BrCSiFYXz2e8C8Ohckc4+kHJDzgOxo4/reSBRE3RO6WQCn3zLeahMEp58uR+/OjAQWa4oYsl5IGpMPwPZA2DLnJ/pPbQPCTPPENFHADyB/DLerxe745FlvPHIYxIrqmWWOrq4LLO0SZg5LW/K4E9evxQ/29ePrz53DOuX1KEho/5rxwePyTJeNaZvZ/sZMx+a/QXgKzYKKwUzP87MFzHzBcz82WIa1W5fXw5ksYkcKGVHH4cDpRaCsHO6cXX+AKrOkSn8z2ePRprLZiw5UEpNqAZCRP9MRClmHpz1syoi+hSAzxBR1Et5lWSzpVc+DQ4OlrweR1zNyWYek1hBx+rqdXQqjfjrNYgIf/57y5FOEp56uR9bjw5FlstmrKj8paONi7/C3oG8DOC/E9GPiOg/F372WQCvAvj/AfypjeJMUO0DaW1tdVSJO1zNyWYek1hBx+rqdXQqjfjrdJY2VOJ9hf0gX/z3w6dOU4wil61YUflLRxsXf4VtIBcA+HcA/wAARPRHAF4H4DFm7gRwzE554ZE7kHjkkTuQ+GA6pzvWd+C8pgxGp7J4bFdPpLlsxJI7EDVhG8guZv4OMz+F/GceKQANzHxymYXdtcEhUC1PVq3SiiOu5mQzj0msoGN19To6lUb8dSapBOGjbzoHMznGv/3uOI7N8y4yG7lsxIrKXzrauPgrbAOZJqItRPQrANuQ34neT0Q3EFE7gCXWKgxJRUXpN4GW25tSAXdzspnHJFbQsbp6HZ1KI/4qzpqOWrzxvEZM57jkB+o+eCwqf+lo4+KvUA2Emb8G4HoAHwPwBmb+C2Z+C/Jv5f2/AfxPaxWGRPaBxCOP7AOJD7bm9MErlyCTSuA3hwax5UjxD9R98JjsA1Fjsoz3YgAfAPDFwuvVwczfYuZPzF6dtVAkk6Vfm1BTE+zdPHHA1Zxs5jGJFXSsrl5Hp9KIv+anpaYC772sAwDwlWeOnjraN4pcJrGi8peONi7+CruM94MAbgPwfOHrNiL6sM3CokbVYOKIqznZzGMSK+hYXb2OTqURf5XmtnXtWFKfxuh0Fk+93B9prrCxovKXjjYu/gp7B5Jg5o8x81eZ+cvM/CfI7wr3BtUqrKEh9Vr0uOFqTjbzmMQKOlZXr6NTacRfpUknE/jT1y/FifEZ/Otvj2F06vT/vfrgsaj8paONi7/CNpBipzWFe2d5RKg+RG9ra3NUiTtczclmHpNYQcfq6nV0Ko34S83VyxtwUWs1Bidm8J0dXZHlChsrKn/paOPir7ANZIKI/hcRfZSI/pKIvgWg9MJux6hOJOzvP/O2Oe64mpPNPCaxgo7V1evoVBrxlxoiwn96fX7B5nd39qBv7LWFLz54LCp/6Wjj4q+wq7DuR36l1SLkD3j6MoDvW6wrcmy/xt4HXM3JZh6TWEHH6up1dCqN+EuPtR21eOO5DZicyeEbW49HkitsrKj8paONi7+0GggRJYho+ewv5O84voz8q0sOA/gfEdYZGNWrTHy5BbSJPMKyo5dHWMWJak4feN0SJAj4yZ4+vDowYT2XPMKKDt07kEYA2wHcW+RrU+HXWyKoLzSqfSBdXV0lr8cRV3OymcckVtCxunodnUoj/tJneWMG71zdirUdtfj2tk7rucLGispfOtq4+Ev3PJABAB9h5m/NJyCiO+2UZAfVMjcfzhO2jas52cxjEivoWF29jk6lEX8F465LF+H9D72IFzoZt1/SjiYPPBaVv3S0cfGXVgPh/AO3bxFRM4CNAFYCqAXQj/yLE3/GzA9GVqUgCGVNS00FblrThodf6Ma9W47jo1cu+IkQggbaH6IT0e0AngRwHYAG5JftLgLwNgA/JaL3RVJhSFT7QEZGIj04cUFwNSebeUxiBR2rq9fRqTTir+C8e307qioSePbwELYf0T/+VkXYuqPyl442Lv4KcqTtBcx8xXwXieivLdRjDdU+kI6ODkeVuMPVnGzmMYkVdKyuXken0oi/gtNYVYFb17bh29u68PjhLDZeaidu2Lqj8peONi7+CrKMV7XT3I91ZQVU+0B6erzatmIFV3OymcckVtCxunodnUoj/grH7Ze0ozadxI7OMTx/bNhKzLB1R+UvHW1c/BXkDuRFItqN/LuvegFMACAAbQAuB/B5++VFh+rM9Djiak4285jECjpWV6+jU2nEX+GorUzhXevasPnlHjy+uxcbFtca5w07Pip/6Wjj4i/tOxBmfgTA6wF8G8Au5FdmHQLwIICrmfmbkVQYEtU+kObmZkeVuMPVnGzmMYkVdKyuXken0oi/wnPLunacmAJ+cfAEth41vwsJW3dU/tLRxsVfQXeiNwPIAHiGmT/HzF9CvplcSURLrVdngGofiC+3gDaRR1h29PIIqziu5lSTTuJt56QBAN/Y2mm861oeYUVHkFVYdyH/+OoTAB4joh8QUS0zHwIwDuDViGoMhWofSH19vaNK3OFqTjbzmMQKOlZXr6NTacRfZty0pg31lUns6h41/iwkbN1R+UtHGxd/BbkDuRXASmZ+HTMvA/A1AP9GRI3INw8/HsppolrmG0dczclmHpNYQcfq6nV0Ko34y4x0gnH7+nYA5nchYeuOyl862rj4K0gDeY6Ze09+w8yPAfgggP8HwDnwbBWW6g94dHTUUSXucDUnm3lMYgUdq6vX0ak04i/zXDetzt+F7OkexY7O8PsewtYdlb90tHHxV5AGcpyI/i8iepWI1gEAMw8x86cBXB1NeeFR7QPx5VB6m7iak808JrGCjtXV6+hUGvGXea7qdBL/8fJFqMukcO+W4+pBJWK5GBdEb+ofX/wVZBXWtwE8DuAjAF6ac+1LAN5stzQzVB+i+3IovU1czclmHpNYQcfq6nV0Ko34y06ut61swUyOsbNzFDuOh/ssJGzdUflLRxsXfwVahcXM+5n5UWY+Y5ceMz9tr6ziENHfEtFRItpW+LqhhLZkLNUdShxxNSebeUxiBR2rq9fRqTTiLzu5atJJ3LI2/+rybz0f7i/NsHVH5S8dbVz8FfZEwoXkH5h5Q+Hr8flEqlVYDQ0N1gtbaFzNyWYek1hBx+rqdXQqjfjLXq5b1rahuiKB54+NYFdX8Gf/YeuOyl862rj4K44NRAvVq0x6e3tLXo8jruZkM49JrKBjdfU6OpVG/GUvV11lCjevCX8XErbuqPylo42Lv+LYQD5CRDuI6OtE1DSfaHBwEBs3bjz1tWnTptOu+9LBbSJ3IHb0cgdSnIW6AwGA2y5pRyaVwG+PDGFPd7C7ELkDiY4g78JyAhE9hfxr4ufyKQD/AuDvkF8y/HcA/juADxSL09TUhM2bN8+bZ2pqyrhW33A1J5t5TGIFHaur19GpNOIvu7kaMvl3ZO3oHMF3XujGp69ZETpWVOOC6E3944u/vGsgzHytjo6Ivgrgsfmu53K5kuPHx8eDFRYDXM3JZh6TWEHH6up1dCqN+Mt+rneuacNDL3RjOss42D+OFc1VoWNFMS6I3tQ/vvgrVo+wiGjxrG9vBbBzPq3sA4lHHtkHEh9c7wOZS3N1Bd6xqgUA8MB2/TPBZR9IdMSqgQD4PBG9QEQ7ALwVwMfmE8o+kHjkkX0g8WEh9oHM5d3rO5Ak4BcHBnB0cNIolu1xsg/Ec5j5D5n5EmZez8w3MfO821MTidJTS6fT1utbaFzNyWYek1hBx+rqdXQqjfgrmlzttWlcu7IZOQYe1LwLCVt3VP7S0cbFX7FqIEFQNZC6ujpHlbjD1Zxs5jGJFXSsrl5Hp9KIv6LLddelHUgQ8NS+fnSPqD9MDlt3VP7S0cbFX2XbQFT7QPr6+hxV4g5Xc7KZxyRW0LG6eh2dSiP+ii7X0oYMblrdhnMaK/HwC91GsWyOC6I39Y8v/irbBqI6kbCpad4tJLHF1Zxs5jGJFXSsrl5Hp9KIv6LNdf2qFhzsn8CPX+rFwHjpzzvD1h2Vv3S0cfFX2TYQWcYbjzyyjDc+LPQy3tmc31KFq5fXYzLL+MHO0qfzyTLe6DhrG8jExISjStzhak4285jECjpWV6+jU2nEX9Hnes+G/FLWR3b1YHRq/vN/wtYdlb90tHHxV9k2ENkHEo88sg8kPiz0PpC5rG6vwaWLazE2ncOju+a/C5F9INFRtg1E9oHEI4/sA4kPPuwDmct7NnQAAL63swcTM8WfOsg+kOgo2waiWsabyWQcVeIOV3OymcckVtCxunodnUoj/nKT67IldVjVVo3BiRk89XLxlUlh647KXzrauPjrrG0gVVV679GJE67mZDOPSaygY3X1OjqVRvzlJhcR4X0bFmF5YyXu39aF6eyZdyFh647KXzrauPirbBuIah/IwMCAo0rc4WpONvOYxAo6Vlevo1NpxF/ucl21vB4EQs/oNH6+/8xxYeuOyl862rj4q2wbiGofSEtLi6NK3OFqTjbzmMQKOlZXr6NTacRf7nIliHDnpfnPQh7Y3oVsjkPHMhkXRG/qH1/8VbYNRLWMd3h42FEl7nA1J5t5TGIFHaur19GpNOIvt7neckETOmrTODI4iV8fGjSKFXZcEL2pf3zx11nbQHw5kMUmcqCUHb0cKFWchTxQSkUqQbhjfTsA4P5tnWB+7S5EDpSKjrJtILIPJB55ZB9IfPBtH8hcrruoBe01FaiqSGDr0df+hS77QKKjbBuI7AOJRx7ZBxIffNwHMpvKVAI3rWnDC52juH/ba696l30g0VG2DUSW8cYjjyzjjQ8+LuOdyx+sbkVNOokdnSPY1TVqFEuW8aop2wZCRCWv+3Igi03kQL+a31IAACAASURBVCk7ejlQqjg+HCiloiadxE2rWwEAD2zvNIolB0qpKdsGks3O/3I1ABgcHCx5PY64mpPNPCaxgo7V1evoVBrx18LlumVdG9JJwjOvDuFg/3joWFH5S0cbF3+VbQNR7QNpbW11VIk7XM3JZh6TWEHH6up1dCqN+GvhcjVVVeAdq07ehXSFjhWVv3S0cfFX2TYQuQOJRx65A4kPcbkDAYA71rcjScDTBwfw8rFwp/fJHYiasm0gs9eBF0O1SiuOuJqTzTwmsYKO1dXr6FQa8dfC5mqvTeP2S9pRU5nCj/aPOKkhiN7UP774q2wbiOwDiUce2QcSH3zfBzKXt61swYnxGTx9bAp9Y8H/wpV9IGrKtoHIPpB45JF9IPHB930gc1nelMHvndeImRzjey90R16D7AMpI5LJZMnrNTU1jipxh6s52cxjEivoWF29jk6lEX/5keuuwoFTj73Ui+HJ0m/oNq0hiN7UP774q2wbiApVg4kjruZkM49JrKBjdfU6OpVG/OVHrotaq7G+PYPx6Rwe2dUbaQ1B9Kb+8cVfZdtAVKuwhoaGHFXiDldzspnHJFbQsbp6HZ1KI/7yJ9fbz6lAYyaJXV0jGJ8u/feCSQ1B9Kb+8cVfZdtAVB+it7W1OarEHa7mZDOPSaygY3X1OjqVRvzlT67fu2gxljVm8Lsjw3j8Jf0lvVH5S0cbF3952UCI6A4iepGIckR05ZxrnySifUS0h4iumy+G6kTC/v5+S9X6g6s52cxjEivoWF29jk6lEX/5k2tgYADvXp//LOThF7oxVeTYWxs1BNGb+scXf3nZQADsBHAbgF/O/iERrQFwF4C1AK4H8GUiCvUwULVPJI64mpPNPCaxgo7V1evoVBrxlz+5mBmvP6ce5zdn0Dc2jade1vvLNyp/6Wjj4i8vGwgz72bmPUUu3QzgAWaeZOaDAPYBuKpYDNWrTHy5BbSJPMKyo5dHWMWJ6yOstrY2EBHuvDS/d+KhHWcee2ujBnmE5T9LARye9f2Rws/OoKenBxs3bjz1tWnTptOud3V1FRsWa1zNyWYek1hBx+rqdXQqjfjLn1wnY715RSOW1KdxbGgKvzx4wnoNQfSm/vHFX6X/mR4hRPQUgGLbKT/FzI/MN6zIz4r+U6KlpQWbN2+eN39tba2yxrjhak4285jECjpWV6+jU2nEX/7kOhkrmSC8e30H/vHfD+One3vxlvMbSx77EJW/dLRx8deCNRBmvjbEsCMAzpn1/TIAx+xUJAhCuXPtymY8/coJ/O7IMJ49PISrlzcsdEmxJm6PsB4FcBcRVRLRCgArATxXTKjaBzIyEu4Faz7jak4285jECjpWV6+jU2nEX/7kmh0rnUzg8qX1YAD3b+ss+WF0VP7S0cbFX142ECK6lYiOAHgDgB8R0RMAwMwvAngIwC4APwHwYWYu2ilU+0A6Ojqs1uwDruZkM49JrKBjdfU6OpVG/OVPrrmxbri4BfWVSezuHsP24/P/RRyVv3S0cfGXlw2Emb/PzMuYuZKZO5j5ulnXPsvMFzDzKmb+8XwxVPtAenp6LFbsB67mZDOPSaygY3X1OjqVRvzlT665saoqkrh1XTuA/F2IrRqC6E3944u/vGwgLlCdmR5HXM3JZh6TWEHH6up1dCqN+MufXMVi3bSmFdUVCbwyMIE9PaNWagiiN/WPL/4q2wai2gfS3NzsqBJ3uJqTzTwmsYKO1dXr6FQa8Zc/uYrFqqtM4T0bFmFoYgbf3lZ8SWxU/tLRxsVfZdtAVOeB+HILaBN5hGVHL4+wilMuj7BO8vaVzUgmCL85NIiD/ePGNcgjrDJC9brj+vp6R5W4w9WcbOYxiRV0rK5eR6fSiL/8yTVfrKbqCrxjVSsA4IHtZ96FROUvHW1c/FW2DUSFaplvHHE1J5t5TGIFHaur19GpNOIvf3KVinXH+nYkCfjFgQEcHZw0qiGI3tQ/vvirbBuI6g94dLT4B2dxxtWcbOYxiRV0rK5eR6fSiL/8yVUqVnttGteubMa5jRn8eM/pB05F5S8dbVz8Rb681dE2Tz/9NK9Zs2be65OTk6isrHRYUfS4mpPNPCaxgo7V1evoVBrxlz+5VLGODE7gjx/ejQQRNr17Ddpr06FqCKI39U9U/y2ampoCLe8q2zsQ1YfovhxKbxNXc7KZxyRW0LG6eh2dSiP+8ieXKtayhgzevKIRMznGwy90h64hiN7UP774q2wbiGqdtGqnehxxNSebeUxiBR2rq9fRqTTiL39y6cR6z4b8e10ff6kXA2PToWoIojf1jy/+KtsGolqF1dBQfi9RczUnm3lMYgUdq6vX0ak04i9/cunEWtFchTec24CpLON7O7tD1RBEb+ofX/xVtg1E9SqT3t7ektfjiKs52cxjEivoWF29jk6lEX/5k0s31ns3dIAAvNQzhqGJmcj8paONi7/KtoHIHUg88sgdSHwo5zsQAFjVVoM3r2jE9uMjeGRXj9yBaFC2DUS1umxqaspRJe5wNSebeUxiBR2rq9fRqTTiL39yBYn1zjX5o2J/8GIPToxORJbH1D+++KtsG0gulyt5fXz8zFcXxB1Xc7KZxyRW0LG6eh2dSiP+8idXkFjrF9di3aIaDE9m8ZOX1cfehs1j6h9f/FW2DUS1SmHRomKn6cYbV3OymcckVtCxunodnUoj/vInV9BY7y2syNp8ZAoTM6X/IRo2j6l/fPFX2TYQ2QcSjzyyDyQ+lOs+kLlcsbQOly2pRVuG8MQe/Q+rZR9IGZFIlJ5aOp12VIk7XM3JZh6TWEHH6up1dCqN+MufXEFjERFuXtuGl0/M4IHt3ZjK6t2FBMlj6h9f/HXWNpC6ujpHlbjD1Zxs5jGJFXSsrl5Hp9KIv/zJFSbW1csbcG5jGn1j0/jp3n7reUz944u/yraBqPaB9PX1OarEHa7mZDOPSaygY3X1OjqVRvzlT64wsRJEuO6c/OeoD27vwkxO/c7AIHlM/eOLv8q2gahOJGxqanJUiTtczclmHpNYQcfq6nV0Ko34y59cYWNds6oD5zRUgpnxq4MDVvOY+scXf5VtA5FlvPHII8t448PZsIx3NlOTE/jDKxahd2wa923pRFZxFyLLeMsIVQOZmAi2SSgOuJqTzTwmsYKO1dXr6FQa8Zc/ucLGmpiYwO+f14RFdWkcHZrELw6UvgsJksfUP774q2wbiOwDiUce2QcSH86WfSCzxyUThDsvzY+/f1sXciXecCH7QMoI2QcSjzyyDyQ+nC37QOaOu/bCJrTXVmB4cgbPHBq0kkf2gXiOahlvJpNxVIk7XM3JZh6TWEHH6up1dCqN+MufXGFjnRxXkUzg7ssWY2gyi/u2ds77nr0geUz944u/ztoGUlVV5agSd7iak808JrGCjtXV6+hUGvGXP7nCxpo97i0XNKE+k8SB/nE88+qQcR5T//jiLy8bCBHdQUQvElGOiK6c9fPziGiciLYVvr4yXwzVPpCBAfWyvLjhak4285jECjpWV6+jU2nEX/7kChtr9rh0KoE713cAAL659XjRRTpB8pj6xxd/edlAAOwEcBuAXxa5tp+ZNxS+PjRfANU+kJaWFrMKPcTVnGzmMYkVdKyuXken0oi//MkVNtbcce+4uBWXLanF+EwOvzs6bJTH1D+++MvLBsLMu5l5j0kM1TLe4eEzDRB3XM3JZh6TWEHH6up1dCqN+MufXGFjzR2XSSVw5bJ6HBmcxLeeP/OzkCB5TP3ji7+8bCAKVhDR80T0CyL6/flEqgbiy4EsNpEDpezo5UCp4pwNB0qpxt24uhUNmRR2d4/h+WPDSn3YmuLir9LPeSKEiJ4CUGwx86eY+ZF5hh0HsJyZ+4joCgA/IKK1zHzGp1pDQ0PYuHHjqe/vvvtu3HPPPae+92UdtU1kH4gdvewDKc7ZuA9kLlUVSdy+rg3PHB7CD3f34vKl9aHyyD4QQ5j5WmZeV+RrvuYBZp5k5r7C77cA2A/gomLa+vp6bN68+dTX7OYB+LOO2iayD8SOXvaBFOds3QcylxvXtOHVExN4+pVB7Dg+rNSHqSku/orVIywiaiOiZOH35wNYCeBAMa0s441HHlnGGx/O5mW8s6lJJ3HrunYA+RVZYfLIMt4IIaJbiegIgDcA+BERPVG49GYAO4hoO4CHAXyImYu+rJ+ISubw5UAWm8iBUnb0cqBUcc6WA6V0xt2yphWXLq5F58g0dnaOBM4jB0pFCDN/n5mXMXMlM3cw83WFn3+Xmdcy86XMfDkz/3C+GNlstmSOwcH5X0kQV1zNyWYek1hBx+rqdXQqjfjLn1xhY5UaV1uZwiWLatE5PIVvPt8ZOI+pf3zxl5cNxAaqfSCtra2OKnGHqznZzGMSK+hYXb2OTqURf/mTK2ws1bhb1rahuiKBrUeHsatrNFAeU//44q+ybSByBxKPPHIHEh/kDuR06jMp3LauDZcsqsF3X+iSO5ByYr4Xnp1E9bbeOOJqTjbzmMQKOlZXr6NTacRf/uQKG0tn3C1r27Gvbxy/emUQe3v1D3ky9Y8v/irbBiLngcQjj+wDiQ+yD+RM6jMp3LSmDQDw1NHSTz2CxI6Lv8q2gch5IPHII/tA4oPsAynO7Ze0Y8PiWuzpGcPenjErsePir7JtIMlksuT1mpoaR5W4w9WcbOYxiRV0rK5eR6fSiL/8yRU2lu64hkwKF7VVY3CK8Y1Z+0JMYsfFX2XbQFSoGkwccTUnm3lMYgUdq6vX0ak04i9/coWNFWTcuy5pR2WS8OzhIeztVd+FmPrHF3+VbQNRrcIaGip+KEyccTUnm3lMYgUdq6vX0ak04i9/coWNFWRcU1UFNp6TLqzI6jaOHRd/lW0DUX2I3tbW5qgSd7iak808JrGCjtXV6+hUGvGXP7nCxgo67s7LlmFvzxh+vn8A+xR3Iab+8cVfZdtAVCcS9vcXfQNKrHE1J5t5TGIFHaur19GpNOIvf3KFjRV0XG58CDeuzm/w+8bzpT/kNvWPL/4q2waiQrVPJI64mpPNPCaxgo7V1evoVBrxlz+5wsYK46871nfgvKYMToxPl7wLMfWPL/4q2waiepWJL7eANpFHWHb08girOPIIS61vrq7AFUvrsLt77NQ7ssLEjou/yraBqPaBdHV1OarEHa7mZDOPSaygY3X1OjqVRvzlT66wscL66471HUgnCb8+NIj9fcXvQkz944u/yraBqJa51dbWOqrEHa7mZDOPSaygY3X1OjqVRvzlT66wscL6q7m6AjeubgUB+PGevlCx4+Kvsm0ggiAIC8Udl7RjSX0lHt3VO+9dSDlQtg1EtQ9kZGTEUSXucDUnm3lMYgUdq6vX0ak04i9/coWNZeKvlpo0rlqePy/9m1vP/CzE1D+++KtsG4hqH0hHR4ejStzhak4285jECjpWV6+jU2nEX/7kChvL1F93Fj4L2dc3dsZdiKl/fPFX2TYQ1T6Qnp4eR5W4w9WcbOYxiRV0rK5eR6fSiL/8yRU2lqm/mqsrcNeGDnSPTOMbc+5CTP3ji7/KtoGoUJ2ZHkdczclmHpNYQcfq6nV0Ko34y59cYWPZ8NcNq1pRUViRNXtfiKl/fPFX2TYQ1T6Q5uZmR5W4w9WcbOYxiRV0rK5eR6fSiL/8yRU2lg1/NVdX4MaLW7C6rRqP7OopqQ2S2xd/lW0DUe0D8eUW0CbyCMuOXh5hFUceYYXTv/vSDhzoH8cTe/vxcuEuRB5heY5qH0h9fb2jStzhak4285jECjpWV6+jU2nEX/7kChvLlr+aq9OvvSOrcF6IqX988VfZNhAVqmW+ccTVnGzmMYkVdKyuXken0oi//MkVNpZNf717fQcyKcLgxAz29owZ+8cXf5VtA1H9AY+OjjqqxB2u5mQzj0msoGN19To6lUb85U+usLFs+qupugK3rWvH7u4xfGPrcWP/+OKvsm0gqn0gvhxKbxNXc7KZxyRW0LG6eh2dSiP+8idX2Fi2/XXz2jZUphJ49vAQhlINRrF88VfZNhDVh+i+HEpvE1dzspnHJFbQsbp6HZ1KI/7yJ1fYWLb91VRVgZtWt6I2ncCjO44ZxfLFX2XbQFTrpFV3KHHE1Zxs5jGJFXSsrl5Hp9KIv/zJFTZWFP66Y307UokEfnF0Eru7538MFRd/edlAiOgLRPQSEe0gou8TUeOsa58kon1EtIeIrpsvhmoVVkND6VvIOOJqTjbzmMQKOlZXr6NTacRf/uQKGysKfzVWVeC6VS0AXluRFSaWL/7ysoEAeBLAOmZeD2AvgE8CABGtAXAXgLUArgfwZSIq2ilUrzLp7e21Wa8XuJqTzTwmsYKO1dXr6FQa8Zc/ucLGispfd1zSjsok8Lsjw9jVVfwuJC7+8rKBMPNPmflkB3gGwLLC728G8AAzTzLzQQD7AFxVLIbcgcQjj9yBxAe5A7Gjr8+kcOvFjVjVVo375rkLiYu/vGwgc/gAgB8Xfr8UwOFZ144UfnYG/f392Lhx46mvTZs2nXZ9amoqglIXFldzspnHJFbQsbp6HZ1KI/7yJ1fYWFH5CwDeck4VDp+YwNajw9jZeear2ePir9IvjIoQInoKQLG1aJ9i5kcKmk8BmAHwrZPDiuiLni7f0NCAzZs3z5t/fHw8UL1xwNWcbOYxiRV0rK5eR6fSiL/8yRU2VlT+AoBkdhK3rWvHN5/vxH1bj+PzN6wMFMsXfy1YA2Hma0tdJ6L3A7gRwDXMfLJJHAFwzizZMgBF18PJPpB45JF9IPFB9oHY0y9atAi3LUrisd09mMkxdhwfwfrFtaddt1lbVHj5CIuIrgfwCQA3MfPsk1geBXAXEVUS0QoAKwE8VyyG7AOJRx7ZBxIfZB+IPX1nZydqK1O4dV07dnaO4t4tx/Hav5Pj4y8vGwiALwGoA/AkEW0joq8AADO/COAhALsA/ATAh5m56DtLEonSU0un01YL9gFXc7KZxyRW0LG6eh2dSiP+8idX2FhR+Wu29qY1bairTOKFzhFsOz5yxnVbtUXFgj3CKgUzX1ji2mcBfFYVQ9VA6urqghfmOa7mZDOPSaygY3X1OjqVRvzlT66wsaLy12xtTTqJd61rw68PDeKxXb3YsLgWRBQbf/l6B2KMah9IX1+fo0rc4WpONvOYxAo6Vlevo1NpxF/+5AobKyp/zdXesrYNXSPT+NUrJ7Dl6LBWLF/8VbYNRHUiYVNTk6NK3OFqTjbzmMQKOlZXr6NTacRf/uQKGysqf83VVqdTuGN9OwDg3i3HkcvlYuOvsm0guVyu5HVflsHZRJbx2tHLMt7iyDJee/q52neubsXa9hpkc4znDg/Fxl9nbQOZmJhwVIk7XM3JZh6TWEHH6up1dCqN+MufXGFjReWvYtqqiiTetKIR+/rGcd/WTmWD8MVfZdtAZB9IPPLIPpD4IPtA7OmLaW9c3Yrm6hT29Y3jlekaq7VFRdk2ENkHEo88sg8kPsg+EHv6YtrKVAJ3re/ARa1VeHRnJ3Jc9CUboWqLirJtIKplvJlMxlEl7nA1J5t5TGIFHaur19GpNOIvf3KFjRWVv0pp33FxC/rHZ7Czbwa/OnjCWm1RcdY2kKqqKkeVuMPVnGzmMYkVdKyuXken0oi//MkVNlZU/iqlrUwl8d4N+cdT39jaiWyu+F2IL/4q2wai2gcyMDDgqBJ3uJqTzTwmsYKO1dXr6FQa8Zc/ucLGispfKu11FzWjJZMAM+Pf57kL8cVfZdtAVPtAWlpaHFXiDldzspnHJFbQsbp6HZ1KI/7yJ1fYWFH5S6WtSCbwHze04fDgJDZtOV70LsQXf5VtA1Et4x0eHnZUiTtczclmHpNYQcfq6nV0Ko34y59cYWNF5S8d7aVNwJL6ShwdmsT/PnDm3YYv/jprG4gvB7LYRA6UsqOXA6WKIwdK2dOrtNmZafzRFYuxvLESm353HNPZ0/8+88VfZdtAZB9IPPLIPpD4IPtA7Ol1/POmFY0ACF0jU3hib79RbVFRtg1E9oHEI4/sA4kPsg/Enl7HP8kE4Q8vXwQC8Oyrg5iayZ123QfKtoHIMt545JFlvPFBlvHa0+v65/dXNOLypXV49vAQHt/Td8b1haZsGwhRsePTX8OXA1lsIgdK2dHLgVLFkQOl7Ol1/ZMgwjvXtAIAHtjWiYnCXYgv/irbBpLNFj2o8BSDg4OOKnGHqznZzGMSK+hYXb2OTqURf/mTK2ysqPylo519/Q3LG3BRaxXaa9N4Yk9vqNqiomwbiGofSGtrq6NK3OFqTjbzmMQKOlZXr6NTacRf/uQKGysqf+loZ18nItxzxRK81DOGbz7fhbGprDf+KtsGIncg8cgjdyDxQe5A7OmD+ueKZXVY016DyZksfvpynzf+KtsGwiXeZAmoV2nFEVdzspnHJFbQsbp6HZ1KI/7yJ1fYWFH5S0c79zoR4QOvW4xUIoH7tnRicGwyUG1RUbYNRPaBxCOP7AOJD7IPxJ4+jH/WL67DBS1VGJnK4td9pR/Ru6JsG4jsA4lHHtkHEh9kH4g9fVj/3HPFYlzQksGzhwYwOFH6hbEuKNsGkkwmS16vqSl94lcccTUnm3lMYgUdq6vX0ak04i9/coWNFZW/dLTzXV+7qBZNVRV4ZSiL7+zoClRfFJRtA1GhajBxxNWcbOYxiRV0rK5eR6fSiL/8yRU2VlT+0tGWun7PFUsAAM8dHkLf2MK+E6tsG4hqFdbQ0JCjStzhak4285jECjpWV6+jU2nEX/7kChsrKn/paEtdv6itGm9dVolDAxN4cHu3ds4oKNsGovoQva2tzVEl7nA1J5t5TGIFHaur19GpNOIvf3KFjRWVv3S0qus3r18MAPjZy33oGl64FVll20BUJxL29/eXvB5HXM3JZh6TWEHH6up1dCqN+MufXGFjReUvHa3qen1uFLetawOIcP/2hfssxMsGQkRfIKKXiGgHEX2fiBoLPz+PiMaJaFvh6ythc6j2icQRV3OymcckVtCxunodnUoj/vInV9hYUflLR6tz/YaLWzE6lcWWI8M4NjShndsmXjYQAE8CWMfM6wHsBfDJWdf2M/OGwteH5gugepWJPGLwI488wooP8gjLnt7UP21tbTinMYPbL2lH7+gUvrl1YZaNe9lAmPmnzHzyGdQzAJYFjaHaB9LVtfBL4Gzjak4285jECjpWV6+jU2nEX/7kChsrKn/paHWv/8HqVhARth4dxqGBce38tvCygczhAwB+POv7FUT0PBH9goh+f75Bg4OD2Lhx46mvTZs2nXa9trY2mmoXEFdzspnHJFbQsbp6HZ1KI/7yJ1fYWFH5S0ere31xXSXuXN+B4cks7luAu5AF2w9PRE8BKLaf/1PM/EhB8ykAMwC+Vbh2HMByZu4joisA/ICI1jLzGWvempubsXnz5oiqFwRB8IM/WN2C7+zoRO/oFPb1juHC1mpnuRfsDoSZr2XmdUW+TjaP9wO4EcD7uPCJEjNPMnNf4fdbAOwHcFGx+Kp9ICMjIxZn4weu5mQzj0msoGN19To6lUb85U+usLGi8peONsj11po0bl/fgd3dY7h3y3HtGmzg5SMsIroewCcA3MTMY7N+3kZEycLvzwewEsCBYjFU+0A6Ojqs1esLruZkM49JrKBjdfU6OpVG/OVPrrCxovKXjjbo9ZvXtqEuncDYdBa7utw1ei8bCIAvAagD8OSc5bpvBrCDiLYDeBjAh5i56IJp1T6Qnp4ei+X6gas52cxjEivoWF29jk6lEX/5kytsrKj8paMNer2pqgI3rW3HC52jTu9C/Hgn8ByY+cJ5fv5dAN+1kUN1ZnoccTUnm3lMYgUdq6vX0ak04i9/coWNFZW/dLRhrt+2rg0/39+PK5fVI8eMhIP/Xl42EBtUVlaWvN7c3OyoEne4mpPNPCaxgo7V1evoVBrxlz+5wsaKyl862jDX6ypT+Poda5w0jpP4+gjLmEwmU/K6PGLwI488wooP8gjLnt72I6yTuGweQBk3kPr6eqPrccTVnGzmMYkVdKyuXkcn/opPrrCxovKXjjYu/irbBqJaxqu6HkdczclmHpNYQcfq6nV04q/45AobKyp/6Wjj4q+ybSCjo6NG1+OIqznZzGMSK+hYXb2OTvwVn1xhY0XlLx1tXPxF5fjWUADo7OzkUh+kT05OKj9ojxuu5mQzj0msoGN19To6lUb85U+usLGi8peOdqH81dTUFOhDlLK9Awl7aH2ccTUnm3lMYgUdq6vX0Ym/4pMrbKyo/KWjjYu/yraBqHail7o+98WLcUE1Zx/zmMQKOlZXr6MTf8UnV9hYUflLRxsXf5VtA3nuuedCX7/vvvtsl+ME1Zx9zGMSK+hYXb2OTvwVn1xhY0XlLx1tXPxVtg3kscceM7oeR1zNyWYek1hBx+rqdXTir/jkChsrKn/paOPir7L9EP3BBx/c0traOu/khoaGGurr6weLXevv729tbm7uja66aCg1J1/zmMQKOlZXr6NTacRf/uQKGysqf+loF9Bfvddcc831uuKybSCCIAhCtJTtIyxBEAQhWqSBCIIgCKGQBiIIgiCEQhqIJkR0PhH9KxE9vNC1COUFEdUQ0b1E9FUiet9C1yOUF1H+3XXWNRAi+joRdRPRzjk/v56I9hDRPiL6q7njmPkAM3/QXaVCnAnos9sAPMzM/wnATc6LFWJHEH9F+XfXWddAAGwCcNoytcI56/8M4B0A1gB4DxGtcV+aUEZsgr7PlgE4XJD58ZpVwXc2wYO/x866BsLMvwQw9xz1qwDsK3TqKQAPALiZiO4mon8koqXOCxViTRCfATiCfBMBzsL/TQrBCeivyBCz5lmK1/4FCOT/B72Ume9j5o8y81EiaiGirwC4jIg+uTBlCjGnqM8AfA/Au4joXwD8cCEKE8qCov6K8u+usj0TPSDFXmF82g5LZu4D8CE35QhlSlGfMfMogD9yXYxQdsznbmO9wwAAAX5JREFUr8j+7pI7kDxHAJwz6/tlAI4tUC1C+SI+E6LEub+kgeT5LYCVRLSCiNIA7gLw6ALXJJQf4jMhSpz766xrIER0P4DfAFhFREeI6IPMPAPgIwCeALAbwEPM/OJC1inEG/GZECW++EtepigIgiCE4qy7AxEEQRDsIA1EEARBCIU0EEEQBCEU0kAEQRCEUEgDEQRBEEIhDUQQBEEIhTQQQRAEIRTSQARBEIRQSAMRBEEQQiENRBAEQQiFNBBBEAQhFNJABEEQzmKIqJGIbizy898Q0ZJSY6WBCIIgnN1cA+BxACCiK2f9/IcAcqUGSgMRBEE4y2Hmk43i47N+3MnMnaXGSQMRBEE4u7kaAIjobQBGC7+/A0CvaqA0EEEQhLObMSLaC+BaAEREBwAsY2blaYZyoJQgCIIQCrkDEQRBEEIhDUQQBEEIhTQQQRAEIRTSQARBEIRQSAMRBEEQQiENRBAEQQiFNBBBEAQhFNJABEEQhFBIAxEEQRBC8X8AP8LisKjsWToAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZMAAAEZCAYAAABSN8jfAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nO2dd5hd1XX233Xv3Hun99GIGY2EhOogY4qQbHDASPQmY9xIAWzi4ILjdDtf8hliG8cl+dxwTJw4lguxcRxjBMgUIzAgMCAwRRUJ1ZE0vfe2vz9mJEbSnXP23mefPaes3/PMw8y971prb+lFa865e59NQggwDMMwjBcSMz0AhmEYJvxwM2EYhmE8w82EYRiG8Qw3E4ZhGMYz3EwYhmEYz3AzYRiGYTzDzYRhGIbxDDcThmEYxjPcTBiGYRjP5KgGEFEhgPMALAJQDKAPQCOAZ4UQDWaHxzAMw4QBkn2cChHVA7gNQBrAqwAOA+gEkAegHMAZAEoBPCaEuNeX0TIMwzCBRKqZENEHAeQD+G8hxJCL9lwAFwH4thBiwMgoGYZhmEAj20zmCiEOnPDabADjQojmLPokgCohRKOxkTIMwzCBRfo210mBRM8CWI+Jz0tahRAPmhwYwzAMEx60m8lxSYjeB6BWCPFN70NiGIZhwoaRZgIARLRbCLHQSDKGYRgmVCgvDZ4KEZ0D4O8A9AJ4ysiIGIZhmNDhadOiEOIlIcQHAfwMQJOZITEMwzBhQ7uZENGVR78XQjwG4DojI2IYhmFCh5fVXCUAVgMgAO8A0C+EuMPc0BiGYZiwoNRMiOi7QoiPT35/BoBqAE8LIQZ9Gh/DMAwTAlSbyUohxAuT338dQArABZh4tMojAH4lhNjrx0C9sHfvXlFaWjrt+52dnXB6P4zYnJPJWrq5VONU9DJaJw37Kzi1vOTyy2NB9ldZWRnJapU+MznaSCZ5QQhxmxDiDAAfBzAA4N8nH70SKPLy8jy9H0ZszslkLd1cqnEqehmtk4b9FZxaXnL55bGo+MvLaq4HiGg1AAgh9goh7hZCXAqgyMzQzNHY6PxUF7f3w4jNOZmspZtLNU5FL6N10rC/glPLSy6/PBYVf2k3EyFErxBi49TXiOhyAB/2PCrDpFIpT++HEZtzMllLN5dqnIpeRuukYX8Fp5aXXH55LCr+Mno4lhDiYQCXmMpHRJcT0U4i2k1En83yfoaI7p18/3kiOjVbnpKSEsc6bu+HEZtzMllLN5dqnIpeRuukYX8Fp5aXXH55LCr+cm0mRDSfiD6kkDOPiG71MKajdZMAvgPgCgD1AG6YPFNlKrcA6Jh8jMvXAXwlW67W1lbHWm7vhxGbczJZSzeXapyKXkbrpGF/BaeWl1x+eSwq/nJ9nIoQYi8RgYi+AuAggCcAbBNTloERUQGAlQAuBtAG4BsGxrYSwG4hxJ7JGj8DsBbAtimatQDumPz+FwDuIiISJyxR4yuT8NTiK5NwEDd/6cTG7cpE6tlck8t9PzO5t+Q9AO4kojwASQAjAJoB/BbAvwghOgyNrRYTzesoDQBWTacRQowSUReACgDHteqXXnoJd95557Gfb7zxRtx8883Hfh4eHjY05OBgc04ma+nmUo1T0ctonTTsr+DU8pLLL49FxV9KD3oUQrwG4DUAIKIlAC7ExNXDRsdAPbKtbz5xU4yMBpWVldi4cfohDgxMfyDkyNg4UkmjHy1ZwWlOQa6lm0s1TkUvo3XS2Py7sEXc/KUTK6uPir+8PDX4LgBXAqgkok8BuOvE20seaQBQN+XnOZjYHJlN00BEOQBKALSfmMhttcPs2bOnfe9P7t2K3qExFGVyUJRJoiiTg8JMEsWT3xdlkihMv/V9UW4OitJJFGWSyE8nkSDpPT9GcZpTkGvp5lKNU9HLaJ00Nv8ubBE3f+nEyuqj4i8vzaRXCDEC4AgR/RrAJzDxgbkpXgSwiIjmAzgE4EMA/vAEzXoANwF4DsD7AGzM1tBGRkYcCzU2NmLevHlZ3xscGcfwmEBb/wja+p3znEiCgMJ0EoXHGlHyuKZ09LXCdM7xzSmT9Hw15DQn05ispZtLNU5FL6N10tj8u7BF3PylEyurj4q/vDSTO4jobwB8Qwixm4i+CIPNZPIzkNsw8ZiWJID/EkJsJaLPA9gshFgP4PsAfkxEuzFxRZJ11Vki4fwPczqdnva9+248A4Oj4+gZGkPP0Ch6h8aOfd8zNIae4Snfn/B+/8g4uofG0D00pjz/3JzESU1narM5rilNuTLKSyVARI5zMo3JWrq5VONU9DJaJ43NvwtbxM1fOrGy+qj4S7uZCCFeJaI3AXyAiCoBLCeiBUdXX5lACLEBwIYTXvvclO8HAbzfLY9bMykqmn7TPhEhL5VEXiqJWYVqf2mj4wK9xxrNGHqHR9E9+Fbz6Z3SiHqHxtA9pSkNjo5jcHQcLX1qV0NJAgozOShMEUryerI2n8J0EsW5J9+mSyb0bsk5/fnZyqUap6KX0TppTP75BAWbcwqCv3RiZfVR8Zd2MyGihBCiF8B/T/68FsCtRHSuEGK1qQGaYHR01PH9trY2FBYWGq+bkyCU5qVQmqe2Q1UIgYGR8ROugLJf/fSc8P3g6Di6BkfRNQgc6lFrRPmpBIoyOVhalY+RcYGa4gxqijOonfxvZUEqa8Mx+eenm0s1TkUvo3XS+OWvmcTmnILgL51YWX1U/OXlNtcNRNSAic8rPg7gbiHE/5gZlllycpynWVZWZmkkchAR8tMTH+BXF6ldDY2MjaN3aAxH2rsgcnLRPXlFdOzqaGgU3UPHXxH1DI2id3gM/SPj6B8ZRlleDna09J+UO5UgzC5KTzSZkreaTEmqEGPjQvvKZiq6fxeqcSp6Ga2TJmj+MoHNOZms5SWXXx6Lir+83Oa6h4hmA7gKwONCiC3mhmWW8fFxx/cHBgZQXFxsaTT+kkomUJafwHDPGKqr5X9bGRcC/cMTnwF1DoyiuXcYh7uHcLh7CIcm/9veP4qDXUM42DV0/A4gAEk6gNlFmWNXMzXFadSWTHxfXZiWXlCg+3ehGqeil9E6aaLkr6PYnJPJWl5y+eWxqPjLy5UJhBCNAO4zNBbfcGsmg4PRO9tLdU4JoonPWjI5OKUog2WzCk7SDIyM4Uj3yU3mQHs/OobGcWjytZNzA7MK01MazdGrmjROKcognfNWo9H9u1CNU9HLaJ007K/g1PKSyy+PRcVf2sf2holNmzaJ+voTH+v1FkNDQ8hkMhZH5D825zQ0NAQkUzjSM9FcDncN4XD38LFm09I3jPFpbEYAKgtSb13F5CextLoIi6sKUJBOKo1BZb4qehmtk4b9FZxaXnL55bEg+0vlcCxPVyZhwcs+k7AyE/sATi3Lw6llJx/UMzw2jqaet65o3rqqGUZjzxBa+kbQ0jeCVw73oigF9LzcDAJwalku6qsLcHp1IeqrC3BKURo0zSZQ3mdiF95nYk4fFX/Fopm4LQ3Ozc21NBJ72JyTW610MoG60lzUlZ6sGx0XxzWa/c0d2NMD7Grtx96OQeztGMRDO9oAAGV5OaifVYDTqwtQX12IhZV5SE9+FqM6XxW9jNZJw/4KTi0vufzyWFT8xc0EwTn20iRhOVY1J0GoLcmgtmTiMr27LoPi4mIMj45jV2s/tjb1YWtzH7Y19aFjYBSb9ndh0/4uAEAqSVhSmY/66gLML0ogUzwivQybj+31Rlj8ZTIXH9vrTCyaids+k46OjkCshjCJzTmZrHU0VzongdNnF+L02RMr0oQQONw9NNFcmiaay/7OQWxp6sOWpr6J4E2NmFOSmXL1UoC60tysz0dTGbOM1knD/gpOLS+5VGNl9VHxVyyaids+k4qKCksjsYfNOZmsNV0uIkJtSS5qS3Jx6eIJTffgKHa09GFrYx9eP9KNXW2DaOgaQkPXEB7dNfG8z6JMEssmm8vp1QVYXFWA3JyE0phltE4a9ldwannJpRorq4+Kv2LRTNyWBvf09ARiB6lJbM7JZC2VXMW5OVhZV4KVdSU4coRQVb0Ee9oGsLWpF9smr2Ba+0fwwsFuvHCwG8DE42YWVubjrIok3rWkBosq86b9UF9lTE4a9ldwannJpRorq4+Kv7iZIDiHy5gkbocXDQ8PIydBWFyVj8VV+bhu+cStsZa+EWxt6j12a2xP+wDebOvHm63Az3bsRE1xGhfML8OFC0qxoDx7Y4nK4UUmiZu/dGLjdjgW7zMB7wMIUi3dXLJx/cNj2NrUi+f2deDZAz1oH3jr87Q5JRlcML8UFy4ow/zytz7UDPI+gJkibv7SiY3bPpPwHSGogcw+k6hhc04ma+nmko3LTydxbl0J1s4l3HPDcnztyoW4emklSnJz0NA1hP9+pQm3/nIHPvqL7fjxy0dwoHNQKreThv0VnFpecqnGyuqj4q9Y3ObipcHhqaWbS2fZZjJBeHtNEd5eU4RPnjcHrx7pwW/3dOKZfZ3Y3zmIH7/ciB+/3Ii5xTlY3d6ICxeUHVvCrFKf/RWcWrw02D9i0UzcPmANyuEyJonb4UVeDy5KJghn1xbj7NpifOr8Ovz+UA+e2tuBTfu6cKB7FOteOoJ1Lx3Bwoo8XLigDJcsKkd5fmrafF7GFgbi5i+d2LgdjhWL21xjY84nHXZ1dVkaiT1szslkLd1cqnFO+pwE4dy6Yvz1BfNw7x8tx21nFuLihWXITyWwu20A929twY33bsVXntyHN9v6XfOxv4JTy0sukx5T1YXBX7G4MnHbZ1JZWWlpJPawOSeTtXRzqcbJ6lPJBNYsq8G1BQUYHh3H5kPd2NzQgw07WvH47g48vrsDZ9cW4ZpFxZgrRNarYPZXcGp5yeWXx2R0Tpqg+IuvTBCczm6SuP3m6NdvjVO16ZwEzptXij8/vw7rPlCP65ZXITcngZcP9eCfnjyEj/1yBx7b1YaRsfGs8VEibv7SiY3blUksmonb8me31V5hxOacTNbSzaUap6LPpp1dlMHH3zEH99xwOj5y7ikoSRP2dgzia789gJvu3Yafv9aEvuExrbGFgbj5SydWVi+jc9IExV+8zwS8DyBItfzeZ6Kjl9H29g9gU0M/fvFaM/Z3ThxWlJ9K4IolFbh6cQlqy4ukxxYG4uYvnVjeZxJBeJ9JeGr5vc9ERy+jbWtpxmWLK/C965fii5ctwJk1hegfGcf/bmnBFx/fhx9sPoyBEefbrWEibv7SieV9JhEkmXQ+sa+g4OQjasOOzTmZrKWbSzVORS+jPaohomPPC9vV2o8HtrXi4Tfa8OYrTXhsVzv+bGUtLlxQ6rpcPejEzV86sbJ6FX95qeM3sbgyccOt2YQRm3MyWUs3l2qcil5Gm02zqDIff3XBXHzh3bOxqDIPrX0j+NIT+/C3D+3GnrYBpfEGjbj5SydWVq/rL9U6fhOLZuK2mqu7u9vSSOxhc04ma+nmUo1T0ctonTSzU8P41rVL8JfvqkNJbg5ea+zFJ361A3c9exDdg85n7QSVuPlLJ1ZW79VfQfn3K5AfwBNROYB7AZwKYB+ADwghOrLoxgC8PvnjASHEtdnyuX0A39/fj/z8fI+jDhY252Sylm4u1TgVvYzWSTP1vZ6hUfzopUY8sL0F4wIoziRx84oaXLGkAslEeG59xc1fOrGyepP+Mk0UPoD/LIDHhRCLADw++XM2BoQQZ05+ZW0kgPtJi+3t7doDDSo252Sylm4u1TgVvYzWSTP1vaJMDj553hx897qlePsphegeGsO3Nh3EbffvxBstfdJjmmni5i+dWFm9SX/NJEFtJmsB/HDy+x8CeI+fxYJ4deYVm3MyWUs3l2qcil5G66TJ9t788jx89cqF+MfVp6KqIIWDHQP45yf246evNGI8BH6Mm790YmX1fvhrJgjqba5OIUTplJ87hBBlWXSjAF4BMArgy0KIX2XLt379enH77bcf+/nGG2/EzTfffOznwcFB5ObmmptAALA5J5O1dHOpxqnoZbROGrf4gZEx/M9rzfjJ7yeWeK6qK8bfXjgPxbnBXWwZN3/pxMrq/faXF0Jxm4uIfkNEW7J8rVVIM1cIsQLAHwL4BhGdlk1UXFyMjRs3Hvua2kgAoKmpSXseQcXmnEzW0s2lGqeil9E6adzi81JJ3HjOKfjCpQtQlEni+YPd+OSvdmJngG97xc1fOrGyer/9ZYsZayZCiIuFEMuzfN0PoImITgGAyf82T5Pj8OR/9wB4EsBZ2XRuS+eCcH6yaWzOyWQt3VyqcSp6Ga2TRrbWqrkl+Lf3LMWSqnw09Q7jrx7YhfXbWgJzG2MqcfOXTqys3pa//Caon5msB3DT5Pc3Abj/RAERlRFRZvL7SgDnA9hmbYQM4wPVRWn869WLcG19JUbGBe56tgFffnJ/pHbPM9EkqM3kywAuIaJdAC6Z/BlEtIKI/nNSswzAZiJ6FcATmPjMJGszcdtn0tvba2rcgcHmnEzW0s2lGqeil9E6aVTHlk4mcNt5dfj7i05Fbk4CT7zZgU/d/wb2dwRno2Pc/KUTK6u37S+/COQH8KZx22fCH8AHp1YcP4B34kDHIL7w+F7s7xxEJieBv3xXHVYvLNfKZZK4+Usnlj+AjyBu+0xaWlosjcQeNudkspZuLtU4Fb2M1knj5c9nblkuvrV2MdYsLMPQ6Dj+7bkG3PtK44x/jhI3f+nEyupn0l8miUUzcSPsD93Lhs05maylm0s1TkUvo3XSeP3zyUsl8XcXzsOfnz8HZXkpfH/zEdz9u0Mz2lDi5i+dWFn9TPvLFLFoJm7H9paXz/xtA9PYnJPJWrq5VONU9DJaJ42JPx8iwtXLqvCRc2uQShDu29qCbz/bMGMbHOPmL51YWX0Q/GWCWDQTt/NMgnKZaJK43YaI6m2uE3nnvBLcfsl8pJKEB7e34pvPHJyRhhI3f+nE8m2uCOK2z6S4uNjSSOxhc04ma+nmUo1T0ctonTSm/y5W1pXg85csQDpJ+PXONvzrUwcwNm63ocTNXzqxsvqg+UuXWDQTN9yWDocRm3MyWUs3l2qcil5G66Tx4+/inDnF+OJlpyGTk8Bju9rx1d/ut9pQ4uYvnVhZfRD9pUMsmonbH3ZfX3AfW6GLzTmZrKWbSzVORS+jddL49XdxZk0RvnT5achLTexF+fIT+zBqqaHEzV86sbL6oPpLFd5nAmBoaAiZTMbiiPzH5pxM1tLNpRqnopfROmn8/rvY2tSLf3j4TfSPjOP6t1XhoytrkfB5hU/c/KUTK6sPsr94n8kJuH0A39jYaGkk9rA5J5O1dHOpxqnoZbROGr//Lk6vLsRXrlyI+lkFWL+tFT/cfMTXekD8/KUTK6sPur9kiUUzcVuHnUqlLI3EHjbnZLKWbi7VOBW9jNZJY+PvYklVAW465xSMjQv89NUmPPnmSQeTGiVu/tKJldWHwV8yxKKZuK3mKikpsTQSe9ick8laurlU41T0Mlonja2/i7Nqi3DrqloAwL8+tR+7Wvt9qxU3f+nEyurD4i83YtFM3B6n0traamkk9rA5J5O1dHOpxqnoZbROGpt/F+85vQqXLS7H0JjA7Y/tQUe/8y1eXeLmL51YWX2Y/OVELJoJX5mEpxZfmXiDiPCp8+tQP6sArX0j+PzjezE8Nm68Ttz8pRPLVyYRxG3F2vDwsKWR2MPmnEzW0s2lGqeil9E6aWz7K51M4HMXz0dlfgpbm/rwnWcbjD/HK27+0omV1YfNX9MRi2YyPu78m9nAQHDOiTCFzTmZrKWbSzVORS+jddLMhL/K81O4Y8ou+fXbzN4KiZu/dGJl9WH0VzZ4nwl4n0mQavE+E7Ns3N2OLz+5HwkC/vmKhTirpshI3rj5SyeW95lEEN5nEp5avM/ELKsXluMDZ8zCuAC+/vR+tPWZuSUSN3/pxPI+kwiSSDhPM51OWxqJPWzOyWQt3VyqcSp6Ga2TZqb99eEVNXj3glKMjwP/8tQBI5+fxM1fOrGy+rD76yjcTAAUFZm59A8SNudkspZuLtU4Fb2M1kkz0/5KJggff8ccDIyO46VDPXh0V7vnnHHzl06srD7s/jpKLJqJ2z6TtrY2SyOxh805maylm0s1TkUvo3XSBMFfZfkpfOKdcwAAd//uEFo93u6Km790YmX1UfAXEJNm4nbSYllZmaWR2MPmnEzW0s2lGqeil9E6aYLir9WnlWFVXTH6hsfwzWcOerrdFTd/6cTK6qPir1g0E14aHJ5avDTYP4gIn35XHfJTCTx/sBtPeHh+V9z8pRMbt6XB3EwADA4OWhqJPWzOyWQt3VyqcSp6Ga2TJkj+qixI49Z3TNzu+s5zDdqPW4mbv3RiZfVR8VcsmonbUzVnz55taST2sDknk7V0c6nGqehltE6aoPnr8sXlOLu2CD1DY/jOcw1aOeLmL51YWX1U/BWLZsL7TMJTi/eZ+A8R4S/fNRd5qQSe2tuJp/d2KueIm790YnmfSQAgovcT0VYiGieiFQ66y4loJxHtJqLPTqdzWxqcm5vrYbTBxOacTNbSzaUap6KX0Tppguiv6qI0bjm3BgDw7U0H0T3ovOLxROLmL51YWX1U/BXIZgJgC4D3AnhqOgERJQF8B8AVAOoB3EBEWZ+Z4tZM8vLytAcaVGzOyWQt3VyqcSp6Ga2TJqj+unpZJd42uxCdg6P47u/UbnfFzV86sbL6qPgrkM1ECLFdCLHTRbYSwG4hxB4hxDCAnwFYm03ots+ko8PfU+lmAptzMllLN5dqnIpeRuukCaq/EkT4qz+Yi3QCaOwexu8P90jHxs1fOrGy+qj4K5DNRJJaAAen/Nww+dpJuO0zqaioMDeqgGBzTiZr6eZSjVPRy2idNEH2V21JBjedU4OtzX349981YGxcbu9J3PylEyurj4q/ZqyZENFviGhLlq+sVxfZUmR5Lev/Ca2trVi9evWxr3Xr1h33fk+P/G9kYcHmnEzW0s2lGqeil9E6aYLur2tPr8KswhT2tA/i8d1yj1qJm790YmX1UfGX86/sPiKEuNhjigYAdVN+ngPgcDZhaWkpNm7cOG2ioBwuY5K4HV7Eh2Ppk8lJ4OZzavDV3+7Hus1HcMGCMuTmOP+eGTd/6cTy4Vjh4UUAi4hoPhGlAXwIwPpsQt5nEp5avM9kZli9sAwLK/LQ2j+CX77e7KqPm790YnmfSQAgouuIqAHAOwE8RESPTL5eQ0QbAEAIMQrgNgCPANgO4OdCiK3Z8vE+k/DU4n0mM0OCCB9dNfGR489fa0LHQHD+nwmCv3RieZ9JABBC3CeEmCOEyAghqoUQl02+flgIceUU3QYhxGIhxGlCiDuny8dLg8NTi5cGzxxn1RRhVV0x+kfG8ZOXnf+Bipu/dGJ5aXAEIXI+eTIoh8uYJG6HF/HhWGb405U1SBDw0I5WHOyc/plPcfOXTiwfjhVBxsbGHN/v6uqyNBJ72JyTyVq6uVTjVPQyWidNmPw1rywPly2uwLgA/vPFrOtZAMTPXzqxsvqo+CsWzcRtn0llZaWlkdjD5pxM1tLNpRqnopfROmnC5q8bzzkFuTkJPLe/C6839mbVxM1fOrGy+qj4KxbNhK9MwlOLr0xmnor8FN5/xixUFaTw8M62rIdoxc1fOrF8ZRJB3E6Uc1vtFUZszslkLd1cqnEqehmtkyaM/nrv8lkYGRd4bFc7Xjl88tVJ3PylEyurj4q/YtFMeJ9JeGrxPpNgUJBO4rrTqwAA9/z+5JVdcfOXTizvM4kgvM8kPLV4n0lwuLa+CoXpJF5r7D3ps5O4+UsnlveZRJBkMun4fkFBgaWR2MPmnEzW0s2lGqeil9E6acLqr4J0Eu+Z5uokbv7SiZXVR8VfsWgmbrg1mzBic04ma+nmUo1T0ctonTRh9td7Tq9CfiqBlw/1YHtz37HX4+YvnVhZfVT8FYtm4raaq7u729JI7GFzTiZr6eZSjVPRy2idNGH2V3FuDq6pn7g6+e8pVydx85dOrKw+Kv6KRTNx+wC+qqrK0kjsYXNOJmvp5lKNU9HLaJ00YffX9curkMlJ4PmD3djV2g8gfv7SiZXVR8VfsWgmbicttrfLneEQJmzOyWQt3VyqcSp6Ga2TJuz+Ks1L4eqlEwcw/fSViauTuPlLJ1ZWHxV/xaKZuOG2DyWM2JyTyVq6uVTjVPQyWidNFPz1vjOqkUoSntnXhb3tA7Hzl06srD4q/opFM3F7nEpQLhNNErfbEHyby18q8lO4csnE1cnPXmmMnb90Yvk2VwRx22fS1NRkaST2sDknk7V0c6nGqehltE6aqPjr/WdU422zC/BaYx+27J3+IZCmCYK/dGJl9VHxVyyaidvSucLCQksjsYfNOZmspZtLNU5FL6N10kTFX7MK05hdlEFb/wh+e8R5haRJguAvnVhZfVT8FYtmwjCMGa5fPgsA8OT+PnQPOi9sYeJFLJqJ2z6T3t7sj9kOMzbnZLKWbi7VOBW9jNZJEyV/LajIwzm1RRgaE3hoR6uVmkHwl06srD4q/opFM3HbZ1JdXW1pJPawOSeTtXRzqcap6GW0Tpqo+et9b5u4Orl/awuGx8Z9rxcEf+nEyuqj4q9YNBO3fSYtLS2WRmIPm3MyWUs3l2qcil5G66SJmr/Ori3CnMIk2gdG8cSbHb7XC4K/dGJl9VHxVyyaiRtuZ8SHEZtzMllLN5dqnIpeRuukiZq/iAiXzc8HAPzi9Wbf9zkEwV86sbL6qPgrFs3EbZ9JeXm5pZHYw+acTNbSzaUap6KX0Tppouivy+tPQUV+Cvs7BrG5ocfXWkHwl06srD4q/opFM3HbZxKUy0ST8G0uc/qo3IYwSWd767HDs+7f2uxrrSD4SyeWb3NFELd9JsXFxZZGYg+bczJZSzeXapyKXkbrpImqv65cWoGzawqxpakPe9oGfK0VhFx+eSwq/opFM3HDbelwGLE5J5O1dHOpxqnoZbROmqj6qzCTg7rSXPSPjONXW/377TgI/tKJldVHxV+BbCZE9H4i2kpE40S0wkG3j4heJ6JXiGjzdDq3P+y+vj7H98OIzTmZrKWbSzVORS+jddJE2V9HT2J8/M12dA443072Wmumc/nlsaj4K5DNBMAWAO8F8JSE9iIhxJlCiGmbjts+kzM0RUAAAB7vSURBVNmzZ6uNLgTYnJPJWrq5VONU9DJaJ02U/VVbkotVdcUYGRPYsKPN11ozncsvj0XFX4FsJkKI7UKInabyuX0A39jY6Ph+GLE5J5O1dHOpxqnoZbROmqj767rlE1cn67e3YMSHTYxB8JdOrKw+Kv4KZDNRQAB4lIheIqI/m07ktg7b7coljNick8laurlU41T0MlonTdT9dVZNEeaV5aK9fxRP7+30tdZM5vLLY1Hx14w1EyL6DRFtyfK1ViHN+UKIswFcAeCTRHRBNlFXVxdWr1597GvdunXHvV9SUqI9j6Bic04ma+nmUo1T0ctonTRR9xcRHVsmfN/WFuObGIPgL51YWX1U/OW8m89HhBAXG8hxePK/zUR0H4CVyPI5S3FxMTZu3DhtntbWVhQUFHgdTqCwOSeTtXRzqcap6GW0Tpo4+GvNwnL814uHsbOlH9ub+1FfbW6+QfCXTqysPir+Cu1tLiIqIKKio98DuBQTH9yfhNs+k6B0dpPwlYk5fVR+czTJiXPK5CRw5dJKAMB9W8xuYgyCv3Ri43ZlEshmQkTXEVEDgHcCeIiIHpl8vYaINkzKqgE8Q0SvAngBwENCiIez5XO77B4eHjY29qBgc04ma+nmUo1T0ctonTRx8dc19ZVIEvD0vk409Qz5Wmsmcvnlsaj4a8ZuczkhhLgPwH1ZXj8M4MrJ7/cAeLtMvvFx5xUmAwP+7d6dKWzOyWQt3VyqcSp6Ga2TJi7+qipI46pllXijpR8Pbm/DLStrfKs1E7n88lhU/BXIKxPT8D6T8NTifSbhYLo5rVlYjh0t/diwsxUDI2Z2ZgfBXzqxvM8kgvA+k/DU4n0m4WC6OS2bVYClVfnoGRrD47vNnHUSBH/pxPI+kwiSSDhPM51OWxqJPWzOyWQt3VyqcSp6Ga2TJm7+OrqJ8X5Dy4SD4C+dWFl9VPzFzQRAUVGRpZHYw+acTNbSzaUap6KX0Tpp4uavP5hfNnHWSecgXj7k/ayTIPhLJ1ZWHxV/xaKZuB3b29bmzzOFZhKbczJZSzeXapyKXkbrpImbv3IShGuWTSwTNvE04SD4SydWVh8Vf8WimbidtFhWVmZpJPawOSeTtXRzqcap6GW0Tpo4+uvKpRVIJQnPH+zGoa5BX2vZyuWXx6Lir1g0E14aHJ5avDQ4HLjNqTQvhTWnlSMB4De7232tZSsXLw12hpsJgMFBb785BRGbczJZSzeXapyKXkbrpImrv65bXoWSvBz87+st6B1yvtXstZaNXH55LCr+ikUz4X0m4anF+0zCgcyc5pfn4dSyPAyOjmPDTv37+kHwl04s7zOJILzPJDy1eJ9JOJCd0/Vvm1gm/KutLRgd11smHAR/6cTyPpMI4rY0ODc319JI7GFzTiZr6eZSjVPRy2idNHH214o5xZhbmovWvhE8vVdvE2MQ/KUTK6uPir+4mQDIy8uzNBJ72JyTyVq6uVTjVPQyWidNnP2VIDq2ifF/X9fbxBgEf+nEyuqj4q9YNBO3fSYdHWYe+xAkbM7JZC3dXKpxKnoZrZMm7v66eGE5ijNJvNHaj61Nfb7W8jOXXx6Lir9i0Uzc9plUVFRYGok9bM7JZC3dXKpxKnoZrZMm7v7K5CRwTf3RqxP1s06C4C+dWFl9VPwVi2bitjS4p8f7Ix+Chs05maylm0s1TkUvo3XSsL+Aa5ZVIpUgPH+wCw2daktZg+AvnVhZfVT8xc0EwTlcxiR8OJY5fVQOLzKJ6pzK81N439tmoSiTg19uUXvEShD8pRMbt8OxYtFMeJ9JeGrxPpNwoDOnNQvL0Tkwikd2taG933m5vtdafuTifSbOxKKZ8D6T8NTifSbhQGdOc8tycd68EoyMCaVz4oPgL51Y3mcSQXhpcHhq8dLgcKA7pw++vRoA8MD2VvQNy53EGAR/6cTy0uAIQkSO7wflcBmT8OFY5vRRObzIJLpzWjqrAGfWFKJ/ZBwPbJf77CQI/tKJ5cOxIsjYmPNvQF1dXZZGYg+bczJZSzeXapyKXkbrpGF/Hc8Hz5i4OrlvSwuGRp0Xx3itZTKXXx6Lir9i0Uzc9plUVlZaGok9bM7JZC3dXKpxKnoZrZOG/XU8Z9cWYWFFHjoGRvHoG+4PgAyCv3RiZfVR8VcsmglfmYSnFl+ZhAMvcyIifOjMiauT/3m9GWMuD4AMgr90YvnKJIK4PQ/IbbVXGLE5J5O1dHOpxqnoZbROGvbXyZw/rxS1xRk09gzjKZcHQAbBXzqxsvqo+It0HrwWNjZt2iTq6+unfX9oaAiZTMbiiPzH5pxM1tLNpRqnopfROmnYX9l5eGcrHn2jHUSEr165EMlE9oUyQfCXTqysPsj+Kisrc169NIVAXpkQ0deIaAcRvUZE9xFR6TS6y4loJxHtJqLPTpeP95mEpxbvMwkHJua0ZmE5WvpG8HpjL367Z/qrkyD4SyeW95kEg8cALBdCnAHgDQB/f6KAiJIAvgPgCgD1AG4goqyXH8lk0rFYQUGB1/EGDptzMllLN5dqnIpeRuukYX9lJ5VM4A/Pmti9/eOXG6f97CQI/tKJldVHxV+BbCZCiEeFEEefG/87AHOyyFYC2C2E2COEGAbwMwBrdeq5NZswYnNOJmvp5lKNU9HLaJ007K/puWRROWqK0zjUPYTHd7f7WstrLr88FhV/BbKZnMBHAPw6y+u1AA5O+blh8rWTcFvN1d3drTu2wGJzTiZr6eZSjVPRy2idNOyv6clJEP74rFMAAD/5fWPWo32D4C+dWFl9VPw1Y82EiH5DRFuyfK2dovkHAKMA7smWIstrWa+Tu7u7sXr16mNf69atO+79qqoq/YkEFJtzMllLN5dqnIpeRuukYX85c9FpZZhbmovGnmE8kmXfSRD8pRMrq4+Kv5x38/mIEOJip/eJ6CYAVwNYI7IvOWsAUDfl5zkADmfLVVJSgo0bN05bq729Hfn5+a5jDhM252Sylm4u1TgVvYzWScP+ciaZIPzJ2bNx58Z9uOf3jbhkYTnSOW/9nhsEf+nEyuqj4q9A3uYiossBfAbAtUKI/mlkLwJYRETziSgN4EMA1uvUi+LyaJtzMllLN5dqnIpeRuukYX+58wfzS7GgPBetfSPYsPP4q5Mg+EsnVlYfFX8FspkAuAtAEYDHiOgVIrobAIiohog2AMDkB/S3AXgEwHYAPxdCbM2WzO1xKkG5TDQJ3+Yyp4/KbQiTmJ5Tggh/cvYpKMlN4vkDXeif8kThIPhLJzZut7kC2UyEEAuFEHVCiDMnvz42+fphIcSVU3QbhBCLhRCnCSHunC6f2z6TpqYmY2MPCjbnZLKWbi7VOBW9jNZJw/6S47x5JTi1LA8vHerBva+9lT8I/tKJldVHxV+BbCamcVs6V1hYaGkk9rA5J5O1dHOpxqnoZbROGvaXHESED6+oAQD87+vNaO4dNl7LSy6/PBYVf8WimTAMEw7qqwvw7gWlGB4T+P6LWdfTMAElFs3EbZ9Jb2+vpZHYw+acTNbSzaUap6KX0Tpp2F9q3HJuLdJJwhNvdmB7c18g/KUTK6uPir9i0UxSqZTj+9XV1ZZGYg+bczJZSzeXapyKXkbrpGF/KeYuSuP65bMAAHf/rgGzZs0yl9vDuP3yWFT8FYtmMjo66vh+S4vc8aFhwuacTNbSzaUap6KX0Tpp2F/qfPDt1SjLy8H25n48+FqDsbxexu2Xx6Lir1g0EzfczogPIzbnZLKWbi7VOBW9jNZJw/5SJz+dxC0ravC22QX4xa5+9A0736qWxcu4/fJYVPwVi2bits+kvLzc0kjsYXNOJmvp5lKNU9HLaJ007C89Ll5cjpExgY7BcazbfMRITi/j9stjUfFXLJqJ2z6ToFwmmoRvc5nTR+U2hElszClBhL9411wkCFi/rQU7W/o85+TbXP4Ri2bits+kuLjY0kjsYXNOJmvp5lKNU9HLaJ007C99FlTk4aqFxRAAvvnMQdfz4t3wMm6/PBYVf8WimbjhtnQ4jNick8laurlU41T0MlonDfvLG9ctKcKswhR2tw3gwR3efgv3Mm6/PBYVf8Wimbj9Yff1eb98Dho252Sylm4u1TgVvYzWScP+8sbY0AD+/Pw6LK3Kx388fxgHOge1c3kZt18ei4q/YtFM3PaZzJ4929JI7GFzTiZr6eZSjVPRy2idNOwv77VW1pWgrjQXw2MCX/vtfu3bXV7G7ZfHouKvWDQTtw/gGxsbLY3EHjbnZLKWbi7VOBW9jNZJw/4yU+sT75yDqoIUdrb042ev6j3c0Mu4/fJYVPwVi2bitg7b7coljNick8laurlU41T0MlonDfvLTK2CdBJ/c8E8AMBPXj6CXa3THXXknsvLOEzro+KvWDQTt9VcJSUllkZiD5tzMllLN5dqnIpeRuukYX+Zq3VWbRHW1ldhTABfeXIfBkfUPnz2Mm6/PBYVf8Wimbg9TqW1tdXSSOxhc04ma+nmUo1T0ctonTTsL7O1bllZg/pZBUgnE7j7+UOecvkZK6uPir9i0Uz4yiQ8tfjKJBzMpL9ycxL45Dtrsb9zEBt2tOHRN9qmiXTP5WUcpvRR8VcsmonbGcnDw8OWRmIPm3MyWUs3l2qcil5G66Rhf5mvtaiqALedVwcA+Namg9jTNqCdy8s4TOij4q9YNJPx8XHH9wcG5IwYJmzOyWQt3VyqcSp6Ga2Thv3lT60rllTgssXlGB4T+Pzje6UeBull3H55LCr+Irff2qPApk2bRH19/bTvDw0NIZPJWByR/9ick8laurlU41T0MlonDfvLv1pDo+P49Po3sKd9AOfNK8HtF893XL3pZdx+eSzI/iorK5N+JHEsrkx4n0l4avE+k3AQFH9lchL4v2vmIz+VQPfgKH7ye+dx8T4T/4hFM0kknKeZTqctjcQeNudkspZuLtU4Fb2M1knD/vK3Vm1JBp+7eD62Nffhxy834vHd7dq5vIxDVx8Vf3EzAVBUVGRpJPawOSeTtXRzqcap6GW0Thr2l/+1zq4txq2ragEA/++pA3i9Mfu56F7G7ZfHouKvWDQTt30mbW3ySwvDgs05maylm0s1TkUvo3XSsL/s1Lpu+Sysra/CyLjA9353CAc6Tn4gpJdx++WxqPgrFs3E7aTFsrIySyOxh805maylm0s1TkUvo3XSsL/s1frYO2pxzbIK7OscwGd/vRuNPUPaubyMQ0UfFX8FspkQ0deIaAcRvUZE9xFR6TS6fUT0OhG9QkSbp8vHS4PDU4uXBoeDoPormSB8dNUcLK4sQGv/CD77691o639rAQ4vDfaPQDYTAI8BWC6EOAPAGwD+3kF7kRDiTCHEiukEbs1kcFD/fISgYnNOJmvp5lKNU9HLaJ007C+7tXJzEvj8pQuwqDIPh7uH8dUn96FzYEQrl5dxyOqj4q/A7zMhousAvE8I8UdZ3tsHYIUQwvHhNLzPJDy1eJ9JOAiDv7oGR/HVJ/dhR0s/yvNT+OoVC5GfHOd9JgpEbZ/JRwD8epr3BIBHieglIvqz6RLwPpPw1OJ9JuEgDP4qyc3BX18wD2V5KezvGMTfPLQL2/apPRjSyzh4n4kliOg3RLQly9faKZp/ADAK4J5p0pwvhDgbwBUAPklEF2QTdXV1YfXq1ce+1q1bd9z7ubm5RuYUJGzOyWQt3VyqcSp6Ga2Thv01c7XK81P42lULcWpZLgSAb7/Sh8PdQ65xJsYhq4+Kv5yXOfmIEOJip/eJ6CYAVwNYI6a5FyeEODz532Yiug/ASgBPnairqKjAxo0bp62Vl5enMPJwYHNOJmvp5lKNU9HLaJ007K+ZrVWWl8LXrlqEf35iH14+1IO/WP8GvnT5aVhYme/rOGT1UfFXIG9zEdHlAD4D4FohRNbj1IiogIiKjn4P4FIAW7Jp3faZdHR0eBpvELE5J5O1dHOpxqnoZbROGvbXzNcqyc3B59bMx7LyHHQOjuKuZw9ic0O3r+OQ1UfFX4FsJgDuAlAE4LHJZb93AwAR1RDRhklNNYBniOhVAC8AeEgI8XC2ZG77TCoqKowNPCjYnJPJWrq5VONU9DJaJw37Kxi18tNJ3LHmVFxbX4k97YP4x0fexAPbWnwbh6w+Kv4KZDMRQiwUQtRNLvk9UwjxscnXDwshrpz8fo8Q4u2TX6cLIe6cLp/b0uCenh6j4w8CNudkspZuLtU4Fb2M1knD/gpOrcH+XnzinXNw3fIqCAFs2NmGbz5zACNjzv9G6IxDVh8Vf83YZyY2cWsmQTlcxiQzfXiR7Vx8OJZdwuyvBBE+vKIGp1Xk4StP7sebbQNo7R3Bp/+gDpUF0z80kQ/Hcibw+0xMwPtMwlOL95mEg6j4a2dLH760cR9yEoTuoTF89t1zcc6c7Mfg8j4TZwJ5m8s0vM8kPLV4n0k4iIq/llQV4JvXLkZlQRpdg6P48ctN+P6LhzE6fvIv2bzPxJlY3OZyewR9UJbWmSRMSzdN5OKlwXaJkr9K81L40uWn4f5tLfje84ewrbkPTT3D+OOzZ2Nuaa5jrGotXV0Y/BWLZuJ0jCcQnMNlTBKkw4ts5OLDsewSNX8lE4T3Lp+FxZX5+PmrTXhyTwee3d+JW1fV4sqllUgmiA/HciEWt7nGxsYc3+/q6rI0EnvYnJPJWrq5VONU9DJaJw37Kzi13HItn12Iz1x0Ki5dVI7S3Bzc/btD+MsH3sDe9n7fPBYVf8WimbjtM6msrLQ0EnvYnJPJWrq5VONU9DJaJw37Kzi1ZHIVpJP4mwvn4dPvmouS3BzsaOnHXc824NcNAgMjzr+YqtaS1YXBX7FoJnxlEp5afGUSDuLgr3PrivEf71uGD50xC1ub+vDL7R34+H078NTeDsisguUrkwji9hfvttorjNick8laurlU41T0MlonDfsrOLVUcxWkk/jIylp8/ZrFmFuURGVBGl98fB/+bsMuvNGS9UlPyrWi4i/eZwLeBxCkWrzPJBzEzV8A0D8wiCf29eAHm4+griQXW5v7cNFpZbjpnFNQU3xyTt5nEkF4n0l4avE+k3AQN38BQEtzE65aVoUffKAeZ9YUIpUgvHiwC5+6fye+9cxBtPQe/2h73mcSQZLJpOP7BQUFlkZiD5tzMllLN5dqnIpeRuukYX8Fp5aXXEdjizI5uGlFDS5fUokHd7Tg568249FdbXh2fyfOP7UEHzijGtVFGelaUfFXLK5M3HBrNmHE5pxM1tLNpRqnopfROmnYX8Gp5SXXibHVRWnccm4tvnf9UlyzrAodA6PY3TaAm3++Dd94ej8O9cqt/IqKv2LRTNxWc3V3q51rEAZszslkLd1cqnEqehmtk4b9FZxaXnJNFzuvLA+3vmOiqSyuzIcAcLBrCH/7m8P4+tMHsLmh23ERUFT8lbzjjjtmegy+c+jQoTuqqqqmfT+dTiOVSlkckf/YnJPJWrq5VONU9DJaJw37Kzi1vORyiy3NS2FlXQnWLCxHe/8o3mzrQ+fAGO7f1ordbf3oGhxDbUkGmZzjf4cPsr/y8vL+SVYbiysTt5MW29vbLY3EHjbnZLKWbi7VOBW9jNZJw/4KTi0vuWRjTynO4KOravHVCytwxdIKLKnMx/MHuvGDFw/hI/+zDd9/8RC2N/cdu1qJir9i8QG8G1FcHm1zTiZr6eZSjVPRy2idNOyv4NTykks1tjBFuOHM2Xj/GdV4dn8nNh/sxsNvtOOlhh48uK0Vs4szuHJpBebljGKOh9pB8RfvMwEwODiI3Nzcad8PIzbnZLKWbi7VOBW9jNZJw/4KTi0vuUx47GDnAB7e2Y79nYPYfLAbBZkkSjNJVBZmcNnicqyaW4KC9MkfqM+Uv3ifyQm47TNpamqyNBJ72JyTyVq6uVTjVPQyWicN+ys4tbzkMuGxutI8fHRVLe64ZAH+6dIFePsphchPjuP3h3tw/7YW3HTvVtz+6B48uacDvUOjjrl0x+UXsbjN5bZ0rrCw0NJI7GFzTiZr6eZSjVPRy2idNOyv4NTyksukx3IShFVzS7Bqbgn2H2nGlk7Cpv1dqCvNxXMHutA9NIp7Xm5EVWEK7zq1FAsLp7/yCIq/YtFMGIZhgkphOomrllXgqmVVaOsfxqZ9Xdjc0I2cBGF/xyA2NxzEssoMyrf34dTyPKycU4TFVQVIJqTvQFkhFre53PaZ9Pb2WhqJPWzOyWQt3VyqcSp6Ga2Thv0VnFpecvnlsam6ivw0rq2vwucvPQ3/56JTccu5NThvXgk6BkbQPTSKe19txN9u2I3PbNiFb286iA07WrG3uVNpXH7BH8CDPyANUi3+AD4cxM1fOrGyehldV28/dnWMYGtzH57e24nGnmEsqcpH3/AYEhAoK0hjXmkellTmY1l1AWYVmjl9kT+APwG3fSYtLS2WRmIPm3MyWUs3l2qcil5G66RhfwWnlpdcfnlMRtfd0YYVdSW46Zwa/Of76vHv712GSxaV44zZhcjQOAZHxrGzpQ/rt7fgK0/ux/95eDe+9/whbG6wtzuePzOB+xnxYcTmnEzW0s2lGqeil9E6adhfwanlJZdfHtPxV21JBrUlE4+dP3AQGMwtx46Wfuxs6cfBzkEAhO3NfSjJzcGKOcVK49YlkM2EiL4AYC2AcQDNAG4WQhzOorsJwD9O/vhFIcQPs+VzO7a3vLzc03iDiM05maylm0s1TkUvo3XSsL+CU8tLLr885tVflRUVyM/Px+KqiacHj40L7G0fwM6Wfrxttr2VXkG9zfU1IcQZQogzATwI4HMnCoioHMDtAFYBWAngdiIqy5bMbZ8J34YITi2+zRUO4uYvnViTt7lU/JVMEBZW5uOqZZWYW2bvs7pANhMhxNQbfQUAsq0SuAzAY0KIdiFEB4DHAFyeLZ/bPpPiYjuXgTaxOSeTtXRzqcap6GW0Thr2V3Bqecnll8ei4q9A3uYCACK6E8CNALoAXJRFUgvg4JSfGyZfU8Zt6XAYsTknk7V0c6nGqehltE4a9ldwannJ5ZfHouKvGbsyIaLfENGWLF9rAUAI8Q9CiDoA9wC4LVuKLK9lXefc2NiI1atXH/tat27dce/39fV5m0wAsTknk7V0c6nGqehltE4a9ldwannJ5ZfHouKvwO8zIaJ5AB4SQiw/4fUbALxbCHHr5M//DuBJIcRPT8zR2NgoMpnMtDWGhobg9H4YsTknk7V0c6nGqehltE4a9ldwannJ5ZfHguyv0O8zIaJFU368FsCOLLJHAFxKRGWTH7xfOvnaSTQ2NjrWc3s/jNick8laurlU41T0MlonDfsrOLW85PLLY1HxVyCbCYAvT97yeg0TTeLTAEBEK4joPwFACNEO4AsAXpz8+vzkayfhdgqZ0/sn3hILCzZP9jNZSzeXapyKXkbrpGF/BaeWl1x+eSwq/gpkMxFCXC+EWD65PPgaIcShydc3CyH+dIruv4QQCye/fjBdvhdeeMGxntP7P/rRj9QnEADc5hzUWrq5VONU9DJaJw37Kzi1vOTyy2NR8Vcgm4lpHnzwQU/vhxGbczJZSzeXapyKXkbrpGF/BaeWl1x+eSwq/gr8B/AmuPfee1+qrKycdqLd3d0lxcXFXdnea29vrywvL2/1b3T+4DSnINfSzaUap6KX0Tpp2F/BqeUll18eC7i/WtesWZN1/96JxKKZMAzDMP4Si9tcDMMwjL9wM2EYhmE8w82EYRiG8Qw3Ew2IaAERfZ+IfjHTY2GiBREVENEPieg/iOiPZno8TLTw89+uWDcTIvovImomoi0nvH45Ee0kot1E9NkT44QQe4QQt9gbKRNmFH32XgC/EEJ8FBNPf2AYR1T85ee/XbFuJgDW4YTH1hNREsB3AFwBoB7ADUQ0/QHyDOPOOsj7bA7eehp2MB4HywSddQjAv2OxbiZCiKcAnPgIlpUAdk928GEAPwOwlohuJKJvEJHWY+6Z+KLiM0wcpTBnUhPr/z8ZORT95Rts1pPJek6KEOJHQoi/EEIcIqIKIrobwFlE9PczM0wm5Ex3Hs8vAVxPRN8F8MBMDIyJBFn95ee/XYE9HGsGcT0nRQjRBuBjdobDRJSsPhNC9AH4sO3BMJFjOn/59m8XX5mcTAOAuik/zwFweIbGwkQX9hnjJ9b9xc3kZF4EsIiI5hNRGsCHAKyf4TEx0YN9xviJdX/FupkQ0U8BPAdgCRE1ENEtQohRTBwT/AiA7QB+LoTYOpPjZMIN+4zxk6D4ix/0yDAMw3gm1lcmDMMwjBm4mTAMwzCe4WbCMAzDeIabCcMwDOMZbiYMwzCMZ7iZMAzDMJ7hZsIwDMN4hpsJwzAM4xluJgzDMIxnuJkwDMMwnuFmwjAMw3iGmwnDMAwDACCiUiK6OsvrzxFRjVMsNxOGYRjmKGsAbAAAIlox5fUHAIw7BXIzYRiGYY4hhDjaNP5uysuNQohGpzhuJgzDMMxR3gEARHQJgL7J798PoNUtkJsJwzAMc5R+InoDwMUAiIj2AJgjhHA9pZEPx2IYhmE8w1cmDMMwjGe4mTAMwzCe4WbCMAzDeIabCcMwDOMZbiYMwzCMZ7iZMAzDMJ7hZsIwDMN4hpsJwzAM4xluJgzDMIxn/j90nNSQmc6wKgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"from sympy.plotting.plot import MatplotlibBackend\n",
"\n",
"def logx_plot(Hw, wrange, **kwargs):\n",
" 'create plot with logarithmic x-axis'\n",
" p = sym.plot(Hw, wrange, show=False, **kwargs)\n",
" backend = MatplotlibBackend(p)\n",
" backend.process_series()\n",
" backend.ax.spines['left'].set_position(('axes', 0))\n",
" backend.ax.spines['bottom'].set_position(('axes', 0))\n",
" plt.xscale('log')\n",
" plt.grid(which='both')\n",
"\n",
"def db(x):\n",
" 'compute dB value'\n",
" return 20 * sym.log(sym.Abs(x), 10)\n",
"\n",
"\n",
"RLC = {R: 1, L: sym.Rational('.5'), C: sym.Rational('.4')}\n",
"logx_plot(db(H.subs(RLC)), (w, 0.1, 10),\n",
" xlabel='$\\omega$', ylabel='$20 \\log_{10} | H(j \\omega) |$ in dB')\n",
"logx_plot(sym.arg(H.subs(RLC)), (w, 0.1, 10),\n",
" xlabel='$\\omega$', ylabel=r'$\\varphi(j \\omega)$')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Retraso de Fase y de Grupo (Phase and Group Delay)\n",
"\n",
"El retraso de fase y grupo caracterizan las propiedades de fase y retraso de un sistema LTI. Ambos cuantifican el retraso dependiente de la frecuencia que se imprime en una señal cuando pasa a través de un sistema. En muchas aplicaciones, el retraso introducido por un sistema debe ser lo más pequeño posible o dentro de límites razonables.\n",
"\n",
"## Retraso de Fase\n",
"\n",
"\n",
"Para un sistema LTI con función de transferencia $H(j \\omega)$, el retardo de fase se define de la siguiente manera\n",
"\n",
"$$\n",
"t_p(\\omega) = - \\frac{\\varphi(j \\omega)}{\\omega}\n",
"$$\n",
"\n",
"donde $\\varphi(j \\omega) = \\arg \\{ H(j \\omega) \\}$ denota la fase de la función de transferencia. El retardo de fase cuantifica el retraso de una señal exponencial armónica única $e^{j \\omega t}$ con frecuencia $\\omega$ cuando pasa a través del sistema. El signo negativo en la definición del retraso de fase resulta en un retraso de fase positivo $t_p(\\omega) > 0$ cuando un sistema retrasa una señal. Tenga en cuenta que el retraso de fase no esta definido para $\\omega = 0$.\n",
"\n",
"Como ejemplo, el retardo de fase $t_p(\\omega)$ se calcula para el filtro de paso bajo de segundo orden. Primero, la función de transferencia $H(j \\omega)$ se define en `SymPy`"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAALgAAAAtCAYAAAAdmKE3AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAGfElEQVR4Ae2djXEUORCFvZQD8G0IkIHhIjjIAO4iADIwRQRXkIEhArAzMETg4zIwIYAzMO+T1VMazXh2GUu2PG5VyTv6a7VeP7V6ZodldXFxsePJEVgqAg+WurAW17VarZ4r/1Tea1G/Jeq0u8RFtbSmSOaP0umH8lrZyX2DBnIPXhlshYDnyi+UX2uq08rTufgMASd4BogXl4WAE3xZ9vTVZAg4wTNAvLgsBJzgy7KnryZDwAmeAeLFZSHgBF+WPX01GQJO8AwQLy4LASf4suzpq8kQcIJngHhxWQis/GWr+gbV1/WHmoWv6Z8q81X9/8rflU+E/wd9eqqEgBO8ErAutg0EPERpww6uRSUEnOCVgHWxbSDgBG/DDq5FJQSc4JWAdbFtIOAEb8MOrkUlBJzglYB1sW0g4ARvww6uRSUEnOCVgHWxbSCwkhr+uxFt2MK1qICAf5NZAVQX2Q4CHqK0YwvXpAIC9/p3UfQS1DthystPD5V5+emNXn4616enhSBwb0OUSO5DERpi76h8pI+HKj9eiG19GULgPocozzMG/KvyvoiON/e0EASqhSgiCkf/K+VnyumxH96BjkR6LY/5JsdSbTbOSFjr/WkLTVDBdEzrctWqlrVuTpE9YQJmo6kwrsdxEmxl6UjzL+cddS1mp3QWUgfKP5Vf5bJVB2n5BwCj7Wl/9eER5llaV+ta86AX80Gw4phsI1NzQ/ABZjZWbSVxxdH01in5bG4wgOS9ttbL0hn7wame/YouAuHKJ8pn+UQpQGqD4ABJzDuqg9r41y/0eXdVn5L1mgedD+bK1FgAnj1+al7JLYnrvuSB66iuqmeT0b4/pVOpNs0zGzeNBRf0hU+md4/gD9RQMn2VMIj5WACcTwhGmXP1CTd4V/SzY5oNUzXp2Odpyhfp877qRPOFl8QV+5C+XH4M/rIBSFP2u+xxy3/hmPLkD5sWI7hIwi4CHCbcBA4/Jfx5Az7BEJJ1lSE2DN+uWXoT77Pr+fXX5lIFXMM9kdbLfU0vaS68KWEKm33K+fTGtVwoQnABAygQ5buAsRuXqXUDHl5zKrFZBkYYG6D5J708+inzw/PmvYKYWH5k5KasbB5sbKridZpvT/lA+ZDPdAKVa+AKBgOnobkgN79jfiw87PQM6qhtFr5h8C3/KUJwrcG8H158YxKAk+GJADUiDgyRC1dfNtamzcKJQbzWkVfjuGbcqa75nxcwME90btpzvRUehEaEbW+V01Qa13T9bCryiTIxN6T+S7q8SBVQ2yx8Uxm3eb1baHLIQdpIyMtuG/+aB5n0HFEK8f7kYy02lAwFiVLyEtdCeojVJfp2hcoX0gkPfRqngVipflSXxtUcx8tkne8jidlMg0e2qpuLL/rfegoE1wIxtBl8G6UgASBZCLGOg3IDjcpivgTgsT7BEOpz5YaJOj/R4B5BEaa2bxqbfyN5pibTlyc3f9D3d5Nk4/WNKOlwMFyr/Z+0Ml4TuvU8Y6z/oXoL6fCUOcFK42rxd28TS4cP0pvTlxOk00F1rHMWvhrXS4Vx68meLGhxo4/pfqdeE0AeDdksS/3wSpOPoJClPHhOa/LVBhnwfoNHXarjGOYr+N66VFf1caPks66BPrkeY+U4ljWz8Tu9Va6B6+AZt+YBS+bvtak8WI/qiuIrebNxy7Di/mWAYakYPHha7VKA2pSeSbHOk+ado9egeio84djktHiUj1cZr9Mbu6VeI6JurArPyc0doRQngaWSuEJMUg+by6ru3oR7lTTdeXxLEdxu8uymKAWpu5bx6NcdgV1D/8Li79HwRDLYqd/iEJ6OmOEITbhmDpMRu4VjliO4uSSdITR6f4rKQXZLJXG1sOo/E558/hmvOTFCinrdeXx3bUHX+cSbChBizCN98tV676ZPdRxDkG6b11HpyzE98PKSg8EhuMXP9PmqeuaDKH8rmx5rXePlQ2yLjrpuMT1BKel3rHVwAnYkQ2fV2Xqui2u4NxjDNZ0TXTQnGw5d7j6+WnAX8133WoBAMjwlxyA3J2TKT6dkq51x9MUzE0eFeDDWDepNltoZx1z0Z2yI7fXJJuC9BPIgjrTxJT81z+xYUmNZIxtx9D0U1c/ClfUpgX+O62Ce2A8swS5gps/q+GqO2bgl6wM/bG08CHjSfm/fBxcYRZO8Hobi3ZpWv+4vut5Swmrj5gQvZCkZCm+3FsFbDYUKrbSsmNq4/QIKys06ux6nMAAAAABJRU5ErkJggg==\n",
"text/latex": [
"$\\displaystyle \\frac{1}{- C L \\omega^{2} + i C R \\omega + 1}$"
],
"text/plain": [
" 1 \n",
"──────────────────────\n",
" 2 \n",
"- C⋅L⋅ω + ⅈ⋅C⋅R⋅ω + 1"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"%matplotlib inline\n",
"import sympy as sym\n",
"sym.init_printing()\n",
"\n",
"L, R, C = sym.symbols('L R C', positive=True)\n",
"w = sym.symbols('omega', real=True)\n",
"s = sym.I * w\n",
"\n",
"H = 1 / (C*L*s**2 + C*R*s + 1)\n",
"H"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Ahora se calcula el retraso de fase $t_p(\\omega)$"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAANUAAAA8CAYAAADxC//JAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAKzklEQVR4Ae2di3XVOBCGk5wUELIVbOiARwVAB0AqADqAkwo40EGgAh4dABWwmw6WrQBIB+z/KZJXfsjW9ZXNjT1zjq9lafSYXzPSSH7c/V+/fu2tifb3958ir+R+sya5TdZxCEhfjpTzrfTlUW4Jh7mMS+ATQM8lx6kAur0EeUyG6RGQrlxKb851/J2rN/tinL5lO1CDQLmvZnzQ8SdA7UCTrAnXCAE/IN+V7gzOWKswKgHCFP6vjnsC5eIa9aU1dYcQYLZSc86lQ71Lh7UYFTMU66jBUWaH+tCasmMIyKhO1KR/dNyQLiW9ncUblYC4JRAYYW4KiG86G3Ug4HFiQW7rzQ58QpRwGhyg12BUGNQ3m6WCWtTP3pieKfZYxy3hdLPOYVcxAtEgnZytFm1UAiBM1zZLxZrRERZWDxX9yoyqA5xGlLBioH4nrF43ktzlQVfkguJeSBZmKXP7FtSpOyDKudpwlmrH0o3qsQQHACNDoCQCn1XYkWYsbtO0aLFG5V0/ttIBwMgQKIaA93zY/XvQVehijUrCulFEANh9qa6et7htEWCwXtdMJYHZGra11LaqY/lTCHxVArdrWrT0mcqMqtXlFlEIAadbfplRK3LJRnUiSc2oat09eMG9KqM8BIJutWarw7z8+VyyXF6tYIMA+kPH93g/3++YvFI8Sv9SB427qwP/9FHY/vZ83JQknfK4NxDKfSC+zkWieGLikRKjHgT8SMutB/BnR4snBr7GfdaTfc1JwajaA5HA45m4IocQ5gYiinwSylSYLe0P4TqcFffTp5EHY+Fx+aeki+hgAkcRP+WG9OchvutMPp/f8XfxWFyZPl8zjl7HWrpYfKZSRVhumFEUdK9bfNIIiIFcEuEJS7+vOGYjaP/q5H7dDNXgZxePEfWN4jvvZEf526NHlGhBQ6AgAnhjNSpqVFL2jyr9owzolg5eCKTCYGAoemxUutxLbXf/UNo2hhHqpJxBUlvd9DjIaAyrQUC6HA/yfXIHXat4ihoVs5FK/qIDZX6mhn3DwBSO11m6rCil9Ky5npJXZVz4cnEJn1Q58wJZhrkBgHm1/gYuj/OprxrMHf6/oSmrr7KoUQlNFrm4edwjapE3DtZvzRmrxasIXL1T5cGYmPE2ecEwp3wVWZbUVgYP3tmifgYMzmzGEP9RcofF7Z54WUvy/BgGwI3EC6Uj81jiYVi3eeMx+6SCij1xrjLxPHgwObjrtXbmyu7bhpz0K54NODH4Hen4pPKHXHuxlSW1iT7Y6LUX5aG9EH1cJwlRZJOCckT80LlVmbpGeYin4QDJ7KOT283jLcqKN4SVRh7WW620nDjlRWAqaS0ic/JvyqN62Mlkd7JWn66douj8s6tMxWNsShonZ5xP5fANBYeXwkH+aqMnpI09q0z6r9qACuUQp2Mj2cWP3C1MFMdmVE1/Qj1TnFUXMrmNNOrepA7xIzc61toMO1BkScJqaWhMbJcHoiFhtKbjU0Q5rxjVGEX8Qd4sEjjkh1qLyKvocr9qG+1CGV6o3too69vB7P1XokZmliLPJqqu2Dtg8OLp/IBDonrtDvmX7pIMPkFlMZOGvnOxW8iO3F2YXCieAbUIDcnmZWLmfTeiwqC/rSXM4YjC+rLQsRgD1o+iodS4P991vNVB4+8onekfZWTdxJkZC1fAkcKfFU8YF6YixaEk75Xe6YJUjFcBeLMNsZF3k0va+Jo2JzKhPKEDmiwoP/gUI2FEXbiVzhXMKDjVtoysrn/GyB5miGYdpfHYRrZm25rXxz7ispkwyr2SAk2aT41EUR+GehQGHAyEUQxjrblZgS8+i4cyKpcoTisVph06cAGSbhZpXek+nrxJN5c0HRUOcbsVjwtVu/+na+oK69qsPhI/65gkr9JpA3I26xolu8qhjcjtlgHU7eMYiGuun643kr8ph/L3yhb4xef0KlznnJXHue46t/o+CWZOwVPweAGTYHhhkumhTeJjB7Hlt4f0EmeVj4EPtqWrLuWjI5XUq9A1RY55lZfRvloHKIyyopgMPoRrChrnjcPi620/5fjyaoOH4kbJrnwYCmVhlBy0mQcButZr2fLHMoWwyuyVLeIbY1RJ/TpQxbtGuFEncmOaa7PQTnbX6Igh+ioGHrtBwaYiFLi2ztigItaarCE6Se2m7Mr9RQ4djI6OpBDkjV1ONgtIR9lRUhRlK/JtwD3FEJprtLGy45ayPsNt5MCVf6+jklVh1nqbyk+2OQl8Y/yrug+r0I4EBPKlAGVtdqbzqc6sxyDWZxgIGwJJZYTRUxD4sa57v9MGv+oCpJy1Gs8nXpJHhEGFsIuIf7xi4N511Y+ithbrysNggr+OrEEGBfeQgzhH4iOMATlSHYPb58qDa4iyxsQAhkHG9E7lofBuwFA6uDQHsrGyI18sF/WGAYFwoCZfr/ybyhYqGXNWXWAPjsxWbRJwO+cClmqTpGX0S7oQ29ajslG0pIuhtKQLpjRcoNZ6SXGuvTrjGsXrDgyiWn8pTIe2XKZNZVIZyfZTlggFcq6fznF7Rsnuy6rJrTjKqrnqut5afpXRK1vASnwbuX+eH0w68T9QwpLJKeJUAqpTGMEZ6Su3jLoYyXSg9M3RnWTSGYWh2oyreBQpEGnspD7UEWYYvunNNeWyQB7reoY6cs7MqLhrlzrjOTgaI7vaHeRuzlTHKvQHBcOjg1lgbvlpQy4FF7Ybf4Gz5JkqjLK1kbG0zOoJDAjFR9kJYxytXSHq9em4bVzAz0HeEBfPRsy0rI/cjKczvFwXm31VVu9ornQwpH2dM6OPH5Td8wUZ4a9GeYUxNlxAcKt2dhXeSn7y9/W10jFeMI3bVdWfyit++qB10zfwL/q7fxKckY+Osn/6AIwOEj4oXu49rY4SdjdqCtm8Pp0JsxspyZfu/jEL85RD325iChuLNwS6EDhTJA8vJGnxMxWSa3RhzcNT2+wqGkUICBvcsO61QcR3HYOlZfOz1KDXswqjQiEECD672yq+jgpibf69CGCgagE6dHtoEFq8+xd1xT2FnwmcsAMVJVnQEEgjIJ1hs4ZNkydDBkUpq5mpnLD/36XnwzGLdHmQ06gsAjKqcL+z6yZ+q7JVGRXS+2mc7e7aPaIWMhZhCFzpC7PUHelL895aEp/VGVUSCUswBAohwEtLWOIXf84p9lJM+JY20uegZTyrQ6DYTCW3yj0usDoETWBDoIFAMaNqlGuXhsBqEVjTlvpqO9kEnxcBM6p58bbaVoCAGdUKOtlEnBcBM6p58bbaVoCAGdUKOtlEnBcBM6p58bbaVoCAGdUKOtlEnBcBM6p58bbaVoCAGdUKOtlEnBcBM6p58S5Wm38dIVkeT+Pr+KmDryEZzYiAGdWMYJeqSobC5wH4ulEf8ckvHpa2lzL7UJogzYxqAlBnKJJXunvf71E6bxPw0Rt7GXOGDomrMKOK0bgGYe/O8d28Gime7yc0ie/Z2Ss6TVQmvjajmhjgCYrn08u1WUoGhYvX+i674vg7UZupJuiEviLNqPrQ2c20rj8iYDOC7yhUJEM7qS4sMCsCZlSzwl2kstqHQf0sxaZF8yuz4VPMRSq1QvIROMxnNc4dQYA10hcZE1/2YXfvsQ7+s+uD4o51xt1jd5C/HDLXT0DMTfbm79yIb1mfDAdDYhZy/8ahs/teiOL5ZjyfJIZeyqBqf+p9FW2/cyDwH3AmGEET7pfPAAAAAElFTkSuQmCC\n",
"text/latex": [
"$\\displaystyle - \\frac{\\arg{\\left(\\frac{1}{- C L \\omega^{2} + i C R \\omega + 1} \\right)}}{\\omega}$"
],
"text/plain": [
" ⎛ 1 ⎞ \n",
"-arg⎜──────────────────────⎟ \n",
" ⎜ 2 ⎟ \n",
" ⎝- C⋅L⋅ω + ⅈ⋅C⋅R⋅ω + 1⎠ \n",
"─────────────────────────────\n",
" ω "
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"phi = sym.arg(H)\n",
"tp = - phi/w\n",
"tp"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"y el resultado se visualiza utilizando los valores normalizados $R=1$, $L=0.5$ y $C=0.4$ para los elementos del filtro de paso bajo"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD3CAYAAADmBxSSAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nOydeXybxbX3f492WZZkyXa8xkv2PSQOWSCYhCQkgUIhBApv2UtLe8tSbktYWpbbS3Mhb3kJ2y0FWlq2EmgSCNAACSEUCJDghOyLHcdyvMiWLVuSZe163j9kKXYs21pmpGfs5/v58PkQSxr/njMzx6OZM+dwPM9DRERERGR4IUm3ABERERER8ojOXURERGQYIjp3ERERkWGI6NxFREREhiGicxcREREZhojOXURERGQYIjp3ERERkWGI6NxFREREhiGydAsQGb5wHJcJ4DwA4wHoADgBmAHs4nm+IZ3aRESGO5x4Q1WENBzHTQFwBwAFgP0AmgB0AlADMAKYASALwDae5zekS6eIyHBGdO4iROE47kcAMgC8yfO8Z4j3ngtgMYBneZ53pUKfiMhIQXTuIkThOK6E5/n6ON4vBZDL87yZoiwRkRGH6NxFqMNxXD6AIM/zrenWIiIyUhCduwh1OI7bBWALQoepbTzPf5BmSSIiwx7RuYukFI7jVgMo4nn+6XRrEREZzojOXSTlcBxXw/P8uHTrEBEZzohx7iIpgeO4CgBrAHQB+Hea5YiIDHvEG6oiKYHn+Sqe538E4C0ALenWIyIy3BGduwh1OI67JPz/PM9vA3BlGuWIiIwIxD13EepwHKcHcBEADsB8AN08zz+aVlEiIsMc0bmLUIHjuD/xPP+Lnv+fASAPwBc8z7vTq0xEZGRAzbmfOnWKz8rKotI2STo7OyHqJEdYZ1VVFSoqKgAADz74IPx+P3bt2oX8/HxcdNFFuPTSS1FaWpp2nUJH1EkOFjQCgMFg4Ei0Qy1aRq1W02qaKKJOsoR1hh17+P+vuuoqAIDJZMKOHTtwzz334Prrr8eqVavSqlPoiDrJwYJGklA7UDWb2UgVIuokSzSdy5cvx7//HYp+LC0txS233IJNmzahq6sr1fIisGxPIcKCThY0koSac5fL5bSaJoqokyzRdGZmZqKysrLPz7Zv344333wzVbL6wbI9hQgLOlnQSBJqzl2v19NqmiiiTnKYTCbs3LkzpvcuXboUL7/8Mv72t79R1TQQLNgTEHWShAWNJKG2597W1gaNRkOreWKIOslRWlqKxsZGPProoygqKsLChQsxadIkcNyZ8yGn04m9e/fi888/h8FgwC9+8Yu0aGXBnoCokyQsaCSJGC3DyAk6azoPHz6Mjz76CPv27YPL5UIwGIRMJkNubi7OO+88/OAHP0jr87BmT6HDgk4WNAIMRMt4vV5aTRNF1EmWsM6pU6di6tSpaVYzMKzZU+iwoJMFjSShtufucrFRNU3USZZYdLa0pD+1zHCypxBgQScLGklCbVvGbDbzSqWSStsk8Xg8EHUmRofLh9OdbnS4/FhQqodCKhlS51NPPYXW1la0trbi7rvvxowZM1Ko+AxCtGc03G43Dlg8cHgC4HngonEGSDgi39qJwoI9WdAIMLAtYzab03oDMVZEnYnxfZMDj39WB6cvCI8/iDKDCvctKoWsyzKozlmzZmHRokUAgNdffz1tzv3EiROYPn16Wn53rLR3+/D8zlp81+qD2x+EViHFhgMtuPfCUkzIyUi3vD4IbXxGgwWNJKHm3BUKBa2miSLqjI9AkMcb+8x4Y58ZPICxRjWcvgDqOty4870TWDVBg5+U8H0iZHqzc+dOfPDBB9DpdPD7/WhoaIDD4cDkyZNT+yACJxDksXZHHQ6aPSjQKjBplAamDhdqrW48uq0Wz/9wIgwZwonbFsr4HAwWNJKEmnPXarW0miaKqDN2gjyPfx5swev7zOAAXD8rHz+elQ9vIIiXdzfh/aNtONEZxBenOlE5xhC1jZUrV6KkpARGoxH79u3Du+++i08++QRbtmxJ6bNIJMLOdv2375pw0NwFg0qK9ZdNgCFDDm8giDUf1uBIqxP/veMUnlg5DnKpMJ5DCONzKFjQSBJqI6O9vZ1W00QRdcbOv2s78ffvmlGSpcLjK8fhxooCSCUc1HIp7jx/NG6ZU4Dvzd14aXcTAkEefr8fAPD2229H2rBarVAqlVAqlZg/fz7uuOMOvPrqqyl/lrA2IXKs1YkNB1oh4YDbpmVEVugKqQQPLS1HdoYch8xOvPBNY5qVnkEI43MoWNBIEmrO3WCIvnITGqLO2AgEeby2txl+Hlg1LRezivqvgn40Mw/5mXK0dHnxVV0nVq9ejSuuuALbt2/H999/D57nsXLlSnz22Wd9PpeO2GOZTLgVJt/Y14zx2Wpcd04e5o0Z1ee17Aw5Hl5aDrmEw/tH27D1WFuaVPYl3eMzFljQSBIxFFLUGRM7aztw2uZBvlaBiydkR32PhOOwvDx00PfPg63YvHkz/vd//xd+vx/PP/88FixYgBtvvLGfc08HwWAw3RKi0uHyYfdpB+o63Lh6el7Ufp88SoO7Fo4GADy7qwGHW9KXgC1MusdnLLCgkSTUli9uNxs1GUSdQxMI8nh9byij3o9n5UMmGThS69xcCTYppThm6caRViemFhbixhtvjETIHDt2TBArKKE692/q7eABnFOoRYZCCssA/b58QjZq2lx474gFf/uuCY8uGwuNQppasb1gYR6xoJEk1Fbu+fn5tJomiqhzaD6tsaLR7kGhToGl44yDvre0qAA/mJQDANh40AIAEccOAJMmTUJeXh41rbEi1AyBu+o6AQDnlYWSXA3W77fPL8K8Eh2OtnZj82FLSvQNBAvziAWNJBHzuYs6B8XfE/oIANfPCh2gDobZbMblU3Ihk3Co63DB6hTmlW+fz5duCf1w+QLY2+QAB2BBSci5D9bvMgmHVVNHwRvg8d5hCzz+9H0bYWEesaCRJNScu0qlotU0UUSdg7Ot2opmhxfFeiUWjx16O0WlUiFbI8fCMj0abB7sqrenQGX8CDEU8rsGB3wBHpNHaWDsiZAZqt/PKczEuGw1bG4/tlVbUyEzKizMIxY0koTaCGelpJWoc2B8gSDe7Fm13zA7f8hVO3BG54yCUDTN900OegKTQIjO/WtTz5ZM6Zm840P1O8dxuHpGaJvrnwdbEQimp+A9C/OIBY0koTbCOzo6aDVNFFHnwHx8woqWLi9Ks1SoLI/tEDSs85zCTADA/uYuBAnmL9q+fTvmzp2LiooKrF+/vt/rDz74ICorK1FZWYlzzz0XZWVlUdsRWpy7P8jj29Ohbznh/XYgtn6vLM9CXqYCTXYPdpls1DQOBgvziAWNJKEWLZOdHT1cTmiIOqPj9Qfx5vfxrdqBMzqLdErkaORoc/pwyurC2Ozkc6EEAgGsWbMGmzZtQmFhIZYsWYIVK1Zg0qRJkfesXbs28v8vvvgiDhw4ELUtocW5HzR3weEJYLReiWL9me2DWPpdKuFw1fRR+N+vG/D2gRYsLNMPmP6BFizMIxY0koTayt3hEObX8bMRdUZn6/F2tDl9KDeosLA89ktGYZ0cx2FWYXhrhkwcdlVVFcrLy1FWVgaFQoFVq1Zh69atA75/48aNuOqqq6K+JrRQyF11oRX3eWV9bR1rvy+fYIRWKcVxSzcOmp3E9Q0FC/OIBY0kobZ8sdvt8Hq9yMnJgc1mg8/nQ35+PsxmMzQaDaRSKex2O3Jzc2G1WsHzPHJzc9HS0oLMzNBX+q6uLuTl5cFisYDjOBiNRlgsFuh0OgQCATidzkibcrkcer0ebW1t0Ov18Hq9cLlckdcVCgW0Wi3a29thMBjgcrngdrsRCARgMpmgUqmgVqvR0dGB7OxsOBwOeL3eyOfVajUUCgVsNltansntdkMqlcb0TOHXE30mQ84ovF4Vutq+aqIWp+vrY36mzs5O6PV6WCwWjNdLsA3ArpOt+MEEfVL9lJ+fjwMHDsBoNMJut6OjowNGoxG7d++GyWTq90xHjx6FyWTCuHHj+rwe7qe2tjYsWrQosj1z8803Y9myZSkde+HXlUolvqoLbRnMGqVAc3NzpJ8sFgukUmlMY+/CQjk+OBXAa7tNuGu2LqXzqaOjo8/YEuJ8cjgc0Ol0CfdTqp6J1D0QMZ87IzmeU6lz06FWvPBNI8Zlq/H8FRPj+orfW2eb04v/84/DUMsl2HjDjEEvP8XCu+++ix07duCZZ54BAGzYsAF79+7FE0880e+9Tz/9NJqamqK+BgBHjhzBlClTktJDiuq2bvzy3eMwZsjw5nXT+uRrj6ffO1w+3PDWYXgDPF66ahJKDak7QGRhHrGgESCXz12Mcxd19iEQ5LG/2YECrQI3zM6Pe++2t84cjQLFeiVcviBOWLqT1lZYWIjGxjPJspqamga8mLJp0yasWrVqwLaEFOcePgQ9rySrXyGOePrdoJbj4vHZ0Cql+Ly2k6jGoWBhHrGgkSRiKKSosw97Guz42mSHhAPmjdbF/fmzdZ7Ts+++j0BI5OzZs1FbWwuTyQSv14tNmzZhxYoV/d5XXV2Nzs5OzJ07d8C2hBQKGQmB7BUlEybefv/h1By4fEH882Arur0BIvpigYV5xIJGklAb4awkxhd19uWj46G0qCsm5iTkAM/WeeZQNXnnLpPJsG7dOqxevRrz58/HFVdcgcmTJ2Pt2rV9DlY3btyIVatWDfqtI9XRJAPRbPeg1upGhlyCGQWZ/V6Pt99LDWpMys2A2x/E56dSt3pnYR6xoJEk1A5UbTZbWlK5xouo8wwd3T58W2+DhAOWjh88h8xAnK1zZkEmOABHWp3w+INQypJbTyxbtgzLli3r87MHH3ywz7/vv//+IdsJBFK3qh2MI61OjM1WY2JuBhRRCm8k0u8rJmbjUIsTHx9vx8qJqQn/Y2EesaCRJNRW7jk5ObSaJoqo8wzba6wI8MDc0TpkJ1jC7WydOpUMY7PV8AV4HGlJfYjeQAglzv1YazdOtruQr42+qkyk3y8oz0KGXIIjrU7Ud6QmEyIL84gFjSSh5txttvTclIsXUWcInud7bckkvtqLpjO8737MIhznLpSVe601lGN8jDH6fnAi/a6WS3FhT5nDj06kpvoQC/OIBY0koebchRSNMBiizhBHW7tx2uaBQS3D3NH9D/ZiJZrOqXkaZCqkxC4zkYBWCHC8GsLOfawx+g3eRPs9/Ad6W7UVvgD9C1sszCMWNJJEzOcu6gRw5iB16ThjUvHo0XSOMarR5Q2grkM4lXCEkM+9tcsHpzcAvUoGY0b0baJE+31SbgZKDSrY3H58m4LMnCzMIxY0kkSMcxd1wuUL4PNToRuSy5M8gIumM0+rgEomQYfLj06XMFZPQljFnbSGYv/HGNUDRu8k2u8cx2FFTznEVGzNsDCPWNBIEmrOXaPR0GqaKKJO4N+nOuHyBTE1T4OSrORyXkfTKeE4lBlC7Z5K0QHfUEil6StJF6a2vWdLJnvg+Otk+n3p+NC3sO8a7GijXDSFhXnEgkaSUHPuQpg8sSDqPLMls3yAwtfxMJDO8p4DwzqrcLZm0s1Qh6lAcv2uV8mwoFSPIA98coJuIQ8W5hELGklCzbnb7cKswHM2I13n6U43Drc4oZZLcOGY5GOAB9IZWblbhbFyF0K0TOQwdZCVe7L9Ht6a+fhEO9G8+mfDwjxiQSNJqDn33NxcWk0TZaTr/LhnP/bCcgPU8uRXNgPpDK/cTwnkUDXdB6rd3gCa7F7IJRxGD7IVlmy/zy7SIlcjR7PDiwPN9KKVWJhHLGgkCTXnbrWmr55jPIxknf4gH6m7uXxiYjdSz2YgnWHnbupwU11Bxkq6KzGd6lm1lxhUg0YnJdvvUgmH5ROyMTk3A9/W04vzZmEesaCRJNScuxDiiGNhJOusarCjw+XHaL0SU0aROWwaSGc43M/tD8LsoHu4xwInY9hvB8j0+7LxRhy1dOODY+1w+ehsR7Ewj1jQSBJxW2YE6/zoeDuyM+S4YmousURag+ks78kvfkoAh6rpTj8Qy347QKbfC3RKTMvTwOMP4ss6OsnEWJhHLGgkCTXn3tLSQqtpooxUnXa3H9+etqPD5etX2i0ZBtN5Zt89/Yeq6Y5zD4dBDrVyJ9Xv4URw26vpbE2wMI9Y0EgSas49XDJK6IxUnTtrO+AP8phdpE04SVg0BtMZjpgRQjhkOsPiAkE+8u1lKOdOqt8ry7Mgl3L4vqkLrV3kt8VYmEcsaCSJcCoWiKSU8ApuWYKpfRMhsnIXgHNPJ012DzwBHrkaOXSq1GwPZSplOK9UDx7AjpMj62BxpELNuXd1CSdJ1GCMRJ2nO904ZulGhlyCBaVk81sPprMkSwUJBzTaPfD66SezGox0xrnHcnkpDMl+D/8h33bCSvxwkYV5xIJGklBz7nl5ebSaJspI1Lm9JrRyu6A8C6oki2eczWA6lTIJCnVKBHmgvjO9++7pjHOP7LcPcZgKkO33iiIdslQynLZ5cKIt+Zq2vWFhHrGgkSTUnLvFYqHVNFFGms4gz+PTGnpbMkPpFMplpnTGuZ+MpPkd2rmTHJ9SCYeLxoXyvJM+WGVhHrGgkSTUnLtQalQOxUjTeaC5C61dPuRlKjAtn/wB01A6ywWWhiAdxJIwLAzp8Rn+g/7ZyQ6ied5ZmEcsaCQJNeduNKbuoC4ZRprO8IptyTgDJBQG+1A6y8IJxNK8ck9XnLvd7Udbtw8qmQQFOuWQ7yc9PscY1Sg3qGD3BLCngVyuFRbmEQsaSSJuy4wgnS5fAF/0XGJJtAD2UAy5LRO5yJTelXu64tzDWzLlRlVMf1xJj0+O46jEvLMwj1jQSBJqzl2n09FqmigjSecukw0uXxCTR2WgWJ9c3vaBGEpngU4BpUyC9m4f7O707XunK879ZPvgZfXOhsb4vGisERIO+KbeTqwPWJhHLGgkCTXnLoSUqrEwknSeiW1PPm/7QAyls3fhjnRvzaSDSBhkDPvtAJ3xma2RY3aRFv4gj89rO4i0ycI8YkEjSag5d6dTOJXuB2Ok6GxzerGvyQG5hENlOdnY9t7EolMIud3TNdFjTTsQhtb4XDruzMEqCViYRyxoJIlYIHuE6NxR04EgD8wr0VO9FRmLTiGEQ6Yjzt0XCKK+0w0OoT33WKA1Ps8ry8I5BZk40dZN5M4BC/OIBY0kEQtkjwCdPH8mbzvtdAOx6AwfqtalceWejgPV+k43/EEehTplzIVRaI1PlUyCPK0C3sCZsZEMLMwjFjSShJpzT3elm1gZCTpr2l0wdbqhV8kwp1hLUFV/YtFZZjyz556uHNvpiHmOd78doDs+L+4pwfdptRWBYHL9wMI8YkEjSag5d71eT6tpoowEneGD1EVjDJBL6eaKi0WnQS1HlkqGbl8QLRQyFMZCOqJl4t1vB+iOz2l5GhRoFWjr9mFfkyOptliYRyxoJAm1md7W1karaaIMd53+II9DLaGESanIABmrzvCec7oOVdORfiCehGFhaI5PjuPOJBNLcmuGhXnEgkaSiCv3Ya5z92kbqttcOLdYi/E5sTuVRIlVZ7pvqqZ65c7zPByeADjElnYgDO3xGb7Q9FVdJ5zexCOIWJhHLGgkCTXn7vWyUSdzuOv8+ERoRTazUJuSfeZYdaa75F6q9/o7XX7UtLugV0mRkxF7tBLt8ZmvVWJmQSa8geRi3lmYRyxoJAk15+5ysXFBZTjr7HD5sLveBgl3Jq6ZNrHqjGzLpKnkXjCY2nzypp5ww0KdChJJ7NMuFeOTxNYMC/OIBY0kEePch7HOHTUdCPDAucU6GAmW0huMWHWWGtTgADR0uolmJ4yVVEdOhGPJS7LiS/uQivEZzut/uMWJRltif2xZmEcsaCSJGOc+THXyPI9PTrQDAJZPoJdu4Gxi1RnOihjggdOdHsqq+pPqOPe6nm8opYb4nHsqxqdaLsUFPbeWE129szCPWNBIEmrOXaFQ0GqaKMNVZ3W7C6c63NAppZhXkrqESfHojOR2T8OhajxbIySoT9C5p2p8hrdmttdYEUzgPIKFecSCRpJQG+FaLd3LMqQYrjq39azaLxpnpB7b3pt4dIbTENSl4VA11c7dlOC2TKrG54yCTORlKtDa5cP+5vhrjbIwj1jQSBJqI7y9vZ1W00QZjjq9gSB29CSEWj4htQUK4tFZlsCh6vbt2zF37lxUVFRg/fr1Ud+zefNmzJ8/HwsWLMBPf/rTqO9JZZx7p8sHm9sPtVyCXE18e/2pGp+S3jHvJ+L/nSzMIxY0koRaBimDwUCraaIMR53fmGxweAIYm63G2OzY8oaTIh6d8YZDBgIBrFmzBps2bUJhYSGWLFmCFStWYNKkSZH3nDx5EuvXr8dHH32ErKysAQs0pLISU+/D1HjDUVM5PpeON+L1fWbUWl1wevzQKGO3EQvziAWNJBFDIYehznBs+8UpuJF6NvHoLNQpoZBysDh96PIMvZKuqqpCeXk5ysrKoFAosGrVKmzdurXPe1599VX85Cc/QVZW6IAwNzc3alupDIU0hffb49ySAVI7Pgt1SlxQloVaqxv/PtUZ12dZmEcsaCQJteVLZ2cn3G43cnJyYLPZ4PP5kJ+fD7PZDI1GA6lUCrvdjtzcXFitVvA8j9zcXLS0tCAzM1S4uaurC3l5ebBYLOA4DkajERaLBTqdDoFAAE6nM9KmXC6HXq9HW1sb9Ho9vF4vXC5X5HWFQgGtVov29nYYDAa4XC643W4EAgGYTCaoVCqo1Wp0dHQgOzsbDocDXq838nm1Wg2FQgGbzZaWZ3K73eA4bshnMnd2o6rRDikHTNf5YbfbU/pMnZ2d0Gq1MfdTYaYMdTYfTrQ6kB20D9hP+fn5OHDgAIxGY+SZjEYjdu/eDZPJFGn/yJEj8Hg8WLx4MSQSCW6//XbMmzev3zO1tbVh0aJFke2Zm2++GcuWLaMy9o42hpy7Di7Y7fY+z2Q2mwcdey0tLeA4LmVjb05hBr6o68R7h8yoHK2OeT61t7fH/Ezpmk8OhwOZmZlx+4hUPxOpbxgcrZt6ZrOZVyqHLgCcbjweD4aTzg37W/CXPU1YWKbHw0vHpEBZX+K15zNf1uNoazeunJYbyVI4EO+++y527NiBZ555BgCwYcMG7N27F0888UTkPddeey3kcjn++te/oqmpCZdccgl27drV7+r5kSNHMGXKlDieLHHW/Ksa3zd14bHlYzB3dHxX4FM9Pt3+IK594yC6fUH8edWkyKH3ULAwj1jQCAAGg4HIVXIxzn0Y6eR5HnsbQ9n9hnKUtIjXnoU6JU5aXThu6R76vYWFaGxsjPy7qamp38WUwsJCrFy5EnK5HKWlpRg/fjxOnjzZr61UxrmHwyDjjZQBUj8+VTIJLuq5zfxRHAerLMwjFjSShJpzV6noFGAmzXDSeajFiX1NDkzL0+Dc4vQUA47XnqU9h6qmGCJmZs+ejdraWphMJni9XmzatAkrVqzo855LLrkEX375JYBQdERNTQ3Kysr6tZWqUEi72w+ryw+lTIJRmfHHWadjfK6YGFoYbK+2whvj7WEW5hELGklCbYSr1fQzEJJgOOn817FQStPpBZmQSlJfjAKI356lvYplD7VFKJPJsG7dOqxevRrz58/HFVdcgcmTJ2Pt2rWRg9UlS5bAYDBg/vz5uPzyy/Ff//VfMBr7HyynyrmfiZRRQpJA4rZ0jM/x2WqMzVbD4QlgV50tps+wMI9Y0EgSageqHR0d0OnSs3qMh+Gi0+7249+nOsEBWDkxPVsyQPz2zNXIkSGXwO4JoNPlh2GIHDjLli3DsmXL+vzswQcfjPw/x3H4wx/+gD/84Q+DtpOqOPfw5aVEImWA9IxPjuOwcmI2ntvVgK3H27Fo7NAHfCzMIxY0koTa8iU7O30OJh6Gi87tNVb4AjwqirXI16bv0Chee3Ich7JwTVUChZpjJVVx7mfSDiS2akzX+Fw81gCFlMO+JgeaHUPn/mFhHrGgkSTUnLvDkVzZrlQxHHTyPI8Pj4a2ZC6ZlJMqSVFJxJ7hrZlY9t1Jkao490TTDoRJ1/jUKmVYWBa6K/DJiaGTibEwj1jQSBKxWMcw0HmoxYnTNg+MGTLML0lvtZlE7HnGuafukknKnHuCCcPCpHN8hrf3Pj7ePmQBbRbmEQsaSSLmcx8GOsOr9uUTsiFL00FqmETsGd6PTuXKPRX53Ls8frR3+6CQcshLIFIGSO/4nFGQiUKdEm3dPuw5bR/0vSzMIxY0kkSMc2dcp93txxd16T9IDZOIPc/UU3WnrPxdKuLc63vy1I/OUiUcvZTO8clxHK6cmosJOWpsPT54zDsL84gFjSQRQyEZ17mtWhgHqWESsadRLYNWKUWXNwBrd2qiWFIRCplspAyQ/vFZOSaUa+bb0za0dg28rZFunbHAgkaSiMU6GNbJ83wktv3SNB+khknEnhzHRRxgXYr23VNRLLy+51kS3W8H0j8+DWo5FpbpEeTP3KOIRrp1xgILGklCzbnbbLFdfkg3LOs8aD5zkDovzQepYRK1Z+RQNUXhkIFAgPrvSDZSBhDG+LxsSiiz5tbj7QPWuxWCzqFgQSNJqDn3nBxhrCSHgmWd4ZXUCgEcpIZJ1J7hOPA6a2qceyri3JONlAGEMT6n5WlQalChw+XHLlN0BykEnUPBgkaSiCt3RnX2PUgVzqBN1J5lkZV7arZlaK/cnd4ALE4f5BIOBUmchQhhfHIch8smh8bYB0ejb80IQedQsKCRJNSce6qryycKqzrDB6lzinXI0wpnLzFRe/a+yJSKiBnav+N0z5ZMsV6ZVJ4foYzPJeOMUMkk2N/cFbl12xuh6BwMFjSSRIxzZ1Anz/P4riEUd3zJpPSHP/YmUXsa1HLoVTJ0+4KwOOlPQtpx7uGEYclsyQDCGZ8ahRRLxoVyzLwfZfUuFJ2DwYJGkohx7gzq3NvoQFWjA9PzM9N+I/VskrFnKi8z0V7F1YVzuCeYUyaMkMbnD3q2ZrZVt8Pl67utJSSdA8GCRpJQc+4ajYZW00RhUee7h0NFnyuKtGlL7TsQydizzJi6cEipVEq1/XoCMe6AsMbn2PWOy/sAACAASURBVOwMTBmlQbcviJ0nO/q8JiSdA8GCRpJQc+60Jw8pWNPZaPNg92k75FJOcFsyQHL2TEcaAlokUxS7N0Ibn+HV+/tH2/qcWwhNZzRY0EgSas7dbh88F4VQYE3nlqMW8AAWjzEgS00/P0q8JGPPSFWmFMS604yWcfkCaOnyQsoBhfrkbg0LbXxWlmdhVmEm/EEeh1u6Ij8Xms5osKCRJNSce25uLq2micKSTpcvgI97cnz8cKowdSdjz7JeETNBytEsNA9UT9s8GGNUYWKuJun7B0IbnwqZBJNyNajrcOPdw2cOVoWmMxosaCQJNedutQ6dA1oIsKRzW7UV3b4gpuVpMD4nI92SopKMPXUqGQxqGdz+IFoGyWNCApqVmE62daPW6iYSoirE8XnZlBxIOeDLuk60OEL9JESdZ8OCRpJQc+6pyu6XLKzoDASDeK/nIFWoq3YgeXuWpaFwB2lq2kMHwuOyk09UJcTxmaNRoHKMAUEe2HIkNCaFqPNsWNBIEnFbhhGdTf4MnLZ5kJMhx/k9FXKESLL2jOy7U3buNNMP1LR3AwDGEfh2JdTxeeXUM/lmXL6AYHX2hgWNJKHm3FtaWmg1TRRWdP7zQChG97IpOYLJIxONZO2ZqqpMtOLcA0EetQRX7kIdn5NGaTBllAZd3gC2VVsFq7M3LGgkCTXnnpmZSatporCgs9HmxsE2H+RSThAFOQYjWXuWRVL/0l250wqLO21zwxPgka9VQKtM/tuBkMfnqmmhlfC7hy3IYCCGXMi2pAH9igUiSbO9ugOjdXJcNFaY4Y8kCa/c6zvdQ9btFCI1beRW7ULn/LIs5GrkaLB5sL+F3TOS4Qo1597V1TX0mwSA0HXa3X7881ArTtt9kZWSkEnWnplKGXIy5PAGeJgd9CJmaMW5V4f327PJRDMJeXxKJVzkcP+D4x1DvDv9CNmWNKDm3PPy8mg1TRSh63z/aBs8/iBmF2pQbhRm+GNvSNhzfokeU/M0VNMQ0IpzPxleueeQWbkLfXyunJgNpUyCI1Y/TllTk645UYRuS9JQc+4Wi4VW00QRsk6PPxjJI3NRIRtXp0nYU6uU4nCLE8cs3QQURYdGnHuQ5yORMuMJrdyFPD4BQKuU4eLxRhiUHHbUCDuOXOi2JA01556KGpUkELLObdVW2Nx+jM9RY3K2cHK2DwYJe07IDTnGExZn0m2lkma7F92+ILIz5DBkkPlmIOTxGWbVtFzYvTw2HbKgPQXpmhOFBVuShJpzNxqNtJomilB1BoI8/nmwFQBw9fQ8ZGcLO0omDAl7Tgw79zYXtTQENOLcI/HtBA9ThTo+e1OkV2FecSZ8QR6bDrWmW86AsGBLkojbMgLVuctkQ5Pdg3ytAheUZwlW59mQ0JmjUcCYIYPTG0CT3UNAVX9oxLnXtJG7vBSGlX5fXBByJR8ea0OXh15qh2RgxZakoObcdTodraaJIkSdPM/j7QOhCxerp4+CVMIJUmc0SOmcmBOKmz5Oad+dRpx7NcHLS2FY6fcZo42YVZiJbl8waqUmIcCKLUlBzbnTLkBMCiHqPGh24rilGzqlFBdPCG3HCFFnNEjpPLPvTu9QlSQ8z+Nkj3MnmdSNpX6/ZkYoGmXzIQs8/mCaFfWHFVuSgppzf/XVV2k1TRQh6nynZ9V++ZRcqGShLhKizmiQ0hned6e1cm9vbyfansXpg83th04pRa6GXJglS/0+u0iLcdlqdLr92FYtvMgZVmzJcdzPSLRDzblv2bKFVtNEEZrOOqsL3562QyHlcPmUnMjPhaZzIEjpnNCz+j3Z3k3lpmpnZyfR9sKHqWOzM4hGZbDU7xzH4dqZodX7OwdaBHfDmBVbAhC2c6ddgJgUQtP51n4zJuSosXr6qD6pBoSmcyBI6dSpZCjQKuAJ8FQuM5FO/xpOOzCe0OWlMKz1+/llWSjUKdHs8OKLU2T/gCYLK7YkBUcrx/E777zDFxcXU2mbJC0tLYK5ueYNBFHX4QaHUF5zufTM314h6RwMkjqb7R44PAHkaRXQq8iGLjocDmi1WmLtNdo8cHoDKNCRSRgWhsV+73T70erwQi2XoFivFEx8OSu2rKmpOXzDDTdMS7Ydas69oaGBZ6HauNPpFExV9HWfm7C92oqVE7NxzwUlfV4Tks7BIKnznwda8OLuJlwyKRu/Wlgy9Afi4PDhw5g6dSqx9q578xDau3145erJKNInVxS7Nyz2u9cfxGM7TmHPaTseXjoGC0r1aVYXghVbGgwGIn8NqW3LtLUJMxzqbISis9HmwY4aKyQccO05/VcXQtE5FCR1TsgNTcTeETPbt2/H3LlzUVFRgfXr1/f7zJtvvonx48ejsrISlZWVAx6ikUw/0NHtQ3u3DxlyCQp0yRXEPhsW+10hk2BWoRYBHnhtb7NgKiCxYktSUCtHo9cL46/1UAhF51v7zQjywPIJRhRo+zsIoegcCpI6x+eoIeGAU1YXvP4gpByPNWvWYNOmTSgsLMSSJUuwYsUKTJo0qc/nrrzySqxbt27QtknGuYfL6o3JVkNCeAuC1X6/ZFIONuxvQU27C9/U2wWxemfFlqRIauXOcdzVHMcd5jguyHHcnN6vPfvss6ioqMDcuXPx6aefRv28yWTC0qVLMWfOHNx6663weukWRQaAW2+9NbKqmzlzJi655JKo75s5cybOP/98VFZW4qKLLqKqqdnuwbbq0Kr9unPyAQCPP/44pk6dGtG6bdu2qJ8daiVLm4cffhjz5s3DwoULccMNNwy4OkrEnmq5FKOzVAjwwEmrC1VVVSgvL0dZWRkUCgVWrVqFrVu3DtrGQPYJryY9Hg9uvfVWVFRUYOnSpaivr4/xyc+QTLKwhoYGXH755Zg3bx4WLFiAF154oc/rXq8XX375JUpLSyNjYag/XLQYrA+9Xi94nsf999+PiooKLFlUiYU5objyVK7eq6urI3aqrKxESUkJ/vSnP0U0AkibPe+44w5MmDAB5513XuRnHR0duPLKKzFnzhxceeWVA0ZxcRx3E8dx1T3/3RTL70t25X4IwCoAfz5LyJQVK1bgnXfeQSAQwPPPP4+xY8eioKAAZrMZGo0GUqkU7733Hu644w7MmTMHH374Id566y1ceOGFkYopXV1dyMvLg8ViAcdxMBqNsFgs0Ol0CAQCcDqdyM/Ph9lshlwuh16vR1tbG/R6PbxeL1wuV+R1hUIBrVaLRx55BAaDAS6XC1u3boXJZILJZIJKpYJarUZHRweys7OxcOFC3HnnnSgvL4fZbEZraysUCgVsNhtycnJgs9ng8/ki7YefyW63Izc3F1arFTzPIzc3Fy0tLYM+08tf1SHIAxeMzoCvwwyPMh8lJSX43e9+h8svvxxtbW1wu91obW3t80xyuRzPPvssXnrpJRQXF+P3v/89qqqqMG3aNJjN5n7P5HA44PV6I59Xq9VJP9PixYtxyy23oKCgAG+99RY++eQTFBYW9usnvV6PF198ETqdDnq9HiaTadB+am9vh8FgQGkmB1MHcLjZjs4DB2A0GmG329HR0QGj0Yjdu3fDZDJFPm+32/Hee+/h888/x7hx45CRkYGXXnoJY8eOxR//+Efs378fJSUlaGtrw6JFi2Cz2eD3+3H33XejuLgYf/nLX3DXXXfFNfYONoQSnGWhG52dnUM+k8vlgtvtRn5+Pmw2Gx5++GFMmDABLS0tWLNmDebNmwej0Rj5PACsXr0ad911V6Sfej9zMmMvnvl0ySWX4O6774bH44FCoUBXV1fkmdra2nD48GGYzWZs2rQJzc3NeOGl56C/8A7UtLuwdX8dphokRMdetGcqKirCa6+9Bp1OB5/Phz/+8Y9YsWIFTCYTHA5HZM999erVuO+++yL9ZDKZBu0nEvPpuuuuwy233IItW7agu7sbVqsV27Ztw7Jly3DppZdix44deP311/HQQw/hLH9qBPAIgDkAeABVHMdt4Xl+0CT6RA5UOY7bCeA3PM9/1/PvBx544IG19957LwDgqquuwn333Ye5c+dGPsPzPMaPH49jx45BJpNh9+7deOKJJ7Bx48ak9cQCz/OYPn063nnnHUyePLnf6zNnzsSOHTuoJ+wyOzy45e0j4AG8vHoyinsO4x5//HFoNBrceeedAEIrTKWy73bN2TZ76qmnAAD33HMPVc0D8cEHH2Dz5s34y1/+0u+1RO35/hELnt3VgKXjDJjQ+T127NiBZ555BgCwYcMG7N27F0888UTk/VarFRqNBkqlEo888ghee+011NbWAuhrnyNHjmDKlCl9xqbf78ekSZNQXV0dV4THjRsOw+zw4s+rJqHcmFwo5I9//GPcdtttWLx4MYBQv+/ZswfPPfcc3nrrraTaTpbB+tDj8eD+++/HwoULcdVVVwEA5s6di1+u/wfeOGLHuGw1nr9iYkojZ3bs2IF169bho48+imhUKpX48ssv02bP+vp6XHvttdi1axeAkI22bNkS+QNw+eWXo7q6uo+ROI67DsAinudv7/n3nwHs5Hn+H4P9LloHqkW9T6ULCwvR3Nzc5w1WqxV6vT6SnS/ae2jy9ddfY9SoUcjIiP5VmuM4XHXVVVi8eDH+9re/UdOxYX8LAjywaIwh4tjDvPzyy1i4cCHuuOMOnDhxot9nm5ubUVRUFPl3qm14Nm+88QYqKiqivpaoPSfmnskxU1hYiMbGxshrTU1NyM/P7/N+o9EY+SN4zjnnwOk8kza4t33CMc+9bSiTyaDT6WC1xn670uHxw+zwQiHlUJKVXJRMfX09Dhw40MeG4ZX7nj17cMEFF+Dqq6/G0aNHk/o9iTJYH5rN5qjjcbLSDqNaFtl7TyWbNm2K/KEJawwjBHsCQGtra2QM5+fnD5TcrAjA6V7/buj52aAMuS3Dcdx2APlRXvotz/PvDfSxs1Oqnv0XO9o3BlJ/1a+88sqolc5/97vfRfbYN27ciFWrVkGhiJ4nfevWrSgoKIDFYsGqVav67ZWR4IfX3oTuC38ByOR4f9092PLblojOW2+9Fffeey84jsPatWuxfv36fitimjbsTSz2fPLJJyGTyXDFFVdEbSNRe5YbVZBLODTYPJg0bSZqa2thMplQUFCATZs24cUXX+zzfrPZHJkse/fu7XeIFraPRBJa1yRrw3A+mXKjGlJJ4rbv6urCTTfdhLVr1/ZJcKVQKDBjxgzs378fmZmZ2LZtG2644QZ89913Cf+uRBmsDxUKRVRbKqQcfjQzD3/6phGv7W3G/BJdSlbvXq8XH330ER5++OEzWnrmulDsGQfRDDbklsuQzp3n+aUJiGnovfqJtsLKzs6O7HfKZLKo70mUzZs3D/q63+/HBx98gB07dgx4kaWgoAAAkJubi0svvRRVVVXEnfuF//Hf+Pa0DUvGGfGznw6s+cYbb8Q111zT7+exrGRJMJQ9//GPf+Djjz/Gu+++i2AwesKoRO0pl0owJluN45Zu1HZ6sW7dOqxevRqBQAA//vGPMXnyZKxduxazZs3CypUr8eKLL2Lr1q2QyWSQSqUYM2ZMpK3e9gk797ANi4qK4Pf7YbfbYTAYYrILcCbNbzKVl3w+H2666SasXr0al112WZ/XtFptZH8ZAJYtW4bf/OY3aG9vT3mO/8H6UKvVDjgeJ+eciZz52mTDeWVZ1LVu374dM2bMwKhRoyI/C8/13n8802lPABg1alRkQWI2m5GbG7VOcgOARb3+XQxg51Bt09qW2bJ582Z4PB6YTCbU1tb2+7rOcRwWLlyI994LLf7feuutASNXSLNz506MHz8eRUVFURNIOZ1OOByOyP9/9tlnUfflk6G+041Pqtthc/tx6aT+g6r3V8gPPvgAZWVl/d4ze/bsyErW6/Vi06ZNWLFiBVGdQ7F9+3Y8/fTTePPNN5GRkUHFnuE8Mycs3Vi2bBn27NmDvXv34te//jUA4MEHH8TKlSsBhKJ3vv76a3zxxRfYvn07WlpaotonHOe+cuXKyN7re++9hwsuuCCulWWt1Q0g8ZqpPM/jrrvuwoQJE/DLX/6y3+vt7e1oaWmJrIqrqqoQDAZTXnhiqD5sb2+P2JLneezZswc6nQ75+flQyiS47px8zMjX4J2DrdQKsPRm48aNfbZkwhoBCMKeYVasWBEZf2+99VZkHJ/FxwAu5jjOwHGcAcDFPT8blKSiZTiOuxLAswByAXzIcdz3PM8v53n+8L333osFCxZAJpNh3bp1kbjia665Bk8//TQKCgrw6KOP4rbbbsPatWsxffp0XH/99cnIiZnNmzdHOj68Smtubsbdd9+Nt99+GxaLBTfccAOAkBNYvXo1li5N5AvMwPy9qhlBHrh0UnbUG42PPvooDh48CI7jUFJSgscee6yfzrBtz17JppL77rsPHo8Hq1atAhD6yvvcc88RtefE3Ay8fxQ43hZfhsiB7LN27drIgeX111+Pn//856ioqIDBYMDLL78cc/s8z2NfkwMGtQzT8hK7+fjtt99iw4YNmDJlCiorKwEADz30EBoaGgCEghE2bNiAv/71r5DJZFCpVHj55ZdTfqV/oD585ZVXIjqXLVuGbdu2oaKiAmq1Gs8991zk8ysnZuPtAy2wOH3YUdOBpePpOdPu7m7s3LkzcoAOAK+88gpcLhf+4z/+A1u2bEmLPW+77TZ89dVXaG9vx9SpU3H//ffjV7/6FW699Va8/vrrKC4ujtizJ7T85zzP38bzvJXjuP8GsKenqd/zPD/kwRC19APHjh3jWcjjkI58E8ctTtz53gkopBz+fs1UZMeQIpaVvBg0dNZ1uPCzjceQl6nAa9eSSRlw8OBBTJ8+Pak2TllduH3TMRgzZPjHddOoOIjh1O8fn2jHk/+uR16mAn+5ejIUUmoX5KPCii0Fn37A7XbTapoo6dD51z2hiI0rp+bG5NiBkW3P0XoVVDIJWrq86HSRyew30NlAPOxpCEV/zCmid0g4nPp96TgjSg0qtHR58WEaqjWxYktSUHPuNA72aJBqnXsb7djX5IBGIcU1M2NfRYxke0olXKS60Yk4t2YGQi5PvqBGVY9zryimV75tOPW7VMLh1jmFAIA3v2+B05vaykis2JIU1Jx77wNBIZNKnTzPR1bt18wYFVdq2JFuz5kFGkzIUaO2nUxu92Rze7t8ARwyO8EBqCgilzr4bIZbv88v0WFqngY2tx//PNhKWVVfWLElKag5d5WKXNpTmqRS55d1Npxo64ZRLcMVU6OGPA3ISLfnxFwNTrS58JXJRqS9cChkouxv7oIvyGNibgZ0hHPN92a49TvHcbjt3NDqfePBVli7U1dAgxVbkoKac1eryVakoUWqdPoCQWyvbodBLcOPZ+VDLY8vK+FIt+fMQi3kUg7HLd3oIOAQknXu4S2ZORS3ZIDh2e9T8zOxoEQPtz+IN/albjXNii1JQc25d3QMmtNGMKRK55Yjbfi63g6DWoYVE+O/LDHS7amSSTCzIHSZ57vG5K+xJ5vPfU9DKOabtnMfrv1+y7kFkHDAv461odHmoaSqL6zYkhTUnHs6bnslQip0drp8eL1nhXLznMI+5fNiRbQncG6PI91zOnnnfnZ6jHhosnvQZPcgUyHFxNzEb6bGwnDt9zKDGismZGNKngZ/r2qipKovrNiSFNSce/g2m9BJhc5Xq8xwegOYU6zFvNGJrfREewJzR4fyxFQ1OhAIJnc/I5lQyO96tmRmF2mTyicTC8O536+fnY8TbS7srO3E/ib6z8mKLUlBzbmnovAGCWjrrG134V/H2yDhgNvnFSUcDy3aEyjSK1GoU8LhCeCYxTn0BwYhGede1bMlQzMEMsxw7vccjQLX9oQD/+mbhqT/YA8FK7YkhRjnTlEnz/P40zcNCPLAZZNzUWpI/EBHtGeIuT3ffHYnuTWTaJy7LxDEvqbwfju9EMgww73fV08fhbxMBWqtbmw93j8vEUlYsSUpxDh3ijq/Mtmwv7kLWqUUN8xObmCJ9gxBat890Tj3wy1OuP1BlBlUyNVETxdNkuHe70qZBLfNDYVG/r2qGV0ecoXLz0bItrTZbPj44/65wDiO+5rjuMJE2hRDISnp9AaCeOnbUPrTmyoKko6FHun2DDOjIBNKKYeadhfakwiJTDQUMlUhkGFGQr9XlmdhWn7oYhPN0Egh2/Lzzz/HsmXLAESShoV5H0BCe4jUnPtARTCEBi2dmw9Z0OzwotSgwqWTcpJub6TbM4xSJsE5haHtkPDBZiIkevZxJgSS/pYMMDL6neM4/GJ+MTgA7x624HQnnRwwQrdlrwXHml4/NvM8n9BfPGrO3WYjc5OQNjR0Wrt9ePP7UH/8fF4RkYiKkWzPszl3dPJbM4FA/HlN2rt9qLW6oJRymJaXOfQHCDBS+n18TgaWT8hGjkaODftbolZ1ShYh2zJcCeqzzz4DACcAcBx3NYCEM6xRc+45OcmvVlMBDZ1/q2qGyxfE/BIdsYiKkWzPswnvu1c1OuBPMMIikTj38JbMzEItFLLUpKsdSf1+y7kF8Ph5fFJtxZd15B2xkG2pVqtx7rnn4vPPPwcAjuO4WgDFPM9vSbRNceVOWOdhcxe+quvEzIJM3D5vyBq2MTNS7RmNAp0So/VKOL0BHGlJLCQykZV7VWNPCCTFRGFnM5L63aCWRwIP/vR1A7oJZ40Usi0feOAB7NmzB48++ih4nr+Z5/kxPM8/NfQnB4aac082616qIKnTFwhi/Zen4fAEMDVPE7XCUsJtj0B7DkZkaybBffd4v/YHgnxk5X5ughfREmGk9fslk3IwMTcDbd0+vLq3mUibYVixJSnEOHeCOv95sBWmTjcKdUpcdw7Z5x+J9hyMuZF998RWY/HGuVe3dcPuCSBfq0CRTpnQ70yEkdbvUgmHu88fDQkXOlw92U4mfz/Aji1JIca5E9LZaPNE8sfcff5oKAnvyY40ew7FtPxMqGQS1FrdMDviTzwV7yruu54tGZpVl6IxEvt9XE4GfjglF0EeePrL08QKarNiS1JQc+4aTWIFg1MNCZ08z+OZr07DF+CxdJwBsyjsyY4ke8aCQirB5VNyUKhT4tOa+LP9hQu2x0r4G8Kc0anbbwdGbr/fWFGA7Aw5jlm68a9jZG6usmJLUlBz7vFOnnRBQuenNR3Y1+SAVinFzwgeovZmJNkzVs4p1KLJ7sH7Ry3wBZKviToQpg4XTnd6sKBEh5kFqXXuI7XfNQopfjE/NJf+uqcJHQRq57JiS1JQc+52e/JpWVNBsjrtbj/+3HMT9WfzipClTr42Z9TfM0LsGQ8VRVqUZqlg7fbj36c64/psPNEyGw60ossbQLZGAY0itQ5iJPf7BeVZmFOsRaZCgjf2Jr+lwootSUHNuefmxldGLl0kq/Ol3Y2wuf2YkZ+Ji8cbCanqz0ixZzxwHIcrp4V+36ZDrXFFwMR6oGp2eLCjxgoJB1w9Y1RCOpNhJPc7x3G467xidHmD2HK0DV8nWWKRFVuSgppzt1qttJomSjI69zc5UNXggFzC4e6Fo6ketI0EeybCknFG6FUyVLe5cCiOmPdYKzG9c6AVQR5YPNaAAm3qomTCjPR+z9epIrHvT39VD0cSicVYsSUpqDl3GteHaZCoTpcvgCe/CA22n84rxOgsusV3h7s9E0Upk+DSSaEKO5sPtRJt29rtw0cnQod5P+rJO55qxH4Hfjg1F1PzNLB2+/HCN40Jt8OKLUkhbsskqPOlb5tgdnhRnEUmMdhQDHd7JsNlU3Ihk3DYZbKhOcawyFjSD2w+1ApfgMeCUj3KksjFnwxivwMSjsOvK0ugkHLYVm3F7gTvNrBiS1JQc+4tLS20miZKIjqrGuz44FgbZBIOay4sTagmarwMZ3smS3aGHIvGGhDkQxdfYmGoOPcujx/vHw3lbLo2Tat2QOz3MMV6FW6qKAAArP/iNJwJpCZgxZakoOaVMjNTkzUvWeLV6fSGtmMA4IbZ+Sg3pmZFN1ztSYpVU0Orso+Pt8c08YcKi9typA3dviBmFWZi8qj0xUeL/X6GVdNGRVIT/Pmbhrg/z4otSZGa1HbDiBe+aUCb04eJuRm4Zkb6VnQifRmXk4EZ+Zno9gXx8YnkLr24fAFs7vkGcO3MkXVlXchIJRx+U1mC0iwVDpqdCW/PjBSoOfeuri5aTRMlHp3f1tvw8Qkr5FIO91aWEsnTHivD0Z6kWTU9tHrffKgVXv/gl5oGi3P/6Hg7bG4/JuZm4JzC9K72xH7vS6lBjWUTjGi0e/DHz+vjutzEii1JQc255+WxsaqNVafd7cc/vg/t2d1SUYASA93omLMZbvakwbzRepxXooNcKsH/ftMwaHTEQHHuvkAQ7xwMRd1cd05eSvPIREPs9/6snj4KMwsy0en2Y/0Xp2OOgmHFlqSg5twtltgOttJNLDp5nseTX9TjWKsTKyYYceW01F9mGU72pIVUwuFH5+SjpcuLfx1rx5vfD3yANlCc+zsHW9Hm9KE0S4X5JXpaUmNG7Pf+SDgO915YCo1Ciq/rbdh6PLZtOFZsSQpqzj3dK55YiUXn+z2349QKKX48qyCl2zFhhpM9aTJ5lAYPLC6DhAP+XtWMrcdir1L2xalO/P27ZszIz8TP5hVCIgCbp9uesZJqnaMyFbjr/GIAwJ++aUSjbei6q6zYkhTUnLvRSO8qPkmG0nnK6sKLPblj7lk4Gnna9BTZHS72TAULy7Jwx3mjAQBPf3U66rX1s+Pcv6zrxNodp8ADmJynwRxC5RGTRQj2jIV06Fw81ojFYw3w+IN4fKdpyJKLrNiSFOK2zCA6Pf4g1n5WB2+Ax8qJ2agcY0ihsr4MB3uSYPv27Zg7dy4qKiqwfv36Ad8XOPEVmra/hiAP/GHHKRxu6XuY1jvOfZepE3/49BQCPHDNjFG4dU6BYFZ5Yr8Pzp3nFSNXI4NMwuHVqsErN7FiS1JQc+46nTBWPkMxmM4/va9bcAAAExpJREFUf9sIU4cbo/VK/Hw+nVS+sTIc7JksgUAAa9aswdtvv42vv/4aGzduxLFjx/q9z+Fw4MUXX0RB+0Gcmw14Azwe/qQWx1ud6PL4YXf7AYkUHS4fPq224rFP6xDggaunj8JPzi0UjGMHxH4fikylDL+9aAyOtjrx1v6WQcMjWbElKag590QKEKeDgXR+VdeJD462QS7h8OBFZVDL05sLmnV7kqCqqgrl5eUoKyuDQqHAqlWrsHXr1n7vW7t2Le666y6oVCpcWQrMG62DwxPAr94/gVWvHcTq1w/C1OnFj944hBd3N8If5LF6+ijcNldYjh0Q+z0WpuRpIrdX1+00weL0Rn0fK7YkBTXn7nQmVpU+1UTT2eLw4p0DoXC42+YWYmx2Rqpl9YNle5KiubkZRUVnvkEVFhaiubnvV/EDBw6gsbERy5cvBwBIOeC3S8rxwOIyaJUyaBRSaJVSSDhAr5JhyqgMrLmwFD8VoGMHxH6PlR/NzMOcYi3sngDW7qhDIMr+e7o1ppqhsyclSEZGBkwmE3JycmCz2eDz+ZCfnw+z2QyNRgOpVAq73Y7c3FxYrVbwPI/c3Fy0tLRErgl3dXUhLy8PFosFHMfBaDTCYrFAp9MhEAjA6XRG2pTL5dDr9Whra4Ner4fX64XL5Yq8rlAooNVq0d7eDoPBAJfLBbfbDaPRCJPJBJVKBbVajdY2K57c142THR5cNFqJleN0MJlMUKvVUCgUsNlsaXmmjIwMtLa2xvRM4dfDz9TR0YHs7Gw4HA54vd7I6zSeCQC6u7uJ91N+fj4sFgtcLhfsdjs6OjrgdrvR3d0Nk8mE/Px8NDU14d5778WTTz4Jk8mEQCAAi8UCY+NpnFecjzEX6CLPtH//flhefhTb/H5sA1B3881YtmxZSsdeLP0UCATQ2tqa1rEXyzPJZLJIP6Rr7F0/QYFT7TIcbnHihS9r8aMp+j7PxHEcnE4nlX4i+UwGA5mzPY5WGszvv/+eLy0tpdI2SUwmE3rrfOqLemw93o68TAWev2IidCpqf//i4mydQoWmzt27d+OJJ57Axo0bAQBPPfUUAOCee+4BEKq0M3v27EitzNbWVhgMBrzxxhuYNWtWn7b279+PmTNnUtFJErHf4+OQuQu/+bAaQR54bPkYzB195q6CUDQOhcFgIPIVktq2TKyVbtJNb51bj7Vh6/F2KKQcHllaLhjHDrBpT9LMnj0btbW1MJlM8Hq92LRpE1asWBF5XafToaamBvv378f+/fsxZ86cqI4dYCfmWez3+JiWn4mb54T235/YaYK5VwpooWhMFdScu16f/tt9sRDWecLSjee+DmWau+v80RiXk/599t6wZk8ayGQyrFu3DqtXr8b8+fNxxRVXYPLkyVi7dm3Ug9XBYKVYstjv8XPNjDzMG61FuUGFxz6tg6cnz5CQNKYCcVvGZEJWXhF++e4xtHb5cOmkbNy9sCTdsvrByldKVnSK2zJkEZpOm9uHO987AbPDiyXjDFhzYSnq6+sFpXEgBL8tw8pfSa1Oh8c/q0NrVyiN7y8WFKdbUlRYsScrOsWVO1mEplOvkuPRpWOglEnwaU0HNh6yCE4jbag5d683eqyp0PjHgTZUNTqgV8nw0JJyKFJQVSkRWLEnKzpZqafJij2FqHNMthprLgyt1F/e3YiqBnuaFaUWap7M5XLRapoYO092YHdjN7Iz5HhwcRlGZaYnb0wssGBPgB2dweDg+d6FAiv2FKrOC8qz8ONZ+QjywLPfWdFoi63G7nCAmnPPzxd2BZsjLU7833+b0NwdxI9m5mFWkTbdkgZF6PYMw4pOViInWLGnkHXeMDsfC0r06PbzeHRbLboTqL/KItScu9lsptV00jQ7PHhkWy18AR4XFivxwyk56ZY0JEK2Z29Y0TlUgWyhwIo9haxTwnFYs6gUBRoJTJ1urPvchCAj23LJQM25KxTC3OJwegN4+ONa2Nx+VBRpceP0LCZinoVqz7NhRadEIsyzlbNhxZ5C16lRSPGrc43IVEhxyurC63uF+8eIFNRGuFYrvG2OQJDHY5+egqnTjdIsFX63pBwGPRuZ4oRoz2iwopMV586KPVnQOT7fgIeXlqHLE8Dr+8z4VxyFXFiE2ghvb0+uAj1peJ7H87saIpExv18+BhqFVHA6B0LUSZaByuwJDVbsyYLO9vZ2nFOow0/mFgIAnvnq9KApglmHmnMnlfyGFJsPW/DBsTbIpRz+a9kYFGiVAISncyBEnWQ5uxKTUGHFnizoDGu8ZFIOrjsnL5R/5tM61LR1p1kZHUZEKOTXpk78+ZtQqbx7K0sxJU8TeU1IOgdD1EkWMRSSLCzo7K3x5ooCLBlngNsfxO8+OYnWLuHF6ScLNefudg9dsDYVHGjuwmOfnsL0gkzcNDsfi8b2XWEIRedQiDrJwopzZ8WeLOjsrZHjOPznBSWYWZAJa7cfv/34JLo8bGzVxcqwjnOvaevGw5+chC8IjNYr8X9m9dckBJ2xIOokixjnThYWdJ6tUS6V4OGl5SjNUsHtC+D/fl4fSTI2HBi2ce4NNjce+Ogkun1BXFiehTvOGx015DHdOmNF1EkWMc6dLCzojKZRq5ThseVjoJZL8XW9DX/YcQr+KFWcWISac1epVLSaHhKL04v7t9ZEYtnXLCqFVBI9lj2dOuNB1EkWVkIhWbEnCzoH0pinVeLBi8qgVUrxTb0d/+/fw+OSE7URrlaraTU9KDa3Hw9sPYnWLh8mj8rAw0vLIR8kGVi6dMaLqJMsrDh3VuzJgs7BNJYZ1PjD8rFQySTYXtOBP33dyExyuYGgNsI7OjpoNT0g3d4AfvfxSdR3ulFmUOG/Lx4LtXzw1K7p0JkIok6ysBLnzoo9WdA5lMZJozT4r2VjIJdw+PCoBW8faEmRMjpQc+7Z2dm0mo6Kxx/Es7tO47ilG/laBf5n5biYyuSlWmeiiDrJwkqcOyv2ZEFnLBpnFWlx/+JSjMlW4y97mvHGPuGfJQwENefucDhoNd0Pjz+Ihz+pxc6THTi3WIvHV45DdkZs0RCp1JkMok6ysBIKyYo9WdAZq8YLyg24ctoocAD+XtWMt/ezuYJnvliHu8ex72tyQKeS4fZ5xSjUKWP+vBCLDERD1EkWVpw7K/ZkQWc8GpeMM+LXlSXgALy8pwmbDrXSE0YJpuPc3f4gHulx7Aa1DP/3kvEoMcR3as9CfC4g6iSNGOdOFhZ0xqvx4gnZ+NXC0QCAF75pZC7RGLNx7iHHfjIpxw6wEZ8LiDpJI8a5k4UFnYloXDkpB3eeV4wZ+Rqs//I0/nmQnRU8tVMlmqFRZxx7V8ixXzoeJVmJxdmyEMIFiDpJI4ZCkoUFnYlqvGxKLjiOwwGzEy9+2whfIIjrzhH+NxXminV0ewN4btdpIo4dEH6RgTCiTrKwUKAFYMeeLOhMRuMPJudE9uBf+a4Zf69qFnwcPDXnbrORz5Nsd/tx39YafHLCivkluqQdO0BHJw1EnWQJBNioo8mKPVnQmazG5ROycd+iUkg44I19Zry8u0nQDp7atkxODtm6pO1OH+7/qAamDjfyMhW4fV4xivSxR8UMBGmdtBB1koWVOHdW7MmCThIaLxpnhFwqwdodp7CztgP+II+fzSsaML1JOmFi5d5k9+CeD07A1BEqj/fUZeOJOHaAjRUHIOokjbhyJwsLOklpvKA8C48sDd1k3XzYgsc/q4M3ILzQWmrOnVQ0wimrC//5/gmYHV5MzM3Akz8YjxwNuf09VqImRJ1kEfLX6d6wYk8WdJLUOL9Uj/+sLEGGXILPT3XioY9r0e0V1oJB0HHuB5q78MI3DbC6/DinMBNPxJhSIB5YiM8FRJ2kEePcycKCTtIaZxRo8eQPxsOglmFfkwNr/lWDTpdw/sgJNs79s5NWPLC1BvuauvDDKTl47OKxyFAMngQsEViIzwVEnaRhYaUJsGNPFnTS0Dg2OwNPXTYBBVoFTrR1438+q0Oz3UP89yQCNeeu0WiGflMUeJ7HP743438+M8EX5PHDKTn4+fxiKGR0pCaqM9WIOskilZJfKNCAFXuyoJOWxkKdEk9dNgFzirSotbpx15YTONrqpPK74oGac09k8gSCPNZ/eRqvfNcMDsDt84rwHwuKqZ5EszLJRZ0jE1bsyYJOmhqNGXL8dkk5xueoYXP7ce+H1fjiVCe13xcL1Jy73W6P6/3d3gAe+uQkth5vh0LK4XdLynHV9FHUL5vEqzNdiDrJwkq0DCv2ZEEnbY0ahRS/v3gsVk7MhjfA47FPT+GdAy1pO7yn5txzc3Njfm9rlxe//qAa3zU4oFfJsO6S8bigPIuWtD7EozOdiDrJwsqBKiv2ZEFnKjTKJBx+tXA0fnJuIXgAL+1uwl/3NKWlLis15261WmN635EWJ+567zgyFBIU6ZR4+vIJmJKXuv27WHWmG1EnWVipxMSKPVnQmSqNHMfhRzPz8NuLylBuUOHdIxY80FPTOZVQc+6xfBXZerwd935YDavLDynHYf1l4+PKxU4CVuKdRZ0jE1bsyYLOVGu8cIwBv7pgNDRyKfY3d+HO947jlNWVst+flm0Zf5DH87tO46kv6nsiYnKxduU46NWp/6rMwtdJQNRJGlbSD7BiTxZ0pkPj5FGZePaKiRifo4bZ4cWv3j+Br+pSc9BKzbm3tEQvTdXp8uGBrTV470gb5BIO/3lBCX55XjFkacrNMJBOoSHqJAsrce6s2JMFnenSmKtR4P/9YAIWjzXA7Qvi9X1mvFrVjADlfXhqzj0zM7Pfz060deOxHXXY39wFY0+63hUT01tYN5pOISLqDLF9+3bMnTsXFRUVWL9+fb/XX3nlFZx//vmorKzEypUrcezYsajtsBC6B4j9TpJ0alTKJLh/USnuPL8Yp6wuvL7PjIc+OQk7xX34lFQs4HkeW45YcM+WEzjd6UbF/2/vfkIaueI4gH/T1JismOyMBqPWopVqvUjXk9Jihda2h8La6KknYaGXgpeC9OClF4telormoLkW1Kr1IoKUFGStYKuHtKVdWoOpf4hJdJr/Ohqnh8VAdrfdsPt7yYz8PqfIjOP3+eIP896befWVmOxrLerEKTO+bDaL4eFhzM/PY3NzE4uLi08U7/7+fmxsbGB9fR1DQ0MYGRkpUVrG8plMJnzU5sToh82wl5vx80ECny0/xF/RtJCfJ6y4J5NJAI/Wr3/1wx4mfzzAxZWGtxtv48ve10gf/vUirnPqHecEtre30dTUhMbGRlgsFrjdbqyuruadY7fbc6/T6fR/3idhlHXu3O909JKxo94Oz8dvoKX6Fo6TKu4/+Burf0TJJ3yFbrO38esuZn7L4ChxgXIzMNRVjxZbBvF/TmE2mxGPx+F0OnF6egpN0+B0OnF8fJz7+JRMJlFTU4NIJAKTyQRZlhGJRGC325HNZpFKpeByuRAKhVBWVgaHw4FoNAqHwwFVVZHJZHLHLRYLKisrcXJyAkmSkMlkcHZ2BkmSEAwGYbVaYbPZoCgKqqqqkEgkoKpq7vttNhssFgtisRiqq6sRi8VwcXGRO15RUSG0TTabDeFwuKA2XR8vRZs0TUM6nSbvJ5fLBb/fD1mWEY/HoSgKZFnG1tYWgsFgXptmZ2fh9XqRzWbh9Xrzjl+3SVEU9PT05JZEDg4Oore3t6jvvUL66fLyEuFwuKTvvULaZDab837Pevx7AoBUKiWkn56nTZ/fuYVvH17hp2MV9x/sY2vvBPfelCFJEkkNNolaHuRZ3dK++T0FNauhSbJi5N0mNLzgrkki7O/vo6GhodQxnolzAsvLy/D5fJiYmAAAzM3NYWdnB2NjY089f2FhAT6fDx6P54ljfr8f7e3tQnJS4n6no9eM3/95iomNfZxdXuEVRzm++/QtktUlwoZl1vYyULMaPmiR8fXdVl0WdsA4e2lyTqCurg6Hh4e5r4+Ojv73Ma5utxsrKyvC8hQD9zsdvWZ873UZk32taJSsOIjRPVFS2LDMF+80IJi4wvstpV0N8yyyLJc6QkE4J9DR0YFAIIBgMIja2losLS1heno675zd3V00NzcDANbW1nKvH1deXtyb5Z4X9zsdPWd89bYVE3dbsfRLmOyawv5zt6px3Rd2AIhEIqWOUBDO+ejGo/HxcQwMDKCzsxN9fX1oa2vD6OhobmJ1ZmYGXV1d6O7uhsfjwdTU1FOvZbXq85Pk47jf6eg9o/Xll/DJHboNRYSNuQcCAY1qYkAkRVHIJjBE4py0OCctI+Q0QkYAkCRJ32PuRllqxjlpcU5anJOOETJSElbcU6nS70RSCM5Ji3PS4px0jJCRkrBhmVAopBlh0ur8/NwQk2uckxbnpGWEnEbICBhgWMYIG+YCnJMa56TFOekYISMlYcXdKDvdcE5anJMW56RjhIyUhBV3h8Mh6tKkOCctzkmLc9IxQkZKwop7NBoVdWlSnJMW56TFOekYISMlYROqjDHGSqcoz3NnjDFWXFzcGWPsBuLizhhjNxAXd8YYu4G4uDPG2A3ExZ0xxm6gfwFO29CTNKDAlgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"RLC = {R: 1, L: sym.Rational('.5'), C: sym.Rational('.4')}\n",
"sym.plot(tp.subs(RLC), (w, -10, 10),\n",
" xlabel='$\\omega$', ylabel='$t_p(j \\omega)$');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Retraso de Grupo\n",
"\n",
"El retraso de grupo se define como la derivada de la fase con respecto a la frecuencia\n",
"\n",
"$$\n",
"t_g(\\omega) = - \\frac{d \\varphi(j \\omega)}{d \\omega}\n",
"$$\n",
"\n",
"El retraso de grupo cuantifica el retraso que observa la envolvente de amplitud de un grupo de señales exponenciales cuando pasa a través de un sistema. El signo negativo en la definición anterior da como resultado un retraso de grupo positivo para un sistema que impone un retraso en la señal de entrada. Tenga en cuenta que la fase $\\varphi(j \\omega)$ en general solo es única para $- \\pi < \\varphi(j \\omega) \\leq \\pi$. Si la fase excede este rango, se envuelve. Para obtener resultados significativos, se requiere desenvolver la fase antes de calcular el retraso del grupo.\n",
"\n",
"**Ejemplo**\n",
"\n",
"El Retardo de grupo $t_g(\\omega)$ del filtro de paso bajo de segundo orden anterior se calcula y se representa gráficamente para los valores normalizados"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAEQCAYAAABLMTQcAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nO29eXyb1Zn3/TvaZUnW5kW2k9hJSMgGIXEISRoCpaQNlEIItEMZ2gLTzjtM23kLT4ehzLyFmT7NU+hCykuXoUw7LS1TQhOWUkIhDUshaQPZSXD2KPEiWba1W7vu5w8t8SLbknyOdB/nfD8ffxLrvnX8u69z7ktH17nu6xBJkiAQCASCqYWi2gIEAoFAQB/h3AUCgWAKIpy7QCAQTEGEcxcIBIIpiHDuAoFAMAURzl0gEAimIMK5CwQCwRREOHeBQCCYgqiqLUAwdSGEGAGsAjAHQC2AMAAXgJ2SJHVWU5tAMNUh4glVAW0IIQsAfAWABsABAN0AfAD0AGwALgVgAfC6JEnPVkunQDCVEc5dQBVCyN8AqAHwjCRJsQnOvRzARwH8/5IkRSqhTyC4UBDOXUAVQsgMSZLOlnC+EkC9JEkuhrIEggsO4dwFzCGEOACkJUnqrbYWgeBCQTh3AXMIITsBvITMYmqfJEkvV1mSQDDlEc5dUFEIIbcCaJEk6YfV1iIQTGWEcxdUHELICUmSLqq2DoFgKiPy3AUVgRDSDuB+ACEAb1dZjkAw5RFPqAoqgiRJeyRJ+hsAvwXgrrYegWCqI5y7gDmEkOtz/5ck6XUAN1dRjkBwQSBi7gLmEELMAK4BQACsADAoSdLDVRUlEExxhHMXMIEQ8hNJku7J/v9SAI0A/ixJUrS6ygSCCwNmzv306dOSxWJh0jZNfD4fhE565HTu2bMH7e3tAIAHH3wQyWQSO3fuhMPhwDXXXINPfvKTaG1trbpOuSN00oMHjQBgtVoJjXaYZcvo9XpWTVNF6KRLTmfOsef+f8sttwAAnE4nduzYgXvvvRd33HEHNmzYUFWdckfopAcPGmnCbEHV5eKjVIjQSZdCOj/xiU/g7bcz2Y+tra246667sHXrVoRCoUrLy8OzPeUIDzp50EgTZs5drVazapoqQiddCuk0Go1Ys2bNsNe2b9+OZ555plKyRsGzPeUIDzp50EgTZs7dbDazapoqQic9nE4n3nzzzaLOvfbaa/HUU0/hv//7v5lqGgse7AkInTThQSNNmMXc+/r6YDAYWDVPDaGTHq2trejq6sLDDz+MlpYWrF69GvPmzQMh59eHwuEw9u7di7feegtWqxX33HNPVbTyYE9A6KQJDxppIrJlOFlB503n4cOH8eqrr2Lfvn2IRCJIp9NQqVSor6/HqlWrcMMNN1T1enizp9zhQScPGgEOsmXi8TirpqkidNIlp3PhwoVYuHBhldWMDW/2lDs86ORBI02YxdwjET52TRM66SJ00kXopAcPGmnCLCzjcrkkrVbLpG2axGIxCJ30GE9nXziOL/9//wd1WgKrMo4lS5ZgxYoVaGlpqbDK6tpTkiT85WwAALB8uglKxdhzrKnQ73KBB40AvbCMyHMXOqkyls6O3jB+sqsT2svWQbfqNlz7+a/i+PHjePrpp/HjH/+4wiqBY8eOVfxvAhnHvumdc3juoAv/s9+FR99yIpJIjXk+7/0uJ3jQSBNmzl2j0bBqmipCJ10K6ZQkCc8ecMMTjiOaSOEDVwA//PNZ6GsteOCBB7Bo0aIqKK0OfznrR28ojtMDEUQSKfz1bAB/PDYw5vk897vc4EEjTZg5d5PJxKppqgiddCmk84g7jEOuEPRqJX75ueVY1lQDiRCYL7sWfr8fL730UsV1KsYJhbDknTM+BGNJfPYyB/5x5TQ0GDX4n/0uJNOFw6M897vc4EEjTZiN8P7+flZNU0XopMtQnclkEgDwX6/tRiCWwty6Grz5p9fxkVYTBtNK/NWdhNlsxve+972K68xpqyTuYAxvnPThrC+GG+bX4bJmE9KSBItOhQPdwYLv4bHf5QoPGmnCzLlbrVZWTVNF6KTLUJ233norblq/HofDWtRpgatmW3DdddchdHQ35tbpYdQocc5XnQrAKlXld5h854wfOhXBx+fYUKNRgRCCa2bbcNobxZunvAXfw2O/yxUeNNJEpEIKnVQZqvOFF17AP2/8ISR1DbyBAO745Mfw+c9/Hm+/+QammXU40BPCe52BquhMp9MV/5t7ugIIxdOY13D+KckVM2oxzaxBIJpEocw1HvtdrvCgkSbMpi/RKB97MgiddBmp05XUoVGTwkcXz8HdX/4LOjo6YLVacdCvwt6uIDr91bmuSjv3eDKNgz2ZKpjt087Hfmfa9BhMpLHrbADnfDHMsOqGvY/XfpcjPGikCbOZu8PhYNU0VYROuozUub8nBHdciZm2jNOaN28eGhsbcVmzCb5oEn864UVqjMVEllS6QuBRzyCaTFpcZNfDqj//twkhuNRhBAAc6Bkdd+e13+UIDxppIvLchU6qDNWZliQcdocBAAsbjcPOqzdq4DBpEEmkcXqg+K/LX/nKVzB37lysWrWq4HFJkvDAAw+gvb0dq1evxoEDBwqel0gkiv6bNNjfE4TTF8078qG0T6vFnDo9TvaPtgOP/S5XeNBIE2bOXafTTXySDBA66TJUZ6cvhlk2HS6fZkKDcXSO8aLGTOz5qGew6PZvv/12PPfcc2Me3759O06ePIn3338fjz32GP7X//pfBc+rdCrkh72ZD7kFjaOrEs626XG8L4IDPaM3L+Gx3+UKDxppwmyE87KlldBJl6E6j/cP4pArDLWy8DC7pMmIGrUCh93F78i0atWqcbMeXnnlFdx2220ghODyyy9HIBAoOGOrpHNPSxI6ejMfYPMLOPc2mx4aJUFXIIZAdHiKJo/9Lld40EgTZiPc6y2c2iU3hE66DNWZCzNcZC98U7VZM4uJJwqEI8qlp6dnWK2a5uZm9PT0jDqvknnu3f4YmkwaLJ9ei3rD6G8wKgXB6jYLLmk04OSIEBWP/S5XeNBIE2bZMhqNBk6nE3V1dfD7/UgkEnA4HHC5XDAYDFAqlQgEAqivr8fAwAAkSUJ9fT3cbjeMxkxcMhQKobGxER6PB4QQ2Gw2eDwe1NbWIpVKIRwO59tUq9Uwm83o6+uD2WxGPB5HJBLJH9doNDCZTOjv74fVakUkEkE0GkVtbS2cTid0Oh30ej28Xi/sdjuCwSDi8Xj+/Xq9HhqNBn6/vyrXpNFo0NvbW9Q15Y5X45pSqRQGBwfh8XjQ4crMVk2pEGKx2KhrshtNUBDA6Y3CH47A19db1DUFg0EkEgmEQqFR1xSLxRAMBvNjL/d3c//mrsnr9eLqq6/OO/k777wTa9euZTL29valcLw/gsUkiUAgUPCaNCSFQ+4wDnf54CCh/DXF43H09vZWdewVcz8BmZ24qjn2JrqmdDqNcDhcso+o9DXRysdnVhXyyJEjUlNTE5O2adLT0wOhkx45nZIk4dO/PoRALIVf37awYMwdAP5+y4c4443ihzfOxfyG4nbJOXv2LG677Tbs3Llz1LF7770Xq1evxi233AIAWL58OV566aVRmRKHDh3CJZdcUuLVlcdTu7uw+WAv7ljiwOfbC/fhto4+PPbOOXx0thXf+Ghb/nXe+l3O8KAR4KAqJC+F8YVOuuR0esIJBGIpmLRK1BvGTju8qK4GAHCir/hF1fG47rrr8Nvf/haSJOG9995DbW1twRS4Sua5h+MpzLBoMXuM8BQAzLZn7HDWOzwsw1u/yxkeNNKEWViGl5xSoZMuOZ1D4+1D91AdyRy7HtuPA2e8xT1g8sUvfhHvvvsu+vv7sXDhQjzwwAP50Mpdd92FtWvX4vXXX0d7ezv0ej2eeOKJgu1UMs99l9OPgUgSs8Zx7jMsWjhMGpz1x5BIpfOL0Lz1u5zhQSNNmDl3l8uF1tZWVs1TQ+ikS05nTyCGSxwGXNI0Oq97KLPtelh0Khwrcub+1FNPjXucEILvfve7E7ZTqTx3fzSJgUgSOpUCjWOEpgBAp1aCAEikJHQHYmi1Zj4IeOt3OcODRpqIVEihkyo5ncf6MmmQ9prxa2i3WvXwRZM464sWrK3CikqlQp7JZr+0WXVQjPMNBgBmWDJ52Gd9sfxrvPW7nOFBI03EZh1CJ1VyOs9mqz3OsIy/rZlZp4JZp0IkkUZvqHJPjY4XKqJJLtzUZp3YseScu3NIpUze+l3O8KCRJsycu9/vZ9U0VYROuvj9fqQlCef8mdnndPPETwW2WXNOrXJV+1Kpsbe2o8mZ7AJpm21iO+SKhg0tg8xTv8sdHjTShJlzr6urY9U0VYROutTV1aEvnEAsmYZFp0KtbuJlndaccy9yUZUGlarnfn7mXoRzz4dlztuBp36XOzxopImYuQudVPH7/UNCMsXV8mi1VN65V2LmLkkSdCoFWq26/DWOR85e53zRfKVMnvpd7vCgkSbMnHulq+6Vi9BJl0QikQ8rTJ8g3p4jlxnirOCuTJVYvPVFktjTFUR/OAFbzcSplwaNEvYaNeIpCb2hTE42T/0ud3jQSBNRz13opIrD4cC5bLZHsTP3GRYtFjUaUKNWVCxjphJ57p2BjB1azNqiF3AXNxlxSaMBXYHMBx1P/S53eNBIE1HPXeikisvlQjydxiUOQ9HO3aJX46wvin3dIQwMVqagVyVmcZ25bzDm4r7BAECNWolD7nD+A5Knfpc7PGikCTPnbjAUVyek2giddDEYDNjbGcQhVxjNtcU7tWnZrJpzFdp2T6lUMv8buYyhliIyhnI01WbS9XqCmbAMT/0ud3jQSBNmzr0SNw8NhE66JCWCvsEElARjFgsrxLTs7LbTH5vgTH7oyqeDFv8h15T9QOzJhnR46XcedPKgkSbMnHsgUJ1d7UtF6KTLqV4fgIyTUiqKf1CoJesAuyo0c69EtkzuW8i0EmbuzaaMHbqzzp2XfudBJw8aacLMudfX17NqmipCJ12iqkwtmVJCMsB5B1ipmTvrBdVkWsrPvptLmLk7TJlvO65QHOlsrW8e4EEnDxppwsy5DwwMsGqaKkInXU72ZnKJS3fu2Zl7oDLOnfVOTO5gDCkJaDCqoVMVf5vVaJSw6FRIpCT0Dya46XcedPKgkSbMnHsli0BNBqGTLr3hTLijpUTn3lyrBUEm1pxM83Gt45FfTK0tfVPm5iFxd176nQedPGikiQjLCJ1UGUhkhlSpM3etSoEGowYpKTPrZQ3r8gOdJT7INZRcxkx3IM5Nv/OgkweNNGHm3N1uN6umqSJ00iW3IFqqcwfOL6qeq0DcnXWee/4BpjLs0GQ6P3Pnpd950MmDRpowc+65zV7ljtBJj1gyjYFoGkpyfmGwFCqZDsk6La4z+xDS9CIf5BrK+Vz3GBf9DvAxPnnQSJPKlMYTXBC4gjE01qjQaqspKQ0yR26WW6l0SJZ0BnJpkKXP3HPpkLkHmQSCcmA2cw+FQqyaporQSY+eYBzuwSRSZS5cVTIdkmWeeziewsBgEmolQb2h9G8wuQeZugMxLvod4GN88qCRJsyce2NjI6umqSJ00iOX191URpwZAKZZcjN39s6dZZ57l/98vL2cbzBWvQpalQLBWAoGKx81yHkYnzxopAkz5+7xeFg1TRWhkx6ubBihqYx4OwA0GDRQKzLlCyIJtk+Qssxz7/SXH5IBMlsA5mz44dlearpYwsP45EEjTZg590rtUTlZhE569GRTGHPZHqWiVJB8lk0lZu+syIWVSik7MJLct5++aJqKJtbwMD550EgTZs7dZrOxapoqQic9egLZmXtt+RsRt1QoY4ZlnvtgIoWL7PqiSx4Xojk7cw9JfGzqzMP45EEjTURYRuikgiRJ+Zm7o8yZOzAkHZJxGQKWee4He0I40R8pK9c/R27mfqYvSEsWU+Q+PgE+NNKEmXOvra1l1TRVhE46DESSiKckmDQKGDTl55BPM2vRaFQjFGNb+4VVnrskSUPCMuU799wHw0Ccj1CC3McnwIdGmjBz7pUoqUoDoZMOruxMu8EwuXDHNLMO7lACh91hGrIqTv9gAtFkGrVaJWp15dsit6DqDvGx76fcxyfAh0aaMHPu4TAfN6fQSYfubEjGNskQ8fm67myLZrG60c9RWEwFMhudKAjQH0khkZL/oqrcxyfAh0aaiA2yhU4q5BZTZ9ZP7quvRaeCQaNEKJ6CP8ouNMMqz72LQkgGANRKBeoNGkgA3CH5P6kq9/EJ8KGRJmKDbKGTCq7szF2fjkyqHULI+druDDNmWC2o5ndfKqMa5Eia89Uh5Z8WKvfxCfChkSbMnDvrnW5oIXTSIVcHpZyCYSPJ1ZgplDGzfft2LF++HO3t7di0adOo452dnbjxxhtx1VVXYfXq1Xj99dcL/g1WOc/5mXsZddxHcn4/VfnP3OU+PgE+NNKEmXM3m82smqaK0EmHXOmB2Y2WSbc1VnXIVCqF+++/H5s3b8auXbuwZcsWdHR0DDvne9/7HtavX4+33noLTz31FL7+9a8X/BussmU6Kc7ccw+DdVegvv1kkfv4BPjQSBNmzr2vr49V01QROidPNJnGQCQJlYJAGvRNur2W7GLkyOqQe/bswcyZM9HW1gaNRoMNGzZg27Ztw84hhCAYzOSGBwKBMeOsLMoPJFJpuIJxEJyv7DgZcg+DuTiYuct5fObgQSNNmD2mx8unpNA5eVz5h5c0sFomP3Mf6ynVnp4etLS05H9vbm7Gnj17hp3zL//yL7jlllvw5JNPYnBwEM8//3zBv8Fi5t4TiCMtZeygKWHf1LFoFjN3qvCgkSbMnLvP54Pf70ddXR38fj8SiQQcDgdcLhcMBgOUSiUCgQDq6+sxMDAAKbvTu9vtzhfVD4VCaGxshMfjASEENpsNHo8HtbW1SKVSCIfD+TbVajXMZjP6+vpgNpsRj8cRiUTyxzUaDUwmE/r7+2G1WhGJRBCNRqFWq+H3+6HT6aDX6+H1emG32xEMBhGPx/Pv1+v10Gg0VbsmSZKKvqbc8Upd08HTmY2HLep0Xtdk+smiqwGQiV/3uFyIx2JwOBzweDyIRCIIBALwer2IRqMYHByE0+nMv/+3v/0tbr75Znz605+G0+nEF7/4RTz33HNobm4edk0ejwdXX311fgZ/5513Yu3atZPqp30nugEA9ToyTFO5/WS3ZbaF6wnE4PV6EQgEZHs/eTwe+P3+io+9Uq4pd7+X6iMqfU1Wq5WKDyascon3798vtba2MmmbJk6nE0Ln5Nj6QS9++pcufGp+HW6clqai87bfHMJAJImn/2YhGrOLtLt378YjjzyCLVu2AAAee+wxAMC9996bf9/KlSvx3HPPYdq0aQCAJUuW4LXXXhu1f+aBAwewePHiSescyuYDbjz1XjfWL6zHP66cRqXNDb/cj1BCwv98dhHsBvkuCMp5fObgQSMAWK1WKqv9Is9d6Jw0+YJhJg01nbm4e+eQuPvSpUtx6tQpOJ1OxONxbN26FevWrRv2vmnTpuHtt98GABw9ehSxWAx1daNrorPInKBRdmAkuTIEPTIPzch5fObgQSNNRJ670DlpcjH3plotNZ35XPch6ZAqlQqPPvoobr31VqxYsQLr16/H/PnzsXHjxvzC6re+9S386le/wpVXXokvfelLeOKJJwqmPbLIc59sHfdCWNSZp1Plnusu5/GZgweNNGEWc9do+ChVKnROnp78Jh1aaOJ0dLaM8SDT2rVrsXbt2mGvPfjgg/n/z5s3D6+++uqE7SsU9Oc1NOq4j8RhVAOIy34/VTmPzxw8aKQJM+duMplYNU0VoXNypCVpWLZMOk5H51i57rSg7dxDsSR80SS0SoI6irHxVrsR0zxJDMblXfRKruNzKDxopAmzsEx/fz+rpqkidE6OgcEE4ikJZp0KNRolNZ25Jzy7AtEJziwP2nnuuQ+hFrMOCopPv+pSg+j0x/Bhr7yLXsl1fA6FB400YebcaaXzsEbonBy5cEGuDgotnY7aTFVEVzDOpCoi7Z2YWCymAsCcpszuQXKPuct1fA6FB400YebcI5HJFZCqFELn5MiVHcjtvkRLp0apQKNRg7QEJvHmdJruBwaLxVQA0ElxaJUEgViK+QYmk0Gu43MoPGikCTPnHo2y+TpNG6FzcriC59MgAbo6x1pUpQFt597FYDEVAGKxWL6AWLeMF1XlOj6HwoNGmog8d6FzUuTCBTkHRFPntAK57rSgned+jlFYxuFwnM91l3FoRq7jcyg8aKSJyHMXOieFa0gaJEBXJ8uMGZp57mlJyufj03buLpcr79zlHHeX6/gcCg8aacIsFVKno/v1lBVC5+ToyT/AlAnL0NSZq+vOIixDMxWyL5xALJmGRaeCUUv3ltLpdGiuzRQ5k7Nzl+v4HAoPGmnCzLnr9XpWTVNF6CyfSCIFbyQJtYLAXpMJc9DUmQ/LMEiHpOncaW2tVwi9Xo+mbHp2t4xL/8pxfI6EB400YRaW8Xq9rJqmitBZPrmQTKNJk8/tpqmz3qjGDIsW9QY1wpQzRWjmuee31qO8mApk7MlDzF2O43MkPGikCTPnbrfbWTVNFaGzfPIhmSEbU9DUqSAEKoUCRz0RnKUcmqGZ585y5m6329Fg1EBJgL7BTPhHjshxfI6EB400Yebcc7vhyB2hs3xy1SBzDzAB9HW2WjOzYaeXbmiGZiokzU2xRxIMBqFUEDSa5F0dUo7jcyQ8aKQJM+cej8s3PjgUobN8zteUOe/UaOtsyzt3ug+g0HTuNDfFHknOnrkPULluli3H8TkSHjTSROS5C51lk1vgaxoyc6etMz9z99GdudPKc4+n0nCH4lCQ4XagRc6eubh7l0zj7nIcnyPhQSNNRJ670Fk2hWLutHW2WjIZDmcoh2Vo5bn3BGL5fVPVSvq3U86ecl9UleP4HAkPGmnCzLnzknYkdJZHWpLgzmbLOEznZ6y0dTpMGmiUBH3hBMIUy97SSoU852OXKQOct2fuA1Suue5yG5+F4EEjTZg5d14K4wud5dE/mEAiLcGqV0GvVuZfp61TqSCYbqG/qFpod6ZyOOuLwaBW4OL6GirtjSRnz3zMXaYLqnIbn4XgQSNNmDl3v9/PqmmqCJ3lcX7f1OEZIix0tlroL6qmUnS+BZz2RhBOpNFoZOM4cvZsMmlBkHm2IJlms6n9ZJDb+CwEDxppwsy5F9qUWI4IneXhDsUxv6EGCx2GYa+z0JlbVD1DcVGVVp776YGMpjYbm6/8OXtqVArYDWqkJaA3JL+sD7mNz0LwoJEmYuYudJbFWW8EH/YODgvJAGx0tlkzjpNmWIbGzD2eSqPTH4WCnP92QZuh9myRcQExuY3PQvCgkSbMnDuL3eVZIHSWR77Ebe3wsAwLnSweZJKkyYc2zvmiSEuZTBatis2tNNSecl5Uldv4LAQPGmki8tyFzrIY65F7FjodJg20SoL+wQS13Yho5LnnQzJWdlkYQ+3ZbM7E9eXo3OU2PgvBg0aaiDx3obNkUmkp72BaRjh3FjoVhH7GDI1Z3OmBzALvTBu7UrJD7dmcK0Egw6dU5TQ+x4IHjTRh5twNBsPEJ8kAobN0esNxJNIS7DXqUTF3VjpzZQhOU3LuSqVy4pMm4HQ2e2cmw5n7UHvKedMOOY3PseBBI02YOXcaN08lEDpLZ7wqiKx0tjJYVJ0sZ7JhGZYz96H2zG1l2BOMIU1hzYAmchqfY8GDRpowc+6BQIBV01QROkuncxznzkrn+RozdHLdJ5stE4wl0TeYgFZJhhVOo81Qexo0Sph1KsRTEvoH5bU4KKfxORY8aKQJM+deX1/PqmmqCJ2l05UtcdtS4JF7VjrbrDosajRAqaDzZOlkF1Rzi6mtVj01TYUYac/z1SHlFZqR0/gcCx400oSZcx8YGGDVNFWEztI5N87MnZXORqMGp71R7OkMUpm1TnYnpjNe9oupwGh7nk+HlNeiqpzG51jwoJEmzJw7jTziSiB0ls54MXdWOgkhuMieibuf6Btk8jdKIZcpwzINEhhtz1aLFq0WLXwReYVl5DQ+x4IHjTQRYRmhsyRiyTR6s/XLC8WaWeqcU5cpzvX1bz+G9vZ2bNq0qeB5zz//PFasWIGVK1fiS1/6UsFzJlt+IJpMY159DWbb2Tr3kfZsNGnh9MVwTAYfcEORy/gcDx400oSZc3e73ayaporQWRrdgRgkZMIDqgKxZpY6Z1kzHyYrr78Vu3btwpYtW9DR0THsnJMnT2LTpk149dVXsWvXLmzcuLFgW5PJc0+mJfz5tA8dnkHMYlRTJsdIe87I5vuf88kr5i6X8TkePGikCTPnbjQaWTVNFaGzNCbaDJqlzqjrFACgO5Ip37phwwZs27Zt2Dm/+tWv8Hd/93ewWCwAxp6tTSYtzumNIJ6S0FyrRa2O3kbbhRhpz9xDY12BGFIyqg4pl/E5HjxopAkz5y6YmnQGcpky7NL/xiIx0AOSTqA3lIA/mkRzczN6enqGnXPy5EmcPHkS69atw9q1a7F9+3bqOjo8mZAIqxru46FXK9FgVCOZlmRb210gD5hNO/r6+hAKhVBXVwe/349EIgGHwwGXywWDwQClUolAIID6+noMDAxAkiTU19fD7XbnP2FDoRAaGxvh8XhACIHNZoPH40FtbS1SqRTC4XC+TbVaDbPZjL6+PpjNZsTjcUQikfxxjUYDk8mE/v5+WK1WRCIRRKNRpFIphEIh6HQ66PV6eL1e2O12BINBxOPx/Pv1ej00Gg38fn9VrimntZhryh1ncU1HuzO5wvpkGP39/aOuyefzQa/XU+8nh8OB/j4PNGE1YqYm7DxyBtFoFIODg3A6nfn3h8NhHD16FE888QQSiQQ2bNiA5557DnPmzBl2TR6PB1dffXU+a+bOO+/E2rVri+qnA+cyWRezrRo4nc5JXdNE/dTV1YVUKjWsnxp0BL0h4JQnhJTPLYv7ye12IxQKMR17k72mYDAInU7HpJ9oXpPVaqXigwmrFeSenh5Jp2ObJkaDaDQKobN47v39MRx2h/HI9RdhSbNp1HGWOnfv3o1/f2k/Em2X4+8ub0b3jmcymu69N3/Offfdh2XLluH220YqUbQAACAASURBVG8HAKxfvx7f/OY3sXTp0mFtHTlyBAsWLChLxz9s/RCnBqJ47FNzsLCR7Vf9Qvb8ya5OPH/Ygy9e3ozPLG5k+veLRS7jczx40AgAVquVyoMTzMIyHo+HVdNUETpLY7ynUwG2OpcuXYr+Y3swx6KCOxjF1q1bsW7dumHnXH/99XjnnXcAAP39/Thx4gTa2tpGtVVunnskkcIZb6aG+0V29mGZQvbMFVE755dPKQa5jM/x4EEjTZg5d1p7VLJG6CyeQDQJfzQJrUqBuprCT3iy1KlSqfD/fuFvcNyXxIvvHcf69esxf/58bNy4Mb+w+rGPfQxWqxUrVqzAjTfeiH//93+HzWajpuFEfwRpCZhp0zOr4T6UQvacnv1glVPGjBzG50TwoJEmzGLuNG8olgidxdMZOD9rH+tGYa3zb67/KJ791UEMmuz4wme/CgB48MEH88cJIfj2t7+Nb3/72+O2U26e+9EKL6YWsmcuHfKsLwpJkmThtOQwPieCB400EWEZobNozvmi0KkIFjaMXTqVtU4FIZiX/ftHesNlt1NunvtRT+ZvXlxfmfKxhexp0atg1CgRiqfgi9DZvGSyyGF8TgQPGmnCzLnX1tayapoqQmfxnB6IIJqUYDeMXXSrEjoXZJ17R2/5T2mWm+een7nXVWbmXsiehBBMt2RDMzKJu8thfE4EDxppwsy509iAuBIIncVTzLZyldA5Pzdzd5c/cy8HfzQJVzAOrUqRL0HMmrHsOd2cC83II+4uh/E5ETxopAkz5x4OV/bGKxehs3iKqYRYCZ3zGjKz5uP9g0ik0mW1Uc6NftQTxkzKpYcnYix7zpBZxowcxudE8KCRJmKDbKGzKHyRBLyRJPRqBRqMmjHPq4ROk1aFZS0mXFxXg+NlFtAqp577vq4gTnujmFuhkAwwtj1n2vRY0GCAVyabdlR7fBYDDxppIjbIFjqLIrd3aZtVB8U42RmV0tlo0uADdxgHekJlvb+cBdW9XUEAwGUtox/eYsVY9pxm1uJIb/nXT5tqj89i4EEjTZg598nudFMphM7iOFNk/fJK6bws+3Ts/u7ynFup6YMDgwmc9kahVRIsbKzcRstj2bPRpIFerYA3kpRFbfdqj89i4EEjTZg5d7PZzKppqgidxXE6vxn0+M69Ujovbco89n/YHUK8jLh7qdky+7ozs/ZLmozQKCtXb28seyoIQVt2Ufe0DDYNr/b4LAYeNNKE2Sjt6+tj1TRVhM7iOJ1bTJ0gS6RSOq16NWZadYinJHSUke9eavmBXEhmaYF6OiwZz565b1G5b1XVpNrjsxh40EgTMXMXOickLUlweuU1cwcmF5opZeYuSVLeuS+pYLwdGN+euY1CTsnAufNwH/GgkSbMnHs8Lq8NfMdC6JwYVzCOaDINW41qws0pKqnzvHMPlvzeUqqhnvPF0D+YgEWnmvDDjTbj2TOXknpGBmEZHu4jHjTShJlzj0SqP5soBqFzYnKbQc8sYjPoSuq8xGGAgmS2/huMl5a3nk4XH6ff05WpYb+kxTRuphALxrNnPizjjSJd5c2febiPeNBIE5HnLnROyOkiQzJAZXUatSp8pNWCgUgSe0ucvZeSOZELybRXOCQDjG/PWp0KdTVqxJJp9ASqOyvl4T7iQSNNRJ670Dkh59MgJ37kvtI659RnPnB2Ov0lva/YPPdkWsJBVyamX+l4OzCxPduyoZnTVY6783Af8aCRJsycu0Yz9lOMckLonJic42grYuZeaZ2rWjMbYf/1rL+kDaMViuKGfkdvGJFEGtPNWtQbKt8HE9kzFyrLZTNVCx7uIx400oSZczeZKj/LKQehc3ziyTS6AjEoCNBqmXjmXmmdMyw6TDNrEYyl8IGr+KyZYp37vq4g5jfU4CNtlnIlToqJ7DmnTo85dj380eqW/uXhPuJBI02YOffc5slyR+gcn7O+KNIS0FyrLWrnoWroXNWaSXHbebb40Ewxee6ptIRXjvbjw95BLJtWnXKxE9lzlq0Gx/sj2FViWIo2PNxHPGikCTPnTmsHb9YInePj9EVRo1ZMWHYgRzV0rsw697+e9Red4ljMTkx7ugLoH0yguVaLSxyVKzkwlInsOc2iRY1aAU84gYEqFhHj4T7iQSNNRCqk0DkuRz2DGEykMb+huEqI1dA5v8GAj7SZ0RdOYH+RhbSKSYV87dgAAODjc2xV28puInsqCMGcbJXK3EYi1YCH+4gHjTRh5tyj0eo/WFEMQuf45B7tn1XkwzvV0KkgBLNtesRTEl46XNxWahM590A0iV1OPwiAtXOrt/dmMfacV59z7tWrV87DfcSDRpqIPHehc0wSqTRO9mdmO8VuCF0te14/rw4qBcGus364gxPnfE+U577jpBeJtIT2aaaqZMnkKMaec7P7uVZz5s7DfcSDRpqIPHehc0xODUSQSEuYbtbCqJ04Rg1Uz562GjWunGlBWgJe7pi4QNREee5/PJZZfPvEXDsVfeVSjD1zH7zH+gZLKqtAEx7uIx400oSZc9fpKrPH5GQROscmtwH1xQ3FLyZW0543LagHAGzr6EM8OX7YZbxUyBN9gzjZH4FJq8TKGdUtNlWMPesNatj0KgRjKXRX6UlVHu4jHjTShJlz1+srW2CpXITOscnFcOcVGZIBqmvP+Q01uMiuRyCWwpunvOOeO55z/2N2IfWa2VZoikj/ZEkx9iSEYG6V4+483Ec8aKQJs5Hr9Y5/c8kFoXNsOrIx3HklzNyraU9CCG5amJm9v3jEM26IYqw890A0ieN9g6g3qPHxKodkgOLteXEu7l7mnrKThYf7iAeNNGHm3O326t8YxSB0FiYYS6LTH4NaSSbcoGMo1bbn1bOsMGmVON4XwaFxnlgdK8/9F+9340hvGBfZ9bjIXv2ZXrH2zMXdj/ZWx7lXu9+LgQeNNGHm3IPB0mtsVwOhszC5zIs59hqoS9hWrtr21KoUuG1xIxY1GvCz3d1j1psplAp5vG8Qr3T0Q0mAuy9vrlpu+1CKtefcbK77if5BJEuosUOLavd7MfCgkSZisw6hsyC5kEyxKZA55GDP6y62wxWK46hnEM8ecBc8Z6RzT0sSfrSzExKA9Qvr0VrkE7msKdaetToVmmu1iKckOKtQREwO/T4RPGikichzFzoLcjT78NK8Ip9MzSEHexq1Knx9zQwAwNN7e3CiQBx6ZJ779uMDONIbhlWvwh1LmyqisxhKsWfug7ijCvnucuj3ieBBI01EnrvQOQpJks4vptaXVlNFLvZc2lKLmxbUIyUB33nzDCIjdmoamuf+fmcAz+x3waJT4YvLm2HQFL+/KmtKsWc14+5y6ffx4EEjTUQqpNA5ClcoDn80CbNOBYeptKczWevcvn07li9fjvb2dmzatGnM81588UU8dPPlqNNmyhN8/ZXj6PKff/w8lwr58od9+Lc/nkR3II4b5tvxsYuqV2qgEKXY8/zDTJVPh+ThPuJBI03EZh1C5yiOewbRYFDj4vqakhcVWepMpVK4//77sXnzZuzatQtbtmxBR0fHqPOCwSCefPJJLLl0Ef6fuQABcLwvgn94/iie2e/CwZ4gIkkJj7x5Bo+/ew5pCfjs4kbcsbSp4nukTkQp9rzIXoOFjQbUqJUIl7in7GTh4T7iQSNNmDl3v7+69aWLRegczd7uIHrDCSxuMpb8XpY69+zZg5kzZ6KtrQ0ajQYbNmzAtm3bRp23ceNG/NM//RN0Oh1qNcD3bpiDa2ZbEUumsa2jH1//wwm4QkmcHohASYD7rpyBuy5vlp1jB0qzp1algCQBH7jDJW1cQgMe7iMeNNKkuIIhZaDVauF0OlFXVwe/349EIgGHwwGXywWDwQClUolAIID6+noMDAxAkiTU19fD7XbDaMw4lVAohMbGRng8HhBCYLPZ4PF4UFtbi1QqhXA4nG9TrVbDbDajr68PZrMZ8XgckUgkf1yj0cBkMqG/vx9WqxWRSATRaBRmsxlOpxM6nQ56vR5erxd2ux3BYBDxeDz/fr1eD41GA7/fX5Vr0mq16O3tLeqacsfLvaZ92Q2hp+uT8Hq9JV1TKpXC4OAg9X5yOBw4ePAgbDYbAoEAvF4vbDYbdu/eDafTmX//6dOncebMGcybNw+pVAoejwc2VxfuXdWEuYYEwmkV/tpDoJJCOLb9OSScB/G/f+FC5513Yu3atRUde8X0UyKRQG9vb9Fjb2G9Dkd6w3j7aDcWN2grdj8RQob1gxzvJ0mSEA6HmfQTzWuiVXeesCo0dPjwYam5uZlJ2zTp7u6G0HkeVzCGzz97BAaNEr+74xIoFaXNZlnqfOGFF7Bjxw48/vjjAIBnn30We/fuxSOPPAIgk95400034Uc/+hFmzJiBT33qU/iP//gPLFmyZFRbBw8exKWXXspEJ01Ktef+7iDuf+UEZtn0+OmGeQyVDYeH+4gHjQBgtVqpfIVkFpYpdnf5aiN0Dmdfd+br/OImY8mOHWCrs7m5GV1dXfnfu7u7h6W3hUIhfPjhh/jUpz6FxYsX4/3338ff/u3fYt++faPaqlb1xFIp1Z4LGgzQKAlODUQquq8qD/cRDxppIvLchc5h7O/OhGSWNJe3mTBLnUuXLsWpU6fgdDoRj8exdetWrFu3Ln+8trYWJ06cwIEDB3DgwAEsW7YMv/nNbwrO3Ceq5y4XSrWnRqXAwsZM+uqB7so9kcnDfcSDRpqIPHehM48kSfl4e7nOnaVOlUqFRx99FLfeeitWrFiB9evXY/78+di4cWPBhdXx4GUWV449L8v23f7uyi2q8nAf8aCRJswWVA2G6mwoXCpC53nOeKPwRZOw16gx3aItqw3WOteuXYu1a9cOe+3BBx8seO7vf//7MdtRKuXzoNJ4lGPPjHPvwf6eys3cebiPeNBIE2Yzd15uHqHzPPvyIRlj2UWzeLEnL5Rjz7l1NahRK9Dpj8ETrkw9FR76nQeNNGHm3AOBAKumqSJ0nicXkrmszJAMwI89U6nKPuRTLuXYU6kguMSRSavbX6G4Ow/9zoNGmjBz7vX19ayaporQmSGZlnAw++DLkpbynTsv9uRlQbVce1Y67s5Dv/OgkSbMnPvAwACrpqkidGY46gkjkkhjmlmLekP5j2nzYs+xdmKSG+Xa87ImI2bZdPAOJpCuQNonD/3Og0aaMHPuvOQRC50ZDnSHQAAsncSsHeDHnrxQrj1n2fUIx9N4vyuII272hcR46HceNNJEhGWETgDA26e9MGqVWNVqnlQ7vNhzrG325Ea59iSEYM1MCwDgrQk2C6cBD/3Og0aaMHPubnfhHXDkhtAJnB6I4NRAphxubiGuXHixJy957pOx51WzMjVK/nzaN+Z2g7Tgod950EgTZs49VwRH7gidwJsnMzO7K2daStovtRC82JOXtLjJ2HNOnR5NJg0GIslxNwunAQ/9zoNGmjBz7gI+kCQJO7LO/ZrZdKrRCeQBISQ/e3/7lK/KagSVhplzD4UqW0+6XC50nR/2DsIdiqOuRo1FkwzJAPzYk5c898na86pZmbj7n8+wDc3w0O88aKQJM+fe2NjIqmmqXOg63ziZSQ+7eraVymYVvNiTlzz3ydpzlk2PaWYt/NEk0weaeOh3HjTShJlz93g8rJqmyoWsM5WW8Fb26/pHKYVkeLEnL3nuk7Xn0NDMWwxDMzz0Ow8aacLMuZdbm6TSXMg693UH4YsmMc2sxUV2OpsH82JPXqBhz1xo5l2nD0lGoRke+p0HjTRh5txtNnntIj8WF7LON4YspNIa+LzYk5c8dxr2bLPq0WrVIRhLYW8Xm/oqPPQ7DxppIsIyF6jOWDKNd8/QDckA/NiTlzx3WvZkHZrhod950EgTZs69traWVdNUuVB1/vWcH4OJNObW1aDFrKPWLi/25CXPnZY9r8o+rbrT6Uc8labS5lB46HceNNKEmXPnJdXsQtX5xolMSIbmrB3gx568QMue0y06zLLpEY6nsKeTftYMD/3Og0aaMHPu4TD7YkU0uBB1hmJJ7D4XAAFw9Sy6zp0Xe/Jyo9O0Z25hlUWtGR76nQeNNBEbZF+AOt91+pFIS1jcbITdQDffmxd78pLnTtOeV8+yYrpZA3cojkCUbiooD/3Og0aaiA2yL0Cdb5/KhWToZw/wYk9eFlRp2rOpVguHSYfD7jCeP0x3cZGHfudBI02YOXdeZkYXms5jnkG81xnE0mYTrmybXHnfQvBiT15ynmnb87OXZZ7SfOGwB6EYvdk7D/3Og0aaMHPuZjN9x8GCC03nr/b2AAAuqtPDqKWf682LPXnJlqFtz0UOIxY3GRGOp/DCkT5q7fLQ7zxopAkz597XR2/gsORC0vlhbxi7zwWgVyvw6UvZ1NngxZ68lB9gYc+/XZKJPT//QS8G43QWlnnodx400kTM3C8gnb/ak5m1r19QD7OOzROavNjzQp25A8DiJiMWNRoQjKXw0od0Yu889DsPGmnCzLnH43FWTVPlQtH5gSuEPV1B1KgVuOWSBkqqRsOLPXnZT5OFPQkhuD07e99yyINIYvKzdx76nQeNNGHm3CORCKumqXKh6MzF2jcsakAto1k7wI8902n6T2mygJU921tMmFdfA380iT98OPlwBQ/9zoNGmog89wtA54HuIPZ3h2DQKLFhEdtNgnmxJy+ZE6zsSQjJx96fO9SLWHJyH3Y89DsPGmki8tynuE5JkvCrvZn33nJJA5MMmaHwYs8LMc99JMun1+Iiux7eSBKvdExu9s5Dv/OgkSbMnLtGo2HVNFWmus79PSEccoVg0ipx80K2s3aAH3sqFHxsH8zSnsNm7wd7J1VQjId+50EjTZiNcJPJxKppqkxlnZIk5TNkbr2kAQYN+wwR1vbcvn07li9fjvb2dmzatGnU8R/96EdYsWIFVq9ejfXr1+PcuXMF2+HFubO258pWM2bZdOgbTOC1YwNlt8PDfcSDRpowG+H9/f2smqbKVNa5pyuIw+4wzDoVblrAftYOsLVnKpXC/fffj82bN2PXrl3YsmULOjo6hp1z6aWXYseOHXjnnXdw44034qGHHirYFi957qzHp4IQ3H5ZZva+4+QAwmXmvfNwH/GgkSbMnLvVSrfaICumqs54Mo3fHXKjwajGpy9tQE0FZu0AW3vu2bMHM2fORFtbGzQaDTZs2IBt27YNO+fKK69ETU0NAGDZsmXo7u4u2BYvOzFVYnyunmnBurk2fOAK4/F3z5WVJsrDfcSDRpowG+H9/f3wer2oq6uD3+9HIpGAw+GAy+WCwWCAUqlEIBBAfX09BgYGIEkS6uvr4Xa7YTQaAQChUAiNjY3weDwghMBms8Hj8aC2thapVArhcDjfplqthtlsRl9fH8xmM+LxOCKRSP64RqOByWRCf38/rFYrIpEIotEoVCoVvF4vdDod9Ho9vF4v7HY7gsEg4vF4/v16vR4ajQZ+v78q15ROpxGNRou6JofDgcfePIm9XTHMtGiwxDiIUChUkWsKh8NQqVTU+8nhcODgwYOw2WwIBALwer2w2WzYvXs3nE5nwWv6xS9+gSuuuGLY8dw19fb24stf/nJ+Bn/nnXdi7dq1FR17uePjjb3Ozk7U1dUxH3vXTtdgx4nM1outujiubjWWdE1utxter7eoa6rW/RSNRqFUKpn0E81rovUhRFg9zLF//36ptbWVSds0cTqdmGo6dzn9eOj1U1ApCDbdOBdz62oYqzsPS3u+8MIL2LFjBx5//HEAwLPPPou9e/fikUceGXXu5s2b8bOf/Qwvv/wytFrtqOMHDhzA4sWLmeikSSXH52vH+vG9t89Cq1Lgx+svxnRL8Tt08XAf8aARAKxWK5WqdiLPfYrp7A8n8P23nQCAu5Y1VdSxA2zt2dzcjK6urvzv3d3dBf/em2++ie9///t45plnCjp2QOS5F2LtHBs+OtuKWDKNjW+cQbyE3Hce7iMeNNJE5LlPIZ1pScKjb51BIJZCe4uJaZmBsWBpz6VLl+LUqVNwOp2Ix+PYunUr1q1bN+ycgwcP4r777sMzzzyD+vqxF5FFnvtoCCH4p49MR3OtBif7I/jZ7sLrFYXg4T7iQSNNmDl3nY7epsssmUo6nzvYi33dIVh0KvzzVa1QVKFmOUt7qlQqPProo7j11luxYsUKrF+/HvPnz8fGjRvzC6sPPfQQwuEw7rrrLqxZswa33357wbZ4SYWs9Pg0aJR48KMzoVIQvHjEg11Of1Hv4+E+4kEjTZjF3J1Op8TDbuOBQICLXdEn0tnRG8a9vz+GlAT870/MwvLp1amAx4s9Dx8+jIULF1ZbxoRUy56/O+jGk7u7YdIq8dMN81BvGP8BIB76nQeNAAcxd6+X/ia8LJgKOn2RBP7PG2eQkoANi+qr5tgBfuzJS557tey54ZIGLJtmQjCWwnfecCKVHn8SyEO/86CRJsycu91uZ9U0VXjXGUmk8O+vn4KtRo159TW4+/LmCisbDi/25CXPvVr2VBCCf76qFTa9CodcIfx6X8+45/PQ7zxopAkz5x4MBlk1TRWedUYSKfzbH0/hcO8g3KE4Hrp2JjTK6saSebEnLyV/q2lPq16Nf7m6DbYaFd446cPL45QG5qHfedBIE7FZB6c6o8k0vvnaKRxyhWCvUeO718+BfYK4aCXgxZ68OPdq23NJiwl3tjehOxDD4++ew0tHCu/cVG2dxcCDRpqIPHcOdcaSaTz02ikc6AnBVqPCdz95EVrMhfO5Kw0v9hR57sWz7uI63LOiBQDwxM5OvHB4tIOXg86J4EEjTUSeO2c648k0Hn79FPZ1B2HVq/Do9XMwzSyfFC9e7Cny3Evj5kUN+PLKaQCAH+/qxNYPeocdl4vO8eBBI02YOXe9Xs+qaarwpLM3FMeDr57EaW8EFp0Kj15/EWaU8Ih4JeDFnrzkucvJnjctrMdXV2Uc/OvHBvCff+3MZ9HISedY8KCRJsxSBngpjM+Lzg/6k/jRHzsQjKVwWbMR/7hyGlqt8husvNiTVOEBr3KQmz0/taAeZp0Kj71zFlsORXDME8G/XtMmO52F4EEjTZhNX/z+4p5sqzZy15lMS3hqdxe+864bwVgKy6fX4l+vmYk2GTp2QP72zJFKlVe3vNLI0Z5rZlnxrY/Phq0mkyb5jy904P0zk99kmzVytCVLmDn3uro6Vk1TRc46e0NxfP3l49h8sBcKAnzx8mb8x8dnwayTb462nO05FF7y3OVqz0UOI368fh4udRgxMJjE9/cE8buDbqQZPfFOA7nakhVi5i5Tne+e8eGe5ztwpDeMuho1vnGFFZ9Z3FiVejGlIFd7jkTM3CePrUaNR66/CLde0oCUBLx92of7fn8cJ/sHqy2tIHK2JQuYTV94yUaQm85zvih+trsL53xRhOOZMMw/X9UKn7tr4jfLALnZcyxY1VSijdztqVQQ/P0VLZiujuCXH0YwEEniyy8cxU0L6vH59qaK7NtbLHK3JW2YFQ5zuVzSWLW05UQsFhuz5nclCUST+PU+F35/xIOUBOjVCnx11XRcc5EVCkJko3MieNF55MgRLFiwoNoyJoQXe8ZiMSSJCr/c04OXjniQlgCbXoUvXdGCa2ZbZbGAzYstZV84jJec0mrrjCVT2HKoF3c9dwQvHM7cFNddbMcvPr0A186x5cMw1dZZLLzo5GUWx4s9XS4XDBol/nHlNPxo/cVY0GDAQCSJTX8+i6//4Th2On1Vj8fzYktaMAvLGAwGVk1TpVo6vYMJvNzRh98f6UO9UY1gLIUlzUb8/RUtmG0fvXuSsCddlEr5hAvGgxd7DtU5216DH3xqDl4/PoC/OP141+nHIddptFp0+MziBnx0tg0qReVn8rzYkhbMnDsvN0+ldZ7sH8QLhz3YccKLRPYBkAUNNbhjbRNWzKgd8+ursOeFCS/2HKlTQQg+MdeONTMtePVoP5471AunL4rvvnUWv9zTg1sXNeDjc+2oqWBMnhdb0oKZcw8EAtR28WZJJXRGk2nsPOPDtqP9ONATAgAQACtnmLFhUT0ubTJOGJMU9qQLL9kyvNhzLJ16tRI3L2rADfPr8MZJL5494MY5fwxvnPLi5+/3YM1MCz5xsR2LGg3M4/K82JIWzBZUu7q6pJqaym7OXA6Dg4NgoTOeSmNPZxBvnvJil9OPaDKNVosOveE4PjHXjpsW1JdU7IuVTtrwopOXBVVe7FmszrQkYafTj3fP+PCnE+c3z2gyafDxOTasarOgzapj4uh5sSWtBVVmM/eBgQEuDElT52A8hf3dQfzlrB9/PuNHOH5+dnhxfQ1unF+Hla1mGLWlm/1CtCdLeNmJiRd7FqtTQQhWt1mwus2CO5Y48NqxAbx2fABKBcEv97rwy70uNNdqsbrNjI+0WXBxfQ21Zzt4sSUtmDl3XvKIJ6MzLUk40R/Bns4A3u8M4og7hJQEXFxXg3A8hVk2Ha6aZcXVs6xoqp1cCtaFYE/BaHixZzk6W8w63HV5Mz7f3oRDrhDeOOnFTqcf3YEYNh/sxeaDvWi16NBm02FJswlLmk2Tuo94sSUtmIVlenp6JB52G49Go0Xvih5PpXGiL4LD7hCOuMMIxJI45ArnjysIMK/egI/OtuCyZhPVwl6l6KwmvOjkJSzDiz1p6UylJRx2h/HuGR9O9Q/iwJD7CwAajRosaTZhkcOABY0GtNRqiw7h8GJL2Ydl3G43WltbWTVPjbF0ptISzvqiONkfwemBCA67wzjeN5jPcAGASx0GNBjVaG+pxbJptVjSbCwr5DIZnXKDF5285LnzYk9aOpUKgkubjLi0yQhJktDpj2FfdxD7u4M40BOCOxTHX8768OqxfgCASavExfU1mFdfgzl1mR97jbqgw+fFlrRg5tyNRiOrpqliMBjgCcfh9EZx1heFN5LA/u4QTg9EEE+dd+QmrRKJtIRWqw4LGw1Y0GDAwkYDmkuYOUwGXuzJi05ee8BGuwAADpVJREFU0uJ4sScLnYQQTLfoMN2iw40L6pFKSzg5EMFxzyDe6wygozeMgUgS73cGcXogil/vcwMAarVKzLbrcYnDiDqDBq1WHWZYdNzYkhZ8lMabJJIkwR9NojsQR3cghu5ADF2BGLr8UbgCMQTi5/LnzrBocdYXAwA4TBpcZNdjtr0G8xsMmFOnh4nRzFwgEIyPUkEwt64Gc+tq8Mn5dZAkCZ5wAh/2htHlj2JfdwinBiIIxFLY1x1CMg0ccoXy77folLisOYAajRIttVo0Z38cJg30aj4+7EuBmacKhUKw2+2smh9GNJlGfziOvnACnnACwXgS53wx9IbicAfjcIfimG3T43BveNR7G2oUAFFihlWXXbzRo9Wiw2y7vBx5Je05GXjRyUueOy/2rIZOQggajBo0GDObcNy+BHmHf7I/AlcwhjqDGud8UZzzReGLpvBeZwDheGZzdKteBW8kkzVl1qngMGkw26ZHjUaJeoMajUYNbDVq1BnUsOrVUFbhqdrJwMx7NTY2Tur98WQavmgS/uxPOJZCbzgObyQJbySBgcEk9GoFDrlCCMaG36hDZ985dGoF5tTp85/WLdkfuxZwWOX/dW2y9qwUvOjkZYNsXuwpF50jHX6OtCThbF8AnihBV/bbeySewuHeMNyheN7P9ARiCGT9yWy7Hif7IwAyyRKXT6vFQCQBmz7j7KdbtFArFbDoVLDqVbDoVajVqVCrVcnig4CZc/d4PGhumYZwPIVwPIVQPIVIIo1ANIlQPIVQLIlgPIVkSkJvOI5gLIVANIlgLIUWswZ7u0LD2ptbp8exvsiw19qsOgRjKagVBHaDGnU1atgNajSbtPjkPBUaTRo0GjM/Yy10njt3DuDAuXs8HkyfPr3aMiaEF5285LnzYk+561QQAmU0gMunT8flI46lJQnewSR6AlH0Zr/994bikJB5krwvnIAv65uO90UAZPzQpQ4jDg4J+1ziMOSz50xaJWq1Ksyp0yOSSMOkVcKkVcGYfd2gUcKoVcKoyfzUaJQwaJTQq+nVcmTm3P+nI4ztf9w/7LWhF5+jzarDGW902GsNRjVUCgKzTpX/mW7RYqHDmP3UVMFWk/nXXqOGWacqe1FTDqVIi0HovDDhxZ486BxLo4JkJod2w9jf5hKpNAYGExgYEjmIJVNotergi2Zes+jUqNUqEYyl8j8qJYFziH8jAEYmnxs1SoSyDzwSALv/+ZpJXmkGZs7dbNBDQSIwaJSoUWc+lZpqtTBqVZlPK60SJo0SdoMaWqUCJq0KtbrMp5pJmzm/EgPGZrMx/xs0EDrpwss2e7zYkwedk9GoVirQaNKi0TTxQ1SptIRQPAV/NIlgNIlALIVgLDPzD8dTCAz5fyiWQiSRglalQDieQjSZLlvjSJiN8OBftmLbvV+T/Sf6T3/6U9x3333VljEhQmeG7du348EHH0QqlcLnPvc5fO1rXxt2PBaL4Z577sGBAwdgtVrx85//HDNmzBjVjsfjYaaRJqLf6VEpjcohUYdSSaUlEEL+XpKkJyerg9lmHS+98LzsHTsAvPDCC9WWUBRCZybD5f7778fmzZuxa9cubNmyBR0dHcPO+fWvfw2LxYI9e/bgnnvuwcMPP1ywLa/XW/B1uSH6nR48aMwuxP49jbaYOXeBgDZ79uzBzJkz0dbWBo1Ggw0bNmDbtm3DznnllVdw2223AQBuuukmvP322xdcTRGBAGBYW2br1q2SzWaDSqVCKpWCJElQq9VIJBL5pwNTqRTUanU+c0GlUpV1PJFIgBACpVKJZDIJpVIJSZKQTqfzxxUKBRQKBZLJJFQqFdLpNNLpNPx+P8xm85jHh76fEIJUKlWVawoEArBYLEVdUynHaV9TMBiE1Wql3k9qtRr9/f0Ih8OYPn16/m+Fw2E4HI78+0+dOoW2tjYoFAqoVCp0dHRg5syZ0Ol0wzSFQiG43e6847fb7aitra3o2CvmuM/ng8lkqurYK+aafD4fjEZjVcfeRNcUCoVgsViY9BPNazpz5szhz33uc4sm9rLjIzbI5mTTXKEz87V6x44dePzxxwEAzz77LPbu3YtHHnkkf87KlSvxu9/9Di0tLQCApUuXYvv27aMW04Q96cKDTh40AmKDbGoInXRhqbO5uRldXV3537u7u+FwOMY8J/eNp9DuO8KedOFBJw8aacLMufPyBKDQSReWOpcuXYpTp07B6XQiHo9j69atWLdu3bBzrrvuOvz2t78FALz44ou48sorCy7sC3vShQedPGikyaScOyHk04SQw4SQNCFk2dBjTz/9NNrb27F8+XL86U9/Kvh+p9OJa6+9FsuWLcPdd9+NeDw+GTlFcffdd2PNmjVYs2YNFi9ejM985jMFz1u8eDE+8pGPYM2aNbjmGjoPFZTCd77zHSxcuDCvdc+ePQXP2759O5YvX4729nZs2rSpwiqBb37zm7jiiiuwevVqfO5znxvzPBr2VKlUePTRR3HrrbdixYoVWL9+PebPn4+NGzfmF1bvuOMODAwMoL29HT/5yU9w7bXXFrSP2WwGkPmqfvfdd6O9vR3XXnstzp49W5a2cuns7MSNN96IK664AitXrsRPf/rTYcfNZjPeeecdtLa25sfCo48+WlGNOcbrQ7PZDEmS8MADD6C9vR2rV6/GgQMHKq7x+PHjeTutWbMGM2bMwE9+8pO8RgBVs+dXvvIVzJ07F6tWrcq/5vV6cfPNN2PZsmW4+eab4fP5Cr6XEPIFQsjx7M8Xivl7k4q5E0LmA0gD+E8AX5ck6f3s6wvmzJlz+O2334bL5cLNN9+M9957b1SZ1bvuugs33HADbrnlFtx3331YtGgR7r777rL1lMq//du/IZ1OY+PGjaOOLV68GDt27Kha0abvfOc7MBgM+OpXvwog80E4shZ1KpXC5Zdfjq1bt6K5uRkf+9jH8LOf/Qzz5s2rmM4dO3ZgzZo1UKlUePjhhxEIBPCDH/xg1HnVsOd49snZ87/+679w+PBh/OAHP8CWLVvwhz/8AT//+c8rptHlcsHtdmPx4sUIBoO45ppr8PTTT+f70Ol04ty5c3jiiSfy30iqxXh96HQ6cezYMTz55JPYvHkz3n//fXzjG9/A9u3bq6A0QyqVwsKFC/H6669j+vTp+T5/5513qmLPnTt3wmAw4J577sHOnTsBAA899BCsViu+9rWvYdOmTfD5fPjhD3847KsmIcQG4H0Ay5B5wHUPgHZJksbP55UkadI/AN4EsGzI798A8I0hv/8RwMoR7yEA+gCosr+vBPBHGnqK1EwAnAMwZ4zjZwDUVUpPgb//MDIfmOOdM8xmI+1eBc03A/iNXOxZjH2Gjk1kHurrQ3bSUyUbvghg7YjXrgbwcrU0FduHyEzyPjvk96MAmqqo9+MA3i3wetXsCaANwAeFbASgCcDRAu/5LID/HMvOY/2wirm3IOM4c3RmXxuKHYBPkqTkOOew5EoAbkmSjo9xXALwGiFkDyGEykMFZfAVQshBQsjPCSGjVwWLs3MluRvAtjGOVcOexdgnf052LPqRGZsVhxDSBmAJgL8WOLySEHKAELKNELKwosLOM1Efym083gbgf8Y4Jgd7AkCjJEk9AJD9t6HAOWXZdcLnYwkh2wE4Chz6V0mSXhzrbQVeGxn/KeacsihS82cxdscDwEckSeomhDQAeJ0Q0iFJ0ts09BWjE8BPAHwLGZt8C8D3kXGew5oo8F7qua3F2JMQ8q8AkgB+M0YzzO1ZgKqOw1IghBgBbAHwNUmSAiMO7wXQKklSiBByPYAXAMyptEZM3IeysCUAEEI0AG5E5tvaSORiz2Ipy64TOndJkq4tQ0wngKH1P6cB6B5xTh8ACyFElZ0xFTqnLCbSTAhRAdgAoH2cNrqz//YSQp4HsBwAVWdUrG0JIT8D8HKBQ8XYedIUYc8vALgBwMek7PfGAm0wt2cBirFP7pzO7LgwAxhgrGsYhBA1Mo79N5IkbR15fKizlyTpFULIjwkhdZIk9VVSZxF9WJHxWCTXAdgrSZJ75AG52DOLmxDSJElSDyGkCUBvgXM6kQkl5ZiGTCh8XFiFZV4CcBshREsImYnMp+LuoSdkncAbAG7NvvQFZOKNleBaAB2SJHUWOkgIMRBCTLn/IxO7+6BC2nIamob8evMYf/89AHMIITOzM5XbkLF9xSCErAPwLwBulCRpcIxzqmXPYuzzEjJjD8iMxR1jfUCxgGTyNP8LwIeSJI1eic6c48ieB0LIcmTu2/5Kacz+3WL68CUAnycZVgDw50IOVWDMb+ZysOcQho6/sXzgHwF8nBBizYZnP559bXwmuThwMzKfKjEAbgxfvPpXACeRWTC4bsjrrwBozv5/FjJO/wSA5wBoK7So8d8A/mHEa80AXhmi60D25zAy4YdKL7w8DeAQgIPZAdA0Umf29+sBHMvauho6TyATD9yf/fmpnOxZyD4A/gOZDyMA0GXH3onsWJxVYfutRuYr9sEhNrwewD/kxiiAr2TtdgDAXwCsqkI/F+zDEToJgB9lbX0IQ5IsKqy1BhlnbR7yWtXticyHTQ+ARNZv/h0y6zt/AnA8+68te+4yAE8Nee/d2TF6AsBdxfw9ZuUHBAKBQFA9RFVIgUAgmIII5y4QCARTEOHcBQKBYAoinLtAIBBMQYRzFwgEgimIcO4CgUAwBRHOXSAQCKYgwrkLBALBFEQ4d4FAIJiCCOcuEAgEUxDh3AUCgaDKEEIshJAbCry+ixDSXE6bwrkLBAJB9fkYMkUVMWI/6t8js5VpyQjnLhAIBDJAkqScE79/yMsuSZJc5bQnnLtAIBBUnxUAQAhZCyCc/f+nkdnUqCyEcxcIBILqM0gIOYbMRkKEEHIKwDRJksrefEfUcxcIBIIpiJi5CwQCwRREOHeBQCCYggjnLhAIBFMQ4dwFAoFgCiKcu0AgEExBhHMXCASCKYhw7gKBQDAFEc5dIBAIpiDCuQsEAsEU5P8CXAtp83m7aEkAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"tg = - sym.diff(phi, w)\n",
"sym.plot(tg.subs(RLC), (w, -10, 10),\n",
" xlabel='$\\omega$', ylabel='$t_g(j \\omega)$');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Combinacion de Sistemas\n",
"\n",
"## Sistemas en Serie\n",
"Cuando dos sistemas lineales invariantes en el tiempo (LTI) se combinan en serie conectando la salida del primer sistema a la entrada de un segundo sistema, esto se denomina *concatenación* de dos sistemas o sistemas en *serie*. Denotando las respuestas de impulso de los dos sistemas por $h_1(t)$ y $h_2(t)$, la señal de salida $y(t)$ del segundo sistema se da como\n",
"\n",
"$$\n",
"y(t) = x(t) * h_1(t) * h_2(t)\n",
"$$\n",
"\n",
"donde $x(t)$ denota la señal de entrada del primer sistema. La transformación de Laplace de las respectivas señales y respuestas de impulso, y la aplicación repetida del teorema de convolución produce\n",
"\n",
"$$\n",
"Y(s) = \\underbrace{H_1(s) \\cdot H_2(s)}_{H(s)} \\cdot X(s)\n",
"$$\n",
"\n",
"Se puede concluir que la concatenación de dos sistemas puede considerarse como un sistema LTI con la función de transferencia $H(s) = H_1(s) \\cdot H_2(s)$. Por lo tanto, las siguientes estructuras son equivalentes\n",
"\n",
"\n",
"\n",
"La extensión a una concatenación de sistemas $N$ es sencilla. La función de transferencia general viene dada por la multiplicación de todas las funciones de transferencia individuales $H_n(s)$\n",
"\n",
"$$\n",
"H(s) = \\prod_{n=1}^{N} H_n(s)\n",
"$$\n",
"\n",
"Las aplicaciones de los sistemas concatenados incluyen, por ejemplo, el modelado de sistemas de transmisión inalámbrica y filtros en cascada."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Ejemplo**\n",
"\n",
"La concatenación de sistemas LTI puede usarse para construir filtros de orden superior a partir de prototipos de orden inferior. Dichos filtros se conocen como *filtros en cascada*. La función de transferencia $H_0(s)$ del paso bajo se da como\n",
"\n",
"$$\n",
"H_0(s) = \\frac{1}{LC s^2 + RC s + 1}\n",
"$$\n",
"\n",
"donde $R$, $L$ y $C$ denotan los valores de la resistencia, el condensador y el inductor. La concatenación de los filtros de segundo orden $N$ conduce a un filtro con el orden $2 N$. Su función de transferencia se lee\n",
"\n",
"$$\n",
"H_N(s) = \\left( \\frac{1}{LC s^2 + RC s + 1} \\right)^N\n",
"$$\n",
"\n",
"La función de transferencia resultante se ilustra mediante su diagrama de Bode para un número variable de filtros en cascada utilizando los valores normalizados $L = .5$, $R = 1$, $C = .4$ . Primero se define la función de transferencia $H_N(s)$"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAMQAAAAgCAYAAABNc9f/AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAHuklEQVR4Ae2ci1EcORCGWYoAMCHgDLAdgSEDfI7AXAa4HIELZ2AcwZ3JAIjAnDMwGfiODLj/06rHox1pZj07T1ZdpXno2f2rW93SLCweHx93MmUEnjICi8XiVPL9qXTMXTp/afKqjLzPSgdKl4tsEAZNvj9lBKT4Z5LvjdKhdP55WVaVnev9Rvnfd8sF+Tkj8IQRwAjwEofeK5RFfY4xkJENogxLfn7SCEjp7yXgjdL7lKB7qYI55cviL8TvvtKhEkK/l/APumfKCOxIP9CNnx4KdOVaeYRO977sh8E0ew/hjeGzhGOzdCLB2BzdmoD5nhEQAmyc8Qw70hHubtHkXUSZC5d4qRiEFOxIiUpzIU4QyvRRL8iAt8g0cQQ0T2xo+6ZXMoRC6TUYXuJMY+M5KHPGAhNByKQKR8q78Cst5XMhC5Xg10Klct5c5NhGPr9L775K5zgBSpLq2NFpso4veKO+TAesLopfkMov1Z8zCmUGZYFBqPCL0uui5QweJFxwhCaWMWrobnnL1ykjoPm7kXKeKJ2hqCleVXalMlIbWjUQ+mCsD/7Ou6PiO4QY4uPEDw38yZfN8iY52CCxp5i1HLMEfwOm/by90LzFlLd1z+qX8H/fG1TRj/LxDP8p4VEKQ3MGoULCCxTp2ToM+c740MEmtizAtdrjjuiPTW5wvKV8a2NxP3EdGxzXTveNSP270yaNy3nz6NQWJxiPYGWTxkQaEWokV1WrNIe75GUvwfeAzuZOfbLI/6H0rxL6WOwV9A7GlLNFQAeXpBceUCRWVXbhtUn1YBzLwsUFdZWHojNItNzqq5xB8UZB+03e1R/GtpYMm4yzblvxsjFOjCXiwoIRYKU8Fh3KMIqgbGrv4hG9QCdYqaO8qszJkyofKt8x55k9rRsUYZSulfAkdYJhEEwU57wV4ZWPC6Mcy6yUt8nzfRb9+fejln0xeedt2tJG1AlOvi/2Q3Qa5Uf5X315K1mbZFTfrbFQW3CAP/TB+EzqjZcX3aostE18dlm+K7cB6DAfuBO9r9KtMlDmpjgP4R/E5C83FPZEmAVhXBuT5x8P903PpyQ9E6qlxt94zIYOusKJYcAbSs2NHSA8LKtN56r5RweIzwmBvq3JGXLWnjat2U/rantq+VIJ5pOgSsmwcsCPHWkpOyDitb+DnPDFTbLGS01yWLv5DQW01aioXSdPUanjh45xgju3R5Ms5TN0x7U3fMIMfpQ2lvE7Xjq84CGI+UcjDOKFUhJQAQ/oxOf3At42dnpNEn2xYqcIw6pMcKoy+eKB/uzTO4Z7Z0qi+zPqjE094IRILB4VzL0xcER+JfmjK2odZnQ8UUIv9sU7oVVyge6TdwwChWdVT5Ht+vESjeQFiQojQZ13UCdrewe1+Uf1+W2Sa6N3Qi2M2PjS4yTI+NkYJ6SRnBYO8cwGHcJjgCEnS6+FSXRhmRFmEiMg00N0MipbULuHFwziQCnpIVRGTA6trcTL6tHrb+0fNLEAw4axPPaY+4OoUD6zS5zo0haPd36RIe+TMMFbY3zBkTaF0MwwWzL962oLKTo5CmEQ+0pmmTEmjLk6oynaaULq3J2b5BUFL9rysNLe8aU8juzYl3DEWDYOmrQi9UkYZkpX7gM8DlT+tpzpnwkboyEKbaxOpF0la0XOSrkybP9gSuLqaHy+8+CFPijFjOK3MesBC8frBhfmYDQiJEmeZauMjY7mofmIVPVYJZNHgPSjVDlTt75VxuoXHNfqHaUlTKJtbXvrZ5O7xkCG6DFnXb9q0xlOjCPiUpkX5eE1o2XGn8o7wUz9tMLC+LC7+iHkg2cWy+RRu8pNtuO6en2W7YqJJrLYHWab6ETMRmM/rUK2Gtcdt3Kk6zyR6vOXTXwb4RSF1ZLNMyviMWVNjIxQ3glO8C35jjz/MaysrOLVZ4jZ6jSZZ1grGllt3MU7BsHgxkisTzsxsk1jrA6TSL2YC7f6tn+IhjxqzyqCtzLie8YXe5FRcDTsfp+k+2iAGT+Re1c40bUtHneRcV75PDySI2Fn8zc3zEwEu1vYWTF2q9D3HYPgo8nL1EBe+YibzwU8IU1AyuNjGDHtR5Q2KAxfcL+4y4oHUXuUiVT+fgEonCYVpHoYTZ3RFXWHfugQJ1h/yyWGlbILQ6COMMFjmAHNCjP4XyE8PwtfnR6tNOn2dU/doaC1Z79i8ErAE7Jc6I4bN4aZAOLcqPdQXVYuVnkEJTGBrGJG5FkIwJm69Us5fWJsPJNPX+t+C6HN4NQWJ2NUsrKwsDg5TDxWwQ8fNQabahYKfjLtmirPeU69TAozLw+rvhnsrfLw7oFMTojlBbliXrFUpd9H+7Urpzh8hY6GM/2yMK3eNWF4Mjb2pmTTYnBAbobGQuMRMv81JvZmEKxMuKpJhiMD6gAeDE90ICymuE8ZEopBsfC4szCv9ScIfQFhBoGLvpUSTOJnEH0Jm/udLgIyCPannFKmvvMMwrwzCEYSQ8T2uKvKb2cG4SQPstUISP84LCBsZ087GpUNglABLxGc7IzGWR54axDw3oG/lhs9ZC8MAvTFGBtK3Fb01GhrZigLOhgC0jlOGvlLR/tONdjYsYECg6CCNwo22Ft/4hQDLOd1i4D0jQOdyfynxYpBdCtu7i0jMC8E/gcQEKEGj5AuOQAAAABJRU5ErkJggg==\n",
"text/latex": [
"$\\displaystyle \\left(C L s^{2} + C R s + 1\\right)^{- N}$"
],
"text/plain": [
" -N\n",
"⎛ 2 ⎞ \n",
"⎝C⋅L⋅s + C⋅R⋅s + 1⎠ "
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"%matplotlib inline\n",
"import sympy as sym\n",
"sym.init_printing()\n",
"\n",
"s = sym.symbols('s', complex=True)\n",
"w, R, L, C = sym.symbols('omega R L C', real=True)\n",
"N = sym.symbols('N', integer=True)\n",
"\n",
"H0 = 1/(L*C*s**2 + R*C*s + 1)\n",
"HN = H0**N\n",
"HN"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"El diagrama de bode para la función de transferencia $H_N(j \\omega)$ se muestra para $N = \\{1, 2, 3\\}$ (línea roja, verde, azul)"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZYAAAFBCAYAAABUw4kBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy8QZhcZAAAgAElEQVR4nOydd3zURf7/n7M1CSkQQm8BBKSJ9CYdAjZAEThQadb7enq2s53nz/POcud5eqjnCSqgVBFFVJTQQXpT6dJCLyYkhNTN7s7vjw2QsuWzm89md2Gej0cebOY98/68lvdOZufzmXmPkFKiUCgUCoVeGEItQKFQKBRXF2pgUSgUCoWuqIFFoVAoFLqiBhaFQqFQ6IoaWBQKhUKhK2pgUSgUCoWuqIFFoVAoFLqiBhaFQqFQ6IrfA4sQIiYYQhQKhUJxdeDXwCKEeBnIEUL8p/j3pkKIYUKIKsEQp1AoFIrIw98ZS1UgDrgohLgfSAX+CuwSQtTXW5xCoVAoIg9/B5adUspcKeWLQDegpZTyRuAPwCu6q1MoFApFxOHvwFIyY+WXUkobgJTyOyBNL1EKhUKhiFz8HVjuFkLcLISIAuxlbBk6aVIoFApFBGPys34+MB74AEgXQnQCfgQ2UXo2o1AoFIprFOHPeSxCiI5Sym3Fr1sB/YC+QA/AJKWsFQyRCoVCoYgc/BpYPDoRQgCvSSmfr7gkhUKhUEQy/u5jaeKuXLpGp891UaRQKBSKiMbfZyzLhRDZwHZgGbBcSnlGCDEYiAd26C1QoVAoFJGFv89YUoClQAfgL7g2S8YBGwG7lPLJYIhUKBQKReQQ8DMWIcTNUsrvhRAWYABQW0o5TVd1CoVCoYg4KpLduIcQIkFKaZNSfg+c0UuUQqFQKCIXf5+xlORTYLUQYifwE1Af+F4XVQqFQqGIWCq03Lg4hf6dQA1gjpRSzVoUCoXiGkevfSyDgXNSSrUqTKFQKK5xAn7GIoT4RAhxWAjxJRANtNNPlkKhUCgilYo8Y1kopZwkhOgBjANydNKkUCgUigimIgOLA0BKuR5Yr48chUKhUEQ6FVlu3F0I8aUQ4k4hRIJuihQKhUIR0VRkYDkFvAd0BlKFED/oI0mhUCgUkUxFdt53AGpKKX8o/j1aSpmvpziFQqFQRB7+ZjcedOm1lHJ7iUFlAGDVWZtCoVAoIhB/b4UNuPRCCPG5EGKzEOIRYAtwi67KFAqFQhGR+DWwSCmfK/HrAiAF18qypcBtOupSKBQKRYRSkWcsiUAHKeUyfSUpFAqFIpLRJaWLQqFQKBSXqMhyY4VCoVAoyqFp570Q4hkgqmSRm2qyhC1PSvlmBbUpFAqFIgJRt8IUCoVCoSt+5woTQsQCPYBmQDyQi+v0yPVSyhP6ylMoFApFpKF5xiKEaAX8AbAAP+NK6ZKFK2V+InADUBVYKqWcFxS1CoVCoQh7NA0sQojRQAwwW0pZ6KNuZ6Af8K5K8aJQKBTXHloHloZSymOanQphBGqoo4oVCoXi2qMiGyRrA04p5Tl9JSkUCoUikqnIwLIeWITrwX26lPJbPYUpFAqFIjLRZbmxEOIuoJ6U8j8Vl6RQKBSKSEa3fSxCiINSyut0caZQKBSKiKUiZ94jhOgIPAPkAGt0UaRQKBSKiKZCucKklNuklKOBucBZfSQpFAqFIpIJeGARQlw+2EtKuRS4QxdFCoVCoYhoKrIqLAHojyvpZDdciSdf1k+aQqFQKCIRvwYWIcQHUsrfF7++AagFrJVSFgRJn0KhUCgiDH8Hli5Sys3Fr98GzEBvXHnDlgALpZRHgiFUoVAoFJFBRW6FjZFSzil+3RgYDNwJfKySUCoUCsW1S0UGlligi5RyRZny+6WUH+khTqFQKBSRR8CrwqSUOW4GlSHAxAqrUigUCkXE4nPGUnybq6uUcq4mh0I0BG6WUn6ogz6FQqFQRBha0+Y3Bh4GjgMrgT2yREMhRBWgCzAQyADekVI6g6JYoVAoFGGNv6vCbgBuBzrjOjnSCBQB54DVwFdSyswg6FQoFApFhKBbEkqFQqFQKKCCucIUCoVCoShLhbIbX6L4gX0MkA3UkVJu08NvMMjMzCw3RcvKyqJq1ao+y0KJHnoC8aG1ja963uyebOEeF720BCsu12JMQPUVf/VopVq1akJrXV0GFuA+wA60wfW8JWwHFndER0drKgsleugJxIfWNr7qebN7soV7XPTSEqy4XIsxAdVX/NUTDPS6FbZMSvk3KeVoKeWjOvmsNM6cOaOpLJTooScQH1rb+Krnze7JFu5x0UtLsOJyLcYEVF/xV08w0GvGcrMQYhyQDqySUi7RyW+lYDabNZWFEj30BOJDaxtf9bzZPdnCPS56aQlWXK7FmIDqK/7qCQZ+zViEEJ09mL4DXgbeAGwV1FQhhBBDhBD7hRAHhRDPaWmTkJCgqSyU6KEnEB9a2/iq583uyRbucdFLS7Dici3GBFRf8VdPMPD3Vti9QghL2UIp5Top5Ukp5QUp5UqdtPmNEMIIvA/cDLQCxgghWvlql56erqkslOihJxAfWtv4qufN7skW7nHRS0uw4nItxgRUX/FXTzDwd2AZC5wXQqwQQvxFCHGTEMIMIIToob88v+kCHJRSHpZS2nAdmTzMV6NwG+3dob6F+aenMlAzFu1aKhPVV/zTEwz8HVgeBxoCU4EUYCaQKYRIBf6us7ZAqIcr7cwlThSXecVmK3/3zl1ZKNFDTyA+tLbxVc+b3ZMt3OOil5ZgxeVajAmovuKvnmDg18N7KeXM4pdzhBAWKeUMIUQ9XId9PaK7Ov9xt8661L6V1atX89e//vXy7+PGjaNfv37lGuXn55f35HCA0VhhkYHgVk8l+NDaxlc9b3ZPNnflevw/6IVeWoIVl2sxJqD6ir96goG/ucLGSilnF78eJ6X8tIRtdKgP+BJCdAdellIOLv79eQAp5euX6mzYsEFef/31pdoVFhZitVp9lsV36ICw2XA2aICjYUOcDRvirF/f9W/xa8q00Qt3eirDh9Y2vup5s3uyaY1LqNBLS7Dici3GBFRf8VePVvzZIOnvrbD/E0IMKz7kqxShHlSK2QI0E0I0Ll5k8Dtgka9GmtaAOxzstp+k4LdTmDZtwjp/PtFvvUWVJ54gbsQIEjp3plqdOiS0akXc4MFUeeABol55Bcv06ZiWL8fw669QgW8Qam2+f3oqA7WPRbuWykT1Ff/0BAN/97HkAJNwPWPJEEI0BdYBG4E7pJQzdNbnF1JKuxDiD8ASXJmXP5FS7vbVzmIpt9CtXJk0GBjyxyQy88/TK7YNQxxNuCU9kcbHsjEcP47h2DEMJ09iOHMGw5kzsGWL22s5a9YsPcu5NPtp0ABngwZQpYpmjf4SiA+tbXzV82b3ZNMSl1Cil5ZgxeVajAmovuKvnmDg78Dy/6SUm4QQBqAD0B94AuiB61lGSAcWACnlYmCxP23i4uJ8lmXkZ2DZPZEC62KW1tnGUrbxVDS06N6ClDEpDEp+hq41OmL5LQPjsWNXBptLr48fx3DiBIZz5zCcOwfbt7vV4qxevfwttgYNSExKcg068fH+vDWf71OvNr7qebN7smmJSyjRS0uw4nItxgT00aP6SsXw9+H9puJ/ncDW4p9/Fi85fkN/eZVDRkYGsbGxXsss9iTS5/8dcl8ludUZqt40lwN1X2X/+f3sP7+fd7e/S7wlnn4N+5HSOIWBNw6kRkyN0hdyOBBnzmA4fhzjpYGn5L8nTmDIyMCQkQE7dpRqekmJs2rVUs90Lr8uHoCklyWG7t5nIP83gdTzZvdk0xKXUKKXlmDF5VqMCeijR/WViqFLShcpZZEQYqbvmuFJtWrVfJbZbIJ77ilk7lwLaXtqw57HqVbtMQbcdpjYHjPZYpvNgcwDfH3wa74++DUCQfta7UlJTiGlcQo31LgBg9GIrFcPR716OLp1Ky/E6UScO1dqlnNp9kNaGqaTJzFkZWHIyoJffnH7Xpzx8ZcHGWeDBldeN2xI9WrVQEoQmp/Buf2/CaSeN7snm5a4hBK9tATiR0ubazEmoI+eYMVES72rIS7X3EFf7laFnT17llq1avksA8jLgy+/tDBtmpUdO66My336FHHb6OPYmn/B8mNL+PHEj9icV9aR14qpxcDkgaQkp9C3YV/iLP5NU8+ePUutmjUR6enlbrEZL/1+4gQiN9erHxkbW+65TsnBR1avXmrg8fT/4Fafl3re7J5s/sQlFOilJRA/WtpcizEBffQEKyZa6oVrXHRPmy+EeAaI0uhTAHlSyje1igg1BQUFmsoAYmLgnnts3HOPjR07jEybZmXBAgurV5tZvboJdeo8zb33PsobYzM5YF9FaloqqUdSOZ17mll7ZjFrzyzMBjM96vVgYKOBpDRO4bqq1yF8zCIKCgpACGSNGjhq1MDRsWP5SlIizp8vf4ut+LU4ehRjTg7GvXsx7t3r9joyJubyLTZHw4bEx8ZivuGGK7faatZ0O+Px9P+lxe7J5k9cQoFeWgLxo6XNtRgT0EdPsGKipd7VEBc1Y6Hia8AvXBDMnWvhk0+sHDjg2kBpNEpuvrmIiRML6d27iL3nd7sGmbRUtp7ZilM6L7dvnNCYQcmDSElOoWe9nlhN2tap+0thQQFRBQWlZzxlBh/DhQtefcioKNfspsTzHUeDBhTWro2xaVNkrVpgKL+KPVzX5lcEtY9Fu5bKRO1j8U+PVvyZsaiBBTh69CiNGjXyWeYLKWHdOhOffGLl22/N2O2uODRp4mDChELGjrWRmCg5n3+e5UeXk5qWyvKjy8kqzLrso4q5Cn0a9GFQ8iAGJQ+ibmzdgPWURZOP7OwrCwuOHSNn1y6qXrhwZeDJzPT+f2CxuAadMrfYTlks1OjUCVmnTrnsBZ506RWXYKGXlkD8aGnjq443e6TGBCqxrwTYJlLjUmknSAohOgJPApeeEl0AJkspN1TEb2UTFVX+Lp+7Ml8IATfdZOemm+ycPSuYOdPKjBkWDh828tJLMbz6ajR33GFjwgQjd3UeycjrR2J32tl6ZitL05aSmpbK7vTdLD68mMWHXSum2ya1JaVxCh3jO1LfWR+jIfCUMpreU3w8jtatcbRuDcD5s2cxl7xPe/HilVVtJQYgx5EjWE+fxpCejvHwYYyHD5dy26z4X2kyXRl4igedmgkJmNq0cQ1EdeqAyeRRbyBxCRZ6aQnEj5Y2vup4s3uyhXtMQB89wYqJlnpXQ1wqNGMRQkwAZkop7cW/W4FxUsqp+sjTH3czluzsbOLL7A9xVxYIDgcsXWrmk0+sLF9uQkrXoN+mjZ1Jkwq56y4bJVcEnrh4gmVpy0hNS2XN8TXk2fMu2xKjEhnQaAApySn0b9SfalH+rfoI5D1pbXO5Xm6ua9l08S22S7MfeeQI5tOnMZw969WPNBpx1q2Ls2FDCmvVwti0aanl1FlxccRXr+7XewgWen1GghUXX3W82T3ZgtlX9EIPPZXSVwKwhzIulXnmfS2ggxDiNOAAagJVK+iz0snMzCwXAHdlgWA0wpAhRQwZUkRamoEZM6zMnGlh1y4TTz5p4qWXYhg9upCJEwtp1cpJ/bj6TGg7gQltJ1BgL+DHEz+yNG0piw8u5mTeSebvn8/8/fMxCANd6nRxLWdOTqFl9ZY+FwAE8p60trlcr0oVnC1a4GzRopT98rQ8P9818JR4vpO/bx/xGRkYjh9HnDmDsXhAcnf+XbzBgKxTB0eDBth790bWqIG9SxccrVpVeoJQvT4jwYqLrzre7J5swewreqGHnkrpKwHYIyUuFZ2xVAHGAy1x5R3bB8yWUmboI09/3M1YcnJyym0kclemF4WF8M03rlnMxo1X/nx261bEpEmF3H57UblclhcvXuRU0SlS01JZlraMDac2YHfaL9vrx9W/vACgV/1exJhjyl03kPektY2vet7spWyFha7UOMeOUXTgANHnzl0ehIzHjyNOnUIUf2btHTpgKs5gIGNjsXfsiL1rV9dPx44VylKgBb0+I8GKi24x8VEezL4SCHroiYi+4qNc77hU2oxFSpkL/LciPsKBixcvlguAuzK9sFrhrruKuOuuIvbsMTBtmpV581yDzMaNZpKSnNx9t40JEwpp1Mi1eiwnJ4cWdVrQIrEFj3Z4lOzCbFYeW3l5oDlx8QTTdk5j2s5pRBmjuKn+TaQkpzAoeRCNEhoF/J60tvFVz5u9lM1qxdmkCc4mTTjTogV16tQpVff00aPUk9I12Pz6K46mTTFt3ozx6FHMq1djXr0acOV2c7Rq5ZrNdO2KvUsXnA0b+rU51Bd6fUaCFRfdYuKjPJh9JRD00BMRfcVHeSjjosvO+5IIIVprSfwYToTykJxWrZy8+WY+L72Uz4IFriXLu3aZ+M9/opg82cqAAa5nMc2bl9YTb41nWLNhDGs2DKd08tO5n0g9ksrStKXsOLeDZUeXsezoMlgNzas1J6VxCu2i2zG05lDMRnc3mdwTdocXAc7kZJzJydCrF7b77gNAnDmDafNmTJs2uQaaX37BtGsXpl274JNPAHDWro29SxfXT9euONq2hQok6lMHfWnXUpmog7780xMMKnor7HkodStcAB2llEMrKixYBGMfi55ICVu2uDZeLlxoobDQ9Q27Xj0HEybYuOeeQmrV8h6zs7lnWXZ0GalHUll5bCU5RTmXbaXymTVyk8+sDBG7Nj8/H9OOHRhLDDZll0rLqCjsHTpcmdV07oxMTPTt218tQfCj9rF4Ru1j8U+PViptH4sQ4k5gW5niu6SUbwXsNMgEcx+L3pw/L5g1y8L06VaOHHE9mDaZJLfd5noW07On3eedHZvDxqZTm0hNS2XxgcUcyTly2eY2n5kovbnxqlmbLyWGAwdKz2oOHChXzdGsmesZTfGsxnnddR5vn6l9LNq1VCZqH4t/erRSmavClkspS23VFkL8r4I+K53o6GhNZZVNYqLk0UcLeeSRQhYuzGHhwlp8/72ZhQstLFxooVkzBxMnFjJmjI2EBPdfECxGC70a9KJXg1482uJR8qx5l9PMrDu5ju1nt7P97Hbe2PTG5Xxmg5IH0bdBX+Kt8Zr/H3zV82b3ZNM1LkLgbN4cW/Pm2O65x1WUkYFpy5Yrs5odOzAeOIDxwAGsM105VZ2JiZdvnzm6dsV+441QrEGvz0ggfrS0CfuYBAk99AQrJlrqXQ1xCWjGIoR4H/jjpf0rxWXRuDZLJgCvSSmzPLUPJe5mLFlZWVStWtVnWSi5pOfkScFnn1n57DMrp0+7ZhfR0ZIRI2xMmlTIjTc6fPq4RG5RLmuOryE1zfVs5lTOqcs2s8FM97rduan2TQxrOcxnPjNf/1/e7J5slR4Xm831bKbk7bMy+26k2YxtxAhkzZpktWuHdcCACq8+C+Q9aWlzVcQkAPTQE6yYaKkXrnEJ5tHElzgAvCWE+E4I8fvisleBY8C/gYcC9BsSLrjJj+WuLJRc0lOvnuS55wr46acLzJiRQ58+ReTnu3b59+8fz8CBccycaSEvz7OPS1QxV+HmJjfzdv+32TlxJ2vGrOHF7i/SpU4XHNLBmhNreG3ra3T9rCudPu3Ec6ufY8XRFRTaC3369sfuyVbpcbFYcHTqROH//R+5M2ZwYc8eLuzYQe7//kfBpEnYW7cGux3T5s1ETZ5M7fvuo2qTJsT170/0iy9i/v57RJb/36cCeU9a2lwVMQkAPfQEKyZa6l0NcQl0xvIusAbIxJWtowDXkcVDpZSZQoh7pZSf6apUJ9zNWHJzc6lS5khgd2WhxJuegwcNTJ9uZfZsC1lZru8KCQlOfvc7GxMnFtK8udOnj7Kczz/PimMrWHxwMatPriaz4MqDb3f5zHz59mb3ZAvLuGRnu2YzGzZgWLsWy88/I+xX9hNJIXC0bo29Rw/sPXti79HDdRSBFwJ5T1raXDMxKYMeeoIVEy31wjUulfGMZY+Ucj6AEGI5cD+QIKW89NcnojJbXrhwoVwA3JWFEm96rrvOyd//ns+f/5zPwoWuJcvbtpn48MMoPvwwil69XFmW27fX/p4SoxO5q8Vd9IjrQc2ba3rNZ9YmqQ3dk7pzZ9s76VSrk9t8Zt70e7KFZVzi47EPGoR90CBOnTpF3YQETFu2YFq3DtP69Zi2bbuyzHnKFAAcLVtSVDzI2Hv0cB09UIJA3pOWNr7qXDUxKYMeeoIVEy31roa4BDqwFAkhtgF5QDywHDgvhLgF13HFdXXSVykUFRVpKgslWvRER8OYMTbGjLHxyy9GPvnEyhdfWFi71szatWaSkpozfryd8eMLqV9f29hfVFSEyWCiW91udKvbjb/0+Eu5fGa70nexK30XU/dN9ZjPzJt+T7Zwj0tRURFUqYK9b1/sffu6CvPzXYPLjz+6BpqtW6+cf/PRR4Br5ZntlltwtGmD/aabAnpPWtr4qnM1xgT00ROsmGipdzXEJeDlxkKIGkAjXLOXvOKyu4EbcD28D68br8WE+z4WTwSqJzsb5s2z8sknVvbvd80kDAbJ4MGuWUz//nZ3x6dovm6BvYB1J9fxw6EfWH5sOWnZaZdtJfOZ9a3bl3Z12rldABCpeyY0aSksxLR9u2tGs24dpi1bEHl5FPXogXn9egDs112HvXdv7DfdhL1nT2QN73uLtF47UvdLVBS1j8U/PVqplH0sQohewBhcGyQXSCl/CMhRJRNJ+1hKUlE9UsJXX6WzeHEjvvnGTFGR6zOSnHzlrJikpPKfBX/W5jds2JADmQcurzIrm8+sXmw9UhqnlMtnFql7JgLSUlSEcccOTDt2YE5NxbRpE6LMSgvH9ddT1KvXlYHGzaZNtY/FM2ofi396tBL0gUUIcR/QBtiDa2C5EfhZSvm+384qGXcDS3p6OklJST7LQokeei75OHdOMGuWlenTLRw/7prFWCySYcNcD/u7dnVc3hOo9bru6pXMZ5Z6JJWMgiu5Sa1G6+V8Zp0SOtE+ub0mn+EUF1202GzkrFpF0s6drttnmzYhyhwpa2/d2jXI9OpFUffuUK2apmv7quPN7skW7jEBfftKMNpEalwq4+G9QUr5RMkCIcRjAfoKOUY36dbdlYUSPfRc8lGzpuSJJwp47LECli93nXi5dKmZ+fOtzJ9vpVWrK2fFaL2uu3ol85llnM/gaNFRUo+ksuzoMraf3c7yo8tZfnQ5cCWfWUpyCl3rdMVsNId9XHTRYrFQ1LkzBSkp8NRTV26drV3runW2eTOm3bsx7d4NH36IIzkZWbUqonNnjIMGYe/WDTwkGvSlz5vdky3cYwL69pVgtLkW4hLoPha7mzLPO/PCnOzsbE1loUQPPWV9GI2QkmJn7txcduzI5okn8qlRw8mePSaefroKbdpU5Zln4tm1y/cH1Je+nIs5dKjVgee6Pcey0cvYd/8+3hv4HkOvG0qsKZZfM3/lve3vMfTLoTSb2oyJiycyc9dMfsv7za/rVCZ6aSnlx2rF3r07Bc88Q87XX5N15AgXFy0i/5lnsA0ciOHUKUw//UTVqVOJGzXKtY9myBCiXn0V09q1UGK240ufN7sn27XaV/Rscy3EJdBbYWOAfpS+Ffa1lPJzfeWVu+7LwAPApb82L0gpFxfbngfuwzXAPSalXOLOh7tbYXl5ecTExPgsCyV66NHiw2ZznRUzbZqV9euv5Bft0sU1ixk61Ia7E099+fZmz7qYxc6sna5bZmmpHMi8ksOrZD6zQcmDaBbbjNgq4ZGiXa/PiF9+8vIwbdoEK1cSvWEDxh07EE7nZbO0Wl25znr1IqdLF0zduoHZfTZrb9f1ZFN9peJtKtJXQhmXynp43xEYCUQB84HNUsqgrm8rHlhypJT/KlPeCpgDdMG11HkZ0FxKWW4W5W5gOXHiBPXr1/dZFkr00OOvj717Dbz3XhHffludixddn6nERCdjx7qexTRufOUPmi/f3uxlbWkX0khNS2XR3kVsy9hGoePKTv8kaxIpTV23zC7lMwsVen1GAvFzuU12NuYNGzCtWeO6fbZrV6l6MjYWe/fuFBU/o3G0bXv5pE1/YuKtXPUV/9ro2Ve8lesdF92fsQghDEBZhb9R+pCvycDvCQ3DgLlSykLgiBDiIK5BZoOWxu4G14pkfQ4Geujx10fLlk6ee+4U//ynkS++sDBtmpVffjHx3ntRvPdeFP36ubIsDx5c5NO3N3tZW3JCMg+2e5CbE28msXYia4+vvTybOZVzitl7ZjN7z+zL+cwGJQ8ipXGKz3xmeqPXZyQQP5fbxMdTNHgwRYMHA8WJNX/80XVbbMUKotLSMC9dinnpUuxt2mA4ccK1EKB3byzNm0O9em6zN3vSpPpKxdvo2Ve8lYcyLppmLEKIROAQ8JMbs8R1Dsv1Uso6buy6UTxjmQBk49qI+VRxCpn3gI1SypnF9T4GvpdSflHWh7sZS0FBAVFl7u+4KwsleugJxEfJNlLC9u2ujZdffWWhoMD1B6luXSdjx+YycaKDOnXcf568XduTrWy5lJIdp3aw+tRqUtNS2XJmC055ZdbUOKHx5eOZe9bridUU3L0Ven1GKhoXb3WiMzMx//gjpjVrEJmZWBYvLlXHWaeOa2lzr14U9emDLP6GqzUmgeoPJuHQVypST4++4o8ereh+K0y4vgaOlVLO8lJntJRyntYLe/GzDKjtxvRnYCOQjmsw+xtQR0o5qTjb8oYyA8tiKeWCsk6++eYb+dJLL13+fdy4cfTr10+tzfezTWamYM4c11kxBw+6bq0YjZJbbnHNYnr3Ln1WTDDW5l/KZ5aalsryo8t95jPTm0g8j8Vw9Cim1asxr1mDWLUK8/nzpeyOJk2w9+rF6VatqHrHHcgyy1XVPpaKt1H7WMpWds1c+uNKPBkLnAdO4TqX5ZyfOiuEECIZ+FZK2ab4wT1SyteLbUuAl6WU5W6FuZuxZGRkUL1MokB3ZaFEDz2B+PDVRkpYs8bE//4nWLasCg6H67N33XVXNl5WrSq9+vFk8ycuDqeDLWe2lMpnVpI2SW1cCwAaD/KYz8xf9PqMBCMuWupkpKdT49w5zMXPZ8w//oi4ePGy3d6hAxQWYu/dm6I+fbB3706Gzab6SgXb+IxLkPtKoARlH4sQ4gP+oc0AACAASURBVC7geWA7kIHr+PHaQGvgWSHEm95mNHoghKgjpTxd/OsdwKUnlYuA2UKIf+N6eN8M2BxMLQoXQkCfPnbatMnAZkvis8+szJjhmsW8+GIMf/97NHfcYWPEiBz69fN4GGOFMRqMpfKZnbx4kqVHl7L0yFJWH199OZ/Zv7f+22M+s2sOIXC2akVhq1YUPvww2O0Yf/4Z85o1yGXLiDpwAEN6Oqbdu4n64AOkyUTUDTdA//7Y+/TB3qkThFEqF0X44M8GyaZSyo6ejEKIv+igxxf/FELciOtWWBrF575IKXcLIT7HtfzZDjzibkWYJ3JycsqN7O7KQokeegLxobVNTk4OjRpV55lnCnjyyQKWLDHzySdWVq40M2eOlTlzGtCunZ2JEwsZMcJGyaSrnq5RkbjUi6vHhDYTmNBmwuV8ZkvTlpJ6JJW07DTm75/P/P3zS+UzS0lOoWX1lpoXAOj1GQlWXHzVKWc3mXB07IijY0eO3nknjWrVcm3QXLMG8+rVGHfsIHr7dti+Hf71L2R0NLaUFPIaN8Y4bJhrxZm3xHOVRCT0Fb/iosEWbn/DNN8KE0K8IKV8zYv9RSnl33VTFiTUw/vKfSB5+LDrrJhZsyxkZrr+6MTHu86KmTChkOuvd1bqA0kppc98ZpcWAPRu0PtyPjN3RMLDe10fEmdnI1euJGbDBsxr1mDct4+irl0xb9oEgLNaNVe25r59sffujbNJk+BNUb0QqX1Fi/2qengPIIQYBrwB7MD1AL0A12qwGkAH4J+XHp6HM+4GluPHj9OgQQOfZaFEDz2B+NDaxle9gwdPsG1bEz75xMqWLVcmyj16FDF06CkmTIjHYvHtU++4lMxntvzocs7lXXlUWDKfWUpyCo0SSj8I1UtLsOLiq443uydbyXJx7hymjRuxLVxIwrZtGI8fL1W3qHt3nI0buwaaXr2QtWr5elu6EOl9paJx8VePVoLyjEVK+bUQYiXQG9eelmrARWAF8H+XUudHIu5ufVTmfggt6KEnEB9a2/iqFxUFo0fbGD3axq5driXL8+dbWL/ezPr1jXjrLSf33lvI+PE2GjRwevSpd1xK5jNzSic/n/v58mymZD6zZ1c/y7jW4+jToA/Dmg3DIAy6aQlWXHzV8Wb3ZCtZLmvWpGjoUE526ICoVw9DWpprxdnq1a59NEJgnT0b6+zZQPGBZ717Y+/Th6IePSA+OJtbI72vVDQu/uoJBv6uCksGOgEHpZQ/FZc1wnUuyyEp5ckgaNQVldIlfNJUZGfD/PlWPvrIzP79rrQjQkgGDXItWe7ePZu4uNDF5VzeucsHmq09vpY8ex6FjkJaJLbg6S5Pk1I3hbjYuApfJ1hxCWnqEKcTw+7dmFetcg00GzeWOh5AGo3YRo7EWb++7gsBrsa+4ssWbildND9pE0L8DtdtsGeBb4UQC4UQsVLKo0A+cMxvpWHCb7/9pqkslOihJxAfWtv4qufOHh8P991XyJw5u1m8OJu77irEbIbUVAu/+10c3bsn8fbbUfz2m/DqJ1jUjKnJ2FZjmX7LdHZN2sXrfV6nQVwD9p/fzwM/PEDfz/uyYP8CHM6K5V8NVlwCiYkvm+a+YjDgbNuWwkcfJeeLL8g6dIiL335L/tNPY+/SBQDjzp1E/+tfxN1+O1WbNiV25Eis776LcedOKJH/zF+uxr7iyxZuf8P8ecYyD9dqq/Ti328DxuNKCmkFTkspQ78kxAfuZiyZmZlUq1bNZ1ko0UNPID60tvFVz5u9pC09XTBrlmvj5dGjrr0mZrPk9ttds5jrr/+NxMTQxcXmsDFn7xze3vo2x7Jd36WaVWvG052f5s7mdwa0PyZYcdErJr7KA/psZmdj2rABc/GtM+PevZdNzpo1weFw7Z/p3Rt73744/djod630FV/lev8NC8qMBVeSyfRLv0gpv8WVTfhpoAGuJcARicNR/hunu7JQooeeQHxobeOrnjd7SVtSkuSPfyxk27Zspk49yZAhNhwO+PJLC7fdFsfNN9dj6lQrocoIbjFaGN9mPFvu3cKrXV+lYbzr1MyHUh+i+8zufL7v81KrzLQQrLjoFRNf5QF9NuPjsQ8eTP5rr5G9bh1Ze/aQ++GHFI4di719ewwZGVi++ooqTzxBQvv2xHftSswTT2D+6itERoZX19dKX/FVHsq/Yf4MLKeFEI8KIY4JIdoASCmzpZQvAt2CI69yyM3N1VQWSvTQE4gPrW181fNmd2czGKBTp9+YPTuXn366wFNP5VOrlpMDB6w8+2wMrVtX5fHHY/jll9AcZmQ2mrml9i1suXcLkwdMJjk+mYNZB3k49WG6z+zO3L1zNQ8wwYqL3jHxVK7HZ1PWro1t5Ejy3nuP3NmzubB5M3lvvonttttwJiQgo6KwzphB7H33UbVZM+L69MH6j39gWr4cyhztfK31FU/lofwb5u/D+6a4dtovllLay9h6SinX6axPd9zdCissLMRa5sGhu7JQooeeQHxobeOrnje7J1vZ8qIi+Ppr+OyzWNauvXLGSMeOrrNihg+3ER3tU6pulNRX5Chi/v75vLXlLY5cOAJAk4QmPNn5SUZdPwqTwfMCzGDFpTJiolVLhXA4MOzcWWohACYT5OcjnE6kxYK9SxeKbr0Ve8eO5LVsibXkDtwAiPS+4o8erQTrVhhSykNSykVlB5ViW9gPKp44c+aMprJQooeeQHxobeOrnje7J1vZcrMZOnc+ytdf57Bx4wUeeqiA+Hgn27aZeOSRKrRuncCLL0Zz6FDlPOorqc9sNDO21Vg23buJ9we9T5OEJhy+cJg/LPsDXT7twqw9syhyuD+uKFhxqYyYaNVSIYxGnDfeSOHjj5Pz1VdkHT5MzuzZFDz2GPb27aGoCPOPP2J9/33iU1Ko0bIlVe65B8uMGRh+/dWV0M5PIr2v+KMnGIT9w/bKwOzmhD13ZaFEDz2B+NDaxlc9b3ZPNm9xad7cyeuv57NnzwUmT86lfXs7WVkG/vvfKDp3TuCOO2L55hszRUE8es6dPpPBxJiWY9h470Y+GPQBTas2JS07jUeXPUqXz7rw2e7Pyg0wwYpLZcek0oiOxt6rFwUvvcTF5cu5cPAgOTNmUDRoEI6mTTHm5GBevZqYp58moVs3Etq0Ierll7F8/jlC4x/bq6mvhALjyy+/HLKLh4ITJ068nFQmFbjBYMBSZtu3u7JQooeeQHxobeOrnje7J5uWuJjNcMMNDsaPt5GSUoTDAQcPGjl40MjChRZmzbKSnS1o0sSh+348r+9JGGhTow2T2k6iadWm7MvYx5ELR/jhyA98vv9zYkwxtKzeEqPBGLS4hComlU50NM4WLbAPHkzhgw+SNXw4ol07hMWC+O03DOfOgcNB1JQpRL3/PqYNGzD+/LMrCWeNGm73z1yNfaWiREdH/1VrXTVjAdLT0zWVhRI99ATiQ2sbX/W82T3Z/I1L+/YO3n03j927L/Daa3k0a+bg9GkDb74ZzY03JnDvvVVYscJUkS0SmrVcwmQwMer6UWy4ZwNTBk+hWbVmHMs+xuMrHqfzp52Zvms6p8+d9uknkGuHQ0xCwdmoKIpGjSJ36lQu7NtH9tq12EaMoGjgQBzJyZjXrCHqww+J+sc/qNq0KTGTJhH1xhsYN27k0hT3au8rwUbNWIpxl6wtnJJQgj56AvGhtY2vet7snmyBxCUqCjp1cnD//YX07GknP19w4ICR/ftNfP65lS++cH2La9vWcen494DR+n9jEAZaJbViUttJNK/WnP3n93PkwhGWHFnCdye/I8YcQ6ukVn7tg9Fy7XCJSWVzWY8QyJo1cXTqhG3kSAonTnTti6lbF0NGBoajR5HVqmGdOxfrrFmYf/gBc2oqUdnZGKtWdR105kdqlEjrK/7gz4zFn7T5Vy02m01TWSjRQ08gPrS28VXPm92TraJxEQJ69bLTq5edM2cEM2e6zoo5fNjIokVmpk61MmVKLu3bB7beP5D/T6PByIgWIxjebDhfH/yaNze/yf7z+3ly5ZO8teUtnuj0BHe3utvnscparh2OMakMvOqxWLD36IG9Rw/X78UbNR1t2mBetQoZF4dlyRKqL1lC0dKlGI8coahPH4oGDcLerRuyXr3ArutHvashLupWGJCfn6+pLJTooScQH1rb+Krnze7JpmdcateWPP10ATt2XGDmzBwKCgSHDhkZMiSOyZOtAd0eq0hMjAYjdza/k3V3r+Mfnf7B9YnXczLnJE+vepqOn3bk418+ptBeWKFrh3tMgoVfei5t1HzjDbI3biR36lRy//tfzt96K1itGM6exfr550R98AFV27YlvmtXol5+GfPixXDhQkDXvRbi4tc+lqsBtY9Frc0HKCiAl1+OZsoU162Cvn2L+OCDXGrV0t4f9NJSWFiI2WLmm4Pf8M/N/2Rvhiu9SZ0qdXi80+Pc2/peokxR5dpcM/tY/ES3vmKxYNi3z5VyZtMmLMuXI61WDMU7/+033ghmM7bbb8fRsSO5bdpgjfOdlDRS4xK0fSxXK+G2Btwdah+Lf3p8ERUFb7yRz5w5OVSv7mTVKjO9esWzdKn2u8N6aTlz5gwGYWBYs2GsHbuW6bdMp3VSa07nnubZ1c/ScUZHpvw8hQJ7gV/XjrSY6IVufUUInC1bUvjww+RNm0bWoUPkzJpF/rPPUtSjB8YDBzBt2YLl22+Ju/VWqtx1F7GjR7v2z+zZ43H/zLUQFzWwgNsleeG01Bj00ROID61tfNXzZvdkq4y4DB5cxJo12fTpU0R6uoHRo+N44YVoCj3fhdJdS0k/BmFg6HVDWT1mNZ/e+iltktpwOvc0z61+jp6zejL156kU2gs1XTtSY1JRgtZXzGYcXbpQ8Oyz5Hz7LVl79pAzZw5F3bvjaN6c6MOHMS9divWzz0i46SaqjBxJzMMPY5k5E1HiELRrIS5qVRiuA3HKBsFdWSjRQ08gPrS28VXPm92TrbLiEhcHo0bZiI6WrFtnYvNmM6mpZnr2tFO9uudbY3pp8fQ+myc2Z3yb8bSt0ZaDmQdJjE5k2q5pzN07l4SYBNrVaud1FVkkx6QiVFpfsVpxXncd9r59Kbz/frJuuQVjhw5gs2E4exbDqVOIvDyiPv0U488/EzV5MuLcOcwFBRjq1fN4/ky4xkXtY/GTDDfZUt2VhRI99ATiQ2sbX/W82T3ZKjMuBgP88Y+FfP/9RZKTHezcaaJ//3g++8ziMSOIXlq8+TEIA7c2vZVVY1bxSPtHaFW9FSdzTvL8+ufp+llX5u6d6/E8mEiPSaCEqq/8ZjZjGz2a/Hfe4cKuXVz89lsKH3oI2803uw4+S0sj6v33iZ482XX+zPDhWCdPdu2fKbGC62qIi5qx4NqhWvYhl7uyUKKHnkB8aG3jq543uydbKOJSt65kzJhCTp0y8NNPJn74wcKvvxrp29dO2S0BemnR4kcIQbPEZkxoO4Hmic3ZdW4XR7KP8N3h71h4YCHVo6vTIrFFqeNor5aY+EtY9BUhkElJONq1o2jECGyjR2Pr1w9ZqxZSCIwOB6bt2zFv2+Y6k2bpUsyLFmE4exZj1aqY69Z1u38mlHFRMxY/Cbeleu5Qy43901MR4uPhf//L44MPcomNlSxcaKF37zg2bSp920kvLf74MQgDdza/k68Hf81/B/2XRvGNOJB5gPt/uJ8+c/qw+NBiLq30vJpi4g9h2VfMZpzFz2dO/P3vXFyyhJx58ygYNw4sFgynT2M4eZKYF1+k1qhRxA0eTNSLL2JesABx8qTPa4RbXNTAAhQUFGgqCyV66AnEh9Y2vup5s3uyhTouo0fbWLUqmw4d7Bw/buS22+J4880oLp2fpJeWQPzYbXZ+1/J3bL53M//u/2/qxtZld/pu7vnuHgbOG8iytGU+/7BEYky0EBF9JS4O+8CBFPztb2SvX8/Fr74i//HHKXjgAQpr1MC0dSvWefOIeu894kaMoMrddxP12muYly6FrCxN1w5lXNQ+Fq6xtflqH4vf2Gzw2mvRTJ7suhfWs6drz0uNGgW67WOpaFwK7AV8uvtT/r3l35zLOwdA59qd+UuPv3BT/Zv8vm64x8QbEd9XCgqIPnoU88qVGLdswbR1K7J2baTJBJmZGAoKsLdti6NdO+zdu+Po2JFCKdU+lnAj3NaAu0PtY/FPj55YLPDyy/ksWHCRWrWcrFtnpnfveGbP1udWgx5xiTJF8WC7B9k+fjt/vemvJEYlsuXMFoZ+OZThXw5n8+nNfl033GPijYjvK2fP4mzRwrV/5uOPyd66lby//Y2ilBRya9YEITCcPYt5+XKiX32V2BEjMD76KJbp0137Z4rTSKh9LGUQQowUQuwWQjiFEJ3K2J4XQhwUQuwXQgwuUT6kuOygEOI5f64XUUn1KtnH1ZxUz1/69bOzdm02KSk2srIMPPVUY556Kqbsybh+o2dcYswxPNrhUXZM2MFjbR4j3hLPmhNrGDJ/CKMXjebnsz9rum6kxMQdV11fKd4/U/jHP3Lmww/JXrmSgj/9CXufPhAdjeHECWKOHMH62WfEjhlDlZEjiXrpJWosX444dcrv96EHYXkrTAjREnACHwJPSym3Fpe3AuYAXYC6wDKgeXGzX4FBwAlgCzBGSrmnrG93t8Kys7OJL3NYh7uyUKKHnkB8aG3jq543uydbuMZFSpgyxcr/+3/R2GyCFi0cfPxxDq1aBZaPP1hxyc7Oxmlx8v6O9/nwpw/JKcqhfc321IurxwvdXqCuue5VE5OSXHN95fRp7CtXErtzJ8b9+xGFhYi8POwGA0azGWetWjhbtqSob18c3br59Z5KEvG3wqSUe6WU+92YhgFzpZSFUsojwEFcg0wX4KCU8rCU0gbMLa6riczMTE1loUQPPYH40NrGVz1vdk+2cI2LEPDQQ4V8+umvNGvmYP9+IwMGxPPRR9ZATsENWlwyMzOpGlWVP3f/Mzsm7ODZLs+yN2Mv3x76lp6zevLIskdIu5Dml/9wjUlJrrm+UqcOJ3v2pOD118ldsIC8t96iYOJELl53HTIqCuPZs5i/+w7zmjWa9OlBWA4sXqgHHC/x+4niMk/lmqhevbqmslCih55AfGht46ueN7snW7jHpUePGFasyGbcuEIKCwXPPBPDPfdUISND+/kdELy4lKxTPbo6z3Z7lm3jtzGp7SSMBiPfnfiOLp914amVT3Eq55THtr7KwykmcI33FSFwXn89RePGUfDWW+TOn0/uK69QOGYMRbfeqkmfHoRsYBFCLBNC7HLz422m4a7HSi/l5UhPT6d///6Xf6ZPn87FixfL1XNXFkr00BOID61tfNXzZvdkC/e4XLx4kSpV4J138pg2LYeEBCfff2+hd+941q7VnswyWHFxV6dObB3+1e9fbLl3C8MaDcMpnUzbOY1OMzrx4toXSc9L9+o/3GMCqq+UKiveP2P7v//D0bq1Jn16ELKDvqSUAwNodgJoUOL3+sClr1qeykuRlJTEihUrSpUdPXq0XL2IOrwoiD7U4UWeKall2LAiOnbM5sEHq7Bxo5nhw2N54okCnn22ALNZu59Arh1InUYJjXj5xpd5rtdzvL7xdRYdXMR/d/yXT3d9ysPtH2Zo0lDqUEeTz3CKCai+4q+eYBCWD+8vIYRYRemH962B2Vx5eL8caIZrxvIrMAA4ievh/Vgp5e6yPtU+FrWPRS/cabHb4V//iuJf/4rC6RR07Ghn6tRckpM9P9gPVlz8ickv537h1Y2vsjRtKQBVrVV5rONjPNDuAaqYq3j1GU4xAdVX/NWjlYh/eC+EuEMIcQLoDnwnhFgCUDxQfA7sAX4AHpFSOqSUduAPwBJgL/C5u0HFE2ptfsXbXM37WDzhTovJBM89V8A33+RQr56TbdtM9O4dz4IFnqctwYqLPzG5oeYNzBs6j8V3LaZnvZ5kFWbxyvpX6Dij9GmW4R4TUH3FXz3BICwHFinlV1LK+lJKq5SylpRycAnbq1LKplLKFlLK70uUL5ZSNi+2verP9aKjozWVhRI99ATiQ2sbX/W82T3Zwj0u3rR07+7a83L77TZycgQPPBDLI4/E4O4WebDiEkhMutXtxqI7F/Fx34/pUKsD5/LO8dWBr+jyWRdm75mN2Vp+gAynmIDqK/7qCQZhObBUNuF2SI471EFf/umpDHxpqVpVMn16Lm+/nUt0tGTOHCv9+sXz00+lk1kGKy6BxkQIQb+G/Vg6aikzb51Jri2X4xeP84dlf2DYkmF8feBrnNLp00+oUH3FPz3BQA0swIULFzSVhRI99ATiQ2sbX/W82T3Zwj0uWrQIAePH21ixIpvWre0cPmxk8OA43n/feinzRtDiUtGYCCG4pektLBu9jA9TPiQ5PplDFw4x8fuJDJg7gGVpy5BShlVMQPUVf/UEA3UeC2A2m8uN7u7KQokeegLxobWNr3re7J5s4R4Xf7QkJUnGjrVx8aJgyxYzNhssWmRhwIAi4uNNQYmLXjExCAOtk1ozqe0kEs2J7D6/m0NZh5i/fz5rT6ylZa2WNE5s7Jf+YKL6in96tKLOY/GTcBvt3aG+hfmnpzLwV0tUFLzxRj5z515k714jS5ea6ds3jh9/9H9ZaGXMWMpiNpoZWnco28Zv4683/ZVqUdXYcGoDI74bwciFI9n5207fwisB1Vf80xMM1MACFBUVaSoLJXroCcSH1ja+6nmze7KFe1wC1ZKSYmflyot06GDnxAkj996bzJQp/qWD0XLtYMUk2hTtSnQ5fgd/6vInYowxpBek02dOHyZ9P4mDmQd9agsmqq/4pycYhPU+lmCg9rGotfl6UVEtNhu89FI0U6a4stkOG2bjP//JRUvuQ733sWi1uSs/mXWSmftm8s62dyh0FGIURsa0HMMzXZ+hflx9329GZ1Rf8U+PViJ+H0tlE25rwN2h1ub7p6cyqKgWi8V1a+yf/zxCbKzk668tDBgQz+7dRp9t9d7HotXmrtx+wc6z3Z5l67itjGs9DoCZe2bSaUYnXljzwuU0MZWF6iv+6QkGamABqlSpoqkslOihJxAfWtv4qufN7skW7nHRS8vw4XZWrMimVSs7hw4ZGTQojlmzvD901XLtyo5Jvbh6vDPgHTbcs4E7m9+JzWnjfz/9j/uX3M/rG18nuzDbp2Y9UH3FPz3BQA0sgNFY/huiu7JQooeeQHxobeOrnje7J1u4x0UvLUajkeuuc5KaepGxYwspKBA8+mgV/vAHz4eIabl2qGJyXbXr+GjIR6wes5q7WtzFuhPreHPzm3SY0YH3tr9Hvl2fkzc9ofqKf3qCgRpYcB2eo6UslOihJxAfWtv4qufN7skW7nHRS8slPzEx8N57ebz7rmtD5ezZVlJS4jh4sHw31XLtUMekbY22TBk8hW9GfEO3ut04X3Cel358iU4zOjFj1wzsTrtXfYGi+op/eoKB2seCa4equUwKWndloUQPPYH40NrGVz1vdk+2cI+LXlrK+rnhBgc332xjzRoz+/ebmDPHSnKyg5YtnR7bBKKvsmJSP64+Y1uOpWPtjuzL2MfhC4dZcmQJiw8tplpUNVoktkAI/86w8YbqK/7p0Yrax+In58+f11QWSvTQE4gPrW181fNm92QL97jopcWdn1atnCxbls3w4a5cY/fdF8tzz0VzKRO6lmuHU0yEEAxKHsSqMav4aMhHNK3alISoBO774T76z+1/eRe/Hqi+4p+eYKAGFnD7gQ63Zdh66AnEh9Y2vup5s3uyhXtc9NLiyU98PHz8cS7/+EceZrNkypQobrkljuPHDZquHY4xMQgDdza/k/V3r2dUi1HUqVKHX377hVGLRnH7gtvZdHqTZl+eUH3FPz3BQO1jAQoKCoiKivJZFkr00BOID61tfNXzZvdkC/e46KVFi59t24xMnFiFEyeMVK3qZPLkLG67zfvto0iISb49n49++Yh3tr5DZkEmceY4+jXqx5+6/InWSYGdeKj6in96tKL2sfjJ2bNnNZWFEj30BOJDaxtf9bzZPdnCPS56adHip2NHB6tXXyQlxUZWloFx4xL529+isHt5/h0JMSm5i//pLk/ToXYHFh1cRO/ZvXloyUOkXUjz26fqK/7pCQZqYAFiY2M1lYUSPfQE4kNrG1/1vNk92cI9Lnpp0eqnWjXJ7Nm5vPRSHgaD5O23o7njjljOnHH/RTKSYhJvjeeFbi8wZfAUHmz3IGaDmfn759Plsy78aeWfOJOrfbOf6iv+6QkGamBRKCIIgwEef7yQTz89Sa1aTtatM9O3bzzr14fP/p6KUCOmBm/0eYPN4zYzpuUYnNLJxzs/5sElD/LKulfIKsgKtUSFBtTAAuTk5GgqCyV66AnEh9Y2vup5s3uyhXtc9NISiJ/WrdNZtSqbXr2KSEhwMnJkHP/5T+lElpEck4bxDXl/0Pv8OPZHbm96OwczD/LOtndoP6M972x9h7wiDztHddKj+krFUPtYgKioKEwmk8+yUKKHnkB8aG3jq543uydbuMdFLy2BxqVqVROjRtnIzjawcqWZ1avN7NplZODAIqzWqyMmSTFJ3NH8DrrW7UrahTR+zfyV1cdXM3vvbKpHV6dFYguMhtKzNdVX/NOjFbWPxU9+++03TWWhRA89gfjQ2sZXPW92T7Zwj4teWioSF6MRnn66gNmzc4iPd7J4sYX+/V2JLK+mmHSq3YmFdyxkwfAF3FjzRi4UXOAva/9C95ndWbB/QamjklVf8U9PMFADC7jd9avnTmA90ENPID60tvFVz5vdky3c46KXFj3iMmRIEStXXqRNG9fxxykpcXz7bbWArxuOMRFC0K9hP5aPXs7Um6dSLaoahy8c5oElD9B3Tl+Wpi1FSqn6ip96goG6FQaYTKZyqQ/clYUSPfQE4kNrG1/1vNk92cI9Lnpp0Ssu1apJfvc7G6dPG9ixw8SKFQmcO2egb98i3N0RidSYCCFohPHjeAAAIABJREFUVq0ZE9tOpF5sPX4+9zOHLxzmi/1fcCjrEA2rNaRRtUYVuobqK+VRt8L8JNymke5Q03v/9FQG4XArrCzR0a5Elm+/nYvZ7GTaNCu33hrHiRPlv71GekxMBhPj2oxj6/itvHLTK/Su35sFvy5g+DfDGfvNWPak7wnYt+orFUPNWHClPoiOjvZZFkr00BOID61tfNXzZvdkC/e46KVF77gIATfe6KBLl/OsX1+F/ftNzJtnoU0bB40bOzX5iKSYmA1mutTpwi1NbsFoMPLT2Z/Yd34f03ZOI+1CGm2T2lI1qqpfPlVfKY+asfiJw+HQVBZK9NATiA+tbXzV82b3ZAv3uOilJVhxad06n5UrLzJgQBHnzxsYOTKWN9+Mwun07SMSYxJvjefP3f/M8qHLebDdg5gMJubtm8fd397Nc6uf41zeOc2+VF+pGGE5sAghRgohdgshnEKITiXKk4UQ+UKIn4p//lfC1lEIsVMIcVAIMVn48eQqNzdXU1ko0UNPID60tvFVz5vdky3c46KXlmDFJTc3l8REybx5OTz7rOtwrddfj2bMmFgyM8VVGROAaGe0a5PlvZt5pP0j7M3Yy5Sfp9BxRkfe2PiGppMsVV+pGGGZhFII0RJwAh8CT0sptxaXJwPfSinbuGmzGfgjsBFYDEyWUn5ftp67JJSFhYVYrVafZaFEDz2B+NDaxlc9b3ZPtnCPi15aghWXsnWWLTPx0ENVyMw00LChg6lTM+nc2f2O/UiNCZTXsyd9D3/f8Hd+OPIDPer2YN/5fTzR6Qnuu+E+okzukzSqvlKeiE9CKaXcK6Xcr7W+EKIOEC+l3CBdI+WnwHCt7c+cKZ+HyF1ZKNFDTyA+tLbxVc+b3ZMt3OOil5ZgxaVsnYED7axceZEbb7Rz7JiRoUOr8fnn7lcNRWpMoLyeVkmtmH37bBbftZhYSyznC87zlx//QudPO/P53s/dnmSp+krFCMuBxQeNhRA7hBCrhRC9isvqASdK1DlRXKYJd0vywmVJ6yX00BOID61tfNXzZvdkC/e46KUlWHFxV6dhQyeLF19k/PhC2rYt4OGHY3n88RgKCrT5D/eYgGc93ep2Y87tc5g3dB6tk1pzMuck725/l56zevLNwW9KnV+i+krFCNnAIoRYJoTY5eZnmJdmp4GGUsr2wJPAbCFEPOBuiub2Hl96ejr9+/e//DN9+nQSEhLK1XNXFkr00BOID61tfNXzZvdkC/e46KUlWHHxVCcqCt5+O48xYwqxWiWfflp+SXKkxgS867l0kuXqMav5ZMgn5BblciDzAOMXj+f3qb9nzfE1Pn0Ecl1/6l0NfSVkA4uUcqCUso2bn6+9tCmUUmYUv94GHAKa45qh1C9RtT5wyp2PpKQkVqxYcflnwoQJpKenl6vnriyU6KEnEB9a2/iq583uyRbucdFLS7Di4qtO//7H+OGHizRs6GDHDhN9+8azapXJa9twjwlo02MQBoY3H87GezfyZt83uT7xehYdWsTwr4Yz8uuRrDm4JijX1VLvaugrEXUrTAhRQwhhLH7dBGgGHJZSngYuCiG6Fa8GGwd4HKDKEm6jvTvUjMU/PZVBpM5YStrbtXOwYsWVJcl33RXL229HERcXmTEB//RYjBbuu+E+Ukel8nTnp4mzxJFXlMfdq+9m0veTOHj+oO7XvRb6SlgOLEKIO4QQJ4DuwHdCiCXFpt7AL0KIn4EvgIellOeLbb8HPgIO4prJlFsR5gmbzaapLJTooScQH1rb+Krnze7JFu5x0UtLsOKiNSaJiZK5c3P405/ycToFf/tbNA89lES2m1W54R4TCExPrCWWJzs/yY7xO+hZrycWg4WFBxZy3w/38cSKJziV4/YGSEDXvRb6SnjkHy+DlPIr4Cs35QuABR7abAXKLUPWQn5+vqayUKKHnkB8aG3jq543uydbuMdFLy3Bios/MTEa4fnnC+jQwcHDD8ewfHkcAwY4mDEjh1atnG7b+KOlMqmInsToRF7o/gIDqw1kcfpi3tvxHjvTd3I46zDta7Xn8Y6Pe9zFr/rKFcJyH0swUftY1Np8vYi0fSxa7UeOGLj33hj27DETEyP5z39yGTGiyGObcIoJ6NtXfj3/K+9ue5d5++dhd9rp37A/N9W/iQfbPUiMOSag60ZqX4n4fSyVTbitAXeH2sfin57KINL2sWi1N27s5KOP9jBqVCF5eYIHHojl+eejKSoK/5iAvn2leWJz3h30Lj+M/IHByYPZcmYLr6x/hQmLJzBt5zSKHEV+X/da6CtqYAEsFoumslCih55AfGht46ueN7snW7jHRS8twYpLRWKSkGDmgw/y+Oc/8zCZJB9+GMXDD8dw4UL5pIbhFBMITl/pUKsDc4bOYcYtM+hcuzO//PYLT618igmLJ/Dlr1/ilE7VV0qgshvjWtteNgjuykKJHnoC8aG1ja963uyebOEeF720BCsuFY2J1WqhQwcHvXsXsXWrkYMHTXz+eSKdO9upX19q8hMKgtlXkhOSuafVPTSIb8C+8/s4mn2U2XtnczjrMFVjqnJd9es0HeQViX1FZTf2k4yMDE1loUQPPYH40NrGVz1vdk+2cI+LXlqCFRe9YtK1q4OFC3No2tTBuXNGhg6N46OPrFx6PBtOMYHg9xUhBMObDWfNmDU80/UZ2iS14ZtD33DPknv4/dLfs+3Mtgrpuxr6ipqxAAaDodxDLndloUQPPYH40NrGVz1vdk+2cI+LXlqCFRc9YxIbCyNH2sjKKmLr1iiWLjVz7JiB/v2LsFjCJyZQeX3FaDByY80bGdViFFUsVciz5ZF6NJWFvy5kd8ZuWlRrQVJMUrl2kdpX1IzFT8JtqZ471HJj//RUBlfTcmMtNrMZnnrqFFOn5hATI5k718qQIXEcOFA+iWMoqey+UsVShcc6Pvb/2zv38Kiqc/9/VjKTSQIJBhBQ4ShaWosUpaVYqeLhUgoWpS22Sj1FfnqqYpGKR6t4qVbbah/rI95qEbker229gRWQi/VUC634U7EeL0VPrQgitwNJICGZrPNHBg1k9t5rNmvPXpl5P88zzwPvu9Y73/j1ZWVmr7U3dw69k+mDpzOo5yAef+dxpiyfwtTlU/mw9sOcahdCr8jCAjQceAc+j1ic2NATpobpnKBxfnmvnOu+2NISlS9ReTJhQhPPPruLo49O8/rrCSZMOJKVK905EhdXr6RaUlw39DruHX0v0744jde3vM4b295g8MLB3P7S7exo2GFUuxB6Rc6xUHx786OY01H35h8MhXqOxS/XNr5zp2LKlEqWLi1DKc2MGQ1Mn95AafZHvOQNV3rl3f99l3tfuZdn3nuG7Xu2M/SIoZzc+2TOPfZculV1C/Xeco6lA+HaHvBsyDmW3PTkg0I9x+KXaxvv0kXzwAP1TJmyCYBnn03w/e93ynormHziSq8cc8gx/Gr4r3j49IcZ/i/DWbdlHY+++SgnPXQSD77x4H5nYEzfu6P0iiwsQHl5+6fIZYvFiQ09YWqYzgka55f3yrnuiy0tUfmSD09KSmDatJ08+mgdGzeWsnRpGSNHVvPmm/H90+Jarxzf43gePuNh5o6dS//u/dnWuI3bXrqN8Y+P57F3HqNFtxjV8cu51iuysAAVFe0PfWWLxYkNPWFqmM4JGueX98q57ostLVH5kk9PRo1qZvHiWo47rpl33y1l9OhqnngingdNudorw/oMY+7Yudw34j6SpUladAsXLL2Asxedzcp/rPzkQWOF0CuysAA7duwwisWJDT1hapjOCRrnl/fKue6LLS1R+ZJvT/r2bWHZslrOPLOR+nrF+ed35ic/qaA5z5vGXO4VpRSDqwbz4jkvcs5x5zD6qNGseH8Ft6+9nW898S3WblpbEL0i51iARCLR7oRqtlic2NATpobpnKBxfnmvnOu+2NISlS9xeJJMwrhxTdTUaJ5/PsGaNUnWrEnwta81UVnZrlwkdIReKU+Vc3yP4/nGMd+gS6oLq95fRVVZFTf/5WbqVT3H1BxDt4r2F/jj7BU5x5IjtbW1RrE4saEnTA3TOUHj/PJeOdd9saUlKl/i8kQpuPDCRp58so4ePVr405+SDB9ezauv5uefm47UKxWJCi754iW8cM4LnNrn1NZ7kr31MN9d9F2uf+F6NtRuMHoP13pFFhbce0hONuRBX7npyQeF8qCvXHK5eDJ0aDOrVu1i8OBmevZMc9pp1TzwQPSfNjtir3RJdeHHJ/6Y//zGf3LeZ89jY+1GlvzPEs5fcj43vngj2/ds930P13pFzrHg/nkJcGdvfthxru7NPxiK/RyL+fvADTdUMGtW6y6lyZMbufnm3URlYyH0yod7PuTnq3/Oa1teo1dlL9I6zfjPjOesfmdR07nGqKacY4kZ1/aAZ8OVvflhxxXC3vwDKfZzLKbvk0rBzTfv4c4760mlNPPnpzj99Co2bjT+dyonCqFXjj7kaOaMncPsr8+mOlXN1t1beejNh5j8h8k89N8PtTsD41qvyMKCe1v1suHqFkrTcYWwhfJAZLuxuRaAf/u3vTzzTC1HHNHC2rUJRoyoZvVq+7eCKaReGdRzEA+d/hC3j7ydnp168uq2V7npzzfxrSe+xeNvP/7JGRjXekUWFtx7SE425EFfuenJB4X8oK+oPBk0KM1zz+1i2LAmPv64hPHjOzNr1qe34LdBIfbKyb1P5rdn/JbbTr6NEw8/EY1mzro5/PuSf+f5fz5PMtn+zFCcvSILC7Bz506jWJzY0BOmhumcoHF+ea+c677Y0hKVL6560r275ve/r2Pq1AaamxWLFye5+OJKdu/OqYwnhdorSim+3OXL3D/mfiYeO5HaplrWbVnH9FXTmbpqarvnwMTZK3KOBUgmk+1W92yxOLGhJ0wN0zlB4/zyXjnXfbGlJSpfXPakpASGD2+mf/80c+eW88orCZYvTzJyZDNduhzcx5dC75XyVDkDewzkrGPPoiJRwdY9W9nSuIXn/vkcr215jaO6HEW3im7We0XOseSI678ZQ+H+FuaXc90X+cRirsWL009vYtmyXfTt23oL/uHDq3juuYO77lIsvVKZrOS8gecxe8xshh46FKUUf9n0F85adBbXPH8Nb216y0x4BMjCAjQ1tb/LaLZYnNjQE6aG6ZygcX55r5zrvtjSEpUvHcWT/v1bWLmylq99rYkdO0r4znc68+tfl4W+7lJsvVJTXsMP+v2AeWPnMerIUfTs1JOXN7/MtBem8au//uqTMzD5RM6x4P55CSiMvflyjsVenY50jsWUlha45ZZy7rmnnMMOa2HAgDR33VVPVVVudYq9V/6+/e/MeX0Or21+DaUUlclKxvQdw8TPT6RTWSfDn6Y9Hf4ci1LqVqXUW0qpdUqpJ5RSh7TJzVBKrVdKva2U+nqb+JhMbL1S6qpc3s+1PeDZKIS9+bnmXPdFzrGYazGhpASuvrqBefPq+PjjEhYtKmP06GrWr8/tn6li75V+Xftxy6m3cMlnL6FfTT8amhtYtH4Rl//xciN9NnByYQGWAwO01gOBd4AZAEqp/sDZwHHAGODXSqlSpVQpcA8wFugPTMyMNaJTp/areLZYnNjQE6aG6ZygcX55r5zrvtjSEpUvHdWT0aObWblyF/36pXn77VJGjqxm2TLzW/BLr7QypPcQ7hh1Bz8+8ccc0fkIJn5+opE+Gzi5sGitn9Va77vZ9hqgd+bP44FHtNaNWuv/AdYDQzKv9Vrr97TWe4FHMmONKM3yLNVssTixoSdMDdM5QeP88l45132xpSUqXzqyJ/36tbBixS7GjdtLba3ie9/rxD33pGhpCZ4rvbJ/bFifYfx69K8Z1meYkT4bOLmwHMB5wJLMn48APmiT25CJecWN2JXlWarZYnFiQ0+YGqZzgsb55b1yrvtiS0tUvnR0T6qqYMGCeq67bg9DhzZz3XWVRo8+ll5pH1MqmtvneGH/fgqGKKVWAL2ypK7RWj+VGXMN0Aw8uG9alvGa7Atk1l0JW7duZcSIEZ/8fdKkSXz3u99tN+7QQw/1k593bOgJU8N0TtA4v7xXLlvcJV9saYnKl0LwRCmYPr2BgQMTvPFGKUuWlDFqVCkLF9Zx7LHZP75Ir+SmJwpi+8SitR6ltR6Q5bVvUTkXGAecoz/durYB6NOmTG9go0+8Hd27d2fVqlWfvCZPnsz27e2342WLxYkNPWFqmM4JGueX98q57ostLVH5UkiejBzZzKpVrY8+Xr++9dHHixdnv+4ivZKbnihw8qswpdQY4ErgDK112xs9LALOVkqllFJ9gX7AX4GXgH5Kqb5KqTJaL/AvMn2/bFuuXduGbUNPmBqmc4LG+eW9cq77YktLVL4UmidHHdXC0qW1TJiwl7o6xbnndmLmzBTptH090isHh5PnWJRS64EUsC0TWqO1viiTu4bW6y7NwKVa6yWZ+GnATKAUmKu1/nm22tnOsTQ0NFBeXh4YixMbesLUMJ0TNM4v75Vz3RdbWqLypVA90RruvTfF0qVJXnghyYgRTcyeXU9NjbamR3qlPR3+HIvW+jNa6z5a6xMyr4va5H6utT5Ga/25fYtKJv6M1vqzmVzWRcWLzZs3G8XixIaeMDVM5wSN88t75Vz3xZaWqHwpVE+UgosvbuSKKxro1q2FVauSjBhRxRtvlFrTI71ycDi5sOSbzp07G8XixIaeMDVM5wSN88t75Vz3xZaWqHwpdE9OOaWZ557bxQknNPP++6V8/etVLF6ckF7JUU8UyMIiCEKHpXdvzR/+UMvEiY306pXmwgs7c8st3WhuDp4rRIcsLEBdXZ1RLE5s6AlTw3RO0Di/vFfOdV9saYnKl2LxpKIC7r57N1OnNtLcDHPm1HDmmZ3Zti382Q3plYPDyYv3USIX7+WCpC3k4r25lnyxenWCyZMr2bKllOOPb+b223dzwgnp4IkHIL3Sng5/8T7fbNmyxSgWJzb0hKlhOidonF/eK+e6L7a0ROVLMXpy0knNPPjg25x0UhMNDYrTTqvi0Udzf9iV9MrBIQsL2W93kO9bIARhQ0+YGqZzgsb55b1yrvtiS0tUvhSjJwC9eqV57LE6hgxppqFBMWVKJ666qoJcHrEivXJwyKOJgUQiQTKZDIzFiQ09YWqYzgka55f3yrnuiy0tUflSjJ5Aq56KiiRjxzbRs2frduR33y1l7doEp5zSjMlNiKVX2iOPJs4R1z5GZkO+CstNTz6Qr8LMteSTtnomT97L4sW1HHdcmiVLyhg+vJqXXw6+C7H0ysEhCwtQXV1tFIsTG3rC1DCdEzTOL++Vc90XW1qi8qUYPYH2eoYMSTNrVj1DhjSzaVMJN95YwQMP+F93kV45OGRhAdIH3mzIIxYnNvSEqWE6J2icX94r57ovtrRE5UsxegLZ9fTqpVm0qJbLLtvDn/6UZNq0Tlx+eQV795rXCPO+YcYVgi+ysAD19fVGsTixoSdMDdM5QeP88l45132xpSUqX4rRE/DWU1YG117bwB131FNWppk7t5zp0yvZvLn9RW7plYNDzrEAjY2NpFKpwFic2NATpobpnKBxfnmvnOu+2NISlS/F6AmY6Vm7tpTbbitn2bIyDjushfnz6/jylz/9DV96pT1yjiVHPvroI6NYnNjQE6aG6ZygcX55r5zrvtjSEpUvxegJmOkZPDjNHXfs5qSTmti0qYTx46t45JFPd1BJrxwcsrBA1i15Lm2fBDt6wtQwnRM0zi/vlXPdF1taovKlGD0Bcz09emiefLKOCy5o4ItfbObiiztz2WWVNDZKrxwsco4FKCkpoaysLDAWJzb0hKlhOidonF/eK+e6L7a0ROVLMXoCuekpLYVRo1rvWLlyZZKXX07wz3+WcOKJmq5dc/uHudB7Rc6x5MjWrVuNYnFiQ0+YGqZzgsb55b1yrvtiS0tUvhSjJxBOz/e+t5dnnqll7Ni9/O53KcaOPZS//CX4vEuY9y0GX2RhAbp06WIUixMbesLUMJ0TNM4v75Vz3RdbWqLypRg9gfB6Bg1KM3Pmbr761Sa2bk3y/e93ZsGCMkz3N0mvfIosLMDeLJvZs8XixIaeMDVM5wSN88t75Vz3xZaWqHwpRk/g4PQceqjm8cfrmDRpO4cf3sL06Z249NLW6y623rcYfJGFBdizZ49RLE5s6AlTw3RO0Di/vFfOdV9saYnKl2L0BA5eTzIJ06f/kylTGikv16xYkeDsszuzcaP/blvplU+RcywUzt78KGoU+t78g0HOsZhrySc2e+W110q59toKXnwxSY8eLcybV8dJJ2U/0V7ovSLnWHLEtT3g2ZBzLLnpyQdyjsVcSz6x2SvHH59m3rx6TjmliaYmuOiiTsyZk8p63UV65VNkYYGsW/Jc2j4JdvSEqWE6J2icX94r57ovtrRE5UsxegL2e6V7d81jj9VxwQWNfPBBKVdcUclNN5XT0BDufYvBF1lYgKqqKqNYnNjQE6aG6ZygcX55r5zrvtjSEpUvxegJRNMriQRceWUDs2bVM2hQM3fdVc64cVV8+KHynBNWXyH4IgsLsG3bNqNYnNjQE6aG6ZygcX55r5zrvtjSEpUvxegJRNsr3/nOXm6/fTeHH94CaEaOrGb16kRO71sMvsjCAtTU1BjF4sSGnjA1TOcEjfPLe+Vc98WWlqh8KUZPIPpeGTgwzapVtXTvrvn44xIuu6yC2bNTHHKI9Mo+nFxYlFK3KqXeUkqtU0o9oZQ6JBM/Sim1Ryn1aub1mzZzvqSUel0ptV4pdafK4YHPrm3Vy4ZsN85NTz6Q7cbmWvJJPnqlWzfNAw/UM23aHmprS7jyykouu6xLu+suYWoXgi9OLizAcmCA1nog8A4wo03uXa31CZnXRW3i9wIXAP0yrzGmb9aQ5f+GbLE4saEnTA3TOUHj/PJeOdd9saUlKl+K0RPIX68kEnDDDQ389Ke7qajQPPHEIUydWsmGDf6/0xaDL86fY1FKfQs4U2t9jlLqKOBprfWAA8YcBjyntT428/eJwL9qrS88sJ6cY5FzLLaQcyzmWvJJHL3yt7+V8otflLF0aTmHHtrC3Ll1fPWr4c67uOpLoZ1jOQ9Y0ubvfZVSryilnldKnZKJHQFsaDNmQyZmhGt7wLMh51hy05MP5ByLuZZ8EkevDBiQ5sor/86ppzbR0ACXXNKJ++4Ld96lEHxJxPXGSqkVQK8sqWu01k9lxlwDNAMPZnKbgH/RWm9TSn0JeFIpdRyQbSXN+lFs69atjBgx4pO/T5o0ibFjx7YbV15ensNPEz029ISpYTonaJxf3iuXLe6SL7a0ROVLMXoC8fVKr15Jfve7OmbOTPGLX1Tys59VsH59CTfeuIe25YrBl9gWFq31KL+8UupcYBwwUme+r9NaNwKNmT+/rJR6F/gsrZ9QereZ3hvYmK1u9+7dWbVq1X6xXbt2tRtXUVFh+qPkBRt6wtQwnRM0zi/vlcsWd8kXW1qi8qUYPYF4eyWRgMsvb6Rv3xbuvz/F/feX8/LLCRYsqKN3b21UuxB8cfKrMKXUGOBK4Ayt9e428UOVUqWZPx9N60X697TWm4BapdRXMrvBJgFPmb7fjh07jGJxYkNPmBqmc4LG+eW9cq77YktLVL4UoyfgRq9MmNDErbfu4cgj0yilGTWqmhdfTBjVLgRfnFxYgLuBKmD5AduKhwHrlFKvAb8HLtJab8/kpgD3A+uBd9n/uowv3bp1M4rFiQ09YWqYzgka55f3yrnuiy0tUflSjJ6AO70yYECalStr6dmz9bzLL39Zzn33pejatfB9cXJh0Vp/Rmvd58BtxVrrx7TWx2mtj9daf1FrvbjNnLVa6wFa62O01lN1DtvdamtrjWJxYkNPmBqmc4LG+eW9cq77YktLVL4UoyfgVq907apZsKCeGTN28+c/J5gxo4Kf/KQCvyMmheCLkwtLvnHtITnZkAd95aYnH8iDvsy15BPXeiWRgCuuaOS+++oZNqyZBQu6c9FF3uddCsEX58+x2EbOscg5FlvIORZzLfnE5V55441SLrmknA8+SFBSAvPm1TF06P7nXVz1pdDOsUSOa3vAsyHnWHLTkw/kHIu5lnzicq8cd1yamTPfZuDANP36pRk/vopZs/Y/71IIvsjCgntb9bIh241z05MPZLuxuZZ84nqv9OpVxqOP1jF4cJp0WvHUU0l++MPKT667FIIvsrDg3kNysiEP+spNTz6QB32Za8knHaFXWu8ztoeFC2tZty7Bn/+cYMKEzmzYoArCF1lYgJ07dxrF4sSGnjA1TOcEjfPLe+Vc98WWlqh8KUZPoGP1yrhxzSxbVsvhh7ewZk2SH/2okpUrm3N+D9d8Kb3hhhtie/M42LBhww3du3ffL5ZMJtut7tlicWJDT5gapnOCxvnlvXKu+2JLS1S+FKMn0PF6pUcPzWmnNbFrFzz5ZIotWzpRV1fKl76U5sCHf8TpS0VFxU9Nx8onFtxb7bPRkX4LyzXfUX4LOxD5xGKuJZ90xF6pqdHceuseZszYw9q1KRYuLGPq1Mp25106ii+ysABNTU1GsTixoSdMDdM5QeP88l45132xpSUqX4rRE+i4vVJaCldc0cDPfvYP6uoUr7xSyre/3Xm/8y4dxRc5x4LszbcxpxjPTMg5FnMt+aQQeuWddyq59NJKUinN5s0l3HFHPSefnJZzLB0J1/aAZ8Plvfkm4wphb/6ByDkWcy35pBB65QtfSPPb39ZSUQHV1Zqf/rSC3/wmxaZNHcMXWViATp06GcXixIaeMDVM5wSN88t75Vz3xZaWqHwpRk+gcHqlWzd49NE6Ro/eyzvvJHj66SQzZx6Z9T5jrvkiCwtQWlpqFIsTG3rC1DCdEzTOL++Vc90XW1qi8qUYPYHC6pVEAmbMaOTuu+v5xz9KePbZKqZNq+SDD5TnnFz1RIEsLGR/0Fe2WJzY0BOmhumcoHF+ea986uZ4AAAI+klEQVSc677Y0hKVL8XoCRRmr5x+ehOPPFLHscfWsXx5knPO6czq1aW+c+L0Rc6x0HpCNZlMBsbixIaeMDVM5wSN88t75Vz3xZaWqHwpRk+gcHulRw/NySc38PHHKXbvVjz4YIpkUjNoUDovvsg5lhzZvn27USxObOgJU8N0TtA4v7xXznVfbGmJypdi9AQKu1e03srMmbsZMqSZykp48skybrihgk2b2j8tMk5fZGEBsm25dm0btg09YWqYzgka55f3yrnuiy0tUflSjJ5A4fdKIgHXX9/A1VfvYccOxcKFZVx1VW8+/FC1GxsX8lUYkEqlSCQSgbE4saEnTA3TOUHj/PJeOdd9saUlKl+K0RMonl753OdaOPHEZt5/v5RduxL88Y9l9OnTQu/eOvTP4Id8FZYjmzdvNorFiQ09YWqYzgka55f3yrnuiy0tUflSjJ5AcfXKgAEt3HXXbnr1quWjj0q47LJK5s9PonW8vsjCAnTu3NkoFic29ISpYTonaJxf3ivnui+2tETlSzF6AsXXK127am6++X8ZM2Yv6bTi7rsruPrqCkpL4/NFFhZBEIQOzr7zLtdcs4devVp49dVSLr+81373GcsnsrAAdXV1RrE4saEnTA3TOUHj/PJeOdd9saUlKl+K0RMo7l4544wmbr55N+k0vPRSiv/4j0rWrMn/QUm5eA+Ul5e3u8iVLRYnNvSEqWE6J2icX94r57ovtrRE5UsxegLSKz17tj7f5YMP4M03k6xYkSSRgIED2z/fJRfk4n2ObNmyxSgWJzb0hKlhOidonF/eK+e6L7a0ROVLMXoC0isA3bppLr/8Xb75zSaUgltvLefaayvI1w5kd37NiBGVZRnPFosTG3rC1DCdEzTOL++Vc90XW1qi8qUYPQHplX0kk4qrrmrg859PM3t2irIyDuoTSy44ubAopW4CxgMtwMfAZK31RtX6X+8O4DRgdyb+/zNzzgWuzZT4mdZ6gen7de3a1SgWJzb0hKlhOidonF/eK+e6L7a0ROVLMXoC0isHxsaPb6J//zRHH91ipM8Grn4VdqvWeqDW+gTgaeAnmfhYoF/mdQFwL4BSqitwPXAiMAS4XilVY/pm8vH+4OcU49cu8lWYuZZ8Ir3SPtavXwv5vNmxkwuL1rrtbTk7Afu+GRwPLNStrAEOUUodBnwdWK613q613gEsB8aYvl91dbVRLE5s6AlTw3RO0Di/vFfOdV9saYnKl2L0BKRXctUTBU5+FQaglPo5MAnYCQzPhI8APmgzbEMm5hU3Ip1OG8XixIaeMDVM5wSN88t75Vz3xZaWqHwpRk9AeiVXPVEQ2ycWpdQKpdTfsrzGA2itr9Fa9wEeBKbum5allPaJt2Pz5s2MGDHik9f8+fOpr69vNy5bLE5s6AlTw3RO0Di/vFfOdV9saYnKl2L0BKRXctUTBcq1O5MeiFLqSOAPWusBSqlZwB+11g9ncm8D/7rvpbW+MBPfb1xbduzY0e4HbmxsJJVKBcbixIaeMDVM5wSN88t75Vz3xZaWqHwpRk9AeiVXPabU1NQY7ylz8hqLUqpfm7+eAbyV+fMiYJJq5SvATq31JmAZMFopVZO5aD86EzPio48+MorFiQ09YWqYzgka55f3yrnuiy0tUflSjJ6A9EqueqLAyYUFuCXztdg6WheJH2XizwDvAeuB2cDFAFrr7cBNwEuZ142ZmBHZnrKWLTZ//vxcfgar2HgSXJgapnOCxvnlvXKu+2Lr6XxR+VKMnoD0ilcsn544ubBorSdorQdkthyfrrX+MBPXWusfaq2P0Vp/QWu9ts2cuVrrz2Re83J5v7/+9a9GsYULF+b+w1gim5581DCdEzTOL++Vc90XG56ErWMypxg9AekVr1g+PXFyYck3Tz/9tFEsTmzoCVPDdE7QOL+8V851X2xpicqXYvQEpFdy1RMFzl+8t83KlSuXAvvdhXLXrl1dqqurdwbFtm/f3r1r165b8yCzHdn05KOG6ZygcX55r5zrvtjwJGwdkznF6ImXnnzUcL1XLHiydeTIkUbnA4tuYREEQRCiRb4KEwRBEKwiC4sgCIJgFVlYBEEQBKvIwnKQKKWOVkrNUUr9Pm4tAiilOimlFiilZiulzolbj9CK9Il7KKW+memTp5RSo23WloUlg1JqrlLqY6XU3w6Ij1FKva2UWq+UuurAeVrr97TW5+dPafGRozffBn6vtf4BrXdtECIiF1+kT/JDjp48memTycBZNnXIwvIp8zngVvtKqVLgHlqfA9MfmKiU6p9/aUXPfMy96c2nd7p267a7hcd8pGdcYz65e3JtJm8NWVgyaK3/CzjwNjBDgPWZ37b2Ao8A45VSk5RSM5VSxrfmF8KTize0PjKhd2aM/P8dITn6IuSBHP8dU0qpXwJL9j2J1xbSeP5kfc6L1nqh1vpSrfWHSqluSqnfAIOUUjPikVmUeD2D53FgglLqXmBxHMKKnKy+SJ/EilevXAKMAs5USl1k8w2dfdCXIwQ+50VrvQ2waopgRFZvtNb1wP/LtxjhE7x8kT6JDy9P7gTujOIN5ROLPxuAPm3+3hvYGJMWYX/EGzcRX9wj757IwuLPS0A/pVRfpVQZcDatz4QR4ke8cRPxxT3y7oksLBmUUg8Dq4HPKaU2KKXO11o30/pY5GXAm8BvtdZvxKmzGBFv3ER8cQ9XPJGbUAqCIAhWkU8sgiAIglVkYREEQRCsIguLIAiCYBVZWARBEASryMIiCIIgWEUWFkEQBMEqsrAIgiAIVpGFRRAEQbCKLCyCIAiCVWRhEQRBEKwiC4sgCIJgFVlYBEEQhHYopQ5RSo3LEl+tlDrcb64sLIIgCEI2RgLPACilBreJLwZa/CbKwiIIgiBkRWu9bwH5cZvwR1rrj/zmycIiCIIgZOMrAEqprwH1mT9/B9gaNFEWFkEQBCEbu5VS7wCjAKWUeg/orbUOfPqkPOhLEARBsIp8YhEEQRCsIguLIAiCYBVZWARBEASryMIiCIIgWEUWFkEQBMEqsrAIgiAIVpGFRRAEQbCKLCyCIAiCVWRhEQRBEKzyf/XEmNZXSi9vAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"import matplotlib.pyplot as plt\n",
"from sympy.plotting.plot import MatplotlibBackend\n",
"\n",
"RLC = {R: 1, L: sym.Rational('.5'), C: sym.Rational('.4')}\n",
"HNlog = 20*sym.log(sym.Abs(HN.subs(RLC).subs(s, 2*sym.pi*w)), 10)\n",
"\n",
"p1 = sym.plot(HNlog.subs(N, 1), (w, 0.1, 100), xlabel='$\\omega$', ylabel='$20 \\log_{10} | H_n(j \\omega) | in dB$', line_color='r', show=False);\n",
"p2 = sym.plot(HNlog.subs(N, 2), (w, 0.1, 100), xlabel='$\\omega$', ylabel='$20 \\log_{10} | H_n(j \\omega) | in dB$', line_color='g', show=False);\n",
"p3 = sym.plot(HNlog.subs(N, 3), (w, 0.1, 100), xlabel='$\\omega$', ylabel='$20 \\log_{10} | H_n(j \\omega) | in dB$', line_color='b', show=False);\n",
"p1.extend(p2)\n",
"p1.extend(p3)\n",
"\n",
"backend = MatplotlibBackend(p1)\n",
"backend.process_series()\n",
"backend.ax.spines['left'].set_position(('axes', 0))\n",
"backend.ax.spines['bottom'].set_position(('axes', 0))\n",
"plt.xscale('log')\n",
"plt.grid(which='both')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Sistemas en Paralelo\n",
"\n",
"Una estructura donde dos sistemas LTI comparten la misma señal de entrada y las señales de salida se superponen se llama *conexión en paralelo*. La señal de salida general $y(t)$ se da como la superposición de las señales de salida de los sistemas individuales\n",
"\n",
"$$\n",
"y(t) = h_1(t) * x(t) + h_2(t) * x(t)\n",
"$$\n",
"\n",
"La Transformación de Laplace de las respectivas señales y respuestas de impulso, y la aplicación del teorema de convolución produce\n",
"\n",
"$$\n",
"Y(s) = \\underbrace{\\left( H_1(s) + H_2(s) \\right)}_{H(s)} \\cdot X(s)\n",
"$$\n",
"\n",
"La función de transferencia global $H(s)$ de una conexión paralela de dos sistemas se da como la superposición de las funciones de transferencia de los sistemas individuales. Por lo tanto, las siguientes estructuras son equivalentes\n",
"\n",
"\n",
"\n",
"La extensión a una conexión paralela de sistemas $N$ es sencilla. La función de transferencia general viene dada por la superposición de todas las funciones de transferencia individuales $H_n(s)$\n",
"\n",
"\\begin{equation}\n",
"H(s) = \\sum_{n=1}^{N} H_n(s)\n",
"\\end{equation}\n",
"\n",
"Una aplicación destacada de una conexión paralela de sistemas son bancos de filtros como se utilizan en el análisis de señales y muchos esquemas de codificación con pérdida como MP3, AAC, etc."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Sistema Realimentado\n",
"\n",
"La conexión de dos sistemas LTI, donde la entrada del segundo sistema está conectada a la salida del primero y la salida del segundo sistema se superpone a la entrada del primero se llama *circuito realimentado*. Esta estructura se representa en la siguiente ilustración \n",
"\n",
"\n",
"\n",
"La señal de salida $y(t)$ se da como\n",
"\n",
"$$\n",
"y(t) = x(t) * h_1(t) + y(t) * h_2(t) * h_1(t)\n",
"$$\n",
"\n",
"La transformada de Laplace de las señales y las respuestas a los impulsos, la aplicación del teorema de convolución y la reordenación de los rendimientos de los términos\n",
"\n",
"$$\n",
"Y(s) = \\frac{H_1(s)}{1 - H_1(s) \\cdot H_2(s)} \\cdot X(s)\n",
"$$\n",
"\n",
"La función de transferencia general $H(s)$ del ciclo de realimentación se da como\n",
"\n",
"$$\n",
"H(s) = \\frac{H_1(s)}{1 - H_1(s) \\cdot H_2(s)}\n",
"$$\n",
"\n",
"Esta equivalencia se representa en el diagrama de bloques inferior de la estructura anterior.\n",
"\n",
"Las aplicaciones de los circuitos de retroalimentación incluyen sistemas de control, diseño de amplificadores, entre otros."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# REFERENCIAS\n",
"- https://nbviewer.jupyter.org/github/spatialaudio/signals-and-systems-lecture/blob/master/systems_spectral_domain/transfer_function.ipynb\n",
"- https://nbviewer.jupyter.org/github/spatialaudio/signals-and-systems-lecture/blob/master/systems_spectral_domain/bode_plot.ipynb\n",
"- https://nbviewer.jupyter.org/github/spatialaudio/signals-and-systems-lecture/blob/master/systems_spectral_domain/phase_group_delay.ipynb\n",
"- https://nbviewer.jupyter.org/github/spatialaudio/signals-and-systems-lecture/blob/master/systems_spectral_domain/combination.ipynb"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Phd. Jose R. Zapata**\n",
"- [https://joserzapata.github.io/](https://joserzapata.github.io/)\n",
"- https://twitter.com/joserzapata\n",
""
]
}
],
"metadata": {
"hide_input": false,
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.4"
},
"nbTranslate": {
"displayLangs": [
"es",
"en"
],
"hotkey": "alt-t",
"langInMainMenu": true,
"sourceLang": "en",
"targetLang": "es",
"useGoogleTranslate": true
},
"toc": {
"base_numbering": 1,
"nav_menu": {},
"number_sections": true,
"sideBar": true,
"skip_h1_title": false,
"title_cell": "Contenido",
"title_sidebar": "Contenido",
"toc_cell": true,
"toc_position": {},
"toc_section_display": true,
"toc_window_display": false
},
"varInspector": {
"cols": {
"lenName": 16,
"lenType": 16,
"lenVar": 40
},
"kernels_config": {
"python": {
"delete_cmd_postfix": "",
"delete_cmd_prefix": "del ",
"library": "var_list.py",
"varRefreshCmd": "print(var_dic_list())"
},
"r": {
"delete_cmd_postfix": ") ",
"delete_cmd_prefix": "rm(",
"library": "var_list.r",
"varRefreshCmd": "cat(var_dic_list()) "
}
},
"types_to_exclude": [
"module",
"function",
"builtin_function_or_method",
"instance",
"_Feature"
],
"window_display": false
}
},
"nbformat": 4,
"nbformat_minor": 2
}