{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"nbsphinx": "hidden"
},
"source": [
"# The Laplace Transform\n",
"\n",
"*This Jupyter notebook is part of a [collection of notebooks](../index.ipynb) in the bachelors module Signals and Systems, Communications Engineering, Universität Rostock. Please direct questions and suggestions to [Sascha.Spors@uni-rostock.de](mailto:Sascha.Spors@uni-rostock.de).*"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Inverse Transform\n",
"\n",
"So far only the [(forward) Laplace transform](definition.ipynb) has been introduced. The Laplace transform features also an [inverse transform](https://en.wikipedia.org/wiki/Inverse_Laplace_transform). The inverse Laplace transform maps a complex-valued Laplace transform $X(s) \\in \\mathbb{C}$ with complex-valued independent variable $s \\in \\mathbb{C}$ into the complex-valued signal $x(t) \\in \\mathbb{C}$ with real-valued independent variable $t \\in \\mathbb{R}$. It can be shown that the inverse Laplace transform $x(t) = \\mathcal{L}^{-1} \\{ X(s) \\}$ is uniquely determined for most practically relevant signals. This section discusses two different techniques for the computation of the inverse Laplace transform."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Integral Formula\n",
"\n",
"Using results from complex analysis, the inverse Laplace transform is given by the following complex line integral\n",
"\n",
"\\begin{equation}\n",
"x(t) = \\frac{1}{2 \\pi j} \\int_{\\sigma - j \\infty}^{\\sigma + j \\infty} X(s) \\, e^{s t} \\; ds\n",
"\\end{equation}\n",
"\n",
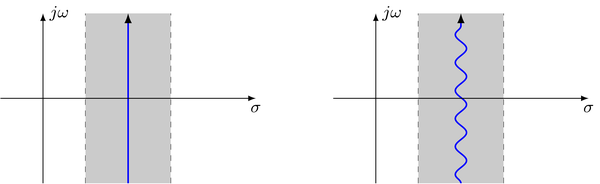
"where $X(s) = \\mathcal{L} \\{ x(t) \\}$ is assumed to be analytic in its simply connected region of convergence (ROC). The notation $\\sigma \\mp j \\infty$ for the lower/upper integration limit denotes an arbitrary integration path which lies in the ROC and ranges from $\\Im \\{s\\} = - \\infty$ to $\\Im \\{s\\} = + \\infty$. The integration path can be chosen parallel to the imaginary axis but also all other paths in the ROC are possible. This results from [Cauchy's integral theorem](https://en.wikipedia.org/wiki/Cauchy's_integral_theorem). Two equivalent paths are shown in the following illustration\n",
"\n",
"\n",
"\n",
"where the blue line indicates the integration path and the gray area the ROC."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Rational Laplace Transforms\n",
"\n",
"Computing the inverse Laplace transform by above integral formula can be challenging. The [Cauchy residue theorem](https://en.wikipedia.org/wiki/Residue_theorem) provides a practically tractable solution for Laplace transforms $X(s) = \\mathcal{L} \\{ x(t) \\}$ which are given as rational functions. It states that the value of a line integral of an holomorphic function over a closed contour is given by summing up its [residues](https://en.wikipedia.org/wiki/Residue_theorem). The residue is the value of the line integral for a path enclosing a singularity. Consequently, the inverse Laplace transform of a rational Laplace transform can be computed by summing up the individual contributions from its poles. This procedure is detailed in the following."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Basic Procedure\n",
"\n",
"A rational Laplace transform $X(s)$ can be written in terms of its numerator and denominator polynomial\n",
"\n",
"\\begin{equation}\n",
"X(s) = \\frac{\\sum_{m=0}^{M} \\beta_m s^m}{\\sum_{n=0}^{N} \\alpha_n s^n}\n",
"\\end{equation}\n",
"\n",
"where $M$, $N$ denote the order of the numerator and denominator polynomial and $\\beta_m$, $\\alpha_n$ their coefficients, respectively. It is assumed that $\\alpha_N \\neq 0$ and that $M \\leq N$. If $M > N$, $X(s)$ can be decomposed by [polynomial division](https://en.wikipedia.org/wiki/Polynomial_long_division) into a sum of powers of $s$ and a rational function fulfilling $M \\leq N$. \n",
"\n",
"Now a [partial fraction decomposition](https://en.wikipedia.org/wiki/Partial_fraction_decomposition) of $X(s)$ is performed resulting in\n",
"\n",
"\\begin{equation}\n",
"X(s) = A_0 + \\sum_{\\mu = 1}^{L} \\sum_{\\nu = 1}^{R_\\mu} \\frac{A_{\\mu \\nu}}{(s - s_{\\infty \\mu})^\\nu}\n",
"\\end{equation}\n",
"\n",
"where $s_{\\infty \\mu}$ denotes the $\\mu$-th unique pole of $X(s)$, $R_\\mu$ its degree and $L$ the total number of different poles $\\mu = 1 \\dots L$. Using the known Laplace transforms (cf. [example for the modulation theorem](theorems.ipynb#Modulation-Theorem) or [table of selected transforms](table_theorems_transforms.ipynb#Selected-Transforms))\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{L} \\{ t^n e^{-s_0 t} \\epsilon(t) \\} = \\frac{n!}{(s + s_0)^{n+1}} \\qquad \\text{for } \\Re \\{ s \\} > \\Re \\{ - s_0 \\}\n",
"\\end{equation}\n",
"\n",
"and $\\mathcal{L} \\{ \\delta(t) \\} = 1$, together with the linearity of the Laplace transform yields a generic result for the inverse Laplace transform $x(t) = \\mathcal{L}^{-1} \\{ X(s) \\}$ of a right-sided signal\n",
"\n",
"\\begin{equation}\n",
"x(t) = A_0 \\cdot \\delta(t) + \\epsilon(t) \\sum_{\\mu = 1}^{L} e^{s_{\\infty \\mu} t} \\sum_{\\nu = 1}^{R_\\mu} \\frac{A_{\\mu \\nu} \\, t^{\\mu - 1}}{(\\nu -1)!}\n",
"\\end{equation}\n",
"\n",
"It remains to compute the coefficients $A_0$ and $A_{\\mu \\nu}$ of the partial fraction decomposition. The constant coefficient $A_0$ is given as\n",
"\n",
"\\begin{equation}\n",
"A_0 = \\lim_{s \\to \\infty} X(s)\n",
"\\end{equation}\n",
"\n",
"For a pole $s_{\\infty \\mu}$ with degree $R_\\mu = 1$, the coefficient $A_{\\mu 1}$ reads\n",
"\n",
"\\begin{equation}\n",
"A_{\\mu 1} = \\lim_{s \\to s_{\\infty \\mu}} \\left( X(s) \\cdot (s - s_{\\infty \\mu}) \\right)\n",
"\\end{equation}\n",
"\n",
"For a pole $s_{\\infty \\mu}$ of degree $R_\\mu > 1$, the coefficients $A_{\\mu \\nu}$ are given as\n",
"\n",
"\\begin{equation}\n",
"A_{\\mu \\nu} = \\frac{1}{(R_\\mu - \\nu)!} \\lim_{s \\to s_{\\infty \\mu}} \\frac{d^{R_\\mu - \\nu}}{d s^{R_\\mu - \\nu}} \\left( X(s) \\cdot (s - s_{\\infty \\mu})^{R_\\mu} \\right)\n",
"\\end{equation}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Example - Inverse transform of a rational Laplace transform\n",
"\n",
"The inverse transform $x(t) = \\mathcal{L}^{-1} \\{ X(s) \\}$ of \n",
"\n",
"\\begin{equation}\n",
"X(s) = \\frac{1}{(s+1) (s+2)^2} \\qquad \\text{for } \\Re \\{s \\} > -1\n",
"\\end{equation}\n",
"\n",
"is computed using the procedure outline above. First the function $X(s)$ is defined in `SymPy`"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAIkAAAAzBAMAAABRWzbpAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMt0Qq5nNdrvvIlSJZkTVYgFVAAAACXBIWXMAAA7EAAAOxAGVKw4bAAACl0lEQVRIDe1WO4gTURQ9+Uw2M0lmVxtBhB1Ht1CbKUQsUwi2wc/aKAQsLEQIWKRQIWELUVgMWtlIEAURZIMgNhZBBRth0yhiFQR/xUJ0GxFhvPe+mdk3YUKWzRYiuZDLuefcnHnvzjxmgHGR2jeuYxP64cX1TXSNbZmZuiTOaDqXxLHgv5tL9sbP48lbnbLTCWx1Av42xGCrF/8X/5d5e8ybfF0GDGdyl9m+9WNyl5K3HS5AMdhRe8SSQt4aoSt+p5ruTGdE19eAvzJCt2skWEtKfZHUxF8tgX2hm9DwcLEJsP0D7GY5U6U0HOqr5bzQR4ZFqq0yVvvIebCaO06ybvS0Ljss5C30TpRzmo41VWQ9mC2UKjB9f8CUqTcVeKsc4mJ6DFucwniugLmO7G/gTkjjS4QIxF1yPaLsqt4QuGQdZOlpuxRJZxm9uSqXHXIplkkyupSK9VeUKQIXQukB8Fo4TuyXn7MrQsTXUqoSKQtq4rPomst8DXivSMqH6LeCfE+IuEvBITLdoVsywLLomssCEU8VSfke/VaW25QN1z1w23XLBNV0UwNCZp9cfn1k8oTr3nXd/QxhVCjNC+TELkX/j6rja7FbxLILVv0uZYpoLvIUfFck5YuM7FueEHEX2VGuw8q34Ks3dCl08Vjf0XU5lrNJLqUG/T9fA14CQy57gMvAB76ABN2tXA3PVBFfi0EG4Nt9AYWKagjWYi2cPuUAZxRJ+ROQqtd7qg5d1FdLuk2s7QC76teUHs4lR++fKnAwYOlOzkVQe3aFuy95r6aHLoqynEiiI7URdrAmxahzqM5k0LO20Rs/yDd1QcdWQ6p8Wyd1/Egrjmo4BvOelJlGjNWKJQ1bsV1ogjyvVD/ROB2W2mH1F9Dq1aTb8ANEAAAAAElFTkSuQmCC\n",
"text/latex": [
"$$\\frac{1}{\\left(s + 1\\right) \\left(s + 2\\right)^{2}}$$"
],
"text/plain": [
" 1 \n",
"────────────────\n",
" 2\n",
"(s + 1)⋅(s + 2) "
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import sympy as sym\n",
"%matplotlib inline\n",
"sym.init_printing()\n",
"\n",
"s = sym.symbols('s', complex=True)\n",
"t = sym.symbols('t', real=True)\n",
"\n",
"X = 1/((s+1)*(s+2)**2)\n",
"X"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Since $X(s)$ has two real-values poles, $x_{\\infty 1} = -1$ with degree $R_1 = 1$ and $x_{\\infty 2} = -2$ with degree $R_2 = 2$, the following partial fraction decomposition is chosen as ansatz in accordance with above given formula"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAARMAAAA0BAMAAABbWcGxAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAIs1UmauJMnZmRLsQ3e++988cAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAEXUlEQVRYCc2YTWgTQRTH3zYhadO0DYIilJqAIIqF9iAiiJhDFAWFHvSk0nqweFAaQdCLmINIRcQoHj2IerCIUEGogtA9ieClIB4EqwUv4qFNK34r68y+2d2ZyczsLKStA9u8/3u/ee9l9rXJFiB2OaVYhABOifywXE7JEpSxtobsUWk7CncmYYVau61asaMwcRJWaGXPoiA1wo7CzUlYvlxm3Xdeamw7CjcnYYVy69u/CFot7Cjcm4QVqpVTPwWtFnYU7k3C8tVyg9lvvFbbdhTuTcIK1dLgfAXI38RLCHECqRcnjvokF1CYEUv5BOtqZc9vgPPX8NJtRKoMB31SR6E/Yilvv/I1gL8E38Uu9U5G/YJi1SfVFHo51udNrBBLE/WeXOZWGHXbphWO9XmhnElMkOBAbCsBBaexaZuMlPUvE8zFnDkipgsxpxJS2XexrQgs5aW1RtKBzE8vubDT22RuJaJ63bhWRJby0qK3wLzMs8L2OkPZQuzYcqzPi3VTnqgVyqqV3nNnXdtWKOvzYrH0MJmGcNEZlNe6gX1Ar2ipqAXPs6AwB2XpJa3jY1XOs4Oz9WYrqaiKU7s+GCloZRG7XFHxNOyuR2pVW7kHF0f+k1bKUBwCGL3M2rE71FZS4Tm0P6kMT0KmlpskroOzs/Ozs29osMdTroZIKRn8zeByaSjeTfO+JFVnoLsK7Ot0K9+vXS76xv1VBuiag2IBPqK2295KCusC5OoA5BnpogtvV62V/OhhlxTfQK7ORdrKp1VrJQ3pGYBXXj+kppdGyA1iDxmtPHq7XNBzx+EetuzG9gI9R3/piziVrdV4KiD81w6Xb4X8MpcwrPqgw0j+0ICLFoCeWguZX/FUQLDXDLlB4Rq95Ia2bIR1r+uZsDvyQDEvJyC6oPBRF/qj49ZggTu8G8ZWGLXggvClA5O0DwbJpNcHVDvPJa9WJmrlGMBwtSnV9iYPaYBOld/jWjijiHOuzPgpVMZWTl52JQo+oIP7mS9xIjBxqvpJT1PnDgRO9esU3MeAqZXOaq4sUdkfTfnSdd7FZg+n6hZAt+c1+HiT7TTgGTpNrRShk5UJqa5yU65uwcNInKpuV4gphfP7BvVzH7CgGNvis4JMVZrT3RVcrBWcqjbhwAQuEmPeCIrw/SpayXjBPz0CqqMcpQisvdRQT1VmKIBMrw//YDQoojoVyE27IrUdHP+g+MxbiNBMVUeJB9U2eaiNb4X8mexxcT9rODsC7cwT5X1NTM1UpWYiTGdthlQZY4ZTaavBNpaAUX2VChkCaX0mWjNV2YbEKuT58SvMG7RyZOFNTQKz4+N1kRrwvCUJAqCtaKYqN9dEGxxBKwaEhEzURrpVPVU2NygqPBGZBstEPSWHopmqjklDzmUInSDfWjVTla4tQz1DykcAuqnqKhj2LUOoq8onFaaqj4+sgC3+BRamav8KlBdKPBYUJ5wVnlryZMFVF8xOV5ArIJy6poj/6U9j/wBPy4xPOXnUhQAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$A_{0} + \\frac{A_{11}}{s + 1} + \\frac{A_{21}}{s + 2} + \\frac{A_{22}}{\\left(s + 2\\right)^{2}}$$"
],
"text/plain": [
" A_{11} A_{21} A_{22} \n",
"A₀ + ────── + ────── + ────────\n",
" s + 1 s + 2 2\n",
" (s + 2) "
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A0, A11, A21, A22 = sym.symbols('A_0 A_{11} A_{21} A_{22}', real=True)\n",
"Xp = A0 + A11/(s+1) + A21/(s+2) + A22/(s+2)**2\n",
"Xp"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The four real-valued constants $A_0$, $A_{11}$, $A_{21}$ and $A_{22}$ of the partial fraction decomposition will be determined later. First a look is taken at the inverse Laplace transforms of the individual summands composed from the constant and the individual poles. For the constant we get"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAADsAAAAVBAMAAAAKrYvGAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAIs1UmauJMnZmRLsQ3e++988cAAAACXBIWXMAAA7EAAAOxAGVKw4bAAABdElEQVQoFW1QPUsDURCc5C7fl3jYaw6shIAp1DYhiGCX3iJnYbAz/yBXiNgZwV+gBGyEExS0ypVCmoggiE3ARqwupgiKEGffy1llYWdndt7t23fA3LClq0DIooBErPYmzXRZxJWAxJouQBLdgHxTaX0IMKaRnVMDLQewnoCSbpuN6Jp0XTpmh5+EwLm29w5bmsAaCykwTYc1IEHMOy1LlegFhAtm3gXinMKDqKhKul7xidtAt3fnIVkX+xJtVyqQcRK/LKvMipIEVFHkseYxULSNCRvPzBrTGBDSt1sNH0kv62MXKbE/mS/MVEh4BBYGKLQwwrfu0LZ+6GSHhCrXHHIu3q0Jb2dnhU6IQA3PdviCEO0Ar5ggXqZ9z7/rGDYyPrBMnRuJ/YEDbFBhH0jUeafpoT8tweh9uRw+RvLEpYtr/qoHDs3bolSo1WY839JkaaZZ+DAnUpmqZjtRg7V5FPyrG8Vi3Gxu9FU3F8w1uRj3As6AP4N5USa6GOfTAAAAAElFTkSuQmCC\n",
"text/latex": [
"$$A_{0} \\delta\\left(t\\right)$$"
],
"text/plain": [
"A₀⋅δ(t)"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x0 = sym.inverse_laplace_transform(Xp.args[0], s, t)\n",
"x0"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For the first pole $s_{\\infty 1}$ with degree zero we get"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAGIAAAAYBAMAAADzMjWaAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAIs1UmauJMnZmRLsQ3e++988cAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAB6UlEQVQ4EX1SS2sTYRQ9k4l5fnYGd1Ko40YQBOMPkMbiIt11UyiIZCwURBDzDzKglu4MIoi4cKDdViO4KQqG0kVFSlMQu80P6CK+aKuLeu43mQeTMAfOfZxzb+4kEyATlzPdCaYaThAzJdPJtMdN4+GVVqQaUukgxQUJE5CrxeJjKSveSLg+yulk9aiUVuSQ6TIAeo/dme4SofiReI+3Im2pPuM2uWcj12MG8k1b57HwVNkodHFMY56cBcp1PXTvkdydgEYBaPv4RWtAzpFHJAzvWU3yODZeAndRPOVXduh+J6/KVB6zHckjqPtPemENqBOYfznjonLn3xKwItY62m48gs1WMdGWjlH4AeT4meaQU89lso5LC8AXJ6BxipIvcoDqn8XmADhf4x2H0k2y9OF2s4viWl8T1ZPVB1RDTHWx7wFTPrdcim1yF7D6vDmixXsJWB7e9IKNfZ+6vKI6tweJDZdaDI59Yyf/l3dQ+qkqHfbDeENu0w5h+aa8gqoHLOMG8BqYkZ6/RvhUZQc7djgPnOvstdgVFoBFxbUGvp5dg/n5pxttYHWNRgTVuCV1pQ9Mv2JxEDnxRiwlq8OgMbgZInyqsE/lF0Gf70S6sfzbE0ZCqqjaWphOyRmt6mrzU8ZI2rooQtnGf0c/cOTzd0xoAAAAAElFTkSuQmCC\n",
"text/latex": [
"$$A_{11} e^{- t} \\theta\\left(t\\right)$$"
],
"text/plain": [
" -t \n",
"A_{11}⋅ℯ ⋅Heaviside(t)"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x1 = sym.inverse_laplace_transform(Xp.args[1], s, t)\n",
"x1"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For the second pole $s_{\\infty 2}$ with degree two we get two contributions"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAGsAAAAYBAMAAAAPJx5QAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAIs1UmauJMnZmRLsQ3e++988cAAAACXBIWXMAAA7EAAAOxAGVKw4bAAACJklEQVQ4EYVSTYvTUBQ9aTJtmsa2CAoudApuByz+gRnFhQOz6GaW0ig4urNudCEyATfFjVHcGxDBZRaKDAqNLkQRaRRxtv0BLurHWBWhnvvSNJm2xAv365x737svuUCO2FubIQr1nIqFlAEjQn8hlQfWfG2Ek3kVC7lyqI0Of7yUcpoKp1MfTJn9UTHC8QxyS8WPE+REEsz6myH+CmZe7NDqDg2TpnLQx7FP7Y3nlDq0F7AGgu7YEe0rqv0BWBEIMNrTcWMgsYdw1Wy9BIoBRsTWqfoQuB/z5690ksJ9Xnt2fcNwHWDbx3cyA6rRAKohA2junab4OamOx0NrnUeeQ+k3YDVYccABCp6UGlhVXmLK6+5GHEyt/Qv6H9Y5wKPeUxfFllAPsU0gEWsX15J44s0Ril8nl6wSKzeEWMNyC2r/3jJf9nBb0IxU9jbbA87XJHaaqkc05pMz7YCTGlGpy7zX3fKJZqUaoO/yS/gEP1NLQ5o3QC2C2j85Zo/QjNRcPAjjNptvjP/lGq8fQPZP3f5zpodp38cnukKTHUOEqszyCMit3D+5jVPoM501X/9CqOKyqKHXUQ6AYwLwO4H7J233YJ9ilpUl732HuXz3pRbfZLh4N16B3vvmyP6pNvNyN9sisX1WHWTxUG3H45vqaQX3T7WlyFy0O0GOpozs3//aJiusVnrSKfunXfjhpgfNR5V4OC2Yp/IQO66vhHlFC7gjCrsL/AOqC4ZRhtSFIQAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$A_{21} e^{- 2 t} \\theta\\left(t\\right)$$"
],
"text/plain": [
" -2⋅t \n",
"A_{21}⋅ℯ ⋅Heaviside(t)"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x2 = sym.inverse_laplace_transform(Xp.args[2], s, t)\n",
"x2"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAHEAAAAYBAMAAAA/qw9xAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAIs1UmauJMnZmRLsQ3e++988cAAAACXBIWXMAAA7EAAAOxAGVKw4bAAACT0lEQVQ4EYVSS2gTURQ900kz+UwzQXBVNBFBEArGjdtGEamgkE1AUEkUIiIUpyB0VToLW9wZQRBBMPgBN9UUFC0KnYWIUEojiisXWYtgVCRtXYznvkmcEabJhXM/59w3793LAEPsXe0csG9IU6RcxGmYnUhpCLmNnK3nhzRFyveQm5k+YAdaVlLlJNklbiebxkgh0BIqf9InDvWTiGh8geWST9RsUY+Ig38e0D1V9ty6/xTjNW0ZGHfxVJQVs0Vv5okPwIRQQKziN/vVpB96XisZ2QUzi3gTXWmt86IOcNuXL1y1Q93HQjmvnL3mTsWB+QZ+UcgQsTyjywSac7MgsWef+4mK3z0Pj+4A52FskXhAjFWBEd7Nb2BSRcmROvvnDMzL111V/XPmJvRtVieAx6svHMRLIj3EfFWibzLFkm1U+7UfE13EfzA9SMgiknk6FJErwbxUdgUyhbaFREOUwNK/y5U2y4+ELEJv0SWeH680+eRYSyBTpDcXr1AIW6aJDYfEV0IWYfBleA9YLVgNrSvARgOWGoJSYJaD+y5LnjRl3lSbrshttZF0ta4Az2BaVdL/G7/3SZj9PNSBq16bqnPHcne8pXARh2XtBekLzGro36R6xZ68nkWyCexlnZa1zbkKZdPh4t5myYRstL5uS1kDRkucL+ZgzZuAvvqzCu0N/wli/C6weMNhV9jMqaOqXGLTSp3zhb68GzMQDLYxdTOwJ2jTXs6eEgRMZJYs+vTJQM14XkcQMNHZsqK1ZrQ6iF1TYtod1BOtaXXhbwF/AXm3kQIRUQrCAAAAAElFTkSuQmCC\n",
"text/latex": [
"$$A_{22} t e^{- 2 t} \\theta\\left(t\\right)$$"
],
"text/plain": [
" -2⋅t \n",
"A_{22}⋅t⋅ℯ ⋅Heaviside(t)"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x3 = sym.inverse_laplace_transform(Xp.args[3], s, t)\n",
"x3"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The inverse Laplace transform of $X(s)$ is now composed from the superposition of the four individual parts"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAc0AAAAYBAMAAABq77sGAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAIs1UmauJMnZmRLsQ3e++988cAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAE/klEQVRYCa1WXWgcVRT+JjPZv0yTRTAIQbMiFIRCg6gIUhJLKym0kJc+qWR9SAxCcQtiBZHMg4agiLEIvgguakEfKltQtCjsCFKEIon/SN0S8EXEn01LTVOV9XxzZ3Z+MrPT7OTAmXvPvef77nf23pm9wG7ZnZmILsw9CmSjkPXN+eM2BsqZlKSAzXZKQu/pKRxDRgpZwICxhtXeK2Wc1SuZCG5gvJaRQtYfqWubuGcHQpyt38n+ayf21nz+HcPxJsZPZqSQ5Yu2tjn6zRO+EISV3OLNaAcvcaYwwYH3vNFgq1WCkd8fcCAq7gMOnEBmClk9t4a7fFHRQvZ7UzmcsaV/vxMrud6U2w60IwNuOGJLpzBXY9gHHPmfkZWCSz9v41+2sUr0DqdoQ2U+zYr418A+BhGbjNaZ/1TsHD5g3nlzTZ79wDFm90VBmbTnqKIM7TOU1hnHKjFmnfJkujDDJGMF0NvA6wzEShJ7dnjD64XbF80ycg1symg/cG0mX+5Bgff91UIKKDNgt+JkYeZzOb6xSh5/qubmmlfZGRY3KtLa0hHTLafhIzfKSmJsOgcs1kF8P/CxU0/bPSjwQHfJsALK9E37+NRRw6omKNGsVye83KYtvbfF91SBAXcfA3XeVnB+CUmI2LtvAI8hvyXD/cD/6nTQgyJQZ1gBZfo23Om0S0dk02KVGJh0C8K9kw1BPQycaX5kITejKAJ1TumsxDNz4QXb68t7eR36DQn7hJMoiSJQZ0iBI/PC8lFfhNOLp3kHi1WVWKwM8mt1t/ikeLEiDzG/ztJE/m815jzP1vJVPyxsIse3t084iZIo/DojCkRm6Uc844twevE0UxiXjZtfAsbLOl+/b8UPiutrDipQpwHtmvzqp5VrWyjUVQqfQ9eOz65LmwbnXZYUEXgvCr9OpYAUzpVYZI6v4CViAxarpPDhodkGclapgUeQZ52/if8gnm/Lw2i1Lv/Raqkj/PKhw/8Az76ifOj60pOS4dlwA6uWBGlw3mVJEYGTJpYCx1qtP1ut75kApYAUdMpsLs/XnSn/EUvzpdwL1zBcwwa2VGki1OSLVlpX0O65NS3gPxk7oHxEFa+ShMXCW7YEaXDeZUkRgZMmiaK7n64CUtApUw5Y1GJppuTjui5HFr+Ym+qVlJtTqQ17+7k1hPCyuFdnVfq+rdbxHaM0uNxlVZ1VH+v2kii6dboKSEGnzOAHowcNLwFymVu08ZP8yzt3zE/kf7Kil1FsKFx3P/lvzTuiWyc/6hMqhc+Ruv4721S43GVJEYH3oujW6SkghThlytHViQ1YnJI7ZH5og3X+igXcx+w5YHBGjrNhSSDm1amtS9Asd+ssVvCFRJ4NrnxVYz8VLndZ1hmBE5pE4dXZVUAKcco8DfMhYgMWQ3Oxsw9680pVzu1V5JarzD4r38LzK/KDu0W4dZrNKzYe7Ozt1omlZYv5rpnTar1U+JitKMJwsiRRuHX6CkghTpmFhWVCg5ZII186fodc2+NsC3C7G3v76c1757YbhztpcN5lHYowLBhFKbz99HJI4dB4A/HtNhp5Ia1SxUsuTqneEXegJHsbsgMS0eMtDc67bA84SaMUwXs850nh0DBItm00kjofuMKdc6BaI4FhdP806EmWAuddthectDdBQZo0S6G56OCH7DSahPmMcLLuAsVN0GjOQX0toYzU4Yxw8u8CRYjmf8QP7O/IwwTdAAAAAElFTkSuQmCC\n",
"text/latex": [
"$$A_{0} \\delta\\left(t\\right) + A_{11} e^{- t} \\theta\\left(t\\right) + A_{21} e^{- 2 t} \\theta\\left(t\\right) + A_{22} t e^{- 2 t} \\theta\\left(t\\right)$$"
],
"text/plain": [
" -t -2⋅t -2⋅t\n",
"A₀⋅δ(t) + A_{11}⋅ℯ ⋅Heaviside(t) + A_{21}⋅ℯ ⋅Heaviside(t) + A_{22}⋅t⋅ℯ \n",
"\n",
" \n",
"⋅Heaviside(t)"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = x0 + x1 + x2 + x3\n",
"x"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For the final solution the four coefficients are determined using the given limit formulas for the coefficients of a partial fraction decomposition"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAAVBAMAAABPpbMoAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEER2zVSJ3ZkiZjKru+/kt61jAAAACXBIWXMAAA7EAAAOxAGVKw4bAAADv0lEQVRIDdWWPWgUQRTH33q5j82Z3IJiIYoi2giSAy0s1JwWWuZSWsgdnESEqKdNFEUucGCKFAeKWBjvrOw0nUoCiYhgocSAheBH0tiYIolEkxjlfG9m3+zO7my4lHnwbt6895+Z387tzi4AWPtg85l9VjIf6RWtnWv1Eu61KiTdhsQ8cQss49Mkji/KIW0LPJTbvqM1DrW2R+tx57nDkdaaxSxJX+VIa8MsWlks9YVSibIsFILwbXnrhjbG7cSbhqz1tscIbxSr8buq7s6pjAxCLP66u9QFyjH88KpfgfETgEuBlOimpmqmdLcRPkLME8TM8CEW1stWLOWHT9xf0xWA/0vBBHTxymhAKbpm+AgxT2CGD7OwXrYh+LuxX7oCVgC68oEcdu1styELYISPEvO0ZvgwC+tlG4KvxP94iusYWgTf8HIcpaCgZ5MVUTLCR4l5MjO8xkJS4vGZB5/KUXpLPv1bla0lDG3sT2RVTgUHYKKoOhTsyYmuET5KLEbgjxFeYyGl4OEh2IqlTlCi3qDfFNh/8eEtFakDDrqAL1JPtwrUJwF25qRjzZJ1I7wQW33vHDHAE8shEfCSZUf/KyAnIx6fiaXqePOOXxPZ40PD/wBKcEhpLNz5rvDOxz4NTX2A9OGycKU23/NSnIJUmQZ4tn2A7GYEvGSpwB0gV2adEaNG3aXsj3mwqg6WLaRcBpiDTE2J8Z4v5FWPg20AmTK+2lzntBleijN77TUxwBNzZLptXJafUB8lZ6mvFTufOIWZjkn8SaHfBnsVOj3crwDPHMzrVgFIzrYKL8XtzobgJQs8RnByCJuAL9SwIF5SBzHogfQiJBtK+xSgyje0Sm7BOr28zTsfuFYW0xo0IGy08+4zo4qSBbv0GiIPmYC/TGmCt2cxmKkhfGcWI/l0J/PWHB8lmJT2CJsOfBf74L3TJngqsBjwY8SFd8U8HcEHUi4LAH33yG+f4LwCXlwWwlszSw6ca57G2yaTp3nFuWqVjo1CEmfw2e7mSYjPLBX98PKcfz9/KwsDjk8LSmxPy6vFovtScGVbvy2/DizBLAAjOBk5mn7Oi6XkfyJuG3cy7YGVuV63FGh8O++rxDV4VXgIL3nnVc4XmJewJ9M1cp9QC3nnVbIE+1XsBsVgQvbN8Amj2P48NrgevHmJkbEXDrlxSkwK+NisV06UBr2OiOjcMph9fiVLHijh0WiwzmZzwSBmZcQS880mkEdZlQrW96gy5dvXK4ZqjVCmhcTGluAJrR8ievCGE5uoTffnAf4D3pn+qxyRmogAAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\left \\{ A_{0} : 0, \\quad A_{11} : 1, \\quad A_{21} : -1, \\quad A_{22} : -1\\right \\}$$"
],
"text/plain": [
"{A₀: 0, A_{11}: 1, A_{21}: -1, A_{22}: -1}"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"coeffs = {A0 : sym.limit(X, s, sym.oo)}\n",
"coeffs.update({A11 : sym.limit(X*(s+1), s, -1)})\n",
"coeffs.update({A21 : sym.limit(sym.diff(X*(s+2)**2, s), s, -2)})\n",
"coeffs.update({A22 : sym.limit(X*(s+2)**2, s, -2)})\n",
"coeffs"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Substitution into the inverse Laplace transform yields the final solution $x(t) = \\mathcal{L}^{-1}\\{ X(s) \\}$"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAASIAAAAYBAMAAACsBu36AAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEM3dMiJUmYlEq7t2Zu/qvyblAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAD70lEQVRIDZVWTYhTVxT+3kxefibJ5OFQFFqYFLF0U4jNqMXVgyoVXEzAjTiUCS2FLoqOitDFDITahY5Cgy4KpT8p7SpaHEE3/jBvVa0MNEpLF6V0XEqhHWEsjo6dfue+F/LuzXvJ5MC999xzvnO/c++5eTdAtGyb/xbYEe2Lsw4Et840HQxV4tbqts/gJKyVbnsPy2DwFFIljPdYznStYdpNFk1rz/lg8ELdXsV7PRfUnfcxvf/0627HaIuquo5N02wNrsrRqyZ5x149/OannSX6EuA0hqodPH4UPeOFLKYahueq4v3ShGjzdAmvhQx9CRI7UXAk4O730idr0vt5Ka27U/DcvCueD5Xbz0upEd3bDh6LOZZgzD/jxE3KdWDKwdeCz7bGZNjCRsSQSlIMIQlCFPy2VaLHKrLtAl6l3iUHhaEC+yoyy3TGExzTQu1GonLPYpLnUHDpmWMjIj8ToL4KxtAg8PQCVmlKtXiqK8BvIbepHsH+XOOlWALCT2ghU/vecWbTQGINhSo9y2yCeMgm8pE/hHuBT9bxL22jbKkiRycM0HT72r7jKa8WS0DwW1rAPxsb+PwXYKSESW44UwwQbwSoiIwE/h0SL4i4wDZcA4YYGiOjGxsrmTk3lgCZS88vwzp/x9zUuIdjdW645iMwHxC0M9JDrHUk14j4GPhi8YaHdMPIZ9vSccMSR+CX/aKbqBkBP7v4rOJvVi4GHgT+dkZ6SG4V6SdEyEnKvcwX2YUkM4EDoamocQSq7PYL5Hgemiw2m//RMFz1Lwbe50QkyMgIyT5rXlmmdzeb3LpkiV1Iplv4KTQVtZtgS1lkQsqeXb971sDjL7ASvKLMVC4GJgVwslz+u1zeS80IGV0AqwA8YpN7mZBjtbYrCpfq4tIZc8uRBIQC43UUGkrTunXk5TMmGREB/xvFMTgjI6Tg4U+HXmZkyX1SHxyObXnWVjpjHAHwDaxCrQMMNK47PENdXggiYFbNCGHSeySSr0NmBU5X1Z6KU5NYAuATfCBlqWp4YA1HZdNZTyGA3wN/cEZGSKGeVB+sW0C6mKwgv6Avx0omdUssAdC0PP4ytlaMgB+sCbGkGwoBzAb+ICMjZKQ15gqA34iRxiv8MXgy68gDWKc6M6XFEfAd+4Nv3pJn4LH1jsoxU/IR4GOlJMjICLFmfcKL/ONyu8Ufg7HB3PmlzRKYuK65OinyMDMl7Yy6gMow7Pr2Q9HuKKtJEIXRbMGbKU+okoiXNoRvP8hzIVsf1SToA+fV9s9/qi/QB1xXg72wSThhAxLw8+IvfnWTFC8rXNbZJJywAQkY8a4snvdPStTeYrfE/2tvkO5tE/wPEJoKOpmaogUAAAAASUVORK5CYII=\n",
"text/latex": [
"$$- t e^{- 2 t} \\theta\\left(t\\right) + e^{- t} \\theta\\left(t\\right) - e^{- 2 t} \\theta\\left(t\\right)$$"
],
"text/plain": [
" -2⋅t -t -2⋅t \n",
"- t⋅ℯ ⋅Heaviside(t) + ℯ ⋅Heaviside(t) - ℯ ⋅Heaviside(t)"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = x.subs(coeffs)\n",
"x"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The solution is plotted for illustration"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM4OC42Nzk1NDU0NTQ1IDMwNy43NTk3NSBdIC9QYXJlbnQgMiAwIFIgL1Jlc291cmNlcyA4IDAgUgovVHlwZSAvUGFnZSA+PgplbmRvYmoKOSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDExIDAgUiA+PgpzdHJlYW0KeJyFmEuvHDUQhff9K7xMFjiu8ntJBFyJXeBKLIBVXhBlIgUQ4efzVU97bvcd3wlSSKZOHR+3Xa9ucR8Wce9dcB/488X96n7n7zdO3B1/3i+BX6cltuZL7Tllfn7c/4yh+pp7zZjD4dcfy/JuefEti/wN6W5ZpPkQglSn2adUcWLhmr3owfhxb+zi87beA31n3ET0LPKeLfMYvu0eBGlDlhx8KrkoW64+p7jK74zJh9X4cVleciJflpf37sUP4iS4+3dLql5b7uag6nt292+WZ+G5u//gvr9fVsVFJPvYS45pL7G33tYQUa9SGjvqoe909JFOCz5qTSkedHbWr+jU6sWOOpcmbaeTjjqastfcYta9zt56W0eT+lBbKWhp3emUo06U4KV1LbLX2Vtv61jQhdBzja3EstNpj3QuYbWXeTB+RaU0X0tYoz7to0AuYXD0r9FL7hp1zZPutTbRM+Wf48amoZmK74+MTxyzeK4i+ppKq1tgch5PSTSetyTJctB4sN4QaeJj4SoLQdaGkD4lJFF9bSnneFDamW9IiTbfWy21Nv4/tNKTWgR/ComTPmo9mG9p1eJLaFxtjJKGVnlKS9la0BxzOWjtzDe0VJPHM6FWyaBNqz2pRXSWlGuuR60H8y2tKh6l1lSlb1IPwfqZci3uG6E4iqWAWPBo0620vj6xolV/DrCcw/bFD7ot/+w/W2XJvkvta9SFs8PQf/bbs9Uj+h6EmJGdz2WRf4aLhtbbGuFXyzxffdjuq+WzGx0gnDNwNIyYqWc8bimeEur+eut+cZ8cPYIuEOzJqHOFI1vsWLf/KkgNmbOhkHX305178d3bf/98/fanu5fu9d8PzeZQ+Tyn33I7ZOTPMzt1xZSzSnrkPLHjnH3jIK9WntgJA/Wp9ZDjI+eJHWfqjpXGx75XZnqhEh05cdeJThIpXfXsPANwT75XolhcztSe1Grb3CfAaSnB0z4Jfa6WdJNEBzn7TxEIhUkip04sUHljjr0Nwgw5LZXQ7a10IkHsqWooG2GKQKg+KbFOq6W9R46uxY0wQ05Lo8gq00ddUytYbd+OaIpA6D5aWcbaib3L8U/sp6VTGXKpydag1bSqsm1nitDxg5XfXNXWoXK0GIKeGXPIKORIYchIpA+HbbU8DsoMOq1TSRBpttvYzR5lqEwho3B+LVcR6h3B03toaVBmEBSlW5LXNToN0Td6kWyMGWIETk5z752yEKmGVfrQmEJQYvEaAwMJgWPNudYyRKYQFEuqFCwShPIbYk8jbOeQUcgtO0bCk41oqzFfKDMICgUsMYQQZCLU7JAljI1NISiFmJDAxOM6T1sJ78GYIUbovnUSU1wn4QoZNG5xhkCgx6jaUzkOUVsIpW+EGXIeQAkBbsrRUJsS3yO0ZogR6GJKbqkjaQobT+MZZggEBv8S1IYPaoByxXUQZogRKOMx0KJcYXaJpNrwvwYo8IGhjm7EUJwbvSSRyFuJnyFGYErhB2lG1Ws0mloHYYJAsFabmGmSy9xmL0VGE5khEJQ+lWzodAQPfYxxaCPMECNkOnikM7rEM2Yc4iBMEAh0pGxVWhxhTHFPI1eniBHo+5a3zdmrgPRaL4QJYn2TXkxpCZiTJUrXS+ecIEZgoJc1a1Nk6pPLM08A3Dkw2g2N0pGTMWgchXOKGIFSl5oIZhxs+hj+1wDuhAjlMzLvY6VUEMCb/wwxAifdSKNkHZNhI6kMwgSBQI3mbUnsHPhXpnuMJ54hRrCXyk5NpO5STu1fm/81YO4WIY3HwkolJQiG+zWAO2nNhMqbi5ljDu2y/xliBALKRuhVlvSQSwzNEAiddUJvvObGxoxTim7FZYoYgXWSJm4ec2U2i+MOZojNX/SKlO3tsRFjEuuYv67s5tx9t9tTs1INeGcb7hPEXk4zXT4QgWZmdmGfG2GGQLCJPGRLuWgFROIWcjPA3LMFLjdj1hAruTH8JwgEcrXCXYe/TlyNyjUDzJ3huVK5z+ZAmKThP0EgEH3dAncdRVvWMrrtFDECU1oo6yqNMhhluF/Zbf4lO7UVu/TKW7aUMo5nhhiBq2YoDesnA0avFsb5zxAIdEXm6JDWuZtRsOWxoRliBPKn8Ma+fvwoDLR5KMyQ0/HrQskUne2AXrnPTt2P5y9sh09Tx1eOr3ygejRCXj6sfVk/rk2+o52e+I62fLp8MFt3Y/TZ687kc8lMefJZ7obyq+V/kQcIvQplbmRzdHJlYW0KZW5kb2JqCjExIDAgb2JqCjE2NjMKZW5kb2JqCjE2IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTc4ID4+CnN0cmVhbQp4nD2QSxIDIQhE956ijyA/0fMkldXk/ts0zpiF9hMobLCl6BjOy9WQXfGWVhie+DbvC56Jq6n1hyQVMvumDhmLZ/IUJyQUryZjQNyx1dajcTLCDLssJmZgroqvRC6oUALqUfJqZqPgaqaCvn3EVpn1FhcIRQImLGcr/p8D0+sWHQwWmO03y7M89grTdCzMe4Z5D0UjfgblWm5gZa2Dn4Ydmve2aCj/5Cd7Fni1zw/eq0KhCmVuZHN0cmVhbQplbmRvYmoKMTcgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA5MiA+PgpzdHJlYW0KeJw9jLENwDAIBHum+AUiYYxt2CdK5ezf5i0naeD0D9fSoDiscXZVNB84i3x4S/WEjcSUppVHU5zd2hYOK4MUu9gWFl5hEaTyapjxeVPVwJJSlOXN+n93PcerG7oKZW5kc3RyZWFtCmVuZG9iagoxNCAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMtT2JsaXF1ZSAvQ2hhclByb2NzIDE1IDAgUgovRW5jb2RpbmcgPDwgL0RpZmZlcmVuY2VzIFsgMTE2IC90IDEyMCAveCBdIC9UeXBlIC9FbmNvZGluZyA+PiAvRmlyc3RDaGFyIDAKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udERlc2NyaXB0b3IgMTMgMCBSCi9Gb250TWF0cml4IFsgMC4wMDEgMCAwIDAuMDAxIDAgMCBdIC9MYXN0Q2hhciAyNTUgL05hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxMiAwIFIgPj4KZW5kb2JqCjEzIDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyA5NgovRm9udEJCb3ggWyAtMTAxNiAtMzUxIDE2NjAgMTA2OCBdIC9Gb250TmFtZSAvRGVqYVZ1U2Fucy1PYmxpcXVlCi9JdGFsaWNBbmdsZSAwIC9NYXhXaWR0aCAxMzUwIC9TdGVtViAwIC9UeXBlIC9Gb250RGVzY3JpcHRvciAvWEhlaWdodCAwID4+CmVuZG9iagoxMiAwIG9iagpbIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwCjYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgMzE4IDQwMSA0NjAgODM4IDYzNgo5NTAgNzgwIDI3NSAzOTAgMzkwIDUwMCA4MzggMzE4IDM2MSAzMTggMzM3IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYKNjM2IDYzNiAzMzcgMzM3IDgzOCA4MzggODM4IDUzMSAxMDAwIDY4NCA2ODYgNjk4IDc3MCA2MzIgNTc1IDc3NSA3NTIgMjk1CjI5NSA2NTYgNTU3IDg2MyA3NDggNzg3IDYwMyA3ODcgNjk1IDYzNSA2MTEgNzMyIDY4NCA5ODkgNjg1IDYxMSA2ODUgMzkwIDMzNwozOTAgODM4IDUwMCA1MDAgNjEzIDYzNSA1NTAgNjM1IDYxNSAzNTIgNjM1IDYzNCAyNzggMjc4IDU3OSAyNzggOTc0IDYzNCA2MTIKNjM1IDYzNSA0MTEgNTIxIDM5MiA2MzQgNTkyIDgxOCA1OTIgNTkyIDUyNSA2MzYgMzM3IDYzNiA4MzggNjAwIDYzNiA2MDAgMzE4CjM1MiA1MTggMTAwMCA1MDAgNTAwIDUwMCAxMzUwIDYzNSA0MDAgMTA3MCA2MDAgNjg1IDYwMCA2MDAgMzE4IDMxOCA1MTggNTE4CjU5MCA1MDAgMTAwMCA1MDAgMTAwMCA1MjEgNDAwIDEwMjggNjAwIDUyNSA2MTEgMzE4IDQwMSA2MzYgNjM2IDYzNiA2MzYgMzM3CjUwMCA1MDAgMTAwMCA0NzEgNjE3IDgzOCAzNjEgMTAwMCA1MDAgNTAwIDgzOCA0MDEgNDAxIDUwMCA2MzYgNjM2IDMxOCA1MDAKNDAxIDQ3MSA2MTcgOTY5IDk2OSA5NjkgNTMxIDY4NCA2ODQgNjg0IDY4NCA2ODQgNjg0IDk3NCA2OTggNjMyIDYzMiA2MzIgNjMyCjI5NSAyOTUgMjk1IDI5NSA3NzUgNzQ4IDc4NyA3ODcgNzg3IDc4NyA3ODcgODM4IDc4NyA3MzIgNzMyIDczMiA3MzIgNjExIDYwOAo2MzAgNjEzIDYxMyA2MTMgNjEzIDYxMyA2MTMgOTk1IDU1MCA2MTUgNjE1IDYxNSA2MTUgMjc4IDI3OCAyNzggMjc4IDYxMiA2MzQKNjEyIDYxMiA2MTIgNjEyIDYxMiA4MzggNjEyIDYzNCA2MzQgNjM0IDYzNCA1OTIgNjM1IDU5MiBdCmVuZG9iagoxNSAwIG9iago8PCAvdCAxNiAwIFIgL3ggMTcgMCBSID4+CmVuZG9iagoyMiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDM5MiA+PgpzdHJlYW0KeJw9UktuBTEI288puECl8E1ynqne7t1/W5vMVKoKLwO2MZSXDKklP+qSiDNMfvVyXeJR8r1samfmIe4uNqb4WHJfuobYctGaYrFPHMkvyLRUWKFW3aND8YUoEw8ALeCBBeG+HP/xF6jB17CFcsN7ZAJgStRuQMZD0RlIWUERYfuRFeikUK9s4e8oIFfUrIWhdGKIDZYAKb6rDYmYqNmgh4SVkqod0vGMpPBbwV2JYVBbW9sEeGbQENnekY0RM+3RGXFZEWs/PemjUTK1URkPTWd88d0yUvPRFeik0sjdykNnz0InYCTmSZjncCPhnttBCzH0ca+WT2z3mClWkfAFO8oBA7393pKNz3vgLIxc2+xMJ/DRaaccE62+HmL9gz9sS5tcxyuHRRSovCgIftdBE3F8WMX3ZKNEd7QB1iMT1WglEAwSws7tMPJ4xnnZ3hW05vREaKNEHtSOET0ossXlnBWwp/yszbEcng8me2+0j5TMzKiEFdR2eqi2z2Md1Hee+/r8AS4AoRkKZW5kc3RyZWFtCmVuZG9iagoyMyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDkwID4+CnN0cmVhbQp4nE2NQRLAIAgD77wiT1BE0P90etL/X6vUDr3ATgKJFkWC9DVqSzDuuDIVa1ApmJSXwFUwXAva7qLK/jJJTJ2G03u3A4Oy8XGD0kn79nF6AKv9egbdD9IcIlgKZW5kc3RyZWFtCmVuZG9iagoyNCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDgwID4+CnN0cmVhbQp4nEWMuw3AMAhEe6ZgBH4mZp8olbN/GyBK3HBPunu4OhIyU95hhocEngwshlPxBpmjYDW4RlKNneyjsG5fdYHmelOr9fcHKk92dnE9zcsZ9AplbmRzdHJlYW0KZW5kb2JqCjI1IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ3ID4+CnN0cmVhbQp4nD1PuQ0DMQzrPQUXOMB6LFvzXJDqsn8bykZSCCJA8ZFlR8cKXGICk445Ei9pP/hpGoFYBjVH9ISKYVjgbpICD4MsSleeLV4MkdpCXUj41hDerUxkojyvETtwJxejBz5UG1keekA7RBVZrknDWNVWXWqdsAIcss7CdT3MqgTl0SdrKR9QVEK9dP+fe9r7CwBvL+sKZW5kc3RyZWFtCmVuZG9iagoyNiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE0OSA+PgpzdHJlYW0KeJw1j0sOAyEMQ/c5hS8wUn6EcB6qrqb33zZhWgkJC9svwRaDkYxLTGDsmGPhJVRPrT4kI4+6STkQqVA3BE9oTAwzbNIl8Mp03zKeW7ycVuqCTkjk6aw2GqKMZl7D0VPOCpv+y9wkamVGmQMy61S3E7KyYAXmBbU89zPuqFzohIedyrDoTjGi3GZGGn7/2/T+AnsyMGMKZW5kc3RyZWFtCmVuZG9iagoyNyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDQ5ID4+CnN0cmVhbQp4nDM2tFAwUDA0MAeSRoZAlpGJQoohF0gAxMzlggnmgFkGQBqiOAeuJocrDQDG6A0mCmVuZHN0cmVhbQplbmRvYmoKMjggMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzMTcgPj4Kc3RyZWFtCnicNVJLckMxCNu/U3CBzpi/fZ50smruv62EJyuwLUBCLi9Z0kt+1CXbpcPkVx/3JbFCPo/tmsxSxfcWsxTPLa9HzxG3LQoEURM9+DInFSLUz9ToOnhhlz4DrxBOKRZ4B5MABq/hX3iUToPAOxsy3hGTkRoQJMGaS4tNSJQ9Sfwr5fWklTR0fiYrc/l7cqkUaqPJCBUgWLnYB6QrKR4kEz2JSLJyvTdWiN6QV5LHZyUmGRDdJrFNtMDj3JW0hJmYQgXmWIDVdLO6+hxMWOOwhPEqYRbVg02eNamEZrSOY2TDePfCTImFhsMSUJt9lQmql4/T3AkjpkdNdu3Csls27yFEo/kzLJTBxygkAYdOYyQK0rCAEYE5vbCKveYLORbAiGWdmiwMbWglu3qOhcDQnLOlYcbXntfz/gdFW3ujCmVuZHN0cmVhbQplbmRvYmoKMjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxMzEgPj4Kc3RyZWFtCnicRY/LDQQhDEPvVOES8hk+qYfVntj+r+swmkFC+EEiO/EwCKzz8jbQxfDRosM3/jbVq2OVLB+6elJWD+mQh7zyFVBpMFHEhVlMHUNhzpjKyJYytxvhtk2DrGyVVK2DdjwGD7anZasIfqltYeos8QzCVV64xw0/kEutd71Vvn9CUzCXCmVuZHN0cmVhbQplbmRvYmoKMzAgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDggPj4Kc3RyZWFtCnicLVE5kgNBCMvnFXpCc9PvscuR9//pCsoBg4ZDIDotcVDGTxCWK97yyFW04e+ZGMF3waHfynUbFjkQFUjSGFRNqF28Hr0HdhxmAvOkNSyDGesDP2MKN3pxeEzG2e11GTUEe9drT2ZQMisXccnEBVN12MiZw0+mjAvtXM8NyLkR1mUYpJuVxoyEI00hUkih6iapM0GQBKOrUaONHMV+6csjnWFVI2oM+1xL29dzE84aNDsWqzw5pUdXnMvJxQsrB/28zcBFVBqrPBAScL/bQ/2c7OQ33tK5s8X0+F5zsrwwFVjx5rUbkE21+Dcv4vg94+v5/AOopVsWCmVuZHN0cmVhbQplbmRvYmoKMzEgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyMTAgPj4Kc3RyZWFtCnicNVDLDUMxCLtnChaoFAKBZJ5WvXX/a23QO2ER/0JYyJQIeanJzinpSz46TA+2Lr+xIgutdSXsypognivvoZmysdHY4mBwGiZegBY3YOhpjRo1dOGCpi6VQoHFJfCZfHV76L5PGXhqGXJ2BBFDyWAJaroWTVi0PJ+QTgHi/37D7i3koZLzyp4b+Ruc7fA7s27hJ2p2ItFyFTLUszTHGAgTRR48eUWmcOKz1nfVNBLUZgtOlgGuTj+MDgBgIl5ZgOyuRDlL0o6ln2+8x/cPQABTtAplbmRzdHJlYW0KZW5kb2JqCjIwIDAgb2JqCjw8IC9CYXNlRm9udCAvRGVqYVZ1U2FucyAvQ2hhclByb2NzIDIxIDAgUgovRW5jb2RpbmcgPDwKL0RpZmZlcmVuY2VzIFsgNDAgL3BhcmVubGVmdCAvcGFyZW5yaWdodCA0NiAvcGVyaW9kIDQ4IC96ZXJvIC9vbmUgL3R3byA1MiAvZm91ciA1NCAvc2l4CjU2IC9laWdodCAxMTYgL3QgXQovVHlwZSAvRW5jb2RpbmcgPj4KL0ZpcnN0Q2hhciAwIC9Gb250QkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZvbnREZXNjcmlwdG9yIDE5IDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zCi9TdWJ0eXBlIC9UeXBlMyAvVHlwZSAvRm9udCAvV2lkdGhzIDE4IDAgUiA+PgplbmRvYmoKMTkgMCBvYmoKPDwgL0FzY2VudCA5MjkgL0NhcEhlaWdodCAwIC9EZXNjZW50IC0yMzYgL0ZsYWdzIDMyCi9Gb250QkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZvbnROYW1lIC9EZWphVnVTYW5zIC9JdGFsaWNBbmdsZSAwCi9NYXhXaWR0aCAxMzQyIC9TdGVtViAwIC9UeXBlIC9Gb250RGVzY3JpcHRvciAvWEhlaWdodCAwID4+CmVuZG9iagoxOCAwIG9iagpbIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwCjYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgMzE4IDQwMSA0NjAgODM4IDYzNgo5NTAgNzgwIDI3NSAzOTAgMzkwIDUwMCA4MzggMzE4IDM2MSAzMTggMzM3IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYKNjM2IDYzNiAzMzcgMzM3IDgzOCA4MzggODM4IDUzMSAxMDAwIDY4NCA2ODYgNjk4IDc3MCA2MzIgNTc1IDc3NSA3NTIgMjk1CjI5NSA2NTYgNTU3IDg2MyA3NDggNzg3IDYwMyA3ODcgNjk1IDYzNSA2MTEgNzMyIDY4NCA5ODkgNjg1IDYxMSA2ODUgMzkwIDMzNwozOTAgODM4IDUwMCA1MDAgNjEzIDYzNSA1NTAgNjM1IDYxNSAzNTIgNjM1IDYzNCAyNzggMjc4IDU3OSAyNzggOTc0IDYzNCA2MTIKNjM1IDYzNSA0MTEgNTIxIDM5MiA2MzQgNTkyIDgxOCA1OTIgNTkyIDUyNSA2MzYgMzM3IDYzNiA4MzggNjAwIDYzNiA2MDAgMzE4CjM1MiA1MTggMTAwMCA1MDAgNTAwIDUwMCAxMzQyIDYzNSA0MDAgMTA3MCA2MDAgNjg1IDYwMCA2MDAgMzE4IDMxOCA1MTggNTE4CjU5MCA1MDAgMTAwMCA1MDAgMTAwMCA1MjEgNDAwIDEwMjMgNjAwIDUyNSA2MTEgMzE4IDQwMSA2MzYgNjM2IDYzNiA2MzYgMzM3CjUwMCA1MDAgMTAwMCA0NzEgNjEyIDgzOCAzNjEgMTAwMCA1MDAgNTAwIDgzOCA0MDEgNDAxIDUwMCA2MzYgNjM2IDMxOCA1MDAKNDAxIDQ3MSA2MTIgOTY5IDk2OSA5NjkgNTMxIDY4NCA2ODQgNjg0IDY4NCA2ODQgNjg0IDk3NCA2OTggNjMyIDYzMiA2MzIgNjMyCjI5NSAyOTUgMjk1IDI5NSA3NzUgNzQ4IDc4NyA3ODcgNzg3IDc4NyA3ODcgODM4IDc4NyA3MzIgNzMyIDczMiA3MzIgNjExIDYwNQo2MzAgNjEzIDYxMyA2MTMgNjEzIDYxMyA2MTMgOTgyIDU1MCA2MTUgNjE1IDYxNSA2MTUgMjc4IDI3OCAyNzggMjc4IDYxMiA2MzQKNjEyIDYxMiA2MTIgNjEyIDYxMiA4MzggNjEyIDYzNCA2MzQgNjM0IDYzNCA1OTIgNjM1IDU5MiBdCmVuZG9iagoyMSAwIG9iago8PCAvZWlnaHQgMjIgMCBSIC9mb3VyIDIzIDAgUiAvb25lIDI0IDAgUiAvcGFyZW5sZWZ0IDI1IDAgUgovcGFyZW5yaWdodCAyNiAwIFIgL3BlcmlvZCAyNyAwIFIgL3NpeCAyOCAwIFIgL3QgMjkgMCBSIC90d28gMzAgMCBSCi96ZXJvIDMxIDAgUiA+PgplbmRvYmoKMyAwIG9iago8PCAvRjEgMjAgMCBSIC9GMiAxNCAwIFIgPj4KZW5kb2JqCjQgMCBvYmoKPDwgL0ExIDw8IC9DQSAwIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4KL0EyIDw8IC9DQSAxIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4gPj4KZW5kb2JqCjUgMCBvYmoKPDwgPj4KZW5kb2JqCjYgMCBvYmoKPDwgPj4KZW5kb2JqCjcgMCBvYmoKPDwgPj4KZW5kb2JqCjIgMCBvYmoKPDwgL0NvdW50IDEgL0tpZHMgWyAxMCAwIFIgXSAvVHlwZSAvUGFnZXMgPj4KZW5kb2JqCjMyIDAgb2JqCjw8IC9DcmVhdGlvbkRhdGUgKEQ6MjAxOTA1MDgxNTA1MTErMDInMDAnKQovQ3JlYXRvciAobWF0cGxvdGxpYiAzLjAuMywgaHR0cDovL21hdHBsb3RsaWIub3JnKQovUHJvZHVjZXIgKG1hdHBsb3RsaWIgcGRmIGJhY2tlbmQgMy4wLjMpID4+CmVuZG9iagp4cmVmCjAgMzMKMDAwMDAwMDAwMCA2NTUzNSBmIAowMDAwMDAwMDE2IDAwMDAwIG4gCjAwMDAwMDg3NDMgMDAwMDAgbiAKMDAwMDAwODUzOCAwMDAwMCBuIAowMDAwMDA4NTgxIDAwMDAwIG4gCjAwMDAwMDg2ODAgMDAwMDAgbiAKMDAwMDAwODcwMSAwMDAwMCBuIAowMDAwMDA4NzIyIDAwMDAwIG4gCjAwMDAwMDAwNjUgMDAwMDAgbiAKMDAwMDAwMDQwMiAwMDAwMCBuIAowMDAwMDAwMjA4IDAwMDAwIG4gCjAwMDAwMDIxNDAgMDAwMDAgbiAKMDAwMDAwMzEwNyAwMDAwMCBuIAowMDAwMDAyODk5IDAwMDAwIG4gCjAwMDAwMDI1NzYgMDAwMDAgbiAKMDAwMDAwNDE2MCAwMDAwMCBuIAowMDAwMDAyMTYxIDAwMDAwIG4gCjAwMDAwMDI0MTIgMDAwMDAgbiAKMDAwMDAwNzMyNSAwMDAwMCBuIAowMDAwMDA3MTI1IDAwMDAwIG4gCjAwMDAwMDY3NDIgMDAwMDAgbiAKMDAwMDAwODM3OCAwMDAwMCBuIAowMDAwMDA0MjAyIDAwMDAwIG4gCjAwMDAwMDQ2NjcgMDAwMDAgbiAKMDAwMDAwNDgyOSAwMDAwMCBuIAowMDAwMDA0OTgxIDAwMDAwIG4gCjAwMDAwMDUyMDEgMDAwMDAgbiAKMDAwMDAwNTQyMyAwMDAwMCBuIAowMDAwMDA1NTQ0IDAwMDAwIG4gCjAwMDAwMDU5MzQgMDAwMDAgbiAKMDAwMDAwNjEzOCAwMDAwMCBuIAowMDAwMDA2NDU5IDAwMDAwIG4gCjAwMDAwMDg4MDMgMDAwMDAgbiAKdHJhaWxlcgo8PCAvSW5mbyAzMiAwIFIgL1Jvb3QgMSAwIFIgL1NpemUgMzMgPj4Kc3RhcnR4cmVmCjg5NTcKJSVFT0YK\n",
"image/svg+xml": [
"\n",
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sym.plot(x, (t, -1, 10), ylabel=r'$x(t)$')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise**\n",
"\n",
"* Derive the inverse Laplace transform of $X(s)$ by manual calculation."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Classification of Poles\n",
"\n",
"Above procedure allows to compute the inverse Laplace transform $x(t) = \\mathcal{L}^{-1} \\{ X(s) \\}$ of a rational Laplace transform $X(s)$ in a systematic way. It is well suited for an algorithmic realization. However, for manual calculus it may be more efficient to classify the poles with respect to their location in the $s$-plane and their symmetries. The classification can then be used to formulate a modified partial fraction decomposition which limits the need for later algebraic simplification of the inverse Laplace transform. Three classes of poles are typically considered\n",
"\n",
"| Type | Pole-Zero Diagramm | $X(s)$ | $x(t) = \\mathcal{L}^{-1} \\{ X(s) \\} \\qquad \\qquad$ |\n",
"|---|:---:|:---:|:---:|\n",
"| Single complex pole | 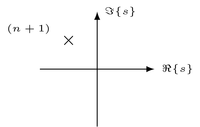 | $\\frac{n!}{(s + s_0)^{n+1}}$ | $t^n e^{-s_0 t} \\epsilon(t)$ |\n",
"| Conjugated imaginary poles | 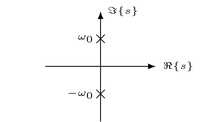 | $\\frac{A s + B}{s^2 + \\omega_0^2}$ | $\\begin{cases} \\sin(\\omega_0 t) \\epsilon(t) \\\\ \\cos(\\omega_0 t) \\epsilon(t) \\end{cases}$ |\n",
"| Conjugated complex poles | 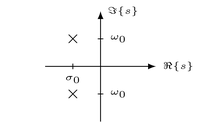 | $\\frac{A s + B}{(s + \\sigma_0)^2 + \\omega_0^2}$ | $\\begin{cases} e^{-\\sigma_0 t} \\sin(\\omega_0 t) \\epsilon(t) \\\\ e^{-\\sigma_0 t} \\cos(\\omega_0 t) \\epsilon(t) \\end{cases}$ |\n",
"\n",
"where $s_0 \\in \\mathbb{C}$ and $\\omega_0, \\sigma_0 \\in \\mathbb{R}$. The expansion coefficients $A, B \\in \\mathbb{R}$ can be derived by comparison of coefficients. Whether $x(t)$ contains a sine or cosine depends on the coefficient $A$. If $A \\neq 0$ then $x(t)$ contains a cosine (cf. [table of selected transforms](table_theorems_transforms.ipynb#Selected-Transforms))."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Example - Inverse transform of a rational Laplace transform with symmetric poles\n",
"\n",
"The inverse transform $x(t) = \\mathcal{L}^{-1} \\{ X(s) \\}$ of \n",
"\n",
"\\begin{equation}\n",
"X(s) = \\frac{2 s^2 + 14 s + 124}{s^3 + 8 s^2 + 46 s + 68} \\qquad \\text{for } \\Re \\{s \\} > -2\n",
"\\end{equation}\n",
"\n",
"is computed. First the function $X(s)$ is defined in `SymPy`"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAALAAAAAwBAMAAABDKe21AAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAIpnNuzKriUQQ7912ZlSugimNAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAEO0lEQVRYCe1XT2gUVxz+Zjezs5vsJnsIpdCWDCsUW6lYKIUWISnowVZxK1gPWhhEVoq12YpWigGXthR6EAdaKvTSehFUMIIQ2u6hWw96MNK1PQmWBi9eCgqJaP3T6e/33vvNvpnZSIT0lneY+b3v+33fvn07efMFyI4Tn3yQBZcD8bFmOWyyHvcxVs+iy4BcX15jp/ZavM4j6eXtDBnZloZ57v4EGK3r92t4Bt59g3OvPUq7x5XxjA2a+ttV/wBGOxT0aQA9CWcMPqpsaHJMGn9jpJwwFq5MxkZ7JZB++z4dYrKqACdwdYG/pUEZv/+6TPkuHBtrrftHYDdIvQ+YrKvJ6PZtoUZFDGXcXNRYa718oGWZ6y+AN/sppqPIUAnjcpWNpy6nPpRXTIO0v+YDrrLDfQRsxGcWkTB+AWQ8UC/6ukE4bUxap5sPNJW+Dvlw7mCLBYtYbUWTjccw0NUNwmlj0nrIB5pKX2v0QC5ci9E17faZdntGzWmPK1VlvKXKgMVpY9JeQz4gKjsqPmFHo6bFyKp4xc+Djb3onuGFU8akdTrIB4ZL3m7BodV8oX8LTYmYjb9sNB7sBYpbwySnjEn7bKMxecpelbi7TZRD+ltezJj6TsE7j5E+xkoLDAZiZt+fq9X2YT2GfQu0V0zwAvId3DS8cLxipQVGJixtXI5H0Tx2zV6NASpEvGd6pgOsija7s7Nd02C4wtsPP4TSIje+QF1LGmLcr/lJXL/+BCYHTQI0kydx/fpXsJUdAKL/aazsbWoHnKuX6ilIpqXDDXNOCvI090Kz/MMi/Tnkzi9CLQF26966ZNuJy6s1MNJy7iYpims+vaMOH0rDPGe4NHWgFXND3bhUhY/CnCoqYdaYMprzIyilZIaCc8BHwpTXm8ochpUuSvId6HWkRjH+bMpoeR8bREx34RT8J/B1zH3T0aU5vr2JnrGOsMCwaQFntNthLOVCOAUftI1ds5HGuLgQ5swCnU3GQsTgjPamAVOcgo9vwiuMUxr7ru481i3ywpl8tFZTlH3f1VRszBltfsfFFv1UlPTUEE7BhejiHKGcxobCymndIcZe9KqmnI3bX9KUiDmjlea7OGclPcMZ+Oh8lSScxtypS1zSEONbo1FLUYNRdEdTYswZrUR59OXQiZOeGCt4+OOt/L/BmE5jLO4lsoqP26dtKtdu/3y23Q6oS2W0h8BfLZP0LE7Bv2P4QWinMfY2Kx4M4fxrBTWmzKp0RrtAxt1e0pNvo2Da1bE5EsRpjNXG+Hsq96coIy6qjPYOr7iX9MSY4a9o6wpdO41ZxoO05W9ZQY0pEauMdpz2GEfipCecgk/Sz16105hlXHwDlY4V1JLGIxMYaJbOWUlPjBX8eYgbdKD00phljPdqq9OUiHVGO/Bi3Up6Mcewu7vWYq/EkMctAepJLH5KTrebQ6iPNj5olsb9BxeNt+pXnWxXAAAAAElFTkSuQmCC\n",
"text/latex": [
"$$\\frac{2 s^{2} + 14 s + 124}{s^{3} + 8 s^{2} + 46 s + 68}$$"
],
"text/plain": [
" 2 \n",
" 2⋅s + 14⋅s + 124 \n",
"─────────────────────\n",
" 3 2 \n",
"s + 8⋅s + 46⋅s + 68"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"X = (2*s**2 + 14*s + 124)/(s**3 + 8 * s**2 + 46*s + 68)\n",
"X"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The poles of $X(s)$ are derived by computing the roots of the denominator polynomial"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAUYAAAAVBAMAAADIlFouAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEER2zVSJ3ZkiZjKru+/kt61jAAAACXBIWXMAAA7EAAAOxAGVKw4bAAADZElEQVRIDc1WS2sTURT+Jmke0zw6UBcKYoMbXdWILoqIzULpRjD9BY0g4s7URaeoaMQsArZUF5UoSAfciBsDQl0oOCBCUYtPcCFoFKQbpa1aSu0i3sfM3DvJ5DaKoHcxc893vnPON3fuPTMAtO34f8f0ZaZt7/DfkViDxhP+WboEsKU1MjFvEDCyLHmq5XeSlRiVjKbp1ROvmpDFgybJNyCh92j+4KEfn8z4PekfQ6RcuCRQVj5lEyBaFKhu42TGM7eWZfkezCZaCXfyfshcPUqAMQ/U5o6017gZ3Ssek01i58cIPVbwUF6eyZM1Jg2k6x4J4fYawyvoywkmndl+k1iD7TUO5rUfnB+y+D3Jb9KVlW/RmF5Gck2wFBpDn9CTE0w6s/0msRQa+zNwNEayPK5TjckikuuilEIjIY1Ygklntt8klkIjOQc/Of93NZKo2BINHWfxSo2h04wjLk/2XII2wFYlVmKwUuMOi4d6Gm8O1NB7kYFSefau4znOda4PaRFnr6g0JvY/9cUBLzGTiYbqFHW2qkrj3Wc1Hu9qTBn6NxT6KSiXD9cJMGORixj8EQwGqDSSd50XUXyWKk7zJ9a4rdKIiHOuXY0k5K2eL7NIqbxOaA9OEVQbMukgTxYvMRK/BGgUTJADBmxigWc4P75m9GSl+ACNEn+RKImb5rkF07R50NQVfJfCefkbh6CVuWjHd0viqHpPooaUv8GlcoivY0TOFqDRTX8f+JBnhruOb4Cpmu+DwjUeywCskbuhkQKuuXPS9Nv3x77lZo1p0hOWcFhEq8611jCaNS4Az9FlS/GsfIT2QrmHYxbYLViU5GwtAfJZ2ubvWuBRIP1CWyE3b9B1lNfVcwBfAPquyXDXsQB8RV+e3NzBNEbrxJQ16uOViSLBpIPV/DVxEnRbzf1RL+GAEVq6TgniXLtfEyfMu91u6Y9VhD9il24RilSey5M1djUajRzNw0538v3qI8RGqd06dlaa/ymqExeA1xal8v44v3g2C/qfETBClckMh9111CtzBlL7GCjKt2oMSIbhILBzLBKsUSRwNQrEN2NLKK+jz+sYhSCwc0zen4FR7j9FoNPZiqyRtyEQWMu293Xi6e2EpOCwj4L2WcEAupXejZ3WxhQlYxtLUH2sJP1b5ywR9ws1ccwXxFD59wAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$\\left \\{ -2 : 1, \\quad -3 - 5 i : 1, \\quad -3 + 5 i : 1\\right \\}$$"
],
"text/plain": [
"{-2: 1, -3 - 5⋅ⅈ: 1, -3 + 5⋅ⅈ: 1}"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"poles = sym.roots(sym.denom(X))\n",
"poles"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The result is a real-valued pole and a conjugate complex pair of poles. According to above introduced classification of poles, the following ansatz is chosen for the partial fraction decomposition of the Laplace transform\n",
"\n",
"\\begin{equation}\n",
"X_p(s) = \\frac{A}{s + 2} + \\frac{B s + C}{s^2 + 6s + 34}\n",
"\\end{equation}\n",
"\n",
"The coefficients $A, B, C \\in \\mathbb{R}$ are derived by equating coefficients with $X(s)$"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAPIAAAAVBAMAAACOB66tAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEER2zVSJ3ZkiZjKru+/kt61jAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAC4ElEQVRIDb1UO2gUURQ9s5ud3cm6yUAs/QTBOgsKKgiJhY2QX5NGMCOIKBaJQVC0cBCLLVS28FeoO4WNVVKlEjJCJM3IpougkhW18++KiIT13jdv/i/CFubB3Hfvuee98+a+DwBtD7a63akLxf2TvvDtrdMvvzBJrPBNKo4nlMt2IuSgd33DW36VgWHURheyKAZee87dLK6fPgdUXEros3620EmwipxLtb5VoJkVeQD9e4pJYf6dianLGdyYw4oUDZRLzXqcdsCNR77fqAJDdgZ/BnzOgNqaCZR+Z/AeG29Symdn4n9TfuxmBmGeGPOknmpfTCRXzfmet2RyLXYTbZoWlFQ2qsMTMYre48Yi6TapH6tncKpedg9meDbFYRkTw0WhZbVLmHYYLNpscUil/AnYcUWkLwkbmauR63vGL+61BbYJcnvx4KD859IIZ7EXSxb3u0fYGo5Cubyx7/AxzkJriy405R+hKx09QhJkre3gAx2/FvEajiDbaLjsaCLSoVDO03k54Yi8KWxoZKHCmEr3JwriZI1u0C0Txk/g6Zyg5F/WmqsR+YlKudKiMsVm3H6RG5e/Fo2UXp94JfzfEFBApl2YHwQeHoV2XSxpAOifDccbVZVyv0uvSVTFkI1eO/KlV/zKzvEMjguk7ACnBuVzApsK1ELQcp7X/GgFUdAvOcA2xZuBKRj1gCR7/yZbKZTCNfHPBb7o4mznHLqBYpkBt8+VWx4AwDBNvzQSxYFXtpA3Y4Vl3ODa6GZAifoh2mfKtDg9S+YRfRVehzzbVPvV0GWYG13F3HsxWeK44l6ttpIh0x0tnBTDkuSKpdHZDu/zzs4RFNbbFjHlMS2Nb1SL58XIwCx3PG90wo8SV3S802kjRYZ207smRybIOHNjIaYcTJ7qJ1PxP8OuyOE/bzKltQmuhLsiC2XxnCjn0qpKWA12RYZ4OHnD1a1XDavRrsjY5fAs95+r5/qP6CJJ/gXYxK5e4qQiDQAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$\\left \\{ A : 4, \\quad B : -2, \\quad C : -6\\right \\}$$"
],
"text/plain": [
"{A: 4, B: -2, C: -6}"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A, B, C = sym.symbols('A B C', real=True)\n",
"\n",
"Xp = A / (s+2) + (B*s + C)/(s**2 + 6*s + 34)\n",
"coeffs = sym.solve(sym.Eq(X, Xp), (A, B, C))\n",
"coeffs"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Introducing the coefficients into $X_p(s)$ yields"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAALsAAAAsBAMAAADP3dSiAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEM3dMiKZu6uJRO92ZlRfaCDxAAAACXBIWXMAAA7EAAAOxAGVKw4bAAADQElEQVRYCe2XzWsTQRjGn6S7STZpmuA/0IIHBYUGI0UUMeAHFBQDolRQXHsIBS+KBUEsrughnrKiFApCc6reFLwUBY2IohAhCPXangRPTapS/KDrzO7OZmd2sgmtBUH30LzzzPP+MjvZTJ4CwevU+GRQBLSZezI5oCl6QPILqoHZql9wanUvbgZVidJnSMS2lMgi9bg9ZFVUxxVWh76+MkKnUy0kvgUdy9mgJlOUD4ZM9rREDomv3sgrdnhVeKFFjXAD0NcE7r/jl7sy+qbarY/Ov+6OP15DvJDU/bTISgPP/UKHWm10x48A5xBv+AkRC7jA349/2qs1dMBHtubpVQBiOsFPFWnLFlvbTaovwGKVSuHXQid8u+0jKTXre1ug1S6C5+6Hn3ZHaq0rfsDESSB5nd+Kyz2tPlkuV+ZN6TszcRR4qeWQ4fGPyN4zR+hrygidVkdKE7loDZ94V9yM9PLkAJmLfKMwilqWNaTU6w1Bn54oCIp0GBterUkn/jkxKe7gn92Bgc3d5v/4kI+r6+aQ79B6riZ5z1g+v+9JPm+QMiNnUNdGrq6r3wgc+CvwkZlydl230dvqY4jlNhGfqapispEnytPTV+kyjrC1hKxeLW0ruLZ0VsTLE2VEx+IS6dnj9iHkSBuD9oPZQH787Iv5hUTpyv1rGBwC+j28198uGOEG8MxTD7ofLbtbIVG6cvIpMgR/bLvXFywY4UUWlaI7rV5yCzYpJEomA8sNwOwFT9J6pUCoNEyO4bDDZxwnUWr1O7yM5H6yN0UJPmgFDpBmGibVyUPnOY6bKCcxx8lQ3t4CzkKCD1gB5RdppmEyZVlNjuMkSrWJKU4mg+UlmBK8zNqnE78bJknlPwLtRKmuLggykGqlizK8xFqizXyYZHvvJMpZy6QW7+hSCoivnYEED9EKpHW7lQuTDO8mygct28JOxsEWwT8sl3/edmT/X8EKfIZapN8nf5hkeDtR3gV4PImP5D8vYN7PteuAFYqJ/iyEMMnwdqLciQHdAblyumE/91gN4ANWnCiVyKMvhEmGB02UR+vvXQ6T50r0SBu3ron8oHXYslZEF9tkUWd4UZeMQ63sQBL6OsiCyx5y1t9oRzorOcS90gAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$\\frac{- 2 s - 6}{s^{2} + 6 s + 34} + \\frac{4}{s + 2}$$"
],
"text/plain": [
" -2⋅s - 6 4 \n",
"───────────── + ─────\n",
" 2 s + 2\n",
"s + 6⋅s + 34 "
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Xp = Xp.subs(coeffs)\n",
"Xp"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The first fraction belongs to the complex conjugate poles. Applying [completion of the square](https://en.wikipedia.org/wiki/Completing_the_square) to the denominator, its inverse can be identified in the [table of Laplace transforms](table_theorems_transforms.ipynb#Transforms) as exponentially decaying cosine signal. Performing the inverse Laplace transform with `SymPy` yields"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAKgAAAAYBAMAAACcr6vyAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEM3dMiKZu6uJRO92ZlRfaCDxAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAC9klEQVQ4EZ2UT0gUURzHv7M7u6vjrg5KSkS42KFLf6z04Mm5RScnAi0k2oIWiqR/RMcMwyQKFylqQWiv4SElw0OH9pJorLZ0qEvBUnSIAktEczPs+97Mmx2lZcnf4b3v9/P7/d68N/N2gTIRmpuxELDLZLeIq1LRcTRvsblcm25Vx/GpXHbLPJg/cfD+P7tDHi0pgaTbiLxKR0T3APs2MdfOQwe2CWNkXSSneTH6USi525IZb2jK4qdn/KI2hZrFXQckkutg9pYw5CIcJOVxVBelwOHrDH52fckYd8imsR4IdnaYQIONACdE8g2ihNxDwgM3gReOcsYdVuhPtF+e0Y+F7gOqJFsAYgmqh6izOJFDIUrGSxPD3J4XQTM2Ec6mPO8T42rRM4QTPFIRdQVKcriISsQAMGxJ5Qz66Ixt9PmJShpxtWgH0V6aVnTl+YXI4SIqNzqB7bnTynmzdi5dQGPuPPS5XJw0zO1XfZi2jNsrd4FHQHMWCxnJPeQ162sw2nDE80r0FoxJvR2RbBPQShjgriJmqIjaH3RvgTcWHtsOV0j1IpjAqTxee16JFtQ+D6Z4GcZMpAiDBZm5inCc4jNwY2joN5XgLqo/JKKNMMl0Lp2h2hDaKm1XAVgNrrwSmZqMGHHR5pOYAaagrVEJrhCtDHE5frnaP/Gt8KZkgBVtZD1BLZqvcFGrmQJjwBpi4lciuEK0Mr4iZItNbQ5tmUTsdPkodi5RB6if8a7gKTRxfK2IYAIOdxGdDD2FqMkLUauAN7cQ1iRgLH0H7pFGshDvdgoj+AK8B4r4ZrpcIbf5WDI5wE+pnXV9aerN44E+iUCKrdeIq/uBbkQnMKRlgQt8kiY+ieQKCc/Yv76+iOhoznH+URtM2+hO38GTD7MZJoxW/sklB030fKRrBxqnbVEvuELC/1/IfbktIa6kwuV+pFKV53e+knC+ZFzuR6VkJRWRp3WqenzFLvcjX7aC1C6VCi6XJFzuR75sJXnSK4j5Ng1ITvQXP/K8BmC+odwAAAAASUVORK5CYII=\n",
"text/latex": [
"$$- 2 e^{- 3 t} \\cos{\\left (5 t \\right )} \\theta\\left(t\\right)$$"
],
"text/plain": [
" -3⋅t \n",
"-2⋅ℯ ⋅cos(5⋅t)⋅Heaviside(t)"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x1 = sym.inverse_laplace_transform(Xp.args[1], s, t)\n",
"x1"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The second fraction belongs to a real-valued pole of first degree. Its inverse Laplace transform can be looked-up directly in the [table of Laplace transforms](table_theorems_transforms.ipynb#Transforms) as exponentially decaying signal. Performing the inverse Laplace transform again with `SymPy` yields"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAFMAAAAYBAMAAAB0A9ycAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMpndq3ZmzYkiRO+7EFRAb64nAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAB2UlEQVQ4EX1SP0gbYRx9p15yaXJ30UFwqiD+20Q61KESaAYXMUgLjqebg5ihiA7KgXFxOih1EgzV0qGLQ6eCmEGFQsGjpdBB0NHNCCr4h8b3+6Le5Th88Pt+773fu+++5Dsgin+lUWAh6sbqTnTBrMaOouYNNrJWMerG6hlsdCzPZ4OZJ1QtgffIlpE8eeSArviXutEW+MK0N7B9dr2ktj5V0/oDeKUEtF/ET2DdxzdxDswBrmaRNQQsiqU/RIUTqZzmvTM9GBWcUzY5gFUFpmTW/kHWJ6y3tvndBvCyjP8006wm7pz2SdzG6G6ths+TwFtoV5x+ZTW7QNLh+z1GzZVxeSoE8xLWDXUfsHW4V4CRA9bA6GZWc0M5Uv0cxjX7HOuMleAhXEZTV9DL1CFkLvJj29TDrF6WNYCEx2jmcmI1FBOaruC4wP6D9ZqlVfEJjNo5ikbYBczK8Rk15cwvtrGVz9+O2G5jjuq4jEExl5iqwpcDEN/Vv3EiNIBdtnZE7QNG0fKQqFDgTn7eb09ogBbnT1ZUCWjJ/eU1FCh6a/uYeC8sDLO7X8lNXvWBw2uIbBXOPvBmtTfwMWYWsRKddaMn4sdJfpZEqqLa88uRGmf851NqmnKkTQP3B5Bn8nog9oQAAAAASUVORK5CYII=\n",
"text/latex": [
"$$4 e^{- 2 t} \\theta\\left(t\\right)$$"
],
"text/plain": [
" -2⋅t \n",
"4⋅ℯ ⋅Heaviside(t)"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x2 = sym.inverse_laplace_transform(Xp.args[0], s, t)\n",
"x2"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The inverse Laplace transform of $X(s)$ is given by summing up these two parts"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAQcAAAAYBAMAAAAFciVuAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMpndq3ZmzYkiRO+7EFRAb64nAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAD90lEQVRIDaWVXWgcVRTH/5PNbPZrdsc+iILQNdoPhUI0gu2DupggIkgWyZaoL1tBxAdxwY8oaB1pglEQhlZFaCWLrSj0JQVfVEr2wRaESoeK0mIh+yIWfHC3NrGN0fV/7uzs3tlMzIcH7rnn/O85v7k7d2YW6LWLU48Dr/eq6+bJ/eM2Btx16zZWkMcdsBobq9Wq+h1zDgua8L/CZcza2cqmEYadqODXTbet0fACZm899JrdXVW3WLmuFhXFyh/f/3bUArrN3UgK/4t8CAN1lrTNrEvwWTtbezJfAQ5GLpNgw1JXDGFC5G3hVuMB5DxK5pQtC1fUqt+gQt8lB99Qy13pchF/dzMtImF+cliQ8DFR5Pv8BuMc7TvgmIeTopy1huitCsc+4E2/qOM/QGLZT26TPhcwmqm5zrIWCGH4j/c1TATZbG+i3ZcsGO44b16ihialvjKQbQDPaFgJ+R5/o0s/28kls3BJl9qxEAoSB5go8s0vS0XHjt20zduRALZX8Q/FNEcff0va61SoYN7DmKtJMS9+uq/oaEoQCqEgSYCJIjvhTcy3Wvj0ADACY4mdn3PEHGCgzECzEWDM1nJjetxN7dSVYFEIBUkCTATZdLkJa/qJnl9qLSIrh74bOHH+2yISiiOsjj0EXCzt6aRBYO2eqeNC6W4Y+0sViiTgkdLtHUwU+SNwE8dtwwkg/mw2kbjB8FWO3zniwguZsYjUPbglpElytJ46ZexDpngZGGIuhO8xWw0wUWSHm0guwayyVrPMtdGxOeYPcuziyAovZLE8Zst4KqRJMonsV7zzRvOkB4e5EIDMUICJIMddbiKzOPGeKu26dA0LRaZfc+zlMBp01kvDYjZDYBA4X5qpqlhz1nUm2+vA9djKk6ILgU/ljQATQf4Q3ESuoAp1lyviRY8CEdYy51XfgHgeuKZ3tGOeEg+wCqxY77TyjEnIVNDXDDAR5BOjo389mnNYHLaFKu4V5SCv34C3+jiuIOnKj+416yoVuRNXP8FP8qUhIT2E/kaAiSZ/qV4etumWq2ZPS34GSFSyLuI1JprxQTa9vXxWNM0PJymm80g1f+FbQUkI3EctwESTV+TRv+CGaf3lH9TRTwH9hR95psXw+pHBwRE8B+uusMzsaBnvGqcw4Pzmgf8CICGZx9NegIkk72qdwUSp5xqwdvj440ScLfNL07PJt1qtP2FOl1btAdbDMy4OzzyGL56dqHKZBBy+c08Hsx55NRExdT+AIxFrG5MCgqrWMIGuSWsB5SUQ2+lPW/ABQbVqmEDXpDXpcqw8kpqatuR8gmoNYTZB5seXlvHUtCXnE1RrCLMJcrIs7c8rxtacT1C9IUyH/C9CfCoWJg8ArgAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$4 e^{- 2 t} \\theta\\left(t\\right) - 2 e^{- 3 t} \\cos{\\left (5 t \\right )} \\theta\\left(t\\right)$$"
],
"text/plain": [
" -2⋅t -3⋅t \n",
"4⋅ℯ ⋅Heaviside(t) - 2⋅ℯ ⋅cos(5⋅t)⋅Heaviside(t)"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = x1 + x2\n",
"x"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The resulting signal is plotted for illustration"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDQwNy42NjkxMzEwOTc2IDMwNy43NTk3NSBdIC9QYXJlbnQgMiAwIFIgL1Jlc291cmNlcyA4IDAgUgovVHlwZSAvUGFnZSA+PgplbmRvYmoKOSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDExIDAgUiA+PgpzdHJlYW0KeJyFmsuuHLcRhvf9FL2UF6bI4n0ZIbGA7OQIyCLJyhclgsaA4iDK4+crdrOnZ7p0ZEDwmfrrZzXJuvZMWD8uYf2w+vUj/76sf1v/wf9/XsP6ln8fFs+n25J8daX0EAMfP50/Rv6sudeM2D98+uey/Lq8/gOL/A7p7bLE7GIv3pdVskuponVbYheXw6P004O0B5f3JU8rnKS7IdkMfeCx2Yprp81gXpElJRd8kbzG6nKK4wHusuT8kH1aljecyZflzfv19Q9hDX59/+sSiws5BhRFXM/r+5+XV97579b3H9c/vV+GwaVxLrmmejZwl71soHZXwVPKQeTBSH40wrE78a20fjZzlr5sKEh0knMuyUtKJ0vheTuhJr3O7h8tnaTfsFSKa77UFnMs5cHS054kNBdDCNLOls7Sly1J8C7m5n30qbWTJXnek5TgWpGYHi2dpN+wlKNj6yKSS3gw9LSl6PHnEHN58Iaz9BuGenWp+JTE13h2iPi8JZ7a9ZJqe7R0kn7DtRM3H7iskFtOD5ae93SPy7Olk/QbllpyuUhrwfd6doh039PnRZPM9544jt3vCw/17qQ2jcCfbiyrqcn1NqyxxOsfZDfy6j+61MJS7/bHNuPeu/Io+5pnOVljdDWVVr8S9sf6Xf+IRPvZwF34ggV2Gj05tXN8wY77w0rILF1i7O1s5iR9wU5IhGQpWSK5IthhfxjC85xIxNfPhk7SFwyJjy5JiakG6WJH/d1Q4YAbsVseDN2lLxnKHTcooYZQRZ6D/vOijvS9ulTILpBRuERpslePuyelYfLRkf43HCm7Hmoft+83hWn/1d9fDQ3NCCGWGk46T96ICtl5d9fLMt/dPfbzelS5LUZmVcSDeH4OhULE///9y/rX9beVM6XQed1ZLmSwmjnbVPb/Kkj1uTWJWfr649v19R9/+e+/fvrlx7dv1p9+PxXUp8iAyqWdQ+MvlhxlQRh8Dc/KVznK0TVNMxflq3woEw1F+lX5WT6quC+x5PisfJXvJR+vTFflZ/mmHMnafXNHrrn0u/oFGYTUfasqFtdikXLoXwDUs/M95kzRKtrT5Nrarm8hg5AyvVdFTBj1FIochCsyCLX2GtsQxyYhlYNwRSAU5ynwtCwjtji/Mk/IQgYhSYgcnIozf4R0EK7IIJTua93EklPOd8IVgVCpUCWNdbSsBQJuJ1jIILB7nzdxoylo/SBckUGIkTYtDHGV0iick3BFBiGH3OOQlkCPc6g/y4dyaSSAOqT0kcHLoX5FBqFT/rZVOEKy26F/AVBvWmN63TZFKprHeZUPZUk1T6H0frichQxCovSmTSw9q8tMwhUZBLKKT9uRkZR6vD/QFRkE/mw0ekNcmjZIk3BFBqF7Ckve11G3PAhXBELXTBB638QsOO/LAIa6sJ28raJRHvqhf0UGIfs2ssF20vc4tpBBqD1NR6HTK3f9C3BbqO5UhJzK5ieUuho3fRMZhCjcx2a20ob3Q/8CDPXi6cz2sKjBp7v+FRmEHuu4F04QT5l5zgJQp1bHVPqQ4lmt7hdsAUO9dbLrlge6BLzs0L8iEMQlapmOGeSy1DpJYSdYCITIXOZrk5FeudAe9pA0EQjk4yqxxJHve8Zl5glZyG3BGiNjocWVykOzS9mvzEQgBBKGD6SCSkWsmd531zcA1JkECG4aPuIIhZza1LcQCImjlu7VbOHoIh92goUMQqNQJU6ialprOiBNwhWBQAmqAYND3LmnsuctE4Gg3QwtIkdXcfbEve5xaSKDkNSnZIgLflbKQbgig9CYOzReEbeMeTkIVwQCBQIn8XraODCHF+YjWcgg5ITpPMSBijWTl4kMAiNQ1E4AsRRa/nIQrggEEhMXmssQEy06BW0ECxkE7fG7DHEicGf5MxEIPF6iU9zWSeVoiixgqGf6hbgJM0n20H6WD2VirpZtU4kK3cuhfkVuSyVDMSPvWyIT7s9iyIcyZkLcNsTO4rxfE4HAwMNNaF+ll0Lj2XenNpFB4AS89lVVW4xSWjwIVwQCA0jQfkH9MHLAeyYy5EOZidi3IRU58qIhRzlSoHPUuYAoqtHL7INMZBB6bpL6EJO5o+8H4YpASA6vo0MdmUBItTNHmAiEzNMFrmPkGqpzj/vtmsggMAhpvhBdMnpa0INwRSAUndZiaSP90btpat4IFgKBAbXh4noWJH9fj37URCDQJmXdF21z8L7PM72Ib0uj2oZedQXNH8XX2RybCAQhn7au5Serj4ej2zIRCLgeHXAkiKK+8qh9dqImclt60fFP30YFiklmxtjUDfltob101Ce9ldAK/T8ht5+mDSmFhC08X1oDlYXz63JQLAhKkJFbmSwDUwZzqRxWTEgp2uwIi62UdN1onuXMhm7jTWbPPnEggS3WVKiMO8WElMLGRGjIGL4p29rXTCsmpBSyVC+JJqCzW0I8pckwEH0VGzX3NfqBToKgPZ75zkSUUPXtj/asjYk8kcbjJBgIhKQvLDKPubZAfm4M+TvBQpSgU3PSfKbBTiVqB8FAlFBGRSRiCUXRF1jz/iwEAm2faG8rK1mRgakc52ohSuAsfPKUH8qAbznMDttElFBGAiIMKZOEbp81ykQgMGZ3vJisP3xT695OsBAlkMRjZl5d6bg47TqTsYnoq/DsOhMkqVZbafzluGkLgcCltKovRlaemSPJc5IyESVUPCZmWoiccDGcbN6DhUDoHF5Llf6YY8R1YpwhYSFK0DlbOuZorRmEeNhJMJDbwuxMXkkNNqMKWTqm/ZRM5DZezqc2/ETn0a7j006wECWwTi8MoquO9/oCYVqwECUwM8Uxh5JSeittVjkTgSBEE8M5+TPRyTLezx7ARCBEWvYq+jZCA4apafYAJqIEqh+dDeGHmJHDzzphIhCSrtMZNtZEaeqhzabKRJSgLsbhxTXhO6GWmfhNBILeYpY0pKJb213JAlQ96/DTQlvTeJ2kyXTXNxD9EoUPRLqetacPrDITpYkoodB4MERkFQvnMGdOE4FAAsGtOn5IAeyelD0JFqIEeiEwijLiEmKZ711MBEKLLup3VqJi/tJBfyNYiBK0lyODjHX0DfBsf0wEgn4fEInCqmLvMwP+TrAQ/cpIB2p9ZRKZUhj0Z3xagKpXnbrpSZEWrmYmPQtAXatj8SGqNJPZpptagKrTcuFYMsSMJ8eVmQgEwQO5x6TSyCHOhtUCVL1yaDXVsQptr5+nYyIQomiTpl97arfWZHb/FqDqRb/r0rFKxRzeTMAmctu+HOMmalOx17o0H8hClFC0E09pvFTv2mEfBAOBQPTlXrmPIeZWjwu2ECXoiK73rWK6lDTTo4lA0PcB4vv27ar2v/N1q4koQUfDULZ3/bSZc6C1ANQpdl6/eB2v2WtpYbZhJqIEHfxGklVxoo5NJ7UQCHQ/lUS2fbVeKQF5PpGF3J6+qSydg9j94t36eZX1z9svHh5+JvD43ciLPxZ4GpKPnzl8GT91sH7UcPvajxqW344fL4ynGQtY38tYX76a1o1fSbxk/d3yf73IruMKZW5kc3RyZWFtCmVuZG9iagoxMSAwIG9iagoyNjQ1CmVuZG9iagoxNiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE3OCA+PgpzdHJlYW0KeJw9kEsSAyEIRPeeoo8gP9HzJJXV5P7bNM6YhfYTKGywpegYzsvVkF3xllYYnvg27wueiaup9YckFTL7pg4Zi2fyFCckFK8mY0DcsdXWo3Eywgy7LCZmYK6Kr0QuqFAC6lHyamaj4Gqmgr59xFaZ9RYXCEUCJixnK/6fA9PrFh0MFpjtN8uzPPYK03QszHuGeQ9FI34G5VpuYGWtg5+GHZr3tmgo/+QnexZ4tc8P3qtCoQplbmRzdHJlYW0KZW5kb2JqCjE3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggOTIgPj4Kc3RyZWFtCnicPYyxDcAwCAR7pvgFImGMbdgnSuXs3+YtJ2ng9A/X0qA4rHF2VTQfOIt8eEv1hI3ElKaVR1Oc3doWDiuDFLvYFhZeYRGk8mqY8XlT1cCSUpTlzfp/dz3Hqxu6CmVuZHN0cmVhbQplbmRvYmoKMTQgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zLU9ibGlxdWUgL0NoYXJQcm9jcyAxNSAwIFIKL0VuY29kaW5nIDw8IC9EaWZmZXJlbmNlcyBbIDExNiAvdCAxMjAgL3ggXSAvVHlwZSAvRW5jb2RpbmcgPj4gL0ZpcnN0Q2hhciAwCi9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnREZXNjcmlwdG9yIDEzIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTIgMCBSID4+CmVuZG9iagoxMyAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgOTYKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udE5hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovSXRhbGljQW5nbGUgMCAvTWF4V2lkdGggMTM1MCAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTIgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM1MCA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDI4IDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxNyA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjE3IDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDgKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk5NSA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMTUgMCBvYmoKPDwgL3QgMTYgMCBSIC94IDE3IDAgUiA+PgplbmRvYmoKMjIgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDcgPj4Kc3RyZWFtCnicTVG7bUQxDOvfFFzgAOtreZ4LUl32b0PJCJDCIKEvKaclFvbGSwzhB1sPvuSRVUN/Hj8x7DMsPcnk1D/muclUFL4VqpuYUBdi4f1oBLwWdC8iK8oH349lDHPO9+CjEJdgJjRgrG9JJhfVvDNkwomhjsNBm1QYd00ULK4VzTPI7VY3sjqzIGx4JRPixgBEBNkXkM1go4yxlZDFch6oCpIFWmDX6RtRi4IrlNYJdKLWxLrM4Kvn9nY3Qy/y4Ki6eH0M60uwwuileyx8rkIfzPRMO3dJI73wphMRZg8FUpmdkZU6PWJ9t0D/n2Ur+PvJz/P9CxUoXCoKZW5kc3RyZWFtCmVuZG9iagoyMyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDkwID4+CnN0cmVhbQp4nE2NQRLAIAgD77wiT1BE0P90etL/X6vUDr3ATgKJFkWC9DVqSzDuuDIVa1ApmJSXwFUwXAva7qLK/jJJTJ2G03u3A4Oy8XGD0kn79nF6AKv9egbdD9IcIlgKZW5kc3RyZWFtCmVuZG9iagoyNCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDgwID4+CnN0cmVhbQp4nEWMuw3AMAhEe6ZgBH4mZp8olbN/GyBK3HBPunu4OhIyU95hhocEngwshlPxBpmjYDW4RlKNneyjsG5fdYHmelOr9fcHKk92dnE9zcsZ9AplbmRzdHJlYW0KZW5kb2JqCjI1IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ3ID4+CnN0cmVhbQp4nD1PuQ0DMQzrPQUXOMB6LFvzXJDqsn8bykZSCCJA8ZFlR8cKXGICk445Ei9pP/hpGoFYBjVH9ISKYVjgbpICD4MsSleeLV4MkdpCXUj41hDerUxkojyvETtwJxejBz5UG1keekA7RBVZrknDWNVWXWqdsAIcss7CdT3MqgTl0SdrKR9QVEK9dP+fe9r7CwBvL+sKZW5kc3RyZWFtCmVuZG9iagoyNiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE0OSA+PgpzdHJlYW0KeJw1j0sOAyEMQ/c5hS8wUn6EcB6qrqb33zZhWgkJC9svwRaDkYxLTGDsmGPhJVRPrT4kI4+6STkQqVA3BE9oTAwzbNIl8Mp03zKeW7ycVuqCTkjk6aw2GqKMZl7D0VPOCpv+y9wkamVGmQMy61S3E7KyYAXmBbU89zPuqFzohIedyrDoTjGi3GZGGn7/2/T+AnsyMGMKZW5kc3RyZWFtCmVuZG9iagoyNyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDQ5ID4+CnN0cmVhbQp4nDM2tFAwUDA0MAeSRoZAlpGJQoohF0gAxMzlggnmgFkGQBqiOAeuJocrDQDG6A0mCmVuZHN0cmVhbQplbmRvYmoKMjggMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzMzggPj4Kc3RyZWFtCnicNVI5rt1ADOt9Cl0ggHbNnOcFqX7u34aUXwpDtFaKmo4WlWn5ZSFVLZMuv+1JbYkb8vfJCokTklcl2qUMkVD5PIVUv2fLvL7WnBEgS5UKk5OSxyUL/gyX3i4c52NrP48jdz16YFWMhBIByxQTo2tZOrvDmo38PKYBP+IRcq5YtxxjFUgNunHaFe9D83nIGiBmmJaKCl1WiRZ+QfGgR61991hUWCDR7RxJcIyNUJGAdoHaSAw5sxa7qC/6WZSYCXTtiyLuosASScycYl06+g8+dCyovzbjy6+OSvpIK2tM2nejSWnMIpOul0VvN299PbhA8y7Kf17NIEFT1ihpfNCqnWMomhllhXccmgw0xxyHzBM8hzMSlPR9KH5fSya6KJE/Dg2hf18eo4ycBm8Bc9GftooDF/HZYa8cYIXSxZrkfUAqE3pg+v/X+Hn+/AMctoBUCmVuZHN0cmVhbQplbmRvYmoKMjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDggPj4Kc3RyZWFtCnicLVE5kgNBCMvnFXpCc9PvscuR9//pCsoBg4ZDIDotcVDGTxCWK97yyFW04e+ZGMF3waHfynUbFjkQFUjSGFRNqF28Hr0HdhxmAvOkNSyDGesDP2MKN3pxeEzG2e11GTUEe9drT2ZQMisXccnEBVN12MiZw0+mjAvtXM8NyLkR1mUYpJuVxoyEI00hUkih6iapM0GQBKOrUaONHMV+6csjnWFVI2oM+1xL29dzE84aNDsWqzw5pUdXnMvJxQsrB/28zcBFVBqrPBAScL/bQ/2c7OQ33tK5s8X0+F5zsrwwFVjx5rUbkE21+Dcv4vg94+v5/AOopVsWCmVuZHN0cmVhbQplbmRvYmoKMzAgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyMTAgPj4Kc3RyZWFtCnicNVDLDUMxCLtnChaoFAKBZJ5WvXX/a23QO2ER/0JYyJQIeanJzinpSz46TA+2Lr+xIgutdSXsypognivvoZmysdHY4mBwGiZegBY3YOhpjRo1dOGCpi6VQoHFJfCZfHV76L5PGXhqGXJ2BBFDyWAJaroWTVi0PJ+QTgHi/37D7i3koZLzyp4b+Ruc7fA7s27hJ2p2ItFyFTLUszTHGAgTRR48eUWmcOKz1nfVNBLUZgtOlgGuTj+MDgBgIl5ZgOyuRDlL0o6ln2+8x/cPQABTtAplbmRzdHJlYW0KZW5kb2JqCjIwIDAgb2JqCjw8IC9CYXNlRm9udCAvRGVqYVZ1U2FucyAvQ2hhclByb2NzIDIxIDAgUgovRW5jb2RpbmcgPDwKL0RpZmZlcmVuY2VzIFsgNDAgL3BhcmVubGVmdCAvcGFyZW5yaWdodCA0NiAvcGVyaW9kIDQ4IC96ZXJvIC9vbmUgL3R3byAvdGhyZWUgL2ZvdXIKL2ZpdmUgXQovVHlwZSAvRW5jb2RpbmcgPj4KL0ZpcnN0Q2hhciAwIC9Gb250QkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZvbnREZXNjcmlwdG9yIDE5IDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zCi9TdWJ0eXBlIC9UeXBlMyAvVHlwZSAvRm9udCAvV2lkdGhzIDE4IDAgUiA+PgplbmRvYmoKMTkgMCBvYmoKPDwgL0FzY2VudCA5MjkgL0NhcEhlaWdodCAwIC9EZXNjZW50IC0yMzYgL0ZsYWdzIDMyCi9Gb250QkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZvbnROYW1lIC9EZWphVnVTYW5zIC9JdGFsaWNBbmdsZSAwCi9NYXhXaWR0aCAxMzQyIC9TdGVtViAwIC9UeXBlIC9Gb250RGVzY3JpcHRvciAvWEhlaWdodCAwID4+CmVuZG9iagoxOCAwIG9iagpbIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwCjYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgMzE4IDQwMSA0NjAgODM4IDYzNgo5NTAgNzgwIDI3NSAzOTAgMzkwIDUwMCA4MzggMzE4IDM2MSAzMTggMzM3IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYKNjM2IDYzNiAzMzcgMzM3IDgzOCA4MzggODM4IDUzMSAxMDAwIDY4NCA2ODYgNjk4IDc3MCA2MzIgNTc1IDc3NSA3NTIgMjk1CjI5NSA2NTYgNTU3IDg2MyA3NDggNzg3IDYwMyA3ODcgNjk1IDYzNSA2MTEgNzMyIDY4NCA5ODkgNjg1IDYxMSA2ODUgMzkwIDMzNwozOTAgODM4IDUwMCA1MDAgNjEzIDYzNSA1NTAgNjM1IDYxNSAzNTIgNjM1IDYzNCAyNzggMjc4IDU3OSAyNzggOTc0IDYzNCA2MTIKNjM1IDYzNSA0MTEgNTIxIDM5MiA2MzQgNTkyIDgxOCA1OTIgNTkyIDUyNSA2MzYgMzM3IDYzNiA4MzggNjAwIDYzNiA2MDAgMzE4CjM1MiA1MTggMTAwMCA1MDAgNTAwIDUwMCAxMzQyIDYzNSA0MDAgMTA3MCA2MDAgNjg1IDYwMCA2MDAgMzE4IDMxOCA1MTggNTE4CjU5MCA1MDAgMTAwMCA1MDAgMTAwMCA1MjEgNDAwIDEwMjMgNjAwIDUyNSA2MTEgMzE4IDQwMSA2MzYgNjM2IDYzNiA2MzYgMzM3CjUwMCA1MDAgMTAwMCA0NzEgNjEyIDgzOCAzNjEgMTAwMCA1MDAgNTAwIDgzOCA0MDEgNDAxIDUwMCA2MzYgNjM2IDMxOCA1MDAKNDAxIDQ3MSA2MTIgOTY5IDk2OSA5NjkgNTMxIDY4NCA2ODQgNjg0IDY4NCA2ODQgNjg0IDk3NCA2OTggNjMyIDYzMiA2MzIgNjMyCjI5NSAyOTUgMjk1IDI5NSA3NzUgNzQ4IDc4NyA3ODcgNzg3IDc4NyA3ODcgODM4IDc4NyA3MzIgNzMyIDczMiA3MzIgNjExIDYwNQo2MzAgNjEzIDYxMyA2MTMgNjEzIDYxMyA2MTMgOTgyIDU1MCA2MTUgNjE1IDYxNSA2MTUgMjc4IDI3OCAyNzggMjc4IDYxMiA2MzQKNjEyIDYxMiA2MTIgNjEyIDYxMiA4MzggNjEyIDYzNCA2MzQgNjM0IDYzNCA1OTIgNjM1IDU5MiBdCmVuZG9iagoyMSAwIG9iago8PCAvZml2ZSAyMiAwIFIgL2ZvdXIgMjMgMCBSIC9vbmUgMjQgMCBSIC9wYXJlbmxlZnQgMjUgMCBSCi9wYXJlbnJpZ2h0IDI2IDAgUiAvcGVyaW9kIDI3IDAgUiAvdGhyZWUgMjggMCBSIC90d28gMjkgMCBSIC96ZXJvIDMwIDAgUiA+PgplbmRvYmoKMyAwIG9iago8PCAvRjEgMjAgMCBSIC9GMiAxNCAwIFIgPj4KZW5kb2JqCjQgMCBvYmoKPDwgL0ExIDw8IC9DQSAwIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4KL0EyIDw8IC9DQSAxIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4gPj4KZW5kb2JqCjUgMCBvYmoKPDwgPj4KZW5kb2JqCjYgMCBvYmoKPDwgPj4KZW5kb2JqCjcgMCBvYmoKPDwgPj4KZW5kb2JqCjIgMCBvYmoKPDwgL0NvdW50IDEgL0tpZHMgWyAxMCAwIFIgXSAvVHlwZSAvUGFnZXMgPj4KZW5kb2JqCjMxIDAgb2JqCjw8IC9DcmVhdGlvbkRhdGUgKEQ6MjAxOTA1MDgxNTA1MTUrMDInMDAnKQovQ3JlYXRvciAobWF0cGxvdGxpYiAzLjAuMywgaHR0cDovL21hdHBsb3RsaWIub3JnKQovUHJvZHVjZXIgKG1hdHBsb3RsaWIgcGRmIGJhY2tlbmQgMy4wLjMpID4+CmVuZG9iagp4cmVmCjAgMzIKMDAwMDAwMDAwMCA2NTUzNSBmIAowMDAwMDAwMDE2IDAwMDAwIG4gCjAwMDAwMDkzNzMgMDAwMDAgbiAKMDAwMDAwOTE2OCAwMDAwMCBuIAowMDAwMDA5MjExIDAwMDAwIG4gCjAwMDAwMDkzMTAgMDAwMDAgbiAKMDAwMDAwOTMzMSAwMDAwMCBuIAowMDAwMDA5MzUyIDAwMDAwIG4gCjAwMDAwMDAwNjUgMDAwMDAgbiAKMDAwMDAwMDQwMiAwMDAwMCBuIAowMDAwMDAwMjA4IDAwMDAwIG4gCjAwMDAwMDMxMjIgMDAwMDAgbiAKMDAwMDAwNDA4OSAwMDAwMCBuIAowMDAwMDAzODgxIDAwMDAwIG4gCjAwMDAwMDM1NTggMDAwMDAgbiAKMDAwMDAwNTE0MiAwMDAwMCBuIAowMDAwMDAzMTQzIDAwMDAwIG4gCjAwMDAwMDMzOTQgMDAwMDAgbiAKMDAwMDAwNzk2NCAwMDAwMCBuIAowMDAwMDA3NzY0IDAwMDAwIG4gCjAwMDAwMDczOTYgMDAwMDAgbiAKMDAwMDAwOTAxNyAwMDAwMCBuIAowMDAwMDA1MTg0IDAwMDAwIG4gCjAwMDAwMDU1MDQgMDAwMDAgbiAKMDAwMDAwNTY2NiAwMDAwMCBuIAowMDAwMDA1ODE4IDAwMDAwIG4gCjAwMDAwMDYwMzggMDAwMDAgbiAKMDAwMDAwNjI2MCAwMDAwMCBuIAowMDAwMDA2MzgxIDAwMDAwIG4gCjAwMDAwMDY3OTIgMDAwMDAgbiAKMDAwMDAwNzExMyAwMDAwMCBuIAowMDAwMDA5NDMzIDAwMDAwIG4gCnRyYWlsZXIKPDwgL0luZm8gMzEgMCBSIC9Sb290IDEgMCBSIC9TaXplIDMyID4+CnN0YXJ0eHJlZgo5NTg3CiUlRU9GCg==\n",
"image/svg+xml": [
"\n",
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sym.plot(x, (t, -0.1, 4), xlabel='$t$', ylabel='$x(t)$');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The same result can be derived directly from $X(s)$ by using the inverse Laplace transform of `SymPy`"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAOIAAAAaBAMAAABY/52QAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAIpnNuzKriUQQ7912ZlSugimNAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAES0lEQVRIDZ1VXYgbVRT+Jskkmfy7FMUWaUx1a8FCYEUQ/yJUoWDZeRB8zKB1UWrtSLWrsNCAoNAKjtuCYJWNYMH60nSl9GFBxz50taYaf55khYgPLSp0Wzd2q1vid252m7vZZDfrgXvud8937rln7jkzA3SVYKareR1G48I5G2uEuaTFm9BwPzCywinsJspYPUwqq+36TcP9QLPQ6WXakTxWD3NE23PbZ69qq66wfe0Kzax0iteWhTHEQ6kl111LQOZH9EU3nKjDhqUOe1v4uNfplXhoeZhvxSHq89TcfbZgowwMbHlcIOV6a+qtLwInh6bUMTwcSDgrfI/6rTDTzwmVcpUDz70VkXnBAReGg4MlZY+W1dRbWXlg6t/XAesU8AD9rHaOT+2gZACzocKEasckjhTtWAZBDy8An4olXULYQ6wsmBm/q+aeKlADHGFTs8APAh4Wpcn7tnFDhXkFaZv27RyXgWQWJz3sY0Io8rjrCF9RmwK+q+aeKkbGETaQB2IewV2y0iTuJU9IGHMe6TrtZY4tHCewB9hnE30DhCsINwhZ4O1iWkXeIOcIH3eBYI3gvKw0McfOZSQMgxbJR/PkznCou/hCHJ8VhfgsrLGznsK6sraO1jFevQfmhars3cqxt3o33hx+wkfE4eodtem96jZiXSZ8XC6pNonunnsROEDSXBCPHaJQ9HHYNl2FdbWxHj1unkLIPwpUSEimO7G5JKVBUnIo2lTR03iaky7f2TiYad2D1Bw/csSz4nG/KEzCuIFESWFdDSH1ES/QbBzy4JL4XJGhiipNqsIVT6eq4SvFtNXwyMg/XMXrrZrjDy5yip4UHcgitDD9mjKw4x+cErGJrtFUrAPX4nNfCvuJKASuqNKYkvtEiWq4OiqTLh/DkjuMlVo1R1H1q3ioZ2Sfpx1ZdYi6eCnHnLW/mSXJE0N5BBqWvMvqtdvMxPA3R4csICmvqpyokjoEXISRoUlOTLm4Je0SdIp1lRZ5xqu340NpZ34FY+zs2egsPKhbLUoQuYrlwpRU1YJ1Nhcs8FbZJgmPXrs5WPWvpd3JdsgQ04llEW38yR4l9yQQ4aGFSD6VQbJAi+rVM3Tr2DmP3yV8yAf241fgJ2zK5faIE98nYzI3WGHjjUu6y2VjDS+bxxF0uf0xUgfoncV5L+x8wHL6tPzMwUa07pRZk73WaVlFHGDE8oF78Wiz+ZeYmGOw2WzmMV2lvVOsZ0YzGBh9Hm/NTJdIHuYYGNwGY1eNHSEZDnIgMVaVSZfxsyr/aAXY8AsJfocXRUrbv8RtzXeT4M7vqsYrqJ6UN8OTF4X/jnVIMqs5y0da+3dojAbV554VqN20meWbsB8gxVwUo0CQdBZXvaZQRjEbNP4lDa8N+bVbkpBHpGq5ZOk2WwVl3alxRzS8NjTat/O9eM+sueUO8Ui2nrTlnMq25v+l1c2ue+elde9ob4jIzfYn/wHc+wEXT/3miAAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$2 \\left(2 e^{t} - \\cos{\\left (5 t \\right )}\\right) e^{- 3 t} \\theta\\left(t\\right)$$"
],
"text/plain": [
" ⎛ t ⎞ -3⋅t \n",
"2⋅⎝2⋅ℯ - cos(5⋅t)⎠⋅ℯ ⋅Heaviside(t)"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sym.inverse_laplace_transform(X, s, t).simplify()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise**\n",
"\n",
"* Derive the inverse Laplace transform of $X(s)$ by manual calculation."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbsphinx": "hidden"
},
"source": [
"**Copyright**\n",
"\n",
"The notebooks are provided as [Open Educational Resource](https://de.wikipedia.org/wiki/Open_Educational_Resources). Feel free to use the notebooks for your own educational purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Lecture Notes on Signals and Systems* by Sascha Spors."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 1
}