{ "cells": [ { "cell_type": "markdown", "metadata": { "nbsphinx": "hidden" }, "source": [ "# The Fourier Transform\n", "\n", "*This Jupyter notebook is part of a [collection of notebooks](../index.ipynb) in the bachelors module Signals and Systems, Communications Engineering, Universität Rostock. Please direct questions and suggestions to [Sascha.Spors@uni-rostock.de](mailto:Sascha.Spors@uni-rostock.de).*" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Properties\n", "\n", "The Fourier transform has a number of specific properties. They can be concluded from its definition. The most important ones in the context of signals and systems are reviewed in the following." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Invertibility\n", "\n", "According to the [Fourier inversion theorem](https://en.wikipedia.org/wiki/Fourier_inversion_theorem), for many types of signals it is possible to recover the signal $x(t)$ from its Fourier transformation $X(j \\omega) = \\mathcal{F} \\{ x(t) \\}$\n", "\n", "\\begin{equation}\n", "x(t) = \\mathcal{F}^{-1} \\left\\{ \\mathcal{F} \\{ x(t) \\} \\right\\}\n", "\\end{equation}\n", "\n", "A sufficient condition for the theorem to hold is that both the signal $x(t)$ and its Fourier transformation are absolutely integrable and $x(t)$ is continuous at the considered time $t$. For this type of signals, above relation can be proven by applying the definition of the inverse Fourier transform to the Fourier transform and rearranging terms\n", "\n", "\\begin{equation}\n", "\\begin{split}\n", "x(t) &= \\frac{1}{2 \\pi} \\int_{-\\infty}^{\\infty} \\underbrace{\\int_{-\\infty}^{\\infty} x(\\tau) e^{-j \\omega \\tau} d\\tau}_{X(j \\omega)} \\; e^{j \\omega t} d\\omega \\\\\n", "&= \\int_{-\\infty}^{\\infty} x(\\tau) \\left( \\frac{1}{2 \\pi} \\int_{-\\infty}^{\\infty} e^{-j \\omega \\tau} e^{j \\omega t} d\\omega \\right) d\\tau \\\\\n", "&= \\int_{-\\infty}^{\\infty} x(\\tau) \\delta(t - \\tau) d\\tau = x(t)\n", "\\end{split}\n", "\\end{equation}\n", "\n", "The solution $\\delta(t - \\tau)$ of the inverse Fourier transform $\\mathcal{F}^{-1} \\{ e^{-j \\omega \\tau} \\}$ in the brackets can be deduced from the [Fourier transform of the Dirac impulse](definition.ipynb#Transformation-of-the-Dirac-Impulse). The invertibility of the Fourier transformation holds also for more general signals $x(t)$, composed for instance from Dirac delta distributions." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "**Example**\n", "\n", "The invertibility of the Fourier transform is illustrated at the example of the [rectangular signal](../continuous_signals/standard_signals.ipynb#Rectangular-Signal) $x(t) = \\text{rect}(t)$. The inverse of [its Fourier transform](definition.ipynb#Transformation-of-the-Rectangular-Signal) $X(j \\omega) = \\text{sinc} \\left( \\frac{\\omega}{2} \\right)$ is computed to show that the rectangular signal, although it has discontinuities, can be recovered by inverse Fourier transformation." ] }, { "cell_type": "code", "execution_count": 1, "metadata": {}, "outputs": [], "source": [ "%matplotlib inline\n", "import sympy as sym\n", "sym.init_printing()\n", "\n", "def fourier_transform(x):\n", " return sym.transforms._fourier_transform(x, t, w, 1, -1, 'Fourier')\n", "\n", "def inverse_fourier_transform(X):\n", " return sym.transforms._fourier_transform(X, w, t, 1/(2*sym.pi), 1, 'Inverse Fourier')" ] }, { "cell_type": "code", "execution_count": 2, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAJMAAABCBAMAAAChqfmsAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAIruZZhDNMomrdlTvRN05z604AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAEQ0lEQVRYCa2XX2gcRRzHv5t0d++ul8thVKgv0UiRaMUr1CIUZSnFhyDpoSLogz0tiD4l5EEQbHNVGoKgSa2CEYonrdpGqdeX+gfh1Fbqn0oPH4qgNilBoSht07RNGtvEmfnd3s7ezs7unVm4zOx3ft/P/mZ2dvcXIOaRleIMqd9C93XJk6hKJ813CXVTnjs1KOPOaLRA2WeiUFvXxkQhE4FaNRdNAk0wCtVdWDHUwOBKoeyrMUg0QfuTTTw29A4mFmKjaoGhqOTiyqEux0Qt06GZYPLfmCgWtvrgPvY3fIJqVF/VdwXaV2lsi4Gy//RZrc9u+M4JZeBlNWqneAxogk9uvOKz9htv+845ag373ct+gQmaewckFFJ+1IQPBLGv+oB2vp0DKOBTDWpvEJWaKWN3wkM94XgxTaIwDWt5yUOZb5TqLA3qpZMTeGzyQZz58fNnRDxbK7NQc9YneHi3y9KgMAH7LNpKmDtCO/gjtqlyDjlTfMHE0X9/raNHZYqw53EeYkG5w9iQrRm95uh66utRw2VgAS94NmXvNO0ZPapSBS5hOwFqz5/bXKxjT9PLXI/iWc3h+bpJ2Tm6h2Q9Kp1Dx3wEqr+2VLUt2kaPc8Nu74F9AlYRM/5kCr7Txs1gzfLh5Lqld6WwoVN3o2t0H365fo+kIuUtEttnh0vu2JunzvF+59euEN3+JqOedhoNU7lGJfTc/EBGBcMG8kEtREmZWlQi1qud2Ef0qEopJIWgbDhaVOqnoCVMsUdfXSiHDQKZXPhYcMTwv2r9AeZzWb+gPdt8TZMVrO+05mYGzVjVRzzimC7neAg3qnva7f3vNq27K83R2/xf9ObM/uh4lYzfE3K28qjR/cq9+uIxVQbGcZUKysoqm2cDw7xAOBdQmdChLvUJ1Q+8EjB1MaU3oHIhr1QJxRyVwPh+ZlCjlKTaBFnGU43b3ubTaBplcpQjXYuXMV8sTZTRe9uhEtA1mev45+ORmy/8/fDV6nvHb/0B9oHJApclD2VlsP8DhpnFPaiM4R/BHseehf0NPkTnpm5nW8m8gbYsuxmPAtNCdi2sFWslUEVPpTKGo9YBl/kLsrOcmTaRLOAY2I3txe95FIXsmQhlsqymSp5KZYzICljEsMO+1NY4q7FmV4/hD47KXHqfZM9EKFZooCItO5UxdVRlw5YtgxZfl+8T6XKRo8yR5ZyQA6geYGveU6mMmUERbIBlxa/CKgjgoafab2dtL27B4/NCZqJ70L56BNjoKqylMma7i0qPA1WBGt5jL2Y56kvgLSFLLkJlyuYJSaQyZoShnuVZ2T8jkRUfp0wBf7G4HnyVxx1CllyEMl87NCiJooxB8p3s0PW7Ni+NY80Duzru+5ZNM+XgADB0cu2vfQerXJZN7U186WWfor/qmkJsUVpu0aewjZUUYmuSNd+aT+EyB6oKtTWpmWot6go7ogLijP8HVYZhxNJHP6UAAAAASUVORK5CYII=\n", "text/latex": [ "$$\\begin{cases} 1 & \\text{for}\\: \\frac{\\left|{\\frac{1}{t^{2}}}\\right|}{4} > 1 \\\\0 & \\text{otherwise} \\end{cases}$$" ], "text/plain": [ "⎧ │1 │ \n", "⎪ │──│ \n", "⎪ │ 2│ \n", "⎪ │t │ \n", "⎨1 for ──── > 1\n", "⎪ 4 \n", "⎪ \n", "⎪0 otherwise \n", "⎩ " ] }, "execution_count": 2, "metadata": {}, "output_type": "execute_result" } ], "source": [ "t, w = sym.symbols('t omega')\n", "\n", "X = sym.sinc(w/2)\n", "x = inverse_fourier_transform(X)\n", "x" ] }, { "cell_type": "code", "execution_count": 3, "metadata": {}, "outputs": [ { "data": { "application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM5Ny45NzMxMjUgMzA3Ljc1OTc1IF0gL1BhcmVudCAyIDAgUiAvUmVzb3VyY2VzIDggMCBSCi9UeXBlIC9QYWdlID4+CmVuZG9iago5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTEgMCBSID4+CnN0cmVhbQp4nKVZTVOcNwy++1f4SA4Yf8r2sUwaZnojMO2h7SFDCA3D0klJSn9+H73vLvuupd1lBhgCq+eRJVuyLDvB3ptg76y39/h5tr/bP/H7sw32Aj93xuPTyqReXa8pxIKPD8uPyVdXS68FYr/z6S9jvpiznzDIE5QujInRlehTSDYWl3MFCyPX7ijvSh92pD24sh5yMcJCujYUZ0N3cBtTcW0xGZhnZKGfqis5TR4shNn5SfhgzDlW5dl8w7/ennqMWV20oPZib1bm/NqefQg2eHv9xTSXauuepsW5/mxOgvP+nb2+Nz9fYwTvPA+C780fGODs/e39p19/XH16fDpdfX388WTf/20u8T05bqi6QKOjC+EhR0twLb/WVY9wvc3VEGDPj74upYec7eRye72z5Y3rGgrsZeHsQnrI2ZCDC6/OAu/iG5c2emRSE/m6kApvd1wKrbueAc8ez07NqWnh1NpILq7KTbGQHjYSgZc2GJlnvjDSvUsioZfSI0ZQD2IcjJRhJikVzG40spQeNpJico0GI3WYyaIyLY0spEeMUIPjO0bCIia73Fod1c6DYfq1cb1lhe/D4qppElCjyyDdkya1uVDzlLopuZqJw7nOlr2mWnE91tHUi/S4qRZdSH5rKu41FbCmKYTR1lZ83BgsuRLy1lrebw2OUS/C2ov4Fdbwd+tta432WosJf9Y+WtuKj1vDxnCxxa21tt8a8jSTSJCt+BXWanFELykStimCIociecrVLdTofC9T6sK19VE9lUzuKNw8FPTPPsS1jZP/pmKJ/Am1T8P7mbBx4uSPk4mRXPchUQ0Lzssg3zeU6BGAKenFMO82VfnSfLOb059ntuk/UqlTnSdyAb//ubW/2UeLhgMthQeC86IR1gHrm2n9VYFUX1qLqcRuP15YFPd/v97cfrw4tzdPe1qP6pJPre/s0CtFjAoT4RxHeeAqci5HCDhFiiNZylcmI68rRhi9UOQgw7XQicJIlvKVQSfSAz7QQFbkIHPl6NhlI1nKQe6upNiCGFnK0TchjLEhAweyIl+ZCt+w9GKCihxkwvmakecjWcpXBtsAJyqOy4GsyEHGhstJ+qzIV6ajaGOHtTSQFTnIvJUTzpKRLOWoET6imWyNxoXWAKZ310qLCl0C3CRiz1AlGtdPA+aeMoVcyui6Bsz0Uj1OdYU+AjOdUHjiGB8NmOm15li00Udg3Q9jo9a8W2yvdIQVEv7uhSRfAkxHyoXQUpR8BYECChIRClkSChrCCg3jeCpBKigIFLgxjNwLCQUNgUJGv4ES0gVfAZie+azADpZ8BeE2nw8enJNyTTVkfS9oaFBl0DQECoTYJ99JTllDWAHB8ZmCDJuGQAF1CAdf61JBQ1gB9bPkoExaQ6DQPPdlqchJawgrZNdaiSTjpiGr6VqCcxOnuFRQEO5UisOxWkjmqobwFQntJKHoiDmoCCsgnhRR1aSCgkABuzCgWMpJqwi/MvDFL8tAawDTcaCm0orIJBWBAjp3QmjkGqkI3/BQY0NA7yAUNIQVyKVYQpQuaQgUCprAim0rNqiKsEKDuBVl0hoCBcrTk4gSNg3hhgs3ThxETYZNQ1iB0CQTjlypoCBQaNjoJeNLKGgIK2CjE/pMGTgNmW/NgddC8BVgfclmR8VuU5G1Qq9e9B4aMNNzQjTHU1kDZjouYuhLFPoIzPTuYXLsezWA6TjaPfbG2IBoANO5i0GVHc98DWB6Q2M+nb0jXQLown12FHtP41Q1APSATRFwWRu7IQ1genW94ao0NiAawPcHXJZ96cIXKWdyR6piN4ixFWB+YsGWRtMw0hUAdNSX1lMX9x4NYDqhQU6pjkHSANAL+qNUfRZ0BWB6n96gRMZoAOjEbw7Zd3EPU4DV9NrT4WMerxMawPc2JAZ6QRklBVipb1ET/dLiYmt/mR/1d17Ch0vpsQfGoWK8vOY/Ty/62tv9at/bvXl8eaOfPOIB1Evx3lkN1rX/DDhk/dL8D7uR9LMKZW5kc3RyZWFtCmVuZG9iagoxMSAwIG9iagoxNDk3CmVuZG9iagoxNiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE3OCA+PgpzdHJlYW0KeJw9kEsSAyEIRPeeoo8gP9HzJJXV5P7bNM6YhfYTKGywpegYzsvVkF3xllYYnvg27wueiaup9YckFTL7pg4Zi2fyFCckFK8mY0DcsdXWo3Eywgy7LCZmYK6Kr0QuqFAC6lHyamaj4Gqmgr59xFaZ9RYXCEUCJixnK/6fA9PrFh0MFpjtN8uzPPYK03QszHuGeQ9FI34G5VpuYGWtg5+GHZr3tmgo/+QnexZ4tc8P3qtCoQplbmRzdHJlYW0KZW5kb2JqCjE3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggOTIgPj4Kc3RyZWFtCnicPYyxDcAwCAR7pvgFImGMbdgnSuXs3+YtJ2ng9A/X0qA4rHF2VTQfOIt8eEv1hI3ElKaVR1Oc3doWDiuDFLvYFhZeYRGk8mqY8XlT1cCSUpTlzfp/dz3Hqxu6CmVuZHN0cmVhbQplbmRvYmoKMTQgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zLU9ibGlxdWUgL0NoYXJQcm9jcyAxNSAwIFIKL0VuY29kaW5nIDw8IC9EaWZmZXJlbmNlcyBbIDExNiAvdCAxMjAgL3ggXSAvVHlwZSAvRW5jb2RpbmcgPj4gL0ZpcnN0Q2hhciAwCi9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnREZXNjcmlwdG9yIDEzIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTIgMCBSID4+CmVuZG9iagoxMyAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgOTYKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udE5hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovSXRhbGljQW5nbGUgMCAvTWF4V2lkdGggMTM1MCAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTIgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM1MCA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDI4IDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxNyA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjE3IDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDgKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk5NSA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMTUgMCBvYmoKPDwgL3QgMTYgMCBSIC94IDE3IDAgUiA+PgplbmRvYmoKMjIgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzOTIgPj4Kc3RyZWFtCnicPVJLbgUxCNvPKbhApfBNcp6p3u7df1ubzFSqCi8DtjGUlwypJT/qkogzTH71cl3iUfK9bGpn5iHuLjam+FhyX7qG2HLRmmKxTxzJL8i0VFihVt2jQ/GFKBMPAC3ggQXhvhz/8ReowdewhXLDe2QCYErUbkDGQ9EZSFlBEWH7kRXopFCvbOHvKCBX1KyFoXRiiA2WACm+qw2JmKjZoIeElZKqHdLxjKTwW8FdiWFQW1vbBHhm0BDZ3pGNETPt0RlxWRFrPz3po1EytVEZD01nfPHdMlLz0RXopNLI3cpDZ89CJ2Ak5kmY53Aj4Z7bQQsx9HGvlk9s95gpVpHwBTvKAQO9/d6Sjc974CyMXNvsTCfw0WmnHBOtvh5i/YM/bEubXMcrh0UUqLwoCH7XQRNxfFjF92SjRHe0AdYjE9VoJRAMEsLO7TDyeMZ52d4VtOb0RGijRB7UjhE9KLLF5ZwVsKf8rM2xHJ4PJntvtI+UzMyohBXUdnqots9jHdR3nvv6/AEuAKEZCmVuZHN0cmVhbQplbmRvYmoKMjMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDcgPj4Kc3RyZWFtCnicTVG7bUQxDOvfFFzgAOtreZ4LUl32b0PJCJDCIKEvKaclFvbGSwzhB1sPvuSRVUN/Hj8x7DMsPcnk1D/muclUFL4VqpuYUBdi4f1oBLwWdC8iK8oH349lDHPO9+CjEJdgJjRgrG9JJhfVvDNkwomhjsNBm1QYd00ULK4VzTPI7VY3sjqzIGx4JRPixgBEBNkXkM1go4yxlZDFch6oCpIFWmDX6RtRi4IrlNYJdKLWxLrM4Kvn9nY3Qy/y4Ki6eH0M60uwwuileyx8rkIfzPRMO3dJI73wphMRZg8FUpmdkZU6PWJ9t0D/n2Ur+PvJz/P9CxUoXCoKZW5kc3RyZWFtCmVuZG9iagoyNCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDkwID4+CnN0cmVhbQp4nE2NQRLAIAgD77wiT1BE0P90etL/X6vUDr3ATgKJFkWC9DVqSzDuuDIVa1ApmJSXwFUwXAva7qLK/jJJTJ2G03u3A4Oy8XGD0kn79nF6AKv9egbdD9IcIlgKZW5kc3RyZWFtCmVuZG9iagoyNSAwIG9iago8PCAvQkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzNwovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJzjMjQwUzA2NVXI5TI3NgKzcsAsI3MjIAski2BBZNMAAV8KCgplbmRzdHJlYW0KZW5kb2JqCjI2IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggODAgPj4Kc3RyZWFtCnicRYy7DcAwCER7pmAEfiZmnyiVs38bIErccE+6e7g6EjJT3mGGhwSeDCyGU/EGmaNgNbhGUo2d7KOwbl91geZ6U6v19wcqT3Z2cT3Nyxn0CmVuZHN0cmVhbQplbmRvYmoKMjcgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNDcgPj4Kc3RyZWFtCnicPU+5DQMxDOs9BRc4wHosW/NckOqyfxvKRlIIIkDxkWVHxwpcYgKTjjkSL2k/+GkagVgGNUf0hIphWOBukgIPgyxKV54tXgyR2kJdSPjWEN6tTGSiPK8RO3AnF6MHPlQbWR56QDtEFVmuScNY1VZdap2wAhyyzsJ1PcyqBOXRJ2spH1BUQr10/5972vsLAG8v6wplbmRzdHJlYW0KZW5kb2JqCjI4IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ5ID4+CnN0cmVhbQp4nDWPSw4DIQxD9zmFLzBSfoRwHqqupvffNmFaCQkL2y/BFoORjEtMYOyYY+ElVE+tPiQjj7pJORCpUDcET2hMDDNs0iXwynTfMp5bvJxW6oJOSOTprDYaooxmXsPRU84Km/7L3CRqZUaZAzLrVLcTsrJgBeYFtTz3M+6oXOiEh53KsOhOMaLcZkYafv/b9P4CezIwYwplbmRzdHJlYW0KZW5kb2JqCjI5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggNDkgPj4Kc3RyZWFtCnicMza0UDBQMDQwB5JGhkCWkYlCiiEXSADEzOWCCeaAWQZAGqI4B64mhysNAMboDSYKZW5kc3RyZWFtCmVuZG9iagozMCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDY4ID4+CnN0cmVhbQp4nDMzNlMwULAwAhKmpoYK5kaWCimGXEA+iJXLBRPLAbPMLMyBLCMLkJYcLkMLYzBtYmykYGZiBmRZIDEgutIAcvgSkQplbmRzdHJlYW0KZW5kb2JqCjMxIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzE3ID4+CnN0cmVhbQp4nDVSS3JDMQjbv1Nwgc6Yv32edLJq7r+thCcrsC1AQi4vWdJLftQl26XD5Fcf9yWxQj6P7ZrMUsX3FrMUzy2vR88Rty0KBFETPfgyJxUi1M/U6Dp4YZc+A68QTikWeAeTAAav4V94lE6DwDsbMt4Rk5EaECTBmkuLTUiUPUn8K+X1pJU0dH4mK3P5e3KpFGqjyQgVIFi52AekKykeJBM9iUiycr03VojekFeSx2clJhkQ3SaxTbTA49yVtISZmEIF5liA1XSzuvocTFjjsITxKmEW1YNNnjWphGa0jmNkw3j3wkyJhYbDElCbfZUJqpeP09wJI6ZHTXbtwrJbNu8hRKP5MyyUwccoJAGHTmMkCtKwgBGBOb2wir3mCzkWwIhlnZosDG1oJbt6joXA0JyzpWHG157X8/4HRVt7owplbmRzdHJlYW0KZW5kb2JqCjMyIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTMxID4+CnN0cmVhbQp4nEWPyw0EIQxD71ThEvIZPqmH1Z7Y/q/rMJpBQvhBIjvxMAis8/I20MXw0aLDN/421atjlSwfunpSVg/pkIe88hVQaTBRxIVZTB1DYc6YysiWMrcb4bZNg6xslVStg3Y8Bg+2p2WrCH6pbWHqLPEMwlVeuMcNP5BLrXe9Vb5/QlMwlwplbmRzdHJlYW0KZW5kb2JqCjMzIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjQ4ID4+CnN0cmVhbQp4nC1ROZIDQQjL5xV6QnPT77HLkff/6QrKAYOGQyA6LXFQxk8Qlive8shVtOHvmRjBd8Gh38p1GxY5EBVI0hhUTahdvB69B3YcZgLzpDUsgxnrAz9jCjd6cXhMxtntdRk1BHvXa09mUDIrF3HJxAVTddjImcNPpowL7VzPDci5EdZlGKSblcaMhCNNIVJIoeomqTNBkASjq1GjjRzFfunLI51hVSNqDPtcS9vXcxPOGjQ7Fqs8OaVHV5zLycULKwf9vM3ARVQaqzwQEnC/20P9nOzkN97SubPF9Phec7K8MBVY8ea1G5BNtfg3L+L4PePr+fwDqKVbFgplbmRzdHJlYW0KZW5kb2JqCjM0IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjEwID4+CnN0cmVhbQp4nDVQyw1DMQi7ZwoWqBQCgWSeVr11/2tt0DthEf9CWMiUCHmpyc4p6Us+OkwPti6/sSILrXUl7MqaIJ4r76GZsrHR2OJgcBomXoAWN2DoaY0aNXThgqYulUKBxSXwmXx1e+i+Txl4ahlydgQRQ8lgCWq6Fk1YtDyfkE4B4v9+w+4t5KGS88qeG/kbnO3wO7Nu4SdqdiLRchUy1LM0xxgIE0UePHlFpnDis9Z31TQS1GYLTpYBrk4/jA4AYCJeWYDsrkQ5S9KOpZ9vvMf3D0AAU7QKZW5kc3RyZWFtCmVuZG9iagoyMCAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMgL0NoYXJQcm9jcyAyMSAwIFIKL0VuY29kaW5nIDw8Ci9EaWZmZXJlbmNlcyBbIDQwIC9wYXJlbmxlZnQgL3BhcmVucmlnaHQgNDYgL3BlcmlvZCA0OCAvemVybyAvb25lIC90d28gNTIgL2ZvdXIgL2ZpdmUKL3NpeCAvc2V2ZW4gL2VpZ2h0IDExNiAvdCBdCi9UeXBlIC9FbmNvZGluZyA+PgovRmlyc3RDaGFyIDAgL0ZvbnRCQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRm9udERlc2NyaXB0b3IgMTkgMCBSCi9Gb250TWF0cml4IFsgMC4wMDEgMCAwIDAuMDAxIDAgMCBdIC9MYXN0Q2hhciAyNTUgL05hbWUgL0RlamFWdVNhbnMKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTggMCBSID4+CmVuZG9iagoxOSAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgMzIKL0ZvbnRCQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRm9udE5hbWUgL0RlamFWdVNhbnMgL0l0YWxpY0FuZ2xlIDAKL01heFdpZHRoIDEzNDIgL1N0ZW1WIDAgL1R5cGUgL0ZvbnREZXNjcmlwdG9yIC9YSGVpZ2h0IDAgPj4KZW5kb2JqCjE4IDAgb2JqClsgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAKNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCAzMTggNDAxIDQ2MCA4MzggNjM2Cjk1MCA3ODAgMjc1IDM5MCAzOTAgNTAwIDgzOCAzMTggMzYxIDMxOCAzMzcgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNgo2MzYgNjM2IDMzNyAzMzcgODM4IDgzOCA4MzggNTMxIDEwMDAgNjg0IDY4NiA2OTggNzcwIDYzMiA1NzUgNzc1IDc1MiAyOTUKMjk1IDY1NiA1NTcgODYzIDc0OCA3ODcgNjAzIDc4NyA2OTUgNjM1IDYxMSA3MzIgNjg0IDk4OSA2ODUgNjExIDY4NSAzOTAgMzM3CjM5MCA4MzggNTAwIDUwMCA2MTMgNjM1IDU1MCA2MzUgNjE1IDM1MiA2MzUgNjM0IDI3OCAyNzggNTc5IDI3OCA5NzQgNjM0IDYxMgo2MzUgNjM1IDQxMSA1MjEgMzkyIDYzNCA1OTIgODE4IDU5MiA1OTIgNTI1IDYzNiAzMzcgNjM2IDgzOCA2MDAgNjM2IDYwMCAzMTgKMzUyIDUxOCAxMDAwIDUwMCA1MDAgNTAwIDEzNDIgNjM1IDQwMCAxMDcwIDYwMCA2ODUgNjAwIDYwMCAzMTggMzE4IDUxOCA1MTgKNTkwIDUwMCAxMDAwIDUwMCAxMDAwIDUyMSA0MDAgMTAyMyA2MDAgNTI1IDYxMSAzMTggNDAxIDYzNiA2MzYgNjM2IDYzNiAzMzcKNTAwIDUwMCAxMDAwIDQ3MSA2MTIgODM4IDM2MSAxMDAwIDUwMCA1MDAgODM4IDQwMSA0MDEgNTAwIDYzNiA2MzYgMzE4IDUwMAo0MDEgNDcxIDYxMiA5NjkgOTY5IDk2OSA1MzEgNjg0IDY4NCA2ODQgNjg0IDY4NCA2ODQgOTc0IDY5OCA2MzIgNjMyIDYzMiA2MzIKMjk1IDI5NSAyOTUgMjk1IDc3NSA3NDggNzg3IDc4NyA3ODcgNzg3IDc4NyA4MzggNzg3IDczMiA3MzIgNzMyIDczMiA2MTEgNjA1CjYzMCA2MTMgNjEzIDYxMyA2MTMgNjEzIDYxMyA5ODIgNTUwIDYxNSA2MTUgNjE1IDYxNSAyNzggMjc4IDI3OCAyNzggNjEyIDYzNAo2MTIgNjEyIDYxMiA2MTIgNjEyIDgzOCA2MTIgNjM0IDYzNCA2MzQgNjM0IDU5MiA2MzUgNTkyIF0KZW5kb2JqCjIxIDAgb2JqCjw8IC9laWdodCAyMiAwIFIgL2ZpdmUgMjMgMCBSIC9mb3VyIDI0IDAgUiAvb25lIDI2IDAgUiAvcGFyZW5sZWZ0IDI3IDAgUgovcGFyZW5yaWdodCAyOCAwIFIgL3BlcmlvZCAyOSAwIFIgL3NldmVuIDMwIDAgUiAvc2l4IDMxIDAgUiAvdCAzMiAwIFIKL3R3byAzMyAwIFIgL3plcm8gMzQgMCBSID4+CmVuZG9iagozIDAgb2JqCjw8IC9GMSAyMCAwIFIgL0YyIDE0IDAgUiA+PgplbmRvYmoKNCAwIG9iago8PCAvQTEgPDwgL0NBIDAgL1R5cGUgL0V4dEdTdGF0ZSAvY2EgMSA+PgovQTIgPDwgL0NBIDEgL1R5cGUgL0V4dEdTdGF0ZSAvY2EgMSA+PiA+PgplbmRvYmoKNSAwIG9iago8PCA+PgplbmRvYmoKNiAwIG9iago8PCA+PgplbmRvYmoKNyAwIG9iago8PCAvRGVqYVZ1U2Fucy1taW51cyAyNSAwIFIgPj4KZW5kb2JqCjIgMCBvYmoKPDwgL0NvdW50IDEgL0tpZHMgWyAxMCAwIFIgXSAvVHlwZSAvUGFnZXMgPj4KZW5kb2JqCjM1IDAgb2JqCjw8IC9DcmVhdGlvbkRhdGUgKEQ6MjAxOTA1MTYxODIxMzErMDInMDAnKQovQ3JlYXRvciAobWF0cGxvdGxpYiAzLjAuMywgaHR0cDovL21hdHBsb3RsaWIub3JnKQovUHJvZHVjZXIgKG1hdHBsb3RsaWIgcGRmIGJhY2tlbmQgMy4wLjMpID4+CmVuZG9iagp4cmVmCjAgMzYKMDAwMDAwMDAwMCA2NTUzNSBmIAowMDAwMDAwMDE2IDAwMDAwIG4gCjAwMDAwMDkyNjIgMDAwMDAgbiAKMDAwMDAwOTAzMiAwMDAwMCBuIAowMDAwMDA5MDc1IDAwMDAwIG4gCjAwMDAwMDkxNzQgMDAwMDAgbiAKMDAwMDAwOTE5NSAwMDAwMCBuIAowMDAwMDA5MjE2IDAwMDAwIG4gCjAwMDAwMDAwNjUgMDAwMDAgbiAKMDAwMDAwMDM5OCAwMDAwMCBuIAowMDAwMDAwMjA4IDAwMDAwIG4gCjAwMDAwMDE5NzAgMDAwMDAgbiAKMDAwMDAwMjkzNyAwMDAwMCBuIAowMDAwMDAyNzI5IDAwMDAwIG4gCjAwMDAwMDI0MDYgMDAwMDAgbiAKMDAwMDAwMzk5MCAwMDAwMCBuIAowMDAwMDAxOTkxIDAwMDAwIG4gCjAwMDAwMDIyNDIgMDAwMDAgbiAKMDAwMDAwNzc5MiAwMDAwMCBuIAowMDAwMDA3NTkyIDAwMDAwIG4gCjAwMDAwMDcyMDIgMDAwMDAgbiAKMDAwMDAwODg0NSAwMDAwMCBuIAowMDAwMDA0MDMyIDAwMDAwIG4gCjAwMDAwMDQ0OTcgMDAwMDAgbiAKMDAwMDAwNDgxNyAwMDAwMCBuIAowMDAwMDA0OTc5IDAwMDAwIG4gCjAwMDAwMDUxNDkgMDAwMDAgbiAKMDAwMDAwNTMwMSAwMDAwMCBuIAowMDAwMDA1NTIxIDAwMDAwIG4gCjAwMDAwMDU3NDMgMDAwMDAgbiAKMDAwMDAwNTg2NCAwMDAwMCBuIAowMDAwMDA2MDA0IDAwMDAwIG4gCjAwMDAwMDYzOTQgMDAwMDAgbiAKMDAwMDAwNjU5OCAwMDAwMCBuIAowMDAwMDA2OTE5IDAwMDAwIG4gCjAwMDAwMDkzMjIgMDAwMDAgbiAKdHJhaWxlcgo8PCAvSW5mbyAzNSAwIFIgL1Jvb3QgMSAwIFIgL1NpemUgMzYgPj4Kc3RhcnR4cmVmCjk0NzYKJSVFT0YK\n", "image/svg+xml": [ "\n", "\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "\n" ], "text/plain": [ "
" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "sym.plot(x, (t,-1,1), ylabel=r'$x(t)$');" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Duality\n", "\n", "Comparing the [definition of the Fourier transform](definition.ipynb) with its inverse\n", "\n", "\\begin{align}\n", "X(j \\omega) &= \\int_{-\\infty}^{\\infty} x(t) \\, e^{-j \\omega t} \\; dt \\\\\n", "x(t) &= \\frac{1}{2 \\pi} \\int_{-\\infty}^{\\infty} X(j \\omega) \\, e^{j \\omega t} \\; d\\omega\n", "\\end{align}\n", "\n", "reveals that both are very similar in their structure. They differ only with respect to the normalization factor $2 \\pi$ and the sign of the exponential function. The duality principle of the Fourier transform can be deduced from this observation. Let's assume that we know the Fourier transformation $x_2(j \\omega)$ of a signal $x_1(t)$ \n", "\n", "\\begin{equation}\n", "x_2(j \\omega) = \\mathcal{F} \\{ x_1(t) \\}\n", "\\end{equation}\n", "\n", "It follows that the Fourier transformation of the signal \n", "\n", "\\begin{equation}\n", "x_2(j t) = x_2(j \\omega) \\big\\vert_{\\omega=t}\n", "\\end{equation}\n", "\n", "is given as\n", "\n", "\\begin{equation}\n", "\\mathcal{F} \\{ x_2(j t) \\} = 2 \\pi \\cdot x_1(- \\omega)\n", "\\end{equation}\n", "\n", "The duality principle of the Fourier transformation allows to carry over results from the time-domain to the spectral-domain and vice-versa. It can be used to derive new transforms from known transforms. This is illustrated at an example. Note, that the Laplace transformation shows no duality. This is due to the mapping of a complex signal $x(t)$ with real valued independent variable $t \\in \\mathbb{R}$ to its complex transform $X(s) \\in \\mathbb{C}$ with complex valued independent variable $s \\in \\mathbb{C}$." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "#### Transformation of the exponential signal\n", "\n", "The Fourier transform of a shifted Dirac impulse $\\delta(t - \\tau)$ is derived by introducing it into the definition of the Fourier transform and exploiting the sifting property of the Dirac delta function\n", "\n", "\\begin{equation}\n", "\\mathcal{F} \\{ \\delta(t - \\tau) \\} = \\int_{-\\infty}^{\\infty} \\delta(t - \\tau) \\, e^{-j \\omega t} \\; dt = e^{-j \\omega \\tau}\n", "\\end{equation}\n", "\n", "Using the duality principle, the Fourier transform of $e^{-j \\omega_0 t}$ can be derived from this result by \n", "\n", "1. substituting $\\omega$ with $t$ and $\\tau$ with $\\omega_0$ on the right-hand side to yield the time-domain signal $e^{-j \\omega_0 t}$\n", "2. substituting $t$ by $- \\omega$, $\\tau$ with $\\omega_0$ and multiplying the result by $2 \\pi$ on the left-hand side\n", "\n", "\\begin{equation}\n", "\\mathcal{F} \\{ e^{-j \\omega_0 t} \\} = 2 \\pi \\cdot \\delta(\\omega + \\omega_0)\n", "\\end{equation}" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Linearity\n", "\n", "The Fourier transform is a linear operation. For two signals $x_1(t)$ and $x_2(t)$ with Fourier transforms $X_1(j \\omega) = \\mathcal{F} \\{ x_1(t) \\}$ and $X_2(j \\omega) = \\mathcal{F} \\{ x_2(t) \\}$ the following holds\n", "\n", "\\begin{equation}\n", "\\mathcal{F} \\{ A \\cdot x_1(t) + B \\cdot x_2(t) \\} = A \\cdot X_1(j \\omega) + B \\cdot X_2(j \\omega)\n", "\\end{equation}\n", "\n", "with $A, B \\in \\mathbb{C}$. The Fourier transform of a weighted superposition of signals is equal to the weighted superposition of the individual Fourier transforms. This property is useful to derive the Fourier transform of signals that can be expressed as superposition of other signals for which the Fourier transforms are known or can be calculated easier. Note, linearity holds also for the inverse Fourier transform." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "#### Transformation of the cosine and sine signal\n", "\n", "The Fourier transform of $\\cos(\\omega_0 t)$ and $\\sin(\\omega_0 t)$ is derived by expressing both as harmonic exponential signals using [Euler's formula](https://en.wikipedia.org/wiki/Euler's_formula)\n", "\n", "\\begin{align}\n", "\\cos(\\omega_0 t) &= \\frac{1}{2} \\left( e^{j \\omega_0 t} + e^{-j \\omega_0 t} \\right) \\\\\n", "\\sin(\\omega_0 t) &= \\frac{1}{2j} \\left( e^{j \\omega_0 t} - e^{-j \\omega_0 t} \\right)\n", "\\end{align}\n", "\n", "together with the Fourier transform $\\mathcal{F} \\{ e^{-j \\omega_0 t} \\} = 2 \\pi \\cdot \\delta(\\omega - \\omega_0)$ from above yields\n", "\n", "\\begin{align}\n", "\\mathcal{F} \\{ \\cos(\\omega_0 t) \\} &= \\pi \\left( \\delta(\\omega + \\omega_0) + \\delta(\\omega - \\omega_0) \\right) \\\\\n", "\\mathcal{F} \\{ \\sin(\\omega_0 t) \\} &= j \\pi \\left( \\delta(\\omega + \\omega_0) - \\delta(\\omega - \\omega_0) \\right)\n", "\\end{align}" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Symmetries\n", "\n", "In order to investigate the symmetries of the Fourier transform $X(j \\omega) = \\mathcal{F} \\{ x(t) \\}$ of a signal $x(t)$ with specific properties, first the case of a real valued signal $x(t) \\in \\mathbb{R}$ is considered. The results are then generalized to complex signals $x(t) \\in \\mathbb{C}$." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "#### Real valued signals\n", "\n", "Decomposing a real valued signal $x(t) \\in \\mathbb{R}$ into its even and odd part $x(t) = x_\\text{e}(t) + x_\\text{o}(t)$ and introducing these into the definition of the Fourier transform yields\n", "\n", "\\begin{align}\n", "X(j \\omega) &= \\int_{-\\infty}^{\\infty} \\left[ x_\\text{e}(t) + x_\\text{o}(t) \\right] e^{-j \\omega t} \\; dt \\\\\n", "&= \\int_{-\\infty}^{\\infty} \\left[ x_\\text{e}(t) + x_\\text{o}(t) \\right] \\cdot \\left[ \\cos(\\omega t) - j \\sin(\\omega t) \\right] \\; dt \\\\\n", "&= \\underbrace{\\int_{-\\infty}^{\\infty} x_\\text{e}(t) \\cos(\\omega t) \\; dt}_{X_\\text{e}(j \\omega)} + \n", "j \\underbrace{\\int_{-\\infty}^{\\infty} - x_\\text{o}(t) \\sin(\\omega t) \\; dt}_{X_\\text{o}(j \\omega)}\n", "\\end{align}\n", "\n", "For the last equality the fact was exploited that an integral with symmetric limits is zero for odd functions. Note that the multiplication of an odd function with an even/odd function results in an even/odd function. In order to conclude on the symmetry of $X(j \\omega)$ its behavior for a reverse of the sign of $\\omega$ has to be investigated. Due to the symmetry properties of $\\cos(\\omega t)$ and $\\sin(\\omega t)$, it follows that the Fourier transform of the\n", "\n", "* even part $x_\\text{e}(t)$ is real valued with even symmetry $X_\\text{e}(j \\omega) = X_\\text{e}(-j \\omega)$\n", "* odd part $x_\\text{o}(t)$ is imaginary valued with odd symmetry $X_\\text{o}(j \\omega) = - X_\\text{o}(-j \\omega)$\n", "\n", "Combining this, it can be concluded that the Fourier transform $X(j \\omega)$ of a real-valued signal $x(t) \\in \\mathbb{R}$ shows complex conjugate symmetry\n", "\n", "\\begin{equation}\n", "X(j \\omega) = X^*(- j \\omega)\n", "\\end{equation}\n", "\n", "It follows that the magnitude spectrum $|X(j \\omega)|$ of a real-valued signal shows even symmetry\n", "\n", "\\begin{equation}\n", "|X(j \\omega)| = |X(- j \\omega)|\n", "\\end{equation}\n", "\n", "and the phase $\\varphi(j \\omega) = \\arg \\{ X(j \\omega) \\}$ odd symmetry\n", "\n", "\\begin{equation}\n", "\\varphi(j \\omega) = - \\varphi(- j \\omega)\n", "\\end{equation}\n", "\n", "Due to these symmetries, both are often plotted only for positive frequencies $\\omega \\geq 0$. However, without the information that the signal is real-valued it is not possible to conclude on the magnitude spectrum and phase for the negative frequencies $\\omega < 0$." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "#### Complex Signals\n", "\n", "By following the same procedure as above for an imaginary signal, the symmetries of the Fourier transform of the even and odd part of an imaginary signal can be derived. The results can be combined, by decomposing a complex signal $x(t) \\in \\mathbb{C}$ and its Fourier transform into its even and odd part for both the real and imaginary part. 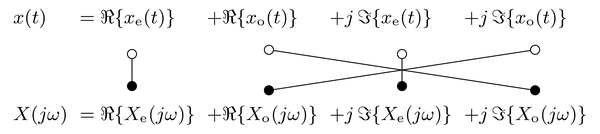This results in the following symmetry relations of the Fourier transform\n", "\n", "![Symmetries of the Fourier transform](symmetries.png)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "**Example**\n", "\n", "The Fourier transform $X(j \\omega)$ of the signal $x(t) = \\text{sgn}(t) \\cdot \\text{rect}(t)$ is computed. The signal is real valued with odd symmetry due to the sign function. It follows from the symmetry relations of the Fourier transform, that $X(j \\omega)$ is imaginary with odd symmetry." ] }, { "cell_type": "code", "execution_count": 4, "metadata": {}, "outputs": [ { "data": { "application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM5MS42MTM3NSAyOTMuMDEyIF0gL1BhcmVudCAyIDAgUiAvUmVzb3VyY2VzIDggMCBSCi9UeXBlIC9QYWdlID4+CmVuZG9iago5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTEgMCBSID4+CnN0cmVhbQp4nLWZTW8cNwyG7/MrdHQOkSXq+9ggjYHeEhvtoe0hcD4aw+siddP05/flzNg7IrVrB04TON598o7IkSiKnPHmavLmo3HmCj9fza/md/x+Z7w5w8/HyeHbbgrN2+xDSfh2vflGLVjnCcxtPv8xTR+m0x9w+S30Z9Pkmw3RZUrGO1t4vJJtzHtyvSWEj3UeaH/dnq2D0zL4RzgJx23duA6T/D9bqzHYkjIMb5mzBHY9TS8wA1+nz/jXmecOIxZLxlOzPhOUl7vpxYU5feXhq7n4MFUbSm3zIPj+bjoh656Zi6vpxwsM4jAJhmft/gOuP335/urtz1/O397cPt99uvlya17+Ob3G39nzKQfbqvB0yw57mryt8Vt89TY9zVfvqs0kp3ULD3vbsMb127x94sz6FCxl6e0WHvbWR2/9NwWCe/LktmKbUzG7gcLdzh9fm20R23Lv8uLVPIkGXi1WKJJNcmd08JgVCtGmOrCShJVarJdR3cGjVkqzRMqKl/cSAnaADMcOHrMSKNiaB1bEvWzz1d7KFh61kqtNTlmh/b1soi6UeD+qTzY2x4l2Dj1OxkgKkQEGOH1Fq4GTv+/CbhBIRLa0JY4wcseGUZ9xK9n4altr/pGb9Km7dO8ttqYLwtuVHfE2IljC47zFcfP9NmlFIinC25Ud8RahHctjvU3fb269DzZ54e4dPBYLrtniH+sw/T85cO/wCg/kQOy1HKAKyIVp9nnNgSJxbM0UnLVyi9zBB8wUZ33bmKF00Ay5iCiVO3GFx82QczaGjZl0+G44P0cZlHfwATPB2Vw2ZsqRu8kRQSHNrPABMwir5u/N+M3aIGQQd885VnyKOCo8nzSUy1z97bPgclD1SfDfOe4ShkZuq2WNyL35k99OZgXW1fmQi99oRCaFhFxdU60a5tk+2342orYNqXDRQDlbj99/vTe/mBuDAwUFKkKFfMo187mGe8jrn4LZLS7VSiFRM2/ODLbIP58u3785e2Eub4eFLPEhnEvs9sP5AOOcgilfYKCXagxpgosx1SakCnNLgFqDJ0hIFd5NMdmA2qRSL9V4NyXMRC6uCanGkGZcnpPLQqowammON5d97KUaQ5psSpSFfUV3EzZ+oCbnX1EIE2+ZFoSfGu+myn1VDKn2Uo0hTTjBEaNSqvBuatjUseboe6nGkCbrcqtiTRWFECFJFdtdKBXm3iAjkRK50GsHHGI+jUKIXszWgENMSIQxhiBWa8BZjGoNB0JoUqw4xCggEwo1L5Z3wFlcAGtoRYoVhxifEiYzi9UYcG5UOO0jUckb1JzFKOpqjSR91nxpgVyhlpRY8bVfChSrXEHNV3FxxYdNlXk+wIs0uBC7gvR8gFdpqakOpB1epM3FFLOS9pilSGwpObTQvVRiSJEsUmoltl6qMEuxtTPvWCGVGNKCFtOFKidLYZZyYqvFC18VhhQJozbCMdhLFWZpsYQ+o3ohlZiP+WCz4yc8nVJSFmbranHyphReWtvYfG7CvMKLtLYY5bIqvDbMqLBdV5Ccj/gqbqXwYitxz1lcrWsleamVeJEGNHxhoBWcxc26VEILUqw4jn6UjBkpC+dBJx5wFjduJ+ew78WKQ4wsW0tFDSPEmrO42VpzaiTFikNMOJgCzjDphuYQc2nigndi6gacxcnmOrfXQqw4i9EolsBhIsSKc4mFXZhc82JRBnx5fOJC4zzQayVen7SQQ17WWsFXcYny8NZ4kWZsbyKtFXwRl8gzr8WCL2KEdypViwVncbM4J5s84QYcYhT5paBgkm5oDnGe62RqojgYcBYnJIZQ5GQoDCmqthRQtIpqZsBZjLgi4twkxIrz4y7UCyVTlCNrzuKMvs7FIkfWHOJGNlYXVQOgOYs5P3ENIMWKc7uANOKoyNpuwCH26N74aaDsGDRnMT8uQLJWYsUhRmYglNJiMjTmx33oTgMyjqhPBpzFOIYr2s8sxYpDjK0eEsoG2eVozmIUtCi9pRcKc5/F5SyWX46rOYsbPqF1lAuiOcRcZSCrBjlvmvMTTO4sSqxSrPlu9Ax0Fr82nw2Zn5Y3SN2LGNnFjh5JqucJ85j3L4++zi+Q5Oui3fh10XRz/2Jo9oMvHfXOh+5EWNVvnw7bfT39B9uYcDMKZW5kc3RyZWFtCmVuZG9iagoxMSAwIG9iagoxNTk2CmVuZG9iagoxNiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE3OCA+PgpzdHJlYW0KeJw9kEsSAyEIRPeeoo8gP9HzJJXV5P7bNM6YhfYTKGywpegYzsvVkF3xllYYnvg27wueiaup9YckFTL7pg4Zi2fyFCckFK8mY0DcsdXWo3Eywgy7LCZmYK6Kr0QuqFAC6lHyamaj4Gqmgr59xFaZ9RYXCEUCJixnK/6fA9PrFh0MFpjtN8uzPPYK03QszHuGeQ9FI34G5VpuYGWtg5+GHZr3tmgo/+QnexZ4tc8P3qtCoQplbmRzdHJlYW0KZW5kb2JqCjE3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggOTIgPj4Kc3RyZWFtCnicPYyxDcAwCAR7pvgFImGMbdgnSuXs3+YtJ2ng9A/X0qA4rHF2VTQfOIt8eEv1hI3ElKaVR1Oc3doWDiuDFLvYFhZeYRGk8mqY8XlT1cCSUpTlzfp/dz3Hqxu6CmVuZHN0cmVhbQplbmRvYmoKMTQgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zLU9ibGlxdWUgL0NoYXJQcm9jcyAxNSAwIFIKL0VuY29kaW5nIDw8IC9EaWZmZXJlbmNlcyBbIDExNiAvdCAxMjAgL3ggXSAvVHlwZSAvRW5jb2RpbmcgPj4gL0ZpcnN0Q2hhciAwCi9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnREZXNjcmlwdG9yIDEzIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTIgMCBSID4+CmVuZG9iagoxMyAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgOTYKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udE5hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovSXRhbGljQW5nbGUgMCAvTWF4V2lkdGggMTM1MCAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTIgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM1MCA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDI4IDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxNyA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjE3IDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDgKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk5NSA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMTUgMCBvYmoKPDwgL3QgMTYgMCBSIC94IDE3IDAgUiA+PgplbmRvYmoKMjIgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDcgPj4Kc3RyZWFtCnicTVG7bUQxDOvfFFzgAOtreZ4LUl32b0PJCJDCIKEvKaclFvbGSwzhB1sPvuSRVUN/Hj8x7DMsPcnk1D/muclUFL4VqpuYUBdi4f1oBLwWdC8iK8oH349lDHPO9+CjEJdgJjRgrG9JJhfVvDNkwomhjsNBm1QYd00ULK4VzTPI7VY3sjqzIGx4JRPixgBEBNkXkM1go4yxlZDFch6oCpIFWmDX6RtRi4IrlNYJdKLWxLrM4Kvn9nY3Qy/y4Ki6eH0M60uwwuileyx8rkIfzPRMO3dJI73wphMRZg8FUpmdkZU6PWJ9t0D/n2Ur+PvJz/P9CxUoXCoKZW5kc3RyZWFtCmVuZG9iagoyMyAwIG9iago8PCAvQkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzNwovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJzjMjQwUzA2NVXI5TI3NgKzcsAsI3MjIAski2BBZNMAAV8KCgplbmRzdHJlYW0KZW5kb2JqCjI0IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggODAgPj4Kc3RyZWFtCnicRYy7DcAwCER7pmAEfiZmnyiVs38bIErccE+6e7g6EjJT3mGGhwSeDCyGU/EGmaNgNbhGUo2d7KOwbl91geZ6U6v19wcqT3Z2cT3Nyxn0CmVuZHN0cmVhbQplbmRvYmoKMjUgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNDcgPj4Kc3RyZWFtCnicPU+5DQMxDOs9BRc4wHosW/NckOqyfxvKRlIIIkDxkWVHxwpcYgKTjjkSL2k/+GkagVgGNUf0hIphWOBukgIPgyxKV54tXgyR2kJdSPjWEN6tTGSiPK8RO3AnF6MHPlQbWR56QDtEFVmuScNY1VZdap2wAhyyzsJ1PcyqBOXRJ2spH1BUQr10/5972vsLAG8v6wplbmRzdHJlYW0KZW5kb2JqCjI2IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ5ID4+CnN0cmVhbQp4nDWPSw4DIQxD9zmFLzBSfoRwHqqupvffNmFaCQkL2y/BFoORjEtMYOyYY+ElVE+tPiQjj7pJORCpUDcET2hMDDNs0iXwynTfMp5bvJxW6oJOSOTprDYaooxmXsPRU84Km/7L3CRqZUaZAzLrVLcTsrJgBeYFtTz3M+6oXOiEh53KsOhOMaLcZkYafv/b9P4CezIwYwplbmRzdHJlYW0KZW5kb2JqCjI3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggNDkgPj4Kc3RyZWFtCnicMza0UDBQMDQwB5JGhkCWkYlCiiEXSADEzOWCCeaAWQZAGqI4B64mhysNAMboDSYKZW5kc3RyZWFtCmVuZG9iagoyOCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDY4ID4+CnN0cmVhbQp4nDMzNlMwULAwAhKmpoYK5kaWCimGXEA+iJXLBRPLAbPMLMyBLCMLkJYcLkMLYzBtYmykYGZiBmRZIDEgutIAcvgSkQplbmRzdHJlYW0KZW5kb2JqCjI5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjQ4ID4+CnN0cmVhbQp4nC1ROZIDQQjL5xV6QnPT77HLkff/6QrKAYOGQyA6LXFQxk8Qlive8shVtOHvmRjBd8Gh38p1GxY5EBVI0hhUTahdvB69B3YcZgLzpDUsgxnrAz9jCjd6cXhMxtntdRk1BHvXa09mUDIrF3HJxAVTddjImcNPpowL7VzPDci5EdZlGKSblcaMhCNNIVJIoeomqTNBkASjq1GjjRzFfunLI51hVSNqDPtcS9vXcxPOGjQ7Fqs8OaVHV5zLycULKwf9vM3ARVQaqzwQEnC/20P9nOzkN97SubPF9Phec7K8MBVY8ea1G5BNtfg3L+L4PePr+fwDqKVbFgplbmRzdHJlYW0KZW5kb2JqCjMwIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjEwID4+CnN0cmVhbQp4nDVQyw1DMQi7ZwoWqBQCgWSeVr11/2tt0DthEf9CWMiUCHmpyc4p6Us+OkwPti6/sSILrXUl7MqaIJ4r76GZsrHR2OJgcBomXoAWN2DoaY0aNXThgqYulUKBxSXwmXx1e+i+Txl4ahlydgQRQ8lgCWq6Fk1YtDyfkE4B4v9+w+4t5KGS88qeG/kbnO3wO7Nu4SdqdiLRchUy1LM0xxgIE0UePHlFpnDis9Z31TQS1GYLTpYBrk4/jA4AYCJeWYDsrkQ5S9KOpZ9vvMf3D0AAU7QKZW5kc3RyZWFtCmVuZG9iagoyMCAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMgL0NoYXJQcm9jcyAyMSAwIFIKL0VuY29kaW5nIDw8Ci9EaWZmZXJlbmNlcyBbIDQwIC9wYXJlbmxlZnQgL3BhcmVucmlnaHQgNDYgL3BlcmlvZCA0OCAvemVybyAvb25lIC90d28gNTMgL2ZpdmUgNTUKL3NldmVuIF0KL1R5cGUgL0VuY29kaW5nID4+Ci9GaXJzdENoYXIgMCAvRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250RGVzY3JpcHRvciAxOSAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2FucwovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxOCAwIFIgPj4KZW5kb2JqCjE5IDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyAzMgovRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250TmFtZSAvRGVqYVZ1U2FucyAvSXRhbGljQW5nbGUgMAovTWF4V2lkdGggMTM0MiAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTggMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM0MiA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDIzIDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxMiA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjEyIDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDUKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk4MiA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMjEgMCBvYmoKPDwgL2ZpdmUgMjIgMCBSIC9vbmUgMjQgMCBSIC9wYXJlbmxlZnQgMjUgMCBSIC9wYXJlbnJpZ2h0IDI2IDAgUgovcGVyaW9kIDI3IDAgUiAvc2V2ZW4gMjggMCBSIC90d28gMjkgMCBSIC96ZXJvIDMwIDAgUiA+PgplbmRvYmoKMyAwIG9iago8PCAvRjEgMjAgMCBSIC9GMiAxNCAwIFIgPj4KZW5kb2JqCjQgMCBvYmoKPDwgL0ExIDw8IC9DQSAwIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4KL0EyIDw8IC9DQSAxIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4gPj4KZW5kb2JqCjUgMCBvYmoKPDwgPj4KZW5kb2JqCjYgMCBvYmoKPDwgPj4KZW5kb2JqCjcgMCBvYmoKPDwgL0RlamFWdVNhbnMtbWludXMgMjMgMCBSID4+CmVuZG9iagoyIDAgb2JqCjw8IC9Db3VudCAxIC9LaWRzIFsgMTAgMCBSIF0gL1R5cGUgL1BhZ2VzID4+CmVuZG9iagozMSAwIG9iago8PCAvQ3JlYXRpb25EYXRlIChEOjIwMTkwNTE2MTgyMTMyKzAyJzAwJykKL0NyZWF0b3IgKG1hdHBsb3RsaWIgMy4wLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZykKL1Byb2R1Y2VyIChtYXRwbG90bGliIHBkZiBiYWNrZW5kIDMuMC4zKSA+PgplbmRvYmoKeHJlZgowIDMyCjAwMDAwMDAwMDAgNjU1MzUgZiAKMDAwMDAwMDAxNiAwMDAwMCBuIAowMDAwMDA4MDY2IDAwMDAwIG4gCjAwMDAwMDc4MzYgMDAwMDAgbiAKMDAwMDAwNzg3OSAwMDAwMCBuIAowMDAwMDA3OTc4IDAwMDAwIG4gCjAwMDAwMDc5OTkgMDAwMDAgbiAKMDAwMDAwODAyMCAwMDAwMCBuIAowMDAwMDAwMDY1IDAwMDAwIG4gCjAwMDAwMDAzOTUgMDAwMDAgbiAKMDAwMDAwMDIwOCAwMDAwMCBuIAowMDAwMDAyMDY2IDAwMDAwIG4gCjAwMDAwMDMwMzMgMDAwMDAgbiAKMDAwMDAwMjgyNSAwMDAwMCBuIAowMDAwMDAyNTAyIDAwMDAwIG4gCjAwMDAwMDQwODYgMDAwMDAgbiAKMDAwMDAwMjA4NyAwMDAwMCBuIAowMDAwMDAyMzM4IDAwMDAwIG4gCjAwMDAwMDY2NDUgMDAwMDAgbiAKMDAwMDAwNjQ0NSAwMDAwMCBuIAowMDAwMDA2MDc3IDAwMDAwIG4gCjAwMDAwMDc2OTggMDAwMDAgbiAKMDAwMDAwNDEyOCAwMDAwMCBuIAowMDAwMDA0NDQ4IDAwMDAwIG4gCjAwMDAwMDQ2MTggMDAwMDAgbiAKMDAwMDAwNDc3MCAwMDAwMCBuIAowMDAwMDA0OTkwIDAwMDAwIG4gCjAwMDAwMDUyMTIgMDAwMDAgbiAKMDAwMDAwNTMzMyAwMDAwMCBuIAowMDAwMDA1NDczIDAwMDAwIG4gCjAwMDAwMDU3OTQgMDAwMDAgbiAKMDAwMDAwODEyNiAwMDAwMCBuIAp0cmFpbGVyCjw8IC9JbmZvIDMxIDAgUiAvUm9vdCAxIDAgUiAvU2l6ZSAzMiA+PgpzdGFydHhyZWYKODI4MAolJUVPRgo=\n", "image/svg+xml": [ "\n", "\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "\n" ], "text/plain": [ "
" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "x = - sym.Heaviside(t + 1/2) + 2 * sym.Heaviside(t) - sym.Heaviside(t - 1/2)\n", "sym.plot(x, (t, -2, 2), xlabel=r'$t$', ylabel=r'$x(t)$');" ] }, { "cell_type": "code", "execution_count": 5, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAMUAAAAtBAMAAADsAbIsAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAdpndiRBE7yJUzatmuzJRAygPAAAACXBIWXMAAA7EAAAOxAGVKw4bAAADy0lEQVRYCe1WXWgUVxT+sjt3dzb7k01ARPsyLpGKiizGB33RFbRVojhUQVAkK4UKfTEWowiig+lDRcUFBfEpC7VQ/zAopS9F1/ZBKYibB0EQdfqDxaesWkWjuH5ndnZmopm0Dy76kAP3nu+e77v3nPszmwCuWU0Q7ieU6OF6MuOmtJUm1QoZkNhQzdmx7GQTt7pkl/jjwIG595yItnyOy4x3lDSp/Wd6zCY5owlcr+fO2w5c0WV5dS1iRJWhD2NdkRCnsd4S/5apsk/1PFnpse1etkboELRngtpLajHwg6dDpIKkiXg/I6k8tKrPeIgSjxr2otQbgQHhT8BuifwGrAV+9ck4EH+K5HNG0sNIPPUZD1HiUcEcGPAkDthv4opFdAcYYtmmx34NJPNIvmagw0DshUf4gBKPGpfjnK8RdAm4YtM/BraX0F4hVF1Z9t1sQLTGro85XtF/sWI11KyuIv64OlNISpoUfulcAEiiQRvoFXacLeNISY4KNFFpsX72jVpGs4RHC8g8AvQ92Gb/ZWFEVRFlWCQuBdzC0WKiJGLO+F3YoMl06P8CXC9VJj4YkX4JG7BQOlmIfHsZJyw+udEHA9AkTolLySidj4jTmOiYgKBFDY6cHAUk8sRmB0vBLjZEDOn7CoixEDpkeC8dhWUjlsQpcSkZRZ5/BVSRslgFh+r7HjGbEMhJp1jn9iwyNRnw8t0cjXfGi01wbe4TCT70juqGCzxaR+JSSJcRec35hrPDbcIGLGU4A04aKsG5CZyVyGm2RAHf0aVZHd8u77exjzmmumkzTolLIc4nWDPkI/6WxNtndRy6xfBd4KbZOCv1Qk57hO1vYBpdqh9yRbwPlL7hfh9mkawwTolLSfXx6j2MGko+4xtsAcsU0CZHcw2YyylVwljtMHu+P31hbl5ejcnlbrQ53AvN+sfGqcQA0hYaT1QoSnQD083Pe/e8/LRCYhZbwAZzuUvoKyNaUvt4bzxy1ldh9yULr9frZXlaGzovS3xz9yro3b3F2JrOz2RMSYOi5MC82dgyZk3fIQR/lYJ2oV4fA5+WWv6JzU/O8rgoh/9hYRI9P9nEQZ9034IfeBeFSSKVd7V+ZL4PcTuAQ2CI5EiI3AnrcuVN29IE4T5Ecit8Bl+7GWD1SmAwMZxYIl96uF0Pp6aYD3YC/LpbbLUPtrepxFMnMHUCH+sJJFmYvrS11Z2UHI9am8OQ5Ve3NEesiDTQ2j+gbcCfQKGl+4gAM6C3NkfazjzGpuD/M+9/S9rOn4cu7n3/6wZXVPd/bNudDUb+D34DOxxHLUT6348AAAAASUVORK5CYII=\n", "text/latex": [ "$$\\frac{i \\left(2.0 \\cos{\\left (0.5 \\omega \\right )} - 2.0\\right)}{\\omega}$$" ], "text/plain": [ "ⅈ⋅(2.0⋅cos(0.5⋅ω) - 2.0)\n", "────────────────────────\n", " ω " ] }, "execution_count": 5, "metadata": {}, "output_type": "execute_result" } ], "source": [ "X = fourier_transform(x)\n", "X = X.rewrite(sym.cos).simplify()\n", "X" ] }, { "cell_type": "code", "execution_count": 6, "metadata": {}, "outputs": [ { "data": { "application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM4OC40MjYyNSAzMDcuMDEyIF0gL1BhcmVudCAyIDAgUiAvUmVzb3VyY2VzIDggMCBSCi9UeXBlIC9QYWdlID4+CmVuZG9iago5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTEgMCBSID4+CnN0cmVhbQp4nLWYTZMUxxGG7/0r+ogOFFVZ30cTsgn74kBsWI6wfcBowawZFIAxB4f/u5/s7prpmc1lpJAsArSbb72V2Vn5VRXmuynMb2Y/3/H3y/yX+W/8/4c5zM/4+2by/HaYYmsuSZHMb+92v0VfnQ+CzO9+/sc0vZ6e/Ab6J9Y/m6ZQXU2l1TwH76ruV5Nr5SR5t5dILa4tG514J9m2uaybv8FIDHdtZzoqFdlrTclJC0EE3Xsxulfxu2l6ih++TB/418+PPftWJ3OQ7lgbq0jme18dpqc385PfBcyeb15PzcXaul8dc/PD9Cj6b+abu+m3N2zkcces/jv+AP3Jt7d3L//0+cXL958eH96+//xp/vbH6Tl/lm+YKkrLfZv34q/aXIqrP99q+YVWh4jaZrh6L/+q3UGKk/SzDQ+/1PBeXPSG4Xv5fcPPjAo9uiA1LIvP7VcTFwtnLFw1Ss6uyX2NZ/IrGiV1l4qtLlzoiyG7aGTBmfyKvuib6w98nlzq22X2mb69/Jq+0lz2tr541LeLnli9i9vmoXD8OfV6iqAlPuZ78eFyDOuSfZT88e/v3n74fPv4x8Ptm5cPRkuKrhTfQl2CRVy7FJtBXrLzkpfC2fFG7Cn0RthfjXPvyq8W6FpLvO+hn5t+El8xvUaXPH9ijT38FNPTr5ej2ixS8HJu+kl8xfTgi+sphUR85PZTbJf/V305GX+SP1BfFocvVmnmpJYk1VN5cRcJuFfJmTZh53Sh8iS/rpK89ZJi6gSH7L1iqpQQyMQQpZyr3MmvqhQGiVxSogSU3PdBZKvEgd2HJO1C5Ul+XWUKLviU8aocHVtOlUbj6LEeeshtBJPkuIwka4khsKqUBcDYZVN2OSl79J8lkrC6SPRr4fXrEhlL/rwtadnnlns8LTnu8tdHy5qoXxbL2nQut7lbluDwkCUmc5dvHtjl0X+P8W7Uy/WzHqiXv3/98eU///X545oAl3TaeytHc76+01nl/TBfDI8xV9otGxZH0swfb+fv5/dzcJkJ0IOEXFqRVUvZ/qtETcWnTWKWPn/3bEbvv9++uv3u2dP51af9SFhwSk6pR+3J4mpk2O2I2UBCXWPphY1AqC7mXCvizOSTkz8SLISuGJ0vHgsRB1I7ElorwUR0EHe9yFo3cGltLaeNYCGHiSQInY+rS6HJ1OyUV4KJHKZMK81Uh7CIeyjBbwQTgcDYX2JMuk8nvJOPm0kmcphwcUl0P/20qmkX0uYlE4GA8xLOJsKLMAinHONGsBDGZTzWKaoNMflKSW+bBhOBULT0LyMV9S609R6j6w3gMDWKQ/OMRUh1l9pzWNebCITsRLxUxKwIWtq2LzCRw9TxtScMGYkrw14mejeLTAQC83NOTffB0FI5/e2TTYRK6TWsQu44GzeWFlPazs2GlMIvXXyU5XyISdJtUCwISojM9WnpXYw8xLEfSixECQ2FQiAjp3H7JFIHw4KgSHSxrwMjgan1NQ6KCSmFCVOa+L5ol+yZTQfFgvQuQ7fIuee8NAGqfarjU0xIKUQ92ZjwI4FUaurlSLEgKJqKlCLdioPL3Usf32JCSmFIrqETBtQhEsi32AfFgqDkhMG9EZvCFS320ts4SBOCQp3LPkbGFL2qCOYOuyxECZlU4wAKtVpLDdbGwbAgvZkHmmutNH2V1zCO5L5cF1NdGqU3oVY0+GrMY70FQWl07JpDijOzj6P/17pllQ0ppdMkhbZAfjIfUujz0GJCOoJwk2tULq2TDNVsJONDTIi+QcJRuaonsrlr+RzqSBMbUgo9K1IrZS6dhkLPG4T7AMvJtsp1p4SZUadz8ynb8ZmIEppLISZ8TUKkSnsYrcxCtFlSvGlSzNXaHXsZnfJSrEsbCc/xJJ0Lig6ieaw2EAgkWO614uqI24if0QBMRAnsQ1TR7LPWPDlZbyEQtKNlahD3G5KeSW7LBwvQ2zqnIuoCeiBzBqk4vtdClKCdqi79nPjCaXqiG8OCoGhHi4EcnvUdheAKo3rYkFJI8oxKQpKrKCXWj8+2EB1YOJ1OF1ykpRzrkwXocpzXozYQLWBCKxnDgQ1BaXwS7UDHjOi5fbXeB8WEoNDici5aqWkihHDZLtQvHoCUkl1kbNbPC3rdk977oFgQkxSJ5TvtX+fKrvOf9DFKmZBS9JGqkX+aisLcMU7dRPSRJegVobS03FFj7T0MHSakFD2oxNmuTxmeziiDYkFQiJoSw2KuZC3ZOkGtFBPSuZPrWI5Je0mkrdBXwpg7DUQJnCkXHw0fYcruZRyJiUCgQycKnY7IesOlaI+ZyoagkDoMpMzpy1ZF29DGsBAl4OvAxV8DiB+5o8Yjw4KgFL1tewoxcuoRzpRhlgnpyxU3GO6+RZ8n9aLgZQy4NnT+2KUn4Oldm5bn84dZ5j+s7+1nz9YXV5LdBXfUzb1s3x+PT+1fluf2y8f1g/24Pr0/PqMvdij1gSdz+1HP0n3/xf5h7c+n/wEO//MmCmVuZHN0cmVhbQplbmRvYmoKMTEgMCBvYmoKMTg2MQplbmRvYmoKMTYgMCBvYmoKPDwgL0JCb3ggWyAtMTAxNiAtMzUxIDE2NjAgMTA2OCBdIC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzMyCi9TdWJ0eXBlIC9Gb3JtIC9UeXBlIC9YT2JqZWN0ID4+CnN0cmVhbQp4nE2SS25rMQxD53cV2kAB62+vp0BHefufviPfDgokoGJLJEXnSZMI+feoLVFL+TyaJeotelyUO3O9+P1YnPdk0+tL3EJ0zY33ki7xc6RcQtfA9xPx/t4pfFI3EofzDChLJROJfS6azsStMiTDxDCQZuJIwXXg74ZsBPaLOeK32iXTkfDPTG7lpqyk8PB5amEJq7lbsuxF+lDcw9kyHRH02+yxZzpcvDghI9dz0fLeTGXMcKoNGz7OtYJlWMNcvtjHIy8SEN1T2WlZsKTYTVQJgTBxS07K9+amblMcMpuV5KavrdKavJWtknbIoqV/gxpExt/KG/QgqGRmLAeSvaCCtIaYFx4kgH6roq+JqPJIX3cTVPFUnyd1glGJnj5Y/FxEEe2pHJvFf8gVNq/ZbdsbGQxVLDkaNU+p+VaKu2L9nrXtz4qf5+c/tip78QplbmRzdHJlYW0KZW5kb2JqCjE3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggOTMgPj4Kc3RyZWFtCnicPY07DsAwCEN3TsEFKoVPArlP1Sm9/1qXfhb0ZGN7ZOfGmytuNOPQybuQWBSepC8tsqHsY4B65qt9kUUOspRyHWVQqho5S7YW97eW8Kwt0gljKkj+keMC4l0b9wplbmRzdHJlYW0KZW5kb2JqCjE4IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTUyID4+CnN0cmVhbQp4nD1PyxFDIQi8W8U2wIwggtbzMjmZ/q8BTTyxsrgf8YEKYhaQVIe4w63ixYW1o6vjU6QdtAqLg+YGlr8SsYK8gevW6Rg9Zpt4iufGGDpjhrBwzJEMWdrFM+62L0WODYK7YVah6SmWPuR6YRsHUnqztF2hpnAupiJjhnHbaZ9bJdKO0y9K/ZquIr3D1JK1i8affX8BvPc2ZwplbmRzdHJlYW0KZW5kb2JqCjE5IDAgb2JqCjw8IC9CQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE4MQovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJw1UDkOBCEM63mFP7ASucN7Rtpq9v/thjBToBgcBzuDSfEhwW9ENpCJFHiCw3GNZIgxiA2qAloO0yiClzS6B79cavUSKGaJpXpISyl1XOEMltjlGjL7LqYgXZAMSA25hpZ0o3uoHE5twglGeaS25gausyaXzza6//J2SvCIduOFj9PQfJxGZdxcpHWqCHpiRs3KPTZ6CUbctRyxnLXUUqRUizpRZbDVD3M2/+7xGt8/5jc/HgplbmRzdHJlYW0KZW5kb2JqCjE0IDAgb2JqCjw8IC9CYXNlRm9udCAvRGVqYVZ1U2Fucy1PYmxpcXVlIC9DaGFyUHJvY3MgMTUgMCBSCi9FbmNvZGluZyA8PCAvRGlmZmVyZW5jZXMgWyA4OCAvWCAxMDYgL2ogXSAvVHlwZSAvRW5jb2RpbmcgPj4gL0ZpcnN0Q2hhciAwCi9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnREZXNjcmlwdG9yIDEzIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTIgMCBSID4+CmVuZG9iagoxMyAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgOTYKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udE5hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovSXRhbGljQW5nbGUgMCAvTWF4V2lkdGggMTM1MCAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTIgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM1MCA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDI4IDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxNyA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjE3IDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDgKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk5NSA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMTUgMCBvYmoKPDwgL1ggMTcgMCBSIC9qIDE4IDAgUiA+PgplbmRvYmoKMjQgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNzkgPj4Kc3RyZWFtCnicPVI7ksUgDOtzCl+AGfAXzpOdrbL3b1eCvFdkrERGkh3SUroMDWkjVWIMqezyMy7CtlT+DiL7XD6/0NY60JyHo4uNCaAp96WrA3YVrZIWvusoMgTmENhommhOUXAKCbV92nCQh/oA6zIidr0vBiV6NrKtQ/Yg9hOpGVJBOfCOhFCEh82+Y/g4cTztzRNgTp4MOCN79TNOKV05YTkUMDK3wy2w3tdnX89GuYi85gdhDiLHInJiUxMMkkCxHF6OdPDUU6M2A+RRXDBRx2yxwM+9Zz7oMaRT6JHt2FwupF5k8IX52aHwYD+3AAYqqrWdBjtYvb+OY72GDb+P4VrkjtuKLRygTRcOxDvBEVnv7y15rt9/B3JuBgplbmRzdHJlYW0KZW5kb2JqCjI1IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjc2ID4+CnN0cmVhbQp4nD1SS47oMAjb5xRcIFL4Jj1PR7Pqu//22bSaFRZgY0jKS5aopUwtk1SVXUt+dHTuMvk3NK9Gz7D15sxD5kmxODK3yj0M5JlbrNBrb9SrCwCxSO7UEtslxpZLxZJkh6ztEHdk0OHFKtnM+NrCDjdrjkdSFypepwcF+Yww8E7Mfb6JZSE0Vxltt8BBDxaoAz0wCxO5IuPdaxM9jXgLoKwPmb+ILjfUXI9sTIBTuNoL3qmU1jEPFYmiHOxGGr2fo+Y4ocPbPWI59nIJRwbe4mjHe/BFiJ5GVkSsfsizEfmGDalIj5jKG+puH3r8ja3YaH92JknB11/W20w10rng1Fyt1l+DR2jw3qjh8/dLnvH7HyEmbhIKZW5kc3RyZWFtCmVuZG9iagoyNiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDkwID4+CnN0cmVhbQp4nE2NQRLAIAgD77wiT1BE0P90etL/X6vUDr3ATgKJFkWC9DVqSzDuuDIVa1ApmJSXwFUwXAva7qLK/jJJTJ2G03u3A4Oy8XGD0kn79nF6AKv9egbdD9IcIlgKZW5kc3RyZWFtCmVuZG9iagoyNyAwIG9iago8PCAvQkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzNwovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJzjMjQwUzA2NVXI5TI3NgKzcsAsI3MjIAski2BBZNMAAV8KCgplbmRzdHJlYW0KZW5kb2JqCjI4IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggODAgPj4Kc3RyZWFtCnicRYy7DcAwCER7pmAEfiZmnyiVs38bIErccE+6e7g6EjJT3mGGhwSeDCyGU/EGmaNgNbhGUo2d7KOwbl91geZ6U6v19wcqT3Z2cT3Nyxn0CmVuZHN0cmVhbQplbmRvYmoKMjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNDcgPj4Kc3RyZWFtCnicPU+5DQMxDOs9BRc4wHosW/NckOqyfxvKRlIIIkDxkWVHxwpcYgKTjjkSL2k/+GkagVgGNUf0hIphWOBukgIPgyxKV54tXgyR2kJdSPjWEN6tTGSiPK8RO3AnF6MHPlQbWR56QDtEFVmuScNY1VZdap2wAhyyzsJ1PcyqBOXRJ2spH1BUQr10/5972vsLAG8v6wplbmRzdHJlYW0KZW5kb2JqCjMwIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ5ID4+CnN0cmVhbQp4nDWPSw4DIQxD9zmFLzBSfoRwHqqupvffNmFaCQkL2y/BFoORjEtMYOyYY+ElVE+tPiQjj7pJORCpUDcET2hMDDNs0iXwynTfMp5bvJxW6oJOSOTprDYaooxmXsPRU84Km/7L3CRqZUaZAzLrVLcTsrJgBeYFtTz3M+6oXOiEh53KsOhOMaLcZkYafv/b9P4CezIwYwplbmRzdHJlYW0KZW5kb2JqCjMxIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggNDkgPj4Kc3RyZWFtCnicMza0UDBQMDQwB5JGhkCWkYlCiiEXSADEzOWCCeaAWQZAGqI4B64mhysNAMboDSYKZW5kc3RyZWFtCmVuZG9iagozMiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDMxNyA+PgpzdHJlYW0KeJw1UktyQzEI279TcIHOmL99nnSyau6/rYQnK7AtQEIuL1nSS37UJdulw+RXH/clsUI+j+2azFLF9xazFM8tr0fPEbctCgRREz34MicVItTP1Og6eGGXPgOvEE4pFngHkwAGr+FfeJROg8A7GzLeEZORGhAkwZpLi01IlD1J/Cvl9aSVNHR+Jitz+XtyqRRqo8kIFSBYudgHpCspHiQTPYlIsnK9N1aI3pBXksdnJSYZEN0msU20wOPclbSEmZhCBeZYgNV0s7r6HExY47CE8SphFtWDTZ41qYRmtI5jZMN498JMiYWGwxJQm32VCaqXj9PcCSOmR0127cKyWzbvIUSj+TMslMHHKCQBh05jJArSsIARgTm9sIq95gs5FsCIZZ2aLAxtaCW7eo6FwNCcs6Vhxtee1/P+B0Vbe6MKZW5kc3RyZWFtCmVuZG9iagozMyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDMzOCA+PgpzdHJlYW0KeJw1Ujmu3UAM630KXSCAds2c5wWpfu7fhpRfCkO0VoqajhaVafllIVUtky6/7UltiRvy98kKiROSVyXapQyRUPk8hVS/Z8u8vtacESBLlQqTk5LHJQv+DJfeLhznY2s/jyN3PXpgVYyEEgHLFBOja1k6u8Oajfw8pgE/4hFyrli3HGMVSA26cdoV70PzecgaIGaYlooKXVaJFn5B8aBHrX33WFRYINHtHElwjI1QkYB2gdpIDDmzFruoL/pZlJgJdO2LIu6iwBJJzJxiXTr6Dz50LKi/NuPLr45K+kgra0zad6NJacwik66XRW83b309uEDzLsp/Xs0gQVPWKGl80KqdYyiaGWWFdxyaDDTHHIfMEzyHMxKU9H0ofl9LJrookT8ODaF/Xx6jjJwGbwFz0Z+2igMX8dlhrxxghdLFmuR9QCoTemD6/9f4ef78Axy2gFQKZW5kc3RyZWFtCmVuZG9iagozNCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI0OCA+PgpzdHJlYW0KeJwtUTmSA0EIy+cVekJz0++xy5H3/+kKygGDhkMgOi1xUMZPEJYr3vLIVbTh75kYwXfBod/KdRsWORAVSNIYVE2oXbwevQd2HGYC86Q1LIMZ6wM/Ywo3enF4TMbZ7XUZNQR712tPZlAyKxdxycQFU3XYyJnDT6aMC+1czw3IuRHWZRikm5XGjIQjTSFSSKHqJqkzQZAEo6tRo40cxX7pyyOdYVUjagz7XEvb13MTzho0OxarPDmlR1ecy8nFCysH/bzNwEVUGqs8EBJwv9tD/Zzs5Dfe0rmzxfT4XnOyvDAVWPHmtRuQTbX4Ny/i+D3j6/n8A6ilWxYKZW5kc3RyZWFtCmVuZG9iagozNSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDIxMCA+PgpzdHJlYW0KeJw1UMsNQzEIu2cKFqgUAoFknla9df9rbdA7YRH/QljIlAh5qcnOKelLPjpMD7Yuv7EiC611JezKmiCeK++hmbKx0djiYHAaJl6AFjdg6GmNGjV04YKmLpVCgcUl8Jl8dXvovk8ZeGoZcnYEEUPJYAlquhZNWLQ8n5BOAeL/fsPuLeShkvPKnhv5G5zt8DuzbuEnanYi0XIVMtSzNMcYCBNFHjx5RaZw4rPWd9U0EtRmC06WAa5OP4wOAGAiXlmA7K5EOUvSjqWfb7zH9w9AAFO0CmVuZHN0cmVhbQplbmRvYmoKMjIgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zIC9DaGFyUHJvY3MgMjMgMCBSCi9FbmNvZGluZyA8PAovRGlmZmVyZW5jZXMgWyA0MCAvcGFyZW5sZWZ0IC9wYXJlbnJpZ2h0IDQ2IC9wZXJpb2QgNDggL3plcm8gL29uZSAvdHdvIC90aHJlZSAvZm91ciA1NAovc2l4IDEyMyAvYnJhY2VsZWZ0IDEyNSAvYnJhY2VyaWdodCBdCi9UeXBlIC9FbmNvZGluZyA+PgovRmlyc3RDaGFyIDAgL0ZvbnRCQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRm9udERlc2NyaXB0b3IgMjEgMCBSCi9Gb250TWF0cml4IFsgMC4wMDEgMCAwIDAuMDAxIDAgMCBdIC9MYXN0Q2hhciAyNTUgL05hbWUgL0RlamFWdVNhbnMKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMjAgMCBSID4+CmVuZG9iagoyMSAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgMzIKL0ZvbnRCQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRm9udE5hbWUgL0RlamFWdVNhbnMgL0l0YWxpY0FuZ2xlIDAKL01heFdpZHRoIDEzNDIgL1N0ZW1WIDAgL1R5cGUgL0ZvbnREZXNjcmlwdG9yIC9YSGVpZ2h0IDAgPj4KZW5kb2JqCjIwIDAgb2JqClsgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAKNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCAzMTggNDAxIDQ2MCA4MzggNjM2Cjk1MCA3ODAgMjc1IDM5MCAzOTAgNTAwIDgzOCAzMTggMzYxIDMxOCAzMzcgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNgo2MzYgNjM2IDMzNyAzMzcgODM4IDgzOCA4MzggNTMxIDEwMDAgNjg0IDY4NiA2OTggNzcwIDYzMiA1NzUgNzc1IDc1MiAyOTUKMjk1IDY1NiA1NTcgODYzIDc0OCA3ODcgNjAzIDc4NyA2OTUgNjM1IDYxMSA3MzIgNjg0IDk4OSA2ODUgNjExIDY4NSAzOTAgMzM3CjM5MCA4MzggNTAwIDUwMCA2MTMgNjM1IDU1MCA2MzUgNjE1IDM1MiA2MzUgNjM0IDI3OCAyNzggNTc5IDI3OCA5NzQgNjM0IDYxMgo2MzUgNjM1IDQxMSA1MjEgMzkyIDYzNCA1OTIgODE4IDU5MiA1OTIgNTI1IDYzNiAzMzcgNjM2IDgzOCA2MDAgNjM2IDYwMCAzMTgKMzUyIDUxOCAxMDAwIDUwMCA1MDAgNTAwIDEzNDIgNjM1IDQwMCAxMDcwIDYwMCA2ODUgNjAwIDYwMCAzMTggMzE4IDUxOCA1MTgKNTkwIDUwMCAxMDAwIDUwMCAxMDAwIDUyMSA0MDAgMTAyMyA2MDAgNTI1IDYxMSAzMTggNDAxIDYzNiA2MzYgNjM2IDYzNiAzMzcKNTAwIDUwMCAxMDAwIDQ3MSA2MTIgODM4IDM2MSAxMDAwIDUwMCA1MDAgODM4IDQwMSA0MDEgNTAwIDYzNiA2MzYgMzE4IDUwMAo0MDEgNDcxIDYxMiA5NjkgOTY5IDk2OSA1MzEgNjg0IDY4NCA2ODQgNjg0IDY4NCA2ODQgOTc0IDY5OCA2MzIgNjMyIDYzMiA2MzIKMjk1IDI5NSAyOTUgMjk1IDc3NSA3NDggNzg3IDc4NyA3ODcgNzg3IDc4NyA4MzggNzg3IDczMiA3MzIgNzMyIDczMiA2MTEgNjA1CjYzMCA2MTMgNjEzIDYxMyA2MTMgNjEzIDYxMyA5ODIgNTUwIDYxNSA2MTUgNjE1IDYxNSAyNzggMjc4IDI3OCAyNzggNjEyIDYzNAo2MTIgNjEyIDYxMiA2MTIgNjEyIDgzOCA2MTIgNjM0IDYzNCA2MzQgNjM0IDU5MiA2MzUgNTkyIF0KZW5kb2JqCjIzIDAgb2JqCjw8IC9icmFjZWxlZnQgMjQgMCBSIC9icmFjZXJpZ2h0IDI1IDAgUiAvZm91ciAyNiAwIFIgL29uZSAyOCAwIFIKL3BhcmVubGVmdCAyOSAwIFIgL3BhcmVucmlnaHQgMzAgMCBSIC9wZXJpb2QgMzEgMCBSIC9zaXggMzIgMCBSCi90aHJlZSAzMyAwIFIgL3R3byAzNCAwIFIgL3plcm8gMzUgMCBSID4+CmVuZG9iagozIDAgb2JqCjw8IC9GMSAyMiAwIFIgL0YyIDE0IDAgUiA+PgplbmRvYmoKNCAwIG9iago8PCAvQTEgPDwgL0NBIDAgL1R5cGUgL0V4dEdTdGF0ZSAvY2EgMSA+PgovQTIgPDwgL0NBIDEgL1R5cGUgL0V4dEdTdGF0ZSAvY2EgMSA+PiA+PgplbmRvYmoKNSAwIG9iago8PCA+PgplbmRvYmoKNiAwIG9iago8PCA+PgplbmRvYmoKNyAwIG9iago8PCAvRGVqYVZ1U2Fucy1PYmxpcXVlLUlmcmFrdHVyIDE2IDAgUiAvRGVqYVZ1U2Fucy1PYmxpcXVlLW9tZWdhIDE5IDAgUgovRGVqYVZ1U2Fucy1taW51cyAyNyAwIFIgPj4KZW5kb2JqCjIgMCBvYmoKPDwgL0NvdW50IDEgL0tpZHMgWyAxMCAwIFIgXSAvVHlwZSAvUGFnZXMgPj4KZW5kb2JqCjM2IDAgb2JqCjw8IC9DcmVhdGlvbkRhdGUgKEQ6MjAxOTA1MTYxODIxMzMrMDInMDAnKQovQ3JlYXRvciAobWF0cGxvdGxpYiAzLjAuMywgaHR0cDovL21hdHBsb3RsaWIub3JnKQovUHJvZHVjZXIgKG1hdHBsb3RsaWIgcGRmIGJhY2tlbmQgMy4wLjMpID4+CmVuZG9iagp4cmVmCjAgMzcKMDAwMDAwMDAwMCA2NTUzNSBmIAowMDAwMDAwMDE2IDAwMDAwIG4gCjAwMDAwMTA0NDEgMDAwMDAgbiAKMDAwMDAxMDE0MiAwMDAwMCBuIAowMDAwMDEwMTg1IDAwMDAwIG4gCjAwMDAwMTAyODQgMDAwMDAgbiAKMDAwMDAxMDMwNSAwMDAwMCBuIAowMDAwMDEwMzI2IDAwMDAwIG4gCjAwMDAwMDAwNjUgMDAwMDAgbiAKMDAwMDAwMDM5NSAwMDAwMCBuIAowMDAwMDAwMjA4IDAwMDAwIG4gCjAwMDAwMDIzMzEgMDAwMDAgbiAKMDAwMDAwNDA1MyAwMDAwMCBuIAowMDAwMDAzODQ1IDAwMDAwIG4gCjAwMDAwMDM1MjMgMDAwMDAgbiAKMDAwMDAwNTEwNiAwMDAwMCBuIAowMDAwMDAyMzUyIDAwMDAwIG4gCjAwMDAwMDI4MTggMDAwMDAgbiAKMDAwMDAwMjk4MyAwMDAwMCBuIAowMDAwMDAzMjA4IDAwMDAwIG4gCjAwMDAwMDg5MDIgMDAwMDAgbiAKMDAwMDAwODcwMiAwMDAwMCBuIAowMDAwMDA4MzAxIDAwMDAwIG4gCjAwMDAwMDk5NTUgMDAwMDAgbiAKMDAwMDAwNTE0OCAwMDAwMCBuIAowMDAwMDA1NTAwIDAwMDAwIG4gCjAwMDAwMDU4NDkgMDAwMDAgbiAKMDAwMDAwNjAxMSAwMDAwMCBuIAowMDAwMDA2MTgxIDAwMDAwIG4gCjAwMDAwMDYzMzMgMDAwMDAgbiAKMDAwMDAwNjU1MyAwMDAwMCBuIAowMDAwMDA2Nzc1IDAwMDAwIG4gCjAwMDAwMDY4OTYgMDAwMDAgbiAKMDAwMDAwNzI4NiAwMDAwMCBuIAowMDAwMDA3Njk3IDAwMDAwIG4gCjAwMDAwMDgwMTggMDAwMDAgbiAKMDAwMDAxMDUwMSAwMDAwMCBuIAp0cmFpbGVyCjw8IC9JbmZvIDM2IDAgUiAvUm9vdCAxIDAgUiAvU2l6ZSAzNyA+PgpzdGFydHhyZWYKMTA2NTUKJSVFT0YK\n", "image/svg+xml": [ "\n", "\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "\n" ], "text/plain": [ "
" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "sym.plot(sym.im(X), (w, -30, 30), xlabel=r'$\\omega$', ylabel=r'$\\Im \\{ X(j \\omega) \\}$');" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "**Exercise**\n", "\n", "* What symmetry do you expect for the Fourier transform of the signal $x(t) = j \\cdot \\text{sgn}(t) \\cdot \\text{rect}(t)$? Check your results by modifying above example." ] }, { "cell_type": "markdown", "metadata": { "nbsphinx": "hidden" }, "source": [ "**Copyright**\n", "\n", "The notebooks are provided as [Open Educational Resource](https://de.wikipedia.org/wiki/Open_Educational_Resources). Feel free to use the notebooks for your own educational purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Lecture Notes on Signals and Systems* by Sascha Spors." ] } ], "metadata": { "kernelspec": { "display_name": "Python 3", "language": "python", "name": "python3" }, "language_info": { "codemirror_mode": { "name": "ipython", "version": 3 }, "file_extension": ".py", "mimetype": "text/x-python", "name": "python", "nbconvert_exporter": "python", "pygments_lexer": "ipython3", "version": "3.7.3" } }, "nbformat": 4, "nbformat_minor": 1 }