{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"nbsphinx": "hidden"
},
"source": [
"# The Fourier Transform\n",
"\n",
"*This Jupyter notebook is part of a [collection of notebooks](../index.ipynb) in the bachelors module Signals and Systems, Communications Engineering, Universität Rostock. Please direct questions and suggestions to [Sascha.Spors@uni-rostock.de](mailto:Sascha.Spors@uni-rostock.de).*"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Theorems\n",
"\n",
"The theorems of the Fourier transform relate basic time-domain operations to their equivalents in the Fourier domain. They are of use for the computation of Fourier transforms of signals composed from modified [standard signals](../continuous_signals/standard_signals.ipynb) and for the computation of the response of systems to an input signal. The theorems allow further to predict the consequences of modifying a signal or system by certain operations."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Temporal Scaling Theorem\n",
"\n",
"A signal $x(t)$ for which the Fourier transform $X(j \\omega) = \\mathcal{F} \\{ x(t) \\}$ is existing and known is given. The Fourier transform of the [temporally scaled signal](../continuous_signals/operations.ipynb#Temporal-Scaling) $x(a t)$ with $a \\in \\mathbb{R} \\setminus \\{0\\}$ reads\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{F} \\{ x(a t) \\} = \\frac{1}{|a|} \\cdot X \\left( \\frac{j \\omega}{a} \\right)\n",
"\\end{equation}\n",
"\n",
"The Fourier transformation of a temporally scaled signal is given by inverse scaling of the Fourier transform of the unscaled signal and weighting with $\\frac{1}{|a|}$. This relation is known as scaling theorem of the Fourier transform. It can be proven by introducing the scaled signal $x(a t)$ into the definition of the Fourier transformation together with the substitution $t' = a t$. For $a>0$ this reads\n",
"\n",
"\\begin{equation}\n",
"\\begin{split}\n",
"\\mathcal{F} \\{ x(a t) \\} &= \\int_{-\\infty}^{\\infty} x(a t) e^{-j \\omega t} dt \\\\\n",
"&= \\frac{1}{a} \\int_{-\\infty}^{\\infty} x(t') e^{-j \\frac{\\omega}{a} t'} dt' \\\\\n",
"&= \\frac{1}{a} X \\left( \\frac{\\omega}{a} \\right)\n",
"\\end{split}\n",
"\\end{equation}\n",
"\n",
"\n",
"\n",
"Note that the cases $a<0$ and $a>0$ have to be regarded separately."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Example**\n",
"\n",
"According to the scaling theorem and the [Fourier transform of the rectangular signal](definition.ipynb#Transformation-of-the-Rectangular-Signal) $\\mathcal{F} \\{ \\text{rect}(t) \\} = \\text{sinc} \\left( \\frac{\\omega}{2} \\right)$, the transform of the scaled rectangular signal $\\text{rect}(a t)$ is given as\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{F} \\{ \\text{rect}(a t) \\} = \\frac{1}{|a|} \\cdot \\text{sinc} \\left( \\frac{\\omega}{2 a} \\right)\n",
"\\end{equation}\n",
"\n",
"This can be confirmed by explicitly calculating the Fourier transformation of $\\text{rect}(a t)$"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAFUAAAAvBAMAAABgYpvOAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAIpnNuzKriUQQ7912ZlSugimNAAAACXBIWXMAAA7EAAAOxAGVKw4bAAACXElEQVRIDe1VTWjUUBD+kk2ym822rgqCojT4U+lBWMGrsIIr1Iu1VAT3sMGDB0FY6cGTNicFUQzqdenSwyoFIRTreT2oKCoqIih7qB6l6FosWH9YZ97bhKxtai715EBmvpn53svkZd57QIz0u5FEOoJXgB+iMb0Y9f7EZoEj+hzwhkGLFbBhR0kCKHe6gIz2grFKT5mB5bFWHEy4DIDMgrSstwi4DTXBR85h3/CQrTMgEYMl3C3Me3p5jZG5xDq7BOMLg175JtwH2IX7Au1nbfgwFoUbVbqYBxdH716pivjObtZq0xc/e1rY2EB5auvDJoVzvsilpoyGAHgiDSpN4Cbg4x7QaOpckVHo5gJzzZNohsxlD1UcAg4Dv8jVijIV6sqIgKpNxvpK30Dcg8BPclMOqagMuMJ7xdoc79gRrmVTrBMI4UmXFPqrWA9sRm0xwk05nIrIgKjhOPAYmAfOrMat5GmgMrN90Ac+ejjAxe6T9RpFSpnnTnnB1GIdUlRUAbjUeuSOTQ+PfS+9/uHQ+taJpEKlWaS8C8Bym+H/ts5Vwj86uJwTRm4T6vOIe711loOiH8JsL5B9lvbNWdEass96KaF3QqCyp9p6nWCfQypOjDnKKMNUs2hzKx9HpLjYb5twdDKvvaWF6+63mAG0j5XSsaFsvnKVUDGGJcN0PmQ7nXZmz/x5IE1Tr6EEffd3217DKv5P/W9XwKDXKbPJ3vmJuXyoJRCbORcSEOmGcaEBLxNxc8Ao6DBOInSnPYeSjKuN6Au4kWyDpW+d/nwycoOuVot5ZG9uurkS4zfPH7SOO/LjZAAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$\\frac{2 \\sin{\\left (\\frac{\\omega}{2 a} \\right )}}{\\omega}$$"
],
"text/plain": [
" ⎛ ω ⎞\n",
"2⋅sin⎜───⎟\n",
" ⎝2⋅a⎠\n",
"──────────\n",
" ω "
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import sympy as sym\n",
"%matplotlib inline\n",
"sym.init_printing()\n",
"\n",
"\n",
"def fourier_transform(x):\n",
" return sym.transforms._fourier_transform(x, t, w, 1, -1, 'Fourier')\n",
"\n",
"\n",
"t, w = sym.symbols('t omega')\n",
"a = sym.symbols('a', positive=True)\n",
"\n",
"x = sym.Heaviside(t + sym.S.Half/a) - sym.Heaviside(t - sym.S.Half/a)\n",
"X = fourier_transform(x)\n",
"X"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For illustration both the signal $x(t)$ and its Fourier transform $X(j \\omega)$ are plotted for a specific value of $a$"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM3OC41MiAzMTcuNzU5NzUgXSAvUGFyZW50IDIgMCBSIC9SZXNvdXJjZXMgOCAwIFIKL1R5cGUgL1BhZ2UgPj4KZW5kb2JqCjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxMSAwIFIgPj4Kc3RyZWFtCnicpVjLchU3EN3PV2hpFpal1qu1DEVwVXaAK1kEFpQxBJevU+AQfj+nZ+5jRt3YSQWX8b19Tj9GanX3KLrbKbpPLrhb/H53v7t3+PvBRXeJ309TwLfdlBr7Qvh4d/iYYvOt9FYgCptvf0zTx+niJyg/QOFyisE3R8Xn3IDDVm2e6SS5O0p69GVvZFFaCfZWabH6CbEhXs+riOFLkClXnyMCbL7kNHs8SLIPs+Rump7job9PX/B/cOcB1lIHmDlScUS+F3e9m55fuYuX0cXgrj5O7PHkPVQQ8P3DdJafuavb6ecrWAk+iCH8HD5A++LFze37X7+9eX//cL77fP/twb34c3qFnznsKWLJONV1nEfRY4FGLE2u/F8ipf8ZKXdP20D3EhXnJo7I1QcO6RSpBBMkGIdgFuNUg6+c19aPosfNU4EKCFvztDWfEvkYeG3+KHrcfCL2nXgwnw/m16lTi6QvlqTNuzLvhxwc33l2AMWLl7S3e/bXYTceW9/i20ryg/Wt1acieEq+ISfafoX9sMZ7BzDaqa0dHCVPOWAsWQonB2Q6iFjShCReeTiJnnIB+77EfPKRbR8Ipfay8XEUPekDtYs7n3xU0wel6EPrax8n0VM+iJonppMPtn20jmO82e6T6EkfrfhajxseTxuOE46MPJfcjDhGIEoZoEb7QnrKzTwXiDk1Dw7Ovs6pmX2MEekfjwXkZpZXHwulOSEX8fUsRh3vHJb0W+RLhifkVuD9EViAt2cHJEQU/XhUWR2P9wdfWA7q/8LqKv63z05n64vbNp6EcoEmQFjEiL9fb9xv7t6hwaCFBCCxVK4kRrEJ+38Ne9ZCYaZUqLvXlw6l8u/P1zevL5+764elS63PbfUdD8Vtc3TfWHKUOZwpKmg5A9mQg8yeIkIZuUqM+paxRCmV0a4hR2vE0zZU0jqQDfncRwuqQKaRrOW7qZBPlXvNA9mQg9yQErwp1AtZy3dTRTWOqXAfyIYcZPYNJyGMW2LId1PLHimHLBjIhnw3McpHzLmPD2jIQUalZaThuIGGfDfJ2IPD2UeyIQe5+lo66sJI1nIkaEAh6K1XlaEGIHT0wJpCHvfFAmR+KR45Q2HcGQsAnaKPlWlMVEMuZHymyHFcFAsAHS0xhI6qNNINQOg4SCGGqiI3ANBz8pFTauPeW4DQGQ9UeDw3hhzkElGAQsnjkbQAoScZ96hougYWeuZUulp0A1joBTVD1QcL2NMbRti2bWZvbGRRwHsDeqKloBBRwFEMPYasFQxkUeiYKjhZCgqRGo4ClWOf2+ZWwUJEAaWkJAy6WsFAoIDujXxtxjNYiMwH5EPCCKKX1UJEAa9jjAavl9VCoNATRlgcf61gIaKAKQYDSdAhWQgaWMBYgS7a1EObiCjgPaZjuVkrGAgUInmuAf1CKViIKLBMOrnqkCxEOnbyUpeKVrAQUcD023vAq5ZSMJBFoaVmZKuJLApoprGZCgpZFHotqZsKChGFgoKZiiqNFrCnZ65l7DAWIPTqCS/nY30x5ELGeWLs+1hILQD0+d2j4jyNdAMAHTMPoR6oIcQChI6hjmtXzc4CQMfc03sh1e0sQOiMl1uMoIqt5PLCjBMU0HWUbQMQevetIfdU5AYAOqafXNB21DIagEyqGIp7LKxnVQ0IXS4JahrHF0MOcsdYyhja1LIYgNDxXsWp69Q1AAzOAZNbLaRmBgsQOl77u/RARdeA0LvcB2ADFV0DoMfsK2FwGhfGAoTePQfqTVk3ANClmqA49HFlLECuTIJcmWyuqxa6AQgdpSe3EsdzagFC75glqARN14C83yCpe0ctVC84GgC9IDVyaUk9qgEIvXpu1OI42lmAXGaiAWckq4rdAI53n1vqK/fFkftluYLdXGkOb5s/uocbCvnx7vX7fP863rfurPvW6f54uTpHcLy4fSr4wdlwb/sjX6+mfwDwFXSRCmVuZHN0cmVhbQplbmRvYmoKMTEgMCBvYmoKMTQ2MwplbmRvYmoKMTYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzNDkgPj4Kc3RyZWFtCnicRZLJjWMxDETvPwom0IC4SoqnB33y5H+dR9qNOdhVnzuLKnVZEipfkIwtWUv+6JO+xdXk7xO7iHg9ft4Yy+V4G3DkEo8SqwnWJd+P7SNfKfapaWsNfj+aPkw1ReUQcrFmSu4e4Hr/qx+MEFsmReWkrG6x08FaR5xmRpRHwt9IBsWbMV9iq/vLtkrkBeODe6Jhh71Z1plk8Fp7YGHkxOFHjsV48bBIa+HFuCfonYNsfN/MqnExHbi7mq3ODlG+ekINavhskohnxpR6l6STbX0AsBXJUfJwjmxp75zF442tjw+LMnJK4lJNW7l0rF2RU0bHg44XTzN27XjfNr08JyeM2t19jaK/t6cPFtvJK/B8sxf3rWHG9L2xMqXNDTQ5G6oo2+j9YLZCw9pDF+WwWjyAHkr3lU1ldGIV82rozefbbQsBXv1ouo7fS407V1G2Cq/R6/+kr+fnH+XehrEKZW5kc3RyZWFtCmVuZG9iagoxNyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE3OCA+PgpzdHJlYW0KeJw9kEsSAyEIRPeeoo8gP9HzJJXV5P7bNM6YhfYTKGywpegYzsvVkF3xllYYnvg27wueiaup9YckFTL7pg4Zi2fyFCckFK8mY0DcsdXWo3Eywgy7LCZmYK6Kr0QuqFAC6lHyamaj4Gqmgr59xFaZ9RYXCEUCJixnK/6fA9PrFh0MFpjtN8uzPPYK03QszHuGeQ9FI34G5VpuYGWtg5+GHZr3tmgo/+QnexZ4tc8P3qtCoQplbmRzdHJlYW0KZW5kb2JqCjE0IDAgb2JqCjw8IC9CYXNlRm9udCAvRGVqYVZ1U2Fucy1PYmxpcXVlIC9DaGFyUHJvY3MgMTUgMCBSCi9FbmNvZGluZyA8PCAvRGlmZmVyZW5jZXMgWyA5NyAvYSAxMTYgL3QgXSAvVHlwZSAvRW5jb2RpbmcgPj4gL0ZpcnN0Q2hhciAwCi9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnREZXNjcmlwdG9yIDEzIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTIgMCBSID4+CmVuZG9iagoxMyAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgOTYKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udE5hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovSXRhbGljQW5nbGUgMCAvTWF4V2lkdGggMTM1MCAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTIgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM1MCA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDI4IDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxNyA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjE3IDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDgKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk5NSA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMTUgMCBvYmoKPDwgL2EgMTYgMCBSIC90IDE3IDAgUiA+PgplbmRvYmoKMjIgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyMzAgPj4Kc3RyZWFtCnicNVFJbsMwDLzrFfOBAOIuv8dBT+3/rx3SCWBgaEuczREbGxF4icHPQeTGW9aMmvibyV3xuzwVHgm3gidRBF6Ge9kJLm8Yl/04zHzwXlo5kxpPMiAX2fTwRMhgl0DowOwa1GGbaSf6hoTPjkg1G1lOX0vQS6sQKE/ZfqcLSrSt6s/tsy607WtPONntqSeVTyCeW7ICl41XTBZjGfRE5S7F9EGqs4WehPKifA6y+aghEl2inIEnBgejQDuw57afiVeFoHV1n7aNoRopHU//NjQ1SSLkEyWc2dK4W/j+nnv9/AOmVFOfCmVuZHN0cmVhbQplbmRvYmoKMjMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDUgPj4Kc3RyZWFtCnicRVC7jUMxDOs9BRcIYP0se553SJXbvz1KRnCFIVo/kloSmIjASwyxlG/iR0ZBPQu/F4XiM8TPF4VBzoSkQJz1GRCZeIbaRm7odnDOvMMzjDkCF8VacKbTmfZc2OScBycQzm2U8YxCuklUFXFUn3FM8aqyz43XgaW1bLPTkewhjYRLSSUml35TKv+0KVsq6NpFE7BI5IGTTTThLD9DkmLMoJRR9zC1jvRxspFHddDJ2Zw5LZnZ7qftTHwPWCaZUeUpnecyPiep81xOfe6zHdHkoqVV+5z93pGW8iK126HV6VclUZmN1aeQuDz/jJ/x/gOOoFk+CmVuZHN0cmVhbQplbmRvYmoKMjQgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzOTIgPj4Kc3RyZWFtCnicPVJLbgUxCNvPKbhApfBNcp6p3u7df1ubzFSqCi8DtjGUlwypJT/qkogzTH71cl3iUfK9bGpn5iHuLjam+FhyX7qG2HLRmmKxTxzJL8i0VFihVt2jQ/GFKBMPAC3ggQXhvhz/8ReowdewhXLDe2QCYErUbkDGQ9EZSFlBEWH7kRXopFCvbOHvKCBX1KyFoXRiiA2WACm+qw2JmKjZoIeElZKqHdLxjKTwW8FdiWFQW1vbBHhm0BDZ3pGNETPt0RlxWRFrPz3po1EytVEZD01nfPHdMlLz0RXopNLI3cpDZ89CJ2Ak5kmY53Aj4Z7bQQsx9HGvlk9s95gpVpHwBTvKAQO9/d6Sjc974CyMXNvsTCfw0WmnHBOtvh5i/YM/bEubXMcrh0UUqLwoCH7XQRNxfFjF92SjRHe0AdYjE9VoJRAMEsLO7TDyeMZ52d4VtOb0RGijRB7UjhE9KLLF5ZwVsKf8rM2xHJ4PJntvtI+UzMyohBXUdnqots9jHdR3nvv6/AEuAKEZCmVuZHN0cmVhbQplbmRvYmoKMjUgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA5MCA+PgpzdHJlYW0KeJxNjUESwCAIA++8Ik9QRND/dHrS/1+r1A69wE4CiRZFgvQ1aksw7rgyFWtQKZiUl8BVMFwL2u6iyv4ySUydhtN7twODsvFxg9JJ+/ZxegCr/XoG3Q/SHCJYCmVuZHN0cmVhbQplbmRvYmoKMjYgMCBvYmoKPDwgL0JCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzcKL1N1YnR5cGUgL0Zvcm0gL1R5cGUgL1hPYmplY3QgPj4Kc3RyZWFtCnic4zI0MFMwNjVVyOUyNzYCs3LALCNzIyALJItgQWTTAAFfCgoKZW5kc3RyZWFtCmVuZG9iagoyNyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDgwID4+CnN0cmVhbQp4nEWMuw3AMAhEe6ZgBH4mZp8olbN/GyBK3HBPunu4OhIyU95hhocEngwshlPxBpmjYDW4RlKNneyjsG5fdYHmelOr9fcHKk92dnE9zcsZ9AplbmRzdHJlYW0KZW5kb2JqCjI4IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ3ID4+CnN0cmVhbQp4nD1PuQ0DMQzrPQUXOMB6LFvzXJDqsn8bykZSCCJA8ZFlR8cKXGICk445Ei9pP/hpGoFYBjVH9ISKYVjgbpICD4MsSleeLV4MkdpCXUj41hDerUxkojyvETtwJxejBz5UG1keekA7RBVZrknDWNVWXWqdsAIcss7CdT3MqgTl0SdrKR9QVEK9dP+fe9r7CwBvL+sKZW5kc3RyZWFtCmVuZG9iagoyOSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE0OSA+PgpzdHJlYW0KeJw1j0sOAyEMQ/c5hS8wUn6EcB6qrqb33zZhWgkJC9svwRaDkYxLTGDsmGPhJVRPrT4kI4+6STkQqVA3BE9oTAwzbNIl8Mp03zKeW7ycVuqCTkjk6aw2GqKMZl7D0VPOCpv+y9wkamVGmQMy61S3E7KyYAXmBbU89zPuqFzohIedyrDoTjGi3GZGGn7/2/T+AnsyMGMKZW5kc3RyZWFtCmVuZG9iagozMCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDQ5ID4+CnN0cmVhbQp4nDM2tFAwUDA0MAeSRoZAlpGJQoohF0gAxMzlggnmgFkGQBqiOAeuJocrDQDG6A0mCmVuZHN0cmVhbQplbmRvYmoKMzEgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNTcgPj4Kc3RyZWFtCnicRZC5EUMxCERzVUEJErAI6rHH0Xf/qRf5SrRvAC2HryVTqh8nIqbc12j0MHkOn00lVizYJraTGnIbFkFKMZh4TjGro7ehmYfU67ioqrh1ZpXTacvKxX/zaFczkz3CNeon8E3o+J88tKnoW6CvC5R9QLU4nUlQMX2vYoGjnHZ/IpwY4D4ZR5kpI3Fibgrs9xkAZr5XuMbjBd0BN3kKZW5kc3RyZWFtCmVuZG9iagozMiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDMxNyA+PgpzdHJlYW0KeJw1UktyQzEI279TcIHOmL99nnSyau6/rYQnK7AtQEIuL1nSS37UJdulw+RXH/clsUI+j+2azFLF9xazFM8tr0fPEbctCgRREz34MicVItTP1Og6eGGXPgOvEE4pFngHkwAGr+FfeJROg8A7GzLeEZORGhAkwZpLi01IlD1J/Cvl9aSVNHR+Jitz+XtyqRRqo8kIFSBYudgHpCspHiQTPYlIsnK9N1aI3pBXksdnJSYZEN0msU20wOPclbSEmZhCBeZYgNV0s7r6HExY47CE8SphFtWDTZ41qYRmtI5jZMN498JMiYWGwxJQm32VCaqXj9PcCSOmR0127cKyWzbvIUSj+TMslMHHKCQBh05jJArSsIARgTm9sIq95gs5FsCIZZ2aLAxtaCW7eo6FwNCcs6Vhxtee1/P+B0Vbe6MKZW5kc3RyZWFtCmVuZG9iagozMyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDEzMSA+PgpzdHJlYW0KeJxFj8sNBCEMQ+9U4RLyGT6ph9We2P6v6zCaQUL4QSI78TAIrPPyNtDF8NGiwzf+NtWrY5UsH7p6UlYP6ZCHvPIVUGkwUcSFWUwdQ2HOmMrIljK3G+G2TYOsbJVUrYN2PAYPtqdlqwh+qW1h6izxDMJVXrjHDT+QS613vVW+f0JTMJcKZW5kc3RyZWFtCmVuZG9iagozNCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI0OCA+PgpzdHJlYW0KeJwtUTmSA0EIy+cVekJz0++xy5H3/+kKygGDhkMgOi1xUMZPEJYr3vLIVbTh75kYwXfBod/KdRsWORAVSNIYVE2oXbwevQd2HGYC86Q1LIMZ6wM/Ywo3enF4TMbZ7XUZNQR712tPZlAyKxdxycQFU3XYyJnDT6aMC+1czw3IuRHWZRikm5XGjIQjTSFSSKHqJqkzQZAEo6tRo40cxX7pyyOdYVUjagz7XEvb13MTzho0OxarPDmlR1ecy8nFCysH/bzNwEVUGqs8EBJwv9tD/Zzs5Dfe0rmzxfT4XnOyvDAVWPHmtRuQTbX4Ny/i+D3j6/n8A6ilWxYKZW5kc3RyZWFtCmVuZG9iagozNSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDIxMCA+PgpzdHJlYW0KeJw1UMsNQzEIu2cKFqgUAoFknla9df9rbdA7YRH/QljIlAh5qcnOKelLPjpMD7Yuv7EiC611JezKmiCeK++hmbKx0djiYHAaJl6AFjdg6GmNGjV04YKmLpVCgcUl8Jl8dXvovk8ZeGoZcnYEEUPJYAlquhZNWLQ8n5BOAeL/fsPuLeShkvPKnhv5G5zt8DuzbuEnanYi0XIVMtSzNMcYCBNFHjx5RaZw4rPWd9U0EtRmC06WAa5OP4wOAGAiXlmA7K5EOUvSjqWfb7zH9w9AAFO0CmVuZHN0cmVhbQplbmRvYmoKMjAgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zIC9DaGFyUHJvY3MgMjEgMCBSCi9FbmNvZGluZyA8PAovRGlmZmVyZW5jZXMgWyA0MCAvcGFyZW5sZWZ0IC9wYXJlbnJpZ2h0IDQ2IC9wZXJpb2QgNDggL3plcm8gL29uZSAvdHdvIDUyIC9mb3VyIDU0IC9zaXgKNTYgL2VpZ2h0IDk5IC9jIDEwMSAvZSAxMTQgL3IgMTE2IC90IF0KL1R5cGUgL0VuY29kaW5nID4+Ci9GaXJzdENoYXIgMCAvRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250RGVzY3JpcHRvciAxOSAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2FucwovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxOCAwIFIgPj4KZW5kb2JqCjE5IDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyAzMgovRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250TmFtZSAvRGVqYVZ1U2FucyAvSXRhbGljQW5nbGUgMAovTWF4V2lkdGggMTM0MiAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTggMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM0MiA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDIzIDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxMiA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjEyIDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDUKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk4MiA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMjEgMCBvYmoKPDwgL2MgMjIgMCBSIC9lIDIzIDAgUiAvZWlnaHQgMjQgMCBSIC9mb3VyIDI1IDAgUiAvb25lIDI3IDAgUgovcGFyZW5sZWZ0IDI4IDAgUiAvcGFyZW5yaWdodCAyOSAwIFIgL3BlcmlvZCAzMCAwIFIgL3IgMzEgMCBSIC9zaXggMzIgMCBSCi90IDMzIDAgUiAvdHdvIDM0IDAgUiAvemVybyAzNSAwIFIgPj4KZW5kb2JqCjMgMCBvYmoKPDwgL0YxIDIwIDAgUiAvRjIgMTQgMCBSID4+CmVuZG9iago0IDAgb2JqCjw8IC9BMSA8PCAvQ0EgMCAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+Ci9BMiA8PCAvQ0EgMSAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+ID4+CmVuZG9iago1IDAgb2JqCjw8ID4+CmVuZG9iago2IDAgb2JqCjw8ID4+CmVuZG9iago3IDAgb2JqCjw8IC9EZWphVnVTYW5zLW1pbnVzIDI2IDAgUiA+PgplbmRvYmoKMiAwIG9iago8PCAvQ291bnQgMSAvS2lkcyBbIDEwIDAgUiBdIC9UeXBlIC9QYWdlcyA+PgplbmRvYmoKMzYgMCBvYmoKPDwgL0NyZWF0aW9uRGF0ZSAoRDoyMDE5MDUxNjE4Mzc1MiswMicwMCcpCi9DcmVhdG9yIChtYXRwbG90bGliIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcpCi9Qcm9kdWNlciAobWF0cGxvdGxpYiBwZGYgYmFja2VuZCAzLjAuMykgPj4KZW5kb2JqCnhyZWYKMCAzNwowMDAwMDAwMDAwIDY1NTM1IGYgCjAwMDAwMDAwMTYgMDAwMDAgbiAKMDAwMDAwOTg4OCAwMDAwMCBuIAowMDAwMDA5NjU4IDAwMDAwIG4gCjAwMDAwMDk3MDEgMDAwMDAgbiAKMDAwMDAwOTgwMCAwMDAwMCBuIAowMDAwMDA5ODIxIDAwMDAwIG4gCjAwMDAwMDk4NDIgMDAwMDAgbiAKMDAwMDAwMDA2NSAwMDAwMCBuIAowMDAwMDAwMzk0IDAwMDAwIG4gCjAwMDAwMDAyMDggMDAwMDAgbiAKMDAwMDAwMTkzMiAwMDAwMCBuIAowMDAwMDAzMTU2IDAwMDAwIG4gCjAwMDAwMDI5NDggMDAwMDAgbiAKMDAwMDAwMjYyNiAwMDAwMCBuIAowMDAwMDA0MjA5IDAwMDAwIG4gCjAwMDAwMDE5NTMgMDAwMDAgbiAKMDAwMDAwMjM3NSAwMDAwMCBuIAowMDAwMDA4NDE1IDAwMDAwIG4gCjAwMDAwMDgyMTUgMDAwMDAgbiAKMDAwMDAwNzgxMiAwMDAwMCBuIAowMDAwMDA5NDY4IDAwMDAwIG4gCjAwMDAwMDQyNTEgMDAwMDAgbiAKMDAwMDAwNDU1NCAwMDAwMCBuIAowMDAwMDA0ODcyIDAwMDAwIG4gCjAwMDAwMDUzMzcgMDAwMDAgbiAKMDAwMDAwNTQ5OSAwMDAwMCBuIAowMDAwMDA1NjY5IDAwMDAwIG4gCjAwMDAwMDU4MjEgMDAwMDAgbiAKMDAwMDAwNjA0MSAwMDAwMCBuIAowMDAwMDA2MjYzIDAwMDAwIG4gCjAwMDAwMDYzODQgMDAwMDAgbiAKMDAwMDAwNjYxNCAwMDAwMCBuIAowMDAwMDA3MDA0IDAwMDAwIG4gCjAwMDAwMDcyMDggMDAwMDAgbiAKMDAwMDAwNzUyOSAwMDAwMCBuIAowMDAwMDA5OTQ4IDAwMDAwIG4gCnRyYWlsZXIKPDwgL0luZm8gMzYgMCBSIC9Sb290IDEgMCBSIC9TaXplIDM3ID4+CnN0YXJ0eHJlZgoxMDEwMgolJUVPRgo=\n",
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
"<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
" \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
"<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
"<svg height=\"317.57225pt\" version=\"1.1\" viewBox=\"0 0 378.52 317.57225\" width=\"378.52pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
" <defs>\n",
" <style type=\"text/css\">\n",
"*{stroke-linecap:butt;stroke-linejoin:round;}\n",
" </style>\n",
" </defs>\n",
" <g id=\"figure_1\">\n",
" <g id=\"patch_1\">\n",
" <path d=\"M 0 317.57225 \n",
"L 378.52 317.57225 \n",
"L 378.52 0 \n",
"L 0 0 \n",
"z\n",
"\" style=\"fill:#ffffff;\"/>\n",
" </g>\n",
" <g id=\"axes_1\">\n",
" <g id=\"patch_2\">\n",
" <path d=\"M 10.7 292.112 \n",
"L 367.82 292.112 \n",
"L 367.82 26 \n",
"L 10.7 26 \n",
"z\n",
"\" style=\"fill:#ffffff;\"/>\n",
" </g>\n",
" <g id=\"matplotlib.axis_1\">\n",
" <g id=\"xtick_1\">\n",
" <g id=\"line2d_1\">\n",
" <defs>\n",
" <path d=\"M 0 0 \n",
"L 0 3.5 \n",
"\" id=\"m5f42d28f26\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
" </defs>\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"46.412\" xlink:href=\"#m5f42d28f26\" y=\"280.016\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_1\">\n",
" <!-- −4 -->\n",
" <defs>\n",
" <path d=\"M 10.59375 35.5 \n",
"L 73.1875 35.5 \n",
"L 73.1875 27.203125 \n",
"L 10.59375 27.203125 \n",
"z\n",
"\" id=\"DejaVuSans-8722\"/>\n",
" <path d=\"M 37.796875 64.3125 \n",
"L 12.890625 25.390625 \n",
"L 37.796875 25.390625 \n",
"z\n",
"M 35.203125 72.90625 \n",
"L 47.609375 72.90625 \n",
"L 47.609375 25.390625 \n",
"L 58.015625 25.390625 \n",
"L 58.015625 17.1875 \n",
"L 47.609375 17.1875 \n",
"L 47.609375 0 \n",
"L 37.796875 0 \n",
"L 37.796875 17.1875 \n",
"L 4.890625 17.1875 \n",
"L 4.890625 26.703125 \n",
"z\n",
"\" id=\"DejaVuSans-52\"/>\n",
" </defs>\n",
" <g transform=\"translate(39.040906 294.614437)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-52\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_2\">\n",
" <g id=\"line2d_2\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"117.836\" xlink:href=\"#m5f42d28f26\" y=\"280.016\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_2\">\n",
" <!-- −2 -->\n",
" <defs>\n",
" <path d=\"M 19.1875 8.296875 \n",
"L 53.609375 8.296875 \n",
"L 53.609375 0 \n",
"L 7.328125 0 \n",
"L 7.328125 8.296875 \n",
"Q 12.9375 14.109375 22.625 23.890625 \n",
"Q 32.328125 33.6875 34.8125 36.53125 \n",
"Q 39.546875 41.84375 41.421875 45.53125 \n",
"Q 43.3125 49.21875 43.3125 52.78125 \n",
"Q 43.3125 58.59375 39.234375 62.25 \n",
"Q 35.15625 65.921875 28.609375 65.921875 \n",
"Q 23.96875 65.921875 18.8125 64.3125 \n",
"Q 13.671875 62.703125 7.8125 59.421875 \n",
"L 7.8125 69.390625 \n",
"Q 13.765625 71.78125 18.9375 73 \n",
"Q 24.125 74.21875 28.421875 74.21875 \n",
"Q 39.75 74.21875 46.484375 68.546875 \n",
"Q 53.21875 62.890625 53.21875 53.421875 \n",
"Q 53.21875 48.921875 51.53125 44.890625 \n",
"Q 49.859375 40.875 45.40625 35.40625 \n",
"Q 44.1875 33.984375 37.640625 27.21875 \n",
"Q 31.109375 20.453125 19.1875 8.296875 \n",
"z\n",
"\" id=\"DejaVuSans-50\"/>\n",
" </defs>\n",
" <g transform=\"translate(110.464906 294.614437)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-50\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_3\">\n",
" <g id=\"line2d_3\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m5f42d28f26\" y=\"280.016\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_3\">\n",
" <!-- 0 -->\n",
" <defs>\n",
" <path d=\"M 31.78125 66.40625 \n",
"Q 24.171875 66.40625 20.328125 58.90625 \n",
"Q 16.5 51.421875 16.5 36.375 \n",
"Q 16.5 21.390625 20.328125 13.890625 \n",
"Q 24.171875 6.390625 31.78125 6.390625 \n",
"Q 39.453125 6.390625 43.28125 13.890625 \n",
"Q 47.125 21.390625 47.125 36.375 \n",
"Q 47.125 51.421875 43.28125 58.90625 \n",
"Q 39.453125 66.40625 31.78125 66.40625 \n",
"z\n",
"M 31.78125 74.21875 \n",
"Q 44.046875 74.21875 50.515625 64.515625 \n",
"Q 56.984375 54.828125 56.984375 36.375 \n",
"Q 56.984375 17.96875 50.515625 8.265625 \n",
"Q 44.046875 -1.421875 31.78125 -1.421875 \n",
"Q 19.53125 -1.421875 13.0625 8.265625 \n",
"Q 6.59375 17.96875 6.59375 36.375 \n",
"Q 6.59375 54.828125 13.0625 64.515625 \n",
"Q 19.53125 74.21875 31.78125 74.21875 \n",
"z\n",
"\" id=\"DejaVuSans-48\"/>\n",
" </defs>\n",
" <g transform=\"translate(186.07875 294.614437)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_4\">\n",
" <g id=\"line2d_4\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"260.684\" xlink:href=\"#m5f42d28f26\" y=\"280.016\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_4\">\n",
" <!-- 2 -->\n",
" <g transform=\"translate(257.50275 294.614437)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-50\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_5\">\n",
" <g id=\"line2d_5\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"332.108\" xlink:href=\"#m5f42d28f26\" y=\"280.016\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_5\">\n",
" <!-- 4 -->\n",
" <g transform=\"translate(328.92675 294.614437)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-52\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_6\">\n",
" <!-- $t$ -->\n",
" <defs>\n",
" <path d=\"M 42.28125 54.6875 \n",
"L 40.921875 47.703125 \n",
"L 23 47.703125 \n",
"L 17.1875 18.015625 \n",
"Q 16.890625 16.359375 16.75 15.234375 \n",
"Q 16.609375 14.109375 16.609375 13.484375 \n",
"Q 16.609375 10.359375 18.484375 8.9375 \n",
"Q 20.359375 7.515625 24.515625 7.515625 \n",
"L 33.59375 7.515625 \n",
"L 32.078125 0 \n",
"L 23.484375 0 \n",
"Q 15.484375 0 11.546875 3.125 \n",
"Q 7.625 6.25 7.625 12.59375 \n",
"Q 7.625 13.71875 7.765625 15.0625 \n",
"Q 7.90625 16.40625 8.203125 18.015625 \n",
"L 14.015625 47.703125 \n",
"L 6.390625 47.703125 \n",
"L 7.8125 54.6875 \n",
"L 15.28125 54.6875 \n",
"L 18.3125 70.21875 \n",
"L 27.296875 70.21875 \n",
"L 24.3125 54.6875 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-116\"/>\n",
" </defs>\n",
" <g transform=\"translate(365.82 308.292562)scale(0.1 -0.1)\">\n",
" <use transform=\"translate(0 0.78125)\" xlink:href=\"#DejaVuSans-Oblique-116\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"matplotlib.axis_2\">\n",
" <g id=\"ytick_1\">\n",
" <g id=\"line2d_6\">\n",
" <defs>\n",
" <path d=\"M 0 0 \n",
"L -3.5 0 \n",
"\" id=\"m95474cd3f1\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
" </defs>\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m95474cd3f1\" y=\"280.016\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_7\">\n",
" <!-- 0.0 -->\n",
" <defs>\n",
" <path d=\"M 10.6875 12.40625 \n",
"L 21 12.40625 \n",
"L 21 0 \n",
"L 10.6875 0 \n",
"z\n",
"\" id=\"DejaVuSans-46\"/>\n",
" </defs>\n",
" <g transform=\"translate(166.356875 283.815219)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_2\">\n",
" <g id=\"line2d_7\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m95474cd3f1\" y=\"231.632\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_8\">\n",
" <!-- 0.2 -->\n",
" <g transform=\"translate(166.356875 235.431219)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-50\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_3\">\n",
" <g id=\"line2d_8\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m95474cd3f1\" y=\"183.248\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_9\">\n",
" <!-- 0.4 -->\n",
" <g transform=\"translate(166.356875 187.047219)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-52\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_4\">\n",
" <g id=\"line2d_9\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m95474cd3f1\" y=\"134.864\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_10\">\n",
" <!-- 0.6 -->\n",
" <defs>\n",
" <path d=\"M 33.015625 40.375 \n",
"Q 26.375 40.375 22.484375 35.828125 \n",
"Q 18.609375 31.296875 18.609375 23.390625 \n",
"Q 18.609375 15.53125 22.484375 10.953125 \n",
"Q 26.375 6.390625 33.015625 6.390625 \n",
"Q 39.65625 6.390625 43.53125 10.953125 \n",
"Q 47.40625 15.53125 47.40625 23.390625 \n",
"Q 47.40625 31.296875 43.53125 35.828125 \n",
"Q 39.65625 40.375 33.015625 40.375 \n",
"z\n",
"M 52.59375 71.296875 \n",
"L 52.59375 62.3125 \n",
"Q 48.875 64.0625 45.09375 64.984375 \n",
"Q 41.3125 65.921875 37.59375 65.921875 \n",
"Q 27.828125 65.921875 22.671875 59.328125 \n",
"Q 17.53125 52.734375 16.796875 39.40625 \n",
"Q 19.671875 43.65625 24.015625 45.921875 \n",
"Q 28.375 48.1875 33.59375 48.1875 \n",
"Q 44.578125 48.1875 50.953125 41.515625 \n",
"Q 57.328125 34.859375 57.328125 23.390625 \n",
"Q 57.328125 12.15625 50.6875 5.359375 \n",
"Q 44.046875 -1.421875 33.015625 -1.421875 \n",
"Q 20.359375 -1.421875 13.671875 8.265625 \n",
"Q 6.984375 17.96875 6.984375 36.375 \n",
"Q 6.984375 53.65625 15.1875 63.9375 \n",
"Q 23.390625 74.21875 37.203125 74.21875 \n",
"Q 40.921875 74.21875 44.703125 73.484375 \n",
"Q 48.484375 72.75 52.59375 71.296875 \n",
"z\n",
"\" id=\"DejaVuSans-54\"/>\n",
" </defs>\n",
" <g transform=\"translate(166.356875 138.663219)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-54\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_5\">\n",
" <g id=\"line2d_10\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m95474cd3f1\" y=\"86.48\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_11\">\n",
" <!-- 0.8 -->\n",
" <defs>\n",
" <path d=\"M 31.78125 34.625 \n",
"Q 24.75 34.625 20.71875 30.859375 \n",
"Q 16.703125 27.09375 16.703125 20.515625 \n",
"Q 16.703125 13.921875 20.71875 10.15625 \n",
"Q 24.75 6.390625 31.78125 6.390625 \n",
"Q 38.8125 6.390625 42.859375 10.171875 \n",
"Q 46.921875 13.96875 46.921875 20.515625 \n",
"Q 46.921875 27.09375 42.890625 30.859375 \n",
"Q 38.875 34.625 31.78125 34.625 \n",
"z\n",
"M 21.921875 38.8125 \n",
"Q 15.578125 40.375 12.03125 44.71875 \n",
"Q 8.5 49.078125 8.5 55.328125 \n",
"Q 8.5 64.0625 14.71875 69.140625 \n",
"Q 20.953125 74.21875 31.78125 74.21875 \n",
"Q 42.671875 74.21875 48.875 69.140625 \n",
"Q 55.078125 64.0625 55.078125 55.328125 \n",
"Q 55.078125 49.078125 51.53125 44.71875 \n",
"Q 48 40.375 41.703125 38.8125 \n",
"Q 48.828125 37.15625 52.796875 32.3125 \n",
"Q 56.78125 27.484375 56.78125 20.515625 \n",
"Q 56.78125 9.90625 50.3125 4.234375 \n",
"Q 43.84375 -1.421875 31.78125 -1.421875 \n",
"Q 19.734375 -1.421875 13.25 4.234375 \n",
"Q 6.78125 9.90625 6.78125 20.515625 \n",
"Q 6.78125 27.484375 10.78125 32.3125 \n",
"Q 14.796875 37.15625 21.921875 38.8125 \n",
"z\n",
"M 18.3125 54.390625 \n",
"Q 18.3125 48.734375 21.84375 45.5625 \n",
"Q 25.390625 42.390625 31.78125 42.390625 \n",
"Q 38.140625 42.390625 41.71875 45.5625 \n",
"Q 45.3125 48.734375 45.3125 54.390625 \n",
"Q 45.3125 60.0625 41.71875 63.234375 \n",
"Q 38.140625 66.40625 31.78125 66.40625 \n",
"Q 25.390625 66.40625 21.84375 63.234375 \n",
"Q 18.3125 60.0625 18.3125 54.390625 \n",
"z\n",
"\" id=\"DejaVuSans-56\"/>\n",
" </defs>\n",
" <g transform=\"translate(166.356875 90.279219)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-56\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_6\">\n",
" <g id=\"line2d_11\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m95474cd3f1\" y=\"38.096\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_12\">\n",
" <!-- 1.0 -->\n",
" <defs>\n",
" <path d=\"M 12.40625 8.296875 \n",
"L 28.515625 8.296875 \n",
"L 28.515625 63.921875 \n",
"L 10.984375 60.40625 \n",
"L 10.984375 69.390625 \n",
"L 28.421875 72.90625 \n",
"L 38.28125 72.90625 \n",
"L 38.28125 8.296875 \n",
"L 54.390625 8.296875 \n",
"L 54.390625 0 \n",
"L 12.40625 0 \n",
"z\n",
"\" id=\"DejaVuSans-49\"/>\n",
" </defs>\n",
" <g transform=\"translate(166.356875 41.895219)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_13\">\n",
" <!-- $\\mathrm{rect}(a t)$ -->\n",
" <defs>\n",
" <path d=\"M 41.109375 46.296875 \n",
"Q 39.59375 47.171875 37.8125 47.578125 \n",
"Q 36.03125 48 33.890625 48 \n",
"Q 26.265625 48 22.1875 43.046875 \n",
"Q 18.109375 38.09375 18.109375 28.8125 \n",
"L 18.109375 0 \n",
"L 9.078125 0 \n",
"L 9.078125 54.6875 \n",
"L 18.109375 54.6875 \n",
"L 18.109375 46.1875 \n",
"Q 20.953125 51.171875 25.484375 53.578125 \n",
"Q 30.03125 56 36.53125 56 \n",
"Q 37.453125 56 38.578125 55.875 \n",
"Q 39.703125 55.765625 41.0625 55.515625 \n",
"z\n",
"\" id=\"DejaVuSans-114\"/>\n",
" <path d=\"M 56.203125 29.59375 \n",
"L 56.203125 25.203125 \n",
"L 14.890625 25.203125 \n",
"Q 15.484375 15.921875 20.484375 11.0625 \n",
"Q 25.484375 6.203125 34.421875 6.203125 \n",
"Q 39.59375 6.203125 44.453125 7.46875 \n",
"Q 49.3125 8.734375 54.109375 11.28125 \n",
"L 54.109375 2.78125 \n",
"Q 49.265625 0.734375 44.1875 -0.34375 \n",
"Q 39.109375 -1.421875 33.890625 -1.421875 \n",
"Q 20.796875 -1.421875 13.15625 6.1875 \n",
"Q 5.515625 13.8125 5.515625 26.8125 \n",
"Q 5.515625 40.234375 12.765625 48.109375 \n",
"Q 20.015625 56 32.328125 56 \n",
"Q 43.359375 56 49.78125 48.890625 \n",
"Q 56.203125 41.796875 56.203125 29.59375 \n",
"z\n",
"M 47.21875 32.234375 \n",
"Q 47.125 39.59375 43.09375 43.984375 \n",
"Q 39.0625 48.390625 32.421875 48.390625 \n",
"Q 24.90625 48.390625 20.390625 44.140625 \n",
"Q 15.875 39.890625 15.1875 32.171875 \n",
"z\n",
"\" id=\"DejaVuSans-101\"/>\n",
" <path d=\"M 48.78125 52.59375 \n",
"L 48.78125 44.1875 \n",
"Q 44.96875 46.296875 41.140625 47.34375 \n",
"Q 37.3125 48.390625 33.40625 48.390625 \n",
"Q 24.65625 48.390625 19.8125 42.84375 \n",
"Q 14.984375 37.3125 14.984375 27.296875 \n",
"Q 14.984375 17.28125 19.8125 11.734375 \n",
"Q 24.65625 6.203125 33.40625 6.203125 \n",
"Q 37.3125 6.203125 41.140625 7.25 \n",
"Q 44.96875 8.296875 48.78125 10.40625 \n",
"L 48.78125 2.09375 \n",
"Q 45.015625 0.34375 40.984375 -0.53125 \n",
"Q 36.96875 -1.421875 32.421875 -1.421875 \n",
"Q 20.0625 -1.421875 12.78125 6.34375 \n",
"Q 5.515625 14.109375 5.515625 27.296875 \n",
"Q 5.515625 40.671875 12.859375 48.328125 \n",
"Q 20.21875 56 33.015625 56 \n",
"Q 37.15625 56 41.109375 55.140625 \n",
"Q 45.0625 54.296875 48.78125 52.59375 \n",
"z\n",
"\" id=\"DejaVuSans-99\"/>\n",
" <path d=\"M 18.3125 70.21875 \n",
"L 18.3125 54.6875 \n",
"L 36.8125 54.6875 \n",
"L 36.8125 47.703125 \n",
"L 18.3125 47.703125 \n",
"L 18.3125 18.015625 \n",
"Q 18.3125 11.328125 20.140625 9.421875 \n",
"Q 21.96875 7.515625 27.59375 7.515625 \n",
"L 36.8125 7.515625 \n",
"L 36.8125 0 \n",
"L 27.59375 0 \n",
"Q 17.1875 0 13.234375 3.875 \n",
"Q 9.28125 7.765625 9.28125 18.015625 \n",
"L 9.28125 47.703125 \n",
"L 2.6875 47.703125 \n",
"L 2.6875 54.6875 \n",
"L 9.28125 54.6875 \n",
"L 9.28125 70.21875 \n",
"z\n",
"\" id=\"DejaVuSans-116\"/>\n",
" <path d=\"M 31 75.875 \n",
"Q 24.46875 64.65625 21.28125 53.65625 \n",
"Q 18.109375 42.671875 18.109375 31.390625 \n",
"Q 18.109375 20.125 21.3125 9.0625 \n",
"Q 24.515625 -2 31 -13.1875 \n",
"L 23.1875 -13.1875 \n",
"Q 15.875 -1.703125 12.234375 9.375 \n",
"Q 8.59375 20.453125 8.59375 31.390625 \n",
"Q 8.59375 42.28125 12.203125 53.3125 \n",
"Q 15.828125 64.359375 23.1875 75.875 \n",
"z\n",
"\" id=\"DejaVuSans-40\"/>\n",
" <path d=\"M 53.71875 31.203125 \n",
"L 47.609375 0 \n",
"L 38.625 0 \n",
"L 40.28125 8.296875 \n",
"Q 36.328125 3.421875 31.265625 1 \n",
"Q 26.21875 -1.421875 20.015625 -1.421875 \n",
"Q 13.03125 -1.421875 8.5625 2.84375 \n",
"Q 4.109375 7.125 4.109375 13.8125 \n",
"Q 4.109375 23.390625 11.75 28.953125 \n",
"Q 19.390625 34.515625 32.8125 34.515625 \n",
"L 45.3125 34.515625 \n",
"L 45.796875 36.921875 \n",
"Q 45.90625 37.3125 45.953125 37.765625 \n",
"Q 46 38.234375 46 39.203125 \n",
"Q 46 43.5625 42.453125 45.96875 \n",
"Q 38.921875 48.390625 32.515625 48.390625 \n",
"Q 28.125 48.390625 23.5 47.265625 \n",
"Q 18.890625 46.140625 14.015625 43.890625 \n",
"L 15.578125 52.203125 \n",
"Q 20.65625 54.109375 25.515625 55.046875 \n",
"Q 30.375 56 34.90625 56 \n",
"Q 44.578125 56 49.625 51.796875 \n",
"Q 54.6875 47.609375 54.6875 39.59375 \n",
"Q 54.6875 37.984375 54.4375 35.8125 \n",
"Q 54.203125 33.640625 53.71875 31.203125 \n",
"z\n",
"M 44 27.484375 \n",
"L 35.015625 27.484375 \n",
"Q 23.96875 27.484375 18.671875 24.53125 \n",
"Q 13.375 21.578125 13.375 15.375 \n",
"Q 13.375 11.078125 16.078125 8.640625 \n",
"Q 18.796875 6.203125 23.578125 6.203125 \n",
"Q 30.90625 6.203125 36.375 11.453125 \n",
"Q 41.84375 16.703125 43.609375 25.484375 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-97\"/>\n",
" <path d=\"M 8.015625 75.875 \n",
"L 15.828125 75.875 \n",
"Q 23.140625 64.359375 26.78125 53.3125 \n",
"Q 30.421875 42.28125 30.421875 31.390625 \n",
"Q 30.421875 20.453125 26.78125 9.375 \n",
"Q 23.140625 -1.703125 15.828125 -13.1875 \n",
"L 8.015625 -13.1875 \n",
"Q 14.5 -2 17.703125 9.0625 \n",
"Q 20.90625 20.125 20.90625 31.390625 \n",
"Q 20.90625 42.671875 17.703125 53.65625 \n",
"Q 14.5 64.65625 8.015625 75.875 \n",
"z\n",
"\" id=\"DejaVuSans-41\"/>\n",
" </defs>\n",
" <g transform=\"translate(160.277188 44.8)rotate(-90)scale(0.1 -0.1)\">\n",
" <use transform=\"translate(0 0.125)\" xlink:href=\"#DejaVuSans-114\"/>\n",
" <use transform=\"translate(41.113281 0.125)\" xlink:href=\"#DejaVuSans-101\"/>\n",
" <use transform=\"translate(102.636719 0.125)\" xlink:href=\"#DejaVuSans-99\"/>\n",
" <use transform=\"translate(157.617188 0.125)\" xlink:href=\"#DejaVuSans-116\"/>\n",
" <use transform=\"translate(196.826172 0.125)\" xlink:href=\"#DejaVuSans-40\"/>\n",
" <use transform=\"translate(235.839844 0.125)\" xlink:href=\"#DejaVuSans-Oblique-97\"/>\n",
" <use transform=\"translate(297.119141 0.125)\" xlink:href=\"#DejaVuSans-Oblique-116\"/>\n",
" <use transform=\"translate(336.328125 0.125)\" xlink:href=\"#DejaVuSans-41\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"LineCollection_1\">\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 10.7 280.016 \n",
"L 16.918787 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 16.918787 280.016 \n",
"L 22.125481 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 22.125481 280.016 \n",
"L 28.21705 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 28.21705 280.016 \n",
"L 34.923351 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 34.923351 280.016 \n",
"L 40.472576 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 40.472576 280.016 \n",
"L 46.530842 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 46.530842 280.016 \n",
"L 52.368964 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 52.368964 280.016 \n",
"L 57.908108 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 57.908108 280.016 \n",
"L 62.913589 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 62.913589 280.016 \n",
"L 68.716007 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 68.716007 280.016 \n",
"L 74.296627 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 74.296627 280.016 \n",
"L 80.614494 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 80.614494 280.016 \n",
"L 85.987755 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 85.987755 280.016 \n",
"L 91.562595 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 91.562595 280.016 \n",
"L 96.659353 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 96.659353 280.016 \n",
"L 102.597967 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 102.597967 280.016 \n",
"L 108.963048 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 108.963048 280.016 \n",
"L 115.257209 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 115.257209 280.016 \n",
"L 121.16821 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 121.16821 280.016 \n",
"L 127.521815 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 127.521815 280.016 \n",
"L 133.009468 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 133.009468 280.016 \n",
"L 138.201069 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 138.201069 280.016 \n",
"L 143.183374 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 143.183374 280.016 \n",
"L 148.16582 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 148.16582 280.016 \n",
"L 151.460546 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 151.460546 280.016 \n",
"L 153.378256 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 153.378256 280.016 \n",
"L 153.483591 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 153.483591 280.016 \n",
"L 153.533576 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 153.533576 280.016 \n",
"L 153.578367 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 153.578367 38.096 \n",
"L 153.759189 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 153.759189 38.096 \n",
"L 154.209104 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 154.209104 38.096 \n",
"L 154.948783 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 154.948783 38.096 \n",
"L 162.341925 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 162.341925 38.096 \n",
"L 168.753803 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 168.753803 38.096 \n",
"L 175.181704 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 175.181704 38.096 \n",
"L 182.032317 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 182.032317 38.096 \n",
"L 187.780629 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 187.780629 38.096 \n",
"L 193.827969 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 193.827969 38.096 \n",
"L 199.216607 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 199.216607 38.096 \n",
"L 204.135274 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 204.135274 38.096 \n",
"L 208.394198 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 208.394198 38.096 \n",
"L 212.860908 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 212.860908 38.096 \n",
"L 218.111464 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 218.111464 38.096 \n",
"L 223.682154 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 223.682154 38.096 \n",
"L 224.399001 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 224.399001 38.096 \n",
"L 224.737783 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 224.737783 38.096 \n",
"L 224.896173 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 224.896173 38.096 \n",
"L 224.965393 38.096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 224.965393 38.096 \n",
"L 225.003569 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 225.003569 280.016 \n",
"L 225.048657 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 225.048657 280.016 \n",
"L 226.24126 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 226.24126 280.016 \n",
"L 228.781982 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 228.781982 280.016 \n",
"L 234.316817 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 234.316817 280.016 \n",
"L 240.248708 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 240.248708 280.016 \n",
"L 246.986909 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 246.986909 280.016 \n",
"L 252.995221 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 252.995221 280.016 \n",
"L 258.50666 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 258.50666 280.016 \n",
"L 264.103371 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 264.103371 280.016 \n",
"L 269.779009 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 269.779009 280.016 \n",
"L 274.455467 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 274.455467 280.016 \n",
"L 280.791585 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 280.791585 280.016 \n",
"L 286.08633 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 286.08633 280.016 \n",
"L 290.480076 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 290.480076 280.016 \n",
"L 295.783969 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 295.783969 280.016 \n",
"L 300.665268 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 300.665268 280.016 \n",
"L 305.893357 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 305.893357 280.016 \n",
"L 309.984258 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 309.984258 280.016 \n",
"L 314.621153 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 314.621153 280.016 \n",
"L 319.802978 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 319.802978 280.016 \n",
"L 324.796199 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 324.796199 280.016 \n",
"L 330.108836 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 330.108836 280.016 \n",
"L 334.847512 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 334.847512 280.016 \n",
"L 339.532502 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 339.532502 280.016 \n",
"L 344.199377 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 344.199377 280.016 \n",
"L 350.445739 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 350.445739 280.016 \n",
"L 356.872714 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 356.872714 280.016 \n",
"L 362.042862 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb0c5c2a97e)\" d=\"M 362.042862 280.016 \n",
"L 367.82 280.016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" </g>\n",
" <g id=\"patch_3\">\n",
" <path d=\"M 189.26 280.016 \n",
"L 189.26 38.096 \n",
"\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
" </g>\n",
" <g id=\"patch_4\">\n",
" <path d=\"M 367.82 292.112 \n",
"L 367.82 26 \n",
"\" style=\"fill:none;\"/>\n",
" </g>\n",
" <g id=\"patch_5\">\n",
" <path d=\"M 10.7 280.016 \n",
"L 367.82 280.016 \n",
"\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
" </g>\n",
" <g id=\"patch_6\">\n",
" <path d=\"M 10.7 26 \n",
"L 367.82 26 \n",
"\" style=\"fill:none;\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <defs>\n",
" <clipPath id=\"pb0c5c2a97e\">\n",
" <rect height=\"266.112\" width=\"357.12\" x=\"10.7\" y=\"26\"/>\n",
" </clipPath>\n",
" </defs>\n",
"</svg>\n"
],
"text/plain": [
"<Figure size 614.4x460.8 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM4OC40MjYyNSAzMTIuNTEyIF0gL1BhcmVudCAyIDAgUiAvUmVzb3VyY2VzIDggMCBSCi9UeXBlIC9QYWdlID4+CmVuZG9iago5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTEgMCBSID4+CnN0cmVhbQp4nLWaS48UyRWF9/krYsksSCJuvJdGM0bjhS2GHtuSx4s204NBVCOGwSws/3d/NzMjq7rqNm2EDOLRceLE8z7Ojarg3kzBvXLeveHPJ/c393f+/dkF94w/rybPT4cptjYnKZL56e3JTzHInIPQ5k/+/89p+mV68jvoH+j/bJpCnWsqrWYX/Fx1vJrmVo4tb09bpJa5LQMdece2bXBZB3/FIln43E6WzpSKnLBLnnv1XTpTn7TKnNbWt9P0lFP4NL3nb+8ee0ats7gc5lhrqD30ltzLw/T0yj35fWDN7uqXqQG27tdTufp5eiT+G3f1ZvruinH87HUofo//QH/y7c2b6z9/fHF9++Hx4fXtxw/u23fTc34vG5hYUGwXCz5p/eyCWSyL/MIlh/x1Sw6+zl4uD/mk+bOL7mVO7YsX/ZXnHJivlMtFnzR/dtEhpVl6X3p+4dK/9rg5r+gvV37SfLnyOysKPc5Barhcuy5vOVjH8tbpJPm5X7rQafMD00nE3cp90+Wz6Vqe86UDnDY/NF3ts4g5VzjbW4yerheTnTY/MFmUSMiyJzvb2Ul0uzPZSfNDk5U2Z29OJvvOTmw0Vj/HdWi9Ap+jT0cTXSzQXVjgnAni+dwO//SPt6/ff7x5/O5w8+r6XnsMZZaGV9TFHmVu582mJ3EaXrL6B9kjtRJEfI3ysCOx1v+TK+1LPzbf40o1zskva+L2Qk0+p6MnzWf2dnpUIc8lN3Z7dlbH9gdnDIFwX5iuYIbl9EjsKdlMTKX2eH49e/vDU5Yw59R7aCm1utr5Z3Yp7MbHVKXcnfKk/cEphV0SQlr2uca+TXn/LqWkueK9uZ1NeWx/eMpCcJNcmxS2ujrYfOJharaP1chCbkRBHT1hnWGz2akggnrHVkOs2GNaBmWU42SP/r1YLqsuglcuK1yN+tcFSDOXG6WF3dhvNkLIElPcu79cmvOcerszzG9Le2QbvmGPR8JPjwbC6rao7NfFyVjc9ZiLWCr9fxj1ZGM/fXPP+I/+szurEXXWM1KXfXH1/V//+O72x9vX3/92/fjj7evvhGCw+e17d6YjY64skxtjtfz76437i7t1GAhi0IOEXFrRbMAUZftVsRqiYWsSM579wzNHnPjX65c3Pzx76l5+OJGHFTNNMXlZMh6X5bsjqPrme01qRy+MZmI6blhDqk2DQs8+rq71wgTojgAKOTbEJpLJE+Jl624AhylFbB1DLS4n4iXbK2t3C6B7n0OpLegYOUupdet92X6Yctb4n+IS+SSU5Pva2wLQpX4u0ip3WFGohai9DW4BdM8zp5pxwdo4rZrqdi4WcJg40pZLzNk1Dnf5z9LbaKez+hK+Xl1FtgPHtvU2gMMEs+N7mQWSTKPHytfuFkD3Qo7yLSwXl0vArLfuBnCYOvcccg9Rb6KnloYBWADdGYSJHEGk1k6HrfNFM12RAC1WfCXVubH1MfBlu0rwMAcNaU3HiKmnrbcFaPc45145fpe9qtvo9/4GogS8LoraQo7o5kp2HgQDgUCGZ17MR80I/9usy2jXzlhoZdvcs5ACeup1dDcQCILfk5pacVxLScSnMb6FKAE/KSorHRdDrGhRBsFAlICvdO9jdD0g1rIM3zMRCHg80YFo6Vqfa+SGxgwWooQ4SyoxBIfkrYU6Y9yBhSgBicJfxBSEb8YC8jglC4GQAonQhxYdXpqxgriFMhNRgsZDTERcbIiT0Ed8MhEtorQ2aMVXJ10lbQhjSRaiBNK0nnF3gvxpKe8zWIgSSOa+RdwOAY6EljbuwUKUgFk1dpScMKIE2U3bQpRAxO2l56TjeCxg738JaPdGydDUImntRLKw9zcQJXSuv3RuU5bU1cu+AwOBwJXgfxED4+gQB0nCRrAQJYSZAjWG4iKhiTi2b8FClKAHJoFsR7nQo3gZhmEhSkhEM3KII/NgXWHEUAvQ7phtJRdXR+6hHMhluKeFKIGAXQvh1XEmqsfSsCML0XcdTcLYV1aLr5ykHzuwECWgnAr1RnfqwEm1+7A8E4LSCJ1MRz4JBJ8kJfZxESakFC4+1oKrC3Gx17BHDQtRQtHmFNWIUTG91j0KmJBSUKJUhJy5JJlrbyrONooFKaUjjntT9Vpn1ipDGpiIqmlCVo1VDY0SlJS0J3AbUgrB0OeS1H8pdNHE43wtZFXsgs7HNgXP8fHoqBZyWB4z0Pak+EW2I0vJI4NhQUpJs6DrsHoha2tNuRuWCa2Uxq/ManEG/ud3QzEhpRCwIvV3WGqPjGov40ZMaH3DwY8TUy7lShhmctmunStyrxIqlkbKnxr38S1opfRMZbMuNbfe5ci4QJSA9MCOU16OA5W9Bx0LUQLBa3laWo484NSy358Foas90jx1LcxwZH19KyNQ2ZBSKAmR7mkxnRqCT3kwDGQl9MTlb8aJbR/7nwPanSOgzEIkCBGs1txG2rYhpaDnOGe1NfIumj2kfQ4LUgrhnZBUsDUivea2sG/cgpTSCPWoGS7WM1Qo/bgwC4Ki0grZi9DUkIad1qGMbUgpVZ8yci5L6BOROISaDUEhd3pcnuNrKhVJW2NdFqIEBBY2gM4uWlqgg8ogGIgS9GHE62KzTpybH3duIUqoWiyjsFTjCkVIGSWbhSgBDY3C6g4dFConGEb/S0C7q2wTleXcauuJFDH6GwgE4rW+1YTkIqVF0XeUjWAhShCVnpoMWTHVVKo7wUCUwAnH5qvaMwZEYh/9LwHtjmFSH6vSIMGjj30d/Q1ECdRSavFVtVLdb+yi+bA++nL3bZFJQhk7IoeJKKFTiCSvW2JyJtz3egls78/IkCx6AhURsx+mhSgBb9XL0zcDsgf17k4wECV0yq+myoIShqwe9/u1EAgoSW6SslvfDWL2YZ/BQpSArsgFM0Q4aHXdhmMagHZHG6GEUSSIABJmG/WQiUDQkpRaiZipRUysIQyntBAlsH/cgh+WIqbvYdIAtDvLjDnEZRROOo6q2ESUgOhnMzSjSRrCcD9SC4FQtQyLBKal1EeT7AQLUQLlLNkb8UH57hMaZmzBQvSDBSEBiIoPklIUljD2YCFKaFqVh7B8zpawlT1oWwgEPQGkKlJQC3mMYPdKC1ECopDMhezXWp6UOXSAiSih4HWI8qjjdJTRkWAg+j6l7yZBVXzWwrvqM9D2QGUgStB3cGRqd9QOqYzOZ610JKXoOwGCtuLcLVN/bZ0tRAkYLLPU5XmmJdnfbUwEgqA0gwZ7hHyXEMZriQUclg9oYidfF21upWL6o7+BKKHoA7y2NiJlT3kcjQHoZ0WoxNi1nMCsyOx7NWAiSsC+k1ay+mKEIpW0EwwEAuGpIWWRZkt624tpC9DuhEuKzJTWV0BWMK7LQiDwA1KMzO6yltjkq0GwECVoQM76iqlxh30ODzARfd9M+jglXL1+nqIf9fTxwGkgSmAclFZefFWFkOwEA7nzIdrxyXYhPHfvnbg/rN9tuPMVgbM33/s+xbI+WFhG3r/c8Gn5gsP51xkO9tcZptv9iwvLapRqf0nB/LzQmvnyGxL3z/18+i+4j8ReCmVuZHN0cmVhbQplbmRvYmoKMTEgMCBvYmoKMjY1MwplbmRvYmoKMTYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzNDkgPj4Kc3RyZWFtCnicRZLJjWMxDETvPwom0IC4SoqnB33y5H+dR9qNOdhVnzuLKnVZEipfkIwtWUv+6JO+xdXk7xO7iHg9ft4Yy+V4G3DkEo8SqwnWJd+P7SNfKfapaWsNfj+aPkw1ReUQcrFmSu4e4Hr/qx+MEFsmReWkrG6x08FaR5xmRpRHwt9IBsWbMV9iq/vLtkrkBeODe6Jhh71Z1plk8Fp7YGHkxOFHjsV48bBIa+HFuCfonYNsfN/MqnExHbi7mq3ODlG+ekINavhskohnxpR6l6STbX0AsBXJUfJwjmxp75zF442tjw+LMnJK4lJNW7l0rF2RU0bHg44XTzN27XjfNr08JyeM2t19jaK/t6cPFtvJK/B8sxf3rWHG9L2xMqXNDTQ5G6oo2+j9YLZCw9pDF+WwWjyAHkr3lU1ldGIV82rozefbbQsBXv1ouo7fS407V1G2Cq/R6/+kr+fnH+XehrEKZW5kc3RyZWFtCmVuZG9iagoxNyAwIG9iago8PCAvQkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxODEKL1N1YnR5cGUgL0Zvcm0gL1R5cGUgL1hPYmplY3QgPj4Kc3RyZWFtCnicNVA5DgQhDOt5hT+wErnDe0baavb/7YYwU6AYHAc7g0nxIcFvRDaQiRR4gsNxjWSIMYgNqgJaDtMogpc0uge/XGr1EihmiaV6SEspdVzhDJbY5Roy+y6mIF2QDEgNuYaWdKN7qBxObcIJRnmktuYGrrMml882uv/ydkrwiHbjhY/T0HycRmXcXKR1qgh6YkbNyj02eglG3LUcsZy11FKkVIs6UWWw1Q9zNv/u8RrfP+Y3Px4KZW5kc3RyZWFtCmVuZG9iagoxOCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE3OCA+PgpzdHJlYW0KeJw9kEsSAyEIRPeeoo8gP9HzJJXV5P7bNM6YhfYTKGywpegYzsvVkF3xllYYnvg27wueiaup9YckFTL7pg4Zi2fyFCckFK8mY0DcsdXWo3Eywgy7LCZmYK6Kr0QuqFAC6lHyamaj4Gqmgr59xFaZ9RYXCEUCJixnK/6fA9PrFh0MFpjtN8uzPPYK03QszHuGeQ9FI34G5VpuYGWtg5+GHZr3tmgo/+QnexZ4tc8P3qtCoQplbmRzdHJlYW0KZW5kb2JqCjE0IDAgb2JqCjw8IC9CYXNlRm9udCAvRGVqYVZ1U2Fucy1PYmxpcXVlIC9DaGFyUHJvY3MgMTUgMCBSCi9FbmNvZGluZyA8PCAvRGlmZmVyZW5jZXMgWyA5NyAvYSAxMTYgL3QgXSAvVHlwZSAvRW5jb2RpbmcgPj4gL0ZpcnN0Q2hhciAwCi9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnREZXNjcmlwdG9yIDEzIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTIgMCBSID4+CmVuZG9iagoxMyAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgOTYKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udE5hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovSXRhbGljQW5nbGUgMCAvTWF4V2lkdGggMTM1MCAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTIgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM1MCA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDI4IDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxNyA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjE3IDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDgKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk5NSA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMTUgMCBvYmoKPDwgL2EgMTYgMCBSIC90IDE4IDAgUiA+PgplbmRvYmoKMjMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNzkgPj4Kc3RyZWFtCnicPVI7ksUgDOtzCl+AGfAXzpOdrbL3b1eCvFdkrERGkh3SUroMDWkjVWIMqezyMy7CtlT+DiL7XD6/0NY60JyHo4uNCaAp96WrA3YVrZIWvusoMgTmENhommhOUXAKCbV92nCQh/oA6zIidr0vBiV6NrKtQ/Yg9hOpGVJBOfCOhFCEh82+Y/g4cTztzRNgTp4MOCN79TNOKV05YTkUMDK3wy2w3tdnX89GuYi85gdhDiLHInJiUxMMkkCxHF6OdPDUU6M2A+RRXDBRx2yxwM+9Zz7oMaRT6JHt2FwupF5k8IX52aHwYD+3AAYqqrWdBjtYvb+OY72GDb+P4VrkjtuKLRygTRcOxDvBEVnv7y15rt9/B3JuBgplbmRzdHJlYW0KZW5kb2JqCjI0IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjc2ID4+CnN0cmVhbQp4nD1SS47oMAjb5xRcIFL4Jj1PR7Pqu//22bSaFRZgY0jKS5aopUwtk1SVXUt+dHTuMvk3NK9Gz7D15sxD5kmxODK3yj0M5JlbrNBrb9SrCwCxSO7UEtslxpZLxZJkh6ztEHdk0OHFKtnM+NrCDjdrjkdSFypepwcF+Yww8E7Mfb6JZSE0Vxltt8BBDxaoAz0wCxO5IuPdaxM9jXgLoKwPmb+ILjfUXI9sTIBTuNoL3qmU1jEPFYmiHOxGGr2fo+Y4ocPbPWI59nIJRwbe4mjHe/BFiJ5GVkSsfsizEfmGDalIj5jKG+puH3r8ja3YaH92JknB11/W20w10rng1Fyt1l+DR2jw3qjh8/dLnvH7HyEmbhIKZW5kc3RyZWFtCmVuZG9iagoyNSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDIzMCA+PgpzdHJlYW0KeJw1UUluwzAMvOsV84EA4i6/x0FP7f+vHdIJYGBoS5zNERsbEXiJwc9B5MZb1oya+JvJXfG7PBUeCbeCJ1EEXoZ72QkubxiX/TjMfPBeWjmTGk8yIBfZ9PBEyGCXQOjA7BrUYZtpJ/qGhM+OSDUbWU5fS9BLqxAoT9l+pwtKtK3qz+2zLrTta0842e2pJ5VPIJ5bsgKXjVdMFmMZ9ETlLsX0QaqzhZ6E8qJ8DrL5qCESXaKcgScGB6NAO7Dntp+JV4WgdXWfto2hGikdT/82NDVJIuQTJZzZ0rhb+P6ee/38A6ZUU58KZW5kc3RyZWFtCmVuZG9iagoyNiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI0NSA+PgpzdHJlYW0KeJxFULuNQzEM6z0FFwhg/Sx7nndIldu/PUpGcIUhWj+SWhKYiMBLDLGUb+JHRkE9C78XheIzxM8XhUHOhKRAnPUZEJl4htpGbuh2cM68wzOMOQIXxVpwptOZ9lzY5JwHJxDObZTxjEK6SVQVcVSfcUzxqrLPjdeBpbVss9OR7CGNhEtJJSaXflMq/7QpWyro2kUTsEjkgZNNNOEsP0OSYsyglFH3MLWO9HGykUd10MnZnDktmdnup+1MfA9YJplR5Smd5zI+J6nzXE597rMd0eSipVX7nP3ekZbyIrXbodXpVyVRmY3Vp5C4PP+Mn/H+A46gWT4KZW5kc3RyZWFtCmVuZG9iagoyNyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI0NyA+PgpzdHJlYW0KeJxNUbttRDEM698UXOAA62t5ngtSXfZvQ8kIkMIgoS8ppyUW9sZLDOEHWw++5JFVQ38ePzHsMyw9yeTUP+a5yVQUvhWqm5hQF2Lh/WgEvBZ0LyIrygffj2UMc8734KMQl2AmNGCsb0kmF9W8M2TCiaGOw0GbVBh3TRQsrhXNM8jtVjeyOrMgbHglE+LGAEQE2ReQzWCjjLGVkMVyHqgKkgVaYNfpG1GLgiuU1gl0otbEuszgq+f2djdDL/LgqLp4fQzrS7DC6KV7LHyuQh/M9Ew7d0kjvfCmExFmDwVSmZ2RlTo9Yn23QP+fZSv4+8nP8/0LFShcKgplbmRzdHJlYW0KZW5kb2JqCjI4IDAgb2JqCjw8IC9CQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDM3Ci9TdWJ0eXBlIC9Gb3JtIC9UeXBlIC9YT2JqZWN0ID4+CnN0cmVhbQp4nOMyNDBTMDY1VcjlMjc2ArNywCwjcyMgCySLYEFk0wABXwoKCmVuZHN0cmVhbQplbmRvYmoKMjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA4MCA+PgpzdHJlYW0KeJxFjLsNwDAIRHumYAR+JmafKJWzfxsgStxwT7p7uDoSMlPeYYaHBJ4MLIZT8QaZo2A1uEZSjZ3so7BuX3WB5npTq/X3BypPdnZxPc3LGfQKZW5kc3RyZWFtCmVuZG9iagozMCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE0NyA+PgpzdHJlYW0KeJw9T7kNAzEM6z0FFzjAeixb81yQ6rJ/G8pGUggiQPGRZUfHClxiApOOORIvaT/4aRqBWAY1R/SEimFY4G6SAg+DLEpXni1eDJHaQl1I+NYQ3q1MZKI8rxE7cCcXowc+VBtZHnpAO0QVWa5Jw1jVVl1qnbACHLLOwnU9zKoE5dEnaykfUFRCvXT/n3va+wsAby/rCmVuZHN0cmVhbQplbmRvYmoKMzEgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNDkgPj4Kc3RyZWFtCnicNY9LDgMhDEP3OYUvMFJ+hHAeqq6m9982YVoJCQvbL8EWg5GMS0xg7Jhj4SVUT60+JCOPukk5EKlQNwRPaEwMM2zSJfDKdN8ynlu8nFbqgk5I5OmsNhqijGZew9FTzgqb/svcJGplRpkDMutUtxOysmAF5gW1PPcz7qhc6ISHncqw6E4xotxmRhp+/9v0/gJ7MjBjCmVuZHN0cmVhbQplbmRvYmoKMzIgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA0OSA+PgpzdHJlYW0KeJwzNrRQMFAwNDAHkkaGQJaRiUKKIRdIAMTM5YIJ5oBZBkAaojgHriaHKw0AxugNJgplbmRzdHJlYW0KZW5kb2JqCjMzIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTU3ID4+CnN0cmVhbQp4nEWQuRFDMQhEc1VBCRKwCOqxx9F3/6kX+Uq0bwAth68lU6ofJyKm3Ndo9DB5Dp9NJVYs2Ca2kxpyGxZBSjGYeE4xq6O3oZmH1Ou4qKq4dWaV02nLysV/82hXM5M9wjXqJ/BN6PifPLSp6FugrwuUfUC1OJ1JUDF9r2KBo5x2fyKcGOA+GUeZKSNxYm4K7PcZAGa+V7jG4wXdATd5CmVuZHN0cmVhbQplbmRvYmoKMzQgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxMzEgPj4Kc3RyZWFtCnicRY/LDQQhDEPvVOES8hk+qYfVntj+r+swmkFC+EEiO/EwCKzz8jbQxfDRosM3/jbVq2OVLB+6elJWD+mQh7zyFVBpMFHEhVlMHUNhzpjKyJYytxvhtk2DrGyVVK2DdjwGD7anZasIfqltYeos8QzCVV64xw0/kEutd71Vvn9CUzCXCmVuZHN0cmVhbQplbmRvYmoKMzUgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDggPj4Kc3RyZWFtCnicLVE5kgNBCMvnFXpCc9PvscuR9//pCsoBg4ZDIDotcVDGTxCWK97yyFW04e+ZGMF3waHfynUbFjkQFUjSGFRNqF28Hr0HdhxmAvOkNSyDGesDP2MKN3pxeEzG2e11GTUEe9drT2ZQMisXccnEBVN12MiZw0+mjAvtXM8NyLkR1mUYpJuVxoyEI00hUkih6iapM0GQBKOrUaONHMV+6csjnWFVI2oM+1xL29dzE84aNDsWqzw5pUdXnMvJxQsrB/28zcBFVBqrPBAScL/bQ/2c7OQ33tK5s8X0+F5zsrwwFVjx5rUbkE21+Dcv4vg94+v5/AOopVsWCmVuZHN0cmVhbQplbmRvYmoKMzYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyMTAgPj4Kc3RyZWFtCnicNVDLDUMxCLtnChaoFAKBZJ5WvXX/a23QO2ER/0JYyJQIeanJzinpSz46TA+2Lr+xIgutdSXsypognivvoZmysdHY4mBwGiZegBY3YOhpjRo1dOGCpi6VQoHFJfCZfHV76L5PGXhqGXJ2BBFDyWAJaroWTVi0PJ+QTgHi/37D7i3koZLzyp4b+Ruc7fA7s27hJ2p2ItFyFTLUszTHGAgTRR48eUWmcOKz1nfVNBLUZgtOlgGuTj+MDgBgIl5ZgOyuRDlL0o6ln2+8x/cPQABTtAplbmRzdHJlYW0KZW5kb2JqCjIxIDAgb2JqCjw8IC9CYXNlRm9udCAvRGVqYVZ1U2FucyAvQ2hhclByb2NzIDIyIDAgUgovRW5jb2RpbmcgPDwKL0RpZmZlcmVuY2VzIFsgNDAgL3BhcmVubGVmdCAvcGFyZW5yaWdodCA0NiAvcGVyaW9kIDQ4IC96ZXJvIC9vbmUgL3R3byA1MyAvZml2ZSA5OSAvYwoxMDEgL2UgMTE0IC9yIDExNiAvdCAxMjMgL2JyYWNlbGVmdCAxMjUgL2JyYWNlcmlnaHQgXQovVHlwZSAvRW5jb2RpbmcgPj4KL0ZpcnN0Q2hhciAwIC9Gb250QkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZvbnREZXNjcmlwdG9yIDIwIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zCi9TdWJ0eXBlIC9UeXBlMyAvVHlwZSAvRm9udCAvV2lkdGhzIDE5IDAgUiA+PgplbmRvYmoKMjAgMCBvYmoKPDwgL0FzY2VudCA5MjkgL0NhcEhlaWdodCAwIC9EZXNjZW50IC0yMzYgL0ZsYWdzIDMyCi9Gb250QkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZvbnROYW1lIC9EZWphVnVTYW5zIC9JdGFsaWNBbmdsZSAwCi9NYXhXaWR0aCAxMzQyIC9TdGVtViAwIC9UeXBlIC9Gb250RGVzY3JpcHRvciAvWEhlaWdodCAwID4+CmVuZG9iagoxOSAwIG9iagpbIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwCjYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgMzE4IDQwMSA0NjAgODM4IDYzNgo5NTAgNzgwIDI3NSAzOTAgMzkwIDUwMCA4MzggMzE4IDM2MSAzMTggMzM3IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYKNjM2IDYzNiAzMzcgMzM3IDgzOCA4MzggODM4IDUzMSAxMDAwIDY4NCA2ODYgNjk4IDc3MCA2MzIgNTc1IDc3NSA3NTIgMjk1CjI5NSA2NTYgNTU3IDg2MyA3NDggNzg3IDYwMyA3ODcgNjk1IDYzNSA2MTEgNzMyIDY4NCA5ODkgNjg1IDYxMSA2ODUgMzkwIDMzNwozOTAgODM4IDUwMCA1MDAgNjEzIDYzNSA1NTAgNjM1IDYxNSAzNTIgNjM1IDYzNCAyNzggMjc4IDU3OSAyNzggOTc0IDYzNCA2MTIKNjM1IDYzNSA0MTEgNTIxIDM5MiA2MzQgNTkyIDgxOCA1OTIgNTkyIDUyNSA2MzYgMzM3IDYzNiA4MzggNjAwIDYzNiA2MDAgMzE4CjM1MiA1MTggMTAwMCA1MDAgNTAwIDUwMCAxMzQyIDYzNSA0MDAgMTA3MCA2MDAgNjg1IDYwMCA2MDAgMzE4IDMxOCA1MTggNTE4CjU5MCA1MDAgMTAwMCA1MDAgMTAwMCA1MjEgNDAwIDEwMjMgNjAwIDUyNSA2MTEgMzE4IDQwMSA2MzYgNjM2IDYzNiA2MzYgMzM3CjUwMCA1MDAgMTAwMCA0NzEgNjEyIDgzOCAzNjEgMTAwMCA1MDAgNTAwIDgzOCA0MDEgNDAxIDUwMCA2MzYgNjM2IDMxOCA1MDAKNDAxIDQ3MSA2MTIgOTY5IDk2OSA5NjkgNTMxIDY4NCA2ODQgNjg0IDY4NCA2ODQgNjg0IDk3NCA2OTggNjMyIDYzMiA2MzIgNjMyCjI5NSAyOTUgMjk1IDI5NSA3NzUgNzQ4IDc4NyA3ODcgNzg3IDc4NyA3ODcgODM4IDc4NyA3MzIgNzMyIDczMiA3MzIgNjExIDYwNQo2MzAgNjEzIDYxMyA2MTMgNjEzIDYxMyA2MTMgOTgyIDU1MCA2MTUgNjE1IDYxNSA2MTUgMjc4IDI3OCAyNzggMjc4IDYxMiA2MzQKNjEyIDYxMiA2MTIgNjEyIDYxMiA4MzggNjEyIDYzNCA2MzQgNjM0IDYzNCA1OTIgNjM1IDU5MiBdCmVuZG9iagoyMiAwIG9iago8PCAvYnJhY2VsZWZ0IDIzIDAgUiAvYnJhY2VyaWdodCAyNCAwIFIgL2MgMjUgMCBSIC9lIDI2IDAgUiAvZml2ZSAyNyAwIFIKL29uZSAyOSAwIFIgL3BhcmVubGVmdCAzMCAwIFIgL3BhcmVucmlnaHQgMzEgMCBSIC9wZXJpb2QgMzIgMCBSIC9yIDMzIDAgUgovdCAzNCAwIFIgL3R3byAzNSAwIFIgL3plcm8gMzYgMCBSID4+CmVuZG9iago0MSAwIG9iago8PCAvQkJveCBbIC0xNDEgLTI0MCAxMTI4IDc5NSBdIC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzgxCi9TdWJ0eXBlIC9Gb3JtIC9UeXBlIC9YT2JqZWN0ID4+CnN0cmVhbQp4nDWTuXEGMQhG862CEsQpqZ5/xpHdf+oHa0cwy/EdaJ+8kh7y84RLpsn3c5fkLVHfUpaix6Viyecxu1IZYkelysT9TPw8fnOyiCAuiVN0bippe2ay6Aj6l/5tq97vRj8ztqQO+Qoqe8HgHNlKrPvGyK50ZiabvlzwumDSybYD6u5tLjFYNpGK1ftFu4KCRWX3TN5musFKiXsmpraeyQyMruJOgpOhM8OX0fHaVQv/slmXMpM1WjLPeJelw4CeVona1jNxD7fO4N/c8tK18WQNN9BKN7zoR3E0ljW3cH2/KFh6JBYz+l6heZX4Vba5eKvY3hU74uz+Zm/9Z06Hd+bgvJnRrfAh44rKNS22KK4b3adlmkLziOGi33kc1ndW9GGAsp4BBHevQkvlXOG6S+boTAbreR9E5TGgRvsybYe2ZSz1Eh5D71JEgsnyNB2C/RSgtWPMnTgSJztdWXOumbltpeWecxkYbY/Za1OTfr9oHxHEv3/h83z9Ai8TlAoKZW5kc3RyZWFtCmVuZG9iagozOSAwIG9iago8PCAvQmFzZUZvbnQgL1NUSVhOb25Vbmljb2RlLUl0YWxpYyAvQ2hhclByb2NzIDQwIDAgUgovRW5jb2RpbmcgPDwgL0RpZmZlcmVuY2VzIFsgXSAvVHlwZSAvRW5jb2RpbmcgPj4gL0ZpcnN0Q2hhciAwCi9Gb250QkJveCBbIC0xNDEgLTI0MCAxMTI4IDc5NSBdIC9Gb250RGVzY3JpcHRvciAzOCAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NQovTmFtZSAvU1RJWE5vblVuaWNvZGUtSXRhbGljIC9TdWJ0eXBlIC9UeXBlMyAvVHlwZSAvRm9udCAvV2lkdGhzIDM3IDAgUiA+PgplbmRvYmoKMzggMCBvYmoKPDwgL0FzY2VudCAxNDUwIC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtNTUyIC9GbGFncyA5NgovRm9udEJCb3ggWyAtMTQxIC0yNDAgMTEyOCA3OTUgXSAvRm9udE5hbWUgL1NUSVhOb25Vbmljb2RlLUl0YWxpYwovSXRhbGljQW5nbGUgNDM5MDkgL01heFdpZHRoIDI1MCAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMAo+PgplbmRvYmoKMzcgMCBvYmoKWyAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MAoyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAKMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwCjI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MAoyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAKMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwCjI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MAoyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAKMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwCjI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MAoyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAKMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwCjI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MAoyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgXQplbmRvYmoKNDAgMCBvYmoKPDwgPj4KZW5kb2JqCjMgMCBvYmoKPDwgL0YxIDIxIDAgUiAvRjIgMTQgMCBSIC9GMyAzOSAwIFIgPj4KZW5kb2JqCjQgMCBvYmoKPDwgL0ExIDw8IC9DQSAwIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4KL0EyIDw8IC9DQSAxIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4gPj4KZW5kb2JqCjUgMCBvYmoKPDwgPj4KZW5kb2JqCjYgMCBvYmoKPDwgPj4KZW5kb2JqCjcgMCBvYmoKPDwgL0RlamFWdVNhbnMtT2JsaXF1ZS1vbWVnYSAxNyAwIFIgL0RlamFWdVNhbnMtbWludXMgMjggMCBSCi9TVElYTm9uVW5pSXRhLXVuaUUyMzIgNDEgMCBSID4+CmVuZG9iagoyIDAgb2JqCjw8IC9Db3VudCAxIC9LaWRzIFsgMTAgMCBSIF0gL1R5cGUgL1BhZ2VzID4+CmVuZG9iago0MiAwIG9iago8PCAvQ3JlYXRpb25EYXRlIChEOjIwMTkwNTE2MTgzNzUyKzAyJzAwJykKL0NyZWF0b3IgKG1hdHBsb3RsaWIgMy4wLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZykKL1Byb2R1Y2VyIChtYXRwbG90bGliIHBkZiBiYWNrZW5kIDMuMC4zKSA+PgplbmRvYmoKeHJlZgowIDQzCjAwMDAwMDAwMDAgNjU1MzUgZiAKMDAwMDAwMDAxNiAwMDAwMCBuIAowMDAwMDEzNjAxIDAwMDAwIG4gCjAwMDAwMTMyOTcgMDAwMDAgbiAKMDAwMDAxMzM1MSAwMDAwMCBuIAowMDAwMDEzNDUwIDAwMDAwIG4gCjAwMDAwMTM0NzEgMDAwMDAgbiAKMDAwMDAxMzQ5MiAwMDAwMCBuIAowMDAwMDAwMDY1IDAwMDAwIG4gCjAwMDAwMDAzOTUgMDAwMDAgbiAKMDAwMDAwMDIwOCAwMDAwMCBuIAowMDAwMDAzMTIzIDAwMDAwIG4gCjAwMDAwMDQ2NjIgMDAwMDAgbiAKMDAwMDAwNDQ1NCAwMDAwMCBuIAowMDAwMDA0MTMyIDAwMDAwIG4gCjAwMDAwMDU3MTUgMDAwMDAgbiAKMDAwMDAwMzE0NCAwMDAwMCBuIAowMDAwMDAzNTY2IDAwMDAwIG4gCjAwMDAwMDM4ODEgMDAwMDAgbiAKMDAwMDAwOTkzOCAwMDAwMCBuIAowMDAwMDA5NzM4IDAwMDAwIG4gCjAwMDAwMDkzMjIgMDAwMDAgbiAKMDAwMDAxMDk5MSAwMDAwMCBuIAowMDAwMDA1NzU3IDAwMDAwIG4gCjAwMDAwMDYxMDkgMDAwMDAgbiAKMDAwMDAwNjQ1OCAwMDAwMCBuIAowMDAwMDA2NzYxIDAwMDAwIG4gCjAwMDAwMDcwNzkgMDAwMDAgbiAKMDAwMDAwNzM5OSAwMDAwMCBuIAowMDAwMDA3NTY5IDAwMDAwIG4gCjAwMDAwMDc3MjEgMDAwMDAgbiAKMDAwMDAwNzk0MSAwMDAwMCBuIAowMDAwMDA4MTYzIDAwMDAwIG4gCjAwMDAwMDgyODQgMDAwMDAgbiAKMDAwMDAwODUxNCAwMDAwMCBuIAowMDAwMDA4NzE4IDAwMDAwIG4gCjAwMDAwMDkwMzkgMDAwMDAgbiAKMDAwMDAxMjIzMSAwMDAwMCBuIAowMDAwMDEyMDE4IDAwMDAwIG4gCjAwMDAwMTE3MDUgMDAwMDAgbiAKMDAwMDAxMzI3NSAwMDAwMCBuIAowMDAwMDExMTkyIDAwMDAwIG4gCjAwMDAwMTM2NjEgMDAwMDAgbiAKdHJhaWxlcgo8PCAvSW5mbyA0MiAwIFIgL1Jvb3QgMSAwIFIgL1NpemUgNDMgPj4Kc3RhcnR4cmVmCjEzODE1CiUlRU9GCg==\n",
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
"<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
" \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
"<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
"<svg height=\"312.412pt\" version=\"1.1\" viewBox=\"0 0 388.434844 312.412\" width=\"388.434844pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
" <defs>\n",
" <style type=\"text/css\">\n",
"*{stroke-linecap:butt;stroke-linejoin:round;}\n",
" </style>\n",
" </defs>\n",
" <g id=\"figure_1\">\n",
" <g id=\"patch_1\">\n",
" <path d=\"M 0 312.412 \n",
"L 388.434844 312.412 \n",
"L 388.434844 0 \n",
"L 0 0 \n",
"z\n",
"\" style=\"fill:#ffffff;\"/>\n",
" </g>\n",
" <g id=\"axes_1\">\n",
" <g id=\"patch_2\">\n",
" <path d=\"M 17.752344 301.712 \n",
"L 374.872344 301.712 \n",
"L 374.872344 35.6 \n",
"L 17.752344 35.6 \n",
"z\n",
"\" style=\"fill:#ffffff;\"/>\n",
" </g>\n",
" <g id=\"matplotlib.axis_1\">\n",
" <g id=\"xtick_1\">\n",
" <g id=\"line2d_1\">\n",
" <defs>\n",
" <path d=\"M 0 0 \n",
"L 0 3.5 \n",
"\" id=\"m082e5440ed\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
" </defs>\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"17.752344\" xlink:href=\"#m082e5440ed\" y=\"246.441071\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_1\">\n",
" <!-- −20 -->\n",
" <defs>\n",
" <path d=\"M 10.59375 35.5 \n",
"L 73.1875 35.5 \n",
"L 73.1875 27.203125 \n",
"L 10.59375 27.203125 \n",
"z\n",
"\" id=\"DejaVuSans-8722\"/>\n",
" <path d=\"M 19.1875 8.296875 \n",
"L 53.609375 8.296875 \n",
"L 53.609375 0 \n",
"L 7.328125 0 \n",
"L 7.328125 8.296875 \n",
"Q 12.9375 14.109375 22.625 23.890625 \n",
"Q 32.328125 33.6875 34.8125 36.53125 \n",
"Q 39.546875 41.84375 41.421875 45.53125 \n",
"Q 43.3125 49.21875 43.3125 52.78125 \n",
"Q 43.3125 58.59375 39.234375 62.25 \n",
"Q 35.15625 65.921875 28.609375 65.921875 \n",
"Q 23.96875 65.921875 18.8125 64.3125 \n",
"Q 13.671875 62.703125 7.8125 59.421875 \n",
"L 7.8125 69.390625 \n",
"Q 13.765625 71.78125 18.9375 73 \n",
"Q 24.125 74.21875 28.421875 74.21875 \n",
"Q 39.75 74.21875 46.484375 68.546875 \n",
"Q 53.21875 62.890625 53.21875 53.421875 \n",
"Q 53.21875 48.921875 51.53125 44.890625 \n",
"Q 49.859375 40.875 45.40625 35.40625 \n",
"Q 44.1875 33.984375 37.640625 27.21875 \n",
"Q 31.109375 20.453125 19.1875 8.296875 \n",
"z\n",
"\" id=\"DejaVuSans-50\"/>\n",
" <path d=\"M 31.78125 66.40625 \n",
"Q 24.171875 66.40625 20.328125 58.90625 \n",
"Q 16.5 51.421875 16.5 36.375 \n",
"Q 16.5 21.390625 20.328125 13.890625 \n",
"Q 24.171875 6.390625 31.78125 6.390625 \n",
"Q 39.453125 6.390625 43.28125 13.890625 \n",
"Q 47.125 21.390625 47.125 36.375 \n",
"Q 47.125 51.421875 43.28125 58.90625 \n",
"Q 39.453125 66.40625 31.78125 66.40625 \n",
"z\n",
"M 31.78125 74.21875 \n",
"Q 44.046875 74.21875 50.515625 64.515625 \n",
"Q 56.984375 54.828125 56.984375 36.375 \n",
"Q 56.984375 17.96875 50.515625 8.265625 \n",
"Q 44.046875 -1.421875 31.78125 -1.421875 \n",
"Q 19.53125 -1.421875 13.0625 8.265625 \n",
"Q 6.59375 17.96875 6.59375 36.375 \n",
"Q 6.59375 54.828125 13.0625 64.515625 \n",
"Q 19.53125 74.21875 31.78125 74.21875 \n",
"z\n",
"\" id=\"DejaVuSans-48\"/>\n",
" </defs>\n",
" <g transform=\"translate(7.2 261.039508)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_2\">\n",
" <g id=\"line2d_2\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"62.392344\" xlink:href=\"#m082e5440ed\" y=\"246.441071\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_2\">\n",
" <!-- −15 -->\n",
" <defs>\n",
" <path d=\"M 12.40625 8.296875 \n",
"L 28.515625 8.296875 \n",
"L 28.515625 63.921875 \n",
"L 10.984375 60.40625 \n",
"L 10.984375 69.390625 \n",
"L 28.421875 72.90625 \n",
"L 38.28125 72.90625 \n",
"L 38.28125 8.296875 \n",
"L 54.390625 8.296875 \n",
"L 54.390625 0 \n",
"L 12.40625 0 \n",
"z\n",
"\" id=\"DejaVuSans-49\"/>\n",
" <path d=\"M 10.796875 72.90625 \n",
"L 49.515625 72.90625 \n",
"L 49.515625 64.59375 \n",
"L 19.828125 64.59375 \n",
"L 19.828125 46.734375 \n",
"Q 21.96875 47.46875 24.109375 47.828125 \n",
"Q 26.265625 48.1875 28.421875 48.1875 \n",
"Q 40.625 48.1875 47.75 41.5 \n",
"Q 54.890625 34.8125 54.890625 23.390625 \n",
"Q 54.890625 11.625 47.5625 5.09375 \n",
"Q 40.234375 -1.421875 26.90625 -1.421875 \n",
"Q 22.3125 -1.421875 17.546875 -0.640625 \n",
"Q 12.796875 0.140625 7.71875 1.703125 \n",
"L 7.71875 11.625 \n",
"Q 12.109375 9.234375 16.796875 8.0625 \n",
"Q 21.484375 6.890625 26.703125 6.890625 \n",
"Q 35.15625 6.890625 40.078125 11.328125 \n",
"Q 45.015625 15.765625 45.015625 23.390625 \n",
"Q 45.015625 31 40.078125 35.4375 \n",
"Q 35.15625 39.890625 26.703125 39.890625 \n",
"Q 22.75 39.890625 18.8125 39.015625 \n",
"Q 14.890625 38.140625 10.796875 36.28125 \n",
"z\n",
"\" id=\"DejaVuSans-53\"/>\n",
" </defs>\n",
" <g transform=\"translate(51.84 261.039508)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_3\">\n",
" <g id=\"line2d_3\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"107.032344\" xlink:href=\"#m082e5440ed\" y=\"246.441071\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_3\">\n",
" <!-- −10 -->\n",
" <g transform=\"translate(96.48 261.039508)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_4\">\n",
" <g id=\"line2d_4\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"151.672344\" xlink:href=\"#m082e5440ed\" y=\"246.441071\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_4\">\n",
" <!-- −5 -->\n",
" <g transform=\"translate(144.30125 261.039508)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_5\">\n",
" <g id=\"line2d_5\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m082e5440ed\" y=\"246.441071\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_5\">\n",
" <!-- 0 -->\n",
" <g transform=\"translate(193.131094 261.039508)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_6\">\n",
" <g id=\"line2d_6\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"240.952344\" xlink:href=\"#m082e5440ed\" y=\"246.441071\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_6\">\n",
" <!-- 5 -->\n",
" <g transform=\"translate(237.771094 261.039508)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_7\">\n",
" <g id=\"line2d_7\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"285.592344\" xlink:href=\"#m082e5440ed\" y=\"246.441071\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_7\">\n",
" <!-- 10 -->\n",
" <g transform=\"translate(279.229844 261.039508)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_8\">\n",
" <g id=\"line2d_8\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"330.232344\" xlink:href=\"#m082e5440ed\" y=\"246.441071\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_8\">\n",
" <!-- 15 -->\n",
" <g transform=\"translate(323.869844 261.039508)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_9\">\n",
" <g id=\"line2d_9\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"374.872344\" xlink:href=\"#m082e5440ed\" y=\"246.441071\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_9\">\n",
" <!-- 20 -->\n",
" <g transform=\"translate(368.509844 261.039508)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_10\">\n",
" <!-- $\\omega$ -->\n",
" <defs>\n",
" <path d=\"M 21.390625 -1.421875 \n",
"Q 1.125 -1.421875 6.78125 27.59375 \n",
"Q 8.984375 39.0625 19.625 54.6875 \n",
"L 29.296875 54.6875 \n",
"Q 19.234375 39.0625 17 27.34375 \n",
"Q 12.796875 6.203125 23.734375 6.203125 \n",
"Q 33.84375 6.203125 38.71875 32.46875 \n",
"L 47.015625 32.46875 \n",
"Q 41.703125 6.0625 51.8125 6.203125 \n",
"Q 62.703125 6.296875 66.796875 27.34375 \n",
"Q 69.046875 39.0625 65.140625 54.6875 \n",
"L 74.8125 54.6875 \n",
"Q 79.296875 39.0625 77.09375 27.59375 \n",
"Q 71.53125 -1.46875 51.21875 -1.421875 \n",
"Q 37.9375 -1.375 39.109375 13.1875 \n",
"Q 34.28125 -1.421875 21.390625 -1.421875 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-969\"/>\n",
" </defs>\n",
" <g transform=\"translate(370.672344 274.717633)scale(0.1 -0.1)\">\n",
" <use transform=\"translate(0 0.3125)\" xlink:href=\"#DejaVuSans-Oblique-969\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"matplotlib.axis_2\">\n",
" <g id=\"ytick_1\">\n",
" <g id=\"line2d_10\">\n",
" <defs>\n",
" <path d=\"M 0 0 \n",
"L -3.5 0 \n",
"\" id=\"ma4a54ac4e4\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
" </defs>\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#ma4a54ac4e4\" y=\"296.129003\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_11\">\n",
" <!-- −0.5 -->\n",
" <defs>\n",
" <path d=\"M 10.6875 12.40625 \n",
"L 21 12.40625 \n",
"L 21 0 \n",
"L 10.6875 0 \n",
"z\n",
"\" id=\"DejaVuSans-46\"/>\n",
" </defs>\n",
" <g transform=\"translate(165.029531 299.928222)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"179.199219\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_2\">\n",
" <g id=\"line2d_11\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#ma4a54ac4e4\" y=\"246.441071\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_12\">\n",
" <!-- 0.0 -->\n",
" <g transform=\"translate(173.409219 250.24029)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_3\">\n",
" <g id=\"line2d_12\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#ma4a54ac4e4\" y=\"196.753139\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_13\">\n",
" <!-- 0.5 -->\n",
" <g transform=\"translate(173.409219 200.552357)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_4\">\n",
" <g id=\"line2d_13\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#ma4a54ac4e4\" y=\"147.065207\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_14\">\n",
" <!-- 1.0 -->\n",
" <g transform=\"translate(173.409219 150.864425)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_5\">\n",
" <g id=\"line2d_14\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#ma4a54ac4e4\" y=\"97.377274\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_15\">\n",
" <!-- 1.5 -->\n",
" <g transform=\"translate(173.409219 101.176493)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_6\">\n",
" <g id=\"line2d_15\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#ma4a54ac4e4\" y=\"47.689342\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_16\">\n",
" <!-- 2.0 -->\n",
" <g transform=\"translate(173.409219 51.488561)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_17\">\n",
" <!-- $\\mathcal{F} \\{ \\mathrm{rect}(a t) \\}$ -->\n",
" <defs>\n",
" <path d=\"M 5.90625 53.40625 \n",
"L 4.296875 55.203125 \n",
"Q 11.40625 61.796875 18.34375 64 \n",
"Q 25.296875 66.203125 33.796875 66.203125 \n",
"Q 42.40625 66.203125 48.59375 65.75 \n",
"Q 54.796875 65.296875 60.140625 64.046875 \n",
"Q 65.5 62.796875 68.25 60.4375 \n",
"Q 71 58.09375 71 54.5 \n",
"Q 71 51.09375 69.203125 48.796875 \n",
"Q 67.40625 46.5 64.203125 46.5 \n",
"Q 61.90625 46.5 60.203125 47.84375 \n",
"Q 58.5 49.203125 58.5 51.203125 \n",
"Q 58.5 53.09375 59.25 54.140625 \n",
"Q 60 55.203125 60.890625 55.453125 \n",
"Q 61.796875 55.703125 62.5 56.140625 \n",
"Q 63.203125 56.59375 63.203125 57.5 \n",
"Q 63.203125 59.5 57.75 60.84375 \n",
"Q 52.296875 62.203125 45.203125 62.203125 \n",
"Q 42.09375 62.203125 40.75 61.25 \n",
"Q 39.40625 60.296875 38.5 57.296875 \n",
"L 32.796875 37.703125 \n",
"L 54.59375 37.703125 \n",
"L 53.296875 33.703125 \n",
"L 31.703125 33.703125 \n",
"L 27.296875 18.796875 \n",
"Q 25.40625 12.296875 23.296875 8.390625 \n",
"Q 21.203125 4.5 18.34375 2.703125 \n",
"Q 15.5 0.90625 12.953125 0.453125 \n",
"Q 10.40625 0 6 0 \n",
"L 6.796875 2.40625 \n",
"Q 9.5 2.40625 11.34375 4.5 \n",
"Q 13.203125 6.59375 14.59375 11.59375 \n",
"L 26.40625 52.09375 \n",
"Q 27.40625 55.59375 27.40625 57.296875 \n",
"Q 27.40625 59 26.40625 59.796875 \n",
"Q 25.40625 60.59375 22.796875 60.59375 \n",
"Q 13.40625 60.59375 5.90625 53.40625 \n",
"z\n",
"\" id=\"STIXNonUnicode-Italic-57906\"/>\n",
" <path d=\"M 51.125 -9.28125 \n",
"L 51.125 -16.3125 \n",
"L 48.09375 -16.3125 \n",
"Q 35.9375 -16.3125 31.8125 -12.6875 \n",
"Q 27.6875 -9.078125 27.6875 1.703125 \n",
"L 27.6875 13.375 \n",
"Q 27.6875 20.75 25.046875 23.578125 \n",
"Q 22.40625 26.421875 15.484375 26.421875 \n",
"L 12.5 26.421875 \n",
"L 12.5 33.40625 \n",
"L 15.484375 33.40625 \n",
"Q 22.46875 33.40625 25.078125 36.203125 \n",
"Q 27.6875 39.015625 27.6875 46.296875 \n",
"L 27.6875 58.015625 \n",
"Q 27.6875 68.796875 31.8125 72.390625 \n",
"Q 35.9375 75.984375 48.09375 75.984375 \n",
"L 51.125 75.984375 \n",
"L 51.125 69 \n",
"L 47.796875 69 \n",
"Q 40.921875 69 38.8125 66.84375 \n",
"Q 36.71875 64.703125 36.71875 57.8125 \n",
"L 36.71875 45.703125 \n",
"Q 36.71875 38.03125 34.5 34.5625 \n",
"Q 32.28125 31.109375 26.90625 29.890625 \n",
"Q 32.328125 28.5625 34.515625 25.09375 \n",
"Q 36.71875 21.625 36.71875 14.015625 \n",
"L 36.71875 1.90625 \n",
"Q 36.71875 -4.984375 38.8125 -7.125 \n",
"Q 40.921875 -9.28125 47.796875 -9.28125 \n",
"z\n",
"\" id=\"DejaVuSans-123\"/>\n",
" <path d=\"M 41.109375 46.296875 \n",
"Q 39.59375 47.171875 37.8125 47.578125 \n",
"Q 36.03125 48 33.890625 48 \n",
"Q 26.265625 48 22.1875 43.046875 \n",
"Q 18.109375 38.09375 18.109375 28.8125 \n",
"L 18.109375 0 \n",
"L 9.078125 0 \n",
"L 9.078125 54.6875 \n",
"L 18.109375 54.6875 \n",
"L 18.109375 46.1875 \n",
"Q 20.953125 51.171875 25.484375 53.578125 \n",
"Q 30.03125 56 36.53125 56 \n",
"Q 37.453125 56 38.578125 55.875 \n",
"Q 39.703125 55.765625 41.0625 55.515625 \n",
"z\n",
"\" id=\"DejaVuSans-114\"/>\n",
" <path d=\"M 56.203125 29.59375 \n",
"L 56.203125 25.203125 \n",
"L 14.890625 25.203125 \n",
"Q 15.484375 15.921875 20.484375 11.0625 \n",
"Q 25.484375 6.203125 34.421875 6.203125 \n",
"Q 39.59375 6.203125 44.453125 7.46875 \n",
"Q 49.3125 8.734375 54.109375 11.28125 \n",
"L 54.109375 2.78125 \n",
"Q 49.265625 0.734375 44.1875 -0.34375 \n",
"Q 39.109375 -1.421875 33.890625 -1.421875 \n",
"Q 20.796875 -1.421875 13.15625 6.1875 \n",
"Q 5.515625 13.8125 5.515625 26.8125 \n",
"Q 5.515625 40.234375 12.765625 48.109375 \n",
"Q 20.015625 56 32.328125 56 \n",
"Q 43.359375 56 49.78125 48.890625 \n",
"Q 56.203125 41.796875 56.203125 29.59375 \n",
"z\n",
"M 47.21875 32.234375 \n",
"Q 47.125 39.59375 43.09375 43.984375 \n",
"Q 39.0625 48.390625 32.421875 48.390625 \n",
"Q 24.90625 48.390625 20.390625 44.140625 \n",
"Q 15.875 39.890625 15.1875 32.171875 \n",
"z\n",
"\" id=\"DejaVuSans-101\"/>\n",
" <path d=\"M 48.78125 52.59375 \n",
"L 48.78125 44.1875 \n",
"Q 44.96875 46.296875 41.140625 47.34375 \n",
"Q 37.3125 48.390625 33.40625 48.390625 \n",
"Q 24.65625 48.390625 19.8125 42.84375 \n",
"Q 14.984375 37.3125 14.984375 27.296875 \n",
"Q 14.984375 17.28125 19.8125 11.734375 \n",
"Q 24.65625 6.203125 33.40625 6.203125 \n",
"Q 37.3125 6.203125 41.140625 7.25 \n",
"Q 44.96875 8.296875 48.78125 10.40625 \n",
"L 48.78125 2.09375 \n",
"Q 45.015625 0.34375 40.984375 -0.53125 \n",
"Q 36.96875 -1.421875 32.421875 -1.421875 \n",
"Q 20.0625 -1.421875 12.78125 6.34375 \n",
"Q 5.515625 14.109375 5.515625 27.296875 \n",
"Q 5.515625 40.671875 12.859375 48.328125 \n",
"Q 20.21875 56 33.015625 56 \n",
"Q 37.15625 56 41.109375 55.140625 \n",
"Q 45.0625 54.296875 48.78125 52.59375 \n",
"z\n",
"\" id=\"DejaVuSans-99\"/>\n",
" <path d=\"M 18.3125 70.21875 \n",
"L 18.3125 54.6875 \n",
"L 36.8125 54.6875 \n",
"L 36.8125 47.703125 \n",
"L 18.3125 47.703125 \n",
"L 18.3125 18.015625 \n",
"Q 18.3125 11.328125 20.140625 9.421875 \n",
"Q 21.96875 7.515625 27.59375 7.515625 \n",
"L 36.8125 7.515625 \n",
"L 36.8125 0 \n",
"L 27.59375 0 \n",
"Q 17.1875 0 13.234375 3.875 \n",
"Q 9.28125 7.765625 9.28125 18.015625 \n",
"L 9.28125 47.703125 \n",
"L 2.6875 47.703125 \n",
"L 2.6875 54.6875 \n",
"L 9.28125 54.6875 \n",
"L 9.28125 70.21875 \n",
"z\n",
"\" id=\"DejaVuSans-116\"/>\n",
" <path d=\"M 31 75.875 \n",
"Q 24.46875 64.65625 21.28125 53.65625 \n",
"Q 18.109375 42.671875 18.109375 31.390625 \n",
"Q 18.109375 20.125 21.3125 9.0625 \n",
"Q 24.515625 -2 31 -13.1875 \n",
"L 23.1875 -13.1875 \n",
"Q 15.875 -1.703125 12.234375 9.375 \n",
"Q 8.59375 20.453125 8.59375 31.390625 \n",
"Q 8.59375 42.28125 12.203125 53.3125 \n",
"Q 15.828125 64.359375 23.1875 75.875 \n",
"z\n",
"\" id=\"DejaVuSans-40\"/>\n",
" <path d=\"M 53.71875 31.203125 \n",
"L 47.609375 0 \n",
"L 38.625 0 \n",
"L 40.28125 8.296875 \n",
"Q 36.328125 3.421875 31.265625 1 \n",
"Q 26.21875 -1.421875 20.015625 -1.421875 \n",
"Q 13.03125 -1.421875 8.5625 2.84375 \n",
"Q 4.109375 7.125 4.109375 13.8125 \n",
"Q 4.109375 23.390625 11.75 28.953125 \n",
"Q 19.390625 34.515625 32.8125 34.515625 \n",
"L 45.3125 34.515625 \n",
"L 45.796875 36.921875 \n",
"Q 45.90625 37.3125 45.953125 37.765625 \n",
"Q 46 38.234375 46 39.203125 \n",
"Q 46 43.5625 42.453125 45.96875 \n",
"Q 38.921875 48.390625 32.515625 48.390625 \n",
"Q 28.125 48.390625 23.5 47.265625 \n",
"Q 18.890625 46.140625 14.015625 43.890625 \n",
"L 15.578125 52.203125 \n",
"Q 20.65625 54.109375 25.515625 55.046875 \n",
"Q 30.375 56 34.90625 56 \n",
"Q 44.578125 56 49.625 51.796875 \n",
"Q 54.6875 47.609375 54.6875 39.59375 \n",
"Q 54.6875 37.984375 54.4375 35.8125 \n",
"Q 54.203125 33.640625 53.71875 31.203125 \n",
"z\n",
"M 44 27.484375 \n",
"L 35.015625 27.484375 \n",
"Q 23.96875 27.484375 18.671875 24.53125 \n",
"Q 13.375 21.578125 13.375 15.375 \n",
"Q 13.375 11.078125 16.078125 8.640625 \n",
"Q 18.796875 6.203125 23.578125 6.203125 \n",
"Q 30.90625 6.203125 36.375 11.453125 \n",
"Q 41.84375 16.703125 43.609375 25.484375 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-97\"/>\n",
" <path d=\"M 42.28125 54.6875 \n",
"L 40.921875 47.703125 \n",
"L 23 47.703125 \n",
"L 17.1875 18.015625 \n",
"Q 16.890625 16.359375 16.75 15.234375 \n",
"Q 16.609375 14.109375 16.609375 13.484375 \n",
"Q 16.609375 10.359375 18.484375 8.9375 \n",
"Q 20.359375 7.515625 24.515625 7.515625 \n",
"L 33.59375 7.515625 \n",
"L 32.078125 0 \n",
"L 23.484375 0 \n",
"Q 15.484375 0 11.546875 3.125 \n",
"Q 7.625 6.25 7.625 12.59375 \n",
"Q 7.625 13.71875 7.765625 15.0625 \n",
"Q 7.90625 16.40625 8.203125 18.015625 \n",
"L 14.015625 47.703125 \n",
"L 6.390625 47.703125 \n",
"L 7.8125 54.6875 \n",
"L 15.28125 54.6875 \n",
"L 18.3125 70.21875 \n",
"L 27.296875 70.21875 \n",
"L 24.3125 54.6875 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-116\"/>\n",
" <path d=\"M 8.015625 75.875 \n",
"L 15.828125 75.875 \n",
"Q 23.140625 64.359375 26.78125 53.3125 \n",
"Q 30.421875 42.28125 30.421875 31.390625 \n",
"Q 30.421875 20.453125 26.78125 9.375 \n",
"Q 23.140625 -1.703125 15.828125 -13.1875 \n",
"L 8.015625 -13.1875 \n",
"Q 14.5 -2 17.703125 9.0625 \n",
"Q 20.90625 20.125 20.90625 31.390625 \n",
"Q 20.90625 42.671875 17.703125 53.65625 \n",
"Q 14.5 64.65625 8.015625 75.875 \n",
"z\n",
"\" id=\"DejaVuSans-41\"/>\n",
" <path d=\"M 12.5 -9.28125 \n",
"L 15.921875 -9.28125 \n",
"Q 22.75 -9.28125 24.828125 -7.171875 \n",
"Q 26.90625 -5.078125 26.90625 1.90625 \n",
"L 26.90625 14.015625 \n",
"Q 26.90625 21.625 29.09375 25.09375 \n",
"Q 31.296875 28.5625 36.71875 29.890625 \n",
"Q 31.296875 31.109375 29.09375 34.5625 \n",
"Q 26.90625 38.03125 26.90625 45.703125 \n",
"L 26.90625 57.8125 \n",
"Q 26.90625 64.75 24.828125 66.875 \n",
"Q 22.75 69 15.921875 69 \n",
"L 12.5 69 \n",
"L 12.5 75.984375 \n",
"L 15.578125 75.984375 \n",
"Q 27.734375 75.984375 31.8125 72.390625 \n",
"Q 35.890625 68.796875 35.890625 58.015625 \n",
"L 35.890625 46.296875 \n",
"Q 35.890625 39.015625 38.515625 36.203125 \n",
"Q 41.15625 33.40625 48.09375 33.40625 \n",
"L 51.125 33.40625 \n",
"L 51.125 26.421875 \n",
"L 48.09375 26.421875 \n",
"Q 41.15625 26.421875 38.515625 23.578125 \n",
"Q 35.890625 20.75 35.890625 13.375 \n",
"L 35.890625 1.703125 \n",
"Q 35.890625 -9.078125 31.8125 -12.6875 \n",
"Q 27.734375 -16.3125 15.578125 -16.3125 \n",
"L 12.5 -16.3125 \n",
"z\n",
"\" id=\"DejaVuSans-125\"/>\n",
" </defs>\n",
" <g transform=\"translate(158.949844 64)rotate(-90)scale(0.1 -0.1)\">\n",
" <use transform=\"translate(0 0.015625)\" xlink:href=\"#STIXNonUnicode-Italic-57906\"/>\n",
" <use transform=\"translate(65.199997 0.015625)\" xlink:href=\"#DejaVuSans-123\"/>\n",
" <use transform=\"translate(128.823044 0.015625)\" xlink:href=\"#DejaVuSans-114\"/>\n",
" <use transform=\"translate(169.936325 0.015625)\" xlink:href=\"#DejaVuSans-101\"/>\n",
" <use transform=\"translate(231.459763 0.015625)\" xlink:href=\"#DejaVuSans-99\"/>\n",
" <use transform=\"translate(286.440231 0.015625)\" xlink:href=\"#DejaVuSans-116\"/>\n",
" <use transform=\"translate(325.649216 0.015625)\" xlink:href=\"#DejaVuSans-40\"/>\n",
" <use transform=\"translate(364.662888 0.015625)\" xlink:href=\"#DejaVuSans-Oblique-97\"/>\n",
" <use transform=\"translate(425.942184 0.015625)\" xlink:href=\"#DejaVuSans-Oblique-116\"/>\n",
" <use transform=\"translate(465.151169 0.015625)\" xlink:href=\"#DejaVuSans-41\"/>\n",
" <use transform=\"translate(504.164841 0.015625)\" xlink:href=\"#DejaVuSans-125\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"LineCollection_1\">\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 17.752344 237.368598 \n",
"L 24.366369 242.331026 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 24.366369 242.331026 \n",
"L 30.576946 249.461607 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 30.576946 249.461607 \n",
"L 36.420851 255.406928 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 36.420851 255.406928 \n",
"L 43.305535 257.923374 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 43.305535 257.923374 \n",
"L 49.173279 254.859323 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 49.173279 254.859323 \n",
"L 55.536903 247.195591 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 55.536903 247.195591 \n",
"L 60.63417 240.044673 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 60.63417 240.044673 \n",
"L 65.881027 234.324527 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 65.881027 234.324527 \n",
"L 70.861824 232.34845 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 70.861824 232.34845 \n",
"L 76.373536 235.155662 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 76.373536 235.155662 \n",
"L 80.94172 241.081032 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 80.94172 241.081032 \n",
"L 86.026287 249.850813 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 86.026287 249.850813 \n",
"L 90.521382 257.463507 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 90.521382 257.463507 \n",
"L 96.015068 263.632485 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 96.015068 263.632485 \n",
"L 98.589194 264.57647 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 98.589194 264.57647 \n",
"L 101.106097 264.06257 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 101.106097 264.06257 \n",
"L 103.603343 262.112697 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 103.603343 262.112697 \n",
"L 106.137877 258.744094 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 106.137877 258.744094 \n",
"L 112.105633 246.5881 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 112.105633 246.5881 \n",
"L 119.180624 230.172503 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 119.180624 230.172503 \n",
"L 121.597355 225.767621 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 121.597355 225.767621 \n",
"L 124.474156 222.196168 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 124.474156 222.196168 \n",
"L 127.595502 220.936774 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 127.595502 220.936774 \n",
"L 130.614558 222.678278 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 130.614558 222.678278 \n",
"L 133.25178 226.650557 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 133.25178 226.650557 \n",
"L 135.919046 232.839443 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 135.919046 232.839443 \n",
"L 141.725652 251.911366 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 141.725652 251.911366 \n",
"L 147.754901 273.760028 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 147.754901 273.760028 \n",
"L 150.954075 282.941883 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 150.954075 282.941883 \n",
"L 152.821308 286.727428 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 152.821308 286.727428 \n",
"L 154.713787 289.037714 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 154.713787 289.037714 \n",
"L 155.885533 289.590797 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 155.885533 289.590797 \n",
"L 157.102423 289.39047 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 157.102423 289.39047 \n",
"L 158.233624 288.456187 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 158.233624 288.456187 \n",
"L 159.61238 286.299034 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 159.61238 286.299034 \n",
"L 160.879802 283.298579 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 160.879802 283.298579 \n",
"L 162.001785 279.815147 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 162.001785 279.815147 \n",
"L 163.377571 274.479976 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 163.377571 274.479976 \n",
"L 164.522249 269.156832 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 164.522249 269.156832 \n",
"L 165.778226 262.414431 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 165.778226 262.414431 \n",
"L 167.281676 253.154153 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 167.281676 253.154153 \n",
"L 170.090334 232.696096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 170.090334 232.696096 \n",
"L 175.467678 184.970018 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 175.467678 184.970018 \n",
"L 181.190236 129.985609 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 181.190236 129.985609 \n",
"L 183.943158 105.44074 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 183.943158 105.44074 \n",
"L 186.942906 82.214257 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 186.942906 82.214257 \n",
"L 188.923446 69.613625 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 188.923446 69.613625 \n",
"L 189.815319 64.772723 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 189.815319 64.772723 \n",
"L 190.679202 60.616527 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 190.679202 60.616527 \n",
"L 191.411118 57.52298 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 191.411118 57.52298 \n",
"L 192.279385 54.37997 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 192.279385 54.37997 \n",
"L 193.269836 51.513999 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 193.269836 51.513999 \n",
"L 194.209822 49.521353 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 194.209822 49.521353 \n",
"L 194.894328 48.523918 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 194.894328 48.523918 \n",
"L 195.63913 47.877635 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 195.63913 47.877635 \n",
"L 196.438916 47.696 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 196.438916 47.696 \n",
"L 197.313075 48.105265 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 197.313075 48.105265 \n",
"L 197.964727 48.82208 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 197.964727 48.82208 \n",
"L 198.748114 50.14579 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 198.748114 50.14579 \n",
"L 199.632656 52.239277 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 199.632656 52.239277 \n",
"L 200.455126 54.745347 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 200.455126 54.745347 \n",
"L 201.258409 57.700955 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 201.258409 57.700955 \n",
"L 201.945569 60.616902 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 201.945569 60.616902 \n",
"L 203.528947 68.636178 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 203.528947 68.636178 \n",
"L 204.912237 77.029852 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 204.912237 77.029852 \n",
"L 206.154131 85.566287 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 206.154131 85.566287 \n",
"L 208.876685 107.095078 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 208.876685 107.095078 \n",
"L 212.131161 136.526262 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 212.131161 136.526262 \n",
"L 217.180024 185.189661 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 217.180024 185.189661 \n",
"L 222.052867 228.820878 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 222.052867 228.820878 \n",
"L 224.422719 246.881104 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 224.422719 246.881104 \n",
"L 225.656161 255.186195 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 225.656161 255.186195 \n",
"L 227.158377 264.175236 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 227.158377 264.175236 \n",
"L 228.530158 271.238839 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 228.530158 271.238839 \n",
"L 229.737984 276.517559 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 229.737984 276.517559 \n",
"L 230.991783 281.046501 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 230.991783 281.046501 \n",
"L 232.221038 284.541521 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 232.221038 284.541521 \n",
"L 233.54354 287.26515 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 233.54354 287.26515 \n",
"L 234.962279 289.020193 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 234.962279 289.020193 \n",
"L 236.381296 289.616 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 236.381296 289.616 \n",
"L 237.727753 289.170479 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 237.727753 289.170479 \n",
"L 239.349537 287.43121 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 239.349537 287.43121 \n",
"L 240.90792 284.652301 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 240.90792 284.652301 \n",
"L 243.722786 277.375221 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 243.722786 277.375221 \n",
"L 249.014316 258.935659 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 249.014316 258.935659 \n",
"L 255.236331 237.061821 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 255.236331 237.061821 \n",
"L 257.461549 230.880512 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 257.461549 230.880512 \n",
"L 259.989378 225.522103 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 259.989378 225.522103 \n",
"L 262.517422 222.174888 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 262.517422 222.174888 \n",
"L 265.09628 220.93202 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 265.09628 220.93202 \n",
"L 267.440602 221.652613 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 267.440602 221.652613 \n",
"L 269.454302 223.556859 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 269.454302 223.556859 \n",
"L 274.469326 232.331059 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 274.469326 232.331059 \n",
"L 278.340842 241.362142 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 278.340842 241.362142 \n",
"L 282.948371 252.083163 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 282.948371 252.083163 \n",
"L 288.014583 260.934087 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 288.014583 260.934087 \n",
"L 290.76756 263.625715 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 290.76756 263.625715 \n",
"L 293.916535 264.584884 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 293.916535 264.584884 \n",
"L 296.797492 263.508784 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 296.797492 263.508784 \n",
"L 300.066493 260.304219 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 300.066493 260.304219 \n",
"L 305.982368 250.952 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 305.982368 250.952 \n",
"L 312.984257 239.126572 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 312.984257 239.126572 \n",
"L 316.883346 234.569662 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 316.883346 234.569662 \n",
"L 320.622399 232.490885 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 320.622399 232.490885 \n",
"L 323.398945 232.544738 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 323.398945 232.544738 \n",
"L 326.664228 234.262549 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 326.664228 234.262549 \n",
"L 332.845373 241.197609 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 332.845373 241.197609 \n",
"L 338.852313 249.611759 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 338.852313 249.611759 \n",
"L 343.824828 255.19083 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 343.824828 255.19083 \n",
"L 349.363613 257.928004 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 349.363613 257.928004 \n",
"L 354.277686 256.723054 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 354.277686 256.723054 \n",
"L 359.350947 252.478787 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 359.350947 252.478787 \n",
"L 364.588758 246.455741 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 364.588758 246.455741 \n",
"L 369.325822 241.263371 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#p27aa9de179)\" d=\"M 369.325822 241.263371 \n",
"L 374.872344 237.368598 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" </g>\n",
" <g id=\"patch_3\">\n",
" <path d=\"M 196.312344 296.129003 \n",
"L 196.312344 47.689342 \n",
"\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
" </g>\n",
" <g id=\"patch_4\">\n",
" <path d=\"M 374.872344 301.712 \n",
"L 374.872344 35.6 \n",
"\" style=\"fill:none;\"/>\n",
" </g>\n",
" <g id=\"patch_5\">\n",
" <path d=\"M 17.752344 246.441071 \n",
"L 374.872344 246.441071 \n",
"\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
" </g>\n",
" <g id=\"patch_6\">\n",
" <path d=\"M 17.752344 35.6 \n",
"L 374.872344 35.6 \n",
"\" style=\"fill:none;\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <defs>\n",
" <clipPath id=\"p27aa9de179\">\n",
" <rect height=\"266.112\" width=\"357.12\" x=\"17.752344\" y=\"35.6\"/>\n",
" </clipPath>\n",
" </defs>\n",
"</svg>\n"
],
"text/plain": [
"<Figure size 614.4x460.8 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"values = {a: 1/2}\n",
"\n",
"sym.plot(x.subs(values), (t, -5, 5), xlabel=r'$t$', ylabel=r'$\\mathrm{rect}(a t)$');\n",
"sym.plot(X.subs(values), (w, -20, 20), xlabel=r'$\\omega$', ylabel=r'$\\mathcal{F} \\{ \\mathrm{rect}(a t) \\}$');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise**\n",
"\n",
"* Change the width $1/a$ of the rectangular signal. How does its spectrum change?\n",
"* On a qualitative level, what happens when $1/a$ increases towards infinity?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Convolution Theorem\n",
"\n",
"The [convolution theorem](https://en.wikipedia.org/wiki/Convolution_theorem) states that the Fourier transform of the convolution of two signals $x(t)$ and $y(t)$ is equal to the scalar multiplication of their Fourier transforms $X(j \\omega) = \\mathcal{F} \\{ x(t) \\}$ and $Y(j \\omega) = \\mathcal{F} \\{ y(t) \\}$\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{F} \\{ x(t) * y(t) \\} = X(j \\omega) \\cdot Y(j \\omega)\n",
"\\end{equation}\n",
"\n",
"The theorem can be proven by introducing the [definition of the convolution](../systems_time_domain/convolution.ipynb) into the [definition of the Fourier transform](definition.ipynb) and changing the order of integration\n",
"\n",
"\\begin{align}\n",
"\\mathcal{F} \\{ x(t) * y(t) \\} &= \\int_{-\\infty}^{\\infty} \\left( \\int_{-\\infty}^{\\infty} x(\\tau) \\cdot y(t-\\tau) \\; d \\tau \\right) e^{-j \\omega t} \\; dt \\\\\n",
"&= \\int_{-\\infty}^{\\infty} \\left( \\int_{-\\infty}^{\\infty} y(t-\\tau) \\, e^{-j \\omega t} \\; dt \\right) x(\\tau) \\; d\\tau \\\\\n",
"&= Y(j \\omega) \\cdot \\int_{-\\infty}^{\\infty} x(\\tau) \\, e^{-j \\omega \\tau} \\; d \\tau \\\\\n",
"&= Y(j \\omega) \\cdot X(j \\omega)\n",
"\\end{align}\n",
"\n",
"under the assumption that both Fourier transforms $X(j \\omega)$ and $Y(j \\omega)$ exist.\n",
"\n",
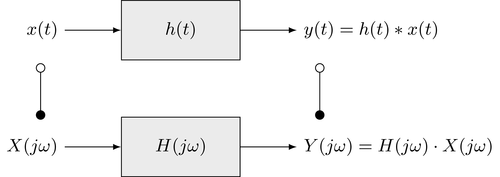
"The convolution theorem is very useful in the context of linear time-invariant (LTI) systems. The output signal $y(t)$ of an LTI system is given as the convolution of the input signal $x(t)$ with the impulse response $h(t)$. Hence, the signals and the system can be represented equivalently in the time and frequency domain\n",
"\n",
"\n",
"\n",
"\n",
"where $H(j \\omega) = \\mathcal{F} \\{ h(t) \\}$.\n",
"Calculation of the system response by transforming the problem into the Fourier domain can be beneficial since this replaces the evaluation of the convolution integral by a scalar multiplication. The (inverse) Fourier transforms are known for many signals or can be derived by applying the properties and theorems to standard signals and their transforms. This procedure simplifies the calculation of the system response significantly in many cases.\n",
"\n",
"The convolution theorem can also be useful to derive an unknown Fourier transform. The key is here to express the signal as convolution of two other signals for which the Fourier transforms are known. This is illustrated by the following example."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Transformation of the triangular signal\n",
"\n",
"A prominent example for the derivation of a Fourier transform by the convolution theorem is the [trianguar signal](https://en.wikipedia.org/wiki/Triangular_function)\n",
"\n",
"\\begin{equation}\n",
"\\Lambda(t) = \\begin{cases} 1- |t| & \\text{for } |t| < 1 \\\\ 0 & \\text{otherwise} \\end{cases}\n",
"\\end{equation}\n",
"\n",
"which can be expressed as the convolution of two rectangular signals\n",
"\n",
"\\begin{equation}\n",
"\\Lambda(t) = \\text{rect}(t) * \\text{rect}(t)\n",
"\\end{equation}\n",
"\n",
"Applying the convolution theorem yields\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{F} \\{ \\Lambda(t) \\} = \\text{sinc}\\left( \\frac{\\omega}{2} \\right) \\cdot \\text{sinc}\\left( \\frac{\\omega}{2} \\right) = \\text{sinc}^2 \\left( \\frac{\\omega}{2} \\right)\n",
"\\end{equation}\n",
"\n",
"Both the signal and its transform are plotted for illustration"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM5MS42MTM3NSAzMDguMjU5NzUgXSAvUGFyZW50IDIgMCBSIC9SZXNvdXJjZXMgOCAwIFIKL1R5cGUgL1BhZ2UgPj4KZW5kb2JqCjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxMSAwIFIgPj4Kc3RyZWFtCnicpVhLbxw3DL7Pr9AxOUQWKYmSjg3SGCh6SWK0h7YHN6/G8LpI3TR/vx9nZ3ZnJdobIDb8WH6kSFF8SeRuJnIfXXA3+PnqfnN/4O87R+4SPx+ngE+7KTbyQrFkfLrdfIqhes4N/92Cc/vpr2n6MF38gCXuIXM5TdR8TEE4O84+pQIurFvEJzml3p5QoSovS25W2FAXRbxX9BFGYyO+brYC9Yps5GPxOcXZgg0x+TATb6fpOXzydfqM38E9C1izeHbMvmX3djc9v3IXL8lRcFcfpupjqW1eAZ/fTU/Yh6fu6mb68QoLBB90DXyv/0D+4sX7m+tfvry5vrt/tvt09+Xevfh7eoXv2e5Jom+1t3NDfMzOTL6mb7UUTvw+SwkHLjy4dEN9zNaGU67fbut3epVy9CyDrRvqY7ZSIk/fHALhux3bim9hjNUjdTD2xCKqzbcEeG/w3qbZgQ427XVwYqzc69hSH9fBwHPtdORORy2ehljeUs/oKM0zn+igfh8xIuaHINxSH9cROfoqnY5uH5uKtNWxoZ7RIdXncKKDj/vYxFksaV0SOy+VeAk3LcSoALMOiF+85GXpJ/+uoXYueLByR30geGBDazNDjL4kqeWBENpoqtm3yJT4VNWRfFZXZU8xs0hhokUfP6iP4PHIIcd4qnBDP6uRIgKWo+SaEvOiMj2sEhaWUBt37tzQz6ss1TeCfYEEJu5VyoMqGVEcWolUTlVu6GdVIn98DCElqtjnorI+rBIpl2ouoXUqj/TzKkv2UmuNUUIe0hYlEZH+TGOeRN0xLw8nhrml78Nd0McCEjhqBuBUZhvmwF/1Pfn9yRz5aIyBohSqZam/Q3KAhXFA++wJ/TJPD7XaDbV6UdxV7J+vd3++u15L9mdnzDYxl7lhiHjC33/eu1/dnUNhwWASgFCWKlrZoEKWr4LTKCHXysiD5l5fOij979Pb968vn7u39/YAA41ELSB+t2n9xqKjYiGlAo6lZzboYEbuhpZazzuQdxO6Y2Ph1q9r0MGMKTHG1mLPPNJ3U06emlDIHbNBB3PzIYYS+5UNOiaq5Lm2XKRjNuhgRvDHGjL1zCN9NyERIjadS8ds0MEM21rLvZdH8m6qmFVqqNTzGnQwa0bHGAbmkb6bGtpS1UrYMRt0MOOcqDXpt2fQdRjEPAHfDxu0gP3smDDahz6SLADshNRG2FYdfBtyI9aF3QCUvaHHJM7JIS9DTPXAPgJgZ4QCgqxEV1EQGMut1lgIBFCWU0C4V9fQvlG+0ipgISpQ1GclR0eUMUJkagcJC4JIQk9G3JOgf7GXqOVjETEhFcHuBDMqlkrFJ8LEy6uIBelcjIGG0aewlKBLYhJJbRExIRWpvlKI2hFLxP0MqUyriAVBBLcaDFHIHtJBAUF8sMtCVAD9ImKcKI6DzkOUjhIWtJvbUkQ4EIoz/JglpMMpmpCKVI+BvnKdm6c0aRRXEQuCSE2+cEIlcKynUAMfjt6EtLeiDyCkkS8M/6QS0NEXERNSEYHBrUCltlgOhIxYRSxof2egrPpBxwEXtJ60iljQXkQKvCeg4+AKSYpHkRHai+gAhG4zzwlyzFsLWa4yGZNFnMkxIy42EiOkItWDGkKd6Thk4sPmLWgvgogQjQk1lxtGhaPICKlI85Jy0Fs0wqPkik6+ilgQOnCIuM5kLXws6LrCNS4ZaUMqgmBte4ORgRjNQqFVxIIgohUNkYAjQkH2ukVeDtKGIMIBDSc1FAEm3MkD7qirYSakIvAkrJbk5pMTTCKrFhPazffAEoog8gjOL4lyW3LShvSSiQTlCKejhDDiQ4iXCLMhFZF5UELqaKHCrKdlbhGxIJ2MWIfLKG2e9GMrSKZ1OLIgFalaOVj3qE4VHN5BxIIggoYREeCluYaLZClF1q1YCARQAXFUrbqilyMMgqu3DEDZcXXEOIgQEnVNCmsymojertGb0lz9EopaqDoY7AUsZH8d16lE+uHGAsCO4oQoQOHo2Q1A2bPHcIK8H9hHQCdU3Eiw+VKHEXUElB0+1kbRj3wWAHbCNJA1qHp2A1D2gjSfHzl69hEAO6aClELhfqS0AH2iQJUXhN5guwEou3iU9tiG1Q0A7EikLGhPw6xvAMqOpiGoIcO4bwB6N8BVhWWwfCArK+5EIY0ToAWAXUjHkNT6eLEAZcdNUaTGIV4MQJ9sSJt2CYPlBrAz331m9lfus2P30/7Z/OS1ub+ynXnIO71Wvzk+mX+dn82tB/LdQw/k093hIXw2SRcw74wPbqvTbr24P6b91fQ/r17YkAplbmRzdHJlYW0KZW5kb2JqCjExIDAgb2JqCjE3MTMKZW5kb2JqCjE2IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTc4ID4+CnN0cmVhbQp4nD2QSxIDIQhE956ijyA/0fMkldXk/ts0zpiF9hMobLCl6BjOy9WQXfGWVhie+DbvC56Jq6n1hyQVMvumDhmLZ/IUJyQUryZjQNyx1dajcTLCDLssJmZgroqvRC6oUALqUfJqZqPgaqaCvn3EVpn1FhcIRQImLGcr/p8D0+sWHQwWmO03y7M89grTdCzMe4Z5D0UjfgblWm5gZa2Dn4Ydmve2aCj/5Cd7Fni1zw/eq0KhCmVuZHN0cmVhbQplbmRvYmoKMTQgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zLU9ibGlxdWUgL0NoYXJQcm9jcyAxNSAwIFIKL0VuY29kaW5nIDw8IC9EaWZmZXJlbmNlcyBbIDExNiAvdCBdIC9UeXBlIC9FbmNvZGluZyA+PiAvRmlyc3RDaGFyIDAKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udERlc2NyaXB0b3IgMTMgMCBSCi9Gb250TWF0cml4IFsgMC4wMDEgMCAwIDAuMDAxIDAgMCBdIC9MYXN0Q2hhciAyNTUgL05hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxMiAwIFIgPj4KZW5kb2JqCjEzIDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyA5NgovRm9udEJCb3ggWyAtMTAxNiAtMzUxIDE2NjAgMTA2OCBdIC9Gb250TmFtZSAvRGVqYVZ1U2Fucy1PYmxpcXVlCi9JdGFsaWNBbmdsZSAwIC9NYXhXaWR0aCAxMzUwIC9TdGVtViAwIC9UeXBlIC9Gb250RGVzY3JpcHRvciAvWEhlaWdodCAwID4+CmVuZG9iagoxMiAwIG9iagpbIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwCjYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgMzE4IDQwMSA0NjAgODM4IDYzNgo5NTAgNzgwIDI3NSAzOTAgMzkwIDUwMCA4MzggMzE4IDM2MSAzMTggMzM3IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYKNjM2IDYzNiAzMzcgMzM3IDgzOCA4MzggODM4IDUzMSAxMDAwIDY4NCA2ODYgNjk4IDc3MCA2MzIgNTc1IDc3NSA3NTIgMjk1CjI5NSA2NTYgNTU3IDg2MyA3NDggNzg3IDYwMyA3ODcgNjk1IDYzNSA2MTEgNzMyIDY4NCA5ODkgNjg1IDYxMSA2ODUgMzkwIDMzNwozOTAgODM4IDUwMCA1MDAgNjEzIDYzNSA1NTAgNjM1IDYxNSAzNTIgNjM1IDYzNCAyNzggMjc4IDU3OSAyNzggOTc0IDYzNCA2MTIKNjM1IDYzNSA0MTEgNTIxIDM5MiA2MzQgNTkyIDgxOCA1OTIgNTkyIDUyNSA2MzYgMzM3IDYzNiA4MzggNjAwIDYzNiA2MDAgMzE4CjM1MiA1MTggMTAwMCA1MDAgNTAwIDUwMCAxMzUwIDYzNSA0MDAgMTA3MCA2MDAgNjg1IDYwMCA2MDAgMzE4IDMxOCA1MTggNTE4CjU5MCA1MDAgMTAwMCA1MDAgMTAwMCA1MjEgNDAwIDEwMjggNjAwIDUyNSA2MTEgMzE4IDQwMSA2MzYgNjM2IDYzNiA2MzYgMzM3CjUwMCA1MDAgMTAwMCA0NzEgNjE3IDgzOCAzNjEgMTAwMCA1MDAgNTAwIDgzOCA0MDEgNDAxIDUwMCA2MzYgNjM2IDMxOCA1MDAKNDAxIDQ3MSA2MTcgOTY5IDk2OSA5NjkgNTMxIDY4NCA2ODQgNjg0IDY4NCA2ODQgNjg0IDk3NCA2OTggNjMyIDYzMiA2MzIgNjMyCjI5NSAyOTUgMjk1IDI5NSA3NzUgNzQ4IDc4NyA3ODcgNzg3IDc4NyA3ODcgODM4IDc4NyA3MzIgNzMyIDczMiA3MzIgNjExIDYwOAo2MzAgNjEzIDYxMyA2MTMgNjEzIDYxMyA2MTMgOTk1IDU1MCA2MTUgNjE1IDYxNSA2MTUgMjc4IDI3OCAyNzggMjc4IDYxMiA2MzQKNjEyIDYxMiA2MTIgNjEyIDYxMiA4MzggNjEyIDYzNCA2MzQgNjM0IDYzNCA1OTIgNjM1IDU5MiBdCmVuZG9iagoxNSAwIG9iago8PCAvdCAxNiAwIFIgPj4KZW5kb2JqCjIxIDAgb2JqCjw8IC9CQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDU4Ci9TdWJ0eXBlIC9Gb3JtIC9UeXBlIC9YT2JqZWN0ID4+CnN0cmVhbQp4nOMyNDRSMFDI5bIAkjlcRhZmCuZGlkCWsaUFlGVmbgaWMzU3BtPGJkYKZsZGQBZEbw5XGgDSKg1wCmVuZHN0cmVhbQplbmRvYmoKMjIgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzOTIgPj4Kc3RyZWFtCnicPVJLbgUxCNvPKbhApfBNcp6p3u7df1ubzFSqCi8DtjGUlwypJT/qkogzTH71cl3iUfK9bGpn5iHuLjam+FhyX7qG2HLRmmKxTxzJL8i0VFihVt2jQ/GFKBMPAC3ggQXhvhz/8ReowdewhXLDe2QCYErUbkDGQ9EZSFlBEWH7kRXopFCvbOHvKCBX1KyFoXRiiA2WACm+qw2JmKjZoIeElZKqHdLxjKTwW8FdiWFQW1vbBHhm0BDZ3pGNETPt0RlxWRFrPz3po1EytVEZD01nfPHdMlLz0RXopNLI3cpDZ89CJ2Ak5kmY53Aj4Z7bQQsx9HGvlk9s95gpVpHwBTvKAQO9/d6Sjc974CyMXNvsTCfw0WmnHBOtvh5i/YM/bEubXMcrh0UUqLwoCH7XQRNxfFjF92SjRHe0AdYjE9VoJRAMEsLO7TDyeMZ52d4VtOb0RGijRB7UjhE9KLLF5ZwVsKf8rM2xHJ4PJntvtI+UzMyohBXUdnqots9jHdR3nvv6/AEuAKEZCmVuZHN0cmVhbQplbmRvYmoKMjMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDcgPj4Kc3RyZWFtCnicTVG7bUQxDOvfFFzgAOtreZ4LUl32b0PJCJDCIKEvKaclFvbGSwzhB1sPvuSRVUN/Hj8x7DMsPcnk1D/muclUFL4VqpuYUBdi4f1oBLwWdC8iK8oH349lDHPO9+CjEJdgJjRgrG9JJhfVvDNkwomhjsNBm1QYd00ULK4VzTPI7VY3sjqzIGx4JRPixgBEBNkXkM1go4yxlZDFch6oCpIFWmDX6RtRi4IrlNYJdKLWxLrM4Kvn9nY3Qy/y4Ki6eH0M60uwwuileyx8rkIfzPRMO3dJI73wphMRZg8FUpmdkZU6PWJ9t0D/n2Ur+PvJz/P9CxUoXCoKZW5kc3RyZWFtCmVuZG9iagoyNCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDkwID4+CnN0cmVhbQp4nE2NQRLAIAgD77wiT1BE0P90etL/X6vUDr3ATgKJFkWC9DVqSzDuuDIVa1ApmJSXwFUwXAva7qLK/jJJTJ2G03u3A4Oy8XGD0kn79nF6AKv9egbdD9IcIlgKZW5kc3RyZWFtCmVuZG9iagoyNSAwIG9iago8PCAvQkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzNwovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJzjMjQwUzA2NVXI5TI3NgKzcsAsI3MjIAski2BBZNMAAV8KCgplbmRzdHJlYW0KZW5kb2JqCjI2IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggODAgPj4Kc3RyZWFtCnicRYy7DcAwCER7pmAEfiZmnyiVs38bIErccE+6e7g6EjJT3mGGhwSeDCyGU/EGmaNgNbhGUo2d7KOwbl91geZ6U6v19wcqT3Z2cT3Nyxn0CmVuZHN0cmVhbQplbmRvYmoKMjcgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNDcgPj4Kc3RyZWFtCnicPU+5DQMxDOs9BRc4wHosW/NckOqyfxvKRlIIIkDxkWVHxwpcYgKTjjkSL2k/+GkagVgGNUf0hIphWOBukgIPgyxKV54tXgyR2kJdSPjWEN6tTGSiPK8RO3AnF6MHPlQbWR56QDtEFVmuScNY1VZdap2wAhyyzsJ1PcyqBOXRJ2spH1BUQr10/5972vsLAG8v6wplbmRzdHJlYW0KZW5kb2JqCjI4IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ5ID4+CnN0cmVhbQp4nDWPSw4DIQxD9zmFLzBSfoRwHqqupvffNmFaCQkL2y/BFoORjEtMYOyYY+ElVE+tPiQjj7pJORCpUDcET2hMDDNs0iXwynTfMp5bvJxW6oJOSOTprDYaooxmXsPRU84Km/7L3CRqZUaZAzLrVLcTsrJgBeYFtTz3M+6oXOiEh53KsOhOMaLcZkYafv/b9P4CezIwYwplbmRzdHJlYW0KZW5kb2JqCjI5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggNDkgPj4Kc3RyZWFtCnicMza0UDBQMDQwB5JGhkCWkYlCiiEXSADEzOWCCeaAWQZAGqI4B64mhysNAMboDSYKZW5kc3RyZWFtCmVuZG9iagozMCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDMxNyA+PgpzdHJlYW0KeJw1UktyQzEI279TcIHOmL99nnSyau6/rYQnK7AtQEIuL1nSS37UJdulw+RXH/clsUI+j+2azFLF9xazFM8tr0fPEbctCgRREz34MicVItTP1Og6eGGXPgOvEE4pFngHkwAGr+FfeJROg8A7GzLeEZORGhAkwZpLi01IlD1J/Cvl9aSVNHR+Jitz+XtyqRRqo8kIFSBYudgHpCspHiQTPYlIsnK9N1aI3pBXksdnJSYZEN0msU20wOPclbSEmZhCBeZYgNV0s7r6HExY47CE8SphFtWDTZ41qYRmtI5jZMN498JMiYWGwxJQm32VCaqXj9PcCSOmR0127cKyWzbvIUSj+TMslMHHKCQBh05jJArSsIARgTm9sIq95gs5FsCIZZ2aLAxtaCW7eo6FwNCcs6Vhxtee1/P+B0Vbe6MKZW5kc3RyZWFtCmVuZG9iagozMSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI0OCA+PgpzdHJlYW0KeJwtUTmSA0EIy+cVekJz0++xy5H3/+kKygGDhkMgOi1xUMZPEJYr3vLIVbTh75kYwXfBod/KdRsWORAVSNIYVE2oXbwevQd2HGYC86Q1LIMZ6wM/Ywo3enF4TMbZ7XUZNQR712tPZlAyKxdxycQFU3XYyJnDT6aMC+1czw3IuRHWZRikm5XGjIQjTSFSSKHqJqkzQZAEo6tRo40cxX7pyyOdYVUjagz7XEvb13MTzho0OxarPDmlR1ecy8nFCysH/bzNwEVUGqs8EBJwv9tD/Zzs5Dfe0rmzxfT4XnOyvDAVWPHmtRuQTbX4Ny/i+D3j6/n8A6ilWxYKZW5kc3RyZWFtCmVuZG9iagozMiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDIxMCA+PgpzdHJlYW0KeJw1UMsNQzEIu2cKFqgUAoFknla9df9rbdA7YRH/QljIlAh5qcnOKelLPjpMD7Yuv7EiC611JezKmiCeK++hmbKx0djiYHAaJl6AFjdg6GmNGjV04YKmLpVCgcUl8Jl8dXvovk8ZeGoZcnYEEUPJYAlquhZNWLQ8n5BOAeL/fsPuLeShkvPKnhv5G5zt8DuzbuEnanYi0XIVMtSzNMcYCBNFHjx5RaZw4rPWd9U0EtRmC06WAa5OP4wOAGAiXlmA7K5EOUvSjqWfb7zH9w9AAFO0CmVuZHN0cmVhbQplbmRvYmoKMTkgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zIC9DaGFyUHJvY3MgMjAgMCBSCi9FbmNvZGluZyA8PAovRGlmZmVyZW5jZXMgWyA0MCAvcGFyZW5sZWZ0IC9wYXJlbnJpZ2h0IDQ2IC9wZXJpb2QgNDggL3plcm8gL29uZSAvdHdvIDUyIC9mb3VyIC9maXZlCi9zaXggNTYgL2VpZ2h0IF0KL1R5cGUgL0VuY29kaW5nID4+Ci9GaXJzdENoYXIgMCAvRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250RGVzY3JpcHRvciAxOCAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2FucwovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxNyAwIFIgPj4KZW5kb2JqCjE4IDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyAzMgovRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250TmFtZSAvRGVqYVZ1U2FucyAvSXRhbGljQW5nbGUgMAovTWF4V2lkdGggMTM0MiAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTcgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM0MiA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDIzIDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxMiA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjEyIDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDUKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk4MiA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMjAgMCBvYmoKPDwgL2VpZ2h0IDIyIDAgUiAvZml2ZSAyMyAwIFIgL2ZvdXIgMjQgMCBSIC9vbmUgMjYgMCBSIC9wYXJlbmxlZnQgMjcgMCBSCi9wYXJlbnJpZ2h0IDI4IDAgUiAvcGVyaW9kIDI5IDAgUiAvc2l4IDMwIDAgUiAvdHdvIDMxIDAgUiAvemVybyAzMiAwIFIgPj4KZW5kb2JqCjMgMCBvYmoKPDwgL0YxIDE5IDAgUiAvRjIgMTQgMCBSID4+CmVuZG9iago0IDAgb2JqCjw8IC9BMSA8PCAvQ0EgMCAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+Ci9BMiA8PCAvQ0EgMSAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+ID4+CmVuZG9iago1IDAgb2JqCjw8ID4+CmVuZG9iago2IDAgb2JqCjw8ID4+CmVuZG9iago3IDAgb2JqCjw8IC9EZWphVnVTYW5zLUxhbWJkYSAyMSAwIFIgL0RlamFWdVNhbnMtbWludXMgMjUgMCBSID4+CmVuZG9iagoyIDAgb2JqCjw8IC9Db3VudCAxIC9LaWRzIFsgMTAgMCBSIF0gL1R5cGUgL1BhZ2VzID4+CmVuZG9iagozMyAwIG9iago8PCAvQ3JlYXRpb25EYXRlIChEOjIwMTkwNTE2MTgzNzUyKzAyJzAwJykKL0NyZWF0b3IgKG1hdHBsb3RsaWIgMy4wLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZykKL1Byb2R1Y2VyIChtYXRwbG90bGliIHBkZiBiYWNrZW5kIDMuMC4zKSA+PgplbmRvYmoKeHJlZgowIDM0CjAwMDAwMDAwMDAgNjU1MzUgZiAKMDAwMDAwMDAxNiAwMDAwMCBuIAowMDAwMDA5MTM0IDAwMDAwIG4gCjAwMDAwMDg4NzggMDAwMDAgbiAKMDAwMDAwODkyMSAwMDAwMCBuIAowMDAwMDA5MDIwIDAwMDAwIG4gCjAwMDAwMDkwNDEgMDAwMDAgbiAKMDAwMDAwOTA2MiAwMDAwMCBuIAowMDAwMDAwMDY1IDAwMDAwIG4gCjAwMDAwMDAzOTcgMDAwMDAgbiAKMDAwMDAwMDIwOCAwMDAwMCBuIAowMDAwMDAyMTg1IDAwMDAwIG4gCjAwMDAwMDI5ODEgMDAwMDAgbiAKMDAwMDAwMjc3MyAwMDAwMCBuIAowMDAwMDAyNDU3IDAwMDAwIG4gCjAwMDAwMDQwMzQgMDAwMDAgbiAKMDAwMDAwMjIwNiAwMDAwMCBuIAowMDAwMDA3NjYyIDAwMDAwIG4gCjAwMDAwMDc0NjIgMDAwMDAgbiAKMDAwMDAwNzA4MyAwMDAwMCBuIAowMDAwMDA4NzE1IDAwMDAwIG4gCjAwMDAwMDQwNjYgMDAwMDAgbiAKMDAwMDAwNDI1NyAwMDAwMCBuIAowMDAwMDA0NzIyIDAwMDAwIG4gCjAwMDAwMDUwNDIgMDAwMDAgbiAKMDAwMDAwNTIwNCAwMDAwMCBuIAowMDAwMDA1Mzc0IDAwMDAwIG4gCjAwMDAwMDU1MjYgMDAwMDAgbiAKMDAwMDAwNTc0NiAwMDAwMCBuIAowMDAwMDA1OTY4IDAwMDAwIG4gCjAwMDAwMDYwODkgMDAwMDAgbiAKMDAwMDAwNjQ3OSAwMDAwMCBuIAowMDAwMDA2ODAwIDAwMDAwIG4gCjAwMDAwMDkxOTQgMDAwMDAgbiAKdHJhaWxlcgo8PCAvSW5mbyAzMyAwIFIgL1Jvb3QgMSAwIFIgL1NpemUgMzQgPj4Kc3RhcnR4cmVmCjkzNDgKJSVFT0YK\n",
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
"<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
" \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
"<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
"<svg height=\"308.07225pt\" version=\"1.1\" viewBox=\"0 0 391.612969 308.07225\" width=\"391.612969pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
" <defs>\n",
" <style type=\"text/css\">\n",
"*{stroke-linecap:butt;stroke-linejoin:round;}\n",
" </style>\n",
" </defs>\n",
" <g id=\"figure_1\">\n",
" <g id=\"patch_1\">\n",
" <path d=\"M 0 308.07225 \n",
"L 391.612969 308.07225 \n",
"L 391.612969 0 \n",
"L 0 0 \n",
"z\n",
"\" style=\"fill:#ffffff;\"/>\n",
" </g>\n",
" <g id=\"axes_1\">\n",
" <g id=\"patch_2\">\n",
" <path d=\"M 19.341406 282.612 \n",
"L 376.461406 282.612 \n",
"L 376.461406 16.5 \n",
"L 19.341406 16.5 \n",
"z\n",
"\" style=\"fill:#ffffff;\"/>\n",
" </g>\n",
" <g id=\"matplotlib.axis_1\">\n",
" <g id=\"xtick_1\">\n",
" <g id=\"line2d_1\">\n",
" <defs>\n",
" <path d=\"M 0 0 \n",
"L 0 3.5 \n",
"\" id=\"m1e1d50d76d\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
" </defs>\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"19.341406\" xlink:href=\"#m1e1d50d76d\" y=\"270.516\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_1\">\n",
" <!-- −2.0 -->\n",
" <defs>\n",
" <path d=\"M 10.59375 35.5 \n",
"L 73.1875 35.5 \n",
"L 73.1875 27.203125 \n",
"L 10.59375 27.203125 \n",
"z\n",
"\" id=\"DejaVuSans-8722\"/>\n",
" <path d=\"M 19.1875 8.296875 \n",
"L 53.609375 8.296875 \n",
"L 53.609375 0 \n",
"L 7.328125 0 \n",
"L 7.328125 8.296875 \n",
"Q 12.9375 14.109375 22.625 23.890625 \n",
"Q 32.328125 33.6875 34.8125 36.53125 \n",
"Q 39.546875 41.84375 41.421875 45.53125 \n",
"Q 43.3125 49.21875 43.3125 52.78125 \n",
"Q 43.3125 58.59375 39.234375 62.25 \n",
"Q 35.15625 65.921875 28.609375 65.921875 \n",
"Q 23.96875 65.921875 18.8125 64.3125 \n",
"Q 13.671875 62.703125 7.8125 59.421875 \n",
"L 7.8125 69.390625 \n",
"Q 13.765625 71.78125 18.9375 73 \n",
"Q 24.125 74.21875 28.421875 74.21875 \n",
"Q 39.75 74.21875 46.484375 68.546875 \n",
"Q 53.21875 62.890625 53.21875 53.421875 \n",
"Q 53.21875 48.921875 51.53125 44.890625 \n",
"Q 49.859375 40.875 45.40625 35.40625 \n",
"Q 44.1875 33.984375 37.640625 27.21875 \n",
"Q 31.109375 20.453125 19.1875 8.296875 \n",
"z\n",
"\" id=\"DejaVuSans-50\"/>\n",
" <path d=\"M 10.6875 12.40625 \n",
"L 21 12.40625 \n",
"L 21 0 \n",
"L 10.6875 0 \n",
"z\n",
"\" id=\"DejaVuSans-46\"/>\n",
" <path d=\"M 31.78125 66.40625 \n",
"Q 24.171875 66.40625 20.328125 58.90625 \n",
"Q 16.5 51.421875 16.5 36.375 \n",
"Q 16.5 21.390625 20.328125 13.890625 \n",
"Q 24.171875 6.390625 31.78125 6.390625 \n",
"Q 39.453125 6.390625 43.28125 13.890625 \n",
"Q 47.125 21.390625 47.125 36.375 \n",
"Q 47.125 51.421875 43.28125 58.90625 \n",
"Q 39.453125 66.40625 31.78125 66.40625 \n",
"z\n",
"M 31.78125 74.21875 \n",
"Q 44.046875 74.21875 50.515625 64.515625 \n",
"Q 56.984375 54.828125 56.984375 36.375 \n",
"Q 56.984375 17.96875 50.515625 8.265625 \n",
"Q 44.046875 -1.421875 31.78125 -1.421875 \n",
"Q 19.53125 -1.421875 13.0625 8.265625 \n",
"Q 6.59375 17.96875 6.59375 36.375 \n",
"Q 6.59375 54.828125 13.0625 64.515625 \n",
"Q 19.53125 74.21875 31.78125 74.21875 \n",
"z\n",
"\" id=\"DejaVuSans-48\"/>\n",
" </defs>\n",
" <g transform=\"translate(7.2 285.114437)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"179.199219\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_2\">\n",
" <g id=\"line2d_2\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"63.981406\" xlink:href=\"#m1e1d50d76d\" y=\"270.516\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_2\">\n",
" <!-- −1.5 -->\n",
" <defs>\n",
" <path d=\"M 12.40625 8.296875 \n",
"L 28.515625 8.296875 \n",
"L 28.515625 63.921875 \n",
"L 10.984375 60.40625 \n",
"L 10.984375 69.390625 \n",
"L 28.421875 72.90625 \n",
"L 38.28125 72.90625 \n",
"L 38.28125 8.296875 \n",
"L 54.390625 8.296875 \n",
"L 54.390625 0 \n",
"L 12.40625 0 \n",
"z\n",
"\" id=\"DejaVuSans-49\"/>\n",
" <path d=\"M 10.796875 72.90625 \n",
"L 49.515625 72.90625 \n",
"L 49.515625 64.59375 \n",
"L 19.828125 64.59375 \n",
"L 19.828125 46.734375 \n",
"Q 21.96875 47.46875 24.109375 47.828125 \n",
"Q 26.265625 48.1875 28.421875 48.1875 \n",
"Q 40.625 48.1875 47.75 41.5 \n",
"Q 54.890625 34.8125 54.890625 23.390625 \n",
"Q 54.890625 11.625 47.5625 5.09375 \n",
"Q 40.234375 -1.421875 26.90625 -1.421875 \n",
"Q 22.3125 -1.421875 17.546875 -0.640625 \n",
"Q 12.796875 0.140625 7.71875 1.703125 \n",
"L 7.71875 11.625 \n",
"Q 12.109375 9.234375 16.796875 8.0625 \n",
"Q 21.484375 6.890625 26.703125 6.890625 \n",
"Q 35.15625 6.890625 40.078125 11.328125 \n",
"Q 45.015625 15.765625 45.015625 23.390625 \n",
"Q 45.015625 31 40.078125 35.4375 \n",
"Q 35.15625 39.890625 26.703125 39.890625 \n",
"Q 22.75 39.890625 18.8125 39.015625 \n",
"Q 14.890625 38.140625 10.796875 36.28125 \n",
"z\n",
"\" id=\"DejaVuSans-53\"/>\n",
" </defs>\n",
" <g transform=\"translate(51.84 285.114437)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"179.199219\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_3\">\n",
" <g id=\"line2d_3\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"108.621406\" xlink:href=\"#m1e1d50d76d\" y=\"270.516\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_3\">\n",
" <!-- −1.0 -->\n",
" <g transform=\"translate(96.48 285.114437)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"179.199219\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_4\">\n",
" <g id=\"line2d_4\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"153.261406\" xlink:href=\"#m1e1d50d76d\" y=\"270.516\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_4\">\n",
" <!-- −0.5 -->\n",
" <g transform=\"translate(141.12 285.114437)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"179.199219\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_5\">\n",
" <g id=\"line2d_5\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"197.901406\" xlink:href=\"#m1e1d50d76d\" y=\"270.516\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_5\">\n",
" <!-- 0.0 -->\n",
" <g transform=\"translate(189.949844 285.114437)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_6\">\n",
" <g id=\"line2d_6\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"242.541406\" xlink:href=\"#m1e1d50d76d\" y=\"270.516\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_6\">\n",
" <!-- 0.5 -->\n",
" <g transform=\"translate(234.589844 285.114437)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_7\">\n",
" <g id=\"line2d_7\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"287.181406\" xlink:href=\"#m1e1d50d76d\" y=\"270.516\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_7\">\n",
" <!-- 1.0 -->\n",
" <g transform=\"translate(279.229844 285.114437)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_8\">\n",
" <g id=\"line2d_8\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"331.821406\" xlink:href=\"#m1e1d50d76d\" y=\"270.516\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_8\">\n",
" <!-- 1.5 -->\n",
" <g transform=\"translate(323.869844 285.114437)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_9\">\n",
" <g id=\"line2d_9\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"376.461406\" xlink:href=\"#m1e1d50d76d\" y=\"270.516\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_9\">\n",
" <!-- 2.0 -->\n",
" <g transform=\"translate(368.509844 285.114437)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_10\">\n",
" <!-- $t$ -->\n",
" <defs>\n",
" <path d=\"M 42.28125 54.6875 \n",
"L 40.921875 47.703125 \n",
"L 23 47.703125 \n",
"L 17.1875 18.015625 \n",
"Q 16.890625 16.359375 16.75 15.234375 \n",
"Q 16.609375 14.109375 16.609375 13.484375 \n",
"Q 16.609375 10.359375 18.484375 8.9375 \n",
"Q 20.359375 7.515625 24.515625 7.515625 \n",
"L 33.59375 7.515625 \n",
"L 32.078125 0 \n",
"L 23.484375 0 \n",
"Q 15.484375 0 11.546875 3.125 \n",
"Q 7.625 6.25 7.625 12.59375 \n",
"Q 7.625 13.71875 7.765625 15.0625 \n",
"Q 7.90625 16.40625 8.203125 18.015625 \n",
"L 14.015625 47.703125 \n",
"L 6.390625 47.703125 \n",
"L 7.8125 54.6875 \n",
"L 15.28125 54.6875 \n",
"L 18.3125 70.21875 \n",
"L 27.296875 70.21875 \n",
"L 24.3125 54.6875 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-116\"/>\n",
" </defs>\n",
" <g transform=\"translate(374.461406 298.792562)scale(0.1 -0.1)\">\n",
" <use transform=\"translate(0 0.78125)\" xlink:href=\"#DejaVuSans-Oblique-116\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"matplotlib.axis_2\">\n",
" <g id=\"ytick_1\">\n",
" <g id=\"line2d_10\">\n",
" <defs>\n",
" <path d=\"M 0 0 \n",
"L -3.5 0 \n",
"\" id=\"m55750aa264\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
" </defs>\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"197.901406\" xlink:href=\"#m55750aa264\" y=\"270.516\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_11\">\n",
" <!-- 0.0 -->\n",
" <g transform=\"translate(174.998281 274.315219)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_2\">\n",
" <g id=\"line2d_11\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"197.901406\" xlink:href=\"#m55750aa264\" y=\"222.127608\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_12\">\n",
" <!-- 0.2 -->\n",
" <g transform=\"translate(174.998281 225.926827)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-50\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_3\">\n",
" <g id=\"line2d_12\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"197.901406\" xlink:href=\"#m55750aa264\" y=\"173.739217\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_13\">\n",
" <!-- 0.4 -->\n",
" <defs>\n",
" <path d=\"M 37.796875 64.3125 \n",
"L 12.890625 25.390625 \n",
"L 37.796875 25.390625 \n",
"z\n",
"M 35.203125 72.90625 \n",
"L 47.609375 72.90625 \n",
"L 47.609375 25.390625 \n",
"L 58.015625 25.390625 \n",
"L 58.015625 17.1875 \n",
"L 47.609375 17.1875 \n",
"L 47.609375 0 \n",
"L 37.796875 0 \n",
"L 37.796875 17.1875 \n",
"L 4.890625 17.1875 \n",
"L 4.890625 26.703125 \n",
"z\n",
"\" id=\"DejaVuSans-52\"/>\n",
" </defs>\n",
" <g transform=\"translate(174.998281 177.538435)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-52\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_4\">\n",
" <g id=\"line2d_13\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"197.901406\" xlink:href=\"#m55750aa264\" y=\"125.350825\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_14\">\n",
" <!-- 0.6 -->\n",
" <defs>\n",
" <path d=\"M 33.015625 40.375 \n",
"Q 26.375 40.375 22.484375 35.828125 \n",
"Q 18.609375 31.296875 18.609375 23.390625 \n",
"Q 18.609375 15.53125 22.484375 10.953125 \n",
"Q 26.375 6.390625 33.015625 6.390625 \n",
"Q 39.65625 6.390625 43.53125 10.953125 \n",
"Q 47.40625 15.53125 47.40625 23.390625 \n",
"Q 47.40625 31.296875 43.53125 35.828125 \n",
"Q 39.65625 40.375 33.015625 40.375 \n",
"z\n",
"M 52.59375 71.296875 \n",
"L 52.59375 62.3125 \n",
"Q 48.875 64.0625 45.09375 64.984375 \n",
"Q 41.3125 65.921875 37.59375 65.921875 \n",
"Q 27.828125 65.921875 22.671875 59.328125 \n",
"Q 17.53125 52.734375 16.796875 39.40625 \n",
"Q 19.671875 43.65625 24.015625 45.921875 \n",
"Q 28.375 48.1875 33.59375 48.1875 \n",
"Q 44.578125 48.1875 50.953125 41.515625 \n",
"Q 57.328125 34.859375 57.328125 23.390625 \n",
"Q 57.328125 12.15625 50.6875 5.359375 \n",
"Q 44.046875 -1.421875 33.015625 -1.421875 \n",
"Q 20.359375 -1.421875 13.671875 8.265625 \n",
"Q 6.984375 17.96875 6.984375 36.375 \n",
"Q 6.984375 53.65625 15.1875 63.9375 \n",
"Q 23.390625 74.21875 37.203125 74.21875 \n",
"Q 40.921875 74.21875 44.703125 73.484375 \n",
"Q 48.484375 72.75 52.59375 71.296875 \n",
"z\n",
"\" id=\"DejaVuSans-54\"/>\n",
" </defs>\n",
" <g transform=\"translate(174.998281 129.150044)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-54\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_5\">\n",
" <g id=\"line2d_14\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"197.901406\" xlink:href=\"#m55750aa264\" y=\"76.962433\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_15\">\n",
" <!-- 0.8 -->\n",
" <defs>\n",
" <path d=\"M 31.78125 34.625 \n",
"Q 24.75 34.625 20.71875 30.859375 \n",
"Q 16.703125 27.09375 16.703125 20.515625 \n",
"Q 16.703125 13.921875 20.71875 10.15625 \n",
"Q 24.75 6.390625 31.78125 6.390625 \n",
"Q 38.8125 6.390625 42.859375 10.171875 \n",
"Q 46.921875 13.96875 46.921875 20.515625 \n",
"Q 46.921875 27.09375 42.890625 30.859375 \n",
"Q 38.875 34.625 31.78125 34.625 \n",
"z\n",
"M 21.921875 38.8125 \n",
"Q 15.578125 40.375 12.03125 44.71875 \n",
"Q 8.5 49.078125 8.5 55.328125 \n",
"Q 8.5 64.0625 14.71875 69.140625 \n",
"Q 20.953125 74.21875 31.78125 74.21875 \n",
"Q 42.671875 74.21875 48.875 69.140625 \n",
"Q 55.078125 64.0625 55.078125 55.328125 \n",
"Q 55.078125 49.078125 51.53125 44.71875 \n",
"Q 48 40.375 41.703125 38.8125 \n",
"Q 48.828125 37.15625 52.796875 32.3125 \n",
"Q 56.78125 27.484375 56.78125 20.515625 \n",
"Q 56.78125 9.90625 50.3125 4.234375 \n",
"Q 43.84375 -1.421875 31.78125 -1.421875 \n",
"Q 19.734375 -1.421875 13.25 4.234375 \n",
"Q 6.78125 9.90625 6.78125 20.515625 \n",
"Q 6.78125 27.484375 10.78125 32.3125 \n",
"Q 14.796875 37.15625 21.921875 38.8125 \n",
"z\n",
"M 18.3125 54.390625 \n",
"Q 18.3125 48.734375 21.84375 45.5625 \n",
"Q 25.390625 42.390625 31.78125 42.390625 \n",
"Q 38.140625 42.390625 41.71875 45.5625 \n",
"Q 45.3125 48.734375 45.3125 54.390625 \n",
"Q 45.3125 60.0625 41.71875 63.234375 \n",
"Q 38.140625 66.40625 31.78125 66.40625 \n",
"Q 25.390625 66.40625 21.84375 63.234375 \n",
"Q 18.3125 60.0625 18.3125 54.390625 \n",
"z\n",
"\" id=\"DejaVuSans-56\"/>\n",
" </defs>\n",
" <g transform=\"translate(174.998281 80.761652)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-56\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_6\">\n",
" <g id=\"line2d_15\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"197.901406\" xlink:href=\"#m55750aa264\" y=\"28.574041\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_16\">\n",
" <!-- 1.0 -->\n",
" <g transform=\"translate(174.998281 32.37326)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_17\">\n",
" <!-- $\\Lambda(t)$ -->\n",
" <defs>\n",
" <path d=\"M 11.1875 0 \n",
"L 0.78125 0 \n",
"L 28.609375 72.90625 \n",
"L 39.796875 72.90625 \n",
"L 67.578125 0 \n",
"L 57.328125 0 \n",
"L 34.1875 63.1875 \n",
"z\n",
"\" id=\"DejaVuSans-923\"/>\n",
" <path d=\"M 31 75.875 \n",
"Q 24.46875 64.65625 21.28125 53.65625 \n",
"Q 18.109375 42.671875 18.109375 31.390625 \n",
"Q 18.109375 20.125 21.3125 9.0625 \n",
"Q 24.515625 -2 31 -13.1875 \n",
"L 23.1875 -13.1875 \n",
"Q 15.875 -1.703125 12.234375 9.375 \n",
"Q 8.59375 20.453125 8.59375 31.390625 \n",
"Q 8.59375 42.28125 12.203125 53.3125 \n",
"Q 15.828125 64.359375 23.1875 75.875 \n",
"z\n",
"\" id=\"DejaVuSans-40\"/>\n",
" <path d=\"M 8.015625 75.875 \n",
"L 15.828125 75.875 \n",
"Q 23.140625 64.359375 26.78125 53.3125 \n",
"Q 30.421875 42.28125 30.421875 31.390625 \n",
"Q 30.421875 20.453125 26.78125 9.375 \n",
"Q 23.140625 -1.703125 15.828125 -13.1875 \n",
"L 8.015625 -13.1875 \n",
"Q 14.5 -2 17.703125 9.0625 \n",
"Q 20.90625 20.125 20.90625 31.390625 \n",
"Q 20.90625 42.671875 17.703125 53.65625 \n",
"Q 14.5 64.65625 8.015625 75.875 \n",
"z\n",
"\" id=\"DejaVuSans-41\"/>\n",
" </defs>\n",
" <g transform=\"translate(168.918594 25.8)rotate(-90)scale(0.1 -0.1)\">\n",
" <use transform=\"translate(0 0.125)\" xlink:href=\"#DejaVuSans-923\"/>\n",
" <use transform=\"translate(68.408203 0.125)\" xlink:href=\"#DejaVuSans-40\"/>\n",
" <use transform=\"translate(107.421875 0.125)\" xlink:href=\"#DejaVuSans-Oblique-116\"/>\n",
" <use transform=\"translate(146.630859 0.125)\" xlink:href=\"#DejaVuSans-41\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"LineCollection_1\">\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 19.341406 270.516 \n",
"L 25.119803 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 25.119803 270.516 \n",
"L 30.209113 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 30.209113 270.516 \n",
"L 35.910271 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 35.910271 270.516 \n",
"L 41.927074 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 41.927074 270.516 \n",
"L 48.234774 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 48.234774 270.516 \n",
"L 54.196887 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 54.196887 270.516 \n",
"L 59.031514 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 59.031514 270.516 \n",
"L 64.290357 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 64.290357 270.516 \n",
"L 69.438832 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 69.438832 270.516 \n",
"L 74.363738 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 74.363738 270.516 \n",
"L 79.100372 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 79.100372 270.516 \n",
"L 83.2816 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 83.2816 270.516 \n",
"L 87.904091 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 87.904091 270.516 \n",
"L 92.983146 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 92.983146 270.516 \n",
"L 98.220748 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 98.220748 270.516 \n",
"L 102.53154 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 102.53154 270.516 \n",
"L 108.456683 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 108.456683 270.516 \n",
"L 113.934061 256.119112 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 113.934061 256.119112 \n",
"L 119.135036 242.02487 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 119.135036 242.02487 \n",
"L 124.296955 228.036465 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 124.296955 228.036465 \n",
"L 131.403709 208.777705 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 131.403709 208.777705 \n",
"L 137.220534 193.014555 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 137.220534 193.014555 \n",
"L 143.711297 175.425084 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 143.711297 175.425084 \n",
"L 149.164564 160.647148 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 149.164564 160.647148 \n",
"L 154.022837 147.481601 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 154.022837 147.481601 \n",
"L 158.811106 134.505759 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 158.811106 134.505759 \n",
"L 163.377291 122.131748 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 163.377291 122.131748 \n",
"L 168.932208 107.078348 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 168.932208 107.078348 \n",
"L 174.312096 92.499265 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 174.312096 92.499265 \n",
"L 178.790609 80.362837 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 178.790609 80.362837 \n",
"L 184.725586 64.279505 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 184.725586 64.279505 \n",
"L 190.146349 49.589653 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 190.146349 49.589653 \n",
"L 196.320495 32.858191 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 196.320495 32.858191 \n",
"L 197.158029 30.588536 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 197.158029 30.588536 \n",
"L 197.674807 29.188107 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 197.674807 29.188107 \n",
"L 197.893303 28.596 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 197.893303 28.596 \n",
"L 197.950844 28.708015 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 197.950844 28.708015 \n",
"L 198.006789 28.859621 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 198.006789 28.859621 \n",
"L 198.143409 29.229849 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 198.143409 29.229849 \n",
"L 199.645866 33.301393 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 199.645866 33.301393 \n",
"L 203.186749 42.896914 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 203.186749 42.896914 \n",
"L 208.996789 58.641679 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 208.996789 58.641679 \n",
"L 213.947795 72.058526 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 213.947795 72.058526 \n",
"L 220.365747 89.450684 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 220.365747 89.450684 \n",
"L 228.021145 110.196226 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 228.021145 110.196226 \n",
"L 234.708394 128.318158 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 234.708394 128.318158 \n",
"L 240.92461 145.163627 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 240.92461 145.163627 \n",
"L 246.467426 160.184234 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 246.467426 160.184234 \n",
"L 252.91715 177.662492 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 252.91715 177.662492 \n",
"L 258.982045 194.097892 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 258.982045 194.097892 \n",
"L 266.39336 214.181987 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 266.39336 214.181987 \n",
"L 273.015761 232.128188 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 273.015761 232.128188 \n",
"L 278.553748 247.135707 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 278.553748 247.135707 \n",
"L 284.242183 262.550931 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 284.242183 262.550931 \n",
"L 287.296542 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 287.296542 270.516 \n",
"L 290.037353 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 290.037353 270.516 \n",
"L 295.809418 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 295.809418 270.516 \n",
"L 300.893959 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 300.893959 270.516 \n",
"L 306.338435 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 306.338435 270.516 \n",
"L 311.959743 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 311.959743 270.516 \n",
"L 317.756656 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 317.756656 270.516 \n",
"L 324.441507 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 324.441507 270.516 \n",
"L 330.170504 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 330.170504 270.516 \n",
"L 336.276177 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 336.276177 270.516 \n",
"L 340.567693 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 340.567693 270.516 \n",
"L 345.2678 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 345.2678 270.516 \n",
"L 350.727081 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 350.727081 270.516 \n",
"L 355.40554 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 355.40554 270.516 \n",
"L 361.413278 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 361.413278 270.516 \n",
"L 366.867619 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 366.867619 270.516 \n",
"L 371.697484 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa18adb9c5a)\" d=\"M 371.697484 270.516 \n",
"L 376.461406 270.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" </g>\n",
" <g id=\"patch_3\">\n",
" <path d=\"M 197.901406 270.516 \n",
"L 197.901406 28.574041 \n",
"\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
" </g>\n",
" <g id=\"patch_4\">\n",
" <path d=\"M 376.461406 282.612 \n",
"L 376.461406 16.5 \n",
"\" style=\"fill:none;\"/>\n",
" </g>\n",
" <g id=\"patch_5\">\n",
" <path d=\"M 19.341406 270.516 \n",
"L 376.461406 270.516 \n",
"\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
" </g>\n",
" <g id=\"patch_6\">\n",
" <path d=\"M 19.341406 16.5 \n",
"L 376.461406 16.5 \n",
"\" style=\"fill:none;\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <defs>\n",
" <clipPath id=\"pa18adb9c5a\">\n",
" <rect height=\"266.112\" width=\"357.12\" x=\"19.341406\" y=\"16.5\"/>\n",
" </clipPath>\n",
" </defs>\n",
"</svg>\n"
],
"text/plain": [
"<Figure size 614.4x460.8 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM4OC40MjYyNSAzMTcuNzYyOTcyNjgxNyBdIC9QYXJlbnQgMiAwIFIgL1Jlc291cmNlcyA4IDAgUgovVHlwZSAvUGFnZSA+PgplbmRvYmoKOSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDExIDAgUiA+PgpzdHJlYW0KeJylWFtvVDcQfj+/wo/wEOMZj2+PRdCIqmoFpBep9CFASIPYIAqUh6r/vd/4HO+e3Z0kSCTKZeeb8Yw9V5vc24ncpQvuLX6+uD/cn/j72pE7xc/lFPBpM8VavXDmhE/vVp8iFV8ytxJBDvsf/5qmN9OD77DIR0idTpOCkmtJjpOXFJQNSxfxNR+Q3+2RG/k0Vl0tsiYvynhWdgnTsR1fVxuCCYqsFojFJ4n4Z7Mmig+d+G6aHuJkvkwf8Du4k4A1i2fH7FtyrzbTwzP34HtyFNzZm6n6WGoL8wmdvZ7ucbjvzt5Oj88gH3zQJfA9/oH4g0cXb89//fz8/Prjyebq+vNH9+j99BTf3ewps4/10MwV8TYzE/kqX2sopW8zlELxgY8OdEW9zdSWvdSvNvUbz5RwMDkfmbqi3mYqiXhubY69rzP4W48WpxPDkb0r6pG9e/ZQi5640M5iNaofooNRsxKW4NtRQqyptyvhqDl/qCQdKKnJp6NwXlPvUFKaZ97TQAf7iDGA5VDFmnq7isgRBWdfxcEuVjVprWJFvUNFrj6FPRW83cUq0mIJPs4rYtulEi+x1kPJHYWST3FhWQfUzy/fXX34fHHyfnNxef51gcW+HlBvCKwSvYQe6DGOytljyx94ZaUJzm5cW5R9VTvynboqe4ocUqPQaNHHN+ojeCOSENV9hSv6nRoJ4ZOosESmyotKuVklLMytxcAHKnf0u1WW6ltg4RK5yKIy36iSI/lQRWreV7mi36kSmeW5lkwkMQ9H1ptVIhklN+T8gcod/W6VJflcIJGSpDxnm1/lgqbBiQY35eIjdwme2z2ymcqSDxneaQ01l2JBHkhfG4vtdN77t9dgip5Dz5K5Mr+418nRq+hSvcIsyUPy02DhUFvt6RAOFn9x/4Zl7v23Lf1Gvs52ar4+P3vy+0/vr3+5vnry6fzk8/XVY448J+uhIOGgK3NDdSDeW2SV9D+eb16+3mb7B3c8c83HF1NBa3Ccsyf8/fvC/eauHQYqTEwBCKVcM5wE70tevvSES0gwIiZu7tmpg+Z/rl5dPDt96F59XA9R1XNqJWmA9LJKUliLiuquvao8NwGwN09JWi29BuE/rgu7AaD4iidEOWnRxPGEIHlmtwCdY31mDi2qiQmdP8jCbgCbSVDcIiFrYwOREbozt0EHc0XCEQ4GrTO2GmTZp0HfTCn6ULKg6gl5hDCnhdsCwI6aELPkqNTEObW2sBsA5kREe0kpFaUiZFJZDtECwI5xPpRGs4kSQ+WF3QA2ExKxIieQcdg+N9Hs7OwWAHa4KyD34hIWdWzVAjYTSqXAD232cyulxZndAsBekJ+Ix+7mWENZFjfomwnzEBRWlFUYiMq1jRYLAHvxgjqcuysqI+QW7mO6TryCBEuIT0lweM6Lhww6mAl5hcOUbiXJ4p5jsrLmfqdKcAKcLZFGApkIBDBdhIqpQXSdLKXU5QRNRAWQuCEGSg4jbkwxJBkCBgKBiPklx4hKhbhIgtMam7UQFai+oINS9x1qCBJiCBgIBJBhmLT1bqcMhbHoImAhKtBwNdJMcJLhS4RtHgIGolO/9LGJyWXENibYka8mogLNN8wOsLSqCQG1dAgYCARyQiHVMujQWFFGMbosAWRDeg1FjGeCU52yVE4cR2iYkIogRyuGaFT4gNhFeanDGSYEEVhZaylIDowZSNlQ6tiKCakI2kUJuP2gjzQEEW7/wyEmpIOBtiiOEXTMs5quI6osZNNvKyIYfRrIyDAMeW1s3oTmqxDqTWpj+Mjza0AXsSAVQapg+pPSl0IxBOcQsSC0pEC97yGodQihmqUt4WtDKpJRdQICFYfCiHDmOvqYCUEE/V3wxfrEoHGn7WgRMSEVqVpmMz6Q7jEgV4dhJgQRdF0cinqV4OBMrLk6i5iQimhvRAMDHbd6DKU1bEUsSHs+uq82RnEFNSoh+8buLWS+buIehUkk9Uoc0uJGC1B2nCEStPbGJIFKKYPfQCCAk84o1Kh3/WpTUhgKLEQFqq8Y6RDK6Ajo2gjrIWAgEMha5vstAaUyYLCiJdxNBAJ6ycPdIhQtxqkQdrkIWIgKJM+ITvRLlPuK0aANDRay6Zfm2rCfpORUuG75j4H5No4oaVCGQ4wVMbOwG4AOamh+mIF0lkB2ImRGEzARFcgY+TFOzK4R1PqtgIFgWAusvtTBUweEgGvGGO4sRAU0gYPIPCLIrhqYCAS0+MI/iEasQzrfLHFqIhBA+kmLSCl1PqK9jJHQRFQAA3YWQthiayUiu2gIGIg+WBCKFUp1HwBx72wjpU1EBbRUVZ2LQI4VDaUNAQPRkRl5jio0T3V5VwAsQNlR1JFPKIV9Y3E72ZgIBNA/Mb3k2o8u6gPP2IGFQABtFlNUkJ6CWCSM3mIiKoCNodjMoyAMzWPqM5H9J5rt1aQLPHUfHLsf5ufvvffig7vNXU9x+5ff57uH7y/98dt85d7c+Mo9XW8fs7tRuoT5cG09SVn6zWfzW/U/nf4HD6DYDAplbmRzdHJlYW0KZW5kb2JqCjExIDAgb2JqCjE4ODIKZW5kb2JqCjE2IDAgb2JqCjw8IC9CQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE4MQovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJw1UDkOBCEM63mFP7ASucN7Rtpq9v/thjBToBgcBzuDSfEhwW9ENpCJFHiCw3GNZIgxiA2qAloO0yiClzS6B79cavUSKGaJpXpISyl1XOEMltjlGjL7LqYgXZAMSA25hpZ0o3uoHE5twglGeaS25gausyaXzza6//J2SvCIduOFj9PQfJxGZdxcpHWqCHpiRs3KPTZ6CUbctRyxnLXUUqRUizpRZbDVD3M2/+7xGt8/5jc/HgplbmRzdHJlYW0KZW5kb2JqCjE3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTc4ID4+CnN0cmVhbQp4nD2QSxIDIQhE956ijyA/0fMkldXk/ts0zpiF9hMobLCl6BjOy9WQXfGWVhie+DbvC56Jq6n1hyQVMvumDhmLZ/IUJyQUryZjQNyx1dajcTLCDLssJmZgroqvRC6oUALqUfJqZqPgaqaCvn3EVpn1FhcIRQImLGcr/p8D0+sWHQwWmO03y7M89grTdCzMe4Z5D0UjfgblWm5gZa2Dn4Ydmve2aCj/5Cd7Fni1zw/eq0KhCmVuZHN0cmVhbQplbmRvYmoKMTQgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zLU9ibGlxdWUgL0NoYXJQcm9jcyAxNSAwIFIKL0VuY29kaW5nIDw8IC9EaWZmZXJlbmNlcyBbIDExNiAvdCBdIC9UeXBlIC9FbmNvZGluZyA+PiAvRmlyc3RDaGFyIDAKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udERlc2NyaXB0b3IgMTMgMCBSCi9Gb250TWF0cml4IFsgMC4wMDEgMCAwIDAuMDAxIDAgMCBdIC9MYXN0Q2hhciAyNTUgL05hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxMiAwIFIgPj4KZW5kb2JqCjEzIDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyA5NgovRm9udEJCb3ggWyAtMTAxNiAtMzUxIDE2NjAgMTA2OCBdIC9Gb250TmFtZSAvRGVqYVZ1U2Fucy1PYmxpcXVlCi9JdGFsaWNBbmdsZSAwIC9NYXhXaWR0aCAxMzUwIC9TdGVtViAwIC9UeXBlIC9Gb250RGVzY3JpcHRvciAvWEhlaWdodCAwID4+CmVuZG9iagoxMiAwIG9iagpbIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwCjYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgMzE4IDQwMSA0NjAgODM4IDYzNgo5NTAgNzgwIDI3NSAzOTAgMzkwIDUwMCA4MzggMzE4IDM2MSAzMTggMzM3IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYKNjM2IDYzNiAzMzcgMzM3IDgzOCA4MzggODM4IDUzMSAxMDAwIDY4NCA2ODYgNjk4IDc3MCA2MzIgNTc1IDc3NSA3NTIgMjk1CjI5NSA2NTYgNTU3IDg2MyA3NDggNzg3IDYwMyA3ODcgNjk1IDYzNSA2MTEgNzMyIDY4NCA5ODkgNjg1IDYxMSA2ODUgMzkwIDMzNwozOTAgODM4IDUwMCA1MDAgNjEzIDYzNSA1NTAgNjM1IDYxNSAzNTIgNjM1IDYzNCAyNzggMjc4IDU3OSAyNzggOTc0IDYzNCA2MTIKNjM1IDYzNSA0MTEgNTIxIDM5MiA2MzQgNTkyIDgxOCA1OTIgNTkyIDUyNSA2MzYgMzM3IDYzNiA4MzggNjAwIDYzNiA2MDAgMzE4CjM1MiA1MTggMTAwMCA1MDAgNTAwIDUwMCAxMzUwIDYzNSA0MDAgMTA3MCA2MDAgNjg1IDYwMCA2MDAgMzE4IDMxOCA1MTggNTE4CjU5MCA1MDAgMTAwMCA1MDAgMTAwMCA1MjEgNDAwIDEwMjggNjAwIDUyNSA2MTEgMzE4IDQwMSA2MzYgNjM2IDYzNiA2MzYgMzM3CjUwMCA1MDAgMTAwMCA0NzEgNjE3IDgzOCAzNjEgMTAwMCA1MDAgNTAwIDgzOCA0MDEgNDAxIDUwMCA2MzYgNjM2IDMxOCA1MDAKNDAxIDQ3MSA2MTcgOTY5IDk2OSA5NjkgNTMxIDY4NCA2ODQgNjg0IDY4NCA2ODQgNjg0IDk3NCA2OTggNjMyIDYzMiA2MzIgNjMyCjI5NSAyOTUgMjk1IDI5NSA3NzUgNzQ4IDc4NyA3ODcgNzg3IDc4NyA3ODcgODM4IDc4NyA3MzIgNzMyIDczMiA3MzIgNjExIDYwOAo2MzAgNjEzIDYxMyA2MTMgNjEzIDYxMyA2MTMgOTk1IDU1MCA2MTUgNjE1IDYxNSA2MTUgMjc4IDI3OCAyNzggMjc4IDYxMiA2MzQKNjEyIDYxMiA2MTIgNjEyIDYxMiA4MzggNjEyIDYzNCA2MzQgNjM0IDYzNCA1OTIgNjM1IDU5MiBdCmVuZG9iagoxNSAwIG9iago8PCAvdCAxNyAwIFIgPj4KZW5kb2JqCjIyIDAgb2JqCjw8IC9CQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDU4Ci9TdWJ0eXBlIC9Gb3JtIC9UeXBlIC9YT2JqZWN0ID4+CnN0cmVhbQp4nOMyNDRSMFDI5bIAkjlcRhZmCuZGlkCWsaUFlGVmbgaWMzU3BtPGJkYKZsZGQBZEbw5XGgDSKg1wCmVuZHN0cmVhbQplbmRvYmoKMjMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNzkgPj4Kc3RyZWFtCnicPVI7ksUgDOtzCl+AGfAXzpOdrbL3b1eCvFdkrERGkh3SUroMDWkjVWIMqezyMy7CtlT+DiL7XD6/0NY60JyHo4uNCaAp96WrA3YVrZIWvusoMgTmENhommhOUXAKCbV92nCQh/oA6zIidr0vBiV6NrKtQ/Yg9hOpGVJBOfCOhFCEh82+Y/g4cTztzRNgTp4MOCN79TNOKV05YTkUMDK3wy2w3tdnX89GuYi85gdhDiLHInJiUxMMkkCxHF6OdPDUU6M2A+RRXDBRx2yxwM+9Zz7oMaRT6JHt2FwupF5k8IX52aHwYD+3AAYqqrWdBjtYvb+OY72GDb+P4VrkjtuKLRygTRcOxDvBEVnv7y15rt9/B3JuBgplbmRzdHJlYW0KZW5kb2JqCjI0IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjc2ID4+CnN0cmVhbQp4nD1SS47oMAjb5xRcIFL4Jj1PR7Pqu//22bSaFRZgY0jKS5aopUwtk1SVXUt+dHTuMvk3NK9Gz7D15sxD5kmxODK3yj0M5JlbrNBrb9SrCwCxSO7UEtslxpZLxZJkh6ztEHdk0OHFKtnM+NrCDjdrjkdSFypepwcF+Yww8E7Mfb6JZSE0Vxltt8BBDxaoAz0wCxO5IuPdaxM9jXgLoKwPmb+ILjfUXI9sTIBTuNoL3qmU1jEPFYmiHOxGGr2fo+Y4ocPbPWI59nIJRwbe4mjHe/BFiJ5GVkSsfsizEfmGDalIj5jKG+puH3r8ja3YaH92JknB11/W20w10rng1Fyt1l+DR2jw3qjh8/dLnvH7HyEmbhIKZW5kc3RyZWFtCmVuZG9iagoyNSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDM5MiA+PgpzdHJlYW0KeJw9UktuBTEI288puECl8E1ynqne7t1/W5vMVKoKLwO2MZSXDKklP+qSiDNMfvVyXeJR8r1samfmIe4uNqb4WHJfuobYctGaYrFPHMkvyLRUWKFW3aND8YUoEw8ALeCBBeG+HP/xF6jB17CFcsN7ZAJgStRuQMZD0RlIWUERYfuRFeikUK9s4e8oIFfUrIWhdGKIDZYAKb6rDYmYqNmgh4SVkqod0vGMpPBbwV2JYVBbW9sEeGbQENnekY0RM+3RGXFZEWs/PemjUTK1URkPTWd88d0yUvPRFeik0sjdykNnz0InYCTmSZjncCPhnttBCzH0ca+WT2z3mClWkfAFO8oBA7393pKNz3vgLIxc2+xMJ/DRaaccE62+HmL9gz9sS5tcxyuHRRSovCgIftdBE3F8WMX3ZKNEd7QB1iMT1WglEAwSws7tMPJ4xnnZ3hW05vREaKNEHtSOET0ossXlnBWwp/yszbEcng8me2+0j5TMzKiEFdR2eqi2z2Md1Hee+/r8AS4AoRkKZW5kc3RyZWFtCmVuZG9iagoyNiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI0NyA+PgpzdHJlYW0KeJxNUbttRDEM698UXOAA62t5ngtSXfZvQ8kIkMIgoS8ppyUW9sZLDOEHWw++5JFVQ38ePzHsMyw9yeTUP+a5yVQUvhWqm5hQF2Lh/WgEvBZ0LyIrygffj2UMc8734KMQl2AmNGCsb0kmF9W8M2TCiaGOw0GbVBh3TRQsrhXNM8jtVjeyOrMgbHglE+LGAEQE2ReQzWCjjLGVkMVyHqgKkgVaYNfpG1GLgiuU1gl0otbEuszgq+f2djdDL/LgqLp4fQzrS7DC6KV7LHyuQh/M9Ew7d0kjvfCmExFmDwVSmZ2RlTo9Yn23QP+fZSv4+8nP8/0LFShcKgplbmRzdHJlYW0KZW5kb2JqCjI3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggOTAgPj4Kc3RyZWFtCnicTY1BEsAgCAPvvCJPUETQ/3R60v9fq9QOvcBOAokWRYL0NWpLMO64MhVrUCmYlJfAVTBcC9ruosr+MklMnYbTe7cDg7LxcYPSSfv2cXoAq/16Bt0P0hwiWAplbmRzdHJlYW0KZW5kb2JqCjI4IDAgb2JqCjw8IC9CQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDM3Ci9TdWJ0eXBlIC9Gb3JtIC9UeXBlIC9YT2JqZWN0ID4+CnN0cmVhbQp4nOMyNDBTMDY1VcjlMjc2ArNywCwjcyMgCySLYEFk0wABXwoKCmVuZHN0cmVhbQplbmRvYmoKMjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA4MCA+PgpzdHJlYW0KeJxFjLsNwDAIRHumYAR+JmafKJWzfxsgStxwT7p7uDoSMlPeYYaHBJ4MLIZT8QaZo2A1uEZSjZ3so7BuX3WB5npTq/X3BypPdnZxPc3LGfQKZW5kc3RyZWFtCmVuZG9iagozMCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE0NyA+PgpzdHJlYW0KeJw9T7kNAzEM6z0FFzjAeixb81yQ6rJ/G8pGUggiQPGRZUfHClxiApOOORIvaT/4aRqBWAY1R/SEimFY4G6SAg+DLEpXni1eDJHaQl1I+NYQ3q1MZKI8rxE7cCcXowc+VBtZHnpAO0QVWa5Jw1jVVl1qnbACHLLOwnU9zKoE5dEnaykfUFRCvXT/n3va+wsAby/rCmVuZHN0cmVhbQplbmRvYmoKMzEgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNDkgPj4Kc3RyZWFtCnicNY9LDgMhDEP3OYUvMFJ+hHAeqq6m9982YVoJCQvbL8EWg5GMS0xg7Jhj4SVUT60+JCOPukk5EKlQNwRPaEwMM2zSJfDKdN8ynlu8nFbqgk5I5OmsNhqijGZew9FTzgqb/svcJGplRpkDMutUtxOysmAF5gW1PPcz7qhc6ISHncqw6E4xotxmRhp+/9v0/gJ7MjBjCmVuZHN0cmVhbQplbmRvYmoKMzIgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA0OSA+PgpzdHJlYW0KeJwzNrRQMFAwNDAHkkaGQJaRiUKKIRdIAMTM5YIJ5oBZBkAaojgHriaHKw0AxugNJgplbmRzdHJlYW0KZW5kb2JqCjMzIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzE3ID4+CnN0cmVhbQp4nDVSS3JDMQjbv1Nwgc6Yv32edLJq7r+thCcrsC1AQi4vWdJLftQl26XD5Fcf9yWxQj6P7ZrMUsX3FrMUzy2vR88Rty0KBFETPfgyJxUi1M/U6Dp4YZc+A68QTikWeAeTAAav4V94lE6DwDsbMt4Rk5EaECTBmkuLTUiUPUn8K+X1pJU0dH4mK3P5e3KpFGqjyQgVIFi52AekKykeJBM9iUiycr03VojekFeSx2clJhkQ3SaxTbTA49yVtISZmEIF5liA1XSzuvocTFjjsITxKmEW1YNNnjWphGa0jmNkw3j3wkyJhYbDElCbfZUJqpeP09wJI6ZHTXbtwrJbNu8hRKP5MyyUwccoJAGHTmMkCtKwgBGBOb2wir3mCzkWwIhlnZosDG1oJbt6joXA0JyzpWHG157X8/4HRVt7owplbmRzdHJlYW0KZW5kb2JqCjM0IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjQ4ID4+CnN0cmVhbQp4nC1ROZIDQQjL5xV6QnPT77HLkff/6QrKAYOGQyA6LXFQxk8Qlive8shVtOHvmRjBd8Gh38p1GxY5EBVI0hhUTahdvB69B3YcZgLzpDUsgxnrAz9jCjd6cXhMxtntdRk1BHvXa09mUDIrF3HJxAVTddjImcNPpowL7VzPDci5EdZlGKSblcaMhCNNIVJIoeomqTNBkASjq1GjjRzFfunLI51hVSNqDPtcS9vXcxPOGjQ7Fqs8OaVHV5zLycULKwf9vM3ARVQaqzwQEnC/20P9nOzkN97SubPF9Phec7K8MBVY8ea1G5BNtfg3L+L4PePr+fwDqKVbFgplbmRzdHJlYW0KZW5kb2JqCjM1IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjEwID4+CnN0cmVhbQp4nDVQyw1DMQi7ZwoWqBQCgWSeVr11/2tt0DthEf9CWMiUCHmpyc4p6Us+OkwPti6/sSILrXUl7MqaIJ4r76GZsrHR2OJgcBomXoAWN2DoaY0aNXThgqYulUKBxSXwmXx1e+i+Txl4ahlydgQRQ8lgCWq6Fk1YtDyfkE4B4v9+w+4t5KGS88qeG/kbnO3wO7Nu4SdqdiLRchUy1LM0xxgIE0UePHlFpnDis9Z31TQS1GYLTpYBrk4/jA4AYCJeWYDsrkQ5S9KOpZ9vvMf3D0AAU7QKZW5kc3RyZWFtCmVuZG9iagoyMCAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMgL0NoYXJQcm9jcyAyMSAwIFIKL0VuY29kaW5nIDw8Ci9EaWZmZXJlbmNlcyBbIDQwIC9wYXJlbmxlZnQgL3BhcmVucmlnaHQgNDYgL3BlcmlvZCA0OCAvemVybyAvb25lIC90d28gNTIgL2ZvdXIgL2ZpdmUKL3NpeCA1NiAvZWlnaHQgMTIzIC9icmFjZWxlZnQgMTI1IC9icmFjZXJpZ2h0IF0KL1R5cGUgL0VuY29kaW5nID4+Ci9GaXJzdENoYXIgMCAvRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250RGVzY3JpcHRvciAxOSAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2FucwovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxOCAwIFIgPj4KZW5kb2JqCjE5IDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyAzMgovRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250TmFtZSAvRGVqYVZ1U2FucyAvSXRhbGljQW5nbGUgMAovTWF4V2lkdGggMTM0MiAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTggMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM0MiA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDIzIDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxMiA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjEyIDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDUKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk4MiA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMjEgMCBvYmoKPDwgL2JyYWNlbGVmdCAyMyAwIFIgL2JyYWNlcmlnaHQgMjQgMCBSIC9laWdodCAyNSAwIFIgL2ZpdmUgMjYgMCBSCi9mb3VyIDI3IDAgUiAvb25lIDI5IDAgUiAvcGFyZW5sZWZ0IDMwIDAgUiAvcGFyZW5yaWdodCAzMSAwIFIKL3BlcmlvZCAzMiAwIFIgL3NpeCAzMyAwIFIgL3R3byAzNCAwIFIgL3plcm8gMzUgMCBSID4+CmVuZG9iago0MCAwIG9iago8PCAvQkJveCBbIC0xNDEgLTI0MCAxMTI4IDc5NSBdIC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzgxCi9TdWJ0eXBlIC9Gb3JtIC9UeXBlIC9YT2JqZWN0ID4+CnN0cmVhbQp4nDWTuXEGMQhG862CEsQpqZ5/xpHdf+oHa0cwy/EdaJ+8kh7y84RLpsn3c5fkLVHfUpaix6Viyecxu1IZYkelysT9TPw8fnOyiCAuiVN0bippe2ay6Aj6l/5tq97vRj8ztqQO+Qoqe8HgHNlKrPvGyK50ZiabvlzwumDSybYD6u5tLjFYNpGK1ftFu4KCRWX3TN5musFKiXsmpraeyQyMruJOgpOhM8OX0fHaVQv/slmXMpM1WjLPeJelw4CeVona1jNxD7fO4N/c8tK18WQNN9BKN7zoR3E0ljW3cH2/KFh6JBYz+l6heZX4Vba5eKvY3hU74uz+Zm/9Z06Hd+bgvJnRrfAh44rKNS22KK4b3adlmkLziOGi33kc1ndW9GGAsp4BBHevQkvlXOG6S+boTAbreR9E5TGgRvsybYe2ZSz1Eh5D71JEgsnyNB2C/RSgtWPMnTgSJztdWXOumbltpeWecxkYbY/Za1OTfr9oHxHEv3/h83z9Ai8TlAoKZW5kc3RyZWFtCmVuZG9iagozOCAwIG9iago8PCAvQmFzZUZvbnQgL1NUSVhOb25Vbmljb2RlLUl0YWxpYyAvQ2hhclByb2NzIDM5IDAgUgovRW5jb2RpbmcgPDwgL0RpZmZlcmVuY2VzIFsgXSAvVHlwZSAvRW5jb2RpbmcgPj4gL0ZpcnN0Q2hhciAwCi9Gb250QkJveCBbIC0xNDEgLTI0MCAxMTI4IDc5NSBdIC9Gb250RGVzY3JpcHRvciAzNyAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NQovTmFtZSAvU1RJWE5vblVuaWNvZGUtSXRhbGljIC9TdWJ0eXBlIC9UeXBlMyAvVHlwZSAvRm9udCAvV2lkdGhzIDM2IDAgUiA+PgplbmRvYmoKMzcgMCBvYmoKPDwgL0FzY2VudCAxNDUwIC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtNTUyIC9GbGFncyA5NgovRm9udEJCb3ggWyAtMTQxIC0yNDAgMTEyOCA3OTUgXSAvRm9udE5hbWUgL1NUSVhOb25Vbmljb2RlLUl0YWxpYwovSXRhbGljQW5nbGUgNDM5MDkgL01heFdpZHRoIDI1MCAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMAo+PgplbmRvYmoKMzYgMCBvYmoKWyAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MAoyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAKMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwCjI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MAoyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAKMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwCjI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MAoyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAKMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwCjI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MAoyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAKMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwCjI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MAoyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgMjUwIDI1MCAyNTAgXQplbmRvYmoKMzkgMCBvYmoKPDwgPj4KZW5kb2JqCjMgMCBvYmoKPDwgL0YxIDIwIDAgUiAvRjIgMTQgMCBSIC9GMyAzOCAwIFIgPj4KZW5kb2JqCjQgMCBvYmoKPDwgL0ExIDw8IC9DQSAwIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4KL0EyIDw8IC9DQSAxIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4gPj4KZW5kb2JqCjUgMCBvYmoKPDwgPj4KZW5kb2JqCjYgMCBvYmoKPDwgPj4KZW5kb2JqCjcgMCBvYmoKPDwgL0RlamFWdVNhbnMtTGFtYmRhIDIyIDAgUiAvRGVqYVZ1U2Fucy1PYmxpcXVlLW9tZWdhIDE2IDAgUgovRGVqYVZ1U2Fucy1taW51cyAyOCAwIFIgL1NUSVhOb25VbmlJdGEtdW5pRTIzMiA0MCAwIFIgPj4KZW5kb2JqCjIgMCBvYmoKPDwgL0NvdW50IDEgL0tpZHMgWyAxMCAwIFIgXSAvVHlwZSAvUGFnZXMgPj4KZW5kb2JqCjQxIDAgb2JqCjw8IC9DcmVhdGlvbkRhdGUgKEQ6MjAxOTA1MTYxODM3NTMrMDInMDAnKQovQ3JlYXRvciAobWF0cGxvdGxpYiAzLjAuMywgaHR0cDovL21hdHBsb3RsaWIub3JnKQovUHJvZHVjZXIgKG1hdHBsb3RsaWIgcGRmIGJhY2tlbmQgMy4wLjMpID4+CmVuZG9iagp4cmVmCjAgNDIKMDAwMDAwMDAwMCA2NTUzNSBmIAowMDAwMDAwMDE2IDAwMDAwIG4gCjAwMDAwMTI1NzEgMDAwMDAgbiAKMDAwMDAxMjI0MSAwMDAwMCBuIAowMDAwMDEyMjk1IDAwMDAwIG4gCjAwMDAwMTIzOTQgMDAwMDAgbiAKMDAwMDAxMjQxNSAwMDAwMCBuIAowMDAwMDEyNDM2IDAwMDAwIG4gCjAwMDAwMDAwNjUgMDAwMDAgbiAKMDAwMDAwMDQwMiAwMDAwMCBuIAowMDAwMDAwMjA4IDAwMDAwIG4gCjAwMDAwMDIzNTkgMDAwMDAgbiAKMDAwMDAwMzQ3MCAwMDAwMCBuIAowMDAwMDAzMjYyIDAwMDAwIG4gCjAwMDAwMDI5NDYgMDAwMDAgbiAKMDAwMDAwNDUyMyAwMDAwMCBuIAowMDAwMDAyMzgwIDAwMDAwIG4gCjAwMDAwMDI2OTUgMDAwMDAgbiAKMDAwMDAwODg4MyAwMDAwMCBuIAowMDAwMDA4NjgzIDAwMDAwIG4gCjAwMDAwMDgyNzMgMDAwMDAgbiAKMDAwMDAwOTkzNiAwMDAwMCBuIAowMDAwMDA0NTU1IDAwMDAwIG4gCjAwMDAwMDQ3NDYgMDAwMDAgbiAKMDAwMDAwNTA5OCAwMDAwMCBuIAowMDAwMDA1NDQ3IDAwMDAwIG4gCjAwMDAwMDU5MTIgMDAwMDAgbiAKMDAwMDAwNjIzMiAwMDAwMCBuIAowMDAwMDA2Mzk0IDAwMDAwIG4gCjAwMDAwMDY1NjQgMDAwMDAgbiAKMDAwMDAwNjcxNiAwMDAwMCBuIAowMDAwMDA2OTM2IDAwMDAwIG4gCjAwMDAwMDcxNTggMDAwMDAgbiAKMDAwMDAwNzI3OSAwMDAwMCBuIAowMDAwMDA3NjY5IDAwMDAwIG4gCjAwMDAwMDc5OTAgMDAwMDAgbiAKMDAwMDAxMTE3NSAwMDAwMCBuIAowMDAwMDEwOTYyIDAwMDAwIG4gCjAwMDAwMTA2NDkgMDAwMDAgbiAKMDAwMDAxMjIxOSAwMDAwMCBuIAowMDAwMDEwMTM2IDAwMDAwIG4gCjAwMDAwMTI2MzEgMDAwMDAgbiAKdHJhaWxlcgo8PCAvSW5mbyA0MSAwIFIgL1Jvb3QgMSAwIFIgL1NpemUgNDIgPj4Kc3RhcnR4cmVmCjEyNzg1CiUlRU9GCg==\n",
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
"<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
" \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
"<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
"<svg height=\"317.725473pt\" version=\"1.1\" viewBox=\"0 0 388.434844 317.725473\" width=\"388.434844pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
" <defs>\n",
" <style type=\"text/css\">\n",
"*{stroke-linecap:butt;stroke-linejoin:round;}\n",
" </style>\n",
" </defs>\n",
" <g id=\"figure_1\">\n",
" <g id=\"patch_1\">\n",
" <path d=\"M 0 317.725473 \n",
"L 388.434844 317.725473 \n",
"L 388.434844 0 \n",
"L 0 0 \n",
"z\n",
"\" style=\"fill:#ffffff;\"/>\n",
" </g>\n",
" <g id=\"axes_1\">\n",
" <g id=\"patch_2\">\n",
" <path d=\"M 17.752344 292.262 \n",
"L 374.872344 292.262 \n",
"L 374.872344 26.15 \n",
"L 17.752344 26.15 \n",
"z\n",
"\" style=\"fill:#ffffff;\"/>\n",
" </g>\n",
" <g id=\"matplotlib.axis_1\">\n",
" <g id=\"xtick_1\">\n",
" <g id=\"line2d_1\">\n",
" <defs>\n",
" <path d=\"M 0 0 \n",
"L 0 3.5 \n",
"\" id=\"mb69c81a97a\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
" </defs>\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"17.752344\" xlink:href=\"#mb69c81a97a\" y=\"280.169223\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_1\">\n",
" <!-- −20 -->\n",
" <defs>\n",
" <path d=\"M 10.59375 35.5 \n",
"L 73.1875 35.5 \n",
"L 73.1875 27.203125 \n",
"L 10.59375 27.203125 \n",
"z\n",
"\" id=\"DejaVuSans-8722\"/>\n",
" <path d=\"M 19.1875 8.296875 \n",
"L 53.609375 8.296875 \n",
"L 53.609375 0 \n",
"L 7.328125 0 \n",
"L 7.328125 8.296875 \n",
"Q 12.9375 14.109375 22.625 23.890625 \n",
"Q 32.328125 33.6875 34.8125 36.53125 \n",
"Q 39.546875 41.84375 41.421875 45.53125 \n",
"Q 43.3125 49.21875 43.3125 52.78125 \n",
"Q 43.3125 58.59375 39.234375 62.25 \n",
"Q 35.15625 65.921875 28.609375 65.921875 \n",
"Q 23.96875 65.921875 18.8125 64.3125 \n",
"Q 13.671875 62.703125 7.8125 59.421875 \n",
"L 7.8125 69.390625 \n",
"Q 13.765625 71.78125 18.9375 73 \n",
"Q 24.125 74.21875 28.421875 74.21875 \n",
"Q 39.75 74.21875 46.484375 68.546875 \n",
"Q 53.21875 62.890625 53.21875 53.421875 \n",
"Q 53.21875 48.921875 51.53125 44.890625 \n",
"Q 49.859375 40.875 45.40625 35.40625 \n",
"Q 44.1875 33.984375 37.640625 27.21875 \n",
"Q 31.109375 20.453125 19.1875 8.296875 \n",
"z\n",
"\" id=\"DejaVuSans-50\"/>\n",
" <path d=\"M 31.78125 66.40625 \n",
"Q 24.171875 66.40625 20.328125 58.90625 \n",
"Q 16.5 51.421875 16.5 36.375 \n",
"Q 16.5 21.390625 20.328125 13.890625 \n",
"Q 24.171875 6.390625 31.78125 6.390625 \n",
"Q 39.453125 6.390625 43.28125 13.890625 \n",
"Q 47.125 21.390625 47.125 36.375 \n",
"Q 47.125 51.421875 43.28125 58.90625 \n",
"Q 39.453125 66.40625 31.78125 66.40625 \n",
"z\n",
"M 31.78125 74.21875 \n",
"Q 44.046875 74.21875 50.515625 64.515625 \n",
"Q 56.984375 54.828125 56.984375 36.375 \n",
"Q 56.984375 17.96875 50.515625 8.265625 \n",
"Q 44.046875 -1.421875 31.78125 -1.421875 \n",
"Q 19.53125 -1.421875 13.0625 8.265625 \n",
"Q 6.59375 17.96875 6.59375 36.375 \n",
"Q 6.59375 54.828125 13.0625 64.515625 \n",
"Q 19.53125 74.21875 31.78125 74.21875 \n",
"z\n",
"\" id=\"DejaVuSans-48\"/>\n",
" </defs>\n",
" <g transform=\"translate(7.2 294.76766)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_2\">\n",
" <g id=\"line2d_2\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"62.392344\" xlink:href=\"#mb69c81a97a\" y=\"280.169223\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_2\">\n",
" <!-- −15 -->\n",
" <defs>\n",
" <path d=\"M 12.40625 8.296875 \n",
"L 28.515625 8.296875 \n",
"L 28.515625 63.921875 \n",
"L 10.984375 60.40625 \n",
"L 10.984375 69.390625 \n",
"L 28.421875 72.90625 \n",
"L 38.28125 72.90625 \n",
"L 38.28125 8.296875 \n",
"L 54.390625 8.296875 \n",
"L 54.390625 0 \n",
"L 12.40625 0 \n",
"z\n",
"\" id=\"DejaVuSans-49\"/>\n",
" <path d=\"M 10.796875 72.90625 \n",
"L 49.515625 72.90625 \n",
"L 49.515625 64.59375 \n",
"L 19.828125 64.59375 \n",
"L 19.828125 46.734375 \n",
"Q 21.96875 47.46875 24.109375 47.828125 \n",
"Q 26.265625 48.1875 28.421875 48.1875 \n",
"Q 40.625 48.1875 47.75 41.5 \n",
"Q 54.890625 34.8125 54.890625 23.390625 \n",
"Q 54.890625 11.625 47.5625 5.09375 \n",
"Q 40.234375 -1.421875 26.90625 -1.421875 \n",
"Q 22.3125 -1.421875 17.546875 -0.640625 \n",
"Q 12.796875 0.140625 7.71875 1.703125 \n",
"L 7.71875 11.625 \n",
"Q 12.109375 9.234375 16.796875 8.0625 \n",
"Q 21.484375 6.890625 26.703125 6.890625 \n",
"Q 35.15625 6.890625 40.078125 11.328125 \n",
"Q 45.015625 15.765625 45.015625 23.390625 \n",
"Q 45.015625 31 40.078125 35.4375 \n",
"Q 35.15625 39.890625 26.703125 39.890625 \n",
"Q 22.75 39.890625 18.8125 39.015625 \n",
"Q 14.890625 38.140625 10.796875 36.28125 \n",
"z\n",
"\" id=\"DejaVuSans-53\"/>\n",
" </defs>\n",
" <g transform=\"translate(51.84 294.76766)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_3\">\n",
" <g id=\"line2d_3\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"107.032344\" xlink:href=\"#mb69c81a97a\" y=\"280.169223\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_3\">\n",
" <!-- −10 -->\n",
" <g transform=\"translate(96.48 294.76766)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_4\">\n",
" <g id=\"line2d_4\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"151.672344\" xlink:href=\"#mb69c81a97a\" y=\"280.169223\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_4\">\n",
" <!-- −5 -->\n",
" <g transform=\"translate(144.30125 294.76766)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_5\">\n",
" <g id=\"line2d_5\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#mb69c81a97a\" y=\"280.169223\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_5\">\n",
" <!-- 0 -->\n",
" <g transform=\"translate(193.131094 294.76766)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_6\">\n",
" <g id=\"line2d_6\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"240.952344\" xlink:href=\"#mb69c81a97a\" y=\"280.169223\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_6\">\n",
" <!-- 5 -->\n",
" <g transform=\"translate(237.771094 294.76766)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_7\">\n",
" <g id=\"line2d_7\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"285.592344\" xlink:href=\"#mb69c81a97a\" y=\"280.169223\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_7\">\n",
" <!-- 10 -->\n",
" <g transform=\"translate(279.229844 294.76766)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_8\">\n",
" <g id=\"line2d_8\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"330.232344\" xlink:href=\"#mb69c81a97a\" y=\"280.169223\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_8\">\n",
" <!-- 15 -->\n",
" <g transform=\"translate(323.869844 294.76766)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_9\">\n",
" <g id=\"line2d_9\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"374.872344\" xlink:href=\"#mb69c81a97a\" y=\"280.169223\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_9\">\n",
" <!-- 20 -->\n",
" <g transform=\"translate(368.509844 294.76766)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_10\">\n",
" <!-- $\\omega$ -->\n",
" <defs>\n",
" <path d=\"M 21.390625 -1.421875 \n",
"Q 1.125 -1.421875 6.78125 27.59375 \n",
"Q 8.984375 39.0625 19.625 54.6875 \n",
"L 29.296875 54.6875 \n",
"Q 19.234375 39.0625 17 27.34375 \n",
"Q 12.796875 6.203125 23.734375 6.203125 \n",
"Q 33.84375 6.203125 38.71875 32.46875 \n",
"L 47.015625 32.46875 \n",
"Q 41.703125 6.0625 51.8125 6.203125 \n",
"Q 62.703125 6.296875 66.796875 27.34375 \n",
"Q 69.046875 39.0625 65.140625 54.6875 \n",
"L 74.8125 54.6875 \n",
"Q 79.296875 39.0625 77.09375 27.59375 \n",
"Q 71.53125 -1.46875 51.21875 -1.421875 \n",
"Q 37.9375 -1.375 39.109375 13.1875 \n",
"Q 34.28125 -1.421875 21.390625 -1.421875 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-969\"/>\n",
" </defs>\n",
" <g transform=\"translate(370.672344 308.445785)scale(0.1 -0.1)\">\n",
" <use transform=\"translate(0 0.3125)\" xlink:href=\"#DejaVuSans-Oblique-969\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"matplotlib.axis_2\">\n",
" <g id=\"ytick_1\">\n",
" <g id=\"line2d_10\">\n",
" <defs>\n",
" <path d=\"M 0 0 \n",
"L -3.5 0 \n",
"\" id=\"m10b5189419\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
" </defs>\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m10b5189419\" y=\"280.169223\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_11\">\n",
" <!-- 0.0 -->\n",
" <defs>\n",
" <path d=\"M 10.6875 12.40625 \n",
"L 21 12.40625 \n",
"L 21 0 \n",
"L 10.6875 0 \n",
"z\n",
"\" id=\"DejaVuSans-46\"/>\n",
" </defs>\n",
" <g transform=\"translate(173.409219 283.968441)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_2\">\n",
" <g id=\"line2d_11\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m10b5189419\" y=\"231.784039\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_12\">\n",
" <!-- 0.2 -->\n",
" <g transform=\"translate(173.409219 235.583257)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-50\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_3\">\n",
" <g id=\"line2d_12\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m10b5189419\" y=\"183.398854\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_13\">\n",
" <!-- 0.4 -->\n",
" <defs>\n",
" <path d=\"M 37.796875 64.3125 \n",
"L 12.890625 25.390625 \n",
"L 37.796875 25.390625 \n",
"z\n",
"M 35.203125 72.90625 \n",
"L 47.609375 72.90625 \n",
"L 47.609375 25.390625 \n",
"L 58.015625 25.390625 \n",
"L 58.015625 17.1875 \n",
"L 47.609375 17.1875 \n",
"L 47.609375 0 \n",
"L 37.796875 0 \n",
"L 37.796875 17.1875 \n",
"L 4.890625 17.1875 \n",
"L 4.890625 26.703125 \n",
"z\n",
"\" id=\"DejaVuSans-52\"/>\n",
" </defs>\n",
" <g transform=\"translate(173.409219 187.198073)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-52\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_4\">\n",
" <g id=\"line2d_13\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m10b5189419\" y=\"135.01367\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_14\">\n",
" <!-- 0.6 -->\n",
" <defs>\n",
" <path d=\"M 33.015625 40.375 \n",
"Q 26.375 40.375 22.484375 35.828125 \n",
"Q 18.609375 31.296875 18.609375 23.390625 \n",
"Q 18.609375 15.53125 22.484375 10.953125 \n",
"Q 26.375 6.390625 33.015625 6.390625 \n",
"Q 39.65625 6.390625 43.53125 10.953125 \n",
"Q 47.40625 15.53125 47.40625 23.390625 \n",
"Q 47.40625 31.296875 43.53125 35.828125 \n",
"Q 39.65625 40.375 33.015625 40.375 \n",
"z\n",
"M 52.59375 71.296875 \n",
"L 52.59375 62.3125 \n",
"Q 48.875 64.0625 45.09375 64.984375 \n",
"Q 41.3125 65.921875 37.59375 65.921875 \n",
"Q 27.828125 65.921875 22.671875 59.328125 \n",
"Q 17.53125 52.734375 16.796875 39.40625 \n",
"Q 19.671875 43.65625 24.015625 45.921875 \n",
"Q 28.375 48.1875 33.59375 48.1875 \n",
"Q 44.578125 48.1875 50.953125 41.515625 \n",
"Q 57.328125 34.859375 57.328125 23.390625 \n",
"Q 57.328125 12.15625 50.6875 5.359375 \n",
"Q 44.046875 -1.421875 33.015625 -1.421875 \n",
"Q 20.359375 -1.421875 13.671875 8.265625 \n",
"Q 6.984375 17.96875 6.984375 36.375 \n",
"Q 6.984375 53.65625 15.1875 63.9375 \n",
"Q 23.390625 74.21875 37.203125 74.21875 \n",
"Q 40.921875 74.21875 44.703125 73.484375 \n",
"Q 48.484375 72.75 52.59375 71.296875 \n",
"z\n",
"\" id=\"DejaVuSans-54\"/>\n",
" </defs>\n",
" <g transform=\"translate(173.409219 138.812889)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-54\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_5\">\n",
" <g id=\"line2d_14\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m10b5189419\" y=\"86.628486\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_15\">\n",
" <!-- 0.8 -->\n",
" <defs>\n",
" <path d=\"M 31.78125 34.625 \n",
"Q 24.75 34.625 20.71875 30.859375 \n",
"Q 16.703125 27.09375 16.703125 20.515625 \n",
"Q 16.703125 13.921875 20.71875 10.15625 \n",
"Q 24.75 6.390625 31.78125 6.390625 \n",
"Q 38.8125 6.390625 42.859375 10.171875 \n",
"Q 46.921875 13.96875 46.921875 20.515625 \n",
"Q 46.921875 27.09375 42.890625 30.859375 \n",
"Q 38.875 34.625 31.78125 34.625 \n",
"z\n",
"M 21.921875 38.8125 \n",
"Q 15.578125 40.375 12.03125 44.71875 \n",
"Q 8.5 49.078125 8.5 55.328125 \n",
"Q 8.5 64.0625 14.71875 69.140625 \n",
"Q 20.953125 74.21875 31.78125 74.21875 \n",
"Q 42.671875 74.21875 48.875 69.140625 \n",
"Q 55.078125 64.0625 55.078125 55.328125 \n",
"Q 55.078125 49.078125 51.53125 44.71875 \n",
"Q 48 40.375 41.703125 38.8125 \n",
"Q 48.828125 37.15625 52.796875 32.3125 \n",
"Q 56.78125 27.484375 56.78125 20.515625 \n",
"Q 56.78125 9.90625 50.3125 4.234375 \n",
"Q 43.84375 -1.421875 31.78125 -1.421875 \n",
"Q 19.734375 -1.421875 13.25 4.234375 \n",
"Q 6.78125 9.90625 6.78125 20.515625 \n",
"Q 6.78125 27.484375 10.78125 32.3125 \n",
"Q 14.796875 37.15625 21.921875 38.8125 \n",
"z\n",
"M 18.3125 54.390625 \n",
"Q 18.3125 48.734375 21.84375 45.5625 \n",
"Q 25.390625 42.390625 31.78125 42.390625 \n",
"Q 38.140625 42.390625 41.71875 45.5625 \n",
"Q 45.3125 48.734375 45.3125 54.390625 \n",
"Q 45.3125 60.0625 41.71875 63.234375 \n",
"Q 38.140625 66.40625 31.78125 66.40625 \n",
"Q 25.390625 66.40625 21.84375 63.234375 \n",
"Q 18.3125 60.0625 18.3125 54.390625 \n",
"z\n",
"\" id=\"DejaVuSans-56\"/>\n",
" </defs>\n",
" <g transform=\"translate(173.409219 90.427705)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-56\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_6\">\n",
" <g id=\"line2d_15\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m10b5189419\" y=\"38.243302\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_16\">\n",
" <!-- 1.0 -->\n",
" <g transform=\"translate(173.409219 42.042521)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_17\">\n",
" <!-- $\\mathcal{F} \\{ \\Lambda(t) \\}$ -->\n",
" <defs>\n",
" <path d=\"M 5.90625 53.40625 \n",
"L 4.296875 55.203125 \n",
"Q 11.40625 61.796875 18.34375 64 \n",
"Q 25.296875 66.203125 33.796875 66.203125 \n",
"Q 42.40625 66.203125 48.59375 65.75 \n",
"Q 54.796875 65.296875 60.140625 64.046875 \n",
"Q 65.5 62.796875 68.25 60.4375 \n",
"Q 71 58.09375 71 54.5 \n",
"Q 71 51.09375 69.203125 48.796875 \n",
"Q 67.40625 46.5 64.203125 46.5 \n",
"Q 61.90625 46.5 60.203125 47.84375 \n",
"Q 58.5 49.203125 58.5 51.203125 \n",
"Q 58.5 53.09375 59.25 54.140625 \n",
"Q 60 55.203125 60.890625 55.453125 \n",
"Q 61.796875 55.703125 62.5 56.140625 \n",
"Q 63.203125 56.59375 63.203125 57.5 \n",
"Q 63.203125 59.5 57.75 60.84375 \n",
"Q 52.296875 62.203125 45.203125 62.203125 \n",
"Q 42.09375 62.203125 40.75 61.25 \n",
"Q 39.40625 60.296875 38.5 57.296875 \n",
"L 32.796875 37.703125 \n",
"L 54.59375 37.703125 \n",
"L 53.296875 33.703125 \n",
"L 31.703125 33.703125 \n",
"L 27.296875 18.796875 \n",
"Q 25.40625 12.296875 23.296875 8.390625 \n",
"Q 21.203125 4.5 18.34375 2.703125 \n",
"Q 15.5 0.90625 12.953125 0.453125 \n",
"Q 10.40625 0 6 0 \n",
"L 6.796875 2.40625 \n",
"Q 9.5 2.40625 11.34375 4.5 \n",
"Q 13.203125 6.59375 14.59375 11.59375 \n",
"L 26.40625 52.09375 \n",
"Q 27.40625 55.59375 27.40625 57.296875 \n",
"Q 27.40625 59 26.40625 59.796875 \n",
"Q 25.40625 60.59375 22.796875 60.59375 \n",
"Q 13.40625 60.59375 5.90625 53.40625 \n",
"z\n",
"\" id=\"STIXNonUnicode-Italic-57906\"/>\n",
" <path d=\"M 51.125 -9.28125 \n",
"L 51.125 -16.3125 \n",
"L 48.09375 -16.3125 \n",
"Q 35.9375 -16.3125 31.8125 -12.6875 \n",
"Q 27.6875 -9.078125 27.6875 1.703125 \n",
"L 27.6875 13.375 \n",
"Q 27.6875 20.75 25.046875 23.578125 \n",
"Q 22.40625 26.421875 15.484375 26.421875 \n",
"L 12.5 26.421875 \n",
"L 12.5 33.40625 \n",
"L 15.484375 33.40625 \n",
"Q 22.46875 33.40625 25.078125 36.203125 \n",
"Q 27.6875 39.015625 27.6875 46.296875 \n",
"L 27.6875 58.015625 \n",
"Q 27.6875 68.796875 31.8125 72.390625 \n",
"Q 35.9375 75.984375 48.09375 75.984375 \n",
"L 51.125 75.984375 \n",
"L 51.125 69 \n",
"L 47.796875 69 \n",
"Q 40.921875 69 38.8125 66.84375 \n",
"Q 36.71875 64.703125 36.71875 57.8125 \n",
"L 36.71875 45.703125 \n",
"Q 36.71875 38.03125 34.5 34.5625 \n",
"Q 32.28125 31.109375 26.90625 29.890625 \n",
"Q 32.328125 28.5625 34.515625 25.09375 \n",
"Q 36.71875 21.625 36.71875 14.015625 \n",
"L 36.71875 1.90625 \n",
"Q 36.71875 -4.984375 38.8125 -7.125 \n",
"Q 40.921875 -9.28125 47.796875 -9.28125 \n",
"z\n",
"\" id=\"DejaVuSans-123\"/>\n",
" <path d=\"M 11.1875 0 \n",
"L 0.78125 0 \n",
"L 28.609375 72.90625 \n",
"L 39.796875 72.90625 \n",
"L 67.578125 0 \n",
"L 57.328125 0 \n",
"L 34.1875 63.1875 \n",
"z\n",
"\" id=\"DejaVuSans-923\"/>\n",
" <path d=\"M 31 75.875 \n",
"Q 24.46875 64.65625 21.28125 53.65625 \n",
"Q 18.109375 42.671875 18.109375 31.390625 \n",
"Q 18.109375 20.125 21.3125 9.0625 \n",
"Q 24.515625 -2 31 -13.1875 \n",
"L 23.1875 -13.1875 \n",
"Q 15.875 -1.703125 12.234375 9.375 \n",
"Q 8.59375 20.453125 8.59375 31.390625 \n",
"Q 8.59375 42.28125 12.203125 53.3125 \n",
"Q 15.828125 64.359375 23.1875 75.875 \n",
"z\n",
"\" id=\"DejaVuSans-40\"/>\n",
" <path d=\"M 42.28125 54.6875 \n",
"L 40.921875 47.703125 \n",
"L 23 47.703125 \n",
"L 17.1875 18.015625 \n",
"Q 16.890625 16.359375 16.75 15.234375 \n",
"Q 16.609375 14.109375 16.609375 13.484375 \n",
"Q 16.609375 10.359375 18.484375 8.9375 \n",
"Q 20.359375 7.515625 24.515625 7.515625 \n",
"L 33.59375 7.515625 \n",
"L 32.078125 0 \n",
"L 23.484375 0 \n",
"Q 15.484375 0 11.546875 3.125 \n",
"Q 7.625 6.25 7.625 12.59375 \n",
"Q 7.625 13.71875 7.765625 15.0625 \n",
"Q 7.90625 16.40625 8.203125 18.015625 \n",
"L 14.015625 47.703125 \n",
"L 6.390625 47.703125 \n",
"L 7.8125 54.6875 \n",
"L 15.28125 54.6875 \n",
"L 18.3125 70.21875 \n",
"L 27.296875 70.21875 \n",
"L 24.3125 54.6875 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-116\"/>\n",
" <path d=\"M 8.015625 75.875 \n",
"L 15.828125 75.875 \n",
"Q 23.140625 64.359375 26.78125 53.3125 \n",
"Q 30.421875 42.28125 30.421875 31.390625 \n",
"Q 30.421875 20.453125 26.78125 9.375 \n",
"Q 23.140625 -1.703125 15.828125 -13.1875 \n",
"L 8.015625 -13.1875 \n",
"Q 14.5 -2 17.703125 9.0625 \n",
"Q 20.90625 20.125 20.90625 31.390625 \n",
"Q 20.90625 42.671875 17.703125 53.65625 \n",
"Q 14.5 64.65625 8.015625 75.875 \n",
"z\n",
"\" id=\"DejaVuSans-41\"/>\n",
" <path d=\"M 12.5 -9.28125 \n",
"L 15.921875 -9.28125 \n",
"Q 22.75 -9.28125 24.828125 -7.171875 \n",
"Q 26.90625 -5.078125 26.90625 1.90625 \n",
"L 26.90625 14.015625 \n",
"Q 26.90625 21.625 29.09375 25.09375 \n",
"Q 31.296875 28.5625 36.71875 29.890625 \n",
"Q 31.296875 31.109375 29.09375 34.5625 \n",
"Q 26.90625 38.03125 26.90625 45.703125 \n",
"L 26.90625 57.8125 \n",
"Q 26.90625 64.75 24.828125 66.875 \n",
"Q 22.75 69 15.921875 69 \n",
"L 12.5 69 \n",
"L 12.5 75.984375 \n",
"L 15.578125 75.984375 \n",
"Q 27.734375 75.984375 31.8125 72.390625 \n",
"Q 35.890625 68.796875 35.890625 58.015625 \n",
"L 35.890625 46.296875 \n",
"Q 35.890625 39.015625 38.515625 36.203125 \n",
"Q 41.15625 33.40625 48.09375 33.40625 \n",
"L 51.125 33.40625 \n",
"L 51.125 26.421875 \n",
"L 48.09375 26.421875 \n",
"Q 41.15625 26.421875 38.515625 23.578125 \n",
"Q 35.890625 20.75 35.890625 13.375 \n",
"L 35.890625 1.703125 \n",
"Q 35.890625 -9.078125 31.8125 -12.6875 \n",
"Q 27.734375 -16.3125 15.578125 -16.3125 \n",
"L 12.5 -16.3125 \n",
"z\n",
"\" id=\"DejaVuSans-125\"/>\n",
" </defs>\n",
" <g transform=\"translate(167.329531 45.1)rotate(-90)scale(0.1 -0.1)\">\n",
" <use transform=\"translate(0 0.015625)\" xlink:href=\"#STIXNonUnicode-Italic-57906\"/>\n",
" <use transform=\"translate(65.199997 0.015625)\" xlink:href=\"#DejaVuSans-123\"/>\n",
" <use transform=\"translate(128.823044 0.015625)\" xlink:href=\"#DejaVuSans-923\"/>\n",
" <use transform=\"translate(197.231247 0.015625)\" xlink:href=\"#DejaVuSans-40\"/>\n",
" <use transform=\"translate(236.244919 0.015625)\" xlink:href=\"#DejaVuSans-Oblique-116\"/>\n",
" <use transform=\"translate(275.453903 0.015625)\" xlink:href=\"#DejaVuSans-41\"/>\n",
" <use transform=\"translate(314.467575 0.015625)\" xlink:href=\"#DejaVuSans-125\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"LineCollection_1\">\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 17.752344 279.453221 \n",
"L 23.866941 280.031187 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 23.866941 280.031187 \n",
"L 29.160456 280.158045 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 29.160456 280.158045 \n",
"L 34.18988 279.832927 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 34.18988 279.832927 \n",
"L 38.627562 279.197869 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 38.627562 279.197869 \n",
"L 43.736489 278.200967 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 43.736489 278.200967 \n",
"L 48.086759 277.314928 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 48.086759 277.314928 \n",
"L 53.081903 276.513718 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 53.081903 276.513718 \n",
"L 58.941932 276.186374 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 58.941932 276.186374 \n",
"L 63.281026 276.483395 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 63.281026 276.483395 \n",
"L 68.413388 277.36989 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 68.413388 277.36989 \n",
"L 72.897506 278.418748 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 72.897506 278.418748 \n",
"L 77.505782 279.453117 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 77.505782 279.453117 \n",
"L 82.414866 280.115179 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 82.414866 280.115179 \n",
"L 87.928989 279.874898 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 87.928989 279.874898 \n",
"L 93.009343 278.520926 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 93.009343 278.520926 \n",
"L 97.448229 276.53048 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 97.448229 276.53048 \n",
"L 104.461338 272.626283 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 104.461338 272.626283 \n",
"L 110.487469 269.789825 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 110.487469 269.789825 \n",
"L 116.768427 268.769788 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 116.768427 268.769788 \n",
"L 122.093283 270.065189 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 122.093283 270.065189 \n",
"L 127.708484 273.359918 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 127.708484 273.359918 \n",
"L 132.968801 277.172503 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 132.968801 277.172503 \n",
"L 138.727286 280.007892 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 138.727286 280.007892 \n",
"L 143.974442 278.940009 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 143.974442 278.940009 \n",
"L 149.389115 271.708897 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 149.389115 271.708897 \n",
"L 154.536689 257.336227 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 154.536689 257.336227 \n",
"L 159.918886 233.752876 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 159.918886 233.752876 \n",
"L 165.131443 203.249771 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 165.131443 203.249771 \n",
"L 172.467231 151.887735 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 172.467231 151.887735 \n",
"L 178.494154 108.608384 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 178.494154 108.608384 \n",
"L 183.893221 74.822186 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 183.893221 74.822186 \n",
"L 187.176465 58.63035 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 187.176465 58.63035 \n",
"L 190.407805 46.933632 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 190.407805 46.933632 \n",
"L 193.454498 40.301975 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 193.454498 40.301975 \n",
"L 196.209064 38.246 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 196.209064 38.246 \n",
"L 198.919616 39.957777 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 198.919616 39.957777 \n",
"L 201.711301 45.526481 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 201.711301 45.526481 \n",
"L 206.836437 64.990685 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 206.836437 64.990685 \n",
"L 212.449891 97.340763 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 212.449891 97.340763 \n",
"L 218.300078 138.305941 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 218.300078 138.305941 \n",
"L 223.365256 175.100641 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 223.365256 175.100641 \n",
"L 228.626766 210.43817 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 228.626766 210.43817 \n",
"L 234.156673 240.959325 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 234.156673 240.959325 \n",
"L 240.379589 264.709919 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 240.379589 264.709919 \n",
"L 246.827658 277.311196 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 246.827658 277.311196 \n",
"L 252.630451 280.165469 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 252.630451 280.165469 \n",
"L 258.819092 277.732147 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 258.819092 277.732147 \n",
"L 264.45765 273.686359 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 264.45765 273.686359 \n",
"L 270.357175 270.141232 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 270.357175 270.141232 \n",
"L 275.246881 268.813679 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 275.246881 268.813679 \n",
"L 279.900504 269.140133 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 279.900504 269.140133 \n",
"L 285.70941 271.328902 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 285.70941 271.328902 \n",
"L 291.115726 274.298703 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 291.115726 274.298703 \n",
"L 296.676267 277.272463 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 296.676267 277.272463 \n",
"L 302.828136 279.504907 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 302.828136 279.504907 \n",
"L 308.915916 280.166 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 308.915916 280.166 \n",
"L 314.431873 279.582145 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 314.431873 279.582145 \n",
"L 320.498648 278.232267 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 320.498648 278.232267 \n",
"L 326.169622 276.975102 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 326.169622 276.975102 \n",
"L 331.465923 276.280041 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 331.465923 276.280041 \n",
"L 337.763866 276.331824 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 337.763866 276.331824 \n",
"L 343.326088 277.089652 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 343.326088 277.089652 \n",
"L 349.024465 278.229304 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 349.024465 278.229304 \n",
"L 354.929153 279.354292 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 354.929153 279.354292 \n",
"L 360.829511 280.043949 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 360.829511 280.043949 \n",
"L 367.732965 280.089298 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pa941f7fcec)\" d=\"M 367.732965 280.089298 \n",
"L 374.872344 279.453221 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" </g>\n",
" <g id=\"patch_3\">\n",
" <path d=\"M 196.312344 280.169223 \n",
"L 196.312344 38.243302 \n",
"\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
" </g>\n",
" <g id=\"patch_4\">\n",
" <path d=\"M 374.872344 292.262 \n",
"L 374.872344 26.15 \n",
"\" style=\"fill:none;\"/>\n",
" </g>\n",
" <g id=\"patch_5\">\n",
" <path d=\"M 17.752344 280.169223 \n",
"L 374.872344 280.169223 \n",
"\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
" </g>\n",
" <g id=\"patch_6\">\n",
" <path d=\"M 17.752344 26.15 \n",
"L 374.872344 26.15 \n",
"\" style=\"fill:none;\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <defs>\n",
" <clipPath id=\"pa941f7fcec\">\n",
" <rect height=\"266.112\" width=\"357.12\" x=\"17.752344\" y=\"26.15\"/>\n",
" </clipPath>\n",
" </defs>\n",
"</svg>\n"
],
"text/plain": [
"<Figure size 614.4x460.8 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"x = sym.Piecewise((1 - abs(t), abs(t) < 1), (0, True))\n",
"X = sym.sinc(w/2)**2\n",
"\n",
"sym.plot(x, (t, -2, 2), xlabel=r'$t$', ylabel=r'$\\Lambda(t)$')\n",
"sym.plot(X, (w, -20, 20), xlabel=r'$\\omega$', ylabel=r'$\\mathcal{F} \\{ \\Lambda(t) \\}$');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise**\n",
"\n",
"* Extend above example by temporal scaling of the triangular signal.\n",
"* Derive the Fourier transform of a trapezoidal shaped signal by convolving two rectangular signals of different width."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Temporal Shift Theorem\n",
"\n",
"The [temporal shift](../continuous_signals/operations.ipynb#Temporal-Shift) $x(t-\\tau)$ of a signal $x(t)$ can be expressed by a convolution with a shifted Dirac impulse\n",
"\n",
"\\begin{equation}\n",
"x(t - \\tau) = x(t) * \\delta(t - \\tau)\n",
"\\end{equation}\n",
"\n",
"for $\\tau \\in \\mathbb{R}$. This follows from the sifting property of the Dirac impulse. Applying a Fourier transform to the left- and right-hand side and exploiting the convolution theorem yields\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{F} \\{ x(t - \\tau) \\} = X(j \\omega) \\cdot e^{- j \\omega \\tau}\n",
"\\end{equation}\n",
"\n",
"where $X(j \\omega) = \\mathcal{F} \\{ x(t) \\}$. Note that $\\mathcal{F} \\{ \\delta(t - \\tau) \\} = e^{- j \\omega \\tau}$ can be derived from the definition of the Fourier transform together with the sifting property of the Dirac impulse. Above relation is known as shift theorem of the Fourier transform.\n",
"\n",
"Expressing $X(j \\omega)$ by its absolute value $|X(j \\omega)|$ and phase $\\varphi(j \\omega)$ results in\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{F} \\{ x(t - \\tau) \\} = | X(j \\omega) | \\cdot e^{j (\\varphi(j \\omega) - \\omega \\tau)}\n",
"\\end{equation}\n",
"\n",
"Temporal shifting of a signal does not change the absolute value of its spectrum but it subtracts the linear contribution $\\omega \\tau$ from the phase of its spectrum."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Differentiation Theorem\n",
"\n",
"Let's assume a signal $x(t)$ whose temporal derivative $\\frac{d x(t)}{dt}$ exists. Using the [derivation property of the Dirac impulse](../continuous_signals/standard_signals.ipynb#Dirac-Impulse), the derivative of the signal can be expressed by the convolution\n",
"\n",
"\\begin{equation}\n",
"\\frac{d x(t)}{dt} = \\frac{d \\delta(t)}{dt} * x(t)\n",
"\\end{equation}\n",
"\n",
"Fourier transformation of the left- and right-hand side together with the [convolution theorem](#Convolution-Theorem) yields the Fourier transform of the derivative of $x(t)$\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{F} \\left\\{ \\frac{d x(t)}{dt} \\right\\} = j \\omega \\cdot X(j \\omega)\n",
"\\end{equation}\n",
"\n",
"where $X(j \\omega) = \\mathcal{F} \\{ x(t) \\}$. The Fourier transform $\\mathcal{F} \\{ \\frac{d \\delta(t)}{dt} \\} = j \\omega$ can be derived by applying the definition of the Fourier transform together with the derivation property of the Dirac impulse. Above result is known as differentiation theorem of the Fourier transform. It states that the differentiation of a signal in the time domain is equivalent to a multiplication of its spectrum by $j \\omega$. Splitting the spectrum of the differentiated signal into its magnitude and phase\n",
"\n",
"\\begin{equation}\n",
"j \\omega \\cdot X(j \\omega) = |\\omega \\, X(j \\omega)| \\; e^{j (\\varphi(j \\omega) + \\frac{\\pi}{2} )}\n",
"\\end{equation}\n",
"\n",
"reveals that differentiation of a signal results in an attenuation of the higher frequencies of its magnitude spectrum and adds a phase shift of $\\frac{\\pi}{2}$.\n",
"\n",
"The main applications of the differentiation theorem are the transformation of differential equations or the derivation of transforms of signals which can be expressed as derivatives of other signals. This latter is illustrated by the following example. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Transformation of the sign signal\n",
"\n",
"The derivative of the [sign signal](../continuous_signals/standard_signals.ipynb#Sign-Signal) $\\text{sgn}(t)$ [is given by the Dirac impulse](https://en.wikipedia.org/wiki/Sign_function#Properties)\n",
"\n",
"\\begin{equation}\n",
"\\frac{d}{dt} \\text{sgn}(t) = 2 \\cdot \\delta(t)\n",
"\\end{equation}\n",
"\n",
"Fourier transformation of the left- and right-hand side and application of the differentiation theorem yields\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{F} \\{ \\text{sgn}(t) \\} = \\frac{2}{j \\omega}\n",
"\\end{equation}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Transformation of the Heaviside signal\n",
"\n",
"The transformation of the [Heaviside signal](../continuous_signals/standard_signals.ipynb#Heaviside-Signal) $\\epsilon(t)$ is derived by expressing it in terms of the sign signal\n",
"\n",
"\\begin{equation}\n",
"\\epsilon(t) = \\frac{1}{2} ( \\text{sgn}(t) + 1 )\n",
"\\end{equation}\n",
"\n",
"Using the linearity of the Fourier transform yields\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{F} \\{ \\epsilon(t) \\} = \\frac{1}{j \\omega} + \\pi \\cdot \\delta(\\omega)\n",
"\\end{equation}\n",
"\n",
"The Fourier transformation of the Heaviside signal plays an important role in the context of [analytic signals](https://en.wikipedia.org/wiki/Analytic_signal) and their generation by the [Hilbert transform](https://en.wikipedia.org/wiki/Hilbert_transform)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Integration Theorem\n",
"\n",
"Let's assume a signal $x(t)$ for which the integral $\\int_{-\\infty}^{t} x(\\tau) \\; d\\tau$ exists. The integration can be regarded as inverse operation to the temporal derivative. The integration can be represented as convolution with the rectangular signal $\\epsilon(t)$ ([see integration theorem of the Laplace transform](../laplace_transform/theorems.ipynb#Integration-Theorem))\n",
"\n",
"\\begin{equation}\n",
"\\int_{-\\infty}^{t} x(\\tau) \\; d\\tau = \\int_{-\\infty}^{\\infty} x(\\tau) \\cdot \\epsilon(t - \\tau) \\; d\\tau = x(t) * \\epsilon(t)\n",
"\\end{equation}\n",
"\n",
"Fourier transformation of the left- and right-hand side, application of the convolution theorem and using the Fourier transform of the Heaviside signal $\\epsilon(t)$ yields the integration theorem of the Fourier transform\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{F} \\left\\{ \\int_{-\\infty}^{t} x(\\tau) \\; d\\tau \\right\\} \n",
"= X(j \\omega) * \\left( \\frac{1}{j \\omega} + \\pi \\delta(\\omega) \\right) \n",
"= \\frac{1}{j \\omega} X(j \\omega) + \\pi X(0) \\delta(\\omega)\n",
"\\end{equation}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Example**\n",
"\n",
"A signal whose amplitude increases linear over a finite temporal interval to a finite value can be defined as\n",
"\n",
"\\begin{equation}\n",
"x(t) = \\begin{cases}\n",
"0 & \\text{for } t < - \\frac{1}{2} \\\\\n",
"t + \\frac{1}{2} & \\text{for } - \\frac{1}{2} < t < \\frac{1}{2} \\\\\n",
"1 & \\text{for } t > \\frac{1}{2}\n",
"\\end{cases}\n",
"\\end{equation}\n",
"\n",
"Such functions are known as [ramp functions](https://en.wikipedia.org/wiki/Ramp_function). In order to derive the Fourier transform of the ramp signal $x(t)$ it is important to note that it can be expressed as integration over the rectangular signal $\\text{rect}(t)$\n",
"\n",
"\\begin{equation}\n",
"x(t) = \\int_{-\\infty}^{t} \\text{rect}(\\tau) \\; d\\tau \n",
"\\end{equation}\n",
"\n",
"Now its straightforward to apply the integration theorem to yield the desired Fourier transform\n",
"\n",
"\\begin{equation}\n",
"X(j \\omega) = \\frac{1}{j \\omega} \\text{sinc}\\left( \\frac{\\omega}{2} \\right) + \\pi \\cdot \\text{sinc}(0) \\cdot \\delta(\\omega)\n",
"\\end{equation}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Multiplication Theorem\n",
"\n",
"The Fourier transform of a multiplication of two signals $x(t)$ and $y(t)$ is given as\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{F} \\{ x(t) \\cdot y(t) \\} = \\frac{1}{2 \\pi} X(j \\omega) * Y(j \\omega)\n",
"\\end{equation}\n",
"\n",
"The Fourier transform of a multiplication of two signals $x(t) \\cdot y(t)$ is given by the convolution of their Fourier transforms $X(j \\omega) = \\mathcal{F} \\{ x(t) \\}$ and $Y(j \\omega) = \\mathcal{F} \\{ y(t) \\}$ weighted by $\\frac{1}{2 \\pi}$. Note, the convolution is performed with respect to the angular frequency $\\omega$.\n",
"\n",
"The multiplication theorem can be proven in a similar way as the convolution theorem by computing the inverse Fourier transform of the convolved spectra\n",
"\n",
"\\begin{equation}\n",
"\\begin{split}\n",
"\\mathcal{F}^{-1} \\left\\{ \\frac{1}{2 \\pi} X(j \\omega) * Y(j \\omega) \\right\\} &= \\frac{1}{2 \\pi} \\int_{-\\infty}^{\\infty} \\left( \\frac{1}{2 \\pi} \\int_{-\\infty}^{\\infty} X(j \\nu) \\cdot Y(j (\\omega-\\nu)) \\; d \\nu \\right) e^{j \\omega t} \\; d\\omega \\\\\n",
"&= \\frac{1}{2 \\pi} \\int_{-\\infty}^{\\infty} \\left( \\frac{1}{2 \\pi} \\int_{-\\infty}^{\\infty} Y(j (\\omega-\\nu)) \\, e^{j \\omega t} \\; d\\omega \\right) X(j \\nu) \\; d\\nu \\\\\n",
"&= y(t) \\cdot \\frac{1}{2 \\pi} \\int_{-\\infty}^{\\infty} X(j \\nu) \\, e^{j \\nu t} \\; d \\nu \\\\\n",
"&= y(t) \\cdot x(t)\n",
"\\end{split}\n",
"\\end{equation}\n",
"\n",
"Alternatively the duality of the Fourier transform can be applied to the [convolution theorem](#Convolution-Theorem). Applications of the multiplication theorem include the modulation and windowing of signals. The former leads to the modulation theorem introduced later, the latter is illustrated by the following example."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Example**\n",
"\n",
"Windowing of signals is often applied to derive signals of finite duration from signals of infinite duration. Here the signal $x(t)$ is multiplied by a weighting function $w(t)$ in order to derive the finite length signal \n",
"\n",
"\\begin{equation}\n",
"y(t) = w(t) \\cdot x(t)\n",
"\\end{equation}\n",
"\n",
"The following example considers the Fourier transform of a finite-length cosine signal. Following the concept of windowing, the signal can be defined as\n",
"\n",
"\\begin{equation}\n",
"y(t) = \\text{rect}(a t) \\cdot \\cos(\\omega_0 t) \n",
"\\end{equation}\n",
"\n",
"where $\\text{rect}(a t)$ denotes the scaled [rectangular signal](../continuous_signals/standard_signals.ipynb#Rectangular-Signal) which is zero for $|t| > \\frac{1}{2 a}$. The Fourier transform $Y(j \\omega) = \\mathcal{F} \\{ y(t) \\}$ is derived by the multiplication theorem, the [Fourier transform of the rectangular signal](definition.ipynb#Transformation-of-the-Rectangular-Signal), and the [Fourier transform of the cosine signal](properties.ipynb#Transformation-of-the-cosine-and-sine-signal) as\n",
"\n",
"\\begin{align}\n",
"Y(j \\omega) &= \\frac{1}{2 \\pi} \\cdot \\frac{1}{|a|} \\text{sinc}\\left( \\frac{\\omega}{2 a} \\right) * \\pi \\left( \\delta(\\omega + \\omega_0) + \\delta(\\omega - \\omega_0) \\right) \\\\\n",
"&= \\frac{1}{2 |a|} \\left( \\text{sinc}\\left( \\frac{\\omega + \\omega_0}{2 a} \\right) + \\text{sinc}\\left( \\frac{\\omega - \\omega_0}{2 a} \\right) \\right)\n",
"\\end{align}\n",
"\n",
"The latter identity results from the sifting property of the Dirac impulse. The convolution is computed in the following in `SymPy` by symbolic evaluation of the convolution integral."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"def convolve(x, y, var):\n",
" tau = sym.symbols('tau')\n",
" return sym.integrate(x.subs(var, tau) * y.subs(var, var - tau), (tau, -sym.oo, sym.oo))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Using above function, both the Fourier transform of the cosine signal and the rectangular window are convolved which each other"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAOsAAAA0BAMAAACZTNIcAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMnZmzRC73UTviSKZVKsmUdgqAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAEf0lEQVRYCe1XbWgcRRh+NpfNXbJ3yVkh4he5pop4QjgCKoIfh4rQP7rSLyyl2Ro8LAVz/iihWur9rQg9kUQkWg8/sETUozSBfkAXLC3UUoO/rP5Z4wcICrbSGm0lvu/uzO7s5W4UoQtSX7iZ531n5nn2nZmbnQXa25ftw0Bfp4aWuELgxpoaMS/u5Ny4H3mGE2ENUgniIwY1o9ZT261AyhN9FDyqGRY1qQQOhSOCVEH2sl6TSNbjBFzAqIqAgtO2iKnV4ZLqEVYJHPLdiGwnub5lrkgkaqsOWCWzxL3ZAnzkqybhLo8jLbbPjQdiBE6cYCTs2ppAtgHkmqmCWTIqZDsCXEaZRpgXxbCMkqEpYrKKCLKVynRlXCUYa1WTgzBQo6zy2XwXp0fm47k6pth5hAuyXMGv2hYxAidO0K08bnzwED1Q5ptTzxZF2MdWFc+zf1IEdbIxAkeQCYIs+TDWDJcP7ccNbx4cKQBbZj+iGO7gYq37o8c1G2OzjhnGd3JBJmVXjd5mrfWMXZ8NL9ISnJ5doLYYgUMBhaCrTv5GoIo9wP6CcRnWW9ibp+B39FtpwdpiH00Fm5A1HaSR9tC7iKEmDi9kXqW2GIFDAd8Cggxvjr02GngO2A78iu4yzjUpWAm6tZTBTsYQPxiZkM1M0cnV46GnjoESHkWOpyRG4HJvtoDAOE8wfekusCx1vICxBrcCjwdV+/J4jeLZycldr09OegRferrpyzoYKJh/UIBMR2AtUQfzvWU3lB0q8BhgN/0GltsZNYzVqCCTa7v5iSuhrHEhaNMRmCw7h3XnQ9kxNxile1gcj0+yZZsP5XmS/WzFwaMjsHiSvwC+DWVpbbFAQd0o3ji+iWyp6i9JWVpb5P6GgLYucM7GDl7Yx3ht6XDuY9IffF6/2Pzx95Hjo5adnJtCT5NS7eZsQYfzh9RLR+Dv5JdHi7XBN54Z/H3bPb952HqaB4V/TYIuTnFEsfsEljv53eEDxvbpJyemr5/YA/OnWX5u+d8muIIgVVfIYlAmRMGlcC1lj7MCyC0l42qtI8h6ak8V99ZC726SNT8tcgrC5Jmsvgpkm6x1BJ3PZH6BhPYBNuX5jBUWvoFkoF2tI+j8BjKU6Td24gxujLjDG0cUWol0BA+u7C4jP0sAzNu0viORn1bmO4q2Ig3Bi619I5+vQoFZnjF3GeMbpI9/fpdqTxDdpULKEORcCeevu8WeMZZK0rccibR1Z4J53bjwmvv28jJeeaAYyvbZumFRW0eC96M+1wxq93a76rFfrpnp/W8masnHbkqQSN1XEzIHEpEDjp3YRkpJy1oePqFMk5btt9FbT1629yL66fKXeLZV9NNVN2lZ2k5pOt1Y9tg7B4GkdjLAHy0km5nBhJ2gLH/ikOxTJb5EJ5Zt1g1kP7fxQoKy95MqZzsN/npLKttcA0dZlj5mU7S3kpK9Cbjdl/0TPeWvk5K1dp85W/Un+WHc6zaSku2mO0/Zl91avHkxn5Qs7ycyPi58S2ptA7X/ZcW0X82qKy/YV/8Llb8ADjHizn8iLSYAAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\frac{\\operatorname{sinc}{\\left (\\frac{\\omega - \\omega_{0}}{2 a} \\right )} + \\operatorname{sinc}{\\left (\\frac{\\omega + \\omega_{0}}{2 a} \\right )}}{2 \\left|{a}\\right|}$$"
],
"text/plain": [
" ⎛ω - ω₀⎞ ⎛ω + ω₀⎞\n",
"sinc⎜──────⎟ + sinc⎜──────⎟\n",
" ⎝ 2⋅a ⎠ ⎝ 2⋅a ⎠\n",
"───────────────────────────\n",
" 2⋅│a│ "
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"w0, a = sym.symbols('omega0 a')\n",
"\n",
"class rect(sym.Function):\n",
"\n",
" @classmethod\n",
" def eval(cls, arg):\n",
" return sym.Heaviside(arg + sym.S.Half) - sym.Heaviside(arg - sym.S.Half)\n",
"\n",
" \n",
"y = rect(a*t) * sym.cos(w0*t)\n",
"W = 1/abs(a) * sym.sinc(w/(2*a))\n",
"X = sym.pi*(sym.DiracDelta(w + w0) + sym.DiracDelta(w - w0))\n",
"\n",
"Y = 1/(2*sym.pi) * convolve(W, X, w)\n",
"Y"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Both the signal and its Fourier transform are plotted for specific values $\\omega_0$, $a$"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM3OC41MiAyOTMuMDEyIF0gL1BhcmVudCAyIDAgUiAvUmVzb3VyY2VzIDggMCBSIC9UeXBlIC9QYWdlCj4+CmVuZG9iago5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTEgMCBSID4+CnN0cmVhbQp4nK2cTbMstZGG9/0raokXFJJSSknLIWwT4R2GsBeeWRAYYxMcHBh7iPn3flOpLqkrkznEDJfg3nP06impVFJ+SNUdj28e8fj6CMc3+P/H40/Hf+HfPx/x+AT/f/0I+O3tQbWdJeHHb58/pk5niAkFYfv5r4/HXx4f/QfAH1D5k0cMZz3GX7gG17Ml/e3b52+p8tkGOsrXr/NKSa/0NfqC/p1t6yGuL8oj85mBxExnLRxbRFtXWTiTln37eHyMG/3x8T3+DseHAVekfoac0V45Yupn5JQpptbb8eXb4+PPj49+G9Hd4/O/PNqJ2+6BURO///nxQf7V8fk3j998jssF3Pshw3T9APqjX3/1zRd/+NdnX3z3w4dvf/vuXz8cv/7741P8N+7hESPunvi106vwf+11xEhlbv+nbqf/Z7dbP9O9188y2+mXvsTGZ2iBnG5Lz4L07EDPtKXE4eSWX5tahe+0lUo9S8g/1VZ6bYsonTG017ZW4TttUWpnT+2n2srPtvZ5x2WshFjO3EMpvB6erLezt0y1CP7Rb9Ns5oN/Ph/d7WGkdNZeeqnjWZSz7kXu/Cnx5NilhYiu9x5aClTT+7MnniH8IhOowF4Qh0irz6vonT5nXIF6pBZDyO/3GVal/CJ9bnTCOgXuq8+r6J0+137m2mPPkan8nD6XX2acY6SzRJapeXV6K3tvdoR+1thTCSkx/5xup19mqG/2Rbu9yn7CvpSOyTwWToRhx/ynwMu8zKm7Vv2zrUrAONG2fray99uq4Yy9E2qX1F/GwbSVQsbcZbjLba2usnfbSgGWnzCLGibSy0yxTVHGlGPK23Tdyt5vimBqa881Y+Kml5Vk2+KMecI58NbWKnu/LZh1LI5CoeREL5ZGDafMyw9lDsWcn5MzSfwQ02Y185iKr0bzf8Z8LLh87dzqnKmrFx/85wejBp43TA/XuNW5WV5USaFN02wu86tlnb8/VtRDcEToJJbPGfHvP746/nh8d8SzII7BvEmxcOMkF4RLn38qRreG0prOqN9/cmDV/Pffvvzq9598fHz5w4ypXpZIPSvGAsvsdZV85itwpOUk6kxkAFeBN4xnpAw/aABXkYDxpNycHnkC4jU6KRKKTH1XAQBHi1iJbAOu8vYo+Wyce7J34CoA+tlqq8m24CpvD8z43mN7DSQG4CoAuhhimXEG8JS3R8X6bQktG8BVAEg4QmTM52e+8vZo+SxY77YBT0B1rP8We+i2vqe8PTqmF0vwagBXwdQOshgagio7t11JEOQQCI+bHVdfksg7nRxaTrZfviRIQzgLm2PH1peAJMQLsDLdDpcvCdJOzjlTdhBPAkLlDKmG7ty+KwHJEeYnFqoWcSVBMJIpBWeq+BKQgoi65Fyc23clQTAsrcbgtOJKihQqmEkuYqWJMMxtOnC3CGlqoo24KwogVA3UpTj10hCJXoBRJlBKqPFAOkEwgFw34K4oUFtGXHFQG36irPp3QaojiEg5op+wx9xjUB//ma8oUBKcTD8wjSjE1ngBRlGA4aJhVhMjMih53bKjKNBqDghUxKeEFLgswCgCYHKGEjqKhzXr9QIcZQIV3SMpDjDgY+PgCdwVBSIH5A4IbxCdNEJweAFGUQA+H4mkFBfCz7wAo0xAHmGSYoILX3PPUSbQCfGfFKMC+rABd0UBpKb4I8VYnYU2wCgT4EZN4r8TyWbcWzCKAjlUSlXyyC75DS3AKBOgjoxzFKcohm8Bd2UClWTOoxhe7rWFu6JAiaHmkdo2KpzrAowygZLGaKM4oKvbXDLKBDr8G2nyvN3Aa7FW5dwakV4BQed2baNMoCEn0ZtCqFS3J2AUBSqWYMmjGJlF3ia2USbAJVGc49xT34C7ogAmb9P76h2B96p/F2Z1QswzZnvAaorbwjHKBLgT3JnMRfRy689d0Opoiuu4Cqwtbd25C7M60pI8LiKZV9iel1EEYOSgQSI2Wa2wC2vhO8oE4MNKk+LWalhPwFEUgN+Lw+DEzjHWVf8uaHUxe6VKMR5PJVr1jaIAsgFJj2AzMxxG4gUYRYHcuYoJZIRuoS074SgKMG4f7gd2H2617F0yigBVjCxSuIPGVKlXfStodeSSBfcPx1Wwtvf6RhGgYSQS97E3lGuqfD00R3kbGWVucKVHq+LC+HpkphyVOcFsM9zhEaUYUeE1iVxJEITxGSYJiy/DNfZe07NHriQI7AfljDAYi1uqIGV+Ip6kSBvPZ+TFCYv3mqyuJAjmZJJsHeXxxIxp13pzJUWQFpJMM9wuwUVeNtiVFMEKbEHSWaz1ynx5EldSBGuWScuR3betX0ZRAHEzBmMU95CobW1YaSIZCWgeew5YjrHlDTHSRGC1kGtIecRSiNvNW0mRkjCH+ihPHX/aQqw0EbiAWkc5DAt8w4YYSRGODCM9ypEClm28jDIBSeO0tNd2TXpPUaDC3I0NFMRtJV/Oy1MmAKPSdQwR6JWwPRErTQTLv5e5CwSrvCNGUqTB7dO1cbTq38pn5VqGm5XCkLbnfRe0eo/IrPT5wJfE/TlYaSJFHI+WYwXU7Q6sJEgVR0JxPiBEMWtBedJEkIJkHb8xUXlDjKRIhPtveinCcr6ialeaCMzrbD0hyww7YqSJyITR1pEBh7IjRlIkxVp1OcP6cV7AXZjVcZGqixkBIpW6AUZShHLslEc50t5Yt05ZSZEcEcs0NUsU90aMokAJCFLzMH2SKy4T50kTqa2M+ZCQprSyZpcnKYKwgSVQh00OxPLjhVhJEVxIgqsEb8Yt47ktxEqCwFdzY+bhX1JEsHV1zJMUqTBehKFHDj8MVFyIlWTnMWDWZXHFeMpItdpycK4kSIKRhIWVXB+OfPdWriSI7D412cuvyFmQQF7Ty1MEKLI1lBEH5ooxkQxk1reCVIc3ygi2DoLvQzJRniPlCFqdGwIbkpyaMqMDq75RBMD9F0nOjoSpCt9VnwvdUxSAi8+yzJAiIOS/4k9PUYAYz2SEjZ0QEdECjKIAnK5k+RhB+OsrA3CEWb0jNmtSnEKUfZdV/64ogHA6avpaa4YLWoBRFGAKnUZx6bGkDTDKBCq8yQjdsfxX1uYpCsDCSzCnGXVaj81RJgAWkaMkK+J8V/XXcq2MdFLOcUY2nTEZV3WjTEB2QTQ5xnLsW3eMMgEe+wBSTLji1iGjTKAjJRu5bg8YiL2Fu6JARzqquXFNKW0jehdmdRr3hVJJw/fqN2FWLxg3LU4tl22OGmUC+I01uY/whztwVwRoYmbT3D4Ioa+F7CgTwOKLfeb3tKa1o0ygwBA2Lca6og24KxOAfS5zvwHef+/SXVEA99OipviYjFcM6CkTyLJFPYpRuh6Do0ygwh5rMULctnXJKBPoNZDOljjc+QLuigKYIpHGdTDUPWwtGGUCSALyWLEBUUXegbsyATnSa7rvwEisN+CuKCA2pOjuGCEj2lowygSIuyb68JEtbsNqlAlIa2PvIfXKvAN3RQGJWuK4Tq651+0ejDIBzrLli2JGxkhbC0ZRAKuvt3FrWCPh2nb2lAnUJlv3sl3BibYe3QWtzjk31r0KPKeyqt8FrY6EIY5QZWyfhq2+URRANAAfIVsVEW51HyGjCNAxR4q8IwR3ilymXDGipyiQYG0kq0TwFMfGzgUYRQF58wRxiZxkEh5mXIBRADQ5pcp4NkfJskT42jvzlLdxgC6v48iJZ+tnQbJxZRKu9DZerZJXS2SXSTbtZSf32StXEgSBPNJOiSNyhjPAM3pGAK6kSJOTXgkbJdiicMV6riTIWO5y3KvBaU/XE3QlRagjlq8jBE4JM7MuxEqKFKyXrLE5Vn+5JpYrKYLsuFQtbxxeOmYlRSpcYEszy0jt2iFzJUXgc6jVUY5gtl/5uStNhDPNzKTXvIytKyki2yGdZk4W8uUyXGkiWQMeHu+flGvTxJUm0rAMouaXuYXL+rjS23g9JKRY4kxi8bSufjnKBBjGO89MGQs2b4SRJjLe1ZkbHTlfmw2upAjsI89BgZ2C+V+IlSYijmFudbTCe8espEgahmluRiDpaAux0kRqSHOTp8YiicRCjKQIxVwpPbc80gLuwqyOnFLHHT/0uN2GURTIKdV5d2i17jdupYn0UOZ+GNwSvSBGUgRxUO1zAsGKXtmCKymCMKLPckw+zlsrVpoII/yeexFUK+2IkRSpWDRVVym8Buz6Qqw0ESbdU5I37aiFbUJaSZEm4YFeKoRhey/ESoogAQlRjVQOIey3byUgPZwho8dxWE+k8uHKsFxJkRRg//vYcM4sZmohVlIk48ZknRYEJaWu7SZXUqRiPchIwhHixxQXYRQBxKcV+E157zxxudyQI0h1sc4wMkmyeDkeWj1yFAEkVmhIGgmRPEKGa/fAEbQ65cDiydpwl9exgKcoUGLKiA8kFsGTujJXT1FA4k1xfEj60dHLjXiKArVTk31WhAwRc3trwSgKNInvxjlVCRzz1oJRFMBzoTjicmQ9tW+AUd4e8u4i8syuOTb8cHraNleZAFOqIwhm2PunrXIVBWIqxHrCPg4Zr/p3YVZHyBX0gL2SZGKr/l2ZQEeQOq4zdkG3OzCKAgi6qpw/YD4icHmmEK4yATyQzDPZufaJXEUBCnC4mvjDNjwPxl1lAhmZRZ0ZXti7ZJQJNJZUcxywX1bWE7Q6fGbMM89GVLRd3ygT4FZDnXk2stQNuCsKYKRlzWom3/YxMsoEcnl2VLb7t8dmlAnAJReaaXOmHbgrCjBsVdaha7K5tQCjTKBQ07HuOYjjWcBdmUCPiXQLSV5D3UbJKApUeM0+pjBK0/bY7sKszsRVj+XFQGzXN8oEMFlIU1pOL0/BKAq0EoKezGMyXqmcqyjQY0ttpLSIka59EFeZQC9juz2fCDJa3daCUQSIElIOY5slaO/LYDiKAgnPUuwCstSGYCQuwCgKEEIR2SmAZ+Ia9xaMokBBHiUhvmz21B54AUZRoEfEUVFcEoL7XDbAKAIkXIdL4iPjp5BavKaeowggL6hVeWmcqxjbmK5hdRQBCuIPBAZpvIcvb2M8c2pfEgQJBFOTmyM8K1xpIZ4kCDwl7KfsYGaSq3K/bsSTgMQgb+RlsUDyXk+43qFwFQVY3kvvI0VNVC/j5ykKjMOxOIIiBK3XUaMvKYJMric9JILet04ZRYAxN8eCl/RUgvyL8CRF4OgT6ZEa1UJpQ6ykCNL5GXZiPV8HEK4ygV5j1DM4DA0ivY0wkiIkpk5TFCyZ60TPlyYCt5k0c8JUCLy1YiVFshwIzqPUQNfeiC8pgjnQ2jw8p5ieG8++NBFkfjwTR8zBa6m7kiIsVuZ5+MwvD9JKEymN+ZnUtbaPmJUUqRHBUp+JY966dRdmdS5h5pnyXmfLG2AkRWAqWr5eHMBMXYiVJlK67Gpq6igOaUOMpEgPaWwpjhcgeixbx6w0kZz6HHj46mu/1JcmgoA10Mw2EVBv895KgqQzyHaR3qOcRPTrmXjSRCoyLR16Of8LO2IkReSlnNE6ITyjuoC7MKtXpJdairCxhrQBRlIEUSVVLScEBpkXYiVFCM61TnvTWg99IVZSRBKisfODKiXEK7hyJUVKoMKanHLBnNhGy0qKcNNTBpbYPyTabt9KisA8JzkFKLJPer2u7CoCIBxqYQRGRfaw6vVSpC8p0hBwSiIiH2sRC5cXYiVBwCPkFHML90clr6jGlQSpsrUAewsny3ISFdez9yRBkLLJC371kB0DuPRyNeIoAJJsv6YKFyYH44zI+TlanqKAvAuPeSMfGKotXx848hQFKoIWSZ07HAAecluAURTojFErkjojFks9L8AoAmAhZBrRf5E3GpZB8RQFEqaxbAwPY5aeBzyuogAxQrBxlp4wdry1YBQFELDNk6Ue5dWDBRhFgRL1pFheX5WzpQUYZQKyqznSBTRb29aCUSbQaGxvYl5iPl/Zk6coID6u6lk6enqZKk+ZwHxFWXLh9jKsRlEAnkvzQnlbJLVV/y7M6gWJjr7SHGEk4lb/rijQkDwGzVTR/v7YjDIBOWWYeWSJlwP0FAU6Ypo2D5dr2u74LszqpYaZdgZK+1M2ygSQCNamJ8W8LKanCDA+fc3c5nvlfS0eR5lAi1EP4Hu63oH3BK0eKTLN3Yu6HoEVZnVZHVWTVHjqutW/KxPoLCe3o0K5jrRdRYEkx/v6Yjnnvf93YVZHPqhZMEkySVv9u6KA7FXra+Upt204b+WzMjIvXdwy1qlv1e+KAohZur5VjoQ2pu36RlFAPvPdh73JiJYaL8AoCsAVj80XOXNEFLM9MaMogHkY+3gNvSb5YNoCjKKAfPxCgjaJo9eujCNIddyOfKPDoaeYV15ly7Uy5mzNI/dlPPXaV3WjKCCvgWJuE1xkbu0K+zxFAfk0RRyf80IKHNaMdpQJMExekew6hrwZFUcRQLZnQ8/286e+pEgMTbJSD7GSImJg7YflXEWAitvr8qEwS3gSEJLYBg7C+bSxKwnS5UNVxfk8pi8ByXDVcHhkPyroS/IpaAlSs3v3rvQ2vlhEwszmDLEryZeWSJqMqMN+HtOXBOnI3uV7ORzEk4BUeXFdPjJuEVcC0uSTrUXeRjOIKwnS5fUssdcW8SQgfXzmNHn34kpvD5L9OoS3zkc4fUmQIr/IfppFPEk+0h5ORgpbnM+ou5IgEtIigrRP35eASHibZYfFIq4kCKLUgFjdIRxFvqoGrjAjX3Ju3pUEGW961ejciSsBkV9gzZyP3PuSIJI9yAGsg3gSkMLyAbHifXOAK8n3SkkwjdjBfkbal9ZXUd2qf3p8f6Tjd/pdWC/fNXX7Bgbvm3fuX4Uxrnh9FdaP4+uw9q/AerNfgfX47vrGq9H6+gatn9H5W1MvX6flt/Xp49+PRtvmCmVuZHN0cmVhbQplbmRvYmoKMTEgMCBvYmoKNTE0NgplbmRvYmoKMTYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNzggPj4Kc3RyZWFtCnicPZBLEgMhCET3nqKPID/R8ySV1eT+2zTOmIX2EyhssKXoGM7L1ZBd8ZZWGJ74Nu8LnomrqfWHJBUy+6YOGYtn8hQnJBSvJmNA3LHV1qNxMsIMuywmZmCuiq9ELqhQAupR8mpmo+BqpoK+fcRWmfUWFwhFAiYsZyv+nwPT6xYdDBaY7TfLszz2CtN0LMx7hnkPRSN+BuVabmBlrYOfhh2a97ZoKP/kJ3sWeLXPD96rQqEKZW5kc3RyZWFtCmVuZG9iagoxNyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDEzOSA+PgpzdHJlYW0KeJw9j7ENxTAIRHumuAWQABsbz5PoV/77t8FxkgLxdKA78GEQsNUs6WhS4LXjVLIaYBf8yaSB1QTaLaEVaF1KKA5aOusIRNsW9ekHfa6TeORSsaRqL7W+KWK5O/SO0W1awKNnTvau0Obgck9GQSZOylPWoZM0fTaZB9QiyWU82vvQ/P6Z9LsAu7wt2wplbmRzdHJlYW0KZW5kb2JqCjE0IDAgb2JqCjw8IC9CYXNlRm9udCAvRGVqYVZ1U2Fucy1PYmxpcXVlIC9DaGFyUHJvY3MgMTUgMCBSCi9FbmNvZGluZyA8PCAvRGlmZmVyZW5jZXMgWyAxMTYgL3QgMTIxIC95IF0gL1R5cGUgL0VuY29kaW5nID4+IC9GaXJzdENoYXIgMAovRm9udEJCb3ggWyAtMTAxNiAtMzUxIDE2NjAgMTA2OCBdIC9Gb250RGVzY3JpcHRvciAxMyAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2Fucy1PYmxpcXVlCi9TdWJ0eXBlIC9UeXBlMyAvVHlwZSAvRm9udCAvV2lkdGhzIDEyIDAgUiA+PgplbmRvYmoKMTMgMCBvYmoKPDwgL0FzY2VudCA5MjkgL0NhcEhlaWdodCAwIC9EZXNjZW50IC0yMzYgL0ZsYWdzIDk2Ci9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnROYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL0l0YWxpY0FuZ2xlIDAgL01heFdpZHRoIDEzNTAgL1N0ZW1WIDAgL1R5cGUgL0ZvbnREZXNjcmlwdG9yIC9YSGVpZ2h0IDAgPj4KZW5kb2JqCjEyIDAgb2JqClsgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAKNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCAzMTggNDAxIDQ2MCA4MzggNjM2Cjk1MCA3ODAgMjc1IDM5MCAzOTAgNTAwIDgzOCAzMTggMzYxIDMxOCAzMzcgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNgo2MzYgNjM2IDMzNyAzMzcgODM4IDgzOCA4MzggNTMxIDEwMDAgNjg0IDY4NiA2OTggNzcwIDYzMiA1NzUgNzc1IDc1MiAyOTUKMjk1IDY1NiA1NTcgODYzIDc0OCA3ODcgNjAzIDc4NyA2OTUgNjM1IDYxMSA3MzIgNjg0IDk4OSA2ODUgNjExIDY4NSAzOTAgMzM3CjM5MCA4MzggNTAwIDUwMCA2MTMgNjM1IDU1MCA2MzUgNjE1IDM1MiA2MzUgNjM0IDI3OCAyNzggNTc5IDI3OCA5NzQgNjM0IDYxMgo2MzUgNjM1IDQxMSA1MjEgMzkyIDYzNCA1OTIgODE4IDU5MiA1OTIgNTI1IDYzNiAzMzcgNjM2IDgzOCA2MDAgNjM2IDYwMCAzMTgKMzUyIDUxOCAxMDAwIDUwMCA1MDAgNTAwIDEzNTAgNjM1IDQwMCAxMDcwIDYwMCA2ODUgNjAwIDYwMCAzMTggMzE4IDUxOCA1MTgKNTkwIDUwMCAxMDAwIDUwMCAxMDAwIDUyMSA0MDAgMTAyOCA2MDAgNTI1IDYxMSAzMTggNDAxIDYzNiA2MzYgNjM2IDYzNiAzMzcKNTAwIDUwMCAxMDAwIDQ3MSA2MTcgODM4IDM2MSAxMDAwIDUwMCA1MDAgODM4IDQwMSA0MDEgNTAwIDYzNiA2MzYgMzE4IDUwMAo0MDEgNDcxIDYxNyA5NjkgOTY5IDk2OSA1MzEgNjg0IDY4NCA2ODQgNjg0IDY4NCA2ODQgOTc0IDY5OCA2MzIgNjMyIDYzMiA2MzIKMjk1IDI5NSAyOTUgMjk1IDc3NSA3NDggNzg3IDc4NyA3ODcgNzg3IDc4NyA4MzggNzg3IDczMiA3MzIgNzMyIDczMiA2MTEgNjA4CjYzMCA2MTMgNjEzIDYxMyA2MTMgNjEzIDYxMyA5OTUgNTUwIDYxNSA2MTUgNjE1IDYxNSAyNzggMjc4IDI3OCAyNzggNjEyIDYzNAo2MTIgNjEyIDYxMiA2MTIgNjEyIDgzOCA2MTIgNjM0IDYzNCA2MzQgNjM0IDU5MiA2MzUgNTkyIF0KZW5kb2JqCjE1IDAgb2JqCjw8IC90IDE2IDAgUiAveSAxNyAwIFIgPj4KZW5kb2JqCjIyIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjQ3ID4+CnN0cmVhbQp4nE1Ru21EMQzr3xRc4ADra3meC1Jd9m9DyQiQwiChLymnJRb2xksM4QdbD77kkVVDfx4/MewzLD3J5NQ/5rnJVBS+FaqbmFAXYuH9aAS8FnQvIivKB9+PZQxzzvfgoxCXYCY0YKxvSSYX1bwzZMKJoY7DQZtUGHdNFCyuFc0zyO1WN7I6syBseCUT4sYARATZF5DNYKOMsZWQxXIeqAqSBVpg1+kbUYuCK5TWCXSi1sS6zOCr5/Z2N0Mv8uCounh9DOtLsMLopXssfK5CH8z0TDt3SSO98KYTEWYPBVKZnZGVOj1ifbdA/59lK/j7yc/z/QsVKFwqCmVuZHN0cmVhbQplbmRvYmoKMjMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA5MCA+PgpzdHJlYW0KeJxNjUESwCAIA++8Ik9QRND/dHrS/1+r1A69wE4CiRZFgvQ1aksw7rgyFWtQKZiUl8BVMFwL2u6iyv4ySUydhtN7twODsvFxg9JJ+/ZxegCr/XoG3Q/SHCJYCmVuZHN0cmVhbQplbmRvYmoKMjQgMCBvYmoKPDwgL0JCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzcKL1N1YnR5cGUgL0Zvcm0gL1R5cGUgL1hPYmplY3QgPj4Kc3RyZWFtCnic4zI0MFMwNjVVyOUyNzYCs3LALCNzIyALJItgQWTTAAFfCgoKZW5kc3RyZWFtCmVuZG9iagoyNSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDgwID4+CnN0cmVhbQp4nEWMuw3AMAhEe6ZgBH4mZp8olbN/GyBK3HBPunu4OhIyU95hhocEngwshlPxBpmjYDW4RlKNneyjsG5fdYHmelOr9fcHKk92dnE9zcsZ9AplbmRzdHJlYW0KZW5kb2JqCjI2IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ3ID4+CnN0cmVhbQp4nD1PuQ0DMQzrPQUXOMB6LFvzXJDqsn8bykZSCCJA8ZFlR8cKXGICk445Ei9pP/hpGoFYBjVH9ISKYVjgbpICD4MsSleeLV4MkdpCXUj41hDerUxkojyvETtwJxejBz5UG1keekA7RBVZrknDWNVWXWqdsAIcss7CdT3MqgTl0SdrKR9QVEK9dP+fe9r7CwBvL+sKZW5kc3RyZWFtCmVuZG9iagoyNyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE0OSA+PgpzdHJlYW0KeJw1j0sOAyEMQ/c5hS8wUn6EcB6qrqb33zZhWgkJC9svwRaDkYxLTGDsmGPhJVRPrT4kI4+6STkQqVA3BE9oTAwzbNIl8Mp03zKeW7ycVuqCTkjk6aw2GqKMZl7D0VPOCpv+y9wkamVGmQMy61S3E7KyYAXmBbU89zPuqFzohIedyrDoTjGi3GZGGn7/2/T+AnsyMGMKZW5kc3RyZWFtCmVuZG9iagoyOCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDQ5ID4+CnN0cmVhbQp4nDM2tFAwUDA0MAeSRoZAlpGJQoohF0gAxMzlggnmgFkGQBqiOAeuJocrDQDG6A0mCmVuZHN0cmVhbQplbmRvYmoKMjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA2OCA+PgpzdHJlYW0KeJwzMzZTMFCwMAISpqaGCuZGlgophlxAPoiVywUTywGzzCzMgSwjC5CWHC5DC2MwbWJspGBmYgZkWSAxILrSAHL4EpEKZW5kc3RyZWFtCmVuZG9iagozMCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI0OCA+PgpzdHJlYW0KeJwtUTmSA0EIy+cVekJz0++xy5H3/+kKygGDhkMgOi1xUMZPEJYr3vLIVbTh75kYwXfBod/KdRsWORAVSNIYVE2oXbwevQd2HGYC86Q1LIMZ6wM/Ywo3enF4TMbZ7XUZNQR712tPZlAyKxdxycQFU3XYyJnDT6aMC+1czw3IuRHWZRikm5XGjIQjTSFSSKHqJqkzQZAEo6tRo40cxX7pyyOdYVUjagz7XEvb13MTzho0OxarPDmlR1ecy8nFCysH/bzNwEVUGqs8EBJwv9tD/Zzs5Dfe0rmzxfT4XnOyvDAVWPHmtRuQTbX4Ny/i+D3j6/n8A6ilWxYKZW5kc3RyZWFtCmVuZG9iagozMSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDIxMCA+PgpzdHJlYW0KeJw1UMsNQzEIu2cKFqgUAoFknla9df9rbdA7YRH/QljIlAh5qcnOKelLPjpMD7Yuv7EiC611JezKmiCeK++hmbKx0djiYHAaJl6AFjdg6GmNGjV04YKmLpVCgcUl8Jl8dXvovk8ZeGoZcnYEEUPJYAlquhZNWLQ8n5BOAeL/fsPuLeShkvPKnhv5G5zt8DuzbuEnanYi0XIVMtSzNMcYCBNFHjx5RaZw4rPWd9U0EtRmC06WAa5OP4wOAGAiXlmA7K5EOUvSjqWfb7zH9w9AAFO0CmVuZHN0cmVhbQplbmRvYmoKMjAgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zIC9DaGFyUHJvY3MgMjEgMCBSCi9FbmNvZGluZyA8PAovRGlmZmVyZW5jZXMgWyA0MCAvcGFyZW5sZWZ0IC9wYXJlbnJpZ2h0IDQ2IC9wZXJpb2QgNDggL3plcm8gL29uZSAvdHdvIDUyIC9mb3VyIC9maXZlCjU1IC9zZXZlbiBdCi9UeXBlIC9FbmNvZGluZyA+PgovRmlyc3RDaGFyIDAgL0ZvbnRCQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRm9udERlc2NyaXB0b3IgMTkgMCBSCi9Gb250TWF0cml4IFsgMC4wMDEgMCAwIDAuMDAxIDAgMCBdIC9MYXN0Q2hhciAyNTUgL05hbWUgL0RlamFWdVNhbnMKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTggMCBSID4+CmVuZG9iagoxOSAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgMzIKL0ZvbnRCQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRm9udE5hbWUgL0RlamFWdVNhbnMgL0l0YWxpY0FuZ2xlIDAKL01heFdpZHRoIDEzNDIgL1N0ZW1WIDAgL1R5cGUgL0ZvbnREZXNjcmlwdG9yIC9YSGVpZ2h0IDAgPj4KZW5kb2JqCjE4IDAgb2JqClsgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAKNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCAzMTggNDAxIDQ2MCA4MzggNjM2Cjk1MCA3ODAgMjc1IDM5MCAzOTAgNTAwIDgzOCAzMTggMzYxIDMxOCAzMzcgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNgo2MzYgNjM2IDMzNyAzMzcgODM4IDgzOCA4MzggNTMxIDEwMDAgNjg0IDY4NiA2OTggNzcwIDYzMiA1NzUgNzc1IDc1MiAyOTUKMjk1IDY1NiA1NTcgODYzIDc0OCA3ODcgNjAzIDc4NyA2OTUgNjM1IDYxMSA3MzIgNjg0IDk4OSA2ODUgNjExIDY4NSAzOTAgMzM3CjM5MCA4MzggNTAwIDUwMCA2MTMgNjM1IDU1MCA2MzUgNjE1IDM1MiA2MzUgNjM0IDI3OCAyNzggNTc5IDI3OCA5NzQgNjM0IDYxMgo2MzUgNjM1IDQxMSA1MjEgMzkyIDYzNCA1OTIgODE4IDU5MiA1OTIgNTI1IDYzNiAzMzcgNjM2IDgzOCA2MDAgNjM2IDYwMCAzMTgKMzUyIDUxOCAxMDAwIDUwMCA1MDAgNTAwIDEzNDIgNjM1IDQwMCAxMDcwIDYwMCA2ODUgNjAwIDYwMCAzMTggMzE4IDUxOCA1MTgKNTkwIDUwMCAxMDAwIDUwMCAxMDAwIDUyMSA0MDAgMTAyMyA2MDAgNTI1IDYxMSAzMTggNDAxIDYzNiA2MzYgNjM2IDYzNiAzMzcKNTAwIDUwMCAxMDAwIDQ3MSA2MTIgODM4IDM2MSAxMDAwIDUwMCA1MDAgODM4IDQwMSA0MDEgNTAwIDYzNiA2MzYgMzE4IDUwMAo0MDEgNDcxIDYxMiA5NjkgOTY5IDk2OSA1MzEgNjg0IDY4NCA2ODQgNjg0IDY4NCA2ODQgOTc0IDY5OCA2MzIgNjMyIDYzMiA2MzIKMjk1IDI5NSAyOTUgMjk1IDc3NSA3NDggNzg3IDc4NyA3ODcgNzg3IDc4NyA4MzggNzg3IDczMiA3MzIgNzMyIDczMiA2MTEgNjA1CjYzMCA2MTMgNjEzIDYxMyA2MTMgNjEzIDYxMyA5ODIgNTUwIDYxNSA2MTUgNjE1IDYxNSAyNzggMjc4IDI3OCAyNzggNjEyIDYzNAo2MTIgNjEyIDYxMiA2MTIgNjEyIDgzOCA2MTIgNjM0IDYzNCA2MzQgNjM0IDU5MiA2MzUgNTkyIF0KZW5kb2JqCjIxIDAgb2JqCjw8IC9maXZlIDIyIDAgUiAvZm91ciAyMyAwIFIgL29uZSAyNSAwIFIgL3BhcmVubGVmdCAyNiAwIFIKL3BhcmVucmlnaHQgMjcgMCBSIC9wZXJpb2QgMjggMCBSIC9zZXZlbiAyOSAwIFIgL3R3byAzMCAwIFIgL3plcm8gMzEgMCBSID4+CmVuZG9iagozIDAgb2JqCjw8IC9GMSAyMCAwIFIgL0YyIDE0IDAgUiA+PgplbmRvYmoKNCAwIG9iago8PCAvQTEgPDwgL0NBIDAgL1R5cGUgL0V4dEdTdGF0ZSAvY2EgMSA+PgovQTIgPDwgL0NBIDEgL1R5cGUgL0V4dEdTdGF0ZSAvY2EgMSA+PiA+PgplbmRvYmoKNSAwIG9iago8PCA+PgplbmRvYmoKNiAwIG9iago8PCA+PgplbmRvYmoKNyAwIG9iago8PCAvRGVqYVZ1U2Fucy1taW51cyAyNCAwIFIgPj4KZW5kb2JqCjIgMCBvYmoKPDwgL0NvdW50IDEgL0tpZHMgWyAxMCAwIFIgXSAvVHlwZSAvUGFnZXMgPj4KZW5kb2JqCjMyIDAgb2JqCjw8IC9DcmVhdGlvbkRhdGUgKEQ6MjAxOTA1MTYxODM3NTUrMDInMDAnKQovQ3JlYXRvciAobWF0cGxvdGxpYiAzLjAuMywgaHR0cDovL21hdHBsb3RsaWIub3JnKQovUHJvZHVjZXIgKG1hdHBsb3RsaWIgcGRmIGJhY2tlbmQgMy4wLjMpID4+CmVuZG9iagp4cmVmCjAgMzMKMDAwMDAwMDAwMCA2NTUzNSBmIAowMDAwMDAwMDE2IDAwMDAwIG4gCjAwMDAwMTE4NDIgMDAwMDAgbiAKMDAwMDAxMTYxMiAwMDAwMCBuIAowMDAwMDExNjU1IDAwMDAwIG4gCjAwMDAwMTE3NTQgMDAwMDAgbiAKMDAwMDAxMTc3NSAwMDAwMCBuIAowMDAwMDExNzk2IDAwMDAwIG4gCjAwMDAwMDAwNjUgMDAwMDAgbiAKMDAwMDAwMDM5MiAwMDAwMCBuIAowMDAwMDAwMjA4IDAwMDAwIG4gCjAwMDAwMDU2MTMgMDAwMDAgbiAKMDAwMDAwNjYyOCAwMDAwMCBuIAowMDAwMDA2NDIwIDAwMDAwIG4gCjAwMDAwMDYwOTcgMDAwMDAgbiAKMDAwMDAwNzY4MSAwMDAwMCBuIAowMDAwMDA1NjM0IDAwMDAwIG4gCjAwMDAwMDU4ODUgMDAwMDAgbiAKMDAwMDAxMDQwOCAwMDAwMCBuIAowMDAwMDEwMjA4IDAwMDAwIG4gCjAwMDAwMDk4MzQgMDAwMDAgbiAKMDAwMDAxMTQ2MSAwMDAwMCBuIAowMDAwMDA3NzIzIDAwMDAwIG4gCjAwMDAwMDgwNDMgMDAwMDAgbiAKMDAwMDAwODIwNSAwMDAwMCBuIAowMDAwMDA4Mzc1IDAwMDAwIG4gCjAwMDAwMDg1MjcgMDAwMDAgbiAKMDAwMDAwODc0NyAwMDAwMCBuIAowMDAwMDA4OTY5IDAwMDAwIG4gCjAwMDAwMDkwOTAgMDAwMDAgbiAKMDAwMDAwOTIzMCAwMDAwMCBuIAowMDAwMDA5NTUxIDAwMDAwIG4gCjAwMDAwMTE5MDIgMDAwMDAgbiAKdHJhaWxlcgo8PCAvSW5mbyAzMiAwIFIgL1Jvb3QgMSAwIFIgL1NpemUgMzMgPj4Kc3RhcnR4cmVmCjEyMDU2CiUlRU9GCg==\n",
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
"<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
" \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
"<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
"<svg height=\"292.862pt\" version=\"1.1\" viewBox=\"0 0 378.52 292.862\" width=\"378.52pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
" <defs>\n",
" <style type=\"text/css\">\n",
"*{stroke-linecap:butt;stroke-linejoin:round;}\n",
" </style>\n",
" </defs>\n",
" <g id=\"figure_1\">\n",
" <g id=\"patch_1\">\n",
" <path d=\"M 0 292.862 \n",
"L 378.52 292.862 \n",
"L 378.52 0 \n",
"L 0 0 \n",
"z\n",
"\" style=\"fill:#ffffff;\"/>\n",
" </g>\n",
" <g id=\"axes_1\">\n",
" <g id=\"patch_2\">\n",
" <path d=\"M 10.7 282.162 \n",
"L 367.82 282.162 \n",
"L 367.82 16.05 \n",
"L 10.7 16.05 \n",
"z\n",
"\" style=\"fill:#ffffff;\"/>\n",
" </g>\n",
" <g id=\"matplotlib.axis_1\">\n",
" <g id=\"xtick_1\">\n",
" <g id=\"line2d_1\">\n",
" <defs>\n",
" <path d=\"M 0 0 \n",
"L 0 3.5 \n",
"\" id=\"mcb4d075ebc\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
" </defs>\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"46.412\" xlink:href=\"#mcb4d075ebc\" y=\"149.105819\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_1\">\n",
" <!-- −4 -->\n",
" <defs>\n",
" <path d=\"M 10.59375 35.5 \n",
"L 73.1875 35.5 \n",
"L 73.1875 27.203125 \n",
"L 10.59375 27.203125 \n",
"z\n",
"\" id=\"DejaVuSans-8722\"/>\n",
" <path d=\"M 37.796875 64.3125 \n",
"L 12.890625 25.390625 \n",
"L 37.796875 25.390625 \n",
"z\n",
"M 35.203125 72.90625 \n",
"L 47.609375 72.90625 \n",
"L 47.609375 25.390625 \n",
"L 58.015625 25.390625 \n",
"L 58.015625 17.1875 \n",
"L 47.609375 17.1875 \n",
"L 47.609375 0 \n",
"L 37.796875 0 \n",
"L 37.796875 17.1875 \n",
"L 4.890625 17.1875 \n",
"L 4.890625 26.703125 \n",
"z\n",
"\" id=\"DejaVuSans-52\"/>\n",
" </defs>\n",
" <g transform=\"translate(39.040906 163.704256)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-52\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_2\">\n",
" <g id=\"line2d_2\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"117.836\" xlink:href=\"#mcb4d075ebc\" y=\"149.105819\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_2\">\n",
" <!-- −2 -->\n",
" <defs>\n",
" <path d=\"M 19.1875 8.296875 \n",
"L 53.609375 8.296875 \n",
"L 53.609375 0 \n",
"L 7.328125 0 \n",
"L 7.328125 8.296875 \n",
"Q 12.9375 14.109375 22.625 23.890625 \n",
"Q 32.328125 33.6875 34.8125 36.53125 \n",
"Q 39.546875 41.84375 41.421875 45.53125 \n",
"Q 43.3125 49.21875 43.3125 52.78125 \n",
"Q 43.3125 58.59375 39.234375 62.25 \n",
"Q 35.15625 65.921875 28.609375 65.921875 \n",
"Q 23.96875 65.921875 18.8125 64.3125 \n",
"Q 13.671875 62.703125 7.8125 59.421875 \n",
"L 7.8125 69.390625 \n",
"Q 13.765625 71.78125 18.9375 73 \n",
"Q 24.125 74.21875 28.421875 74.21875 \n",
"Q 39.75 74.21875 46.484375 68.546875 \n",
"Q 53.21875 62.890625 53.21875 53.421875 \n",
"Q 53.21875 48.921875 51.53125 44.890625 \n",
"Q 49.859375 40.875 45.40625 35.40625 \n",
"Q 44.1875 33.984375 37.640625 27.21875 \n",
"Q 31.109375 20.453125 19.1875 8.296875 \n",
"z\n",
"\" id=\"DejaVuSans-50\"/>\n",
" </defs>\n",
" <g transform=\"translate(110.464906 163.704256)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-50\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_3\">\n",
" <g id=\"line2d_3\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#mcb4d075ebc\" y=\"149.105819\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_3\">\n",
" <!-- 0 -->\n",
" <defs>\n",
" <path d=\"M 31.78125 66.40625 \n",
"Q 24.171875 66.40625 20.328125 58.90625 \n",
"Q 16.5 51.421875 16.5 36.375 \n",
"Q 16.5 21.390625 20.328125 13.890625 \n",
"Q 24.171875 6.390625 31.78125 6.390625 \n",
"Q 39.453125 6.390625 43.28125 13.890625 \n",
"Q 47.125 21.390625 47.125 36.375 \n",
"Q 47.125 51.421875 43.28125 58.90625 \n",
"Q 39.453125 66.40625 31.78125 66.40625 \n",
"z\n",
"M 31.78125 74.21875 \n",
"Q 44.046875 74.21875 50.515625 64.515625 \n",
"Q 56.984375 54.828125 56.984375 36.375 \n",
"Q 56.984375 17.96875 50.515625 8.265625 \n",
"Q 44.046875 -1.421875 31.78125 -1.421875 \n",
"Q 19.53125 -1.421875 13.0625 8.265625 \n",
"Q 6.59375 17.96875 6.59375 36.375 \n",
"Q 6.59375 54.828125 13.0625 64.515625 \n",
"Q 19.53125 74.21875 31.78125 74.21875 \n",
"z\n",
"\" id=\"DejaVuSans-48\"/>\n",
" </defs>\n",
" <g transform=\"translate(186.07875 163.704256)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_4\">\n",
" <g id=\"line2d_4\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"260.684\" xlink:href=\"#mcb4d075ebc\" y=\"149.105819\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_4\">\n",
" <!-- 2 -->\n",
" <g transform=\"translate(257.50275 163.704256)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-50\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_5\">\n",
" <g id=\"line2d_5\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"332.108\" xlink:href=\"#mcb4d075ebc\" y=\"149.105819\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_5\">\n",
" <!-- 4 -->\n",
" <g transform=\"translate(328.92675 163.704256)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-52\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_6\">\n",
" <!-- $t$ -->\n",
" <defs>\n",
" <path d=\"M 42.28125 54.6875 \n",
"L 40.921875 47.703125 \n",
"L 23 47.703125 \n",
"L 17.1875 18.015625 \n",
"Q 16.890625 16.359375 16.75 15.234375 \n",
"Q 16.609375 14.109375 16.609375 13.484375 \n",
"Q 16.609375 10.359375 18.484375 8.9375 \n",
"Q 20.359375 7.515625 24.515625 7.515625 \n",
"L 33.59375 7.515625 \n",
"L 32.078125 0 \n",
"L 23.484375 0 \n",
"Q 15.484375 0 11.546875 3.125 \n",
"Q 7.625 6.25 7.625 12.59375 \n",
"Q 7.625 13.71875 7.765625 15.0625 \n",
"Q 7.90625 16.40625 8.203125 18.015625 \n",
"L 14.015625 47.703125 \n",
"L 6.390625 47.703125 \n",
"L 7.8125 54.6875 \n",
"L 15.28125 54.6875 \n",
"L 18.3125 70.21875 \n",
"L 27.296875 70.21875 \n",
"L 24.3125 54.6875 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-116\"/>\n",
" </defs>\n",
" <g transform=\"translate(365.82 177.382381)scale(0.1 -0.1)\">\n",
" <use transform=\"translate(0 0.78125)\" xlink:href=\"#DejaVuSans-Oblique-116\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"matplotlib.axis_2\">\n",
" <g id=\"ytick_1\">\n",
" <g id=\"line2d_6\">\n",
" <defs>\n",
" <path d=\"M 0 0 \n",
"L -3.5 0 \n",
"\" id=\"m9733e5ac5c\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
" </defs>\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m9733e5ac5c\" y=\"270.066043\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_7\">\n",
" <!-- −1.00 -->\n",
" <defs>\n",
" <path d=\"M 12.40625 8.296875 \n",
"L 28.515625 8.296875 \n",
"L 28.515625 63.921875 \n",
"L 10.984375 60.40625 \n",
"L 10.984375 69.390625 \n",
"L 28.421875 72.90625 \n",
"L 38.28125 72.90625 \n",
"L 38.28125 8.296875 \n",
"L 54.390625 8.296875 \n",
"L 54.390625 0 \n",
"L 12.40625 0 \n",
"z\n",
"\" id=\"DejaVuSans-49\"/>\n",
" <path d=\"M 10.6875 12.40625 \n",
"L 21 12.40625 \n",
"L 21 0 \n",
"L 10.6875 0 \n",
"z\n",
"\" id=\"DejaVuSans-46\"/>\n",
" </defs>\n",
" <g transform=\"translate(151.614688 273.865262)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"179.199219\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"242.822266\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_2\">\n",
" <g id=\"line2d_7\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m9733e5ac5c\" y=\"239.825987\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_8\">\n",
" <!-- −0.75 -->\n",
" <defs>\n",
" <path d=\"M 8.203125 72.90625 \n",
"L 55.078125 72.90625 \n",
"L 55.078125 68.703125 \n",
"L 28.609375 0 \n",
"L 18.3125 0 \n",
"L 43.21875 64.59375 \n",
"L 8.203125 64.59375 \n",
"z\n",
"\" id=\"DejaVuSans-55\"/>\n",
" <path d=\"M 10.796875 72.90625 \n",
"L 49.515625 72.90625 \n",
"L 49.515625 64.59375 \n",
"L 19.828125 64.59375 \n",
"L 19.828125 46.734375 \n",
"Q 21.96875 47.46875 24.109375 47.828125 \n",
"Q 26.265625 48.1875 28.421875 48.1875 \n",
"Q 40.625 48.1875 47.75 41.5 \n",
"Q 54.890625 34.8125 54.890625 23.390625 \n",
"Q 54.890625 11.625 47.5625 5.09375 \n",
"Q 40.234375 -1.421875 26.90625 -1.421875 \n",
"Q 22.3125 -1.421875 17.546875 -0.640625 \n",
"Q 12.796875 0.140625 7.71875 1.703125 \n",
"L 7.71875 11.625 \n",
"Q 12.109375 9.234375 16.796875 8.0625 \n",
"Q 21.484375 6.890625 26.703125 6.890625 \n",
"Q 35.15625 6.890625 40.078125 11.328125 \n",
"Q 45.015625 15.765625 45.015625 23.390625 \n",
"Q 45.015625 31 40.078125 35.4375 \n",
"Q 35.15625 39.890625 26.703125 39.890625 \n",
"Q 22.75 39.890625 18.8125 39.015625 \n",
"Q 14.890625 38.140625 10.796875 36.28125 \n",
"z\n",
"\" id=\"DejaVuSans-53\"/>\n",
" </defs>\n",
" <g transform=\"translate(151.614688 243.625206)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"179.199219\" xlink:href=\"#DejaVuSans-55\"/>\n",
" <use x=\"242.822266\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_3\">\n",
" <g id=\"line2d_8\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m9733e5ac5c\" y=\"209.585931\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_9\">\n",
" <!-- −0.50 -->\n",
" <g transform=\"translate(151.614688 213.38515)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"179.199219\" xlink:href=\"#DejaVuSans-53\"/>\n",
" <use x=\"242.822266\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_4\">\n",
" <g id=\"line2d_9\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m9733e5ac5c\" y=\"179.345875\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_10\">\n",
" <!-- −0.25 -->\n",
" <g transform=\"translate(151.614688 183.145094)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"179.199219\" xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"242.822266\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_5\">\n",
" <g id=\"line2d_10\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m9733e5ac5c\" y=\"149.105819\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_11\">\n",
" <!-- 0.00 -->\n",
" <g transform=\"translate(159.994375 152.905037)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"159.033203\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_6\">\n",
" <g id=\"line2d_11\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m9733e5ac5c\" y=\"118.865763\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_12\">\n",
" <!-- 0.25 -->\n",
" <g transform=\"translate(159.994375 122.664981)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"159.033203\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_7\">\n",
" <g id=\"line2d_12\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m9733e5ac5c\" y=\"88.625707\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_13\">\n",
" <!-- 0.50 -->\n",
" <g transform=\"translate(159.994375 92.424925)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-53\"/>\n",
" <use x=\"159.033203\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_8\">\n",
" <g id=\"line2d_13\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m9733e5ac5c\" y=\"58.385651\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_14\">\n",
" <!-- 0.75 -->\n",
" <g transform=\"translate(159.994375 62.184869)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-55\"/>\n",
" <use x=\"159.033203\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_9\">\n",
" <g id=\"line2d_14\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"189.26\" xlink:href=\"#m9733e5ac5c\" y=\"28.145594\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_15\">\n",
" <!-- 1.00 -->\n",
" <g transform=\"translate(159.994375 31.944813)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"159.033203\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_16\">\n",
" <!-- $y(t)$ -->\n",
" <defs>\n",
" <path d=\"M 24.8125 -5.078125 \n",
"Q 18.5625 -15.578125 14.625 -18.1875 \n",
"Q 10.6875 -20.796875 4.59375 -20.796875 \n",
"L -2.484375 -20.796875 \n",
"L -0.984375 -13.28125 \n",
"L 4.203125 -13.28125 \n",
"Q 7.953125 -13.28125 10.59375 -11.234375 \n",
"Q 13.234375 -9.1875 16.5 -3.21875 \n",
"L 19.28125 2 \n",
"L 7.171875 54.6875 \n",
"L 16.703125 54.6875 \n",
"L 25.78125 12.796875 \n",
"L 50.875 54.6875 \n",
"L 60.296875 54.6875 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-121\"/>\n",
" <path d=\"M 31 75.875 \n",
"Q 24.46875 64.65625 21.28125 53.65625 \n",
"Q 18.109375 42.671875 18.109375 31.390625 \n",
"Q 18.109375 20.125 21.3125 9.0625 \n",
"Q 24.515625 -2 31 -13.1875 \n",
"L 23.1875 -13.1875 \n",
"Q 15.875 -1.703125 12.234375 9.375 \n",
"Q 8.59375 20.453125 8.59375 31.390625 \n",
"Q 8.59375 42.28125 12.203125 53.3125 \n",
"Q 15.828125 64.359375 23.1875 75.875 \n",
"z\n",
"\" id=\"DejaVuSans-40\"/>\n",
" <path d=\"M 8.015625 75.875 \n",
"L 15.828125 75.875 \n",
"Q 23.140625 64.359375 26.78125 53.3125 \n",
"Q 30.421875 42.28125 30.421875 31.390625 \n",
"Q 30.421875 20.453125 26.78125 9.375 \n",
"Q 23.140625 -1.703125 15.828125 -13.1875 \n",
"L 8.015625 -13.1875 \n",
"Q 14.5 -2 17.703125 9.0625 \n",
"Q 20.90625 20.125 20.90625 31.390625 \n",
"Q 20.90625 42.671875 17.703125 53.65625 \n",
"Q 14.5 64.65625 8.015625 75.875 \n",
"z\n",
"\" id=\"DejaVuSans-41\"/>\n",
" </defs>\n",
" <g transform=\"translate(145.514688 24.9)rotate(-90)scale(0.1 -0.1)\">\n",
" <use transform=\"translate(0 0.125)\" xlink:href=\"#DejaVuSans-Oblique-121\"/>\n",
" <use transform=\"translate(59.179688 0.125)\" xlink:href=\"#DejaVuSans-40\"/>\n",
" <use transform=\"translate(98.193359 0.125)\" xlink:href=\"#DejaVuSans-Oblique-116\"/>\n",
" <use transform=\"translate(137.402344 0.125)\" xlink:href=\"#DejaVuSans-41\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"LineCollection_1\">\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 10.7 149.105819 \n",
"L 17.781201 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 17.781201 149.105819 \n",
"L 25.339633 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 25.339633 149.105819 \n",
"L 31.134256 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 31.134256 149.105819 \n",
"L 37.34801 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 37.34801 149.105819 \n",
"L 43.313143 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 43.313143 149.105819 \n",
"L 49.183631 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 49.183631 149.105819 \n",
"L 54.864926 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 54.864926 149.105819 \n",
"L 59.878721 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 59.878721 149.105819 \n",
"L 64.991808 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 64.991808 149.105819 \n",
"L 69.516875 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 69.516875 149.105819 \n",
"L 74.482872 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 74.482872 149.105819 \n",
"L 79.163376 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 79.163376 149.105819 \n",
"L 84.57922 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 84.57922 149.105819 \n",
"L 89.281909 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 89.281909 149.105819 \n",
"L 95.364688 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 95.364688 149.105819 \n",
"L 100.708162 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 100.708162 149.105819 \n",
"L 106.888185 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 106.888185 149.105819 \n",
"L 112.608428 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 112.608428 149.105819 \n",
"L 118.084066 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 118.084066 149.105819 \n",
"L 123.213699 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 123.213699 149.105819 \n",
"L 128.644434 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 128.644434 149.105819 \n",
"L 135.027095 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 135.027095 149.105819 \n",
"L 141.461537 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 141.461537 149.105819 \n",
"L 146.822022 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 146.822022 149.105819 \n",
"L 152.154459 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 152.154459 149.105819 \n",
"L 153.287102 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 153.287102 149.105819 \n",
"L 153.535468 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 153.535468 149.105819 \n",
"L 153.568232 250.971277 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 153.568232 250.971277 \n",
"L 153.601039 251.566196 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 153.601039 251.566196 \n",
"L 153.655071 252.527133 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 153.655071 252.527133 \n",
"L 153.784993 254.74045 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 153.784993 254.74045 \n",
"L 154.224132 261.170951 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 154.224132 261.170951 \n",
"L 154.520589 264.560114 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 154.520589 264.560114 \n",
"L 154.695331 266.186596 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 154.695331 266.186596 \n",
"L 154.874016 267.559935 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 154.874016 267.559935 \n",
"L 155.005096 268.379025 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.005096 268.379025 \n",
"L 155.078863 268.769388 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.078863 268.769388 \n",
"L 155.160913 269.143602 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.160913 269.143602 \n",
"L 155.208043 269.329914 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.208043 269.329914 \n",
"L 155.248672 269.473719 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.248672 269.473719 \n",
"L 155.293362 269.613909 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.293362 269.613909 \n",
"L 155.332222 269.720469 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.332222 269.720469 \n",
"L 155.368386 269.806809 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.368386 269.806809 \n",
"L 155.407327 269.885937 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.407327 269.885937 \n",
"L 155.439795 269.940934 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.439795 269.940934 \n",
"L 155.473071 269.986937 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.473071 269.986937 \n",
"L 155.510746 270.026353 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.510746 270.026353 \n",
"L 155.552672 270.054395 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.552672 270.054395 \n",
"L 155.599223 270.066 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.599223 270.066 \n",
"L 155.648833 270.055745 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.648833 270.055745 \n",
"L 155.681391 270.036329 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.681391 270.036329 \n",
"L 155.720554 269.999658 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.720554 269.999658 \n",
"L 155.765231 269.940071 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.765231 269.940071 \n",
"L 155.804823 269.87146 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.804823 269.87146 \n",
"L 155.838783 269.800782 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.838783 269.800782 \n",
"L 155.869399 269.72771 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.869399 269.72771 \n",
"L 155.905673 269.62966 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.905673 269.62966 \n",
"L 155.947949 269.499694 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 155.947949 269.499694 \n",
"L 156.010721 269.275602 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 156.010721 269.275602 \n",
"L 156.082258 268.974958 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 156.082258 268.974958 \n",
"L 156.14613 268.665883 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 156.14613 268.665883 \n",
"L 156.206557 268.338267 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 156.206557 268.338267 \n",
"L 156.352423 267.406974 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 156.352423 267.406974 \n",
"L 156.496763 266.291169 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 156.496763 266.291169 \n",
"L 156.663967 264.759467 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 156.663967 264.759467 \n",
"L 157.078943 259.87127 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 157.078943 259.87127 \n",
"L 157.447517 254.274427 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 157.447517 254.274427 \n",
"L 158.202696 239.389232 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 158.202696 239.389232 \n",
"L 159.48507 205.34138 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 159.48507 205.34138 \n",
"L 162.536104 105.273194 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 162.536104 105.273194 \n",
"L 164.945064 44.462272 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 164.945064 44.462272 \n",
"L 165.534409 35.916811 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 165.534409 35.916811 \n",
"L 165.849676 32.596702 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 165.849676 32.596702 \n",
"L 166.026794 31.128171 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.026794 31.128171 \n",
"L 166.120357 30.469337 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.120357 30.469337 \n",
"L 166.232802 29.785309 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.232802 29.785309 \n",
"L 166.323632 29.31911 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.323632 29.31911 \n",
"L 166.406945 28.959619 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.406945 28.959619 \n",
"L 166.444254 28.819816 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.444254 28.819816 \n",
"L 166.483888 28.685687 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.483888 28.685687 \n",
"L 166.525079 28.562002 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.525079 28.562002 \n",
"L 166.562577 28.463352 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.562577 28.463352 \n",
"L 166.616192 28.34541 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.616192 28.34541 \n",
"L 166.66337 28.264138 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.66337 28.264138 \n",
"L 166.707275 28.20745 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.707275 28.20745 \n",
"L 166.755094 28.166499 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.755094 28.166499 \n",
"L 166.789495 28.150449 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.789495 28.150449 \n",
"L 166.830736 28.146 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.830736 28.146 \n",
"L 166.875833 28.1596 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.875833 28.1596 \n",
"L 166.916999 28.188852 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.916999 28.188852 \n",
"L 166.959056 28.235329 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 166.959056 28.235329 \n",
"L 167.010312 28.314637 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 167.010312 28.314637 \n",
"L 167.061844 28.419454 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 167.061844 28.419454 \n",
"L 167.105582 28.528135 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 167.105582 28.528135 \n",
"L 167.144712 28.640695 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 167.144712 28.640695 \n",
"L 167.178624 28.749945 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 167.178624 28.749945 \n",
"L 167.21772 28.88936 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 167.21772 28.88936 \n",
"L 167.262475 29.066643 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 167.262475 29.066643 \n",
"L 167.341934 29.427825 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 167.341934 29.427825 \n",
"L 167.418238 29.83043 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 167.418238 29.83043 \n",
"L 167.500664 30.326509 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 167.500664 30.326509 \n",
"L 167.578556 30.853452 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 167.578556 30.853452 \n",
"L 167.704622 31.825378 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 167.704622 31.825378 \n",
"L 167.855218 33.177856 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 167.855218 33.177856 \n",
"L 168.168666 36.650652 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 168.168666 36.650652 \n",
"L 168.799835 46.236229 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 168.799835 46.236229 \n",
"L 170.104696 75.763811 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 170.104696 75.763811 \n",
"L 172.298889 144.628171 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 172.298889 144.628171 \n",
"L 174.578898 217.546536 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 174.578898 217.546536 \n",
"L 175.708449 245.17405 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 175.708449 245.17405 \n",
"L 176.34523 256.687342 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 176.34523 256.687342 \n",
"L 176.689903 261.515212 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 176.689903 261.515212 \n",
"L 177.053322 265.471724 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.053322 265.471724 \n",
"L 177.260424 267.189958 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.260424 267.189958 \n",
"L 177.367717 267.924317 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.367717 267.924317 \n",
"L 177.42889 268.295046 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.42889 268.295046 \n",
"L 177.495878 268.660898 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.495878 268.660898 \n",
"L 177.586162 269.087403 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.586162 269.087403 \n",
"L 177.630932 269.270473 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.630932 269.270473 \n",
"L 177.677891 269.442204 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.677891 269.442204 \n",
"L 177.731806 269.613712 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.731806 269.613712 \n",
"L 177.779607 269.7428 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.779607 269.7428 \n",
"L 177.807293 269.807685 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.807293 269.807685 \n",
"L 177.840165 269.875302 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.840165 269.875302 \n",
"L 177.868091 269.924708 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.868091 269.924708 \n",
"L 177.891212 269.960022 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.891212 269.960022 \n",
"L 177.91392 269.989774 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.91392 269.989774 \n",
"L 177.93293 270.010924 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.93293 270.010924 \n",
"L 177.957963 270.033547 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.957963 270.033547 \n",
"L 177.982866 270.050157 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 177.982866 270.050157 \n",
"L 178.008271 270.061042 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.008271 270.061042 \n",
"L 178.032219 270.065698 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.032219 270.065698 \n",
"L 178.059988 270.064287 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.059988 270.064287 \n",
"L 178.085552 270.056522 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.085552 270.056522 \n",
"L 178.118814 270.037141 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.118814 270.037141 \n",
"L 178.146084 270.013424 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.146084 270.013424 \n",
"L 178.170984 269.985612 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.170984 269.985612 \n",
"L 178.197032 269.950228 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.197032 269.950228 \n",
"L 178.226134 269.903092 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.226134 269.903092 \n",
"L 178.254241 269.849952 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.254241 269.849952 \n",
"L 178.279688 269.795389 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.279688 269.795389 \n",
"L 178.309352 269.724052 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.309352 269.724052 \n",
"L 178.336958 269.650184 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.336958 269.650184 \n",
"L 178.366119 269.564334 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.366119 269.564334 \n",
"L 178.419318 269.387029 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.419318 269.387029 \n",
"L 178.464155 269.216864 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.464155 269.216864 \n",
"L 178.510982 269.018933 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.510982 269.018933 \n",
"L 178.578022 268.69969 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.578022 268.69969 \n",
"L 178.64486 268.339455 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.64486 268.339455 \n",
"L 178.755118 267.653995 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.755118 267.653995 \n",
"L 178.888774 266.671629 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 178.888774 266.671629 \n",
"L 179.015684 265.586425 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 179.015684 265.586425 \n",
"L 179.245345 263.249742 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 179.245345 263.249742 \n",
"L 179.810029 255.522239 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 179.810029 255.522239 \n",
"L 180.704415 237.950382 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 180.704415 237.950382 \n",
"L 185.037243 103.302937 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 185.037243 103.302937 \n",
"L 186.416313 64.510089 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 186.416313 64.510089 \n",
"L 187.186424 47.969456 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 187.186424 47.969456 \n",
"L 187.842566 37.548911 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 187.842566 37.548911 \n",
"L 188.226801 33.172729 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 188.226801 33.172729 \n",
"L 188.399347 31.641323 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 188.399347 31.641323 \n",
"L 188.541944 30.582495 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 188.541944 30.582495 \n",
"L 188.633574 30.001729 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 188.633574 30.001729 \n",
"L 188.739282 29.429167 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 188.739282 29.429167 \n",
"L 188.827387 29.032038 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 188.827387 29.032038 \n",
"L 188.864338 28.887228 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 188.864338 28.887228 \n",
"L 188.902393 28.751541 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 188.902393 28.751541 \n",
"L 188.941806 28.625416 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 188.941806 28.625416 \n",
"L 188.981221 28.513964 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 188.981221 28.513964 \n",
"L 189.02151 28.415221 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.02151 28.415221 \n",
"L 189.067964 28.320436 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.067964 28.320436 \n",
"L 189.099623 28.267549 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.099623 28.267549 \n",
"L 189.136693 28.217691 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.136693 28.217691 \n",
"L 189.179484 28.176336 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.179484 28.176336 \n",
"L 189.219037 28.153552 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.219037 28.153552 \n",
"L 189.270292 28.146097 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.270292 28.146097 \n",
"L 189.314732 28.1598 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.314732 28.1598 \n",
"L 189.36621 28.199086 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.36621 28.199086 \n",
"L 189.422784 28.271236 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.422784 28.271236 \n",
"L 189.490579 28.397636 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.490579 28.397636 \n",
"L 189.552791 28.551903 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.552791 28.551903 \n",
"L 189.613991 28.739356 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.613991 28.739356 \n",
"L 189.665432 28.924266 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.665432 28.924266 \n",
"L 189.710477 29.106661 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.710477 29.106661 \n",
"L 189.763999 29.348199 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.763999 29.348199 \n",
"L 189.861197 29.855576 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.861197 29.855576 \n",
"L 189.960014 30.461956 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 189.960014 30.461956 \n",
"L 190.041041 31.026973 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 190.041041 31.026973 \n",
"L 190.209259 32.393701 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 190.209259 32.393701 \n",
"L 190.413864 34.404695 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 190.413864 34.404695 \n",
"L 190.721977 38.14079 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 190.721977 38.14079 \n",
"L 196.41515 199.835411 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 196.41515 199.835411 \n",
"L 198.734462 255.914095 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 198.734462 255.914095 \n",
"L 199.01896 260.093505 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 199.01896 260.093505 \n",
"L 199.340601 263.969472 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 199.340601 263.969472 \n",
"L 199.512461 265.660504 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 199.512461 265.660504 \n",
"L 199.695847 267.167238 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 199.695847 267.167238 \n",
"L 199.793895 267.845344 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 199.793895 267.845344 \n",
"L 199.878023 268.355858 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 199.878023 268.355858 \n",
"L 199.977311 268.873208 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 199.977311 268.873208 \n",
"L 200.019906 269.066797 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.019906 269.066797 \n",
"L 200.063278 269.246386 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.063278 269.246386 \n",
"L 200.12536 269.472601 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.12536 269.472601 \n",
"L 200.161802 269.588448 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.161802 269.588448 \n",
"L 200.195116 269.683377 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.195116 269.683377 \n",
"L 200.228754 269.768584 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.228754 269.768584 \n",
"L 200.265646 269.849724 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.265646 269.849724 \n",
"L 200.303481 269.919553 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.303481 269.919553 \n",
"L 200.349317 269.985984 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.349317 269.985984 \n",
"L 200.386859 270.02556 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.386859 270.02556 \n",
"L 200.430141 270.054604 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.430141 270.054604 \n",
"L 200.468707 270.065515 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.468707 270.065515 \n",
"L 200.511462 270.061124 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.511462 270.061124 \n",
"L 200.545859 270.045007 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.545859 270.045007 \n",
"L 200.584453 270.013567 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.584453 270.013567 \n",
"L 200.619047 269.973384 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.619047 269.973384 \n",
"L 200.653817 269.921568 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.653817 269.921568 \n",
"L 200.691233 269.853015 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.691233 269.853015 \n",
"L 200.727992 269.77276 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.727992 269.77276 \n",
"L 200.763679 269.682615 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.763679 269.682615 \n",
"L 200.793139 269.599124 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.793139 269.599124 \n",
"L 200.850049 269.414629 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.850049 269.414629 \n",
"L 200.918285 269.153141 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.918285 269.153141 \n",
"L 200.995556 268.804123 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 200.995556 268.804123 \n",
"L 201.067461 268.429001 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 201.067461 268.429001 \n",
"L 201.204702 267.578899 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 201.204702 267.578899 \n",
"L 201.361358 266.394801 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 201.361358 266.394801 \n",
"L 201.542538 264.744094 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 201.542538 264.744094 \n",
"L 201.916431 260.402544 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 201.916431 260.402544 \n",
"L 202.546526 250.359188 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 202.546526 250.359188 \n",
"L 203.657349 225.246873 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 203.657349 225.246873 \n",
"L 205.962592 153.382542 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 205.962592 153.382542 \n",
"L 208.963838 61.910742 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 208.963838 61.910742 \n",
"L 209.575412 48.899308 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 209.575412 48.899308 \n",
"L 210.295441 37.36174 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 210.295441 37.36174 \n",
"L 210.619539 33.62456 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 210.619539 33.62456 \n",
"L 210.786241 32.070852 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 210.786241 32.070852 \n",
"L 210.974926 30.62004 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 210.974926 30.62004 \n",
"L 211.067233 30.030524 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.067233 30.030524 \n",
"L 211.166235 29.486674 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.166235 29.486674 \n",
"L 211.25697 29.068958 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.25697 29.068958 \n",
"L 211.297114 28.908862 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.297114 28.908862 \n",
"L 211.338172 28.760825 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.338172 28.760825 \n",
"L 211.387527 28.603932 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.387527 28.603932 \n",
"L 211.441754 28.458089 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.441754 28.458089 \n",
"L 211.500887 28.330757 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.500887 28.330757 \n",
"L 211.556663 28.241001 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.556663 28.241001 \n",
"L 211.606749 28.185524 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.606749 28.185524 \n",
"L 211.658662 28.153125 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.658662 28.153125 \n",
"L 211.716329 28.1471 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.716329 28.1471 \n",
"L 211.765092 28.166616 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.765092 28.166616 \n",
"L 211.812845 28.207581 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.812845 28.207581 \n",
"L 211.859971 28.269201 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.859971 28.269201 \n",
"L 211.902486 28.342846 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.902486 28.342846 \n",
"L 211.942963 28.428864 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.942963 28.428864 \n",
"L 211.987903 28.542528 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 211.987903 28.542528 \n",
"L 212.033575 28.677605 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 212.033575 28.677605 \n",
"L 212.072619 28.808695 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 212.072619 28.808695 \n",
"L 212.120303 28.9883 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 212.120303 28.9883 \n",
"L 212.173803 29.215298 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 212.173803 29.215298 \n",
"L 212.227373 29.469554 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 212.227373 29.469554 \n",
"L 212.320073 29.973091 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 212.320073 29.973091 \n",
"L 212.406051 30.511867 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 212.406051 30.511867 \n",
"L 212.503561 31.206075 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 212.503561 31.206075 \n",
"L 212.686134 32.741768 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 212.686134 32.741768 \n",
"L 212.862252 34.51135 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 212.862252 34.51135 \n",
"L 213.180679 38.414782 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 213.180679 38.414782 \n",
"L 213.854536 49.528186 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 213.854536 49.528186 \n",
"L 214.458497 62.507123 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 214.458497 62.507123 \n",
"L 217.513711 156.064898 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 217.513711 156.064898 \n",
"L 219.939677 230.388543 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 219.939677 230.388543 \n",
"L 221.222748 256.695005 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 221.222748 256.695005 \n",
"L 221.580446 261.683519 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 221.580446 261.683519 \n",
"L 221.759401 263.758432 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 221.759401 263.758432 \n",
"L 221.968145 265.814706 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 221.968145 265.814706 \n",
"L 222.143859 267.236846 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.143859 267.236846 \n",
"L 222.290974 268.207734 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.290974 268.207734 \n",
"L 222.366439 268.627436 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.366439 268.627436 \n",
"L 222.431958 268.948548 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.431958 268.948548 \n",
"L 222.510165 269.279024 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.510165 269.279024 \n",
"L 222.544303 269.405218 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.544303 269.405218 \n",
"L 222.583484 269.536507 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.583484 269.536507 \n",
"L 222.620976 269.648563 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.620976 269.648563 \n",
"L 222.665231 269.763734 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.665231 269.763734 \n",
"L 222.71607 269.873172 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.71607 269.873172 \n",
"L 222.758923 269.946409 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.758923 269.946409 \n",
"L 222.808701 270.009636 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.808701 270.009636 \n",
"L 222.854199 270.046881 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.854199 270.046881 \n",
"L 222.901189 270.06474 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.901189 270.06474 \n",
"L 222.957053 270.058724 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.957053 270.058724 \n",
"L 222.998578 270.035075 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 222.998578 270.035075 \n",
"L 223.036668 269.999006 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 223.036668 269.999006 \n",
"L 223.081166 269.93945 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 223.081166 269.93945 \n",
"L 223.13163 269.849209 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 223.13163 269.849209 \n",
"L 223.164397 269.777703 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 223.164397 269.777703 \n",
"L 223.196948 269.696612 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 223.196948 269.696612 \n",
"L 223.232213 269.59745 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 223.232213 269.59745 \n",
"L 223.274679 269.462447 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 223.274679 269.462447 \n",
"L 223.31001 269.33716 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 223.31001 269.33716 \n",
"L 223.346558 269.195171 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 223.346558 269.195171 \n",
"L 223.433913 268.804876 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 223.433913 268.804876 \n",
"L 223.516199 268.371714 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 223.516199 268.371714 \n",
"L 223.605707 267.828649 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 223.605707 267.828649 \n",
"L 223.705193 267.137557 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 223.705193 267.137557 \n",
"L 223.80766 266.330007 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 223.80766 266.330007 \n",
"L 224.00431 264.51052 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 224.00431 264.51052 \n",
"L 224.366741 260.245421 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 224.366741 260.245421 \n",
"L 224.699994 255.313128 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 224.699994 255.313128 \n",
"L 224.921919 251.512909 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 224.921919 251.512909 \n",
"L 224.963435 250.757636 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 224.963435 250.757636 \n",
"L 225.010941 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 225.010941 149.105819 \n",
"L 225.108539 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 225.108539 149.105819 \n",
"L 225.52318 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 225.52318 149.105819 \n",
"L 227.929886 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 227.929886 149.105819 \n",
"L 233.853253 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 233.853253 149.105819 \n",
"L 239.532528 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 239.532528 149.105819 \n",
"L 245.610132 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 245.610132 149.105819 \n",
"L 252.324318 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 252.324318 149.105819 \n",
"L 257.655989 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 257.655989 149.105819 \n",
"L 263.794725 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 263.794725 149.105819 \n",
"L 269.839082 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 269.839082 149.105819 \n",
"L 276.488235 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 276.488235 149.105819 \n",
"L 282.605315 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 282.605315 149.105819 \n",
"L 289.828163 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 289.828163 149.105819 \n",
"L 295.027282 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 295.027282 149.105819 \n",
"L 300.921468 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 300.921468 149.105819 \n",
"L 305.756358 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 305.756358 149.105819 \n",
"L 310.638451 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 310.638451 149.105819 \n",
"L 316.160479 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 316.160479 149.105819 \n",
"L 321.546623 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 321.546623 149.105819 \n",
"L 327.00217 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 327.00217 149.105819 \n",
"L 333.045018 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 333.045018 149.105819 \n",
"L 338.170719 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 338.170719 149.105819 \n",
"L 343.790931 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 343.790931 149.105819 \n",
"L 349.931226 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 349.931226 149.105819 \n",
"L 356.869501 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 356.869501 149.105819 \n",
"L 362.361274 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pb26932ca60)\" d=\"M 362.361274 149.105819 \n",
"L 367.82 149.105819 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" </g>\n",
" <g id=\"patch_3\">\n",
" <path d=\"M 189.26 270.066043 \n",
"L 189.26 28.145594 \n",
"\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
" </g>\n",
" <g id=\"patch_4\">\n",
" <path d=\"M 367.82 282.162 \n",
"L 367.82 16.05 \n",
"\" style=\"fill:none;\"/>\n",
" </g>\n",
" <g id=\"patch_5\">\n",
" <path d=\"M 10.7 149.105819 \n",
"L 367.82 149.105819 \n",
"\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
" </g>\n",
" <g id=\"patch_6\">\n",
" <path d=\"M 10.7 16.05 \n",
"L 367.82 16.05 \n",
"\" style=\"fill:none;\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <defs>\n",
" <clipPath id=\"pb26932ca60\">\n",
" <rect height=\"266.112\" width=\"357.12\" x=\"10.7\" y=\"16.05\"/>\n",
" </clipPath>\n",
" </defs>\n",
"</svg>\n"
],
"text/plain": [
"<Figure size 614.4x460.8 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM4OC40MjYyNSAyOTcuMDEyIF0gL1BhcmVudCAyIDAgUiAvUmVzb3VyY2VzIDggMCBSCi9UeXBlIC9QYWdlID4+CmVuZG9iago5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTEgMCBSID4+CnN0cmVhbQp4nLWZTa8VxxGG9/MreokXNN3V30sjx0jZRNgokZVkgTEmIA4WQYS/n6fmTM8ZzqnLDUKxjbm333qnarrrsye6N0t0r1xwb/jzyf3d/ZO/f3PRPeHPqyXw22lJvfssVQq/vT38JqP5EIW1cPj5X8vy+/Loe+gfkH+yLLH5lmtvxcXgmz6vZd/rZeXtcUVa9X190IV3WdseLueHv8JIDPf9YDoqFTmwa/elhNwiqg+rxYfz6ttlecwufFre8//gHgae2ry4kvwotUmoqSb34rQ8fuYe/Rix2T37fek+tT7CeVee/bY8kPCde/Zm+dMznhPYC6ebt/8A/dEPL988/+vHn5+/+/Dw9Prdxw/uhz+Wp/y7vsBSxad+Y/Bh9YsGl+h7/lqTY/k2k2Pg0OV2kw/LXzR6VJ/7Vxv9jfsc2apab40+LH/R6JizlzFWya80/Vu3m/1K4dbyw/Kt5Z9ZFEfyUVq8tV3NWzfWYd5ZneTgx20IHZfvUSeJcKt3qStX6nrx5TYAjsv3qWvDi5i64tW7pRQQvVF2XL5HWZJEyrKVXb3ZIbt9puywfJ8y5QVTmexvdvDR1IJP50dzWtJzz+XioqsHuhsP9CVFXPXKD//y69vX7z++fPjH6eWr53f6Y4o+pJxyW/1RfL9eNiNJX1vKWkpIuOxHE8HU+wOJd/o/hdJu+mX5jlBqyeew2lSzbyWVUS6R5K/87aAvhupDrWXkzxUe1u/VGIN4qaPFESSn45bYKnMihoj7q+M5rN+vMg3feulZchTZVOa7VXaOfvSer7b1sH6/ytZ4HA8tPYSpst6pUmL3NeZRrzb2sH6vSonEZOyhj9h73FT2u1WW6mOKofcrlZf1+1UWSnzKQuy1elYZ/SGoNVIeql/H0vdwqWltiM7hrJ6f12dBfvSjbDoe/LLGCJaEnkbPqW3hczHjwT8erDJklRDTlqnD1WPerCIx+lgk2U/5bo/Gq7QSBadhO8tYeZuZ/0uKee+u+sZUGrWLV+eF+PvfL93f3DsXfaH5CyCx1F7lrKVu/zSOrIXSu6Qiw/30xKH3P69fvPzpyWP34sOhHeQQYm091bXC6T6XNDQv1ypd1mP82QQQHz4NST25ThDmkXrZxA2AtJ99aZSq4Ub0I5Uy6lncAhAfnJ8QAtot1Upm355uAacl0wey11kXQ2kt57O0sY5w8bGXSA+GRo4opu3ZFnBaCpuZAr+6VnwbIadtXywAccIkt7E20rnXIJvwzfLa5bYcRquOAlwDhSGehS0A8UJBKJX94UQG+xQ3uy0A8e5JJSEPJzxubvfNKoKkOOrVIMBIjLhN3l7QAk5LIyQarWAmhsFDnAdvAYijRiS0xrDkiwblFDcAxHG23iuujmNIHETfJm4AiBefh/DOWvFxBpxzEzcAxAkm6lvILuOlMnoYm7gBnJau1NI4V96tEASyHZAFIK67xJCIu1FGB8l0M8YCEEcnCahRZJJvjSKzSd+un5aRSZed43ASWOX157abCITmyT+RuJJElA+q3uYCJgJheFIhlRgv0sxYimwGmYgOPNFr4LZzMg9pzMgwESWIrzmHRD4jrVFxNI43hgUphcOulapCCtSKUWRaZUNKIdaHLmZfNbXs8jfr56GtcTZkK12Pjda0THkLUkonOktZtTZKZ62TcAuo+CCtYRqay2BcjZLGJFgQlKhpa8wySfHJY76ECSmFo6cPa50zQnvRSJwUC1IKaSPmuIY3jxqd8jwpFqSUhsGBgknLgOvkvUaYCAShLJVciabYB4mPc51vYkJKYfIhr7Zz8xUzRWy+iQlBSVoJiUFZ8zx5eD9DC1GCxgwRHB0tBT1Pkil/C6h41fgdJE2yQ09hd0EDUHH8gFGFh2DliOoKU95AIFCmijDtiY4OleDf7bEQJaxhyJmIPrD3scvfAipeNVJEEy3zxkX4ellFO8mV7DdU4eCAZk0yEb1AwD9yzNQqdAvzXJguYSFKoL3FT5KrkdQw4h4+BoA4sVSlanpjzq1k6FnbTUQJOMnIZAdHIg01l90gC1ECjXLWbmkt+4TK7tQWordpZDcOMVQ31AT6w+luFqIEalcjoHhO8EMk7v5pIUqgCJUcmjgGB6I25Z1gIBA6XRSjGAW6sotkiDB31UK0a6dRpUUcrmS9amv7OxvAuckfgjcldXQSexvTIAs5387khDKW6TgIPGmTYCC0kxQA5k5NsXRINOV1bFFvIkpoVN6gpZRz7aOQFybBQCCQB2mUmzambF2nu9s8yUSUwPHX0antHH+oYW8rTQQCLVUII+lpcvyBAJwmWYgSaJRkaNbv2jXHvc01ESWQKaN0Jiy1lPE710kwEAik79HrIMvSzVVaOJkEC1HCoNtnIiJq6UPqOnhtBAPRsUF0RKKNcEmXQ5rJy0SUkLXURdSRSCKFaTfJQpTQsA/Pj5rV6KM0R2wEA4FAZx5bobJq/xxa1Xb3TLAQJRDeHDt5k13RPZmdjIkoIeGTZEwKQGcaCdMxbtdVmLzD+JR13zgnfp7St4CKa1jg8biv3neEMtOLiUCoOqSmjksR7HqSecvZJqKE4keTVDuTqt4SMEXODTIhKI1BZJDbMgNq0QGvzlO2ECUwsNaatbwwlWDFJRhMSCmdxjTz39qoVJJjmvtqQnpNGrURp/twupnSOdK5WSakFB2u4qDnZQeZ1km/0zATUgpZumpO1BuI0GPdX95Czre3HH5qdW0d6Z2n+M26Cjf1mRxkXRQK3+4gJqQUarHo5KmtJv458m6QgShh6G2L9u1rp8mw2KePmJDO99pwtJR1ndpUu0bNNuFbkFKYc6iBXTtNujsExnwTE1IKcxrxqLOF8LJMj33XYkGnJQViOERdp2XUUabOvGxDStF9x390por61JrbpFgQFBptumuaNcdsSNnsM8ZNRAl5/ciAxxS9/8915kETUULV8Tpp80inxO7sVyIWogStBCHSY+sNM1PkiJNgIBBosRtORj5iA2ngwuy1TEQJzFHS9DqJwCThlzmqmIgSyNi9Mi/rdULPPDdNgoEoofkc2DKd8zTn5TTfwULO3yawTmdnpmHibcwx2USUQAucR8BX9JNVUg+aBAPRmymchq6kah2kXR2z8bAAFSdpR3QN7SJp4GX20yaiBFpxWngGQ4JgMELHPgkGAoGaQ8Ff76Eqk7cw9G0EC1ECvt57YMOGznqtzlRrIhC0fDAckBtIecz2FIqNYCGn9UsMjR0makvFppR5R2Qin33ludwxroSn7r0T9+fzx/fPvmFfXVIe7pvnTdVx7ZhX9+/un9Zv79df2k/2l/bl3f5NfbVDqfb3c/NTlqX59uP93bqfLv8FqIZ8BgplbmRzdHJlYW0KZW5kb2JqCjExIDAgb2JqCjI1MDQKZW5kb2JqCjE2IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggNzggPj4Kc3RyZWFtCnicNYy7EcAwCEN7pmAE8w/75FI5+7fBHGnQk3TIiXChyznhGJx4E5Q/9AJ5Nm2QZahN5jbZ/1GtGopGEcdVWxsospXVp5nRDc8HJmsWtQplbmRzdHJlYW0KZW5kb2JqCjE3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTUyID4+CnN0cmVhbQp4nD1PyxFDIQi8W8U2wIwggtbzMjmZ/q8BTTyxsrgf8YEKYhaQVIe4w63ixYW1o6vjU6QdtAqLg+YGlr8SsYK8gevW6Rg9Zpt4iufGGDpjhrBwzJEMWdrFM+62L0WODYK7YVah6SmWPuR6YRsHUnqztF2hpnAupiJjhnHbaZ9bJdKO0y9K/ZquIr3D1JK1i8affX8BvPc2ZwplbmRzdHJlYW0KZW5kb2JqCjE4IDAgb2JqCjw8IC9CQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE4MQovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJw1UDkOBCEM63mFP7ASucN7Rtpq9v/thjBToBgcBzuDSfEhwW9ENpCJFHiCw3GNZIgxiA2qAloO0yiClzS6B79cavUSKGaJpXpISyl1XOEMltjlGjL7LqYgXZAMSA25hpZ0o3uoHE5twglGeaS25gausyaXzza6//J2SvCIduOFj9PQfJxGZdxcpHWqCHpiRs3KPTZ6CUbctRyxnLXUUqRUizpRZbDVD3M2/+7xGt8/5jc/HgplbmRzdHJlYW0KZW5kb2JqCjE0IDAgb2JqCjw8IC9CYXNlRm9udCAvRGVqYVZ1U2Fucy1PYmxpcXVlIC9DaGFyUHJvY3MgMTUgMCBSCi9FbmNvZGluZyA8PCAvRGlmZmVyZW5jZXMgWyA4OSAvWSAxMDYgL2ogXSAvVHlwZSAvRW5jb2RpbmcgPj4gL0ZpcnN0Q2hhciAwCi9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnREZXNjcmlwdG9yIDEzIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTIgMCBSID4+CmVuZG9iagoxMyAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgOTYKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udE5hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovSXRhbGljQW5nbGUgMCAvTWF4V2lkdGggMTM1MCAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTIgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM1MCA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDI4IDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxNyA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjE3IDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDgKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk5NSA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMTUgMCBvYmoKPDwgL1kgMTYgMCBSIC9qIDE3IDAgUiA+PgplbmRvYmoKMjMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzOTIgPj4Kc3RyZWFtCnicPVJLbgUxCNvPKbhApfBNcp6p3u7df1ubzFSqCi8DtjGUlwypJT/qkogzTH71cl3iUfK9bGpn5iHuLjam+FhyX7qG2HLRmmKxTxzJL8i0VFihVt2jQ/GFKBMPAC3ggQXhvhz/8ReowdewhXLDe2QCYErUbkDGQ9EZSFlBEWH7kRXopFCvbOHvKCBX1KyFoXRiiA2WACm+qw2JmKjZoIeElZKqHdLxjKTwW8FdiWFQW1vbBHhm0BDZ3pGNETPt0RlxWRFrPz3po1EytVEZD01nfPHdMlLz0RXopNLI3cpDZ89CJ2Ak5kmY53Aj4Z7bQQsx9HGvlk9s95gpVpHwBTvKAQO9/d6Sjc974CyMXNvsTCfw0WmnHBOtvh5i/YM/bEubXMcrh0UUqLwoCH7XQRNxfFjF92SjRHe0AdYjE9VoJRAMEsLO7TDyeMZ52d4VtOb0RGijRB7UjhE9KLLF5ZwVsKf8rM2xHJ4PJntvtI+UzMyohBXUdnqots9jHdR3nvv6/AEuAKEZCmVuZHN0cmVhbQplbmRvYmoKMjQgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDcgPj4Kc3RyZWFtCnicTVG7bUQxDOvfFFzgAOtreZ4LUl32b0PJCJDCIKEvKaclFvbGSwzhB1sPvuSRVUN/Hj8x7DMsPcnk1D/muclUFL4VqpuYUBdi4f1oBLwWdC8iK8oH349lDHPO9+CjEJdgJjRgrG9JJhfVvDNkwomhjsNBm1QYd00ULK4VzTPI7VY3sjqzIGx4JRPixgBEBNkXkM1go4yxlZDFch6oCpIFWmDX6RtRi4IrlNYJdKLWxLrM4Kvn9nY3Qy/y4Ki6eH0M60uwwuileyx8rkIfzPRMO3dJI73wphMRZg8FUpmdkZU6PWJ9t0D/n2Ur+PvJz/P9CxUoXCoKZW5kc3RyZWFtCmVuZG9iagoyNSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDkwID4+CnN0cmVhbQp4nE2NQRLAIAgD77wiT1BE0P90etL/X6vUDr3ATgKJFkWC9DVqSzDuuDIVa1ApmJSXwFUwXAva7qLK/jJJTJ2G03u3A4Oy8XGD0kn79nF6AKv9egbdD9IcIlgKZW5kc3RyZWFtCmVuZG9iagoyNiAwIG9iago8PCAvQkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzNwovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJzjMjQwUzA2NVXI5TI3NgKzcsAsI3MjIAski2BBZNMAAV8KCgplbmRzdHJlYW0KZW5kb2JqCjI3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggODAgPj4Kc3RyZWFtCnicRYy7DcAwCER7pmAEfiZmnyiVs38bIErccE+6e7g6EjJT3mGGhwSeDCyGU/EGmaNgNbhGUo2d7KOwbl91geZ6U6v19wcqT3Z2cT3Nyxn0CmVuZHN0cmVhbQplbmRvYmoKMjggMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNDcgPj4Kc3RyZWFtCnicPU+5DQMxDOs9BRc4wHosW/NckOqyfxvKRlIIIkDxkWVHxwpcYgKTjjkSL2k/+GkagVgGNUf0hIphWOBukgIPgyxKV54tXgyR2kJdSPjWEN6tTGSiPK8RO3AnF6MHPlQbWR56QDtEFVmuScNY1VZdap2wAhyyzsJ1PcyqBOXRJ2spH1BUQr10/5972vsLAG8v6wplbmRzdHJlYW0KZW5kb2JqCjI5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ5ID4+CnN0cmVhbQp4nDWPSw4DIQxD9zmFLzBSfoRwHqqupvffNmFaCQkL2y/BFoORjEtMYOyYY+ElVE+tPiQjj7pJORCpUDcET2hMDDNs0iXwynTfMp5bvJxW6oJOSOTprDYaooxmXsPRU84Km/7L3CRqZUaZAzLrVLcTsrJgBeYFtTz3M+6oXOiEh53KsOhOMaLcZkYafv/b9P4CezIwYwplbmRzdHJlYW0KZW5kb2JqCjMwIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggNDkgPj4Kc3RyZWFtCnicMza0UDBQMDQwB5JGhkCWkYlCiiEXSADEzOWCCeaAWQZAGqI4B64mhysNAMboDSYKZW5kc3RyZWFtCmVuZG9iagozMSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDMxNyA+PgpzdHJlYW0KeJw1UktyQzEI279TcIHOmL99nnSyau6/rYQnK7AtQEIuL1nSS37UJdulw+RXH/clsUI+j+2azFLF9xazFM8tr0fPEbctCgRREz34MicVItTP1Og6eGGXPgOvEE4pFngHkwAGr+FfeJROg8A7GzLeEZORGhAkwZpLi01IlD1J/Cvl9aSVNHR+Jitz+XtyqRRqo8kIFSBYudgHpCspHiQTPYlIsnK9N1aI3pBXksdnJSYZEN0msU20wOPclbSEmZhCBeZYgNV0s7r6HExY47CE8SphFtWDTZ41qYRmtI5jZMN498JMiYWGwxJQm32VCaqXj9PcCSOmR0127cKyWzbvIUSj+TMslMHHKCQBh05jJArSsIARgTm9sIq95gs5FsCIZZ2aLAxtaCW7eo6FwNCcs6Vhxtee1/P+B0Vbe6MKZW5kc3RyZWFtCmVuZG9iagozMiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI0OCA+PgpzdHJlYW0KeJwtUTmSA0EIy+cVekJz0++xy5H3/+kKygGDhkMgOi1xUMZPEJYr3vLIVbTh75kYwXfBod/KdRsWORAVSNIYVE2oXbwevQd2HGYC86Q1LIMZ6wM/Ywo3enF4TMbZ7XUZNQR712tPZlAyKxdxycQFU3XYyJnDT6aMC+1czw3IuRHWZRikm5XGjIQjTSFSSKHqJqkzQZAEo6tRo40cxX7pyyOdYVUjagz7XEvb13MTzho0OxarPDmlR1ecy8nFCysH/bzNwEVUGqs8EBJwv9tD/Zzs5Dfe0rmzxfT4XnOyvDAVWPHmtRuQTbX4Ny/i+D3j6/n8A6ilWxYKZW5kc3RyZWFtCmVuZG9iagozMyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDIxMCA+PgpzdHJlYW0KeJw1UMsNQzEIu2cKFqgUAoFknla9df9rbdA7YRH/QljIlAh5qcnOKelLPjpMD7Yuv7EiC611JezKmiCeK++hmbKx0djiYHAaJl6AFjdg6GmNGjV04YKmLpVCgcUl8Jl8dXvovk8ZeGoZcnYEEUPJYAlquhZNWLQ8n5BOAeL/fsPuLeShkvPKnhv5G5zt8DuzbuEnanYi0XIVMtSzNMcYCBNFHjx5RaZw4rPWd9U0EtRmC06WAa5OP4wOAGAiXlmA7K5EOUvSjqWfb7zH9w9AAFO0CmVuZHN0cmVhbQplbmRvYmoKMjEgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zIC9DaGFyUHJvY3MgMjIgMCBSCi9FbmNvZGluZyA8PAovRGlmZmVyZW5jZXMgWyA0MCAvcGFyZW5sZWZ0IC9wYXJlbnJpZ2h0IDQ2IC9wZXJpb2QgNDggL3plcm8gL29uZSAvdHdvIDUyIC9mb3VyIC9maXZlCi9zaXggNTYgL2VpZ2h0IF0KL1R5cGUgL0VuY29kaW5nID4+Ci9GaXJzdENoYXIgMCAvRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250RGVzY3JpcHRvciAyMCAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2FucwovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxOSAwIFIgPj4KZW5kb2JqCjIwIDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyAzMgovRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250TmFtZSAvRGVqYVZ1U2FucyAvSXRhbGljQW5nbGUgMAovTWF4V2lkdGggMTM0MiAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTkgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM0MiA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDIzIDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxMiA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjEyIDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDUKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk4MiA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMjIgMCBvYmoKPDwgL2VpZ2h0IDIzIDAgUiAvZml2ZSAyNCAwIFIgL2ZvdXIgMjUgMCBSIC9vbmUgMjcgMCBSIC9wYXJlbmxlZnQgMjggMCBSCi9wYXJlbnJpZ2h0IDI5IDAgUiAvcGVyaW9kIDMwIDAgUiAvc2l4IDMxIDAgUiAvdHdvIDMyIDAgUiAvemVybyAzMyAwIFIgPj4KZW5kb2JqCjMgMCBvYmoKPDwgL0YxIDIxIDAgUiAvRjIgMTQgMCBSID4+CmVuZG9iago0IDAgb2JqCjw8IC9BMSA8PCAvQ0EgMCAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+Ci9BMiA8PCAvQ0EgMSAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+ID4+CmVuZG9iago1IDAgb2JqCjw8ID4+CmVuZG9iago2IDAgb2JqCjw8ID4+CmVuZG9iago3IDAgb2JqCjw8IC9EZWphVnVTYW5zLU9ibGlxdWUtb21lZ2EgMTggMCBSIC9EZWphVnVTYW5zLW1pbnVzIDI2IDAgUiA+PgplbmRvYmoKMiAwIG9iago8PCAvQ291bnQgMSAvS2lkcyBbIDEwIDAgUiBdIC9UeXBlIC9QYWdlcyA+PgplbmRvYmoKMzQgMCBvYmoKPDwgL0NyZWF0aW9uRGF0ZSAoRDoyMDE5MDUxNjE4Mzc1NSswMicwMCcpCi9DcmVhdG9yIChtYXRwbG90bGliIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcpCi9Qcm9kdWNlciAobWF0cGxvdGxpYiBwZGYgYmFja2VuZCAzLjAuMykgPj4KZW5kb2JqCnhyZWYKMCAzNQowMDAwMDAwMDAwIDY1NTM1IGYgCjAwMDAwMDAwMTYgMDAwMDAgbiAKMDAwMDAxMDE5NCAwMDAwMCBuIAowMDAwMDA5OTMxIDAwMDAwIG4gCjAwMDAwMDk5NzQgMDAwMDAgbiAKMDAwMDAxMDA3MyAwMDAwMCBuIAowMDAwMDEwMDk0IDAwMDAwIG4gCjAwMDAwMTAxMTUgMDAwMDAgbiAKMDAwMDAwMDA2NSAwMDAwMCBuIAowMDAwMDAwMzk1IDAwMDAwIG4gCjAwMDAwMDAyMDggMDAwMDAgbiAKMDAwMDAwMjk3NCAwMDAwMCBuIAowMDAwMDA0MjE1IDAwMDAwIG4gCjAwMDAwMDQwMDcgMDAwMDAgbiAKMDAwMDAwMzY4NSAwMDAwMCBuIAowMDAwMDA1MjY4IDAwMDAwIG4gCjAwMDAwMDI5OTUgMDAwMDAgbiAKMDAwMDAwMzE0NSAwMDAwMCBuIAowMDAwMDAzMzcwIDAwMDAwIG4gCjAwMDAwMDg3MTUgMDAwMDAgbiAKMDAwMDAwODUxNSAwMDAwMCBuIAowMDAwMDA4MTM2IDAwMDAwIG4gCjAwMDAwMDk3NjggMDAwMDAgbiAKMDAwMDAwNTMxMCAwMDAwMCBuIAowMDAwMDA1Nzc1IDAwMDAwIG4gCjAwMDAwMDYwOTUgMDAwMDAgbiAKMDAwMDAwNjI1NyAwMDAwMCBuIAowMDAwMDA2NDI3IDAwMDAwIG4gCjAwMDAwMDY1NzkgMDAwMDAgbiAKMDAwMDAwNjc5OSAwMDAwMCBuIAowMDAwMDA3MDIxIDAwMDAwIG4gCjAwMDAwMDcxNDIgMDAwMDAgbiAKMDAwMDAwNzUzMiAwMDAwMCBuIAowMDAwMDA3ODUzIDAwMDAwIG4gCjAwMDAwMTAyNTQgMDAwMDAgbiAKdHJhaWxlcgo8PCAvSW5mbyAzNCAwIFIgL1Jvb3QgMSAwIFIgL1NpemUgMzUgPj4Kc3RhcnR4cmVmCjEwNDA4CiUlRU9GCg==\n",
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
"<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
" \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
"<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
"<svg height=\"296.562pt\" version=\"1.1\" viewBox=\"0 0 388.434844 296.562\" width=\"388.434844pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
" <defs>\n",
" <style type=\"text/css\">\n",
"*{stroke-linecap:butt;stroke-linejoin:round;}\n",
" </style>\n",
" </defs>\n",
" <g id=\"figure_1\">\n",
" <g id=\"patch_1\">\n",
" <path d=\"M 0 296.562 \n",
"L 388.434844 296.562 \n",
"L 388.434844 0 \n",
"L 0 0 \n",
"z\n",
"\" style=\"fill:#ffffff;\"/>\n",
" </g>\n",
" <g id=\"axes_1\">\n",
" <g id=\"patch_2\">\n",
" <path d=\"M 17.752344 285.862 \n",
"L 374.872344 285.862 \n",
"L 374.872344 19.75 \n",
"L 17.752344 19.75 \n",
"z\n",
"\" style=\"fill:#ffffff;\"/>\n",
" </g>\n",
" <g id=\"matplotlib.axis_1\">\n",
" <g id=\"xtick_1\">\n",
" <g id=\"line2d_1\">\n",
" <defs>\n",
" <path d=\"M 0 0 \n",
"L 0 3.5 \n",
"\" id=\"me07ba06aba\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
" </defs>\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"17.752344\" xlink:href=\"#me07ba06aba\" y=\"228.011529\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_1\">\n",
" <!-- −20 -->\n",
" <defs>\n",
" <path d=\"M 10.59375 35.5 \n",
"L 73.1875 35.5 \n",
"L 73.1875 27.203125 \n",
"L 10.59375 27.203125 \n",
"z\n",
"\" id=\"DejaVuSans-8722\"/>\n",
" <path d=\"M 19.1875 8.296875 \n",
"L 53.609375 8.296875 \n",
"L 53.609375 0 \n",
"L 7.328125 0 \n",
"L 7.328125 8.296875 \n",
"Q 12.9375 14.109375 22.625 23.890625 \n",
"Q 32.328125 33.6875 34.8125 36.53125 \n",
"Q 39.546875 41.84375 41.421875 45.53125 \n",
"Q 43.3125 49.21875 43.3125 52.78125 \n",
"Q 43.3125 58.59375 39.234375 62.25 \n",
"Q 35.15625 65.921875 28.609375 65.921875 \n",
"Q 23.96875 65.921875 18.8125 64.3125 \n",
"Q 13.671875 62.703125 7.8125 59.421875 \n",
"L 7.8125 69.390625 \n",
"Q 13.765625 71.78125 18.9375 73 \n",
"Q 24.125 74.21875 28.421875 74.21875 \n",
"Q 39.75 74.21875 46.484375 68.546875 \n",
"Q 53.21875 62.890625 53.21875 53.421875 \n",
"Q 53.21875 48.921875 51.53125 44.890625 \n",
"Q 49.859375 40.875 45.40625 35.40625 \n",
"Q 44.1875 33.984375 37.640625 27.21875 \n",
"Q 31.109375 20.453125 19.1875 8.296875 \n",
"z\n",
"\" id=\"DejaVuSans-50\"/>\n",
" <path d=\"M 31.78125 66.40625 \n",
"Q 24.171875 66.40625 20.328125 58.90625 \n",
"Q 16.5 51.421875 16.5 36.375 \n",
"Q 16.5 21.390625 20.328125 13.890625 \n",
"Q 24.171875 6.390625 31.78125 6.390625 \n",
"Q 39.453125 6.390625 43.28125 13.890625 \n",
"Q 47.125 21.390625 47.125 36.375 \n",
"Q 47.125 51.421875 43.28125 58.90625 \n",
"Q 39.453125 66.40625 31.78125 66.40625 \n",
"z\n",
"M 31.78125 74.21875 \n",
"Q 44.046875 74.21875 50.515625 64.515625 \n",
"Q 56.984375 54.828125 56.984375 36.375 \n",
"Q 56.984375 17.96875 50.515625 8.265625 \n",
"Q 44.046875 -1.421875 31.78125 -1.421875 \n",
"Q 19.53125 -1.421875 13.0625 8.265625 \n",
"Q 6.59375 17.96875 6.59375 36.375 \n",
"Q 6.59375 54.828125 13.0625 64.515625 \n",
"Q 19.53125 74.21875 31.78125 74.21875 \n",
"z\n",
"\" id=\"DejaVuSans-48\"/>\n",
" </defs>\n",
" <g transform=\"translate(7.2 242.609967)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_2\">\n",
" <g id=\"line2d_2\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"62.392344\" xlink:href=\"#me07ba06aba\" y=\"228.011529\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_2\">\n",
" <!-- −15 -->\n",
" <defs>\n",
" <path d=\"M 12.40625 8.296875 \n",
"L 28.515625 8.296875 \n",
"L 28.515625 63.921875 \n",
"L 10.984375 60.40625 \n",
"L 10.984375 69.390625 \n",
"L 28.421875 72.90625 \n",
"L 38.28125 72.90625 \n",
"L 38.28125 8.296875 \n",
"L 54.390625 8.296875 \n",
"L 54.390625 0 \n",
"L 12.40625 0 \n",
"z\n",
"\" id=\"DejaVuSans-49\"/>\n",
" <path d=\"M 10.796875 72.90625 \n",
"L 49.515625 72.90625 \n",
"L 49.515625 64.59375 \n",
"L 19.828125 64.59375 \n",
"L 19.828125 46.734375 \n",
"Q 21.96875 47.46875 24.109375 47.828125 \n",
"Q 26.265625 48.1875 28.421875 48.1875 \n",
"Q 40.625 48.1875 47.75 41.5 \n",
"Q 54.890625 34.8125 54.890625 23.390625 \n",
"Q 54.890625 11.625 47.5625 5.09375 \n",
"Q 40.234375 -1.421875 26.90625 -1.421875 \n",
"Q 22.3125 -1.421875 17.546875 -0.640625 \n",
"Q 12.796875 0.140625 7.71875 1.703125 \n",
"L 7.71875 11.625 \n",
"Q 12.109375 9.234375 16.796875 8.0625 \n",
"Q 21.484375 6.890625 26.703125 6.890625 \n",
"Q 35.15625 6.890625 40.078125 11.328125 \n",
"Q 45.015625 15.765625 45.015625 23.390625 \n",
"Q 45.015625 31 40.078125 35.4375 \n",
"Q 35.15625 39.890625 26.703125 39.890625 \n",
"Q 22.75 39.890625 18.8125 39.015625 \n",
"Q 14.890625 38.140625 10.796875 36.28125 \n",
"z\n",
"\" id=\"DejaVuSans-53\"/>\n",
" </defs>\n",
" <g transform=\"translate(51.84 242.609967)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_3\">\n",
" <g id=\"line2d_3\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"107.032344\" xlink:href=\"#me07ba06aba\" y=\"228.011529\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_3\">\n",
" <!-- −10 -->\n",
" <g transform=\"translate(96.48 242.609967)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_4\">\n",
" <g id=\"line2d_4\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"151.672344\" xlink:href=\"#me07ba06aba\" y=\"228.011529\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_4\">\n",
" <!-- −5 -->\n",
" <g transform=\"translate(144.30125 242.609967)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_5\">\n",
" <g id=\"line2d_5\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#me07ba06aba\" y=\"228.011529\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_5\">\n",
" <!-- 0 -->\n",
" <g transform=\"translate(193.131094 242.609967)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_6\">\n",
" <g id=\"line2d_6\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"240.952344\" xlink:href=\"#me07ba06aba\" y=\"228.011529\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_6\">\n",
" <!-- 5 -->\n",
" <g transform=\"translate(237.771094 242.609967)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_7\">\n",
" <g id=\"line2d_7\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"285.592344\" xlink:href=\"#me07ba06aba\" y=\"228.011529\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_7\">\n",
" <!-- 10 -->\n",
" <g transform=\"translate(279.229844 242.609967)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_8\">\n",
" <g id=\"line2d_8\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"330.232344\" xlink:href=\"#me07ba06aba\" y=\"228.011529\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_8\">\n",
" <!-- 15 -->\n",
" <g transform=\"translate(323.869844 242.609967)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_9\">\n",
" <g id=\"line2d_9\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"374.872344\" xlink:href=\"#me07ba06aba\" y=\"228.011529\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_9\">\n",
" <!-- 20 -->\n",
" <g transform=\"translate(368.509844 242.609967)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_10\">\n",
" <!-- $\\omega$ -->\n",
" <defs>\n",
" <path d=\"M 21.390625 -1.421875 \n",
"Q 1.125 -1.421875 6.78125 27.59375 \n",
"Q 8.984375 39.0625 19.625 54.6875 \n",
"L 29.296875 54.6875 \n",
"Q 19.234375 39.0625 17 27.34375 \n",
"Q 12.796875 6.203125 23.734375 6.203125 \n",
"Q 33.84375 6.203125 38.71875 32.46875 \n",
"L 47.015625 32.46875 \n",
"Q 41.703125 6.0625 51.8125 6.203125 \n",
"Q 62.703125 6.296875 66.796875 27.34375 \n",
"Q 69.046875 39.0625 65.140625 54.6875 \n",
"L 74.8125 54.6875 \n",
"Q 79.296875 39.0625 77.09375 27.59375 \n",
"Q 71.53125 -1.46875 51.21875 -1.421875 \n",
"Q 37.9375 -1.375 39.109375 13.1875 \n",
"Q 34.28125 -1.421875 21.390625 -1.421875 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-969\"/>\n",
" </defs>\n",
" <g transform=\"translate(370.672344 256.288092)scale(0.1 -0.1)\">\n",
" <use transform=\"translate(0 0.3125)\" xlink:href=\"#DejaVuSans-Oblique-969\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"matplotlib.axis_2\">\n",
" <g id=\"ytick_1\">\n",
" <g id=\"line2d_10\">\n",
" <defs>\n",
" <path d=\"M 0 0 \n",
"L -3.5 0 \n",
"\" id=\"m0e8ed92520\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
" </defs>\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m0e8ed92520\" y=\"265.527653\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_11\">\n",
" <!-- −0.2 -->\n",
" <defs>\n",
" <path d=\"M 10.6875 12.40625 \n",
"L 21 12.40625 \n",
"L 21 0 \n",
"L 10.6875 0 \n",
"z\n",
"\" id=\"DejaVuSans-46\"/>\n",
" </defs>\n",
" <g transform=\"translate(165.029531 269.326872)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"179.199219\" xlink:href=\"#DejaVuSans-50\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_2\">\n",
" <g id=\"line2d_11\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m0e8ed92520\" y=\"228.011529\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_12\">\n",
" <!-- 0.0 -->\n",
" <g transform=\"translate(173.409219 231.810748)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_3\">\n",
" <g id=\"line2d_12\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m0e8ed92520\" y=\"190.495406\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_13\">\n",
" <!-- 0.2 -->\n",
" <g transform=\"translate(173.409219 194.294625)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-50\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_4\">\n",
" <g id=\"line2d_13\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m0e8ed92520\" y=\"152.979283\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_14\">\n",
" <!-- 0.4 -->\n",
" <defs>\n",
" <path d=\"M 37.796875 64.3125 \n",
"L 12.890625 25.390625 \n",
"L 37.796875 25.390625 \n",
"z\n",
"M 35.203125 72.90625 \n",
"L 47.609375 72.90625 \n",
"L 47.609375 25.390625 \n",
"L 58.015625 25.390625 \n",
"L 58.015625 17.1875 \n",
"L 47.609375 17.1875 \n",
"L 47.609375 0 \n",
"L 37.796875 0 \n",
"L 37.796875 17.1875 \n",
"L 4.890625 17.1875 \n",
"L 4.890625 26.703125 \n",
"z\n",
"\" id=\"DejaVuSans-52\"/>\n",
" </defs>\n",
" <g transform=\"translate(173.409219 156.778501)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-52\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_5\">\n",
" <g id=\"line2d_14\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m0e8ed92520\" y=\"115.463159\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_15\">\n",
" <!-- 0.6 -->\n",
" <defs>\n",
" <path d=\"M 33.015625 40.375 \n",
"Q 26.375 40.375 22.484375 35.828125 \n",
"Q 18.609375 31.296875 18.609375 23.390625 \n",
"Q 18.609375 15.53125 22.484375 10.953125 \n",
"Q 26.375 6.390625 33.015625 6.390625 \n",
"Q 39.65625 6.390625 43.53125 10.953125 \n",
"Q 47.40625 15.53125 47.40625 23.390625 \n",
"Q 47.40625 31.296875 43.53125 35.828125 \n",
"Q 39.65625 40.375 33.015625 40.375 \n",
"z\n",
"M 52.59375 71.296875 \n",
"L 52.59375 62.3125 \n",
"Q 48.875 64.0625 45.09375 64.984375 \n",
"Q 41.3125 65.921875 37.59375 65.921875 \n",
"Q 27.828125 65.921875 22.671875 59.328125 \n",
"Q 17.53125 52.734375 16.796875 39.40625 \n",
"Q 19.671875 43.65625 24.015625 45.921875 \n",
"Q 28.375 48.1875 33.59375 48.1875 \n",
"Q 44.578125 48.1875 50.953125 41.515625 \n",
"Q 57.328125 34.859375 57.328125 23.390625 \n",
"Q 57.328125 12.15625 50.6875 5.359375 \n",
"Q 44.046875 -1.421875 33.015625 -1.421875 \n",
"Q 20.359375 -1.421875 13.671875 8.265625 \n",
"Q 6.984375 17.96875 6.984375 36.375 \n",
"Q 6.984375 53.65625 15.1875 63.9375 \n",
"Q 23.390625 74.21875 37.203125 74.21875 \n",
"Q 40.921875 74.21875 44.703125 73.484375 \n",
"Q 48.484375 72.75 52.59375 71.296875 \n",
"z\n",
"\" id=\"DejaVuSans-54\"/>\n",
" </defs>\n",
" <g transform=\"translate(173.409219 119.262378)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-54\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_6\">\n",
" <g id=\"line2d_15\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m0e8ed92520\" y=\"77.947036\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_16\">\n",
" <!-- 0.8 -->\n",
" <defs>\n",
" <path d=\"M 31.78125 34.625 \n",
"Q 24.75 34.625 20.71875 30.859375 \n",
"Q 16.703125 27.09375 16.703125 20.515625 \n",
"Q 16.703125 13.921875 20.71875 10.15625 \n",
"Q 24.75 6.390625 31.78125 6.390625 \n",
"Q 38.8125 6.390625 42.859375 10.171875 \n",
"Q 46.921875 13.96875 46.921875 20.515625 \n",
"Q 46.921875 27.09375 42.890625 30.859375 \n",
"Q 38.875 34.625 31.78125 34.625 \n",
"z\n",
"M 21.921875 38.8125 \n",
"Q 15.578125 40.375 12.03125 44.71875 \n",
"Q 8.5 49.078125 8.5 55.328125 \n",
"Q 8.5 64.0625 14.71875 69.140625 \n",
"Q 20.953125 74.21875 31.78125 74.21875 \n",
"Q 42.671875 74.21875 48.875 69.140625 \n",
"Q 55.078125 64.0625 55.078125 55.328125 \n",
"Q 55.078125 49.078125 51.53125 44.71875 \n",
"Q 48 40.375 41.703125 38.8125 \n",
"Q 48.828125 37.15625 52.796875 32.3125 \n",
"Q 56.78125 27.484375 56.78125 20.515625 \n",
"Q 56.78125 9.90625 50.3125 4.234375 \n",
"Q 43.84375 -1.421875 31.78125 -1.421875 \n",
"Q 19.734375 -1.421875 13.25 4.234375 \n",
"Q 6.78125 9.90625 6.78125 20.515625 \n",
"Q 6.78125 27.484375 10.78125 32.3125 \n",
"Q 14.796875 37.15625 21.921875 38.8125 \n",
"z\n",
"M 18.3125 54.390625 \n",
"Q 18.3125 48.734375 21.84375 45.5625 \n",
"Q 25.390625 42.390625 31.78125 42.390625 \n",
"Q 38.140625 42.390625 41.71875 45.5625 \n",
"Q 45.3125 48.734375 45.3125 54.390625 \n",
"Q 45.3125 60.0625 41.71875 63.234375 \n",
"Q 38.140625 66.40625 31.78125 66.40625 \n",
"Q 25.390625 66.40625 21.84375 63.234375 \n",
"Q 18.3125 60.0625 18.3125 54.390625 \n",
"z\n",
"\" id=\"DejaVuSans-56\"/>\n",
" </defs>\n",
" <g transform=\"translate(173.409219 81.746255)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-56\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_7\">\n",
" <g id=\"line2d_16\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m0e8ed92520\" y=\"40.430912\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_17\">\n",
" <!-- 1.0 -->\n",
" <g transform=\"translate(173.409219 44.230131)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_18\">\n",
" <!-- $Y(j \\omega)$ -->\n",
" <defs>\n",
" <path d=\"M 6.296875 72.90625 \n",
"L 16.890625 72.90625 \n",
"L 30.515625 42.921875 \n",
"L 56.5 72.90625 \n",
"L 67.578125 72.90625 \n",
"L 34.515625 34.71875 \n",
"L 27.78125 0 \n",
"L 17.921875 0 \n",
"L 24.609375 34.71875 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-89\"/>\n",
" <path d=\"M 31 75.875 \n",
"Q 24.46875 64.65625 21.28125 53.65625 \n",
"Q 18.109375 42.671875 18.109375 31.390625 \n",
"Q 18.109375 20.125 21.3125 9.0625 \n",
"Q 24.515625 -2 31 -13.1875 \n",
"L 23.1875 -13.1875 \n",
"Q 15.875 -1.703125 12.234375 9.375 \n",
"Q 8.59375 20.453125 8.59375 31.390625 \n",
"Q 8.59375 42.28125 12.203125 53.3125 \n",
"Q 15.828125 64.359375 23.1875 75.875 \n",
"z\n",
"\" id=\"DejaVuSans-40\"/>\n",
" <path d=\"M 14.5 54.6875 \n",
"L 23.484375 54.6875 \n",
"L 12.703125 -0.984375 \n",
"L 12.640625 -1.21875 \n",
"Q 10.84375 -10.546875 8.5 -14.015625 \n",
"Q 6.296875 -17.28125 2.0625 -19.03125 \n",
"Q -2.15625 -20.796875 -7.90625 -20.796875 \n",
"L -11.28125 -20.796875 \n",
"L -9.8125 -13.1875 \n",
"L -7.515625 -13.1875 \n",
"Q -2.25 -13.1875 -0.015625 -10.984375 \n",
"Q 2.203125 -8.796875 3.71875 -0.984375 \n",
"z\n",
"M 18.703125 75.984375 \n",
"L 27.6875 75.984375 \n",
"L 25.484375 64.59375 \n",
"L 16.5 64.59375 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-106\"/>\n",
" <path d=\"M 8.015625 75.875 \n",
"L 15.828125 75.875 \n",
"Q 23.140625 64.359375 26.78125 53.3125 \n",
"Q 30.421875 42.28125 30.421875 31.390625 \n",
"Q 30.421875 20.453125 26.78125 9.375 \n",
"Q 23.140625 -1.703125 15.828125 -13.1875 \n",
"L 8.015625 -13.1875 \n",
"Q 14.5 -2 17.703125 9.0625 \n",
"Q 20.90625 20.125 20.90625 31.390625 \n",
"Q 20.90625 42.671875 17.703125 53.65625 \n",
"Q 14.5 64.65625 8.015625 75.875 \n",
"z\n",
"\" id=\"DejaVuSans-41\"/>\n",
" </defs>\n",
" <g transform=\"translate(158.929531 32.3)rotate(-90)scale(0.1 -0.1)\">\n",
" <use transform=\"translate(0 0.015625)\" xlink:href=\"#DejaVuSans-Oblique-89\"/>\n",
" <use transform=\"translate(61.083984 0.015625)\" xlink:href=\"#DejaVuSans-40\"/>\n",
" <use transform=\"translate(100.097656 0.015625)\" xlink:href=\"#DejaVuSans-Oblique-106\"/>\n",
" <use transform=\"translate(127.880859 0.015625)\" xlink:href=\"#DejaVuSans-Oblique-969\"/>\n",
" <use transform=\"translate(211.621094 0.015625)\" xlink:href=\"#DejaVuSans-41\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"LineCollection_1\">\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 17.752344 244.394164 \n",
"L 24.031008 230.899172 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 24.031008 230.899172 \n",
"L 29.397852 216.312615 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 29.397852 216.312615 \n",
"L 34.578268 204.626404 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 34.578268 204.626404 \n",
"L 39.108127 199.898295 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 39.108127 199.898295 \n",
"L 41.899209 200.504256 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 41.899209 200.504256 \n",
"L 45.190617 204.968865 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 45.190617 204.968865 \n",
"L 50.736061 220.771562 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 50.736061 220.771562 \n",
"L 56.353388 243.07598 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 56.353388 243.07598 \n",
"L 62.746445 265.960349 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 62.746445 265.960349 \n",
"L 65.381164 271.602385 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 65.381164 271.602385 \n",
"L 68.182517 273.766 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 68.182517 273.766 \n",
"L 69.708963 273.003152 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 69.708963 273.003152 \n",
"L 71.178463 270.861815 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 71.178463 270.861815 \n",
"L 72.727545 267.051165 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 72.727545 267.051165 \n",
"L 74.09408 262.342848 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 74.09408 262.342848 \n",
"L 75.498427 256.191718 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 75.498427 256.191718 \n",
"L 77.160473 247.232191 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 77.160473 247.232191 \n",
"L 80.381207 225.059479 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 80.381207 225.059479 \n",
"L 83.559733 197.962818 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 83.559733 197.962818 \n",
"L 87.195639 162.78616 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 87.195639 162.78616 \n",
"L 94.344172 92.770415 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 94.344172 92.770415 \n",
"L 97.864668 64.370564 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 97.864668 64.370564 \n",
"L 99.677128 52.656476 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 99.677128 52.656476 \n",
"L 101.285438 44.258062 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 101.285438 44.258062 \n",
"L 102.649501 38.743342 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 102.649501 38.743342 \n",
"L 104.271599 34.226776 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 104.271599 34.226776 \n",
"L 106.096468 31.904726 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 106.096468 31.904726 \n",
"L 107.760951 32.383335 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 107.760951 32.383335 \n",
"L 108.750968 33.840534 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 108.750968 33.840534 \n",
"L 109.937709 36.720761 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 109.937709 36.720761 \n",
"L 111.905094 44.124506 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 111.905094 44.124506 \n",
"L 113.741846 53.810271 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 113.741846 53.810271 \n",
"L 115.319663 64.063827 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 115.319663 64.063827 \n",
"L 117.936187 84.41372 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 117.936187 84.41372 \n",
"L 120.460078 107.080136 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 120.460078 107.080136 \n",
"L 125.578544 157.419641 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 125.578544 157.419641 \n",
"L 130.130681 200.518135 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 130.130681 200.518135 \n",
"L 134.33922 233.37368 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 134.33922 233.37368 \n",
"L 136.560418 246.73176 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 136.560418 246.73176 \n",
"L 138.71182 256.644786 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 138.71182 256.644786 \n",
"L 141.534151 264.942968 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 141.534151 264.942968 \n",
"L 143.911199 267.853108 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 143.911199 267.853108 \n",
"L 146.271669 267.32408 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 146.271669 267.32408 \n",
"L 148.223568 264.616549 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 148.223568 264.616549 \n",
"L 152.446945 253.356992 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 152.446945 253.356992 \n",
"L 157.377298 235.252834 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 157.377298 235.252834 \n",
"L 162.632172 216.961556 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 162.632172 216.961556 \n",
"L 165.599573 209.497492 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 165.599573 209.497492 \n",
"L 168.651351 204.988372 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 168.651351 204.988372 \n",
"L 171.268975 203.936765 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 171.268975 203.936765 \n",
"L 174.07861 205.639835 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 174.07861 205.639835 \n",
"L 179.359541 215.319655 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 179.359541 215.319655 \n",
"L 184.565016 229.172094 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 184.565016 229.172094 \n",
"L 190.011359 242.175272 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 190.011359 242.175272 \n",
"L 192.934392 246.564205 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 192.934392 246.564205 \n",
"L 196.445372 248.418173 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 196.445372 248.418173 \n",
"L 202.053133 243.194301 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 202.053133 243.194301 \n",
"L 207.505651 230.666693 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 207.505651 230.666693 \n",
"L 213.281251 215.280646 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 213.281251 215.280646 \n",
"L 218.67529 205.501256 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 218.67529 205.501256 \n",
"L 222.014811 203.954913 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 222.014811 203.954913 \n",
"L 225.734707 207.170295 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 225.734707 207.170295 \n",
"L 229.418357 215.308454 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 229.418357 215.308454 \n",
"L 232.992378 226.873574 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 232.992378 226.873574 \n",
"L 239.027345 249.396375 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 239.027345 249.396375 \n",
"L 242.15766 259.401668 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 242.15766 259.401668 \n",
"L 244.846594 265.398274 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 244.846594 265.398274 \n",
"L 247.68726 268.019817 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 247.68726 268.019817 \n",
"L 250.180791 266.485951 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 250.180791 266.485951 \n",
"L 251.586842 263.871062 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 251.586842 263.871062 \n",
"L 253.054669 259.735496 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 253.054669 259.735496 \n",
"L 255.559408 249.332447 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 255.559408 249.332447 \n",
"L 258.145941 234.301465 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 258.145941 234.301465 \n",
"L 261.159356 211.873559 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 261.159356 211.873559 \n",
"L 265.977837 167.949841 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 265.977837 167.949841 \n",
"L 270.698103 121.16938 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 270.698103 121.16938 \n",
"L 276.171931 72.408913 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 276.171931 72.408913 \n",
"L 278.860322 53.944566 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 278.860322 53.944566 \n",
"L 281.380586 41.281235 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 281.380586 41.281235 \n",
"L 282.747405 36.544683 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 282.747405 36.544683 \n",
"L 284.071359 33.480338 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 284.071359 33.480338 \n",
"L 285.655845 31.846 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 285.655845 31.846 \n",
"L 287.05487 32.270347 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 287.05487 32.270347 \n",
"L 288.231399 33.980058 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 288.231399 33.980058 \n",
"L 289.339993 36.705019 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 289.339993 36.705019 \n",
"L 291.622812 45.593678 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 291.622812 45.593678 \n",
"L 293.522657 56.127507 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 293.522657 56.127507 \n",
"L 295.458728 69.462518 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 295.458728 69.462518 \n",
"L 300.106728 109.702356 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 300.106728 109.702356 \n",
"L 305.660956 165.108353 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 305.660956 165.108353 \n",
"L 311.442531 218.662196 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 311.442531 218.662196 \n",
"L 314.132585 238.797368 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 314.132585 238.797368 \n",
"L 316.708818 254.110204 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 316.708818 254.110204 \n",
"L 319.395587 265.470109 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 319.395587 265.470109 \n",
"L 320.777161 269.413934 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 320.777161 269.413934 \n",
"L 322.332743 272.322461 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 322.332743 272.322461 \n",
"L 324.891767 273.718797 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 324.891767 273.718797 \n",
"L 327.41527 271.332569 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 327.41527 271.332569 \n",
"L 330.811733 263.277016 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 330.811733 263.277016 \n",
"L 333.95455 252.326675 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 333.95455 252.326675 \n",
"L 340.125129 227.414001 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 340.125129 227.414001 \n",
"L 345.525318 209.347708 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 345.525318 209.347708 \n",
"L 348.792324 202.637682 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 348.792324 202.637682 \n",
"L 351.922617 199.889889 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 351.922617 199.889889 \n",
"L 356.8935 202.824313 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 356.8935 202.824313 \n",
"L 362.294411 213.890739 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 362.294411 213.890739 \n",
"L 368.801393 231.442452 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pfebcd40d30)\" d=\"M 368.801393 231.442452 \n",
"L 374.872344 244.394164 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" </g>\n",
" <g id=\"patch_3\">\n",
" <path d=\"M 196.312344 273.766 \n",
"L 196.312344 31.846 \n",
"\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
" </g>\n",
" <g id=\"patch_4\">\n",
" <path d=\"M 374.872344 285.862 \n",
"L 374.872344 19.75 \n",
"\" style=\"fill:none;\"/>\n",
" </g>\n",
" <g id=\"patch_5\">\n",
" <path d=\"M 17.752344 228.011529 \n",
"L 374.872344 228.011529 \n",
"\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
" </g>\n",
" <g id=\"patch_6\">\n",
" <path d=\"M 17.752344 19.75 \n",
"L 374.872344 19.75 \n",
"\" style=\"fill:none;\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <defs>\n",
" <clipPath id=\"pfebcd40d30\">\n",
" <rect height=\"266.112\" width=\"357.12\" x=\"17.752344\" y=\"19.75\"/>\n",
" </clipPath>\n",
" </defs>\n",
"</svg>\n"
],
"text/plain": [
"<Figure size 614.4x460.8 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"values = {w0: 10, a: 1/2}\n",
"\n",
"sym.plot(y.subs(values), (t, -5, 5), xlabel=r'$t$', ylabel=r'$y(t)$')\n",
"sym.plot(Y.subs(values), (w, -20, 20), xlabel=r'$\\omega$', ylabel=r'$Y(j \\omega)$');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise**\n",
"\n",
"* Change the length $1/a$ of the signal by modifying the substitution in the example. How does the Fourier transform change if you decrease or increase the length $1/a$?\n",
"\n",
"* What happens if you change the angular frequency $\\omega_0$ of the signal?\n",
"\n",
"* Assume a signal that is composed from a superposition of two finite length cosine signals with different frequencies. What qualitative condition has to hold that you can derive these frequencies from the spectrum of the superposition?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Modulation Theorem\n",
"\n",
"The complex modulation of a signal $x(t)$ is defined as $e^{j \\omega_0 t} \\cdot x(t)$ with $\\omega_0 \\in \\mathbb{R}$. Its Fourier transform can be derived by applying the multiplication theorem\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{F} \\left\\{ e^{j \\omega_0 t} \\cdot x(t) \\right\\} = \\frac{1}{2 \\pi} \\cdot 2 \\pi \\cdot \\delta(\\omega - \\omega_0) * X(j \\omega) \n",
"= X \\big( j \\, (\\omega - \\omega_0) \\big)\n",
"\\end{equation}\n",
"\n",
"where $X(j \\omega) = \\mathcal{F} \\{ x(t) \\}$. Above result states that the complex modulation of a signal leads to a shift of its spectrum. For $\\omega_0 > 0$ the spectrum is shifted to higher frequencies. This lays the ground for wireless transmission of signals. Above result is known as modulation theorem."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Example**\n",
"\n",
"Lets assume a signal $x(t)$ which has a triangular spectrum $X(j \\omega) = 2 \\pi \\cdot \\Lambda(\\omega)$. Due to the definition of the triangular function, the spectrum has only non-zero contributions for $|\\omega| < 1$. Applying the duality principle to the [Fourier transform of $\\Lambda(t)$ derived above](#Transformation-of-the-triangular-signal) yields the corresponding signal $x(t) = \\mathcal{F}^{-1} \\{ X(j \\omega) \\}$\n",
"\n",
"\\begin{equation}\n",
"x(t) = \\text{sinc}^2 \\left( \\frac{t}{2} \\right)\n",
"\\end{equation}\n",
"\n",
"Now lets consider the complex modulation $y(t) = e^{-j \\omega_0 t} \\cdot x(t)$ of the signal $x(t)$. The Fourier transform of the modulated signal is given as\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{F} \\{ e^{j \\omega_0 t} \\cdot x(t) \\} = 2 \\pi \\cdot \\Lambda(\\omega - \\omega_0)\n",
"\\end{equation}\n",
"\n",
"The spectrum of the modulated signal has non-zero contributions for $\\omega_0 -1 < \\omega < \\omega_0 + 1$. For large $\\omega_0$ it only occupies a small part of the spectrum. This is an important property of signals used for wireless transmission. The signal $y(t)$ is defined"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAIYAAAAyBAMAAABrDL7BAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEIl2mUTdMiJmu6tUze/kkN0jAAAACXBIWXMAAA7EAAAOxAGVKw4bAAADpklEQVRIDZ1XXWgUVxT+ZrO7s8nsrotIMRXcwaIt1JBtFLRIcRFRRGwXBV8EsxXpg0VZilgQJGMV0UAxxSKoYBTBnwpliyBYoQYE8UWzQp/Eh7T4YNnGJsa/pGKce869d2bcNebmPpzzne9+35mdO3d+FpjBcErSZJ2dgZst17RzX05DM+C4Wp8ua2gGjpP8A0+k9YSNQ+oFWQYpJvuM/cKQdMm2gWL6L0qm4TQbtnH609RO+r9FTPw+cYWqbo+SWWgZJX16hG2Zopmd1MkqpXiNvWlu6ReWx8w0Yk+FRHJlYY0pT6ygEJDxAhyg2Z/+xsUfnPIlOXc+0AQoH8AQKmINV3VO3bAY9HucI/FOpFLFMxylk7DHmenAbQb5Ps6JFbAHgFOi+mHnx0xG40+yR+wl89ctefrZKhOxfC7uoz1UPWCuIS4ipm2IJ3pPSEFbmcH+WziCdsRTiz8B1MVK/SNVnOyvKWfPRFggNiKJc/7ZHUN7BhkkhiSXeBpR9+aozBcjLND6jAlrtLIMa7F8PrK5lupcqWKTLFJV2xOwpyAJlWy5QdI1d8vuHZvcQ0hW4gVXTYdz7/e7qefgQJj1sSV/rnXFyzx06vB/h5dYV3lLReV/k5OU+xtm//f7fLSUDiAUYj1o2J8vqf1Yx56HB1YUgDkLFjPtx5WehhJMAJsrtqtoui6i+BAo41ugXrBfIvUvtuqjd+oDKtMwUuNoKalS5605uLgM/AqMI1PDXU9NfdXQ4xu0jXUtVPNBTk4sh+jxCzCGvBtM4AbjSTFGCO/CrGpIoKHVMVnUPSKXU/bQSsDv4YZKDfej/YXuEdlWzc5FPEsGtFeBm8A13cNfj0DS6SmNysNorWFOA427OVwUi3FfrId/48S0ZGVFeVWuA11LCqoK8sZjXaW9j8/ufX3h5PMq5q3yb0U5GvdY9LZSuqnyYIlnD264wMB6MpW86VxPH9GpKjq5m7rnmqqbk7OKxDs5ZIcIpV9RMgnJGqmzo3D4qdgiH44GTZwhEjtlOPz+d0YM3CxtVY9KJNmcPWPcw9anL2+BowXjHvC3FI/tnJq+o5TmHflLyceLDK6+QzcV3V3i2Z+lSL+zpzK9NZcsEpF2cViAYI2Jnl6Qpu+Az4RBfo5Mz6tV9C2V2r56fVlQ3Z6IpqM/5zsy/qOwJpyXTe2kz7ghW0JvuRD5fmg/CmmyA6HCAH4R0l4PYRMY/uanNTExK+0lBTDj/x5ok1sV1j3R7Q2xEshA9JphigAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$e^{i \\omega_{0} t} \\operatorname{sinc}^{2}{\\left (\\frac{t}{2} \\right )}$$"
],
"text/plain": [
" ⅈ⋅ω₀⋅t 2⎛t⎞\n",
"ℯ ⋅sinc ⎜─⎟\n",
" ⎝2⎠"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"y = sym.exp(sym.I*w0*t) * sym.sinc(t/2)**2\n",
"y"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"and the real part of the complex modulated signal is plotted for illustration"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM4OC40MjYyNSAzMDMuNTEyIF0gL1BhcmVudCAyIDAgUiAvUmVzb3VyY2VzIDggMCBSCi9UeXBlIC9QYWdlID4+CmVuZG9iago5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTEgMCBSID4+CnN0cmVhbQp4nLWdS89tuXGe59+v2EN5oN28kzW04LiBTALJjWTgeKDoZnV0FEgtRQiC/Pe8bxU3ybNZ3ceCbBmyvsN3PXtxcZHFKt5WfHz7ER+/eYTHt/jvXx7//PgX/O8vH/HxNf77m4+Af336yGM8S2qp4l+/O/6VQ37WmJAWjr//9ePj1x9f/T3w73D91x8fsT97aaPXRwzPzt/r5TnaTvndmZJ6ew79oc3ttPnjyX78N8gkMv4cR9ZxSyrnXUt89t5zz7j3kZzHM1ny7z4+foJy+MvHH/D/w+PHAb/bn+kRU3/GkVtKuGw8fvHp4yffPL76x4hsP7759cd4IlWCFcw3v/z4UQp/9/jm24//9A1+KDwDfwv/9/oD+Ff/8Ktvf/5f//xPP//9dz/+9Nvf//m7xz/8r4+f4v/0GT5aeuZx5/lI/uE81/gc5a/Odax/W65j6M+QnKI+0n8439KeZfz1+f4bSzuiuFpz8n2k/3C+YynPJGKX/pW5/1sLHWWWg5P5I93J/Gd5ipKfyHZ0ss8cavE+kEO7YyrhKU6LOtO/dMeU0fza996xvt1x1Gd12sOZ/sU7dnniDu7t4tsT5hxw7X2/M/1L98spw5J9z/3enu+0g5/d70j/4v3aeNbg3y+t5zvqbO5p/XikzY699F1lafKfMkqGjt/46h/TvNGP/vSqsF4VHM+RQyhWA3GD92S39dTBdoYWEesz5BxRbB3XfrnhP8Pf2vR31os8qxXHZ1nfyT+c9VLx3gL+E2NNX846urt/v4Y/Av7KPYzPs76Tfzjr6FQriJxabfHfkvX671fqMeIlllDLW4VZyV+oMOhaUsmtVfym/Fvynv7D7O3O/E7/Hnvb0CGWyPzDDsoIRfq2trNSb/Nw3hKNtsaSwlstPdK/eEsYih47bFnqo39WKu4tExy6VGPIb7XrSP/iLUWepZbY0sAPf1aJ/FvmjFJh7j6/40r+0g0TDHWUIFJzC+WzBuffsJVnT6WHtzd5pH/xlg3mEiWKfibE/Jl5MsPLivtj1rLpVpCp/ZnjtBaorDFLK2Zyw7NotVXT+7rbj/6v1l1ku+EJrasNb9b5/+gl9Smxy3nB+o3//iO9AkWJfM4u+P1H/vS6JIUx+4DrZ/7ue37mR/9vNbDH1cDmU701s//yP3732z/8+Vc//tmv//jz//mnP//x1eL+8HgLGTIKDOWVWntG/O8ff/X4b4/fP+Kzwu/HG0+xttGSFV+b/+l43T3UMVKuSR4/+/qBW//v3/7iVz/7+iePX3z3WXyQnkFiLKzp6L5rlz5mc44wMpGV4J98BZ01MoBOFNnS5FFQFwxwFQAVzm5Do9DkVoMswFM+feBvtNkSu+Y0tpqyXe8JuLyh7qI2iv5KTE3GvNwRcDk7OrgYSIQ3CAsh83k94dMHKnEKrRfR5FxLDcWudxUACdVJUhLLJFpZrRPwFADoUVuoDTfO8hwplTrLx1UAtCfsKAMfeKIhhdjn5Xc6Lh7qyqGpshBQK6O8LvcUBF8R1gIWxcqhhyZxFr+raLTWSx01WjkUQSc1AU8BgCAixob+WmtiQVWcb8xVAHTeOIs+WMrqbtr1jvDpo9PoIoSeP9IHLtDLPQGXIxjLUhmQoRzgZzeZP+8qnz4G3yNetsx63kVmCbkKAHTjKOliJQ1LDUdrAp7y6UMKml5Gh645HTmOWaKegMvrcwhafbGq21p5FairAIB5KWwO/JWOEkdvZdc7Ai4X9PO59FkPQ+1hlpCrMBJmexvF/HmJ6GbmK3AVAgj58Tsl6g8VOGkLcBQCBZ1LzWrO8rPROo8X4UlEGjqq2vTtoFzgMb4qqi8ZwhYV+FMNzR0RRNvILdkgQEkx52Y/1WIt61E8ichA82ulVQ2wJaOZ5BfiSYa0OmKzF4vUUsZGbokI3hVau3RtLehB4n4pngQEnZHkjmBXHbiWS+ivjLkSEVTjUnpFjc7wtwveX3ohnkQkoe2GzG4A6ei+5FUdfcmQ0dFLzp+SGkLayC0RQXcGvz+aM4pKW1YVcyUiCEvxcml/0TpZa0t/IZ5EBLkcCE+tIrWOurcy5kmGoJctmVYSXhYMd8gbuSUiHdYoWt3DnzAbpbwQTzIEhiDqK0Y1FPT+spFbIoKwIguMhqbDuUXDfSGeRERQXWuNQ59RZKBPfyGeBCTBS0VEyVpR+OeI6fUsrkQE1jvVRCsIIxJKWU/vKQZ0uMHVKis8Aby5TdwSEXRYcMR71GokBQHmi3AUAwYMbSz6Q/gDvsEmbolIecIeh55mfMRo5YV4EpHK7ArTC/29EVdlcSUiqDnsqq0XrnA6Xr2JLxkC/2eEpFYH/c2yrZ5CYLBMtBtDJDEkxlet9xQCqA1oZcnsGrwEZP1FeJIhTfBbdQ5D1pE3cSkAMryakWo2j7fBQ1t2xZWIwN4gdovWrGF5Yl+IJxHJzGMUq6SId1J75cuViDSYZfgGdfb6zPkkHAUAvY+olZl/jiTxBXgKATUc5nkxJpH+Kl1P4RAwe1kR/gzC5pbbeL1xTzGA4YT67ojoKmLyvolbMoTxfzFrVkdHvdjILRHJNPpF+2X0t1XKK3bwJUMQrSNOMzOL31pG25UMQZmnMOtP41DKRm6JSGFtKGKhC4LZUdezeBIRWL2eOPTECosfym0hnkQEIXAc6pag4SFEDbJeiycZAucn6PQCOhxYjlE3ckuGoMBtzLjCv4T9TBu5JSIcDmDV1nSGVsvOu5IhCc6LptMSjLzarysZkgc6DktvUnI57nJLhqDDV3Ou6am0TVyKAQ1Fz/qNZHp+fQOXYkBHerHfQd0YqzG6kiEDhc16hyKBlU1y3OSWiLD3iqMkTe8IovJ6dE8yJKUKE6uvt+YdBfiSIQXZ1TLB0yLorcddbskQdpGxaVWF61RT38gtGYIm0BM7THRM47zHu8DLRSM/dsgJVS7V5XN6CgCEmQg8Ct23Bkc2wrV6NSxXMiT2kuCARQSFcMT7avGuZEgOXRKMeYfRRdhZ6kZuyRB0+ogzddwSPV8+bnIpBtQE76BpcoMPsyqKKxnSMvwJVKCeac/zOJBbMqTDWIqlZ9idkjZyS4agLjdG2khHUJyOZ7+UCcA1ipaMxt3yka1bMkSajh4xOSH6zJu4FAJ4qITwoNmtZdDmTsKTDIl4OWk+X8lpP4gnTUQqB4OYzlGVnS9PMiQhvBG7e2Cn3DdyS4agVYZhFaKhgS9L70qGlJ4je4DOap7S8uhdyZDaEKsNragI21s87nJLhjQ0IBooNgcY2nA8yy0ZAg+xchSBjU767rRdyZAxGv1QjtoPlOlBXIoBMuiOPTg03WTkeLzIWyJS4POx/TQGn2Usn9YR7HLUNDhs/AsRclrRsqcYUGqjax85UlakHDe4FAM4Ps7RLnYDaeRaN3FLRNCjZhSCeWMNQcXyIVzJkJpRe2yQLMAo17aRWyLS1G/lCEKkaWvb0jnKJ50dgHHW/iWgcErZ3a4rGQK3Eu/pwSGhFPt2513JkFpCgl8p6M/QEFaX6CkGNDbj8hAGOvh32sClGNBzSLB5Ao8spD1C4ikGwNVj8IvkEODDxg1cygSko0t9CEojRVxyAO+KAdJCRgwhaG6D4+UbuBQCg3PLFfWFqx3Y1S/AUQxAPE+XS9DHCB4ub+BSJiAZ/2FyQj5FDuBdMQBBLzoJJgeE9bt/dpQJjF5RxhIZOsOWHcC7YkDOsL+VyTogeTzDpUygxwCDJRyVGochdBQD4BS0wdTa2xqC9oR5OVoKvGUmo8XXo4wuxQC0K4RXmgynrhwZupQJ4J2I5rNycrUdwLtiAAPKor9D67IdBUeZQGHwzZKDF1SPMn0X5uXCKTImC2xROoroUgzomUMW+vIHIurjLV/KBAZjMK1eo4+jTN8Fu3zgxQSrvl1aPkroUiaA9wGvAclyDCs5gl0uKAYYQ1Ff6Wj8jkJA2OOzQqGJB1b7ZY8cxYDIdRaFyYNLl/oGLsUARGgc/+LIf0Kv0zZwKRMQ4VAGDWGlr3wA74oBWaqAhqnlioRwAJdiAPxcbeLo8WEb0gFcigFwJzsjj8C3E/quSJ5kCF8iHfCAkAh1ORwFdUuGcN6YY3JBOPy7jZijAICLA0NCF5qjn4MDba97uBIRzoxnXRyVOVGStvF2JSLoVfF8dBUG4sGe4MW9EE8yBC6ojl5zXWEPcbUjVyIC15MT1P0Bp/WJ1lXXIIErGRJDLygLLojIidHXRm7JkMTVCQ3pVQeRlk/rSoagFkhNSG+IoOM2Iq5kCOwvQzy4S/gTkduB3JIhNdJvTXzB8BvWuKCnTABNAU4CQjA4cDBhx5PckiGNIz+Wjlpe+pGtW5oIF1ciuxF+T0txdXuuZEiHswNTzPTa+ijHo9zSRKTQ4jEdfu8yQp5iwCiJ/0iRCwd6kONJbmki8Bvg/DAdbhZcuAO5JEMkB7xVTUchSjzq1y1NpMMW290LzH85HuWWiNC6ImSzn6qhh2XjXWkiHLq1dISScXnDrmQITAccIUtHx7GGX11pIpzbLPaMDYV63OWWJoI7InjWkoQrno9nuSVD0AWwoUaOOpS6huk9ZQK15zq0SqDnk9XHudJEEOD0oukd3mM4snVLhnCKN1vtxrOeD3IpE2iI66ympqKO+SYuyRD+rZUowMC3seINV5pI4XQzkxl3nw9yKQbUOAaLBOYDr2zXekcxAI5XUXuDjiO1no+KcksT6Vx4kQJHGxGvtoN4VwzonDWOajcLOquzdG/JEOF0dlGD3tFvnDe5JSIIcjrH15DOZUCjLEfClQxJPTAwhEeSMixP38SlGNBgzivX2eIFwKtvaRO3ZIjA7Qk2qNNDqGucz5WIIMSlsbEJklj2yKCnEEDQM/B26qNzRXIIaybLUwwoEhDbPhi3StoBuacYwIF73I4jYelwiDzFAPi3XKnDIVOUxbbxjmKA1IJu5VHxkI0DjRu4FAKgKwKx+qiVa4f6ipQ9xYCI9whnr7LTkLwm1jxlAsLVf0yG2egrXPEUA9DWGclzAqrBHuUNXMoERq2o/pzjgvMtxzNcigEZuZPCjSdSQhjHHS5lAvC1O1NbHm13nLdglyNk7nAgkIxK3Hb/7ygT6InhiC5GK3GNBnmKAYglOzwiJMNnG/3I0aVMoDHYe1SYRmm1pgN4VwxoMXC1J5NHq0eO3oV5eRttaD5DlcN5cxQDOvyfrCWRULvG8dIuZQI0n7pbiOF8Ol7apRgw8AZh3XV7Uf7sLVzKBEbkyFvlqsRjHNZTDJDUGW9XRjGxnHe4lAkMuAqdNR42OJbjLVwKgMHhPAQkicnwsODXTcBTJsCFJnj9tJ81r4kHTzEgwhNBtMdmjrayughPmQDKogwmI5huazGJpxiQch+w/VzYiDu/Vtm5igE5c1nlow56sjEcd7gUAwoDnPRo4Yn/2ZXbUwzQ6bb+aHy0sBu0pxgAe4OG+ECMWNB3lCNLl0Ig0o2GbXiMxBnqtIJMTyHAySD0k+gsm+7a6btcPYmIRlKIONG/cmKQS0VfiCcZ0uDdM/iKXLtUeh8buSUi8EERpet69sjFLHsphSsZgnpGo8V9U7r6oW7klgyBORx0YbhyjWshDuSWDEGd5JK6xDWUVdrqsF3JkIZWQ0efqwDQQefjLrc0kcY5dqRzYheV7nj8WzKkRwQqKMnS6F+04yaXMoGexFIR4uyxGE8xYOQS4CIWDoDnPTzkKROQYQXCjVlS4pGnWzJE0IKLaDpbqRw3uSUi3A7VAr3jwr4dVWi9EU+aCEcPCgedSlj93p1uF8ciTaKmlyZrzZSnGIA+U+AbajICqdQ2cUsTqYWrM/XemYu1D+SSDMkRPZtlN/JX00ZuaSKVpa4lOGLbw8SuZAg8e2sGHNoOa72+L00E3kmz2tC5FzceyCUZgpbDwInp3KEwjjK+pYng3jFqJS09HuX1LtjlLRfROl0531HOl35LE+HgX9W2KchEPJFLMgSxSg6souhQ8XhylNYtGQLLPwYLPqIUy/nkl2IAXOrIMDjjTfW2l8i6EpFGF4jtP3PLCxfGvwhHMSBx6B9lmFDnOMHVNnFLhsDcBY3OYaEQqPYDuSUiiFJy4qotTnEiwFm+lacQQGWu7ExbY2wwdoW/BbucNSE/UA/g2bW1/McR7HKEERXOUIZbBKu6rbSjGCAZ94qPzIi+x11IjgJA4AzJ6OiGuEW21+0xeIoBXF3KsQUEgzDJ+QAuxQC4rlxTkBrH/OJyoD3FgMw9sHg3rDzSVujmKRNAN83uh1bmCN08xYACA9FY8RGVhnBc/y7MyxH0RlpIvMuR1tiypxhQYYb4M1xRgHBrbOBSJtBKxcvhWtw8ynGDd8Eub9zNo78S6naeHWFejibBITruHO6Sj5+/FAM6vCuYWy4m5j6yvIFLmUDPHDXFz3DbylGg74JdzrWqfPEI8uFbxuMBLmUCY2hNyRr5hqMOXYoBwlG2ruVcuHliA5cyARmJg6Uc0NxeqiPwcu5yla7+C3yfeLwCRzEgBs7ja00cLay1+p4yAcTrNbNxBGRgdfGeYgAX7ATuaNQVJvXI0qVMoLaAcInrLYfslUOeYkCOHCPiYrjCKbp9/btgl5dUOTAIn7gJPMnj9y/FAFRZ1vFMf7rHcZTRpRjQYHHMCI6RohyPfCkGoLFmmCi6B7nVcDzCpXzSHaWI+xjacxItS16etacQqFyubU4knRH0GCtPnmRIjakyeECM3EbbjrUrGQJ/m6vaEiNM9hdjI7dkSK8cmUE6p/TgVOaN3JIhIwXuv+MeWXSrY79BT5qIBDo6XBfENakn8a4YgOZIPyK1xJBuL3lzpU+6+5cnEkjVdKnHqLQrTYQLiNCIuSxM8p6ZdyVDEC839JLcSxy4sylt5JYm0mLmnENjdAe3px/IJRmC6NSaJnqcimyXjdzSRDrnqGyTc0BMcDzLLRmCeG7+Ut+16z15XtoRMduztcz9ncfll2QIOs2Q7a4Fbowcz3BLExnafWsJIrLb1s2TDKnc4Fjme5Jaj8e+JUMaXDzOM7E29NrPinJLE+Eu3FnnShjHTS7FAJRcEKvXyHk873FLE4Hvkoe2HTpAu1l5kiGDO6Hpx3BA7Zi5caWJwCkWa9O59xN4E+xyqa3SOHFVfToL913g5VxkVtivc9ANb2s7dY5iQA6l0GBws1SKe+WHKxlS6aYWjQRgOnac50pEBmoMzaTNMQ2YpfU2PIkIu6zKFbu6GxOlv/LlKJ8+OOUTEATV9tCZhBpea/BcxYCKHxOdcECFWMN+rmIAfBounOPBPAF1s2zgUgjQhRicWsuccNBp4gk4igEpRe4Whm8/GnfIbuBSDIDHwS1biSuZ9qoaV5lA7xojc5sC1+YdwLtiAOoAXGI6KfAgZLQNXIoBNYjalkovv73CbVeZgK0zoGc21mYVT7DLYXFRzdS3j3nZTVeZAN46vSYu05BwPvKlGNDhZ/DBuOCER/9s4FIM4OB7Uu94oAHI8QiXMoFe6e+pu348wOfJdqnAsg0LBXKv6bj6UibQddmouuojh6MOXQoBbmVE/5H1oUbNq3huYV7eOnPHQmv5ZS88wS5Hp4zgh6mov/W1GtpVJgC3W9Sx5wlNqR7Au2JACtyHzeQR4trV6ioTqEMdGB1kip8B74oBOeTEG3NQlIv8N3ApE0DAMNRRj0FXJG7gXTGgRD36Ba0VAeKaB3cVA2oIow369gjIxrZ2jjIBSfg7J55mldJxg3fBLu898NyIzG4AGS77+ksxQPLgehOOWbHn29e/C7ycOx8qgiSd9whl1HW9oxDg4hTh6hour+N6XFmEJxHBPziaxOl9ZDrl3lZd9SRDYMa4wITjTzwwodWN3BIRuF+jcIqVh+RkCWtphS8ZwhMYkk4x5L4GszxhXo5oTwcnBLFxlG1SPckQrsez6QVUgbaNqqMYMBAEaXiMp4OzvSuIJxnC0+mizS7A2+5yPPgtEeHe8t51UBftBV3y7kI9aSKtc4Is6Y7SfUiLLxkSOeRQbI6h0avfyC1NhJPj2eYYhJ3+gVySIQkhTbF0DmYdxKVMQLi/lSPtYbATP4B3xQD0BXHOGcBa1yGbuCVDEIpy55pOGtQs56Pf0kS6lDnNQNelHcS7YkDlvESa965r/5QvGaKT3vp8qEXhAN6FeXlPI1kBImyuchTVLRnSU2s6HMRRTo0IFnJLhnCHEJcLlW7TtnEjtzSR3nlSEWtcHuPozTzJEEGzZFDK0YVQ14EjvkQEhj5ywZ42uMh1patqedJE5jq8ovvkQhoHckmGRFQCLcnIwy+Ox/ckQ3iODxx0ThqgW5JdIT3JENScwglY9AOIOnrexKUYACdicOiW+1Q5aXRk65aIMCAQnpNAIx2brlKYiCcB4Wl4XEpSdOcPur3tA7iSIRXlDRdx6CrEtt6jpxiA1ib1oTtDytqt7wm8PHFxMw8wYOQb6Ze+rncUAxKPhxjsKAM62LGvfxfs8sytWulRO4+HKq8xNlcxoAQ0+sIoCEVYViP0FAPgedBS1sL1Vf213MxVJmDrbZAMl6KlI0uXYkCLGjbpgqxQ91tzlAk0nhrE9VicZj/K9F2wy7n9uNlyrBDS8qo8ZQLcfZ24UAcFEeLxyJdiAEKm2DUZVSv2o1AvxQC8QY4vcnXSqGtzjKsQ4Lr6wNO2dPlTX/sNXGUCGoDzZ+Db7Ge+Bbucq+iqLfiC25Hbvv5SDNAdWpoMq7iMmSPMyzl1UFnSdJCP7LwLdnkuJcKkcyETj1bal78LdnkJJbBiZd1Sua9+S58X8yS+oQsGa5Q4jsvfFQMqp51Zayt6g5L39e/CvHxwWIzrkRr3jh1FcykGwMnhBADHfPJYG4dcxQBOR6K/4HqkUtZWclcxgCvmKk0Hly8ddect3S7mgTY1Prh1uKCjOH79Ugigz+KZLsLBea5T7ev3HcWAxrHQ9tC1LCIjb+BSCDQdzOdGFBizwu3ri/AkQ2AvuNCCS58qrMi2jJ5EhEcRcd/zQ+eVahkrGHElQ9hH8NA8TjgErkXayC0ZgvCY44Yc82qIPvJxl1sypAlipqarpmuQdSqULxkCS0C7wy6SK8FlE5diwICXx90b8PMrxwXjJm7JEHgTtnGHi6pCWdGFKxEZNFYyxwWRjdEW4kkT6Z0b69nv8wCZXA7kkgyJTYMmLrCv3MPTN3JLhuDhgu2pEW4uOm5yKRMoWd2WqOtFx6gHcUkTGTrrq85FyXU7D55kSM5hiKUP3cu4kVuaSNdjInVTDV5cPx7llgzhITu2QyQh7+XI16VMoGUeGaNuBkxCPV7jLRnCDVEtzp0r3Di+kVuaSK488UzTORR73OWWJsLYsc1dOLImBH3JkBbb0BrBXTi51aOy3NJEKs8qtfS610T50kRQc5LtKMo9HI6mJxnSucEpzl04so6P86WJtD73U0UeiXPUyUsxAEU3slVV9E35bI+3NJHCY7BtF07kfMCBXNJEIDRLL51bFw/kkgxBP9nSbHZcV7KJS5kAjy+15Ar7IUe2bokIz4MJOswXOa0a+jq71pUMiYk7RdTioM6O7at60kTgiOouGTbZWlYc40qGwMfUdSscpyjhqJKeZEhuOggcOPUbz2y9C3Z54aIAWs7C8bjDJ/AkQ1oM3DKs0xbcgXggt2QIzLNuxOGpXPAYxiYuBUAKXG9QeKbsGHp22+rnXYlIfHJvIk+VzXpg4Vpl4EtEtJXpOcCRZ7qv/TCuYgCaDo9DsaGQtQ7QVQwQ1AJOZgXd4LmHB1yJSGaAqme/Bi43L2vLvy8ZEhEgILeCGp7GdjQ9xQD4VoimWOhR1pDQnW4XZ65Da/zcCDcNrhboKQYUznDaiRW9tSM374JdXtF2a+IWdFjZNU/nCHZ5KygG4Z74ynmCo3guxYAeeZqubrqXdZyiJ8zL4W6ipxa12+tYZFcxYMACj2KHVYQ8juK8FAM4F5X1FAO4UOMon3dhXm7H4PGoCtj4FTJ5ygSkIB7RcxVCyuME3hUCCMLpMOvvNISQu8Y5ygREz6zVoyT6WDOfnmJALLoxX5PDWpTkKhOQyAEnPQ7jGOH2FAN4KEzWwkPPm5bL7ikT4A5i/Z2ux58fwLtiQOZWUz0Og8sKwnGHS5kAT6jq8/SJHQ55igE8O75ErS9S6ugbuJQJSE2vg1VGLUexXooBXNLSh1b5ihoZN3ApBvDosqptCiF/DsebvhQDGLhEa7NV2lFI74JdPkLlUnvaBLydeLznSzFAYuF2Ltqc2ls6MnQpBLjyP3DZgTBEiutIB1cxIA4JPBJD0B6l74rhKAZwar10PU1CUl3jXJ5iQM92hC2PB0B4vkvVk4hw0oRLRfVoCPR/shxtVyLS8XhSux14jWa8DpLyJUOKtK6nsnK7AMepNnJLhsBv4wSmngsp4TD3nkQEMU5kDeaBbPRe8yIcxYDMSUbRVeADxbgG+lzJkMozwZse3gUTLMv/dyVDetIpXj2nhUN0fSO3ZMjgMcdDTy7LoeTjJpdigIzETXB6ckcKYU2uuBIRPe9YzxXjoYCy1037kiF4r1W3JPOA+rZOWvAlQ7hvfx4kyDNn1gSLKxmSQ9YztflppIQO6LjLLU2kJ84K6PkgPeY1QehKhsB48+B5nvXRuDFzE5diAD9uM08rLLG0A7iUCcAr4VlyesYfamA8iEsypHGbbp8nCeZejke/JUN6iDXnmR73mJIrTYQnTszDBzud8QO5JEOGnkM0Dx/kkX0buSVDhONTlo6Xm8qRsVsCkvlZiJqHHQs4OND4enxXMoSzbHFWIpG03qMrGZJ6CFa5O9rHMqueYkBJekAA2xzP3SgbuBQDGpwszgVxWFK4tmATt2QIqgOXO+hhcaiwctzklojwiJ5GV4sH5WXEBsvau5IhCG64PkAPeixtHVHlS0R0eY6WInch80DFlTFPMgTRbBr2WYrBs+fTRm6JCJumLoLX48S5unLdxZMM4VcvaT74PaLWd5V0JUO4359nSGZ6wmFXSVcyZCRdZ8cjYJH/scZIXMkQlLee3U1DCnOw4iBXIlJ4CGGa31yk37Z8QFcyJEc99pq7APh1hLKJSzGgdOH6UKbHFNf+NF8yBDY567HP9clTFsKB3JIhg6uz7PBfTp/0A7klIgzaEnf56enKeAdr2ZMrGRJH1yNHbY2fpLKRWzKEJxoEO5B5xHgUmCcZUvl5mGEZ7r0cxKUYAG+ES6GYzBMd8gYuxYBRM0fmmIwIKpyZuiUiXDCWOW6gHxjEn8sTdiUiujC46LcgGCD0NTjmKQTYmVe1BfycntR1PLsvGVLoJRX74AJP94kbuSVDuGo322cdBE7/zpcnfdIvW4ZRWOnK4Ac69kJXTzGg8KsBVdPhzK4vw/iSIZzi7JYMy7PWN3gKAZ5H0dR0cG1JXuvlXcUANJyu332CY5p1l/0ibokI57l65MFyPLM9xbRGJ1zJEEGRBPvcAg/lXQGKKxHhofOIrV9n77e0nFtXIsJPymZWZ/0pHq+9nsWTgFR+5k64/kr7gELvbCKuRKQyJuSOW/3sACz6qiquRITjnWjW82sT3OHxevOuRIQHdHQ9/Lfoyuy9CsqVgDSu+mj8PqJ9tKxsZ8KViKAP4ArOoW1ucDJyIZ5EBLav8oAATYevufZX+BKRqvuLmn38K3EX3quQXYlI5zg0D1TQVyyxrhEtVyIyuAhUhg2Awkbt8RdXIsLYQudQmc4Tzda4nCsZUjnE3OcHTdo6QNCXDOFpNNm+aBJ5NGzfyC0B6Xo63utjkNyvvRBXIpLZIYdgn3jg2MYaQnMlInhJXGxun7/hcShrFsGVDNFtCPPbE3gZq1txJSKV4/6hWzpixLF8I1cyhBuf9KsQtNI5LHPhSoYwlaMQfEZEZquDdCUi/EfSmK/owqp19LYvfbLvBfPAByt83ZywMuZJhsBfVvuGWlFK3g6oKwHh+Sh4z/bNHHYLywfxFAJRvxzCQYjMbT7cdPYiPMmQxjl3sWrEw07TRm6JCAcla7Sv06S4P+7nKgYwptAPlcxjCtombumTfryZVbXZu2JnsLPlSUS4377ZJ3C4dXCUFXW5EpGuS754qr5+aKet0298CYjoAAe/I2A7dtr6uogvEYn6hXP1yQcchxzWUKcrGQLLrO4Jx6y4W7Js5JaI8CijEOeXjPiBzzVT5UpE+EkpXQpBoxvC2F2rK/E7lty2G9LrOy08P3w+iy8R6c/E5dCvL1zKmoLxJSBccFY7vXftP1tYq0Z9icjgyeqv70Sm9bXMOx0X8xtZ7G00jQvmXlc7wif9Wjf6Zm6J0m9i8sTO1xO4EhFd/FLmV4zgaI7XqJQvEYHlQ1yU7LOGPM64rrt4EhF4AFXPaNNes6ewbuIo9o3yAZcna2rHnV97jV2FAIfsI4900K9R8hO28UV4EhF+40+aWjN+3rCP1xyRLwHhytwOT8Zymzn1MhuVLxHhRsHB/UXqL/F4ldezuxI/qcovUHV9xKSnK76exBF4edPjn16Vs8la6u1LQFrgeOko5vfxJNmXCfIlIvzmTRsy07nJ+ZUtVyLCvTBibZNNoKwzun3p82/F7+/YKvLTxx8e6fGfH+Hx7UM/ffz458e/4F+/fP8S7vd9x937TrL+8ld/Hx+/+Q4/9Rf89+vP8sDP9X6WK3a0w4zP7wEmBTU3RM+v8B5f1f7sqc6val/33j/wutH33/2nH/8fQUH2qwplbmRzdHJlYW0KZW5kb2JqCjExIDAgb2JqCjk0ODUKZW5kb2JqCjE2IDAgb2JqCjw8IC9CQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDUzMgovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJw9k0tuJjEIhPd9Cl9gJAMG2+eJNKs/99/OV3Qyixa0ebqq/JTX+GMxvp+8d6wceWrYtNdmjK+nvXs48eFRI3cOr1KkfITPkStGrD3Sdlsi8z1Z1MSaNFamauLGcLp9Xo9Jr2exRuwaxyiIsTQ55h2adXtF99X267F92rNgK7bNN32bqpMTv22OVqHaToyzhm3cObGpJvKCLJt9YQsbu7unCQjjhyO7W+brcS6K48sV9Yo32+mtcr8M4KZtz1UELy25X3sUKLeUi18xlUO3yjMc5Ip+dk5btih7T2J3hln91NykiY8DV7oxJjROzqxBdAGj0tc6agRly7h5QcPMHiHLcANyTj8My/bMRcIdFwSseYRCkFzAClwyKSxwtALRgmSy6zSklG9nZ9ptbqYBsoxCL/LEqDJE8VsTKEP3jLyjpCdqK1Wz6ow9tV66quAa3rcqu69QKkV0wrdBv1h2RzXteFC2hRu4t/VsmaBhWN2AIFa0R3p340+KLXhe0vN/HMpme+UCj00XQN2uYWIguxKEKfaIgAMRJOd8dWerpu2cvRtQK5ctzLiTQacCm+GGsD/PmVoM5/eB8kpaPZenGugrz7tBQkJb3z+vK1KYCb04Up80uFCGqFu8skQeirIH2yR6LOandCa73/uyL5OVUVldU9WKoLJK7wsU0F+u1xLx856oo5BUZkvwd/PP8/cfiKjUdQplbmRzdHJlYW0KZW5kb2JqCjE3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTc4ID4+CnN0cmVhbQp4nD2QSxIDIQhE956ijyA/0fMkldXk/ts0zpiF9hMobLCl6BjOy9WQXfGWVhie+DbvC56Jq6n1hyQVMvumDhmLZ/IUJyQUryZjQNyx1dajcTLCDLssJmZgroqvRC6oUALqUfJqZqPgaqaCvn3EVpn1FhcIRQImLGcr/p8D0+sWHQwWmO03y7M89grTdCzMe4Z5D0UjfgblWm5gZa2Dn4Ydmve2aCj/5Cd7Fni1zw/eq0KhCmVuZHN0cmVhbQplbmRvYmoKMTggMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxMzkgPj4Kc3RyZWFtCnicPY+xDcUwCER7prgFkAAbG8+T6Ff++7fBcZIC8XSgO/BhELDVLOloUuC141SyGmAX/MmkgdUE2i2hFWhdSigOWjrrCETbFvXpB32uk3jkUrGkai+1viliuTv0jtFtWsCjZ072rtDm4HJPRkEmTspT1qGTNH02mQfUIsllPNr70Pz+mfS7ALu8LdsKZW5kc3RyZWFtCmVuZG9iagoxNCAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMtT2JsaXF1ZSAvQ2hhclByb2NzIDE1IDAgUgovRW5jb2RpbmcgPDwgL0RpZmZlcmVuY2VzIFsgMTE2IC90IDEyMSAveSBdIC9UeXBlIC9FbmNvZGluZyA+PiAvRmlyc3RDaGFyIDAKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udERlc2NyaXB0b3IgMTMgMCBSCi9Gb250TWF0cml4IFsgMC4wMDEgMCAwIDAuMDAxIDAgMCBdIC9MYXN0Q2hhciAyNTUgL05hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxMiAwIFIgPj4KZW5kb2JqCjEzIDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyA5NgovRm9udEJCb3ggWyAtMTAxNiAtMzUxIDE2NjAgMTA2OCBdIC9Gb250TmFtZSAvRGVqYVZ1U2Fucy1PYmxpcXVlCi9JdGFsaWNBbmdsZSAwIC9NYXhXaWR0aCAxMzUwIC9TdGVtViAwIC9UeXBlIC9Gb250RGVzY3JpcHRvciAvWEhlaWdodCAwID4+CmVuZG9iagoxMiAwIG9iagpbIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwCjYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgMzE4IDQwMSA0NjAgODM4IDYzNgo5NTAgNzgwIDI3NSAzOTAgMzkwIDUwMCA4MzggMzE4IDM2MSAzMTggMzM3IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYKNjM2IDYzNiAzMzcgMzM3IDgzOCA4MzggODM4IDUzMSAxMDAwIDY4NCA2ODYgNjk4IDc3MCA2MzIgNTc1IDc3NSA3NTIgMjk1CjI5NSA2NTYgNTU3IDg2MyA3NDggNzg3IDYwMyA3ODcgNjk1IDYzNSA2MTEgNzMyIDY4NCA5ODkgNjg1IDYxMSA2ODUgMzkwIDMzNwozOTAgODM4IDUwMCA1MDAgNjEzIDYzNSA1NTAgNjM1IDYxNSAzNTIgNjM1IDYzNCAyNzggMjc4IDU3OSAyNzggOTc0IDYzNCA2MTIKNjM1IDYzNSA0MTEgNTIxIDM5MiA2MzQgNTkyIDgxOCA1OTIgNTkyIDUyNSA2MzYgMzM3IDYzNiA4MzggNjAwIDYzNiA2MDAgMzE4CjM1MiA1MTggMTAwMCA1MDAgNTAwIDUwMCAxMzUwIDYzNSA0MDAgMTA3MCA2MDAgNjg1IDYwMCA2MDAgMzE4IDMxOCA1MTggNTE4CjU5MCA1MDAgMTAwMCA1MDAgMTAwMCA1MjEgNDAwIDEwMjggNjAwIDUyNSA2MTEgMzE4IDQwMSA2MzYgNjM2IDYzNiA2MzYgMzM3CjUwMCA1MDAgMTAwMCA0NzEgNjE3IDgzOCAzNjEgMTAwMCA1MDAgNTAwIDgzOCA0MDEgNDAxIDUwMCA2MzYgNjM2IDMxOCA1MDAKNDAxIDQ3MSA2MTcgOTY5IDk2OSA5NjkgNTMxIDY4NCA2ODQgNjg0IDY4NCA2ODQgNjg0IDk3NCA2OTggNjMyIDYzMiA2MzIgNjMyCjI5NSAyOTUgMjk1IDI5NSA3NzUgNzQ4IDc4NyA3ODcgNzg3IDc4NyA3ODcgODM4IDc4NyA3MzIgNzMyIDczMiA3MzIgNjExIDYwOAo2MzAgNjEzIDYxMyA2MTMgNjEzIDYxMyA2MTMgOTk1IDU1MCA2MTUgNjE1IDYxNSA2MTUgMjc4IDI3OCAyNzggMjc4IDYxMiA2MzQKNjEyIDYxMiA2MTIgNjEyIDYxMiA4MzggNjEyIDYzNCA2MzQgNjM0IDYzNCA1OTIgNjM1IDU5MiBdCmVuZG9iagoxNSAwIG9iago8PCAvdCAxNyAwIFIgL3kgMTggMCBSID4+CmVuZG9iagoyMyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI3OSA+PgpzdHJlYW0KeJw9UjuSxSAM63MKX4AZ8BfOk52tsvdvV4K8V2SsREaSHdJSugwNaSNVYgyp7PIzLsK2VP4OIvtcPr/Q1jrQnIeji40JoCn3pasDdhWtkha+6ygyBOYQ2GiaaE5RcAoJtX3acJCH+gDrMiJ2vS8GJXo2sq1D9iD2E6kZUkE58I6EUISHzb5j+DhxPO3NE2BOngw4I3v1M04pXTlhORQwMrfDLbDe12dfz0a5iLzmB2EOIscicmJTEwySQLEcXo508NRTozYD5FFcMFHHbLHAz71nPugxpFPoke3YXC6kXmTwhfnZofBgP7cABiqqtZ0GO1i9v45jvYYNv4/hWuSO24otHKBNFw7EO8ERWe/vLXmu338Hcm4GCmVuZHN0cmVhbQplbmRvYmoKMjQgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNzYgPj4Kc3RyZWFtCnicPVJLjugwCNvnFFwgUvgmPU9Hs+q7//bZtJoVFmBjSMpLlqilTC2TVJVdS350dO4y+Tc0r0bPsPXmzEPmSbE4MrfKPQzkmVus0Gtv1KsLALFI7tQS2yXGlkvFkmSHrO0Qd2TQ4cUq2cz42sION2uOR1IXKl6nBwX5jDDwTsx9vollITRXGW23wEEPFqgDPTALE7ki491rEz2NeAugrA+Zv4guN9Rcj2xMgFO42gveqZTWMQ8ViaIc7EYavZ+j5jihw9s9Yjn2cglHBt7iaMd78EWInkZWRKx+yLMR+YYNqUiPmMob6m4fevyNrdhof3YmScHXX9bbTDXSueDUXK3WX4NHaPDeqOHz90ue8fsfISZuEgplbmRzdHJlYW0KZW5kb2JqCjI1IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjQ3ID4+CnN0cmVhbQp4nE1Ru21EMQzr3xRc4ADra3meC1Jd9m9DyQiQwiChLymnJRb2xksM4QdbD77kkVVDfx4/MewzLD3J5NQ/5rnJVBS+FaqbmFAXYuH9aAS8FnQvIivKB9+PZQxzzvfgoxCXYCY0YKxvSSYX1bwzZMKJoY7DQZtUGHdNFCyuFc0zyO1WN7I6syBseCUT4sYARATZF5DNYKOMsZWQxXIeqAqSBVpg1+kbUYuCK5TWCXSi1sS6zOCr5/Z2N0Mv8uCounh9DOtLsMLopXssfK5CH8z0TDt3SSO98KYTEWYPBVKZnZGVOj1ifbdA/59lK/j7yc/z/QsVKFwqCmVuZHN0cmVhbQplbmRvYmoKMjYgMCBvYmoKPDwgL0JCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzcKL1N1YnR5cGUgL0Zvcm0gL1R5cGUgL1hPYmplY3QgPj4Kc3RyZWFtCnic4zI0MFMwNjVVyOUyNzYCs3LALCNzIyALJItgQWTTAAFfCgoKZW5kc3RyZWFtCmVuZG9iagoyNyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDgwID4+CnN0cmVhbQp4nEWMuw3AMAhEe6ZgBH4mZp8olbN/GyBK3HBPunu4OhIyU95hhocEngwshlPxBpmjYDW4RlKNneyjsG5fdYHmelOr9fcHKk92dnE9zcsZ9AplbmRzdHJlYW0KZW5kb2JqCjI4IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ3ID4+CnN0cmVhbQp4nD1PuQ0DMQzrPQUXOMB6LFvzXJDqsn8bykZSCCJA8ZFlR8cKXGICk445Ei9pP/hpGoFYBjVH9ISKYVjgbpICD4MsSleeLV4MkdpCXUj41hDerUxkojyvETtwJxejBz5UG1keekA7RBVZrknDWNVWXWqdsAIcss7CdT3MqgTl0SdrKR9QVEK9dP+fe9r7CwBvL+sKZW5kc3RyZWFtCmVuZG9iagoyOSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE0OSA+PgpzdHJlYW0KeJw1j0sOAyEMQ/c5hS8wUn6EcB6qrqb33zZhWgkJC9svwRaDkYxLTGDsmGPhJVRPrT4kI4+6STkQqVA3BE9oTAwzbNIl8Mp03zKeW7ycVuqCTkjk6aw2GqKMZl7D0VPOCpv+y9wkamVGmQMy61S3E7KyYAXmBbU89zPuqFzohIedyrDoTjGi3GZGGn7/2/T+AnsyMGMKZW5kc3RyZWFtCmVuZG9iagozMCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDQ5ID4+CnN0cmVhbQp4nDM2tFAwUDA0MAeSRoZAlpGJQoohF0gAxMzlggnmgFkGQBqiOAeuJocrDQDG6A0mCmVuZHN0cmVhbQplbmRvYmoKMzEgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA2OCA+PgpzdHJlYW0KeJwzMzZTMFCwMAISpqaGCuZGlgophlxAPoiVywUTywGzzCzMgSwjC5CWHC5DC2MwbWJspGBmYgZkWSAxILrSAHL4EpEKZW5kc3RyZWFtCmVuZG9iagozMiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI0OCA+PgpzdHJlYW0KeJwtUTmSA0EIy+cVekJz0++xy5H3/+kKygGDhkMgOi1xUMZPEJYr3vLIVbTh75kYwXfBod/KdRsWORAVSNIYVE2oXbwevQd2HGYC86Q1LIMZ6wM/Ywo3enF4TMbZ7XUZNQR712tPZlAyKxdxycQFU3XYyJnDT6aMC+1czw3IuRHWZRikm5XGjIQjTSFSSKHqJqkzQZAEo6tRo40cxX7pyyOdYVUjagz7XEvb13MTzho0OxarPDmlR1ecy8nFCysH/bzNwEVUGqs8EBJwv9tD/Zzs5Dfe0rmzxfT4XnOyvDAVWPHmtRuQTbX4Ny/i+D3j6/n8A6ilWxYKZW5kc3RyZWFtCmVuZG9iagozMyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDIxMCA+PgpzdHJlYW0KeJw1UMsNQzEIu2cKFqgUAoFknla9df9rbdA7YRH/QljIlAh5qcnOKelLPjpMD7Yuv7EiC611JezKmiCeK++hmbKx0djiYHAaJl6AFjdg6GmNGjV04YKmLpVCgcUl8Jl8dXvovk8ZeGoZcnYEEUPJYAlquhZNWLQ8n5BOAeL/fsPuLeShkvPKnhv5G5zt8DuzbuEnanYi0XIVMtSzNMcYCBNFHjx5RaZw4rPWd9U0EtRmC06WAa5OP4wOAGAiXlmA7K5EOUvSjqWfb7zH9w9AAFO0CmVuZHN0cmVhbQplbmRvYmoKMjEgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zIC9DaGFyUHJvY3MgMjIgMCBSCi9FbmNvZGluZyA8PAovRGlmZmVyZW5jZXMgWyA0MCAvcGFyZW5sZWZ0IC9wYXJlbnJpZ2h0IDQ2IC9wZXJpb2QgNDggL3plcm8gL29uZSAvdHdvIDUzIC9maXZlIDU1Ci9zZXZlbiAxMjMgL2JyYWNlbGVmdCAxMjUgL2JyYWNlcmlnaHQgXQovVHlwZSAvRW5jb2RpbmcgPj4KL0ZpcnN0Q2hhciAwIC9Gb250QkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZvbnREZXNjcmlwdG9yIDIwIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zCi9TdWJ0eXBlIC9UeXBlMyAvVHlwZSAvRm9udCAvV2lkdGhzIDE5IDAgUiA+PgplbmRvYmoKMjAgMCBvYmoKPDwgL0FzY2VudCA5MjkgL0NhcEhlaWdodCAwIC9EZXNjZW50IC0yMzYgL0ZsYWdzIDMyCi9Gb250QkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZvbnROYW1lIC9EZWphVnVTYW5zIC9JdGFsaWNBbmdsZSAwCi9NYXhXaWR0aCAxMzQyIC9TdGVtViAwIC9UeXBlIC9Gb250RGVzY3JpcHRvciAvWEhlaWdodCAwID4+CmVuZG9iagoxOSAwIG9iagpbIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwCjYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgMzE4IDQwMSA0NjAgODM4IDYzNgo5NTAgNzgwIDI3NSAzOTAgMzkwIDUwMCA4MzggMzE4IDM2MSAzMTggMzM3IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYKNjM2IDYzNiAzMzcgMzM3IDgzOCA4MzggODM4IDUzMSAxMDAwIDY4NCA2ODYgNjk4IDc3MCA2MzIgNTc1IDc3NSA3NTIgMjk1CjI5NSA2NTYgNTU3IDg2MyA3NDggNzg3IDYwMyA3ODcgNjk1IDYzNSA2MTEgNzMyIDY4NCA5ODkgNjg1IDYxMSA2ODUgMzkwIDMzNwozOTAgODM4IDUwMCA1MDAgNjEzIDYzNSA1NTAgNjM1IDYxNSAzNTIgNjM1IDYzNCAyNzggMjc4IDU3OSAyNzggOTc0IDYzNCA2MTIKNjM1IDYzNSA0MTEgNTIxIDM5MiA2MzQgNTkyIDgxOCA1OTIgNTkyIDUyNSA2MzYgMzM3IDYzNiA4MzggNjAwIDYzNiA2MDAgMzE4CjM1MiA1MTggMTAwMCA1MDAgNTAwIDUwMCAxMzQyIDYzNSA0MDAgMTA3MCA2MDAgNjg1IDYwMCA2MDAgMzE4IDMxOCA1MTggNTE4CjU5MCA1MDAgMTAwMCA1MDAgMTAwMCA1MjEgNDAwIDEwMjMgNjAwIDUyNSA2MTEgMzE4IDQwMSA2MzYgNjM2IDYzNiA2MzYgMzM3CjUwMCA1MDAgMTAwMCA0NzEgNjEyIDgzOCAzNjEgMTAwMCA1MDAgNTAwIDgzOCA0MDEgNDAxIDUwMCA2MzYgNjM2IDMxOCA1MDAKNDAxIDQ3MSA2MTIgOTY5IDk2OSA5NjkgNTMxIDY4NCA2ODQgNjg0IDY4NCA2ODQgNjg0IDk3NCA2OTggNjMyIDYzMiA2MzIgNjMyCjI5NSAyOTUgMjk1IDI5NSA3NzUgNzQ4IDc4NyA3ODcgNzg3IDc4NyA3ODcgODM4IDc4NyA3MzIgNzMyIDczMiA3MzIgNjExIDYwNQo2MzAgNjEzIDYxMyA2MTMgNjEzIDYxMyA2MTMgOTgyIDU1MCA2MTUgNjE1IDYxNSA2MTUgMjc4IDI3OCAyNzggMjc4IDYxMiA2MzQKNjEyIDYxMiA2MTIgNjEyIDYxMiA4MzggNjEyIDYzNCA2MzQgNjM0IDYzNCA1OTIgNjM1IDU5MiBdCmVuZG9iagoyMiAwIG9iago8PCAvYnJhY2VsZWZ0IDIzIDAgUiAvYnJhY2VyaWdodCAyNCAwIFIgL2ZpdmUgMjUgMCBSIC9vbmUgMjcgMCBSCi9wYXJlbmxlZnQgMjggMCBSIC9wYXJlbnJpZ2h0IDI5IDAgUiAvcGVyaW9kIDMwIDAgUiAvc2V2ZW4gMzEgMCBSCi90d28gMzIgMCBSIC96ZXJvIDMzIDAgUiA+PgplbmRvYmoKMyAwIG9iago8PCAvRjEgMjEgMCBSIC9GMiAxNCAwIFIgPj4KZW5kb2JqCjQgMCBvYmoKPDwgL0ExIDw8IC9DQSAwIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4KL0EyIDw8IC9DQSAxIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4gPj4KZW5kb2JqCjUgMCBvYmoKPDwgPj4KZW5kb2JqCjYgMCBvYmoKPDwgPj4KZW5kb2JqCjcgMCBvYmoKPDwgL0RlamFWdVNhbnMtT2JsaXF1ZS1SZnJha3R1ciAxNiAwIFIgL0RlamFWdVNhbnMtbWludXMgMjYgMCBSID4+CmVuZG9iagoyIDAgb2JqCjw8IC9Db3VudCAxIC9LaWRzIFsgMTAgMCBSIF0gL1R5cGUgL1BhZ2VzID4+CmVuZG9iagozNCAwIG9iago8PCAvQ3JlYXRpb25EYXRlIChEOjIwMTkwNTE2MTgzNzU5KzAyJzAwJykKL0NyZWF0b3IgKG1hdHBsb3RsaWIgMy4wLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZykKL1Byb2R1Y2VyIChtYXRwbG90bGliIHBkZiBiYWNrZW5kIDMuMC4zKSA+PgplbmRvYmoKeHJlZgowIDM1CjAwMDAwMDAwMDAgNjU1MzUgZiAKMDAwMDAwMDAxNiAwMDAwMCBuIAowMDAwMDE3NDc0IDAwMDAwIG4gCjAwMDAwMTcyMDggMDAwMDAgbiAKMDAwMDAxNzI1MSAwMDAwMCBuIAowMDAwMDE3MzUwIDAwMDAwIG4gCjAwMDAwMTczNzEgMDAwMDAgbiAKMDAwMDAxNzM5MiAwMDAwMCBuIAowMDAwMDAwMDY1IDAwMDAwIG4gCjAwMDAwMDAzOTUgMDAwMDAgbiAKMDAwMDAwMDIwOCAwMDAwMCBuIAowMDAwMDA5OTU1IDAwMDAwIG4gCjAwMDAwMTE2MzYgMDAwMDAgbiAKMDAwMDAxMTQyOCAwMDAwMCBuIAowMDAwMDExMTA1IDAwMDAwIG4gCjAwMDAwMTI2ODkgMDAwMDAgbiAKMDAwMDAwOTk3NiAwMDAwMCBuIAowMDAwMDEwNjQyIDAwMDAwIG4gCjAwMDAwMTA4OTMgMDAwMDAgbiAKMDAwMDAxNTk4MCAwMDAwMCBuIAowMDAwMDE1NzgwIDAwMDAwIG4gCjAwMDAwMTUzODEgMDAwMDAgbiAKMDAwMDAxNzAzMyAwMDAwMCBuIAowMDAwMDEyNzMxIDAwMDAwIG4gCjAwMDAwMTMwODMgMDAwMDAgbiAKMDAwMDAxMzQzMiAwMDAwMCBuIAowMDAwMDEzNzUyIDAwMDAwIG4gCjAwMDAwMTM5MjIgMDAwMDAgbiAKMDAwMDAxNDA3NCAwMDAwMCBuIAowMDAwMDE0Mjk0IDAwMDAwIG4gCjAwMDAwMTQ1MTYgMDAwMDAgbiAKMDAwMDAxNDYzNyAwMDAwMCBuIAowMDAwMDE0Nzc3IDAwMDAwIG4gCjAwMDAwMTUwOTggMDAwMDAgbiAKMDAwMDAxNzUzNCAwMDAwMCBuIAp0cmFpbGVyCjw8IC9JbmZvIDM0IDAgUiAvUm9vdCAxIDAgUiAvU2l6ZSAzNSA+PgpzdGFydHhyZWYKMTc2ODgKJSVFT0YK\n",
"image/svg+xml": [
"<?xml version=\"1.0\" encoding=\"utf-8\" standalone=\"no\"?>\n",
"<!DOCTYPE svg PUBLIC \"-//W3C//DTD SVG 1.1//EN\"\n",
" \"http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd\">\n",
"<!-- Created with matplotlib (https://matplotlib.org/) -->\n",
"<svg height=\"303.312pt\" version=\"1.1\" viewBox=\"0 0 388.434844 303.312\" width=\"388.434844pt\" xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\">\n",
" <defs>\n",
" <style type=\"text/css\">\n",
"*{stroke-linecap:butt;stroke-linejoin:round;}\n",
" </style>\n",
" </defs>\n",
" <g id=\"figure_1\">\n",
" <g id=\"patch_1\">\n",
" <path d=\"M 0 303.312 \n",
"L 388.434844 303.312 \n",
"L 388.434844 0 \n",
"L 0 0 \n",
"z\n",
"\" style=\"fill:#ffffff;\"/>\n",
" </g>\n",
" <g id=\"axes_1\">\n",
" <g id=\"patch_2\">\n",
" <path d=\"M 17.752344 292.612 \n",
"L 374.872344 292.612 \n",
"L 374.872344 26.5 \n",
"L 17.752344 26.5 \n",
"z\n",
"\" style=\"fill:#ffffff;\"/>\n",
" </g>\n",
" <g id=\"matplotlib.axis_1\">\n",
" <g id=\"xtick_1\">\n",
" <g id=\"line2d_1\">\n",
" <defs>\n",
" <path d=\"M 0 0 \n",
"L 0 3.5 \n",
"\" id=\"m059963db52\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
" </defs>\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"17.752344\" xlink:href=\"#m059963db52\" y=\"161.534627\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_1\">\n",
" <!-- −20 -->\n",
" <defs>\n",
" <path d=\"M 10.59375 35.5 \n",
"L 73.1875 35.5 \n",
"L 73.1875 27.203125 \n",
"L 10.59375 27.203125 \n",
"z\n",
"\" id=\"DejaVuSans-8722\"/>\n",
" <path d=\"M 19.1875 8.296875 \n",
"L 53.609375 8.296875 \n",
"L 53.609375 0 \n",
"L 7.328125 0 \n",
"L 7.328125 8.296875 \n",
"Q 12.9375 14.109375 22.625 23.890625 \n",
"Q 32.328125 33.6875 34.8125 36.53125 \n",
"Q 39.546875 41.84375 41.421875 45.53125 \n",
"Q 43.3125 49.21875 43.3125 52.78125 \n",
"Q 43.3125 58.59375 39.234375 62.25 \n",
"Q 35.15625 65.921875 28.609375 65.921875 \n",
"Q 23.96875 65.921875 18.8125 64.3125 \n",
"Q 13.671875 62.703125 7.8125 59.421875 \n",
"L 7.8125 69.390625 \n",
"Q 13.765625 71.78125 18.9375 73 \n",
"Q 24.125 74.21875 28.421875 74.21875 \n",
"Q 39.75 74.21875 46.484375 68.546875 \n",
"Q 53.21875 62.890625 53.21875 53.421875 \n",
"Q 53.21875 48.921875 51.53125 44.890625 \n",
"Q 49.859375 40.875 45.40625 35.40625 \n",
"Q 44.1875 33.984375 37.640625 27.21875 \n",
"Q 31.109375 20.453125 19.1875 8.296875 \n",
"z\n",
"\" id=\"DejaVuSans-50\"/>\n",
" <path d=\"M 31.78125 66.40625 \n",
"Q 24.171875 66.40625 20.328125 58.90625 \n",
"Q 16.5 51.421875 16.5 36.375 \n",
"Q 16.5 21.390625 20.328125 13.890625 \n",
"Q 24.171875 6.390625 31.78125 6.390625 \n",
"Q 39.453125 6.390625 43.28125 13.890625 \n",
"Q 47.125 21.390625 47.125 36.375 \n",
"Q 47.125 51.421875 43.28125 58.90625 \n",
"Q 39.453125 66.40625 31.78125 66.40625 \n",
"z\n",
"M 31.78125 74.21875 \n",
"Q 44.046875 74.21875 50.515625 64.515625 \n",
"Q 56.984375 54.828125 56.984375 36.375 \n",
"Q 56.984375 17.96875 50.515625 8.265625 \n",
"Q 44.046875 -1.421875 31.78125 -1.421875 \n",
"Q 19.53125 -1.421875 13.0625 8.265625 \n",
"Q 6.59375 17.96875 6.59375 36.375 \n",
"Q 6.59375 54.828125 13.0625 64.515625 \n",
"Q 19.53125 74.21875 31.78125 74.21875 \n",
"z\n",
"\" id=\"DejaVuSans-48\"/>\n",
" </defs>\n",
" <g transform=\"translate(7.2 176.133065)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_2\">\n",
" <g id=\"line2d_2\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"62.392344\" xlink:href=\"#m059963db52\" y=\"161.534627\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_2\">\n",
" <!-- −15 -->\n",
" <defs>\n",
" <path d=\"M 12.40625 8.296875 \n",
"L 28.515625 8.296875 \n",
"L 28.515625 63.921875 \n",
"L 10.984375 60.40625 \n",
"L 10.984375 69.390625 \n",
"L 28.421875 72.90625 \n",
"L 38.28125 72.90625 \n",
"L 38.28125 8.296875 \n",
"L 54.390625 8.296875 \n",
"L 54.390625 0 \n",
"L 12.40625 0 \n",
"z\n",
"\" id=\"DejaVuSans-49\"/>\n",
" <path d=\"M 10.796875 72.90625 \n",
"L 49.515625 72.90625 \n",
"L 49.515625 64.59375 \n",
"L 19.828125 64.59375 \n",
"L 19.828125 46.734375 \n",
"Q 21.96875 47.46875 24.109375 47.828125 \n",
"Q 26.265625 48.1875 28.421875 48.1875 \n",
"Q 40.625 48.1875 47.75 41.5 \n",
"Q 54.890625 34.8125 54.890625 23.390625 \n",
"Q 54.890625 11.625 47.5625 5.09375 \n",
"Q 40.234375 -1.421875 26.90625 -1.421875 \n",
"Q 22.3125 -1.421875 17.546875 -0.640625 \n",
"Q 12.796875 0.140625 7.71875 1.703125 \n",
"L 7.71875 11.625 \n",
"Q 12.109375 9.234375 16.796875 8.0625 \n",
"Q 21.484375 6.890625 26.703125 6.890625 \n",
"Q 35.15625 6.890625 40.078125 11.328125 \n",
"Q 45.015625 15.765625 45.015625 23.390625 \n",
"Q 45.015625 31 40.078125 35.4375 \n",
"Q 35.15625 39.890625 26.703125 39.890625 \n",
"Q 22.75 39.890625 18.8125 39.015625 \n",
"Q 14.890625 38.140625 10.796875 36.28125 \n",
"z\n",
"\" id=\"DejaVuSans-53\"/>\n",
" </defs>\n",
" <g transform=\"translate(51.84 176.133065)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_3\">\n",
" <g id=\"line2d_3\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"107.032344\" xlink:href=\"#m059963db52\" y=\"161.534627\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_3\">\n",
" <!-- −10 -->\n",
" <g transform=\"translate(96.48 176.133065)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_4\">\n",
" <g id=\"line2d_4\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"151.672344\" xlink:href=\"#m059963db52\" y=\"161.534627\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_4\">\n",
" <!-- −5 -->\n",
" <g transform=\"translate(144.30125 176.133065)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_5\">\n",
" <g id=\"line2d_5\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m059963db52\" y=\"161.534627\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_5\">\n",
" <!-- 0 -->\n",
" <g transform=\"translate(193.131094 176.133065)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_6\">\n",
" <g id=\"line2d_6\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"240.952344\" xlink:href=\"#m059963db52\" y=\"161.534627\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_6\">\n",
" <!-- 5 -->\n",
" <g transform=\"translate(237.771094 176.133065)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_7\">\n",
" <g id=\"line2d_7\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"285.592344\" xlink:href=\"#m059963db52\" y=\"161.534627\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_7\">\n",
" <!-- 10 -->\n",
" <g transform=\"translate(279.229844 176.133065)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_8\">\n",
" <g id=\"line2d_8\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"330.232344\" xlink:href=\"#m059963db52\" y=\"161.534627\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_8\">\n",
" <!-- 15 -->\n",
" <g transform=\"translate(323.869844 176.133065)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"xtick_9\">\n",
" <g id=\"line2d_9\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"374.872344\" xlink:href=\"#m059963db52\" y=\"161.534627\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_9\">\n",
" <!-- 20 -->\n",
" <g transform=\"translate(368.509844 176.133065)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_10\">\n",
" <!-- $t$ -->\n",
" <defs>\n",
" <path d=\"M 42.28125 54.6875 \n",
"L 40.921875 47.703125 \n",
"L 23 47.703125 \n",
"L 17.1875 18.015625 \n",
"Q 16.890625 16.359375 16.75 15.234375 \n",
"Q 16.609375 14.109375 16.609375 13.484375 \n",
"Q 16.609375 10.359375 18.484375 8.9375 \n",
"Q 20.359375 7.515625 24.515625 7.515625 \n",
"L 33.59375 7.515625 \n",
"L 32.078125 0 \n",
"L 23.484375 0 \n",
"Q 15.484375 0 11.546875 3.125 \n",
"Q 7.625 6.25 7.625 12.59375 \n",
"Q 7.625 13.71875 7.765625 15.0625 \n",
"Q 7.90625 16.40625 8.203125 18.015625 \n",
"L 14.015625 47.703125 \n",
"L 6.390625 47.703125 \n",
"L 7.8125 54.6875 \n",
"L 15.28125 54.6875 \n",
"L 18.3125 70.21875 \n",
"L 27.296875 70.21875 \n",
"L 24.3125 54.6875 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-116\"/>\n",
" </defs>\n",
" <g transform=\"translate(372.872344 189.81119)scale(0.1 -0.1)\">\n",
" <use transform=\"translate(0 0.78125)\" xlink:href=\"#DejaVuSans-Oblique-116\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"matplotlib.axis_2\">\n",
" <g id=\"ytick_1\">\n",
" <g id=\"line2d_10\">\n",
" <defs>\n",
" <path d=\"M 0 0 \n",
"L -3.5 0 \n",
"\" id=\"m4eba6a592e\" style=\"stroke:#000000;stroke-width:0.8;\"/>\n",
" </defs>\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m4eba6a592e\" y=\"284.481957\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_11\">\n",
" <!-- −1.00 -->\n",
" <defs>\n",
" <path d=\"M 10.6875 12.40625 \n",
"L 21 12.40625 \n",
"L 21 0 \n",
"L 10.6875 0 \n",
"z\n",
"\" id=\"DejaVuSans-46\"/>\n",
" </defs>\n",
" <g transform=\"translate(158.667031 288.281176)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"179.199219\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"242.822266\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_2\">\n",
" <g id=\"line2d_11\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m4eba6a592e\" y=\"253.745125\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_12\">\n",
" <!-- −0.75 -->\n",
" <defs>\n",
" <path d=\"M 8.203125 72.90625 \n",
"L 55.078125 72.90625 \n",
"L 55.078125 68.703125 \n",
"L 28.609375 0 \n",
"L 18.3125 0 \n",
"L 43.21875 64.59375 \n",
"L 8.203125 64.59375 \n",
"z\n",
"\" id=\"DejaVuSans-55\"/>\n",
" </defs>\n",
" <g transform=\"translate(158.667031 257.544344)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"179.199219\" xlink:href=\"#DejaVuSans-55\"/>\n",
" <use x=\"242.822266\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_3\">\n",
" <g id=\"line2d_12\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m4eba6a592e\" y=\"223.008292\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_13\">\n",
" <!-- −0.50 -->\n",
" <g transform=\"translate(158.667031 226.807511)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"179.199219\" xlink:href=\"#DejaVuSans-53\"/>\n",
" <use x=\"242.822266\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_4\">\n",
" <g id=\"line2d_13\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m4eba6a592e\" y=\"192.27146\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_14\">\n",
" <!-- −0.25 -->\n",
" <g transform=\"translate(158.667031 196.070679)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-8722\"/>\n",
" <use x=\"83.789062\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"147.412109\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"179.199219\" xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"242.822266\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_5\">\n",
" <g id=\"line2d_14\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m4eba6a592e\" y=\"161.534627\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_15\">\n",
" <!-- 0.00 -->\n",
" <g transform=\"translate(167.046719 165.333846)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"159.033203\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_6\">\n",
" <g id=\"line2d_15\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m4eba6a592e\" y=\"130.797795\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_16\">\n",
" <!-- 0.25 -->\n",
" <g transform=\"translate(167.046719 134.597013)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-50\"/>\n",
" <use x=\"159.033203\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_7\">\n",
" <g id=\"line2d_16\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m4eba6a592e\" y=\"100.060962\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_17\">\n",
" <!-- 0.50 -->\n",
" <g transform=\"translate(167.046719 103.860181)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-53\"/>\n",
" <use x=\"159.033203\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_8\">\n",
" <g id=\"line2d_17\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m4eba6a592e\" y=\"69.32413\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_18\">\n",
" <!-- 0.75 -->\n",
" <g transform=\"translate(167.046719 73.123348)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-55\"/>\n",
" <use x=\"159.033203\" xlink:href=\"#DejaVuSans-53\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"ytick_9\">\n",
" <g id=\"line2d_18\">\n",
" <g>\n",
" <use style=\"stroke:#000000;stroke-width:0.8;\" x=\"196.312344\" xlink:href=\"#m4eba6a592e\" y=\"38.587297\"/>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_19\">\n",
" <!-- 1.00 -->\n",
" <g transform=\"translate(167.046719 42.386516)scale(0.1 -0.1)\">\n",
" <use xlink:href=\"#DejaVuSans-49\"/>\n",
" <use x=\"63.623047\" xlink:href=\"#DejaVuSans-46\"/>\n",
" <use x=\"95.410156\" xlink:href=\"#DejaVuSans-48\"/>\n",
" <use x=\"159.033203\" xlink:href=\"#DejaVuSans-48\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"text_20\">\n",
" <!-- $\\Re \\{ y(t) \\}$ -->\n",
" <defs>\n",
" <path d=\"M 62.59375 -1.421875 \n",
"Q 58.59375 7.515625 58.59375 15.28125 \n",
"Q 58.59375 22.125 57.515625 26.5625 \n",
"Q 55.5625 34.671875 51.703125 34.671875 \n",
"Q 49.65625 34.671875 45.171875 32.5625 \n",
"L 39.3125 29.828125 \n",
"L 39.3125 20.125 \n",
"Q 39.3125 10.0625 34.28125 4.296875 \n",
"Q 29.25 -1.421875 22.40625 -1.421875 \n",
"Q 15.53125 -1.421875 10.546875 4.296875 \n",
"Q 5.515625 10.0625 5.515625 18.65625 \n",
"Q 7.71875 18.0625 9.96875 17.484375 \n",
"Q 9.96875 11.53125 13.09375 7.328125 \n",
"Q 16.21875 3.078125 19.734375 3.078125 \n",
"Q 23.25 3.078125 26.3125 7.328125 \n",
"Q 29.4375 11.578125 29.4375 18.890625 \n",
"L 29.4375 51.46875 \n",
"Q 29.4375 58.734375 26.3125 63.03125 \n",
"Q 23.25 67.28125 18.75 67.28125 \n",
"Q 14.796875 67.28125 11.625 63.03125 \n",
"Q 8.5 58.84375 8.5 53.90625 \n",
"Q 8.5 48.96875 11.625 44.78125 \n",
"Q 14.75 40.53125 18.796875 40.53125 \n",
"L 21.4375 36.03125 \n",
"Q 14.0625 36.03125 9.078125 41.75 \n",
"Q 4.046875 47.515625 4.046875 55.125 \n",
"Q 4.046875 62.796875 9.078125 68.5 \n",
"Q 14.0625 74.21875 21.4375 74.21875 \n",
"Q 29.34375 74.21875 34.28125 68.5 \n",
"Q 35.75 66.796875 36.53125 65.234375 \n",
"L 46.828125 70.015625 \n",
"Q 55.953125 74.265625 61.421875 74.265625 \n",
"Q 63.71875 74.265625 65.484375 73.578125 \n",
"Q 71.625 71.1875 71.625 62.546875 \n",
"Q 71.625 58.296875 68.453125 52.296875 \n",
"Q 65.234375 46.234375 59.125 41.65625 \n",
"Q 61.96875 41.65625 64.359375 39.265625 \n",
"Q 66.109375 37.5 67.4375 32.421875 \n",
"Q 69 26.421875 69 20.015625 \n",
"Q 69 13.765625 71.1875 8.015625 \n",
"L 78.21875 11.28125 \n",
"L 80.28125 6.84375 \n",
"z\n",
"M 38.28125 60.890625 \n",
"Q 39.3125 57.234375 39.3125 52.734375 \n",
"L 39.3125 35.015625 \n",
"L 46.828125 38.484375 \n",
"Q 53.859375 41.75 57.625 46.828125 \n",
"Q 61.234375 51.8125 61.234375 57.71875 \n",
"Q 61.234375 65.09375 57.625 66.65625 \n",
"Q 56.453125 67.140625 54.9375 67.140625 \n",
"Q 51.8125 67.140625 46.828125 64.84375 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-8476\"/>\n",
" <path d=\"M 51.125 -9.28125 \n",
"L 51.125 -16.3125 \n",
"L 48.09375 -16.3125 \n",
"Q 35.9375 -16.3125 31.8125 -12.6875 \n",
"Q 27.6875 -9.078125 27.6875 1.703125 \n",
"L 27.6875 13.375 \n",
"Q 27.6875 20.75 25.046875 23.578125 \n",
"Q 22.40625 26.421875 15.484375 26.421875 \n",
"L 12.5 26.421875 \n",
"L 12.5 33.40625 \n",
"L 15.484375 33.40625 \n",
"Q 22.46875 33.40625 25.078125 36.203125 \n",
"Q 27.6875 39.015625 27.6875 46.296875 \n",
"L 27.6875 58.015625 \n",
"Q 27.6875 68.796875 31.8125 72.390625 \n",
"Q 35.9375 75.984375 48.09375 75.984375 \n",
"L 51.125 75.984375 \n",
"L 51.125 69 \n",
"L 47.796875 69 \n",
"Q 40.921875 69 38.8125 66.84375 \n",
"Q 36.71875 64.703125 36.71875 57.8125 \n",
"L 36.71875 45.703125 \n",
"Q 36.71875 38.03125 34.5 34.5625 \n",
"Q 32.28125 31.109375 26.90625 29.890625 \n",
"Q 32.328125 28.5625 34.515625 25.09375 \n",
"Q 36.71875 21.625 36.71875 14.015625 \n",
"L 36.71875 1.90625 \n",
"Q 36.71875 -4.984375 38.8125 -7.125 \n",
"Q 40.921875 -9.28125 47.796875 -9.28125 \n",
"z\n",
"\" id=\"DejaVuSans-123\"/>\n",
" <path d=\"M 24.8125 -5.078125 \n",
"Q 18.5625 -15.578125 14.625 -18.1875 \n",
"Q 10.6875 -20.796875 4.59375 -20.796875 \n",
"L -2.484375 -20.796875 \n",
"L -0.984375 -13.28125 \n",
"L 4.203125 -13.28125 \n",
"Q 7.953125 -13.28125 10.59375 -11.234375 \n",
"Q 13.234375 -9.1875 16.5 -3.21875 \n",
"L 19.28125 2 \n",
"L 7.171875 54.6875 \n",
"L 16.703125 54.6875 \n",
"L 25.78125 12.796875 \n",
"L 50.875 54.6875 \n",
"L 60.296875 54.6875 \n",
"z\n",
"\" id=\"DejaVuSans-Oblique-121\"/>\n",
" <path d=\"M 31 75.875 \n",
"Q 24.46875 64.65625 21.28125 53.65625 \n",
"Q 18.109375 42.671875 18.109375 31.390625 \n",
"Q 18.109375 20.125 21.3125 9.0625 \n",
"Q 24.515625 -2 31 -13.1875 \n",
"L 23.1875 -13.1875 \n",
"Q 15.875 -1.703125 12.234375 9.375 \n",
"Q 8.59375 20.453125 8.59375 31.390625 \n",
"Q 8.59375 42.28125 12.203125 53.3125 \n",
"Q 15.828125 64.359375 23.1875 75.875 \n",
"z\n",
"\" id=\"DejaVuSans-40\"/>\n",
" <path d=\"M 8.015625 75.875 \n",
"L 15.828125 75.875 \n",
"Q 23.140625 64.359375 26.78125 53.3125 \n",
"Q 30.421875 42.28125 30.421875 31.390625 \n",
"Q 30.421875 20.453125 26.78125 9.375 \n",
"Q 23.140625 -1.703125 15.828125 -13.1875 \n",
"L 8.015625 -13.1875 \n",
"Q 14.5 -2 17.703125 9.0625 \n",
"Q 20.90625 20.125 20.90625 31.390625 \n",
"Q 20.90625 42.671875 17.703125 53.65625 \n",
"Q 14.5 64.65625 8.015625 75.875 \n",
"z\n",
"\" id=\"DejaVuSans-41\"/>\n",
" <path d=\"M 12.5 -9.28125 \n",
"L 15.921875 -9.28125 \n",
"Q 22.75 -9.28125 24.828125 -7.171875 \n",
"Q 26.90625 -5.078125 26.90625 1.90625 \n",
"L 26.90625 14.015625 \n",
"Q 26.90625 21.625 29.09375 25.09375 \n",
"Q 31.296875 28.5625 36.71875 29.890625 \n",
"Q 31.296875 31.109375 29.09375 34.5625 \n",
"Q 26.90625 38.03125 26.90625 45.703125 \n",
"L 26.90625 57.8125 \n",
"Q 26.90625 64.75 24.828125 66.875 \n",
"Q 22.75 69 15.921875 69 \n",
"L 12.5 69 \n",
"L 12.5 75.984375 \n",
"L 15.578125 75.984375 \n",
"Q 27.734375 75.984375 31.8125 72.390625 \n",
"Q 35.890625 68.796875 35.890625 58.015625 \n",
"L 35.890625 46.296875 \n",
"Q 35.890625 39.015625 38.515625 36.203125 \n",
"Q 41.15625 33.40625 48.09375 33.40625 \n",
"L 51.125 33.40625 \n",
"L 51.125 26.421875 \n",
"L 48.09375 26.421875 \n",
"Q 41.15625 26.421875 38.515625 23.578125 \n",
"Q 35.890625 20.75 35.890625 13.375 \n",
"L 35.890625 1.703125 \n",
"Q 35.890625 -9.078125 31.8125 -12.6875 \n",
"Q 27.734375 -16.3125 15.578125 -16.3125 \n",
"L 12.5 -16.3125 \n",
"z\n",
"\" id=\"DejaVuSans-125\"/>\n",
" </defs>\n",
" <g transform=\"translate(152.567031 45.8)rotate(-90)scale(0.1 -0.1)\">\n",
" <use transform=\"translate(0 0.015625)\" xlink:href=\"#DejaVuSans-Oblique-8476\"/>\n",
" <use transform=\"translate(81.396484 0.015625)\" xlink:href=\"#DejaVuSans-123\"/>\n",
" <use transform=\"translate(145.019531 0.015625)\" xlink:href=\"#DejaVuSans-Oblique-121\"/>\n",
" <use transform=\"translate(204.199219 0.015625)\" xlink:href=\"#DejaVuSans-40\"/>\n",
" <use transform=\"translate(243.212891 0.015625)\" xlink:href=\"#DejaVuSans-Oblique-116\"/>\n",
" <use transform=\"translate(282.421875 0.015625)\" xlink:href=\"#DejaVuSans-41\"/>\n",
" <use transform=\"translate(321.435547 0.015625)\" xlink:href=\"#DejaVuSans-125\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <g id=\"LineCollection_1\">\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 17.752344 161.220852 \n",
"L 23.585253 161.597639 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 23.585253 161.597639 \n",
"L 30.156581 161.527218 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 30.156581 161.527218 \n",
"L 35.49163 161.661018 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 35.49163 161.661018 \n",
"L 41.032886 161.14677 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 41.032886 161.14677 \n",
"L 46.733377 162.18502 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 46.733377 162.18502 \n",
"L 49.568239 160.140209 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 49.568239 160.140209 \n",
"L 51.212218 159.957496 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 51.212218 159.957496 \n",
"L 52.934697 161.192745 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 52.934697 161.192745 \n",
"L 55.766036 163.489548 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 55.766036 163.489548 \n",
"L 56.983309 163.29183 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 56.983309 163.29183 \n",
"L 58.232281 162.249803 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 58.232281 162.249803 \n",
"L 61.315426 159.605087 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 61.315426 159.605087 \n",
"L 62.751319 159.962349 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 62.751319 159.962349 \n",
"L 64.217077 161.262882 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 64.217077 161.262882 \n",
"L 67.314859 163.073325 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 67.314859 163.073325 \n",
"L 70.508229 161.264161 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 70.508229 161.264161 \n",
"L 76.445017 161.725305 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 76.445017 161.725305 \n",
"L 82.930518 161.524007 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 82.930518 161.524007 \n",
"L 88.632312 161.707332 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 88.632312 161.707332 \n",
"L 94.579375 160.48019 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 94.579375 160.48019 \n",
"L 95.898992 160.145582 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 95.898992 160.145582 \n",
"L 97.152449 160.600304 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 97.152449 160.600304 \n",
"L 99.778946 163.506295 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 99.778946 163.506295 \n",
"L 101.133919 164.393931 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 101.133919 164.393931 \n",
"L 102.340209 163.82871 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 102.340209 163.82871 \n",
"L 104.670844 159.621862 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 104.670844 159.621862 \n",
"L 106.011118 157.474949 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 106.011118 157.474949 \n",
"L 106.783874 157.110864 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 106.783874 157.110864 \n",
"L 107.426804 157.450451 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 107.426804 157.450451 \n",
"L 108.071933 158.375487 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 108.071933 158.375487 \n",
"L 108.663632 159.660552 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 108.663632 159.660552 \n",
"L 109.786866 162.743831 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 109.786866 162.743831 \n",
"L 110.943415 165.677927 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 110.943415 165.677927 \n",
"L 111.650222 166.770978 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 111.650222 166.770978 \n",
"L 112.23583 167.076004 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 112.23583 167.076004 \n",
"L 112.879042 166.716998 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 112.879042 166.716998 \n",
"L 113.561584 165.577571 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 113.561584 165.577571 \n",
"L 114.820135 162.027453 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 114.820135 162.027453 \n",
"L 116.286228 157.641868 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 116.286228 157.641868 \n",
"L 116.9839 156.309997 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 116.9839 156.309997 \n",
"L 117.586874 155.807356 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 117.586874 155.807356 \n",
"L 117.940666 155.820511 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 117.940666 155.820511 \n",
"L 118.344635 156.112872 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 118.344635 156.112872 \n",
"L 119.070987 157.313491 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 119.070987 157.313491 \n",
"L 120.882521 162.433876 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 120.882521 162.433876 \n",
"L 122.030675 165.26756 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 122.030675 165.26756 \n",
"L 122.725125 166.185534 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 122.725125 166.185534 \n",
"L 123.32884 166.37163 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 123.32884 166.37163 \n",
"L 123.857882 166.070933 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 123.857882 166.070933 \n",
"L 124.423541 165.330267 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 124.423541 165.330267 \n",
"L 125.725441 162.603897 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 125.725441 162.603897 \n",
"L 127.074599 159.786419 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 127.074599 159.786419 \n",
"L 127.723271 158.92162 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 127.723271 158.92162 \n",
"L 128.328899 158.522888 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 128.328899 158.522888 \n",
"L 129.048394 158.566281 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 129.048394 158.566281 \n",
"L 129.698704 159.01617 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 129.698704 159.01617 \n",
"L 131.088004 160.676504 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 131.088004 160.676504 \n",
"L 132.287386 162.008824 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 132.287386 162.008824 \n",
"L 133.750662 162.649737 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 133.750662 162.649737 \n",
"L 136.663464 161.70965 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 136.663464 161.70965 \n",
"L 141.519913 161.48285 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 141.519913 161.48285 \n",
"L 146.98432 163.29221 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 146.98432 163.29221 \n",
"L 152.345409 154.548312 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 152.345409 154.548312 \n",
"L 152.75233 155.157793 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 152.75233 155.157793 \n",
"L 152.98281 155.724766 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 152.98281 155.724766 \n",
"L 153.240918 156.552518 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 153.240918 156.552518 \n",
"L 153.515655 157.653253 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 153.515655 157.653253 \n",
"L 153.804674 159.043094 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 153.804674 159.043094 \n",
"L 154.28696 161.827146 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 154.28696 161.827146 \n",
"L 155.97803 173.421636 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 155.97803 173.421636 \n",
"L 156.324118 175.413902 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 156.324118 175.413902 \n",
"L 156.670516 177.013815 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 156.670516 177.013815 \n",
"L 156.877744 177.736798 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 156.877744 177.736798 \n",
"L 157.049988 178.185091 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 157.049988 178.185091 \n",
"L 157.256788 178.523617 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 157.256788 178.523617 \n",
"L 157.386668 178.617651 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 157.386668 178.617651 \n",
"L 157.506125 178.61954 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 157.506125 178.61954 \n",
"L 157.678062 178.47493 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 157.678062 178.47493 \n",
"L 157.772715 178.319185 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 157.772715 178.319185 \n",
"L 157.887356 178.056703 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 157.887356 178.056703 \n",
"L 158.047311 177.553461 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 158.047311 177.553461 \n",
"L 158.231257 176.775582 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 158.231257 176.775582 \n",
"L 158.430125 175.694841 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 158.430125 175.694841 \n",
"L 158.652085 174.198473 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 158.652085 174.198473 \n",
"L 158.860189 172.5261 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 158.860189 172.5261 \n",
"L 159.054628 170.739427 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 159.054628 170.739427 \n",
"L 162.062884 133.595296 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 162.062884 133.595296 \n",
"L 162.179701 132.696294 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 162.179701 132.696294 \n",
"L 162.313392 131.802655 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 162.313392 131.802655 \n",
"L 162.419947 131.19964 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 162.419947 131.19964 \n",
"L 162.526535 130.698103 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 162.526535 130.698103 \n",
"L 162.636145 130.292613 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 162.636145 130.292613 \n",
"L 162.753766 129.986358 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 162.753766 129.986358 \n",
"L 162.821108 129.87275 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 162.821108 129.87275 \n",
"L 162.899488 129.798363 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 162.899488 129.798363 \n",
"L 162.966588 129.784887 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 162.966588 129.784887 \n",
"L 163.027774 129.813508 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 163.027774 129.813508 \n",
"L 163.139996 129.968775 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 163.139996 129.968775 \n",
"L 163.20126 130.110287 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 163.20126 130.110287 \n",
"L 163.259665 130.282843 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 163.259665 130.282843 \n",
"L 163.369557 130.707802 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 163.369557 130.707802 \n",
"L 163.478618 131.259711 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 163.478618 131.259711 \n",
"L 163.571817 131.834382 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 163.571817 131.834382 \n",
"L 163.679656 132.617693 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 163.679656 132.617693 \n",
"L 163.786067 133.514518 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 163.786067 133.514518 \n",
"L 163.891778 134.526208 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 163.891778 134.526208 \n",
"L 163.99366 135.613685 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 163.99366 135.613685 \n",
"L 164.092069 136.767162 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 164.092069 136.767162 \n",
"L 164.277099 139.202731 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 164.277099 139.202731 \n",
"L 164.461536 141.96252 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 164.461536 141.96252 \n",
"L 164.671677 145.483645 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 164.671677 145.483645 \n",
"L 165.144042 154.659536 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 165.144042 154.659536 \n",
"L 165.536358 163.276744 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 165.536358 163.276744 \n",
"L 166.750633 191.00555 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 166.750633 191.00555 \n",
"L 167.165258 199.067754 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 167.165258 199.067754 \n",
"L 167.345349 202.094417 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 167.345349 202.094417 \n",
"L 167.545731 205.051561 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 167.545731 205.051561 \n",
"L 167.637723 206.250328 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 167.637723 206.250328 \n",
"L 167.735711 207.409831 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 167.735711 207.409831 \n",
"L 167.819597 208.302229 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 167.819597 208.302229 \n",
"L 167.902596 209.090859 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 167.902596 209.090859 \n",
"L 167.965862 209.627139 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 167.965862 209.627139 \n",
"L 168.039024 210.175589 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.039024 210.175589 \n",
"L 168.123852 210.712977 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.123852 210.712977 \n",
"L 168.198802 211.097801 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.198802 211.097801 \n",
"L 168.247032 211.299996 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.247032 211.299996 \n",
"L 168.293038 211.459269 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.293038 211.459269 \n",
"L 168.335644 211.577227 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.335644 211.577227 \n",
"L 168.376476 211.663382 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.376476 211.663382 \n",
"L 168.429149 211.735325 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.429149 211.735325 \n",
"L 168.47997 211.762541 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.47997 211.762541 \n",
"L 168.522105 211.753452 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.522105 211.753452 \n",
"L 168.565466 211.713954 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.565466 211.713954 \n",
"L 168.607814 211.645713 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.607814 211.645713 \n",
"L 168.652658 211.541347 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.652658 211.541347 \n",
"L 168.69914 211.398175 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.69914 211.398175 \n",
"L 168.742668 211.231689 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.742668 211.231689 \n",
"L 168.788157 211.02411 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.788157 211.02411 \n",
"L 168.842272 210.732364 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.842272 210.732364 \n",
"L 168.899974 210.36756 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.899974 210.36756 \n",
"L 168.952633 209.986229 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 168.952633 209.986229 \n",
"L 169.035087 209.296368 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 169.035087 209.296368 \n",
"L 169.116993 208.499283 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 169.116993 208.499283 \n",
"L 169.207675 207.487434 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 169.207675 207.487434 \n",
"L 169.304644 206.256259 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 169.304644 206.256259 \n",
"L 169.401434 204.875399 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 169.401434 204.875399 \n",
"L 169.484032 203.578679 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 169.484032 203.578679 \n",
"L 169.645225 200.741275 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 169.645225 200.741275 \n",
"L 169.801791 197.609693 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 169.801791 197.609693 \n",
"L 169.974183 193.75501 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 169.974183 193.75501 \n",
"L 170.335856 184.412273 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 170.335856 184.412273 \n",
"L 171.009144 163.539139 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 171.009144 163.539139 \n",
"L 172.381136 118.039686 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 172.381136 118.039686 \n",
"L 172.796584 106.841889 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 172.796584 106.841889 \n",
"L 173.011726 102.000415 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.011726 102.000415 \n",
"L 173.112968 99.984743 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.112968 99.984743 \n",
"L 173.224565 97.972002 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.224565 97.972002 \n",
"L 173.32742 96.320175 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.32742 96.320175 \n",
"L 173.428884 94.889675 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.428884 94.889675 \n",
"L 173.517338 93.809304 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.517338 93.809304 \n",
"L 173.597241 92.970612 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.597241 92.970612 \n",
"L 173.654011 92.455525 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.654011 92.455525 \n",
"L 173.705154 92.049869 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.705154 92.049869 \n",
"L 173.749387 91.744154 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.749387 91.744154 \n",
"L 173.800105 91.44568 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.800105 91.44568 \n",
"L 173.848101 91.214905 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.848101 91.214905 \n",
"L 173.889297 91.057242 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.889297 91.057242 \n",
"L 173.936386 90.923083 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.936386 90.923083 \n",
"L 173.979911 90.843058 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 173.979911 90.843058 \n",
"L 174.025046 90.804956 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.025046 90.804956 \n",
"L 174.071697 90.813855 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.071697 90.813855 \n",
"L 174.115402 90.866921 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.115402 90.866921 \n",
"L 174.153793 90.949365 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.153793 90.949365 \n",
"L 174.186906 91.047466 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.186906 91.047466 \n",
"L 174.226459 91.197488 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.226459 91.197488 \n",
"L 174.262827 91.367029 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.262827 91.367029 \n",
"L 174.300343 91.573696 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.300343 91.573696 \n",
"L 174.340204 91.82866 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.340204 91.82866 \n",
"L 174.373785 92.071758 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.373785 92.071758 \n",
"L 174.407887 92.345117 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.407887 92.345117 \n",
"L 174.448759 92.707896 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.448759 92.707896 \n",
"L 174.524327 93.47942 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.524327 93.47942 \n",
"L 174.607956 94.485261 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.607956 94.485261 \n",
"L 174.684599 95.546554 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.684599 95.546554 \n",
"L 174.7706 96.894966 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.7706 96.894966 \n",
"L 174.916833 99.564954 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 174.916833 99.564954 \n",
"L 175.082636 103.153559 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 175.082636 103.153559 \n",
"L 175.276359 108.072533 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 175.276359 108.072533 \n",
"L 175.628924 118.881838 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 175.628924 118.881838 \n",
"L 175.925676 129.611494 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 175.925676 129.611494 \n",
"L 176.714649 163.16494 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 176.714649 163.16494 \n",
"L 178.192864 226.131981 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 178.192864 226.131981 \n",
"L 178.49557 235.719744 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 178.49557 235.719744 \n",
"L 178.670475 240.391275 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 178.670475 240.391275 \n",
"L 178.842425 244.295768 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 178.842425 244.295768 \n",
"L 178.960089 246.549894 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 178.960089 246.549894 \n",
"L 179.064223 248.249231 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.064223 248.249231 \n",
"L 179.152232 249.462624 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.152232 249.462624 \n",
"L 179.198515 250.017213 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.198515 250.017213 \n",
"L 179.248141 250.547027 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.248141 250.547027 \n",
"L 179.291 250.950101 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.291 250.950101 \n",
"L 179.343163 251.371917 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.343163 251.371917 \n",
"L 179.387939 251.673305 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.387939 251.673305 \n",
"L 179.425257 251.881369 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.425257 251.881369 \n",
"L 179.477912 252.107836 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.477912 252.107836 \n",
"L 179.522183 252.237125 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.522183 252.237125 \n",
"L 179.57194 252.315448 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.57194 252.315448 \n",
"L 179.615781 252.32546 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.615781 252.32546 \n",
"L 179.674153 252.252675 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.674153 252.252675 \n",
"L 179.731707 252.084311 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.731707 252.084311 \n",
"L 179.78814 251.825877 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.78814 251.825877 \n",
"L 179.845498 251.468369 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.845498 251.468369 \n",
"L 179.887042 251.149711 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.887042 251.149711 \n",
"L 179.932815 250.740569 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.932815 250.740569 \n",
"L 179.990546 250.137858 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 179.990546 250.137858 \n",
"L 180.039341 249.553206 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 180.039341 249.553206 \n",
"L 180.089784 248.876603 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 180.089784 248.876603 \n",
"L 180.131835 248.256654 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 180.131835 248.256654 \n",
"L 180.187016 247.366372 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 180.187016 247.366372 \n",
"L 180.243336 246.368407 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 180.243336 246.368407 \n",
"L 180.336661 244.517892 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 180.336661 244.517892 \n",
"L 180.417051 242.729448 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 180.417051 242.729448 \n",
"L 180.590866 238.261305 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 180.590866 238.261305 \n",
"L 180.770193 232.820152 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 180.770193 232.820152 \n",
"L 181.10285 220.653773 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 181.10285 220.653773 \n",
"L 182.617428 143.085272 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 182.617428 143.085272 \n",
"L 183.326755 105.091799 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 183.326755 105.091799 \n",
"L 183.702521 87.637222 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 183.702521 87.637222 \n",
"L 184.115744 71.893824 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 184.115744 71.893824 \n",
"L 184.320912 65.709645 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 184.320912 65.709645 \n",
"L 184.4363 62.760555 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 184.4363 62.760555 \n",
"L 184.539934 60.452381 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 184.539934 60.452381 \n",
"L 184.608797 59.101865 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 184.608797 59.101865 \n",
"L 184.66845 58.052584 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 184.66845 58.052584 \n",
"L 184.724891 57.16435 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 184.724891 57.16435 \n",
"L 184.778388 56.417399 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 184.778388 56.417399 \n",
"L 184.839499 55.678434 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 184.839499 55.678434 \n",
"L 184.903934 55.032585 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 184.903934 55.032585 \n",
"L 184.968317 54.525204 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 184.968317 54.525204 \n",
"L 185.041527 54.117221 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.041527 54.117221 \n",
"L 185.101469 53.917936 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.101469 53.917936 \n",
"L 185.155159 53.84297 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.155159 53.84297 \n",
"L 185.210376 53.868274 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.210376 53.868274 \n",
"L 185.259982 53.979755 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.259982 53.979755 \n",
"L 185.316065 54.207098 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.316065 54.207098 \n",
"L 185.365315 54.495452 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.365315 54.495452 \n",
"L 185.4233 54.941218 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.4233 54.941218 \n",
"L 185.487932 55.573319 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.487932 55.573319 \n",
"L 185.540351 56.190417 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.540351 56.190417 \n",
"L 185.58858 56.8405 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.58858 56.8405 \n",
"L 185.640461 57.627536 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.640461 57.627536 \n",
"L 185.685103 58.377186 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.685103 58.377186 \n",
"L 185.776777 60.125108 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.776777 60.125108 \n",
"L 185.859355 61.93717 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.859355 61.93717 \n",
"L 185.959643 64.435978 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 185.959643 64.435978 \n",
"L 186.064689 67.397089 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 186.064689 67.397089 \n",
"L 186.26527 73.995274 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 186.26527 73.995274 \n",
"L 186.624543 88.691024 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 186.624543 88.691024 \n",
"L 187.537878 138.831977 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 187.537878 138.831977 \n",
"L 189.160988 237.249198 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 189.160988 237.249198 \n",
"L 189.588599 256.688351 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 189.588599 256.688351 \n",
"L 189.769046 263.370365 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 189.769046 263.370365 \n",
"L 189.943489 268.864874 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 189.943489 268.864874 \n",
"L 190.104213 273.036448 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.104213 273.036448 \n",
"L 190.201986 275.139068 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.201986 275.139068 \n",
"L 190.28226 276.612846 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.28226 276.612846 \n",
"L 190.328203 277.352394 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.328203 277.352394 \n",
"L 190.37295 277.999231 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.37295 277.999231 \n",
"L 190.430338 278.72191 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.430338 278.72191 \n",
"L 190.479386 279.243715 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.479386 279.243715 \n",
"L 190.523338 279.635812 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.523338 279.635812 \n",
"L 190.56999 279.97355 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.56999 279.97355 \n",
"L 190.623388 280.26058 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.623388 280.26058 \n",
"L 190.678102 280.444065 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.678102 280.444065 \n",
"L 190.728117 280.513567 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.728117 280.513567 \n",
"L 190.778789 280.488131 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.778789 280.488131 \n",
"L 190.83086 280.361388 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.83086 280.361388 \n",
"L 190.894259 280.069396 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.894259 280.069396 \n",
"L 190.952826 279.665463 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 190.952826 279.665463 \n",
"L 191.003746 279.20973 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 191.003746 279.20973 \n",
"L 191.055191 278.650858 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 191.055191 278.650858 \n",
"L 191.111512 277.925971 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 191.111512 277.925971 \n",
"L 191.158622 277.229297 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 191.158622 277.229297 \n",
"L 191.207174 276.425648 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 191.207174 276.425648 \n",
"L 191.261562 275.422775 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 191.261562 275.422775 \n",
"L 191.322528 274.170729 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 191.322528 274.170729 \n",
"L 191.430727 271.619895 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 191.430727 271.619895 \n",
"L 191.520314 269.194811 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 191.520314 269.194811 \n",
"L 191.702045 263.429808 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 191.702045 263.429808 \n",
"L 191.922787 254.975499 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 191.922787 254.975499 \n",
"L 192.372123 233.372681 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 192.372123 233.372681 \n",
"L 195.300934 57.899588 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 195.300934 57.899588 \n",
"L 195.518044 50.625584 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 195.518044 50.625584 \n",
"L 195.634766 47.388352 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 195.634766 47.388352 \n",
"L 195.761855 44.421037 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 195.761855 44.421037 \n",
"L 195.826252 43.144195 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 195.826252 43.144195 \n",
"L 195.895578 41.942755 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 195.895578 41.942755 \n",
"L 195.952951 41.085508 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 195.952951 41.085508 \n",
"L 196.009863 40.358742 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.009863 40.358742 \n",
"L 196.070717 39.718689 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.070717 39.718689 \n",
"L 196.121095 39.296508 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.121095 39.296508 \n",
"L 196.166868 38.997823 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.166868 38.997823 \n",
"L 196.218174 38.759376 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.218174 38.759376 \n",
"L 196.279731 38.607939 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.279731 38.607939 \n",
"L 196.333519 38.596 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.333519 38.596 \n",
"L 196.378684 38.672708 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.378684 38.672708 \n",
"L 196.429501 38.853606 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.429501 38.853606 \n",
"L 196.495075 39.234797 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.495075 39.234797 \n",
"L 196.553303 39.712449 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.553303 39.712449 \n",
"L 196.612892 40.336242 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.612892 40.336242 \n",
"L 196.670701 41.07119 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.670701 41.07119 \n",
"L 196.72156 41.822842 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.72156 41.822842 \n",
"L 196.765107 42.544095 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.765107 42.544095 \n",
"L 196.81135 43.387896 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.81135 43.387896 \n",
"L 196.865359 44.47426 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.865359 44.47426 \n",
"L 196.962034 46.6869 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 196.962034 46.6869 \n",
"L 197.069789 49.551346 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 197.069789 49.551346 \n",
"L 197.309953 57.390283 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 197.309953 57.390283 \n",
"L 197.576733 68.300218 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 197.576733 68.300218 \n",
"L 198.082333 94.424192 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 198.082333 94.424192 \n",
"L 199.151105 163.85233 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 199.151105 163.85233 \n",
"L 200.090825 224.356928 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 200.090825 224.356928 \n",
"L 200.52546 247.151407 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 200.52546 247.151407 \n",
"L 200.893596 262.406246 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 200.893596 262.406246 \n",
"L 201.113956 269.467558 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 201.113956 269.467558 \n",
"L 201.227308 272.450531 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 201.227308 272.450531 \n",
"L 201.321202 274.576259 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 201.321202 274.576259 \n",
"L 201.383352 275.808359 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 201.383352 275.808359 \n",
"L 201.454145 277.040014 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 201.454145 277.040014 \n",
"L 201.514501 277.944385 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 201.514501 277.944385 \n",
"L 201.567599 278.62836 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 201.567599 278.62836 \n",
"L 201.63004 279.298284 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 201.63004 279.298284 \n",
"L 201.701063 279.882959 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 201.701063 279.882959 \n",
"L 201.755645 280.203638 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 201.755645 280.203638 \n",
"L 201.82119 280.440706 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 201.82119 280.440706 \n",
"L 201.880821 280.516 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 201.880821 280.516 \n",
"L 201.931752 280.474474 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 201.931752 280.474474 \n",
"L 201.977638 280.353691 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 201.977638 280.353691 \n",
"L 202.028682 280.12669 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 202.028682 280.12669 \n",
"L 202.073265 279.84883 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 202.073265 279.84883 \n",
"L 202.120648 279.472462 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 202.120648 279.472462 \n",
"L 202.165967 279.034675 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 202.165967 279.034675 \n",
"L 202.212122 278.510997 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 202.212122 278.510997 \n",
"L 202.263952 277.829897 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 202.263952 277.829897 \n",
"L 202.308767 277.162151 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 202.308767 277.162151 \n",
"L 202.365752 276.208329 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 202.365752 276.208329 \n",
"L 202.416507 275.260954 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 202.416507 275.260954 \n",
"L 202.506337 273.361128 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 202.506337 273.361128 \n",
"L 202.598189 271.128774 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 202.598189 271.128774 \n",
"L 202.775724 266.009156 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 202.775724 266.009156 \n",
"L 202.944402 260.20612 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 202.944402 260.20612 \n",
"L 203.351295 242.807142 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 203.351295 242.807142 \n",
"L 204.15541 197.784602 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 204.15541 197.784602 \n",
"L 205.567378 110.588233 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 205.567378 110.588233 \n",
"L 205.99244 89.043535 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 205.99244 89.043535 \n",
"L 206.389716 72.921261 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 206.389716 72.921261 \n",
"L 206.610088 65.94177 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 206.610088 65.94177 \n",
"L 206.694437 63.670085 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 206.694437 63.670085 \n",
"L 206.796619 61.224336 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 206.796619 61.224336 \n",
"L 206.90089 59.080874 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 206.90089 59.080874 \n",
"L 206.95228 58.157201 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 206.95228 58.157201 \n",
"L 207.013232 57.176346 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.013232 57.176346 \n",
"L 207.073051 56.335477 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.073051 56.335477 \n",
"L 207.129732 55.650583 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.129732 55.650583 \n",
"L 207.192422 55.020395 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.192422 55.020395 \n",
"L 207.249412 54.56385 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.249412 54.56385 \n",
"L 207.305409 54.223386 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.305409 54.223386 \n",
"L 207.35766 54.002411 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.35766 54.002411 \n",
"L 207.422385 53.858083 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.422385 53.858083 \n",
"L 207.484939 53.854454 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.484939 53.854454 \n",
"L 207.55454 54.006887 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.55454 54.006887 \n",
"L 207.617769 54.287597 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.617769 54.287597 \n",
"L 207.678292 54.682406 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.678292 54.682406 \n",
"L 207.732147 55.136767 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.732147 55.136767 \n",
"L 207.811436 55.980809 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.811436 55.980809 \n",
"L 207.883254 56.923462 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.883254 56.923462 \n",
"L 207.947395 57.906671 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 207.947395 57.906671 \n",
"L 208.019976 59.177845 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 208.019976 59.177845 \n",
"L 208.086906 60.496972 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 208.086906 60.496972 \n",
"L 208.159392 62.081809 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 208.159392 62.081809 \n",
"L 208.273577 64.900011 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 208.273577 64.900011 \n",
"L 208.462919 70.405427 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 208.462919 70.405427 \n",
"L 208.683286 78.033689 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 208.683286 78.033689 \n",
"L 209.15484 98.146923 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 209.15484 98.146923 \n",
"L 211.105123 202.128897 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 211.105123 202.128897 \n",
"L 211.53961 221.367371 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 211.53961 221.367371 \n",
"L 211.922418 234.977737 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 211.922418 234.977737 \n",
"L 212.112812 240.392441 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 212.112812 240.392441 \n",
"L 212.228846 243.21862 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 212.228846 243.21862 \n",
"L 212.330111 245.382599 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 212.330111 245.382599 \n",
"L 212.413013 246.940506 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 212.413013 246.940506 \n",
"L 212.506422 248.462244 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 212.506422 248.462244 \n",
"L 212.564794 249.286379 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 212.564794 249.286379 \n",
"L 212.623956 250.021497 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 212.623956 250.021497 \n",
"L 212.670239 250.526031 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 212.670239 250.526031 \n",
"L 212.72143 251.011728 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 212.72143 251.011728 \n",
"L 212.798281 251.597984 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 212.798281 251.597984 \n",
"L 212.87264 252.001826 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 212.87264 252.001826 \n",
"L 212.938885 252.226347 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 212.938885 252.226347 \n",
"L 213.006282 252.324301 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 213.006282 252.324301 \n",
"L 213.074109 252.290528 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 213.074109 252.290528 \n",
"L 213.152222 252.088064 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 213.152222 252.088064 \n",
"L 213.219662 251.77345 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 213.219662 251.77345 \n",
"L 213.294344 251.27528 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 213.294344 251.27528 \n",
"L 213.349602 250.80636 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 213.349602 250.80636 \n",
"L 213.409493 250.2028 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 213.409493 250.2028 \n",
"L 213.472657 249.460082 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 213.472657 249.460082 \n",
"L 213.527049 248.734257 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 213.527049 248.734257 \n",
"L 213.595424 247.710245 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 213.595424 247.710245 \n",
"L 213.657563 246.673556 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 213.657563 246.673556 \n",
"L 213.768976 244.567655 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 213.768976 244.567655 \n",
"L 213.870918 242.37091 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 213.870918 242.37091 \n",
"L 213.97112 239.969695 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 213.97112 239.969695 \n",
"L 214.183498 234.131921 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 214.183498 234.131921 \n",
"L 214.638275 218.642017 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 214.638275 218.642017 \n",
"L 216.300884 145.850617 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 216.300884 145.850617 \n",
"L 216.911375 121.793599 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 216.911375 121.793599 \n",
"L 217.202783 112.257102 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 217.202783 112.257102 \n",
"L 217.346952 108.110183 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 217.346952 108.110183 \n",
"L 217.522573 103.613362 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 217.522573 103.613362 \n",
"L 217.695954 99.802868 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 217.695954 99.802868 \n",
"L 217.774641 98.28711 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 217.774641 98.28711 \n",
"L 217.860404 96.790289 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 217.860404 96.790289 \n",
"L 217.928968 95.711574 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 217.928968 95.711574 \n",
"L 218.006433 94.620134 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.006433 94.620134 \n",
"L 218.082995 93.675166 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.082995 93.675166 \n",
"L 218.167383 92.788583 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.167383 92.788583 \n",
"L 218.211489 92.390096 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.211489 92.390096 \n",
"L 218.249286 92.084115 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.249286 92.084115 \n",
"L 218.293403 91.768437 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.293403 91.768437 \n",
"L 218.336364 91.503969 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.336364 91.503969 \n",
"L 218.384698 91.257026 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.384698 91.257026 \n",
"L 218.426209 91.087657 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.426209 91.087657 \n",
"L 218.468566 90.955444 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.468566 90.955444 \n",
"L 218.50813 90.868912 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.50813 90.868912 \n",
"L 218.541228 90.823874 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.541228 90.823874 \n",
"L 218.581294 90.802588 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.581294 90.802588 \n",
"L 218.622284 90.818343 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.622284 90.818343 \n",
"L 218.65698 90.861218 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.65698 90.861218 \n",
"L 218.695891 90.941371 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.695891 90.941371 \n",
"L 218.73094 91.042453 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.73094 91.042453 \n",
"L 218.772789 91.198805 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.772789 91.198805 \n",
"L 218.818306 91.412634 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.818306 91.412634 \n",
"L 218.852301 91.601883 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.852301 91.601883 \n",
"L 218.890131 91.841964 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.890131 91.841964 \n",
"L 218.961091 92.37526 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 218.961091 92.37526 \n",
"L 219.003251 92.742803 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 219.003251 92.742803 \n",
"L 219.045767 93.151239 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 219.045767 93.151239 \n",
"L 219.127814 94.045197 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 219.127814 94.045197 \n",
"L 219.2024 94.976523 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 219.2024 94.976523 \n",
"L 219.287338 96.171343 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 219.287338 96.171343 \n",
"L 219.367159 97.42097 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 219.367159 97.42097 \n",
"L 219.447995 98.807891 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 219.447995 98.807891 \n",
"L 219.615993 102.063451 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 219.615993 102.063451 \n",
"L 219.781359 105.728572 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 219.781359 105.728572 \n",
"L 220.122881 114.566217 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 220.122881 114.566217 \n",
"L 221.683926 165.807499 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 221.683926 165.807499 \n",
"L 222.375886 186.80475 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 222.375886 186.80475 \n",
"L 222.737959 195.762186 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 222.737959 195.762186 \n",
"L 222.926406 199.720671 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 222.926406 199.720671 \n",
"L 223.104518 202.977541 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 223.104518 202.977541 \n",
"L 223.191085 204.383245 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 223.191085 204.383245 \n",
"L 223.286339 205.79254 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 223.286339 205.79254 \n",
"L 223.381025 207.048426 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 223.381025 207.048426 \n",
"L 223.489239 208.304335 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 223.489239 208.304335 \n",
"L 223.572921 209.14307 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 223.572921 209.14307 \n",
"L 223.646468 209.784261 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 223.646468 209.784261 \n",
"L 223.717973 210.32133 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 223.717973 210.32133 \n",
"L 223.805354 210.861983 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 223.805354 210.861983 \n",
"L 223.852653 211.101614 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 223.852653 211.101614 \n",
"L 223.909598 211.340815 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 223.909598 211.340815 \n",
"L 223.952331 211.485028 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 223.952331 211.485028 \n",
"L 223.999684 211.609618 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 223.999684 211.609618 \n",
"L 224.051601 211.703841 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.051601 211.703841 \n",
"L 224.103873 211.754158 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.103873 211.754158 \n",
"L 224.14879 211.761895 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.14879 211.761895 \n",
"L 224.196576 211.734336 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.196576 211.734336 \n",
"L 224.249702 211.660702 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.249702 211.660702 \n",
"L 224.293856 211.565334 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.293856 211.565334 \n",
"L 224.343776 211.420492 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.343776 211.420492 \n",
"L 224.394876 211.231921 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.394876 211.231921 \n",
"L 224.44301 211.017413 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.44301 211.017413 \n",
"L 224.500752 210.713455 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.500752 210.713455 \n",
"L 224.558147 210.361619 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.558147 210.361619 \n",
"L 224.621228 209.918698 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.621228 209.918698 \n",
"L 224.715879 209.146032 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.715879 209.146032 \n",
"L 224.810565 208.246886 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.810565 208.246886 \n",
"L 224.920153 207.054378 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 224.920153 207.054378 \n",
"L 225.036277 205.620693 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 225.036277 205.620693 \n",
"L 225.194493 203.402234 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 225.194493 203.402234 \n",
"L 225.383316 200.38679 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 225.383316 200.38679 \n",
"L 225.740987 193.737598 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 225.740987 193.737598 \n",
"L 226.144148 185.137044 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 226.144148 185.137044 \n",
"L 227.04504 164.265052 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 227.04504 164.265052 \n",
"L 227.502171 154.208899 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 227.502171 154.208899 \n",
"L 227.889507 146.621335 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 227.889507 146.621335 \n",
"L 228.221338 141.057265 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 228.221338 141.057265 \n",
"L 228.399368 138.486731 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 228.399368 138.486731 \n",
"L 228.586165 136.127088 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 228.586165 136.127088 \n",
"L 228.735318 134.501823 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 228.735318 134.501823 \n",
"L 228.896957 133.00768 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 228.896957 133.00768 \n",
"L 228.987784 132.291987 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 228.987784 132.291987 \n",
"L 229.071334 131.712991 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 229.071334 131.712991 \n",
"L 229.144976 131.265905 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 229.144976 131.265905 \n",
"L 229.226447 130.840367 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 229.226447 130.840367 \n",
"L 229.30883 130.483735 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 229.30883 130.483735 \n",
"L 229.378214 130.240646 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 229.378214 130.240646 \n",
"L 229.447709 130.049377 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 229.447709 130.049377 \n",
"L 229.525145 129.89737 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 229.525145 129.89737 \n",
"L 229.589267 129.819849 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 229.589267 129.819849 \n",
"L 229.643166 129.788255 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 229.643166 129.788255 \n",
"L 229.707002 129.790102 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 229.707002 129.790102 \n",
"L 229.774414 129.837748 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 229.774414 129.837748 \n",
"L 229.863432 129.971478 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 229.863432 129.971478 \n",
"L 229.939611 130.148752 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 229.939611 130.148752 \n",
"L 230.030858 130.435645 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 230.030858 130.435645 \n",
"L 230.124587 130.812777 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 230.124587 130.812777 \n",
"L 230.275529 131.589179 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 230.275529 131.589179 \n",
"L 230.432636 132.60756 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 230.432636 132.60756 \n",
"L 230.624022 134.116727 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 230.624022 134.116727 \n",
"L 230.804402 135.784506 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 230.804402 135.784506 \n",
"L 231.011851 137.962198 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 231.011851 137.962198 \n",
"L 231.193491 140.065211 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 231.193491 140.065211 \n",
"L 232.072587 151.844586 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 232.072587 151.844586 \n",
"L 232.766757 161.427458 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 232.766757 161.427458 \n",
"L 233.078622 165.363086 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 233.078622 165.363086 \n",
"L 233.431746 169.344478 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 233.431746 169.344478 \n",
"L 233.633116 171.341752 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 233.633116 171.341752 \n",
"L 233.82991 173.079153 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 233.82991 173.079153 \n",
"L 233.986004 174.297354 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 233.986004 174.297354 \n",
"L 234.164717 175.511292 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 234.164717 175.511292 \n",
"L 234.325408 176.433866 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 234.325408 176.433866 \n",
"L 234.485243 177.190536 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 234.485243 177.190536 \n",
"L 234.63883 177.765796 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 234.63883 177.765796 \n",
"L 234.820641 178.255526 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 234.820641 178.255526 \n",
"L 235.008299 178.547129 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 235.008299 178.547129 \n",
"L 235.192557 178.628076 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 235.192557 178.628076 \n",
"L 235.387878 178.500866 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 235.387878 178.500866 \n",
"L 235.551327 178.23456 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 235.551327 178.23456 \n",
"L 235.695695 177.88527 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 235.695695 177.88527 \n",
"L 235.858891 177.369966 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 235.858891 177.369966 \n",
"L 236.149193 176.168232 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 236.149193 176.168232 \n",
"L 238.842936 158.92464 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 238.842936 158.92464 \n",
"L 239.140491 157.516021 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 239.140491 157.516021 \n",
"L 239.487993 156.193859 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 239.487993 156.193859 \n",
"L 239.786305 155.350464 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 239.786305 155.350464 \n",
"L 240.090079 154.770531 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 240.090079 154.770531 \n",
"L 240.431054 154.444295 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 240.431054 154.444295 \n",
"L 240.775439 154.438809 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 240.775439 154.438809 \n",
"L 241.082117 154.67806 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 241.082117 154.67806 \n",
"L 241.367178 155.077276 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 241.367178 155.077276 \n",
"L 244.182625 161.890761 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 244.182625 161.890761 \n",
"L 244.913871 162.892193 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 244.913871 162.892193 \n",
"L 245.66125 163.295788 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 245.66125 163.295788 \n",
"L 247.029141 162.865386 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 247.029141 162.865386 \n",
"L 250.265051 161.464726 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 250.265051 161.464726 \n",
"L 255.62058 161.615264 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 255.62058 161.615264 \n",
"L 258.33929 162.600435 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 258.33929 162.600435 \n",
"L 259.733067 162.423083 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 259.733067 162.423083 \n",
"L 261.101522 161.217179 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 261.101522 161.217179 \n",
"L 263.915837 158.479199 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 263.915837 158.479199 \n",
"L 264.760983 158.792797 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 264.760983 158.792797 \n",
"L 265.691938 160.029466 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 265.691938 160.029466 \n",
"L 267.16567 163.220433 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 267.16567 163.220433 \n",
"L 268.598455 165.891895 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 268.598455 165.891895 \n",
"L 269.066851 166.292407 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 269.066851 166.292407 \n",
"L 269.541636 166.365889 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 269.541636 166.365889 \n",
"L 269.984303 166.112973 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 269.984303 166.112973 \n",
"L 270.346594 165.677073 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 270.346594 165.677073 \n",
"L 273.805478 156.808128 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 273.805478 156.808128 \n",
"L 274.530044 155.897703 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 274.530044 155.897703 \n",
"L 274.85903 155.785227 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 274.85903 155.785227 \n",
"L 275.20154 155.879178 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 275.20154 155.879178 \n",
"L 275.55476 156.198993 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 275.55476 156.198993 \n",
"L 275.934716 156.781656 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 275.934716 156.781656 \n",
"L 276.538447 158.146518 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 276.538447 158.146518 \n",
"L 279.268824 165.996263 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 279.268824 165.996263 \n",
"L 279.89887 166.868458 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 279.89887 166.868458 \n",
"L 280.532479 167.056129 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 280.532479 167.056129 \n",
"L 281.159707 166.555476 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 281.159707 166.555476 \n",
"L 281.675338 165.689938 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 281.675338 165.689938 \n",
"L 284.200599 159.097496 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 284.200599 159.097496 \n",
"L 284.95821 157.728884 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 284.95821 157.728884 \n",
"L 285.805536 157.113938 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 285.805536 157.113938 \n",
"L 286.622394 157.483577 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 286.622394 157.483577 \n",
"L 287.376888 158.525892 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 287.376888 158.525892 \n",
"L 290.310366 163.855902 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 290.310366 163.855902 \n",
"L 291.032311 164.348913 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 291.032311 164.348913 \n",
"L 291.826992 164.302366 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 291.826992 164.302366 \n",
"L 293.175641 163.132351 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 293.175641 163.132351 \n",
"L 295.997957 160.303788 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 295.997957 160.303788 \n",
"L 301.25576 161.871733 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 301.25576 161.871733 \n",
"L 307.20624 161.522054 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 307.20624 161.522054 \n",
"L 312.762673 161.651845 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 312.762673 161.651845 \n",
"L 318.311698 161.03 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 318.311698 161.03 \n",
"L 320.891928 160.71508 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 320.891928 160.71508 \n",
"L 323.338595 162.114904 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 323.338595 162.114904 \n",
"L 325.206962 163.059105 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 325.206962 163.059105 \n",
"L 327.486792 162.155644 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 327.486792 162.155644 \n",
"L 329.758141 160.03995 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 329.758141 160.03995 \n",
"L 330.871599 159.583081 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 330.871599 159.583081 \n",
"L 332.08649 159.933729 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 332.08649 159.933729 \n",
"L 336.785071 163.504114 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 336.785071 163.504114 \n",
"L 341.283061 160.003842 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 341.283061 160.003842 \n",
"L 346.63382 162.529535 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 346.63382 162.529535 \n",
"L 351.312599 161.23489 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 351.312599 161.23489 \n",
"L 356.23224 161.542597 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 356.23224 161.542597 \n",
"L 360.816309 161.568077 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 360.816309 161.568077 \n",
"L 365.00236 161.533949 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 365.00236 161.533949 \n",
"L 369.964957 161.647364 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" <path clip-path=\"url(#pe717969085)\" d=\"M 369.964957 161.647364 \n",
"L 374.872344 161.220852 \n",
"\" style=\"fill:none;stroke:#1f77b4;stroke-width:1.5;\"/>\n",
" </g>\n",
" <g id=\"patch_3\">\n",
" <path d=\"M 196.312344 284.481957 \n",
"L 196.312344 38.587297 \n",
"\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
" </g>\n",
" <g id=\"patch_4\">\n",
" <path d=\"M 374.872344 292.612 \n",
"L 374.872344 26.5 \n",
"\" style=\"fill:none;\"/>\n",
" </g>\n",
" <g id=\"patch_5\">\n",
" <path d=\"M 17.752344 161.534627 \n",
"L 374.872344 161.534627 \n",
"\" style=\"fill:none;stroke:#000000;stroke-linecap:square;stroke-linejoin:miter;stroke-width:0.8;\"/>\n",
" </g>\n",
" <g id=\"patch_6\">\n",
" <path d=\"M 17.752344 26.5 \n",
"L 374.872344 26.5 \n",
"\" style=\"fill:none;\"/>\n",
" </g>\n",
" </g>\n",
" </g>\n",
" <defs>\n",
" <clipPath id=\"pe717969085\">\n",
" <rect height=\"266.112\" width=\"357.12\" x=\"17.752344\" y=\"26.5\"/>\n",
" </clipPath>\n",
" </defs>\n",
"</svg>\n"
],
"text/plain": [
"<Figure size 614.4x460.8 with 1 Axes>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"values = {w0: 5}\n",
"sym.plot(sym.re(y.subs(values)), (t, -20, 20), xlabel=r'$t$', ylabel=r'$\\Re \\{ y(t) \\}$');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise**\n",
"\n",
"* Derive the spectrum of the signal $x(t)$ modulated by $\\cos(\\omega_0 t)$. Hint: Express $\\cos(\\omega_0 t)$ by Euler's formula and exploit the linearity of the Fourier transform. What is different in the resulting spectrum when comparing to above result?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Parseval's Theorem\n",
"\n",
"[Parseval's theorem](https://en.wikipedia.org/wiki/Parseval's_theorem) relates the energy of a signal in the time domain to its spectrum. The squared absolute value of a signal $x(t)$ represents its instantaneous power. It can be expressed as\n",
"\n",
"\\begin{equation}\n",
"| x(t) |^2 = x(t) \\cdot x^*(t)\n",
"\\end{equation}\n",
"\n",
"where $x^*(t)$ denotes the complex conjugate of $x(t)$. Fourier transformation of the right-hand side and application of the multiplication theorem results in\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{F} \\{ x(t) \\cdot x^*(t) \\} = \\frac{1}{2 \\pi} \\cdot X(j \\omega) * X^*(-j \\omega)\n",
"\\end{equation}\n",
"\n",
"Introducing the definition of the Fourier transform and the convolution\n",
"\n",
"\\begin{equation}\n",
"\\int_{-\\infty}^{\\infty} x(t) \\cdot x^*(t) \\, e^{-j \\omega t} \\; dt =\n",
"\\frac{1}{2 \\pi} \\int_{-\\infty}^{\\infty} X(j \\eta) \\cdot X^*(-j (\\omega - \\eta)) \\, d\\eta\n",
"\\end{equation}\n",
"\n",
"and setting $\\omega = 0$ yields the desired relation\n",
"\n",
"\\begin{equation}\n",
"\\int_{-\\infty}^{\\infty} | x(t) |^2 \\; dt = \\frac{1}{2 \\pi} \\int_{-\\infty}^{\\infty} | X(j \\omega) |^2 \\; d\\omega\n",
"\\end{equation}\n",
"\n",
"The integral over the squared absolute signal in the time-domain is equal to the integral over its squared absolute spectrum divided by $2 \\pi$. Since the left-hand side represents the energy $E$ of the signal $x(t)$, Parseval's theorem states that the energy can be computed either in the time or spectral domain by integrating over the squared absolute value of the signal/spectrum. Parseval's theorem can be generalized to the [Plancherel theorem](https://en.wikipedia.org/wiki/Plancherel_theorem) which considers the product of two signals $x(t) \\cdot y^*(t)$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Example**\n",
"\n",
"The energy of the rectangular signal $\\text{rect}(t)$ is computed in the time and spectral domain by evaluation of the respective integrals. First the time domain is evaluated\n",
"\n",
"\\begin{equation}\n",
"E_t = \\int_{-\\infty}^{\\infty} | \\text{rect}(t) |^2 \\; dt = \\int_{- \\frac{1}{2}}^{\\frac{1}{2}} 1 \\; dt\n",
"\\end{equation}"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAAgAAAAOBAMAAADgeEClAAAAIVBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADdcGRXAAAACnRSTlMAMt0Qq5nNdrvvxbMB0AAAAAlwSFlzAAAOxAAADsQBlSsOGwAAABtJREFUCB1jYGBUZmAwCVvMwMDAThbB0rnIHQBAqQoWQ8kakgAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$1$$"
],
"text/plain": [
"1"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"E_t = sym.integrate(1, (t, -sym.S.Half, sym.S.Half))\n",
"E_t"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The energy in the spectral domain is computed by evaluating\n",
"\n",
"\\begin{equation}\n",
"E_f = \\frac{1}{2 \\pi} \\int_{-\\infty}^{\\infty} \\left| \\text{sinc}\\left(\\frac{\\omega}{2}\\right) \\right|^2 \\; d\\omega\n",
"\\end{equation}"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAAgAAAAOBAMAAADgeEClAAAAIVBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADdcGRXAAAACnRSTlMAMt0Qq5nNdrvvxbMB0AAAAAlwSFlzAAAOxAAADsQBlSsOGwAAABtJREFUCB1jYGBUZmAwCVvMwMDAThbB0rnIHQBAqQoWQ8kakgAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$1$$"
],
"text/plain": [
"1"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"E_f = 1/(2*sym.pi) * sym.integrate(sym.sinc(w/2)**2, (w, -sym.oo, sym.oo))\n",
"E_f"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbsphinx": "hidden"
},
"source": [
"**Copyright**\n",
"\n",
"The notebooks are provided as [Open Educational Resource](https://de.wikipedia.org/wiki/Open_Educational_Resources). Feel free to use the notebooks for your own educational purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Lecture Notes on Signals and Systems* by Sascha Spors."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 1
}