{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"nbsphinx": "hidden"
},
"source": [
"# Characterization of Systems in the Time Domain\n",
"\n",
"*This Jupyter notebook is part of a [collection of notebooks](../index.ipynb) in the bachelors module Signals and Systems, Communications Engineering, Universität Rostock. Please direct questions and suggestions to [Sascha.Spors@uni-rostock.de](mailto:Sascha.Spors@uni-rostock.de).*"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Analysis of a Passive Electrical Network\n",
"\n",
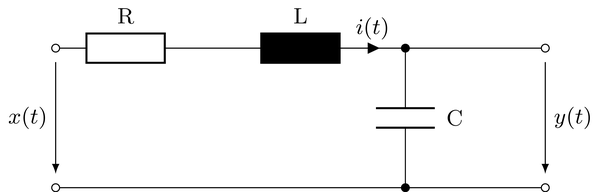
"[Electrical networks](https://en.wikipedia.org/wiki/Electrical_network) composed of linear passive elements, like resistors, capacitors and inductors can be described by linear ordinary differential equations (ODEs) with constant coefficients. Hence, in view of the theory of signals and systems they can be interpreted as linear time-invariant (LTI) systems. The different ways to characterize the properties of an LTI system introduced before are illustrated at the example of a second-order analog [low-pass filter](https://en.wikipedia.org/wiki/Low-pass_filter).\n",
"\n",
"\n",
"\n",
"It is assumed that no energy is stored in the capacitor and inductor for $t<0$. It is furthermore assumed that $x(t) = 0$ for $t<0$. Hence $y(t) = 0$ and $\\frac{d y(t)}{dt} = 0$ for $t<0$. For illustration, the normalized values $L = 0.5$, $R = 1$, $C = 0.4$ are used for the elements of the electrical network."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Differential Equation\n",
"\n",
"The differential equation describing the input/output relation of the electrical network is derived by applying [Kirchhoff's circuit laws](https://en.wikipedia.org/wiki/Kirchhoff's_circuit_laws) to the network. This results in the following ODE\n",
"\n",
"\\begin{equation}\n",
"C L \\frac{d^2 y(t)}{dt^2} + C R \\frac{d y(t)}{dt} + y(t) = x(t)\n",
"\\end{equation}\n",
"\n",
"This ODE is defined in `SymPy`"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAUwAAAAuBAMAAACxCz2JAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEHa7q2Yiie9U3ZnNRDKmwYvPAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAGI0lEQVRYCdVYb4hUVRT/3Z3dN/P27ayT+kE08qVFxoKu2xpUlpOu+CGhgUjoD/ggI6oPThJIIu1kFP0hGvzgRkFOUVkb5GaJIBtOQbDRh5ZIkCh2PllUtLNaimG7nftv5r43b2Zn3rhgB947957f+d1z3r133rtzgHBhe4dS4chVZXXgFK6qhMKTWTRpzYYjV5W1K/U/SPOPV4F4Ieq89U6MRaW2yLsE/Bb9J7Qo32K4iO7JGVjrI3KJNhX9CVsKSgu+C2dbopjO+8zOArZ7xqy7/vw0coBvIzNbIT65ZzqfmJsrt8Kp+lon1tLOXnhJvohNbWyuM15sZuGTBJZlMB49DnsBTjE6vXnmqRSONO8d9HRm0J0NGhei/zzYv9HHTfRj5WR0etNMdhFdEX89PMbKLHY2HasNR3YJseKhyAOszGOj7UWmN0/8Cg+O1ewui/PFbZ6Betyuj+Omj8c74sYbQfG4Qdx4o0YahF1609nNpSDhZm5IukFzbZ9tfnbXWsPckeed7w2L2WyMAkZYtnpoq5VFx72XN5gj+Nq2nF7B8gFYPDiUeQxYPTd4y21+RPZGhJLp1OKNUZhh11wPe18GWFSoHUZbrqXGcg89KW3QuuNACiPvU+88MJ3W1qpmRYB9AHxZNRmtxihghF3yDvFOeRRFzpgxSrV5nJqHga4xZTqtNLudEncuAL3ngBjpoDgZwC4DDykgSf2qBNEqIltG2AkKhDN0rZsMelX7OWryT9NzynRQ6R5uSOaADvpL0hOSZoJw/lVK8CgktiuUugVRE+PtHF0ybFycE36n/nd01ZFkkYAjdH2tHHSaw3ky9I5RimVajn6FGuonandnCc9Ioz/NIGoQedMIu7vADdfRdZk3gsL6XCyFk0Vyy/nNwNMKV2la//A+K9HG7of1ngKlWnwMLI0TwA+bBl3E09Kq0wxHKwOwVXf/8owZdthVWPJixcloxO0cfVX4XNhlMj+sIJVm/Jx2nRrou6OkO0Jn3+BfMz79tKnRVRTGyqKHoSdHuYiHdXCDe9IMe7Qk+YiHfsgfp421Bd15ucPwpnJWaXZX/iQPe2xLSoFCWflxdPbjI+qM02UXhFWnWQeVPnTfgXXeVjPs62JwuvHdRTLnE6QSLg4gMSl3GKa5Cz31S/KpE+Jkycg2QeueNdhlxmkuXiOMb+peProzOvrhK6OjadonISg5VKSEjdQ2wh7lkF2iKEVaGo86fplK9c4Kf3Hu4W8ELno2xaO9TYa/6NCR5khF6G/fdImnKc5byZwEbFfqcFRi4s63E09ThT3lUT9O15QLdJIOyDg6cujJE05TEFx0/sYEsvSb/Ju24JiPSrtlDfANYWWkgovOX1I1qLE3kbyAa8ywu10a/Cm6hkvAjaQDMohYGjEX2I9DwH0KVbNp8WeOp2g5afWH3V6TS7RBYIDwIp2YuvolpmczHNV8dmdnmZ7eCGvTPIxQINDqx80/Maom9zmmMuJ1MsRc4JgaSKWJwxnY9IzsV2LudH9WqFBOmk8xvcE604vpOYjMRacZjkof8ppdkUvmfWFXDN4zSYG2zw1tn0trP9KqJrd0D22LZAF45H4y0tdZiE6TfTb0BRnie/dm4AxkFCoU29ZHW+JHOv5tIHu3JzGdZjiq+eyY+9YDtF0KgbAaF1rWgCo1uf1k/EQ6WAWp9U9I9XyqWkGKFym9kgSfUD46Tb4XalHlVFHBsBVANKgGtNyTNTmnyF4mmzo5OHq+TvsJvp5g87flsnz1sHJcueijRzjqG4c6wbB+nGpA/MtBJRp0u51ZasY8utEKiPs8N8V+F9u4463C2+oPkBqj2jnmiVadsFQDGiec1+TsVXzvgckw6wVrnptiH+yb5I5LhHeMhvJJY1S7Ng5LNSD6cvhqco9yZsjbXw9oaMnWBivDWzt0N6Abo0D9sLwGJI5DkWpyFXYgnyveFTUgu4xoNTnNvuJpBQaUNSD6lkWqyVXYgVGveFfWgPiBO4q0x24hYkLUgKKWgdpjt5CmrAGJ41ALLO3aHluP0oSWNSBxHGrCO+jSHjs4WoO+rAGJ41ADr3pQe+x6o4bYZQ1IHIdC0PlM7bHrj/4fekCxr3eUiKUAAAAASUVORK5CYII=\n",
"text/latex": [
"$$C L \\frac{d^{2}}{d t^{2}} y{\\left (t \\right )} + C R \\frac{d}{d t} y{\\left (t \\right )} + y{\\left (t \\right )} = x{\\left (t \\right )}$$"
],
"text/plain": [
" 2 \n",
" d d \n",
"C⋅L⋅───(y(t)) + C⋅R⋅──(y(t)) + y(t) = x(t)\n",
" 2 dt \n",
" dt "
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import sympy as sym\n",
"%matplotlib inline\n",
"sym.init_printing()\n",
"\n",
"t, L, R, C = sym.symbols('t L R C', real=True)\n",
"x = sym.Function('x')(t)\n",
"y = sym.Function('y')(t)\n",
"\n",
"ode = sym.Eq(L*C*y.diff(t, 2) + R*C*y.diff(t) + y, x)\n",
"ode"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The normalized values of the network elements are stored in a dictionary for later substitution"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAOIAAAAyBAMAAACzABrLAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAIrt2EIlmRJmrMu/dzVR9PQywAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAD+klEQVRYCb1YTWgTQRR+22yanyZNFIQKgsGKWBUNKiJ4cKEnaaE92HNy9GZuHhS6SMHUUggqQsHSXDx5aKXeFFqxSIWKwWuRerAXL621/tKyvvnZZGYzs7uBxHeYfe/73rwv2Z2/XQC0gznSdtySi65EZMdy3c5eb7/m9QtFpVDf9Ckl7gGTKx5AH5rrWUrGfitzjAoUSkpGAq9N70qxbzCUo3TXtjIrYUHPgpKRwUgLitG/tG8mJ5fgUc8uJL4pGRlsRTH5nfYdqcgleJRYhgT7SUq6DraiaLAHOGLXe3uclPp+y1mtKJpBivN5ubgyaqviqlLCA7ZTMW57iivDdireUCp4wTYq9o7CAW95RdxGxacAFxUKXqh9isZqeXLZW14Rt08x7ThOTaHggRKn9x56IH3omY+DAzPFQ/pszkTm9k8EJgGcdwaOnRXy2A4jK0YWLdh8KyRp3MyyhpDhHYD5xvLJdxhJ0TxjAcRDLN3zo3JpdUTW7C6hGnva5h+azUqkX2AQW1D3F9GrJTHS+RHcBNJNioD/HI2VKHxGN2ljE2AbATyj09t4V3ONVD6iWedXBDf2SGtWSeu/nO6TFLSUTS+aJpMD4x3heBpX3CoiFH9OiCjbK4lrujVJ0GSxHxwaqTVxAjDef/lklcQ8jSvSgTJFiZSw+VokU2fRX5wxdRkUL2TNBxbxeBpXhKkSDNsEBzxjoIlVcAFwHHwaHiMPSLAMTRMA7q4DZEYF2FXsXYThCYqz7f6rkKNxMzWA7qyGbMA4DaTTjKsYewPA7iqbieKvavSWvPE8QEJCVEHsJ8CWLTCuIlFjI8cgIydqCTncFW80gQpVgEucEy6W4KMbx4dUyCcbIFdkx8f3FMdx23udevJY9Q7JD/jD6DOXCLkPmM8w5Wb+FtaTx+p4kUiwFcC8O3OPRGh8PlbBxOeVWmEga81ZZ2bWqZBAno9rFktgbXRsrAjx/iJGLM3dYc5RXrdQLn2iZb7QJG1jlD9Wkey1tBkiwaa67ry6tkfvcsBoOgx0hkbFulqfr+Q6RXrvwMxr+1PiEcBLdAb9szgr7VbNPZhidzMhIUsWzGUBihKoC0Ip6jq7+BOAuaobBF0DFB9fuB9UgfE4YUJagOJxOFoKU4m/ooVJDVDEY8NymDLyxPTtEagY5tgDUPYVkUh/xa4axIVNU+opBt22GPn7/oo9+I687V+Asptg4OwIZ/6KuIr05IILJUchYgWnsQxXsaLsYNhwJUSpI+UyTsmQ5q8IfZMTIQptOI7vSUwqwb88ZHIS2skgyQ6CXXSD7aRQvTY5qaNx4TrcQWeoxorTF4AO6tRLu18CIcK+69SJjjl33K+d//eL7j/AZQfnGLm0TQAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$\\left \\{ C : \\frac{2}{5}, \\quad L : \\frac{1}{2}, \\quad R : 1\\right \\}$$"
],
"text/plain": [
"{C: 2/5, L: 1/2, R: 1}"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"RLC = {R: 1, L: sym.Rational('.5'), C: sym.Rational('.4')}\n",
"RLC"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Impulse Response\n",
"\n",
"The passive electrical network and the ODE describing its input/output relation can be interpreted as an LTI system. Hence, the system can be characterized by its [impulse response](impulse_response.ipynb) $h(t)$ which is defined as the output of the system for a Dirac Delta impulse $x(t) = \\delta(t)$ at the input. For the given system, the impulse response is calculated by explicit solution of the ODE"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA8AAAABdCAMAAABdGP+pAAAAPFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAo1xBWAAAAE3RSTlMAELvv3c2ZVESJZnYiqzKBxeNgQeo2UQAAAAlwSFlzAAAOxAAADsQBlSsOGwAAEsdJREFUeAHtXYm2q6gSRTOo0aTfa///XxspZpBJSMBj1rr3KJPsQgSKXQVC1++SgCqBTr0Nu/tMa/4fSqpKWIV5qpRnfPJjXdFX0HLY18VZJTC+UpD1n5RcvjzL5EtxOD4JbrNoD4vrKqB2CXTvlBp++pRc/jzz6E9zKEUS3GbRHhLVlbkJCbxTppToXaqj9UnVCZd0Etxm0YbL5UrZqASGpEnr8jDgDosRBAHDPHk7wMzzLkkTAp7dd5EE10S7CxZVhdYnjSu+fQk8kka8pzEAv4wQJpsb1tZgjY379+TR/d6HgKc4cpEE10C7DxZVhfaIpK68TUjgI3pORH07NgDP8/watiLY0pIHoGmd5+mJPw+4Q37wa239TesEyrCRTwRIcdbEGQKT4DK0HBsDi3hInWgzCOwqonIJeCe31vo/BxK8kNFy2HozDFJSABq34BkmxL05PMNad7yz8sXQeE+aE7By3H+T4AJaCRsdkaWQOtG6ZXHFnkECe0OjE1sH3a67k9Gz2wZPEiIHoHkL7sni9mluOb2gm858AjDBNwHneSZtazkrzCNT4AJaGZsJv060HPZ1cVYJDEm7QRN0MTq8brIBNY8UgND7ObygV04d4hNkKshhgQ7c884qZs5DOTVWElxAK2GjOi0ppE60Z31pL1xCApPes0SUeTWwiTCd98LwStKN5EMgBSB069By3xRSD8xiojlYmZ8RQQe+cY0VlLAlWLwaL1ZM9N8YuBpaCRutqhRSJ9po8VwZmpNAzyeu/qrPN6q6mummz5sOxDgrjJpSAOq22apS/PKE34g6nJF0YOirpDiJK7HyXu2vVFwKpT7urDpaCRudIkghdaJ1A7xizyABMQJ60SzdtMJalg2nH9Khhy0Qup8UgMhs9TZ2No3UgrW364S7KUk0k1LFFBrdI74q3morCcLhGmglbPRbI4XUiVaBnn5ja0FvaY2Qx1vH5t+flVuqW8nq9MVZF+Nzfs0wXEKnFgHD44H75XPiaeWC8K4T6cA40Tz3kJUN6zidMjdV8x27i4KroxXYQGOHkAipEu0xWfHcSdxx1AZ5vHlsY5xW9kkmt7B65Q0MF4fpF1IBE1dNaw85ehsHdx+tVNfEKkklFEObWDUtG9/z1sLdt9KCyJ0wMjYvVb59bGQLN1yGy4q7lp2MKIgY4cXJKTtJHa6od+VER6/j4O6jPQoWfQXtUWlB/iTueCNU+faxvahaKrSt+7VDgnGh5Hoe0zzhrSb+myNrxTP6LiLh7qM9CBZ9Ba1PGkHx9s+1L6tJHke77PHfkcdzYcsEDSWYAczSuCcahZMgRRC9GtdZUjap0fJLqcYE3Cnk4sh+FlA8TWKFm4T2EFj0HbThcnGk3PlcO3JsUQZ5XIWs5MarOL9uQiyqpMWHUkzCTSZsSmsq1YiEhiKw0c7+z/+UB9IbmQSpxT9uj92RVhpDtVz+WyXv8H9/hrgULrgKWnVb3IFWqXBcZfALK2fIj1Yu/eB1EnccGeTxKqnymbDxhbRJjMddJcYKAO0OjmYrUk2yvQNLJEg95wCKaD047/2/2TuwC66CVnzpN0iNos3YGknccWSQx6ukymfC5ibGR1kBUHZTQPvNd5CxdU4pkSDNogi3ygzOGjKwjeZcpTrhCsonfpzagVGTaHNJbSsnbpeCPtkkj1dJlc+EDV5WmSovEePjrAAizABoF7F3YE6ClF+FAl7djCLp87J3YLZxa4WroGUd2KhagYBiaOVmO3adxB1HBnm8Sqp8JmxOYjxWlaiLMjyrc1gBUEJjQJvxRQpTYgmaI16hbZ+mjXQoBwYUqiYRKwI1POAuewfW4crAOFo0YabnHf9jjO+AmvIkNaHllTp+EcMdR/vkcVQjVT4TNhcxPtYKINwMAK+WCY/ZOiS5SJCh74RsKhuah6fL3oFdcFW0bATmdQm6qAttUJXDEkVwx5GDPF4lVT4TthBivBgwPFYAKNQMYHm+iDLZ1oE9tMCglldWBEE55ETZO7ADroY2qQNXhlYW5cHrcO44cpHHq6TKZ8IWR4z3WAFEmwHYtdAHWx1nP8alyq+Fpoj8cJM6cKVojzejf39WfoaDPE6VEDWRx7Nho+qkUGxOK4BoMwDbCCy3Ser1MXOE7xI5FIy6ykGJ3LupFO1edcPD47jjaJ88HkNRsFdP4jjkIY9nwybVzF51X6hcQCy2Ul1FNpX11d+ML/VZQYXgVorWFGxsSBx3HKtg8ATGzk88yh7PTx7Phi0ntOipK2EhxTZrQHrZVDYguZakWAcuBLdStJpUE25jP3j75HF0kD0uU1fzUOXzYcsIDcVi++SmTLC3RKwIWEjE36mUU6xScOtEGyHxnaTWL+k+dxy1RJW3YhPegQ2JOLDJXxcjny9AZVLHflYKup/yVdwR/0xaiToKZFFVwi2GlqFO+BvMHdfKdpDHVQK4ls93m5M87sKmeAfWOBgObEr1fFi0eDVvLDG+w+aB9f1iduiial8l3GJoo0SjJg7mjqvZmiCPu7BJJEiMTN2SqJMYfwMvV1o7/Pg2YocusqY1wi2HNlI4Ink4d1zkgav6yeNObKoZgNqB6yTG1/j5j9uh018h532FcAuidYrCGemiyivccV5KAa64USR92EGejwub8IW8PYt1YKMiBQJSsYmTEWgJFfwppWrC0CqEWxBtcluGcccFQTDhQT8jj+vYFMZ/e8T4QhsrCS0qsrzYl08E5bqqEG5BtMlSC+eOJz7ih+RxFzbNO3Dae/hlbElGkYnNFpitjEdSeHh9cEuiDRS4kSycO25kDQr4JXncgQ21SIwXZ4oFif4LiejJaWWeVB3comiPytDPHU97Qg3k8QBsSSPwt7GVcuCb1rJbrlepXeCt8OrgFkW7IT7ys5MdjpQIeWsgjwdgS3oRv45t30nd8YZKKqFshcqWHg+4tvooCGJ5QUpmx00N5PHTYEvzzedonYNRvvoIp5jiKuKRvuIjisqR1FcdgVFc5XhuWBmldH41kMfPg+0gFzvsVQhP1bu5YbM4+GzcOXfJ/ay64JZG65aFL7bYFlcF5PHzYJMttXwtWj7+JToofdg8vQVdTDFWkzpzeMWqglscbbhcbCmr5I7jE/NsdY0NOxG2tJEsVmBh6RdD89e/kNDUsl34Dih7Sa71K4L7BbRhYt9JVSV3XD10eqfm/uCmsRWgguUvEtpg2vxm0nOJMbkNjhTHpHkSG0iCyF+3/CXmQwsl5fm/Ru44ykQePzO2lNaf1knMdFMKsOb5rJuT15XNqxkP40mPP8O83N/8/gjaCrnjAQcphb0SZ8YWJgGSip8tNxbxDfDeSv2sdODlmsM7XQY9aEREhQ8l/Vtoq+SOo1zapwp58T5s3TTPz8xjFh4TwZ6miDy6ddM0D2QYxhegvhjf/dq/iQra6bujANyK0R76MO1l5l/MvQQ/CA9cN3lr1h628Y7nuJ8sKjwhHbw9CQewYWVT/t9MVr8Tc3fNBly6BMasLcdJwiXg1os2v+xJiWzNUqj4lGKzkcdbw7aQieiccnCIW85wAFsm1YL6qH5949/KRH2na2G2BEYO09BScOtEq4ot31113HFpS+Ioytaw9es8T1P+/gsHsMG2WhK1wtEQt00HDfPoLdWN1p4tgfHqeDdzIbiVot0Vw8GI6rjjGanyrWErdLIvPYCNHDE059ZDkyXwizvuoh24Y2ti5PDOXQZurWgP9tP97NVxtTNWKGNR+wKMiXFXaM28+oWa0QPYsCXlPPe5FdHQU++c3PGAKfS4jbtEGeeYQheBWy3amNckKq2PrB1VWIbEOeuTs6wM0JCnPnTeybZUczyxeBnbUDuIzV5qqjVh1dVAyP0vdjyqWZMG4SaiFWYO4sqUR2pIXdxx5CGPx6FsCxvR2HaV1dkjcGx3Rr03kIR01+j9Rh2stp/7i+4G4aahlRjhJViiVXHHkUke97xBzujGsM14G3j/hXci/VVk95zlLw4liyz9i+5ZubyYtgc3EG3X36S1SpJ5Rzf3WLv/QkvAsqrEVyH1fTLJ42ZJZ8Zmom0sZNvJln6L9CJLwWe53EX74FoBlGTeMd/mTYUwTHfr5n1+pneBEvca+QTY9qCdIFxj4TDbhhMgs0HYRcu54UnmHV1/p3Q8OA/U9ujsYWXI46Sao/QVOhu27O3w6wLls1TRoqmw5Jb8dUWzPH8H7cj31fDWOH0Q47YIjd9uDR48jWMXbjd3XERh8jipzCCtC8+GLU7aDaRW1A66RlJuyQaw+Ku4g3YSKwdO6GXcFsY23S98EuO3Z99iv4zgGPx9KUiVh2pIzX46bMGCbibhIuZLL33XRGrJZvC4K2pH+3gOrxlG5zjzju1hyyq6f6eoFAoYfyDcRAWp8iA80eznw+Z+Pc4WK1rybMgUPN26MXbwXhr+sQHXZt7xvEs/fuQyPt5XKY3flDD+2AovSB6HuotmPx823jp/4kK05KnhDsRE600UADHmHSCUO3dvAvcdtegqZfxRkjwOCESza9i6aXq/N31du9gA4V/5X7TkqRGDvupGBtIY8w4Qyk3SgOGX+zPPMKUuZPxRlDwOc4zbjcw08BxDw7Zttj03dC1i6x7S/Glb6hTYiqukSNJMG1rRkieGixDRVy0wkMaYd2A54d9dGHANZAlM+eRljD+KkscBEBLfbQ3bRk0lcmoXG4X4R/6IljwzYLDwoJpol3mHfQ0s7f0CDYt14ABSVp1iFc2uYXvhGQZ04Gax1SnxUrUSLVnqCTWU+yJD6G1C2/sZY94BlV+4EgvPbrcf7cANGn8AIGkENrAhRD507WKjEP/In7/RgUF7hWfQ27ASY97B3ndwETjQ/ss6cIPGHwyQUKsPGjbsJW77SrWLjUI88OfX69yYqh/vwH0DcMH52DSR1zbKvIPKsntiS4Ynd83CbKrbM/6geORm17AtlOvTLLaY19+a9sP3D63RdQXKLZlUs6bQAsJdg4dgAbAOHJyhtoT7zb7gt/ej031qq37Z+mRzAVi2mlD6fksGPr0ptIBp1+AhEDJfAwenry7hLgV+6T+fT24/ytXBd1bI5fcr5MvGt9KdT7FFhpSu59ttST3hzn1baCmIHYOHHYhG8DI9VodbBCN9SwE3siBqqcbZ6yqdC6iXLTmC0KPEPd9KF0GBV78wI28S7Y7BQ6CYr2SnlsDC/KabXg6EIwgtbsaKoP7d9+ToGb6V7hYTs4qZ3+v6oB7igz4Q7mIjYzla7LBHc1hRM1q7wUMk9iv5KSXwpqpK08sBcwSBj88xvDushKX72egvfCvdLZ47V5VJpjJJZ4e6n+OOZWhNSGdE65bFFXsGCdAhyeblgPnCsMR9KFOgpweiSNarO0KZeQf+SM5gNfXMTt58wWwAtkA6Idp8crtKqlYCT3BBa/NywBxBWOLgPCNs6QYdGLbSXRg/rwcbgedtzs1+3HEECyj7l6JFFkgnRFtWllfpNUiAThxtXg6YIwhb3APY8h+YSbOtdAegCfEOTPNCYmbr6siaMYpNky2QTog2o+CuomqVABz+ZPVyAI4g7N4daMeFaXHAVvq8iA68Mq3ZJhPn2aHZhUaPurLBPSHa7OK7CqxOAh3YiVq9HNDB0RY3rj0+hbindtz+rfRNicpG4FFaArvPDs0uLYoW2SCdD2128V0F1iKBDkxUcHVm8D6leTmAelJHELY4cphv9wYSasBW+kbJZx14kpfAjGVfUjIGWmwuq/iJIg8/C9qSkrzKrkMCnxv3GU59n2leDqCa1I7cFvcAjY8ylkImw8fAFkw807EOrCyBXWeHQoGH/zfR6k4dyCOS0GKX65pLhV+jPSyuq4DqJTAMPXPYwE5h0bwcAAT6StviwPtBF+gEYSE2NawDsyUw+Jss7rXYgtZ0WIEBnwNt9S/fVcEcEhjBohK7XqGlaV4OIJQ6grDE0fzDykdyZ61GfETP+73e3ttMemS25rCr9AUzGQMtskBCZ0HrbIkr8iQSuEPPfTEvJBYvB9wRhCXuCT7TiC7IXE3uyOgGPXai60+6+nacHbpTTnywjhYr1pl5ODN4PxHaePlcOZqTwAsUSez4HGxupns5wJDYDo8e133osviF+8EokTLcYoCdJzZ9najfxG8YyRhobXBPg9bdClfsOSRAepNg7+OzMVQPDhtK6gjCiJu2H9FeP3s6jvqF8sSuC/u5e+M/eDq9/Q95XGeH+ksNTGGgtcA9D9pAoVzJWpYAWQX6LAk0RxAl8H7n7NC/hbZEO11lViaBBeufRp8K6guWBsyCoKx4/hbasrK8Sq9DAngnaTt8x/1THEG4k6bF6meHppXiz/W30PrlcaVoXgIjXop6QSiOILypExLoZ4cmFBGU5W+hDRLJlahxCdypJa8ThuQIwpkuMdI4OzSxHH+2v4XWL48rRfMSePkH4OYxCgCNof0P8JE6A73MN7UAAAAASUVORK5CYII=\n",
"text/latex": [
"$$h{\\left (t \\right )} = C_{1} e^{\\frac{t \\left(- R - \\frac{\\sqrt{C \\left(C R^{2} - 4 L\\right)}}{C}\\right)}{2 L}} + C_{2} e^{\\frac{t \\left(- R + \\frac{\\sqrt{C \\left(C R^{2} - 4 L\\right)}}{C}\\right)}{2 L}} - \\frac{e^{\\frac{t \\left(- R - \\frac{\\sqrt{C \\left(C R^{2} - 4 L\\right)}}{C}\\right)}{2 L}} \\theta\\left(t\\right)}{\\sqrt{C \\left(C R^{2} - 4 L\\right)}} + \\frac{e^{\\frac{t \\left(- R + \\frac{\\sqrt{C \\left(C R^{2} - 4 L\\right)}}{C}\\right)}{2 L}} \\theta\\left(t\\right)}{\\sqrt{C \\left(C R^{2} - 4 L\\right)}}$$"
],
"text/plain": [
" \n",
" ⎛ ________________⎞ ⎛ ________________⎞ \n",
" ⎜ ╱ ⎛ 2 ⎞ ⎟ ⎜ ╱ ⎛ 2 ⎞ ⎟ \n",
" ⎜ ╲╱ C⋅⎝C⋅R - 4⋅L⎠ ⎟ ⎜ ╲╱ C⋅⎝C⋅R - 4⋅L⎠ ⎟ \n",
" t⋅⎜-R - ───────────────────⎟ t⋅⎜-R + ───────────────────⎟ \n",
" ⎝ C ⎠ ⎝ C ⎠ \n",
" ──────────────────────────── ──────────────────────────── \n",
" 2⋅L 2⋅L ℯ\n",
"h(t) = C₁⋅ℯ + C₂⋅ℯ - ─\n",
" \n",
" \n",
" \n",
"\n",
" ⎛ ________________⎞ ⎛ ________________⎞ \n",
" ⎜ ╱ ⎛ 2 ⎞ ⎟ ⎜ ╱ ⎛ 2 ⎞ ⎟ \n",
" ⎜ ╲╱ C⋅⎝C⋅R - 4⋅L⎠ ⎟ ⎜ ╲╱ C⋅⎝C⋅R - 4⋅L⎠ ⎟ \n",
"t⋅⎜-R - ───────────────────⎟ t⋅⎜-R + ───────────────────⎟ \n",
" ⎝ C ⎠ ⎝ C ⎠ \n",
"──────────────────────────── ──────────────────────────── \n",
" 2⋅L 2⋅L \n",
" ⋅Heaviside(t) ℯ ⋅Heav\n",
"───────────────────────────────────────── + ──────────────────────────────────\n",
" ________________ ________________ \n",
" ╱ ⎛ 2 ⎞ ╱ ⎛ 2 ⎞ \n",
" ╲╱ C⋅⎝C⋅R - 4⋅L⎠ ╲╱ C⋅⎝C⋅R - 4⋅L⎠ \n",
"\n",
" \n",
" \n",
" \n",
" \n",
" \n",
" \n",
" \n",
"iside(t)\n",
"────────\n",
" \n",
" \n",
" "
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"solution_h = sym.dsolve(\n",
" ode.subs(x, sym.DiracDelta(t)).subs(y, sym.Function('h')(t)))\n",
"solution_h"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The integration constants $C_1$ and $C_2$ have to be determined from the initial conditions $y(t) = 0$ and $\\frac{d y(t)}{dt} = 0$ for $t<0$. "
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAJcAAAAVBAMAAAC5yWGZAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAEER2zVSJ3ZkiZjKru+/kt61jAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAB90lEQVQ4EaWUv0vkQBTHv1GS2+yiLginKLriHyB7eK2LHNjK2ghWrijaiK6CWOqBjZWWFkL2T9jOO7SwEUQtFOy0sLGxUfEHooW+9zKZTLJuEJxi5vvefN43Q+YlAKxefH+4Y77H75HvewF7Z+xi3/NsDZwcuSVWejiT61qHoi54yYxT5rnwC/ZMhZUeQ2jb1IEWdcEZRsSsa4HURqQ2XYZzqj0CUR8MzYazRPcFFbI27as3EMnWB7WZ88QV/yJlLatokLSZTQC1mVfmis6g7McqqRyZvQaZYE0AxSw1CMznA1rWHKXglZB5iKQpSAALzHoVYKXKCugYlMXimc2eJTQmBVrTJ/ySYYJekZptkZK3spXN9JfDwlwJDTUnU2AKqZBUoHtehLVGRivsYVdhhwjoAuyaC1BgS4/7ph+rQOcPZagF/A5zyM8wazpFWj4OXUVCWtFBOmuYKXB8k/a5ab08iYmoWfoKdDdZ0yoE1Xcjmz6IOQ7YzKYeGKU6dTK5TSyhu2o9Rs0CEDvylBAEdJ+h/fKwh8qUmfQZfvYfA8uxoynQlX8EDNAwU88335mfsmNmCtzGf6X0Ep5MpWrN6FY+Ge7F7t94Wswar3TanXrJ68AXrbHYD5vf3+/iG2ucsK7jaTOumEGStm5kd+sgCfriXma2CHwAJpmAO532qpoAAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\left \\{ C_{1} : 0, \\quad C_{2} : 0\\right \\}$$"
],
"text/plain": [
"{C₁: 0, C₂: 0}"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"integration_constants = sym.solve((solution_h.rhs.limit(\n",
" t, 0, '-'), solution_h.rhs.diff(t).limit(t, 0, '-')), ['C1', 'C2'])\n",
"integration_constants"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Substitution of the values for the integration constants $C_1$ and $C_2$ into the result from above yields the impulse response of the low-pass"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAiIAAABeCAMAAAApFY+LAAAAPFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAo1xBWAAAAE3RSTlMAELvv3c2ZVESJZnYiqzKBxeNgQeo2UQAAAAlwSFlzAAAOxAAADsQBlSsOGwAADY9JREFUeAHtXYm2qyoPRts613/w/d/1Mg8KGCK4aXu71jlbIQS+EDFAiITc+Gswda3jlv9HUE3BNJ+VwVT2BbAR4homRCHSrphSZ2WW8YwiXz4K9+fDRgiweSMKkbXFlDovMw/nNHkoULg/HzZGeG/MeEvepbqyRTUHARyF+/NhIyTVo4b25XWoql8OSSKhn8dTyc667IIa1HRx8AUK9+fDBsvHInyhntruMIhMhxRVyYMahpu6Cf3tdEYbUjVNkeUChfvzYSNkt5q+SSjdqEFknuepZyzUm10nkHGb57GjCki7fKVq4v2N2yjM3kEPZpydlzhnIgr358PGiPD0FeBl2vU8eeFPfM/0RTxfVgIZWPIsXhvtcYgRNsfwVPzNU/1EjWuKD/AvCvfnwwZKxyELPd4O0f6mER3bPPkI0LABgKfYCWRmyS03MrrjBHkSijDrQWwUWkfLdKhJ+L6NJ/cY3F8A+0QqvuweNXcdRSfKIYLxFXaclUDIu+sn0e9jQ/RrRDaiX4SKtFodzPulv8FgReH+fNg+FThLG/d9FyvQq9eFfDuIIYKXGLiqWQmEPBqyPJnp+aKrsPp9IvivAxEq8tC2qeDAspdT21YwufJ/Cu4vgo0RWauH9/PS80MaqbOcor7lYEKLiiffSiANG8od9ksnfgNpaEGuIkIbODtrUWrTenPeKCSF07A4j2+CHUfqzzVPsT/fSl2acRM2hRoSVq4yPUsUHWwlED6UP4bGZ3sudN6zjVQRONHMuZoXDXkm6K3VwJRLOO6vgp0iIkl7vl5hM202biVMep1r6OZpFo+8UBuT0L9etOe7UdPajOgcmasIJZrnVhRVQxOlc95XbrlMd0m4vwc2RnpDmmHf8VeAsCJ21V1e8LIYjHqas6sk220a7q+BjZEfX9KAF1w22nn+lWuz9AVnZ1M21tTKmRjZRNmu03B/DWyM/CZpgELLtltDzBqXU6q7ZmPSibH+zYmt0gXBF4m4vwU2WD4W4Ww9uyZZL52bJHk1bLNlVrrZdie7OYA7Z4cnsQMB7PckXtzfD3svhui93E/9z399VPbS+S7/9XgFRwtrHNiVOr91yvb/Oy+ApIjhdmC760WfDhsjLTkr8auItXS+592LSc0+Oe/9/8upSAy3A9u1mD8dNqJ/5qfYkfIOuNbS+ZE1Xy89JmdN6dXCS1aujFkUt9kxoJSuipDPho2So+wEv4ropXObdX5f5iNHWV85FRG7jVRVfDaYA1upyLGR+VPKw7Y7EnitHB+0qMziOF3W0kvndiqQsyYzjiM6CXpRTkX2uG2ABvZINwqe9J/akoK2m9PhcZeDnQRAEtNpCd9f0SpiM4ktndt0sWvbcSRG580rJ6sYbhe2GkW8DQwnXsFdDna4veGcpZv4xMSnIidL52GmVo7jOGKlwy7LySqCewcbpyKXcJeDDRO7n8o/o/HTpqReWx8tOKORIM5x41TkEu7ysFO6UNH6RhGVd+XvtY24P1o6cwC76yJOVuTmEu7ysCMtD2aVapXtOBKsPJhRSnFNhVXiLg/bCAB+xRcU4eRgSttxBFxIE5aXVZW4y8PWEk64WEstUhnHkYTWKNKxuPNqlbjLw1YCTvl7h5toSnsEbYczBBIqqhJ3edgJEtKkDd3cr++X4FiKbHyVuMvDRknrIbxRUWWLFYI7lqKbUCPuG2Bj5FWj5iY5lmJA0zIV4r4DNkZa5jQcpnSZMsVsSau5FeK+A7YlAfBlqdkfuAEewgm3sunhFE6qEPcdsMMCieSkucBHGOXLKhMrate++nDfAnsnBdCtOW0NIr+BSB6uLlxTdbjvgY2RqnVOElO8QJmp+KoIa3R1uO+BjeqvsLsyit31Qjc16KZqwPKorT1Ww1HheqzyuS/P2mMc8M0Vpg1n9WB4Xihz1hwD1lxdqC6t6MUzUmmVnVOfREyczZHwIXBe+LwOTlEX7ttgA6XjkNlHJZ2MP7mZjArI+mm8RbME7JwWtdQF0daqcN8HGyEpQi4+jag6Q4WWw5oIjWNkjH3lntyIQwuBs6Mh5rv0inDfCXsnhcBtfj//AhxF20d2nEHGNTFh0HoRyCh1talAK7OzLAA7oAVfkrxu7KTCpt4+asGrkwfD6dGXr/x9J2wdQTVrn72Zz9O6yaB5etn8KddOXjIja51JzL4MdjPOM4uVm/Ono3ebCKoZ2Tcbm7X0fCihF8LpZni3W/vm0xmYo1YB3J8AG9EPAwuTumZeu6RDv9jFLrJ3OnMrZFTx8dSgIU0RQkBuyiVwfwBshIYsfLjO/TEPupAjonebCKqItoWKtNub/jZlgqg4ecoUIZDTSUVw1w87JNJYestiso+oc6oxttQ9h/Ms4jP1YPMZ8bZhbXjI1itThFop8aax3FK4K4d9LpgjRanIICJ6txVB9Vg1OoWbIpN2sJUq0ijbhEDC2hXCXTtsjMy3zFaIbIOM3m1FUMU0zl9G6MJTL6e9xOR3YGMHN7shL5oyuKuH7ZdoPFWOzmqJIU4MzpXRu+0IquCy54RsuOjN4oc8DznSVRHxgaTJFydkx7YI7iphmw0+c7UTRvyWW/9NXZtX8RbTTw2w1XezQyPnuO83De3Li3aAnbwPxI2DbW1ZYfcWZrosAhDpWbfdmd90s63Tcu1laSe5ZAaKL/V5uIGwm/ZhnabMuMN5ZxfnrssaURjrxZJQ7qpq4heE/dJmGsm6w1kT+MS27Pbtbvm4UWITS5AHYevNq8s7nCWa/Tc8rUjxdBDxGauoDzT/DRh4rQHYg14OoGtGkptaVjRGPryar6B0/IC8nlr9h5lboG4JwB7Ni7bCHU4QsgJEi9nbFeHa9nV8pYoQP+wX/bbcLEYY5A7nXno/cf+dKuLtumZjbvN0CYD+ojuc3dP6FQ/e4m1rTYk/pCI93wd/c4sMtcNZU7/d2JYfUhFhmT648YXY4Wxe1tjC1iezO1lWw1DpnxhOHw8OXA+n1TQzd0PoFyjZrtsiHHtRO5xKcj/293dGEbHJKWc10R3Of20R5yH4HRWZuLPMYyQT3fVG7XA6gvudm99REWGn0vcMe9+gdjh/RyscpL+jIsIVdBTfucXtcDqSw960ua2sVH6pDc+jIh8HmwS3+lIFmEq/6plBasm/os+iIp8HmwS3+kp3RCS6EsSzqRnH9xt1cgfC3Qs+yzZeBDYBtAwPG8LdC5sarHbDvDucgYLXkiOxfCwfp3AdzJ2hM3tNYcJDDtZv6sAIkxCBTSC48bAvnMEPbPVh8KeU0WEbmrmlB1omsigfaePjtMua6Wu8fbctj2zKfE/l2k6sWhV/ZX5v20seyIF0RYznlbwwbOtb5y5uDGySF7d/q++KHABlF/XZ7fkxs9dFPz7lRqvycaJfItxnkY1vGqzscAKbsQNU5Kktns0MOdciQwDQBUnCsLVvlwd3OmxSGe6gQCIZb3G0qWmf0p7o1NFJ5e/lyVr54Rd2xEm8HC2nhkBVsxbVap1o2NlfgbIlksOwSRh3Omz6SVj1aNSBGyFL9TS9tAeTPtqkfJw8WeIcLt2eFiqyKvUKNmCdXkpUsz5ERal1rcGSZTIisLVv1xF3MmxSG26MNMXnnsloPCTVy1P5OHmyqGrwulYx8C5e1zCnNSPRKiLLimzlAuEQ33AThk0iuJNh00XRunAjRCvtjcWyDxp5pkV+OsWXJU2RRQyiCx0fVns2dmzHvBhRbcr4YWSwyBBHhhdTIrBl9ApqXhmTSYlEPhFg2KQ23BixyQDHo7QtbBbyAfdlDVtLo5i08shru65rPKQJs8PV0zRYpggwMoTdqjzXEdjKt8uDOxU2dzWsCjdCeioI3VM4JDgcpI+TL4sHA2ne4v3y4MvtTtH9DZtFK1GNtikCigyx53b9PgabhHGnwuZ7bzXhhkuu0Wuhs5zfPixPfJUpHVh8WS9hyTrjgaz+4OZE07mPshKVY4qAIkPAgcUpYbBV9AoP7kTYteCOS8Wbuz70+S71un2aGB69Ol4rVcSXJWI1NMCQDQv3qlMqokwR4duup0/elmZNBMJWKuLBnQabVIIbIcS+b5VC6OO/ei2EGpCKpfRx8mQNInRdv2lVU2W8fwcWhYiGIXoz1oOyesQcGBIZwss0OREKmwRxJ8ImdeBOFhQvILFSx0hVflEdR2hMDfmTPk6erE68lrhBp8YcVSr49yF0YpRWj3zFQSJDBFkmZsBgK9+uI24UbPL3uBPFJMifQjesb1/0cmAwGqLno/usZpWv6Ynq1SDDTp03Q0wYiRy/R2n8QCJDnPMGUoBgh3AjYcv1gT/FDRSPQzaJWYW9Jtp0dA+vsztcR9DcZY3sx83crlXmrsPdd9PReC7t3LzpH/rSYf8LKlBkCB9DTBoINgngRsEmVeDGyEqottnI9fPY+Tj5ia6l3hwZgo9kZ7D3vl3XEPpL34zb34h4KrdBz7ZZb9hjUztm8dZmywXB3vt2ZavdYnQzbqtm8OVCJyPD6XzE8XEC804gvM9vSjQKBtv17UqAAya9Gze4YTYhnfeef4XL8XGyS+e6Pt/+y1WT5AOCTb4PN0aMA7Uaz8tZPk7nxOkU/sgQ6XzgJWCw7TAOcN5wyvtxw9tmUT6V45CV9gOXPwob1bMTYBBBMa670IfB/geXx9FKv4zeLQAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$h{\\left (t \\right )} = - \\frac{e^{\\frac{t \\left(- R - \\frac{\\sqrt{C \\left(C R^{2} - 4 L\\right)}}{C}\\right)}{2 L}} \\theta\\left(t\\right)}{\\sqrt{C \\left(C R^{2} - 4 L\\right)}} + \\frac{e^{\\frac{t \\left(- R + \\frac{\\sqrt{C \\left(C R^{2} - 4 L\\right)}}{C}\\right)}{2 L}} \\theta\\left(t\\right)}{\\sqrt{C \\left(C R^{2} - 4 L\\right)}}$$"
],
"text/plain": [
" ⎛ ________________⎞ ⎛ ____________\n",
" ⎜ ╱ ⎛ 2 ⎞ ⎟ ⎜ ╱ ⎛ 2 \n",
" ⎜ ╲╱ C⋅⎝C⋅R - 4⋅L⎠ ⎟ ⎜ ╲╱ C⋅⎝C⋅R - 4\n",
" t⋅⎜-R - ───────────────────⎟ t⋅⎜-R + ───────────────\n",
" ⎝ C ⎠ ⎝ C \n",
" ──────────────────────────── ───────────────────────\n",
" 2⋅L 2⋅L \n",
" ℯ ⋅Heaviside(t) ℯ \n",
"h(t) = - ────────────────────────────────────────── + ────────────────────────\n",
" ________________ __________\n",
" ╱ ⎛ 2 ⎞ ╱ ⎛ 2 \n",
" ╲╱ C⋅⎝C⋅R - 4⋅L⎠ ╲╱ C⋅⎝C⋅R -\n",
"\n",
"____⎞ \n",
" ⎞ ⎟ \n",
"⋅L⎠ ⎟ \n",
"────⎟ \n",
" ⎠ \n",
"───── \n",
" \n",
" ⋅Heaviside(t)\n",
"──────────────────\n",
"______ \n",
" ⎞ \n",
" 4⋅L⎠ "
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"h = solution_h.subs(integration_constants)\n",
"h"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The impulse response is plotted for the values of $R$, $L$ and $C$ given above"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM5MC4zNjcwNDU0NTQ1IDI5My4wNTEwNjI1IF0gL1BhcmVudCAyIDAgUiAvUmVzb3VyY2VzIDggMCBSCi9UeXBlIC9QYWdlID4+CmVuZG9iago5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTEgMCBSID4+CnN0cmVhbQp4nIWZT48ctxHF7/0p+mgfRJHF/8cITgTkJmuRHOIcDFmWLWgUKLKjr59fsZs9M9u1WC1WO8NXj8Umi1WP7LB+XML6YfXrR36/rf9a/83fX9awvub3w+L5dlli9y6W6lPm66fbr9Kj8zn4IrT7+6+/Lcuvy8u/0M1XaK+X0F1ptdQ1eFe111pc80fDp5sG0U9BOzlI16a9X9n6/cA4GbtrN6PHmyJLFhdyDJLXklwKUXzB702rd31r/bQsr5iIb8urh/Xl3wIjWh9+XVJzvcYUa15Tx3tPuSTxaX34ZfnOf78+fFz/+rAM30sI1fmWfEx3zm6bn/EWQnTdp5hK7r4bHuWRxybOh9RTvPd40/ycx9pci1lyLi00w2O69yipOPCW5c7jbfMzHiVFV0sJJdUq1fBY7j3GEJwufwl3Hm+bn/EYfXOlV19jK7EYHtsjj0cQ3jm8tj7nr3qXUpOeEz+Gv3AEziNeci2VGgdzjcWFVHMLB++P+3FeozhGJ6nzjIyTiC2PW49xfuF/v77w7Bihkxpa1R3sUpYmIs239d3lflTNxdo6+1l3/oh6N6JwYRxfGInXHvmZH+C//OH9x5//8efbnz9/fXH5/fOfX9cf/rO84efxuG/n9zrua+sTEdR5rqIjZyUIpBivU8Qwnpqknl1m+cK9s2vrc856cLV2NnLOvd/OhOUsSHE1eeHjrbeb5ufcBRG2VIy6gj3v/tKT/nIlc0RS1b2/a/Oz/nJypO2WW4vz8cqT7lp3vlT28r27a/Oz7lp2Uj1FpNdWdn/tKX9CtEr0lfxy6++m+Tl/EopjNlutgfS4bcOnY0VycLEnIbvc+bs2P+svVZe7phzJte7+xNz3uhtf6OYJydWupUZKJdZkfH64jBKsHfz203d//PT97OPLOiujH3lmlNDIglMipZA8+Pvf9+s/189rcJna6EECeb4I3RJLZf9XefzqWXehEPT1x9crG/h/v797/+PrV+u7r9cCfJ/xXY09kk/vtutbE7joxJTWss8ncwMg2WZKZsgSHptbACuEGslUn9NgLADzpAm8l1PvFjDWv5YmoZ/MDQBxwWxXKvhpMBYwzFuvbFTD/AQM6eJ78dTqx+YGsCmdyJIb1o/bN2MeJyIbMrmA8hCv1o+BYS6lkzNWwjW0krZK89YEhjmh59l8jZ2XIwXxMD8BmCOFpAqzFXxyBVFUp72FQGCDk1/Rkhhozit9tzcAzBE+jcrR2UbB9RyCD7u9hVwWik0LRdpIJaGUOKQo9haAuS5fQrOSpSo1NPp9Mi0Ac832lZ2wCoW/dq9berO3EAjR5eSrdpMCesPrE24EC4FAfk941tyU2aM59fkAFjIIFEbPWiMjnE813BDOCARSekTodBIlIZCC95NgIYPAfgvaT9Y6TES2g3BGILCUlXrIXGtlYxLrfGgLGYRKuBIgkrU25TijyEQgELFMAMpUWFehCvdJsJBByKGTO2mmOrCTmhyEMzII4zSAY5Y20JzKQTgjEBplqfg6Wpv39LPbG8AwT4VOtApE0l+/MT8Bw7zWmrS60YpqRS4f9mcEgq44RVvdEjhEo8zxW8ggsBwp99FMxW/1sD8BwzxzIIGqrWTv5Pthf0YGoRGHupIjMJHP8SCckcuCPieXhZJH86793hrNwzRX5nV7pIJwm+FgIoPQfG95a0a8pXQlnBEImvP07LRNgmeW9zxkIoOQC8EaxrJUMudM6iYyCC2n2rdmtmG+8XBGIGzFwYctsFCPhwcLGQQGOmQPkd5Lkd4OwhmBECkjYUQi2gMF0/YltoBhzokxqbBhr0rw1V/tzwgEwo+s18LIBihu1nUnWAgEdEVChhBa6GBOPGXaG8Aw7xLGWmZkcq1HMTARCCSPTtZnnIiMRMmdudREIDTdG5FyLrE5/Ic248hCLkvT81xsKH0OcogkBN2+zUwEAufZ1rVuBY62bJJW90UzkctCMYwtVLQXE06k9TzDwkQgFCcsCUsYvOZzQXvvBAuB0Mk4UcjcjaLHWWQqCgu4LMETg4E9hUQqmi/r3r0FqDlrH1XlrsRKidJKmfYGogSqYcisyErVYmd5aZNgIEqgoAfEb19T0Ywf0zEiA1ECOZYMRVoapZpCmifBQPQyiaBCXOWA1Ce5EWT7TjARJXBs7TWHtEamzot+2gkGogTZboT6GukRKZAODwZyGZdWLF/VvNkcCU7K4cFAlEC+zFUIKgRQku6vHgxECeOQXkYeR6qUY/OYiBIKUVizV/ngPIHQ5rRayHZHl1XYqmaicmXNWDvBQJRAMfWtoaBF5RYxdhAMRAmdxIAoptgx28jpfDyDgUAQdlIX9KE21z5D9dSspmTNRiZL6jLwdHmGnYUoIbN+VHMeSY8Mxz44t6sxWUaY2KyLEjP9zUe1EAgRNp79iEQOgwjEnWAhEJLqqRJJraTAlkM+PFiIElhF3ytxQlKuzMfUjSYCgVzcs9Q+7icrU9x3iWAiSiBDIbtT0wxCqMdZ900EAuWNvE9tWVVHCMe8uQYWogTyALWOHEWRlF7ykVwsBILqATIxy0PV86m06cAA1JzR5U4Y0gk699DiFrDdGVcKCoqb7oSj4Tx/mIgSqEM5lsg8dOaBmjdnyEIg9KQ5gKOMHgv1JmJmdxO5LMiXcb1HeeM4kNlHM45MRAlMHIJ4ux1g3o8pNREIpEAUsUYL+ke6ZpKdYCFKaBwVStQzPLMS41FkTQQC247S6/VKgUJBeYx74JmIEpiylpreg9IPuzH2STAQCOyp3nseA0WPkrB2ewPQexskAPUtijZnFJ+f9haiBE4l7DxqNc2dw3mfA7IQCBzYutcHGpcLnD7nQdxEIOjzS+vbbQTR5fdAsgA17+Thmuu4MkIJRZn9WwgENBmFTrZrnapTOB/ZQiC0qKWUbDOahe/7XjARvd3SeyZBZY2Bcm49FsFClJBd4sATRz8Z1T4luYlclkjE67Vx3W5sOApMoWAiSlDhWmS7PUJ3zLscC9DXKSQ/ZNPohLDkPLObG4CaM3GN7D1eA3EqjvMcbiIQRI8agW+jOdY894GJKIEkElAleytlddqfAcwJdhITAmA0p67H3M3eQiBoZamayEczJ+04rxgtRAmFBW/7uzZST0wHwUD0DnM8GGszmlEaYd5hngE1L3rmlP1KblwD7OZnAHP2BpV3riOCMu+7wESUUDlO5rDNA6f6457CRPSFV9B3emF/1UdmmIrFRC6P3ptJj9P+zfpllfXv2yvmu9e09xfNt/f9u7S5abo9qh/vlL+N98qP3iNfzPfIy+fjlfEYw90L6Sfe9N1fmj7yenox/aTfN8v/ASCyK7gKZW5kc3RyZWFtCmVuZG9iagoxMSAwIG9iagoyNDkzCmVuZG9iagoxNiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDM5MiA+PgpzdHJlYW0KeJw9UktuBTEI288puECl8E1ynqne7t1/W5vMVKoKLwO2MZSXDKklP+qSiDNMfvVyXeJR8r1samfmIe4uNqb4WHJfuobYctGaYrFPHMkvyLRUWKFW3aND8YUoEw8ALeCBBeG+HP/xF6jB17CFcsN7ZAJgStRuQMZD0RlIWUERYfuRFeikUK9s4e8oIFfUrIWhdGKIDZYAKb6rDYmYqNmgh4SVkqod0vGMpPBbwV2JYVBbW9sEeGbQENnekY0RM+3RGXFZEWs/PemjUTK1URkPTWd88d0yUvPRFeik0sjdykNnz0InYCTmSZjncCPhnttBCzH0ca+WT2z3mClWkfAFO8oBA7393pKNz3vgLIxc2+xMJ/DRaaccE62+HmL9gz9sS5tcxyuHRRSovCgIftdBE3F8WMX3ZKNEd7QB1iMT1WglEAwSws7tMPJ4xnnZ3hW05vREaKNEHtSOET0ossXlnBWwp/yszbEcng8me2+0j5TMzKiEFdR2eqi2z2Md1Hee+/r8AS4AoRkKZW5kc3RyZWFtCmVuZG9iagoxNyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDkwID4+CnN0cmVhbQp4nE2NQRLAIAgD77wiT1BE0P90etL/X6vUDr3ATgKJFkWC9DVqSzDuuDIVa1ApmJSXwFUwXAva7qLK/jJJTJ2G03u3A4Oy8XGD0kn79nF6AKv9egbdD9IcIlgKZW5kc3RyZWFtCmVuZG9iagoxOCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE2MyA+PgpzdHJlYW0KeJxFkLl1BDEMQ3NVgRJ4gDrqGT9Hs/2nC2m83kD6eIR4iD0Jw3JdxYXRDT/etsw0vI4y3I31Zcb4qLFATtAHGCITV6NJ9e2KM1Tp4dVirqOiXC86IhLMkuOrQCN8OrLHQ1vbmX46r3/sIe8T/yoq525hAS6q7kD5Uh/x1I/ZUeqaoY8qK2seatq/CLsilLZ9XE5lnLp7B7TCZytX+30DqOc6gAplbmRzdHJlYW0KZW5kb2JqCjE5IDAgb2JqCjw8IC9CQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDM3Ci9TdWJ0eXBlIC9Gb3JtIC9UeXBlIC9YT2JqZWN0ID4+CnN0cmVhbQp4nOMyNDBTMDY1VcjlMjc2ArNywCwjcyMgCySLYEFk0wABXwoKCmVuZHN0cmVhbQplbmRvYmoKMjAgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA4MCA+PgpzdHJlYW0KeJxFjLsNwDAIRHumYAR+JmafKJWzfxsgStxwT7p7uDoSMlPeYYaHBJ4MLIZT8QaZo2A1uEZSjZ3so7BuX3WB5npTq/X3BypPdnZxPc3LGfQKZW5kc3RyZWFtCmVuZG9iagoyMSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE0NyA+PgpzdHJlYW0KeJw9T7kNAzEM6z0FFzjAeixb81yQ6rJ/G8pGUggiQPGRZUfHClxiApOOORIvaT/4aRqBWAY1R/SEimFY4G6SAg+DLEpXni1eDJHaQl1I+NYQ3q1MZKI8rxE7cCcXowc+VBtZHnpAO0QVWa5Jw1jVVl1qnbACHLLOwnU9zKoE5dEnaykfUFRCvXT/n3va+wsAby/rCmVuZHN0cmVhbQplbmRvYmoKMjIgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNDkgPj4Kc3RyZWFtCnicNY9LDgMhDEP3OYUvMFJ+hHAeqq6m9982YVoJCQvbL8EWg5GMS0xg7Jhj4SVUT60+JCOPukk5EKlQNwRPaEwMM2zSJfDKdN8ynlu8nFbqgk5I5OmsNhqijGZew9FTzgqb/svcJGplRpkDMutUtxOysmAF5gW1PPcz7qhc6ISHncqw6E4xotxmRhp+/9v0/gJ7MjBjCmVuZHN0cmVhbQplbmRvYmoKMjMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA0OSA+PgpzdHJlYW0KeJwzNrRQMFAwNDAHkkaGQJaRiUKKIRdIAMTM5YIJ5oBZBkAaojgHriaHKw0AxugNJgplbmRzdHJlYW0KZW5kb2JqCjI0IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzE3ID4+CnN0cmVhbQp4nDVSS3JDMQjbv1Nwgc6Yv32edLJq7r+thCcrsC1AQi4vWdJLftQl26XD5Fcf9yWxQj6P7ZrMUsX3FrMUzy2vR88Rty0KBFETPfgyJxUi1M/U6Dp4YZc+A68QTikWeAeTAAav4V94lE6DwDsbMt4Rk5EaECTBmkuLTUiUPUn8K+X1pJU0dH4mK3P5e3KpFGqjyQgVIFi52AekKykeJBM9iUiycr03VojekFeSx2clJhkQ3SaxTbTA49yVtISZmEIF5liA1XSzuvocTFjjsITxKmEW1YNNnjWphGa0jmNkw3j3wkyJhYbDElCbfZUJqpeP09wJI6ZHTXbtwrJbNu8hRKP5MyyUwccoJAGHTmMkCtKwgBGBOb2wir3mCzkWwIhlnZosDG1oJbt6joXA0JyzpWHG157X8/4HRVt7owplbmRzdHJlYW0KZW5kb2JqCjI1IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTMxID4+CnN0cmVhbQp4nEWPyw0EIQxD71ThEvIZPqmH1Z7Y/q/rMJpBQvhBIjvxMAis8/I20MXw0aLDN/421atjlSwfunpSVg/pkIe88hVQaTBRxIVZTB1DYc6YysiWMrcb4bZNg6xslVStg3Y8Bg+2p2WrCH6pbWHqLPEMwlVeuMcNP5BLrXe9Vb5/QlMwlwplbmRzdHJlYW0KZW5kb2JqCjI2IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjQ4ID4+CnN0cmVhbQp4nC1ROZIDQQjL5xV6QnPT77HLkff/6QrKAYOGQyA6LXFQxk8Qlive8shVtOHvmRjBd8Gh38p1GxY5EBVI0hhUTahdvB69B3YcZgLzpDUsgxnrAz9jCjd6cXhMxtntdRk1BHvXa09mUDIrF3HJxAVTddjImcNPpowL7VzPDci5EdZlGKSblcaMhCNNIVJIoeomqTNBkASjq1GjjRzFfunLI51hVSNqDPtcS9vXcxPOGjQ7Fqs8OaVHV5zLycULKwf9vM3ARVQaqzwQEnC/20P9nOzkN97SubPF9Phec7K8MBVY8ea1G5BNtfg3L+L4PePr+fwDqKVbFgplbmRzdHJlYW0KZW5kb2JqCjI3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjEwID4+CnN0cmVhbQp4nDVQyw1DMQi7ZwoWqBQCgWSeVr11/2tt0DthEf9CWMiUCHmpyc4p6Us+OkwPti6/sSILrXUl7MqaIJ4r76GZsrHR2OJgcBomXoAWN2DoaY0aNXThgqYulUKBxSXwmXx1e+i+Txl4ahlydgQRQ8lgCWq6Fk1YtDyfkE4B4v9+w+4t5KGS88qeG/kbnO3wO7Nu4SdqdiLRchUy1LM0xxgIE0UePHlFpnDis9Z31TQS1GYLTpYBrk4/jA4AYCJeWYDsrkQ5S9KOpZ9vvMf3D0AAU7QKZW5kc3RyZWFtCmVuZG9iagoxNCAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMgL0NoYXJQcm9jcyAxNSAwIFIKL0VuY29kaW5nIDw8Ci9EaWZmZXJlbmNlcyBbIDQwIC9wYXJlbmxlZnQgL3BhcmVucmlnaHQgNDYgL3BlcmlvZCA0OCAvemVybyAvb25lIC90d28gNTIgL2ZvdXIgNTQgL3NpeAo1NiAvZWlnaHQgMTA0IC9oIDExNiAvdCBdCi9UeXBlIC9FbmNvZGluZyA+PgovRmlyc3RDaGFyIDAgL0ZvbnRCQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRm9udERlc2NyaXB0b3IgMTMgMCBSCi9Gb250TWF0cml4IFsgMC4wMDEgMCAwIDAuMDAxIDAgMCBdIC9MYXN0Q2hhciAyNTUgL05hbWUgL0RlamFWdVNhbnMKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTIgMCBSID4+CmVuZG9iagoxMyAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgMzIKL0ZvbnRCQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRm9udE5hbWUgL0RlamFWdVNhbnMgL0l0YWxpY0FuZ2xlIDAKL01heFdpZHRoIDEzNDIgL1N0ZW1WIDAgL1R5cGUgL0ZvbnREZXNjcmlwdG9yIC9YSGVpZ2h0IDAgPj4KZW5kb2JqCjEyIDAgb2JqClsgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAKNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCAzMTggNDAxIDQ2MCA4MzggNjM2Cjk1MCA3ODAgMjc1IDM5MCAzOTAgNTAwIDgzOCAzMTggMzYxIDMxOCAzMzcgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNgo2MzYgNjM2IDMzNyAzMzcgODM4IDgzOCA4MzggNTMxIDEwMDAgNjg0IDY4NiA2OTggNzcwIDYzMiA1NzUgNzc1IDc1MiAyOTUKMjk1IDY1NiA1NTcgODYzIDc0OCA3ODcgNjAzIDc4NyA2OTUgNjM1IDYxMSA3MzIgNjg0IDk4OSA2ODUgNjExIDY4NSAzOTAgMzM3CjM5MCA4MzggNTAwIDUwMCA2MTMgNjM1IDU1MCA2MzUgNjE1IDM1MiA2MzUgNjM0IDI3OCAyNzggNTc5IDI3OCA5NzQgNjM0IDYxMgo2MzUgNjM1IDQxMSA1MjEgMzkyIDYzNCA1OTIgODE4IDU5MiA1OTIgNTI1IDYzNiAzMzcgNjM2IDgzOCA2MDAgNjM2IDYwMCAzMTgKMzUyIDUxOCAxMDAwIDUwMCA1MDAgNTAwIDEzNDIgNjM1IDQwMCAxMDcwIDYwMCA2ODUgNjAwIDYwMCAzMTggMzE4IDUxOCA1MTgKNTkwIDUwMCAxMDAwIDUwMCAxMDAwIDUyMSA0MDAgMTAyMyA2MDAgNTI1IDYxMSAzMTggNDAxIDYzNiA2MzYgNjM2IDYzNiAzMzcKNTAwIDUwMCAxMDAwIDQ3MSA2MTIgODM4IDM2MSAxMDAwIDUwMCA1MDAgODM4IDQwMSA0MDEgNTAwIDYzNiA2MzYgMzE4IDUwMAo0MDEgNDcxIDYxMiA5NjkgOTY5IDk2OSA1MzEgNjg0IDY4NCA2ODQgNjg0IDY4NCA2ODQgOTc0IDY5OCA2MzIgNjMyIDYzMiA2MzIKMjk1IDI5NSAyOTUgMjk1IDc3NSA3NDggNzg3IDc4NyA3ODcgNzg3IDc4NyA4MzggNzg3IDczMiA3MzIgNzMyIDczMiA2MTEgNjA1CjYzMCA2MTMgNjEzIDYxMyA2MTMgNjEzIDYxMyA5ODIgNTUwIDYxNSA2MTUgNjE1IDYxNSAyNzggMjc4IDI3OCAyNzggNjEyIDYzNAo2MTIgNjEyIDYxMiA2MTIgNjEyIDgzOCA2MTIgNjM0IDYzNCA2MzQgNjM0IDU5MiA2MzUgNTkyIF0KZW5kb2JqCjE1IDAgb2JqCjw8IC9laWdodCAxNiAwIFIgL2ZvdXIgMTcgMCBSIC9oIDE4IDAgUiAvb25lIDIwIDAgUiAvcGFyZW5sZWZ0IDIxIDAgUgovcGFyZW5yaWdodCAyMiAwIFIgL3BlcmlvZCAyMyAwIFIgL3NpeCAyNCAwIFIgL3QgMjUgMCBSIC90d28gMjYgMCBSCi96ZXJvIDI3IDAgUiA+PgplbmRvYmoKMyAwIG9iago8PCAvRjEgMTQgMCBSID4+CmVuZG9iago0IDAgb2JqCjw8IC9BMSA8PCAvQ0EgMCAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+Ci9BMiA8PCAvQ0EgMSAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+ID4+CmVuZG9iago1IDAgb2JqCjw8ID4+CmVuZG9iago2IDAgb2JqCjw8ID4+CmVuZG9iago3IDAgb2JqCjw8IC9EZWphVnVTYW5zLW1pbnVzIDE5IDAgUiA+PgplbmRvYmoKMiAwIG9iago8PCAvQ291bnQgMSAvS2lkcyBbIDEwIDAgUiBdIC9UeXBlIC9QYWdlcyA+PgplbmRvYmoKMjggMCBvYmoKPDwgL0NyZWF0aW9uRGF0ZSAoRDoyMDE5MDQxNjA5MzE1OSswMicwMCcpCi9DcmVhdG9yIChtYXRwbG90bGliIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcpCi9Qcm9kdWNlciAobWF0cGxvdGxpYiBwZGYgYmFja2VuZCAzLjAuMykgPj4KZW5kb2JqCnhyZWYKMCAyOQowMDAwMDAwMDAwIDY1NTM1IGYgCjAwMDAwMDAwMTYgMDAwMDAgbiAKMDAwMDAwNzk3MSAwMDAwMCBuIAowMDAwMDA3NzUyIDAwMDAwIG4gCjAwMDAwMDc3ODQgMDAwMDAgbiAKMDAwMDAwNzg4MyAwMDAwMCBuIAowMDAwMDA3OTA0IDAwMDAwIG4gCjAwMDAwMDc5MjUgMDAwMDAgbiAKMDAwMDAwMDA2NSAwMDAwMCBuIAowMDAwMDAwNDA0IDAwMDAwIG4gCjAwMDAwMDAyMDggMDAwMDAgbiAKMDAwMDAwMjk3MiAwMDAwMCBuIAowMDAwMDA2NTI5IDAwMDAwIG4gCjAwMDAwMDYzMjkgMDAwMDAgbiAKMDAwMDAwNTkzOSAwMDAwMCBuIAowMDAwMDA3NTgyIDAwMDAwIG4gCjAwMDAwMDI5OTMgMDAwMDAgbiAKMDAwMDAwMzQ1OCAwMDAwMCBuIAowMDAwMDAzNjIwIDAwMDAwIG4gCjAwMDAwMDM4NTYgMDAwMDAgbiAKMDAwMDAwNDAyNiAwMDAwMCBuIAowMDAwMDA0MTc4IDAwMDAwIG4gCjAwMDAwMDQzOTggMDAwMDAgbiAKMDAwMDAwNDYyMCAwMDAwMCBuIAowMDAwMDA0NzQxIDAwMDAwIG4gCjAwMDAwMDUxMzEgMDAwMDAgbiAKMDAwMDAwNTMzNSAwMDAwMCBuIAowMDAwMDA1NjU2IDAwMDAwIG4gCjAwMDAwMDgwMzEgMDAwMDAgbiAKdHJhaWxlcgo8PCAvSW5mbyAyOCAwIFIgL1Jvb3QgMSAwIFIgL1NpemUgMjkgPj4Kc3RhcnR4cmVmCjgxODUKJSVFT0YK\n",
"image/svg+xml": [
"\n",
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sym.plot(h.rhs.subs(RLC), (t,-1,10), ylabel=r'h(t)');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Step Response\n",
"\n",
"The [step response](step_response.ipynb) is derived by integrating over the impulse response $h(t)$. For ease of illustration this is performed for the specific values of the elements given above"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAvwAAAA8BAMAAADoAXMhAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMhAi783diatmdpm7RFShYZRwAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAJx0lEQVR4Ae1bfYwbRxV/3vWdz5/nii/RqrpFKElVPs5EQIpScUdAVaUAOSG1fAgRNyAXKVKxKkFDJCQLBDoKIhYhfzRQapGStskfuIWGXg+oW8RHigSOVFBTCWpVAkT7x/lSUaCQHPNmd2ZnZmfHY985va1uJO+893vvzbzfu9nZXa8PQG75pqy/0przkREyWBohZowh2zzrwR+x9rxMjq+zz51llG8waXP0KesllF2IZlwsRzGC5DwtLIDnBDkUB8eFvkTKdiTVRjmmcRo1l1HjpBS+J2kG5bWeYrwO4I0B5D4RCM8f6sIEQFtxlVS3AalgHxsqThqEKk9GITOS2qPY1VwyxD4KB9s4ZXqAQisC6YGPqvBxgEaAXX0gEOadPkrnA1XbZVswFRiGiosONleJYkZkoq6Y1VzyxD4KB9s4ZXoA98UIpAVKFxQ4d7Dncjas/JXUfOkU8PIqIW+m+slfwC5msItj3kLvYOXzHQGxEVc8xUvNBcs4CofBccrEqFIOP9MYNNAkLzUzVqHUZDIrIxS6pRfIKcVw3u849GWAw1SdBPgHwwfGOdHd2rlj0YNMiwxhu3TYbHArlwJBzQXLOAoHY5yRg+UZPOMFGbPOWYBsE9zl5eWfAxxgwoMAjwNu/0prwxmGbAO4i7kPjLvyJAvjfR7y1UD5DQethJR6BoOcS2b5DJIZmsOAOCOHQmRZa6l8U0VL7WaqzUC2ijNe3al2Nav/IsyVA+cXsnCVdRz8jbnyfrrrrgbKdzhIhQoe6UHGmTbVYRLr1VxwFY/CwRhn5JCdZ7n4vcCh7G9PFP+P5LXjVNNdqkAnAK/c2/Ol/WtVuNODNwR42H2blP+ZBjiHH4DdR/mfZ3CcJvWs564W76dDz/XCGcj9LtWeESGAFIB/ySHwdFO06XLBMo7CwRhn5OBeEnOSOOy7qeYBnEZ7SrpCO7f4Nz13S6Gh0g5FLn0Bbr8A28v0pifb5bAkaOKiq5+sz2pm1sPAST8gd6iM2t/xEBCgIh7S/7yZnJo56jhT4TARdLlgGYPmD800v4/lYI4zcjjoD63hUHvpdmKj16tsX0xkqrGriXpO4sM9SmUuciF1wH17FRbdL1LkBMdFQRenS/313k4fzi/Q8LNOlfTkYgTOpwHkB8nJz93qkb9THR3vwQNvulwy3KrLJZ6DOc7I4WF/Sg2HBk8GpnyiAZBees6XvNBDkBwuhw8A13v4iLH3+35E6MFdiRCixSbDNanjw5r/xJXro1umA3gxwO+kSgT4LgulPXvEQOWrksU2lzBo3RxCWiGHH9HxdRwa4cxpQSabaDm0GKXnmdVtpCqzb6JlYpCpL7WYVVP+6+A1zgWaQYleg2e6gBtomnzwdEh7LBZ7sfw3igbrXHjQ+jmEtEIOK5SJjkODzwzT9VAmd8Y9aIl6rMzLf/0VV3l/zcDvIRfrKxrCPKPldx+/4qHSAs0nRa9bX4MU3hj8kXxwk5loiiOJ5f+XaLDOhQetnwOnJXCY6eEEOg5fP/UgOKdbaFZuGpaOe4gObLz8+9bW4JoT8Ja7fjAwBh14nrv2P6oGpNfW+s6dFYQdLLvzMpQukv6nAE//4bctyDSIwtvU8dNluNYfBL3DZpsLj1g/B05L4DCLq0XL4QmY62aK8zi/fIuHiFXj5bfyDp14niGklV4maG4VMnhf9nHyWSGf7AI58Fbw3ItQfwp15R6Pu4xJ0HDQQDDdIvPHcChU34vbKYB/iqA0VBt3+XE7Kfx78cg86W8jH7yNKFXJQWy/dnv09sLfqkTLWGVNrTWQv63HcMi/6NG/DjzbJak6N9ewlS2zPlOrfaBW+6yld+iWr9U+c0Ot1ggRgG105ltECOX/kk+6A7Mt0n+IfPAmOdUnB7E9thPwLIEiblFDchjSnU+r4aCB0H26TQ46DoUFyK/CiodO8upfG9iCErDVPz0wgDngZOHeT+N8iB8DTzoDlp+sj3s80pPyO1hgf7ckAm2/Anis7H9dK6/+wSkpf8bBAWJmWg589QuetPw6DukqTPXhY5SFXP6A2uCOlX+wp+zB85RhVSNXLIDZLhxEw6dI5fvgKZvPDQBHYKKBDnL5ERlr03DQQP6Zq+NAHuXSHecSfaKba46U6pjL7+K9zHS3tAeTe5I8gC2UKso7yDrAB2G2Rzqg3uh5eZqm1hoIaGV1HNw23OsV++/BbGdbhpzdL53v6s2G8scHkaF4nrv+fHd0ZA7S9TzV3F5Gn0PkGatxLXn0aokRuyG3B551mwSj54pok2Q+qISalWE5cFoAfDq6r2g57H7kIbKoMHNItw2JFPfhJU/XDOWPDyID8TyfeqkeHZeD/sX00R9Tlz+R9X2WJDtZESPc5W+QrzseoNBe0aDKfFDVYNCH5cBpAfDp/JsaIwfyKNkxZVGOM5rKHxtEBuN5ntONzMGs+P5kMhjw3boQin0y1kIMfFCTk2KL+aWH76XhwCFhOnrbwMaN45CfZx6avnj1cxoUofMxOIHjg9DYDALP/cULJKHjYL4qoNm2rywJmCz+RFZljQ8qw0ZtWA6cFik/I8bfAuJMcRykdaamVPzKNT0VG6jbBT2981vRkTg42RCNv6SK2xExSZYWmmQhCh9UNRj0jeAgPxfFcHAuGbLQPOoYvQNjqm/jNaNzCkD6fQm3v5VKBY8DqjDbUxFJ184keUSVdXOgX1uF48Zx+F3oEpFK/vNOBDcCdkE9vK1XGwdXKqKJ3t7AURGS5UKwPclooPFBtVY9uAEcStJrRIjjoLzVltKZLg/9kw9yu24VtAqaX2JwMHhTJCVjULLzBiMf1OCjmjaAQ35BHVSraxYh98tArsEVW8EuqA73Rwfk4IejNhNCv5OIc+CDxjlo8A3gkO5pxo1CGcNfyTl8RzRgEGIXtOO+enQgBubmozYj8nmDlQ1qcImYNoDDvZFB9cD79PAriVqunDDFdDmUN4lkewIf2yT5Cmn8UJCtRPlNjFXImJ1yhk1FmnqiJambQHHfP3QSnxg6YswB76xYToA/odlcbXtv6Hy227IdeuTRApzbrOPe5Vm7Xh7Hs8NP48q/wRp+gA2OKDStB3TL1q6XxdHpjjDNO0aIGWPI28Y49tbQWxVIbgXY2+/k9eHvGazfj286ksldN1uZb1VgqwJbFdiqwFYFtioQqUD4X5ERU2KABHOQ35InpuJSognmcLIhMUmkklwOqWPJL3+COWT8Hx0nctGzpBPM4cSroPzJ5eA2k1/+BHPIBP/xwM7jJPYJ5nD0VVD+5HJwW8kvf4I5FBcXj9xYT+KOE+acbA7pRsgkqVKCOUx3klr0MO/kcsjv/18r5JFMabwc/g9zNN6WVeCaJQAAAABJRU5ErkJggg==\n",
"text/latex": [
"$$\\frac{5 i \\left(- \\frac{e^{t \\left(-1 - 2 i\\right)}}{5} + \\frac{2 i e^{t \\left(-1 - 2 i\\right)}}{5} + \\frac{1}{5} - \\frac{2 i}{5}\\right) \\theta\\left(t\\right)}{4} - \\frac{5 i \\left(- \\frac{e^{t \\left(-1 + 2 i\\right)}}{5} - \\frac{2 i e^{t \\left(-1 + 2 i\\right)}}{5} + \\frac{1}{5} + \\frac{2 i}{5}\\right) \\theta\\left(t\\right)}{4}$$"
],
"text/plain": [
" ⎛ t⋅(-1 - 2⋅ⅈ) t⋅(-1 - 2⋅ⅈ) ⎞ ⎛ t⋅(\n",
" ⎜ ℯ 2⋅ⅈ⋅ℯ 1 2⋅ⅈ⎟ ⎜ ℯ \n",
"5⋅ⅈ⋅⎜- ───────────── + ───────────────── + ─ - ───⎟⋅Heaviside(t) 5⋅ⅈ⋅⎜- ────\n",
" ⎝ 5 5 5 5 ⎠ ⎝ \n",
"──────────────────────────────────────────────────────────────── - ───────────\n",
" 4 \n",
"\n",
"-1 + 2⋅ⅈ) t⋅(-1 + 2⋅ⅈ) ⎞ \n",
" 2⋅ⅈ⋅ℯ 1 2⋅ⅈ⎟ \n",
"───────── - ───────────────── + ─ + ───⎟⋅Heaviside(t)\n",
" 5 5 5 5 ⎠ \n",
"─────────────────────────────────────────────────────\n",
" 4 "
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"tau = sym.symbols('tau', real=True)\n",
"\n",
"he = sym.integrate(h.rhs.subs(RLC).subs(t, tau), (tau, 0, t))\n",
"he"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's plot the step response"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM4Mi4zMjAxNzA0NTQ1IDMxMC4yNTk3NSBdIC9QYXJlbnQgMiAwIFIgL1Jlc291cmNlcyA4IDAgUgovVHlwZSAvUGFnZSA+PgplbmRvYmoKOSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDExIDAgUiA+PgpzdHJlYW0KeJyFmU1zHLcRhu/zK+YoHwQBje9jVI5VlUtKNis5JDk4Mi1LxZWjyI7+fp6eAZazy+ZaKha5/faLxjT6C7Nh/biE9f3q14/8fF3/sf6L3z+tYX3Dz/vF8+m0xCYuig+VTw+HTzF4J7nXjNRffPplWX5eXv2JJb7AebMsIbiSfO15lexSqmixbmmulkvpw4W0B5fHkocVDtJhSHZD79k0D+La4VEwr8iSkgu+SF5jdTnFbQOPsuT8JntYltd45Ovy+m599V1Yg1/vfl6Sd11KVk0Rxxbuflpe+G/Wu4/rn++Wzd4SfHc+1pD70cJRettG8Nm1XJPq+n6wI1d2anS9NF/ahZ2D9A/sVO9qa1F1QzvYSZd2JDbXeuu1Hu0cpbftSMyuhi6qK/Vgp1zaiT66Jr21crRzlN62E713JfugurEc7LQrO49hdbRzkP6BnSIu+ZDEp5yOcRDOgXClX1ztnSPtqt+d1BZkp/x2uTUzNHmqS9kzbg5O1hhdTaXVEZjOP7N+rSwqpYajgUfhDQuEV/P6KC1JHFbkGSshsGIhjOVo5iC9YScEDBWSoJSW6jCUnjOUq6vic4gXhh6ltwxlEkZiwbMy7ZTn7HRWrD3FSzuP0lt2Onaa5Nxi6dNz7RlDwmGTmTGno6GD9IYh2eI3pNolhLJH5rOBIBw6iSmXoXaQ3jJUdRWfvPfsaLdzDoXPNIKwvgyU3JBdkKBBKY2Q3Ar2uxMLalchlcqeDK++k7H6i190FQqhi10TOscgrLPpzB28+OeLTQmn+hAJWl3fX63z21QRT63akufJMt9sOrpjNuO9tjY//iouxtr6tsGXPFvcVmDrr769//jj337/4cdPX17+9d8PHz7/fv/y/j9fPjz8+mn99tflLf8/r+c+tZeJ2dciUcnjCFUh8Pu/9+vf108rjYxW5dVRubSC5zmpVMY/NuWqz61RS6Wv379Z2cH/Pry7//7N6/Xdl0NLPHaC4nyTVMJF5fjBklPOOfqUpaUrZUOOcnI99ZDztfJTuRZwR67XY1XflA05yniJnlTlWvmpfAvXmHpP1ysbcpSj87WUeP2AhnwbB1L26ncV9l59GdoGsKlXMlu2NWpu3oez+hMAdfIhEte4qTET5NbjUDeATb0ycpSi0uZreNS+lqNcXApS6X+x05e81rRd2wBQr040e9uaAmv42ob2U/mm3PAqrkrak3Mv9az9BECdhhoapWTFtk4kZycaAOrd1bhFWqZGkWpZhroBnBb+ztVTEdeMkyXK3LoFoC6avo2eU6Irwgw3jsgCUM/kSM+UzxY4Qtr9cLoFoK7HRa1qVJXoJEjqwzUmcloKlTOlngvFMbjQ0Og7wUQg6LSV8dpKodMoyTNoTOS0VCoKqchJ0AFd6Yx444lNBEJyyJJQmshjio3G4U6wEAiF4Tv5FreO0wONYBIsBALnngIldZWk+ey1se8ECzktdAvmpq6GOcvmEz12J5gIBA6zMJox/eXO3SSFYcACUI8uSe/UKylaBhJlY+hbCAQ2R18QfJ6YTcoIuadiVAnt7r0OvDicqMUVQ9tCIFAhepYYEGM95dDHgZkIhIYPKncRxJl1GpPfIFjIaenURYqXOo3+7qP0OCyYCATaSuPM1XBzokPv0DcA1EUnNirLJu0MiXUcl4lA0J5IbyZOasd156JsAajjXoZvDVxWSTn2cVoWoDeuwCEKNynE9LzMnDJKig0pJWn05aYbZcqnPdU0KRa03+twdRNCi9zdptUzxYKgMBClzkPhPuoJh3qOJBuCogOXl6AJQiEvTF3j2U1ECVstYIJYx01NzjZMCAqXh84kpW6MXGo8aTUCyoag0GqD9mUqA12lVWaQwbAQJRQnQq8qm5zyFlKYDAuCQoWmXZTW96W4eJyP0YSUQtC03rWeRPoXEZHn8GNCOixlR8r00vf5ObY866UN6U1bmA9TqTpy60xVUp8uNiGlaOvL2zVYJwJifPZnG4LSqKAMfcwQ22mV3NOMLxOCQnpyPY1aMKKmT8tzILEhpRQadyCONjkBGGe5siGdGOkj1NFUN3kuIcxzsSGlMFYkKnDf5NJ9z+c504Kg6DXQcwkcz5hjmVOHDSmFB+OWFDdxykVzdjAMBAKzea502rbJfelpnooN6dsPKmBhrpf9tKqkmSs2tL8woYxTRzY5DbLO0LchnbOZYLww92/yxA11MiwEAiMDnaiVMMSMHnNbJqSUSmpzxdq3y282PCkWBIWWiOc02FRefCeLBsWElNJcDCWN6C7cTdOZYkFQ9E1D8W3fL3W0zBnMRJRAqGXCc/cJdyWsT4YFQaFzMzllvz9hq5ScUcBsSCmdD6Xsu+WSXOqMFQuB0Cn9ocSwy3vgLjrKhA0ppTNz5NTjkBdayaRY0P6ajOzJwyk9xNDmPctAlEAj3nrgLvZMj3EyLAgKCUeg6Si0PWHjRj3i0YaUQsVgIB1+rz7OMd1EIJBwniG8DS9yBRlPbiIQor4lqFOaQpuTvYkoQUfSwj17vE+JyZ8ZFgRFb5SN44kjfIo2z51iQkqhGTPBhDTk5I5MigXp3VdfMdA6ZpDKTEQTUQJzNjE08lNfDpTpLBM6be8u9e4V89xunZFlQ5fv5jen+DSvHm/Xz6usf9m/NLh41375euLmG/er0e/8XcHX7fsC65uB03PfDCyfzt8AbLvRBcxXI9YrYMu69VXDLetvl/8DRMcAwQplbmRzdHJlYW0KZW5kb2JqCjExIDAgb2JqCjIwMzIKZW5kb2JqCjE2IDAgb2JqCjw8IC9CQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDMzMgovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJwtkkluQzEMQ/f/FLxAAGvwdJ4AXaX33/ZJ6cIgY30xFOXH7pbfqd/HlitGyGIrbMuc33H0fsyGYlIZqdj2xWtVgWUueobyDtlJTfrej/vUzCPfR3OZIr3x/cRa35vLzbxKu+CkUkpzmnJXL2dwcEMF7ZxLnycXbE1lON9xxgZX6R46Tznl5pT3bMQL8xXzFXybcqYqHSrVjTPDS/pojJs1WTF0faBIMm4L5e5BN2K1WvglM2vEAd8X+zzdMRPmOP9nTFTMx1VxOyHvPkt2MCrxKyOvxoyqFHMSx7ENfM6j0ythnI2yHRGlr4aatEn4VrkjidXGzhSZprlORXd0O1U2ZVF2K17GNL0qt9CrAyX+F6v3vUHMsppC/n1HM6tnInKPCoYXMis+MVjcfj+I1Eg8it0JEq1n+/fSZTAW7weV/2f4fn7+AKXrejcKZW5kc3RyZWFtCmVuZG9iagoxNyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDIxMyA+PgpzdHJlYW0KeJw9UDGSAzEI6/0KngAIsP2evbkq+X8bYWdS7IpBSEYUQlSQ/GWVzFL5s5E5BVB5j9gg9RqhXywyPk+1BeES06hPIgRknxEzBXOzU4K1Lu48TEk4NZyLgEQqv90M2ikklPPLqb/4jN6jK2+nSvGkDiDjRhdVsR3cYIotojZjnmdbXLCFk+w1fP4q48plXYE228SZP9mFuuR5AGQyGY+LJVVhF7lu+e3sLRmccmrdyGQyCMP2NSPXRTtM9Rk4zxBY1FQc52YYuPQ4Iuj0Pf8z/j+cDk48CmVuZHN0cmVhbQplbmRvYmoKMTggMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNzggPj4Kc3RyZWFtCnicPZBLEgMhCET3nqKPID/R8ySV1eT+2zTOmIX2EyhssKXoGM7L1ZBd8ZZWGJ74Nu8LnomrqfWHJBUy+6YOGYtn8hQnJBSvJmNA3LHV1qNxMsIMuywmZmCuiq9ELqhQAupR8mpmo+BqpoK+fcRWmfUWFwhFAiYsZyv+nwPT6xYdDBaY7TfLszz2CtN0LMx7hnkPRSN+BuVabmBlrYOfhh2a97ZoKP/kJ3sWeLXPD96rQqEKZW5kc3RyZWFtCmVuZG9iagoxNCAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMtT2JsaXF1ZSAvQ2hhclByb2NzIDE1IDAgUgovRW5jb2RpbmcgPDwgL0RpZmZlcmVuY2VzIFsgMTA0IC9oIDExNiAvdCBdIC9UeXBlIC9FbmNvZGluZyA+PiAvRmlyc3RDaGFyIDAKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udERlc2NyaXB0b3IgMTMgMCBSCi9Gb250TWF0cml4IFsgMC4wMDEgMCAwIDAuMDAxIDAgMCBdIC9MYXN0Q2hhciAyNTUgL05hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxMiAwIFIgPj4KZW5kb2JqCjEzIDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyA5NgovRm9udEJCb3ggWyAtMTAxNiAtMzUxIDE2NjAgMTA2OCBdIC9Gb250TmFtZSAvRGVqYVZ1U2Fucy1PYmxpcXVlCi9JdGFsaWNBbmdsZSAwIC9NYXhXaWR0aCAxMzUwIC9TdGVtViAwIC9UeXBlIC9Gb250RGVzY3JpcHRvciAvWEhlaWdodCAwID4+CmVuZG9iagoxMiAwIG9iagpbIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwCjYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgMzE4IDQwMSA0NjAgODM4IDYzNgo5NTAgNzgwIDI3NSAzOTAgMzkwIDUwMCA4MzggMzE4IDM2MSAzMTggMzM3IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYKNjM2IDYzNiAzMzcgMzM3IDgzOCA4MzggODM4IDUzMSAxMDAwIDY4NCA2ODYgNjk4IDc3MCA2MzIgNTc1IDc3NSA3NTIgMjk1CjI5NSA2NTYgNTU3IDg2MyA3NDggNzg3IDYwMyA3ODcgNjk1IDYzNSA2MTEgNzMyIDY4NCA5ODkgNjg1IDYxMSA2ODUgMzkwIDMzNwozOTAgODM4IDUwMCA1MDAgNjEzIDYzNSA1NTAgNjM1IDYxNSAzNTIgNjM1IDYzNCAyNzggMjc4IDU3OSAyNzggOTc0IDYzNCA2MTIKNjM1IDYzNSA0MTEgNTIxIDM5MiA2MzQgNTkyIDgxOCA1OTIgNTkyIDUyNSA2MzYgMzM3IDYzNiA4MzggNjAwIDYzNiA2MDAgMzE4CjM1MiA1MTggMTAwMCA1MDAgNTAwIDUwMCAxMzUwIDYzNSA0MDAgMTA3MCA2MDAgNjg1IDYwMCA2MDAgMzE4IDMxOCA1MTggNTE4CjU5MCA1MDAgMTAwMCA1MDAgMTAwMCA1MjEgNDAwIDEwMjggNjAwIDUyNSA2MTEgMzE4IDQwMSA2MzYgNjM2IDYzNiA2MzYgMzM3CjUwMCA1MDAgMTAwMCA0NzEgNjE3IDgzOCAzNjEgMTAwMCA1MDAgNTAwIDgzOCA0MDEgNDAxIDUwMCA2MzYgNjM2IDMxOCA1MDAKNDAxIDQ3MSA2MTcgOTY5IDk2OSA5NjkgNTMxIDY4NCA2ODQgNjg0IDY4NCA2ODQgNjg0IDk3NCA2OTggNjMyIDYzMiA2MzIgNjMyCjI5NSAyOTUgMjk1IDI5NSA3NzUgNzQ4IDc4NyA3ODcgNzg3IDc4NyA3ODcgODM4IDc4NyA3MzIgNzMyIDczMiA3MzIgNjExIDYwOAo2MzAgNjEzIDYxMyA2MTMgNjEzIDYxMyA2MTMgOTk1IDU1MCA2MTUgNjE1IDYxNSA2MTUgMjc4IDI3OCAyNzggMjc4IDYxMiA2MzQKNjEyIDYxMiA2MTIgNjEyIDYxMiA4MzggNjEyIDYzNCA2MzQgNjM0IDYzNCA1OTIgNjM1IDU5MiBdCmVuZG9iagoxNSAwIG9iago8PCAvaCAxNyAwIFIgL3QgMTggMCBSID4+CmVuZG9iagoyMyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDM5MiA+PgpzdHJlYW0KeJw9UktuBTEI288puECl8E1ynqne7t1/W5vMVKoKLwO2MZSXDKklP+qSiDNMfvVyXeJR8r1samfmIe4uNqb4WHJfuobYctGaYrFPHMkvyLRUWKFW3aND8YUoEw8ALeCBBeG+HP/xF6jB17CFcsN7ZAJgStRuQMZD0RlIWUERYfuRFeikUK9s4e8oIFfUrIWhdGKIDZYAKb6rDYmYqNmgh4SVkqod0vGMpPBbwV2JYVBbW9sEeGbQENnekY0RM+3RGXFZEWs/PemjUTK1URkPTWd88d0yUvPRFeik0sjdykNnz0InYCTmSZjncCPhnttBCzH0ca+WT2z3mClWkfAFO8oBA7393pKNz3vgLIxc2+xMJ/DRaaccE62+HmL9gz9sS5tcxyuHRRSovCgIftdBE3F8WMX3ZKNEd7QB1iMT1WglEAwSws7tMPJ4xnnZ3hW05vREaKNEHtSOET0ossXlnBWwp/yszbEcng8me2+0j5TMzKiEFdR2eqi2z2Md1Hee+/r8AS4AoRkKZW5kc3RyZWFtCmVuZG9iagoyNCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDkwID4+CnN0cmVhbQp4nE2NQRLAIAgD77wiT1BE0P90etL/X6vUDr3ATgKJFkWC9DVqSzDuuDIVa1ApmJSXwFUwXAva7qLK/jJJTJ2G03u3A4Oy8XGD0kn79nF6AKv9egbdD9IcIlgKZW5kc3RyZWFtCmVuZG9iagoyNSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDgwID4+CnN0cmVhbQp4nEWMuw3AMAhEe6ZgBH4mZp8olbN/GyBK3HBPunu4OhIyU95hhocEngwshlPxBpmjYDW4RlKNneyjsG5fdYHmelOr9fcHKk92dnE9zcsZ9AplbmRzdHJlYW0KZW5kb2JqCjI2IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ3ID4+CnN0cmVhbQp4nD1PuQ0DMQzrPQUXOMB6LFvzXJDqsn8bykZSCCJA8ZFlR8cKXGICk445Ei9pP/hpGoFYBjVH9ISKYVjgbpICD4MsSleeLV4MkdpCXUj41hDerUxkojyvETtwJxejBz5UG1keekA7RBVZrknDWNVWXWqdsAIcss7CdT3MqgTl0SdrKR9QVEK9dP+fe9r7CwBvL+sKZW5kc3RyZWFtCmVuZG9iagoyNyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE0OSA+PgpzdHJlYW0KeJw1j0sOAyEMQ/c5hS8wUn6EcB6qrqb33zZhWgkJC9svwRaDkYxLTGDsmGPhJVRPrT4kI4+6STkQqVA3BE9oTAwzbNIl8Mp03zKeW7ycVuqCTkjk6aw2GqKMZl7D0VPOCpv+y9wkamVGmQMy61S3E7KyYAXmBbU89zPuqFzohIedyrDoTjGi3GZGGn7/2/T+AnsyMGMKZW5kc3RyZWFtCmVuZG9iagoyOCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDQ5ID4+CnN0cmVhbQp4nDM2tFAwUDA0MAeSRoZAlpGJQoohF0gAxMzlggnmgFkGQBqiOAeuJocrDQDG6A0mCmVuZHN0cmVhbQplbmRvYmoKMjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzMTcgPj4Kc3RyZWFtCnicNVJLckMxCNu/U3CBzpi/fZ50smruv62EJyuwLUBCLi9Z0kt+1CXbpcPkVx/3JbFCPo/tmsxSxfcWsxTPLa9HzxG3LQoEURM9+DInFSLUz9ToOnhhlz4DrxBOKRZ4B5MABq/hX3iUToPAOxsy3hGTkRoQJMGaS4tNSJQ9Sfwr5fWklTR0fiYrc/l7cqkUaqPJCBUgWLnYB6QrKR4kEz2JSLJyvTdWiN6QV5LHZyUmGRDdJrFNtMDj3JW0hJmYQgXmWIDVdLO6+hxMWOOwhPEqYRbVg02eNamEZrSOY2TDePfCTImFhsMSUJt9lQmql4/T3AkjpkdNdu3Csls27yFEo/kzLJTBxygkAYdOYyQK0rCAEYE5vbCKveYLORbAiGWdmiwMbWglu3qOhcDQnLOlYcbXntfz/gdFW3ujCmVuZHN0cmVhbQplbmRvYmoKMzAgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxMzEgPj4Kc3RyZWFtCnicRY/LDQQhDEPvVOES8hk+qYfVntj+r+swmkFC+EEiO/EwCKzz8jbQxfDRosM3/jbVq2OVLB+6elJWD+mQh7zyFVBpMFHEhVlMHUNhzpjKyJYytxvhtk2DrGyVVK2DdjwGD7anZasIfqltYeos8QzCVV64xw0/kEutd71Vvn9CUzCXCmVuZHN0cmVhbQplbmRvYmoKMzEgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDggPj4Kc3RyZWFtCnicLVE5kgNBCMvnFXpCc9PvscuR9//pCsoBg4ZDIDotcVDGTxCWK97yyFW04e+ZGMF3waHfynUbFjkQFUjSGFRNqF28Hr0HdhxmAvOkNSyDGesDP2MKN3pxeEzG2e11GTUEe9drT2ZQMisXccnEBVN12MiZw0+mjAvtXM8NyLkR1mUYpJuVxoyEI00hUkih6iapM0GQBKOrUaONHMV+6csjnWFVI2oM+1xL29dzE84aNDsWqzw5pUdXnMvJxQsrB/28zcBFVBqrPBAScL/bQ/2c7OQ33tK5s8X0+F5zsrwwFVjx5rUbkE21+Dcv4vg94+v5/AOopVsWCmVuZHN0cmVhbQplbmRvYmoKMzIgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyMTAgPj4Kc3RyZWFtCnicNVDLDUMxCLtnChaoFAKBZJ5WvXX/a23QO2ER/0JYyJQIeanJzinpSz46TA+2Lr+xIgutdSXsypognivvoZmysdHY4mBwGiZegBY3YOhpjRo1dOGCpi6VQoHFJfCZfHV76L5PGXhqGXJ2BBFDyWAJaroWTVi0PJ+QTgHi/37D7i3koZLzyp4b+Ruc7fA7s27hJ2p2ItFyFTLUszTHGAgTRR48eUWmcOKz1nfVNBLUZgtOlgGuTj+MDgBgIl5ZgOyuRDlL0o6ln2+8x/cPQABTtAplbmRzdHJlYW0KZW5kb2JqCjIxIDAgb2JqCjw8IC9CYXNlRm9udCAvRGVqYVZ1U2FucyAvQ2hhclByb2NzIDIyIDAgUgovRW5jb2RpbmcgPDwKL0RpZmZlcmVuY2VzIFsgNDAgL3BhcmVubGVmdCAvcGFyZW5yaWdodCA0NiAvcGVyaW9kIDQ4IC96ZXJvIC9vbmUgL3R3byA1MiAvZm91ciA1NCAvc2l4CjU2IC9laWdodCAxMTYgL3QgXQovVHlwZSAvRW5jb2RpbmcgPj4KL0ZpcnN0Q2hhciAwIC9Gb250QkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZvbnREZXNjcmlwdG9yIDIwIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zCi9TdWJ0eXBlIC9UeXBlMyAvVHlwZSAvRm9udCAvV2lkdGhzIDE5IDAgUiA+PgplbmRvYmoKMjAgMCBvYmoKPDwgL0FzY2VudCA5MjkgL0NhcEhlaWdodCAwIC9EZXNjZW50IC0yMzYgL0ZsYWdzIDMyCi9Gb250QkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZvbnROYW1lIC9EZWphVnVTYW5zIC9JdGFsaWNBbmdsZSAwCi9NYXhXaWR0aCAxMzQyIC9TdGVtViAwIC9UeXBlIC9Gb250RGVzY3JpcHRvciAvWEhlaWdodCAwID4+CmVuZG9iagoxOSAwIG9iagpbIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwCjYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgMzE4IDQwMSA0NjAgODM4IDYzNgo5NTAgNzgwIDI3NSAzOTAgMzkwIDUwMCA4MzggMzE4IDM2MSAzMTggMzM3IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYKNjM2IDYzNiAzMzcgMzM3IDgzOCA4MzggODM4IDUzMSAxMDAwIDY4NCA2ODYgNjk4IDc3MCA2MzIgNTc1IDc3NSA3NTIgMjk1CjI5NSA2NTYgNTU3IDg2MyA3NDggNzg3IDYwMyA3ODcgNjk1IDYzNSA2MTEgNzMyIDY4NCA5ODkgNjg1IDYxMSA2ODUgMzkwIDMzNwozOTAgODM4IDUwMCA1MDAgNjEzIDYzNSA1NTAgNjM1IDYxNSAzNTIgNjM1IDYzNCAyNzggMjc4IDU3OSAyNzggOTc0IDYzNCA2MTIKNjM1IDYzNSA0MTEgNTIxIDM5MiA2MzQgNTkyIDgxOCA1OTIgNTkyIDUyNSA2MzYgMzM3IDYzNiA4MzggNjAwIDYzNiA2MDAgMzE4CjM1MiA1MTggMTAwMCA1MDAgNTAwIDUwMCAxMzQyIDYzNSA0MDAgMTA3MCA2MDAgNjg1IDYwMCA2MDAgMzE4IDMxOCA1MTggNTE4CjU5MCA1MDAgMTAwMCA1MDAgMTAwMCA1MjEgNDAwIDEwMjMgNjAwIDUyNSA2MTEgMzE4IDQwMSA2MzYgNjM2IDYzNiA2MzYgMzM3CjUwMCA1MDAgMTAwMCA0NzEgNjEyIDgzOCAzNjEgMTAwMCA1MDAgNTAwIDgzOCA0MDEgNDAxIDUwMCA2MzYgNjM2IDMxOCA1MDAKNDAxIDQ3MSA2MTIgOTY5IDk2OSA5NjkgNTMxIDY4NCA2ODQgNjg0IDY4NCA2ODQgNjg0IDk3NCA2OTggNjMyIDYzMiA2MzIgNjMyCjI5NSAyOTUgMjk1IDI5NSA3NzUgNzQ4IDc4NyA3ODcgNzg3IDc4NyA3ODcgODM4IDc4NyA3MzIgNzMyIDczMiA3MzIgNjExIDYwNQo2MzAgNjEzIDYxMyA2MTMgNjEzIDYxMyA2MTMgOTgyIDU1MCA2MTUgNjE1IDYxNSA2MTUgMjc4IDI3OCAyNzggMjc4IDYxMiA2MzQKNjEyIDYxMiA2MTIgNjEyIDYxMiA4MzggNjEyIDYzNCA2MzQgNjM0IDYzNCA1OTIgNjM1IDU5MiBdCmVuZG9iagoyMiAwIG9iago8PCAvZWlnaHQgMjMgMCBSIC9mb3VyIDI0IDAgUiAvb25lIDI1IDAgUiAvcGFyZW5sZWZ0IDI2IDAgUgovcGFyZW5yaWdodCAyNyAwIFIgL3BlcmlvZCAyOCAwIFIgL3NpeCAyOSAwIFIgL3QgMzAgMCBSIC90d28gMzEgMCBSCi96ZXJvIDMyIDAgUiA+PgplbmRvYmoKMyAwIG9iago8PCAvRjEgMjEgMCBSIC9GMiAxNCAwIFIgPj4KZW5kb2JqCjQgMCBvYmoKPDwgL0ExIDw8IC9DQSAwIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4KL0EyIDw8IC9DQSAxIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4gPj4KZW5kb2JqCjUgMCBvYmoKPDwgPj4KZW5kb2JqCjYgMCBvYmoKPDwgPj4KZW5kb2JqCjcgMCBvYmoKPDwgL0RlamFWdVNhbnMtT2JsaXF1ZS1lcHNpbG9uIDE2IDAgUiA+PgplbmRvYmoKMiAwIG9iago8PCAvQ291bnQgMSAvS2lkcyBbIDEwIDAgUiBdIC9UeXBlIC9QYWdlcyA+PgplbmRvYmoKMzMgMCBvYmoKPDwgL0NyZWF0aW9uRGF0ZSAoRDoyMDE5MDQxNjA5MzIwMSswMicwMCcpCi9DcmVhdG9yIChtYXRwbG90bGliIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcpCi9Qcm9kdWNlciAobWF0cGxvdGxpYiBwZGYgYmFja2VuZCAzLjAuMykgPj4KZW5kb2JqCnhyZWYKMCAzNAowMDAwMDAwMDAwIDY1NTM1IGYgCjAwMDAwMDAwMTYgMDAwMDAgbiAKMDAwMDAwOTczNSAwMDAwMCBuIAowMDAwMDA5NDk1IDAwMDAwIG4gCjAwMDAwMDk1MzggMDAwMDAgbiAKMDAwMDAwOTYzNyAwMDAwMCBuIAowMDAwMDA5NjU4IDAwMDAwIG4gCjAwMDAwMDk2NzkgMDAwMDAgbiAKMDAwMDAwMDA2NSAwMDAwMCBuIAowMDAwMDAwNDAyIDAwMDAwIG4gCjAwMDAwMDAyMDggMDAwMDAgbiAKMDAwMDAwMjUwOSAwMDAwMCBuIAowMDAwMDA0MDY0IDAwMDAwIG4gCjAwMDAwMDM4NTYgMDAwMDAgbiAKMDAwMDAwMzUzMyAwMDAwMCBuIAowMDAwMDA1MTE3IDAwMDAwIG4gCjAwMDAwMDI1MzAgMDAwMDAgbiAKMDAwMDAwMjk5NiAwMDAwMCBuIAowMDAwMDAzMjgyIDAwMDAwIG4gCjAwMDAwMDgyODIgMDAwMDAgbiAKMDAwMDAwODA4MiAwMDAwMCBuIAowMDAwMDA3Njk5IDAwMDAwIG4gCjAwMDAwMDkzMzUgMDAwMDAgbiAKMDAwMDAwNTE1OSAwMDAwMCBuIAowMDAwMDA1NjI0IDAwMDAwIG4gCjAwMDAwMDU3ODYgMDAwMDAgbiAKMDAwMDAwNTkzOCAwMDAwMCBuIAowMDAwMDA2MTU4IDAwMDAwIG4gCjAwMDAwMDYzODAgMDAwMDAgbiAKMDAwMDAwNjUwMSAwMDAwMCBuIAowMDAwMDA2ODkxIDAwMDAwIG4gCjAwMDAwMDcwOTUgMDAwMDAgbiAKMDAwMDAwNzQxNiAwMDAwMCBuIAowMDAwMDA5Nzk1IDAwMDAwIG4gCnRyYWlsZXIKPDwgL0luZm8gMzMgMCBSIC9Sb290IDEgMCBSIC9TaXplIDM0ID4+CnN0YXJ0eHJlZgo5OTQ5CiUlRU9GCg==\n",
"image/svg+xml": [
"\n",
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sym.plot(he, (t,-1,10), ylabel=r'$h_\\epsilon(t)$');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Transfer Function\n",
"\n",
"For an exponential input signal $x(t) = e^{s t}$, the [transfer function](eigenfunctions.ipynb#Transfer-Function) $H(s)$ represents the complex weight of the exponential output signal $y(t) = H(s) \\cdot e^{s t}$. The transfer function is derived by introducing $x(t)$ and $y(t)$ into the ODE and solving for $H(s)$"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAJkAAAAsBAMAAACEdQdPAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMt0Qq5nNdrvvZiKJVETbNVTtAAAACXBIWXMAAA7EAAAOxAGVKw4bAAACnElEQVRIDe1WPWhTURT+0tck1bz8KBRxanl20aURFB0EA6a1uBg6iJO6Sac+EEktQqtUqgVRdBCnPHB0MGMHIaEVXArRQVwK7SKog42t1OJPn9+59z7pi1aClCKYD+459zvn3O+ed94LBGgKu7NNlTVVZPUNb6EaMNZSa2rujUWtuTVOpDn+38xtoNTjNjeSVlVrAts4AX8LUd/Gvv/Jq449O7GFfRUw+NdqRyby3lMgfnp1ymiso5JpkLNG8qcSVWDEn7h5uyGnaGSfcvEHWcwf4DbdrTjNo1/VrlxCcsZjbg3oytE34NCZFYlY1/kfI/qVu66qcI0Z498bf1RuPl8GIp+BDqk2SHlmE1dqsfukqbs0Y4smwTO6beC1CQ3xSrzjin8EYhvUkq6p0Gq1F6SRAs2widNNy2GBUbO/C+nkitX5EOPCNMJqiWWJWhmaVZW3i7NI5CJlRQK1SrfQg1zpcSR66J9f1ReG1WzOQSP1TflreIPpXZ26NlCruUHV0uTlGxmOLpMqqFBYrY1z0LDXxSfqmELJ903QPGkvBTRqZWsgC1TQ4alAWG2HfrHMyESotvZYVYkZdJyHjiPPVaIAIGaID1ul2lSZJOo4++85To5bqLfQpjRekqYvADvLqPlVkgBBb8KTGZpPwPEcYPt6Lgj3pr40VFm35ALt9G9Vt9wIjJp8abC5Ul+AhYJs7mRpeQVPKajeEvIWbMnUMsAo+Nn+Rq0iZ2a5okzW3IjdjbScaVTDgoek1KGXqiu4iGRBmIHpLcmW5nnc2ku1J+6HmItXuiLcG6yz+XNMWP1+vt/PYU9xNFASb9RweKJvkdSem/MQnfQixaJHSgRq7beWT+rIH2ygtmlJoLZpwcZE8KvfGAvtf/7qJfoDjYD0c3qrEq4AAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\frac{1}{C L s^{2} + C R s + 1}$$"
],
"text/plain": [
" 1 \n",
"──────────────────\n",
" 2 \n",
"C⋅L⋅s + C⋅R⋅s + 1"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"s = sym.symbols('s')\n",
"H = sym.Function('H')(s)\n",
"\n",
"H, = sym.solve(ode.subs(x, sym.exp(s*t)).subs(y, H*sym.exp(s*t)).doit(), H)\n",
"H"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The transfer characteristic of an LTI system for harmonic exponential signals $e^{j \\omega t} = \\cos(\\omega t) + j \\sin(\\omega t)$ is of special interest for the analysis of electrical circuits. It can be derived from $H(s)$ by substituting the complex frequency $s$ by $s = j \\omega$. The resulting transfer function $H(j \\omega)$ provides the attenuation/amplification and phase the system adds to an harmonic input signal."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAALgAAAAsBAMAAAAk6m+hAAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMt0Qq5nNdrvvZiKJVETbNVTtAAAACXBIWXMAAA7EAAAOxAGVKw4bAAACbUlEQVRIDe2XP2jUUBzHv3fPXNom155u4nDldNEpQ6FuzXCgY0CouojootPdoKBOV620DoLo0KmQvYOHOAoGdBEOLu5Cu7q02h6tqHj+3iXvT2KkTcHF5gePvD+f3/fy++bleAHyROl0HjofOzO/ky8hF20W4ll+FbZkuYLClv/LlmNPti9kVlRMFg4cZQeG/zCOsq+Hr531ms7hs/fJNGBM74MccHl2sem/Ae4Mb/kiY2rD+ir68dX0qBOj94aLy09T6/Ewdaw0Vxx8Okdr2wqfcP4QLweARL8BdVfhqpc6VrKH5K7xAyj9VAxgT0ejSV/NKnQPGKMUFRJLHhQqLwiZfEa39UuxwIn4gVbbalah5FklIS6xpHg/pOySR/QXJQPrUTyQWTROoPWOhkNiCXFr5DSrAVPXOe1Se1XDa5ziI8is2cvQ0A6sM5LVseT5ySb7otgK6FrldbxtWwvHL0Wz4paCz9DQpbuPa4IdcQJLipfllutvEGZw1A7Hh8PYpDjLCuehoV120REsz5AFRuLsRoNHbXz00cBovcWhTaCDiS7vUhiNxtnnjYYLMOxBobfJxECxCqNtoX+ElEd3+JGUdqmttfmztaknQtRb3YFCB8CcC50VWFKc73AgoN3IzXc9mCHodZUhsiru6GWI0O/AugedFVhS3OKatkONzDf9BdQ9dlNKKzPnwkCiBpXeb5d0Nlsc6z6q70iNF913PrxfHVz1M8S3LF+g7CSJv2xv6uxfxNmV5jUSm2kNmq0Bzu92769o2nIbjD2gpxqhdq/nw1jydVaI5ztWiiz9BzP6B8RSmfIfKTWfGiaw3zwKHDV1Am3VAAAAAElFTkSuQmCC\n",
"text/latex": [
"$$\\frac{1}{- C L \\omega^{2} + i C R \\omega + 1}$$"
],
"text/plain": [
" 1 \n",
"──────────────────────\n",
" 2 \n",
"- C⋅L⋅ω + ⅈ⋅C⋅R⋅ω + 1"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"w = sym.symbols('omega', real=True)\n",
"\n",
"Hjw = H.subs(s, sym.I * w)\n",
"Hjw"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The magnitude of the transfer function $|H(j \\omega)|$ is plotted for illustration for the specific values of the elements given above"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM5Ny45NzMxMjUgMzI2LjE1NTc4Nzg2OTkgXSAvUGFyZW50IDIgMCBSIC9SZXNvdXJjZXMgOCAwIFIKL1R5cGUgL1BhZ2UgPj4KZW5kb2JqCjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxMSAwIFIgPj4Kc3RyZWFtCnicpZlNs1S3EYb351doiRcIqfW9DOWYVDYpbCpZJFkQjAkUg4tQhE1+fJ4+czRzZqbvh8vcAu70q1fdkvpLmug+LNG9c8F94O8393f3T/7/2UX3gr/vlsCnw5JG86OlKIWPH/cfk1QfS2m9Iw+XH/+9LL8sz/7ANF+gvVgWEV8kpJhcKr7npMOYvA1f85X444U4RD/mrLtJ9uJNmRyVvcN4FuT7bkmYoMhpAnGp+YK6ghE7YfZhFX5clufszbflM/8G9zQwZ/PiGDqKe3NYnr9yz36ILgb36pele+weoa5b9Orn5UkMPnznXn1Y/viKGfigk/Azf2GCZ9+//fD6r19/ev3py9PD+09fv7jvf11e8rMavtTmYz2u9GzoTnifoaWgZ9QO/Eh7UfH7zI0x+h6u7d1L7zN4cNrlNxlcfu/+xlJ9zjcG76T3GRxz9jJ+k8Xye7dY8PjQry3eS28svrAojuSjtHi2Wc3aHNVh1qYmF9/kRs1Oer8agdXqtZpt9Ts1I/h04+B76QNquvgcrtWU69Ukskq48cu99H41SRr4tZp2vZp9vtqp2UkfUFO7L+FCR9ydzM7zmMNHnRPHGl5a119W51s9y914li9pG7L3r7/86+P7z1/fPv318Pbd68f4WSTtlyvpHX7Wuo8tr66fkm95jRLb186qGlUlZrLApa6z+GFlLfsYW+uptNw3hXKnwhi7l15KbZcad/KHVcaYfe69Dol5tE1nvltn6SS6mlu90nmWP0Jnyb6TLUNoROWms96tk+QapKWer3Se5Y/QOYqXFEoYZL206ex36pQ0fBpdGHqhcyd/WKcQpDXEjKxlOcbEPQ4kBFvjIPD6S51n+SN0El2jCZ1MzmNTKeco1AB8qlEVWzxzej52Ig0/GFssauClMtLR88/KnvxvLQKJLIdfn8vDsx9kjvjTOgL72fSt67qc4h9PtjlGiGnLtNeTfFiHUH5jkbQG680s390xy2aikU0iRtW+Leu0vsdkls/u1GOVU6N33C+ilbLkpNI88v9/3rq/uU8u+kL3FkAoyb1yLpx4rtufBtJC6R0fkeF+fOGw4L/v37z98cVz9+bLrqHL5A861rXX1FTeU8TkrNl2MLO6xE8mQPamwLQoObpMos05p+NoQ87gipMRjkmFvWfWto02gMOSA24WE3MUEnQtfZpiAQwn+upINbsSfZLYa9mGGwDDB86fqSNFqBVj5L6NvpUfFrJJyhKKuEJ/UBIfjqMtgOGD1RcaG6d46VLiNtwA6FjJVa120Z60oTuO42hDzmB2KPWYm8MnpKYx2jbaAA5L09xLgmCS7jvtzcjH4RbAcFafQsvZVbyHFiBue24Bh6UTGdxzhrgqJOdEsB6HWwDDyeCpacJhaXhQS5sxFnBY6MXYq9ijo6evI4ywLdUCGK6eFmOiyEWfWVmaww2A9BdoN2IdnJ22C6nQ6xzHm4gSSMyaj5rrhHpqNcZJMBDt7DNr76Mm1ytistnmNiYCQcjUtVO8HLWEnD1k208TUQJRiV+0RsZiooEVJ4YFQSE02erR8lrFC3HUN3+zIaU0n0fqjYJIs9JHpvZPigVByYnOs5CUKMXkLrJFm4aZkFIqm9ioFMfKgSuPPikWpBRcd/TeSLu9aJ6pJU+KBenlJWvBDNpFsqV6anP1FgIBf6c/HbWSfumVWimnxZuQUthHxEPlRHwpQ9qkWJBS2LwcSbCU1+ormX4uxEKUkH3j/lq1tgY9XqnTuUxIKYWwGdR55MkHMufJgU1IKdrZd+3zpGuSLnOzDOA4nAtdIXCEkA5D7T4TbiGlEPqBjVPNA2/oHO6kWJBStEGq2qyovPYe8mkdFgSlcTxUU+JN5XSGxzcRpZiQUqI+4WgwqMHkx1P9sSGl4NmN7U7rptAjxToNMyGlDH2tqKKnS87E68Y8RhOCQitVM7vSnVBP6G/bmA5pQkohezMBG0l5yynF0+otRFvD6omCvMoJuEFdm4s3Ib1jU/IHFrS1gy151LadvQ0phVsEWY3aICQFvJQ+dlIsCEokGkItesBU8xYC2XyjmJBSSP8oJzSpin6Qe2qfFAvSty7tqrNolBJBlYiKk2JCSumURbZTfYLYKGurtFEsCEpSz4taU1c36ufyaUNKwfMiYRqnsxaZWkxIKXheCZpuVS6k0TI32YSUQuNRKTFpNRhXCmku34SUQmfKKZW+tvr4eZmub0OH9Q2Ey5yEvF4/hjYAeVIsSCnsZF3bWaF/qdxATw5jQvoms2ZADpYjVp/KtU6KCSlFO+Mmmj+pCXHk2ZCZiBLo+alO1BoRelMCoshkWBAUuksSeSCXE3Gka5x9KjEhpdDrUMX0pkkVIV5znmdvQlCqJip95nRadas2YpNiQkqh1I5RVDt+qwc8E5IN6ZWB+x+uSnuhfU0LSWYVtiGlVO0KO62J4LXhFMO38sP6ioV9pAA3+C1p778NtxAldHVmIobKz4YQGnP8LaDvaVkjDP/UhxSSbJ3TGwC3mMC1Gs0kyibrRUS21ZqIEqh3wjEOV/U3rjdlEgwEAltF1AitG6W85D5vGxagdzBuQYP+llm4EvZI/zpvYQaiBFJ4Cdr6Uy6Zb7qeBehDIAk46NOzK5Qu7sCzlTMRJShbBrc4bi4iREyfBAOBwBWtiB6kXqNq05vgcbwBMJxrHxWkq1oCMnEV2ELaRJTQ9YmdnKA3RlpiavwkGIjeVCuZUWic9UbahPwwt9RC9BWTnSB9snU0ni23fNojC7l49jxfv1fCS/fZifvz8Quni+9nru7vDz11X3c6py+avq1fNpnfKh3u/FZp+XT68mg1Sqcwvyiynnkt/TvyWc+9+l8u/wdE5YIRCmVuZHN0cmVhbQplbmRvYmoKMTEgMCBvYmoKMjEzNQplbmRvYmoKMTYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA4OCA+PgpzdHJlYW0KeJw9jbkRwDAIBHOqoASBeKR+PI7k/lOf8BMAO+zcXLpyY02sVMdMPoQkZuFFGqNokUpj6w3k+D0UGq/9wrCj83Y2rK6joVuCZNpHyG1XveuvW3TeyQsbzgplbmRzdHJlYW0KZW5kb2JqCjE3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTUyID4+CnN0cmVhbQp4nD1PyxFDIQi8W8U2wIwggtbzMjmZ/q8BTTyxsrgf8YEKYhaQVIe4w63ixYW1o6vjU6QdtAqLg+YGlr8SsYK8gevW6Rg9Zpt4iufGGDpjhrBwzJEMWdrFM+62L0WODYK7YVah6SmWPuR6YRsHUnqztF2hpnAupiJjhnHbaZ9bJdKO0y9K/ZquIr3D1JK1i8affX8BvPc2ZwplbmRzdHJlYW0KZW5kb2JqCjE4IDAgb2JqCjw8IC9CQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE4MQovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJw1UDkOBCEM63mFP7ASucN7Rtpq9v/thjBToBgcBzuDSfEhwW9ENpCJFHiCw3GNZIgxiA2qAloO0yiClzS6B79cavUSKGaJpXpISyl1XOEMltjlGjL7LqYgXZAMSA25hpZ0o3uoHE5twglGeaS25gausyaXzza6//J2SvCIduOFj9PQfJxGZdxcpHWqCHpiRs3KPTZ6CUbctRyxnLXUUqRUizpRZbDVD3M2/+7xGt8/5jc/HgplbmRzdHJlYW0KZW5kb2JqCjE0IDAgb2JqCjw8IC9CYXNlRm9udCAvRGVqYVZ1U2Fucy1PYmxpcXVlIC9DaGFyUHJvY3MgMTUgMCBSCi9FbmNvZGluZyA8PCAvRGlmZmVyZW5jZXMgWyA3MiAvSCAxMDYgL2ogXSAvVHlwZSAvRW5jb2RpbmcgPj4gL0ZpcnN0Q2hhciAwCi9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnREZXNjcmlwdG9yIDEzIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTIgMCBSID4+CmVuZG9iagoxMyAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgOTYKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udE5hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovSXRhbGljQW5nbGUgMCAvTWF4V2lkdGggMTM1MCAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTIgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM1MCA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDI4IDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxNyA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjE3IDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDgKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk5NSA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMTUgMCBvYmoKPDwgL0ggMTYgMCBSIC9qIDE3IDAgUiA+PgplbmRvYmoKMjMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA1NCA+PgpzdHJlYW0KeJwzNjZXMFAwNDJX0DUyNlUwMjRQMDczUUgx5IIxc8EssGwOF1whhAmSz4GrzOFKAwBMkA8VCmVuZHN0cmVhbQplbmRvYmoKMjQgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzOTIgPj4Kc3RyZWFtCnicPVJLbgUxCNvPKbhApfBNcp6p3u7df1ubzFSqCi8DtjGUlwypJT/qkogzTH71cl3iUfK9bGpn5iHuLjam+FhyX7qG2HLRmmKxTxzJL8i0VFihVt2jQ/GFKBMPAC3ggQXhvhz/8ReowdewhXLDe2QCYErUbkDGQ9EZSFlBEWH7kRXopFCvbOHvKCBX1KyFoXRiiA2WACm+qw2JmKjZoIeElZKqHdLxjKTwW8FdiWFQW1vbBHhm0BDZ3pGNETPt0RlxWRFrPz3po1EytVEZD01nfPHdMlLz0RXopNLI3cpDZ89CJ2Ak5kmY53Aj4Z7bQQsx9HGvlk9s95gpVpHwBTvKAQO9/d6Sjc974CyMXNvsTCfw0WmnHBOtvh5i/YM/bEubXMcrh0UUqLwoCH7XQRNxfFjF92SjRHe0AdYjE9VoJRAMEsLO7TDyeMZ52d4VtOb0RGijRB7UjhE9KLLF5ZwVsKf8rM2xHJ4PJntvtI+UzMyohBXUdnqots9jHdR3nvv6/AEuAKEZCmVuZHN0cmVhbQplbmRvYmoKMjUgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDcgPj4Kc3RyZWFtCnicTVG7bUQxDOvfFFzgAOtreZ4LUl32b0PJCJDCIKEvKaclFvbGSwzhB1sPvuSRVUN/Hj8x7DMsPcnk1D/muclUFL4VqpuYUBdi4f1oBLwWdC8iK8oH349lDHPO9+CjEJdgJjRgrG9JJhfVvDNkwomhjsNBm1QYd00ULK4VzTPI7VY3sjqzIGx4JRPixgBEBNkXkM1go4yxlZDFch6oCpIFWmDX6RtRi4IrlNYJdKLWxLrM4Kvn9nY3Qy/y4Ki6eH0M60uwwuileyx8rkIfzPRMO3dJI73wphMRZg8FUpmdkZU6PWJ9t0D/n2Ur+PvJz/P9CxUoXCoKZW5kc3RyZWFtCmVuZG9iagoyNiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDkwID4+CnN0cmVhbQp4nE2NQRLAIAgD77wiT1BE0P90etL/X6vUDr3ATgKJFkWC9DVqSzDuuDIVa1ApmJSXwFUwXAva7qLK/jJJTJ2G03u3A4Oy8XGD0kn79nF6AKv9egbdD9IcIlgKZW5kc3RyZWFtCmVuZG9iagoyNyAwIG9iago8PCAvQkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzNwovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJzjMjQwUzA2NVXI5TI3NgKzcsAsI3MjIAski2BBZNMAAV8KCgplbmRzdHJlYW0KZW5kb2JqCjI4IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggODAgPj4Kc3RyZWFtCnicRYy7DcAwCER7pmAEfiZmnyiVs38bIErccE+6e7g6EjJT3mGGhwSeDCyGU/EGmaNgNbhGUo2d7KOwbl91geZ6U6v19wcqT3Z2cT3Nyxn0CmVuZHN0cmVhbQplbmRvYmoKMjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNDcgPj4Kc3RyZWFtCnicPU+5DQMxDOs9BRc4wHosW/NckOqyfxvKRlIIIkDxkWVHxwpcYgKTjjkSL2k/+GkagVgGNUf0hIphWOBukgIPgyxKV54tXgyR2kJdSPjWEN6tTGSiPK8RO3AnF6MHPlQbWR56QDtEFVmuScNY1VZdap2wAhyyzsJ1PcyqBOXRJ2spH1BUQr10/5972vsLAG8v6wplbmRzdHJlYW0KZW5kb2JqCjMwIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ5ID4+CnN0cmVhbQp4nDWPSw4DIQxD9zmFLzBSfoRwHqqupvffNmFaCQkL2y/BFoORjEtMYOyYY+ElVE+tPiQjj7pJORCpUDcET2hMDDNs0iXwynTfMp5bvJxW6oJOSOTprDYaooxmXsPRU84Km/7L3CRqZUaZAzLrVLcTsrJgBeYFtTz3M+6oXOiEh53KsOhOMaLcZkYafv/b9P4CezIwYwplbmRzdHJlYW0KZW5kb2JqCjMxIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggNDkgPj4Kc3RyZWFtCnicMza0UDBQMDQwB5JGhkCWkYlCiiEXSADEzOWCCeaAWQZAGqI4B64mhysNAMboDSYKZW5kc3RyZWFtCmVuZG9iagozMiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDY4ID4+CnN0cmVhbQp4nDMzNlMwULAwAhKmpoYK5kaWCimGXEA+iJXLBRPLAbPMLMyBLCMLkJYcLkMLYzBtYmykYGZiBmRZIDEgutIAcvgSkQplbmRzdHJlYW0KZW5kb2JqCjMzIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzE3ID4+CnN0cmVhbQp4nDVSS3JDMQjbv1Nwgc6Yv32edLJq7r+thCcrsC1AQi4vWdJLftQl26XD5Fcf9yWxQj6P7ZrMUsX3FrMUzy2vR88Rty0KBFETPfgyJxUi1M/U6Dp4YZc+A68QTikWeAeTAAav4V94lE6DwDsbMt4Rk5EaECTBmkuLTUiUPUn8K+X1pJU0dH4mK3P5e3KpFGqjyQgVIFi52AekKykeJBM9iUiycr03VojekFeSx2clJhkQ3SaxTbTA49yVtISZmEIF5liA1XSzuvocTFjjsITxKmEW1YNNnjWphGa0jmNkw3j3wkyJhYbDElCbfZUJqpeP09wJI6ZHTXbtwrJbNu8hRKP5MyyUwccoJAGHTmMkCtKwgBGBOb2wir3mCzkWwIhlnZosDG1oJbt6joXA0JyzpWHG157X8/4HRVt7owplbmRzdHJlYW0KZW5kb2JqCjM0IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjQ4ID4+CnN0cmVhbQp4nC1ROZIDQQjL5xV6QnPT77HLkff/6QrKAYOGQyA6LXFQxk8Qlive8shVtOHvmRjBd8Gh38p1GxY5EBVI0hhUTahdvB69B3YcZgLzpDUsgxnrAz9jCjd6cXhMxtntdRk1BHvXa09mUDIrF3HJxAVTddjImcNPpowL7VzPDci5EdZlGKSblcaMhCNNIVJIoeomqTNBkASjq1GjjRzFfunLI51hVSNqDPtcS9vXcxPOGjQ7Fqs8OaVHV5zLycULKwf9vM3ARVQaqzwQEnC/20P9nOzkN97SubPF9Phec7K8MBVY8ea1G5BNtfg3L+L4PePr+fwDqKVbFgplbmRzdHJlYW0KZW5kb2JqCjM1IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjEwID4+CnN0cmVhbQp4nDVQyw1DMQi7ZwoWqBQCgWSeVr11/2tt0DthEf9CWMiUCHmpyc4p6Us+OkwPti6/sSILrXUl7MqaIJ4r76GZsrHR2OJgcBomXoAWN2DoaY0aNXThgqYulUKBxSXwmXx1e+i+Txl4ahlydgQRQ8lgCWq6Fk1YtDyfkE4B4v9+w+4t5KGS88qeG/kbnO3wO7Nu4SdqdiLRchUy1LM0xxgIE0UePHlFpnDis9Z31TQS1GYLTpYBrk4/jA4AYCJeWYDsrkQ5S9KOpZ9vvMf3D0AAU7QKZW5kc3RyZWFtCmVuZG9iagoyMSAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMgL0NoYXJQcm9jcyAyMiAwIFIKL0VuY29kaW5nIDw8Ci9EaWZmZXJlbmNlcyBbIDQwIC9wYXJlbmxlZnQgL3BhcmVucmlnaHQgNDYgL3BlcmlvZCA0OCAvemVybyAvb25lIC90d28gNTIgL2ZvdXIgL2ZpdmUKL3NpeCAvc2V2ZW4gL2VpZ2h0IDEyNCAvYmFyIF0KL1R5cGUgL0VuY29kaW5nID4+Ci9GaXJzdENoYXIgMCAvRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250RGVzY3JpcHRvciAyMCAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2FucwovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxOSAwIFIgPj4KZW5kb2JqCjIwIDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyAzMgovRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250TmFtZSAvRGVqYVZ1U2FucyAvSXRhbGljQW5nbGUgMAovTWF4V2lkdGggMTM0MiAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTkgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM0MiA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDIzIDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxMiA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjEyIDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDUKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk4MiA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMjIgMCBvYmoKPDwgL2JhciAyMyAwIFIgL2VpZ2h0IDI0IDAgUiAvZml2ZSAyNSAwIFIgL2ZvdXIgMjYgMCBSIC9vbmUgMjggMCBSCi9wYXJlbmxlZnQgMjkgMCBSIC9wYXJlbnJpZ2h0IDMwIDAgUiAvcGVyaW9kIDMxIDAgUiAvc2V2ZW4gMzIgMCBSCi9zaXggMzMgMCBSIC90d28gMzQgMCBSIC96ZXJvIDM1IDAgUiA+PgplbmRvYmoKMyAwIG9iago8PCAvRjEgMjEgMCBSIC9GMiAxNCAwIFIgPj4KZW5kb2JqCjQgMCBvYmoKPDwgL0ExIDw8IC9DQSAwIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4KL0EyIDw8IC9DQSAxIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4gPj4KZW5kb2JqCjUgMCBvYmoKPDwgPj4KZW5kb2JqCjYgMCBvYmoKPDwgPj4KZW5kb2JqCjcgMCBvYmoKPDwgL0RlamFWdVNhbnMtT2JsaXF1ZS1vbWVnYSAxOCAwIFIgL0RlamFWdVNhbnMtbWludXMgMjcgMCBSID4+CmVuZG9iagoyIDAgb2JqCjw8IC9Db3VudCAxIC9LaWRzIFsgMTAgMCBSIF0gL1R5cGUgL1BhZ2VzID4+CmVuZG9iagozNiAwIG9iago8PCAvQ3JlYXRpb25EYXRlIChEOjIwMTkwNDE2MDkzMjAzKzAyJzAwJykKL0NyZWF0b3IgKG1hdHBsb3RsaWIgMy4wLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZykKL1Byb2R1Y2VyIChtYXRwbG90bGliIHBkZiBiYWNrZW5kIDMuMC4zKSA+PgplbmRvYmoKeHJlZgowIDM3CjAwMDAwMDAwMDAgNjU1MzUgZiAKMDAwMDAwMDAxNiAwMDAwMCBuIAowMDAwMDEwMTQ4IDAwMDAwIG4gCjAwMDAwMDk4ODUgMDAwMDAgbiAKMDAwMDAwOTkyOCAwMDAwMCBuIAowMDAwMDEwMDI3IDAwMDAwIG4gCjAwMDAwMTAwNDggMDAwMDAgbiAKMDAwMDAxMDA2OSAwMDAwMCBuIAowMDAwMDAwMDY1IDAwMDAwIG4gCjAwMDAwMDA0MDMgMDAwMDAgbiAKMDAwMDAwMDIwOCAwMDAwMCBuIAowMDAwMDAyNjEzIDAwMDAwIG4gCjAwMDAwMDM4NjQgMDAwMDAgbiAKMDAwMDAwMzY1NiAwMDAwMCBuIAowMDAwMDAzMzM0IDAwMDAwIG4gCjAwMDAwMDQ5MTcgMDAwMDAgbiAKMDAwMDAwMjYzNCAwMDAwMCBuIAowMDAwMDAyNzk0IDAwMDAwIG4gCjAwMDAwMDMwMTkgMDAwMDAgbiAKMDAwMDAwODY0MyAwMDAwMCBuIAowMDAwMDA4NDQzIDAwMDAwIG4gCjAwMDAwMDgwNTEgMDAwMDAgbiAKMDAwMDAwOTY5NiAwMDAwMCBuIAowMDAwMDA0OTU5IDAwMDAwIG4gCjAwMDAwMDUwODUgMDAwMDAgbiAKMDAwMDAwNTU1MCAwMDAwMCBuIAowMDAwMDA1ODcwIDAwMDAwIG4gCjAwMDAwMDYwMzIgMDAwMDAgbiAKMDAwMDAwNjIwMiAwMDAwMCBuIAowMDAwMDA2MzU0IDAwMDAwIG4gCjAwMDAwMDY1NzQgMDAwMDAgbiAKMDAwMDAwNjc5NiAwMDAwMCBuIAowMDAwMDA2OTE3IDAwMDAwIG4gCjAwMDAwMDcwNTcgMDAwMDAgbiAKMDAwMDAwNzQ0NyAwMDAwMCBuIAowMDAwMDA3NzY4IDAwMDAwIG4gCjAwMDAwMTAyMDggMDAwMDAgbiAKdHJhaWxlcgo8PCAvSW5mbyAzNiAwIFIgL1Jvb3QgMSAwIFIgL1NpemUgMzcgPj4Kc3RhcnR4cmVmCjEwMzYyCiUlRU9GCg==\n",
"image/svg+xml": [
"\n",
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sym.plot(abs(Hjw.subs(RLC)), (w, -10, 10),\n",
" ylabel=r'$|H(j \\omega)|$', xlabel=r'$\\omega$');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"It now becomes obvious, that the low frequencies pass through the system and that high frequencies are attenuated. This motivates the term 'low-pass' for such systems.\n",
"\n",
"As alternative to the solution of the ODE, the transfer function $H(s)$ is [computed from the impulse response](eigenfunctions.ipynb#Link-between-Transfer-Function-and-Impulse-Response) and plotted for the specific values of the elements given above"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAGUAAAAtBAMAAABFWbj9AAAAMFBMVEX///8AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAv3aB7AAAAD3RSTlMAMhAi783diatmdpm7RFShYZRwAAAACXBIWXMAAA7EAAAOxAGVKw4bAAABrElEQVRIDe2UvUvDQBjGn5q0jba1FUFHD/wHCi5Ch4pIJwcn5+AQhQ52E1x0FBx01qW4CHURQRE6lAoWnOzqv6CLH4iTxEvurrmrecUu0sEbcn2f3z33kVwfIL4lgNl4Qqv2++oaTeNJanOdxRNadWhEkj/zHJ0VyE0QIMusTwL9JHd+ggRrFQlAybdAa9ADVYADaj5KrwHLFKP0EsYWKUbpVnOfUexfH/I34A/cnof8RHx7I1t7bNBdZpBxf+PRUzzftV5MT+mybQphpaf4KOvzWLvY6X43mSmedsWIB9E5DPaC+Bk+laxJwBQT5aPo7Fc4b9oAKRspbt3IAQq6cPQTKllNs33KMI9JUUrIixS/IwEKm/LIFM8WcudWe+LCgLyYqSNAhqxSvIzsoe378uZF61SBABkeXnQCoXxXFDpw5XlLnrcRlhm+gkS6jDDF0/6H8vC+t84xLyIk5V6K5+5ZZFKe8RrmgB6SckWkOP+Y+RjPNHCiIempiRRP1vEULaP2ZlWb166GpEemeKLRkO8mdEqY5P/4FQ1JOT7FJdRW1qfql0UtL2M/NOQvt3ibbsdYS6UAAAAASUVORK5CYII=\n",
"text/latex": [
"$$\\frac{5}{s^{2} + 2 s + 5}$$"
],
"text/plain": [
" 5 \n",
"────────────\n",
" 2 \n",
"s + 2⋅s + 5"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"H2 = sym.integrate(h.rhs.subs(RLC)*sym.exp(-s*t), (t, 0, sym.oo), conds='none')\n",
"H2.simplify()"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM5Ny45NzMxMjUgMzI2LjE1NjIwMjA4OTYgXSAvUGFyZW50IDIgMCBSIC9SZXNvdXJjZXMgOCAwIFIKL1R5cGUgL1BhZ2UgPj4KZW5kb2JqCjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxMSAwIFIgPj4Kc3RyZWFtCnicpZnLkhW5EYb39RRaMguElLovTYwHhzcOBsJe2F5gpgdD0ExgArPxw/vLqtI51aezLxPQQfc5+vUrpVReq6L7sET3zgX3gf/f3N/dP/n7i4vuBf/fLYFv10sazY+WohS+fjx+TVJ9LFWCMB5ufv33svy6PPsDy3yB9mJZRHyRkGJyqfies05j8TZ8zRfDH28Mh+jHXPWwyHF4FyabsHdsngP5fjgSW1DktIC41HzJqRU2cRjMPqyDH5flObr5tnzmd3BPA2s2L46po7i318vz1+7ZT9HF4F7/unSfWh+hrip6/cvyJAYffnCvPyx/fM0KfNFF+JkfWODZj1cf3vz166s3n748vX7/6esX9+Nvy0t+1o0vtflYt5OeN3oYvG+jpSBn1A78yP0i4vu2G2P0PVzu9zh634YHt11+14bL9+oXQ/U539rwYfS+DcecvYzftWP5XhULFh/65Y6Po7d2fGNHcSQfpcXznnVbu6E6trWLycU3uSXmMHq/GIHV6qWY/fQHMSP4dMvAj6MPiOnic7gUUy5Pk4gq4ZZdHkfvF5OkgV+KaZenOcarg5jD6ANiavcl3JARDzdzsDzW8FHXxLCGl9b1w2p8q2W5W5blS9qnHO3rL//6+P7z16unv11fvXvzGDuLhP1yMXqHnbXuY8ur6afkW169xLa1s6hGVolVarsp6zz8sLCWfcTIh0SImzy5U16M3UvvreebAg/jD0uMMfs84ghDpMZdZr5bZum+1kjqupB5Hn+EzJJ9ryTKmtKYMuvdMomtIaUe+4XM8/gjZI7iJdWRUy4iu8x+p0xJA99kf/WmzMP4wzIFH61h5BpKLZvMeI/9CL7WWu8lXcg8jz9CJs41OmwCWJ8y5eyF6oBP1atii2dSz3slEvqouy+q46Uy0mb5Z2lP/rcmgUSUGzGf08Ozn2TO+NM6gwOg9b3qurnEP57sa4wQ0x5pLxf5sE4h/cYiaXXWW6v8cMcq+xaNaBLZVO37sU7ne0xk+exONVY5F3qrvlKhqKGwqhSP/P3Plfub++SiL1RvAYSU3CsXw5Xnuv9rIC2U3jESGe7nF44d/Pf926ufXzx3b78cCrpM/MhhqzVlYBToo7nc2UEsbY0qr0yA6E0pEMuIjA7fU6ybq7wygesli29Ydq6uYJy1s+I23QKYTmrQo7kiWjTjW/vs2+PXixZ00gtXULCc0NJmza9MgDIRow0Z+3HEijYqDrRNt4C1qhRpNbMIJ6tkO9mnG8D10pKX2Ao3X7TIGRLGNt0CmN59IyC36GpQ71c1b9MN4HrpLFJF8PgqPomg3W26BTCdaB1D53PNvg68cD+qBVwvg7vgBlCqni3ISPvqFsB04nLOGS214McgXu63ZAGEnYBWu5TeHIGkDTJ+3eabiNbHyh69FNe1Us5pGo2JKKHighRxw3HAjAPkOf82wHQcoY0oWZx2bbnVMte3ECUM4lrku9Md1ER0nUcwISiUNoV02ckpgqo53LwyG4KSORx1AVYec0XxoZQpxYSUktQzU68kQDaiWaRPigUppfo+QFiK0gCLydMPbEjLf3TdQySoB8yttThDhIls/cLIow/NV1U12uTEsCAoVe8zURWtMY+4U8O8RBNSClUhqguNDCUafEqYhzchpVBwDnRXGW++dvYxVWxCSik+UT714dbiWkIdaVIsSCnVV0kUyIwT1SlIZuywIaU030tVkaI+Grjh0/EtSCmdBJsyGVk6FYSw+ZMUC4LSND1JHW0d7zVsDwqUYkJKiTShax2n49QqoU1zMSGlJNJiydSK0ldNltPxTUgpmBu6aZta6hhZTlIsSCnVpyQl6FIkdGqGNibFgqBwSSGijboaUsptphcTUQJ7zG0tmMgkQVvb6cQmpDWWEJAL5bbT5jBJOOvLhJRSudVW1nFSUaT2mgwD0eZWo2DLp9Kxl5myLUQJFBNkKjVU8i5BP7c8GRYEJSZa/tZUhzg5oZ9qcaeYkFKoncmLrFQTpQOOOibDQPQBE4EwUFjK6nJ9yFSViSihkUEzuXotL0sfe3Pw6g5IKVhmoM4oq8URoeo8uYVASFqO0AVvrkOKnMnERJQQqbrUADbPyTlJnQwLUoqsjw24TR0natJDTIoFKQXFJer1zaVjpsE6SbEgpejTmBBEtsCB7ifhNqDTi4oLLa6OlgNOM83KhK7XhxoxhLCGpuhxhnAqHk1IKV3DsdCjUUN5rVzSaVsWpBTtVaKGzKqRacjMcSaiT2Xw5kozrgba6Of4Pc3EhJRCuxNwHNROPY+P9tMlmhAU3B5DboNsSfggwdKw7hQTUgoiO9dD71i1Peo1TRcxIShUgTVriUfmJ6pTaszoYENKqdp5kfCpL6h/cKQmk2JBUIjLlbUS0gMmxHlnoLMhpXBbo+vzFpyhtXNEMQCmdzVSomZzA3OgGDntyUKUQMygOkCH+DO7Lf1EMBDtY1Bb7a2uT0eIaCf/MAD6GEIlpUvCkKkQBo45/dxElEAXjOvQZmFsqdCrjUkwEAjUg7hZocTWrI/YGQ9NRAn6EEtQiFuLkZQlToKBQBBawa7tgqNGahQvM2uaiBK09ERzNFIDXWA7MgkGogS+pMD9a/ei9fas3U1EnyFWQj0WL9odRe1sJ8FCIJDYWs7a5tB90Wr0tIcQE1GCdl00XUm7u0zfOO/NAJhOx0g4LSRCPklB7VNHFqIEOjDJVdtBzaZxjKkjC9GOOPtM8aPrBFYs53u2ECXgR9SXWCR9LZ0yBfEkGIg+MdXLidp94ehFr3OewUJuPGI9t/or4aX77MT9eXu5deNd0MWzgoceq18WkKeXWt/WF1vmG6zrO99gLZ9OL6rWTekS5ksp65GyJf9APsu5V/7L5f+e9JWxCmVuZHN0cmVhbQplbmRvYmoKMTEgMCBvYmoKMjE1MwplbmRvYmoKMTYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA4OCA+PgpzdHJlYW0KeJw9jbkRwDAIBHOqoASBeKR+PI7k/lOf8BMAO+zcXLpyY02sVMdMPoQkZuFFGqNokUpj6w3k+D0UGq/9wrCj83Y2rK6joVuCZNpHyG1XveuvW3TeyQsbzgplbmRzdHJlYW0KZW5kb2JqCjE3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTUyID4+CnN0cmVhbQp4nD1PyxFDIQi8W8U2wIwggtbzMjmZ/q8BTTyxsrgf8YEKYhaQVIe4w63ixYW1o6vjU6QdtAqLg+YGlr8SsYK8gevW6Rg9Zpt4iufGGDpjhrBwzJEMWdrFM+62L0WODYK7YVah6SmWPuR6YRsHUnqztF2hpnAupiJjhnHbaZ9bJdKO0y9K/ZquIr3D1JK1i8affX8BvPc2ZwplbmRzdHJlYW0KZW5kb2JqCjE4IDAgb2JqCjw8IC9CQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE4MQovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJw1UDkOBCEM63mFP7ASucN7Rtpq9v/thjBToBgcBzuDSfEhwW9ENpCJFHiCw3GNZIgxiA2qAloO0yiClzS6B79cavUSKGaJpXpISyl1XOEMltjlGjL7LqYgXZAMSA25hpZ0o3uoHE5twglGeaS25gausyaXzza6//J2SvCIduOFj9PQfJxGZdxcpHWqCHpiRs3KPTZ6CUbctRyxnLXUUqRUizpRZbDVD3M2/+7xGt8/5jc/HgplbmRzdHJlYW0KZW5kb2JqCjE0IDAgb2JqCjw8IC9CYXNlRm9udCAvRGVqYVZ1U2Fucy1PYmxpcXVlIC9DaGFyUHJvY3MgMTUgMCBSCi9FbmNvZGluZyA8PCAvRGlmZmVyZW5jZXMgWyA3MiAvSCAxMDYgL2ogXSAvVHlwZSAvRW5jb2RpbmcgPj4gL0ZpcnN0Q2hhciAwCi9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnREZXNjcmlwdG9yIDEzIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTIgMCBSID4+CmVuZG9iagoxMyAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgOTYKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udE5hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovSXRhbGljQW5nbGUgMCAvTWF4V2lkdGggMTM1MCAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTIgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM1MCA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDI4IDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxNyA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjE3IDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDgKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk5NSA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMTUgMCBvYmoKPDwgL0ggMTYgMCBSIC9qIDE3IDAgUiA+PgplbmRvYmoKMjMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA1NCA+PgpzdHJlYW0KeJwzNjZXMFAwNDJX0DUyNlUwMjRQMDczUUgx5IIxc8EssGwOF1whhAmSz4GrzOFKAwBMkA8VCmVuZHN0cmVhbQplbmRvYmoKMjQgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzOTIgPj4Kc3RyZWFtCnicPVJLbgUxCNvPKbhApfBNcp6p3u7df1ubzFSqCi8DtjGUlwypJT/qkogzTH71cl3iUfK9bGpn5iHuLjam+FhyX7qG2HLRmmKxTxzJL8i0VFihVt2jQ/GFKBMPAC3ggQXhvhz/8ReowdewhXLDe2QCYErUbkDGQ9EZSFlBEWH7kRXopFCvbOHvKCBX1KyFoXRiiA2WACm+qw2JmKjZoIeElZKqHdLxjKTwW8FdiWFQW1vbBHhm0BDZ3pGNETPt0RlxWRFrPz3po1EytVEZD01nfPHdMlLz0RXopNLI3cpDZ89CJ2Ak5kmY53Aj4Z7bQQsx9HGvlk9s95gpVpHwBTvKAQO9/d6Sjc974CyMXNvsTCfw0WmnHBOtvh5i/YM/bEubXMcrh0UUqLwoCH7XQRNxfFjF92SjRHe0AdYjE9VoJRAMEsLO7TDyeMZ52d4VtOb0RGijRB7UjhE9KLLF5ZwVsKf8rM2xHJ4PJntvtI+UzMyohBXUdnqots9jHdR3nvv6/AEuAKEZCmVuZHN0cmVhbQplbmRvYmoKMjUgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDcgPj4Kc3RyZWFtCnicTVG7bUQxDOvfFFzgAOtreZ4LUl32b0PJCJDCIKEvKaclFvbGSwzhB1sPvuSRVUN/Hj8x7DMsPcnk1D/muclUFL4VqpuYUBdi4f1oBLwWdC8iK8oH349lDHPO9+CjEJdgJjRgrG9JJhfVvDNkwomhjsNBm1QYd00ULK4VzTPI7VY3sjqzIGx4JRPixgBEBNkXkM1go4yxlZDFch6oCpIFWmDX6RtRi4IrlNYJdKLWxLrM4Kvn9nY3Qy/y4Ki6eH0M60uwwuileyx8rkIfzPRMO3dJI73wphMRZg8FUpmdkZU6PWJ9t0D/n2Ur+PvJz/P9CxUoXCoKZW5kc3RyZWFtCmVuZG9iagoyNiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDkwID4+CnN0cmVhbQp4nE2NQRLAIAgD77wiT1BE0P90etL/X6vUDr3ATgKJFkWC9DVqSzDuuDIVa1ApmJSXwFUwXAva7qLK/jJJTJ2G03u3A4Oy8XGD0kn79nF6AKv9egbdD9IcIlgKZW5kc3RyZWFtCmVuZG9iagoyNyAwIG9iago8PCAvQkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzNwovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJzjMjQwUzA2NVXI5TI3NgKzcsAsI3MjIAski2BBZNMAAV8KCgplbmRzdHJlYW0KZW5kb2JqCjI4IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggODAgPj4Kc3RyZWFtCnicRYy7DcAwCER7pmAEfiZmnyiVs38bIErccE+6e7g6EjJT3mGGhwSeDCyGU/EGmaNgNbhGUo2d7KOwbl91geZ6U6v19wcqT3Z2cT3Nyxn0CmVuZHN0cmVhbQplbmRvYmoKMjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNDcgPj4Kc3RyZWFtCnicPU+5DQMxDOs9BRc4wHosW/NckOqyfxvKRlIIIkDxkWVHxwpcYgKTjjkSL2k/+GkagVgGNUf0hIphWOBukgIPgyxKV54tXgyR2kJdSPjWEN6tTGSiPK8RO3AnF6MHPlQbWR56QDtEFVmuScNY1VZdap2wAhyyzsJ1PcyqBOXRJ2spH1BUQr10/5972vsLAG8v6wplbmRzdHJlYW0KZW5kb2JqCjMwIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ5ID4+CnN0cmVhbQp4nDWPSw4DIQxD9zmFLzBSfoRwHqqupvffNmFaCQkL2y/BFoORjEtMYOyYY+ElVE+tPiQjj7pJORCpUDcET2hMDDNs0iXwynTfMp5bvJxW6oJOSOTprDYaooxmXsPRU84Km/7L3CRqZUaZAzLrVLcTsrJgBeYFtTz3M+6oXOiEh53KsOhOMaLcZkYafv/b9P4CezIwYwplbmRzdHJlYW0KZW5kb2JqCjMxIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggNDkgPj4Kc3RyZWFtCnicMza0UDBQMDQwB5JGhkCWkYlCiiEXSADEzOWCCeaAWQZAGqI4B64mhysNAMboDSYKZW5kc3RyZWFtCmVuZG9iagozMiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDY4ID4+CnN0cmVhbQp4nDMzNlMwULAwAhKmpoYK5kaWCimGXEA+iJXLBRPLAbPMLMyBLCMLkJYcLkMLYzBtYmykYGZiBmRZIDEgutIAcvgSkQplbmRzdHJlYW0KZW5kb2JqCjMzIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzE3ID4+CnN0cmVhbQp4nDVSS3JDMQjbv1Nwgc6Yv32edLJq7r+thCcrsC1AQi4vWdJLftQl26XD5Fcf9yWxQj6P7ZrMUsX3FrMUzy2vR88Rty0KBFETPfgyJxUi1M/U6Dp4YZc+A68QTikWeAeTAAav4V94lE6DwDsbMt4Rk5EaECTBmkuLTUiUPUn8K+X1pJU0dH4mK3P5e3KpFGqjyQgVIFi52AekKykeJBM9iUiycr03VojekFeSx2clJhkQ3SaxTbTA49yVtISZmEIF5liA1XSzuvocTFjjsITxKmEW1YNNnjWphGa0jmNkw3j3wkyJhYbDElCbfZUJqpeP09wJI6ZHTXbtwrJbNu8hRKP5MyyUwccoJAGHTmMkCtKwgBGBOb2wir3mCzkWwIhlnZosDG1oJbt6joXA0JyzpWHG157X8/4HRVt7owplbmRzdHJlYW0KZW5kb2JqCjM0IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjQ4ID4+CnN0cmVhbQp4nC1ROZIDQQjL5xV6QnPT77HLkff/6QrKAYOGQyA6LXFQxk8Qlive8shVtOHvmRjBd8Gh38p1GxY5EBVI0hhUTahdvB69B3YcZgLzpDUsgxnrAz9jCjd6cXhMxtntdRk1BHvXa09mUDIrF3HJxAVTddjImcNPpowL7VzPDci5EdZlGKSblcaMhCNNIVJIoeomqTNBkASjq1GjjRzFfunLI51hVSNqDPtcS9vXcxPOGjQ7Fqs8OaVHV5zLycULKwf9vM3ARVQaqzwQEnC/20P9nOzkN97SubPF9Phec7K8MBVY8ea1G5BNtfg3L+L4PePr+fwDqKVbFgplbmRzdHJlYW0KZW5kb2JqCjM1IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjEwID4+CnN0cmVhbQp4nDVQyw1DMQi7ZwoWqBQCgWSeVr11/2tt0DthEf9CWMiUCHmpyc4p6Us+OkwPti6/sSILrXUl7MqaIJ4r76GZsrHR2OJgcBomXoAWN2DoaY0aNXThgqYulUKBxSXwmXx1e+i+Txl4ahlydgQRQ8lgCWq6Fk1YtDyfkE4B4v9+w+4t5KGS88qeG/kbnO3wO7Nu4SdqdiLRchUy1LM0xxgIE0UePHlFpnDis9Z31TQS1GYLTpYBrk4/jA4AYCJeWYDsrkQ5S9KOpZ9vvMf3D0AAU7QKZW5kc3RyZWFtCmVuZG9iagoyMSAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMgL0NoYXJQcm9jcyAyMiAwIFIKL0VuY29kaW5nIDw8Ci9EaWZmZXJlbmNlcyBbIDQwIC9wYXJlbmxlZnQgL3BhcmVucmlnaHQgNDYgL3BlcmlvZCA0OCAvemVybyAvb25lIC90d28gNTIgL2ZvdXIgL2ZpdmUKL3NpeCAvc2V2ZW4gL2VpZ2h0IDEyNCAvYmFyIF0KL1R5cGUgL0VuY29kaW5nID4+Ci9GaXJzdENoYXIgMCAvRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250RGVzY3JpcHRvciAyMCAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2FucwovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxOSAwIFIgPj4KZW5kb2JqCjIwIDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyAzMgovRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250TmFtZSAvRGVqYVZ1U2FucyAvSXRhbGljQW5nbGUgMAovTWF4V2lkdGggMTM0MiAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTkgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM0MiA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDIzIDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxMiA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjEyIDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDUKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk4MiA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMjIgMCBvYmoKPDwgL2JhciAyMyAwIFIgL2VpZ2h0IDI0IDAgUiAvZml2ZSAyNSAwIFIgL2ZvdXIgMjYgMCBSIC9vbmUgMjggMCBSCi9wYXJlbmxlZnQgMjkgMCBSIC9wYXJlbnJpZ2h0IDMwIDAgUiAvcGVyaW9kIDMxIDAgUiAvc2V2ZW4gMzIgMCBSCi9zaXggMzMgMCBSIC90d28gMzQgMCBSIC96ZXJvIDM1IDAgUiA+PgplbmRvYmoKMyAwIG9iago8PCAvRjEgMjEgMCBSIC9GMiAxNCAwIFIgPj4KZW5kb2JqCjQgMCBvYmoKPDwgL0ExIDw8IC9DQSAwIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4KL0EyIDw8IC9DQSAxIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4gPj4KZW5kb2JqCjUgMCBvYmoKPDwgPj4KZW5kb2JqCjYgMCBvYmoKPDwgPj4KZW5kb2JqCjcgMCBvYmoKPDwgL0RlamFWdVNhbnMtT2JsaXF1ZS1vbWVnYSAxOCAwIFIgL0RlamFWdVNhbnMtbWludXMgMjcgMCBSID4+CmVuZG9iagoyIDAgb2JqCjw8IC9Db3VudCAxIC9LaWRzIFsgMTAgMCBSIF0gL1R5cGUgL1BhZ2VzID4+CmVuZG9iagozNiAwIG9iago8PCAvQ3JlYXRpb25EYXRlIChEOjIwMTkwNDE2MDkzMjA2KzAyJzAwJykKL0NyZWF0b3IgKG1hdHBsb3RsaWIgMy4wLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZykKL1Byb2R1Y2VyIChtYXRwbG90bGliIHBkZiBiYWNrZW5kIDMuMC4zKSA+PgplbmRvYmoKeHJlZgowIDM3CjAwMDAwMDAwMDAgNjU1MzUgZiAKMDAwMDAwMDAxNiAwMDAwMCBuIAowMDAwMDEwMTY2IDAwMDAwIG4gCjAwMDAwMDk5MDMgMDAwMDAgbiAKMDAwMDAwOTk0NiAwMDAwMCBuIAowMDAwMDEwMDQ1IDAwMDAwIG4gCjAwMDAwMTAwNjYgMDAwMDAgbiAKMDAwMDAxMDA4NyAwMDAwMCBuIAowMDAwMDAwMDY1IDAwMDAwIG4gCjAwMDAwMDA0MDMgMDAwMDAgbiAKMDAwMDAwMDIwOCAwMDAwMCBuIAowMDAwMDAyNjMxIDAwMDAwIG4gCjAwMDAwMDM4ODIgMDAwMDAgbiAKMDAwMDAwMzY3NCAwMDAwMCBuIAowMDAwMDAzMzUyIDAwMDAwIG4gCjAwMDAwMDQ5MzUgMDAwMDAgbiAKMDAwMDAwMjY1MiAwMDAwMCBuIAowMDAwMDAyODEyIDAwMDAwIG4gCjAwMDAwMDMwMzcgMDAwMDAgbiAKMDAwMDAwODY2MSAwMDAwMCBuIAowMDAwMDA4NDYxIDAwMDAwIG4gCjAwMDAwMDgwNjkgMDAwMDAgbiAKMDAwMDAwOTcxNCAwMDAwMCBuIAowMDAwMDA0OTc3IDAwMDAwIG4gCjAwMDAwMDUxMDMgMDAwMDAgbiAKMDAwMDAwNTU2OCAwMDAwMCBuIAowMDAwMDA1ODg4IDAwMDAwIG4gCjAwMDAwMDYwNTAgMDAwMDAgbiAKMDAwMDAwNjIyMCAwMDAwMCBuIAowMDAwMDA2MzcyIDAwMDAwIG4gCjAwMDAwMDY1OTIgMDAwMDAgbiAKMDAwMDAwNjgxNCAwMDAwMCBuIAowMDAwMDA2OTM1IDAwMDAwIG4gCjAwMDAwMDcwNzUgMDAwMDAgbiAKMDAwMDAwNzQ2NSAwMDAwMCBuIAowMDAwMDA3Nzg2IDAwMDAwIG4gCjAwMDAwMTAyMjYgMDAwMDAgbiAKdHJhaWxlcgo8PCAvSW5mbyAzNiAwIFIgL1Jvb3QgMSAwIFIgL1NpemUgMzcgPj4Kc3RhcnR4cmVmCjEwMzgwCiUlRU9GCg==\n",
"image/svg+xml": [
"\n",
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sym.plot(abs(H2.subs(s, sym.I*w)), (w, -10, 10),\n",
" ylabel=r'$|H(j \\omega)|$', xlabel=r'$\\omega$');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The phase of the transfer function $\\varphi(j \\omega) = \\arg \\{ H(j \\omega) \\}$ provides insight into the phase added to an harmonic signal when passing through the system. It is computed and plotted for the specific values of the elements given above"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM5Ny45NzMxMjUgMjk3LjAxMiBdIC9QYXJlbnQgMiAwIFIgL1Jlc291cmNlcyA4IDAgUgovVHlwZSAvUGFnZSA+PgplbmRvYmoKOSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDExIDAgUiA+PgpzdHJlYW0KeJy1mU2TFEUQhu/9K+qIB4r6/jhKqER4MZANPagHxBXZYFAkkL/vk91dPT1N7gKBsgHs5FtZmVWV+WZWjTc3kzfPjTM3/H1nfjK/8P9vxptH/H0+OT6dptir7TX6kPn4cv8x8KvzAaHb/f7HNP0+PfiSCd6g8GiaQrA5uOij8c5WmbF2W9JZ8nIvCbXYNk901jvL1snDMvlz3MR123bOY1KQTTsYn6KtuWB4L3M2IHs5TQ/Zg3fTa/515r5jxmrBQ7e+BBb57DQ9vDIPvvH4aq5+n5qNtXVX5u24+m26xxLcF+bqZvr6iln4IBPxM35hggdfXd88/eHtk6ev3tw/vXj19o356s/pMT+z61Op2Fq2Y3N1L7vd1Zyx0kur+VM8rjZ/nsPee9vcweML4e0ud046f7LL+XP32OdiUzq6vBfe7rJPyYb+yT6Hz93m4Lx17eDzhfDg84U/vkfrQ/WXXotja8AaHFsNpWxrOBraC+8yFGK1tWiG1h3YGerOxmOoXwjvNNSCTU4zlI8rihHRMUIvhHcZigEyS5qhelzRnsvOhvbCOw2VZrN7z4rfndAuDmPN1su0DPM+29QdoiUQ5ygz70WZzfPoQ6x99+vLF6/fXt//83T9/OmtMReYpHbXomQK9J6PYjVXWHpMuYtjvliOLDBd7+HD+RL/s2wp3kbOL4RLz8/iD3meqxxLS9WV8hGeh/8uzx05E10s/tL1nfxDvvdma4ypkVHRf0T5+h84au/4KryFo1oVjlmiJXbbc/eDpA7MsbPTku3Nl9gPps7yj7DWvEWhMrqUft4J1WIIRLKrobZDKpzlH7YY6D6Sd8mFHmM7x41ukfqfYui+Hiye5R9hsURbYNbku3PtnGMLrUjc3Jdj9jVswSMq0mktnFIslbrUpfI5uLcsh3M2d+/ne3P8RNudj2sRcMuYMMbczENoD3wOMcXziPMsX2xRqHDYYvcWDvvrjxdLRB41fbT0jZtPd89ywYSvzdYo5qVDjRACuxJKsZ7//742P5pXxttM4+lAaCRaCYuZsv6pnGp1ubUQc+jm+0cGw/+8eHb9/aOH5tmbXTMaSrLVz6VQuj5KXJ1l0I+LSQ76iY5QaYItREZaxD4338qioCIoUHBq40Dno669pYUOn+jIaaL3ab2mMkvhjjG/Ij9NGYbtJXSRBkIii8PzcBVBgWXl3lqexSnFnNYFqwh9MbvmPDGJ2HMRybWv/qvI3EiXzk+ZxQlS7+t4BThNlZTJLRE/oZCVqfnql/EqgkKzrcByi5heKITVgIqcpkZbVSmJiDOs7Xsr65JV5DR18S7XyMHkZlPOLudFQUVQ4LaUY4UHgxQy6Cmsa1ARCAbiybFlCRZa4uIZsprQIVEpwi29irO0IoRXiENFg5YLQk8ON5ETkr66NqyokKgUTjK0KHLOlybcDysqhAp55WAsyatMBpbW14hVEVEgEIIrzJOkOnrodigoCAqkVibnWZ60yLmkceIqIgpcKVPqHf5OpCUnG9LQ0CBU+FCzp9xLd91bdGXY0BBRyNJnNmIeviHXchqJoUOiUsVbOBm5TCpN+FDRIFHpnGfm/o8c4iMhBh/okNyxJEhjkyBlP0PpnNyqokKikuQtoWbCNHCJcUTTpqJBy02ueJqHZIJvTMU2jS1WIVSEJbiwZraFiM0t8/uqokKiwr2gUChpNnqSqWofx6JCqFBce3di0jfHAbta1mTUIVGhxpcmC4Ni4Eq2fzimQqJC70TVl7KHI1WIfzimQqjQAJEMFEXkCWqj0x07pkKiksgzTzkzskMuyDVgqGjQaW5HCiWQD14YvaeUxvJVSLodAq6mVpmKACk1hcF3OiQq1C72JctdnRLtINwRMCok12gCieTxfb6iQVZpjX0VEQX20YUkj0eSRYTecEuHUBGKKvR78p5EfNcYBhHrkLxQSaXAPO5CV8RQGtVBh0SFMCqEHcGdi3OjnityGQwv0bE2JqFBqiWR6mO8BonKnDROIts1qVDebyoahEokNblt0+bKayE0MnZKAWQ408CtEC0lkFxlwBivIPI0QYBS7Vo38jJIearDgIYsbxk0zZ09Lt3WlLk+DwUFEQVZDlSRjLQ3IW9LVgCGSzTCqqEYCnFzkOYafyoiCpgNIbluhNEypXhTUBBRaDJPzM1Quyjcbhv/PsBwYbAEsxYDlWM9lhEWGiIKGe9IdSOPXbFtZKAB0qh629hegpEcwXzbwkhDRKHaVgtNH1WrsG/biSkAw1u03F/FGBlVJM9HSGiIKHSuYpSQYoix0tj3sQANkVenJKWwsW9UuEgqppXLVEQUJMurNMjRy/NQGWVfRWi1XaajpnRQeBgQ6c7WNagICh5zdGSJhoMoa7X61YKKiEKTfo6bABxC/xpGZdUAuSxk6+kWpXeYH7jyNr+GyIMZwcvdUe6d0FoL45A1QIZLdUqwshEuSXKXHeMVBAVpebjUSItM1MulZjikIaJAjNCXSBPO/SNDuX4oKAgKmWhhWRQZxClSY4cFDREFuQZJvyBiinMbcaQiKBSp9lHumDQkpbrU1jhSEVHoVtoWiCPMN6cweggVkddEOuJO2Zb+jdJU/MhlFbl4fpwLxRoUjw0XW/Pt8nXPxXcmh4up/gSov07MM2/f9rybv/E5fr9z0r/fmV5t3+TM3oiq9q2N8sSqWd3dp1cTt9t9PP0LBbdtSwplbmRzdHJlYW0KZW5kb2JqCjExIDAgb2JqCjIwMjAKZW5kb2JqCjE2IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTUyID4+CnN0cmVhbQp4nD1PyxFDIQi8W8U2wIwggtbzMjmZ/q8BTTyxsrgf8YEKYhaQVIe4w63ixYW1o6vjU6QdtAqLg+YGlr8SsYK8gevW6Rg9Zpt4iufGGDpjhrBwzJEMWdrFM+62L0WODYK7YVah6SmWPuR6YRsHUnqztF2hpnAupiJjhnHbaZ9bJdKO0y9K/ZquIr3D1JK1i8affX8BvPc2ZwplbmRzdHJlYW0KZW5kb2JqCjE3IDAgb2JqCjw8IC9CQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE4MQovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJw1UDkOBCEM63mFP7ASucN7Rtpq9v/thjBToBgcBzuDSfEhwW9ENpCJFHiCw3GNZIgxiA2qAloO0yiClzS6B79cavUSKGaJpXpISyl1XOEMltjlGjL7LqYgXZAMSA25hpZ0o3uoHE5twglGeaS25gausyaXzza6//J2SvCIduOFj9PQfJxGZdxcpHWqCHpiRs3KPTZ6CUbctRyxnLXUUqRUizpRZbDVD3M2/+7xGt8/5jc/HgplbmRzdHJlYW0KZW5kb2JqCjE4IDAgb2JqCjw8IC9CQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI4MQovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJw9kTlyRDEIBXOdggu4SqySzjNVjsb3T93ojx1pAR7NY0SFxAr5GRF2b2FLIqeEbonp8hqeLrXlPXzfS0d2klSiekiIM0XjSKqLTZVEwlaXph/x4MdL/DgZJeHz1iCUR2Lr0/YDQmShlApSWt5bFqfxe0DbRU45VTGlWr+OlNmnY02ooMsFk3JqkNWypQJfTJMvVXFf93wNO0e+bC4GNJ3/19g3/h66nwp1bwGd8xEESnm3C/gC+gNwDCL+jPm8Y9i6ey6DMfHLIEs8cas7HQbTNlb3ss2EqFu7EbjIjEEd1TPE0dHd7LSu82moEDSzFhNn3gxlRUSYjBKjEWtrzepvx8reLAulRbIwx9hG+bP+Nb5/AXuPZFAKZW5kc3RyZWFtCmVuZG9iagoxNCAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMtT2JsaXF1ZSAvQ2hhclByb2NzIDE1IDAgUgovRW5jb2RpbmcgPDwgL0RpZmZlcmVuY2VzIFsgMTA2IC9qIF0gL1R5cGUgL0VuY29kaW5nID4+IC9GaXJzdENoYXIgMAovRm9udEJCb3ggWyAtMTAxNiAtMzUxIDE2NjAgMTA2OCBdIC9Gb250RGVzY3JpcHRvciAxMyAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2Fucy1PYmxpcXVlCi9TdWJ0eXBlIC9UeXBlMyAvVHlwZSAvRm9udCAvV2lkdGhzIDEyIDAgUiA+PgplbmRvYmoKMTMgMCBvYmoKPDwgL0FzY2VudCA5MjkgL0NhcEhlaWdodCAwIC9EZXNjZW50IC0yMzYgL0ZsYWdzIDk2Ci9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnROYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL0l0YWxpY0FuZ2xlIDAgL01heFdpZHRoIDEzNTAgL1N0ZW1WIDAgL1R5cGUgL0ZvbnREZXNjcmlwdG9yIC9YSGVpZ2h0IDAgPj4KZW5kb2JqCjEyIDAgb2JqClsgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAKNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCAzMTggNDAxIDQ2MCA4MzggNjM2Cjk1MCA3ODAgMjc1IDM5MCAzOTAgNTAwIDgzOCAzMTggMzYxIDMxOCAzMzcgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNgo2MzYgNjM2IDMzNyAzMzcgODM4IDgzOCA4MzggNTMxIDEwMDAgNjg0IDY4NiA2OTggNzcwIDYzMiA1NzUgNzc1IDc1MiAyOTUKMjk1IDY1NiA1NTcgODYzIDc0OCA3ODcgNjAzIDc4NyA2OTUgNjM1IDYxMSA3MzIgNjg0IDk4OSA2ODUgNjExIDY4NSAzOTAgMzM3CjM5MCA4MzggNTAwIDUwMCA2MTMgNjM1IDU1MCA2MzUgNjE1IDM1MiA2MzUgNjM0IDI3OCAyNzggNTc5IDI3OCA5NzQgNjM0IDYxMgo2MzUgNjM1IDQxMSA1MjEgMzkyIDYzNCA1OTIgODE4IDU5MiA1OTIgNTI1IDYzNiAzMzcgNjM2IDgzOCA2MDAgNjM2IDYwMCAzMTgKMzUyIDUxOCAxMDAwIDUwMCA1MDAgNTAwIDEzNTAgNjM1IDQwMCAxMDcwIDYwMCA2ODUgNjAwIDYwMCAzMTggMzE4IDUxOCA1MTgKNTkwIDUwMCAxMDAwIDUwMCAxMDAwIDUyMSA0MDAgMTAyOCA2MDAgNTI1IDYxMSAzMTggNDAxIDYzNiA2MzYgNjM2IDYzNiAzMzcKNTAwIDUwMCAxMDAwIDQ3MSA2MTcgODM4IDM2MSAxMDAwIDUwMCA1MDAgODM4IDQwMSA0MDEgNTAwIDYzNiA2MzYgMzE4IDUwMAo0MDEgNDcxIDYxNyA5NjkgOTY5IDk2OSA1MzEgNjg0IDY4NCA2ODQgNjg0IDY4NCA2ODQgOTc0IDY5OCA2MzIgNjMyIDYzMiA2MzIKMjk1IDI5NSAyOTUgMjk1IDc3NSA3NDggNzg3IDc4NyA3ODcgNzg3IDc4NyA4MzggNzg3IDczMiA3MzIgNzMyIDczMiA2MTEgNjA4CjYzMCA2MTMgNjEzIDYxMyA2MTMgNjEzIDYxMyA5OTUgNTUwIDYxNSA2MTUgNjE1IDYxNSAyNzggMjc4IDI3OCAyNzggNjEyIDYzNAo2MTIgNjEyIDYxMiA2MTIgNjEyIDgzOCA2MTIgNjM0IDYzNCA2MzQgNjM0IDU5MiA2MzUgNTkyIF0KZW5kb2JqCjE1IDAgb2JqCjw8IC9qIDE2IDAgUiA+PgplbmRvYmoKMjMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDcgPj4Kc3RyZWFtCnicTVG7bUQxDOvfFFzgAOtreZ4LUl32b0PJCJDCIKEvKaclFvbGSwzhB1sPvuSRVUN/Hj8x7DMsPcnk1D/muclUFL4VqpuYUBdi4f1oBLwWdC8iK8oH349lDHPO9+CjEJdgJjRgrG9JJhfVvDNkwomhjsNBm1QYd00ULK4VzTPI7VY3sjqzIGx4JRPixgBEBNkXkM1go4yxlZDFch6oCpIFWmDX6RtRi4IrlNYJdKLWxLrM4Kvn9nY3Qy/y4Ki6eH0M60uwwuileyx8rkIfzPRMO3dJI73wphMRZg8FUpmdkZU6PWJ9t0D/n2Ur+PvJz/P9CxUoXCoKZW5kc3RyZWFtCmVuZG9iagoyNCAwIG9iago8PCAvQkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzNwovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJzjMjQwUzA2NVXI5TI3NgKzcsAsI3MjIAski2BBZNMAAV8KCgplbmRzdHJlYW0KZW5kb2JqCjI1IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggODAgPj4Kc3RyZWFtCnicRYy7DcAwCER7pmAEfiZmnyiVs38bIErccE+6e7g6EjJT3mGGhwSeDCyGU/EGmaNgNbhGUo2d7KOwbl91geZ6U6v19wcqT3Z2cT3Nyxn0CmVuZHN0cmVhbQplbmRvYmoKMjYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNDcgPj4Kc3RyZWFtCnicPU+5DQMxDOs9BRc4wHosW/NckOqyfxvKRlIIIkDxkWVHxwpcYgKTjjkSL2k/+GkagVgGNUf0hIphWOBukgIPgyxKV54tXgyR2kJdSPjWEN6tTGSiPK8RO3AnF6MHPlQbWR56QDtEFVmuScNY1VZdap2wAhyyzsJ1PcyqBOXRJ2spH1BUQr10/5972vsLAG8v6wplbmRzdHJlYW0KZW5kb2JqCjI3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ5ID4+CnN0cmVhbQp4nDWPSw4DIQxD9zmFLzBSfoRwHqqupvffNmFaCQkL2y/BFoORjEtMYOyYY+ElVE+tPiQjj7pJORCpUDcET2hMDDNs0iXwynTfMp5bvJxW6oJOSOTprDYaooxmXsPRU84Km/7L3CRqZUaZAzLrVLcTsrJgBeYFtTz3M+6oXOiEh53KsOhOMaLcZkYafv/b9P4CezIwYwplbmRzdHJlYW0KZW5kb2JqCjI4IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggNDkgPj4Kc3RyZWFtCnicMza0UDBQMDQwB5JGhkCWkYlCiiEXSADEzOWCCeaAWQZAGqI4B64mhysNAMboDSYKZW5kc3RyZWFtCmVuZG9iagoyOSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDY4ID4+CnN0cmVhbQp4nDMzNlMwULAwAhKmpoYK5kaWCimGXEA+iJXLBRPLAbPMLMyBLCMLkJYcLkMLYzBtYmykYGZiBmRZIDEgutIAcvgSkQplbmRzdHJlYW0KZW5kb2JqCjMwIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzM4ID4+CnN0cmVhbQp4nDVSOa7dQAzrfQpdIIB2zZznBal+7t+GlF8KQ7RWipqOFpVp+WUhVS2TLr/tSW2JG/L3yQqJE5JXJdqlDJFQ+TyFVL9ny7y+1pwRIEuVCpOTksclC/4Ml94uHOdjaz+PI3c9emBVjIQSAcsUE6NrWTq7w5qN/DymAT/iEXKuWLccYxVIDbpx2hXvQ/N5yBogZpiWigpdVokWfkHxoEetffdYVFgg0e0cSXCMjVCRgHaB2kgMObMWu6gv+lmUmAl07Ysi7qLAEknMnGJdOvoPPnQsqL8248uvjkr6SCtrTNp3o0lpzCKTrpdFbzdvfT24QPMuyn9ezSBBU9YoaXzQqp1jKJoZZYV3HJoMNMcch8wTPIczEpT0fSh+X0smuiiRPw4NoX9fHqOMnAZvAXPRn7aKAxfx2WGvHGCF0sWa5H1AKhN6YPr/1/h5/vwDHLaAVAplbmRzdHJlYW0KZW5kb2JqCjMxIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjQ4ID4+CnN0cmVhbQp4nC1ROZIDQQjL5xV6QnPT77HLkff/6QrKAYOGQyA6LXFQxk8Qlive8shVtOHvmRjBd8Gh38p1GxY5EBVI0hhUTahdvB69B3YcZgLzpDUsgxnrAz9jCjd6cXhMxtntdRk1BHvXa09mUDIrF3HJxAVTddjImcNPpowL7VzPDci5EdZlGKSblcaMhCNNIVJIoeomqTNBkASjq1GjjRzFfunLI51hVSNqDPtcS9vXcxPOGjQ7Fqs8OaVHV5zLycULKwf9vM3ARVQaqzwQEnC/20P9nOzkN97SubPF9Phec7K8MBVY8ea1G5BNtfg3L+L4PePr+fwDqKVbFgplbmRzdHJlYW0KZW5kb2JqCjMyIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjEwID4+CnN0cmVhbQp4nDVQyw1DMQi7ZwoWqBQCgWSeVr11/2tt0DthEf9CWMiUCHmpyc4p6Us+OkwPti6/sSILrXUl7MqaIJ4r76GZsrHR2OJgcBomXoAWN2DoaY0aNXThgqYulUKBxSXwmXx1e+i+Txl4ahlydgQRQ8lgCWq6Fk1YtDyfkE4B4v9+w+4t5KGS88qeG/kbnO3wO7Nu4SdqdiLRchUy1LM0xxgIE0UePHlFpnDis9Z31TQS1GYLTpYBrk4/jA4AYCJeWYDsrkQ5S9KOpZ9vvMf3D0AAU7QKZW5kc3RyZWFtCmVuZG9iagoyMSAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMgL0NoYXJQcm9jcyAyMiAwIFIKL0VuY29kaW5nIDw8Ci9EaWZmZXJlbmNlcyBbIDQwIC9wYXJlbmxlZnQgL3BhcmVucmlnaHQgNDYgL3BlcmlvZCA0OCAvemVybyAvb25lIC90d28gL3RocmVlIDUzIC9maXZlCjU1IC9zZXZlbiBdCi9UeXBlIC9FbmNvZGluZyA+PgovRmlyc3RDaGFyIDAgL0ZvbnRCQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRm9udERlc2NyaXB0b3IgMjAgMCBSCi9Gb250TWF0cml4IFsgMC4wMDEgMCAwIDAuMDAxIDAgMCBdIC9MYXN0Q2hhciAyNTUgL05hbWUgL0RlamFWdVNhbnMKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTkgMCBSID4+CmVuZG9iagoyMCAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgMzIKL0ZvbnRCQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRm9udE5hbWUgL0RlamFWdVNhbnMgL0l0YWxpY0FuZ2xlIDAKL01heFdpZHRoIDEzNDIgL1N0ZW1WIDAgL1R5cGUgL0ZvbnREZXNjcmlwdG9yIC9YSGVpZ2h0IDAgPj4KZW5kb2JqCjE5IDAgb2JqClsgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAKNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCAzMTggNDAxIDQ2MCA4MzggNjM2Cjk1MCA3ODAgMjc1IDM5MCAzOTAgNTAwIDgzOCAzMTggMzYxIDMxOCAzMzcgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNgo2MzYgNjM2IDMzNyAzMzcgODM4IDgzOCA4MzggNTMxIDEwMDAgNjg0IDY4NiA2OTggNzcwIDYzMiA1NzUgNzc1IDc1MiAyOTUKMjk1IDY1NiA1NTcgODYzIDc0OCA3ODcgNjAzIDc4NyA2OTUgNjM1IDYxMSA3MzIgNjg0IDk4OSA2ODUgNjExIDY4NSAzOTAgMzM3CjM5MCA4MzggNTAwIDUwMCA2MTMgNjM1IDU1MCA2MzUgNjE1IDM1MiA2MzUgNjM0IDI3OCAyNzggNTc5IDI3OCA5NzQgNjM0IDYxMgo2MzUgNjM1IDQxMSA1MjEgMzkyIDYzNCA1OTIgODE4IDU5MiA1OTIgNTI1IDYzNiAzMzcgNjM2IDgzOCA2MDAgNjM2IDYwMCAzMTgKMzUyIDUxOCAxMDAwIDUwMCA1MDAgNTAwIDEzNDIgNjM1IDQwMCAxMDcwIDYwMCA2ODUgNjAwIDYwMCAzMTggMzE4IDUxOCA1MTgKNTkwIDUwMCAxMDAwIDUwMCAxMDAwIDUyMSA0MDAgMTAyMyA2MDAgNTI1IDYxMSAzMTggNDAxIDYzNiA2MzYgNjM2IDYzNiAzMzcKNTAwIDUwMCAxMDAwIDQ3MSA2MTIgODM4IDM2MSAxMDAwIDUwMCA1MDAgODM4IDQwMSA0MDEgNTAwIDYzNiA2MzYgMzE4IDUwMAo0MDEgNDcxIDYxMiA5NjkgOTY5IDk2OSA1MzEgNjg0IDY4NCA2ODQgNjg0IDY4NCA2ODQgOTc0IDY5OCA2MzIgNjMyIDYzMiA2MzIKMjk1IDI5NSAyOTUgMjk1IDc3NSA3NDggNzg3IDc4NyA3ODcgNzg3IDc4NyA4MzggNzg3IDczMiA3MzIgNzMyIDczMiA2MTEgNjA1CjYzMCA2MTMgNjEzIDYxMyA2MTMgNjEzIDYxMyA5ODIgNTUwIDYxNSA2MTUgNjE1IDYxNSAyNzggMjc4IDI3OCAyNzggNjEyIDYzNAo2MTIgNjEyIDYxMiA2MTIgNjEyIDgzOCA2MTIgNjM0IDYzNCA2MzQgNjM0IDU5MiA2MzUgNTkyIF0KZW5kb2JqCjIyIDAgb2JqCjw8IC9maXZlIDIzIDAgUiAvb25lIDI1IDAgUiAvcGFyZW5sZWZ0IDI2IDAgUiAvcGFyZW5yaWdodCAyNyAwIFIKL3BlcmlvZCAyOCAwIFIgL3NldmVuIDI5IDAgUiAvdGhyZWUgMzAgMCBSIC90d28gMzEgMCBSIC96ZXJvIDMyIDAgUiA+PgplbmRvYmoKMyAwIG9iago8PCAvRjEgMjEgMCBSIC9GMiAxNCAwIFIgPj4KZW5kb2JqCjQgMCBvYmoKPDwgL0ExIDw8IC9DQSAwIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4KL0EyIDw8IC9DQSAxIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4gPj4KZW5kb2JqCjUgMCBvYmoKPDwgPj4KZW5kb2JqCjYgMCBvYmoKPDwgPj4KZW5kb2JqCjcgMCBvYmoKPDwgL0RlamFWdVNhbnMtT2JsaXF1ZS1vbWVnYSAxNyAwIFIgL0RlamFWdVNhbnMtT2JsaXF1ZS1waGkgMTggMCBSCi9EZWphVnVTYW5zLW1pbnVzIDI0IDAgUiA+PgplbmRvYmoKMiAwIG9iago8PCAvQ291bnQgMSAvS2lkcyBbIDEwIDAgUiBdIC9UeXBlIC9QYWdlcyA+PgplbmRvYmoKMzMgMCBvYmoKPDwgL0NyZWF0aW9uRGF0ZSAoRDoyMDE5MDQxNjA5MzIwNyswMicwMCcpCi9DcmVhdG9yIChtYXRwbG90bGliIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcpCi9Qcm9kdWNlciAobWF0cGxvdGxpYiBwZGYgYmFja2VuZCAzLjAuMykgPj4KZW5kb2JqCnhyZWYKMCAzNAowMDAwMDAwMDAwIDY1NTM1IGYgCjAwMDAwMDAwMTYgMDAwMDAgbiAKMDAwMDAwOTUxMCAwMDAwMCBuIAowMDAwMDA5MjE2IDAwMDAwIG4gCjAwMDAwMDkyNTkgMDAwMDAgbiAKMDAwMDAwOTM1OCAwMDAwMCBuIAowMDAwMDA5Mzc5IDAwMDAwIG4gCjAwMDAwMDk0MDAgMDAwMDAgbiAKMDAwMDAwMDA2NSAwMDAwMCBuIAowMDAwMDAwMzk2IDAwMDAwIG4gCjAwMDAwMDAyMDggMDAwMDAgbiAKMDAwMDAwMjQ5MSAwMDAwMCBuIAowMDAwMDAzOTkxIDAwMDAwIG4gCjAwMDAwMDM3ODMgMDAwMDAgbiAKMDAwMDAwMzQ2NyAwMDAwMCBuIAowMDAwMDA1MDQ0IDAwMDAwIG4gCjAwMDAwMDI1MTIgMDAwMDAgbiAKMDAwMDAwMjczNyAwMDAwMCBuIAowMDAwMDAzMDUyIDAwMDAwIG4gCjAwMDAwMDgwMTEgMDAwMDAgbiAKMDAwMDAwNzgxMSAwMDAwMCBuIAowMDAwMDA3NDM2IDAwMDAwIG4gCjAwMDAwMDkwNjQgMDAwMDAgbiAKMDAwMDAwNTA3NiAwMDAwMCBuIAowMDAwMDA1Mzk2IDAwMDAwIG4gCjAwMDAwMDU1NjYgMDAwMDAgbiAKMDAwMDAwNTcxOCAwMDAwMCBuIAowMDAwMDA1OTM4IDAwMDAwIG4gCjAwMDAwMDYxNjAgMDAwMDAgbiAKMDAwMDAwNjI4MSAwMDAwMCBuIAowMDAwMDA2NDIxIDAwMDAwIG4gCjAwMDAwMDY4MzIgMDAwMDAgbiAKMDAwMDAwNzE1MyAwMDAwMCBuIAowMDAwMDA5NTcwIDAwMDAwIG4gCnRyYWlsZXIKPDwgL0luZm8gMzMgMCBSIC9Sb290IDEgMCBSIC9TaXplIDM0ID4+CnN0YXJ0eHJlZgo5NzI0CiUlRU9GCg==\n",
"image/svg+xml": [
"\n",
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"phi = sym.arg(Hjw)\n",
"sym.plot(phi.subs(RLC), (w, -10, 10),\n",
" ylabel=r'$\\varphi(j \\omega)$', xlabel=r'$\\omega$');"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbsphinx": "hidden"
},
"source": [
"**Copyright**\n",
"\n",
"The notebooks are provided as [Open Educational Resource](https://de.wikipedia.org/wiki/Open_Educational_Resources). Feel free to use the notebooks for your own educational purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Lecture Notes on Signals and Systems* by Sascha Spors."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 1
}