{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Optimization of cycles on surfaces"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In this notebook we use MOSEK Fusion to solve some geometric optimization problems on surfaces. The code demonstrates setting up a linear optimization problem, extending the `Model` class and shows the practical difference between interior-point and basic solution."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Requirements"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [],
"source": [
"%matplotlib notebook\n",
"import mosek \n",
"from mosek.fusion import *\n",
"import numpy as np \n",
"import sys, io, math, plyfile\n",
"from mpl_toolkits.mplot3d import Axes3D\n",
"import matplotlib.pyplot as plt\n",
"\n",
"#Fetching examples predefined for this presentation\n",
"def getExample(name):\n",
" return plyfile.PlyData.read(open(name, 'rb'))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### References\n",
"`plyfile` is a package for reading the descriptions of surfaces in PLY format. It can be installed with `pip install plyfile`. You will also need some data files with examples used in this presentation. The complete code and additional files are available from GitHub.\n",
"\n",
"One of the models used in this tutorial comes from John Burkardt's library of PLY files and the other ones were generated using CGAL. A comprehensive survey of topological optimization problems can be found in the survey paper by Jeff Erickson. The model used in this tutorial comes from the paper Optimal Homologous Cycles, Total Unimodularity, and Linear Programming by Dey, Hirani and Krishnamoorthy. The experts in the field are kindly asked to fill in some vague statements in the following text with the precise algebro-topological language on their own."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## A crash-course in homotopy\n",
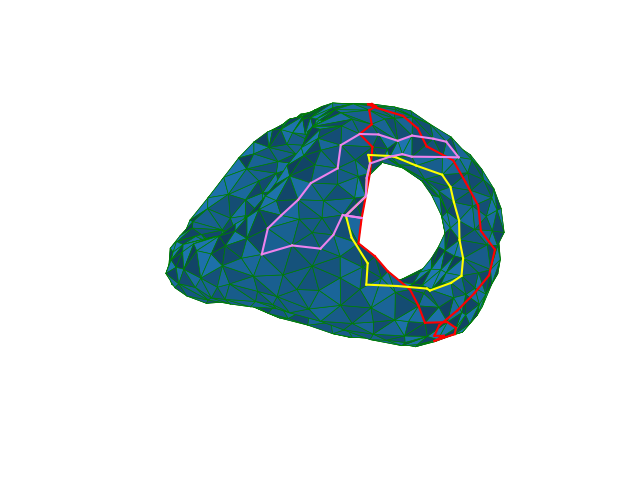
"A triangulated surface is a mesh of 2D triangles in 3D that fit together to form a surface. The vertices and edges of a triangulation form a graph. The *cycles* in that graph can be used to detect interesting *topological features*. For an example of what that means, see the three loops on the surface below:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now imagine that each loop is a rubber band that can be stretched in a continuous way and slide on the surface. Then the violet loop is not very interesting - it lies in a small patch of the surface and if we start shrinking it, it will collapse to a point (in other words, it is *contractible*). The yellow loop is different - it circles around a hole in the surface, and no matter how much we deform it, it will not disappear. We say this loop *detects a feature* - in this case the feature is one of the holes. The red loop has the same property. Moreover, the yellow and red loops are *homotopic* - each of them can be continuosly moulded into the second one - i.e. they detect the same feature (hole).\n",
"\n",
"In some applications it is useful to have *small* representations of topological features, in this case the shortest possible loops in a given homotopy class. There are at least two reasonable ways of measuring the length of a path on a surface: with the Euclidean metric on the edges, or just counting the number of edges."
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [],
"source": [
"#Two ways of assigning edge weights\n",
"def euclideanM(x, y):\n",
" return math.sqrt(sum([(x[i]-y[i])**2 for i in range(3)]))\n",
"def graphM(x,y):\n",
" return 1"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## First problem: shortest equivalent representation of a cycle\n",
"Suppose the surface has $v$ vertices, $e$ edges and $t$ triangles. It is convenient to represent it by *boundary matrices*, which are just variants of the incidence matrix of a graph. Specifically, let $V(i)$, $E(ij)$ and $T(ijk)$ denote the vertex, edge and triangle with the given vertex set. Then we have a linear map $D_1:\\mathbb{R}^e\\to\\mathbb{R}^v$ given on the basis vectors by:\n",
"\n",
"$$D_1(\\mathbf{e}_{E(ij)})=\\mathbf{e}_{V(j)}-\\mathbf{e}_{V(i)}$$\n",
"\n",
"and we identify $D_1\\in \\mathbb{R}^{v\\times e}$ with the matrix of this map. Similarly, we can record the incidence between triangles and edges by $D_2:\\mathbb{R}^t\\to\\mathbb{R}^e$:\n",
"\n",
"$$D_2(\\mathbf{e}_{T(ijk)})=\\mathbf{e}_{E(jk)}-\\mathbf{e}_{E(ik)}+\\mathbf{e}_{E(ij)}$$\n",
"\n",
"and let $D_2\\in \\mathbb{R}^{e\\times t}$ be its matrix. We refer to other sources for more details. Note that matrices $D_1,D_2$ are extremely sparse - they have just two, resp. three, nonzeros in each column.\n",
"\n",
"### Shortest homologous cycle problem\n",
"A *chain* (more precisely, *1-chain*) is just a vector $c\\in \\mathbb{R}^e$, that is an assignment of a real coefficient to every edge. If $c$ is an actual path or cycle in the graph, then these coefficients are $\\pm1$ for edges in the cycle, and $0$ otherwise, but more general chains are allowed. We will mostly concentrate on cycles.\n",
"\n",
"We can now formulate the following problem: given a cycle $c\\in\\mathbb{R}^e$, find the shortest cycle that detects the same topological features as $c$ (strictly speaking, the shortest cycle *homologous* to $c$). Suppose $w_1,\\ldots,w_e$ are the weights (lengths) of the edges.\n",
"\n",
"$$\n",
"\\begin{array}{ll}\n",
"\\textrm{minimize} & \\sum_{i=1}^e w_i|x_i| \\\\\n",
"\\textrm{subject to} & x-c=D_2y \\\\\n",
" & x\\in\\mathbb{R}^e, y\\in\\mathbb{R}^t\n",
"\\end{array}\n",
"$$\n",
"\n",
"### Implementation\n",
"This optimization problem can easily be formulated as a linear program. Below is the implementation of this program in a class `Surface`, which extends a Mosek Fusion `Model`."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [],
"source": [
"#A model of a surface (or a more general 2D complex in 3D)\n",
"class Surface:\n",
" #Initialize from plydata using edge weights given by metric\n",
" def __init__(self, plydata, metric):\n",
"\n",
" ### Initialize basic data\n",
" self.v = plydata.elements[0].count # number of vertices\n",
" self.t = plydata.elements[1].count # number of triangles\n",
" self.coo = plydata['vertex'] # coordinates of vertices in 3D\n",
" self.xc, self.yc, self.zc = zip(*self.coo)\n",
" self.tri = [tuple(sorted(f[0])) for f in plydata['face']] # list of triangles, as sorted triples of vertices\n",
" self.edg = list(set([tuple(sorted([f[i],f[j]])) # list of edges, as sorted pairs of vertices\n",
" for f in self.tri for i,j in [(0,1),(0,2),(1,2)]]))\n",
" self.e = len(self.edg) # number of edges\n",
" self.wgh = [metric(self.coo[f[0]],self.coo[f[1]]) # weights of edges\n",
" for f in self.edg]\n",
"\n",
" ### Homological algebra\n",
" # Construct the sparse matrix D2\n",
" d1 = [ (self.edg[i][k], i, sgn) for i in range(self.e) for k,sgn in [(1,+1),(0,-1)] ]\n",
" s1, s2, val = zip(*d1)\n",
" self.D1 = Matrix.sparse(self.v, self.e, list(s1), list(s2), list(val))\n",
" # Construct the sparse matrix D3\n",
" d2 = [ (self.edg.index((self.tri[i][k],self.tri[i][l])), i, sgn) \n",
" for i in range(self.t) for k,l,sgn in [(1,2,+1),(0,2,-1),(0,1,+1)] ]\n",
" s1, s2, val = zip(*d2)\n",
" self.D2 = Matrix.sparse(self.e, self.t, list(s1), list(s2), list(val))\n",
"\n",
" #Plot the surface and a number of chains\n",
" def plot(self, chains=[], colors=[]):\n",
" fig = plt.figure()\n",
" ax = fig.gca(projection='3d')\n",
" ax.plot_trisurf(self.xc, self.yc, self.zc, triangles=self.tri, linewidth=0.5, alpha=1.0, edgecolor='green')\n",
" i = 0\n",
" for C in chains:\n",
" for j in range(self.e):\n",
" if abs(C[j])>0.0001:\n",
" # Extract the edge and plot with intensity depending on its coefficient in C\n",
" xc,yc,zc = zip(*[ self.coo[self.edg[j][0]], self.coo[self.edg[j][1]] ])\n",
" ax.plot(xc, yc, zc, color=colors[i], alpha=min(1,abs(C[j])))\n",
" i += 1\n",
" plt.axis('off')\n",
" plt.show()\n",
"\n",
" #Find the shortest chain homologous to a given chain C\n",
" def short(self, C):\n",
" ### Set up a MOSEK Fusion model for solving shortest homologous cycles\n",
" with Model(\"short\") as M:\n",
" x = M.variable(self.e, Domain.unbounded()) # the chain we are looking for\n",
" xabs = M.variable(self.e, Domain.unbounded()) # absolute value of x\n",
" y = M.variable(self.t, Domain.unbounded()) # a 2-chain whose boundary is x-C\n",
"\n",
" # -xabs <= x <= xabs\n",
" M.constraint(Expr.add(xabs, x), Domain.greaterThan(0))\n",
" M.constraint(Expr.sub(xabs, x), Domain.greaterThan(0))\n",
"\n",
" # x - c = D2*y, so x-c is a boundary\n",
" M.constraint(Expr.sub(Expr.sub(x, C), Expr.mul(self.D2, y)), Domain.equalsTo(0))\n",
"\n",
" # min weighted 1-norm of x\n",
" M.objective(ObjectiveSense.Minimize, Expr.dot(self.wgh, xabs))\n",
"\n",
" # solve\n",
" M.solve()\n",
" return x.level()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The inititlization part processes the PLY description of the surface and initializes the sparse boundary matrices. Every time we optimize for the shortest cycle a new Fusion model is constructed and solved from the input data.\n",
"\n",
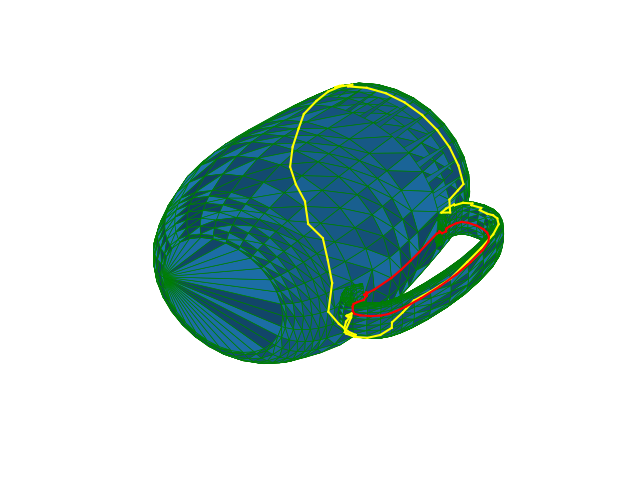
"### Example\n",
"We predefined the yellow cycle on the mug, and Mosek finds the red cycle - its shortest topological equivalent."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Indeed, if we again imagine the yellow loop is made out of rubber, then once it starts contracting it will reach its minimum length when it sits tightly around the mug's handle."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Detecting features\n",
"OK, but what if we don't have any predefined cycle, and we would simply like to visualize all topological features on a given input surface using shortest possible loops? In general, this is a hard problem, for which some algorithms are known on surfaces. However, we can use our model to try a more pedestrian approach, which is not perfect, but often good enough for visualization.\n",
"\n",
"Without going into too much algebra, the space of features on the surface can be identified with the nullspace of the matrix $$A=\\left[\\begin{array}{l} D_1 \\\\ D_2^T\\end{array}\\right]$$ (for the experts, we are now computing first homology with real coefficients). This can be easily found using singular value decomposition:"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [],
"source": [
"#Find the basis for the nullspace of a matrix\n",
"def nullspace(A):\n",
" u, s, vh = np.linalg.svd(A)\n",
" nnz = (s >= 1e-13).sum()\n",
" ns = vh[nnz:].conj().T\n",
" return ns, ns.shape[1]\n",
"\n",
"def homology(S):\n",
" return nullspace(np.reshape(\n",
" np.concatenate((S.D1.getDataAsArray(), S.D2.transpose().getDataAsArray())),\n",
" [S.v+S.t, S.e]))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For an orientable surface the dimension of the nullspace of $A$ equals $2g$, where $g$ is the genus, or the number of holes. For example, the torus has one hole and two essential features: the parallel and the meridian cycle.\n",
"\n",
"Since the SVD decomposition is oblivious to the underlying geometry, the chains it returns are typically dense vectors with real coordinates, not very useful for visualization. However, we can replace them with their shortest equivalents and see if they are any better. It turns out in practice they often are. To make this easier to see we also normalize so that the maximal coefficient of each chain is 1."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [
{
"data": {
"application/javascript": [
"/* Put everything inside the global mpl namespace */\n",
"window.mpl = {};\n",
"\n",
"\n",
"mpl.get_websocket_type = function() {\n",
" if (typeof(WebSocket) !== 'undefined') {\n",
" return WebSocket;\n",
" } else if (typeof(MozWebSocket) !== 'undefined') {\n",
" return MozWebSocket;\n",
" } else {\n",
" alert('Your browser does not have WebSocket support.' +\n",
" 'Please try Chrome, Safari or Firefox 6. ' +\n",
" 'Firefox 4 and 5 are also supported but you ' +\n",
" 'have to enable WebSockets in about:config.');\n",
" };\n",
"}\n",
"\n",
"mpl.figure = function(figure_id, websocket, ondownload, parent_element) {\n",
" this.id = figure_id;\n",
"\n",
" this.ws = websocket;\n",
"\n",
" this.supports_binary = (this.ws.binaryType != undefined);\n",
"\n",
" if (!this.supports_binary) {\n",
" var warnings = document.getElementById(\"mpl-warnings\");\n",
" if (warnings) {\n",
" warnings.style.display = 'block';\n",
" warnings.textContent = (\n",
" \"This browser does not support binary websocket messages. \" +\n",
" \"Performance may be slow.\");\n",
" }\n",
" }\n",
"\n",
" this.imageObj = new Image();\n",
"\n",
" this.context = undefined;\n",
" this.message = undefined;\n",
" this.canvas = undefined;\n",
" this.rubberband_canvas = undefined;\n",
" this.rubberband_context = undefined;\n",
" this.format_dropdown = undefined;\n",
"\n",
" this.image_mode = 'full';\n",
"\n",
" this.root = $('');\n",
" this._root_extra_style(this.root)\n",
" this.root.attr('style', 'display: inline-block');\n",
"\n",
" $(parent_element).append(this.root);\n",
"\n",
" this._init_header(this);\n",
" this._init_canvas(this);\n",
" this._init_toolbar(this);\n",
"\n",
" var fig = this;\n",
"\n",
" this.waiting = false;\n",
"\n",
" this.ws.onopen = function () {\n",
" fig.send_message(\"supports_binary\", {value: fig.supports_binary});\n",
" fig.send_message(\"send_image_mode\", {});\n",
" if (mpl.ratio != 1) {\n",
" fig.send_message(\"set_dpi_ratio\", {'dpi_ratio': mpl.ratio});\n",
" }\n",
" fig.send_message(\"refresh\", {});\n",
" }\n",
"\n",
" this.imageObj.onload = function() {\n",
" if (fig.image_mode == 'full') {\n",
" // Full images could contain transparency (where diff images\n",
" // almost always do), so we need to clear the canvas so that\n",
" // there is no ghosting.\n",
" fig.context.clearRect(0, 0, fig.canvas.width, fig.canvas.height);\n",
" }\n",
" fig.context.drawImage(fig.imageObj, 0, 0);\n",
" };\n",
"\n",
" this.imageObj.onunload = function() {\n",
" fig.ws.close();\n",
" }\n",
"\n",
" this.ws.onmessage = this._make_on_message_function(this);\n",
"\n",
" this.ondownload = ondownload;\n",
"}\n",
"\n",
"mpl.figure.prototype._init_header = function() {\n",
" var titlebar = $(\n",
" '');\n",
" var titletext = $(\n",
" '');\n",
" titlebar.append(titletext)\n",
" this.root.append(titlebar);\n",
" this.header = titletext[0];\n",
"}\n",
"\n",
"\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._init_canvas = function() {\n",
" var fig = this;\n",
"\n",
" var canvas_div = $('');\n",
"\n",
" canvas_div.attr('style', 'position: relative; clear: both; outline: 0');\n",
"\n",
" function canvas_keyboard_event(event) {\n",
" return fig.key_event(event, event['data']);\n",
" }\n",
"\n",
" canvas_div.keydown('key_press', canvas_keyboard_event);\n",
" canvas_div.keyup('key_release', canvas_keyboard_event);\n",
" this.canvas_div = canvas_div\n",
" this._canvas_extra_style(canvas_div)\n",
" this.root.append(canvas_div);\n",
"\n",
" var canvas = $('');\n",
" canvas.addClass('mpl-canvas');\n",
" canvas.attr('style', \"left: 0; top: 0; z-index: 0; outline: 0\")\n",
"\n",
" this.canvas = canvas[0];\n",
" this.context = canvas[0].getContext(\"2d\");\n",
"\n",
" var backingStore = this.context.backingStorePixelRatio ||\n",
"\tthis.context.webkitBackingStorePixelRatio ||\n",
"\tthis.context.mozBackingStorePixelRatio ||\n",
"\tthis.context.msBackingStorePixelRatio ||\n",
"\tthis.context.oBackingStorePixelRatio ||\n",
"\tthis.context.backingStorePixelRatio || 1;\n",
"\n",
" mpl.ratio = (window.devicePixelRatio || 1) / backingStore;\n",
"\n",
" var rubberband = $('');\n",
" rubberband.attr('style', \"position: absolute; left: 0; top: 0; z-index: 1;\")\n",
"\n",
" var pass_mouse_events = true;\n",
"\n",
" canvas_div.resizable({\n",
" start: function(event, ui) {\n",
" pass_mouse_events = false;\n",
" },\n",
" resize: function(event, ui) {\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" stop: function(event, ui) {\n",
" pass_mouse_events = true;\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" });\n",
"\n",
" function mouse_event_fn(event) {\n",
" if (pass_mouse_events)\n",
" return fig.mouse_event(event, event['data']);\n",
" }\n",
"\n",
" rubberband.mousedown('button_press', mouse_event_fn);\n",
" rubberband.mouseup('button_release', mouse_event_fn);\n",
" // Throttle sequential mouse events to 1 every 20ms.\n",
" rubberband.mousemove('motion_notify', mouse_event_fn);\n",
"\n",
" rubberband.mouseenter('figure_enter', mouse_event_fn);\n",
" rubberband.mouseleave('figure_leave', mouse_event_fn);\n",
"\n",
" canvas_div.on(\"wheel\", function (event) {\n",
" event = event.originalEvent;\n",
" event['data'] = 'scroll'\n",
" if (event.deltaY < 0) {\n",
" event.step = 1;\n",
" } else {\n",
" event.step = -1;\n",
" }\n",
" mouse_event_fn(event);\n",
" });\n",
"\n",
" canvas_div.append(canvas);\n",
" canvas_div.append(rubberband);\n",
"\n",
" this.rubberband = rubberband;\n",
" this.rubberband_canvas = rubberband[0];\n",
" this.rubberband_context = rubberband[0].getContext(\"2d\");\n",
" this.rubberband_context.strokeStyle = \"#000000\";\n",
"\n",
" this._resize_canvas = function(width, height) {\n",
" // Keep the size of the canvas, canvas container, and rubber band\n",
" // canvas in synch.\n",
" canvas_div.css('width', width)\n",
" canvas_div.css('height', height)\n",
"\n",
" canvas.attr('width', width * mpl.ratio);\n",
" canvas.attr('height', height * mpl.ratio);\n",
" canvas.attr('style', 'width: ' + width + 'px; height: ' + height + 'px;');\n",
"\n",
" rubberband.attr('width', width);\n",
" rubberband.attr('height', height);\n",
" }\n",
"\n",
" // Set the figure to an initial 600x600px, this will subsequently be updated\n",
" // upon first draw.\n",
" this._resize_canvas(600, 600);\n",
"\n",
" // Disable right mouse context menu.\n",
" $(this.rubberband_canvas).bind(\"contextmenu\",function(e){\n",
" return false;\n",
" });\n",
"\n",
" function set_focus () {\n",
" canvas.focus();\n",
" canvas_div.focus();\n",
" }\n",
"\n",
" window.setTimeout(set_focus, 100);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items) {\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) {\n",
" // put a spacer in here.\n",
" continue;\n",
" }\n",
" var button = $('');\n",
" button.addClass('ui-button ui-widget ui-state-default ui-corner-all ' +\n",
" 'ui-button-icon-only');\n",
" button.attr('role', 'button');\n",
" button.attr('aria-disabled', 'false');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
"\n",
" var icon_img = $('');\n",
" icon_img.addClass('ui-button-icon-primary ui-icon');\n",
" icon_img.addClass(image);\n",
" icon_img.addClass('ui-corner-all');\n",
"\n",
" var tooltip_span = $('');\n",
" tooltip_span.addClass('ui-button-text');\n",
" tooltip_span.html(tooltip);\n",
"\n",
" button.append(icon_img);\n",
" button.append(tooltip_span);\n",
"\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" var fmt_picker_span = $('');\n",
"\n",
" var fmt_picker = $('');\n",
" fmt_picker.addClass('mpl-toolbar-option ui-widget ui-widget-content');\n",
" fmt_picker_span.append(fmt_picker);\n",
" nav_element.append(fmt_picker_span);\n",
" this.format_dropdown = fmt_picker[0];\n",
"\n",
" for (var ind in mpl.extensions) {\n",
" var fmt = mpl.extensions[ind];\n",
" var option = $(\n",
" '', {selected: fmt === mpl.default_extension}).html(fmt);\n",
" fmt_picker.append(option)\n",
" }\n",
"\n",
" // Add hover states to the ui-buttons\n",
" $( \".ui-button\" ).hover(\n",
" function() { $(this).addClass(\"ui-state-hover\");},\n",
" function() { $(this).removeClass(\"ui-state-hover\");}\n",
" );\n",
"\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"}\n",
"\n",
"mpl.figure.prototype.request_resize = function(x_pixels, y_pixels) {\n",
" // Request matplotlib to resize the figure. Matplotlib will then trigger a resize in the client,\n",
" // which will in turn request a refresh of the image.\n",
" this.send_message('resize', {'width': x_pixels, 'height': y_pixels});\n",
"}\n",
"\n",
"mpl.figure.prototype.send_message = function(type, properties) {\n",
" properties['type'] = type;\n",
" properties['figure_id'] = this.id;\n",
" this.ws.send(JSON.stringify(properties));\n",
"}\n",
"\n",
"mpl.figure.prototype.send_draw_message = function() {\n",
" if (!this.waiting) {\n",
" this.waiting = true;\n",
" this.ws.send(JSON.stringify({type: \"draw\", figure_id: this.id}));\n",
" }\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" var format_dropdown = fig.format_dropdown;\n",
" var format = format_dropdown.options[format_dropdown.selectedIndex].value;\n",
" fig.ondownload(fig, format);\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_resize = function(fig, msg) {\n",
" var size = msg['size'];\n",
" if (size[0] != fig.canvas.width || size[1] != fig.canvas.height) {\n",
" fig._resize_canvas(size[0], size[1]);\n",
" fig.send_message(\"refresh\", {});\n",
" };\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_rubberband = function(fig, msg) {\n",
" var x0 = msg['x0'] / mpl.ratio;\n",
" var y0 = (fig.canvas.height - msg['y0']) / mpl.ratio;\n",
" var x1 = msg['x1'] / mpl.ratio;\n",
" var y1 = (fig.canvas.height - msg['y1']) / mpl.ratio;\n",
" x0 = Math.floor(x0) + 0.5;\n",
" y0 = Math.floor(y0) + 0.5;\n",
" x1 = Math.floor(x1) + 0.5;\n",
" y1 = Math.floor(y1) + 0.5;\n",
" var min_x = Math.min(x0, x1);\n",
" var min_y = Math.min(y0, y1);\n",
" var width = Math.abs(x1 - x0);\n",
" var height = Math.abs(y1 - y0);\n",
"\n",
" fig.rubberband_context.clearRect(\n",
" 0, 0, fig.canvas.width, fig.canvas.height);\n",
"\n",
" fig.rubberband_context.strokeRect(min_x, min_y, width, height);\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_figure_label = function(fig, msg) {\n",
" // Updates the figure title.\n",
" fig.header.textContent = msg['label'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_cursor = function(fig, msg) {\n",
" var cursor = msg['cursor'];\n",
" switch(cursor)\n",
" {\n",
" case 0:\n",
" cursor = 'pointer';\n",
" break;\n",
" case 1:\n",
" cursor = 'default';\n",
" break;\n",
" case 2:\n",
" cursor = 'crosshair';\n",
" break;\n",
" case 3:\n",
" cursor = 'move';\n",
" break;\n",
" }\n",
" fig.rubberband_canvas.style.cursor = cursor;\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_message = function(fig, msg) {\n",
" fig.message.textContent = msg['message'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_draw = function(fig, msg) {\n",
" // Request the server to send over a new figure.\n",
" fig.send_draw_message();\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_image_mode = function(fig, msg) {\n",
" fig.image_mode = msg['mode'];\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Called whenever the canvas gets updated.\n",
" this.send_message(\"ack\", {});\n",
"}\n",
"\n",
"// A function to construct a web socket function for onmessage handling.\n",
"// Called in the figure constructor.\n",
"mpl.figure.prototype._make_on_message_function = function(fig) {\n",
" return function socket_on_message(evt) {\n",
" if (evt.data instanceof Blob) {\n",
" /* FIXME: We get \"Resource interpreted as Image but\n",
" * transferred with MIME type text/plain:\" errors on\n",
" * Chrome. But how to set the MIME type? It doesn't seem\n",
" * to be part of the websocket stream */\n",
" evt.data.type = \"image/png\";\n",
"\n",
" /* Free the memory for the previous frames */\n",
" if (fig.imageObj.src) {\n",
" (window.URL || window.webkitURL).revokeObjectURL(\n",
" fig.imageObj.src);\n",
" }\n",
"\n",
" fig.imageObj.src = (window.URL || window.webkitURL).createObjectURL(\n",
" evt.data);\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
" else if (typeof evt.data === 'string' && evt.data.slice(0, 21) == \"data:image/png;base64\") {\n",
" fig.imageObj.src = evt.data;\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
"\n",
" var msg = JSON.parse(evt.data);\n",
" var msg_type = msg['type'];\n",
"\n",
" // Call the \"handle_{type}\" callback, which takes\n",
" // the figure and JSON message as its only arguments.\n",
" try {\n",
" var callback = fig[\"handle_\" + msg_type];\n",
" } catch (e) {\n",
" console.log(\"No handler for the '\" + msg_type + \"' message type: \", msg);\n",
" return;\n",
" }\n",
"\n",
" if (callback) {\n",
" try {\n",
" // console.log(\"Handling '\" + msg_type + \"' message: \", msg);\n",
" callback(fig, msg);\n",
" } catch (e) {\n",
" console.log(\"Exception inside the 'handler_\" + msg_type + \"' callback:\", e, e.stack, msg);\n",
" }\n",
" }\n",
" };\n",
"}\n",
"\n",
"// from http://stackoverflow.com/questions/1114465/getting-mouse-location-in-canvas\n",
"mpl.findpos = function(e) {\n",
" //this section is from http://www.quirksmode.org/js/events_properties.html\n",
" var targ;\n",
" if (!e)\n",
" e = window.event;\n",
" if (e.target)\n",
" targ = e.target;\n",
" else if (e.srcElement)\n",
" targ = e.srcElement;\n",
" if (targ.nodeType == 3) // defeat Safari bug\n",
" targ = targ.parentNode;\n",
"\n",
" // jQuery normalizes the pageX and pageY\n",
" // pageX,Y are the mouse positions relative to the document\n",
" // offset() returns the position of the element relative to the document\n",
" var x = e.pageX - $(targ).offset().left;\n",
" var y = e.pageY - $(targ).offset().top;\n",
"\n",
" return {\"x\": x, \"y\": y};\n",
"};\n",
"\n",
"/*\n",
" * return a copy of an object with only non-object keys\n",
" * we need this to avoid circular references\n",
" * http://stackoverflow.com/a/24161582/3208463\n",
" */\n",
"function simpleKeys (original) {\n",
" return Object.keys(original).reduce(function (obj, key) {\n",
" if (typeof original[key] !== 'object')\n",
" obj[key] = original[key]\n",
" return obj;\n",
" }, {});\n",
"}\n",
"\n",
"mpl.figure.prototype.mouse_event = function(event, name) {\n",
" var canvas_pos = mpl.findpos(event)\n",
"\n",
" if (name === 'button_press')\n",
" {\n",
" this.canvas.focus();\n",
" this.canvas_div.focus();\n",
" }\n",
"\n",
" var x = canvas_pos.x * mpl.ratio;\n",
" var y = canvas_pos.y * mpl.ratio;\n",
"\n",
" this.send_message(name, {x: x, y: y, button: event.button,\n",
" step: event.step,\n",
" guiEvent: simpleKeys(event)});\n",
"\n",
" /* This prevents the web browser from automatically changing to\n",
" * the text insertion cursor when the button is pressed. We want\n",
" * to control all of the cursor setting manually through the\n",
" * 'cursor' event from matplotlib */\n",
" event.preventDefault();\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" // Handle any extra behaviour associated with a key event\n",
"}\n",
"\n",
"mpl.figure.prototype.key_event = function(event, name) {\n",
"\n",
" // Prevent repeat events\n",
" if (name == 'key_press')\n",
" {\n",
" if (event.which === this._key)\n",
" return;\n",
" else\n",
" this._key = event.which;\n",
" }\n",
" if (name == 'key_release')\n",
" this._key = null;\n",
"\n",
" var value = '';\n",
" if (event.ctrlKey && event.which != 17)\n",
" value += \"ctrl+\";\n",
" if (event.altKey && event.which != 18)\n",
" value += \"alt+\";\n",
" if (event.shiftKey && event.which != 16)\n",
" value += \"shift+\";\n",
"\n",
" value += 'k';\n",
" value += event.which.toString();\n",
"\n",
" this._key_event_extra(event, name);\n",
"\n",
" this.send_message(name, {key: value,\n",
" guiEvent: simpleKeys(event)});\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype.toolbar_button_onclick = function(name) {\n",
" if (name == 'download') {\n",
" this.handle_save(this, null);\n",
" } else {\n",
" this.send_message(\"toolbar_button\", {name: name});\n",
" }\n",
"};\n",
"\n",
"mpl.figure.prototype.toolbar_button_onmouseover = function(tooltip) {\n",
" this.message.textContent = tooltip;\n",
"};\n",
"mpl.toolbar_items = [[\"Home\", \"Reset original view\", \"fa fa-home icon-home\", \"home\"], [\"Back\", \"Back to previous view\", \"fa fa-arrow-left icon-arrow-left\", \"back\"], [\"Forward\", \"Forward to next view\", \"fa fa-arrow-right icon-arrow-right\", \"forward\"], [\"\", \"\", \"\", \"\"], [\"Pan\", \"Pan axes with left mouse, zoom with right\", \"fa fa-arrows icon-move\", \"pan\"], [\"Zoom\", \"Zoom to rectangle\", \"fa fa-square-o icon-check-empty\", \"zoom\"], [\"\", \"\", \"\", \"\"], [\"Download\", \"Download plot\", \"fa fa-floppy-o icon-save\", \"download\"]];\n",
"\n",
"mpl.extensions = [\"eps\", \"jpeg\", \"pdf\", \"png\", \"ps\", \"raw\", \"svg\", \"tif\"];\n",
"\n",
"mpl.default_extension = \"png\";var comm_websocket_adapter = function(comm) {\n",
" // Create a \"websocket\"-like object which calls the given IPython comm\n",
" // object with the appropriate methods. Currently this is a non binary\n",
" // socket, so there is still some room for performance tuning.\n",
" var ws = {};\n",
"\n",
" ws.close = function() {\n",
" comm.close()\n",
" };\n",
" ws.send = function(m) {\n",
" //console.log('sending', m);\n",
" comm.send(m);\n",
" };\n",
" // Register the callback with on_msg.\n",
" comm.on_msg(function(msg) {\n",
" //console.log('receiving', msg['content']['data'], msg);\n",
" // Pass the mpl event to the overriden (by mpl) onmessage function.\n",
" ws.onmessage(msg['content']['data'])\n",
" });\n",
" return ws;\n",
"}\n",
"\n",
"mpl.mpl_figure_comm = function(comm, msg) {\n",
" // This is the function which gets called when the mpl process\n",
" // starts-up an IPython Comm through the \"matplotlib\" channel.\n",
"\n",
" var id = msg.content.data.id;\n",
" // Get hold of the div created by the display call when the Comm\n",
" // socket was opened in Python.\n",
" var element = $(\"#\" + id);\n",
" var ws_proxy = comm_websocket_adapter(comm)\n",
"\n",
" function ondownload(figure, format) {\n",
" window.open(figure.imageObj.src);\n",
" }\n",
"\n",
" var fig = new mpl.figure(id, ws_proxy,\n",
" ondownload,\n",
" element.get(0));\n",
"\n",
" // Call onopen now - mpl needs it, as it is assuming we've passed it a real\n",
" // web socket which is closed, not our websocket->open comm proxy.\n",
" ws_proxy.onopen();\n",
"\n",
" fig.parent_element = element.get(0);\n",
" fig.cell_info = mpl.find_output_cell(\"\");\n",
" if (!fig.cell_info) {\n",
" console.error(\"Failed to find cell for figure\", id, fig);\n",
" return;\n",
" }\n",
"\n",
" var output_index = fig.cell_info[2]\n",
" var cell = fig.cell_info[0];\n",
"\n",
"};\n",
"\n",
"mpl.figure.prototype.handle_close = function(fig, msg) {\n",
" var width = fig.canvas.width/mpl.ratio\n",
" fig.root.unbind('remove')\n",
"\n",
" // Update the output cell to use the data from the current canvas.\n",
" fig.push_to_output();\n",
" var dataURL = fig.canvas.toDataURL();\n",
" // Re-enable the keyboard manager in IPython - without this line, in FF,\n",
" // the notebook keyboard shortcuts fail.\n",
" IPython.keyboard_manager.enable()\n",
" $(fig.parent_element).html(' ');\n",
" fig.close_ws(fig, msg);\n",
"}\n",
"\n",
"mpl.figure.prototype.close_ws = function(fig, msg){\n",
" fig.send_message('closing', msg);\n",
" // fig.ws.close()\n",
"}\n",
"\n",
"mpl.figure.prototype.push_to_output = function(remove_interactive) {\n",
" // Turn the data on the canvas into data in the output cell.\n",
" var width = this.canvas.width/mpl.ratio\n",
" var dataURL = this.canvas.toDataURL();\n",
" this.cell_info[1]['text/html'] = '
');\n",
" fig.close_ws(fig, msg);\n",
"}\n",
"\n",
"mpl.figure.prototype.close_ws = function(fig, msg){\n",
" fig.send_message('closing', msg);\n",
" // fig.ws.close()\n",
"}\n",
"\n",
"mpl.figure.prototype.push_to_output = function(remove_interactive) {\n",
" // Turn the data on the canvas into data in the output cell.\n",
" var width = this.canvas.width/mpl.ratio\n",
" var dataURL = this.canvas.toDataURL();\n",
" this.cell_info[1]['text/html'] = ' ';\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Tell IPython that the notebook contents must change.\n",
" IPython.notebook.set_dirty(true);\n",
" this.send_message(\"ack\", {});\n",
" var fig = this;\n",
" // Wait a second, then push the new image to the DOM so\n",
" // that it is saved nicely (might be nice to debounce this).\n",
" setTimeout(function () { fig.push_to_output() }, 1000);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items){\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) { continue; };\n",
"\n",
" var button = $('');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" // Add the status bar.\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"\n",
" // Add the close button to the window.\n",
" var buttongrp = $('');\n",
" var button = $('');\n",
" button.click(function (evt) { fig.handle_close(fig, {}); } );\n",
" button.mouseover('Stop Interaction', toolbar_mouse_event);\n",
" buttongrp.append(button);\n",
" var titlebar = this.root.find($('.ui-dialog-titlebar'));\n",
" titlebar.prepend(buttongrp);\n",
"}\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(el){\n",
" var fig = this\n",
" el.on(\"remove\", function(){\n",
"\tfig.close_ws(fig, {});\n",
" });\n",
"}\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(el){\n",
" // this is important to make the div 'focusable\n",
" el.attr('tabindex', 0)\n",
" // reach out to IPython and tell the keyboard manager to turn it's self\n",
" // off when our div gets focus\n",
"\n",
" // location in version 3\n",
" if (IPython.notebook.keyboard_manager) {\n",
" IPython.notebook.keyboard_manager.register_events(el);\n",
" }\n",
" else {\n",
" // location in version 2\n",
" IPython.keyboard_manager.register_events(el);\n",
" }\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" var manager = IPython.notebook.keyboard_manager;\n",
" if (!manager)\n",
" manager = IPython.keyboard_manager;\n",
"\n",
" // Check for shift+enter\n",
" if (event.shiftKey && event.which == 13) {\n",
" this.canvas_div.blur();\n",
" event.shiftKey = false;\n",
" // Send a \"J\" for go to next cell\n",
" event.which = 74;\n",
" event.keyCode = 74;\n",
" manager.command_mode();\n",
" manager.handle_keydown(event);\n",
" }\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" fig.ondownload(fig, null);\n",
"}\n",
"\n",
"\n",
"mpl.find_output_cell = function(html_output) {\n",
" // Return the cell and output element which can be found *uniquely* in the notebook.\n",
" // Note - this is a bit hacky, but it is done because the \"notebook_saving.Notebook\"\n",
" // IPython event is triggered only after the cells have been serialised, which for\n",
" // our purposes (turning an active figure into a static one), is too late.\n",
" var cells = IPython.notebook.get_cells();\n",
" var ncells = cells.length;\n",
" for (var i=0; i= 3 moved mimebundle to data attribute of output\n",
" data = data.data;\n",
" }\n",
" if (data['text/html'] == html_output) {\n",
" return [cell, data, j];\n",
" }\n",
" }\n",
" }\n",
" }\n",
"}\n",
"\n",
"// Register the function which deals with the matplotlib target/channel.\n",
"// The kernel may be null if the page has been refreshed.\n",
"if (IPython.notebook.kernel != null) {\n",
" IPython.notebook.kernel.comm_manager.register_target('matplotlib', mpl.mpl_figure_comm);\n",
"}\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"
';\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Tell IPython that the notebook contents must change.\n",
" IPython.notebook.set_dirty(true);\n",
" this.send_message(\"ack\", {});\n",
" var fig = this;\n",
" // Wait a second, then push the new image to the DOM so\n",
" // that it is saved nicely (might be nice to debounce this).\n",
" setTimeout(function () { fig.push_to_output() }, 1000);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items){\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) { continue; };\n",
"\n",
" var button = $('');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" // Add the status bar.\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"\n",
" // Add the close button to the window.\n",
" var buttongrp = $('');\n",
" var button = $('');\n",
" button.click(function (evt) { fig.handle_close(fig, {}); } );\n",
" button.mouseover('Stop Interaction', toolbar_mouse_event);\n",
" buttongrp.append(button);\n",
" var titlebar = this.root.find($('.ui-dialog-titlebar'));\n",
" titlebar.prepend(buttongrp);\n",
"}\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(el){\n",
" var fig = this\n",
" el.on(\"remove\", function(){\n",
"\tfig.close_ws(fig, {});\n",
" });\n",
"}\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(el){\n",
" // this is important to make the div 'focusable\n",
" el.attr('tabindex', 0)\n",
" // reach out to IPython and tell the keyboard manager to turn it's self\n",
" // off when our div gets focus\n",
"\n",
" // location in version 3\n",
" if (IPython.notebook.keyboard_manager) {\n",
" IPython.notebook.keyboard_manager.register_events(el);\n",
" }\n",
" else {\n",
" // location in version 2\n",
" IPython.keyboard_manager.register_events(el);\n",
" }\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" var manager = IPython.notebook.keyboard_manager;\n",
" if (!manager)\n",
" manager = IPython.keyboard_manager;\n",
"\n",
" // Check for shift+enter\n",
" if (event.shiftKey && event.which == 13) {\n",
" this.canvas_div.blur();\n",
" event.shiftKey = false;\n",
" // Send a \"J\" for go to next cell\n",
" event.which = 74;\n",
" event.keyCode = 74;\n",
" manager.command_mode();\n",
" manager.handle_keydown(event);\n",
" }\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" fig.ondownload(fig, null);\n",
"}\n",
"\n",
"\n",
"mpl.find_output_cell = function(html_output) {\n",
" // Return the cell and output element which can be found *uniquely* in the notebook.\n",
" // Note - this is a bit hacky, but it is done because the \"notebook_saving.Notebook\"\n",
" // IPython event is triggered only after the cells have been serialised, which for\n",
" // our purposes (turning an active figure into a static one), is too late.\n",
" var cells = IPython.notebook.get_cells();\n",
" var ncells = cells.length;\n",
" for (var i=0; i= 3 moved mimebundle to data attribute of output\n",
" data = data.data;\n",
" }\n",
" if (data['text/html'] == html_output) {\n",
" return [cell, data, j];\n",
" }\n",
" }\n",
" }\n",
" }\n",
"}\n",
"\n",
"// Register the function which deals with the matplotlib target/channel.\n",
"// The kernel may be null if the page has been refreshed.\n",
"if (IPython.notebook.kernel != null) {\n",
" IPython.notebook.kernel.comm_manager.register_target('matplotlib', mpl.mpl_figure_comm);\n",
"}\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
" "
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"application/javascript": [
"/* Put everything inside the global mpl namespace */\n",
"window.mpl = {};\n",
"\n",
"\n",
"mpl.get_websocket_type = function() {\n",
" if (typeof(WebSocket) !== 'undefined') {\n",
" return WebSocket;\n",
" } else if (typeof(MozWebSocket) !== 'undefined') {\n",
" return MozWebSocket;\n",
" } else {\n",
" alert('Your browser does not have WebSocket support.' +\n",
" 'Please try Chrome, Safari or Firefox 6. ' +\n",
" 'Firefox 4 and 5 are also supported but you ' +\n",
" 'have to enable WebSockets in about:config.');\n",
" };\n",
"}\n",
"\n",
"mpl.figure = function(figure_id, websocket, ondownload, parent_element) {\n",
" this.id = figure_id;\n",
"\n",
" this.ws = websocket;\n",
"\n",
" this.supports_binary = (this.ws.binaryType != undefined);\n",
"\n",
" if (!this.supports_binary) {\n",
" var warnings = document.getElementById(\"mpl-warnings\");\n",
" if (warnings) {\n",
" warnings.style.display = 'block';\n",
" warnings.textContent = (\n",
" \"This browser does not support binary websocket messages. \" +\n",
" \"Performance may be slow.\");\n",
" }\n",
" }\n",
"\n",
" this.imageObj = new Image();\n",
"\n",
" this.context = undefined;\n",
" this.message = undefined;\n",
" this.canvas = undefined;\n",
" this.rubberband_canvas = undefined;\n",
" this.rubberband_context = undefined;\n",
" this.format_dropdown = undefined;\n",
"\n",
" this.image_mode = 'full';\n",
"\n",
" this.root = $('');\n",
" this._root_extra_style(this.root)\n",
" this.root.attr('style', 'display: inline-block');\n",
"\n",
" $(parent_element).append(this.root);\n",
"\n",
" this._init_header(this);\n",
" this._init_canvas(this);\n",
" this._init_toolbar(this);\n",
"\n",
" var fig = this;\n",
"\n",
" this.waiting = false;\n",
"\n",
" this.ws.onopen = function () {\n",
" fig.send_message(\"supports_binary\", {value: fig.supports_binary});\n",
" fig.send_message(\"send_image_mode\", {});\n",
" if (mpl.ratio != 1) {\n",
" fig.send_message(\"set_dpi_ratio\", {'dpi_ratio': mpl.ratio});\n",
" }\n",
" fig.send_message(\"refresh\", {});\n",
" }\n",
"\n",
" this.imageObj.onload = function() {\n",
" if (fig.image_mode == 'full') {\n",
" // Full images could contain transparency (where diff images\n",
" // almost always do), so we need to clear the canvas so that\n",
" // there is no ghosting.\n",
" fig.context.clearRect(0, 0, fig.canvas.width, fig.canvas.height);\n",
" }\n",
" fig.context.drawImage(fig.imageObj, 0, 0);\n",
" };\n",
"\n",
" this.imageObj.onunload = function() {\n",
" fig.ws.close();\n",
" }\n",
"\n",
" this.ws.onmessage = this._make_on_message_function(this);\n",
"\n",
" this.ondownload = ondownload;\n",
"}\n",
"\n",
"mpl.figure.prototype._init_header = function() {\n",
" var titlebar = $(\n",
" '');\n",
" var titletext = $(\n",
" '');\n",
" titlebar.append(titletext)\n",
" this.root.append(titlebar);\n",
" this.header = titletext[0];\n",
"}\n",
"\n",
"\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._init_canvas = function() {\n",
" var fig = this;\n",
"\n",
" var canvas_div = $('');\n",
"\n",
" canvas_div.attr('style', 'position: relative; clear: both; outline: 0');\n",
"\n",
" function canvas_keyboard_event(event) {\n",
" return fig.key_event(event, event['data']);\n",
" }\n",
"\n",
" canvas_div.keydown('key_press', canvas_keyboard_event);\n",
" canvas_div.keyup('key_release', canvas_keyboard_event);\n",
" this.canvas_div = canvas_div\n",
" this._canvas_extra_style(canvas_div)\n",
" this.root.append(canvas_div);\n",
"\n",
" var canvas = $('');\n",
" canvas.addClass('mpl-canvas');\n",
" canvas.attr('style', \"left: 0; top: 0; z-index: 0; outline: 0\")\n",
"\n",
" this.canvas = canvas[0];\n",
" this.context = canvas[0].getContext(\"2d\");\n",
"\n",
" var backingStore = this.context.backingStorePixelRatio ||\n",
"\tthis.context.webkitBackingStorePixelRatio ||\n",
"\tthis.context.mozBackingStorePixelRatio ||\n",
"\tthis.context.msBackingStorePixelRatio ||\n",
"\tthis.context.oBackingStorePixelRatio ||\n",
"\tthis.context.backingStorePixelRatio || 1;\n",
"\n",
" mpl.ratio = (window.devicePixelRatio || 1) / backingStore;\n",
"\n",
" var rubberband = $('');\n",
" rubberband.attr('style', \"position: absolute; left: 0; top: 0; z-index: 1;\")\n",
"\n",
" var pass_mouse_events = true;\n",
"\n",
" canvas_div.resizable({\n",
" start: function(event, ui) {\n",
" pass_mouse_events = false;\n",
" },\n",
" resize: function(event, ui) {\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" stop: function(event, ui) {\n",
" pass_mouse_events = true;\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" });\n",
"\n",
" function mouse_event_fn(event) {\n",
" if (pass_mouse_events)\n",
" return fig.mouse_event(event, event['data']);\n",
" }\n",
"\n",
" rubberband.mousedown('button_press', mouse_event_fn);\n",
" rubberband.mouseup('button_release', mouse_event_fn);\n",
" // Throttle sequential mouse events to 1 every 20ms.\n",
" rubberband.mousemove('motion_notify', mouse_event_fn);\n",
"\n",
" rubberband.mouseenter('figure_enter', mouse_event_fn);\n",
" rubberband.mouseleave('figure_leave', mouse_event_fn);\n",
"\n",
" canvas_div.on(\"wheel\", function (event) {\n",
" event = event.originalEvent;\n",
" event['data'] = 'scroll'\n",
" if (event.deltaY < 0) {\n",
" event.step = 1;\n",
" } else {\n",
" event.step = -1;\n",
" }\n",
" mouse_event_fn(event);\n",
" });\n",
"\n",
" canvas_div.append(canvas);\n",
" canvas_div.append(rubberband);\n",
"\n",
" this.rubberband = rubberband;\n",
" this.rubberband_canvas = rubberband[0];\n",
" this.rubberband_context = rubberband[0].getContext(\"2d\");\n",
" this.rubberband_context.strokeStyle = \"#000000\";\n",
"\n",
" this._resize_canvas = function(width, height) {\n",
" // Keep the size of the canvas, canvas container, and rubber band\n",
" // canvas in synch.\n",
" canvas_div.css('width', width)\n",
" canvas_div.css('height', height)\n",
"\n",
" canvas.attr('width', width * mpl.ratio);\n",
" canvas.attr('height', height * mpl.ratio);\n",
" canvas.attr('style', 'width: ' + width + 'px; height: ' + height + 'px;');\n",
"\n",
" rubberband.attr('width', width);\n",
" rubberband.attr('height', height);\n",
" }\n",
"\n",
" // Set the figure to an initial 600x600px, this will subsequently be updated\n",
" // upon first draw.\n",
" this._resize_canvas(600, 600);\n",
"\n",
" // Disable right mouse context menu.\n",
" $(this.rubberband_canvas).bind(\"contextmenu\",function(e){\n",
" return false;\n",
" });\n",
"\n",
" function set_focus () {\n",
" canvas.focus();\n",
" canvas_div.focus();\n",
" }\n",
"\n",
" window.setTimeout(set_focus, 100);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items) {\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) {\n",
" // put a spacer in here.\n",
" continue;\n",
" }\n",
" var button = $('');\n",
" button.addClass('ui-button ui-widget ui-state-default ui-corner-all ' +\n",
" 'ui-button-icon-only');\n",
" button.attr('role', 'button');\n",
" button.attr('aria-disabled', 'false');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
"\n",
" var icon_img = $('');\n",
" icon_img.addClass('ui-button-icon-primary ui-icon');\n",
" icon_img.addClass(image);\n",
" icon_img.addClass('ui-corner-all');\n",
"\n",
" var tooltip_span = $('');\n",
" tooltip_span.addClass('ui-button-text');\n",
" tooltip_span.html(tooltip);\n",
"\n",
" button.append(icon_img);\n",
" button.append(tooltip_span);\n",
"\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" var fmt_picker_span = $('');\n",
"\n",
" var fmt_picker = $('');\n",
" fmt_picker.addClass('mpl-toolbar-option ui-widget ui-widget-content');\n",
" fmt_picker_span.append(fmt_picker);\n",
" nav_element.append(fmt_picker_span);\n",
" this.format_dropdown = fmt_picker[0];\n",
"\n",
" for (var ind in mpl.extensions) {\n",
" var fmt = mpl.extensions[ind];\n",
" var option = $(\n",
" '', {selected: fmt === mpl.default_extension}).html(fmt);\n",
" fmt_picker.append(option)\n",
" }\n",
"\n",
" // Add hover states to the ui-buttons\n",
" $( \".ui-button\" ).hover(\n",
" function() { $(this).addClass(\"ui-state-hover\");},\n",
" function() { $(this).removeClass(\"ui-state-hover\");}\n",
" );\n",
"\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"}\n",
"\n",
"mpl.figure.prototype.request_resize = function(x_pixels, y_pixels) {\n",
" // Request matplotlib to resize the figure. Matplotlib will then trigger a resize in the client,\n",
" // which will in turn request a refresh of the image.\n",
" this.send_message('resize', {'width': x_pixels, 'height': y_pixels});\n",
"}\n",
"\n",
"mpl.figure.prototype.send_message = function(type, properties) {\n",
" properties['type'] = type;\n",
" properties['figure_id'] = this.id;\n",
" this.ws.send(JSON.stringify(properties));\n",
"}\n",
"\n",
"mpl.figure.prototype.send_draw_message = function() {\n",
" if (!this.waiting) {\n",
" this.waiting = true;\n",
" this.ws.send(JSON.stringify({type: \"draw\", figure_id: this.id}));\n",
" }\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" var format_dropdown = fig.format_dropdown;\n",
" var format = format_dropdown.options[format_dropdown.selectedIndex].value;\n",
" fig.ondownload(fig, format);\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_resize = function(fig, msg) {\n",
" var size = msg['size'];\n",
" if (size[0] != fig.canvas.width || size[1] != fig.canvas.height) {\n",
" fig._resize_canvas(size[0], size[1]);\n",
" fig.send_message(\"refresh\", {});\n",
" };\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_rubberband = function(fig, msg) {\n",
" var x0 = msg['x0'] / mpl.ratio;\n",
" var y0 = (fig.canvas.height - msg['y0']) / mpl.ratio;\n",
" var x1 = msg['x1'] / mpl.ratio;\n",
" var y1 = (fig.canvas.height - msg['y1']) / mpl.ratio;\n",
" x0 = Math.floor(x0) + 0.5;\n",
" y0 = Math.floor(y0) + 0.5;\n",
" x1 = Math.floor(x1) + 0.5;\n",
" y1 = Math.floor(y1) + 0.5;\n",
" var min_x = Math.min(x0, x1);\n",
" var min_y = Math.min(y0, y1);\n",
" var width = Math.abs(x1 - x0);\n",
" var height = Math.abs(y1 - y0);\n",
"\n",
" fig.rubberband_context.clearRect(\n",
" 0, 0, fig.canvas.width, fig.canvas.height);\n",
"\n",
" fig.rubberband_context.strokeRect(min_x, min_y, width, height);\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_figure_label = function(fig, msg) {\n",
" // Updates the figure title.\n",
" fig.header.textContent = msg['label'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_cursor = function(fig, msg) {\n",
" var cursor = msg['cursor'];\n",
" switch(cursor)\n",
" {\n",
" case 0:\n",
" cursor = 'pointer';\n",
" break;\n",
" case 1:\n",
" cursor = 'default';\n",
" break;\n",
" case 2:\n",
" cursor = 'crosshair';\n",
" break;\n",
" case 3:\n",
" cursor = 'move';\n",
" break;\n",
" }\n",
" fig.rubberband_canvas.style.cursor = cursor;\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_message = function(fig, msg) {\n",
" fig.message.textContent = msg['message'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_draw = function(fig, msg) {\n",
" // Request the server to send over a new figure.\n",
" fig.send_draw_message();\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_image_mode = function(fig, msg) {\n",
" fig.image_mode = msg['mode'];\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Called whenever the canvas gets updated.\n",
" this.send_message(\"ack\", {});\n",
"}\n",
"\n",
"// A function to construct a web socket function for onmessage handling.\n",
"// Called in the figure constructor.\n",
"mpl.figure.prototype._make_on_message_function = function(fig) {\n",
" return function socket_on_message(evt) {\n",
" if (evt.data instanceof Blob) {\n",
" /* FIXME: We get \"Resource interpreted as Image but\n",
" * transferred with MIME type text/plain:\" errors on\n",
" * Chrome. But how to set the MIME type? It doesn't seem\n",
" * to be part of the websocket stream */\n",
" evt.data.type = \"image/png\";\n",
"\n",
" /* Free the memory for the previous frames */\n",
" if (fig.imageObj.src) {\n",
" (window.URL || window.webkitURL).revokeObjectURL(\n",
" fig.imageObj.src);\n",
" }\n",
"\n",
" fig.imageObj.src = (window.URL || window.webkitURL).createObjectURL(\n",
" evt.data);\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
" else if (typeof evt.data === 'string' && evt.data.slice(0, 21) == \"data:image/png;base64\") {\n",
" fig.imageObj.src = evt.data;\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
"\n",
" var msg = JSON.parse(evt.data);\n",
" var msg_type = msg['type'];\n",
"\n",
" // Call the \"handle_{type}\" callback, which takes\n",
" // the figure and JSON message as its only arguments.\n",
" try {\n",
" var callback = fig[\"handle_\" + msg_type];\n",
" } catch (e) {\n",
" console.log(\"No handler for the '\" + msg_type + \"' message type: \", msg);\n",
" return;\n",
" }\n",
"\n",
" if (callback) {\n",
" try {\n",
" // console.log(\"Handling '\" + msg_type + \"' message: \", msg);\n",
" callback(fig, msg);\n",
" } catch (e) {\n",
" console.log(\"Exception inside the 'handler_\" + msg_type + \"' callback:\", e, e.stack, msg);\n",
" }\n",
" }\n",
" };\n",
"}\n",
"\n",
"// from http://stackoverflow.com/questions/1114465/getting-mouse-location-in-canvas\n",
"mpl.findpos = function(e) {\n",
" //this section is from http://www.quirksmode.org/js/events_properties.html\n",
" var targ;\n",
" if (!e)\n",
" e = window.event;\n",
" if (e.target)\n",
" targ = e.target;\n",
" else if (e.srcElement)\n",
" targ = e.srcElement;\n",
" if (targ.nodeType == 3) // defeat Safari bug\n",
" targ = targ.parentNode;\n",
"\n",
" // jQuery normalizes the pageX and pageY\n",
" // pageX,Y are the mouse positions relative to the document\n",
" // offset() returns the position of the element relative to the document\n",
" var x = e.pageX - $(targ).offset().left;\n",
" var y = e.pageY - $(targ).offset().top;\n",
"\n",
" return {\"x\": x, \"y\": y};\n",
"};\n",
"\n",
"/*\n",
" * return a copy of an object with only non-object keys\n",
" * we need this to avoid circular references\n",
" * http://stackoverflow.com/a/24161582/3208463\n",
" */\n",
"function simpleKeys (original) {\n",
" return Object.keys(original).reduce(function (obj, key) {\n",
" if (typeof original[key] !== 'object')\n",
" obj[key] = original[key]\n",
" return obj;\n",
" }, {});\n",
"}\n",
"\n",
"mpl.figure.prototype.mouse_event = function(event, name) {\n",
" var canvas_pos = mpl.findpos(event)\n",
"\n",
" if (name === 'button_press')\n",
" {\n",
" this.canvas.focus();\n",
" this.canvas_div.focus();\n",
" }\n",
"\n",
" var x = canvas_pos.x * mpl.ratio;\n",
" var y = canvas_pos.y * mpl.ratio;\n",
"\n",
" this.send_message(name, {x: x, y: y, button: event.button,\n",
" step: event.step,\n",
" guiEvent: simpleKeys(event)});\n",
"\n",
" /* This prevents the web browser from automatically changing to\n",
" * the text insertion cursor when the button is pressed. We want\n",
" * to control all of the cursor setting manually through the\n",
" * 'cursor' event from matplotlib */\n",
" event.preventDefault();\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" // Handle any extra behaviour associated with a key event\n",
"}\n",
"\n",
"mpl.figure.prototype.key_event = function(event, name) {\n",
"\n",
" // Prevent repeat events\n",
" if (name == 'key_press')\n",
" {\n",
" if (event.which === this._key)\n",
" return;\n",
" else\n",
" this._key = event.which;\n",
" }\n",
" if (name == 'key_release')\n",
" this._key = null;\n",
"\n",
" var value = '';\n",
" if (event.ctrlKey && event.which != 17)\n",
" value += \"ctrl+\";\n",
" if (event.altKey && event.which != 18)\n",
" value += \"alt+\";\n",
" if (event.shiftKey && event.which != 16)\n",
" value += \"shift+\";\n",
"\n",
" value += 'k';\n",
" value += event.which.toString();\n",
"\n",
" this._key_event_extra(event, name);\n",
"\n",
" this.send_message(name, {key: value,\n",
" guiEvent: simpleKeys(event)});\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype.toolbar_button_onclick = function(name) {\n",
" if (name == 'download') {\n",
" this.handle_save(this, null);\n",
" } else {\n",
" this.send_message(\"toolbar_button\", {name: name});\n",
" }\n",
"};\n",
"\n",
"mpl.figure.prototype.toolbar_button_onmouseover = function(tooltip) {\n",
" this.message.textContent = tooltip;\n",
"};\n",
"mpl.toolbar_items = [[\"Home\", \"Reset original view\", \"fa fa-home icon-home\", \"home\"], [\"Back\", \"Back to previous view\", \"fa fa-arrow-left icon-arrow-left\", \"back\"], [\"Forward\", \"Forward to next view\", \"fa fa-arrow-right icon-arrow-right\", \"forward\"], [\"\", \"\", \"\", \"\"], [\"Pan\", \"Pan axes with left mouse, zoom with right\", \"fa fa-arrows icon-move\", \"pan\"], [\"Zoom\", \"Zoom to rectangle\", \"fa fa-square-o icon-check-empty\", \"zoom\"], [\"\", \"\", \"\", \"\"], [\"Download\", \"Download plot\", \"fa fa-floppy-o icon-save\", \"download\"]];\n",
"\n",
"mpl.extensions = [\"eps\", \"jpeg\", \"pdf\", \"png\", \"ps\", \"raw\", \"svg\", \"tif\"];\n",
"\n",
"mpl.default_extension = \"png\";var comm_websocket_adapter = function(comm) {\n",
" // Create a \"websocket\"-like object which calls the given IPython comm\n",
" // object with the appropriate methods. Currently this is a non binary\n",
" // socket, so there is still some room for performance tuning.\n",
" var ws = {};\n",
"\n",
" ws.close = function() {\n",
" comm.close()\n",
" };\n",
" ws.send = function(m) {\n",
" //console.log('sending', m);\n",
" comm.send(m);\n",
" };\n",
" // Register the callback with on_msg.\n",
" comm.on_msg(function(msg) {\n",
" //console.log('receiving', msg['content']['data'], msg);\n",
" // Pass the mpl event to the overriden (by mpl) onmessage function.\n",
" ws.onmessage(msg['content']['data'])\n",
" });\n",
" return ws;\n",
"}\n",
"\n",
"mpl.mpl_figure_comm = function(comm, msg) {\n",
" // This is the function which gets called when the mpl process\n",
" // starts-up an IPython Comm through the \"matplotlib\" channel.\n",
"\n",
" var id = msg.content.data.id;\n",
" // Get hold of the div created by the display call when the Comm\n",
" // socket was opened in Python.\n",
" var element = $(\"#\" + id);\n",
" var ws_proxy = comm_websocket_adapter(comm)\n",
"\n",
" function ondownload(figure, format) {\n",
" window.open(figure.imageObj.src);\n",
" }\n",
"\n",
" var fig = new mpl.figure(id, ws_proxy,\n",
" ondownload,\n",
" element.get(0));\n",
"\n",
" // Call onopen now - mpl needs it, as it is assuming we've passed it a real\n",
" // web socket which is closed, not our websocket->open comm proxy.\n",
" ws_proxy.onopen();\n",
"\n",
" fig.parent_element = element.get(0);\n",
" fig.cell_info = mpl.find_output_cell(\"\");\n",
" if (!fig.cell_info) {\n",
" console.error(\"Failed to find cell for figure\", id, fig);\n",
" return;\n",
" }\n",
"\n",
" var output_index = fig.cell_info[2]\n",
" var cell = fig.cell_info[0];\n",
"\n",
"};\n",
"\n",
"mpl.figure.prototype.handle_close = function(fig, msg) {\n",
" var width = fig.canvas.width/mpl.ratio\n",
" fig.root.unbind('remove')\n",
"\n",
" // Update the output cell to use the data from the current canvas.\n",
" fig.push_to_output();\n",
" var dataURL = fig.canvas.toDataURL();\n",
" // Re-enable the keyboard manager in IPython - without this line, in FF,\n",
" // the notebook keyboard shortcuts fail.\n",
" IPython.keyboard_manager.enable()\n",
" $(fig.parent_element).html('
"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"application/javascript": [
"/* Put everything inside the global mpl namespace */\n",
"window.mpl = {};\n",
"\n",
"\n",
"mpl.get_websocket_type = function() {\n",
" if (typeof(WebSocket) !== 'undefined') {\n",
" return WebSocket;\n",
" } else if (typeof(MozWebSocket) !== 'undefined') {\n",
" return MozWebSocket;\n",
" } else {\n",
" alert('Your browser does not have WebSocket support.' +\n",
" 'Please try Chrome, Safari or Firefox 6. ' +\n",
" 'Firefox 4 and 5 are also supported but you ' +\n",
" 'have to enable WebSockets in about:config.');\n",
" };\n",
"}\n",
"\n",
"mpl.figure = function(figure_id, websocket, ondownload, parent_element) {\n",
" this.id = figure_id;\n",
"\n",
" this.ws = websocket;\n",
"\n",
" this.supports_binary = (this.ws.binaryType != undefined);\n",
"\n",
" if (!this.supports_binary) {\n",
" var warnings = document.getElementById(\"mpl-warnings\");\n",
" if (warnings) {\n",
" warnings.style.display = 'block';\n",
" warnings.textContent = (\n",
" \"This browser does not support binary websocket messages. \" +\n",
" \"Performance may be slow.\");\n",
" }\n",
" }\n",
"\n",
" this.imageObj = new Image();\n",
"\n",
" this.context = undefined;\n",
" this.message = undefined;\n",
" this.canvas = undefined;\n",
" this.rubberband_canvas = undefined;\n",
" this.rubberband_context = undefined;\n",
" this.format_dropdown = undefined;\n",
"\n",
" this.image_mode = 'full';\n",
"\n",
" this.root = $('');\n",
" this._root_extra_style(this.root)\n",
" this.root.attr('style', 'display: inline-block');\n",
"\n",
" $(parent_element).append(this.root);\n",
"\n",
" this._init_header(this);\n",
" this._init_canvas(this);\n",
" this._init_toolbar(this);\n",
"\n",
" var fig = this;\n",
"\n",
" this.waiting = false;\n",
"\n",
" this.ws.onopen = function () {\n",
" fig.send_message(\"supports_binary\", {value: fig.supports_binary});\n",
" fig.send_message(\"send_image_mode\", {});\n",
" if (mpl.ratio != 1) {\n",
" fig.send_message(\"set_dpi_ratio\", {'dpi_ratio': mpl.ratio});\n",
" }\n",
" fig.send_message(\"refresh\", {});\n",
" }\n",
"\n",
" this.imageObj.onload = function() {\n",
" if (fig.image_mode == 'full') {\n",
" // Full images could contain transparency (where diff images\n",
" // almost always do), so we need to clear the canvas so that\n",
" // there is no ghosting.\n",
" fig.context.clearRect(0, 0, fig.canvas.width, fig.canvas.height);\n",
" }\n",
" fig.context.drawImage(fig.imageObj, 0, 0);\n",
" };\n",
"\n",
" this.imageObj.onunload = function() {\n",
" fig.ws.close();\n",
" }\n",
"\n",
" this.ws.onmessage = this._make_on_message_function(this);\n",
"\n",
" this.ondownload = ondownload;\n",
"}\n",
"\n",
"mpl.figure.prototype._init_header = function() {\n",
" var titlebar = $(\n",
" '');\n",
" var titletext = $(\n",
" '');\n",
" titlebar.append(titletext)\n",
" this.root.append(titlebar);\n",
" this.header = titletext[0];\n",
"}\n",
"\n",
"\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._init_canvas = function() {\n",
" var fig = this;\n",
"\n",
" var canvas_div = $('');\n",
"\n",
" canvas_div.attr('style', 'position: relative; clear: both; outline: 0');\n",
"\n",
" function canvas_keyboard_event(event) {\n",
" return fig.key_event(event, event['data']);\n",
" }\n",
"\n",
" canvas_div.keydown('key_press', canvas_keyboard_event);\n",
" canvas_div.keyup('key_release', canvas_keyboard_event);\n",
" this.canvas_div = canvas_div\n",
" this._canvas_extra_style(canvas_div)\n",
" this.root.append(canvas_div);\n",
"\n",
" var canvas = $('');\n",
" canvas.addClass('mpl-canvas');\n",
" canvas.attr('style', \"left: 0; top: 0; z-index: 0; outline: 0\")\n",
"\n",
" this.canvas = canvas[0];\n",
" this.context = canvas[0].getContext(\"2d\");\n",
"\n",
" var backingStore = this.context.backingStorePixelRatio ||\n",
"\tthis.context.webkitBackingStorePixelRatio ||\n",
"\tthis.context.mozBackingStorePixelRatio ||\n",
"\tthis.context.msBackingStorePixelRatio ||\n",
"\tthis.context.oBackingStorePixelRatio ||\n",
"\tthis.context.backingStorePixelRatio || 1;\n",
"\n",
" mpl.ratio = (window.devicePixelRatio || 1) / backingStore;\n",
"\n",
" var rubberband = $('');\n",
" rubberband.attr('style', \"position: absolute; left: 0; top: 0; z-index: 1;\")\n",
"\n",
" var pass_mouse_events = true;\n",
"\n",
" canvas_div.resizable({\n",
" start: function(event, ui) {\n",
" pass_mouse_events = false;\n",
" },\n",
" resize: function(event, ui) {\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" stop: function(event, ui) {\n",
" pass_mouse_events = true;\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" });\n",
"\n",
" function mouse_event_fn(event) {\n",
" if (pass_mouse_events)\n",
" return fig.mouse_event(event, event['data']);\n",
" }\n",
"\n",
" rubberband.mousedown('button_press', mouse_event_fn);\n",
" rubberband.mouseup('button_release', mouse_event_fn);\n",
" // Throttle sequential mouse events to 1 every 20ms.\n",
" rubberband.mousemove('motion_notify', mouse_event_fn);\n",
"\n",
" rubberband.mouseenter('figure_enter', mouse_event_fn);\n",
" rubberband.mouseleave('figure_leave', mouse_event_fn);\n",
"\n",
" canvas_div.on(\"wheel\", function (event) {\n",
" event = event.originalEvent;\n",
" event['data'] = 'scroll'\n",
" if (event.deltaY < 0) {\n",
" event.step = 1;\n",
" } else {\n",
" event.step = -1;\n",
" }\n",
" mouse_event_fn(event);\n",
" });\n",
"\n",
" canvas_div.append(canvas);\n",
" canvas_div.append(rubberband);\n",
"\n",
" this.rubberband = rubberband;\n",
" this.rubberband_canvas = rubberband[0];\n",
" this.rubberband_context = rubberband[0].getContext(\"2d\");\n",
" this.rubberband_context.strokeStyle = \"#000000\";\n",
"\n",
" this._resize_canvas = function(width, height) {\n",
" // Keep the size of the canvas, canvas container, and rubber band\n",
" // canvas in synch.\n",
" canvas_div.css('width', width)\n",
" canvas_div.css('height', height)\n",
"\n",
" canvas.attr('width', width * mpl.ratio);\n",
" canvas.attr('height', height * mpl.ratio);\n",
" canvas.attr('style', 'width: ' + width + 'px; height: ' + height + 'px;');\n",
"\n",
" rubberband.attr('width', width);\n",
" rubberband.attr('height', height);\n",
" }\n",
"\n",
" // Set the figure to an initial 600x600px, this will subsequently be updated\n",
" // upon first draw.\n",
" this._resize_canvas(600, 600);\n",
"\n",
" // Disable right mouse context menu.\n",
" $(this.rubberband_canvas).bind(\"contextmenu\",function(e){\n",
" return false;\n",
" });\n",
"\n",
" function set_focus () {\n",
" canvas.focus();\n",
" canvas_div.focus();\n",
" }\n",
"\n",
" window.setTimeout(set_focus, 100);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items) {\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) {\n",
" // put a spacer in here.\n",
" continue;\n",
" }\n",
" var button = $('');\n",
" button.addClass('ui-button ui-widget ui-state-default ui-corner-all ' +\n",
" 'ui-button-icon-only');\n",
" button.attr('role', 'button');\n",
" button.attr('aria-disabled', 'false');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
"\n",
" var icon_img = $('');\n",
" icon_img.addClass('ui-button-icon-primary ui-icon');\n",
" icon_img.addClass(image);\n",
" icon_img.addClass('ui-corner-all');\n",
"\n",
" var tooltip_span = $('');\n",
" tooltip_span.addClass('ui-button-text');\n",
" tooltip_span.html(tooltip);\n",
"\n",
" button.append(icon_img);\n",
" button.append(tooltip_span);\n",
"\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" var fmt_picker_span = $('');\n",
"\n",
" var fmt_picker = $('');\n",
" fmt_picker.addClass('mpl-toolbar-option ui-widget ui-widget-content');\n",
" fmt_picker_span.append(fmt_picker);\n",
" nav_element.append(fmt_picker_span);\n",
" this.format_dropdown = fmt_picker[0];\n",
"\n",
" for (var ind in mpl.extensions) {\n",
" var fmt = mpl.extensions[ind];\n",
" var option = $(\n",
" '', {selected: fmt === mpl.default_extension}).html(fmt);\n",
" fmt_picker.append(option)\n",
" }\n",
"\n",
" // Add hover states to the ui-buttons\n",
" $( \".ui-button\" ).hover(\n",
" function() { $(this).addClass(\"ui-state-hover\");},\n",
" function() { $(this).removeClass(\"ui-state-hover\");}\n",
" );\n",
"\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"}\n",
"\n",
"mpl.figure.prototype.request_resize = function(x_pixels, y_pixels) {\n",
" // Request matplotlib to resize the figure. Matplotlib will then trigger a resize in the client,\n",
" // which will in turn request a refresh of the image.\n",
" this.send_message('resize', {'width': x_pixels, 'height': y_pixels});\n",
"}\n",
"\n",
"mpl.figure.prototype.send_message = function(type, properties) {\n",
" properties['type'] = type;\n",
" properties['figure_id'] = this.id;\n",
" this.ws.send(JSON.stringify(properties));\n",
"}\n",
"\n",
"mpl.figure.prototype.send_draw_message = function() {\n",
" if (!this.waiting) {\n",
" this.waiting = true;\n",
" this.ws.send(JSON.stringify({type: \"draw\", figure_id: this.id}));\n",
" }\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" var format_dropdown = fig.format_dropdown;\n",
" var format = format_dropdown.options[format_dropdown.selectedIndex].value;\n",
" fig.ondownload(fig, format);\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_resize = function(fig, msg) {\n",
" var size = msg['size'];\n",
" if (size[0] != fig.canvas.width || size[1] != fig.canvas.height) {\n",
" fig._resize_canvas(size[0], size[1]);\n",
" fig.send_message(\"refresh\", {});\n",
" };\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_rubberband = function(fig, msg) {\n",
" var x0 = msg['x0'] / mpl.ratio;\n",
" var y0 = (fig.canvas.height - msg['y0']) / mpl.ratio;\n",
" var x1 = msg['x1'] / mpl.ratio;\n",
" var y1 = (fig.canvas.height - msg['y1']) / mpl.ratio;\n",
" x0 = Math.floor(x0) + 0.5;\n",
" y0 = Math.floor(y0) + 0.5;\n",
" x1 = Math.floor(x1) + 0.5;\n",
" y1 = Math.floor(y1) + 0.5;\n",
" var min_x = Math.min(x0, x1);\n",
" var min_y = Math.min(y0, y1);\n",
" var width = Math.abs(x1 - x0);\n",
" var height = Math.abs(y1 - y0);\n",
"\n",
" fig.rubberband_context.clearRect(\n",
" 0, 0, fig.canvas.width, fig.canvas.height);\n",
"\n",
" fig.rubberband_context.strokeRect(min_x, min_y, width, height);\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_figure_label = function(fig, msg) {\n",
" // Updates the figure title.\n",
" fig.header.textContent = msg['label'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_cursor = function(fig, msg) {\n",
" var cursor = msg['cursor'];\n",
" switch(cursor)\n",
" {\n",
" case 0:\n",
" cursor = 'pointer';\n",
" break;\n",
" case 1:\n",
" cursor = 'default';\n",
" break;\n",
" case 2:\n",
" cursor = 'crosshair';\n",
" break;\n",
" case 3:\n",
" cursor = 'move';\n",
" break;\n",
" }\n",
" fig.rubberband_canvas.style.cursor = cursor;\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_message = function(fig, msg) {\n",
" fig.message.textContent = msg['message'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_draw = function(fig, msg) {\n",
" // Request the server to send over a new figure.\n",
" fig.send_draw_message();\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_image_mode = function(fig, msg) {\n",
" fig.image_mode = msg['mode'];\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Called whenever the canvas gets updated.\n",
" this.send_message(\"ack\", {});\n",
"}\n",
"\n",
"// A function to construct a web socket function for onmessage handling.\n",
"// Called in the figure constructor.\n",
"mpl.figure.prototype._make_on_message_function = function(fig) {\n",
" return function socket_on_message(evt) {\n",
" if (evt.data instanceof Blob) {\n",
" /* FIXME: We get \"Resource interpreted as Image but\n",
" * transferred with MIME type text/plain:\" errors on\n",
" * Chrome. But how to set the MIME type? It doesn't seem\n",
" * to be part of the websocket stream */\n",
" evt.data.type = \"image/png\";\n",
"\n",
" /* Free the memory for the previous frames */\n",
" if (fig.imageObj.src) {\n",
" (window.URL || window.webkitURL).revokeObjectURL(\n",
" fig.imageObj.src);\n",
" }\n",
"\n",
" fig.imageObj.src = (window.URL || window.webkitURL).createObjectURL(\n",
" evt.data);\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
" else if (typeof evt.data === 'string' && evt.data.slice(0, 21) == \"data:image/png;base64\") {\n",
" fig.imageObj.src = evt.data;\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
"\n",
" var msg = JSON.parse(evt.data);\n",
" var msg_type = msg['type'];\n",
"\n",
" // Call the \"handle_{type}\" callback, which takes\n",
" // the figure and JSON message as its only arguments.\n",
" try {\n",
" var callback = fig[\"handle_\" + msg_type];\n",
" } catch (e) {\n",
" console.log(\"No handler for the '\" + msg_type + \"' message type: \", msg);\n",
" return;\n",
" }\n",
"\n",
" if (callback) {\n",
" try {\n",
" // console.log(\"Handling '\" + msg_type + \"' message: \", msg);\n",
" callback(fig, msg);\n",
" } catch (e) {\n",
" console.log(\"Exception inside the 'handler_\" + msg_type + \"' callback:\", e, e.stack, msg);\n",
" }\n",
" }\n",
" };\n",
"}\n",
"\n",
"// from http://stackoverflow.com/questions/1114465/getting-mouse-location-in-canvas\n",
"mpl.findpos = function(e) {\n",
" //this section is from http://www.quirksmode.org/js/events_properties.html\n",
" var targ;\n",
" if (!e)\n",
" e = window.event;\n",
" if (e.target)\n",
" targ = e.target;\n",
" else if (e.srcElement)\n",
" targ = e.srcElement;\n",
" if (targ.nodeType == 3) // defeat Safari bug\n",
" targ = targ.parentNode;\n",
"\n",
" // jQuery normalizes the pageX and pageY\n",
" // pageX,Y are the mouse positions relative to the document\n",
" // offset() returns the position of the element relative to the document\n",
" var x = e.pageX - $(targ).offset().left;\n",
" var y = e.pageY - $(targ).offset().top;\n",
"\n",
" return {\"x\": x, \"y\": y};\n",
"};\n",
"\n",
"/*\n",
" * return a copy of an object with only non-object keys\n",
" * we need this to avoid circular references\n",
" * http://stackoverflow.com/a/24161582/3208463\n",
" */\n",
"function simpleKeys (original) {\n",
" return Object.keys(original).reduce(function (obj, key) {\n",
" if (typeof original[key] !== 'object')\n",
" obj[key] = original[key]\n",
" return obj;\n",
" }, {});\n",
"}\n",
"\n",
"mpl.figure.prototype.mouse_event = function(event, name) {\n",
" var canvas_pos = mpl.findpos(event)\n",
"\n",
" if (name === 'button_press')\n",
" {\n",
" this.canvas.focus();\n",
" this.canvas_div.focus();\n",
" }\n",
"\n",
" var x = canvas_pos.x * mpl.ratio;\n",
" var y = canvas_pos.y * mpl.ratio;\n",
"\n",
" this.send_message(name, {x: x, y: y, button: event.button,\n",
" step: event.step,\n",
" guiEvent: simpleKeys(event)});\n",
"\n",
" /* This prevents the web browser from automatically changing to\n",
" * the text insertion cursor when the button is pressed. We want\n",
" * to control all of the cursor setting manually through the\n",
" * 'cursor' event from matplotlib */\n",
" event.preventDefault();\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" // Handle any extra behaviour associated with a key event\n",
"}\n",
"\n",
"mpl.figure.prototype.key_event = function(event, name) {\n",
"\n",
" // Prevent repeat events\n",
" if (name == 'key_press')\n",
" {\n",
" if (event.which === this._key)\n",
" return;\n",
" else\n",
" this._key = event.which;\n",
" }\n",
" if (name == 'key_release')\n",
" this._key = null;\n",
"\n",
" var value = '';\n",
" if (event.ctrlKey && event.which != 17)\n",
" value += \"ctrl+\";\n",
" if (event.altKey && event.which != 18)\n",
" value += \"alt+\";\n",
" if (event.shiftKey && event.which != 16)\n",
" value += \"shift+\";\n",
"\n",
" value += 'k';\n",
" value += event.which.toString();\n",
"\n",
" this._key_event_extra(event, name);\n",
"\n",
" this.send_message(name, {key: value,\n",
" guiEvent: simpleKeys(event)});\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype.toolbar_button_onclick = function(name) {\n",
" if (name == 'download') {\n",
" this.handle_save(this, null);\n",
" } else {\n",
" this.send_message(\"toolbar_button\", {name: name});\n",
" }\n",
"};\n",
"\n",
"mpl.figure.prototype.toolbar_button_onmouseover = function(tooltip) {\n",
" this.message.textContent = tooltip;\n",
"};\n",
"mpl.toolbar_items = [[\"Home\", \"Reset original view\", \"fa fa-home icon-home\", \"home\"], [\"Back\", \"Back to previous view\", \"fa fa-arrow-left icon-arrow-left\", \"back\"], [\"Forward\", \"Forward to next view\", \"fa fa-arrow-right icon-arrow-right\", \"forward\"], [\"\", \"\", \"\", \"\"], [\"Pan\", \"Pan axes with left mouse, zoom with right\", \"fa fa-arrows icon-move\", \"pan\"], [\"Zoom\", \"Zoom to rectangle\", \"fa fa-square-o icon-check-empty\", \"zoom\"], [\"\", \"\", \"\", \"\"], [\"Download\", \"Download plot\", \"fa fa-floppy-o icon-save\", \"download\"]];\n",
"\n",
"mpl.extensions = [\"eps\", \"jpeg\", \"pdf\", \"png\", \"ps\", \"raw\", \"svg\", \"tif\"];\n",
"\n",
"mpl.default_extension = \"png\";var comm_websocket_adapter = function(comm) {\n",
" // Create a \"websocket\"-like object which calls the given IPython comm\n",
" // object with the appropriate methods. Currently this is a non binary\n",
" // socket, so there is still some room for performance tuning.\n",
" var ws = {};\n",
"\n",
" ws.close = function() {\n",
" comm.close()\n",
" };\n",
" ws.send = function(m) {\n",
" //console.log('sending', m);\n",
" comm.send(m);\n",
" };\n",
" // Register the callback with on_msg.\n",
" comm.on_msg(function(msg) {\n",
" //console.log('receiving', msg['content']['data'], msg);\n",
" // Pass the mpl event to the overriden (by mpl) onmessage function.\n",
" ws.onmessage(msg['content']['data'])\n",
" });\n",
" return ws;\n",
"}\n",
"\n",
"mpl.mpl_figure_comm = function(comm, msg) {\n",
" // This is the function which gets called when the mpl process\n",
" // starts-up an IPython Comm through the \"matplotlib\" channel.\n",
"\n",
" var id = msg.content.data.id;\n",
" // Get hold of the div created by the display call when the Comm\n",
" // socket was opened in Python.\n",
" var element = $(\"#\" + id);\n",
" var ws_proxy = comm_websocket_adapter(comm)\n",
"\n",
" function ondownload(figure, format) {\n",
" window.open(figure.imageObj.src);\n",
" }\n",
"\n",
" var fig = new mpl.figure(id, ws_proxy,\n",
" ondownload,\n",
" element.get(0));\n",
"\n",
" // Call onopen now - mpl needs it, as it is assuming we've passed it a real\n",
" // web socket which is closed, not our websocket->open comm proxy.\n",
" ws_proxy.onopen();\n",
"\n",
" fig.parent_element = element.get(0);\n",
" fig.cell_info = mpl.find_output_cell(\"\");\n",
" if (!fig.cell_info) {\n",
" console.error(\"Failed to find cell for figure\", id, fig);\n",
" return;\n",
" }\n",
"\n",
" var output_index = fig.cell_info[2]\n",
" var cell = fig.cell_info[0];\n",
"\n",
"};\n",
"\n",
"mpl.figure.prototype.handle_close = function(fig, msg) {\n",
" var width = fig.canvas.width/mpl.ratio\n",
" fig.root.unbind('remove')\n",
"\n",
" // Update the output cell to use the data from the current canvas.\n",
" fig.push_to_output();\n",
" var dataURL = fig.canvas.toDataURL();\n",
" // Re-enable the keyboard manager in IPython - without this line, in FF,\n",
" // the notebook keyboard shortcuts fail.\n",
" IPython.keyboard_manager.enable()\n",
" $(fig.parent_element).html(' ');\n",
" fig.close_ws(fig, msg);\n",
"}\n",
"\n",
"mpl.figure.prototype.close_ws = function(fig, msg){\n",
" fig.send_message('closing', msg);\n",
" // fig.ws.close()\n",
"}\n",
"\n",
"mpl.figure.prototype.push_to_output = function(remove_interactive) {\n",
" // Turn the data on the canvas into data in the output cell.\n",
" var width = this.canvas.width/mpl.ratio\n",
" var dataURL = this.canvas.toDataURL();\n",
" this.cell_info[1]['text/html'] = '
');\n",
" fig.close_ws(fig, msg);\n",
"}\n",
"\n",
"mpl.figure.prototype.close_ws = function(fig, msg){\n",
" fig.send_message('closing', msg);\n",
" // fig.ws.close()\n",
"}\n",
"\n",
"mpl.figure.prototype.push_to_output = function(remove_interactive) {\n",
" // Turn the data on the canvas into data in the output cell.\n",
" var width = this.canvas.width/mpl.ratio\n",
" var dataURL = this.canvas.toDataURL();\n",
" this.cell_info[1]['text/html'] = ' ';\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Tell IPython that the notebook contents must change.\n",
" IPython.notebook.set_dirty(true);\n",
" this.send_message(\"ack\", {});\n",
" var fig = this;\n",
" // Wait a second, then push the new image to the DOM so\n",
" // that it is saved nicely (might be nice to debounce this).\n",
" setTimeout(function () { fig.push_to_output() }, 1000);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items){\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) { continue; };\n",
"\n",
" var button = $('');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" // Add the status bar.\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"\n",
" // Add the close button to the window.\n",
" var buttongrp = $('');\n",
" var button = $('');\n",
" button.click(function (evt) { fig.handle_close(fig, {}); } );\n",
" button.mouseover('Stop Interaction', toolbar_mouse_event);\n",
" buttongrp.append(button);\n",
" var titlebar = this.root.find($('.ui-dialog-titlebar'));\n",
" titlebar.prepend(buttongrp);\n",
"}\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(el){\n",
" var fig = this\n",
" el.on(\"remove\", function(){\n",
"\tfig.close_ws(fig, {});\n",
" });\n",
"}\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(el){\n",
" // this is important to make the div 'focusable\n",
" el.attr('tabindex', 0)\n",
" // reach out to IPython and tell the keyboard manager to turn it's self\n",
" // off when our div gets focus\n",
"\n",
" // location in version 3\n",
" if (IPython.notebook.keyboard_manager) {\n",
" IPython.notebook.keyboard_manager.register_events(el);\n",
" }\n",
" else {\n",
" // location in version 2\n",
" IPython.keyboard_manager.register_events(el);\n",
" }\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" var manager = IPython.notebook.keyboard_manager;\n",
" if (!manager)\n",
" manager = IPython.keyboard_manager;\n",
"\n",
" // Check for shift+enter\n",
" if (event.shiftKey && event.which == 13) {\n",
" this.canvas_div.blur();\n",
" event.shiftKey = false;\n",
" // Send a \"J\" for go to next cell\n",
" event.which = 74;\n",
" event.keyCode = 74;\n",
" manager.command_mode();\n",
" manager.handle_keydown(event);\n",
" }\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" fig.ondownload(fig, null);\n",
"}\n",
"\n",
"\n",
"mpl.find_output_cell = function(html_output) {\n",
" // Return the cell and output element which can be found *uniquely* in the notebook.\n",
" // Note - this is a bit hacky, but it is done because the \"notebook_saving.Notebook\"\n",
" // IPython event is triggered only after the cells have been serialised, which for\n",
" // our purposes (turning an active figure into a static one), is too late.\n",
" var cells = IPython.notebook.get_cells();\n",
" var ncells = cells.length;\n",
" for (var i=0; i= 3 moved mimebundle to data attribute of output\n",
" data = data.data;\n",
" }\n",
" if (data['text/html'] == html_output) {\n",
" return [cell, data, j];\n",
" }\n",
" }\n",
" }\n",
" }\n",
"}\n",
"\n",
"// Register the function which deals with the matplotlib target/channel.\n",
"// The kernel may be null if the page has been refreshed.\n",
"if (IPython.notebook.kernel != null) {\n",
" IPython.notebook.kernel.comm_manager.register_target('matplotlib', mpl.mpl_figure_comm);\n",
"}\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"
';\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Tell IPython that the notebook contents must change.\n",
" IPython.notebook.set_dirty(true);\n",
" this.send_message(\"ack\", {});\n",
" var fig = this;\n",
" // Wait a second, then push the new image to the DOM so\n",
" // that it is saved nicely (might be nice to debounce this).\n",
" setTimeout(function () { fig.push_to_output() }, 1000);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items){\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) { continue; };\n",
"\n",
" var button = $('');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" // Add the status bar.\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"\n",
" // Add the close button to the window.\n",
" var buttongrp = $('');\n",
" var button = $('');\n",
" button.click(function (evt) { fig.handle_close(fig, {}); } );\n",
" button.mouseover('Stop Interaction', toolbar_mouse_event);\n",
" buttongrp.append(button);\n",
" var titlebar = this.root.find($('.ui-dialog-titlebar'));\n",
" titlebar.prepend(buttongrp);\n",
"}\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(el){\n",
" var fig = this\n",
" el.on(\"remove\", function(){\n",
"\tfig.close_ws(fig, {});\n",
" });\n",
"}\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(el){\n",
" // this is important to make the div 'focusable\n",
" el.attr('tabindex', 0)\n",
" // reach out to IPython and tell the keyboard manager to turn it's self\n",
" // off when our div gets focus\n",
"\n",
" // location in version 3\n",
" if (IPython.notebook.keyboard_manager) {\n",
" IPython.notebook.keyboard_manager.register_events(el);\n",
" }\n",
" else {\n",
" // location in version 2\n",
" IPython.keyboard_manager.register_events(el);\n",
" }\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" var manager = IPython.notebook.keyboard_manager;\n",
" if (!manager)\n",
" manager = IPython.keyboard_manager;\n",
"\n",
" // Check for shift+enter\n",
" if (event.shiftKey && event.which == 13) {\n",
" this.canvas_div.blur();\n",
" event.shiftKey = false;\n",
" // Send a \"J\" for go to next cell\n",
" event.which = 74;\n",
" event.keyCode = 74;\n",
" manager.command_mode();\n",
" manager.handle_keydown(event);\n",
" }\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" fig.ondownload(fig, null);\n",
"}\n",
"\n",
"\n",
"mpl.find_output_cell = function(html_output) {\n",
" // Return the cell and output element which can be found *uniquely* in the notebook.\n",
" // Note - this is a bit hacky, but it is done because the \"notebook_saving.Notebook\"\n",
" // IPython event is triggered only after the cells have been serialised, which for\n",
" // our purposes (turning an active figure into a static one), is too late.\n",
" var cells = IPython.notebook.get_cells();\n",
" var ncells = cells.length;\n",
" for (var i=0; i= 3 moved mimebundle to data attribute of output\n",
" data = data.data;\n",
" }\n",
" if (data['text/html'] == html_output) {\n",
" return [cell, data, j];\n",
" }\n",
" }\n",
" }\n",
" }\n",
"}\n",
"\n",
"// Register the function which deals with the matplotlib target/channel.\n",
"// The kernel may be null if the page has been refreshed.\n",
"if (IPython.notebook.kernel != null) {\n",
" IPython.notebook.kernel.comm_manager.register_target('matplotlib', mpl.mpl_figure_comm);\n",
"}\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
" "
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"#Normalize a chain so that l_\\infty norm is 1\n",
"def normalize(C):\n",
" return C/max(abs(C))\n",
"\n",
"S = Surface(getExample('torus.ply'), euclideanM)\n",
"generators, betti1 = homology(S)\n",
"\n",
"G = [ normalize(generators[:,i]) for i in range(betti1) ]\n",
"GS= [ normalize(S.short(g)) for g in G ]\n",
"\n",
"for i in range(betti1):\n",
" S.plot([G[i], GS[i]], ['yellow', 'red'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The two projections of the torus do not reveal where the holes are. In yellow we see the dense cycles found by SVD. Their shortest homologous red versions make this a bit more clear. For example, the coil-shaped part of the first cycle clearly detects the hole in the middle of the torus.\n",
"\n",
"Here is an example of this on a more complicated surface."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Number of features: 6\n"
]
},
{
"data": {
"application/javascript": [
"/* Put everything inside the global mpl namespace */\n",
"window.mpl = {};\n",
"\n",
"\n",
"mpl.get_websocket_type = function() {\n",
" if (typeof(WebSocket) !== 'undefined') {\n",
" return WebSocket;\n",
" } else if (typeof(MozWebSocket) !== 'undefined') {\n",
" return MozWebSocket;\n",
" } else {\n",
" alert('Your browser does not have WebSocket support.' +\n",
" 'Please try Chrome, Safari or Firefox 6. ' +\n",
" 'Firefox 4 and 5 are also supported but you ' +\n",
" 'have to enable WebSockets in about:config.');\n",
" };\n",
"}\n",
"\n",
"mpl.figure = function(figure_id, websocket, ondownload, parent_element) {\n",
" this.id = figure_id;\n",
"\n",
" this.ws = websocket;\n",
"\n",
" this.supports_binary = (this.ws.binaryType != undefined);\n",
"\n",
" if (!this.supports_binary) {\n",
" var warnings = document.getElementById(\"mpl-warnings\");\n",
" if (warnings) {\n",
" warnings.style.display = 'block';\n",
" warnings.textContent = (\n",
" \"This browser does not support binary websocket messages. \" +\n",
" \"Performance may be slow.\");\n",
" }\n",
" }\n",
"\n",
" this.imageObj = new Image();\n",
"\n",
" this.context = undefined;\n",
" this.message = undefined;\n",
" this.canvas = undefined;\n",
" this.rubberband_canvas = undefined;\n",
" this.rubberband_context = undefined;\n",
" this.format_dropdown = undefined;\n",
"\n",
" this.image_mode = 'full';\n",
"\n",
" this.root = $('');\n",
" this._root_extra_style(this.root)\n",
" this.root.attr('style', 'display: inline-block');\n",
"\n",
" $(parent_element).append(this.root);\n",
"\n",
" this._init_header(this);\n",
" this._init_canvas(this);\n",
" this._init_toolbar(this);\n",
"\n",
" var fig = this;\n",
"\n",
" this.waiting = false;\n",
"\n",
" this.ws.onopen = function () {\n",
" fig.send_message(\"supports_binary\", {value: fig.supports_binary});\n",
" fig.send_message(\"send_image_mode\", {});\n",
" if (mpl.ratio != 1) {\n",
" fig.send_message(\"set_dpi_ratio\", {'dpi_ratio': mpl.ratio});\n",
" }\n",
" fig.send_message(\"refresh\", {});\n",
" }\n",
"\n",
" this.imageObj.onload = function() {\n",
" if (fig.image_mode == 'full') {\n",
" // Full images could contain transparency (where diff images\n",
" // almost always do), so we need to clear the canvas so that\n",
" // there is no ghosting.\n",
" fig.context.clearRect(0, 0, fig.canvas.width, fig.canvas.height);\n",
" }\n",
" fig.context.drawImage(fig.imageObj, 0, 0);\n",
" };\n",
"\n",
" this.imageObj.onunload = function() {\n",
" fig.ws.close();\n",
" }\n",
"\n",
" this.ws.onmessage = this._make_on_message_function(this);\n",
"\n",
" this.ondownload = ondownload;\n",
"}\n",
"\n",
"mpl.figure.prototype._init_header = function() {\n",
" var titlebar = $(\n",
" '');\n",
" var titletext = $(\n",
" '');\n",
" titlebar.append(titletext)\n",
" this.root.append(titlebar);\n",
" this.header = titletext[0];\n",
"}\n",
"\n",
"\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._init_canvas = function() {\n",
" var fig = this;\n",
"\n",
" var canvas_div = $('');\n",
"\n",
" canvas_div.attr('style', 'position: relative; clear: both; outline: 0');\n",
"\n",
" function canvas_keyboard_event(event) {\n",
" return fig.key_event(event, event['data']);\n",
" }\n",
"\n",
" canvas_div.keydown('key_press', canvas_keyboard_event);\n",
" canvas_div.keyup('key_release', canvas_keyboard_event);\n",
" this.canvas_div = canvas_div\n",
" this._canvas_extra_style(canvas_div)\n",
" this.root.append(canvas_div);\n",
"\n",
" var canvas = $('');\n",
" canvas.addClass('mpl-canvas');\n",
" canvas.attr('style', \"left: 0; top: 0; z-index: 0; outline: 0\")\n",
"\n",
" this.canvas = canvas[0];\n",
" this.context = canvas[0].getContext(\"2d\");\n",
"\n",
" var backingStore = this.context.backingStorePixelRatio ||\n",
"\tthis.context.webkitBackingStorePixelRatio ||\n",
"\tthis.context.mozBackingStorePixelRatio ||\n",
"\tthis.context.msBackingStorePixelRatio ||\n",
"\tthis.context.oBackingStorePixelRatio ||\n",
"\tthis.context.backingStorePixelRatio || 1;\n",
"\n",
" mpl.ratio = (window.devicePixelRatio || 1) / backingStore;\n",
"\n",
" var rubberband = $('');\n",
" rubberband.attr('style', \"position: absolute; left: 0; top: 0; z-index: 1;\")\n",
"\n",
" var pass_mouse_events = true;\n",
"\n",
" canvas_div.resizable({\n",
" start: function(event, ui) {\n",
" pass_mouse_events = false;\n",
" },\n",
" resize: function(event, ui) {\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" stop: function(event, ui) {\n",
" pass_mouse_events = true;\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" });\n",
"\n",
" function mouse_event_fn(event) {\n",
" if (pass_mouse_events)\n",
" return fig.mouse_event(event, event['data']);\n",
" }\n",
"\n",
" rubberband.mousedown('button_press', mouse_event_fn);\n",
" rubberband.mouseup('button_release', mouse_event_fn);\n",
" // Throttle sequential mouse events to 1 every 20ms.\n",
" rubberband.mousemove('motion_notify', mouse_event_fn);\n",
"\n",
" rubberband.mouseenter('figure_enter', mouse_event_fn);\n",
" rubberband.mouseleave('figure_leave', mouse_event_fn);\n",
"\n",
" canvas_div.on(\"wheel\", function (event) {\n",
" event = event.originalEvent;\n",
" event['data'] = 'scroll'\n",
" if (event.deltaY < 0) {\n",
" event.step = 1;\n",
" } else {\n",
" event.step = -1;\n",
" }\n",
" mouse_event_fn(event);\n",
" });\n",
"\n",
" canvas_div.append(canvas);\n",
" canvas_div.append(rubberband);\n",
"\n",
" this.rubberband = rubberband;\n",
" this.rubberband_canvas = rubberband[0];\n",
" this.rubberband_context = rubberband[0].getContext(\"2d\");\n",
" this.rubberband_context.strokeStyle = \"#000000\";\n",
"\n",
" this._resize_canvas = function(width, height) {\n",
" // Keep the size of the canvas, canvas container, and rubber band\n",
" // canvas in synch.\n",
" canvas_div.css('width', width)\n",
" canvas_div.css('height', height)\n",
"\n",
" canvas.attr('width', width * mpl.ratio);\n",
" canvas.attr('height', height * mpl.ratio);\n",
" canvas.attr('style', 'width: ' + width + 'px; height: ' + height + 'px;');\n",
"\n",
" rubberband.attr('width', width);\n",
" rubberband.attr('height', height);\n",
" }\n",
"\n",
" // Set the figure to an initial 600x600px, this will subsequently be updated\n",
" // upon first draw.\n",
" this._resize_canvas(600, 600);\n",
"\n",
" // Disable right mouse context menu.\n",
" $(this.rubberband_canvas).bind(\"contextmenu\",function(e){\n",
" return false;\n",
" });\n",
"\n",
" function set_focus () {\n",
" canvas.focus();\n",
" canvas_div.focus();\n",
" }\n",
"\n",
" window.setTimeout(set_focus, 100);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items) {\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) {\n",
" // put a spacer in here.\n",
" continue;\n",
" }\n",
" var button = $('');\n",
" button.addClass('ui-button ui-widget ui-state-default ui-corner-all ' +\n",
" 'ui-button-icon-only');\n",
" button.attr('role', 'button');\n",
" button.attr('aria-disabled', 'false');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
"\n",
" var icon_img = $('');\n",
" icon_img.addClass('ui-button-icon-primary ui-icon');\n",
" icon_img.addClass(image);\n",
" icon_img.addClass('ui-corner-all');\n",
"\n",
" var tooltip_span = $('');\n",
" tooltip_span.addClass('ui-button-text');\n",
" tooltip_span.html(tooltip);\n",
"\n",
" button.append(icon_img);\n",
" button.append(tooltip_span);\n",
"\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" var fmt_picker_span = $('');\n",
"\n",
" var fmt_picker = $('');\n",
" fmt_picker.addClass('mpl-toolbar-option ui-widget ui-widget-content');\n",
" fmt_picker_span.append(fmt_picker);\n",
" nav_element.append(fmt_picker_span);\n",
" this.format_dropdown = fmt_picker[0];\n",
"\n",
" for (var ind in mpl.extensions) {\n",
" var fmt = mpl.extensions[ind];\n",
" var option = $(\n",
" '', {selected: fmt === mpl.default_extension}).html(fmt);\n",
" fmt_picker.append(option)\n",
" }\n",
"\n",
" // Add hover states to the ui-buttons\n",
" $( \".ui-button\" ).hover(\n",
" function() { $(this).addClass(\"ui-state-hover\");},\n",
" function() { $(this).removeClass(\"ui-state-hover\");}\n",
" );\n",
"\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"}\n",
"\n",
"mpl.figure.prototype.request_resize = function(x_pixels, y_pixels) {\n",
" // Request matplotlib to resize the figure. Matplotlib will then trigger a resize in the client,\n",
" // which will in turn request a refresh of the image.\n",
" this.send_message('resize', {'width': x_pixels, 'height': y_pixels});\n",
"}\n",
"\n",
"mpl.figure.prototype.send_message = function(type, properties) {\n",
" properties['type'] = type;\n",
" properties['figure_id'] = this.id;\n",
" this.ws.send(JSON.stringify(properties));\n",
"}\n",
"\n",
"mpl.figure.prototype.send_draw_message = function() {\n",
" if (!this.waiting) {\n",
" this.waiting = true;\n",
" this.ws.send(JSON.stringify({type: \"draw\", figure_id: this.id}));\n",
" }\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" var format_dropdown = fig.format_dropdown;\n",
" var format = format_dropdown.options[format_dropdown.selectedIndex].value;\n",
" fig.ondownload(fig, format);\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_resize = function(fig, msg) {\n",
" var size = msg['size'];\n",
" if (size[0] != fig.canvas.width || size[1] != fig.canvas.height) {\n",
" fig._resize_canvas(size[0], size[1]);\n",
" fig.send_message(\"refresh\", {});\n",
" };\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_rubberband = function(fig, msg) {\n",
" var x0 = msg['x0'] / mpl.ratio;\n",
" var y0 = (fig.canvas.height - msg['y0']) / mpl.ratio;\n",
" var x1 = msg['x1'] / mpl.ratio;\n",
" var y1 = (fig.canvas.height - msg['y1']) / mpl.ratio;\n",
" x0 = Math.floor(x0) + 0.5;\n",
" y0 = Math.floor(y0) + 0.5;\n",
" x1 = Math.floor(x1) + 0.5;\n",
" y1 = Math.floor(y1) + 0.5;\n",
" var min_x = Math.min(x0, x1);\n",
" var min_y = Math.min(y0, y1);\n",
" var width = Math.abs(x1 - x0);\n",
" var height = Math.abs(y1 - y0);\n",
"\n",
" fig.rubberband_context.clearRect(\n",
" 0, 0, fig.canvas.width, fig.canvas.height);\n",
"\n",
" fig.rubberband_context.strokeRect(min_x, min_y, width, height);\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_figure_label = function(fig, msg) {\n",
" // Updates the figure title.\n",
" fig.header.textContent = msg['label'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_cursor = function(fig, msg) {\n",
" var cursor = msg['cursor'];\n",
" switch(cursor)\n",
" {\n",
" case 0:\n",
" cursor = 'pointer';\n",
" break;\n",
" case 1:\n",
" cursor = 'default';\n",
" break;\n",
" case 2:\n",
" cursor = 'crosshair';\n",
" break;\n",
" case 3:\n",
" cursor = 'move';\n",
" break;\n",
" }\n",
" fig.rubberband_canvas.style.cursor = cursor;\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_message = function(fig, msg) {\n",
" fig.message.textContent = msg['message'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_draw = function(fig, msg) {\n",
" // Request the server to send over a new figure.\n",
" fig.send_draw_message();\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_image_mode = function(fig, msg) {\n",
" fig.image_mode = msg['mode'];\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Called whenever the canvas gets updated.\n",
" this.send_message(\"ack\", {});\n",
"}\n",
"\n",
"// A function to construct a web socket function for onmessage handling.\n",
"// Called in the figure constructor.\n",
"mpl.figure.prototype._make_on_message_function = function(fig) {\n",
" return function socket_on_message(evt) {\n",
" if (evt.data instanceof Blob) {\n",
" /* FIXME: We get \"Resource interpreted as Image but\n",
" * transferred with MIME type text/plain:\" errors on\n",
" * Chrome. But how to set the MIME type? It doesn't seem\n",
" * to be part of the websocket stream */\n",
" evt.data.type = \"image/png\";\n",
"\n",
" /* Free the memory for the previous frames */\n",
" if (fig.imageObj.src) {\n",
" (window.URL || window.webkitURL).revokeObjectURL(\n",
" fig.imageObj.src);\n",
" }\n",
"\n",
" fig.imageObj.src = (window.URL || window.webkitURL).createObjectURL(\n",
" evt.data);\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
" else if (typeof evt.data === 'string' && evt.data.slice(0, 21) == \"data:image/png;base64\") {\n",
" fig.imageObj.src = evt.data;\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
"\n",
" var msg = JSON.parse(evt.data);\n",
" var msg_type = msg['type'];\n",
"\n",
" // Call the \"handle_{type}\" callback, which takes\n",
" // the figure and JSON message as its only arguments.\n",
" try {\n",
" var callback = fig[\"handle_\" + msg_type];\n",
" } catch (e) {\n",
" console.log(\"No handler for the '\" + msg_type + \"' message type: \", msg);\n",
" return;\n",
" }\n",
"\n",
" if (callback) {\n",
" try {\n",
" // console.log(\"Handling '\" + msg_type + \"' message: \", msg);\n",
" callback(fig, msg);\n",
" } catch (e) {\n",
" console.log(\"Exception inside the 'handler_\" + msg_type + \"' callback:\", e, e.stack, msg);\n",
" }\n",
" }\n",
" };\n",
"}\n",
"\n",
"// from http://stackoverflow.com/questions/1114465/getting-mouse-location-in-canvas\n",
"mpl.findpos = function(e) {\n",
" //this section is from http://www.quirksmode.org/js/events_properties.html\n",
" var targ;\n",
" if (!e)\n",
" e = window.event;\n",
" if (e.target)\n",
" targ = e.target;\n",
" else if (e.srcElement)\n",
" targ = e.srcElement;\n",
" if (targ.nodeType == 3) // defeat Safari bug\n",
" targ = targ.parentNode;\n",
"\n",
" // jQuery normalizes the pageX and pageY\n",
" // pageX,Y are the mouse positions relative to the document\n",
" // offset() returns the position of the element relative to the document\n",
" var x = e.pageX - $(targ).offset().left;\n",
" var y = e.pageY - $(targ).offset().top;\n",
"\n",
" return {\"x\": x, \"y\": y};\n",
"};\n",
"\n",
"/*\n",
" * return a copy of an object with only non-object keys\n",
" * we need this to avoid circular references\n",
" * http://stackoverflow.com/a/24161582/3208463\n",
" */\n",
"function simpleKeys (original) {\n",
" return Object.keys(original).reduce(function (obj, key) {\n",
" if (typeof original[key] !== 'object')\n",
" obj[key] = original[key]\n",
" return obj;\n",
" }, {});\n",
"}\n",
"\n",
"mpl.figure.prototype.mouse_event = function(event, name) {\n",
" var canvas_pos = mpl.findpos(event)\n",
"\n",
" if (name === 'button_press')\n",
" {\n",
" this.canvas.focus();\n",
" this.canvas_div.focus();\n",
" }\n",
"\n",
" var x = canvas_pos.x * mpl.ratio;\n",
" var y = canvas_pos.y * mpl.ratio;\n",
"\n",
" this.send_message(name, {x: x, y: y, button: event.button,\n",
" step: event.step,\n",
" guiEvent: simpleKeys(event)});\n",
"\n",
" /* This prevents the web browser from automatically changing to\n",
" * the text insertion cursor when the button is pressed. We want\n",
" * to control all of the cursor setting manually through the\n",
" * 'cursor' event from matplotlib */\n",
" event.preventDefault();\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" // Handle any extra behaviour associated with a key event\n",
"}\n",
"\n",
"mpl.figure.prototype.key_event = function(event, name) {\n",
"\n",
" // Prevent repeat events\n",
" if (name == 'key_press')\n",
" {\n",
" if (event.which === this._key)\n",
" return;\n",
" else\n",
" this._key = event.which;\n",
" }\n",
" if (name == 'key_release')\n",
" this._key = null;\n",
"\n",
" var value = '';\n",
" if (event.ctrlKey && event.which != 17)\n",
" value += \"ctrl+\";\n",
" if (event.altKey && event.which != 18)\n",
" value += \"alt+\";\n",
" if (event.shiftKey && event.which != 16)\n",
" value += \"shift+\";\n",
"\n",
" value += 'k';\n",
" value += event.which.toString();\n",
"\n",
" this._key_event_extra(event, name);\n",
"\n",
" this.send_message(name, {key: value,\n",
" guiEvent: simpleKeys(event)});\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype.toolbar_button_onclick = function(name) {\n",
" if (name == 'download') {\n",
" this.handle_save(this, null);\n",
" } else {\n",
" this.send_message(\"toolbar_button\", {name: name});\n",
" }\n",
"};\n",
"\n",
"mpl.figure.prototype.toolbar_button_onmouseover = function(tooltip) {\n",
" this.message.textContent = tooltip;\n",
"};\n",
"mpl.toolbar_items = [[\"Home\", \"Reset original view\", \"fa fa-home icon-home\", \"home\"], [\"Back\", \"Back to previous view\", \"fa fa-arrow-left icon-arrow-left\", \"back\"], [\"Forward\", \"Forward to next view\", \"fa fa-arrow-right icon-arrow-right\", \"forward\"], [\"\", \"\", \"\", \"\"], [\"Pan\", \"Pan axes with left mouse, zoom with right\", \"fa fa-arrows icon-move\", \"pan\"], [\"Zoom\", \"Zoom to rectangle\", \"fa fa-square-o icon-check-empty\", \"zoom\"], [\"\", \"\", \"\", \"\"], [\"Download\", \"Download plot\", \"fa fa-floppy-o icon-save\", \"download\"]];\n",
"\n",
"mpl.extensions = [\"eps\", \"jpeg\", \"pdf\", \"png\", \"ps\", \"raw\", \"svg\", \"tif\"];\n",
"\n",
"mpl.default_extension = \"png\";var comm_websocket_adapter = function(comm) {\n",
" // Create a \"websocket\"-like object which calls the given IPython comm\n",
" // object with the appropriate methods. Currently this is a non binary\n",
" // socket, so there is still some room for performance tuning.\n",
" var ws = {};\n",
"\n",
" ws.close = function() {\n",
" comm.close()\n",
" };\n",
" ws.send = function(m) {\n",
" //console.log('sending', m);\n",
" comm.send(m);\n",
" };\n",
" // Register the callback with on_msg.\n",
" comm.on_msg(function(msg) {\n",
" //console.log('receiving', msg['content']['data'], msg);\n",
" // Pass the mpl event to the overriden (by mpl) onmessage function.\n",
" ws.onmessage(msg['content']['data'])\n",
" });\n",
" return ws;\n",
"}\n",
"\n",
"mpl.mpl_figure_comm = function(comm, msg) {\n",
" // This is the function which gets called when the mpl process\n",
" // starts-up an IPython Comm through the \"matplotlib\" channel.\n",
"\n",
" var id = msg.content.data.id;\n",
" // Get hold of the div created by the display call when the Comm\n",
" // socket was opened in Python.\n",
" var element = $(\"#\" + id);\n",
" var ws_proxy = comm_websocket_adapter(comm)\n",
"\n",
" function ondownload(figure, format) {\n",
" window.open(figure.imageObj.src);\n",
" }\n",
"\n",
" var fig = new mpl.figure(id, ws_proxy,\n",
" ondownload,\n",
" element.get(0));\n",
"\n",
" // Call onopen now - mpl needs it, as it is assuming we've passed it a real\n",
" // web socket which is closed, not our websocket->open comm proxy.\n",
" ws_proxy.onopen();\n",
"\n",
" fig.parent_element = element.get(0);\n",
" fig.cell_info = mpl.find_output_cell(\"\");\n",
" if (!fig.cell_info) {\n",
" console.error(\"Failed to find cell for figure\", id, fig);\n",
" return;\n",
" }\n",
"\n",
" var output_index = fig.cell_info[2]\n",
" var cell = fig.cell_info[0];\n",
"\n",
"};\n",
"\n",
"mpl.figure.prototype.handle_close = function(fig, msg) {\n",
" var width = fig.canvas.width/mpl.ratio\n",
" fig.root.unbind('remove')\n",
"\n",
" // Update the output cell to use the data from the current canvas.\n",
" fig.push_to_output();\n",
" var dataURL = fig.canvas.toDataURL();\n",
" // Re-enable the keyboard manager in IPython - without this line, in FF,\n",
" // the notebook keyboard shortcuts fail.\n",
" IPython.keyboard_manager.enable()\n",
" $(fig.parent_element).html('
"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"#Normalize a chain so that l_\\infty norm is 1\n",
"def normalize(C):\n",
" return C/max(abs(C))\n",
"\n",
"S = Surface(getExample('torus.ply'), euclideanM)\n",
"generators, betti1 = homology(S)\n",
"\n",
"G = [ normalize(generators[:,i]) for i in range(betti1) ]\n",
"GS= [ normalize(S.short(g)) for g in G ]\n",
"\n",
"for i in range(betti1):\n",
" S.plot([G[i], GS[i]], ['yellow', 'red'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The two projections of the torus do not reveal where the holes are. In yellow we see the dense cycles found by SVD. Their shortest homologous red versions make this a bit more clear. For example, the coil-shaped part of the first cycle clearly detects the hole in the middle of the torus.\n",
"\n",
"Here is an example of this on a more complicated surface."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Number of features: 6\n"
]
},
{
"data": {
"application/javascript": [
"/* Put everything inside the global mpl namespace */\n",
"window.mpl = {};\n",
"\n",
"\n",
"mpl.get_websocket_type = function() {\n",
" if (typeof(WebSocket) !== 'undefined') {\n",
" return WebSocket;\n",
" } else if (typeof(MozWebSocket) !== 'undefined') {\n",
" return MozWebSocket;\n",
" } else {\n",
" alert('Your browser does not have WebSocket support.' +\n",
" 'Please try Chrome, Safari or Firefox 6. ' +\n",
" 'Firefox 4 and 5 are also supported but you ' +\n",
" 'have to enable WebSockets in about:config.');\n",
" };\n",
"}\n",
"\n",
"mpl.figure = function(figure_id, websocket, ondownload, parent_element) {\n",
" this.id = figure_id;\n",
"\n",
" this.ws = websocket;\n",
"\n",
" this.supports_binary = (this.ws.binaryType != undefined);\n",
"\n",
" if (!this.supports_binary) {\n",
" var warnings = document.getElementById(\"mpl-warnings\");\n",
" if (warnings) {\n",
" warnings.style.display = 'block';\n",
" warnings.textContent = (\n",
" \"This browser does not support binary websocket messages. \" +\n",
" \"Performance may be slow.\");\n",
" }\n",
" }\n",
"\n",
" this.imageObj = new Image();\n",
"\n",
" this.context = undefined;\n",
" this.message = undefined;\n",
" this.canvas = undefined;\n",
" this.rubberband_canvas = undefined;\n",
" this.rubberband_context = undefined;\n",
" this.format_dropdown = undefined;\n",
"\n",
" this.image_mode = 'full';\n",
"\n",
" this.root = $('');\n",
" this._root_extra_style(this.root)\n",
" this.root.attr('style', 'display: inline-block');\n",
"\n",
" $(parent_element).append(this.root);\n",
"\n",
" this._init_header(this);\n",
" this._init_canvas(this);\n",
" this._init_toolbar(this);\n",
"\n",
" var fig = this;\n",
"\n",
" this.waiting = false;\n",
"\n",
" this.ws.onopen = function () {\n",
" fig.send_message(\"supports_binary\", {value: fig.supports_binary});\n",
" fig.send_message(\"send_image_mode\", {});\n",
" if (mpl.ratio != 1) {\n",
" fig.send_message(\"set_dpi_ratio\", {'dpi_ratio': mpl.ratio});\n",
" }\n",
" fig.send_message(\"refresh\", {});\n",
" }\n",
"\n",
" this.imageObj.onload = function() {\n",
" if (fig.image_mode == 'full') {\n",
" // Full images could contain transparency (where diff images\n",
" // almost always do), so we need to clear the canvas so that\n",
" // there is no ghosting.\n",
" fig.context.clearRect(0, 0, fig.canvas.width, fig.canvas.height);\n",
" }\n",
" fig.context.drawImage(fig.imageObj, 0, 0);\n",
" };\n",
"\n",
" this.imageObj.onunload = function() {\n",
" fig.ws.close();\n",
" }\n",
"\n",
" this.ws.onmessage = this._make_on_message_function(this);\n",
"\n",
" this.ondownload = ondownload;\n",
"}\n",
"\n",
"mpl.figure.prototype._init_header = function() {\n",
" var titlebar = $(\n",
" '');\n",
" var titletext = $(\n",
" '');\n",
" titlebar.append(titletext)\n",
" this.root.append(titlebar);\n",
" this.header = titletext[0];\n",
"}\n",
"\n",
"\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._init_canvas = function() {\n",
" var fig = this;\n",
"\n",
" var canvas_div = $('');\n",
"\n",
" canvas_div.attr('style', 'position: relative; clear: both; outline: 0');\n",
"\n",
" function canvas_keyboard_event(event) {\n",
" return fig.key_event(event, event['data']);\n",
" }\n",
"\n",
" canvas_div.keydown('key_press', canvas_keyboard_event);\n",
" canvas_div.keyup('key_release', canvas_keyboard_event);\n",
" this.canvas_div = canvas_div\n",
" this._canvas_extra_style(canvas_div)\n",
" this.root.append(canvas_div);\n",
"\n",
" var canvas = $('');\n",
" canvas.addClass('mpl-canvas');\n",
" canvas.attr('style', \"left: 0; top: 0; z-index: 0; outline: 0\")\n",
"\n",
" this.canvas = canvas[0];\n",
" this.context = canvas[0].getContext(\"2d\");\n",
"\n",
" var backingStore = this.context.backingStorePixelRatio ||\n",
"\tthis.context.webkitBackingStorePixelRatio ||\n",
"\tthis.context.mozBackingStorePixelRatio ||\n",
"\tthis.context.msBackingStorePixelRatio ||\n",
"\tthis.context.oBackingStorePixelRatio ||\n",
"\tthis.context.backingStorePixelRatio || 1;\n",
"\n",
" mpl.ratio = (window.devicePixelRatio || 1) / backingStore;\n",
"\n",
" var rubberband = $('');\n",
" rubberband.attr('style', \"position: absolute; left: 0; top: 0; z-index: 1;\")\n",
"\n",
" var pass_mouse_events = true;\n",
"\n",
" canvas_div.resizable({\n",
" start: function(event, ui) {\n",
" pass_mouse_events = false;\n",
" },\n",
" resize: function(event, ui) {\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" stop: function(event, ui) {\n",
" pass_mouse_events = true;\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" });\n",
"\n",
" function mouse_event_fn(event) {\n",
" if (pass_mouse_events)\n",
" return fig.mouse_event(event, event['data']);\n",
" }\n",
"\n",
" rubberband.mousedown('button_press', mouse_event_fn);\n",
" rubberband.mouseup('button_release', mouse_event_fn);\n",
" // Throttle sequential mouse events to 1 every 20ms.\n",
" rubberband.mousemove('motion_notify', mouse_event_fn);\n",
"\n",
" rubberband.mouseenter('figure_enter', mouse_event_fn);\n",
" rubberband.mouseleave('figure_leave', mouse_event_fn);\n",
"\n",
" canvas_div.on(\"wheel\", function (event) {\n",
" event = event.originalEvent;\n",
" event['data'] = 'scroll'\n",
" if (event.deltaY < 0) {\n",
" event.step = 1;\n",
" } else {\n",
" event.step = -1;\n",
" }\n",
" mouse_event_fn(event);\n",
" });\n",
"\n",
" canvas_div.append(canvas);\n",
" canvas_div.append(rubberband);\n",
"\n",
" this.rubberband = rubberband;\n",
" this.rubberband_canvas = rubberband[0];\n",
" this.rubberband_context = rubberband[0].getContext(\"2d\");\n",
" this.rubberband_context.strokeStyle = \"#000000\";\n",
"\n",
" this._resize_canvas = function(width, height) {\n",
" // Keep the size of the canvas, canvas container, and rubber band\n",
" // canvas in synch.\n",
" canvas_div.css('width', width)\n",
" canvas_div.css('height', height)\n",
"\n",
" canvas.attr('width', width * mpl.ratio);\n",
" canvas.attr('height', height * mpl.ratio);\n",
" canvas.attr('style', 'width: ' + width + 'px; height: ' + height + 'px;');\n",
"\n",
" rubberband.attr('width', width);\n",
" rubberband.attr('height', height);\n",
" }\n",
"\n",
" // Set the figure to an initial 600x600px, this will subsequently be updated\n",
" // upon first draw.\n",
" this._resize_canvas(600, 600);\n",
"\n",
" // Disable right mouse context menu.\n",
" $(this.rubberband_canvas).bind(\"contextmenu\",function(e){\n",
" return false;\n",
" });\n",
"\n",
" function set_focus () {\n",
" canvas.focus();\n",
" canvas_div.focus();\n",
" }\n",
"\n",
" window.setTimeout(set_focus, 100);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items) {\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) {\n",
" // put a spacer in here.\n",
" continue;\n",
" }\n",
" var button = $('');\n",
" button.addClass('ui-button ui-widget ui-state-default ui-corner-all ' +\n",
" 'ui-button-icon-only');\n",
" button.attr('role', 'button');\n",
" button.attr('aria-disabled', 'false');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
"\n",
" var icon_img = $('');\n",
" icon_img.addClass('ui-button-icon-primary ui-icon');\n",
" icon_img.addClass(image);\n",
" icon_img.addClass('ui-corner-all');\n",
"\n",
" var tooltip_span = $('');\n",
" tooltip_span.addClass('ui-button-text');\n",
" tooltip_span.html(tooltip);\n",
"\n",
" button.append(icon_img);\n",
" button.append(tooltip_span);\n",
"\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" var fmt_picker_span = $('');\n",
"\n",
" var fmt_picker = $('');\n",
" fmt_picker.addClass('mpl-toolbar-option ui-widget ui-widget-content');\n",
" fmt_picker_span.append(fmt_picker);\n",
" nav_element.append(fmt_picker_span);\n",
" this.format_dropdown = fmt_picker[0];\n",
"\n",
" for (var ind in mpl.extensions) {\n",
" var fmt = mpl.extensions[ind];\n",
" var option = $(\n",
" '', {selected: fmt === mpl.default_extension}).html(fmt);\n",
" fmt_picker.append(option)\n",
" }\n",
"\n",
" // Add hover states to the ui-buttons\n",
" $( \".ui-button\" ).hover(\n",
" function() { $(this).addClass(\"ui-state-hover\");},\n",
" function() { $(this).removeClass(\"ui-state-hover\");}\n",
" );\n",
"\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"}\n",
"\n",
"mpl.figure.prototype.request_resize = function(x_pixels, y_pixels) {\n",
" // Request matplotlib to resize the figure. Matplotlib will then trigger a resize in the client,\n",
" // which will in turn request a refresh of the image.\n",
" this.send_message('resize', {'width': x_pixels, 'height': y_pixels});\n",
"}\n",
"\n",
"mpl.figure.prototype.send_message = function(type, properties) {\n",
" properties['type'] = type;\n",
" properties['figure_id'] = this.id;\n",
" this.ws.send(JSON.stringify(properties));\n",
"}\n",
"\n",
"mpl.figure.prototype.send_draw_message = function() {\n",
" if (!this.waiting) {\n",
" this.waiting = true;\n",
" this.ws.send(JSON.stringify({type: \"draw\", figure_id: this.id}));\n",
" }\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" var format_dropdown = fig.format_dropdown;\n",
" var format = format_dropdown.options[format_dropdown.selectedIndex].value;\n",
" fig.ondownload(fig, format);\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_resize = function(fig, msg) {\n",
" var size = msg['size'];\n",
" if (size[0] != fig.canvas.width || size[1] != fig.canvas.height) {\n",
" fig._resize_canvas(size[0], size[1]);\n",
" fig.send_message(\"refresh\", {});\n",
" };\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_rubberband = function(fig, msg) {\n",
" var x0 = msg['x0'] / mpl.ratio;\n",
" var y0 = (fig.canvas.height - msg['y0']) / mpl.ratio;\n",
" var x1 = msg['x1'] / mpl.ratio;\n",
" var y1 = (fig.canvas.height - msg['y1']) / mpl.ratio;\n",
" x0 = Math.floor(x0) + 0.5;\n",
" y0 = Math.floor(y0) + 0.5;\n",
" x1 = Math.floor(x1) + 0.5;\n",
" y1 = Math.floor(y1) + 0.5;\n",
" var min_x = Math.min(x0, x1);\n",
" var min_y = Math.min(y0, y1);\n",
" var width = Math.abs(x1 - x0);\n",
" var height = Math.abs(y1 - y0);\n",
"\n",
" fig.rubberband_context.clearRect(\n",
" 0, 0, fig.canvas.width, fig.canvas.height);\n",
"\n",
" fig.rubberband_context.strokeRect(min_x, min_y, width, height);\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_figure_label = function(fig, msg) {\n",
" // Updates the figure title.\n",
" fig.header.textContent = msg['label'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_cursor = function(fig, msg) {\n",
" var cursor = msg['cursor'];\n",
" switch(cursor)\n",
" {\n",
" case 0:\n",
" cursor = 'pointer';\n",
" break;\n",
" case 1:\n",
" cursor = 'default';\n",
" break;\n",
" case 2:\n",
" cursor = 'crosshair';\n",
" break;\n",
" case 3:\n",
" cursor = 'move';\n",
" break;\n",
" }\n",
" fig.rubberband_canvas.style.cursor = cursor;\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_message = function(fig, msg) {\n",
" fig.message.textContent = msg['message'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_draw = function(fig, msg) {\n",
" // Request the server to send over a new figure.\n",
" fig.send_draw_message();\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_image_mode = function(fig, msg) {\n",
" fig.image_mode = msg['mode'];\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Called whenever the canvas gets updated.\n",
" this.send_message(\"ack\", {});\n",
"}\n",
"\n",
"// A function to construct a web socket function for onmessage handling.\n",
"// Called in the figure constructor.\n",
"mpl.figure.prototype._make_on_message_function = function(fig) {\n",
" return function socket_on_message(evt) {\n",
" if (evt.data instanceof Blob) {\n",
" /* FIXME: We get \"Resource interpreted as Image but\n",
" * transferred with MIME type text/plain:\" errors on\n",
" * Chrome. But how to set the MIME type? It doesn't seem\n",
" * to be part of the websocket stream */\n",
" evt.data.type = \"image/png\";\n",
"\n",
" /* Free the memory for the previous frames */\n",
" if (fig.imageObj.src) {\n",
" (window.URL || window.webkitURL).revokeObjectURL(\n",
" fig.imageObj.src);\n",
" }\n",
"\n",
" fig.imageObj.src = (window.URL || window.webkitURL).createObjectURL(\n",
" evt.data);\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
" else if (typeof evt.data === 'string' && evt.data.slice(0, 21) == \"data:image/png;base64\") {\n",
" fig.imageObj.src = evt.data;\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
"\n",
" var msg = JSON.parse(evt.data);\n",
" var msg_type = msg['type'];\n",
"\n",
" // Call the \"handle_{type}\" callback, which takes\n",
" // the figure and JSON message as its only arguments.\n",
" try {\n",
" var callback = fig[\"handle_\" + msg_type];\n",
" } catch (e) {\n",
" console.log(\"No handler for the '\" + msg_type + \"' message type: \", msg);\n",
" return;\n",
" }\n",
"\n",
" if (callback) {\n",
" try {\n",
" // console.log(\"Handling '\" + msg_type + \"' message: \", msg);\n",
" callback(fig, msg);\n",
" } catch (e) {\n",
" console.log(\"Exception inside the 'handler_\" + msg_type + \"' callback:\", e, e.stack, msg);\n",
" }\n",
" }\n",
" };\n",
"}\n",
"\n",
"// from http://stackoverflow.com/questions/1114465/getting-mouse-location-in-canvas\n",
"mpl.findpos = function(e) {\n",
" //this section is from http://www.quirksmode.org/js/events_properties.html\n",
" var targ;\n",
" if (!e)\n",
" e = window.event;\n",
" if (e.target)\n",
" targ = e.target;\n",
" else if (e.srcElement)\n",
" targ = e.srcElement;\n",
" if (targ.nodeType == 3) // defeat Safari bug\n",
" targ = targ.parentNode;\n",
"\n",
" // jQuery normalizes the pageX and pageY\n",
" // pageX,Y are the mouse positions relative to the document\n",
" // offset() returns the position of the element relative to the document\n",
" var x = e.pageX - $(targ).offset().left;\n",
" var y = e.pageY - $(targ).offset().top;\n",
"\n",
" return {\"x\": x, \"y\": y};\n",
"};\n",
"\n",
"/*\n",
" * return a copy of an object with only non-object keys\n",
" * we need this to avoid circular references\n",
" * http://stackoverflow.com/a/24161582/3208463\n",
" */\n",
"function simpleKeys (original) {\n",
" return Object.keys(original).reduce(function (obj, key) {\n",
" if (typeof original[key] !== 'object')\n",
" obj[key] = original[key]\n",
" return obj;\n",
" }, {});\n",
"}\n",
"\n",
"mpl.figure.prototype.mouse_event = function(event, name) {\n",
" var canvas_pos = mpl.findpos(event)\n",
"\n",
" if (name === 'button_press')\n",
" {\n",
" this.canvas.focus();\n",
" this.canvas_div.focus();\n",
" }\n",
"\n",
" var x = canvas_pos.x * mpl.ratio;\n",
" var y = canvas_pos.y * mpl.ratio;\n",
"\n",
" this.send_message(name, {x: x, y: y, button: event.button,\n",
" step: event.step,\n",
" guiEvent: simpleKeys(event)});\n",
"\n",
" /* This prevents the web browser from automatically changing to\n",
" * the text insertion cursor when the button is pressed. We want\n",
" * to control all of the cursor setting manually through the\n",
" * 'cursor' event from matplotlib */\n",
" event.preventDefault();\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" // Handle any extra behaviour associated with a key event\n",
"}\n",
"\n",
"mpl.figure.prototype.key_event = function(event, name) {\n",
"\n",
" // Prevent repeat events\n",
" if (name == 'key_press')\n",
" {\n",
" if (event.which === this._key)\n",
" return;\n",
" else\n",
" this._key = event.which;\n",
" }\n",
" if (name == 'key_release')\n",
" this._key = null;\n",
"\n",
" var value = '';\n",
" if (event.ctrlKey && event.which != 17)\n",
" value += \"ctrl+\";\n",
" if (event.altKey && event.which != 18)\n",
" value += \"alt+\";\n",
" if (event.shiftKey && event.which != 16)\n",
" value += \"shift+\";\n",
"\n",
" value += 'k';\n",
" value += event.which.toString();\n",
"\n",
" this._key_event_extra(event, name);\n",
"\n",
" this.send_message(name, {key: value,\n",
" guiEvent: simpleKeys(event)});\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype.toolbar_button_onclick = function(name) {\n",
" if (name == 'download') {\n",
" this.handle_save(this, null);\n",
" } else {\n",
" this.send_message(\"toolbar_button\", {name: name});\n",
" }\n",
"};\n",
"\n",
"mpl.figure.prototype.toolbar_button_onmouseover = function(tooltip) {\n",
" this.message.textContent = tooltip;\n",
"};\n",
"mpl.toolbar_items = [[\"Home\", \"Reset original view\", \"fa fa-home icon-home\", \"home\"], [\"Back\", \"Back to previous view\", \"fa fa-arrow-left icon-arrow-left\", \"back\"], [\"Forward\", \"Forward to next view\", \"fa fa-arrow-right icon-arrow-right\", \"forward\"], [\"\", \"\", \"\", \"\"], [\"Pan\", \"Pan axes with left mouse, zoom with right\", \"fa fa-arrows icon-move\", \"pan\"], [\"Zoom\", \"Zoom to rectangle\", \"fa fa-square-o icon-check-empty\", \"zoom\"], [\"\", \"\", \"\", \"\"], [\"Download\", \"Download plot\", \"fa fa-floppy-o icon-save\", \"download\"]];\n",
"\n",
"mpl.extensions = [\"eps\", \"jpeg\", \"pdf\", \"png\", \"ps\", \"raw\", \"svg\", \"tif\"];\n",
"\n",
"mpl.default_extension = \"png\";var comm_websocket_adapter = function(comm) {\n",
" // Create a \"websocket\"-like object which calls the given IPython comm\n",
" // object with the appropriate methods. Currently this is a non binary\n",
" // socket, so there is still some room for performance tuning.\n",
" var ws = {};\n",
"\n",
" ws.close = function() {\n",
" comm.close()\n",
" };\n",
" ws.send = function(m) {\n",
" //console.log('sending', m);\n",
" comm.send(m);\n",
" };\n",
" // Register the callback with on_msg.\n",
" comm.on_msg(function(msg) {\n",
" //console.log('receiving', msg['content']['data'], msg);\n",
" // Pass the mpl event to the overriden (by mpl) onmessage function.\n",
" ws.onmessage(msg['content']['data'])\n",
" });\n",
" return ws;\n",
"}\n",
"\n",
"mpl.mpl_figure_comm = function(comm, msg) {\n",
" // This is the function which gets called when the mpl process\n",
" // starts-up an IPython Comm through the \"matplotlib\" channel.\n",
"\n",
" var id = msg.content.data.id;\n",
" // Get hold of the div created by the display call when the Comm\n",
" // socket was opened in Python.\n",
" var element = $(\"#\" + id);\n",
" var ws_proxy = comm_websocket_adapter(comm)\n",
"\n",
" function ondownload(figure, format) {\n",
" window.open(figure.imageObj.src);\n",
" }\n",
"\n",
" var fig = new mpl.figure(id, ws_proxy,\n",
" ondownload,\n",
" element.get(0));\n",
"\n",
" // Call onopen now - mpl needs it, as it is assuming we've passed it a real\n",
" // web socket which is closed, not our websocket->open comm proxy.\n",
" ws_proxy.onopen();\n",
"\n",
" fig.parent_element = element.get(0);\n",
" fig.cell_info = mpl.find_output_cell(\"\");\n",
" if (!fig.cell_info) {\n",
" console.error(\"Failed to find cell for figure\", id, fig);\n",
" return;\n",
" }\n",
"\n",
" var output_index = fig.cell_info[2]\n",
" var cell = fig.cell_info[0];\n",
"\n",
"};\n",
"\n",
"mpl.figure.prototype.handle_close = function(fig, msg) {\n",
" var width = fig.canvas.width/mpl.ratio\n",
" fig.root.unbind('remove')\n",
"\n",
" // Update the output cell to use the data from the current canvas.\n",
" fig.push_to_output();\n",
" var dataURL = fig.canvas.toDataURL();\n",
" // Re-enable the keyboard manager in IPython - without this line, in FF,\n",
" // the notebook keyboard shortcuts fail.\n",
" IPython.keyboard_manager.enable()\n",
" $(fig.parent_element).html(' ');\n",
" fig.close_ws(fig, msg);\n",
"}\n",
"\n",
"mpl.figure.prototype.close_ws = function(fig, msg){\n",
" fig.send_message('closing', msg);\n",
" // fig.ws.close()\n",
"}\n",
"\n",
"mpl.figure.prototype.push_to_output = function(remove_interactive) {\n",
" // Turn the data on the canvas into data in the output cell.\n",
" var width = this.canvas.width/mpl.ratio\n",
" var dataURL = this.canvas.toDataURL();\n",
" this.cell_info[1]['text/html'] = '
');\n",
" fig.close_ws(fig, msg);\n",
"}\n",
"\n",
"mpl.figure.prototype.close_ws = function(fig, msg){\n",
" fig.send_message('closing', msg);\n",
" // fig.ws.close()\n",
"}\n",
"\n",
"mpl.figure.prototype.push_to_output = function(remove_interactive) {\n",
" // Turn the data on the canvas into data in the output cell.\n",
" var width = this.canvas.width/mpl.ratio\n",
" var dataURL = this.canvas.toDataURL();\n",
" this.cell_info[1]['text/html'] = ' ';\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Tell IPython that the notebook contents must change.\n",
" IPython.notebook.set_dirty(true);\n",
" this.send_message(\"ack\", {});\n",
" var fig = this;\n",
" // Wait a second, then push the new image to the DOM so\n",
" // that it is saved nicely (might be nice to debounce this).\n",
" setTimeout(function () { fig.push_to_output() }, 1000);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items){\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) { continue; };\n",
"\n",
" var button = $('');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" // Add the status bar.\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"\n",
" // Add the close button to the window.\n",
" var buttongrp = $('');\n",
" var button = $('');\n",
" button.click(function (evt) { fig.handle_close(fig, {}); } );\n",
" button.mouseover('Stop Interaction', toolbar_mouse_event);\n",
" buttongrp.append(button);\n",
" var titlebar = this.root.find($('.ui-dialog-titlebar'));\n",
" titlebar.prepend(buttongrp);\n",
"}\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(el){\n",
" var fig = this\n",
" el.on(\"remove\", function(){\n",
"\tfig.close_ws(fig, {});\n",
" });\n",
"}\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(el){\n",
" // this is important to make the div 'focusable\n",
" el.attr('tabindex', 0)\n",
" // reach out to IPython and tell the keyboard manager to turn it's self\n",
" // off when our div gets focus\n",
"\n",
" // location in version 3\n",
" if (IPython.notebook.keyboard_manager) {\n",
" IPython.notebook.keyboard_manager.register_events(el);\n",
" }\n",
" else {\n",
" // location in version 2\n",
" IPython.keyboard_manager.register_events(el);\n",
" }\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" var manager = IPython.notebook.keyboard_manager;\n",
" if (!manager)\n",
" manager = IPython.keyboard_manager;\n",
"\n",
" // Check for shift+enter\n",
" if (event.shiftKey && event.which == 13) {\n",
" this.canvas_div.blur();\n",
" event.shiftKey = false;\n",
" // Send a \"J\" for go to next cell\n",
" event.which = 74;\n",
" event.keyCode = 74;\n",
" manager.command_mode();\n",
" manager.handle_keydown(event);\n",
" }\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" fig.ondownload(fig, null);\n",
"}\n",
"\n",
"\n",
"mpl.find_output_cell = function(html_output) {\n",
" // Return the cell and output element which can be found *uniquely* in the notebook.\n",
" // Note - this is a bit hacky, but it is done because the \"notebook_saving.Notebook\"\n",
" // IPython event is triggered only after the cells have been serialised, which for\n",
" // our purposes (turning an active figure into a static one), is too late.\n",
" var cells = IPython.notebook.get_cells();\n",
" var ncells = cells.length;\n",
" for (var i=0; i= 3 moved mimebundle to data attribute of output\n",
" data = data.data;\n",
" }\n",
" if (data['text/html'] == html_output) {\n",
" return [cell, data, j];\n",
" }\n",
" }\n",
" }\n",
" }\n",
"}\n",
"\n",
"// Register the function which deals with the matplotlib target/channel.\n",
"// The kernel may be null if the page has been refreshed.\n",
"if (IPython.notebook.kernel != null) {\n",
" IPython.notebook.kernel.comm_manager.register_target('matplotlib', mpl.mpl_figure_comm);\n",
"}\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"
';\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Tell IPython that the notebook contents must change.\n",
" IPython.notebook.set_dirty(true);\n",
" this.send_message(\"ack\", {});\n",
" var fig = this;\n",
" // Wait a second, then push the new image to the DOM so\n",
" // that it is saved nicely (might be nice to debounce this).\n",
" setTimeout(function () { fig.push_to_output() }, 1000);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items){\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) { continue; };\n",
"\n",
" var button = $('');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" // Add the status bar.\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"\n",
" // Add the close button to the window.\n",
" var buttongrp = $('');\n",
" var button = $('');\n",
" button.click(function (evt) { fig.handle_close(fig, {}); } );\n",
" button.mouseover('Stop Interaction', toolbar_mouse_event);\n",
" buttongrp.append(button);\n",
" var titlebar = this.root.find($('.ui-dialog-titlebar'));\n",
" titlebar.prepend(buttongrp);\n",
"}\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(el){\n",
" var fig = this\n",
" el.on(\"remove\", function(){\n",
"\tfig.close_ws(fig, {});\n",
" });\n",
"}\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(el){\n",
" // this is important to make the div 'focusable\n",
" el.attr('tabindex', 0)\n",
" // reach out to IPython and tell the keyboard manager to turn it's self\n",
" // off when our div gets focus\n",
"\n",
" // location in version 3\n",
" if (IPython.notebook.keyboard_manager) {\n",
" IPython.notebook.keyboard_manager.register_events(el);\n",
" }\n",
" else {\n",
" // location in version 2\n",
" IPython.keyboard_manager.register_events(el);\n",
" }\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" var manager = IPython.notebook.keyboard_manager;\n",
" if (!manager)\n",
" manager = IPython.keyboard_manager;\n",
"\n",
" // Check for shift+enter\n",
" if (event.shiftKey && event.which == 13) {\n",
" this.canvas_div.blur();\n",
" event.shiftKey = false;\n",
" // Send a \"J\" for go to next cell\n",
" event.which = 74;\n",
" event.keyCode = 74;\n",
" manager.command_mode();\n",
" manager.handle_keydown(event);\n",
" }\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" fig.ondownload(fig, null);\n",
"}\n",
"\n",
"\n",
"mpl.find_output_cell = function(html_output) {\n",
" // Return the cell and output element which can be found *uniquely* in the notebook.\n",
" // Note - this is a bit hacky, but it is done because the \"notebook_saving.Notebook\"\n",
" // IPython event is triggered only after the cells have been serialised, which for\n",
" // our purposes (turning an active figure into a static one), is too late.\n",
" var cells = IPython.notebook.get_cells();\n",
" var ncells = cells.length;\n",
" for (var i=0; i= 3 moved mimebundle to data attribute of output\n",
" data = data.data;\n",
" }\n",
" if (data['text/html'] == html_output) {\n",
" return [cell, data, j];\n",
" }\n",
" }\n",
" }\n",
" }\n",
"}\n",
"\n",
"// Register the function which deals with the matplotlib target/channel.\n",
"// The kernel may be null if the page has been refreshed.\n",
"if (IPython.notebook.kernel != null) {\n",
" IPython.notebook.kernel.comm_manager.register_target('matplotlib', mpl.mpl_figure_comm);\n",
"}\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
" "
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"application/javascript": [
"/* Put everything inside the global mpl namespace */\n",
"window.mpl = {};\n",
"\n",
"\n",
"mpl.get_websocket_type = function() {\n",
" if (typeof(WebSocket) !== 'undefined') {\n",
" return WebSocket;\n",
" } else if (typeof(MozWebSocket) !== 'undefined') {\n",
" return MozWebSocket;\n",
" } else {\n",
" alert('Your browser does not have WebSocket support.' +\n",
" 'Please try Chrome, Safari or Firefox 6. ' +\n",
" 'Firefox 4 and 5 are also supported but you ' +\n",
" 'have to enable WebSockets in about:config.');\n",
" };\n",
"}\n",
"\n",
"mpl.figure = function(figure_id, websocket, ondownload, parent_element) {\n",
" this.id = figure_id;\n",
"\n",
" this.ws = websocket;\n",
"\n",
" this.supports_binary = (this.ws.binaryType != undefined);\n",
"\n",
" if (!this.supports_binary) {\n",
" var warnings = document.getElementById(\"mpl-warnings\");\n",
" if (warnings) {\n",
" warnings.style.display = 'block';\n",
" warnings.textContent = (\n",
" \"This browser does not support binary websocket messages. \" +\n",
" \"Performance may be slow.\");\n",
" }\n",
" }\n",
"\n",
" this.imageObj = new Image();\n",
"\n",
" this.context = undefined;\n",
" this.message = undefined;\n",
" this.canvas = undefined;\n",
" this.rubberband_canvas = undefined;\n",
" this.rubberband_context = undefined;\n",
" this.format_dropdown = undefined;\n",
"\n",
" this.image_mode = 'full';\n",
"\n",
" this.root = $('');\n",
" this._root_extra_style(this.root)\n",
" this.root.attr('style', 'display: inline-block');\n",
"\n",
" $(parent_element).append(this.root);\n",
"\n",
" this._init_header(this);\n",
" this._init_canvas(this);\n",
" this._init_toolbar(this);\n",
"\n",
" var fig = this;\n",
"\n",
" this.waiting = false;\n",
"\n",
" this.ws.onopen = function () {\n",
" fig.send_message(\"supports_binary\", {value: fig.supports_binary});\n",
" fig.send_message(\"send_image_mode\", {});\n",
" if (mpl.ratio != 1) {\n",
" fig.send_message(\"set_dpi_ratio\", {'dpi_ratio': mpl.ratio});\n",
" }\n",
" fig.send_message(\"refresh\", {});\n",
" }\n",
"\n",
" this.imageObj.onload = function() {\n",
" if (fig.image_mode == 'full') {\n",
" // Full images could contain transparency (where diff images\n",
" // almost always do), so we need to clear the canvas so that\n",
" // there is no ghosting.\n",
" fig.context.clearRect(0, 0, fig.canvas.width, fig.canvas.height);\n",
" }\n",
" fig.context.drawImage(fig.imageObj, 0, 0);\n",
" };\n",
"\n",
" this.imageObj.onunload = function() {\n",
" fig.ws.close();\n",
" }\n",
"\n",
" this.ws.onmessage = this._make_on_message_function(this);\n",
"\n",
" this.ondownload = ondownload;\n",
"}\n",
"\n",
"mpl.figure.prototype._init_header = function() {\n",
" var titlebar = $(\n",
" '');\n",
" var titletext = $(\n",
" '');\n",
" titlebar.append(titletext)\n",
" this.root.append(titlebar);\n",
" this.header = titletext[0];\n",
"}\n",
"\n",
"\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._init_canvas = function() {\n",
" var fig = this;\n",
"\n",
" var canvas_div = $('');\n",
"\n",
" canvas_div.attr('style', 'position: relative; clear: both; outline: 0');\n",
"\n",
" function canvas_keyboard_event(event) {\n",
" return fig.key_event(event, event['data']);\n",
" }\n",
"\n",
" canvas_div.keydown('key_press', canvas_keyboard_event);\n",
" canvas_div.keyup('key_release', canvas_keyboard_event);\n",
" this.canvas_div = canvas_div\n",
" this._canvas_extra_style(canvas_div)\n",
" this.root.append(canvas_div);\n",
"\n",
" var canvas = $('');\n",
" canvas.addClass('mpl-canvas');\n",
" canvas.attr('style', \"left: 0; top: 0; z-index: 0; outline: 0\")\n",
"\n",
" this.canvas = canvas[0];\n",
" this.context = canvas[0].getContext(\"2d\");\n",
"\n",
" var backingStore = this.context.backingStorePixelRatio ||\n",
"\tthis.context.webkitBackingStorePixelRatio ||\n",
"\tthis.context.mozBackingStorePixelRatio ||\n",
"\tthis.context.msBackingStorePixelRatio ||\n",
"\tthis.context.oBackingStorePixelRatio ||\n",
"\tthis.context.backingStorePixelRatio || 1;\n",
"\n",
" mpl.ratio = (window.devicePixelRatio || 1) / backingStore;\n",
"\n",
" var rubberband = $('');\n",
" rubberband.attr('style', \"position: absolute; left: 0; top: 0; z-index: 1;\")\n",
"\n",
" var pass_mouse_events = true;\n",
"\n",
" canvas_div.resizable({\n",
" start: function(event, ui) {\n",
" pass_mouse_events = false;\n",
" },\n",
" resize: function(event, ui) {\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" stop: function(event, ui) {\n",
" pass_mouse_events = true;\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" });\n",
"\n",
" function mouse_event_fn(event) {\n",
" if (pass_mouse_events)\n",
" return fig.mouse_event(event, event['data']);\n",
" }\n",
"\n",
" rubberband.mousedown('button_press', mouse_event_fn);\n",
" rubberband.mouseup('button_release', mouse_event_fn);\n",
" // Throttle sequential mouse events to 1 every 20ms.\n",
" rubberband.mousemove('motion_notify', mouse_event_fn);\n",
"\n",
" rubberband.mouseenter('figure_enter', mouse_event_fn);\n",
" rubberband.mouseleave('figure_leave', mouse_event_fn);\n",
"\n",
" canvas_div.on(\"wheel\", function (event) {\n",
" event = event.originalEvent;\n",
" event['data'] = 'scroll'\n",
" if (event.deltaY < 0) {\n",
" event.step = 1;\n",
" } else {\n",
" event.step = -1;\n",
" }\n",
" mouse_event_fn(event);\n",
" });\n",
"\n",
" canvas_div.append(canvas);\n",
" canvas_div.append(rubberband);\n",
"\n",
" this.rubberband = rubberband;\n",
" this.rubberband_canvas = rubberband[0];\n",
" this.rubberband_context = rubberband[0].getContext(\"2d\");\n",
" this.rubberband_context.strokeStyle = \"#000000\";\n",
"\n",
" this._resize_canvas = function(width, height) {\n",
" // Keep the size of the canvas, canvas container, and rubber band\n",
" // canvas in synch.\n",
" canvas_div.css('width', width)\n",
" canvas_div.css('height', height)\n",
"\n",
" canvas.attr('width', width * mpl.ratio);\n",
" canvas.attr('height', height * mpl.ratio);\n",
" canvas.attr('style', 'width: ' + width + 'px; height: ' + height + 'px;');\n",
"\n",
" rubberband.attr('width', width);\n",
" rubberband.attr('height', height);\n",
" }\n",
"\n",
" // Set the figure to an initial 600x600px, this will subsequently be updated\n",
" // upon first draw.\n",
" this._resize_canvas(600, 600);\n",
"\n",
" // Disable right mouse context menu.\n",
" $(this.rubberband_canvas).bind(\"contextmenu\",function(e){\n",
" return false;\n",
" });\n",
"\n",
" function set_focus () {\n",
" canvas.focus();\n",
" canvas_div.focus();\n",
" }\n",
"\n",
" window.setTimeout(set_focus, 100);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items) {\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) {\n",
" // put a spacer in here.\n",
" continue;\n",
" }\n",
" var button = $('');\n",
" button.addClass('ui-button ui-widget ui-state-default ui-corner-all ' +\n",
" 'ui-button-icon-only');\n",
" button.attr('role', 'button');\n",
" button.attr('aria-disabled', 'false');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
"\n",
" var icon_img = $('');\n",
" icon_img.addClass('ui-button-icon-primary ui-icon');\n",
" icon_img.addClass(image);\n",
" icon_img.addClass('ui-corner-all');\n",
"\n",
" var tooltip_span = $('');\n",
" tooltip_span.addClass('ui-button-text');\n",
" tooltip_span.html(tooltip);\n",
"\n",
" button.append(icon_img);\n",
" button.append(tooltip_span);\n",
"\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" var fmt_picker_span = $('');\n",
"\n",
" var fmt_picker = $('');\n",
" fmt_picker.addClass('mpl-toolbar-option ui-widget ui-widget-content');\n",
" fmt_picker_span.append(fmt_picker);\n",
" nav_element.append(fmt_picker_span);\n",
" this.format_dropdown = fmt_picker[0];\n",
"\n",
" for (var ind in mpl.extensions) {\n",
" var fmt = mpl.extensions[ind];\n",
" var option = $(\n",
" '', {selected: fmt === mpl.default_extension}).html(fmt);\n",
" fmt_picker.append(option)\n",
" }\n",
"\n",
" // Add hover states to the ui-buttons\n",
" $( \".ui-button\" ).hover(\n",
" function() { $(this).addClass(\"ui-state-hover\");},\n",
" function() { $(this).removeClass(\"ui-state-hover\");}\n",
" );\n",
"\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"}\n",
"\n",
"mpl.figure.prototype.request_resize = function(x_pixels, y_pixels) {\n",
" // Request matplotlib to resize the figure. Matplotlib will then trigger a resize in the client,\n",
" // which will in turn request a refresh of the image.\n",
" this.send_message('resize', {'width': x_pixels, 'height': y_pixels});\n",
"}\n",
"\n",
"mpl.figure.prototype.send_message = function(type, properties) {\n",
" properties['type'] = type;\n",
" properties['figure_id'] = this.id;\n",
" this.ws.send(JSON.stringify(properties));\n",
"}\n",
"\n",
"mpl.figure.prototype.send_draw_message = function() {\n",
" if (!this.waiting) {\n",
" this.waiting = true;\n",
" this.ws.send(JSON.stringify({type: \"draw\", figure_id: this.id}));\n",
" }\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" var format_dropdown = fig.format_dropdown;\n",
" var format = format_dropdown.options[format_dropdown.selectedIndex].value;\n",
" fig.ondownload(fig, format);\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_resize = function(fig, msg) {\n",
" var size = msg['size'];\n",
" if (size[0] != fig.canvas.width || size[1] != fig.canvas.height) {\n",
" fig._resize_canvas(size[0], size[1]);\n",
" fig.send_message(\"refresh\", {});\n",
" };\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_rubberband = function(fig, msg) {\n",
" var x0 = msg['x0'] / mpl.ratio;\n",
" var y0 = (fig.canvas.height - msg['y0']) / mpl.ratio;\n",
" var x1 = msg['x1'] / mpl.ratio;\n",
" var y1 = (fig.canvas.height - msg['y1']) / mpl.ratio;\n",
" x0 = Math.floor(x0) + 0.5;\n",
" y0 = Math.floor(y0) + 0.5;\n",
" x1 = Math.floor(x1) + 0.5;\n",
" y1 = Math.floor(y1) + 0.5;\n",
" var min_x = Math.min(x0, x1);\n",
" var min_y = Math.min(y0, y1);\n",
" var width = Math.abs(x1 - x0);\n",
" var height = Math.abs(y1 - y0);\n",
"\n",
" fig.rubberband_context.clearRect(\n",
" 0, 0, fig.canvas.width, fig.canvas.height);\n",
"\n",
" fig.rubberband_context.strokeRect(min_x, min_y, width, height);\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_figure_label = function(fig, msg) {\n",
" // Updates the figure title.\n",
" fig.header.textContent = msg['label'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_cursor = function(fig, msg) {\n",
" var cursor = msg['cursor'];\n",
" switch(cursor)\n",
" {\n",
" case 0:\n",
" cursor = 'pointer';\n",
" break;\n",
" case 1:\n",
" cursor = 'default';\n",
" break;\n",
" case 2:\n",
" cursor = 'crosshair';\n",
" break;\n",
" case 3:\n",
" cursor = 'move';\n",
" break;\n",
" }\n",
" fig.rubberband_canvas.style.cursor = cursor;\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_message = function(fig, msg) {\n",
" fig.message.textContent = msg['message'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_draw = function(fig, msg) {\n",
" // Request the server to send over a new figure.\n",
" fig.send_draw_message();\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_image_mode = function(fig, msg) {\n",
" fig.image_mode = msg['mode'];\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Called whenever the canvas gets updated.\n",
" this.send_message(\"ack\", {});\n",
"}\n",
"\n",
"// A function to construct a web socket function for onmessage handling.\n",
"// Called in the figure constructor.\n",
"mpl.figure.prototype._make_on_message_function = function(fig) {\n",
" return function socket_on_message(evt) {\n",
" if (evt.data instanceof Blob) {\n",
" /* FIXME: We get \"Resource interpreted as Image but\n",
" * transferred with MIME type text/plain:\" errors on\n",
" * Chrome. But how to set the MIME type? It doesn't seem\n",
" * to be part of the websocket stream */\n",
" evt.data.type = \"image/png\";\n",
"\n",
" /* Free the memory for the previous frames */\n",
" if (fig.imageObj.src) {\n",
" (window.URL || window.webkitURL).revokeObjectURL(\n",
" fig.imageObj.src);\n",
" }\n",
"\n",
" fig.imageObj.src = (window.URL || window.webkitURL).createObjectURL(\n",
" evt.data);\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
" else if (typeof evt.data === 'string' && evt.data.slice(0, 21) == \"data:image/png;base64\") {\n",
" fig.imageObj.src = evt.data;\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
"\n",
" var msg = JSON.parse(evt.data);\n",
" var msg_type = msg['type'];\n",
"\n",
" // Call the \"handle_{type}\" callback, which takes\n",
" // the figure and JSON message as its only arguments.\n",
" try {\n",
" var callback = fig[\"handle_\" + msg_type];\n",
" } catch (e) {\n",
" console.log(\"No handler for the '\" + msg_type + \"' message type: \", msg);\n",
" return;\n",
" }\n",
"\n",
" if (callback) {\n",
" try {\n",
" // console.log(\"Handling '\" + msg_type + \"' message: \", msg);\n",
" callback(fig, msg);\n",
" } catch (e) {\n",
" console.log(\"Exception inside the 'handler_\" + msg_type + \"' callback:\", e, e.stack, msg);\n",
" }\n",
" }\n",
" };\n",
"}\n",
"\n",
"// from http://stackoverflow.com/questions/1114465/getting-mouse-location-in-canvas\n",
"mpl.findpos = function(e) {\n",
" //this section is from http://www.quirksmode.org/js/events_properties.html\n",
" var targ;\n",
" if (!e)\n",
" e = window.event;\n",
" if (e.target)\n",
" targ = e.target;\n",
" else if (e.srcElement)\n",
" targ = e.srcElement;\n",
" if (targ.nodeType == 3) // defeat Safari bug\n",
" targ = targ.parentNode;\n",
"\n",
" // jQuery normalizes the pageX and pageY\n",
" // pageX,Y are the mouse positions relative to the document\n",
" // offset() returns the position of the element relative to the document\n",
" var x = e.pageX - $(targ).offset().left;\n",
" var y = e.pageY - $(targ).offset().top;\n",
"\n",
" return {\"x\": x, \"y\": y};\n",
"};\n",
"\n",
"/*\n",
" * return a copy of an object with only non-object keys\n",
" * we need this to avoid circular references\n",
" * http://stackoverflow.com/a/24161582/3208463\n",
" */\n",
"function simpleKeys (original) {\n",
" return Object.keys(original).reduce(function (obj, key) {\n",
" if (typeof original[key] !== 'object')\n",
" obj[key] = original[key]\n",
" return obj;\n",
" }, {});\n",
"}\n",
"\n",
"mpl.figure.prototype.mouse_event = function(event, name) {\n",
" var canvas_pos = mpl.findpos(event)\n",
"\n",
" if (name === 'button_press')\n",
" {\n",
" this.canvas.focus();\n",
" this.canvas_div.focus();\n",
" }\n",
"\n",
" var x = canvas_pos.x * mpl.ratio;\n",
" var y = canvas_pos.y * mpl.ratio;\n",
"\n",
" this.send_message(name, {x: x, y: y, button: event.button,\n",
" step: event.step,\n",
" guiEvent: simpleKeys(event)});\n",
"\n",
" /* This prevents the web browser from automatically changing to\n",
" * the text insertion cursor when the button is pressed. We want\n",
" * to control all of the cursor setting manually through the\n",
" * 'cursor' event from matplotlib */\n",
" event.preventDefault();\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" // Handle any extra behaviour associated with a key event\n",
"}\n",
"\n",
"mpl.figure.prototype.key_event = function(event, name) {\n",
"\n",
" // Prevent repeat events\n",
" if (name == 'key_press')\n",
" {\n",
" if (event.which === this._key)\n",
" return;\n",
" else\n",
" this._key = event.which;\n",
" }\n",
" if (name == 'key_release')\n",
" this._key = null;\n",
"\n",
" var value = '';\n",
" if (event.ctrlKey && event.which != 17)\n",
" value += \"ctrl+\";\n",
" if (event.altKey && event.which != 18)\n",
" value += \"alt+\";\n",
" if (event.shiftKey && event.which != 16)\n",
" value += \"shift+\";\n",
"\n",
" value += 'k';\n",
" value += event.which.toString();\n",
"\n",
" this._key_event_extra(event, name);\n",
"\n",
" this.send_message(name, {key: value,\n",
" guiEvent: simpleKeys(event)});\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype.toolbar_button_onclick = function(name) {\n",
" if (name == 'download') {\n",
" this.handle_save(this, null);\n",
" } else {\n",
" this.send_message(\"toolbar_button\", {name: name});\n",
" }\n",
"};\n",
"\n",
"mpl.figure.prototype.toolbar_button_onmouseover = function(tooltip) {\n",
" this.message.textContent = tooltip;\n",
"};\n",
"mpl.toolbar_items = [[\"Home\", \"Reset original view\", \"fa fa-home icon-home\", \"home\"], [\"Back\", \"Back to previous view\", \"fa fa-arrow-left icon-arrow-left\", \"back\"], [\"Forward\", \"Forward to next view\", \"fa fa-arrow-right icon-arrow-right\", \"forward\"], [\"\", \"\", \"\", \"\"], [\"Pan\", \"Pan axes with left mouse, zoom with right\", \"fa fa-arrows icon-move\", \"pan\"], [\"Zoom\", \"Zoom to rectangle\", \"fa fa-square-o icon-check-empty\", \"zoom\"], [\"\", \"\", \"\", \"\"], [\"Download\", \"Download plot\", \"fa fa-floppy-o icon-save\", \"download\"]];\n",
"\n",
"mpl.extensions = [\"eps\", \"jpeg\", \"pdf\", \"png\", \"ps\", \"raw\", \"svg\", \"tif\"];\n",
"\n",
"mpl.default_extension = \"png\";var comm_websocket_adapter = function(comm) {\n",
" // Create a \"websocket\"-like object which calls the given IPython comm\n",
" // object with the appropriate methods. Currently this is a non binary\n",
" // socket, so there is still some room for performance tuning.\n",
" var ws = {};\n",
"\n",
" ws.close = function() {\n",
" comm.close()\n",
" };\n",
" ws.send = function(m) {\n",
" //console.log('sending', m);\n",
" comm.send(m);\n",
" };\n",
" // Register the callback with on_msg.\n",
" comm.on_msg(function(msg) {\n",
" //console.log('receiving', msg['content']['data'], msg);\n",
" // Pass the mpl event to the overriden (by mpl) onmessage function.\n",
" ws.onmessage(msg['content']['data'])\n",
" });\n",
" return ws;\n",
"}\n",
"\n",
"mpl.mpl_figure_comm = function(comm, msg) {\n",
" // This is the function which gets called when the mpl process\n",
" // starts-up an IPython Comm through the \"matplotlib\" channel.\n",
"\n",
" var id = msg.content.data.id;\n",
" // Get hold of the div created by the display call when the Comm\n",
" // socket was opened in Python.\n",
" var element = $(\"#\" + id);\n",
" var ws_proxy = comm_websocket_adapter(comm)\n",
"\n",
" function ondownload(figure, format) {\n",
" window.open(figure.imageObj.src);\n",
" }\n",
"\n",
" var fig = new mpl.figure(id, ws_proxy,\n",
" ondownload,\n",
" element.get(0));\n",
"\n",
" // Call onopen now - mpl needs it, as it is assuming we've passed it a real\n",
" // web socket which is closed, not our websocket->open comm proxy.\n",
" ws_proxy.onopen();\n",
"\n",
" fig.parent_element = element.get(0);\n",
" fig.cell_info = mpl.find_output_cell(\"\");\n",
" if (!fig.cell_info) {\n",
" console.error(\"Failed to find cell for figure\", id, fig);\n",
" return;\n",
" }\n",
"\n",
" var output_index = fig.cell_info[2]\n",
" var cell = fig.cell_info[0];\n",
"\n",
"};\n",
"\n",
"mpl.figure.prototype.handle_close = function(fig, msg) {\n",
" var width = fig.canvas.width/mpl.ratio\n",
" fig.root.unbind('remove')\n",
"\n",
" // Update the output cell to use the data from the current canvas.\n",
" fig.push_to_output();\n",
" var dataURL = fig.canvas.toDataURL();\n",
" // Re-enable the keyboard manager in IPython - without this line, in FF,\n",
" // the notebook keyboard shortcuts fail.\n",
" IPython.keyboard_manager.enable()\n",
" $(fig.parent_element).html('
"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"application/javascript": [
"/* Put everything inside the global mpl namespace */\n",
"window.mpl = {};\n",
"\n",
"\n",
"mpl.get_websocket_type = function() {\n",
" if (typeof(WebSocket) !== 'undefined') {\n",
" return WebSocket;\n",
" } else if (typeof(MozWebSocket) !== 'undefined') {\n",
" return MozWebSocket;\n",
" } else {\n",
" alert('Your browser does not have WebSocket support.' +\n",
" 'Please try Chrome, Safari or Firefox 6. ' +\n",
" 'Firefox 4 and 5 are also supported but you ' +\n",
" 'have to enable WebSockets in about:config.');\n",
" };\n",
"}\n",
"\n",
"mpl.figure = function(figure_id, websocket, ondownload, parent_element) {\n",
" this.id = figure_id;\n",
"\n",
" this.ws = websocket;\n",
"\n",
" this.supports_binary = (this.ws.binaryType != undefined);\n",
"\n",
" if (!this.supports_binary) {\n",
" var warnings = document.getElementById(\"mpl-warnings\");\n",
" if (warnings) {\n",
" warnings.style.display = 'block';\n",
" warnings.textContent = (\n",
" \"This browser does not support binary websocket messages. \" +\n",
" \"Performance may be slow.\");\n",
" }\n",
" }\n",
"\n",
" this.imageObj = new Image();\n",
"\n",
" this.context = undefined;\n",
" this.message = undefined;\n",
" this.canvas = undefined;\n",
" this.rubberband_canvas = undefined;\n",
" this.rubberband_context = undefined;\n",
" this.format_dropdown = undefined;\n",
"\n",
" this.image_mode = 'full';\n",
"\n",
" this.root = $('');\n",
" this._root_extra_style(this.root)\n",
" this.root.attr('style', 'display: inline-block');\n",
"\n",
" $(parent_element).append(this.root);\n",
"\n",
" this._init_header(this);\n",
" this._init_canvas(this);\n",
" this._init_toolbar(this);\n",
"\n",
" var fig = this;\n",
"\n",
" this.waiting = false;\n",
"\n",
" this.ws.onopen = function () {\n",
" fig.send_message(\"supports_binary\", {value: fig.supports_binary});\n",
" fig.send_message(\"send_image_mode\", {});\n",
" if (mpl.ratio != 1) {\n",
" fig.send_message(\"set_dpi_ratio\", {'dpi_ratio': mpl.ratio});\n",
" }\n",
" fig.send_message(\"refresh\", {});\n",
" }\n",
"\n",
" this.imageObj.onload = function() {\n",
" if (fig.image_mode == 'full') {\n",
" // Full images could contain transparency (where diff images\n",
" // almost always do), so we need to clear the canvas so that\n",
" // there is no ghosting.\n",
" fig.context.clearRect(0, 0, fig.canvas.width, fig.canvas.height);\n",
" }\n",
" fig.context.drawImage(fig.imageObj, 0, 0);\n",
" };\n",
"\n",
" this.imageObj.onunload = function() {\n",
" fig.ws.close();\n",
" }\n",
"\n",
" this.ws.onmessage = this._make_on_message_function(this);\n",
"\n",
" this.ondownload = ondownload;\n",
"}\n",
"\n",
"mpl.figure.prototype._init_header = function() {\n",
" var titlebar = $(\n",
" '');\n",
" var titletext = $(\n",
" '');\n",
" titlebar.append(titletext)\n",
" this.root.append(titlebar);\n",
" this.header = titletext[0];\n",
"}\n",
"\n",
"\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(canvas_div) {\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._init_canvas = function() {\n",
" var fig = this;\n",
"\n",
" var canvas_div = $('');\n",
"\n",
" canvas_div.attr('style', 'position: relative; clear: both; outline: 0');\n",
"\n",
" function canvas_keyboard_event(event) {\n",
" return fig.key_event(event, event['data']);\n",
" }\n",
"\n",
" canvas_div.keydown('key_press', canvas_keyboard_event);\n",
" canvas_div.keyup('key_release', canvas_keyboard_event);\n",
" this.canvas_div = canvas_div\n",
" this._canvas_extra_style(canvas_div)\n",
" this.root.append(canvas_div);\n",
"\n",
" var canvas = $('');\n",
" canvas.addClass('mpl-canvas');\n",
" canvas.attr('style', \"left: 0; top: 0; z-index: 0; outline: 0\")\n",
"\n",
" this.canvas = canvas[0];\n",
" this.context = canvas[0].getContext(\"2d\");\n",
"\n",
" var backingStore = this.context.backingStorePixelRatio ||\n",
"\tthis.context.webkitBackingStorePixelRatio ||\n",
"\tthis.context.mozBackingStorePixelRatio ||\n",
"\tthis.context.msBackingStorePixelRatio ||\n",
"\tthis.context.oBackingStorePixelRatio ||\n",
"\tthis.context.backingStorePixelRatio || 1;\n",
"\n",
" mpl.ratio = (window.devicePixelRatio || 1) / backingStore;\n",
"\n",
" var rubberband = $('');\n",
" rubberband.attr('style', \"position: absolute; left: 0; top: 0; z-index: 1;\")\n",
"\n",
" var pass_mouse_events = true;\n",
"\n",
" canvas_div.resizable({\n",
" start: function(event, ui) {\n",
" pass_mouse_events = false;\n",
" },\n",
" resize: function(event, ui) {\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" stop: function(event, ui) {\n",
" pass_mouse_events = true;\n",
" fig.request_resize(ui.size.width, ui.size.height);\n",
" },\n",
" });\n",
"\n",
" function mouse_event_fn(event) {\n",
" if (pass_mouse_events)\n",
" return fig.mouse_event(event, event['data']);\n",
" }\n",
"\n",
" rubberband.mousedown('button_press', mouse_event_fn);\n",
" rubberband.mouseup('button_release', mouse_event_fn);\n",
" // Throttle sequential mouse events to 1 every 20ms.\n",
" rubberband.mousemove('motion_notify', mouse_event_fn);\n",
"\n",
" rubberband.mouseenter('figure_enter', mouse_event_fn);\n",
" rubberband.mouseleave('figure_leave', mouse_event_fn);\n",
"\n",
" canvas_div.on(\"wheel\", function (event) {\n",
" event = event.originalEvent;\n",
" event['data'] = 'scroll'\n",
" if (event.deltaY < 0) {\n",
" event.step = 1;\n",
" } else {\n",
" event.step = -1;\n",
" }\n",
" mouse_event_fn(event);\n",
" });\n",
"\n",
" canvas_div.append(canvas);\n",
" canvas_div.append(rubberband);\n",
"\n",
" this.rubberband = rubberband;\n",
" this.rubberband_canvas = rubberband[0];\n",
" this.rubberband_context = rubberband[0].getContext(\"2d\");\n",
" this.rubberband_context.strokeStyle = \"#000000\";\n",
"\n",
" this._resize_canvas = function(width, height) {\n",
" // Keep the size of the canvas, canvas container, and rubber band\n",
" // canvas in synch.\n",
" canvas_div.css('width', width)\n",
" canvas_div.css('height', height)\n",
"\n",
" canvas.attr('width', width * mpl.ratio);\n",
" canvas.attr('height', height * mpl.ratio);\n",
" canvas.attr('style', 'width: ' + width + 'px; height: ' + height + 'px;');\n",
"\n",
" rubberband.attr('width', width);\n",
" rubberband.attr('height', height);\n",
" }\n",
"\n",
" // Set the figure to an initial 600x600px, this will subsequently be updated\n",
" // upon first draw.\n",
" this._resize_canvas(600, 600);\n",
"\n",
" // Disable right mouse context menu.\n",
" $(this.rubberband_canvas).bind(\"contextmenu\",function(e){\n",
" return false;\n",
" });\n",
"\n",
" function set_focus () {\n",
" canvas.focus();\n",
" canvas_div.focus();\n",
" }\n",
"\n",
" window.setTimeout(set_focus, 100);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items) {\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) {\n",
" // put a spacer in here.\n",
" continue;\n",
" }\n",
" var button = $('');\n",
" button.addClass('ui-button ui-widget ui-state-default ui-corner-all ' +\n",
" 'ui-button-icon-only');\n",
" button.attr('role', 'button');\n",
" button.attr('aria-disabled', 'false');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
"\n",
" var icon_img = $('');\n",
" icon_img.addClass('ui-button-icon-primary ui-icon');\n",
" icon_img.addClass(image);\n",
" icon_img.addClass('ui-corner-all');\n",
"\n",
" var tooltip_span = $('');\n",
" tooltip_span.addClass('ui-button-text');\n",
" tooltip_span.html(tooltip);\n",
"\n",
" button.append(icon_img);\n",
" button.append(tooltip_span);\n",
"\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" var fmt_picker_span = $('');\n",
"\n",
" var fmt_picker = $('');\n",
" fmt_picker.addClass('mpl-toolbar-option ui-widget ui-widget-content');\n",
" fmt_picker_span.append(fmt_picker);\n",
" nav_element.append(fmt_picker_span);\n",
" this.format_dropdown = fmt_picker[0];\n",
"\n",
" for (var ind in mpl.extensions) {\n",
" var fmt = mpl.extensions[ind];\n",
" var option = $(\n",
" '', {selected: fmt === mpl.default_extension}).html(fmt);\n",
" fmt_picker.append(option)\n",
" }\n",
"\n",
" // Add hover states to the ui-buttons\n",
" $( \".ui-button\" ).hover(\n",
" function() { $(this).addClass(\"ui-state-hover\");},\n",
" function() { $(this).removeClass(\"ui-state-hover\");}\n",
" );\n",
"\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"}\n",
"\n",
"mpl.figure.prototype.request_resize = function(x_pixels, y_pixels) {\n",
" // Request matplotlib to resize the figure. Matplotlib will then trigger a resize in the client,\n",
" // which will in turn request a refresh of the image.\n",
" this.send_message('resize', {'width': x_pixels, 'height': y_pixels});\n",
"}\n",
"\n",
"mpl.figure.prototype.send_message = function(type, properties) {\n",
" properties['type'] = type;\n",
" properties['figure_id'] = this.id;\n",
" this.ws.send(JSON.stringify(properties));\n",
"}\n",
"\n",
"mpl.figure.prototype.send_draw_message = function() {\n",
" if (!this.waiting) {\n",
" this.waiting = true;\n",
" this.ws.send(JSON.stringify({type: \"draw\", figure_id: this.id}));\n",
" }\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" var format_dropdown = fig.format_dropdown;\n",
" var format = format_dropdown.options[format_dropdown.selectedIndex].value;\n",
" fig.ondownload(fig, format);\n",
"}\n",
"\n",
"\n",
"mpl.figure.prototype.handle_resize = function(fig, msg) {\n",
" var size = msg['size'];\n",
" if (size[0] != fig.canvas.width || size[1] != fig.canvas.height) {\n",
" fig._resize_canvas(size[0], size[1]);\n",
" fig.send_message(\"refresh\", {});\n",
" };\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_rubberband = function(fig, msg) {\n",
" var x0 = msg['x0'] / mpl.ratio;\n",
" var y0 = (fig.canvas.height - msg['y0']) / mpl.ratio;\n",
" var x1 = msg['x1'] / mpl.ratio;\n",
" var y1 = (fig.canvas.height - msg['y1']) / mpl.ratio;\n",
" x0 = Math.floor(x0) + 0.5;\n",
" y0 = Math.floor(y0) + 0.5;\n",
" x1 = Math.floor(x1) + 0.5;\n",
" y1 = Math.floor(y1) + 0.5;\n",
" var min_x = Math.min(x0, x1);\n",
" var min_y = Math.min(y0, y1);\n",
" var width = Math.abs(x1 - x0);\n",
" var height = Math.abs(y1 - y0);\n",
"\n",
" fig.rubberband_context.clearRect(\n",
" 0, 0, fig.canvas.width, fig.canvas.height);\n",
"\n",
" fig.rubberband_context.strokeRect(min_x, min_y, width, height);\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_figure_label = function(fig, msg) {\n",
" // Updates the figure title.\n",
" fig.header.textContent = msg['label'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_cursor = function(fig, msg) {\n",
" var cursor = msg['cursor'];\n",
" switch(cursor)\n",
" {\n",
" case 0:\n",
" cursor = 'pointer';\n",
" break;\n",
" case 1:\n",
" cursor = 'default';\n",
" break;\n",
" case 2:\n",
" cursor = 'crosshair';\n",
" break;\n",
" case 3:\n",
" cursor = 'move';\n",
" break;\n",
" }\n",
" fig.rubberband_canvas.style.cursor = cursor;\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_message = function(fig, msg) {\n",
" fig.message.textContent = msg['message'];\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_draw = function(fig, msg) {\n",
" // Request the server to send over a new figure.\n",
" fig.send_draw_message();\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_image_mode = function(fig, msg) {\n",
" fig.image_mode = msg['mode'];\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Called whenever the canvas gets updated.\n",
" this.send_message(\"ack\", {});\n",
"}\n",
"\n",
"// A function to construct a web socket function for onmessage handling.\n",
"// Called in the figure constructor.\n",
"mpl.figure.prototype._make_on_message_function = function(fig) {\n",
" return function socket_on_message(evt) {\n",
" if (evt.data instanceof Blob) {\n",
" /* FIXME: We get \"Resource interpreted as Image but\n",
" * transferred with MIME type text/plain:\" errors on\n",
" * Chrome. But how to set the MIME type? It doesn't seem\n",
" * to be part of the websocket stream */\n",
" evt.data.type = \"image/png\";\n",
"\n",
" /* Free the memory for the previous frames */\n",
" if (fig.imageObj.src) {\n",
" (window.URL || window.webkitURL).revokeObjectURL(\n",
" fig.imageObj.src);\n",
" }\n",
"\n",
" fig.imageObj.src = (window.URL || window.webkitURL).createObjectURL(\n",
" evt.data);\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
" else if (typeof evt.data === 'string' && evt.data.slice(0, 21) == \"data:image/png;base64\") {\n",
" fig.imageObj.src = evt.data;\n",
" fig.updated_canvas_event();\n",
" fig.waiting = false;\n",
" return;\n",
" }\n",
"\n",
" var msg = JSON.parse(evt.data);\n",
" var msg_type = msg['type'];\n",
"\n",
" // Call the \"handle_{type}\" callback, which takes\n",
" // the figure and JSON message as its only arguments.\n",
" try {\n",
" var callback = fig[\"handle_\" + msg_type];\n",
" } catch (e) {\n",
" console.log(\"No handler for the '\" + msg_type + \"' message type: \", msg);\n",
" return;\n",
" }\n",
"\n",
" if (callback) {\n",
" try {\n",
" // console.log(\"Handling '\" + msg_type + \"' message: \", msg);\n",
" callback(fig, msg);\n",
" } catch (e) {\n",
" console.log(\"Exception inside the 'handler_\" + msg_type + \"' callback:\", e, e.stack, msg);\n",
" }\n",
" }\n",
" };\n",
"}\n",
"\n",
"// from http://stackoverflow.com/questions/1114465/getting-mouse-location-in-canvas\n",
"mpl.findpos = function(e) {\n",
" //this section is from http://www.quirksmode.org/js/events_properties.html\n",
" var targ;\n",
" if (!e)\n",
" e = window.event;\n",
" if (e.target)\n",
" targ = e.target;\n",
" else if (e.srcElement)\n",
" targ = e.srcElement;\n",
" if (targ.nodeType == 3) // defeat Safari bug\n",
" targ = targ.parentNode;\n",
"\n",
" // jQuery normalizes the pageX and pageY\n",
" // pageX,Y are the mouse positions relative to the document\n",
" // offset() returns the position of the element relative to the document\n",
" var x = e.pageX - $(targ).offset().left;\n",
" var y = e.pageY - $(targ).offset().top;\n",
"\n",
" return {\"x\": x, \"y\": y};\n",
"};\n",
"\n",
"/*\n",
" * return a copy of an object with only non-object keys\n",
" * we need this to avoid circular references\n",
" * http://stackoverflow.com/a/24161582/3208463\n",
" */\n",
"function simpleKeys (original) {\n",
" return Object.keys(original).reduce(function (obj, key) {\n",
" if (typeof original[key] !== 'object')\n",
" obj[key] = original[key]\n",
" return obj;\n",
" }, {});\n",
"}\n",
"\n",
"mpl.figure.prototype.mouse_event = function(event, name) {\n",
" var canvas_pos = mpl.findpos(event)\n",
"\n",
" if (name === 'button_press')\n",
" {\n",
" this.canvas.focus();\n",
" this.canvas_div.focus();\n",
" }\n",
"\n",
" var x = canvas_pos.x * mpl.ratio;\n",
" var y = canvas_pos.y * mpl.ratio;\n",
"\n",
" this.send_message(name, {x: x, y: y, button: event.button,\n",
" step: event.step,\n",
" guiEvent: simpleKeys(event)});\n",
"\n",
" /* This prevents the web browser from automatically changing to\n",
" * the text insertion cursor when the button is pressed. We want\n",
" * to control all of the cursor setting manually through the\n",
" * 'cursor' event from matplotlib */\n",
" event.preventDefault();\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" // Handle any extra behaviour associated with a key event\n",
"}\n",
"\n",
"mpl.figure.prototype.key_event = function(event, name) {\n",
"\n",
" // Prevent repeat events\n",
" if (name == 'key_press')\n",
" {\n",
" if (event.which === this._key)\n",
" return;\n",
" else\n",
" this._key = event.which;\n",
" }\n",
" if (name == 'key_release')\n",
" this._key = null;\n",
"\n",
" var value = '';\n",
" if (event.ctrlKey && event.which != 17)\n",
" value += \"ctrl+\";\n",
" if (event.altKey && event.which != 18)\n",
" value += \"alt+\";\n",
" if (event.shiftKey && event.which != 16)\n",
" value += \"shift+\";\n",
"\n",
" value += 'k';\n",
" value += event.which.toString();\n",
"\n",
" this._key_event_extra(event, name);\n",
"\n",
" this.send_message(name, {key: value,\n",
" guiEvent: simpleKeys(event)});\n",
" return false;\n",
"}\n",
"\n",
"mpl.figure.prototype.toolbar_button_onclick = function(name) {\n",
" if (name == 'download') {\n",
" this.handle_save(this, null);\n",
" } else {\n",
" this.send_message(\"toolbar_button\", {name: name});\n",
" }\n",
"};\n",
"\n",
"mpl.figure.prototype.toolbar_button_onmouseover = function(tooltip) {\n",
" this.message.textContent = tooltip;\n",
"};\n",
"mpl.toolbar_items = [[\"Home\", \"Reset original view\", \"fa fa-home icon-home\", \"home\"], [\"Back\", \"Back to previous view\", \"fa fa-arrow-left icon-arrow-left\", \"back\"], [\"Forward\", \"Forward to next view\", \"fa fa-arrow-right icon-arrow-right\", \"forward\"], [\"\", \"\", \"\", \"\"], [\"Pan\", \"Pan axes with left mouse, zoom with right\", \"fa fa-arrows icon-move\", \"pan\"], [\"Zoom\", \"Zoom to rectangle\", \"fa fa-square-o icon-check-empty\", \"zoom\"], [\"\", \"\", \"\", \"\"], [\"Download\", \"Download plot\", \"fa fa-floppy-o icon-save\", \"download\"]];\n",
"\n",
"mpl.extensions = [\"eps\", \"jpeg\", \"pdf\", \"png\", \"ps\", \"raw\", \"svg\", \"tif\"];\n",
"\n",
"mpl.default_extension = \"png\";var comm_websocket_adapter = function(comm) {\n",
" // Create a \"websocket\"-like object which calls the given IPython comm\n",
" // object with the appropriate methods. Currently this is a non binary\n",
" // socket, so there is still some room for performance tuning.\n",
" var ws = {};\n",
"\n",
" ws.close = function() {\n",
" comm.close()\n",
" };\n",
" ws.send = function(m) {\n",
" //console.log('sending', m);\n",
" comm.send(m);\n",
" };\n",
" // Register the callback with on_msg.\n",
" comm.on_msg(function(msg) {\n",
" //console.log('receiving', msg['content']['data'], msg);\n",
" // Pass the mpl event to the overriden (by mpl) onmessage function.\n",
" ws.onmessage(msg['content']['data'])\n",
" });\n",
" return ws;\n",
"}\n",
"\n",
"mpl.mpl_figure_comm = function(comm, msg) {\n",
" // This is the function which gets called when the mpl process\n",
" // starts-up an IPython Comm through the \"matplotlib\" channel.\n",
"\n",
" var id = msg.content.data.id;\n",
" // Get hold of the div created by the display call when the Comm\n",
" // socket was opened in Python.\n",
" var element = $(\"#\" + id);\n",
" var ws_proxy = comm_websocket_adapter(comm)\n",
"\n",
" function ondownload(figure, format) {\n",
" window.open(figure.imageObj.src);\n",
" }\n",
"\n",
" var fig = new mpl.figure(id, ws_proxy,\n",
" ondownload,\n",
" element.get(0));\n",
"\n",
" // Call onopen now - mpl needs it, as it is assuming we've passed it a real\n",
" // web socket which is closed, not our websocket->open comm proxy.\n",
" ws_proxy.onopen();\n",
"\n",
" fig.parent_element = element.get(0);\n",
" fig.cell_info = mpl.find_output_cell(\"\");\n",
" if (!fig.cell_info) {\n",
" console.error(\"Failed to find cell for figure\", id, fig);\n",
" return;\n",
" }\n",
"\n",
" var output_index = fig.cell_info[2]\n",
" var cell = fig.cell_info[0];\n",
"\n",
"};\n",
"\n",
"mpl.figure.prototype.handle_close = function(fig, msg) {\n",
" var width = fig.canvas.width/mpl.ratio\n",
" fig.root.unbind('remove')\n",
"\n",
" // Update the output cell to use the data from the current canvas.\n",
" fig.push_to_output();\n",
" var dataURL = fig.canvas.toDataURL();\n",
" // Re-enable the keyboard manager in IPython - without this line, in FF,\n",
" // the notebook keyboard shortcuts fail.\n",
" IPython.keyboard_manager.enable()\n",
" $(fig.parent_element).html(' ');\n",
" fig.close_ws(fig, msg);\n",
"}\n",
"\n",
"mpl.figure.prototype.close_ws = function(fig, msg){\n",
" fig.send_message('closing', msg);\n",
" // fig.ws.close()\n",
"}\n",
"\n",
"mpl.figure.prototype.push_to_output = function(remove_interactive) {\n",
" // Turn the data on the canvas into data in the output cell.\n",
" var width = this.canvas.width/mpl.ratio\n",
" var dataURL = this.canvas.toDataURL();\n",
" this.cell_info[1]['text/html'] = '
');\n",
" fig.close_ws(fig, msg);\n",
"}\n",
"\n",
"mpl.figure.prototype.close_ws = function(fig, msg){\n",
" fig.send_message('closing', msg);\n",
" // fig.ws.close()\n",
"}\n",
"\n",
"mpl.figure.prototype.push_to_output = function(remove_interactive) {\n",
" // Turn the data on the canvas into data in the output cell.\n",
" var width = this.canvas.width/mpl.ratio\n",
" var dataURL = this.canvas.toDataURL();\n",
" this.cell_info[1]['text/html'] = ' ';\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Tell IPython that the notebook contents must change.\n",
" IPython.notebook.set_dirty(true);\n",
" this.send_message(\"ack\", {});\n",
" var fig = this;\n",
" // Wait a second, then push the new image to the DOM so\n",
" // that it is saved nicely (might be nice to debounce this).\n",
" setTimeout(function () { fig.push_to_output() }, 1000);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items){\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) { continue; };\n",
"\n",
" var button = $('');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" // Add the status bar.\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"\n",
" // Add the close button to the window.\n",
" var buttongrp = $('');\n",
" var button = $('');\n",
" button.click(function (evt) { fig.handle_close(fig, {}); } );\n",
" button.mouseover('Stop Interaction', toolbar_mouse_event);\n",
" buttongrp.append(button);\n",
" var titlebar = this.root.find($('.ui-dialog-titlebar'));\n",
" titlebar.prepend(buttongrp);\n",
"}\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(el){\n",
" var fig = this\n",
" el.on(\"remove\", function(){\n",
"\tfig.close_ws(fig, {});\n",
" });\n",
"}\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(el){\n",
" // this is important to make the div 'focusable\n",
" el.attr('tabindex', 0)\n",
" // reach out to IPython and tell the keyboard manager to turn it's self\n",
" // off when our div gets focus\n",
"\n",
" // location in version 3\n",
" if (IPython.notebook.keyboard_manager) {\n",
" IPython.notebook.keyboard_manager.register_events(el);\n",
" }\n",
" else {\n",
" // location in version 2\n",
" IPython.keyboard_manager.register_events(el);\n",
" }\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" var manager = IPython.notebook.keyboard_manager;\n",
" if (!manager)\n",
" manager = IPython.keyboard_manager;\n",
"\n",
" // Check for shift+enter\n",
" if (event.shiftKey && event.which == 13) {\n",
" this.canvas_div.blur();\n",
" event.shiftKey = false;\n",
" // Send a \"J\" for go to next cell\n",
" event.which = 74;\n",
" event.keyCode = 74;\n",
" manager.command_mode();\n",
" manager.handle_keydown(event);\n",
" }\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" fig.ondownload(fig, null);\n",
"}\n",
"\n",
"\n",
"mpl.find_output_cell = function(html_output) {\n",
" // Return the cell and output element which can be found *uniquely* in the notebook.\n",
" // Note - this is a bit hacky, but it is done because the \"notebook_saving.Notebook\"\n",
" // IPython event is triggered only after the cells have been serialised, which for\n",
" // our purposes (turning an active figure into a static one), is too late.\n",
" var cells = IPython.notebook.get_cells();\n",
" var ncells = cells.length;\n",
" for (var i=0; i= 3 moved mimebundle to data attribute of output\n",
" data = data.data;\n",
" }\n",
" if (data['text/html'] == html_output) {\n",
" return [cell, data, j];\n",
" }\n",
" }\n",
" }\n",
" }\n",
"}\n",
"\n",
"// Register the function which deals with the matplotlib target/channel.\n",
"// The kernel may be null if the page has been refreshed.\n",
"if (IPython.notebook.kernel != null) {\n",
" IPython.notebook.kernel.comm_manager.register_target('matplotlib', mpl.mpl_figure_comm);\n",
"}\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
"
';\n",
"}\n",
"\n",
"mpl.figure.prototype.updated_canvas_event = function() {\n",
" // Tell IPython that the notebook contents must change.\n",
" IPython.notebook.set_dirty(true);\n",
" this.send_message(\"ack\", {});\n",
" var fig = this;\n",
" // Wait a second, then push the new image to the DOM so\n",
" // that it is saved nicely (might be nice to debounce this).\n",
" setTimeout(function () { fig.push_to_output() }, 1000);\n",
"}\n",
"\n",
"mpl.figure.prototype._init_toolbar = function() {\n",
" var fig = this;\n",
"\n",
" var nav_element = $('')\n",
" nav_element.attr('style', 'width: 100%');\n",
" this.root.append(nav_element);\n",
"\n",
" // Define a callback function for later on.\n",
" function toolbar_event(event) {\n",
" return fig.toolbar_button_onclick(event['data']);\n",
" }\n",
" function toolbar_mouse_event(event) {\n",
" return fig.toolbar_button_onmouseover(event['data']);\n",
" }\n",
"\n",
" for(var toolbar_ind in mpl.toolbar_items){\n",
" var name = mpl.toolbar_items[toolbar_ind][0];\n",
" var tooltip = mpl.toolbar_items[toolbar_ind][1];\n",
" var image = mpl.toolbar_items[toolbar_ind][2];\n",
" var method_name = mpl.toolbar_items[toolbar_ind][3];\n",
"\n",
" if (!name) { continue; };\n",
"\n",
" var button = $('');\n",
" button.click(method_name, toolbar_event);\n",
" button.mouseover(tooltip, toolbar_mouse_event);\n",
" nav_element.append(button);\n",
" }\n",
"\n",
" // Add the status bar.\n",
" var status_bar = $('');\n",
" nav_element.append(status_bar);\n",
" this.message = status_bar[0];\n",
"\n",
" // Add the close button to the window.\n",
" var buttongrp = $('');\n",
" var button = $('');\n",
" button.click(function (evt) { fig.handle_close(fig, {}); } );\n",
" button.mouseover('Stop Interaction', toolbar_mouse_event);\n",
" buttongrp.append(button);\n",
" var titlebar = this.root.find($('.ui-dialog-titlebar'));\n",
" titlebar.prepend(buttongrp);\n",
"}\n",
"\n",
"mpl.figure.prototype._root_extra_style = function(el){\n",
" var fig = this\n",
" el.on(\"remove\", function(){\n",
"\tfig.close_ws(fig, {});\n",
" });\n",
"}\n",
"\n",
"mpl.figure.prototype._canvas_extra_style = function(el){\n",
" // this is important to make the div 'focusable\n",
" el.attr('tabindex', 0)\n",
" // reach out to IPython and tell the keyboard manager to turn it's self\n",
" // off when our div gets focus\n",
"\n",
" // location in version 3\n",
" if (IPython.notebook.keyboard_manager) {\n",
" IPython.notebook.keyboard_manager.register_events(el);\n",
" }\n",
" else {\n",
" // location in version 2\n",
" IPython.keyboard_manager.register_events(el);\n",
" }\n",
"\n",
"}\n",
"\n",
"mpl.figure.prototype._key_event_extra = function(event, name) {\n",
" var manager = IPython.notebook.keyboard_manager;\n",
" if (!manager)\n",
" manager = IPython.keyboard_manager;\n",
"\n",
" // Check for shift+enter\n",
" if (event.shiftKey && event.which == 13) {\n",
" this.canvas_div.blur();\n",
" event.shiftKey = false;\n",
" // Send a \"J\" for go to next cell\n",
" event.which = 74;\n",
" event.keyCode = 74;\n",
" manager.command_mode();\n",
" manager.handle_keydown(event);\n",
" }\n",
"}\n",
"\n",
"mpl.figure.prototype.handle_save = function(fig, msg) {\n",
" fig.ondownload(fig, null);\n",
"}\n",
"\n",
"\n",
"mpl.find_output_cell = function(html_output) {\n",
" // Return the cell and output element which can be found *uniquely* in the notebook.\n",
" // Note - this is a bit hacky, but it is done because the \"notebook_saving.Notebook\"\n",
" // IPython event is triggered only after the cells have been serialised, which for\n",
" // our purposes (turning an active figure into a static one), is too late.\n",
" var cells = IPython.notebook.get_cells();\n",
" var ncells = cells.length;\n",
" for (var i=0; i= 3 moved mimebundle to data attribute of output\n",
" data = data.data;\n",
" }\n",
" if (data['text/html'] == html_output) {\n",
" return [cell, data, j];\n",
" }\n",
" }\n",
" }\n",
" }\n",
"}\n",
"\n",
"// Register the function which deals with the matplotlib target/channel.\n",
"// The kernel may be null if the page has been refreshed.\n",
"if (IPython.notebook.kernel != null) {\n",
" IPython.notebook.kernel.comm_manager.register_target('matplotlib', mpl.mpl_figure_comm);\n",
"}\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/html": [
" "
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"S = Surface(getExample('surface.ply'), euclideanM)\n",
"generators, betti1 = homology(S)\n",
"print(\"Number of features: {0}\".format(betti1))\n",
"\n",
"G = [ normalize(generators[:,i]) for i in range(betti1) ]\n",
"for i in [2,5]:\n",
" S.plot([G[i], normalize(S.short(G[i]))], ['yellow', 'red'])\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"
"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"S = Surface(getExample('surface.ply'), euclideanM)\n",
"generators, betti1 = homology(S)\n",
"print(\"Number of features: {0}\".format(betti1))\n",
"\n",
"G = [ normalize(generators[:,i]) for i in range(betti1) ]\n",
"for i in [2,5]:\n",
" S.plot([G[i], normalize(S.short(G[i]))], ['yellow', 'red'])\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"
This work is licensed under a GNU GPL Version 3 License. The **MOSEK** logo and name are trademarks of Mosek ApS. The code is provided as-is. Compatibility with future release of **MOSEK** or the `Fusion API` are not guaranteed. For more information contact our [support](mailto:support@mosek.com). "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.4"
}
},
"nbformat": 4,
"nbformat_minor": 1
}