1.1. Balance equations for open systems

This section is a recall of results obtained in thermodynamics and fluid mechanics. We are going to obtain balance equations of mass, energy and entropy for an open system.

1.1.1. Prerequisities

1.1.1.1. General balance equation

Let us consider a material volume (closed system) \mathcal{V} as defined in Figure 1.1: .

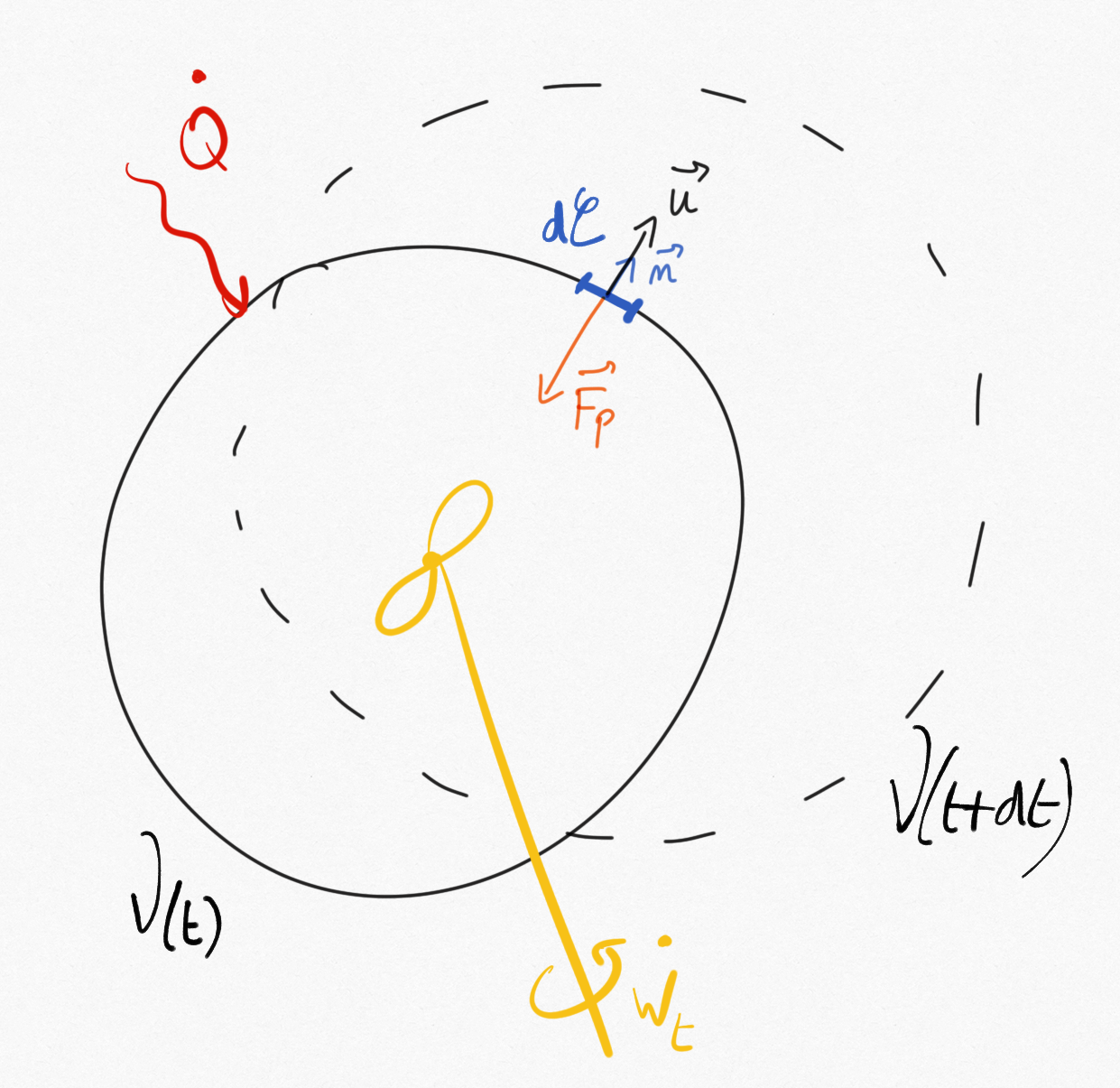
_images/volumeControl.png

Figure 1.1: A material volume representing a closed system.

For any extensive variable \phi associated to the intensive variable \eta in this volume, we have:

(1.1)\phi=\int_{\mathcal{V}}\eta dV

And the general balance equation of \phi in the material volume \mathcal{V} is:

(1.2)\frac{d\phi}{dt} = \dot{\phi_E} + \dot{\phi_C}

where:

  • \dot{\phi_E} represents the sum of all quantities of \phi exchanged by time unit dt between the control volume and exterior but not linked with flow.

  • \dot{\phi_C} represents the creation of quantity \phi by time unit dt in the control volume.

Introducing equation Eq.1.1 in Eq.1.2:

(1.3)\frac{d}{dt} \int_{\mathcal{V}}\eta dV = \dot{\phi_E} + \dot{\phi_C}

Thanks to the transport theorem, equation Eq.1.3 becomes:

(1.4)\int_{\mathcal{V}} \frac{\partial \eta}{\partial t} dV + \int_{\mathcal{C}} \eta \vec{u}\cdot\vec{n} dC = \dot{\phi_E} + \dot{\phi_C}

where:

  • \mathcal{C} represent the contour surrounding the control volume \mathcal{V}.

  • \vec{u} is the local fluid velocity.

  • \vec{n} is the local normal (directed to the exterior).

For a machine with a fix control volume V_{machine}, thanks to the transport theorem we also may write:

(1.5)\frac{d}{dt} \int_{V_{machine}} \eta dV = \int_{V_{machine}} \frac{\partial \eta}{\partial t} dV

If we consider the machine volume exactly fits the material volume at instant t, we can write:

\int_{V_{machine}} \frac{\partial \eta}{\partial t} dV = \int_{\mathcal{V}} \frac{\partial \eta}{\partial t} dV \qquad \text{and} \qquad \int_{C_{machine}} \eta \vec{u}\cdot\vec{n} dC = \int_{\mathcal{C}} \eta \vec{u}\cdot\vec{n} dC

Important

And thanks to Eq.1.4, we finally obtain the general balance equation for a fix control volume:

(1.6)\int_{V_{machine}} \frac{\partial \eta}{\partial t} dV + \int_{C_{machine}} \eta \vec{u}\cdot\vec{n} dC = \dot{\phi_E} + \dot{\phi_C}

1.1.1.2. Steady flow

In practical engineering problems, when studying thermodynamic cycles of thermal machines, the flow is steady. In that case equation Eq.1.4 becomes:

(1.7)\int_{C_{machine}} \eta \vec{u}\cdot\vec{n} dC = \dot{\phi_E} + \dot{\phi_C}

1.1.1.3. One dimensional hypothesis in fluid sections of \mathcal{C}

It is also common in thermal machines study to consider that flow variables are constant in inflow and outflow sections of the control volume.

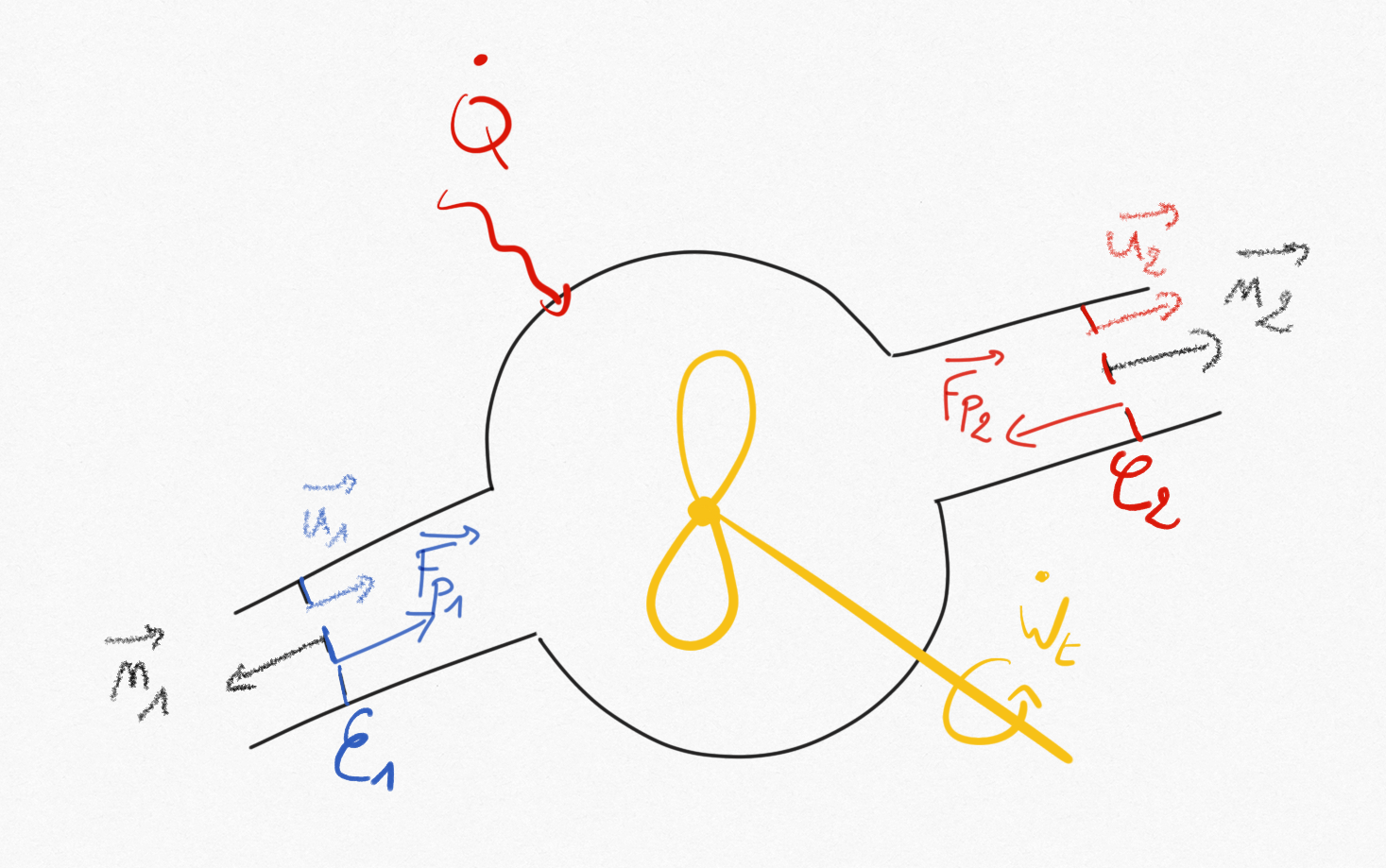
_images/volumeControl2.png

Figure 1.2: Component of a thermal machine with two fluid sections.

Thus, for a steady flow assumption with one dimensional hypothesis in fluid sections, we simply obtain:

(1.8)\sum_{k=1}^n \eta_k \vec{u}_k\cdot\vec{n}_k C_{k} = \dot{\phi_E} + \dot{\phi_C}

Where the contour C_{machine} has been splited in n fluid contours of section \mathcal{C}_{k}.

We then apply this balance equation to mass, energy and entropy extensive variables.

1.1.2. Mass

Applying equation Eq.1.8 to mass conservation is very simple as we use:

  • \phi = M: the mass in the control volume,

  • \eta = \rho: the specific mass,

  • \dot{\phi_E} = 0: the mass being only exchanged thanks to the flow,

  • \dot{\phi_C} = 0: there is no chemical, phase change or nuclear reactions in the control volume.

Important

The mass balance for an open system simply reads:

(1.9)\sum_{k} \dot{m_k} = 0

Where \dot{m_k} = \rho_k \vec{u}\cdot\vec{n} C_{k} is the mass flow rate throught C_{k}.

1.1.3. Momentum

Momentum balance can be usefull to determine forces acting on solid walls into systems. This is not the aim of present course, and the interested student is encouraged to go back in his fluid mechanics course to catch details on that point.

1.1.4. Energy

We apply equation Eq.1.8 to energy conservation:

  • \phi = E: the total energy in the control volume,

  • \eta = \rho e_t: the volumic total energy,

  • \dot{\phi_E}: the sum of all exchanged energies per time unit

  • \dot{\phi_C} = 0: there is no energy creation in the control volume.

The specific total energy e_t in the volume control contains:

  • the specific internal energy \epsilon,

  • the specific kinetic energy 1/2 u^2,

  • the potential specific energy e_p,

The term \dot{\phi_E} contains different contributions, we will retain:

  • the rate of pressure forces work \dot{W_p}

  • the heat flux \dot{Q}

  • the rate of technical work echanged with a machine (pumps, turbines, etc.)

such that we obtain:

(1.10)\sum_{k} \dot{m}_k e_{t,k} = \dot{W_p} + \dot{Q} + \dot{W}_{t}

1.1.4.1. Expression of rate of pressure forces work

In the control volume, pressure forces only acts on fluid contours such that we can write:

(1.11)\dot{W_p} = \frac{1}{dt}\sum_{k} \vec{F}_{p,k}\cdot \vec{dl}_k

With the pressure force \vec{F}_{p,k} = -p_k \mathcal{C}_{k} \vec{n_k} and the elementary displacement \vec{dl}_k = \vec{u}_k dt, we obtain:

(1.12)\dot{W_p} = -\sum_{k} p_k C_{k} \vec{n_k}\cdot \vec{u}_k

Thanks to this expression, equation Eq.1.10 becomes:

(1.13)\sum_{k} \dot{m}_k (e_{t,k}+\frac{p_k}{\rho_k}) = \dot{Q} + \dot{W}_{t}

Important

We define h_t = e_{t,k}+\frac{p_k}{\rho_k} the total specific enthalpy (or the stagnation enthalpy). Thus we have the final usefull form of energy balance for thermodynamic machines that traduces the first principle of thermodynamics for an open system:

(1.14)\sum_{k} \dot{m}_k h_{t,k} = \dot{Q} + \dot{W}_{t}

  • \dot{Q} represents the heat exchanges between the system and its surrounding.

  • \dot{W}_{t} is called technical work and is exchanged between the system and a machine.

1.1.5. Entropy

We apply equation Eq.1.8 to entropy extensive variable:

  • \phi = S: the entropy in the control volume,

  • \eta = \rho s: the volumic entropy,

  • \dot{\phi_E} = \sum_i \frac{\dot{Q}_i}{T_i}: the rate of exchanged entropies.

  • \dot{\phi_C} = \dot{S_c}: the rate of entropy creation thanks to non reversible processes (internal or external).

Important

We thus obtain the entropy balance equation for an open system:

(1.15)\sum_{k} \dot{m}_k s_{k} = \sum_i \frac{\dot{Q}_i}{T_i} + \dot{S_c}