1.2. Applications¶

Balance equations presented in Section 1.1: are applied here to the constituting elements of engineering machines: nozzles, heat exchangers, compressors and turbines, etc. These elements are made for continuous processes (steady flow) and generally present one fluid entry and one fluid exit.

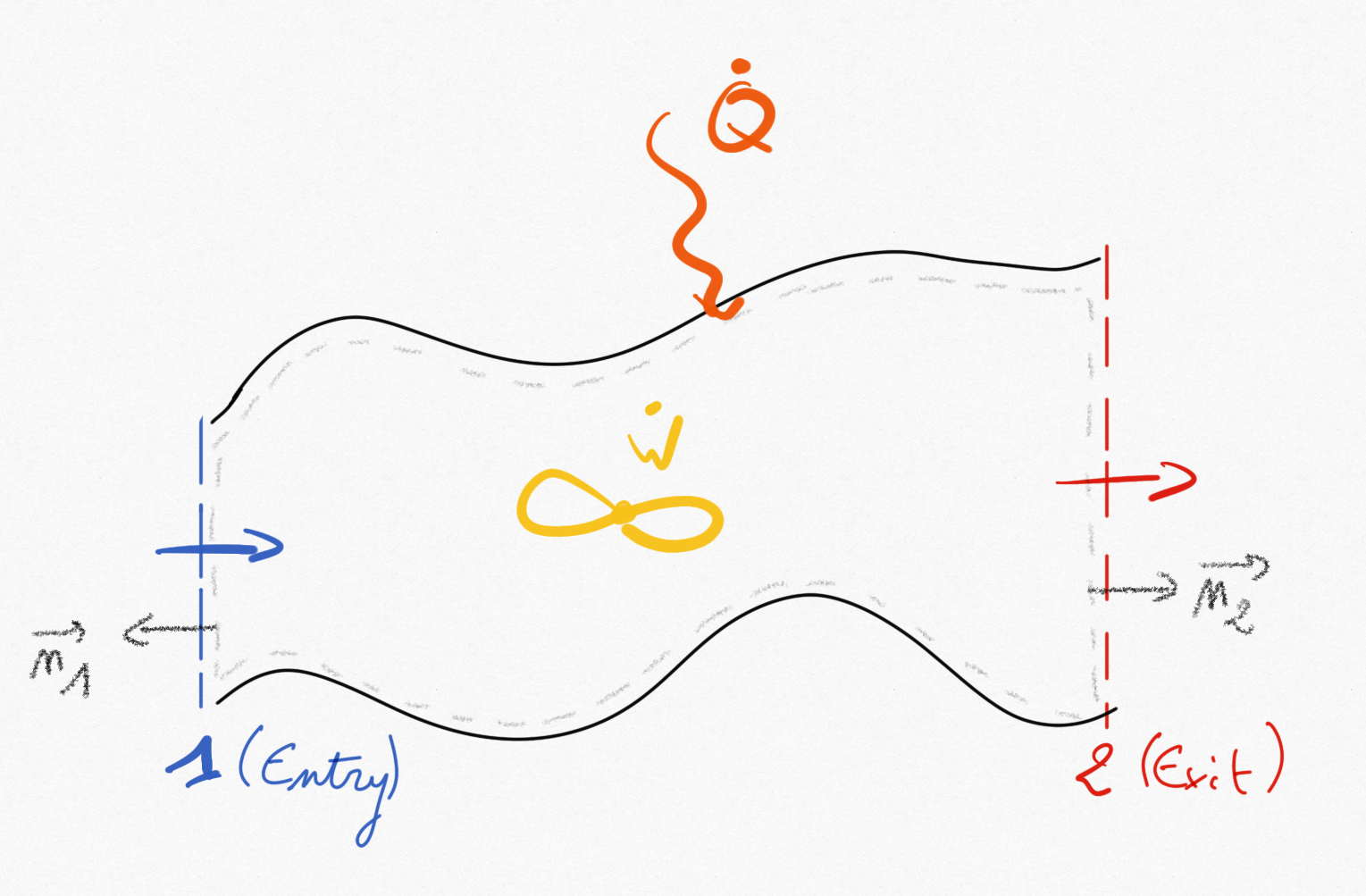
Figure 1.3: A fluid system with one entry and one exit¶

In that specific case, balance equations Eq.1.9 and Eq.1.10 simplify in:

(1.16)¶ $\dot{m_2} = - \dot{m_1} = \dot{m}$

and

(1.17)¶ $\dot{m} (h_{t,2} - h_{t,1}) = \dot{Q} + \dot{W}_{t}$

1.2.1. Acceleration in a nozzle¶

Nozzles can be found in gas turbine or on aircrafts/rocket engines. They are basic components used to accelerate/decelerate a flow.

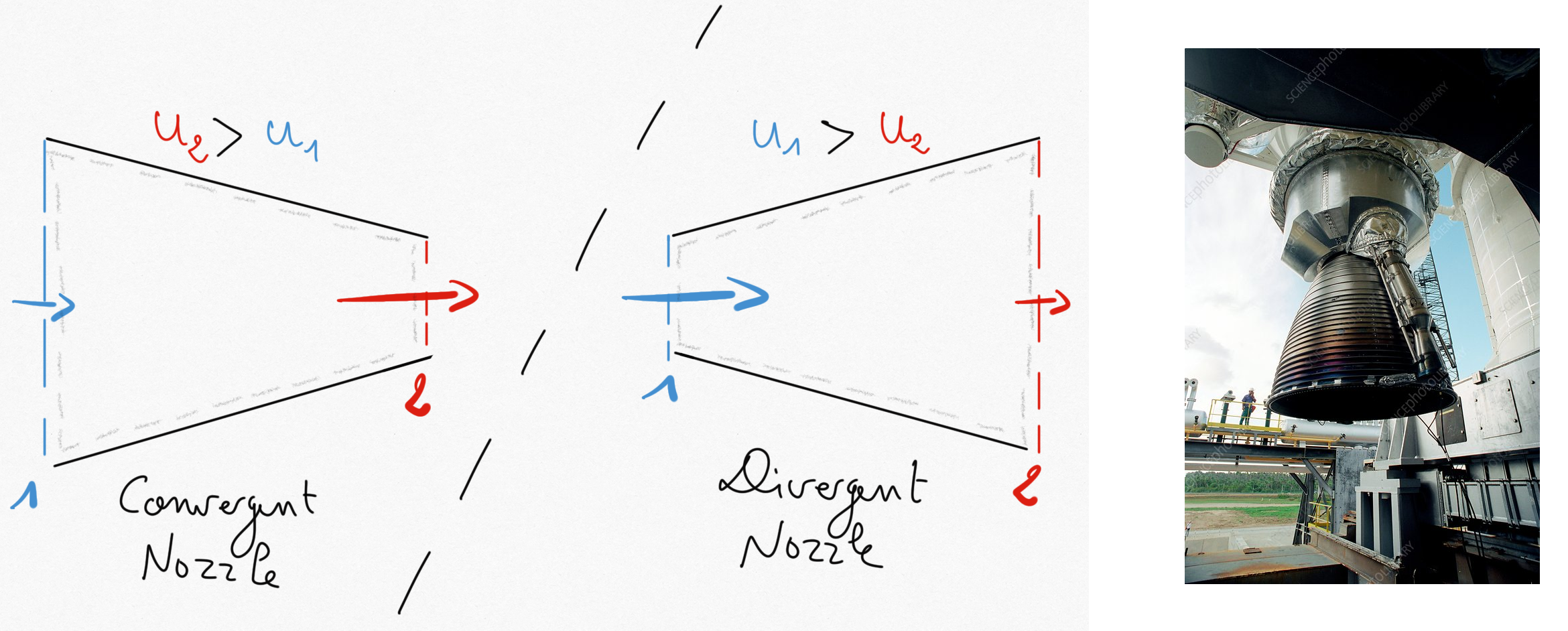
Figure 1.4: Left: subsonic convergent nozzle, Middle: subsonic divergent nozzle, Right: Ariane’5 Vulcain engine nozzle.¶

In nozzle systems:

It is commonly accepted that no thermal energy is exchanged ( $\dot{Q}=0$ ) due to important fluid velocities.

Moreover, no working machine is present ( $\dot{W}_{t}$ )

Potential energy is negligible.

such that relation Eq.1.17 becomes:

(1.18)¶ $h_{2} - h_{1} = - \frac{1}{2}(u_2^2-u_1^2)$

1.2.2. Heat exchanger¶

Heat exchangers allow to exchange a thermal energy between two fluids without mixing. The simpler heat exchanger is the double-tube presented in Figure 1.5: .

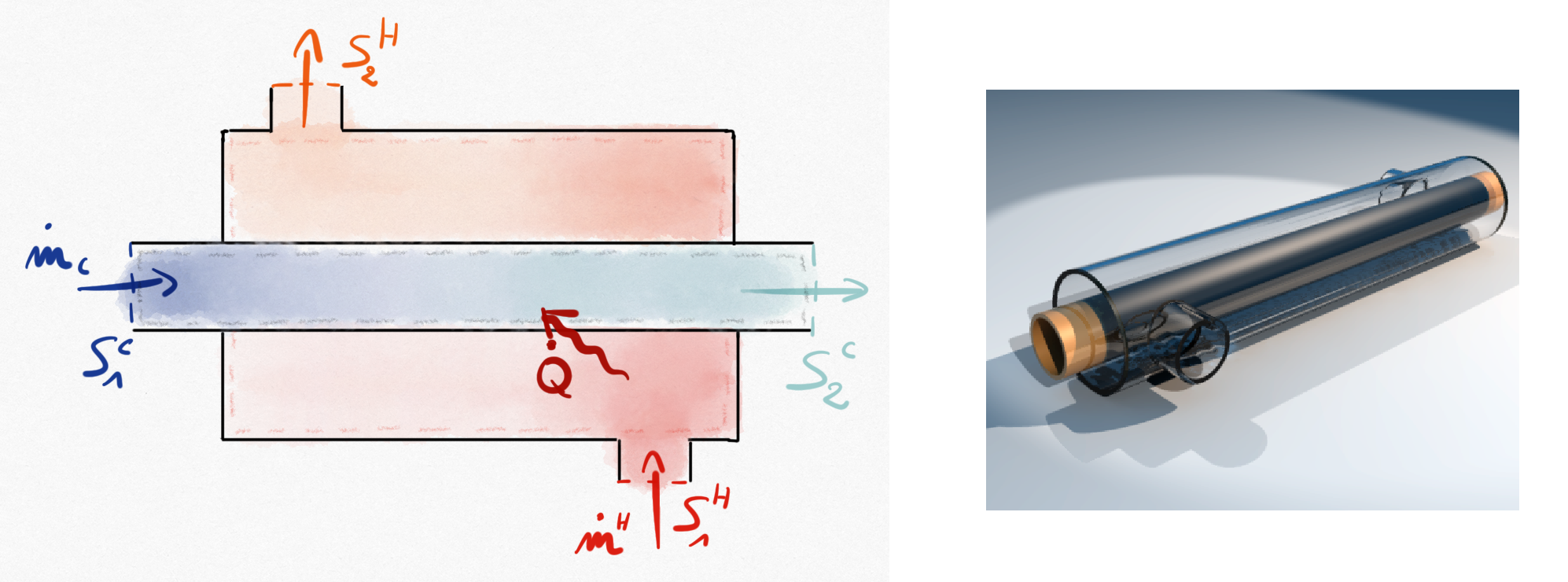
Figure 1.5: Double-tube heat exchanger. The cold fluid is absorbing thermal energy provided by the hot fluid.¶

In heat exchanger systems:

Kinetic energy variation is commonly negligible.

Potential energy is negligible.

No working machine is present ( $\dot{W}_{t}$ )

Such that for example if considering the cold fluid system, the balance energy equation Eq.1.17 becomes:

(1.19)¶ $\dot{m}_C (h_{2}^C - h_{1}^C) = \dot{Q}$

If the heat exchanger is insulated, the hot fluid system balance energy will read:

$\dot{m}_H (h_{2}^H - h_{1}^H) = -\dot{Q}$

1.2.3. Compressor/Turbine¶

These elements contains a rotary mechanical device to convert flow energy into mechanical work (turbine) and reversely (compressor). The mechanical work is transmitted thanks to a shaft.

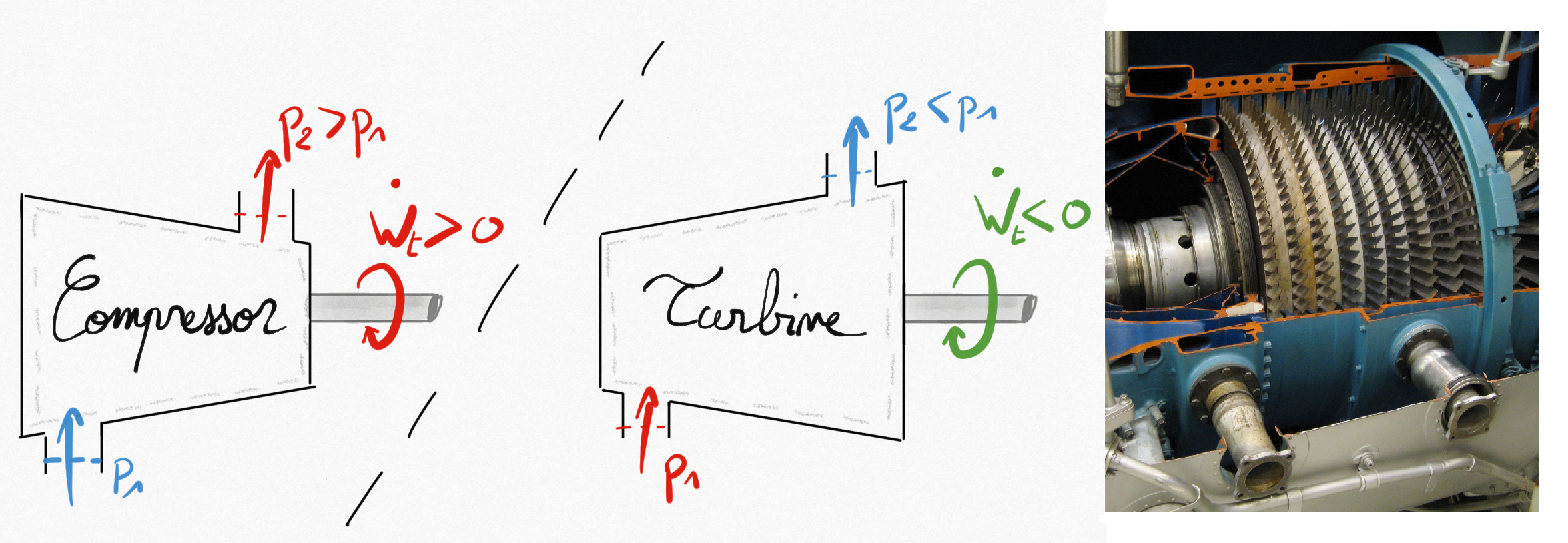
Figure 1.6: Left: schematic representation of a compressor and a turbine. Right: multi-stage compressor.¶

In these elements, this is commonly accepted that:

Kinetic energy variation is negligible.

Potential energy negligible.

No heat exchanges unless they are cooled (or heated) $\dot{Q} =0$ .

Balance energy equation becomes:

(1.20)¶ $\dot{m} (h_{2} - h_{1}) = \dot{W}_{t}$

In a turbine, a work is produced on the shaft ( $W_t < 0$ because lost by the turbine), and the flow enthalpy is decreasing because of fluid expansion resulting in a lower pressure at the turbine exit than at the entry.

In a compressor, as for a pump or a ventilator, the fluid’s enthalpy is increasing because of fluid compression resulting in an increase of flow pressure as a work is provided on the shaft ( $W_t > 0$ because earned by the compressor).

1.2.4. Throttling Valves¶

Throttling valves produce a pressure drop in a flow. It can be obtained thanks to adjustable valve or thanks to a porous.

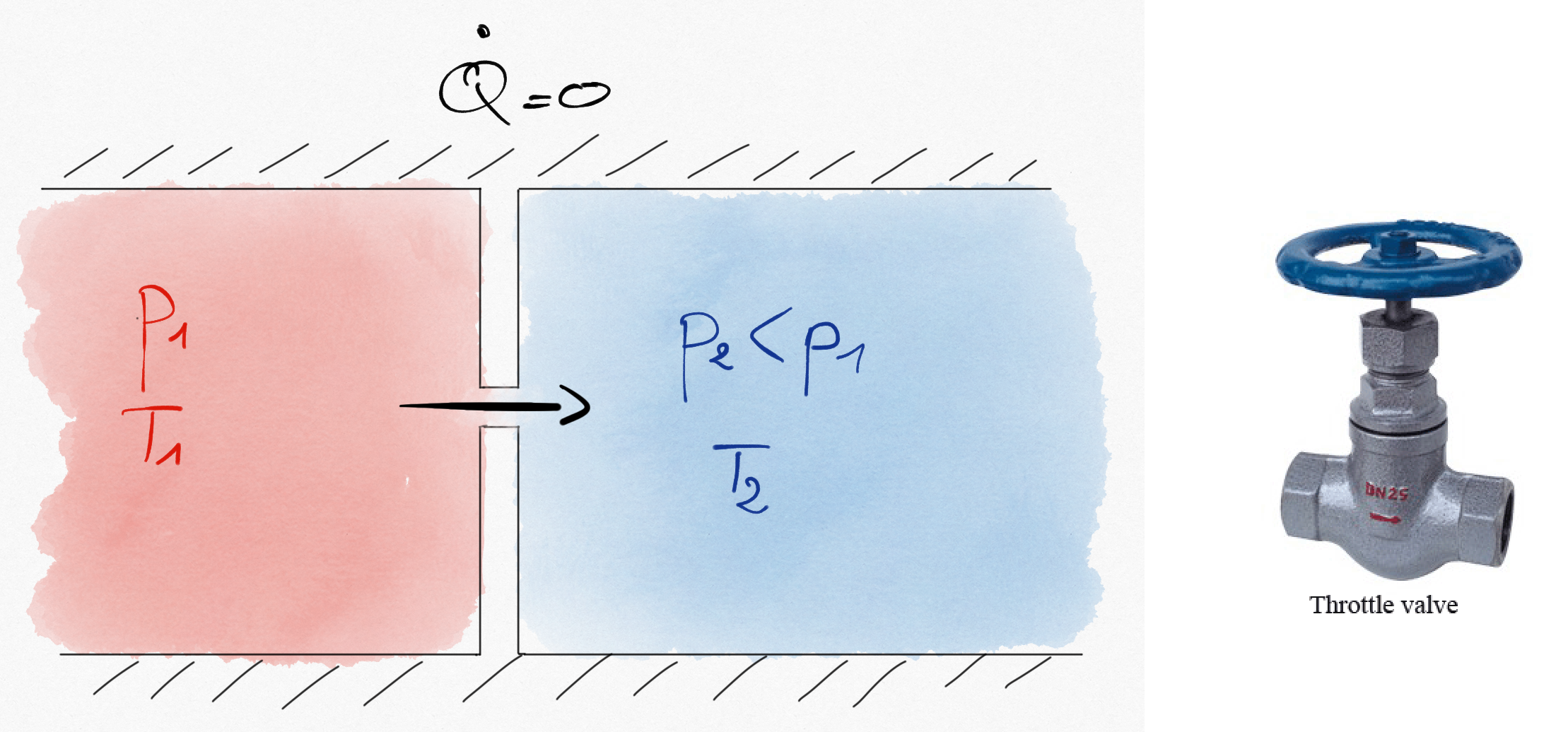
Figure 1.7: A high pressure gas is expanded through a hole. This kind of expansion is isenthalpic.¶

Common hypothesis are:

No heat echanges (insulated walls),

No working machine,

Kinetic energy variation is negligible.

Such that the first principle reduces to:

(1.21)¶ $h_1 = h_2$

If the fluid can be considered as ideal gas, the isenthalpic expansion is also isothermal:

$T_1 = T_2$