2.1. Energy conversion¶

Definitions of energy converters and energy reservoirs are given first, then the specific case of thermal energy converters (thermal machines) are studied.

2.1.1. Definitions¶

2.1.1.1. Energy converter¶

An energy converter is a thermodynamic system able to transfer energy from a system in a given form to another system in another form.

This energy conversion should remain in time thanks to a cyclic operation of the converter.

Examples of energy converters

An electric resistance converts electrical energy to heat energy.
A thermo-alternator group from an hydraulic power plant converts kinetic and potential energies of water in electrical energy.
A car engine converts chemical energy into mechanical energy.
etc.

An energy converter is said perfect if he follows a reversible cycle.

2.1.1.2. Energy reservoirs¶

A reservoir (source or sink) associated to a given energy type is a system with an infinite size such that if he exchange energy, the intensive variable corresponding to this energy type remains unchanged.

Examples of energy reservoirs

A lake upstream from a dam represents a reservoir of potential energy since its can provide energy to a turbine ( $\delta{e}_p = gz dM$ ) with a mass change ( $dM$ ) while remaining its surface at the same altitude ( $gz$ ).
Outside air represents a reservoir of thermal energy since it can, during winter, draw heat energy from a building ( $\delta Q = T dS$ ) with an entropy variation ( $dS$ ) while its temperature ( $T$ ) remains constant.

2.1.2. Thermal energy converters¶

Energy converters under interest in this course are thermo-mecanical energy converters. They are classed in three families:

Heat engines: they are converting thermal energy into mechanical energy. We can cite for example reciprocating internal combustion engines (car engines), steam locomotive, gas turbine, turboreactors, etc.

Heat pumps: they are converting thermal energy from mechanical energy, providing thermal energy to a hot sink.

Refrigerators: they are converting thermal energy from mechanical energy, drawing thermal energy from a cold source.

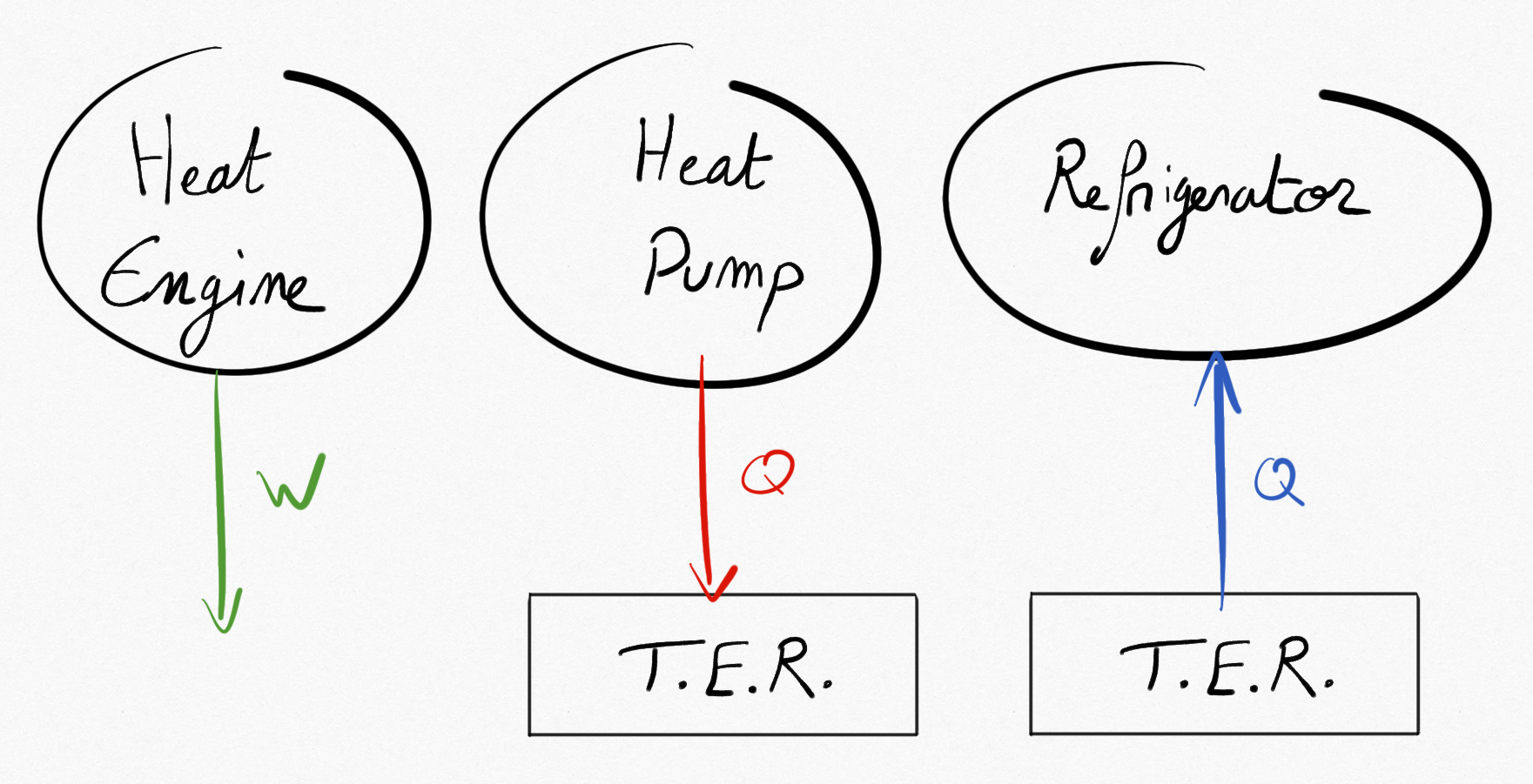
Figure 2.1: 3 kind of thermal machines¶

Thus thermal energy converters are exchanging thermal energy between thermal energy reservoirs (TER) and draws or produces mechanical energy.

The energy is transmitted between the different elements of a thermal converter thanks to a working fluid also named refrigerant or coolant. This can be a gas (air, carbon dioxyde, helium, etc.) or a liquid that can vaporize (water, ammonia, freon, etc.) that follows a thermodynamic cycle.

During this cycle, the final state $f$ of the working fluid is the same as its initial $i$ one such that its internal energy variation is nul:

(2.1)¶ $\Delta [E]_{cycle} = E_f - E_i = 0$

We also have no variation of entropy:

(2.2)¶ $\Delta [S]_{cycle} = S_f - S_i = 0$

Thanks to the first and second principle of thermodynamics, we are going to analyse the possibilities if we put the system in contact with one or more TER.

Let us consider that our system exchange thermal energies with $n$ TER. The thermal energy $Q_k$ is associated to the TER $k$ at temperature $T_k$ .

The general application of the first principle reads:

(2.3)¶ $\Delta [E]_{cycle} = 0 = W + \sum_k^n Q_k$

where $W$ represents the mechanical energy echanged during the cycle.

The second principle reads:

$\Delta [S]_{cycle} = 0 = \sum_k^n \frac{Q_k}{T_k} + S_c$

Important

Because the creation of entropy during the cycle is necessarly positive or nul, we thus have :

(2.4)¶ $\sum_k^n \frac{Q_k}{T_k} \le 0 \text{ (0 if reversible cycle)}$

Relation Eq.2.4 is the traduction of second principle for cycles. It is known as the Clausius relation.

2.1.2.1. Monotherm thermal energy converters¶

If the system exchange thermal energy with a unique TER

Equation Eq.2.4 traduces that $Q \le 0$ , that is to say that the system provides thermal energy to the TER.

Equation Eq.2.3 traduces that $W = -Q \ge 0$ , thus the system is absorbing mechanical energy.

Important

Thermal machine exchanging thermal energy with only one TER is necessarilly a heat pump

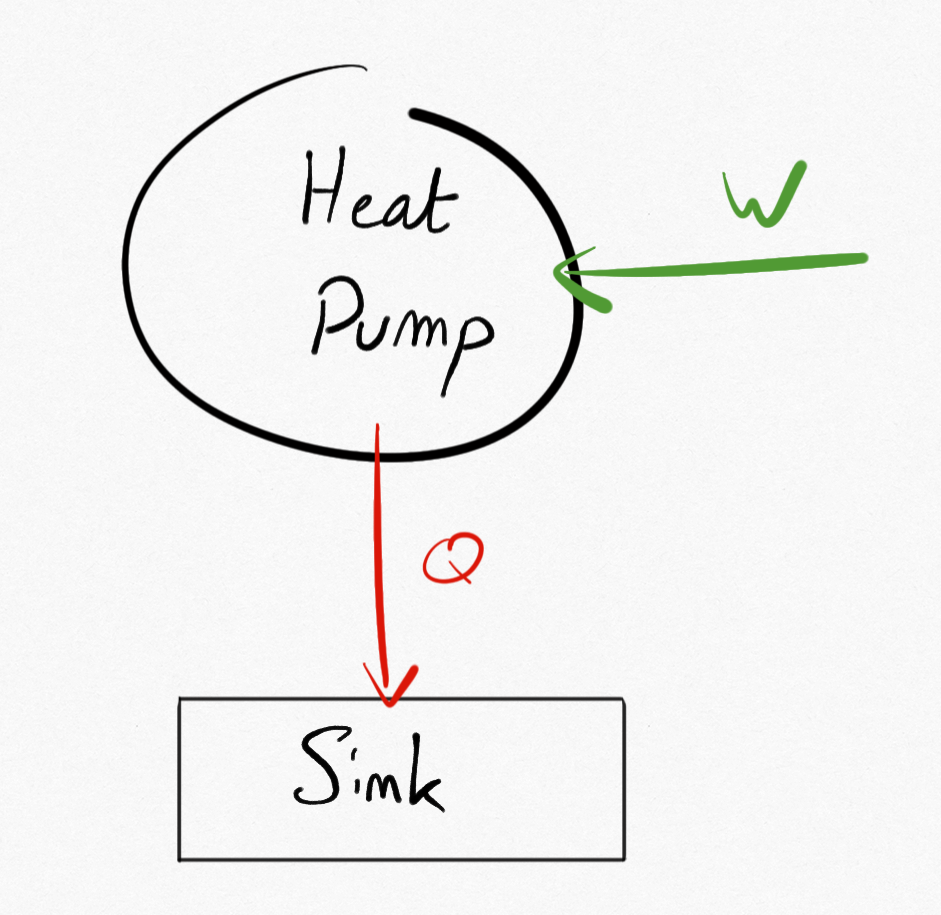
Figure 2.2: A heat pump with a unique TER¶

Examples of such system can be found in nature as for example friction between bodies are consumming mechanical energy to supply thermal energy (heating).

2.1.2.2. Thermal energy converters with two TER¶

We consider that the system is now connected to two TER at different temperatures $T_H$ for the hot one and $T_C$ for the cold one Thanks to equations Eq.2.3 and Eq.2.4 We thus have the two relations:

(2.5)¶ $W + Q_C + Q_H = 0$

and

(2.6)¶ $\frac{Q_C}{T_C} + \frac{Q_H}{T_H} \le 0$

2.1.2.2.1. Case 1: $W < 0$ ¶

The thermal converter is a heat engine.

With equation Eq.2.5, we obtain that:

$-Q_C - Q_H = W < 0$

(2.7)¶ $-\frac{Q_C}{T_C} - \frac{Q_H}{T_C} < 0$

Addig relations Eq.2.6 and Eq.2.7 brings:

$Q_H (\frac{1}{T_H} -\frac{1}{T_C}) < 0$

And because $T_H>T_C$ , necessarily we obtain that $Q_H>0$ . In other words, the machine is absorbing thermal energy to the hot source and provides thermal energy to the cold sink with:

$Q_H > -Q_C > 0$

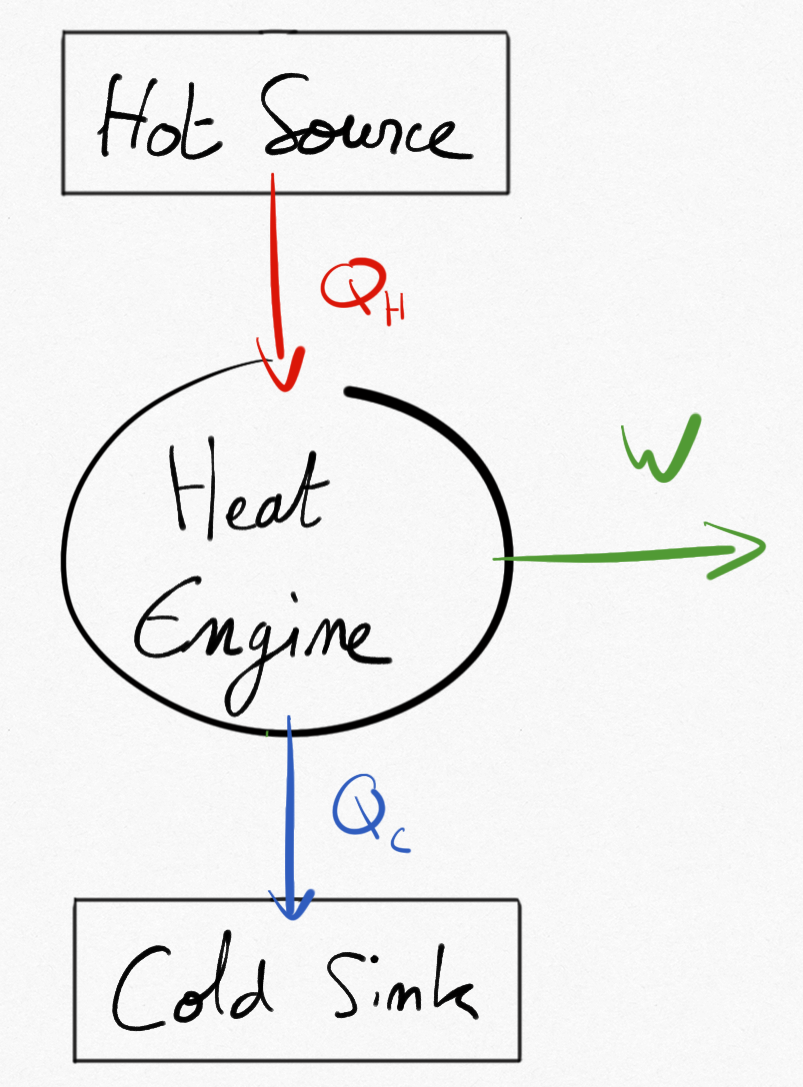
Figure 2.3: Heat Engine between two TER.¶

Important

A heat engine necessarily absorbs thermal energy to a hot source and releases thermal energy to a cold sink.

2.1.2.2.2. Case 2: $W = 0$ ¶

It is easy to show that in this case, the thermal energy is spontaneously exchanged from the hot source to the cold sink with the relation:

$Q_H = -Q_C > 0$

2.1.2.2.3. Case 3: $W > 0$ ¶

The thermal converter is absorbing mechanical energy.

With equation Eq.2.5, we obtain that:

$-Q_C - Q_H = W > 0$

Several possibilities occur:

2.1.2.2.3.1. $Q_H > 0$ : the converter absorbs thermal energy from the hot source¶

In that case, we have

(2.8)¶ $Q_C < - Q_H < 0$

The converter supplies thermal heat to the cold sink.

But equation Eq.2.6 brings:

$-\frac{|Q_C|}{T_C} + \frac{|Q_H|}{T_H} \le 0$

$|Q_H| \le |Q_C|\frac{{T_H}}{T_C}$

If the transformation is reversible, we have $|Q_H| = |Q_C|\frac{{T_H}}{T_C} > |Q_C|$ that is incompatible with Eq.2.8.

2.1.2.2.3.2. $Q_H < 0$ : the converter supplies thermal energy to the hot source¶

if $Q_C < 0$ , the machine is providing $-Q_C-Q_H = W$ . This is a non interesting case for a heat pump.

if $Q_C > 0$ , the machine is absorbing thermal energy from the cold source and supplies thermal energy to the hot sink. This can be a heat pump or a refrigerator.

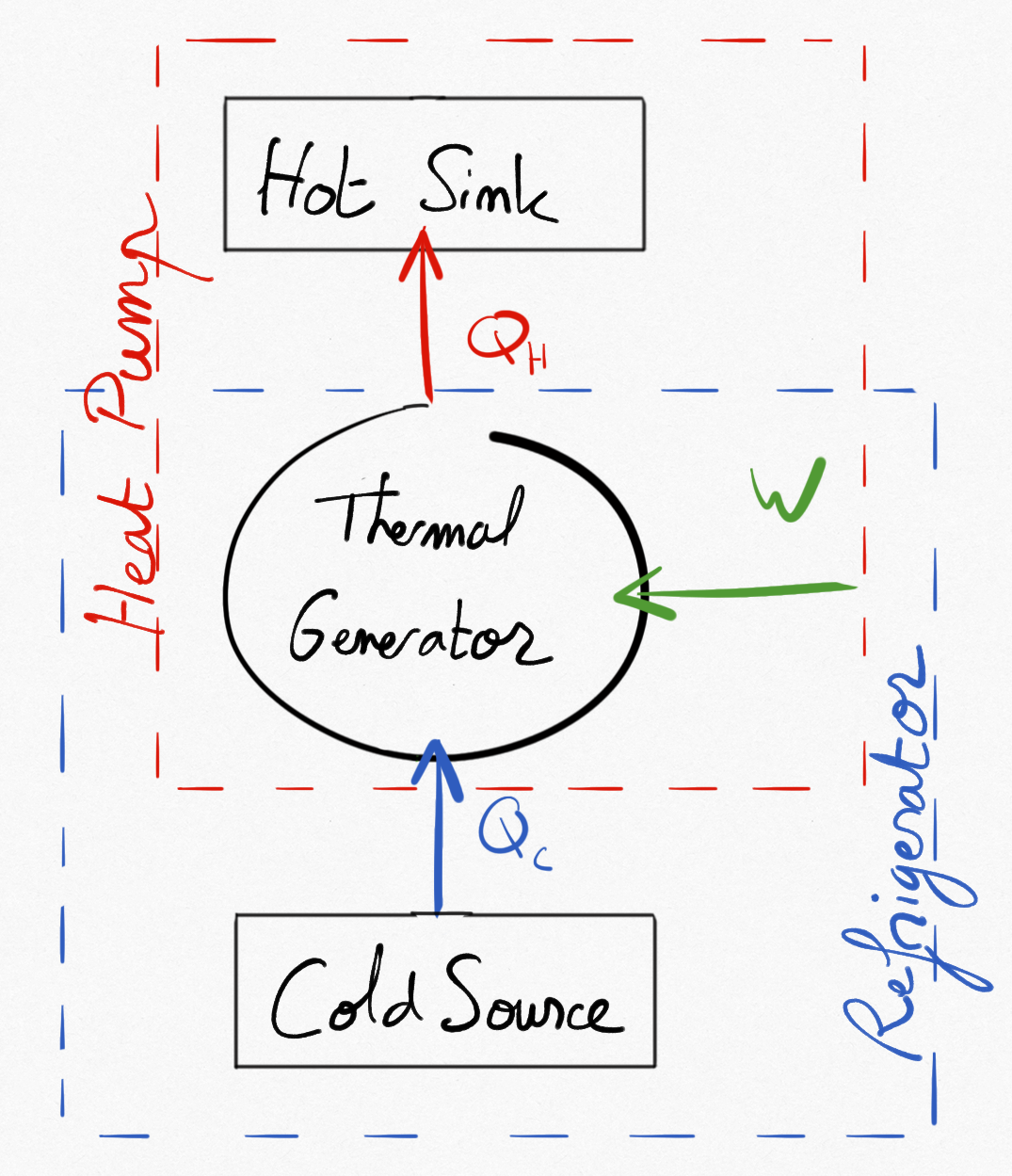
Figure 2.4: Two different heat generators: the heat pump and the refrogerator.¶

Important

A heat pump or a refrigerators absorbs thermal energy to a cold source and releases thermal energy to a hot sink and necessarily riquires a mechanical energy.

2.1. Energy conversion¶

2.1.1. Definitions¶

2.1.1.1. Energy converter¶

2.1.1.2. Energy reservoirs¶

2.1.2. Thermal energy converters¶

2.1.2.1. Monotherm thermal energy converters¶

2.1.2.2. Thermal energy converters with two TER¶

2.1.2.2.1. Case 1: ¶

2.1.2.2.2. Case 2: ¶

2.1.2.2.3. Case 3: ¶

2.1.2.2.3.1. : the converter absorbs thermal energy from the hot source¶

2.1.2.2.3.2. : the converter supplies thermal energy to the hot source¶

2.1.2.2.1. Case 1: $W < 0$ ¶

2.1.2.2.2. Case 2: $W = 0$ ¶

2.1.2.2.3. Case 3: $W > 0$ ¶

2.1.2.2.3.1. $Q_H > 0$ : the converter absorbs thermal energy from the hot source¶

2.1.2.2.3.2. $Q_H < 0$ : the converter supplies thermal energy to the hot source¶