2.2. Cycles¶

2.2.1. Thermal machines cycles and efficiency (def)¶

We consider in this section thermal machines working between two thermal reservoirs. In these machines, the working fluid is the thermodynamic system that exchange thermal energies between a hot reservoir (at temperature $T_H$ ) and a cold one (at temperature $T_C$ ). Following results of Section 2.1: , it can supply mechanical energy (it is thus a heat engine) or absorb mechanical energy (it can be a heat pump or refrigerator).

2.2.1.1. Evolutions during a cycle¶

In a thermal machine, the working fluid is evolving on a thermodynamic cycle. Let us consider a transformation $a$ from a state 1 to a state 2 as represented on Figure 2.5:

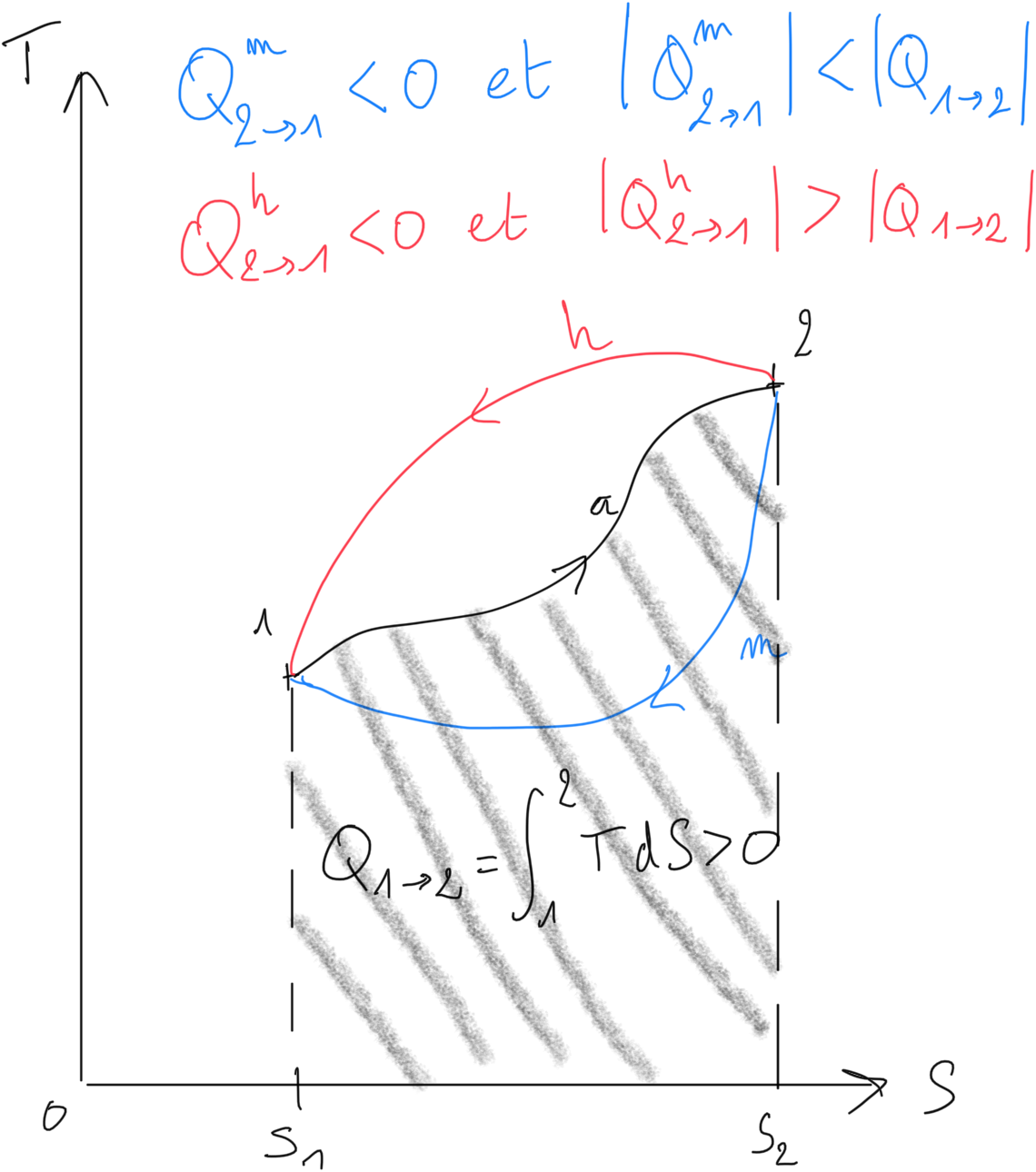
Figure 2.5: Entropic diagram representing thermal energy exchanged during a cycle.¶

During reversible transformation from 1 to 2, the heat exchanged is positive and corresponds to the hatched area. During this transformation, the fluid is absorbing thermal energy $Q_{1\rightarrow 2}>0$ .

For the return from state 2 to 1, the fluid will supply thermal energy $Q_{2\rightarrow 1}<0$ . Thus two possibilities occurs:

The fluid follows transformation $m$ (in blue): $|Q_{2\rightarrow 1}|<|Q_{1\rightarrow 2}|$ such that the thermal energy exchanged during cycle is positive. The application of first principle immplies that the mechanical work will be negative: this is a heat engine.

The fluid follows transformation $h$ (in red): $|Q_{2\rightarrow 1}|>|Q_{1\rightarrow 2}|$ such that the thermal energy exchanged during cycle is negative. The application of first principle immplies that the mechanical work will be positive: this can be a heat pump or a refirgerators.

From this observation, one can observe several things:

Remarks

When a cycle is followed clockwise in the entropic diagram (T,S), the cycle is describing a heat engine
When a cycle is followed reversed clockwise in the entropic diagram (T,S), the cycle is describing a heat pump or a refrigerator
Any cycle can be used as a basis to develop a thermal machine.

2.2.1.2. Energy conversion efficiency¶

The economice notion of efficiency is generally defined by the ratio bewteen the usefull energy provided by the machine and its energy absorption, or in other words the ratio between benefits of a thermodynamic system and costs:

$\eta \equiv \frac{\text{benefits}}{\text{costs}}$

2.2.1.2.1. Heat engine and thermal efficiency¶

For a heat engine, a mechanical energy $-W$ is produced (benefit) from a thermal energy absorption from hot source $Q_H$ (cost). This defines the thermal efficiency of the heat engine:

$\eta_{th} = \frac{-W}{Q_H}$

Thanks to the first principle, it can also be written as:

(2.9)¶ $\eta_{th} = \frac{Q_H + Q_C}{Q_H} = 1 + \frac{Q_C}{Q_H} = 1 - \frac{|Q_C|}{|Q_H|}$

Remark

For internal combustion engines, the thermal efficiency is about 25% for gasoline engines and 40% for diesel engines. For gas turbine, the thermal efficiency can reach 60%.
A great part of chemical energy (from fuel combustion) is then dissipated in heat and released in environnement (to the cold sink).

2.2.1.2.2. Heat generators and coefficient of performance (COP)¶

For a heat pump or refrigerators, a mechanical energy $W$ is consumed (cost) and the benefits depend on the usefull thermal energy exchanged. Because these ratio are generally greater than 1, we talk about coefficient of performance:

For a heat pump :

(2.10)¶ $COP_{HP} = \frac{-Q_H}{W} = \frac{Q_H}{Q_H+Q_C} = \frac{1}{1 + \frac{Q_C}{Q_H}} = \frac{1}{1 - \frac{|Q_C|}{|Q_H|}}$

For a refrigerator :

(2.11)¶ $COP_{R} = \frac{Q_C}{W} = \frac{Q_C}{-Q_H-Q_C} = \frac{1}{-\frac{Q_H}{Q_C}-1} = \frac{1}{\frac{|Q_H|}{|Q_C|}-1}$

2.2.2. Carnot cycle¶

If a thermal machine is working between two TER in a reversible maneer, then it must exchange with both TER following isothermal transformation. These two isothermal transformation can thus be linked using:

2 isentropes: this is the Carnot cycle

2 isochores: this is the Stirling cycle

2 isobares: this is the Ericsson cycle

These three cycles are ideal cycles for a thermal machine working between two TER and serve as reference cycle providing the maximum thermal efficiencies/COP.

2.2.2.1. Carnot heat engine¶

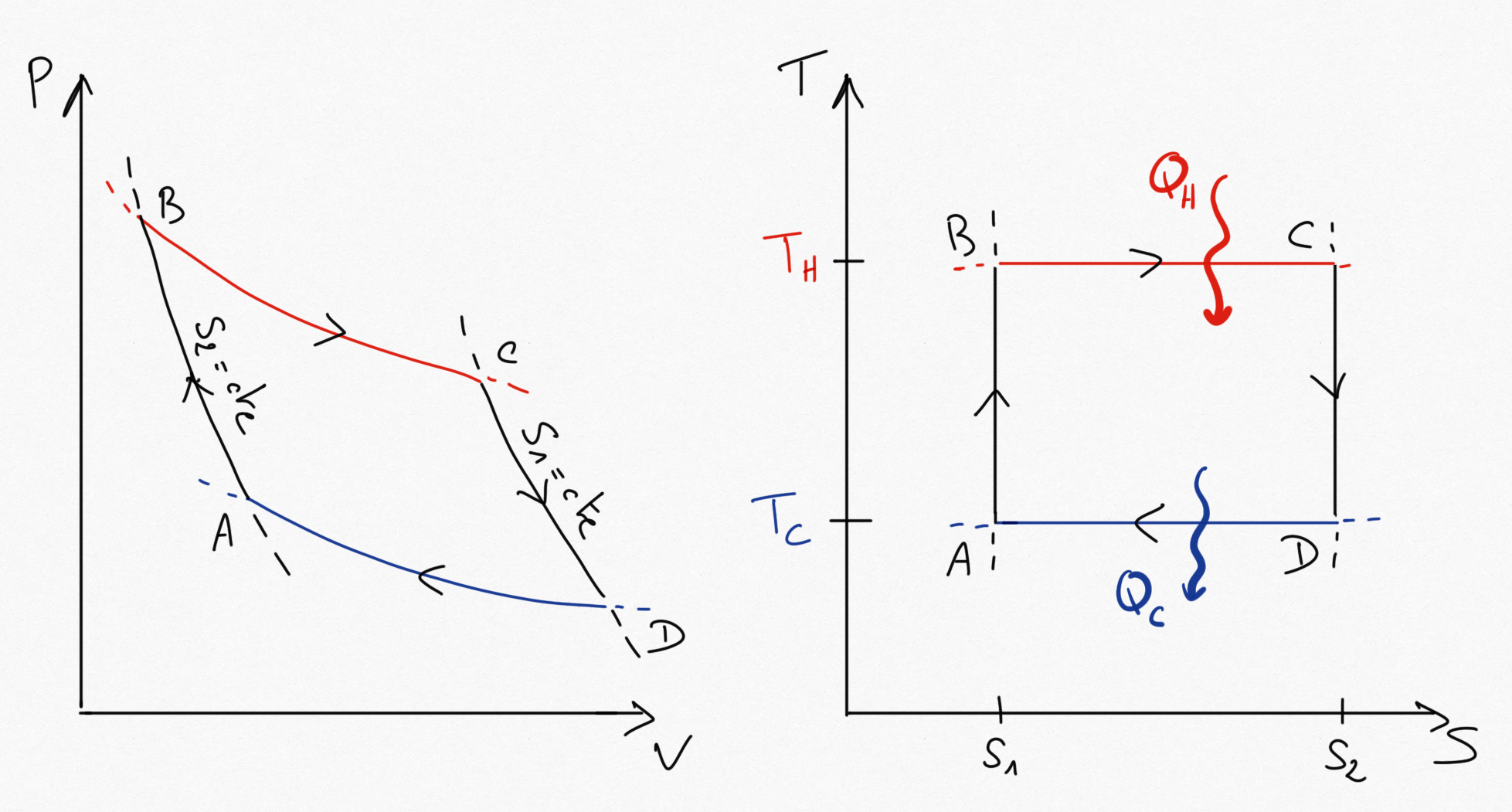
Figure 2.6: Carnot cycle (for a heat engine).¶

It is easy to remark that in the reversible isothermes, we have $Q_C = T_C (S_1-S_2)$ and $Q_H = T_H (S_2-S_1)$ , such that thanks to equation Eq.2.9, it is easy to show that:

(2.12)¶ $\eta_{th,C} = 1 - \frac{T_C}{T_H}$

As $T_H>T_C$ , the carnot thermal efficiency is always lower than 1.

Remark

The Carnot thermal efficiency gives the maximum efficiency that can be reached by a heat engine between two TER.
For example, the Carnot thermal efficiency of a thermal power plant beteen $T_H = 1000 K$ (combustion temperature) and $T_C = 300 K$ (ambiant) is about 70%. Real thermal efficiency of such power plant reaches 40% because of non reversibility.

2.2.2.2. Carnot heat pump/refrigerators¶

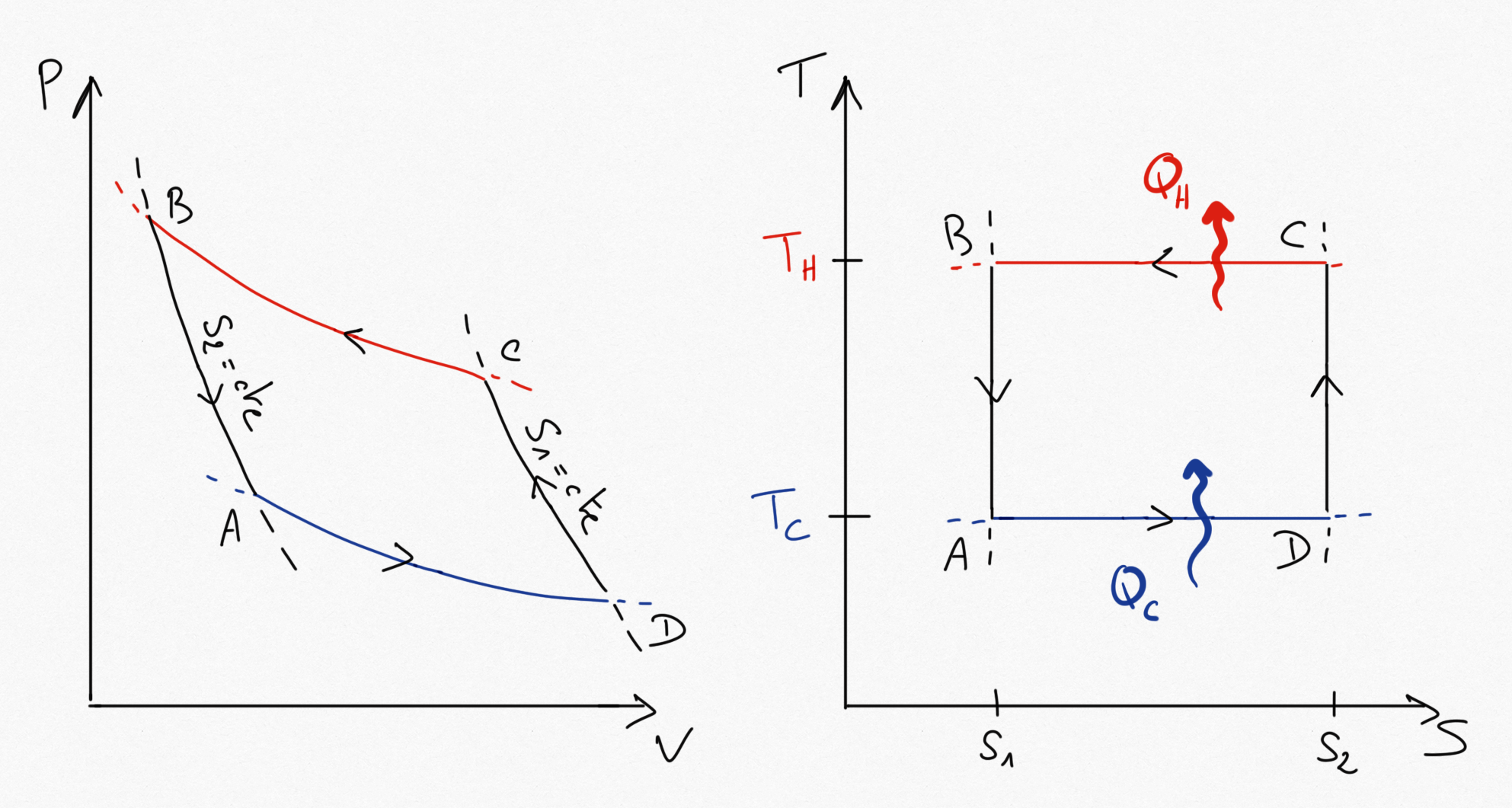
Figure 2.7: Carnot cycle (for a heat generator: heat pump or refrigerator).¶

This times, in the reversible isothermes, we have $Q_C = T_C (S_2-S_1)$ and $Q_H = T_H (S_1-S_2)$ .

If this is a heat pump, the coefficient of performance Eq.2.10 becomes:

(2.13)¶ $COP_{HP,C} = \frac{1}{1 - \frac{T_C}{T_H}} > 1$

If this is a refrigerator, the coefficient of performance Eq.2.11 becomes:

(2.14)¶ $COP_{R,C} = \frac{1}{\frac{T_H}{T_C}-1}$

If the $COP_{HP,C}$ of a heat pump is greater than 1, we cannot conclude for a refrigerator.

2.2.3. Other cycles¶

It is shown that the thermal efficiency of a Carnot’s cycle is the better thermal efficiency a heat engine can reach between two TER. It is let to the reader to apply the same reasonement to a heat pump or refrigerator.

2.2.3.1. Heat engine Reversible cycles¶

If we consider any reversible cycle, there are two possibilities:

If the cycle is working between the two TER $T_C$ and $T_H$ , then it will have the same thermal efficiency as Carnot cycle.

Otherwise, it can be decomposed in an infinity of reversible cycles $i$ working between two TER whith temperatures $T_{Ci} > T_C$ and $T_{Hi} < T_H$ who have a thermal efficiency lower than Carnot efficiency between $T_C$ and $T_H$ . As a result, the global efficiency will be lower than Carnot’s efficiency.

2.2.3.2. Heat engine irreversible cycles¶

Thanks to second principle of thermodynamics, a heat engine that exchange between two TER during a cycle will guarantee that (equation Eq.2.4):

$\frac{Q_H}{T_H} + \frac{Q_C}{T_C} \le 0 \text{ (0 if reversible cycle)}$

That can be rewritten as:

$\frac{|Q_H|}{T_H} - \frac{|Q_C|}{T_C} \le 0$

Or:

$-\frac{T_C}{T_H} \ge -\frac{|Q_C|}{|Q_H|}$

And finally, thanks to relation Eq.2.9, the thermal efficiency of a heat pump reads:

$\eta_{th} = 1 - \frac{|Q_C|}{|Q_H|} \le 1 - \frac{T_C}{T_H}$

In other words, the thermal efficiency of any irreversible cycle between two TER will be lower than the Carnot’s thermal efficiency.

2.2.4. Importance of Carnot cycle¶

Caution

Carnot cycle, as any reversible cycle working between two TER (Ericsson, Stirling, etc.) may serve as reference for real cycles describing thermal machines :

In a heat engine, thermal exchanged cannot be represented by isothermal transformations. It is more often isobaric/isochore transformations (or a combination of both).
In a heat pump (or refrigerator), it is possible to be close to isothermal transformations during heat exchanges using phase change properties of a liquid-vapor couple ( $p^{sat}(T)$ ).
Whatever the system is, transformations will be non reversibles.