3.1. Compressions/Expansions¶

3.1.1. Expression of technical work¶

For a closed system (cf. thermodynamics course), the work of reversible pressure forces for a transformation between state 1 and 2 expresses as:

(3.1)¶ $w_{12} = -\int_1^2 pdv$

For an open system (crossed by a fluid flow), the balance energy equation has been obtained in Section 1.1: and reads per unit of mass crossing the system:

(3.2)¶ $h_2 - h_1 = w_{t,12} + q_{12}$

During the transformation and thanks to the Gibbs equation, we also have:

(3.3)¶ $dh = Tds + vdp$

Such that between state 1 and 2:

(3.4)¶ $h_2 - h_1 = \int_1^2 Tds + \int_1^2 vdp$

Relations Eq.3.2 and Eq.3.4 applied to a reversible transformation allows to express the technical work $w_t$ :

(3.5)¶ $w_{t,12} = \int_1^2 vdp$

Important

For a reversible transformation:

The specific pressure work in a closed system expresses as:

$w_{12} = - \int_1^2 pdv$
The specific technical work in an open system expresses as:

$w_{t,12} = \int_1^2 vdp$

According to the system under study, the work will be:

The opposite of the aera under the curve in (p,v) plane for closed systems

The aera on the left of the curve in the (p,v) plane for open systems

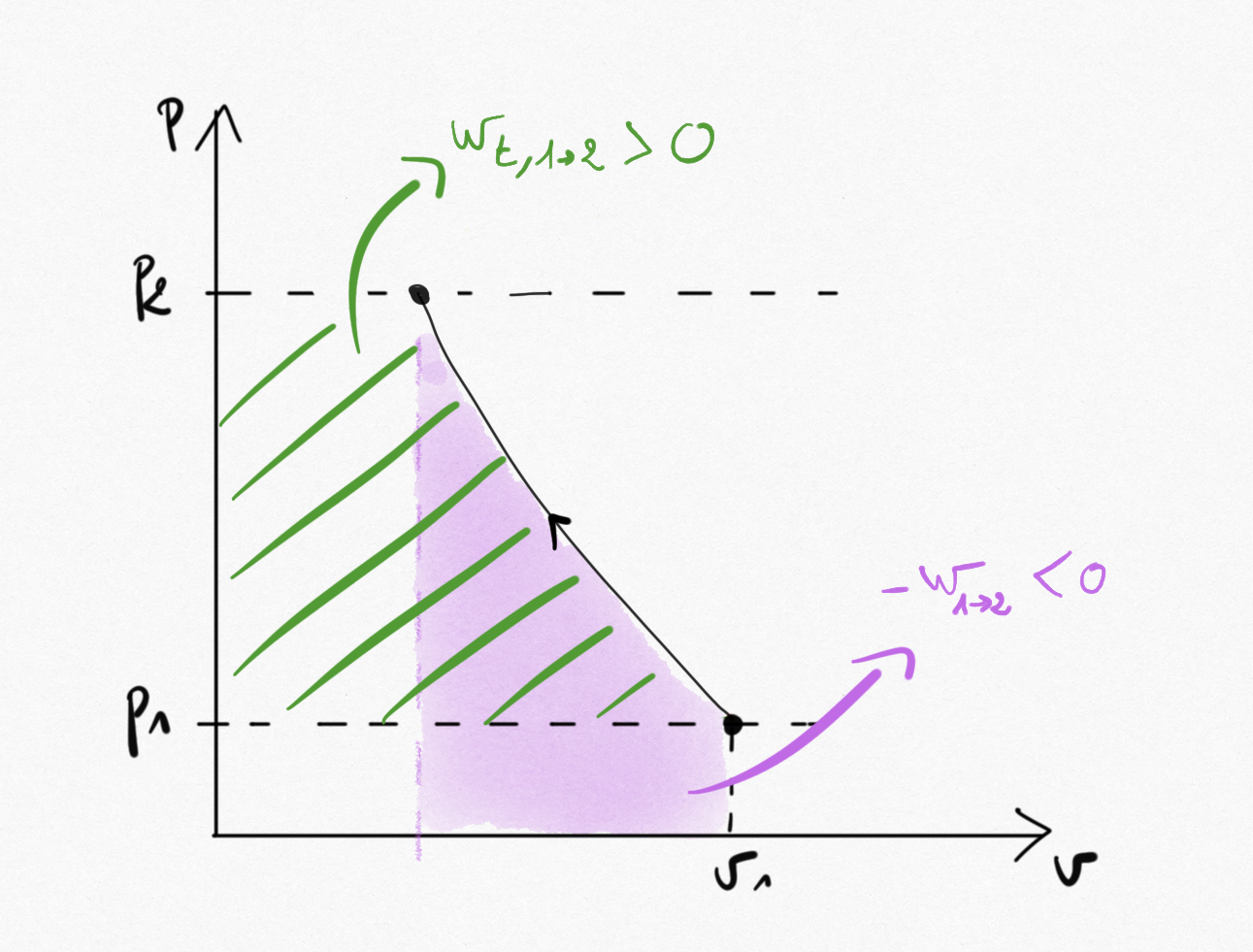
Figure 3.1: work for a closed system transformation between state 1 and 2 (pink aera) and for an open system between same states (green stripes aera).¶

3.1.2. Reversible compression/expansion¶

Reversible compressions (or expansions) can be:

Isotherme: $T=cte$

Polytropic: $pv^k=cte$

Isentropic: $s=cte$

A representation of these transformations in the Clapeyron diagram is presented in figure Figure 3.2:

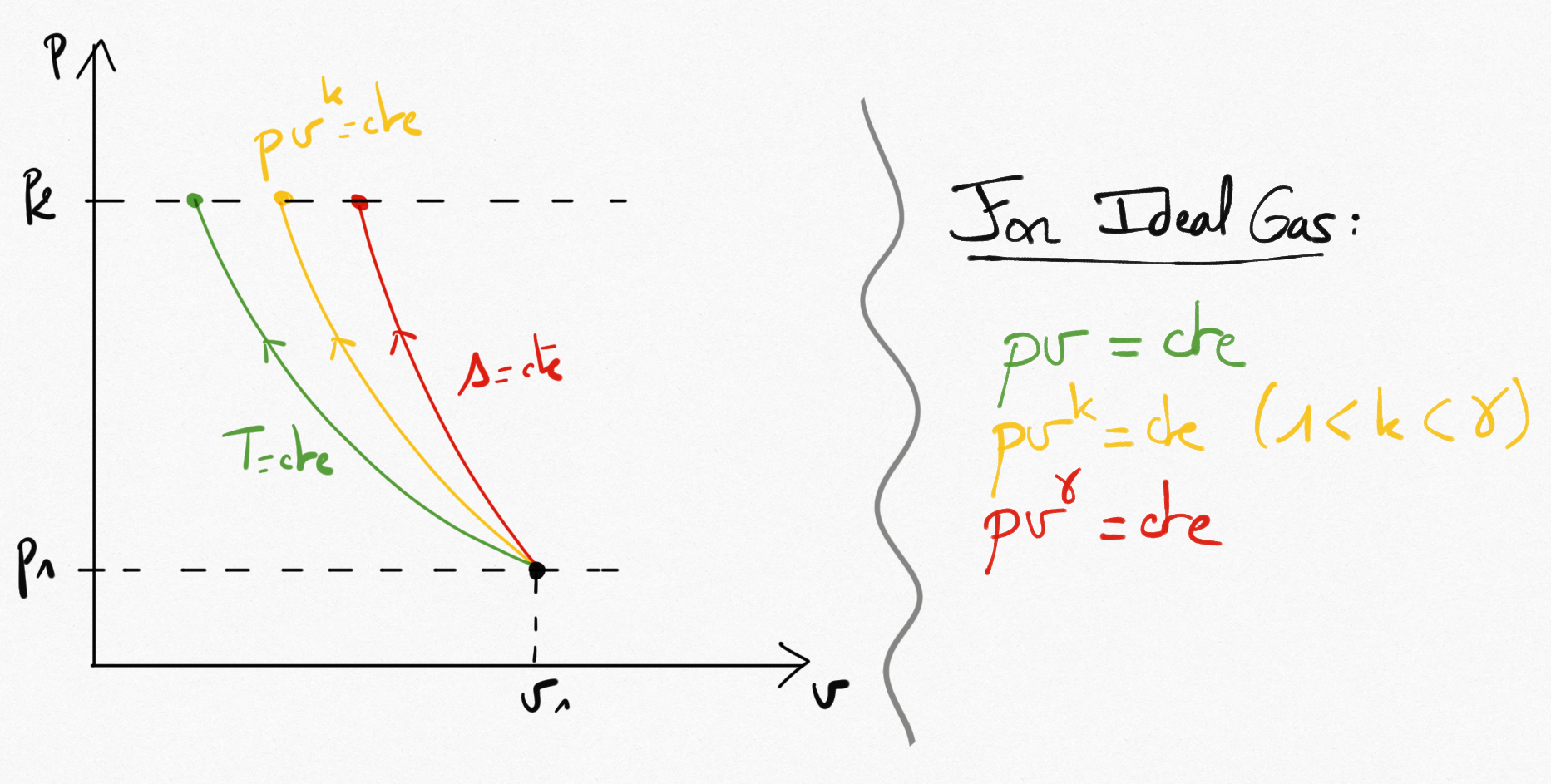
Figure 3.2: Isotherme, Polytropic and Isentropic reversible compressions in (p,v).¶

For ideal gas equation of state, the expressions of specific works are recalled hereafter.

3.1.2.1. Isothermal transformation¶

(3.6)¶ $w_{12}^T = w_{t,12}^T = rT ln \left( \frac{p_2}{p_1} \right)$

3.1.2.2. Isentropic transformation¶

(3.7)¶ $w_{12}^s = \frac{rT_1}{\gamma-1} \left[ \left( \frac{p_2}{p_1} \right)^{\frac{\gamma-1}{\gamma}} -1 \right]$

and

(3.8)¶ $w_{t,12}^s = \frac{\gamma rT_1}{\gamma-1} \left[ \left( \frac{p_2}{p_1} \right)^{\frac{\gamma-1}{\gamma}} -1 \right]$

3.1.2.3. Polytropic transformation¶

(3.9)¶ $w_{12}^p = \frac{rT_1}{k-1} \left[ \left( \frac{p_2}{p_1} \right)^{\frac{k-1}{k}} -1 \right]$

and

(3.10)¶ $w_{t,12}^p = \frac{krT_1}{k-1} \left[ \left( \frac{p_2}{p_1} \right)^{\frac{k-1}{k}} -1 \right]$

3.1.3. Real Compressions/Expansions¶

If during a real compression (or expansion) the transformation remains irreversible, calculs are performed thanks to associated reversible transformations and the knowledge of corresponding efficiencies that are known as manufacturer’s data.

For a compression, real work (positive) is always greater than the corresponding theoretical reversible transformation, such that we define the compression efficiency of a compressor by:

(3.11)¶ $\eta_{C} = \frac{w_{t,rev}}{w_{t,real}} \leq 1$

For an expansion, the reversed situation appears as the technical work provided by the machine is always lower than the corresponding theoretical reversible transformation such that we define the expansion efficiency of a turbine by:

(3.12)¶ $\eta_{T} = \frac{w_{t,real}}{w_{t,rev}} \leq 1$

Thus depending on insulating of compressor/turbine, one will talk about isentropic, isothermic or polytropic efficiency.

3.1.3.1. Adiabatic transformations/ isentropic efficiencies¶

When the compression/expansion machine is thermically insulated, we use the isentropic efficiency that provides the ratio between the real work and those associated to the corresponding reversbile transformation (isentropic). The real transformation induces an increase of the entropy.

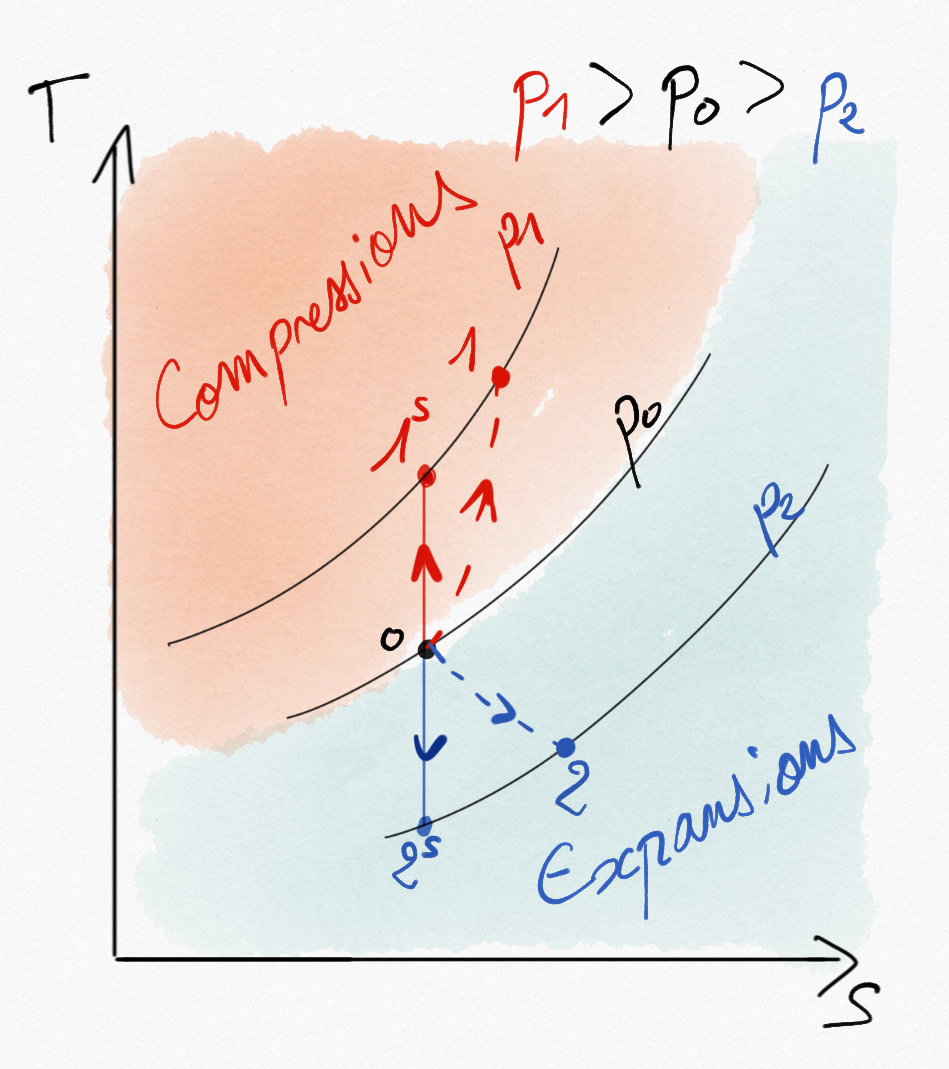
Figure 3.3: Adiabatic compression and expansion. Comparaison between isentropic path and real path.¶

Because the transformations are adiabatics, the isentropic efficiencies for compressors or turbines become:

(3.13)¶ $\eta_{C}^S = \frac{h_{t,1}^S-h_{t,0}}{h_{t,1}-h_{t,0}} \qquad \text{and} \qquad \eta_{T}^S = \frac{h_{t,2}-h_{t,0}}{h_{t,2}^S-h_{t,0}}$

Simplifications

When Kinetic energy variations are negligible
When the working fluid is consiered as an ideal gas

Isentropic efficiencies become:

$\eta_{C}^S = \frac{T_{1}^S-T_{0}}{T_{1}-T_{0}} \qquad \text{and} \qquad \eta_{T}^S = \frac{T_{2}-T_{0}}{T_{2}^S-T_{0}}$

Using Laplace relations for isentropic transformation, we get:

(3.14)¶ $\eta_{C}^S = \frac{T_{0} r_p^{\frac{\gamma-1}{\gamma}}-T_{0}}{T_{1}-T_{0}} \qquad \text{and} \qquad \eta_{T}^S = \frac{T_{2}-T_{0}}{T_{0} r_p^{\frac{\gamma-1}{\gamma}}-T_{0}}$

Then, it is possible to determine easily the final temperature of the working fluid by knowledge of the pressure ratio ( $r_p = p_{final}/p_{init}$ ) and isentropic efficiencies.

3.1.3.2. Non adibatic transformations/ polytropic efficiencies¶

When the compression/expansion is not thermically insulated, isentropic efficiencies are no longer valid and we use the polytropic efficiency providing the ratio between the real work and those associated to the corresponding reversible polytropic transformation leading to the same thermodynamic state at the end of compression/expansion.

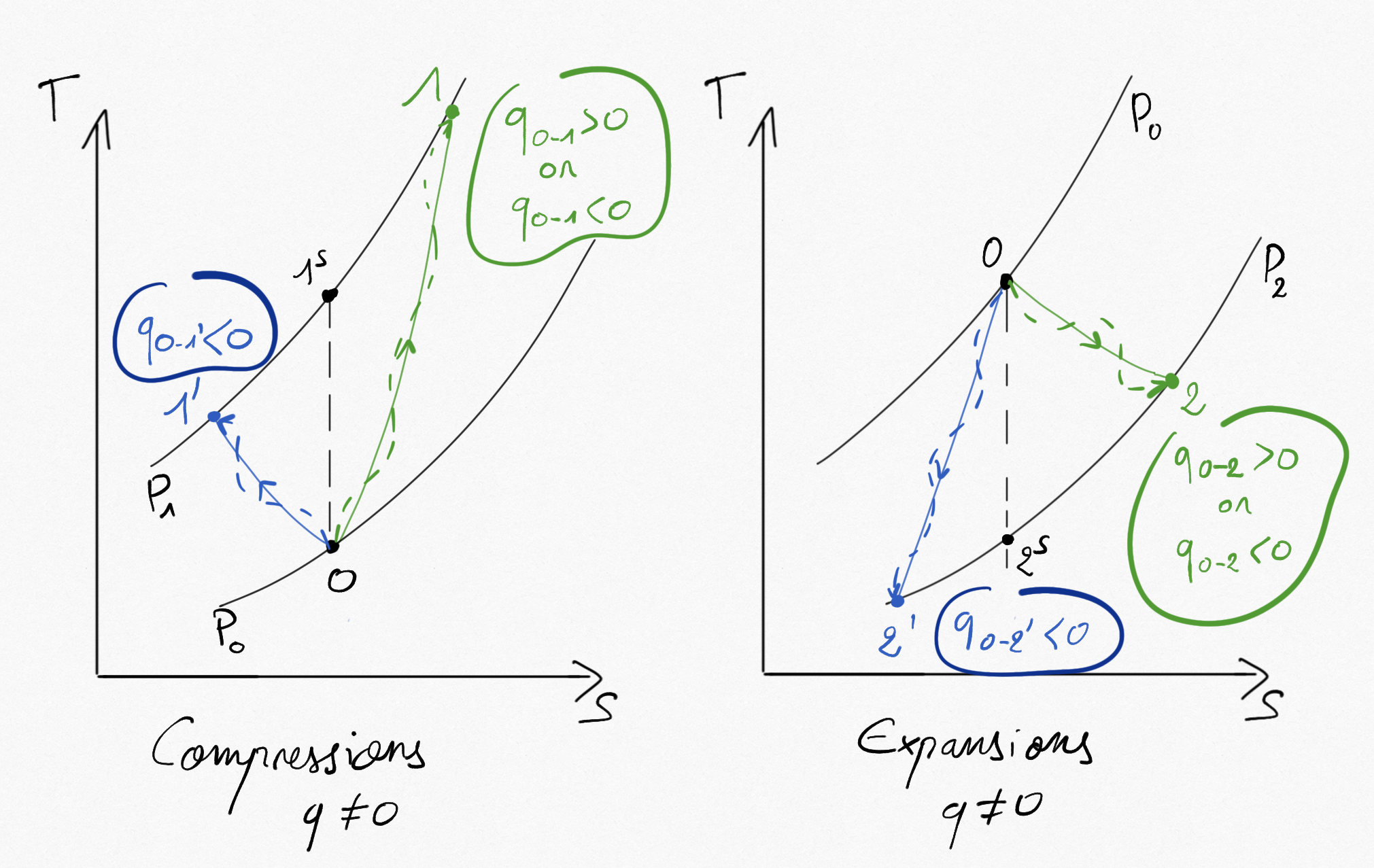
Figure 3.4: Non adiabatic compressions and expansions. Comparaison between polytropic path (lines) and real path (dash lines).¶

Possible transformation with heat exchanges during compression/expansions can lead to different possibilities summarized in Figure 3.4: . Whatever the case is, we have for the polytropic ( $p$ ) and real transformation:

$w_{t}^P = (h_{t,i}-h_{t,0}) - q_P \qquad \text{and} \qquad w_{t} = (h_{t,i}-h_{t,0}) - q$

Such that the polytropic efficiencies express as:

(3.15)¶ $\eta_{C}^P = \frac{(h_{t,1}-h_{t,0})-q_P}{(h_{t,1}-h_{t,0})-q} \qquad \text{and} \qquad \eta_{T}^P = \frac{(h_{t,2}-h_{t,0}) - q}{(h_{t,2}-h_{t,0}) -q_P}$

Simplifications

When Kinetic energy variations are negligible
When the working fluid is consiered as an ideal gas

The technical work for a polytropic transformation is given by relation Eq.3.10, and the real technical work expresses as:

$w_t = (h_{t,i}-h_{t,0}) - q = \frac{\gamma r}{\gamma -1} T_0 (r_p^{\frac{k-1}{k}}-1) - q$

Polytropic efficiencies thus become:

(3.16)¶ $\eta_{C}^P = \frac{ \frac{k}{k-1} (r_p^{\frac{k-1}{k}}-1)} { \frac{\gamma }{\gamma -1} (r_p^{\frac{k-1}{k}}-1) - \frac{q (\gamma-1)}{r T_0} } \qquad \text{and} \qquad \eta_{T}^P = \frac{ \frac{\gamma }{\gamma -1} (r_p^{\frac{k-1}{k}}-1) - \frac{q (\gamma-1)}{r T_0} } {\frac{k}{k-1} (r_p^{\frac{k-1}{k}}-1)}$