4.3. Steam turbines¶

In the preceding section, gas turbines have been studied. We have seen that gas turbine cycles are generally linking two isentropes to other transformations (isobare, isochores, etc.). It is indeed diffult to approach isothermal transformations in such cyles (only approach with an important number of compression/expansion stages Section 4.2.5: ). When using phase change it becomes easier as isobare are also isothermes in the equilibirum two-phase flow. Machine using phase change are named steam turbines and they are commonly found in power plants (nuclear or not) where they use water as working fluid.

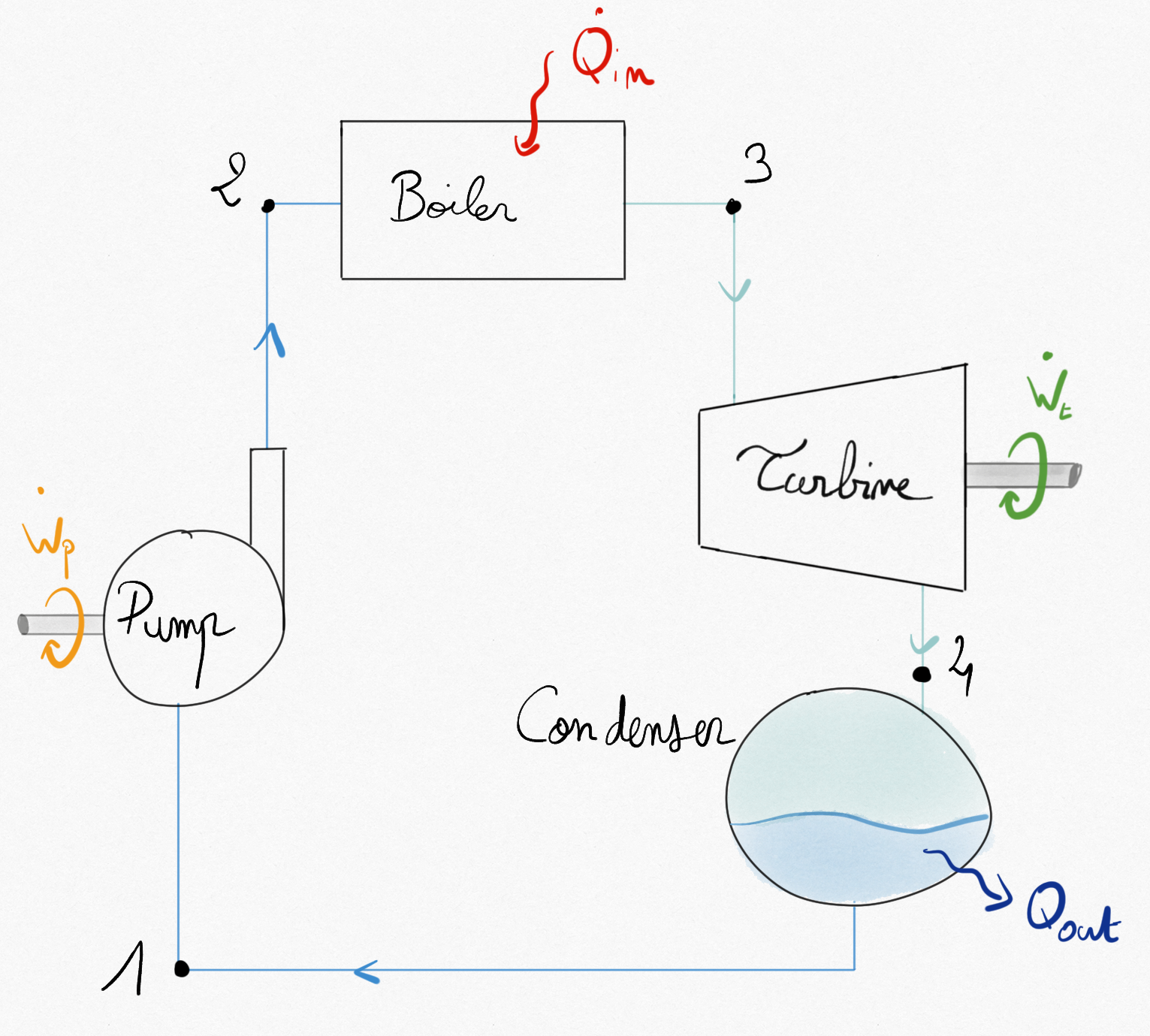
Figure 4.22: Component of a simple steam turbine.¶

4.3.1. Vapor Carnot cycle¶

The better thermal efficiency for thermal engine is obtain thanks to the Carnot cycle

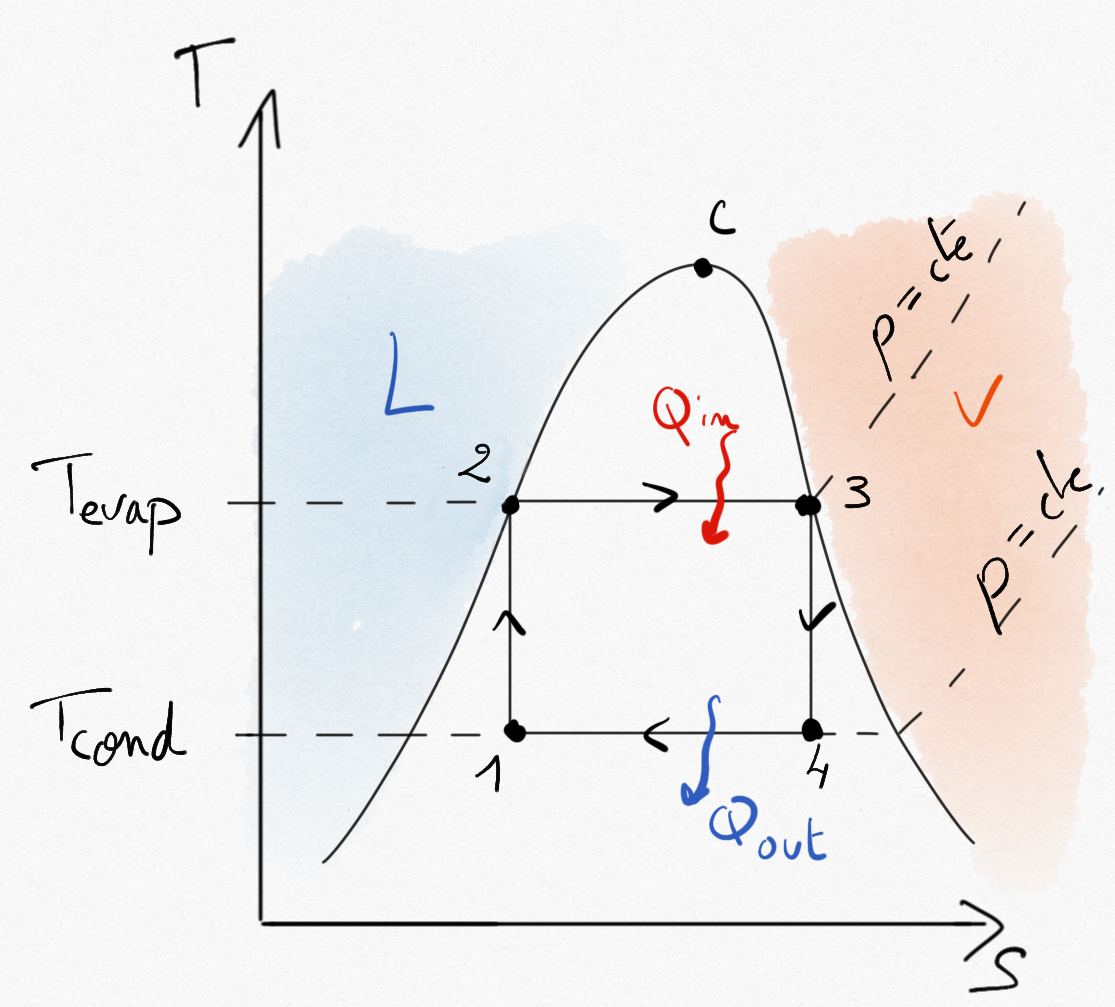
Figure 4.23: Carnot cycle using phase change for a steam turbine. The cycle is included under the saturation curve.¶

As seen in Section 2.2.2.1: the maximum efficiency with phase change between $T_{cond}$ and $T_{evap}$ is:

$\eta_{th,C} = 1 - \frac{T_{cond}}{T_{evap}}$

Important

The Carnot cycle cannot been used without modifications because of technical difficulties:

It is very difficult to compress at constant entropy a two-phase mixture $\rightarrow$ The fluid is entirely condensed to be compress by a pump: We obtain the Rankine cycle (Section 4.3.2: ).

Presence of liquid droplets in the turbine will erode the blades $\rightarrow$ The fluid is then entirely evaporated and the vapor is overheated: We obtain the Hirn cycle (Section 4.3.3: ).

4.3.2. Rankine cycle¶

To prevent the presence of liquid-vapor mixture during the compression, the fluid is entirely condensed.

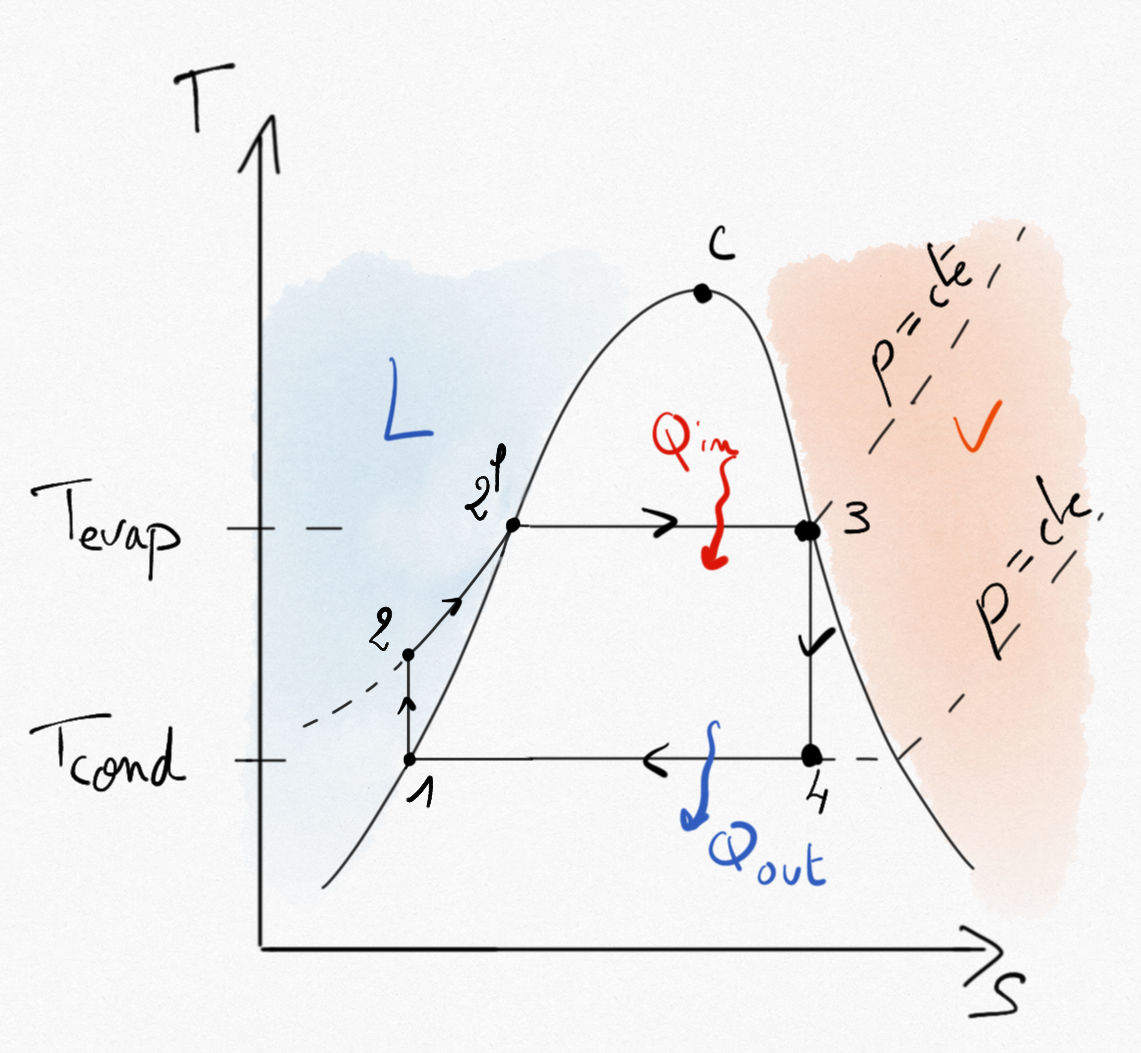
Figure 4.24: Rankine cycle for a steam turbine.¶

As for any heat engine (Eq.2.9), the thermal efficiency for a steam turbine is:

$\eta_{th} = 1 - \frac{|q_{41}|}{|q_{23}|}$

Because no machine is working in transformations 2-3 and 4-1, application of the balance energy equation reads:

$|q_{23}| = \dot{m} (h_3-h_2) \qquad \text{ and } \qquad |q_{41}| = \dot{m} (h_4-h_1)$

such that the thermal efficiency of steam turbines becomes:

(4.15)¶ $\eta_{th} = 1 - \frac{h_4-h_1}{h_3-h_2}$

Caution

The fluid can not be considered as an ideal gas since a phase change occurs from liquid to vapor and reversely. In practice calculs are performed thanks to thermodynamics tables.

4.3.3. Hirn cycle¶

To limit a two important quantity of liquid droplets in the turbine, the vapor is overheated.

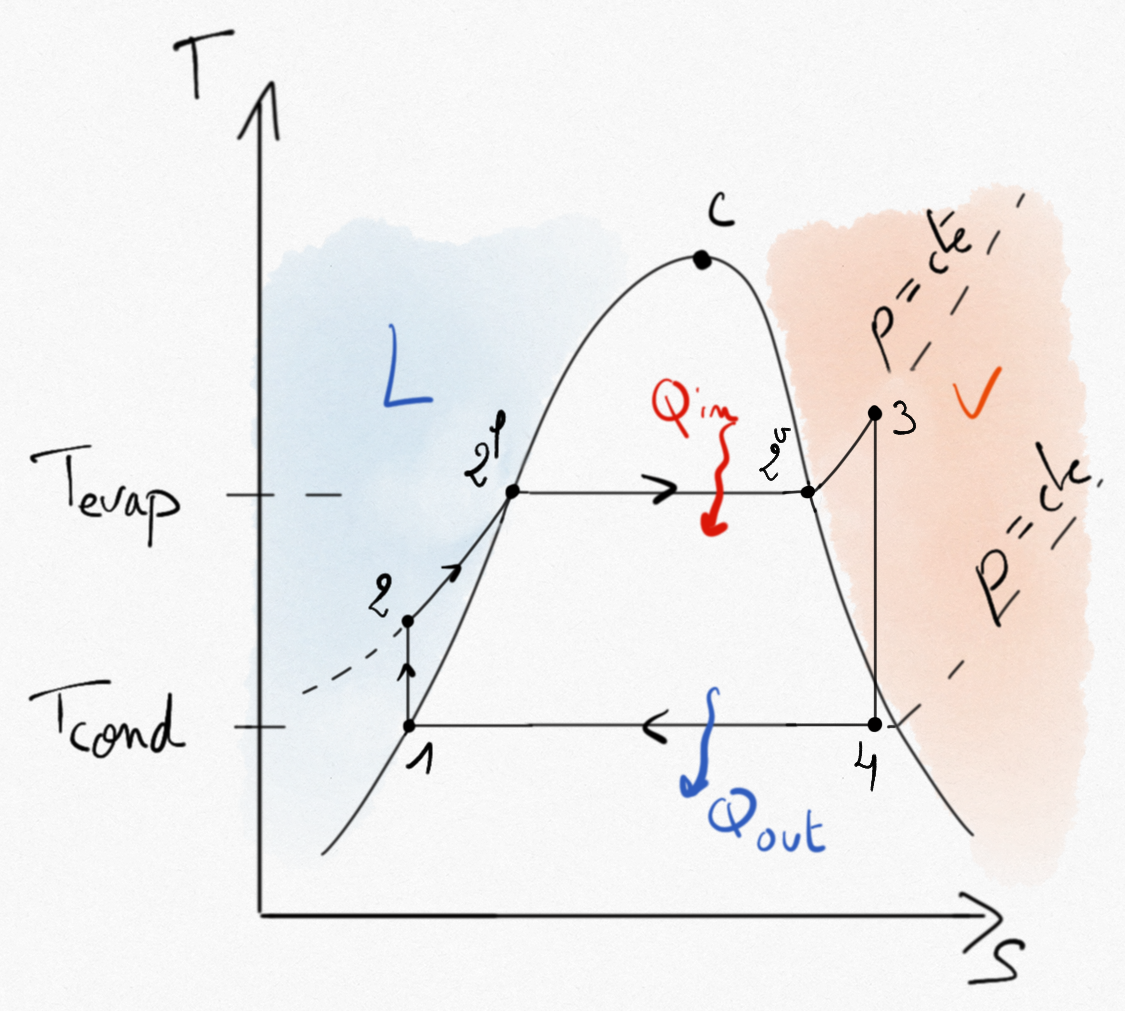
Figure 4.25: Hirn cycle for a steam turbine.¶

Expression of thermal efficiency Eq.4.15 remains unchanged.

4.3.3.1. Improving the Hirn cycle¶

The net specific technical work during cycle is obtain thanks to the first principle applied to the cycle:

$w_{t,net} = -q_{cycle}$

The net specific work supplied by the steam turbine is thus represented by the aera inside the Hirn cycle in the (T,s) plane.

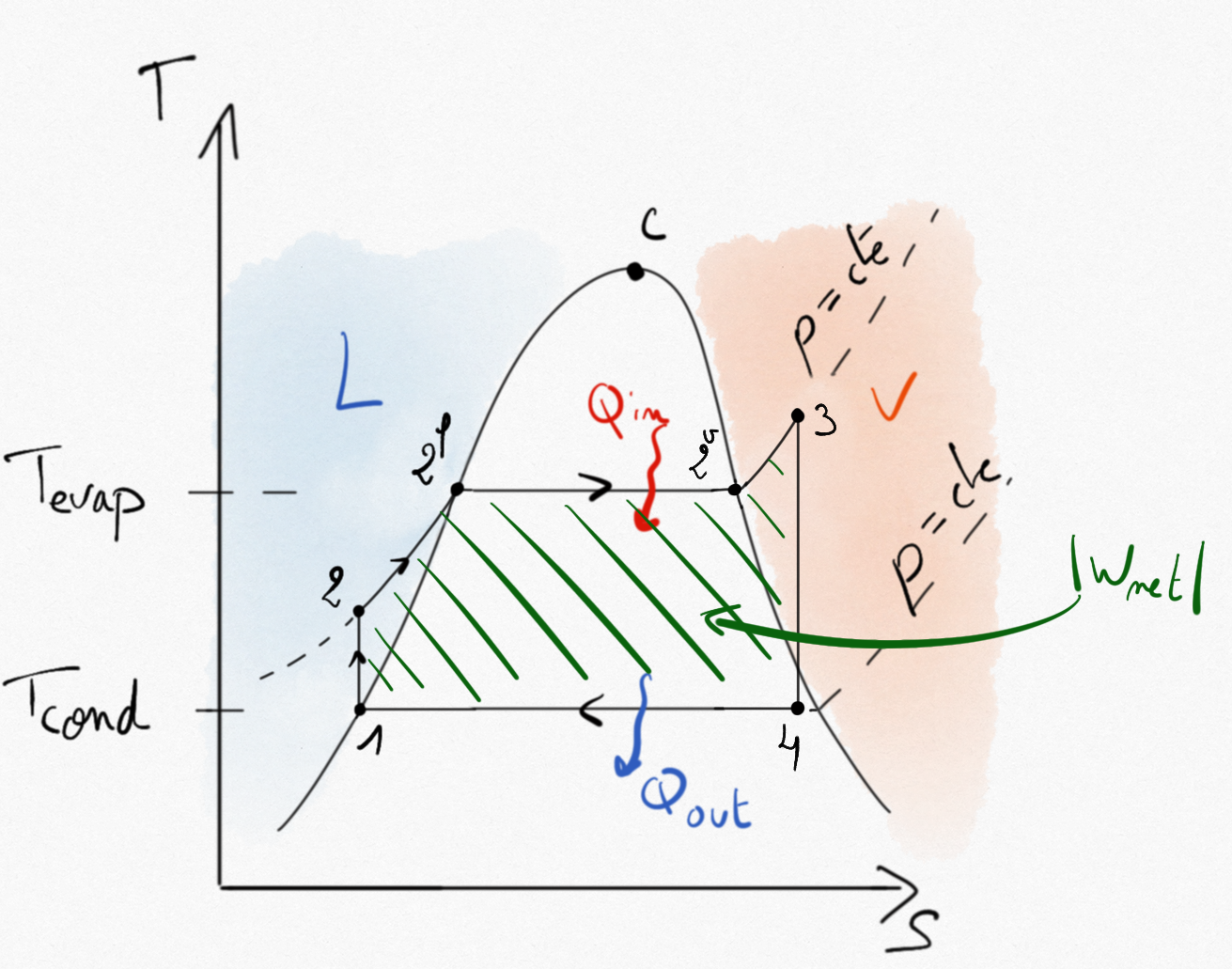
Figure 4.26: The specific technical work supplied by the steam turbine corresponds to the aera inluded in the Hirn cycle.¶

As seen before, phase change induces the use of Hirn cycle to prevent the presence of two-phase mixtures in the pump and in the turbine. This implies also that some portion of heat echanges in the Hirn cycle are not isothermal transformations ( $2-2^l$ and $2^v-3$ ). Consequentely, the thermal efficiency is not as good as it can be. Nevertheless, some improvements permit to increase the thermal efficiency of steam turbines and are represented in Figure 4.27: .

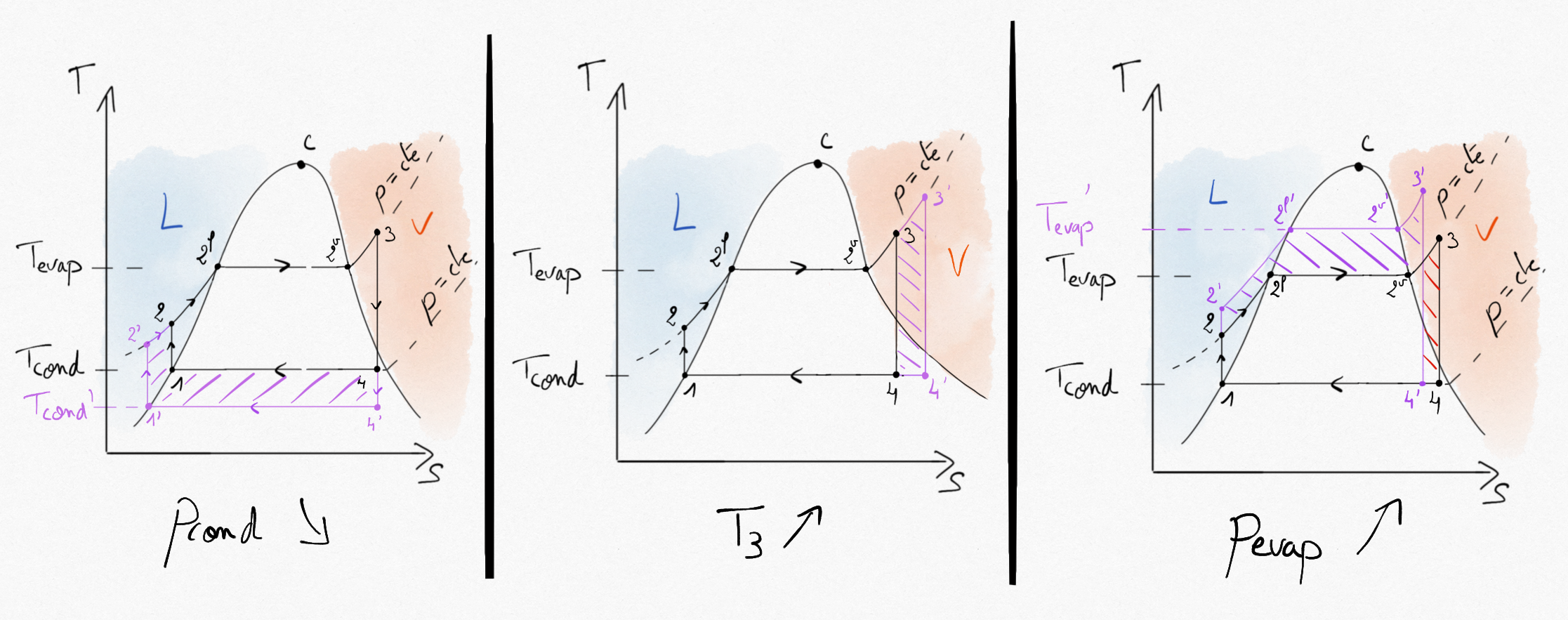
Figure 4.27: Possible improvements in the Hirn cycle. Pink hashed zone represents earned specific technical work.¶

Analyse of these improvements reveal that:

Decrease condenser pressure: By decreasing the pressure in the condenser, the temperature decreases. This improvement is limited by the requested temperature needed for ensuring heat transfers between the working fluid and the cold sink (generally the exterior temperature). When water is used as working fluid, this temperature can not decrease below 25°C, corresponding to a condensation pressure of nearly 3200 Pa. Moreover, with the lower the pressure is, the more the infiltration risks are higher.

Increase vapor temperature: Overheating the vapor in the boiler increases the thermal efficiency and reduces the quantity of liquid droplets in the turbine. Nevertheless, it is limited by mechanical properties of blades in the turbine. The typical maximum value is 600°C.

Increase boiler pressure: This also improves the thermal efficiency of the steam turbine. It has the drawback to increase the amount of liquid droplets in the turbine. Today’s typicall pressure in the boiler reaches 300 Bar in power plants (less for nuclear plants).

4.3.4. Hirn cycle with reheat¶

Increasing the average tempearture in the boiler represent an interesting direction to improve the thermal efficiency of steam turbines but is limited by the maximum temperature admitted by the turbine. A better way to improve the thermal efficiency is to use a multi-stage expansion with reheat between the turbines.

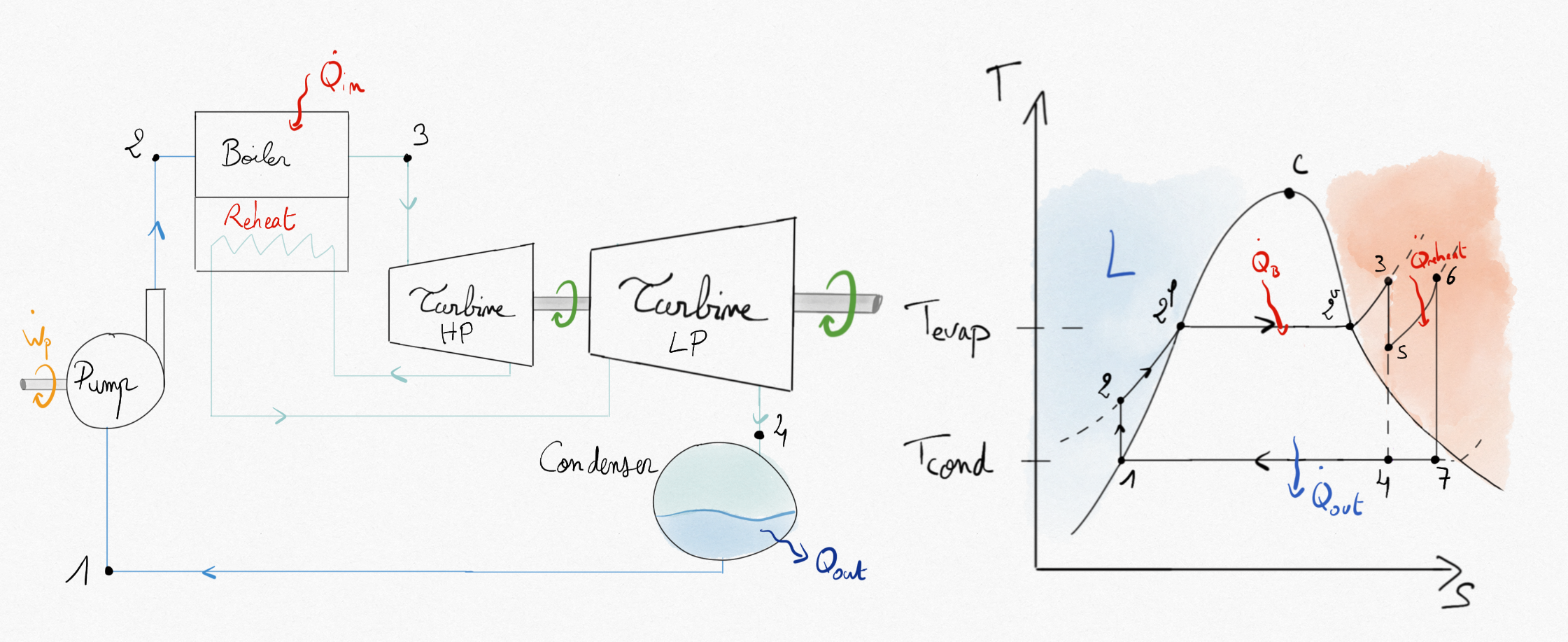
Figure 4.28: Hirn cycle with reheat between a high and low pressure turbine.¶

The thermal efficiency becomes:

$\eta_{th,reheat} = 1 - \frac{|q_{71}|}{|q_{23}|+|q_{56}|} = 1 - \frac{h_7-h_1}{h_3-h_2+h_6-h_5}$

In the bigger installations, reheat allows an increase in thermal efficiency of 5%.

4.3.5. Regenerative cycle¶

In the Rankine (or Hirn) cycle, thermal efficiency is lower than the Carnot’s one because of the transformation $2-2^l$ which is not at constant temperature. The temperature of the fluid entering the boiler is low. In order to increase the thermal efficiency, it is possible to increase this temperature by a regenerative process. This is done by extracting a part of the steam from the turbine after partial expansion. This extracted steam is then used in a heater (or regenerator) to increase the liquid temperature before entering the boiler.

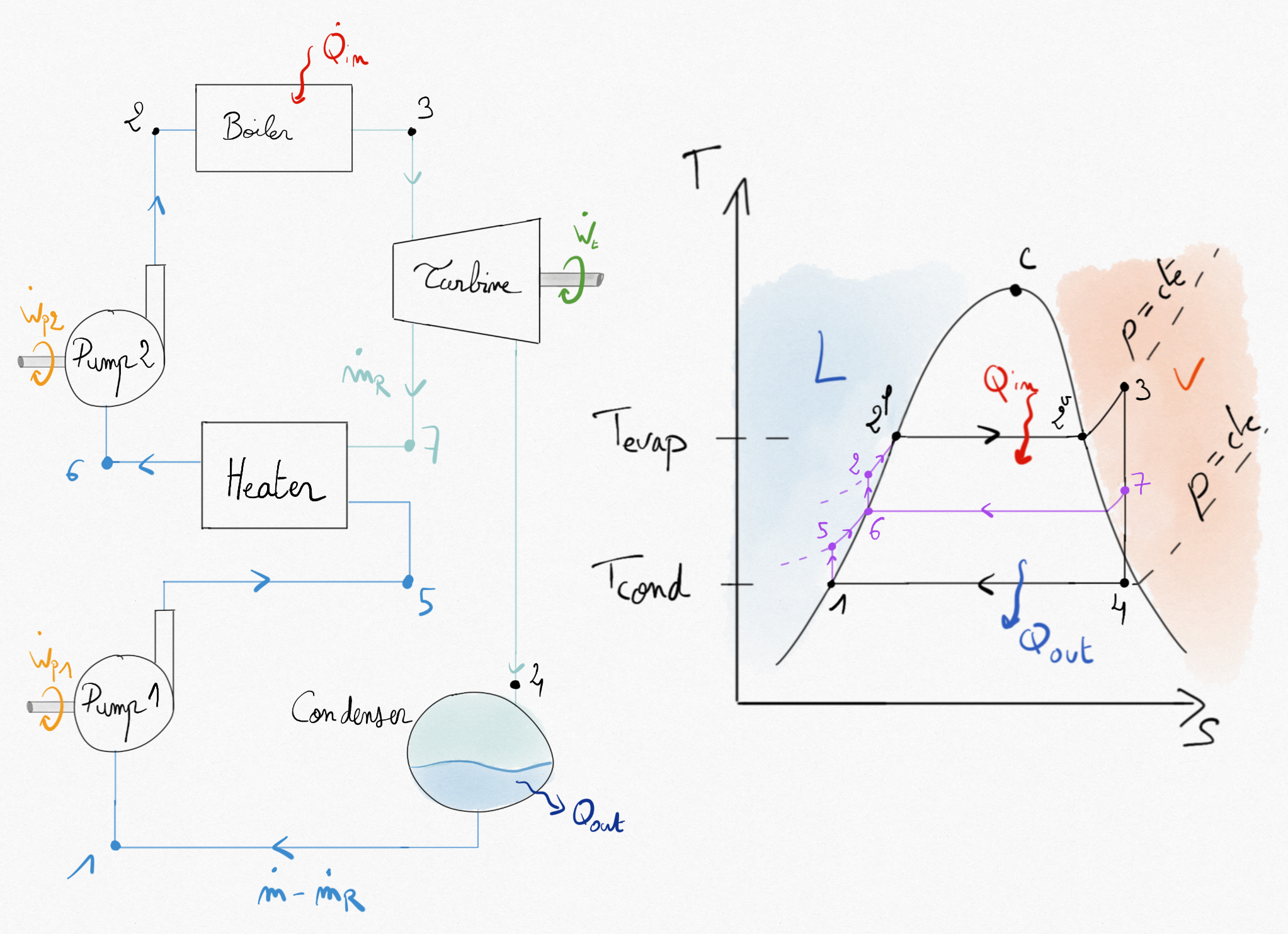
Figure 4.29: Regenerative Hirn cycle. A part of fluid ( $\dot{m}_R$ ) is extracted from the turbine to increase the liquid temperature before entering the boiler.¶

The thermal efficiency of the regenerative cycle is:

$\eta_{th,regen} = 1 - \frac{|q_{41}|}{|q_{23}|} = 1 - \frac{(\dot{m}-\dot{m}_R)(h_4-h_1)}{\dot{m}(h_3-h_2)}$

If the number of extraction is increased, the thermal efficiency increases. In the bigger installation, 7 or 8 extractions occur.