<!DOCTYPE html>
<html class="writer-html5" lang="en" >
<head>
<meta charset="utf-8">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>5.1. Gas heat pump and refrigeration cycle — Thermal machines 1.0 documentation</title>
<link rel="stylesheet" href="_static/css/theme.css" type="text/css" />
<link rel="stylesheet" href="_static/pygments.css" type="text/css" />
<!--[if lt IE 9]>
<script src="_static/js/html5shiv.min.js"></script>
<![endif]-->
<script type="text/javascript" id="documentation_options" data-url_root="./" src="_static/documentation_options.js"></script>
<script src="_static/jquery.js"></script>
<script src="_static/underscore.js"></script>
<script src="_static/doctools.js"></script>
<script type="text/javascript" src="_static/js/theme.js"></script>
<link rel="index" title="Index" href="genindex.html" />
<link rel="search" title="Search" href="search.html" />
<link rel="next" title="5.2. Vapor compression machines" href="chap5_2VaporCompMachines.html" />
<link rel="prev" title="5. Heat pumps and refrigerators" href="chap5_ThermalGenerators_Chap.html" />
</head>
<body class="wy-body-for-nav">
<div class="wy-grid-for-nav">
<nav data-toggle="wy-nav-shift" class="wy-nav-side">
<div class="wy-side-scroll">
<div class="wy-side-nav-search" >
<a href="index.html" class="icon icon-home" alt="Documentation Home"> Thermal machines
</a>
<div class="version">
1.0
</div>
<div role="search">
<form id="rtd-search-form" class="wy-form" action="search.html" method="get">
<input type="text" name="q" placeholder="Search docs" />
<input type="hidden" name="check_keywords" value="yes" />
<input type="hidden" name="area" value="default" />
</form>
</div>
</div>
<div class="wy-menu wy-menu-vertical" data-spy="affix" role="navigation" aria-label="main navigation">
<p class="caption"><span class="caption-text">Contents:</span></p>
<ul class="current">
<li class="toctree-l1"><a class="reference internal" href="chap1_balanceEquations_Chap.html">1. Balance equations</a></li>
<li class="toctree-l1"><a class="reference internal" href="chap2_thermMachinesBasics_Chap.html">2. Thermal machines: Basics</a></li>
<li class="toctree-l1"><a class="reference internal" href="chap3_CompExpGas_Chap.html">3. Compression / Expansion of Gas and vapors</a></li>
<li class="toctree-l1"><a class="reference internal" href="chap4_ThermalEngines_Chap.html">4. Heat engines</a></li>
<li class="toctree-l1 current"><a class="reference internal" href="chap5_ThermalGenerators_Chap.html">5. Heat pumps and refrigerators</a><ul class="current">
<li class="toctree-l2 current"><a class="current reference internal" href="#">5.1. Gas heat pump and refrigeration cycle</a></li>
<li class="toctree-l2"><a class="reference internal" href="chap5_2VaporCompMachines.html">5.2. Vapor compression machines</a></li>
</ul>
</li>
<li class="toctree-l1"><a class="reference internal" href="zBibliography.html">6. References</a></li>
</ul>
</div>
</div>
</nav>
<section data-toggle="wy-nav-shift" class="wy-nav-content-wrap">
<nav class="wy-nav-top" aria-label="top navigation">
<i data-toggle="wy-nav-top" class="fa fa-bars"></i>
<a href="index.html">Thermal machines</a>
</nav>
<div class="wy-nav-content">
<div class="rst-content">
<div role="navigation" aria-label="breadcrumbs navigation">
<ul class="wy-breadcrumbs">
<li><a href="index.html" class="icon icon-home"></a> »</li>
<li><a href="chap5_ThermalGenerators_Chap.html"><span class="section-number">5. </span>Heat pumps and refrigerators</a> »</li>
<li><span class="section-number">5.1. </span>Gas heat pump and refrigeration cycle</li>
<li class="wy-breadcrumbs-aside">
<a href="_sources/chap5_1GasGenerator.rst.txt" rel="nofollow"> View page source</a>
</li>
</ul>
<hr/>
</div>
<div role="main" class="document" itemscope="itemscope" itemtype="http://schema.org/Article">
<div itemprop="articleBody">
<div class="section" id="gas-heat-pump-and-refrigeration-cycle">
<h1><span class="section-number">5.1. </span>Gas heat pump and refrigeration cycle<a class="headerlink" href="#gas-heat-pump-and-refrigeration-cycle" title="Permalink to this headline">¶</a></h1>
<p><em>Gas heat pumps</em> and <em>gas regrigerators</em> are basically following the reverse <strong>Brayton cycle</strong> (or Joule cycle).</p>
<div class="figure align-center" id="id1">
<span id="fig-chap5-braytonreverse"></span><a class="reference internal image-reference" href="_images/BraytonReverse.png"><img alt="_images/BraytonReverse.png" src="_images/BraytonReverse.png" style="width: 572.6999999999999px; height: 323.09999999999997px;" /></a>
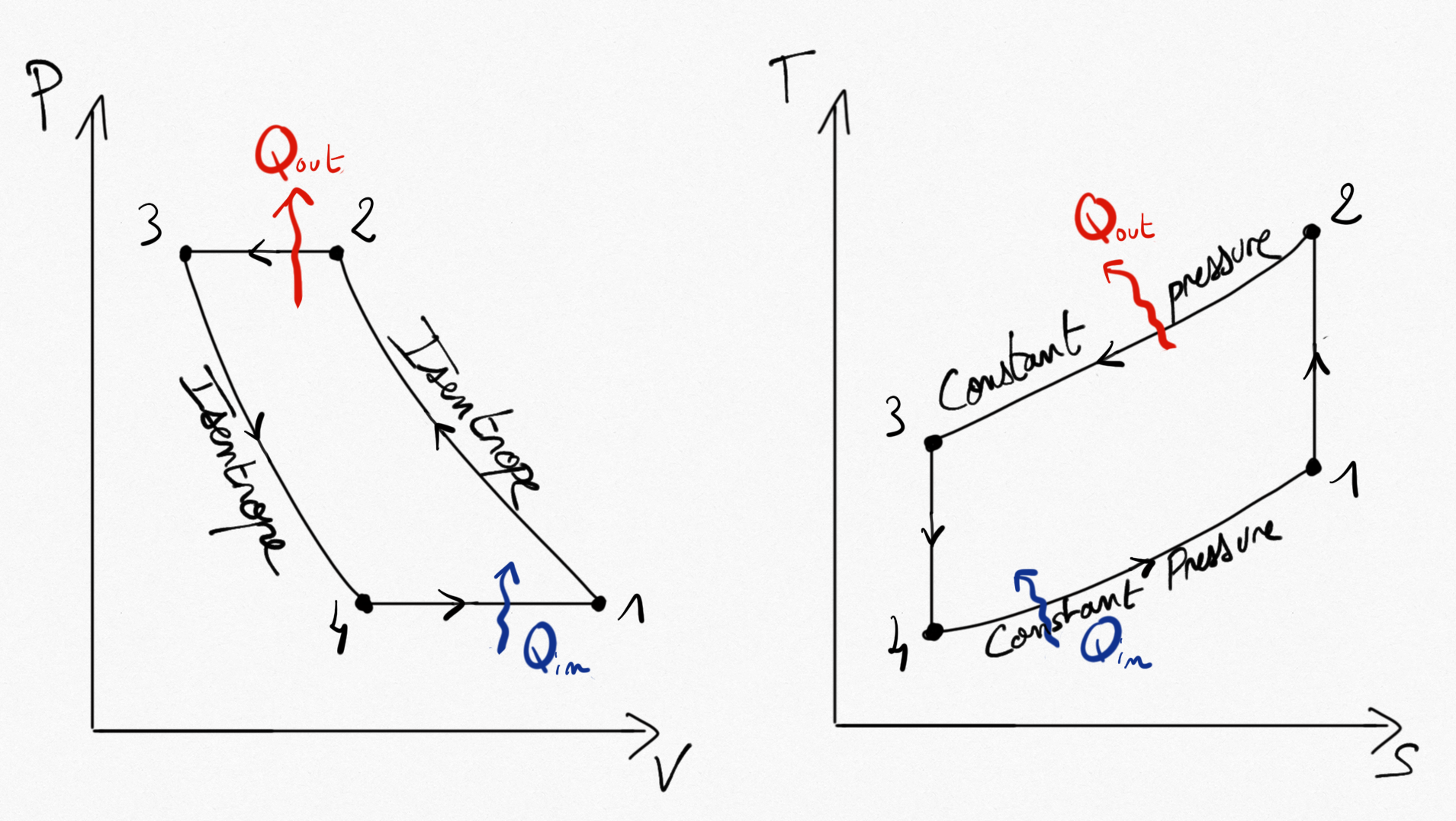
<p class="caption"><span class="caption-number">Figure 5.1: </span><span class="caption-text">Reverse <em>Brayton</em> cycle for gas refrigeration.</span><a class="headerlink" href="#id1" title="Permalink to this image">¶</a></p>
</div>
<p>As for any heat pump or refrigerator, (<a class="reference internal" href="chap2_2Cycles.html#equation-copr">Eq.2.11</a>, and <a class="reference internal" href="chap2_2Cycles.html#equation-cophp">Eq.2.10</a>) the <em>coefficients of performance</em> of <em>Reverse Brayton cycle</em> are:</p>
<div class="math">
<p><img src="_images/math/59409faabacf7321c5b01836c67d07705586eb80.svg" alt="COP_{R,Joule} = \frac{1}{\frac{|q_{23}|}{|q_{41}|}-1} \qquad \text{and} \qquad COP_{HP,Joule} = \frac{1}{1-\frac{|q_{41}|}{|q_{23}|}}"/></p>
</div><p>Considering the working fluid as an <strong>ideal gas</strong>, and because no machine is working in transformations 2-3 and 4-1, application of the balance energy equation reads:</p>
<div class="math">
<p><img src="_images/math/58c0cb5f8c32bbaae3bc60a697c4b2613abe8fcd.svg" alt="|q_{23}| = \dot{m} c_p (T_2-T_3) \qquad \text{ and } \qquad |q_{41}| = \dot{m} c_p (T_1-T_4)"/></p>
</div><p>such that the COPs of <em>Reverse Brayton cycle</em> become:</p>
<div class="math">
<p><img src="_images/math/f55f377eb40ddaaac469646cd991b108d9bbba46.svg" alt="COP_{R,Joule} = \frac{1}{\frac{T_2-T_3}{T_1-T_4}-1} \qquad \text{and} \qquad COP_{HP,Joule} = \frac{1}{1-\frac{T_1-T_4}{T_2-T_3}}"/></p>
</div><p>As for gas turbine, it is possible to determine gas temperatures after the compressor and the turbine thanks to isentropic relations for ideal gases:</p>
<div class="math">
<p><img src="_images/math/ae5ce554aee712c1bc5bcae176e89147d7e73dce.svg" alt="\frac{T_1}{T_2} = \frac{p_2}{p_1}^{\frac{1-\gamma}{\gamma}} = \frac{p_3}{p_4}^{\frac{1 - \gamma}{\gamma}} = \frac{T_4}{T_3}"/></p>
</div><p>we finally obtain:</p>
<div class="math" id="equation-copeffbraytonigrev">
<p><span class="eqno">(5.1)<a class="headerlink" href="#equation-copeffbraytonigrev" title="Permalink to this equation">¶</a></span><img src="_images/math/69b9f208d1a9026bbc6feae63543a09ffdd5eeee.svg" alt="COP_{R,Joule} = \frac{1}{r_p^{\frac{\gamma-1}{\gamma}}-1} \qquad \text{and} \qquad COP_{HP,Joule} = \frac{1}{1-r_p^{\frac{1-\gamma}{\gamma}}}"/></p>
</div><p>where <img class="math" src="_images/math/f2db6382816f4474fde28717c3dbfd86ae542e39.svg" alt="r_p=\frac{p_2}{p_1}" style="vertical-align: -8px"/> is the <strong>pressure ratio</strong>.</p>
<div class="figure align-center" id="id2">
<span id="fig-chap5-copjoule"></span><a class="reference internal image-reference" href="_images/COPJoule.png"><img alt="_images/COPJoule.png" src="_images/COPJoule.png" style="width: 420.0px; height: 300.0px;" /></a>
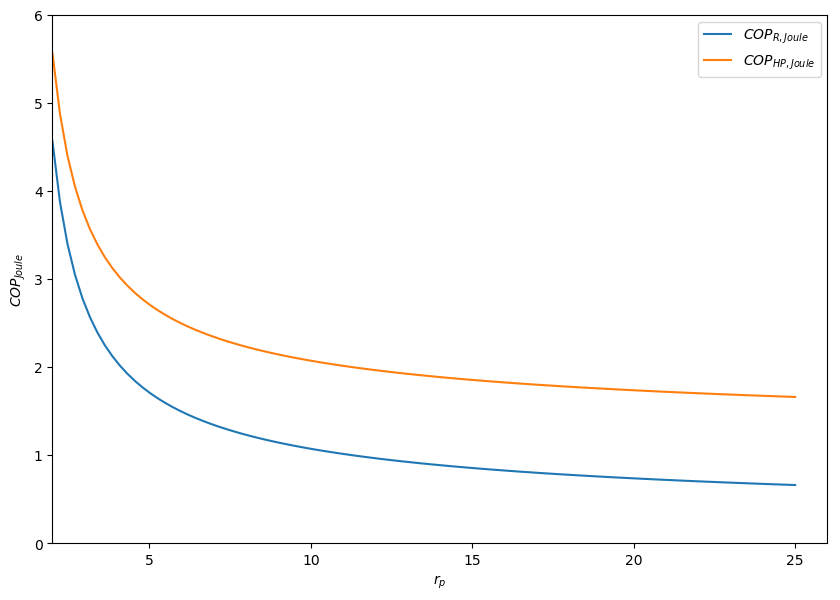
<p class="caption"><span class="caption-number">Figure 5.2: </span><span class="caption-text">COP for <em>reverse Brayton cycle</em> (Joule cycle) for heat pump or refrigerators as a function of the pressure ratio for IG with <img class="math" src="_images/math/9049d1a8815b484e4c2de416b6b17e4cc067c9e8.svg" alt="\gamma=1.4" style="vertical-align: -3px"/>.</span><a class="headerlink" href="#id2" title="Permalink to this image">¶</a></p>
</div>
<p><a class="reference internal" href="#fig-chap5-copjoule"><span class="std std-numref">Figure 5.2: </span></a> reveals that the performance of such machine is good for low pressure ratio.</p>
<div class="admonition-remarks admonition">
<p class="admonition-title">Remarks</p>
<ul class="simple">
<li><p>As for gas turbine, it is possible to easily account for the adiabatic compressor and adiabatic turbine irreversibilities by using the isentropic efficiency of both components (see <a class="reference internal" href="chap4_3GasTurbines.html#sec-chap4-realgasturbinecycle"><span class="std std-numref">Section 4.2.3: </span></a>).</p></li>
<li><p>It is also possible to improve the cycle using <strong>regeneration</strong> (see <a class="reference internal" href="chap4_3GasTurbines.html#sec-chap4-regeneration"><span class="std std-numref">Section 4.2.4: </span></a>)</p></li>
<li><p>Heat pumps and Refrigerators using the <em>reverse Brayton cycle</em> have low performances and are used only for specific applications.</p></li>
</ul>
</div>
</div>
</div>
</div>
<footer>
<div class="rst-footer-buttons" role="navigation" aria-label="footer navigation">
<a href="chap5_2VaporCompMachines.html" class="btn btn-neutral float-right" title="5.2. Vapor compression machines" accesskey="n" rel="next">Next <span class="fa fa-arrow-circle-right"></span></a>
<a href="chap5_ThermalGenerators_Chap.html" class="btn btn-neutral float-left" title="5. Heat pumps and refrigerators" accesskey="p" rel="prev"><span class="fa fa-arrow-circle-left"></span> Previous</a>
</div>
<hr/>
<div role="contentinfo">
<p>
© Copyright 2019, Fabien Petitpas, AMU, Polytech Marseille ME
</p>
</div>
Built with <a href="http://sphinx-doc.org/">Sphinx</a> using a
<a href="https://github.com/rtfd/sphinx_rtd_theme">theme</a>
provided by <a href="https://readthedocs.org">Read the Docs</a>.
</footer>
</div>
</div>
</section>
</div>
<script type="text/javascript">
jQuery(function () {
SphinxRtdTheme.Navigation.enable(true);
});
</script>
</body>
</html>