{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"\n",
"\n",
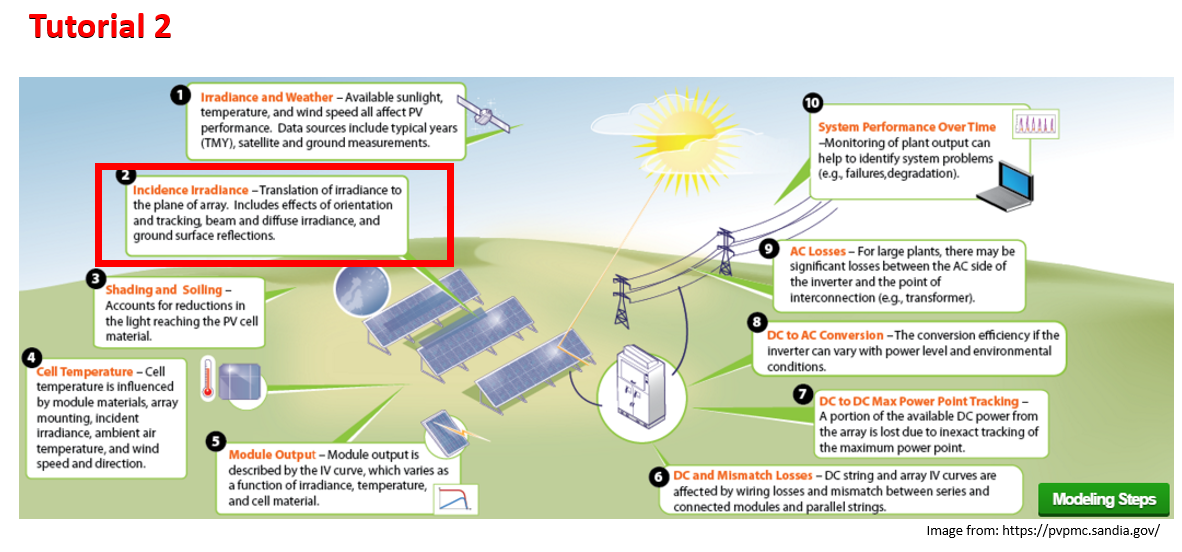
"# Tutorial 2 - POA Irradiance\n",
"\n",
"This notebook shows how to use pvlib to transform the three irradiance components (GHI, DHI, and DNI) into POA irradiance, the main driver of a PV system.\n",
"\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## PV Concepts\n",
"- Plane of Array Irradiance\n",
"- Angle of Incidence\n",
"- Time delta for solar position\n",
"- GHI vs POA for fixed tilt system and tracked systems\n",
"\n",
"## Python Concepts\n",
"- pandas Timedelta\n",
"- making a new dataframe from existing columns\n",
"- resampling\n",
"- bar ploting"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## What is transposition?\n",
"\n",
"The amount of sunlight collected by a PV panel depends on how well the panel orientation matches incoming sunlight. For example, a rooftop array facing West will produce hardly any energy in the morning when the sun is in the East because the panel can only \"see\" the dim part of the sky away from the sun. \n",
"\n",
"\n",
"\n",
"\n",
"As the sun comes into view and moves towards the center of the panel's field of view, the panel will collect more and more irradiance. This concept is what defines plane-of-array irradiance -- the amount of sunlight available to be collected at a given panel orientation. Like the three \"basic\" irradiance components, POA irradiance is measured in watts per square meter."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"\n",
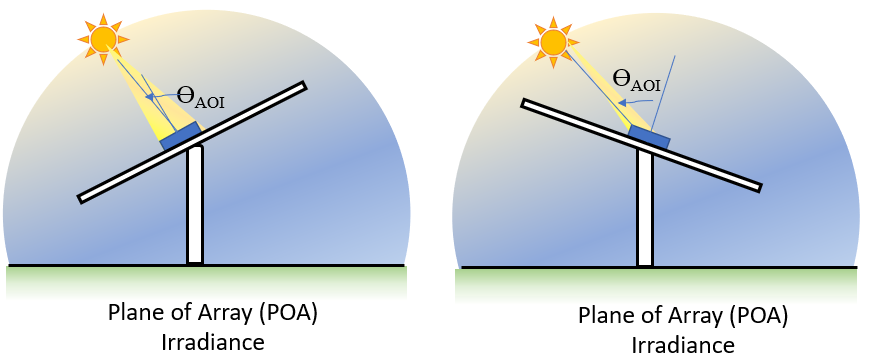
"Each irradiance component is considered separately when modeling POA irradiance. For example, calculating the component of direct irradiance (DNI) that is incident on a panel is solved with straightforward geometry based on the angle of incidence. Finding the POA component of diffuse irradiance (DHI) is more complex and can vary based on atmospheric conditions. Many models, ranging from simple models with lots of assumptions to strongly empirical models, have been published to transpose DHI into the diffuse POA component. A third component of POA irradiance is light that reflects off the ground before being collected by the PV panel. Functions to calculate each of these components are provided by pvlib.\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## How is array orientation defined?\n",
"\n",
"Two parameters define the panel orientation, one that measures the cardinal direction (North, East, South, West), and one that measures how high in the sky the panel faces:\n",
"\n",
"- tilt; measured in degrees from horizontal. A flat panel is at tilt=0 and a panel standing on its edge has tilt=90.\n",
"- azimuth; measured in degrees from North. The direction along the horizon the panel is facing. N=0, E=90, S=180, W=270.\n",
"\n",
"A fixed array has fixed tilt and azimuth, but a tracker array constantly changes its orientation to best match the sun's position. So depending on the system configuration, tilt and azimuth may or may not be time series values.\n",
"\n",
"## Modeling POA from GHI, DHI, and DNI\n",
"\n",
"As mentioned earlier, pvlib makes it easy to calculate POA irradiance. First, let's load in the example TMY dataset from the previous tutorial:"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# if running on google colab, uncomment the next line and execute this cell to install the dependencies and prevent \"ModuleNotFoundError\" in later cells:\n",
"# !pip install -r https://raw.githubusercontent.com/PV-Tutorials/pyData-2021-Solar-PV-Modeling/main/requirements.txt"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.8.1\n"
]
}
],
"source": [
"import pvlib\n",
"import pandas as pd # for data wrangling\n",
"import matplotlib.pyplot as plt # for visualization\n",
"import pathlib # for finding the example dataset\n",
"\n",
"print(pvlib.__version__)\n",
"\n",
"DATA_DIR = pathlib.Path(pvlib.__file__).parent / 'data'\n",
"df_tmy, metadata = pvlib.iotools.read_tmy3(DATA_DIR / '723170TYA.CSV', coerce_year=1990)\n",
"\n",
"# make a Location object corresponding to this TMY\n",
"location = pvlib.location.Location(latitude=metadata['latitude'],\n",
" longitude=metadata['longitude'])"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"We are looking at data from \"GREENSBORO PIEDMONT TRIAD INT\" , NC\n"
]
}
],
"source": [
"print(\"We are looking at data from \", metadata['Name'], \",\", metadata['State'])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Because part of the transposition process requires knowing where the sun is in the sky, let's use pvlib to calculate solar position. There is a gotcha here! TMY data represents the average weather conditions across each hour, meaning we need to calculate solar position in the middle of each hour. pvlib calculates solar position for the exact timestamps you specify, so we need to adjust the times by half an interval (30 minutes):"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"
\n",
"\n",
"
\n",
" \n",
"
\n",
"
\n",
"
apparent_zenith
\n",
"
zenith
\n",
"
apparent_elevation
\n",
"
elevation
\n",
"
azimuth
\n",
"
equation_of_time
\n",
"
\n",
" \n",
" \n",
"
\n",
"
1990-01-01 01:00:00-05:00
\n",
"
166.841893
\n",
"
166.841893
\n",
"
-76.841893
\n",
"
-76.841893
\n",
"
6.889661
\n",
"
-3.395097
\n",
"
\n",
"
\n",
"
1990-01-01 02:00:00-05:00
\n",
"
160.512529
\n",
"
160.512529
\n",
"
-70.512529
\n",
"
-70.512529
\n",
"
52.424214
\n",
"
-3.414863
\n",
"
\n",
"
\n",
"
1990-01-01 03:00:00-05:00
\n",
"
149.674856
\n",
"
149.674856
\n",
"
-59.674856
\n",
"
-59.674856
\n",
"
73.251821
\n",
"
-3.434619
\n",
"
\n",
"
\n",
"
1990-01-01 04:00:00-05:00
\n",
"
137.777090
\n",
"
137.777090
\n",
"
-47.777090
\n",
"
-47.777090
\n",
"
85.208599
\n",
"
-3.454365
\n",
"
\n",
"
\n",
"
1990-01-01 05:00:00-05:00
\n",
"
125.672180
\n",
"
125.672180
\n",
"
-35.672180
\n",
"
-35.672180
\n",
"
94.134730
\n",
"
-3.474102
\n",
"
\n",
" \n",
"
\n",
"
"
],
"text/plain": [
" apparent_zenith zenith apparent_elevation \\\n",
"1990-01-01 01:00:00-05:00 166.841893 166.841893 -76.841893 \n",
"1990-01-01 02:00:00-05:00 160.512529 160.512529 -70.512529 \n",
"1990-01-01 03:00:00-05:00 149.674856 149.674856 -59.674856 \n",
"1990-01-01 04:00:00-05:00 137.777090 137.777090 -47.777090 \n",
"1990-01-01 05:00:00-05:00 125.672180 125.672180 -35.672180 \n",
"\n",
" elevation azimuth equation_of_time \n",
"1990-01-01 01:00:00-05:00 -76.841893 6.889661 -3.395097 \n",
"1990-01-01 02:00:00-05:00 -70.512529 52.424214 -3.414863 \n",
"1990-01-01 03:00:00-05:00 -59.674856 73.251821 -3.434619 \n",
"1990-01-01 04:00:00-05:00 -47.777090 85.208599 -3.454365 \n",
"1990-01-01 05:00:00-05:00 -35.672180 94.134730 -3.474102 "
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Note: TMY datasets are right-labeled hourly intervals, e.g. the\n",
"# 10AM to 11AM interval is labeled 11. We should calculate solar position in\n",
"# the middle of the interval (10:30), so we subtract 30 minutes:\n",
"times = df_tmy.index - pd.Timedelta('30min')\n",
"solar_position = location.get_solarposition(times)\n",
"# but remember to shift the index back to line up with the TMY data:\n",
"solar_position.index += pd.Timedelta('30min')\n",
"\n",
"solar_position.head()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The two values needed here are the solar zenith (how close the sun is to overhead) and azimuth (what direction along the horizon the sun is, like panel azimuth). The difference between `apparent_zenith` and `zenith` is that `apparent_zenith` includes the effect of atmospheric refraction.\n",
"\n",
"Now that we have a time series of solar position that matches our irradiance data, let's run a transposition model using the convenient wrapper function [`pvlib.irradiance.get_total_irradiance`](https://pvlib-python.readthedocs.io/en/latest/generated/pvlib.irradiance.get_total_irradiance.html). The more complex transposition models like Perez and Hay Davies require additional weather inputs, so for simplicity we'll just use the basic `isotropic` model here, which is the default if nothing is passed for `model` keyword argument. As an example, we'll model a fixed array tilted south at 20 degrees."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Fixed Tilt POA"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"df_poa = pvlib.irradiance.get_total_irradiance(\n",
" surface_tilt=20, # tilted 20 degrees from horizontal\n",
" surface_azimuth=180, # facing South\n",
" dni=df_tmy['DNI'],\n",
" ghi=df_tmy['GHI'],\n",
" dhi=df_tmy['DHI'],\n",
" solar_zenith=solar_position['apparent_zenith'],\n",
" solar_azimuth=solar_position['azimuth'],\n",
" model='isotropic')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"`get_total_irradiance` returns a DataFrame containing each of the POA components mentioned earlier (direct, diffuse, and ground), along with the total in-plane irradiance. "
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"Index(['poa_global', 'poa_direct', 'poa_diffuse', 'poa_sky_diffuse',\n",
" 'poa_ground_diffuse'],\n",
" dtype='object')"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df_poa.keys()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### What angle should you tilt your modules at?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[PVEducation Solar Radiation on a Tilted Surface](https://www.pveducation.org/pvcdrom/properties-of-sunlight/solar-radiation-on-a-tilted-surface)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The total POA irradiance is called `poa_global` and is the one we'll focus on. Like the previous tutorial, let's visualize monthly irradiance to summarize the difference between the insolation received by a flat panel (GHI) and that of a tilted panel (POA):"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZ0AAAF3CAYAAAB+AJZGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjAsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+17YcXAAAgAElEQVR4nO2de5gdVZnufy8BgiKESyIwJCFRg4oiEcLFER1GBAIKUUcUOCMJolGRGT0zKvEcz3ARR/AujoAoKDhIQJSLgFwGQcaRQAKBBAghEQIGkDuIlyDB7/xRq8NOZ3end/baq3tXv7/nqadrr6pd77rsqq9rrW+tTxGBMcYYU4L1BjsDxhhjhg82OsYYY4pho2OMMaYYNjrGGGOKYaNjjDGmGOsPdgaGOqNHj44JEyYMdjaMMaaruOWWWx6PiDG902101sKECROYN2/eYGfDGGO6Ckn3N0t395oxxphi2OgYY4wpho2OMcaYYnhMxxhjCvD888+zfPlyVqxYMdhZycpGG23E2LFj2WCDDQZ0vo2OMcYUYPny5WyyySZMmDABSYOdnSxEBE888QTLly9n4sSJA/qOu9eMMaYAK1asYMstt6yNwQGQxJZbbtnS25uNjjHGFKJOBqeHVstko2OMMaYYHtMxxphBYMKsy7Neb9lJ71jn7+6111585StfYcqUKaulz5s3j3POOYdTTjml3eytwkbHmCFOXw+ndh4yxgyEKVOmrGGI2sVGx5h1pL//VG0QzFDl85//POeeey7jxo1j9OjR7LLLLgD8+Mc/5qijjuLpp5/mzDPP5C1veQvXX389X/nKV7jsssuy6XtMxxhjhgnz5s3jJz/5CfPnz+enP/3pautKrly5kptvvplvfOMbHH/88R3Lg990jOlWjhvVz7FnyuXDdA2/+tWvmDZtGi95yUsAOPDAA1cde8973gPALrvswrJlyzqWB7/pGGPMMCEi+jw2cuRIAEaMGMHKlSs7lgcbHWOMGSbsueee/OxnP2PFihX84Q9/4PLL83rQDQR3rxnTCfrq+nK3l0kMhrPJrrvuykEHHcROO+3Edtttx5QpUxg1qp9u2g7gNx1jjBlGfOpTn2Lx4sVcfPHFLF68mF122YXrr79+lWv06NGjV43p7LXXXlk918BvOsYYM6yYOXMmd911FytWrGD69OnsvPPORfVtdIwxZhjxox/9aFD13b1mjDGmGMWNjqSzJD0q6Y6GtPMl3Za2ZZJuS+kTJP254djpDd/ZRdJCSUslnaK01KmkLSRdI2lJ+rt5Slc6b6mkBZLKvlMaY4wZlO61HwD/AZzTkxAR7+/Zl/RVoNHF5zcRMbnJdU4DZgJzgCuAqcDPgVnAtRFxkqRZ6fMxwP7ApLTtnr6/e7ZSGVNX7IlnMlL8TScibgCebHYsva28Dzivv2tI2gbYNCJujGq20znAu9LhacDZaf/sXunnRMUcYLN0HWOMMYUYao4EbwEeiYglDWkTJc0Hfg98LiL+G9gWWN5wzvKUBrBVRDwMEBEPS3p5St8W+G2T7zycvxjGGLMW+lvGaJ2u1x1vnkPN6BzK6m85DwPjI+IJSbsAF0t6HdAsVF3f6ztUDPg7kmZSdd0xfvz4tWbaDC28+rMxQ5chY3QkrQ+8B9ilJy0ingOeS/u3SPoNsD3VW8rYhq+PBR5K+49I2ia95WwDPJrSlwPj+vjOakTEGcAZAFOmTFmbMTPdhMcn+qTPuD0bFc6I6RjLli1j6tSp7L777syfP5/tt9+ec845hxtvvJFPfepTrFy5kl133ZXTTjuNkSNHcsIJJ/Czn/2MP//5z/zt3/4t3/nOd9oOuT2UXKbfDtwdEau6zSSNkTQi7b+Cygng3tR99qykPdI40OHAJelrlwLT0/70XumHJy+2PYBnerrhjDFmuLB48WJmzpzJggUL2HTTTfna177GjBkzOP/881m4cCErV67ktNNOA+Doo49m7ty53HHHHfz5z3/OsjrBYLhMnwfcCLxa0nJJR6ZDh7CmA8FbgQWSbgcuBD4aET1OCB8DvgcsBX5D5bkGcBKwj6QlwD7pM1Qebvem878LHJW7bMYYM9QZN24cb37zmwH4x3/8R6699lomTpzI9ttvD8D06dO54YYbALjuuuvYfffd2XHHHfnFL37BnXfe2bZ+8e61iDi0j/QZTdJ+Avykj/PnAa9vkv4EsHeT9AA+3mJ2jTGmVgy0e2zFihUcddRRzJs3j3HjxnHcccexYsWKtvWHUveaMcaYDvPAAw9w4403AnDeeefx9re/nWXLlrF06VIAfvjDH/J3f/d3qwzM6NGj+cMf/sCFF16YRX/IOBKYYY4H+M1wY5B+26997Ws5++yz+chHPsKkSZP45je/yR577MHBBx+8ypHgox/9KCNHjuTDH/4wO+64IxMmTGDXXXfNom+jY4wxw4j11luP008/fbW0vffem/nz569x7oknnsiJJ56YVz/r1Ywxxph+sNExxphhwoQJE7jjjjvWfmIHsdExxphCVE609aLVMtnoGGNMATbaaCOeeOKJWhmeiOCJJ55go40GvmyFHQmMMaYAY8eOZfny5Tz22GODnZWsbLTRRowdO3btJyZsdExRvL6XGa5ssMEGTJw4cbCzMei4e80YY0wxBvSmI2mLAZz214h4us38GGOMqTED7V57KG39LdozAnDwGWOMMX0yUKOzKCLe2N8JKbqnMcYY0ycDHdN5U6ZzjDHGDGMGZHQiYq3rWQ/kHGOMMcObtRodSftI+q6kyenzzM5nyxhjTB0ZyJjOUcARwOeSF9vkzmbJGGNMXRlI99pjEfF0RHwK2BfIE1TBGGPMsGMgRmfVFPKImAWc07nsGGOMqTNrNToRcUmvz99qR1DSWZIelXRHQ9pxkh6UdFvaDmg49llJSyUtlrRfQ/rUlLZU0qyG9ImSbpK0RNL5kjZM6SPT56Xp+IR2ymGMMaZ1WloGR9IUSRdJulXSAkkLJS1oUfMHwNQm6V+PiMlpuyLp7QAcArwufedUSSMkjQC+DewP7AAcms4FODldaxLwFHBkSj8SeCoiXgV8PZ1njDGmIK0u+Hku8GlgIfDXdRGMiBtaeMuYBsyOiOeA+yQtBXZLx5ZGxL0AkmYD0yQtAt4GHJbOORs4DjgtXeu4lH4h8B+SFHVaZ9wYY4Y4rS74+VhEXBoR90XE/T1bprwcnd6ezpK0eUrbFvhtwznLU1pf6VsCT0fEyl7pq10rHX8mnb8GkmZKmidpXt2WITfGmMGkVaNzrKTvSTpU0nt6tgz5OA14JZU79sPAV1N6s7XeYh3S+7vWmokRZ0TElIiYMmbMmP7ybYwxpgVa7V47AngNsAEvdq8F8NN2MhERj/TsS/oucFn6uBwY13DqWKqFR+kj/XFgM0nrp7eZxvN7rrVc0vrAKODJdvJtjDGmNVo1OjtFxI65MyFpm4h4OH18N9Dj2XYp8CNJXwP+BpgE3Ez11jJJ0kTgQSpng8MiIiRdB7wXmA1MBy5puNZ04MZ0/BcezxkAx43q59gz5fJhjKkFrRqdOZJ2iIi71lVQ0nnAXsBoScuBY4G90jI7ASwDPgIQEXdKugC4C1gJfDwiXkjXORq4iiqkwlkRcWeSOAaYLelEYD5wZko/E/hhckZ4kspQGWOMKUirRmdPYLqk+4DnqN44IiLeMNALRMShTZLPbJLWc/4XgC80Sb8CuKJJ+r286OHWmL4COHig+TTGGJOfgUYOfRMwh+bza4wxxpgBMdA3nelUkzHvAa4EroyI33UsV8aY4Udf44ceO6wVAzI6EfFRAEmvoVoF4AeSRgHXURmh/+kZazHGGGP6oqV5OhFxd0R8PSKmUs38/xXVOMlNncicMcaYetGSI4GkkcA/ABMavvtYREzJnC9jjDE1pFXvtUuolo+5hcp7DfqY1W+MMcb0plWjMzZ1rRljjDEt0+raa7+WlH1FAmOMMcODgc7TWUjVjbY+cISke1nHyaHGGGOGLwPtXntnR3NhjDFmWDDQeTq5YuYYY4wZxrQ6pmOMMcasMzY6xhhjitGqy7QxxqwzE2Zd3uexZRsVzIgZNAbqvfZJ4H+A+Skip6kZfT0M/CAwxuRkoG86Y4FvAq+RtAD4NZURujEiHPLZGGPMgBio99qnACRtCEwB/hb4IPBdSU9HxA6dy6IxxmTEIRQGlVbHdF4CbAqMSttDwMLcmTLGGFNPBuS9JukMSf8DnA+8iap77eCImBIRR7QiKOksSY9KuqMh7cuS7pa0QNJFkjZL6RMk/VnSbWk7veE7u0haKGmppFMkKaVvIekaSUvS381TutJ5S5POzq3k2xhjTPsM1GV6PDAS+B3wILAceHodNX/AmmGvrwFen5bTuQf4bMOx30TE5LR9tCH9NGAmMCltPdecBVwbEZOAa9NnqILP9Zw7M33fGGNMQQZkdNLK0rsCX0lJ/wrMlXS1pONbEYyIG4Ane6Vd3eAVN4fKcaFPJG0DbBoRN0ZEAOcA70qHpwFnp/2ze6WfExVzgM3SdYwxxhRiwJND08P6DuAK4OdU3muvBD6ROU8fTNfvYaKk+ZJ+KektKW1bqretHpanNICtIuLhlOeHgZc3fOe3fXxnNSTNlDRP0rzHHnusvdIYY4xZxUDn6XyCaiznzcDzJHdp4CwyOhJI+r/ASuDclPQwMD4inpC0C3CxpNdRrW7dm7UFkxvwdyLiDOAMgClTpjhInTHGZGKg3mvbARcC/7vnLSI3kqZTrWa9d+oyIyKeI0UojYhbJP0G2J7qLaWxC24slScdwCOStomIh1P32aMpfTkwro/vGGOMKcBAu9f2iogL+zM4km5d10xImgocAxwUEX9qSB8jaUTafwWVE8C9KR/PStojea0dThVKG+BSYHran94r/fDkxbYH8EynDKgxxpjmDPRNp2clgr4Q1bydtSLpPGAvYLSk5cCxVN5qI4FrkufznOSp9lbgBEkrgReAjzasgPAxKk+4l1CNAfWMA50EXCDpSOAB4OCUfgVwALAU+BPQkqu3McaY9hmo0XntAM55YSAXiohDmySf2ce5PwF+0sexecDrm6Q/AezdJD2Ajw8kj8YYYzqDg7gZY4wphuPpGGOMKYaNjjHGmGLY6BhjjClGS6tMSxoJ/AMwofG7EXFC3mwZY4ypI62GNrgEeAa4hTRp0xhjjBkorRqdsWnxT2OMMaZlWh3T+bWkHTuSE2OMMbWn1TedPYEZku6j6l4T1bzLN2TPmTHGmNrRqtHZvyO5MMaYjEyYdXmfx5ZtVDAjZg1a6l5LKxNsBhyYts28WoExxpiB0pLRSXF1zqUKjPZy4D8l/VMnMmaMMaZ+tNq9diSwe0T8EUDSyVTB3L6VO2PGGGPqR6vea2L11aRfoHlETmOMMWYNWn3T+T5wk6SL0ud30UdYAmOMMaY3LRmdiPiapF8Cb6Z6wzkiIuZ3JGdm7RzXR9y8454pmw9jjBkgrb7pEBG3UC2DY4wxxrTEgIyOpF9FxJ6SngWi8RDV5NBNO5I7Y4wxtWKgkUP3TH836Wx2jDHG1JlW5+mcPJC0tVzjLEmPSrqjIW0LSddIWpL+bp7SJekUSUslLZC0c8N3pqfzl0ia3pC+i6SF6TunSFJ/GsYYY8rRqsv0Pk3SWl0a5wdA75WqZwHXRsQk4Nr0uefak9I2EzgNKgMCHAvsDuwGHNtgRE5L5/Z8b+paNIwxxhRiQEZH0sckLQRend44erb7gIWtCEbEDcCTvZKnAWen/bOpXLF70s+JijnAZpK2AfYDromIJyPiKeAaYGo6tmlE3BgRAZzT61rNNIwxxhRioN5rPwJ+DnyR1d8Qno2I3gZkXdgqIh4GiIiHJb08pW8L/LbhvOUprb/05U3S+9NYA0kzqd6WGD9+/LqWyRhjTC8G9KYTEc9ExLKIOBT4PbAVsB3weklv7WD+mq12EOuQ3hIRcUZETImIKWPGjGn168YYY/qgVUeCDwE3AFcBx6e/x2XIxyOpa4z099GUvhwY13DeWOChtaSPbZLen4YxxphCtOpI8AlgV+D+iPh74I3AYxnycSnQ44E2HbikIf3w5MW2B/BM6iK7CthX0ubJgWBf4Kp07FlJeySvtcN7XauZhjHGmEK0uiLBiohYIQlJIyPibkmvbuUCks4D9gJGS1pO5YV2EnCBpCOBB4CD0+lXAAcAS4E/AUcARMSTkj4PzE3nndAwtvQxKg+5l1CNQ/08pfelkR8vT2OMMU1p1egsl7QZcDFwjaSneLH7akCkcaFm7N3k3AA+3sd1zgLOapI+D3h9k/QnmmkYY4wpR6sLfr477R4n6TpgFHBl9lwZY4ypJS0v+NlDRPwyZ0aMMca0SBd25Q90wc+mC33iBT+NMWZN+jIGMKQNQgkGuuCnF/o0xhjTNi13r0naCXhL+nhDRCzImyVjjDF1pdXJoZ8AzgVenrZzJf1TJzJmjDGmfrT6pnMksHtE/BFWhTW4EfhW7owZY4ypH62uSCDghYbPL9B8vTNjjDFmDVp90/k+cJOki6iMzTTgzOy5MsYYU0tanRz6NUnXA3umpBkRcVv2XBljjKklLRkdSQcDV0bErZL+H/Bvkj4fEfM7kz0zYdblfR5btlHBjBhjTAZaHdP5fxHxrKQ9qUJXnw2cnj9bxhhj6kirRqfHieAdwOkRcQmwYd4sGWOMqSutGp0HJX0HeD9whaSR63ANY4wxw5RWDcb7qAKo7RcRTwObA5/OnitjjDG1pFWX6ReAjYCDJTV+9+p8WTLGGFNXWjU6lwBPA7cCz+XPjjHGmDrTqtEZGxFTO5ITY4wxtafVMZ1fS9qxExmR9GpJtzVsv5f0SUnHSXqwIf2Ahu98VtJSSYsl7deQPjWlLZU0qyF9oqSbJC2RdL4ke94ZY0xBWjU6ewK3pAf6AkkLJWUJbRARiyNickRMBnYB/gRclA5/vedYRFwBIGkH4BDgdcBU4FRJIySNAL4N7A/sAByazgU4OV1rEvAU1QKmxhhjCtFq99r+HcnFmuwN/CYi7pf6XE90GjA7Ip4D7pO0FNgtHVsaEfcCSJoNTJO0CHgbcFg652zgOOC0zhTBGGNMb1pde+3+TmWkF4cA5zV8PlrS4cA84F8j4ilgW2BOwznLUxrAb3ul7w5sCTwdESubnL8akmYCMwHGjx/fNINensYYY1pnQN1rkp5NYyy9t2cl/T5nhtI4y0HAj1PSacArgcnAw8BXe05t8vVYh/Q1EyPOiIgpETFlzJgxLeTeGGNMfwzoTSciNul0RhrYH7g1Ih5J2o/0HJD0XeCy9HE5MK7he2OBh9J+s/THgc0krZ/edhrPN8aYlumrx8O9HX0zFJewOZSGrjVJ2zQcezdwR9q/FDhE0khJE4FJwM3AXGBS8lTbkKqr7tKICOA64L3p+9Op5h0ZY4wpRKuOBB1F0kupVq/+SEPylyRNpuoKW9ZzLCLulHQBcBewEvh4RLyQrnM01XI9I4CzIuLOdK1jgNmSTgTm4wB0xhhTlCFldCLiT1QD/o1pH+jn/C8AX2iSfgVwRZP0e3nRw80YY0xhWg3idjRwbvIeM8YYU4A6jR21OqazNTBX0gVp1n+fk2iMMcaY3rRkdCLic1QD9mcCM4Alkv5d0is7kDdjjDE1o2XvteQF9ru0raSKqXOhpC9lzpsxxpia0eqYzj9TuRo/DnwP+HREPC9pPWAJ8Jn8WTTGGFMXWvVeGw28p/dyOBHxV0nvzJctY4wxdaTVtdf+rZ9ji9rPjjHGmDozIKMj6VleXKest8daRMSmWXNljDGmlgzFtdeMMcbUlFYdCUYC/wBMaPxuRJyQN1vGGGPqSKuOBJcAzwC3AM/lz44xxpg606rRGRsRUzuSE2OMMbWn1cmhv5a0Y0dyYowxpvYM1HttIZX32vrAEZLupepeE5X32hs6l0VjjDF1YaDda574aYwxpm0G1L0WEfenVQiO6tlvTOtsFo0xxtSFVsd09mmStn+OjBhjjKk/Ax3T+RjVG80rJC1oOLQJ8D+dyJgxxpj6MdAxnR8BPwe+CMxqSH82Ip7MnitjjDG1ZKBjOs9ExLKIOLTXmE5WgyNpmaSFkm6TNC+lbSHpGklL0t/NU7oknSJpqaQFknZuuM70dP4SSdMb0ndJ11+avuvIp8YYU5ChuAzO30fE4w2fZwHXRsRJkmalz8dQjSVNStvuwGnA7pK2AI4FplC5ed8i6dKIeCqdMxOYA1wBTKV6gzPGGFOAVh0JLgGmUUUM/WPD1kmmAWen/bOBdzWknxMVc4DNJG0D7AdcExFPJkNzDTA1Hds0Im5M0U/PabiWMcaYAgy1ZXACuFpSAN+JiDOArSLiYYCIeFjSy9O52wK/bfju8pTWX/ryJulrIGkm1RsR48ePb7dMxhhjEkNtGZw3R8TOVF1nH5f01n7ObTYeE+uQvmZixBkRMSUipowZM2ZteTbGGDNAWjU6e1KNkSxOg/cLe7lQt0VEPJT+PgpcBOwGPJK6xkh/H02nLwfGNXx9LPDQWtLHNkk3xhhTiFaNTs/g/b7AgVTL4xyYIyOSNpa0Sc9+0rgDuBTo8UCbTjWuREo/PHmx7QE8k7rhrgL2lbR58nTbF7gqHXtW0h7Ja+3whmsZY4wpQEtjOhFxv6SdgLekpP+OiNsz5WUr4KLkxbw+8KOIuFLSXOACSUcCDwAHp/OvAA4AlgJ/Ao5IeXxS0ueBuem8Expcuz8G/AB4CZXXmj3XjDGmIK26TH8C+DDw05T0n5LOiIhvtZuRiLgX2KlJ+hPA3k3SA/h4H9c6CzirSfo84PXt5tUYY8y60ar32pHA7hHxRwBJJwM3Am0bHWOMMfWn1TEdAS80fH6B5l5hxhhjzBq0+qbzfeAmSRdRGZtpNOnGMsYYY5rRqiPB1yRdT+U6DTAjIm7LnitjjDG1ZKChDS7tnZT+vl0SEXFQ3mwZY4ypIwN903kT1dIy5wE34XEcY4wx68BAjc7WVFFDDwUOAy4HzouIOzuVMWOMMfVjoPF0XoiIKyNiOrAH1YTM6yX9U0dzZ4wxplYM2JEgxdJ5B9XbzgTgFF6cJGqMMcaslYE6EpxNNZP/58DxEXFHR3NljDGmlgz0TecDVMHatgf+uSHKs6hWpNm0A3kzxhhTMwZkdCKi1ZULjDHGmDWwMTHGGFMMGx1jjDHFsNExxhhTDBsdY4wxxbDRMcYYUwwbHWOMMcUYMkZH0jhJ10laJOnOFBobScdJelDSbWk7oOE7n5W0VNJiSfs1pE9NaUslzWpInyjpJklLJJ0vacOypTTGmOHNkDE6wErgXyPitVTru31c0g7p2NcjYnLargBIxw4BXgdMBU6VNELSCODbwP7ADsChDdc5OV1rEvAUVfhtY4wxhRgyRiciHo6IW9P+s8AiYNt+vjINmB0Rz0XEfVSLkO6WtqURcW9E/AWYDUxTtYzC24AL0/fPBt7VmdIYY4xpxpAxOo1ImgC8kSp2D8DRkhZIOkvS5iltW6oYPz0sT2l9pW8JPB0RK3ulN9OfKWmepHmPPfZYhhIZY4yBIWh0JL0M+AnwyYj4PXAa8EpgMvAw8NWeU5t8PdYhfc3EiDMiYkpETBkzZkyLJTDGGNMXAw5tUAJJG1AZnHMj4qcAEfFIw/HvApelj8uBcQ1fHws8lPabpT8ObCZp/fS203i+McaYAgyZN5005nImsCgivtaQvk3Dae8GesIqXAocImmkpInAJOBmYC4wKXmqbUjlbHBpRARwHfDe9P3pwCWdLJMxxpjVGUpvOm+mCqGwUNJtKe3/UHmfTabqClsGfAQgIu6UdAFwF5Xn28cj4gUASUcDVwEjgLMawmofA8yWdCIwn8rIGWOMKcSQMToR8Suaj7tc0c93vgB8oUn6Fc2+FxH3Unm3GWOMGQSGTPeaMcaY+mOjY4wxphg2OsYYY4pho2OMMaYYNjrGGGOKYaNjjDGmGDY6xhhjimGjY4wxphg2OsYYY4pho2OMMaYYNjrGGGOKYaNjjDGmGDY6xhhjimGjY4wxphg2OsYYY4pho2OMMaYYNjrGGGOKYaNjjDGmGDY6xhhjijHsjI6kqZIWS1oqadZg58cYY4YTw8roSBoBfBvYH9gBOFTSDoObK2OMGT4MK6MD7AYsjYh7I+IvwGxg2iDnyRhjhg2KiMHOQzEkvReYGhEfSp8/AOweEUf3Om8mMDN9fDWwuEWp0cDjbWZ3qOjUqSx106lTWeqmU6eyrKvOdhExpnfi+nny0zWoSdoaVjcizgDOWGcRaV5ETFnX7w8lnTqVpW46dSpL3XTqVJbcOsOte205MK7h81jgoUHKizHGDDuGm9GZC0ySNFHShsAhwKWDnCdjjBk2DKvutYhYKelo4CpgBHBWRNzZAal17pobgjp1KkvddOpUlrrp1KksWXWGlSOBMcaYwWW4da8ZY4wZRGx0jDHGFMNGxwwakraQtPlg58MYUw6P6bSJJFGtdLAt1Zyfh4CbI3PFFtTZqlEjIh7JfP3xwJeAvYGnqeZObQr8ApgVEcsyahWps6TV6XqrTVlK6pSot4L35ihgai+dqyLi6W7SsdFpA0n7AqcCS4AHU/JY4FXAURFxdbfoSJoMnA6M6qXxdNK4tV2NpHMj8A3gwoh4IaWNAA4GPhkRe2TSKdU2Ha+3OpWlsE6J+6ZU2xwOHAtc3UtnH+D4iDina3Qiwts6bsAiYEKT9InAom7SAW6jWhKod/oewO0Zy7JkXY4NxTorVW91KkthnRL3Tam2WQxs1iR9c+CebtIZVvN0OsD6VKsc9OZBYIMu09k4Im7qnRgRcyRtnEkD4BZJpwJnA79NaeOA6cD8jDql2qZEvdWpLCV1StRbqbYRTZbsAv5K8+W9hqyOjU57nAXMlTSb1R+ghwBndpnOzyVdDpzTS+Nw4MpMGqTrHQkcT9VnLKqb9lK6r86gTL3VqSwldUrUW6m2+QJwq6SrG3TGU3V7fb6bdDym0yYpHs9B9HqARsRd3aYjaX+qUA+9Na7IpVGSgm3T8XqrU1kK65S4b0q1zebAfr10roqIp7pJx0YnE5K2ACL3D2CwdDqFpPWp3nTexereMZcAZ0bE8x3Q7Oo6a6ROZSlJiXorpAYCQzQAAB3SSURBVNH1noWep9MGksZLmi3pUeAm4GZJj6a0Cd2kI2mUpJMkLZL0RNoWpbTNcmgkfghMpupeOwB4R9rfCfjPXCIF26bj9VanshTWKXHflGqbyZLmANcDJwNfBn4paY6knbtKJ5fXw3DcgBuB9wMjGtJGUPXnzukmHapFUI8Btm5I2xqYBVyTsSyL+zmW0wunVNt0vN7qVJbCOiXum1JtUxvPwiwZHa4b5dx/O66zFmPQ57F10JlDNSdnvYa09dKNe1M31VmpeqtTWQrrlLhvhsIzYGk36dh7rT1Kuf+W0Llf0meAsyP136Z+3RkNmjk4hOq1/VRJPX3fmwHXpWO5KNU2JeqtTmUpqVOi3kq1TW08C+1I0AaqAsEdyepeOL8FfkY1KP5ct+gkj5VZSWMrqgHER6hcmU+OiCfb1WiiuSXVbzB7jPeCbdPxeqtTWQrrlLhvirRN0qqFZ6GNjhk0JG0dEb/r67Mxpn7Yey0Tkt7Z3+du0untpZLTO6YXvSfP5ZxMt4qCbdPxeqtTWQrrlLhvSrXNzP4+D3UdG5187LqWz92k87G1fM5CRLyjv88ZKdU2JeqtTmUpqVOi3kq1Te/laHIug9NxHXevmUFH0hadGDMyxgw9/KaTEUkTJb1H0mu6XUfSyyTtnHOyXrru5xr2d5B0D5UH0DJJu+fU6qVbqm06Um+9NGpTlsI6Je6bUm2zp6R/URVaoat0bHTaQNLFDfvTqAKRHQhcImlGN+kkt8+e/T2Bu4CvAgslHZBDI/Gehv0vA5+IiInA+4Cv5xIp2DYdr7c6laWwTon7plTb3Nyw/2HgP4BNgGMlzeoqnVyTiobjBsxv2P81MDHtjybvLOGO6wC3NuxfB+yc9l8BzMtYlkad+b2Ozc+oU6ptOl5vdSpLYZ0S981gPAPmAmPS/sbAwm7S8eTQ9mgcEFs/Iu4DiIjHJf21C3V62DRS9MaIuFdVZM9cvELSpVSDkmMlvTQi/pSO5Yw/UrrOoHP1VqeylNQpUW+l2ma9NL9pPaqx+MeSzh8lrewmHRud9thJ0u+pHqAje+aZqJowlvPmKaHzGkkLksYESZtHxFOS1iOvMZjW6/MIWDUj/bSMOqXapkS91aksJXVK1FupthkF3JJ0okHnZeT1Xuu4jr3XOkAaEH1tRNzYLTqStuuV9HBE/EXSaOCtEfHTdjWGArnbZjDrrVvLMti/tRL3Z8FnwEuBrXresLpBx0YnA6pBjIteOh2LCyJpFPBZqng6Y1Lyo1TxdE6KiKcz6xWps6TV0XgqdSpLSZ0S9VZIQ8BurB6H6ubI/BDvtI6NThtIeiNVl9AoqpjoAGOBp4GPRUSWBf9K6EgaD3wJ2DtdV8CmVN44syJiWbsaSeeqdM2zIy15I2lrqgUS3x4R+2TSKdU2Ha+3OpWlsE6J+6ZU2+wLnAos6aXzKuCoiLi6a3RyeT0Mx406xbgoFxek1LL2pdqmRMyW2pSlsE6J+6ZU2ywCJjRJnwgs6iYdz9Npj40j4qbeiRExh8rFsJt0RkfE+RHxQsP1X4iI2cCWmTQgLWufuiOAqmtC0jHkXda+VNuUqLc6laWkTol6K9U261Ot9tybB8nrfNFxHXuvtUdtYlxQLi7I+6mWtf+lpJentJ5l7d+XUadU25SotzqVpaROiXor1TZnAXMlzW7QGU91P+VcKLfjOh7TaRPVJcZF87ggy6mMQda4IKUo0Tal6q1mZSn2WytUb6WeAa/tQ+eubtKx0cmMCsWEKaVTAkmXRURHloHvpVOnOqtNWUpSot4KPgN2jjSxtpt0PKaTn6z/3QymjqSO/6AT2xbSKdI2heqtTmUp+VsrUW+lngHf60YdG538dCq2xWDolCpLzn78/nDbWMdtM8g6diTIz3drpHN5Jy/eMDHwg53UaaBU23S03hJ1KktJnRL1Vqptju9GHRudNmkye/cWSYrMg2UFdRpnVn8r57XT9deYGCgp+8TApFWkzpJWp+utNmUpqVOi3grem6OAqQ06D0naLPKv4tFRHTsStEGdZglLmgycTvOZ1UflGkiUdCPwDeDCnnkaqlYWPhj4ZETskUmnVNt0vN7qVJbCOiXum1JtczhwLHB1L519gOMj4pyu0ck1k3U4btRoljDlZlYvWZdjQ7HOStVbncpSWKfEfVOqbRYDmzVJ3xy4p5t03L3WHrWZJUw/M6sl5ZxZXWpiYKm2KVFvdSpLSZ0S9VaqbcTqsXt6+Ct5B/o7rmOj0x7NZu+Oo1pDqtOzhHPrlJpZfTjVxMDjaTIxMKNOqbYpUW91KktJnRL1VqptvgDcKulqVl8pYB/g892k4zGdNpG0A3AQnZ8l3HGdUjOrS1GwbUrMeq9NWQrrlLhvSrXN5sB+vXSuisxhITqtY6OTCdUo/kgnkbQ+1ZvOu1g9XsclVEugPN8Bza6us0bqVJaSlKi3QhpdH7vLk0PbQNJ4SbMlPQrcBNws6dGUNqGbdCSNknSSpEWSnkjbopS2WQ6NxA+ByVTdawcA70j7OwH/mUukYNt0vN7qVJbCOiXum1JtM1nSHOB64GTgy1SL5s6RtHNX6eTyehiOGzWKPwJcBRwDbN2QtjXVitDXZCxLf/F0cnrhlGqbjtdbncpSWKfEfVOb2ECldLJkdLhulHP/7bjOWoxBzuBqc6jm5KzXkLZeunFv6qY6K1VvdSpLYZ0S981QeAYs7SYde6+1R53ij9wv6TNUYaQfgVX9ujPIG1ztEKrX9lMl9fR9bwZcl47lolTblKi3OpWlpE6JeqtTbKAiOnYkaAM1jwvyW+BndD7+SFad5LEyK2lsRTWA2BNc7eSIeLJdjSaaW1L9Bh/vwLVLtU3H661OZSmsU+K+KdI2SasWnoU2OmbQUK+4I70/G2Pqh73XMiHpnf197iad3l4qOb1jetF78lzOyXSrKNg2Ha+3OpWlsE6J+6ZU28zs7/NQ17HRyceua/ncTTofW8vnLETEO/r7nJFSbVOi3upUlpI6JeqtVNv0Xo6mU3F1OqLj7jVTHGmNpeAfAm4O/xiNqT02Om0i6TW8OOjW8wC9NCIWdZuOmsTRoFr+Ilu8DhVaCj5plWqbEvVWm7IU1ilx35Rqm/1ospJHROT0Xuu4jrvX2kDSMcBsqtfOm4G5af88SbO6SUdVHI1bgb2AlwIbA39P5RJ6eA6NxDeBt0fE/hHxobRNpVpQ8Ju5RAq2TcfrrU5lKaxT4r4p1TbfAD4B/JIqCOKX0/4/S8p533ReJ9ekouG4AfcAGzRJ35C8E8M6rkO5eB1LgPX7KEvOSW6l2qbj9VanshTWKXHfFHsG9JGubtPxm057/BX4mybp26Rj3aRTKl5Hz1Lwx0g6LG3HUK1bldN7rVTblKi3OpWlpE6JeivVNisk7dYkfVdgRTfpeEWC9vgkcK2kJawee+JVwNFdplMkXkdEfFHSJVRLwb+JFyef/a/IuxR8qbYpUW91KktJnRL1VqptZgCnSdqEF4PGjQN+n451jY4dCdpE0nq86InV8wCdGxEvdJuOCsXraNDr6FLwBdum4/VWp7IU1ilx3xRpm6S1daNOdGgydSd1/KbTPtGw/bXhb9fpRMRTkq5j9TgauR8C46kGKN8GPJPSRgG/AGZFxLKMckXapkS9Ua+yFNOhTL0VaZt0n/wdDXUmqVOehR3T8ZtOG5Ry/y2hI2kycDowiuo/NSWNp5PGre1qJJ0bgW8AF/b8JyhpBNXK05+MiD0y6ZRqm47XW53KUlinxH1Tqm0OB44Fru6lsw9wfESc0zU6ubwehuMGLAImNEmfCCzqJh3KxesotRR8qbbpfPyRGpWlsE6J+6ZU29TGs9Dda+2xPi8OtjXyILBBl+lsHBE39U6MiDmSNs6kAeWWgi/VNiXqrU5lKalTot5KtU1tPAttdNqjx/13Nqs/QA8hr/tvCZ1S8ToOp1oK/niaLAWfUadU25SotzqVpaROiXor1Ta18Sz0mE6bSHotzWNP5HT/LaKjQvE6SlGwbTpeb3UqS2GdEvdNqbaphWehjY4ZNCS9MyIu6+uzMaZ+eEWCTEg6rr/P3aSjQvE6KLQUfMG26Xi91akshXWO6+9zt2ik657R3+ehrmOjk49b1vK5m3SKxOuIiGP7+5yRUm1Tot7qVJaSOiXqrVTbfGctn4e0jrvXTHFUaCl4Y8zQw0anDSStT+WJ9W6qRf9WxZ4AzoyI57tMp+PxOtLinodSLQff42o6lsrbZ3ZEnJRJp0idJa2O1ludylJSp0S9Fbw3RwGfpaqzMSn50aRzUuRaLaCAjo1OG0g6j2oW9dms/gCdDmwREe/vFh1VcTS2p3JjbdQ4nGrS5ifa1Ug69wCv630zStoQuDMiJmXSKdU2Ha+3OpWlsE6J+6ZU21xFtVTU2ZHWQUvro02nik+1T9fo5JrJOhw3YHE/x7LOEu60Tl/XgezxOu4GtmuSvl1/5RyKdVaq3upUlsI6Je6bofAMKHXfZNGxI0F7PCXp4LTKLACS1pP0fiCn73wJnVLxOnqWgv+5pDPSdiVwLVXEwlyUapsS9VanspTUKVFvpdrmfkmfkbRVg85Wqbv6t/18b8jpuHutDSRNAE6mWjH5Kar/1DbjxRWT7+sWHUk7A6cBzeJoHBUR2TxxVGa5+QmUaZuO11udylJYZwKdv286rpF0NgdmUTng9BiE3wGXAidHxJPdomOjkwlJW1LV5+PdrKMC8TokiReNTs/A683RoR9jibYpUW9Jp05lKaKTtErUW5FnQLfjtdfapLf7r6QeL5y7u01HBeJ1qJ+l4CVlWwo+aZVqmxL1VpuyFNYpcd+UaptaeBZ6TKcNUj/nbKr/1G4G5qb92ZJmdZOOqjgatwJ7AS8FNgb+nmpV6MNzaCS+SeUFs39EfChtU6kWFPxmLpGCbdPxeqtTWQrrlLhvSrXNN6jGPH9JFQTxy2n/nyXlvG86r5PL62E4bsA9wAZN0jcks7dPp3UoF69jCbB+H2VZ2k11Vqre6lSWwjol7ptiz4A+0rvOs9BvOu3xV6oJYb3ZhrzhakvolIrX0bMU/DGSDkvbMcBN5F0KvlTblKi3OpWlpE6JeivVNrXxLPSYTnv0uP8uYfXYE68Cju4ynSLxOiLii5IupuoDfxMveq/9r8i7FHyptilRb3UqS0mdEvVWqm1mAKdJaubxN6ObdOy91iYl3H9L6ahQvI5SFGybjtdbncpSWKfEfVOkbZJW13sW2ugYY4wphsd0jDHGFMNGxxhjTDFsdLoEVUuo9+y/TNIUSVsMZp7WBUmjJJ0k6W5JT6RtUUrbbLDz1w6StkhjFWaA1KXO0vpkO0t6Y+O6ZYW0X9ZNOjY6HULSwozXmgE8IukeSfsDC6jWe7pd0qG5dPrR/3nGy11AtUbVXhGxZURsSTUx8Cngxxl1+iRz24yXNFvSY1Ru33MlPZrSJuTS6Uc/W1nWopPtNzDYdZbykKXeJE2WNAe4nobJlJLmqFpjrgQ5vT47rmOX6TaQ9J6+DgFbZ5T6V+DVVAsk3g68MSJ+k/6jugY4r12Bfm4QAZPbvX4DEyLi5MaE5BlzsqQP5hIp2DbnA9+gcvl+IWmPAA6mmqm+R7sCpcpS8DfQ8TpL1yxRbz8APhIRN/XS3gP4PrBTDhFJ/9LXISDbm04JHRud9jgfOJfmE902yqjzQlSLCD4u6Q8R8RuAiHhEyjaXbi7VchfNLpiz2+t+SZ+hChL1CFRdE1RzAHIu0V6qbUZHxPmNCelBOltSrjknpcpS6jdQos6gTL1t3NvgAETEHEkbZ9IA+Heqt6iVTY7l7LHquI6NTnssAL4SEXf0PiDp7Rl1HpD0Rao3nbslfRX4KfB24OFMGouo/mNb0vuApJzG4P1US6f/UtLLU9ojVEunvy+jTqm2uUXSqVSRI3vqaRxVpMX5mTRKlaXUb6BEnUGZevu5pMupoqA2luVwIOdCnLcCF0eTsA+SPtRNOp6n0waS3gLcHxEPNDk2JSLmZdLZFPg41X9s/0E1qe4I4H7gxIho2/BIei+wMCIWNzn2roi4uF2NkhRsmw2BI3lxleGeyYGXAmdGxHMZNEqVpchvoESdJZ1S9XYAcBC9yhIRV+S4ftJ4NfBkRDzW5NhWPb0G3aBjo2OKoqo/8GAqA3ohVfCraVRhrE+PiJzrVRljhhj2XmsDSS9VFdr105I2kjRD0qWSvpTTjVHSCEkfkfR5SW/udexzmTQk6X2qQu9K0t6STpF0lBpC8Wbg21TdaB8Afgh8FJgHvBX4ei6Rgm3TW2d6bp2CZSnyGyhRZ33oZK83SVtLOk3StyVtKek4SQskXSBpmxwa/egs7EYdv+m0gaQLqPpxX0LlXbaIyiX4QGDriPhAJp3vUcUduZnqYf3LiPiXdOzWiGjbNVNVH/vLqZZk/z0wEvgZcADwSER8ol2NpLMwInaUtAFVGNxtIuIvquYhzY+IHTPplGqbjusULEup30Cd2uZK4HKqmECHUTkunEf19v72iJjWrkbtdHLFYRiOG3BbvBhr4ne8aMQFLMios6Bhf33gDCpHgpFUD+ocGgvT3w2AJ4ANG/QWZizL/Ib9K5vVZ5e1Tcd1Cpal1G+gTm3T+Ht+oJm+dVbf3L2Wgaha5Ir0t+dzzlfIDRu0VkbETOA24Bfk89Ffma7/PNUKuX/p0QNyrpb7u56ujagihgKrVrX9S0Ydkkan26aYTgGNUr8B0nXr0DaNz9Bz+jlmnZwXGcbMa3iArprYKOmVwLOZdaY2JkTECVSTzyZk0ihiDKIKU/2HJoeeBd6ZS4eybdNpnVJlKfUPQZ3a5pIGjVXjq5JeRRVVNBe10fGYToeQpKhB5aqa4LZxRDzaQY3jIuK4Tl2/iV6RtimhU0ij47+BBq3atI1pjt90MiPpDFj1Ct9xnQ5rHBcRfyzwsDmow9cHyrdNJ3UKlqXIb6BmbXNZp65dBx0bnfxMqZFOEWNA82VXOkGd2qZUWUr9BurUNtsW0OhaHRud/HS8C6KgTiljsEshnTq1TamylPoN1Kltci7lUzsdj+mYPpG0XhRYIUDSPRGxfad1TOt47MPkxm86HSLnmIvKrEiwxuxt4OIOzBJ/VtLv0/aspGeBV/akZ9R5Q8P+BpI+l2aj/7ukl2bUOVrS6LT/Kkk3SHpK0k2Sck10/amkf8zZDn3ovELSWZJOVBUo8LvAQkk/VsY4N5LWk/RBSZdLul3SLapi6eyVSyPpDGrAQOWNQbSppC9K+qGkw3odOzWXzlrykKU8ftNpA/UduVPA7RExNpNOiRUJSs0S/xYwCvh0vBja4L6ImJjj+g06q+pF1arcW1K5mL8L2DIiDs+kc2dEvC7tXw58LyIuSg/QL0TEm/u9wMA0HgRupFqn7r+oZohf3jOPJheSbkjXHgX8I1V9XQDsSxX75m2ZdL5PtVjtfwHvpVr94L+BY4BLIuJbmXSuoprLdnZUMZt63L+nU82u3yeDRn8xiC6LiDxLx0g/AZYAc4APAs8Dh0XEc7meAUmn4+Wx0WkDSS9Q3TyN/d6RPm8bERs2/WLrOgsi4g1pf33gVGA0cCgwJyLemEHjtoiYLElU4RK2iYhIn2/v0c+BpF2oYnZcTLVq9tKIeEWu6yeN+T31Iuk2YNeIeD53eSQtjohXp/25EbFrw7EFOXR6yiJpEyqjeSiwK3AZcF5EXN2uRqNO2n8gIsY3O5ZBZ7V6kTQnIvaQNJJq1vtrM+msaptWjrWo8QJ9xyDaIyJe0q5G0rktIiY3fP6/VMsTHQRck9HodLw8jqfTHvcCe0fzpdNzxh9ZbUUCYKakfyPvigQ91w9Jq83elpR7Zv0tquKZHE31A88ZiKyHUZLeTdWFPDLNsu9EeS6U9APgBOAiSZ+kWqJob2CN38U60tMWz1ItkvrD9Jb9PqrYRFmMDvBXSdtTvem8VGn5f1UTA0dk0gB4XtIro4p+uzNp4mn6rz1n29yvzgcMLBWDaKQaxlgj4guSlgM3kPcZ0PnyRKY1e4bjRhXjZqc+jv1TRp3/BKY2Sf8Q8Hwmje8BL2uS/krgVx2sw22AAzpw3e/32rZK6VsD12bWmgHcBDxONdP9LqoIjKMyXf+GTtV/L529gcXpwbMn8BNgKZXH17SMOm+jMshLgPuA3VP6GOBLGXU2B06mCpvxZNoWpbQtMmm8F3h1H8felbEsX6LqEuydPhVYklGn4+Vx95pZK1JeDyZJr+HFAF4BPEQV9GpRLg2Th+Qk8VRU4aRzXldUY2uP57yuGfrY6LRJqQdoCZ1CGsdQjUnMpoqwCDAWOASYHREnZdRy2+TRuSQi7i6gU+wfD0lHRMT3u12jEzqS9qMaO+z9G8gSfttGpw1KPUBL6BQsyz3A6yKNsTSkbwjcGRGTMum4bYa5zlrysJqjRLdq5NaR9A1ge6oVphvb5nCqbry2YyrZ6LRBwQdox3UKluVuYL+IuL9X+nbA1ZHBoyhdz21jnQV9HQK2j4iR3aBRWKfpRO3UHXpPjrax91p7/BX4Gyq36Ua2Sce6SadUWT4JXCtpCS96EI0HXkXlzZYLt411tgL2A57qlS7g112kUVJnhaTdIuLmXum7AityCNjotEepB2gJnSJliYgrk1vublR9xqJ6jZ+bebDabWOdy6g8Mm/rfUDS9V2kUVJnBnBamhPW0702jmoC74wcAu5eaxNJ69H5B2gRnVJlaaI7MyKyh2pw21jHrBuqVm5Y1TaRVnTIQi7/bm+rfNln1kWnYFlurUud1bBtrDMENQrrHJfzel7wMz8frZFOqbKUWj7fbWMdt03rZI2pZKOTn1IP0BI6pcpyYCEdt4113DaDrOMxncxIGhsRy9d+5tDX6ZRGpyef9aPrtrGO26Z1naxxtWx02qTUA7SETiGNjk8+a9By21jHbZNP/98i4oS2r2Ojs+6UeoAWmSVcriwdn3yWrue2sY7bJiPZVj4o4f1Q143qIdksXeRd+bXjOgXLsgDYrUn6bsDCbqqzGraNdYagRmGd3/exPQuszKFhR4L2WCFptybp2WbvFtQpVZYZwLck3SXp6rQtAr5FpslnCbeNddw2rfM0MCkiNu21bUIV3LFtvCJBe8ygw7N3C+qU0CAibgV27+jks4oZuG2s47ZplXOA7YBHmhz7UQ4Bj+lkoMADtJhOwbJMobppVlJ1D2RdOr9Bx21jHbfNEMJvOnkYy4sP0D8AnfohlNDpqIakvwO+SvUavwvwP8Dmkp4HPhAROUP8gtvGOm6blunkP4V+02mDvh6gQNYHaAmdgmWZD+wbEY9Jmgh8LSLeLWkf4NMRsW8mHbeNddw2Q1Enl9fDcNyA+cCYtD8RuCjt70MVG6ZrdAqWZUHD/gga1l2jiqXSNXVWw7axzhDUqJuOvdfaY0REPJb2H6AagCMirqHqd+0mnVJlmSfpTEmHUQ1MXg8g6aVURigXbhvruG2GoI7HdNpjnqQzgWup4r1fDx15gJbQKVWWjwAfBv4W+C/grJQeVEGqcuG2sY7bZgjqeEynDSRtQPUA3QG4HTgrIl6Q9BLg5dErJPNQ1ilVllK4bazjthmaOjY6piiSXgZ8BngPlXfMX4DfAKdHxA8GMWvGmAJ4TKcNJL1M0gmS7pD0jKTHJM2RNKPbdEqVBTgXuBeYChwPnAJ8APh7Sf+eS8RtYx23zdDU8ZtOG0i6BLiIamzifcDGwGzgc8CDEfF/ukWnYFluj4idGj7PjYhdVYUvvisiXpNJx21jHbfNUNTJ5Wo3HDfg9l6f56a/6wF3d5NOwbL8Gtgz7R8IXNVwbHE31VkN28Y6Q1CjbjruXmuPP0raE0DSgcCTAFEFPMoZba+ETqmyfBT4mqSngWOAf0qaY4BvZ9Rx21jHbTMUdXJZyOG4AW8AbqaavfsrYPuUPgb4527SKVUWt83Q1LDO0NWom47HdMyQQdIREfH9wc6HMaZzuHutQ0g6oi46pcpC5c3Wcdw21nHbDJ6O33Q6hHKFdh0COjk1JC3o6xDVq/zIHDpryYPbxjpum0HS8TI4bbCWB+hW3aRTqizpWvsBTzXR+XUuEbeNddw2Q1PHRqc9ijxAC+mUKstlwMsi4rbeByRdn1HHbWMdt80Q1LHRaY9SD9ASOkXKEhFH9nPssFw6uG2s47YZkjoe0zHGGFMMe68ZY4wpho2OMcaYYtjoGGOMKYaNjjHGmGLY6BhjjCnG/wfECdOdw4sbQwAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"df = pd.DataFrame({\n",
" 'ghi': df_tmy['GHI'],\n",
" 'poa': df_poa['poa_global'],\n",
"})\n",
"df_monthly = df.resample('M').sum()\n",
"df_monthly.plot.bar()\n",
"plt.ylabel('Monthly Insolation [W h/m$^2$]');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This plot shows that, compared with a flat array, a tilted array receives significantly more insolation in the winter. However, it comes at the cost of slightly less insolation in the summer. The difference is all about solar position -- tilting up from horizontal gives a better match to solar position in winter, when the sun is low in the sky. However it gives a slightly worse match in summer when the sun is very high in the sky.\n",
"\n",
"As an example, here's a sunny day in winter vs a sunny day in summer. Note that the daily profile doesn't just change its height, it also changes its width (summer POA is \"skinnier\" than GHI)."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEECAYAAAA2xHO4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjAsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+17YcXAAAgAElEQVR4nO3deXxU9bn48c+ThJAAgRB2SCBsgbALYZPFBRFQEOu1P7UuVG2pVa+12t7a5br12uqtW63VW9eitdpqqyLggigKKGBQhLCHPUBCwhqWJCR5fn+cE4wwSWbCzJyZ5Hm/XvOamXO+58wDhDxzvt/veb6iqhhjjDE1ifE6AGOMMZHNEoUxxphaWaIwxhhTK0sUxhhjamWJwhhjTK0sURhjjKlVnNcBhELbtm01PT3d6zCMMSZqrFixokhV2/na1yATRXp6OtnZ2V6HYYwxUUNEtte0z7qejDHG1MoShTHGmFpZojDGGFOrBjlGYYwxwXDixAny8vIoKSnxOpSgSUhIIDU1lSZNmvh9jCUKY4ypQV5eHklJSaSnpyMiXodzxlSVffv2kZeXR/fu3f0+zrqejDGmBiUlJbRp06ZBJAkAEaFNmzYBXyFZojAm2pWXQmWF11E0WA0lSVSpz5/HEoUx0WzzR/D4IPjzCNixzOtoTBide+65Pu8Xy87O5rbbbgvqZ3mSKETkpyKyRkRyRORVEUkQke4iskxENonIP0Qk3m3b1H2f6+5P9yJmYyJKeSm8/2t4+TuQ0ArKy+CFSfDuXVB21OvojIeysrJ44okngnrOsCcKEekC3AZkqeoAIBa4EngIeExVewMHgBvdQ24EDqhqL+Axt50xjdfe9fDsBPj8SRj+A5i5EG7+zHm97Gl4+mzYusjrKE0Q/fa3v6Vv375MnDiRq666iocffhiA119/nREjRpCRkcGiRc6/+cKFC5k6dWpQP9+rWU9xQKKInACaAXuA84HvuftnAfcCTwPT3dcAbwBPioioreFqGhtVyH7euZKIbw5XvQZ9pnyz/+KHof+l8PatMGsqZN0IE++DpknexdyA3PfOGtbuPhzUc/br3JJ7pvWvtU12djb/+te/+OqrrygvL2fo0KEMGzYMgPLycpYvX868efO47777+PDDD4MaX5WwX1Go6i7gYWAHToI4BKwADqpqudssD+jivu4C7HSPLXfbtwlnzMZ47mgRvPY9mHsndDsbfvzZt5NElfSxzr5Rt0D2C/DUaMhdEP54TdAsXryY6dOnk5iYSFJSEtOmTTu577LLLgNg2LBhbNu2LWQxhP2KQkRa41wldAcOAq8DPn7iqbpi8DVEf9rVhIjMBGYCdO3aNSixGhMRNn8Eb94Exw/ApN/DyJsgppbvePHNYPLv3KuLW+Bvl8FZ18CFD0BicvjibmDq+uYfKrV1njRt2hSA2NhYysvLa2x3prwYzL4A2Kqqhap6Avg3cDaQLCJViSsV2O2+zgPSANz9rYD9p55UVZ9R1SxVzWrXzmelXGOiS/UB68TW8MOPYPTNtSeJ6tJGwI8Wwdifwsq/w1OjYMN7oY3ZBN3YsWN55513KCkp4ciRI8ydOzfsMXiRKHYAo0SkmTgTeicAa4GPgcvdNjOAt93Xs933uPs/svEJ0+AVboDnqg1Y//Bj6Dgw8PM0SYAL7oUfLHCSzatXwL9nwrHTvmuZCDV8+HAuueQSBg8ezGWXXUZWVhatWrUKawzixe9cEbkPuAIoB74CfoAzFvEakOJuu0ZVS0UkAXgZOAvnSuJKVd1S2/mzsrLU1qMwUUnVGVt4/9dOF9L0P/sei6iP8jJY9DAsegQSU+DiR6DfJcE5dwO1bt06MjMzvQ6DI0eO0KJFC44dO8b48eN55plnGDp0aL3P5+vPJSIrVDXLV3tPZj2p6j3APads3gKM8NG2BPhuOOIyxlNH98HsW2HDPOh5Plz6NCR1DN754+LhvF9B5jR462b457XQ/zvO5zRJDN7nmKCbOXMma9eupaSkhBkzZpxRkqgPKwpoTCTYux5emg7H9/s3YH0mOg50xjsWPwYfPwBdsuDsW0PzWSYo/v73v3v6+VbCw5hIsOB+KC8JfMC6vmKbwDn/Benj4LM/OQPnxtTAEoUxXsvPgQ1zYdTN9RuwPhPj7oQj+bDylfB+rokqliiM8dqiRyA+CUbODP9n9zgXugyDxY9DRejm4ZvoZonCGC8VbYI1b8KIHzrTV8NNxLmqOLgdcv4V/s83UcEShTFeWvQoxCXA6Fu8iyFjCrTvB4sfhcpK7+IwEcsShTFeObANVv0Dsq6H5m29iyMmxrmqKFwP6+d4F4eJWJYojPHK4schJhbO/k+vI4F+l0Lr7s4NeVb4IKJs27aNvn37MmPGDAYNGsTll1/OsWPHWLBgAWeddRYDBw7khhtuoLTUmbl2//33M3z4cAYMGMDMmTNrrRXlL7uPwhgvHNrlzDQ66xpo2dnraCA2zqkJ9c5tsHkB9LrA64giz7t3Qf7q4J6z40CY8mCdzTZs2MDzzz/PmDFjuOGGG3j00Uf5y1/+woIFC8jIyOC6667j6aef5vbbb+fWW2/l7rvvBuDaa69lzpw536o4Wx92RWGMFz77k7PO9ZjbvY7kG4OvgpZd4NNHvI7EnCItLY0xY8YAcM0117BgwQK6d+9ORkYGADNmzODTTz8F4OOPP2bkyJEMHDiQjz76iDVr1pzx59sVhTHhdqQQVvwVBl8Jrbt5Hc034uLh7NvgvV/A9s+cdS/MN/z45h8qTv3UupWUlHDzzTeTnZ1NWloa9957LyUlJWf8+XZFYUy4Lf2zcxf22Du8juR0Q6+DZm2deztMxNixYweff/45AK+++ioXXHAB27ZtIzc3F4CXX36Zc84552RSaNu2LUeOHOGNN94IyudbojAmnI7th+XPwoDLoG0vr6M5XXwzp4RI7oew+yuvozGuzMxMZs2axaBBg9i/fz8//elPefHFF/nud7/LwIEDiYmJ4aabbiI5OZkf/vCHDBw4kEsvvZThw4cH5fM9KTMealZm3ESshQ/Cwt87y5V28GbFtDqVHILHBkKP8XDF37yOxlORUGZ827ZtTJ06lZycnKCdM9Ay43ZFYUy4lByGpU9Dn4sjN0kAJLRyyomse8epamsavbAnChHpIyIrqz0Oi8jtIpIiIvNFZJP73NptLyLyhIjkisgqEQlvIXZjgiX7eSg5COPv9DqSuo38MTRp5pQiN55KT08P6tVEfYQ9UajqBlUdoqpDgGHAMeBN4C5ggar2Bha47wGmAL3dx0zg6XDHbMwZKzsGnz0JPSc4RfgiXfM2MOx6WP067N/qdTTGY153PU0ANqvqdmA6MMvdPgu41H09HXhJHUuBZBHpFP5QjTkDX86CY0Uw/udeR+K/s2917hxf8kevI/FUQxvHrc+fx+tEcSXwqvu6g6ruAXCf27vbuwA7qx2T524zJjqUlzq/bLuNhW6jvY7Gfy07w5DvOXeQH97jdTSeSEhIYN++fQ0mWagq+/btIyEhIaDjPLvhTkTigUuAX9bV1Me20/7VRGQmTtcUXbt2PeP4jAmalX+H4j3O2tTRZszt8OXL8PmTMOkBr6MJu9TUVPLy8igsLPQ6lKBJSEggNTU1oGO8vDN7CvClqha47wtEpJOq7nG7lva62/OAtGrHpQK7Tz2Zqj4DPAPO9NjQhW1MACpOOOW7u2Q5iwRFm5TuMPByyH7BuUGweRuvIwqrJk2a0L17d6/D8JyXXU9X8U23E8BsYIb7egbwdrXt17mzn0YBh6q6qIyJeKvfgIM7nLEJP8swRJyxd8CJY7Ds/7yOxHjEk0QhIs2AicC/q21+EJgoIpvcfVWFVeYBW4Bc4Fng5jCGakz9VVY4pTA6DISMSV5HU3/t+0LfqbD8L869IKbR8aTrSVWPAW1O2bYPZxbUqW0V8HD5L2Pqae3bsG8TfPev0Xs1UWX8z5xFjb54DsZFYI0qE1Jez3oypmGqrIRPH4a2GZB5idfRnLnOZzn3gHz+Z+eeENOoWKIwJhQ2vgd71zhLjMbEeh1NcIy707kX5KuXvY7EhJklCmOCTRU+/QMkd4MBl3sdTfCkj4Guo517QsrLvI7GhJElCmOCbfNHsPtLpy8/toGtDTbuZ3B4F6x6zetITBhZojAm2BY94iwpOvgqryMJvl4ToNNgp1hgZYXX0ZgwsURhTDBtWwLbl8CYn0BcU6+jCT4RZ6xi/xZY86bX0ZgwsURhTDAtehiat3OWFG2o+k6Dtn2cGVCmUbBEYUywlB2DLQvhrGuhSaLX0YROTAwMucoZhzm4s+72JupZojAmWPauA6107jlo6PpOc57Xz/E2DhMWliiMCZaC1c5zxwHexhEObXtBu0xYZ4miMbBEYUywFKyB+BaQnO51JOGROQ12fAZHGk4JbuObJQpjgiU/Bzr0d/rwG4PMaU5X24Z5XkdiQqyR/EQbE2KqzhVFh0bQ7VSl40Dn7nMbp2jwLFEYEwwHd0DpocYxPlFFxLmq2LIQSg55HY0JIUsUxgRDQY7z3GGgt3GEW+Y0qCiDTfO9jsSEkCUKY4IhPwcQ6NDP60jCK3UEtOgA697xOhITQl6tcJcsIm+IyHoRWScio0UkRUTmi8gm97m121ZE5AkRyRWRVSIy1IuYjalVwWpI6QHxzb2OJLxiYqDPRc4VxYnjXkdjQsSrK4o/Au+pal9gMLAOuAtYoKq9gQXue4ApQG/3MRN4OvzhGlOHqhlPjVHmNDhxFDZ/7HUkJkTCnihEpCUwHngeQFXLVPUgMB2Y5TabBVzqvp4OvKSOpUCyiHQKc9jG1Ky0GA5sdWYBNUbp4yChlc1+asC8uKLoARQCL4rIVyLynIg0Bzqo6h4A97m9274LUL2gTJ677VtEZKaIZItIdmGh3QBkwqhgrfPcmKbGVhcXDxlTnPspKk54HY0JAS8SRRwwFHhaVc8CjvJNN5Mvvlal19M2qD6jqlmqmtWuXbvgRGqMP6pmPDWmqbGnypwKxw84JdZNg+NFosgD8lR1mfv+DZzEUVDVpeQ+763WPq3a8anA7jDFakzdCnKcrpdWaXW3bah6ToC4RKv91ED5lSjcGUl1PZL9OZeq5gM7RaSPu2kCsBaYDcxwt80A3nZfzwauc2c/jQIOVXVRGRMR8nOcbifxdfHbSMQ3g94XOOMUlZVeR2OCzN8FfXe7j9r+J8QCXf08338Cr4hIPLAFuB4naf1TRG4EdgDfddvOAy4CcoFjbltjIkNlpVO646xrPAvh0LETxMUKzZt6vD5332nO/RS7VkDacG9jMUHl70/WOnc8oUYi8pW/H6qqK4EsH7sm+GirwC3+ntuYsDqw1Zka6sH4xJHScp76OJfnFm8lsUkst57Xi2tHdyOhSWzYYwEgYxLExMG62ZYoGhh/xyhGB6mNMQ3LydId4UsUFZXKa8t3cO4fFvLUws1cNKAjQ9KSeWDeOiY88glvfbWLysrT5nuEXmIydD/H6X5SDz7fhIxfVxSqWhKMNsY0OPk5IDHQPjMsH7ckt4jfzlnL+vxisrq15rkZWQxJc4YHF28q4vfvruP2f6zkucVb+NWUTM7u1TYscZ2UOQ3m3A571zbeGxAboDqvKERkoog8KyJD3PczQx+WMVGiIAfa9Ar5GtmbC49w41+/4OrnlnGktJw/f28or980+mSSABjbuy3v3DqWx68YwoGjJ/jec8v4/ovL2ZBfHNLYvqXvxYBY7acGxp8riptxBpB/IyIpwJDQhmRMFMnPgVRfw23BceBoGX9csIm/Ld1OQpNYfjG5L9ePSa9xHCImRrj0rC5MHtCRlz7fxpMf5TLlj59y+bBU7pjYh46tEkIWKwAt2kPXUc402XNruz3KRBN/EkWhW2LjZyLyIGCjVMYAHD8Ih3ZA1veDfuqy8kpeXrqdJxZsorjkBFeO6ModEzNo26KpX8cnNIll5vie/L+sNJ78KJeXPt/O7K9384OxPfjROT1ISmgS9JhPypwG7/8K9m9xCiWaqOfPYPbcqheqehfwUujCMSaK7K0q3RG8Gk+qygdr8pn0+Kf8ds5aBqW2Yt5PxvG77wz0O0lUl9wsnt9M7ceCO89hUv+OPPlxLuf8YSGzPtvGiYoQ3e/Qd6rzbDffNRh1JgpVffuU938KXTjGRJH84JbuWLP7EN97dhkzX15BjMCL3x/OSzeMoG/Hlmd87rSUZvzxyrOYfesYMjq04J7Za7jwsU95LycE96627gYdB1mRwAYkoBIeIpIlIm+KyJfu2hCrRWRVqIIzJqIVrIbEFEg682LGc1ftYeqfFrM+/zD3T+/Pe7eP57y+7ZEg3+09KDWZV384ihe/P5wmscJNf/uSd74OQUWczEtg5zIozg/+uU3YBVrr6RXgReA/gGnAVPfZmMYnP8e5mjjDX+aHS05wz+w1DOjcioU/O4/rRqfTJDZ0ZdhEhPP6tmfebePo37klD8xdx9HS8uB+SKb7a8GuKhqEQH8aC1V1tqpuVdXtVY+QRGZMJKusgL3rgjI+8egHG9l3tJTffWcgrZqFcJD5FHGxMdw/fQD5h0v400e5wT15uz7OtGEbp2gQAk0U97jrR1wlIpdVPUISmTGRbN9mKD9+xuMTObsO8dLn27h2VDcGprYKTmwBGNatNZcPS+X5xVvYXHgkeCcWca4qti2CY/uDd17jiUATxfU491FMxulyqup+MqZxKVjtPJ/B3ceVlcpv3sohpXk8d17Yp+4DQuQXk/uS0CSWe2evQYNZeiNzGlSWw8b3g3dO44lAE8Vgd3GgGap6vfu4ISSRGRPJ8nOcAnjt+tb7FP/I3snKnQf51UWZtEoMX5fTqdolNeWOiRks2lTE+2uCOPjceSi07GLjFA1AoIliqYj0C0kkxkSTghxomwFxgd/bALD/aBkPvbeeEd1T+M5Zp63sG3bXjupG345J/HbOOo6XVQTnpCLOPRW5H0LZ0eCc03gi0EQxFlgpIhtseqxp1KoWK6qnh95dz5GScv7n0gFBnwJbH3GxMdx3SX92HTzOUwuDOLCdOQ3KS5xkYaKWvyvcjRbnp3ky0Bu4kDOYHisi29wks1JEst1tKSIyX0Q2uc+t3e0iIk+ISK6bnIYG+nnGBNWx/VC8u94D2Su27+cf2Tu5cWx3MjokBTm4+hvZow2XDunMXz7ZwraiIF0BdB3t3GtiRQKjmr9XFDOAFcBDwHlAaRCmx56nqkNUtaqi2l3AAlXtDSxw3wNMwUlOvYGZwNP1/DxjguMM1qAor6jk12/m0KlVArdN6B3kwM7cLy/KpEmscP+ctcE5YWwc9L3IGdAuLwvOOU3Y+ZUoVPUmVR0K3Au0Bv4qIp+LyO9EZLyIBGNJrenALPf1LODSattfUsdSIFlEzvxWWGPq62TpjsDvoXjp8+2szy/m7qn9vF+61IcOLRO4/YIMPlq/lw/XFgTnpJmXQOlh2PppcM5nwi6gMQpVXa+qj6nqZOB8YDHO2tbLAvxcBT4QkRXV1rfooKp73M/ZA7R3t3cBdlY7Ns/d9i0iMlNEskUku7CwMMBwjAlAQQ40b++U1A7ksMMlPDp/I+dktGPygI4hCu7MfX9MOr3at+C+OWsoORGEge3u50B8krNEqolK/o5R3C4iw0Xk5FcgVT2uqvNU9T+rdR/5a4x7hTIFuEVExtf28T62nTbZW1WfcafuZrVr1y7AcIwJQP7qeo1P/M/cdZRVVHLfJf0jYgC7Jk1iY7j/kv7s3H+cv3yyJQgnTIDeE2HDPOeOdhN1/L2iSAX+COwVkYVul9PF7kJGAVPV3e7zXuBNYARQUNWl5D7vdZvnAWmnxBKCKmbG+KHiBBSuD3h8YkluEe98vZsfn9OT9LbNQxRc8Jzdqy0XD+rEUwtz2bn/2JmfMHMaHC10CgWaqOPvGMXPVPVsoCPwK2A/cAOQIyIBjXqJSHMRSap6jTODKgeYjTNojvtcVd58NnCdO/tpFHCoqovKmLAr2gQVZQElitLyCv777Ry6tWnGj8/tGcLgguvXF2USI8JvgzGw3XsixDa12U9RKtD7KBKBlkAr97GbwMcnOgCLReRrYDkwV1XfAx4EJorIJmCi+x5gHrAFyAWexVma1RhvFAS+BsVzi7aypfAo917Sv8YlTCNR5+RE/nNCLz5YW8DCDXvrPqA2TZOg53lOkcBglgkxYeHXtAsReQboDxTjJIbPgEdV9UCgH6iqW4DBPrbvAyb42K7ALYF+jjEhkb8aYuOdu7L9sHP/Mf700SYm9+/IeX0CG/yOBDeO7c7r2Xnc985aRvdsQ9O4M0h0mdNg43uw52voPCR4QZqQ8/eKoivQFMgHduGMGxwMVVDGRKyCHKeEdqx/tZnue2ctMSLcPS06K980jYvl3kv6s7XoKM8v3npmJ8uYAhJr3U9RyN8xisnAcOBhd9OdwBci8oGI3Beq4IyJOAVr/F6D4sO1BXy4roCfTOhN5+TEEAcWOudktGNS/w78aUEuuw8er/+JmreB9DFWJDAK+T1G4d7wloMzZvAusAToCfwkRLEZE1mOFMKRAr/GJ46XVXDvO2vo3b4FN4ztHobgQus3F/ejUpUH5q47sxP1nebMGivcGJzATFj4ex/FbSLymojsBD7FqfG0AbgMqNcUWWOizsk1KOpOFH/+OJe8A8f57aUDQrqsabikpTTjlvN6MXf1HpbkFtX/RH0vcp6tSGBU8fcnOB14Axihqj1U9VpVfUpVv1bVytCFZ0wE8bN0x+bCI/zl081cdlYXRvVoE4bAwmPm+B50TWnGPbPXUFZez//2rVIhpQdsWxzc4ExI+TtGcYeqvmH3L5hGrSAHkjpDs5ovolWVu9/OIaFJLL+8KDOMwYVeQpNY7pnWj9y9R5j12bb6nyh9LGxfApX2HTNa+Nv19GUw2hgT1fJz6hyfmLNqD0ty9/HzSX1ol1S/RY0i2YTMDpzftz2Pf7iRgsMl9TtJ+jgoOfjNPSkm4vnb9ZTprgVR02M10DaUgRrjqfJSKNpQ6xrZlZXK7+etY0CXllw9slsYgwuve6b140Sl8tB76+t3gm5jnGfrfooa/tY59mdhYKv2ZRquwg1QWV7rQPaGgmJ2HyrhpxMziI2J3KJ/Z6pbm+ZcM7IbL32+jbum9KV9UkJgJ2jV5ZtxitFWaCEa+DtGsd2PR16ogzXGMwV1D2RXzQYa27vhX1xfPaor5ZXK69n1/G9v4xRRJfrn7RkTDvk5EJcAKTUX9VucW0TPds3p1Cp6b67zV892LTi7Zxv+vmwHFZX1qN1k4xRRxRKFMf4oyIH2mc7Snj6UllewbMt+xvZq+FcTVa4Z1Y1dB4/z6cZ6LBRm4xRRJaBE4Zb6vkZE7nbfdxWREaEJzZgIoeokilrGJ77acZDjJyoY04gSxcR+HWiX1JRXlm0P/ODq4xQm4gV6RfEUMBq4yn1fDPw5qBEZE2mK8+HYvjrHJ2JjhFE9G84NdnVpEhvDFVlpfLR+L7vqUwPKximiRqCJYqSq3gKUALhlxuODHpUxkaSqH72WK4rFuUUMTm1FywT/qso2FFeOSEOBfyzfEfjBNk4RNQJNFCdEJBZ3zWoRaQcE/HVARGJF5CsRmeO+7y4iy0Rkk4j8Q0Ti3e1N3fe57v70QD/LmDOWX1Xjyfc9FIdLTvD1zoONanyiSmrrZpzXpz2vfbGTExUB/io4OU6xKPiBmaAKNFE8gbPGdXsReQBYDPyuHp/7E6B6GcqHgMdUtTdwALjR3X4jcEBVewGPue2MCa+CHGjVFRKTfe7+fPM+KpVGNT5R3dUju7K3uJQF6woCO9DGKaJGQIlCVV8B/gv4PbAHuFRVXw/kHCKSClwMPOe+F+B8nKKDALOAS93X0933uPsnuO2NCZ/8nFrvyF6SW0Rik1jO6to6jEFFjnP7tKdzqwT+trQ+3U9V4xR2v24kC3h6rKquV9U/q+qTqlqf4vSP4ySbquvUNsBBVS133+cBXdzXXYCd7ueWA4fc9saEx4njsG9TrTWeFucWMbJHCvFxjXO2eWyMcNWIrizOLWJr0dHADk4fByWHbJwiwgU6PXaWiCRXe99aRF4I4PipwF5VXVF9s4+m6se+U889U0SyRSS7sLAe87qN8WXvOtDKGgeydx88zpbCo41yfKK6K4anERcjvBrooLbdTxEVAv0KNEhVT66V7c56OiuA48cAl4jINuA1nC6nx4FkEam6kykV2O2+zgPSANz9rYD9vk6sqs+oapaqZrVr1y6AkIypRR2lOxpT2Y7atG+ZwIX9O/B69k5KTgTQjWTjFFEh0EQRIyInO2JFJAX/Cwuiqr9U1VRVTQeuBD5S1auBj4HL3WYzgLfd17Pd97j7P1LVetQLMKaeCtZAk+bQ2vdypotzi2jbIp4+HZLCHFjkuXpkNw4cO8F7OfmBHZg+zsYpIlygieIR4HMR+a2I/Bb4DPhDEOL4BXCHiOTijEE8725/Hmjjbr8DuCsIn2WM//JzoEM/iDn9v4qqsiS3iDG92mJzLGB0jzZ0b9s88Du1bZwi4vl9NQCgqi+JSDZOlxHAZaq6tj4frKoLgYXu6y3AaaVAVLUE+G59zm/MGVN11snuf5nP3RsKiik6UtZop8WeKiZG+N6Irjwwbx0b8ovp09HPq6z0auMUnQaHLkBTb4EOZjcFhgAtgRTg8qq6T8Y0OIfynG+6Ncx4WrzJHZ+wRHHSfwxLJT4uhr8HclXRsrNTldfGKSJWoF1Pb+Pc21AOHK32MKbhOVm6o+aB7B7tmtM5ueGXFfdXSvN4Lh7YiX9/uYtjZeV1H1DF7qeIaIEmilRVvUJV/1dVH6l6hCQyY7yWX5Uo+p22q6y8kmVbG1dZcX9dPbIrxaXlzF65u+7GVWycIqIFmig+E5GaS2ga05AUrIbW6dD09L72r3Yc4FhZ4yor7q9h3VrTp0MSrywL4J6KdLufIpIFmijGAitEZIOIrBKR1SKyKhSBGeO5/JrXoFiSW0SMwKgeVijgVCLCNaO6snrXIVblHaz7ALBxiggXaKKYAvQGLgSmAVPdZ2MalrKjsH9LjTfaLc4tYnBaMq0SG1dZcX9delYXmsXH8kog9Z9snCJiBVoUcDtwGB4id3sAAB8hSURBVOgAdKv2MKZhKVgLqM8risMlJ/g675CNT9QiKaEJ04d0ZvbXuzl0/IR/B9k4RcQKdHrsD4BPgfeB+9zne4MfljEeO1m64/REsXTzPioq1cYn6vC9Ed04fqKCt77a5d8BNk4RsQLtevoJMBzYrqrn4dR5sgp8puEpyIGmLSH59Avmb8qK+16fwjgGprZicGorXlm2Hb8q71SNU2y1hYwiTaCJosS9WxoRaaqq64E+wQ/LGI9VrUHhozTH4twiRnRPoWlcrAeBRZerR3ZjY8ERsrcf8O+A9LGw/TMbp4gwgSaKPLfM+FvAfBF5m28qvRrTMFRWOsUAfYxP7Dl0nM2FRxnXyKvF+mvq4E4kJcTxylI/79ROHwelh75ZftZEhEAHs7+jqgdV9V7gv3GK9l1a+1HGRJmD26Gs2Of4xJLcfUDjXfY0UM3i4/iPoanMW53PviOldR9g4xQRqd5LcqnqJ6o6W1XLghmQMZ47Wbrj9ESxeFOhlRUP0NUju1JWUckbK/Lqbmz3U0QkvxKFiCx2n4tF5PCpz6EN0Zgw27oIJBbaZ35rs6qyOHcfZ/dsS0yMlRX3V+8OSYzonsLfl++gstKPQe3u42ycIsL4lShUdaz7nKSqLU99Dm2IxoRRcT58OQsGXQHxzb+1a2PBEYqOlNr9E/Vw9ciubN93jCWbi+pubOMUEcev9ShE5I7a9qvqo/5+oIgk4NyL0dT9/DdU9R4R6Y6zPGoK8CVwraqWuaXNXwKGAfuAK1R1m7+fZ0xAFj8OFSfgnJ+fvstd9nSMDWQHbPKAjqQ0j+eVpTsY17uOpYqrr6PdeUjogzN18neMIsl9ZAE/Brq4j5uA00tr1q4UOF9VB+OsbTFZREYBDwGPqWpv4ABwo9v+RuCAqvYCHnPbGRN8h3dD9gsw5CpnHedTLMktokfb5nSxsuIBaxoXy3ezUpm/roCCwyW1N27ZCdr0snGKCOJv19N9qnof0BYYqqp3quqdON/yUwP5QHUccd82cR+Ks2reG+72WXwzm2q6+x53/wSxdSdNKCx+DLQCxp9+NVFWXsnSLftsttMZ+N6IrlRUKv/4Ymfdje1+iogS6KynrkD1WU5lQHqgHyoisSKyEtgLzAc2AwdVtWqlkzycKxbc550A7v5DOOtqGxM8h3bBir/CkKud0uKnWLnzoJUVP0Pd2jRnXO+2vLp8B+UVlbU3tnGKiBJoongZWC4i94rIPcAynPGDgKhqhaoOwbkaGQFk+mrmPvu6ejht6oSIzBSRbBHJLiy0qiImQIsecdbIHv8zn7sXu2XFR1tZ8TNy9chu7DlUwicb6/g/2s3up4gkgd5w9wBwPc4YwkHgelX9XX0/XFUPAguBUUCyiFQNrqfyzR3feUAagLu/FbDfx7meUdUsVc1q166OwTJjqju4E758Cc66BpK7+myyJLeIganJtGpmZcXPxITM9rRu1oTZX9dR0MHGKSJKfW642wp8DnwFJInI+EAOFpF2bhkQRCQRuABYB3wMXO42m4GzPjfAbPc97v6P1K8KY8b4adEjTk2ncXf63F1ccoKVOw8yzrqdzliT2BimDOzE/LUFHC+rY/zBxikihhdlxjsBH7sr430BzFfVOcAvgDtEJBdnDOJ5t/3zQBt3+x3AXQF+njE1O7AdvnoZhl4HyWk+myzdst/KigfRtEGdOVZWwUfr99be0MYpIoZf91FUU1VmfKmqnicifXESht9UdRVOefJTt2/BGa84dXsJ8N0A4zTGP4seBomBsTXfKrQkt4iEJjEM7WZlxYNhRPcU2ic15Z2vd3PxoE41N7T7KSKGlRk3jdf+rbDy7zDsemjVpcZmTlnxNlZWPEhiY4SLB3Xiow17KS6pZfW7k+MUtj6F16zMuGm8Pn0YYuJg7E9rbJJ/qITcvUcY28tmOwXTtMGdKSuvZP7agtob2jhFRPA7Ubg3ud1mZcZNg7BvM3z9qnM10bLm7o8lbtmOsb1sJl0wnZWWTJfkRN6pa/ZT+jgoPQz5q8ITmPHJ70ThzjR6q9p7KzNuotenD0NsfK1XE+B0O7VpHk/fjlZWPJhEhGmDO7NoUxEHjtbyK8Tup4gIgXY9LRWR4SGJxJhwKcqFVa/B8BshqUONzZyy4kWc3cvKiofCtMGdKK9U3luTX3Mju58iIgSaKM4DPheRzSKySkRWu9NcjYken/4vxDaFMT+ptdmmvUcoLC618YkQ6depJT3aNWf2yrq6n2ycwmuBJoopQE+cAn7TgKnuszHRoXAjrH4dRvwQWrSvteniTW5Zcbt/IiREhGmDOrN06z721lZR1sYpPBfoYHalqm4/9RHC+IwJrk8egrjEOq8mwBnI7t62Oamtm4UhsMZp2uBOqMLc1XtqbpQ+1nm27ifP1Hsw25ios3c95PzLuZpoXvtVwomKqrLi1u0USr3aJ5HZqWXts5+SOkKb3pYoPGSD2abx+OQhZ3nTs2+rs+nKnQc5WlZhy56GwbTBnfhyx0F27j9WcyMbp/BUfQazl9pgtok6BWthzZsw8kfQvO6rhMWbihCB0T0sUYTatEGdAT+6n2ycwjOB1nqazDfrQ1gFVxM9PnkQ4lvA6Fv9ar4kt4hBXVpZWfEwSEtpxpC0ZN75ejc3ndPTd6Pq4xSdTysVZ0LMrysKESkWkcNADrDafeQAa9xnYyJXfg6sfRtG/RiapdTZvLjkBF/tPMjY3nY1ES7TBndmze7DbC484ruBjVN4yt81s5NUtaWPR5Kqtgx1kMackYW/h6atYPTNfjVfZmXFw+7igZ0QgTlf19L91H0cbFsC5VYMItzqs3CRMdFjzypYP8e5mkhsXWdzVWXW59tIahrH0K51tzfB0bFVAiPSU5j99S5qXJes94VQVgw7PgtvcCb8iUJE0kTkYxFZJyJrROQn7vYUEZkvIpvc59budhGRJ0Qk1x1AHxrumE0UW/igczUx6sd+NZ+7eg+LNhVxx4UZJDSxsuLhNG1wZzYXHmV9frHvBt3PgbgE2Ph+eAMznlxRlAN3qmomzlrZt4hIP5yV6xaoam9gAd+sZDcF6O0+ZgJPhz9kE5V2fwUb5sLZt0Ji3YsOFZec4P531tK/c0uuHdUtDAGa6qYM6EhsjNR8T0V8M+g+Hja8C7YacliFPVGo6h5V/dJ9XYyzXnYXYDowy202i2/Kl08HXlLHUiBZRGpZFssY18IHISEZRt7kV/NH52+k8EgpD3xnIHGx1isbbm1aNGVMr7a8s2p3zd1PGZPgwFbYlxve4Bo5T/83iEg6zrKoy4AOqroHnGQCVBXi6QLsrHZYnrvNmJod2AYb34NRN0NC3fMtcnYdYtZn27h6ZFeGpNmSp16ZNqgTO/cf5+u8Q74b9J7kPG98L3xBGe8ShYi0AP4F3K6qh2tr6mPbaV83RGSmiGSLSHZhYWGwwjTRav0853lQ3cutV1Qqv34rh5Tm8fx8Ut8QB2Zqc2H/jsTHxtTc/ZScBh0G2DhFmHmSKESkCU6SeEVV/+1uLqjqUnKf97rb84C0aoen4mP5VVV9RlWzVDWrXTtbjazRWz8X2veDlB51Nn11+Q6+3nmQX1+cSatEu8HOS60Sm3BOn3bMWbWbyspaZj9t/wyOHwxvcI2YF7OeBGcJ1XWq+mi1XbOBGe7rGcDb1bZf585+GgUcquqiMsanY/udKZR9L66zaWFxKf/73npG92jDpUOsRzMSTBvcmYLDpSzftt93g4zJoBWweUF4A2vEvLiiGANcC5wvIivdx0XAg8BEEdkETHTfA8wDtgC5wLOAf3dNmcZr43uglX4lit/PW8fxExX89tIBON9hjNcuyGxPYpPYmrufUrMgMQU2fhDewBqxQGs9nTFVXYzvcQeACT7aK3BLSIMyDcv6udCyC3QaUmuzzzYX8e+vdnHreb3o1b5FmIIzdWkWH8eEzPa8m5PPvZf0p8mpM9BiYp3up00fONVkY+x+l1CzOYCmYSk7BrkLoM9FUMsVQll5Jf/9Vg5pKYncen6vMAZo/HHJ4M7sP1rGZ5v3+W6QMQmO74e87PAG1khZojANy5aFUH68zm6nZxdtYXPhUe6/ZIDdgR2BzunTjqSEuJq7n3qeDzFxNk02TCxRmIZl/VynZEdVWWofdu4/xhMLNjG5f0fO61v7utnGG03jYpnUvyPv5+RTWu5jsaLEZOg62qbJhoklCtNwVFbAxnch40KI9T3NVVW5++0c4mKEey7pF+YATSCmDe5McWk5n2yo4b6ojMmwdw0c3BHewBohSxSm4di5DI7tq7Xb6f01+Xy8oZCfTsygU6vEMAZnAnV2zzakNI/nnVU1zIbPmOw821VFyFmiMA3H+rkQGw+9LvC5+2hpOfe9s5a+HZP4/tnp4Y3NBKxJbAxTBnTkw7UFHCsrP71B216Q0tMSRRhYojANg6qz7kT3c6Bpks8mj3+4kT2HSnjgOwOs6F+UmDa4M8dPVLBg3V7fDTImw9ZPoexoeANrZOx/i2kY9q5zCgHW0O20bs9hXliyjatGpDGsW93LoZrIMDw9hQ4tm9Y8+ynjQqgohS2fhDewRsYShWkY1s91nvtMOW1XZaXym7dyaJXYhF9MtqJ/0SQ2Rrh4YGcWbijkcMmJ0xt0PRvik2yabIhZojANw/o5kDockjqetuuf2TtZsf0Av5zSl+Rm8R4EZ87EtMGdKKuo5IM1BafvjIuHXuc74xS2mFHIWKIw0e9QHuxZ6bPbaf/RMh58bz0j0lO4fFiqB8GZMzUkLZnU1om1dD9NhiP5sOfr8AbWiFiiMNFvw7vOc9+pp+36/bx1HCkp53++Y0X/opWIMG1wZxbnFrH/aNnpDXpNBMRmP4WQJQoT/dbPgTa9oW3vb21evnU/r6/I4wfjepDRwfdMKBMdpg3qTEWl8m6Oj3sqWrRzKspuskQRKpYoTHQ7fhC2LT6t26m8opLfvLWaLsmJ3DbBiv5Fu8xOSfRs15y3v6qp+2kS7FoBR2qYRmvOiCUKE902zYfK8tO6nf6ZncfGgiP899R+NIsPezV9E2QiwlUjurJ8234WbvCRDKru0t5ka1SEgiUKE93Wz4EWHaDLsJObjpdV8PiHGxnWrTWT+nfwMDgTTNeO7kaPts25/521lJVXfntnhwHOGiQ2TTYkvFgK9QUR2SsiOdW2pYjIfBHZ5D63dreLiDwhIrkiskpEhoY7XhPByksh90Pn3omYb36UX1iylb3Fpdw1pa8NYDcgTeNiuXtaP7YUHeWFJVu/vVPE6X7a/LHzc2GCyosrir8Ck0/ZdhewQFV7Awvc9wBTgN7uYybwdJhiNNFg66dQduRb3U4Hjpbxf59s5oLM9gxPtzuwG5pz+7TngswO/GnBJgoOl3x7Z8Zk5+dh+xJvgmvAwp4oVPVT4NRV06cDs9zXs4BLq21/SR1LgWQR6RSeSE3EWz8H4ltA9/EnNz21MJcjpeX8fJLdgd1Q3T21Hycqld/PW/ftHd3HQ1yiTZMNgUgZo+igqnsA3Oeq1WS6ADurtctzt51GRGaKSLaIZBcW1lC/3jQclZXO/RO9LoC4pgDsOnicWZ9t5z+GptKno02Hbai6tmnGj8b34K2Vu/liW7XvnE0SnWSx4V27SzvIIiVR1MRXB7PPnwBVfUZVs1Q1q127diEOy3hu1wo4UvCtbqfH5m8EgZ9OzPAwMBMON5/bi86tErjn7TVUVFb7lZAxCQ5uh6KN3gXXAEVKoiio6lJyn6vmv+UBadXapQI1TKQ2jcr6Oc6ayb0nArAhv5h/fZnHjNHd6JJsCxI1dInxsfz64n6s3XOYvy+vtsJdxiTn2WY/BVWkJIrZwAz39Qzg7Wrbr3NnP40CDlV1UZlGbv1cZ13sxGQA/vD+elo0jePmc+3musbiooEdGd2jDY98sIEDVaU9WqVCh4E2ThFkXkyPfRX4HOgjInkiciPwIDBRRDYBE933APOALUAu8Cxwc7jjNRGocCPs23Sy22n51v18uG4vN53Tk9bNrTpsYyEi3De9P8Ul5fzhgw3f7MiYBDuWwrFT58yY+vJi1tNVqtpJVZuoaqqqPq+q+1R1gqr2dp/3u21VVW9R1Z6qOlBVs8Mdr4lAG75Ze0JVefDddbRPasoNY7p7G5cJu4wOSVw3uhuvLt9Bzq5D7sbJoBWw+SNvg2tAIqXryRj/rZ8LnYZAq1Tmry3gyx0Huf2CDBLjY72OzHjg9gsySGkWzz2z16Cq0GUoNGtr4xRBZInCRJfifMjLhr5TKa+o5H/f30CPts35f1m21kRjVbVy4YrtB3jzq10QEwu9L3Tu2q8o9zq8BsEShYkuG94FFPpexL+/3EXu3iP81+Q+xMXaj3JjdvmwVAanJfP7d9dTXHLCGac4fgDyvvA6tAbB/neZ6LJ+LrROp6R1Hx6dv5EhaclM6n/68qemcYmJEe67pD+FxaX86aNc6Hm+M33aup+CwhKFiR6lxbD1E+g7lb9+vp38wyVW+M+cNCQtmSuy0nhh8VZyD8dAtzE2TTZILFGY6JH7IVSUcST9Qp76OJdz+7RjVI82XkdlIsjPJ/chMT6W+95Zg/a+EArXwYFtXocV9SxRmOixfi40a8OTm1MoLi3nv6zwnzlF2xZNuWNiBos2FbE4JsvZuNEWMzpTlihMdKg4ARs/4Fj3ibz4WR7fGdKFfp1beh2ViUDXjupGnw5J/PKTY1Sm9LJxiiCwRGGiw7bFUHqIfxYPRtUK/5maxcXGcO8l/ck7cJyVCSNh2yIoPeJ1WFHNEoWJDuvnUhmXwP9u6sg1o7qRltLM64hMBBvdsw0XD+rE4zt7QEUZbFnodUhRzRKFiXyqsGEeX8cPIya+Obeeb4X/TN1+fVEmX9GX4zHNrfvpDFmiMJFvz0o4vIu/HRzIj8b3IMUK/xk/dE5O5Efn9WHBiYGUrXvPWezK1IslChPxdN0cKolhZeJIbhxnhf+M/34wrgcrE0cSX1JI+Y6lXocTtSxRmIh3dNVsllf24fsTh9EsPs7rcEwUSWgSy7gpV3FUmyJ/vZgdj01gz4d/Ro/srftgc5IlChPRKoq20OLQRrITRnPl8LS6DzDmFOOH9GXhuW/wZvMrOXFgF50W/4rKh/uw9ZHz2frek1QUF3odYsQTjYJFyEVkMvBHIBZ4TlUfrK19VlaWZmfb0hXRSFU5uL+I/K2rOZy3nsQt7zHo8CcsmDSfCaNHeB2eiXJFxSV8sWwxJ1b/mwEHP6KH7KGCGLY0P4uKzOmkj72ShOQOXofpCRFZoapZPvdFeqIQkVhgI87Kd3nAF8BVqrq2pmMsUUS+40ePsGfbWg7sXEdp/kZiD26m5dHtdDiRRwqHT7arUCGnxdkMvHMuMTFW08kET/HxMr7MXsLxlf+iT9GHdJc9lGsMuc2HUJoxnZ7jr6BFSievwwybaE8Uo4F7VXWS+/6XAKr6+5qOyezRRV/8nx+HKULjl8oTcHAHzYu30bZ0Jx20iBj55mevkNYUxqdxtEU3KlN6kdgpg5Su/ejYrS9x8QkeBm4ag9IT5Xy9YglHvnyDnnvn0w0naaxPHMKRzmMhrqnXIYbc6Kv/u8ZEEQ0jg12AndXe5wEjT20kIjOBmQDDOsUwauMfwhOd8VuxJrKnSRq7Wg5he3IPmnToTXJaJh3T+9OuZWvaeR2gabSaNoljxKhzYNQ5VFRUsubrzzj4xT/pmj+fAVue8Do8z0VDovDV33DaZZCqPgM8A3DWkCF66Lb5oY7LBEBiYkhq2ZqMGJs/YSJbbGwM/YeOhaFj0cpKDh3a79z02dDd177GXdGQKPKA6tNdUoHdtR0QGxdHqxT7fmqMOTMSE0Or1m29DsNz0fD17gugt4h0F5F44EpgtscxGWNMoxHxVxSqWi4itwLv40yPfUFV13gcljHGNBoRnygAVHUeMM/rOIwxpjGKhq4nY4wxHrJEYYwxplaWKIwxxtTKEoUxxphaRXwJj/oQkWJgg9dx+KkVcMjrIAJg8YZONMUKFm8oeRFrH1VN8rUjKmY91cOGmmqWRBoReUZVZ3odh78s3tCJpljB4g0lL2IVkRorqVrXk/fe8TqAAFm8oRNNsYLFG0oRFWtD7XrKjpYrCmOMiQS1/d5sqFcUz3gdgDHGRJkaf282yCsKY4wxwdNQryg8IyKTRWSDiOSKyF3utudF5GsRWSUib4hIixqO/aV73AYRmVTbOUMYq4jIAyKyUUTWichtNRw7Q0Q2uY8Z1bYPE5HV7jmfEJGgLUtXQ7zni8iXIpIjIrNExOcEjXDHKyIviMheEcmptu0PIrLe/Tl4U0SS/f1zutu7i8gy98/wD7dIZlDUEO+9IrJLRFa6j4siPN4hIrLUjTVbRHyunevBz0KaiHzs/n9aIyI/cbd/131fKSI1dpV78fd7GlW1R5AeOEULNwM9gHjga6Af0LJam0eBu3wc289t3xTo7p4ntqZzhjDW64GXgBi3XXsfx6YAW9zn1u7r1u6+5cBonHVE3gWmhPjvdieQ4ba5H7gxQuIdDwwFcqptuxCIc18/BDzk75/T3fdP4Er39f8BPw7iz66veO8FflaffxeP4v2g6t8PuAhYGCE/C52Aoe7rJJylnfsBmUAfYCGQFUl/v6c+Iv6KooZvkX5lUgnzN3RgBJCrqltUtQx4DZiuqofdzxUgER8LLwHTgddUtVRVtwK57vl8njNUsQI/Bu5X1UoAVd3r49hJwHxV3a+qB4D5wGQR6YSTFD9X56f3JeDSIMRaU7z/AZSq6ka3zXx3m+fxquqnwP5Ttn2gquXu26U4a6ucyue/i/uzcz7whttuVrBirSleP0VSvAq0dF+3wve6NV78LOxR1S/d18XAOqCLqq5T1bru9/Lk7/dUEZ0oRCQW+DMwBScDXyUi/XC+jT2mqr2BA8CNPo7th7N2RX9gMvCUiMTWcs5g8LVsaxc3nheBfKAv8Cd32yUicn8dx9Z4zhDF2hO4wr10f1dEeruxZonIc37EmheCWGv6zI5Ak2qX7ZfjLnIVAfHW5Qacb62ISGcRqaqOXFOsbYCD1RJNuGK91e0qe0FEWkd4vLcDfxCRncDDwC/deCPmZ0FE0oGzgGW1tIm4v9+IThTU/K3Xn0wa7m/oUMuyrap6PdAZ59vEFe622ap6dx3H+rUUbD3UdN6mQIk60+SeBV5wY81W1R94FGtNn1mJ82XgMRFZDhQD5RAR8dZIRH6NE+crAKq6W1Wr+v8jKdancb44DAH2AI9ARMf7Y+CnqpoG/BR4HiLnZ0Gcscl/AbdX9TL4Eol/v5GeKGrKpj4zqcff0KvOVeOyrapaAfwD390jNR0b8FKwZxhrHs4PM8CbwKAAj031sT0YfH6m21UwTlVHAJ8CmyIkXp/cwdOpwNVuF8epaoq1CEiWbwbrQx6rqhaoaoXbDfkszpesiI0XmAH82339OoHFG9KfBRFpgvP/6hVV/Xdd7auJiL/fSE8UvrJmrI9tVd/avfyGDjUs2yoiveDkGMU0YL2PY2cDV4pIUxHpDvTGGVwL1VKwNZ33LZwrNoBzcAbeTvU+cKGItHa7Iy4E3lfVPUCxiIxy/6zXAW8HIdYa4xWR9gAi0hT4Bc6gXiTEexoRmezGeImqHquhmc8/p5tUPsbpXgPnl2LIYnXj7VTt7XeAHB/NIiZenF+U57ivz8f3l4aw/yy453seWKeqjwZ4eGT8/YZqlDwYD5wZCO9Xe/9L91HEN7NHvtXm1LbV3r/vtvV5ziDGfBHOL9fNwK9xkvESYDXOf7RXcGdBAZfgDBxXHftr97gNVJtxceo5QxWruy0ZmOvG+zkw2N2eBTxX7dgbcLrzcoHrq23Pcv+cm4Ence/VCWG8f8DpztuAc0lPJMQLvIrTXXMC51vhje5n7wRWuo//c9t2BubV9e+NM/NluXue14GmQfy79RXvy+7PwSqcLxGdIjzescAKnJlBy4BhEfKzMBbny+iqav/2F+Ek3zygFCjA/b0UCX+/pz4i+oY797JqIzAB2IWTXb+HM23vX6r6moj8H7BKVZ865dj+wN9xLj87AwtwvqWLr3OqrcNtjDE+RXTXkzrjELfiXA2sA/7p/kL/BXCHiOTijP4/D98eo3Db/RNYC7wH3KJOf2tN5zTGGONDRF9RGGOM8V5EX1EYY4zxniUKY4wxtYrYRCFnVqTsryJyua99xhhjAhOxiQL4K07pjVM9pqpD3Mc8H/uNMcYEUcQmCq1/kbJvEZG7ReQLccpQP+Pe/IKILBSRh0RkuTgltcedcdDGGNMARWyiqMVpRcrq8KSqDlfVATiVW6dW2xenTumH24F7QhGsMcZEu2hLFD6LlNXhPHFKkq/Gua2/f7V9VTVXVgDpQYzTGGMajKhKFFpDkTIRedEd3P7WmIWIJABPAZer6kD3mIRqTUrd5wrA58poxhjT2EXVL0cR6aRO8S6oVqRMnRLevlQlhSK3xO/lfFOe3BhjjB8iNlGIyKvAuUBbEcnDGUM4V0SG4BTY2gb8qIbD43BWPjsoIs/iFDbbhlPXyRhjTAAaXAkPEYnBSQjXWQ0nY4w5c1E1RlEXEemM0x211JKEMcYER4O7ojDGGBNcDeqKwhhjTPBZojDGGFMrSxTGGGNqZYnCGGNMrSxRGGOMqZUlCmOMMbX6/6tqwiMsH+pQAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"df.loc['1990-01-15'].plot()\n",
"plt.ylabel('Irradiance [W/m$^2$]');"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZAAAAEFCAYAAADNFLE8AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjAsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+17YcXAAAgAElEQVR4nO3deXxU1f3/8dcnk52ELCRhSQJhXxMghE1wxQ0UEVRcqlK1Urdqa9tv7ff7a7XVWrtYu9cN1wqiCIKKC4KAIPsStrATQgiQQCCQhOzn98e90YgJTMJM7kzyeT4e85iZm3sn7wmTfLjnnHuOGGNQSimlGivA6QBKKaX8kxYQpZRSTaIFRCmlVJNoAVFKKdUkWkCUUko1iRYQpZRSTdLsBUREXhGRfBHZUmdbrIgsEJFd9n2MvV1E5O8isltENolIep1jptj77xKRKc39PpRSqrWT5r4OREQuAoqBN4wxA+xtfwQKjTHPiMhjQIwx5hciMg74ETAOGA78zRgzXERigbVABmCAdcAQY8zxs33vuLg4k5KS4q23ppRSLdK6deuOGmPiz9we2NxBjDFLRSTljM0TgEvsx68Di4Ff2NvfMFaVWyki0SLS0d53gTGmEEBEFgBXAzPO9r1TUlJYu3atR96HUkq1FiKyv77tvtIH0t4YcwjAvk+wtycCB+rsl2tva2i7UkqpZuIrBaQhUs82c5bt330BkakislZE1hYUFHg0nFJKtWa+UkCO2E1T2Pf59vZcILnOfklA3lm2f4cx5kVjTIYxJiM+/jtNeEoppZqo2ftAGjAPmAI8Y9/PrbP9IRF5G6sTvcgYc0hEPgWerh2tBVwJ/LKZMyulWqnKykpyc3MpKytzOopHhYaGkpSURFBQkFv7N3sBEZEZWJ3gcSKSCzyOVTjeEZF7gBzgJnv3+VgjsHYDpcBdAMaYQhF5Elhj7/fb2g51pZTyttzcXCIjI0lJSUGkvhZ1/2OM4dixY+Tm5tK1a1e3jnFiFNatDXxpTD37GuDBBl7nFeAVD0ZTSim3lJWVtajiASAitGvXjsb0FftKH4hSqiHlp6CmxukU6gwtqXjUaux70gKilC/bvwL+2A2e6QyvjIWPH4ON0+HIVqiucjqd8kGXXHJJvde7rV27locfftij38tXOtGVUmcqOQaz7oa2idDjcji8Cda/DpWl1tcDQyGhH3QcaN/SIKE/BIU6m1v5pIyMDDIyMjz6mlpAlPJFNTUw54dQegx+sMAqEAA11XBsNxzaBIc2wqFM2Dob1r1qfV1cEN/nm6IS3xsiEqBNPITFgkt/5VuSJ598krfeeovk5GTi4uIYMmQIAO+++y4PPPAAJ06cYNq0aVx44YUsXryYP//5z3z44Yce+/76aVLKFy3/K+xewMFRv2PCtHziIpaS3iWGIZ1jSO+SREpqLyTNHqxoDJzYbxWTQ5us+92fQ+b0M15UIDwWwuOsgtKm9r7u4zrbwqKb/W37o998sJVteSc9+pr9OrXl8fH9z7rP2rVree+999iwYQNVVVWkp6d/XUCqqqpYvXo18+fP5ze/+Q2ff/65R/PV0gKilK/Z/xUseorTvSYwaXVvglwBxEeG8MHGPKavygEgtk0w6Z2jSe8SQ3rnGAYmJRPWLwX6TfjmdU4dhqO7oPQolNTeCuzbUcjfZj0+3cAcpOP/BkO+7/W3q5pm2bJlTJgwgbCwMADGjx//9dcmTZoEwJAhQ8jOzvZaBi0gSvmSkqMw6x5qortwe/73KKmoYdb9w+nToS3VNYbd+cWs23+c9TnHWb//OJ9nWZM2BAYIfTu2ZUiXGAZ3jmZIlxgSo9sjkR3O/T2rK62mstrCUnIUljwDG2doAXHDuc4UvOVsM6mHhIQA4HK5qKry3mALLSBK+Qq738OUHuPJ9n9jw74qpn1/KH06tAXAFSD07hBJ7w6R3Da8MwDHSyrYcOC4VVT2n2DmmgO89lU2AAmRIfTuEElIoIuQwACCAwMIdgUQEmTdBwd+cwsJdBEc2JYQVzTBgb3o334cPbb9Azl1BCLbO/UTUWcxevRofvjDH/LLX/6SqqoqPvroI+69995mzaAFRClfsfyvsPtzPunyc17d0ZYnxvfj0t4JZz0kpk0wl/Vpz2V9rD/yVdU1bD98ig05VlHZd6yUiqoKKqqqqaiuoaLKupXb91U19f8vtqcksSDEwI6PIONuj79Vdf6GDh3Kddddx8CBA+nSpQsZGRlERUU1a4ZmX1DKSRkZGUbXA1E+af9X8Nq1ZHe4kkv23c6UkSn8ZsIAr3/bmhpDRbVVUMqrqr8uMI/P3cLvDn6f5K59kTvneD2Hv8nKyqJv375Ox6C4uJiIiAhKS0u56KKLePHFF0lPTz/3gWdR33sTkXXGmO+MAdYzEKWcVnIUZt3N6YhkJuy/kUt6J/Cra/s1y7cOCBBCA1yEBrmAbybQu2FIMh9lZ/DDfR8jp0/oiCwfNXXqVLZt20ZZWRlTpkw57+LRWFpAlHJSTQ3MnkpNaSF3VD9Jh/gE/nHrYAJdzk4ScXm/9nz/veHcbz6AnZ/CwJsdzaPqN336mUO1m5dOZaKUk5Y/B3sW8peAu8kO7Ma072cQGereVNreFBESSPs+IzhCLDXb5jkdR/koLSBKOWX/V5hFT7Es5GJeOn0RL92ZQVJMuNOpvnbtwCQ+rsrA7P4cKkqdjqN8kBYQpZxQchQz624KgjpxX9EdPDt5EIM7x5z7uGZ0aZ8ElrhG4Kougz0LnY6jfJAWEKWam93vUV18jO+feoAfXjGIa9M6OZ3qO0KDXLTrezHHiaR6qzZjqe/SAqJUc7P7PX5VcQd9Bo3ioct6OJ2oQdcM6syCqnRqdnwCVRVOx1E+RguIUs0pezlm0VN8UHMBe5Ju5Pc3pPr0wkSjesSxLGgEQZUnIftLp+MoH6MFRKnmUlxA1bt3k2Pa86+IH/H8nRmEBLqcTnVWwYEBRPW/glITQpU2Y/mU7Oxs+vTpw5QpU0hLS+PGG2+ktLSUhQsXMnjwYFJTU7n77rspLy8H4Le//S1Dhw5lwIABTJ069axzablLr0RXqjnU1FD15iRq9i3jNn7HMw98jx4JEU6ncstXe45S+Nr3uDx8N6G/2AkBvl30msO3rtb++DE4vNmz36BDKox95qy7ZGdn07VrV5YtW8aoUaO4++676datGy+88AILFy6kV69e3HnnnaSnp/PjH/+YwsJCYmNjAbjjjjuYPHnyt2bwrfe92Rq6El3PQJRqBtXL/07gvi/4TdUUHr39Br8pHgDDu7bjq+CRhJYfhdw1TsdRdSQnJzNq1CgAbr/9dhYuXEjXrl3p1asXAFOmTGHp0qUAfPHFFwwfPpzU1FQWLVrE1q1bz/v765XoSnlbeTEVi59lefVgUsc/zAU94pxO1CiuACFywDgqNv4DtswluPMIpyP5lnOcKXiTu/1nZWVlPPDAA6xdu5bk5GSeeOIJysrKzvv76xmIUl52Yvk0wqpPsq3HD7lleBen4zTJlek9WVYzgMot86wVEJVPyMnJYcWKFQDMmDGDyy+/nOzsbHbv3g3Am2++ycUXX/x1sYiLi6O4uJhZs2Z55PtrAVHKm6qrqFnxb9bU9OHGCdc7nabJ0jtHsypkFG1Kcz3f3q+arG/fvrz++uukpaVRWFjIT37yE1599VVuuukmUlNTCQgI4L777iM6Opp7772X1NRUrr/+eoYOHeqR769NWEp5Uf6qt0moPMynPR9laHSY03GaTEQITxtP9bp/U7FpLmEd05yOpICAgACef/75b20bM2YMGzZs+M6+Tz31FE899ZRnv79HX00p9Q1jKF/yV/aYToyZcIfTac7b5Rn9WGP6UL75faejKB+hBUQpLzmw7hOSy3exo9tdJLT1nUkSm6pfx7asCRtFdPFuOLbH6TitXkpKClu2bHE0gxYQpbzk5MJnKTDRXDDxfqejeISIEJo6AYDijbpKodICopRX7MpcSf/Ta9iZchvRbSOdjuMxlw5LJ7OmG6WZ2ozVEi/Cbux70gKilBfkf/YnSgkhbeKjTkfxqB4JEWwIH03Cyc1wMs/pOI4JDQ3l2LFjLaqIGGM4duwYoaGhbh+jo7CU8rDMrVsYVvwFWck3kxYd73QcjwtJnQBr3uD4ujnEXPqg03EckZSURG5uLgUFBU5H8ajQ0FCSkpLc3l8LiFIedmD+X+gvhp4T/sfpKF4xeuQF7FqVSFhm6y0gQUFBdO3a1ekYjvOpJiwR+YmIbBWRLSIyQ0RCRaSriKwSkV0iMlNEgu19Q+znu+2vpzibXilYuW0fFxfPZ3+HqwiLb5l/YJJjw9kYMZqOJ9ZBaaHTcZSDfKaAiEgi8DCQYYwZALiAW4A/AM8ZY3oCx4F77EPuAY4bY3oAz9n7KeUYYww7PvobkXKa5GsfczqOVwUPmICLGo6s1dFYrZnPFBBbIBAmIoFAOHAIuAyonbjldaB2PogJ9nPsr48RX16ZR7V4i7flclXx+xxuN4LgpEFOx/GqkaMu46CJo3iDFpDWzGcKiDHmIPBnIAercBQB64ATxpgqe7dcINF+nAgcsI+tsvdv15yZlapVU2PY8NHLdJDjxF31c6fjeF1CVBibIkaTfHwlpvyU03GUQ3ymgIhIDNZZRVegE9AGGFvPrrXj5uo72/jOmDoRmSoia0VkbUsbMaF8xydbDnFN8SxOtO1NYM8xTsdpFoEDJhBMJblrdKXC1spnCghwObDPGFNgjKkEZgMXANF2kxZAElA7+DwXSAawvx4FfKdHzxjzojEmwxiTER/f8oZUKudV1xiWfTyD3gG5tL3sUWglLalDRo/lmGnLKW3GarV8qYDkACNEJNzuyxgDbAO+AG6095kCzLUfz7OfY399kWlJV/UovzEv8yDji2dxOqwjAak3OB2n2cRGhrElchRdji3DVJ7/4kTK//hMATHGrMLqDF8PbMbK9iLwC+BREdmN1ccxzT5kGtDO3v4o0LKHvSifVFldw/xPPmakaxshox8EV5DTkZpVYP8JtOE0e1bPdzqKcoBPXUhojHkcePyMzXuBYfXsWwbc1By5lGrIrHW5TCidRWVoJEEZ33c6TrNLu3A8p1b+hJPrZ8OoSU7HUc3MZ85AlPI3ZZXVzPr8S8a6VhM47B4IaTmTJrorMiKCrMiRdD22hOqqqnMfoFoULSBKNdGM1TmML30fCXAhw+9zOo5jXP2vI4aTZK3+1OkoqplpAVGqCUorqvjvoo3cErSEgLSboW1HpyM5pt+Fkyg3QRSt19FYrY0WEKWa4I0V+xlX9iGhphwu+JHTcRwVFhHFzshhdDu6iMqqaqfjqGakBUSpRjpVVsmri7dxb8jn0PMqSOjjdCTHBfQbT0eOkbl6sdNRVDPSAqJUI01bto8xFV/QtuYEjHrY6Tg+oeeFk6kigOPrZjsdRTUjnxrGq5SvO15Swatf7uGz8E8hPh26jHI6kk8IjmzHrjaD6X70C8oqqwkNcjkdSTUDPQNRqhFe/HIvI6pW0b4y1zr7aCXTlrgjoO94uslB1qxZ4XQU1Uy0gCjlpqPF5by2PJvH2n4GMSnQ9zqnI/mUlNGTAbQZqxXRAqKUm2auOUC/qm10Pb0VRj4EAdpMU5crOpED4f3pdvQL9h0tcTqOagZaQJRyQ02NYcbqHH4Z9RmExcKg7zkdySdFZkxmgOzl1Vefp6xSh/S2dFpAlHLD0l0FBJ7Yy5CylTDsXggOdzqST4q+6H6Ko3rzo+K/8cx7y5yOo7xMC4hSbpi+Koc7Q5dbneYZdzsdx3cFhhBx6zRiA0oYuvUp3lmd43Qi5UVaQJQ6h8NFZSzafpgbgr5Cuo+ByA5OR/JtHVKRS/+Pa1yrWfXBC2zNK3I6kfISLSBKncPMNQfIIIuoisMw8Ban4/iFgNGPUNlpKI+7XuXxNz/jZFml05GUF2gBUeosqmsMM9fkcH/MGgiOhN7jnI7kHwJcBN3wAm0Ca/hxyd/4+Tsb0QVDWx63CoiIxLpxi/Z2WKWa2+Id+RQWFTGqfBn0m6Cd543Rrjuuq37H6IDNxO94i5e/3Od0IuVh7k5lkmffznbZrQvofN6JlPIh01flcEObTAKrSrT5qiky7sZs/4hf753O2E9SGdQ5mqEpsU6nUh7ibhNWljGmmzGma0M34Jg3gyrV3A6eOM0XO/K5J3I1RCXrvFdNIYJM+CdBIWH8PfQFHv7vGgpOlTudSnmIuwVkpIf2UcpvzFydQztO0LVoJaRNhgDtMmyStp2Qa56lf80Obip/j0fe3kB1jfaHtARu/UYYY8o8sY9S/qKquoaZaw/waIdNiKmBNG2+Oi+pN0L/Sfw48D2K9q7juQU7nU6kPOCcBURErhCRl0RkkP18qvdjKeWshdvzOXKynGvMEuiUDvG9nI7k/655loA2cbzc9mVe+mIbi7YfcTqROk/unIE8APwcuF1ELgMGeTeSUs6bviqHURFHaHsiSzvPPSU8Fib8k47le/ld1Dx+MjOT3OOlTqdS58GdAlJgjDlhjPkZcCUw1MuZlHLUgcJSlu4q4Cft10NAIAy4welILUfPK2DIXdxQPodBZhsPvLWecl1H3W+5U0A+qn1gjHkMeMN7cZRy3ttrcnBRw+ATC6DnldAmzulILcuVTyExXfhPm5fYk3uYpz7McjqRaqJzFhBjzNwznv/De3GUclZldQ0z1+TyQJeDuEoOQ9rNTkdqeUIiYOILhJcc5L/J83hz5X7mbjzodCrVBI0alygiGSIyR0TWi8gmEdksIpu8FU6p5rZg2xGOFpdzW8hyCI2CXlc7Hall6jwCRj3C4IK5/LDDLh57bzO7jpxyOpVqpMYObH8LeBW4ARgPXGvfK9UiTF+VQ48oaJ/3OfSfCEGhTkdquS79X0joz/9U/JNOwSXc9991lJRXOZ1KNUJjC0iBMWaeMWafMWZ/7c0ryZRqZtlHS1i2+yi/6LITqSyFgbc6HallCwyBSS/gKjvBzMR32Xe0mD9+st3pVKoRGltAHheRl0XkVhGZVHvzSjKlmtmMNTm4AoSLyhZBTAokD3c6UsvXIRUu/SVxOR/zu+47eHvNAY4V61Qn/qKxBeQurOtArsZquqptxlLKr1VU1TBrbS439hRCcr60rjyXs80dqjzmgkcgaRiTC/5GTFUBr6/QRg1/4e5svLUGGmNSvZJEKQd9uvUwx0oq+GHMRthvrLmvVPNwBcLE53E9P5rn4uZy/4oO3HdxN8KDG/vnSTW3xp6BrBSRfl5JAohItIjMEpHtIpIlIiPttUYWiMgu+z7G3ldE5O8istseEZburVyq5Zu+KofkmFC6HvzAarpq193pSK1Lu+4w+A6Gly4hsPQo76w54HQi5YbGFpDRwEYR2eGlYbx/Az4xxvQBBgJZwGPAQmNMT2Ch/RxgLNDTvk0F/uPBHKoV2VNQzIq9x3io72mkIEuv/XDK0B8QUFPJo+1W8PKyfVRV1zidSJ2DuysSjhQRwer76Ik1pYlHh/GKSFvgImAagDGmwhhzApgAvG7v9jpwvf14AvCGsawEokWkoyeyqNZlxqocAgOE8SwBV7A1fFc1v/he0O0SJtV8xqHjxczfctjpROoc3D0DmQKsA/4AXAqUe2EYbzegAHhVRDbYo73aAO2NMYcA7PsEe/9EoO55bq69TSm3lVVWM2t9Llf3iyN8xxzodZU16Z9yxrCphJ4+zO3RW3lhyR5dR93HubseyH3GmHTgCSAGeE1EVojI0yJykYi4PJAlEEgH/mOMGQyU8E1zVX3qGyLznU+biEwVkbUisragoMADMVVL8smWw5woreT+pP1QUqDXfjit19UQlcwDbRaxNe8ky3frQqe+rFF9IMaY7caY54wxVwOXAcuAm4BVHsiSC+QaY2pfaxZWQTlS2zRl3+fX2T+5zvFJWOu2n5n5RWNMhjEmIz4+3gMxVUsyfVUOKe3C6VfwMYTFQo8rnI7UugW4IONu2h9bzbCIfF5YusfpROos3O0D+bGIDBWRr8fVGWNOG2PmG2N+ZIzJON8gxpjDwAER6W1vGgNsA+ZhNaFh39dO7jgPuNMejTUCKKpt6lLKHbuOnGJ1diFT0mOQHR9Z07YHBjsdS6XfCa5gfpWwnC93HWVrXpHTiVQD3D0DScIaIZUvIovtpqtrRMTTjcU/At6yR3YNAp4GngGuEJFdwBX2c4D5wF5gN/AS1sJXSrlt+uocgl0B3BS+AarKdOEoX9EmDgbcwICj80kILufFpXudTqQa4NaVOvZiUohIMJABXADcDbwkIieMMR65NsQYs9F+/TONqWdfAzzoie+rWp+yymreW5fLVQM6ELH9n9CuByQOcTqWqjXsXiRzBk+mbOaBTaH87MreJMeGO51KnaGx14GEAW2BKPuWh2f6P5RqVh9uOsTJsiq+388F+5fp1CW+JnEIdEpnTPEHCIZpy/Y5nUjVw90+kBdFZDkwExgJfAXcZHdO3+XNgEp5w/RV++kW34b0E59aG3TqEt8zbCqBhbv4aY/DzFxzgOMlFU4nUmdw9wykMxACHAYOYo2AOuGtUEp50/bDJ1mfc4LbhiYjm96GLqMgpovTsdSZ+k+E8HbcHvAppyur+e9KnWTR17h7HcjVwFDgz/amnwJrROQzEfmNt8Ip5Q3TV+UQHBjA5E4FcGy3dp77qqBQSL+TyP0LuKG74bWvsimrrHY6larD7T4Qe8qQLVijnz4GlgPdgUe8lE0pj6uoqmHuxjyu7t+BtjtmQWAo9JvgdCzVkIy7AXg0ZhnHSiqYtS7X4UCqLnf7QB4WkbdF5ACwFGsOrB3AJEDnfVB+Y+nOAopOVzIxLQ62vAe9x1lrnyvfFN0Zeo2l0953yEgM4+Uv91Jdo9Ob+Ap3z0BSsK4MH2aM6WaMucMY829jTKYxRqfMVH5jXmYe0eFBjCYTThfq1CX+YNi9SOkx/l/XnWQfK+WzrTrJoq9wtw/kUWPMLL3SW/mz0ooqFmw7wtgBHQnaMhPaxEP3y5yOpc6l2yXQricD896hS7twntdJFn2Gu01Y6z2xj1JO+jwrn9OV1Uzs0wZ2fgKpN1mr4SnfJmKdheSt47G0UjJzi1i1r9DpVAr3m7D62gtINXTbDMR5M6hS52vexjzatw0ho2QxVFfowlH+ZOAtENSGK0s+oF2bYJ3exEe4+9+vPm7so+PrlM8qKq1kyc587hyZQsCmP0F8H+g40OlYyl2hUTDwFlwb/ssPh97D04vz2XH4FL07RDqdrFVztw9kvxs3HV+nfNYnWw9RWW2Y1CMADqyEATfq1CX+Zti9UF3O7cFLCAty6VmID2jsXFhK+aV5mXl0aRdOv6Il1ga99sP/JPSFlAsJz3ydWzI6MXfjQQ4VnXY6VaumBUS1ePmnylix5xjXDeyEbJsH8X2t9beV/xl2LxTl8EDiHgzw6vJspxO1ao0qIPbiTbeLyK/t551FZJh3oinlGR9tOkSNgYk9g2D/cj378Ge9r4HITsRnvcE1qR2ZviqHotOVTqdqtRp7BvJvrNl4a6++OgX8y6OJlPKweZl59OkQSbejXwBGC4g/cwVa05vsWcRDaYbi8iqmr8pxOlWr1dgCMtwY8yBQBmCMOQ7oGqDKZx0oLGVDzgmuG9QJts21Fo5K6Ot0LHU+hkyBgCB65czkwp5xvLJ8H+VVOgjUCY0tIJUi4gIMgIjEAzqVifJZ8zLzAJjQMwSyl1lnHzr6yr9FJED/62HjdO4b2Z6CU+XM3ZDndKpWqbEF5O/AHCBBRH4HLMNat1wpn/RBZh5DusSQeOQLMNXafNVSDJsK5Se5oGQh/Tq25YWle6jRSRabXaMKiDHmLeB/gN8Dh4DrjTHveiOYUudr55FTbD98iusG2s1XMSnQIc3pWMoTkoZChzRkzctMvbArewpKWLH3mNOpWp1GD+M1xmw3xvzLGPNPY0yWN0Ip5QnzNuYRIHBNzzDYu1ibr1oSEessJH8bY9vuJTIkkDkbDjqdqtVp7DDe10Ukus7zGBF5xfOxlDo/xhjmZeYxqkcccQcXQk2VNl+1NANugNBoQtZPY2xqBz7efIjTFdqZ3pwaewaSZoz5ei10exTWYM9GUur8ZeYWkVNYyvja5quoZOiU7nQs5UnB4ZB+B2R9wOTeLkoqqvlsm64V0pwaW0ACRCSm9omIxOL+hIxKNZt5G/MIdgVwVY82sGcR9L1Om69aoox7wNQwpGAunaJCeV+bsZpVYwvIs8AKEXlSRJ4EvgL+5PlYSjVddY3hw015XNI7nqichdbU7dp81TLFdoWeVyLrXmPiwASW7jpKwalyp1O1Go0dhfUG1jroR+zbJHubUj5j1b5j5J8qty8efB8iO1qjdlTLNPQeKMnnttgdVNcYPsjUa0KaS2M70UOAQUBbIBa4sXZeLKV8xQeZebQJdjGmWxvY/bnVfBWg84a2WN0vg/A4EnM+oH+ntry/UZuxmktjf6vmAhOAKqCkzk0pn1BRVcP8zYe5ol97wrIXQlWZNl+1dK4g6D8Rdn7C5NQoNuUWsTu/2OlUrUJjC0iSMeZmY8wfjTHP1t68kkypJvhyVwFFpyu/mfuqTTx0HuF0LOVtaZOhqoyJoRsIEJizQde3aw6NLSBfiUiqV5Io5QHzMvOIDg9idJc2sGsB9B0PAS6nYylvSxoKMSm03TWH0T3jeX9Dnk5t0gwaW0BGA+tEZIeIbBKRzSKyyRvBlGqs0xXVLNh2hLEDOhKc/QVUlmjzVWshAqk3wb4l3No3mIMnTrMmu9DpVC1eYwvIWKAncCUwHrjWvlfKcZ9nHaG0ovqbua/CYqHLaKdjqeaSOhlMDWOqlxEe7NKpTZpBY4fx7gdOAu2BLnVuHiMiLhHZICIf2s+7isgqEdklIjNFJNjeHmI/321/PcWTOZT/mZeZR/u2IQxLDocdn0Dfa60FiFTrEN8LOg4keNssru7fgY82H6KsUqc28abGDuP9AbAU+BT4jX3/hIczPQLUnaTxD8BzxpiewHHgHnv7PcBxY0wP4Dl7P9VKFZVWsmRHAdemdcK1bzFUnIK+2nzV6qROhrwN3Nq9glNlVSzanu90ohatsU1YjwBDgf3GmEux5sEq8FQYEbYz/eoAAByPSURBVEkCrgFetp8LcBkwy97ldeB6+/EE+zn218fY+6tW6JOth6iorvmm+So0Crpe5HQs1dwGTAKEIScXkBAZwuz12ozlTY0tIGXGmDKwmpCMMduB3h7M81es9UZqVzlsB5wwxlTZz3OBRPtxInAAwP56kb2/aoXmZebRpV04aR3DYMd86H0NBOpqy61O207Q9UICtsxiwsCOLN6RT2FJhdOpWqzGFpBcezr394EFIjIX8Mi8ASJyLZBvjFlXd3M9uxo3vlb3daeKyFoRWVtQ4LGTJeVD8k+VsWLPMa4b2AnZ9yWUFenoq9YsdTIU7uXWpKNU1Rg+2qRTm3hLYzvRJxpjThhjngB+BUzjmyal8zUKuE5EsoG3sZqu/gpEi0htT2gS3xSsXCAZwP56FPCdcXvGmBeNMRnGmIz4+HgPRVW+5KNNh6gx2M1X70NwJHS/1OlYyin9rgNXCF3zPqJ3+0hm62gsr2nyBEHGmCXGmHnGGI+cHxpjfmmMSTLGpAC3AIuMMd8DvgButHebgjWdCsA8+zn21xcZY/TKoVZoXmYefTpE0jMuFLZ/CL3HQmCI07GUU0KjoNdVyNbZTBrUng05J8g+qjMueYNbBUREltn3p0Tk5Jn33o3IL4BHRWQ3Vh/HNHv7NKCdvf1R4DEv51A+6EBhKRtyTlhTl2Qvg9PHrf+BqtYtbTKUFHBj7B5E0GtCvMStQfLGmNH2faR343z9/RYDi+3He4Fh9exTBtzUHHmU75pnT909Pq0TLP8nBLWBHpc7nEo5rueVEBJFuz1zGdntLt7feJAfX94THajpWW4VEBF59GxfN8b8xTNxlGqcDzLzSO8cTXJ0iNV81etKCApzOpZyWmCIdSa6dQ43jvkpj87ZxfqcEwzpEnPuY5Xb3O0DibRvGcD9WENoE4H7gH7eiabU2e08corth09Znec5K6CkQEdfqW+kTYaKYsYGbyQkMEBn6PUCtwqIMeY3xpjfAHFAujHmp8aYnwJDsEZGKdXs5m3MI0DgmjT74sHAMOhxhdOxlK/oMhoiOxGWNZsr+3fgw02HqKiqOfdxym2NHYXVGag76qoCSPFYGqXcZIxhXmYeF3SPI75NEGybBz0vh5AIp6MpXxEQAKk3wO4FTO4XzonSShbv0KlNPKmxBeRNYLWIPCEijwOrAF0TXTW7zNwicgpLrear3NVQfFjnvlLflToZaqq4oPxL2rUJ1tFYHtbYCwl/B9yFNanhCeAuY8zT3gim1Nm8v+EgwYEBXDWgg9V85QqGXlc5HUv5mg6pEN8H15ZZjB/YiYVZ+RSVVjqdqsVoyoWE+4AVwAYgUkR0xjrVrCqra/ggM4/L+yYQFRpoNV91HwOhbZ2OpnxN7UJTOSuY3MNQUV3D/C2HnE7VYvjidO5KndXSnQUcK6lg4uAkOLgeTubq6CvVsFRrIou+xz6jW3wb5ugMvR7jU9O5K+WO2RsOEtsmmIt7xVtzXwUEQe+rnY6lfFVMCiQPRza/y6TBiazOLuRAYanTqVoEX5vOXamzOllWyYJtRxif1pFgl1j9H90ugTC9QEydRepNkL+NG5OKAJi7Uc9CPMFnpnNXyh0fb7bG8k9MT4JDmXBiv859pc6t/yQICKTD/nkMS4ll9oaD6Nyr58/tAmKv9vewF6dzV+qcZq8/SLe4NgxMirLOPsRlLR6l1Nm0aWcNtNj8HhMHd2RvQQmbcoucTuX33C4g9lTp79d57tHp3JU6lwOFpazaV8jEwYnWamLb5kLXC60/DkqdS9pkOJnL+Khsgl0Bek2IBzS2CWuliAz1ShKlzqG23fr6wYmQvw0K9+joK+W+3mMhqA0RO2czpm8CH2TmUVmtU5ucj8YWkEuBFSKyR0Q2ichmEdnkjWBK1WWMYfaGgwxLiSU5Nhw2v2s1X/W51uloyl8Et4E+18C2uUxKi+dYSQVf7tJBpOfDrenc6xjrlRRKncOm3CL2FpRw74XdoKYaMmda635EJDgdTfmTtMmw+R0ucW0iOjyYORvyuKxPe6dT+a3GdqLXGGP2n3nzYj6lAGtFueDAAMaldoR9S+BUHgy61elYyt90uxTC4wja+i7XpnXks62HOVWmU5s0VZM70ZVqLrVTl1zRtz1RYUGwcYa97rWeEKtGcgXCgEmw8xNu6B9FeVUNH2857HQqv6Wd6MrnfTN1SSKUnYSsD6xx/UGhTkdT/ih1MlSVMah4KV3ahTNrnS401VRN6URfqZ3oqjnNXm9PXdI7HrLmQdVpGHSb07GUv0rKgJiuyOZ3uWVoZ1bvK2TnkVNOp/JLjS0gVwPdgMuAa4Fr7HulvKLodCULsqypS4JcAVbzVWx3SNITYdVEtTP07lvKzX2CCHYF8NZK7cptCrcKiIicEpGTwBZgs33bAmy175Xyim9NXXI8G/Yvg4G3Wn8ElGqq1JvA1BC770PGpXbgvfUHKSmvcjqV33F3TfRIY0zbem6RxhhdhEF5zewNdaYuyZxpbRx4s7OhlP+L7wUdB8Lmd7h9RBeKy6uYu1Gn9WuspiwopVSzOFBYyuq6U5dkzoCUCyG6s9PRVEuQOhnyNjAk4hh9OkTy5sr9OsFiI2kBUT7rW1OXHFgFx/dp57nynAE3AIJsfpfbR3Qh69BJ1ueccDqVX9EConzS11OXdLWnLtk4HYLCoa9O3a48pG1H6H4prH+T69MSiAgJ5L/amd4oWkCUT8q0py6ZNDgRKk/D1jlW8QiJcDqaakmG3wen8ojY8xETByfy0aZDFJboBOPu0gKifNKc9bkEBwYwNrUj7JgP5Sd16hLleT2usIaFr/wPt4/oQkV1De+sPeB0Kr+hBUT5nMrqGj7YdOjbU5e0TYKUi5yOplqagAAYcT8cXEvvyu0MS4nlrVX7qanRznR3aAFRPmfJjgIKa6cuOXUY9iy0hu4G6MdVecHAW6251Vb+m9tHduFA4WmW6DTvbtHfSOVz5myoM3XJpnfA1Fi/5Ep5Q0gEpE+BbXO5OqmSuIhgvTLdTVpAlE+pnbrkuoGdCAoQ69qPxAyI6+l0NNWSDZsKQPD6adw8NJmF2/PJPV7qcCjf5zMFRESSReQLEckSka0i8oi9PVZEFojILvs+xt4uIvJ3EdltT+yY7uw7UJ7w9dQlgxPh8CZr6VrtPFfeFp0MfcfDute4bXAcADNW5zgcyvf5TAEBqoCfGmP6AiOAB0WkH/AYsNAY0xNYaD8Ha3XEnvZtKvCf5o+sPG32+oN0i29DWlKU1XnuCramblfK20Y8AGVFJO5/nzF9Epi55gAVVbpm+tn4TAExxhwyxqy3H58CsoBEYALwur3b68D19uMJwBvGshKIFpGOzRxbedCBwlJWZxcyaXAiUlNlrXveeyyExzodTbUGycOgUzqsfJ7vDU/maHEFn2zVxabOxmcKSF0ikgIMBlYB7Y0xh8AqMkDtItiJQN0B27n2tjNfa6qIrBWRtQUFOrLCl72/wZq6ZMKgRNi1AEqPaue5aj4i1lnIsV1cLJtIjg3TK9PPwecKiIhEAO8BPzbGnDzbrvVs+87gbWPMi8aYDGNMRnx8vKdiKg8zxjCn7tQlmTMgPA56XO50NNWa9L8eIjsSsOrf3D68C6v3FbLjsC421RCfKiAiEoRVPN4yxsy2Nx+pbZqy7/Pt7blAcp3DkwCdj9lPZeYWsfeoPXVJaSHs/ATSJoMryOloqjVxBcGwe2HvF9ySUkJwYABvrdKzkIb4TAEREQGmAVnGmL/U+dI8YIr9eAowt872O+3RWCOAotqmLuV/vjV1yZb3oLpCm6+UM4bcBYGhRGW+zLWpHZmti001yGcKCDAKuAO4TEQ22rdxwDPAFSKyC7jCfg4wH9gL7AZeAh5wILPygIoqe+qSfvbUJZkzIKE/dEh1OppqjcJjYeAtsGkmdw6KpLi8ivftpQXUtwU6HaCWMWYZ9fdrAIypZ38DPOjVUKpZLNlpTV0yaXAiFOyEg+vgyqd02VrlnOH3w7rXGHhkDv06DufNFfu5bVhnRD+T3+JLZyCqlZqzIZd2bYK5qFe8dfYhLmu1OKWcktAHul+GrHmZO4d1YvvhU6zPOe50Kp+jBUQ5quh0JZ9n5TN+YCeCxMCmmdBjDES2dzqaau1GPACnDnF98GoiQwJ5c4V2pp9JC4hy1Py6U5fsWwonD1rtz0o5rfsYiOtF6LoXmDS4E/M3H+ZYcbnTqXyKFhDlqNnrc7+ZuiTzbQiJgt7XOB1LKWv5gOH3Qd4GfpBSYC82let0Kp+iBUQ5ZsnOAtZkH7c6JyuKIWseDJgIQaFOR1PKMvAWCI0meedrDO8ay/TV+6nWxaa+pgVEOaKquoanPtxG59hw7hjZBbbNg8pSGHib09GU+kZwGxjyfcj6gKkDAzlQeJqlO3VKpFpaQJQjZqzOYVd+Mf87ri8hgS5r9FVsN2tCO6V8ybB7AeGSE+8TFxGi82PVoQVENbui0kr+smAnI7rFclX/9nAiB7K/tK4813H2ytdEJUG/Cbg2vMmdQ9qxaEc+Bwp1sSnQAqIc8PdFuzhxupJfXdvPujArc6b1hbSbnQ2mVENGPgjlRdwZthxBF5uqpQVENau9BcW8/lU2N2ck079TFBhjNV+lXAgxXZyOp1T9kjIgaSjRm6ZxeZ94Zq45QHlVtdOpHKcFRDWrp+dnERrk4qdX9rY2HFgNhXt04kTl+0bcD4V7+VHnfRwrqeCTLbrYlBYQ1Wy+3FXA51n5PHhpD+IjQ6yNmdMhKBz6XedsOKXOpe910DaRATlv0aVduHamowVENRNr2G4WybFh3DUqxdp4ZCtsesf6xQyJdDSfUudkrxUi+5bwUP9y1mQfZ93+1j0/lhYQ1SzeXnOAHUdO8b9j+xIa5LIWjXr7NghpC5c/4XQ8pdyTPgUCw5hQNo/E6DAeeXsDRacrnU7lGC0gyuuKTlvDdod1jeXqAR2gugpm3QUn8+Dm/0Lbjk5HVMo94bEw6FaCt87iPxOTOVxUxv/MysRaXaL10QKivO6fi3ZxvLSCX9cO2/38cdi7GK75CyQPdTqeUo0z/H6oLift8BweG9uHT7ce4bWvsp1O5QgtIMqr9h0t4bWvsrlpSBIDEu0JE1f8E4ZNhfQ7nI6nVOPF94IeV8Dql7hnRCcu75vA0/OzyDxwwulkzU4LiPKqp+dnEewK4GdX9oaD62Hew9Y1H1c97XQ0pZpu5INQko989Ch/vjGVhMhQHpy+vtX1h2gBUV6zfPdRFmw7wgOX9iAh4CTMvB0i2sNNr1kjWpTyV90vhUt+CRvfInrJr/jHrYNaZX+IFhDlFdU1hic/3EZidBj3jEyEd+60Rl7d8l9oE+d0PKXO38W/gAt+BKtfJH3X37/uD3l1ebbTyZpNoNMBVMs0c80Bth8+xb9uSyf08/+FnBVwwzToONDpaEp5hghc8SRUlMCy57jnsghW9r2E33+cRXqXGAYlRzud0Ov0DER53MmySp79bAdDU2IYV/EJrH0FRj0CqTc6HU0pzxKBcc9C2i3Ioif5e9cVJESG8tD09RSVtvz+EC0gyuP+tWg3haUVPJNRisz/OfS4HMY87nQspbwjIAAm/Av6jid80f9jesZODheV8fNW0B+iBUR5VPbREl5Zvo+7U4Pp/sX9EJ0MN7wMAS6noynlPa5Aq4m2x+V0WfYYLw7O5rNtLb8/RAuI8qjff5xFhKuKx4qespaovWUGhMU4HUsp7wsMgclvQpcLuDTrV/y08x5+/3EWG1vw9SFaQJTHfLXnKJ9uPcyMDjMIOrIRJr0ICX2cjqVU8wkOh9tmIh0H8tCxJxkXvoMH32q5/SFaQJRHWMN2s3g04nP65M+HS/4X+lzjdCylml9IJHxvFhLXi7+YP5BUnMnPWmh/iBYQ5RHvrj1A7JHl/KjqdehzLVz0c6cjKeWc8Fi4Yw6uqETeDPkzh7JW8EoL7A/RAqLO26mySmZ8upTnQ/4J8b1h4vPWyBSlWrOIBLhzLkERMcwI+yOzPv6sxfWH6G+5arIDhaX85bMdTHz2Y56pfIawoADk1um6OJRStaKSkCnzaBMWxptBv+fpNz9qUf0heiW6apSKqhoWbDvC3FVZhGcvYFzAKn7k2kSgqxq5+T2I7eZ0RKV8S2w3AqbMI/qVsTx3+tc8/XY0z9w1zlrawM+JP3fsiMjVwN8AF/CyMeaZs+2fkZFh1q5d2yzZWprd+cW8v2IrRRvncXHVci5ybSaYKqojOuLqPwHSbobEdKdjKuW78jZS/so1HKyIYPaglxiTkUrfjm2tFTp9nIisM8ZkfGe7vxYQEXEBO4ErgFxgDXCrMWZbQ8doAWmc0xXVfLYui9wVs+h3fBGjArYQLNWUhXckOHUiAQMmQmKG9nco5SaTs5KKVydQU1PDDpPELjpzIrIXrg4DiOueTr8eKXSLiyAgwLfOThoqIP7chDUM2G2M2QsgIm8DE4AGC4hyT9aefWxfPIOEnE8YxxaCpJqTbTpRNeA+ggfdQGhiujUHkFKqUaTzCIJ/8Akl62aQlLuJXoUbCS9ZDHuAPXDk02i+ogvHI3pB+37EdhtMt76D6RAb5ZNNXv5cQBKBA3We5wLDz3ZASeEhVk5/yquh/FlNZTlhuUtJrdhEX6mhIDiR/N730mnkLbTtNEiLhlIeIImDiUgcTASAMVCcT/XhrRTuXc/pA5l0O7ad+JI5BO19F/ZC5QIXe6UTR9v0pDquNwEhEU6/ha/5cwGp76/Zd9rjRGQqMBVgSMcARuz8k7dz+bXcgES2dbuHrhfdRnzKYC0aSnmTCES2xxXZnvielxFfu726ivIjO8jbuY6T+zcSWLCNLiVb6LB/kZNpv8Of+0BGAk8YY66yn/8SwBjz+4aOGTxokFm8aEEzJfRDIrSNikW0T0Mpn1RaXERlRUWzf9/odgktrg9kDdBTRLoCB4FbgNvOdoArMJCo2Piz7aKUUj4rPCLK6Qjf4rcFxBhTJSIPAZ9iDeN9xRiz1eFYSinVavhtAQEwxswH5judQymlWiNt7FZKKdUkWkCUUko1iRYQpZRSTaIFRCmlVJNoAVFKKdUkfnshYVOIyClgh9M5GiEKKHI6hJv8KStoXm/yp6yged3R2xjznYV+/HoYbxPsqO9qSl8lIi8aY6Y6ncMd/pQVNK83+VNW0Lxufs96pzHXJizf9oHTARrBn7KC5vUmf8oKmrfJWlsT1lp/OgNRSilf0NDfztZ2BvKi0wGUUsoP1fu3s1WdgSillPKc1nYG4hgRuVpEdojIbhF5zN42TUQyRWSTiMwSkXpXihGRX9rH7RCRq872ml7OKyLyOxHZKSJZIvJwA8dOEZFd9m1Kne1DRGSz/Zp/Fw8tsdZA1stEZL2IbBGR10Wk3gEjDmR9RUTyRWRLnW1/EpHt9udgjohEu/s+7e1dRWSV/R5mikiwJ7KeJe8TInJQRDbat3E+nneQiKy0s64VkWENHNvcn4VkEfnC/l3aKiKP2Ntvsp/XiEiDTe5O/Hy/wxjjlzfgaqwhubuBx+xtXYFVwC5gJhDcwLG/tI/bAVx1ttf0UFYX1qKV3YBgIBPoB7Sts89f6vue9n6ZQIj9/vbYr1fva3o5713AG0CAvV9CPcfGAnvt+xj7cYz9tdXASKzFwD4Gxnox6wGgl73Pb4F7nM5qv+5FQDqwpc62K4FA+/EfgD+4+z7tr70D3GI/fh6434Of3fryPgH8rCn/Lg7l/az23w8YByz2kc9CRyDdfhwJ7LQ/u32B3sBiIMOXfr5n3vzyDEREXMC/gLFYP/BbRaQf1i/fc8aYnsBx4J56ju2HtXZIf6yC8W8RcZ3lNT3h6/XbjTEVwNvABGPMSTuTAGHUs6Ii1jrvbxtjyo0x+7CK27CGXtObeYH7gd8aY2oAjDH59Rx7FbDAGFNojDkOLACuFpGOWAVzhbE+2W8A13sp6w1AuTFmp73PAnub01kxxiwFCs/Y9pkxpsp+uhJIqufQev9N7M/OZcAse7/XPZW1obxu8qW8BmhrP44C8uo51InPwiFjzHr78SkgC0g0xmQZY851vZojP98z+WUBoeE/cO784Jz4g1zf+u2JACLyKnAY6AP8w952nYj89hzHNviaXszbHbjZbgb4WER62nkzRORlN/LmeiFvfd+vAxBU5/T/RiDZB7K6426s/+UiIp1EpHa5goaytgNO1ClAzZX1IbvJ7RURifHxvD8G/iQiB4A/Y7VA+NRnQURSgMFYLSgN7eNzP19/LSAN/fDq/cH5wB/kBtdvN8bcBXTC+t/Hzfa2ecaYX5/jWLfWhG+ihl47BCgz1nC+l4BXAIwxa40xPzjHsd7KW9/r1mCdZT4nIquBU0CVD2Q9KxH5P6ycbwEYY/KMMbX9C76U9T9Y/5kYBBwCngWfzns/8BNjTDLwE2Aa+M5nQay+z/eAH9e2StTHF3++/lpA6vshuerZVvtH2uk/yLnY/wO2JVHnNNoYU43VZ1NfM0tDx571Nb2UNxfrgw4wB0hr5LFJ9Wz3Sla7yeFCY8wwYClWv5jTWRtkd9peC3zPbio5U0NZjwLR8s0gAa9nNcYcMcZU202ZL2GdvftsXmAKMNt+/C6Ny+vVz4KIBGH9Tr1ljJl9rv3r8Imfr78WkPp+eDm494Nz4g/y1+u32yMibgHmiUgP+LoPZDywvZ5j5wG3iEiIWOu/98Tq1Kv3Nb2ZF3gfq5kQ4GKsTr8zfQpcKSIxdtPGlcCnxphDwCkRGWG/3zuBud7KKiIJACISAvwCqzPR6az1EpGr7YzXGWNKG9it3vdpF5svsJrpwPpj6bWsdt6OdZ5OBLbUs5vP5MX6Pb7YfnwZ9f9notk/C/brTQOyjDF/aeThvvHz9VbvvDdvWHN47cUalVQ7AqE/1v8u6o4+eKCeY/vz7VFNe7HOXup9TQ9mHof1B3cP8H9YxXs5sBnrF/At7FFZwHVYndW1x/6ffdwO6owAOfM1Pfwz/s5rA9HAR3bmFcBAe3sG8HKdY+/G6lvaDdxVZ3uG/V73AP/Evg7JS1n/hNUsuAOraQAfyToDq9mnEus/LffY3/sAsNG+PW/v2wmYf65/b6yROKvt13kXCPHg56C+vG/an4FNWP+x6OjjeUcD67B+p1cBQ3zkszAaq5VjU51/+3FYRTkXKAeOYBUyn/j5nnnz2wsJxRp7/lesP/6vGGN+JyLdsDq/Y4ENwO3GmHIRuQ5rONyv7WP/D+vDUoX1x+Xjhl6zud+XUkr5C78tIEoppZzlr30gSimlHKYFRCmlVJNoAVFKKdUkfltA6ptITETGiDWB3kYRWVY7TLaeY7NFJO4cr/+aiNx4tn2UUqo188sCcpZ5q/6DdSHWIGA68P+cS6mUUi2bXxYQGp63yp1J074mIiny7WmffyYiT3gnslJKtSz1rpHgB+qbt2o48ANgvoicBk4CIxzIppRSrYK/noE0NG/VT4Bxxpgk4FWsNTaUUkp5gb8WkPrmrcrHmlqjdjrkmcAF9loftSun/faM16ni2z+DUK8lVkqpFsZfC0hDk/1FiUgve58rsCYpqzbGDLJvvz7jdY4ACSLSzp5079pmewdKKeXn/LIPxBhTJSIPYc2gWTtvVaaI3Au8JyI1WCsS3t3ASwRirVhXaZ+VrAL2Uf9suEopperR6ubCEpF4YKMxprlWmFNKqRbJX5uwmsSelfdL7CUtlVJKNV2rOwNRSinlGa3qDEQppZTnaAFRSinVJFpAlFJKNYkWEKWUUk2iBUQppVSTaAFRSinVJP8f64cNjA54+esAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"df.loc['1990-07-08'].plot()\n",
"plt.ylabel('Irradiance [W/m$^2$]');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The difference between GHI and POA is of course dependent on the tilt defining POA, but because it also depends on solar position, it varies from location to location. Luckily, tools like pvlib make it easy to model!\n",
"\n",
"## Modeling POA for a tracking system\n",
"\n",
"The previous section calculated the transposition assuming a fixed array tilt and azimuth. Now we'll do the same for a tracking array that follows the sun across the sky. The most common type of tracking array is what's called a single-axis tracker (SAT) that rotates from East to West to follow the sun. We can calculate the time-dependent orientation of a SAT array with pvlib:"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZcAAAEECAYAAADklHngAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjAsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+17YcXAAAgAElEQVR4nO3deXxU9bn48c+TFZJAErIQICRhDQiCxIiKK27gvl+t1tqqte21t7a9XfTa3tv6a2/XW3vtbe11txYvdUGlbrhULFVZw76HNQlbIBAgkIRknt8f50QDzkwGMjMnM/O8X695kTlzzvk+CZM8891FVTHGGGPCKcnrAIwxxsQfSy7GGGPCzpKLMcaYsLPkYowxJuwsuRhjjAk7Sy7GGGPCLsXrAMIhPz9fy8rKvA7DGGNiyqJFi3arakEk7h0XyaWsrIyFCxd6HYYxxsQUEdkSqXtbs5gxxpiws+RijDEm7Cy5GGOMCTtLLsYYY8LOkosxxpiws+RijDEm7Cy5GGNC0tLW7nUIJoZYcjHGdGnh5gbG/scsFmxu8DoUEyMsuRhjgvL5lB//dRVH2pU56+q9DsfECEsuxpigXllSx/K6RtKSk1hcs8/rcEyMiIvlX4wxkXGotY1fvrWWccXZjBmYzWtLt+HzKUlJ4nVopoezmosxJqDH/r6JHfub+eEVJ3FqaS4HWtpYv+ug12GZGGDJxRjj147GZv74wQYuO7mI08r6UVGSA0DV1r0eR2ZigSUXY4xfv357Le0+5b6powEYkp9JTkYqiy25mBBYcjHGfMaKukZeqqrlS2eVUZKXAYCIMGFwDlVbrVPfdM3T5CIiOSLyooisEZHVInKmiPQTkXdEZL37b66XMRqTaFSV//faKnIz0rjnguFHvVZRkkv1roM0HjriUXQmVnhdc/lv4C1VHQWMB1YD9wHvqeoI4D33uTEmSt5etZN5mxr41sUj6dsr9ajXKkqdz3pLaq32YoLzLLmISF/gXOAJAFVtVdV9wNXAM+5pzwDXeBOhMYmntc3Hz95YzYjCLD532uDPvD5+cA4iULXF+l1McF7WXIYC9cBTIrJYRB4XkUygv6puB3D/LfR3sYjcLSILRWRhfb3NGjYmHP708WY27znEA5ePJiX5s38estJTKO/fx0aMmS55mVxSgArgEVWdADRxHE1gqvqoqlaqamVBQUGkYjQmYextauXh99Zz7sgCzi/3+5kOgAkluSyp2YfPp1GMzsQaL5NLLVCrqvPc5y/iJJudIjIAwP13l0fxGZNQ/vu99RxsaeMHl48Oel5FSQ4HmtvYUG+TKU1gniUXVd0B1IhIuXvoQmAVMBO43T12O/CqB+EZk1Cqdx3k2blb+NzEEkb27xP03AklTqe+NY2ZYLxeW+xfgGkikgZsBL6Ek/CeF5E7ga3AjR7GZ0xC+Nkbq8lITeZbF4/s8tyh+Zlk906lass+bjqtJArRmVjkaXJR1SVApZ+XLox2LMYkqn+s3817a3Zx36WjyM9K7/L8pCRhQkkOi2us5mIC83qeizHGQ+0+5Sevr2Jwv958cVJZyNdVlOSyftdB9jfbZErjnyUXYxLYCwtrWLPjAPdNHU2v1OSQr5tQkoMqLLGlYEwAllyMSVAHW9r49dvrqCzN5bKTi47r2lM6JlNap74JwJKLMQnqkdnV7D7Ywg+vOAmR49v8q0+vVEYW9mGx1VxMAJZcjElAtXsP8dicTVw7YRDjB+ec0D0mlOSweOtem0xp/LLkYkwC+uVba0kS+O6U8q5PDqCiJJf9zW1s3G2TKc1nWXIxJsFUbd3LzKXbuPucoQzM6X3C96ko7diZ0prGzGdZcjEmgagqP3ltFYV90vnKecO6da+h+Vn07ZViO1Mavyy5GJNAXlu2naqt+/jOlHIy07s3hzopSTilJJeqLVZzMZ9lycWYBOHzKb95Zx2jB/Tl+orisNyzoiSHdbsO2GRK8xmWXIxJEO+u3smm3U3cM3kYyUnHN/Q4kIqSXFRhWU1jWO5n4oclF2MSxONzNjEopzdTxxzfhMlgOoYx22RKcyxLLsYkgKU1+5i/uYE7zh7id4fJE5XdO5URhVmWXMxnWHIxJgE8NmcjfXqlcNNpg8N+74qSXBZvtZ0pzdEsuRgT52r3HuLNFTu4ZWIJWd0cIeZPRWkOjYePsGlPU9jvbWKXJRdj4txTH25GgC+eVRaR+3+yM+UWaxozn7LkYkwc2998hL8sqOGKcQMYkH3is/GDGV6QRZ9eKTZT3xwlYB1ZRH4TwvX7VfVH4QvHGBNO0+dv5WBLG3edMzRiZSQlCacMzrGZ+uYowWou1wMru3jcFOkAjTEn5ki7j6c+3MyZQ/MYOyg7omVVlOSybucBDra0RbQcEzuC9e79TlWfCHaxiOSGOR5jTJi8sXw72xub+em1YyNe1oSSHHzqDHk+a3h+xMszPV/Amouq/rqri0M5xxgTfarKY3M2Mqwgk/NHFka8vAmDrVPfHK3LDn0R+ZmI9BWRFBGZJSI7ReSWcAUgIskislhEXnOfDxGReSKyXkT+IiJp4SrLmEQxd2MDK+r2c+fZQ0kK01IvwWRnpDK8MIvFNdapbxyhjBa7VFX3A1cAu4AxwPfDGMO9wOpOz38BPKSqI4C9wJ1hLMuYhPD4nI3kZaZxXcWgqJU5we3UV7XJlCa05NLRL3MZ8H+quhsIy7tHRIqBy4HH3ecCXAC86J7yDHBNOMoyJlFU7zrIe2t28fkzSumVmhy1citKc9l76AibdttkShNacnlTRFYApwPviEg+0BKm8n8LfA/wuc/zgH2q2jHkpBaI3kcvY+LAE//YRFpKEredWRrVcivcyZSLbb6LIYTkoqrfxalNnKqqR4Bm4LruFiwiVwC7VHVR58P+Qghw/d0islBEFtbX13c3HGPiwp6DLcyoquX6ikHkZ6VHtewRhVn0SU+xRSwNEFqHfm/gDuB37qEiYFwYyj4LuEpENgPTcRLYb4EcEeloiisGtvm7WFUfVdVKVa0sKCgIQzjGxL5n526hpc3HnWdHbtJkIElJwvjBOTZT3wChNYs96Z53jvt8G/Cf3S1YVe9X1WJVLQNuBv6mqrcC7wM3uKfdDrza3bKMSQTNR9p59uMtXDCqkOGFWZ7EUFGSw9od+20ypQkpuYxQ1f8EjgCo6iH8N1+Fy/eBb4tINU4fTNCJnMYYxyuL69jT1Mpd5wzxLIYJpbn4FJbVWu0l0YWy/nariPTC7fsQkSFAaziDUNXZwGz3643AxHDe35h45/Mpj/9jE2MG9uXMoXmexTHB3Zly8dZ9TBpmM/UTWSg1lweBt4BiEXkGp9nq/ohGZYw5Lh+sq6d610G+fM5QnBH93sjJSGNoQabN1Ddd11xU9S0RWQRMwmkO+66q7op4ZMaYkD02ZyMDsntx+bgBXodCRUkuf1uzC1X1NNEZb4W6n8uFwFhVfQVIF5FTIxiTMeY4rNzWyEcb9vDFSWWkJnu/RVNFSS4NTa1s2XPI61CMh0IZivw/wGTg8+6hJuCPkQzKGBO6x+dsIjMtmZsnlngdCuCskAzYfJcEF8rHnEmq+hWcyZOoagNgi0ka0wNsbzzMX5du46bTSsjunep1OACM7N+HLJtMmfBCSS5HRCSJT0eL5fHpci3GGA89/dFmfKp86awyr0P5RHKSMH5wti0Dk+BCSS6/B14CCkTkx8A/cFYuNsZ46GBLG8/N28qlJw9gcL8Mr8M5SkVJLmt2HOBQq02mTFShjBb7kzta7CKc0WI3quqKiEdmjAnq+QU1HGhu48vnRH+pl65MKMmh3acsrWnkzGHezbsx3gmaXEQkGahS1fHAyuiEZIzpSlu7jyc/3MRpZbmc4k5c7Ek6dqZcXLPXkkuCCtospqrtwCoRsWXvjelBZq3cSe3ew9zVA2stALmZaQzNz6Rqi/W7JKpQln/JB1aLyMc4w5ABUNVuL7tvjDl+qspjczZSmpfBRaP7ex1OQKeU5PDB2nqbTJmgQkkuP494FMaYkFVt3ceSmn08ePUYkpN67h/tipJcZlTVsbXhEKV5mV6HY6IslA7996IRiDEmNM8vqCEjLZnrK4q9DiWozjtTWnJJPKHM0N8rIg3HPDaJyAsiUhb5EI0xHQ61tvH68u1cfvIAMtNDaXjwTnlRHzLSkm0yZYIK5d35O2An8BzOUOSbgQKgGngKZ2kYY0wUzFq5g4Mtbdxwas+utYA7mbI4x5JLggplEuUlqvp7Vd2rqg2q+gfgUlWdBvSLcHzGmE5eXFRLSb8MTiuLjV+9itIcVm8/wOHWdq9DMVEW0hKqInLdMV939CLaMjDGREnt3kN8tGEP11cUk9SDO/I7qyjJpd2ntjNlAgoluXwe+LLb17IH+DJwm4hkAN+MaHTGmE/MqKpDFa4/NXamnXVM8KyydcYSTiijxaqBSwO8/EF4wzHG+KOqvLiolknD8ijO7VnriAWTl5VOWV6G9bskoFBGiw0XkVkistR9Pk5EbJtjY6Jowea9bG04FBMd+ceaOKQfczfssUUsE0wozWKPAz/m0/6V5Xy6cZgxJgpeXFRDZloyU8cWeR3KcbuxcjAHWtr469JtXodioiiU5JKpqh91PFFVBY50t2ARGSwi74vIahFZKSL3usf7icg7IrLe/Te3u2UZE8sOtbbx+rLtXD5uABlpPXtuiz+VpbmM7J/FtHlbvQ7FRFEoyWWPiAzh083CrgF2hKHsNuBfVXU0cAZwj4icBNwHvKeqI4D33OfGJKy3VuygqbWdG04d7HUoJ0REuPX0UpbVNtqosQQSSnL5OvAEMEpEtuD8sf9adwtW1e2qWuV+fQBYDQwCrgaecU97Brimu2UZE8s+ndsSu5X4aysG0Ts1mWlzrfaSKLpMLqparaoXAAOA8ap6hqpuCmcQ7jIyE4B5QH9V3e6WvR0oDGdZxsSSmgZnbssNpxbH9MrCfXulcvUpA5m5dBuNh7vdqm5iQMAGXBH5RoDjAKjqw+EIQESycLZR/qaq7g/1F0hE7gbuBigpKQlHKMb0ODOq6hCB62NwlNixbj29lOkLanhlcR23TyrzOhwTYcFqLgXuYxLOZMlh7uNe4JRwFC4iqTiJZZqqznAP7xSRAe7rA4Bd/q5V1UdVtVJVKwsKCsIRjjE9is+nvFhVw6RheQzK6e11ON12cnE244uz+fPcLTjjgkw8C5hcVPWHqvpDIBc4RVXvVdV7cZqvBnS3YHGqKE8Aq1X1N51emgnc7n59O/Bqd8syJhYt2NxATcPhmJzbEsitp5eyftdBFmy2SZXxLpQO/VKgudPzFmBIGMo+C7gNuEBElriPy3A2J7tYRNYDF2OblZkE9eKiWrLSU5gyJvbmtgRyxfgB9OmVwrR5W7wOxURYKIPmnwPmichLOMORrwP+3N2CVfUffLoA5rEu7O79jYllTS3Ovi1XjhsYk3NbAslIS+H6imKem7eVf7+ihbysdK9DMhESymixB3E6zg/j1GC+qqo/iXRgxiSyt1bs4FBrOzdUxk+TWIdbTy+htd3HC4tqvQ7FRFBIH4lUdQGwIMKxGGNcLyyqoTQvg8rS2J3bEsiI/n2YOKQfz83byt3nDI2Z7QPM8QlYcxGR+V1dHMo5xpjjU9NwiLkbG7ihIrbntgTz+TNK2dpwiDnVu70OxURIsJrLySJSFeR1AfLCHI8xCe+lqlpE4Lo4GiV2rClj+pOXmca0uVs4b6RNJYhHwZLL2BCutzW0jQkjn095qaqWs4blx8XclkDSU5K5sXIwj83ZyPbGwwzIjt/vNVEFm+eyIYSHjSc0Jozmx+HclkBumViCT5Xp82u8DsVEQCjzXIwxURKPc1sCKcnL4NwRBUxfsJW2dl/XF5iYYsnFmB6iqaWNN5Zv54pxA+idlux1OFFx6+kl7Nzfwntr/K7yZGKYJRdjeog3O+a2JECTWIcLRhUyILsXf55rLezxpsvkIiJXu7tFNorIfhE5ICL7oxGcMYnkhYU1lOVlcGoczm0JJCU5iZtPK2HO+t1s2dPkdTgmjEKpufwX8E+qmq2qfVW1j6r2jXRgxiSSrXsOMW9TQ8zv23IibjptMMlJwnPzbSOxeBJKctmpqssjHokxCeyTuS0VidMk1qEouxcXjS7khYW1tLS1ex2OCZNQkssCEZkmIjeKyFUdj4hHZkyC6JjbcvbwfAbG8dyWYD5/RikNTa28tWKH16GYMAklueQBPuAq4Eb3cUMkgzImkczb1EDt3sSY2xLIWcPyKc3LYNpcaxqLF10uXKmqt0UjEGMS1YuLaumTnsIlJ8X/3JZAkpKEWyaW8LM317B2xwHKi/p4HZLpplBGiw0UkRdEZLv7+IuIDIxGcMbEu6aWNt5csZ0rxifO3JZAbqwcTFpyEs/ZRmJxIZRmsaeAt4Ey9/GOe8wY002vL9+ecHNbAumXmcZlJxcxo6qOQ622bGGsCyW59FfVx1S1xX08DvSPdGDGJIIXF9UyJD+TipLEmdsSzK1nlHKgpY2ZS7Z5HYrpplCSS4OI3CyfugloiHRgxsS7LXuamJ+gc1sCqSzNpbx/H6bNs479WBdKcrkD+AKwG6gHbgPujGRQxiSCl6rq3Lktg7wOpccQEW49o4TldY0sq93ndTimG7pMLqq6WVUvU9U8Vc1X1StUdVM0gjMmXvl8ykuLnLkttpfJ0a6ZMIjeqcm23liMC7bN8b+6/z4kIr859hHpwERkqoisFZFqEbkv0uUZE03zNzdQty+x57YE0rdXKtdMGMjMpdtoPHzE63DMCQpWc9ng/rsCWOnnETEikgz8HrgUOAn4nIicFMkyjYmmGVW1ZKYlJ/TclmBumVhK8xEfL1fVeh2KOUEBJ1Gq6ivul3tVdUbn10TkuohGBROBalXd6JY3HbgaWBXhco2JuMOt7byxfAeXnWxzWwI5uTib8cXZ/HneVm6fVGYDHmJQlzP0gR8AM4459oCfY+E0COi892ktcHqgk7fsaeKuZxZEMBxzIs4Ymsdd5wz1Oowe5+1VOzjY0paQi1Qej1vPKOV7Ly7jC0/OJz3Ftp6KNQGTi4hMAaYCg47pY+mLs9ZYJPn7mKJHnSByN3A3QMaAYWxvbI5wSOZ47D7Ywt/X7+bW00vt0/kxZlTVMSinN6cP6ed1KD3aleMG8vqy7ew+2OJ1KOYEBKu57MLpb2nm6D6WA0CkO9hrgcGdnhcDR82qUtVHgUcBKisr9fVvnBPhkMzxmLO+ntuemM/HG3dzwSibc9th5/5m5qyv55/PH05SkjX1BNM7LZln7pjodRhxTe6N3L2D9bksBhaLyDRVjXa1YAEwQkSGAHXAzcAtUY7BdMPEIf3onZrM7LX1llw6eXVJHT6Fa21ui4lzoTRkDhKR6SKyTETWdTwiGZSqtgFfB2YBq4HnVTWiI9RMeKWnJHPW8Dz+tmYXqtr1BQlAVXlpUR2nDM5hWEGW1+EYE1GhJJencRaqFJyhwc8D0yMYEwCq+oaqjlTVYar600iXZ8Lv/PJCavceZkO97Y0OsGr7ftbuPMD1NrfFJIBQkkuGqs4CUNUNqvoDYHJkwzLx4PzyAgBmr93lcSQ9w4yqOlKThSvHDfA6FGMiLpTk0iLOIPMNIvJVEbkSKIxwXCYOFOdmMLJ/Fu9bcqGt3cerS+q4cFR/cjLSvA7HmIgLJbl8C8gCvgGcBdwFfCmSQZn4Mbm8kPmbGjjYktj7c8xZv5vdB1ttkUqTMELq0FfVA6q6VVVvU9WrAVuzwoTk/PJCjrQrH1bv9joUT71UVUtuRirnl1ul3ySGUJLLD/wceyDcgZj4VFmWS1Z6SkL3uzQePsLbq3Zy1fiBpNlMc5MgeuoMfRMnUpOTOHt4PrPX1qOqCblG1BvLt9Pa5rPlXkxCCfYx6tgZ+h2Pt3GGJBsTksmjCtje2MzanQe8DsUTM6pqGVaQybjibK9DMSZqQpqhD7QBw92Xqt1JjsaEpKOf4f019Ywq6utxNNG1ZU8TCzbv5XtTyxOy1mYSVygNwJVANfAE8CSwTkTOimhUJq7079uLkwb0TcghyS8vdrYyvuYUGyVmEksoyeW3wGWqepaqTgIuB/47smGZeDN5VAGLtuxNqJ0FVZUZVXVMGpbHwBzbytgkllCSS5qqfrJJl6quBmwWmDkuk8sLafcp/1ifOEOSF23Zy9aGQ1w3wTryTeIJJblUicj/isjZ7uMRYHGkAzPx5ZTBOWT3Tk2oprGXquronZrM1LE2LcwknlB2ovwqzuz87+EsXvl34HeRDMrEn5TkJM4Zkc8H6+rx+TTu9zJpPtLOa8u2cenYIjLTQ/k1Mya+dFlzUdVmVf2lql6lqleq6q+A8VGIzcSZyeWF1B9oYdX2/V6HEnHvrt7JgWbbytgkroDJRUSSRORGEfmmiIx2j00Vkb8Dj0ctQhM3znNXSX5/Tfw3jc2oqqOoby/OHJbndSjGeCJYzeVx4B5gEPCIiDyG0xz2sKqeHI3gTHzJz0pnfHF23Pe71B9o4YN19VxbMYjkOG/+MyaQYI3BpwPjVLVdRHoDu4Hhqro9OqGZeHR+eSEP/209DU2t9MuMz0GHM5duo92nXDfB5raYxBWs5tKiqu0AqnoYWGuJxXTX5FGFqMKc9fVehxIxM6pqGVeczYj+fbwOxRjPBEsuo0Skyn0s7vR8sYhURStAE1/GDcqmX2Za3Pa7rNmxn5Xb9lutxSS8YM1i1q9iwi4pSThvZAEfrKun3adx1yfxclUdKUnCleMHeh2KMZ4KtnDlhmgGYhLH+eUFvLy4jmW1+5hQkut1OGHT1u7j5cV1nF9eSF5WutfhGOMp27nIRN25IwpIEnh/bXz1u3y4YQ+7DrRwvW1lbIw3yUVEfiUia0RkmYi8LCI5nV67X0SqRWStu2GZiTO5mWlMKMmNu90pZ1TVkt07lQtG21bGxgRNLiKSLCLPRKDcd4CxqjoOWAfc75Z3EnAzMAZnF8w/iEhyBMo3HptcXsCy2kbqD7R4HUpYHGg+wqyVO7hy/ADSU+wta0zQ5OIORR4gIqnhLFRV3+604dhcoGONjKuB6araoqqbcPaRmRjOsk3P0LGB2Afr4qNp7M0VO2g+YlsZG9MhlBX1NgJzRORVoKnjoKo+HKYY7gD+4n49CCfZdKh1j32GiNwN3A1QUlISplBMtIwZ2JeCPum8v3YXN5wa+3+QZ1TVMiQ/kwmDc7o+2ZgEEEqfSz1OM1YGUNDpEZSIvCsiK/w8ru50zgM4WyhP6zjk51bq7/6q+qiqVqpqZUFBl+GYHkZEOH9kAXPW1dPW7vM6nG6p3XuIuRsbuG7CINvK2BhXlzUXVf0hgIikq2rIDeSqelGw10XkduAK4EJV7UggtcDgTqcVA9tCLdPElsmjCnlhUS2La/ZxWlk/r8M5Ya8srgPgGps4acwnuqy5iMhEEVkOrHefjxeRbu3nIiJTge8DV6nqoU4vzQRuFpF0ERkCjADmd6cs03OdPSKf5CSJ6dn6qspLVXWcPqQfg/tleB2OMT1GKM1iD+PUMPYAqOpSYHI3y/0foA/wjogsEZE/uvdeCTwPrALeAu7pWN/MxJ++vVKpLM2N6fkui2v2sWl3E9dbR74xRwmlQz9JVbcc05bcrT/4qjo8yGs/BX7anfub2DF5VCE/f3MNOxqbKcru5XU4x+25eVvJSEvm0pNtK2NjOgul5lIjIhMBdee9fBNnboox3TbZHZIcixMq9xxsYebSbVxXMYg+vcI6Wt+YmBdKcvka8G2gBNgJnOEeM6bbRvbPYkB2r5jcQGz6ghpa23zcfmaZ16EY0+OE0izWqqo3dz4gIqU4m4cZ0y0iwvnlhcxcUkdrm4+0lNhY7u5Iu49nP97C2cPzbd8WY/wI5Tf5ryKS1fFERMqB1yMXkkk0k8sLaGptZ+GWBq9DCdnbK3eyY38zX5xU5nUoxvRIoSSXXwGviUiGiJwCzAC+ENmwTCI5a3g+qcnC7BgaNfb0R5so6ZfB5FG2SKUx/nSZXFR1JvA74G3gWeB6VbWdKE3YZKancPqQvJiZ77KirpEFm/fyhTNL426zM2PCJWCfi4g8xKdLrwiQg7OQ5N0igqp+OwrxmQRxfnkBP3l9NTUNh3r8ZMRnPtpM79Rkbqwc3PXJxiSoYDWXFcBK97ECeAj4a6djxoRNxyrJs3v4Ksl7Drbwqjv8OLu3DT82JpBg2xw/ASAivXBGjPnc50lAWnTCM4liWEEmg/v1ZvaaXdx2RqnX4QTUMfzYOvKNCS6UDv33gcxOzzOBv0UmHJOoRITJ5YV8uGE3zUd65oo/be0+/jzXhh8bE4pQkktvVT3Q8cT9umc3ipuYNLm8kOYjPuZv6plDkt9etZPtjc3cbrUWY7oUSnI5JCLjO564w5GbIxeSSVRnDM0jPSWpx87Wf/rDzQzu15sLbPixMV0KJbl8C3hZRN4XkfeBl4BvRDYsk4h6pyVz5rC8HjnfZeW2RuZvbuALZ5TZ8GNjQhDKPJd5wGicJPNtYLSq2h4rJiImlxeyaXcTm3Y3dX1yFHUMP/4nG35sTEhCXchpCDAUJ8ncICK3RC4kk8g6Vkn+Ww+aUNnQ1MorS9zhxxk2/NiYUISyE+UPgEeBPwKXAr8FbohwXCZBleRlUN6/D7NW7vA6lE9MX7DVWf3YOvKNCVkoNZebcHae3K6qtwHjCW01ZWNOyJQx/Vm4uYHdB1u8DsUZfvzxFs4ansdIG35sTMhCSS6H3a2G20SkD7ADp4nMmIi4ZEwRPoV3V+30OhTeWbWTbY3NtmeLMccplOSyWERygCeBhcB8wBauNBEzZmBfinN794imsac+2kxxbm8uHN3f61CMiSlBk4uICPAjVd2nqr8HLge+oqq25L6JGBFhypgiPqzew4HmI57FsWrbfuZvauD2M234sTHHK2hyUVUFXuv0vNqW2zfRMHVsEa3tPt73cM6LDT825sSF0iw2X0QqIlG4iHxHRFRE8t3nIiIPi0i1iCyLVLmm56soySU/K82zprG9Ta28sqSOa234sTEnJGByEZGOEWFn4ySYtSJSJSKLRaTbtRcRGQxcDGztdPhSYIT7uBt4pLvlmNiUnCRcfFJ/Zq/Z5clCltMX1OMXjdcAAA83SURBVNDS5rOOfGNOULCaS8cs/GuAcuAy4EacOS43hqHsh4Dv8emGZABXA39Sx1wgR0QGhKEsE4OmjCmiqbWdD6t3R7XctnYfz368mUnD8igvsuHHxpyIYMlFAFR1g79HdwoVkauAOlVdesxLg4CaTs9r3WP+7nG3iCwUkYX19T1vLSrTfZOG5dMnPSXqTWMdw49tzxZjTlywyZAFIhJwK2NV/U2wG4vIu0CRn5ceAP4NuMTfZf6KClD+ozgrB1BZWen3HBPb0lKSmDyqkHdW7aSt3UdKcqirFXXP0zb82JhuC5ZckoEs/P/B75KqXuTvuIicjLNW2VJnpDPFQJWITMSpqXQemlMMbDuR8k18mDq2iJlLt7Fg817OHJYX8fJWb9/PvE0N/Ntlo2z4sTHdECy5bFfVB8NdoKouBz7ZEENENgOVqrpbRGYCXxeR6cDpQKOqbg93DCZ2nDeygLSUJGat3BGV5PLMR5vplZpkw4+N6aYu+1yi7A1gI1ANPAb8swcxmB4kMz2Fc0fk8/bKHTjTriJnb1MrLy+u49oJxeRkpEW0LGPiXbDkcmE0AlDVMlXd7X6tqnqPqg5T1ZNVdWE0YjA925QxRWxrbGZ5XWNEy+kYfmwd+cZ0X8Dkoqo9cyNzk3AuGt2f5CSJ6KixtnYff567hTOH2vBjY8IhOsNvjOmG3Mw0Jpb1460VkUsu767eSd2+w3zxrLKIlWFMIrHkYmLC1LFFbKhvonrXwYjc/+mPNjMopzcX2fBjY8LCkouJCZeMcf7oR6JpbO7GPczd2MAXJ9nqx8aEiyUXExMGZPdmfHF22JOLqvLzN9dQ1LcXt51ZGtZ7G5PILLmYmDFlbBHLahvZtu9w2O45a+VOltTs41sXj6BXanLY7mtMorPkYmLGlDHOakJvh6n20tbu45ez1jCsIJPrK4rDck9jjMOSi4kZwwqyGFGYxVthSi4vLqplY30T35s6KmrrlhmTKOw3ysSUKWOKmL+pgYam1m7d53BrOw+9u46KkhwuOclGiBkTbpZcTEyZMqYInzrzUrrj6Y82s3N/C9+fOgp3AVVjTBhZcjExZeygvgzK6c2sbkyo3HeolT/MruaCUYWcPjTyi2Eak4gsuZiYIiJcMqY/c6p3c7Cl7YTu8cjsDRxsaeN7U8vDHJ0xpoMlFxNzpowporXNxwdrj38H0m37DvPUR5u5dsIgRhX1jUB0xhiw5GJi0Gll/cjLTDuhUWO/fXcdKHz74pERiMwY08GSi4k5yUnCRaP78/6aXbS0tYd83fqdB3hxUS23nVlKcW5GBCM0xlhyMTFpytj+HGxp46PqPSFf88tZa8lMS+GeycMjGJkxBiy5mBg1aVg+WekpIa81tnBzA++s2slXzhtKv0zbZdKYSLPkYmJSr9Rkzi8v4J1VO2n3Bd/+WFX5xVtrKOiTzh1nD4lShMYkNksuJmZNGVPEnqZWFm4Ovmnqe6t3sWDzXu69cAQZaSlRis6YxGbJxcSsyaMKSUtOYtbKwLP1233KL2etYUh+JjedNjiK0RmT2Cy5mJiVlZ7C2SPymbVyB6r+m8ZmVNWybudBvnNJOam2OKUxUePZb5uI/IuIrBWRlSLyy07H7xeRave1KV7FZ2LD1DFF1O07zMpt+z/zWvORdh56Zx3jirO57OQiD6IzJnF50gAtIpOBq4FxqtoiIoXu8ZOAm4ExwEDgXREZqaqhT2YwCeXC0YUkibP98dhB2Ue99uzHW9jW2Myvbxxvi1MaE2Ve1Vy+BvxcVVsAVHWXe/xqYLqqtqjqJqAamOhRjCYG5GWlc1pZv88MSW48fITfz67mnBH5TBqe71F0xiQur5LLSOAcEZknIh+IyGnu8UFATafzat1jxgQ0dWwR63YeZGP9wU+O/e8HG9h36AjfnzrKw8iMSVwRSy4i8q6IrPDzuBqnOS4XOAP4LvC8OO0W/tou/PbUisjdIrJQRBbW1x//AoYmflzibn/cMWps5/5mnvxwE1eNH/iZpjJjTHRELLmo6kWqOtbP41WcGskMdcwHfEC+e7zzeNFiYFuA+z+qqpWqWllQUBCpb8PEgEE5vTl5UPYnTWO/fXc97T7lO5fYkvrGeMWrZrFXgAsARGQkkAbsBmYCN4tIuogMAUYA8z2K0cSQqWOLWFKzj4+qd/P8whpumVhCSZ4tTmmMV7xKLk8CQ0VkBTAduN2txawEngdWAW8B99hIMROKKWP6A/DVPy+iV0oS/3LhCI8jMiaxeTIUWVVbgc8HeO2nwE+jG5GJdcML+zC0IJON9U3ce+EI8rPSvQ7JmIRmU5ZN3Ljh1GIG5fTmy+cO9ToUYxKereJn4sY/nz+cr547jKQkmzBpjNes5mLiiiUWY3oGSy7GGGPCzpKLMcaYsLPkYowxJuwsuRhjjAk7Sy7GGGPCzpKLMcaYsLPkYowxJuwk0N7jsUREDgBro1xsNtAY5TK7w+KNnFiKFSzeSIqlWAHKVbVPJG4cLzP016pqZTQLFJFHVfXuaJbZHRZv5MRSrGDxRlIsxQogIgsjdW9rFjtxf/U6gONk8UZOLMUKFm8kxVKsERUvzWILo11zMcaYWBfJv53xUnN51OsAjDEmBkXsb2dc1FyMMcb0LPFSc+k2EZkqImtFpFpE7nOPPSEiS0VkmYi8KCJZAa69371urYhMCXbPCMYqIvJTEVknIqtF5BsBrr1dRNa7j9s7HT9VRJa793xYRMK2vHCAeC8QkSoRWSEiz4iI38El0Y5XRJ4UkV3uLqkdx34lImvc98HLIpIT6vfpHh8iIvPc7+EvIpIWjliDxPsjEakTkSXu47IeHu8pIjLXjXWhiEwMcG203wuDReR99/dppYjc6x6/0X3uE5GATUpe/Hx7FFVN+AeQDGwAhgJpwFLgJKBvp3N+A9zn59qT3PPTgSHufZID3TOCsX4J+BOQ5J5X6OfafsBG999c9+tc97X5wJmAAG8Cl0b4Z1sDjHTPeRC4s4fEey5QAazodOwSIMX9+hfAL0L9Pt3Xngdudr/+I/C1ML53/cX7I+A7J/L/4lG8b3f8/wGXAbN7yHthAFDhft0HWOe+d0cD5cBsoLIn/Xx70sNqLo6JQLWqblRnC+bpwNWquh+cWgHQG/DXhng1MF1VW1R1E1Dt3s/vPSMVK/A14EFV9QGo6i4/104B3lHVBlXdC7wDTBWRATiJ9GN13vF/Aq4JQ6yB4r0eaFHVde4577jHPI9XVf8ONBxz7G1VbXOfzgWK/Vzq9//Ffe9cALzonvdMuGINFG+IelK8CvR1v84Gtvm51Iv3wnZVrXK/PgCsBgap6mpV7WpeXdR/vgFaCEKqJUkEWl8suTgG4XyS7lDrHkNEngJ2AKOA37nHrhKRB7u4NuA9IxTrMOAmt1nhTREZ4cZaKSKPhxBrbQRiDVRmEZDaqUnhBmBwD4m3K3fgfDpGRAaKyBvu8UCx5gH7OiWnaMX6dbcZ70kRye3h8X4T+JWI1AC/Bu534+0x7wURKQMmAPOCnOPZz1dEkoHfA5fi1K4+JyIn4dS0H1LVEcBe4E4/154E3AyMAaYCfxCR5CD3DIklF4e/NloFUNUvAQNxPrXc5B6bqar/3sW1Ae/ZTYHumw40qzOs8DHgSTfWhap6l0exBirTh/NmfkhE5gMHgDboEfEGJCIP4MQ5DUBVt6lqR39GT4r1EZwPG6cA24H/gh4d79eAb6nqYOBbwBPQc94L4vS1vgR8s6M1wx+Pf76BWjRCqSVFpPXFkoujFveTs6uYTlVzVW0H/oL/pptA1wa9ZwRircX5BQB4GRh3nNcW+zkeDn7LdJsxzlHVicDfgfU9JF6/3A7kK4Bb3eaXYwWKdTeQI58OWIh4rKq6U1Xb3SbSx3D+SPTYeIHbgRnu1y9wfPFG9L0gIqk4v1fTVHVGV+d3Eu2fb6Cakt9aUjRaXyy5OBYAI9z2yTScT9UzRWQ4fNLnciWwxs+1M4GbRSRdRIYAI3A6GP3eM1KxAq/gfEoBOA+n8/FYs4BLRCTXbSq5BJilqtuBAyJyhvu9fgF4NQyxBoxXRAoBRCQd+D5Ox2ZPiPczRGSqG+NVqnoowGl+v083Eb2P0/QHzh/SiMXqxjug09NrgRV+Tusx8eL8cT3P/foC/H/QiPp7wb3fE8BqVf3NcV4e7Z+vvxpRsp9jHS0ykW998XI0QU964IxSWYczwuMBnMT7IbAc55dzGu7oMeAqnM7zjmsfcK9bS6eRKsfeM1KxusdygNfdeD8GxrvHK4HHO117B061txr4Uqfjle73uQH4H9w5UBGM91c4TY1rcZob6AnxAv+H05R0BOeT2p1u2TXAEvfxR/fcgcAbXf1/44wYmu/e5wUgPYw/W3/xPuu+D5bhfPAY0MPjPRtYhDOiah5wag95L5yN88d0Waf/+8twEnYt0ALsxElynv58cUbLzer0/H73sZtPRzoedc6x53Z6Pss91+89Q43JJlEaY0yMc5vZ1gEXAnU4NadbcIalv6Sq00Xkj8AyVf3DMdeOAZ7DaY4cCLyH0wIj/u6pqitDicmaxYwxJsap06/ydZxax2rgeTcJfB/4tohU44xUewKO7nNxz3seWAW8BdyjTp9doHuGxGouxhhjws5qLsYYY8LOkosxxpiws+RijDExLsDSL9PcYyvclRpSA1w7W4IswHmiLLkYY0wMC7JMyzScZatOxlkb8a6AN4kASy7GGBPbAi28+4a6cObV+Ftw9Sgi8oi7PuFKEflxp+ObReTH4myTsVxERnV1L0suxhgT24Iu0+I2h92GM8y4Kw+osz7hOOA8Eem8jNRuVa3AWbvuO13dyJKLMcbEtq6WafkD8HdVnRPCvf5JRKqAxTirJHdeBbljbbVFQFlXN/K7+58xxpiYEXCRXBH5D6AA+ErHiyIyC+gPdF51GndtxO8Ap6nqXhF5GujV6b4t7r/thJA7LLkYY0xs+2SRTJxlWm4GbhGRu3A2WbtQ3U0EAVR1iv/b0BdoAhpFpD/OAIHZJxqUJRdjjIlhqtomIh3LtCQDT6rqShFZCmwBPnYWeGaGqj7o5xYpODvDLheRxcBKnG2kP+xOXLb8izHGJCh3y4tqYKyqNobz3tahb4wxCcidOLkE+EO4EwtYzcUYY0wEWM3FGGNM2FlyMcYYE3aWXIwxxoSdJRdjjDFhZ8nFGGNM2FlyMcYYE3b/H4KyKktpDscFAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"tracker_data = pvlib.tracking.singleaxis(\n",
" solar_position['apparent_zenith'],\n",
" solar_position['azimuth'],\n",
" axis_azimuth=180, # axis is aligned N-S\n",
" ) # leave the rest of the singleaxis parameters like backtrack and gcr at their defaults\n",
"tilt = tracker_data['surface_tilt'].fillna(0)\n",
"azimuth = tracker_data['surface_azimuth'].fillna(0)\n",
"\n",
"# plot a day to illustrate:\n",
"tracker_data['tracker_theta'].fillna(0).head(24).plot()\n",
"plt.ylabel('Tracker Rotation [degrees]');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This plot shows a single day of tracker operation. The y-axis shows the tracker rotation from horizontal, so 0 degrees means the panels are flat. In the morning, the trackers rotate to negative angles to face East towards the morning sun; in the afternoon they rotate to positive angles to face West towards the evening sun. In the middle of the day, the trackers are flat because the sun is more or less overhead.\n",
"\n",
"Now we can model the irradiance collected by a tracking array -- we follow the same procedure as before, but using the timeseries tilt and azimuth this time:"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [],
"source": [
"df_poa_tracker = pvlib.irradiance.get_total_irradiance(\n",
" surface_tilt=tilt, # time series for tracking array\n",
" surface_azimuth=azimuth, # time series for tracking array\n",
" dni=df_tmy['DNI'],\n",
" ghi=df_tmy['GHI'],\n",
" dhi=df_tmy['DHI'],\n",
" solar_zenith=solar_position['apparent_zenith'],\n",
" solar_azimuth=solar_position['azimuth'])\n",
"tracker_poa = df_poa_tracker['poa_global']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Like before, let's compare GHI and POA:"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEECAYAAAA2xHO4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjAsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+17YcXAAAgAElEQVR4nO3deXxV5bXw8d/KTELmgSmBJAwyyCCEQUBUVMSpWodr1SpaFa22V2v79nrv7WDtvX3tra9erYqi2Kq1znWqWqeCijIFhDCTAIEchpAEMhEyP+8fewcjZDjDPkOS9f18zufk7LOHZTxknWfY6xFjDEoppVRnwoIdgFJKqdCmiUIppVSXNFEopZTqkiYKpZRSXdJEoZRSqkuaKJRSSnUpItgB+ENaWprJzs4OdhhKKdVjrF27ttwYk97Re70yUWRnZ5Ofnx/sMJRSqscQkT2dvaddT0oppbqkiUIppVSXNFEopZTqUq8co1BK9VxNTU24XC7q6+uDHUqvFBMTQ2ZmJpGRkW4fo4lCKRVSXC4X8fHxZGdnIyLBDqdXMcZQUVGBy+UiJyfH7eO060kpFVLq6+tJTU3VJOEHIkJqaqrHrTVNFEopz7U0Q321306vScJ/vPndateTUsozhR/De/dA5V6IToDETEjMsp6Tsr75OTEL4gdCWHiwI3bEWWedxYMPPkheXt63tufn5/P888/z6KOPBiky/9NEoZSTjIHe+m245iD8417Y/CakjYJzfm1tq3JB1V5wrYZjR759TFgExA+2E0im9UjOgfFXQWRMcP47HJaXl3dS8uhtNFEo5RRj4IkZ1rfsC/8HBp8W7Iic0doKa5+FT34DzQ1w9i9g1r9CRPTJ+zbU2onDBVUl9sMFlSWwZwVU7wPTAuGRMPF7gf9vcdNvf/tbXnzxRbKyskhLS2PKlCkAvPbaa9xxxx1UVlayZMkSzjjjDJYtW8aDDz7I3//+9yBH7T+aKJRyyuFdULbN+ha9+GyYsgDm/griUoMdmfcOboK/3w2uNZBzJlz8MKQO73z/6P6QMdp6dKS5Ef5vJpRucuvyv3l3M1v2OzsWMnZwAr++ZFyn7+fn5/PGG2/w9ddf09zczOTJk48niubmZlavXs3777/Pb37zGz755BNHYwtVmiiUcoprjfV843uw5R1Y9SRsfgvm/gLyftCz+uobj8Jnv4evHoN+SfDdxTDhX3zvVouIgrSRcGibM3H6wfLly7n00kvp168fAJdccsnx9y6//HIApkyZQnFxcTDCCwpNFEo5xbUGouIhcyoMnQGTr4cPfg7v/wzWPgcX/gGGnR7sKLvXfrD6tOvhvPshNsW586ePhpLVbu3a1Td/fzHGdPpedLTV3RYeHk5zc3OgQgq6oEyPFZEkEXldRLaJyFYROV1EUkTkYxEptJ+T7X1FRB4VkSIRKRCRycGIWalulayGzCnftBwyxsAN78BVf7YGef80H964FaoPBDXMTtUchNduhBevhIgYuPF9uPQxZ5MEWN1SVXut8YwQNHv2bN59913q6+upra3lvffeC3ZIQRes+ygeAf5hjBkNTAS2AvcCnxpjRgKf2q8BLgBG2o+FwKLAh6tUNxqPQulmyJz27e0iMO678KPVcMbPYMtb8FgefPmI1V8fClpbYc0z8NhU2Pa+NVh9+3LInuWf66WPsZ7Ltvvn/D6aOnUq3/nOd5g4cSKXX345eXl5JCYmBjus4DLGBPQBJAC7ATlh+3ZgkP3zIGC7/fNTwDUd7dfZY8qUKUapgNr9hTG/TjBm+4dd71ex05gXr7b2fXSKMYWfBCa+zhzYaMzT51jx/PkSY8qL/H/N8iLreute6PDtLVu2+D+GbtTU1BhjjDl69KiZMmWKWbt2bZAjclZHv2Mg33TyNzUYLYpcoAz4k4h8LSLPiEgcMMAYcwDAfs6w9x8ClLQ73mVvUyp0tPW5Z3Yznz4lF659Ga59zZom+pfL4eXr4Eix30P8lv1fwxu3wFNzrNla310MN7zd9YwmpyRnQ3g0HNrq/2t5aeHChUyaNInJkydzxRVXMHly3+7xDsZgdgQwGfixMWaViDzCN91MHelomsVJo00ishCra4qhQ4c6EadS7nOtgdSR7vfnj5oHuWfCisfg8wfh8ekw88cw+QZI8tPnt7UVdvzDuuaeL62B9xk/hDN+6vw4RFfCwq0b9spCd+bTX//612CHEFKCkShcgMsYs8p+/TpWoigVkUHGmAMiMgg41G7/rHbHZwL7TzypMWYxsBggLy+v82kLSjnNGCtRjDjPs+Mioq0/0hOuho9+CZ//wXpkToVTr4Cxl0HCIN/jazwK6/8KKxfB4Z1WaY15/20lpZgE38/vjYzRsHdlcK6tPBbwridjzEGgREROsTedA2wB3gEW2NsWAG/bP78D3GDPfpoBVLV1USkVEo4Uw9EyyJrq3fGJmXDVn+DH62DuL6HpmFUq46Ex8KcLYfXTUHuo+/OcqOYgfHo/PDzOmqLbLwmu/BP863qY+aPgJQmwpshWlUBDTfBiUG4L1n0UPwZeFJEoYBdwE1bSelVEbgb2AlfZ+74PXAgUAXX2vkqFjrYb7U6c8eSp1OEw52fWo2wHbP4bbPqb9Uf+g59D9hlw6uUw+pKu7/Y+uBFWPAEbX4PWZhhzMZz+I8iaHjp1qDLazXzqblxHBV1QEoUxZj3Q0afjnA72NcCdfg9KKW+51kBU/2/++DkhfRScdS+c+W9waIuVMDb/Dd69C/5+D+SeZSeNi62WQmsrFH1ijT/s/gwi46y7wWfcbg2gh5p0u8THoa2aKHoAvTNbKV+VrIYhk/1TokMEBoyzHnN/AQc2WAlj85vw9p3w7t0wfK7V/VW+HeIHwbn3wZQboV+y8/E4JTnbuqkvhAe01Td04SKlfNFYZxW4y/RyfMITIjB4klVS464CuOVTjk2+hYriDeyvExq/86S1ffZPQjtJgD3zaWRIT5ENpGXLlnHxxRd3uc99993Hgw8+6NF5+/fv70tYx2mLQilfHFhvjQP4Oj7hKRFWNuZwd8F5VNTNoanFMHxpHI8MOMapQ6ICG4u30sdY03RVyNNEoZQvjt9oF4AWha25pZU//rOIP/6zkOzUOJ5ZMIvKuiZ++tp6vvvEl/yf80/hltm5hIWFyMB1ZzJGw8ZXrSVVO5uB9cG91uC8kwaOhwse6PTt4uJi5s+fz/Tp0/n6668ZNWoUzz//PCtWrOBnP/sZzc3NTJ06lUWLFhEdHc3999/Pu+++y7Fjx5g5cyZPPfVUp8uNrlmzhptvvpm4uDhmz57NBx98wKZN3y65fvjwYX7wgx+wa9cuYmNjWbx4MRMmTABgw4YNzJ07l5KSEn7+859z6623Ultby6WXXsqRI0doamriv/7rv7j00kud+32hXU9K+ca1xhosDtCaEweqjnHtM6t45NNCvntaJu/+eDanDklk9sg0/nHXHOaOzuB372/j+mdXcbCqPiAxeS2Eaz5t376dhQsXUlBQQEJCAg899BA33ngjr7zyChs3bqS5uZlFi6yycz/60Y9Ys2YNmzZt4tixY10uYHTTTTfx5JNPsmLFCsLDOx7T+vWvf81pp51GQUEBv/vd77jhhhuOv1dQUMB7773HihUruP/++9m/fz8xMTG8+eabrFu3jqVLl/LTn/60ywq43tAWhVLearvRLvfsgFzu4y2l/J/XN9DY3MpD/zKRyydnfuv95Lgonvz+FF7NL+G+d7Yw/5HPeeDy8cw/1YGb9vyhbXGjsq2d34PSxTd/f8rKymLWLKso4ve//31++9vfkpOTw6hRowBYsGABjz/+OHfffTdLly7lf/7nf6irq+Pw4cOMGzfuW2tYtKmsrKSmpoaZM2cCcO2113aYVJYvX84bb7wBwNy5c6moqKCqqgrg+DoZ/fr14+yzz2b16tVcdNFF/Md//Aeff/45YWFh7Nu3j9LSUgYOHOjY70MThVLeqtwLtaXe32jnpvqmFh74YBt//qqYcYMT+OM1p5Gb3vEgpYhw9dShTM1O4e5X1nP7X9ZxdV4Wv7pkLHHRIfbPPSkbIvqF5CJGnXUdnai+vp477riD/Px8srKyuO+++6iv77gl5+63/I72a4vnxLhEhBdffJGysjLWrl1LZGQk2dnZncbgLe16Uspbx2+081+i2FlWy+VPfMWfvyrmB7Ny+NsdMztNEu3lpvfn9dtncsdZw3l1bQkX/3E5G0oq/RanV8LCrPtFykJv5tPevXtZsWIFAC+99BLnnnsuxcXFFBUVAfDCCy9w5plnHv+DnJaWRm1tLa+//nqn50xOTiY+Pp6VK63SJS+//HKH+82ZM4cXX3wRsGZDpaWlkZBgjeG8/fbb1NfXU1FRwbJly5g6dSpVVVVkZGQQGRnJ0qVL2bNnjzO/hHZC7CuGUj2Ia411Y1uG86uwGWN4Y90+fvX2JqIjwliyII9zxgzw6BxREWH8fP5o5oxK555X1nPFoq/4yXmjuP3M4YSHykB3+mjY/UWwozjJmDFjeO6557jtttsYOXIkjzzyCDNmzOCqq646Pph9++23Ex0dza233sr48ePJzs5m6tSuvzQsWbKEW2+9lbi4OM4666wO17m47777uOmmm5gwYQKxsbE899xzx9+bNm0aF110EXv37uWXv/wlgwcP5rrrruOSSy4hLy+PSZMmMXp0J+uV+0CcHvQIBXl5eSY/Pz/YYajebvHZEBUHN3Y+eOmN2oZmfvnWJt78eh/Tc1J45HunMTAxxqdzVtU18R9vbeS9ggNMy0nh4asnMSSpn0MR++CLh+DT38C9eyHG+qO5detWxoxx8C53DxUXF3PxxRefNBvJCbW1tcfvbXjggQc4cOAAjzzyiOPX6U5Hv2MRWWuM6fA2ee16UsobTcfgYIHj5Sc2uqq4+NEveHv9Pn5y7ij+eusMn5MEQGJsJI9dcxoPXjWRzfuqmP+/n/PuhpOKMAdeRujOfPKH9957j0mTJnHqqafyxRdf8Itf/CLYIblFu56U8saBDY7eaGeM4dkvi3ngg62k9Y/mpVtnMD3X2Sm3IsKVUzKZmp3MXS+v58cvfc3S7Yd44PIJREUE6Ttj+5pPWQG+abET2dnZPrcm7rzzTr788ts3E951113cdNNNXH311T6dOxg0USjlDYdvtHtx1V5++/ctnDtmAH+4cgLJcf67u3pYahyv3X46j3xSyGNLi5gyLJnrpg/z2/W6lDQMImN7Xc2nxx9/PNghOEq7npTyhmu1Vdiuf7rPp2pqaWXRsp1MHprE0zdM8WuSaBMZHsZP541iYmYiT3++i5bWII1VhoVZq92dUPOpN46dhgpvfreaKJTylDFQssaxbqf3Cg6wr/IYd5w1wu35+04QERbOGU5xRR0fbzkYsOueJH30t1oUMTExVFRUaLLwA2MMFRUVxMR4Nu6lXU9KearKBbUHHelTN8awaNlORg3oz9zRGQ4E55n5pw5kaEosiz7bxfnjBgY0UR2XMRoKXoZjldAviczMTFwuF2VlZYGPpQ+IiYkhMzOz+x3b0UShlKdcbeMTvs94Wrr9ENtLa3joXyYGpYhfeJhw6xk5/PLtzazefdjxAXS3tK/5NHQ6kZGR5OTkBD4O1SntelLKU658q/TEgFN9PtWiZTsZktSPSyYOdiAw71w5JYuUuCgWf74rOAG0r/mkQpImCqU81baiXXikT6dZU3yYNcVHuPWMHCLDg/dPsV9UOAtOz+bTbYcoLK0JfACJQ62ZTyFY80lZNFEo5YmmeuseCge6nZ5ctpOUuCiunjrUgcB8c/3pw4iJDAtOqyIsDNJP0RZFCNNEoZQnDhZAa5PPM562Hazm022HuHFmNv2i/LDWtodS4qK4Oi+Lt9bvC846FuljtEURwjRRKOUJh260e+qzXcRGhXPD6UG60a0Dt5yRS0ur4U9f7Q78xdNPsWaSHTsS+GurbmmiUMoTrtWQNBTiPavk2l7J4Tre2bCfa6cNJSk2dNa3zkqJ5cLxg/jryr1U1zcF9uJtNZ+0VRGSgpIoRKRYRDaKyHoRybe3pYjIxyJSaD8n29tFRB4VkSIRKRCRycGIWSnAmvHkY7fTM1/sIkzg5jNCbwrobXOGU9PQzEur9gb2wm01n3pZKY/eIpgtirONMZPalbW9F/jUGDMS+NR+DXABMNJ+LAQWBTxSpQCq9kH1Pp+6ncprG3h5TQmXTRrCoMQQKPN9gvGZicwcnsqzX+6msbk1cBdOzLLW9tBEEZJCqevpUqBthY7ngMvabX/eWFYCSSISoosAq16t7UY7H5Y+fe6rYhpbWrntzFyHgnLewjm5lFY38Pb6fYG7aNvMp0M68ykUBStRGOAjEVkrIgvtbQOMMQcA7Oe2egZDgJJ2x7rsbd8iIgtFJF9E8vXWf+UXrnyIiIEB4706vLahmee+Kmbe2AGMyIh3ODjnnDkqndED43n6i120BrJYYMYYbVGEqGAlilnGmMlY3Up3isicLvbtqK7BSZ9eY8xiY0yeMSYvPd33ip5KnaRkNQyaBBHeDUC/tGov1fXN3H7mcIcDc5aIcNuZueworWXZjkOBu3D6KVBbCnWHA3dN5ZagJApjzH77+RDwJjANKG3rUrKf2z6hLiCr3eGZQAgszaX6lOYGOLDe626nhuYWnlm+i9NzUzltaLLDwTnv4gmDGZwYw5OfBfAGvOM1n7RVEWoCnihEJE5E4tt+BuYBm4B3gAX2bguAt+2f3wFusGc/zQCq2rqolAqYgxuhpdHrGU9vfb2P0uoGfnhWaLcm2kSGh/GD2Tms3n2Yr/cG6N6GDJ35FKqC0aIYACwXkQ3AauA9Y8w/gAeA80SkEDjPfg3wPrALKAKeBu4IfMiqz/PhRruWVsNTn+1i3OAEzhiZ5nBg/vO9aUOJj4kIXFmPxCyI6q/3UoSggJcZN8bsAiZ2sL0COKeD7Qa4MwChKdU512rrD1mC5xPuPtp8kF3lR3ns2tOCs96Dl/pHR3D9jGEs+mwnxeVHyU6L8+8FRbTmU4gKpemxSoUuV75XrQljDIs+28mw1FguOLXnzeq+cWY2kWFhPP1FgFoVWvMpJGmiUKo71QegqsSrRPHVzgoKXFXcNmc44UFYmMhXGQkxXD55CK+tdVFe2+D/C6afAkcP6cynEKOJQqnuHL/RzvOB7EXLdpIeH83lk0+69afHuHVOLk0trTz/VbH/L3a85pN2P4USTRRKdce1BsKjYeAEjw7b6KpieVE5N8/OISYy+KXEvTU8vT/njhnA8yv3UNfY7N+Lpetqd6FIE4VS3SlZA4Mmenyj3ZOf7SQ+JoLrpgd/YSJf3X5mLpV1Tby6pqT7nX2RmAlR8db62SpkaKJQqivNjbD/a4+7nXaXH+X9TQe4fsYw4mN8WzI1FEwZlsKUYck8s3w3zS1+LBbYNvNJu55CiiYKpbpSuhFaGjweyF78+U4iw8O4aVbolRL31m1zcnEdOcb7mw7690IZo/WmuxCjiUKprpSssZ49SBSl1fW8sXYfV03JJD0+2k+BBd65YwaQmx7HU5/txLq9yU/Sx8DRMjha4b9rKI9oolCqK67VkDAEEt2ftfTs8t00t7aycE7olhL3RliYsPCMXDbvr+bLIj/+EdcB7ZDjVqKwV5/r7pHk72CVCjjXGo9aE1V1Tfxl5R4umjCYYal+vpM5CC47bQhp/aN56vOd/rtIW80nHacIGe6W8NhvP7q6Yygc6PnTO5RqU1MKlXth2m1uH/KXVXs42tjC7SG8MJEvYiLDuWlWNn/4cDub91cxbnCi8xdJGALRCTrzKYS42/W01RiTa4zJ6ewBaIei6l08vNHOGMNzXxUzZ1S6f/6AhojvTx9GXFQ4z3yx2z8XOF7zSQe0Q4W7ieJ0h/ZRqudwrYGwSLdvtCs5fIxDNQ2cP26AnwMLrsTYSC49bQgfbj5IfVOLfy6SPlq7nkKIW4nCGFPvxD5K9ShtN9pFxri1e8G+SgAmDOn9w3XnjxtIXWMLXxaV++cCGWOgrhyO+un8yiPdJgoROU9EnhaRSfbrhd0do1SP19Lk8Y12Ba4qosLDOGVg6K6H7ZTTc1OJj47go82l/rlA+inWs7YqQoI7LYo7gP8DfF9E5gKT/BuSUiGgdBM0H4PMPLcPKXBVMmZQPFERvX/WeVREGGeNzuCTraW0tPrhngpdFjWkuPOJLjPGVBpjfoa1bKl3iwYr1ZMcv9HOvRZFa6th075qJmT2/m6nNuePG0DF0UbW+WOp1ITB1swnbVGEBHcSxXttPxhj7gWe9184SoUI12qIH2QVqXPDrvKj1DY0Mz6z9852OtGZo9KJCg/jQ3+U9BCxBrR1imxI6DZRGGPePuH1H/0XjlIhwrXG6nZyc+nSApc1kD2xD7Uo4mMimTkilY+2lPqnpEfGaL07O0R41JkqInki8qaIrBORAhHZKCIF/gpOqaCoLYMjxW53O4E1kN0vMpzh6b3vbuyuzBs7kL2H69heWuP8ydPHQF2F9f9DBZWno24vAn8CrgAuAS62n5XqPbxY0a7AVcmpQxKICO/9A9ntnTs2AxH8M/spQ2s+hQpPP9Vlxph3jDG7jTF72h5+iUypYCn82FrRbtBEt3Zvamll8/6+NZDdJiM+hslDk/lwsx/GKdqKAx7SmU/B5mmi+LWIPCMi14jI5W0PTy8qIuEi8rWI/N1+nSMiq0SkUEReEZEoe3u0/brIfj/b02sp5ZFjR6DgFRh/FUT2c+uQwtJaGppbmdCHBrLbmzd2AJv3V+M6UufsieMHQXSitihCgKeJ4ias+yjmY3U5tXU/eeouoP3//d8DDxtjRgJHgJvt7TcDR4wxI4CH7f2U8p91z0NTHcy43e1D2gay+2KLAmDeuIEAfLzF4e4nEav7SVsUQedpophojMkzxiwwxtxkP37gyQlEJBO4CHjGfi3AXOB1e5fngMvsny+1X2O/f469v1LOa2mG1U/DsNkwcLzbhxXsqyI+JoJhKbF+DC505aTFMWpAf/+MU6TbM5/8uVCS6paniWKliIz18Zr/C/wcaFt4NxWoNMY0269dQNsqMUOAEgD7/Sp7f6Wct+3vUFUCM37o0WEFrkomZCYSFtZ3v8PMGzuQ1cWHOXK00dkTZ4yxugOP6synYPI0UcwG1ovIdm+mx4rIxcAhY8za9ps72NW48d6J514oIvkikl9Wph8q5YVVT0LSMDjlArcPqW9qYfvBGsb3gUKAXZk3bgAtrYZPtx1y9sTpuohRKHB3hbvT7S6f+cBIrFIe3kyPnQV8R0SKgZexupz+F0gSkbZFlDKxFkkCq3WRZccQASQChzs6sTFmsd0tlpeenu5BSEoB+9fD3hUwbSGEhbt92LaDNTS1GCb20YHsNuOHJDIoMYaPnJ79dHxZVB2nCCZ3WxQLgLVYg8lnAw3eTI81xvy7MSbTGJMNfA/4pzHmOmApcGW7a7XdDf6O/Rr7/X8av67qrvqsVU9CVH+YfL1Hh220B7L7UumOjogI88YO4PPCMo41OrhGRfxAiEnUFkWQubsexe3GmMnAfUAy8GcRWSEivxOROSLi/lewjv0bcI+IFGGNQSyxty8BUu3t9wD3+ngdpU5WUwobX4dJ11p/lDywwVVFalwUQ5Lcm0rbm80bN5D6plY+L3Sw61fEukNbWxRB5e6a2QAYY7YB24CHRaQfVuviKuAhwP16zNa5lgHL7J93ASfdBmsvhnSVJ+dVymP5z0Jrk0drY7fZ6KpifGYiOhkPpuWkkBBjrVFxvj1l1hEZo2HzW9bMJ/09B4W7YxR3i8jUduMIGGOOGWPeN8b82BjjUZJQKmQ0N0D+Ehh5PqSN8OjQusZmCg/V9Nn7J04UGR7GOWMG8Om2UppbWrs/wF3pY6C+EmodHihXbnN3jCITeAQ4JCLL7C6ni0QkxY+xKeV/m96wpl56cIPd8UP3VdNq6PMD2e2dP24AlXVNrCl2cI0KrfkUdO6OUfzMGDMTGAj8B9bMox8Am0Rkix/jU8p/jIGVi6yZNblne3x4gQ5kn2TOqHSiI8Kcrf2kNZ+CztP7KPoBCVjTVBOxprGucjoopQJi7wo4WADTb/eq77vAVcWgxBgy4mP8EFzPFBsVwRkj0/jYyTUq+g+AmCRtUQSRW4PZIrIYGAfUYCWGr4CHjDF+WANRqQBZ+QT0S4YJV3t1+MZ9VYwfoq2JE80bO5BPth5i8/5qTnXi9yNi3aGtLYqgcbdFMRSIBg4C+7BuhKv0V1BK+d2RPbDtPZi8AKI8r9FUdayJ3eVHmZilA9knOmdMBmECHzlZJFBrPgWVu2MU84GpwIP2pp8Ca0TkIxH5jb+CU8pv1jwNCEy71avDN+2rAtAWRQdS+0eTl53i7F3aGWOgvgpq/VB4UHXL7TEKY9kEvA98AHwJDMcqGa5Uz9FQC2ufh7HfgcRMr06x4XhpcU0UHZk3dgDbDtawt8KhNSq05lNQuXsfxb+KyMsiUgJ8jlXjaTtwOaBTZFXPsuElaKiC6Z5ViW1vo6uKoSmxJMVGORhY7zFvrHXD3UdbHGpVZIyxnvUO7aBw987sbKz1IH5ijDngv3CU8rPWVlj1FAye7NGa2CcqcFVx2lAdn+jM0NRYRg+M56PNpdxyRq7vJ4xLtyYeaIsiKNwdo7jHGPO6JgnV4+38FCoKrTUnvCwHUV7bwL7KY9rt1I3zxw0kf89hymsbfD+Z1nwKKne7ntY5sY9SQbdyEfQfCGMv637fTmx0WQPZWrqja/PGDaDVwKdbHRqATj8FyrY7cy7lEXe7nsZ0s0CRYN2Ap1ToKtthtSjO/gVEeD+2sMFViQjO3CPQi40dlMCQpH58tLmUq6cO9f2EKblWzadjR6xuKBUw7iaK0W7s42AReqX8YNWTEB4NeTf5dJqNriqGp/enf7RHxZf7HBFh3rgBvLhqL0cbmonz9feVkmM9H94NQzRRBJK7YxR73Hi4/B2sUl47dsSa7TT+KohL8/o0xhg2uKp0fMJN548bSGNzK5/vcGCNimQ7URzZ7fu5lEc8rfWkVM+07nloqvOqSmx7B6vrKa9tYIJ2O7klb1gyybGRzhQJbN+iUAGliUL1fi3NsPppyD4DBo736VQbSo5LvcsAACAASURBVOyBbC3d4ZaI42tUHKLJ1zUqouKsAoGaKALOo0Qhlu+LyK/s10NFxPvJ6EoFwra/Q1WJVSXWRxv3VRIRJowdlOBAYH3DvLEDqKlvZtWuw76fLDlHu56CwNMWxRPA6cA19usa4HFHI1LKaauehKRhcMoFPp+qwFXFqAHxxET6ukx83zFnVDr9IsOduUs7JUdbFEHgaaKYboy5E6gHsMuMaw0DFbr2f22tOzH9Ngjz7Y+7MYYCHcj2WExkOHNGpfHR5lJaW32s/pqcAzX7oemYM8Ept3iaKJpEJBwwACKSDji4OK5SDlv5JET1h9O+7/Op9h6uo+pYk95o54V5YwdysLqejXbVXa+l2OVAjuzxPSjlNk8TxaPAm0CGiPw3sBz4neNRKeWEmlJrTexJ10GM762AguN3ZGuLwlPnjMkgPEx87346PvNpl+9BKbd5lCiMMS8CPwf+L3AAuMwY85o/AlPKZ/nPQmuz1e3kgAJXJVERYYwaEO/I+fqSpNgopuek8NFmH8t56L0UQeHx9FhjzDZjzOPGmMeMMR6XchSRGBFZLSIbRGRz28JHIpIjIqtEpFBEXhGRKHt7tP26yH4/29Nrqj6opRnyl8DIeZA63JFTbnBVMWZQAlEROqvcG/PGDqDwUC27ymq9P0lsCkQn6IB2gHk6PfY5EUlq9zpZRJ718JoNwFxjzERgEjBfRGYAvwceNsaMBI4AN9v73wwcMcaMAB6291Oqa0d2w9EyGOd98b/2WloNm/dVMVG7nbx23ri2NSp8aFWIQHK2tigCzNOvRhOMMcfXyrZnPZ3myQnslfLavlJE2g8DzMVa8wLgOaDtX/il9mvs988R8bI+tOo7ygut57RTHDndrrJajja26EC2D4Yk9ePUIQm+L5GakqstigDzNFGEicjxalwikoL7hQWPE5FwEVkPHAI+BnYClcaYZnsXFzDE/nkIUAJgv18FpHZwzoUiki8i+WVlDtSVUT1b+Q7rOW2EI6fTgWxnzBs7kK9LKjlUXe/9SVJyoHKP1b2oAsLTRPH/gBUi8lsR+S3wFfAHTy9qjGkxxkwCMoFpwJiOdrOfO2o9nDQZ2xiz2BiTZ4zJS09P9zQk1duUF1rrTjgw2wmsgezYqHCGp/d35Hx91bxxAzAGlm4/5P1JknOsSQrVWoc0UDyd9fQ81jrZpfbjcnubV+xurGXADCBJRNpaJ5nAfvtnF5AFYL+fCDhQC0D1auU7IG2kY6cr2FfFqYMTCQ/TXk9fnDIgnvT4aJYXVXh/Ei0OGHCeDmZHYw1AJwApwJVtdZ88OEd624C4iPQDzgW2AkuBK+3dFgBv2z+/Y7/Gfv+fxhgfb+9UvZoxdqIY5cjpmlpa2bK/WrudHCAizB6RxldF5d7fpa1TZAPO066nt7EGl5uBo+0enhgELLVXzFsDfGyM+Tvwb8A9IlKENQaxxN5/CZBqb78HuNfD66m+5mi5tRKaQ4liR2kNDc2tjNdE4YhZI9KoONrI9tIa706QMMRagEpbFAHj6UB0pjFmvi8XNMYU0MFMKWPMLqzxihO31wNX+XJN1cdUtM14cnYge6LOeHLErBHWXJQvi8oZ400V3rAwSB6md2cHkKctiq9ExLeC/kr52/EZT860KApcVSTERDAsNdaR8/V1gxL7MTw9juVF5d6fJDkHjhQ7FpPqmqeJYjawVkS2i0iBiGy0u5CUCh3lhRDRDxIyHTldgauSCZlJ6O07zpk1Io1Vuw7T2OxlTdG2cuM6XBkQniaKC4CRwDzgEuBi+1mp0FG+w+p2CvO91EZ9UwvbD9bo+ITDZo1I41hTC1/vPeLdCVJyoemodfe98jtPp8fuAaqBAcCwdg+lQoeDM562HqimudVo6Q6HzchNJUyscQqvJOsU2UDydHrsLcDnwIfAb+zn+5wPSykvNdVbaxU4OD4BaOkOhyX2i2RCZpL34xRabjygPG2b3wVMBfYYY87Gmr2kbT8VOg7vBAykOjfjKa1/FIMSYxw5n/rG7BFpbHBVUVPf5PnBSUMB0XspAsTTRFFvT1dFRKKNMdsAZ6quKeWE48UAnWpR6EC2v8wakUZLq2HVLi8KLUREQ2Kmdj0FiKeJwmXfVf0W8LGIvM03pTaUCr62ROFAi+JoQzNFZbWMH6LjE/4weVgSMZFhvnU/aYsiIDy64c4Y8137x/tEZClW3aV/OB6VUt4q3wGJQyHK93seNu2rwhiYmKWJwh+iI8KZmp3i24D2tvecDUp1yOv5g8aYz4wx7xhjGp0MSCmfOFgMcOM+ayB7/BAdyPaX2SPSKDxUS6k3ZcdTcqCuHOqrnQ9MfYtbiUJEltvPNSJSfeKzf0NUyk3GWF1PDo1PbHBVMTgxhvT4aEfOp042a0Qa4OU0WS0OGDBuJQpjzGz7Od4Yk3Dis39DVMpN1futm7AcqvG00VWpN9r52dhBCSTHRvKlN2XHtdx4wLg1RiEi93T1vjHmIWfCUcoHFc7NeKqqa6K4oo6r8rJ8PpfqXFiYMHNEGl8WlWOM8Wx2mbYoAsbdMYp4+5EH/BBredIhwO3AWP+EppSHHJwaW7DPWhpe16Dwv9kj0jhYXc/OMg9XLIhJgNg0bVEEgFstCmPMbwBE5CNgsjGmxn59H/Ca36JTyhPlOyA6AfoP8PlUx+/I1oFsv5vdbpxiRIaHS82m5Ojd2QHg6aynoUD7WU6NQLZj0Sjli7YZTw7cHFfgqiQ7NZbE2EgHAlNdyUqJJSuln3f3U2i58YDwNFG8AKwWkftE5NfAKsDrNbOVcpSDM542uqoYr/WdAmb2iDRW7qygucXDsuMpOVDlguYG/wSmAM+rx/43cBNwBKgEbjLG/M4fgSnlkYZaqN7nyB3ZZTUN7K+q14qxATRrRBo1Dc0U2PeuuC0lFzBQudcvcSmLNzfc7QZWAF8D8SIyx9mQlPJCRZH17ECLYqM9kK2lOwJn5nBrnOIrT7uftNx4QGiZcdU7ODjj6cuiCsLDhFM1UQRMSlwU4wYneD5OoeXGA0LLjKveoXwHSPg3fzi8VFXXxMur93LR+EHERXtUCk35aPaINNbtqaSusdn9g+LSITJO76XwMy0zrnqH8h2QnG2Vn/bBcyuKOdrYwg/PGu5IWMp9M0ek0djSyppiD5ZHFflm/WzlNwEvMy4iWSKyVES2ishmEbnL3p4iIh+LSKH9nGxvFxF5VESKRKRARCZ7GLPqCxyY8VTX2MyfvtzN3NEZjBmklWkCbWp2MlHhYZ7XfdJy437ndqIQ6976fzXGVBpj7gN+CSwBLvPwms3AT40xY4AZwJ0iMha4F/jUGDMS+NR+DXABMNJ+LAQWeXg91du1tliD2T7WeHp5dQlH6pq4Q1sTQREbFcHkYUksL/RiQPtIsfU5UH7hdqIwxhislkTba6/KjBtjDhhj1tk/1wBbscqBXAo8Z+/2HN8koEuB541lJZAkIoM8uabq5apKoKXBpxZFY3MrT3+xi2nZKeRlpzgYnPLE7BFpbDlQzeGjHvxZScmBlkarKKTyC0+7nlaKyFSnLi4i2VgD4quAAcaYA2AlEyDD3m0IUNLuMJe9TSmLAzOe3lq/jwNV9fzwbG1NBFNb2fGvdnrQqtDigH7naaI4G1ghIjvt8YKNIlLgzYVFpD/wBnC3MaarNS06qsdgOjjfQhHJF5H8sjKdiNWnlO+wnr1MFC2thic/28nYQQmcNSrdwcCUp8YPSSQ+JsKzcYqUXOtZB7T9xtP5fxc4cVERicRKEi8aY/5mby4VkUHGmAN219Ihe7sLaF/rOZMOBtCNMYuBxQB5eXknJRLVi5XvgNhUiPWuy+jDzQfZVXaUx649zbMy18pxEeFhnJ6b6tn9FImZEBapLQo/8nQwu9UYs+fEhycXtM+zBNh6wjoW7wAL7J8XAG+3236DPftpBlDV1kWlFODTjCdjDE8sKyInLY4LTtWhr1Awa0QaJYePsbeizr0DwsIhaajedOdHXg9m+2AWcD0wV0TW248LgQeA80SkEDjPfg3wPrALKAKeBu5wIAbVm5Tv8LrG0xeF5WzaV81tc3IJD9PWRChoG6fwqFWh91L4laddTytFZKoxZo23FzTGLKfjcQeAczrY3wB3ens91csdOwJHy7xuUTyxrIgBCdF8d7LOjwgVw9PjGJgQw5dF5Vw7fah7ByXnQMlqa9107T50nDeD2SudGMxWyhHl3hcDXLf3CCt3HebWM3KJjgh3ODDlLRFh1og0vtpZTmurm8ONKbnQUA11h/0bXB/laYtiPt+0BnTAWAXf8RlPIz0+9ImlO0mKjeSaaW5+a1UBM3tkKm+sc7HlQLV7xRlT2k2RjUv1b3B9kFuJQkRq6DgxiL1d6x2o4CjfAeFRkDTMo8O2H6zhk62l3H3uSC3+F4JmDf9meVS3EkVyuyqymXl+jKxvcqvryRgTb4xJ6OARb4zRJKGCp7wQUoZDuGd/7BctKyI2KpwbZ2b7Jy7lk4yEGEZm9Hd/QDvZ/qKgA9p+4c3CRUqFjvIdHtd4Kjlcx7sFB7h22lCSYqP8FJjy1awRaawpPkx9kxs1nCL7QfxgvZfCTzRRqJ6rpcn6w+DhQPZTn+8kTOCWM3L9FJhywuwRadQ3tbJur5tlx1NytUXhJ5ooVM91pBhamz1KFIdq6nk138UVkzMZmBjjv9iUz6bnphAeJnxVVOHeASnZ2qLwE00UqufyYsbTs8uLaW5p5bYztfhfqIuPiWRSVpIH4xQ5UFsKDbX+DawP0kSheq62RJHqXqKoOtbEX1bu4YLxg8hJi/NjYMops0akUeCqpOpYU/c7H58iW+zXmPoiTRSq5yovhPhBEOPexLu/rNxDbUOzLkzUg8wekUargZW73Oh+0nLjfqOJQvVcHtR4OtbYwrPLd3PWKemMG+zGvHwVEiZlJdEvMty9suNtLQod0HacJgrVMxnjUdXYV9bspeJoI3ec5dtyqSqwoiLCmJ6b4t44Rb9k66EtCsdpolA909FyqK90K1E0tbTy9Be7yRuWzLQcXea0p5k9Io1dZUc5UHWs+52Tc7TcuB9oolA9kwcznt5ev599lce4Q5c57ZHayo5/6c40WS037heaKFTP5Obyp632MqejB8Zz9ikZXe6rQtMpA+JJ6x/l3jhFcg5UuaybMZVjNFGonqm8ECJjIaHrdSQ+2lJK0aFafnjWcF3mtIcKCxNmDk9jeVE51vI0XUjJBdMClXsDE1wfoYlC9UzlOyB1OIR1/hE2xrBoWRHDUmO5aLwuc9qTzRqRSllNA4WHurmZLkWnyPqDJgrVM1V0P+Ppq50VbHBVcduc4USE60e9Jzu+PGphN91PyTpF1h/0X4/qeZrq4ciebhPF40uLyIiP5oopusxpT5eZHEt2amz34xTxAyGinyYKh2miUD3P4Z2A6XLG05b91Xy1s4KbZ+foMqe9xJmj0lleVE5FbUPnO4lY3U/a9eQoTRSq53FjxtNfVu0hJjKM703VZU57i+tPH0ZDcysvrNzT9Y7JOkXWaZooVM9TXgiItbJdB6rrm3jr6318Z+JgEmMjAxub8psRGfGcMzqD51fs6Xoxo5QcuwR9a8Bi6+0CnihE5FkROSQim9ptSxGRj0Wk0H5OtreLiDwqIkUiUiAikwMdrwpB5TsgKQuiYjt8+811+6hrbOH6GdmBjUv53cI5uRw+2sjra12d75ScDc3HoPZgwOLq7YLRovgzMP+EbfcCnxpjRgKf2q8BLgBG2o+FwKIAxahCWXlhp6XFjTG8sHIPE7OSGJ+pxf96m2k5KUzMTGTJ8t20tHZyT4UWB3RcwBOFMeZz4PAJmy8FnrN/fg64rN32541lJZAkIjohvi/rphjgil0VFB2q5foZwwIcmAoEEWHhnOHsLj/Kx1tKO94pxV7iVge0HRMqYxQDjDEHAOzntloLQ4CSdvu57G2qr6reD01HO53x9JeVe0iKjeTiCfp9orc6f9wAslL68fQXnRT/S8wCCdcWhYNCJVF0pqOaCx22N0VkoYjki0h+WVmZn8NSQdPFjKfS6no+3FzKv+RlEROpU2J7q4jwMG6ZncvaPUdYu+fEzgkgPNIaw9IWhWNCJVGUtnUp2c+H7O0uIKvdfpnA/o5OYIxZbIzJM8bkpaen+zVYFUTlhdZzB4nipdV7aWk1XDddp8T2dlflZZLYL5LFn3fSqtBy444KlUTxDrDA/nkB8Ha77TfYs59mAFVtXVSqjyrfAdGJ0P/blWCbWlp5afVezhyVzrBUXQ+7t4uNiuD6GcP4aEspu8uPnryDlht3VDCmx74ErABOERGXiNwMPACcJyKFwHn2a4D3gV1AEfA0cEeg41UhpqIQ0kZYd+C288mWUkqrG3QQuw9ZMDObyLAwnulorCIl11rY6tiRwAfWC0UE+oLGmGs6eeucDvY1wJ3+jUj1KOWFkDPnpM0vrNzDkKR+nD1a15zoK9Ljo7l88hBeX+vinvNGkdo/+ps32xcHHJIcnAB7kVDpelKqew01UL3vpBlPRYdq+GpnBddOH0p4mK450ZfcckYuDc2tPL/ihLIeWm7cUZooVM9RUWQ9nzCQ/ZeVe4kMF66emtXBQao3G5HRn3PHZPDCyj0ca2xX1iM523rWAW1HaKJQPUcHM57qGpt5Y62LC8cPIq1914PqMxbOGW6V9VjXrqxHVBz0HwCHi4MWV2+iiUL1HOU7rBup2vqfgbfX76emoVkHsfuwqdnJTMxKYskXu75d1iMlV7ueHKKJQvUc5YVWl0JEFGDXdVqxh9ED45kyTAcs+yoRYeEZuRRX1H27rIeWG3eMJgrVc5xQ42nd3kq2HKjm+tOHIaKD2H3Z/FMHkpXSj8Wf7/xmY0oO1OyHpmPBC6yX0ESheobWFmswu92Mp7+s3EP/6Agum6Tlv/q68DDhltm5rNtb+U1Zj7YuyiPFQYurt9BEoXqGyr3Q0nC8RVFR28B7BQe4YvIQ4qIDfjuQCkFX5WWSFBvJU5/ZM5203LhjNFGonuGEGU+v5rtobGnl+tN1EFtZ2sp6fLy1lF1ltVpu3EGaKFTPcLxq7EhaWg0vrtrD6bmpjMiID25cKqTccHo2keFhPLN8N/RLtuqCaYvCZ5ooVM9QUQixqRCbwmc7DuE6ckxbE+ok6fHRXDF5CG+sdVF+tBFSsvWmOwdoolA9Q7sZTy+s2ENGfDTnjR0Q5KBUKLp5tlXW44UVe6wBbe168pkmCtUzlO+AtJHsrahj2Y4yrpk2lMhw/fiqk1llPQbw/IpimpJy7IkQzcEOq0fTf2kq9NUdhqNlkDaKF1fvIUyEa6bp4kSqcwvn5HKkron86kRobYZqV/cHqU5polChzy4G2Jg0glfXlDBv7AAGJsYEOSgVyqZmJzMpK4mXi+wlcXVA2yeaKFTos2c8La1I5Ehdk9Z1Ut0SERbOyWV1ZZK1QQe0faKJQoW+8kIIj2JxQTO56XGcPjw12BGpHuD8cQOJSh5CI5EYbVH4RBOFCn3lhdQnZLO2pIbrZ2hdJ+We8DDh5jnD2dOaQeW+HcEOp0fTRKFCX/kOClsG0S8ynMsnZwY7GtWDXDklk/1hA6k9WBjsUHo0TRQqtLU0YY7sZnllCpedNpjEfpHBjkj1ILFREcQPGklKwz4KSo4EO5weSxOFCm2HdyOtzWxvHsT3dRBbeWHUmAnESQM3P/4+1y9ZxYebD9Lc0hrssHoUTRQqpJny7QBEDhjFuMGJQY5G9UT9B1ql6X8+LYqiQ7Xc9sJaZv9+Kf/7yQ5Kq+uDHF3PoIlChazWlhZ2bvgSgDmnnx7kaFSPZVeRvSryS774fiJPXzeeUQPj+d9PCpn5wD+5/YW1LC8sp7X9MqrqW8SY0P/liMh84BEgHHjGGPNAV/vn5eWZ/Pz8gMSmnNHU2EDJjvWUF67G7F9PQuVWhjbuJE7q2U8GKf+5jZjI8GCHqXqiliZ4cjaUbbNeh0fDoIlUp03knzVDeXpXMpuPJZOT1p/rpg/lismZJMdFBTfmIBCRtcaYvA7fC/VEISLhwA7gPMAFrAGuMcZs6ewYTRShrb6ulr3b8jlStAYOFpBSvZWhTcVESxMAdSaaPVHDqU4aiwyeRHbefDKyRnZzVqW6YAxUuWBfPrjyYd9a2P81NFtdT/XRqWw0I1h2dBibw0YyeOxMrpw1jtOykvrMdOyuEkVPWBpsGlBkjNkFICIvA5cCnSaKo4cPsPKv/xWg8JRbmhsIr9hOWs12slr2MkqswcQq4iiJHsnXaf9CROYkMkZNY0juqYyJ6AkfTdVjiEBSlvUY911rW0sTlG6GffnEuNYy1bWGqY2rAGjdJhRtHczHMWOIyzqV8PC+PduuJ/xrHAKUtHvtAqafuJOILAQWAkwZFMaMHX8ITHTKbWUks7/fKNakziU6azKDRk9jYNZITg3ToTIVBOGRMHiS9Zh6i7Xt2BHYt46mPWuI27ac6eWrSNz5SXDjDAE9oevpKuB8Y8wt9uvrgWnGmB93dsxpkyaZZf/8OFAhKjeEhYcTn5gS7DCU8ohpbaW66rDVddXLJaVm9OiuJxeQ1e51JrC/qwPCIyJITEn3a1BKqd5PwsJITE4LdhhB1xPa/GuAkSKSIyJRwPeAd4Ick1JK9Rkh36IwxjSLyI+AD7Gmxz5rjNkc5LCUUqrPCPlEAWCMeR94P9hxKKVUX9QTup6UUkoFkSYKpZRSXdJEoZRSqkuaKJRSSnUp5G+484aI1ADbgx2HmxKBqmAH4QGN1396Uqyg8fpTMGI9xRgT39EbPWLWkxe2d3aHYagRkcXGmIXBjsNdGq//9KRYQeP1p2DEKiKdVlLVrqfgezfYAXhI4/WfnhQraLz+FFKx9taup/ye0qJQSqlQ0NXfzd7aolgc7ACUUqqH6fTvZq9sUSillHJOb21RBI2IzBeR7SJSJCL32tuWiMgGESkQkddFpH8nx/67fdx2ETm/q3P6MVYRkf8WkR0islVE/rWTYxeISKH9WNBu+xQR2Wif81FxcHmwTuKdKyLrRGSTiDwnIh1O0Ah0vCLyrIgcEpFN7bb9QUS22Z+DN0Ukyd3/Tnt7joissv8bXrGLZDqik3jvE5F9IrLeflwY4vFOEpGVdqz5IjKtk2MD/VnIEpGl9r+nzSJyl739Kvt1q4h02lUejN/vSYwx+nDogVW0cCeQC0QBG4CxQEK7fR4C7u3g2LH2/tFAjn2e8M7O6cdYbwKeB8Ls/TI6ODYF2GU/J9s/J9vvrQZOBwT4ALjAz7/bEmCUvc/9wM0hEu8cYDKwqd22eUCE/fPvgd+7+99pv/cq8D375yeBHzr42e0o3vuAn3nz/yVI8X7U9v8PuBBYFiKfhUHAZPvneKylnccCY4BTgGVAXij9fk98hHyLopNvkW5lUgnwN3TaLdtqjGkEXgYuNcZU29cVoB/QUX/fpcDLxpgGY8xuoMg+X4fn9FeswA+B+40xrQDGmEMdHHs+8LEx5rAx5gjwMTBfRAZhJcUVxvr0Pg9c5kCsncV7BdBgjNlh7/OxvS3o8RpjPgcOn7DtI2NMs/1yJdbaKifq8P+L/dmZC7xu7/ecU7F2Fq+bQileAyTYPyfS8bo1wfgsHDDGrLN/rgG2AkOMMVuNMd3d7xWU3++JQjpRiEg48DhwAVYGvkZExmJ9G3vYGDMSOALc3MGxY7HWrhgHzAeeEJHwLs7phI6WbR1ix/Mn4CAwGvijve07InJ/N8d2ek4/xTocuNpuun8gIiPtWPNE5Bk3YnX5IdbOrjkQiGzXbL8Se5GrEIi3Oz/A+taKiAwWkbbqyJ3FmgpUtks0gYr1R3ZX2bMikhzi8d4N/EFESoAHgX+34w2Zz4KIZAOnAau62Cfkfr8hnSjo/FuvO5k00N/QwWqynsgAGGNuAgZjfZu42t72jjHmV90c2+k5fdTZeaOBemNNk3saeNaONd/Yy9EGIdbOrtmK9WXgYRFZDdQAzRAS8XZKRP4TK84XAYwx+40xbf3/oRTrIqwvDpOAA8D/g5CO94fAT4wxWcBPgCUQOp8FscYm3wDubutl6Ego/n5DPVF0lk07zKRB/obedq5Ol201xrQAr9Bx90hnx3q8FKyPsbqwPswAbwITPDw2s4PtTujwmnZXwRnGmGnA50BhiMTbIXvw9GLgOruL40SdxVoOJMk3g/V+j9UYU2qMabG7IZ/G+pIVsvECC4C/2T+/hmfx+vWzICKRWP+uXjTG/K27/dsJid9vqCeKjrJmeAfb2r61B/MbOnSybKuIjIDjYxSXANs6OPYd4HsiEi0iOcBIrME1fy0F29l538JqsQGciTXwdqIPgXkikmx3R8wDPjTGHABqRGSG/d96A/C2A7F2Gq+IZACISDTwb1iDeqEQ70lEZL4d43eMMXWd7Nbhf6edVJZida+B9UfRb7Ha8Q5q9/K7wKYOdguZeLH+UJ5p/zyXjr80BPyzYJ9vCbDVGPOQh4eHxu/XX6PkTjywZiB82O71v9uPcr6ZPfKtfU7ct93rD+19OzyngzFfiPXHdSfwn1jJ+EtgI9Y/tBexZ0EB38EaOG479j/t47bTbsbFief0V6z2tiTgPTveFcBEe3se8Ey7Y3+A1Z1XBNzUbnue/d+5E3gM+14dP8b7B6zuvO1YTXpCIV7gJazumiasb4U329cuAdbbjyftfQcD73f3/xtr5stq+zyvAdEO/m47ivcF+3NQgPUlYlCIxzsbWIs1M2gVMCVEPguzsb6MFrT7f38hVvJ1AQ1AKfbfpVD4/Z74COkb7uxm1Q7gHGAfVna9Fmva3hvGmJdF5EmgwBjzxAnHjgP+itX8HAx8ivUtXTo6p9F1uJVSqkMh3fVkrHGIH2G1BrYCr9p/0P8NuEdEirBG/5fAt8co7P1eBbYA/wDuNFZ/a2fnVEop1YGQblEopZQKvpBuUSillAo+TRRKKaW6FLKJQnwrUvZnEbmy6Z0WOgAAAWZJREFUo/eUUkp5JmQTBfBnrNIbJ3rYGDPJfrzfwftKKaUcFLKJwnhfpOxbRORXIrJGrDLUi+2bXxCRZSLyexFZLVZJ7TN8DloppXqhkE0UXTipSFk3HjPGTDXGnIpVufXidu9FGKv0w93Ar/0RrFJK9XQ9LVF0WKSsG2eLVZJ8I9Zt/ePavddWc2UtkO1gnEop1Wv0qERhOilSJiJ/sge3vzVmISIxwBPAlcaY8fYxMe12abCfW4AOV0ZTSqm+rkf9cRSRQcYq3gXtipQZq4R3R9qSQrld4vdKvilPrpRSyg0hmyhE5CXgLCBNRFxYYwhnicgkrAJbxcBtnRwegbXyWaWIPI1V2KwYq66TUkopD/S6Eh4iEoaVEG7QGk5KKeW7HjVG0R0RGYzVHbVSk4RSSjmj17UolFJKOatXtSiUUko5TxOFUkqpLmmiUEop1SVNFEoppbqkiUIppVSXNFEopZTq0v8HLETroUWgqS4AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"df.loc['1990-01-15', 'ghi'].plot()\n",
"tracker_poa.loc['1990-01-15'].plot()\n",
"plt.legend()\n",
"plt.ylabel('Irradiance [W/m$^2$]');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Notice how different the daily profile is for the tracker array! This is because the array can tilt steeply East and West to face towards the sun in early morning and late afternoon, meaning the edges of day get much higher irradiance than for a south-facing array.\n",
"\n",
"Note also that in the middle of the day, GHI and POA just touch each other -- this is because at solar noon, the array lies flat, and so POA is momentarily identical to GHI."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note that the POA calculations discussed above do not address the partial blocking of diffuse light in arrays with multiple tilted rows of PV modules, so the results will be slightly (typically 1-3%) optimistic relative to real conditions or to commercial modeling software. Such corrections are likely to be added to pvlib in the future for specific generic geometries like fixed racks."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"[](http://creativecommons.org/licenses/by/4.0/)\n",
"\n",
"This work is licensed under a [Creative Commons Attribution 4.0 International License](http://creativecommons.org/licenses/by/4.0/)."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3 (ipykernel)",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.11.4"
}
},
"nbformat": 4,
"nbformat_minor": 4
}