{ "cells": [ { "cell_type": "markdown", "metadata": {}, "source": [ "> **前言：** 学习了 Sutton 的《强化学习（第二版）》第6章时序差分学习的控制部分，将笔记提炼如下。\n", "\n", "笔者阅读的是中文书籍，所提到的公式，笔者将给出其在英文书籍上的页码。英文书籍见 Sutton 个人主页：\n", "[http://incompleteideas.net/book/the-book.html](http://incompleteideas.net/book/the-book.html)\n", "\n", "本次笔记内容：\n", "\n", "- 6.4 Sarsa：同轨策略下的时序差分控制\n", "- 6.5 Q 学习：离轨策略下的时序差分控制\n", "- 6.6 期望 Sarsa\n", "- 6.7 最大化偏差与双学习\n", "- 6.8 游戏、后位状态和其他特殊例子\n", "- 6.9 本章小结\n", "\n", "在上一次笔记中，我们讨论了 [动态规划（ Dynamic Programming, DP ）、蒙特卡洛方法（ Monte Carlo Method, MC ）与时序差分学习（ Temporal Difference Learning, TD ）的异同](https://blog.csdn.net/weixin_42815609/article/details/104034967)，以及时序差分学习中的预测算法。本次笔记中我们讨论其控制部分算法，其概述如下。\n", "\n", "- Sarsa 是同轨策略下的时序差分控制，；\n", "- Q-learning 是离轨策略下的时序差分控制；\n", "- 期望 Sarsa 的表现比上述二者表现都更好（ van Hasselt, 2011），并且被称为“广义 Q 学习”；\n", "- 然而，单纯的最大化操作带来了“最大化偏差”，因此我们提出“双学习”来消除“最大化偏差”；\n", "- 此外，我们还引出了如“后位状态”的概念，没有具体讨论。\n", "\n", "书中展示了4段实例， Zhang 都有相应代码进行实现，分别介绍如下知识点：\n", "- 有风的网格世界（Example 6.5: Windy Gridworld）介绍 Sarsa 的性能；\n", "- 在悬崖边行走（Example 6.6: Cliff Walking）对比了基于$\\epsilon$-贪心方法的 Sarsa 与 Q-learning 的控制效果；\n", "- 接着，在介绍 期望 Sarsa 时也使用了 Cliff Walking 实例对其效果进行展示；\n", "- 最大化偏差实例（Example 6.7: Maximization Bias Example）用于表达：双 Q 学习优于 Q 学习。\n", "\n", "我对其代码进行了标注，请见[https://github.com/PiperLiu/Reinforcement-Learning-practice-zh/blob/master/practice/05-02-Temporal-Difference-Control.ipynb](https://github.com/PiperLiu/Reinforcement-Learning-practice-zh/blob/master/practice/05-02-Temporal-Difference-Control.ipynb)。**并且，我还由代码及实验结果，复述了我对于书上提出的算法对比特性的理解。**\n", "\n", "### Sarsa\n", "\n", "基于同轨策略，其更新公式为：\n", "\n", "$$Q(S_t,A_t) \\leftarrow Q(S_t,A_t) + \\alpha [ R_{t+1} + \\gamma Q( S_{t+1}, A_{t+1} ) - Q_(S_t , A_t ) ]$$\n", "\n", "可以看出与之前“时序差分预测”中的价值预测公式很像。\n", "\n", "如果 $S_{t+1}$ 是终止状态，那么$Q( S_{t+1}, A_{t+1}$则定义为0。这个公式用到了元组$(S_t,A_t,R_{t+1},S_{t+1},A_{t+1})$，因此该算法命名为 Sarsa 。\n", "\n", "Sarsa 想要以1的概率收敛到最优的策略和动作价值函数，需要满足2个条件：\n", "1. 所有的“状态-动作”二元组都被无限多次访问到；\n", "2. 贪心策略在极限情况下能够收敛（收敛过程可以通过令 $\\epsilon = 1/t$ 来实现）。\n", "\n", "算法框架中，每幕中的每步都要更新 Q ，不具体展示框架了，可见书第6章。\n", "\n", "### Q-learning\n", "\n", "更新公式为：\n", "\n", "$$Q(S_t,A_t) \\leftarrow Q(S_t, A_t) + \\alpha [R_{t+1} + \\gamma \\max_a Q(S_{t+1}, a) - Q(S_t, A_t)]$$\n", "\n", "只是变了个更新公式而已，连算法框图都没变，**为什么说 Q-learning 是离轨策略呢？**\n", "- 书上的解释：In this case, the learned action-value function, Q, directly approximates q*, the optimal action-value function, independent of the policy being followed.\n", "- 我的理解：在公式中用于更新的动作为 $\\argmax_a Q(S' , a)$ ，而下一步却未必是 $\\argmax_a Q(S' , a)$ ，因此为离轨策略。\n", "\n", "**我的理解方式没有错，并且，这个理解会辅助对于“最大化偏差”部分的学习。**\n", "\n", "### 期望 Sarsa\n", "\n", "$$\\begin{aligned}Q(S_t, A_t) & \\leftarrow Q(S_t, A_t) + \\alpha [R_{t+1} + \\gamma \\mathbb{E}[ Q(S_{t+1}, A_{t+1}) | S_{t+1}] - Q(S_t, A_t)]\\\\\n", "& \\leftarrow Q(S_t, A_t) + \\alpha [R_{t+1} + \\gamma \\sum_a \\pi(a | S_{t+1}) Q(S_{t+1},a) - Q(S_t, A_t)]\\\\\\end{aligned}$$\n", "\n", "虽然计算上更为复杂，但它消除了 Sarsa 中因为随机选择 $A_{t+1}$ 而带来的方差。并且，对于 cliff walking 中的情况，期望 Sarsa 将保持 Sarsa 相对于 Q-learning 的“能学到迂回策略”的优势。\n", "\n", "### 最大化偏差与双学习\n", "\n", "#### 最大化偏差\n", "\n", "上述算法中，通常是基于 $\\epsilon-$贪心 来产生策略的，这其中都用到了“最大化操作”。\n", "\n", "**但是，如果在估计值的基础上进行最大化操作，就是隐式地对最大值进行估计，而这就会产生一个显著的正偏差。例子如下。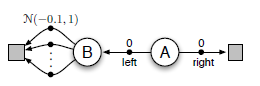**\n", "\n", "![](images/05-05.png)\n", "\n", "如图的MDP，A为起点，做动作 left ，则0收益；做动作 right ，之后获得的收益服从 正态分布 N(-0.1, 1)。\n", "\n", "我们知道最优策略应该是 100% 做动作 left 。\n", "\n", "但是，如果使用了最大化操作，动作 right 的估计值是不确定的，有些可能大于0，则估计值的最大值就产生了正数，就产生了正偏差。**就是最大化偏差。**\n", "\n", "#### 双学习\n", "\n", "双学习可以消除最大化偏差。双学习使用了2倍的内存，但计算量无需双倍。\n", "\n", "**以双Q学习为例：**\n", "\n", "使用 $Q1$ 来估计 $A^* = \\argmax_a Q_1(a)$ ，而 $Q_2$ 负责估计 $Q_2(A^*) = Q_2(\\argmax_a Q_1 (a))$ ，由于 $\\mathbb{E} [Q_2 (A^*)] = q(A^*)$ ，因此这个估计是无偏的。\n", "\n", "即更新公式换为：\n", "\n", "$$\\begin{aligned}\n", "& With \\; 0.5 \\; probabilility: \\\\\n", "& \\quad Q_1(S_t,A_t) \\leftarrow Q_1(S_t, A_t) + \\alpha [R_{t+1} + \\gamma Q_2(S_{t+1}, \\argmax_a Q_1(S_{t+1}, a)) - Q_1(S_t, A_t)] \\\\\n", "& else: \\\\\n", "& \\quad Q_2(S_t,A_t) \\leftarrow Q_2(S_t, A_t) + \\alpha [R_{t+1} + \\gamma Q_1(S_{t+1}, \\argmax_a Q_2(S_{t+1}, a)) - Q_2(S_t, A_t)] \\\\\n", "\\end{aligned}$$\n", "\n", "### 后位状态\n", "\n", "后位状态我读了两遍，差不多明白了其意思：类似下棋的游戏中，可以由不同的状态，经过不同的动作，达到同一状态（棋盘摆放位置同），我们叫这个为后位状态。在这种情况中，后位状态显然更为重要。这很有趣，应该找些实例继续了解。\n", "\n", "Van Roy, Bertsekas, Lee, Tsitsiklis, 1997; Powell, 2011 对其进行了研究。\n" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Example 6.5: Windy Gridworld\n", "\n", "![](/images/05-03.png)\n", "\n", "Shown inset below is a standard gridworld, with start and goal states, but with one di↵erence: there is a crosswind running upward through the middle of the grid. The actions are the standard four—up, down, right, and left—but in the middle region the resultant next states are shifted upward by a “wind,” the strength of which varies from column to column. The strength of the wind is given below each column, in number of cells shifted upward. For example, if you are one cell to the right of the goal, then the action left takes you to the cell just above the goal. This is an undiscounted episodic task, with constant rewards of −1 until the goal state is reached." ] }, { "cell_type": "code", "execution_count": 2, "metadata": {}, "outputs": [ { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZMAAAEKCAYAAADXdbjqAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzt3Xl8FPX9x/HXhyNAIBCSEI4ECEcEQeQKp+2vCt53rQdeIKB41draarWtbW1/v9aeivWC4sGtgCJqtWpVShEFEu5DIIQrhCOBECAJkOP7+2MnNUCAJdnNbpL38/HYx858Z3b3w5DsOzPfmfmacw4REZGqqBfqAkREpOZTmIiISJUpTEREpMoUJiIiUmUKExERqTKFiYiIVJnCREREqkxhIiIiVaYwERGRKmsQ6gKqIi4uziUlJYW6DBGRGiUtLS3HOdcqkO9Zo8MkKSmJ1NTUUJchIlKjmNm2QL+nDnOJiEiVKUxERKTKFCYiIlJlChMREakyhYmIiFRZUMPEzLaa2WozW2FmqV5bjJl9YmabvOeWXruZ2XNmlm5mq8ysXzBrExGRwKmOPZOLnHN9nHMp3vzjwKfOuWTgU28e4Aog2XuMA16qhtpERCQAQnGY6zpgsjc9Gbi+XPsU5/MVEG1mbUNQn4hI2Dp8tJinP/yaHfsLQl3KcYIdJg742MzSzGyc19baObcLwHuO99oTgB3lXpvptR3HzMaZWaqZpWZnZwexdBGR8LIrr5Brn1/Iy//ezPyN4fX9F+wr4C9wzmWZWTzwiZl9fZp1rYI2d1KDcxOBiQApKSknLRcRqY225ORzx6TF5BUWMeOeQQztEhfqko4T1DBxzmV5z3vNbC4wENhjZm2dc7u8w1h7vdUzgfblXp4IZAWzPhGRmmBtVh6jXl1CqYOZ9wymV2KLUJd0kqAd5jKzpmYWVTYNXAqsAd4FRnmrjQLmedPvAiO9s7oGA3llh8NEROqqT9bt4aaXv6Rh/XrMundIWAYJBHfPpDUw18zKPmeGc+6fZrYUmGVmY4HtwE3e+h8AVwLpQAEwOoi1iYiEvUWbc3hw+jLObRvFxJEptG7eONQlnVLQwsQ5lwH0rqB9HzC8gnYHPBisekREapJ1WQe5d0oaHWMjmTJmEC0iG4a6pNPSFfAiImFmxY4DjJj4Jc0aN+D1MQPDPkhAYSIiEla+3LyPu15bQnRkBLPuHUJCdJNQl+QXhYmISJh4Ky2TO15ZTEzTCKaOHUj7mMhQl+S3Gj3SoohIbbBh9yFeWZjBrNRMLugay8t39Ceqcfgf2ipPYSIiEkIfr93NA9OXUa+eMfZbnXjs8m40alA/1GWdNYWJiEiIzF2eyaOzV9EzoQWv3TWAmKYRoS6p0hQmIiIh8NoXW3jqvXUM6RzLxJE177DWiRQmIiLVbO7yTJ56bx2X9WzN+BF9adyw5h3WOpHCRESkGr29LJPH5qxicOcY/nZrPyIa1I6TahUmIiLV5O8LMvi/D9YztEssE+7sX2uCBBQmIiLV4i8fb+Bvn6VzVa+2/PWW3jXyjK3TUZiIiARRaanj2U838bfP0rklpT2/u6EX9etVNHxTzaYwEREJot99sJ5JC7dwQ7+EWhskoDAREQmaiQs2M2nhFkYN6civr+2JNyRHrVR7en9ERMLI28sy+d0HX3PV+W355TW1O0hAYSIiEnDzN+zlsTmrGNollr/e3LvWHtoqT2EiIhJAX6TncP+0ZZzTOooJd/avdWdtnYrCREQkQKYv3sbtkxbTpkVjXh8zoMbfIuVsqANeRCQA5i7P5BfvrGFY93heuK0fTSLqxh5JGYWJiEgVfb5hLz+ZvYrBnWJ58fZ+teJeW2dLh7lERKpgxY4DPDBtGd1aRzFxZP86GSSgMBERqbT3VmZxx6TFxEVF1Lk+khMpTEREKuHNpdt5aOZyurWJ4o1xQ4iPahzqkkJKfSYiImdp/L828cy/NvKdc1oxcWTdOf33dBQmIiJ+Olpcwp/+ucF3r62+vnttKUh8FCYiIn4oOFbMuClpLEzPYeSQjvzy6h40qK+egjIKExGRMzh0pIixr6eSum0/f7rxfG5KaR/qksKOwkRE5DTyCosY9eoSVu/MY/yIvlzTu12oSwpLChMRkVPYd/goo15bwobdh3jx9n5c1rNNqEsKWwoTEZEK7NhfwJ2vLGZX3hEmjkzhom7xoS4prAW998jM6pvZcjN735vvZGaLzWyTmb1pZhFeeyNvPt1bnhTs2kREKnKg4BijXlvC/vxjzLhnkILED9VxKsLDwPpy838AnnHOJQO5wFivfSyQ65zrCjzjrSciUq32HT7K7ZMWk7m/kEmjBtC/Y0yoS6oRghomZpYIXAVM8uYNGAbM8VaZDFzvTV/nzeMtH261fWgyEQkrWQcKuXnCl2zOPsyEkf0Z2ElB4q9g95k8CzwGRHnzscAB51yxN58JJHjTCcAOAOdcsZnleevnBLlGERGyDhRy08tfcrCwiCljBilIzlLQ9kzM7Gpgr3MurXxzBas6P5aVf99xZpZqZqnZ2dkBqFRE6rqsA4WMfHUJBwuLmH6PgqQygnmY6wLgWjPbCryB7/DWs0C0mZXtESUCWd50JtAewFveAth/4ps65yY651KccymtWrUKYvkiUhcs357Ltc9/we68I0walcL5idGhLqlGClqYOOeecM4lOueSgBHAZ86524HPgRu91UYB87zpd715vOWfOedO2jMREQmURZtzuH3SYiIj6jP3gaEM6hwb6pJqrFDcWOanwCNmlo6vT+QVr/0VINZrfwR4PAS1iUgdMX/DXka/tpSE6CbMuW8Iya2jzvwiOaVquWjROTcfmO9NZwADK1jnCHBTddQjInXbp+v3cN+0NJLjo5g6diCxzRqFuqQaT1fAi0idsig9h/unL+Pcts2ZOmYQLSLr7uiIgaT7J4tInbFocw5jJi8lKTaSyaMHKkgCSGEiInXCgo3ZjHl9KR1iIplxz2BaNo0IdUm1isJERGq9L9JzuHtyKp3imjHjnsHEqY8k4NRnIiK1Wtq2XMZNSSUpLpKZ9wwiOlJ7JMGgPRMRqbU+XL2L2/7+FXFRjZg6VkESTAoTEamVPly9iwdnLKNnu+a8ff9QWjdvHOqSajUd5hKRWmf+hr384I3l9GkfzdSxg2jaSF91waY9ExGpVRZszObeqWmc0zqK10YPVJBUE4WJiNQai9JzuHtKKp1bNWPq2EG0aKLrSKqLIltEaoVFm31B0im2KTPuHqTrSKqZ9kxEpMZbuCmHsa+nkhDdhKl3D1SQhID2TESkxiopdfz+g/VMWriFpNhIpt8ziPgonbUVCgoTEamRNu45xE9mr2RVZh53Du7IE1d2JzJCX2mhoi0vIjXOwk053D8tjUYN6zF+RB+u7d0Os4pG/pbqojARkRrlk3V7eGB6Gp3jmvHa6AG0i24S6pIEhYmI1CAfrt7FQzOX07Ndc6ZoLJKworO5RKRGeH9VFg/OWMb5iS2YereCJNxoz0REwt6/N2bzozdXkNIxhtdGD9BV7WFIeyYiEtYWpecwbkoqXeOjmHRXioIkTClMRCRsLc7Yx9jJqXSMjWTa2IE0b6xDW+FKYSIiYenr3Qe5e3Iq7aIbM/3uwcRqdMSwpjARkbCzK6+Qu15dStNGDZg6dhCtohQk4U4HH0UkrOzKK2TExK84fLSYWfcO0XUkNYT2TEQkbBwoOMbIV5aw7/AxJo8ZSI92zUNdkvhJYSIiYaHwWAljJ6eybV8BE0f2p3/HlqEuSc6CDnOJSMgVl5Ty/RnLWLY9lxdu68fQLnGhLknOkvZMRCSknHM88fZqPv16L7+57jyu7NU21CVJJShMRCSk/vjRBmanZfLw8GTuHNwx1OVIJSlMRCRkXlm4hZfmb+a2QR344cXJoS5HqkBhIiIhMW/FTn77/jou79mG3153nsYjqeGCFiZm1tjMlpjZSjNba2ZPee2dzGyxmW0yszfNLMJrb+TNp3vLk4JVm4iE1oKN2fx41koGd47h2RF9qF9PQVLTBXPP5CgwzDnXG+gDXG5mg4E/AM8455KBXGCst/5YINc51xV4xltPRGqZFTsOcN+0NJJbRzFxZAqNG9YPdUkSAEELE+dz2Jtt6D0cMAyY47VPBq73pq/z5vGWDzft94rUKpv2HGLM60uJbRbB5NEDdOPGWiSofSZmVt/MVgB7gU+AzcAB51yxt0omkOBNJwA7ALzleUBsBe85zsxSzSw1Ozs7mOWLSACtzszj5glfUr+eMXXMIOKbNw51SRJAfoWJmT1sZs3N5xUzW2Zml57pdc65EudcHyARGAicW9FqZR9zmmXl33Oicy7FOZfSqlUrf8oXkRBbunU/t/39KyIjGjD73iEkxTUNdUkSYP7umYxxzh0ELgVaAaOBp/39EOfcAWA+MBiINrOyK+8TgSxvOhNoD+AtbwHs9/czRCQ8Ld+ey12vLqFV80bMuV9BUlv5GyZlew1XAq8551ZS8Z7ENy8wa2Vm0d50E+BiYD3wOXCjt9ooYJ43/a43j7f8M+fcSXsmIlJzLM7Yx+2TFhPbrBFv3DOYti10B+Dayt97c6WZ2cdAJ+AJM4sCSs/wmrbAZDOrjy+0Zjnn3jezdcAbZva/wHLgFW/9V4CpZpaOb49kxFn+W0QkjGzJyef+6cto06Ixb4wbTHyU+khqM3/DZCy+03sznHMFZhaL71DXKTnnVgF9K2jPwNd/cmL7EeAmP+sRkTC2bV8+33tpESWljr+PTFGQ1AH+HuZyQA/gB958U0A/HSJykk/W7eHK8f+huKSUt+4fSpdWzUJdklQDf8PkRWAIcKs3fwh4ISgViUiNVFLq+OM/v+aeKal0iW/G+w99m67xCpK6wt/DXIOcc/3MbDmAcy637DYoIiLFJaX8ePZK5q3I4taB7fnVNT11ZXsd42+YFHkd6Q58Z2px5g54EakDikpKeWjGcv65djePXd6NBy7sGuqSJAT8Pcz1HDAXiDez/wMWAr8LWlUiUiOUlDp+Mnsl/1y7myev7qEgqcP82jNxzk03szRgOL7rS653zq0PamUiEtZKSx2Pv7WKeSuyePSyboz9VqdQlyQhdNowMbOYcrN7gZnllznndIW6SB3knOPJeWuYnZbJD4Yn8+BF2iOp6860Z5KGr5/EgA74bhlvQDSwHd9FjCJShzjneOq9dUxfvJ37vtOFH2mEROEMfSbOuU7Ouc7AR8A1zrk451wscDXwdnUUKCLhwznH0x9+zeuLtjLmgk789PJuGiFRAP874Ac45z4om3HOfQh8JzgliUi4euaTjUxYkMGdgzvy5NXnKkjkv/w9NTjHzH4BTMN32OsOYF/QqhKRsPP8Z5t47rN0Rgxoz1PX9lSQyHH8DZNbgV/hOz0YYAHfXA0vIrVYXmERv5y3hnkrsrihbwK/+24v6mnMdjmBv6cG7wceNrPmQGm54XhFpBY7dKSIG19aREZOPo9ccg4PXtRVQSIV8itMzKwXMAWI8eZzgFHOuTVBrE1EQij/aDFjJ6eSkZPP66MH8O1kjWwqp+ZvB/wE4BHnXEfnXEfgx8DE4JUlIqGUf7SY0a8vJXXrfp65pY+CRM7I3zBp6pz7vGzGOTcf323oRaSWKSop5f7py0jdup/xI/pybe92oS5JagB/O+AzzOxJYKo3fwewJTgliUioOOf4+dzVLNiYzR++14trFCTiJ3/3TMYArfBdqDgXiOMMIy2KSM1SWup4ZNZKZqVm8oNhXbllQIdQlyQ1iL9nc+XijbLo3Yq+qXPuYDALE5Hq9cy/NjJ3+U5+eHEyDw/XLVLk7Pi1Z2JmM8ysuZk1BdYCG8zs0eCWJiLV5e1lmfzts3RuTknk4eHJuiBRzpq/h7l6eHsi1wMf4Lvp451Bq0pEqs2spTt4bM4qhnSO5X+v76UgkUrxN0wamllDfGEyzzlXhDfqoojUXFO+3Mpjb61iSJdYXr6zPxEN/P1KEDmev2dzTQC2AiuBBWbWEVCfiUgNday4lKfeW8v0xdu5+Nx4Xri9H40aaMx2qTx/O+Cfwzd0b5ltZnZRcEoSkWDKzT/GPVNSSd2Wy33f6cKjl3Wjvm6RIlV0ppEW73DOTTOzR06xyl+DUJOIBEnZle3rdh3kb7f21XUkEjBn2jMpu8o9KtiFiEhwHSkq4b5paazKPMBLd/Tnsp5tQl2S1CKnDRPn3ATv+anqKUdEgiE3/xh3T0ll2fZc/nDD+QoSCTh/rzPpbGbvmVm2me01s3lm1jnYxYlI1e3YX8D3Xl7E6p15vHhbP24e0D7UJUkt5O95gDOAWUBboB0wG5gZrKJEpOqcc3yRnsMNLy0i59BRpo0dxBW92oa6LKml/D012JxzU8vNTzOz7wejIBGpuoJjxdw3bRkLNmaTEN2EGXcPIrm1uj4lePzdM/nczB43syQz62hmjwH/MLMYM4up6AVm1t7MPjez9Wa21swe9tpjzOwTM9vkPbf02s3MnjOzdDNbZWb9AvNPFKk7jhSV8J9N2dw+aTELN2Xz5NU9+OSR/1GQSND5u2dyi/d87wntY/BdCV9R/0kx8GPn3DIziwLSzOwT4C7gU+fc02b2OPA48FPgCiDZewwCXvKeRcQP81bs5Ml31nDwSDFRjRrwwm39dFhLqo2/Fy12Ots3ds7tAnZ504fMbD2QAFwHXOitNhmYjy9MrgOmOOcc8JWZRZtZW+99ROQ0Pl67mx+9uYJ+HVry4LCuDEyKoWkjf/9WFKm60x7m8g5nlU3fdMKy3/n7IWaWBPQFFgOtywLCe473VksAdpR7WabXJiKn8en6PTw0czm9ElowZexALuoWryCRanemPpMR5aafOGHZ5f58gJk1A94CfniGMVAqup/DSTeTNLNxZpZqZqnZ2dn+lCBSa/3l4w2MnZxKp7imvHrXACIjFCISGmcKEzvFdEXzJ7/Yd6fht4Dpzrm3veY9ZtbWW94W2Ou1ZwLlT4BPBLJOfE/n3ETnXIpzLqVVq1ZnKkGkVjpWXMpPZq/87xgk7zx4AbHNGoW6LKnDzhQm7hTTFc0fx3yDIrwCrHfOlb+H17vAKG96FDCvXPtI76yuwUCe+ktETnakqIR7p6YyJy2T71/Uld/fcD6NG+qOvxJaZ9on7m1mB/HthTTxpvHmG5/htRfgG0BrtZmt8Np+BjwNzDKzscB2oKwv5gPgSiAdKEBjzIucpOBYMfdMSWXR5n387ru9uG2QxmmX8HCme3NV+s8d59xCTn0obHgF6zvgwcp+nkhtd+hIEWNeX0ratlz+fGNvvtc/MdQlifyXeutEaoAv0nP4xTtr2LG/gL/d2o+rztf1IxJeFCYiYazgWDE/n7uGuct30jE2kqljBzGkS2yoyxI5icJEJEzl5h/jgenLWLxlHw8N68qDF3VVR7uELYWJSBjKP1rMyFeXsGH3If5yc2++21f9IxLeFCYiYWZ//jHufGUxX+8+xMQ7+zP83NahLknkjPy9a7CIVIP8o8WMnbyUTXsPK0ikRlGYiISJPQePMPq1pazKzOO5EX0VJFKj6DCXSBh4Y8l2fvHOGgDGj+jD5edpjHapWRQmIiE29attPPnOGr6dHMf/Xn8eHWObhrokkbOmMBEJEeccExdk8PsPv2Z493hevKMfjRro1F+pmRQmIiGQmVvAz+auYcHGbK44rw3jR/QlooG6MKXmUpiIVKODR4r4v/fX886KndSvZ/zmup7cObgjvptsi9RcChORarJky36eeHsV2/YVcPOA9jxwYRcSW0aGuiyRgFCYiARZcUkpv//wayYv2kqbFo2ZMmYgQ7vGhboskYBSmIgEUXFJKT+atZL3VmZxS0p7nriyO9GREaEuSyTgFCYiQbIu6yBPzltD2rZcnriiO/d+p0uoSxIJGoWJSBDMW7GTR2evIqpxA/56c29u6KcbNUrtpjARCSDnHC98ns6fP97IwKQYXr6zPzFNdVhLaj+FiUiAHCsu5WdzVzMnLZPr+7TjDzeer4sQpc5QmIgEQF5BEfdNS+PLjH08PDyZH16crGtHpE5RmIhU0fZ9BYx+fQnb9xeof0TqLIWJSBWkbctl3JRUiksdU8cOYnBnjc8udZPCRKQSSkodry/ayh//+TVtWjTm1bsG0KVVs1CXJRIyChORs5SRfZhfv7eOBRuzGdY9nj/f1FtnbEmdpzAROQtvpWXyi3fWUM/QTRpFylGYiPhha04+f/lkI++tzGJQpxieu7UvrZs3DnVZImFDYSJyGvlHi5nw7828MH8zDeoZPxiezA+GdaVBfY09IlKewkSkAoXHSpj61VZe/ncG+/OPcX2fdvzsqnOJj9LeiEhFFCYi5RwrLmV22g6e/dcmsg8d5dvJcTxyyTn07dAy1KWJhDWFiQiw80Ahr/xnC7NSd3D4aDEDk2J44bZ+DOwUE+rSRGoEhYnUWcUlpcxOy2Tmku2syswD4Po+7bimdzuGdY/XWVoiZyFoYWJmrwJXA3udc+d5bTHAm0ASsBW42TmXa77f2vHAlUABcJdzblmwahNZnZnHo3NW8vXuQ/Ro25yfXt6dK85rQ1Jc01CXJlIjBXPP5HXgeWBKubbHgU+dc0+b2ePe/E+BK4Bk7zEIeMl7FgmofYePMnFBBpMWbqFVs0a8eHs/rjivjfZCRKooaGHinFtgZkknNF8HXOhNTwbm4wuT64ApzjkHfGVm0WbW1jm3K1j1Sd2yK6+QiQsymLlkO0eLS/lev0SevLoHLZo0DHVpIrVCdfeZtC4LCOfcLjOL99oTgB3l1sv02hQmUiXb9uUzK3UHf//PFkpKHdf3SeD+C7vQNV730RIJpHDpgK/oGIOrcEWzccA4gA4dOgSzJqnBvkjPYeaS7Xy0djfFpY5Le7TmF1f1oH1MZKhLE6mVqjtM9pQdvjKztsBerz0TaF9uvUQgq6I3cM5NBCYCpKSkVBg4UjcdKSrhlYVbeCstk4ycfGKbRjBiQAcevKgrbVroYkORYKruMHkXGAU87T3PK9f+fTN7A1/He576S8RfRSWlzN+QzVPvrSUzt5ChXWIZ/a1O3JySqGFzRapJME8Nnomvsz3OzDKBX+ELkVlmNhbYDtzkrf4BvtOC0/GdGjw6WHVJ7ZFXWMTfF2TwxtLt5Bw+RkJ0E2bcM4ihXeJCXZpInRPMs7luPcWi4RWs64AHg1WL1C6Fx0p4fdFWXv73ZvIKi7ikR2tu6p/Ihd3iiWigGzCKhEK4dMCLnFFpqWPm0u2M/9cm9h46yrDu8fzk0m70aNc81KWJ1HkKEwl7+UeLmfbVNt5blcWanQfp37Elz+u+WSJhRWEiYW3FjgM8NHMZO/YXcn5iC359TQ9GDU3SFesiYUZhImEpr7CIaV9t46+fbKR1VCNm3TtEeyIiYUxhImGhtNSRlVfItn0FvLcyi7nLd3K0uJQLu7Vi/Ii+uu2JSJhTmEhIlZY6ZqXu4LfvryP/WAkAEfXrcWNKIiMGtKdXQgsd0hKpARQmEjIrdhzgV++uZeWOA/RpH80tA9rTMTaS7m2aE9M0ItTlichZUJhItTt0xHex4QvzNxPbNII/39SbG/omUK+e9kBEaiqFiVSbjOzDTPlyG3PSMjl8tJjr+7TjN9efR/PG6g8RqekUJhJUzjkycvKZvGgrU77cRsP6xtXnt2P0BUmcnxgd6vJEJEAUJhJwBceKWb/rEPM37OXNpTvYe+go9QxuHdiBH12STHyU7uArUtsoTCRgdh4o5PnPNjE7NZPiUt/oAMO6xzP83HiGdY+nbYsmIa5QRIJFYSJVUlrqWJOVx1tpmcxc4hssc8TA9nznnHh6tmtOu2gFiEhdoDCRStmSk8/8DXuZlZrJ+l0HqV/PuDklke8PSyZBASJS5yhM5KwUl5Qy/tNNvDh/MyWljvYxTXj6hl5c0qM1sc0ahbo8EQkRhYn4Zc3OPL7K2Mc/Vu9i+fYDfK9fIj+8OFljqosIoDCR09i05xBzl+9k8Zb9pG3LBSAhugl/vbk3N/RLDHF1IhJOFCYC+O7Suyg9h637Cti2L5/l2w+wYc8hGtQzzktowWOXd+PG/ok6rVdEKqQwqaNKSx1b9uWzcfchFm/Zz+zUHf+90WJcswi6tYnippRz+W7fBPWFiMgZKUzqmF15hcxcsoO5yzPZsb8QgPr1jKvPb8udgzvSrU0UUbq9iYicJYVJHVF4rIQJCzbz8r83c7S4lG91jePBC7vSs10LusY3o0lE/VCXKCI1mMKkltqw+xCp2/aTmVvIjv0FfJGeQ25BEVed35bHL++us7BEJKAUJrVASanj/VVZfLl5HzsPFLIzt5CMnHwAGtQz2kU3YWjXOO4amsSAJA19KyKBpzCpgY4Wl7A26yDLtuWyfPsBFm327XVERzakY0wk3dtG8b3+iVzXpx1tWzShvsYJEZEgU5jUEPlHi/nX+j28uyKL/2zK4VhJKeC77uPCbvFc2qM1l/VsowGmRCQkFCZh6EhRCfM3ZLM5+zA7DxSSmVvI0i37KSwqoW2LxtwxuCMDO8XQt0M0rZvrug8RCT2FSZg4UlTC8u0HeG9VFh+s3sWBgiIAWkY2JKFlE27ol8B1fRJI6dhSex8iEnYUJiFw8EgRizP2s2ZnHht2H2LjnkNs3ZdPqYMmDetzSY/W3JSSSL8OLWnaSP9FIhL+9E1VTUpLHWnbc3lz6Q7mLt9JSanDDJJim9KtdRTX9G5Hj3bN+XZyHJER+m8RkZpF31pBtvfgEd5atpOpX24lK+8IjRrU445BHbiiV1t6J0brYkERqRUUJkGQc/go/1i1i3+s3sXSrftxDr7VNY6fXtGd4ee2ppkOXYlILRNW32pmdjkwHqgPTHLOPR3ikk6ruKSUrANHyMg5zNacfLbk5LNlXwFLtuzjSFEp57RuxsPDk7mqV1uSW0eFulwRkaAJmzAxs/rAC8AlQCaw1Mzedc6tC+bnFpeUcqCwiNz8Y+QWFHGwsIi8wiIOHvGeC4vLTfueDx0pJq+wiMNHi497r2aNGpAUF8l3+yZy19AkurVRgIhI3RA2YQIMBNKdcxkAZvYGcB0Q8DB5c+l2Xpq/mdwCXzicTrNGDWjeuAHNmzSkeZOGtI/03KDoAAAJO0lEQVSJpHnjhjRv0oAWTRrSrkUTkuKa0imuKXHNIjDTabsiUveEU5gkADvKzWcCg05cyczGAeMAOnToUKkPimnaiF6J0cRENqRl0whimkYQHRlBy8iGtGjiezRv3JCoxg1oUL9epT5DRKQuCacwqehPendSg3MTgYkAKSkpJy33xyU9WnNJj9aVeamIiFQgnP7szgTal5tPBLJCVIuIiJyFcAqTpUCymXUyswhgBPBuiGsSERE/hM1hLudcsZl9H/gI36nBrzrn1oa4LBER8UPYhAmAc+4D4INQ1yEiImcnnA5ziYhIDaUwERGRKlOYiIhIlSlMRESkysy5Sl33FxbMLBvYFuo6TiMOyAl1EX5QnYGlOgNLdQZWHNDUOdcqkG9ao8Mk3JlZqnMuJdR1nInqDCzVGViqM7CCVacOc4mISJUpTEREpMoUJsE1MdQF+El1BpbqDCzVGVhBqVN9JiIiUmXaMxERkSpTmJwFM2tvZp+b2XozW2tmD3vtMWb2iZlt8p5beu1mZs+ZWbqZrTKzfuXea5S3/iYzGxWkeuub2XIze9+b72Rmi73PfNO7OzNm1sibT/eWJ5V7jye89g1mdlkQaow2szlm9rW3XYeE4/Y0sx95/+drzGymmTUOh+1pZq+a2V4zW1OuLWDbz8z6m9lq7zXPWSWHEj1FnX/y/t9XmdlcM4sut6zC7WRml3tt6Wb2eLn2Cv8vAlFnuWU/MTNnZnHefFhtT6/9IW/7rDWzP5ZrD/72dM7p4ecDaAv086ajgI1AD+CPwONe++PAH7zpK4EP8Q38NRhY7LXHABnec0tvumUQ6n0EmAG8783PAkZ40y8D93vTDwAve9MjgDe96R7ASqAR0AnYDNQPcI2Tgbu96QggOty2J75RQLcATcptx7vCYXsC/wP0A9aUawvY9gOWAEO813wIXBHAOi8FGnjTfyhXZ4XbyXtsBjp7PysrgR6n+9kORJ1ee3t8dzTfBsSF6fa8CPgX0Mibj6/O7RnQL6+69gDmAZcAG4C2XltbYIM3PQG4tdz6G7zltwITyrUft16AaksEPgWGAe97P7w55X55hwAfedMfAUO86QbeegY8ATxR7j3/u16AamyO70vaTmgPq+3JN0NKx3jb533gsnDZnkDSCV8qAdl+3rKvy7Uft15V6zxh2XeB6d50hdup/DYuv97pfrYDVScwB+gNbOWbMAmr7YkvAC6uYL1q2Z46zFVJ3qGLvsBioLVzbheA9xzvrVbRuPYJp2kPpGeBx4BSbz4WOOCcK67gM/9bj7c8z1s/2HV2BrKB18x3OG6SmTUlzLanc24n8GdgO7AL3/ZJI/y2Z5lAbb8EbzrY9QKMwfeXemXqPN3PdpWZ2bXATufcyhMWhdv2PAf4tnd46t9mNqCSdVZqeypMKsHMmgFvAT90zh083aoVtLnTtAeEmV0N7HXOpflRy+mWBbVOfH+19wNecs71BfLxHZY5lVBtz5bAdfgOEbQDmgJXnOYzQ7U9z+Rs66qWes3s50AxML2s6SzrCVqdZhYJ/Bz4ZUWLz7Ke6vh9aonvkNujwCyvT6Za6lSYnCUza4gvSKY75972mveYWVtveVtgr9d+qnHtgz3e/QXAtWa2FXgD36GuZ4FoMysbEK38Z/63Hm95C2B/NdSZCWQ65xZ783PwhUu4bc+LgS3OuWznXBHwNjCU8NueZQK1/TK96aDV63VOXw3c7rxjKpWoM4dT/19UVRd8f0Ss9H6fEoFlZtamEnUGe3tmAm87nyX4jkrEVaLOym3Pyh6vq4sPfIk9BXj2hPY/cXyH5x+96as4voNuidceg6+voKX32ALEBKnmC/mmA342x3eqPeBNP8jxHcazvOmeHN9xl0HgO+D/A3Tzpn/tbcuw2p7AIGAtEOl99mTgoXDZnpx87Dxg2w9Y6q1b1mF8ZQDrvBxYB7Q6Yb0KtxO+v7wzvLayDuOep/vZDkSdJyzbyjd9JuG2Pe8DfuNNn4PvEJZV1/YM+JdXbX4A38K3u7cKWOE9rsR3jPFTYJP3XPaDY8AL+M6YWA2klHuvMUC69xgdxJov5Jsw6YzvbJJ074el7KyPxt58ure8c7nX/9yrfwOVPPPkDPX1AVK9bfqO98sXdtsTeAr4GlgDTPV+MUO+PYGZ+PpxivD9pTk2kNsPSPH+zZuB5znhZIkq1pmO7wuv7Hfp5TNtJ+/3baO37Ofl2iv8vwhEnScs38o3YRJu2zMCmOa9/zJgWHVuT10BLyIiVaY+ExERqTKFiYiIVJnCREREqkxhIiIiVaYwERGRKmtw5lVEagczKztlFqANUILvdi4ABc65odVQQzRwm3PuxWB/lkh10qnBUieZ2a+Bw865P1fz5ybhu+7nvOr8XJFg02EuEcDMDnvPF3o3yZtlZhvN7Gkzu93MlnjjUHTx1mtlZm+Z2VLvcUEF79nTe90Kb7yLZOBpoIvX9idvvUe991hlZk95bUneWB+TvfY53n2i8Gpa57VXaxiKnIoOc4mcrDdwLr77aWUAk5xzA803GNpDwA+B8cAzzrmFZtYB3229zz3hfe4DxjvnpnuDC9XHd3uT85xzfQDM7FIgGRiI74rqd83sf/DdobgbviuwvzCzV4EHvOfvAt2dc87KDSglEkraMxE52VLn3C7n3FF8t5n42Gtfje9+SOC7+ePzZrYCeBdobmZRJ7zPl8DPzOynQEfnXGEFn3Wp91iO7xYY3fGFC8AO59wX3vQ0fLfzOQgcASaZ2Q1AQZX+pSIBoj0TkZMdLTddWm6+lG9+Z+rhG9iqooAAwDk3w8wW47sh4Edmdje+PZ3yDPi9c27CcY2+vpUTOzSdc67YzAYCw/HdRPL7+O4KLRJS2jMRqZyP8X2RA2BmfU5cwcw6AxnOuefw7b2cDxzCN+RzmY+AMd4YOZhZgpmVDWbVwcyGeNO3Agu99Vo45z7Ad7jtpM8VCQXtmYhUzg+AF8xsFb7fowX4+kjKuwW4w8yKgN34bg++38y+MLM1wIfOuUfN7FzgS984RhwG7sB32vJ6YJSZTcB3B+CX8I2NMs/MGuPbq/lRsP+hIv7QqcEiYUinEEtNo8NcIiJSZdozERGRKtOeiYiIVJnCREREqkxhIiIiVaYwERGRKlOYiIhIlSlMRESkyv4fylw0DsO7KC4AAAAASUVORK5CYII=\n", "image/svg+xml": [ "\r\n", "\r\n", "\r\n", "\r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", "\r\n" ], "text/plain": [ "
" ] }, "metadata": { "needs_background": "light" }, "output_type": "display_data" }, { "name": "stdout", "output_type": "stream", "text": [ "Optimal policy is:\n", "['R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R']\n", "['R', 'R', 'R', 'U', 'R', 'R', 'R', 'R', 'R', 'D']\n", "['U', 'R', 'R', 'R', 'R', 'R', 'R', 'L', 'L', 'D']\n", "['R', 'U', 'R', 'R', 'R', 'R', 'R', 'G', 'R', 'D']\n", "['R', 'R', 'R', 'R', 'R', 'R', 'U', 'D', 'L', 'L']\n", "['R', 'R', 'R', 'R', 'R', 'U', 'U', 'R', 'R', 'D']\n", "['R', 'R', 'R', 'R', 'U', 'U', 'U', 'U', 'U', 'U']\n", "Wind strength for each column:\n", "['0', '0', '0', '1', '1', '1', '2', '2', '1', '0']\n" ] } ], "source": [ "#######################################################################\n", "# Copyright (C) #\n", "# 2016-2018 Shangtong Zhang(zhangshangtong.cpp@gmail.com) #\n", "# 2016 Kenta Shimada(hyperkentakun@gmail.com) #\n", "# Permission given to modify the code as long as you keep this #\n", "# declaration at the top #\n", "#######################################################################\n", "\n", "import numpy as np\n", "import matplotlib\n", "%matplotlib inline\n", "import matplotlib.pyplot as plt\n", "\n", "# world height\n", "WORLD_HEIGHT = 7\n", "\n", "# world width\n", "WORLD_WIDTH = 10\n", "\n", "# wind strength for each column\n", "WIND = [0, 0, 0, 1, 1, 1, 2, 2, 1, 0]\n", "\n", "# possible actions\n", "ACTION_UP = 0\n", "ACTION_DOWN = 1\n", "ACTION_LEFT = 2\n", "ACTION_RIGHT = 3\n", "\n", "# probability for exploration\n", "EPSILON = 0.1\n", "\n", "# Sarsa step size\n", "ALPHA = 0.5\n", "\n", "# reward for each step\n", "REWARD = -1.0\n", "\n", "START = [3, 0]\n", "GOAL = [3, 7]\n", "ACTIONS = [ACTION_UP, ACTION_DOWN, ACTION_LEFT, ACTION_RIGHT]\n", "\n", "def step(state, action):\n", " i, j = state\n", " if action == ACTION_UP:\n", " return [max(i - 1 - WIND[j], 0), j]\n", " elif action == ACTION_DOWN:\n", " return [max(min(i + 1 - WIND[j], WORLD_HEIGHT - 1), 0), j]\n", " elif action == ACTION_LEFT:\n", " return [max(i - WIND[j], 0), max(j - 1, 0)]\n", " elif action == ACTION_RIGHT:\n", " return [max(i - WIND[j], 0), min(j + 1, WORLD_WIDTH - 1)]\n", " else:\n", " assert False\n", "\n", "# play for an episode\n", "def episode(q_value):\n", " # track the total time steps in this episode\n", " time = 0\n", "\n", " # initialize state\n", " state = START\n", "\n", " # choose an action based on epsilon-greedy algorithm\n", " '''\n", " 使用 np.random.binomial(1, EPSILON) 二项分布\n", " 来生产随机数据，表示随机性，我认为要比 random < 值 要好\n", " '''\n", " if np.random.binomial(1, EPSILON) == 1:\n", " action = np.random.choice(ACTIONS)\n", " else:\n", " values_ = q_value[state[0], state[1], :]\n", " '''\n", " choice() 里 [] 的生成，使用了迭代器以及 if\n", " '''\n", " action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])\n", "\n", " # keep going until get to the goal state\n", " while state != GOAL:\n", " next_state = step(state, action)\n", " if np.random.binomial(1, EPSILON) == 1:\n", " next_action = np.random.choice(ACTIONS)\n", " else:\n", " values_ = q_value[next_state[0], next_state[1], :]\n", " next_action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])\n", "\n", " # Sarsa update\n", " q_value[state[0], state[1], action] += \\\n", " ALPHA * (REWARD + q_value[next_state[0], next_state[1], next_action] -\n", " q_value[state[0], state[1], action])\n", " state = next_state\n", " action = next_action\n", " time += 1\n", " return time\n", "\n", "def figure_6_3():\n", " q_value = np.zeros((WORLD_HEIGHT, WORLD_WIDTH, 4))\n", " episode_limit = 500\n", "\n", " steps = []\n", " ep = 0\n", " while ep < episode_limit:\n", " steps.append(episode(q_value))\n", " # time = episode(q_value)\n", " # episodes.extend([ep] * time)\n", " ep += 1\n", "\n", " steps = np.add.accumulate(steps)\n", "\n", " plt.plot(steps, np.arange(1, len(steps) + 1))\n", " plt.xlabel('Time steps')\n", " plt.ylabel('Episodes')\n", "\n", " plt.show()\n", "\n", " # display the optimal policy\n", " optimal_policy = []\n", " for i in range(0, WORLD_HEIGHT):\n", " optimal_policy.append([])\n", " for j in range(0, WORLD_WIDTH):\n", " if [i, j] == GOAL:\n", " optimal_policy[-1].append('G')\n", " continue\n", " bestAction = np.argmax(q_value[i, j, :])\n", " if bestAction == ACTION_UP:\n", " optimal_policy[-1].append('U')\n", " elif bestAction == ACTION_DOWN:\n", " optimal_policy[-1].append('D')\n", " elif bestAction == ACTION_LEFT:\n", " optimal_policy[-1].append('L')\n", " elif bestAction == ACTION_RIGHT:\n", " optimal_policy[-1].append('R')\n", " print('Optimal policy is:')\n", " for row in optimal_policy:\n", " print(row)\n", " print('Wind strength for each column:\\n{}'.format([str(w) for w in WIND]))\n", "\n", "\n", "figure_6_3()\n" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### 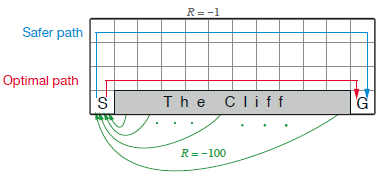Example 6.6: Cliff Walking\n", "\n", "This gridworld example compares Sarsa and Q-learning, highlighting the difference between on-policy (Sarsa) and o↵-policy (Q-learning) methods.\n", "\n", "Consider the gridworld shown to the right. This is a standard undiscounted, episodic task, with start and goal states, and the usual actions causing movement up, down, right, and left. Reward is −1 on all\n", "transitions except those into the region marked “The Cliff.” Stepping\n", "into this region incurs a reward of −100 and sends the agent instantly\n", "back to the start.\n", "\n", "![](images/05-04.png)" ] }, { "cell_type": "code", "execution_count": 3, "metadata": {}, "outputs": [], "source": [ "#######################################################################\n", "# Copyright (C) #\n", "# 2016-2018 Shangtong Zhang(zhangshangtong.cpp@gmail.com) #\n", "# 2016 Kenta Shimada(hyperkentakun@gmail.com) #\n", "# Permission given to modify the code as long as you keep this #\n", "# declaration at the top #\n", "#######################################################################\n", "\n", "import numpy as np\n", "import matplotlib\n", "%matplotlib inline\n", "import matplotlib.pyplot as plt\n", "from tqdm import tqdm\n", "\n", "# world height\n", "WORLD_HEIGHT = 4\n", "\n", "# world width\n", "WORLD_WIDTH = 12\n", "\n", "# probability for exploration\n", "EPSILON = 0.1\n", "\n", "# step size\n", "ALPHA = 0.5\n", "\n", "# gamma for Q-Learning and Expected Sarsa\n", "GAMMA = 1\n", "\n", "# all possible actions\n", "ACTION_UP = 0\n", "ACTION_DOWN = 1\n", "ACTION_LEFT = 2\n", "ACTION_RIGHT = 3\n", "ACTIONS = [ACTION_UP, ACTION_DOWN, ACTION_LEFT, ACTION_RIGHT]\n", "\n", "# initial state action pair values\n", "START = [3, 0]\n", "GOAL = [3, 11]\n", "\n", "def step(state, action):\n", " i, j = state\n", " if action == ACTION_UP:\n", " next_state = [max(i - 1, 0), j]\n", " elif action == ACTION_LEFT:\n", " next_state = [i, max(j - 1, 0)]\n", " elif action == ACTION_RIGHT:\n", " next_state = [i, min(j + 1, WORLD_WIDTH - 1)]\n", " elif action == ACTION_DOWN:\n", " next_state = [min(i + 1, WORLD_HEIGHT - 1), j]\n", " else:\n", " assert False\n", "\n", " reward = -1\n", " if (action == ACTION_DOWN and i == 2 and 1 <= j <= 10) or (\n", " action == ACTION_RIGHT and state == START):\n", " reward = -100\n", " next_state = START\n", "\n", " return next_state, reward\n", "\n", "# reward for each action in each state\n", "# actionRewards = np.zeros((WORLD_HEIGHT, WORLD_WIDTH, 4))\n", "# actionRewards[:, :, :] = -1.0\n", "# actionRewards[2, 1:11, ACTION_DOWN] = -100.0\n", "# actionRewards[3, 0, ACTION_RIGHT] = -100.0\n", "\n", "# set up destinations for each action in each state\n", "# actionDestination = []\n", "# for i in range(0, WORLD_HEIGHT):\n", "# actionDestination.append([])\n", "# for j in range(0, WORLD_WIDTH):\n", "# destinaion = dict()\n", "# destinaion[ACTION_UP] = [max(i - 1, 0), j]\n", "# destinaion[ACTION_LEFT] = [i, max(j - 1, 0)]\n", "# destinaion[ACTION_RIGHT] = [i, min(j + 1, WORLD_WIDTH - 1)]\n", "# if i == 2 and 1 <= j <= 10:\n", "# destinaion[ACTION_DOWN] = START\n", "# else:\n", "# destinaion[ACTION_DOWN] = [min(i + 1, WORLD_HEIGHT - 1), j]\n", "# actionDestination[-1].append(destinaion)\n", "# actionDestination[3][0][ACTION_RIGHT] = START\n", "\n", "# choose an action based on epsilon greedy algorithm\n", "def choose_action(state, q_value):\n", " if np.random.binomial(1, EPSILON) == 1:\n", " return np.random.choice(ACTIONS)\n", " else:\n", " values_ = q_value[state[0], state[1], :]\n", " return np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])\n", "\n", "# an episode with Sarsa\n", "# @q_value: values for state action pair, will be updated\n", "# @expected: if True, will use expected Sarsa algorithm\n", "# @step_size: step size for updating\n", "# @return: total rewards within this episode\n", "def sarsa(q_value, expected=False, step_size=ALPHA):\n", " state = START\n", " action = choose_action(state, q_value)\n", " rewards = 0.0\n", " while state != GOAL:\n", " next_state, reward = step(state, action)\n", " next_action = choose_action(next_state, q_value)\n", " rewards += reward\n", " if not expected:\n", " target = q_value[next_state[0], next_state[1], next_action]\n", " else:\n", " # calculate the expected value of new state\n", " target = 0.0\n", " q_next = q_value[next_state[0], next_state[1], :]\n", " best_actions = np.argwhere(q_next == np.max(q_next))\n", " for action_ in ACTIONS:\n", " if action_ in best_actions:\n", " target += ((1.0 - EPSILON) / len(best_actions) + EPSILON / len(ACTIONS)) * q_value[next_state[0], next_state[1], action_]\n", " else:\n", " target += EPSILON / len(ACTIONS) * q_value[next_state[0], next_state[1], action_]\n", " target *= GAMMA\n", " q_value[state[0], state[1], action] += step_size * (\n", " reward + target - q_value[state[0], state[1], action])\n", " state = next_state\n", " action = next_action\n", " return rewards\n", "\n", "# an episode with Q-Learning\n", "# @q_value: values for state action pair, will be updated\n", "# @step_size: step size for updating\n", "# @return: total rewards within this episode\n", "def q_learning(q_value, step_size=ALPHA):\n", " state = START\n", " rewards = 0.0\n", " while state != GOAL:\n", " action = choose_action(state, q_value)\n", " next_state, reward = step(state, action)\n", " rewards += reward\n", " # Q-Learning update\n", " q_value[state[0], state[1], action] += step_size * (\n", " reward + GAMMA * np.max(q_value[next_state[0], next_state[1], :]) -\n", " q_value[state[0], state[1], action])\n", " state = next_state\n", " return rewards\n", "\n", "# print optimal policy\n", "def print_optimal_policy(q_value):\n", " optimal_policy = []\n", " for i in range(0, WORLD_HEIGHT):\n", " optimal_policy.append([])\n", " for j in range(0, WORLD_WIDTH):\n", " if [i, j] == GOAL:\n", " optimal_policy[-1].append('G')\n", " continue\n", " bestAction = np.argmax(q_value[i, j, :])\n", " if bestAction == ACTION_UP:\n", " optimal_policy[-1].append('U')\n", " elif bestAction == ACTION_DOWN:\n", " optimal_policy[-1].append('D')\n", " elif bestAction == ACTION_LEFT:\n", " optimal_policy[-1].append('L')\n", " elif bestAction == ACTION_RIGHT:\n", " optimal_policy[-1].append('R')\n", " for row in optimal_policy:\n", " print(row)\n", "\n", "# Use multiple runs instead of a single run and a sliding window\n", "# With a single run I failed to present a smooth curve\n", "# However the optimal policy converges well with a single run\n", "# Sarsa converges to the safe path, while Q-Learning converges to the optimal path\n", "def figure_6_4():\n", " # episodes of each run\n", " episodes = 500\n", "\n", " # perform 40 independent runs\n", " runs = 50\n", " '''\n", " runs 求平均之用\n", " 防止一次计算带来的误差\n", " 多次计算\n", " '''\n", "\n", " rewards_sarsa = np.zeros(episodes)\n", " rewards_q_learning = np.zeros(episodes)\n", " for r in tqdm(range(runs)):\n", " q_sarsa = np.zeros((WORLD_HEIGHT, WORLD_WIDTH, 4))\n", " q_q_learning = np.copy(q_sarsa)\n", " for i in range(0, episodes):\n", " # cut off the value by -100 to draw the figure more elegantly\n", " # rewards_sarsa[i] += max(sarsa(q_sarsa), -100)\n", " # rewards_q_learning[i] += max(q_learning(q_q_learning), -100)\n", " rewards_sarsa[i] += sarsa(q_sarsa)\n", " rewards_q_learning[i] += q_learning(q_q_learning)\n", "\n", " # averaging over independt runs\n", " rewards_sarsa /= runs\n", " rewards_q_learning /= runs\n", "\n", " # draw reward curves\n", " plt.plot(rewards_sarsa, label='Sarsa')\n", " plt.plot(rewards_q_learning, label='Q-Learning')\n", " plt.xlabel('Episodes')\n", " plt.ylabel('Sum of rewards during episode')\n", " plt.ylim([-100, 0])\n", " plt.legend()\n", "\n", " plt.show()\n", "\n", " # display optimal policy\n", " print('Sarsa Optimal Policy:')\n", " print_optimal_policy(q_sarsa)\n", " print('Q-Learning Optimal Policy:')\n", " print_optimal_policy(q_q_learning)\n", "\n", "# Due to limited capacity of calculation of my machine, I can't complete this experiment\n", "# with 100,000 episodes and 50,000 runs to get the fully averaged performance\n", "# However even I only play for 1,000 episodes and 10 runs, the curves looks still good.\n", "def figure_6_6():\n", " step_sizes = np.arange(0.1, 1.1, 0.1)\n", " episodes = 1000\n", " runs = 10\n", "\n", " ASY_SARSA = 0\n", " ASY_EXPECTED_SARSA = 1\n", " ASY_QLEARNING = 2\n", " INT_SARSA = 3\n", " INT_EXPECTED_SARSA = 4\n", " INT_QLEARNING = 5\n", " methods = range(0, 6)\n", "\n", " performace = np.zeros((6, len(step_sizes)))\n", " for run in range(runs):\n", " for ind, step_size in tqdm(list(zip(range(0, len(step_sizes)), step_sizes))):\n", " q_sarsa = np.zeros((WORLD_HEIGHT, WORLD_WIDTH, 4))\n", " q_expected_sarsa = np.copy(q_sarsa)\n", " q_q_learning = np.copy(q_sarsa)\n", " '''\n", " 注意作者的命名规范，所有的期望都是\n", " q_ + 方法名，即便出现 q_q_learning\n", " '''\n", " for ep in range(episodes):\n", " sarsa_reward = sarsa(q_sarsa, expected=False, step_size=step_size)\n", " expected_sarsa_reward = sarsa(q_expected_sarsa, expected=True, step_size=step_size)\n", " q_learning_reward = q_learning(q_q_learning, step_size=step_size)\n", " performace[ASY_SARSA, ind] += sarsa_reward\n", " performace[ASY_EXPECTED_SARSA, ind] += expected_sarsa_reward\n", " performace[ASY_QLEARNING, ind] += q_learning_reward\n", " '''\n", " 所谓 “长期性能” 与 “短期性能” 的区别就是\n", " 经历的幕数的多少，短期性能的幕数限制在了 100 以内\n", " '''\n", "\n", " if ep < 100:\n", " performace[INT_SARSA, ind] += sarsa_reward\n", " performace[INT_EXPECTED_SARSA, ind] += expected_sarsa_reward\n", " performace[INT_QLEARNING, ind] += q_learning_reward\n", "\n", " performace[:3, :] /= episodes * runs\n", " performace[3:, :] /= 100 * runs\n", " labels = ['Asymptotic Sarsa', 'Asymptotic Expected Sarsa', 'Asymptotic Q-Learning',\n", " 'Interim Sarsa', 'Interim Expected Sarsa', 'Interim Q-Learning']\n", "\n", " for method, label in zip(methods, labels):\n", " plt.plot(step_sizes, performace[method, :], label=label)\n", " plt.xlabel('alpha')\n", " plt.ylabel('reward per episode')\n", " plt.legend()\n", "\n", " plt.show()\n" ] }, { "cell_type": "code", "execution_count": 4, "metadata": {}, "outputs": [ { "name": "stderr", "output_type": "stream", "text": [ "100%|██████████| 50/50 [00:30<00:00, 1.64it/s]\n" ] }, { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZAAAAEKCAYAAAA8QgPpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzsXXecFdXZfs7cun1hl95BUGkKSJWIxm4QiSXGFmMlUdQYv0SsWGI3xhYLGnvBXrACgiKI9F4ERMpSdtlle7n1fH+cOTNnzpQ7dwtF5vn9FnbnTjkz98z7vs/bDqGUwoMHDx48eEgXyv4egAcPHjx4ODjhKRAPHjx48NAoeArEgwcPHjw0Cp4C8eDBgwcPjYKnQDx48ODBQ6PgKRAPHjx48NAoHHQKhBByGiHkJ0LIJkLIpP09Hg8ePHg4VEEOpjoQQogPwAYAJwMoArAIwAWU0rX7dWAePHjwcAjiYGMgwwBsopRuppRGAUwFcNZ+HpMHDx48HJLw7+8BpIlOALYLfxcBGC7uQAi5GsDVAJCVlTXkiCOO2Hej8+DBg4dfAZYsWVJKKW2Tar+DTYEQi20GHxyldAqAKQBwzDHH0MWLF++LcXnw4MHDrwaEkK1u9jvYXFhFALoIf3cGsHM/jcWDBw8eDmkcbApkEYDehJAehJAggD8C+HQ/j8mDBw8eDkkcVC4sSmmcEDIRwNcAfABeopSu2c/D8uDBg4dDEgeVAgEASukXAL7Y3+Pw4MFDyyEWi6GoqAgNDQ37eyi/aoTDYXTu3BmBQKBRxx90CsSDBw+/fhQVFSEnJwfdu3cHIVa5Mx6aCkopysrKUFRUhB49ejTqHAdbDMSDBw+HABoaGlBQUOApjxYEIQQFBQVNYnmeAvHgwcMBCU95tDya+ow9BeLBgwcPHhoFT4F48ODBgw3uu+8+9OvXDwMHDsTRRx+NBQsW7O8hHVDwgugePHjwYIH58+fjs88+w9KlSxEKhVBaWopoNOrq2Hg8Dr//1y9ef/136MGDBw+NwK5du1BYWIhQKAQAKCwsBADcc889mDZtGurr6zFq1Cg8//zzIITg+OOPx6hRozBv3jyMGzcOXbt2xd133w2fz4e8vDzMmTMHW7ZswSWXXILa2loAwNNPP41Ro0btt3tsKjwF4sGDhwMad09bg7U7q5r1nH075mLymf0c9znllFNwzz33oE+fPjjppJNw/vnnY8yYMZg4cSLuvPNOAMAll1yCzz77DGeeeSYAoKKiAt999x0AYMCAAfj666/RqVMnVFRUAADatm2LGTNmIBwOY+PGjbjgggtwMPfr82IgHjx48GCB7OxsLFmyBFOmTEGbNm1w/vnn45VXXsHs2bMxfPhwDBgwALNmzcKaNXozjPPPP1/7/dhjj8Wf//xnvPDCC0gkEgBYgeRVV12FAQMG4LzzzsPatQf3UkYeA/HgwcMBjVRMoSXh8/lw/PHH4/jjj8eAAQPw/PPPY+XKlVi8eDG6dOmCu+66y1BHkZWVpf3+3HPPYcGCBfj8889x9NFHY/ny5XjqqafQrl07rFixAslkEuFweH/cVrPBYyAePHjwYIGffvoJGzdu1P5evnw5Dj/8cAAsHlJTU4P333/f9viff/4Zw4cPxz333IPCwkJs374dlZWV6NChAxRFweuvv64xk4MVHgPx4MGDBwvU1NTguuuuQ0VFBfx+Pw477DBMmTIF+fn5GDBgALp3746hQ4faHv+Pf/wDGzduBKUUJ554Io466ihcc801OOecc/Dee+/hhBNOMDCWgxEH1Zro6cJbUMqDh4MT69atw5FHHrm/h3FIwOpZE0KWUEqPSXWs58Ly4MGDBw+NgqdAPHjw4MFDo+ApEA8ePHjw0Ch4CsSDBw8ePDQKngLx4MGDBw+NgqdAPHjw4MFDo+ApEA8ePHiwQFFREc466yz07t0bPXv2xMSJExGJREz7/fnPf3YsKGxufPrpp3jwwQf32fWc4CkQDx48eJBAKcXZZ5+N8ePHY+PGjdi4cSPq6+vxz3/+c59c36lCfdy4cZg0adI+GUcqeArEgwcPHiTMmjUL4XAYl112GQDWE+s///kPXnvtNdTU1Lg6xyOPPIKhQ4di4MCBmDx5srZ9/PjxGDJkCPr164cpU6Zo27Ozs3HnnXdi+PDhmD9/Prp3747Jkydj8ODBGDBgANavXw8AeOWVVzBx4kQAjP1cf/31GDVqFHr27KkxoWQyiWuuuQb9+vXD2LFjccYZZ7QIS/JamXjw4OHAxpeTgN2rmvec7QcAp9u7gdasWYMhQ4YYtuXm5qJ79+7YtGkTjj76aMfTT58+HRs3bsTChQtBKcW4ceMwZ84cHHfccXjppZfQunVr1NfXY+jQoTjnnHNQUFCA2tpa9O/fH/fcc492nsLCQixduhTPPPMMHn30Ubz44ouma+3atQtz587F+vXrMW7cOJx77rn48MMPsWXLFqxatQolJSU48sgjcfnll6f5kFLDYyAePHjwIIFSCkKI5XY3mD59OqZPn45BgwZh8ODBWL9+vdaY8cknn8RRRx2FESNGYPv27dp2n8+Hc845x3Ces88+GwAwZMgQbNmyxfJa48ePh6Io6Nu3L4qLiwEAc+fOxXnnnQdFUdC+fXuccMIJrsadLjwG4sGDhwMbDkyhpdCvXz988MEHhm1VVVUoLi7GE088gWXLlqFjx4744osvLI+nlOKWW27BhAkTDNu//fZbzJw5E/Pnz0dmZiaOP/54rR18OByGz+cz7M9XQ/T5fIjH45bX4vvw64r/tzQ8BuLBgwcPEk488UTU1dXhtddeA8CC2jfddBMmTpyIl19+GcuXL7dVHgBw6qmn4qWXXtLiJTt27EBJSQkqKyvRqlUrZGZmYv369fjxxx9bZPyjR4/GBx98gGQyieLiYnz77bctch1PgXjw4MGDBEIIPvroI7z//vvo3bs3CgoKoCgKbrvtNsv9J0yYgM6dO6Nz584YOXIkTjnlFFx44YUYOXIkBgwYgHPPPRfV1dU47bTTEI/HMXDgQNxxxx0YMWJEi4z/nHPOQefOndG/f39MmDABw4cPR15eXrNfJ2U7d8IcgRcB6EkpvYcQ0hVAe0rpwmYfTTPDa+fuwcPBiQOtnfsPP/yACy64AB9++KEpuH6goqamBtnZ2SgrK8OwYcMwb948tG/f3rRfU9q5u4mBPAMgCeC3AO4BUA3gAwD2K6l48ODBw68Io0aNwtatW/f3MNLC2LFjUVFRgWg0ijvuuMNSeTQVbhTIcErpYELIMgCglJYTQoLNPhIPHjx48NBsaKm4hwg3MZAYIcQHgAIAIaQNGCPx4MGDhxbDr3m11AMFTX3GbhTIkwA+AtCWEHIfgLkA7m/SVT148ODBAeFwGGVlZZ4SaUFQSlFWVoZwONzoc6R0YVFK3ySELAFwIgACYDyldF2jr+jBgwcPKdC5c2cUFRVhz549+3sov2qEw2F07ty50cfbKhBCSGvhzxIAb4ufUUr3NvqqHjx48OCAQCCAHj167O9heEgBJwayBCzuQQB0BVCu/p4PYBsA79v14MGDh0MYtjEQSmkPSmlPAF8DOJNSWkgpLQAwFsCHLTUgQsgjhJD1hJCVhJCPCCH5wme3EEI2EUJ+IoSc2lJj8ODBgwcPqeEmiD6UUqrV7FNKvwQwpuWGhBkA+lNKBwLYAOAWACCE9AXwRwD9AJwG4Bk1O8yDBw+HCGKJJMpro/t7GB5UuFEgpYSQ2wkh3Qkh3QghtwEoa6kBUUqnU0p517AfAfAIz1kAplJKI5TSXwBsAjCspcbhwcOvBbFE47LuqxtiGPXAN1iwmb3upTURfLFqV3MOLW3c+M5yDLp3xiGXnRVPJDFzbbHlfVc1xLCjon4/jMqdArkAQBuwVN6PAbRVt+0LXA7gS/X3TgC2C58VqdsMIIRcTQhZTAhZ7GVweNjfqI8m8JuHZ2HeptIWv9bG4moUVzUYts3bVIqBd01HRV36VvuOinrsrGzApj2sIeA1by7FNW8uRWmNeVnXxmD1jkoMu28m9qqMorw2it2VDY7HfLaSKbD6mP2Kfb9GPD17E658bTHmbDTPo8emb8CFL7RMU8ZUSKlAKKV7KaU3gLmtfkMpvaGpGViEkJmEkNUWP2cJ+9wGIA7gTb7JangW451CKT2GUnpMmzZtmjLMQwr726L7fuMelFQ5Cw83KKluwPa9dc0woubBhuJqbN9bjwe/XN/i1zr5P3Nw7IOzDNs2l9aiPpbA0ffMwLQVO1OeY9IHK3HPtLUAgMq6GAAgGmcMprSaKY69zeRCWrerCiXVEexUreeh983EiAe+cTwmHGAiq0Idm1t8v3EP6qOplU5xVQO6T/oc36wrTuv8zYG9tVFsKa21/GztzioAjBXK2Fxaiz3VzaPU00VKBUIIGaC2MVkFYA0hZAkhpH9TLkopPYlS2t/i5xP1mpeCBesvorpkKwLQRThNZwCp3wgPKdF90uf4+7sr9tv144kkLvnfQlz04oImn2fYfd/gNw/PbvKY3l9ShNEPzbJ8YdNBbYR5Y7NC+yZcF08aDYEGQWi+8WPqXk5TF23HS/N+AQBU1rN75y6wnDBL2iypchZWkXgCf31jCdbtqnLcjz+baCIJSqk29vLaKC5+cYGlQZEZZGNIR4H8vKcGl/xvIW772HlVw9fnb8Gz3/4MAPho2Q7X528ujH5oFo5/9FvLz+rU7zGRNBt6uyvrURdNIJnct2uBAO5cWM8D+DultBultBuAmwBMSXFMo0EIOQ3AzQDGUUpFU/JTAH8khIQIIT0A9AZwwHcEPliwP14YjtIaZtH+YmN9ucVht33p+HlVQwyvzd9ieMHiiaTJok4mKf7vvRUoKq/Hz3uaNqZa9cXPCrbs2m1xKc5xzrM/4OGv1muCh40ljnOf/QHHuVSwXIFwBpKbEQAAXPw/o3DfWxvFWwu2ac91+bYKfLl6N+74eLXj+Wu4AoknMXNdibZ96qLtmLupFP+b+4vpmMygzzC2dO7D6buklOKOT9bglR+2AAC6FWS6Pn8qbCiuxg1TlyESd2ZAdRYMKZ5I4u2F27CrkrE0q/vmbr861a039qm5+P0z80xzoiXgRoFkUUq1GUcp/RZAVouNCHgaQA6AGYSQ5YSQ59TrrgHwLoC1AL4CcC2l9NByhP5Kwf32XDi0FP7+znLc+ckarBUs47unrcXge2cYXu4SwR3A3WF10ThOfuw7LNpi9N5+snwH7v/CvjGDzkBaVoFUNeir1S3bVo4lW8vxzLc/oy6mb6+NJLB4azm2CS6+txZsQ/dJn6M+msDUhdsM5xQVyCfLd+B7wf8+fa3u4hnz8Gzc+tEqLT7Cn19hdghOqIkktPPf9ekabXtSVURJC0s6W32OlfX2brRPlu/AtjL9Hrli81k5wbWxGFf7C/hSi8bSmghKayL49qcSdJ/0ueaK2763TnM5AcBlLy/CJ8t3Ytm2CsPxv5TWoqwmgls/WoUlW8u17Zv31KD7pM/x39mbcP3UZbjlw1Wa8pOZV20krn33tZE4tu+tw5qdVVi2rQLrd1envIemws2s3kwIuQPA6+rfFwMwmwbNBErpYQ6f3Qfgvpa69qEI0Rr/bsMeDOveGhktLMhlcIHTFCHrhrbzl1QUDtPX7gbArLhuBcwu2l6uC5+iciYU1u2qxsaSGtwzbS2mXTda+/yGqcsBALeeYb12RW2UvdyZQR8+X7kLG4qrcePJfWzv4YXvN+P3gzqjTY6z8AWA2T+VYGTPAoQDPoNlyu+zfW7Y4PcXhSSlFI/N2ICnZm0CAAy/f6ZBCQFAFVcgCardJ0e7XNY/KRJPoFo975erdyMr5MeRHXIBwHQPd3y8Gm8s2IpnLxqM0/p3QE2Enf+9JUWG4D8fJ/9KP162A7PWl+DJCwZpc9OOgSSTbKx+hWDT/WcAALghrliscc4hC2a7eElJdQPOfGou3rhiOE7+zxwAwDHdWgEANu+pRcf8DM2FuuXB34FSqmVIrSqqxIieBdq5ThDcVW8t0JX3l6vZnHzk659M15fve7fw3FYWVeKq1/T1j2Sl2BJww0AuB8vC+hAsE6sQwGUtOSgP+w5RgeZe+tJCPDlr4z657r+n/4RLX2IeyJJq9hLEEhTHPTwbq4oq0z5fQ8xI10WFQinFu4u2o1wKCgNA6ywm5HaU12PW+mKc+dRcgyutqLwOy7dXaNtSuSFkcAaSGfTj2reW4olvNmJTSTWSSYrukz7Ho4KQWLOzCvd/sR6TPliZ8rzrd1fhspcX4fq3l+GGqcs06xfQ2QgFNbhFxPqJ8rqYpjzEY0TILiwRfJscvPURom1rlWVc9eH1H7eCUuAvbyzFL6W1qFUZyLQVOxFPUrTKZC6yGm38DH97Zzk+XbETf5u6TLPi7WIg3I0jxoK4K6c+lsDTszZa3o8smK3cSQDw9erdKK6K4GXV1QUAW8rY3AgFzOJUfL9ElmE1Bo6tZfauNvm+i4WstQ3FRsZReyAoEEppOaX0ekrpYADHALiTUlqe6jgP+x6TP1mN6WuY9fLi95sxb1MpkknqaInIE9lNpkpz4KlZm/DdBpZmXawGZUtrIti2tw5PfJO+EuOWPkdEuK+vVu/GPwWhLNZFFGYzIVdUUY8rX12MVTsqsXoHU2C922ZjR0U9xv93Hv7vPZZkYPfi2zEgLiSzQj70bpsNAHhn0XaUqcJ8yvebATDLefZ6FgfYmSKVFdAzpKavLcYny3dqvntAz9Spbogb0l1FoSqn+1rdD1cq0YR5TvBtsgJpnR3Uzu3ECrftrTPNywLV5cW3yy6sj5frOTN2DEQUmt+sK8bqHZVoUJX+mp1VeHT6BszdZE7v54L59P7t0T43jLooUzYTXjeuaMrnVcivi04ew6uPJkxCW5yH36wv1mIZeyxSoflcXL69wvQZh+y62yXMFTkF+oBgIISQtwghuYSQLABrAPxECPlHi4/MQ9p4df5WXP36EgDAvz5fh4teXID7vliH/pO/trWcZYGYnaYbKRpPYvC9M/DZSvZyz/+5DKMfmoWfdlfj259KUhzNLPoy6WUK2Dirj/nXTNt897qI8f64BRmNJzHvZ2PufCyhC6Y8NTC8o7weXL5uLatDQVYQbXNDpoyjLWV1+Ngi4SBio1i4QCEA/Krr7MvVuzXGUKBa6W8v2oZ/z9gAwJ07rlyyRCuFv6tVwV8XTWhuKBnvLylyPH8kntSEdLHwDDq3ygCgz5sSSYEkKdXqRKIOQdyi8jqNaXDwZ8EVoNNjqLC5L1FoXvHqYox9aq6JnXIXJqVUu48KVTDfeHIfZIf9qI/F8ej0Dfh6TTHmbizVlKKuQMxu3ts/Xo1+k7/W/o4nkoio175gWFfEEhSLtjDb26repUBlwxuKa2zve+a6ElzxyiJMW7ETox+apWXMATDEtgB9HrQk3Liw+lJKqwCMB/AFWGPFS1p0VB6aBFGY8EwWO2bBX/L7ft8fOSF/2lZLVUMMe2ujuPVDliL5wJfrUFRej1Mfn4M/v7zI8pikYAnvqY6YlJhPsVYgpTUR/PCzdRMEmYG8+sMWjHlkNvrc/iXe+NEYHBYZCE+LFF1A5XVR5IT9yAz6LSt8b7fILrJ7vlWqMExQqgnzovJ6LPyFBeNbq0KTs55jlVX4e+WDoEl74fvDplJTimy5UCgoph7vtKlQtspwElEXTWgKRAxIB1XLO6oqYZmB1EbimuCKxSkq62Ka1S1i+95603fGg+5u6kzs3DOyIQEADVLRIRfqN727An1u/xKUUo2B5GcEkBn0GVxYF/9vAUY/xOpruAIJ+s2iUxbgtdGEZri1V2NGdeq4rVKUC3N0l985g80t1jMCTGl9s74E1729DEXl9VgjBOvl6x8QDARAgBASAFMgn1BKY7Ao4POwfyGm7O20eGHtXC9RwaLKDvsb7Tfl7g4iBSqtrOnSWl3o7KmOmGoX/DYKxAl1kjB64puN2FpmXVAoWsbcxSNWV1fUxZAR9CMr6LN0lQzr0dq0TRaGHFyYJpIsKH1U5zwAwCzVXcUVyPa97Dt7M/gATqHzMGXOz1hh48q48MUFJjcfH6dfIQbLU7R0F912En554AyMO6ojAKas/pJvXXtTG4lr5ywSkgr4d7OpuBp3T1uDkqoGEALMummMelxCE1yxRBKnPj4HIx+Yhd9K9Q2WDER14XBW48TE7OYpvzZ3BwHmqnWuBD5UmeTWsjrtXnNVBVLdEIc4lTlrjVq4sJzGyNlP6yzGdHlat5ULkTMQAHjk3IEYfVih4fMB6tyRwbMXt5bVonVWEBv+dToUcoDEQMDqQLaApe7OIYR0A+BcIeRhn0N0y8jCFLB3sXBrPOhXTJaXG8QTxpdclv1W191Rriu4kuqIqVfTzHUsLXLzHmsqb1VMVWthedohJoyJMwfRWiuviyIjoCDTwp03sHMekpSipKoBHwhuoFQMJJZIojoSxzHdmfKZr/aX4lbl+t3VmmAHgIe/Woez/jvPdD673H4+/niSoqohpgn6WmFcQb8CQghuOKk3AKasJjU8YXk+kYGI5+CZTK/O34qX523Bgl/2Ij8jgJ5tsnFE+xzUROKaYoglklqW0GapxqeovN4cA1EFKGc1sutJhJ17hgvNtjn6KnuyoorEE1izs1JjPHM3laKiLopwQEE44ENm0I8lW8stXWjpJFHUROLa/vmZTKFxBmIdAwmp/wehKARy0tjATkyB+BSChbeeiBf+dAwAPSMuSYE22SEE/QqyQv4Dw4VFKX2SUtqJUnoGZdgK4IQWH5kHE95euA3zbVw4IsOoqrdSICzWUNUQw1WvLdaKvDRK7lOQ3QgXVlxytfikWW+lkMRMkpLqiEkJ8TE8993Pli8sz9oyXsf9uJdsK9eUUIN6/zWCAqpuiCNTZSAch7XNxm+PaItwwIf6aAJXvb4EN72nV+9b3WdtJI7yWnavXBh3zM/Q4ggAe/6UUpTXRdGltb5dsSH5dTY9oMTr762JGq7Bwa3mrq1TF8nVRuOW7Et2L8YSSa06PDvkV11YPP03RQxEmmt5Gew8fE7WxxKWxgIfn4jVOypx7ZtLtTG3y9WteVmQNsSS+N2TczXWubOCVXLz+J8T/+XusLkWPalkfLh0h1YPkh32I+Aj2vdn9Wxzwn48feEgfH79byzPxxlIz8IstM0N4+S+7fDGFcPx1AWDtH24G6wx7ujGwGlFwosppW8QQv5us8tjLTQmDza4RY0zbHnwd6bPxJe1yqL9Rm0kgZMem4mebbKwWS1Kund8fwMlzwym78KSX3A5174uGtfcNABr7ifS9z0WDITj3cVFOLJDLs4e1BnVEaNfv0OeUUCmw0Ce/24zgj4FN51yuNbqQ77vcMBnqEt568rhaJsbxqUvLURFXdTk+5cVCKXUEFDlKbS5YT+OaJ+j1Zd8t2EPXvh+MxJJarieAv2ZvLtoOzaWVOPiEd0w5pFvU97fzsoGDOvRGlskFx5XIAGfgtP7t2f9rAHkZwZM6aF7a6K2bk+fQnQFHEtq6atZIT/21kY1xiIbBiJ45pKIrJAfCoGWzFAfs08CkFnF9VOXYfOeWixQY0siA5Hb0azZaUwTr4sm2H2ogfFiCwOFg7tqOYN0wnPf/awxTP5+cQZiZeQF/QrGDuxo2s7RryOrrxneU3ehju7N3Fw5IT+qI3GNxTXFHZ0OnBgIrzbPsfnxcABBVCBW1k2ZGnfYLLRzaIglNCHBaW9tNGGpgKxw60er8M6i7YZtijSjRNdOcVUDLnpxASZ9qPck2lPdgJgqMazqvJZvr8BvHp6F0Q/p7Tf21prHlw4DAVga8eItezX/uPyyZQZ9hvYj3AWRGfShPpbQMqo46mPG44vKjXGovWqQOy8jgN7tjK/PC9+zgHaOoECIykBKqhrwzw9W4oXvf8HKNOpjrHz0Ynzq2YuHaL8vv/MU075XvrbYtA1gBoOYJVcdiWlCMjvkNxgHdgqotVQfwhH0MxcSR0MsYZuuWyMZDAF14nFW4cRA5mw0pvHWReNoiCc0Rbi7kp3js+tGG7IS524sxecr02tnz+cXc43pLmKrd0zOPuyrFmRyxtirTTamTRyNO8b2NR3Liza5G6wx3oTGwGlFwufV/++2+mnxkXlwxIC7vsYFU/SU1pjBhaVPTj4prSy+8rqopniCfgXZIR/W7arCwLumm6w0K8xYW2x4GRtiCRMDqWqI4Y6PV2NHRb1JoHQvyGRB9EQSx3RrhZ/vOwN/GtnNsM+qHZWmIjerBoe1NjGIU/q2sx3/uc/N117waullywj4kCk0QORZNxkBJgTkl11mQLKw55lxOeEA8tXUYQ7OZrLDIgNhCmTY/Xp3WvnZ8sI7K/Rqk237WVOQSFIEBeVZVR/XhH5WyGdI6+VKsyArqFnPfz+5D6ZcMgRWCPkVTRkBrEDvlg+tGyDWRIxzwC99H21ydQYizx+esMBRF00gEksirDKQXPV76Nkmy/A981T1xiAkxRir6mNaZpZ2D5L19X+nHo6pV4/AzL+PwbI7TgYhBAM651mmEPO5wxMRDpgYCCGkJyFkGiFkDyGkhBDyCSGkZ4uPzANDTQkQrTNlpFQ3xA00WmQgYsCSWyRWazhU1MV0BuIzBo2d2kNzP3c8kTS4EiKxpMlHPmdDKV7/cSv+8d4KQ0BdIUDXgiwtBuL3ESgKMWSiAEbGxGFlWdXZWFttc51bgnCftqzcMgQGIgrMcNCHhljC1CvpureXGVxxqyUFzH32GUEfxh7VEQVZQRwuMZHskK4QRBeWfA6O9nnmOAfArO/rfmvbEcgSnwntWUSIAh1g6chBQYBVNcS0FutyKxrORm4940gMUAPA2SE/2ucZBSdHwGdkINv31mtzfPXdp+L23+ntYhpiSUNCgcwIcwVlnKqjcp2absvv49XLh+GJPx6NzKAfr16ur1nnpj+WHUJ+n8rwVRdWQxxHdjB+/wGJNQZ8Ckb0LEDQr5iq+mVwdsmzz24+7Qj8a3yTmqa7gpsn8hZYE8MOADoCeA/A2y05KA8CHu0NvDrWlOoqQ2x09+FSvdCNWyRldgxEcGFFDQLePpQ4+qFZOPbBWYhLVe7RRNKUxssVW62QkQIwQdIuhxWBBN6RAAAgAElEQVTqxZJJ7eXskG8tXESIltXy7RXod+dX2FhinbGVG7a30uVzicgI+rT0yDzB0s9Qg+hWdQAriyq1/H55XQdenxDyK+iUn4Eld5yMgVJaZnbIzEBEyEZAB0kQc2t5SLdWWudct+jfKU9jCSLCUnuO3m2zDe4xSqFZ7kd1zjfsyxVI6+yg1go+Ek+iVaaTC8v8XPt3ykV2yG9yy4msLyAZLqKVnsqVUxeNoyGW0JRXl9aZOOtotlbdwM75ePz8owGwvlNW37sVckJ+FmfSxqNo7BVgbmZZkQaduj2mAL99bjD275SH/p2s036bE26eBqGUvk4pjas/b8CrA9m32LHENg0XYCvR3fvZWsvPuEUvV3sDzK3yidoeIuhXDPEKObuKoyGWQHldDFUNccQT1CCA48mkqeOpvuYDNaRl5oQDaJMTQmkNKyTUFIiNdSpCvObr87eiNprQGtDJsCtKTIVMIYguuop4DERWlABroc5dTnIAu07whdsh2yIGIkKuXpafFU/lbpsTbpS1LBsN4YCCIWqjwPa5YbxxxXD8+w9Hm4RoWFW0Zx2tB4CDPkX7vnPDAY1d1URipq7L/cgW+BFHUGIgALOop149EoC5+rtGYGSiC2vtPaca9kvlytGD6NbPLFfNDpuxtti2Y3SepLD//YejMKaPvqBdKMBijDxWV1UfMxk3TWE4/O7T7STRVLgZ8WxCyCRhTfR/AvicENKaEGKuqPLQIpCraUXIwkoEt/ysYiDfrC/BV2rvrKBPwR1j+2LCGOadjCUodlXWo//krw1Vz2JDuPpYwqDYYnFqEkKc+UTjCQMDyQn7UZgdQjxJUVYT1eoWZKHYzsIFJfq/rT53C6c1HzKCPq0OIF+wmMMBH5IUqBQqv/u0M8YbKKVCQzyKv/o+RWGyTD1ef+Xk7DNjDMSswHdWOCuQP43shrEDO+CGE3vb3pcTZF276q5TNQMkM+jD6N6FyA75DS49QGcghBB8dt1oDOvRGn0FNpMd8mNgF56Cmm1Qvt3IbnweuhW3+d9EQIqBAEwwc6EoNys89sFZeGcR6zIgEvTMoN+QkCFXaMtYWVSJVTsqbZV7z0L9+82U9rnxpD646eQ+2vfKg9nldVGttxfAlF9m0IfVO6pw6UsLEYknkZsRwElHttX2aYoCObUfYzsd863dmi0FNyM+H8AEALMBfAvgr2AdepcAsE7V8NDsMAhqSfDYtasA9IWMrGIgYvfOkF9B+7wwfj+IUfdEkmrFXqJ7yKnNRDSRhCJJIX7dSFzvCwQwocKtueqGmPbyiH79t64cbtnWXLQo3bQ9twO/VytkBH1aTr0YiOcCTowRXffb3gYL9OlZmzRXxWFkB24OTMV/g08CMFrRMSnNNZULa3eV8XtuLcWLOuVn4OkLB6f0l9tClbo3ndwHE8b0RMCnaGxDFK4Bv5mpcPTvlId3J4w0rAWSGfThhMPb4qu//QZnDzY+89Zgc/Bo5WcEfYrWrp0fXymku/I5InYq4C3PDVl0j/XFqL0fp3PnpnsU0b0wC38e1R0ATEsdjO5dgOtO7K09pzvH9kW3gkyccHhbQzV8yK9obXF4E1FCgBcvHartZ9cDzg2uPq4nFt52Irq4qPFpTrgpJOzh8OMF0/cRfhQKCGUhbtWviYO7YcqkYzKDPkOmEH8BeCZITGgEJ2Z12RV2AcyFJb8C/LrReNLAomqjus+5NprQXBBciA7v0RqjDitEfoZRGAZ8xBC4T+WiclIwxx/eFq9ePgxXju5h+iwj4MMR7XPx3T+OxxXC51yAiFlffoVg4gl60PrfMzZgSLdWmHHjcTipDyPpWWDfkShs5UK7HAcGQgiweoexAYTsThnUtZXtvbrB2AEdAADnHdMFt5zOAtZcaIuC08RALARvUFAyfA4e0T7X3OpGnTEEFCG/oinYkb3YuhmdhIJIzm5FlsuZtUGBVO1Azjc3462rhjvfsASr+AtHvurGtMqAAvRnMqRbK3z3jxPQNjdsEObs3tg+947vj0tHdsOZUs1Hk1xYhBhqX/YVUjrMCCGZAP4OoCul9GpCSG8Ah1NKP2vx0XnQIFY9yxlSzgqETXg5BtK3Qy4WC+4oXYGwlzORpJrLSbT4nRRILE5Nn/PrllRH8Nc3l2rbfYqxVkF8eRbeeiJyVP+wLJzaZIcM47GqNRjavRW2lNVh0mlHYPygThjWozVOe/x70345YT+O7pJvmbLMhTNfZEreDrBnFU9SJCjFVcf1RCig4M5P2Mp6z1w0GO1yw5h02uGsGZAqKI0MhI29VWYA1Q1xw/O4ZkwP3P2d3gvrkhHd8Np845rmfh/BrJvGoHVWEDnhgKMyHdQ13/Yzjit/0wN/HNZFe/aAMX1Z3sYhu50A4/fptNIkny0EFAGfolnhvdpk4ZmLBmOwoBT5/SkKAMmjWxtNoG+HXDz5x6OAZ9VxOgjk3LDflN5rpxzY/uyZyC3m5e68+UK8rEBggoQQPPnHQdi6tw5Duxs9//yUTVEg+wtuIi4vg7mrRql/F4FlYnkKpIWxansFBlhsl91RTi4sbtEnqS7wANYWwaBAuHtAfYHjCaq9HGIapJMCqWqImap45bbjAPDfCwdjQKc8/Cz0uhLpe1shP14ObLbJDWs1G/d+ttayq+y4ozvhkhF6PckR7XOx+PaTUFIVwRlP6oqEW/yWefUh6ywmUaH97aTe6N0uBycd2c70mZ7SStV/CQI+YhDyXIH8YWgXgBoL/fp2yAbAFMiQbq0womeBSYH4CEFPF/Ue0288Dn3ElOGyn4GNM0z7EUKY8ojUAPV7gfyuWgKBWKgZlJ6XleXOhaFPIY6NB9+8agTwGlMgQb+isdSCrCDOUBkRB390cpytqLwOtZE4zjqqIw5royt8ObVXRGF2yKxAHBgIz2oTWePowwo1BRf0K8wFJ8wBmW21zQ0b5raMg1GBuBlxL0rpwwBiAEAprYdzuxgPzYDVOyox/r9zLD+TU3KdFMgp/dprAcXD2+tCRO70yV82PonjAgMRq2YTDh1SL3pxgeZmucn/LhaF/mK538heBehakImwkkAPwip75SIqDi58uODtlB9GdUMMD3y5LmVLchGF2SFDYBcAcmJ7gYrtlgKuV9ss0zaABXV7kF0YQDYjLzOIU/u118YmCg8t2Eq5AtGDzRzH9WZZOhcO64pbpCVxQ6pCDQcUvDthpMG9xSHHm+xgYgj/OwX46mb7A14bBzzOTJehaufhVTt0liZf1cqFxedRZtBnmbH21pXD8ZcxvTRFzRkIdw3K8R3A2oUFAKMfmo26aILVMVFdwItGiTwEqzhRKAVjAYztWd64crh270G/gtyMgOW9ukVTYiD7C24USJQQkgHVlCKE9AJgX2XmoVmwq7IBPotMHMDYqiQaT5oW9eHY8K/T0aMwS6PIlx2r+/JPPLIdVkw+BU9fOMgQJObCMJ7UYyDGVF13GdzX+T9GG2LdtJlbrO23f46vgjcjG3WmSmIObhXedWZfrLjzFOSGA4jGk3j+u81ojSpwC//rvx2nZZBlObhMRGQ8eSTweH9LBSJXCXN0bpWB2aGbMC10u6lhoSiodeGuMxDZwr36uJ5YP3Aqus35P9N1eBF8wKfApxBDyucHfx2FdrkhDLdoK28F0xr3kRTNtHewRcmQTGgFgGLvMTETDwBClgqE3b/YDkbEqMMKMen0IzTJTsCEMGc6BdlmAc9ls52Mzgz6DApEdGE9ePYAg0vJasmAmMPc5gwknkhaKvOQX9HdV/EIcFcesPR1fPW339hW3sv4tTKQyQC+AtCFEPImgG8A/LNFR+UBSUotUzkBmNZ7sCMFskVz7GEFhr/zMgIYO7AjpqhtoQG9p5DowhKD6EmXCsQJoT2rgLvy0GrndwiRODIRsfVXc/dSJJ5EXibz8ycpxRFkG5aG/4Lzfd+CEMaubjypD+4c21crAnPCG1foAVYrAWhnSYqKpUsrY8aLpa9fradJgphcZYQQhDd8Cqx4y3QYZyBcoYuFgUO6tcKCW08ypBc7wTQu4lJQRWsQ8Cn46JpRmHr1CG2zrJCcYiBO8Q8AGkPjQXRecGnVL6uTmqI6rLu14gz6FCApJDcIc+r8oV2x5I6TNSbBWczAznlahlXEoX08z7KLJSlm3DgGH197rOHz3w3ogHOHqItA1bGGjph1L45on4tT+rWHGxyMCiRlDIRSOoMQshTACDBD4QZKaepexh6aBEqpLQMRYxJ2AfTVd59qEoJ2VrUIn09nIDw+XVYbxaItezG0e2vXDMTxGhu+BADk//wpACCAuC0DuWJ0Dyzashfj1CI1nxrH6UVYAeRxygq8m2SrC4QDPlxukVFlBd7FFDDGWa49oRf6d7Sv4BWFksxAwpYKhCl7CuKY5SODn4q3x7eyet1Cdp2ZFAil1mZ9QxUQzjNld707YSR2VzbgAnV5YacYiNhPzBIqYyDqMTx2ZNVBoHe7HMy48ThE4kl8s968XHLAr9i6sDjm/PME1McSuOldlpTiVwh6qXETp7U+RAbSPi9sqiL/47Cu4k2p/7tzSfG9g/6Dz4XlalZSSssAfN7CY/EgIEkBn5xqokJkIHbxD6uKVDf+WU7tt++tx0fqim0riypx3nPz8c7VI5qFgcgvlp8kbGMgXVpnGtZH4K3E8zJDQBzwgTqune0GogK57NgehhoGAMDDvYChVwIn3GLYLPv+rSxxJHVl75TlI4PLZNIMCsQUKzEpkCRALMZm4+rqUZiFHoV6jMjKTcXbcmQGUow7yZd8DcGnEDx3yRDMXFts2y+rd7scbBTql0SEfIqtC4sjPzOIfBjjKdoyvQ7dHvj7lGnjkrNEmvEQu3fgQMbBN+JDAD/vqcE1by61ZSBiUNsu/iHi+hN746Fz9Hyujg7tQrgCef3HraYeQt9u2GPJQM5W5qAQepDVTcqo4Zowd7e1g48wBRKlqovH5hmlA1EoBKxe4rpS4LsHzdt3rwYqtml/WiqQBPuuKJzrDGRw9yWXgSbl8+xo4ImjHc/Rv5O5txUAawXCERF6ikWsBbUMq4A0Z2NOi0oB0BhaazV+0Ck/A5eqLiU72KUrB/wEoNYuLBn/2XUJngk8DkJ0V6RTZ4K8jABuPeMIvHGli9qSNC2annQ7bva/fVAG0fdt4xQPrnDLB6yFtc+m5ZioQIqrGhAO6H2HFt9+kilX/e8n99F+X3/vaY6GEXs5Ke7yv4r3EsdjDe2ufbaqqFIr8OJog3I8FnwOS5OH4ezoPQCcLTkAJsvMjwQ616wCalsDWQU2B6nj86kKJKlakGkqkHcnsL5K4kueJbhZ7FxplnhO9YPfxZSnKVgNaAISFjEQA+r2At//W/uzIDOAC4d3xUXDu1rvX2zd5lzEuxNG2jQSlO5RVCAPCPGjBncrV7e2iMUc36ctHv7qJyy3Wdddv3bCPIYUsIsVBH0+w/fqJJDbJIpxhq8YrxCCUYcV4q2rhtvGVjiuPq6XuwFqSszdXHo+eRcK/JXYE6sAsG8ryZsKN+3cW1v8pNfq04Mj/vXZWox9itUnrCyqwMItLAhnJxznbdKr0ndW1KMwO6S5OAqzQ44VqeGAz1GQEULQSqnHn/3T8XbwX4bPtpfXmVaZC6hutnZEz8xJqUBkFxYSGL/0MuCVM1IcJzCQROMYyLAerTGsR2sgprv+coSaj7QUiARLBaIykGSqGMjXtwLzn9b+VAjF/b8fgH4O8ZhUyAz6reeCbEEkbXz/qbK1VLS2yJjq2zEXJ/dth/t+n6KluN21HWDLQHxEioGkZnz8VKN6FToyFleY/QDLvkq4W5CNI1PtUuDewXngwA0DWQqgC4BysDc/H8AuQkgJgKsopUtacHyHBF5U6xlKqhsw7ul52nY3wnF3VQMKskN4d8JIUwtxDeVbgGA2kFVo/bkEn/oihWEuWLRbflbsHiu7LdrkhBzXFwlBfeH2rE85Nr9CkKAUkSQAJX0GokFwz4hNDE0urDTcEU4xEBZEdxARUem7s7DIe7fNtl/fJJkE4vVA0Lp+xQAnF5aIBncrINqlTb8gZPfZQrPW3T9nqxRcQA2iCwrJjQIhzVnSNucR9j83TlzGQIJgLNFHW34BqOaGG5X7FYAzKKWFlNICAKeDrQ9yDYBnWnJwvyp8cw/wi7mdhog/v7TI8LePpBaOuyob0CY7iI75GRh1mI2CeOIo4DHzMph2CKqzIkjYy/g3//sYQDYjlqDYWVEPnyC4feo+4qsiMxCxQ+iqu04xvVhhYt+gUYaiEFAKzYVlULKJmHuBLygQ0YVlCjjLwnXncttTcoFlEKhJXSiY6k3EscrXsRDqM/4+Bm9eOcK0HQCwcirwn/5A3MWzNCkQOwbiLgbSlOI5TeCn4cKyYyByEN1NK39FAfse1nzs7tk5gT/HOO/G4DKup87hvODBt0qGGwVyDKX0a/4HpXQ6gOMopT8CaHwr1EMN3/8beHWs4y5rd1UZ/Laydc2zRc5W5mBT+E8IIoY91RHTKn6WSESYnz0RB36ezei2DYKKOJEp/ub/ENNCtwNgy4x+FrgFK0JXsX1V68nAQAwKhKKNkNXE+iwZX6wMuS71m3uBty80W+XQrc+kOnUNSvbeQuDjv9reFwCgvoL9RHTr2jE2kZSswiljHE//1AWDDFljSLDj+5KteHz98cCuldbnll056bp2KotY+5GGFDEHwD0DcenCahI0BZIGA7FhFnIarxsQEOCXOcB7lwLf3G2/YzIBPHIY8N3DzE21fZH9vjG1fXy6ijUd11cyAbwyFtj0Tep9WxBuFMheQsjN6logfD2QckKID2iGFJhDHHHJ3cMX8AFYbEBEjppK+GDgBfgRR7bqO3W9JsbDPYDP/ga8Pt46q0iF6KqX24pvLavDkWQrcgi7No+BiApEbD1PQNEmR/KRS+9VBiTL7/tHgZ8+Zz2bJHCGwLu4akq2Rl2bfUWKxTIf6sZ+XFrXJgWSAmce1RHdhRRX7sLK4Czrpy/0z+KC4pRZgFuBqiooJNTzu3E7yQrEZvEwRJ3X0WgWNKMLK+hT7NmUDQiBzhj2/GS/Y6weqN0DzL6P/b38DYd902MgGhJpMKCGSmDL98D7l6d3jWaGmxjIhWDV6B+DPZG56jYfgD+03NAODcgLPfVqk40fN1sH0bW+O6rbiAv3i0d2g2usej/lLkGFat1ORSVGiNqeXY3LBhGDX2MgOiil2gYCYFCXVnh74Xbb62UQm/hI0myRceHBFZbmwtqtdivOs8lakuFagaQf5DVAtipFC1kUGPJ13FrSsVrAlycoEBesQbaM+bVkpWXx/EU8c9Hgpq+A1wgGYh9ENzOQZy8ajD7tjWuPi89aIUSPG1kwXh3S+Jyq+eMN9p85IR0FoqisWTRw4hEABPA3cj2YRsDNeiCllNLrKKWDKKVHU0onUkr3UEqjlNJN+2KQv2aUSN1rO5I9+PYm5iaRg+hyLyUfEsgN22Ta2EEWHhtnAh9fa9gkuurFYka5kr0DKTO5sDICPrzDU2UBzL/5ePQz1SNIMRCZgXAkzNY/LwAzKxA1rbXtkaZjLNFCDCTl8aKicGQgLhUIZwn8WTXKhcV995IiTyHQzhjQAccJy7Y2Ctrzca9AbNN4LVxYpw/ogF5yx2LhPgkBoKhZeNEa2EJW8G4UCJ/mqz8AKuwNKA1uXFiJOHNFc4UrfkcPdAb+4z7W2Rxwk8bbhxAyhRAynRAyi//si8EdChDz9AeTDbh2+e/RvYitpiYqkAw0IORTDKzEjwQKm7AiHwDgzXNMdDwkxEB6EH2tcV5wxZeN6kz2CAyFHXPnmX3Rv5OeetouJ2gOHktKrHO2GEwWfndgIJx9ac+DW95Bl3n0XIEoNhnp0VomNJrKQGQFIgo40VK1YyANVcAHV+n9lWRwf3tTXFj8WnGpq0Ga6aiNgh37cYBdbJy5sFycJ6ErEIUIxYfNpUC0FHHCxvP+5cCLJ7kYlwsG8vnfmSuaK0H+HX1yLTu+dk/qczQj3MRA3gOwDMDtAP4h/HhoBojra/RRitgv21iPIVFZrAtfjgtiH2pxDwBQSNLcdiMlhLfP5mUTs02/CN2q/c57P+0Gy/bqTEoRIEYXljnTKMkKvAzbjNedMEJY90EUWhYCTFtUiGeB8WfEhYBbxhBxUDjJBHB/R+CrSWn71E1w68Kyy8Ja9AKw6l1g3hPW5+dul7QUiE0dCPfd53UFstqk51JpLJLpx0Dssr4CfuJO4QvfCQH0OePkwpLngVXrFw4xjZePp2a3/f7auFw875XvqvtyJUjZNZY5xGRaEG4USJxS+iyldCGldAn/aemBEUL+jxBCCSGF6t+EEPIkIWQTIWQlIWRwS4+h2eBgFcmFeRwhv2JyYY2JzNZrJgD4kTRkOLm6tvjy2bxsQWI9Js52ygir2O1M9iAgubBMtQ40aVrBznTdmBCsFVmHhTLwqXUaJgbCz+mWMUgM5NR+7dCWs7lqtkYJlr5mHENjLHKZRVEbF5YdA+GppX6b71ljIOp1moOBnHArkFm4jxhI+jEQOwQtYiCWMLiwiDsFIs9FRxeWyEBSzEfxvt0oEI2x2TDZfQw3CmQaIeQaQkgHsRq9JQdFCOkC4GQA24TNpwPorf5cDW3hyoMAwpc9fc1u1Avradt1t10x+RSTAvERICTUTPiQwCn92smHGiELAXHiiy+FoQWE9Zh4fYjowgpqdSBcgVgwEJMCkV5GoSrcMF5LBQLD9XwmBeKWgVRr48Pcx/H8sFIsvE11M/D+VuE84/lijchKkuM4osBwEwPhlqbPJjDaGAZiamUiMZBAGPAF9o0CaUQMRMS0iaO1312n8QqCWiHQ505aLiyHDCsnw8C0ryD8+bgqi4Aac7dhAMK8kIPn+wduFMilYC6rH8CWtl0CYHFLDgrAf8DWHBFn1VkAXqMMPwLIJ4R0sDz6QIMwqa9+fQkmf7pa+zthk0IZDvjMCgRJAwN558pjUq99YbJqRAYiKhAhtmLzcmQTNtm59d+JlCLHz9dzYOjaWqqEpklzTyLZKhcVSAqLX2cgTXVhCQpk5mTg7fP1z7gCCeUaBUDEQcDYQb5X8XwJNwxE3ScVA0kKDKShCtiglm5F64B10urTVu3cAd1y9mcwhdUYF1ZtKfDZjew7dZMGrCn+JLBlnvO+FhBXjnSVxhupBqp1dxIhMM6ZknU240yDgYjzOZVCMxhP6vP+Tz/g0d42B1gEzw9kBkIp7WHx07OlBkQIGQdgB6V0hfRRJwBiKkORuk0+/mpCyGJCyOI9e/ZtQMkW0iTaWqa/WDHBhUUly1CuRFdAERYUSEGGi+45sgAjNp8JAiyoWE/6LMopPhtzZ7IH2QF9QSAAOKytlPFCqQsGIggaAwOxUiDsf8WOgThZzQZlwBWIYKPEGoDiNYICybE+Jh04BtFdMBBNgdhk2kUtXFgfTQDe+gO7j69vBd65CCgSbD47F5aBgTRSgWz+Flj8EvDqmcD9HYDtC4H1X5j3q9jOnj2/dlUR64UmK7sUEFugu3JhPXGUoeeaIrqwAFYoaAX5vDyNllKW4LDgef0zMQaSSqEZDAoXjI/PV/HdiNkvad3SsE3iJoT8llI6ixByttXnlNIPG3tRQshMAFbLdN0G4FYAp1gdZjUMi3FNATAFAI455pgDozeAzaQurYngy9W7rA4AdizFQGIspPORJEJiyqubAK9pUtrEQAwMRNg9nKe5RWR3VXuUIy8QB+JsAaBl/zzZ4laS5nUZTDEQkYGIQXRJ+CZiOHzT/xDCQLMC0RiIwzMRBXZ9uTY+DZ/dyFYHPELtGBBvMAqXxigQpyC6wdUhB9G5pZnChcWFPP8/UsV6nwFMuVSqiRm1whpwpkJCnsYrMhB/41p78DTiIrVS+3/qnLhLcK3tXs06GZ/2kPn4ShfprgLEokJFIakVSF2Z4U8TA8m06QZtx0DmPArMNjYdNcRAUrmwxHfYlcLm8+LAcGE5VQGNATALwJkWn1EAjVYglFLLnDZCyAAAPQCsUDMtOgNYSggZBsY4ugi7dwaws7Fj2KewCRBe9vIirNqhv1iGvV44AbdKGaYKkggRa9ZgC1MMJLULy9DKJKbT45AaGyHqvgqhaKdUa79brQsBSs1ZM/KYYrXWn8kMZNkb6LvmMfzVfzbWJ7uq100jBiJSfS5QRYGz/Uf1M5W5NlQaz+fkI7eDEwNJuGEgqlCxUyD8OEMMhD9vqru+xGvZMhBV8HEGIrrslr7OlJG0qJYJ9S7qUMpZ81D8MgfoNkr6ML3qbVPvMruqehsQIgl5u+JJuzTe9dPM+/J3hrhQaAaXrZsgugUD2Y8uLFsFQimdTAhRAHxJKX13XwyGUroKQFv+NyFkC1gvrlJCyKcAJhJCpgIYDqCSUmplvh8QoJTi8lcW4ZKR3fDbHsa4ABfPxaVlYAX9BAFf6r6gCqiRgbjx9zvFQERhLQgwnxYsV6AIgidIKHJQh6DgRmujqArQjutZvUBug+iyolEDxtmot4iBcEXipEAEIVpnoUC4b5y/kPUVRsHuWKlsAxMDEbOwog77cQXSYB6nCNl1JwfRuQKJOykQKYjOYyCikPp0Ivs/lQJxlQXG3T/J9NKkGyqZAM1gC5Z1JcXAj88CELoPOAlsC1ePyYVlUbwKwIKBqPfQ5ghgl+RtF5sppjLy0nVhaQxEVCAHaBCdUpoEMHEfjSUVvgCwGcAmAC+AdQM+YBFNJDH7pz24/JXF1pO6bi8Wkj9hoo8VDbpZ7lSRguiOwjIRZx1GG8VA2O8xYrR6g0oSq8JXoje2IUbZeIe05kLQRoMI59WMRccgusP9CWMXXViHt8tJn4FwQSd+NzwWwwV7rNbAwGwVyMMWIcHKHSyQ7RREN2TgSEKAJtl3x91RdvelZeXYZGH5rBSITSuTeDNkYdlVwov3zRUYTbNQ88GurI+ZiqnBe4GvJiETwoYDcuoAACAASURBVHN0UiDcnSdAoUn92RLFngWY6kDUe7BKrBC/15RpvOm6sFQYWpjsvxiImyysGWpNRpd9lcbLQSntTiktVX+nlNJrKaW9KKUDKKUtnQnWJBg60kqTeu3OKox7mCmOs32sxfvYgR1SJjIqSBrbftil+gHA/KdYh9HnRksfuI+BJKR1w8TgeiLMmj4WUFVg2OXxq+edevUIfPePE8zXBRyC6NZCsw2pxLV+9vxaZfjw7l9G6vu6ZSDa+CxecFEA1AsV4HYuLMmvDgB44bcskG3KrhLdg8J9y/EGmgBm3gXsXmk/TsCagXAFQe1cWDaFhFzZKYHGB9HtGIh4r1z4VmxrUsffVmDfh6FnnJPAtlAgfsT1+/dnuHdhadXrFnExq0JCO4gut0TUfT2MqQfW/oGbTmi83aPYMIkCaLFMrF8DnBRITSSOehIDQnpAetLpR0Bp3weYAVtjXgE1xkA+uIJZin3PMu9cpYaHZMvWwEBEYa2PMaDGQOJKEOK7KcZGwnltgZJSoJYrMWcFMqKnEJw0xUDcp/ECwFm+H7Tf/UgiLyPgLo3XylKz2l8cT72+0mJaMRBeeSwLYSvGY7ffFmH9GDtBRCUFEqsz1lZoLizh/HZpvPwail9VII1gIHYxkGgty2oD1EU4wBYQc7GImB04Cx3SJRffbVfv2YmBWCRBBEhCf16BDPt7NrXbj+vnDGQZ43ixNAoJ5fnu9pkbXFgHYAyEg1LaY18M5NcGw6p8FlaFgXaDNYLLDDhHQRSaxA1jurKKHI6t860ViG1EJbULKzvI9kkokgsLFtkqnAXZCjg3MRD3aby253flwnJpqYmuKtFF0ZgYiOx3NygQm9gP3y+ng+5ft3u+GgMRFATvC5ZMMAMDSBFElzLYFB9TIo1iIA4KRB+A/fFVO5j7dfuPrJ3/kEttdyWqdfPSJUcjmaU2dXSMgZjrUnwQ3GiOCkRuiskVSA2LyYgKJC4E0dPJwopH3CsDQxrvAaxACCF/stpOKX2t+Yfz60EkZs9AACBTbWHOXyWfQpyFHwC/QtEpW3r50l20xkUMpCCTTYu4FAMJUUEIhfMAEN0FYStsLJiJfJ9Rm1YmdgFNw7l4Kww3QXSXL5ooDEQXRWMUiGmpWjEoLypOixhIjpDpzu+rpsSY6ioyEOJjf3M3UjJuEwOxycLi11B8ugtr9yoWKHYLOxfWOxcDf5nLzu0kVH94kv1wOCgQPQ6W0JZhNr1rsQamRKt3W7a6DyCus+hAhvsYiFi9ntGaKT7tmlIzRRHrpgFt+wIFvYznAdh36NbIOVgYCIChwu9hACeCrZPuKRAHGBmIWYFkSQzEryhG14MF/EhaWBvpLicqZmEJwvbDK4Hz3wTCuSjIYlZrRJoewaRwbcXPLC+tnkK15BQpGeDbh4BxT+rb924G1gvFYjL9N9RGSNag1csdq2UrxeWrmThu60AAXeDKEL8vAwNpRBqvbPW6dmFRIJwv/K2O8/kxQLWQvS4ykKxCoKZYV0Y0CW0uOTEATQlLLqz6chZDaz/QuK/8HYuwc2GVrGUxiFbd3DFLFyBWGUny939fO6DDUYzJ+czV/KeUvAL8xOJp8IftDRC7tvyRGqB1L+NndkF0SpkiVQLAnaXmz9dNA4ZPMF9700yWkHHGI/q2gyELCwDUtUD4z1UABgHYdyuWHKRwioEAugtL6+mkEH1S2E3iWL3Z2mguBvLLHGDuY0C0FkPXs4lan5SC6FS4NlGY8BdhJeCXv8FeDI43zjV+HpIW+xGFtPwc7F6U2j3AjiXWxxiOl56dXW2F3XicGEikBnjzD0D5Vul4JwXikD3zwRXAvMf1v/l9VUulTxp7iJmL4JJx/Thx7KkYCPHpri9AD+QD1t9B0WLgmVEsHuAUFNfarjRxjRV1WWAfb/pp09NN3191A8osD8CA6jn6H4FM4xxOxIF3L2XHy/UlyTjbFq3R0oo1GGJ6CeMxAOw6QKByG7DyHfP43zgHWDhFuv6BwUDcZGHJqANraOjBAZG4dYYTAGwJX4gng/81H8QnmNUkAtikaUw1tAi7ZooAi6fMfRw5FawfUH3SaGn6qeQG8UkE1k4g8tYggFGQ+cNmIR61iYc4nV+EUxBSFn5OK7fxdULcxkB++gLY+LV5XW2ZtRgUSBouMbsCOTELKyQt3JWM6yzTKgtKHhO/BmcgVrAQwpj2N6BkDWtb4hSD4O6tpjZpfP43MLB0G1esGxCRAQTCxrGVbgDWfgx8eLWFCyuufn9UdecKEGMgBpelBYOVGZPbrLSmNvlsJrhZUGoaIeRT9eczAD8B+KTlh3Zw4qvVuzD0vpmoiYgToxGpeXaQF4whBPjgSmDaDebtlrDJwgKYpSkqKKn/ksGFRYh5MSa7yV8t1HsGhHMGMiyUkBgPcclARDi6sGQG4tAKX1vm1KULK8DWSjG5GOWXWxyfG4WY0Uo9Lm5dcyBWostszpaB2HTjlWMgVrD6Diq3ma9hBS02k0bthw0M9VA2BbFuYEgB9mdYxxZ8QfNcpAn9+wjbMRApiG4VH5LHK2b9OaX0iu5nN8sYtxDcxEAeFX6PA9hKKTUnVHsAAEz+dA32VEewq0IXDjSZcMiJEtcDcGGZmRSIAqx6j/1+0t1M8PlsVtmTYVWPIVD4IzoXAkI7rtaLhUWNiGK+jt1E3rkc2Pwd0HMMe0k5AplmJRS1aWsCuCuYSicLy8mFFcxmGUURl0F0fl+ywmisC0scI1G7zD5g0Xl5ziNA1xHpKRBZMGlrTCTYtQixn0NWCoQLxuoUiyZpCiQNBkKppTEkLqzWNAYiPAtfQHINCY0sTWm8Cd2g4EpeH4T+v6ggaiyau/LznvYQ8NXNxtquZMLIFu1W62xCLU1T4SYG8p3wM89THu4gLlUbjdtbRQWkCvf7X2SWhxsGUryaCV4Nwsv1UDfg9d879yOyi4FwiK1LQhmGj3wNQlEdUczBVLuJvO0H4LVxzEUiMpAuw5i7RITd4lKASwbi8Axlge3kwgqpXYVdK5Cg9TVk1iIqRTdZXUqAxSSc7uuNc5jgNCkQocp69ypzxpq4H8D25S067BSIU2pvqlX3ihYB2xaw5VfdwoatfHzVUcI+TVAgIgORiyfFynyrNF4+N+QYiLZPwuh6LNtosY963g4D2fVFJZyMGQ1Gu7YnkSq2guTwv5rdmC0MWwVCCKkmhFTZ/ezLQR5M4EZCeZ0+EWsa7F+6LBLBhf5ZrOrYjQKpLwcGCmtXyP7sLd+r7R5cuLCsGI9YcGa3BgU/j8mFlSI+E602usXOe8XswuJCVfEzmh6rF/z4+5KBcBeWmNLrYsU6kz9asvY3zQDuymPPyhUD8bNn4WZuhC1iIFzo1JboHXLtGjcmE7pCt3VhOQRsufCTl3s99X72/8IpwEtWjbYdYMNWumQKz0N8Nmm6xwweAF9A6nLLXVghC6Ub140D2YXFQRPGZ11qoUD458THziMykETU6P4Vx2BgIOp7pfj0fd65GHjNqj6seWGrQCilOZTSXACPA5gEtvZGZwA3A/iX3XEeGP47W/f9bN3jIvC9c7m9C+v4W4EjhabIgy7Wf7eLddhuF363EkqigHBSIKILK6havql8sfUVeqyAw04JBTLZ+O5rD0y9QB2bCwZCE/a+43SysDjL40IikOkcA+GK121GTMU2pkBSWYxKQFUgLixrqyB6Mg6E1CDv9gXsf9P660IhoZKCgcgtV0SBzYVddlvjPnKQORXOexXoqnbptWM8YjzIEANJj4EoooCXXVjcYPCHrNN4XTEQUYFssNiHJy742HMSWVxCYiCGvlnSMgP+EHsntTXYS9J+Fo2BmyysUymlz1BKqymlVZTSZwGc09IDO1hhJbpWFemBsd8qS60P3LUcWGnT9HjktcCJd+l/iwVmdkxj9yqbEaZYE110QzkFmcUgelaB8Vg7AW4VRJQFlSawM/TzbZzO/nddpRtna078+BwwY7I+nngDDPfvpCAVP7t/LiSCWc4MhLv+3FYFR+tYFk8w23k/X4C1/nDFQCRBlowzgZhVCOR10eeESYEILixNgbhgIPGo8ZlUF7P/s6Vllu0Ww7KDLwD0G89+tysmNaR7x9hCVk8PTXtxJUMQXQkYFZY4F61amdgF0TlkBlK2yXofQFcgIhJRIyOxZSA17BnzWBnAjDW7cTUj3ATRE4SQiwBMBZOPFwBoehrFIYJ2uSG8Nn8zLlVl1UvBR+13jthU8So+o3/bMDFshLXYR8kAm0AcR50Q53BkIER3P2UWsK6xmgKxsXwaKswCVo6BRISXli8vyl0i6SiQ547V/+5wFND/bMZgQrn6c3ZiIIqPjYErvWC2OYFBhNbBtw5Y9X7qMdbvZcIusxBwJKiEPSM32UX5XY3uLt5p1hcA2hxur0DeuRi4dSe7RioXlpjG+87FQFCIx5WsYd9VVqHxGDf1NiLEOhRbBiI8tGQC+HoSs/D3ClkfVoaMP2yYRz4qKChf0KiwUjEQ3qXAFETn+ySNz1ps5rh7NSsQ5BXpxGdmMjIDcYqB5HYyVvk3VNozo2aEGwZyIYA/AChWf85Tt3mwgDxn+7TL0VouNBqK36hARKv959npncuqsEmEmEaYyoXFhU0wm1lvDepqeF/ebH1MQ6X+8l6osi1bBpIJVKhFea3VdmzpKBARO5fqx4sCz0mwEVWB8O8umGW/L6ALulg9KwJMhboy83gsQVMH0Tnyuxqz3HgMRPEzQbVXXcjJSrA2VBmD6HZrfosurKodQInUDHHQRVKSB5jQ/t1jqcfPofh1dmuXsRWVXFj8uxQNFCtDRh6bCJ/U/4srEF9IV+CDLgHaDzAyEFFQH3O5/rvYrt4XMo75uWOBmZP1zy0ZiOzCEhmI7MIKq50V1H0aKtJ3HTYCbrKwtlBKz6KUFlJK21BKx1NKt7T4yH4l6FmYZaTJjYEmzFSIVvtOG5eYiG5CS/dkHJobx0ooGRiIg+uBKPpL7guyAG6kGnjnEmDRC9bH1FcwoXnEWKDPqWybKQZSY742b1Pi1j0h31d1MbBnA7u2eF5HF5b0zFO9jNwyt0w1tnAz1pWxl93JTQgwYa/43QWH87sa74nHQBSfWmUdYedzaszI55ZduxJRiScTxnb3ANB3vFnZ+kNArxNSj59DUXSFYBcXjEguLG6IiIs5WSkQpzktL6KlsRzhmZ04WW95Eq1h74HohhRjlcmEPgY7Q4HfH/GZn5uTC8uQzVfDnrHiY2PlHSv2gQurMZXoHhxhtO66FWQ1AwNRjEFxO+vQDqKVn4zr57LyL4vV0Y6uB8GF5Qsy11BDpX03VkBnIOJLrI1NHVO0Wo0/CGPmVrFVevLv/m1UkIBZQK6bBvx3KKuXsby2BYhitOZ5t1cAGGPBsLhlbiW0rOIcfEndlDU7NHUDQoC5wkLZxvvTFIhQWZ6IWo8xGTMG0eVMKg7RQk/GzWuhZOSbEyWCWWZXpRMUvz63bBWI6MKK6/cnJlpYMhAHBaIE2Lk4Q+MMRMxm452KqRpED2Ybv8NsIT4pMhC57Q8HV3iK36zc5DReuxgIwJ45lwvcCDxAXFge0kAiaVQWrbICxlRBt+hzuvX2w89Iv/+VOMG55Qukdou4ZiABFjit3u0caG6oZC4G8SXmAou76CI1auaRqPRi7KW2Wrhp8KXMpSDCqQBRtNAdkwQUo9UoZhZZCX2rFh8cVtanpkBcxAcUm6aPIvI6s/8DkgJJxIzCKR6xFqyJmBoD8enXtEKsThewNGGeQ+F8s5soo1V6CoQIlfDcjSnD4MKKCwxE+K4dGEiC+BGnkvjT4i7q/NEUiHCfXIEk1Ur0UI7RoJONNf69yUqVQ1Mgivl9S8TMsR7tM+m58ywsQGeFHgM5+FAbTeBO/2u4zPclAIqurTLcKZDLvjT+3XWEeZ+7KoE/vpX+oOyEVEoF4hQjEGIgvgCQ34W1tHBUIBXsBRcte64ouJXeUKkuqSoIHF71m4yByoLIqiLe6b7ScWHldtT/FhmI1fOccaf9uaz87tyyTMVAqMsYCM98MjCQpO6W0lYmtGEgiZgUA7FRINNuAJ44itWy7N1s/jyjVdMViBgDeesP+uJoIsRtIgMRVwO0VCDsOVDiQxWkccqBe66kuHLlYyNqVlxUZSCiQSfeJ3/+gIMLS70W8VkokKixrsiJgfA6EEBnIAeCAiGE3EAIySUM/yOELCWEpFkNdGgglkgiGk/icv9XmBx4HRf7ZmLIKz1xwZHWgjhKhZdUFFaAuaqYI132ATgokBQtJRwZiNDuwhdkaaJVO50D3Q2VzAI2sAD1HPx+kzGmYMRrJ2I6+xBdBICkQBxiOxwBty4sH9BKWEtNzCyS4zYyCg4z/m3lwtICtG5cWC5iIDwTKJULK95go0Ci+r6AvmqgFexYAcBiRbK1Hc63Vkj9fm99DtmFWVtqroMRY39JIYguMhNLBcLGRkFQRSW3Ej8Hfy/4nNu5VF+bnnAGogbRQ9J36wsA1y8Huv/GmMZrF7znLjfFZ3avJWJSCxqbIDqgMhCuQNRxHyAurMsppVUATgHQBsBlAB5s0VEdpKiPGV/yi4IslXZgVrnV7qiHIEgzpGXmU9UHyBj/nP1ndkIqlVByzFISGIjiZwwklZVcX8EsRKuEAPFFDISNqZHJmG5V5XSQxiHUo2gCQCwOk1iGIQaSwoXVWlAg4veTkjUkgV6/1f+2sj55rCmVMqI8BpLi2fLnZ6dAUrmwtBiI+n3YMZBUUCyCwYpF2xvAXC8i7i8/Yy6IT7gdOPkeXaADahaWOu5ICgWiCmlKFFRDLmqV4i7czVi2CVj8kr4PV+jRGvN7qvjZvOk0xFhImFKBWMRAEjHGQPi8NhQSygxEiIGIqectDDcKhJu8ZwB4mVK6QtjmQUAiYXRVHdmRZe703vSS5f6BDKFyWH7p3DZE5GjfX6/elWGrQCShJAfnU8VADAyka+ox1pYA4jrd4tjE+/dnSAokriuQXEmBALrw4EJKvK9MSTFbXdsKisRAxPOkilvE6o0CwyoFmDdZTBkDURVIquVlOYOTYyCaAkkRRH//CrYYFWceTotGpYKVv9/KhaUZD7nm7aJirdyut2FRfOYVEmN1uutKs9jtXFicgSj2DCQhMRDD2MQYSLXZU8DHzeNWqbKwtNbvdi6sel0R2GVhAUIWFvRn4diKqHngRoEsIYRMB1MgXxNCcoCm5qX+OhFPyrEOpmcz6q2bzGVmCZNPfmG1F86lrk7E7F9626IwCz+qCJmeyxCLztzQZV6pbBUD8Wfo55MZSDwCvMmaHxCZgYjn4ApQVCDyC25gICnqQMTgvMhAUr2Y0VqjArGyPuVYkV2aME2ysXBBk9XWmh0ELRgID3KL1u2X/7RuCVP+CxPSTWUggPX9WikQrsBlX70YRAeAmXfrC5HxlGQRM+5kRXkAUPqTupHaFBKq3x0hqHaKgSQTxpoobWxE7wzAg+iGcwjPzw0D4YuGyWnjgBpnqdXfQ0MNl8W7y78zHjdJtwNAI+BGgVwB1gtrKKW0Dmw1wstadFQHKeQMLNmivz460fi5XXHaRe/rk9ntJCjsY29R2yqQFFZtYR/7zwxBdIcFiETw1fQMxXxCJhd3KckMREzflWNF4jk0BSK8XPLzE8fpGERXGOs4+V7g8N8Zg+ipAsLRGiMTsPqeuQuroBfQ5kjn5AiisBUjAfx/e+cdbldVLfrf2CUNkkAKEBJKgCTUECD0jvSgSFGKKFxRkIs0O6JP4tVrefbrez4QUPlEEcQrRVAgIKBSvYYQQNqlyANFlICSQHLOmfePtebec609V9tn13PG7/v2t/dedc5V5pijzDHZ82y/sJ4UpnqPjAOxAsRpkJ++sz4HuPdcGVFYacwIM+Tm1kCsAJncuK0bRPG3J+rXS8o5Bl+GeE1YdQ3kHyZWTlcDWfl3ErM8WB+IdaJH1jkaiJvO3RUgb/8ObLJndD8pNT6Pa1YGx7C55pJGokPoAxFnPzqigSS+CSKyY2zRZtKMA3cUMRB39MUEyOr45Y43LGMmwvS5MOcgeOKWYFlaJJTl1FuCXkpSw9ZMam5It6G66dzLY4qlq3AbjFrYaBgptOZ1jwYS9r7nLWpM1AeNGogb4hhvzFwHcJYTHYIGe8+zo73ZrLqaoeg27n0eOzm47lYDGTcZzrwn5VgmqjFYG7zLpnvXMzQ3jEQPQ1zzNibNaiCn31kXIO65rFnVJ5DiARS1MsQ0EFcQlCrpo8ldUqOwhNcZ513Hn+5Jz/BQGweS4ESH+vWzDb1b5gUnBud69rfRY1Ziz6oN4bXXJz4Gx6U6vismrLSu1FfD73HATsAyAnvKfOBeYK+E/UYtjRpIVOCuIfYSxV+E8/9U38e+yHk0EPugJAqQnLPLxVV+34DFyRsFNmmR+vpSNZ+gs0QEiONHsXWtjIv2su2Ls/n+/rrUBjR68ifFr59N5wHZTvTIf+de5hq74dwL9z6f/xzc+DG47yL/eRow0VBOnwDZ+X1134V3JLrHQZtYbivQiw5Wda6Jvacb7Qan3BD8FglTbbiBG+E1bXC6l8EkCHefqcdL1kh0YWWDAAn/X3dW+qFLlcCHNbTG70SH+vWrCZAEh33tf7mxwbe55ayQcsca+TQQez2tAMnKctAC0tK572+M2R94FtjJGLPQGLMTsAPgSSupNPhAYo3DQIMGEhMgvnjyPA+BffCH6wOJUyoHppV9PlpfNmWzsKylusAplYo9rOMc7cI1YdkXqDo+2ui6c0z7elU1s0Elur09lmWPs+CYS+r/s8aBJJEnwMFtIOINpGveytLqjYmmcClVUvxlROtrbfBpc5w3lDtjHEjifs41qZ3LRMsaL7cV9L7GNekaSymnBmL8kWvhPR+SMiuNc//nH+cXsnGtAIJrY/0j8QAAez9rGkhYR/uu10yEsfrF0xWBkwk6FCADKRqIOw5kzcowyKXA2JsmydPN2NIYU8sNboxZDixoX5H6lwYNJOYAbzBhJaU3AMcHkuPFrzkGE25nogkrpoGc9FPY9tj6fynBlovggE9Fl9W+bX1lGCYsJxTY1qMyLvoy2Z5k3LlqKacIELdROPhz0QGaeUxYLhM3zN7P4jaWDQLEaQAzG+qYAClXGxsfV4C4QvFvTwbaYskT4bPN0UHepqMu8h+rqA+k7BEgDSbSmLC0z1+8F+9m442T14RlhoIBj3Gc610Lo990bzj6Yr8A8fpuyvWyJwWalGICxJbZ1jWXBmJNWFYDcQWIz4kevptrVnbEgQ75BMgfReQSEdlPRPYVke8Cj7a7YP3EIy+8xtdveZyBWBhvXIUeMLGXMi3Da5YGsuUR9d9ZD4t9sCZvFF0eN2Ftuhcce6mzn6cRqQkpqWsgIs2bsNxQYFcD2WB72PcT0XrGbeO15bFGz21wd07JjJumNfka0NN+DSdena93nqaBuPcry4RlyDZhRQSII3gfuzE8R7nx/qy9Phz3Q9h49+jyrJHoSbj3xZofrbZqiZuUbI+6wYSVojHlNmHh10DCc/1l8oK6D6TWyPsEiOf+REK0kwSI7cy8Gd3HaiLx5yueew0cDcTjA2lIZeJGYa0q1qEbBnkEyCnAw8A5wLnAI2gUVoR3XnQ3P1pyH7OuP471cbKTxnr4g/HLnSeaJMnMcvwV2dvUThw+bBvtCrv9a335Sxn9AF/jVlPR43mEMsrgCi936lU3n5brAymVYP/zYd1NnXN7eml2X2jUQA76LKy/bXKZUlO1eExLE9eHuQdHtbBDE8bUlqr1UfNxTdNtAPMkxnR7m14B4jRGvuuz6pXG+2PPG+/pZ+XCSsJtsKZuDu+6Bt76reg28Xxe9j7F3wM71sKHlJuLELOsNR1Ov5Pbt1pcN2HZhtnXEfMJ0unz6r+TNJDayP+wM2OFpBUkDSl5PObZuBM9PomWy7jJ0Q5UhzSQVCOZiJSBS4wxJwFf70iJ+pCBoSHeVr6bSS/+jnPchyA2/edQXICk3WTbc8kTSWGPkzQToH3Y3MFGEJ18x0eaI9U1YUkpu8czeVZgTrHlsLiN/4QwXUhkpHrMhu4TVPFecy0fksd045I1DiRxnSNANkkYvFmqBOnV//nnxgaviAYSDyWNh7jaZRZf73zFs43PkRWQ8Wtge+2FNZCYIJpzYOM2rgYizuDIBkd0igBJC6Feb2t46ZH0cpYqMGN7Bh5/qu5Et75ArwnLcx3cTknSlMTx+UnsfbHC0meiS/KBWCEVmcY3Zh6cMKU+pfDq14tZBIZB6tNrjBkEpotIZ0rTp1RLJZ43wTiBHUpOo7w6OtXcUNwGnGZLt72zPKpoVu9/0BEgwxkg5iKOCQvJjtpJM0nY9WuHYy3cF9m19/tMMbYs0KiB+Gz/ecrklsuHK0ASG7oyzNrZv66IBhI3+xTxgVhWPOcRIDaCLlZ+2zANJwori0P+HT7xrKOBFDFhpZQrqQMVPzbBI7PS+kBqnbWcPpD1tqr/TjJh1QSIzThgzbNrJR83fv64E93NzBs3YY1f1/GBdE4DyfOUPAP8VkQ+LSIfsp82l6uvqFZKlMNZfrcqPVdfEZu/olGApDT8dhDfDidlFyDrZR9yelhFsqJ6sSYsIXGglXe3hGgj14RlB+u5vhlXyJYSNJ2aOSas2xpnjoVULSpNSOQQIHa6WR+lChx4IRx1McyJ5R6NCMgMgb7tMY3HTfWBeBqOmQtTTFix6znYIg0kjQlTA7PM/hcE40S2XBQrW+hEP/GqulbqrkskjwBxnOg1E5b1U6SYsI65FD78ePB77NrBDItzD4uaWF1sR8cKyVrAgBUgnnpkmbDic6C4jF83asLqQAgv5BMgLwA3hNtOdD5KSLUsVHzTxL8RneP8s2+PzVuR1nissxF8ZgXMf2f+giQ10nZQ3qSZLRAg9lylqBM9C2MCu/gxl0aX+0xYK1+ur3fLm2Qqi/emrd05TjPrwAAAIABJREFUqXe/3ycBSS93mmbg+oGSGjSbf2r74xobhkgUVsp5Pv4sHLi48bipPpBYI/i+2+DYyzxmL6v5xRr+mgZSQIC4g0rzYO/h1M3hvTc1zilu6zf3kCAp5dQ5jess7/g+zD8++O0b9xHHKefruUxY4f2ZMDXwgVl2PhVOvDJ5gqp4enkrBKz24nsPqxOCwbLH/TD43+ADcQVIzAdSrjom3JUdGUQIGT4QAGPM4qxtRjuVUomqT4DEekQ7bjI1tj6j4S068j9JhV9wEkyaBdsdC3cVmJs6lSayEvjs4m4+LZso0bXvRgRIghM9LkDWOCYsH/t9PPjY0cbT5sG7roZvznfOm8eEJcnbueWOm5zyjgPxpSzJGgcSbwRn7ug/R5IJyzZMRTSQohE/8e0bTHLOuY/5Ljx9F/zgiMZ1EKSEX7UCll2ZbsKSUiBgnPo2mLB8WpS9DkUb5HJMA9l072BM1RYHhfXwNL0icMKP6ok2ayastaL/wT+baMSE1SMaiIhMF5H/LSI3isht9tOJwvUL1bJQlYx025A+urkZDv9KdA7mJMrVoCdcKhe3bcdxe9/GcaI3izuQcN4i2OtDwbzT8fWQ4kSP+0AcJ3oabiRSQ+8z5d7UGrEUE5bb429woheMwtr5/c5xq57IKdeJHqtH0jPmCkEX2xtvRqPIS7xx80UkJR3fd0/t9UjSQN55eT0U1jlX3YSVNqA2fMaLmoQiTvRQ291yUd20lZbG332O3SSj8XngG/ZzNJAeCuO9AvgjMBtYTOATub+NZUJEzhKRx0TkYRH5srP8fBF5Mlx3SDvLUIRqueQ3YTUQf5mHKUB2eX9d3U09bcKMacMh0vANox7uKPJyBQ78TPLkTUkDzCKDG8nWQOL7lSqehjajN2u/82gg8WO7++QRIIu+Uk+WWKrA9idE17vXJM15epYzCVPSeQcLaiATN2ycoyWLNAHoww2csNduwx3rQqE2X0aCAHEjBp1rX9NA0qYjtgkMm9VA1qz0PyNpz2ZkEOqE+r2IaCAeAVK7p6Y3wnhDphpjLhWRc4wxdwB3iMgd7SqQiOwPHAnMN8a8KSLrhcu3Bo4HtgE2BG4VkblhpFhXqZRLVOmCBpIXtzFoNgrrjLuDB/vmcFS6SD2x4YS4aa4A7kBCH/Ew3jQTls3PFddA3v7//OnSXQ1k/LpBYzh2YpASPM2eHjFhNRFuWsq4H9scFYzZ8e1TqgSmyO2ODaaVjR/PNhxbH9k4RiWP78X2bPNqqvt+LChLEeK9+cwIPmd7W9fTnGSHtWudIPQjaXccDYSxvFFei3GHfS753PY5yBIg5zwYbdRdJ7rvHqc9H+69qU6o/7fjQNycYvOPD3xJEHsOOqOB5BEg9qq8KCKLCJzqs9pXJM4AvmiMeRPAGGNzTx8JXBkuf1pEngR2Ae5uY1lykehEB9j1DLj3O8Hvhpe2QwIk0gg3qYGsv3X4wzFh7X5G0Pvc7h3RbWftHGgOz/0uf9kSU9G7GkiGE92YYH1cA1lwQuM+7n6l0Cz04Ufh9i/AHV9srwCRBA3kuCuCHqsvcEIcAZJ2LitApm7RmPo+HpDgo6gGUh2fPP1yEsMxeaWasFIESG3Mkru/8NUdb+WChVv79gqwGkhWmePRWJkaSNrzIXWfTXVCXcC++Rq1nFlWmLz1G/WwcPee9lAY7+dEZDLwYeAjwCXAeW0s01xgbxG5V0TuEBEbTD8T+JOz3fPhsggicpqIPCAiD/z1r39tYzHrVNM0kMjD79FAdjkdjvhGi0qS9gKFDGcUb/yY5UroW4nV690/D3IL5aFmwkrKfRQTICJwYTS6raYBTZsbvLi15IsZj3c8/BfqWmGWQzb4kXyOvCYKd/+tjkiOunNzhiWtAycvWobZJEuA5H1OmtFoi/aOI5l+PfV3kzf6iDz/BTtQZpgmrFeeiaaiyVsOe13HOBrIm/8IHOpJFgX3d4d8IHmu5q3GmDeAV4H9W3FSEbkV2MCz6oKwTOsCuwE7A1eJyGb4u+sNT4wx5mLgYoCFCxcWGKjQPJWSJERhERMgnioc/uXGZa1GWqCBNB40eVVlbH7HuutET1sPyY3a+tvAydfDrF1g+U/hv29P397iaiD1heF3Hh9IizWQNFIFkmckepbdPVGArG4sY2q5mgigGE7UVlpv3phgTpIXH4yuTxEgmWMPrQZS9L3JqmPWuJlSOTAnVteKCpDqhKjPJqlz2EM+kOUi8hfgLuBO4LfGmFcz9knFGOOJ5wwQkTOAnxljDHCfiAwB0wg0Djcb4CwCc1rXqZSFiiQIEHcCpPhLO2th+wrl4j5Y4xJSL+QlKRdW5HyV1gmQLH+BZfY+wbc79qZIFFZ8WV4NJFGAxOqzwXZBKCcUd6JD/Ty+BIG5NZAcJix7/LwaSDMdksImrLxRWAbe+yu45n3wxxucfZysCUU18Nl7wyPX5k/gWCtTRh0zOzeuBmKd6P+EyTPhDecZcO9jxITVI2G8xpgtgBOAh4AjgAdFZGkby/Rz4AAAEZlLMIXuy8B1wPEiMlZEZgNzgPvaWI7cDA6ZZBPWOpvUf7s3+H23wYY7tKdAG8yP/nfPu/VRcPDnYYtEGZ6P1EF4KaadOOtvB3ueW29c45RyaCBJZL6ksfBfcBSQPD4QTyoT23DEl3/gN3DoFxrLlbcHb8/pFSBu1M7aQRbcaVt4tksQIGutV59itagG0owJq7AG4nGiu9SeERM09A3p4d0orOh9aXiMT7gSDv1S/f9RF8GZ96dnzvaWOUuAOOWIT28L9XpWx9fv1eCbgUYS6YA4FXDvRdHyNkmecSCzgD2BvQkmk3oY+Ekby3QZwfS5y4ErgZNNwMPAVQTZgH8JnNmVCKxnfgP/jPpWBgYNVQZ5wzeLmpuF1n1p887rXIjwYZp3WGyxG8Zbgj0+OHwbaVYEWV4BUhkDBy1O1ozKsTDeIjSjgRQyYYV+oHMfqq/LmtwrXq681+mwLwVzp7t5mCyRQYtlOPsPQSRX2nbueT/6BJwc9tinbxluW1AzKoKvd+ym7U/b3js1biyMNz5GIhKFFd2/QdGcdxhse3T9f3V8MM10UbL8PO51+5cbPeutAIkJjEg+O2l8ty15p/0dJnnu/nME4z7+3RjzgTaXB2PMasCbAMoY83ng8+0uQyrfXwRTNoez6zH1a4YMFQZYxVjGEXt410kQIK1KahjBF2mSwFCzsjeHCSvP+rxEGseCx8za3ucDKeJEt9uus3F9XZIGEilXEwJkkz2S507P24inBVOUSoEfab1t8h0r6Th58Jkrj7+iHpacdg6vCcvxgUBjptqiTvQieb0Sj+EIkF1Ob1zfjBMdohm1G4JyelADIdA6LgdOFJG7ReRyETm1zeXqbWJp0AeHhqgywBqfPHZvZDuioXzkOfbMHZPXjZ+Svb+v4XPNUEUG5qURT2VShOH4QPKU13cNahpIi53oaeQWIK65w3Pe2fvAWgXH9DQlQIZhn88yYYEnzYeT+DOXAGlBBJN7jEM8fd6s6+YzYdnj2mM3CJAe1ECMMQ+KyFPAUwRmrJOAfYBLU3ccRVgT1hqch+LoSxpjw7Ne4FaR56Xe56PBy3TbvzWuO2dpfSxFIh4T1nuurWs2rRok6W3cc1JkJHp9YfCVmpjPSWMfp1JUA2lBR6KZZ6lV96cTPhAIknAu+SxM9ARv1kxYKRpIESd6KwSIe55mNJpaDq5xNGggkzYMOrHx+x4fwd4B8vhAHiAYrHcUQUqTfYwxm7a5XL1JglljzeAQFRmMTlk7ZTZsFJsPot0aiJ3oZlKOcZ6lMuzwbv+6cZOjmUd9+BqtUrnegLZq0ORwnOjtisJKy0Jse9etNmH5OMDJClCUIudd+N7kdc34QJJMiydeDW/7tn/ddsfCucv8GQVqJqxQ6Me3KeJE92zTFdwJvyLCaEx9gGj8Hrq+ovgsmG0iz5U6zBjTmRF5vU5Cr3RgyGogKQn0oP0+kH0+Cpvt3zgCOYmJ6weD8pJsz2kU9oE0a8IaRm+9mXEguRrjlCSSNQGaFqXWIgGyz0eDTzPE598uwlu/CdefE/xuZUdo7sHZ2/iIm7CO+BpsvBvc9LHgf8p75+0ndCrFUBq1EfBVvwYCjeV0Tc895AMpicilInITgIhsPWp9IEkCZNCEPpCMAXvt1kBKZdh41/b6VyytisLKIs9AwsQy5NVAPNFJqU708Lh2AiwXq4HEzSgurdJAhkPRcQ0u629bn/CsLcEgBYmnMhm/LuzqOK6HMxK9WxgnhUp8hLlNrBkf4e5qXr1iwgK+D/yKIIEhwOPAue0qUE+T0KgMDA1RYZCBTAGSELPdatrZKOUZSNjKMsRTmRTaN+84EE8Yb5oPZPLMoBd+wo8b11kzwkBKhteIBtKl3u5wBEg8wWW3KcVMWHGK+kB6ATcHV9yJnmRhcJ+lDpmw8ryR04wxVwFDAMaYAciVu3zkkaaByAADERNWFzSQ2nk6oYF0SIAU1UBOvzP/9l4fSI5xIAA7neJ36G6yR/C91rTGdb5ydatBKyRAYkJOmiz/2Uvr403aQlIurMYoLMnjk9t4j9YUK415i/zLTYoJy6f5xumQBpJHn3tdRKYS3gER2Y0gL9boI0GArBkcYkJ5iNWDRXwgXY7CGjYdMmEVNffM2N7ZvgkfiI3AaXYswL4fDyb5Wj9lPEWnnoM0ioR5xuf7KFWo3f8iJqEps4NPqxm3TpBZYY+z/OsjGkhQXpPVQTj/+fbPKx5PCupiy+tzovsCCeL0Shgv8CGCNCKbi8hvgelAwQkARggJAmRwyDC+algxUGbICCUxXdZA2tkoWRNWVg+uRaaZ+IRShfZtwgeyw0mw4tnmndOlcpD3KvW8HQrnTqNIsr29zg0GxP7yE7DqleQR7d2iVIKTrkleH4nCyvkMFU1R7+NdP803pspHxITlPC+VsfkESC840UWkBIwD9gX2AE4HtjHGLOtA2XqQhDDeIcP48hADlFltZbIvPXnbR6KHdMSJ3qMmrEgZmtBAKmPhoM+2pgHJQz840ctV2P546lpHuTcilfIipXq2gPCZyGXCGi5zDoJZOzW3b8SE5WogY2FsjoSovZDO3RgzJCJfNcbsTpADa3Tj0UBWrFzN6oEhxpUHWU2F1VSCdCYj3geSZcJqlQYyjJHozfhAmmWnU5qbmbEfTFgWcQSIJTMfeg8gJTjlRnj+vpq2mWnC6jZJTvTKmHThf+CFcP9lHRPweUxYN4vIMdRTrI9eXAGy5N/grq+yy5ogEmeMDIYaSBVYhV9b6VAUVjPCaWLOsSO5o7DaIEDceh393WwzTFYZx6wVHCOPUzKLt36zuf26FQbbTBRWbQBlGfIknewVpBREzk32JJjsVVwNJO4DSXu39jov+HSIvD6QtYABEXmD4MkxxphhTizRh7jy866vALB6MBAqZRMIkJ8N7s1plV/4X9Be1UD+9d7ovCX5TpJ/0y2PCHpGzZCUyiRp5j6XrGs8blIQGVS47i2kL8N4+2QshcXTkeiICWs42M6qL4y3h8jUn40xE40xJWPMGGPMpPD/6BMekKqul4bWsIYKXxg4AT7+rN+GHvGBtPEBLmoWWW9LmNCksy8Px18B0+Y0t287U5kATJrR3bEB3TJhNdMQ+eZP6Qc813jrDYMmbIeN1+10aYoRH0jYoYmi8tIDIRR9hMcHso08w3mVnzLxzT+z2lQwlGD8Ov79RTqjXjYzzWivMpxR2/0waKxbAmQ4HRgpwTHfha3fDtPmta5M7cJT1z23mMbd5x/AovkzPDv0EPFxIO0OLS5In3UluoxHgFw/5oIgbBc4Yud57LDrPsn7iwSmnAMvbEfp/Jx8fefO1Q7svONDA/lNc0W37ya9EAZbFJEgVPmdP+h2SfKRcI1nTB6GGa9TlMdEO4RZE1V1mEQBIiKzjTFPd7IwPY9HgFjhAbD25CnM26BD4Z95mZ0i0IZFDufpvh8PkjsOl1I1EAh5NQopAwW27yb9UEZLj9nfc9OPQtoSv+ZWAznzflj5t86XJ0aaBvJTYCcRWWKMeUunCtTbZDSanRo70E2KmD72/2RrzlmuwsCqYhrI4Jv90XD0Qxkt77kWll0VJCvsJ/rpGseJh5hbDaSZaXbbQJoAKYnIZ4C5IvKh+EpjzNfaV6weJXWSIfIN8Ol3uhHJbXvp7Zynu1v0U+M2fR685dPdLkVx+ukax4kPSO4xLTDtyh4PvEEgZCZ6PqOPTAEyOi9L2ylVi/kzdjo5+C6SrqNbdLpxO3tpYP4YTfSzAEkyYfUIiV01Y8xjwJdEZJkx5qYOlql3yep9jxsFGkg3xi3EB1NlceBi2P8CqKoAaaAdyQx7nb4WIDENpENZdvOSR9f/nYh8jWAedIA7gM8aY0ZfRl41YXWHUqVYI1AqQakPhAf0duN2wKdgzRvdLsXw6eVrnEVcA5m6RXfKkUAeAXIZsBywQ3/fDXwPOLpdhepZVIDU6aQvpFTpj5DcZujlxq3ZjMS9Ri9f4yziAqTHBhLmESCbG2OOcf4vFpGl7SpQT5PVaCb5QE74CTy1pPXlSWPuoa0JoW2gD0xY/UQ/N279Qj9lDo7jmrCmbN69ciSQR4CsEpG9jDG/ARCRPQmyBY5CmvSBzDs0+HSSE3/S2fO1k1J15Da0I7VevUQ/X2Mr/M57OJg4q8fII0A+AFwuInYWk1eAk9tXpB4mwYT1m3kXsNfKWzs2C1hv0EkTVlk1EKV5RsI1njyr2yXwkilAjDEPAtuLyKTw/2ttL1WvkiBA/v+GB8O+H+twYbpEt6KwRqoPZKQKxl5iJAiQHiX3iKtRLTgsCQKkUtFGoK2oCUsZDv14jU+/C/7S+3P49dGQ3R4gwYleacWMdv1GJ6OwypWR21Pvx8at3+jHazxjfvDpcfrwynaRJA2kOkIbNy9dMGGN6DDePo4Q6hf6UYD0CZkaiIiUgUXApu72mgurTrUyCjWQTlKqjqw5TpTOogKkbeQxYV1PkBPrISBjJN0IJ1GAjNDecSqdNGGNYCe60n5UgLSNPAJkljGm941xHSHBB1IZRa6kbphcxk6CsWt3/rzKyEDNhG0jT8t3k4gcbIy5ue2l6XUSHMdjRpMA6QYHfgZWv97tUij9igqQtpFHt7sH+E8RWSUir4nIP0SkbSG9IrJARO4RkaUi8oCI7BIuFxH5log8KSLLRGTHdpUhkSQTVnUUCpBORmFN3ACm9l4aB0UZ7eRp+b4K7A48ZExHWo0vA4uNMTeJyOHh//2Aw4A54WdX4Dvhd+dIECCjqn9z6BeDEfdbvbXbJVEUpcvk0UCeAJZ3SHhA4GiwSaUmAy+Ev48ELjcB9wDriMiMDpUpLJn/EsxcZ3xHi9FVJm4Ab/+/PZcVVFGUzpNHA3kR+LWI3AS8aRe2MYz3XOBXIvIVAgG3R7h8JvAnZ7vnw2UvujuLyGnAaQAbb7xxa0uWoIGsN6lP5p5QFEVpIXk0kKeBJcAYWjSlrYjcKiLLPZ8jgTOA84wxGwHnAZfa3TyHalAJjDEXG2MWGmMWTp8+fTjF9JxtdEcxK0pfseCkbpdgxJMnmeLiVp/UGHNg0joRuRw4J/x7NXBJ+Pt5YCNn01nUzVsd4YUVr7NhJ0+oKErzHPnt4KO0jTwj0W/H39M/oC0lCoTCvsCvgQMIfDAA1wEfFJErCZznrxpjXvQeoU185OoH+dGY7O0UJZNTfgEvLut2KUY2Gr7bdvL4QD7i/B4HHAMMtKc4ALwf+KaIVAhGwJ8WLr8ROBx4ElgJ/Esby+Cl1MnR18rIZtO9go+i9DF5TFi/jy36rYjc0abyEM58uJNnuQHObNd581Aa5ZlcFEVRXPKYsKY4f0sEjfsGbStRD6MKsaIoSp08JqzfE/hAhMB09TRwajsL1auIaiCKoig18piwZneiIP2A+kAURVHqJI4DEZGdRWQD5/97ROTaMB/VlKT9RjIqQBRFUeqkDSS8CFgNICL7AF8ELgdeBS5uf9F6j5KoAFEURbGkmbDKxpi/h7+PAy42xlwDXCMiS9tftN5jjM5LoyiKUiOtSSyHYzEA3gLc5qwbhfnLYYxOiqcoilIjTRD8GLhDRF4GVgF3AYjIFgRmrFFHtSSjfVJfRVGUGokCxBjzeRFZAswAbnbSuZeAszpRuF5jTFkFiKIoiiXVFBXOuxFf9nj7itPbjCkbWNPtUiiKovQG6hYuQFWvlqIoSg1tEgugF0tRFKWOtokFMDqhlKIoSg0VIAVQAaIoilJHBUgRhlSAKIqiWFSAFMCoAFEURamhAqQAasJSFEWpowKkACpAFEVR6qgAKYIKEEVRlBoqQApQz+aiKIqiqAApgjrRFUVRaqgAKYD6QBRFUeqoACmCChBFUZQaKkByYoxRH4iiKIqDCpCcDBkQnQxEURSlhgqQnAwMDVFCNRBFURSLCpCcDA4ZFSCKoigOKkByMjBkEBUgiqIoNVSA5GRwUDUQRVEUFxUgORk0qoEoiqK4qADJSeAD0SgsRVEUiwqQnAQ+EEVRFMWiAiQng4OGkqgGoiiKYlEBkpOBoSH1gSiKojioAMmJjgNRFEWJ0hUBIiLvEJGHRWRIRBbG1p0vIk+KyGMicoiz/NBw2ZMi8olOlzlxHMjcwzpdFEVRlJ6g0qXzLgeOBi5yF4rI1sDxwDbAhsCtIjI3XP1/gIOA54H7ReQ6Y8wjnSqwVwO54M9QqnaqCIqiKD1FVwSIMeZRAJGGuKYjgSuNMW8CT4vIk8Au4bonjTH/He53ZbhtRwTICytW8a0lT7BjXIBUx3fi9IqiKD1JtzSQJGYC9zj/nw+XAfwptnxX3wFE5DTgtPDvP0XksWGUZxrwsrvgDPfP4hEZ2NtQ51GA1nl0oHXOzyZ5NmqbABGRW4ENPKsuMMZcm7SbZ5nB76vxerSNMRcDF+cqZAYi8oAxZmH2liMHrfPoQOs8Omh3ndsmQIwxBzax2/PARs7/WcAL4e+k5YqiKEoX6LUw3uuA40VkrIjMBuYA9wH3A3NEZLaIjCFwtF/XxXIqiqKMerriAxGRo4D/AKYDvxCRpcaYQ4wxD4vIVQTO8QHgTGPMYLjPB4FfAWXgMmPMwx0oaktMYX2G1nl0oHUeHbS1zqLzfCuKoijN0GsmLEVRFKVPUAGiKIqiNIUKEA/dTpvSLkTkMhF5SUSWO8umiMgtIvJE+L1uuFxE5FvhNVgmIjt2r+TNIyIbicjtIvJomD7nnHD5iK23iIwTkftE5MGwzovD5bNF5N6wzj8JA1IIg1Z+Etb5XhHZtJvlHw4iUhaRP4jIDeH/EV1nEXlGRB4SkaUi8kC4rGPPtgqQGCJSJkibchiwNXBCmGJlJPB94NDYsk8AS4wxc4Al4X8I6j8n/JwGfKdDZWw1A8CHjTFbAbsBZ4b3cyTX+03gAGPM9sAC4FAR2Q34EvD1sM6vAKeG258KvGKM2QL4erhdv3IO8KjzfzTUeX9jzAJnvEfnnm1jjH6cD7A78Cvn//nA+d0uVwvrtymw3Pn/GDAj/D0DeCz8fRFwgm+7fv4A1xLkVBsV9QYmAP9FkLnhZaASLq895wTRjbuHvyvhdtLtsjdR11lhg3kAcAPBwOSRXudngGmxZR17tlUDaWQmjWlTZiZsOxJY3xjzIkD4vV64fMRdh9BMsQNwLyO83qEpZynwEnAL8BSwwhgzEG7i1qtW53D9q8DUzpa4JXwD+BjU5p6eysivswFuFpHfh2mcoIPPdq/lwuoFktKpjDZG1HUQkbWBa4BzjTGveRJ51jb1LOu7eptg/NQCEVkH+E9gK99m4Xff11lEjgBeMsb8XkT2s4s9m46YOofsaYx5QUTWA24RkT+mbNvyOqsG0khaOpWRyF9EZAZA+P1SuHzEXAcRqRIIjyuMMT8LF4/4egMYY1YAvybw/6wjIrbT6NarVudw/WTg750t6bDZE3ibiDwDXElgxvoGI7vOGGNeCL9fIugo7EIHn20VII2MtrQp1wEnh79PJvAR2OXvCSM3dgNetWpxPyGBqnEp8Kgx5mvOqhFbbxGZHmoeiMh44EACx/LtwLHhZvE622txLHCbCY3k/YIx5nxjzCxjzKYE7+xtxph3MYLrLCJrichE+xs4mGCupc492912AvXiBzgceJzAbnxBt8vTwnr9GHgRWEPQGzmVwO67BHgi/J4SbisE0WhPAQ8BC7td/ibrvBeBmr4MWBp+Dh/J9QbmA38I67wc+F/h8s0Icss9CVwNjA2Xjwv/Pxmu36zbdRhm/fcDbhjpdQ7r9mD4edi2VZ18tjWViaIoitIUasJSFEVRmkIFiKIoitIUKkAURVGUplABoiiKojSFChBFURSlKVSAKEoORGQwzHhqP6lZmkXkAyLynhac9xkRmTbc4yhKO9AwXkXJgYj80xizdhfO+wxBvP7LnT63omShGoiiDINQQ/hSOP/GfSKyRbj8QhH5SPj7bBF5JJyD4cpw2RQR+Xm47B4RmR8unyoiN4dzWlyEk79IRE4Kz7FURC4KEyaWReT7IrI8nBfivC5cBmWUogJEUfIxPmbCOs5Z95oxZhfg2wT5l+J8AtjBGDMf+EC4bDHwh3DZJ4HLw+WfAX5jjNmBIPXExgAishVwHEHyvAXAIPAugvk+ZhpjtjXGbAd8r4V1VpRUNBuvouRjVdhw+/ix8/11z/plwBUi8nPg5+GyvYBjAIwxt4Wax2RgH+DocPkvROSVcPu3ADsB94eZhMcTJMm7HthMRP4D+AVwc/NVVJRiqAaiKMPHJPy2LCLIQbQT8Psw+2taam3fMQT4gQlmnltgjJlnjLnQGPMKsD1Bxt0zgUuarIOiFEYFiKIMn+Oc77vdFSJSAjYyxtxOMNnROsDawJ0EJijC+SteNsa8Flt+GLBueKglwLHhvA/Wh7JJGKFVMsZcA3wa6Ls53JX+RU1YipKP8eEMf5ZfGmNsKO+YyWVsAAAAjUlEQVRYEbmXoEN2Qmy/MvDD0DwlBPNzrxCRC4HvicgyYCX19NuLgR+LyH8BdwDPARhjHhGRTxHMPlciyKh8JrAqPI7tDJ7fuiorSjoaxqsow0DDbJXRjJqwFEVRlKZQDURRFEVpCtVAFEVRlKZQAaIoiqI0hQoQRVEUpSlUgCiKoihNoQJEURRFaYr/Afdp/EpCgl4+AAAAAElFTkSuQmCC\n", "image/svg+xml": [ "\r\n", "\r\n", "\r\n", "\r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", "\r\n" ], "text/plain": [ "
" ] }, "metadata": { "needs_background": "light" }, "output_type": "display_data" }, { "name": "stdout", "output_type": "stream", "text": [ "Sarsa Optimal Policy:\n", "['D', 'L', 'R', 'R', 'R', 'R', 'R', 'D', 'R', 'R', 'R', 'D']\n", "['R', 'R', 'U', 'U', 'U', 'R', 'R', 'R', 'U', 'U', 'R', 'D']\n", "['U', 'U', 'U', 'U', 'U', 'L', 'U', 'U', 'U', 'U', 'R', 'D']\n", "['U', 'U', 'U', 'U', 'U', 'U', 'U', 'U', 'U', 'U', 'U', 'G']\n", "Q-Learning Optimal Policy:\n", "['L', 'R', 'R', 'R', 'D', 'D', 'R', 'R', 'R', 'R', 'D', 'D']\n", "['D', 'D', 'D', 'D', 'R', 'R', 'R', 'R', 'D', 'D', 'R', 'D']\n", "['R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'R', 'D']\n", "['U', 'U', 'U', 'U', 'U', 'U', 'U', 'U', 'U', 'U', 'U', 'G']\n" ] } ], "source": [ "figure_6_4()" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "由上图可以看出， Q-learning 学习了最优策略，但是智能体偶尔会调入悬崖（因为是贪心探索策略）。\n", "\n", "虽然 Q-learning 学到了最优策略的价值，但是在线性性能却比学到迂回策略的 Sarsa 差。但如果 $\\epsilon$逐渐减小，那么两种方法都会渐进地收敛到最优策略。" ] }, { "cell_type": "code", "execution_count": 5, "metadata": {}, "outputs": [ { "name": "stderr", "output_type": "stream", "text": [ "100%|██████████| 10/10 [00:30<00:00, 3.28s/it]\n", "100%|██████████| 10/10 [00:25<00:00, 2.80s/it]\n", "100%|██████████| 10/10 [00:25<00:00, 2.86s/it]\n", "100%|██████████| 10/10 [00:24<00:00, 2.73s/it]\n", "100%|██████████| 10/10 [00:25<00:00, 2.93s/it]\n", "100%|██████████| 10/10 [00:24<00:00, 2.71s/it]\n", "100%|██████████| 10/10 [00:25<00:00, 2.80s/it]\n", "100%|██████████| 10/10 [00:26<00:00, 3.05s/it]\n", "100%|██████████| 10/10 [00:24<00:00, 2.72s/it]\n", "100%|██████████| 10/10 [00:25<00:00, 2.90s/it]\n" ] }, { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAEKCAYAAADTgGjXAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzsnXd8VceZv5+5/V71hoQQkhCIDhICCTC4YGyKsbGNU5zNJo4Tx5viJC4pju1f1ptN2/TibIrtxHE2LnFiHBeaMRibXgQCAQJEVQP1evs98/vjXF1JIEC9MY99P2fOzJxz3iuJ+Z73nSaklCgUCoVC0RMMg22AQqFQKIYvSkQUCoVC0WOUiCgUCoWixygRUSgUCkWPUSKiUCgUih6jREShUCgUPUaJiEKhUCh6jBIRhUKhUPQYJSIKhUKh6DGmwTagv4mPj5fp6emDbYZCoVAMG/bt21ctpUzoSt0RLyLp6ens3bt3sM1QKBSKYYMQ4mxX6w65cJYQ4idCiCIhxEEhxGohRHS7sm8LIYqFEMeEEEsH006FQqFQDEERAd4FpkspZwLHgW8DCCGmAvcC04BlwP8KIYyDZqVCoVAohp6ISCk3SCn9wdOdQEowfSfwipTSI6U8DRQDeYNho0KhUCh0hpyIXMRngbXB9BigpF1ZaTDvEoQQDwoh9goh9lZVVfWziQqFQnHtMigd60KIjUBSJ0VPSin/FazzJOAH/tZ6WSf1O90MRUr5R+CPAHPmzFEbpigUCkU/MSgiIqW85UrlQoj7gNuBxbJt16xSYGy7ailAef9YqFAoFIquMOTCWUKIZcC3gJVSSme7ojeBe4UQViHEOCAT2D0YNioUCoVCZyjOE3kGsALvCiEAdkopvyClPCyE+DtwBD3M9WUpZWAQ7VQoFFKC1PS0MIDoLOo8hJASAj7QfBDwQsAfTPva5bce/Xqd1nSn13hB8190bbBZCv08RMfjJXmXq2dol0cneVe5h9kOU1f2+490yImIlHLCFcq+D3x/AM1RKPoOKcHvAb+77eNrn3YFy4PHrpxrfr0R1wL6UQbanUv9/JIyre28y2Wy43lrutNuyYsbQcNlzsWVy7tTt/W8U0HwtzX419J7Z9ioa1NEFIpBRdPA2wTuRvA0Bo9NwXRDW9rbcqkIdOW8NxgtYLK1+1j1PGEAgyHYoBrBYGyXNun1LikLfgxGPT+U7kGZaI2KB72SkHfS2bm8SvnF53SjrtS/r9Gs/1xa0wZzMK81bQqWt+Z15ZqL0obgPdpfHyoLTl9r/a5cdGxv75XyoO07dijrLO/iezBgXqESEcXIwe9pa/wvEYCL84NlF6e9TVd/jjCAJVxvyM22jg272Qa2yI7nF5eH0na9gTcFj52etxMMg5pbO6wQYsAa8sFEiYhi4NE08Dn1cIyvRT96ncG84KfDuUt/8289XiwGrWIR8Fz92SY7WCP0ht4aqacjEsEadWl+a9oWLLNG6nlmxzXROCgUXUGJiOLySAnuemipAVdtsCG/qFG/oghcprwnYZ3WN3dzWFvjHpYAcePbGndrhC4GofRF+dYIMFn6/uekUFzDKBG5lgiJQrX+cVZDS5UuEs5gXksVOGvayjX/1e+LAEuY/oZutgfTdv08PAksjmCZoy3/4rzQNcHjxeUqlKNQDEmUiAxnNE0XBWdNUAxahSF4HhKGYL6z5vKiYI2EsHhwxEN0KiTP0t/0W/MccW0NfXuRMDuCHbcqvKNQXIsoERnKNJTBqc3QWN7OS6ju6DlcbsiiNQrC4nQBiEmHlNl6OiQMcfoxLEFPm6wD+tUUCsXIQInIUEJKqCiAY2vh2Bo4f7CtzBoVbPRbRWFOm5fQmt+a7gdRCGidL0HWmf9xsVMilJeiUIxYlIgMNj43nPlQF41j66CpXB9CmpIHt/wXTFwKseP7tENY0yT1Lh+1LV7qnF792OKl1umltlk/6uc+/djipdnTlb6R3tGZ1lycZTQIHBYTYRYjDmvwaDERZr3oeNVyEw6rkTCLCZvZoIROoeghSkQGg5ZqOL4ejq+F4k36CCZzGEy4GSb9P8hconsUXUBKSYs3QF2Ll5pWMWgvDk4vNc3tz33UO71cxrHAbjYSG2YhNsxCTJiFcXEOYsIsRNrMGA3iomd3Ys9FM5g7r9PpF+lSPV9A4vL6afEGcHr9tHj0Y3m9Tz/3BnB69GNXEQJdVCxGwqzBYzuR6ZAfPCZEWJmcFEl6nAOTccgtQadQDBhKRAYCKaH6eJu3UbILkBCRDFn3wqTbIH2hPhGtHeX1LgpK6qls8lxWGOpafHgDWqePNRkEMWEWYh0WYsLMTE6KJCbMHDwPCoXD0iYaDgt2y8gYBaVpErc/EBKZ0LGdyHTIv6TcT22Ll5JaJ05vgJbgNReH9awmA5mJ4UxOimRyUgRTRkcyKSmC+HDVx6S4NlAi0l8E/HBuh96/cXwt1J7S80dnwU2Pw6TlkDQzFMPxBTSOltaz72wd+87WkX+2jvKGjvMpouxm4oIeQkqMg5kpUcSEWfQ8R5v3EOuwEBtuIcJqumbDNIZg2MthMaGv59l7pJR4AxotngAVDS6KKpooOt9I0fkmthyv4h/7SkN148OtTBkdweSkCCYFBWbCqHBs5pEh0gpFK0pE+hJ3AxRv1L2NExv04bdGC4y7EeY/BBOXQZS+GWO900v+scqQaBSUNODy6SGY5Cgbs9NjeTA1mlmpMYyJsRNtN6uwySAjhMBqMmI16SG/aclRHcqrmz0cO9/E0YpGjp1vouh8Ey/uOIvHr3uKRoMgIz6MSUGPZXJSBJNHR5IcZbtmxV4x/BGys6D1CGLOnDly7969/feAujO6aBxfC2e26vMwHHG6YExaDhmLkJYwTlW3sO+MLhj7ztVRXNkM6A3LtORIZqfFMDsthpzUGJKj7f1nr2JA8Qc0ztQ4g6LSyNGg91Ja5wrVibCZdEFJimRy0HuZmBhBhM08iJYrrmWEEPuklHO6VFeJSDfRNCjPDw7DXQuVh/X8+Em6aExajmtUDgfLm9gbDEvln6ujzukD9JBUq2DMTothZkpUMOSiuJZocvs4fqEpJCrHzjdRVNFEU7tRcGNj7aG+llaBSY8Lu2SAg0LR1ygRaUefiIjXCae3tHWMt1Tqy2CnXQeTllOVfDO7G6KDoalaDpc34g92wI5PCGN2Wgxz0mLJSYshIz4Mg2oEFJ0gpaSsXu9rOXZBD4sVnW/iVFVzaDSd1WRgYmJEKBSWER9GcrSdMTF2wq3qZUTRNygRaUePRaTpAhxfp3sbpzbriwZaI9HGL6YscRFbyWZHuca+s3WU1euhCZvZQFZKtC4a6THMGhtDTJha8E/RO9y+AMWVzRSdb6IoKCxF55uobu64anGU3cyYaDvJ0XZSYuyMCYpLcrSejg+3qL4XRZdQItKOHomI1wn/kw4BD1pUKmWJN7HTlMeb9ensK23BGZyDkBRpY3Z6DLNTddGYMjoSs+r8VgwQVU0eztU6Kat3UVbnorzeFUqX1bsumSBqNRlCItMqMO1FJynKpv5+FUD3RET5v53gMVh5I/mbvFeXwIYLcXBBYDQIpo4WfGzOWHLSYpiTpjrAFYNLQoSVhAgrs9NiLimTUtLo9ocEpazOSXmDm7I6F6X1Lt4rqrzEkzEISIy0XSIy7dNhKmSmuAj1F9EJFqOBPzflMTrOxtdzYshJiyF7bLTqAFcMG4QQRNnNRNnNTE2O7LSO2xegIigsZfVOyurb0vtL6lhzqCLUt9dKa8isvcCkxNhZmBmvRpNdowzZcJYQ4uvAT4AEKWW10IO5vwJuA5zAZ6SU+Ve7T78P8VUoRigBTVLV5KGs3klpnYvyercuNnVtYbPW5WViwyx8edEE/n1eKlaTmlA53Bn24SwhxFjgVuBcu+zlQGbwMxf4XfCoUCj6AaNBkBRlIynKxuy0S8ullDS6/Bw938hvNp3gv98+wp+2nubRWydy16wxaijyNcJQ7UX7BfBNOq7BdyfwotTZCUQLIUYPinUKhUIPmTnMzMuI428PzOOvn8sjJszMY68VsOLXH7Kp6AJDNdKh6DuGnIgIIVYCZVLKgouKxgAl7c5Lg3kKhWIIcH1mAm9+eSG/+cQsXL4An31hLx//w072na0bbNMU/cighLOEEBuBpE6KngSeAJZ0dlkneZ2+5gghHgQeBEhNTe2hlQqForsYDII7spJZNj2JV/aU8KuNJ7jnd9u5dWoi31w6iczEiME2UdHHDKmOdSHEDOA99I5zgBSgHMgD/gt4X0r5crDuMeAmKWXFle6pOtYVisGjxePnz9tO84ctp2jx+rknJ4VHbp2ohscPcUbMZEMhxBlgTnB01grgIfTRWXOBX0sp8652DyUiCsXgU9vi5X83F/PijrMg4L75aXzppglqRYchSndEZMj1iVyBNcApoBh4FvjS4JqjUCi6SmyYhadun8qmr9/IHTOTeW7raW748WZ+u7kYp7f/t15W9B9D2hPpC5QnolAMPY6db+In64vYeLSShAgrX1ucycdzx6plV4YII9UTUSgUI4RJSRE8d18ur31hPmmxDp56o5Alv/iAtw+Wq2HBwwwlIgqFYtDITY/ltS/M57lPz8FsFDz00n5WPrONrSeqB9s0RRdR4SyFQjEkCGiS1fvL+MW7xymrd7FwQjzfWjaZGSlRV7/4GkdqEi0gCQQ0NL9+lJokPMbWo/uNmNFZfYESEYVieOH2Bfi/nWf57eZi6pw+VswczdeXTGJcfNhgm3ZFPE4fDVUumus8BPwaml8jEJD60d+xge9wvLhu6NhWfmlZ6331Opp2aTvuiLRw/48X9ui7DPu1sxQKxbWLzWzkgesz+FjuWJ794BTPfXia9YXnuTdvLF9dnMmoiJ69XfcWKSXuZl0oGiqd+rH1U+nC3eLr8r0MJoHRaAgdjaZg2mTAYGx3NBsw20wYW8tC1xkwGkXHY+h6PW22DcxCmMoTUSgUQ5rKJje/ea+Yl3efw2w08LmF43jwxgwi+2HpeSklzgYvDVVO6ivbBKKxWhcOrzvQVllARIyNqFF2ohLsRCbYiU5wEB5rxWQ2hkShgzCYBAaDGPI7TKpwVjuUiCgUI4Mz1S387N3jvFVQTozDHFx6Pg2buXtv3Jomaa51X+RJ6J5FY5ULv08L1TUYBBHxNqIS7EQlOPRjq2jE2TGaR+bYJCUi7VAiolCMLArLGvifdUV8eKKa5Cgbj9w6kVU5KR2Wng8ENJqqW4XCSUOli4bqNq9CC7S1e0aTgcgEe5tAxLcKhYOIWCuGa3DuihKRdigRUSj6Hyn1zl0Z0EcJacHRQvpHC53Ly+SHygNtI4uudp+zVS3sKK6mpslDrMNCzphoIgLQWOWiqdaDbNfZbLYag+GmNoFoDUGFR1sRau+TDqiOdYVC0adIKXG3+Ki/4KL+gpP6SicNlU7qL+hv+n6vdvWb9DUCJhgF47HgaZCU19diCDcxJTOWiXlJwRCUnahRDuwR5iHfDzFcUSKiUChCeN1+Gipd1Fc624mFLhweZ9saVwaD0N/sEx2kTI7BYjdhMAgMRv0jDAJj8GgwGkL5rXX0cgPionw9bQjVCeWF6hg63KMVX0DjD1tO8vN3jzO2QeOZ21KZrOaXDAgqnKVQXGME/BqN1UGP4kJHwXA2eDvUDY+1Ej3KoX8SHUSN0oUjMs42JPsK9pyp5asv76e62cMTt03hM9elKw+kB6hwlkLRAwJaAK/mxRvw4tN8+AI+vJo3dGyfH5ABhBC0/qf/L0J5BqE3sO3zWo8ABmHomNd6fSf1L1fPIAwIoR8N6GmjMOp1pcBV76e52ktzpZfGKg+NVW4aK90017hp/+5ojzATleAgdWos0YltghGZYMds6dlcAyklfs2PJ+DBE/DgDXg7pN0Bdyjv4rKr5mmX5nkD+u/HIAxEZJrwNwf4SaHk98VW0mIjsJusmAym0MdsMLedi455Fx8ve13w3Gwwt93DaMZitBBrjSXGFoPNNDhzWgYSJSKKIYOUEnfAjdPnxOl34vQ5cfldtPhaOpz7NJ/eaAQb+Nbzy+V7tXai0FqvE7HQ5CDE9XuDBLsvgih3AlHuBKJdo0LHSHc8Jtk2j8JrcNNgr6LBVkV9cmUwXUmDvRq/2aOLEQaMNUZEjcBQ1CZKrYJnEIYOH4HAaDAiEKGfdfuGXXa+8WiXMRvMWI1WLEYLVqO1Q9pitBBuDsdiayszG8wEZAC/5sef4OdEVT3HLzRw3B1gYhLYLX7cfjc+zYdf+vEFfHpd6cev+fV8zR/6BGTg6kZehTBzGDHWGGLtscTaYomzxRFr09MxtphQOs4eR7Q1GpNh+DXJw89ixZCgtcFv8bXg8rn0Rj7Y0Dv9Tr3hv0gMLpvfeu53drshNwojFqMl9EZoMVouOTcbzHqDY7VgNnbM76yuxWjBYui8bmu+QRhCq81KJFLKDkcATWod82Swbif1Q8d29ULXI5EaeOvAcx48FwTeCwa8Fwxo7nahGoPEGB3AODqAIcaLiG5BRPkg2ovDHiCSAClEo8lINJmBJrXQRyIJyIA+yqpdfmtZZ3kBGdDTUoZ+Pp019l3J66xOqzfXGw6W1vPQS/vZd9bFo7dO5Is3jsfQxZFYmtRCguLTfJeITAfhaRWigA93wE2du45ad22HT3lzOYXVhdS56y4rUNHW6A7i0io8HfLsel6EJaJPfka9RfWJDFECWoDDNYfZe2EvTp+zR//QNamhoYX+oV9ybWdlXHTfYFlABjo2+D5nl980DcJAmCkMu9mOw+TAYXYQZg7T08Fzu8mu55nb8tqXt57bTLa2xtxgxmgYmKUdBhItoFF33klVSRNV5/RPdUkzPo/e8BhMgrjkcBJSI4gdHUZ0kh6CulbnNFyNRrePJ14/xNsHK7g+M56ffyybhAjroNmjSY0mbxM17hpqXbWXiM3FnwZPQ6f3MQkT0bboDoLT6tXEWGNIcCRwQ8oNPbJRzRNpx3ASkWpXNdvLt7O1dCvbK7Z3+OMJhRG4KKQQjIkbhfGqIYdOy1rDFeKicjo+wyiMlzToXTmGmcOwGCyqc/MyBHwatRUtIbGoKmmiurSZQHDWtMlsIH5sOAljI4hPjQgJh9GkxKI7SCl5ZU8JT795mAibmV9+PJuFmfGDbVaX8Gk+GjwN1LhqLhGYOnedLkbu2pAgOf1OAOLt8Wz+2OYePVOJSDuGsoj4NB8Hqw6yrWwbW8u2crT2KACxtlgWjlnIguQFzE+eT4wtZpAtVfQFPm+AmtLmkFhUnWuitrwlNHvaYjMSP1YXioTUCBLGRhCd5Ohy+EVxdYrON/LQS/s5WdXMl2+awMO3ZGIaYd6b26+H01p8LUyImdCjeygRacdQE5HzLedDorGzYifNvmaMwkhWQhYLxyxk4ZiFTIqdNCRinYqe43X5qS5toupcm2jUVbSERkXZwswkpEWQMDY8JBxR8XY1c3oAcHr9PP3mYf6+t5Tc9Bh+/YlZjI6yD7ZZQwolIu0YbBHxBrzkV+aHhKO4vhiAREdiSDTmjp5LhCVi0GxU9A53s6+t/yJ4bKh0hcrDoiwkpAbDUUHBCI+xqhDfIPOvA2U88fohzCYDP/1IFrdMTRxsk4YMSkTaMRgiUtJUwraybWwr28au87tw+V2YDWZyEnO4fsz1LEhewPjo8aoRGYZoAY2Kkw1UFNeHvIymWneoPCLOFgpFJaRGED82nLCowevEVVyZ09UtPPRSPofLG/nsgnE8vnwyFtXfNPxFRAjxFeAhwA+8I6X8ZjD/28DngADwVSnl+qvdayBExOV3sff8XraV697G2cazAKSEp4S8jdykXBxmR7/aoegffJ4AJUdqOVVQxZlD1Xha9OU/ohMdejiqXR+GLazv97hQ9C8ef4Afrinihe1nmJkSxW8+MYu0uKG9i2J/0+ciIoSwA6lSymO9Na4Lz1oEPAmskFJ6hBCjpJSVQoipwMtAHpAMbAQmSnnlGUH9ISJSSk43ng55G3sv7MUT8GAz2shNymXBmAUsHLOQ1IhU5W0MU5yNXs4cqub0gSpKiuoI+DSsDhNpM+LIyEogZUosVruaZjWSWFd4nm/+owBNwg9XzeCOrOTBNmnQ6NNlT4QQdwA/BSzAOCFENvBdKeXK3pl5Wb4I/EhK6QGQUlYG8+8EXgnmnxZCFKMLyo5+sqMDLb4WdlXs0oWjfBtlzWUAZERl8LFJH2Nh8kJyEnOuiWUORir1F5y6t1FQTcWpBpAQEWtj2sJkxmUnMHpCFMYRNpJH0cay6UlMHxPJV17ez1de3s/2k9V85/Zp2Hu49Mu1QldepZ5Gb6zfB5BSHhBCpPebRTARuF4I8X3ADXxdSrkHGAPsbFevNJjXL0gpOV53nG3lureRX5mPX/PjMDmYN3oen53+WRaMWcCY8H4zQdHPSE1y4Wwjpw9Uc7qgirrzwfH1Y8PJXTGOcVnxxKeEK2/yGiIlxsHf/2M+P9twnN9vOcm+s3X89t9yyExUA18uR1dExC+lbOjLf0hCiI1AUidFTwZtigHmAbnA34UQGUBnBnQaixNCPAg8CJCamtpt+9x+N7evvp0LzgsATIqZxKenfpqFYxaSnZCN2aji3sOVgE+j9Fid7nEcrMbZ4EUYBMmZ0Uy/cQzpM+OJjFPDPa9lzEYDjy+fzPzxcTz66gHueGYr3105nY/OSVEvFJ3QFREpFEL8G2AUQmQCXwW29+ahUspbLlcmhPgi8LrUO2t2CyE0IB7d8xjbrmoKUH6Z+/8R+CPofSLdtc9msrEiYwXpkeksGLOAUY5R3b2FYgjhbvFxtrCG0wVVnDtci88TwGw1kjotlnFZCaRNj1Md4opLuHFiAmu/dj0Pv3qAb/7zINtPVvO9u2cQblV9Ye25ase6EMKB7iEsQfcG1gP/LaV0X/HCnhokxBeAZCnld4QQE4H3gFRgKvASbR3r7wGZg9Gxrhj6NNW6OV1QxemCasqP16NpEkekhfSseMbNjCdlcgwms4p1K65OQJP8dnMxv9x4nLS4MH7ziVlMHzOyN7wa1kN8hRAW4E9ANuBF7xPZFCx7Evgs+tDfh6WUa692PyUi1wZSSmrKmjkV7N+oLmkGICbJwbisBMZlxZOYHqlmhCt6zK5TNXz1lf3Utfh44rbJ3DeCN7zqExERQrzFZfocAPpxdFafokRk5KIFNMqLG3SP40C1PulPQNK4KMZlx5ORlUB0opqbo+g7alu8fP21AjYVVbJkaiI/+UgWUY6RFwrtKxG5MZhchd4J/n/B808AZ6SUT/TW0IFAicjIwuv2U3KkltMF1frEP6cfo8nA2CkxjMtOIH1GPI5Iy2CbqRjBSCl5futp/mddEaMibPz6E7OYnTayFknt03CWEOIDKeUNV8sbqigRGRnUlrewf8NZTuytJODXsIaZSJ8Rz7iseMZOicViU52dioHlQEk9X3k5n/J6N0/MHcVH7HW4Cw7gv1BJ+PULCV+0CGNk5GCb2SP6eo/1BCFEhpTyVPDm44CE3hioUHSV86cbyF93ltMF1ZgsBqYsGM2EnFGMnhClNmAaZKTPR/OWLTSu34AxIgLbtKnYpk7FOn48wjJyvUHp9+M+dozUAwf4a0U+53fsIer1Kn2oqNmMMTKSxrffBrOZ8OuuI2LpUiIW34wxamR2xndFRB4B3hdCnAqepxOcg6FQ9AdSSkqO1JK//ixlx+uxOkzkrkhnxqIU7OEjt3EaLnhOnKD+9dU0vPkmgZoajDExSI+HupdeAkCYzVgnTsQ2daouLFOmYJ00CYNteK7m4K+rw3XgAK79B/TjoUNIl75KsykhgZS8WRyNS+PX5+1Uj07nZ/fOZpargsZ162lav57mLVuoMJsJmz+PyKVLiVi8GGN09CB/q76jq2tnWYHJwdOi1iVJhgMqnDV80DTJyfxK8tefpbqkmbBoK9m3jGXqwmQVrhpkAk1NNL6zhvrVr+MuOAgmExGLFhG16m7Cr78eDAa8Z8/iPnKk3ecoWkNwd06jEWtGRpuwTJ2KdfIUjOFDa6FDGQjgKT6Ja//+oHDsx3tWX1AVkwnb5MnYs7Oxz8rGkZ2NKTk5NELraEUjD72Uz7laJ9sev5lRETaklLgLC2lct46mdevxlZWByUTY3LlELFtKxC23YIoZev0pfd0nYkZfz6q1D+R94A9SSl9vjBwolIgMfQI+jaKdFezfcI6GKhfRiQ5mLUll0twktQ3sICI1Defu3dS//jpNG95Fut1YMzOJumcVUXfcgSku7srXS4mvrBz30XbCcvgIgepqvYIQWNLSOgiLbcqUAX1LDzQ24iooCHoZ+3EVHERraQHAGBvbQTBs06djsF95NYODpfWsfGYbv7o3mzuzOy6JJKXEffgITevX0bhuPb6SEjAaCZubR8TSZUTcegum2Nh++67doa9F5DnADPwlmPUpICClfKBXVg4QSkSGLl6Xn8IPyyh4rwRng5dRaRHkLEtjXFaC2hJ2EPGVlVH/xhs0vL4aX1kZhogIIm9fQfSqe7BNn9bruRG+ysqLPJYj+MsrQuXm5OQ2UQl+TAm974aVmob39GlcBw7gDHoa3uKTeqHBgHXixJBg2GfNwjx2bLe/a0CTZH93A7fPHM0PV828vC1S4jl6lMb1G2hat073dgwGHHl5RC5dQsStt2KKH7w94PtaRAqklFlXyxuqKBEZejgbvRzcVMKhLWV4XX5SJseQsyyNlEkxw2LyluZyIX2+YTvypjM0j4emjRtp+OfrtOzYAVLimD+P6FX3EHHrLf3en+Gvq8Nz9GgHjyUURkLve+jgsUydimn06Cv+vQSaW3AfOhgSDFfBwVB4zRAVhT07KyQYtukz+iy09sBf9lBc2cz731jUpfpSSjzHj4dCXt7Tp3VBmTOHiKVLiFyypE9EtDv0tYjkAx+VUp4MnmcA/5BS5vTa0gFAicjQobHaxYF3z3FkewUBv8b47ARylqUxKm1oN8aay4XrwAFadu3CuWs3rkOHwO/Hkp6OPSsLW9ZM/ThxIsI8fCaetYZXGl7/Jw1vv4PW2Ig5OZmoVauIuusuLCmDu0J1oLm5o7AcOYLn5CnQNACM0dHYpk4JiYo5LQ3PiRNSOAfeAAAgAElEQVShTnDPiROhutbMCXpoKigalvR0hKF/QqXPfXiK771zlB3fvrnbe7dLKfGcOEHTuvU0rl+P9+RJEALH7Nn6KK8lSzAn9v9afn0tIouBPwOn0NfOSgPul1Ju7q2hA4ESkcGnpqyZ/PX6HA8hYNK8JGbdmkpM0tDqVG1F83hw7T+Ac/cuWnbvxl1wEOnzgdGIbfo0wvLmYggLw3XwIK6CAgI1NQAImw3btGnYs7Kwz5yJPTsLc1Jni1UPLv7aWhrfeov611fjOXYMYbUSsWQJ0avuxjF3br81rr1FSom3oZ7GQ4doPFxI84kTNJ85jfPCBXxI/MEh3wazBUtSEubkZKwpKVhSxmAMC8NgMCCCH4PB2C5tuCRtEAaEwYjB2Fpm7LReW7qtvLjOx93P5fPzj2WxKielV9/ZU1wcGuXlOXEChMA+axaRy4KC0k9/X/2xs6EVmIQuImp0lqJLVJxsIH/dGc4cqsFkNTLt+mSyF48lPGZoDfXUvF7cBQW07NqNc9cuXAUFSK8XDAZs06bhyMslbO5c7DmzLwl5hDqPDxboHbQFB3EfPqyLDmAaNUoXlVZvZdo0DI6BX4pF+v20bNtG/T9fp2nzZvD5sM2YQfQ9q4i87bYBC81JKfG6XHhamnG3NONubm5LtzTjaWkJHoPnzcGjswV3czNawD8gdvYKIai0JWGbkMXDn7ubmNF949F5Tp2iaf16Gtetx3NM32TWnp1NxLKlRC5Zgjm573Zi7GtP5KPAOillkxDiKSAH+J6UMr/3pvY/SkQGFiklZwtryF9/loriBmxhZmbenMKMm1KGzHLr0uvFdeiQHp7avQfX/v1IjweEwDZlCo65c3Hk5eKYMwdjRPc3I9K8XjxFRbgKdE/FdfAgvnPn9EKjUe/AzZqJfWYW9uysfg2teE6fpuH11TS88Qb+qiqMsbFErVxJ1Kq7sU2c2Ov7B/w+zhefoLmutqMYNDfjdrboee2EwtPSgpTaZe8nDAasYeHYwsKwhYVjDX7an9vCw7E6wrG1psP0tMWhh46kpqFpGjL46ZgOtKUDgSvU05DBuleq0+F+wXRzbQ2bN7yPrVEfLBCXksr4OXOZkDuPpIzMPvlde06fpmn9BhrXr8dz9CgAtqyZRC5ZSsTSpb0ORfa1iByUUs4UQiwEfoi+Ve4TUsq5vbJygFAiMjBoAY3i/Ery152jpqyZ8Bgr2bemMnVBMmbr4C65Ln0+XIcKce7ejXP3Lpz5+5FuNwiBdfJkwvJydeGYM6ff3sj9tbWh8Je7oADXwUNozfpKw4aICD38FfRYbDNn9mruQKC5hab166h/fTWuffvAYCD8hhuIumcVETfe2KvZ5FJK6s+Xc6YgnzMF+ZQcPoTP03FXCKPJdNnG3xYWjtURhjWYvlgYLHb7sBhccTX+vO00P399F7+6zkzNkX2UHClEahrhMbGMnzOPCbnzGDttBkZT71+svGfP6qO81q/HffgwALYZM4hcuoTY++7rUT9dX4vIfinlLCHED4FDUsqXWvO6bdkgoESkf/F7AxTtqGD/u+dorHYTk+QgZ2kamXmJg7YfufT7cR8+rIendu/GmZ+PdOpb31onTgx5GmG5uYM2c1hqGt5Tpzp4K57jx0Mdwea01GDfSpYeBps08YqNv5QSV34+9f98ncZ165BOJ5Zx4/Rw1cqVmEf1vDPW42zhXGEBZw/u50xBPg2V+o6f0YmjScvKIX3mLKITk0LCYLJYR4QQ9Iai840s++WH/PgjM/nYnLG4mps4nb+H4j07OV2wD7/Hg8XuICMnlwm58xiXPRuLvfdhTm9JiR7yWr8BramJjLVrevS76GsReRsoA24BZgMuYLca4ntt43H5KdxSSsGmUlyNXhLHRZKzNI1xM+MHfM8O6ffjPnoU5+7dtOzahWvvPrRW0cicgCM3LyQcQ3F2cCtaSwuuw4d1b+XgQVwHCvBXVQEgrFZsU6d26F8xjR6Nv7KShjf+RcPrr+M9exaDw0HkituIunsV9lnZPWpANC1A5amTurdxMJ/y40VITcNitzN2WhbprcKRNLqvfwQjBk2TzPn+Rm6amMDPP57doczn9XDu0AGK9+zk5N5duJoaMZpMpE7PYkLufMbPmUtYdO//TrWWFgxhPRu80tci4gCWoXshJ4QQo4EZUsoNPbJugFEi0re0NHg4uKmEwi1leN0BUqfGkrM0jeSJ0QP29ikDAdxFRThbPY29e0OhIUtGBo65eYTl5eHIy7vqrOqhjJQS//nzuqdyQPdW3IcP6/03gDEujkBdHWgajjlziLrnHiKXLulRx31zbU0oRHW2sAB3UyMAiRkTgqKRw+iJkzGa1PIzXeVLf9vH/nP1bH/85sv+29C0AOXHjlK8ZyfFe3fScOE8CMHozElMmDOPCbnziU0e+KHWfbWfSKSUslEI0ek8fCllbS9sHDCUiPQNDVVO9r9bQtH2CrSAxvicUeQsTSMhtfsdzz3BX1dH08aNNG9+XxeNRr2Rs6Sl6V7G3Dwcubm9CtsMB6TPh/vYcVwFB3AfKsSUlEj0XXdhSU/v1n38Xi+lRYd10SjIp7pEn9gXFh1DelYOaTNnkTZzFo7Ikbny7EDw1x1n+H//Osz7X7+J9PirewRSSqpLzlK8ZwfFe3ZSeVqfTR87ZiwTcuf1acf81egrEXlbSnm7EOI0+g6H7aVUSikzem9q/6NEpHf4vQF2v3WaAxvPIYyCyfNGM+vW1AHZMTDQ2EjTxvdoXLtWn0Xt92MeMwbH/HmEzZ2LIy8Pc2Jiv9sxEpBSUltWwpmC/Zw5mE/pkUL8Xg9Gk4kxk6fp3kZWDvGpI3fL14GmuLKJW37+AT9cNYNP5KV2+/rG6kpO7t1F8Z6dlBw51G8d850xrPdY72uUiPSc86caeO8vR6m/4GTqgtHk3ZFBWLS1X58ZaG6medMmGtespXnbNvD5MI8ZQ+TyZUQsX45t6lTVyHURd3MzZw8d0L2Ng/tpqtH7V2KTU3RvI2sWY6fMwDxMl2gf6kgpyfvBe1w3Po5f3du7cUiu5iZO799L8Z4dnD5wacd8etZsrH04/6ivN6VCCLEKWIjukXwopXyjF/Yphjg+b4Bdb56i4L0SwmOsrPxaNmOn9N/qoprTSdPmzbrH8cGHSK8XU1ISsZ/8JJG3Lcc2Y4YSji6gBQJUFB8PikY+54tPIKWG1RFG6ows5t3zcdJn5hCZMLJDfkMFIQTzMuLYcbIGKWWv/obt4RFMvX4RU69fFOyYL9A75vftomjbln7pmO8qXelY/19gAvByMOvjwEkp5Zf72bY+QXki3aOiuJ73XjxKQ6WLaTeM4bpV4/tlLw/N7aZ5ywc0rl1L8/vvI91uTAkJRCxbRuTyZdizs4fs8htDicbqylCH+LnCAjwtLQhhIGlCZihElTR+Igbj4M7VuVZ5adc5nlh9iPceu5HxCeF9fn9NC1B+vEjvmN+z45KO+dkr7urRYIi+9kRuBKbLoNoIIf4CHOq2VV1ECJEN/B6wAX7gS1LK3UKX8V8BtwFO4DPDZdb8cMDnDbDrjVMUbC4hItbGnQ9nkzK5b70PzeOhZetWGtespWnzZqTTqc+gvvsuIpcvxzF7NuIaaOykpuHzuPG6XHjdLrwuFz53W7o13+d2XbaOz+3C43TibKgHIDwunsy8BaRn5ZA6Iwt7+MAMeFBcmfnj9dGBO07W9IuIGAxGUiZPI2XyNG78989SU3I2NNKrcPMGclfe0+fPvJiuiMgxIBVoXZd5LHCw3yyCHwP/JaVcK4S4LXh+E7AcyAx+5gK/Cx4VvaT8RD2bXjxKQ5WL6TeOYf7dfed9SK+X5u3baVq7lqb3NqE1N2OMiiJqxQoib1uOIzcXMcyGjTZWV1F/vuIyDb0Tr9vd1uhfLAgu1yUzvK+E2WrDYrdjsdsx2+xYbHbCY2L1tN1O3JixpGflEDum+3tfKPqf9DgHiZFWdpyq4d/npfXrs4QQxKemE5+azrx77sXrdg3I30RX/vXGAUeFELuD57nADiHEmwBSypV9bJMEWteeiALKg+k7gReDHtFOIUS0EGK0lLKis5soro7PE2DnGyc5+H4pkXE27nxkFimTeh9LlT4fLbt207h2DU0b30NraMAQGUnEkiVELl9O2Ly5w2bJdCkl9RcqKD1aSOmRQkqPHqax6sJl67c27habLZQOj4nFYndgttmwhMrtbXUvPg8ezVabCukNc4QQzM+IY2txda/7RbqLxda9Zeh7SldE5Dv9bkVHHgbWCyF+ChiA64L5Y4CSdvVKg3mXiIgQ4kHgQYDU1O4PrbsWKDtex6YXj9JY7WbGTSnMuyujV96HDARw7tmjh6o2bCBQX48hLIzwxTcTuXw54QsW9GrNpoGidShsyZFCSo8WUna0kOY6fUqUPTKKlCnTmL3iTuLHpmN1ODqKhmr0FZ0wf3wcbxwo50RlMxMTR16Y8aqthpRyixAiDciUUm4UQtgBk5SyqacPFUJsBDpbCP9JYDHwiJTyn0KIjwHPoy+50pmEdzoqQEr5R+CPoHes99TOkYjX7WfnG6c49H4pkfE27np0FmMm9sz7kJqGa98+Gteuo3HDBgLV1QiHg4ibbiLytuWEXX89Bmv/DgnuLZoWoOrsGcqOFlJypJCyosO4grO1w2NiSZk6g5Qp00mZMp3YMSkqZKToNvMz9G1ud5ysuTZFRAjxefS3+lhgPJCC3vG9uKcPlVLecoXnvQh8LXj6GvBcMF2K3h/TSgptoS5FFyg9Vsfmv+rex8xFKcy7a3y3V9iVmobrQAGN69bStG49/spKhM1G+I036h7HjTdgsA+MG90TAn4/ladP6uGpo4WUFR3B42wBIGpUIhk5uSHRiEpMUqKh6DVjY+2Mibaz42QN912XPtjm9DldiV98GcgDdgEE18/qz4Hm5egjwt4HbgZOBPPfBB4SQryC3qHeoPpDuobX7WfH6pMUbikjKsHO3Y/lkJzZvdVrXYcKaVyzhsZ16/BXVCAsFsJuuJ7IZcuJWHRTjxd662/8Xi/nTx7X+zOKDlN+7GioYzsmOYVJ868nZco0xkyZTmT8wO5jrbg2aJ0v8l7RBTRNYhjgBUr7m66IiEdK6W19IxNCmLhMGKmP+Dzwq+Bz3AT7NoA16MN7i9GH+N7fjzaMGEqLatn01yKaat1k3TyWuXdlYLZ03fuQPh/nv/d96l99Fcxmwq+7jsiHv0b44sUYw/t+yGJv8bndlB8vorRI9zQqThwjENxlMCE1nWk33RL0NKYN6IQsxbXN/PFx/DO/lKLzTUxNHphdJAeKrojIFiHEE4BdCHEr8CXgrf4ySEq5FX3J+YvzJbpXpOgCXref7a+f5PAHZUSNsrPqsRxGT+ie9xGor6f04Udw7txJ7Gc/S/x/PIgxamgtyOdxtlB27AilRw9TeuQQF04VowUCCGFg1LjxZC9ZQcrUGYyZPFXNnVAMGqH5IqdqrkkReRz4HPoEw/9A9wieu+IVikGl5Ggtm/56lOY6D1m3jGXuyu55HwCeU6cp/eIX8ZWXM/pHPyT6rrv6ydru4WpqpLTocHC4bSFVZ04jpYbBaCJpfCZz7lhFypTpJE+c0qdrCSkUvWFMtJ3UWAc7T9XwuYXjBtucPqUro7M04NngRzGE8br8bHu9mCMflhOd6GDV12czenz3PYeW7dspffgRhMlE6l9ewJGT0w/Wdh0tEOBk/m4OrHubc4UFAJjMFkZPnMy8ez5OypTpjM6chNmqFhJUDF3mZ8SxtrCCgCYxjqB+keE1VVhxWc4dqWHzX4toqfcw69ZU8u4Yh6mb3gdA3csvc/5738eakUHK736HJWXgN8RpxdnYwKFNGyh4dw1N1VVExCUw/yOfIG3GLBLHZ2IaJhMWFQrQQ1qv7i3haEUj08cMrbBwb1AiMszxuPxs/8cJjmyrICbJwapvzCYpo/t/oNLv58IPf0Td3/5G+I03kvyznw5ax/mFU8XsX/c2Rdu3EPD5GDttJovu+zzjZ89VCwkqhi3t19G6ZkRECGEEfiSl/MYA2aPoBmcP1/D+/+neR87SVHJvH4fJ3P1GNtDYSNkjj9KybRux99/PqK8/NuALIQb8Po7v3Mb+9W9TcbwIs9XG9JtuJXvpCuLH9u+aQwrFQJAYaSMjPowdp2r4/A3DYk+/LnFFEZFSBoQQs4UQQl5tzXjFgOFx+tj6j2KKtuvexz3fnEPiuJ6N+PCePUvJF7+E99w5Rn/vv4n+yEf62Nor01xbQ8HGdRzcuBZnQz0xo5NZdN/nmXrjYmxhQ28IsULRG+ZmxPFWQTn+gIbJODKWyOlKOGs/8C8hxGtAS2umlPL1frNKcVnOHKrm/b8dw9ngIWdZGrkr0nvkfQC07NpN2Ve/CkDqn54nLC+vL029LFJKyo4dYf+6tynevR1N08iYNYfspbeTPnOWWn9KMWKZPz6Ol3efo7C8keyx3RtyP1TpiojEAjXos8dbkYASkQHE3eJj22snKNp5ntjkMJZ/YQaJ6T0fb1732muc/6/vYklNZezvf4dlABaq9HncHN26hQPr36bq7GmsYWHMWnYH2UtWEJ00ut+fr1AMNvMy9D16dpysuXZEREqpZoYPMmcOVvP+34pwNvmYvTyN3NvGYTT37G1dBgJU/vgn1P7lL4QtXMiYX/wcY0T/TsKrv3CegnfXULhpA+6WZuJT07n1wYeYsuAmtb+34ppiVISNCaPC2XGqhi/eNH6wzekTurIA40T0DaASpZTThRAzgZVSyu/1u3XXOFpAY/Nfi0Lex21fmsmotJ57H4HmZsoee4yWLR8Q86lPkfitb/bbhlBS0zh76AD717/Nqfw9CCHIzLuOWctuZ8zkaWphQ8U1y/wMfQkUX0DDPAL6RbrSgjwLfAP4A4CU8qAQ4iVAiUg/c3R7BUU7z5OzNJW82zN67H0AeEtLKf3iF/GcOk3S0/9JzL339qGlbXicTg5veY8D69+mrqIMR1Q081Z9nJm3LCMiNr5fnqlQDCfmj4/jrzvPcrC0ntlpfbsF9WDQFRFxBPc4b5/n7yd7FEH83gB73jlDUkYk8+4a36s3d+e+fZQ+9BVkIEDqc88SNn9+H1qqU1N6jv3r3+HIB5vwuV2MzpzEbQ89Rua8hWpSoELRjnkZbfNFrhURqRZCjCe4cq8Q4iN0spugom8p/KCMlnoPt94/tVcCUv/6air+8z+xJCeT8vvfYR3Xd+v2tC1H8hbnCg9iNJuZfN0NZC+9naTxmX32HIViJBEbZmFyUgQ7T9Xy0M1Xrz/U6ep+In8EJgshyoDTwCf71aprHK/Lz761Zxk7NZYxPdzzXAYCVP3iF9Q89zyO+fNI+eUv+2wF3s6WI1l476eZsXgpjsiRMxNXoegv5mXE8cqec3j8Aaym4b0KQ1dGZ50CbhFChAGG3myLq+gaBzaew93iY96dPZvVqrW0UPaNb9K8aRPR936cpCefRPRBSEktR6JQ9A3zx8fxwvYzFJQ0kDdueIe0ujI6Kw74T2AhIIUQW4HvSilr+tu4axFXs5cDG0sYPyuhRyOxfOXllHzxS3hOnCDxqaeI+eS/9XokVOmRQj54+QW1HIlC0UfMGxeHEHq/yIgXEeAV4APgnuD5J4FXgcvuk67oOfvWncXvDZC3svteiHP/fr0D3eNh7B/+QPj1C3tli7Ohni3/9yeOfLCJiPgEtRyJQtFHRDnMTB0dyY5T1XyN4d1/2KUZ61LK/253/j0hxNDYoWiE0VTrpvD9MibNSyJ2dPf2LG946y0qnnwKU2IiY1/8C9bxPZ/IJDWNQ5s28OFLL+B1u8m766PMW/VxtV+HQtGHzM+I48WdZ3H7Ath6uHTRUKArIrJZCHEv8Pfg+UeAd/rPpGuXvWvOIJHk3t71EVRS06j69a+p+f0fcOTmMubXv8IU0/O9wyvPnGLjc7+l4sQxUqZO55bPfZm4lLE9vp9Coeic+ePjeG7rafLP1XHd+OE7h6orIvIfwKPAX4PnRqBFCPEo+tbnI2vD4EGi/oKTo9srmHHjGCLj7F26RnM6Kf/W4zS9+y5RH7mH0d/5DsJi6dHzvS4n2/7+N/avfQtbRATLv/woU65fpGaWKxT9RO64WAwCdp6sGdkiIqXs84WVhBAfBZ4GpgB5Usq97cq+jb6newD4qpRyfTB/GfArdBF7Tkr5o762azDZ9dYpjGYDs5end6m+7/x5Sr/0ZdxHjzLq8W8Re999PWrwpZSc2LWNzS/8keb6OrJuWcbCe+/D1m5DKp/PR2lpKW63u9v3VygGEpvNRkpKCuZhMME10mZm+pgodpwa3mOUBmtnw0JgFcGlVFoRQkwF7gWmAcnAxuDaXQC/BW4FSoE9Qog3pZRHBs7k/qOqpInivZXMXp6GI/LqnoTr0CFKv/RltJYWUn73v0TcdFOPnlt/voL3/vx7zhzYx6j08ax87ElGZ066pF5paSkRERGkp6crz0QxZJFSUlNTQ2lpKeP6cFJtfzI/I44/bTuNyxvA3oPtrIcCgyIiUsqjQGcN0p3AK1JKD3BaCFEMtG5yURycs4IQ4pVg3REhIrv+dQqrw8SsW6++HHvj2rWUP/5tTPHxpD3/HLaJE696zcX4fT72vPkPdq9+DYPJyKLPPEj2khWXnevhdruVgCiGPEII4uLiqKqqGmxTusy88XH84YNT7D1by/WZCYNtTo8YanusjwF2tjsvDeYBlFyUP3egjOpPyovrOVtYw/y7x2N1XN4Fl1JS/dv/pfqZZ7Dn5JDym19jiovr9vPOHjrAe8//jrqKMibOv55Fn36A8Nir30cJiGI4MNz+TnPTYzEaBDtO1gxbEbnssrBCiNgrfa52YyHERiFEYSefO690WSd58gr5l3v2g0KIvUKIvUP5rURKyc43TuKIsjBjUcpl62luN+WPPUb1M88QdeedpL7w524LSEt9He/8+if843tPITWNe574Lnc8/K0uCchQYfXq1QghKCoqGpTnnzlzhpdeeumq9Q4cOMCaNWtC52+++SY/+lHXu/D+9Kc/MWPGDGbOnMn06dP517/+1SN7FUOfcKuJmSnDu1/kSp7IPtoa8FSgLpiOBs4BVww6Sil7MhmxFGg/njQFKA+mL5ff2bP/iL7eF3PmzBmye8OfO1xLRXEDN35iIubLxEN9lZWUfvkh3IWFjPr6Y8R+7nPdetvStAAFG9aw9ZW/EvB5mf+RT5B350cx9XAU12Dy8ssvs3DhQl555RWefvrpAX9+q4j827/92xXrHThwgL1793LbbbcBsHLlSlauXNmlZ5SWlvL973+f/Px8oqKiaG5u7lZ4xu/3Y+qnPWIU/cP8DD2k1eLxE2Ydfr+7y3oiUspxUsoMYD1wh5QyXkoZB9xO/22N+yZwrxDCKoQYB2QCu4E9QKYQYpwQwoLe+f5mP9kwIEhNsvNfJ4mMtzFlQXKndfw1NZz52MfxnDxJym9+TdwDD3RLQM6fPMFLTz7Gpj//gdGZk7jvp7/luo9+clgKSHNzM9u2beP555/nlVdeCeVXVFRwww03kJ2dzfTp0/nwww95/vnneeSRR0J1nn32WR599FHOnDnD5MmTeeCBB5g+fTqf/OQn2bhxIwsWLCAzM5Pdu3cD8PTTT/OpT32Km2++mczMTJ599lkAHn/8cT788EOys7P5xS9+gdvt5v7772fGjBnMmjWLzZs34/V6+c53vsOrr75KdnY2r776Ki+88AIPPfQQABcuXODuu+8mKyuLrKwstm/f3uF7VlZWEhERQXhwdFx4eHiok/jZZ58lNzeXrKws7rnnHpxOJwCf+cxnePTRR1m0aBHf+ta32LJlC9nZ2WRnZzNr1iyamppobm5m8eLF5OTkMGPGDOXdDCHmj48joEn2nKkdbFN6RFdkL1dK+YXWEynlWiHEf1/pgqshhLgb+A2QALwjhDggpVwqpTwshPg7eoe5H/iylDIQvOYhdEEzAn+SUh7ujQ2DTXF+JdUlzdxy/1SMps61vOqXv8JfXU36yy9jnzG9y/d2tzSz7dW/cmDDGsKiY1jxtW8yaf71fRIv/q+3DnOkvLHX92nP1ORI/vOOaVes88Ybb7Bs2TImTpxIbGws+fn55OTk8NJLL7F06VKefPJJAoEATqeTnJwcZs6cyY9//GPMZjN//vOf+cMf9IGAxcXFvPbaa/zxj38kNzeXl156ia1bt/Lmm2/ygx/8gDfeeAOAgwcPsnPnTlpaWpg1axYrVqzgRz/6ET/96U95++23AfjZz34GwKFDhygqKmLJkiUcP36c7373u+zdu5dnnnkGgBdeeCH0Pb761a9y4403snr1agKBAM3NzR2+Z1ZWFomJiYwbN47FixezatUq7rjjDgBWrVrF5z//eQCeeuopnn/+eb7yla8AcPz4cTZu3IjRaOSOO+7gt7/9LQsWLKC5uRlbcAvi1atXExkZSXV1NfPmzWPlypXDrg9hJDInLRazUbDjVA03TRo12OZ0m67uJ/IU8H/o4a1/B3oVwJNSrgZWX6bs+8D3O8lfA6y59IrhhxbQ2P3WaWKTw8jMTey0jvvoUer/8Q9iP/2pLguIlJKibVt4/8XncDU2MmvZ7Sz42L9jdXRvCZWhyMsvv8zDDz8MwL333svLL79MTk4Oubm5fPazn8Xn83HXXXeRnZ0NwM0338zbb7/NlClT8Pl8zJgxgzNnzjBu3DhmzJgBwLRp01i8eDFCiFB5K3feeSd2ux273c6iRYvYvXs30dHRHWzaunVrqBGfPHkyaWlpHD9+/IrfY9OmTbz44osAGI1Goi5ant9oNLJu3Tr27NnDe++9xyOPPMK+fft4+umnKSws5KmnnqK+vp7m5maWLl0auu6jH/0oxuDougULFvDoo4/yyU9+klWrVpGSkoLP5+OJJ57ggw8+wGAwUFZWxoULF0hKSurur0LRx/LgkvgAACAASURBVNgtRrLHRrPz5PDsF+mKiHwCfRXf1egi8kEwT9FDinacp/6Ck+VfmIHBcOmboJSSCz/4IcaoKOK/9KUu3bO2vJT3nv8d5woLSBqfyarHnyYxY0Jfm35Vj6E/qKmpYdOmTRQWFiKEIBAIIITgxz/+MTfccAMffPAB77zzDp/61Kf4xje+wac//WkeeOABfvCDHzB58mTuv//+0L2sVmsobTAYQucGgwG/v23Dzovf0Dt7Y5eyf7rbhBDk5eWRl5fHrbfeyv3338/TTz/NZz7zGd544w2ysrJ44YUXeP/990PXhIW1vSg8/vjjrFixgjVr1jBv3jw2btzIzp07qaqqYt++fZjNZtLT09Xk0SHE/Iw4ntlcTKPbR6Rt6E+UbM8VN+0WQhiBb0spvyalnCWlzJFSPiylHJ7BuyGA3xdgzzunSRwXybiszpc6aNrwLs49e0j42levupGUz+th29//jxe/8f/bO/O4Kqvt/783g6CiooBTOKHhwCiDgCNep0qz0szMMrSblddrv763UvOWZtattMxuN8tyqrRBTSs1MxNKDTVwHkOchxBQFASZzvr9ceAIMh0QzgHc79frvODZz36evc7m4ayz99r7syaScPwY/Z6YwKhZc6rEgViLlStXMmbMGE6dOsXJkyc5c+YM7dq1Y+vWrZw6dYqmTZvy5JNP8sQTT7Br1y4AQkJCOHPmDMuXL2fUqPJ/5/nuu++4fv06ycnJREVFERwcTIMGDUhNvZFOp3fv3ixbtgwwTiedPn2ajh07FqlXkH79+jF//nwAcnNzuXq18NTg+fPnTe8BjEH6Nm2Mkvupqam0aNGC7OxsU7vFER8fj4+PD5MnTyYoKIgjR45w5coVmjZtir29PZGRkZw6darcfaKpOkLbu2AQ+ONEzftoLXUkIiK5SqlASxlzO3Dg13OkXc6k3+Odi/12a8jM5OLbb+Pg6YnziBGl3uvEnlh+WTSfKwl/0blXX/o8Oo76zhUXX6yufPnll0yZMqVQ2fDhw1m+fDmhoaHMnj0be3t7nJycTFNFAA899BB79uyhcQUEKbt168bgwYM5ffo0L7/8Mi1btsTNzQ07Ozv8/PyIiIhgwoQJPP300/j4+GBnZ8eSJUtwcHCgb9++vPnmm/j7+zN16tRC9503bx7jx49n4cKF2NraMn/+fMIK5LzPzs7m+eef5/z58zg6OuLm5sZHH30EwGuvvUZISAht2rTBx8enREf13nvvERkZia2tLV26dOHuu+8mNTWVe++9l6CgIPz9/enUqVO5+0RTdQS0bkwdOxui45Pp17n4Ke7qiiprSK6UegfjKqkVwLX8chGpqhValUpQUJDExMSUXdECZF3P4fN/R+Pq7sR9/69rsXWSPvqYxPfeo/WSxdQPDS22TuqlJKKWfMKfO7bRpKU7/Z6YQGtv3yqz+/Dhw3Tu3LnK7l9VDBkyhOeee45+/fqV67oZM2bg5OTE888/X0WWaaqSmvq8jvw4mrTMHNZN6mVtU1BKxYpIkDl1zcongjGQXjClvFB1y3xrLXt/OcP1tGxC7y8+10d2wkWSFizAqX+/Yh2IITeX3Rt+YNs3y5DcXHo+PIagex/A1q5mzaFWNSkpKXTr1g0/P79yOxCNxlqEtXdh3i9xpKRn4Vyv5izDN0fFd2xZdTRlk5GWxe6fT+Ph70aztsWr5yfOnQvZ2TR78cUi587/eZhNn35I4qkTtOsaRL9xT9OoqV5ZUxzOzs5lrpIqDWtsZNRowjxceG9THDtOXGKQV8353zYnx7ojRml2L8CU2k5ExlWhXbWOXRtOkZOZS0gJaW8z9u/nypo1uPz9Ceq0viHEmJGWypblS9j/y084ubgy9P9eokO3ML2+X6OpZfi3dsYhLy5Sq5wIxmRUR4BBwEyMOdYPV6VRtY20y9fZH3WOjiHNadKy6J4NESHh9TewdXXF5WnTvk6uJiWy7KXnyEi9SuCQB+g+4hHqOJqXsEqj0dQsHOxsCWrbmO01TEer1CW+eXQQkZeBayKyFBgM+FStWbWLP9afRKTktLdX164jY88emj73/7AtkAxqy/IlZKWnM/r1dwl/7AntQDSaWk6YhwtH/krl0rUsa5tiNuY4key8nylKKW+gEdC2yiyqZaQkpHN42wW8et1BQ9eiTsCQns7Fd97BsUsXGj3wgKn87JGDHNn2K0FDh9WqPR8ajaZkwtobVbV31KDRiDlOZIFSqjHwMkbRw0PAW1VqVS1i59oT2NopAu9uU+z55IWLyPnrL5q9NBVlY/xzGAy5RC5ZgJOLK92GPmhJc6s1t4sUfNu2bfHx8TGJKE6aNKlC9paXN954o9zXFBSXLEhCQgJDhgzBz8+PLl26mBSNNaXj6+5MvTq2NUoavkwnIiKfishlEflVRDxEpKmIfFzWdRpIOptK3B8J+P6tFfUbORQ5n33+PMkLF9Lg7ruoF3RjSfbBqF+4eCKe3qPHYu/oWOS625WCUvDWoKJOZOjQoUU2S5ZFZGQke/bsYc+ePbz//vvltrUiVMSJlMQrr7zCgAED2Lt3L4cOHSqXExURDAZDpdlSk7C3tSGobROia5COVplORCkVr5RappR6Oi8HusZMtpeR9vbinHdAhGYFNrVlpl9j61ef0bJjFzp1720pU6s9t4sUfEnk5OQQHBxs0suaOnUq06ZNA4wjl8mTJ5v0to4dOwZAYmIiw4cPJzg4mODgYLZt22bqy3y7fX19WbVqFVOmTCEjIwN/f39Gjx4NwBdffEG3bt3w9/fnqaeeIjc3F4DFixfj6elJnz59TPe8mQsXLuDufiPRmq+vr6nt4iTpT548SefOnZkwYQIBAQGcOXOGiIgIvL298fHxYe7cuaa/ZXFy+LWJMA8X4i6mkZiaaW1TzENESn0BDkBvYBpGFd3jwOqyrqsur8DAQLEG5+MuywdP/SIxP54o9vy12Fg51LGTXJw3r1B55GefypyRQ+Sv+DgLWGkehw4dunGwfrLIonsq97V+cpk2fP755zJu3DgREQkLC5PY2FgREZkzZ47MmjVLRERycnLk6tWrkpaWJh4eHpKVlWWqv2/fPjlx4oTY2trKvn37JDc3VwICAmTs2LFiMBhkzZo1ct9994mIyPTp08XX11fS09MlMTFR3N3d5dy5cxIZGSmDBw822TRnzhyJiIgQEZHDhw9Lq1atJCMjQxYvXiz/+Mc/TPUKHj/00EMyd+5ck70pKSlF3mubNm3E29tb/Pz8xM/PT959910RETlw4IB06tRJNm7cKP7+/pKZmWmqn98HS5cuNdk4atQo2bJli4iInDp1Sjp16iQiIi+++KI8++yzpvYuXbokIiL169cv9DcfMmSIqQ+feeYZWbp0qZw/f15atWolFy9elMzMTOnevXuh95rPhg0bpFGjRhIeHi6zZs2Sc+fOiYhIdna2XLlyRUREEhMTpX379mIwGOTEiROilJLo6GgREYmJiZH+/fub7nf58mUREUlKSjKVTZs2Td5///0ibRd6Xmsgu09fljaT18r3e85ZzQYgRsz8jDVniW8uxuB6LmAAEoCLVeHQagsiwvbvjlO3YR18+7Yqet5gIOH1N7Br1gyXv//dVH7p/Fl2//g93uEDdDD9Jm4XKfh8IiMjcXUtLNDp5eXFY489xr333kt0dDR1CiQXyxeZHDVqlGkUtmnTJg4dOmSqc/XqVVJTU9m0aVOh0Vxx2mK//PILsbGxBAcHA5CRkUHTpk3ZsWMH4eHhuLkZ84GPHDmy2Pc8aNAgjh8/zoYNG/jxxx/p2rUrBw4cwNnZuVhJeoA2bdoQmqfU4OHhwfHjx/nnP//J4MGDGThwIECpcvi1Be+WDXFysCP6eDL3+hWfsK46YY4TuQrsB94FPhGRmjNZZyVOH7rE+bgUej/sib1D0bS3V9Z8x/WDB2n59lvY1KtnKo/67FPs6jjQ8+HHLGlu+bjb/LntyuJ2k4Ivjf379+Ps7Gz64M2noH35vxsMBqKjo6lbt/CqQBEpc7OqiPD444/zn//8p1D5mjVrzN7o2qRJEx555BEeeeQRhgwZwm+//UZqamqJkvQF5ewbN27M3r17+emnn/jf//7HN998w6JFi0qVw68t2Nna0K1dkxqTX8Sc1VmjMOYQmQB8pZR6VSmlBYlKQAzC9jXxNHBxpEvPot8ictOucXHuu9T186PhkCGm8uO7/+DE7hjChj9cK5V4b4XbSQq+NL799luSk5P57bffmDRpEikpKaZzX3/9telnvirwwIEDTdkVwRjwL6788uXLANjb25OdnW2yc+XKlVy8aJx0uHTpEqdOnSIkJISoqCiSk5PJzs5mxYoVxdq6efNmU7wiNTWV+Ph4WrdubbYkfVJSEgaDgeHDh/Paa6+Z/q7myuHXdEI9mnA86RoJV6t/zhdzVmd9JyIvAE9hjIlEAGur2K4aS/zuRJLOpNHt3nbFpr1N/vhjchOTaDbtJdOS3tycbKKWfkrjFnfQ9e57LW1ytefLL7/kgQJ7aOCGFHxUVJQpl/iqVat49tlnTXUeeughevTocUtS8KGhoSYpeF9fX5MU/Ny5c5kwYQK5ubn4+PgwcuTIQlLwhw4dMgXWCzJv3jwiIyPx8fEhMDCQgweLz/Lct29f0xLfMWPGkJSUxJQpU1i4cCGenp5MnDix0HvNzMwkJCSEefPmmYLQ77//PjExMfj6+tKlSxeTpPy///1vLl++jLe3N35+fkRGRgIwfvx4fH19GT16NF26dGHWrFkMHDgQX19fBgwYwIULF2jRogUzZswgLCyM/v37ExAQUKz9sbGxBAUF4evrS1hYGH//+98JDg5m9OjRxMTEEBQUxLJly0qUpD937hzh4eH4+/sTERFhGhHly+EPGDCgVsvZh3kYpzJrxCqtsoImwCogHmN+838DfQBHc4Mu1n5ZMrCem5MrX7wSLctf3S65uYYi5zNPn5bD3j5y7sUXC5X/8cO3MuehwRK/a6elTC0XNTVQOXjwYNm0aVO5r5s+fbrMnj27CiyqGtq0aSOJiYnWNqPaUFOf14Lk5BrEZ/oGeXHFXqu0TyUH1t8EdolIblU5strCke2lp729+PZssLPD7f/+z1SWfiWF6JVf0s4/EI+uwZY0t9aipeA1NR1bG0W3di41YtOhOU7kIDBVKdVaRMYrpe4EOoqIntIqQE52Ln+sPUHTtsWnvb22YyepP/+M27OTsG92I3PZ1q8+Iycrk/DHn7SkubWa200KvuCqMk3tIay9C5sOJ3AuJYM7nKuvbp45gfXFQBbQPe/4LDDrVhpVSo1QSh1UShmUUkEFygcopWKVUvvzfv6twLnAvPJjSqn3VTXTQj/423nSLmcSer9HkdUrkptLwhtvYN+yJU0KrBRKOH6M/ZE/0/Wue2nS0v3mW2o0mtuYMA+jjlZ1X6VljhNpLyJvkyfEKCIZwK1+gB8AhmFc9VWQJOBeEfEBHscoQ5/PfGA8xlS9dwJ33aINlUbW9RxiN5zkjo6NadWpSZHzKStWknn0KE1ffAGbPBkTESFy6QLqNmhI6PCHLW2yRqOp5nRq3oDG9eyr/ZSWOU4kSylVF2NKXJRS7YFb2o8vIodF5Ggx5btF5Hze4UHAUSnloJRqATQUkei8oM9nwP23YkNlsveXM2SkZhN6f9GEU7lXr5I4bx51gwJpUGBj1NHff+PckUP0fHgMjvWdilyn0Whub2xsFCHtXKr9Ci1znMh0YAPQSim1DPgFKJq/tfIZDuwWkUzgDozTaPmczSuzOtfTstnz82na+bnSvF3R3cdJH84nNyWF5i+9ZJrmys68zq/LFtO0bXu8+/a3tMkajaaGENbehXMpGZy5VH01wkp1InlxhyMYp54igC+BIBGJKuvGSqlNSqkDxbzuM+NaL4xy80/lFxVTrcTtwkqp8UqpGKVUTGJiYlnN3RK7fjpFVglpbzOPn+DSF1/g/OBwHLvc0K7c+d0q0pKT6Dt2PDY2RXe0a4rndpGCv3LlCmPGjKF9+/a0b9+e0aNHmzYE3syMGTOYM2eO2fe+VWJiYiwmTa+5kV+kOo9GSnUieVNHa0QkWUTWichaEUky58Yi0l9EvIt5fVfadUopd2A1MEZE4vOKzwIFI8/uwPmbry3Q9gIRCRKRoHyNn6og7XIm+6LO0rFbc1zuKDoldfGtt7BxcMCtwKawq4kXifl+FR2798a9k1eV2VYbuV2k4J944gk8PDyIj48nPj6eDh06EBERURGTK0S+Wm9xBAUFWUyaXgN3NnXC1alOtY6LmDOdtV0pZZENDEopZ2AdMFVETBrTInIBSFVKheaNjsYApTojSxDz40nEIHS7t2ja27QtW0n79VdcJzyDXQEhvV+XLQal6D16bJFrNCVzu0jBHzt2jNjYWF5++WVT2SuvvMLevXs5erRIGLFESpJxf+aZZwgKCsLLy4vp06eb6rdt25aZM2fSs2dPVqxYQXh4uEle3tPTky1btgAQFRXFkDy5nhkzZjBu3DjCw8Px8PAo5Fxee+01OnXqxIABAxg1apRFR0u1CaUUIR7GuIhYQavNHMzZJ9IXeEopdQq4hnFqSUTEt6KNKqUeAP4LuAHrlFJ7RGQQMBHoALyslMr/LxooIheBZ4AlQF3gx7yX1biSmM7hrefp0qtlkbS3kp1NwptvYt+6NY0fuyGmeObQfv6M3kL3EaNp6Fp1I6Sq5K2db3HkUuVOJ3Vq0onJ3SaXWmfNmjXcddddeHp60qRJE3bt2kVAQADLly9n0KBBTJs2jdzcXNLT0wkICMDX15e3334be3t7Fi9ezMcfG/OoHTt2jBUrVrBgwQKCg4NZvnw5W7du5fvvv+eNN95gzZo1AOzbt4/t27dz7do1unbtyuDBg3nzzTeZM2cOa9cat0i98847gFEU8ciRIwwcOJA///yTmTNnEhMTY9KnWrJkiel9TJo0iT59+rB69Wpyc3NJS0sr9D7z5VJsbW9Mc9ra2tK1a1cOHz5Mx44dy+zPw4cP8/XXX7Nt2zbs7e2ZMGECy5YtY8yYMbz++us0adKE3Nxc+vXrx759+0y5PhwdHdm6dSsAH330ETk5OezcuZP169fz6quvsmnTpiJtHTlyhMjISFJTU+nYsSPPPPMMe/fuZdWqVezevZucnBwCAgIIDAws025N8YR5uLBu3wVOJqfTzrV+2RdYGHOcyN2V3aiIrMY4ZXVz+SxK2IMiIjGAd2XbUlF2fH8CG1tF0D1ti5y7/NXXZMXH4/6/D7DJk+vOT3nbwNWNoHsfKHKNpnRuFyl4KUFhtzzfQkuScQf45ptvWLBgATk5OVy4cIFDhw6ZnMjIkSML3WfYsGEABAYGlrihcfDgwTg4OODg4EDTpk1JSEhg69atpv4DuPderQd3K4R63IiL1EgnIiLFy2zexiSdTSMuJoGAgW2KpL3NuXyZxA8+oH73MJz+Ztoryf5fNpJ46gRD/t9k7B1qbsrbskYMVcHtJAXv5eXF7t27MRgM2OQJdBoMBvbt20dAQADTpk1j3bp1wA1V3uLsKk7G/cSJE8yZM4c//viDxo0bExERYZJhh8JS7HCjr2xtbQv1TXF1CtarrtMuNZX2bvVxa+BA9PFkHgkpPkuqNTEnJqK5iR3fH6eOox1dBxb9gyb99wMMqak0nTLF9MFzPS2NrV9/jntnbzxDe1ra3BrP7SQF36FDB7p27cqsWTcG5LNmzaJfv360bt2a119/3ZR7vSRKknG/evUq9evXp1GjRiQkJPDjj1UzI9yzZ09++OEHrl+/TlpamsnpaSqGUoqwahwX0U6knFyIv8LJfUl0Hdgax/r2hc5lxsVx+euvafzwSBw9PU3l0au+JDMtjb4R481O6KO5we0mBb9o0SLi4uLo0KEDbm5ubN++3STjXhyzZs3C3d3d9CpJxt3Pz4+uXbvi5eXFuHHj6NGjR7n7xRyCg4MZOnQofn5+DBs2jKCgoBIzOGrMI6y9C0lpmcQnppVd2dKYK/dbU1+VKQVvMBjk2zmxsvD53yTrek6Rc6fGjpMjwd0kOy9ntYhI0pnT8u6oobJxwX8rzQ5LU1OltWuDFPyRI0fEw8ND1q1bZ21TykVqaqqIiFy7dk0CAwMlNjbWYm3X1Oe1NE4kpkmbyWvls+iTFmmPckjB65FIOThz2Jj2NuietkXS3qZFRnHt999xmzgRu7xvvpKnj2Xv4EiPkdU45W0tIyUlBU9PT+rWrVvjpeA7duxIfHw899xzj7VNKRfjx4/H39+fgIAAhg8fXmLyKo15tHGpR4tGjtVSjNGc1VkajA5h+5rjNGjiiFfPwoorkpVFwltvUqd9exqPuiGmeHzXH5zat5vwMU9Sr6EezluK200KvjpizqZMjfnkx0V+/TOxxBV81kKPRMzk+O5EEk+nGtPe2hfutkuff0H2qdM0mzIZZW+Mk+RkZxP12Sc0aemO/6DB1jBZo9HUIkLbu5B8LYs/E6pXXEQ7ETMw5BrY8f1xGjevh2dI80LncpKTSZo/n/p9euPUq5epfPeP35Py1wX6Pv4ktnZ6wKfRaG6NMNN+EbOUpyyGdiJmcHTHX1z+K52Q+zyKpL1NfG8ehuvXaTb5hjbStZTLbP/2KzwCgmnrr3fqajSaW6dVk3q4N65b7XS0tBMpg9xsAzvXnqBpmwZ4+BeWKrl++DApK1fSZPRoHDxu6Gdt+XIpOVnZhI/5u6XN1Wg0tZgwDxd2nLiEwVB99otoJ1IGB7acI+1SJqH3tS8UzBIREl5/A1tnZ1z/McFU/texPzkYtYmAe4bSuEW1SHlSK3ByKjtx13vvvUd6evnzLrzyyivF6kKZy+uvv46Xlxe+vr74+/uzY8eOCt9LoymNsPYupKRnc/ivq2VXthB6sr4Usq7nEPvjSe7o6Ix758Ib1lJ/2kh6TAzNZ0zHtmFDwOhYNi9dQL1GzoQO0ylvLc17773Ho48+Sr169cy+Jjc3l5kzZ1a4zejoaNauXcuuXbtwcHAgKSmJrKwss6/PycnBTsfMNGZSML+IV8vqseJTj0RKYd/ms8a0tzeNQgyZmVycPRsHT0+cH3zQVH5kaxQX/jxCr1GP41CODzKN+URFRREeHs6DDz5Ip06dGD16NCLC+++/z/nz5+nbty99+/YFYOPGjYSFhREQEMCIESNMirk3y55HRESwcuVK07mXXnqJsLAwgoKC2LVrF4MGDaJ9+/bF7hq/cOECrq6uJg0pV1dXWrZsCcDMmTMJDg7G29ub8ePHmyQrwsPDeemll+jTpw/z5s1jxYoVeHt74+fnR+/evQFj7pJevXoREBBAQEBAEcl4ze1Ji0Z1aetSj+3VKC6ivwKVwPVr2ez++TRtfV1p7lHY419avITsc+dovWQxKu9bZNb1DH5btphmHnfi1admb3Arjb/eeIPMw5UrBe/QuRPNX3rJ7Pq7d+/m4MGDtGzZkh49erBt2zYmTZrEu+++S2RkJK6uriQlJTFr1iw2bdpE/fr1eeutt3j33Xd55ZVXgMKy5xs2bCh0/1atWhEdHc1zzz1HREQE27Zt4/r163h5efH0008Xqjtw4EBmzpyJp6cn/fv3Z+TIkfTp0weAiRMnmtp77LHHWLt2rUnRNiUlhV9//RUAHx8ffvrpJ+644w5SUlIAaNq0KT///DOOjo7ExcUxatQoYmJiytu1mlpIqIcL6/ZfINcg2NpYf7+IHomUwK6fTpF1PYfQ+wqnvc1OuEjSggU0GNCf+qGhpvKda1aSdvkSfxs7HmWju7Uq6datG+7u7tjY2ODv71+sTPn27ds5dOgQPXr0wN/fn6VLl3Lq1A1B6ptlzwsydOhQwPjhHhISQoMGDXBzc8PR0dH0IZ+Pk5MTsbGxLFiwADc3N5OGFkBkZCQhISH4+PiwefPmQjpZBdvv0aMHERERfPLJJ6bkUdnZ2Tz55JP4+PgwYsQIDh06VO5+0tROwtq7kHo9h4Pnr1jbFECPRIolMyOH/VFn8QxuViTtbeK770J2Nk1ffNFUduXiX8Ss/ZbOPcNp6dnZ0uZalPKMGKqK4uTHb0ZEGDBgAF9++WWx97hZ9ry4+xeUis8/Lq4tW1tbwsPDCQ8Px8fHh6VLl/Lwww8zYcIEYmJiaNWqFTNmzChRdv2jjz5ix44drFu3Dn9/f/bs2cN///tfmjVrxt69ezEYDDg61tz0AZrKJX+/yPbjyfi6O5dRu+rRX5mLwaGuHcOeDyTkplFIxr59XPnuO5pEPE6dVq1M5b9+vghlY0Ov0REWtlRTkIIS7KGhoWzbto1jx44BkJ6efktSKCVx9OhR4uLiTMd79uyhTZs2Jofh6upKWlqaKeZSHPHx8YSEhDBz5kxcXV05c+YMV65coUWLFtjY2PD555+Xmvdcc3vRtKEjHm71ia4mOlp6JFICbq0bFDoWERLe+A+2rq64PHVjXvz0gb3E7fydHiMfo0ET15tvo7Eg48eP5+6776ZFixZERkayZMkSRo0aRWZmJmCUTPcsINFfGaSlpfHPf/6TlJQU7Ozs6NChAwsWLMDZ2dk0HdW2bVtTlsHieOGFF4iLi0NE6NevH35+fkyYMIHhw4ezYsUK+vbtW+rISXP7Eebhwnd7zpOTa8DO1rpjAZW/YqS2EhQUJJURkLzyw1rOv/ACLV5/HefhxrShhtxcPp/yLFkZGUS8+yH2dRzKuEvN5PDhw3TuXLun6TS1h9vheV277zwTl+9m9YTudG1d/nw5ZaGUihWRIHPq6uksMzCkp3Nxzhwcvbxo9MD9pvJ9mzaQdPok4Y89UWsdiEajqX6Y8q5Xg6W+2omYQfKnC8lJSKDZS1NNK68y0lLZ9s0XtPLypUO3MCtbqNFobidcnRzwbOZULeIiVnEiSqkRSqmDSimDUqrIkEkp1VoplaaUer5A2V1KqaNKqWNKqSk3X1NVZJ8/T/LChTS8VGR+uQAAE5VJREFU527qBd4QU/z9m2VkXrtG38efrFba/hqN5vYgzMOFmJOXycoxWNUOa41EDgDDgN9KOD8X+DH/QCllC/wPuBvoAoxSSnWpaiMBLs55B4Cmz5v8GUmnT7L35/X4DrgbtzbtSrpUo9Foqoyw9i5kZOey72xK2ZWrEKs4ERE5LCJHizunlLofOA4cLFDcDTgmIsdFJAv4Crivqu1Mj43l6vr1uDzxBPZ5UhbGlLef4FC3Hj0eGl3VJmg0Gk2xhLRzQSmsPqVVrWIiSqn6wGTg1ZtO3QGcKXB8Nq+spPuMV0rFKKViEhMTK2SLGAwkvPEf7Jo1w+XvT5jKj8Vs5/SBvXR/aDR1GzSs0L01Go3mVmlcvw6dmje0enC9ypyIUmqTUupAMa/SRhCvAnNF5Ob8j8UFHUpcmywiC0QkSESC3NzcSqpWKldWr+H6wYM0ff5f2OSJKeZkZfHr5wtxcW+N34B7KnRfTcWozlLwtra2+Pv7m15vvvlmhe9lLikpKXz44Yflvm7GjBnMmTOnSPnRo0cJDw/H39+fzp07M378+MowU1PFhHm4EHvqMpk51tuMWmWbDUWkfwUuCwEeVEq9DTgDBqXUdSAWaFWgnjtw/tatLJ7ctGtcfG8udf38aDhkiKk8dt0ariT8xYPTZmFja1tVzWsqiDWk4AHq1q3Lnj17buke5SXfiUyYMKHsymYwadIknnvuOe67z/gdb//+/WZfm5ubi63+f7AKoR5NWLTtBLtPp5iW/VqaajWdJSK9RKStiLQF3gPeEJEPgD+AO5VS7ZRSdYCHge+ryg4bRwfc/vEPmv17mmnlVdqlZHas/oYOwaG08fWvqqY1ZVDdpOBL4sqVK3Ts2JGjR42hv1GjRvHJJ58AxlHVv/71LwICAujXrx/5U67x8fHcddddBAYG0qtXL44cMaolJyQk8MADD+Dn54efnx+///47U6ZMIT4+Hn9/f1544QUAZs+eTXBwML6+vkyfPt1ky+uvv07Hjh3p37+/yZ6buXDhAu7u7qZjHx8foGRJ+qioKPr27csjjzyCj48P165dY/Dgwfj5+eHt7c3XX38NlCyHr6kcqkNcxCqyJ0qpB4D/Am7AOqXUHhEZVFJ9EclRSk0EfgJsgUUicrCk+rdsn50djR8unFRqy5dLMeTm0OfRJ0q46vZgyzd/knTm5tnGW8O1lRO9HjJfjqQ6ScEDZGRk4O9/44vF1KlTGTlyJB988AERERE8++yzXL58mSeffBKAa9euERAQwDvvvMPMmTN59dVX+eCDDxg/fjwfffQRd955Jzt27GDChAls3ryZSZMm0adPH1avXk1ubi5paWm8+eabHDhwwDQC2rhxI3FxcezcuRMRYejQofz222/Ur1+fr776it27d5OTk0NAQACBBZaq5/Pcc8/xt7/9je7duzNw4EDGjh2Ls7NzqZL0O3fu5MCBA7Rr145Vq1bRsmVL1q1bBxidKJQuh6+5dRrVs8erZUOr5hexihMRkdXA6jLqzLjpeD2wvgrNKpELcUc59Ntmut33IM7NW1jDBE0B8qXgAZMUfM+ePQvVKSgFD5CVlUVY2I1NoeZKwaelpdGgQQMaNGhgkoJ3di6snFrSdNaAAQNYsWIF//jHP9i7d6+p3MbGxtT+o48+yrBhw0hLS+P3339nxIgRpnr5ml+bN2/ms88+A4zxl0aNGnH58uVCbW3cuJGNGzfStWtXwKjpFRcXR2pqKg888IBpii//vd3M2LFjGTRoEBs2bOC7777j448/Zu/evWRnZzNx4kT27NmDra1tIRHLbt260a5dO1NfPf/880yePJkhQ4bQq1cvwCiH//bbb5Oens6lS5fw8vLSTqSSCfNwYenvp7ienYujveWnFbUAYxmIwcDmJR9Tv3ETQh54yNrmWJ3yjBiqiuomBV8SBoOBw4cPU7duXS5dulRouqggSikMBgPOzs4Vjq2ICFOnTuWpp54qVP7ee++ZvRm2ZcuWjBs3jnHjxuHt7c2BAwf44YcfSpSkL9iHnp6exMbGsn79eqZOncrAgQN58cUXS5XD11QOYe1d+GTLCXadukz3DpYXga1WMZHqyKEtkfx17E96jXqcOnV1ytvqjDWk4Etj7ty5dO7cmS+//JJx48aRnZ0NGJ1Lfgxm+fLl9OzZk4YNG9KuXTtWrFgBGJ1C/uilX79+zJ8/HzAGsa9evVrovQIMGjSIRYsWmeI+586d4+LFi/Tu3ZvVq1eTkZFBamoqP/zwQ7G2btiwwWTfX3/9RXJyMnfccYfZkvTnz5+nXr16PProozz//PPs2rWrXHL4mooT3LYJtjbKakt99UikFLIy0tmyfAktOnSkS6++1jZHUwbWkIKHojGRu+66i3HjxvHpp5+yc+dOGjRoQO/evZk1axavvvoq9evX5+DBgwQGBtKoUSNTEHrZsmU888wzzJo1i+zsbB5++GH8/PyYN28e48ePZ+HChdja2jJ//nzCwsLo0aMH3t7e3H333cyePZvDhw+bpuycnJz44osvCAgIYOTIkfj7+9OmTRvTNNPNbNy4kWeffdY00pg9ezbNmzc3W5J+//79vPDCC9jY2GBvb8/8+fPLJYevqTgNHO3xvqOR1YLrWgq+FLYsX8LO71byyKx3aHFnx0q2rOZwO0hrWxInJyfTiEFT+dyOz+ubPx5h4dbj7J0+kHp1bn1soKXgK4HLf50ndt0auvT+223tQDQaTfUnrL0L2blCzMnLZVeuZLQTKYFfP1+EjZ09vR6JsLYpmlqGHoVoKpugNo2xs1JcRDuRYrh+LY1L584Q8sBDODVuYm1zNBqNplTqO9jh18rZKnERHVgvBsf6Tjw+5wNrm6HRaDRmE+bhwvxf40nLzMHJwXIf7XokUgK2dvbY2tlb2wyNRqMxi7D2LuQahD9OXLJou9qJaDQaTS0goHVj7G0tHxfRTkRTI6jOUvBnz57lvvvu484778TDw4OJEyea9qbcTEGxR0vw/fffW0SaXmN96taxpWurxhbX0dJORFNrqIgTyZeC79+/IpkLjDvLhw0bxv33309cXBxxcXFkZGTw4osvVuh+FaGkXeRg1MqaMmWKxWzRWJfQ9i4cOHeFq9ezLdamdiKaGkV1k4LfvHkzjo6OjB07FjBqec2dO5fPPvusXEt5S5Jxv//++wkMDMTLy4sFCxaYyp2cnHjllVcICQkhOjqatm3bMn36dAICAvDx8THJyC9ZsoSJEycCxlHQpEmT6N69Ox4eHqb3bDAYmDBhAl5eXgwZMoR77rlHS5TUUMI8XDAI7DxuubiIXp2lKReRSxZw8dTxSr1n0zYe9I0wP5NedZKCz5cvKUjDhg1p27Ytx44dKySHUhIlybj37t2bRYsW0aRJEzIyMggODmb48OG4uLhw7do1vL29CyXUcnV1ZdeuXXz44YfMmTOHTz/9tEhbFy5cYOvWrRw5coShQ4fy4IMP8u2333Ly5En279/PxYsX6dy5M+PGjTPvj6GpVnRt7UwdOxuijyfTv0szi7SpnYimxlGdpOBFpFiV3PLICZUk4967d2/ef/99Vq82Zk04c+YMcXFxuLi4YGtry/DhwwvdZ9iwYQAEBgby7bffFtvW/fffj42NDV26dCEhIQGArVu3MmLECGxsbGjevLlpJKepeTja2xLYurFF94toJ6IpF+UZMVQV1UkK3svLi1WrVhUqu3r1KgkJCXTs2JGxY8eye/duWrZsyfr1xafDKUnGPSoqik2bNhEdHU29evUIDw83KeM6OjoWSUmbb2tJfVKwTn67BX9qagdh7V2Yu+lPUtKzcK5Xp8rb0zERTa3BGlLw/fr1Iz093ZQ0Kjc3l3/9619MnDiRunXrsnjxYvbs2VOiA4GSZdyvXLlC48aNqVevHkeOHGH79u2Vbj9Az549WbVqFQaDgYSEBKKioqqkHY1lCGvvgghst1BcRDsRTa0hXwq+b9++uLm5maTgfX19CQ0NNQWbKxOlFKtXr2blypXceeeduLi4YGNjw7Rp00q85qmnnsLd3R13d3fCwsIYOHAgjzzyCGFhYfj4+PDggw+SmprKXXfdRU5ODr6+vrz88suEhoZWuv0Aw4cPx93dHW9vb5566ilCQkJo1KhRlbSlqXr83J2pa29rsaW+WgpeUya3o7R2Rfn9998ZNWoU3377bbG5zKsraWlpODk5kZycTLdu3di2bRvNmze3tlkVQj+v8NjCHVy8mslPz/Wu0PXlkYLXMRGNphLp3r07p06dsrYZ5WbIkCGkpKSQlZXFyy+/XGMdiMbIYJ8W7D17hVyDYGtjXnrkimIVJ6KUGgHMADoD3UQkpsA5X+BjoCFgAIJF5LpSKhBYAtQF1gPPSm0fRmk0FkLHQWoXD3drzcPdLNOWtWIiB4BhwG8FC5VSdsAXwNMi4gWEA/lbL+cD44E78153WcpYjUaj0RSPVZyIiBwWkaPFnBoI7BORvXn1kkUkVynVAmgoItF5o4/PgPstaPJtjx70aWoC+jm1PNVtdZYnIEqpn5RSu5RS+QJEdwBnC9Q7m1emsQCOjo4kJyfrf1BNtUZESE5OxtHR0dqm3FZUWUxEKbUJKC46N01EvivFnp5AMJAO/KKUigWuFlO3xE80pdR4jFNftG7dujxma4rB3d2ds2fPkpiYaG1TNJpScXR0NKkZaCxDlTkREamILOpZ4FcRSQJQSq0HAjDGSQo+Ge7A+VLaXgAsAOMS3wrYoSmAvb097dq1s7YZGo2mGlLdprN+AnyVUvXygux9gEMicgFIVUqFKqNQ0RigpNGMRqPRaCyEVZyIUuoBpdRZIAxYp5T6CUBELgPvAn8Ae4BdIrIu77JngE+BY0A88KPFDddoNBpNIfSOdY1Go9EUojw71mu9E1FKJQI1bwtxYVyBJGsbUU3QfVEY3R+F0f1xg1vpizYi4mZOxVrvRGoDSqkYc78V1HZ0XxRG90dhdH/cwFJ9Ud0C6xqNRqOpQWgnotFoNJoKo51IzWCBtQ2oRui+KIzuj8Lo/riBRfpCx0Q0Go1GU2H0SESj0Wg0FUY7kWqCUuoupdRRpdQxpdSUYs7/n1LqkFJqn1LqF6VUG2vYaSnK6o8C9R5USolSqlavyDGnP5RSD+U9IweVUsstbaOlMON/pbVSKlIptTvv/+Uea9hpCZRSi5RSF5VSB0o4r5RS7+f11T6lVEClGyEi+mXlF2CLcRe+B1AH2At0ualOX6Be3u/PAF9b225r9kdevQYYc9JsB4KsbbeVn487gd1A47zjpta224p9sQB4Ju/3LsBJa9tdhf3RG6O+4IESzt+DUd1DAaHAjsq2QY9EqgfdgGMiclxEsoCvgPsKVhCRSBFJzzvcTmFBytpGmf2Rx2vA28B1SxpnBczpjyeB/4lROggRuWhhGy2FOX0hGDOjAjSiFLHWmo6I/AZcKqXKfcBnYmQ74JyXn6nS0E6kenAHcKbAcVn5Up6gdmuHldkfSqmuQCsRWWtJw6yEOc+HJ+CplNqmlNqulKqtmT/N6YsZwKN5+nzrgX9axrRqSXk/W8qNVXKsa4qgiikrdtmcUupRIAijwnFtpdT+UErZAHOBCEsZZGXMeT7sME5phWMcpW5RSnmLSEoV22ZpzOmLUcASEXlHKRUGfJ7XF4aqN6/aYfZnS0XRI5HqwVmgVYHjYvOlKKX6A9OAoSKSaSHbrEFZ/dEA8AailFInMc71fl+Lg+vmPB9nge9EJFtETgBHMTqV2oY5ffEE8A2AiEQDjhh1pG5HzPpsuRW0E6ke/AHcqZRqp5SqAzwMfF+wQt70zccYHUhtne/Op9T+EJErIuIqIm1FpC3GGNFQEamtcs1lPh/AGoyLL1BKuWKc3jpuUSstgzl9cRroB6CU6ozRidyuaTm/B8bkrdIKBa6IMT9TpaGns6oBIpKjlJqIMSmXLbBIRA4qpWYCMSLyPTAbcAJWGPNycVpEhlrN6CrEzP64bTCzP34CBiqlDgG5wAsikmw9q6sGM/viX8AnSqnnME7dREjeUqXahlLqS4xTmK55MaDpgD2AiHyEMSZ0D8Y8TOnA2Eq3oZb2rUaj0WgsgJ7O0mg0Gk2F0U5Eo9FoNBVGOxGNRqPRVBjtRDQajUZTYbQT0Wg0Gk2F0U5Eo6lClFIn8/Zt3FIdjaa6op2IRqPRaCqMdiIaTSWhlFqjlIrNy+cx/qZzbZVSR5RSS/PyOqxUStUrUOWfSqldSqn9SqlOedd0U0r9npcX43elVEeLviGNxgy0E9FoKo9xIhKIUSBzklLK5abzHYEFIuILXAUmFDiXJCIBwHzg+byyI0BvEekKvAK8UaXWazQVQDsRjabymKSU2otRy6sVRQUQz4jItrzfvwB6Fjj3bd7PWKBt3u+NMMrcHMCoWuxVFUZrNLeCdiIaTSWglAoH+gNhIuKHMcug403VbtYYKnicr8qcyw1Nu9eASBHxBu4t5n4ajdXRTkSjqRwaAZdFJD0vphFaTJ3WefktwJjzYqsZ9zyX93tEpVip0VQy2oloNJXDBsBOKbUP4whiezF1DgOP59VpgjH+URpvA/9RSm3DqFir0VQ7tIqvRmMBlFJtgbV5U1MaTa1Bj0Q0Go1GU2H0SESj0Wg0FUaPRDQajUZTYbQT0Wg0Gk2F0U5Eo9FoNBVGOxGNRqPRVBjtRDQajUZTYbQT0Wg0Gk2F+f8XGWPIqkU/KAAAAABJRU5ErkJggg==\n", "image/svg+xml": [ "\r\n", "\r\n", "\r\n", "\r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", "\r\n" ], "text/plain": [ "
" ] }, "metadata": { "needs_background": "light" }, "output_type": "display_data" } ], "source": [ "figure_6_6()" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Example 6.7: Maximization Bias Example\n", "\n", "The small MDP shown inset in Figure provides a simple example of how maximization bias can harm the performance of TD control algorithms. The MDP has two non-terminal states A and B. Episodes always start in A with a choice between two actions, left and right. The right action ransitions immediately to the terminal state with a reward and return of zero. The left action transitions to B, also with a reward of zero, from which here are many possible actions all of which cause immediate termination with a reward drawn from a normal distribution with mean −0.1 and variance 1.0.\n", "\n", "![](images/05-05.png)" ] }, { "cell_type": "code", "execution_count": 10, "metadata": {}, "outputs": [], "source": [ "#######################################################################\n", "# Copyright (C) #\n", "# 2016-2018 Shangtong Zhang(zhangshangtong.cpp@gmail.com) #\n", "# 2016 Kenta Shimada(hyperkentakun@gmail.com) #\n", "# Permission given to modify the code as long as you keep this #\n", "# declaration at the top #\n", "#######################################################################\n", "\n", "import numpy as np\n", "import matplotlib\n", "%matplotlib inline\n", "import matplotlib.pyplot as plt\n", "from tqdm import tqdm\n", "import copy\n", "\n", "# state A\n", "STATE_A = 0\n", "\n", "# state B\n", "STATE_B = 1\n", "\n", "# use one terminal state\n", "STATE_TERMINAL = 2\n", "\n", "# starts from state A\n", "STATE_START = STATE_A\n", "\n", "# possible actions in A\n", "ACTION_A_RIGHT = 0\n", "ACTION_A_LEFT = 1\n", "\n", "# probability for exploration\n", "EPSILON = 0.1\n", "\n", "# step size\n", "ALPHA = 0.1\n", "\n", "# discount for max value\n", "GAMMA = 1.0\n", "\n", "# possible actions in B, maybe 10 actions\n", "ACTIONS_B = range(0, 10)\n", "\n", "# all possible actions\n", "STATE_ACTIONS = [[ACTION_A_RIGHT, ACTION_A_LEFT], ACTIONS_B]\n", "\n", "# state action pair values, if a state is a terminal state, then the value is always 0\n", "INITIAL_Q = [np.zeros(2), np.zeros(len(ACTIONS_B)), np.zeros(1)]\n", "\n", "# set up destination for each state and each action\n", "TRANSITION = [[STATE_TERMINAL, STATE_B], [STATE_TERMINAL] * len(ACTIONS_B)]\n", "\n", "# choose an action based on epsilon greedy algorithm\n", "def choose_action(state, q_value):\n", " if np.random.binomial(1, EPSILON) == 1:\n", " return np.random.choice(STATE_ACTIONS[state])\n", " else:\n", " values_ = q_value[state]\n", " return np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])\n", "\n", "# take @action in @state, return the reward\n", "def take_action(state, action):\n", " if state == STATE_A:\n", " return 0\n", " return np.random.normal(-0.1, 1)\n", "\n", "# if there are two state action pair value array, use double Q-Learning\n", "# otherwise use normal Q-Learning\n", "def q_learning(q1, q2=None):\n", " state = STATE_START\n", " # track the # of action left in state A\n", " left_count = 0\n", " while state != STATE_TERMINAL:\n", " if q2 is None:\n", " action = choose_action(state, q1)\n", " else:\n", " # derive a action form Q1 and Q2\n", " '''\n", " zip() 还可用在 [ for ] 中，直接对元素运算 来生成 list()\n", " '''\n", " action = choose_action(state, [item1 + item2 for item1, item2 in zip(q1, q2)])\n", " if state == STATE_A and action == ACTION_A_LEFT:\n", " left_count += 1\n", " reward = take_action(state, action)\n", " next_state = TRANSITION[state][action]\n", " if q2 is None:\n", " active_q = q1\n", " target = np.max(active_q[next_state])\n", " else:\n", " if np.random.binomial(1, 0.5) == 1:\n", " active_q = q1\n", " target_q = q2\n", " else:\n", " active_q = q2\n", " target_q = q1\n", " best_action = np.random.choice([action_ for action_, value_ in enumerate(active_q[next_state]) if value_ == np.max(active_q[next_state])])\n", " target = target_q[next_state][best_action]\n", "\n", " # Q-Learning update\n", " active_q[state][action] += ALPHA * (\n", " reward + GAMMA * target - active_q[state][action])\n", " state = next_state\n", " return left_count\n", "\n", "# Figure 6.7, 1,000 runs may be enough, # of actions in state B will also affect the curves\n", "def figure_6_7():\n", " # each independent run has 300 episodes\n", " episodes = 300\n", " runs = 1000\n", " left_counts_q = np.zeros((runs, episodes))\n", " left_counts_double_q = np.zeros((runs, episodes))\n", " for run in tqdm(range(runs)):\n", " q = copy.deepcopy(INITIAL_Q)\n", " q1 = copy.deepcopy(INITIAL_Q)\n", " q2 = copy.deepcopy(INITIAL_Q)\n", " for ep in range(0, episodes):\n", " left_counts_q[run, ep] = q_learning(q)\n", " left_counts_double_q[run, ep] = q_learning(q1, q2)\n", " left_counts_q = left_counts_q.mean(axis=0)\n", " left_counts_double_q = left_counts_double_q.mean(axis=0)\n", "\n", " plt.plot(left_counts_q, label='Q-Learning')\n", " plt.plot(left_counts_double_q, label='Double Q-Learning')\n", " plt.plot(np.ones(episodes) * 0.05, label='Optimal')\n", " plt.xlabel('episodes')\n", " plt.ylabel('% left actions from A')\n", " plt.legend()\n", "\n", " plt.show()" ] }, { "cell_type": "code", "execution_count": 11, "metadata": {}, "outputs": [ { "name": "stderr", "output_type": "stream", "text": [ "100%|██████████| 1000/1000 [00:24<00:00, 40.57it/s]\n" ] }, { "data": { "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAEKCAYAAAD9xUlFAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvIxREBQAAIABJREFUeJzs3Xd4VMX6wPHv7KZ30kkjAQIhIdTQEekg0kQF8YKKXjtY8Cfq9apYruXaC15FUcSCDSuColJDDxB6SCCEJEBII73tZuf3x0lCDwtks5tkPs+zz+6enD3n3RD23Tkz846QUqIoiqIoADprB6AoiqLYDpUUFEVRlDoqKSiKoih1VFJQFEVR6qikoCiKotRRSUFRFEWpo5KCoiiKUkclBUVRFKWOSgqKoihKHTtrB3CpfH19ZXh4uLXDUBRFaVK2bduWK6X0u9h+TS4phIeHk5CQYO0wFEVRmhQhxBFz9lOXjxRFUZQ6KikoiqIodVRSUBRFUeo0uT4FRVEuzGAwkJmZSUVFhbVDUazEycmJkJAQ7O3tL+v1KikoSjOSmZmJu7s74eHhCCGsHY7SyKSU5OXlkZmZSURExGUdQ10+UpRmpKKiAh8fH5UQWighBD4+PlfUUlRJQVGaGZUQWrYr/fdXSaEBSClZsi2T7CJ1HVdRlKZNJYUG8MP2ozzy3U7e/CvF2qEoik3IzMxkwoQJREZG0rZtW2bOnEllZeU5+9122218//33jRbXL7/8wssvv9xo52uKVFK4QuVV1Ty3dB+AaikoClrLedKkSUycOJGUlBRSUlIoLy9nzpw5jXL+6urqC/5s/PjxPP74440SR1OlksJF5JZUcssnW9icmkdGfhlSStLzyvjHx5vYmpbPjvSTFJYbcHO0IymrmBmfbuG3XcetHbaiWM3KlStxcnJixowZAOj1et58800WLVpESUmJWcd49dVX6dWrF126dOGZZ56p2z5x4kR69uxJTEwM8+fPr9vu5ubG008/TZ8+fdi4cSPh4eE888wz9OjRg9jYWJKSkgBYuHAhM2fOBLRWygMPPED//v1p27ZtXYvFZDJx3333ERMTw9ixYxkzZkyjtmasTQ1JvYg/9maxNjmHtck5ANzWP5yVSdmk55dxomg3o2IC0An4R98wPlyTytGCchKOnCQ6yIOZX23nxp4h3Dbg8oaGKcqVePbXvew7VtSgx4wO8uCZcTH17rN371569ux5xjYPDw/Cw8M5ePAg3bp1q/f1K1asICUlhS1btiClZPz48axdu5ZBgwbxySef4O3tTXl5Ob169eL666/Hx8eH0tJSOnfuzHPPPVd3HF9fX7Zv387777/Pa6+9xscff3zOuY4fP058fDxJSUmMHz+eG264gR9++IG0tDR2795NdnY2nTp14vbbb7+E31LTploKFxGfkosQcG2X1vRv58PCDWkUlht4cFgkB7NLmLfqENFBHsS18QbAyV6HsVoy7t149h4r4qN1hzGZpJXfhaI0HinleUfASGne/4MVK1awYsUKunfvTo8ePUhKSiIlReuve+edd+jatSt9+/YlIyOjbrter+f6668/4ziTJk0CoGfPnqSlpZ33XBMnTkSn0xEdHc2JEycAiI+P58Ybb0Sn0xEYGMiQIUPMiru5UC2FelSbJOsP5jK5Zyiv3NCFsiojH6w+xITuwbT1deVwbim/7DxGTGtPogLdARga5c+k7iHc/cU2gr2cOVpQzoZDeQyM9OVIXilezg54ulzeTENFuRQX+0ZvKTExMSxZsuSMbUVFRZw4cYK3336bHTt2EBQUxLJly877eiklTzzxBHffffcZ21evXs1ff/3Fxo0bcXFxYfDgwXXj8Z2cnNDr9Wfs7+joCGgJw2g0nvdctfvUnvf0+5ZKtRTqsflwHkUVRgZG+gLg4mDH7JEdaefnhhCCl6+PZWrvUG4fGEFIK2fuGBjBvVe3Z3h0ACsfuZrlD12Fp7M93yZkUFppZNy78Vz/wQZKK8//B6oozcGwYcMoKytj0aJFgNbx+8gjjzBz5kw+/fRTEhMTL5gQAEaNGsUnn3xS1/9w9OhRsrOzKSwspFWrVri4uJCUlMSmTZssEv/AgQNZsmQJJpOJEydOsHr1aoucx1appFCPj9cdxsfVgRHRAef9uYuDHS9N6kLHQHeEEDw1NprYEE8A2vi44uFkz8RuQfy+N4uFG9IoqjByMLuEN/9Mbsy3oSiNSgjBjz/+yPfff09kZCQ+Pj7odDqefPLJ8+5/9913ExISQkhICP369WPkyJHcfPPN9OvXj9jYWG644QaKi4sZPXo0RqORLl268NRTT9G3b1+LxH/99dcTEhJC586dufvuu+nTpw+enp4WOZctEk2tqRQXFyctvciOsdrEqysO8OGaVGaP6MADwyIv+1h7jxVy7Tvx6HWCTq3daeXiQG5JFcsfvKoBI1YUzf79++nUqZO1wzjDhg0bmDp1Kj/88MM5HdC2qqSkBDc3N/Ly8ujduzfr168nMDDQ2mGZ7Xx/B0KIbVLKuIu9VvUpnMdf+0/w4ZpUxsQGMmNA+BUdKybIk6m9w8gvrWTW0Ej+2JvF+6sPUV5VjbOD/uIHUJQmrn///hw5YtaiXzZj7NixFBQUUFVVxVNPPdWkEsKVUknhPHZkFGCvF7w5pRuOdlf+wf3SpNi6x8cLK6g2Sdal5PDVlnTCvF2YObQ99jodrVwdrvhciqJcuZbWj3A6lRTOY1dGIdGtPRokIZyta02fw31fbsdYM1R10cYj9I7w5tu7+zX4+RRFUS6F6mg+S7VJsvtoIV1DvSxyfH8PJ8K8XXB3suO7e/oxqUcwAFsO55NVqMpkKIpiXaqlcJbUnBJKKo10CbFMUgD48p99cLLX4+fuSK9wb+4f0p5hr6/h9z3H1exnRVGsSiWFs/ydlA1A73Bvi50j1NvljOft/NyICnTny83pbE8vwNFOx6s3drXY+RVFUS5EXT46y087jtIt1IswH5eL79yAHh3VkZTsEn7ZeYyfEo9SVGFo1PMrSkPR6/V069aNmJgYunbtyhtvvIHJZLrs47m5uZ13++WU3Z4/fz5RUVFERUURFxd3wQ7ltLQ0OnfufKmhXpExY8ZQUFDQqOc8H5UUTpN8opikrGImdgtq9HMP6xTAfYPbMSzKH0O1ZM2BnEaPQVEagrOzM4mJiezdu5c///yTZcuW8eyzz1o7LJYuXcqHH35YVwBv/vz5TJs2jaNHjzbK+S9UaqPWsmXL8PKy3GVrc6mkcJp1KbkAjOpsnTHJc0ZHMf+WOHxcHfh4XSo70k9aJQ5FaSj+/v7Mnz+f9957DyklFRUVzJgxg9jYWLp3786qVauAM0tagzZP4PRv8Y888gg9evRg2LBh5OSc+4Vp27ZtXH311fTs2ZNRo0Zx/Pi55etfeeUVXn31VXx9tbI1PXr0YMaMGcybN8/s93Po0CFGjx5Nz549ueqqq+pKcv/666/06dOH7t27M3z48LrienPnzuWuu+5i5MiR3HLLLSxcuJBJkyYxevRoIiMjz1hjIjw8nNzcXNLS0ujUqRN33nknMTExjBw5kvLycgC2bt1Kly5d6NevH48++qhFWjOqT+E0247kE+zlTGtPZ6vFoNcJZg5tz6t/HOCWBVtYM2cI3mr+gnI5lj8OWbsb9piBsXDNpa1c1rZtW0wmE9nZ2XzxxRcA7N69m6SkJEaOHElycv1lX0pLS+nRowevv/46zz33HM8++yzvvfde3c8NBgOzZs3i559/xs/Pj2+++YYnn3ySTz755IzjnK+kd1xcHJ9++qnZ7+Wuu+7igw8+IDIyks2bN3PfffexcuVKBg4cyKZNmxBC8PHHH/Pf//6X119/HdASVnx8PM7OzixcuJDExER27NiBo6MjHTt2ZNasWYSGhp5xnpSUFBYvXsxHH33E5MmTWbJkCdOmTWPGjBnMnz+f/v37W2yxIJUUakgpSUg7Sb92PtYOhRkDIhjY3pdRb63lvZUHeXpctLVDUpQrUltOJz4+nlmzZgEQFRVFmzZtLpoUdDodU6ZMAWDatGl1JbFrHThwgD179jBixAhAK8DXunXrS4rLHCUlJWzYsIEbb7yxblvtEqOZmZlMmTKF48ePU1VVRUTEqVGE48ePx9n51BfNYcOG1dVSio6O5siRI+ckhYiIiLp1J2pLfxcUFFBcXEz//v0BuPnmm1m6dKnZ8ZtLJYUamSfLyS6uJK5NK2uHAkBkgDuT40L5fFMat/UPb/SOb6UZuMRv9JaSmpqKXq/H39//gh/CdnZ2Z3RG15bEPp+z12qQUhITE8PGjRvrjSM6Oppt27YxdOjQum3bt28nLi6OzZs315Xqfu655+jSpcs5rzeZTHh5eZGYmHjOz2bNmsXs2bMZP348q1evZu7cuXU/c3V1PWPf08t1X6is99n7lJeXN1pJb9WnUGNnptbr3z3MNpICwMMjOqDXCV5dccDaoSjKZcnJyeGee+5h5syZCCEYNGgQX375JQDJycmkp6fTsWNHwsPDSUxMxGQykZGRwZYtW+qOYTKZ6kYZffXVVwwcOPCMc3Ts2JGcnJy6pGAwGNi7d+85scyZM4fHHnuMvLw8ABITE/nxxx/rKqEmJiaSmJjI+PHjz/tePDw8iIiI4LvvvgO0ZLRz504ACgsLCQ7WJqJ+9tlnl/37qk+rVq1wd3evKxn+9ddfW+Q8qqVQIzWnFNDmDNiKAA8n7h7Ujrf/TmFS92CGRPlbOyRFuajy8nK6deuGwWDAzs6O6dOnM3v2bADuu+8+7rnnHmJjY7Gzs2PhwoU4OjoyYMAAIiIiiI2NpXPnzvTo0aPueK6urnX9AZ6ennzzzTdnnM/BwYHvv/+eBx54gMLCQoxGIw899BAxMWcuMjR+/HiOHTvGgAEDMBqNZGVlsXPnTvz8/M77Pg4cOEBISEjd8zfffJMvv/ySe++9lxdeeAGDwcBNN91E165dmTt3LjfeeCPBwcH07duXw4cPN9Sv8wwLFizgzjvvxNXVlcGDB1ukpLcqnV3j4W8S2Zyax4YnhjX4sa9EpbGace/GU1pZzepHB2OvV4075cJssXS2LTIajcyYMQOTycQXX3xx3uVDbVFtSW+Al19+mePHj/P222+fs58qnd0AUnNLifBzvfiOjczRTs9jo6O447MEftt1nIndg60dkqI0eXZ2dnz++efWDuOS/fbbb7z00ksYjUbatGnDwoULG/wcKimgXRs8nFPChG62+YE7pKM/HQLcmLfqIGNiW+Ngp1oLitISTZkypW4klqWoTxcgv7SKogojEb6211IA0OkEc0ZFkZJdwv9WH7J2OIqiNGMqKQCHc7VOZlu8fFRreHQAY2IDmb/2EIbqy68joyiKUh+VFID0/DIA2njb9lyAcV2CKK2qZldmobVDURSlmbJoUhBCjBZCHBBCHBRCnDMnWwgRJoRYJYTYIYTYJYQYY8l4LiSrSJsoE+jpZI3Tm61PW2229a2fbKHDv5cz7t34RpvQoihKy2CxpCCE0APzgGuAaGCqEOLseg3/Br6VUnYHbgLet1Q89ckuqsTdyQ4XB9vud/d2dUAnoKTSiKezPbuPFnK0oNzaYSnKOTIzM5kwYQKRkZG0a9eOBx98kKqqqgvuX1BQwPvvn/rvf+zYMW644YYGiWXu3Lm89tprDXKslsCSLYXewEEpZaqUsgr4Gphw1j4S8Kh57Akcs2A8F3SiqIIAD9tuJdR6cFgHfN0ceGOytgjPnqPqUpJiW6SUTJo0iYkTJ5KSkkJycjIlJSU8+eSTF3zN2UkhKCjoktdKUBqGJb8aBwMZpz3PBPqctc9cYIUQYhbgCgy3YDwXlFVUQYCH48V3tAEPDo9k5tD2GKpN2OkEu48WMrqzecW/FKUxrFy5EicnJ2bMmAFotXvefPNNIiIiiIiI4I8//qCyspLDhw9z880388wzz/D4449z6NAhunXrxogRI7j//vsZO3Yse/bsYeHChfz0009UV1ezZ88eHnnkEaqqqvj8889xdHRk2bJleHt789FHHzF//nyqqqpo3749n3/+OS4utt1PaIssmRTON0Xw7AvgU4GFUsrXhRD9gM+FEJ2llGcMrxFC3AXcBRAWFtbggWYXVdInwnLLbzY0vU6g1+npEODO7qNF1g5HsVGvbHmFpPykBj1mlHcUj/V+rN59zlei2sPDg7CwMIxGI1u2bGHPnj24uLjQq1cvrr32Wl5++WX27NlTV2wuLS3tjNfv2bOHHTt2UFFRQfv27XnllVfYsWMHDz/8MIsWLeKhhx5i0qRJ3HnnnQD8+9//ZsGCBXUVWRXzWfLyUSZwej3YEM69PHQH8C2AlHIj4AT4nn0gKeV8KWWclDLuQnVKLpfJJMkuriDAxjuZzyc22JNdmQUYa4aoqk5nxRZIKc9bNqJ2+4gRI/Dx8cHZ2ZlJkyYRHx9/0WMOGTIEd3d3/Pz88PT0ZNy4cQDExsbWJZA9e/Zw1VVXERsby5dffnneonjKxVmypbAViBRCRABH0TqSbz5rn3RgGLBQCNEJLSk06jqU+WVVGKolAe5N4/LR6YZ28uebhAye+nkva5NzkFKy8v8G42Svt3Zoig242Dd6S4mJiWHJkiVnbCsqKiIjIwO9Xn9OwjCn7tDppaR1Ol3dc51OV1d6+rbbbuOnn36ia9euLFy48ILrLyv1s1hLQUppBGYCfwD70UYZ7RVCPCeEqK1N+whwpxBiJ7AYuE028tfdEzXDUZtKR/PphkX5E+TpxOIt6VRVmzhWWEFCmlrCU7GuYcOGUVZWxqJFiwBt0ZtHHnmE2267DRcXF/7880/y8/MpLy/np59+YsCAAbi7u1NcXHxF5y0uLqZ169YYDIa68tzKpbPoPAUp5TIpZQcpZTsp5X9qtj0tpfyl5vE+KeUAKWVXKWU3KeUKS8ZzPtlF2spJTfHykZ1exwPDImnn58q3d/fDXi9Yl9KoDS1FOYcQgh9//JHvvvuOyMhIOnTogJOTEy+++CIAAwcOZPr06XTr1o3rr7+euLg4fHx8GDBgAJ07d+bRRx+9rPM+//zz9OnThxEjRhAVFdWQb6lFafGls7/dmsGcJbtYN2cIoTY+o/lCaq/V3jR/I0XlRpY9eJW1Q1KsxNZLZy9cuJCEhIQz1lhWGt6VlM5u8WUu8su0CTXerg5WjuTy1V6THdTBj33Hi0jNKbFyRIqiNFUtPimcLKvCQa/DxaHpd87e2DMUBzsdH62zzKpPinKlbrvtNtVKsHEqKZRW0crVvsmsvFQfP3dHbugZwuIt6Ux6fz2F5QZrh6RYQVO7JKw0rCv992/xSSG/1EArl6Z76ehs/xrTiYeHd2BHRgHv/J1i7XCURubk5EReXp5KDC2UlJK8vDycnC5/4IxtV4BrBAVlVU26P+Fsbo52PDg8kuOF5SyIP0zCkZN8+c8+uDm2+H/qFiEkJITMzExyctQotJbKycmJkJCQy359i/+kyC+rolOgx8V3bGKeHheNj5sD81YdYm1yDmNiVX2klsDe3p6IiAhrh6E0YS3+8lFtn0Jz4+Jgx8PDO+DhZMeqpGxrh6MoShPRopNCtUlSWG7Auxn1KZzOTq9jUAc/VifnYDKpa8yKolxci04KReUGTBK8mmlSALi6gx85xZUcOHFlJQQURWkZLjkpCCGchBA3WiKYxtYcJq5dTJ8IbQnPhCOqJpKiKBdnVlIQQuiFENcIIRYBR4Aplg2rcRTUJIVWzTgphHo74+fuyLa0fGuHoihKE1Dv6CMhxCC0ctfXAluAAUCElLKsEWKzuPxSbXJXc+1TAK0ERlybVqqloCiKWS7YUhBCZAIvA+uBaCnl9UB5c0kIADnFWoVUb7fmmxQA4sK9yTxZzr1fbKO4Qs1yVhTlwuq7fLQEbZ3lKcA4IYQr5y6n2aSl5ZXiYKejdRNcS+FSTOwWxNTeYSzfk8UXm9KtHY6iKDbsgklBSvkgEA68AQwBkgE/IcRkIYRb44RnWYdzS2nj7YJO1/TrHtXHx82RlybFclWkLwviU/nf6kMYqk0Xf6GiKC1OvR3NUrNSSnknWoK4GZgIpFk+NMtLyy0l3NfV2mE0mgeGRVJSaeSV35NYm6zKICiKci6zh6RKKQ1Syl+llDcDoRaMqVGYTJIj+WWE+zTNhXUuR69wbxKfHomDXsfa5Bw+iT9MhaHa2mEpimJDLqv2kZSyvKEDaWzHCsupMppaVEsBwMleT9dQTxZtOoKU4Olsz/U9L794lqIozUuLndGclqsNoorwaVlJAaB3hDe1lZX/3HfCusEoimJTWmxSOFqgJYWmui7zlbi6gz9CQEyQB2tTctQlJEVR6lw0KQgh4oQQPwohtgshdgkhdgshdjVGcJZUXGEEwNOl+VVIvZjeEd5s+/cI5oyOoqyqmr/2q9aCoigac/oUvgQeBXYDzWYcY0mllhRcHVrmkhLerg4MbO9LuI8LH61N5drY1s1iSVJFUa6MOZePcqSUv0gpD0spj9TeLB6ZhZVUGHFx0KNv5nMU6qPXCe4c1JadmYWsTcm1djiKotgAc5LCM0KIj4UQU4UQk2pvFo/MwkqrjLiqJSq5oWcIYd4uvLB0H0Y1oU1RWjxzksIMoBswGhhXcxtryaAaQ3GFUa1bDDja6fnXmChSskv4Y6/qW1CUls6cT8WuUspYi0fSyEorVVKoNSI6EG9XB1bsy2J058AWfUlNUVo6c1oKm4QQ0RaPpJGVVBpxddRbOwyboNcJhkb583PiMTo9/TuPL9lFeZUapqooLZE5SWEgkCiEONCchqSWVFbj5tjyhqNeyIjoAEBbt/rrrRl8sOYQB7NL1NrOitLCmHP9ZLTFo7CCkkoDbo7NothrgxgW5c+L18UyKiaAOd/vYt6qg7z9dwrPT4hher9wa4enKEojuWhLoWb4qRenOpm9msOQ1NLKatycVJ9CLTu9jpv7hOHj5si9g9thrGkh/J2UbeXIFEVpTObMaH4QbQKbf83tCyHELEsHZmlan4JKCucTF+7NiocHcVOvULYezqfKqIaqKkpLYU6fwh1AHynl01LKp4G+wJ2WDcuyqowmqowm3FrobGZzdAhwZ0iUP6VV1WxPV+s7K0pLYU5SEMDpQ1Gqa7Y1WaU1JS7U5aP69W/ng4OdjuW7j1s7FEVRGok5SeFTYLMQYq4QYi6wCVhg0agsrK7ukbp8VC93J3tGxwTyU+IxVUlVUVoIczqa30Cb1ZwPnARmSCnfMufgQojRNUNZDwohHr/APpOFEPuEEHuFEF9dSvCXqzYpuKukcFGT40IpLDeoSqqK0kLU+6kohNABu6SUnYHtl3JgIYQemAeMADKBrUKIX6SU+07bJxJ4AhggpTwphPC/1DdwOVRLwXz92vng4qAnIe0kY7sEWTscRVEsrN6WgpTSBOwUQoRdxrF7AwellKlSyirga2DCWfvcCcyTUp6sOV+jjH8sUX0KZtPrBDFBHuw+WmjtUBRFaQTmfCq2BvYKIbYApbUbpZTjL/K6YCDjtOeZQJ+z9ukAIIRYD+iBuVLK382I6YqU1Cywo2ofmSc22IuvthzBWG3CTt9iF+tTlBbhgp+KQghHKWUl8OxlHvt8I5TOrplgB0QCg4EQYJ0QorOUsuCsWO4C7gIIC7ucRsuZStXlo0sSG+JBxXoTh3JK6Rjobu1wFEWxoPq+9m2suf+nlHLN2Tczjp0JhJ72PAQ4dp59fpZSGqSUh4EDaEniDFLK+VLKOCllnJ+fnxmnrl/tUpwe6vKRWWKDPQHYdkTNV1CU5q6+pOAghLgV6H/64jqXsMjOViBSCBEhhHAAbgJ+OWufn4AhAEIIX7TLSamX/jYuTVGFAZ1ouUtxXqq2vm50DHDnf2sOqqGpitLM1ZcU7kGbvXx63SOzF9mRUhqBmcAfwH7gWynlXiHEc0KI2v6IP4A8IcQ+YBXwqJQy73LfjLmKyg24O9mjU+sGmEWnEzw9LpqM/HK+2pxu7XAURbGgC35VllLGA/FCiAQp5WVNVpNSLgOWnbXt6dMeS2B2za3RFFUY8XBWrYRLMaC9L91CvVi8JZ0ZA8JJPlFCqLczLqq1pSjNijmT15r07OXzKSo34OGk1lK4VFN6hZKSXcKGQ3mMemstY9+JR8vriqI0Fy1yfGFRhUoKl2Nsl9Y42et4+uc9AKTmlvKbqoukKM1Ky0wK5ery0eVwd7JncAd/DuWUYqcT+Lo5sHSnSgqK0pyYs57CACGEa83jaUKIN4QQbSwfmuWolsLlG9OlNQA92rRicEd/tqTlq0tIitKMmNNS+B9QJoToCswBjgCLLBqVhRWVG/BwVknhcgyN8sfT2Z7hnfzpHeFNfmkVB7NLrB2WoigNxJxrKEYppRRCTADellIuqJm/0CQZq02UVlWrlsJlcnO0I/6xIbg42JF5sgyATal5RAaomc6K0hyY01IoFkI8AUwDfqupftpkP1HrZjOrPoXL5u5kj14nCPN2ob2/Gx+uTa0rHaIoStNmTlKYAlQCd0gps9AK3b1q0agsqKjCAKBaCg1ACMFLk2I5WlDO/LUWn4iuKEojMGeeQpaU8g0p5bqa5+lSyibbp1BUXttSUEmhIfQK96ZbqBcbD1l8IrqiKI3AnNFHk4QQKUKIQiFEkRCiWAhR1BjBWcKploK6fNRQuoe2YtfRAgzVJmuHoijKFTLn8tF/gfFSSk8ppYeU0l1K6WHpwCylqLwmKaiWQoPpHuZFhcFE0vFia4eiKMoVMicpnJBS7rd4JI2kqMLAUN12OnzWFSrUamINoXuYFwA3zd/I1rR8K0ejKMqVMCcpJAghvhFCTL3E0tk26VhBBf11e9FX5EPOAWuH0ywEeznTzs+V0qpq3vk7xdrhKIpyBcxJCh5AGTCSSyidbXNSV8O3t5CSVUBXx5rSDHmHrBpScyGE4PeHBnFLvzZsTcunyqj6FhSlqbpob6uUckZjBGJxpbmw72e6OLYisnbp6HyVFBqKvV7HgPa+LNp4hIS0fPq09UGv1qtQlCbHnNFHIUKIH4UQ2UKIE0KIJUKIkMYIrkF1vp6ytqO4p3IhXtU1wydVS6FB9Y3wAeDmjzfz6Hc7rRyNoiiXw5zLR58rtSzrAAAgAElEQVSiLaMZhDZx7deabU3KB2tTGbFvzKkNds6QkwSZ20AVdGsQni723NY/nE6tPfhhx1H2H2+yI5cVpcUyJyn4SSk/lVIaa24LAT8Lx9XgRscEchQ/NpuitA2RwyF7H3w8FLYthJNpsOxRMJRbM8wmb+74GBbf2Qd3Rzs+WqdmOStKU2PODK5cIcQ0YHHN86lAk5u+Gu7rysIZvfh84+vEXWVCf3wb7P8VHD1h+RyortJ2jLkO2vS3brBNnJeLA1d39GPDwTyklAih+hYUpakwJyncDrwHvAlIYEPNtiZncEd/Bnf0154EdQG3QIgcCT/fD8nLte1Fx6wXYDPSJ8KbpbuOk5FfTpiPi7XDURTFTOaMPkoHxjdCLI3L2Qu6TdUeT10MhZnwVmeVFBpI75pO582H81RSUJQm5IJJQQgxR0r5XyHEu2gthDNIKR+waGSNSQjwDAF7VyhWy0s2hEh/N1q52LMuJZcb40KtHY6iKGaqr6O5trRFArDtPLfmRQjwCIKio9aOpFnQ6QQTugXz2+7jpOWWWjscRVHMdMGkIKX8teZhmZTys9NvaDOcmx+P1lCkWgoN5b7B7bDTCd5bddDaoSiKYiZzhqQ+Yea2ps8jWF0+akD+Hk5Mjgvll8Rj5JVUWjscRVHMcMGkIIS4pqY/IVgI8c5pt4VA81x70b21lhRMqnZPQ7mlXxuqqk18vTXD2qEoimKG+loKx9D6Eyo4sy/hF2CU5UOzAo8gMBmhNMfakTQbkQHuDOrgxwdrDpFVWGHtcBRFuYj6+hR21vQfxAJfnNaf8DPams3Nj0ewdl+Uad04mpnnxsdgqDYxZ8kuTCZVUkRRbJk5fQorAOfTnjsDf1kmHCvzqhk6WZBu3TiamXBfV54aG83a5BzmqU5nRbFp5sxodpJSltQ+kVKWCCGa52wkrzba/ckj1o2jGbq5dxibU/N5++8U7PQ6ooM8uLpDkyuhpSjNnjkthVIhRI/aJ0KInkDzrBrn5AHOraBAJYWGJoTguQkxeLk48MrvSdzz+TZ1KUlRbJA5SeEh4DshxDohxDrgG2CmZcOyIq82qqVgIV4uDnxzd19u6x9OuaGaHRkF1g5JUZSzXDQpSCm3AlHAvcB9QCcpZfOb0VyrVRvVUrCgdn5uPDyiA3Y6wYp9WdYOR1GUs5jTpwDQEYgGnIDuQgiklIssF5YVeYXBgeXaXAWdOQ0p5VJ5OtszMNKX+WtTWZ2Uw4D2vjw9LtraYSmKgnnLcT4DvFtzGwL8l+ZYNbWWVxttbYWSE9aOpFl7Y3I3Zg2NxMlexyfrD6tV2hTFRpjzVfgGYBiQJaWcAXQFHM05uBBitBDigBDioBDi8Xr2u0EIIYUQcWZFbUmtIrT7fLVqmCV5uzowe0QHPru9Ny4Oej5co9bLVhRbYE5SKJdSmgCjEMIDyAbaXuxFQgg9MA+4Bu3S01QhxDnXCIQQ7sADwOZLCdxi/Dtp99n7rBtHC+Hl4sAt/cL5KfEYm1Kb3IJ+itLsmJMUEoQQXsBHaGUutgNbzHhdb+CglDJVSlkFfA1MOM9+z6NdkrKNGggeQeDkCSf2WjuSFuPBYZG08XHh8SW7qDRWWzscRWnRzBl9dJ+UskBK+QEwAri15jLSxQQDp1dBy6zZVkcI0R0IlVIuvYSYLUsICOisWgqNyNlBz3MTOpOWV8bC9WnWDkdRWrRLGl4jpUyTUu4yc/fzrdZeN1tJCKFDW/f5kYseSIi7hBAJQoiEnJxGKFbnHw0n9oFUk6say9Ud/Bga5c+8VQepMKjWgqJYiyXHXGYCp6/DGIJWebWWO9AZWC2ESAP6Ar+cr7NZSjlfShknpYzz82uE0ggBMVBVrGogNbI7BkZQVGHkj71ZSCmpMqoS5orS2CyZFLYCkUKICCGEA3ATWtltAKSUhVJKXylluJQyHNgEjJdSJlgwJvME11T1SF1t1TBamn5tfQj1dubbhAzeW3mQqKeWq8V5FKWRmTNP4XNztp1NSmlEK4fxB9p6z99KKfcKIZ4TQtj2PIfALuDdDnZ/Z+1IWhSdTjC2SxCbUvP535pDmCTM/VX17ShKYzKnpRBz+pOaoaY9zTm4lHKZlLKDlLKdlPI/NduellL+cp59B9tEKwG0zuYukyEtHgqPWjuaFqV3uDfVJklZldav8OvOY+xIP8meo4WsTFITChXF0upbjvMJIUQx0EUIUVRzK0abp/Bzo0VoLZ3GARIOr7V2JC1Kj7BWdY9fmNgZb1cHblmwhbHvxnP7wgQy8susGJ2iNH/1tRTWSindgdeklB41N3cppY+U8onGCtBq/DqBowdkmjMlQ2koni72dAhwA6BfOx8eHx1FkJczDwxtD8DyPcetGZ6iNHv1JYV3au5HNkYgNken0zqcM7daO5IWp387X3zdHInwcWVyr1D+eHgQs0d2JDbYk992q8qqimJJ9SUFgxDiUyBYCPHO2bfGCtCqQnpD1m5YcieU5lo7mhbjsdFR/PbAQHS6M6e6TOgWxM6MAl5Yug+p5pAoikXUVzp7LDAcGIpW3qLlCe2t3e/+FsL6QK9/WjeeFsLZQY+zg/6c7TMGRHAkr4yP4w8zuKM/TvY6Pt2QxgsTOrPnWCFXRarlPRXlSomLfeMSQnSVUu5spHguKi4uTiYkNNIgJZMJ9v0EP94DMdfBpA8b57zKBVUaqxny6mpauTpQUGbgaEE5djqB0SRZ/uBVdGrtYe0QFcUmCSG2SSkvWonarCqpQoi/hRB7ag7cRQjx7yuOsCnQ6aDzJIgcofoWbISjnZ7Hx3Ri//EijheWE+TphLFmredEtbynolwxc5LCR8ATgAGgpvbRTZYMyuaExEH+ISjLt3YkCjC+axA7nh7JmkeH8MSYTjjZa3/GO1VSUJQrZk5ScJFSnj0u02iJYGxWSC/tXrUWbIansz2h3i6M6xrEzmdGMqiDHzszC60dlqI0eeYkhVwhRDtqKpwKIW4AWtZg8aDuIPQqKdgoRzs93UI8ST5RzKoD2Xy8LlUV01OUy1Tf6KNa9wPzgSghxFHgMDDNolHZGgdXrXKqSgo2a0R0IB+sSWXGp9q/kYezPZPjQi/yKkVRzmbOIjupUsrhgB8QJaUcKKVMs3hktiakF2RuA5Oq9W+LYkM8iX98CB9M60GkvxuLNqapuQyKchku2FIQQsy+wHYApJRvWCgm2xTSCxIWQM4BCDhnqWnFBvi7OzG6c2tyS6r49097ePT7Xew/XsSz42OIC/e2dniK0iTU11Jwv8itZWnTT7tP+cO6cSgXNTkulLFdWvP9tkxSskuYsXArf+9XFVYVxRwXnbxmaxp18trZFoyCslyYmaCV11ZslskkScoqxt3JjjsXJZCUVcxXd/ahfztfa4emKFbRkJPXlFo9pkPeQcjYbO1IlIvQ6QTRQR6Eervw0/0DcHHQ89uuljVoTlEuh0oKlyJ6Iji4wfaLLjyn2BAnez2DIv34a/8JTKam1TJWlMamksKlcHTTaiDt/REqi60djXIJRkQHcKKokid/2sNN8zeyPf2ktUNSFJtkdlIQQvQVQqwUQqwXQky0ZFA2rfs0MJRCsupwbkquiQ1kWJQ/i7eksyO9gHu/2EZuSaW1w1IUm1PfcpyBZ22aDYwHRgPPWzIomxYcB3ZOcHS7tSNRLoGLgx0LbuvFvudG8eN9A8grqeKdv1OsHZai2Jz6WgofCCGeEkI41TwvAG4GpgBFFo/MVuntIKAzZO2ydiTKZXBxsCM6yIMb40JZvCWdzJNqzWdFOd0Fk4KUciKQCCwVQkwHHgJMgAvQci8fAbTuAsd3QRMbzqucMmtoe6pNkq+3ZJBdXMHLy5NIzSmxdliKYnX19ilIKX8FRgFewA/AASnlO1LKnMYIzmYFdoHKQjiZZu1IlMsU5OXMgPa+fJuQwei31vHBmkPM+X6XKo2htHj19SmMF0LEAyuBPWhrKFwnhFhcUzW15WrdVbs/pvoVmrKJ3YLJLq7EJCX3D2lHwpGT/L4ny9phKYpV1ddSeAGtlXA98IqUskBKORt4GvhPYwRnswJjwS0Adn5t7UiUKzC6cyCjYgKYd3MPZo/oSICHIz8nHrN2WIpiVfUlhUK01sFNQHbtRillipSyZa28dja9PfScASl/QnaStaNRLpOrox0fTo9jQHtf9DrB8E4BrE3JocKgVcJdl5LDydIqK0epKI2rvqRwHVqnshFt1JFyup63abObF4yAtHhrR6M0gBHRAZRVVTNl/iYeX7KL6Qu28Mwve60dlqI0qvpGH+VKKd+VUn4gpWy5Q1AvxKM13LMWXP3gx3vVDOdmoF87H7qGeFJYVsXXWzOw0wl+35vF99sySc87NXTVZJIUlhl4489k/tynqq8qzYuqknqlMrbAgpHQZQpc94GqntoMSCnZlJqPlJKbP9aKH7bxceGXmQPRCbhp/ib2HtO+JwV7ObNuzhB0OvXvrtg2c6ukmrMcp1Kf0N4w+AlY/SJ0HK3VRlKaNCEE/dr5APDQ8EikhHmrDjLzq+3Y6QRJWcXMGtoek5TMW3WI9YdyuSrSz8pRK0rDUEmhIQx6FLZ+BAd+V0mhmXloeAcAQlo58+j3u9DrBHPHRTO9XzgVhmq+3JzOfV9sZ0qvUB6/Jgo7vXZF9q2/kpESHh7RwZrhK8olU0mhIeh0ENoHMjZB3iHwCAJ7Z2tHpTSgG+NC8XN3JMDDiU6tPQCtJPeCW3uxcEMaH8cfZvPhfO4c1Jac4kre+isFJ3sd91zdDmcHvZWjVxTzqdLZDSWsrzbD+d0esPIFa0ejWMDgjv51CaFWzzateHdqd96a0o2SSiMPLN7B80v3EebtQoXBxLqUU5P/jdUmiisMjR22olwS1VJoKKF9Tz0+us16cShWMbF7MOO7BhF/MBeAPm296TJ3BXd9vo2hUf68fVM3pi/YQubJcn6dNYDWnqolqdgm1VJoKK27gl8n7XGxWvaxJdLpBIM6+DGogx+Odnpu7R9OsJczK5OyGfLaGnYfLaS00siDXyeqGkuKzbJoUhBCjBZCHBBCHBRCPH6en88WQuwTQuwSQvwthGhjyXgsys4B7t8EQ/6tXUaqVBU3W7p/jelE/GNDGB0TiE7A/Ok9+ffYTmw5nM/KpOyLH0BRrMBil4+EEHpgHjACyAS2CiF+kVLuO223HUCclLJMCHEv8F+09RqaroBo7T57P4T2sm4sitUJIXj/Hz2QgF4nMFSbmL82lVf/OMDVHfzqRispiq2w5F9kb+CglDJVSlkFfA1MOH0HKeUqKWXtVNFNQIgF42kc/jVJ4cRu68ah2AydTqCvmdxmr9fxxDVRJGUV88GaQ2fstyD+MNe+s47yqmprhKkogGU7moOBjNOeZwJ96tn/DmC5BeNpHF5twCsM4t+E6Ing4m3tiBQbM7pza66Nbc1rK5JZvieLKqOJNj6urEw6gUnC73uPc133pv/9SGmaLNlSON+8//P2rgkhpgFxwKsX+PldQogEIURCTo6Nr++j08ENn0LRcVj5PFSVgclk7agUG/P65K7MGtoeVwc7wrxdOJJXyrBOAYR6O7N4cwbGau1vpsJQzbYjJwGoNKoWhGJ5Fqt9JIToB8yVUo6qef4EgJTypbP2Gw68C1wtpbxo75vN1T66kF8fhMTFUF0Jg+bA0CetHZHSBHy0NpX/LNtPsJczU3uHsjE1j/UH87gq0pdtR06ydNZA2vq5WTtMpQkyt/aRJVsKW4FIIUSEEMIBbV2GX07fQQjRHfgQGG9OQmhS+s2C6ppa/HuWWDcWpcm4Y2AE86f3JMzbhddWJLP+YB5tfV1Zl5JLWVU181Yd4uN1qVQZVetTsQyL9SlIKY1CiJnAH4Ae+ERKuVcI8RyQIKX8Be1ykRvwndCqi6ZLKcdbKqZG5dsepn0PWxfAoVWweCq0Gwp+HcG9NfhGWjtCxQbpdIKRMYGMjAkku7iCiioTns72rDqQza87j7FkeyYAfu6OTOgWTKWxmp93HGNi92Ac7HQczC6hnZ8rQlXrVS6TRWc0SymXAcvO2vb0aY+HW/L8Vtd+OJSdhAPLtFv2PijJgXZD4KYvrR2dYuP83Z3qHk/sHkygpxP7jhdRbqjmu4RMXBzs2JF+kvdXa6OYjCbJv37czQfTejK6c6C1wlaaOFXmwtKCe5x6fDJNu89RS3gql65vWx82PD6Ul5cn8eHa1LqSGgCfbzrCoRxtwuSO9JMqKSiXTSUFS/NuC+5B2qS2g39p2/JTwVgJdo7WjU1pcoQQTO/XhiN5ZfRp682m1Dw8ne35NiETd0c7HO107MgoYN6qg4zvGkSot4u1Q1aaGLXyWmMoyQFHd/htNhRmwuE1EDtZ62PoNtXa0SlN3LGCcmZ/m8jsER35YXsmX2/Vpge18XHhizv6XDAxHMwuIaSVM072l1baO7u4AiT4ezhddF8p5Rn9G1JKpEStVGcF5o4+UkmhsWXtgQ8GaI/tXWBmAngGWzcmpdn4YtMR/v3THoK9nCkqN2A0Sab1DWPm0Eg8ne2pMpq478vteLnY88P2TPq38+Wz23vXzbi+kL3HCnGy19PW15Vr3l6Hq6Mdo2MCKSivYnJcKMUVRjoHe57xmvdXH+T7bZn89fDVdUngi01HeOuvZFb932Dcnewt9ntQzqWW47RVPu1PPTZVw0/3wE1faS0JRblCPcJaAXDv4HYMjfLn5eVJfLI+jXUpuZRWGekR1oq/9p8AtPWl4w/m8sDiHbx4XSyeLvYknyhmVVI2AyN96Rjgjl4nqDSauGXBFrxdHXh2QgxJWcXodYK03FJKKo2sS8klLbeUid2DOZJXxsIZvRBCsPpADqk5pezPKiImSEsY3yVkkFtSxa87j3NznzCz3pOx2lRXIyo9r4x/LNjEu1N70C3UiyqjCQe7Sx9Zn55XhoezHV4uDnXbTCbtC3JLb8WopNDY7J3AwQ08gmHgw/Dz/fDrQ3DVbECAEFBtgNZdznzd9kWQuRXGv2uVsJWmITrIg19nDiQmyAOdTvDO1O6MiW3NfV9uw06n4+fEYwR4ODJ/ehyRAW58uj6NN/9MxsPZjrsHtWP8e/FUGEx03uWByQQ+bg4MbO9LXmkVeaVVPPGDVtOr2iTJK9Xm4ezKLARg0cYjAPy44yih3i7srtken5JLkKczSVnF7KzZ9m1CBlN7h3KyzEArF3tySirrRlvlFFfi5+7I8cJyUk6UMPOr7XwwvSf92/mycEMaGfnlfLX5CG6Odox7N563burGsCh//rf6ENfEBtLe370uxrs/T2BKrzBGRAfU/Y6qjCYmvr+eIR39eX1y17rtt3+2FS9ne966qTugzSY3VJtaXItGJQVrmL0f9Pbakp1H1sO+X+DYDi0Z6O3AWAVR10LJCZj8mfaazfO1IntDnwI3f+vGr9i02JAzL+OM7hzIpn8N43hBBRPfX8/kuFC6hnoBcP+Q9hzKLmHpruMczC7BXq/j9gERdcNcAdal5NI1xJP0/DLS88uYOy6a53/bT7VJ4qDXUVVtoq2fKwVlBgzVJmZ/u/OM87+0PImXlp8acTe9bxs+33SEF5ftZ0H8YXqFe7MlLZ9Pbu3FoZwSXvhtP8M7BfDX/hO4OdpRUmnkmZ/3cu/gdny3LQMhYPnuLPJLDZQbqlm8JR2A1/9M5rttmfwycwBeLg6sTcnhr/3ZmCQEejiRebKMuHBvdqSfJL+0im1H8utiqjKa2HAoDwG8VFVNcYWBGz7YSCsXe6b2DiOvtIr7h7SnJVB9Cta2+3tYcscFfijg/5K1h6/VTHab9DF0ubFRQlOan+QTxYR5u5zRubwmOYdbP9kCwOs3dmVU50D6vvg3bf1c+b+RHck4WcaYzq1JyS5BSkmftj5c9/56iiuMdAx0JzO/jIUzelNaZWTpruP8sTeLxIwCpISxXVqzdNdx7h3cjghfV+z1gp5h3gx6dRVCQO3Hj5eLPQajCYNJYjJJjCZJqLczmSfLuaUmiZgkeDjZMXNoe15cpiUZH1cHCsoNRLf24GhBOcUVBnxcHfn41jjmrTrI8j1ZONnrMJmgqtqEh5MdAR5OpGRrw3efuCaKDoHu+Lo6Mu69eEBb92LxlnRWHdDqrDnodZik5Nb+4RSVG3j1xlOtC4CswgoOZpcwMNLXov92V0p1NDcVxSfg9Q7aYxcfEHqoKgVDqbZt/Ltg5wQ/3Kn9rMsUbZ2GnGS45mXrxa00G8ZqE2PfjadfOx+eGRcDwJ6jhbRydSDY6/zLhqblllItJcFezpikxMXhzIsO93+5nc2H89j4xDAqDNXnXIIZ9eZaDpwo5r7B7ejXzodwH1deW3GArMIKnhobzcqkbG4fGEF1tcTTxZ5jBeWUVVXTxscFO51g+Z4syqqq6RDgxvj31gMwZ3RHBrTz5a7PE3Cy13P0ZDkRvq6kZJegE/C/aT35anM6Gw/lERviWVdo0MVBz/R+bfhwTSoOeh1Xd/RjVVI2U3qF8v22TCrPKiny9yNX0+60+lP//CyBNcnZ7J476rwjuSoM1ew9VkjPNtatmKySQlPyfj9tzsI1r4I0QfLvUJINh9eCm592Oan4GEQMgr0/nnrdvRsgIObyznnyCHw7HSbMg8DYhnkfSpN19tDRK1VaaeRkWRUhrc4/HPaNFQd4Z+VBVv3fYCJ8Xa/oXLszCymuMNArwht7vY5fdh7jgcU7CGnlzNd39WXoa2sYERPAvJu1iaQmk6SkykjXZ1dgpxM46HWU1qxh8Y8+YXy5WbscteTe/vy1/wQ5xZUczi0lOauYMkM1d17Vlht6hpBdVEGotwtXv7oKk4TFd/YlzMelLpGuP5jL23+nMKSjP6/8nsSL18We0bmeV1LJ23+n8Oiojo3Sb6FGHzUlkz/X+hJahWvPw2qWnUj4BJbN0fofbvwMAjtDYBetM/rv52HXtzDiWdj2GcS/AffEmz+KKXU1HN8JC0bB40e0cygtVkPXSnJ1tMPV8cIfL/cMbsdVHfyuOCHAuX0o47q0Jr+kkoGRfoS0cuHbe/oR7nMqOel0Ag8ne/q19aFjoDvDogKYtmAzo2ICuH9Ie75LyMTD2Y7uoV70bKON5so8WUZJpZE3/0xmQXwqn21Iw1BtYlgn/7r1AGYt3kFJpYH4x4bi6+bIF5uOsOVwfl1L49lf93JN50Ds7XS4OdrxU+IxFm08QmSAO9P7nrsScWmlsd7foaWoloKtK8kBYwV4hZ65/YsbIHUVhPWD0lzI2Q+jXoR+90PWbm200qiXtGRTbdRKbPie1lG24inY8I72+LoPoetNjfaWFMVW1LaQTpZWoddryeKbrenY63VM6nHuQkf5pVU8v3QfRwvKScwooMpo4pZ+bVix9wRZRRUAPDqqI3cMjKDH839SdtYqencNasvC9Wksf+gqnl+6j9UHcohr04rv7+0PaP07r/1xgNkjO3D3om18fGscgzr4Nch7VS2F5sLtAn8Qw5+BzYGw43Ptud4RNs6DrlPh+9shNxk8Q+DAcigv0JLGtCUQ0gs2fQDHE8E/BgxlsOMLlRSUFqm2hdTK9dR8hSm9Ljx/wtvVgTendAPg3b9T+H1vFo+NjuJEUQVZeyvwdXPko3Wp7EgvOCMhDOnox6oDOSzenE5VtYlvtmawOTUfN0c7Eo6cJCO/jH3Hi7j7820APPPzXqqqTaxLyWmwpGAutWp4UxUYCxPeg6ixoLODSfOh6Cj8r7+WEIQe/nwGjiWCTg8eIfD7v2DLfFj9otZf4R8F3f8BaevgxD6txPf/Bmqzrk/s0ybXXcjen6AgvfHer6LYmFnDIlk6ayCujnZM6BbM4I5+LJzRi6hAd3ZlFtA11Kvu8liftj60crGnuNIIwML1aZQbqnl4hDbI5P3Vh5i1eAfdQr0IaeVMer62dP22Iyd55+8UBr+6ijXJjbPqpLp81NRVFEH+IQjqDr/9HyQsgNGvwKG/tQ7rgbO1VsWB5bD4JtDZg8mgvXbIk9DjVi2RmIxQUaBtj5kEe3/QEs75SnwXZ8HrHSG0D9z+h9bHcSEr/wOuvtDn7oZ/74pi42Yt3sGvO4/x8S1xfLQulc2H8wnydOJYYQXXxrbmzSndGPvuOpJPlOBop2P940N59+8UPquZCFjL2V5PqLczyx8cdNGSJBdiCyuvKY3ByUNLCADX/Bce2gN97oIuk7WZ03G3az/rMForwGcygFdN89gvCtwDtMtKXmHQ/wHtvnaEU9LSU5VdTdXwx5OQvunUtozNWvK4kGoDbHwPNrx7akC6Las2wEfDtASqKA2gY4A2dLW9vxsdA7VBIA8MiyT+sSHM+0cPHOx0dbOtx3cNwtfNkd4RPgB1EwyjAt15+fpYkk+UsHTXMYvHrJJCc6LTnSquFzMJHj10qoNaCBjzGkRPhJu/1X4ecZX2s6BucM86GPk8tBsGSK3ct70LJK/Q9jm0SvuA//pmWP+OtnqcTyRs/vDU+Y/t0IbS1jq+U+uzKMyAvINnxvrLLPhy8qW/x/ICOLzu1HND+akYr1TeQTia0DSTQlUZ/PWs9vtRbMZNvcN4aVIsbXxc6NTaA4AuIV5nDNWd2C2YIE8n7rgqAoBBHXwZ1zWI/0zsTEgrZ/41phPjugQxrW/YGfMjLEV1NDdXQmh1lk7n0+5U2YwbPz3/60J6wbZPtVZFwRHI2KR94Gz7FJy8tJFMuQeg+3Tw7QB/PgU5B7QhrQtGQuuucMef2vnT4k8d99CqU0uQSglJy6CqRDue/qw/Qym1lsnZ26uN2rKm6Ru0y1ZhfbUEtfpFbTiuk6c2VPfa17UWVK3SXPj9cRj5ArjXs/hM9r5T96W52mzz9sPPHLVlS4qOw/bPAKENSIh/Q/tS0Ouf59/fUKHNh1FLdTYaXzdHpvbWWubXdQ/G392R6CCPM/aJDHBnwxPD6p67O9nz7lSt9R//2NC67S9MbJz5RKqloJwpfHwA4ysAABHbSURBVIDWcd1hlPahe3wnvBymXUrq9g+YlaBNsrt6jjbSSWcHHw2FT6+F6iqtaN9fz0DuQa2uk08ktIrQ+jdASzBZu6AsVxtqW7sKXfIf2jfdk0fg9yfgjU6Q9Js2cztrDxz8G7Z8qCUEexdY+QKYTJD4hfb61DWw40vY/a32OtBaEfmpWgtn93fadpMJDvyuzRo/W/Z+7f7EXq2f5ffH4Jtp2oJIZzu6DfIPN+zvvj5VZbD/11OX4f6/vTOPk6q49vj3yL4JDIhBRHZF9BECBhcQFxADUUElH4yyKHF5xt2Ia57iHkSj0WgwAQQVBRWNPBEUcAGVAIJsIutTlEVARIYdBur98avuacYZGJiRnnHO9/PpT9+urnvvqVvddeqcOvfcdUvh6RPhg79IKY67U+VfTvrxvhtXw7OnwYOHK9JsVxaM7Knt/WHVHAUgOAdE+TKlaH/s4fuumGbcUnD2pHp9JeyrdBiUjSbu7p1wzuNw3PlQobrWLBL0elORSCs/U6bXaf+Ej/8GX7wlS6P1Vbqh7sP+GlRe6wPrFmfvv3w6bF4Dr/SGrK1yR+3cIstjxMV7ylapFtQ9CY6/EMb2hRcvUASUHaLBcHOMzlg4RlbR811jupA4M14xU+sG426DY8+DTv2l1CodBtMHweLxqrdzi14nXyuF8tETUoqr5+n7M/8Hpg6UpXTpW4Vz3dcthRlDoUI1KdsqtRVFtm0D1G0NHzys+0r6vKubG+e+Ctsz4Zqp8HZfPbgJZJ1t+R7evgWO7iTL4JOnZM1VrSvLIqMhfDFar3VL1EdVfgHPdVIixlOuy13GV3tLOXV+BCpkZLsf82LreslSo1HhXKOfM1nbYfpgrQHmtPAPMh595OTN9o0w6Cw4/TYphPywayfMHgGjr1VY7PWfQamy8MTxyuG0cyuEGOp6SGlFPYEGwe7DYcxNim66fKJm7pvXSo4PHtIA2eVpWSyjr9M9Gk3OVnTT3FdlqZSuICWR0UCDUsveMGekyjat1vnKV4WNq7JlbnWpBmRQSvPMFXq/cZ4itpaMV/qRlr1g2SewfRNs+lbHbNZFdavXV/baZl32cj03SdkkstxOH6wbELsNhVF9lC0XdJ3qt9V5AS4ZFS2WrdCiB1SqAYsnSGlfPkFW0vNdoMXFMGs4NOkIi1PWWUqVg67P6Kl/E+5RVNmCt2K98QpZbnUZTP+XQpevn6nyCtV1DTMayDp7skX2MSv/Am6er30XjtO1bdU7+/tVs+HZdtr+81oonX0fwE/C7l2yHlv2lNIrDqyYKeX9+xEKC3+tj3KdrVkAp/5J/VyIeO4jJ33s3gWDOigtR+L5D+89qGilVpfCd4s1yM5+WdZEpwHwX92gYoZcGzu37LkmALox7+Mn4boZUK6y3CibVmuGu3g8DO+meuc8DmNvk4K4cLCOC/D+w/BhTCB4wxy5iDavgSnPaI0kQYtLYN7rcNLVCuVd9olm0DWPhj9OhfcfhMmP5t7uclXh5s/3TDXyzTQNrGUqKhvuzq1w6RjN8oedq+vQ8QG5zlpfAa2vVL0VM6DNDUqZTlxjqXaUwo8TnH6nFDZoDQSDZ05Su5p1UfLESrV0T0uZ8lIKTzSXUm50JvR8Qy6w16+E5dOyj1uplo6R2q7jL9C6UvPukLlSg1ivN6H+qTrmlnVw61IoW0lrMW9cla3wLxsH9U7W9peTpbi6PKPAiILy9VSo01K/raG/1WDa/u4f15v1kqL0ah2rz1nbNVlZOBYOrZ0dwVcY7Ngit2X5qvDWTbLSrvxgz0E+azs8ECcHFw7W9ZwxNHtScsr1muh0+bvWtQoBVwpOeglh3wuaq2bLEsjvj35vx9z4rSKfajdXapAN32iwSJC4T6NRe+iZEkY7Yyj87w2yhI7uBI3OkGVS9Ui5XkKAifcpGWGjM7IVUKmykNFIs/4G7dSOqQM1S214upRT5ip45kQt8FasoYE5Sw+mocrhkrN81eiWCnD1FDi8meqv/0o3F46+Xi6fM+6SZTXxXgUDrJgBV02W4k1l/TIprXZ9s0OPU1k8XgrojDuhaWeVfTMdBneAem3UJ6XLSZnviK63CfdooCpbGe5YrrWgAU1kzbTsBSPic8bPe0qhz8O7Sbl3fwGeagWn36G2TB+ka7JusRTjlu+h2Xn56/vcWD4DBp2p9C4bVsB/nlbaFzsE2twIR3dUvc3fwYDGuq/mD+/o+g5sI2vn6ymyUq+bof1++FoTjaxtCr2uefSev6OcbMvU7yNzpe7p2bUTXvqdrLc6LbUGk7UVOvSTTD98DdXrweyR8EZ0w7a9Geb/W4okQcKKrnmMEl8uflfrfeWr5iZFvnCl4DipZO2Ajx7XbLxiSgrjHVtg1OWaYR7Zat/H2foD9K8PdVpB79H685Yup+9e/r0si20/QLtbYdFYWUW7d2ldpscoKZNh56r+2Q9pIJ4xVH733Hz5m9Yo8eGJV2kAmj5IFsTOLXu2o6BMHwxHniCXX8Uamj2nyjDxXqjdQtcP4MNHZDWB3ExZ2yVTwuXU4V5oe6NcSGUry6pLDUuuWFPBBv/9kSyZ+aNhzJ/gqkk697ZMWR3v3a8F8Ute08DY4DQNqm/3VfTa0vcU8bYtE9anLPzXa6M1lIan6ZonnlnS5x0pvrG36nOpcrBrO5Q7VNYbyIVGkCI8pAycdR80OUvrVgveklXRpKOUx0vds4MlUt2QiZtE29woBb5+mazPd+7Qb23DcgVPVK4FGKz5PPvaJShTUde0WVcpjabnQPcXDzh6zJWC4/xUvH4l1DlhzwX3BLuy5G5aPk0L2Oc9pVQj3y2CbkP0hx52Liz/VD75CtUPvvyFxZeT5Lape6L844vG6eZGAlz7qUKQ33sAJg1Q/V9fIdfanJEacEHWWcUMhSxvXAln3a/nmL/SU1bIp0NUr3qD7EH/0CMhc7m2EwMnwFGnKDotN8pXlcI7ooVchzUaa6Cv1Uxums1roV5buSbffwgw+N0QWVXfzpFi252l963r5YIrVU7rP50HZM/6azWDdrfI0pv8V12HVbPh5e46f5mKsGOjJhPNumpNZs5I7dv+Hinf+qfKndT2JvjqY/2WrJTO2e05ufIOAFcKjpMudmVpraRK7ewIrlQ2rdVCd87ncP8cGHeHItH6xBDkrO3yq6/8TH710uVg1BUKHa6QAVsTj8Q0zbwr1dSsfZkenEOt4xSRtexjuesad1Bo8q96yEVz1r0woZ/WOo47X6HER50st1Cj9lI4c1/VQFuvTfa60mVjod4pubdh3VIp74yGcgd9O1cusZ1bNchXqKaItHWLZUVUOwoGtlW9RMbhEOSGTKyNjeypaK+LXpbSWT1XQROZK2Vx1WklmaY8rf3H3AJnP6Bw4uc6ad1pzXxZjLV/mbvc+8CVguM4RYfU9aAlE2Dy4wphnjQAzn1SM+YlE7LdOlXral3onCe0tvHuXdkL699/mf3skVRXyu7dMLGfIrTWLpAFUzFD52j6W1kYTxyv8l7/3j/51y7MDg/OjcmPKfvwDbNznwhsy1S48DGdFIb9dl+5xNZ/CYPPgh6vQ+P2P94PpKSqNyjwwrwrhRz0n9afBd8v2HdFx3HSQwiaOW/P1Cx981o49AityaxbonWXUgUMbd2xWcf4KR4qFXZrsfon3K9pRlNua33b/p8Df56C4zjFDbOYuyvm76oaH3JT6pDsUNKCUrbgT3rLkwNRCAXZ7yeixCiFA9WujuM4JYmipaIcx3GctOJKwXEcx0niSsFxHMdJ4krBcRzHSeJKwXEcx0niSsFxHMdJ4krBcRzHSeJKwXEcx0lS7NJcmNlaYNkB7l4T+K4QxUkn3paiibelaOJtgXohhMP2VanYKYWCYGaf5if3R3HA21I08bYUTbwt+cfdR47jOE4SVwqO4zhOkpKmFP6ZbgEKEW9L0cTbUjTxtuSTErWm4DiO4+ydkmYpOI7jOHuhxCgFM/uNmS00syVmdnu65dlfzOwrM5trZrPM7NNYlmFm481scXwvkk+BN7MhZrbGzOallOUqu4knYz/NMbOW6ZP8x+TRln5mtiL2zSwz65zy3R2xLQvN7Oz0SP1jzKyumb1vZl+Y2edmdkMsL3b9spe2FMd+KW9m08xsdmzLvbG8gZlNjf0y0szKxvJy8fOS+H39AgsRQvjZv4BSwFKgIVAWmA00S7dc+9mGr4CaOcoeAW6P27cD/dMtZx6ytwNaAvP2JTvQGRgLGHASMDXd8uejLf2AW3Kp2yz+1soBDeJvsFS62xBlqw20jNtVgEVR3mLXL3tpS3HsFwMqx+0ywNR4vV8BLorlA4Gr4/YfgYFx+yJgZEFlKCmWQmtgSQjh/0IIO4ARQJc0y1QYdAGGxe1hQNc0ypInIYRJwPc5ivOSvQvwfBD/AaqZWe2DI+m+yaMtedEFGBFC2B5C+BJYgn6LaSeEsCqEMDNubwS+QM/BLHb9spe25EVR7pcQQtgUP5aJrwCcCbwWy3P2S6K/XgPam5kVRIaSohTqAN+kfF7O3n80RZEAvGtmM8zsylh2eAhhFeiPAdRKm3T7T16yF9e+uja6VYakuPGKRVuiy+FXaFZarPslR1ugGPaLmZUys1nAGmA8smR+CCFkxSqp8ibbEr/fANQoyPlLilLITXMWt7CrNiGElkAn4Boza5dugX4iimNf/QNoBLQAVgGPxfIi3xYzqwyMAm4MIWTurWouZUW9LcWyX0IIu0IILYAjkQVzbG7V4nuht6WkKIXlQN2Uz0cCK9MkywERQlgZ39cAb6Afy+qECR/f16RPwv0mL9mLXV+FEFbHP/Ju4F9kuyKKdFvMrAwaRIeHEF6PxcWyX3JrS3HtlwQhhB+AD9CaQjUzKx2/SpU32Zb4fVXy797MlZKiFKYDTeIKflm0IDM6zTLlGzOrZGZVEttAR2AeakPvWK038GZ6JDwg8pJ9NNArRrucBGxIuDOKKjl86+ejvgG15aIYIdIAaAJMO9jy5Ub0Ow8Gvggh/DXlq2LXL3m1pZj2y2FmVi1uVwA6oDWS94FusVrOfkn0VzfgvRBXnQ+YdK+2H6wXip5YhPxzd6Vbnv2UvSGKlpgNfJ6QH/kOJwKL43tGumXNQ/6Xkfm+E81s/pCX7Mgcfjr201zghHTLn4+2vBBlnRP/pLVT6t8V27IQ6JRu+VPkaovcDHOAWfHVuTj2y17aUhz7pTnwWZR5HnB3LG+IFNcS4FWgXCwvHz8vid83LKgMfkez4ziOk6SkuI8cx3GcfOBKwXEcx0niSsFxHMdJ4krBcRzHSeJKwXEcx0niSsFx8oGZ3WdmHQrhOJv2Xctx0oeHpDrOQcTMNoUQKqdbDsfJC7cUnBKLmfWIuetnmdmzMRHZJjN7zMxmmtlEMzss1h1qZt3i9l/MbH5MtPZoLKsX68+J70fF8gZmNsXMppvZ/TnO3zeWz0nJm1/JzMbEfPrzzKz7wb0qTknHlYJTIjGzY4HuKNFgC2AXcAlQCZgZlHzwQ+CeHPtloJQJx4UQmgMPxK/+jlJLNweGA0/G8r8B/wgh/Br4NuU4HVF6hdYoYVurmOTwN8DKEMIvQwjHA+MKvfGOsxdcKTgllfZAK2B6TFPcHqUS2A2MjHVeRCkUUskEtgGDzOwCYEssPxl4KW6/kLJfG5QaI1GeoGN8fQbMBJoiJTEX6GBm/c3s1BDChgK203H2C1cKTknFgGEhhBbxdUwIoV8u9fZYdAvKWd8aZeTsSt4z+ZDHdur5H045f+MQwuAQwiKkrOYCD5vZ3fvXLMcpGK4UnJLKRKCbmdWC5LOJ66H/RCIb5cXAR6k7xZz9VUMIbwM3ItcPwCco+y7IDZXY7+Mc5QneAfrE42FmdcyslpkdAWwJIbwIPIoe/ek4B43S+67iOD8/QgjzzezP6Gl2h6Csp9cAm4HjzGwGeopVzoXeKsCbZlYezfZviuXXA0PMrC+wFrgslt8AvGR6mPyolPO/G9c1psSnJ24CegCNgQFmtjvKdHXhttxx9o6HpDpOCh4y6pR03H3kOI7jJHFLwXEcx0niloLjOI6TxJWC4ziOk8SVguM4jpPElYLjOI6TxJWC4ziOk8SVguM4jpPk/wEw/CUBLcTteQAAAABJRU5ErkJggg==\n", "image/svg+xml": [ "\r\n", "\r\n", "\r\n", "\r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", " \r\n", "\r\n" ], "text/plain": [ "
" ] }, "metadata": { "needs_background": "light" }, "output_type": "display_data" } ], "source": [ "figure_6_7()" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "实验结果证明，相比Q学习，双Q学习是有效的。" ] }, { "cell_type": "code", "execution_count": null, "metadata": {}, "outputs": [], "source": [] } ], "metadata": { "file_extension": ".py", "kernelspec": { "display_name": "Python 3.7.0 64-bit ('base': conda)", "language": "python", "name": "python37064bitbasecondaf1f4ce8bd9ee468caf98567667ef0765" }, "language_info": { "codemirror_mode": { "name": "ipython", "version": 3 }, "file_extension": ".py", "mimetype": "text/x-python", "name": "python", "nbconvert_exporter": "python", "pygments_lexer": "ipython3", "version": "3.7.0" }, "mimetype": "text/x-python", "name": "python", "npconvert_exporter": "python", "pygments_lexer": "ipython3", "toc": { "base_numbering": 1, "nav_menu": {}, "number_sections": true, "sideBar": true, "skip_h1_title": false, "title_cell": "Table of Contents", "title_sidebar": "Contents", "toc_cell": false, "toc_position": {}, "toc_section_display": true, "toc_window_display": false }, "varInspector": { "cols": { "lenName": 16, "lenType": 16, "lenVar": 40 }, "kernels_config": { "python": { "delete_cmd_postfix": "", "delete_cmd_prefix": "del ", "library": "var_list.py", "varRefreshCmd": "print(var_dic_list())" }, "r": { "delete_cmd_postfix": ") ", "delete_cmd_prefix": "rm(", "library": "var_list.r", "varRefreshCmd": "cat(var_dic_list()) " } }, "types_to_exclude": [ "module", "function", "builtin_function_or_method", "instance", "_Feature" ], "window_display": false }, "version": 3 }, "nbformat": 4, "nbformat_minor": 2 }