{"cells":[{"metadata":{},"cell_type":"markdown","source":"![En tête general](https://raw.githubusercontent.com/PythonLycee/PyLyc/master/img/En_tete_general.png)\n\n\n<i>© Copyright Franck CHEVRIER 2019-2022 https://www.python-lycee.com.</i><br>\n<i>Les activités partagées sur <a href=\"https://capytale2.ac-paris.fr/web/accueil\"><strong>Capytale</strong></a> sont sous licence <a href=\"https://creativecommons.org/licenses/by-sa/3.0/fr/\">Creative Commons</a>.</i>\n\n<span style=\"color: #9317B4\"> Pour exécuter une saisie Python, sélectionner la cellule et valider avec </span><span style=\"color: #B317B4\"><strong>SHIFT+Entrée</strong></span>.\n"},{"metadata":{},"cell_type":"markdown","source":"# Approximation par balayage"},{"metadata":{},"cell_type":"markdown","source":"On considère la fonction $f$ définie sur $[0;+\\infty[$ par $f(x)=x^2$.\n\n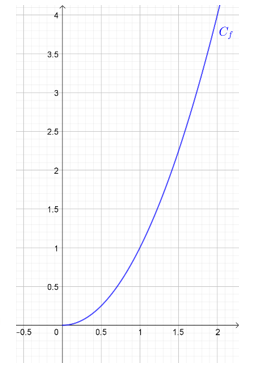![Fonction carré](https://raw.githubusercontent.com/PythonLycee/PyLyc/master/img/Approximation_par_balayage_carre.png)\n\nOn admet que la fonction $f$ est croissante sur $[0;+\\infty[$ et que l’équation $f(x)=2$ \na une unique solution sur $[0;+\\infty[$, notée $\\sqrt{2}$. \nLe but de l’exercice est d’obtenir des valeurs approchées de $\\sqrt{2}$.\n"},{"metadata":{},"cell_type":"markdown","source":"__1. Ecrire une fonction Python $f$ qui reçoit une valeur $x$ en argument et renvoie l’image de $x$ par la fonction $f$.__\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"# Ecrire la fonction\n","execution_count":2,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__2. La fonction ci-dessous permet d’obtenir des images successives par la fonction $f$ sur l’intervalle $[1;2]$, avec un pas de $10^{-1}=0,1$.__\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"def balayage(f):\n    \n    x=1\n    while x<2:\n        print(\"f(\",x,\")=\",f(x))\n        x = x+0.1\n    \n    return None","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__Utiliser cette fonction pour compléter le tableau :__\n\n|   $x$      | $1  $ | $1.1$ |$1.2$ |$1.3$ |$1.4$ |$1.5$ |$1.6$ |$1.7$ |$1.8$ |$1.9$ |$2  $ |\n| :-------:  |:--:   | :--:  | :--: | :--: | :--: | :--: | :--: | :--: | :--: | :--: | :--: |\n|   $f$$($$x$$)$   |       |       |      |      |      |      |      |      |      |      |      |\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"# Effectuer les saisies nécessaires\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__Pour quelle valeur $x_1$ du tableau a-t-on $x_1 \\leqslant \\sqrt{2} \\leqslant x_1+0,1$ ? Justifier.__\n\n__Modifier la fonction précédente pour qu’elle renvoie cette valeur $x_1$.__\n\n\n\n\n<span style=\"color: #888888\">Aides : On pourra, entre autres, modifier la condition de la boucle while.\nOn pourra supprimer les affichages réalisés avec l’instruction print.</span> \n"},{"metadata":{"trusted":false},"cell_type":"code","source":"# Modifier la fonction puis effectuer les tests ici\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__3. Compléter la fonction pour qu’elle effectue, à partir de cette valeur $x_1$, un nouveau balayage de pas $10^{-2}=0,01$.__\n\n__La fonction renverra une valeur $x_2$ telle que $x_2 \\leqslant \\sqrt{2} \\leqslant x_2+0,01$.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"# Modifier la fonction puis effectuer les tests ici\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__4. Compléter la fonction pour qu’elle renvoie une valeur $x_3$ telle que $x_3 \\leqslant \\sqrt{2} \\leqslant x_3+0,001$.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"# Modifier la fonction puis effectuer les tests ici\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__5. \tEn ajoutant une boucle, modifier la fonction précédente pour qu’elle renvoie une valeur $x_n$ telle que $x_n \\leqslant \\sqrt{2} \\leqslant x_n+10^{-n}$, où $n$ est une valeur donnée en argument de la fonction.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"# Modifier la fonction puis effectuer les tests ici\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__Donner une valeur approchée de $\\sqrt{2}$ à $10^{-7}$ près.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"# Effectuer les saisies nécessaires ici\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__6. Prolongement :__\n\n__On admet que l’équation $x^3=5$ admet une unique solution sur $[0;+\\infty[$, notée $\\sqrt[3]{5}$.__\n\n__Déterminer une valeur approchée de $\\sqrt[3]{5}$ à $10^{-8}$ près.__\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"# Effectuer les saisies nécessaires ici\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"![Cardan](https://raw.githubusercontent.com/PythonLycee/PyLyc/master/img/Cardan.jpg)\n\n<center> <a href=\"https://fr.wikipedia.org/wiki/J%C3%A9r%C3%B4me_Cardan\">Jérôme Cardan</a> (1501-1576) fut un des premiers à justifier la méthode d'approximation par balayage.</center>"},{"metadata":{},"cell_type":"markdown","source":"<i>© Copyright Franck CHEVRIER 2019-2022 https://www.python-lycee.com.</i><br>\n<i>Les activités partagées sur <a href=\"https://capytale2.ac-paris.fr/web/accueil\"><strong>Capytale</strong></a> sont sous licence <a href=\"https://creativecommons.org/licenses/by-sa/3.0/fr/\">Creative Commons</a>.</i>\n<br><br>\n<span style=\"font-size:8px\">Dernière modification de l'activité : Juillet 2022</span>"}],"metadata":{"celltoolbar":"Raw Cell Format","kernelspec":{"display_name":"Python 3","language":"python","name":"python3"}},"nbformat":4,"nbformat_minor":2}