{"cells":[{"metadata":{},"cell_type":"markdown","source":"\n\n\n© Copyright Franck CHEVRIER 2019-2022 https://www.python-lycee.com.
\nLes activités partagées sur Capytale sont sous licence Creative Commons.\n\n Pour exécuter une saisie Python, sélectionner la cellule et valider avec SHIFT+Entrée.\n"},{"metadata":{},"cell_type":"markdown","source":"# Chiffrement matriciel de Hill \n\n### Activité sur le chiffrement n°2\n##### (prérecquis: calcul matriciel, déterminant, inverse d'une matrice, congruences, théorème de Bézout)\n\n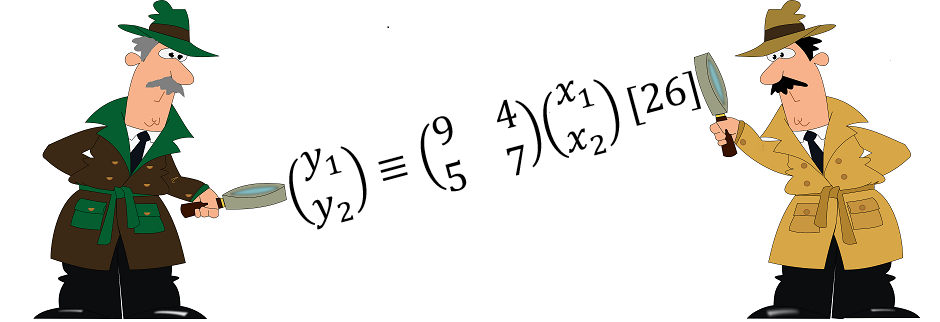"},{"metadata":{},"cell_type":"markdown","source":"### Sommaire\n\n0. Notation : matrices congruentes
\n1. Chiffrement de Hill dans un cas particulier
\n2. Généralisation
\n"},{"metadata":{},"cell_type":"markdown","source":"## 0. Notation : matrices congruentes"},{"metadata":{},"cell_type":"markdown","source":"Dans cette activité, on étend la notion de congruence modulo $n$ ( $n \\geqslant 2$ ) à des matrices à coefficients entiers.
\nOn dira que deux matrices $A$ et $B$ à coefficients entiers sont congrues modulo $n$ si leurs coefficients correspondants sont deux à deux congrus modulo $n$.
On notera alors $A \\equiv B \\;[n]$.\n
\n\n\nAinsi, pour des matrices de dimension $2 \\times 2$ à coefficients entiers, on a :
\n$ \\begin{pmatrix} a & b \\\\ c & d \\end{pmatrix} \\equiv \\begin{pmatrix} a' & b' \\\\ c' & d' \\end{pmatrix} [n]$ si et seulement si $\\begin{Bmatrix} a \\equiv a' [n] \\\\ b \\equiv b' [n] \\\\ c \\equiv c' [n] \\\\ d \\equiv d' [n] \\end{Bmatrix}$\n\n\n__0.0. On considère des matrices $A$; $B$ et $C$ de dimension $2 \\times 2$ à coefficients entiers, telles que $A \\equiv B \\;[n]$.__
\n$\\;\\;\\;\\;\\;\\;$__Démontrer que $CA \\equiv CB \\;[n]$.__\n\n"},{"metadata":{},"cell_type":"markdown","source":"## 1. Chiffrement de Hill dans un cas particulier"},{"metadata":{},"cell_type":"markdown","source":"Deux détectives, Archibald et Balthazar, souhaitent échanger des messages secrets, de telle sorte qu'ils soient difficilement déchiffrables s'ils tombaient en de mauvaises mains. Pour simplifier, on supposera que les messages à coder sont écrits en majuscules, sans accents, et ne comportent pas d'espaces.
\n
\nIls décident de coder leurs messages avec un chiffrement matriciel de Hill, à l'aide d'une matrice de chiffrement $ H= \\begin{pmatrix} 9 & 4 \\\\ 5 & 7 \\end{pmatrix} $.
\n
\nPour cela, ils commencent par remplacer chaque lettre du message à coder par son rang dans l'alphabet, comme l'indique le tableau ci-dessous:
\n\n| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | \n|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|:--|\n| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10| 11| 12| 13| 14| 15| 16| 17| 18| 19| 20| 21| 22| 23| 24| 25|\n\n
\nLes valeurs sont ensuite regroupées par deux dans des matrices colonnes (S'il manque une valeur, on complète arbitrairement le texte avec une lettre).
\nA chaque matrice colonne $ X= \\begin{pmatrix} x_1 \\\\ x_2 \\end{pmatrix} $ ainsi construite, on associe la matrice colonne $HX$, définie modulo $26$, ce qui permet d'obtenir une matrice colonne $Y= \\begin{pmatrix} y_1 \\\\ y_2 \\end{pmatrix}$ de coefficients compris entre $0$ et $25$.
\nOn peut alors, en considérant les rangs dans l'alphabet, associer un couple de lettres au couple de lettres initial.
\n\nPar exemple:
\nArchibald souhaite coder le mot \"EUREKA\". Les premières lettres \"EU\" correspondent à la matrice $ X=\\begin{pmatrix} 4 \\\\ 20 \\end{pmatrix} $ qui donne la matrice codée $ HX= \\begin{pmatrix} 9 & 4 \\\\ 5 & 7 \\end{pmatrix} \\begin{pmatrix} 4 \\\\ 20 \\end{pmatrix}=\\begin{pmatrix} 116 \\\\ 160 \\end{pmatrix} \\equiv \\begin{pmatrix} 12 \\\\ 4 \\end{pmatrix} [26]$. On obtient donc les lettres codées \"ME\".
\n"},{"metadata":{},"cell_type":"markdown","source":"__1.1. Coder complètement le mot \"EUREKA\".__\n"},{"metadata":{},"cell_type":"markdown","source":"__1.2. On donne la fonction Python codage_Hill ci-dessous, qui permet de coder un message à l'aide d'une matrice de chiffrement H.__
\n$\\;\\;\\;\\;\\;\\;$__Exécuter les deux cellules pour vérifier le résultat de la question 1.1.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"import numpy as np\n\n#Mise en mémoire de l'alphabet\nAlphabet=\"ABCDEFGHIJKLMNOPQRSTUVWXYZ\"\n\ndef codage_Hill(message,H):\n \"\"\"\n fonction réalisant le codage du message\n à l'aide de la matrice de chiffrement H\n \"\"\"\n code=\"\"\n if len(message)%2 !=0: message += \"A\" # s'il n'y a pas un nombre pair de lettres, on complète le message avec un A\n \n for k in range(len(message)//2): # pour chaque couple de lettres:\n X = np.array([[ Alphabet.index(message[2*k])], # on crée la matrice X\n [ Alphabet.index(message[2*k+1])]]) \n Y = np.dot( H , X ) %26 # on calcule la matrice Y\n code += Alphabet[Y[0][0]]+Alphabet[Y[1][0]] # on complète le code avec les deux lettres obtenues\n \n return code\n","execution_count":null,"outputs":[]},{"metadata":{"trusted":false},"cell_type":"code","source":"#définition de la matrice de chiffrement H\nH = np.array([ [ 9 , 4 ],\n [ 5 , 7 ] ])\n\n#Appel à la fonction codage_Hill pour la construction du message codé\ncode = codage_Hill(\"EUREKA\",H)\ncode","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"Archibald et Balthazar ont convenu d'une matrice $H$ pour coder leurs messages, mais il leur faut maintenant aussi une méthode pour déchiffrer les messages. On cherche à déterminer une matrice $D$ qui, utilisée comme précédemment, permette ce décodage.\n\n\n__1.3. Vérifier que la matrice $H$ a pour déterminant $43$. En déduire que $H$ est une matrice inversible et calculer $H^{-1}$.__
\n$\\;\\;\\;\\;\\;$__Pourquoi la matrice $H^{-1}$ ne peut-elle pas être la matrice $D$ cherchée ?__\n"},{"metadata":{},"cell_type":"markdown","source":"__1.4. a. Sans chercher à déterminer sa valeur, justifier qu'il existe un unique $m$ tel que $1 \\leqslant m \\leqslant 25$ et $43m \\equiv 1 [26]$.__
\n$\\;\\;\\;\\;\\;\\;\\;\\;\\;$__On dit que $m$ est l'inverse de $43$ modulo $26$__
\n$\\;\\;\\;\\;\\;\\;\\;\\;\\;$(pour démontrer l'existence, on pourra appliquer le théorème de Bézout)
\n\n\n$\\;\\;\\;\\;\\;$__b. Ecrire une fonction Python inv qui renvoie une valeur $m$ qui convient.__
\n$\\;\\;\\;\\;\\;\\;\\;\\;$(on pourra écrire une boucle qui teste un à un les candidats pour la valeur de $m$ à partir de $1$)
\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"#Ecrire ici la fonction inv\n\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"$\\;\\;\\;\\;\\;$__c. A l'aide d'un appel à la fonction Python inv, déterminer une valeur de $m$ qui convient.__
\n\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"#Effectuer ici l'appel à la fonction inv\n\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__1.5. a. Vérifier que la matrice $D_0=43H^{-1}$ est à coefficients entiers.__
\n\n\n$\\;\\;\\;\\;\\;$__b. Déterminer une matrice $D$, dont les coefficients sont entiers compris entre $0$ et $25$, telle que $D \\equiv m D_0[26]$.__
\n\n\n$\\;\\;\\;\\;\\;$__c. On considère deux matrices colonnes $X=\\begin{pmatrix} x_1 \\\\ x_2 \\end{pmatrix}$ et $Y=\\begin{pmatrix} y_1 \\\\ y_2 \\end{pmatrix}$. Démontrer que $Y \\equiv HX [26]$ est équivalent à $X \\equiv DY [26]$.__\n
\nLa matrice $D$ ainsi construite est donc la matrice de déchiffrement cherchée.
\n"},{"metadata":{},"cell_type":"markdown","source":"__1.6. Définir ci-dessous la matrice $D$ en langage Python (s'inspirer de la syntaxe utilisée pour $H$ dans la question 1.2).__"},{"metadata":{"trusted":false},"cell_type":"code","source":"# définir ici la matrice de déchiffrement D\n\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__1.7. Effectuer un appel à la fonction Python codage_Hill pour décoder le message qui a été codé à la question 1.2.__
\n$\\;\\;\\;\\;\\;$__Vérifier qu'on retrouve bien le mot \"EUREKA\".__"},{"metadata":{"trusted":false},"cell_type":"code","source":"# Effectuer ici l'appel à la fonction codage_Hill\n\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__1.8. Balthazar a reçu de la part d'Archibald le message suivant: \"IWVZHSGENJSSMQMVSIINAJ\". Décoder ce message.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"# Utiliser cette zone de saisie pour décoder le message\n\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"## 2. Généralisation"},{"metadata":{},"cell_type":"markdown","source":"On considère une matrice $H$ de dimension $2 \\times 2$ à coefficients entiers, de déterminant $d=det(H)$.
\nOn suppose que $d$ est non nul et premier avec $26$.\n"},{"metadata":{},"cell_type":"markdown","source":"__2.1. Justifier qu'il existe un entier $m$ tel que $dm \\equiv 1[26]$ ($m$ est inverse de $d$ modulo $26$)__
\n$\\;\\;\\;\\;\\;\\;$(on pourra utiliser le théorème de Bézout)\n\n\n__2.2. Adapter la fonction inv de la question 1.4 pour qu'elle reçoive en argument une valeur d et renvoie son inverse m modulo $26$.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"#Ecrire ici la fonction inv modifiée\n\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__2.3. a. Justifier que la matrice $D_0=dH^{-1}$ est à coefficients entiers.__
\n\n\n$\\;\\;\\;\\;\\;$__b. On considère une matrice $D$ à coefficients entiers telle que $D \\equiv mD_0 [26]$.__
\n$\\;\\;\\;\\;\\;\\;\\;\\;$__On considère deux matrices colonnes $X=\\begin{pmatrix} x_1 \\\\ x_2 \\end{pmatrix}$ et $Y=\\begin{pmatrix} y_1 \\\\ y_2 \\end{pmatrix}$ à coefficients entiers.__
\n$\\;\\;\\;\\;\\;\\;\\;\\;$__Démontrer que $Y \\equiv HX [26]$ est équivalent à $X \\equiv DY [26]$.__\n\n"},{"metadata":{},"cell_type":"markdown","source":"__2.4. Convenir avec une autre personne d'une matrice de chiffrement $H$ (dont le déterminant est premier avec $26$).__
\n$\\;\\;\\;\\;\\;$__Chacun code alors un message à l'aide de la fonction Python codage_Hill en utilisant cette matrice, et le donne à l'autre.__
\n$\\;\\;\\;\\;\\;$__Enfin, après avoir déterminé la matrice de décodage $D$, chacun décode le message reçu à l'aide de la fonction Python codage_Hill.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"#Utiliser les zones de saisie ci-dessous\n","execution_count":null,"outputs":[]},{"metadata":{"trusted":false},"cell_type":"code","source":"","execution_count":null,"outputs":[]},{"metadata":{"trusted":false},"cell_type":"code","source":"","execution_count":null,"outputs":[]},{"metadata":{"trusted":false},"cell_type":"code","source":"","execution_count":null,"outputs":[]},{"metadata":{"trusted":false},"cell_type":"code","source":"","execution_count":null,"outputs":[]},{"metadata":{"trusted":false},"cell_type":"code","source":"","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"\n\nLester S. Hill (1891-1961)"},{"metadata":{},"cell_type":"markdown","source":"© Copyright Franck CHEVRIER 2019-2022 https://www.python-lycee.com.
\nLes activités partagées sur Capytale sont sous licence Creative Commons.\n
\nDernière modification de l'activité : Juillet 2022"}],"metadata":{"celltoolbar":"Raw Cell Format","kernelspec":{"display_name":"Python 3","language":"python","name":"python3"},"language_info":{"codemirror_mode":{"name":"ipython","version":3},"file_extension":".py","mimetype":"text/x-python","name":"python","nbconvert_exporter":"python","pygments_lexer":"ipython3","version":"3.7.10"}},"nbformat":4,"nbformat_minor":2}