{"cells":[{"metadata":{},"cell_type":"markdown","source":"\n\n\n© Copyright Franck CHEVRIER 2019-2022 https://www.python-lycee.com.
\nLes activités partagées sur Capytale sont sous licence Creative Commons.\n\n Pour exécuter une saisie Python, sélectionner la cellule et valider avec SHIFT+Entrée.\n"},{"metadata":{},"cell_type":"markdown","source":"# 1. Dérivation (corrigé) "},{"metadata":{},"cell_type":"markdown","source":"*But de l’activité : Ecrire des fonctions Python permettant le calcul de taux de variation, de nombres dérivés, du coefficient directeur et de l’ordonnée à l’origine d’une tangente à une courbe.*\n"},{"metadata":{},"cell_type":"markdown","source":"On considère la fonction __$f$__ définie sur $\\mathbb{R}$ par $\\displaystyle f(x)=\\frac{1}{4} x^3+x-3$.\n"},{"metadata":{},"cell_type":"markdown","source":"__1. Ecrire une fonction Python f qui :__\n* __reçoit en argument une valeur $x$ ;__\n* __renvoie son image par la fonction $f$.__\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"def f(x):\n return 1/4*x**3+x-3","execution_count":null,"outputs":[]},{"metadata":{"trusted":false},"cell_type":"code","source":"f(5)","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__2. Ecrire une fonction Python coeff_dir qui :__\n* __reçoit en arguments les coordonnées de deux points $A(x_A;y_A )$ et $B(x_B;y_B )$ (avec $x_A≠x_B$) ;__\n* __renvoie le coefficient directeur de la droite $(AB)$.__\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"def coeff_dir(xA,yA,xB,yB):\n return (yB-yA)/(xB-xA)\n","execution_count":null,"outputs":[]},{"metadata":{"trusted":false},"cell_type":"code","source":"coeff_dir(2,5,3,-2)\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__3. A l’aide de la fonction précédente, écrire une fonction Python taux_variation qui :__\n* __reçoit en arguments une fonction $f$ et deux valeurs $a$ et $h$ ;__\n* __renvoie le taux de variation de la fonction $f$ entre $a$ et $a+h$.__\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"def taux_variation(f,a,h):\n return coeff_dir(a,f(a),a+h,f(a+h))\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__4. A l’aide de cette fonction, calculer le taux de variation de $f$ entre $3$ et $3,000001$. Conjecturer la valeur du nombre dérivé $f'(3)$, puis effectuer un calcul pour vérifier.__\n\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"taux_variation(f,3,0.000001)","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__5. L’import « from scipy import misc » permet d’utiliser la fonction misc.derivative qui :__\n* __reçoit en arguments une fonction $f$ et une valeur $a$;__\n* __renvoie le nombre dérivé de $f$ en $a$.__\n\n__Tester cette fonction pour calculer $f'(3)$.__\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"from scipy import misc\nec=10**-9\n\nmisc.derivative(f,3,ec)\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__6. Ecrire une fonction Python coeff_tang qui :__\n* __reçoit en arguments une fonction $f$ et une valeur $a$ ;__\n* __renvoie le coefficient directeur et l’ordonnée à l’origine de la tangente à $f$ en $a$.__\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"def coeff_tang(f,a):\n derive=misc.derivative(f,a,ec)\n return derive , f(a)-derive*a","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__Tester cette fonction pour déterminer l’équation de la tangente à la courbe de $f$ en $2$.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"coeff_tang(f,2)","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__7. La fonction tab_val ci-dessous permet d’obtenir une liste de valeurs de la fonction $f$.__\n* __Quelle est la valeur initiale de cette liste ? le pas ? le nombre de valeurs obtenues ?__\n* __Adapter cette fonction pour qu’elle reçoive en argument la valeur initiale $x_0$, le pas $p$ et le nombre de valeurs n.__\n\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"#(Tester puis) modifier la fonction\ndef tab_val(f,x0,p,n):\n t=[]\n x=x0\n for k in range(n):\n t.append(f(x))\n x=x+p\n return t","execution_count":null,"outputs":[]},{"metadata":{"trusted":false},"cell_type":"code","source":"# Tester la fonction modifiée\ntab_val(f,3,0.5,10)","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__8. Ecrire une fonction Python cdir_secantes qui :__\n* __reçoit en arguments une fonction $f$, une valeur $x_0$, un pas $p$ et un entier $n$.__\n* __renvoie la liste des $n$ coefficients directeurs des sécantes à la courbe de $f$ à partir de $x_0$ avec un pas en abscisse $p$.__\n\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"# Ecrire la fonction\ndef cdir_secantes(f,x_0,p,n):\n t=[]\n x=x_0\n for k in range(n):\n x=x+p #Attention: incrément préalable pour éviter une division par 0\n t.append(coeff_dir(x_0,f(x_0),x,f(x)))\n return t \n\ncdir_secantes(f,3,0.5,10)","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"# 2. Méthode de Newton (corrigé) "},{"metadata":{},"cell_type":"markdown","source":"*Prérequis : Fonctions Python réalisées dans l’activité « Fonctions élémentaires autour de la dérivation »* \n\n*But de l’activité : Approcher la solution d’une équation à l’aide de la méthode de Newton.*\n"},{"metadata":{},"cell_type":"markdown","source":"On considère la fonction __$f$__ définie sur $\\mathbb{R}$ par $\\displaystyle f(x)=\\frac{1}{4} x^3+x-3$."},{"metadata":{},"cell_type":"markdown","source":"__1. Démontrer que $f$ est croissante sur $\\mathbb{R}$.__ \n__On admettra pour la suite que l’équation $f(x)=0$ a une unique solution sur $\\mathbb{R}$, notée $α$.__\n"},{"metadata":{},"cell_type":"markdown","source":"__2. Justifier que pour toute abscisse $a$, la tangente $T_a$ à la courbe de $f$ en $a$ coupe l’axe des abscisses en un point $P$.__ \n\n__Déterminer l’expression de l’abscisse de $P$ en fonction de $a$, $f'(a)$ et $f(a)$.__\n\n__Ecrire une fonction Python etap_Newton qui :__\n* __reçoit en argument une fonction $f$ et une valeur $a$__ ;\n* __renvoie l’abscisse du point $P$ correspondant.__\n\n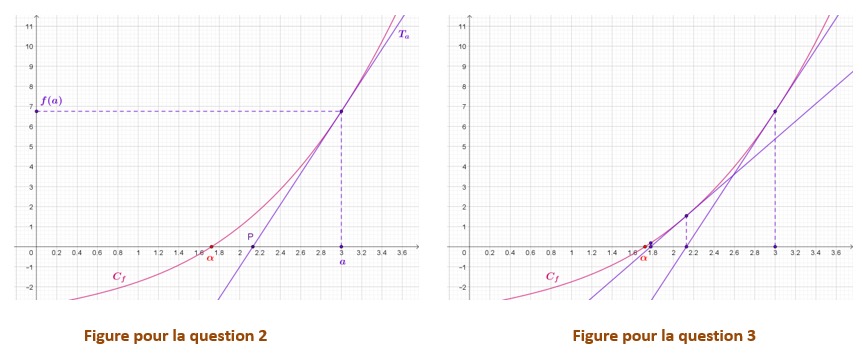\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"def etap_Newton(f,a):\n return a-f(a)/misc.derivative(f,a,ec)","execution_count":null,"outputs":[]},{"metadata":{"trusted":false},"cell_type":"code","source":"# Tester la fonction\netap_Newton(f,3)","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__3. A partir d’un point de l’axe des abscisses, on peut donc construire une suite de points.\nOn admettra ici que la suite des abscisses de ces points a pour limite $α$.__\n\n__La fonction Python appl_Newton donnée ci-dessous :__\n\n* __reçoit en arguments une fonction $f$, une valeur $a$ et un entier $n$;__\n* __renvoie une liste de valeurs.__ \n\n__Expliquer ce que représentent les termes de la liste renvoyée.__\n\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"def appl_Newton(f,a,n):\n t=[a]\n for k in range(n): \n a=etap_Newton(f,a)\n t.append(a) \n return t","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__4. Tester cette fonction appl_Newton pour la fonction $f$ de l’énoncé avec $a=3$ et $n=10$.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"appl_Newton(f,3,10)","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__5. Proposer et coder en Python des fonctions polynomiales $g$ et $h$ à coefficients entiers s’annulant respectivement en $\\sqrt{5}$ et $\\sqrt[3]{7}$.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"def g(x):\n return x**2-5\n\ndef h(x):\n return x**3-7","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__A l’aide des fonctions Python précédentes, proposer des valeurs approchées de ces deux nombres.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"# Effectuer les saisies nécessaires\nappl_Newton(g,3,5) , appl_Newton(h,3,5)","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"# 3. Algorithme de Dichotomie (corrigé) "},{"metadata":{},"cell_type":"markdown","source":"*Prérequis : Aucun, mais les question 1)a)b) peuvent être supprimées si l’activité « Méthode de Newton » a été traitée.*\n\n*But de l’activité : Approcher la solution d’une équation à l’aide d’un algorithme de dichotomie (méthode plus lente que la méthode de Newton, mais pour laquelle la précision du résultat est connue).*\n"},{"metadata":{},"cell_type":"markdown","source":"On considère la fonction __$f$__ définie sur $\\mathbb{R}$ par $\\displaystyle f(x)=\\frac{1}{4} x^3+x-3$."},{"metadata":{},"cell_type":"markdown","source":"__1. Démontrer que $f$ est croissante sur $\\mathbb{R}$.__ \n__On admettra pour la suite que l’équation $f(x)=0$ a une unique solution sur $\\mathbb{R}$, notée $α$.__\n\n__Ecrire une fonction Python $f$ qui:__\n* __reçoit en argument une valeur $x$ ;__\n* __renvoie son image par la fonction $f$.__\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"def f(x):\n return 1/4*x**3+x-3","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__Déterminer les images de $0$ et $3$ par $f$, et en déduire que $α∈[0;3]$.__\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"f(0) , f(3)","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__2. On considère un intervalle $[a;b]$ contenant $α$ et on pose $\\displaystyle m= \\frac{a+b}{2}$.__\n\n__Justifier que : (*) si $f(a) \\times f(m)<0$ alors $α∈[a;m]$ , et sinon $α∈[m;b]$ .__\n\n__En utilisant (*), écrire une fonction Python etap_dichoto qui :__\n* __reçoit en arguments une fonction $f$ et les bornes $a$ et $b$ d’un intervalle contenant $α$ ;__\n* __renvoie les bornes $a$ et $b$ d’un nouvel intervalle contenant $α$.__\n\n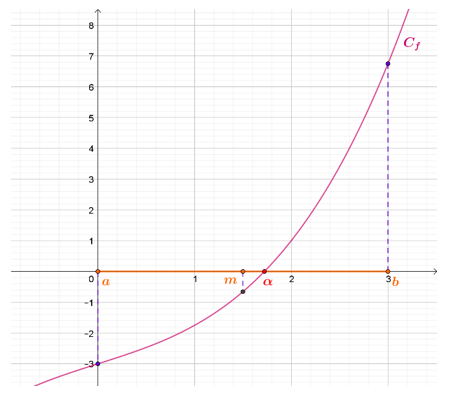"},{"metadata":{"trusted":false},"cell_type":"code","source":"def etap_dichoto(f,a,b):\n m=(a+b)/2\n if f(a)*f(m)<0:\n return a,m\n else:\n return m,b","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__A partir de l’intervalle $[a;b]=[0;3]$, obtenir successivement 3 nouveaux intervalles contenant $α$.__\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"int1=etap_dichoto(f,0,3)\nint2=etap_dichoto(f,*int1)\nint3=etap_dichoto(f,*int2)\n\nint1 , int2 , int3","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__Que peut-on dire de la longueur de chaque intervalle obtenu par rapport à la précédente ?__"},{"metadata":{},"cell_type":"markdown","source":"__3. Ecrire une fonction Python dichoto_iter qui :__\n* __reçoit en arguments une fonction $f$, les bornes $a$ et $b$ d’un intervalle contenant $α$ et un entier $n$ ;__\n* __renvoie les bornes d’un nouvel intervalle contenant $α$ obtenu en répétant $n$ fois la fonction précédente.__\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"def dichoto_iter(f,a,b,n):\n for k in range(n):\n a,b=etap_dichoto(f,a,b)\n return a,b","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__Tester avec la fonction $f$ de l’énoncé en partant de l’intervalle $[0;3]$ et en répétant $10$ fois la méthode.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"dichoto_iter(f,0,3,10)","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__4. Ecrire une fonction Python dichoto_test qui :__\n* __reçoit en arguments la fonction $f$, les bornes $a$ et $b$ d’un intervalle contenant $α$ et une valeur $h$ ;__\n* __renvoie les bornes du premier intervalle de longueur inférieure à $h$ obtenu avec la méthode décrite précédemment.__\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"def dichoto_test(f,a,b,h):\n while b-a>h:\n a,b=etap_dichoto(f,a,b)\n return a,b","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__Tester avec la fonction $f$ de l’énoncé pour obtenir un encadrement de α à $10^{-5}$ près.__\n"},{"metadata":{"trusted":false},"cell_type":"code","source":"dichoto_test(f,0,3,10**-5)","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__5. Proposer et coder en Python des fonctions polynomiales $g$ et $h$ à coefficients entiers s’annulant respectivement en $\\sqrt{5}$ et $\\sqrt[3]{7}$.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"def g(x):\n return x**2-5\n\ndef h(x):\n return x**3-7","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"__A l’aide des fonctions Python précédentes, proposer des encadrements de ces deux nombres à $10^{-7}$ près.__"},{"metadata":{"trusted":false},"cell_type":"code","source":"dichoto_test(g,0,3,10**-7) , dichoto_test(f,0,3,10**-7)\n","execution_count":null,"outputs":[]},{"metadata":{},"cell_type":"markdown","source":"© Copyright Franck CHEVRIER 2019-2022 https://www.python-lycee.com.
\nLes activités partagées sur Capytale sont sous licence Creative Commons.\n
\nDernière modification de l'activité : Juillet 2022"}],"metadata":{"celltoolbar":"Raw Cell Format","kernelspec":{"display_name":"Python 3","language":"python","name":"python3"}},"nbformat":4,"nbformat_minor":2}