{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "![En tête general](https://raw.githubusercontent.com/PythonLycee/PyLyc/master/img/En_tete_general.png)\n",
    "\n",
    "\n",
    "<i>© Copyright Franck CHEVRIER 2019-2021 https://www.python-lycee.com.</i><br>\n",
    "<i>Les activités partagées sur <a href=\"https://capytale2.ac-paris.fr/web/accueil\"><strong>Capytale</strong></a> sont sous licence <a href=\"https://creativecommons.org/licenses/by-sa/3.0/fr/\">Creative Commons</a>.</i>\n",
    "\n",
    "<span style=\"color: #9317B4\"> Pour exécuter une saisie Python, sélectionner la cellule et valider avec </span><span style=\"color: #B317B4\"><strong>SHIFT+Entrée</strong></span>.\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "# Algorithme de Dijkstra"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "*Le but de l’activité est de découvrir et mettre en oeuvre l'algorithme Dijkstra, permettant d'optimiser un trajet en minimisant distance, temps de parcours ou coût.*\n",
    "\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
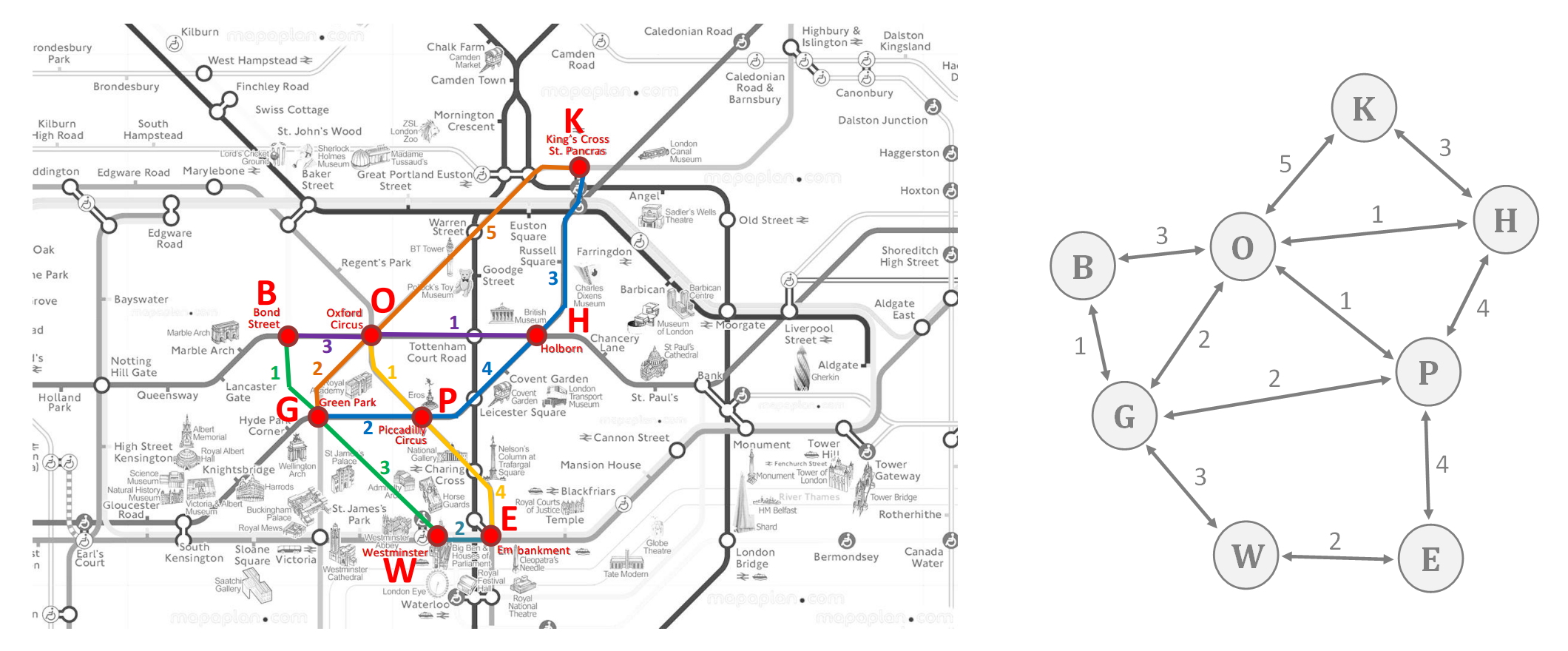
    "<span style=\"color: #7C39C9\">__1. a. On considère le plan du métro londonien. Les temps de parcours étant donnés en minute, on souhaite minimiser le temps de trajet pour se rendre de la station Westminster (W) à la station King's Cross (K). Suivre la vidéo ci-dessous, qui détaille la modélisation du problème à l'aide d'un graphe et la mise en oeuvre de l'algorithme de Dijkstra sur cet exemple.__</span>\n",
    "\n",
    "\n",
    "![MetroLondres](https://raw.githubusercontent.com/PythonLycee/PyLyc/master/SNT/img/Dijkstra1.png)\n",
    "\n",
    "\n",
    "\n",
    "<video controls src=\"https://raw.githubusercontent.com/PythonLycee/PyLyc/master/SNT/video/Dijkstra.mp4\" width=\"960\" height=\"540\" />"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<span style=\"color: #7C39C9\">__1. b. On code en Python le graphe précédent à l'aide de la structure <mark>G1</mark> ci-dessous. Expliquer brièvement comment sont stockées les informations du graphe dans <mark>G1</mark>.__</span>\n",
    "\n",
    "<em style=\"color:#A9A9A9\">Attention : Penser ensuite à exécuter la zone ci-dessous (et les suivantes) avec <strong>SHIFT+Entrée</strong></em>."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "G1 = { 'B':{'G':1,'O':3} , \n",
    "       'E':{'W':2,'P':4} , \n",
    "       'G':{'B':1,'O':2,'P':2,'W':3} , \n",
    "       'H':{'P':4,'O':1,'K':3} , \n",
    "       'K':{'O':5,'H':3} , \n",
    "       'O':{'B':3,'G':2,'P':1,'H':1,'K':5} , \n",
    "       'P':{'E':4,'G':2,'O':1,'H':4} , \n",
    "       'W':{'G':3,'E':2} \n",
    "     }"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<span style=\"color: #7C39C9\">__1. c. La fonction Python <mark>Dijkstra</mark> ci-dessous permet d'appliquer l'algorithme de Dijkstra. Tester l'appel à la fonction pour <mark>G1</mark> afin d'optimiser le trajet de W à K. Vérifier la cohérence avec le résultat obtenu dans la question 1.a.__</span>\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "def etapes(Graphe,depart,final,s_traites,dist,prec):\n",
    "    \"\"\"\n",
    "    Etapes de l'algorithme de Dijkstra (version récursive)\n",
    "        \n",
    "    s_traites:  Liste des sommets déjà traités\n",
    "    dist:       Distances minimales trouvées pour chaque sommet\n",
    "    prec:       Indique pour chaque sommet, celui qui le précède dans le trajet le plus court trouvé    \n",
    "    \"\"\"    \n",
    "    #on choisit le sommet à traiter:\n",
    "    if not dist:\n",
    "        #si aucune distance n'a été calculée, on choisit depart(et on note 0 comme distance pour le depart)\n",
    "        s_courant=depart\n",
    "        dist[s_courant]=0 \n",
    "    else:\n",
    "        #sinon on choisit un sommet non encore traité dont la distance calculée est minimale \n",
    "        non_traites={ s:dist.get(s,float('inf'))  for s in Graphe if s not in s_traites }\n",
    "        s_courant=min(non_traites, key=non_traites.get)\n",
    "\n",
    "    #si le sommet courant est celui à atteindre\n",
    "    if s_courant==final:\n",
    "        #construction de la liste des sommets, à rebours\n",
    "        Chaine=[final]\n",
    "        while Chaine[-1]!=depart:\n",
    "            Chaine.append(prec[Chaine[-1]])\n",
    "        #on renvoie la distance minimale trouvée et la liste des sommets\n",
    "        Chaine.reverse()\n",
    "        return dist[final],Chaine\n",
    "\n",
    "    #on traite tous les voisins du sommet courant\n",
    "    for voisin in Graphe[s_courant]:\n",
    "        #on récupère la distance précédemment calculée pour ce voisin (+inf si non atteint)\n",
    "        dist_voisin_prec=dist.get(voisin,float('+inf'))\n",
    "        #on calcule la nouvelle distance obtenue\n",
    "\n",
    "        dist_voisin_new=dist[s_courant]+Graphe[s_courant][voisin]\n",
    "        #on compare les deux distances et on modifie si nécessaire\n",
    "        if dist_voisin_new<dist_voisin_prec:\n",
    "            dist[voisin]=dist_voisin_new\n",
    "            prec[voisin]=s_courant\n",
    "\n",
    "    #on ajoute le sommet courant à la liste des sommets traites\n",
    "    s_traites.append(s_courant)\n",
    "\n",
    "    #on réitère la méthode pour traiter le sommet suivant\n",
    "    return etapes(Graphe,depart,final,s_traites,dist,prec)\n",
    "\n",
    "def Dijkstra(Graphe,depart,final):\n",
    "    \"\"\"\n",
    "    Application de l'algorithme de Dijkstra\n",
    "    \n",
    "    Graphe:     Graphe fourni sous forme d'un dictionnaire\n",
    "    depart:     Sommet initial du trajet cherché \n",
    "    final:      Sommet final du trajet cherché\n",
    "    \"\"\"  \n",
    "    return etapes(Graphe,depart,final,[],{},{})\n",
    "    "
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "#Appel à la fonction pour le graphe G1, du sommet W au sommet K\n",
    "Dijkstra(G1,'W','K')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<span style=\"color: #7C39C9\">__2. a. Le graphe ci-dessous indique les frais de déplacement occasionnés (péage, essence,...) pour un trajet entre deux villes, exprimés en euro. Appliquer l'algorithme de Dijkstra à l'aide d'un tableau pour déterminer le trajet le moins onéreux pour se rendre de Calais à Mulhouse, et indiquer ce coût.__</span>\n",
    "\n",
    "<ul style=\"color: #7C39C9\">\n",
    "    <li> C : Calais </li>\n",
    "    <li> L : Lille </li>\n",
    "    <li> N : Nancy </li>\n",
    "    <li> S : Strasbourg </li>\n",
    "    <li> A : Amiens </li>\n",
    "    <li> T : Troyes </li>\n",
    "    <li> D : Dijon </li>\n",
    "    <li> M : Mulhouse </li>\n",
    "</ul>\n",
    "\n",
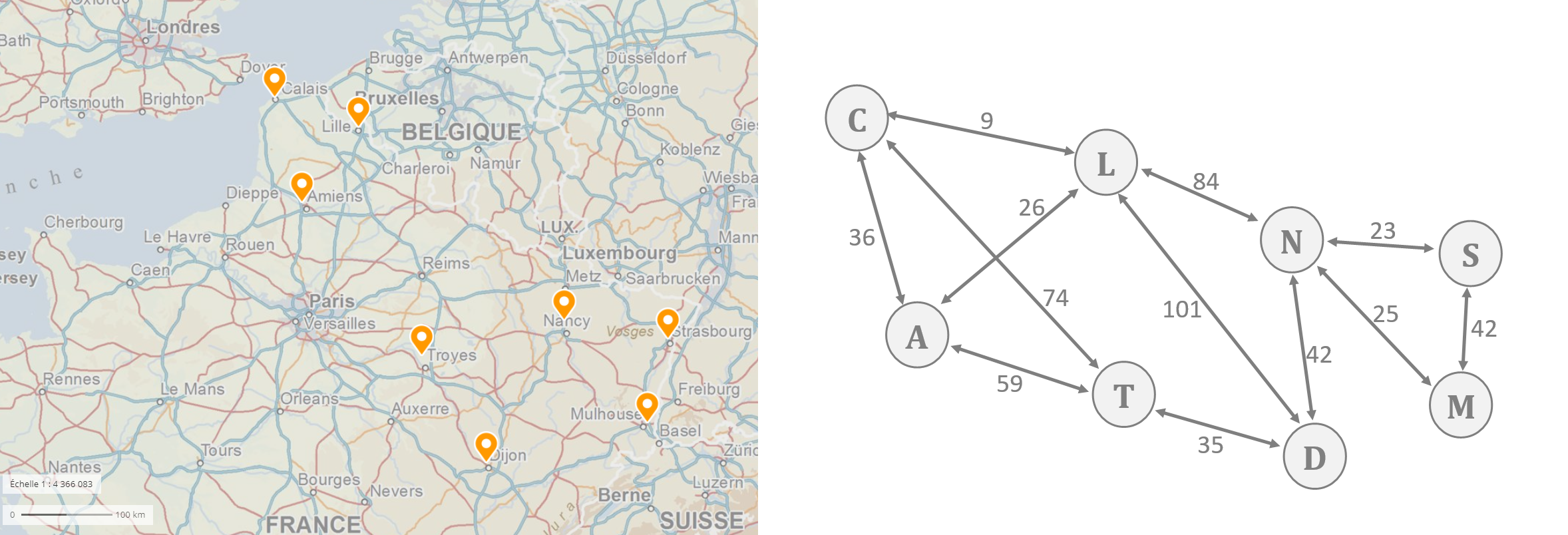    "![Villes](https://raw.githubusercontent.com/PythonLycee/PyLyc/master/SNT/img/Dijkstra2.png)\t\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<span style=\"color: #7C39C9\">__2. b. Créer une structure Python <mark>G2</mark> pour coder ce graphe.__</span>\n",
    "\n",
    "\t"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "#Créer la structure G2 (sur le même modèle que G1)\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<span style=\"color: #7C39C9\">__2. c. Effectuer un appel à la fonction Python <mark>Dijkstra</mark> pour vérifier votre réponse à la question 2.a.__</span>\n",
    "\n",
    "\t"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {},
   "outputs": [],
   "source": [
    "#Effectuer l'appel à la fonction \n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<i>© Copyright Franck CHEVRIER 2019-2021 https://www.python-lycee.com.</i><br>\n",
    "<i>Les activités partagées sur <a href=\"https://capytale2.ac-paris.fr/web/accueil\"><strong>Capytale</strong></a> sont sous licence <a href=\"https://creativecommons.org/licenses/by-sa/3.0/fr/\">Creative Commons</a>.</i>"
   ]
  }
 ],
 "metadata": {
  "celltoolbar": "Raw Cell Format",
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.7.10"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 2
}