{
"cells": [
{
"cell_type": "markdown",
"id": "2b0e6bfc",
"metadata": {},
"source": [
"\n",
""
]
},
{
"cell_type": "markdown",
"id": "abb97b05",
"metadata": {},
"source": [
"# Orthogonal Projections and Their Applications\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"id": "ddd0c1e3",
"metadata": {},
"source": [
"## Contents\n",
"\n",
"- [Orthogonal Projections and Their Applications](#Orthogonal-Projections-and-Their-Applications) \n",
" - [Overview](#Overview) \n",
" - [Key Definitions](#Key-Definitions) \n",
" - [The Orthogonal Projection Theorem](#The-Orthogonal-Projection-Theorem) \n",
" - [Orthonormal Basis](#Orthonormal-Basis) \n",
" - [Projection Via Matrix Algebra](#Projection-Via-Matrix-Algebra) \n",
" - [Least Squares Regression](#Least-Squares-Regression) \n",
" - [Orthogonalization and Decomposition](#Orthogonalization-and-Decomposition) \n",
" - [Exercises](#Exercises) "
]
},
{
"cell_type": "markdown",
"id": "53e1f122",
"metadata": {},
"source": [
"## Overview\n",
"\n",
"Orthogonal projection is a cornerstone of vector space methods, with many diverse applications.\n",
"\n",
"These include\n",
"\n",
"- Least squares projection, also known as linear regression \n",
"- Conditional expectations for multivariate normal (Gaussian) distributions \n",
"- Gram–Schmidt orthogonalization \n",
"- QR decomposition \n",
"- Orthogonal polynomials \n",
"- etc \n",
"\n",
"\n",
"In this lecture, we focus on\n",
"\n",
"- key ideas \n",
"- least squares regression \n",
"\n",
"\n",
"We’ll require the following imports:"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "91aa6927",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"import numpy as np\n",
"from scipy.linalg import qr"
]
},
{
"cell_type": "markdown",
"id": "91164af1",
"metadata": {},
"source": [
"### Further Reading\n",
"\n",
"For background and foundational concepts, see our lecture [on linear algebra](https://python-intro.quantecon.org/linear_algebra.html).\n",
"\n",
"For more proofs and greater theoretical detail, see [A Primer in Econometric Theory](http://www.johnstachurski.net/emet.html).\n",
"\n",
"For a complete set of proofs in a general setting, see, for example, [[Rom05](https://python-advanced.quantecon.org/zreferences.html#id111)].\n",
"\n",
"For an advanced treatment of projection in the context of least squares prediction, see [this book chapter](http://www.tomsargent.com/books/TOMchpt.2.pdf)."
]
},
{
"cell_type": "markdown",
"id": "726ccd11",
"metadata": {},
"source": [
"## Key Definitions\n",
"\n",
"Assume $ x, z \\in \\mathbb R^n $.\n",
"\n",
"Define $ \\langle x, z\\rangle = \\sum_i x_i z_i $.\n",
"\n",
"Recall $ \\|x \\|^2 = \\langle x, x \\rangle $.\n",
"\n",
"The **law of cosines** states that $ \\langle x, z \\rangle = \\| x \\| \\| z \\| \\cos(\\theta) $ where $ \\theta $ is the angle between the vectors $ x $ and $ z $.\n",
"\n",
"When $ \\langle x, z\\rangle = 0 $, then $ \\cos(\\theta) = 0 $ and $ x $ and $ z $ are said to be **orthogonal** and we write $ x \\perp z $.\n",
"\n",
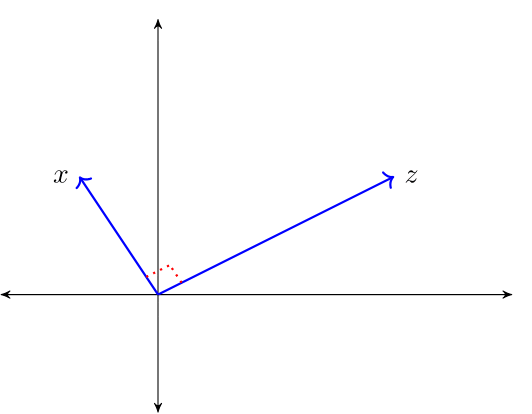"\n",
"\n",
" \n",
"For a linear subspace $ S \\subset \\mathbb R^n $, we call $ x \\in \\mathbb R^n $ **orthogonal to** $ S $ if $ x \\perp z $ for all $ z \\in S $, and write $ x \\perp S $.\n",
"\n",
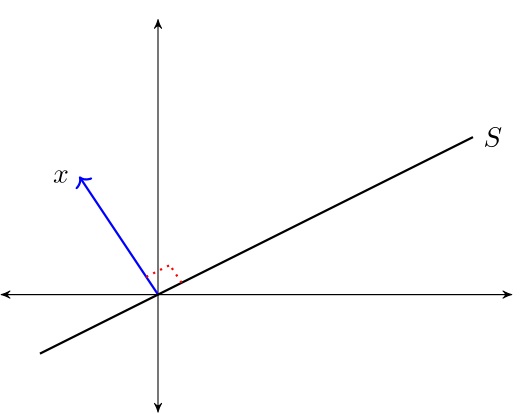"\n",
"\n",
" \n",
"The **orthogonal complement** of linear subspace $ S \\subset \\mathbb R^n $ is the set $ S^{\\perp} := \\{x \\in \\mathbb R^n \\,:\\, x \\perp S\\} $.\n",
"\n",
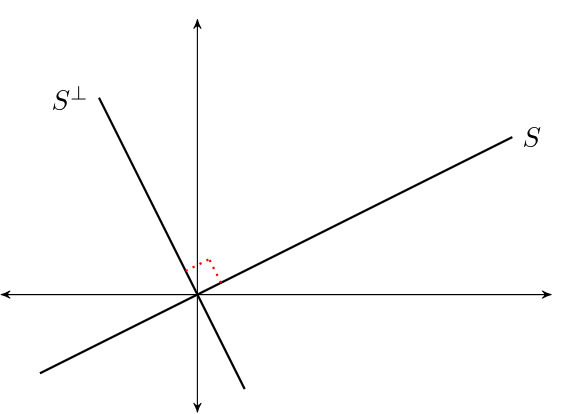"\n",
"\n",
" \n",
"$ S^\\perp $ is a linear subspace of $ \\mathbb R^n $\n",
"\n",
"- To see this, fix $ x, y \\in S^{\\perp} $ and $ \\alpha, \\beta \\in \\mathbb R $. \n",
"- Observe that if $ z \\in S $, then \n",
"\n",
"\n",
"$$\n",
"\\langle \\alpha x + \\beta y, z \\rangle\n",
"= \\alpha \\langle x, z \\rangle + \\beta \\langle y, z \\rangle\n",
" = \\alpha \\times 0 + \\beta \\times 0 = 0\n",
"$$\n",
"\n",
"- Hence $ \\alpha x + \\beta y \\in S^{\\perp} $, as was to be shown \n",
"\n",
"\n",
"A set of vectors $ \\{x_1, \\ldots, x_k\\} \\subset \\mathbb R^n $ is called an **orthogonal set** if $ x_i \\perp x_j $ whenever $ i \\not= j $.\n",
"\n",
"If $ \\{x_1, \\ldots, x_k\\} $ is an orthogonal set, then the **Pythagorean Law** states that\n",
"\n",
"$$\n",
"\\| x_1 + \\cdots + x_k \\|^2\n",
"= \\| x_1 \\|^2 + \\cdots + \\| x_k \\|^2\n",
"$$\n",
"\n",
"For example, when $ k=2 $, $ x_1 \\perp x_2 $ implies\n",
"\n",
"$$\n",
"\\| x_1 + x_2 \\|^2\n",
" = \\langle x_1 + x_2, x_1 + x_2 \\rangle\n",
" = \\langle x_1, x_1 \\rangle + 2 \\langle x_2, x_1 \\rangle + \\langle x_2, x_2 \\rangle\n",
" = \\| x_1 \\|^2 + \\| x_2 \\|^2\n",
"$$"
]
},
{
"cell_type": "markdown",
"id": "7cb822b3",
"metadata": {},
"source": [
"### Linear Independence vs Orthogonality\n",
"\n",
"If $ X \\subset \\mathbb R^n $ is an orthogonal set and $ 0 \\notin X $, then $ X $ is linearly independent.\n",
"\n",
"Proving this is a nice exercise.\n",
"\n",
"While the converse is not true, a kind of partial converse holds, as we’ll [see below](#gram-schmidt)."
]
},
{
"cell_type": "markdown",
"id": "6a6491f6",
"metadata": {},
"source": [
"## The Orthogonal Projection Theorem\n",
"\n",
"What vector within a linear subspace of $ \\mathbb R^n $ best approximates a given vector in $ \\mathbb R^n $?\n",
"\n",
"The next theorem answers this question.\n",
"\n",
"**Theorem** (OPT) Given $ y \\in \\mathbb R^n $ and linear subspace $ S \\subset \\mathbb R^n $,\n",
"there exists a unique solution to the minimization problem\n",
"\n",
"$$\n",
"\\hat y := \\argmin_{z \\in S} \\|y - z\\|\n",
"$$\n",
"\n",
"The minimizer $ \\hat y $ is the unique vector in $ \\mathbb R^n $ that satisfies\n",
"\n",
"- $ \\hat y \\in S $ \n",
"- $ y - \\hat y \\perp S $ \n",
"\n",
"\n",
"The vector $ \\hat y $ is called the **orthogonal projection** of $ y $ onto $ S $.\n",
"\n",
"The next figure provides some intuition\n",
"\n",
""
]
},
{
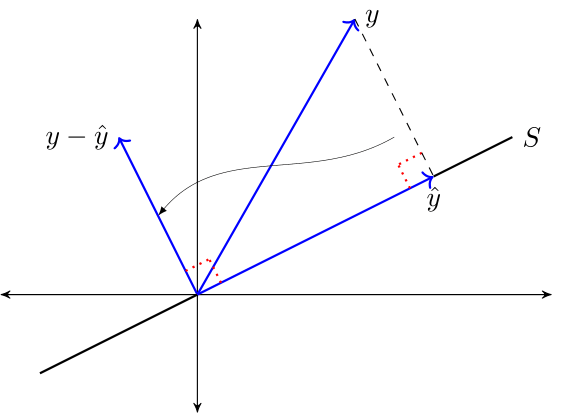"cell_type": "markdown",
"id": "66b1349d",
"metadata": {},
"source": [
"### Proof of Sufficiency\n",
"\n",
"We’ll omit the full proof.\n",
"\n",
"But we will prove sufficiency of the asserted conditions.\n",
"\n",
"To this end, let $ y \\in \\mathbb R^n $ and let $ S $ be a linear subspace of $ \\mathbb R^n $.\n",
"\n",
"Let $ \\hat y $ be a vector in $ \\mathbb R^n $ such that $ \\hat y \\in S $ and $ y - \\hat y \\perp S $.\n",
"\n",
"Let $ z $ be any other point in $ S $ and use the fact that $ S $ is a linear subspace to deduce\n",
"\n",
"$$\n",
"\\| y - z \\|^2\n",
"= \\| (y - \\hat y) + (\\hat y - z) \\|^2\n",
"= \\| y - \\hat y \\|^2 + \\| \\hat y - z \\|^2\n",
"$$\n",
"\n",
"Hence $ \\| y - z \\| \\geq \\| y - \\hat y \\| $, which completes the proof."
]
},
{
"cell_type": "markdown",
"id": "f1b26096",
"metadata": {},
"source": [
"### Orthogonal Projection as a Mapping\n",
"\n",
"For a linear space $ Y $ and a fixed linear subspace $ S $, we have a functional relationship\n",
"\n",
"$$\n",
"y \\in Y\\; \\mapsto \\text{ its orthogonal projection } \\hat y \\in S\n",
"$$\n",
"\n",
"By the OPT, this is a well-defined mapping or *operator* from $ \\mathbb R^n $ to $ \\mathbb R^n $.\n",
"\n",
"In what follows we denote this operator by a matrix $ P $\n",
"\n",
"- $ P y $ represents the projection $ \\hat y $. \n",
"- This is sometimes expressed as $ \\hat E_S y = P y $, where $ \\hat E $ denotes a **wide-sense expectations operator** and the subscript $ S $ indicates that we are projecting $ y $ onto the linear subspace $ S $. \n",
"\n",
"\n",
"The operator $ P $ is called the **orthogonal projection mapping onto** $ S $.\n",
"\n",
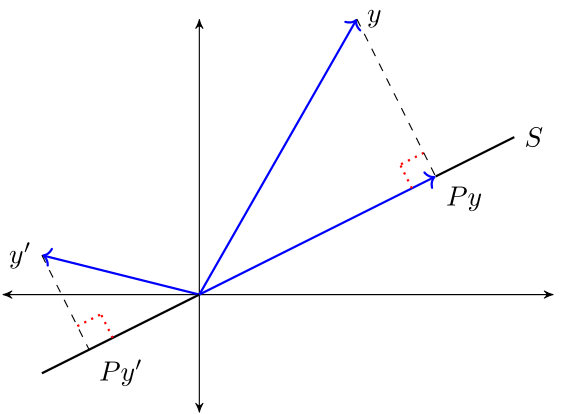"\n",
"\n",
" \n",
"It is immediate from the OPT that for any $ y \\in \\mathbb R^n $\n",
"\n",
"1. $ P y \\in S $ and \n",
"1. $ y - P y \\perp S $ \n",
"\n",
"\n",
"From this, we can deduce additional useful properties, such as\n",
"\n",
"1. $ \\| y \\|^2 = \\| P y \\|^2 + \\| y - P y \\|^2 $ and \n",
"1. $ \\| P y \\| \\leq \\| y \\| $ \n",
"\n",
"\n",
"For example, to prove 1, observe that $ y = P y + y - P y $ and apply the Pythagorean law."
]
},
{
"cell_type": "markdown",
"id": "4cdc5c0f",
"metadata": {},
"source": [
"#### Orthogonal Complement\n",
"\n",
"Let $ S \\subset \\mathbb R^n $.\n",
"\n",
"The **orthogonal complement** of $ S $ is the linear subspace $ S^{\\perp} $ that satisfies\n",
"$ x_1 \\perp x_2 $ for every $ x_1 \\in S $ and $ x_2 \\in S^{\\perp} $.\n",
"\n",
"Let $ Y $ be a linear space with linear subspace $ S $ and its orthogonal complement $ S^{\\perp} $.\n",
"\n",
"We write\n",
"\n",
"$$\n",
"Y = S \\oplus S^{\\perp}\n",
"$$\n",
"\n",
"to indicate that for every $ y \\in Y $ there is unique $ x_1 \\in S $ and a unique $ x_2 \\in S^{\\perp} $\n",
"such that $ y = x_1 + x_2 $.\n",
"\n",
"Moreover, $ x_1 = \\hat E_S y $ and $ x_2 = y - \\hat E_S y $.\n",
"\n",
"This amounts to another version of the OPT:\n",
"\n",
"**Theorem**. If $ S $ is a linear subspace of $ \\mathbb R^n $, $ \\hat E_S y = P y $ and $ \\hat E_{S^{\\perp}} y = M y $, then\n",
"\n",
"$$\n",
"P y \\perp M y\n",
" \\quad \\text{and} \\quad\n",
"y = P y + M y\n",
" \\quad \\text{for all } \\, y \\in \\mathbb R^n\n",
"$$\n",
"\n",
"The next figure illustrates\n",
"\n",
""
]
},
{
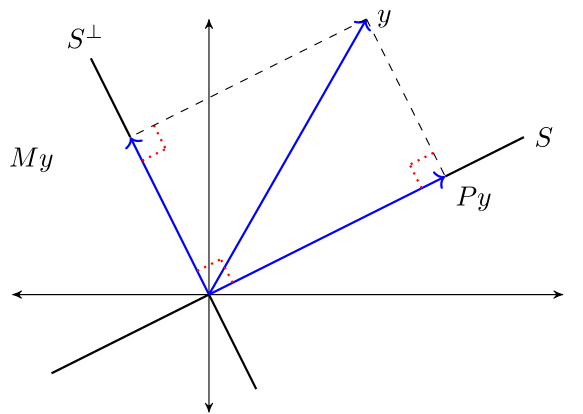"cell_type": "markdown",
"id": "fdc48ec9",
"metadata": {},
"source": [
"## Orthonormal Basis\n",
"\n",
"An orthogonal set of vectors $ O \\subset \\mathbb R^n $ is called an **orthonormal set** if $ \\| u \\| = 1 $ for all $ u \\in O $.\n",
"\n",
"Let $ S $ be a linear subspace of $ \\mathbb R^n $ and let $ O \\subset S $.\n",
"\n",
"If $ O $ is orthonormal and $ \\mathop{\\mathrm{span}} O = S $, then $ O $ is called an **orthonormal basis** of $ S $.\n",
"\n",
"$ O $ is necessarily a basis of $ S $ (being independent by orthogonality and the fact that no element is the zero vector).\n",
"\n",
"One example of an orthonormal set is the canonical basis $ \\{e_1, \\ldots, e_n\\} $\n",
"that forms an orthonormal basis of $ \\mathbb R^n $, where $ e_i $ is the $ i $ th unit vector.\n",
"\n",
"If $ \\{u_1, \\ldots, u_k\\} $ is an orthonormal basis of linear subspace $ S $, then\n",
"\n",
"$$\n",
"x = \\sum_{i=1}^k \\langle x, u_i \\rangle u_i\n",
"\\quad \\text{for all} \\quad\n",
"x \\in S\n",
"$$\n",
"\n",
"To see this, observe that since $ x \\in \\mathop{\\mathrm{span}}\\{u_1, \\ldots, u_k\\} $, we can find\n",
"scalars $ \\alpha_1, \\ldots, \\alpha_k $ that verify\n",
"\n",
"\n",
"\n",
"$$\n",
"x = \\sum_{j=1}^k \\alpha_j u_j \\tag{1.1}\n",
"$$\n",
"\n",
"Taking the inner product with respect to $ u_i $ gives\n",
"\n",
"$$\n",
"\\langle x, u_i \\rangle\n",
"= \\sum_{j=1}^k \\alpha_j \\langle u_j, u_i \\rangle\n",
"= \\alpha_i\n",
"$$\n",
"\n",
"Combining this result with [(1.1)](#equation-pob) verifies the claim."
]
},
{
"cell_type": "markdown",
"id": "fa75ecfb",
"metadata": {},
"source": [
"### Projection onto an Orthonormal Basis\n",
"\n",
"When a subspace onto which we project is orthonormal, computing the projection simplifies:\n",
"\n",
"**Theorem** If $ \\{u_1, \\ldots, u_k\\} $ is an orthonormal basis for $ S $, then\n",
"\n",
"\n",
"\n",
"$$\n",
"P y = \\sum_{i=1}^k \\langle y, u_i \\rangle u_i,\n",
"\\quad\n",
"\\forall \\; y \\in \\mathbb R^n \\tag{1.2}\n",
"$$\n",
"\n",
"Proof: Fix $ y \\in \\mathbb R^n $ and let $ P y $ be defined as in [(1.2)](#equation-exp-for-op).\n",
"\n",
"Clearly, $ P y \\in S $.\n",
"\n",
"We claim that $ y - P y \\perp S $ also holds.\n",
"\n",
"It sufficies to show that $ y - P y \\perp $ any basis vector $ u_i $.\n",
"\n",
"This is true because\n",
"\n",
"$$\n",
"\\left\\langle y - \\sum_{i=1}^k \\langle y, u_i \\rangle u_i, u_j \\right\\rangle\n",
"= \\langle y, u_j \\rangle - \\sum_{i=1}^k \\langle y, u_i \\rangle\n",
"\\langle u_i, u_j \\rangle = 0\n",
"$$\n",
"\n",
"(Why is this sufficient to establish the claim that $ y - P y \\perp S $?)"
]
},
{
"cell_type": "markdown",
"id": "748bea1a",
"metadata": {},
"source": [
"## Projection Via Matrix Algebra\n",
"\n",
"Let $ S $ be a linear subspace of $ \\mathbb R^n $ and let $ y \\in \\mathbb R^n $.\n",
"\n",
"We want to compute the matrix $ P $ that verifies\n",
"\n",
"$$\n",
"\\hat E_S y = P y\n",
"$$\n",
"\n",
"Evidently $ Py $ is a linear function from $ y \\in \\mathbb R^n $ to $ P y \\in \\mathbb R^n $.\n",
"\n",
"[This reference](https://en.wikipedia.org/wiki/Linear_map#Matrices) is useful.\n",
"\n",
"**Theorem.** Let the columns of $ n \\times k $ matrix $ X $ form a basis of $ S $. Then\n",
"\n",
"$$\n",
"P = X (X'X)^{-1} X'\n",
"$$\n",
"\n",
"Proof: Given arbitrary $ y \\in \\mathbb R^n $ and $ P = X (X'X)^{-1} X' $, our claim is that\n",
"\n",
"1. $ P y \\in S $, and \n",
"1. $ y - P y \\perp S $ \n",
"\n",
"\n",
"Claim 1 is true because\n",
"\n",
"$$\n",
"P y = X (X' X)^{-1} X' y = X a\n",
"\\quad \\text{when} \\quad\n",
"a := (X' X)^{-1} X' y\n",
"$$\n",
"\n",
"An expression of the form $ X a $ is precisely a linear combination of the\n",
"columns of $ X $ and hence an element of $ S $.\n",
"\n",
"Claim 2 is equivalent to the statement\n",
"\n",
"$$\n",
"y - X (X' X)^{-1} X' y \\, \\perp\\, X b\n",
"\\quad \\text{for all} \\quad\n",
"b \\in \\mathbb R^K\n",
"$$\n",
"\n",
"To verify this, notice that if $ b \\in \\mathbb R^K $, then\n",
"\n",
"$$\n",
"(X b)' [y - X (X' X)^{-1} X'\n",
"y]\n",
"= b' [X' y - X' y]\n",
"= 0\n",
"$$\n",
"\n",
"The proof is now complete."
]
},
{
"cell_type": "markdown",
"id": "5e79e4bf",
"metadata": {},
"source": [
"### Starting with the Basis\n",
"\n",
"It is common in applications to start with $ n \\times k $ matrix $ X $ with linearly independent columns and let\n",
"\n",
"$$\n",
"S := \\mathop{\\mathrm{span}} X := \\mathop{\\mathrm{span}} \\{\\col_1 X, \\ldots, \\col_k X \\}\n",
"$$\n",
"\n",
"Then the columns of $ X $ form a basis of $ S $.\n",
"\n",
"From the preceding theorem, $ P = X (X' X)^{-1} X' y $ projects $ y $ onto $ S $.\n",
"\n",
"In this context, $ P $ is often called the **projection matrix**\n",
"\n",
"- The matrix $ M = I - P $ satisfies $ M y = \\hat E_{S^{\\perp}} y $ and is sometimes called the **annihilator matrix**. "
]
},
{
"cell_type": "markdown",
"id": "2cfb7ae0",
"metadata": {},
"source": [
"### The Orthonormal Case\n",
"\n",
"Suppose that $ U $ is $ n \\times k $ with orthonormal columns.\n",
"\n",
"Let $ u_i := \\mathop{\\mathrm{col}} U_i $ for each $ i $, let $ S := \\mathop{\\mathrm{span}} U $ and let $ y \\in \\mathbb R^n $.\n",
"\n",
"We know that the projection of $ y $ onto $ S $ is\n",
"\n",
"$$\n",
"P y = U (U' U)^{-1} U' y\n",
"$$\n",
"\n",
"Since $ U $ has orthonormal columns, we have $ U' U = I $.\n",
"\n",
"Hence\n",
"\n",
"$$\n",
"P y\n",
"= U U' y\n",
"= \\sum_{i=1}^k \\langle u_i, y \\rangle u_i\n",
"$$\n",
"\n",
"We have recovered our earlier result about projecting onto the span of an orthonormal\n",
"basis."
]
},
{
"cell_type": "markdown",
"id": "46e6f9ed",
"metadata": {},
"source": [
"### Application: Overdetermined Systems of Equations\n",
"\n",
"Let $ y \\in \\mathbb R^n $ and let $ X $ be $ n \\times k $ with linearly independent columns.\n",
"\n",
"Given $ X $ and $ y $, we seek $ b \\in \\mathbb R^k $ that satisfies the system of linear equations $ X b = y $.\n",
"\n",
"If $ n > k $ (more equations than unknowns), then $ b $ is said to be **overdetermined**.\n",
"\n",
"Intuitively, we may not be able to find a $ b $ that satisfies all $ n $ equations.\n",
"\n",
"The best approach here is to\n",
"\n",
"- Accept that an exact solution may not exist. \n",
"- Look instead for an approximate solution. \n",
"\n",
"\n",
"By approximate solution, we mean a $ b \\in \\mathbb R^k $ such that $ X b $ is close to $ y $.\n",
"\n",
"The next theorem shows that a best approximation is well defined and unique.\n",
"\n",
"The proof uses the OPT.\n",
"\n",
"**Theorem** The unique minimizer of $ \\| y - X b \\| $ over $ b \\in \\mathbb R^K $ is\n",
"\n",
"$$\n",
"\\hat \\beta := (X' X)^{-1} X' y\n",
"$$\n",
"\n",
"Proof: Note that\n",
"\n",
"$$\n",
"X \\hat \\beta = X (X' X)^{-1} X' y =\n",
"P y\n",
"$$\n",
"\n",
"Since $ P y $ is the orthogonal projection onto $ \\mathop{\\mathrm{span}}(X) $ we have\n",
"\n",
"$$\n",
"\\| y - P y \\|\n",
"\\leq \\| y - z \\| \\text{ for any } z \\in \\mathop{\\mathrm{span}}(X)\n",
"$$\n",
"\n",
"Because $ Xb \\in \\mathop{\\mathrm{span}}(X) $\n",
"\n",
"$$\n",
"\\| y - X \\hat \\beta \\|\n",
"\\leq \\| y - X b \\| \\text{ for any } b \\in \\mathbb R^K\n",
"$$\n",
"\n",
"This is what we aimed to show."
]
},
{
"cell_type": "markdown",
"id": "d762254c",
"metadata": {},
"source": [
"## Least Squares Regression\n",
"\n",
"Let’s apply the theory of orthogonal projection to least squares regression.\n",
"\n",
"This approach provides insights about many geometric properties of linear regression.\n",
"\n",
"We treat only some examples."
]
},
{
"cell_type": "markdown",
"id": "ff09dc91",
"metadata": {},
"source": [
"### Squared Risk Measures\n",
"\n",
"Given pairs $ (x, y) \\in \\mathbb R^K \\times \\mathbb R $, consider choosing $ f \\colon \\mathbb R^K \\to \\mathbb R $ to minimize\n",
"the **risk**\n",
"\n",
"$$\n",
"R(f) := \\mathbb{E}\\, [(y - f(x))^2]\n",
"$$\n",
"\n",
"If probabilities and hence $ \\mathbb{E}\\, $ are unknown, we cannot solve this problem directly.\n",
"\n",
"However, if a sample is available, we can estimate the risk with the **empirical risk**:\n",
"\n",
"$$\n",
"\\min_{f \\in \\mathcal{F}} \\frac{1}{N} \\sum_{n=1}^N (y_n - f(x_n))^2\n",
"$$\n",
"\n",
"Minimizing this expression is called **empirical risk minimization**.\n",
"\n",
"The set $ \\mathcal{F} $ is sometimes called the hypothesis space.\n",
"\n",
"The theory of statistical learning tells us that to prevent overfitting we should take the set $ \\mathcal{F} $ to be relatively simple.\n",
"\n",
"If we let $ \\mathcal{F} $ be the class of linear functions, the problem is\n",
"\n",
"$$\n",
"\\min_{b \\in \\mathbb R^K} \\;\n",
"\\sum_{n=1}^N (y_n - b' x_n)^2\n",
"$$\n",
"\n",
"This is the sample **linear least squares problem**."
]
},
{
"cell_type": "markdown",
"id": "ca70b4d9",
"metadata": {},
"source": [
"### Solution\n",
"\n",
"Define the matrices\n",
"\n",
"$$\n",
"y :=\n",
"\\left(\n",
"\\begin{array}{c}\n",
" y_1 \\\\\n",
" y_2 \\\\\n",
" \\vdots \\\\\n",
" y_N\n",
"\\end{array}\n",
"\\right),\n",
"\\quad\n",
"x_n :=\n",
"\\left(\n",
"\\begin{array}{c}\n",
" x_{n1} \\\\\n",
" x_{n2} \\\\\n",
" \\vdots \\\\\n",
" x_{nK}\n",
"\\end{array}\n",
"\\right)\n",
"= n\\text{-th obs on all regressors}\n",
"$$\n",
"\n",
"and\n",
"\n",
"$$\n",
"X :=\n",
"\\left(\n",
"\\begin{array}{c}\n",
" x_1' \\\\\n",
" x_2' \\\\\n",
" \\vdots \\\\\n",
" x_N'\n",
"\\end{array}\n",
"\\right)\n",
":=:\n",
"\\left(\n",
"\\begin{array}{cccc}\n",
" x_{11} & x_{12} & \\cdots & x_{1K} \\\\\n",
" x_{21} & x_{22} & \\cdots & x_{2K} \\\\\n",
" \\vdots & \\vdots & & \\vdots \\\\\n",
" x_{N1} & x_{N2} & \\cdots & x_{NK}\n",
"\\end{array}\n",
"\\right)\n",
"$$\n",
"\n",
"We assume throughout that $ N > K $ and $ X $ is full column rank.\n",
"\n",
"If you work through the algebra, you will be able to verify that $ \\| y - X b \\|^2 = \\sum_{n=1}^N (y_n - b' x_n)^2 $.\n",
"\n",
"Since monotone transforms don’t affect minimizers, we have\n",
"\n",
"$$\n",
"\\argmin_{b \\in \\mathbb R^K} \\sum_{n=1}^N (y_n - b' x_n)^2\n",
"= \\argmin_{b \\in \\mathbb R^K} \\| y - X b \\|\n",
"$$\n",
"\n",
"By our results about overdetermined linear systems of equations, the solution is\n",
"\n",
"$$\n",
"\\hat \\beta := (X' X)^{-1} X' y\n",
"$$\n",
"\n",
"Let $ P $ and $ M $ be the projection and annihilator associated with $ X $:\n",
"\n",
"$$\n",
"P := X (X' X)^{-1} X'\n",
"\\quad \\text{and} \\quad\n",
"M := I - P\n",
"$$\n",
"\n",
"The **vector of fitted values** is\n",
"\n",
"$$\n",
"\\hat y := X \\hat \\beta = P y\n",
"$$\n",
"\n",
"The **vector of residuals** is\n",
"\n",
"$$\n",
"\\hat u := y - \\hat y = y - P y = M y\n",
"$$\n",
"\n",
"Here are some more standard definitions:\n",
"\n",
"- The **total sum of squares** is $ := \\| y \\|^2 $. \n",
"- The **sum of squared residuals** is $ := \\| \\hat u \\|^2 $. \n",
"- The **explained sum of squares** is $ := \\| \\hat y \\|^2 $. \n",
"\n",
"\n",
"> TSS = ESS + SSR\n",
"\n",
"\n",
"We can prove this easily using the OPT.\n",
"\n",
"From the OPT we have $ y = \\hat y + \\hat u $ and $ \\hat u \\perp \\hat y $.\n",
"\n",
"Applying the Pythagorean law completes the proof."
]
},
{
"cell_type": "markdown",
"id": "38f0ef62",
"metadata": {},
"source": [
"## Orthogonalization and Decomposition\n",
"\n",
"Let’s return to the connection between linear independence and orthogonality touched on above.\n",
"\n",
"A result of much interest is a famous algorithm for constructing orthonormal sets from linearly independent sets.\n",
"\n",
"The next section gives details.\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"id": "ea18c40e",
"metadata": {},
"source": [
"### Gram-Schmidt Orthogonalization\n",
"\n",
"**Theorem** For each linearly independent set $ \\{x_1, \\ldots, x_k\\} \\subset \\mathbb R^n $, there exists an\n",
"orthonormal set $ \\{u_1, \\ldots, u_k\\} $ with\n",
"\n",
"$$\n",
"\\mathop{\\mathrm{span}} \\{x_1, \\ldots, x_i\\} =\n",
"\\mathop{\\mathrm{span}} \\{u_1, \\ldots, u_i\\}\n",
"\\quad \\text{for} \\quad\n",
"i = 1, \\ldots, k\n",
"$$\n",
"\n",
"The **Gram-Schmidt orthogonalization** procedure constructs an orthogonal set $ \\{ u_1, u_2, \\ldots, u_n\\} $.\n",
"\n",
"One description of this procedure is as follows:\n",
"\n",
"- For $ i = 1, \\ldots, k $, form $ S_i := \\mathop{\\mathrm{span}}\\{x_1, \\ldots, x_i\\} $ and $ S_i^{\\perp} $ \n",
"- Set $ v_1 = x_1 $ \n",
"- For $ i \\geq 2 $ set $ v_i := \\hat E_{S_{i-1}^{\\perp}} x_i $ and $ u_i := v_i / \\| v_i \\| $ \n",
"\n",
"\n",
"The sequence $ u_1, \\ldots, u_k $ has the stated properties.\n",
"\n",
"A Gram-Schmidt orthogonalization construction is a key idea behind the Kalman filter described in [A First Look at the Kalman filter](https://python-intro.quantecon.org/kalman.html).\n",
"\n",
"In some exercises below, you are asked to implement this algorithm and test it using projection."
]
},
{
"cell_type": "markdown",
"id": "6c771be4",
"metadata": {},
"source": [
"### QR Decomposition\n",
"\n",
"The following result uses the preceding algorithm to produce a useful decomposition.\n",
"\n",
"**Theorem** If $ X $ is $ n \\times k $ with linearly independent columns, then there exists a factorization $ X = Q R $ where\n",
"\n",
"- $ R $ is $ k \\times k $, upper triangular, and nonsingular \n",
"- $ Q $ is $ n \\times k $ with orthonormal columns \n",
"\n",
"\n",
"Proof sketch: Let\n",
"\n",
"- $ x_j := \\col_j (X) $ \n",
"- $ \\{u_1, \\ldots, u_k\\} $ be orthonormal with the same span as $ \\{x_1, \\ldots, x_k\\} $ (to be constructed using Gram–Schmidt) \n",
"- $ Q $ be formed from cols $ u_i $ \n",
"\n",
"\n",
"Since $ x_j \\in \\mathop{\\mathrm{span}}\\{u_1, \\ldots, u_j\\} $, we have\n",
"\n",
"$$\n",
"x_j = \\sum_{i=1}^j \\langle u_i, x_j \\rangle u_i\n",
"\\quad \\text{for } j = 1, \\ldots, k\n",
"$$\n",
"\n",
"Some rearranging gives $ X = Q R $."
]
},
{
"cell_type": "markdown",
"id": "d8c0b414",
"metadata": {},
"source": [
"### Linear Regression via QR Decomposition\n",
"\n",
"For matrices $ X $ and $ y $ that overdetermine $ \\beta $ in the linear\n",
"equation system $ y = X \\beta $, we found the least squares approximator $ \\hat \\beta = (X' X)^{-1} X' y $.\n",
"\n",
"Using the QR decomposition $ X = Q R $ gives\n",
"\n",
"$$\n",
"\\begin{aligned}\n",
" \\hat \\beta\n",
" & = (R'Q' Q R)^{-1} R' Q' y \\\\\n",
" & = (R' R)^{-1} R' Q' y \\\\\n",
" & = R^{-1} (R')^{-1} R' Q' y\n",
" = R^{-1} Q' y\n",
"\\end{aligned}\n",
"$$\n",
"\n",
"Numerical routines would in this case use the alternative form $ R \\hat \\beta = Q' y $ and back substitution."
]
},
{
"cell_type": "markdown",
"id": "4b6e2aaf",
"metadata": {},
"source": [
"## Exercises"
]
},
{
"cell_type": "markdown",
"id": "a3b75e7c",
"metadata": {},
"source": [
"## Exercise 1.1\n",
"\n",
"Show that, for any linear subspace $ S \\subset \\mathbb R^n $, $ S \\cap S^{\\perp} = \\{0\\} $."
]
},
{
"cell_type": "markdown",
"id": "d8565307",
"metadata": {},
"source": [
"## Solution to[ Exercise 1.1](https://python-advanced.quantecon.org/#op_ex1)\n",
"\n",
"If $ x \\in S $ and $ x \\in S^\\perp $, then we have in particular\n",
"that $ \\langle x, x \\rangle = 0 $, but then $ x = 0 $."
]
},
{
"cell_type": "markdown",
"id": "ac4b156c",
"metadata": {},
"source": [
"## Exercise 1.2\n",
"\n",
"Let $ P = X (X' X)^{-1} X' $ and let $ M = I - P $. Show that\n",
"$ P $ and $ M $ are both idempotent and symmetric. Can you give any\n",
"intuition as to why they should be idempotent?"
]
},
{
"cell_type": "markdown",
"id": "cca31e2c",
"metadata": {},
"source": [
"## Solution to[ Exercise 1.2](https://python-advanced.quantecon.org/#op_ex2)\n",
"\n",
"Symmetry and idempotence of $ M $ and $ P $ can be established\n",
"using standard rules for matrix algebra. The intuition behind\n",
"idempotence of $ M $ and $ P $ is that both are orthogonal\n",
"projections. After a point is projected into a given subspace, applying\n",
"the projection again makes no difference (A point inside the subspace\n",
"is not shifted by orthogonal projection onto that space because it is\n",
"already the closest point in the subspace to itself)."
]
},
{
"cell_type": "markdown",
"id": "e35b5d68",
"metadata": {},
"source": [
"## Exercise 1.3\n",
"\n",
"Using Gram-Schmidt orthogonalization, produce a linear projection of $ y $ onto the column space of $ X $ and verify this using the projection matrix $ P := X (X' X)^{-1} X' $ and also using QR decomposition, where:\n",
"\n",
"$$\n",
"y :=\n",
"\\left(\n",
"\\begin{array}{c}\n",
" 1 \\\\\n",
" 3 \\\\\n",
" -3\n",
"\\end{array}\n",
"\\right),\n",
"\\quad\n",
"$$\n",
"\n",
"and\n",
"\n",
"$$\n",
"X :=\n",
"\\left(\n",
"\\begin{array}{cc}\n",
" 1 & 0 \\\\\n",
" 0 & -6 \\\\\n",
" 2 & 2\n",
"\\end{array}\n",
"\\right)\n",
"$$"
]
},
{
"cell_type": "markdown",
"id": "0b241117",
"metadata": {},
"source": [
"## Solution to[ Exercise 1.3](https://python-advanced.quantecon.org/#op_ex3)\n",
"\n",
"Here’s a function that computes the orthonormal vectors using the GS\n",
"algorithm given in the lecture"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "990119bc",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"def gram_schmidt(X):\n",
" \"\"\"\n",
" Implements Gram-Schmidt orthogonalization.\n",
"\n",
" Parameters\n",
" ----------\n",
" X : an n x k array with linearly independent columns\n",
"\n",
" Returns\n",
" -------\n",
" U : an n x k array with orthonormal columns\n",
"\n",
" \"\"\"\n",
"\n",
" # Set up\n",
" n, k = X.shape\n",
" U = np.empty((n, k))\n",
" I = np.eye(n)\n",
"\n",
" # The first col of U is just the normalized first col of X\n",
" v1 = X[:,0]\n",
" U[:, 0] = v1 / np.sqrt(np.sum(v1 * v1))\n",
"\n",
" for i in range(1, k):\n",
" # Set up\n",
" b = X[:, i] # The vector we're going to project\n",
" Z = X[:, 0:i] # First i-1 columns of X\n",
"\n",
" # Project onto the orthogonal complement of the col span of Z\n",
" M = I - Z @ np.linalg.inv(Z.T @ Z) @ Z.T\n",
" u = M @ b\n",
"\n",
" # Normalize\n",
" U[:, i] = u / np.sqrt(np.sum(u * u))\n",
"\n",
" return U"
]
},
{
"cell_type": "markdown",
"id": "10eb84da",
"metadata": {},
"source": [
"Here are the arrays we’ll work with"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "685cf8a8",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"y = [1, 3, -3]\n",
"\n",
"X = [[1, 0],\n",
" [0, -6],\n",
" [2, 2]]\n",
"\n",
"X, y = [np.asarray(z) for z in (X, y)]"
]
},
{
"cell_type": "markdown",
"id": "05688fd3",
"metadata": {},
"source": [
"First, let’s try projection of $ y $ onto the column space of\n",
"$ X $ using the ordinary matrix expression:"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "ef1fcfab",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"Py1 = X @ np.linalg.inv(X.T @ X) @ X.T @ y\n",
"Py1"
]
},
{
"cell_type": "markdown",
"id": "2424ea7f",
"metadata": {},
"source": [
"Now let’s do the same using an orthonormal basis created from our\n",
"`gram_schmidt` function"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "d87e4a67",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"U = gram_schmidt(X)\n",
"U"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "734c19c5",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"Py2 = U @ U.T @ y\n",
"Py2"
]
},
{
"cell_type": "markdown",
"id": "133313c7",
"metadata": {},
"source": [
"This is the same answer. So far so good. Finally, let’s try the same\n",
"thing but with the basis obtained via QR decomposition:"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "cda8cd9b",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"Q, R = qr(X, mode='economic')\n",
"Q"
]
},
{
"cell_type": "code",
"execution_count": null,
"id": "349ccdff",
"metadata": {
"hide-output": false
},
"outputs": [],
"source": [
"Py3 = Q @ Q.T @ y\n",
"Py3"
]
},
{
"cell_type": "markdown",
"id": "c1339c92",
"metadata": {},
"source": [
"Again, we obtain the same answer."
]
}
],
"metadata": {
"date": 1705369587.1547778,
"filename": "orth_proj.md",
"kernelspec": {
"display_name": "Python",
"language": "python3",
"name": "python3"
},
"title": "Orthogonal Projections and Their Applications"
},
"nbformat": 4,
"nbformat_minor": 5
}