{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Tài liệu này mang giấy phép Creative Commons Attribution (CC BY).\n",
"(c) Nguyễn Ngọc Sáng, Zhukovsky 12/2018.\n",
"\n",
"[@SangVn](https://github.com/SangVn) [@VnCFD](https://vncfdgroup.wordpress.com/)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"*Thực hành CFD với Python!*\n",
"\n",
"# Thực hành CFD với Python !"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Ở [phần I](https://vncfdgroup.wordpress.com/2018/12/12/thuc-hanh-cfd-voi-python/), chúng ta đã tìm hiểu và thực hành phương pháp `sai phân hữu hạn`, sang phần II chúng ta sẽ sử dụng `phương pháp thể tích hữu hạn` để `tính toán động lực học lưu chất`.\n",
"\n",
"\n",
"\n",
"## Bài 11. Phương trình liên tục, phương pháp thể tích hữu hạn\n",
"\n",
"### 1. Phương trình liên tục ([tham khảo](https://vncfdgroup.wordpress.com/2012/02/24/ph%C6%B0%C6%A1ng-trinh-lien-t%E1%BB%A5c/))\n",
"\n",
"Hệ phương trình động lực học lưu chất mô tả ba định luật bảo toàn: bảo toàn khối lượng, bảo toàn động lượng và bảo toàn năng lượng. Định luật bảo toàn khối lượng được sử dụng như sau:\n",
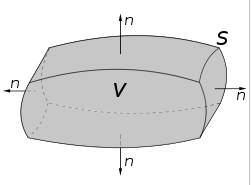
"Xét một `thể tích hữu hạn` V được bao quanh bởi `bề mặt kiểm soát` S, lưu chất có khối lượng riêng là $\\rho(x, y, z, t)$ và vận tốc $\\vec v(x, y, z, t)$. Sự `biến đổi khối lượng` lưu chất trong thể tích hữu hạn V được gây ra bởi hai yếu tố: \n",
"\n",
" \n",
"\n",
"* khối lượng riêng thay đổi theo thời gian, dẫn đến khối lượng thay đổi:\n",
"$$\\int_V\\frac{\\partial \\rho}{\\partial t}dV$$\n",
"\n",
"* dòng lưu chất đi vào ra qua bề mặt kiểm soát, tương ứng:\n",
"$$\\oint_S \\rho \\vec v d\\vec S $$ \n",
"\n",
"Mặt khác, theo định luật bảo toàn khối lượng, khối lượng lưu chất trong thể tích V không đổi hay ta có:\n",
"\n",
"$$\\int_V\\frac{\\partial \\rho}{\\partial t} dV + \\oint_S \\rho \\vec v d\\vec S = 0 \\qquad (1)$$\n",
"\n",
"Sử dụng định lý Gauss-Ostrogradsky (định lý phân kì) ta có:\n",
"\n",
"$$\\int_V\\frac{\\partial \\rho}{\\partial t} dV + \\int_V \\nabla (\\rho \\vec v) dV = 0$$\n",
"$$=> \\int_V\\left(\\frac{\\partial \\rho}{\\partial t} + \\nabla (\\rho \\vec v)\\right) dV = 0$$\n",
"Thu được `phương trình liên tục` dạng vector:\n",
"$$\\frac{\\partial \\rho}{\\partial t} + \\nabla (\\rho \\vec v) = 0 \\qquad (2)$$\n",
"hay là: $\\frac{\\partial \\rho}{\\partial t} + \\nabla \\vec F = 0 $ với $\\vec F=\\rho \\vec v$ - dòng (flux, thông lượng) khối lượng.\n",
"\n",
"Trường hợp dòng hai chiều, phương trình (2) có thể viết lại ở dạng:\n",
"$$\\frac{\\partial \\rho}{\\partial t} + \\frac{\\partial H}{\\partial x} + \\frac{\\partial G}{\\partial y} = 0; H=\\rho u, G=\\rho v \\qquad (3)$$\n",
"Hay là: \n",
"$$\\frac{\\partial \\rho}{\\partial t} + \\rho\\frac{\\partial u}{\\partial x} + u\\frac{\\partial \\rho}{\\partial x} + \\rho\\frac{\\partial v}{\\partial y} + v\\frac{\\partial \\rho}{\\partial y} = 0 \\qquad (4)$$\n",
"\n",
"Phương trình vi phân được viết ở dạng (2) hoặc (3) được gọi là `dạng phân kì (dạng bảo toàn)`, dạng (4) - `không phân kì`.\n",
"Ta có thể xây dựng rất nhiều `sơ đồ sai phân` cho phương trình liên tục, tuy nhiên không phải tất cả các sơ đồ thu được đều đảm bảo rằng định luật bảo toàn khối lượng được thỏa mãn. Nếu đảm bảo điều này thì sơ đồ sai phân được gọi là `có tính chất bảo toàn`. Khi sử dụng phương pháp `sai phân hữu hạn` để có được sơ đồ sai phân bảo toàn thường biến đổi phương trình vi phân dạng phân kì (3) thay vì dạng không phân kì (4).\n",
"\n",
"Tuy nhiên phương pháp `sai phân hữu hạn` sử dụng các biến đổi toán học đơn thuần cho `phương trình vi phân` (2), nghĩa là định luật bảo toàn chỉ sử dụng để thu được phương trình (2) mà không được áp dụng khi xây dựng sơ đồ sai phân, do đó tính bảo toàn của sơ đồ không được bảo đảm chắc chắn. Trái lại, phương pháp `thể tích hữu hạn` sử dụng định luật bảo toàn để xây dựng sơ đồ sai phân và thay vì biến đổi phương trình vi phân (2) ta biến đổi `phương trình dạng tích phân` (1). Phương trình (1) có thể thu được từ phương trình (2) bằng các biến đổi theo thứ tự ngược lại.\n",
"\n",
"### 2. Phương pháp thể tích hữu hạn\n",
"\n",
"**Lưới rời rạc**. \n",
"\n",
"Chia các `điểm lưới` dọc theo biên, sau đó chia vùng tính toán thành các `thể tích hữu hạn`, mỗi thể tích hữu hạn chứa một điểm lưới (hình trái - lưới trong tạo độ Đềcac, hình phải - trường hợp tổng quát):\n",
"\n",
"
\n",
"\n",
"* khối lượng riêng thay đổi theo thời gian, dẫn đến khối lượng thay đổi:\n",
"$$\\int_V\\frac{\\partial \\rho}{\\partial t}dV$$\n",
"\n",
"* dòng lưu chất đi vào ra qua bề mặt kiểm soát, tương ứng:\n",
"$$\\oint_S \\rho \\vec v d\\vec S $$ \n",
"\n",
"Mặt khác, theo định luật bảo toàn khối lượng, khối lượng lưu chất trong thể tích V không đổi hay ta có:\n",
"\n",
"$$\\int_V\\frac{\\partial \\rho}{\\partial t} dV + \\oint_S \\rho \\vec v d\\vec S = 0 \\qquad (1)$$\n",
"\n",
"Sử dụng định lý Gauss-Ostrogradsky (định lý phân kì) ta có:\n",
"\n",
"$$\\int_V\\frac{\\partial \\rho}{\\partial t} dV + \\int_V \\nabla (\\rho \\vec v) dV = 0$$\n",
"$$=> \\int_V\\left(\\frac{\\partial \\rho}{\\partial t} + \\nabla (\\rho \\vec v)\\right) dV = 0$$\n",
"Thu được `phương trình liên tục` dạng vector:\n",
"$$\\frac{\\partial \\rho}{\\partial t} + \\nabla (\\rho \\vec v) = 0 \\qquad (2)$$\n",
"hay là: $\\frac{\\partial \\rho}{\\partial t} + \\nabla \\vec F = 0 $ với $\\vec F=\\rho \\vec v$ - dòng (flux, thông lượng) khối lượng.\n",
"\n",
"Trường hợp dòng hai chiều, phương trình (2) có thể viết lại ở dạng:\n",
"$$\\frac{\\partial \\rho}{\\partial t} + \\frac{\\partial H}{\\partial x} + \\frac{\\partial G}{\\partial y} = 0; H=\\rho u, G=\\rho v \\qquad (3)$$\n",
"Hay là: \n",
"$$\\frac{\\partial \\rho}{\\partial t} + \\rho\\frac{\\partial u}{\\partial x} + u\\frac{\\partial \\rho}{\\partial x} + \\rho\\frac{\\partial v}{\\partial y} + v\\frac{\\partial \\rho}{\\partial y} = 0 \\qquad (4)$$\n",
"\n",
"Phương trình vi phân được viết ở dạng (2) hoặc (3) được gọi là `dạng phân kì (dạng bảo toàn)`, dạng (4) - `không phân kì`.\n",
"Ta có thể xây dựng rất nhiều `sơ đồ sai phân` cho phương trình liên tục, tuy nhiên không phải tất cả các sơ đồ thu được đều đảm bảo rằng định luật bảo toàn khối lượng được thỏa mãn. Nếu đảm bảo điều này thì sơ đồ sai phân được gọi là `có tính chất bảo toàn`. Khi sử dụng phương pháp `sai phân hữu hạn` để có được sơ đồ sai phân bảo toàn thường biến đổi phương trình vi phân dạng phân kì (3) thay vì dạng không phân kì (4).\n",
"\n",
"Tuy nhiên phương pháp `sai phân hữu hạn` sử dụng các biến đổi toán học đơn thuần cho `phương trình vi phân` (2), nghĩa là định luật bảo toàn chỉ sử dụng để thu được phương trình (2) mà không được áp dụng khi xây dựng sơ đồ sai phân, do đó tính bảo toàn của sơ đồ không được bảo đảm chắc chắn. Trái lại, phương pháp `thể tích hữu hạn` sử dụng định luật bảo toàn để xây dựng sơ đồ sai phân và thay vì biến đổi phương trình vi phân (2) ta biến đổi `phương trình dạng tích phân` (1). Phương trình (1) có thể thu được từ phương trình (2) bằng các biến đổi theo thứ tự ngược lại.\n",
"\n",
"### 2. Phương pháp thể tích hữu hạn\n",
"\n",
"**Lưới rời rạc**. \n",
"\n",
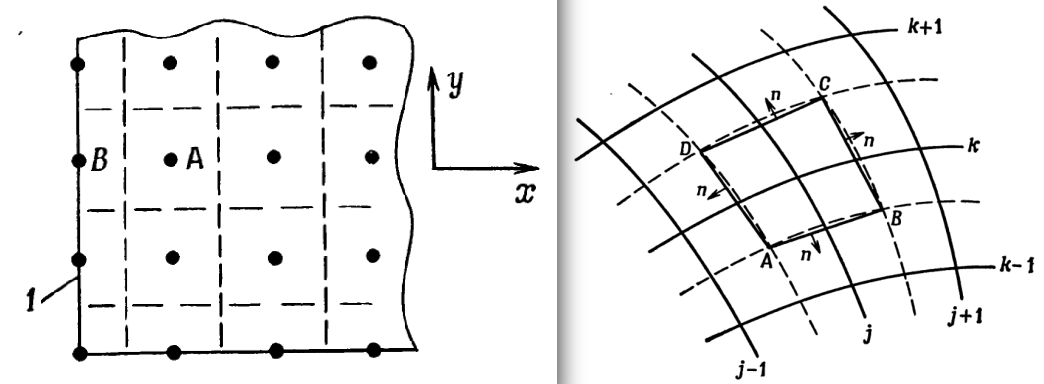
"Chia các `điểm lưới` dọc theo biên, sau đó chia vùng tính toán thành các `thể tích hữu hạn`, mỗi thể tích hữu hạn chứa một điểm lưới (hình trái - lưới trong tạo độ Đềcac, hình phải - trường hợp tổng quát):\n",
"\n",
" \n",
"\n",
"Trong trường hợp lưới đều, điểm lưới là tâm thể tích hữu hạn. Chỉ số tại các bề mặt của thể tích hữu hạn tương ứng là $i-1/2, i+1/2, j-1/2, j+1/2$\n",
"\n",
"**Sơ đồ sai phân**\n",
"\n",
"Xét thể tích hữu hạn ABCD (hình phải) không nằm trên biên, lấy tích phân phương trình (3):\n",
"\n",
"$$\\int_{ABCD} \\left(\\frac{\\partial \\rho}{\\partial t} + \\frac{\\partial H}{\\partial x} + \\frac{\\partial G}{\\partial y} \\right)dxdy = 0$$\n",
"\n",
"áp dụng định lý Green ta thu được phương trình dạng tích phân (1)\n",
"$$\\frac{d}{dt}\\int \\rho dV + \\oint_{ABCD} \\vec F. \\vec n ds = 0 \\qquad (5)$$\n",
"với $\\vec F = (H, G)$. Trong tọa độ Đềcac ta có:\n",
"$$\\vec F. \\vec n ds = Hdy - Gdx$$\n",
"\n",
"Một dạng xấp xỉ phương trình (5) đó là:\n",
"$$\\frac {d}{dt} (V_{i,j}\\rho_{i,j}) + \\sum_{AB}^{DA}(F \\Delta y - G \\Delta x) = 0 \\qquad (6) $$\n",
"hay là:\n",
"\n",
"$$\\frac {d}{dt} (V_{i,j}\\rho_{i,j}) + F_{AB}\\Delta y_{AB} - G_{AB} \\Delta x_{AB} + \n",
"F_{BC}\\Delta y_{BC} - G_{BC}\\Delta x_{BC} + F_{CD}\\Delta y_{CD} - G_{CD}\\Delta x_{CD} +\n",
"F_{DA}\\Delta y_{DA} - G_{DA}\\Delta x_{DA} = 0 \\qquad (7) $$\n",
"\n",
"với $V_{i,j}$ - diện tích hình ABCD, $\\rho_{i,j}$ - khối lượng riêng `trung bình` trong tứ giác. Trong phương trình (7)\n",
"$$\\Delta y_{AB} = y_B - y_A, \\Delta x_{AB} = x_B - x_A$$\n",
"giá trị dòng khối lượng trên biên có thể lấy xấp xỉ bằng:\n",
"$$H_{AB} = 0.5(H_{i, j-1} + H_{i, j}), G_{AB} = 0.5(G_{i, j-1} + G_{i, j}) \\qquad (8)$$\n",
"tương tự cho các giá trị còn lại.\n",
"\n",
"\n",
"Trường hợp lưới vuông đơn giản như trên hình bên trái, phương trình (7) có dạng:\n",
"\n",
"$$\\Delta x\\Delta y \\frac{d\\rho_{i,j}}{dt} - G_{i, j-1/2}\\Delta x + H_{i+1/2,j}\\Delta y - G_{i, j+1/2}(-\\Delta x) + H_{i-1/2, j}(-\\Delta y) = 0$$\n",
"Sử dụng xấp xỉ (8) ta có:\n",
"$$\\frac{d\\rho_{i,j}}{dt} + \\frac{H_{i+i, j} - H_{i-1, j}}{2\\Delta x} +\\frac{G_{i, j+1} - G_{i, j-1}}{2\\Delta y} = 0 \\qquad (9)$$\n",
"\n",
"Sơ đồ sai phân (9) cũng chính là sơ đồ sai phân trung tâm khi sử dụng phương pháp sai phân hữu hạn cho phương trình (3).\n",
"\n",
"Nếu áp dụng định luật bảo toàn cho `thể tích hữu hạn` kề biên chúng ta sẽ thu được điều kiện biên cho sơ đồ sai phân."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Bài 11 chúng ta tập trung làm rõ khái niệm `phương pháp thể tích hữu hạn`, so sánh với `phương pháp sai phân hữu hạn`. Sang bài 12 chúng ta sẽ thực hành với python để hiểu rõ hơn vấn đề.\n",
"\n",
"### Bài 12. [Sơ đồ Godunov, bài toán Riemann](Bai_12.ipynb)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.15rc1"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
\n",
"\n",
"Trong trường hợp lưới đều, điểm lưới là tâm thể tích hữu hạn. Chỉ số tại các bề mặt của thể tích hữu hạn tương ứng là $i-1/2, i+1/2, j-1/2, j+1/2$\n",
"\n",
"**Sơ đồ sai phân**\n",
"\n",
"Xét thể tích hữu hạn ABCD (hình phải) không nằm trên biên, lấy tích phân phương trình (3):\n",
"\n",
"$$\\int_{ABCD} \\left(\\frac{\\partial \\rho}{\\partial t} + \\frac{\\partial H}{\\partial x} + \\frac{\\partial G}{\\partial y} \\right)dxdy = 0$$\n",
"\n",
"áp dụng định lý Green ta thu được phương trình dạng tích phân (1)\n",
"$$\\frac{d}{dt}\\int \\rho dV + \\oint_{ABCD} \\vec F. \\vec n ds = 0 \\qquad (5)$$\n",
"với $\\vec F = (H, G)$. Trong tọa độ Đềcac ta có:\n",
"$$\\vec F. \\vec n ds = Hdy - Gdx$$\n",
"\n",
"Một dạng xấp xỉ phương trình (5) đó là:\n",
"$$\\frac {d}{dt} (V_{i,j}\\rho_{i,j}) + \\sum_{AB}^{DA}(F \\Delta y - G \\Delta x) = 0 \\qquad (6) $$\n",
"hay là:\n",
"\n",
"$$\\frac {d}{dt} (V_{i,j}\\rho_{i,j}) + F_{AB}\\Delta y_{AB} - G_{AB} \\Delta x_{AB} + \n",
"F_{BC}\\Delta y_{BC} - G_{BC}\\Delta x_{BC} + F_{CD}\\Delta y_{CD} - G_{CD}\\Delta x_{CD} +\n",
"F_{DA}\\Delta y_{DA} - G_{DA}\\Delta x_{DA} = 0 \\qquad (7) $$\n",
"\n",
"với $V_{i,j}$ - diện tích hình ABCD, $\\rho_{i,j}$ - khối lượng riêng `trung bình` trong tứ giác. Trong phương trình (7)\n",
"$$\\Delta y_{AB} = y_B - y_A, \\Delta x_{AB} = x_B - x_A$$\n",
"giá trị dòng khối lượng trên biên có thể lấy xấp xỉ bằng:\n",
"$$H_{AB} = 0.5(H_{i, j-1} + H_{i, j}), G_{AB} = 0.5(G_{i, j-1} + G_{i, j}) \\qquad (8)$$\n",
"tương tự cho các giá trị còn lại.\n",
"\n",
"\n",
"Trường hợp lưới vuông đơn giản như trên hình bên trái, phương trình (7) có dạng:\n",
"\n",
"$$\\Delta x\\Delta y \\frac{d\\rho_{i,j}}{dt} - G_{i, j-1/2}\\Delta x + H_{i+1/2,j}\\Delta y - G_{i, j+1/2}(-\\Delta x) + H_{i-1/2, j}(-\\Delta y) = 0$$\n",
"Sử dụng xấp xỉ (8) ta có:\n",
"$$\\frac{d\\rho_{i,j}}{dt} + \\frac{H_{i+i, j} - H_{i-1, j}}{2\\Delta x} +\\frac{G_{i, j+1} - G_{i, j-1}}{2\\Delta y} = 0 \\qquad (9)$$\n",
"\n",
"Sơ đồ sai phân (9) cũng chính là sơ đồ sai phân trung tâm khi sử dụng phương pháp sai phân hữu hạn cho phương trình (3).\n",
"\n",
"Nếu áp dụng định luật bảo toàn cho `thể tích hữu hạn` kề biên chúng ta sẽ thu được điều kiện biên cho sơ đồ sai phân."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Bài 11 chúng ta tập trung làm rõ khái niệm `phương pháp thể tích hữu hạn`, so sánh với `phương pháp sai phân hữu hạn`. Sang bài 12 chúng ta sẽ thực hành với python để hiểu rõ hơn vấn đề.\n",
"\n",
"### Bài 12. [Sơ đồ Godunov, bài toán Riemann](Bai_12.ipynb)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.15rc1"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
 \n",
"\n",
"* khối lượng riêng thay đổi theo thời gian, dẫn đến khối lượng thay đổi:\n",
"$$\\int_V\\frac{\\partial \\rho}{\\partial t}dV$$\n",
"\n",
"* dòng lưu chất đi vào ra qua bề mặt kiểm soát, tương ứng:\n",
"$$\\oint_S \\rho \\vec v d\\vec S $$ \n",
"\n",
"Mặt khác, theo định luật bảo toàn khối lượng, khối lượng lưu chất trong thể tích V không đổi hay ta có:\n",
"\n",
"$$\\int_V\\frac{\\partial \\rho}{\\partial t} dV + \\oint_S \\rho \\vec v d\\vec S = 0 \\qquad (1)$$\n",
"\n",
"Sử dụng định lý Gauss-Ostrogradsky (định lý phân kì) ta có:\n",
"\n",
"$$\\int_V\\frac{\\partial \\rho}{\\partial t} dV + \\int_V \\nabla (\\rho \\vec v) dV = 0$$\n",
"$$=> \\int_V\\left(\\frac{\\partial \\rho}{\\partial t} + \\nabla (\\rho \\vec v)\\right) dV = 0$$\n",
"Thu được `phương trình liên tục` dạng vector:\n",
"$$\\frac{\\partial \\rho}{\\partial t} + \\nabla (\\rho \\vec v) = 0 \\qquad (2)$$\n",
"hay là: $\\frac{\\partial \\rho}{\\partial t} + \\nabla \\vec F = 0 $ với $\\vec F=\\rho \\vec v$ - dòng (flux, thông lượng) khối lượng.\n",
"\n",
"Trường hợp dòng hai chiều, phương trình (2) có thể viết lại ở dạng:\n",
"$$\\frac{\\partial \\rho}{\\partial t} + \\frac{\\partial H}{\\partial x} + \\frac{\\partial G}{\\partial y} = 0; H=\\rho u, G=\\rho v \\qquad (3)$$\n",
"Hay là: \n",
"$$\\frac{\\partial \\rho}{\\partial t} + \\rho\\frac{\\partial u}{\\partial x} + u\\frac{\\partial \\rho}{\\partial x} + \\rho\\frac{\\partial v}{\\partial y} + v\\frac{\\partial \\rho}{\\partial y} = 0 \\qquad (4)$$\n",
"\n",
"Phương trình vi phân được viết ở dạng (2) hoặc (3) được gọi là `dạng phân kì (dạng bảo toàn)`, dạng (4) - `không phân kì`.\n",
"Ta có thể xây dựng rất nhiều `sơ đồ sai phân` cho phương trình liên tục, tuy nhiên không phải tất cả các sơ đồ thu được đều đảm bảo rằng định luật bảo toàn khối lượng được thỏa mãn. Nếu đảm bảo điều này thì sơ đồ sai phân được gọi là `có tính chất bảo toàn`. Khi sử dụng phương pháp `sai phân hữu hạn` để có được sơ đồ sai phân bảo toàn thường biến đổi phương trình vi phân dạng phân kì (3) thay vì dạng không phân kì (4).\n",
"\n",
"Tuy nhiên phương pháp `sai phân hữu hạn` sử dụng các biến đổi toán học đơn thuần cho `phương trình vi phân` (2), nghĩa là định luật bảo toàn chỉ sử dụng để thu được phương trình (2) mà không được áp dụng khi xây dựng sơ đồ sai phân, do đó tính bảo toàn của sơ đồ không được bảo đảm chắc chắn. Trái lại, phương pháp `thể tích hữu hạn` sử dụng định luật bảo toàn để xây dựng sơ đồ sai phân và thay vì biến đổi phương trình vi phân (2) ta biến đổi `phương trình dạng tích phân` (1). Phương trình (1) có thể thu được từ phương trình (2) bằng các biến đổi theo thứ tự ngược lại.\n",
"\n",
"### 2. Phương pháp thể tích hữu hạn\n",
"\n",
"**Lưới rời rạc**. \n",
"\n",
"Chia các `điểm lưới` dọc theo biên, sau đó chia vùng tính toán thành các `thể tích hữu hạn`, mỗi thể tích hữu hạn chứa một điểm lưới (hình trái - lưới trong tạo độ Đềcac, hình phải - trường hợp tổng quát):\n",
"\n",
"
\n",
"\n",
"* khối lượng riêng thay đổi theo thời gian, dẫn đến khối lượng thay đổi:\n",
"$$\\int_V\\frac{\\partial \\rho}{\\partial t}dV$$\n",
"\n",
"* dòng lưu chất đi vào ra qua bề mặt kiểm soát, tương ứng:\n",
"$$\\oint_S \\rho \\vec v d\\vec S $$ \n",
"\n",
"Mặt khác, theo định luật bảo toàn khối lượng, khối lượng lưu chất trong thể tích V không đổi hay ta có:\n",
"\n",
"$$\\int_V\\frac{\\partial \\rho}{\\partial t} dV + \\oint_S \\rho \\vec v d\\vec S = 0 \\qquad (1)$$\n",
"\n",
"Sử dụng định lý Gauss-Ostrogradsky (định lý phân kì) ta có:\n",
"\n",
"$$\\int_V\\frac{\\partial \\rho}{\\partial t} dV + \\int_V \\nabla (\\rho \\vec v) dV = 0$$\n",
"$$=> \\int_V\\left(\\frac{\\partial \\rho}{\\partial t} + \\nabla (\\rho \\vec v)\\right) dV = 0$$\n",
"Thu được `phương trình liên tục` dạng vector:\n",
"$$\\frac{\\partial \\rho}{\\partial t} + \\nabla (\\rho \\vec v) = 0 \\qquad (2)$$\n",
"hay là: $\\frac{\\partial \\rho}{\\partial t} + \\nabla \\vec F = 0 $ với $\\vec F=\\rho \\vec v$ - dòng (flux, thông lượng) khối lượng.\n",
"\n",
"Trường hợp dòng hai chiều, phương trình (2) có thể viết lại ở dạng:\n",
"$$\\frac{\\partial \\rho}{\\partial t} + \\frac{\\partial H}{\\partial x} + \\frac{\\partial G}{\\partial y} = 0; H=\\rho u, G=\\rho v \\qquad (3)$$\n",
"Hay là: \n",
"$$\\frac{\\partial \\rho}{\\partial t} + \\rho\\frac{\\partial u}{\\partial x} + u\\frac{\\partial \\rho}{\\partial x} + \\rho\\frac{\\partial v}{\\partial y} + v\\frac{\\partial \\rho}{\\partial y} = 0 \\qquad (4)$$\n",
"\n",
"Phương trình vi phân được viết ở dạng (2) hoặc (3) được gọi là `dạng phân kì (dạng bảo toàn)`, dạng (4) - `không phân kì`.\n",
"Ta có thể xây dựng rất nhiều `sơ đồ sai phân` cho phương trình liên tục, tuy nhiên không phải tất cả các sơ đồ thu được đều đảm bảo rằng định luật bảo toàn khối lượng được thỏa mãn. Nếu đảm bảo điều này thì sơ đồ sai phân được gọi là `có tính chất bảo toàn`. Khi sử dụng phương pháp `sai phân hữu hạn` để có được sơ đồ sai phân bảo toàn thường biến đổi phương trình vi phân dạng phân kì (3) thay vì dạng không phân kì (4).\n",
"\n",
"Tuy nhiên phương pháp `sai phân hữu hạn` sử dụng các biến đổi toán học đơn thuần cho `phương trình vi phân` (2), nghĩa là định luật bảo toàn chỉ sử dụng để thu được phương trình (2) mà không được áp dụng khi xây dựng sơ đồ sai phân, do đó tính bảo toàn của sơ đồ không được bảo đảm chắc chắn. Trái lại, phương pháp `thể tích hữu hạn` sử dụng định luật bảo toàn để xây dựng sơ đồ sai phân và thay vì biến đổi phương trình vi phân (2) ta biến đổi `phương trình dạng tích phân` (1). Phương trình (1) có thể thu được từ phương trình (2) bằng các biến đổi theo thứ tự ngược lại.\n",
"\n",
"### 2. Phương pháp thể tích hữu hạn\n",
"\n",
"**Lưới rời rạc**. \n",
"\n",
"Chia các `điểm lưới` dọc theo biên, sau đó chia vùng tính toán thành các `thể tích hữu hạn`, mỗi thể tích hữu hạn chứa một điểm lưới (hình trái - lưới trong tạo độ Đềcac, hình phải - trường hợp tổng quát):\n",
"\n",
" \n",
"\n",
"Trong trường hợp lưới đều, điểm lưới là tâm thể tích hữu hạn. Chỉ số tại các bề mặt của thể tích hữu hạn tương ứng là $i-1/2, i+1/2, j-1/2, j+1/2$\n",
"\n",
"**Sơ đồ sai phân**\n",
"\n",
"Xét thể tích hữu hạn ABCD (hình phải) không nằm trên biên, lấy tích phân phương trình (3):\n",
"\n",
"$$\\int_{ABCD} \\left(\\frac{\\partial \\rho}{\\partial t} + \\frac{\\partial H}{\\partial x} + \\frac{\\partial G}{\\partial y} \\right)dxdy = 0$$\n",
"\n",
"áp dụng định lý Green ta thu được phương trình dạng tích phân (1)\n",
"$$\\frac{d}{dt}\\int \\rho dV + \\oint_{ABCD} \\vec F. \\vec n ds = 0 \\qquad (5)$$\n",
"với $\\vec F = (H, G)$. Trong tọa độ Đềcac ta có:\n",
"$$\\vec F. \\vec n ds = Hdy - Gdx$$\n",
"\n",
"Một dạng xấp xỉ phương trình (5) đó là:\n",
"$$\\frac {d}{dt} (V_{i,j}\\rho_{i,j}) + \\sum_{AB}^{DA}(F \\Delta y - G \\Delta x) = 0 \\qquad (6) $$\n",
"hay là:\n",
"\n",
"$$\\frac {d}{dt} (V_{i,j}\\rho_{i,j}) + F_{AB}\\Delta y_{AB} - G_{AB} \\Delta x_{AB} + \n",
"F_{BC}\\Delta y_{BC} - G_{BC}\\Delta x_{BC} + F_{CD}\\Delta y_{CD} - G_{CD}\\Delta x_{CD} +\n",
"F_{DA}\\Delta y_{DA} - G_{DA}\\Delta x_{DA} = 0 \\qquad (7) $$\n",
"\n",
"với $V_{i,j}$ - diện tích hình ABCD, $\\rho_{i,j}$ - khối lượng riêng `trung bình` trong tứ giác. Trong phương trình (7)\n",
"$$\\Delta y_{AB} = y_B - y_A, \\Delta x_{AB} = x_B - x_A$$\n",
"giá trị dòng khối lượng trên biên có thể lấy xấp xỉ bằng:\n",
"$$H_{AB} = 0.5(H_{i, j-1} + H_{i, j}), G_{AB} = 0.5(G_{i, j-1} + G_{i, j}) \\qquad (8)$$\n",
"tương tự cho các giá trị còn lại.\n",
"\n",
"\n",
"Trường hợp lưới vuông đơn giản như trên hình bên trái, phương trình (7) có dạng:\n",
"\n",
"$$\\Delta x\\Delta y \\frac{d\\rho_{i,j}}{dt} - G_{i, j-1/2}\\Delta x + H_{i+1/2,j}\\Delta y - G_{i, j+1/2}(-\\Delta x) + H_{i-1/2, j}(-\\Delta y) = 0$$\n",
"Sử dụng xấp xỉ (8) ta có:\n",
"$$\\frac{d\\rho_{i,j}}{dt} + \\frac{H_{i+i, j} - H_{i-1, j}}{2\\Delta x} +\\frac{G_{i, j+1} - G_{i, j-1}}{2\\Delta y} = 0 \\qquad (9)$$\n",
"\n",
"Sơ đồ sai phân (9) cũng chính là sơ đồ sai phân trung tâm khi sử dụng phương pháp sai phân hữu hạn cho phương trình (3).\n",
"\n",
"Nếu áp dụng định luật bảo toàn cho `thể tích hữu hạn` kề biên chúng ta sẽ thu được điều kiện biên cho sơ đồ sai phân."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Bài 11 chúng ta tập trung làm rõ khái niệm `phương pháp thể tích hữu hạn`, so sánh với `phương pháp sai phân hữu hạn`. Sang bài 12 chúng ta sẽ thực hành với python để hiểu rõ hơn vấn đề.\n",
"\n",
"### Bài 12. [Sơ đồ Godunov, bài toán Riemann](Bai_12.ipynb)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.15rc1"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
\n",
"\n",
"Trong trường hợp lưới đều, điểm lưới là tâm thể tích hữu hạn. Chỉ số tại các bề mặt của thể tích hữu hạn tương ứng là $i-1/2, i+1/2, j-1/2, j+1/2$\n",
"\n",
"**Sơ đồ sai phân**\n",
"\n",
"Xét thể tích hữu hạn ABCD (hình phải) không nằm trên biên, lấy tích phân phương trình (3):\n",
"\n",
"$$\\int_{ABCD} \\left(\\frac{\\partial \\rho}{\\partial t} + \\frac{\\partial H}{\\partial x} + \\frac{\\partial G}{\\partial y} \\right)dxdy = 0$$\n",
"\n",
"áp dụng định lý Green ta thu được phương trình dạng tích phân (1)\n",
"$$\\frac{d}{dt}\\int \\rho dV + \\oint_{ABCD} \\vec F. \\vec n ds = 0 \\qquad (5)$$\n",
"với $\\vec F = (H, G)$. Trong tọa độ Đềcac ta có:\n",
"$$\\vec F. \\vec n ds = Hdy - Gdx$$\n",
"\n",
"Một dạng xấp xỉ phương trình (5) đó là:\n",
"$$\\frac {d}{dt} (V_{i,j}\\rho_{i,j}) + \\sum_{AB}^{DA}(F \\Delta y - G \\Delta x) = 0 \\qquad (6) $$\n",
"hay là:\n",
"\n",
"$$\\frac {d}{dt} (V_{i,j}\\rho_{i,j}) + F_{AB}\\Delta y_{AB} - G_{AB} \\Delta x_{AB} + \n",
"F_{BC}\\Delta y_{BC} - G_{BC}\\Delta x_{BC} + F_{CD}\\Delta y_{CD} - G_{CD}\\Delta x_{CD} +\n",
"F_{DA}\\Delta y_{DA} - G_{DA}\\Delta x_{DA} = 0 \\qquad (7) $$\n",
"\n",
"với $V_{i,j}$ - diện tích hình ABCD, $\\rho_{i,j}$ - khối lượng riêng `trung bình` trong tứ giác. Trong phương trình (7)\n",
"$$\\Delta y_{AB} = y_B - y_A, \\Delta x_{AB} = x_B - x_A$$\n",
"giá trị dòng khối lượng trên biên có thể lấy xấp xỉ bằng:\n",
"$$H_{AB} = 0.5(H_{i, j-1} + H_{i, j}), G_{AB} = 0.5(G_{i, j-1} + G_{i, j}) \\qquad (8)$$\n",
"tương tự cho các giá trị còn lại.\n",
"\n",
"\n",
"Trường hợp lưới vuông đơn giản như trên hình bên trái, phương trình (7) có dạng:\n",
"\n",
"$$\\Delta x\\Delta y \\frac{d\\rho_{i,j}}{dt} - G_{i, j-1/2}\\Delta x + H_{i+1/2,j}\\Delta y - G_{i, j+1/2}(-\\Delta x) + H_{i-1/2, j}(-\\Delta y) = 0$$\n",
"Sử dụng xấp xỉ (8) ta có:\n",
"$$\\frac{d\\rho_{i,j}}{dt} + \\frac{H_{i+i, j} - H_{i-1, j}}{2\\Delta x} +\\frac{G_{i, j+1} - G_{i, j-1}}{2\\Delta y} = 0 \\qquad (9)$$\n",
"\n",
"Sơ đồ sai phân (9) cũng chính là sơ đồ sai phân trung tâm khi sử dụng phương pháp sai phân hữu hạn cho phương trình (3).\n",
"\n",
"Nếu áp dụng định luật bảo toàn cho `thể tích hữu hạn` kề biên chúng ta sẽ thu được điều kiện biên cho sơ đồ sai phân."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Bài 11 chúng ta tập trung làm rõ khái niệm `phương pháp thể tích hữu hạn`, so sánh với `phương pháp sai phân hữu hạn`. Sang bài 12 chúng ta sẽ thực hành với python để hiểu rõ hơn vấn đề.\n",
"\n",
"### Bài 12. [Sơ đồ Godunov, bài toán Riemann](Bai_12.ipynb)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.15rc1"
}
},
"nbformat": 4,
"nbformat_minor": 2
}