{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### 网络科学理论\n",
"***\n",
"***\n",
"# 网络科学简介\n",
"***\n",
"***\n",
"\n",
"王成军 \n",
"\n",
"wangchengjun@nju.edu.cn\n",
"\n",
"计算传播网 http://computational-communication.com"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# FROM SADDAM HUSSEIN TO NETWORK THEORY \n",
"### A SIMPLE STORY (1) The fate of Saddam and network science\n",
"\n",
"- Invasion that started in March 19, 2003. Many of the regime's high ranking officials, including Saddam Hussein, avoided capture. \n",
"- Hussein was last spotted kissing a baby in Baghdad in April 2003, and then his trace went cold. \n",
"\n",
"- Designed a deck of cards, each card engraved with the images of the 55 most wanted. \n",
" - It worked: by May 1, 2003, 15 men on the cards were captured, and by the end of the month another 12 were under custody. \n",
" - Yet, the ace of spades, i.e. Hussein himself, remained at large.\n",
"\n",
"\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
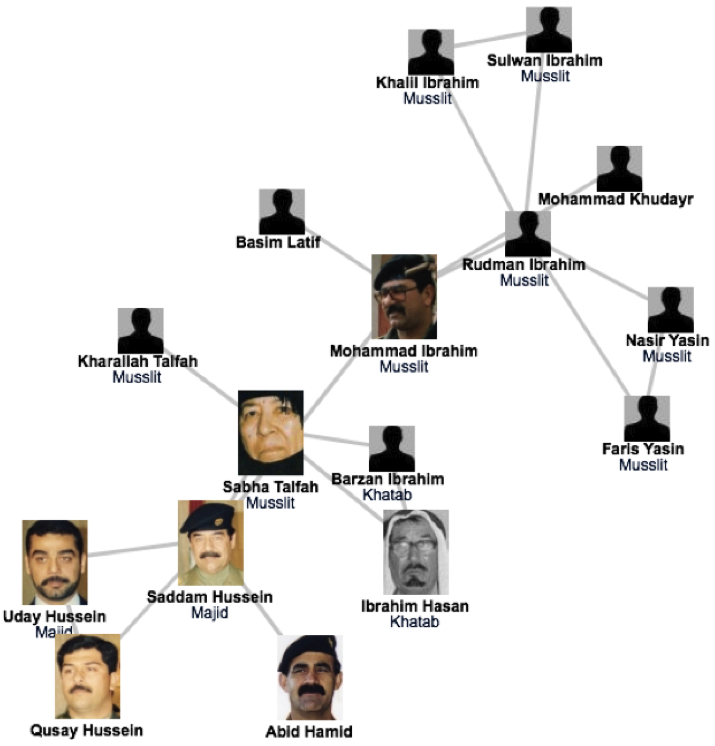
"# The capture of Saddam Hussein\n",
"\n",
"- shows the strong predictive power of networks. \n",
"\n",
"- underlies the need to obtain accurate maps of the networks we aim to study; and the often heroic difficulties we encounter during the mapping process.\n",
"\n",
"- demonstrates the remarkable stability of these networks: The capture of Hussein was not based on fresh intelligence, but rather on his pre-invasion social links, unearthed from old photos stacked in his family album.\n",
"\n",
"- shows that the choice of network we focus on makes a huge difference: the hierarchical tree, that captured the official organization of the Iraqi government, was of no use when it came to Saddam Hussein's whereabouts. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# A SIMPLE STORY (2): August 15, 2003 blackout.\n",
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# The capture of Saddam Hussein\n",
"\n",
"- shows the strong predictive power of networks. \n",
"\n",
"- underlies the need to obtain accurate maps of the networks we aim to study; and the often heroic difficulties we encounter during the mapping process.\n",
"\n",
"- demonstrates the remarkable stability of these networks: The capture of Hussein was not based on fresh intelligence, but rather on his pre-invasion social links, unearthed from old photos stacked in his family album.\n",
"\n",
"- shows that the choice of network we focus on makes a huge difference: the hierarchical tree, that captured the official organization of the Iraqi government, was of no use when it came to Saddam Hussein's whereabouts. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# A SIMPLE STORY (2): August 15, 2003 blackout.\n",
"\n",
"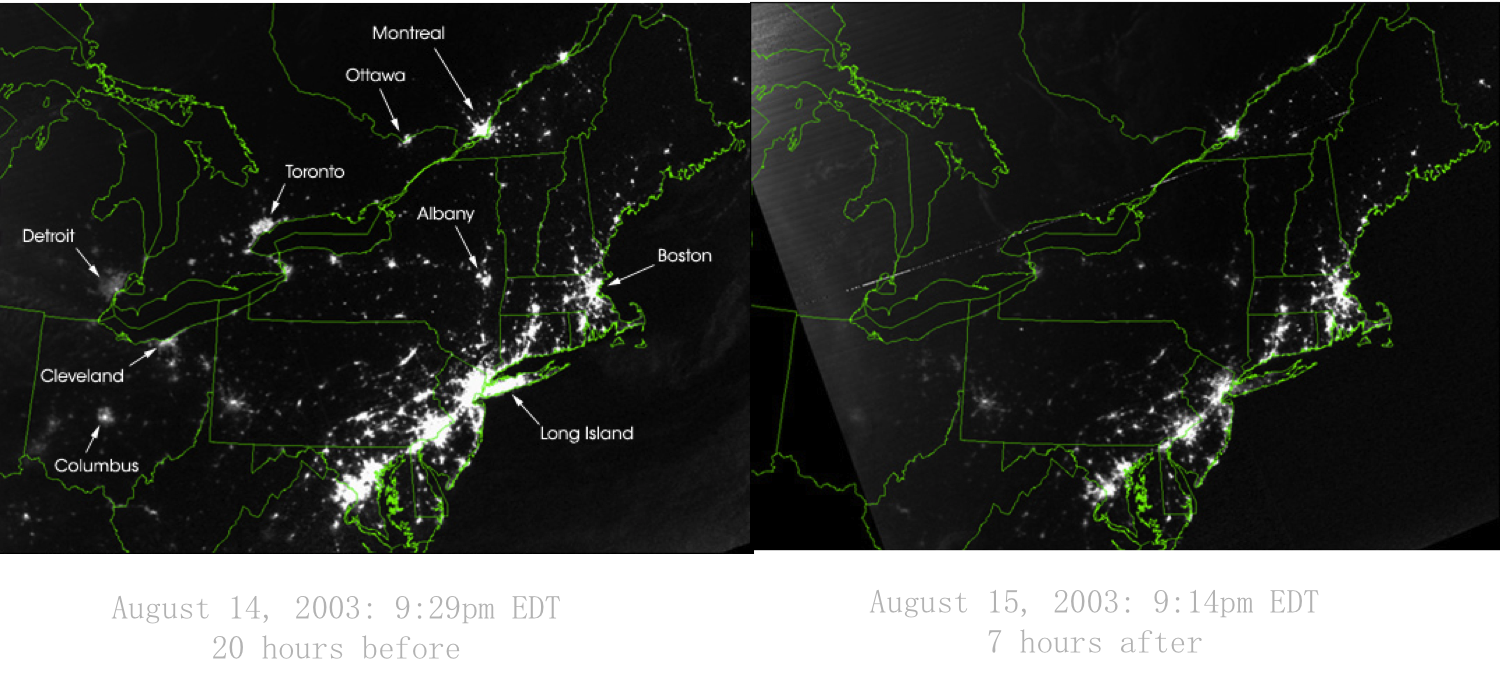 \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# VULNERABILITY \n",
"DUE TO INTERCONNECTIVITY \n",
"\n",
"- The 2003 blackout is a typical example of a cascading failure. \n",
"- 1997, when the International Monetary Fund pressured the central banks of several Pacific nations to limit their credit. \n",
"- 2009-2011 financial melt-down"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"An important theme of this class: \n",
"\n",
"- we must understand **how network structure affects the robustness of a complex system**. \n",
"\n",
"- develop quantitative tools to assess the interplay between network structure and the dynamical processes on the networks, and their impact on failures. \n",
"\n",
"- We will learn that failures reality failures follow reproducible laws, that can be quantified and even predicted using the tools of network science.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"NETWORKS AT THE HEART OF \n",
"# COMPLEX SYSTEMS \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Complex\n",
"\n",
"[adj., v. kuh m-pleks, kom-pleks; n. kom-pleks] \n",
"–adjective \n",
"- composed of many interconnected parts; compound; composite: a complex highway system. \n",
"- characterized by a very complicated or involved arrangement of parts, units, etc.: complex machinery. \n",
"- so complicated or intricate as to be hard to understand or deal with: a complex problem. \n",
"\t\t\t\tSource: Dictionary.com\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"\n",
"# Complexity\n",
"\n",
"a scientific theory which asserts that some systems display behavioral phenomena that are completely inexplicable by any conventional analysis of the systems’ constituent parts. These phenomena, commonly referred to as emergent behaviour, seem to occur in many complex systems involving living organisms, such as a stock market or the human brain.\n",
" \n",
"Source: John L. Casti, Encyclopædia Britannica\n",
" \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# COMPLEX SYSTEMS\n",
"\n",
"- society\n",
"- brain\n",
"- market\n",
"- cell\n",
"\n",
"## Stephen Hawking: I think the next century will be the century of complexity. "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Behind each complex system there is a network, that defines the interactions between the component. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"
\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# VULNERABILITY \n",
"DUE TO INTERCONNECTIVITY \n",
"\n",
"- The 2003 blackout is a typical example of a cascading failure. \n",
"- 1997, when the International Monetary Fund pressured the central banks of several Pacific nations to limit their credit. \n",
"- 2009-2011 financial melt-down"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"An important theme of this class: \n",
"\n",
"- we must understand **how network structure affects the robustness of a complex system**. \n",
"\n",
"- develop quantitative tools to assess the interplay between network structure and the dynamical processes on the networks, and their impact on failures. \n",
"\n",
"- We will learn that failures reality failures follow reproducible laws, that can be quantified and even predicted using the tools of network science.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"NETWORKS AT THE HEART OF \n",
"# COMPLEX SYSTEMS \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Complex\n",
"\n",
"[adj., v. kuh m-pleks, kom-pleks; n. kom-pleks] \n",
"–adjective \n",
"- composed of many interconnected parts; compound; composite: a complex highway system. \n",
"- characterized by a very complicated or involved arrangement of parts, units, etc.: complex machinery. \n",
"- so complicated or intricate as to be hard to understand or deal with: a complex problem. \n",
"\t\t\t\tSource: Dictionary.com\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"\n",
"# Complexity\n",
"\n",
"a scientific theory which asserts that some systems display behavioral phenomena that are completely inexplicable by any conventional analysis of the systems’ constituent parts. These phenomena, commonly referred to as emergent behaviour, seem to occur in many complex systems involving living organisms, such as a stock market or the human brain.\n",
" \n",
"Source: John L. Casti, Encyclopædia Britannica\n",
" \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# COMPLEX SYSTEMS\n",
"\n",
"- society\n",
"- brain\n",
"- market\n",
"- cell\n",
"\n",
"## Stephen Hawking: I think the next century will be the century of complexity. "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Behind each complex system there is a network, that defines the interactions between the component. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"- Social graph\n",
"- Organization\n",
"- Brain\n",
"- finantial network\n",
"- business \n",
"- Internet\n",
"- Genes"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Behind each system studied in complexity there is an intricate wiring diagram, or a network, that defines the interactions between the component. \n",
"\n",
"# We will never understand complex system unless we map out and understand the networks behind them.\n",
" \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# TWO FORCES HELPED THE EMERGENCE OF NETWORK SCIENCE \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE HISTORY OF NETWORK ANALYSIS\n",
"\n",
"- Graph theory: 1735, Euler\n",
"\n",
"- Social Network Research: 1930s, Moreno\n",
"\n",
"- Communication networks/internet: 1960s\n",
"\n",
"- Ecological Networks: May, 1979.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"\n",
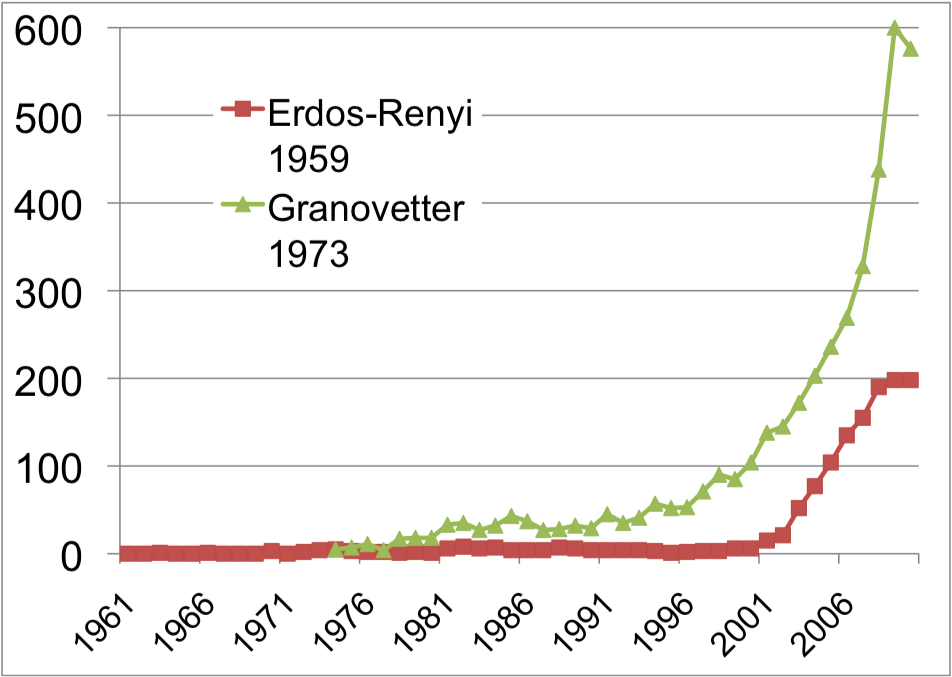
"While the study of networks has a long history from graph theory to sociology, **the modern chapter of network science emerged only during the first decade of the 21st century, following the publication of two seminal papers in 1998 and 1999**. \n",
"\n",
"The explosive interest in network science is well documented by the citation pattern of two classic network papers, the 1959 paper by Paul Erdos and Alfréd Rényi that marks the beginning of the study of random networks in graph theory [4] and the 1973 paper by Mark Granovetter, the most cited social network paper [5]. \n",
"\n",
"Both papers were hardly or only moderately cited before 2000. The explosive growth of citations to these papers in the 21st century documents the emergence of network science, drawing a new, interdisciplinary audience to these classic publications. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"- Social graph\n",
"- Organization\n",
"- Brain\n",
"- finantial network\n",
"- business \n",
"- Internet\n",
"- Genes"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Behind each system studied in complexity there is an intricate wiring diagram, or a network, that defines the interactions between the component. \n",
"\n",
"# We will never understand complex system unless we map out and understand the networks behind them.\n",
" \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# TWO FORCES HELPED THE EMERGENCE OF NETWORK SCIENCE \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE HISTORY OF NETWORK ANALYSIS\n",
"\n",
"- Graph theory: 1735, Euler\n",
"\n",
"- Social Network Research: 1930s, Moreno\n",
"\n",
"- Communication networks/internet: 1960s\n",
"\n",
"- Ecological Networks: May, 1979.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"\n",
"While the study of networks has a long history from graph theory to sociology, **the modern chapter of network science emerged only during the first decade of the 21st century, following the publication of two seminal papers in 1998 and 1999**. \n",
"\n",
"The explosive interest in network science is well documented by the citation pattern of two classic network papers, the 1959 paper by Paul Erdos and Alfréd Rényi that marks the beginning of the study of random networks in graph theory [4] and the 1973 paper by Mark Granovetter, the most cited social network paper [5]. \n",
"\n",
"Both papers were hardly or only moderately cited before 2000. The explosive growth of citations to these papers in the 21st century documents the emergence of network science, drawing a new, interdisciplinary audience to these classic publications. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE EMERGENCE OF NETWORK SCIENCE\n",
"- Movie Actor Network, 1998;\n",
"- World Wide Web, 1999.\n",
"- C elegans neural wiring diagram 1990\n",
"- Citation Network, 1998\n",
"- Metabolic Network, 2000; \n",
"- PPI network, 2001\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# The universality of network characteristics: \n",
"The architecture of networks emerging in various domains of science, nature, and technology are more similar to each other than one would have expected. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE CHARACTERISTICS OF NETWORK SCIENCE \n",
"- Interdisciplinary \n",
"- Empirical\n",
"- Quantitative and Mathematical \n",
"- Computational \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE IMPACT OF NETWORK SCIENCE \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Google\n",
"Market Cap(2010 Jan 1): \n",
"$189 billion\n",
"\n",
"# Cisco Systems\n",
"networking gear Market cap (Jan 1, 2919): \n",
"$112 billion\n",
"\n",
"# Facebook\n",
"market cap: \n",
"$50 billion\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Health: From drug design to metabolic engineering. \n",
"The human genome project, completed in 2001, offered the first comprehensive list of all human genes. \n",
"\n",
"- Yet, to fully understand how our cells function, and the origin of disease, we need accurate maps that tell us how these genes and other cellular components interact with each other. "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Security: Fighting Terrorism. \n",
"Terrorism is one of the maladies of the 21st century, absorbing significant resources to combat it worldwide. \n",
"\n",
"- **Network thinking** is increasingly present in the arsenal of various law enforcement agencies in charge of limiting terrorist activities. \n",
" - It is used to disrupt the financial network of terrorist organizations, to map terrorist networks, and to uncover the role of their members and their capabilities. \n",
" - While much of the work in this area is classified, several success stories have surfaced. Examples include the use of social networks to capture Saddam Hussein or \n",
" - the capture of the individuals behind the March 11, 2004 Madrid train bombings through the examination of the mobile call network. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Epidemics: From forecasting to halting deadly viruses. \n",
"While the H1N1 pandemic was not as devastating as it was feared at the beginning of the outbreak in 2009, it gained a special role in the history of epidemics: it was the first pandemic whose course and time evolution was accurately predicted months before the pandemic reached its peak. \n",
"- This was possible thanks to fundamental advances in understanding the role of networks in the spread of viruses. \n",
"- Indeed, before 2000 epidemic modeling was dominated by compartment models, assuming that everyone can infect everyone else one word the same socio-physical compartment. \n",
"- The emergence of a network-based framework has fundamentally changed this, offering a new level of predictability in epidemic phenomena. \n",
"\n",
"In January 2010 network science tools have predicted the conditions necessary for the emergence of viruses spreading through mobile phones. \n",
" - The first major mobile epidemic outbreak that started in the fall of 2010 in China, infecting over 300,000 phones each day, closely followed the predicted scenario. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Brain Research: Mapping neural network. \n",
"The human brain, consisting of hundreds of billions of interlinked neurons, is one of the least understood networks from the perspective of network science. \n",
"\n",
"The reason is simple: \n",
"- we lack maps telling us which neurons link to each other. \n",
"- The only fully mapped neural map available for research is that of the C.Elegans worm, with only 300 neurons. \n",
"\n",
"Driven by the potential impact of such maps, in 2010 the **National Institutes of Health** has initiated the Connectome project, aimed at developing the technologies that could provide an accurate neuron-level map of mammalian brains. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
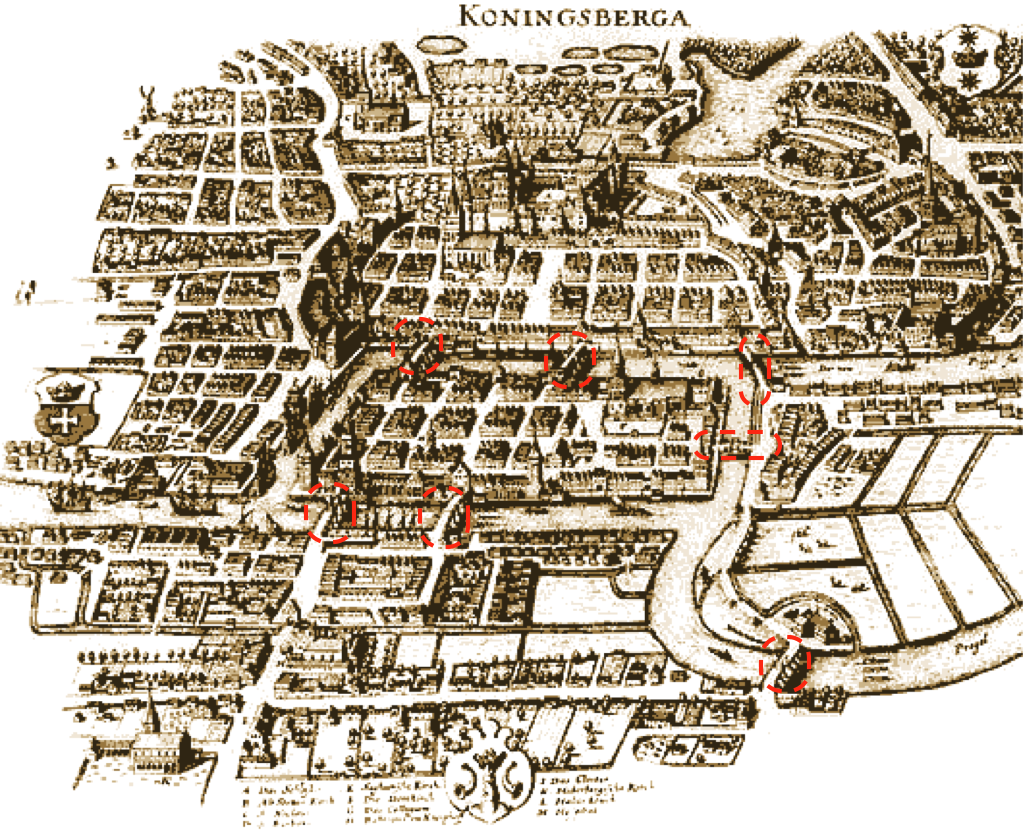
"# The Bridges of Konigsberg\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE EMERGENCE OF NETWORK SCIENCE\n",
"- Movie Actor Network, 1998;\n",
"- World Wide Web, 1999.\n",
"- C elegans neural wiring diagram 1990\n",
"- Citation Network, 1998\n",
"- Metabolic Network, 2000; \n",
"- PPI network, 2001\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# The universality of network characteristics: \n",
"The architecture of networks emerging in various domains of science, nature, and technology are more similar to each other than one would have expected. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE CHARACTERISTICS OF NETWORK SCIENCE \n",
"- Interdisciplinary \n",
"- Empirical\n",
"- Quantitative and Mathematical \n",
"- Computational \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE IMPACT OF NETWORK SCIENCE \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Google\n",
"Market Cap(2010 Jan 1): \n",
"$189 billion\n",
"\n",
"# Cisco Systems\n",
"networking gear Market cap (Jan 1, 2919): \n",
"$112 billion\n",
"\n",
"# Facebook\n",
"market cap: \n",
"$50 billion\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Health: From drug design to metabolic engineering. \n",
"The human genome project, completed in 2001, offered the first comprehensive list of all human genes. \n",
"\n",
"- Yet, to fully understand how our cells function, and the origin of disease, we need accurate maps that tell us how these genes and other cellular components interact with each other. "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Security: Fighting Terrorism. \n",
"Terrorism is one of the maladies of the 21st century, absorbing significant resources to combat it worldwide. \n",
"\n",
"- **Network thinking** is increasingly present in the arsenal of various law enforcement agencies in charge of limiting terrorist activities. \n",
" - It is used to disrupt the financial network of terrorist organizations, to map terrorist networks, and to uncover the role of their members and their capabilities. \n",
" - While much of the work in this area is classified, several success stories have surfaced. Examples include the use of social networks to capture Saddam Hussein or \n",
" - the capture of the individuals behind the March 11, 2004 Madrid train bombings through the examination of the mobile call network. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Epidemics: From forecasting to halting deadly viruses. \n",
"While the H1N1 pandemic was not as devastating as it was feared at the beginning of the outbreak in 2009, it gained a special role in the history of epidemics: it was the first pandemic whose course and time evolution was accurately predicted months before the pandemic reached its peak. \n",
"- This was possible thanks to fundamental advances in understanding the role of networks in the spread of viruses. \n",
"- Indeed, before 2000 epidemic modeling was dominated by compartment models, assuming that everyone can infect everyone else one word the same socio-physical compartment. \n",
"- The emergence of a network-based framework has fundamentally changed this, offering a new level of predictability in epidemic phenomena. \n",
"\n",
"In January 2010 network science tools have predicted the conditions necessary for the emergence of viruses spreading through mobile phones. \n",
" - The first major mobile epidemic outbreak that started in the fall of 2010 in China, infecting over 300,000 phones each day, closely followed the predicted scenario. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Brain Research: Mapping neural network. \n",
"The human brain, consisting of hundreds of billions of interlinked neurons, is one of the least understood networks from the perspective of network science. \n",
"\n",
"The reason is simple: \n",
"- we lack maps telling us which neurons link to each other. \n",
"- The only fully mapped neural map available for research is that of the C.Elegans worm, with only 300 neurons. \n",
"\n",
"Driven by the potential impact of such maps, in 2010 the **National Institutes of Health** has initiated the Connectome project, aimed at developing the technologies that could provide an accurate neuron-level map of mammalian brains. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# The Bridges of Konigsberg\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"# Can one walk across the seven bridges and never cross the same bridge twice and get back to the starting place? \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
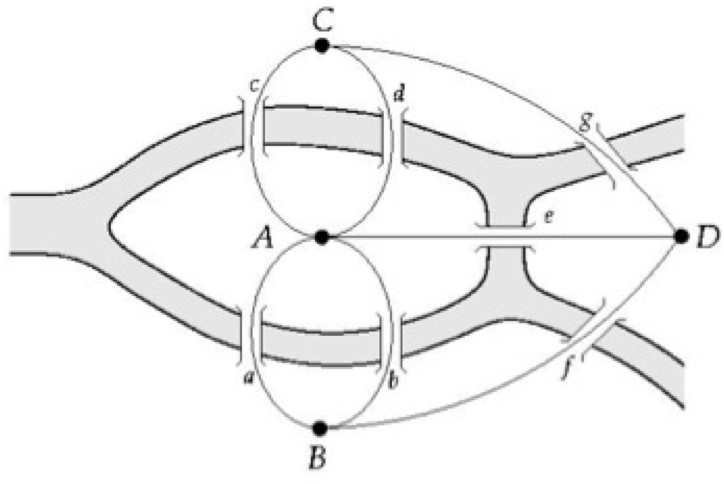
"source": [
"Can one walk across the seven bridges and never cross the same bridge twice and get back to the starting place? \n",
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"# Can one walk across the seven bridges and never cross the same bridge twice and get back to the starting place? \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Can one walk across the seven bridges and never cross the same bridge twice and get back to the starting place? \n",
"\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Euler’s theorem (1735):\n",
"\n",
"- If a graph has more than two nodes of odd degree, there is no path. \n",
"- If a graph is connected and has no odd degree nodes, it has at least one path.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"COMPONENTS OF A COMPLEX SYSTEM\n",
"\n",
"# Networks and graphs\n",
" - components: nodes, vertices\t\t N\n",
" - interactions: links, edges\t\t\t L\n",
" - system: \t network, graph\t\t(N,L)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"network often refers to real systems\n",
"- www, \n",
"- social network\n",
"- metabolic network. \n",
"\n",
"Language: (Network, node, link)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"graph: mathematical representation of a network\n",
"- web graph, \n",
"- social graph (a Facebook term)\n",
"\n",
"Language: (Graph, vertex, edge)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Euler’s theorem (1735):\n",
"\n",
"- If a graph has more than two nodes of odd degree, there is no path. \n",
"- If a graph is connected and has no odd degree nodes, it has at least one path.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"COMPONENTS OF A COMPLEX SYSTEM\n",
"\n",
"# Networks and graphs\n",
" - components: nodes, vertices\t\t N\n",
" - interactions: links, edges\t\t\t L\n",
" - system: \t network, graph\t\t(N,L)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"network often refers to real systems\n",
"- www, \n",
"- social network\n",
"- metabolic network. \n",
"\n",
"Language: (Network, node, link)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"graph: mathematical representation of a network\n",
"- web graph, \n",
"- social graph (a Facebook term)\n",
"\n",
"Language: (Graph, vertex, edge)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# CHOOSING A PROPER REPRESENTATION\n",
"\n",
"The choice of the proper network representation determines our ability to use network theory successfully.\n",
"\n",
"In some cases there is a unique, unambiguous representation. \n",
"In other cases, the representation is by no means unique.\n",
" \n",
"For example, the way we assign the links between a group of individuals will determine the nature of the question we can study.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"If you connect individuals that work with each other, you will explore the professional network.\n",
"\n",
"http://www.theyrule.net"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"If you connect those that have a romantic and sexual relationship, you will be exploring the sexual networks.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"If you connect individuals based on their first name (all Peters connected to each other), you will be exploring what? \n",
"\n",
"# It is a network, nevertheless.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# UNDIRECTED VS. DIRECTED NETWORKS\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
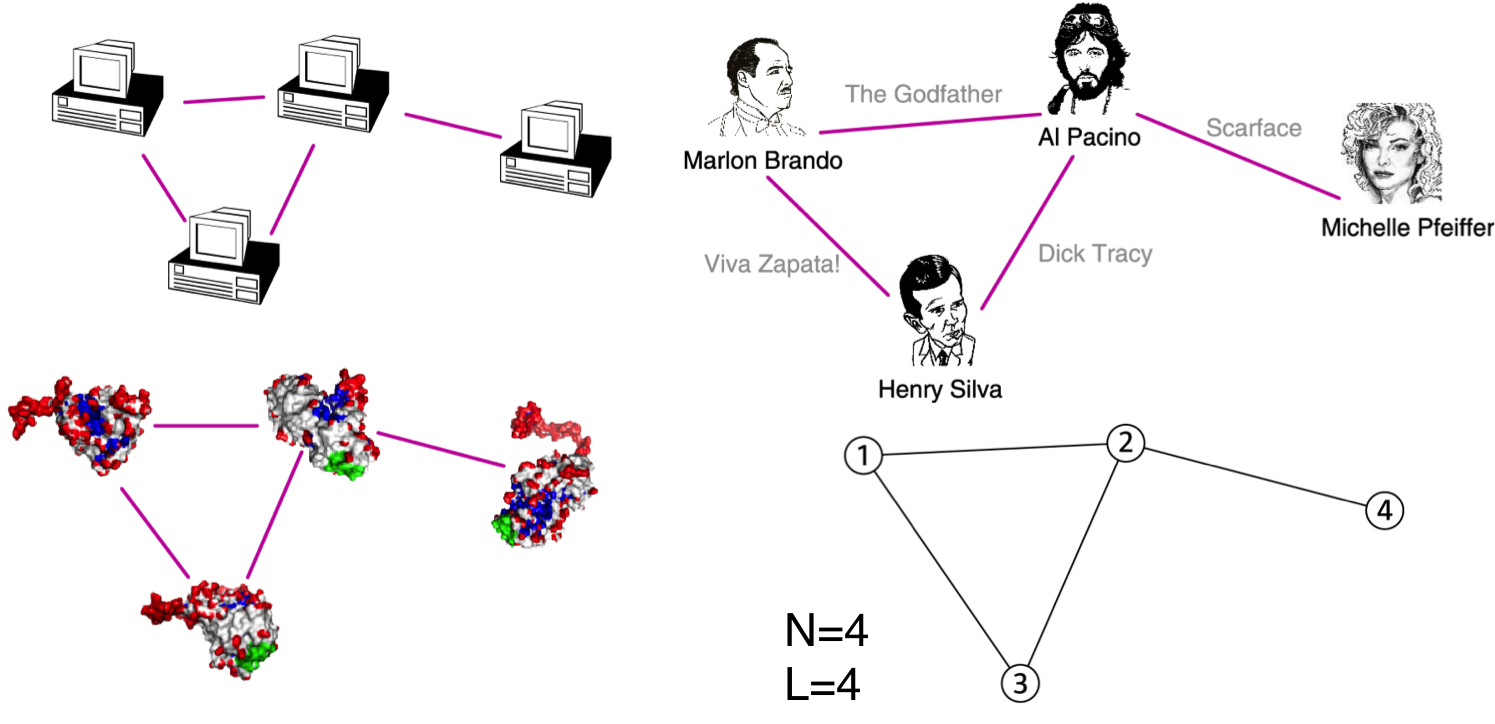
"# Undirected\n",
"Links: undirected\n",
"- coauthorship \n",
"- actor network\n",
"- protein interactions"
]
},
{
"cell_type": "code",
"execution_count": 174,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8jWfi///3sWZppNZq7VuoiSifhEQYSxwtLR1MVami\n1cV00SVIPv11WjOjifKp6rSfzPCZaUqULkopGU0EERGNNWFobGN9WEoQTVKS3N8/6PmphiLLdZbX\n8/HwUOfcOed9HjTvXNd93fdlsyzLEgAAMKKK6QAAAHgyihgAAIMoYgAADKKIAQAwiCIGAMAgihgA\nAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIG\nAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKI\nAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMo\nYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKpmOgAAwDmdPHlSc+PjlZOVpQvnzukOf38FBAVp9Nix\nql+/vul4bsNmWZZlOgQAwHlkZmZqVkyMlicmaoikkMJC+UnKk/Stt7cWW5Ye7N9fE6KjFRISYjit\n66OIAQAOs+Pi9GZkpCYXFGi0Zal2KcfkSoq32fSOt7emzJihZ8aPr+yYboUiBgBIulzC0yIjtTI/\nX61v4vi9ku738dFkyrhMKGIAgDIzMzWoVy+tu6aER0lKlpQvqZ6kJyW9ftXzeyX18PHRsrVrFRwc\nXHmB3QirpgEAmhUTo8kFBb8YCUdLOiDpnKRESX+VtPKq51tLmlRQoFkxMZUT1A0xIgYAD3fy5Em1\nbdZM+wsLSz0n/JPvJPWV9JWkzlc9fkZSKy8v5Rw6xGrq28CIGAA83Nz4eA2WrlvCz0vylRSoy9PS\nna95vo6kwTab5sbHV1hGd0YRA4CHy8nKUpfCwus+/6GkC7p8rvj/k5RZyjEhBQXKyc6umIBujiIG\nAA934dw5+f3KMTZJPSU9ImlBKc/7ScrLzS3vaB6BIgYAD3eHv7/ybvLYIkk+pTyeJ8mv9o3OMON6\nKGIA8HABQUH61svrF4+fkvSppB8klejyaunPJT1cymtkensroEOHiozptlg1DQAe7nqrpr+X9HtJ\nWZIsSW0kvSFp4DVfz6rpsmFEDAAerkGDBnqwf3/F22w/e7yepDW6XLS5kr7VL0tYkj622fTQgAGU\n8G2iiAEACouI0BTL0t5b/Lq9kt7x9taE6OiKiOURKGIA8HBz5szRn//8Z417+WXd7+Nz02X8072m\np8yYwe0ty4D9iAHAQxUXF2vSpEn6+uuvtW7dOrVp00YBAQHqERmpSQUFGnOd3ZfO6PLuS9PZfalc\nsFgLADxQXl6eRowYofz8fH3xxReqfdWlR5s2bdKsmBh9vWKFBttsCikocOxHnHllP+KHBgzQhOho\nRsLlgCIGAA9z6NAhDRw4UKGhofrggw9UvXr1Uo87deqU5sbHKyc7W3m5ufKrXVsBHTroiTFjWJhV\njihiAPAgGzdu1JAhQxQZGamXX35ZtmtWSqPycY4YADzEp59+qhdeeEH//Oc/NXBgaRciwQSKGADc\nnGVZ+vOf/6x//OMfWrVqlYKCgkxHwlUoYgBwY4WFhXryySe1b98+bdy4UQ0bNjQdCdfgOmIAcFMn\nTpxQnz59VFJSojVr1lDCTooiBgA3tGPHDoWGhqpfv35asGCBvL29TUfCdTA1DQBuZsWKFRozZoze\ne+89jRgxwnQc/AqKGADchGVZev/99zVt2jR99dVXCgsLMx0JN4EiBgA3cOnSJb300ktKS0tTenq6\nmjdvbjoSbhJFDAAu7uzZs3rkkUdUvXp1rV+/XrVq1TIdCbeAxVoA4ML27dunsLAw/eY3v9HSpUsp\nYRdEEQOAi0pNTVV4eLgmTJig9957T9WqMcnpivhbAwAXFB8fr8mTJ2v+/Pnq27ev6TgoA4oYAFxI\nSUmJXn/9dX3++edau3at2rVrZzoSyogiBgAX8cMPP2jUqFH6/vvvlZGRoXr16pmOhHLAOWIAcAFH\njx5Vjx495O/vr6SkJErYjVDEAODkNm/erNDQUD366KP65z//qZo1a5qOhHLE1DQAOLEvv/xSzz77\nrGbPnq3BgwebjoMKQBEDgBOyLEvTpk3Thx9+qJUrV6pz586mI6GCUMQA4GR+/PFHPfvss8rOzlZG\nRoYaNWpkOhIqEOeIAcCJfP/997Lb7crLy1Nqaiol7AEoYgBwErt27VLXrl3VvXt3ff755/L19TUd\nCZWAqWkAcAJJSUkaOXKkpk+frtGjR5uOg0rEiBgADIuLi9OoUaO0aNEiStgDMSIGAEOKior02muv\n6ZtvvtH69evVqlUr05FgAEUMAAacP39ew4cPV1FRkTZs2KA777zTdCQYwtQ0AFSy//znP+rWrZua\nN2+uFStWUMIejiIGgEqUnp6ubt266dlnn9WHH37IHsJgahoAKsv8+fP1yiuv6OOPP1b//v1Nx4GT\noIgBoIKVlJTorbfe0rx585SSkqLAwEDTkeBEKGIAqEAFBQUaM2aMDh8+rI0bN6pBgwamI8HJcI4Y\nACrI8ePH1atXL1WrVk0pKSmUMEpFEQNABdi+fbu6du2qgQMHKiEhQV5eXqYjwUkxNQ0A5WzZsmV6\n6qmn9MEHH2jYsGGm48DJUcQAUE4sy9LMmTP1P//zP/r666/VpUsX05HgAihiACgHly5d0vPPP6+N\nGzdqw4YNatq0qelIcBEUMQCU0ZkzZ/TII4/I19dXaWlp8vPzMx0JLoTFWgBQBjk5OQoNDVWnTp20\nePFiShi3jCIGgNu0evVq9ejRQxMnTtSMGTNUtWpV05HggpiaBoDb8H//9396/fXXtXDhQvXu3dt0\nHLgwihgAbkFxcbGioqL01Vdfad26dQoICDAdCS6OIgaAm3ThwgWNHDlSeXl5ysjIUJ06dUxHghvg\nHDEA3ITDhw+re/fuql+/vv71r39Rwig3FDEA/IrMzEyFhYVp1KhRmjNnjmrUqGE6EtwIU9MAcAOf\nffaZnn/+ef3jH//QoEGDTMeBG6KIAaAUlmVp6tSpmj17tpKSknTfffeZjgQ3RREDwDUKCws1btw4\n5eTkaOPGjbr77rtNR4Ib4xwxAFzl5MmTioiI0MWLF7V27VpKGBWOIgaAK3bu3KnQ0FBFRERo4cKF\n8vb2Nh0JHoCpaQCQ9K9//UtPPPGEZs6cqZEjR5qOAw9CEQPweB988IGmTp2qxYsXKzw83HQceBiK\nGIDHKioq0oQJE7RmzRqlp6erRYsWpiPBA1HEADzS2bNn9eijj6pKlSpKT0+Xv7+/6UjwUCzWAuBx\n9u/fr27duqldu3ZatmwZJQyjKGIAHiUtLU3h4eF64YUXNGvWLFWrxsQgzOJfIACPMXfuXEVGRioh\nIUH9+vUzHQeQRBED8AAlJSV64403tHDhQq1Zs0bt27c3HQlwoIgBuLX8/Hw98cQTOnHihDIyMlS/\nfn3TkYCf4RwxALd17Ngx/fa3v5Wvr6+Sk5MpYTglihiAW9qyZYu6du2qoUOHKj4+XjVr1jQdCSgV\nU9MA3M6SJUv09NNP629/+5uGDh1qOg5wQxQxALdhWZamT5+u999/X4mJiQoODjYdCfhVFDEAt3Dx\n4kU999xz2rZtmzIyMtS4cWPTkYCbQhEDcHmnT5/WkCFDVKdOHa1bt06+vr6mIwE3jcVaAFza7t27\nFRoaqrCwMC1atIgShsuhiAG4rOTkZPXs2VP//d//rdjYWFWpwrc0uB7+1QJwSX//+9/1+OOP67PP\nPtPYsWNNxwFuG+eIAbiU4uJiRUZGKjExUWlpaWrdurXpSECZUMQAXEZeXp4ee+wxFRYWasOGDapd\nu7bpSECZMTUNwCUcPHhQ4eHhaty4sRITEylhuA2KGIDTy8jIUFhYmJ566inFxcWpevXqpiMB5Yap\naQBObeHChXrppZf00Ucf6cEHHzQdByh3FDEAp2RZlqZMmaL4+HitWrVKHTp0MB0JqBAUMQCnU1BQ\noCeffFL/+c9/tHHjRt11112mIwEVhnPEAJzK8ePH1bt3b0lSSkoKJQy3RxEDcBpZWVkKDQ1V//79\n9cknn8jb29t0JKDCMTUNwCksX75cY8eO1fvvv6/hw4ebjgNUGooYQLk7efKk5sbHKycrSxfOndMd\n/v4KCArS6LFjVb9+/Z8da1mWZs2apXfeeUdLly5VaGioodSAGTbLsizTIQC4h8zMTM2KidHyxEQN\nkRRSWCg/SXmSvvX21mLL0oP9+2tCdLRCQkJ06dIlvfjii0pPT9eyZcvUrFkzw58AqHwUMYByMTsu\nTm9GRmpyQYFGW5ZKu+9VrqR4m03veHtr0p/+pOWJifLy8tKCBQvk5+dX2ZEBp0ARAyiz2XFxmhYZ\nqZX5+bqZLRj2SvqtzabA3r2V+M03qlq1akVHBJwWq6YBlElmZqbevEEJ75HkLemJqx5rLSnVspSd\nkaGtW7dWSk7AWVHEAMpkVkyMJhcUXHck/IKkLqU83lrSpIICzYqJqbhwgAtgahrAbTt58qTaNmum\n/YWFpZ4TXihpiaT2ujwdPfea589IauXlpZxDh36xmhrwFIyIAdy2ufHxGiyVWsLnJb0p6V1J1/tp\nv46kwTab5sbHV0xAwAVQxABuW05WlroUFpb63B8lPS3pnl95jZCCAuVkZ5d3NMBlcEMPALftwrlz\nKu2io22Skq/8/mv8JOXl5pZrLsCVUMQAbpuPn5/ySnl8raSDkprq8rT0BUnFkv4tadM1x+ZJ8qtd\n2uQ24BkoYgA3zbIs7d69W0lJSUpKSlJyUpLybTY9d82az2clPXbVn6frcjH/rZTXzPT21m/Yaxge\njFXTAG7oxIkTSk5Ovly8ycmqWrWq7Ha77Ha7goKC1K1z5+uumv7JFEn7xKppoDQUMYCfyc/PV2pq\nqqN8Dx06pF69ejnKt3Xr1rLZbI7jHx8yRMFLlujl2/hWMtNm05bBgzVv0aLy/AiAS6GIAQ9XXFys\nrVu3OqabMzMz1alTJ0fxBgcHq1q165/FyszM1KBevbTuJm9v+ZO9knr4+GjZ2rUKDg4u8+cAXBVF\nDHigAwcOOIo3JSVFDRs2VN++fWW329WzZ89b3oDhdu41fb+PjybPmKFnxo+/rc8AuAuKGPAAubm5\nSklJcZznvXDhgqN4+/btq0aNGpX5PX7afWliQYHGXmf3pTO6vPvSdG9vTaGEAUkUMeCWLl68qPT0\ndMd53l27dik8PNwx3RwYGPiz87zlZdOmTXpy+HAdOHhQj1SvrpCCAsd+xJlX9iN+aMAATYiOZjoa\nuIIiBtyAZVnauXOnY7o5LS1N7dq1c4x4u3Xrppo1a1Z4jkuXLqlx48ZaunSp0lJTlZOdrbzcXPnV\nrq2ADh30xJgxrI4GrkERAy7q2LFjP7usyNvb2zHi7dOnj+rUqVPpmZYvX66pU6cqPT290t8bcFXc\n0ANwERcuXNDatWsd5Xvs2DH16dNHdrtdU6ZMUcuWLU1HVEJCgh5//HHTMQCXwogYcFJFRUXavHmz\nY7p5y5YtCg4Odkw3/9d//ZeqVq1qOqbD+fPn1aRJE+3fv19169Y1HQdwGYyIASdhWZb27dvnKN7V\nq1erSZMm6tu3r6KiovTb3/5Wvr6+pmNe15dffqlevXpRwsAtoogBg06fPq1Vq1Y5ppt//PFH2e12\nDRkyRP/7v/+rhg0bmo540+bNm6fxXI4E3DKmpoFKVFhYqPT0dMeod8+ePerRo4djkdW9995bIZcV\nVbQjR44oKChIx44dk5eXl+k4gEthRAxUoJKSEmVnZzuKNz09XYGBgbLb7Xr33XcVGhqqGjVqmI5Z\nZgsWLNDQoUMpYeA2MCIGytmRI0cclxQlJyerVq1ajhFv7969deedd5qOWO6CgoL017/+VT179jQd\nBXA5FDFQRufPn9fatWsdo95Tp04pIiLCsbq5efPmpiNWqKysLA0cOFAHDhxQlSpVTMcBXA5T08At\nKioq0rfffuso3u3bt6tr166y2+1KSEhQp06dPKqQ5s2bp5EjR3rUZwbKEyNi4FdYlqWcnBxH8a5d\nu1bNmzd3TDd3795dPj4+pmMaUVxcrKZNmyopKUnt27c3HQdwSYyIgVKcOnXKcY43KSlJlmXJbrdr\n+PDhmjNnjho0aGA6olNYvXq1GjZsSAkDZUARA5IKCgqUlpbmGPUeOHBAPXv2lN1u16RJkxQQEOCS\nlxVVNG5pCZQdU9PwSCUlJdq2bZujeDdu3KiOHTs69ujt0qWLqlevbjqmU8vPz1ejRo20a9cul7rx\nCOBsGBHDYxw8eNBxWdGqVatUt25d2e12vfTSS+rVq5dq1aplOqJL+eqrr9S1a1dKGCgjihhu6+zZ\ns1qzZo1j1Hv27Fn17dtX999/v6ZPn64mTZqYjujS5s2bp1GjRpmOAbg8pqbhNi5duqSMjAxH8e7Y\nsUPdunVzXM8bFBTEJTbl5MSJE2rbtq2OHj3q1BtRAK6AETFclmVZ2rVrl2O6OTU1Va1bt5bdbtdf\n/vIXhYeHc8vFCvLpp59q0KBBlDBQDhgRw6UcP35cq1atcpRvtWrVHNfz9unTR/Xq1TMd0SOEhIRo\n6tSp6tevn+kogMujiOHU8vPzlZqa6phuPnz4sHr37u2Ybm7dujWXFVWy3bt3q0+fPjp8+LCqVq1q\nOg7g8piahlMpLi7Wli1bHMWbmZmpzp07y263a/bs2QoODla1avyzNSkhIUGPPfYYJQyUE0bEMG7/\n/v2OqeaUlBQ1bNjQMd3cs2dP3XHHHaYj4oqSkhK1atVKixcv1n333Wc6DuAWGFqg0uXm5iolJcUx\n6s3Pz1ffvn01cOBAzZo1S/fcc4/piLiO9evXy9fXVx07djQdBXAbFDEq3I8//qgNGzY4inf37t0K\nDw+X3W7X888/r8DAQM7zuoiEhASNGjWKvy+gHDE1jXJnWZZ27NjhmG5OS0tTu3btHNPNYWFhqlmz\npumYuEWFhYVq1KiRtm3bxs1QgHLEiBjl4tixY46dipKTk+Xj4yO73a6nnnpKCQkJqlOnjumIKKMV\nK1aoY8eOlDBQzihi3JYLFy5o7dq1junm48ePq0+fPrLb7ZoyZYpatmxpOiLK2bx589hpCagATE3j\nphQVFWnTpk2OEe+WLVsUHBzsmG7u3Lkzl7O4sTNnzqhFixY6dOiQ/P39TccB3AojYhdw8uRJzY2P\nV05Wli6cO6c7/P0VEBSk0WPHqn79+hXynpZlae/evY7p5tWrV6tJkyay2+2Kjo5Wjx49uL2hB/n8\n88/1wAMPUMJABWBE7MQyMzM1KyZGyxMTNURSSGGh/CTlSfrW21uLLUsP9u+vCdHRCgkJKfP7nT59\n2nH7yKSkJF26dMkx4o2IiGC7Ow/WvXt3TZ48WQMHDjQdBXA7FLGTmh0XpzcjIzW5oECjLUu1Szkm\nV1K8zaZ3vL01ZcYMPTN+/C29R2FhodavX++Ybt6zZ4969OjhKN97772Xy1Sg/fv3q2vXrjp27Jiq\nV69uOg7gdpiadkKz4+I0LTJS6/Lz1foGx9WW9IplaWB+vu6PjJSkG5ZxSUmJsrKyHNPN6enpCgwM\nlN1u18yZM9W1a1fVqFGjfD8MXN78+fP16KOPUsJABWFE7GQyMzM1qFevn5XwRUl/kJSsy6PgVpLe\nlvTAVV+3V1IPHx8tW7tWwcHBjsePHDnimGpetWqV/P39HSPeXr166c4776ycDwaXZFmW2rVrp7lz\n56pr166m4wBuiRGxk5kVE6PJBQU/GwkXSWoqaZ2kJpKWSxomaceVxyWptaRJBQWa8ac/acS4cY7y\nPX36tCIiItS3b1/FxMSoWbNmlflx4OIyMzNlWZa6dOliOgrgthgRO5GTJ0+qbbNm2l9YWOo54at1\nlPSWpMFXPXZGUiNJIT166MEHH5Tdbtd9992nKlWqVFBiuLuXXnpJ9erV0x//+EfTUQC3xYjYicyN\nj9dg6VdL+ISkPZJ+c83jdSQN9/JS4MCBem3ixIqICA9y6dIlLVy4UBs2bDAdBXBrDJWcSE5WlroU\nFt7wmCJJj0saIymglOe7FBYqJzu7/MPB43zzzTdq06aNWrVqZToK4NYoYidy4dw5+d3geUuXS7im\npL9e5xg/SXm5ueUdDR6IW1oClYMidiJ3+Psr7wbPPyXpe0lfSrrezSTzJPnV/rXJbeDGzp8/r8TE\nRA0bNsx0FMDtUcROJCAoSN96eZX63HOSdktaKulGV/pmensroEOHCkgHT/Lll1+qd+/eqlu3ruko\ngNtj1bQTud6q6UOSmkvy0v8/ErZJ+rukx6467oykZtWqacu//602bdpURmS4qYiICI0fP16///3v\nTUcB3B4jYifSoEEDPdi/vz6+5raSTSWVSMrX5annPEnn9fMSli7f7rJJo0YKDQ3VxIkTdezYscqI\nDTdz5MgRbd26VQ899JDpKIBHoIidzIToaE3z9tbeW/y6vZKme3tr7hdfaNu2bSoqKlJgYKCefvpp\n5eTkVERUuKlPPvlEQ4cOldd1TpMAKF8UsZMJCQnRlBkzdL+Pz02X8V5J9/v4aMqMGQoODlaTJk00\nc+ZM7dmzR40bN1b37t31yCOPaNOmTRUZHW4iISFBo0aNMh0D8BgUsRN6Zvx4TZ4xQz18fDTTZtP1\nLkY6I+ldm009fHw0uZTdl+rWras333xTBw4cUPfu3TVkyBDZ7XatWrVKLA1AabZv365z586pe/fu\npqMAHoPFWk5s06ZNmhUTo69XrNBgm00hBQWO/Ygzr+xH/NCAAZoQHf2zjR6u5+LFi1qwYIGmTZsm\nX19fRUVF6Xe/+52qVr3exVDwNBMnTlSNGjU0depU01EAj0ERu4BTp05pbny8crKzlZebK7/atRXQ\noYOeGDNG9evXv+XXKykp0bJlyxQTE6Pc3FxNmjRJjz/+uGrWrFkB6eEqiouL1bRpUyUnJ+vee+81\nHQfwGBSxB7MsS6mpqYqNjVV2drZeeeUVPfPMM/Lzu9H9veCukpOTFRUVxVoCoJJxjtiD2Ww29ezZ\nU4mJiVq2bJk2bdqkli1b6o033tCpU6dMx0Ml45aWgBkUMSRJnTp10oIFC5SRkaHvv/9ebdu21Ysv\nvqiDBw+ajoZK8MMPP2jp0qV67LFrr04HUNEoYvxMq1atFBcXp507d8rX11edO3fWE088oR07dpiO\nhgq0dOlShYaG6q677jIdBfA4FDFKdffddys2Nlb79u1T+/btZbfbNWjQIKWnp5uOhgowb948rh0G\nDGGxFm5KQUGBPv74Y02fPl2NGjVSVFSU+vfvL9s1t+OE6zlx4oTatWunI0eOyNfX13QcwONQxLgl\nRUVF+uKLLxQbG6uSkhJFRUVp2LBhqlatmulouE2zZs3Sli1b9PHHH5uOAngkihi3xbIsrVy5UrGx\nsTp48KAmTpyosWPHytvb23Q03KKQkBC9/fbbstvtpqMAHolzxLgtNptNDzzwgNasWaNPPvlE33zz\njVq0aKG3335bZ8+eNR0PN2n37t06evSo+vTpYzoK4LEoYpRZWFiYlixZopSUFOXk5KhVq1aaNGkS\n2zC6gISEBI0YMYLbnAIGUcQoN+3bt1d8fLy2bt2qixcvKjAwUM8884z27NljOhpKUVJSooSEBG7i\nARhGEaPcNW3aVO+9955ycnJ0zz33qFu3bho2bJg2b95sOhqusn79evn5+aljx46mowAejSJGhalX\nr57eeustHThwQGFhYXr44YfVr18/rV69mm0YncBPt7TkEjTALFZNo9JcvHhR8+fP17Rp0+Tv76+o\nqCg9/PDDqlKFnwcrW2FhoRo1aqRt27apSZMmpuMAHo3vgKg0NWrU0NixY/Xvf/9bUVFRiomJUfv2\n7fXRRx/p4sWLpuN5lBUrVqhjx46UMOAEKGJUuipVqmjw4MHauHGj4uLitHDhQrVq1UozZ87UhQsX\nTMfzCNzSEnAeTE3DKWzZskXTpk1TSkqK/vCHP+jFF19UvXr1TMdyS2fOnFHLli116NAh1apVy3Qc\nwOMxIoZT6Ny5sz799FOlp6fr+PHjCggI0IQJE3To0CHT0dzOZ599pgceeIASBpwERQyn0qZNG/39\n73/Xzp075eXlpU6dOmn06NHauXOn6Whug2uHAedCEcMp3X333Zo2bZr27dundu3aKSIiQg8//LA2\nbNhgOppL279/v3JycnT//febjgLgCooYTu3OO+9UdHS0Dhw4oAceeEAjR45Uz549lZiYyLXIt2H+\n/Pl69NFHVb16ddNRAFzBYi24lKKiIn322WeKjY1VlSpVNHnyZD3yyCNsw3gTLMtS27ZtlZCQoC5d\nupiOA+AKRsRwKdWqVdOIESO0fft2vf3224qLi1Pbtm31t7/9TYWFhabjObXMzExJl7c9BOA8KGK4\nJJvNpgEDBig1NVVz587VihUr1KJFC8XGxurcuXOm4zklbmkJOCempuE2duzYoXfeeUfLly/X008/\nrZdfflkNGzY0HcspXLp0SY0aNVJGRoZatmxpOg6AqzAihtsIDAzU3LlztXnzZuXn56t9+/Z67rnn\ntHfvXtPRjFu5cqXatGlDCQNOiCKG22nevLnef/99fffdd2rQoIHCwsI0fPhwbd261XQ0YxISEril\nJeCkmJqG28vLy9OcOXP07rvvKjAwUFFRUerZs6fHnCs9f/68mjZtqn379qlu3bqm4wC4BiNiuD0/\nPz+9+uqr2rdvn4YNG6Znn31WYWFhWrJkiUpKSkzHq3CLFi1S7969KWHASTEihscpLi7WkiVLFBMT\nox9++EGTJ0/WiBEjVKNGDdPRKkRERIT+8Ic/aOjQoaajACgFRQyPZVmWUlJSFBsbq++++06vvvqq\nxo0bpzvuuMN0tHJz5MgRdezYUUePHpWXl5fpOABKwdQ0PJbNZlNERISSkpL05Zdfav369WrZsqXe\neustnT4x8lf9AAAGfklEQVR92nS8cvHJJ59o6NChlDDgxChiQFJwcLA+//xzpaWl6ejRo2rTpo1e\neeUVHT582HS022ZZlubNm8dqacDJUcTAVQICAjRnzhxlZ2erWrVquu+++zR27Fjt2rXLdLRblpWV\npby8PIWHh5uOAuAGKGKgFI0aNdL06dO1d+9etW7dWr169dLgwYO1ceNG09Fu2k+3tKxShf/NAWfG\nYi3gJuTn5+ujjz7S9OnT1aJFC0VFRalfv35Oey1ycXGxmjRpolWrVunee+81HQfADfCjMnATfHx8\n9Pzzz2vPnj0aN26cIiMj1blzZ3366acqLi42He8XUlJSdM8991DCgAtgRAzcBsuytGLFCsXExOj4\n8eOaOHGiRo8e7TSrk0ePHq3OnTtrwoQJpqMA+BUUMVBGaWlpio2N1ebNm/Xyyy/rueeek7+/v7E8\nP/zwgxo3bqzdu3frrrvuMpYDwM1hahooo+7du+vrr7/WypUrlZ2drZYtWyo6OlrHjx83kuerr75S\nWFgYJQy4CIoYKCdBQUFKSEjQpk2blJeXp/bt22v8+PHat29fpeZISEjQ448/XqnvCeD2UcRAOWvR\nooU++OAD7d69W3Xr1lXXrl01YsQIbd++vcLf+8SJE9qwYYN+97vfVfh7ASgfFDFQQRo0aKC//OUv\n2r9/vzp37qwBAwZowIABSk1NVUUtzVi4cKEGDRokHx+fCnl9AOWPIgYqWK1atRQZGan9+/dryJAh\nGjdunMLDw7V06dJy34aRW1oCrodV00AlKy4u1uLFixUTE6PCwkJNnjxZjz32mKpXr37Tr3Hy5EnN\njY9XTlaWLpw7pzv8/eXfsKHmJSTo6NGjqlq1agV+AgDliSIGDLEsS6tWrVJsbKz27Nmj1157TU89\n9ZR8fX2v+zWZmZmaFROj5YmJGiIppLBQfpLyJK2vVk1LLEsPDxqkCdHRCgkJqayPAqAMKGLACXz7\n7beaNm2a1q1bpxdeeEEvvPCC6tSp87NjZsfF6c3ISE0uKNBoy1LtUl4nV1K8zaZ3vL01ZcYMPTN+\nfKXkB3D7OEcMOIEuXbpo0aJFSk1N1cGDB9W6dWu9+uqrOnLkiKTLJTwtMlLr8vP18nVKWJJqS3rF\nsrQuP1/TIiM1Oy6u0j4DgNvDiBhwQkeOHNHMmTP10UcfKTw8XJnJyUorLFTrq475UFK8pGxJIyT9\n85rX2Cuph4+Plq1dq+Dg4MoJDuCWUcSAEztz5oz6de+ux3bt0mvXPLdEl6e0Vkoq0C+LWJJm2mza\nMniw5i1aVNFRAdwmihhwYidPnlTbZs20v7DwutPRb0g6qtKL+IykVl5eyjl0SPXr16+wnABuH+eI\nASc2Nz5eg6XrlvCvqSNpsM2mufHx5RcKQLmiiAEnlpOVpS6FhWV6jZCCAuVkZ5dTIgDljSIGnNiF\nc+fkV8bX8JOUl5tbHnEAVACKGHBid/j7K6+Mr5Enya/27U5uA6hoFDHgxAKCgvStl1epzxVLKrzy\ne5GkH6/897Uyvb0V0KFDhWUEUDasmgac2I1WTU+58st21WNvSvrjVX9m1TTg/BgRA06sQYMGerB/\nf31ss/3iuTcllejyKPinX3+85piPbTY9NGAAJQw4MUbEgJPLzMzUoF69tC4//2d31vo13FkLcA2M\niAEnFxISoikzZuh+Hx/tvcmv2Svpfh8fTZkxgxIGnBxFDLiAZ8aP1+QZM9TDx0czbTZd72KkM5Le\ntdnUw8dHk9l9CXAJTE0DLmTTpk2aFROjr1es0GCbTSEFBY79iDO9vbXYsvTQgAGaEB3NSBhwERQx\n4IJOnTqlufHxysnOVl5urvxq11ZAhw56YswYFmYBLoYiBgDAIM4RAwBgEEUMAIBBFDEAAAZRxAAA\nGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEA\nAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUM\nAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQR\nAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZR\nxAAAGEQRAwBgEEUMAIBBFDEAAAb9P603wxJf3z2wAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"\n",
"import networkx as nx\n",
"Gu = nx.Graph()\n",
"for i, j in [(1, 2), (1, 4), (4, 2), (4, 3)]:\n",
" Gu.add_edge(i,j)\n",
"nx.draw(Gu, with_labels = True)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Directed\n",
"Links: directed\n",
"- urls on the www\n",
"- phone calls\n",
"- metabolic reactions"
]
},
{
"cell_type": "code",
"execution_count": 173,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XlY1XX+///7AZXFfV8y9xAXcMUFBdxmnBxzsmusfm2i\npWlkTqNo6Ki5hQvWmJ8+TjXlkTY/pWPLjGZqiKgpkCWEBrngMppiEJKCCpzfH9b5SqKhAq+zPG7X\n5TVz3md70GU8ej3fm8Vms9kQERERIzxMBxAREXFnKmIRERGDVMQiIiIGqYhFREQMUhGLiIgYpCIW\nERExSEUsIiJikIpYRETEIBWxiIiIQSpiERERg1TEIiIiBqmIRUREDFIRi4iIGKQiFhERMUhFLCIi\nYpCKWERExCAVsYiIiEEqYhEREYNUxCIiIgapiEVERAxSEYuIiBikIhYRETFIRSwiImKQilhERMQg\nFbGIiIhBKmIRERGDVMQiIiIGqYhFREQMUhGLiIgYVMV0AHd15swZYq1WMlJS+Ck3lxq1a+MXGMjo\nMWNo2LCh6XgiIlJJLDabzWY6hDtJSkpieXQ0/9m4kfuAoIICagJ5QKKPD+ttNv54991MjooiKCjI\ncFoREaloKuJK9NrKlcyZOpXp+fmMttmoW8prcgCrxcISHx/mxsQwfuLEyo4pIiKVSEVcSV5buZLF\nU6ey6cIF2pXh9QeBob6+TFcZi4i4NBVxJUhKSmLEgAEk/KqEXwGsQCrwEPDmr953EAjx9eWT+Hh6\n9uxZOWFFRKRS6ajpSrA8Oprp+fnXrITvAGYBj1/nfe2Aafn5LI+OrtB8IiJijlbEFezMmTO0b9mS\nwwUFpe4Thitl/F+uXREDZANtvb3JOHZMR1OLiLggrYgrWKzVyki4bgn/lnrASIuFWKu1/EKJiIjD\nUBFXsIyUFHoVFNzWZwTl55ORmlpOiURExJGoiCvYT7m51LzNz6gJ5OXklEccERFxMCriClajdm3y\nbvMz8oCadW91uC0iIo5MRVzB/AIDSfT2LvW5IqDg5/8tBC7+/P9/bTvw+a5dvPDCC+zZs4fCwsKK\niisiIpVMR01XsBsdNT335z+Wq7bNAWZf9TgbaOvlxStvvklycjJbtmzh+PHjhIWFMWTIEIYMGUL7\n9u2xWK7+FBERcRYq4krwyH330fPDD/nLLfyjfsliYe/Ikby1bp192+nTp/n888/ZsmULW7ZsobCw\n0F7KgwcPplmzZuUZX0REKpCKuBJc78pav6UsV9ay2WwcOnTIXspxcXE0btzYXsoDBgygdu3a5fJz\niIhI+VMRV5LKutZ0UVERX3/9NVu2bGHr1q188cUXdO7cmcGDBzNkyBD69u2Ll5fXLf8cIiJSvlTE\nleiXuy9Ny88n/Dp3X8rmyt2XlpbT3ZcKCgrYtWsXW7duZcuWLezfv5/g4GD7KLtLly54eOiYPRER\nU1TElSw5OZnl0dH8e8MGRlosBOXn2+9HnGCxsNHLi+HDhjE5KqpCbvTw448/sm3bNvso++zZswwa\nNMg+ym7Tpo0O/BIRqUQqYkOysrKItVrJSE0lLycHn5o1eWftWg6kp9O6detKy3HixAm2bt1qXzF7\neXnZS3nQoEE0atSo0rKIiLgjFbEDCQkJYc6cOQwZMsTI99tsNg4cOGAv5fj4eFq2bGkfY4eEhFCj\nRg0j2UREXJWK2IHMnDkTT09P5s2bZzoKAIWFhfZzl7ds2UJycjLdu3e3r5h79epF1apVTccUEXFq\nKmIHsmnTJqKjo9m2bZvpKKU6f/48O3bssB+RfejQIUJDQ+1HZHfq1En7l0VEbpKK2IHk5eXRtGlT\nfvjhB6c4xSgrK4u4uDj7KPv8+fP2Uh48eDAtWrQwHVFExOGpiB1Mr169WLZsGSEhIaaj3LQjR47Y\nS3nr1q3UrVvXvn954MCB1NWNK0RErqEidjBTp06lbt26zJw503SU21JcXExqaqp9//LOnTtp3769\nfbXcr18/fHx8TMcUETFORexgPv74Y1555RU2bdpkOkq5unTpErt377avllNSUujVq5d9xdy9e3c8\nPT1NxxQRqXQqYgeTnZ1Nq1atyM7OpkqVKqbjVJhz584RHx9vH2WfPHmSAQMG2FfMfn5+OvBLRNyC\nitgBBQYG8sYbbxAUFGQ6SqU5depUiTtKAfZSHjx4ME2bNjWcUESkYqiIHdDTTz9N69atmTJliuko\nRthsNr777jv7GDsuLo5mzZrZj8gOCwujVq1apmOKiJQLFbEDev/993nnnXf46KOPTEdxCEVFRezd\nu9c+xt6zZw8BAQH2FXOfPn2c4nQvEZHSqIgd0Pfff0/Hjh05e/as7oxUivz8fHbt2mUfY6enp9Ov\nXz97MQcGBuqfm4g4DRWxg2rfvj0ffPABgYGBpqM4vOzsbPsdpbZu3Up2drZ93/KQIUMq9SYaIiI3\nS0XsoMaNG0eXLl14+umnTUdxOseOHStxRylfX1/7aVKDBg2iQYMGpiOKiNipiB3UW2+9xSeffML7\n779vOopTs9lspKWl2Ut5+/bttGnTxj7GDgkJoXr16qZjiogbUxE7qKNHj9K7d29OnTql82nL0eXL\nl0lKSrLvX967dy89e/a0j7GDgoJc+vxtEXE8KmIH1rJlSzZv3oyfn5/pKC7rp59+IiEhwb5izszM\nJDQ01D7K7tChg/5DSEQqlIrYgT366KOEhYXxxBNPmI7iNs6cOUNcXJx9xXzx4sUSB341b97cdEQR\ncTEqYgf2+uuvk5CQQGxsrOkobuvw4cP2Uv78889p0KCBff/ygAEDdEcpEbltKmIHlp6ezu9//3uO\nHj1qOopw5Y5S+/bts58mtXPnTjp27GhfLQcHB+Pt7W06pog4GRWxA7PZbDRt2pQ9e/bQsmVL03Hk\nVy5evMgXX3xh37/8zTff0KdPH/uKuVu3brqjlIj8JhWxg7v//vu55557ePTRR01Hkd+Qm5tLfHy8\nfZR9+vRpBg4caF8xt2vXTgd+icg1VMQO7n/+53/Yt28fr7/+uukocpNOnjxpXy1v3boVT09PeykP\nHjyYxo0bm44oIg5ARezgUlJSGDVqFOnp6aajyG2w2Wykp6fbi3nbtm00b97cfppUaGgoNWvWNB1T\nRAxQETu44uJiGjRowP79+2nSpInpOFJOCgsL2bt3r32MnZiYSNeuXe0r5t69e1OtWjXTMUWkEqiI\nncCIESN49NFHGTVqlOkoUkEuXLjAzp077WPsjIwM+vfvb18xd+7c+Zo7ShUVFeHh4aH9ziJOTkXs\nBGJiYjh69CgrVqwwHUUqyQ8//EBcXJx9lH3u3DkGDRpk37/cqlUr3n77bWbMmGHfNnjwYE1NRJyQ\nitgJJCYm8sQTT5CSkmI6ihhy9OjREgd+1axZE09PTzIyMkq8rnPnzvZiDgsL035nESegInYChYWF\n1KtXj8zMTOrVq2c6jhhms9lITU0lLCyMH3/88bqvq1KlCr1799Z+ZxEHpyJ2EkOHDiUiIoIRI0aY\njiIO4MSJE9x1110UFBSU+T3Vq1e339Bi8ODBBAQEXLPfWUQqn4rYSSxcuJCcnBxiYmJMRxEHUVBQ\nwK5du+zj6uTkZIqLi8v8/oYNG5a4oUWrVq0qLqyIXJeK2EkkJCQwZcoUEhMTTUcRB5WTk8O2bdvs\n+5Jv9tzztm3b2kt54MCBNGjQoNwznjlzhlirlYyUFH7KzaVG7dr4BQYyeswYGjZsWO7fJ+IMVMRO\noqCggAYNGnDq1CkdgCNlcuLEiRIHeJ06darM77VYLHTt2tV++lT//v3x9fW95SxJSUksj47mPxs3\nch8QVFBATSAPSPTxYb3Nxh/vvpvJUVEEBQXd8veIOCMVsRMJCwtj5syZ/P73vzcdRZyMzWbjwIED\n9lKOi4sjLy+vzO+vVq0awcHB9v3LPXv2pEqVKmV672srVzJn6lSm5+cz2majtBtH5gBWi4UlPj7M\njYlh/MSJZc4m4uxUxE5k1qxZ2Gw2FixYYDqKOLnCwkKSkpLsK+Zdu3Zx+fLlMr+/Vq1aJW5o4e/v\nX+qFRV5buZLFU6ey6cIF2pXhcw8CQ319ma4yFjeiInYimzdvZt68eSQkJJiOIi7m/Pnz7Nixw37J\nza+//vqm3t+sWbMSN7S44447SEpKYsSAASSUUsLfAYHAKCD2V88dBEJ8ffkkPp6ePXve8s8k4ixU\nxE7k/PnzNG7cmKysLHx8fEzHEReWlZVFXFycfZR9+PDhm3q/v78/VS5dYuyRIzxbyq+YoUAB0JJr\nixjgJYuFvSNH8ta6dbcSX8SpqIidTJ8+fVi8eDFhYWGmo4gbOXz4MFu3brX/OXv27G++xxs4Cdfs\nE14DfAh05Mrqt7QizgbaenuTceyYjqYWl6ez+Z1MaGgo27dvNx1D3EybNm0YN24ca9as4fTp03z1\n1VfExMTwhz/8odSjqS3AvVxbwueAOcCLwI1WAPWAkRYLsVZr+fwAIg5MRexkVMRimoeHB127dmXK\nlCls3LiRnJwc4uPjmTVrFsHBwXh6euINlDazmQ2MA5qV4XuC8vPJSE0t1+wijkhF7GT69evH7t27\nb+oIV5GKVK1aNUJDQ5k3bx47d+4kOzubvkFB/Pps96+BLcBfyvi5NYG8nJxyzSriiFTETqZu3bq0\nbduWvXv3mo4iUqpatWrR1s+PX5+lHA8cBVoATYEYYC1wveOi84CadUs761jEtaiInZDG0+Lo/AID\nSfT2LrHtSeAQV1bG+4AJwHDgs+t8RpKPD34BARUZU8QhqIidUGhoKPHx8aZjiFzXo6NHs66oiKsH\ny95Ao6v+1Ph5W2k39swG1ttsPBYeXtFRRYxTETuh0NBQdu7cSVFRkekoItdITk7mwQcfxMfLC2sp\nV9v6xRxKP3UJYLXFwvBhw3TqkrgFFbETatSoEU2aNCFVR5SKA8nMzOShhx5ixIgRPPTQQ6z/7DOW\n+Phw8CY/5yCwxMeHyVFRFRFTxOGoiJ2U9hOLo8jOzmbq1Kn06NGD9u3bk5GRwbhx4+jbty9zY2IY\n6utb5jL+5VrTc2NidHlLcRsqYielIhbTCgoKWLZsGf7+/vz000+kpaUxZ84catSoYX/N+IkTmR4T\nQ4ivLy9ZLFzvZKRsYCkQ4uOjGz6I29ElLp3U8ePH6dGjB6dPny71rjciFaW4uJg1a9Ywc+ZMAgMD\nWbRoER06dLjhe5KTk1keHc2/N2xgpMVCUH6+/X7EST/fj/jOO+6gWbt2fPrpp5Xyc4g4ChWxE2vd\nujUbN27E39/fdBRxE3FxcURGRuLp6cnSpUsJDQ29qfdnZWURa7WSkZpKXk4ONevWxS8ggMfCw6le\nvTpdunRh6dKl3HvvvRX0E4g4HhWxExs9ejTBwcE8+eSTpqOIi0tLS2P69Ons37+f6Oho7r///gqZ\nxOzYsYP777+f1NRU6tevX+6fL+KItI/YiWk/sVS0kydPMm7cOAYNGsTvfvc7Dhw4wAMPPFBhu0P6\n9+/PAw88wKRJkyrk80UckYrYiYWFhREfH4+GGlLe8vLymD17NgEBAdSrV4/09HQmT56Ml5dXhX/3\nwoULSU5OZv369RX+XSKOQEXsxNq2bUtxcTGZmZmmo4iLuHz5MitXrsTPz4/MzEy++uorFi9eTJ06\ndSotg6+vL6tWrSIiIqJM9z0WcXYqYidmsVg0npZyYbPZ+PDDDwkICGDdunVs2LCB2NhYWrRoYSRP\nv379ePDBBzWiFregInZyKmK5Xbt37yY0NJTZs2ezfPlyNm/eTLdu3UzHYsGCBXz55Zf861//Mh1F\npEKpiJ2cilhu1cGDBxk1ahSjRo1i7NixfPXVVwwdOtRhzkv39fXFarVqRC0uT0Xs5Dp27Eh2djYn\nT540HUWcxNmzZ5k8eTJ9+vShW7dupKenM2bMGDw9PU1Hu0ZwcDAPP/wwTz/9tOkoIhVGRezkPDw8\nCAkJ0apYflN+fj6LFi3C39+f4uJiDhw4wIwZM/D19TUd7Ybmz5/P119/zdq1a01HEakQKmIXoPG0\n3EhRURGrV6+mffv2JCcn88UXX7BixQqnucWgj48Pq1atYtKkSWRlZZmOI1LudGUtF5CcnEx4eDjf\nfPON6SjiYD777DOmTZtG9erViYmJoW/fvqYj3bLIyEiOHj3K+++/bzqKSLlSEbuAwsJC6tevz6FD\nh2jQoIHpOOIA9u3bx7Rp0zhy5AiLFi1i5MiRDnMQ1q3Kz8+nW7duzJ8/n1GjRpmOI1JuNJp2AVWq\nVCE4OJgdO3aYjiKGHT9+nPDwcIYOHcqIESNIS0vjvvvuc/oShisjaqvVyqRJkzhz5ozpOCLlRkXs\nIrSf2L3l5uYSFRVF165dad68ORkZGURERFC1alXT0cpVnz59eOyxx4iIiDAdRaTcqIhdhIrYPV26\ndImXX34ZPz8/zpw5Q0pKCgsWLKBWrVqmo1WYefPm8c0332hfsbgM7SN2ERcvXqR+/fqcPHnSpX8J\nyxU2m421a9cSFRWFn58fixcvJiAgwHSsSrNnzx7+9Kc/kZKSQqNGjUzHEbktWhG7CC8vL4KCgti5\nc6fpKFLBduzYQd++fYmOjubVV19lw4YNblXCAL1792b06NE89dRTuvuYOD0VsQvReNq1paenc++9\n99qvNJWcnMzgwYNNxzJm7ty57N+/XyNqcXoqYheiInZNp0+f5qmnnqJ///7069eP9PR0HnnkETw8\n3PtfX29vb6xWK5MnT+b06dOm44jcMvf+N9nF9O3bl3379nHhwgXTUaQcnD9/nvnz59OpUye8vb35\n9ttviYyMxNvb23Q0h9GrVy/GjBnDxIkTNaIWp6UidiG+vr4EBgayZ88e01HkNhQWFvLPf/4TPz8/\n9u/fT2JiIi+++CL169c3Hc0hPf/886Snp7NmzRrTUURuiYrYxWg87bxsNhv/+c9/6Nq1K2+//TYf\nfvgh7733Hm3atDEdzaF5eXlhtVr5y1/+wvfff286jshNUxG7GBWxc/ryyy8ZPHgwkZGRREdHExcX\nR1BQkOlYTiMoKIjHH39cI2pxSipiF9OvXz8SExO5dOmS6ShSBpmZmTz88MPcc889PPjgg6SkpHDP\nPfe4xCUpK9ucOXP47rvveO+990xHEbkpKmIXU7t2be666y6Sk5NNR5EbyM7OZurUqfTo0QM/Pz8y\nMjIYP348VapUMR3Naf0yon722Wc1ohanoiJ2QRpPO66LFy+ybNky/P39+emnn0hLS2POnDnUqFHD\ndDSX0LNnT5544gkmTJigEbU4DRWxC1IRO57i4mLeffdd/P392b59O/Hx8fzjH/+gSZMmpqO5nNmz\nZ3Po0CHeffdd01FEykTXmnZBWVlZ3HXXXfzwww94enqajuP24uLiiIyMxMPDg6VLlxIWFmY6ksv7\n8ssvGTZsGF9//TVNmzY1HUfkhrQidkENGzbkjjvuYN++faajuLW0tDSGDx/O448/TmRkJHv27FEJ\nV5IePXowfvx4nnzySY2oxeGpiF2UxtPmnDx5knHjxjFw4ECGDBnCgQMHeOCBB3QkdCWbNWsWmZmZ\nvP3226ajiNyQithFqYgrX15eHrNnzyYgIIB69eqRkZHBX/7yF7y8vExHc0vVqlXDarUyZcoUTp48\naTqOyHWpiF1USEgI27dvp7i42HQUl3f58mVWrlyJn58fmZmZ7N27l8WLF1OnTh3T0dxe9+7dmTBh\ngkbU4tBUxC6qefPm1K5dmwMHDpiO4rJsNhsffvghAQEBrFu3jg0bNhAbG0vLli1NR5Or/O1vf+PY\nsWO89dZbpqOIlEpXD3Bhv4ynO3XqZDqKy9m9ezeRkZHk5uby97//naFDh2ofsIP6ZUQ9dOhQhgwZ\nQrNmzUxHEilBK2IXpv3E5e/QoUPcf//9/PnPf2bs2LF89dVX/OEPf1AJO7hu3boxceJExo8frxG1\nOBwVsQsLCwtj+/bt+sVTDs6ePcvkyZPp3bs3Xbt2JSMjgzFjxug8bScyc+ZMTpw4QWxsrOkoIiWo\niF1Y69atsVgsHD582HQUp5Wfn8+iRYvo0KEDxcXF7N+/nxkzZuDr62s6mtykX0bUkZGR/Pe//zUd\nR8RORezCLBaLxtO3qKioiNWrV9O+fXuSk5PZuXMnK1asoFGjRqajyW3o2rUrERERGlGLQ1ERuzgV\n8c3bvHkzPXr04NVXX2XNmjWsXbsWPz8/07GknMyYMYOTJ0+yevVq01FEAF1r2uXt37+f4cOHazxd\nBvv27WPatGkcOXKERYsWMXLkSB2E5aL27dvHkCFD+Oqrr2jevLnpOOLmtCJ2cR06dCAvL4/jx4+b\njuKwjh8/Tnh4OEOHDmXEiBGkpaVx3333qYRdWJcuXZg0aRLjxo3TiFqMUxG7OIvFQkhICAkJCZw4\ncUK/dK6Sm5tLVFQUXbt2pXnz5mRkZBAREUHVqlVNR5NKEBUVxenTp1m1apXpKOLmVMQu7p133uH4\n8eNMmDCBO++8UyNq4NKlS7z88sv4+flx5swZ9u3bx4IFC6hVq5bpaFKJqlatitVqZfr06ZoYiVEq\nYhe3atUqkpOTycvLAyA+Pt5wInNsNhtr166lU6dObNy4kS1btvDGG29oH6EbCwwM5JlnntGIWoxS\nEbu40NDQEo/d9QjqHTt2EBwczAsvvMDKlSvZuHEjAQEBpmOJA3juuefIysrizTffNB1F3JSOmnZx\n27ZtY+DAgfbHrVu3dqvxdHp6Os899xx79+5l4cKFPPTQQ3h46L8/paTU1FQGDRrE3r17ufPOO03H\nETej30gurnfv3iUOPjpy5Ihb7A87ffo0Tz31FP379yc4OJj09HQeeeQRlbCUKiAggMmTJ2tELUbo\nt5KL8/HxoVevXiW2JSQkGEpT8c6fP8+CBQvo1KkTXl5efPvtt0RGRuLt7W06mji46dOnk5WVxRtv\nvGE6irgZFbEbCAsLK/HYFfcTFxUV8cYbb9C+fXvS0tJITEzkpZdeon79+qajiZOoWrUqq1evJioq\nimPHjpmOI25ERewGXPmALZvNxoYNG+jSpQuxsbH861//4r333qNNmzamo4kT6ty5M88++yxPPPGE\nRtRSaXSwlhvIy8ujTp06FBcX27edPn3a6W9g8OWXXxIZGcmpU6dYsmQJw4cP19Ww5LYVFhbSt29f\nxo0bx/jx403HETegFbEbqFmzJt27dy+xbceOHYbS3L7MzEwefvhh7rnnHh544AFSU1O55557VMJS\nLqpUqYLVamXmzJkcPXrUdBxxAypiN/Hr8bQzXtgjJyeHyMhIevbsiZ+fHxkZGTz55JNUqVLFdDRx\nMZ06deKvf/2rRtRSKVTEbsLZ9hOfO3eOWbNmMXbsWC5evMiyZcto3749586dIzU1lTlz5lCjRg3T\nMcWFRUZGkpuby2uvvWY6irg47SN2Ez/88AMNGjSwP7ZYLGRnZ1OnTh2Dqa51+fJlXn/9dZ5//nmy\nsrIAaNq0KT179mTx4sV06NDBcEJxJ/v37ycsLIykpCRatWplOo64KK2I3UT9+vXp3Lmz/bHNZmPn\nzp0GE5Vks9lYv349nTt3JiIiwl7CAA0bNuSjjz5SCUul69ixI1OmTNGIWiqUitiNOOp4+osvviAk\nJIT77ruPjIyMa57//vvv3eJqYOKYpk6dSl5eHq+++qrpKOKiVMRuxNEu7PHdd9/x5z//meDg4FJX\n576+vsyePZuDBw/SokULAwlFrhxFvWrVKmbNmkVmZqbpOOKCtI/YjZw6dYpmzZrZH1epUoUff/yR\n6tWrV2qOrKws5s+fz8qVKyksLLzmeQ8PDx5//HGef/75EnlFTFqyZAmbNm1i8+bNuma5lCv9bXIj\nTZs25a677rI/LiwsZPfu3ZX2/fn5+URHR9OuXTtWrFhRagkPHz6clJQUXnvtNZWwOJQpU6Zw/vx5\njail3KmI3YyJ84mLioqwWq34+fkxY8YMzp07d81revToweeff84nn3xCp06dKjyTyM3y9PTEarUy\na9Ysjhw5YjqOuBAVsZup7AO2Nm3aRPfu3RkzZgwnTpy45vlWrVrx7rvvkpiYWOK+ySKOyN/fn+nT\npzN27NgSl4wVuR3aR+xmMjMzad26tf2xl5cXubm5eHl5lev3fP3110ybNo3NmzeX+nzdunX529/+\nRkRERLl/t0hFKioqon///jzyyCNERESYjiMuQEXsZmw2Gy1btixxOlBCQgL9+/cvl88/duwYs2bN\n4q233ir1vMtq1arxzDPPMGPGDOrWrVsu3ylS2b799lv69+9PYmKi7vQlt02jaTdjsVgqZDz9448/\n8txzz+Hn50dsbGypJfzQQw+Rnp7O0qVLVcLi1Pz9/Xnuuec0opZyoSJ2Q+V5PvGlS5dYvnw57dq1\nY/HixVy8ePGa1wwcOJDk5GTeeecdXSZQXMazzz7LpUuX+N///V/TUcTJaTTthtLT0/H397c/rlGj\nBjk5OTd1FyObzcYHH3xAVFQUhw8fLvU1nTp1YsmSJdx99926RaG4pPT0dPr168eePXto27at6Tji\npFTEbshms9GkSRPOnDmDBfAGBvTvT/OWLfELDGT0mDE0bNjwuu9PSEhg6tSpJCYmlvp806ZNmT9/\nPqNHj9YtCsXlLVu2jI8//pi4uDhd6ENuiYrYDSUlJfHQvfdy4uRJRgKhQE0gD0j08WG9zcYf776b\nyVFRBAUF2d/37bff8txzz/HRRx+V+rk1atRg2rRp/PWvf630q3WJmFJUVERoaCgPPvggkyZNMh1H\nnJCK2M28tnIlc6ZOZVp+PuE2G6UdMpUDWC0Wlvj4MDcmhhEjRzJ37lxef/11ioqKrnm9p6cn48eP\nZ86cOTRu3LjCfwYRR5ORkUFwcLBG1HJLVMRu5LWVK1k8dSqbLlygXRlefxAYVLUqWRYLBZculfqa\ne++9l0WLFtG+fftyzSribF566SXWr1/Ptm3bNKKWm6K/LW4iKSmJOb8q4UvAE0AroDbQHfj0qve0\nAz6/fJlqpZRwnz59SEhIYP369SphEeCZZ56huLiYFStWmI4iTkZF7CaWR0czPT+/xEq4EGgBJAC5\nwHzgfuDz7A+HAAANaUlEQVTYVa9pB8wCfH5+3LZtWz744AN27dpVbhcBEXEFnp6erFq1ivnz5/Pd\nd9+ZjiNORKNpN3DmzBnat2zJ4YKCUvcJX60L8Dww8qpt2UBz4G8LFzJ16lSqVatWQUlFnN/f//53\n1q1bR3x8vEbUUib6W+IGYq1WRsJvlvBp4Dvg1/c+qgc84O2NV9WqKmGR3/DMM88A8PLLLxtOIs5C\nRewGMlJS6FVQcMPXFAKPAOGAXynP9yooICM1tfzDibgYDw8PVq1axYIFCzSiljJREbuBn3JzqXmD\n521cKWEv4HqHmdQE8nJyyjuaiEtq164ds2bNYsyYMaWe8idyNRWxG6hRuzZ5N3j+ceAs8C/A8zqv\nyQNq6kYNImU2adIkPDw8NKKW36QidgN+gYEkenuX+twE4FvgY+BGe3+TfHzwCwiogHQirsnDw4M3\n33yThQsXkpGRYTqOODAdNe0GrnfU9DGunEPszf9bCVuAV4H/76rXZQNtvb3JOHbshtegFpFrrVix\ngjVr1rB9+3Y8Pa83cxJ3phWxG2jUqBF/vPtuVv/qDkgtgGLgAldGz3nAOUqWMMBqi4Xhw4aphEVu\nQUREBFWrVmX58uWmo4iD0orYTSQlJTFiwAASynh5y18cBEJ8ffkkPp6ePXtWVDwRl3b48GF69erF\nzp07dSU6uYZWxG4iKCiIuTExDPX15WAZ33MQGOrry9yYGJWwyG1o06YNzz//vI6illKpiN3I+IkT\nmR4TQ4ivLy9ZLFzvZKRs4EWLhRBfX6bHxDB+4sTKjCnikp566im8vLx46aWXTEcRB6PRtBtKTk5m\neXQ0/96wgZEWC0H5+fb7ESf9fD/i4cOGMTkqSithkXL0y4h6x44d+Pv7m44jDkJF7MaysrKItVrJ\nSE0lLyeHmnXr4hcQwGPh4TowS6SCvPLKK7z99tvs2LFDR1ELoCIWEalUxcXFDB48mGHDhhEZGWk6\njjgAFbGISCU7cuQIQUFBJCQk0KFDB9NxxDAdrCUiUslat27NvHnzdBS1ACpiEREjJkyYQPXq1Vm2\nbJnpKGKYRtMiIoZkZmYSFBREfHw8HTt2NB1HDNGKWETEkFatWjF//nzCw8MpLCw0HUcMURGLiBj0\n5JNPUqtWLWJiYkxHEUM0mhYRMezo0aP07NmTbdu20alTJ9NxpJJpRSwiYljLli1ZsGCBRtRuSkUs\nIuIAxo8fT506dVi6dKnpKFLJNJoWEXEQv4yo4+Li6Ny5s+k4Ukm0IhYRcRAtW7Zk4cKFjBkzRiNq\nN6IiFhFxIOPGjaNu3bosWbLEdBSpJBpNi4g4mGPHjtGjRw+NqN2EVsQiIg6mRYsWREdHEx4ezuXL\nl03HkQqmIhYRcUCPP/44DRo00IjaDWg0LSLioI4fP0737t3ZunUrgYGBpuNIBdGKWETEQd15550s\nWrRII2oXpyIWEXFgY8eOpXHjxixatMh0FKkgGk2LiDi4EydO0K1bN42oXZRWxCIiDq558+YsXrxY\nI2oXpSIWEXECY8aMoUmTJkRHR5uOIuVMo2kRESfxy4h6y5YtdOnSxXQcKSdaEYuIOInmzZuzZMkS\njahdjIpYRMSJhIeH06xZM1544QXTUaScaDQtIuJk/vvf/9KtWzc+++wzunbtajqO3CatiEVEnMwd\nd9zB0qVLGT16NJcuXTIdR26TilhExAk99thj3HnnnSxcuNB0FLlNGk2LiDipkydP0rVrVzZt2kS3\nbt1Mx5FbpBWxiIiTatasGTExMYSHh2tE7cRUxCIiTuzRRx+lRYsWLFiwwHQUuUUaTYuIOLlfRtSf\nfvop3bt3Nx1HbpJWxCIiTq5Zs2YsW7ZMI2onpSIWEXEBjzzyCK1atWL+/Pmmo8hN0mhaRMRFnDp1\niq5du7JhwwZ69OhhOo6UkVbEIiIuomnTprz44ouEh4dz8eJF03GkjLQiFhFxITabjZEjR9KpUydd\n7MNJaEUsIuJCLBYL//jHP/jnP//JunXr+NOf/kRWVpbpWHIDKmIRERfTsGFDfve73zFq1Cg+/vhj\nnn76adOR5AZUxCIiLsZqtfLOO+/wy57H999/n7Vr1xpOJdejfcQiIi7m8uXL9OnTh71799q3NWzY\nkLS0NBo2bGgwmZRGK2IRERdTtWpVrFYrVatWtW/LysoiIiLCYCq5HhWxiIgLCggIYM6cOSW2ffDB\nB3zwwQeGEsn1aDQtIuKiCgsL6dOnD19++aV9W4MGDUhLS6NRo0YGk8nVtCIWEXFRVapUwWq1Uq1a\nNfu2s2fPakTtYFTEIiIurHPnzteMqNeuXcv7779vKJH8mkbTIiIurrCwkL59+5KcnGzfphG149CK\nWETExV1vRP3UU0+htZh5KmIRETfQqVMnnn/++RLb1q1bx//93/+ZCSR2Gk2LiLiJwsJCgoODSUpK\nsm+rX78+aWlpNG7c2GAy96YVsYiImyhtRP3DDz8wceJEjagNUhGLiLiRjh07Mm/evBLb1q9fz5o1\nawwlEo2mRUTcTGFhIf369SMxMdG+rV69eqSlpdGkSRODydyTVsQiIm7mlxG1l5eXfVt2drZG1Iao\niEVE3FCHDh2uGVF/+OGHvPfee4YSuS+NpkVE3FRRURH9+vVjz5499m0aUVc+rYhFRNyUp6dnqSPq\nCRMmaERdiVTEIiJuzN/fn/nz55fY9tFHH/Huu+8aSuR+NJoWEXFzRUVF9O/fn927d9u31a1bl7S0\nNJo2bWowmXvQilhExM15enqyatWqEiPqnJwcnnzySY2oK4GKWERE8Pf3Z+HChSW2ffLJJ7z99tuG\nErkPjaZFRAS4MqIODQ1l165d9m116tQhLS2NZs2aGUzm2rQiFhER4P+NqL29ve3bfvzxR42oK5iK\nWERE7Pz8/K4ZUf/73//mrbfeMpTI9Wk0LSIiJRQVFREWFsbOnTvt2zSirjhaEYuISAmenp68+eab\n14yox48frxF1BVARi4jINfz8/HjhhRdKbPvPf/5DbGysoUSuS6NpEREpVWkj6tq1a5OWlsYdd9xh\nMJlr0YpYRERK9ctR1D4+PvZtubm5jBs3TiPqcqQiFhGR67rrrruuGVFv3LgRq9VqJpAL0mhaRERu\nqLi4mAEDBpCQkGDfVqtWLdLS0mjevLnBZK5BK2IREbkhDw8P3nzzzRIj6nPnzmlEXU5UxCIi8pva\ntWvHokWLSmz79NNPWbVqlaFErkOjaRERKZPi4mIGDhzI9u3b7dtq1arFN998w5133mkwmXNTEYuI\nSJkdOnSIwMBALly4YN82dOhQVq9ezVurV5ORksJPubnUqF0bv8BARo8ZQ8OGDQ0mdnwqYhERuSkr\nVqzgmWeesT/2BTyrVGFUlSoEFRRQE8gDEn18WG+z8ce772ZyVBRBQUGmIjs0FbGIiNyU4uJiBg0a\nxPb4eGoCs4GxQN1SXpsDWC0Wlvj4MDcmhvETJ1ZqVmegg7VEROSmeHh48LvBg2kMfAlMofQS5uft\nz9psJFy4wOKpU3lt5cpKy+kstCIWEZGbkpSUxIgBA0i4cIF2V21/FNgCXAAacGWVPPOq5w8CIb6+\nfBIfT8+ePSsvsIPTilhERG7K8uhopufnlyhhgCjgCJALbARWAJuuer4dMC0/n+XR0ZUT1EloRSwi\nImV25swZ2rdsyeGCguuOowHSgSHAR0D3q7ZnA229vck4dkxHU/9MK2IRESmzWKuVkVx/n3AEUB3o\nzJWxdPdfPV8PGGmxEKtrVdupiEVEpMwyUlLoVVBw3edfAX7iyr7ivwFJpbwmKD+fjNTUignohFTE\nIiJSZj/l5lLzN15jAcKAUcB7pTxfE8jLySnvaE5LRSwiImVWo3Zt8sr42kKuXOzj1/KAmnVvtIfZ\nvaiIRUSkzPwCA0n09r5mexbwf8B5oJgrR0t/APyplM9I8vHBLyCgImM6FR01LSIiZXa9o6bPAn8G\nUgAbcBcwC7jnV+/XUdPX0opYRETKrFGjRvzx7rtZbbGU2N4A2MaVos0BErm2hAFWWywMHzZMJXwV\nrYhFROSmXO/KWr9FV9YqnVbEIiJyU4KCgpgbE8NQX18OlvE9B4Ghvr7MjYlRCf+KilhERG7a+IkT\nmR4TQ4ivLy9ZLFzvZKRs4EWLhRBfX6br7kul0mhaRERuWXJyMsujo/n3hg2MtFgIys+334846ef7\nEQ8fNozJUVFaCV+HilhERG5bVlYWsVYrGamp5OXkULNuXfwCAngsPFwHZv0GFbGIiIhB2kcsIiJi\nkIpYRETEIBWxiIiIQSpiERERg1TEIiIiBqmIRUREDFIRi4iIGKQiFhERMUhFLCIiYpCKWERExCAV\nsYiIiEEqYhEREYNUxCIiIgapiEVERAxSEYuIiBikIhYRETFIRSwiImKQilhERMQgFbGIiIhBKmIR\nERGDVMQiIiIGqYhFREQMUhGLiIgYpCIWERExSEUsIiJikIpYRETEIBWxiIiIQSpiERERg1TEIiIi\nBqmIRUREDFIRi4iIGKQiFhERMUhFLCIiYpCKWERExCAVsYiIiEEqYhEREYNUxCIiIgapiEVERAxS\nEYuIiBikIhYRETFIRSwiImKQilhERMSg/x9X1mG+8y80QgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import networkx as nx\n",
"Gd = nx.DiGraph()\n",
"for i, j in [(1, 2), (1, 4), (4, 2), (4, 3)]:\n",
" Gd.add_edge(i,j)\n",
"nx.draw(Gd, with_labels = True)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# CHOOSING A PROPER REPRESENTATION\n",
"\n",
"The choice of the proper network representation determines our ability to use network theory successfully.\n",
"\n",
"In some cases there is a unique, unambiguous representation. \n",
"In other cases, the representation is by no means unique.\n",
" \n",
"For example, the way we assign the links between a group of individuals will determine the nature of the question we can study.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"If you connect individuals that work with each other, you will explore the professional network.\n",
"\n",
"http://www.theyrule.net"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"If you connect those that have a romantic and sexual relationship, you will be exploring the sexual networks.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"If you connect individuals based on their first name (all Peters connected to each other), you will be exploring what? \n",
"\n",
"# It is a network, nevertheless.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# UNDIRECTED VS. DIRECTED NETWORKS\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Undirected\n",
"Links: undirected\n",
"- coauthorship \n",
"- actor network\n",
"- protein interactions"
]
},
{
"cell_type": "code",
"execution_count": 174,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8jWfi///3sWZppNZq7VuoiSifhEQYSxwtLR1MVami\n1cV00SVIPv11WjOjifKp6rSfzPCZaUqULkopGU0EERGNNWFobGN9WEoQTVKS3N8/6PmphiLLdZbX\n8/HwUOfcOed9HjTvXNd93fdlsyzLEgAAMKKK6QAAAHgyihgAAIMoYgAADKKIAQAwiCIGAMAgihgA\nAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIG\nAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKI\nAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMo\nYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKpmOgAAwDmdPHlSc+PjlZOVpQvnzukOf38FBAVp9Nix\nql+/vul4bsNmWZZlOgQAwHlkZmZqVkyMlicmaoikkMJC+UnKk/Stt7cWW5Ye7N9fE6KjFRISYjit\n66OIAQAOs+Pi9GZkpCYXFGi0Zal2KcfkSoq32fSOt7emzJihZ8aPr+yYboUiBgBIulzC0yIjtTI/\nX61v4vi9ku738dFkyrhMKGIAgDIzMzWoVy+tu6aER0lKlpQvqZ6kJyW9ftXzeyX18PHRsrVrFRwc\nXHmB3QirpgEAmhUTo8kFBb8YCUdLOiDpnKRESX+VtPKq51tLmlRQoFkxMZUT1A0xIgYAD3fy5Em1\nbdZM+wsLSz0n/JPvJPWV9JWkzlc9fkZSKy8v5Rw6xGrq28CIGAA83Nz4eA2WrlvCz0vylRSoy9PS\nna95vo6kwTab5sbHV1hGd0YRA4CHy8nKUpfCwus+/6GkC7p8rvj/k5RZyjEhBQXKyc6umIBujiIG\nAA934dw5+f3KMTZJPSU9ImlBKc/7ScrLzS3vaB6BIgYAD3eHv7/ybvLYIkk+pTyeJ8mv9o3OMON6\nKGIA8HABQUH61svrF4+fkvSppB8klejyaunPJT1cymtkensroEOHiozptlg1DQAe7nqrpr+X9HtJ\nWZIsSW0kvSFp4DVfz6rpsmFEDAAerkGDBnqwf3/F22w/e7yepDW6XLS5kr7VL0tYkj622fTQgAGU\n8G2iiAEACouI0BTL0t5b/Lq9kt7x9taE6OiKiOURKGIA8HBz5szRn//8Z417+WXd7+Nz02X8072m\np8yYwe0ty4D9iAHAQxUXF2vSpEn6+uuvtW7dOrVp00YBAQHqERmpSQUFGnOd3ZfO6PLuS9PZfalc\nsFgLADxQXl6eRowYofz8fH3xxReqfdWlR5s2bdKsmBh9vWKFBttsCikocOxHnHllP+KHBgzQhOho\nRsLlgCIGAA9z6NAhDRw4UKGhofrggw9UvXr1Uo87deqU5sbHKyc7W3m5ufKrXVsBHTroiTFjWJhV\njihiAPAgGzdu1JAhQxQZGamXX35ZtmtWSqPycY4YADzEp59+qhdeeEH//Oc/NXBgaRciwQSKGADc\nnGVZ+vOf/6x//OMfWrVqlYKCgkxHwlUoYgBwY4WFhXryySe1b98+bdy4UQ0bNjQdCdfgOmIAcFMn\nTpxQnz59VFJSojVr1lDCTooiBgA3tGPHDoWGhqpfv35asGCBvL29TUfCdTA1DQBuZsWKFRozZoze\ne+89jRgxwnQc/AqKGADchGVZev/99zVt2jR99dVXCgsLMx0JN4EiBgA3cOnSJb300ktKS0tTenq6\nmjdvbjoSbhJFDAAu7uzZs3rkkUdUvXp1rV+/XrVq1TIdCbeAxVoA4ML27dunsLAw/eY3v9HSpUsp\nYRdEEQOAi0pNTVV4eLgmTJig9957T9WqMcnpivhbAwAXFB8fr8mTJ2v+/Pnq27ev6TgoA4oYAFxI\nSUmJXn/9dX3++edau3at2rVrZzoSyogiBgAX8cMPP2jUqFH6/vvvlZGRoXr16pmOhHLAOWIAcAFH\njx5Vjx495O/vr6SkJErYjVDEAODkNm/erNDQUD366KP65z//qZo1a5qOhHLE1DQAOLEvv/xSzz77\nrGbPnq3BgwebjoMKQBEDgBOyLEvTpk3Thx9+qJUrV6pz586mI6GCUMQA4GR+/PFHPfvss8rOzlZG\nRoYaNWpkOhIqEOeIAcCJfP/997Lb7crLy1Nqaiol7AEoYgBwErt27VLXrl3VvXt3ff755/L19TUd\nCZWAqWkAcAJJSUkaOXKkpk+frtGjR5uOg0rEiBgADIuLi9OoUaO0aNEiStgDMSIGAEOKior02muv\n6ZtvvtH69evVqlUr05FgAEUMAAacP39ew4cPV1FRkTZs2KA777zTdCQYwtQ0AFSy//znP+rWrZua\nN2+uFStWUMIejiIGgEqUnp6ubt266dlnn9WHH37IHsJgahoAKsv8+fP1yiuv6OOPP1b//v1Nx4GT\noIgBoIKVlJTorbfe0rx585SSkqLAwEDTkeBEKGIAqEAFBQUaM2aMDh8+rI0bN6pBgwamI8HJcI4Y\nACrI8ePH1atXL1WrVk0pKSmUMEpFEQNABdi+fbu6du2qgQMHKiEhQV5eXqYjwUkxNQ0A5WzZsmV6\n6qmn9MEHH2jYsGGm48DJUcQAUE4sy9LMmTP1P//zP/r666/VpUsX05HgAihiACgHly5d0vPPP6+N\nGzdqw4YNatq0qelIcBEUMQCU0ZkzZ/TII4/I19dXaWlp8vPzMx0JLoTFWgBQBjk5OQoNDVWnTp20\nePFiShi3jCIGgNu0evVq9ejRQxMnTtSMGTNUtWpV05HggpiaBoDb8H//9396/fXXtXDhQvXu3dt0\nHLgwihgAbkFxcbGioqL01Vdfad26dQoICDAdCS6OIgaAm3ThwgWNHDlSeXl5ysjIUJ06dUxHghvg\nHDEA3ITDhw+re/fuql+/vv71r39Rwig3FDEA/IrMzEyFhYVp1KhRmjNnjmrUqGE6EtwIU9MAcAOf\nffaZnn/+ef3jH//QoEGDTMeBG6KIAaAUlmVp6tSpmj17tpKSknTfffeZjgQ3RREDwDUKCws1btw4\n5eTkaOPGjbr77rtNR4Ib4xwxAFzl5MmTioiI0MWLF7V27VpKGBWOIgaAK3bu3KnQ0FBFRERo4cKF\n8vb2Nh0JHoCpaQCQ9K9//UtPPPGEZs6cqZEjR5qOAw9CEQPweB988IGmTp2qxYsXKzw83HQceBiK\nGIDHKioq0oQJE7RmzRqlp6erRYsWpiPBA1HEADzS2bNn9eijj6pKlSpKT0+Xv7+/6UjwUCzWAuBx\n9u/fr27duqldu3ZatmwZJQyjKGIAHiUtLU3h4eF64YUXNGvWLFWrxsQgzOJfIACPMXfuXEVGRioh\nIUH9+vUzHQeQRBED8AAlJSV64403tHDhQq1Zs0bt27c3HQlwoIgBuLX8/Hw98cQTOnHihDIyMlS/\nfn3TkYCf4RwxALd17Ngx/fa3v5Wvr6+Sk5MpYTglihiAW9qyZYu6du2qoUOHKj4+XjVr1jQdCSgV\nU9MA3M6SJUv09NNP629/+5uGDh1qOg5wQxQxALdhWZamT5+u999/X4mJiQoODjYdCfhVFDEAt3Dx\n4kU999xz2rZtmzIyMtS4cWPTkYCbQhEDcHmnT5/WkCFDVKdOHa1bt06+vr6mIwE3jcVaAFza7t27\nFRoaqrCwMC1atIgShsuhiAG4rOTkZPXs2VP//d//rdjYWFWpwrc0uB7+1QJwSX//+9/1+OOP67PP\nPtPYsWNNxwFuG+eIAbiU4uJiRUZGKjExUWlpaWrdurXpSECZUMQAXEZeXp4ee+wxFRYWasOGDapd\nu7bpSECZMTUNwCUcPHhQ4eHhaty4sRITEylhuA2KGIDTy8jIUFhYmJ566inFxcWpevXqpiMB5Yap\naQBObeHChXrppZf00Ucf6cEHHzQdByh3FDEAp2RZlqZMmaL4+HitWrVKHTp0MB0JqBAUMQCnU1BQ\noCeffFL/+c9/tHHjRt11112mIwEVhnPEAJzK8ePH1bt3b0lSSkoKJQy3RxEDcBpZWVkKDQ1V//79\n9cknn8jb29t0JKDCMTUNwCksX75cY8eO1fvvv6/hw4ebjgNUGooYQLk7efKk5sbHKycrSxfOndMd\n/v4KCArS6LFjVb9+/Z8da1mWZs2apXfeeUdLly5VaGioodSAGTbLsizTIQC4h8zMTM2KidHyxEQN\nkRRSWCg/SXmSvvX21mLL0oP9+2tCdLRCQkJ06dIlvfjii0pPT9eyZcvUrFkzw58AqHwUMYByMTsu\nTm9GRmpyQYFGW5ZKu+9VrqR4m03veHtr0p/+pOWJifLy8tKCBQvk5+dX2ZEBp0ARAyiz2XFxmhYZ\nqZX5+bqZLRj2SvqtzabA3r2V+M03qlq1akVHBJwWq6YBlElmZqbevEEJ75HkLemJqx5rLSnVspSd\nkaGtW7dWSk7AWVHEAMpkVkyMJhcUXHck/IKkLqU83lrSpIICzYqJqbhwgAtgahrAbTt58qTaNmum\n/YWFpZ4TXihpiaT2ujwdPfea589IauXlpZxDh36xmhrwFIyIAdy2ufHxGiyVWsLnJb0p6V1J1/tp\nv46kwTab5sbHV0xAwAVQxABuW05WlroUFpb63B8lPS3pnl95jZCCAuVkZ5d3NMBlcEMPALftwrlz\nKu2io22Skq/8/mv8JOXl5pZrLsCVUMQAbpuPn5/ySnl8raSDkprq8rT0BUnFkv4tadM1x+ZJ8qtd\n2uQ24BkoYgA3zbIs7d69W0lJSUpKSlJyUpLybTY9d82az2clPXbVn6frcjH/rZTXzPT21m/Yaxge\njFXTAG7oxIkTSk5Ovly8ycmqWrWq7Ha77Ha7goKC1K1z5+uumv7JFEn7xKppoDQUMYCfyc/PV2pq\nqqN8Dx06pF69ejnKt3Xr1rLZbI7jHx8yRMFLlujl2/hWMtNm05bBgzVv0aLy/AiAS6GIAQ9XXFys\nrVu3OqabMzMz1alTJ0fxBgcHq1q165/FyszM1KBevbTuJm9v+ZO9knr4+GjZ2rUKDg4u8+cAXBVF\nDHigAwcOOIo3JSVFDRs2VN++fWW329WzZ89b3oDhdu41fb+PjybPmKFnxo+/rc8AuAuKGPAAubm5\nSklJcZznvXDhgqN4+/btq0aNGpX5PX7afWliQYHGXmf3pTO6vPvSdG9vTaGEAUkUMeCWLl68qPT0\ndMd53l27dik8PNwx3RwYGPiz87zlZdOmTXpy+HAdOHhQj1SvrpCCAsd+xJlX9iN+aMAATYiOZjoa\nuIIiBtyAZVnauXOnY7o5LS1N7dq1c4x4u3Xrppo1a1Z4jkuXLqlx48ZaunSp0lJTlZOdrbzcXPnV\nrq2ADh30xJgxrI4GrkERAy7q2LFjP7usyNvb2zHi7dOnj+rUqVPpmZYvX66pU6cqPT290t8bcFXc\n0ANwERcuXNDatWsd5Xvs2DH16dNHdrtdU6ZMUcuWLU1HVEJCgh5//HHTMQCXwogYcFJFRUXavHmz\nY7p5y5YtCg4Odkw3/9d//ZeqVq1qOqbD+fPn1aRJE+3fv19169Y1HQdwGYyIASdhWZb27dvnKN7V\nq1erSZMm6tu3r6KiovTb3/5Wvr6+pmNe15dffqlevXpRwsAtoogBg06fPq1Vq1Y5ppt//PFH2e12\nDRkyRP/7v/+rhg0bmo540+bNm6fxXI4E3DKmpoFKVFhYqPT0dMeod8+ePerRo4djkdW9995bIZcV\nVbQjR44oKChIx44dk5eXl+k4gEthRAxUoJKSEmVnZzuKNz09XYGBgbLb7Xr33XcVGhqqGjVqmI5Z\nZgsWLNDQoUMpYeA2MCIGytmRI0cclxQlJyerVq1ajhFv7969deedd5qOWO6CgoL017/+VT179jQd\nBXA5FDFQRufPn9fatWsdo95Tp04pIiLCsbq5efPmpiNWqKysLA0cOFAHDhxQlSpVTMcBXA5T08At\nKioq0rfffuso3u3bt6tr166y2+1KSEhQp06dPKqQ5s2bp5EjR3rUZwbKEyNi4FdYlqWcnBxH8a5d\nu1bNmzd3TDd3795dPj4+pmMaUVxcrKZNmyopKUnt27c3HQdwSYyIgVKcOnXKcY43KSlJlmXJbrdr\n+PDhmjNnjho0aGA6olNYvXq1GjZsSAkDZUARA5IKCgqUlpbmGPUeOHBAPXv2lN1u16RJkxQQEOCS\nlxVVNG5pCZQdU9PwSCUlJdq2bZujeDdu3KiOHTs69ujt0qWLqlevbjqmU8vPz1ejRo20a9cul7rx\nCOBsGBHDYxw8eNBxWdGqVatUt25d2e12vfTSS+rVq5dq1aplOqJL+eqrr9S1a1dKGCgjihhu6+zZ\ns1qzZo1j1Hv27Fn17dtX999/v6ZPn64mTZqYjujS5s2bp1GjRpmOAbg8pqbhNi5duqSMjAxH8e7Y\nsUPdunVzXM8bFBTEJTbl5MSJE2rbtq2OHj3q1BtRAK6AETFclmVZ2rVrl2O6OTU1Va1bt5bdbtdf\n/vIXhYeHc8vFCvLpp59q0KBBlDBQDhgRw6UcP35cq1atcpRvtWrVHNfz9unTR/Xq1TMd0SOEhIRo\n6tSp6tevn+kogMujiOHU8vPzlZqa6phuPnz4sHr37u2Ybm7dujWXFVWy3bt3q0+fPjp8+LCqVq1q\nOg7g8piahlMpLi7Wli1bHMWbmZmpzp07y263a/bs2QoODla1avyzNSkhIUGPPfYYJQyUE0bEMG7/\n/v2OqeaUlBQ1bNjQMd3cs2dP3XHHHaYj4oqSkhK1atVKixcv1n333Wc6DuAWGFqg0uXm5iolJcUx\n6s3Pz1ffvn01cOBAzZo1S/fcc4/piLiO9evXy9fXVx07djQdBXAbFDEq3I8//qgNGzY4inf37t0K\nDw+X3W7X888/r8DAQM7zuoiEhASNGjWKvy+gHDE1jXJnWZZ27NjhmG5OS0tTu3btHNPNYWFhqlmz\npumYuEWFhYVq1KiRtm3bxs1QgHLEiBjl4tixY46dipKTk+Xj4yO73a6nnnpKCQkJqlOnjumIKKMV\nK1aoY8eOlDBQzihi3JYLFy5o7dq1junm48ePq0+fPrLb7ZoyZYpatmxpOiLK2bx589hpCagATE3j\nphQVFWnTpk2OEe+WLVsUHBzsmG7u3Lkzl7O4sTNnzqhFixY6dOiQ/P39TccB3AojYhdw8uRJzY2P\nV05Wli6cO6c7/P0VEBSk0WPHqn79+hXynpZlae/evY7p5tWrV6tJkyay2+2Kjo5Wjx49uL2hB/n8\n88/1wAMPUMJABWBE7MQyMzM1KyZGyxMTNURSSGGh/CTlSfrW21uLLUsP9u+vCdHRCgkJKfP7nT59\n2nH7yKSkJF26dMkx4o2IiGC7Ow/WvXt3TZ48WQMHDjQdBXA7FLGTmh0XpzcjIzW5oECjLUu1Szkm\nV1K8zaZ3vL01ZcYMPTN+/C29R2FhodavX++Ybt6zZ4969OjhKN97772Xy1Sg/fv3q2vXrjp27Jiq\nV69uOg7gdpiadkKz4+I0LTJS6/Lz1foGx9WW9IplaWB+vu6PjJSkG5ZxSUmJsrKyHNPN6enpCgwM\nlN1u18yZM9W1a1fVqFGjfD8MXN78+fP16KOPUsJABWFE7GQyMzM1qFevn5XwRUl/kJSsy6PgVpLe\nlvTAVV+3V1IPHx8tW7tWwcHBjsePHDnimGpetWqV/P39HSPeXr166c4776ycDwaXZFmW2rVrp7lz\n56pr166m4wBuiRGxk5kVE6PJBQU/GwkXSWoqaZ2kJpKWSxomaceVxyWptaRJBQWa8ac/acS4cY7y\nPX36tCIiItS3b1/FxMSoWbNmlflx4OIyMzNlWZa6dOliOgrgthgRO5GTJ0+qbbNm2l9YWOo54at1\nlPSWpMFXPXZGUiNJIT166MEHH5Tdbtd9992nKlWqVFBiuLuXXnpJ9erV0x//+EfTUQC3xYjYicyN\nj9dg6VdL+ISkPZJ+c83jdSQN9/JS4MCBem3ixIqICA9y6dIlLVy4UBs2bDAdBXBrDJWcSE5WlroU\nFt7wmCJJj0saIymglOe7FBYqJzu7/MPB43zzzTdq06aNWrVqZToK4NYoYidy4dw5+d3geUuXS7im\npL9e5xg/SXm5ueUdDR6IW1oClYMidiJ3+Psr7wbPPyXpe0lfSrrezSTzJPnV/rXJbeDGzp8/r8TE\nRA0bNsx0FMDtUcROJCAoSN96eZX63HOSdktaKulGV/pmensroEOHCkgHT/Lll1+qd+/eqlu3ruko\ngNtj1bQTud6q6UOSmkvy0v8/ErZJ+rukx6467oykZtWqacu//602bdpURmS4qYiICI0fP16///3v\nTUcB3B4jYifSoEEDPdi/vz6+5raSTSWVSMrX5annPEnn9fMSli7f7rJJo0YKDQ3VxIkTdezYscqI\nDTdz5MgRbd26VQ899JDpKIBHoIidzIToaE3z9tbeW/y6vZKme3tr7hdfaNu2bSoqKlJgYKCefvpp\n5eTkVERUuKlPPvlEQ4cOldd1TpMAKF8UsZMJCQnRlBkzdL+Pz02X8V5J9/v4aMqMGQoODlaTJk00\nc+ZM7dmzR40bN1b37t31yCOPaNOmTRUZHW4iISFBo0aNMh0D8BgUsRN6Zvx4TZ4xQz18fDTTZtP1\nLkY6I+ldm009fHw0uZTdl+rWras333xTBw4cUPfu3TVkyBDZ7XatWrVKLA1AabZv365z586pe/fu\npqMAHoPFWk5s06ZNmhUTo69XrNBgm00hBQWO/Ygzr+xH/NCAAZoQHf2zjR6u5+LFi1qwYIGmTZsm\nX19fRUVF6Xe/+52qVr3exVDwNBMnTlSNGjU0depU01EAj0ERu4BTp05pbny8crKzlZebK7/atRXQ\noYOeGDNG9evXv+XXKykp0bJlyxQTE6Pc3FxNmjRJjz/+uGrWrFkB6eEqiouL1bRpUyUnJ+vee+81\nHQfwGBSxB7MsS6mpqYqNjVV2drZeeeUVPfPMM/Lzu9H9veCukpOTFRUVxVoCoJJxjtiD2Ww29ezZ\nU4mJiVq2bJk2bdqkli1b6o033tCpU6dMx0Ml45aWgBkUMSRJnTp10oIFC5SRkaHvv/9ebdu21Ysv\nvqiDBw+ajoZK8MMPP2jp0qV67LFrr04HUNEoYvxMq1atFBcXp507d8rX11edO3fWE088oR07dpiO\nhgq0dOlShYaG6q677jIdBfA4FDFKdffddys2Nlb79u1T+/btZbfbNWjQIKWnp5uOhgowb948rh0G\nDGGxFm5KQUGBPv74Y02fPl2NGjVSVFSU+vfvL9s1t+OE6zlx4oTatWunI0eOyNfX13QcwONQxLgl\nRUVF+uKLLxQbG6uSkhJFRUVp2LBhqlatmulouE2zZs3Sli1b9PHHH5uOAngkihi3xbIsrVy5UrGx\nsTp48KAmTpyosWPHytvb23Q03KKQkBC9/fbbstvtpqMAHolzxLgtNptNDzzwgNasWaNPPvlE33zz\njVq0aKG3335bZ8+eNR0PN2n37t06evSo+vTpYzoK4LEoYpRZWFiYlixZopSUFOXk5KhVq1aaNGkS\n2zC6gISEBI0YMYLbnAIGUcQoN+3bt1d8fLy2bt2qixcvKjAwUM8884z27NljOhpKUVJSooSEBG7i\nARhGEaPcNW3aVO+9955ycnJ0zz33qFu3bho2bJg2b95sOhqusn79evn5+aljx46mowAejSJGhalX\nr57eeustHThwQGFhYXr44YfVr18/rV69mm0YncBPt7TkEjTALFZNo9JcvHhR8+fP17Rp0+Tv76+o\nqCg9/PDDqlKFnwcrW2FhoRo1aqRt27apSZMmpuMAHo3vgKg0NWrU0NixY/Xvf/9bUVFRiomJUfv2\n7fXRRx/p4sWLpuN5lBUrVqhjx46UMOAEKGJUuipVqmjw4MHauHGj4uLitHDhQrVq1UozZ87UhQsX\nTMfzCNzSEnAeTE3DKWzZskXTpk1TSkqK/vCHP+jFF19UvXr1TMdyS2fOnFHLli116NAh1apVy3Qc\nwOMxIoZT6Ny5sz799FOlp6fr+PHjCggI0IQJE3To0CHT0dzOZ599pgceeIASBpwERQyn0qZNG/39\n73/Xzp075eXlpU6dOmn06NHauXOn6Whug2uHAedCEcMp3X333Zo2bZr27dundu3aKSIiQg8//LA2\nbNhgOppL279/v3JycnT//febjgLgCooYTu3OO+9UdHS0Dhw4oAceeEAjR45Uz549lZiYyLXIt2H+\n/Pl69NFHVb16ddNRAFzBYi24lKKiIn322WeKjY1VlSpVNHnyZD3yyCNsw3gTLMtS27ZtlZCQoC5d\nupiOA+AKRsRwKdWqVdOIESO0fft2vf3224qLi1Pbtm31t7/9TYWFhabjObXMzExJl7c9BOA8KGK4\nJJvNpgEDBig1NVVz587VihUr1KJFC8XGxurcuXOm4zklbmkJOCempuE2duzYoXfeeUfLly/X008/\nrZdfflkNGzY0HcspXLp0SY0aNVJGRoZatmxpOg6AqzAihtsIDAzU3LlztXnzZuXn56t9+/Z67rnn\ntHfvXtPRjFu5cqXatGlDCQNOiCKG22nevLnef/99fffdd2rQoIHCwsI0fPhwbd261XQ0YxISEril\nJeCkmJqG28vLy9OcOXP07rvvKjAwUFFRUerZs6fHnCs9f/68mjZtqn379qlu3bqm4wC4BiNiuD0/\nPz+9+uqr2rdvn4YNG6Znn31WYWFhWrJkiUpKSkzHq3CLFi1S7969KWHASTEihscpLi7WkiVLFBMT\nox9++EGTJ0/WiBEjVKNGDdPRKkRERIT+8Ic/aOjQoaajACgFRQyPZVmWUlJSFBsbq++++06vvvqq\nxo0bpzvuuMN0tHJz5MgRdezYUUePHpWXl5fpOABKwdQ0PJbNZlNERISSkpL05Zdfav369WrZsqXe\neustnT4x8lf9AAAGfklEQVR92nS8cvHJJ59o6NChlDDgxChiQFJwcLA+//xzpaWl6ejRo2rTpo1e\neeUVHT582HS022ZZlubNm8dqacDJUcTAVQICAjRnzhxlZ2erWrVquu+++zR27Fjt2rXLdLRblpWV\npby8PIWHh5uOAuAGKGKgFI0aNdL06dO1d+9etW7dWr169dLgwYO1ceNG09Fu2k+3tKxShf/NAWfG\nYi3gJuTn5+ujjz7S9OnT1aJFC0VFRalfv35Oey1ycXGxmjRpolWrVunee+81HQfADfCjMnATfHx8\n9Pzzz2vPnj0aN26cIiMj1blzZ3366acqLi42He8XUlJSdM8991DCgAtgRAzcBsuytGLFCsXExOj4\n8eOaOHGiRo8e7TSrk0ePHq3OnTtrwoQJpqMA+BUUMVBGaWlpio2N1ebNm/Xyyy/rueeek7+/v7E8\nP/zwgxo3bqzdu3frrrvuMpYDwM1hahooo+7du+vrr7/WypUrlZ2drZYtWyo6OlrHjx83kuerr75S\nWFgYJQy4CIoYKCdBQUFKSEjQpk2blJeXp/bt22v8+PHat29fpeZISEjQ448/XqnvCeD2UcRAOWvR\nooU++OAD7d69W3Xr1lXXrl01YsQIbd++vcLf+8SJE9qwYYN+97vfVfh7ASgfFDFQQRo0aKC//OUv\n2r9/vzp37qwBAwZowIABSk1NVUUtzVi4cKEGDRokHx+fCnl9AOWPIgYqWK1atRQZGan9+/dryJAh\nGjdunMLDw7V06dJy34aRW1oCrodV00AlKy4u1uLFixUTE6PCwkJNnjxZjz32mKpXr37Tr3Hy5EnN\njY9XTlaWLpw7pzv8/eXfsKHmJSTo6NGjqlq1agV+AgDliSIGDLEsS6tWrVJsbKz27Nmj1157TU89\n9ZR8fX2v+zWZmZmaFROj5YmJGiIppLBQfpLyJK2vVk1LLEsPDxqkCdHRCgkJqayPAqAMKGLACXz7\n7beaNm2a1q1bpxdeeEEvvPCC6tSp87NjZsfF6c3ISE0uKNBoy1LtUl4nV1K8zaZ3vL01ZcYMPTN+\nfKXkB3D7OEcMOIEuXbpo0aJFSk1N1cGDB9W6dWu9+uqrOnLkiKTLJTwtMlLr8vP18nVKWJJqS3rF\nsrQuP1/TIiM1Oy6u0j4DgNvDiBhwQkeOHNHMmTP10UcfKTw8XJnJyUorLFTrq475UFK8pGxJIyT9\n85rX2Cuph4+Plq1dq+Dg4MoJDuCWUcSAEztz5oz6de+ux3bt0mvXPLdEl6e0Vkoq0C+LWJJm2mza\nMniw5i1aVNFRAdwmihhwYidPnlTbZs20v7DwutPRb0g6qtKL+IykVl5eyjl0SPXr16+wnABuH+eI\nASc2Nz5eg6XrlvCvqSNpsM2mufHx5RcKQLmiiAEnlpOVpS6FhWV6jZCCAuVkZ5dTIgDljSIGnNiF\nc+fkV8bX8JOUl5tbHnEAVACKGHBid/j7K6+Mr5Enya/27U5uA6hoFDHgxAKCgvStl1epzxVLKrzy\ne5GkH6/897Uyvb0V0KFDhWUEUDasmgac2I1WTU+58st21WNvSvrjVX9m1TTg/BgRA06sQYMGerB/\nf31ss/3iuTcllejyKPinX3+85piPbTY9NGAAJQw4MUbEgJPLzMzUoF69tC4//2d31vo13FkLcA2M\niAEnFxISoikzZuh+Hx/tvcmv2Svpfh8fTZkxgxIGnBxFDLiAZ8aP1+QZM9TDx0czbTZd72KkM5Le\ntdnUw8dHk9l9CXAJTE0DLmTTpk2aFROjr1es0GCbTSEFBY79iDO9vbXYsvTQgAGaEB3NSBhwERQx\n4IJOnTqlufHxysnOVl5urvxq11ZAhw56YswYFmYBLoYiBgDAIM4RAwBgEEUMAIBBFDEAAAZRxAAA\nGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEA\nAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUM\nAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQR\nAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZR\nxAAAGEQRAwBgEEUMAIBBFDEAAAb9P603wxJf3z2wAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"\n",
"import networkx as nx\n",
"Gu = nx.Graph()\n",
"for i, j in [(1, 2), (1, 4), (4, 2), (4, 3)]:\n",
" Gu.add_edge(i,j)\n",
"nx.draw(Gu, with_labels = True)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Directed\n",
"Links: directed\n",
"- urls on the www\n",
"- phone calls\n",
"- metabolic reactions"
]
},
{
"cell_type": "code",
"execution_count": 173,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XlY1XX+///7AZXFfV8y9xAXcMUFBdxmnBxzsmusfm2i\npWlkTqNo6Ki5hQvWmJ8+TjXlkTY/pWPLjGZqiKgpkCWEBrngMppiEJKCCpzfH9b5SqKhAq+zPG7X\n5TVz3md70GU8ej3fm8Vms9kQERERIzxMBxAREXFnKmIRERGDVMQiIiIGqYhFREQMUhGLiIgYpCIW\nERExSEUsIiJikIpYRETEIBWxiIiIQSpiERERg1TEIiIiBqmIRUREDFIRi4iIGKQiFhERMUhFLCIi\nYpCKWERExCAVsYiIiEEqYhEREYNUxCIiIgapiEVERAxSEYuIiBikIhYRETFIRSwiImKQilhERMQg\nFbGIiIhBKmIRERGDVMQiIiIGqYhFREQMUhGLiIgYVMV0AHd15swZYq1WMlJS+Ck3lxq1a+MXGMjo\nMWNo2LCh6XgiIlJJLDabzWY6hDtJSkpieXQ0/9m4kfuAoIICagJ5QKKPD+ttNv54991MjooiKCjI\ncFoREaloKuJK9NrKlcyZOpXp+fmMttmoW8prcgCrxcISHx/mxsQwfuLEyo4pIiKVSEVcSV5buZLF\nU6ey6cIF2pXh9QeBob6+TFcZi4i4NBVxJUhKSmLEgAEk/KqEXwGsQCrwEPDmr953EAjx9eWT+Hh6\n9uxZOWFFRKRS6ajpSrA8Oprp+fnXrITvAGYBj1/nfe2Aafn5LI+OrtB8IiJijlbEFezMmTO0b9mS\nwwUFpe4Thitl/F+uXREDZANtvb3JOHZMR1OLiLggrYgrWKzVyki4bgn/lnrASIuFWKu1/EKJiIjD\nUBFXsIyUFHoVFNzWZwTl55ORmlpOiURExJGoiCvYT7m51LzNz6gJ5OXklEccERFxMCriClajdm3y\nbvMz8oCadW91uC0iIo5MRVzB/AIDSfT2LvW5IqDg5/8tBC7+/P9/bTvw+a5dvPDCC+zZs4fCwsKK\niisiIpVMR01XsBsdNT335z+Wq7bNAWZf9TgbaOvlxStvvklycjJbtmzh+PHjhIWFMWTIEIYMGUL7\n9u2xWK7+FBERcRYq4krwyH330fPDD/nLLfyjfsliYe/Ikby1bp192+nTp/n888/ZsmULW7ZsobCw\n0F7KgwcPplmzZuUZX0REKpCKuBJc78pav6UsV9ay2WwcOnTIXspxcXE0btzYXsoDBgygdu3a5fJz\niIhI+VMRV5LKutZ0UVERX3/9NVu2bGHr1q188cUXdO7cmcGDBzNkyBD69u2Ll5fXLf8cIiJSvlTE\nleiXuy9Ny88n/Dp3X8rmyt2XlpbT3ZcKCgrYtWsXW7duZcuWLezfv5/g4GD7KLtLly54eOiYPRER\nU1TElSw5OZnl0dH8e8MGRlosBOXn2+9HnGCxsNHLi+HDhjE5KqpCbvTw448/sm3bNvso++zZswwa\nNMg+ym7Tpo0O/BIRqUQqYkOysrKItVrJSE0lLycHn5o1eWftWg6kp9O6detKy3HixAm2bt1qXzF7\neXnZS3nQoEE0atSo0rKIiLgjFbEDCQkJYc6cOQwZMsTI99tsNg4cOGAv5fj4eFq2bGkfY4eEhFCj\nRg0j2UREXJWK2IHMnDkTT09P5s2bZzoKAIWFhfZzl7ds2UJycjLdu3e3r5h79epF1apVTccUEXFq\nKmIHsmnTJqKjo9m2bZvpKKU6f/48O3bssB+RfejQIUJDQ+1HZHfq1En7l0VEbpKK2IHk5eXRtGlT\nfvjhB6c4xSgrK4u4uDj7KPv8+fP2Uh48eDAtWrQwHVFExOGpiB1Mr169WLZsGSEhIaaj3LQjR47Y\nS3nr1q3UrVvXvn954MCB1NWNK0RErqEidjBTp06lbt26zJw503SU21JcXExqaqp9//LOnTtp3769\nfbXcr18/fHx8TMcUETFORexgPv74Y1555RU2bdpkOkq5unTpErt377avllNSUujVq5d9xdy9e3c8\nPT1NxxQRqXQqYgeTnZ1Nq1atyM7OpkqVKqbjVJhz584RHx9vH2WfPHmSAQMG2FfMfn5+OvBLRNyC\nitgBBQYG8sYbbxAUFGQ6SqU5depUiTtKAfZSHjx4ME2bNjWcUESkYqiIHdDTTz9N69atmTJliuko\nRthsNr777jv7GDsuLo5mzZrZj8gOCwujVq1apmOKiJQLFbEDev/993nnnXf46KOPTEdxCEVFRezd\nu9c+xt6zZw8BAQH2FXOfPn2c4nQvEZHSqIgd0Pfff0/Hjh05e/as7oxUivz8fHbt2mUfY6enp9Ov\nXz97MQcGBuqfm4g4DRWxg2rfvj0ffPABgYGBpqM4vOzsbPsdpbZu3Up2drZ93/KQIUMq9SYaIiI3\nS0XsoMaNG0eXLl14+umnTUdxOseOHStxRylfX1/7aVKDBg2iQYMGpiOKiNipiB3UW2+9xSeffML7\n779vOopTs9lspKWl2Ut5+/bttGnTxj7GDgkJoXr16qZjiogbUxE7qKNHj9K7d29OnTql82nL0eXL\nl0lKSrLvX967dy89e/a0j7GDgoJc+vxtEXE8KmIH1rJlSzZv3oyfn5/pKC7rp59+IiEhwb5izszM\nJDQ01D7K7tChg/5DSEQqlIrYgT366KOEhYXxxBNPmI7iNs6cOUNcXJx9xXzx4sUSB341b97cdEQR\ncTEqYgf2+uuvk5CQQGxsrOkobuvw4cP2Uv78889p0KCBff/ygAEDdEcpEbltKmIHlp6ezu9//3uO\nHj1qOopw5Y5S+/bts58mtXPnTjp27GhfLQcHB+Pt7W06pog4GRWxA7PZbDRt2pQ9e/bQsmVL03Hk\nVy5evMgXX3xh37/8zTff0KdPH/uKuVu3brqjlIj8JhWxg7v//vu55557ePTRR01Hkd+Qm5tLfHy8\nfZR9+vRpBg4caF8xt2vXTgd+icg1VMQO7n/+53/Yt28fr7/+uukocpNOnjxpXy1v3boVT09PeykP\nHjyYxo0bm44oIg5ARezgUlJSGDVqFOnp6aajyG2w2Wykp6fbi3nbtm00b97cfppUaGgoNWvWNB1T\nRAxQETu44uJiGjRowP79+2nSpInpOFJOCgsL2bt3r32MnZiYSNeuXe0r5t69e1OtWjXTMUWkEqiI\nncCIESN49NFHGTVqlOkoUkEuXLjAzp077WPsjIwM+vfvb18xd+7c+Zo7ShUVFeHh4aH9ziJOTkXs\nBGJiYjh69CgrVqwwHUUqyQ8//EBcXJx9lH3u3DkGDRpk37/cqlUr3n77bWbMmGHfNnjwYE1NRJyQ\nitgJJCYm8sQTT5CSkmI6ihhy9OjREgd+1axZE09PTzIyMkq8rnPnzvZiDgsL035nESegInYChYWF\n1KtXj8zMTOrVq2c6jhhms9lITU0lLCyMH3/88bqvq1KlCr1799Z+ZxEHpyJ2EkOHDiUiIoIRI0aY\njiIO4MSJE9x1110UFBSU+T3Vq1e339Bi8ODBBAQEXLPfWUQqn4rYSSxcuJCcnBxiYmJMRxEHUVBQ\nwK5du+zj6uTkZIqLi8v8/oYNG5a4oUWrVq0qLqyIXJeK2EkkJCQwZcoUEhMTTUcRB5WTk8O2bdvs\n+5Jv9tzztm3b2kt54MCBNGjQoNwznjlzhlirlYyUFH7KzaVG7dr4BQYyeswYGjZsWO7fJ+IMVMRO\noqCggAYNGnDq1CkdgCNlcuLEiRIHeJ06darM77VYLHTt2tV++lT//v3x9fW95SxJSUksj47mPxs3\nch8QVFBATSAPSPTxYb3Nxh/vvpvJUVEEBQXd8veIOCMVsRMJCwtj5syZ/P73vzcdRZyMzWbjwIED\n9lKOi4sjLy+vzO+vVq0awcHB9v3LPXv2pEqVKmV672srVzJn6lSm5+cz2majtBtH5gBWi4UlPj7M\njYlh/MSJZc4m4uxUxE5k1qxZ2Gw2FixYYDqKOLnCwkKSkpLsK+Zdu3Zx+fLlMr+/Vq1aJW5o4e/v\nX+qFRV5buZLFU6ey6cIF2pXhcw8CQ319ma4yFjeiInYimzdvZt68eSQkJJiOIi7m/Pnz7Nixw37J\nza+//vqm3t+sWbMSN7S44447SEpKYsSAASSUUsLfAYHAKCD2V88dBEJ8ffkkPp6ePXve8s8k4ixU\nxE7k/PnzNG7cmKysLHx8fEzHEReWlZVFXFycfZR9+PDhm3q/v78/VS5dYuyRIzxbyq+YoUAB0JJr\nixjgJYuFvSNH8ta6dbcSX8SpqIidTJ8+fVi8eDFhYWGmo4gbOXz4MFu3brX/OXv27G++xxs4Cdfs\nE14DfAh05Mrqt7QizgbaenuTceyYjqYWl6ez+Z1MaGgo27dvNx1D3EybNm0YN24ca9as4fTp03z1\n1VfExMTwhz/8odSjqS3AvVxbwueAOcCLwI1WAPWAkRYLsVZr+fwAIg5MRexkVMRimoeHB127dmXK\nlCls3LiRnJwc4uPjmTVrFsHBwXh6euINlDazmQ2MA5qV4XuC8vPJSE0t1+wijkhF7GT69evH7t27\nb+oIV5GKVK1aNUJDQ5k3bx47d+4kOzubvkFB/Pps96+BLcBfyvi5NYG8nJxyzSriiFTETqZu3bq0\nbduWvXv3mo4iUqpatWrR1s+PX5+lHA8cBVoATYEYYC1wveOi84CadUs761jEtaiInZDG0+Lo/AID\nSfT2LrHtSeAQV1bG+4AJwHDgs+t8RpKPD34BARUZU8QhqIidUGhoKPHx8aZjiFzXo6NHs66oiKsH\ny95Ao6v+1Ph5W2k39swG1ttsPBYeXtFRRYxTETuh0NBQdu7cSVFRkekoItdITk7mwQcfxMfLC2sp\nV9v6xRxKP3UJYLXFwvBhw3TqkrgFFbETatSoEU2aNCFVR5SKA8nMzOShhx5ixIgRPPTQQ6z/7DOW\n+Phw8CY/5yCwxMeHyVFRFRFTxOGoiJ2U9hOLo8jOzmbq1Kn06NGD9u3bk5GRwbhx4+jbty9zY2IY\n6utb5jL+5VrTc2NidHlLcRsqYielIhbTCgoKWLZsGf7+/vz000+kpaUxZ84catSoYX/N+IkTmR4T\nQ4ivLy9ZLFzvZKRsYCkQ4uOjGz6I29ElLp3U8ePH6dGjB6dPny71rjciFaW4uJg1a9Ywc+ZMAgMD\nWbRoER06dLjhe5KTk1keHc2/N2xgpMVCUH6+/X7EST/fj/jOO+6gWbt2fPrpp5Xyc4g4ChWxE2vd\nujUbN27E39/fdBRxE3FxcURGRuLp6cnSpUsJDQ29qfdnZWURa7WSkZpKXk4ONevWxS8ggMfCw6le\nvTpdunRh6dKl3HvvvRX0E4g4HhWxExs9ejTBwcE8+eSTpqOIi0tLS2P69Ons37+f6Oho7r///gqZ\nxOzYsYP777+f1NRU6tevX+6fL+KItI/YiWk/sVS0kydPMm7cOAYNGsTvfvc7Dhw4wAMPPFBhu0P6\n9+/PAw88wKRJkyrk80UckYrYiYWFhREfH4+GGlLe8vLymD17NgEBAdSrV4/09HQmT56Ml5dXhX/3\nwoULSU5OZv369RX+XSKOQEXsxNq2bUtxcTGZmZmmo4iLuHz5MitXrsTPz4/MzEy++uorFi9eTJ06\ndSotg6+vL6tWrSIiIqJM9z0WcXYqYidmsVg0npZyYbPZ+PDDDwkICGDdunVs2LCB2NhYWrRoYSRP\nv379ePDBBzWiFregInZyKmK5Xbt37yY0NJTZs2ezfPlyNm/eTLdu3UzHYsGCBXz55Zf861//Mh1F\npEKpiJ2cilhu1cGDBxk1ahSjRo1i7NixfPXVVwwdOtRhzkv39fXFarVqRC0uT0Xs5Dp27Eh2djYn\nT540HUWcxNmzZ5k8eTJ9+vShW7dupKenM2bMGDw9PU1Hu0ZwcDAPP/wwTz/9tOkoIhVGRezkPDw8\nCAkJ0apYflN+fj6LFi3C39+f4uJiDhw4wIwZM/D19TUd7Ybmz5/P119/zdq1a01HEakQKmIXoPG0\n3EhRURGrV6+mffv2JCcn88UXX7BixQqnucWgj48Pq1atYtKkSWRlZZmOI1LudGUtF5CcnEx4eDjf\nfPON6SjiYD777DOmTZtG9erViYmJoW/fvqYj3bLIyEiOHj3K+++/bzqKSLlSEbuAwsJC6tevz6FD\nh2jQoIHpOOIA9u3bx7Rp0zhy5AiLFi1i5MiRDnMQ1q3Kz8+nW7duzJ8/n1GjRpmOI1JuNJp2AVWq\nVCE4OJgdO3aYjiKGHT9+nPDwcIYOHcqIESNIS0vjvvvuc/oShisjaqvVyqRJkzhz5ozpOCLlRkXs\nIrSf2L3l5uYSFRVF165dad68ORkZGURERFC1alXT0cpVnz59eOyxx4iIiDAdRaTcqIhdhIrYPV26\ndImXX34ZPz8/zpw5Q0pKCgsWLKBWrVqmo1WYefPm8c0332hfsbgM7SN2ERcvXqR+/fqcPHnSpX8J\nyxU2m421a9cSFRWFn58fixcvJiAgwHSsSrNnzx7+9Kc/kZKSQqNGjUzHEbktWhG7CC8vL4KCgti5\nc6fpKFLBduzYQd++fYmOjubVV19lw4YNblXCAL1792b06NE89dRTuvuYOD0VsQvReNq1paenc++9\n99qvNJWcnMzgwYNNxzJm7ty57N+/XyNqcXoqYheiInZNp0+f5qmnnqJ///7069eP9PR0HnnkETw8\n3PtfX29vb6xWK5MnT+b06dOm44jcMvf+N9nF9O3bl3379nHhwgXTUaQcnD9/nvnz59OpUye8vb35\n9ttviYyMxNvb23Q0h9GrVy/GjBnDxIkTNaIWp6UidiG+vr4EBgayZ88e01HkNhQWFvLPf/4TPz8/\n9u/fT2JiIi+++CL169c3Hc0hPf/886Snp7NmzRrTUURuiYrYxWg87bxsNhv/+c9/6Nq1K2+//TYf\nfvgh7733Hm3atDEdzaF5eXlhtVr5y1/+wvfff286jshNUxG7GBWxc/ryyy8ZPHgwkZGRREdHExcX\nR1BQkOlYTiMoKIjHH39cI2pxSipiF9OvXz8SExO5dOmS6ShSBpmZmTz88MPcc889PPjgg6SkpHDP\nPfe4xCUpK9ucOXP47rvveO+990xHEbkpKmIXU7t2be666y6Sk5NNR5EbyM7OZurUqfTo0QM/Pz8y\nMjIYP348VapUMR3Naf0yon722Wc1ohanoiJ2QRpPO66LFy+ybNky/P39+emnn0hLS2POnDnUqFHD\ndDSX0LNnT5544gkmTJigEbU4DRWxC1IRO57i4mLeffdd/P392b59O/Hx8fzjH/+gSZMmpqO5nNmz\nZ3Po0CHeffdd01FEykTXmnZBWVlZ3HXXXfzwww94enqajuP24uLiiIyMxMPDg6VLlxIWFmY6ksv7\n8ssvGTZsGF9//TVNmzY1HUfkhrQidkENGzbkjjvuYN++faajuLW0tDSGDx/O448/TmRkJHv27FEJ\nV5IePXowfvx4nnzySY2oxeGpiF2UxtPmnDx5knHjxjFw4ECGDBnCgQMHeOCBB3QkdCWbNWsWmZmZ\nvP3226ajiNyQithFqYgrX15eHrNnzyYgIIB69eqRkZHBX/7yF7y8vExHc0vVqlXDarUyZcoUTp48\naTqOyHWpiF1USEgI27dvp7i42HQUl3f58mVWrlyJn58fmZmZ7N27l8WLF1OnTh3T0dxe9+7dmTBh\ngkbU4tBUxC6qefPm1K5dmwMHDpiO4rJsNhsffvghAQEBrFu3jg0bNhAbG0vLli1NR5Or/O1vf+PY\nsWO89dZbpqOIlEpXD3Bhv4ynO3XqZDqKy9m9ezeRkZHk5uby97//naFDh2ofsIP6ZUQ9dOhQhgwZ\nQrNmzUxHEilBK2IXpv3E5e/QoUPcf//9/PnPf2bs2LF89dVX/OEPf1AJO7hu3boxceJExo8frxG1\nOBwVsQsLCwtj+/bt+sVTDs6ePcvkyZPp3bs3Xbt2JSMjgzFjxug8bScyc+ZMTpw4QWxsrOkoIiWo\niF1Y69atsVgsHD582HQUp5Wfn8+iRYvo0KEDxcXF7N+/nxkzZuDr62s6mtykX0bUkZGR/Pe//zUd\nR8RORezCLBaLxtO3qKioiNWrV9O+fXuSk5PZuXMnK1asoFGjRqajyW3o2rUrERERGlGLQ1ERuzgV\n8c3bvHkzPXr04NVXX2XNmjWsXbsWPz8/07GknMyYMYOTJ0+yevVq01FEAF1r2uXt37+f4cOHazxd\nBvv27WPatGkcOXKERYsWMXLkSB2E5aL27dvHkCFD+Oqrr2jevLnpOOLmtCJ2cR06dCAvL4/jx4+b\njuKwjh8/Tnh4OEOHDmXEiBGkpaVx3333qYRdWJcuXZg0aRLjxo3TiFqMUxG7OIvFQkhICAkJCZw4\ncUK/dK6Sm5tLVFQUXbt2pXnz5mRkZBAREUHVqlVNR5NKEBUVxenTp1m1apXpKOLmVMQu7p133uH4\n8eNMmDCBO++8UyNq4NKlS7z88sv4+flx5swZ9u3bx4IFC6hVq5bpaFKJqlatitVqZfr06ZoYiVEq\nYhe3atUqkpOTycvLAyA+Pt5wInNsNhtr166lU6dObNy4kS1btvDGG29oH6EbCwwM5JlnntGIWoxS\nEbu40NDQEo/d9QjqHTt2EBwczAsvvMDKlSvZuHEjAQEBpmOJA3juuefIysrizTffNB1F3JSOmnZx\n27ZtY+DAgfbHrVu3dqvxdHp6Os899xx79+5l4cKFPPTQQ3h46L8/paTU1FQGDRrE3r17ufPOO03H\nETej30gurnfv3iUOPjpy5Ihb7A87ffo0Tz31FP379yc4OJj09HQeeeQRlbCUKiAggMmTJ2tELUbo\nt5KL8/HxoVevXiW2JSQkGEpT8c6fP8+CBQvo1KkTXl5efPvtt0RGRuLt7W06mji46dOnk5WVxRtv\nvGE6irgZFbEbCAsLK/HYFfcTFxUV8cYbb9C+fXvS0tJITEzkpZdeon79+qajiZOoWrUqq1evJioq\nimPHjpmOI25ERewGXPmALZvNxoYNG+jSpQuxsbH861//4r333qNNmzamo4kT6ty5M88++yxPPPGE\nRtRSaXSwlhvIy8ujTp06FBcX27edPn3a6W9g8OWXXxIZGcmpU6dYsmQJw4cP19Ww5LYVFhbSt29f\nxo0bx/jx403HETegFbEbqFmzJt27dy+xbceOHYbS3L7MzEwefvhh7rnnHh544AFSU1O55557VMJS\nLqpUqYLVamXmzJkcPXrUdBxxAypiN/Hr8bQzXtgjJyeHyMhIevbsiZ+fHxkZGTz55JNUqVLFdDRx\nMZ06deKvf/2rRtRSKVTEbsLZ9hOfO3eOWbNmMXbsWC5evMiyZcto3749586dIzU1lTlz5lCjRg3T\nMcWFRUZGkpuby2uvvWY6irg47SN2Ez/88AMNGjSwP7ZYLGRnZ1OnTh2Dqa51+fJlXn/9dZ5//nmy\nsrIAaNq0KT179mTx4sV06NDBcEJxJ/v37ycsLIykpCRatWplOo64KK2I3UT9+vXp3Lmz/bHNZmPn\nzp0GE5Vks9lYv349nTt3JiIiwl7CAA0bNuSjjz5SCUul69ixI1OmTNGIWiqUitiNOOp4+osvviAk\nJIT77ruPjIyMa57//vvv3eJqYOKYpk6dSl5eHq+++qrpKOKiVMRuxNEu7PHdd9/x5z//meDg4FJX\n576+vsyePZuDBw/SokULAwlFrhxFvWrVKmbNmkVmZqbpOOKCtI/YjZw6dYpmzZrZH1epUoUff/yR\n6tWrV2qOrKws5s+fz8qVKyksLLzmeQ8PDx5//HGef/75EnlFTFqyZAmbNm1i8+bNuma5lCv9bXIj\nTZs25a677rI/LiwsZPfu3ZX2/fn5+URHR9OuXTtWrFhRagkPHz6clJQUXnvtNZWwOJQpU6Zw/vx5\njail3KmI3YyJ84mLioqwWq34+fkxY8YMzp07d81revToweeff84nn3xCp06dKjyTyM3y9PTEarUy\na9Ysjhw5YjqOuBAVsZup7AO2Nm3aRPfu3RkzZgwnTpy45vlWrVrx7rvvkpiYWOK+ySKOyN/fn+nT\npzN27NgSl4wVuR3aR+xmMjMzad26tf2xl5cXubm5eHl5lev3fP3110ybNo3NmzeX+nzdunX529/+\nRkRERLl/t0hFKioqon///jzyyCNERESYjiMuQEXsZmw2Gy1btixxOlBCQgL9+/cvl88/duwYs2bN\n4q233ir1vMtq1arxzDPPMGPGDOrWrVsu3ylS2b799lv69+9PYmKi7vQlt02jaTdjsVgqZDz9448/\n8txzz+Hn50dsbGypJfzQQw+Rnp7O0qVLVcLi1Pz9/Xnuuec0opZyoSJ2Q+V5PvGlS5dYvnw57dq1\nY/HixVy8ePGa1wwcOJDk5GTeeecdXSZQXMazzz7LpUuX+N///V/TUcTJaTTthtLT0/H397c/rlGj\nBjk5OTd1FyObzcYHH3xAVFQUhw8fLvU1nTp1YsmSJdx99926RaG4pPT0dPr168eePXto27at6Tji\npFTEbshms9GkSRPOnDmDBfAGBvTvT/OWLfELDGT0mDE0bNjwuu9PSEhg6tSpJCYmlvp806ZNmT9/\nPqNHj9YtCsXlLVu2jI8//pi4uDhd6ENuiYrYDSUlJfHQvfdy4uRJRgKhQE0gD0j08WG9zcYf776b\nyVFRBAUF2d/37bff8txzz/HRRx+V+rk1atRg2rRp/PWvf630q3WJmFJUVERoaCgPPvggkyZNMh1H\nnJCK2M28tnIlc6ZOZVp+PuE2G6UdMpUDWC0Wlvj4MDcmhhEjRzJ37lxef/11ioqKrnm9p6cn48eP\nZ86cOTRu3LjCfwYRR5ORkUFwcLBG1HJLVMRu5LWVK1k8dSqbLlygXRlefxAYVLUqWRYLBZculfqa\ne++9l0WLFtG+fftyzSribF566SXWr1/Ptm3bNKKWm6K/LW4iKSmJOb8q4UvAE0AroDbQHfj0qve0\nAz6/fJlqpZRwnz59SEhIYP369SphEeCZZ56huLiYFStWmI4iTkZF7CaWR0czPT+/xEq4EGgBJAC5\nwHzgfuDz7A+HAAANaUlEQVTYVa9pB8wCfH5+3LZtWz744AN27dpVbhcBEXEFnp6erFq1ivnz5/Pd\nd9+ZjiNORKNpN3DmzBnat2zJ4YKCUvcJX60L8Dww8qpt2UBz4G8LFzJ16lSqVatWQUlFnN/f//53\n1q1bR3x8vEbUUib6W+IGYq1WRsJvlvBp4Dvg1/c+qgc84O2NV9WqKmGR3/DMM88A8PLLLxtOIs5C\nRewGMlJS6FVQcMPXFAKPAOGAXynP9yooICM1tfzDibgYDw8PVq1axYIFCzSiljJREbuBn3JzqXmD\n521cKWEv4HqHmdQE8nJyyjuaiEtq164ds2bNYsyYMaWe8idyNRWxG6hRuzZ5N3j+ceAs8C/A8zqv\nyQNq6kYNImU2adIkPDw8NKKW36QidgN+gYEkenuX+twE4FvgY+BGe3+TfHzwCwiogHQirsnDw4M3\n33yThQsXkpGRYTqOODAdNe0GrnfU9DGunEPszf9bCVuAV4H/76rXZQNtvb3JOHbshtegFpFrrVix\ngjVr1rB9+3Y8Pa83cxJ3phWxG2jUqBF/vPtuVv/qDkgtgGLgAldGz3nAOUqWMMBqi4Xhw4aphEVu\nQUREBFWrVmX58uWmo4iD0orYTSQlJTFiwAASynh5y18cBEJ8ffkkPp6ePXtWVDwRl3b48GF69erF\nzp07dSU6uYZWxG4iKCiIuTExDPX15WAZ33MQGOrry9yYGJWwyG1o06YNzz//vI6illKpiN3I+IkT\nmR4TQ4ivLy9ZLFzvZKRs4EWLhRBfX6bHxDB+4sTKjCnikp566im8vLx46aWXTEcRB6PRtBtKTk5m\neXQ0/96wgZEWC0H5+fb7ESf9fD/i4cOGMTkqSithkXL0y4h6x44d+Pv7m44jDkJF7MaysrKItVrJ\nSE0lLyeHmnXr4hcQwGPh4TowS6SCvPLKK7z99tvs2LFDR1ELoCIWEalUxcXFDB48mGHDhhEZGWk6\njjgAFbGISCU7cuQIQUFBJCQk0KFDB9NxxDAdrCUiUslat27NvHnzdBS1ACpiEREjJkyYQPXq1Vm2\nbJnpKGKYRtMiIoZkZmYSFBREfHw8HTt2NB1HDNGKWETEkFatWjF//nzCw8MpLCw0HUcMURGLiBj0\n5JNPUqtWLWJiYkxHEUM0mhYRMezo0aP07NmTbdu20alTJ9NxpJJpRSwiYljLli1ZsGCBRtRuSkUs\nIuIAxo8fT506dVi6dKnpKFLJNJoWEXEQv4yo4+Li6Ny5s+k4Ukm0IhYRcRAtW7Zk4cKFjBkzRiNq\nN6IiFhFxIOPGjaNu3bosWbLEdBSpJBpNi4g4mGPHjtGjRw+NqN2EVsQiIg6mRYsWREdHEx4ezuXL\nl03HkQqmIhYRcUCPP/44DRo00IjaDWg0LSLioI4fP0737t3ZunUrgYGBpuNIBdGKWETEQd15550s\nWrRII2oXpyIWEXFgY8eOpXHjxixatMh0FKkgGk2LiDi4EydO0K1bN42oXZRWxCIiDq558+YsXrxY\nI2oXpSIWEXECY8aMoUmTJkRHR5uOIuVMo2kRESfxy4h6y5YtdOnSxXQcKSdaEYuIOInmzZuzZMkS\njahdjIpYRMSJhIeH06xZM1544QXTUaScaDQtIuJk/vvf/9KtWzc+++wzunbtajqO3CatiEVEnMwd\nd9zB0qVLGT16NJcuXTIdR26TilhExAk99thj3HnnnSxcuNB0FLlNGk2LiDipkydP0rVrVzZt2kS3\nbt1Mx5FbpBWxiIiTatasGTExMYSHh2tE7cRUxCIiTuzRRx+lRYsWLFiwwHQUuUUaTYuIOLlfRtSf\nfvop3bt3Nx1HbpJWxCIiTq5Zs2YsW7ZMI2onpSIWEXEBjzzyCK1atWL+/Pmmo8hN0mhaRMRFnDp1\niq5du7JhwwZ69OhhOo6UkVbEIiIuomnTprz44ouEh4dz8eJF03GkjLQiFhFxITabjZEjR9KpUydd\n7MNJaEUsIuJCLBYL//jHP/jnP//JunXr+NOf/kRWVpbpWHIDKmIRERfTsGFDfve73zFq1Cg+/vhj\nnn76adOR5AZUxCIiLsZqtfLOO+/wy57H999/n7Vr1xpOJdejfcQiIi7m8uXL9OnTh71799q3NWzY\nkLS0NBo2bGgwmZRGK2IRERdTtWpVrFYrVatWtW/LysoiIiLCYCq5HhWxiIgLCggIYM6cOSW2ffDB\nB3zwwQeGEsn1aDQtIuKiCgsL6dOnD19++aV9W4MGDUhLS6NRo0YGk8nVtCIWEXFRVapUwWq1Uq1a\nNfu2s2fPakTtYFTEIiIurHPnzteMqNeuXcv7779vKJH8mkbTIiIurrCwkL59+5KcnGzfphG149CK\nWETExV1vRP3UU0+htZh5KmIRETfQqVMnnn/++RLb1q1bx//93/+ZCSR2Gk2LiLiJwsJCgoODSUpK\nsm+rX78+aWlpNG7c2GAy96YVsYiImyhtRP3DDz8wceJEjagNUhGLiLiRjh07Mm/evBLb1q9fz5o1\nawwlEo2mRUTcTGFhIf369SMxMdG+rV69eqSlpdGkSRODydyTVsQiIm7mlxG1l5eXfVt2drZG1Iao\niEVE3FCHDh2uGVF/+OGHvPfee4YSuS+NpkVE3FRRURH9+vVjz5499m0aUVc+rYhFRNyUp6dnqSPq\nCRMmaERdiVTEIiJuzN/fn/nz55fY9tFHH/Huu+8aSuR+NJoWEXFzRUVF9O/fn927d9u31a1bl7S0\nNJo2bWowmXvQilhExM15enqyatWqEiPqnJwcnnzySY2oK4GKWERE8Pf3Z+HChSW2ffLJJ7z99tuG\nErkPjaZFRAS4MqIODQ1l165d9m116tQhLS2NZs2aGUzm2rQiFhER4P+NqL29ve3bfvzxR42oK5iK\nWERE7Pz8/K4ZUf/73//mrbfeMpTI9Wk0LSIiJRQVFREWFsbOnTvt2zSirjhaEYuISAmenp68+eab\n14yox48frxF1BVARi4jINfz8/HjhhRdKbPvPf/5DbGysoUSuS6NpEREpVWkj6tq1a5OWlsYdd9xh\nMJlr0YpYRERK9ctR1D4+PvZtubm5jBs3TiPqcqQiFhGR67rrrruuGVFv3LgRq9VqJpAL0mhaRERu\nqLi4mAEDBpCQkGDfVqtWLdLS0mjevLnBZK5BK2IREbkhDw8P3nzzzRIj6nPnzmlEXU5UxCIi8pva\ntWvHokWLSmz79NNPWbVqlaFErkOjaRERKZPi4mIGDhzI9u3b7dtq1arFN998w5133mkwmXNTEYuI\nSJkdOnSIwMBALly4YN82dOhQVq9ezVurV5ORksJPubnUqF0bv8BARo8ZQ8OGDQ0mdnwqYhERuSkr\nVqzgmWeesT/2BTyrVGFUlSoEFRRQE8gDEn18WG+z8ce772ZyVBRBQUGmIjs0FbGIiNyU4uJiBg0a\nxPb4eGoCs4GxQN1SXpsDWC0Wlvj4MDcmhvETJ1ZqVmegg7VEROSmeHh48LvBg2kMfAlMofQS5uft\nz9psJFy4wOKpU3lt5cpKy+kstCIWEZGbkpSUxIgBA0i4cIF2V21/FNgCXAAacGWVPPOq5w8CIb6+\nfBIfT8+ePSsvsIPTilhERG7K8uhopufnlyhhgCjgCJALbARWAJuuer4dMC0/n+XR0ZUT1EloRSwi\nImV25swZ2rdsyeGCguuOowHSgSHAR0D3q7ZnA229vck4dkxHU/9MK2IRESmzWKuVkVx/n3AEUB3o\nzJWxdPdfPV8PGGmxEKtrVdupiEVEpMwyUlLoVVBw3edfAX7iyr7ivwFJpbwmKD+fjNTUignohFTE\nIiJSZj/l5lLzN15jAcKAUcB7pTxfE8jLySnvaE5LRSwiImVWo3Zt8sr42kKuXOzj1/KAmnVvtIfZ\nvaiIRUSkzPwCA0n09r5mexbwf8B5oJgrR0t/APyplM9I8vHBLyCgImM6FR01LSIiZXa9o6bPAn8G\nUgAbcBcwC7jnV+/XUdPX0opYRETKrFGjRvzx7rtZbbGU2N4A2MaVos0BErm2hAFWWywMHzZMJXwV\nrYhFROSmXO/KWr9FV9YqnVbEIiJyU4KCgpgbE8NQX18OlvE9B4Ghvr7MjYlRCf+KilhERG7a+IkT\nmR4TQ4ivLy9ZLFzvZKRs4EWLhRBfX6br7kul0mhaRERuWXJyMsujo/n3hg2MtFgIys+334846ef7\nEQ8fNozJUVFaCV+HilhERG5bVlYWsVYrGamp5OXkULNuXfwCAngsPFwHZv0GFbGIiIhB2kcsIiJi\nkIpYRETEIBWxiIiIQSpiERERg1TEIiIiBqmIRUREDFIRi4iIGKQiFhERMUhFLCIiYpCKWERExCAV\nsYiIiEEqYhEREYNUxCIiIgapiEVERAxSEYuIiBikIhYRETFIRSwiImKQilhERMQgFbGIiIhBKmIR\nERGDVMQiIiIGqYhFREQMUhGLiIgYpCIWERExSEUsIiJikIpYRETEIBWxiIiIQSpiERERg1TEIiIi\nBqmIRUREDFIRi4iIGKQiFhERMUhFLCIiYpCKWERExCAVsYiIiEEqYhEREYNUxCIiIgapiEVERAxS\nEYuIiBikIhYRETFIRSwiImKQilhERMSg/x9X1mG+8y80QgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import networkx as nx\n",
"Gd = nx.DiGraph()\n",
"for i, j in [(1, 2), (1, 4), (4, 2), (4, 3)]:\n",
" Gd.add_edge(i,j)\n",
"nx.draw(Gd, with_labels = True)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"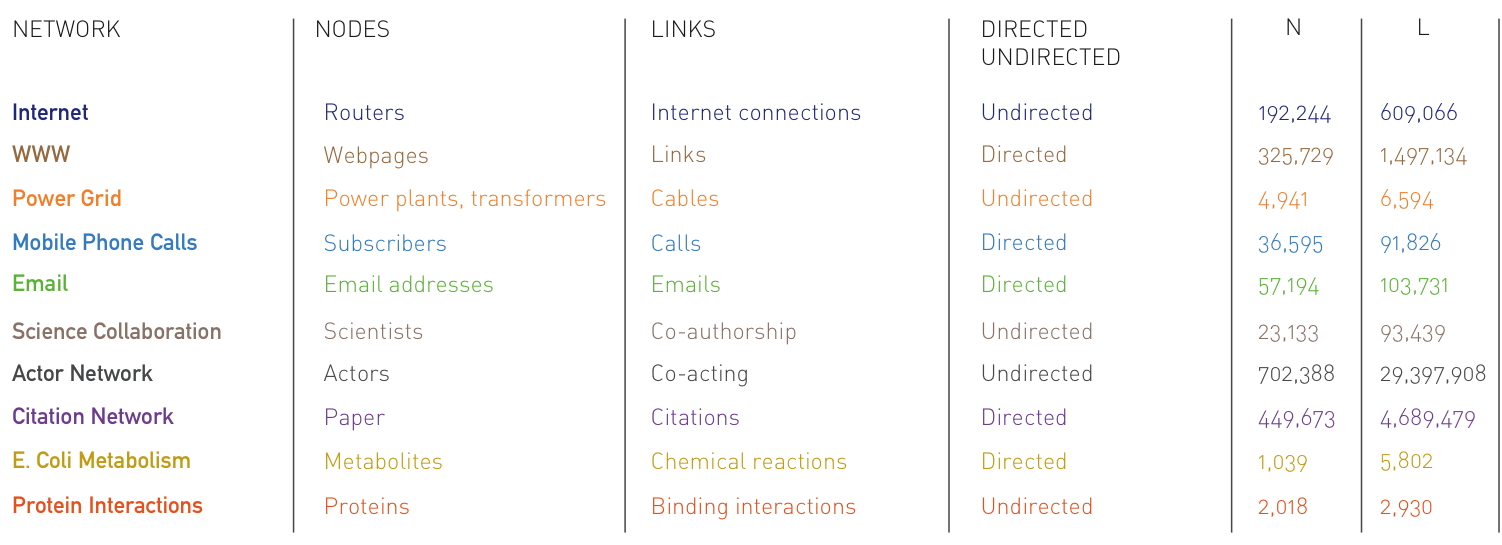 "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Degree, Average Degree and Degree Distribution\n"
]
},
{
"cell_type": "code",
"execution_count": 175,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtYlHX+//HXgAqDIEtqVl6WfdVBU0kQMs9adhnaulFt\nmeUxc6U2qwUlW81DKWVDZVpcaesPMRU7qGVlluVptRSEQlcBzdL023okQh2Iw/z+sPqagoIy8xmY\n5+O6vKqZuelNB55+7vtzz1icTqdTAADACB/TAwAA4M0IMQAABhFiAAAMIsQAABhEiAEAMIgQAwBg\nECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIAAAwixAAAGESIAQAwiBADAGAQIQYAwCBCDACAQYQYAACD\nCDEAAAYRYgAADCLEAAAYRIgBADCIEAMAYBAhBgDAIEIMAIBBhBgAAIMIMQAABhFiAAAMIsQAABhE\niAEAMIgQAwBgECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIAAAwixAAAGESIAQAwiBADAGAQIQYAwCBC\nDACAQYQYAACDCDEAAAYRYgAADKpnegCgLjhy5IhSU1KUl52tkwUFCgwOli0sTMNHjlTTpk1NjwfA\ng1mcTqfT9BBAbZWenq7ZiYn6aPVq3SUpqqhIQZIKJW2zWrXC6dTA6Gg9PnGioqKiDE8LwBMRYuAS\nzUtO1pT4eCU4HBrudCqkgtfkS0qxWDTLatU0u11jYmPdPSYAD0eIgUswLzlZL8THa83p02pdhdfv\nldQ/IEAJxBjAOQgxUE3p6eka1KePNp0T4aGS1ko6LamJpFGS/nnW83sl9QwI0KoNGxQZGem+gQF4\nNHZNA9U0OzFRCQ7HeSvhiZK+k1QgabWkOZLWnPV8a0kTHA7NTkx0z6AAagVWxEA1HDlyRKHXXad9\nRUUVXhP+Ta6kfpLelxRx1uMnJLXy91fegQPspgYgiRUxUC2pKSmKkSqN8KOSGkrqoDOnpSPOef4K\nSTEWi1JTUlw2I4DahRAD1ZCXna2biooqff41SSd15lrxJEnpFbwmyuFQ3o4drhkQQK1DiIFqOFlQ\noKCLvMYiqbekv0paWsHzQZIK8/NrejQAtRQhBqohMDhYhVV8bamkgAoeL5QUFHKhK8wAvAkhBqrB\nFhambf7+5z1+VNIySacklevMbul3JP2lgq+RbrXK1rGjK8cEUIuwaxqohsp2TR+TdI+kbElOSW0k\nTZb053OOZ9c0gHOxIgaq4corr9TA6GgttFj+8HgTSet1JrT5krbp/AhL0kKLRXcMGECEAfyOFTFQ\nTZW9s9bF8M5aACrCihiopqioKE2z29U/IEB7q3jMb+81Pc1uJ8IA/oAQA5dgTGysEux29QwI0MsW\niyq7GemEpJcsFvXkAx8AVIJT08BlyMjI0OzERH348ceKsVgU5XD8/nnE6b9+HvEdAwbo8YkTWQkD\nqBAhBmrA0aNHlZqSorwdO7QvL0/f7t+vR//xDw0bMYKNWQAuiBADNey7775T7969deDAAdOjAKgF\nCDFQw8rKyhQYGKgTJ07IarWaHgeAh2OzFlDDfH191bJlS3377bemRwFQCxBiwAXatGmjPXv2mB4D\nQC1AiAEXsNlsysvLMz0GgFqAEAMuwIoYQFURYsAFCDGAqiLEgAsQYgBVxe1LgAuUl5crMDBQhw8f\nVlBQkOlxAHgwVsSAC/j4+Kh169bau7eqHwsBwFsRYsBFOD0NoCoIMeAihBhAVRBiwEXatGnDvcQA\nLooQAy5is9lYEQO4KEIMuAinpgFUBSEGXKRZs2YqKipSfn6+6VEAeDBCDLiIxWJhVQzgoggx4EJc\nJwZwMYQYcCFWxAAuhhADLkSIAVwMIQZciBADuBg+9AFwoePHj6tVq1bKz8+XxWIxPQ4AD8SKGHCh\nxo0by8fHR8eOHTM9CgAPRYgBF+P0NIALIcSAixFiABdCiAEXs9lsfPgDgEoRYsDFWBEDuBBCDLgY\nIQZwIdy+BLhYQUGBmjdvrsLCQm5hAnAeVsSAiwUHB6thw4b68ccfTY8CwAMRYsANOD0NoDKEGHAD\nQgygMoQYcANCDKAyhBhwgzZt2nAvMYAKEWLADWw2GytiABXi9iXADU6dOqWmTZvq5MmT8vHh978A\n/g8/EQA3aNiwoUJCQnTw4EHTowDwMIQYcBOuEwOoCCEG3ITrxAAqQogBN+EWJgAVIcSAmxBiABUh\nxICbEGIAFeH2JcBNioqK9Kc//UknT55UvXr1TI8DwEOwIgbcxN/fX1dddZX2799vehQAHoQQA27E\n6WkA5yLEgBsRYgDnIsSAG9lsNt7UA8AfEGLAjVgRAzgXIQbciBADOBe3LwFuVFJSoqCgIP38889q\n0KCB6XEAeABWxIAb1a9fXy1atNC+fftMjwLAQxBiwM04PQ3gbIQYcDNCDOBshBhwM0IM4GyEGHAz\n7iUGcDZCDLgZK2IAZ+P2JcDNysrKFBgYqBMnTshqtZoeB4BhrIgBN/P19VXLli317bffmh4FgAcg\nxIABbdq04ToxAEmEGDDCZrNxnRiAJEIMGMGGLQC/IcSAAYQYwG8IMWAAIQbwG25fAgwoLy9XYGCg\nDh8+rKCgINPjADCIFTFggI+Pj1q3bq29e/eaHgWAYYQYMITT0wAkQgwYQ4gBSIQYMIYPfwAgEWLA\nGFbEACRCDBhDiAFIhBgwplmzZioqKlJ+fr7pUQAYRIgBQywWC+85DYAQAyZxehoAIQYMIsQACDFg\nECEGQIgBg7iXGAAf+gAYdPz4cbVq1Ur5+fmyWCymxwFgACtiwKDGjRvLx8dHx44dMz0KAEMIMWAY\n14kB70aIAcO4Tgx4N0IMGMaKGPBuhBgwjBAD3o0QA4YRYsC7cfsSYFhBQYGaN2+uwsJCbmECvBAr\nYsCw4OBgNWzYUD/++KPpUQAYQIgBD8DpacB7EWLAAxBiwHsRYsADEGLAexFiwAPwph6A9yLEgAdg\nRQx4r3qmBwAgNWrUSHtyc/Xwgw/qVEGBAoODZQsL0/CRI9W0aVPT4wFwIe4jBgxKT0/X7MREfbR6\ntaKLitRLUpCkQknbrFatcDo1MDpaj0+cqKioKMPTAnAFQgwYMi85WVPi45XgcGi406mQCl6TLynF\nYtEsq1XT7HaNiY1195gAXIwQAwbMS07WC/HxWnP6tFpX4fV7JfUPCFACMQbqHEIMuFl6eroG9emj\nTRVEeI+kMEl/lZR6znN7JfUMCNCqDRsUGRnpjlEBuAG7pgE3m52YqASHo8KV8N8l3VTJca0lTXA4\nNDsx0XXDAXA7VsSAGx05ckSh112nfUVF510TTpO0UtINOrP6PXdFLEknJLXy91fegQPspgbqCFbE\ngBulpqQoRjovwj9LmiLpJUkX+p3xFZJiLBalpqS4ZkAAbkeIATfKy87WTUVF5z3+jKSHJV1Tha8R\n5XAob8eOmh4NgCG8oQfgRicLChR0zmNfS1r76x+rIkhSYX5+jc4FwBxCDLhRYHCwCs95bIOk/ZKu\n1ZnT0icllUnaJSmjgq9RKCkopKK7jgHURpyaBtzIFhambf7+f3jsb5K+1ZkV8TeSxkq6Q9KnlXyN\ndKtVto4dXTkmADdi1zTgRhfaNf2baToT5kp3Tfv5Ke+HH9g1DdQRrIgBN2rQoIGaXHGFFlzgNVNU\ncYQl6f9Jskhavny5SktLa3w+AO5HiAE32bZtmyIiItSpWzfZAwK0t5rH75VkDwjQ7PnztXTpUt14\n441avXq1OKkF1G6EGHCx8vJy2e123XHHHbLb7XrnnXc0zW5X/2rE+Lf3mp5mt2vo0KFat26dZs6c\nqSeeeEL9+/dXdna2K78FAC7kO3Xq1KmmhwDqqqNHj+ree+9VZmam1qxZo65du0qSOkdFyXrFFRq2\nbp18S0vVVpK1guNPSEq2WDQ6IECTzvrAB4vForZt22rs2LEqLCzUww8/rNzcXEVFRSko6NwbpAB4\nMlbEgIusX79e4eHhCgsL08aNG9WyZcs/PD8mNlarNmxQZkyM/sffX6OsViVLektSsqRRVqta+fsr\nKyZGqzZsqPBTl+rXr6/HHntMubm5CgkJUYcOHTR9+nSdOnXKHd8igBrArmmghpWVlenZZ5/VG2+8\noZSUFPXv3/+ixxw9elSpKSnK27FDhfn5CgoJka1jRw0bMaJau6P37duniRMnavPmzZoxY4aGDh0q\nHx9+vw14MkIM1KBDhw7pgQcekK+vr9566y1dffXVRubYsmWL4uLiVFxcrKSkJPXt29fIHAAujt8q\nAzXk448/VufOndWvXz99+umnxiIsSd26ddOWLVuUkJCgUaNGadCgQcrJyTE2D4DKEWLgMv3yyy+K\nj4/X2LFj9c4772jSpEny9fU1PZYsFovuu+8+7d69Wz179lSPHj3097//XUePHjU9GoCzEGLgMuzb\nt089evRQXl6esrKy1LNnT9Mjncff31/jx49XTk6OLBaL2rVrp1mzZqmogk+BAuB+hBi4RG+//ba6\ndOmiIUOG6P3331fjxo1Nj3RBTZo00Zw5c7R582Zt3rxZ7dq1U1paGm8IAhjGZi2gmhwOh5588kmt\nXbtWaWlpioyMND3SJVm3bp3i4uLk5+enpKQkdevWzfRIgFdiRQxUw+7du9WlSxcVFBQoMzOz1kZY\nkvr27auMjAzFxsbqvvvu07333qt9+/aZHgvwOoQYqAKn06kFCxaoV69eGjdunJYsWaJGjRqZHuuy\n+fj4aNiwYcrNzVXHjh0VFRWl+Ph45efnmx4N8BqEGLiIwsJCDR06VElJSVq/fr1Gjx4ti8Vieqwa\nFRAQoMmTJ2vnzp0qKChQaGioXn31VZWUlJgeDajzCDFwAVlZWercubOsVqvS09PVvn170yO51NVX\nX6358+fr888/10cffaT27dtr5cqVbOgCXIjNWkAFnE6n5s6dq+nTp2vOnDkaPHiw6ZGM+OSTTxQf\nH68mTZooKSlJnTt3Nj0SUOcQYuAcJ06c0KhRo3Tw4EGlpaWpdevWpkcyqrS0VAsWLNCUKVN02223\nacaMGWrRooXpsYA6g1PTwFm2bNmi8PBwXX/99dq8ebPXR1iS6tWrpzFjxigvL0/XXnutOnXqpEmT\nJqmwsND0aECdQIgBSeXl5UpMTFRMTIzmzp2rl19+WX5+fqbH8ihBQUF67rnn9PXXX2v//v2y2Wya\nN2+eSktLTY8G1GqcmobXO3z4sIYOHSqHw6ElS5Zw2rWKMjIyFBcXp+PHj8tut+v22283PRJQK7Ei\nhlf77LPPFB4eri5dumjdunVEuBoiIyO1fv16Pffccxo3bpz69++vHTt2mB4LqHUIMbxSaWmpnn76\naY0YMUKLFi3Ss88+q3r16pkeq9axWCy68847tXPnTg0cOFC33nqrHn74Yf33v/81PRpQaxBieJ0D\nBw6od+/e2r59uzIzM3XrrbeaHqnWa9CggcaNG6fc3FwFBwerffv2eu6553T69GnTowEejxDDq7z/\n/vuKiorSoEGDtHr1ajVr1sz0SHVKSEiI7Ha70tPTlZ2drdDQUKWmpqq8vNz0aIDHYrMWvEJxcbHG\njx+vDz74QEuXLlXXrl1Nj+QVNm/erLi4OJWUlCgpKUl9+vQxPRLgcVgRo87bs2ePunbtqkOHDikr\nK4sIu1H37t315Zdfavz48Ro5cqT+8pe/KDc31/RYgEchxKjTlixZom7dumn06NF69913FRISYnok\nr2OxWDR48GDt3r1b3bt3V/fu3fXYY4/p2LFjpkcDPAIhRp106tQpPfTQQ5o2bZo+++wzPfLII3Xu\nE5NqG39/f02YMEG7d++W0+lUu3bt9OKLL6q4uNj0aIBRhBh1zo4dOxQVFaWSkhJt375dnTp1Mj0S\nztK0aVPNnTtXmzZt0qZNm9SuXTu9/fbbfMITvBabtVBnOJ1OzZs3T5MmTVJSUpKGDRtmeiRUwRdf\nfKG4uDhZrVYlJSVxDR9ehxCjTigoKNCYMWOUk5OjZcuWqW3btqZHQjWUlZVp0aJFmjRpkrp3767n\nn39e119/vemxALfg1DRqvfT0dEVERKhx48b66quviHAt5OvrqxEjRig3N1ft27dXZGSkxo8fr59+\n+sn0aIDLEWLUWuXl5UpKStLAgQM1a9Ysvf7667JarabHwmVo2LChnnnmGe3cuVP5+fkKDQ3VnDlz\nVFJSYno0wGU4NY1a6dixYxo+fLiOHz+utLQ0tWzZ0vRIcIHs7GzFx8dr//79mjVrlgYNGsTud9Q5\nrIhR62zYsEHh4eHq0KGDNm3aRITrsLCwMK1Zs0avvPKKnn76ad1yyy3KzMw0PRZQowgxao2ysjJN\nnz5dgwcP1rx58/TCCy+ofv36pseCi1ksFkVHR+ubb77R4MGDNXDgQA0fPlwHDx40PRpQIwgxaoX/\n/d//Vb9+/bR+/Xpt375d0dHRpkeCm9WrV09/+9vflJubq+bNm+vGG2/U5MmTVVhYaHo04LIQYni8\n1atXq3Pnzrrlllv02Wef6ZprrjE9Egxq1KiRZs6cqaysLH333XcKDQ3V/PnzVVZWZno04JKwWQse\n65dfftE///lPpaWlafHixerVq5fpkeCB0tPTFRcXp/z8fNntdvXv39/0SEC1EGJ4pO+++06DBw9W\n06ZNlZKSoiZNmpgeCR7M6XRq5cqVmjBhglq1aiW73a4OHTqYHguoEk5Nw+O8++676tKli+677z6t\nWrWKCOOiLBaLYmJi9J///EfR0dG65ZZbNGbMGP33v/81PRpwUYQYHsPhcCg2NlYJCQn66KOP9I9/\n/IN7RlEtDRo00OOPP67c3FwFBQWpQ4cOmjFjhk6fPm16NKBShBgeIScnRzfffLPy8/OVmZmpqKgo\n0yOhFgsJCVFSUpK2bt2qrKwstW3bVosWLVJ5ebnp0YDzcI0Yxi1cuFDx8fGaOXOmRo8ezSoYNe7f\n//634uLiVFZWpqSkJPXu3dv0SMDvCDGMKSws1KOPPqqMjAwtW7ZMHTt2ND0S6rDy8nItW7ZMEydO\nVKdOnTRr1izZbDbTYwGcmoYZX3/9tSIjI9WgQQOlp6cTYbicj4+P7r//fuXk5Khr167q1q2bxo0b\np+PHj5seDV6OEMOtnE6n5s6dq9tuu01Tp07Vm2++qYYNG5oeC17E399fCQkJ2r17t8rKytS2bVvZ\n7XYVFxebHg1eilPTcJv8/Hw99NBD2r9/v5YtW6bWrVubHgnQ7t27NWHCBO3atUvPP/+87rnnHvYp\nwK1YEcMtvvzyS4WHh6tFixbasmULEYbHaNeunVatWqV58+ZpxowZ6tGjh7766ivTY8GLsCKGS5WX\nl2vWrFl6+eWXNX/+fA0aNMj0SEClysrKlJqaqsmTJ6tHjx5KTEzU9ddfb3os1HGsiOEyhw8fVnR0\ntD788ENlZGQQYXg8X19fjRw5Urm5uWrXrp0iIyM1YcIE/fTTT6ZHQx1GiOESn3/+uSIiIhQVFaX1\n69erRYsWpkcCqqxhw4aaMmWKduzYoePHjys0NFRz585VSUmJ6dFQB3FqGjWqtLRUU6dO1YIFC5Sa\nmqp+/fqZHgm4bN98843i4+P1ww8/aNasWfrzn//Mhi7UGEKMGvPDDz9oyJAhslqtWrRokZo1a2Z6\nJKDGOJ1OrV69WvHx8brqqquUlJSk8PBw02OhDuDUNGrEBx98oMjISA0cOFCffPIJEUadY7FYNGDA\nAGVnZ+vee+9VdHS0RowYoUOHDpkeDbUcIcZlKS4u1hNPPKFx48ZpxYoVeuqpp+Tjw39WqLvq1aun\nsWPHKi8vT1dffbXCwsL0zDPP6OTJk6ZHQy3FT0xcsr1796pbt27av3+/MjMz1a1bN9MjAW7TqFEj\nJSYmKjMzU99++61sNpvefPNNlZWVmR4NtQwhxiVZunSpunbtqpEjR2r58uW64oorTI8EGHHddddp\n8eLFWrlypRYuXKjw8HB9+umnpsdCLcJmLVTL6dOnNW7cOG3cuFHLli1jswpwFqfTqRUrVmjChAlq\n06aN7Ha72rdvb3oseDhWxKiynTt3KioqSsXFxdq+fTsRBs5hsVh01113adeuXerfv7/69u2rsWPH\n6vDhw6ZHgwcjxLgop9Op+fPnq2/fvho/frxSU1MVFBRkeizAYzVo0EBPPPGEcnJyFBAQoPbt22vm\nzJlyOBymR4MH4tQ0Lujnn3/WmDFjtGvXLi1btkzt2rUzPRJQ6+zdu1cJCQlKT0/XzJkzNWTIEO4u\nwO/4LwGVysjIUEREhEJCQrR161YiDFyi1q1b67333tPixYv16quvqkuXLtq4caPpseAhWBHjPE6n\nU6+88ooSExP12muv6a9//avpkYA6o7y8XGlpaZo4caIiIiI0a9YstWnTxvRYMIgVMf7g2LFjGjRo\nkNLS0rR161YiDNQwHx8fDRkyRDk5OerSpYu6du2qxx9/XMePHzc9GgwhxPjdpk2bFB4errZt22rT\npk18DivgQlarVU899ZR27dqlkpIStW3bVi+99JKKi4tNjwY349Q0VFZWppkzZ+q1117TggULNGDA\nANMjAV5n165dmjBhgnbv3q0XXnhBd999N5/w5CUIsZf78ccf9eCDD6q8vFxvvfWWmjdvbnokwKut\nXbtWcXFxCgoKUlJSkrp06WJ6JLgYp6a92CeffKKIiAj16tVLa9euJcKAB+jXr58yMzM1atQo3XXX\nXbr//vv1/fffmx4LLkSIvVBJSYkSEhI0evRopaWlacqUKfL19TU9FoBf+fr6atSoUcrNzVVoaKg6\nd+6shIQEFRQUmB4NLkCIvcz333+vXr16aefOncrKylLv3r1NjwSgEoGBgZo6daqys7N19OhR2Ww2\nvfbaayopKTE9GmoQIfYiy5cv10033aR77rlHq1atUtOmTU2PBKAKmjdvrgULFmjNmjVasWKFwsLC\n9OGHH4otPnUDm7W8QFFRkeLi4rR69WqlpaXppptuMj0SgEvkdDr18ccfKz4+Xtdcc42SkpLUqVMn\n02PhMrAiruNyc3N188036+jRo8rKyiLCQC1nsVg0cOBAZWdn6+6779btt9+ukSNH6tChQ6ZHwyUi\nxHVYamqqevToodjYWC1btkzBwcGmRwJQQ+rXr69HHnlEubm5atasmcLCwjR16lSdOnXK9GioJk5N\n10EnT57Uo48+qm3btuntt99Wx44dTY8EwMW+//57Pf3009qwYYOeffZZDR8+nLshaglWxHXMN998\no8jISPn6+iojI4MIA16iZcuWWrJkiZYvX64FCxYoIiJCa9euNT0WqoAVcR3hdDqVnJysKVOm6JVX\nXtEDDzxgeiQAhjidTi1fvlwJCQkKDQ3Viy++qBtuuKFKxx45ckSpKSnKy87WyYICBQYHyxYWpuEj\nR3KnhYsQ4jrgp59+0ujRo7Vv3z6lpaXJZrOZHgmAByguLtbrr7+umTNn6p577tG0adN05ZVXVvja\n9PR0zU5M1EerV+suSVFFRQqSVChpm9WqFU6nBkZH6/GJExUVFeXOb6PO49R0LffVV18pPDxc11xz\njb788ksiDOB3fn5+evLJJ5WTkyM/Pz/dcMMNSkxMlMPh+MPr5iUna1CfPopcuVL7ior0r6IijZX0\ngKSxkhY4HNpXVKTOK1dqUJ8+mpecbOLbqbNYEddS5eXlstvtSkpK0htvvKE777zT9EgAPNyePXuU\nkJCg7du3KzExUYMHD9abb7yhF+Ljteb0abWuwtfYK6l/QIAS7HaNiY119chegRDXQkeOHNGwYcNU\nWFiopUuX6tprrzU9EoBaZOPGjYqLi9OpU6d0fN8+bS4u/j3Cv0h6RNJaSfmSWkmaKen2s47fK6ln\nQIBWbdigyMhIt85eF3Fqupb54osvFB4eroiICK1fv54IA6i2Xr16aevWrWoaEKAJZ0VYkkolXStp\nk6QCSc9KulfSgbNe01rSBIdDsxMT3TZzXcaK2JDq7kwsLS3V9OnT9eabb2rhwoW67bbbDEwNoK44\ncuSIQq+7TvuKihRykdfeKGmqpJizHjshqZW/v/IOHGA39WWqZ3oAb3PBnYnLl8s2Zcp5OxMPHjyo\nIUOGyM/PT5mZmbrqqqtMfgsA6oDUlBTFSBeN8GFJeyS1P+fxKyTFWCxKTUlR3PjxrhjRaxBiN5qX\nnKwp8fFKcDg0x+k873+AsQ6HkiSlrFypQWvWaJrdrmtatNDo0aM1btw4PfXUU/Lx4WoC4K2cTqdK\nS0tVUlJS5V+Vvf6TlSt1T1HRBf9+pZIelDRCUkX3Y0Q5HPp6x46a/0a9DCF2k3nJyXohPl6bLrIz\nMUTSk06n/nz6tPqOGydHUJDeX7VK3bt3d9eoQJ3hdDpVVlZWrXBVNWQmji8tLZWvr6/q169fpV/1\n6tWr9LlDBw4o6EL/7HQmwn6S5lTymiBJhfn5Nf2vzesQYjdIT0/XlAoi/JqkFEk7JA2RtOCs51pL\nWldaqp5FRfLz83PfsPBqFYXLk0J0Kcf6+PhUOVzVjdnZv6xWqxo1anRJx1bn722xWGrk3/WYBx9U\n4eLFlT7/kKRjkj6WVNk7VhdKCgq52MltXAwhdoPZiYlKcDjOWwk3lzRZ0hpJjvMPO7MzsahIsxMT\ntei991w9Ji5RVVZcpmNUndefGy5XxKR+/fry8/NTYGBgjYWwsmO5nFMxW1iYtr33nsZWcHp6rKQc\nnbmFqcEFvka61ar2vJ/9ZWPXtItVZWfiZEmH9McV8W/q4s7E8vLyWrWqutjxklwWEhPHEy7vUNnP\npgOSWkry1/+thC2S3pB0/1mvq4s/m0xhRexiVd2ZWJkrJN1psWjBv/6lvz/2mEeGqLrHl5eXuy1E\nAQEBLg8ZHzWH2ujKK6/UwOhoLVy5Uk+ctR67VlJ5FY5faLHojgEDiHANYEXsYmMefFARixdr7AVe\nc6EVsSQlS4q3WOT09681q6oLHevr61tj17kAXLr09HQN6tPnoptIz8U7a9UsVsQudrKg4II7E6si\nSNJfBg7UklWramIkAJAkRUVFaZrdrv6X8F7T0+x2IlxDuBjkYoHBwSq8zK/BzkQArjImNlYJdrt6\nBgToZYt5QuZWAAACEklEQVRFld2MdELSSxaLevKBDzWOELuYLSxM2/z9K3yuTFLRr38slVT865+f\nK91qlY2diQBcZExsrFZt2KDMmBj9j7+/RlmtSpb0ls5cGhtltaqVv7+yYmK0asMGIlzDuEbsYhfa\nNT3t119nXy2dIumZs/6anYkA3Ono0aNn3gd/xw4V5ucrKCREto4dNWzECH4GuQghdoMH77pLkefs\nTKyqly0WZcbEcB8xANRRhNgN2JkIAKgM14jd4PediQEB2lvFY9iZCADegRC7CTsTAQAV4dS0m2Vk\nZGh2YqI+/PhjxVgsinI4fv884nSrVSucTt0xYIAenziRlTAAeAFCbAg7EwEAEiEGAMAorhEDAGAQ\nIQYAwCBCDACAQYQYAACDCDEAAAYRYgAADCLEAAAYRIgBADCIEAMAYBAhBgDAIEIMAIBBhBgAAIMI\nMQAABhFiAAAMIsQAABhEiAEAMIgQAwBgECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIAAAwixAAAGESI\nAQAwiBADAGAQIQYAwCBCDACAQYQYAACDCDEAAAYRYgAADCLEAAAYRIgBADCIEAMAYBAhBgDAIEIM\nAIBBhBgAAIMIMQAABhFiAAAMIsQAABhEiAEAMIgQAwBgECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIA\nAAwixAAAGESIAQAwiBADAGAQIQYAwCBCDACAQf8fHWpWlowNdzgAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"nx.draw(Gu, with_labels = True)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Undirected network: \n",
"Node degree: the number of links connected to the node.\n",
"## $k_1 = k_2 = 2, k_3 = 3, k_4 = 1$"
]
},
{
"cell_type": "code",
"execution_count": 177,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X98z/X+//H724y9Z2soS59OIcuvUNH0kfTN+dQRabMQ\nSn6eSI6PTiktkzAtWspJ7ZNTGYVDORGSc4roSDYS8qONKZVzbH40m/3e3t8/2C72i/f7vfd7z/f7\nvdv1cukSr/fr/Xo9Vpe6e76ej9fzabHZbDYBAAAj6pkuAACAuowgBgDAIIIYAACDCGIAAAwiiAEA\nMIggBgDAIIIYAACDCGIAAAwiiAEAMIggBgDAIIIYAACDCGIAAAwiiAEAMIggBgDAIIIYAACDCGIA\nAAwiiAEAMIggBgDAIIIYAACDCGIAAAwiiAEAMIggBgDAIIIYAACDCGIAAAwiiAEAMIggBgDAIIIY\nAACDCGIAAAwiiAEAMIggBgDAIIIYAACDCGIAAAwiiAEAMIggBgDAIIIYAACD6psuAADg/dLT07Uk\nMVEpe/cqOzNTQSEhatO5s0aMGqVmzZqZLs+jWWw2m810EQAA75ScnKz5cXFav2GDHpQUnpenYElZ\nkpKsVn1ss+n+Pn00KTpa4eHhhqv1TAQxAMApCxMSNH3yZE3JzdUIm01NqjjnjKREi0VzrVbNiI/X\n2PHja7tMj0cQAwActjAhQXMmT9bGnByF2XH+YUm9AwM1hTCuhCAGADgkOTlZEXffra8qhPCjkj6X\nlCPpKkmjJU296PPDknoGBmrtli267bbbaq9gD0fXNADAIfPj4jQlN7fSSDha0lFJmZI2SHpD0saL\nPg+T9GxurubHxdVOoV6CETEAwG7p6elq26KF0vLyqpwTLvWDpHskrZHU5aLjpyW1DghQyrFjdFNf\nwIgYAGC3JYmJ6i9VG8ITJDWS1FHnH0t3qfB5U0lRFouWJCa6rUZvw3vEAIAqZWZm6uDBg+X+2rF5\ns2bm5VX7nTclLZC0VdIASV0lVXxpKTw3V9/t2+e2ur0NQQwAdZjNZlNGRoYOHDhQFralvz5+/Hil\n84MkBV/mmhZJ/0/SIEnLVTmIgyVlnTnjgup9A0EMAHVASUmJfv7553Kj29LAPX36tN3XKdb5xTrs\nUSQpsIrjWZKCm1xqhrluIYgBwIcUFRXpyJEjlcL20KFDOnfuXI2vnydpi6THKxzPkLRJUj9JVkn/\nlPThhb9XlGy16qZOnWpci6+gaxoAvFBeXp5++OGHSoGbkpKiwsJCl9yjfv36CgsLU4cOHdS+fXu1\nb99ezZs318D771dafn65hq2TkgZK2ivJJulGSdMkPVDhmnRNV8aIGAA82NmzZyuF7cGDB5WWliZX\njaOsVqvatWtXFralwRsWFiZ/f/9K59/ft68Wr16tJy+6/1WSvrTjXostFvXr25cQvggjYgDwAL/9\n9pv27NlTLmwPHjyoX3/91WX3aNy4cVnYXhy4LVq0UL169r/NWt3KWpfDylpVY0QMAB5g1apV+uMf\n/+iSazVv3rxS2JY+VrZYLDW+fnh4uGbEx6u3E2tNz4iPJ4QrIIgBwJCMjIyyR86bNm1y+PstW7as\nMnCb1EJHcunGDT0nT9azubkaWc3uS6d1fvelV9h9qVo8mgYAN7LZbPrll1+qfE+3uLi4LERbtmyp\nadOmVfp+acNUxbBt27atGjVqZOAnKm/nzp2aHxendZ9+qiiLReG5uWX7ESdf2I+4X9++mhQdzUi4\nGgQxALhAUVGRjh49WilwDx06pKCgoEpB2qFDB1199dXlHhXfe++9Cg0NLXdO69at1aBBA4M/mX0y\nMjK0JDFRKfv2KevMGQU3aaI2nTpp+MiRNGZdBkEMAA7Iy8tTSkpKpdHt4cOH1bx583JhW5uPiuG9\nCGIAqEJWVlaVrw39/PPPatWqVaXRbdu2bRUYWNU6UsClEcQA6rTShqmKgXvq1Kly79Z626NieA+C\nGIDPK22Yqhi2Bw8eVGFhYaXRrTPv1gLOIogB+Izi4mKlpaVVGbilDVMVA9dV79YCziKIAXid/Px8\npaSkVArb1NTUahezoGEKnoogBuCxsrKydOjQoUqvBJU2THnqu7WAIwhiAMadPHmy0uj2wIEDOnXq\nlNq2bVspcMPCwmiYgs8giAHUCpvNpl9//bXKFaYKCwsrhW1pw5Sfn5/p0gG3IogBuNTFDVMVN6YP\nDAyscoUpGqZQlxHEAJxS2jBVMXBTU1N19dVXV/lKEA1TQGUEMYBLKm2YqvhK0LFjx9SyZcsqV5ii\nYQqwH0EMQNL5hqmqVpg6efJkWcPUxaNbGqYA1yCIATulp6ef311m715lZ2YqKCREbTp31ohRo7xm\nd5nShqmKYXvgwAEVFBRUu8IUDVOA+xDEwGUkJydrflyc1m/YoAclheflle23mnRhv9X7+/TRpOho\nhYeHG672vOLiYh09erTKFaZKG6YqNk1dc801NEwBBhDEwCUsTEjQ9MmTNSU3VyNsNlXVanRGUqLF\norlWq2bEx2vs+PG1Vl9+fr5SU1MrjW5LG6aqeiWoadOmtVYfgMsjiIFqLExI0JzJk7UxJ0dhdpx/\nWFLvwEBNcUMYZ2dnV7nCVGnDVMXAbdeuHQ1TgJcgiIEqJCcnK+Luu/VVNSGcKqmzpEGSllx0/LCk\nnoGBWrtli2677TaH73vq1KkqF7w4efKk2rRpU2l0e+ONN9IwBXg5ghiowrAHH9Rtq1fryWr+8+gt\nKU9SC5UPYkl6zWLRt1FRen/Vqiq/e3HDVMU53Pz8/CoXvKBhCvBdBDFQQXp6utq2aKG0vLwq54T/\nJmm1pA46PwKuGMSnJbUOCNDBo0eVnZ1dZeBardZKo9sOHTrQMAXUQfVNFwB4miWJiYqSqgzhs5Km\nS9os6a/VfL+ppD75+Wpx3XVq/l//VRa4PXr00GOPPUbDFIByCGKggpS9e9UtL6/Kz16Q9Jik/7rM\nNXrabAoYOFDvLV/u6vIA+BiCGKggOzNTwVUc/07S5xf+fjnBkvKys11aFwDfRBADFQSFhCiriuNb\nJP0k6XpJNknZkoolHZC0s8K5WZKC2eAAgB3qmS4A8DRtOndWUkBApePjJB3R+RHxHkmPS+on6R9V\nXCPZalWbTp3cWSYAH0HXNFDB5bqmS83Q+WCurms65dgxr1mDGoA5jIiBCkJDQ3V/nz5KvMxrRNNV\nOYQlabHFon59+xLCAOxCEANV6Nm7t1602XTYwe8dljTXatWk6Gh3lAXABxHEQAVHjx7V1KlTlSWp\np2R3GJeuNT0jPt6p5S0B1E0EMXCR7OxsRUZG6tSpU7JJOiGpq6R5FovOVPOd0xc+7+mmDR8A+DZe\nXwIuKCkp0fDhw7Vv376yYzZJQ8aO1e6TJzXr008VZbEoPDe3bD/i5Av7Effr21dro6MZCQNwGEEM\nXDBz5kx9/PHH5Y4NHDhQCQkJqlevnjIyMrQkMVFfff21vti4Uf0HDtRNnTppzsiRNGYBcBqvLwGS\nPvroIw0aNKjcsZtvvlnbtm2rtK/vqVOn1KZNG506dao2SwTgowhi1HnfffedevTooZycnLJjzZo1\nU3Jyslq0aFHp/KKiIgUEBKiwsJCdkgDUGM1aqNPS09MVGRlZLoTr16+vVatWVRnCpZ9brVZls5Y0\nABcgiFFnFRQUaODAgTp27Fi542+++aZ69ux5ye82btxYv/32mzvLA1BHEMSok2w2myZOnKivvvqq\n3PEJEyZo7Nixl/1+SEgIQQzAJQhi1EkJCQlauHBhuWO9evXSa6+9Ztf3GzdurMzMTHeUBqCOIYhR\n52zevFn/+7//W+5Yq1at9OGHH8rf39+ua/BoGoCrEMSoU9LS0jRo0CAVFxeXHQsKCtInn3yiK6+8\n0u7rEMQAXIUgRp2RlZVVtnzlxT744AN17NjRoWsxRwzAVQhi1AklJSV69NFH9f3335c7PmvWLEVG\nRjp8PUbEAFyFIEad8OKLL2rNmjXljg0aNEhTp0516no0awFwFYIYPm/lypWaNWtWuWO33nqrFi1a\n5PTKWIyIAbgKQQyftnv3bo0cObLcsdDQUK1evbrSGtKOIIgBuApBDJ914sQJRUZGKjc3t+yYv7+/\nVq1apeuvv75G16ZZC4CrEMTwSQUFBRowYIB+/vnncscTEhJ055131vj6jIgBuApBDJ9js9k0YcIE\nbdu2rdzxiRMnasyYMS65B81aAFyFIIbPefPNN/XOO++UO/Y///M/mjdvnsvuwYgYgKuwHzF8yhdf\nfKHevXuXWzmrdevW2rFjh0MrZ11Ofn6+goODlZ+fz57EAGqEETF8xpEjRyotXxkcHKw1a9a4NIQl\nqWHDhvLz8yvXCAYAziCI4RPOnj2riIgInTlzpuyYxWLR0qVLddNNN7nlnswTA3AFghher6SkRMOG\nDdOBAwfKHZ89e7YeeOABt92XeWIArkAQw+u98MILWrt2bbljQ4YM0XPPPefW+xLEAFyBIIbX69mz\np6xWa9nvu3TponfffdftTVQs6gHAFeqbLgCoKavVKqvVqubNmysnJ0erV69WYGCg2+/LiBiAKxDE\n8Go//fSTBg8erOXLl6tbt246duyYrrvuulq5N81aAFyBIIbXOnfunCIiIjRlyhT94Q9/kHQ+HGsL\nI2IArsAcMbxSSUmJRowYoS5dumjSpElGaiCIAbgCI2J4pdjYWB0/flybN282trJVSEiIfvzxRyP3\nBuA7CGJ4nb///e965513lJSUpIYNGxqrgxExAFcgiOFV9u7dq3Hjxumzzz5T8+bNjdZCsxYAV2CO\nGF4jIyNDkZGR+stf/qKuXbuaLocRMQCXIIjhFQoLCzVo0CANHTpUQ4cONV2OJIIYgGsQxPAKkyZN\nUnBwsGJjY02XUoaVtQC4AnPE8HgJCQn68ssv9c0336hePc/5syMjYgCuYLHZbDbTRQDV2bJlix56\n6CFt27ZNYWFhpsspx2azqWHDhsrKyjLavQ3Au3nO8AKo4OjRoxoyZIiWLl3qcSEsnd/vmM5pADVF\nEMMjZWdnKzIyUtHR0brnnntMl1MtHk8DqCmCGB6npKREw4cPV7du3TRx4kTT5VwSDVsAaopmLXic\nmTNn6sSJE1q+fLmx5SvtxYgYQE0RxPAoH330kRYtWmR8+Up7MUcMoKYIYniM7777TuPHj9fGjRt1\n9dVXmy7HLoyIAdQUc8TwCOnp6erfv78WLFigLl26mC7HbswRA6gpghjGFRQUaODAgRo2bJgGDx5s\nuhyHMCIGUFMEMYyy2WyaOHGimjZtqpkzZ5oux2EEMYCaYo4YRiUkJGjbtm3avn27Ry1faS+atQDU\nFEEMYzZt2qSZM2dq27ZtCg4ONl2OUxgRA6gp7xuCwCekpaXp4Ycf1rJly9S6dWvT5TiNZi0ANUUQ\no9ZlZWUpMjJSMTEx+v3vf2+6nBphRAygpghi1KqSkhI9+uij6t69uyZMmGC6nBojiAHUFHPEqFXT\np0/XqVOntHLlSo9fvtIeNGsBqCmCGLVm5cqVev/995WUlKQGDRqYLsclgoKClJubq6KiItWvz39O\nABzHo2nUit27d2vChAlavXq1QkNDTZfjMhaLRVdccQWjYgBOI4jhdidOnFD//v311ltv6ZZbbjFd\njssxTwygJghiuFVBQYEGDBigESNGaNCgQabLcQvmiQHUBEEMt7HZbHriiSfUrFkzvfjii6bLcRtG\nxABqgu4SuM2CBQuUlJSkr7/+2iuXr7QXQQygJghiuMUXX3yh2bNna/v27QoKCjJdjluxuhaAmiCI\n4XJHjhzRww8/rBUrVqhVq1amy3E7RsQAasJ3nxfCiLNnzyoiIkIvvvii7r77btPl1AqatQDUBEEM\nlykpKdGwYcPUs2dPjR8/3nQ5tYYRMYCa4NE0XGbatGnKzMzURx99ZLqUWsUcMYCaIIjhEn/729+0\nbNkyn1q+0l6MiAHUBEGMGtu1a5cmTpyozz//XM2aNTNdTq0jiAHUBHPEqJH//Oc/ioqK0v/93//p\n5ptvNl2OETRrAagJghhOy8/P14MPPqgxY8ZowIABpssxhhExgJqw2Gw2m+ki4H1sNpvGjBmjs2fP\nauXKlT69ctblnDlzRq1atSKMATiFOWI45S9/+Yt27dqlbdu21ekQlqQrrrhCWVlZKikpqfP/LAA4\njiCGw/75z3/q5ZdfrhPLV9rDz89PQUFBOnv2rBo3bmy6HABehj++wyGpqakaNmyYVqxYoZYtW5ou\nx2PQsAXAWQQx7JaZmanIyEjNnDlTd911l+lyPAoNWwCcRRDDLsXFxXrkkUfUq1cvjRs3znQ5HofV\ntQA4iyCGXWJiYnTu3Dm9/vrrpkvxSIyIATiLZi1c1rJly7RixQolJSXJ39/fdDkeiSAG4CyCGJe0\nc+dOTZo0SZs2bdJVV11luhyPRbMWAGfxaBrV+ve//62oqCgtXLhQnTp1Ml2OR2NEDMBZBDGqlJeX\np6ioKI0dO1ZRUVGmy/F4NGsBcBZBjEpsNpsef/xxXX/99YqJiTFdjldgRAzAWcwRo5LXX39de/bs\n0b/+9S9ZLBbT5XgFghiAswhilLNx40bNnTtX33zzjRo1amS6HK9BsxYAZxHEKJOSkqLhw4dr1apV\natGihelyvApzxACcxRwxJJ1fvjIiIkKxsbG68847TZfjdXg0DcBZBDFUXFysoUOH6t5779Vjjz1m\nuhyvRBADcJbFZrPZTBcBs5599lnt2rVLn332GStnOamwsFBWq1WFhYU0uAFwCHPEddwHH3ygVatW\nsXxlDfn7+ysgIEDnzp1jj2YADiGI67CkpCQ99dRT2rRpk6688krT5Xi90oYtghiAI5gjrqOOHz+u\nBx98UO+88446duxouhyfwDwxAGcQxHVQ6fKV48ePV0REhOlyfAZBDMAZBHEdY7PZNHbsWLVq1UrP\nP/+86XJ8Cot6AHAGc8R1zKuvvqrvv/+e5SvdgBExAGcQxHXIhg0bNG/ePO3YsUOBgYGmy/E5rK4F\nwBkEcR1x6NAhjRgxQh9//LGuu+460+X4JEbEAJzBHHEd8NtvvykyMlIvv/yyevToYbocn0UQA3AG\nQezjiouLNWTIEN13330aPXq06XJ8Gs1aAJxBEPu4KVOmqLi4WK+++qrpUnweI2IAzmCO2IctWbJE\na9as0Y4dO1S/Pv+q3Y1mLQDO4P/OPuqbb77R5MmT9eWXX6pp06amy6kTGBEDcAaPpn3Qr7/+qgED\nBujdd99Vhw4dTJdTZxDEAJxBEPuY3Nxc9e/fXxMnTtQDDzxgupw6hWYtAM5gP2IfYrPZ9Oijj6qk\npERLly5l5axalpeXp5CQEOXl5fHPHoDdmCP2Ia+88ooOHTqkrVu3EgQGBAQEyGKxKC8vT1ar1XQ5\nALwEQewj1q9fr/nz57N8pWGl88QEMQB7MUfsAw4ePKhRo0bpo48+0u9+9zvT5dRpNGwBcBRB7OXO\nnDmjiIgIzZkzR927dzddTp1HwxYARxHEXqyoqEiDBw/WAw88oFGjRpkuB2JRDwCOI4i92LPPPitJ\nmjt3ruFKUIpH0wAcRbOWl1q0aJHWrVvH8pUehiAG4Cj+D+6Ftm/frilTpmjLli1q0qSJ6XJwEYIY\ngKN4NO1lfvnlFw0cOFCJiYlq37696XJQAc1aABxFEHuRnJwc9e/fX5MmTVLfvn1Nl4Mq0KwFwFEE\nsZew2WwaM2aM2rVrp2eeecZ0OagGj6YBOIo5Yi8xZ84cHT58mOUrPRxBDMBRBLEXWLt2rRYsWKAd\nO3awdKKHI4gBOIog9nAHDhzQmDFjtHbtWl177bWmy8Fl0KwFwFHMEXuw06dPKyIiQvHx8br99ttN\nlwM70KwFwFHsR2xIenq6liQmKmXvXmVnZiooJERtOnfWiFGj1KxZMxUVFem+++7TLbfcovj4eNPl\nwk7nzp1Ts2bNlJOTY7oUAF6CIK5lycnJmh8Xp/UbNuhBSeF5eQqWlCUpyWrVxzab7u/TR0UNGigz\nM1Pr1q2Tn5+f4aphL5vNpgYNGig7O1sNGzY0XQ4AL8AccS1amJCg6ZMna0purt6w2VRxTazHc3P1\nqqRFq1drpqQX4+MJYS9jsVjK5olDQ0NNlwPACzBHXEsWJiRozuTJ+ionR09eCOE3JYVLCpA0+sJ5\nTSQ9ZbNpp82mN6ZN08KEBFMlw0khISE0bAGwG0FcC5KTkzV98mRtzMlR2EXHr5U0TdKYKr4TJmlj\nTo6mT56snTt31kqdcA1eYQLgCIK4FsyPi9OU3NxyISxJ/SVFSGpazffCJD2bm6v5cXFurQ+uRRAD\ncARB7Gbp6elav2GDRjjZEzfCZtO6Tz9VRkaGiyuDuxDEABxBELvZksRERUmVGrPs1VRSlMWiJYmJ\nrisKbsWiHgAcQRC7WcreveqWl1eja4Tn5ipl3z4XVQR3Y1EPAI4giN0sOzNTwTW8RrCkrDNnXFEO\nagGPpgE4giB2s6CQEGVV81mxpLwLfy+SlH/h1xVlSQpu4uzDbdQ2ghiAIwhiN2vTubOSAgKq/CxW\nUqCkOZKWXvj17CrOSwoIUJtOndxWI1yLIAbgCILYzYaPHKmPJVX1YHm6pBKdHwWX/vVChXNOS1qR\nl6eff/2VzmkvQbMWAEcQxG4WGhqq+/v00WKLxanvL7ZYdF/v3srPz1fbtm311FNP6fjx4y6uEq5E\nsxYARxDEtWBSdLTmWK067OD3Dkuaa7Xq+dhYJSQkaN+FzumOHTvqiSee0I8//ujqUuECPJoG4AiC\nuBaEh4drRny8egcG2h3GhyX1DgzUjPh43XbbbZKka6+9VvPmzdOhQ4fUuHFjde3aVaNHj1Zqaqrb\naofjCGIAjiCIa8nY8eM1JT5ePQMD9ZrFUuWcsXR+TniexaKegYGaEh+vsePHVzonNDRUL730kg4f\nPqyWLVvqjjvu0MMPP6zvv//erT8D7EMQA3AE+xHXsp07d2p+XJzWffqpoiwWhefmlu1HnHxhP+J+\nfftqUnR02Uj4crKyspSQkKB58+bpjjvu0NSpU9W1a1e3/hyoXklJifz9/ZWfn6/69dlpFMClEcSG\nZGRkaEliolL27VPWmTMKbtJEbTp10vCRI9WsWTOnrpmTk6N33nlHc+fOVadOnRQTE6MePXq4uHLY\no0mTJjpy5IiaNq1uSw8AOI8g9kH5+flavHixXn75ZbVo0ULTpk1Tr169ZHGycxv2++yzz/Tcc89p\n//79CgwMVFRUlBJZJxzAJTBH7IMaNmyosWPH6ocfftCoUaP0xBNPqEePHlq/fr34c5d75eXlac+e\nPSoqKtLZs2d1+vRp0yUB8HAEsQ/z9/fX8OHDtX//fj355JN6/vnn1bVrV61atUolJSWmy/NJjRs3\nLvd7mrYAXA5BXAf4+fnpoYce0nfffacZM2Zozpw56tSpk5YuXaqioiLT5fkUghiAowjiOsRiseiB\nBx7Qjh079Prrr+vtt99Wu3bt9O6776qgoMB0eT6BIAbgKIK4DrJYLLr33nu1detWvffee1q5cqVu\nvPFGvfnmm8rNzTVdnlcLCQkp93vWnAZwOXRNQ5KUlJSk2bNnKzk5WU8//bTGjRunoKAg02V5neLi\n4krvDhcVFcnPz89QRQA8HSNiSJK6deumNWvWaMOGDUpKStINN9yg2bNn82jVQX5+frriiivKHTt7\n9qyhagB4A4IY5dx8881asWKFtm7dqpSUFIWFhWnatGk6efKk6dK8BvPEABxBEKNK7dq10+LFi5WU\nlKT09HS1adNGzzzzjP7zn/+YLs3jEcQAHEEQ45JuuOEGvf3229q7d68KCgrUoUMH/elPf9KxY8dM\nl+axaNgC4AiCGHb53e9+p/nz5+vgwYNq1KiRbrnlFv3xj3/U4cOO7rLs+xgRA3AEQQyHXH311Zoz\nZ45SU1N17bXX6r//+781bNgwHThwwHRpHoMgBuAIghhOufLKKzVjxgwdOXJEN910k3r16qWBAwdq\n9+7dpkszjiAG4AiCGDUSEhKi6OhopaWl6c4771S/fv3Ur18/bd++3XRpxhDEABxBEMMlGjVqpCef\nfFJHjhxRv379NHToUN1zzz368ssv69yOTzRrAXAEQQyXCggI0OOPP67U1FQNGzZMY8eOVc+ePfXZ\nZ5/VmUBmRAzAEQQx3MLf318jR47UwYMH9ac//UnPPPOMwsPDtXr1ap/fgpEgBuAIghhu5efnpyFD\nhmjPnj2KiYlRbGysOnfurOXLl6u4uNh0eW5BEANwBEGMWlGvXj31799fycnJio+P14IFC9S+fXst\nWrRIhYWFpstzqYpzxAQxgEshiFGrLBaL7rvvPv3rX//SwoULtXTpUt14441KSEhQXl6e6fJcouKI\nmGYtAJdCEMMIi8Wiu+++W59//rmWL1+u9evXq3Xr1nrttdd07tw50+XVCI+mATiCIIZx3bt317p1\n67Ru3Tp9/fXXuuGGGxQXF+e12wdW9fqSrzeoAXAeQQyPceutt+rDDz/U5s2bdeDAAd1www2aPn26\nTp8+bbo0h/j7+6tRo0Zlvy8pKVF2drbBigB4MoIYHqdDhw56//339c033+j48eO68cYbNWXKFJ04\nccJ0aXajYQuAvQhieKywsDD99a9/1e7du5WTk6P27dtr0qRJ+uWXX0yXdlk0bAGwF0EMj3f99dfr\njTfe0P79+9WgQQN17txZ48aNU1pamunSqkXDFgB7EcTwGtdcc41eeeUVpaSkKDQ0VN26ddPw4cN1\n6NAh06VVQhADsBdBDK9z1VVXadasWTp8+LDatm2ru+66S4MHD9aePXtMl1aGIAZgL4IYXqtx48aa\nOnWq0tLS1K1bN/Xp00cRERFKSkoyXRrNWgDsRhDD6wUFBenpp5/WkSNH1Lt3bw0aNEh/+MMftHXr\nVmM10awFwF4EMXyG1WrVhAkTlJqaqiFDhmj06NG666679I9//KNsC8aVK1fWyuiUR9MA7EUQw+c0\naNBAo0eP1qFDhzRu3Dj9+c9/1u23364FCxZo8ODBatGihaZOnaqMjAy31UAQA7AXQQyfVb9+fT3y\nyCPat2/h5tnOAAAFVklEQVSfnnvuOb3wwguSpLNnz+qll15Sy5Yt9fTTT+vf//63y+9NEAOwF0EM\nn1evXj117ty50jxtTk6O5s2bp1atWmnChAn66aefXHZPmrUA2IsgRp0QGhqq2NhYXXXVVZU+y8/P\n11tvvaWwsDCNGTNGqampNb4fzVoA7EUQo0644oorFB0drR9//FHz5s3TNddcU+mcoqIivffee2rX\nrp0eeeQR7d+/3+n78WgagL0IYtQpjRo10p///GelpaXprbfeUosWLSqdU1JSomXLlqljx44aMGCA\nvv32W4fvQxADsJfFVvpeB1AHFRYWaunSpXrppZcu+Ui6T58+iomJ0R133GHXdfPy8mS1Wst+X79+\nfRUUFMhisdS4ZgC+hSAGJBUXF+vDDz9UbGzsJR9J9+rVSzExMerVq9dlQ7Vhw4YqLChQgCQ/SYMG\nD1aHLl00YtQoNWvWzLU/AACvRRADFykpKdEnn3yi2NhY7dq1q9rzunfvrpiYGPXp06dSICcnJ2t+\nXJz+/vHH6i/pLknBkrIkJVmt+thm0/19+mhSdLTCw8Pd+eMA8AIEMVAFm82mjRs3atasWfr666+r\nPe/WW29VTEyM+vfvr3r16mlhQoKmT56sKbm5GmGzqUkV3zkjKdFi0VyrVTPi4zV2/Hi3/RwAPB9B\nDFyCzWbTli1bFBsbqy+++KLa8zp06KDut9+uzStWaGNOjsLsuPZhSb0DAzWFMAbqNIIYsNP27ds1\ne/ZsrV+/vsrPr5C0SyoL4QJJT0j6XOdHwa0lvSTpvou+c1hSz8BArd2yRbfddpu7SgfgwXh9CbBT\n9+7dtW7dOn377bcaMGBAuc8CJb0glRsJF0m6XtJXkjIlzZL0kKRjF50TJunZ3FzNj4tzZ+kAPBgj\nYsBJ+/fvV1xcnJYtW6aGNpuOS1XOCV/sZkkvSoq66NhpSa0DApRy7Bjd1EAdxIgYcNJNN92kDz74\nQM9OnqwBfn6XDeETklIl3VTheFNJURaLliQmuqNMAB6OIAZq6PTx47qzuPiS5xRJGiZppKQ2VXwe\nnpurlH37XF8cAI9HEAM1lJ2ZqeBLfG7T+RBuKOmNas4JlpR15oyrSwPgBeqbLgDwdkEhIcq6xOdj\nJJ2U9KnOr7BVlSxJwU0u93AbgC9iRAzUUJvOnZUUEFDlZ49LOiTpE0kNLnGNZKtVbTp1ckN1ADwd\nXdNADaWnp6ttixZKy8sr17B1TFJLqWytaUmySHpb0tCLzqNrGqjbGBEDNRQaGqr7+/TR4gprTl8v\nqURSjs4/es6SdFblQ1iSFlss6te3LyEM1FGMiAEXSE5OVsTdd+srO5e3LMXKWgAYEQMuEB4erhnx\n8eodGKjDdn6ndK3pGfHxhDBQhxHEgIuMHT9eU+Lj1TMwUK9ZLKruZaTTkuZZLOrJhg8AxKNpwOV2\n7typ+XFxWvfpp4qyWBSem1u2H3Hyhf2I+/Xtq0nR0YyEARDEgLtkZGRoSWKiUvbtU9aZMwpu0kRt\nOnXS8JEjacwCUIYgBgDAIOaIAQAwiCAGAMAgghgAAIMIYgAADCKIAQAwiCAGAMAgghgAAIMIYgAA\nDCKIAQAwiCAGAMAgghgAAIMIYgAADCKIAQAwiCAGAMAgghgAAIMIYgAADCKIAQAwiCAGAMAgghgA\nAIMIYgAADCKIAQAwiCAGAMAgghgAAIMIYgAADCKIAQAwiCAGAMAgghgAAIMIYgAADCKIAQAwiCAG\nAMAgghgAAIMIYgAADCKIAQAwiCAGAMAgghgAAIMIYgAADCKIAQAwiCAGAMAgghgAAIMIYgAADCKI\nAQAwiCAGAMCg/w835PM8oaEV8wAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"nx.draw(Gd, with_labels = True)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Directed network\n",
"In directed networks we can define an in-degree and out-degree. The (total) degree is the sum of in-and out-degree.\n",
"\n",
"## $k_3^{in} = 2, k_3^{out} = 1, k_3 = 3$\n",
"\n",
"Source: a node with $k^{in}= 0$; Sink: a node with $k^{out}= 0$.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"For a sample of N values: $x_1, x_2, ..., x_N$:\n",
"\n",
"# Average(mean):\n",
"\n",
"## $ = \\frac{x_1 +x_2 + ...+x_N}{N} = \\frac{1}{N}\\sum_{i = 1}^{N} x_i$ "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"For a sample of N values: $x_1, x_2, ..., x_N$:\n",
"\n",
"# The nth moment:\n",
"\n",
"## $ = \\frac{x_1^n +x_2^n + ...+x_N^n}{N} = \\frac{1}{N}\\sum_{i = 1}^{N} x_i^n$ "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"For a sample of N values: $x_1, x_2, ..., x_N$:\n",
"\n",
"# Standard deviation:\n",
"\n",
"## $\\sigma_x = \\sqrt{\\frac{1}{N}\\sum_{i = 1}^{N} (x_i - )^2}$ "
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"(1.6666666666666667, 10, 0.7453559924999299)"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import numpy as np\n",
"x = [1, 1, 1, 2, 2, 3]\n",
"np.mean(x), np.sum(x), np.std(x)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"For a sample of N values: $x_1, x_2, ..., x_N$:\n",
"\n",
"# Distribution of x:\n",
"\n",
"## $p_x = \\frac{The \\: frequency \\: of \\: x}{The\\: Number \\:of\\: Observations}$\n",
"\n",
"其中,$p_x 满足 \\sum_i p_x = 1$"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXkAAAEACAYAAABWLgY0AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAADdtJREFUeJzt3W+IXfWdx/HPR6PSRSaghaQkmoDVLZYd0t0SIy6bLEup\nEdY8EawVBB8FWVHwSRcRkn1S2Id1m5IGbGkUqYsPNLvRRai9NQoNEjMaNNlG6KrNNgOLhqIJS9p+\n9sEcu9ebmbnn3jkzN/n6fsHB8+c753w9/OYzZ34zZ+IkAgDUdNmkGwAALB9CHgAKI+QBoDBCHgAK\nI+QBoDBCHgAKGxrytq+yfdj2Udtv2/7uAnWP2z5pe8b2pu5bBQCMatWwgiT/a/tvk5y1fbmk12zf\nluS1T2tsb5d0Q5Ibbd8iaa+kLcvXNgCgjVbTNUnONqtXNR/z0UDJDkn7m9rDklbbXtNVkwCA8bQK\neduX2T4q6bSkXpJ3BkrWSfqgb/tUsw8AMEFtn+T/mORrktZL+hvbW5e3LQBAF4bOyfdL8jvbByV9\nXdIv+g6dknRd3/b6Zt9n2OYP5QDAGJJ4nI9r89s1X7S9uln/gqRvSJoZKDsg6b6mZoukM0lmF2h1\nosvU1F/ozTffVJJLftm1a9fEe6i0cD+5lxfrshRtnuS/JOkntq25LwpPJvmZ7Z2SkmRfkhds32H7\nXUmfSLp/SV0BADrR5lcoj0n6y3n2/3Bg+8EO+wIAdIA3Xi9h27Ztm3QLpXA/u8O9vHh4qfM9I13M\nztzc+ORMTU3r0KGnND09PdE+AKAt28py/eAVAHDpIuQBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAK\nI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QB\noDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoLChIW97ve2Xbb9t+5jth+ap2Wr7jO03muWx5WkX\nADCKVS1qfi/pkSQztq+WdMT2S0lODNS9kuTO7lsEAIxr6JN8ktNJZpr1jyUdl7RunlJ33BsAYIlG\nmpO3vVHSJkmH5zl8q+0Z2wdt39xBbwCAJWozXSNJaqZqnpX0cPNE3++IpOuTnLW9XdJzkm7qrk0A\nwDhahbztVZoL+CeTPD94vD/0k7xo+we2r0ny4YVn2923vq1ZAACf6vV66vV6nZzLSYYX2fsl/U+S\nRxY4vibJbLO+WdK/Jtk4T12k4ddbTlNT0zp06ClNT09PtA8AaMu2koz1c8+hT/K2b5N0r6Rjto9q\nLqUflbRBUpLsk3SX7QcknZd0TtLd4zQDAOjW0JBP8pqky4fU7JG0p6umAADd4I1XACiMkAeAwgh5\nACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiM\nkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeA\nwgh5AChsaMjbXm/7Zdtv2z5m+6EF6h63fdL2jO1N3bcKABjVqhY1v5f0SJIZ21dLOmL7pSQnPi2w\nvV3SDUlutH2LpL2StixPywCAtoY+ySc5nWSmWf9Y0nFJ6wbKdkja39QclrTa9pqOewUAjGikOXnb\nGyVtknR44NA6SR/0bZ/ShV8IAAArrM10jSSpmap5VtLDzRP9mHb3rW9rFmDy1q7dqNnZ9ybaw5o1\nG3T69H9NtAdMXq/XU6/X6+RcTjK8yF4l6d8lvZjke/Mc3yvp50meabZPSNqaZHagLtLw6y2nqalp\nHTr0lKanpyfaBy4+tjXp8SlZbT4n8fliW0k8zse2na75kaR35gv4xgFJ9zXNbJF0ZjDgAQArb+h0\nje3bJN0r6Zjto5p71HlU0gZJSbIvyQu277D9rqRPJN2/nE0DANoZGvJJXpN0eYu6BzvpCADQGd54\nBYDCCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DC\nCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DCCHkA\nKIyQB4DCCHkAKGxoyNt+wvas7bcWOL7V9hnbbzTLY923CQAYx6oWNT+W9C+S9i9S80qSO7tpCQDQ\nlaFP8klelfTRkDJ30w4AoEtdzcnfanvG9kHbN3d0TgDAErWZrhnmiKTrk5y1vV3Sc5JuWrh8d9/6\ntmYBAHyq1+up1+t1ci4nGV5kb5D0b0mmW9T+WtJfJflwnmORhl9vOU1NTevQoac0PT30fwWfM7Y1\n6fEpWW0+J/H5YltJxpoWbztdYy0w7257Td/6Zs194bgg4AEAK2/odI3tpzU3p3Kt7fcl7ZJ0paQk\n2SfpLtsPSDov6Zyku5evXQDAKIaGfJJvDzm+R9KezjoCAHSGN14BoDBCHgAKI+QBoDBCHgAKI+QB\noDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBC\nHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKGxrytp+wPWv7\nrUVqHrd90vaM7U3dtggAGFebJ/kfS/rmQgdtb5d0Q5IbJe2UtLej3gAASzQ05JO8KumjRUp2SNrf\n1B6WtNr2mm7aAwAsRRdz8uskfdC3farZBwCYsFUrf8ndfevbmgUALk5r127U7Ox7k25jbF2E/ClJ\n1/Vtr2/2LWB3B5cEgJUxF/CZcBce+yPbTtd4kasckHSfJNneIulMktmxOwIAdGbok7ztpzU3p3Kt\n7fcl7ZJ0paQk2ZfkBdt32H5X0ieS7l/OhgEA7Q0N+STfblHzYDftAAC6xBuvAFAYIQ8AhRHyAFAY\nIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8A\nhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhbUK\nedu32z5h+1e2vzPP8a22z9h+o1ke675VAMCoVg0rsH2ZpO9L+jtJ/y3pddvPJzkxUPpKkjuXoUcA\nwJjaPMlvlnQyyXtJzkv6qaQd89S5084AAEvWJuTXSfqgb/s3zb5Bt9qesX3Q9s2ddAcAWJKh0zUt\nHZF0fZKztrdLek7STR2dGwAwpjYhf0rS9X3b65t9f5Lk4771F23/wPY1ST688HS7+9a3NQsA4P/1\nmmXp2oT865K+bHuDpN9K+pake/oLbK9JMtusb5bk+QNe+mzIAwAutE2ffQD+p7HPNDTkk/zB9oOS\nXtLcHP4TSY7b3jl3OPsk3WX7AUnnJZ2TdPfYHQEAOtNqTj7Jf0j684F9P+xb3yNpT7etAQCWijde\nAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAw\nQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4A\nCiPkAaAwQh4ACmsV8rZvt33C9q9sf2eBmsdtn7Q9Y3tTt20CAMYxNORtXybp+5K+Kemrku6x/ZWB\nmu2Sbkhyo6SdkvYuQ68Y0Ov1Jt0CMC/G5sWjzZP8Zkknk7yX5Lykn0raMVCzQ9J+SUpyWNJq22s6\n7RQX4BMJFyvG5sWjTcivk/RB3/Zvmn2L1ZyapwYAsMJWrfQFp6b+fqUv+Rnnzv1aV1xxxUR7AICV\n4iSLF9hbJO1Ocnuz/Y+SkuSf+2r2Svp5kmea7ROStiaZHTjX4hcDAMwricf5uDZP8q9L+rLtDZJ+\nK+lbku4ZqDkg6R8kPdN8UTgzGPBLaRIAMJ6hIZ/kD7YflPSS5ubwn0hy3PbOucPZl+QF23fYflfS\nJ5LuX962AQBtDJ2uAQBcujp/49X2E7Znbb+1SA0vTrU07H7a3mr7jO03muWxle7xUmF7ve2Xbb9t\n+5jthxaoY3y20OZ+Mj7bs32V7cO2jzb39LsL1I02PpN0ukj6a0mbJL21wPHtkg4267dI+mXXPVRa\nWtzPrZIOTLrPS2GRtFbSpmb9akn/KekrAzWMz27vJ+NztHv6Z81/L5f0S0m3DRwfeXx2/iSf5FVJ\nHy1SwotTI2hxPyWJH2i3kOR0kplm/WNJx3Xh+xyMz5Za3k+J8dlakrPN6lWam2kZ/NwfeXxO4g+U\n8eJU925tvnU7aPvmSTdzKbC9UXPfIR0eOMT4HMMi91NifLZm+zLbRyWdltRL8s5Aycjjc8VfhkLn\njki6PsnZ5m8IPSfppgn3dFGzfbWkZyU93DyBYgmG3E/G5wiS/FHS12xPSXrJ9tYkv1jKOSfxJH9K\n0nV92+ubfRhDko8//RYvyYuSrrB9zYTbumjZXqW5QHoyyfPzlDA+RzDsfjI+x5Pkd5IOSvr6wKGR\nx+dyhby18DzcAUn3SX96m3beF6fwGQvez/75ONubNfdrsR+uVGOXoB9JeifJ9xY4zvgczaL3k/HZ\nnu0v2l7drH9B0jckzQyUjTw+O5+usf20pG2SrrX9vqRdkq4UL06NZdj9lHSX7QcknZd0TtLdk+r1\nYmf7Nkn3SjrWzHtG0qOSNojxObI291OMz1F8SdJPbFtzD+BPJvnZUl885WUoACiMf/4PAAoj5AGg\nMEIeAAoj5AGgMEIeAAoj5AGgMEIeAAoj5AGgsP8DlQRse4t0JfQAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.hist(x)\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 113,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"defaultdict(int, {1: 3, 2: 2, 3: 1})"
]
},
"execution_count": 113,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from collections import defaultdict, Counter\n",
"freq = defaultdict(int)\n",
"for i in x:\n",
" freq[i] +=1\n",
"\n",
"freq"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"6"
]
},
"execution_count": 37,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"freq_sum = np.sum(freq.values())\n",
"freq_sum"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"[0.5, 0.3333333333333333, 0.16666666666666666]"
]
},
"execution_count": 38,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"px = [float(i)/freq_sum for i in freq.values()]\n",
"px"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX8AAAEACAYAAABbMHZzAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAH/dJREFUeJzt3XuQVPWZ//H30xizolF3QoSAQpBbuF8mEAj8pIUoKCnQ\nyZaC2bhiFNa7FVIFlWAxLsaIwQiRoKBZTSS7WN4ICRJAyVDMBnAiw3DZAQxBooHVjUbDReT2/P74\ntmxnHJieme4+ffm8qro43efSz3Q13/P09/t8zzF3R0REikss6gBERCT71PiLiBQhNf4iIkVIjb+I\nSBFS4y8iUoTU+IuIFKGUGn8zG21m281sp5lNrWf9cDN738w2Jh7TU91XRESyzxqq8zezGLATGAns\nBaqA8e6+PWmb4cAUdx/b2H1FRCT7Usn8BwGvu/sedz8KLAbG1bOdNWNfERHJolQa/3bAm0nP30q8\nVtcQM9tkZsvMrEcj9xURkSw6I03HeQ1o7+6HzOwKYAnQNU3HFhGRNEul8f8z0D7p+YWJ105y9wNJ\ny8vNbL6ZlaSy78fMTBcZEhFpJHevr8u9Qal0+1QBnc2sg5mdCYwHliZvYGatk5YHEQaS30tl32QO\nHADKe/fGDx/G3fVowmPGjBmRx1BID32e+jxz9dEcDTb+7n4cuB1YCWwDFrt7rZlNNrNJic3+ycy2\nmlk1MAe49nT7nuq9DgIzOnTghtatoV8/WLu2OX+biIicQkp9/u7+G6BbndcWJC3/BPhJqvueyuxv\nfIM7Zs6kQ8eO8MILMGECjBkDs2bB+eencggREUlBTs3wnbFoUWj4AcrKYNs2aNECevaE55+HZv7M\nKRbxeDzqEAqKPs/00ueZGxqc5JUtZuanjOW//gtuvhm6dIF58+Cii7IbnIhIDjIzPIMDvtEbOhSq\nq6G0FAYMCCeA48ejjkpEJG/lR+afrLYWJk2CY8dg4ULo3TvzwYmI5KDCz/yTde8Oa9bAxIkwYgRM\nnw6HD0cdlYhIXsm/xh8gFgvZ/+bNsGMH9OkDFRVRRyUikjfyr9unPkuXwu23w+WXw4MPQklJeoMT\nEclBxdXtU5+xY2HrVjjrrFAWunixykJFRE6jMDL/ZOvXh7LQ9u1h/nzo0KH5xxQRyUHK/JMNHgyv\nvRbKQ0tLYc4clYWKiNRReJl/sp07YfJkOHAAnngC+vZN7/FFRCKkzP9UunaF1avhllvgsstg2jQ4\ndCjqqEREIlfYjT+AGdx4I2zZAnv2hElhL78cdVQiIpEq7G6f+rz0Etx6KwwfDg89BK1aZf49RUQy\nQN0+jXHllaEstKQEevWCRYtUFioiRaf4Mv9kVVWhLLRNG3j0Ufj4ctIiInlAmX9TDRwYTgAjRoTl\n2bPDBeNERApccWf+yXbtgn/9V3j3XXj88TBHQEQkhynzT4dOnWDlSrj77jAuMGUKHDwYdVQiIhmh\nxj+ZGVx/fRgQfuedMCC8YkXUUYmIpJ26fU5nxYowQWzIEHj4YbjggqgjEhE5Sd0+mTJqVJgc1q5d\nmBz21FMqCxWRgqDMP1XV1XDTTXD++bBgAXTuHHVEIlLkMp75m9loM9tuZjvNbOppthtoZkfNrCzp\ntTfMrMbMqs3s1aYEmRP694cNG2DMmHDl0AcegKNHo45KRKRJGsz8zSwG7ARGAnuBKmC8u2+vZ7tV\nwIfAv7v7C4nX/wiUuvtfG3if3M78k+3eHcYC9u0LZaGDBkUdkYgUoUxn/oOA1919j7sfBRYD4+rZ\n7g7gOeCduvGl+D75o2NHWL4cpk6FceNCeej+/VFHJSKSslQa5XbAm0nP30q8dpKZtQWucvdHCY19\nMgdWmVmVmd3cnGBzihlcd10oC/3gg1AWumxZ1FGJiKTkjDQdZw6QPBaQfAIY6u77zOxzhJNArbtX\n1neQ8vLyk8vxeJx4PJ6m8DLos5+FJ58M9w2YPBl+/nOYOzdcL0hEJI0qKiqoqKhIy7FS6fMfDJS7\n++jE82mAu/uspG3++PEi0Ao4CExy96V1jjUD2O/uP6rnffKnz/9UPvwQZs4Mdw27/3741rfCLwQR\nkQxoTp9/Ko1/C2AHYcB3H/AqMMHda0+x/ZPAr9z9BTNrCcTc/YCZnQ2sBO5195X17Jf/jf/HNm8O\nZaEtW4ay0G7doo5IRApQRgd83f04cDuh4d4GLHb3WjObbGaT6tslabk1UGlm1cB6wknhEw1/wenT\nB9atg7KycCP5++6DI0eijkpE5CRN8sq0P/0p3DnsjTdCWeiQIVFHJCIFIqPdPtlSsI0/hEtCPPts\nKAm9+mr4wQ/g3HOjjkpE8pyu7ZPrzOCaa2DbttD907MnLFkSdVQiUsSU+UdhzRqYNCnMDXjkEWjb\nNuqIRCQPKfPPN8OHQ00N9OgBffvCY4/BiRNRRyUiRUSZf9S2bg2/AmIxWLgwnBBERFKgzD+f9eoF\nlZXhUhHDh0N5OXz0UdRRiUiBU+OfC2KxUA5aXQ2bNkG/frB2bdRRiUgBU7dPLnrhBbjzznDvgFmz\nwg1kRETqULdPoSkrC2WhsVgoC33+ed0+UkTSSpl/rqusDAPCXbrAvHlw0UVRRyQiOUKZfyEbNiyM\nBZSWwoAB4QRw/HjUUYlInlPmn09qa8OvgGPHQllo795RRyQiEVLmXyy6dw+zgydOhBEjYPp0OHw4\n6qhEJA+p8c83sVjI/jdvhh07wuWj03RnHxEpHur2yXdLl8Jtt8GoUfDgg1BSEnVEIpIl6vYpZmPH\nhrLQs84Ks4WfeUZloSLSIGX+hWT9erj5ZmjfHubPhw4doo5IRDJImb8EgwfDa6+FW0eWlsKcOSoL\nFZF6KfMvVDt3wuTJcOAAPPFEuHS0iBQUZf7ySV27wurVcMstcNllMG0afPhh1FGJSI5Q41/IzODG\nG2HLFtizJ0wKe/nlqKMSkRygbp9i8tJL4dLRw4fDQw9Bq1ZRRyQizaBuH0nNlVeGO4eVlISy0EWL\nVBYqUqRSavzNbLSZbTeznWY29TTbDTSzo2ZW1th9JUvOOQcefhh+9SuYPRuuuAJ27446KhHJsgYb\nfzOLAfOAUUBPYIKZffEU2z0ArGjsvhKBgQOhqgouvTQsz54dLhgnIkUhlcx/EPC6u+9x96PAYmBc\nPdvdATwHvNOEfSUKn/oUTJ0KGzbAihUwaFCYJyAiBS+Vxr8d8GbS87cSr51kZm2Bq9z9UcAas6/k\ngE6dYOVKuPvuMC4wZQocPBh1VCKSQWek6ThzgGb355eXl59cjsfjxOPx5h5SUmUG118fxgC+/e0w\nIPzYY+GCcSKSEyoqKqhI01V8Gyz1NLPBQLm7j048nwa4u89K2uaPHy8CrYCDwCRCF9Bp9006hko9\nc8mKFWGC2JAhYYD4gguijkhE6sh0qWcV0NnMOpjZmcB4YGnyBu5+ceLRkdDvf6u7L01lX8lRo0aF\nyWFt24bJYT/7mcpCRQpIg42/ux8HbgdWAtuAxe5ea2aTzWxSfbs0tG9aIpfMO/ts+OEPYfly+PGP\n4atfhT/8IeqoRCQNNMNXUnPsWDgB3H8/fOc7YVD4U5+KOiqRotacbh81/tI4u3eHsYB9++Dxx0N5\nqIhEQpd3kOzp2DF0A02dCuPGhfLQ/fujjkpEGkmNvzSeGVx3XbhO0AcfhLLQZcuijkpEGkHdPtJ8\nr7wSbhxTWgpz50KbNlFHJFIU1O0j0Ro5MpSFduoEffqEO4fpRC6S05T5S3pt3gw33QQtW8KCBdCt\nW9QRiRQsZf6SO/r0gXXroKws3Ej+vvvgyJGooxKROtT4S/q1aAF33gkbN8L69TBgQDghiEjOULeP\nZJY7PPtsKAktKwuTxM49N+qoRAqCun0kd5nBNdfAtm3w0UfQsycsWRJ1VCJFT5m/ZNeaNTBpUpgb\n8Mgj4cJxItIkyvwlfwwfDjU10KMH9O0b7hlw4kTUUYkUHWX+Ep2tW8OvgBYtYOFC6N496ohE8ooy\nf8lPvXpBZSWMHw+XXALl5WFcQEQyTo2/RCsWg9tug+pq2LQJ+vWDtWujjkqk4KnbR3LLCy+EOQJj\nxsCsWXD++VFHJJKz1O0jhaOsLJSFxmKhLPT553WdIJEMUOYvuauyMgwId+kCP/kJXHhh1BGJ5BRl\n/lKYhg0LYwEDBkD//jBvHhw/HnVUIgVBmb/kh9ra8Cvg2LFQFtq7d9QRiUROmb8Uvu7dw+zgiRNh\nxAiYPh0OH446KpG8pcZf8kcsFrL/zZthx45w+eiKiqijEslL6vaR/LV0aZgjMGoUPPgglJREHZFI\nVmW828fMRpvZdjPbaWZT61k/1sxqzKzazH5vZiOS1r2RtO7VpgQpUq+xY0NZ6FlnhdnCzzyjslCR\nFDWY+ZtZDNgJjAT2AlXAeHffnrRNS3c/lFjuDbzo7p0Tz/8IlLr7Xxt4H2X+0nTr18PNN0P79jB/\nPnToEHVEIhmX6cx/EPC6u+9x96PAYmBc8gYfN/wJ5wB/SY4vxfcRabrBg+G118KtI0tLYc4clYWK\nnEYqjXI74M2k528lXvs7ZnaVmdUCLwF3Jq1yYJWZVZnZzc0JVuS0zjwTvvtd+N3v4Je/DCeEmpqo\noxLJSWek60DuvgRYYmbDgKeBbolVQ919n5l9jnASqHX3yvqOUV5efnI5Ho8Tj8fTFZ4Uk65dYfVq\nePJJuOwyuPFGmDEjjA2I5LGKigoq0lThlkqf/2Cg3N1HJ55PA9zdZ51mn13AIHd/t87rM4D97v6j\nevZRn7+k39tvw113we9/H24c89WvRh2RSNpkus+/CuhsZh3M7ExgPLC0TgCdkpYHALj7u2bW0szO\nSbx+NnA5sLUpgYo0SevWsHgxzJ0L3/oW/Mu/wF/+0vB+IgWuwcbf3Y8DtwMrgW3AYnevNbPJZjYp\nsdnXzWyrmW0E5gLXJl5vDVSaWTWwHviVu69M+18h0pAxY0JZaElJKAtdtEhloVLUNMlLik9VVSgL\nbdMGHn0UOnaMOiKRJtG1fUQaY+DAcAK49NKwPHt2uGCcSBFR5i/FbdcumDwZ3nsPnngiXD5aJE8o\n8xdpqk6dYNUquPtuuOIK+M534ODBqKMSyThl/iIf+9//hW9/O9xB7LHH2NO1K0/dcw8n/vxnYu3a\nccPMmXTQ+IDkkOZk/mr8RepasYI9N93EI++/z70HDnA2cBCY0akTd6xapROA5Ax1+4ik06hRPDV0\n6MmGH+Bs4N5du3jqnnuijEwkbdT4i9TjxNtvn2z4P3Y2cGLv3ijCEUk7Nf4i9Yi1a0fdYd+DQOy9\n9+Do0ShCEkkrNf4i9bhh5kxmdOp08gRwEJjRvj03nHsufOlL8KruSyT5TQO+IqewZ/fuUO2zdy+x\ntm1Dtc8XvgD/+Z8wZQpcey3MnAmf+UzUoUqRUrWPSLa9+26YE7B6dbhz2JgxUUckRUiNv0hUXnkl\nzBAuLQ1XDm3TJuqIpIio1FMkKiNHwpYtcPHF0KdPuESEkhjJA8r8RdKlpiZcLbRlS1iwALp1a3gf\nkWZQ5i+SC/r2hXXroKws3Ej+vvvgyJGooxKplxp/kXRq0QLuvBM2boT168NVQtetizoqkU9Qt49I\nprjDs8+GK4aWlcH998O550YdlRQQdfuI5CIzuOaacPvIjz6Cnj1hyZKooxIBlPmLZE9FRSgL7dUL\nHnkE2raNOiLJc8r8RfJBPB4qgnr0CIPDjz0GJ05EHZUUKWX+IlHYuhUmTQoDxAsXQvfuUUckeUiZ\nv0i+6dUr3DFs/Hi45BIoLw/jAiJZosZfJCqxGNx2G1RXw6ZN0K8frF0bdVRSJFJq/M1stJltN7Od\nZja1nvVjzazGzKrN7PdmNiLVfUWK3oUXwosvwve/DxMmhEHh99+POiopcA02/mYWA+YBo4CewAQz\n+2KdzV52977u3h+YCCxsxL4iYhbmAmzbFn4R9OwJzz+v6wRJxqSS+Q8CXnf3Pe5+FFgMjEvewN0P\nJT09B/hLqvuKSJLzzoNHH4VnnoF77oGrroI334w6KilAqTT+7YDkb99bidf+jpldZWa1wEvAnY3Z\nV0TqGDYsjAUMGAD9+8O8eXD8eNRRSQE5I10HcvclwBIz+3/A00CjL2lYXl5+cjkejxOPx9MVnkj+\n+fSnYcaMMEt40iT4xS9CWWjv3lFHJhGpqKigoqIiLcdqsM7fzAYD5e4+OvF8GuDuPus0++widPl0\nSXVf1fmLnMaJE+FeAd/7XhgQnj4d/uEfoo5KIpbpOv8qoLOZdTCzM4HxwNI6AXRKWh4A4O7vprKv\niKQgFgvZ/+bNsGNHuHFMmjJAKU4Ndvu4+3Ezux1YSThZ/NTda81scljtC4Gvm9n1wBHgIKGRP+W+\nGfpbRArf5z8frhS6dCl885swahQ8+CCUlEQdmeQZXd5BJF/97W+hG+i55+Dhh+Haa0PJqBQN3cBd\npJitWxduH9mhA8yfH/6VoqBr+4gUsyFDwp3DvvIVKC2FOXNUFioNUuYvUkh27gzVQAcOhOqgvn2j\njkgySJm/iARdu8Lq1XDLLXDZZTBtGhw61PB+UnTU+IsUGjO48UbYsgXeeCNMCnv55aijkhyjbh+R\nQrdsGdx6a7iT2EMPQatWUUckaaJuHxE5tTFjwtVCS0rCTWQWLdLVQkWZv0hRqaoKZaFt2oSrh3bs\nGHVE0gzK/EUkNQMHhhPApZeG5dmz4dixqKOSCCjzFylWu3aFstD33oPHHw9zBCSvKPMXkcbr1AlW\nrYK774Yrr4QpU+DgwaijkixR4y9SzMzg+uth61Z4550wILxiRdRRSRao20dE/s+KFWGC2JAh4WJx\nF1wQdURyGur2EZH0GDUqTA5r2zZMDnvqKZWFFihl/iJSv40bQ1no+efDggXQuXPUEUkdyvxFJP0G\nDIANG8Jg8ODB8MADcPRo1FFJmijzF5GG7d4dxgL27QtloYMGRR2RoMxfRDKtY0dYvhymToVx40J5\n6P79UUclzaDGX0RSYwbXXRfKQj/4IJSF/vrXUUclTaRuHxFpmldeCTOES0th7txwvSDJKnX7iEj2\njRwZykIvvhj69Al3DlMClzeU+YtI89XUhLLQli1DWWi3blFHVBSU+YtItPr2hXXr4OqrYehQuO8+\nOHIk6qjkNFJq/M1stJltN7OdZja1nvXXmVlN4lFpZn2S1r2ReL3azF5NZ/AikkNatIC77gqTw9av\nD/ME1q2LOio5hQa7fcwsBuwERgJ7gSpgvLtvT9pmMFDr7h+Y2Wig3N0HJ9b9ESh197828D7q9hEp\nFO7w7LOhJPTqq+EHP4Bzz406qoKT6W6fQcDr7r7H3Y8Ci4FxyRu4+3p3/yDxdD3QLjm+FN9HRAqF\nGVxzTbh95JEj0LMnLFkSdVSSJJVGuR3wZtLzt/j7xr2um4DlSc8dWGVmVWZ2c+NDFJG89Y//GGYE\nP/10mCD29a/D3r1RRyXAGek8mJldCkwEhiW9PNTd95nZ5wgngVp3r6xv//Ly8pPL8XiceDyezvBE\nJCrxeKgI+v73w+DwzJkwaRLE1CnQGBUVFVRUVKTlWKn0+Q8m9OGPTjyfBri7z6qzXR/geWC0u+86\nxbFmAPvd/Uf1rFOfv0gx2Lr1/xr+hQuhR4+oI8pbme7zrwI6m1kHMzsTGA8srRNAe0LD/83kht/M\nWprZOYnls4HLga1NCVRECkSvXlBZCRMmwPDhUF4OH30UdVRFp8HG392PA7cDK4FtwGJ3rzWzyWY2\nKbHZPUAJML9OSWdroNLMqgkDwb9y95Vp/ytEJL/EYnDbbVBdDZs2Qb9+sHZt1FEVFc3wFZFoucOL\nL8Idd8DXvgazZoUbyEiDNMNXRPKXGZSVhbLQWCyUhT73nK4TlGHK/EUkt1RWhgHhLl1g3jy46KKo\nI8pZyvxFpHAMGxbGAgYMgP79wwng+PGooyo4yvxFJHfV1oZfAceOhbLQ3r2jjiinKPMXkcLUvTus\nWQM33AAjRsD06XD4cNRRFQQ1/iKS22KxcMewmhrYsSPcOOa3v406qrynbh8RyS9Ll4Y5ApdfDj/8\nIZSURB1RZNTtIyLFY+zYUBbasmUoC128WGWhTaDMX0Ty17p14faRHTrA/Pnh3yKizF9EitOQIeHO\nYV/5CpSWwpw5KgtNkTJ/ESkMO3eGgeEDB8I9BPr1izqijFPmLyLStSusXg233BIGg6dOhUOHoo4q\nZ6nxF5HCYQY33ghbtsCePWFS2MsvRx1VTlK3j4gUrmXL4NZbw53EHnoIWrWKOqK0UrePiEh9xowJ\nZaElJeEmMosWqSw0QZm/iBSHqqpQFtq6NTz6KFx8cdQRNZsyfxGRhgwcGE4AI0bAoEEwe3a4YFyR\nUuYvIsVn165QFvree6EstLQ06oiaRJm/iEhjdOoEq1bB3XfDlVfClClw8GDUUWWVGn8RKU5mcP31\nsHUrvP12GBD+zW+ijipr1O0jIgKwYkWYIDZkCDz8MFxwQdQRNUjdPiIizTVqVJgc1rZtmBz21FMF\nXRaqzF9EpK6NG0NZ6Pnnw4IF0Llz1BHVK+OZv5mNNrPtZrbTzKbWs/46M6tJPCrNrE+q+4qI5JwB\nA2DDhjAYPHgwPPAAHD0adVRp1WDmb2YxYCcwEtgLVAHj3X170jaDgVp3/8DMRgPl7j44lX2TjqHM\nX0Ryz+7dYSxg795QFvrlL0cd0UmZzvwHAa+7+x53PwosBsYlb+Du6939g8TT9UC7VPcVEclpHTvC\n8uUwbRqMGwd33QX790cdVbOl0vi3A95Mev4W/9e41+cmYHkT9xURyT1mcN114TpBf/tbKAv99a+j\njqpZzkjnwczsUmAiMKwp+5eXl59cjsfjxOPxtMQlIpIWn/0sPPkkvPJKmCH89NMwdy60aZOVt6+o\nqKCioiItx0qlz38woQ9/dOL5NMDdfVad7foAzwOj3X1XY/ZNrFOfv4jkjw8/hH/7N/jpT+H++8N9\nBGLZrZ5vTp9/Ko1/C2AHYdB2H/AqMMHda5O2aQ+8AnzT3dc3Zt+kbdX4i0j+qakJZaFnnQULF0K3\nbll764wO+Lr7ceB2YCWwDVjs7rVmNtnMJiU2uwcoAeabWbWZvXq6fZsSqIhITurbF9atg7IyGDoU\nZs6EI0eijqpBmuQlIpIuf/pTuHPYG2+EstAhQzL6dhnt9skWNf4iUhDc4dlnwxVDr746jAecd15G\n3krX9hERyRVmcM01oSz0yJFQFrpkSdRRfYIyfxGRTKqoCGWhPXvCvHnhwnFposxfRCRXxeOhIqhn\nzzA4/NhjcOJE1FEp8xcRyZqtW2HSpDAfYOFC6NGjWYdT5i8ikg969YLKSpgwAS65BGbMgI8+iiQU\nNf4iItkUi8Ftt8GmTaE7qG9fWLs262Go20dEJCru8OKLcMcd8LWvwaxZ4QYyKVK3j4hIPjILM4O3\nbQu/CHr2hOeey8rtI5X5i4jkisrKMCDcpUsoC73ootNursxfRKQQDBsG1dXhNpL9+4cTwPHjGXkr\nZf4iIrmotjb8Cjh6NFwnqHfvT2yizF9EpNB07w5r1sDEiTBiBHzve3D4cNoOr8ZfRCRXxWLh0hA1\nNbBjB/TpA7/9LXt27+bef/7nZh1a3T4iIvnil79kz+TJPHLoEPfu3885oG4fEZGCN24cTw0fzr37\n93N2Mw+lxl9EJI+ceOedZjf8oMZfRCSvxNq142A6jpOGY4iISJbcMHMmMzp1avYJQI2/iEge6dCx\nI3esWsXsb3yjWcdRtY+ISJ7SJC8REWmUlBp/MxttZtvNbKeZTa1nfTcz+52ZHTazb9dZ94aZ1ZhZ\ntZm9mq7ARUSk6Rps/M0sBswDRgE9gQlm9sU6m70L3AH8sJ5DnADi7t7f3Qc1M15JQUVFRdQhFBR9\nnumlzzM3pJL5DwJed/c97n4UWAyMS97A3f/i7q8Bx+rZ31J8H0kT/edKL32e6aXPMzek0ii3A95M\nev5W4rVUObDKzKrM7ObGBCciIplxRhbeY6i77zOzzxFOArXuXpmF9xURkVNosNTTzAYD5e4+OvF8\nGuDuPquebWcA+939R6c41inXm5nqPEVEGqmppZ6pZP5VQGcz6wDsA8YDE06z/clAzKwlEHP3A2Z2\nNnA5cG99OzX1DxARkcZrsPF39+NmdjuwkjBG8FN3rzWzyWG1LzSz1sDvgc8AJ8zsLqAH8DngxURW\nfwbwC3dfmak/RkREUpMzM3xFRCR7slqCaWY/NbO3zWzzabb5sZm9bmabzKxfNuPLJw19lmY23Mze\nN7ONicf0bMeYT8zsQjNbbWbbzGyLmd15iu30/WxAKp+lvp+pM7NPm9mGxETZbWZ2/ym2a9x3092z\n9gCGAf2AzadYfwWwLLH8ZWB9NuPLp0cKn+VwYGnUcebLA2gD9EssnwPsAL5YZxt9P9P3Wer72bjP\ntGXi3xbAekIVZfL6Rn83s5r5eyjx/OtpNhkH/Dyx7QbgvMR4gtSRwmcJSYPvcnru/j/uvimxfACo\n5ZPzWfT9TEGKnyXo+5kydz+UWPw0ocem7v/9Rn83c23mbd0JZX+mcRPK5O8NSfwEXGZmPaIOJl+Y\n2RcIv6o21Fml72cjneazBH0/U2ZmMTOrBv4HqHD3/66zSaO/m9mY5CXReA1o7+6HzOwKYAnQNeKY\ncp6ZnQM8B9yVyFqliRr4LPX9bAR3PwH0N7NzgZVmNtzd1zTnmLmW+f8ZuCjp+YWJ16SR3P3Axz8V\n3X058CkzK4k4rJxmZmcQGqun3f2X9Wyi72eKGvos9f1sGnf/G7AM+FKdVY3+bkbR+Bun7utbClwP\nJ2cWv+/ub2crsDx0ys8yub/PzAYRynrfy1Zgeerfgf9297mnWK/vZ+pO+1nq+5k6M2tlZuclls8C\nLgM21dms0d/NrHb7mNl/AHHgs2b2J2AGcCaJyWLu/pKZXWlmfwAOAhOzGV8+aeizBP7JzG4BjgIf\nAtdGFWs+MLOhwDeALYm+VQe+C3RA389GSeWzRN/Pxvg88DMz+/gKyU+7+yvJE22b8t3UJC8RkSKU\na33+IiKSBWr8RUSKkBp/EZEipMZfRKQIqfEXESlCavxFRIqQGn8RkSKkxl9EpAj9f8tV/TmiK9R4\nAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.plot(freq.keys(), px, 'r-o')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Average Degree"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## Undirected\n",
"\n",
"# $ = \\frac{1}{N} \\sum_{i = 1}^{N} k_i = \\frac{2L}{N}$\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## Directed\n",
"# $ = \\frac{1}{N} \\sum_{i=1}^N k_i^{in}= = \\frac{1}{N} \\sum_{i=1}^N k_i^{out} = \\frac{L}{N}$ "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Degree distribution \n",
"P(k): probability that a randomly selected node has degree k\n",
"\n",
"\n",
"$N_k = The \\:number\\: of \\:nodes\\:with \\:degree\\: k$\n",
"\n",
"## $P(k) = \\frac{N_k}{N}$\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Adjacency matrix\n",
"$A_{ij} =1$ if there is a link between node i and j\n",
"\n",
"$A_{ij} =0$ if there is no link between node i and j"
]
},
{
"cell_type": "code",
"execution_count": 182,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYEAAAEACAYAAABVtcpZAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XlcVfW+//HXFkrYYogeh6ysq177OVEamMNpOF7LNBug\nwSEVtYScbmmZeh2SOoYZWWphZnUQTTOvmZma6aljZCI4QhwKrY6mD484EEKiAnvdP0x/ioAMe++1\n917v5+PBw9jDWh97fJbv9V3T12YYhoGIiFhSLbMLEBER8ygEREQsTCEgImJhCgEREQtTCIiIWJhC\nQETEwhQCIiIWphAQEbEwhYCIiIUpBERELEwhICJiYQoBERELUwiIiFiYQkBExMIUAiIiFqYQEBGx\nMIWAiIiFKQRERCxMISAiYmEKARERC1MIiIhYmEJARMTCFAIiIhamEBARsTCFgIiIhSkEREQsTCEg\nImJhCgEREQtTCIiIWJhCQETEwhQCIiIWphAQEbEwhYCIiIX5m12AWFNOTg5JiYlkp6dTkJdHUHAw\nrUJDiRo6lIYNG5pdnki1eGNf2wzDMMwuQqwjLS2NOXFxrF2/nkgg/PRp6gL5QGpgIKsMg/t79eKZ\nSZMIDw83uVqRyvHqvjZE3GRBQoLRxG433rDZjBNgGGX8nABjts1mNLHbjQUJCWaXLHJF3t7XCgFx\niwUJCUZzu93YW85GUvpnLxjNPXCDEbmYL/S1DgeJy6WlpfHg3XeTfOoULavwvX3AHXY7azZvJiws\nzFXliVSLr/S1rg4Sl5sTF8eEwsLLNpRBwLVAMNACmFHq/ZbAC4WFzImLc0OVIlXjK32tkYC4VE5O\nDjffeCM/nz5NSKn3/gk0BwKAbOBOYBHQ86LPnABaBASQfeCAx15dIdbjS32tkYC4VFJiIhFw2YYC\n0IZzGwqAAVwFlN4c6gMRNhtJiYkuq1GkqnyprxUC4lLZ6el0On263PdHAXWAdsBkoGMZnwkvLCQ7\nI8M1BYpUgy/1tUJAXKogL4+6Fbz/NlAAbAKmAGllfKYukJ+b64LqRKrHl/paISAuFRQcTP4VPmMD\n7gIeA5aV8X4+UDekrIG3iDl8qa8VAuJSrUJDSQ0IuPIHgWLAXsbraYGBtGrf3ql1idSEL/W1rg4S\nlyrvKoqjwFdAHyAQ2Aj0/ePPi2+q96SrKETO86W+1khAXKpRo0bc36sXi2y2S163AfOBG4AGwFRg\nMZduKACLbDb69O5t+oYicjFf6muNBMTlfOXOSpGL+UpfayQgLhceHk5sfDw97Xb2VfI7+4Cedjux\n8fEesaGIlBYeHs6Lr73GXbVqeXVfKwTELaJHjODh4cMJs9mYbbNR3oVxJ4DZNht32O1MiI8nesQI\nd5YpUiWGzcZhh4PbgHjwyr7W4SBxi8LCQkJDQxkxYgS7tmzh83XriLDZCC8svPDc9bQ/nrvep3dv\nnpk0yWP2lETKcujQIdq0acPJkyeBcyeCa9WqxWO1a9PJi/paISBuMXnyZLKzs1mxYgUAR48ePTcD\nU0YG+bm51A0JoVX79gweMsQjTpaJXMkjjzzCJ598cuH3oKAgkpOT+fvGjV7V1woBcbmMjAy6d+9O\neno61157rdnliNTY6tWrefjhhy95be7cuYwZM8akiqpPISAu5XA46NatG0OGDCEmJsbsckRq7OTJ\nk7Rp04ZDhw5deK1Tp0589913+Pn5mVhZ9ejEsLjUO++8g5+fH8OHDze7FBGnmDJlyiUB4O/vz8KF\nC70yAEAjAXGhQ4cOceutt7J582batGljdjkiNbZt2za6dOnCxf9sTpgwgZkzZ5pYVc0oBMRlIiMj\nadeuHS+99JLZpYjUWFFREWFhYaSnp194rXnz5mRkZGC3l/V0IO/gb3YB4ps+/fRTMjMzWbp0qdml\niDjF7NmzLwkAOHe405sDADQSEBc4efIkbdu2ZcmSJdx1111mlyNSYz/99BPt2rXj9EUTyQwaNIik\npCQTq3IOnRgWp5s8eTI9e/ZUAIjPeOONNy4JgAYNGvD666+bWJHzaCQgTpWSkkJERASZmZnUr1/f\n7HJEnKKoqIg777yTtLQ0SkpKWLRoEYMHDza7LKfQOQFxmqKiIoYPH87s2bMVAOJTUlNTOXDgADt2\n7GDFihUMGjTI7JKcRiMBcZqZM2eyefNm1q1bh63Uc9ZFvNXZs2fp0KED06dP57HHHjO7HKdTCIhT\n7Nu3j86dO5OWlsZ//Md/mF2OiNP89a9/JSUlhTVr1vjkzo1CQGrMMAzuuece7rvvPp5//nmzyxFx\nmuzsbLp27cqOHTu48cYbzS7HJXR1kNTY4sWLOX78OM8++6zZpYg4jWEYxMTEMGXKFJ8NANCJYamh\nY8eOMX78eNauXYu/v9pJfEdiYiIFBQVe+WTQqtDhIKmRqKgoGjRowOzZs80uRcRpcnJyaNeuHRs2\nbKBDhw5ml+NS2nWTatu0aRObN2/m+++/N7sUEacaN24cUVFRPh8AoBCQajp16hQxMTG8/fbbBAUF\nmV2OiNNs2LCBLVu2WGbnRoeDpFomTZrEzz//zPLly80uRcRpfv/9d9q3b09CQgL33Xef2eW4hUJA\nqiw9PZ0ePXqQnp5OkyZNzC5HxGleeOEFDh06xIcffmh2KW6jw0FSJSUlJURHRzNjxgwFgPiU3bt3\nk5iYaJnDQOfpPgGpkvnz53P11Vfz5JNPml2KiNOUlJQwfPhwZs6cSaNGjcwux600EpBKO3jwINOn\nTyc5OZlatbT/IL7jrbfeIigoiKFDh5pditvpnIBUWkREBLfccgvTp083uxQRpzlw4AAdO3bku+++\no1WrVmaX43YaCUilrFq1iqysLD766COzSxFxGsMwGDVqFM8884wlAwAUAlIJeXl5jBkzhqVLl1K7\ndm2zyxFxmpUrV/Lzzz+zcuVKs0sxjQ4HyRWNGjWKs2fPsnDhQrNLEXGa3377jbZt2/Lxxx/TrVs3\ns8sxjUJAKrR161YeeeQRMjMzCQkJMbscEad5+umnsdlszJ8/3+xSTKXDQVKus2fPEh0dzRtvvKEA\nEJ/y7bffsmbNGjIzM80uxXS6zk/KFR8fT7NmzXj88cfNLkXEac6cOUN0dDRz5syhXr16ZpdjOh0O\nkjLt3buXLl26+PSMSmJNL7/8Mmlpaaxevdonp4usKoWAXMYwDP7rv/6LPn36MG7cOLPLEXGaH3/8\nkW7durFr1y5uuOEGs8vxCDocJJdJSkoiLy+P//7v/za7FBGncTgcREdHM23aNAXARXRiWC5x9OhR\nXnjhBdavX6/pIsWn/O1vf6OwsJBRo0aZXYpH0eEgucSgQYNo3Lgx8fHxZpci4jRHjhyhffv2fPnl\nl9x6661ml+NRtKsnF2zcuJHk5GRdNic+Z+zYsQwdOlQBUAaFgADnpot8+umnSUhIoE6dOmaXI+I0\n69evZ9u2bbz33ntml+KRdDhIAJg4cSL79+9n2bJlZpci4jS///47bdu25d133+Xee+81uxyPpBAQ\n9uzZwz333ENGRgaNGzc2uxwRp3n++ef597//zZIlS8wuxWPpcJDFnZ9RKS4uTgEgPmXnzp0sXryY\njIwMs0vxaLpPwOISEhIIDAxk2LBhZpci4jTFxcVER0fz6quvWm66yKrSSMDCfv31V2JjY/n22291\n+7z4lHnz5nHNNdcQFRVldikeT+cELMowDB566CHCwsKYNm2a2eWIOM2//vUvwsLCLDtdZFVpJGBR\nn3zyCfv27WPFihVmlyLiNOenixw7dqwCoJIUAhZ0/rlAy5cv13SR4lNWrFjB/v37WbVqldmleA0d\nDrKgkSNHUlJSwoIFC8wuRcRpcnNzadu2LStXrqRLly5ml+M1FAIWs2XLFh5//HEyMzM1oYb4lOjo\naPz9/UlISDC7FK+iw0EWcn66yDfffFMBID4lOTmZdevW6blX1aD7BCxk1qxZNG/enEcffdTsUkSc\n5vx0kXPnziU4ONjscryODgdZRHZ2Nl27dmXnzp00a9bM7HJEnCY2NpZdu3axatUq3e9SDQoBCzAM\ng+7du/PQQw/x7LPPml2OiNNkZWVxxx13aLrIGtDhIAtITEykoKCAMWPGmF2KiNM4HA5iYmJ48cUX\nFQA1oBPDPi4nJ4eJEyfyxRdf4OfnZ3Y5Ik7z/vvvc+bMGUaOHGl2KV5Nh4N83MCBA2natCmzZs0y\nuxQRp/n3v/9NaGgomzZtIjQ01OxyvJpGAl4uJyeHpMREstPTKcjLIyg4mFahoUQNHcrOnTv57rvv\n9Chd8ToV9XXDhg159tlnGTZsmALACTQS8FJpaWnMiYtj7fr1RALhp09TF8gHUgMDWeVw4O/nx5RX\nXuGZZ54xuVqRyrliXxsGt3XoQNb+/ezduxe73W5yxT7AEK+zICHBaGK3G2/YbMYJMIwyfk6AEQ9G\nE7vdWJCQYHbJIldU2b5+DYyGtWurr51EIeBlFiQkGM3tdmNvORtJ6Z+9YDRXEIiHU1+bR4eDvEha\nWhoP3n03yadO0bLUe3uBUOAxIKnUe/uAO+x21mzeTFhYmDtKFam0ivoayu9t9bVz6D4BLzInLo4J\nhYVlbiijgU7lfK8l8EJhIXPi4lxXnEg1VdTXUH5vq6+dQyMBL5GTk8PNN97Iz6dPE1LqvY+AT4E2\nnNs7Kj0SADgBtAgIIPvAARo2bOjiakUqp6K+hiv3tvq65jQS8BJJiYlEwGUbykngRWA2UFGa1wci\nbDaSEhNdU6BINZTX11C53lZf15xCwEtkp6fT6fTpy16fBgwHmlZiGeGFhWTrngHxIOX1NVS+t9XX\nNaObxbxEQV4edUu9thvY9MeflVEXyM/NdWpdIjVRVl9D1XpbfV0zCgEvERQcTH6p1zYD+4FmnBsu\nFwAlwD+B7WUsIx+oG1LWwFvEHGX1NVStt9XXNaPDQV6iVWgoqQEBl7wWA/zEub2lPcDTQB/gy3KW\nkRYYSKv27V1ZpkiVtAoNZevVV1/2elV6W31dMwoBLzF4yBBWGQYXD3oDgEYX/QT98Vr9Mr5/Alhl\nGAweMsTVpYpUyr59+9iwcSMfnz1L6YM5le1t9XXNKQS8gGEYJCcn41erFn+r4HMvUvbloQCLbDb6\n9O6ty+jEdKdOnWLq1Km0bduWTZs2UQv44ArfKa+31dc1p/sEPNyPP/7ImDFjOHz4MKNHj2b6uHHl\n3llZHt1ZKZ7AMAw+/fRTxo4dy/79+y957xpgB6ivTaCRgIcqKChg4sSJ/PnPf6Z3797s3LmTmJgY\nYuPj6Wm3s6+Sy9kH9LTbiY2P14YipsnOzqZXr15ERkZeFgAAjVu04J6AAPW1Gcx7bJGUxeFwGMuX\nLzeuv/56Y9CgQcbhw4cv+8z5py3OruBpi8fBeN1m01NExXQOh8Po0KGDwbkLfS75adKkibF48WLD\n4XCor02iEPAgmZmZRvfu3Y3Q0FAjOTm5ws+mpaUZAyMjjSA/P2Ogv7+RAMZiMBLAGBoYaNQLCDAG\nRkYaaWlpbqpepGwlJSXGhAkTLvnH38/Pzxg7dqyRl5d3yWfP93W9gACj3x/9rL52LZ0T8AD5+fnE\nxsayaNEipk2bxogRI/D3r9wtHB06dKBrly4UFxSQn5tL3ZAQWrVvz+AhQ3SyTEy3e/duRo0aRVFR\nEfXq1WPjxo3cddddvPXWW7Rr167c7yUnJxP58MNE3n+/+trFdLOYiQzDYNmyZbzwwgvcc889fP/9\n9zRu3LjS3y8sLCQ7O5stW7ZohiXxKLm5uUydOpUVK1YwY8YMhg0bxuHDh/nmm2/o168fNputwu9n\nZ2dzX+/eLEgq73o3cRaFgEm+//57Ro8ezcmTJ1mxYgVdunSp8jJ27dpF69atFQDiMRwOB4mJifzP\n//wPkZGRZGVlUb/+uav7r7vuOvr371+p5aSkpNC5c2dXlip/0NVBbpaXl8fYsWPp3r07jz/+OGlp\nadUKANCGIp5lx44ddO3alYULF7Ju3ToSEhIuBEBVqbfdRyHgJoZhsHjxYlq3bk1+fj6ZmZmMHDkS\nPz+/ai9TG4p4ghMnTjBixAjuv/9+YmJi2LJlCx07dqz28k6ePMkvv/xCaGioE6uU8igE3GDPnj3c\neeedzJkzh1WrVvHee+855eSWQkDM5HA4WLhwIa1bt8bf35+srCyGDh1KrVo1+2clLS2NDh06cNVV\nVzmpUqmIzgm40G+//ca0adNYvnw5L730Ek899VSN9vwvdujQIU6dOkWLFi2csjyRqkhNTWX06NFc\nffXVbNiwgVtvvdVpy9bOjXtpJOAC50+OtW7dmjNnzvDPf/6TmJgYpwUAwLZt2+jcufMVr7IQcaZj\nx44xfPhwHnroIUaPHk1ycrJTAwAUAu6mEHCyXbt28ec//5n58+ezZs0aFixYQIMGDZy+Hm0o4k4l\nJSW88847tGnThjp16pCVlcXgwYOdvhNiGIZ6280UAk6Sm5vLqFGjuO+++xg2bBhbt2516TNNtKGI\nu6SkpNCpUyeWLl3Kpk2bePPNN6lXr55L1vXzzz8TEBDAdddd55Lly+UUAjXkcDh4//33ad26NYZh\nkJWVxVNPPVXjk2MVKSoqYufOnYSHh7tsHSI5OTkMGzaMyMhIxo0bx+bNm11+xc7WrVu1c+NmOjFc\nA9u3b2f06NHYbDbWrVtXo8viqiI9PZ2bbrqJ4OBgt6xPrKW4uJh33nmHl156iUGDBvHDDz9wzTXX\nuGXdKSkp1b5vRqpHIVANx48fZ/LkyaxevZpXXnmFqKgol+75l6ZDQeIqW7ZsYdSoUYSEhPD111/T\ntm1bt64/JSWFAQMGuHWdVqfDQVVQUlLCu+++S5s2bbj66quddl10VWlvSZztyJEjREVF0bdvXyZO\nnMhXX33l9gA4deoUWVlZdOjQwa3rtTqFQCWlpqbSuXNnkpKS2LBhA3PnznXZybEr0UhAnKW4uJg5\nc+bQrl07GjduTFZWVqUe8OYKO3fupG3btgQGBrp93Vamw0FXcOzYMSZNmsTatWuZOXMmgwYNMvXa\n/GPHjpGTk0Pr1q1Nq0F8wzfffMPo0aNp1KgR33zzjek9pZ0bc2gkUI6SkhLmz59PmzZtCAoKctl1\n0VW1bds2OnXq5PZDUOI7Dh8+zMCBA3niiSeYOnUqGzduND0AQCFgFp8dCeTk5JCUmEh2ejoFeXkE\nBQfTKjSUqKFDr/jcnq1btzJ69Gjq1KnD3//+d9q3b++mqq9MG4pUt7eLioqYN28er7zyCsOHDycr\nK4ugoCA3Vl6xlJQUZs2aZXYZ1mPmtGaukJqaajwREWHUCwgwhgUEGPPBWALG/Iump3siIsJITU29\n7LtHjhwxhg4dajRt2tRYsmSJ4XA4TPgbVKxHjx7G559/bnYZYoKa9PbXX39ttG3b1rj33nuNH374\nwYTqK/brr78aDRs29Mhtztf5VAicn6j6jQomqj4BxuxSE1UXFRUZc+fONf70pz8Z48aNu2zeU09R\nXFxsXHPNNcbRo0fNLkXcrLq9ffDgQaNfv35Gs2bNjJUrV3rsP7IrVqwwHnjgAbPLsCSfCYEFCQlG\nc7vd2FvOBlL6Zy8Yze12Y/xzzxm33HKL8Ze//MX4/vvvzf5rVCgjI8No2bKl2WWIm1W3tx+JiDAa\nNGhgTJ482SgoKDD7r1GhcePGGTNmzDC7DEvyiRBITU01mpSxkbwFRhgYtcEYWs7GEmyzGTNmzPDY\nPaSLLVy40Bg4cKDZZYgbldXbV+rr870dUquWsXLlSrP/CpXStWtX46uvvjK7DEvyiUtM5sTFMaGw\nkJalXr8OmAo8Wc73WgLTgKwdO0y/6qcydFLYesrq7Sv1NZzr7SmGwaoPP3Rpfc5w9uxZdu/e7dIH\nLkr5vD4EcnJyWLt+PVGGcdl7DwMPAhXNcjrEMPh83TqOHj3qqhKdRiFgLeX1dmX6Grynt/fs2UPL\nli2pW7eu2aVYkteHQFJiIhFASDW/Xx+IsNlISkx0XlEukJeXx7/+9S/Nu2ohVult7dyYy+tDIDs9\nnU6nT9doGeGFhWRnZDipItdIS0ujY8eOmnfVQqzS2woBc3l9CBTk5VHTQWRdID831xnluIw2FOtR\nb4s7eH0IBAUHk1/DZeQDdUOqO+h2D20o1mOF3s7JyeH48ePcfPPNZpdiWV4fAq1CQ0kNCCjzvRLg\n9B9/FgNn/vjv0tICA2nlQY+GKM3QvKuWVF5vV7avwfN7e9u2bdx+++16FpaJvP7//OAhQ1gFlDXg\n/StgB14FPvzjv2eU+swJYJVhMHjIEFeWWSM//fQTdrudpk2bml2KuFF5vV2Zvgbv6G3t3JjP60Og\nUaNG3N+rF4vKuM7/RcDBub2k8z/TSn1mkc1Gn969r/hQOTNp3lVrKq+3K9PX4D29rQmSzOX1IQDw\nzKRJvBoYyL4qfm8fMCswkGcmTXJFWU6jvSXr8uXeLikpYfv27XTq1MnsUizNJ0IgPDyc2Ph4etrt\nld5Y9gH3BgYSGx/v8XcqKgSsq7q93dNu9/jezszMpGnTptSvf6Xb3sSVfCIEAKJHjGBCfDx32O28\nYbOVeY4Azh0nnW2z0dnfn6DmzXkqJsadZVaZ5l2VqvT26zYbYTYbPQYMIHrECHeWWWXaufEMPhMC\ncG5jWbN5MzsjImgeEMCwwEDmA0uA+cCwwEBaBASwKyKCz5OTsQcF8eabb5pcdcV27NhBu3btNO+q\nxVW2t3dHRDA3MZFVq1fzyy+/mFx1xRQCnsFmGGU8dMcHHD169NzsSxkZ5OfmUjckhFbt2zN4yJAL\nJ8p++eUXbr/9dtauXUt4eLjJFZfttdde4+DBg8yZM8fsUsRDVKa3Z8+ezccff0xycrLH3mXepk0b\nli5dyq233mp2KZbmsyFQWf/7v//LhAkT2LlzJ8HBwWaXc5lHHnmERx99lP79+5tdingRh8PBAw88\nQLt27Xj11VfNLucyv/32GzfccAO5ubn4+/vsLLdewacOB1XHo48+yr333ktMTAyeloeGYejyUKmW\nWrVqkZiYyIcffsiGDRvMLucyqamp3HbbbQoAD2D5EIBzQ+fMzEw++OADs0u5xMGDBykpKeGmm24y\nuxTxQg0bNmTJkiUMGTKEw4cPm13OJXQ+wHMoBIDAwECWL1/OxIkTyczMNLucC85vKN4w4Y14prvv\nvpvo6GgGDRpESUl5D5dwP4WA51AI/KFNmza8+uqr9O3bl8LCQrPLAXSnsDjH1KlTKSoq8phzAw6H\nQyHgQRQCFxk6dCihoaGMHTvW7FIA7S2Jc/j7+/Phhx8yd+5ctmzZYnY57N27l+DgYJo0aWJ2KYJC\n4BI2m4133nmHTZs2sWLFClNrOXPmDHv27PHoOz7Fe1x//fW89957DBgwgBMnTphai3ZuPItCoJRr\nrrmGjz76iFGjRpl6s43mXRVn69OnD5GRkTz55JOmXgmnEPAsCoEyhIWFMWnSJPr160dRUZEpNWhD\nEVeYOXMmBw4cICEhwbQa1NueRSFQjmeffZaGDRsyefJkU9avDUVcoXbt2ixfvpzp06eze/dut6//\n999/Jzs7W3cJexCFQDlsNhuJiYksW7aML774wu3rT0lJ0XPWxSVatmzJnDlz6Nu3LwUFBW5d9/bt\n2wkNDaV27dpuXa+UTyFQgT/96U8sWbKEoUOHuvVmmyNHjpCbm0urVq3ctk6xlgEDBtCtWzdGjx7t\n1vVqhOt5FAJXcNdddxETE8PAgQPddrON5l0Vd5g3bx7btm1j8eLFblunQsDz6F+ZSpgyZQrFxcXM\nnDnTLevThiLuUKdOHZYvX864cePIzs52+foMw1BveyCFQCWcv9lm3rx5fPvtty5fn+4UFncJDQ3l\npZdeom/fvpw5c8al69q/fz82m41mzZq5dD1SNQqBSjp/s80TTzzh0pttiouLNe+quNXTTz9NixYt\nGD9+vEvXo2dheSaFQBWcv9lm2LBhLrvZJjMzk+uuu07zrorb2Gw2Fi5cyGeffcbq1atdth4dCvJM\nCoEqmjlzJgcPHuTtt992yfK1oYgZQkJCWLZsGdHR0fz6668uWYd62zMpBKqodu3afPTRR8TGxrJr\n1y6nL18bipilS5cujBs3jv79+1NcXOzUZZ85c4aMjAxuu+02py5Xak4hUA0X32yTn5/v1GUrBMRM\n48ePx263Exsb67Rl5uXlsWvXLm6++Wbq1KnjtOWKc1h+juGaePLJJykuLmbRokVOWV5ubi7NmjXT\nvKtiqiNHjtCxY0cWL15M9+7da7Ss4uJigoODCQgIoH79+owZM4aRI0eqvz2IRgI1MHfuXFJTU0lK\nSnLK8lJTUwkLC9MGIqZq3LgxixYtYvDgweTk5NRoWRkZGZw6dYoTJ06wb98+4uLi8PPzc1Kl4gwK\ngRo4f7PNc889x48//ljj5elQkHiKHj16MHjwYKKionA4HNVeztatWy/5XZeIeh6FQA2Fhoby8ssv\n069fP06fPl2jZSkExJPExsaSl5fH7Nmzq72MlJSUS37XQxE9j84JOIFhGDz22GNce+21zJs3r1rL\ncDgcNGjQgKysLE27Jx5j//79dOrUic8++4zbb7+9yt9v1aoVe/fuvfD75s2bufPOO51ZotSQRgJO\nYLPZeO+99/j888/59NNPq7WM7Oxs6tWrpwAQj3LjjTcyf/58+vfvz2+//Val7x4/fvySAPDz89Ml\noh5IIeAk9erVY9myZcTExHDgwIEqf1+HgsRTRUZG0qtXL6Kjo6t0p/y2bdsu+T00NFSXiHoghYAT\nde7cmXHjxjFgwIAq32yjEBBP9vrrr/Pjjz+ycOFCDMOo1I5O6fMB6m/PpBBwsvHjx1OnTh2mT59e\npe8pBMSTBQQEsHz5ciZNmkT37t3p1KkTR44cqfA7CgHvoBBwslq1apGUlMQHH3zApk2bKvWdgoIC\n9u7dq3lXxaMdO3YMwzD4xz/+wZEjRxg8eHC5l486HI7LDgcpBDyTQsAFGjduTFJSElFRUVfcWwLN\nuyreYdOmTeTm5l74/csvv+S1114r87M//PADJ0+evPB7SEgI//mf/+nyGqXqFAIu0qNHD6Kioip1\ns40OBYnOMtJcAAAEi0lEQVQ3mDJlymWXd06ePPmyG8Kg7ENBuknMMykEXCg2Npb8/Hzi4+Mr/JxC\nQLzB+Rn2GjRocOG1kpIS+vfvf8kIAcq+U1g8k0LAha666iqWLl1KfHz8JXtGOTk5xM+aRfTAgQx4\n4AG++eIL0vfs4ejRoyZWK3Jl119/PYmJiZe8tn//foYPH86RI0cu9PXajz4iEDi/768Q8Fy6Y9gN\nPvnkE5577jnef/99PnjrLdauX08kEH76NHWBfGBbYCCfGgb39+rFM5MmER4ebnLVIuUbO3Ysb775\n5oXf7YCfvz+P+ftf0tf/AFYDD/bpw/PTpqmvPZBCwE263303u7/9lqkOB0MMg5AyPpMLJNpszAoM\nJDY+nugRI9xdpkilnDlzhm7durFzxw7qAtOAYaC+9kJ6ZrEbvDt/PvvT0kgtKaFlBZ8LAcYaBg+c\nOkXP558H0AYjHql27do8/OCDHNqxg2RQX3sxjQRcLC0tjQfvvpvkU6cubChngZHAJs7tJbUAXgHu\nu+h7+4A77HbWbN5MWFiYW2sWuRL1te/QiWEXmxMXx4TCwkv2lIqBZkAykAe8DDwOXHwjfkvghcJC\n5sTFua1WkcpSX/sOjQRcKCcnh5tvvJGfT58u81jpxW4BpgMRF712AmgREED2gQM0bNjQVWWKVIn6\n2rdoJOBCSYmJRFD2ybKLHQH2Am1LvV4fiLDZSCp1SZ6ImdTXvkUh4ELZ6el0usJsY8XAQGAI0KqM\n98MLC8nOyHB+cSLVpL72LQoBFyrIy6NuBe8bnNtQagPlzUdWF8gvdTemiJnU175Fl4i6UFBwMPkV\nvP8kcAxYB/iV85l8oG7IlQbeIu6jvvYtGgm4UKvQUFIDAsp872ngB+Az4OoKlpEWGEir9u1dUJ1I\n9aivfYuuDnKh8q6iOADcBATw//eUbMACoP9Fn9NVFOKJ1Ne+RSMBF2rUqBH39+rFolKP0G0GOIBT\nnBsW5wMnuXRDAVhks9Gnd29tKOJR1Ne+RSMBFyvrzsrK0J2V4snU175DIwEXCw8PJzY+np52O/sq\n+Z19QE+7ndj4eG0o4pHU177Db3pVZ0SXKrstPJzA+vUZ/PXX+BUX8/+AwDI+dwKYb7PxlN3OFD1t\nUTyc+to36HCQG23fvp05cXF8vm4dETYb4YWFF567nhYYyCrDoE/v3jwzaZL2lMRrqK+9m0LABEeP\nHiUpMZHsjAzyc3OpGxJCq/btGTxkiE6WiddSX3snhYCIiIXpxLCIiIUpBERELEwhICJiYQoBEREL\nUwiIiFiYQkBExMIUAiIiFqYQEBGxMIWAiIiFKQRERCxMISAiYmEKARERC1MIiIhYmEJARMTCFAIi\nIhamEBARsTCFgIiIhSkEREQsTCEgImJhCgEREQtTCIiIWJhCQETEwhQCIiIWphAQEbEwhYCIiIUp\nBERELEwhICJiYQoBERELUwiIiFiYQkBExMIUAiIiFqYQEBGxMIWAiIiFKQRERCxMISAiYmEKARER\nC1MIiIhYmEJARMTCFAIiIhamEBARsTCFgIiIhSkEREQs7P8AyEbH/RNJMSgAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.figure(1)\n",
"plt.subplot(121)\n",
"pos = nx.spring_layout(Gu) #定义一个布局,此处采用了spring布局方式\n",
"nx.draw(Gu, pos, with_labels = True)\n",
"plt.subplot(122)\n",
"nx.draw(Gd, pos, with_labels = True)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Undirected\n",
"$A_{ij} =1$ if there is a link between node i and j\n",
"\n",
"$A_{ij} =0$ if there is no link between node i and j\n",
"\n",
"## $A_{ij}=\\begin{bmatrix} 0&1 &0 &1 \\\\ 1&0 &0 &1 \\\\ 0 &0 &0 &1 \\\\ 1&1 &1 & 0 \\end{bmatrix}$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Undirected\n",
"## $A_{ij} = A_{ji}, \\: A_{ii} = 0$\n",
"## $k_i = \\sum_{j=1}^N A_{ij}, \\: k_j = \\sum_{i=1}^N A_{ij} $\n",
"## $ L = \\frac{1}{2}\\sum_{i=1}^N k_i = \\frac{1}{2}\\sum_{ij}^N A_{ij} $"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Directed\n",
"$A_{ij} =1$ if there is a link between node i and j\n",
"\n",
"$A_{ij} =0$ if there is no link between node i and j\n",
"\n",
"## $A_{ij}=\\begin{bmatrix} 0&0 &0 &0 \\\\ 1&0 &0 &1 \\\\ 0 &0 &0 &1 \\\\ 1&0 &0 & 0 \\end{bmatrix}$\n",
"\n",
"Note that for a directed graph the matrix is not symmetric.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Directed\n",
"## $A_{ij} \\neq A_{ji}, \\: A_{ii} = 0$\n",
"## $k_i^{in} = \\sum_{j=1}^N A_{ij}, \\: k_j^{out} = \\sum_{i=1}^N A_{ij} $\n",
"## $ L = \\sum_{i=1}^N k_i^{in} = \\sum_{j=1}^N k_j^{out}= \\frac{1}{2}\\sum_{i,j}^N A_{ij} $"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# WEIGHTED AND UNWEIGHTED NETWORKS\n",
"\n",
"## $A_{ij} = W_{ij}$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# BIPARTITE NETWORKS \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"bipartite graph (or bigraph) is a graph whose nodes can be divided into two disjoint sets U and V such that every link connects a node in U to one in V; that is, U and V are independent sets. \n",
"\n",
"- Hits algorithm\n",
"- recommendation system\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Ingredient-Flavor Bipartite Network\n",
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Degree, Average Degree and Degree Distribution\n"
]
},
{
"cell_type": "code",
"execution_count": 175,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtYlHX+//HXgAqDIEtqVl6WfdVBU0kQMs9adhnaulFt\nmeUxc6U2qwUlW81DKWVDZVpcaesPMRU7qGVlluVptRSEQlcBzdL023okQh2Iw/z+sPqagoIy8xmY\n5+O6vKqZuelNB55+7vtzz1icTqdTAADACB/TAwAA4M0IMQAABhFiAAAMIsQAABhEiAEAMIgQAwBg\nECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIAAAwixAAAGESIAQAwiBADAGAQIQYAwCBCDACAQYQYAACD\nCDEAAAYRYgAADCLEAAAYRIgBADCIEAMAYBAhBgDAIEIMAIBBhBgAAIMIMQAABhFiAAAMIsQAABhE\niAEAMIgQAwBgECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIAAAwixAAAGESIAQAwiBADAGAQIQYAwCBC\nDACAQYQYAACDCDEAAAYRYgAADKpnegCgLjhy5IhSU1KUl52tkwUFCgwOli0sTMNHjlTTpk1NjwfA\ng1mcTqfT9BBAbZWenq7ZiYn6aPVq3SUpqqhIQZIKJW2zWrXC6dTA6Gg9PnGioqKiDE8LwBMRYuAS\nzUtO1pT4eCU4HBrudCqkgtfkS0qxWDTLatU0u11jYmPdPSYAD0eIgUswLzlZL8THa83p02pdhdfv\nldQ/IEAJxBjAOQgxUE3p6eka1KePNp0T4aGS1ko6LamJpFGS/nnW83sl9QwI0KoNGxQZGem+gQF4\nNHZNA9U0OzFRCQ7HeSvhiZK+k1QgabWkOZLWnPV8a0kTHA7NTkx0z6AAagVWxEA1HDlyRKHXXad9\nRUUVXhP+Ta6kfpLelxRx1uMnJLXy91fegQPspgYgiRUxUC2pKSmKkSqN8KOSGkrqoDOnpSPOef4K\nSTEWi1JTUlw2I4DahRAD1ZCXna2biooqff41SSd15lrxJEnpFbwmyuFQ3o4drhkQQK1DiIFqOFlQ\noKCLvMYiqbekv0paWsHzQZIK8/NrejQAtRQhBqohMDhYhVV8bamkgAoeL5QUFHKhK8wAvAkhBqrB\nFhambf7+5z1+VNIySacklevMbul3JP2lgq+RbrXK1rGjK8cEUIuwaxqohsp2TR+TdI+kbElOSW0k\nTZb053OOZ9c0gHOxIgaq4corr9TA6GgttFj+8HgTSet1JrT5krbp/AhL0kKLRXcMGECEAfyOFTFQ\nTZW9s9bF8M5aACrCihiopqioKE2z29U/IEB7q3jMb+81Pc1uJ8IA/oAQA5dgTGysEux29QwI0MsW\niyq7GemEpJcsFvXkAx8AVIJT08BlyMjI0OzERH348ceKsVgU5XD8/nnE6b9+HvEdAwbo8YkTWQkD\nqBAhBmrA0aNHlZqSorwdO7QvL0/f7t+vR//xDw0bMYKNWQAuiBADNey7775T7969deDAAdOjAKgF\nCDFQw8rKyhQYGKgTJ07IarWaHgeAh2OzFlDDfH191bJlS3377bemRwFQCxBiwAXatGmjPXv2mB4D\nQC1AiAEXsNlsysvLMz0GgFqAEAMuwIoYQFURYsAFCDGAqiLEgAsQYgBVxe1LgAuUl5crMDBQhw8f\nVlBQkOlxAHgwVsSAC/j4+Kh169bau7eqHwsBwFsRYsBFOD0NoCoIMeAihBhAVRBiwEXatGnDvcQA\nLooQAy5is9lYEQO4KEIMuAinpgFUBSEGXKRZs2YqKipSfn6+6VEAeDBCDLiIxWJhVQzgoggx4EJc\nJwZwMYQYcCFWxAAuhhADLkSIAVwMIQZciBADuBg+9AFwoePHj6tVq1bKz8+XxWIxPQ4AD8SKGHCh\nxo0by8fHR8eOHTM9CgAPRYgBF+P0NIALIcSAixFiABdCiAEXs9lsfPgDgEoRYsDFWBEDuBBCDLgY\nIQZwIdy+BLhYQUGBmjdvrsLCQm5hAnAeVsSAiwUHB6thw4b68ccfTY8CwAMRYsANOD0NoDKEGHAD\nQgygMoQYcANCDKAyhBhwgzZt2nAvMYAKEWLADWw2GytiABXi9iXADU6dOqWmTZvq5MmT8vHh978A\n/g8/EQA3aNiwoUJCQnTw4EHTowDwMIQYcBOuEwOoCCEG3ITrxAAqQogBN+EWJgAVIcSAmxBiABUh\nxICbEGIAFeH2JcBNioqK9Kc//UknT55UvXr1TI8DwEOwIgbcxN/fX1dddZX2799vehQAHoQQA27E\n6WkA5yLEgBsRYgDnIsSAG9lsNt7UA8AfEGLAjVgRAzgXIQbciBADOBe3LwFuVFJSoqCgIP38889q\n0KCB6XEAeABWxIAb1a9fXy1atNC+fftMjwLAQxBiwM04PQ3gbIQYcDNCDOBshBhwM0IM4GyEGHAz\n7iUGcDZCDLgZK2IAZ+P2JcDNysrKFBgYqBMnTshqtZoeB4BhrIgBN/P19VXLli317bffmh4FgAcg\nxIABbdq04ToxAEmEGDDCZrNxnRiAJEIMGMGGLQC/IcSAAYQYwG8IMWAAIQbwG25fAgwoLy9XYGCg\nDh8+rKCgINPjADCIFTFggI+Pj1q3bq29e/eaHgWAYYQYMITT0wAkQgwYQ4gBSIQYMIYPfwAgEWLA\nGFbEACRCDBhDiAFIhBgwplmzZioqKlJ+fr7pUQAYRIgBQywWC+85DYAQAyZxehoAIQYMIsQACDFg\nECEGQIgBg7iXGAAf+gAYdPz4cbVq1Ur5+fmyWCymxwFgACtiwKDGjRvLx8dHx44dMz0KAEMIMWAY\n14kB70aIAcO4Tgx4N0IMGMaKGPBuhBgwjBAD3o0QA4YRYsC7cfsSYFhBQYGaN2+uwsJCbmECvBAr\nYsCw4OBgNWzYUD/++KPpUQAYQIgBD8DpacB7EWLAAxBiwHsRYsADEGLAexFiwAPwph6A9yLEgAdg\nRQx4r3qmBwAgNWrUSHtyc/Xwgw/qVEGBAoODZQsL0/CRI9W0aVPT4wFwIe4jBgxKT0/X7MREfbR6\ntaKLitRLUpCkQknbrFatcDo1MDpaj0+cqKioKMPTAnAFQgwYMi85WVPi45XgcGi406mQCl6TLynF\nYtEsq1XT7HaNiY1195gAXIwQAwbMS07WC/HxWnP6tFpX4fV7JfUPCFACMQbqHEIMuFl6eroG9emj\nTRVEeI+kMEl/lZR6znN7JfUMCNCqDRsUGRnpjlEBuAG7pgE3m52YqASHo8KV8N8l3VTJca0lTXA4\nNDsx0XXDAXA7VsSAGx05ckSh112nfUVF510TTpO0UtINOrP6PXdFLEknJLXy91fegQPspgbqCFbE\ngBulpqQoRjovwj9LmiLpJUkX+p3xFZJiLBalpqS4ZkAAbkeIATfKy87WTUVF5z3+jKSHJV1Tha8R\n5XAob8eOmh4NgCG8oQfgRicLChR0zmNfS1r76x+rIkhSYX5+jc4FwBxCDLhRYHCwCs95bIOk/ZKu\n1ZnT0icllUnaJSmjgq9RKCkopKK7jgHURpyaBtzIFhambf7+f3jsb5K+1ZkV8TeSxkq6Q9KnlXyN\ndKtVto4dXTkmADdi1zTgRhfaNf2baToT5kp3Tfv5Ke+HH9g1DdQRrIgBN2rQoIGaXHGFFlzgNVNU\ncYQl6f9Jskhavny5SktLa3w+AO5HiAE32bZtmyIiItSpWzfZAwK0t5rH75VkDwjQ7PnztXTpUt14\n441avXq1OKkF1G6EGHCx8vJy2e123XHHHbLb7XrnnXc0zW5X/2rE+Lf3mp5mt2vo0KFat26dZs6c\nqSeeeEL9+/dXdna2K78FAC7kO3Xq1KmmhwDqqqNHj+ree+9VZmam1qxZo65du0qSOkdFyXrFFRq2\nbp18S0vVVpK1guNPSEq2WDQ6IECTzvrAB4vForZt22rs2LEqLCzUww8/rNzcXEVFRSko6NwbpAB4\nMlbEgIusX79e4eHhCgsL08aNG9WyZcs/PD8mNlarNmxQZkyM/sffX6OsViVLektSsqRRVqta+fsr\nKyZGqzZsqPBTl+rXr6/HHntMubm5CgkJUYcOHTR9+nSdOnXKHd8igBrArmmghpWVlenZZ5/VG2+8\noZSUFPXv3/+ixxw9elSpKSnK27FDhfn5CgoJka1jRw0bMaJau6P37duniRMnavPmzZoxY4aGDh0q\nHx9+vw14MkIM1KBDhw7pgQcekK+vr9566y1dffXVRubYsmWL4uLiVFxcrKSkJPXt29fIHAAujt8q\nAzXk448/VufOndWvXz99+umnxiIsSd26ddOWLVuUkJCgUaNGadCgQcrJyTE2D4DKEWLgMv3yyy+K\nj4/X2LFj9c4772jSpEny9fU1PZYsFovuu+8+7d69Wz179lSPHj3097//XUePHjU9GoCzEGLgMuzb\nt089evRQXl6esrKy1LNnT9Mjncff31/jx49XTk6OLBaL2rVrp1mzZqmogk+BAuB+hBi4RG+//ba6\ndOmiIUOG6P3331fjxo1Nj3RBTZo00Zw5c7R582Zt3rxZ7dq1U1paGm8IAhjGZi2gmhwOh5588kmt\nXbtWaWlpioyMND3SJVm3bp3i4uLk5+enpKQkdevWzfRIgFdiRQxUw+7du9WlSxcVFBQoMzOz1kZY\nkvr27auMjAzFxsbqvvvu07333qt9+/aZHgvwOoQYqAKn06kFCxaoV69eGjdunJYsWaJGjRqZHuuy\n+fj4aNiwYcrNzVXHjh0VFRWl+Ph45efnmx4N8BqEGLiIwsJCDR06VElJSVq/fr1Gjx4ti8Vieqwa\nFRAQoMmTJ2vnzp0qKChQaGioXn31VZWUlJgeDajzCDFwAVlZWercubOsVqvS09PVvn170yO51NVX\nX6358+fr888/10cffaT27dtr5cqVbOgCXIjNWkAFnE6n5s6dq+nTp2vOnDkaPHiw6ZGM+OSTTxQf\nH68mTZooKSlJnTt3Nj0SUOcQYuAcJ06c0KhRo3Tw4EGlpaWpdevWpkcyqrS0VAsWLNCUKVN02223\nacaMGWrRooXpsYA6g1PTwFm2bNmi8PBwXX/99dq8ebPXR1iS6tWrpzFjxigvL0/XXnutOnXqpEmT\nJqmwsND0aECdQIgBSeXl5UpMTFRMTIzmzp2rl19+WX5+fqbH8ihBQUF67rnn9PXXX2v//v2y2Wya\nN2+eSktLTY8G1GqcmobXO3z4sIYOHSqHw6ElS5Zw2rWKMjIyFBcXp+PHj8tut+v22283PRJQK7Ei\nhlf77LPPFB4eri5dumjdunVEuBoiIyO1fv16Pffccxo3bpz69++vHTt2mB4LqHUIMbxSaWmpnn76\naY0YMUKLFi3Ss88+q3r16pkeq9axWCy68847tXPnTg0cOFC33nqrHn74Yf33v/81PRpQaxBieJ0D\nBw6od+/e2r59uzIzM3XrrbeaHqnWa9CggcaNG6fc3FwFBwerffv2eu6553T69GnTowEejxDDq7z/\n/vuKiorSoEGDtHr1ajVr1sz0SHVKSEiI7Ha70tPTlZ2drdDQUKWmpqq8vNz0aIDHYrMWvEJxcbHG\njx+vDz74QEuXLlXXrl1Nj+QVNm/erLi4OJWUlCgpKUl9+vQxPRLgcVgRo87bs2ePunbtqkOHDikr\nK4sIu1H37t315Zdfavz48Ro5cqT+8pe/KDc31/RYgEchxKjTlixZom7dumn06NF69913FRISYnok\nr2OxWDR48GDt3r1b3bt3V/fu3fXYY4/p2LFjpkcDPAIhRp106tQpPfTQQ5o2bZo+++wzPfLII3Xu\nE5NqG39/f02YMEG7d++W0+lUu3bt9OKLL6q4uNj0aIBRhBh1zo4dOxQVFaWSkhJt375dnTp1Mj0S\nztK0aVPNnTtXmzZt0qZNm9SuXTu9/fbbfMITvBabtVBnOJ1OzZs3T5MmTVJSUpKGDRtmeiRUwRdf\nfKG4uDhZrVYlJSVxDR9ehxCjTigoKNCYMWOUk5OjZcuWqW3btqZHQjWUlZVp0aJFmjRpkrp3767n\nn39e119/vemxALfg1DRqvfT0dEVERKhx48b66quviHAt5OvrqxEjRig3N1ft27dXZGSkxo8fr59+\n+sn0aIDLEWLUWuXl5UpKStLAgQM1a9Ysvf7667JarabHwmVo2LChnnnmGe3cuVP5+fkKDQ3VnDlz\nVFJSYno0wGU4NY1a6dixYxo+fLiOHz+utLQ0tWzZ0vRIcIHs7GzFx8dr//79mjVrlgYNGsTud9Q5\nrIhR62zYsEHh4eHq0KGDNm3aRITrsLCwMK1Zs0avvPKKnn76ad1yyy3KzMw0PRZQowgxao2ysjJN\nnz5dgwcP1rx58/TCCy+ofv36pseCi1ksFkVHR+ubb77R4MGDNXDgQA0fPlwHDx40PRpQIwgxaoX/\n/d//Vb9+/bR+/Xpt375d0dHRpkeCm9WrV09/+9vflJubq+bNm+vGG2/U5MmTVVhYaHo04LIQYni8\n1atXq3Pnzrrlllv02Wef6ZprrjE9Egxq1KiRZs6cqaysLH333XcKDQ3V/PnzVVZWZno04JKwWQse\n65dfftE///lPpaWlafHixerVq5fpkeCB0tPTFRcXp/z8fNntdvXv39/0SEC1EGJ4pO+++06DBw9W\n06ZNlZKSoiZNmpgeCR7M6XRq5cqVmjBhglq1aiW73a4OHTqYHguoEk5Nw+O8++676tKli+677z6t\nWrWKCOOiLBaLYmJi9J///EfR0dG65ZZbNGbMGP33v/81PRpwUYQYHsPhcCg2NlYJCQn66KOP9I9/\n/IN7RlEtDRo00OOPP67c3FwFBQWpQ4cOmjFjhk6fPm16NKBShBgeIScnRzfffLPy8/OVmZmpqKgo\n0yOhFgsJCVFSUpK2bt2qrKwstW3bVosWLVJ5ebnp0YDzcI0Yxi1cuFDx8fGaOXOmRo8ezSoYNe7f\n//634uLiVFZWpqSkJPXu3dv0SMDvCDGMKSws1KOPPqqMjAwtW7ZMHTt2ND0S6rDy8nItW7ZMEydO\nVKdOnTRr1izZbDbTYwGcmoYZX3/9tSIjI9WgQQOlp6cTYbicj4+P7r//fuXk5Khr167q1q2bxo0b\np+PHj5seDV6OEMOtnE6n5s6dq9tuu01Tp07Vm2++qYYNG5oeC17E399fCQkJ2r17t8rKytS2bVvZ\n7XYVFxebHg1eilPTcJv8/Hw99NBD2r9/v5YtW6bWrVubHgnQ7t27NWHCBO3atUvPP/+87rnnHvYp\nwK1YEcMtvvzyS4WHh6tFixbasmULEYbHaNeunVatWqV58+ZpxowZ6tGjh7766ivTY8GLsCKGS5WX\nl2vWrFl6+eWXNX/+fA0aNMj0SEClysrKlJqaqsmTJ6tHjx5KTEzU9ddfb3os1HGsiOEyhw8fVnR0\ntD788ENlZGQQYXg8X19fjRw5Urm5uWrXrp0iIyM1YcIE/fTTT6ZHQx1GiOESn3/+uSIiIhQVFaX1\n69erRYsWpkcCqqxhw4aaMmWKduzYoePHjys0NFRz585VSUmJ6dFQB3FqGjWqtLRUU6dO1YIFC5Sa\nmqp+/fqZHgm4bN98843i4+P1ww8/aNasWfrzn//Mhi7UGEKMGvPDDz9oyJAhslqtWrRokZo1a2Z6\nJKDGOJ1OrV69WvHx8brqqquUlJSk8PBw02OhDuDUNGrEBx98oMjISA0cOFCffPIJEUadY7FYNGDA\nAGVnZ+vee+9VdHS0RowYoUOHDpkeDbUcIcZlKS4u1hNPPKFx48ZpxYoVeuqpp+Tjw39WqLvq1aun\nsWPHKi8vT1dffbXCwsL0zDPP6OTJk6ZHQy3FT0xcsr1796pbt27av3+/MjMz1a1bN9MjAW7TqFEj\nJSYmKjMzU99++61sNpvefPNNlZWVmR4NtQwhxiVZunSpunbtqpEjR2r58uW64oorTI8EGHHddddp\n8eLFWrlypRYuXKjw8HB9+umnpsdCLcJmLVTL6dOnNW7cOG3cuFHLli1jswpwFqfTqRUrVmjChAlq\n06aN7Ha72rdvb3oseDhWxKiynTt3KioqSsXFxdq+fTsRBs5hsVh01113adeuXerfv7/69u2rsWPH\n6vDhw6ZHgwcjxLgop9Op+fPnq2/fvho/frxSU1MVFBRkeizAYzVo0EBPPPGEcnJyFBAQoPbt22vm\nzJlyOBymR4MH4tQ0Lujnn3/WmDFjtGvXLi1btkzt2rUzPRJQ6+zdu1cJCQlKT0/XzJkzNWTIEO4u\nwO/4LwGVysjIUEREhEJCQrR161YiDFyi1q1b67333tPixYv16quvqkuXLtq4caPpseAhWBHjPE6n\nU6+88ooSExP12muv6a9//avpkYA6o7y8XGlpaZo4caIiIiI0a9YstWnTxvRYMIgVMf7g2LFjGjRo\nkNLS0rR161YiDNQwHx8fDRkyRDk5OerSpYu6du2qxx9/XMePHzc9GgwhxPjdpk2bFB4errZt22rT\npk18DivgQlarVU899ZR27dqlkpIStW3bVi+99JKKi4tNjwY349Q0VFZWppkzZ+q1117TggULNGDA\nANMjAV5n165dmjBhgnbv3q0XXnhBd999N5/w5CUIsZf78ccf9eCDD6q8vFxvvfWWmjdvbnokwKut\nXbtWcXFxCgoKUlJSkrp06WJ6JLgYp6a92CeffKKIiAj16tVLa9euJcKAB+jXr58yMzM1atQo3XXX\nXbr//vv1/fffmx4LLkSIvVBJSYkSEhI0evRopaWlacqUKfL19TU9FoBf+fr6atSoUcrNzVVoaKg6\nd+6shIQEFRQUmB4NLkCIvcz333+vXr16aefOncrKylLv3r1NjwSgEoGBgZo6daqys7N19OhR2Ww2\nvfbaayopKTE9GmoQIfYiy5cv10033aR77rlHq1atUtOmTU2PBKAKmjdvrgULFmjNmjVasWKFwsLC\n9OGHH4otPnUDm7W8QFFRkeLi4rR69WqlpaXppptuMj0SgEvkdDr18ccfKz4+Xtdcc42SkpLUqVMn\n02PhMrAiruNyc3N188036+jRo8rKyiLCQC1nsVg0cOBAZWdn6+6779btt9+ukSNH6tChQ6ZHwyUi\nxHVYamqqevToodjYWC1btkzBwcGmRwJQQ+rXr69HHnlEubm5atasmcLCwjR16lSdOnXK9GioJk5N\n10EnT57Uo48+qm3btuntt99Wx44dTY8EwMW+//57Pf3009qwYYOeffZZDR8+nLshaglWxHXMN998\no8jISPn6+iojI4MIA16iZcuWWrJkiZYvX64FCxYoIiJCa9euNT0WqoAVcR3hdDqVnJysKVOm6JVX\nXtEDDzxgeiQAhjidTi1fvlwJCQkKDQ3Viy++qBtuuKFKxx45ckSpKSnKy87WyYICBQYHyxYWpuEj\nR3KnhYsQ4jrgp59+0ujRo7Vv3z6lpaXJZrOZHgmAByguLtbrr7+umTNn6p577tG0adN05ZVXVvja\n9PR0zU5M1EerV+suSVFFRQqSVChpm9WqFU6nBkZH6/GJExUVFeXOb6PO49R0LffVV18pPDxc11xz\njb788ksiDOB3fn5+evLJJ5WTkyM/Pz/dcMMNSkxMlMPh+MPr5iUna1CfPopcuVL7ior0r6IijZX0\ngKSxkhY4HNpXVKTOK1dqUJ8+mpecbOLbqbNYEddS5eXlstvtSkpK0htvvKE777zT9EgAPNyePXuU\nkJCg7du3KzExUYMHD9abb7yhF+Ljteb0abWuwtfYK6l/QIAS7HaNiY119chegRDXQkeOHNGwYcNU\nWFiopUuX6tprrzU9EoBaZOPGjYqLi9OpU6d0fN8+bS4u/j3Cv0h6RNJaSfmSWkmaKen2s47fK6ln\nQIBWbdigyMhIt85eF3Fqupb54osvFB4eroiICK1fv54IA6i2Xr16aevWrWoaEKAJZ0VYkkolXStp\nk6QCSc9KulfSgbNe01rSBIdDsxMT3TZzXcaK2JDq7kwsLS3V9OnT9eabb2rhwoW67bbbDEwNoK44\ncuSIQq+7TvuKihRykdfeKGmqpJizHjshqZW/v/IOHGA39WWqZ3oAb3PBnYnLl8s2Zcp5OxMPHjyo\nIUOGyM/PT5mZmbrqqqtMfgsA6oDUlBTFSBeN8GFJeyS1P+fxKyTFWCxKTUlR3PjxrhjRaxBiN5qX\nnKwp8fFKcDg0x+k873+AsQ6HkiSlrFypQWvWaJrdrmtatNDo0aM1btw4PfXUU/Lx4WoC4K2cTqdK\nS0tVUlJS5V+Vvf6TlSt1T1HRBf9+pZIelDRCUkX3Y0Q5HPp6x46a/0a9DCF2k3nJyXohPl6bLrIz\nMUTSk06n/nz6tPqOGydHUJDeX7VK3bt3d9eoQJ3hdDpVVlZWrXBVNWQmji8tLZWvr6/q169fpV/1\n6tWr9LlDBw4o6EL/7HQmwn6S5lTymiBJhfn5Nf2vzesQYjdIT0/XlAoi/JqkFEk7JA2RtOCs51pL\nWldaqp5FRfLz83PfsPBqFYXLk0J0Kcf6+PhUOVzVjdnZv6xWqxo1anRJx1bn722xWGrk3/WYBx9U\n4eLFlT7/kKRjkj6WVNk7VhdKCgq52MltXAwhdoPZiYlKcDjOWwk3lzRZ0hpJjvMPO7MzsahIsxMT\ntei991w9Ji5RVVZcpmNUndefGy5XxKR+/fry8/NTYGBgjYWwsmO5nFMxW1iYtr33nsZWcHp6rKQc\nnbmFqcEFvka61ar2vJ/9ZWPXtItVZWfiZEmH9McV8W/q4s7E8vLyWrWqutjxklwWEhPHEy7vUNnP\npgOSWkry1/+thC2S3pB0/1mvq4s/m0xhRexiVd2ZWJkrJN1psWjBv/6lvz/2mEeGqLrHl5eXuy1E\nAQEBLg8ZHzWH2ujKK6/UwOhoLVy5Uk+ctR67VlJ5FY5faLHojgEDiHANYEXsYmMefFARixdr7AVe\nc6EVsSQlS4q3WOT09681q6oLHevr61tj17kAXLr09HQN6tPnoptIz8U7a9UsVsQudrKg4II7E6si\nSNJfBg7UklWramIkAJAkRUVFaZrdrv6X8F7T0+x2IlxDuBjkYoHBwSq8zK/BzkQArjImNlYJdrt6\nBgToZYt5QuZWAAACEklEQVRFld2MdELSSxaLevKBDzWOELuYLSxM2/z9K3yuTFLRr38slVT865+f\nK91qlY2diQBcZExsrFZt2KDMmBj9j7+/RlmtSpb0ls5cGhtltaqVv7+yYmK0asMGIlzDuEbsYhfa\nNT3t119nXy2dIumZs/6anYkA3Ono0aNn3gd/xw4V5ucrKCREto4dNWzECH4GuQghdoMH77pLkefs\nTKyqly0WZcbEcB8xANRRhNgN2JkIAKgM14jd4PediQEB2lvFY9iZCADegRC7CTsTAQAV4dS0m2Vk\nZGh2YqI+/PhjxVgsinI4fv884nSrVSucTt0xYIAenziRlTAAeAFCbAg7EwEAEiEGAMAorhEDAGAQ\nIQYAwCBCDACAQYQYAACDCDEAAAYRYgAADCLEAAAYRIgBADCIEAMAYBAhBgDAIEIMAIBBhBgAAIMI\nMQAABhFiAAAMIsQAABhEiAEAMIgQAwBgECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIAAAwixAAAGESI\nAQAwiBADAGAQIQYAwCBCDACAQYQYAACDCDEAAAYRYgAADCLEAAAYRIgBADCIEAMAYBAhBgDAIEIM\nAIBBhBgAAIMIMQAABhFiAAAMIsQAABhEiAEAMIgQAwBgECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIA\nAAwixAAAGESIAQAwiBADAGAQIQYAwCBCDACAQf8fHWpWlowNdzgAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"nx.draw(Gu, with_labels = True)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Undirected network: \n",
"Node degree: the number of links connected to the node.\n",
"## $k_1 = k_2 = 2, k_3 = 3, k_4 = 1$"
]
},
{
"cell_type": "code",
"execution_count": 177,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X98z/X+//H724y9Z2soS59OIcuvUNH0kfTN+dQRabMQ\nSn6eSI6PTiktkzAtWspJ7ZNTGYVDORGSc4roSDYS8qONKZVzbH40m/3e3t8/2C72i/f7vfd7z/f7\nvdv1cukSr/fr/Xo9Vpe6e76ej9fzabHZbDYBAAAj6pkuAACAuowgBgDAIIIYAACDCGIAAAwiiAEA\nMIggBgDAIIIYAACDCGIAAAwiiAEAMIggBgDAIIIYAACDCGIAAAwiiAEAMIggBgDAIIIYAACDCGIA\nAAwiiAEAMIggBgDAIIIYAACDCGIAAAwiiAEAMIggBgDAIIIYAACDCGIAAAwiiAEAMIggBgDAIIIY\nAACDCGIAAAwiiAEAMIggBgDAIIIYAACDCGIAAAwiiAEAMIggBgDAIIIYAACD6psuAADg/dLT07Uk\nMVEpe/cqOzNTQSEhatO5s0aMGqVmzZqZLs+jWWw2m810EQAA75ScnKz5cXFav2GDHpQUnpenYElZ\nkpKsVn1ss+n+Pn00KTpa4eHhhqv1TAQxAMApCxMSNH3yZE3JzdUIm01NqjjnjKREi0VzrVbNiI/X\n2PHja7tMj0cQAwActjAhQXMmT9bGnByF2XH+YUm9AwM1hTCuhCAGADgkOTlZEXffra8qhPCjkj6X\nlCPpKkmjJU296PPDknoGBmrtli267bbbaq9gD0fXNADAIfPj4jQlN7fSSDha0lFJmZI2SHpD0saL\nPg+T9GxurubHxdVOoV6CETEAwG7p6elq26KF0vLyqpwTLvWDpHskrZHU5aLjpyW1DghQyrFjdFNf\nwIgYAGC3JYmJ6i9VG8ITJDWS1FHnH0t3qfB5U0lRFouWJCa6rUZvw3vEAIAqZWZm6uDBg+X+2rF5\ns2bm5VX7nTclLZC0VdIASV0lVXxpKTw3V9/t2+e2ur0NQQwAdZjNZlNGRoYOHDhQFralvz5+/Hil\n84MkBV/mmhZJ/0/SIEnLVTmIgyVlnTnjgup9A0EMAHVASUmJfv7553Kj29LAPX36tN3XKdb5xTrs\nUSQpsIrjWZKCm1xqhrluIYgBwIcUFRXpyJEjlcL20KFDOnfuXI2vnydpi6THKxzPkLRJUj9JVkn/\nlPThhb9XlGy16qZOnWpci6+gaxoAvFBeXp5++OGHSoGbkpKiwsJCl9yjfv36CgsLU4cOHdS+fXu1\nb99ezZs318D771dafn65hq2TkgZK2ivJJulGSdMkPVDhmnRNV8aIGAA82NmzZyuF7cGDB5WWliZX\njaOsVqvatWtXFralwRsWFiZ/f/9K59/ft68Wr16tJy+6/1WSvrTjXostFvXr25cQvggjYgDwAL/9\n9pv27NlTLmwPHjyoX3/91WX3aNy4cVnYXhy4LVq0UL169r/NWt3KWpfDylpVY0QMAB5g1apV+uMf\n/+iSazVv3rxS2JY+VrZYLDW+fnh4uGbEx6u3E2tNz4iPJ4QrIIgBwJCMjIyyR86bNm1y+PstW7as\nMnCb1EJHcunGDT0nT9azubkaWc3uS6d1fvelV9h9qVo8mgYAN7LZbPrll1+qfE+3uLi4LERbtmyp\nadOmVfp+acNUxbBt27atGjVqZOAnKm/nzp2aHxendZ9+qiiLReG5uWX7ESdf2I+4X9++mhQdzUi4\nGgQxALhAUVGRjh49WilwDx06pKCgoEpB2qFDB1199dXlHhXfe++9Cg0NLXdO69at1aBBA4M/mX0y\nMjK0JDFRKfv2KevMGQU3aaI2nTpp+MiRNGZdBkEMAA7Iy8tTSkpKpdHt4cOH1bx583JhW5uPiuG9\nCGIAqEJWVlaVrw39/PPPatWqVaXRbdu2bRUYWNU6UsClEcQA6rTShqmKgXvq1Kly79Z626NieA+C\nGIDPK22Yqhi2Bw8eVGFhYaXRrTPv1gLOIogB+Izi4mKlpaVVGbilDVMVA9dV79YCziKIAXid/Px8\npaSkVArb1NTUahezoGEKnoogBuCxsrKydOjQoUqvBJU2THnqu7WAIwhiAMadPHmy0uj2wIEDOnXq\nlNq2bVspcMPCwmiYgs8giAHUCpvNpl9//bXKFaYKCwsrhW1pw5Sfn5/p0gG3IogBuNTFDVMVN6YP\nDAyscoUpGqZQlxHEAJxS2jBVMXBTU1N19dVXV/lKEA1TQGUEMYBLKm2YqvhK0LFjx9SyZcsqV5ii\nYQqwH0EMQNL5hqmqVpg6efJkWcPUxaNbGqYA1yCIATulp6ef311m715lZ2YqKCREbTp31ohRo7xm\nd5nShqmKYXvgwAEVFBRUu8IUDVOA+xDEwGUkJydrflyc1m/YoAclheflle23mnRhv9X7+/TRpOho\nhYeHG672vOLiYh09erTKFaZKG6YqNk1dc801NEwBBhDEwCUsTEjQ9MmTNSU3VyNsNlXVanRGUqLF\norlWq2bEx2vs+PG1Vl9+fr5SU1MrjW5LG6aqeiWoadOmtVYfgMsjiIFqLExI0JzJk7UxJ0dhdpx/\nWFLvwEBNcUMYZ2dnV7nCVGnDVMXAbdeuHQ1TgJcgiIEqJCcnK+Luu/VVNSGcKqmzpEGSllx0/LCk\nnoGBWrtli2677TaH73vq1KkqF7w4efKk2rRpU2l0e+ONN9IwBXg5ghiowrAHH9Rtq1fryWr+8+gt\nKU9SC5UPYkl6zWLRt1FRen/Vqiq/e3HDVMU53Pz8/CoXvKBhCvBdBDFQQXp6utq2aKG0vLwq54T/\nJmm1pA46PwKuGMSnJbUOCNDBo0eVnZ1dZeBardZKo9sOHTrQMAXUQfVNFwB4miWJiYqSqgzhs5Km\nS9os6a/VfL+ppD75+Wpx3XVq/l//VRa4PXr00GOPPUbDFIByCGKggpS9e9UtL6/Kz16Q9Jik/7rM\nNXrabAoYOFDvLV/u6vIA+BiCGKggOzNTwVUc/07S5xf+fjnBkvKys11aFwDfRBADFQSFhCiriuNb\nJP0k6XpJNknZkoolHZC0s8K5WZKC2eAAgB3qmS4A8DRtOndWUkBApePjJB3R+RHxHkmPS+on6R9V\nXCPZalWbTp3cWSYAH0HXNFDB5bqmS83Q+WCurms65dgxr1mDGoA5jIiBCkJDQ3V/nz5KvMxrRNNV\nOYQlabHFon59+xLCAOxCEANV6Nm7t1602XTYwe8dljTXatWk6Gh3lAXABxHEQAVHjx7V1KlTlSWp\np2R3GJeuNT0jPt6p5S0B1E0EMXCR7OxsRUZG6tSpU7JJOiGpq6R5FovOVPOd0xc+7+mmDR8A+DZe\nXwIuKCkp0fDhw7Vv376yYzZJQ8aO1e6TJzXr008VZbEoPDe3bD/i5Av7Effr21dro6MZCQNwGEEM\nXDBz5kx9/PHH5Y4NHDhQCQkJqlevnjIyMrQkMVFfff21vti4Uf0HDtRNnTppzsiRNGYBcBqvLwGS\nPvroIw0aNKjcsZtvvlnbtm2rtK/vqVOn1KZNG506dao2SwTgowhi1HnfffedevTooZycnLJjzZo1\nU3Jyslq0aFHp/KKiIgUEBKiwsJCdkgDUGM1aqNPS09MVGRlZLoTr16+vVatWVRnCpZ9brVZls5Y0\nABcgiFFnFRQUaODAgTp27Fi542+++aZ69ux5ye82btxYv/32mzvLA1BHEMSok2w2myZOnKivvvqq\n3PEJEyZo7Nixl/1+SEgIQQzAJQhi1EkJCQlauHBhuWO9evXSa6+9Ztf3GzdurMzMTHeUBqCOIYhR\n52zevFn/+7//W+5Yq1at9OGHH8rf39+ua/BoGoCrEMSoU9LS0jRo0CAVFxeXHQsKCtInn3yiK6+8\n0u7rEMQAXIUgRp2RlZVVtnzlxT744AN17NjRoWsxRwzAVQhi1AklJSV69NFH9f3335c7PmvWLEVG\nRjp8PUbEAFyFIEad8OKLL2rNmjXljg0aNEhTp0516no0awFwFYIYPm/lypWaNWtWuWO33nqrFi1a\n5PTKWIyIAbgKQQyftnv3bo0cObLcsdDQUK1evbrSGtKOIIgBuApBDJ914sQJRUZGKjc3t+yYv7+/\nVq1apeuvv75G16ZZC4CrEMTwSQUFBRowYIB+/vnncscTEhJ055131vj6jIgBuApBDJ9js9k0YcIE\nbdu2rdzxiRMnasyYMS65B81aAFyFIIbPefPNN/XOO++UO/Y///M/mjdvnsvuwYgYgKuwHzF8yhdf\nfKHevXuXWzmrdevW2rFjh0MrZ11Ofn6+goODlZ+fz57EAGqEETF8xpEjRyotXxkcHKw1a9a4NIQl\nqWHDhvLz8yvXCAYAziCI4RPOnj2riIgInTlzpuyYxWLR0qVLddNNN7nlnswTA3AFghher6SkRMOG\nDdOBAwfKHZ89e7YeeOABt92XeWIArkAQw+u98MILWrt2bbljQ4YM0XPPPefW+xLEAFyBIIbX69mz\np6xWa9nvu3TponfffdftTVQs6gHAFeqbLgCoKavVKqvVqubNmysnJ0erV69WYGCg2+/LiBiAKxDE\n8Go//fSTBg8erOXLl6tbt246duyYrrvuulq5N81aAFyBIIbXOnfunCIiIjRlyhT94Q9/kHQ+HGsL\nI2IArsAcMbxSSUmJRowYoS5dumjSpElGaiCIAbgCI2J4pdjYWB0/flybN282trJVSEiIfvzxRyP3\nBuA7CGJ4nb///e965513lJSUpIYNGxqrgxExAFcgiOFV9u7dq3Hjxumzzz5T8+bNjdZCsxYAV2CO\nGF4jIyNDkZGR+stf/qKuXbuaLocRMQCXIIjhFQoLCzVo0CANHTpUQ4cONV2OJIIYgGsQxPAKkyZN\nUnBwsGJjY02XUoaVtQC4AnPE8HgJCQn68ssv9c0336hePc/5syMjYgCuYLHZbDbTRQDV2bJlix56\n6CFt27ZNYWFhpsspx2azqWHDhsrKyjLavQ3Au3nO8AKo4OjRoxoyZIiWLl3qcSEsnd/vmM5pADVF\nEMMjZWdnKzIyUtHR0brnnntMl1MtHk8DqCmCGB6npKREw4cPV7du3TRx4kTT5VwSDVsAaopmLXic\nmTNn6sSJE1q+fLmx5SvtxYgYQE0RxPAoH330kRYtWmR8+Up7MUcMoKYIYniM7777TuPHj9fGjRt1\n9dVXmy7HLoyIAdQUc8TwCOnp6erfv78WLFigLl26mC7HbswRA6gpghjGFRQUaODAgRo2bJgGDx5s\nuhyHMCIGUFMEMYyy2WyaOHGimjZtqpkzZ5oux2EEMYCaYo4YRiUkJGjbtm3avn27Ry1faS+atQDU\nFEEMYzZt2qSZM2dq27ZtCg4ONl2OUxgRA6gp7xuCwCekpaXp4Ycf1rJly9S6dWvT5TiNZi0ANUUQ\no9ZlZWUpMjJSMTEx+v3vf2+6nBphRAygpghi1KqSkhI9+uij6t69uyZMmGC6nBojiAHUFHPEqFXT\np0/XqVOntHLlSo9fvtIeNGsBqCmCGLVm5cqVev/995WUlKQGDRqYLsclgoKClJubq6KiItWvz39O\nABzHo2nUit27d2vChAlavXq1QkNDTZfjMhaLRVdccQWjYgBOI4jhdidOnFD//v311ltv6ZZbbjFd\njssxTwygJghiuFVBQYEGDBigESNGaNCgQabLcQvmiQHUBEEMt7HZbHriiSfUrFkzvfjii6bLcRtG\nxABqgu4SuM2CBQuUlJSkr7/+2iuXr7QXQQygJghiuMUXX3yh2bNna/v27QoKCjJdjluxuhaAmiCI\n4XJHjhzRww8/rBUrVqhVq1amy3E7RsQAasJ3nxfCiLNnzyoiIkIvvvii7r77btPl1AqatQDUBEEM\nlykpKdGwYcPUs2dPjR8/3nQ5tYYRMYCa4NE0XGbatGnKzMzURx99ZLqUWsUcMYCaIIjhEn/729+0\nbNkyn1q+0l6MiAHUBEGMGtu1a5cmTpyozz//XM2aNTNdTq0jiAHUBHPEqJH//Oc/ioqK0v/93//p\n5ptvNl2OETRrAagJghhOy8/P14MPPqgxY8ZowIABpssxhhExgJqw2Gw2m+ki4H1sNpvGjBmjs2fP\nauXKlT69ctblnDlzRq1atSKMATiFOWI45S9/+Yt27dqlbdu21ekQlqQrrrhCWVlZKikpqfP/LAA4\njiCGw/75z3/q5ZdfrhPLV9rDz89PQUFBOnv2rBo3bmy6HABehj++wyGpqakaNmyYVqxYoZYtW5ou\nx2PQsAXAWQQx7JaZmanIyEjNnDlTd911l+lyPAoNWwCcRRDDLsXFxXrkkUfUq1cvjRs3znQ5HofV\ntQA4iyCGXWJiYnTu3Dm9/vrrpkvxSIyIATiLZi1c1rJly7RixQolJSXJ39/fdDkeiSAG4CyCGJe0\nc+dOTZo0SZs2bdJVV11luhyPRbMWAGfxaBrV+ve//62oqCgtXLhQnTp1Ml2OR2NEDMBZBDGqlJeX\np6ioKI0dO1ZRUVGmy/F4NGsBcBZBjEpsNpsef/xxXX/99YqJiTFdjldgRAzAWcwRo5LXX39de/bs\n0b/+9S9ZLBbT5XgFghiAswhilLNx40bNnTtX33zzjRo1amS6HK9BsxYAZxHEKJOSkqLhw4dr1apV\natGihelyvApzxACcxRwxJJ1fvjIiIkKxsbG68847TZfjdXg0DcBZBDFUXFysoUOH6t5779Vjjz1m\nuhyvRBADcJbFZrPZTBcBs5599lnt2rVLn332GStnOamwsFBWq1WFhYU0uAFwCHPEddwHH3ygVatW\nsXxlDfn7+ysgIEDnzp1jj2YADiGI67CkpCQ99dRT2rRpk6688krT5Xi90oYtghiAI5gjrqOOHz+u\nBx98UO+88446duxouhyfwDwxAGcQxHVQ6fKV48ePV0REhOlyfAZBDMAZBHEdY7PZNHbsWLVq1UrP\nP/+86XJ8Cot6AHAGc8R1zKuvvqrvv/+e5SvdgBExAGcQxHXIhg0bNG/ePO3YsUOBgYGmy/E5rK4F\nwBkEcR1x6NAhjRgxQh9//LGuu+460+X4JEbEAJzBHHEd8NtvvykyMlIvv/yyevToYbocn0UQA3AG\nQezjiouLNWTIEN13330aPXq06XJ8Gs1aAJxBEPu4KVOmqLi4WK+++qrpUnweI2IAzmCO2IctWbJE\na9as0Y4dO1S/Pv+q3Y1mLQDO4P/OPuqbb77R5MmT9eWXX6pp06amy6kTGBEDcAaPpn3Qr7/+qgED\nBujdd99Vhw4dTJdTZxDEAJxBEPuY3Nxc9e/fXxMnTtQDDzxgupw6hWYtAM5gP2IfYrPZ9Oijj6qk\npERLly5l5axalpeXp5CQEOXl5fHPHoDdmCP2Ia+88ooOHTqkrVu3EgQGBAQEyGKxKC8vT1ar1XQ5\nALwEQewj1q9fr/nz57N8pWGl88QEMQB7MUfsAw4ePKhRo0bpo48+0u9+9zvT5dRpNGwBcBRB7OXO\nnDmjiIgIzZkzR927dzddTp1HwxYARxHEXqyoqEiDBw/WAw88oFGjRpkuB2JRDwCOI4i92LPPPitJ\nmjt3ruFKUIpH0wAcRbOWl1q0aJHWrVvH8pUehiAG4Cj+D+6Ftm/frilTpmjLli1q0qSJ6XJwEYIY\ngKN4NO1lfvnlFw0cOFCJiYlq37696XJQAc1aABxFEHuRnJwc9e/fX5MmTVLfvn1Nl4Mq0KwFwFEE\nsZew2WwaM2aM2rVrp2eeecZ0OagGj6YBOIo5Yi8xZ84cHT58mOUrPRxBDMBRBLEXWLt2rRYsWKAd\nO3awdKKHI4gBOIog9nAHDhzQmDFjtHbtWl177bWmy8Fl0KwFwFHMEXuw06dPKyIiQvHx8br99ttN\nlwM70KwFwFHsR2xIenq6liQmKmXvXmVnZiooJERtOnfWiFGj1KxZMxUVFem+++7TLbfcovj4eNPl\nwk7nzp1Ts2bNlJOTY7oUAF6CIK5lycnJmh8Xp/UbNuhBSeF5eQqWlCUpyWrVxzab7u/TR0UNGigz\nM1Pr1q2Tn5+f4aphL5vNpgYNGig7O1sNGzY0XQ4AL8AccS1amJCg6ZMna0purt6w2VRxTazHc3P1\nqqRFq1drpqQX4+MJYS9jsVjK5olDQ0NNlwPACzBHXEsWJiRozuTJ+ionR09eCOE3JYVLCpA0+sJ5\nTSQ9ZbNpp82mN6ZN08KEBFMlw0khISE0bAGwG0FcC5KTkzV98mRtzMlR2EXHr5U0TdKYKr4TJmlj\nTo6mT56snTt31kqdcA1eYQLgCIK4FsyPi9OU3NxyISxJ/SVFSGpazffCJD2bm6v5cXFurQ+uRRAD\ncARB7Gbp6elav2GDRjjZEzfCZtO6Tz9VRkaGiyuDuxDEABxBELvZksRERUmVGrPs1VRSlMWiJYmJ\nrisKbsWiHgAcQRC7WcreveqWl1eja4Tn5ipl3z4XVQR3Y1EPAI4giN0sOzNTwTW8RrCkrDNnXFEO\nagGPpgE4giB2s6CQEGVV81mxpLwLfy+SlH/h1xVlSQpu4uzDbdQ2ghiAIwhiN2vTubOSAgKq/CxW\nUqCkOZKWXvj17CrOSwoIUJtOndxWI1yLIAbgCILYzYaPHKmPJVX1YHm6pBKdHwWX/vVChXNOS1qR\nl6eff/2VzmkvQbMWAEcQxG4WGhqq+/v00WKLxanvL7ZYdF/v3srPz1fbtm311FNP6fjx4y6uEq5E\nsxYARxDEtWBSdLTmWK067OD3Dkuaa7Xq+dhYJSQkaN+FzumOHTvqiSee0I8//ujqUuECPJoG4AiC\nuBaEh4drRny8egcG2h3GhyX1DgzUjPh43XbbbZKka6+9VvPmzdOhQ4fUuHFjde3aVaNHj1Zqaqrb\naofjCGIAjiCIa8nY8eM1JT5ePQMD9ZrFUuWcsXR+TniexaKegYGaEh+vsePHVzonNDRUL730kg4f\nPqyWLVvqjjvu0MMPP6zvv//erT8D7EMQA3AE+xHXsp07d2p+XJzWffqpoiwWhefmlu1HnHxhP+J+\nfftqUnR02Uj4crKyspSQkKB58+bpjjvu0NSpU9W1a1e3/hyoXklJifz9/ZWfn6/69dlpFMClEcSG\nZGRkaEliolL27VPWmTMKbtJEbTp10vCRI9WsWTOnrpmTk6N33nlHc+fOVadOnRQTE6MePXq4uHLY\no0mTJjpy5IiaNq1uSw8AOI8g9kH5+flavHixXn75ZbVo0ULTpk1Tr169ZHGycxv2++yzz/Tcc89p\n//79CgwMVFRUlBJZJxzAJTBH7IMaNmyosWPH6ocfftCoUaP0xBNPqEePHlq/fr34c5d75eXlac+e\nPSoqKtLZs2d1+vRp0yUB8HAEsQ/z9/fX8OHDtX//fj355JN6/vnn1bVrV61atUolJSWmy/NJjRs3\nLvd7mrYAXA5BXAf4+fnpoYce0nfffacZM2Zozpw56tSpk5YuXaqioiLT5fkUghiAowjiOsRiseiB\nBx7Qjh079Prrr+vtt99Wu3bt9O6776qgoMB0eT6BIAbgKIK4DrJYLLr33nu1detWvffee1q5cqVu\nvPFGvfnmm8rNzTVdnlcLCQkp93vWnAZwOXRNQ5KUlJSk2bNnKzk5WU8//bTGjRunoKAg02V5neLi\n4krvDhcVFcnPz89QRQA8HSNiSJK6deumNWvWaMOGDUpKStINN9yg2bNn82jVQX5+frriiivKHTt7\n9qyhagB4A4IY5dx8881asWKFtm7dqpSUFIWFhWnatGk6efKk6dK8BvPEABxBEKNK7dq10+LFi5WU\nlKT09HS1adNGzzzzjP7zn/+YLs3jEcQAHEEQ45JuuOEGvf3229q7d68KCgrUoUMH/elPf9KxY8dM\nl+axaNgC4AiCGHb53e9+p/nz5+vgwYNq1KiRbrnlFv3xj3/U4cOO7rLs+xgRA3AEQQyHXH311Zoz\nZ45SU1N17bXX6r//+781bNgwHThwwHRpHoMgBuAIghhOufLKKzVjxgwdOXJEN910k3r16qWBAwdq\n9+7dpkszjiAG4AiCGDUSEhKi6OhopaWl6c4771S/fv3Ur18/bd++3XRpxhDEABxBEMMlGjVqpCef\nfFJHjhxRv379NHToUN1zzz368ssv69yOTzRrAXAEQQyXCggI0OOPP67U1FQNGzZMY8eOVc+ePfXZ\nZ5/VmUBmRAzAEQQx3MLf318jR47UwYMH9ac//UnPPPOMwsPDtXr1ap/fgpEgBuAIghhu5efnpyFD\nhmjPnj2KiYlRbGysOnfurOXLl6u4uNh0eW5BEANwBEGMWlGvXj31799fycnJio+P14IFC9S+fXst\nWrRIhYWFpstzqYpzxAQxgEshiFGrLBaL7rvvPv3rX//SwoULtXTpUt14441KSEhQXl6e6fJcouKI\nmGYtAJdCEMMIi8Wiu+++W59//rmWL1+u9evXq3Xr1nrttdd07tw50+XVCI+mATiCIIZx3bt317p1\n67Ru3Tp9/fXXuuGGGxQXF+e12wdW9fqSrzeoAXAeQQyPceutt+rDDz/U5s2bdeDAAd1www2aPn26\nTp8+bbo0h/j7+6tRo0Zlvy8pKVF2drbBigB4MoIYHqdDhw56//339c033+j48eO68cYbNWXKFJ04\nccJ0aXajYQuAvQhieKywsDD99a9/1e7du5WTk6P27dtr0qRJ+uWXX0yXdlk0bAGwF0EMj3f99dfr\njTfe0P79+9WgQQN17txZ48aNU1pamunSqkXDFgB7EcTwGtdcc41eeeUVpaSkKDQ0VN26ddPw4cN1\n6NAh06VVQhADsBdBDK9z1VVXadasWTp8+LDatm2ru+66S4MHD9aePXtMl1aGIAZgL4IYXqtx48aa\nOnWq0tLS1K1bN/Xp00cRERFKSkoyXRrNWgDsRhDD6wUFBenpp5/WkSNH1Lt3bw0aNEh/+MMftHXr\nVmM10awFwF4EMXyG1WrVhAkTlJqaqiFDhmj06NG666679I9//KNsC8aVK1fWyuiUR9MA7EUQw+c0\naNBAo0eP1qFDhzRu3Dj9+c9/1u23364FCxZo8ODBatGihaZOnaqMjAy31UAQA7AXQQyfVb9+fT3y\nyCPat2/h5tnOAAAFVklEQVSfnnvuOb3wwguSpLNnz+qll15Sy5Yt9fTTT+vf//63y+9NEAOwF0EM\nn1evXj117ty50jxtTk6O5s2bp1atWmnChAn66aefXHZPmrUA2IsgRp0QGhqq2NhYXXXVVZU+y8/P\n11tvvaWwsDCNGTNGqampNb4fzVoA7EUQo0644oorFB0drR9//FHz5s3TNddcU+mcoqIivffee2rX\nrp0eeeQR7d+/3+n78WgagL0IYtQpjRo10p///GelpaXprbfeUosWLSqdU1JSomXLlqljx44aMGCA\nvv32W4fvQxADsJfFVvpeB1AHFRYWaunSpXrppZcu+Ui6T58+iomJ0R133GHXdfPy8mS1Wst+X79+\nfRUUFMhisdS4ZgC+hSAGJBUXF+vDDz9UbGzsJR9J9+rVSzExMerVq9dlQ7Vhw4YqLChQgCQ/SYMG\nD1aHLl00YtQoNWvWzLU/AACvRRADFykpKdEnn3yi2NhY7dq1q9rzunfvrpiYGPXp06dSICcnJ2t+\nXJz+/vHH6i/pLknBkrIkJVmt+thm0/19+mhSdLTCw8Pd+eMA8AIEMVAFm82mjRs3atasWfr666+r\nPe/WW29VTEyM+vfvr3r16mlhQoKmT56sKbm5GmGzqUkV3zkjKdFi0VyrVTPi4zV2/Hi3/RwAPB9B\nDFyCzWbTli1bFBsbqy+++KLa8zp06KDut9+uzStWaGNOjsLsuPZhSb0DAzWFMAbqNIIYsNP27ds1\ne/ZsrV+/vsrPr5C0SyoL4QJJT0j6XOdHwa0lvSTpvou+c1hSz8BArd2yRbfddpu7SgfgwXh9CbBT\n9+7dtW7dOn377bcaMGBAuc8CJb0glRsJF0m6XtJXkjIlzZL0kKRjF50TJunZ3FzNj4tzZ+kAPBgj\nYsBJ+/fvV1xcnJYtW6aGNpuOS1XOCV/sZkkvSoq66NhpSa0DApRy7Bjd1EAdxIgYcNJNN92kDz74\nQM9OnqwBfn6XDeETklIl3VTheFNJURaLliQmuqNMAB6OIAZq6PTx47qzuPiS5xRJGiZppKQ2VXwe\nnpurlH37XF8cAI9HEAM1lJ2ZqeBLfG7T+RBuKOmNas4JlpR15oyrSwPgBeqbLgDwdkEhIcq6xOdj\nJJ2U9KnOr7BVlSxJwU0u93AbgC9iRAzUUJvOnZUUEFDlZ49LOiTpE0kNLnGNZKtVbTp1ckN1ADwd\nXdNADaWnp6ttixZKy8sr17B1TFJLqWytaUmySHpb0tCLzqNrGqjbGBEDNRQaGqr7+/TR4gprTl8v\nqURSjs4/es6SdFblQ1iSFlss6te3LyEM1FGMiAEXSE5OVsTdd+srO5e3LMXKWgAYEQMuEB4erhnx\n8eodGKjDdn6ndK3pGfHxhDBQhxHEgIuMHT9eU+Lj1TMwUK9ZLKruZaTTkuZZLOrJhg8AxKNpwOV2\n7typ+XFxWvfpp4qyWBSem1u2H3Hyhf2I+/Xtq0nR0YyEARDEgLtkZGRoSWKiUvbtU9aZMwpu0kRt\nOnXS8JEjacwCUIYgBgDAIOaIAQAwiCAGAMAgghgAAIMIYgAADCKIAQAwiCAGAMAgghgAAIMIYgAA\nDCKIAQAwiCAGAMAgghgAAIMIYgAADCKIAQAwiCAGAMAgghgAAIMIYgAADCKIAQAwiCAGAMAgghgA\nAIMIYgAADCKIAQAwiCAGAMAgghgAAIMIYgAADCKIAQAwiCAGAMAgghgAAIMIYgAADCKIAQAwiCAG\nAMAgghgAAIMIYgAADCKIAQAwiCAGAMAgghgAAIMIYgAADCKIAQAwiCAGAMAgghgAAIMIYgAADCKI\nAQAwiCAGAMCg/w835PM8oaEV8wAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"nx.draw(Gd, with_labels = True)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Directed network\n",
"In directed networks we can define an in-degree and out-degree. The (total) degree is the sum of in-and out-degree.\n",
"\n",
"## $k_3^{in} = 2, k_3^{out} = 1, k_3 = 3$\n",
"\n",
"Source: a node with $k^{in}= 0$; Sink: a node with $k^{out}= 0$.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"For a sample of N values: $x_1, x_2, ..., x_N$:\n",
"\n",
"# Average(mean):\n",
"\n",
"## $ = \\frac{x_1 +x_2 + ...+x_N}{N} = \\frac{1}{N}\\sum_{i = 1}^{N} x_i$ "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"For a sample of N values: $x_1, x_2, ..., x_N$:\n",
"\n",
"# The nth moment:\n",
"\n",
"## $ = \\frac{x_1^n +x_2^n + ...+x_N^n}{N} = \\frac{1}{N}\\sum_{i = 1}^{N} x_i^n$ "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"For a sample of N values: $x_1, x_2, ..., x_N$:\n",
"\n",
"# Standard deviation:\n",
"\n",
"## $\\sigma_x = \\sqrt{\\frac{1}{N}\\sum_{i = 1}^{N} (x_i - )^2}$ "
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"(1.6666666666666667, 10, 0.7453559924999299)"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import numpy as np\n",
"x = [1, 1, 1, 2, 2, 3]\n",
"np.mean(x), np.sum(x), np.std(x)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"For a sample of N values: $x_1, x_2, ..., x_N$:\n",
"\n",
"# Distribution of x:\n",
"\n",
"## $p_x = \\frac{The \\: frequency \\: of \\: x}{The\\: Number \\:of\\: Observations}$\n",
"\n",
"其中,$p_x 满足 \\sum_i p_x = 1$"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXkAAAEACAYAAABWLgY0AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAADdtJREFUeJzt3W+IXfWdx/HPR6PSRSaghaQkmoDVLZYd0t0SIy6bLEup\nEdY8EawVBB8FWVHwSRcRkn1S2Id1m5IGbGkUqYsPNLvRRai9NQoNEjMaNNlG6KrNNgOLhqIJS9p+\n9sEcu9ebmbnn3jkzN/n6fsHB8+c753w9/OYzZ34zZ+IkAgDUdNmkGwAALB9CHgAKI+QBoDBCHgAK\nI+QBoDBCHgAKGxrytq+yfdj2Udtv2/7uAnWP2z5pe8b2pu5bBQCMatWwgiT/a/tvk5y1fbmk12zf\nluS1T2tsb5d0Q5Ibbd8iaa+kLcvXNgCgjVbTNUnONqtXNR/z0UDJDkn7m9rDklbbXtNVkwCA8bQK\neduX2T4q6bSkXpJ3BkrWSfqgb/tUsw8AMEFtn+T/mORrktZL+hvbW5e3LQBAF4bOyfdL8jvbByV9\nXdIv+g6dknRd3/b6Zt9n2OYP5QDAGJJ4nI9r89s1X7S9uln/gqRvSJoZKDsg6b6mZoukM0lmF2h1\nosvU1F/ozTffVJJLftm1a9fEe6i0cD+5lxfrshRtnuS/JOkntq25LwpPJvmZ7Z2SkmRfkhds32H7\nXUmfSLp/SV0BADrR5lcoj0n6y3n2/3Bg+8EO+wIAdIA3Xi9h27Ztm3QLpXA/u8O9vHh4qfM9I13M\nztzc+ORMTU3r0KGnND09PdE+AKAt28py/eAVAHDpIuQBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAK\nI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QB\noDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoLChIW97ve2Xbb9t+5jth+ap2Wr7jO03muWx5WkX\nADCKVS1qfi/pkSQztq+WdMT2S0lODNS9kuTO7lsEAIxr6JN8ktNJZpr1jyUdl7RunlJ33BsAYIlG\nmpO3vVHSJkmH5zl8q+0Z2wdt39xBbwCAJWozXSNJaqZqnpX0cPNE3++IpOuTnLW9XdJzkm7qrk0A\nwDhahbztVZoL+CeTPD94vD/0k7xo+we2r0ny4YVn2923vq1ZAACf6vV66vV6nZzLSYYX2fsl/U+S\nRxY4vibJbLO+WdK/Jtk4T12k4ddbTlNT0zp06ClNT09PtA8AaMu2koz1c8+hT/K2b5N0r6Rjto9q\nLqUflbRBUpLsk3SX7QcknZd0TtLd4zQDAOjW0JBP8pqky4fU7JG0p6umAADd4I1XACiMkAeAwgh5\nACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiM\nkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeAwgh5ACiMkAeA\nwgh5AChsaMjbXm/7Zdtv2z5m+6EF6h63fdL2jO1N3bcKABjVqhY1v5f0SJIZ21dLOmL7pSQnPi2w\nvV3SDUlutH2LpL2StixPywCAtoY+ySc5nWSmWf9Y0nFJ6wbKdkja39QclrTa9pqOewUAjGikOXnb\nGyVtknR44NA6SR/0bZ/ShV8IAAArrM10jSSpmap5VtLDzRP9mHb3rW9rFmDy1q7dqNnZ9ybaw5o1\nG3T69H9NtAdMXq/XU6/X6+RcTjK8yF4l6d8lvZjke/Mc3yvp50meabZPSNqaZHagLtLw6y2nqalp\nHTr0lKanpyfaBy4+tjXp8SlZbT4n8fliW0k8zse2na75kaR35gv4xgFJ9zXNbJF0ZjDgAQArb+h0\nje3bJN0r6Zjto5p71HlU0gZJSbIvyQu277D9rqRPJN2/nE0DANoZGvJJXpN0eYu6BzvpCADQGd54\nBYDCCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DC\nCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DCCHkAKIyQB4DCCHkA\nKIyQB4DCCHkAKGxoyNt+wvas7bcWOL7V9hnbbzTLY923CQAYx6oWNT+W9C+S9i9S80qSO7tpCQDQ\nlaFP8klelfTRkDJ30w4AoEtdzcnfanvG9kHbN3d0TgDAErWZrhnmiKTrk5y1vV3Sc5JuWrh8d9/6\ntmYBAHyq1+up1+t1ci4nGV5kb5D0b0mmW9T+WtJfJflwnmORhl9vOU1NTevQoac0PT30fwWfM7Y1\n6fEpWW0+J/H5YltJxpoWbztdYy0w7257Td/6Zs194bgg4AEAK2/odI3tpzU3p3Kt7fcl7ZJ0paQk\n2SfpLtsPSDov6Zyku5evXQDAKIaGfJJvDzm+R9KezjoCAHSGN14BoDBCHgAKI+QBoDBCHgAKI+QB\noDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBC\nHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKI+QBoDBCHgAKGxrytp+wPWv7\nrUVqHrd90vaM7U3dtggAGFebJ/kfS/rmQgdtb5d0Q5IbJe2UtLej3gAASzQ05JO8KumjRUp2SNrf\n1B6WtNr2mm7aAwAsRRdz8uskfdC3farZBwCYsFUrf8ndfevbmgUALk5r127U7Ox7k25jbF2E/ClJ\n1/Vtr2/2LWB3B5cEgJUxF/CZcBce+yPbTtd4kasckHSfJNneIulMktmxOwIAdGbok7ztpzU3p3Kt\n7fcl7ZJ0paQk2ZfkBdt32H5X0ieS7l/OhgEA7Q0N+STfblHzYDftAAC6xBuvAFAYIQ8AhRHyAFAY\nIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8A\nhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhRHyAFAYIQ8AhbUK\nedu32z5h+1e2vzPP8a22z9h+o1ke675VAMCoVg0rsH2ZpO9L+jtJ/y3pddvPJzkxUPpKkjuXoUcA\nwJjaPMlvlnQyyXtJzkv6qaQd89S5084AAEvWJuTXSfqgb/s3zb5Bt9qesX3Q9s2ddAcAWJKh0zUt\nHZF0fZKztrdLek7STR2dGwAwpjYhf0rS9X3b65t9f5Lk4771F23/wPY1ST688HS7+9a3NQsA4P/1\nmmXp2oT865K+bHuDpN9K+pake/oLbK9JMtusb5bk+QNe+mzIAwAutE2ffQD+p7HPNDTkk/zB9oOS\nXtLcHP4TSY7b3jl3OPsk3WX7AUnnJZ2TdPfYHQEAOtNqTj7Jf0j684F9P+xb3yNpT7etAQCWijde\nAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAw\nQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4ACiPkAaAwQh4A\nCiPkAaAwQh4ACmsV8rZvt33C9q9sf2eBmsdtn7Q9Y3tTt20CAMYxNORtXybp+5K+Kemrku6x/ZWB\nmu2Sbkhyo6SdkvYuQ68Y0Ov1Jt0CMC/G5sWjzZP8Zkknk7yX5Lykn0raMVCzQ9J+SUpyWNJq22s6\n7RQX4BMJFyvG5sWjTcivk/RB3/Zvmn2L1ZyapwYAsMJWrfQFp6b+fqUv+Rnnzv1aV1xxxUR7AICV\n4iSLF9hbJO1Ocnuz/Y+SkuSf+2r2Svp5kmea7ROStiaZHTjX4hcDAMwricf5uDZP8q9L+rLtDZJ+\nK+lbku4ZqDkg6R8kPdN8UTgzGPBLaRIAMJ6hIZ/kD7YflPSS5ubwn0hy3PbOucPZl+QF23fYflfS\nJ5LuX962AQBtDJ2uAQBcujp/49X2E7Znbb+1SA0vTrU07H7a3mr7jO03muWxle7xUmF7ve2Xbb9t\n+5jthxaoY3y20OZ+Mj7bs32V7cO2jzb39LsL1I02PpN0ukj6a0mbJL21wPHtkg4267dI+mXXPVRa\nWtzPrZIOTLrPS2GRtFbSpmb9akn/KekrAzWMz27vJ+NztHv6Z81/L5f0S0m3DRwfeXx2/iSf5FVJ\nHy1SwotTI2hxPyWJH2i3kOR0kplm/WNJx3Xh+xyMz5Za3k+J8dlakrPN6lWam2kZ/NwfeXxO4g+U\n8eJU925tvnU7aPvmSTdzKbC9UXPfIR0eOMT4HMMi91NifLZm+zLbRyWdltRL8s5Aycjjc8VfhkLn\njki6PsnZ5m8IPSfppgn3dFGzfbWkZyU93DyBYgmG3E/G5wiS/FHS12xPSXrJ9tYkv1jKOSfxJH9K\n0nV92+ubfRhDko8//RYvyYuSrrB9zYTbumjZXqW5QHoyyfPzlDA+RzDsfjI+x5Pkd5IOSvr6wKGR\nx+dyhby18DzcAUn3SX96m3beF6fwGQvez/75ONubNfdrsR+uVGOXoB9JeifJ9xY4zvgczaL3k/HZ\nnu0v2l7drH9B0jckzQyUjTw+O5+usf20pG2SrrX9vqRdkq4UL06NZdj9lHSX7QcknZd0TtLdk+r1\nYmf7Nkn3SjrWzHtG0qOSNojxObI291OMz1F8SdJPbFtzD+BPJvnZUl885WUoACiMf/4PAAoj5AGg\nMEIeAAoj5AGgMEIeAAoj5AGgMEIeAAoj5AGgsP8DlQRse4t0JfQAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.hist(x)\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 113,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"defaultdict(int, {1: 3, 2: 2, 3: 1})"
]
},
"execution_count": 113,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from collections import defaultdict, Counter\n",
"freq = defaultdict(int)\n",
"for i in x:\n",
" freq[i] +=1\n",
"\n",
"freq"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"6"
]
},
"execution_count": 37,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"freq_sum = np.sum(freq.values())\n",
"freq_sum"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"text/plain": [
"[0.5, 0.3333333333333333, 0.16666666666666666]"
]
},
"execution_count": 38,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"px = [float(i)/freq_sum for i in freq.values()]\n",
"px"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX8AAAEACAYAAABbMHZzAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAH/dJREFUeJzt3XuQVPWZ//H30xizolF3QoSAQpBbuF8mEAj8pIUoKCnQ\nyZaC2bhiFNa7FVIFlWAxLsaIwQiRoKBZTSS7WN4ICRJAyVDMBnAiw3DZAQxBooHVjUbDReT2/P74\ntmxnHJieme4+ffm8qro43efSz3Q13/P09/t8zzF3R0REikss6gBERCT71PiLiBQhNf4iIkVIjb+I\nSBFS4y8iUoTU+IuIFKGUGn8zG21m281sp5lNrWf9cDN738w2Jh7TU91XRESyzxqq8zezGLATGAns\nBaqA8e6+PWmb4cAUdx/b2H1FRCT7Usn8BwGvu/sedz8KLAbG1bOdNWNfERHJolQa/3bAm0nP30q8\nVtcQM9tkZsvMrEcj9xURkSw6I03HeQ1o7+6HzOwKYAnQNU3HFhGRNEul8f8z0D7p+YWJ105y9wNJ\ny8vNbL6ZlaSy78fMTBcZEhFpJHevr8u9Qal0+1QBnc2sg5mdCYwHliZvYGatk5YHEQaS30tl32QO\nHADKe/fGDx/G3fVowmPGjBmRx1BID32e+jxz9dEcDTb+7n4cuB1YCWwDFrt7rZlNNrNJic3+ycy2\nmlk1MAe49nT7nuq9DgIzOnTghtatoV8/WLu2OX+biIicQkp9/u7+G6BbndcWJC3/BPhJqvueyuxv\nfIM7Zs6kQ8eO8MILMGECjBkDs2bB+eencggREUlBTs3wnbFoUWj4AcrKYNs2aNECevaE55+HZv7M\nKRbxeDzqEAqKPs/00ueZGxqc5JUtZuanjOW//gtuvhm6dIF58+Cii7IbnIhIDjIzPIMDvtEbOhSq\nq6G0FAYMCCeA48ejjkpEJG/lR+afrLYWJk2CY8dg4ULo3TvzwYmI5KDCz/yTde8Oa9bAxIkwYgRM\nnw6HD0cdlYhIXsm/xh8gFgvZ/+bNsGMH9OkDFRVRRyUikjfyr9unPkuXwu23w+WXw4MPQklJeoMT\nEclBxdXtU5+xY2HrVjjrrFAWunixykJFRE6jMDL/ZOvXh7LQ9u1h/nzo0KH5xxQRyUHK/JMNHgyv\nvRbKQ0tLYc4clYWKiNRReJl/sp07YfJkOHAAnngC+vZN7/FFRCKkzP9UunaF1avhllvgsstg2jQ4\ndCjqqEREIlfYjT+AGdx4I2zZAnv2hElhL78cdVQiIpEq7G6f+rz0Etx6KwwfDg89BK1aZf49RUQy\nQN0+jXHllaEstKQEevWCRYtUFioiRaf4Mv9kVVWhLLRNG3j0Ufj4ctIiInlAmX9TDRwYTgAjRoTl\n2bPDBeNERApccWf+yXbtgn/9V3j3XXj88TBHQEQkhynzT4dOnWDlSrj77jAuMGUKHDwYdVQiIhmh\nxj+ZGVx/fRgQfuedMCC8YkXUUYmIpJ26fU5nxYowQWzIEHj4YbjggqgjEhE5Sd0+mTJqVJgc1q5d\nmBz21FMqCxWRgqDMP1XV1XDTTXD++bBgAXTuHHVEIlLkMp75m9loM9tuZjvNbOppthtoZkfNrCzp\ntTfMrMbMqs3s1aYEmRP694cNG2DMmHDl0AcegKNHo45KRKRJGsz8zSwG7ARGAnuBKmC8u2+vZ7tV\nwIfAv7v7C4nX/wiUuvtfG3if3M78k+3eHcYC9u0LZaGDBkUdkYgUoUxn/oOA1919j7sfBRYD4+rZ\n7g7gOeCduvGl+D75o2NHWL4cpk6FceNCeej+/VFHJSKSslQa5XbAm0nP30q8dpKZtQWucvdHCY19\nMgdWmVmVmd3cnGBzihlcd10oC/3gg1AWumxZ1FGJiKTkjDQdZw6QPBaQfAIY6u77zOxzhJNArbtX\n1neQ8vLyk8vxeJx4PJ6m8DLos5+FJ58M9w2YPBl+/nOYOzdcL0hEJI0qKiqoqKhIy7FS6fMfDJS7\n++jE82mAu/uspG3++PEi0Ao4CExy96V1jjUD2O/uP6rnffKnz/9UPvwQZs4Mdw27/3741rfCLwQR\nkQxoTp9/Ko1/C2AHYcB3H/AqMMHda0+x/ZPAr9z9BTNrCcTc/YCZnQ2sBO5195X17Jf/jf/HNm8O\nZaEtW4ay0G7doo5IRApQRgd83f04cDuh4d4GLHb3WjObbGaT6tslabk1UGlm1cB6wknhEw1/wenT\nB9atg7KycCP5++6DI0eijkpE5CRN8sq0P/0p3DnsjTdCWeiQIVFHJCIFIqPdPtlSsI0/hEtCPPts\nKAm9+mr4wQ/g3HOjjkpE8pyu7ZPrzOCaa2DbttD907MnLFkSdVQiUsSU+UdhzRqYNCnMDXjkEWjb\nNuqIRCQPKfPPN8OHQ00N9OgBffvCY4/BiRNRRyUiRUSZf9S2bg2/AmIxWLgwnBBERFKgzD+f9eoF\nlZXhUhHDh0N5OXz0UdRRiUiBU+OfC2KxUA5aXQ2bNkG/frB2bdRRiUgBU7dPLnrhBbjzznDvgFmz\nwg1kRETqULdPoSkrC2WhsVgoC33+ed0+UkTSSpl/rqusDAPCXbrAvHlw0UVRRyQiOUKZfyEbNiyM\nBZSWwoAB4QRw/HjUUYlInlPmn09qa8OvgGPHQllo795RRyQiEVLmXyy6dw+zgydOhBEjYPp0OHw4\n6qhEJA+p8c83sVjI/jdvhh07wuWj03RnHxEpHur2yXdLl8Jtt8GoUfDgg1BSEnVEIpIl6vYpZmPH\nhrLQs84Ks4WfeUZloSLSIGX+hWT9erj5ZmjfHubPhw4doo5IRDJImb8EgwfDa6+FW0eWlsKcOSoL\nFZF6KfMvVDt3wuTJcOAAPPFEuHS0iBQUZf7ySV27wurVcMstcNllMG0afPhh1FGJSI5Q41/IzODG\nG2HLFtizJ0wKe/nlqKMSkRygbp9i8tJL4dLRw4fDQw9Bq1ZRRyQizaBuH0nNlVeGO4eVlISy0EWL\nVBYqUqRSavzNbLSZbTeznWY29TTbDTSzo2ZW1th9JUvOOQcefhh+9SuYPRuuuAJ27446KhHJsgYb\nfzOLAfOAUUBPYIKZffEU2z0ArGjsvhKBgQOhqgouvTQsz54dLhgnIkUhlcx/EPC6u+9x96PAYmBc\nPdvdATwHvNOEfSUKn/oUTJ0KGzbAihUwaFCYJyAiBS+Vxr8d8GbS87cSr51kZm2Bq9z9UcAas6/k\ngE6dYOVKuPvuMC4wZQocPBh1VCKSQWek6ThzgGb355eXl59cjsfjxOPx5h5SUmUG118fxgC+/e0w\nIPzYY+GCcSKSEyoqKqhI01V8Gyz1NLPBQLm7j048nwa4u89K2uaPHy8CrYCDwCRCF9Bp9006hko9\nc8mKFWGC2JAhYYD4gguijkhE6sh0qWcV0NnMOpjZmcB4YGnyBu5+ceLRkdDvf6u7L01lX8lRo0aF\nyWFt24bJYT/7mcpCRQpIg42/ux8HbgdWAtuAxe5ea2aTzWxSfbs0tG9aIpfMO/ts+OEPYfly+PGP\n4atfhT/8IeqoRCQNNMNXUnPsWDgB3H8/fOc7YVD4U5+KOiqRotacbh81/tI4u3eHsYB9++Dxx0N5\nqIhEQpd3kOzp2DF0A02dCuPGhfLQ/fujjkpEGkmNvzSeGVx3XbhO0AcfhLLQZcuijkpEGkHdPtJ8\nr7wSbhxTWgpz50KbNlFHJFIU1O0j0Ro5MpSFduoEffqEO4fpRC6S05T5S3pt3gw33QQtW8KCBdCt\nW9QRiRQsZf6SO/r0gXXroKws3Ej+vvvgyJGooxKROtT4S/q1aAF33gkbN8L69TBgQDghiEjOULeP\nZJY7PPtsKAktKwuTxM49N+qoRAqCun0kd5nBNdfAtm3w0UfQsycsWRJ1VCJFT5m/ZNeaNTBpUpgb\n8Mgj4cJxItIkyvwlfwwfDjU10KMH9O0b7hlw4kTUUYkUHWX+Ep2tW8OvgBYtYOFC6N496ohE8ooy\nf8lPvXpBZSWMHw+XXALl5WFcQEQyTo2/RCsWg9tug+pq2LQJ+vWDtWujjkqk4KnbR3LLCy+EOQJj\nxsCsWXD++VFHJJKz1O0jhaOsLJSFxmKhLPT553WdIJEMUOYvuauyMgwId+kCP/kJXHhh1BGJ5BRl\n/lKYhg0LYwEDBkD//jBvHhw/HnVUIgVBmb/kh9ra8Cvg2LFQFtq7d9QRiUROmb8Uvu7dw+zgiRNh\nxAiYPh0OH446KpG8pcZf8kcsFrL/zZthx45w+eiKiqijEslL6vaR/LV0aZgjMGoUPPgglJREHZFI\nVmW828fMRpvZdjPbaWZT61k/1sxqzKzazH5vZiOS1r2RtO7VpgQpUq+xY0NZ6FlnhdnCzzyjslCR\nFDWY+ZtZDNgJjAT2AlXAeHffnrRNS3c/lFjuDbzo7p0Tz/8IlLr7Xxt4H2X+0nTr18PNN0P79jB/\nPnToEHVEIhmX6cx/EPC6u+9x96PAYmBc8gYfN/wJ5wB/SY4vxfcRabrBg+G118KtI0tLYc4clYWK\nnEYqjXI74M2k528lXvs7ZnaVmdUCLwF3Jq1yYJWZVZnZzc0JVuS0zjwTvvtd+N3v4Je/DCeEmpqo\noxLJSWek60DuvgRYYmbDgKeBbolVQ919n5l9jnASqHX3yvqOUV5efnI5Ho8Tj8fTFZ4Uk65dYfVq\nePJJuOwyuPFGmDEjjA2I5LGKigoq0lThlkqf/2Cg3N1HJ55PA9zdZ51mn13AIHd/t87rM4D97v6j\nevZRn7+k39tvw113we9/H24c89WvRh2RSNpkus+/CuhsZh3M7ExgPLC0TgCdkpYHALj7u2bW0szO\nSbx+NnA5sLUpgYo0SevWsHgxzJ0L3/oW/Mu/wF/+0vB+IgWuwcbf3Y8DtwMrgW3AYnevNbPJZjYp\nsdnXzWyrmW0E5gLXJl5vDVSaWTWwHviVu69M+18h0pAxY0JZaElJKAtdtEhloVLUNMlLik9VVSgL\nbdMGHn0UOnaMOiKRJtG1fUQaY+DAcAK49NKwPHt2uGCcSBFR5i/FbdcumDwZ3nsPnngiXD5aJE8o\n8xdpqk6dYNUquPtuuOIK+M534ODBqKMSyThl/iIf+9//hW9/O9xB7LHH2NO1K0/dcw8n/vxnYu3a\nccPMmXTQ+IDkkOZk/mr8RepasYI9N93EI++/z70HDnA2cBCY0akTd6xapROA5Ax1+4ik06hRPDV0\n6MmGH+Bs4N5du3jqnnuijEwkbdT4i9TjxNtvn2z4P3Y2cGLv3ijCEUk7Nf4i9Yi1a0fdYd+DQOy9\n9+Do0ShCEkkrNf4i9bhh5kxmdOp08gRwEJjRvj03nHsufOlL8KruSyT5TQO+IqewZ/fuUO2zdy+x\ntm1Dtc8XvgD/+Z8wZQpcey3MnAmf+UzUoUqRUrWPSLa9+26YE7B6dbhz2JgxUUckRUiNv0hUXnkl\nzBAuLQ1XDm3TJuqIpIio1FMkKiNHwpYtcPHF0KdPuESEkhjJA8r8RdKlpiZcLbRlS1iwALp1a3gf\nkWZQ5i+SC/r2hXXroKws3Ej+vvvgyJGooxKplxp/kXRq0QLuvBM2boT168NVQtetizoqkU9Qt49I\nprjDs8+GK4aWlcH998O550YdlRQQdfuI5CIzuOaacPvIjz6Cnj1hyZKooxIBlPmLZE9FRSgL7dUL\nHnkE2raNOiLJc8r8RfJBPB4qgnr0CIPDjz0GJ05EHZUUKWX+IlHYuhUmTQoDxAsXQvfuUUckeUiZ\nv0i+6dUr3DFs/Hi45BIoLw/jAiJZosZfJCqxGNx2G1RXw6ZN0K8frF0bdVRSJFJq/M1stJltN7Od\nZja1nvVjzazGzKrN7PdmNiLVfUWK3oUXwosvwve/DxMmhEHh99+POiopcA02/mYWA+YBo4CewAQz\n+2KdzV52977u3h+YCCxsxL4iYhbmAmzbFn4R9OwJzz+v6wRJxqSS+Q8CXnf3Pe5+FFgMjEvewN0P\nJT09B/hLqvuKSJLzzoNHH4VnnoF77oGrroI334w6KilAqTT+7YDkb99bidf+jpldZWa1wEvAnY3Z\nV0TqGDYsjAUMGAD9+8O8eXD8eNRRSQE5I10HcvclwBIz+3/A00CjL2lYXl5+cjkejxOPx9MVnkj+\n+fSnYcaMMEt40iT4xS9CWWjv3lFHJhGpqKigoqIiLcdqsM7fzAYD5e4+OvF8GuDuPus0++widPl0\nSXVf1fmLnMaJE+FeAd/7XhgQnj4d/uEfoo5KIpbpOv8qoLOZdTCzM4HxwNI6AXRKWh4A4O7vprKv\niKQgFgvZ/+bNsGNHuHFMmjJAKU4Ndvu4+3Ezux1YSThZ/NTda81scljtC4Gvm9n1wBHgIKGRP+W+\nGfpbRArf5z8frhS6dCl885swahQ8+CCUlEQdmeQZXd5BJF/97W+hG+i55+Dhh+Haa0PJqBQN3cBd\npJitWxduH9mhA8yfH/6VoqBr+4gUsyFDwp3DvvIVKC2FOXNUFioNUuYvUkh27gzVQAcOhOqgvn2j\njkgySJm/iARdu8Lq1XDLLXDZZTBtGhw61PB+UnTU+IsUGjO48UbYsgXeeCNMCnv55aijkhyjbh+R\nQrdsGdx6a7iT2EMPQatWUUckaaJuHxE5tTFjwtVCS0rCTWQWLdLVQkWZv0hRqaoKZaFt2oSrh3bs\nGHVE0gzK/EUkNQMHhhPApZeG5dmz4dixqKOSCCjzFylWu3aFstD33oPHHw9zBCSvKPMXkcbr1AlW\nrYK774Yrr4QpU+DgwaijkixR4y9SzMzg+uth61Z4550wILxiRdRRSRao20dE/s+KFWGC2JAh4WJx\nF1wQdURyGur2EZH0GDUqTA5r2zZMDnvqKZWFFihl/iJSv40bQ1no+efDggXQuXPUEUkdyvxFJP0G\nDIANG8Jg8ODB8MADcPRo1FFJmijzF5GG7d4dxgL27QtloYMGRR2RoMxfRDKtY0dYvhymToVx40J5\n6P79UUclzaDGX0RSYwbXXRfKQj/4IJSF/vrXUUclTaRuHxFpmldeCTOES0th7txwvSDJKnX7iEj2\njRwZykIvvhj69Al3DlMClzeU+YtI89XUhLLQli1DWWi3blFHVBSU+YtItPr2hXXr4OqrYehQuO8+\nOHIk6qjkNFJq/M1stJltN7OdZja1nvXXmVlN4lFpZn2S1r2ReL3azF5NZ/AikkNatIC77gqTw9av\nD/ME1q2LOio5hQa7fcwsBuwERgJ7gSpgvLtvT9pmMFDr7h+Y2Wig3N0HJ9b9ESh197828D7q9hEp\nFO7w7LOhJPTqq+EHP4Bzz406qoKT6W6fQcDr7r7H3Y8Ci4FxyRu4+3p3/yDxdD3QLjm+FN9HRAqF\nGVxzTbh95JEj0LMnLFkSdVSSJJVGuR3wZtLzt/j7xr2um4DlSc8dWGVmVWZ2c+NDFJG89Y//GGYE\nP/10mCD29a/D3r1RRyXAGek8mJldCkwEhiW9PNTd95nZ5wgngVp3r6xv//Ly8pPL8XiceDyezvBE\nJCrxeKgI+v73w+DwzJkwaRLE1CnQGBUVFVRUVKTlWKn0+Q8m9OGPTjyfBri7z6qzXR/geWC0u+86\nxbFmAPvd/Uf1rFOfv0gx2Lr1/xr+hQuhR4+oI8pbme7zrwI6m1kHMzsTGA8srRNAe0LD/83kht/M\nWprZOYnls4HLga1NCVRECkSvXlBZCRMmwPDhUF4OH30UdVRFp8HG392PA7cDK4FtwGJ3rzWzyWY2\nKbHZPUAJML9OSWdroNLMqgkDwb9y95Vp/ytEJL/EYnDbbVBdDZs2Qb9+sHZt1FEVFc3wFZFoucOL\nL8Idd8DXvgazZoUbyEiDNMNXRPKXGZSVhbLQWCyUhT73nK4TlGHK/EUkt1RWhgHhLl1g3jy46KKo\nI8pZyvxFpHAMGxbGAgYMgP79wwng+PGooyo4yvxFJHfV1oZfAceOhbLQ3r2jjiinKPMXkcLUvTus\nWQM33AAjRsD06XD4cNRRFQQ1/iKS22KxcMewmhrYsSPcOOa3v406qrynbh8RyS9Ll4Y5ApdfDj/8\nIZSURB1RZNTtIyLFY+zYUBbasmUoC128WGWhTaDMX0Ty17p14faRHTrA/Pnh3yKizF9EitOQIeHO\nYV/5CpSWwpw5KgtNkTJ/ESkMO3eGgeEDB8I9BPr1izqijFPmLyLStSusXg233BIGg6dOhUOHoo4q\nZ6nxF5HCYQY33ghbtsCePWFS2MsvRx1VTlK3j4gUrmXL4NZbw53EHnoIWrWKOqK0UrePiEh9xowJ\nZaElJeEmMosWqSw0QZm/iBSHqqpQFtq6NTz6KFx8cdQRNZsyfxGRhgwcGE4AI0bAoEEwe3a4YFyR\nUuYvIsVn165QFvree6EstLQ06oiaRJm/iEhjdOoEq1bB3XfDlVfClClw8GDUUWWVGn8RKU5mcP31\nsHUrvP12GBD+zW+ijipr1O0jIgKwYkWYIDZkCDz8MFxwQdQRNUjdPiIizTVqVJgc1rZtmBz21FMF\nXRaqzF9EpK6NG0NZ6Pnnw4IF0Llz1BHVK+OZv5mNNrPtZrbTzKbWs/46M6tJPCrNrE+q+4qI5JwB\nA2DDhjAYPHgwPPAAHD0adVRp1WDmb2YxYCcwEtgLVAHj3X170jaDgVp3/8DMRgPl7j44lX2TjqHM\nX0Ryz+7dYSxg795QFvrlL0cd0UmZzvwHAa+7+x53PwosBsYlb+Du6939g8TT9UC7VPcVEclpHTvC\n8uUwbRqMGwd33QX790cdVbOl0vi3A95Mev4W/9e41+cmYHkT9xURyT1mcN114TpBf/tbKAv99a+j\njqpZzkjnwczsUmAiMKwp+5eXl59cjsfjxOPxtMQlIpIWn/0sPPkkvPJKmCH89NMwdy60aZOVt6+o\nqKCioiItx0qlz38woQ9/dOL5NMDdfVad7foAzwOj3X1XY/ZNrFOfv4jkjw8/hH/7N/jpT+H++8N9\nBGLZrZ5vTp9/Ko1/C2AHYdB2H/AqMMHda5O2aQ+8AnzT3dc3Zt+kbdX4i0j+qakJZaFnnQULF0K3\nbll764wO+Lr7ceB2YCWwDVjs7rVmNtnMJiU2uwcoAeabWbWZvXq6fZsSqIhITurbF9atg7IyGDoU\nZs6EI0eijqpBmuQlIpIuf/pTuHPYG2+EstAhQzL6dhnt9skWNf4iUhDc4dlnwxVDr746jAecd15G\n3krX9hERyRVmcM01oSz0yJFQFrpkSdRRfYIyfxGRTKqoCGWhPXvCvHnhwnFposxfRCRXxeOhIqhn\nzzA4/NhjcOJE1FEp8xcRyZqtW2HSpDAfYOFC6NGjWYdT5i8ikg969YLKSpgwAS65BGbMgI8+iiQU\nNf4iItkUi8Ftt8GmTaE7qG9fWLs262Go20dEJCru8OKLcMcd8LWvwaxZ4QYyKVK3j4hIPjILM4O3\nbQu/CHr2hOeey8rtI5X5i4jkisrKMCDcpUsoC73ootNursxfRKQQDBsG1dXhNpL9+4cTwPHjGXkr\nZf4iIrmotjb8Cjh6NFwnqHfvT2yizF9EpNB07w5r1sDEiTBiBHzve3D4cNoOr8ZfRCRXxWLh0hA1\nNbBjB/TpA7/9LXt27+bef/7nZh1a3T4iIvnil79kz+TJPHLoEPfu3885oG4fEZGCN24cTw0fzr37\n93N2Mw+lxl9EJI+ceOedZjf8oMZfRCSvxNq142A6jpOGY4iISJbcMHMmMzp1avYJQI2/iEge6dCx\nI3esWsXsb3yjWcdRtY+ISJ7SJC8REWmUlBp/MxttZtvNbKeZTa1nfTcz+52ZHTazb9dZ94aZ1ZhZ\ntZm9mq7ARUSk6Rps/M0sBswDRgE9gQlm9sU6m70L3AH8sJ5DnADi7t7f3Qc1M15JQUVFRdQhFBR9\nnumlzzM3pJL5DwJed/c97n4UWAyMS97A3f/i7q8Bx+rZ31J8H0kT/edKL32e6aXPMzek0ii3A95M\nev5W4rVUObDKzKrM7ObGBCciIplxRhbeY6i77zOzzxFOArXuXpmF9xURkVNosNTTzAYD5e4+OvF8\nGuDuPquebWcA+939R6c41inXm5nqPEVEGqmppZ6pZP5VQGcz6wDsA8YDE06z/clAzKwlEHP3A2Z2\nNnA5cG99OzX1DxARkcZrsPF39+NmdjuwkjBG8FN3rzWzyWG1LzSz1sDvgc8AJ8zsLqAH8DngxURW\nfwbwC3dfmak/RkREUpMzM3xFRCR7slqCaWY/NbO3zWzzabb5sZm9bmabzKxfNuPLJw19lmY23Mze\nN7ONicf0bMeYT8zsQjNbbWbbzGyLmd15iu30/WxAKp+lvp+pM7NPm9mGxETZbWZ2/ym2a9x3092z\n9gCGAf2AzadYfwWwLLH8ZWB9NuPLp0cKn+VwYGnUcebLA2gD9EssnwPsAL5YZxt9P9P3Wer72bjP\ntGXi3xbAekIVZfL6Rn83s5r5eyjx/OtpNhkH/Dyx7QbgvMR4gtSRwmcJSYPvcnru/j/uvimxfACo\n5ZPzWfT9TEGKnyXo+5kydz+UWPw0ocem7v/9Rn83c23mbd0JZX+mcRPK5O8NSfwEXGZmPaIOJl+Y\n2RcIv6o21Fml72cjneazBH0/U2ZmMTOrBv4HqHD3/66zSaO/m9mY5CXReA1o7+6HzOwKYAnQNeKY\ncp6ZnQM8B9yVyFqliRr4LPX9bAR3PwH0N7NzgZVmNtzd1zTnmLmW+f8ZuCjp+YWJ16SR3P3Axz8V\n3X058CkzK4k4rJxmZmcQGqun3f2X9Wyi72eKGvos9f1sGnf/G7AM+FKdVY3+bkbR+Bun7utbClwP\nJ2cWv+/ub2crsDx0ys8yub/PzAYRynrfy1Zgeerfgf9297mnWK/vZ+pO+1nq+5k6M2tlZuclls8C\nLgM21dms0d/NrHb7mNl/AHHgs2b2J2AGcCaJyWLu/pKZXWlmfwAOAhOzGV8+aeizBP7JzG4BjgIf\nAtdGFWs+MLOhwDeALYm+VQe+C3RA389GSeWzRN/Pxvg88DMz+/gKyU+7+yvJE22b8t3UJC8RkSKU\na33+IiKSBWr8RUSKkBp/EZEipMZfRKQIqfEXESlCavxFRIqQGn8RkSKkxl9EpAj9f8tV/TmiK9R4\nAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.plot(freq.keys(), px, 'r-o')\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Average Degree"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## Undirected\n",
"\n",
"# $ = \\frac{1}{N} \\sum_{i = 1}^{N} k_i = \\frac{2L}{N}$\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## Directed\n",
"# $ = \\frac{1}{N} \\sum_{i=1}^N k_i^{in}= = \\frac{1}{N} \\sum_{i=1}^N k_i^{out} = \\frac{L}{N}$ "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Degree distribution \n",
"P(k): probability that a randomly selected node has degree k\n",
"\n",
"\n",
"$N_k = The \\:number\\: of \\:nodes\\:with \\:degree\\: k$\n",
"\n",
"## $P(k) = \\frac{N_k}{N}$\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Adjacency matrix\n",
"$A_{ij} =1$ if there is a link between node i and j\n",
"\n",
"$A_{ij} =0$ if there is no link between node i and j"
]
},
{
"cell_type": "code",
"execution_count": 182,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYEAAAEACAYAAABVtcpZAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XlcVfW+//HXFkrYYogeh6ysq177OVEamMNpOF7LNBug\nwSEVtYScbmmZeh2SOoYZWWphZnUQTTOvmZma6aljZCI4QhwKrY6mD484EEKiAnvdP0x/ioAMe++1\n917v5+PBw9jDWh97fJbv9V3T12YYhoGIiFhSLbMLEBER8ygEREQsTCEgImJhCgEREQtTCIiIWJhC\nQETEwhQCIiIWphAQEbEwhYCIiIUpBERELEwhICJiYQoBERELUwiIiFiYQkBExMIUAiIiFqYQEBGx\nMIWAiIiFKQRERCxMISAiYmEKARERC1MIiIhYmEJARMTCFAIiIhamEBARsTCFgIiIhSkEREQsTCEg\nImJhCgEREQtTCIiIWJhCQETEwhQCIiIWphAQEbEwhYCIiIX5m12AWFNOTg5JiYlkp6dTkJdHUHAw\nrUJDiRo6lIYNG5pdnki1eGNf2wzDMMwuQqwjLS2NOXFxrF2/nkgg/PRp6gL5QGpgIKsMg/t79eKZ\nSZMIDw83uVqRyvHqvjZE3GRBQoLRxG433rDZjBNgGGX8nABjts1mNLHbjQUJCWaXLHJF3t7XCgFx\niwUJCUZzu93YW85GUvpnLxjNPXCDEbmYL/S1DgeJy6WlpfHg3XeTfOoULavwvX3AHXY7azZvJiws\nzFXliVSLr/S1rg4Sl5sTF8eEwsLLNpRBwLVAMNACmFHq/ZbAC4WFzImLc0OVIlXjK32tkYC4VE5O\nDjffeCM/nz5NSKn3/gk0BwKAbOBOYBHQ86LPnABaBASQfeCAx15dIdbjS32tkYC4VFJiIhFw2YYC\n0IZzGwqAAVwFlN4c6gMRNhtJiYkuq1GkqnyprxUC4lLZ6el0On263PdHAXWAdsBkoGMZnwkvLCQ7\nI8M1BYpUgy/1tUJAXKogL4+6Fbz/NlAAbAKmAGllfKYukJ+b64LqRKrHl/paISAuFRQcTP4VPmMD\n7gIeA5aV8X4+UDekrIG3iDl8qa8VAuJSrUJDSQ0IuPIHgWLAXsbraYGBtGrf3ql1idSEL/W1rg4S\nlyrvKoqjwFdAHyAQ2Aj0/ePPi2+q96SrKETO86W+1khAXKpRo0bc36sXi2y2S163AfOBG4AGwFRg\nMZduKACLbDb69O5t+oYicjFf6muNBMTlfOXOSpGL+UpfayQgLhceHk5sfDw97Xb2VfI7+4Cedjux\n8fEesaGIlBYeHs6Lr73GXbVqeXVfKwTELaJHjODh4cMJs9mYbbNR3oVxJ4DZNht32O1MiI8nesQI\nd5YpUiWGzcZhh4PbgHjwyr7W4SBxi8LCQkJDQxkxYgS7tmzh83XriLDZCC8svPDc9bQ/nrvep3dv\nnpk0yWP2lETKcujQIdq0acPJkyeBcyeCa9WqxWO1a9PJi/paISBuMXnyZLKzs1mxYgUAR48ePTcD\nU0YG+bm51A0JoVX79gweMsQjTpaJXMkjjzzCJ598cuH3oKAgkpOT+fvGjV7V1woBcbmMjAy6d+9O\neno61157rdnliNTY6tWrefjhhy95be7cuYwZM8akiqpPISAu5XA46NatG0OGDCEmJsbsckRq7OTJ\nk7Rp04ZDhw5deK1Tp0589913+Pn5mVhZ9ejEsLjUO++8g5+fH8OHDze7FBGnmDJlyiUB4O/vz8KF\nC70yAEAjAXGhQ4cOceutt7J582batGljdjkiNbZt2za6dOnCxf9sTpgwgZkzZ5pYVc0oBMRlIiMj\nadeuHS+99JLZpYjUWFFREWFhYaSnp194rXnz5mRkZGC3l/V0IO/gb3YB4ps+/fRTMjMzWbp0qdml\niDjF7NmzLwkAOHe405sDADQSEBc4efIkbdu2ZcmSJdx1111mlyNSYz/99BPt2rXj9EUTyQwaNIik\npCQTq3IOnRgWp5s8eTI9e/ZUAIjPeOONNy4JgAYNGvD666+bWJHzaCQgTpWSkkJERASZmZnUr1/f\n7HJEnKKoqIg777yTtLQ0SkpKWLRoEYMHDza7LKfQOQFxmqKiIoYPH87s2bMVAOJTUlNTOXDgADt2\n7GDFihUMGjTI7JKcRiMBcZqZM2eyefNm1q1bh63Uc9ZFvNXZs2fp0KED06dP57HHHjO7HKdTCIhT\n7Nu3j86dO5OWlsZ//Md/mF2OiNP89a9/JSUlhTVr1vjkzo1CQGrMMAzuuece7rvvPp5//nmzyxFx\nmuzsbLp27cqOHTu48cYbzS7HJXR1kNTY4sWLOX78OM8++6zZpYg4jWEYxMTEMGXKFJ8NANCJYamh\nY8eOMX78eNauXYu/v9pJfEdiYiIFBQVe+WTQqtDhIKmRqKgoGjRowOzZs80uRcRpcnJyaNeuHRs2\nbKBDhw5ml+NS2nWTatu0aRObN2/m+++/N7sUEacaN24cUVFRPh8AoBCQajp16hQxMTG8/fbbBAUF\nmV2OiNNs2LCBLVu2WGbnRoeDpFomTZrEzz//zPLly80uRcRpfv/9d9q3b09CQgL33Xef2eW4hUJA\nqiw9PZ0ePXqQnp5OkyZNzC5HxGleeOEFDh06xIcffmh2KW6jw0FSJSUlJURHRzNjxgwFgPiU3bt3\nk5iYaJnDQOfpPgGpkvnz53P11Vfz5JNPml2KiNOUlJQwfPhwZs6cSaNGjcwux600EpBKO3jwINOn\nTyc5OZlatbT/IL7jrbfeIigoiKFDh5pditvpnIBUWkREBLfccgvTp083uxQRpzlw4AAdO3bku+++\no1WrVmaX43YaCUilrFq1iqysLD766COzSxFxGsMwGDVqFM8884wlAwAUAlIJeXl5jBkzhqVLl1K7\ndm2zyxFxmpUrV/Lzzz+zcuVKs0sxjQ4HyRWNGjWKs2fPsnDhQrNLEXGa3377jbZt2/Lxxx/TrVs3\ns8sxjUJAKrR161YeeeQRMjMzCQkJMbscEad5+umnsdlszJ8/3+xSTKXDQVKus2fPEh0dzRtvvKEA\nEJ/y7bffsmbNGjIzM80uxXS6zk/KFR8fT7NmzXj88cfNLkXEac6cOUN0dDRz5syhXr16ZpdjOh0O\nkjLt3buXLl26+PSMSmJNL7/8Mmlpaaxevdonp4usKoWAXMYwDP7rv/6LPn36MG7cOLPLEXGaH3/8\nkW7durFr1y5uuOEGs8vxCDocJJdJSkoiLy+P//7v/za7FBGncTgcREdHM23aNAXARXRiWC5x9OhR\nXnjhBdavX6/pIsWn/O1vf6OwsJBRo0aZXYpH0eEgucSgQYNo3Lgx8fHxZpci4jRHjhyhffv2fPnl\nl9x6661ml+NRtKsnF2zcuJHk5GRdNic+Z+zYsQwdOlQBUAaFgADnpot8+umnSUhIoE6dOmaXI+I0\n69evZ9u2bbz33ntml+KRdDhIAJg4cSL79+9n2bJlZpci4jS///47bdu25d133+Xee+81uxyPpBAQ\n9uzZwz333ENGRgaNGzc2uxwRp3n++ef597//zZIlS8wuxWPpcJDFnZ9RKS4uTgEgPmXnzp0sXryY\njIwMs0vxaLpPwOISEhIIDAxk2LBhZpci4jTFxcVER0fz6quvWm66yKrSSMDCfv31V2JjY/n22291\n+7z4lHnz5nHNNdcQFRVldikeT+cELMowDB566CHCwsKYNm2a2eWIOM2//vUvwsLCLDtdZFVpJGBR\nn3zyCfv27WPFihVmlyLiNOenixw7dqwCoJIUAhZ0/rlAy5cv13SR4lNWrFjB/v37WbVqldmleA0d\nDrKgkSNHUlJSwoIFC8wuRcRpcnNzadu2LStXrqRLly5ml+M1FAIWs2XLFh5//HEyMzM1oYb4lOjo\naPz9/UlISDC7FK+iw0EWcn66yDfffFMBID4lOTmZdevW6blX1aD7BCxk1qxZNG/enEcffdTsUkSc\n5vx0kXPnziU4ONjscryODgdZRHZ2Nl27dmXnzp00a9bM7HJEnCY2NpZdu3axatUq3e9SDQoBCzAM\ng+7du/PQQw/x7LPPml2OiNNkZWVxxx13aLrIGtDhIAtITEykoKCAMWPGmF2KiNM4HA5iYmJ48cUX\nFQA1oBPDPi4nJ4eJEyfyxRdf4OfnZ3Y5Ik7z/vvvc+bMGUaOHGl2KV5Nh4N83MCBA2natCmzZs0y\nuxQRp/n3v/9NaGgomzZtIjQ01OxyvJpGAl4uJyeHpMREstPTKcjLIyg4mFahoUQNHcrOnTv57rvv\n9Chd8ToV9XXDhg159tlnGTZsmALACTQS8FJpaWnMiYtj7fr1RALhp09TF8gHUgMDWeVw4O/nx5RX\nXuGZZ54xuVqRyrliXxsGt3XoQNb+/ezduxe73W5yxT7AEK+zICHBaGK3G2/YbMYJMIwyfk6AEQ9G\nE7vdWJCQYHbJIldU2b5+DYyGtWurr51EIeBlFiQkGM3tdmNvORtJ6Z+9YDRXEIiHU1+bR4eDvEha\nWhoP3n03yadO0bLUe3uBUOAxIKnUe/uAO+x21mzeTFhYmDtKFam0ivoayu9t9bVz6D4BLzInLo4J\nhYVlbiijgU7lfK8l8EJhIXPi4lxXnEg1VdTXUH5vq6+dQyMBL5GTk8PNN97Iz6dPE1LqvY+AT4E2\nnNs7Kj0SADgBtAgIIPvAARo2bOjiakUqp6K+hiv3tvq65jQS8BJJiYlEwGUbykngRWA2UFGa1wci\nbDaSEhNdU6BINZTX11C53lZf15xCwEtkp6fT6fTpy16fBgwHmlZiGeGFhWTrngHxIOX1NVS+t9XX\nNaObxbxEQV4edUu9thvY9MeflVEXyM/NdWpdIjVRVl9D1XpbfV0zCgEvERQcTH6p1zYD+4FmnBsu\nFwAlwD+B7WUsIx+oG1LWwFvEHGX1NVStt9XXNaPDQV6iVWgoqQEBl7wWA/zEub2lPcDTQB/gy3KW\nkRYYSKv27V1ZpkiVtAoNZevVV1/2elV6W31dMwoBLzF4yBBWGQYXD3oDgEYX/QT98Vr9Mr5/Alhl\nGAweMsTVpYpUyr59+9iwcSMfnz1L6YM5le1t9XXNKQS8gGEYJCcn41erFn+r4HMvUvbloQCLbDb6\n9O6ty+jEdKdOnWLq1Km0bduWTZs2UQv44ArfKa+31dc1p/sEPNyPP/7ImDFjOHz4MKNHj2b6uHHl\n3llZHt1ZKZ7AMAw+/fRTxo4dy/79+y957xpgB6ivTaCRgIcqKChg4sSJ/PnPf6Z3797s3LmTmJgY\nYuPj6Wm3s6+Sy9kH9LTbiY2P14YipsnOzqZXr15ERkZeFgAAjVu04J6AAPW1Gcx7bJGUxeFwGMuX\nLzeuv/56Y9CgQcbhw4cv+8z5py3OruBpi8fBeN1m01NExXQOh8Po0KGDwbkLfS75adKkibF48WLD\n4XCor02iEPAgmZmZRvfu3Y3Q0FAjOTm5ws+mpaUZAyMjjSA/P2Ogv7+RAMZiMBLAGBoYaNQLCDAG\nRkYaaWlpbqpepGwlJSXGhAkTLvnH38/Pzxg7dqyRl5d3yWfP93W9gACj3x/9rL52LZ0T8AD5+fnE\nxsayaNEipk2bxogRI/D3r9wtHB06dKBrly4UFxSQn5tL3ZAQWrVvz+AhQ3SyTEy3e/duRo0aRVFR\nEfXq1WPjxo3cddddvPXWW7Rr167c7yUnJxP58MNE3n+/+trFdLOYiQzDYNmyZbzwwgvcc889fP/9\n9zRu3LjS3y8sLCQ7O5stW7ZohiXxKLm5uUydOpUVK1YwY8YMhg0bxuHDh/nmm2/o168fNputwu9n\nZ2dzX+/eLEgq73o3cRaFgEm+//57Ro8ezcmTJ1mxYgVdunSp8jJ27dpF69atFQDiMRwOB4mJifzP\n//wPkZGRZGVlUb/+uav7r7vuOvr371+p5aSkpNC5c2dXlip/0NVBbpaXl8fYsWPp3r07jz/+OGlp\nadUKANCGIp5lx44ddO3alYULF7Ju3ToSEhIuBEBVqbfdRyHgJoZhsHjxYlq3bk1+fj6ZmZmMHDkS\nPz+/ai9TG4p4ghMnTjBixAjuv/9+YmJi2LJlCx07dqz28k6ePMkvv/xCaGioE6uU8igE3GDPnj3c\neeedzJkzh1WrVvHee+855eSWQkDM5HA4WLhwIa1bt8bf35+srCyGDh1KrVo1+2clLS2NDh06cNVV\nVzmpUqmIzgm40G+//ca0adNYvnw5L730Ek899VSN9vwvdujQIU6dOkWLFi2csjyRqkhNTWX06NFc\nffXVbNiwgVtvvdVpy9bOjXtpJOAC50+OtW7dmjNnzvDPf/6TmJgYpwUAwLZt2+jcufMVr7IQcaZj\nx44xfPhwHnroIUaPHk1ycrJTAwAUAu6mEHCyXbt28ec//5n58+ezZs0aFixYQIMGDZy+Hm0o4k4l\nJSW88847tGnThjp16pCVlcXgwYOdvhNiGIZ6280UAk6Sm5vLqFGjuO+++xg2bBhbt2516TNNtKGI\nu6SkpNCpUyeWLl3Kpk2bePPNN6lXr55L1vXzzz8TEBDAdddd55Lly+UUAjXkcDh4//33ad26NYZh\nkJWVxVNPPVXjk2MVKSoqYufOnYSHh7tsHSI5OTkMGzaMyMhIxo0bx+bNm11+xc7WrVu1c+NmOjFc\nA9u3b2f06NHYbDbWrVtXo8viqiI9PZ2bbrqJ4OBgt6xPrKW4uJh33nmHl156iUGDBvHDDz9wzTXX\nuGXdKSkp1b5vRqpHIVANx48fZ/LkyaxevZpXXnmFqKgol+75l6ZDQeIqW7ZsYdSoUYSEhPD111/T\ntm1bt64/JSWFAQMGuHWdVqfDQVVQUlLCu+++S5s2bbj66quddl10VWlvSZztyJEjREVF0bdvXyZO\nnMhXX33l9gA4deoUWVlZdOjQwa3rtTqFQCWlpqbSuXNnkpKS2LBhA3PnznXZybEr0UhAnKW4uJg5\nc+bQrl07GjduTFZWVqUe8OYKO3fupG3btgQGBrp93Vamw0FXcOzYMSZNmsTatWuZOXMmgwYNMvXa\n/GPHjpGTk0Pr1q1Nq0F8wzfffMPo0aNp1KgR33zzjek9pZ0bc2gkUI6SkhLmz59PmzZtCAoKctl1\n0VW1bds2OnXq5PZDUOI7Dh8+zMCBA3niiSeYOnUqGzduND0AQCFgFp8dCeTk5JCUmEh2ejoFeXkE\nBQfTKjSUqKFDr/jcnq1btzJ69Gjq1KnD3//+d9q3b++mqq9MG4pUt7eLioqYN28er7zyCsOHDycr\nK4ugoCA3Vl6xlJQUZs2aZXYZ1mPmtGaukJqaajwREWHUCwgwhgUEGPPBWALG/Iump3siIsJITU29\n7LtHjhwxhg4dajRt2tRYsmSJ4XA4TPgbVKxHjx7G559/bnYZYoKa9PbXX39ttG3b1rj33nuNH374\nwYTqK/brr78aDRs29Mhtztf5VAicn6j6jQomqj4BxuxSE1UXFRUZc+fONf70pz8Z48aNu2zeU09R\nXFxsXHPNNcbRo0fNLkXcrLq9ffDgQaNfv35Gs2bNjJUrV3rsP7IrVqwwHnjgAbPLsCSfCYEFCQlG\nc7vd2FvOBlL6Zy8Yze12Y/xzzxm33HKL8Ze//MX4/vvvzf5rVCgjI8No2bKl2WWIm1W3tx+JiDAa\nNGhgTJ482SgoKDD7r1GhcePGGTNmzDC7DEvyiRBITU01mpSxkbwFRhgYtcEYWs7GEmyzGTNmzPDY\nPaSLLVy40Bg4cKDZZYgbldXbV+rr870dUquWsXLlSrP/CpXStWtX46uvvjK7DEvyiUtM5sTFMaGw\nkJalXr8OmAo8Wc73WgLTgKwdO0y/6qcydFLYesrq7Sv1NZzr7SmGwaoPP3Rpfc5w9uxZdu/e7dIH\nLkr5vD4EcnJyWLt+PVGGcdl7DwMPAhXNcjrEMPh83TqOHj3qqhKdRiFgLeX1dmX6Grynt/fs2UPL\nli2pW7eu2aVYkteHQFJiIhFASDW/Xx+IsNlISkx0XlEukJeXx7/+9S/Nu2ohVult7dyYy+tDIDs9\nnU6nT9doGeGFhWRnZDipItdIS0ujY8eOmnfVQqzS2woBc3l9CBTk5VHTQWRdID831xnluIw2FOtR\nb4s7eH0IBAUHk1/DZeQDdUOqO+h2D20o1mOF3s7JyeH48ePcfPPNZpdiWV4fAq1CQ0kNCCjzvRLg\n9B9/FgNn/vjv0tICA2nlQY+GKM3QvKuWVF5vV7avwfN7e9u2bdx+++16FpaJvP7//OAhQ1gFlDXg\n/StgB14FPvzjv2eU+swJYJVhMHjIEFeWWSM//fQTdrudpk2bml2KuFF5vV2Zvgbv6G3t3JjP60Og\nUaNG3N+rF4vKuM7/RcDBub2k8z/TSn1mkc1Gn969r/hQOTNp3lVrKq+3K9PX4D29rQmSzOX1IQDw\nzKRJvBoYyL4qfm8fMCswkGcmTXJFWU6jvSXr8uXeLikpYfv27XTq1MnsUizNJ0IgPDyc2Ph4etrt\nld5Y9gH3BgYSGx/v8XcqKgSsq7q93dNu9/jezszMpGnTptSvf6Xb3sSVfCIEAKJHjGBCfDx32O28\nYbOVeY4Azh0nnW2z0dnfn6DmzXkqJsadZVaZ5l2VqvT26zYbYTYbPQYMIHrECHeWWWXaufEMPhMC\ncG5jWbN5MzsjImgeEMCwwEDmA0uA+cCwwEBaBASwKyKCz5OTsQcF8eabb5pcdcV27NhBu3btNO+q\nxVW2t3dHRDA3MZFVq1fzyy+/mFx1xRQCnsFmGGU8dMcHHD169NzsSxkZ5OfmUjckhFbt2zN4yJAL\nJ8p++eUXbr/9dtauXUt4eLjJFZfttdde4+DBg8yZM8fsUsRDVKa3Z8+ezccff0xycrLH3mXepk0b\nli5dyq233mp2KZbmsyFQWf/7v//LhAkT2LlzJ8HBwWaXc5lHHnmERx99lP79+5tdingRh8PBAw88\nQLt27Xj11VfNLucyv/32GzfccAO5ubn4+/vsLLdewacOB1XHo48+yr333ktMTAyeloeGYejyUKmW\nWrVqkZiYyIcffsiGDRvMLucyqamp3HbbbQoAD2D5EIBzQ+fMzEw++OADs0u5xMGDBykpKeGmm24y\nuxTxQg0bNmTJkiUMGTKEw4cPm13OJXQ+wHMoBIDAwECWL1/OxIkTyczMNLucC85vKN4w4Y14prvv\nvpvo6GgGDRpESUl5D5dwP4WA51AI/KFNmza8+uqr9O3bl8LCQrPLAXSnsDjH1KlTKSoq8phzAw6H\nQyHgQRQCFxk6dCihoaGMHTvW7FIA7S2Jc/j7+/Phhx8yd+5ctmzZYnY57N27l+DgYJo0aWJ2KYJC\n4BI2m4133nmHTZs2sWLFClNrOXPmDHv27PHoOz7Fe1x//fW89957DBgwgBMnTphai3ZuPItCoJRr\nrrmGjz76iFGjRpl6s43mXRVn69OnD5GRkTz55JOmXgmnEPAsCoEyhIWFMWnSJPr160dRUZEpNWhD\nEVeYOXMmBw4cICEhwbQa1NueRSFQjmeffZaGDRsyefJkU9avDUVcoXbt2ixfvpzp06eze/dut6//\n999/Jzs7W3cJexCFQDlsNhuJiYksW7aML774wu3rT0lJ0XPWxSVatmzJnDlz6Nu3LwUFBW5d9/bt\n2wkNDaV27dpuXa+UTyFQgT/96U8sWbKEoUOHuvVmmyNHjpCbm0urVq3ctk6xlgEDBtCtWzdGjx7t\n1vVqhOt5FAJXcNdddxETE8PAgQPddrON5l0Vd5g3bx7btm1j8eLFblunQsDz6F+ZSpgyZQrFxcXM\nnDnTLevThiLuUKdOHZYvX864cePIzs52+foMw1BveyCFQCWcv9lm3rx5fPvtty5fn+4UFncJDQ3l\npZdeom/fvpw5c8al69q/fz82m41mzZq5dD1SNQqBSjp/s80TTzzh0pttiouLNe+quNXTTz9NixYt\nGD9+vEvXo2dheSaFQBWcv9lm2LBhLrvZJjMzk+uuu07zrorb2Gw2Fi5cyGeffcbq1atdth4dCvJM\nCoEqmjlzJgcPHuTtt992yfK1oYgZQkJCWLZsGdHR0fz6668uWYd62zMpBKqodu3afPTRR8TGxrJr\n1y6nL18bipilS5cujBs3jv79+1NcXOzUZZ85c4aMjAxuu+02py5Xak4hUA0X32yTn5/v1GUrBMRM\n48ePx263Exsb67Rl5uXlsWvXLm6++Wbq1KnjtOWKc1h+juGaePLJJykuLmbRokVOWV5ubi7NmjXT\nvKtiqiNHjtCxY0cWL15M9+7da7Ss4uJigoODCQgIoH79+owZM4aRI0eqvz2IRgI1MHfuXFJTU0lK\nSnLK8lJTUwkLC9MGIqZq3LgxixYtYvDgweTk5NRoWRkZGZw6dYoTJ06wb98+4uLi8PPzc1Kl4gwK\ngRo4f7PNc889x48//ljj5elQkHiKHj16MHjwYKKionA4HNVeztatWy/5XZeIeh6FQA2Fhoby8ssv\n069fP06fPl2jZSkExJPExsaSl5fH7Nmzq72MlJSUS37XQxE9j84JOIFhGDz22GNce+21zJs3r1rL\ncDgcNGjQgKysLE27Jx5j//79dOrUic8++4zbb7+9yt9v1aoVe/fuvfD75s2bufPOO51ZotSQRgJO\nYLPZeO+99/j888/59NNPq7WM7Oxs6tWrpwAQj3LjjTcyf/58+vfvz2+//Val7x4/fvySAPDz89Ml\noh5IIeAk9erVY9myZcTExHDgwIEqf1+HgsRTRUZG0qtXL6Kjo6t0p/y2bdsu+T00NFSXiHoghYAT\nde7cmXHjxjFgwIAq32yjEBBP9vrrr/Pjjz+ycOFCDMOo1I5O6fMB6m/PpBBwsvHjx1OnTh2mT59e\npe8pBMSTBQQEsHz5ciZNmkT37t3p1KkTR44cqfA7CgHvoBBwslq1apGUlMQHH3zApk2bKvWdgoIC\n9u7dq3lXxaMdO3YMwzD4xz/+wZEjRxg8eHC5l486HI7LDgcpBDyTQsAFGjduTFJSElFRUVfcWwLN\nuyreYdOmTeTm5l74/csvv+S1114r87M//PADJ0+evPB7SEgI//mf/+nyGqXqFAIu0qNHD6Kioip1\ns40OBYnOMtJcAAAEi0lEQVQ3mDJlymWXd06ePPmyG8Kg7ENBuknMMykEXCg2Npb8/Hzi4+Mr/JxC\nQLzB+Rn2GjRocOG1kpIS+vfvf8kIAcq+U1g8k0LAha666iqWLl1KfHz8JXtGOTk5xM+aRfTAgQx4\n4AG++eIL0vfs4ejRoyZWK3Jl119/PYmJiZe8tn//foYPH86RI0cu9PXajz4iEDi/768Q8Fy6Y9gN\nPvnkE5577jnef/99PnjrLdauX08kEH76NHWBfGBbYCCfGgb39+rFM5MmER4ebnLVIuUbO3Ysb775\n5oXf7YCfvz+P+ftf0tf/AFYDD/bpw/PTpqmvPZBCwE263303u7/9lqkOB0MMg5AyPpMLJNpszAoM\nJDY+nugRI9xdpkilnDlzhm7durFzxw7qAtOAYaC+9kJ6ZrEbvDt/PvvT0kgtKaFlBZ8LAcYaBg+c\nOkXP558H0AYjHql27do8/OCDHNqxg2RQX3sxjQRcLC0tjQfvvpvkU6cubChngZHAJs7tJbUAXgHu\nu+h7+4A77HbWbN5MWFiYW2sWuRL1te/QiWEXmxMXx4TCwkv2lIqBZkAykAe8DDwOXHwjfkvghcJC\n5sTFua1WkcpSX/sOjQRcKCcnh5tvvJGfT58u81jpxW4BpgMRF712AmgREED2gQM0bNjQVWWKVIn6\n2rdoJOBCSYmJRFD2ybKLHQH2Am1LvV4fiLDZSCp1SZ6ImdTXvkUh4ELZ6el0usJsY8XAQGAI0KqM\n98MLC8nOyHB+cSLVpL72LQoBFyrIy6NuBe8bnNtQagPlzUdWF8gvdTemiJnU175Fl4i6UFBwMPkV\nvP8kcAxYB/iV85l8oG7IlQbeIu6jvvYtGgm4UKvQUFIDAsp872ngB+Az4OoKlpEWGEir9u1dUJ1I\n9aivfYuuDnKh8q6iOADcBATw//eUbMACoP9Fn9NVFOKJ1Ne+RSMBF2rUqBH39+rFolKP0G0GOIBT\nnBsW5wMnuXRDAVhks9Gnd29tKOJR1Ne+RSMBFyvrzsrK0J2V4snU175DIwEXCw8PJzY+np52O/sq\n+Z19QE+7ndj4eG0o4pHU177Db3pVZ0SXKrstPJzA+vUZ/PXX+BUX8/+AwDI+dwKYb7PxlN3OFD1t\nUTyc+to36HCQG23fvp05cXF8vm4dETYb4YWFF567nhYYyCrDoE/v3jwzaZL2lMRrqK+9m0LABEeP\nHiUpMZHsjAzyc3OpGxJCq/btGTxkiE6WiddSX3snhYCIiIXpxLCIiIUpBERELEwhICJiYQoBEREL\nUwiIiFiYQkBExMIUAiIiFqYQEBGxMIWAiIiFKQRERCxMISAiYmEKARERC1MIiIhYmEJARMTCFAIi\nIhamEBARsTCFgIiIhSkEREQsTCEgImJhCgEREQtTCIiIWJhCQETEwhQCIiIWphAQEbEwhYCIiIUp\nBERELEwhICJiYQoBERELUwiIiFiYQkBExMIUAiIiFqYQEBGxMIWAiIiFKQRERCxMISAiYmEKARER\nC1MIiIhYmEJARMTCFAIiIhamEBARsTCFgIiIhSkEREQs7P8AyEbH/RNJMSgAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.figure(1)\n",
"plt.subplot(121)\n",
"pos = nx.spring_layout(Gu) #定义一个布局,此处采用了spring布局方式\n",
"nx.draw(Gu, pos, with_labels = True)\n",
"plt.subplot(122)\n",
"nx.draw(Gd, pos, with_labels = True)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Undirected\n",
"$A_{ij} =1$ if there is a link between node i and j\n",
"\n",
"$A_{ij} =0$ if there is no link between node i and j\n",
"\n",
"## $A_{ij}=\\begin{bmatrix} 0&1 &0 &1 \\\\ 1&0 &0 &1 \\\\ 0 &0 &0 &1 \\\\ 1&1 &1 & 0 \\end{bmatrix}$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Undirected\n",
"## $A_{ij} = A_{ji}, \\: A_{ii} = 0$\n",
"## $k_i = \\sum_{j=1}^N A_{ij}, \\: k_j = \\sum_{i=1}^N A_{ij} $\n",
"## $ L = \\frac{1}{2}\\sum_{i=1}^N k_i = \\frac{1}{2}\\sum_{ij}^N A_{ij} $"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Directed\n",
"$A_{ij} =1$ if there is a link between node i and j\n",
"\n",
"$A_{ij} =0$ if there is no link between node i and j\n",
"\n",
"## $A_{ij}=\\begin{bmatrix} 0&0 &0 &0 \\\\ 1&0 &0 &1 \\\\ 0 &0 &0 &1 \\\\ 1&0 &0 & 0 \\end{bmatrix}$\n",
"\n",
"Note that for a directed graph the matrix is not symmetric.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Directed\n",
"## $A_{ij} \\neq A_{ji}, \\: A_{ii} = 0$\n",
"## $k_i^{in} = \\sum_{j=1}^N A_{ij}, \\: k_j^{out} = \\sum_{i=1}^N A_{ij} $\n",
"## $ L = \\sum_{i=1}^N k_i^{in} = \\sum_{j=1}^N k_j^{out}= \\frac{1}{2}\\sum_{i,j}^N A_{ij} $"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# WEIGHTED AND UNWEIGHTED NETWORKS\n",
"\n",
"## $A_{ij} = W_{ij}$"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# BIPARTITE NETWORKS \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"bipartite graph (or bigraph) is a graph whose nodes can be divided into two disjoint sets U and V such that every link connects a node in U to one in V; that is, U and V are independent sets. \n",
"\n",
"- Hits algorithm\n",
"- recommendation system\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Ingredient-Flavor Bipartite Network\n",
"\n",
"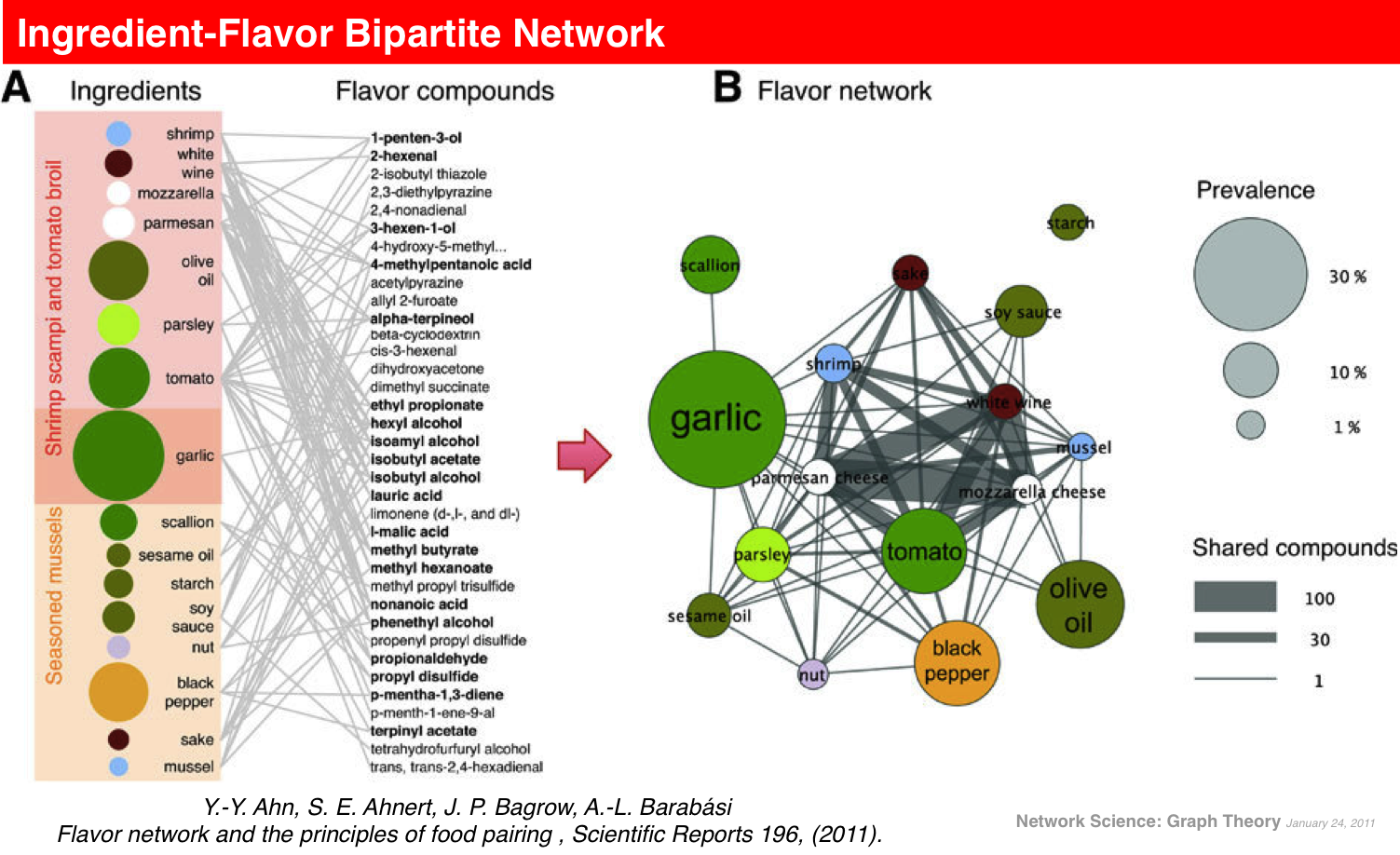 "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Path\n",
"A path is a sequence of nodes in which each node is adjacent to the next one\n",
" - In a directed network, the path can follow only the direction of an arrow. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Distance\n",
"\n",
"The distance (shortest path, geodesic path) between two nodes is defined as the number of edges along the shortest path connecting them.\n",
"\n",
" - *If the two nodes are disconnected, the distance is infinity.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Diameter: \n",
"\n",
"**Diameter $d_{max}$** is the maximum distance between any pair of nodes in the graph. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Shortest Path \n",
"The path with the shortest length between two nodes (distance). \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Average path length/distance, $$\n",
"\n",
"## The average of the shortest paths for all pairs of nodes.\n",
"\n",
"\n",
"- for a connected graph: where $d_{ij}$ is the distance from node i to node j\n",
"\n",
"## $ = \\frac{1}{2 L }\\sum_{i, j \\neq i} d_{ij}$\n",
"\n",
"- In an undirected graph $d_{ij} =d_{ji}$ , so we only need to count them once:\n",
"\n",
"## $ = \\frac{1}{L }\\sum_{i, j > i} d_{ij}$\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Cycle\n",
"A path with the same start and end node. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# CONNECTEDNESS\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Connected (undirected) graph: \n",
"any two vertices can be joined by a path. A disconnected graph is made up by two or more connected components. \n",
"\n",
"- Largest Component: Giant Component\n",
"- The rest: Isolates\n",
"\n",
"## Bridge: \n",
"if we erase it, the graph becomes disconnected. "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## The adjacency matrix of a network with several components can be written in a block-diagonal form, so that nonzero elements are confined to squares, with all other elements being zero:\n",
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Path\n",
"A path is a sequence of nodes in which each node is adjacent to the next one\n",
" - In a directed network, the path can follow only the direction of an arrow. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Distance\n",
"\n",
"The distance (shortest path, geodesic path) between two nodes is defined as the number of edges along the shortest path connecting them.\n",
"\n",
" - *If the two nodes are disconnected, the distance is infinity.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Diameter: \n",
"\n",
"**Diameter $d_{max}$** is the maximum distance between any pair of nodes in the graph. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Shortest Path \n",
"The path with the shortest length between two nodes (distance). \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Average path length/distance, $$\n",
"\n",
"## The average of the shortest paths for all pairs of nodes.\n",
"\n",
"\n",
"- for a connected graph: where $d_{ij}$ is the distance from node i to node j\n",
"\n",
"## $ = \\frac{1}{2 L }\\sum_{i, j \\neq i} d_{ij}$\n",
"\n",
"- In an undirected graph $d_{ij} =d_{ji}$ , so we only need to count them once:\n",
"\n",
"## $ = \\frac{1}{L }\\sum_{i, j > i} d_{ij}$\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Cycle\n",
"A path with the same start and end node. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# CONNECTEDNESS\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Connected (undirected) graph: \n",
"any two vertices can be joined by a path. A disconnected graph is made up by two or more connected components. \n",
"\n",
"- Largest Component: Giant Component\n",
"- The rest: Isolates\n",
"\n",
"## Bridge: \n",
"if we erase it, the graph becomes disconnected. "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"## The adjacency matrix of a network with several components can be written in a block-diagonal form, so that nonzero elements are confined to squares, with all other elements being zero:\n",
"\n",
"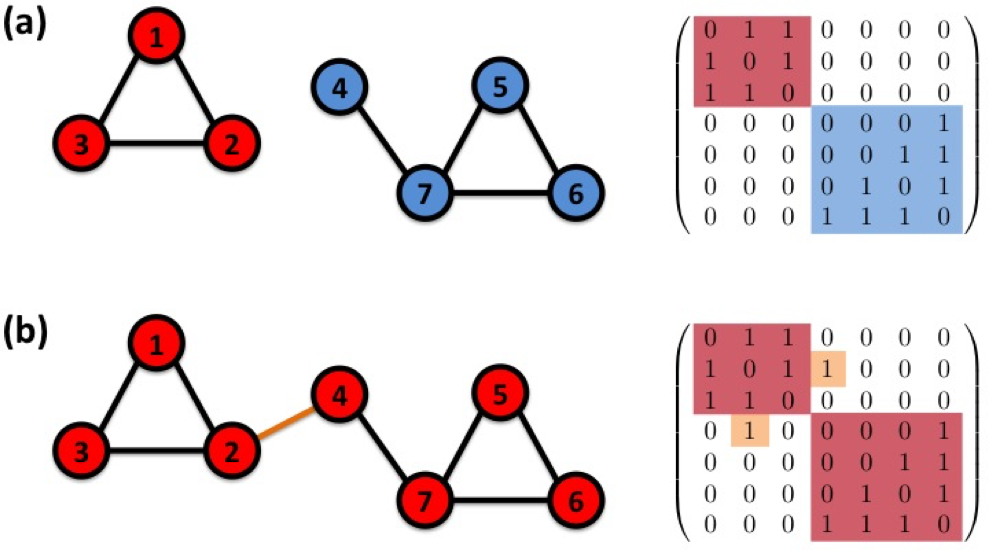 "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Strongly connected directed graph: \n",
"has a path from each node to every other node and vice versa (e.g. AB path and BA path).\n",
"\n",
"# Weakly connected directed graph: \n",
"it is connected if we disregard the edge directions.\n",
"\n",
"Strongly connected components can be identified, but not every node is partof a nontrivial strongly connected component. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"- In-component: nodes that can reach the scc, \n",
"- Out-component: nodes that can be reached from the scc. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Clustering coefficient\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Clustering coefficient: \n",
"what fraction of your neighbors are connected? Watts & Strogatz, Nature 1998.\n",
"\n",
"- Node i with degree $k_i$\n",
"- $C_i$ in [0,1]\n",
"\n",
"# $C_i = \\frac{2e_i}{k_i(k_i -1)}$\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Strongly connected directed graph: \n",
"has a path from each node to every other node and vice versa (e.g. AB path and BA path).\n",
"\n",
"# Weakly connected directed graph: \n",
"it is connected if we disregard the edge directions.\n",
"\n",
"Strongly connected components can be identified, but not every node is partof a nontrivial strongly connected component. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"- In-component: nodes that can reach the scc, \n",
"- Out-component: nodes that can be reached from the scc. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Clustering coefficient\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Clustering coefficient: \n",
"what fraction of your neighbors are connected? Watts & Strogatz, Nature 1998.\n",
"\n",
"- Node i with degree $k_i$\n",
"- $C_i$ in [0,1]\n",
"\n",
"# $C_i = \\frac{2e_i}{k_i(k_i -1)}$\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"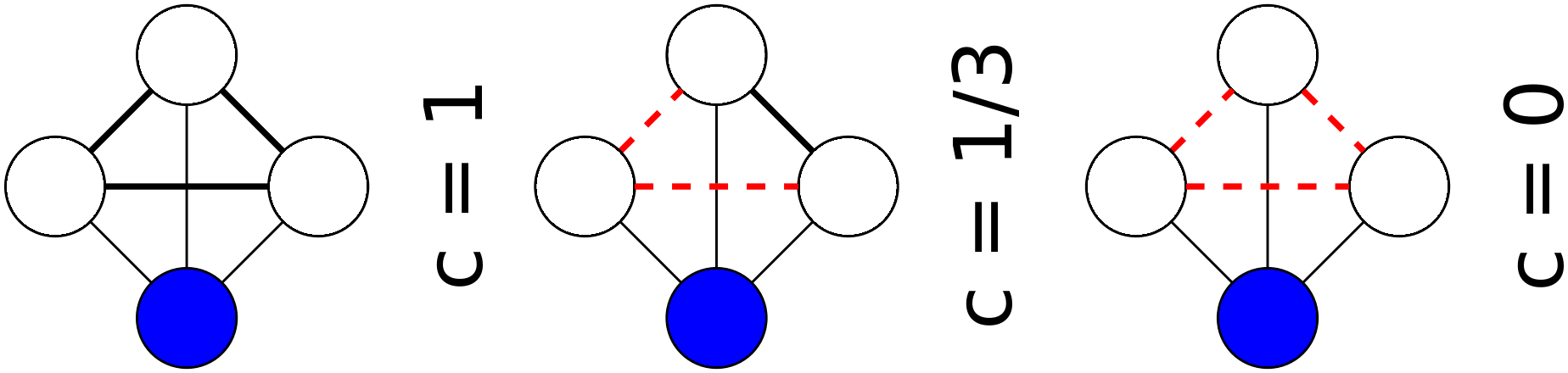 "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Global Clustering Coefficient:\n",
" \n",
"## $C = \\frac{3 \\times \\mbox{number of triangles}}{\\mbox{number of connected triplets of vertices}} = \\frac{\\mbox{number of closed triplets}}{\\mbox{number of connected triplets of vertices}}$\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 215,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xd4jefjBvD7CJnS1CxFokYQYkepkpAdMyqEqoiZxC6J\nPRIh1GhRiVDEqhUzJITEbhFFmxqJndpiRPZ8f3/4tj9FKuOc85xxf67LxXXG+97p98t9nuc87/PK\nJEmSQEREREKUER2AiIhIm7GIiYiIBGIRExERCcQiJiIiEohFTEREJBCLmIiISCAWMRERkUAsYiIi\nIoFYxERERAKxiImIiARiERMREQnEIiYiIhKIRUxERCQQi5iIiEggFjEREZFALGIiIiKBWMREREQC\nsYiJiIgEYhETEREJxCImIiISiEVMREQkEIuYiIhIIBYxERGRQCxiIiIigVjEREREArGIiYiIBGIR\nExERCcQiJiIiEohFTEREJBCLmIiISCAWMRERkUAsYiIiIoFYxERERAKxiImIiARiERMREQnEIiYi\nIhKIRUxERCQQi5iIiEggFjEREZFALGIiIiKBWMREREQCsYiJiIgEYhETEREJxCImIiISiEVMREQk\nEIuYiIhIIBYxERGRQCxiIiIigcqKDkCkSp48eYINYWFI/OMPpKWkoLyJCcybNoWHpyeqVKkiOh4R\naSCZJEmS6BBEosXFxWFpUBAOREWhFwCrrCwYA0gFcM7AALslCV2cnTF2yhRYWVkJTktEmoRFTFpv\nVUgIZk2ciEmZmfCQJFR4z2teAAiTyfCdgQH8Fy3CcG9vZcckIg3FIiattiokBAsmTsShjAzUK8Lr\nbwBwNDTEJJYxEckJi5i0VlxcHLrb2ODkWyX8AsBgAIcBVAEwD0C/N56/AaCDoSEijh9H69atlReY\niDQSV02T1loaFIRJmZnvjIR9AOgDeApgEwBvAFffeL4eAL/MTCwNClJOUCLSaBwRk1Z68uQJGpiZ\n4VZW1r++E84AUAHAFQB1//eYB4AaeD0y/ttzAHX19ZGYlMTV1ERUKhwRk1baEBYGV+CdhVmJAMrh\n/0sYAJoBuPzW6yoCcJXJsCEsTGEZiUg7sIhJKyX+8QfaZGW983gagI/eeuwjvL6M6W1WmZlIjI9X\nQDoi0iYsYtJKaSkpMH7P4+UBvHrrsRTgva81BpD64oW8oxGRlmERk1Yqb2Ly3lGuOYA8ADffeOx3\nAI3f89pUAMYV3nfVMRFR0bGISSuZN22Kc/r67zxuCKAXgJl4vXDrFIAIAN+85xhxBgYwt7RUZEwi\n0gJcNU1aqbBV08C/ryOuDGABgL5vvYarpolIXjgiJq1UtWpVdHF2xnqZ7J3nKgDYjdcLt+7g3RIG\ngPUyGbq6uLCEiajUOCImrVXYzlofcgPAl/r62H/yJHfWIqJS44iYtJaVlRX8Fy2Co6EhbhTxPTcA\n2OrqIrtcOejq6ioyHhFpCd6PmLTa3zdu+GL8ePhlZ2MI3t3kA3j9nfA6mQyL/nf3pY8rVYKDgwMi\nIyPRsmVLZUYmIg3DqWnSenl5eahXrx7q16iB8xcuwFUmg1Vm5j/3I44zMMCO3FyY1ayJsB07/pmO\n3rNnD0aMGIF9+/bh888/F/ozEJH64oiYtN7atWtRp04dRMfEIDk5GRvCwnApPh6pL17AuEIFNLa0\nxHgnJ3Ts2BHm5ub/vK9nz54oV64cunXrhl27duHLL78U+FMQkbriiJi0WlpaGszNzbFv374PLrzq\n3bs3OnfuDB8fn389Hh0djQEDBmD79u2wsbFRYFoi0kRcrEVabcmSJbCxsSnS6mdvb2+EhITg7c+u\nDg4O2LZtG/r06YPDhw8rKioRaSiOiElrPX78GBYWFjh//jw+++yzD75ekiQ0bNgQa9asee809KlT\np9CrVy+EhYXBxcVFEZGJSANxRExay9/fHx4eHkUqYQCQyWTw8vJCSEjIe5//8ssvERERAU9PT+zZ\ns0eeUYlIg3FETFopISEBX375Ja5du4ZKlSoV+X3Pnz9HnTp1cP369UJ31frtt9/QpUsXLF++HG5u\nbvKKTEQaiiNi0kpTpkyBr69vsUoYACpWrAhXV1esW7eu0Ne0atUKhw4dwpgxY7B58+bSRiUiDccR\nMWmd06dPo1+/fkhISICBgUGx33/u3Dn069cP169fR5kyhX+WvXz5MhwcHBAYGAhPT8/SRCYiDcYR\nMWkVSZLg6+uLwMDAEpUw8HprzI8//hjR0dH/+brGjRsjNjYWM2fORGhoaInORUSaj0VMWmX37t3I\nyMjA119/XeJjyGSyfy5l+pAGDRrg2LFjCAoKwvLly0t8TiLSXJyaJq2Rm5uLxo0bY/ny5XB0dCzV\nsdLT02FqaoqLFy/C1NT0g6+/e/cuOnfuDG9vb0ycOLFU5yYizcIRMWmN1atXw8zMDA4ODqU+lpGR\nEfr374/Vq1cX6fVmZmY4fvw4Vq1ahblz55b6/ESkOTgiJq2QmpqK+vXrIyoqCi1atJDLMS9fvgw7\nOzskJSWhXLlyRXrPw4cPYWtrCzc3N8yePRsymUwuWYhIfXFETFph4cKFsLe3l1sJA68XY5mbmxdr\n847q1avj2LFj2L17N6ZMmfLOdplEpH04IiaN9/DhQzRp0gQXLlyAmZmZXI+9detWrFq1CrGxscV6\n37Nnz2Bvbw9ra2ssWbKEI2MiLcYiJo03YsQIfPTRR1i4cKHcj52TkwNTU1McO3YMDRs2LNZ7X7x4\nAScnJ7Ru3RrLly//z2uSiUhzsYhJo129ehUdO3ZEYmIiKlSooJBzTJ06FRkZGfjhhx+K/d5Xr17B\n2dkZFhYWCA0NZRkTaSEWMWm0Hj16oGPHjpgwYYLCznHnzh20atUKf/31FwwNDYv9/rS0NHTt2hVm\nZmZYu3YtdHR0FJCSiFQVP36Txjpx4gR+//13jBw5UqHnqV27Ntq1a4etW7eW6P3ly5dHZGQkHjx4\ngAEDBiA3N1fOCYlIlbGISSP9vZXl3Llzoa+vr/DzFXWnrcIYGhoiIiICKSkpcHd3R05OjhzTEZEq\nYxGTRgoPD0dubi769eunlPM5OTnh6dOnOH/+fImPoa+vj927dyM/Px+9e/dGdna2HBMSkapiEZPG\nycnJwZQpU7Bw4UKlLX7S0dHBiBEjSjUqBgA9PT3s2LEDenp66NGjBzIzM+WUkIhUFRdrkcZZvnw5\nIiMjERUVpdTzPnnyBA0aNMCtW7dKvUI7Ly8PHh4eePToEfbt2wcjIyM5pSQiVcMiJo2SkpICc3Nz\nHD58GE2bNlX6+fv164e2bdti7NixpT5Wfn4+hg4dips3b+LAgQMwNjaWQ0IiUjWcmiaN8t1338HF\nxUVICQOvF22tXLlSLltX6ujoYM2aNWjUqBEcHR2RkpIih4REpGo4IiaNce/ePTRr1gyXLl1CrVq1\nhGSQJAmWlpb48ccfYWNjI7djjhkzBmfOnMGhQ4dQsWJFuRyXiFQDR8SkMWbNmoXhw4cLK2EAkMlk\n8PLyKvWirbePuWzZMlhbW8PW1hbJyclyOzYRiccRMWmE+Ph42NnZITExESYmJkKzpKSkoHbt2rh6\n9SqqVasmt+NKkoTp06dj7969iImJwSeffCK3YxOROBwRk0aYPHkypk6dKryEAcDExARubm5Ys2aN\nXI8rk8kQGBiIPn36wMbGBg8ePJDr8YlIDI6ISe3FxsZi2LBhuHr1KnR1dUXHAQBcvHgRPXv2xK1b\ntxSyd/T8+fOxZs0axMbGCp2KJ6LS44iY1FpBQQH8/Pwwb948lSlhAGjRogWqVauGyMhIhRx/8uTJ\n8PHxgbW1NW7fvq2QcxCRcrCISa1t27YNZcqUgZubm+go7yjt/tMfMn78eEyYMAE2Nja4ceOGws5D\nRIrFqWlSW9nZ2WjYsCHWrVsnt0uF5CkzMxO1atVCXFwcPvvsM4WdZ/Xq1fD398eRI0fQsGFDhZ2H\niBSDI2JSW8HBwWjSpIlKljAAGBgYYODAgQgNDVXoeYYNG4a5c+eic+fO+PPPPxV6LiKSP46ISS29\nePECDRo0wNGjR9G4cWPRcQqVmJiIDh06ICkpCXp6ego919atWzFu3DhERUWhRYsWCj0XEckPR8Sk\nlubPn48ePXqodAkDgLm5OSwtLbFz506Fn8vd3R0rVqyAk5MT4uLiFH4+IpIPjohJ7SQlJaFFixaI\nj4/Hp59+KjrOB+3cuRM//PADTp48qZTzRUREYMiQIdizZw+++OILpZyTiEqORUxqx8PDA6amppgz\nZ47oKEWSm5uL2rVr4+DBg7C0tFTKOQ8ePIiBAwciPDwcHTt2VMo5iahkWMSkVi5dugQnJyckJibi\no48+Eh2nyGbNmoXk5GSsWLFCaeeMiYmBu7s7tm7dCltbW6Wdl4iKh0VMasXR0RHdu3fHyJEjRUcp\nlnv37qFp06ZISkpC+fLllXbeEydOoHfv3tiwYQOcnJyUdl4iKjou1iK1ER0djdu3b2P48OGioxRb\nzZo1YW1tjc2bNyv1vB07dsTevXsxcOBAREREKPXcRFQ0LGJSCwUFBZg0aRLmzZuHcuXKiY5TIn/v\ntKXsSah27drhwIEDGDp0qFJWbxNR8bCISS38/PPP0NPTw1dffSU6SonZ2dkhLS0NZ86cUfq5rays\ncOjQIYwaNQpbtmxR+vmJqHBlRQcg+pCsrCxMmzYNmzZtgkwmEx2nxMqUKQMvLy+sXLkS7dq1U/r5\nmzdvjsOHD8PBwQE5OTnw8PBQegYieheLmFTejz/+iBYtWqBDhw6io5Sap6cn6tWrh2fPnqFSpUpK\nP3+TJk0QGxsLOzs75ObmYujQoUrPQET/xlXTpNKeP3+OBg0a4OTJkxpzQ4OBAweiWbNmmDBhgrAM\n169fh52dHfz8/NRuBTqRpmERk0qbOHEi0tLSsHLlStFR5ObXX3/FwIEDkZCQgDJlxC3TuH37Nmxt\nbTF69GiMHz9eWA4ibcepaVJZd+7cwbp163D58mXRUeSqbdu2MDIyQkxMDOzt7YXl+Oyzz3Ds2DHY\n2toiOzsbkydPFpaFSJtx1TSprOnTp2P06NGoVq2a6ChyJZPJ/rmUSTRTU1McP34cYWFhCAgIUPql\nVUTEqWlSURcuXECXLl2QmJgIY2Nj0XHkLjU1FWZmZoiPj0eNGjVEx8Hjx49ha2uLHj16IDAwUK1X\npxOpG46ISeVIkgRfX1/MmjVLI0sYAIyNjeHu7o7Vq1eLjgIA+OSTT3D06FEcOHAAvr6+HBkTKRFH\nxKRyDh48iHHjxiE+Pl5td9Eqivj4eDg5OeHOnTsq83M+f/4cjo6OaNeuHZYuXcqRMZEScERMKiU/\nPx9+fn6YP3++ypSTolhaWuKzzz5TqT2gK1asiCNHjiAuLg5eXl4oKCgQHYlI47GISaVs3LgRH330\nEXr06CE6ilKoyqKtN5mYmCA6OhpXr17FkCFDkJ+fLzoSkUbj1DSpjMzMTJibm2P79u1CtoAUITs7\nG7Vq1cLp06dRv3590XH+JT09Hd27d0e1atWwfv16lC3Lqx2JFIEjYlIZS5cuxeeff641JQwAenp6\n8PT0VMkNS4yMjLB//348e/YM/fv3R25uruhIRBqJI2JSCcnJyWjYsCF++eUXmJubi46jVLdu3UKb\nNm3w119/wcDAQHScd2RlZcHNzQ06OjrYtm0b9PT0REci0igcEZNKCAwMhLu7u9aVMADUqVMHVlZW\n2L59u+go76Wvr4+dO3dCR0cHvXr1QlZWluhIRBqFI2IS7ubNm/j8889x5coVVK1aVXQcIfbt24d5\n8+YJuVdxUeXm5mLgwIFITk7G3r17YWhoKDoSkUbgiJiEmzZtGsaNG6e1JQwAXbp0wYMHD3Dx4kXR\nUQpVrlw5bNq0CdWrV0eXLl2QlpYmOhKRRmARk1Dnzp3DyZMntf7uPzo6Ohg+fLjKXcr0Nh0dHaxb\ntw5169aFk5MTXr16JToSkdrj1DQJI0kSOnXqhAEDBvAG9QAePXqERo0a4c6dOzAxMREd5z8VFBRg\n1KhR+O2333Dw4EFUqFBBdCQitcURMQlz4MABPH36FIMGDRIdRSVUq1YN9vb22LRpk+goH1SmTBms\nWLECX3zxBWxtbfHs2TPRkYjUFouYhMjLy8OkSZOwYMECbhTxhr932lKHiSqZTIYlS5bAwcEBnTp1\nwpMnT0RHIlJLLGISIiwsDFWqVEGXLl1ER1EpNjY2yM/Px6lTp0RHKRKZTIagoCC4urrCxsYGDx8+\nFB2JSO3wO2JSuvT0dJibm2P37t1o06aN6DgqZ+nSpTh79ix+/vln0VGKZe7cuVi/fj1iY2NRs2ZN\n0XGI1AaLmJQuMDAQf/75J7Zu3So6ikp68eIF6tSpg4SEBLW7pGvRokUICQlBbGwszMzMRMchUgss\nYlKqJ0+ewMLCAmfPnkXdunVFx1FZgwcPhrm5OSZPniw6SrEtW7YMS5YsQUxMDP83JioCFjEp1ahR\no1C2bFn88MMPoqOotLi4OPTp0wc3btyAjo6O6DjFFhoaisDAQBw5cgQNGjQQHYdIpXG5KinN9evX\nsW3bNly9elV0FJVnZWWFSpUq4dChQ3BxcREdp9hGjBgBXV1ddO7cGYcPH4aFhYXoSEQqi6umSWmm\nTp2KCRMmoHLlyqKjqIW/L2VSV56enliwYAFsbW3xxx9/iI5DpLI4NU1KcebMGbi5uSExMVElb/Wn\nitLT02FqaooLFy6o9cKn7du3Y8yYMYiMjETLli1FxyFSORwRk8JJkgRfX1/MmTOHJVwMRkZGGDBg\nAFatWiU6Sqn06dMHK1euhLOzM86ePSs6DpHKYRGTwu3btw8pKSn45ptvREdRO15eXlizZg1ycnJE\nRymVnj17Yu3atejWrZvabFZCpCwsYlKoN7eyVMfVv6I1atQIjRo1wu7du0VHKbUuXbpg06ZNcHV1\nxdGjR0XHIVIZLGJSqDVr1qBGjRpwcnISHUVtqfuirTc5ODhgx44d6Nu3L6Kjo0XHIVIJXKxFCpOW\nlgZzc3NERESgVatWouOorZycHJiZmSEmJkZjLgM6ffo0XF1dsW7dOu43TlqPI2JSmMWLF6NTp04s\n4VLS1dXFkCFDsHLlStFR5KZ9+/aIiIjA4MGDNWLanag0OCImhXj06BEaN26M8+fP47PPPhMdR+0l\nJSWhRYsWSEpKgpGRkeg4cnPhwgW4uLhg2bJl6NOnj+g4REJwREwK4e/vj0GDBrGE5cTU1BTt27fH\nli1bREeRq5YtWyI6Ohpjx47Fpk2bRMchEoIjYpK7a9euoUOHDkhISEDFihVFx9EYUVFRmD59Os6f\nPw+ZTCY6jlxduXIF9vb2mDNnDgYPHiw6DpFScURMcjdlyhT4+fmxhOXM0dERL168wPnz50VHkTsL\nCwscPXoUs2fP1qjvwomKgjd9ILk6deoULly4oHFTqKqgTJkyGDFiBEJCQmBlZSU6jtyZm5vj6NGj\nsLW1RU5ODsaMGSM6EpFScGqa5EaSJHzxxRfw8fHhLloK8vTpU5ibm+PWrVuoUKGC6DgKcffuXXTu\n3BleXl7w9fUVHYdI4Tg1TXKza9cuZGZm4uuvvxYdRWNVqVIFLi4uWL9+vegoCmNmZobjx4/jp59+\nQmBgoOg4RArHETHJRW5uLiwsLBAcHAx7e3vRcTTaqVOnMHToUFy9elXjFm296eHDh7Czs8NXX30F\nf39/jf5ZSbtxRExysWrVKtSpU4clrATt27dH2bJlNX6/5urVq+Po0aPYs2cPJk+eDI4ZSFNxREyl\n9urVK5ibm+PgwYNo3ry56DhaYcWKFTh27Bh27NghOorCPXv2DA4ODujQoQO+//57joxJ47CIqdRm\nzJiBpKQkjf7eUtW8evUKZmZmuHLlCqpXry46jsK9fPkSjo6OaNWqFX788UeUKcPJPNIcLGIqlQcP\nHsDS0hIXL16Eqamp6DhaZcSIEahZsyZmzJghOopSvHr1Ci4uLmjYsCFCQ0N5W03SGCxiKpVhw4ah\nYsWKWLBggegoWufSpUvo1q0bbt++jbJltWNLgLS0NHTr1g21atXC2rVrtebnJs3G+R0qscuXL2Pv\n3r2YMmWK6ChaqXnz5qhZsyYOHDggOorSlC9fHgcOHMCjR48wYMAA5Obmio5EVGosYiqxyZMnY8qU\nKfj4449FR9Fa3t7eCAkJER1DqQwNDbFv3z6kpqaib9++yMnJER2JqFQ4NU0lcuzYMXh6euLatWvQ\n09MTHUdrZWVloVatWjhz5gzq1q0rOo5SZWdno2/fvsjPz8eOHTugr68vOhJRiXBETMUmSRL8/Pww\nb948lrBg+vr68PDwQGhoqOgoSqenp4cdO3bAwMAAPXr0QGZmpuhIRCXCIqZi27FjBwoKCtC3b1/R\nUQivV0+HhYUhKytLdBSlK1euHH7++WdUqVIFXbp0QXp6uuhIRMXGIqZiycnJwZQpU7Bw4UJey6ki\n6tevj+bNmyM8PFx0FCHKli2L9evXw8zMDM7OzkhNTRUdiahY+C8pFcvKlSvRsGFDdOrUSXQUeoM2\nLtp6k46ODtasWQMLCws4ODjg5cuXoiMRFRkXa1GRpaSkwNzcHDExMWjSpInoOPSGvLw81K5dG5GR\nkWjatKnoOMJIkoSxY8fil19+QXR0NCpWrCg6EtEHcURMRbZgwQJ07dqVJayCypYti2HDhmHlypWi\nowglk8mwdOlSdOrUCZ07d8bTp09FRyL6II6IqUju3buHZs2a4ffff0fNmjVFx6H3uH//PiwtLXH3\n7l0YGxuLjiOUJEmYMWMG9uzZgyNHjqBatWqiIxEViiNiKpKZM2fCy8uLJazCatSogU6dOmHz5s2i\nowgnk8kQGBiIvn37wsbGBvfv3xcdiahQHBHTB8XHx8POzg6JiYkwMTERHYf+w5EjRzBhwgRcunSJ\ntwv8nwULFmD16tWIjY3ljUlIJXFETB80adIkTJ8+nSWsBjp37ozMzEz8+uuvoqOojEmTJmHkyJGw\ntrbG7du3RcchegdvXUL/KSYmBomJidizZ4/oKFQEZcqUgZeXF0JCQvDFF1+IjqMyxo8fDz09PVhb\nWyMmJgb169cXHYnoH5yapkIVFBTAysoKkyZNQp8+fUTHoSJ69uwZ6tatixs3bqBy5cqi46iUn376\nCbNnz8bhw4fRqFEj0XGIAHBETP9h69at0NHRgZubm+goVAyVKlVCjx49sHz5chgbGSHxjz+QlpKC\n8iYmMG/aFB6enqhSpYromEIMHToUurq6sLW1RXR0NC/FI5XAETG9V3Z2Nho2bIiwsDBYW1uLjkPF\nEBcXh1m+vjh24gTc9fTQJisLxgBSAZwzMMBuSUIXZ2eMnTIFVlZWouMKsXXrVowbNw5RUVFo0aKF\n6Dik5VjE9F5LlizBsWPHsG/fPtFRqBhWhYRg1sSJ8MvMxCBJQoX3vOYFgDCZDN8ZGMB/0SIM9/ZW\ndkyVsHPnTvj4+GD//v1a+4GEVAOLmN7x4sULNGjQAMeOHYOFhYXoOFREq0JCsGDiRBzKyEC9/z22\nAkAYgHgA/QGsfeP1NwA4GhpikhaXcUREBIYMGYI9e/ZwcRsJwyKmd/j5+eHly5dYtWqV6ChURHFx\ncehuY4OTb5QwAOzB62sUDwHIxL+LGHhdxh0MDRFx/Dhat26tpLSq5eDBgxg4cCDCw8PRsWNH0XFI\nC7GI6V/u3r2Lli1bIj4+Hp9++qnoOFREA3r1Qus9ezCukL/OMwDcx7tFDADfy2S44OqKjTt3KjKi\nSouJiYG7uzu2bt0KW1tb0XFIy7CI6V8GDhyI2rVrIyAgQHQUKqInT56ggZkZbmVlvfc7YeC/i/g5\ngLr6+khMStLa1dQAcOLECfTu3RsbNmyAk5OT6DikRbizFv3j4sWLiI6Ohq+vr+goVAwbwsLgChRa\nwh9SEYCrTIYNYWHyC6WGOnbsiL1792LgwIGIiIgQHYe0CIuY/jFp0iTMnDlT6+/co24S//gDbbKy\nSnUMq8xMJMbHyymR+mrXrh0iIyMxbNgw7NTiqXpSLm7oQQCA6Oho3LlzB8OGDRMdhYopLSUFpf3o\nZAwg9cULecRRe61bt8bBgwfh7OyM7Oxs9O/fX3Qk0nAsYkJ+fj78/Pwwf/58lCtXTnQcKqbyJiZI\nLeS5fAC5//s9D0A2Xv+l13nrdakAjCuUdHJb8zRv3hyHDx+Go6MjcnNz4eHhIToSaTBOTRM2b94M\nQ0NDuLq6io5CxZSZmYlXOTk4WcgtDwMBGAJYAGDz//489z2vO2dgAHNLS4XlVEdNmjRBTEwMpk+f\njtWrV4uOQxqMRazlMjMzMX36dCxcuJD3r1Uj169fx4QJE2Bqaoqnz55hf9myeN/E8iwABXg9Iv77\n18y3XvMcwLbMTMh0dJCTk6PY4GqmYcOGOHr0KAIDA7FixQrRcUhDsYi13PLly9G6dWu0b99edBT6\ngLy8POzZswcODg5o3749ypYti7NnzyImJgbdunbF+hJ+kFovk8HG2hrR0dGoX78+Vq5ciezsbDmn\nV1/16tXD8ePHsXjxYixZskR0HNJEEmmt5ORkqXLlytK1a9dER6H/8ODBAykgIECqWbOm1K5dO2nj\nxo1SZmbmv15z7tw5qZqhoXQdkKRi/LoOSNUMDaW4uDhJkiTp119/lZydnaVatWpJK1aseOc82iwp\nKUmqV6+eNG/ePNFRSMNwRKzF5s6dCzc3NzRo0EB0FHqLJEk4fvw4+vbtCwsLC9y7dw8RERH45Zdf\nMGDAAOjr6//r9VZWVvBftAiOhoa4UcRz/L3XtP+iRf9sb9m2bVtERkYiPDwckZGRqFevHpYvX46s\nUl4epQlq1aqF48ePY8OGDfD394fEvZBIXkR/EiAxbt26JVWqVEl69OiR6Cj0hpcvX0rLly+XLCws\npEaNGknLli2TXr58WeT3hwYHS9UMDaUlMpn0vJBR8DNAWiyTSdUMDaXQ4OD/PN758+el7t27S59+\n+qn0ww8/SBkZGaX9EdXeo0ePpCZNmkhTpkyRCgoKRMchDcAtLrXU119/jQYNGmDmzLeX7pAIv//+\nO4KDg7HnjjQUAAAcLklEQVR9+3bY29vDx8cH1tbWJVpAd/78eSwNCsL+yEi4ymSwysz8537Ecf+7\nH3FXFxeMnTKlyDd6uHjxIgICAnD27Fn4+vpixIgRMDQ0LHY2TZGcnAx7e3t07twZixYt4kJHKhUW\nsRb67bff0K1bNyQmJqJ8+fKi42it7OxshIeHIzg4GHfv3sWIESMwdOhQVK9eXS7Hf/r0KTaEhSEx\nPh6pL17AuEIFmFtaYuCgQSXeU/r333/HnDlzcPr0aUyYMAHe3t4wMjKSS1518/z5czg6OqJt27ZY\nunQpypThN31UMixiLSNJEmxtbeHu7o7hw4eLjqOVbt++jdDQUKxduxbNmzeHt7c3unXrhrJl1Wd/\nnfj4eMyZMwcnTpzAt99+Cx8fH638UJeSkgJnZ2c0adIEK1euZBlTifD/NVrm4MGDePjwIQYPHiw6\nilbJz8/HgQMH0KVLF1hZWSEnJwenTp1CdHQ0XF1d1aqEAcDS0hLbt29HTEwMLly4gLp16yIoKAip\nqYXt8aWZTExMcOjQISQkJGDw4MHIz88XHYnUEEfEWiQ/Px/NmzfH3Llz0b17d9FxtMLTp0+xZs0a\nhIaGonLlyvDx8UHfvn017vvVK1euYO7cuTh8+DDGjh2L0aNH46OPPhIdS2nS09PRvXt3VKtWDevX\nr1e7D1YkFkfEWmTDhg2oUKECunXrJjqKRpMkCadPn8aAAQNQv359JCYmYvv27YiLi4Onp6fGlTAA\nWFhYYPPmzTh58iSuXbuGunXrIiAgACkpKaKjKYWRkRH279+P58+fo1+/fsjNzRUdidQIR8RaIiMj\nAw0aNEB4eDg+//xz0XE0UlpaGjZv3ozg4GBkZmbC29sbHh4eqFixouhoSpeYmIh58+bhwIEDGDly\nJMaNG4ePP/5YdCyFy87OhpubG2QyGbZv3w49PT3RkUgNcESsJZYuXYp27dqxhBXg8uXLGDVqFExN\nTXHo0CEsWrQI165dw/jx47WyhAHA3NwcYWFh+PXXX5GUlIR69eph5syZeP78uehoCqWnp4fw8HCU\nK1cOrq6uyMzMFB2J1ACLWAs8ffoUixcvxrx580RH0Rg5OTnYtm0brK2tYW9vj4oVK+L333/Hrl27\nYG9vz9Wz/1OvXj2sXbsW586dw8OHD1G/fn1MmzYNz549Ex1NYXR1dbF161aYmJige/fuyMjIEB2J\nVBynprXA2LFjIUkSli1bJjqK2ktKSsKqVauwZs0aNGzYED4+PujZsyfv41xEd+7cQVBQEMLDwzF8\n+HBMmDABlStXFh1LIfLz8zF48GDcvXsX+/fv18rLu6ho+LFdw924cQObN2/GjBkzREdRWwUFBYiO\njkbPnj3RvHlzvHr1CjExMTh69Cjc3NxYwsVQu3ZthIaG4uLFi3j58iUaNGgAPz8/PHnyRHQ0udPR\n0cG6detQv359ODo6as3CNSo+FrGGmzZtGr799tsS76SkzZ49e4bFixfD3Nwcfn5+cHFxQVJSEpYt\nWwYLCwvR8dSaqakpQkJCcOnSJWRkZKBRo0aYOHEiHj9+LDqaXJUpUwahoaFo3rw57O3t8eLF++4a\nTdqORazBzp49i9OnT2PcuHGio6gNSZJw7tw5DBo0CHXr1sWlS5ewceNGXLx4EcOHD+f0opzVqlUL\nP/74I/744w/k5OSgUaNG+Pbbb/Ho0SPR0eSmTJky+PHHH/Hll1/C1tYWycnJoiORimERayhJkuDn\n5wd/f3+NvG5V3jIyMrBmzRpYWVnB3d0dFhYWuH79OjZu3Ih27dpxU38Fq1GjBpYtW4Y///wTkiSh\ncePGGDduHB48eCA6mlzIZDIsXrwYjo6O6Ny5s0ZOxVPJsYg11P79+/Hs2TN4eHiIjqLSEhISMH78\neNSqVQt79uxBQEAArl+/Dj8/P07nC/Dpp5/i+++/x+XLl6GjowNLS0uMHj0a9+7dEx2t1GQyGebN\nm4devXrBxsYGDx8+FB2JVASLWAPl5eVh0qRJWLBgAbfae4+8vDzs2rULdnZ26NixI/T19fHbb78h\nIiICLi4u0NHRER1R61WrVg2LFy/GlStXoK+vj2bNmmHkyJH466+/REcrFZlMhtmzZ2PAgAGwtrbW\niA8YVHosYg20bt06fPLJJ3BxcREdRaU8ePAA/v7+MDMzw5IlSzB48GAkJSUhKCgItWvXFh2P3uOT\nTz7BwoULce3aNRgbG6N58+bw8vLC3bt3RUcrlalTp2LEiBGwtrbGnTt3RMchwVjEGiY9PR2zZ8/G\nd999x+818fq78tjYWPTu3RuNGzfGo0ePEBUVhVOnTqF///7cglBNVKlSBfPnz0dCQgIqVqyIli1b\nYvjw4bh9+7boaCU2YcIEjBs3DjY2Nrh586boOCQQi1jDLFmyBB07doSVlZXoKEK9fPnyn8uMxowZ\ng86dO+Pu3bsICQlB06ZNRcejEqpcuTLmzZuHxMREVK1aFa1bt8aQIUNw69Yt0dFKZPTo0Zg6dSps\nbGyQkJAgOg4Jwp21NMjjx49hYWGBuLg41KlTR3QcIS5cuICQkBCEh4fDyckJ3t7e6NChA2cHNNSL\nFy/www8/YMWKFejWrRumTZuGevXqiY5VbOvWrcP06dMRHR2Nxo0bi45DSsYRsQYJCAjAwIEDta6E\ns7KysGHDBrRt2xY9e/ZE7dq1cfXqVWzZsgUdO3ZkCWuwChUqwN/fHzdu3EDt2rXRrl07eHh4IDEx\nUXS0YvH09MR3330HOzs7/P7776LjkJJxRKwhEhIS0L59eyQkJKBSpUqi4yjFzZs3sXLlSoSFhaFV\nq1bw8fGBi4sLV4prsZSUFCxfvhxLly6Fo6Mjpk+fjoYNG4qOVWQ7duzA6NGjceDAAbRq1Up0HFIS\njog1xNSpU+Hr66vxJZyfn4+IiAg4Ozujbdu2AIBff/0VBw8eRPfu3VnCWs7ExATTp0/HzZs3YWFh\ngY4dO6J///64cuWK6GhF4ubmhtDQULi4uODMmTOi45CScESsAX755Re4u7sjISEBBgYGouMoxOPH\nj7FmzRqEhoaievXq8Pb2Rp8+fTT25yX5SE1NxYoVK/D999/DxsYGM2bMQJMmTUTH+qDIyEgMGjQI\nu3btwpdffik6DikYR8RqTpIk+Pr6Ys6cORpXSpIk4eTJk+jXrx8aNmyIW7duYdeuXThz5gw8PDw0\n7ucl+TM2NsbkyZNx8+ZNtG7dGnZ2dnBzc0N8fLzoaP/JxcUFmzdvhqurK44ePSo6DikYi1jN7dmz\nB2lpaRgwYIDoKHLz6tUrBAcHo2nTphg6dCjatm2LW7du4aeffuL3ZlQi5cuXh6+vL27evIm2bdvC\nwcEBX331lUovjLK3t8eOHTvQt29fREdHi45DCsSpaTWWm5uLJk2aYNmyZXB0dBQdp9Ti4+MRHByM\nrVu3wtbWFt7e3ujcuTNXPZPcZWRkYNWqVfjuu+/Qpk0bzJw5Ey1bthQd671Onz4NV1dXrFu3Dl26\ndBEdhxSAI2I1tmbNGpiamsLBwUF0lBLLzs7Gli1b0KFDBzg5OaFatWr4888/ER4eDltbW5YwKYSh\noSHGjRuHmzdvonPnzujWrRu6d++O8+fPi472jvbt2yMiIgKDBw/G7t27RcchBeCIWE2lpqbC3Nwc\nkZGRaNGiheg4xXb37l2EhoZizZo1sLS0hLe3N7p3745y5cqJjkZaKCsrCz/99BPmz5+PZs2aYdas\nWWjTpo3oWP9y4cIFuLi4YNmyZejTp4/oOCRHHBGrqcWLF8POzk6tSrigoABRUVHo1q0bWrZsiYyM\nDBw/fhxHjhzBV199xRImYfT19TFq1CjcvHkTXbt2Re/eveHs7KxSlxC1bNkS0dHRGDt2LDZt2iQ6\nDskRR8Rq6OHDh2jSpAkuXLgAMzMz0XE+KDk5GevWrcPKlSthYmKCkSNHwt3dHUZGRqKjEb1XdnY2\nwsLCEBQUBHNzc8yaNQvt27cXHQsAcOXKFdjb22POnDkYPHiw6DgkByxiNeTl5QVjY2MsXLhQdJRC\nSZKEs2fPIjg4GPv27UPPnj3h7e2NNm3a8HtfUhs5OTnYsGED5s6di7p162LWrFno0KGD6FhITEyE\nnZ0dpk6dCi8vL9FxqJRYxGrm6tWrsLa2RkJCAipUqCA6zjvS09Px888/Izg4GKmpqfDy8oKnp6fG\n7/hFmi03NxcbN27E3LlzYWZmhlmzZsHa2lpoplu3bsHW1hbjxo3D2LFjhWah0mERq5mePXuiQ4cO\nmDBhgugo/3L16lWEhIRg8+bN+PLLL+Hj4wN7e3uUKcNlCKQ5cnNz8fPPPyMwMBCffvopZs2ahU6d\nOgmb5bl79y5sbW0xfPhw+Pn5CclApcciViMnT57EN998g2vXrkFfX190HOTm5mLv3r0IDg7GlStX\nMHToUAwfPhympqaioxEpVF5eHrZs2YLAwEBUrVoVs2bNEna53f3799G5c2cMGDAAM2bMUPr5qfRY\nxGpCkiS0a9cOo0ePxtdffy00y71797B69WqsXr0a9evXh7e3N3r16gVdXV2huYiULT8/H1u3bsWc\nOXNQqVIlzJw5Ew4ODkov5EePHsHW1ha9evVCQEAA12GoGc4bqomdO3ciJycH/fr1E3L+goICHDly\nBL169ULTpk2RnJyM6OhoHD9+HO7u7ixh0ko6Ojr4+uuvcfnyZYwaNQrjx49Hu3btEBUVBWWOcapV\nq4Zjx45h3759mDRpklLPTaXHEbEayMnJQePGjbFy5UrY2toq9dwvXrxAWFgYQkJCoK+vDx8fH3z9\n9dcwNjZWag4idVBQUIDw8HAEBATAyMgIM2fOhIuLi9JGqM+ePYODgwM6dOiA77//niNjNcEiVgM/\n/vgjDhw4gKioKKWd8/z58wgODsauXbvQpUsX+Pj44IsvvuBfbKIiKCgowK5duxAQEABdXV3MnDkT\n3bp1U8rfn5cvX8LJyQktWrTAihUruGBSDbCIVdyrV69gbm6O6OhoNG3aVKHnyszMxLZt2xAcHIwn\nT57Ay8sLgwcPRtWqVRV6XiJNVVBQgL179/7zve3MmTPRo0cPhRfyq1ev0KVLF5ibm2PVqlXQ0dFR\n6PmodFjEKm769Om4f/8+1q1bp7BzXL9+HStXrsT69evx+eefw9vbG87OzvzLSyQnkiRh3759CAgI\nQH5+PmbMmAFXV1eFjlbT0tLQvXt31KhRA+vWrUPZsmUVdi4qHRaxCrt//z6aNm2KS5cuoVatWnI9\ndl5eHvbv34/g4GBcunQJnp6eGDFiBOrUqSPX8xDR/5MkCQcOHIC/vz+ys7MxY8YMfPXVVwor5IyM\nDPTs2RMVKlTApk2buJ+7imIRq7ChQ4eiSpUqCAoKktsxHz58iJ9++gmrVq1CrVq14OPjg969e6vE\ndclE2kKSJERFRcHf3x9paWmYMWMG3NzcFDILlZWVhd69e0NXVxdbt27lFQ4qiEWsov7880/Y2toi\nMTERJiYmpTqWJEk4ceIEgoODER0djT59+sDb2xvNmzeXU1oiKglJknDo0CH4+/sjJSUF06dPR9++\nfeVeyDk5Oejbty9yc3MRHh7OD94qhkWsorp27Qo7OzuMGzeuxMdISUnBxo0bERISAkmS4O3tjYED\nB5a62IlIviRJwpEjR+Dv74/k5GRMnz4d7u7ucv1eNzc3FwMGDMDLly+xe/duGBoayu3YVDosYhV0\n9OhRDBkyBFevXoWenl6x33/p0iWEhIRg+/btsLe3h4+PD6ytrXnpEZGKkyQJsbGx8Pf3x6NHjzB9\n+nT0799fboWcl5cHT09P3L9/HxEREbwVqYpgEQvy5MkTbAgLQ+IffyAtJQXlTUxg3rQpvvHwQNeu\nXTFhwgS4u7sX+XhZWVkIDw9HcHAwkpKSMGLECAwdOhTVq1dX4E9BRIpy7Ngx+Pv746+//sK0adMw\nYMAAuSy2ys/Px7Bhw3D9+nUcOHAAH330kRzSUmmwiJUsLi4OS4OCcCAqCr0AWGVlwRhAKoBzBgbY\nmZeH8kZG2HXwID7//PMPHu/27dsIDQ3F2rVr0bx5c/j4+KBr1668VIFIQ5w4cQL+/v64ffs2pk2b\nhoEDB5a6kAsKCjBy5EhcvHgRBw8exMcffyyntFQiEilNaHCwVM3QUPpeJpOeA5L0nl/PAWmxTCZV\nMzSUQoOD33ucvLw8af/+/ZKLi4tUqVIl6dtvv5USExOV/NMQkTKdPHlSsrOzk2rXri2FhoZK2dnZ\npTpeQUGBNGbMGKlVq1bSs2fP5JSSSoJFrCShwcFSHUND6XohBfz2r+uAVOetMn78+LEUFBQkmZmZ\nSVZWVtLatWul9PR0gT8VESnb6dOnJUdHR8nU1FQKCQmRsrKySnysgoICydfXV2ratKn05MkTOaak\n4uDUtBLExcWhu40NTmZkoN4bj38D4AiADACVAQwGMO2N528A6GBoiMBlyxAbG4vIyEi4urrC29sb\nVlZWyvsBiEjlnDlzBgEBAfjzzz8xefJkDB48uESXJUmShJkzZ2LXrl2IiYlBtWrVFJCW/guLWAkG\n9OqF1nv2YNxb/6mvAKgDQB9AIoCOANYDcHzjNYsAfGdkhClz5sDDwwMVK1ZUUmoiUgdxcXEICAjA\nxYsXMWnSJAwbNqxEhTxnzhxs3rwZMTExqFGjhgKSUmFYxAr25MkTNDAzw62sLFT4j9clALADsBdA\nyzcefw6grr4+EpOSUKVKFUVGJSI19ttvvyEgIADnz5+Hn58fhg8fDgMDg2Id47vvvsOqVasQGxsL\nU1NTBSWlt/H+WAq2ISwMrkChJTwSgBGAJng9Ld3yrecrAnCVybAhLExhGYlI/bVq1Qp79+7F/v37\ncezYMdStWxdLlixBRkZGkY/h5+eHUaNGwdraGrdu3VJgWnqTzuzZs2eLDqHJwkJC0PriRbQu5Pku\nAKYCsAbgBaATgLcnhR7k5WFvair0jY1x9+5dPHjwAMnJyXj16hUyMzNRUFAAHR0d3i2JiFC9enW4\nu7vDzs4OmzdvxsSJEwEAzZo1K9I+023btoWenh6GDh2Krl27olKlSoqOrPV4samCpaWkwPgDr5Hh\ndRG7AdgC4O1lWMYAHt67h507dyItLQ3p6elIS0t7589lypSBkZERypcvj/Lly//z57d/L+5zurq6\n3JWLSM00a9YM4eHhiI+Px5w5c7Bw4UJ8++23GDlyJMqXL/+f7/X29oauri46deqEw4cPo1GjRkpK\nrZ1YxApW3sQEqUV8bR6A9+3+mgqgQ6dOCN2wodD3SpKEnJyc95b027///efHjx8X+tybv0uSJLdS\nf/M5PT09FjyRgllaWmL79u24fPkyAgMDUbduXYwbNw6jRo2CsXHhw4QhQ4ZAV1cXtra2OHToECwt\nLZWYWruwiBXMvGlTnNu5E15ZWf96/CmAWABdARgAOAxgx/9+f1ucgQEaf+AvgUwmg56eHvT09OS+\nsvrNgi9KcScnJxfpw0BeXl6RC7w4hW9gYMCCJ3pL48aNsWXLFly9evWfQh47dixGjx5d6DaX33zz\nDXR1dWFvb4+oqCi0aNFCyam1A1dNK1hhq6aTAfQG8AcACUB9ADMAdHvr/Zq8ajo3Nxfp6elFKvf/\neu7tx3JycmBoaFiiEft/vd7Q0JAFTxojISEBc+fORVRUFEaPHo0xY8YUutXlrl274O3tjYiICLRp\n00bJSTUfi1gJCruOuCi+l8lwwdUVG3fuVEAyzZSXl4eMjIwSlfp/PZednQ0DAwO5T9EbGhqiTBle\nwEBiXL9+HXPnzsX+/fsxatQojB07FhUqvHudx/79+zF48GDs2bMHX3zxhYCkmotFrASF7az1IX/v\nrBVx/Dhaty5s3TUpS35+/j8FX9pSf/O5zMxMGBgYyH2hnZGREVfSU5HduHED8+bNw759++Dt7Y3x\n48e/8zXXoUOH8M0332DHjh2wtrb+13OF3VHOw9NT42bz5I1FrCSrQkKwYOJEHCpiGd8A4GhoiEmL\nFmG4t7ei45FABQUFyMjIkPsUfXp6OvT09OQ+RW9kZMS7e2mwW7duISgoCLt27YKXlxe+/fbbf13C\nFBsbi759+2LLli2ws7P74B3ldksSujg7Y+yUKdyatxAsYiVaFRKCWRMnwi8zE4Mk6b2bfDwHECaT\nYaGBAfxZwlQKkiQhMzNT7lP06enpKFeunNyn6I2MjORyv12Sjzt37iAoKAjh4eEYPnw4JkyYgMqV\nKwMATp48ia+++gruffpgx7p1mJSZCY9C/k17gdf/pn3Hf9MKxSJWsvPnz2NpUBD2R0bCVSaDVWbm\nP58e4/736bGriwvGTpnC6WhSSZIkISsrS+5T9Onp6dDR0VHYtfBUMklJSZg/fz62bduGIUOGYOLE\niahatSom+fpi46JFOAFwlq+UWMSCPH369PX3KfHxSH3xAsYVKsDc0hIDBw3i9ymklSRJQnZ2ttyn\n6NPS0gBALpfGvf2cNm1289dff2HBggXYsmULnJ2dcWTXLpzKzPynhHMA+OD1HeVeAKgLYB4ApzeO\nwXUv78ciJiKNl5OTo5Ap+vz8fLmU+9uP6evrq2zB379/H04dO2LQrVuY8MbjGXh9tzhPALUAHADQ\nD8CfAN68fQSvBHkXi5iIqIT+3uxG3lP0ubm5Cpmil8dmN0W9oxwANAMwG4DrG49p8t4IJcWlj0RE\nJaSrqwtdXd33XndbGnl5ecWahv/rr7+KfC38f62GL8qIfe/u3ehRyMKsNz0GcB1A47cef/OOchN8\nfeX6301dsYiJiFRM2bJlYWJiAhMTE7keNz8/v9DR+PsK/OHDh+88l3jpEqZmZ//nefIADAAwCID5\ne563yszEpfh4uf5s6oxFTESkJXR0dPDRRx8Vurd0UfTv1g3G+/cX+ryE1yWsB2B5Ia8xBpD64kWJ\nM2gaFjERERXZh+4oNwSv99KPBFDYvm6pAIzlPJ2vzrjBLRERFZl506Y4p6//3ue8AFwDsA/Af125\nHWdgAHPeVvEfXDVNRERFVtiq6SQAtQHo4/9HwjIAoXh9GdPfuGr6XRwRExFRkVWtWhVdnJ2x/q3L\noEwBFOD19cSp//v1Cv8uYQBYL5Ohq4sLS/gNHBETEVGx8I5y8sURMRERFYuVlRX8Fy2Co6EhbhTx\nPX/vNe2/aBFL+C0sYiIiKrbh3t6YtGgROhga4nuZDIVdjPQcwBKZDB14w4dCcWqaiIhKjHeUKz0W\nMRERlRrvKFdyLGIiIiKB+B0xERGRQCxiIiIigVjEREREArGIiYiIBGIRExERCcQiJiIiEohFTERE\nJBCLmIiISCAWMRERkUAsYiIiIoFYxERERAKxiImIiARiERMREQnEIiYiIhKIRUxERCQQi5iIiEgg\nFjEREZFALGIiIiKBWMREREQCsYiJiIgEYhETEREJxCImIiISiEVMREQkEIuYiIhIIBYxERGRQCxi\nIiIigVjEREREArGIiYiIBGIRExERCcQiJiIiEohFTEREJBCLmIiISCAWMRERkUAsYiIiIoFYxERE\nRAKxiImIiARiERMREQnEIiYiIhKIRUxERCQQi5iIiEggFjEREZFALGIiIiKBWMREREQCsYiJiIgE\nYhETEREJxCImIiISiEVMREQkEIuYiIhIIBYxERGRQCxiIiIigVjEREREAv0fjYccUo1/HCYAAAAA\nSUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"G1 = nx.complete_graph(4)\n",
"pos = nx.spring_layout(G1) #定义一个布局,此处采用了spring布局方式\n",
"nx.draw(G1, pos = pos, with_labels = True)"
]
},
{
"cell_type": "code",
"execution_count": 206,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1.0\n"
]
}
],
"source": [
"print(nx.transitivity(G1))"
]
},
{
"cell_type": "code",
"execution_count": 216,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xt8zvX/x/HHhbKNJcd0sMnYGBvKxNfXoSLnYwmRIWZb\n+aacC2tzzlL4to2SxVckIWLaNyIStlBz2jCMSk5rxjZzuH5/+NZPDtm4tvd2Xc/77eZWt+v67PN5\nrlv23OtzvT+fj8VqtVoRERERI4qYDiAiIuLIVMQiIiIGqYhFREQMUhGLiIgYpCIWERExSEUsIiJi\nkIpYRETEIBWxiIiIQSpiERERg1TEIiIiBqmIRUREDFIRi4iIGKQiFhERMUhFLCIiYpCKWERExCAV\nsYiIiEEqYhEREYNUxCIiIgapiEVERAxSEYuIiBikIhYRETFIRSwiImKQilhERMQgFbGIiIhBKmIR\nERGDVMQiIiIGqYhFREQMUhGLiIgYpCIWERExSEUsIiJikIpYRETEIBWxiIiIQSpiERERg1TEIiIi\nBqmIRUREDFIRi4iIGKQiFhERMUhFLCIiYpCKWERExCAVsYiIiEEqYhEREYNUxCIiIgapiEVERAxS\nEYuIiBikIhYRETFIRSwiImKQilhERMQgFbGIiIhBxUwHEClITpw4wbzoaJJ++olzaWmULFUKT19f\n/Pv2pXz58qbjiYgdslitVqvpECKmxcXFMX3SJFbFxNAF8MvKwhVIB7Y5O7PMaqVt69a8OmoUfn5+\nhtOKiD1REYvDmx0ZScjQoYzIzMTfaqX0TbZJBaItFt52diY0PJyAoKD8jikidkpFLA5tdmQkU4YO\n5auMDKrmYPsDQEsXF0aojEXERlTE4rDi4uLo0KwZG68r4VSgH/BfoDwwEehxzfsHgMYuLqzcsIF6\n9erlX2ARsUtaNS0Oa/qkSYzIzLxhEg4GnICTwH+AIGDvNe9XBYZnZjJ90qT8CSoidk0TsTikEydO\n4OXuTnJW1l8+E84ASgN7AI//veYPPMzVyfgPZwAPJyeSUlK0mlpE7oomYnFI86Kj6Qw3LMxKAu7h\n/0sYoDaw+7rtygCdLRbmRUfnWUYRcQwqYnFIST/9RP2srBtePwfcd91r93H1Mqbr+WVmkpSQkAfp\nRMSRqIjFIZ1LS8P1Jq+XBM5e91oa3HRbVyA9NdXW0UTEwaiIxSGVLFXqplOuJ3AJOHjNaz8CNW+y\nbTrgWvpmVx2LiOScilgckqevL9ucnG543QXoAozl6sKtTcBK4MWb7CPO2RlPH5+8jCkiDkCrpsUh\n3WrVNPz1OuJywBSg23XbaNW0iNiKJmJxSBUqVKBt69Z8bLHc8F5pYBlXF24d5sYSBvjYYqFdmzYq\nYRG5a5qIxWHd6s5at6M7a4mILWkiFofl5+dHaHg4LV1cOJDDr/njXtOh4eEqYRGxCRWxOLSAoCBG\nhIfzj+LFCefq58M3cwZ4x2KhsR74ICI2plPT4vAuXbpE1apVqfbww8Rv305niwW/zMw/n0cc5+zM\nZxcv4v7II0R/9pkmYRGxqWKmA4iY9tFHH1GlShVi167l1KlTzIuOZmdCAumpqbiWLk1NHx9ea9WK\nJk2a4OnpaTquiNgZTcTi0M6dO4enpycrVqy47aT73HPP8dRTTxEcHJxP6UTEEegzYnFo06ZNo1mz\nZjk63RwUFERkZCT63VVEbEkTsTis3377DW9vb+Lj43n00Udvu73VaqV69erMmTOHf/7zn/mQUEQc\ngSZicVihoaH4+/vnqIQBLBYLgYGBREZG5nEyEXEkmojFISUmJvLPf/6Tffv2UbZs2Rx/3ZkzZ6hS\npQr79+/XXbVExCY0EYtDGjVqFMOGDctVCQOUKVOGzp07M3fu3DxKJiKORhOxOJzvvvuOHj16kJiY\niLOzc66/ftu2bfTo0YP9+/dTpIh+lxWRu6OfIuJQrFYrw4YNY/z48XdUwnD11pj3338/sbGxNk4n\nIo5IRSwOZdmyZWRkZNCzZ8873ofFYvnzUiYRkbulU9PiMC5evEjNmjWZOXMmLVu2vKt9nT9/Hjc3\nN3bs2IGbm5uNEoqII9JELA7jgw8+wN3dnWeeeeau91WiRAleeOEFPvjgAxskExFHpolYHEJ6ejrV\nqlUjJiaGunXr2mSfu3fvpnnz5qSkpHDPPffYZJ8i4ng0EYtDmDp1Ki1atLBZCQPUrFkTT09Pli9f\nbrN9iojj0UQsdu/XX3+lVq1abN++HXd3d5vue9GiRcyePZt169bZdL8i4jhUxGL3Bg4cyH333cfU\nqVNtvu/s7Gzc3NxYv3491atXt/n+RcT+qYjFru3du5cmTZqQlJRE6dKl8+QYb7zxBhkZGbz33nt5\nsn8RsW8qYrFrHTt2pEmTJgwZMiTPjnH48GEef/xxjh49iouLS54dR0TskxZrid369ttv+fHHH3n5\n5Zfz9DiVK1emYcOGLFq0KE+PIyL2SUUsdumPW1lOmDABJyenPD+e7rQlIndKRSx2acmSJVy8eJEe\nPXrky/FatWrFyZMniY+Pz5fjiYj9UBGL3cnOzmbUqFFMnTo1356OVLRoUQYOHKipWERyTYu1xO7M\nnDmT1atXExMTk6/HPXHiBF5eXiQnJ+fZCm0RsT8qYrEraWlpeHp68t///hdfX998P36PHj1o0KAB\nr776ar4fW0QKJ52aFrvy9ttv06ZNGyMlDFcXbUVFRaHfb0Ukp4qZDiBiK8eOHSMqKoqdO3cay9C4\ncWOKFi3Khg0baNasmbEcIlJ4aCIWuxESEkJAQACVKlUylsFisRAYGKhFWyKSY/qMWOxCQkICzZs3\nJykpiVKlShnNkpaWRuXKldm7dy8VK1Y0mkVECj5NxGIXRo4cyRtvvGG8hAFKlSpF165dmTNnjuko\nIlIIaCKWQm/dunUMGDCAvXv3cu+995qOA8COHTvo1KkTycnJFC1a1HQcESnANBFLoXblyhWGDx/O\nxIkTC0wJA9StW5eKFSuyevVq01FEpIBTEUuh9umnn1KkSBG6du1qOsoNdP9pEckJnZqWQuvChQtU\nr16duXPnFshLhTIzM6lUqRJxcXE8+uijpuOISAGliVgKrYiICGrVqlUgSxjA2dmZ3r17M2vWLNNR\nRKQA00QshVJqaipeXl5888031KxZ03ScW0pKSqJx48akpKRQvHhx03FEpADSRCyF0uTJk+nYsWOB\nLmEAT09PfHx8+Pzzz01HEZECShOxFDopKSnUrVuXhIQEHnroIdNxbuvzzz/nvffeY+PGjaajiEgB\npCKWQsff3x83NzfGjRtnOkqOXLx4kcqVK7NmzRp8fHxMxxGRAkZFLIXKzp07adWqFUlJSdx3332m\n4+RYSEgIp06d4v333zcdRUQKGBWxFCotW7akQ4cOvPzyy6aj5MqxY8fw9fUlJSWFkiVLmo4jIgWI\nFmtJoREbG8uhQ4cICAgwHSXXHnnkEZo2bcqCBQtMRxGRAkZFLIXClStXGDFiBBMnTuSee+4xHeeO\n/HGnLZ2EEpFrqYilUPjkk08oXrw4zz77rOkod6x58+acO3eOLVu2mI4iIgWIPiOWAi8rKwsvLy/+\n85//0LhxY9Nx7kp4eDgJCQl8/PHHpqOISAGhIpYCLzw8nE2bNrF8+XLTUe7a6dOnqVq1KgcOHKBs\n2bKm44hIAaAilgLtzJkzeHl5sXHjRqpXr246jk307t2b2rVrM2TIENNRRKQAUBFLgTZ06FDOnTtH\nVFSU6Sg28/3339O7d28SExMpUkTLNEQcXTHTAURu5fDhw8ydO5fdu3ebjmJTDRo0oESJEqxdu5YW\nLVqYjiMihunXcSmwRo8ezaBBg6hYsaLpKDZlsVj+vJRJRESnpqVA2r59O23btiUpKQlXV1fTcWwu\nPT0dd3d3EhISePjhh03HERGDNBFLgWO1Whk2bBghISF2WcIArq6udO/enQ8++MB0FBExTBOxFDhr\n1qxh8ODBJCQkFNq7aOVEQkICrVq14vDhw3b9fYrI39NELAXK5cuXGT58OJMnT7b7cvLx8eHRRx9l\n5cqVpqOIiEEqYilQ5s+fz3333UfHjh1NR8kXWrQlIjo1LQVGZmYmnp6eLF68mIYNG5qOky8uXLhA\npUqV+O6776hWrZrpOCJigCZiKTCmT5/OE0884TAlDFC8eHH69u1rVzcsEZHc0UQsBcKpU6eoXr06\nmzdvxtPT03ScfJWcnEz9+vU5evQozs7OpuOISD7TRCwFwvjx4+nevbvDlTBAlSpV8PPzY/Hixaaj\niIgBmojFuIMHD/LEE0+wZ88eKlSoYDqOEStWrGDixIl6VrGIA9JELMa9+eabDB482GFLGKBt27b8\n8ssv7Nixw3QUEclnKmIxatu2bWzcuJHXXnvNdBSjihYtSkBAgC5lEnFAOjUtxlitVp588kl69epF\n//79Tccx7vjx49SoUYPDhw9TqlQp03FEJJ9oIhZjVq1axcmTJ+nTp4/pKAVCxYoVadGiBf/5z39M\nRxGRfKQiFiMuXbrEiBEjmDJlCsWK6bHYf/jjTls6USXiOFTEYkR0dDTly5enbdu2pqMUKM2aNePy\n5cts2rTJdBQRySf6jFjy3fnz5/H09GTZsmXUr1/fdJwCZ/r06WzdupVPPvnEdBQRyQcqYsl348eP\nZ9euXSxatMh0lAIpNTWVKlWqkJiY6NCXdIk4ChWx5KsTJ07g7e3N1q1b8fDwMB2nwOrXrx+enp6M\nHDnSdBQRyWMqYslXr7zyCsWKFeO9994zHaVAi4uL4/nnn+fAgQMULVrUdBwRyUNarir5Zv/+/Xz6\n6afs3bvXdJQCz8/Pj7Jly/LVV1/Rpk0b03FEJA9p1bTkmzfeeIMhQ4ZQrlw501EKhT8uZRIR+6ZT\n05IvtmzZQteuXUlKStKj/nLo/PnzuLm5sX37dtzd3U3HEZE8oolY8pzVamXYsGGMGzdOJZwLJUqU\noFevXsyePdt0FBHJQypiyXMrVqwgLS2NF1980XSUQicwMJA5c+aQnZ1tOoqI5BEVseSpa29lqdW/\nuVejRg1q1KjBsmXLTEcRkTyiIpY8NWfOHB5++GFatWplOkqhpUVbIvZNi7Ukz5w7dw5PT09WrlzJ\n448/bjpOoZWdnY27uztr167F29vbdBwRsTFNxJJn3nnnHZ588kmV8F269957eemll4iKijIdRUTy\ngCZiyRPHjx+nZs2axMfH8+ijj5qOU+ilpKRQt25dUlJSKFGihOk4ImJDmoglT4SGhtKnTx+VsI24\nubnRqFEjFi5caDqKiNiYJmKxuX379tG4cWMSExMpU6aM6Th2IyYmhtGjRxMfH4/FYjEdR0RsRBOx\n2NyoUaMYPny4StjGWrZsSWpqKvHx8aajiIgNqYjFpjZt2sT27dsZNGiQ6Sh2p0iRIgwcOFCXMonY\nGZ2aFpuxWq384x//IDg4WHfRyiMnT57E09OT5ORkSpcubTqOiNiAJmKxmaVLl5KZmUnPnj1NR7Fb\n5cuXp02bNnz88cemo4iIjWgiFpu4ePEi3t7eRERE0KJFC9Nx7NqmTZvo378/e/fu1aItETugiVhs\nYvbs2VSpUkUlnA8aNWpEsWLF+Oabb0xHEREb0EQsd+3s2bN4enqyZs0a6tSpYzqOQ3j//fdZv349\nn332mekoInKXVMRy18aMGUNKSoo+t8xHZ8+exd3dnT179vDggw+ajiMid0FFLHfll19+wcfHhx07\nduDm5mY6jkMZOHAgjzzyCGPGjDEdRUTugopY7sqAAQMoU6YMU6ZMMR3F4ezcuZP27dtz6NAhihUr\nZjqOiNwh/e2VO7Z7926++OILkpKSTEdxSHXq1OGRRx5h1apVdOzY0XQcEblDWjUtd2zkyJGMGjWK\n+++/33QUhxUUFKQ7bYkUcjo1LXdk/fr19O3bl3379lG8eHHTcRxWVlYWlSpVYsuWLXh4eJiOIyJ3\nQBOx5JrVamX48OFMnDhRJWyYk5MT/v7+zJo1y3QUEblDKmLJtc8++4wrV67QrVs301GEq6uno6Oj\nycrKMh1FRO6AilhyJTs7m1GjRjF16lSKFNH/PgVBtWrVqFOnDkuWLDEdRUTugH6SSq5ERUVRvXp1\nnnzySdNR5BpatCVSeGmxluRYWloanp6erF27llq1apmOI9e4dOkSlStXZvXq1fj6+pqOIyK5oIlY\ncmzKlCm0a9dOJVwAFStWjAEDBhAVFWU6iojkkiZiyZFjx45Ru3ZtfvzxRx555BHTceQmfv75Z3x8\nfDhy5Aiurq6m44hIDmkilhwZO3YsgYGBKuEC7OGHH+bJJ59kwYIFpqOISC5oIpbbSkhIoHnz5iQl\nJVGqVCnTceRvfP311wwZMoSdO3disVhMxxGRHNBELLc1YsQIRo8erRIuBJ566ikyMzP5/vvvTUcR\nkRxSEcvfWrt2LUlJSQwcONB0FMmBIkWKEBgYqEuZRAoRnZqWW7py5Qp+fn6MGDGC559/3nQcyaHT\np0/j4eHBgQMHKFeunOk4InIbegyi3NKiRYsoWrQoXbt2NR1FcqFs2bJ07NiRmTNn4lqiBEk//cS5\ntDRKliqFp68v/n37Ur58edMxReR/NBHLTV24cIHq1asTHR1N06ZNTceRXIiLiyNk2DDWf/st3YsX\np35WFq5AOrDN2ZllVittW7fm1VGj8PPzMx1XxOGpiOWmpk2bxvr161mxYoXpKJILsyMjCRk6lOGZ\nmfSxWil9k21SgWiLhbednQkNDycgKCi/Y4rINVTEcoPU1FS8vLxYv3493t7epuNIDs2OjGTK0KF8\nlZFB1f+99j4QDSQALwAfXbP9AaCliwsjVMYiRqmI5QbDhw/n999/Z/bs2aajSA7FxcXRoVkzNl5T\nwgDLuXppxFdAJn8tYrhaxo1dXFi5YQP16tXLp7Qici0VsfzFkSNHeOyxx0hISOChhx4yHUdyqFeX\nLtRbvpzBt/jrPAb4mRuLGOBdi4XtnTsz//PP8zKiiNyCilj+onfv3lSuXJmwsDDTUSSHTpw4gZe7\nO8lZWTf9TBj+vojPAB5OTiSlpGg1tYgBuqGH/GnHjh3ExsYybNgw01EkF+ZFR9MZblnCt1MG6Gyx\nMC862nahRCTHVMTypxEjRjB27Fg9uaeQSfrpJ+pnZd3VPvwyM0lKSLBRIhHJDRWxABAbG8vhw4cZ\nMGCA6SiSS+fS0rjbX51cgfTUVFvEEZFcUhELly9fZvjw4UyePJl77rnHdBzJpZKlSpF+i/cuA1n/\n++cl4ML//v166YBr6Ts9uS0id0NFLCxYsAAXFxc6d+5sOorkUmZmJmezs9l4i0cejgdcgCnAgv/9\n+4SbbLfN2RlPH588yykit6YidnCZmZmMHj2aqVOn6vm1hcj+/fsZMmQIbm5unDx9mi+LFeNmJ5ZD\ngCtcnYL/+DP2um3OAJ9mZmIpWpTs7Oy8DS4iN1ARO7iZM2dSr149GjVqZDqK3MalS5dYvnw5zzzz\nDI0aNaJYsWJs3bqVtWvX0r5dOz6+w1+kPrZYaNa0KbGxsVSrVo2oqCguXLhg4/Qiciu6jtiBnT59\nmurVq7Np0ya8vLxMx5Fb+PXXX/nwww+ZPXs2lSpVIjg4mOeeew4nJ6c/t7nVnbVu5/o7a23ZsoWw\nsDB27drFyJEj6dev31+OIyK2p4nYgU2YMIGuXbuqhAsgq9XKhg0b6NatG97e3hw7doyVK1eyefNm\nevXqdUM5+vn5ERoeTksXFw7k8Bh/3Gs6NDz8z9tbNmjQgNWrV7NkyRJWr15N1apVmTlzJll3eXmU\niPwNqzik5ORka9myZa3Hjx83HUWu8fvvv1tnzpxp9fb2ttaoUcM6Y8YM6++//57jr58VEWGt6OJi\nnWaxWM+A1XqTP6fB+o7FYq3o4mKdFRHxt/uLj4+3dujQwfrQQw9Z33vvPWtGRsbdfosich2dmnZQ\nPXv2xMvLi7Fjr1+6Iyb8+OOPREREsHjxYlq0aEFwcDBNmza9owV08fHxTJ80iS9Xr6azxYJfZuaf\nzyOO+9/ziNu1acOro0bl+EEPO3bsICwsjK1btzJs2DAGDhyIi4tLrrOJyI1UxA7ohx9+oH379iQl\nJVGyZEnTcRzWhQsXWLJkCRERERw5coSBAwfSv39/HnzwQZvs/+TJk8yLjiYpIYH01FRcS5fG08eH\n3n363PE9pX/88UfGjRvHd999x5AhQwgKCqJEiRI2ySviqFTEDsZqtfL000/TvXt3AgICTMdxSIcO\nHWLWrFl89NFH1KlTh6CgINq3b0+xYsVMR8uxhIQExo0bx7fffsvrr79OcHCwfqkTuUNarOVg1qxZ\nw6+//kq/fv1MR3Eoly9fZtWqVbRt2xY/Pz+ys7PZtGkTsbGxdO7cuVCVMICPjw+LFy9m7dq1bN++\nHQ8PDyZNmkR6+q3u8SUit6KJ2IFcvnyZOnXqMGHCBDp06GA6jkM4efIkc+bMYdasWZQrV47g4GC6\ndetmd5+v7tmzhwkTJvDf//6XV199lUGDBnHfffeZjiVSKGgidiDz5s2jdOnStG/f3nQUu2a1Wvnu\nu+/o1asX1apVIykpicWLFxMXF0ffvn3troQBvL29WbBgARs3bmTfvn14eHgQFhZGWlqa6WgiBZ4m\nYgeRkZGBl5cXS5Ys4YknnjAdxy6dO3eOBQsWEBERQWZmJkFBQfj7+1OmTBnT0fJdUlISEydOZNWq\nVbz88ssMHjyY+++/33QskQJJE7GDmD59Og0bNlQJ54Hdu3fzyiuv4ObmxldffUV4eDj79u3jtdde\nc8gSBvD09CQ6Oprvv/+elJQUqlatytixYzlz5ozpaCIFjiZiB3Dy5Elq1KjBli1bqFo1NzdAlFvJ\nzs5m2bJlREREsH//fvr378+AAQOoVKmS6WgFUnJyMpMmTWLp0qUEBgby+uuvU7ZsWdOxRAoEFbED\nePXVV7FarcyYMcN0lEIvJSWF2bNnM2fOHKpXr05wcDCdOnXSc5xz6PDhw0yaNIklS5YQEBDAkCFD\nKFeunOlYIkbp1LSdO3DgAAsWLGDMmDGmoxRaV65cITY2lk6dOlGnTh3Onj3L2rVr+eabb+jatatK\nOBcqV67MrFmz2LFjB7///jteXl4MHz6cEydOmI4mYowmYjvXrVs3ateuzRtvvGE6SqFz+vRpoqOj\niYyMpGTJkgQHB/PCCy/oxhU2dPToUaZMmcLChQvp27cvw4YN44EHHjAdSyRfaSK2Y1u3buW7775j\n8ODBpqMUGlarlW3bttGnTx88PDzYuXMn8+fPZ8eOHQQEBKiEbaxSpUr8+9//5qeffiI7O5saNWrw\n+uuvc/z4cdPRRPKNithOWa1Whg8fTmhoqF1et2prGRkZzJkzBz8/P7p37463tzf79+9n/vz5NGzY\n8I4eviA59/DDDzNjxgx27dqF1WqlZs2aDB48mF9++cV0NJE8pyK2U19++SWnT5/G39/fdJQCLTEx\nkddee41KlSqxfPlywsLC2L9/P8OHD7/jByPInXvooYd499132b17N0WLFsXHx4dBgwZx7Ngx09FE\n8oyK2A5dunSJESNGMGXKlEJ3D+P8cOnSJZYuXUrz5s1p0qQJTk5O/PDDD6xcuZI2bdpQtGhR0xEd\nXsWKFXnnnXfYs2cPTk5O1K5dm5dffpmjR4+ajiZicypiOzR37lweeOAB2rRpYzpKgfLLL78QGhqK\nu7s706ZNo1+/fqSkpDBp0iQqV65sOp7cxAMPPMDUqVPZt28frq6u1KlTh8DAQI4cOWI6mojNqIjt\nzPnz53nrrbd4++239bkmVz8rX7duHc899xw1a9bk+PHjxMTEsGnTJl544QWKFy9uOqLkQPny5Zk8\neTKJiYmUKVOGxx57jICAAA4dOmQ6mshdUxHbmWnTptGkSRP8/PxMRzHq999/Z8aMGXh7e/Ovf/2L\np556iiNHjhAZGYmvr6/peHKHypUrx8SJE0lKSqJChQrUq1ePl156ieTkZNPRRO6YriO2I7/99hve\n3t7ExcVRpUoV03GM2L59O5GRkSxZsoRWrVoRFBRE48aNdXbATqWmpvLee+/x/vvv0759e958803d\nxlUKHU3EdiQsLIzevXs7XAlnZWUxb948GjRoQKdOnahcuTJ79+5l4cKFNGnSRCVsx0qXLk1oaCgH\nDhygcuXKNGzYEH9/f5KSkkxHE8kxTcR2IjExkUaNGpGYmOgwN9M/ePAgUVFRREdH8/jjjxMcHEyb\nNm20UtyBpaWlMXPmTKZPn07Lli0ZPXo01atXNx1L5G9pIrYTb7zxBsOGDbP7Er58+TIrV66kdevW\nNGjQAIDvv/+eNWvW0KFDB5WwgytVqhSjR4/m4MGDeHt706RJE1544QX27NljOprILWkitgObN2+m\ne/fuJCYm4uzsbDpOnvjtt9+YM2cOs2bN4sEHHyQoKIjnn3/ebr9fsY309HTef/993n33XZo1a8aY\nMWOoVauW6Vgif6GJuJCzWq0MGzaMcePG2V0pWa1WNm7cSI8ePahevTrJycksXbqULVu24O/vb3ff\nr9ieq6srI0eO5ODBg9SrV4/mzZvTtWtXEhISTEcT+ZOKuJBbvnw5586do1evXqaj2MzZs2eJiIjA\n19eX/v3706BBA5KTk/nwww95/PHHTceTQqhkyZIMGzaMgwcP0qBBA5555hmeffZZfvzxR9PRRHRq\nujC7ePEitWrVYsaMGbRs2dJ0nLuWkJBAREQEixYt4umnnyYoKIinnnpKq57F5jIyMpg9ezZvv/02\n9evXZ+zYsTz22GOmY4mD0kRciM2ZMwc3NzeeeeYZ01Hu2IULF1i4cCGNGzemVatWVKxYkV27drFk\nyRKefvpplbDkCRcXFwYPHszBgwd56qmnaN++PR06dCA+Pt50NHFAmogLqfT0dDw9PVm9ejV169Y1\nHSfXjhw5wqxZs5gzZw4+Pj4EBQXRoUMH7rnnHtPRxAFlZWXx4YcfMnnyZGrXrk1ISAj169c3HUsc\nhCbiQuqdd96hefPmhaqEr1y5QkxMDO3bt+exxx4jIyODDRs28PXXX/Pss8+qhMUYJycnXnnlFQ4e\nPEi7du1Rn41EAAAMsklEQVR47rnnaN26NVu2bDEdTRyAJuJC6Ndff6VWrVps374dd3d303Fu69Sp\nU8ydO5eoqChKlSrFyy+/TPfu3SlRooTpaCI3deHCBaKjo5k0aRKenp6EhITQqFEj07HETqmIC6HA\nwEBcXV2ZOnWq6Si3ZLVa2bp1KxEREaxYsYJOnToRFBRE/fr19bmvFBrZ2dnMmzePCRMm4OHhQUhI\nCI0bNzYdS+yMiriQ2bt3L02bNiUxMZHSpUubjnOD8+fP88knnxAREUF6ejqBgYH07dvX7u/4Jfbt\n4sWLzJ8/nwkTJuDu7k5ISAhNmzY1HUvshIq4kOnUqRONGzdmyJAhpqP8xd69e4mMjGTBggX885//\nJDg4mBYtWlCkiJYhiP24ePEin3zyCePHj+ehhx4iJCSEJ598Umd55K6oiAuRjRs38uKLL7Jv3z6c\nnJxMx+HixYt88cUXREREsGfPHvr3709AQABubm6mo4nkqUuXLrFw4ULGjx9PhQoVCAkJ0eV2csdU\nxIWE1WqlYcOGDBo0iJ49exrNcuzYMT744AM++OADqlWrRlBQEF26dOHee+81mkskv12+fJlFixYx\nbtw4ypYty9ixY3nmmWdUyJIrOm9YSHz++edkZ2fTo0cPI8e/cuUKX3/9NV26dMHX15dTp04RGxvL\nhg0b6N69u0pYHFLRokXp2bMnu3fv5pVXXuG1116jYcOGxMTEoBlHckoTcSGQnZ1NzZo1iYqK4umn\nn87XY6emphIdHU1kZCROTk4EBwfTs2dPXF1d8zWHSGFw5coVlixZQlhYGCVKlGDs2LG0adNGE7L8\nLRVxIfDvf/+bVatWERMTk2/HjI+PJyIigqVLl9K2bVuCg4P5xz/+oR8oIjlw5coVli5dSlhYGPfe\ney9jx46lffv2+vsjN6UiLuDOnj2Lp6cnsbGx+Pr65umxMjMz+fTTT4mIiODEiRMEBgbSr18/KlSo\nkKfHFbFXV65c4YsvviAsLAyLxcLYsWPp2LGjCln+QkVcwI0ePZqff/6ZuXPn5tkx9u/fT1RUFB9/\n/DFPPPEEQUFBtG7dmqJFi+bZMUUcidVqZcWKFYSFhXH58mXGjBlD586ddXmfACriAu3nn3/G19eX\nnTt3UqlSJZvu+9KlS3z55ZdERESwc+dO+vbty8CBA6lSpYpNjyMi/89qtbJq1SpCQ0O5cOECY8aM\n4dlnn1UhOzgVcQHWv39/ypcvz6RJk2y2z19//ZUPP/yQ2bNnU6lSJYKDg3nuuecKxHXJIo7CarUS\nExNDaGgo586dY8yYMXTt2lVnoRyUiriA2rVrF08//TRJSUmUKlXqrvZltVr59ttviYiIIDY2luef\nf56goCDq1Kljo7QiciesVitfffUVoaGhpKWlMXr0aLp166ZCdjAq4gKqXbt2NG/enMGDB9/xPtLS\n0pg/fz6RkZFYrVaCgoLo3bv3XRe7iNiW1Wrl66+/JjQ0lFOnTjF69Gi6d+9OsWLFTEeTfKAiLoC+\n+eYbXnrpJfbu3Uvx4sVz/fU7d+4kMjKSxYsX06JFC4KDg2natKlWaooUcFarlXXr1hEaGsrx48cZ\nPXo0L7zwggrZzqmIDTlx4gTzoqNJ+uknzqWlUbJUKTx9fXnR35927doxZMgQunfvnuP9ZWVlsWTJ\nEiIiIkhJSWHgwIH079+fBx98MA+/CxHJK+vXryc0NJSjR4/y5ptv0qtXL+655x7TsSQPqIjzWVxc\nHNMnTWJVTAxdAL+sLFyBdGCbszOfX7pEyRIlWLpmDU888cRt93fo0CFmzZrFRx99RJ06dQgODqZd\nu3b6DVrETnz77beEhoZy6NAh3nzzTXr37q1CtjMq4nw0OzKSkKFDGZGZib/Vys2eJpwKzLVYmOrs\nTGh4OAFBQTdsc/nyZdasWUNERARbt27F39+fwMBAqlWrluffg4iYsWnTJkJDQzlw4ACjRo2iT58+\nuse7nVAR55PZkZFMGTqUrzIyqJqD7Q8ALV1cGHFNGZ84cYKPPvqIqKgoKlSoQFBQEN26dcPFxSVP\ns4tIwbF582bCwsLYu3cvo0aNom/fvne0lkQKDhVxPoiLi6NDs2ZsvK6EXwS+BjKAckA/4M1r3j8A\nNHZxYfyMGaxbt47Vq1fTuXNngoKC8PPzy79vQEQKnC1bthAWFsauXbsYOXIk/fr10/0ACikVcT7o\n1aUL9ZYvZ/B1/6n3AFUAJyAJaAJ8DLS8Zptw4O0SJRg1bhz+/v6UKVMmn1KLSGEQFxdHWFgYO3bs\nYMSIEQwYMECFXMioiPPYiRMn8HJ3Jzkr66afCf8hEWgOfAE8ds3rZwAPJyeSUlIoX758XkYVkULs\nhx9+ICwsjPj4eIYPH05AQADOzs6mY0kO6AaneWxedDSd4ZYl/DJQAqjF1dPSj133fhmgs8XCvOjo\nPMsoIoXf448/zhdffMGXX37J+vXr8fDwYNq0aWRkZJiOJrehIs5jST/9RP2srFu+/z5wjqufFY8G\n4m6yjV9mJkkJCXkTUETsSt26dVm2bBkxMTFs3rwZDw8PwsPDOX/+vOlocgsq4jx2Li0N19tsYwGa\nAl2BhTd53xVIT021dTQRsWO1a9dmyZIlxMbGsm3bNqpUqcKUKVM4d+6c6WhyHRVxHitZqhTpOdz2\nEnCzC5HSAdfSf/cJs4jIzfn4+LB48WLWrVvHzp078fDwYNKkSaSn5/Qnk+Q1FXEe8/T1ZdtNVjCe\nBD4FzgNXgK+Az4CON9lHnLMznj4+eRlTROxczZo1WbhwIevXr2fXrl14eHgwYcIEzp49azqaw9Oq\n6Tx2q1XTp4DngJ8AK1ANGAO0v+7rtWpaRPJCYmIiEyZMICYmhkGDBvGvf/2L+++/33Qsh6SJOI9V\nqFCBtq1b8/F1Tz4qB6znatGmAtu4sYQBPrZYaNemjUpYRGzKy8uLefPmsXnzZpKTk6latSpvvfUW\nqVqPku80EeeDW91Z63b+uLPWyg0bqFevXl7FExHhwIEDTJw4kRUrVhAUFMRrr72WqxsI3eqJcv59\n+2qQuA1NxPnAz8+P0PBwWrq4cCCHX/PHvaZDw8NVwiKS56pWrcpHH33Etm3bOH78ONWqVePNN9/k\n9OnTf/t1cXFx9OrSBS93d/aGhPDYggW0/fJLHluwgD1vvYWnmxu9unQhLu5mF2cKAFbJN7MiIqwV\nXVys0ywW6xmwWm/y5zRY37FYrBVdXKyzIiJMRxYRB3Xo0CFrQECAtUyZMtaRI0daT548ecM2f/xM\ne/dvfqadAes0/Uz7Wzo1nc/i4+OZPmkSX65eTWeLBb/MzD+fRxzn7Mwyq5V2bdrw6qhRmoRFxLiU\nlBQmT57Mp59+yksvvcTQoUOpUKGCTZ4oJ1epiA05efLk1c9TEhJIT03FtXRpPH186N2njz5PEZEC\n5+jRo0yZMoWFCxfSunVrvl66lE2ZmX+WcDYQzNW7BKYCHsBEoNU1+9C6l5tTEYuISI79/PPPtGrS\nhD7JyQy55vUMrj4tri9QCVgF9AB2AW7XbPeuxcL2zp2Z//nn+Za5oFMRi4hIjuX0iXIAtYG3gM7X\nvKZ7I9xIq6ZFRCTHbvdEuT/8BuwHal73up4odyMVsYiI5NjtnigHV++b3wvoA3je5H09Ue6vVMQi\nIpJjt3uinJWrJVwcmHmLbfREub8qZjqAiIgUHrd7otxLXL2X/mqg6C220RPl/koTsYiI5NitnigH\nEAjsA1YA9/7NPvREub/SqmkREcmxW62aTgEqA078/yRsAWZx9TKmP2jV9I00EYuISI7d6olyblx9\ntnoGV089pwNn+WsJg54odzOaiEVEJFf0RDnb0kQsIiK5oifK2ZaKWEREci0gKIgR4eE0dnHhXYuF\nW12MdAaYZrHQWA98uCWdmhYRkTumJ8rdPRWxiIjcNT1R7s6piEVERAzSZ8QiIiIGqYhFREQMUhGL\niIgYpCIWERExSEUsIiJikIpYRETEIBWxiIiIQSpiERERg1TEIiIiBqmIRUREDFIRi4iIGKQiFhER\nMUhFLCIiYpCKWERExCAVsYiIiEEqYhEREYNUxCIiIgapiEVERAxSEYuIiBikIhYRETFIRSwiImKQ\nilhERMQgFbGIiIhBKmIRERGDVMQiIiIGqYhFREQMUhGLiIgYpCIWERExSEUsIiJikIpYRETEIBWx\niIiIQSpiERERg1TEIiIiBqmIRUREDFIRi4iIGKQiFhERMUhFLCIiYpCKWERExCAVsYiIiEEqYhER\nEYNUxCIiIgapiEVERAxSEYuIiBikIhYRETFIRSwiImKQilhERMQgFbGIiIhBKmIRERGDVMQiIiIG\nqYhFREQMUhGLiIgY9H8jVYI4xjKLCgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"G2 = nx.Graph()\n",
"for i, j in [(1, 2), (1, 3), (1, 0), (3, 0)]:\n",
" G2.add_edge(i,j)\n",
"nx.draw(G2,pos = pos, with_labels = True)"
]
},
{
"cell_type": "code",
"execution_count": 198,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.6\n"
]
}
],
"source": [
"print(nx.transitivity(G2))"
]
},
{
"cell_type": "code",
"execution_count": 219,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xt0zXe+//HXliAXkQnl6LQSlYuWCaritOO41FC3MtJS\n6jiIamTvTk/bqWotlzRRk+ovHavTmdyUiajRGqMXLWXKoJRKWipKRQTRi0lKGiGJuOzfH6pHSSoi\nO599eT7Wsmrt/d3bS9eyX3l/9+f7/VjsdrtdAADAiEamAwAA4MkoYgAADKKIAQAwiCIGAMAgihgA\nAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIG\nAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKI\nAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMo\nYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAg\nb9MBAGdSVFSkrMxM5e3erVOlpWoWGKiIzp01ISZGrVq1Mh0PgBuy2O12u+kQgGnZ2dl6JSlJ769Z\nowckRVVWKkBSmaQdvr56y27X0MGD9cT06YqKijKcFoA7oYjh8TJSUxU/daqerajQBLtdQdUcUyIp\n02LRS76+SkhOVqzV2tAxAbgpihgeLSM1VfOmTtXa8nKF1eL4fEkD/fz0LGUMoJ5QxPBY2dnZGt63\nrz66ooRLJE2S9E9JrST9QdLDlz2fL6mXn59Wbdqk7t27N1xgAG6JVdPwWK8kJenZioqrJmGbJB9J\nxZJel2SVtO+y58MkTauo0CtJSQ0TFIBbYyKGRyoqKlKHkBAVVFb+5DvhcklBkvZKCv3hsQmSbtHF\nyfiSE5JCfXyUV1jIamoAN4SJGB4pKzNT0dJVC7PyJDXW/5WwJHWR9MUVx7WQFG2xKCsz02EZAXgG\nihgeKW/3bvWorLzq8VOSml/xWHNdvIzpSlEVFcrLzXVAOgCehCKGRzpVWqqAah5vJunkFY+VStUe\nGyCprKSkvqMB8DAUMTxSs8DAaqfcCEnnJB287LHPJXWq5tgySQFB1V11DAC1RxHDI0V07qwdPj5X\nPe4n6QFJs3Vx4dYWSask/U8175Ht66uIyEhHxgTgAVg1DY9U06pp6afXEd8kaZ6k0Vccw6ppAPWF\niRgeqXXr1ho6eLAWWyxXPRck6S1dXLh1WFeXsCQttlh0/5AhlDCAG8ZEDI9V0521roU7awGoT0zE\n8FhRUVFKSE7WQD8/5dfyNZfuNZ2QnEwJA6gXFDE8WqzVqmeTk9XLz0/zLRbVdDHSCUkvWyzqxYYP\nAOoZp6YBSTk5OXolKUnvrV6taItFURUVP+5HnO3rq7+fPauQW29V5t//ziQMoF5RxMBliouLlZWZ\nqbzcXJWVlCggKEgRkZG6b9Ag9e7dW0eOHFHz5lfeewsA6o4iBmpp5MiR6tevn2w2m+koANwI3xED\ntWS1WpWamip+dgVQnyhioJb69eunqqoqbd261XQUAG6EIgZqyWKxKC4uTqmpqaajAHAjfEcMXIcT\nJ06offv2OnDgAHfVAlAvmIiB69CiRQtFR0frr3/9q+koANwEEzFwnXbs2KGHH35YBw4cUKNG/CwL\n4MbwKQJcp6ioKP3iF7/QunXrTEcB4AYoYuA6WSyWHy9lAoAbxalpoA5Onz6t4OBg7dy5U8HBwabj\nAHBhTMRAHfj7+2vs2LFasGCB6SgAXBwTMVBHX3zxhfr376/CwkI1btzYdBwALoqJGKijTp06KSIi\nQm+//bbpKABcGEUM3AAWbQG4UZyaBm5AVVWVgoODtXHjRt1+++2m4wBwQUzEwA1o0qSJJk2apLS0\nNNNRALgoJmLgBh0+fFh33XWXjh49Kj8/P9NxALgYJmLgBrVr10733HOP3njjDdNRALggihioByza\nAlBXFDFQDwYNGqTi4mLl5OSYjgLAxVDEQD3w8vLSlClTmIoBXDcWawH1pKioSB06dFBBQYGCgoJM\nxwHgIpiIgXrSunVrDRo0SFlZWaajAHAhTMRAPdq8ebOmTJmivXv3ymKxmI4DwAUwEQP1qFevXvLy\n8tKmTZtMRwHgIihioB5ZLBbFxcWxaAtArXFqGqhnpaWlateunfbt26c2bdqYjgPAyTERA/UsMDBQ\no0aN0sKFC01HAeACmIgBB9i5c6dGjBihgoICeXl5mY4DwIkxEQMOcOedd6pNmzZavXq16SgAnBxF\nDDgI958GUBucmgYcpKKiQm3btlV2drZuu+0203EAOCkmYsBBfH19NX78eKWnp5uOAsCJMREDDpSX\nl6devXqpsLBQTZs2NR0HgBNiIgYcKCIiQpGRkfrHP/5hOgoAJ0URAw7Goi0AP4dT04CDnT17Vu3a\ntdMHH3ygyMhI03EAOBkmYsDBGjdurMmTJystLc10FABOiIkYaABfffWVOnfurMLCQjVr1sx0HABO\nhIkYaAC33nqr+vTpo6VLl5qOAsDJUMRAA7m0aIuTUAAuRxEDDaR///46deqUtm/fbjoKACdCEQMN\npFGjRoqLi2PRFoCfYLEW0ICOHz+usLAw5efnq2XLlqbjAHACTMRAA2rZsqWGDRumzMxM01EAOAkm\nYqCBbdu2TePHj9f+/fvVqBE/CwOejk8BoIHdfffd8vf31/r1601HAeAEKGKggVksFu4/DeBHnJoG\nDCgrK1NISIhyc3N1yy23mI4DwCAmYsCAgIAAjRkzRgsWLDAdBYBhTMSAIbm5uRo0aJAOHz6sxo0b\nm44DwBAmYsCQyMhI3XbbbVq1apXpKAAMoogBg1i0BYBT04BBZ86cUdu2bbV161aFh4ebjgPAACZi\nwKCmTZsqJiaG+08DHoyJGDCsoKBAPXr00NGjR+Xr62s6DoAGxkQMGNa+fXtFRUVp+fLlpqMAMIAi\nBpwAi7YAz0URA05g6NCh+uabb7Rz507TUQA0MIoYcAJeXl6KjY1lKgY8EIu1ACdx7Ngx3XHHHTp8\n+LACAwNNxwHQQJiIASfRpk0bDRgwQK+//rrpKAAaEEUMOJFLi7Y4UQV4DooYcCJ9+/bV+fPntWXL\nFtNRADQQihhwIhaLRXFxcSzaAjwIi7UAJ1NSUqL27dtr//79at26tek4AByMiRhwMkFBQYqOjtai\nRYtMRwHQAJiIASeUnZ2thx56SPn5+fLy8jIdB4ADMREDTigqKkotW7bU2rVrTUcB4GAUMeCkuP80\n4Bk4NQ04qdOnTys4OFifffaZQkJCTMcB4CBMxICT8vf317hx45SRkWE6CgAHYiIGnNi+fft07733\nqrCwUE2aNDEdB4ADMBEDTuyOO+7QHXfcobfeest0FAAOQhEDTo5FW4B749Q04OSqqqoUEhKi9evX\nq2PHjqbjAKhnTMSAk2vSpIkeeeQRpaWlmY4CwAGYiAEXUFhYqDvvvFOFhYXy9/c3HQdAPWIiBlxA\ncHCwevbsqWXLlpmOAqCeUcSAi7i0aIuTWIB7oYgBFzFw4ECVlJQoJyfHdBQA9YgiBlxEo0aNNGXK\nFC5lAtwMi7UAF1JcXKyIiAgVFBQoKCjIdBwA9YCJGHAhrVq10pAhQ7R48WLTUQDUEyZiwMVs2bJF\nkydP1r59+2SxWEzHAXCDmIgBF9OzZ095e3vrX//6l+koAOoBRQy4GIvFwv2nATfCqWnABZ08eVIh\nISHau3evbr75ZtNxANwAJmLABTVv3lwPPfSQXnvtNdNRANwgJmLARe3atUvDhg3ToUOH5O3tbToO\ngDpiIgZcVNeuXXXrrbfq/fffNx0FwA2giAEXxqItwPVxahpwYZWVlWrbtq22b9+u0NBQ03EA1AET\nMeDCfHx8NGHCBKWnp5uOAqCOmIgBF3fgwAH17NlThYWF8vHxMR0HwHViIgZcXHh4uLp27aoVK1aY\njgKgDihiwA2waAtwXRQx4AaGDRumI0eOaPfu3aajALhOFDHgBry9vfXoo48qLS3NdBQA14nFWoCb\n+PrrrxUZGakjR44oICDAdBwAtcREDLiJW265Rffee6+WLl1qOgqA60ARA27k0qItTnQBroMiBtxI\nv379VFFRoW3btpmOAqCWKGLAjTRq1EhxcXFcygS4EBZrAW7m+PHjCg0NVX5+vm666SbTcQBcA0UM\nuKEJEyaoXbt2CvD3V97u3TpVWqpmgYGK6NxZE2Ji1KpVK9MRAfyAIgbcTHZ2tuKfeUYbN2/WmKZN\n1aOyUgGSyiTt8PXVW3a7hg4erCemT1dUVJTpuIDHo4gBN5KRmqr4qVM1raJCE+12BVVzTImkTItF\nL/n6KiE5WbFWa0PHBHAZFmsBbiIjNVXzpk7VR+XleuqHEv6LpChJPpIm/XBckKSn7HZ9VF6ueVOn\nKoOFXYBRTMSAG8jOztbwvn31UXm5wi57/G1d/Gl7raQKSYuueF2+pF5+flq1aZO6d+/eQGkBXI6J\nGHADryQl6dmKip+UsCSNkDRcUosaXhcmaVpFhV5JSnJoPgA1YyIGXFxRUZE6hISooLKy2u+EJWmW\npK919UQsSSckhfr4KK+wkNXUgAFMxICLy8rMVLRUYwlfSwtJ0RaLsjIz6y8UgFqjiAEXl7d7t3pU\nVt7Qe0RVVCgvN7eeEgG4HhQx4OJOlZbqRjc9DJBUVlJSH3EAXCeKGHBxzQIDVVbDc+clVf7w33OS\nzvzw+yuVSQoIquvJbQA3giIGXFhFRYVOVlXpI4ul2udfkOQnaZ6kpT/8fm41x+3w9VVEZKTDcgKo\nGUUMuKADBw7o6aefVnBwsIqPH9d73t6q7sRyvKQLujgFX/o1+4pjTkh6s6JCFi8vVVVVOTY4gKtQ\nxICLOHfunN5++23dd9996tmzp7y9vfXJJ59o/fr1Gnb//Vpcw1R8LYstFvXt00fr1q1TeHi40tLS\ndObMmXpOD6AmXEcMOLlvv/1Wr732mjIyMtS2bVvZbDaNHDlSPj4+Px5T0521ruXKO2tt375diYmJ\n2rNnj5577jlNmjTpJ38OgPrHRAw4Ibvdrk2bNmn06NHq2LGjvvrqK61atUoff/yxxo0bd1U5RkVF\nKSE5WQP9/JRfyz8jX9JAPz8lJCf/eHvLu+++W6tXr9aKFSu0evVqhYWF6dVXX1XlDV4eBaBmTMSA\nEyktLdWSJUuUmpoqu90uq9Wq8ePHKzAwsFavr83uSyd0cfel/1eL3Zc+/fRTJSYmKicnR9OmTVNs\nbKx8fX3r9pcDUC2KGHACn3/+uVJSUrR8+XINGDBANptNffr0kaUO3/vm5OTolaQkvbd6taItFkVV\nVPy4H3H2D/sR3z9kiJ6YPr3WGz3s3LlTiYmJ+uSTT/TMM89oypQp8vPzu+5sAK5GEQOGnDlzRitW\nrFBKSoqOHDmiKVOmaPLkybr55pvr5f2Li4uVlZmpvNxclZWUKCAoSBGRkRo/cWKd7yn9+eefa86c\nOdq6dauefvppWa1W+fv710tewFNRxEADO3TokNLT07Vo0SJ17dpVVqtVw4YNk7e3t+lotZabm6s5\nc+Zo8+bN+v3vfy+bzaZmzZqZjgW4JBZrAQ3g/Pnzev/99zV06FBFRUWpqqpKW7Zs0bp16xQdHe1S\nJSxJkZGRWr58udavX6/PPvtMoaGhSkpKUllZTff4AlATJmLAgYqLi7Vw4UKlp6frpptuks1m0+jR\no93u+9W9e/dq7ty5+uc//6knnnhCjz/+uJo3b246FuASmIiBema327V161aNGzdO4eHhysvL0/Ll\ny5Wdna2YmBi3K2FJ6tixo5YuXaqPPvpIX375pUJDQ5WYmKjS0lLT0QCnRxED9eTUqVNKT09X165d\nFRMTo7vuuksFBQVatGiRoqKiTMdrEB06dNCSJUu0detWFRQUKCwsTM8//7y+//5709EAp0URAzfo\niy++0O9+9zsFBwdr7dq1Sk5O1pdffqmnnnpKLVq0MB3PiIiICGVmZmrbtm0qLCxUWFiYZs+erRMn\nTpiOBjgdihiog6qqKr355pvq06ePBgwYoBYtWujzzz/XypUrNWDAADVqxD8tSQoLC9OiRYu0Y8cO\nffvttwoPD9eMGTN0/Phx09EAp8FiLeA6FBYWKiMjQwsXLtTtt98um82mESNGqHHjxqajuYTDhw8r\nKSlJK1asUGxsrJ5++mnddNNNpmMBRvFjO3ANFy5c0Lp16zRixAh17dpVJ0+e1Pr16/Wvf/1Lo0aN\nooSvQ7t27ZSenq6dO3fq+++/V4cOHTRt2jQVFRWZjgYYw0QM1OD48ePKzMxUamqqmjVrJpvNprFj\nx3Ljinp09OhRzZs3T8uWLVNMTIyeeeYZ/cd//IfpWECDYiIGLmO327Vjxw5NnDhRoaGh2rVrl5Ys\nWaKdO3cqNjaWEq5nbdu21Z///Gft3r1bVVVVuuOOO/T73/9ex44dMx0NaDAUMSCpvLxcCxcuVFRU\nlMaMGaOOHTvqwIEDWrJkie655546bb6A2rvlllv0pz/9SXv27JHdblenTp305JNP6ptvvjEdDXA4\nihgebf/+/XrqqafUtm1bvf3220pMTNSBAwc0bdq0Om+MgLr75S9/qfnz5+uLL76Ql5eXIiMj9fjj\nj+urr74yHQ1wGIoYHufcuXNauXKl+vfvr969e8vHx0effvqpVq1apSFDhsjLy8t0RI/Xpk0bvfzy\ny9q7d698fHzUpUsXPfbYYzp69KjpaEC9Y7EWPMY333yjBQsWKCMjQ7fddptsNpsefPBBNW3a1HQ0\nXENxcbFefvllLViwQKNGjdL06dMVEhJiOhZQL5iI4dbsdrs2bNigkSNHqlOnTjp27JjWrFmjLVu2\naOzYsZSwi2jVqpVefPFF7d+/Xy1atFC3bt0UGxurQ4cOmY4G3DAmYril77//XllZWUpNTZWXl5ds\nNpvGjRvHjkBu4vjx45o/f75SU1M1YsQIzZgxQ+3btzcdC6gTJmK4lc8++0yPPvqobrvtNm3btk3p\n6enKzc2VzWajhN1Iy5Yt9cILLyg/P1+33nqrevTooZiYGOXn55uOBlw3ihgur7KyUllZWbr77rs1\nYsQItWvXTvv27dOyZcvUu3dvLj1yY0FBQUpISFB+fr7atWune+65RxMmTFBeXp7paECtcWoaLuvg\nwYNKS0tTZmam7rrrLtlsNg0ZMkTe3t6mo8GQ0tJSvfrqq3rllVc0cOBAzZw5U7fffrvpWMDPYiKG\nSzl//rxWrVqlwYMH6+6775Ykbdu2TR988IGGDx9OCXu4wMBAzZw5UwcPHlTHjh3Vu3dvjR07Vnv3\n7jUdDagREzFcwr///W8tXLhQ6enpuvnmm2W1WvXQQw/J19fXdDQ4sbKyMv3lL3/R/Pnz1bdvX82a\nNUu/+tWvTMcCfoKJGE7Lbrfro48+0sMPP6zbb79dBQUFWrlypbZv364JEyZQwrimgIAAPffcczp4\n8KC6d++u/v37a9SoUcrNzTUdDfgREzGczsmTJ/X6668rNTVVVVVVstlsGj9+vIKCgkxHg4s7ffq0\n0tLSlJycrF//+teaPXu2unTpYjoWPBxFDKeRm5urlJQUvfHGG/rNb34jq9Wqfv36seoZ9a68vFwZ\nGRl66aWX1KNHD82ePVvdunUzHQseilPTMOrMmTNatmyZevXqpUGDBqlNmzbas2ePVqxYod/85jeU\nMBzCz89PTz75pA4ePKh+/fpp2LBhGj58uHJyckxHgwdiIoYRR44cUXp6uhYuXKjIyEhZrVYNHz5c\njRs3Nh0NHqiyslKvvfaaXnzxRXXp0kXx8fHq0aOH6VjwEEzEaDAXLlzQmjVrNGzYMHXr1k3l5eXa\ntGmTPvzwQz344IOUMIzx8fHR7373Ox08eFD333+/Ro4cqcGDB2v79u2mo8EDMBHD4b777jv99a9/\nVVpamgIDA/XYY49pzJgx8vf3Nx0NqNaZM2eUmZmppKQkRUREKD4+Xj179jQdC26KIoZD2O12ffLJ\nJ0pJSdG7776rESNGyGq1qkePHnzvC5dRVVWlrKwszZ07V6GhoYqPj1evXr1Mx4KboYhRr06fPq2/\n/e1vSklJUVlZmeLi4hQTE6OWLVuajgbU2dmzZ7VkyRLNnTtXISEhio+PV58+fUzHgpugiFEv9u3b\np9TUVC1dulT/9V//JZvNpgEDBqhRI5YhwH2cPXtWf/vb3/TCCy/ol7/8peLj43Xvvfdylgc3hCJG\nnZ09e1bvvPOOUlJStHfvXk2ePFmxsbEKDg42HQ1wqHPnzmnZsmV64YUX1Lp1a8XHx3O5HeqMIsZ1\n++qrr7RgwQItWLBA4eHhslqteuCBB9SkSRPT0YAGdf78eb3xxhuaM2eOWrZsqdmzZ+u+++6jkHFd\nKGLUyoULF7RhwwalpKRo48aNevjhh2W1WrmBPqCLhbx8+XLNmTNHzZs3V3x8vAYNGkQho1YoYvys\nkpISZWZmKjU1VT4+PrLZbPrv//5vBQQEmI4GOJ0LFy5oxYoVSkxMlL+/v2bPnq0hQ4ZQyPhZFDGq\nlZOTo5SUFK1cuVJDhw6VzWbTr3/9az5QgFq4cOGCVq5cqcTERDVp0kSzZ8/WsGHD+PeDalHE+FFF\nRYXefPNNpaSkqKioSHFxcZo0aZJat25tOhrgki5cuKB33nlHiYmJslgsmj17tn77299SyPgJihg6\ncOCA0tLStHjxYv3nf/6nrFarBg8eLC8vL9PRALdgt9v17rvvKjExUefPn9esWbMUHR3N5X2QRBF7\nrHPnzum9995TSkqKdu3apZiYGE2ZMkXt27c3HQ1wW3a7Xe+//74SEhJ05swZzZo1Sw8++CCF7OEo\nYg/z7bff6rXXXlNGRobatm0rm82mkSNHysfHx3Q0wGPY7XatWbNGCQkJOnXqlGbNmqVRo0ZxFspD\nUcQewG63a/PmzUpJSdG6dev00EMPyWq1qmvXrqajAR7Nbrdr7dq1SkhIUGlpqWbOnKnRo0dTyB6G\nInZjpaWlWrJkiVJTU2W322W1WjV+/HgFBgaajgbgMna7XR9++KESEhL03XffaebMmRozZoy8vb1N\nR0MDoIjd0K5du5Samqrly5drwIABstls6tOnDys1ASdnt9u1YcMGJSQk6NixY5o5c6bGjh1LIbs5\nitiQoqIiZWVmKm/3bp0qLVWzwEBFdO6sCTExatWq1XW/X2VlpVasWKGUlBQVFhZqypQpmjx5sm6+\n+WYHpAfgaBs3blRCQoKOHj2qGTNmaNy4cWrcuLHpWHAAiriBZWdn65WkJL2/Zo0ekBRVWakASWWS\ndvj66i27XUMHD9YT06crKirqmu936NAhpaena9GiReratatsNpvuv/9+foIG3MTmzZuVkJCgQ4cO\nacaMGRo/fjyF7GYo4gaUkZqq+KlT9WxFhSbY7Qqq5pgSSZkWi17y9VVCcrJirdarjjl//rw++OAD\npaSk6JNPPtGECRMUFxen8PBwh/8dAJixZcsWJSQkKD8/X9OnT9fEiRPZaMVNUMQNJCM1VfOmTtXa\n8nKF1eL4fEkD/fz07GVlXFRUpEWLFiktLU2tW7eW1WrV6NGj5efn59DsAJzHxx9/rMTERO3bt0/T\np09XTEyMmjZtajoWbgBF3ACys7M1vG9ffXRFCf+PpA8llUu6SdIkSTMuez5fUi8/P73wpz9pw4YN\nWr16taKjo2W1Wmt12hqA+9q+fbsSExO1Z88ePffcc5o0aRL3A3BRFHEDGPfAA+r+9tt68or/1Xsl\ntZfkIylPUm9JiyUNvOyYZEkv+ftr+pw5mjBhglq0aNFAqQG4guzsbCUmJmrnzp169tln9eijj1LI\nLoYidrCioiJ1CAlRQWVltd8JX7JfUn9J70jqdtnjJySF+vgor7CwTqupAXiGTz/9VImJicrJydG0\nadMUGxsrX19f07FQC9zg1MGyMjMVLdVYwo9J8pf0K108Ld3tiudbSIq2WJSVmemwjABc31133aV3\n3nlH7733njZu3KjQ0FD98Y9/VHl5uelouAaK2MHydu9Wj8rKGp//i6RTuvhd8UxJ2dUcE1VRobzc\nXMcEBOBW7rzzTr311ltas2aNPv74Y4WGhio5OVmnT582HQ01oIgd7FRpqQKucYxFUh9JoyQtq+b5\nAEllJSX1HQ2AG+vSpYtWrFihdevWaceOHWrfvr3mzZunU6dOmY6GK1DEDtYsMFBltTz2nKTqLkQq\nkxQQ9HPfMANA9SIjI7V8+XJt2LBBu3btUmhoqJKSklRWVttPJjgaRexgEZ07a0c1KxiLJb0p6bSk\nC5LWSvq7pN9W8x7Zvr6KiIx0ZEwAbq5Tp05atmyZNm7cqD179ig0NFRz587VyZMnTUfzeKyadrCa\nVk1/J2mkpN2S7JLCJc2SNOyK17NqGoAj7N+/X3PnztWaNWv0+OOP63//93/1i1/8wnQsj8RE7GCt\nW7fW0MGDtfiKnY9ukrRRF4u2RNIOXV3CkrTYYtH9Q4ZQwgDqVYcOHZSVlaWPP/5YBQUFCgsL0/PP\nP68S1qM0OCbiBlDTnbWu5dKdtVZt2qTu3bs7Kh4AKD8/X3/4wx/07rvvymq16qmnnrquGwjV945y\nnoSJuAFERUUpITlZA/38lF/L11y613RCcjIlDMDhwsLCtGjRIu3YsUPHjh1TeHi4ZsyYoePHj//s\n67KzszXugQfUISRE++Lj1W3pUg197z11W7pUe59/XhHBwRr3wAPKzq7u4kxIkuxoMOkpKfY2fn72\nP1os9hOS3V7Nr+OS/WWLxd7Gz8+enpJiOjIAD3Xo0CF7bGysvUWLFvbnnnvOXlxcfNUxlz7T5v/M\nZ9oJyf5HPtN+FqemG1hOTo5eSUrSe6tXK9piUVRFxY/7EWf/sB/x/UOG6Inp05mEARhXWFioF198\nUW+++aYeeeQRTZ06Va1bt66XHeVwEUVsSHFx8cXvU3JzVVZSooCgIEVERmr8xIl8nwLA6Rw9elTz\n5s3TsmWgRw/nAAAChUlEQVTLNHjwYH24cqW2VFT8WMJVkmy6eJfAEkmhkv4gadBl78G6l+pRxACA\nWvv66681qHdvTSwo0NOXPV6ui7vFxUhqK+l9SQ9L2iMp+LLj5lss+iw6Wkv+8Y8Gy+zsKGIAQK3V\ndkc5Seoi6XlJ0Zc9xr0RrsaqaQBArV1rR7lL/i3pgKROVzzOjnJXo4gBALV2rR3lpIv3zR8naaKk\niGqeZ0e5n6KIAQC1dq0d5ey6WMJNJb1awzHsKPdT3qYDAABcx7V2lHtEF++lv1qSVw3HsKPcTzER\nAwBqraYd5SQpTtKXkt6V1ORn3oMd5X6KVdMAgFqradV0oaR2knz0f5OwRVK6Ll7GdAmrpq/GRAwA\nqLWadpQL1sW91ct18dRzmaST+mkJS+woVx0mYgDAdWFHufrFRAwAuC7sKFe/KGIAwHWLtVr1bHKy\nevn5ab7FopouRjoh6Y8Wi3qx4UONODUNAKgzdpS7cRQxAOCGsaNc3VHEAAAYxHfEAAAYRBEDAGAQ\nRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwAgEEUMQAABlHEAAAY\nRBEDAGAQRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwAgEEUMQAA\nBlHEAAAYRBEDAGAQRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwA\ngEEUMQAABlHEAAAYRBEDAGAQRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwAgEEUMQAABlHEAAAYRBED\nAGAQRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwAgEH/H5PDuRwyg7XtAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"G3 = nx.Graph()\n",
"for i, j in [(1, 2), (1, 3), (1, 0)]:\n",
" G3.add_edge(i,j)\n",
"nx.draw(G3, pos =pos, with_labels = True)"
]
},
{
"cell_type": "code",
"execution_count": 200,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.0\n"
]
}
],
"source": [
"print(nx.transitivity(G3))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"THREE CENTRAL QUANTITIES IN NETWORK SCIENCE\n",
"- A. Degree distribution: \t\t\t $p_k$\n",
"- B. Path length: \t\t\t\t\t\t$$\t\t\t\n",
"- C. Clustering coefficient: $C_i$\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Typical Network Science Research\n",
"\n",
"- Discovering, Modeling, Verification\n",
" - WATTSDJ,STROGATZSH.Collective dynamics of‘small-world’ networks. Nature, 1998, 393(6684): 440–442.\n",
" - BARABÁSI A-L, ALBERT R. Emergence of scaling in random networks. Science, 1999, 286(5439): 509-512."
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Typical Math Style\n",
"Fan Chung & Linyuan Lu, The average distance in random graphs with given expected degree,. PNAS, 19, 15879-15882 (2002)."
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Typical Physical Style\n",
"A.-L.Barabási,R.Albert,H.Jeong Mean-field theory for scale-free random networks. Physica A 272, 173–187 (1999)."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Typical Computer Science Style\n",
"\n",
"- Community detection\n",
"- Link prediction\n",
"- Recommendation algorithms"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Typical control sytle\n",
"Controllability of Complex Networks\n",
"\n",
"Liu Y Y, Slotine J J, Barabási A L. Nature, 2011, 473(7346): 167-173."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# 阅读材料\n",
"- Barabasi 2016 Network Science. Cambridge\n",
"- 汪小帆、李翔、陈关荣 2012 网络科学导论. 高等教育出版社\n",
"- 梅拉妮·米歇尔 2011 复杂,湖南科学技术出版社\n",
"- 菲利普-鲍尔 2004 预知社会:群体行为的内在法则,当代中国出版社\n",
"- 巴拉巴西 2007 链接:网络新科学 湖南科技出版社"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.11"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Global Clustering Coefficient:\n",
" \n",
"## $C = \\frac{3 \\times \\mbox{number of triangles}}{\\mbox{number of connected triplets of vertices}} = \\frac{\\mbox{number of closed triplets}}{\\mbox{number of connected triplets of vertices}}$\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 215,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xd4jefjBvD7CJnS1CxFokYQYkepkpAdMyqEqoiZxC6J\nPRIh1GhRiVDEqhUzJITEbhFFmxqJndpiRPZ8f3/4tj9FKuOc85xxf67LxXXG+97p98t9nuc87/PK\nJEmSQEREREKUER2AiIhIm7GIiYiIBGIRExERCcQiJiIiEohFTEREJBCLmIiISCAWMRERkUAsYiIi\nIoFYxERERAKxiImIiARiERMREQnEIiYiIhKIRUxERCQQi5iIiEggFjEREZFALGIiIiKBWMREREQC\nsYiJiIgEYhETEREJxCImIiISiEVMREQkEIuYiIhIIBYxERGRQCxiIiIigVjEREREArGIiYiIBGIR\nExERCcQiJiIiEohFTEREJBCLmIiISCAWMRERkUAsYiIiIoFYxERERAKxiImIiARiERMREQnEIiYi\nIhKIRUxERCQQi5iIiEggFjEREZFALGIiIiKBWMREREQCsYiJiIgEYhETEREJxCImIiISiEVMREQk\nEIuYiIhIIBYxERGRQCxiIiIigcqKDkCkSp48eYINYWFI/OMPpKWkoLyJCcybNoWHpyeqVKkiOh4R\naSCZJEmS6BBEosXFxWFpUBAOREWhFwCrrCwYA0gFcM7AALslCV2cnTF2yhRYWVkJTktEmoRFTFpv\nVUgIZk2ciEmZmfCQJFR4z2teAAiTyfCdgQH8Fy3CcG9vZcckIg3FIiattiokBAsmTsShjAzUK8Lr\nbwBwNDTEJJYxEckJi5i0VlxcHLrb2ODkWyX8AsBgAIcBVAEwD0C/N56/AaCDoSEijh9H69atlReY\niDQSV02T1loaFIRJmZnvjIR9AOgDeApgEwBvAFffeL4eAL/MTCwNClJOUCLSaBwRk1Z68uQJGpiZ\n4VZW1r++E84AUAHAFQB1//eYB4AaeD0y/ttzAHX19ZGYlMTV1ERUKhwRk1baEBYGV+CdhVmJAMrh\n/0sYAJoBuPzW6yoCcJXJsCEsTGEZiUg7sIhJKyX+8QfaZGW983gagI/eeuwjvL6M6W1WmZlIjI9X\nQDoi0iYsYtJKaSkpMH7P4+UBvHrrsRTgva81BpD64oW8oxGRlmERk1Yqb2Ly3lGuOYA8ADffeOx3\nAI3f89pUAMYV3nfVMRFR0bGISSuZN22Kc/r67zxuCKAXgJl4vXDrFIAIAN+85xhxBgYwt7RUZEwi\n0gJcNU1aqbBV08C/ryOuDGABgL5vvYarpolIXjgiJq1UtWpVdHF2xnqZ7J3nKgDYjdcLt+7g3RIG\ngPUyGbq6uLCEiajUOCImrVXYzlofcgPAl/r62H/yJHfWIqJS44iYtJaVlRX8Fy2Co6EhbhTxPTcA\n2OrqIrtcOejq6ioyHhFpCd6PmLTa3zdu+GL8ePhlZ2MI3t3kA3j9nfA6mQyL/nf3pY8rVYKDgwMi\nIyPRsmVLZUYmIg3DqWnSenl5eahXrx7q16iB8xcuwFUmg1Vm5j/3I44zMMCO3FyY1ayJsB07/pmO\n3rNnD0aMGIF9+/bh888/F/ozEJH64oiYtN7atWtRp04dRMfEIDk5GRvCwnApPh6pL17AuEIFNLa0\nxHgnJ3Ts2BHm5ub/vK9nz54oV64cunXrhl27duHLL78U+FMQkbriiJi0WlpaGszNzbFv374PLrzq\n3bs3OnfuDB8fn389Hh0djQEDBmD79u2wsbFRYFoi0kRcrEVabcmSJbCxsSnS6mdvb2+EhITg7c+u\nDg4O2LZtG/r06YPDhw8rKioRaSiOiElrPX78GBYWFjh//jw+++yzD75ekiQ0bNgQa9asee809KlT\np9CrVy+EhYXBxcVFEZGJSANxRExay9/fHx4eHkUqYQCQyWTw8vJCSEjIe5//8ssvERERAU9PT+zZ\ns0eeUYlIg3FETFopISEBX375Ja5du4ZKlSoV+X3Pnz9HnTp1cP369UJ31frtt9/QpUsXLF++HG5u\nbvKKTEQaiiNi0kpTpkyBr69vsUoYACpWrAhXV1esW7eu0Ne0atUKhw4dwpgxY7B58+bSRiUiDccR\nMWmd06dPo1+/fkhISICBgUGx33/u3Dn069cP169fR5kyhX+WvXz5MhwcHBAYGAhPT8/SRCYiDcYR\nMWkVSZLg6+uLwMDAEpUw8HprzI8//hjR0dH/+brGjRsjNjYWM2fORGhoaInORUSaj0VMWmX37t3I\nyMjA119/XeJjyGSyfy5l+pAGDRrg2LFjCAoKwvLly0t8TiLSXJyaJq2Rm5uLxo0bY/ny5XB0dCzV\nsdLT02FqaoqLFy/C1NT0g6+/e/cuOnfuDG9vb0ycOLFU5yYizcIRMWmN1atXw8zMDA4ODqU+lpGR\nEfr374/Vq1cX6fVmZmY4fvw4Vq1ahblz55b6/ESkOTgiJq2QmpqK+vXrIyoqCi1atJDLMS9fvgw7\nOzskJSWhXLlyRXrPw4cPYWtrCzc3N8yePRsymUwuWYhIfXFETFph4cKFsLe3l1sJA68XY5mbmxdr\n847q1avj2LFj2L17N6ZMmfLOdplEpH04IiaN9/DhQzRp0gQXLlyAmZmZXI+9detWrFq1CrGxscV6\n37Nnz2Bvbw9ra2ssWbKEI2MiLcYiJo03YsQIfPTRR1i4cKHcj52TkwNTU1McO3YMDRs2LNZ7X7x4\nAScnJ7Ru3RrLly//z2uSiUhzsYhJo129ehUdO3ZEYmIiKlSooJBzTJ06FRkZGfjhhx+K/d5Xr17B\n2dkZFhYWCA0NZRkTaSEWMWm0Hj16oGPHjpgwYYLCznHnzh20atUKf/31FwwNDYv9/rS0NHTt2hVm\nZmZYu3YtdHR0FJCSiFQVP36Txjpx4gR+//13jBw5UqHnqV27Ntq1a4etW7eW6P3ly5dHZGQkHjx4\ngAEDBiA3N1fOCYlIlbGISSP9vZXl3Llzoa+vr/DzFXWnrcIYGhoiIiICKSkpcHd3R05OjhzTEZEq\nYxGTRgoPD0dubi769eunlPM5OTnh6dOnOH/+fImPoa+vj927dyM/Px+9e/dGdna2HBMSkapiEZPG\nycnJwZQpU7Bw4UKlLX7S0dHBiBEjSjUqBgA9PT3s2LEDenp66NGjBzIzM+WUkIhUFRdrkcZZvnw5\nIiMjERUVpdTzPnnyBA0aNMCtW7dKvUI7Ly8PHh4eePToEfbt2wcjIyM5pSQiVcMiJo2SkpICc3Nz\nHD58GE2bNlX6+fv164e2bdti7NixpT5Wfn4+hg4dips3b+LAgQMwNjaWQ0IiUjWcmiaN8t1338HF\nxUVICQOvF22tXLlSLltX6ujoYM2aNWjUqBEcHR2RkpIih4REpGo4IiaNce/ePTRr1gyXLl1CrVq1\nhGSQJAmWlpb48ccfYWNjI7djjhkzBmfOnMGhQ4dQsWJFuRyXiFQDR8SkMWbNmoXhw4cLK2EAkMlk\n8PLyKvWirbePuWzZMlhbW8PW1hbJyclyOzYRiccRMWmE+Ph42NnZITExESYmJkKzpKSkoHbt2rh6\n9SqqVasmt+NKkoTp06dj7969iImJwSeffCK3YxOROBwRk0aYPHkypk6dKryEAcDExARubm5Ys2aN\nXI8rk8kQGBiIPn36wMbGBg8ePJDr8YlIDI6ISe3FxsZi2LBhuHr1KnR1dUXHAQBcvHgRPXv2xK1b\ntxSyd/T8+fOxZs0axMbGCp2KJ6LS44iY1FpBQQH8/Pwwb948lSlhAGjRogWqVauGyMhIhRx/8uTJ\n8PHxgbW1NW7fvq2QcxCRcrCISa1t27YNZcqUgZubm+go7yjt/tMfMn78eEyYMAE2Nja4ceOGws5D\nRIrFqWlSW9nZ2WjYsCHWrVsnt0uF5CkzMxO1atVCXFwcPvvsM4WdZ/Xq1fD398eRI0fQsGFDhZ2H\niBSDI2JSW8HBwWjSpIlKljAAGBgYYODAgQgNDVXoeYYNG4a5c+eic+fO+PPPPxV6LiKSP46ISS29\nePECDRo0wNGjR9G4cWPRcQqVmJiIDh06ICkpCXp6ego919atWzFu3DhERUWhRYsWCj0XEckPR8Sk\nlubPn48ePXqodAkDgLm5OSwtLbFz506Fn8vd3R0rVqyAk5MT4uLiFH4+IpIPjohJ7SQlJaFFixaI\nj4/Hp59+KjrOB+3cuRM//PADTp48qZTzRUREYMiQIdizZw+++OILpZyTiEqORUxqx8PDA6amppgz\nZ47oKEWSm5uL2rVr4+DBg7C0tFTKOQ8ePIiBAwciPDwcHTt2VMo5iahkWMSkVi5dugQnJyckJibi\no48+Eh2nyGbNmoXk5GSsWLFCaeeMiYmBu7s7tm7dCltbW6Wdl4iKh0VMasXR0RHdu3fHyJEjRUcp\nlnv37qFp06ZISkpC+fLllXbeEydOoHfv3tiwYQOcnJyUdl4iKjou1iK1ER0djdu3b2P48OGioxRb\nzZo1YW1tjc2bNyv1vB07dsTevXsxcOBAREREKPXcRFQ0LGJSCwUFBZg0aRLmzZuHcuXKiY5TIn/v\ntKXsSah27drhwIEDGDp0qFJWbxNR8bCISS38/PPP0NPTw1dffSU6SonZ2dkhLS0NZ86cUfq5rays\ncOjQIYwaNQpbtmxR+vmJqHBlRQcg+pCsrCxMmzYNmzZtgkwmEx2nxMqUKQMvLy+sXLkS7dq1U/r5\nmzdvjsOHD8PBwQE5OTnw8PBQegYieheLmFTejz/+iBYtWqBDhw6io5Sap6cn6tWrh2fPnqFSpUpK\nP3+TJk0QGxsLOzs75ObmYujQoUrPQET/xlXTpNKeP3+OBg0a4OTJkxpzQ4OBAweiWbNmmDBhgrAM\n169fh52dHfz8/NRuBTqRpmERk0qbOHEi0tLSsHLlStFR5ObXX3/FwIEDkZCQgDJlxC3TuH37Nmxt\nbTF69GiMHz9eWA4ibcepaVJZd+7cwbp163D58mXRUeSqbdu2MDIyQkxMDOzt7YXl+Oyzz3Ds2DHY\n2toiOzsbkydPFpaFSJtx1TSprOnTp2P06NGoVq2a6ChyJZPJ/rmUSTRTU1McP34cYWFhCAgIUPql\nVUTEqWlSURcuXECXLl2QmJgIY2Nj0XHkLjU1FWZmZoiPj0eNGjVEx8Hjx49ha2uLHj16IDAwUK1X\npxOpG46ISeVIkgRfX1/MmjVLI0sYAIyNjeHu7o7Vq1eLjgIA+OSTT3D06FEcOHAAvr6+HBkTKRFH\nxKRyDh48iHHjxiE+Pl5td9Eqivj4eDg5OeHOnTsq83M+f/4cjo6OaNeuHZYuXcqRMZEScERMKiU/\nPx9+fn6YP3++ypSTolhaWuKzzz5TqT2gK1asiCNHjiAuLg5eXl4oKCgQHYlI47GISaVs3LgRH330\nEXr06CE6ilKoyqKtN5mYmCA6OhpXr17FkCFDkJ+fLzoSkUbj1DSpjMzMTJibm2P79u1CtoAUITs7\nG7Vq1cLp06dRv3590XH+JT09Hd27d0e1atWwfv16lC3Lqx2JFIEjYlIZS5cuxeeff641JQwAenp6\n8PT0VMkNS4yMjLB//348e/YM/fv3R25uruhIRBqJI2JSCcnJyWjYsCF++eUXmJubi46jVLdu3UKb\nNm3w119/wcDAQHScd2RlZcHNzQ06OjrYtm0b9PT0REci0igcEZNKCAwMhLu7u9aVMADUqVMHVlZW\n2L59u+go76Wvr4+dO3dCR0cHvXr1QlZWluhIRBqFI2IS7ubNm/j8889x5coVVK1aVXQcIfbt24d5\n8+YJuVdxUeXm5mLgwIFITk7G3r17YWhoKDoSkUbgiJiEmzZtGsaNG6e1JQwAXbp0wYMHD3Dx4kXR\nUQpVrlw5bNq0CdWrV0eXLl2QlpYmOhKRRmARk1Dnzp3DyZMntf7uPzo6Ohg+fLjKXcr0Nh0dHaxb\ntw5169aFk5MTXr16JToSkdrj1DQJI0kSOnXqhAEDBvAG9QAePXqERo0a4c6dOzAxMREd5z8VFBRg\n1KhR+O2333Dw4EFUqFBBdCQitcURMQlz4MABPH36FIMGDRIdRSVUq1YN9vb22LRpk+goH1SmTBms\nWLECX3zxBWxtbfHs2TPRkYjUFouYhMjLy8OkSZOwYMECbhTxhr932lKHiSqZTIYlS5bAwcEBnTp1\nwpMnT0RHIlJLLGISIiwsDFWqVEGXLl1ER1EpNjY2yM/Px6lTp0RHKRKZTIagoCC4urrCxsYGDx8+\nFB2JSO3wO2JSuvT0dJibm2P37t1o06aN6DgqZ+nSpTh79ix+/vln0VGKZe7cuVi/fj1iY2NRs2ZN\n0XGI1AaLmJQuMDAQf/75J7Zu3So6ikp68eIF6tSpg4SEBLW7pGvRokUICQlBbGwszMzMRMchUgss\nYlKqJ0+ewMLCAmfPnkXdunVFx1FZgwcPhrm5OSZPniw6SrEtW7YMS5YsQUxMDP83JioCFjEp1ahR\no1C2bFn88MMPoqOotLi4OPTp0wc3btyAjo6O6DjFFhoaisDAQBw5cgQNGjQQHYdIpXG5KinN9evX\nsW3bNly9elV0FJVnZWWFSpUq4dChQ3BxcREdp9hGjBgBXV1ddO7cGYcPH4aFhYXoSEQqi6umSWmm\nTp2KCRMmoHLlyqKjqIW/L2VSV56enliwYAFsbW3xxx9/iI5DpLI4NU1KcebMGbi5uSExMVElb/Wn\nitLT02FqaooLFy6o9cKn7du3Y8yYMYiMjETLli1FxyFSORwRk8JJkgRfX1/MmTOHJVwMRkZGGDBg\nAFatWiU6Sqn06dMHK1euhLOzM86ePSs6DpHKYRGTwu3btw8pKSn45ptvREdRO15eXlizZg1ycnJE\nRymVnj17Yu3atejWrZvabFZCpCwsYlKoN7eyVMfVv6I1atQIjRo1wu7du0VHKbUuXbpg06ZNcHV1\nxdGjR0XHIVIZLGJSqDVr1qBGjRpwcnISHUVtqfuirTc5ODhgx44d6Nu3L6Kjo0XHIVIJXKxFCpOW\nlgZzc3NERESgVatWouOorZycHJiZmSEmJkZjLgM6ffo0XF1dsW7dOu43TlqPI2JSmMWLF6NTp04s\n4VLS1dXFkCFDsHLlStFR5KZ9+/aIiIjA4MGDNWLanag0OCImhXj06BEaN26M8+fP47PPPhMdR+0l\nJSWhRYsWSEpKgpGRkeg4cnPhwgW4uLhg2bJl6NOnj+g4REJwREwK4e/vj0GDBrGE5cTU1BTt27fH\nli1bREeRq5YtWyI6Ohpjx47Fpk2bRMchEoIjYpK7a9euoUOHDkhISEDFihVFx9EYUVFRmD59Os6f\nPw+ZTCY6jlxduXIF9vb2mDNnDgYPHiw6DpFScURMcjdlyhT4+fmxhOXM0dERL168wPnz50VHkTsL\nCwscPXoUs2fP1qjvwomKgjd9ILk6deoULly4oHFTqKqgTJkyGDFiBEJCQmBlZSU6jtyZm5vj6NGj\nsLW1RU5ODsaMGSM6EpFScGqa5EaSJHzxxRfw8fHhLloK8vTpU5ibm+PWrVuoUKGC6DgKcffuXXTu\n3BleXl7w9fUVHYdI4Tg1TXKza9cuZGZm4uuvvxYdRWNVqVIFLi4uWL9+vegoCmNmZobjx4/jp59+\nQmBgoOg4RArHETHJRW5uLiwsLBAcHAx7e3vRcTTaqVOnMHToUFy9elXjFm296eHDh7Czs8NXX30F\nf39/jf5ZSbtxRExysWrVKtSpU4clrATt27dH2bJlNX6/5urVq+Po0aPYs2cPJk+eDI4ZSFNxREyl\n9urVK5ibm+PgwYNo3ry56DhaYcWKFTh27Bh27NghOorCPXv2DA4ODujQoQO+//57joxJ47CIqdRm\nzJiBpKQkjf7eUtW8evUKZmZmuHLlCqpXry46jsK9fPkSjo6OaNWqFX788UeUKcPJPNIcLGIqlQcP\nHsDS0hIXL16Eqamp6DhaZcSIEahZsyZmzJghOopSvHr1Ci4uLmjYsCFCQ0N5W03SGCxiKpVhw4ah\nYsWKWLBggegoWufSpUvo1q0bbt++jbJltWNLgLS0NHTr1g21atXC2rVrtebnJs3G+R0qscuXL2Pv\n3r2YMmWK6ChaqXnz5qhZsyYOHDggOorSlC9fHgcOHMCjR48wYMAA5Obmio5EVGosYiqxyZMnY8qU\nKfj4449FR9Fa3t7eCAkJER1DqQwNDbFv3z6kpqaib9++yMnJER2JqFQ4NU0lcuzYMXh6euLatWvQ\n09MTHUdrZWVloVatWjhz5gzq1q0rOo5SZWdno2/fvsjPz8eOHTugr68vOhJRiXBETMUmSRL8/Pww\nb948lrBg+vr68PDwQGhoqOgoSqenp4cdO3bAwMAAPXr0QGZmpuhIRCXCIqZi27FjBwoKCtC3b1/R\nUQivV0+HhYUhKytLdBSlK1euHH7++WdUqVIFXbp0QXp6uuhIRMXGIqZiycnJwZQpU7Bw4UJey6ki\n6tevj+bNmyM8PFx0FCHKli2L9evXw8zMDM7OzkhNTRUdiahY+C8pFcvKlSvRsGFDdOrUSXQUeoM2\nLtp6k46ODtasWQMLCws4ODjg5cuXoiMRFRkXa1GRpaSkwNzcHDExMWjSpInoOPSGvLw81K5dG5GR\nkWjatKnoOMJIkoSxY8fil19+QXR0NCpWrCg6EtEHcURMRbZgwQJ07dqVJayCypYti2HDhmHlypWi\nowglk8mwdOlSdOrUCZ07d8bTp09FRyL6II6IqUju3buHZs2a4ffff0fNmjVFx6H3uH//PiwtLXH3\n7l0YGxuLjiOUJEmYMWMG9uzZgyNHjqBatWqiIxEViiNiKpKZM2fCy8uLJazCatSogU6dOmHz5s2i\nowgnk8kQGBiIvn37wsbGBvfv3xcdiahQHBHTB8XHx8POzg6JiYkwMTERHYf+w5EjRzBhwgRcunSJ\ntwv8nwULFmD16tWIjY3ljUlIJXFETB80adIkTJ8+nSWsBjp37ozMzEz8+uuvoqOojEmTJmHkyJGw\ntrbG7du3RcchegdvXUL/KSYmBomJidizZ4/oKFQEZcqUgZeXF0JCQvDFF1+IjqMyxo8fDz09PVhb\nWyMmJgb169cXHYnoH5yapkIVFBTAysoKkyZNQp8+fUTHoSJ69uwZ6tatixs3bqBy5cqi46iUn376\nCbNnz8bhw4fRqFEj0XGIAHBETP9h69at0NHRgZubm+goVAyVKlVCjx49sHz5chgbGSHxjz+QlpKC\n8iYmMG/aFB6enqhSpYromEIMHToUurq6sLW1RXR0NC/FI5XAETG9V3Z2Nho2bIiwsDBYW1uLjkPF\nEBcXh1m+vjh24gTc9fTQJisLxgBSAZwzMMBuSUIXZ2eMnTIFVlZWouMKsXXrVowbNw5RUVFo0aKF\n6Dik5VjE9F5LlizBsWPHsG/fPtFRqBhWhYRg1sSJ8MvMxCBJQoX3vOYFgDCZDN8ZGMB/0SIM9/ZW\ndkyVsHPnTvj4+GD//v1a+4GEVAOLmN7x4sULNGjQAMeOHYOFhYXoOFREq0JCsGDiRBzKyEC9/z22\nAkAYgHgA/QGsfeP1NwA4GhpikhaXcUREBIYMGYI9e/ZwcRsJwyKmd/j5+eHly5dYtWqV6ChURHFx\ncehuY4OTb5QwAOzB62sUDwHIxL+LGHhdxh0MDRFx/Dhat26tpLSq5eDBgxg4cCDCw8PRsWNH0XFI\nC7GI6V/u3r2Lli1bIj4+Hp9++qnoOFREA3r1Qus9ezCukL/OMwDcx7tFDADfy2S44OqKjTt3KjKi\nSouJiYG7uzu2bt0KW1tb0XFIy7CI6V8GDhyI2rVrIyAgQHQUKqInT56ggZkZbmVlvfc7YeC/i/g5\ngLr6+khMStLa1dQAcOLECfTu3RsbNmyAk5OT6DikRbizFv3j4sWLiI6Ohq+vr+goVAwbwsLgChRa\nwh9SEYCrTIYNYWHyC6WGOnbsiL1792LgwIGIiIgQHYe0CIuY/jFp0iTMnDlT6+/co24S//gDbbKy\nSnUMq8xMJMbHyymR+mrXrh0iIyMxbNgw7NTiqXpSLm7oQQCA6Oho3LlzB8OGDRMdhYopLSUFpf3o\nZAwg9cULecRRe61bt8bBgwfh7OyM7Oxs9O/fX3Qk0nAsYkJ+fj78/Pwwf/58lCtXTnQcKqbyJiZI\nLeS5fAC5//s9D0A2Xv+l13nrdakAjCuUdHJb8zRv3hyHDx+Go6MjcnNz4eHhIToSaTBOTRM2b94M\nQ0NDuLq6io5CxZSZmYlXOTk4WcgtDwMBGAJYAGDz//489z2vO2dgAHNLS4XlVEdNmjRBTEwMpk+f\njtWrV4uOQxqMRazlMjMzMX36dCxcuJD3r1Uj169fx4QJE2Bqaoqnz55hf9myeN/E8iwABXg9Iv77\n18y3XvMcwLbMTMh0dJCTk6PY4GqmYcOGOHr0KAIDA7FixQrRcUhDsYi13PLly9G6dWu0b99edBT6\ngLy8POzZswcODg5o3749ypYti7NnzyImJgbdunbF+hJ+kFovk8HG2hrR0dGoX78+Vq5ciezsbDmn\nV1/16tXD8ePHsXjxYixZskR0HNJEEmmt5ORkqXLlytK1a9dER6H/8ODBAykgIECqWbOm1K5dO2nj\nxo1SZmbmv15z7tw5qZqhoXQdkKRi/LoOSNUMDaW4uDhJkiTp119/lZydnaVatWpJK1aseOc82iwp\nKUmqV6+eNG/ePNFRSMNwRKzF5s6dCzc3NzRo0EB0FHqLJEk4fvw4+vbtCwsLC9y7dw8RERH45Zdf\nMGDAAOjr6//r9VZWVvBftAiOhoa4UcRz/L3XtP+iRf9sb9m2bVtERkYiPDwckZGRqFevHpYvX46s\nUl4epQlq1aqF48ePY8OGDfD394fEvZBIXkR/EiAxbt26JVWqVEl69OiR6Cj0hpcvX0rLly+XLCws\npEaNGknLli2TXr58WeT3hwYHS9UMDaUlMpn0vJBR8DNAWiyTSdUMDaXQ4OD/PN758+el7t27S59+\n+qn0ww8/SBkZGaX9EdXeo0ePpCZNmkhTpkyRCgoKRMchDcAtLrXU119/jQYNGmDmzLeX7pAIv//+\nO4KDg7HnjjQUAAAcLklEQVR9+3bY29vDx8cH1tbWJVpAd/78eSwNCsL+yEi4ymSwysz8537Ecf+7\nH3FXFxeMnTKlyDd6uHjxIgICAnD27Fn4+vpixIgRMDQ0LHY2TZGcnAx7e3t07twZixYt4kJHKhUW\nsRb67bff0K1bNyQmJqJ8+fKi42it7OxshIeHIzg4GHfv3sWIESMwdOhQVK9eXS7Hf/r0KTaEhSEx\nPh6pL17AuEIFmFtaYuCgQSXeU/r333/HnDlzcPr0aUyYMAHe3t4wMjKSS1518/z5czg6OqJt27ZY\nunQpypThN31UMixiLSNJEmxtbeHu7o7hw4eLjqOVbt++jdDQUKxduxbNmzeHt7c3unXrhrJl1Wd/\nnfj4eMyZMwcnTpzAt99+Cx8fH638UJeSkgJnZ2c0adIEK1euZBlTifD/NVrm4MGDePjwIQYPHiw6\nilbJz8/HgQMH0KVLF1hZWSEnJwenTp1CdHQ0XF1d1aqEAcDS0hLbt29HTEwMLly4gLp16yIoKAip\nqYXt8aWZTExMcOjQISQkJGDw4MHIz88XHYnUEEfEWiQ/Px/NmzfH3Llz0b17d9FxtMLTp0+xZs0a\nhIaGonLlyvDx8UHfvn017vvVK1euYO7cuTh8+DDGjh2L0aNH46OPPhIdS2nS09PRvXt3VKtWDevX\nr1e7D1YkFkfEWmTDhg2oUKECunXrJjqKRpMkCadPn8aAAQNQv359JCYmYvv27YiLi4Onp6fGlTAA\nWFhYYPPmzTh58iSuXbuGunXrIiAgACkpKaKjKYWRkRH279+P58+fo1+/fsjNzRUdidQIR8RaIiMj\nAw0aNEB4eDg+//xz0XE0UlpaGjZv3ozg4GBkZmbC29sbHh4eqFixouhoSpeYmIh58+bhwIEDGDly\nJMaNG4ePP/5YdCyFy87OhpubG2QyGbZv3w49PT3RkUgNcESsJZYuXYp27dqxhBXg8uXLGDVqFExN\nTXHo0CEsWrQI165dw/jx47WyhAHA3NwcYWFh+PXXX5GUlIR69eph5syZeP78uehoCqWnp4fw8HCU\nK1cOrq6uyMzMFB2J1ACLWAs8ffoUixcvxrx580RH0Rg5OTnYtm0brK2tYW9vj4oVK+L333/Hrl27\nYG9vz9Wz/1OvXj2sXbsW586dw8OHD1G/fn1MmzYNz549Ex1NYXR1dbF161aYmJige/fuyMjIEB2J\nVBynprXA2LFjIUkSli1bJjqK2ktKSsKqVauwZs0aNGzYED4+PujZsyfv41xEd+7cQVBQEMLDwzF8\n+HBMmDABlStXFh1LIfLz8zF48GDcvXsX+/fv18rLu6ho+LFdw924cQObN2/GjBkzREdRWwUFBYiO\njkbPnj3RvHlzvHr1CjExMTh69Cjc3NxYwsVQu3ZthIaG4uLFi3j58iUaNGgAPz8/PHnyRHQ0udPR\n0cG6detQv359ODo6as3CNSo+FrGGmzZtGr799tsS76SkzZ49e4bFixfD3Nwcfn5+cHFxQVJSEpYt\nWwYLCwvR8dSaqakpQkJCcOnSJWRkZKBRo0aYOHEiHj9+LDqaXJUpUwahoaFo3rw57O3t8eLF++4a\nTdqORazBzp49i9OnT2PcuHGio6gNSZJw7tw5DBo0CHXr1sWlS5ewceNGXLx4EcOHD+f0opzVqlUL\nP/74I/744w/k5OSgUaNG+Pbbb/Ho0SPR0eSmTJky+PHHH/Hll1/C1tYWycnJoiORimERayhJkuDn\n5wd/f3+NvG5V3jIyMrBmzRpYWVnB3d0dFhYWuH79OjZu3Ih27dpxU38Fq1GjBpYtW4Y///wTkiSh\ncePGGDduHB48eCA6mlzIZDIsXrwYjo6O6Ny5s0ZOxVPJsYg11P79+/Hs2TN4eHiIjqLSEhISMH78\neNSqVQt79uxBQEAArl+/Dj8/P07nC/Dpp5/i+++/x+XLl6GjowNLS0uMHj0a9+7dEx2t1GQyGebN\nm4devXrBxsYGDx8+FB2JVASLWAPl5eVh0qRJWLBgAbfae4+8vDzs2rULdnZ26NixI/T19fHbb78h\nIiICLi4u0NHRER1R61WrVg2LFy/GlStXoK+vj2bNmmHkyJH466+/REcrFZlMhtmzZ2PAgAGwtrbW\niA8YVHosYg20bt06fPLJJ3BxcREdRaU8ePAA/v7+MDMzw5IlSzB48GAkJSUhKCgItWvXFh2P3uOT\nTz7BwoULce3aNRgbG6N58+bw8vLC3bt3RUcrlalTp2LEiBGwtrbGnTt3RMchwVjEGiY9PR2zZ8/G\nd999x+818fq78tjYWPTu3RuNGzfGo0ePEBUVhVOnTqF///7cglBNVKlSBfPnz0dCQgIqVqyIli1b\nYvjw4bh9+7boaCU2YcIEjBs3DjY2Nrh586boOCQQi1jDLFmyBB07doSVlZXoKEK9fPnyn8uMxowZ\ng86dO+Pu3bsICQlB06ZNRcejEqpcuTLmzZuHxMREVK1aFa1bt8aQIUNw69Yt0dFKZPTo0Zg6dSps\nbGyQkJAgOg4Jwp21NMjjx49hYWGBuLg41KlTR3QcIS5cuICQkBCEh4fDyckJ3t7e6NChA2cHNNSL\nFy/www8/YMWKFejWrRumTZuGevXqiY5VbOvWrcP06dMRHR2Nxo0bi45DSsYRsQYJCAjAwIEDta6E\ns7KysGHDBrRt2xY9e/ZE7dq1cfXqVWzZsgUdO3ZkCWuwChUqwN/fHzdu3EDt2rXRrl07eHh4IDEx\nUXS0YvH09MR3330HOzs7/P7776LjkJJxRKwhEhIS0L59eyQkJKBSpUqi4yjFzZs3sXLlSoSFhaFV\nq1bw8fGBi4sLV4prsZSUFCxfvhxLly6Fo6Mjpk+fjoYNG4qOVWQ7duzA6NGjceDAAbRq1Up0HFIS\njog1xNSpU+Hr66vxJZyfn4+IiAg4Ozujbdu2AIBff/0VBw8eRPfu3VnCWs7ExATTp0/HzZs3YWFh\ngY4dO6J///64cuWK6GhF4ubmhtDQULi4uODMmTOi45CScESsAX755Re4u7sjISEBBgYGouMoxOPH\nj7FmzRqEhoaievXq8Pb2Rp8+fTT25yX5SE1NxYoVK/D999/DxsYGM2bMQJMmTUTH+qDIyEgMGjQI\nu3btwpdffik6DikYR8RqTpIk+Pr6Ys6cORpXSpIk4eTJk+jXrx8aNmyIW7duYdeuXThz5gw8PDw0\n7ucl+TM2NsbkyZNx8+ZNtG7dGnZ2dnBzc0N8fLzoaP/JxcUFmzdvhqurK44ePSo6DikYi1jN7dmz\nB2lpaRgwYIDoKHLz6tUrBAcHo2nTphg6dCjatm2LW7du4aeffuL3ZlQi5cuXh6+vL27evIm2bdvC\nwcEBX331lUovjLK3t8eOHTvQt29fREdHi45DCsSpaTWWm5uLJk2aYNmyZXB0dBQdp9Ti4+MRHByM\nrVu3wtbWFt7e3ujcuTNXPZPcZWRkYNWqVfjuu+/Qpk0bzJw5Ey1bthQd671Onz4NV1dXrFu3Dl26\ndBEdhxSAI2I1tmbNGpiamsLBwUF0lBLLzs7Gli1b0KFDBzg5OaFatWr4888/ER4eDltbW5YwKYSh\noSHGjRuHmzdvonPnzujWrRu6d++O8+fPi472jvbt2yMiIgKDBw/G7t27RcchBeCIWE2lpqbC3Nwc\nkZGRaNGiheg4xXb37l2EhoZizZo1sLS0hLe3N7p3745y5cqJjkZaKCsrCz/99BPmz5+PZs2aYdas\nWWjTpo3oWP9y4cIFuLi4YNmyZejTp4/oOCRHHBGrqcWLF8POzk6tSrigoABRUVHo1q0bWrZsiYyM\nDBw/fhxHjhzBV199xRImYfT19TFq1CjcvHkTXbt2Re/eveHs7KxSlxC1bNkS0dHRGDt2LDZt2iQ6\nDskRR8Rq6OHDh2jSpAkuXLgAMzMz0XE+KDk5GevWrcPKlSthYmKCkSNHwt3dHUZGRqKjEb1XdnY2\nwsLCEBQUBHNzc8yaNQvt27cXHQsAcOXKFdjb22POnDkYPHiw6DgkByxiNeTl5QVjY2MsXLhQdJRC\nSZKEs2fPIjg4GPv27UPPnj3h7e2NNm3a8HtfUhs5OTnYsGED5s6di7p162LWrFno0KGD6FhITEyE\nnZ0dpk6dCi8vL9FxqJRYxGrm6tWrsLa2RkJCAipUqCA6zjvS09Px888/Izg4GKmpqfDy8oKnp6fG\n7/hFmi03NxcbN27E3LlzYWZmhlmzZsHa2lpoplu3bsHW1hbjxo3D2LFjhWah0mERq5mePXuiQ4cO\nmDBhgugo/3L16lWEhIRg8+bN+PLLL+Hj4wN7e3uUKcNlCKQ5cnNz8fPPPyMwMBCffvopZs2ahU6d\nOgmb5bl79y5sbW0xfPhw+Pn5CclApcciViMnT57EN998g2vXrkFfX190HOTm5mLv3r0IDg7GlStX\nMHToUAwfPhympqaioxEpVF5eHrZs2YLAwEBUrVoVs2bNEna53f3799G5c2cMGDAAM2bMUPr5qfRY\nxGpCkiS0a9cOo0ePxtdffy00y71797B69WqsXr0a9evXh7e3N3r16gVdXV2huYiULT8/H1u3bsWc\nOXNQqVIlzJw5Ew4ODkov5EePHsHW1ha9evVCQEAA12GoGc4bqomdO3ciJycH/fr1E3L+goICHDly\nBL169ULTpk2RnJyM6OhoHD9+HO7u7ixh0ko6Ojr4+uuvcfnyZYwaNQrjx49Hu3btEBUVBWWOcapV\nq4Zjx45h3759mDRpklLPTaXHEbEayMnJQePGjbFy5UrY2toq9dwvXrxAWFgYQkJCoK+vDx8fH3z9\n9dcwNjZWag4idVBQUIDw8HAEBATAyMgIM2fOhIuLi9JGqM+ePYODgwM6dOiA77//niNjNcEiVgM/\n/vgjDhw4gKioKKWd8/z58wgODsauXbvQpUsX+Pj44IsvvuBfbKIiKCgowK5duxAQEABdXV3MnDkT\n3bp1U8rfn5cvX8LJyQktWrTAihUruGBSDbCIVdyrV69gbm6O6OhoNG3aVKHnyszMxLZt2xAcHIwn\nT57Ay8sLgwcPRtWqVRV6XiJNVVBQgL179/7zve3MmTPRo0cPhRfyq1ev0KVLF5ibm2PVqlXQ0dFR\n6PmodFjEKm769Om4f/8+1q1bp7BzXL9+HStXrsT69evx+eefw9vbG87OzvzLSyQnkiRh3759CAgI\nQH5+PmbMmAFXV1eFjlbT0tLQvXt31KhRA+vWrUPZsmUVdi4qHRaxCrt//z6aNm2KS5cuoVatWnI9\ndl5eHvbv34/g4GBcunQJnp6eGDFiBOrUqSPX8xDR/5MkCQcOHIC/vz+ys7MxY8YMfPXVVwor5IyM\nDPTs2RMVKlTApk2buJ+7imIRq7ChQ4eiSpUqCAoKktsxHz58iJ9++gmrVq1CrVq14OPjg969e6vE\ndclE2kKSJERFRcHf3x9paWmYMWMG3NzcFDILlZWVhd69e0NXVxdbt27lFQ4qiEWsov7880/Y2toi\nMTERJiYmpTqWJEk4ceIEgoODER0djT59+sDb2xvNmzeXU1oiKglJknDo0CH4+/sjJSUF06dPR9++\nfeVeyDk5Oejbty9yc3MRHh7OD94qhkWsorp27Qo7OzuMGzeuxMdISUnBxo0bERISAkmS4O3tjYED\nB5a62IlIviRJwpEjR+Dv74/k5GRMnz4d7u7ucv1eNzc3FwMGDMDLly+xe/duGBoayu3YVDosYhV0\n9OhRDBkyBFevXoWenl6x33/p0iWEhIRg+/btsLe3h4+PD6ytrXnpEZGKkyQJsbGx8Pf3x6NHjzB9\n+nT0799fboWcl5cHT09P3L9/HxEREbwVqYpgEQvy5MkTbAgLQ+IffyAtJQXlTUxg3rQpvvHwQNeu\nXTFhwgS4u7sX+XhZWVkIDw9HcHAwkpKSMGLECAwdOhTVq1dX4E9BRIpy7Ngx+Pv746+//sK0adMw\nYMAAuSy2ys/Px7Bhw3D9+nUcOHAAH330kRzSUmmwiJUsLi4OS4OCcCAqCr0AWGVlwRhAKoBzBgbY\nmZeH8kZG2HXwID7//PMPHu/27dsIDQ3F2rVr0bx5c/j4+KBr1668VIFIQ5w4cQL+/v64ffs2pk2b\nhoEDB5a6kAsKCjBy5EhcvHgRBw8exMcffyyntFQiEilNaHCwVM3QUPpeJpOeA5L0nl/PAWmxTCZV\nMzSUQoOD33ucvLw8af/+/ZKLi4tUqVIl6dtvv5USExOV/NMQkTKdPHlSsrOzk2rXri2FhoZK2dnZ\npTpeQUGBNGbMGKlVq1bSs2fP5JSSSoJFrCShwcFSHUND6XohBfz2r+uAVOetMn78+LEUFBQkmZmZ\nSVZWVtLatWul9PR0gT8VESnb6dOnJUdHR8nU1FQKCQmRsrKySnysgoICydfXV2ratKn05MkTOaak\n4uDUtBLExcWhu40NTmZkoN4bj38D4AiADACVAQwGMO2N528A6GBoiMBlyxAbG4vIyEi4urrC29sb\nVlZWyvsBiEjlnDlzBgEBAfjzzz8xefJkDB48uESXJUmShJkzZ2LXrl2IiYlBtWrVFJCW/guLWAkG\n9OqF1nv2YNxb/6mvAKgDQB9AIoCOANYDcHzjNYsAfGdkhClz5sDDwwMVK1ZUUmoiUgdxcXEICAjA\nxYsXMWnSJAwbNqxEhTxnzhxs3rwZMTExqFGjhgKSUmFYxAr25MkTNDAzw62sLFT4j9clALADsBdA\nyzcefw6grr4+EpOSUKVKFUVGJSI19ttvvyEgIADnz5+Hn58fhg8fDgMDg2Id47vvvsOqVasQGxsL\nU1NTBSWlt/H+WAq2ISwMrkChJTwSgBGAJng9Ld3yrecrAnCVybAhLExhGYlI/bVq1Qp79+7F/v37\ncezYMdStWxdLlixBRkZGkY/h5+eHUaNGwdraGrdu3VJgWnqTzuzZs2eLDqHJwkJC0PriRbQu5Pku\nAKYCsAbgBaATgLcnhR7k5WFvair0jY1x9+5dPHjwAMnJyXj16hUyMzNRUFAAHR0d3i2JiFC9enW4\nu7vDzs4OmzdvxsSJEwEAzZo1K9I+023btoWenh6GDh2Krl27olKlSoqOrPV4samCpaWkwPgDr5Hh\ndRG7AdgC4O1lWMYAHt67h507dyItLQ3p6elIS0t7589lypSBkZERypcvj/Lly//z57d/L+5zurq6\n3JWLSM00a9YM4eHhiI+Px5w5c7Bw4UJ8++23GDlyJMqXL/+f7/X29oauri46deqEw4cPo1GjRkpK\nrZ1YxApW3sQEqUV8bR6A9+3+mgqgQ6dOCN2wodD3SpKEnJyc95b027///efHjx8X+tybv0uSJLdS\nf/M5PT09FjyRgllaWmL79u24fPkyAgMDUbduXYwbNw6jRo2CsXHhw4QhQ4ZAV1cXtra2OHToECwt\nLZWYWruwiBXMvGlTnNu5E15ZWf96/CmAWABdARgAOAxgx/9+f1ucgQEaf+AvgUwmg56eHvT09OS+\nsvrNgi9KcScnJxfpw0BeXl6RC7w4hW9gYMCCJ3pL48aNsWXLFly9evWfQh47dixGjx5d6DaX33zz\nDXR1dWFvb4+oqCi0aNFCyam1A1dNK1hhq6aTAfQG8AcACUB9ADMAdHvr/Zq8ajo3Nxfp6elFKvf/\neu7tx3JycmBoaFiiEft/vd7Q0JAFTxojISEBc+fORVRUFEaPHo0xY8YUutXlrl274O3tjYiICLRp\n00bJSTUfi1gJCruOuCi+l8lwwdUVG3fuVEAyzZSXl4eMjIwSlfp/PZednQ0DAwO5T9EbGhqiTBle\nwEBiXL9+HXPnzsX+/fsxatQojB07FhUqvHudx/79+zF48GDs2bMHX3zxhYCkmotFrASF7az1IX/v\nrBVx/Dhaty5s3TUpS35+/j8FX9pSf/O5zMxMGBgYyH2hnZGREVfSU5HduHED8+bNw759++Dt7Y3x\n48e/8zXXoUOH8M0332DHjh2wtrb+13OF3VHOw9NT42bz5I1FrCSrQkKwYOJEHCpiGd8A4GhoiEmL\nFmG4t7ei45FABQUFyMjIkPsUfXp6OvT09OQ+RW9kZMS7e2mwW7duISgoCLt27YKXlxe+/fbbf13C\nFBsbi759+2LLli2ws7P74B3ldksSujg7Y+yUKdyatxAsYiVaFRKCWRMnwi8zE4Mk6b2bfDwHECaT\nYaGBAfxZwlQKkiQhMzNT7lP06enpKFeunNyn6I2MjORyv12Sjzt37iAoKAjh4eEYPnw4JkyYgMqV\nKwMATp48ia+++gruffpgx7p1mJSZCY9C/k17gdf/pn3Hf9MKxSJWsvPnz2NpUBD2R0bCVSaDVWbm\nP58e4/736bGriwvGTpnC6WhSSZIkISsrS+5T9Onp6dDR0VHYtfBUMklJSZg/fz62bduGIUOGYOLE\niahatSom+fpi46JFOAFwlq+UWMSCPH369PX3KfHxSH3xAsYVKsDc0hIDBw3i9ymklSRJQnZ2ttyn\n6NPS0gBALpfGvf2cNm1289dff2HBggXYsmULnJ2dcWTXLpzKzPynhHMA+OD1HeVeAKgLYB4ApzeO\nwXUv78ciJiKNl5OTo5Ap+vz8fLmU+9uP6evrq2zB379/H04dO2LQrVuY8MbjGXh9tzhPALUAHADQ\nD8CfAN68fQSvBHkXi5iIqIT+3uxG3lP0ubm5Cpmil8dmN0W9oxwANAMwG4DrG49p8t4IJcWlj0RE\nJaSrqwtdXd33XndbGnl5ecWahv/rr7+KfC38f62GL8qIfe/u3ehRyMKsNz0GcB1A47cef/OOchN8\nfeX6301dsYiJiFRM2bJlYWJiAhMTE7keNz8/v9DR+PsK/OHDh+88l3jpEqZmZ//nefIADAAwCID5\ne563yszEpfh4uf5s6oxFTESkJXR0dPDRRx8Vurd0UfTv1g3G+/cX+ryE1yWsB2B5Ia8xBpD64kWJ\nM2gaFjERERXZh+4oNwSv99KPBFDYvm6pAIzlPJ2vzrjBLRERFZl506Y4p6//3ue8AFwDsA/Af125\nHWdgAHPeVvEfXDVNRERFVtiq6SQAtQHo4/9HwjIAoXh9GdPfuGr6XRwRExFRkVWtWhVdnJ2x/q3L\noEwBFOD19cSp//v1Cv8uYQBYL5Ohq4sLS/gNHBETEVGx8I5y8sURMRERFYuVlRX8Fy2Co6EhbhTx\nPX/vNe2/aBFL+C0sYiIiKrbh3t6YtGgROhga4nuZDIVdjPQcwBKZDB14w4dCcWqaiIhKjHeUKz0W\nMRERlRrvKFdyLGIiIiKB+B0xERGRQCxiIiIigVjEREREArGIiYiIBGIRExERCcQiJiIiEohFTERE\nJBCLmIiISCAWMRERkUAsYiIiIoFYxERERAKxiImIiARiERMREQnEIiYiIhKIRUxERCQQi5iIiEgg\nFjEREZFALGIiIiKBWMREREQCsYiJiIgEYhETEREJxCImIiISiEVMREQkEIuYiIhIIBYxERGRQCxi\nIiIigVjEREREArGIiYiIBGIRExERCcQiJiIiEohFTEREJBCLmIiISCAWMRERkUAsYiIiIoFYxERE\nRAKxiImIiARiERMREQnEIiYiIhKIRUxERCQQi5iIiEggFjEREZFALGIiIiKBWMREREQCsYiJiIgE\nYhETEREJxCImIiISiEVMREQkEIuYiIhIIBYxERGRQCxiIiIigVjEREREAv0fjYccUo1/HCYAAAAA\nSUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"G1 = nx.complete_graph(4)\n",
"pos = nx.spring_layout(G1) #定义一个布局,此处采用了spring布局方式\n",
"nx.draw(G1, pos = pos, with_labels = True)"
]
},
{
"cell_type": "code",
"execution_count": 206,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1.0\n"
]
}
],
"source": [
"print(nx.transitivity(G1))"
]
},
{
"cell_type": "code",
"execution_count": 216,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xt8zvX/x/HHhbKNJcd0sMnYGBvKxNfXoSLnYwmRIWZb\n+aacC2tzzlL4to2SxVckIWLaNyIStlBz2jCMSk5rxjZzuH5/+NZPDtm4tvd2Xc/77eZWt+v67PN5\nrlv23OtzvT+fj8VqtVoRERERI4qYDiAiIuLIVMQiIiIGqYhFREQMUhGLiIgYpCIWERExSEUsIiJi\nkIpYRETEIBWxiIiIQSpiERERg1TEIiIiBqmIRUREDFIRi4iIGKQiFhERMUhFLCIiYpCKWERExCAV\nsYiIiEEqYhEREYNUxCIiIgapiEVERAxSEYuIiBikIhYRETFIRSwiImKQilhERMQgFbGIiIhBKmIR\nERGDVMQiIiIGqYhFREQMUhGLiIgYpCIWERExSEUsIiJikIpYRETEIBWxiIiIQSpiERERg1TEIiIi\nBqmIRUREDFIRi4iIGKQiFhERMUhFLCIiYpCKWERExCAVsYiIiEEqYhEREYNUxCIiIgapiEVERAxS\nEYuIiBikIhYRETFIRSwiImKQilhERMQgFbGIiIhBxUwHEClITpw4wbzoaJJ++olzaWmULFUKT19f\n/Pv2pXz58qbjiYgdslitVqvpECKmxcXFMX3SJFbFxNAF8MvKwhVIB7Y5O7PMaqVt69a8OmoUfn5+\nhtOKiD1REYvDmx0ZScjQoYzIzMTfaqX0TbZJBaItFt52diY0PJyAoKD8jikidkpFLA5tdmQkU4YO\n5auMDKrmYPsDQEsXF0aojEXERlTE4rDi4uLo0KwZG68r4VSgH/BfoDwwEehxzfsHgMYuLqzcsIF6\n9erlX2ARsUtaNS0Oa/qkSYzIzLxhEg4GnICTwH+AIGDvNe9XBYZnZjJ90qT8CSoidk0TsTikEydO\n4OXuTnJW1l8+E84ASgN7AI//veYPPMzVyfgPZwAPJyeSUlK0mlpE7oomYnFI86Kj6Qw3LMxKAu7h\n/0sYoDaw+7rtygCdLRbmRUfnWUYRcQwqYnFIST/9RP2srBtePwfcd91r93H1Mqbr+WVmkpSQkAfp\nRMSRqIjFIZ1LS8P1Jq+XBM5e91oa3HRbVyA9NdXW0UTEwaiIxSGVLFXqplOuJ3AJOHjNaz8CNW+y\nbTrgWvpmVx2LiOScilgckqevL9ucnG543QXoAozl6sKtTcBK4MWb7CPO2RlPH5+8jCkiDkCrpsUh\n3WrVNPz1OuJywBSg23XbaNW0iNiKJmJxSBUqVKBt69Z8bLHc8F5pYBlXF24d5sYSBvjYYqFdmzYq\nYRG5a5qIxWHd6s5at6M7a4mILWkiFofl5+dHaHg4LV1cOJDDr/njXtOh4eEqYRGxCRWxOLSAoCBG\nhIfzj+LFCefq58M3cwZ4x2KhsR74ICI2plPT4vAuXbpE1apVqfbww8Rv305niwW/zMw/n0cc5+zM\nZxcv4v7II0R/9pkmYRGxqWKmA4iY9tFHH1GlShVi167l1KlTzIuOZmdCAumpqbiWLk1NHx9ea9WK\nJk2a4OnpaTquiNgZTcTi0M6dO4enpycrVqy47aT73HPP8dRTTxEcHJxP6UTEEegzYnFo06ZNo1mz\nZjk63RwUFERkZCT63VVEbEkTsTis3377DW9vb+Lj43n00Udvu73VaqV69erMmTOHf/7zn/mQUEQc\ngSZicVihoaH4+/vnqIQBLBYLgYGBREZG5nEyEXEkmojFISUmJvLPf/6Tffv2UbZs2Rx/3ZkzZ6hS\npQr79+/XXbVExCY0EYtDGjVqFMOGDctVCQOUKVOGzp07M3fu3DxKJiKORhOxOJzvvvuOHj16kJiY\niLOzc66/ftu2bfTo0YP9+/dTpIh+lxWRu6OfIuJQrFYrw4YNY/z48XdUwnD11pj3338/sbGxNk4n\nIo5IRSwOZdmyZWRkZNCzZ8873ofFYvnzUiYRkbulU9PiMC5evEjNmjWZOXMmLVu2vKt9nT9/Hjc3\nN3bs2IGbm5uNEoqII9JELA7jgw8+wN3dnWeeeeau91WiRAleeOEFPvjgAxskExFHpolYHEJ6ejrV\nqlUjJiaGunXr2mSfu3fvpnnz5qSkpHDPPffYZJ8i4ng0EYtDmDp1Ki1atLBZCQPUrFkTT09Pli9f\nbrN9iojj0UQsdu/XX3+lVq1abN++HXd3d5vue9GiRcyePZt169bZdL8i4jhUxGL3Bg4cyH333cfU\nqVNtvu/s7Gzc3NxYv3491atXt/n+RcT+qYjFru3du5cmTZqQlJRE6dKl8+QYb7zxBhkZGbz33nt5\nsn8RsW8qYrFrHTt2pEmTJgwZMiTPjnH48GEef/xxjh49iouLS54dR0TskxZrid369ttv+fHHH3n5\n5Zfz9DiVK1emYcOGLFq0KE+PIyL2SUUsdumPW1lOmDABJyenPD+e7rQlIndKRSx2acmSJVy8eJEe\nPXrky/FatWrFyZMniY+Pz5fjiYj9UBGL3cnOzmbUqFFMnTo1356OVLRoUQYOHKipWERyTYu1xO7M\nnDmT1atXExMTk6/HPXHiBF5eXiQnJ+fZCm0RsT8qYrEraWlpeHp68t///hdfX998P36PHj1o0KAB\nr776ar4fW0QKJ52aFrvy9ttv06ZNGyMlDFcXbUVFRaHfb0Ukp4qZDiBiK8eOHSMqKoqdO3cay9C4\ncWOKFi3Khg0baNasmbEcIlJ4aCIWuxESEkJAQACVKlUylsFisRAYGKhFWyKSY/qMWOxCQkICzZs3\nJykpiVKlShnNkpaWRuXKldm7dy8VK1Y0mkVECj5NxGIXRo4cyRtvvGG8hAFKlSpF165dmTNnjuko\nIlIIaCKWQm/dunUMGDCAvXv3cu+995qOA8COHTvo1KkTycnJFC1a1HQcESnANBFLoXblyhWGDx/O\nxIkTC0wJA9StW5eKFSuyevVq01FEpIBTEUuh9umnn1KkSBG6du1qOsoNdP9pEckJnZqWQuvChQtU\nr16duXPnFshLhTIzM6lUqRJxcXE8+uijpuOISAGliVgKrYiICGrVqlUgSxjA2dmZ3r17M2vWLNNR\nRKQA00QshVJqaipeXl5888031KxZ03ScW0pKSqJx48akpKRQvHhx03FEpADSRCyF0uTJk+nYsWOB\nLmEAT09PfHx8+Pzzz01HEZECShOxFDopKSnUrVuXhIQEHnroIdNxbuvzzz/nvffeY+PGjaajiEgB\npCKWQsff3x83NzfGjRtnOkqOXLx4kcqVK7NmzRp8fHxMxxGRAkZFLIXKzp07adWqFUlJSdx3332m\n4+RYSEgIp06d4v333zcdRUQKGBWxFCotW7akQ4cOvPzyy6aj5MqxY8fw9fUlJSWFkiVLmo4jIgWI\nFmtJoREbG8uhQ4cICAgwHSXXHnnkEZo2bcqCBQtMRxGRAkZFLIXClStXGDFiBBMnTuSee+4xHeeO\n/HGnLZ2EEpFrqYilUPjkk08oXrw4zz77rOkod6x58+acO3eOLVu2mI4iIgWIPiOWAi8rKwsvLy/+\n85//0LhxY9Nx7kp4eDgJCQl8/PHHpqOISAGhIpYCLzw8nE2bNrF8+XLTUe7a6dOnqVq1KgcOHKBs\n2bKm44hIAaAilgLtzJkzeHl5sXHjRqpXr246jk307t2b2rVrM2TIENNRRKQAUBFLgTZ06FDOnTtH\nVFSU6Sg28/3339O7d28SExMpUkTLNEQcXTHTAURu5fDhw8ydO5fdu3ebjmJTDRo0oESJEqxdu5YW\nLVqYjiMihunXcSmwRo8ezaBBg6hYsaLpKDZlsVj+vJRJRESnpqVA2r59O23btiUpKQlXV1fTcWwu\nPT0dd3d3EhISePjhh03HERGDNBFLgWO1Whk2bBghISF2WcIArq6udO/enQ8++MB0FBExTBOxFDhr\n1qxh8ODBJCQkFNq7aOVEQkICrVq14vDhw3b9fYrI39NELAXK5cuXGT58OJMnT7b7cvLx8eHRRx9l\n5cqVpqOIiEEqYilQ5s+fz3333UfHjh1NR8kXWrQlIjo1LQVGZmYmnp6eLF68mIYNG5qOky8uXLhA\npUqV+O6776hWrZrpOCJigCZiKTCmT5/OE0884TAlDFC8eHH69u1rVzcsEZHc0UQsBcKpU6eoXr06\nmzdvxtPT03ScfJWcnEz9+vU5evQozs7OpuOISD7TRCwFwvjx4+nevbvDlTBAlSpV8PPzY/Hixaaj\niIgBmojFuIMHD/LEE0+wZ88eKlSoYDqOEStWrGDixIl6VrGIA9JELMa9+eabDB482GFLGKBt27b8\n8ssv7Nixw3QUEclnKmIxatu2bWzcuJHXXnvNdBSjihYtSkBAgC5lEnFAOjUtxlitVp588kl69epF\n//79Tccx7vjx49SoUYPDhw9TqlQp03FEJJ9oIhZjVq1axcmTJ+nTp4/pKAVCxYoVadGiBf/5z39M\nRxGRfKQiFiMuXbrEiBEjmDJlCsWK6bHYf/jjTls6USXiOFTEYkR0dDTly5enbdu2pqMUKM2aNePy\n5cts2rTJdBQRySf6jFjy3fnz5/H09GTZsmXUr1/fdJwCZ/r06WzdupVPPvnEdBQRyQcqYsl348eP\nZ9euXSxatMh0lAIpNTWVKlWqkJiY6NCXdIk4ChWx5KsTJ07g7e3N1q1b8fDwMB2nwOrXrx+enp6M\nHDnSdBQRyWMqYslXr7zyCsWKFeO9994zHaVAi4uL4/nnn+fAgQMULVrUdBwRyUNarir5Zv/+/Xz6\n6afs3bvXdJQCz8/Pj7Jly/LVV1/Rpk0b03FEJA9p1bTkmzfeeIMhQ4ZQrlw501EKhT8uZRIR+6ZT\n05IvtmzZQteuXUlKStKj/nLo/PnzuLm5sX37dtzd3U3HEZE8oolY8pzVamXYsGGMGzdOJZwLJUqU\noFevXsyePdt0FBHJQypiyXMrVqwgLS2NF1980XSUQicwMJA5c+aQnZ1tOoqI5BEVseSpa29lqdW/\nuVejRg1q1KjBsmXLTEcRkTyiIpY8NWfOHB5++GFatWplOkqhpUVbIvZNi7Ukz5w7dw5PT09WrlzJ\n448/bjpOoZWdnY27uztr167F29vbdBwRsTFNxJJn3nnnHZ588kmV8F269957eemll4iKijIdRUTy\ngCZiyRPHjx+nZs2axMfH8+ijj5qOU+ilpKRQt25dUlJSKFGihOk4ImJDmoglT4SGhtKnTx+VsI24\nubnRqFEjFi5caDqKiNiYJmKxuX379tG4cWMSExMpU6aM6Th2IyYmhtGjRxMfH4/FYjEdR0RsRBOx\n2NyoUaMYPny4StjGWrZsSWpqKvHx8aajiIgNqYjFpjZt2sT27dsZNGiQ6Sh2p0iRIgwcOFCXMonY\nGZ2aFpuxWq384x//IDg4WHfRyiMnT57E09OT5ORkSpcubTqOiNiAJmKxmaVLl5KZmUnPnj1NR7Fb\n5cuXp02bNnz88cemo4iIjWgiFpu4ePEi3t7eRERE0KJFC9Nx7NqmTZvo378/e/fu1aItETugiVhs\nYvbs2VSpUkUlnA8aNWpEsWLF+Oabb0xHEREb0EQsd+3s2bN4enqyZs0a6tSpYzqOQ3j//fdZv349\nn332mekoInKXVMRy18aMGUNKSoo+t8xHZ8+exd3dnT179vDggw+ajiMid0FFLHfll19+wcfHhx07\nduDm5mY6jkMZOHAgjzzyCGPGjDEdRUTugopY7sqAAQMoU6YMU6ZMMR3F4ezcuZP27dtz6NAhihUr\nZjqOiNwh/e2VO7Z7926++OILkpKSTEdxSHXq1OGRRx5h1apVdOzY0XQcEblDWjUtd2zkyJGMGjWK\n+++/33QUhxUUFKQ7bYkUcjo1LXdk/fr19O3bl3379lG8eHHTcRxWVlYWlSpVYsuWLXh4eJiOIyJ3\nQBOx5JrVamX48OFMnDhRJWyYk5MT/v7+zJo1y3QUEblDKmLJtc8++4wrV67QrVs301GEq6uno6Oj\nycrKMh1FRO6AilhyJTs7m1GjRjF16lSKFNH/PgVBtWrVqFOnDkuWLDEdRUTugH6SSq5ERUVRvXp1\nnnzySdNR5BpatCVSeGmxluRYWloanp6erF27llq1apmOI9e4dOkSlStXZvXq1fj6+pqOIyK5oIlY\ncmzKlCm0a9dOJVwAFStWjAEDBhAVFWU6iojkkiZiyZFjx45Ru3ZtfvzxRx555BHTceQmfv75Z3x8\nfDhy5Aiurq6m44hIDmkilhwZO3YsgYGBKuEC7OGHH+bJJ59kwYIFpqOISC5oIpbbSkhIoHnz5iQl\nJVGqVCnTceRvfP311wwZMoSdO3disVhMxxGRHNBELLc1YsQIRo8erRIuBJ566ikyMzP5/vvvTUcR\nkRxSEcvfWrt2LUlJSQwcONB0FMmBIkWKEBgYqEuZRAoRnZqWW7py5Qp+fn6MGDGC559/3nQcyaHT\np0/j4eHBgQMHKFeunOk4InIbegyi3NKiRYsoWrQoXbt2NR1FcqFs2bJ07NiRmTNn4lqiBEk//cS5\ntDRKliqFp68v/n37Ur58edMxReR/NBHLTV24cIHq1asTHR1N06ZNTceRXIiLiyNk2DDWf/st3YsX\np35WFq5AOrDN2ZllVittW7fm1VGj8PPzMx1XxOGpiOWmpk2bxvr161mxYoXpKJILsyMjCRk6lOGZ\nmfSxWil9k21SgWiLhbednQkNDycgKCi/Y4rINVTEcoPU1FS8vLxYv3493t7epuNIDs2OjGTK0KF8\nlZFB1f+99j4QDSQALwAfXbP9AaCliwsjVMYiRqmI5QbDhw/n999/Z/bs2aajSA7FxcXRoVkzNl5T\nwgDLuXppxFdAJn8tYrhaxo1dXFi5YQP16tXLp7Qici0VsfzFkSNHeOyxx0hISOChhx4yHUdyqFeX\nLtRbvpzBt/jrPAb4mRuLGOBdi4XtnTsz//PP8zKiiNyCilj+onfv3lSuXJmwsDDTUSSHTpw4gZe7\nO8lZWTf9TBj+vojPAB5OTiSlpGg1tYgBuqGH/GnHjh3ExsYybNgw01EkF+ZFR9MZblnCt1MG6Gyx\nMC862nahRCTHVMTypxEjRjB27Fg9uaeQSfrpJ+pnZd3VPvwyM0lKSLBRIhHJDRWxABAbG8vhw4cZ\nMGCA6SiSS+fS0rjbX51cgfTUVFvEEZFcUhELly9fZvjw4UyePJl77rnHdBzJpZKlSpF+i/cuA1n/\n++cl4ML//v166YBr6Ts9uS0id0NFLCxYsAAXFxc6d+5sOorkUmZmJmezs9l4i0cejgdcgCnAgv/9\n+4SbbLfN2RlPH588yykit6YidnCZmZmMHj2aqVOn6vm1hcj+/fsZMmQIbm5unDx9mi+LFeNmJ5ZD\ngCtcnYL/+DP2um3OAJ9mZmIpWpTs7Oy8DS4iN1ARO7iZM2dSr149GjVqZDqK3MalS5dYvnw5zzzz\nDI0aNaJYsWJs3bqVtWvX0r5dOz6+w1+kPrZYaNa0KbGxsVSrVo2oqCguXLhg4/Qiciu6jtiBnT59\nmurVq7Np0ya8vLxMx5Fb+PXXX/nwww+ZPXs2lSpVIjg4mOeeew4nJ6c/t7nVnbVu5/o7a23ZsoWw\nsDB27drFyJEj6dev31+OIyK2p4nYgU2YMIGuXbuqhAsgq9XKhg0b6NatG97e3hw7doyVK1eyefNm\nevXqdUM5+vn5ERoeTksXFw7k8Bh/3Gs6NDz8z9tbNmjQgNWrV7NkyRJWr15N1apVmTlzJll3eXmU\niPwNqzik5ORka9myZa3Hjx83HUWu8fvvv1tnzpxp9fb2ttaoUcM6Y8YM6++//57jr58VEWGt6OJi\nnWaxWM+A1XqTP6fB+o7FYq3o4mKdFRHxt/uLj4+3dujQwfrQQw9Z33vvPWtGRsbdfosich2dmnZQ\nPXv2xMvLi7Fjr1+6Iyb8+OOPREREsHjxYlq0aEFwcDBNmza9owV08fHxTJ80iS9Xr6azxYJfZuaf\nzyOO+9/ziNu1acOro0bl+EEPO3bsICwsjK1btzJs2DAGDhyIi4tLrrOJyI1UxA7ohx9+oH379iQl\nJVGyZEnTcRzWhQsXWLJkCRERERw5coSBAwfSv39/HnzwQZvs/+TJk8yLjiYpIYH01FRcS5fG08eH\n3n363PE9pX/88UfGjRvHd999x5AhQwgKCqJEiRI2ySviqFTEDsZqtfL000/TvXt3AgICTMdxSIcO\nHWLWrFl89NFH1KlTh6CgINq3b0+xYsVMR8uxhIQExo0bx7fffsvrr79OcHCwfqkTuUNarOVg1qxZ\nw6+//kq/fv1MR3Eoly9fZtWqVbRt2xY/Pz+ys7PZtGkTsbGxdO7cuVCVMICPjw+LFy9m7dq1bN++\nHQ8PDyZNmkR6+q3u8SUit6KJ2IFcvnyZOnXqMGHCBDp06GA6jkM4efIkc+bMYdasWZQrV47g4GC6\ndetmd5+v7tmzhwkTJvDf//6XV199lUGDBnHfffeZjiVSKGgidiDz5s2jdOnStG/f3nQUu2a1Wvnu\nu+/o1asX1apVIykpicWLFxMXF0ffvn3troQBvL29WbBgARs3bmTfvn14eHgQFhZGWlqa6WgiBZ4m\nYgeRkZGBl5cXS5Ys4YknnjAdxy6dO3eOBQsWEBERQWZmJkFBQfj7+1OmTBnT0fJdUlISEydOZNWq\nVbz88ssMHjyY+++/33QskQJJE7GDmD59Og0bNlQJ54Hdu3fzyiuv4ObmxldffUV4eDj79u3jtdde\nc8gSBvD09CQ6Oprvv/+elJQUqlatytixYzlz5ozpaCIFjiZiB3Dy5Elq1KjBli1bqFo1NzdAlFvJ\nzs5m2bJlREREsH//fvr378+AAQOoVKmS6WgFUnJyMpMmTWLp0qUEBgby+uuvU7ZsWdOxRAoEFbED\nePXVV7FarcyYMcN0lEIvJSWF2bNnM2fOHKpXr05wcDCdOnXSc5xz6PDhw0yaNIklS5YQEBDAkCFD\nKFeunOlYIkbp1LSdO3DgAAsWLGDMmDGmoxRaV65cITY2lk6dOlGnTh3Onj3L2rVr+eabb+jatatK\nOBcqV67MrFmz2LFjB7///jteXl4MHz6cEydOmI4mYowmYjvXrVs3ateuzRtvvGE6SqFz+vRpoqOj\niYyMpGTJkgQHB/PCCy/oxhU2dPToUaZMmcLChQvp27cvw4YN44EHHjAdSyRfaSK2Y1u3buW7775j\n8ODBpqMUGlarlW3bttGnTx88PDzYuXMn8+fPZ8eOHQQEBKiEbaxSpUr8+9//5qeffiI7O5saNWrw\n+uuvc/z4cdPRRPKNithOWa1Whg8fTmhoqF1et2prGRkZzJkzBz8/P7p37463tzf79+9n/vz5NGzY\n8I4eviA59/DDDzNjxgx27dqF1WqlZs2aDB48mF9++cV0NJE8pyK2U19++SWnT5/G39/fdJQCLTEx\nkddee41KlSqxfPlywsLC2L9/P8OHD7/jByPInXvooYd499132b17N0WLFsXHx4dBgwZx7Ngx09FE\n8oyK2A5dunSJESNGMGXKlEJ3D+P8cOnSJZYuXUrz5s1p0qQJTk5O/PDDD6xcuZI2bdpQtGhR0xEd\nXsWKFXnnnXfYs2cPTk5O1K5dm5dffpmjR4+ajiZicypiOzR37lweeOAB2rRpYzpKgfLLL78QGhqK\nu7s706ZNo1+/fqSkpDBp0iQqV65sOp7cxAMPPMDUqVPZt28frq6u1KlTh8DAQI4cOWI6mojNqIjt\nzPnz53nrrbd4++239bkmVz8rX7duHc899xw1a9bk+PHjxMTEsGnTJl544QWKFy9uOqLkQPny5Zk8\neTKJiYmUKVOGxx57jICAAA4dOmQ6mshdUxHbmWnTptGkSRP8/PxMRzHq999/Z8aMGXh7e/Ovf/2L\np556iiNHjhAZGYmvr6/peHKHypUrx8SJE0lKSqJChQrUq1ePl156ieTkZNPRRO6YriO2I7/99hve\n3t7ExcVRpUoV03GM2L59O5GRkSxZsoRWrVoRFBRE48aNdXbATqWmpvLee+/x/vvv0759e958803d\nxlUKHU3EdiQsLIzevXs7XAlnZWUxb948GjRoQKdOnahcuTJ79+5l4cKFNGnSRCVsx0qXLk1oaCgH\nDhygcuXKNGzYEH9/f5KSkkxHE8kxTcR2IjExkUaNGpGYmOgwN9M/ePAgUVFRREdH8/jjjxMcHEyb\nNm20UtyBpaWlMXPmTKZPn07Lli0ZPXo01atXNx1L5G9pIrYTb7zxBsOGDbP7Er58+TIrV66kdevW\nNGjQAIDvv/+eNWvW0KFDB5WwgytVqhSjR4/m4MGDeHt706RJE1544QX27NljOprILWkitgObN2+m\ne/fuJCYm4uzsbDpOnvjtt9+YM2cOs2bN4sEHHyQoKIjnn3/ebr9fsY309HTef/993n33XZo1a8aY\nMWOoVauW6Vgif6GJuJCzWq0MGzaMcePG2V0pWa1WNm7cSI8ePahevTrJycksXbqULVu24O/vb3ff\nr9ieq6srI0eO5ODBg9SrV4/mzZvTtWtXEhISTEcT+ZOKuJBbvnw5586do1evXqaj2MzZs2eJiIjA\n19eX/v3706BBA5KTk/nwww95/PHHTceTQqhkyZIMGzaMgwcP0qBBA5555hmeffZZfvzxR9PRRHRq\nujC7ePEitWrVYsaMGbRs2dJ0nLuWkJBAREQEixYt4umnnyYoKIinnnpKq57F5jIyMpg9ezZvv/02\n9evXZ+zYsTz22GOmY4mD0kRciM2ZMwc3NzeeeeYZ01Hu2IULF1i4cCGNGzemVatWVKxYkV27drFk\nyRKefvpplbDkCRcXFwYPHszBgwd56qmnaN++PR06dCA+Pt50NHFAmogLqfT0dDw9PVm9ejV169Y1\nHSfXjhw5wqxZs5gzZw4+Pj4EBQXRoUMH7rnnHtPRxAFlZWXx4YcfMnnyZGrXrk1ISAj169c3HUsc\nhCbiQuqdd96hefPmhaqEr1y5QkxMDO3bt+exxx4jIyODDRs28PXXX/Pss8+qhMUYJycnXnnlFQ4e\nPEi7du1Rn41EAAAMsklEQVR47rnnaN26NVu2bDEdTRyAJuJC6Ndff6VWrVps374dd3d303Fu69Sp\nU8ydO5eoqChKlSrFyy+/TPfu3SlRooTpaCI3deHCBaKjo5k0aRKenp6EhITQqFEj07HETqmIC6HA\nwEBcXV2ZOnWq6Si3ZLVa2bp1KxEREaxYsYJOnToRFBRE/fr19bmvFBrZ2dnMmzePCRMm4OHhQUhI\nCI0bNzYdS+yMiriQ2bt3L02bNiUxMZHSpUubjnOD8+fP88knnxAREUF6ejqBgYH07dvX7u/4Jfbt\n4sWLzJ8/nwkTJuDu7k5ISAhNmzY1HUvshIq4kOnUqRONGzdmyJAhpqP8xd69e4mMjGTBggX885//\nJDg4mBYtWlCkiJYhiP24ePEin3zyCePHj+ehhx4iJCSEJ598Umd55K6oiAuRjRs38uKLL7Jv3z6c\nnJxMx+HixYt88cUXREREsGfPHvr3709AQABubm6mo4nkqUuXLrFw4ULGjx9PhQoVCAkJ0eV2csdU\nxIWE1WqlYcOGDBo0iJ49exrNcuzYMT744AM++OADqlWrRlBQEF26dOHee+81mkskv12+fJlFixYx\nbtw4ypYty9ixY3nmmWdUyJIrOm9YSHz++edkZ2fTo0cPI8e/cuUKX3/9NV26dMHX15dTp04RGxvL\nhg0b6N69u0pYHFLRokXp2bMnu3fv5pVXXuG1116jYcOGxMTEoBlHckoTcSGQnZ1NzZo1iYqK4umn\nn87XY6emphIdHU1kZCROTk4EBwfTs2dPXF1d8zWHSGFw5coVlixZQlhYGCVKlGDs2LG0adNGE7L8\nLRVxIfDvf/+bVatWERMTk2/HjI+PJyIigqVLl9K2bVuCg4P5xz/+oR8oIjlw5coVli5dSlhYGPfe\ney9jx46lffv2+vsjN6UiLuDOnj2Lp6cnsbGx+Pr65umxMjMz+fTTT4mIiODEiRMEBgbSr18/KlSo\nkKfHFbFXV65c4YsvviAsLAyLxcLYsWPp2LGjCln+QkVcwI0ePZqff/6ZuXPn5tkx9u/fT1RUFB9/\n/DFPPPEEQUFBtG7dmqJFi+bZMUUcidVqZcWKFYSFhXH58mXGjBlD586ddXmfACriAu3nn3/G19eX\nnTt3UqlSJZvu+9KlS3z55ZdERESwc+dO+vbty8CBA6lSpYpNjyMi/89qtbJq1SpCQ0O5cOECY8aM\n4dlnn1UhOzgVcQHWv39/ypcvz6RJk2y2z19//ZUPP/yQ2bNnU6lSJYKDg3nuuecKxHXJIo7CarUS\nExNDaGgo586dY8yYMXTt2lVnoRyUiriA2rVrF08//TRJSUmUKlXqrvZltVr59ttviYiIIDY2luef\nf56goCDq1Kljo7QiciesVitfffUVoaGhpKWlMXr0aLp166ZCdjAq4gKqXbt2NG/enMGDB9/xPtLS\n0pg/fz6RkZFYrVaCgoLo3bv3XRe7iNiW1Wrl66+/JjQ0lFOnTjF69Gi6d+9OsWLFTEeTfKAiLoC+\n+eYbXnrpJfbu3Uvx4sVz/fU7d+4kMjKSxYsX06JFC4KDg2natKlWaooUcFarlXXr1hEaGsrx48cZ\nPXo0L7zwggrZzqmIDTlx4gTzoqNJ+uknzqWlUbJUKTx9fXnR35927doxZMgQunfvnuP9ZWVlsWTJ\nEiIiIkhJSWHgwIH079+fBx98MA+/CxHJK+vXryc0NJSjR4/y5ptv0qtXL+655x7TsSQPqIjzWVxc\nHNMnTWJVTAxdAL+sLFyBdGCbszOfX7pEyRIlWLpmDU888cRt93fo0CFmzZrFRx99RJ06dQgODqZd\nu3b6DVrETnz77beEhoZy6NAh3nzzTXr37q1CtjMq4nw0OzKSkKFDGZGZib/Vys2eJpwKzLVYmOrs\nTGh4OAFBQTdsc/nyZdasWUNERARbt27F39+fwMBAqlWrluffg4iYsWnTJkJDQzlw4ACjRo2iT58+\nuse7nVAR55PZkZFMGTqUrzIyqJqD7Q8ALV1cGHFNGZ84cYKPPvqIqKgoKlSoQFBQEN26dcPFxSVP\ns4tIwbF582bCwsLYu3cvo0aNom/fvne0lkQKDhVxPoiLi6NDs2ZsvK6EXwS+BjKAckA/4M1r3j8A\nNHZxYfyMGaxbt47Vq1fTuXNngoKC8PPzy79vQEQKnC1bthAWFsauXbsYOXIk/fr10/0ACikVcT7o\n1aUL9ZYvZ/B1/6n3AFUAJyAJaAJ8DLS8Zptw4O0SJRg1bhz+/v6UKVMmn1KLSGEQFxdHWFgYO3bs\nYMSIEQwYMECFXMioiPPYiRMn8HJ3Jzkr66afCf8hEWgOfAE8ds3rZwAPJyeSUlIoX758XkYVkULs\nhx9+ICwsjPj4eIYPH05AQADOzs6mY0kO6AaneWxedDSd4ZYl/DJQAqjF1dPSj133fhmgs8XCvOjo\nPMsoIoXf448/zhdffMGXX37J+vXr8fDwYNq0aWRkZJiOJrehIs5jST/9RP2srFu+/z5wjqufFY8G\n4m6yjV9mJkkJCXkTUETsSt26dVm2bBkxMTFs3rwZDw8PwsPDOX/+vOlocgsq4jx2Li0N19tsYwGa\nAl2BhTd53xVIT021dTQRsWO1a9dmyZIlxMbGsm3bNqpUqcKUKVM4d+6c6WhyHRVxHitZqhTpOdz2\nEnCzC5HSAdfSf/cJs4jIzfn4+LB48WLWrVvHzp078fDwYNKkSaSn5/Qnk+Q1FXEe8/T1ZdtNVjCe\nBD4FzgNXgK+Az4CON9lHnLMznj4+eRlTROxczZo1WbhwIevXr2fXrl14eHgwYcIEzp49azqaw9Oq\n6Tx2q1XTp4DngJ8AK1ANGAO0v+7rtWpaRPJCYmIiEyZMICYmhkGDBvGvf/2L+++/33Qsh6SJOI9V\nqFCBtq1b8/F1Tz4qB6znatGmAtu4sYQBPrZYaNemjUpYRGzKy8uLefPmsXnzZpKTk6latSpvvfUW\nqVqPku80EeeDW91Z63b+uLPWyg0bqFevXl7FExHhwIEDTJw4kRUrVhAUFMRrr72WqxsI3eqJcv59\n+2qQuA1NxPnAz8+P0PBwWrq4cCCHX/PHvaZDw8NVwiKS56pWrcpHH33Etm3bOH78ONWqVePNN9/k\n9OnTf/t1cXFx9OrSBS93d/aGhPDYggW0/fJLHluwgD1vvYWnmxu9unQhLu5mF2cKAFbJN7MiIqwV\nXVys0ywW6xmwWm/y5zRY37FYrBVdXKyzIiJMRxYRB3Xo0CFrQECAtUyZMtaRI0daT548ecM2f/xM\ne/dvfqadAes0/Uz7Wzo1nc/i4+OZPmkSX65eTWeLBb/MzD+fRxzn7Mwyq5V2bdrw6qhRmoRFxLiU\nlBQmT57Mp59+yksvvcTQoUOpUKGCTZ4oJ1epiA05efLk1c9TEhJIT03FtXRpPH186N2njz5PEZEC\n5+jRo0yZMoWFCxfSunVrvl66lE2ZmX+WcDYQzNW7BKYCHsBEoNU1+9C6l5tTEYuISI79/PPPtGrS\nhD7JyQy55vUMrj4tri9QCVgF9AB2AW7XbPeuxcL2zp2Z//nn+Za5oFMRi4hIjuX0iXIAtYG3gM7X\nvKZ7I9xIq6ZFRCTHbvdEuT/8BuwHal73up4odyMVsYiI5NjtnigHV++b3wvoA3je5H09Ue6vVMQi\nIpJjt3uinJWrJVwcmHmLbfREub8qZjqAiIgUHrd7otxLXL2X/mqg6C220RPl/koTsYiI5NitnigH\nEAjsA1YA9/7NPvREub/SqmkREcmxW62aTgEqA078/yRsAWZx9TKmP2jV9I00EYuISI7d6olyblx9\ntnoGV089pwNn+WsJg54odzOaiEVEJFf0RDnb0kQsIiK5oifK2ZaKWEREci0gKIgR4eE0dnHhXYuF\nW12MdAaYZrHQWA98uCWdmhYRkTumJ8rdPRWxiIjcNT1R7s6piEVERAzSZ8QiIiIGqYhFREQMUhGL\niIgYpCIWERExSEUsIiJikIpYRETEIBWxiIiIQSpiERERg1TEIiIiBqmIRUREDFIRi4iIGKQiFhER\nMUhFLCIiYpCKWERExCAVsYiIiEEqYhEREYNUxCIiIgapiEVERAxSEYuIiBikIhYRETFIRSwiImKQ\nilhERMQgFbGIiIhBKmIRERGDVMQiIiIGqYhFREQMUhGLiIgYpCIWERExSEUsIiJikIpYRETEIBWx\niIiIQSpiERERg1TEIiIiBqmIRUREDFIRi4iIGKQiFhERMUhFLCIiYpCKWERExCAVsYiIiEEqYhER\nEYNUxCIiIgapiEVERAxSEYuIiBikIhYRETFIRSwiImKQilhERMQgFbGIiIhBKmIRERGDVMQiIiIG\nqYhFREQMUhGLiIgY9H8jVYI4xjKLCgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"G2 = nx.Graph()\n",
"for i, j in [(1, 2), (1, 3), (1, 0), (3, 0)]:\n",
" G2.add_edge(i,j)\n",
"nx.draw(G2,pos = pos, with_labels = True)"
]
},
{
"cell_type": "code",
"execution_count": 198,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.6\n"
]
}
],
"source": [
"print(nx.transitivity(G2))"
]
},
{
"cell_type": "code",
"execution_count": 219,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xt0zXe+//HXliAXkQnl6LQSlYuWCaritOO41FC3MtJS\n6jiIamTvTk/bqWotlzRRk+ovHavTmdyUiajRGqMXLWXKoJRKWipKRQTRi0lKGiGJuOzfH6pHSSoi\nO599eT7Wsmrt/d3bS9eyX3l/9+f7/VjsdrtdAADAiEamAwAA4MkoYgAADKKIAQAwiCIGAMAgihgA\nAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIG\nAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKI\nAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMo\nYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAg\nb9MBAGdSVFSkrMxM5e3erVOlpWoWGKiIzp01ISZGrVq1Mh0PgBuy2O12u+kQgGnZ2dl6JSlJ769Z\nowckRVVWKkBSmaQdvr56y27X0MGD9cT06YqKijKcFoA7oYjh8TJSUxU/daqerajQBLtdQdUcUyIp\n02LRS76+SkhOVqzV2tAxAbgpihgeLSM1VfOmTtXa8nKF1eL4fEkD/fz0LGUMoJ5QxPBY2dnZGt63\nrz66ooRLJE2S9E9JrST9QdLDlz2fL6mXn59Wbdqk7t27N1xgAG6JVdPwWK8kJenZioqrJmGbJB9J\nxZJel2SVtO+y58MkTauo0CtJSQ0TFIBbYyKGRyoqKlKHkBAVVFb+5DvhcklBkvZKCv3hsQmSbtHF\nyfiSE5JCfXyUV1jIamoAN4SJGB4pKzNT0dJVC7PyJDXW/5WwJHWR9MUVx7WQFG2xKCsz02EZAXgG\nihgeKW/3bvWorLzq8VOSml/xWHNdvIzpSlEVFcrLzXVAOgCehCKGRzpVWqqAah5vJunkFY+VStUe\nGyCprKSkvqMB8DAUMTxSs8DAaqfcCEnnJB287LHPJXWq5tgySQFB1V11DAC1RxHDI0V07qwdPj5X\nPe4n6QFJs3Vx4dYWSask/U8175Ht66uIyEhHxgTgAVg1DY9U06pp6afXEd8kaZ6k0Vccw6ppAPWF\niRgeqXXr1ho6eLAWWyxXPRck6S1dXLh1WFeXsCQttlh0/5AhlDCAG8ZEDI9V0521roU7awGoT0zE\n8FhRUVFKSE7WQD8/5dfyNZfuNZ2QnEwJA6gXFDE8WqzVqmeTk9XLz0/zLRbVdDHSCUkvWyzqxYYP\nAOoZp6YBSTk5OXolKUnvrV6taItFURUVP+5HnO3rq7+fPauQW29V5t//ziQMoF5RxMBliouLlZWZ\nqbzcXJWVlCggKEgRkZG6b9Ag9e7dW0eOHFHz5lfeewsA6o4iBmpp5MiR6tevn2w2m+koANwI3xED\ntWS1WpWamip+dgVQnyhioJb69eunqqoqbd261XQUAG6EIgZqyWKxKC4uTqmpqaajAHAjfEcMXIcT\nJ06offv2OnDgAHfVAlAvmIiB69CiRQtFR0frr3/9q+koANwEEzFwnXbs2KGHH35YBw4cUKNG/CwL\n4MbwKQJcp6ioKP3iF7/QunXrTEcB4AYoYuA6WSyWHy9lAoAbxalpoA5Onz6t4OBg7dy5U8HBwabj\nAHBhTMRAHfj7+2vs2LFasGCB6SgAXBwTMVBHX3zxhfr376/CwkI1btzYdBwALoqJGKijTp06KSIi\nQm+//bbpKABcGEUM3AAWbQG4UZyaBm5AVVWVgoODtXHjRt1+++2m4wBwQUzEwA1o0qSJJk2apLS0\nNNNRALgoJmLgBh0+fFh33XWXjh49Kj8/P9NxALgYJmLgBrVr10733HOP3njjDdNRALggihioByza\nAlBXFDFQDwYNGqTi4mLl5OSYjgLAxVDEQD3w8vLSlClTmIoBXDcWawH1pKioSB06dFBBQYGCgoJM\nxwHgIpiIgXrSunVrDRo0SFlZWaajAHAhTMRAPdq8ebOmTJmivXv3ymKxmI4DwAUwEQP1qFevXvLy\n8tKmTZtMRwHgIihioB5ZLBbFxcWxaAtArXFqGqhnpaWlateunfbt26c2bdqYjgPAyTERA/UsMDBQ\no0aN0sKFC01HAeACmIgBB9i5c6dGjBihgoICeXl5mY4DwIkxEQMOcOedd6pNmzZavXq16SgAnBxF\nDDgI958GUBucmgYcpKKiQm3btlV2drZuu+0203EAOCkmYsBBfH19NX78eKWnp5uOAsCJMREDDpSX\nl6devXqpsLBQTZs2NR0HgBNiIgYcKCIiQpGRkfrHP/5hOgoAJ0URAw7Goi0AP4dT04CDnT17Vu3a\ntdMHH3ygyMhI03EAOBkmYsDBGjdurMmTJystLc10FABOiIkYaABfffWVOnfurMLCQjVr1sx0HABO\nhIkYaAC33nqr+vTpo6VLl5qOAsDJUMRAA7m0aIuTUAAuRxEDDaR///46deqUtm/fbjoKACdCEQMN\npFGjRoqLi2PRFoCfYLEW0ICOHz+usLAw5efnq2XLlqbjAHACTMRAA2rZsqWGDRumzMxM01EAOAkm\nYqCBbdu2TePHj9f+/fvVqBE/CwOejk8BoIHdfffd8vf31/r1601HAeAEKGKggVksFu4/DeBHnJoG\nDCgrK1NISIhyc3N1yy23mI4DwCAmYsCAgIAAjRkzRgsWLDAdBYBhTMSAIbm5uRo0aJAOHz6sxo0b\nm44DwBAmYsCQyMhI3XbbbVq1apXpKAAMoogBg1i0BYBT04BBZ86cUdu2bbV161aFh4ebjgPAACZi\nwKCmTZsqJiaG+08DHoyJGDCsoKBAPXr00NGjR+Xr62s6DoAGxkQMGNa+fXtFRUVp+fLlpqMAMIAi\nBpwAi7YAz0URA05g6NCh+uabb7Rz507TUQA0MIoYcAJeXl6KjY1lKgY8EIu1ACdx7Ngx3XHHHTp8\n+LACAwNNxwHQQJiIASfRpk0bDRgwQK+//rrpKAAaEEUMOJFLi7Y4UQV4DooYcCJ9+/bV+fPntWXL\nFtNRADQQihhwIhaLRXFxcSzaAjwIi7UAJ1NSUqL27dtr//79at26tek4AByMiRhwMkFBQYqOjtai\nRYtMRwHQAJiIASeUnZ2thx56SPn5+fLy8jIdB4ADMREDTigqKkotW7bU2rVrTUcB4GAUMeCkuP80\n4Bk4NQ04qdOnTys4OFifffaZQkJCTMcB4CBMxICT8vf317hx45SRkWE6CgAHYiIGnNi+fft07733\nqrCwUE2aNDEdB4ADMBEDTuyOO+7QHXfcobfeest0FAAOQhEDTo5FW4B749Q04OSqqqoUEhKi9evX\nq2PHjqbjAKhnTMSAk2vSpIkeeeQRpaWlmY4CwAGYiAEXUFhYqDvvvFOFhYXy9/c3HQdAPWIiBlxA\ncHCwevbsqWXLlpmOAqCeUcSAi7i0aIuTWIB7oYgBFzFw4ECVlJQoJyfHdBQA9YgiBlxEo0aNNGXK\nFC5lAtwMi7UAF1JcXKyIiAgVFBQoKCjIdBwA9YCJGHAhrVq10pAhQ7R48WLTUQDUEyZiwMVs2bJF\nkydP1r59+2SxWEzHAXCDmIgBF9OzZ095e3vrX//6l+koAOoBRQy4GIvFwv2nATfCqWnABZ08eVIh\nISHau3evbr75ZtNxANwAJmLABTVv3lwPPfSQXnvtNdNRANwgJmLARe3atUvDhg3ToUOH5O3tbToO\ngDpiIgZcVNeuXXXrrbfq/fffNx0FwA2giAEXxqItwPVxahpwYZWVlWrbtq22b9+u0NBQ03EA1AET\nMeDCfHx8NGHCBKWnp5uOAqCOmIgBF3fgwAH17NlThYWF8vHxMR0HwHViIgZcXHh4uLp27aoVK1aY\njgKgDihiwA2waAtwXRQx4AaGDRumI0eOaPfu3aajALhOFDHgBry9vfXoo48qLS3NdBQA14nFWoCb\n+PrrrxUZGakjR44oICDAdBwAtcREDLiJW265Rffee6+WLl1qOgqA60ARA27k0qItTnQBroMiBtxI\nv379VFFRoW3btpmOAqCWKGLAjTRq1EhxcXFcygS4EBZrAW7m+PHjCg0NVX5+vm666SbTcQBcA0UM\nuKEJEyaoXbt2CvD3V97u3TpVWqpmgYGK6NxZE2Ji1KpVK9MRAfyAIgbcTHZ2tuKfeUYbN2/WmKZN\n1aOyUgGSyiTt8PXVW3a7hg4erCemT1dUVJTpuIDHo4gBN5KRmqr4qVM1raJCE+12BVVzTImkTItF\nL/n6KiE5WbFWa0PHBHAZFmsBbiIjNVXzpk7VR+XleuqHEv6LpChJPpIm/XBckKSn7HZ9VF6ueVOn\nKoOFXYBRTMSAG8jOztbwvn31UXm5wi57/G1d/Gl7raQKSYuueF2+pF5+flq1aZO6d+/eQGkBXI6J\nGHADryQl6dmKip+UsCSNkDRcUosaXhcmaVpFhV5JSnJoPgA1YyIGXFxRUZE6hISooLKy2u+EJWmW\npK919UQsSSckhfr4KK+wkNXUgAFMxICLy8rMVLRUYwlfSwtJ0RaLsjIz6y8UgFqjiAEXl7d7t3pU\nVt7Qe0RVVCgvN7eeEgG4HhQx4OJOlZbqRjc9DJBUVlJSH3EAXCeKGHBxzQIDVVbDc+clVf7w33OS\nzvzw+yuVSQoIquvJbQA3giIGXFhFRYVOVlXpI4ul2udfkOQnaZ6kpT/8fm41x+3w9VVEZKTDcgKo\nGUUMuKADBw7o6aefVnBwsIqPH9d73t6q7sRyvKQLujgFX/o1+4pjTkh6s6JCFi8vVVVVOTY4gKtQ\nxICLOHfunN5++23dd9996tmzp7y9vfXJJ59o/fr1Gnb//Vpcw1R8LYstFvXt00fr1q1TeHi40tLS\ndObMmXpOD6AmXEcMOLlvv/1Wr732mjIyMtS2bVvZbDaNHDlSPj4+Px5T0521ruXKO2tt375diYmJ\n2rNnj5577jlNmjTpJ38OgPrHRAw4Ibvdrk2bNmn06NHq2LGjvvrqK61atUoff/yxxo0bd1U5RkVF\nKSE5WQP9/JRfyz8jX9JAPz8lJCf/eHvLu+++W6tXr9aKFSu0evVqhYWF6dVXX1XlDV4eBaBmTMSA\nEyktLdWSJUuUmpoqu90uq9Wq8ePHKzAwsFavr83uSyd0cfel/1eL3Zc+/fRTJSYmKicnR9OmTVNs\nbKx8fX3r9pcDUC2KGHACn3/+uVJSUrR8+XINGDBANptNffr0kaUO3/vm5OTolaQkvbd6taItFkVV\nVPy4H3H2D/sR3z9kiJ6YPr3WGz3s3LlTiYmJ+uSTT/TMM89oypQp8vPzu+5sAK5GEQOGnDlzRitW\nrFBKSoqOHDmiKVOmaPLkybr55pvr5f2Li4uVlZmpvNxclZWUKCAoSBGRkRo/cWKd7yn9+eefa86c\nOdq6dauefvppWa1W+fv710tewFNRxEADO3TokNLT07Vo0SJ17dpVVqtVw4YNk7e3t+lotZabm6s5\nc+Zo8+bN+v3vfy+bzaZmzZqZjgW4JBZrAQ3g/Pnzev/99zV06FBFRUWpqqpKW7Zs0bp16xQdHe1S\nJSxJkZGRWr58udavX6/PPvtMoaGhSkpKUllZTff4AlATJmLAgYqLi7Vw4UKlp6frpptuks1m0+jR\no93u+9W9e/dq7ty5+uc//6knnnhCjz/+uJo3b246FuASmIiBema327V161aNGzdO4eHhysvL0/Ll\ny5Wdna2YmBi3K2FJ6tixo5YuXaqPPvpIX375pUJDQ5WYmKjS0lLT0QCnRxED9eTUqVNKT09X165d\nFRMTo7vuuksFBQVatGiRoqKiTMdrEB06dNCSJUu0detWFRQUKCwsTM8//7y+//5709EAp0URAzfo\niy++0O9+9zsFBwdr7dq1Sk5O1pdffqmnnnpKLVq0MB3PiIiICGVmZmrbtm0qLCxUWFiYZs+erRMn\nTpiOBjgdihiog6qqKr355pvq06ePBgwYoBYtWujzzz/XypUrNWDAADVqxD8tSQoLC9OiRYu0Y8cO\nffvttwoPD9eMGTN0/Phx09EAp8FiLeA6FBYWKiMjQwsXLtTtt98um82mESNGqHHjxqajuYTDhw8r\nKSlJK1asUGxsrJ5++mnddNNNpmMBRvFjO3ANFy5c0Lp16zRixAh17dpVJ0+e1Pr16/Wvf/1Lo0aN\nooSvQ7t27ZSenq6dO3fq+++/V4cOHTRt2jQVFRWZjgYYw0QM1OD48ePKzMxUamqqmjVrJpvNprFj\nx3Ljinp09OhRzZs3T8uWLVNMTIyeeeYZ/cd//IfpWECDYiIGLmO327Vjxw5NnDhRoaGh2rVrl5Ys\nWaKdO3cqNjaWEq5nbdu21Z///Gft3r1bVVVVuuOOO/T73/9ex44dMx0NaDAUMSCpvLxcCxcuVFRU\nlMaMGaOOHTvqwIEDWrJkie655546bb6A2rvlllv0pz/9SXv27JHdblenTp305JNP6ptvvjEdDXA4\nihgebf/+/XrqqafUtm1bvf3220pMTNSBAwc0bdq0Om+MgLr75S9/qfnz5+uLL76Ql5eXIiMj9fjj\nj+urr74yHQ1wGIoYHufcuXNauXKl+vfvr969e8vHx0effvqpVq1apSFDhsjLy8t0RI/Xpk0bvfzy\ny9q7d698fHzUpUsXPfbYYzp69KjpaEC9Y7EWPMY333yjBQsWKCMjQ7fddptsNpsefPBBNW3a1HQ0\nXENxcbFefvllLViwQKNGjdL06dMVEhJiOhZQL5iI4dbsdrs2bNigkSNHqlOnTjp27JjWrFmjLVu2\naOzYsZSwi2jVqpVefPFF7d+/Xy1atFC3bt0UGxurQ4cOmY4G3DAmYril77//XllZWUpNTZWXl5ds\nNpvGjRvHjkBu4vjx45o/f75SU1M1YsQIzZgxQ+3btzcdC6gTJmK4lc8++0yPPvqobrvtNm3btk3p\n6enKzc2VzWajhN1Iy5Yt9cILLyg/P1+33nqrevTooZiYGOXn55uOBlw3ihgur7KyUllZWbr77rs1\nYsQItWvXTvv27dOyZcvUu3dvLj1yY0FBQUpISFB+fr7atWune+65RxMmTFBeXp7paECtcWoaLuvg\nwYNKS0tTZmam7rrrLtlsNg0ZMkTe3t6mo8GQ0tJSvfrqq3rllVc0cOBAzZw5U7fffrvpWMDPYiKG\nSzl//rxWrVqlwYMH6+6775Ykbdu2TR988IGGDx9OCXu4wMBAzZw5UwcPHlTHjh3Vu3dvjR07Vnv3\n7jUdDagREzFcwr///W8tXLhQ6enpuvnmm2W1WvXQQw/J19fXdDQ4sbKyMv3lL3/R/Pnz1bdvX82a\nNUu/+tWvTMcCfoKJGE7Lbrfro48+0sMPP6zbb79dBQUFWrlypbZv364JEyZQwrimgIAAPffcczp4\n8KC6d++u/v37a9SoUcrNzTUdDfgREzGczsmTJ/X6668rNTVVVVVVstlsGj9+vIKCgkxHg4s7ffq0\n0tLSlJycrF//+teaPXu2unTpYjoWPBxFDKeRm5urlJQUvfHGG/rNb34jq9Wqfv36seoZ9a68vFwZ\nGRl66aWX1KNHD82ePVvdunUzHQseilPTMOrMmTNatmyZevXqpUGDBqlNmzbas2ePVqxYod/85jeU\nMBzCz89PTz75pA4ePKh+/fpp2LBhGj58uHJyckxHgwdiIoYRR44cUXp6uhYuXKjIyEhZrVYNHz5c\njRs3Nh0NHqiyslKvvfaaXnzxRXXp0kXx8fHq0aOH6VjwEEzEaDAXLlzQmjVrNGzYMHXr1k3l5eXa\ntGmTPvzwQz344IOUMIzx8fHR7373Ox08eFD333+/Ro4cqcGDB2v79u2mo8EDMBHD4b777jv99a9/\nVVpamgIDA/XYY49pzJgx8vf3Nx0NqNaZM2eUmZmppKQkRUREKD4+Xj179jQdC26KIoZD2O12ffLJ\nJ0pJSdG7776rESNGyGq1qkePHnzvC5dRVVWlrKwszZ07V6GhoYqPj1evXr1Mx4KboYhRr06fPq2/\n/e1vSklJUVlZmeLi4hQTE6OWLVuajgbU2dmzZ7VkyRLNnTtXISEhio+PV58+fUzHgpugiFEv9u3b\np9TUVC1dulT/9V//JZvNpgEDBqhRI5YhwH2cPXtWf/vb3/TCCy/ol7/8peLj43Xvvfdylgc3hCJG\nnZ09e1bvvPOOUlJStHfvXk2ePFmxsbEKDg42HQ1wqHPnzmnZsmV64YUX1Lp1a8XHx3O5HeqMIsZ1\n++qrr7RgwQItWLBA4eHhslqteuCBB9SkSRPT0YAGdf78eb3xxhuaM2eOWrZsqdmzZ+u+++6jkHFd\nKGLUyoULF7RhwwalpKRo48aNevjhh2W1WrmBPqCLhbx8+XLNmTNHzZs3V3x8vAYNGkQho1YoYvys\nkpISZWZmKjU1VT4+PrLZbPrv//5vBQQEmI4GOJ0LFy5oxYoVSkxMlL+/v2bPnq0hQ4ZQyPhZFDGq\nlZOTo5SUFK1cuVJDhw6VzWbTr3/9az5QgFq4cOGCVq5cqcTERDVp0kSzZ8/WsGHD+PeDalHE+FFF\nRYXefPNNpaSkqKioSHFxcZo0aZJat25tOhrgki5cuKB33nlHiYmJslgsmj17tn77299SyPgJihg6\ncOCA0tLStHjxYv3nf/6nrFarBg8eLC8vL9PRALdgt9v17rvvKjExUefPn9esWbMUHR3N5X2QRBF7\nrHPnzum9995TSkqKdu3apZiYGE2ZMkXt27c3HQ1wW3a7Xe+//74SEhJ05swZzZo1Sw8++CCF7OEo\nYg/z7bff6rXXXlNGRobatm0rm82mkSNHysfHx3Q0wGPY7XatWbNGCQkJOnXqlGbNmqVRo0ZxFspD\nUcQewG63a/PmzUpJSdG6dev00EMPyWq1qmvXrqajAR7Nbrdr7dq1SkhIUGlpqWbOnKnRo0dTyB6G\nInZjpaWlWrJkiVJTU2W322W1WjV+/HgFBgaajgbgMna7XR9++KESEhL03XffaebMmRozZoy8vb1N\nR0MDoIjd0K5du5Samqrly5drwIABstls6tOnDys1ASdnt9u1YcMGJSQk6NixY5o5c6bGjh1LIbs5\nitiQoqIiZWVmKm/3bp0qLVWzwEBFdO6sCTExatWq1XW/X2VlpVasWKGUlBQVFhZqypQpmjx5sm6+\n+WYHpAfgaBs3blRCQoKOHj2qGTNmaNy4cWrcuLHpWHAAiriBZWdn65WkJL2/Zo0ekBRVWakASWWS\ndvj66i27XUMHD9YT06crKirqmu936NAhpaena9GiReratatsNpvuv/9+foIG3MTmzZuVkJCgQ4cO\nacaMGRo/fjyF7GYo4gaUkZqq+KlT9WxFhSbY7Qqq5pgSSZkWi17y9VVCcrJirdarjjl//rw++OAD\npaSk6JNPPtGECRMUFxen8PBwh/8dAJixZcsWJSQkKD8/X9OnT9fEiRPZaMVNUMQNJCM1VfOmTtXa\n8nKF1eL4fEkD/fz07GVlXFRUpEWLFiktLU2tW7eW1WrV6NGj5efn59DsAJzHxx9/rMTERO3bt0/T\np09XTEyMmjZtajoWbgBF3ACys7M1vG9ffXRFCf+PpA8llUu6SdIkSTMuez5fUi8/P73wpz9pw4YN\nWr16taKjo2W1Wmt12hqA+9q+fbsSExO1Z88ePffcc5o0aRL3A3BRFHEDGPfAA+r+9tt68or/1Xsl\ntZfkIylPUm9JiyUNvOyYZEkv+ftr+pw5mjBhglq0aNFAqQG4guzsbCUmJmrnzp169tln9eijj1LI\nLoYidrCioiJ1CAlRQWVltd8JX7JfUn9J70jqdtnjJySF+vgor7CwTqupAXiGTz/9VImJicrJydG0\nadMUGxsrX19f07FQC9zg1MGyMjMVLdVYwo9J8pf0K108Ld3tiudbSIq2WJSVmemwjABc31133aV3\n3nlH7733njZu3KjQ0FD98Y9/VHl5uelouAaK2MHydu9Wj8rKGp//i6RTuvhd8UxJ2dUcE1VRobzc\nXMcEBOBW7rzzTr311ltas2aNPv74Y4WGhio5OVmnT582HQ01oIgd7FRpqQKucYxFUh9JoyQtq+b5\nAEllJSX1HQ2AG+vSpYtWrFihdevWaceOHWrfvr3mzZunU6dOmY6GK1DEDtYsMFBltTz2nKTqLkQq\nkxQQ9HPfMANA9SIjI7V8+XJt2LBBu3btUmhoqJKSklRWVttPJjgaRexgEZ07a0c1KxiLJb0p6bSk\nC5LWSvq7pN9W8x7Zvr6KiIx0ZEwAbq5Tp05atmyZNm7cqD179ig0NFRz587VyZMnTUfzeKyadrCa\nVk1/J2mkpN2S7JLCJc2SNOyK17NqGoAj7N+/X3PnztWaNWv0+OOP63//93/1i1/8wnQsj8RE7GCt\nW7fW0MGDtfiKnY9ukrRRF4u2RNIOXV3CkrTYYtH9Q4ZQwgDqVYcOHZSVlaWPP/5YBQUFCgsL0/PP\nP68S1qM0OCbiBlDTnbWu5dKdtVZt2qTu3bs7Kh4AKD8/X3/4wx/07rvvymq16qmnnrquGwjV945y\nnoSJuAFERUUpITlZA/38lF/L11y613RCcjIlDMDhwsLCtGjRIu3YsUPHjh1TeHi4ZsyYoePHj//s\n67KzszXugQfUISRE++Lj1W3pUg197z11W7pUe59/XhHBwRr3wAPKzq7u4kxIkuxoMOkpKfY2fn72\nP1os9hOS3V7Nr+OS/WWLxd7Gz8+enpJiOjIAD3Xo0CF7bGysvUWLFvbnnnvOXlxcfNUxlz7T5v/M\nZ9oJyf5HPtN+FqemG1hOTo5eSUrSe6tXK9piUVRFxY/7EWf/sB/x/UOG6Inp05mEARhXWFioF198\nUW+++aYeeeQRTZ06Va1bt66XHeVwEUVsSHFx8cXvU3JzVVZSooCgIEVERmr8xIl8nwLA6Rw9elTz\n5s3TsmWgRw/nAAAChUlEQVTLNHjwYH24cqW2VFT8WMJVkmy6eJfAEkmhkv4gadBl78G6l+pRxACA\nWvv66681qHdvTSwo0NOXPV6ui7vFxUhqK+l9SQ9L2iMp+LLj5lss+iw6Wkv+8Y8Gy+zsKGIAQK3V\ndkc5Seoi6XlJ0Zc9xr0RrsaqaQBArV1rR7lL/i3pgKROVzzOjnJXo4gBALV2rR3lpIv3zR8naaKk\niGqeZ0e5n6KIAQC1dq0d5ey6WMJNJb1awzHsKPdT3qYDAABcx7V2lHtEF++lv1qSVw3HsKPcTzER\nAwBqraYd5SQpTtKXkt6V1ORn3oMd5X6KVdMAgFqradV0oaR2knz0f5OwRVK6Ll7GdAmrpq/GRAwA\nqLWadpQL1sW91ct18dRzmaST+mkJS+woVx0mYgDAdWFHufrFRAwAuC7sKFe/KGIAwHWLtVr1bHKy\nevn5ab7FopouRjoh6Y8Wi3qx4UONODUNAKgzdpS7cRQxAOCGsaNc3VHEAAAYxHfEAAAYRBEDAGAQ\nRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwAgEEUMQAABlHEAAAY\nRBEDAGAQRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwAgEEUMQAA\nBlHEAAAYRBEDAGAQRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwA\ngEEUMQAABlHEAAAYRBEDAGAQRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwAgEEUMQAABlHEAAAYRBED\nAGAQRQwAgEEUMQAABlHEAAAYRBEDAGAQRQwAgEH/H5PDuRwyg7XtAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"G3 = nx.Graph()\n",
"for i, j in [(1, 2), (1, 3), (1, 0)]:\n",
" G3.add_edge(i,j)\n",
"nx.draw(G3, pos =pos, with_labels = True)"
]
},
{
"cell_type": "code",
"execution_count": 200,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"0.0\n"
]
}
],
"source": [
"print(nx.transitivity(G3))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"THREE CENTRAL QUANTITIES IN NETWORK SCIENCE\n",
"- A. Degree distribution: \t\t\t $p_k$\n",
"- B. Path length: \t\t\t\t\t\t$$\t\t\t\n",
"- C. Clustering coefficient: $C_i$\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Typical Network Science Research\n",
"\n",
"- Discovering, Modeling, Verification\n",
" - WATTSDJ,STROGATZSH.Collective dynamics of‘small-world’ networks. Nature, 1998, 393(6684): 440–442.\n",
" - BARABÁSI A-L, ALBERT R. Emergence of scaling in random networks. Science, 1999, 286(5439): 509-512."
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Typical Math Style\n",
"Fan Chung & Linyuan Lu, The average distance in random graphs with given expected degree,. PNAS, 19, 15879-15882 (2002)."
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Typical Physical Style\n",
"A.-L.Barabási,R.Albert,H.Jeong Mean-field theory for scale-free random networks. Physica A 272, 173–187 (1999)."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Typical Computer Science Style\n",
"\n",
"- Community detection\n",
"- Link prediction\n",
"- Recommendation algorithms"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Typical control sytle\n",
"Controllability of Complex Networks\n",
"\n",
"Liu Y Y, Slotine J J, Barabási A L. Nature, 2011, 473(7346): 167-173."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# 阅读材料\n",
"- Barabasi 2016 Network Science. Cambridge\n",
"- 汪小帆、李翔、陈关荣 2012 网络科学导论. 高等教育出版社\n",
"- 梅拉妮·米歇尔 2011 复杂,湖南科学技术出版社\n",
"- 菲利普-鲍尔 2004 预知社会:群体行为的内在法则,当代中国出版社\n",
"- 巴拉巴西 2007 链接:网络新科学 湖南科技出版社"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"celltoolbar": "Slideshow",
"kernelspec": {
"display_name": "Python 2",
"language": "python",
"name": "python2"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 2
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython2",
"version": "2.7.11"
}
},
"nbformat": 4,
"nbformat_minor": 0
}
 "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Degree, Average Degree and Degree Distribution\n"
]
},
{
"cell_type": "code",
"execution_count": 175,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtYlHX+//HXgAqDIEtqVl6WfdVBU0kQMs9adhnaulFt\nmeUxc6U2qwUlW81DKWVDZVpcaesPMRU7qGVlluVptRSEQlcBzdL023okQh2Iw/z+sPqagoIy8xmY\n5+O6vKqZuelNB55+7vtzz1icTqdTAADACB/TAwAA4M0IMQAABhFiAAAMIsQAABhEiAEAMIgQAwBg\nECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIAAAwixAAAGESIAQAwiBADAGAQIQYAwCBCDACAQYQYAACD\nCDEAAAYRYgAADCLEAAAYRIgBADCIEAMAYBAhBgDAIEIMAIBBhBgAAIMIMQAABhFiAAAMIsQAABhE\niAEAMIgQAwBgECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIAAAwixAAAGESIAQAwiBADAGAQIQYAwCBC\nDACAQYQYAACDCDEAAAYRYgAADKpnegCgLjhy5IhSU1KUl52tkwUFCgwOli0sTMNHjlTTpk1NjwfA\ng1mcTqfT9BBAbZWenq7ZiYn6aPVq3SUpqqhIQZIKJW2zWrXC6dTA6Gg9PnGioqKiDE8LwBMRYuAS\nzUtO1pT4eCU4HBrudCqkgtfkS0qxWDTLatU0u11jYmPdPSYAD0eIgUswLzlZL8THa83p02pdhdfv\nldQ/IEAJxBjAOQgxUE3p6eka1KePNp0T4aGS1ko6LamJpFGS/nnW83sl9QwI0KoNGxQZGem+gQF4\nNHZNA9U0OzFRCQ7HeSvhiZK+k1QgabWkOZLWnPV8a0kTHA7NTkx0z6AAagVWxEA1HDlyRKHXXad9\nRUUVXhP+Ta6kfpLelxRx1uMnJLXy91fegQPspgYgiRUxUC2pKSmKkSqN8KOSGkrqoDOnpSPOef4K\nSTEWi1JTUlw2I4DahRAD1ZCXna2biooqff41SSd15lrxJEnpFbwmyuFQ3o4drhkQQK1DiIFqOFlQ\noKCLvMYiqbekv0paWsHzQZIK8/NrejQAtRQhBqohMDhYhVV8bamkgAoeL5QUFHKhK8wAvAkhBqrB\nFhambf7+5z1+VNIySacklevMbul3JP2lgq+RbrXK1rGjK8cEUIuwaxqohsp2TR+TdI+kbElOSW0k\nTZb053OOZ9c0gHOxIgaq4corr9TA6GgttFj+8HgTSet1JrT5krbp/AhL0kKLRXcMGECEAfyOFTFQ\nTZW9s9bF8M5aACrCihiopqioKE2z29U/IEB7q3jMb+81Pc1uJ8IA/oAQA5dgTGysEux29QwI0MsW\niyq7GemEpJcsFvXkAx8AVIJT08BlyMjI0OzERH348ceKsVgU5XD8/nnE6b9+HvEdAwbo8YkTWQkD\nqBAhBmrA0aNHlZqSorwdO7QvL0/f7t+vR//xDw0bMYKNWQAuiBADNey7775T7969deDAAdOjAKgF\nCDFQw8rKyhQYGKgTJ07IarWaHgeAh2OzFlDDfH191bJlS3377bemRwFQCxBiwAXatGmjPXv2mB4D\nQC1AiAEXsNlsysvLMz0GgFqAEAMuwIoYQFURYsAFCDGAqiLEgAsQYgBVxe1LgAuUl5crMDBQhw8f\nVlBQkOlxAHgwVsSAC/j4+Kh169bau7eqHwsBwFsRYsBFOD0NoCoIMeAihBhAVRBiwEXatGnDvcQA\nLooQAy5is9lYEQO4KEIMuAinpgFUBSEGXKRZs2YqKipSfn6+6VEAeDBCDLiIxWJhVQzgoggx4EJc\nJwZwMYQYcCFWxAAuhhADLkSIAVwMIQZciBADuBg+9AFwoePHj6tVq1bKz8+XxWIxPQ4AD8SKGHCh\nxo0by8fHR8eOHTM9CgAPRYgBF+P0NIALIcSAixFiABdCiAEXs9lsfPgDgEoRYsDFWBEDuBBCDLgY\nIQZwIdy+BLhYQUGBmjdvrsLCQm5hAnAeVsSAiwUHB6thw4b68ccfTY8CwAMRYsANOD0NoDKEGHAD\nQgygMoQYcANCDKAyhBhwgzZt2nAvMYAKEWLADWw2GytiABXi9iXADU6dOqWmTZvq5MmT8vHh978A\n/g8/EQA3aNiwoUJCQnTw4EHTowDwMIQYcBOuEwOoCCEG3ITrxAAqQogBN+EWJgAVIcSAmxBiABUh\nxICbEGIAFeH2JcBNioqK9Kc//UknT55UvXr1TI8DwEOwIgbcxN/fX1dddZX2799vehQAHoQQA27E\n6WkA5yLEgBsRYgDnIsSAG9lsNt7UA8AfEGLAjVgRAzgXIQbciBADOBe3LwFuVFJSoqCgIP38889q\n0KCB6XEAeABWxIAb1a9fXy1atNC+fftMjwLAQxBiwM04PQ3gbIQYcDNCDOBshBhwM0IM4GyEGHAz\n7iUGcDZCDLgZK2IAZ+P2JcDNysrKFBgYqBMnTshqtZoeB4BhrIgBN/P19VXLli317bffmh4FgAcg\nxIABbdq04ToxAEmEGDDCZrNxnRiAJEIMGMGGLQC/IcSAAYQYwG8IMWAAIQbwG25fAgwoLy9XYGCg\nDh8+rKCgINPjADCIFTFggI+Pj1q3bq29e/eaHgWAYYQYMITT0wAkQgwYQ4gBSIQYMIYPfwAgEWLA\nGFbEACRCDBhDiAFIhBgwplmzZioqKlJ+fr7pUQAYRIgBQywWC+85DYAQAyZxehoAIQYMIsQACDFg\nECEGQIgBg7iXGAAf+gAYdPz4cbVq1Ur5+fmyWCymxwFgACtiwKDGjRvLx8dHx44dMz0KAEMIMWAY\n14kB70aIAcO4Tgx4N0IMGMaKGPBuhBgwjBAD3o0QA4YRYsC7cfsSYFhBQYGaN2+uwsJCbmECvBAr\nYsCw4OBgNWzYUD/++KPpUQAYQIgBD8DpacB7EWLAAxBiwHsRYsADEGLAexFiwAPwph6A9yLEgAdg\nRQx4r3qmBwAgNWrUSHtyc/Xwgw/qVEGBAoODZQsL0/CRI9W0aVPT4wFwIe4jBgxKT0/X7MREfbR6\ntaKLitRLUpCkQknbrFatcDo1MDpaj0+cqKioKMPTAnAFQgwYMi85WVPi45XgcGi406mQCl6TLynF\nYtEsq1XT7HaNiY1195gAXIwQAwbMS07WC/HxWnP6tFpX4fV7JfUPCFACMQbqHEIMuFl6eroG9emj\nTRVEeI+kMEl/lZR6znN7JfUMCNCqDRsUGRnpjlEBuAG7pgE3m52YqASHo8KV8N8l3VTJca0lTXA4\nNDsx0XXDAXA7VsSAGx05ckSh112nfUVF510TTpO0UtINOrP6PXdFLEknJLXy91fegQPspgbqCFbE\ngBulpqQoRjovwj9LmiLpJUkX+p3xFZJiLBalpqS4ZkAAbkeIATfKy87WTUVF5z3+jKSHJV1Tha8R\n5XAob8eOmh4NgCG8oQfgRicLChR0zmNfS1r76x+rIkhSYX5+jc4FwBxCDLhRYHCwCs95bIOk/ZKu\n1ZnT0icllUnaJSmjgq9RKCkopKK7jgHURpyaBtzIFhambf7+f3jsb5K+1ZkV8TeSxkq6Q9KnlXyN\ndKtVto4dXTkmADdi1zTgRhfaNf2baToT5kp3Tfv5Ke+HH9g1DdQRrIgBN2rQoIGaXHGFFlzgNVNU\ncYQl6f9Jskhavny5SktLa3w+AO5HiAE32bZtmyIiItSpWzfZAwK0t5rH75VkDwjQ7PnztXTpUt14\n441avXq1OKkF1G6EGHCx8vJy2e123XHHHbLb7XrnnXc0zW5X/2rE+Lf3mp5mt2vo0KFat26dZs6c\nqSeeeEL9+/dXdna2K78FAC7kO3Xq1KmmhwDqqqNHj+ree+9VZmam1qxZo65du0qSOkdFyXrFFRq2\nbp18S0vVVpK1guNPSEq2WDQ6IECTzvrAB4vForZt22rs2LEqLCzUww8/rNzcXEVFRSko6NwbpAB4\nMlbEgIusX79e4eHhCgsL08aNG9WyZcs/PD8mNlarNmxQZkyM/sffX6OsViVLektSsqRRVqta+fsr\nKyZGqzZsqPBTl+rXr6/HHntMubm5CgkJUYcOHTR9+nSdOnXKHd8igBrArmmghpWVlenZZ5/VG2+8\noZSUFPXv3/+ixxw9elSpKSnK27FDhfn5CgoJka1jRw0bMaJau6P37duniRMnavPmzZoxY4aGDh0q\nHx9+vw14MkIM1KBDhw7pgQcekK+vr9566y1dffXVRubYsmWL4uLiVFxcrKSkJPXt29fIHAAujt8q\nAzXk448/VufOndWvXz99+umnxiIsSd26ddOWLVuUkJCgUaNGadCgQcrJyTE2D4DKEWLgMv3yyy+K\nj4/X2LFj9c4772jSpEny9fU1PZYsFovuu+8+7d69Wz179lSPHj3097//XUePHjU9GoCzEGLgMuzb\nt089evRQXl6esrKy1LNnT9Mjncff31/jx49XTk6OLBaL2rVrp1mzZqmogk+BAuB+hBi4RG+//ba6\ndOmiIUOG6P3331fjxo1Nj3RBTZo00Zw5c7R582Zt3rxZ7dq1U1paGm8IAhjGZi2gmhwOh5588kmt\nXbtWaWlpioyMND3SJVm3bp3i4uLk5+enpKQkdevWzfRIgFdiRQxUw+7du9WlSxcVFBQoMzOz1kZY\nkvr27auMjAzFxsbqvvvu07333qt9+/aZHgvwOoQYqAKn06kFCxaoV69eGjdunJYsWaJGjRqZHuuy\n+fj4aNiwYcrNzVXHjh0VFRWl+Ph45efnmx4N8BqEGLiIwsJCDR06VElJSVq/fr1Gjx4ti8Vieqwa\nFRAQoMmTJ2vnzp0qKChQaGioXn31VZWUlJgeDajzCDFwAVlZWercubOsVqvS09PVvn170yO51NVX\nX6358+fr888/10cffaT27dtr5cqVbOgCXIjNWkAFnE6n5s6dq+nTp2vOnDkaPHiw6ZGM+OSTTxQf\nH68mTZooKSlJnTt3Nj0SUOcQYuAcJ06c0KhRo3Tw4EGlpaWpdevWpkcyqrS0VAsWLNCUKVN02223\nacaMGWrRooXpsYA6g1PTwFm2bNmi8PBwXX/99dq8ebPXR1iS6tWrpzFjxigvL0/XXnutOnXqpEmT\nJqmwsND0aECdQIgBSeXl5UpMTFRMTIzmzp2rl19+WX5+fqbH8ihBQUF67rnn9PXXX2v//v2y2Wya\nN2+eSktLTY8G1GqcmobXO3z4sIYOHSqHw6ElS5Zw2rWKMjIyFBcXp+PHj8tut+v22283PRJQK7Ei\nhlf77LPPFB4eri5dumjdunVEuBoiIyO1fv16Pffccxo3bpz69++vHTt2mB4LqHUIMbxSaWmpnn76\naY0YMUKLFi3Ss88+q3r16pkeq9axWCy68847tXPnTg0cOFC33nqrHn74Yf33v/81PRpQaxBieJ0D\nBw6od+/e2r59uzIzM3XrrbeaHqnWa9CggcaNG6fc3FwFBwerffv2eu6553T69GnTowEejxDDq7z/\n/vuKiorSoEGDtHr1ajVr1sz0SHVKSEiI7Ha70tPTlZ2drdDQUKWmpqq8vNz0aIDHYrMWvEJxcbHG\njx+vDz74QEuXLlXXrl1Nj+QVNm/erLi4OJWUlCgpKUl9+vQxPRLgcVgRo87bs2ePunbtqkOHDikr\nK4sIu1H37t315Zdfavz48Ro5cqT+8pe/KDc31/RYgEchxKjTlixZom7dumn06NF69913FRISYnok\nr2OxWDR48GDt3r1b3bt3V/fu3fXYY4/p2LFjpkcDPAIhRp106tQpPfTQQ5o2bZo+++wzPfLII3Xu\nE5NqG39/f02YMEG7d++W0+lUu3bt9OKLL6q4uNj0aIBRhBh1zo4dOxQVFaWSkhJt375dnTp1Mj0S\nztK0aVPNnTtXmzZt0qZNm9SuXTu9/fbbfMITvBabtVBnOJ1OzZs3T5MmTVJSUpKGDRtmeiRUwRdf\nfKG4uDhZrVYlJSVxDR9ehxCjTigoKNCYMWOUk5OjZcuWqW3btqZHQjWUlZVp0aJFmjRpkrp3767n\nn39e119/vemxALfg1DRqvfT0dEVERKhx48b66quviHAt5OvrqxEjRig3N1ft27dXZGSkxo8fr59+\n+sn0aIDLEWLUWuXl5UpKStLAgQM1a9Ysvf7667JarabHwmVo2LChnnnmGe3cuVP5+fkKDQ3VnDlz\nVFJSYno0wGU4NY1a6dixYxo+fLiOHz+utLQ0tWzZ0vRIcIHs7GzFx8dr//79mjVrlgYNGsTud9Q5\nrIhR62zYsEHh4eHq0KGDNm3aRITrsLCwMK1Zs0avvPKKnn76ad1yyy3KzMw0PRZQowgxao2ysjJN\nnz5dgwcP1rx58/TCCy+ofv36pseCi1ksFkVHR+ubb77R4MGDNXDgQA0fPlwHDx40PRpQIwgxaoX/\n/d//Vb9+/bR+/Xpt375d0dHRpkeCm9WrV09/+9vflJubq+bNm+vGG2/U5MmTVVhYaHo04LIQYni8\n1atXq3Pnzrrlllv02Wef6ZprrjE9Egxq1KiRZs6cqaysLH333XcKDQ3V/PnzVVZWZno04JKwWQse\n65dfftE///lPpaWlafHixerVq5fpkeCB0tPTFRcXp/z8fNntdvXv39/0SEC1EGJ4pO+++06DBw9W\n06ZNlZKSoiZNmpgeCR7M6XRq5cqVmjBhglq1aiW73a4OHTqYHguoEk5Nw+O8++676tKli+677z6t\nWrWKCOOiLBaLYmJi9J///EfR0dG65ZZbNGbMGP33v/81PRpwUYQYHsPhcCg2NlYJCQn66KOP9I9/\n/IN7RlEtDRo00OOPP67c3FwFBQWpQ4cOmjFjhk6fPm16NKBShBgeIScnRzfffLPy8/OVmZmpqKgo\n0yOhFgsJCVFSUpK2bt2qrKwstW3bVosWLVJ5ebnp0YDzcI0Yxi1cuFDx8fGaOXOmRo8ezSoYNe7f\n//634uLiVFZWpqSkJPXu3dv0SMDvCDGMKSws1KOPPqqMjAwtW7ZMHTt2ND0S6rDy8nItW7ZMEydO\nVKdOnTRr1izZbDbTYwGcmoYZX3/9tSIjI9WgQQOlp6cTYbicj4+P7r//fuXk5Khr167q1q2bxo0b\np+PHj5seDV6OEMOtnE6n5s6dq9tuu01Tp07Vm2++qYYNG5oeC17E399fCQkJ2r17t8rKytS2bVvZ\n7XYVFxebHg1eilPTcJv8/Hw99NBD2r9/v5YtW6bWrVubHgnQ7t27NWHCBO3atUvPP/+87rnnHvYp\nwK1YEcMtvvzyS4WHh6tFixbasmULEYbHaNeunVatWqV58+ZpxowZ6tGjh7766ivTY8GLsCKGS5WX\nl2vWrFl6+eWXNX/+fA0aNMj0SEClysrKlJqaqsmTJ6tHjx5KTEzU9ddfb3os1HGsiOEyhw8fVnR0\ntD788ENlZGQQYXg8X19fjRw5Urm5uWrXrp0iIyM1YcIE/fTTT6ZHQx1GiOESn3/+uSIiIhQVFaX1\n69erRYsWpkcCqqxhw4aaMmWKduzYoePHjys0NFRz585VSUmJ6dFQB3FqGjWqtLRUU6dO1YIFC5Sa\nmqp+/fqZHgm4bN98843i4+P1ww8/aNasWfrzn//Mhi7UGEKMGvPDDz9oyJAhslqtWrRokZo1a2Z6\nJKDGOJ1OrV69WvHx8brqqquUlJSk8PBw02OhDuDUNGrEBx98oMjISA0cOFCffPIJEUadY7FYNGDA\nAGVnZ+vee+9VdHS0RowYoUOHDpkeDbUcIcZlKS4u1hNPPKFx48ZpxYoVeuqpp+Tjw39WqLvq1aun\nsWPHKi8vT1dffbXCwsL0zDPP6OTJk6ZHQy3FT0xcsr1796pbt27av3+/MjMz1a1bN9MjAW7TqFEj\nJSYmKjMzU99++61sNpvefPNNlZWVmR4NtQwhxiVZunSpunbtqpEjR2r58uW64oorTI8EGHHddddp\n8eLFWrlypRYuXKjw8HB9+umnpsdCLcJmLVTL6dOnNW7cOG3cuFHLli1jswpwFqfTqRUrVmjChAlq\n06aN7Ha72rdvb3oseDhWxKiynTt3KioqSsXFxdq+fTsRBs5hsVh01113adeuXerfv7/69u2rsWPH\n6vDhw6ZHgwcjxLgop9Op+fPnq2/fvho/frxSU1MVFBRkeizAYzVo0EBPPPGEcnJyFBAQoPbt22vm\nzJlyOBymR4MH4tQ0Lujnn3/WmDFjtGvXLi1btkzt2rUzPRJQ6+zdu1cJCQlKT0/XzJkzNWTIEO4u\nwO/4LwGVysjIUEREhEJCQrR161YiDFyi1q1b67333tPixYv16quvqkuXLtq4caPpseAhWBHjPE6n\nU6+88ooSExP12muv6a9//avpkYA6o7y8XGlpaZo4caIiIiI0a9YstWnTxvRYMIgVMf7g2LFjGjRo\nkNLS0rR161YiDNQwHx8fDRkyRDk5OerSpYu6du2qxx9/XMePHzc9GgwhxPjdpk2bFB4errZt22rT\npk18DivgQlarVU899ZR27dqlkpIStW3bVi+99JKKi4tNjwY349Q0VFZWppkzZ+q1117TggULNGDA\nANMjAV5n165dmjBhgnbv3q0XXnhBd999N5/w5CUIsZf78ccf9eCDD6q8vFxvvfWWmjdvbnokwKut\nXbtWcXFxCgoKUlJSkrp06WJ6JLgYp6a92CeffKKIiAj16tVLa9euJcKAB+jXr58yMzM1atQo3XXX\nXbr//vv1/fffmx4LLkSIvVBJSYkSEhI0evRopaWlacqUKfL19TU9FoBf+fr6atSoUcrNzVVoaKg6\nd+6shIQEFRQUmB4NLkCIvcz333+vXr16aefOncrKylLv3r1NjwSgEoGBgZo6daqys7N19OhR2Ww2\nvfbaayopKTE9GmoQIfYiy5cv10033aR77rlHq1atUtOmTU2PBKAKmjdvrgULFmjNmjVasWKFwsLC\n9OGHH4otPnUDm7W8QFFRkeLi4rR69WqlpaXppptuMj0SgEvkdDr18ccfKz4+Xtdcc42SkpLUqVMn\n02PhMrAiruNyc3N188036+jRo8rKyiLCQC1nsVg0cOBAZWdn6+6779btt9+ukSNH6tChQ6ZHwyUi\nxHVYamqqevToodjYWC1btkzBwcGmRwJQQ+rXr69HHnlEubm5atasmcLCwjR16lSdOnXK9GioJk5N\n10EnT57Uo48+qm3btuntt99Wx44dTY8EwMW+//57Pf3009qwYYOeffZZDR8+nLshaglWxHXMN998\no8jISPn6+iojI4MIA16iZcuWWrJkiZYvX64FCxYoIiJCa9euNT0WqoAVcR3hdDqVnJysKVOm6JVX\nXtEDDzxgeiQAhjidTi1fvlwJCQkKDQ3Viy++qBtuuKFKxx45ckSpKSnKy87WyYICBQYHyxYWpuEj\nR3KnhYsQ4jrgp59+0ujRo7Vv3z6lpaXJZrOZHgmAByguLtbrr7+umTNn6p577tG0adN05ZVXVvja\n9PR0zU5M1EerV+suSVFFRQqSVChpm9WqFU6nBkZH6/GJExUVFeXOb6PO49R0LffVV18pPDxc11xz\njb788ksiDOB3fn5+evLJJ5WTkyM/Pz/dcMMNSkxMlMPh+MPr5iUna1CfPopcuVL7ior0r6IijZX0\ngKSxkhY4HNpXVKTOK1dqUJ8+mpecbOLbqbNYEddS5eXlstvtSkpK0htvvKE777zT9EgAPNyePXuU\nkJCg7du3KzExUYMHD9abb7yhF+Ljteb0abWuwtfYK6l/QIAS7HaNiY119chegRDXQkeOHNGwYcNU\nWFiopUuX6tprrzU9EoBaZOPGjYqLi9OpU6d0fN8+bS4u/j3Cv0h6RNJaSfmSWkmaKen2s47fK6ln\nQIBWbdigyMhIt85eF3Fqupb54osvFB4eroiICK1fv54IA6i2Xr16aevWrWoaEKAJZ0VYkkolXStp\nk6QCSc9KulfSgbNe01rSBIdDsxMT3TZzXcaK2JDq7kwsLS3V9OnT9eabb2rhwoW67bbbDEwNoK44\ncuSIQq+7TvuKihRykdfeKGmqpJizHjshqZW/v/IOHGA39WWqZ3oAb3PBnYnLl8s2Zcp5OxMPHjyo\nIUOGyM/PT5mZmbrqqqtMfgsA6oDUlBTFSBeN8GFJeyS1P+fxKyTFWCxKTUlR3PjxrhjRaxBiN5qX\nnKwp8fFKcDg0x+k873+AsQ6HkiSlrFypQWvWaJrdrmtatNDo0aM1btw4PfXUU/Lx4WoC4K2cTqdK\nS0tVUlJS5V+Vvf6TlSt1T1HRBf9+pZIelDRCUkX3Y0Q5HPp6x46a/0a9DCF2k3nJyXohPl6bLrIz\nMUTSk06n/nz6tPqOGydHUJDeX7VK3bt3d9eoQJ3hdDpVVlZWrXBVNWQmji8tLZWvr6/q169fpV/1\n6tWr9LlDBw4o6EL/7HQmwn6S5lTymiBJhfn5Nf2vzesQYjdIT0/XlAoi/JqkFEk7JA2RtOCs51pL\nWldaqp5FRfLz83PfsPBqFYXLk0J0Kcf6+PhUOVzVjdnZv6xWqxo1anRJx1bn722xWGrk3/WYBx9U\n4eLFlT7/kKRjkj6WVNk7VhdKCgq52MltXAwhdoPZiYlKcDjOWwk3lzRZ0hpJjvMPO7MzsahIsxMT\ntei991w9Ji5RVVZcpmNUndefGy5XxKR+/fry8/NTYGBgjYWwsmO5nFMxW1iYtr33nsZWcHp6rKQc\nnbmFqcEFvka61ar2vJ/9ZWPXtItVZWfiZEmH9McV8W/q4s7E8vLyWrWqutjxklwWEhPHEy7vUNnP\npgOSWkry1/+thC2S3pB0/1mvq4s/m0xhRexiVd2ZWJkrJN1psWjBv/6lvz/2mEeGqLrHl5eXuy1E\nAQEBLg8ZHzWH2ujKK6/UwOhoLVy5Uk+ctR67VlJ5FY5faLHojgEDiHANYEXsYmMefFARixdr7AVe\nc6EVsSQlS4q3WOT09681q6oLHevr61tj17kAXLr09HQN6tPnoptIz8U7a9UsVsQudrKg4II7E6si\nSNJfBg7UklWramIkAJAkRUVFaZrdrv6X8F7T0+x2IlxDuBjkYoHBwSq8zK/BzkQArjImNlYJdrt6\nBgToZYt5QuZWAAACEklEQVRFld2MdELSSxaLevKBDzWOELuYLSxM2/z9K3yuTFLRr38slVT865+f\nK91qlY2diQBcZExsrFZt2KDMmBj9j7+/RlmtSpb0ls5cGhtltaqVv7+yYmK0asMGIlzDuEbsYhfa\nNT3t119nXy2dIumZs/6anYkA3Ono0aNn3gd/xw4V5ucrKCREto4dNWzECH4GuQghdoMH77pLkefs\nTKyqly0WZcbEcB8xANRRhNgN2JkIAKgM14jd4PediQEB2lvFY9iZCADegRC7CTsTAQAV4dS0m2Vk\nZGh2YqI+/PhjxVgsinI4fv884nSrVSucTt0xYIAenziRlTAAeAFCbAg7EwEAEiEGAMAorhEDAGAQ\nIQYAwCBCDACAQYQYAACDCDEAAAYRYgAADCLEAAAYRIgBADCIEAMAYBAhBgDAIEIMAIBBhBgAAIMI\nMQAABhFiAAAMIsQAABhEiAEAMIgQAwBgECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIAAAwixAAAGESI\nAQAwiBADAGAQIQYAwCBCDACAQYQYAACDCDEAAAYRYgAADCLEAAAYRIgBADCIEAMAYBAhBgDAIEIM\nAIBBhBgAAIMIMQAABhFiAAAMIsQAABhEiAEAMIgQAwBgECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIA\nAAwixAAAGESIAQAwiBADAGAQIQYAwCBCDACAQf8fHWpWlowNdzgAAAAASUVORK5CYII=\n",
"text/plain": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Degree, Average Degree and Degree Distribution\n"
]
},
{
"cell_type": "code",
"execution_count": 175,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3XtYlHX+//HXgAqDIEtqVl6WfdVBU0kQMs9adhnaulFt\nmeUxc6U2qwUlW81DKWVDZVpcaesPMRU7qGVlluVptRSEQlcBzdL023okQh2Iw/z+sPqagoIy8xmY\n5+O6vKqZuelNB55+7vtzz1icTqdTAADACB/TAwAA4M0IMQAABhFiAAAMIsQAABhEiAEAMIgQAwBg\nECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIAAAwixAAAGESIAQAwiBADAGAQIQYAwCBCDACAQYQYAACD\nCDEAAAYRYgAADCLEAAAYRIgBADCIEAMAYBAhBgDAIEIMAIBBhBgAAIMIMQAABhFiAAAMIsQAABhE\niAEAMIgQAwBgECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIAAAwixAAAGESIAQAwiBADAGAQIQYAwCBC\nDACAQYQYAACDCDEAAAYRYgAADKpnegCgLjhy5IhSU1KUl52tkwUFCgwOli0sTMNHjlTTpk1NjwfA\ng1mcTqfT9BBAbZWenq7ZiYn6aPVq3SUpqqhIQZIKJW2zWrXC6dTA6Gg9PnGioqKiDE8LwBMRYuAS\nzUtO1pT4eCU4HBrudCqkgtfkS0qxWDTLatU0u11jYmPdPSYAD0eIgUswLzlZL8THa83p02pdhdfv\nldQ/IEAJxBjAOQgxUE3p6eka1KePNp0T4aGS1ko6LamJpFGS/nnW83sl9QwI0KoNGxQZGem+gQF4\nNHZNA9U0OzFRCQ7HeSvhiZK+k1QgabWkOZLWnPV8a0kTHA7NTkx0z6AAagVWxEA1HDlyRKHXXad9\nRUUVXhP+Ta6kfpLelxRx1uMnJLXy91fegQPspgYgiRUxUC2pKSmKkSqN8KOSGkrqoDOnpSPOef4K\nSTEWi1JTUlw2I4DahRAD1ZCXna2biooqff41SSd15lrxJEnpFbwmyuFQ3o4drhkQQK1DiIFqOFlQ\noKCLvMYiqbekv0paWsHzQZIK8/NrejQAtRQhBqohMDhYhVV8bamkgAoeL5QUFHKhK8wAvAkhBqrB\nFhambf7+5z1+VNIySacklevMbul3JP2lgq+RbrXK1rGjK8cEUIuwaxqohsp2TR+TdI+kbElOSW0k\nTZb053OOZ9c0gHOxIgaq4corr9TA6GgttFj+8HgTSet1JrT5krbp/AhL0kKLRXcMGECEAfyOFTFQ\nTZW9s9bF8M5aACrCihiopqioKE2z29U/IEB7q3jMb+81Pc1uJ8IA/oAQA5dgTGysEux29QwI0MsW\niyq7GemEpJcsFvXkAx8AVIJT08BlyMjI0OzERH348ceKsVgU5XD8/nnE6b9+HvEdAwbo8YkTWQkD\nqBAhBmrA0aNHlZqSorwdO7QvL0/f7t+vR//xDw0bMYKNWQAuiBADNey7775T7969deDAAdOjAKgF\nCDFQw8rKyhQYGKgTJ07IarWaHgeAh2OzFlDDfH191bJlS3377bemRwFQCxBiwAXatGmjPXv2mB4D\nQC1AiAEXsNlsysvLMz0GgFqAEAMuwIoYQFURYsAFCDGAqiLEgAsQYgBVxe1LgAuUl5crMDBQhw8f\nVlBQkOlxAHgwVsSAC/j4+Kh169bau7eqHwsBwFsRYsBFOD0NoCoIMeAihBhAVRBiwEXatGnDvcQA\nLooQAy5is9lYEQO4KEIMuAinpgFUBSEGXKRZs2YqKipSfn6+6VEAeDBCDLiIxWJhVQzgoggx4EJc\nJwZwMYQYcCFWxAAuhhADLkSIAVwMIQZciBADuBg+9AFwoePHj6tVq1bKz8+XxWIxPQ4AD8SKGHCh\nxo0by8fHR8eOHTM9CgAPRYgBF+P0NIALIcSAixFiABdCiAEXs9lsfPgDgEoRYsDFWBEDuBBCDLgY\nIQZwIdy+BLhYQUGBmjdvrsLCQm5hAnAeVsSAiwUHB6thw4b68ccfTY8CwAMRYsANOD0NoDKEGHAD\nQgygMoQYcANCDKAyhBhwgzZt2nAvMYAKEWLADWw2GytiABXi9iXADU6dOqWmTZvq5MmT8vHh978A\n/g8/EQA3aNiwoUJCQnTw4EHTowDwMIQYcBOuEwOoCCEG3ITrxAAqQogBN+EWJgAVIcSAmxBiABUh\nxICbEGIAFeH2JcBNioqK9Kc//UknT55UvXr1TI8DwEOwIgbcxN/fX1dddZX2799vehQAHoQQA27E\n6WkA5yLEgBsRYgDnIsSAG9lsNt7UA8AfEGLAjVgRAzgXIQbciBADOBe3LwFuVFJSoqCgIP38889q\n0KCB6XEAeABWxIAb1a9fXy1atNC+fftMjwLAQxBiwM04PQ3gbIQYcDNCDOBshBhwM0IM4GyEGHAz\n7iUGcDZCDLgZK2IAZ+P2JcDNysrKFBgYqBMnTshqtZoeB4BhrIgBN/P19VXLli317bffmh4FgAcg\nxIABbdq04ToxAEmEGDDCZrNxnRiAJEIMGMGGLQC/IcSAAYQYwG8IMWAAIQbwG25fAgwoLy9XYGCg\nDh8+rKCgINPjADCIFTFggI+Pj1q3bq29e/eaHgWAYYQYMITT0wAkQgwYQ4gBSIQYMIYPfwAgEWLA\nGFbEACRCDBhDiAFIhBgwplmzZioqKlJ+fr7pUQAYRIgBQywWC+85DYAQAyZxehoAIQYMIsQACDFg\nECEGQIgBg7iXGAAf+gAYdPz4cbVq1Ur5+fmyWCymxwFgACtiwKDGjRvLx8dHx44dMz0KAEMIMWAY\n14kB70aIAcO4Tgx4N0IMGMaKGPBuhBgwjBAD3o0QA4YRYsC7cfsSYFhBQYGaN2+uwsJCbmECvBAr\nYsCw4OBgNWzYUD/++KPpUQAYQIgBD8DpacB7EWLAAxBiwHsRYsADEGLAexFiwAPwph6A9yLEgAdg\nRQx4r3qmBwAgNWrUSHtyc/Xwgw/qVEGBAoODZQsL0/CRI9W0aVPT4wFwIe4jBgxKT0/X7MREfbR6\ntaKLitRLUpCkQknbrFatcDo1MDpaj0+cqKioKMPTAnAFQgwYMi85WVPi45XgcGi406mQCl6TLynF\nYtEsq1XT7HaNiY1195gAXIwQAwbMS07WC/HxWnP6tFpX4fV7JfUPCFACMQbqHEIMuFl6eroG9emj\nTRVEeI+kMEl/lZR6znN7JfUMCNCqDRsUGRnpjlEBuAG7pgE3m52YqASHo8KV8N8l3VTJca0lTXA4\nNDsx0XXDAXA7VsSAGx05ckSh112nfUVF510TTpO0UtINOrP6PXdFLEknJLXy91fegQPspgbqCFbE\ngBulpqQoRjovwj9LmiLpJUkX+p3xFZJiLBalpqS4ZkAAbkeIATfKy87WTUVF5z3+jKSHJV1Tha8R\n5XAob8eOmh4NgCG8oQfgRicLChR0zmNfS1r76x+rIkhSYX5+jc4FwBxCDLhRYHCwCs95bIOk/ZKu\n1ZnT0icllUnaJSmjgq9RKCkopKK7jgHURpyaBtzIFhambf7+f3jsb5K+1ZkV8TeSxkq6Q9KnlXyN\ndKtVto4dXTkmADdi1zTgRhfaNf2baToT5kp3Tfv5Ke+HH9g1DdQRrIgBN2rQoIGaXHGFFlzgNVNU\ncYQl6f9Jskhavny5SktLa3w+AO5HiAE32bZtmyIiItSpWzfZAwK0t5rH75VkDwjQ7PnztXTpUt14\n441avXq1OKkF1G6EGHCx8vJy2e123XHHHbLb7XrnnXc0zW5X/2rE+Lf3mp5mt2vo0KFat26dZs6c\nqSeeeEL9+/dXdna2K78FAC7kO3Xq1KmmhwDqqqNHj+ree+9VZmam1qxZo65du0qSOkdFyXrFFRq2\nbp18S0vVVpK1guNPSEq2WDQ6IECTzvrAB4vForZt22rs2LEqLCzUww8/rNzcXEVFRSko6NwbpAB4\nMlbEgIusX79e4eHhCgsL08aNG9WyZcs/PD8mNlarNmxQZkyM/sffX6OsViVLektSsqRRVqta+fsr\nKyZGqzZsqPBTl+rXr6/HHntMubm5CgkJUYcOHTR9+nSdOnXKHd8igBrArmmghpWVlenZZ5/VG2+8\noZSUFPXv3/+ixxw9elSpKSnK27FDhfn5CgoJka1jRw0bMaJau6P37duniRMnavPmzZoxY4aGDh0q\nHx9+vw14MkIM1KBDhw7pgQcekK+vr9566y1dffXVRubYsmWL4uLiVFxcrKSkJPXt29fIHAAujt8q\nAzXk448/VufOndWvXz99+umnxiIsSd26ddOWLVuUkJCgUaNGadCgQcrJyTE2D4DKEWLgMv3yyy+K\nj4/X2LFj9c4772jSpEny9fU1PZYsFovuu+8+7d69Wz179lSPHj3097//XUePHjU9GoCzEGLgMuzb\nt089evRQXl6esrKy1LNnT9Mjncff31/jx49XTk6OLBaL2rVrp1mzZqmogk+BAuB+hBi4RG+//ba6\ndOmiIUOG6P3331fjxo1Nj3RBTZo00Zw5c7R582Zt3rxZ7dq1U1paGm8IAhjGZi2gmhwOh5588kmt\nXbtWaWlpioyMND3SJVm3bp3i4uLk5+enpKQkdevWzfRIgFdiRQxUw+7du9WlSxcVFBQoMzOz1kZY\nkvr27auMjAzFxsbqvvvu07333qt9+/aZHgvwOoQYqAKn06kFCxaoV69eGjdunJYsWaJGjRqZHuuy\n+fj4aNiwYcrNzVXHjh0VFRWl+Ph45efnmx4N8BqEGLiIwsJCDR06VElJSVq/fr1Gjx4ti8Vieqwa\nFRAQoMmTJ2vnzp0qKChQaGioXn31VZWUlJgeDajzCDFwAVlZWercubOsVqvS09PVvn170yO51NVX\nX6358+fr888/10cffaT27dtr5cqVbOgCXIjNWkAFnE6n5s6dq+nTp2vOnDkaPHiw6ZGM+OSTTxQf\nH68mTZooKSlJnTt3Nj0SUOcQYuAcJ06c0KhRo3Tw4EGlpaWpdevWpkcyqrS0VAsWLNCUKVN02223\nacaMGWrRooXpsYA6g1PTwFm2bNmi8PBwXX/99dq8ebPXR1iS6tWrpzFjxigvL0/XXnutOnXqpEmT\nJqmwsND0aECdQIgBSeXl5UpMTFRMTIzmzp2rl19+WX5+fqbH8ihBQUF67rnn9PXXX2v//v2y2Wya\nN2+eSktLTY8G1GqcmobXO3z4sIYOHSqHw6ElS5Zw2rWKMjIyFBcXp+PHj8tut+v22283PRJQK7Ei\nhlf77LPPFB4eri5dumjdunVEuBoiIyO1fv16Pffccxo3bpz69++vHTt2mB4LqHUIMbxSaWmpnn76\naY0YMUKLFi3Ss88+q3r16pkeq9axWCy68847tXPnTg0cOFC33nqrHn74Yf33v/81PRpQaxBieJ0D\nBw6od+/e2r59uzIzM3XrrbeaHqnWa9CggcaNG6fc3FwFBwerffv2eu6553T69GnTowEejxDDq7z/\n/vuKiorSoEGDtHr1ajVr1sz0SHVKSEiI7Ha70tPTlZ2drdDQUKWmpqq8vNz0aIDHYrMWvEJxcbHG\njx+vDz74QEuXLlXXrl1Nj+QVNm/erLi4OJWUlCgpKUl9+vQxPRLgcVgRo87bs2ePunbtqkOHDikr\nK4sIu1H37t315Zdfavz48Ro5cqT+8pe/KDc31/RYgEchxKjTlixZom7dumn06NF69913FRISYnok\nr2OxWDR48GDt3r1b3bt3V/fu3fXYY4/p2LFjpkcDPAIhRp106tQpPfTQQ5o2bZo+++wzPfLII3Xu\nE5NqG39/f02YMEG7d++W0+lUu3bt9OKLL6q4uNj0aIBRhBh1zo4dOxQVFaWSkhJt375dnTp1Mj0S\nztK0aVPNnTtXmzZt0qZNm9SuXTu9/fbbfMITvBabtVBnOJ1OzZs3T5MmTVJSUpKGDRtmeiRUwRdf\nfKG4uDhZrVYlJSVxDR9ehxCjTigoKNCYMWOUk5OjZcuWqW3btqZHQjWUlZVp0aJFmjRpkrp3767n\nn39e119/vemxALfg1DRqvfT0dEVERKhx48b66quviHAt5OvrqxEjRig3N1ft27dXZGSkxo8fr59+\n+sn0aIDLEWLUWuXl5UpKStLAgQM1a9Ysvf7667JarabHwmVo2LChnnnmGe3cuVP5+fkKDQ3VnDlz\nVFJSYno0wGU4NY1a6dixYxo+fLiOHz+utLQ0tWzZ0vRIcIHs7GzFx8dr//79mjVrlgYNGsTud9Q5\nrIhR62zYsEHh4eHq0KGDNm3aRITrsLCwMK1Zs0avvPKKnn76ad1yyy3KzMw0PRZQowgxao2ysjJN\nnz5dgwcP1rx58/TCCy+ofv36pseCi1ksFkVHR+ubb77R4MGDNXDgQA0fPlwHDx40PRpQIwgxaoX/\n/d//Vb9+/bR+/Xpt375d0dHRpkeCm9WrV09/+9vflJubq+bNm+vGG2/U5MmTVVhYaHo04LIQYni8\n1atXq3Pnzrrlllv02Wef6ZprrjE9Egxq1KiRZs6cqaysLH333XcKDQ3V/PnzVVZWZno04JKwWQse\n65dfftE///lPpaWlafHixerVq5fpkeCB0tPTFRcXp/z8fNntdvXv39/0SEC1EGJ4pO+++06DBw9W\n06ZNlZKSoiZNmpgeCR7M6XRq5cqVmjBhglq1aiW73a4OHTqYHguoEk5Nw+O8++676tKli+677z6t\nWrWKCOOiLBaLYmJi9J///EfR0dG65ZZbNGbMGP33v/81PRpwUYQYHsPhcCg2NlYJCQn66KOP9I9/\n/IN7RlEtDRo00OOPP67c3FwFBQWpQ4cOmjFjhk6fPm16NKBShBgeIScnRzfffLPy8/OVmZmpqKgo\n0yOhFgsJCVFSUpK2bt2qrKwstW3bVosWLVJ5ebnp0YDzcI0Yxi1cuFDx8fGaOXOmRo8ezSoYNe7f\n//634uLiVFZWpqSkJPXu3dv0SMDvCDGMKSws1KOPPqqMjAwtW7ZMHTt2ND0S6rDy8nItW7ZMEydO\nVKdOnTRr1izZbDbTYwGcmoYZX3/9tSIjI9WgQQOlp6cTYbicj4+P7r//fuXk5Khr167q1q2bxo0b\np+PHj5seDV6OEMOtnE6n5s6dq9tuu01Tp07Vm2++qYYNG5oeC17E399fCQkJ2r17t8rKytS2bVvZ\n7XYVFxebHg1eilPTcJv8/Hw99NBD2r9/v5YtW6bWrVubHgnQ7t27NWHCBO3atUvPP/+87rnnHvYp\nwK1YEcMtvvzyS4WHh6tFixbasmULEYbHaNeunVatWqV58+ZpxowZ6tGjh7766ivTY8GLsCKGS5WX\nl2vWrFl6+eWXNX/+fA0aNMj0SEClysrKlJqaqsmTJ6tHjx5KTEzU9ddfb3os1HGsiOEyhw8fVnR0\ntD788ENlZGQQYXg8X19fjRw5Urm5uWrXrp0iIyM1YcIE/fTTT6ZHQx1GiOESn3/+uSIiIhQVFaX1\n69erRYsWpkcCqqxhw4aaMmWKduzYoePHjys0NFRz585VSUmJ6dFQB3FqGjWqtLRUU6dO1YIFC5Sa\nmqp+/fqZHgm4bN98843i4+P1ww8/aNasWfrzn//Mhi7UGEKMGvPDDz9oyJAhslqtWrRokZo1a2Z6\nJKDGOJ1OrV69WvHx8brqqquUlJSk8PBw02OhDuDUNGrEBx98oMjISA0cOFCffPIJEUadY7FYNGDA\nAGVnZ+vee+9VdHS0RowYoUOHDpkeDbUcIcZlKS4u1hNPPKFx48ZpxYoVeuqpp+Tjw39WqLvq1aun\nsWPHKi8vT1dffbXCwsL0zDPP6OTJk6ZHQy3FT0xcsr1796pbt27av3+/MjMz1a1bN9MjAW7TqFEj\nJSYmKjMzU99++61sNpvefPNNlZWVmR4NtQwhxiVZunSpunbtqpEjR2r58uW64oorTI8EGHHddddp\n8eLFWrlypRYuXKjw8HB9+umnpsdCLcJmLVTL6dOnNW7cOG3cuFHLli1jswpwFqfTqRUrVmjChAlq\n06aN7Ha72rdvb3oseDhWxKiynTt3KioqSsXFxdq+fTsRBs5hsVh01113adeuXerfv7/69u2rsWPH\n6vDhw6ZHgwcjxLgop9Op+fPnq2/fvho/frxSU1MVFBRkeizAYzVo0EBPPPGEcnJyFBAQoPbt22vm\nzJlyOBymR4MH4tQ0Lujnn3/WmDFjtGvXLi1btkzt2rUzPRJQ6+zdu1cJCQlKT0/XzJkzNWTIEO4u\nwO/4LwGVysjIUEREhEJCQrR161YiDFyi1q1b67333tPixYv16quvqkuXLtq4caPpseAhWBHjPE6n\nU6+88ooSExP12muv6a9//avpkYA6o7y8XGlpaZo4caIiIiI0a9YstWnTxvRYMIgVMf7g2LFjGjRo\nkNLS0rR161YiDNQwHx8fDRkyRDk5OerSpYu6du2qxx9/XMePHzc9GgwhxPjdpk2bFB4errZt22rT\npk18DivgQlarVU899ZR27dqlkpIStW3bVi+99JKKi4tNjwY349Q0VFZWppkzZ+q1117TggULNGDA\nANMjAV5n165dmjBhgnbv3q0XXnhBd999N5/w5CUIsZf78ccf9eCDD6q8vFxvvfWWmjdvbnokwKut\nXbtWcXFxCgoKUlJSkrp06WJ6JLgYp6a92CeffKKIiAj16tVLa9euJcKAB+jXr58yMzM1atQo3XXX\nXbr//vv1/fffmx4LLkSIvVBJSYkSEhI0evRopaWlacqUKfL19TU9FoBf+fr6atSoUcrNzVVoaKg6\nd+6shIQEFRQUmB4NLkCIvcz333+vXr16aefOncrKylLv3r1NjwSgEoGBgZo6daqys7N19OhR2Ww2\nvfbaayopKTE9GmoQIfYiy5cv10033aR77rlHq1atUtOmTU2PBKAKmjdvrgULFmjNmjVasWKFwsLC\n9OGHH4otPnUDm7W8QFFRkeLi4rR69WqlpaXppptuMj0SgEvkdDr18ccfKz4+Xtdcc42SkpLUqVMn\n02PhMrAiruNyc3N188036+jRo8rKyiLCQC1nsVg0cOBAZWdn6+6779btt9+ukSNH6tChQ6ZHwyUi\nxHVYamqqevToodjYWC1btkzBwcGmRwJQQ+rXr69HHnlEubm5atasmcLCwjR16lSdOnXK9GioJk5N\n10EnT57Uo48+qm3btuntt99Wx44dTY8EwMW+//57Pf3009qwYYOeffZZDR8+nLshaglWxHXMN998\no8jISPn6+iojI4MIA16iZcuWWrJkiZYvX64FCxYoIiJCa9euNT0WqoAVcR3hdDqVnJysKVOm6JVX\nXtEDDzxgeiQAhjidTi1fvlwJCQkKDQ3Viy++qBtuuKFKxx45ckSpKSnKy87WyYICBQYHyxYWpuEj\nR3KnhYsQ4jrgp59+0ujRo7Vv3z6lpaXJZrOZHgmAByguLtbrr7+umTNn6p577tG0adN05ZVXVvja\n9PR0zU5M1EerV+suSVFFRQqSVChpm9WqFU6nBkZH6/GJExUVFeXOb6PO49R0LffVV18pPDxc11xz\njb788ksiDOB3fn5+evLJJ5WTkyM/Pz/dcMMNSkxMlMPh+MPr5iUna1CfPopcuVL7ior0r6IijZX0\ngKSxkhY4HNpXVKTOK1dqUJ8+mpecbOLbqbNYEddS5eXlstvtSkpK0htvvKE777zT9EgAPNyePXuU\nkJCg7du3KzExUYMHD9abb7yhF+Ljteb0abWuwtfYK6l/QIAS7HaNiY119chegRDXQkeOHNGwYcNU\nWFiopUuX6tprrzU9EoBaZOPGjYqLi9OpU6d0fN8+bS4u/j3Cv0h6RNJaSfmSWkmaKen2s47fK6ln\nQIBWbdigyMhIt85eF3Fqupb54osvFB4eroiICK1fv54IA6i2Xr16aevWrWoaEKAJZ0VYkkolXStp\nk6QCSc9KulfSgbNe01rSBIdDsxMT3TZzXcaK2JDq7kwsLS3V9OnT9eabb2rhwoW67bbbDEwNoK44\ncuSIQq+7TvuKihRykdfeKGmqpJizHjshqZW/v/IOHGA39WWqZ3oAb3PBnYnLl8s2Zcp5OxMPHjyo\nIUOGyM/PT5mZmbrqqqtMfgsA6oDUlBTFSBeN8GFJeyS1P+fxKyTFWCxKTUlR3PjxrhjRaxBiN5qX\nnKwp8fFKcDg0x+k873+AsQ6HkiSlrFypQWvWaJrdrmtatNDo0aM1btw4PfXUU/Lx4WoC4K2cTqdK\nS0tVUlJS5V+Vvf6TlSt1T1HRBf9+pZIelDRCUkX3Y0Q5HPp6x46a/0a9DCF2k3nJyXohPl6bLrIz\nMUTSk06n/nz6tPqOGydHUJDeX7VK3bt3d9eoQJ3hdDpVVlZWrXBVNWQmji8tLZWvr6/q169fpV/1\n6tWr9LlDBw4o6EL/7HQmwn6S5lTymiBJhfn5Nf2vzesQYjdIT0/XlAoi/JqkFEk7JA2RtOCs51pL\nWldaqp5FRfLz83PfsPBqFYXLk0J0Kcf6+PhUOVzVjdnZv6xWqxo1anRJx1bn722xWGrk3/WYBx9U\n4eLFlT7/kKRjkj6WVNk7VhdKCgq52MltXAwhdoPZiYlKcDjOWwk3lzRZ0hpJjvMPO7MzsahIsxMT\ntei991w9Ji5RVVZcpmNUndefGy5XxKR+/fry8/NTYGBgjYWwsmO5nFMxW1iYtr33nsZWcHp6rKQc\nnbmFqcEFvka61ar2vJ/9ZWPXtItVZWfiZEmH9McV8W/q4s7E8vLyWrWqutjxklwWEhPHEy7vUNnP\npgOSWkry1/+thC2S3pB0/1mvq4s/m0xhRexiVd2ZWJkrJN1psWjBv/6lvz/2mEeGqLrHl5eXuy1E\nAQEBLg8ZHzWH2ujKK6/UwOhoLVy5Uk+ctR67VlJ5FY5faLHojgEDiHANYEXsYmMefFARixdr7AVe\nc6EVsSQlS4q3WOT09681q6oLHevr61tj17kAXLr09HQN6tPnoptIz8U7a9UsVsQudrKg4II7E6si\nSNJfBg7UklWramIkAJAkRUVFaZrdrv6X8F7T0+x2IlxDuBjkYoHBwSq8zK/BzkQArjImNlYJdrt6\nBgToZYt5QuZWAAACEklEQVRFld2MdELSSxaLevKBDzWOELuYLSxM2/z9K3yuTFLRr38slVT865+f\nK91qlY2diQBcZExsrFZt2KDMmBj9j7+/RlmtSpb0ls5cGhtltaqVv7+yYmK0asMGIlzDuEbsYhfa\nNT3t119nXy2dIumZs/6anYkA3Ono0aNn3gd/xw4V5ucrKCREto4dNWzECH4GuQghdoMH77pLkefs\nTKyqly0WZcbEcB8xANRRhNgN2JkIAKgM14jd4PediQEB2lvFY9iZCADegRC7CTsTAQAV4dS0m2Vk\nZGh2YqI+/PhjxVgsinI4fv884nSrVSucTt0xYIAenziRlTAAeAFCbAg7EwEAEiEGAMAorhEDAGAQ\nIQYAwCBCDACAQYQYAACDCDEAAAYRYgAADCLEAAAYRIgBADCIEAMAYBAhBgDAIEIMAIBBhBgAAIMI\nMQAABhFiAAAMIsQAABhEiAEAMIgQAwBgECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIAAAwixAAAGESI\nAQAwiBADAGAQIQYAwCBCDACAQYQYAACDCDEAAAYRYgAADCLEAAAYRIgBADCIEAMAYBAhBgDAIEIM\nAIBBhBgAAIMIMQAABhFiAAAMIsQAABhEiAEAMIgQAwBgECEGAMAgQgwAgEGEGAAAgwgxAAAGEWIA\nAAwixAAAGESIAQAwiBADAGAQIQYAwCBCDACAQf8fHWpWlowNdzgAAAAASUVORK5CYII=\n",
"text/plain": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Path\n",
"A path is a sequence of nodes in which each node is adjacent to the next one\n",
" - In a directed network, the path can follow only the direction of an arrow. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Distance\n",
"\n",
"The distance (shortest path, geodesic path) between two nodes is defined as the number of edges along the shortest path connecting them.\n",
"\n",
" - *If the two nodes are disconnected, the distance is infinity.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Diameter: \n",
"\n",
"**Diameter $d_{max}$** is the maximum distance between any pair of nodes in the graph. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Shortest Path \n",
"The path with the shortest length between two nodes (distance). \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Average path length/distance, $
"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Path\n",
"A path is a sequence of nodes in which each node is adjacent to the next one\n",
" - In a directed network, the path can follow only the direction of an arrow. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Distance\n",
"\n",
"The distance (shortest path, geodesic path) between two nodes is defined as the number of edges along the shortest path connecting them.\n",
"\n",
" - *If the two nodes are disconnected, the distance is infinity.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Diameter: \n",
"\n",
"**Diameter $d_{max}$** is the maximum distance between any pair of nodes in the graph. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Shortest Path \n",
"The path with the shortest length between two nodes (distance). \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Average path length/distance, $ "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Strongly connected directed graph: \n",
"has a path from each node to every other node and vice versa (e.g. AB path and BA path).\n",
"\n",
"# Weakly connected directed graph: \n",
"it is connected if we disregard the edge directions.\n",
"\n",
"Strongly connected components can be identified, but not every node is partof a nontrivial strongly connected component. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"- In-component: nodes that can reach the scc, \n",
"- Out-component: nodes that can be reached from the scc. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Clustering coefficient\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Clustering coefficient: \n",
"what fraction of your neighbors are connected? Watts & Strogatz, Nature 1998.\n",
"\n",
"- Node i with degree $k_i$\n",
"- $C_i$ in [0,1]\n",
"\n",
"# $C_i = \\frac{2e_i}{k_i(k_i -1)}$\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Strongly connected directed graph: \n",
"has a path from each node to every other node and vice versa (e.g. AB path and BA path).\n",
"\n",
"# Weakly connected directed graph: \n",
"it is connected if we disregard the edge directions.\n",
"\n",
"Strongly connected components can be identified, but not every node is partof a nontrivial strongly connected component. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"- In-component: nodes that can reach the scc, \n",
"- Out-component: nodes that can be reached from the scc. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Clustering coefficient\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Clustering coefficient: \n",
"what fraction of your neighbors are connected? Watts & Strogatz, Nature 1998.\n",
"\n",
"- Node i with degree $k_i$\n",
"- $C_i$ in [0,1]\n",
"\n",
"# $C_i = \\frac{2e_i}{k_i(k_i -1)}$\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Global Clustering Coefficient:\n",
" \n",
"## $C = \\frac{3 \\times \\mbox{number of triangles}}{\\mbox{number of connected triplets of vertices}} = \\frac{\\mbox{number of closed triplets}}{\\mbox{number of connected triplets of vertices}}$\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 215,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xd4jefjBvD7CJnS1CxFokYQYkepkpAdMyqEqoiZxC6J\nPRIh1GhRiVDEqhUzJITEbhFFmxqJndpiRPZ8f3/4tj9FKuOc85xxf67LxXXG+97p98t9nuc87/PK\nJEmSQEREREKUER2AiIhIm7GIiYiIBGIRExERCcQiJiIiEohFTEREJBCLmIiISCAWMRERkUAsYiIi\nIoFYxERERAKxiImIiARiERMREQnEIiYiIhKIRUxERCQQi5iIiEggFjEREZFALGIiIiKBWMREREQC\nsYiJiIgEYhETEREJxCImIiISiEVMREQkEIuYiIhIIBYxERGRQCxiIiIigVjEREREArGIiYiIBGIR\nExERCcQiJiIiEohFTEREJBCLmIiISCAWMRERkUAsYiIiIoFYxERERAKxiImIiARiERMREQnEIiYi\nIhKIRUxERCQQi5iIiEggFjEREZFALGIiIiKBWMREREQCsYiJiIgEYhETEREJxCImIiISiEVMREQk\nEIuYiIhIIBYxERGRQCxiIiIigcqKDkCkSp48eYINYWFI/OMPpKWkoLyJCcybNoWHpyeqVKkiOh4R\naSCZJEmS6BBEosXFxWFpUBAOREWhFwCrrCwYA0gFcM7AALslCV2cnTF2yhRYWVkJTktEmoRFTFpv\nVUgIZk2ciEmZmfCQJFR4z2teAAiTyfCdgQH8Fy3CcG9vZcckIg3FIiattiokBAsmTsShjAzUK8Lr\nbwBwNDTEJJYxEckJi5i0VlxcHLrb2ODkWyX8AsBgAIcBVAEwD0C/N56/AaCDoSEijh9H69atlReY\niDQSV02T1loaFIRJmZnvjIR9AOgDeApgEwBvAFffeL4eAL/MTCwNClJOUCLSaBwRk1Z68uQJGpiZ\n4VZW1r++E84AUAHAFQB1//eYB4AaeD0y/ttzAHX19ZGYlMTV1ERUKhwRk1baEBYGV+CdhVmJAMrh\n/0sYAJoBuPzW6yoCcJXJsCEsTGEZiUg7sIhJKyX+8QfaZGW983gagI/eeuwjvL6M6W1WmZlIjI9X\nQDoi0iYsYtJKaSkpMH7P4+UBvHrrsRTgva81BpD64oW8oxGRlmERk1Yqb2Ly3lGuOYA8ADffeOx3\nAI3f89pUAMYV3nfVMRFR0bGISSuZN22Kc/r67zxuCKAXgJl4vXDrFIAIAN+85xhxBgYwt7RUZEwi\n0gJcNU1aqbBV08C/ryOuDGABgL5vvYarpolIXjgiJq1UtWpVdHF2xnqZ7J3nKgDYjdcLt+7g3RIG\ngPUyGbq6uLCEiajUOCImrVXYzlofcgPAl/r62H/yJHfWIqJS44iYtJaVlRX8Fy2Co6EhbhTxPTcA\n2OrqIrtcOejq6ioyHhFpCd6PmLTa3zdu+GL8ePhlZ2MI3t3kA3j9nfA6mQyL/nf3pY8rVYKDgwMi\nIyPRsmVLZUYmIg3DqWnSenl5eahXrx7q16iB8xcuwFUmg1Vm5j/3I44zMMCO3FyY1ayJsB07/pmO\n3rNnD0aMGIF9+/bh888/F/ozEJH64oiYtN7atWtRp04dRMfEIDk5GRvCwnApPh6pL17AuEIFNLa0\nxHgnJ3Ts2BHm5ub/vK9nz54oV64cunXrhl27duHLL78U+FMQkbriiJi0WlpaGszNzbFv374PLrzq\n3bs3OnfuDB8fn389Hh0djQEDBmD79u2wsbFRYFoi0kRcrEVabcmSJbCxsSnS6mdvb2+EhITg7c+u\nDg4O2LZtG/r06YPDhw8rKioRaSiOiElrPX78GBYWFjh//jw+++yzD75ekiQ0bNgQa9asee809KlT\np9CrVy+EhYXBxcVFEZGJSANxRExay9/fHx4eHkUqYQCQyWTw8vJCSEjIe5//8ssvERERAU9PT+zZ\ns0eeUYlIg3FETFopISEBX375Ja5du4ZKlSoV+X3Pnz9HnTp1cP369UJ31frtt9/QpUsXLF++HG5u\nbvKKTEQaiiNi0kpTpkyBr69vsUoYACpWrAhXV1esW7eu0Ne0atUKhw4dwpgxY7B58+bSRiUiDccR\nMWmd06dPo1+/fkhISICBgUGx33/u3Dn069cP169fR5kyhX+WvXz5MhwcHBAYGAhPT8/SRCYiDcYR\nMWkVSZLg6+uLwMDAEpUw8HprzI8//hjR0dH/+brGjRsjNjYWM2fORGhoaInORUSaj0VMWmX37t3I\nyMjA119/XeJjyGSyfy5l+pAGDRrg2LFjCAoKwvLly0t8TiLSXJyaJq2Rm5uLxo0bY/ny5XB0dCzV\nsdLT02FqaoqLFy/C1NT0g6+/e/cuOnfuDG9vb0ycOLFU5yYizcIRMWmN1atXw8zMDA4ODqU+lpGR\nEfr374/Vq1cX6fVmZmY4fvw4Vq1ahblz55b6/ESkOTgiJq2QmpqK+vXrIyoqCi1atJDLMS9fvgw7\nOzskJSWhXLlyRXrPw4cPYWtrCzc3N8yePRsymUwuWYhIfXFETFph4cKFsLe3l1sJA68XY5mbmxdr\n847q1avj2LFj2L17N6ZMmfLOdplEpH04IiaN9/DhQzRp0gQXLlyAmZmZXI+9detWrFq1CrGxscV6\n37Nnz2Bvbw9ra2ssWbKEI2MiLcYiJo03YsQIfPTRR1i4cKHcj52TkwNTU1McO3YMDRs2LNZ7X7x4\nAScnJ7Ru3RrLly//z2uSiUhzsYhJo129ehUdO3ZEYmIiKlSooJBzTJ06FRkZGfjhhx+K/d5Xr17B\n2dkZFhYWCA0NZRkTaSEWMWm0Hj16oGPHjpgwYYLCznHnzh20atUKf/31FwwNDYv9/rS0NHTt2hVm\nZmZYu3YtdHR0FJCSiFQVP36Txjpx4gR+//13jBw5UqHnqV27Ntq1a4etW7eW6P3ly5dHZGQkHjx4\ngAEDBiA3N1fOCYlIlbGISSP9vZXl3Llzoa+vr/DzFXWnrcIYGhoiIiICKSkpcHd3R05OjhzTEZEq\nYxGTRgoPD0dubi769eunlPM5OTnh6dOnOH/+fImPoa+vj927dyM/Px+9e/dGdna2HBMSkapiEZPG\nycnJwZQpU7Bw4UKlLX7S0dHBiBEjSjUqBgA9PT3s2LEDenp66NGjBzIzM+WUkIhUFRdrkcZZvnw5\nIiMjERUVpdTzPnnyBA0aNMCtW7dKvUI7Ly8PHh4eePToEfbt2wcjIyM5pSQiVcMiJo2SkpICc3Nz\nHD58GE2bNlX6+fv164e2bdti7NixpT5Wfn4+hg4dips3b+LAgQMwNjaWQ0IiUjWcmiaN8t1338HF\nxUVICQOvF22tXLlSLltX6ujoYM2aNWjUqBEcHR2RkpIih4REpGo4IiaNce/ePTRr1gyXLl1CrVq1\nhGSQJAmWlpb48ccfYWNjI7djjhkzBmfOnMGhQ4dQsWJFuRyXiFQDR8SkMWbNmoXhw4cLK2EAkMlk\n8PLyKvWirbePuWzZMlhbW8PW1hbJyclyOzYRiccRMWmE+Ph42NnZITExESYmJkKzpKSkoHbt2rh6\n9SqqVasmt+NKkoTp06dj7969iImJwSeffCK3YxOROBwRk0aYPHkypk6dKryEAcDExARubm5Ys2aN\nXI8rk8kQGBiIPn36wMbGBg8ePJDr8YlIDI6ISe3FxsZi2LBhuHr1KnR1dUXHAQBcvHgRPXv2xK1b\ntxSyd/T8+fOxZs0axMbGCp2KJ6LS44iY1FpBQQH8/Pwwb948lSlhAGjRogWqVauGyMhIhRx/8uTJ\n8PHxgbW1NW7fvq2QcxCRcrCISa1t27YNZcqUgZubm+go7yjt/tMfMn78eEyYMAE2Nja4ceOGws5D\nRIrFqWlSW9nZ2WjYsCHWrVsnt0uF5CkzMxO1atVCXFwcPvvsM4WdZ/Xq1fD398eRI0fQsGFDhZ2H\niBSDI2JSW8HBwWjSpIlKljAAGBgYYODAgQgNDVXoeYYNG4a5c+eic+fO+PPPPxV6LiKSP46ISS29\nePECDRo0wNGjR9G4cWPRcQqVmJiIDh06ICkpCXp6ego919atWzFu3DhERUWhRYsWCj0XEckPR8Sk\nlubPn48ePXqodAkDgLm5OSwtLbFz506Fn8vd3R0rVqyAk5MT4uLiFH4+IpIPjohJ7SQlJaFFixaI\nj4/Hp59+KjrOB+3cuRM//PADTp48qZTzRUREYMiQIdizZw+++OILpZyTiEqORUxqx8PDA6amppgz\nZ47oKEWSm5uL2rVr4+DBg7C0tFTKOQ8ePIiBAwciPDwcHTt2VMo5iahkWMSkVi5dugQnJyckJibi\no48+Eh2nyGbNmoXk5GSsWLFCaeeMiYmBu7s7tm7dCltbW6Wdl4iKh0VMasXR0RHdu3fHyJEjRUcp\nlnv37qFp06ZISkpC+fLllXbeEydOoHfv3tiwYQOcnJyUdl4iKjou1iK1ER0djdu3b2P48OGioxRb\nzZo1YW1tjc2bNyv1vB07dsTevXsxcOBAREREKPXcRFQ0LGJSCwUFBZg0aRLmzZuHcuXKiY5TIn/v\ntKXsSah27drhwIEDGDp0qFJWbxNR8bCISS38/PPP0NPTw1dffSU6SonZ2dkhLS0NZ86cUfq5rays\ncOjQIYwaNQpbtmxR+vmJqHBlRQcg+pCsrCxMmzYNmzZtgkwmEx2nxMqUKQMvLy+sXLkS7dq1U/r5\nmzdvjsOHD8PBwQE5OTnw8PBQegYieheLmFTejz/+iBYtWqBDhw6io5Sap6cn6tWrh2fPnqFSpUpK\nP3+TJk0QGxsLOzs75ObmYujQoUrPQET/xlXTpNKeP3+OBg0a4OTJkxpzQ4OBAweiWbNmmDBhgrAM\n169fh52dHfz8/NRuBTqRpmERk0qbOHEi0tLSsHLlStFR5ObXX3/FwIEDkZCQgDJlxC3TuH37Nmxt\nbTF69GiMHz9eWA4ibcepaVJZd+7cwbp163D58mXRUeSqbdu2MDIyQkxMDOzt7YXl+Oyzz3Ds2DHY\n2toiOzsbkydPFpaFSJtx1TSprOnTp2P06NGoVq2a6ChyJZPJ/rmUSTRTU1McP34cYWFhCAgIUPql\nVUTEqWlSURcuXECXLl2QmJgIY2Nj0XHkLjU1FWZmZoiPj0eNGjVEx8Hjx49ha2uLHj16IDAwUK1X\npxOpG46ISeVIkgRfX1/MmjVLI0sYAIyNjeHu7o7Vq1eLjgIA+OSTT3D06FEcOHAAvr6+HBkTKRFH\nxKRyDh48iHHjxiE+Pl5td9Eqivj4eDg5OeHOnTsq83M+f/4cjo6OaNeuHZYuXcqRMZEScERMKiU/\nPx9+fn6YP3++ypSTolhaWuKzzz5TqT2gK1asiCNHjiAuLg5eXl4oKCgQHYlI47GISaVs3LgRH330\nEXr06CE6ilKoyqKtN5mYmCA6OhpXr17FkCFDkJ+fLzoSkUbj1DSpjMzMTJibm2P79u1CtoAUITs7\nG7Vq1cLp06dRv3590XH+JT09Hd27d0e1atWwfv16lC3Lqx2JFIEjYlIZS5cuxeeff641JQwAenp6\n8PT0VMkNS4yMjLB//348e/YM/fv3R25uruhIRBqJI2JSCcnJyWjYsCF++eUXmJubi46jVLdu3UKb\nNm3w119/wcDAQHScd2RlZcHNzQ06OjrYtm0b9PT0REci0igcEZNKCAwMhLu7u9aVMADUqVMHVlZW\n2L59u+go76Wvr4+dO3dCR0cHvXr1QlZWluhIRBqFI2IS7ubNm/j8889x5coVVK1aVXQcIfbt24d5\n8+YJuVdxUeXm5mLgwIFITk7G3r17YWhoKDoSkUbgiJiEmzZtGsaNG6e1JQwAXbp0wYMHD3Dx4kXR\nUQpVrlw5bNq0CdWrV0eXLl2QlpYmOhKRRmARk1Dnzp3DyZMntf7uPzo6Ohg+fLjKXcr0Nh0dHaxb\ntw5169aFk5MTXr16JToSkdrj1DQJI0kSOnXqhAEDBvAG9QAePXqERo0a4c6dOzAxMREd5z8VFBRg\n1KhR+O2333Dw4EFUqFBBdCQitcURMQlz4MABPH36FIMGDRIdRSVUq1YN9vb22LRpk+goH1SmTBms\nWLECX3zxBWxtbfHs2TPRkYjUFouYhMjLy8OkSZOwYMECbhTxhr932lKHiSqZTIYlS5bAwcEBnTp1\nwpMnT0RHIlJLLGISIiwsDFWqVEGXLl1ER1EpNjY2yM/Px6lTp0RHKRKZTIagoCC4urrCxsYGDx8+\nFB2JSO3wO2JSuvT0dJibm2P37t1o06aN6DgqZ+nSpTh79ix+/vln0VGKZe7cuVi/fj1iY2NRs2ZN\n0XGI1AaLmJQuMDAQf/75J7Zu3So6ikp68eIF6tSpg4SEBLW7pGvRokUICQlBbGwszMzMRMchUgss\nYlKqJ0+ewMLCAmfPnkXdunVFx1FZgwcPhrm5OSZPniw6SrEtW7YMS5YsQUxMDP83JioCFjEp1ahR\no1C2bFn88MMPoqOotLi4OPTp0wc3btyAjo6O6DjFFhoaisDAQBw5cgQNGjQQHYdIpXG5KinN9evX\nsW3bNly9elV0FJVnZWWFSpUq4dChQ3BxcREdp9hGjBgBXV1ddO7cGYcPH4aFhYXoSEQqi6umSWmm\nTp2KCRMmoHLlyqKjqIW/L2VSV56enliwYAFsbW3xxx9/iI5DpLI4NU1KcebMGbi5uSExMVElb/Wn\nitLT02FqaooLFy6o9cKn7du3Y8yYMYiMjETLli1FxyFSORwRk8JJkgRfX1/MmTOHJVwMRkZGGDBg\nAFatWiU6Sqn06dMHK1euhLOzM86ePSs6DpHKYRGTwu3btw8pKSn45ptvREdRO15eXlizZg1ycnJE\nRymVnj17Yu3atejWrZvabFZCpCwsYlKoN7eyVMfVv6I1atQIjRo1wu7du0VHKbUuXbpg06ZNcHV1\nxdGjR0XHIVIZLGJSqDVr1qBGjRpwcnISHUVtqfuirTc5ODhgx44d6Nu3L6Kjo0XHIVIJXKxFCpOW\nlgZzc3NERESgVatWouOorZycHJiZmSEmJkZjLgM6ffo0XF1dsW7dOu43TlqPI2JSmMWLF6NTp04s\n4VLS1dXFkCFDsHLlStFR5KZ9+/aIiIjA4MGDNWLanag0OCImhXj06BEaN26M8+fP47PPPhMdR+0l\nJSWhRYsWSEpKgpGRkeg4cnPhwgW4uLhg2bJl6NOnj+g4REJwREwK4e/vj0GDBrGE5cTU1BTt27fH\nli1bREeRq5YtWyI6Ohpjx47Fpk2bRMchEoIjYpK7a9euoUOHDkhISEDFihVFx9EYUVFRmD59Os6f\nPw+ZTCY6jlxduXIF9vb2mDNnDgYPHiw6DpFScURMcjdlyhT4+fmxhOXM0dERL168wPnz50VHkTsL\nCwscPXoUs2fP1qjvwomKgjd9ILk6deoULly4oHFTqKqgTJkyGDFiBEJCQmBlZSU6jtyZm5vj6NGj\nsLW1RU5ODsaMGSM6EpFScGqa5EaSJHzxxRfw8fHhLloK8vTpU5ibm+PWrVuoUKGC6DgKcffuXXTu\n3BleXl7w9fUVHYdI4Tg1TXKza9cuZGZm4uuvvxYdRWNVqVIFLi4uWL9+vegoCmNmZobjx4/jp59+\nQmBgoOg4RArHETHJRW5uLiwsLBAcHAx7e3vRcTTaqVOnMHToUFy9elXjFm296eHDh7Czs8NXX30F\nf39/jf5ZSbtxRExysWrVKtSpU4clrATt27dH2bJlNX6/5urVq+Po0aPYs2cPJk+eDI4ZSFNxREyl\n9urVK5ibm+PgwYNo3ry56DhaYcWKFTh27Bh27NghOorCPXv2DA4ODujQoQO+//57joxJ47CIqdRm\nzJiBpKQkjf7eUtW8evUKZmZmuHLlCqpXry46jsK9fPkSjo6OaNWqFX788UeUKcPJPNIcLGIqlQcP\nHsDS0hIXL16Eqamp6DhaZcSIEahZsyZmzJghOopSvHr1Ci4uLmjYsCFCQ0N5W03SGCxiKpVhw4ah\nYsWKWLBggegoWufSpUvo1q0bbt++jbJltWNLgLS0NHTr1g21atXC2rVrtebnJs3G+R0qscuXL2Pv\n3r2YMmWK6ChaqXnz5qhZsyYOHDggOorSlC9fHgcOHMCjR48wYMAA5Obmio5EVGosYiqxyZMnY8qU\nKfj4449FR9Fa3t7eCAkJER1DqQwNDbFv3z6kpqaib9++yMnJER2JqFQ4NU0lcuzYMXh6euLatWvQ\n09MTHUdrZWVloVatWjhz5gzq1q0rOo5SZWdno2/fvsjPz8eOHTugr68vOhJRiXBETMUmSRL8/Pww\nb948lrBg+vr68PDwQGhoqOgoSqenp4cdO3bAwMAAPXr0QGZmpuhIRCXCIqZi27FjBwoKCtC3b1/R\nUQivV0+HhYUhKytLdBSlK1euHH7++WdUqVIFXbp0QXp6uuhIRMXGIqZiycnJwZQpU7Bw4UJey6ki\n6tevj+bNmyM8PFx0FCHKli2L9evXw8zMDM7OzkhNTRUdiahY+C8pFcvKlSvRsGFDdOrUSXQUeoM2\nLtp6k46ODtasWQMLCws4ODjg5cuXoiMRFRkXa1GRpaSkwNzcHDExMWjSpInoOPSGvLw81K5dG5GR\nkWjatKnoOMJIkoSxY8fil19+QXR0NCpWrCg6EtEHcURMRbZgwQJ07dqVJayCypYti2HDhmHlypWi\nowglk8mwdOlSdOrUCZ07d8bTp09FRyL6II6IqUju3buHZs2a4ffff0fNmjVFx6H3uH//PiwtLXH3\n7l0YGxuLjiOUJEmYMWMG9uzZgyNHjqBatWqiIxEViiNiKpKZM2fCy8uLJazCatSogU6dOmHz5s2i\nowgnk8kQGBiIvn37wsbGBvfv3xcdiahQHBHTB8XHx8POzg6JiYkwMTERHYf+w5EjRzBhwgRcunSJ\ntwv8nwULFmD16tWIjY3ljUlIJXFETB80adIkTJ8+nSWsBjp37ozMzEz8+uuvoqOojEmTJmHkyJGw\ntrbG7du3RcchegdvXUL/KSYmBomJidizZ4/oKFQEZcqUgZeXF0JCQvDFF1+IjqMyxo8fDz09PVhb\nWyMmJgb169cXHYnoH5yapkIVFBTAysoKkyZNQp8+fUTHoSJ69uwZ6tatixs3bqBy5cqi46iUn376\nCbNnz8bhw4fRqFEj0XGIAHBETP9h69at0NHRgZubm+goVAyVKlVCjx49sHz5chgbGSHxjz+QlpKC\n8iYmMG/aFB6enqhSpYromEIMHToUurq6sLW1RXR0NC/FI5XAETG9V3Z2Nho2bIiwsDBYW1uLjkPF\nEBcXh1m+vjh24gTc9fTQJisLxgBSAZwzMMBuSUIXZ2eMnTIFVlZWouMKsXXrVowbNw5RUVFo0aKF\n6Dik5VjE9F5LlizBsWPHsG/fPtFRqBhWhYRg1sSJ8MvMxCBJQoX3vOYFgDCZDN8ZGMB/0SIM9/ZW\ndkyVsHPnTvj4+GD//v1a+4GEVAOLmN7x4sULNGjQAMeOHYOFhYXoOFREq0JCsGDiRBzKyEC9/z22\nAkAYgHgA/QGsfeP1NwA4GhpikhaXcUREBIYMGYI9e/ZwcRsJwyKmd/j5+eHly5dYtWqV6ChURHFx\ncehuY4OTb5QwAOzB62sUDwHIxL+LGHhdxh0MDRFx/Dhat26tpLSq5eDBgxg4cCDCw8PRsWNH0XFI\nC7GI6V/u3r2Lli1bIj4+Hp9++qnoOFREA3r1Qus9ezCukL/OMwDcx7tFDADfy2S44OqKjTt3KjKi\nSouJiYG7uzu2bt0KW1tb0XFIy7CI6V8GDhyI2rVrIyAgQHQUKqInT56ggZkZbmVlvfc7YeC/i/g5\ngLr6+khMStLa1dQAcOLECfTu3RsbNmyAk5OT6DikRbizFv3j4sWLiI6Ohq+vr+goVAwbwsLgChRa\nwh9SEYCrTIYNYWHyC6WGOnbsiL1792LgwIGIiIgQHYe0CIuY/jFp0iTMnDlT6+/co24S//gDbbKy\nSnUMq8xMJMbHyymR+mrXrh0iIyMxbNgw7NTiqXpSLm7oQQCA6Oho3LlzB8OGDRMdhYopLSUFpf3o\nZAwg9cULecRRe61bt8bBgwfh7OyM7Oxs9O/fX3Qk0nAsYkJ+fj78/Pwwf/58lCtXTnQcKqbyJiZI\nLeS5fAC5//s9D0A2Xv+l13nrdakAjCuUdHJb8zRv3hyHDx+Go6MjcnNz4eHhIToSaTBOTRM2b94M\nQ0NDuLq6io5CxZSZmYlXOTk4WcgtDwMBGAJYAGDz//489z2vO2dgAHNLS4XlVEdNmjRBTEwMpk+f\njtWrV4uOQxqMRazlMjMzMX36dCxcuJD3r1Uj169fx4QJE2Bqaoqnz55hf9myeN/E8iwABXg9Iv77\n18y3XvMcwLbMTMh0dJCTk6PY4GqmYcOGOHr0KAIDA7FixQrRcUhDsYi13PLly9G6dWu0b99edBT6\ngLy8POzZswcODg5o3749ypYti7NnzyImJgbdunbF+hJ+kFovk8HG2hrR0dGoX78+Vq5ciezsbDmn\nV1/16tXD8ePHsXjxYixZskR0HNJEEmmt5ORkqXLlytK1a9dER6H/8ODBAykgIECqWbOm1K5dO2nj\nxo1SZmbmv15z7tw5qZqhoXQdkKRi/LoOSNUMDaW4uDhJkiTp119/lZydnaVatWpJK1aseOc82iwp\nKUmqV6+eNG/ePNFRSMNwRKzF5s6dCzc3NzRo0EB0FHqLJEk4fvw4+vbtCwsLC9y7dw8RERH45Zdf\nMGDAAOjr6//r9VZWVvBftAiOhoa4UcRz/L3XtP+iRf9sb9m2bVtERkYiPDwckZGRqFevHpYvX46s\nUl4epQlq1aqF48ePY8OGDfD394fEvZBIXkR/EiAxbt26JVWqVEl69OiR6Cj0hpcvX0rLly+XLCws\npEaNGknLli2TXr58WeT3hwYHS9UMDaUlMpn0vJBR8DNAWiyTSdUMDaXQ4OD/PN758+el7t27S59+\n+qn0ww8/SBkZGaX9EdXeo0ePpCZNmkhTpkyRCgoKRMchDcAtLrXU119/jQYNGmDmzLeX7pAIv//+\nO4KDg7HnjjQUAAAcLklEQVR9+3bY29vDx8cH1tbWJVpAd/78eSwNCsL+yEi4ymSwysz8537Ecf+7\nH3FXFxeMnTKlyDd6uHjxIgICAnD27Fn4+vpixIgRMDQ0LHY2TZGcnAx7e3t07twZixYt4kJHKhUW\nsRb67bff0K1bNyQmJqJ8+fKi42it7OxshIeHIzg4GHfv3sWIESMwdOhQVK9eXS7Hf/r0KTaEhSEx\nPh6pL17AuEIFmFtaYuCgQSXeU/r333/HnDlzcPr0aUyYMAHe3t4wMjKSS1518/z5czg6OqJt27ZY\nunQpypThN31UMixiLSNJEmxtbeHu7o7hw4eLjqOVbt++jdDQUKxduxbNmzeHt7c3unXrhrJl1Wd/\nnfj4eMyZMwcnTpzAt99+Cx8fH638UJeSkgJnZ2c0adIEK1euZBlTifD/NVrm4MGDePjwIQYPHiw6\nilbJz8/HgQMH0KVLF1hZWSEnJwenTp1CdHQ0XF1d1aqEAcDS0hLbt29HTEwMLly4gLp16yIoKAip\nqYXt8aWZTExMcOjQISQkJGDw4MHIz88XHYnUEEfEWiQ/Px/NmzfH3Llz0b17d9FxtMLTp0+xZs0a\nhIaGonLlyvDx8UHfvn017vvVK1euYO7cuTh8+DDGjh2L0aNH46OPPhIdS2nS09PRvXt3VKtWDevX\nr1e7D1YkFkfEWmTDhg2oUKECunXrJjqKRpMkCadPn8aAAQNQv359JCYmYvv27YiLi4Onp6fGlTAA\nWFhYYPPmzTh58iSuXbuGunXrIiAgACkpKaKjKYWRkRH279+P58+fo1+/fsjNzRUdidQIR8RaIiMj\nAw0aNEB4eDg+//xz0XE0UlpaGjZv3ozg4GBkZmbC29sbHh4eqFixouhoSpeYmIh58+bhwIEDGDly\nJMaNG4ePP/5YdCyFy87OhpubG2QyGbZv3w49PT3RkUgNcESsJZYuXYp27dqxhBXg8uXLGDVqFExN\nTXHo0CEsWrQI165dw/jx47WyhAHA3NwcYWFh+PXXX5GUlIR69eph5syZeP78uehoCqWnp4fw8HCU\nK1cOrq6uyMzMFB2J1ACLWAs8ffoUixcvxrx580RH0Rg5OTnYtm0brK2tYW9vj4oVK+L333/Hrl27\nYG9vz9Wz/1OvXj2sXbsW586dw8OHD1G/fn1MmzYNz549Ex1NYXR1dbF161aYmJige/fuyMjIEB2J\nVBynprXA2LFjIUkSli1bJjqK2ktKSsKqVauwZs0aNGzYED4+PujZsyfv41xEd+7cQVBQEMLDwzF8\n+HBMmDABlStXFh1LIfLz8zF48GDcvXsX+/fv18rLu6ho+LFdw924cQObN2/GjBkzREdRWwUFBYiO\njkbPnj3RvHlzvHr1CjExMTh69Cjc3NxYwsVQu3ZthIaG4uLFi3j58iUaNGgAPz8/PHnyRHQ0udPR\n0cG6detQv359ODo6as3CNSo+FrGGmzZtGr799tsS76SkzZ49e4bFixfD3Nwcfn5+cHFxQVJSEpYt\nWwYLCwvR8dSaqakpQkJCcOnSJWRkZKBRo0aYOHEiHj9+LDqaXJUpUwahoaFo3rw57O3t8eLF++4a\nTdqORazBzp49i9OnT2PcuHGio6gNSZJw7tw5DBo0CHXr1sWlS5ewceNGXLx4EcOHD+f0opzVqlUL\nP/74I/744w/k5OSgUaNG+Pbbb/Ho0SPR0eSmTJky+PHHH/Hll1/C1tYWycnJoiORimERayhJkuDn\n5wd/f3+NvG5V3jIyMrBmzRpYWVnB3d0dFhYWuH79OjZu3Ih27dpxU38Fq1GjBpYtW4Y///wTkiSh\ncePGGDduHB48eCA6mlzIZDIsXrwYjo6O6Ny5s0ZOxVPJsYg11P79+/Hs2TN4eHiIjqLSEhISMH78\neNSqVQt79uxBQEAArl+/Dj8/P07nC/Dpp5/i+++/x+XLl6GjowNLS0uMHj0a9+7dEx2t1GQyGebN\nm4devXrBxsYGDx8+FB2JVASLWAPl5eVh0qRJWLBgAbfae4+8vDzs2rULdnZ26NixI/T19fHbb78h\nIiICLi4u0NHRER1R61WrVg2LFy/GlStXoK+vj2bNmmHkyJH466+/REcrFZlMhtmzZ2PAgAGwtrbW\niA8YVHosYg20bt06fPLJJ3BxcREdRaU8ePAA/v7+MDMzw5IlSzB48GAkJSUhKCgItWvXFh2P3uOT\nTz7BwoULce3aNRgbG6N58+bw8vLC3bt3RUcrlalTp2LEiBGwtrbGnTt3RMchwVjEGiY9PR2zZ8/G\nd999x+818fq78tjYWPTu3RuNGzfGo0ePEBUVhVOnTqF///7cglBNVKlSBfPnz0dCQgIqVqyIli1b\nYvjw4bh9+7boaCU2YcIEjBs3DjY2Nrh586boOCQQi1jDLFmyBB07doSVlZXoKEK9fPnyn8uMxowZ\ng86dO+Pu3bsICQlB06ZNRcejEqpcuTLmzZuHxMREVK1aFa1bt8aQIUNw69Yt0dFKZPTo0Zg6dSps\nbGyQkJAgOg4Jwp21NMjjx49hYWGBuLg41KlTR3QcIS5cuICQkBCEh4fDyckJ3t7e6NChA2cHNNSL\nFy/www8/YMWKFejWrRumTZuGevXqiY5VbOvWrcP06dMRHR2Nxo0bi45DSsYRsQYJCAjAwIEDta6E\ns7KysGHDBrRt2xY9e/ZE7dq1cfXqVWzZsgUdO3ZkCWuwChUqwN/fHzdu3EDt2rXRrl07eHh4IDEx\nUXS0YvH09MR3330HOzs7/P7776LjkJJxRKwhEhIS0L59eyQkJKBSpUqi4yjFzZs3sXLlSoSFhaFV\nq1bw8fGBi4sLV4prsZSUFCxfvhxLly6Fo6Mjpk+fjoYNG4qOVWQ7duzA6NGjceDAAbRq1Up0HFIS\njog1xNSpU+Hr66vxJZyfn4+IiAg4Ozujbdu2AIBff/0VBw8eRPfu3VnCWs7ExATTp0/HzZs3YWFh\ngY4dO6J///64cuWK6GhF4ubmhtDQULi4uODMmTOi45CScESsAX755Re4u7sjISEBBgYGouMoxOPH\nj7FmzRqEhoaievXq8Pb2Rp8+fTT25yX5SE1NxYoVK/D999/DxsYGM2bMQJMmTUTH+qDIyEgMGjQI\nu3btwpdffik6DikYR8RqTpIk+Pr6Ys6cORpXSpIk4eTJk+jXrx8aNmyIW7duYdeuXThz5gw8PDw0\n7ucl+TM2NsbkyZNx8+ZNtG7dGnZ2dnBzc0N8fLzoaP/JxcUFmzdvhqurK44ePSo6DikYi1jN7dmz\nB2lpaRgwYIDoKHLz6tUrBAcHo2nTphg6dCjatm2LW7du4aeffuL3ZlQi5cuXh6+vL27evIm2bdvC\nwcEBX331lUovjLK3t8eOHTvQt29fREdHi45DCsSpaTWWm5uLJk2aYNmyZXB0dBQdp9Ti4+MRHByM\nrVu3wtbWFt7e3ujcuTNXPZPcZWRkYNWqVfjuu+/Qpk0bzJw5Ey1bthQd671Onz4NV1dXrFu3Dl26\ndBEdhxSAI2I1tmbNGpiamsLBwUF0lBLLzs7Gli1b0KFDBzg5OaFatWr4888/ER4eDltbW5YwKYSh\noSHGjRuHmzdvonPnzujWrRu6d++O8+fPi472jvbt2yMiIgKDBw/G7t27RcchBeCIWE2lpqbC3Nwc\nkZGRaNGiheg4xXb37l2EhoZizZo1sLS0hLe3N7p3745y5cqJjkZaKCsrCz/99BPmz5+PZs2aYdas\nWWjTpo3oWP9y4cIFuLi4YNmyZejTp4/oOCRHHBGrqcWLF8POzk6tSrigoABRUVHo1q0bWrZsiYyM\nDBw/fhxHjhzBV199xRImYfT19TFq1CjcvHkTXbt2Re/eveHs7KxSlxC1bNkS0dHRGDt2LDZt2iQ6\nDskRR8Rq6OHDh2jSpAkuXLgAMzMz0XE+KDk5GevWrcPKlSthYmKCkSNHwt3dHUZGRqKjEb1XdnY2\nwsLCEBQUBHNzc8yaNQvt27cXHQsAcOXKFdjb22POnDkYPHiw6DgkByxiNeTl5QVjY2MsXLhQdJRC\nSZKEs2fPIjg4GPv27UPPnj3h7e2NNm3a8HtfUhs5OTnYsGED5s6di7p162LWrFno0KGD6FhITEyE\nnZ0dpk6dCi8vL9FxqJRYxGrm6tWrsLa2RkJCAipUqCA6zjvS09Px888/Izg4GKmpqfDy8oKnp6fG\n7/hFmi03NxcbN27E3LlzYWZmhlmzZsHa2lpoplu3bsHW1hbjxo3D2LFjhWah0mERq5mePXuiQ4cO\nmDBhgugo/3L16lWEhIRg8+bN+PLLL+Hj4wN7e3uUKcNlCKQ5cnNz8fPPPyMwMBCffvopZs2ahU6d\nOgmb5bl79y5sbW0xfPhw+Pn5CclApcciViMnT57EN998g2vXrkFfX190HOTm5mLv3r0IDg7GlStX\nMHToUAwfPhympqaioxEpVF5eHrZs2YLAwEBUrVoVs2bNEna53f3799G5c2cMGDAAM2bMUPr5qfRY\nxGpCkiS0a9cOo0ePxtdffy00y71797B69WqsXr0a9evXh7e3N3r16gVdXV2huYiULT8/H1u3bsWc\nOXNQqVIlzJw5Ew4ODkov5EePHsHW1ha9evVCQEAA12GoGc4bqomdO3ciJycH/fr1E3L+goICHDly\nBL169ULTpk2RnJyM6OhoHD9+HO7u7ixh0ko6Ojr4+uuvcfnyZYwaNQrjx49Hu3btEBUVBWWOcapV\nq4Zjx45h3759mDRpklLPTaXHEbEayMnJQePGjbFy5UrY2toq9dwvXrxAWFgYQkJCoK+vDx8fH3z9\n9dcwNjZWag4idVBQUIDw8HAEBATAyMgIM2fOhIuLi9JGqM+ePYODgwM6dOiA77//niNjNcEiVgM/\n/vgjDhw4gKioKKWd8/z58wgODsauXbvQpUsX+Pj44IsvvuBfbKIiKCgowK5duxAQEABdXV3MnDkT\n3bp1U8rfn5cvX8LJyQktWrTAihUruGBSDbCIVdyrV69gbm6O6OhoNG3aVKHnyszMxLZt2xAcHIwn\nT57Ay8sLgwcPRtWqVRV6XiJNVVBQgL179/7zve3MmTPRo0cPhRfyq1ev0KVLF5ibm2PVqlXQ0dFR\n6PmodFjEKm769Om4f/8+1q1bp7BzXL9+HStXrsT69evx+eefw9vbG87OzvzLSyQnkiRh3759CAgI\nQH5+PmbMmAFXV1eFjlbT0tLQvXt31KhRA+vWrUPZsmUVdi4qHRaxCrt//z6aNm2KS5cuoVatWnI9\ndl5eHvbv34/g4GBcunQJnp6eGDFiBOrUqSPX8xDR/5MkCQcOHIC/vz+ys7MxY8YMfPXVVwor5IyM\nDPTs2RMVKlTApk2buJ+7imIRq7ChQ4eiSpUqCAoKktsxHz58iJ9++gmrVq1CrVq14OPjg969e6vE\ndclE2kKSJERFRcHf3x9paWmYMWMG3NzcFDILlZWVhd69e0NXVxdbt27lFQ4qiEWsov7880/Y2toi\nMTERJiYmpTqWJEk4ceIEgoODER0djT59+sDb2xvNmzeXU1oiKglJknDo0CH4+/sjJSUF06dPR9++\nfeVeyDk5Oejbty9yc3MRHh7OD94qhkWsorp27Qo7OzuMGzeuxMdISUnBxo0bERISAkmS4O3tjYED\nB5a62IlIviRJwpEjR+Dv74/k5GRMnz4d7u7ucv1eNzc3FwMGDMDLly+xe/duGBoayu3YVDosYhV0\n9OhRDBkyBFevXoWenl6x33/p0iWEhIRg+/btsLe3h4+PD6ytrXnpEZGKkyQJsbGx8Pf3x6NHjzB9\n+nT0799fboWcl5cHT09P3L9/HxEREbwVqYpgEQvy5MkTbAgLQ+IffyAtJQXlTUxg3rQpvvHwQNeu\nXTFhwgS4u7sX+XhZWVkIDw9HcHAwkpKSMGLECAwdOhTVq1dX4E9BRIpy7Ngx+Pv746+//sK0adMw\nYMAAuSy2ys/Px7Bhw3D9+nUcOHAAH330kRzSUmmwiJUsLi4OS4OCcCAqCr0AWGVlwRhAKoBzBgbY\nmZeH8kZG2HXwID7//PMPHu/27dsIDQ3F2rVr0bx5c/j4+KBr1668VIFIQ5w4cQL+/v64ffs2pk2b\nhoEDB5a6kAsKCjBy5EhcvHgRBw8exMcffyyntFQiEilNaHCwVM3QUPpeJpOeA5L0nl/PAWmxTCZV\nMzSUQoOD33ucvLw8af/+/ZKLi4tUqVIl6dtvv5USExOV/NMQkTKdPHlSsrOzk2rXri2FhoZK2dnZ\npTpeQUGBNGbMGKlVq1bSs2fP5JSSSoJFrCShwcFSHUND6XohBfz2r+uAVOetMn78+LEUFBQkmZmZ\nSVZWVtLatWul9PR0gT8VESnb6dOnJUdHR8nU1FQKCQmRsrKySnysgoICydfXV2ratKn05MkTOaak\n4uDUtBLExcWhu40NTmZkoN4bj38D4AiADACVAQwGMO2N528A6GBoiMBlyxAbG4vIyEi4urrC29sb\nVlZWyvsBiEjlnDlzBgEBAfjzzz8xefJkDB48uESXJUmShJkzZ2LXrl2IiYlBtWrVFJCW/guLWAkG\n9OqF1nv2YNxb/6mvAKgDQB9AIoCOANYDcHzjNYsAfGdkhClz5sDDwwMVK1ZUUmoiUgdxcXEICAjA\nxYsXMWnSJAwbNqxEhTxnzhxs3rwZMTExqFGjhgKSUmFYxAr25MkTNDAzw62sLFT4j9clALADsBdA\nyzcefw6grr4+EpOSUKVKFUVGJSI19ttvvyEgIADnz5+Hn58fhg8fDgMDg2Id47vvvsOqVasQGxsL\nU1NTBSWlt/H+WAq2ISwMrkChJTwSgBGAJng9Ld3yrecrAnCVybAhLExhGYlI/bVq1Qp79+7F/v37\ncezYMdStWxdLlixBRkZGkY/h5+eHUaNGwdraGrdu3VJgWnqTzuzZs2eLDqHJwkJC0PriRbQu5Pku\nAKYCsAbgBaATgLcnhR7k5WFvair0jY1x9+5dPHjwAMnJyXj16hUyMzNRUFAAHR0d3i2JiFC9enW4\nu7vDzs4OmzdvxsSJEwEAzZo1K9I+023btoWenh6GDh2Krl27olKlSoqOrPV4samCpaWkwPgDr5Hh\ndRG7AdgC4O1lWMYAHt67h507dyItLQ3p6elIS0t7589lypSBkZERypcvj/Lly//z57d/L+5zurq6\n3JWLSM00a9YM4eHhiI+Px5w5c7Bw4UJ8++23GDlyJMqXL/+f7/X29oauri46deqEw4cPo1GjRkpK\nrZ1YxApW3sQEqUV8bR6A9+3+mgqgQ6dOCN2wodD3SpKEnJyc95b027///efHjx8X+tybv0uSJLdS\nf/M5PT09FjyRgllaWmL79u24fPkyAgMDUbduXYwbNw6jRo2CsXHhw4QhQ4ZAV1cXtra2OHToECwt\nLZWYWruwiBXMvGlTnNu5E15ZWf96/CmAWABdARgAOAxgx/9+f1ucgQEaf+AvgUwmg56eHvT09OS+\nsvrNgi9KcScnJxfpw0BeXl6RC7w4hW9gYMCCJ3pL48aNsWXLFly9evWfQh47dixGjx5d6DaX33zz\nDXR1dWFvb4+oqCi0aNFCyam1A1dNK1hhq6aTAfQG8AcACUB9ADMAdHvr/Zq8ajo3Nxfp6elFKvf/\neu7tx3JycmBoaFiiEft/vd7Q0JAFTxojISEBc+fORVRUFEaPHo0xY8YUutXlrl274O3tjYiICLRp\n00bJSTUfi1gJCruOuCi+l8lwwdUVG3fuVEAyzZSXl4eMjIwSlfp/PZednQ0DAwO5T9EbGhqiTBle\nwEBiXL9+HXPnzsX+/fsxatQojB07FhUqvHudx/79+zF48GDs2bMHX3zxhYCkmotFrASF7az1IX/v\nrBVx/Dhaty5s3TUpS35+/j8FX9pSf/O5zMxMGBgYyH2hnZGREVfSU5HduHED8+bNw759++Dt7Y3x\n48e/8zXXoUOH8M0332DHjh2wtrb+13OF3VHOw9NT42bz5I1FrCSrQkKwYOJEHCpiGd8A4GhoiEmL\nFmG4t7ei45FABQUFyMjIkPsUfXp6OvT09OQ+RW9kZMS7e2mwW7duISgoCLt27YKXlxe+/fbbf13C\nFBsbi759+2LLli2ws7P74B3ldksSujg7Y+yUKdyatxAsYiVaFRKCWRMnwi8zE4Mk6b2bfDwHECaT\nYaGBAfxZwlQKkiQhMzNT7lP06enpKFeunNyn6I2MjORyv12Sjzt37iAoKAjh4eEYPnw4JkyYgMqV\nKwMATp48ia+++gruffpgx7p1mJSZCY9C/k17gdf/pn3Hf9MKxSJWsvPnz2NpUBD2R0bCVSaDVWbm\nP58e4/736bGriwvGTpnC6WhSSZIkISsrS+5T9Onp6dDR0VHYtfBUMklJSZg/fz62bduGIUOGYOLE\niahatSom+fpi46JFOAFwlq+UWMSCPH369PX3KfHxSH3xAsYVKsDc0hIDBw3i9ymklSRJQnZ2ttyn\n6NPS0gBALpfGvf2cNm1289dff2HBggXYsmULnJ2dcWTXLpzKzPynhHMA+OD1HeVeAKgLYB4ApzeO\nwXUv78ciJiKNl5OTo5Ap+vz8fLmU+9uP6evrq2zB379/H04dO2LQrVuY8MbjGXh9tzhPALUAHADQ\nD8CfAN68fQSvBHkXi5iIqIT+3uxG3lP0ubm5Cpmil8dmN0W9oxwANAMwG4DrG49p8t4IJcWlj0RE\nJaSrqwtdXd33XndbGnl5ecWahv/rr7+KfC38f62GL8qIfe/u3ehRyMKsNz0GcB1A47cef/OOchN8\nfeX6301dsYiJiFRM2bJlYWJiAhMTE7keNz8/v9DR+PsK/OHDh+88l3jpEqZmZ//nefIADAAwCID5\ne563yszEpfh4uf5s6oxFTESkJXR0dPDRRx8Vurd0UfTv1g3G+/cX+ryE1yWsB2B5Ia8xBpD64kWJ\nM2gaFjERERXZh+4oNwSv99KPBFDYvm6pAIzlPJ2vzrjBLRERFZl506Y4p6//3ue8AFwDsA/Af125\nHWdgAHPeVvEfXDVNRERFVtiq6SQAtQHo4/9HwjIAoXh9GdPfuGr6XRwRExFRkVWtWhVdnJ2x/q3L\noEwBFOD19cSp//v1Cv8uYQBYL5Ohq4sLS/gNHBETEVGx8I5y8sURMRERFYuVlRX8Fy2Co6EhbhTx\nPX/vNe2/aBFL+C0sYiIiKrbh3t6YtGgROhga4nuZDIVdjPQcwBKZDB14w4dCcWqaiIhKjHeUKz0W\nMRERlRrvKFdyLGIiIiKB+B0xERGRQCxiIiIigVjEREREArGIiYiIBGIRExERCcQiJiIiEohFTERE\nJBCLmIiISCAWMRERkUAsYiIiIoFYxERERAKxiImIiARiERMREQnEIiYiIhKIRUxERCQQi5iIiEgg\nFjEREZFALGIiIiKBWMREREQCsYiJiIgEYhETEREJxCImIiISiEVMREQkEIuYiIhIIBYxERGRQCxi\nIiIigVjEREREArGIiYiIBGIRExERCcQiJiIiEohFTEREJBCLmIiISCAWMRERkUAsYiIiIoFYxERE\nRAKxiImIiARiERMREQnEIiYiIhKIRUxERCQQi5iIiEggFjEREZFALGIiIiKBWMREREQCsYiJiIgE\nYhETEREJxCImIiISiEVMREQkEIuYiIhIIBYxERGRQCxiIiIigVjEREREAv0fjYccUo1/HCYAAAAA\nSUVORK5CYII=\n",
"text/plain": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Global Clustering Coefficient:\n",
" \n",
"## $C = \\frac{3 \\times \\mbox{number of triangles}}{\\mbox{number of connected triplets of vertices}} = \\frac{\\mbox{number of closed triplets}}{\\mbox{number of connected triplets of vertices}}$\n",
" "
]
},
{
"cell_type": "code",
"execution_count": 215,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xd4jefjBvD7CJnS1CxFokYQYkepkpAdMyqEqoiZxC6J\nPRIh1GhRiVDEqhUzJITEbhFFmxqJndpiRPZ8f3/4tj9FKuOc85xxf67LxXXG+97p98t9nuc87/PK\nJEmSQEREREKUER2AiIhIm7GIiYiIBGIRExERCcQiJiIiEohFTEREJBCLmIiISCAWMRERkUAsYiIi\nIoFYxERERAKxiImIiARiERMREQnEIiYiIhKIRUxERCQQi5iIiEggFjEREZFALGIiIiKBWMREREQC\nsYiJiIgEYhETEREJxCImIiISiEVMREQkEIuYiIhIIBYxERGRQCxiIiIigVjEREREArGIiYiIBGIR\nExERCcQiJiIiEohFTEREJBCLmIiISCAWMRERkUAsYiIiIoFYxERERAKxiImIiARiERMREQnEIiYi\nIhKIRUxERCQQi5iIiEggFjEREZFALGIiIiKBWMREREQCsYiJiIgEYhETEREJxCImIiISiEVMREQk\nEIuYiIhIIBYxERGRQCxiIiIigcqKDkCkSp48eYINYWFI/OMPpKWkoLyJCcybNoWHpyeqVKkiOh4R\naSCZJEmS6BBEosXFxWFpUBAOREWhFwCrrCwYA0gFcM7AALslCV2cnTF2yhRYWVkJTktEmoRFTFpv\nVUgIZk2ciEmZmfCQJFR4z2teAAiTyfCdgQH8Fy3CcG9vZcckIg3FIiattiokBAsmTsShjAzUK8Lr\nbwBwNDTEJJYxEckJi5i0VlxcHLrb2ODkWyX8AsBgAIcBVAEwD0C/N56/AaCDoSEijh9H69atlReY\niDQSV02T1loaFIRJmZnvjIR9AOgDeApgEwBvAFffeL4eAL/MTCwNClJOUCLSaBwRk1Z68uQJGpiZ\n4VZW1r++E84AUAHAFQB1//eYB4AaeD0y/ttzAHX19ZGYlMTV1ERUKhwRk1baEBYGV+CdhVmJAMrh\n/0sYAJoBuPzW6yoCcJXJsCEsTGEZiUg7sIhJKyX+8QfaZGW983gagI/eeuwjvL6M6W1WmZlIjI9X\nQDoi0iYsYtJKaSkpMH7P4+UBvHrrsRTgva81BpD64oW8oxGRlmERk1Yqb2Ly3lGuOYA8ADffeOx3\nAI3f89pUAMYV3nfVMRFR0bGISSuZN22Kc/r67zxuCKAXgJl4vXDrFIAIAN+85xhxBgYwt7RUZEwi\n0gJcNU1aqbBV08C/ryOuDGABgL5vvYarpolIXjgiJq1UtWpVdHF2xnqZ7J3nKgDYjdcLt+7g3RIG\ngPUyGbq6uLCEiajUOCImrVXYzlofcgPAl/r62H/yJHfWIqJS44iYtJaVlRX8Fy2Co6EhbhTxPTcA\n2OrqIrtcOejq6ioyHhFpCd6PmLTa3zdu+GL8ePhlZ2MI3t3kA3j9nfA6mQyL/nf3pY8rVYKDgwMi\nIyPRsmVLZUYmIg3DqWnSenl5eahXrx7q16iB8xcuwFUmg1Vm5j/3I44zMMCO3FyY1ayJsB07/pmO\n3rNnD0aMGIF9+/bh888/F/ozEJH64oiYtN7atWtRp04dRMfEIDk5GRvCwnApPh6pL17AuEIFNLa0\nxHgnJ3Ts2BHm5ub/vK9nz54oV64cunXrhl27duHLL78U+FMQkbriiJi0WlpaGszNzbFv374PLrzq\n3bs3OnfuDB8fn389Hh0djQEDBmD79u2wsbFRYFoi0kRcrEVabcmSJbCxsSnS6mdvb2+EhITg7c+u\nDg4O2LZtG/r06YPDhw8rKioRaSiOiElrPX78GBYWFjh//jw+++yzD75ekiQ0bNgQa9asee809KlT\np9CrVy+EhYXBxcVFEZGJSANxRExay9/fHx4eHkUqYQCQyWTw8vJCSEjIe5//8ssvERERAU9PT+zZ\ns0eeUYlIg3FETFopISEBX375Ja5du4ZKlSoV+X3Pnz9HnTp1cP369UJ31frtt9/QpUsXLF++HG5u\nbvKKTEQaiiNi0kpTpkyBr69vsUoYACpWrAhXV1esW7eu0Ne0atUKhw4dwpgxY7B58+bSRiUiDccR\nMWmd06dPo1+/fkhISICBgUGx33/u3Dn069cP169fR5kyhX+WvXz5MhwcHBAYGAhPT8/SRCYiDcYR\nMWkVSZLg6+uLwMDAEpUw8HprzI8//hjR0dH/+brGjRsjNjYWM2fORGhoaInORUSaj0VMWmX37t3I\nyMjA119/XeJjyGSyfy5l+pAGDRrg2LFjCAoKwvLly0t8TiLSXJyaJq2Rm5uLxo0bY/ny5XB0dCzV\nsdLT02FqaoqLFy/C1NT0g6+/e/cuOnfuDG9vb0ycOLFU5yYizcIRMWmN1atXw8zMDA4ODqU+lpGR\nEfr374/Vq1cX6fVmZmY4fvw4Vq1ahblz55b6/ESkOTgiJq2QmpqK+vXrIyoqCi1atJDLMS9fvgw7\nOzskJSWhXLlyRXrPw4cPYWtrCzc3N8yePRsymUwuWYhIfXFETFph4cKFsLe3l1sJA68XY5mbmxdr\n847q1avj2LFj2L17N6ZMmfLOdplEpH04IiaN9/DhQzRp0gQXLlyAmZmZXI+9detWrFq1CrGxscV6\n37Nnz2Bvbw9ra2ssWbKEI2MiLcYiJo03YsQIfPTRR1i4cKHcj52TkwNTU1McO3YMDRs2LNZ7X7x4\nAScnJ7Ru3RrLly//z2uSiUhzsYhJo129ehUdO3ZEYmIiKlSooJBzTJ06FRkZGfjhhx+K/d5Xr17B\n2dkZFhYWCA0NZRkTaSEWMWm0Hj16oGPHjpgwYYLCznHnzh20atUKf/31FwwNDYv9/rS0NHTt2hVm\nZmZYu3YtdHR0FJCSiFQVP36Txjpx4gR+//13jBw5UqHnqV27Ntq1a4etW7eW6P3ly5dHZGQkHjx4\ngAEDBiA3N1fOCYlIlbGISSP9vZXl3Llzoa+vr/DzFXWnrcIYGhoiIiICKSkpcHd3R05OjhzTEZEq\nYxGTRgoPD0dubi769eunlPM5OTnh6dOnOH/+fImPoa+vj927dyM/Px+9e/dGdna2HBMSkapiEZPG\nycnJwZQpU7Bw4UKlLX7S0dHBiBEjSjUqBgA9PT3s2LEDenp66NGjBzIzM+WUkIhUFRdrkcZZvnw5\nIiMjERUVpdTzPnnyBA0aNMCtW7dKvUI7Ly8PHh4eePToEfbt2wcjIyM5pSQiVcMiJo2SkpICc3Nz\nHD58GE2bNlX6+fv164e2bdti7NixpT5Wfn4+hg4dips3b+LAgQMwNjaWQ0IiUjWcmiaN8t1338HF\nxUVICQOvF22tXLlSLltX6ujoYM2aNWjUqBEcHR2RkpIih4REpGo4IiaNce/ePTRr1gyXLl1CrVq1\nhGSQJAmWlpb48ccfYWNjI7djjhkzBmfOnMGhQ4dQsWJFuRyXiFQDR8SkMWbNmoXhw4cLK2EAkMlk\n8PLyKvWirbePuWzZMlhbW8PW1hbJyclyOzYRiccRMWmE+Ph42NnZITExESYmJkKzpKSkoHbt2rh6\n9SqqVasmt+NKkoTp06dj7969iImJwSeffCK3YxOROBwRk0aYPHkypk6dKryEAcDExARubm5Ys2aN\nXI8rk8kQGBiIPn36wMbGBg8ePJDr8YlIDI6ISe3FxsZi2LBhuHr1KnR1dUXHAQBcvHgRPXv2xK1b\ntxSyd/T8+fOxZs0axMbGCp2KJ6LS44iY1FpBQQH8/Pwwb948lSlhAGjRogWqVauGyMhIhRx/8uTJ\n8PHxgbW1NW7fvq2QcxCRcrCISa1t27YNZcqUgZubm+go7yjt/tMfMn78eEyYMAE2Nja4ceOGws5D\nRIrFqWlSW9nZ2WjYsCHWrVsnt0uF5CkzMxO1atVCXFwcPvvsM4WdZ/Xq1fD398eRI0fQsGFDhZ2H\niBSDI2JSW8HBwWjSpIlKljAAGBgYYODAgQgNDVXoeYYNG4a5c+eic+fO+PPPPxV6LiKSP46ISS29\nePECDRo0wNGjR9G4cWPRcQqVmJiIDh06ICkpCXp6ego919atWzFu3DhERUWhRYsWCj0XEckPR8Sk\nlubPn48ePXqodAkDgLm5OSwtLbFz506Fn8vd3R0rVqyAk5MT4uLiFH4+IpIPjohJ7SQlJaFFixaI\nj4/Hp59+KjrOB+3cuRM//PADTp48qZTzRUREYMiQIdizZw+++OILpZyTiEqORUxqx8PDA6amppgz\nZ47oKEWSm5uL2rVr4+DBg7C0tFTKOQ8ePIiBAwciPDwcHTt2VMo5iahkWMSkVi5dugQnJyckJibi\no48+Eh2nyGbNmoXk5GSsWLFCaeeMiYmBu7s7tm7dCltbW6Wdl4iKh0VMasXR0RHdu3fHyJEjRUcp\nlnv37qFp06ZISkpC+fLllXbeEydOoHfv3tiwYQOcnJyUdl4iKjou1iK1ER0djdu3b2P48OGioxRb\nzZo1YW1tjc2bNyv1vB07dsTevXsxcOBAREREKPXcRFQ0LGJSCwUFBZg0aRLmzZuHcuXKiY5TIn/v\ntKXsSah27drhwIEDGDp0qFJWbxNR8bCISS38/PPP0NPTw1dffSU6SonZ2dkhLS0NZ86cUfq5rays\ncOjQIYwaNQpbtmxR+vmJqHBlRQcg+pCsrCxMmzYNmzZtgkwmEx2nxMqUKQMvLy+sXLkS7dq1U/r5\nmzdvjsOHD8PBwQE5OTnw8PBQegYieheLmFTejz/+iBYtWqBDhw6io5Sap6cn6tWrh2fPnqFSpUpK\nP3+TJk0QGxsLOzs75ObmYujQoUrPQET/xlXTpNKeP3+OBg0a4OTJkxpzQ4OBAweiWbNmmDBhgrAM\n169fh52dHfz8/NRuBTqRpmERk0qbOHEi0tLSsHLlStFR5ObXX3/FwIEDkZCQgDJlxC3TuH37Nmxt\nbTF69GiMHz9eWA4ibcepaVJZd+7cwbp163D58mXRUeSqbdu2MDIyQkxMDOzt7YXl+Oyzz3Ds2DHY\n2toiOzsbkydPFpaFSJtx1TSprOnTp2P06NGoVq2a6ChyJZPJ/rmUSTRTU1McP34cYWFhCAgIUPql\nVUTEqWlSURcuXECXLl2QmJgIY2Nj0XHkLjU1FWZmZoiPj0eNGjVEx8Hjx49ha2uLHj16IDAwUK1X\npxOpG46ISeVIkgRfX1/MmjVLI0sYAIyNjeHu7o7Vq1eLjgIA+OSTT3D06FEcOHAAvr6+HBkTKRFH\nxKRyDh48iHHjxiE+Pl5td9Eqivj4eDg5OeHOnTsq83M+f/4cjo6OaNeuHZYuXcqRMZEScERMKiU/\nPx9+fn6YP3++ypSTolhaWuKzzz5TqT2gK1asiCNHjiAuLg5eXl4oKCgQHYlI47GISaVs3LgRH330\nEXr06CE6ilKoyqKtN5mYmCA6OhpXr17FkCFDkJ+fLzoSkUbj1DSpjMzMTJibm2P79u1CtoAUITs7\nG7Vq1cLp06dRv3590XH+JT09Hd27d0e1atWwfv16lC3Lqx2JFIEjYlIZS5cuxeeff641JQwAenp6\n8PT0VMkNS4yMjLB//348e/YM/fv3R25uruhIRBqJI2JSCcnJyWjYsCF++eUXmJubi46jVLdu3UKb\nNm3w119/wcDAQHScd2RlZcHNzQ06OjrYtm0b9PT0REci0igcEZNKCAwMhLu7u9aVMADUqVMHVlZW\n2L59u+go76Wvr4+dO3dCR0cHvXr1QlZWluhIRBqFI2IS7ubNm/j8889x5coVVK1aVXQcIfbt24d5\n8+YJuVdxUeXm5mLgwIFITk7G3r17YWhoKDoSkUbgiJiEmzZtGsaNG6e1JQwAXbp0wYMHD3Dx4kXR\nUQpVrlw5bNq0CdWrV0eXLl2QlpYmOhKRRmARk1Dnzp3DyZMntf7uPzo6Ohg+fLjKXcr0Nh0dHaxb\ntw5169aFk5MTXr16JToSkdrj1DQJI0kSOnXqhAEDBvAG9QAePXqERo0a4c6dOzAxMREd5z8VFBRg\n1KhR+O2333Dw4EFUqFBBdCQitcURMQlz4MABPH36FIMGDRIdRSVUq1YN9vb22LRpk+goH1SmTBms\nWLECX3zxBWxtbfHs2TPRkYjUFouYhMjLy8OkSZOwYMECbhTxhr932lKHiSqZTIYlS5bAwcEBnTp1\nwpMnT0RHIlJLLGISIiwsDFWqVEGXLl1ER1EpNjY2yM/Px6lTp0RHKRKZTIagoCC4urrCxsYGDx8+\nFB2JSO3wO2JSuvT0dJibm2P37t1o06aN6DgqZ+nSpTh79ix+/vln0VGKZe7cuVi/fj1iY2NRs2ZN\n0XGI1AaLmJQuMDAQf/75J7Zu3So6ikp68eIF6tSpg4SEBLW7pGvRokUICQlBbGwszMzMRMchUgss\nYlKqJ0+ewMLCAmfPnkXdunVFx1FZgwcPhrm5OSZPniw6SrEtW7YMS5YsQUxMDP83JioCFjEp1ahR\no1C2bFn88MMPoqOotLi4OPTp0wc3btyAjo6O6DjFFhoaisDAQBw5cgQNGjQQHYdIpXG5KinN9evX\nsW3bNly9elV0FJVnZWWFSpUq4dChQ3BxcREdp9hGjBgBXV1ddO7cGYcPH4aFhYXoSEQqi6umSWmm\nTp2KCRMmoHLlyqKjqIW/L2VSV56enliwYAFsbW3xxx9/iI5DpLI4NU1KcebMGbi5uSExMVElb/Wn\nitLT02FqaooLFy6o9cKn7du3Y8yYMYiMjETLli1FxyFSORwRk8JJkgRfX1/MmTOHJVwMRkZGGDBg\nAFatWiU6Sqn06dMHK1euhLOzM86ePSs6DpHKYRGTwu3btw8pKSn45ptvREdRO15eXlizZg1ycnJE\nRymVnj17Yu3atejWrZvabFZCpCwsYlKoN7eyVMfVv6I1atQIjRo1wu7du0VHKbUuXbpg06ZNcHV1\nxdGjR0XHIVIZLGJSqDVr1qBGjRpwcnISHUVtqfuirTc5ODhgx44d6Nu3L6Kjo0XHIVIJXKxFCpOW\nlgZzc3NERESgVatWouOorZycHJiZmSEmJkZjLgM6ffo0XF1dsW7dOu43TlqPI2JSmMWLF6NTp04s\n4VLS1dXFkCFDsHLlStFR5KZ9+/aIiIjA4MGDNWLanag0OCImhXj06BEaN26M8+fP47PPPhMdR+0l\nJSWhRYsWSEpKgpGRkeg4cnPhwgW4uLhg2bJl6NOnj+g4REJwREwK4e/vj0GDBrGE5cTU1BTt27fH\nli1bREeRq5YtWyI6Ohpjx47Fpk2bRMchEoIjYpK7a9euoUOHDkhISEDFihVFx9EYUVFRmD59Os6f\nPw+ZTCY6jlxduXIF9vb2mDNnDgYPHiw6DpFScURMcjdlyhT4+fmxhOXM0dERL168wPnz50VHkTsL\nCwscPXoUs2fP1qjvwomKgjd9ILk6deoULly4oHFTqKqgTJkyGDFiBEJCQmBlZSU6jtyZm5vj6NGj\nsLW1RU5ODsaMGSM6EpFScGqa5EaSJHzxxRfw8fHhLloK8vTpU5ibm+PWrVuoUKGC6DgKcffuXXTu\n3BleXl7w9fUVHYdI4Tg1TXKza9cuZGZm4uuvvxYdRWNVqVIFLi4uWL9+vegoCmNmZobjx4/jp59+\nQmBgoOg4RArHETHJRW5uLiwsLBAcHAx7e3vRcTTaqVOnMHToUFy9elXjFm296eHDh7Czs8NXX30F\nf39/jf5ZSbtxRExysWrVKtSpU4clrATt27dH2bJlNX6/5urVq+Po0aPYs2cPJk+eDI4ZSFNxREyl\n9urVK5ibm+PgwYNo3ry56DhaYcWKFTh27Bh27NghOorCPXv2DA4ODujQoQO+//57joxJ47CIqdRm\nzJiBpKQkjf7eUtW8evUKZmZmuHLlCqpXry46jsK9fPkSjo6OaNWqFX788UeUKcPJPNIcLGIqlQcP\nHsDS0hIXL16Eqamp6DhaZcSIEahZsyZmzJghOopSvHr1Ci4uLmjYsCFCQ0N5W03SGCxiKpVhw4ah\nYsWKWLBggegoWufSpUvo1q0bbt++jbJltWNLgLS0NHTr1g21atXC2rVrtebnJs3G+R0qscuXL2Pv\n3r2YMmWK6ChaqXnz5qhZsyYOHDggOorSlC9fHgcOHMCjR48wYMAA5Obmio5EVGosYiqxyZMnY8qU\nKfj4449FR9Fa3t7eCAkJER1DqQwNDbFv3z6kpqaib9++yMnJER2JqFQ4NU0lcuzYMXh6euLatWvQ\n09MTHUdrZWVloVatWjhz5gzq1q0rOo5SZWdno2/fvsjPz8eOHTugr68vOhJRiXBETMUmSRL8/Pww\nb948lrBg+vr68PDwQGhoqOgoSqenp4cdO3bAwMAAPXr0QGZmpuhIRCXCIqZi27FjBwoKCtC3b1/R\nUQivV0+HhYUhKytLdBSlK1euHH7++WdUqVIFXbp0QXp6uuhIRMXGIqZiycnJwZQpU7Bw4UJey6ki\n6tevj+bNmyM8PFx0FCHKli2L9evXw8zMDM7OzkhNTRUdiahY+C8pFcvKlSvRsGFDdOrUSXQUeoM2\nLtp6k46ODtasWQMLCws4ODjg5cuXoiMRFRkXa1GRpaSkwNzcHDExMWjSpInoOPSGvLw81K5dG5GR\nkWjatKnoOMJIkoSxY8fil19+QXR0NCpWrCg6EtEHcURMRbZgwQJ07dqVJayCypYti2HDhmHlypWi\nowglk8mwdOlSdOrUCZ07d8bTp09FRyL6II6IqUju3buHZs2a4ffff0fNmjVFx6H3uH//PiwtLXH3\n7l0YGxuLjiOUJEmYMWMG9uzZgyNHjqBatWqiIxEViiNiKpKZM2fCy8uLJazCatSogU6dOmHz5s2i\nowgnk8kQGBiIvn37wsbGBvfv3xcdiahQHBHTB8XHx8POzg6JiYkwMTERHYf+w5EjRzBhwgRcunSJ\ntwv8nwULFmD16tWIjY3ljUlIJXFETB80adIkTJ8+nSWsBjp37ozMzEz8+uuvoqOojEmTJmHkyJGw\ntrbG7du3RcchegdvXUL/KSYmBomJidizZ4/oKFQEZcqUgZeXF0JCQvDFF1+IjqMyxo8fDz09PVhb\nWyMmJgb169cXHYnoH5yapkIVFBTAysoKkyZNQp8+fUTHoSJ69uwZ6tatixs3bqBy5cqi46iUn376\nCbNnz8bhw4fRqFEj0XGIAHBETP9h69at0NHRgZubm+goVAyVKlVCjx49sHz5chgbGSHxjz+QlpKC\n8iYmMG/aFB6enqhSpYromEIMHToUurq6sLW1RXR0NC/FI5XAETG9V3Z2Nho2bIiwsDBYW1uLjkPF\nEBcXh1m+vjh24gTc9fTQJisLxgBSAZwzMMBuSUIXZ2eMnTIFVlZWouMKsXXrVowbNw5RUVFo0aKF\n6Dik5VjE9F5LlizBsWPHsG/fPtFRqBhWhYRg1sSJ8MvMxCBJQoX3vOYFgDCZDN8ZGMB/0SIM9/ZW\ndkyVsHPnTvj4+GD//v1a+4GEVAOLmN7x4sULNGjQAMeOHYOFhYXoOFREq0JCsGDiRBzKyEC9/z22\nAkAYgHgA/QGsfeP1NwA4GhpikhaXcUREBIYMGYI9e/ZwcRsJwyKmd/j5+eHly5dYtWqV6ChURHFx\ncehuY4OTb5QwAOzB62sUDwHIxL+LGHhdxh0MDRFx/Dhat26tpLSq5eDBgxg4cCDCw8PRsWNH0XFI\nC7GI6V/u3r2Lli1bIj4+Hp9++qnoOFREA3r1Qus9ezCukL/OMwDcx7tFDADfy2S44OqKjTt3KjKi\nSouJiYG7uzu2bt0KW1tb0XFIy7CI6V8GDhyI2rVrIyAgQHQUKqInT56ggZkZbmVlvfc7YeC/i/g5\ngLr6+khMStLa1dQAcOLECfTu3RsbNmyAk5OT6DikRbizFv3j4sWLiI6Ohq+vr+goVAwbwsLgChRa\nwh9SEYCrTIYNYWHyC6WGOnbsiL1792LgwIGIiIgQHYe0CIuY/jFp0iTMnDlT6+/co24S//gDbbKy\nSnUMq8xMJMbHyymR+mrXrh0iIyMxbNgw7NTiqXpSLm7oQQCA6Oho3LlzB8OGDRMdhYopLSUFpf3o\nZAwg9cULecRRe61bt8bBgwfh7OyM7Oxs9O/fX3Qk0nAsYkJ+fj78/Pwwf/58lCtXTnQcKqbyJiZI\nLeS5fAC5//s9D0A2Xv+l13nrdakAjCuUdHJb8zRv3hyHDx+Go6MjcnNz4eHhIToSaTBOTRM2b94M\nQ0NDuLq6io5CxZSZmYlXOTk4WcgtDwMBGAJYAGDz//489z2vO2dgAHNLS4XlVEdNmjRBTEwMpk+f\njtWrV4uOQxqMRazlMjMzMX36dCxcuJD3r1Uj169fx4QJE2Bqaoqnz55hf9myeN/E8iwABXg9Iv77\n18y3XvMcwLbMTMh0dJCTk6PY4GqmYcOGOHr0KAIDA7FixQrRcUhDsYi13PLly9G6dWu0b99edBT6\ngLy8POzZswcODg5o3749ypYti7NnzyImJgbdunbF+hJ+kFovk8HG2hrR0dGoX78+Vq5ciezsbDmn\nV1/16tXD8ePHsXjxYixZskR0HNJEEmmt5ORkqXLlytK1a9dER6H/8ODBAykgIECqWbOm1K5dO2nj\nxo1SZmbmv15z7tw5qZqhoXQdkKRi/LoOSNUMDaW4uDhJkiTp119/lZydnaVatWpJK1aseOc82iwp\nKUmqV6+eNG/ePNFRSMNwRKzF5s6dCzc3NzRo0EB0FHqLJEk4fvw4+vbtCwsLC9y7dw8RERH45Zdf\nMGDAAOjr6//r9VZWVvBftAiOhoa4UcRz/L3XtP+iRf9sb9m2bVtERkYiPDwckZGRqFevHpYvX46s\nUl4epQlq1aqF48ePY8OGDfD394fEvZBIXkR/EiAxbt26JVWqVEl69OiR6Cj0hpcvX0rLly+XLCws\npEaNGknLli2TXr58WeT3hwYHS9UMDaUlMpn0vJBR8DNAWiyTSdUMDaXQ4OD/PN758+el7t27S59+\n+qn0ww8/SBkZGaX9EdXeo0ePpCZNmkhTpkyRCgoKRMchDcAtLrXU119/jQYNGmDmzLeX7pAIv//+\nO4KDg7HnjjQUAAAcLklEQVR9+3bY29vDx8cH1tbWJVpAd/78eSwNCsL+yEi4ymSwysz8537Ecf+7\nH3FXFxeMnTKlyDd6uHjxIgICAnD27Fn4+vpixIgRMDQ0LHY2TZGcnAx7e3t07twZixYt4kJHKhUW\nsRb67bff0K1bNyQmJqJ8+fKi42it7OxshIeHIzg4GHfv3sWIESMwdOhQVK9eXS7Hf/r0KTaEhSEx\nPh6pL17AuEIFmFtaYuCgQSXeU/r333/HnDlzcPr0aUyYMAHe3t4wMjKSS1518/z5czg6OqJt27ZY\nunQpypThN31UMixiLSNJEmxtbeHu7o7hw4eLjqOVbt++jdDQUKxduxbNmzeHt7c3unXrhrJl1Wd/\nnfj4eMyZMwcnTpzAt99+Cx8fH638UJeSkgJnZ2c0adIEK1euZBlTifD/NVrm4MGDePjwIQYPHiw6\nilbJz8/HgQMH0KVLF1hZWSEnJwenTp1CdHQ0XF1d1aqEAcDS0hLbt29HTEwMLly4gLp16yIoKAip\nqYXt8aWZTExMcOjQISQkJGDw4MHIz88XHYnUEEfEWiQ/Px/NmzfH3Llz0b17d9FxtMLTp0+xZs0a\nhIaGonLlyvDx8UHfvn017vvVK1euYO7cuTh8+DDGjh2L0aNH46OPPhIdS2nS09PRvXt3VKtWDevX\nr1e7D1YkFkfEWmTDhg2oUKECunXrJjqKRpMkCadPn8aAAQNQv359JCYmYvv27YiLi4Onp6fGlTAA\nWFhYYPPmzTh58iSuXbuGunXrIiAgACkpKaKjKYWRkRH279+P58+fo1+/fsjNzRUdidQIR8RaIiMj\nAw0aNEB4eDg+//xz0XE0UlpaGjZv3ozg4GBkZmbC29sbHh4eqFixouhoSpeYmIh58+bhwIEDGDly\nJMaNG4ePP/5YdCyFy87OhpubG2QyGbZv3w49PT3RkUgNcESsJZYuXYp27dqxhBXg8uXLGDVqFExN\nTXHo0CEsWrQI165dw/jx47WyhAHA3NwcYWFh+PXXX5GUlIR69eph5syZeP78uehoCqWnp4fw8HCU\nK1cOrq6uyMzMFB2J1ACLWAs8ffoUixcvxrx580RH0Rg5OTnYtm0brK2tYW9vj4oVK+L333/Hrl27\nYG9vz9Wz/1OvXj2sXbsW586dw8OHD1G/fn1MmzYNz549Ex1NYXR1dbF161aYmJige/fuyMjIEB2J\nVBynprXA2LFjIUkSli1bJjqK2ktKSsKqVauwZs0aNGzYED4+PujZsyfv41xEd+7cQVBQEMLDwzF8\n+HBMmDABlStXFh1LIfLz8zF48GDcvXsX+/fv18rLu6ho+LFdw924cQObN2/GjBkzREdRWwUFBYiO\njkbPnj3RvHlzvHr1CjExMTh69Cjc3NxYwsVQu3ZthIaG4uLFi3j58iUaNGgAPz8/PHnyRHQ0udPR\n0cG6detQv359ODo6as3CNSo+FrGGmzZtGr799tsS76SkzZ49e4bFixfD3Nwcfn5+cHFxQVJSEpYt\nWwYLCwvR8dSaqakpQkJCcOnSJWRkZKBRo0aYOHEiHj9+LDqaXJUpUwahoaFo3rw57O3t8eLF++4a\nTdqORazBzp49i9OnT2PcuHGio6gNSZJw7tw5DBo0CHXr1sWlS5ewceNGXLx4EcOHD+f0opzVqlUL\nP/74I/744w/k5OSgUaNG+Pbbb/Ho0SPR0eSmTJky+PHHH/Hll1/C1tYWycnJoiORimERayhJkuDn\n5wd/f3+NvG5V3jIyMrBmzRpYWVnB3d0dFhYWuH79OjZu3Ih27dpxU38Fq1GjBpYtW4Y///wTkiSh\ncePGGDduHB48eCA6mlzIZDIsXrwYjo6O6Ny5s0ZOxVPJsYg11P79+/Hs2TN4eHiIjqLSEhISMH78\neNSqVQt79uxBQEAArl+/Dj8/P07nC/Dpp5/i+++/x+XLl6GjowNLS0uMHj0a9+7dEx2t1GQyGebN\nm4devXrBxsYGDx8+FB2JVASLWAPl5eVh0qRJWLBgAbfae4+8vDzs2rULdnZ26NixI/T19fHbb78h\nIiICLi4u0NHRER1R61WrVg2LFy/GlStXoK+vj2bNmmHkyJH466+/REcrFZlMhtmzZ2PAgAGwtrbW\niA8YVHosYg20bt06fPLJJ3BxcREdRaU8ePAA/v7+MDMzw5IlSzB48GAkJSUhKCgItWvXFh2P3uOT\nTz7BwoULce3aNRgbG6N58+bw8vLC3bt3RUcrlalTp2LEiBGwtrbGnTt3RMchwVjEGiY9PR2zZ8/G\nd999x+818fq78tjYWPTu3RuNGzfGo0ePEBUVhVOnTqF///7cglBNVKlSBfPnz0dCQgIqVqyIli1b\nYvjw4bh9+7boaCU2YcIEjBs3DjY2Nrh586boOCQQi1jDLFmyBB07doSVlZXoKEK9fPnyn8uMxowZ\ng86dO+Pu3bsICQlB06ZNRcejEqpcuTLmzZuHxMREVK1aFa1bt8aQIUNw69Yt0dFKZPTo0Zg6dSps\nbGyQkJAgOg4Jwp21NMjjx49hYWGBuLg41KlTR3QcIS5cuICQkBCEh4fDyckJ3t7e6NChA2cHNNSL\nFy/www8/YMWKFejWrRumTZuGevXqiY5VbOvWrcP06dMRHR2Nxo0bi45DSsYRsQYJCAjAwIEDta6E\ns7KysGHDBrRt2xY9e/ZE7dq1cfXqVWzZsgUdO3ZkCWuwChUqwN/fHzdu3EDt2rXRrl07eHh4IDEx\nUXS0YvH09MR3330HOzs7/P7776LjkJJxRKwhEhIS0L59eyQkJKBSpUqi4yjFzZs3sXLlSoSFhaFV\nq1bw8fGBi4sLV4prsZSUFCxfvhxLly6Fo6Mjpk+fjoYNG4qOVWQ7duzA6NGjceDAAbRq1Up0HFIS\njog1xNSpU+Hr66vxJZyfn4+IiAg4Ozujbdu2AIBff/0VBw8eRPfu3VnCWs7ExATTp0/HzZs3YWFh\ngY4dO6J///64cuWK6GhF4ubmhtDQULi4uODMmTOi45CScESsAX755Re4u7sjISEBBgYGouMoxOPH\nj7FmzRqEhoaievXq8Pb2Rp8+fTT25yX5SE1NxYoVK/D999/DxsYGM2bMQJMmTUTH+qDIyEgMGjQI\nu3btwpdffik6DikYR8RqTpIk+Pr6Ys6cORpXSpIk4eTJk+jXrx8aNmyIW7duYdeuXThz5gw8PDw0\n7ucl+TM2NsbkyZNx8+ZNtG7dGnZ2dnBzc0N8fLzoaP/JxcUFmzdvhqurK44ePSo6DikYi1jN7dmz\nB2lpaRgwYIDoKHLz6tUrBAcHo2nTphg6dCjatm2LW7du4aeffuL3ZlQi5cuXh6+vL27evIm2bdvC\nwcEBX331lUovjLK3t8eOHTvQt29fREdHi45DCsSpaTWWm5uLJk2aYNmyZXB0dBQdp9Ti4+MRHByM\nrVu3wtbWFt7e3ujcuTNXPZPcZWRkYNWqVfjuu+/Qpk0bzJw5Ey1bthQd671Onz4NV1dXrFu3Dl26\ndBEdhxSAI2I1tmbNGpiamsLBwUF0lBLLzs7Gli1b0KFDBzg5OaFatWr4888/ER4eDltbW5YwKYSh\noSHGjRuHmzdvonPnzujWrRu6d++O8+fPi472jvbt2yMiIgKDBw/G7t27RcchBeCIWE2lpqbC3Nwc\nkZGRaNGiheg4xXb37l2EhoZizZo1sLS0hLe3N7p3745y5cqJjkZaKCsrCz/99BPmz5+PZs2aYdas\nWWjTpo3oWP9y4cIFuLi4YNmyZejTp4/oOCRHHBGrqcWLF8POzk6tSrigoABRUVHo1q0bWrZsiYyM\nDBw/fhxHjhzBV199xRImYfT19TFq1CjcvHkTXbt2Re/eveHs7KxSlxC1bNkS0dHRGDt2LDZt2iQ6\nDskRR8Rq6OHDh2jSpAkuXLgAMzMz0XE+KDk5GevWrcPKlSthYmKCkSNHwt3dHUZGRqKjEb1XdnY2\nwsLCEBQUBHNzc8yaNQvt27cXHQsAcOXKFdjb22POnDkYPHiw6DgkByxiNeTl5QVjY2MsXLhQdJRC\nSZKEs2fPIjg4GPv27UPPnj3h7e2NNm3a8HtfUhs5OTnYsGED5s6di7p162LWrFno0KGD6FhITEyE\nnZ0dpk6dCi8vL9FxqJRYxGrm6tWrsLa2RkJCAipUqCA6zjvS09Px888/Izg4GKmpqfDy8oKnp6fG\n7/hFmi03NxcbN27E3LlzYWZmhlmzZsHa2lpoplu3bsHW1hbjxo3D2LFjhWah0mERq5mePXuiQ4cO\nmDBhgugo/3L16lWEhIRg8+bN+PLLL+Hj4wN7e3uUKcNlCKQ5cnNz8fPPPyMwMBCffvopZs2ahU6d\nOgmb5bl79y5sbW0xfPhw+Pn5CclApcciViMnT57EN998g2vXrkFfX190HOTm5mLv3r0IDg7GlStX\nMHToUAwfPhympqaioxEpVF5eHrZs2YLAwEBUrVoVs2bNEna53f3799G5c2cMGDAAM2bMUPr5qfRY\nxGpCkiS0a9cOo0ePxtdffy00y71797B69WqsXr0a9evXh7e3N3r16gVdXV2huYiULT8/H1u3bsWc\nOXNQqVIlzJw5Ew4ODkov5EePHsHW1ha9evVCQEAA12GoGc4bqomdO3ciJycH/fr1E3L+goICHDly\nBL169ULTpk2RnJyM6OhoHD9+HO7u7ixh0ko6Ojr4+uuvcfnyZYwaNQrjx49Hu3btEBUVBWWOcapV\nq4Zjx45h3759mDRpklLPTaXHEbEayMnJQePGjbFy5UrY2toq9dwvXrxAWFgYQkJCoK+vDx8fH3z9\n9dcwNjZWag4idVBQUIDw8HAEBATAyMgIM2fOhIuLi9JGqM+ePYODgwM6dOiA77//niNjNcEiVgM/\n/vgjDhw4gKioKKWd8/z58wgODsauXbvQpUsX+Pj44IsvvuBfbKIiKCgowK5duxAQEABdXV3MnDkT\n3bp1U8rfn5cvX8LJyQktWrTAihUruGBSDbCIVdyrV69gbm6O6OhoNG3aVKHnyszMxLZt2xAcHIwn\nT57Ay8sLgwcPRtWqVRV6XiJNVVBQgL179/7zve3MmTPRo0cPhRfyq1ev0KVLF5ibm2PVqlXQ0dFR\n6PmodFjEKm769Om4f/8+1q1bp7BzXL9+HStXrsT69evx+eefw9vbG87OzvzLSyQnkiRh3759CAgI\nQH5+PmbMmAFXV1eFjlbT0tLQvXt31KhRA+vWrUPZsmUVdi4qHRaxCrt//z6aNm2KS5cuoVatWnI9\ndl5eHvbv34/g4GBcunQJnp6eGDFiBOrUqSPX8xDR/5MkCQcOHIC/vz+ys7MxY8YMfPXVVwor5IyM\nDPTs2RMVKlTApk2buJ+7imIRq7ChQ4eiSpUqCAoKktsxHz58iJ9++gmrVq1CrVq14OPjg969e6vE\ndclE2kKSJERFRcHf3x9paWmYMWMG3NzcFDILlZWVhd69e0NXVxdbt27lFQ4qiEWsov7880/Y2toi\nMTERJiYmpTqWJEk4ceIEgoODER0djT59+sDb2xvNmzeXU1oiKglJknDo0CH4+/sjJSUF06dPR9++\nfeVeyDk5Oejbty9yc3MRHh7OD94qhkWsorp27Qo7OzuMGzeuxMdISUnBxo0bERISAkmS4O3tjYED\nB5a62IlIviRJwpEjR+Dv74/k5GRMnz4d7u7ucv1eNzc3FwMGDMDLly+xe/duGBoayu3YVDosYhV0\n9OhRDBkyBFevXoWenl6x33/p0iWEhIRg+/btsLe3h4+PD6ytrXnpEZGKkyQJsbGx8Pf3x6NHjzB9\n+nT0799fboWcl5cHT09P3L9/HxEREbwVqYpgEQvy5MkTbAgLQ+IffyAtJQXlTUxg3rQpvvHwQNeu\nXTFhwgS4u7sX+XhZWVkIDw9HcHAwkpKSMGLECAwdOhTVq1dX4E9BRIpy7Ngx+Pv746+//sK0adMw\nYMAAuSy2ys/Px7Bhw3D9+nUcOHAAH330kRzSUmmwiJUsLi4OS4OCcCAqCr0AWGVlwRhAKoBzBgbY\nmZeH8kZG2HXwID7//PMPHu/27dsIDQ3F2rVr0bx5c/j4+KBr1668VIFIQ5w4cQL+/v64ffs2pk2b\nhoEDB5a6kAsKCjBy5EhcvHgRBw8exMcffyyntFQiEilNaHCwVM3QUPpeJpOeA5L0nl/PAWmxTCZV\nMzSUQoOD33ucvLw8af/+/ZKLi4tUqVIl6dtvv5USExOV/NMQkTKdPHlSsrOzk2rXri2FhoZK2dnZ\npTpeQUGBNGbMGKlVq1bSs2fP5JSSSoJFrCShwcFSHUND6XohBfz2r+uAVOetMn78+LEUFBQkmZmZ\nSVZWVtLatWul9PR0gT8VESnb6dOnJUdHR8nU1FQKCQmRsrKySnysgoICydfXV2ratKn05MkTOaak\n4uDUtBLExcWhu40NTmZkoN4bj38D4AiADACVAQwGMO2N528A6GBoiMBlyxAbG4vIyEi4urrC29sb\nVlZWyvsBiEjlnDlzBgEBAfjzzz8xefJkDB48uESXJUmShJkzZ2LXrl2IiYlBtWrVFJCW/guLWAkG\n9OqF1nv2YNxb/6mvAKgDQB9AIoCOANYDcHzjNYsAfGdkhClz5sDDwwMVK1ZUUmoiUgdxcXEICAjA\nxYsXMWnSJAwbNqxEhTxnzhxs3rwZMTExqFGjhgKSUmFYxAr25MkTNDAzw62sLFT4j9clALADsBdA\nyzcefw6grr4+EpOSUKVKFUVGJSI19ttvvyEgIADnz5+Hn58fhg8fDgMDg2Id47vvvsOqVasQGxsL\nU1NTBSWlt/H+WAq2ISwMrkChJTwSgBGAJng9Ld3yrecrAnCVybAhLExhGYlI/bVq1Qp79+7F/v37\ncezYMdStWxdLlixBRkZGkY/h5+eHUaNGwdraGrdu3VJgWnqTzuzZs2eLDqHJwkJC0PriRbQu5Pku\nAKYCsAbgBaATgLcnhR7k5WFvair0jY1x9+5dPHjwAMnJyXj16hUyMzNRUFAAHR0d3i2JiFC9enW4\nu7vDzs4OmzdvxsSJEwEAzZo1K9I+023btoWenh6GDh2Krl27olKlSoqOrPV4samCpaWkwPgDr5Hh\ndRG7AdgC4O1lWMYAHt67h507dyItLQ3p6elIS0t7589lypSBkZERypcvj/Lly//z57d/L+5zurq6\n3JWLSM00a9YM4eHhiI+Px5w5c7Bw4UJ8++23GDlyJMqXL/+f7/X29oauri46deqEw4cPo1GjRkpK\nrZ1YxApW3sQEqUV8bR6A9+3+mgqgQ6dOCN2wodD3SpKEnJyc95b027///efHjx8X+tybv0uSJLdS\nf/M5PT09FjyRgllaWmL79u24fPkyAgMDUbduXYwbNw6jRo2CsXHhw4QhQ4ZAV1cXtra2OHToECwt\nLZWYWruwiBXMvGlTnNu5E15ZWf96/CmAWABdARgAOAxgx/9+f1ucgQEaf+AvgUwmg56eHvT09OS+\nsvrNgi9KcScnJxfpw0BeXl6RC7w4hW9gYMCCJ3pL48aNsWXLFly9evWfQh47dixGjx5d6DaX33zz\nDXR1dWFvb4+oqCi0aNFCyam1A1dNK1hhq6aTAfQG8AcACUB9ADMAdHvr/Zq8ajo3Nxfp6elFKvf/\neu7tx3JycmBoaFiiEft/vd7Q0JAFTxojISEBc+fORVRUFEaPHo0xY8YUutXlrl274O3tjYiICLRp\n00bJSTUfi1gJCruOuCi+l8lwwdUVG3fuVEAyzZSXl4eMjIwSlfp/PZednQ0DAwO5T9EbGhqiTBle\nwEBiXL9+HXPnzsX+/fsxatQojB07FhUqvHudx/79+zF48GDs2bMHX3zxhYCkmotFrASF7az1IX/v\nrBVx/Dhaty5s3TUpS35+/j8FX9pSf/O5zMxMGBgYyH2hnZGREVfSU5HduHED8+bNw759++Dt7Y3x\n48e/8zXXoUOH8M0332DHjh2wtrb+13OF3VHOw9NT42bz5I1FrCSrQkKwYOJEHCpiGd8A4GhoiEmL\nFmG4t7ei45FABQUFyMjIkPsUfXp6OvT09OQ+RW9kZMS7e2mwW7duISgoCLt27YKXlxe+/fbbf13C\nFBsbi759+2LLli2ws7P74B3ldksSujg7Y+yUKdyatxAsYiVaFRKCWRMnwi8zE4Mk6b2bfDwHECaT\nYaGBAfxZwlQKkiQhMzNT7lP06enpKFeunNyn6I2MjORyv12Sjzt37iAoKAjh4eEYPnw4JkyYgMqV\nKwMATp48ia+++gruffpgx7p1mJSZCY9C/k17gdf/pn3Hf9MKxSJWsvPnz2NpUBD2R0bCVSaDVWbm\nP58e4/736bGriwvGTpnC6WhSSZIkISsrS+5T9Onp6dDR0VHYtfBUMklJSZg/fz62bduGIUOGYOLE\niahatSom+fpi46JFOAFwlq+UWMSCPH369PX3KfHxSH3xAsYVKsDc0hIDBw3i9ymklSRJQnZ2ttyn\n6NPS0gBALpfGvf2cNm1289dff2HBggXYsmULnJ2dcWTXLpzKzPynhHMA+OD1HeVeAKgLYB4ApzeO\nwXUv78ciJiKNl5OTo5Ap+vz8fLmU+9uP6evrq2zB379/H04dO2LQrVuY8MbjGXh9tzhPALUAHADQ\nD8CfAN68fQSvBHkXi5iIqIT+3uxG3lP0ubm5Cpmil8dmN0W9oxwANAMwG4DrG49p8t4IJcWlj0RE\nJaSrqwtdXd33XndbGnl5ecWahv/rr7+KfC38f62GL8qIfe/u3ehRyMKsNz0GcB1A47cef/OOchN8\nfeX6301dsYiJiFRM2bJlYWJiAhMTE7keNz8/v9DR+PsK/OHDh+88l3jpEqZmZ//nefIADAAwCID5\ne563yszEpfh4uf5s6oxFTESkJXR0dPDRRx8Vurd0UfTv1g3G+/cX+ryE1yWsB2B5Ia8xBpD64kWJ\nM2gaFjERERXZh+4oNwSv99KPBFDYvm6pAIzlPJ2vzrjBLRERFZl506Y4p6//3ue8AFwDsA/Af125\nHWdgAHPeVvEfXDVNRERFVtiq6SQAtQHo4/9HwjIAoXh9GdPfuGr6XRwRExFRkVWtWhVdnJ2x/q3L\noEwBFOD19cSp//v1Cv8uYQBYL5Ohq4sLS/gNHBETEVGx8I5y8sURMRERFYuVlRX8Fy2Co6EhbhTx\nPX/vNe2/aBFL+C0sYiIiKrbh3t6YtGgROhga4nuZDIVdjPQcwBKZDB14w4dCcWqaiIhKjHeUKz0W\nMRERlRrvKFdyLGIiIiKB+B0xERGRQCxiIiIigVjEREREArGIiYiIBGIRExERCcQiJiIiEohFTERE\nJBCLmIiISCAWMRERkUAsYiIiIoFYxERERAKxiImIiARiERMREQnEIiYiIhKIRUxERCQQi5iIiEgg\nFjEREZFALGIiIiKBWMREREQCsYiJiIgEYhETEREJxCImIiISiEVMREQkEIuYiIhIIBYxERGRQCxi\nIiIigVjEREREArGIiYiIBGIRExERCcQiJiIiEohFTEREJBCLmIiISCAWMRERkUAsYiIiIoFYxERE\nRAKxiImIiARiERMREQnEIiYiIhKIRUxERCQQi5iIiEggFjEREZFALGIiIiKBWMREREQCsYiJiIgE\nYhETEREJxCImIiISiEVMREQkEIuYiIhIIBYxERGRQCxiIiIigVjEREREAv0fjYccUo1/HCYAAAAA\nSUVORK5CYII=\n",
"text/plain": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# The capture of Saddam Hussein\n",
"\n",
"- shows the strong predictive power of networks. \n",
"\n",
"- underlies the need to obtain accurate maps of the networks we aim to study; and the often heroic difficulties we encounter during the mapping process.\n",
"\n",
"- demonstrates the remarkable stability of these networks: The capture of Hussein was not based on fresh intelligence, but rather on his pre-invasion social links, unearthed from old photos stacked in his family album.\n",
"\n",
"- shows that the choice of network we focus on makes a huge difference: the hierarchical tree, that captured the official organization of the Iraqi government, was of no use when it came to Saddam Hussein's whereabouts. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# A SIMPLE STORY (2): August 15, 2003 blackout.\n",
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# The capture of Saddam Hussein\n",
"\n",
"- shows the strong predictive power of networks. \n",
"\n",
"- underlies the need to obtain accurate maps of the networks we aim to study; and the often heroic difficulties we encounter during the mapping process.\n",
"\n",
"- demonstrates the remarkable stability of these networks: The capture of Hussein was not based on fresh intelligence, but rather on his pre-invasion social links, unearthed from old photos stacked in his family album.\n",
"\n",
"- shows that the choice of network we focus on makes a huge difference: the hierarchical tree, that captured the official organization of the Iraqi government, was of no use when it came to Saddam Hussein's whereabouts. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# A SIMPLE STORY (2): August 15, 2003 blackout.\n",
"\n",
" \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# VULNERABILITY \n",
"DUE TO INTERCONNECTIVITY \n",
"\n",
"- The 2003 blackout is a typical example of a cascading failure. \n",
"- 1997, when the International Monetary Fund pressured the central banks of several Pacific nations to limit their credit. \n",
"- 2009-2011 financial melt-down"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"An important theme of this class: \n",
"\n",
"- we must understand **how network structure affects the robustness of a complex system**. \n",
"\n",
"- develop quantitative tools to assess the interplay between network structure and the dynamical processes on the networks, and their impact on failures. \n",
"\n",
"- We will learn that failures reality failures follow reproducible laws, that can be quantified and even predicted using the tools of network science.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"NETWORKS AT THE HEART OF \n",
"# COMPLEX SYSTEMS \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Complex\n",
"\n",
"[adj., v. kuh m-pleks, kom-pleks; n. kom-pleks] \n",
"–adjective \n",
"- composed of many interconnected parts; compound; composite: a complex highway system. \n",
"- characterized by a very complicated or involved arrangement of parts, units, etc.: complex machinery. \n",
"- so complicated or intricate as to be hard to understand or deal with: a complex problem. \n",
"\t\t\t\tSource: Dictionary.com\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"\n",
"# Complexity\n",
"\n",
"a scientific theory which asserts that some systems display behavioral phenomena that are completely inexplicable by any conventional analysis of the systems’ constituent parts. These phenomena, commonly referred to as emergent behaviour, seem to occur in many complex systems involving living organisms, such as a stock market or the human brain.\n",
" \n",
"Source: John L. Casti, Encyclopædia Britannica\n",
" \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# COMPLEX SYSTEMS\n",
"\n",
"- society\n",
"- brain\n",
"- market\n",
"- cell\n",
"\n",
"## Stephen Hawking: I think the next century will be the century of complexity. "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Behind each complex system there is a network, that defines the interactions between the component. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"
\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# VULNERABILITY \n",
"DUE TO INTERCONNECTIVITY \n",
"\n",
"- The 2003 blackout is a typical example of a cascading failure. \n",
"- 1997, when the International Monetary Fund pressured the central banks of several Pacific nations to limit their credit. \n",
"- 2009-2011 financial melt-down"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"An important theme of this class: \n",
"\n",
"- we must understand **how network structure affects the robustness of a complex system**. \n",
"\n",
"- develop quantitative tools to assess the interplay between network structure and the dynamical processes on the networks, and their impact on failures. \n",
"\n",
"- We will learn that failures reality failures follow reproducible laws, that can be quantified and even predicted using the tools of network science.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"NETWORKS AT THE HEART OF \n",
"# COMPLEX SYSTEMS \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Complex\n",
"\n",
"[adj., v. kuh m-pleks, kom-pleks; n. kom-pleks] \n",
"–adjective \n",
"- composed of many interconnected parts; compound; composite: a complex highway system. \n",
"- characterized by a very complicated or involved arrangement of parts, units, etc.: complex machinery. \n",
"- so complicated or intricate as to be hard to understand or deal with: a complex problem. \n",
"\t\t\t\tSource: Dictionary.com\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"\n",
"# Complexity\n",
"\n",
"a scientific theory which asserts that some systems display behavioral phenomena that are completely inexplicable by any conventional analysis of the systems’ constituent parts. These phenomena, commonly referred to as emergent behaviour, seem to occur in many complex systems involving living organisms, such as a stock market or the human brain.\n",
" \n",
"Source: John L. Casti, Encyclopædia Britannica\n",
" \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# COMPLEX SYSTEMS\n",
"\n",
"- society\n",
"- brain\n",
"- market\n",
"- cell\n",
"\n",
"## Stephen Hawking: I think the next century will be the century of complexity. "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Behind each complex system there is a network, that defines the interactions between the component. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"- Social graph\n",
"- Organization\n",
"- Brain\n",
"- finantial network\n",
"- business \n",
"- Internet\n",
"- Genes"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Behind each system studied in complexity there is an intricate wiring diagram, or a network, that defines the interactions between the component. \n",
"\n",
"# We will never understand complex system unless we map out and understand the networks behind them.\n",
" \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# TWO FORCES HELPED THE EMERGENCE OF NETWORK SCIENCE \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE HISTORY OF NETWORK ANALYSIS\n",
"\n",
"- Graph theory: 1735, Euler\n",
"\n",
"- Social Network Research: 1930s, Moreno\n",
"\n",
"- Communication networks/internet: 1960s\n",
"\n",
"- Ecological Networks: May, 1979.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"\n",
"While the study of networks has a long history from graph theory to sociology, **the modern chapter of network science emerged only during the first decade of the 21st century, following the publication of two seminal papers in 1998 and 1999**. \n",
"\n",
"The explosive interest in network science is well documented by the citation pattern of two classic network papers, the 1959 paper by Paul Erdos and Alfréd Rényi that marks the beginning of the study of random networks in graph theory [4] and the 1973 paper by Mark Granovetter, the most cited social network paper [5]. \n",
"\n",
"Both papers were hardly or only moderately cited before 2000. The explosive growth of citations to these papers in the 21st century documents the emergence of network science, drawing a new, interdisciplinary audience to these classic publications. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"- Social graph\n",
"- Organization\n",
"- Brain\n",
"- finantial network\n",
"- business \n",
"- Internet\n",
"- Genes"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Behind each system studied in complexity there is an intricate wiring diagram, or a network, that defines the interactions between the component. \n",
"\n",
"# We will never understand complex system unless we map out and understand the networks behind them.\n",
" \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# TWO FORCES HELPED THE EMERGENCE OF NETWORK SCIENCE \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE HISTORY OF NETWORK ANALYSIS\n",
"\n",
"- Graph theory: 1735, Euler\n",
"\n",
"- Social Network Research: 1930s, Moreno\n",
"\n",
"- Communication networks/internet: 1960s\n",
"\n",
"- Ecological Networks: May, 1979.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"\n",
"While the study of networks has a long history from graph theory to sociology, **the modern chapter of network science emerged only during the first decade of the 21st century, following the publication of two seminal papers in 1998 and 1999**. \n",
"\n",
"The explosive interest in network science is well documented by the citation pattern of two classic network papers, the 1959 paper by Paul Erdos and Alfréd Rényi that marks the beginning of the study of random networks in graph theory [4] and the 1973 paper by Mark Granovetter, the most cited social network paper [5]. \n",
"\n",
"Both papers were hardly or only moderately cited before 2000. The explosive growth of citations to these papers in the 21st century documents the emergence of network science, drawing a new, interdisciplinary audience to these classic publications. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE EMERGENCE OF NETWORK SCIENCE\n",
"- Movie Actor Network, 1998;\n",
"- World Wide Web, 1999.\n",
"- C elegans neural wiring diagram 1990\n",
"- Citation Network, 1998\n",
"- Metabolic Network, 2000; \n",
"- PPI network, 2001\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# The universality of network characteristics: \n",
"The architecture of networks emerging in various domains of science, nature, and technology are more similar to each other than one would have expected. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE CHARACTERISTICS OF NETWORK SCIENCE \n",
"- Interdisciplinary \n",
"- Empirical\n",
"- Quantitative and Mathematical \n",
"- Computational \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE IMPACT OF NETWORK SCIENCE \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Google\n",
"Market Cap(2010 Jan 1): \n",
"$189 billion\n",
"\n",
"# Cisco Systems\n",
"networking gear Market cap (Jan 1, 2919): \n",
"$112 billion\n",
"\n",
"# Facebook\n",
"market cap: \n",
"$50 billion\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Health: From drug design to metabolic engineering. \n",
"The human genome project, completed in 2001, offered the first comprehensive list of all human genes. \n",
"\n",
"- Yet, to fully understand how our cells function, and the origin of disease, we need accurate maps that tell us how these genes and other cellular components interact with each other. "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Security: Fighting Terrorism. \n",
"Terrorism is one of the maladies of the 21st century, absorbing significant resources to combat it worldwide. \n",
"\n",
"- **Network thinking** is increasingly present in the arsenal of various law enforcement agencies in charge of limiting terrorist activities. \n",
" - It is used to disrupt the financial network of terrorist organizations, to map terrorist networks, and to uncover the role of their members and their capabilities. \n",
" - While much of the work in this area is classified, several success stories have surfaced. Examples include the use of social networks to capture Saddam Hussein or \n",
" - the capture of the individuals behind the March 11, 2004 Madrid train bombings through the examination of the mobile call network. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Epidemics: From forecasting to halting deadly viruses. \n",
"While the H1N1 pandemic was not as devastating as it was feared at the beginning of the outbreak in 2009, it gained a special role in the history of epidemics: it was the first pandemic whose course and time evolution was accurately predicted months before the pandemic reached its peak. \n",
"- This was possible thanks to fundamental advances in understanding the role of networks in the spread of viruses. \n",
"- Indeed, before 2000 epidemic modeling was dominated by compartment models, assuming that everyone can infect everyone else one word the same socio-physical compartment. \n",
"- The emergence of a network-based framework has fundamentally changed this, offering a new level of predictability in epidemic phenomena. \n",
"\n",
"In January 2010 network science tools have predicted the conditions necessary for the emergence of viruses spreading through mobile phones. \n",
" - The first major mobile epidemic outbreak that started in the fall of 2010 in China, infecting over 300,000 phones each day, closely followed the predicted scenario. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Brain Research: Mapping neural network. \n",
"The human brain, consisting of hundreds of billions of interlinked neurons, is one of the least understood networks from the perspective of network science. \n",
"\n",
"The reason is simple: \n",
"- we lack maps telling us which neurons link to each other. \n",
"- The only fully mapped neural map available for research is that of the C.Elegans worm, with only 300 neurons. \n",
"\n",
"Driven by the potential impact of such maps, in 2010 the **National Institutes of Health** has initiated the Connectome project, aimed at developing the technologies that could provide an accurate neuron-level map of mammalian brains. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# The Bridges of Konigsberg\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE EMERGENCE OF NETWORK SCIENCE\n",
"- Movie Actor Network, 1998;\n",
"- World Wide Web, 1999.\n",
"- C elegans neural wiring diagram 1990\n",
"- Citation Network, 1998\n",
"- Metabolic Network, 2000; \n",
"- PPI network, 2001\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# The universality of network characteristics: \n",
"The architecture of networks emerging in various domains of science, nature, and technology are more similar to each other than one would have expected. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE CHARACTERISTICS OF NETWORK SCIENCE \n",
"- Interdisciplinary \n",
"- Empirical\n",
"- Quantitative and Mathematical \n",
"- Computational \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# THE IMPACT OF NETWORK SCIENCE \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Google\n",
"Market Cap(2010 Jan 1): \n",
"$189 billion\n",
"\n",
"# Cisco Systems\n",
"networking gear Market cap (Jan 1, 2919): \n",
"$112 billion\n",
"\n",
"# Facebook\n",
"market cap: \n",
"$50 billion\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Health: From drug design to metabolic engineering. \n",
"The human genome project, completed in 2001, offered the first comprehensive list of all human genes. \n",
"\n",
"- Yet, to fully understand how our cells function, and the origin of disease, we need accurate maps that tell us how these genes and other cellular components interact with each other. "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Security: Fighting Terrorism. \n",
"Terrorism is one of the maladies of the 21st century, absorbing significant resources to combat it worldwide. \n",
"\n",
"- **Network thinking** is increasingly present in the arsenal of various law enforcement agencies in charge of limiting terrorist activities. \n",
" - It is used to disrupt the financial network of terrorist organizations, to map terrorist networks, and to uncover the role of their members and their capabilities. \n",
" - While much of the work in this area is classified, several success stories have surfaced. Examples include the use of social networks to capture Saddam Hussein or \n",
" - the capture of the individuals behind the March 11, 2004 Madrid train bombings through the examination of the mobile call network. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Epidemics: From forecasting to halting deadly viruses. \n",
"While the H1N1 pandemic was not as devastating as it was feared at the beginning of the outbreak in 2009, it gained a special role in the history of epidemics: it was the first pandemic whose course and time evolution was accurately predicted months before the pandemic reached its peak. \n",
"- This was possible thanks to fundamental advances in understanding the role of networks in the spread of viruses. \n",
"- Indeed, before 2000 epidemic modeling was dominated by compartment models, assuming that everyone can infect everyone else one word the same socio-physical compartment. \n",
"- The emergence of a network-based framework has fundamentally changed this, offering a new level of predictability in epidemic phenomena. \n",
"\n",
"In January 2010 network science tools have predicted the conditions necessary for the emergence of viruses spreading through mobile phones. \n",
" - The first major mobile epidemic outbreak that started in the fall of 2010 in China, infecting over 300,000 phones each day, closely followed the predicted scenario. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Brain Research: Mapping neural network. \n",
"The human brain, consisting of hundreds of billions of interlinked neurons, is one of the least understood networks from the perspective of network science. \n",
"\n",
"The reason is simple: \n",
"- we lack maps telling us which neurons link to each other. \n",
"- The only fully mapped neural map available for research is that of the C.Elegans worm, with only 300 neurons. \n",
"\n",
"Driven by the potential impact of such maps, in 2010 the **National Institutes of Health** has initiated the Connectome project, aimed at developing the technologies that could provide an accurate neuron-level map of mammalian brains. \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# The Bridges of Konigsberg\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"# Can one walk across the seven bridges and never cross the same bridge twice and get back to the starting place? \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Can one walk across the seven bridges and never cross the same bridge twice and get back to the starting place? \n",
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"# Can one walk across the seven bridges and never cross the same bridge twice and get back to the starting place? \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"Can one walk across the seven bridges and never cross the same bridge twice and get back to the starting place? \n",
"\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Euler’s theorem (1735):\n",
"\n",
"- If a graph has more than two nodes of odd degree, there is no path. \n",
"- If a graph is connected and has no odd degree nodes, it has at least one path.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"COMPONENTS OF A COMPLEX SYSTEM\n",
"\n",
"# Networks and graphs\n",
" - components: nodes, vertices\t\t N\n",
" - interactions: links, edges\t\t\t L\n",
" - system: \t network, graph\t\t(N,L)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"network often refers to real systems\n",
"- www, \n",
"- social network\n",
"- metabolic network. \n",
"\n",
"Language: (Network, node, link)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"graph: mathematical representation of a network\n",
"- web graph, \n",
"- social graph (a Facebook term)\n",
"\n",
"Language: (Graph, vertex, edge)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Euler’s theorem (1735):\n",
"\n",
"- If a graph has more than two nodes of odd degree, there is no path. \n",
"- If a graph is connected and has no odd degree nodes, it has at least one path.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"COMPONENTS OF A COMPLEX SYSTEM\n",
"\n",
"# Networks and graphs\n",
" - components: nodes, vertices\t\t N\n",
" - interactions: links, edges\t\t\t L\n",
" - system: \t network, graph\t\t(N,L)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"network often refers to real systems\n",
"- www, \n",
"- social network\n",
"- metabolic network. \n",
"\n",
"Language: (Network, node, link)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"graph: mathematical representation of a network\n",
"- web graph, \n",
"- social graph (a Facebook term)\n",
"\n",
"Language: (Graph, vertex, edge)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# CHOOSING A PROPER REPRESENTATION\n",
"\n",
"The choice of the proper network representation determines our ability to use network theory successfully.\n",
"\n",
"In some cases there is a unique, unambiguous representation. \n",
"In other cases, the representation is by no means unique.\n",
" \n",
"For example, the way we assign the links between a group of individuals will determine the nature of the question we can study.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"If you connect individuals that work with each other, you will explore the professional network.\n",
"\n",
"http://www.theyrule.net"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"If you connect those that have a romantic and sexual relationship, you will be exploring the sexual networks.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"If you connect individuals based on their first name (all Peters connected to each other), you will be exploring what? \n",
"\n",
"# It is a network, nevertheless.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# UNDIRECTED VS. DIRECTED NETWORKS\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Undirected\n",
"Links: undirected\n",
"- coauthorship \n",
"- actor network\n",
"- protein interactions"
]
},
{
"cell_type": "code",
"execution_count": 174,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8jWfi///3sWZppNZq7VuoiSifhEQYSxwtLR1MVami\n1cV00SVIPv11WjOjifKp6rSfzPCZaUqULkopGU0EERGNNWFobGN9WEoQTVKS3N8/6PmphiLLdZbX\n8/HwUOfcOed9HjTvXNd93fdlsyzLEgAAMKKK6QAAAHgyihgAAIMoYgAADKKIAQAwiCIGAMAgihgA\nAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIG\nAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKI\nAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMo\nYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKpmOgAAwDmdPHlSc+PjlZOVpQvnzukOf38FBAVp9Nix\nql+/vul4bsNmWZZlOgQAwHlkZmZqVkyMlicmaoikkMJC+UnKk/Stt7cWW5Ye7N9fE6KjFRISYjit\n66OIAQAOs+Pi9GZkpCYXFGi0Zal2KcfkSoq32fSOt7emzJihZ8aPr+yYboUiBgBIulzC0yIjtTI/\nX61v4vi9ku738dFkyrhMKGIAgDIzMzWoVy+tu6aER0lKlpQvqZ6kJyW9ftXzeyX18PHRsrVrFRwc\nXHmB3QirpgEAmhUTo8kFBb8YCUdLOiDpnKRESX+VtPKq51tLmlRQoFkxMZUT1A0xIgYAD3fy5Em1\nbdZM+wsLSz0n/JPvJPWV9JWkzlc9fkZSKy8v5Rw6xGrq28CIGAA83Nz4eA2WrlvCz0vylRSoy9PS\nna95vo6kwTab5sbHV1hGd0YRA4CHy8nKUpfCwus+/6GkC7p8rvj/k5RZyjEhBQXKyc6umIBujiIG\nAA934dw5+f3KMTZJPSU9ImlBKc/7ScrLzS3vaB6BIgYAD3eHv7/ybvLYIkk+pTyeJ8mv9o3OMON6\nKGIA8HABQUH61svrF4+fkvSppB8klejyaunPJT1cymtkensroEOHiozptlg1DQAe7nqrpr+X9HtJ\nWZIsSW0kvSFp4DVfz6rpsmFEDAAerkGDBnqwf3/F22w/e7yepDW6XLS5kr7VL0tYkj622fTQgAGU\n8G2iiAEACouI0BTL0t5b/Lq9kt7x9taE6OiKiOURKGIA8HBz5szRn//8Z417+WXd7+Nz02X8072m\np8yYwe0ty4D9iAHAQxUXF2vSpEn6+uuvtW7dOrVp00YBAQHqERmpSQUFGnOd3ZfO6PLuS9PZfalc\nsFgLADxQXl6eRowYofz8fH3xxReqfdWlR5s2bdKsmBh9vWKFBttsCikocOxHnHllP+KHBgzQhOho\nRsLlgCIGAA9z6NAhDRw4UKGhofrggw9UvXr1Uo87deqU5sbHKyc7W3m5ufKrXVsBHTroiTFjWJhV\njihiAPAgGzdu1JAhQxQZGamXX35ZtmtWSqPycY4YADzEp59+qhdeeEH//Oc/NXBgaRciwQSKGADc\nnGVZ+vOf/6x//OMfWrVqlYKCgkxHwlUoYgBwY4WFhXryySe1b98+bdy4UQ0bNjQdCdfgOmIAcFMn\nTpxQnz59VFJSojVr1lDCTooiBgA3tGPHDoWGhqpfv35asGCBvL29TUfCdTA1DQBuZsWKFRozZoze\ne+89jRgxwnQc/AqKGADchGVZev/99zVt2jR99dVXCgsLMx0JN4EiBgA3cOnSJb300ktKS0tTenq6\nmjdvbjoSbhJFDAAu7uzZs3rkkUdUvXp1rV+/XrVq1TIdCbeAxVoA4ML27dunsLAw/eY3v9HSpUsp\nYRdEEQOAi0pNTVV4eLgmTJig9957T9WqMcnpivhbAwAXFB8fr8mTJ2v+/Pnq27ev6TgoA4oYAFxI\nSUmJXn/9dX3++edau3at2rVrZzoSyogiBgAX8cMPP2jUqFH6/vvvlZGRoXr16pmOhHLAOWIAcAFH\njx5Vjx495O/vr6SkJErYjVDEAODkNm/erNDQUD366KP65z//qZo1a5qOhHLE1DQAOLEvv/xSzz77\nrGbPnq3BgwebjoMKQBEDgBOyLEvTpk3Thx9+qJUrV6pz586mI6GCUMQA4GR+/PFHPfvss8rOzlZG\nRoYaNWpkOhIqEOeIAcCJfP/997Lb7crLy1Nqaiol7AEoYgBwErt27VLXrl3VvXt3ff755/L19TUd\nCZWAqWkAcAJJSUkaOXKkpk+frtGjR5uOg0rEiBgADIuLi9OoUaO0aNEiStgDMSIGAEOKior02muv\n6ZtvvtH69evVqlUr05FgAEUMAAacP39ew4cPV1FRkTZs2KA777zTdCQYwtQ0AFSy//znP+rWrZua\nN2+uFStWUMIejiIGgEqUnp6ubt266dlnn9WHH37IHsJgahoAKsv8+fP1yiuv6OOPP1b//v1Nx4GT\noIgBoIKVlJTorbfe0rx585SSkqLAwEDTkeBEKGIAqEAFBQUaM2aMDh8+rI0bN6pBgwamI8HJcI4Y\nACrI8ePH1atXL1WrVk0pKSmUMEpFEQNABdi+fbu6du2qgQMHKiEhQV5eXqYjwUkxNQ0A5WzZsmV6\n6qmn9MEHH2jYsGGm48DJUcQAUE4sy9LMmTP1P//zP/r666/VpUsX05HgAihiACgHly5d0vPPP6+N\nGzdqw4YNatq0qelIcBEUMQCU0ZkzZ/TII4/I19dXaWlp8vPzMx0JLoTFWgBQBjk5OQoNDVWnTp20\nePFiShi3jCIGgNu0evVq9ejRQxMnTtSMGTNUtWpV05HggpiaBoDb8H//9396/fXXtXDhQvXu3dt0\nHLgwihgAbkFxcbGioqL01Vdfad26dQoICDAdCS6OIgaAm3ThwgWNHDlSeXl5ysjIUJ06dUxHghvg\nHDEA3ITDhw+re/fuql+/vv71r39Rwig3FDEA/IrMzEyFhYVp1KhRmjNnjmrUqGE6EtwIU9MAcAOf\nffaZnn/+ef3jH//QoEGDTMeBG6KIAaAUlmVp6tSpmj17tpKSknTfffeZjgQ3RREDwDUKCws1btw4\n5eTkaOPGjbr77rtNR4Ib4xwxAFzl5MmTioiI0MWLF7V27VpKGBWOIgaAK3bu3KnQ0FBFRERo4cKF\n8vb2Nh0JHoCpaQCQ9K9//UtPPPGEZs6cqZEjR5qOAw9CEQPweB988IGmTp2qxYsXKzw83HQceBiK\nGIDHKioq0oQJE7RmzRqlp6erRYsWpiPBA1HEADzS2bNn9eijj6pKlSpKT0+Xv7+/6UjwUCzWAuBx\n9u/fr27duqldu3ZatmwZJQyjKGIAHiUtLU3h4eF64YUXNGvWLFWrxsQgzOJfIACPMXfuXEVGRioh\nIUH9+vUzHQeQRBED8AAlJSV64403tHDhQq1Zs0bt27c3HQlwoIgBuLX8/Hw98cQTOnHihDIyMlS/\nfn3TkYCf4RwxALd17Ngx/fa3v5Wvr6+Sk5MpYTglihiAW9qyZYu6du2qoUOHKj4+XjVr1jQdCSgV\nU9MA3M6SJUv09NNP629/+5uGDh1qOg5wQxQxALdhWZamT5+u999/X4mJiQoODjYdCfhVFDEAt3Dx\n4kU999xz2rZtmzIyMtS4cWPTkYCbQhEDcHmnT5/WkCFDVKdOHa1bt06+vr6mIwE3jcVaAFza7t27\nFRoaqrCwMC1atIgShsuhiAG4rOTkZPXs2VP//d//rdjYWFWpwrc0uB7+1QJwSX//+9/1+OOP67PP\nPtPYsWNNxwFuG+eIAbiU4uJiRUZGKjExUWlpaWrdurXpSECZUMQAXEZeXp4ee+wxFRYWasOGDapd\nu7bpSECZMTUNwCUcPHhQ4eHhaty4sRITEylhuA2KGIDTy8jIUFhYmJ566inFxcWpevXqpiMB5Yap\naQBObeHChXrppZf00Ucf6cEHHzQdByh3FDEAp2RZlqZMmaL4+HitWrVKHTp0MB0JqBAUMQCnU1BQ\noCeffFL/+c9/tHHjRt11112mIwEVhnPEAJzK8ePH1bt3b0lSSkoKJQy3RxEDcBpZWVkKDQ1V//79\n9cknn8jb29t0JKDCMTUNwCksX75cY8eO1fvvv6/hw4ebjgNUGooYQLk7efKk5sbHKycrSxfOndMd\n/v4KCArS6LFjVb9+/Z8da1mWZs2apXfeeUdLly5VaGioodSAGTbLsizTIQC4h8zMTM2KidHyxEQN\nkRRSWCg/SXmSvvX21mLL0oP9+2tCdLRCQkJ06dIlvfjii0pPT9eyZcvUrFkzw58AqHwUMYByMTsu\nTm9GRmpyQYFGW5ZKu+9VrqR4m03veHtr0p/+pOWJifLy8tKCBQvk5+dX2ZEBp0ARAyiz2XFxmhYZ\nqZX5+bqZLRj2SvqtzabA3r2V+M03qlq1akVHBJwWq6YBlElmZqbevEEJ75HkLemJqx5rLSnVspSd\nkaGtW7dWSk7AWVHEAMpkVkyMJhcUXHck/IKkLqU83lrSpIICzYqJqbhwgAtgahrAbTt58qTaNmum\n/YWFpZ4TXihpiaT2ujwdPfea589IauXlpZxDh36xmhrwFIyIAdy2ufHxGiyVWsLnJb0p6V1J1/tp\nv46kwTab5sbHV0xAwAVQxABuW05WlroUFpb63B8lPS3pnl95jZCCAuVkZ5d3NMBlcEMPALftwrlz\nKu2io22Skq/8/mv8JOXl5pZrLsCVUMQAbpuPn5/ySnl8raSDkprq8rT0BUnFkv4tadM1x+ZJ8qtd\n2uQ24BkoYgA3zbIs7d69W0lJSUpKSlJyUpLybTY9d82az2clPXbVn6frcjH/rZTXzPT21m/Yaxge\njFXTAG7oxIkTSk5Ovly8ycmqWrWq7Ha77Ha7goKC1K1z5+uumv7JFEn7xKppoDQUMYCfyc/PV2pq\nqqN8Dx06pF69ejnKt3Xr1rLZbI7jHx8yRMFLlujl2/hWMtNm05bBgzVv0aLy/AiAS6GIAQ9XXFys\nrVu3OqabMzMz1alTJ0fxBgcHq1q165/FyszM1KBevbTuJm9v+ZO9knr4+GjZ2rUKDg4u8+cAXBVF\nDHigAwcOOIo3JSVFDRs2VN++fWW329WzZ89b3oDhdu41fb+PjybPmKFnxo+/rc8AuAuKGPAAubm5\nSklJcZznvXDhgqN4+/btq0aNGpX5PX7afWliQYHGXmf3pTO6vPvSdG9vTaGEAUkUMeCWLl68qPT0\ndMd53l27dik8PNwx3RwYGPiz87zlZdOmTXpy+HAdOHhQj1SvrpCCAsd+xJlX9iN+aMAATYiOZjoa\nuIIiBtyAZVnauXOnY7o5LS1N7dq1c4x4u3Xrppo1a1Z4jkuXLqlx48ZaunSp0lJTlZOdrbzcXPnV\nrq2ADh30xJgxrI4GrkERAy7q2LFjP7usyNvb2zHi7dOnj+rUqVPpmZYvX66pU6cqPT290t8bcFXc\n0ANwERcuXNDatWsd5Xvs2DH16dNHdrtdU6ZMUcuWLU1HVEJCgh5//HHTMQCXwogYcFJFRUXavHmz\nY7p5y5YtCg4Odkw3/9d//ZeqVq1qOqbD+fPn1aRJE+3fv19169Y1HQdwGYyIASdhWZb27dvnKN7V\nq1erSZMm6tu3r6KiovTb3/5Wvr6+pmNe15dffqlevXpRwsAtoogBg06fPq1Vq1Y5ppt//PFH2e12\nDRkyRP/7v/+rhg0bmo540+bNm6fxXI4E3DKmpoFKVFhYqPT0dMeod8+ePerRo4djkdW9995bIZcV\nVbQjR44oKChIx44dk5eXl+k4gEthRAxUoJKSEmVnZzuKNz09XYGBgbLb7Xr33XcVGhqqGjVqmI5Z\nZgsWLNDQoUMpYeA2MCIGytmRI0cclxQlJyerVq1ajhFv7969deedd5qOWO6CgoL017/+VT179jQd\nBXA5FDFQRufPn9fatWsdo95Tp04pIiLCsbq5efPmpiNWqKysLA0cOFAHDhxQlSpVTMcBXA5T08At\nKioq0rfffuso3u3bt6tr166y2+1KSEhQp06dPKqQ5s2bp5EjR3rUZwbKEyNi4FdYlqWcnBxH8a5d\nu1bNmzd3TDd3795dPj4+pmMaUVxcrKZNmyopKUnt27c3HQdwSYyIgVKcOnXKcY43KSlJlmXJbrdr\n+PDhmjNnjho0aGA6olNYvXq1GjZsSAkDZUARA5IKCgqUlpbmGPUeOHBAPXv2lN1u16RJkxQQEOCS\nlxVVNG5pCZQdU9PwSCUlJdq2bZujeDdu3KiOHTs69ujt0qWLqlevbjqmU8vPz1ejRo20a9cul7rx\nCOBsGBHDYxw8eNBxWdGqVatUt25d2e12vfTSS+rVq5dq1aplOqJL+eqrr9S1a1dKGCgjihhu6+zZ\ns1qzZo1j1Hv27Fn17dtX999/v6ZPn64mTZqYjujS5s2bp1GjRpmOAbg8pqbhNi5duqSMjAxH8e7Y\nsUPdunVzXM8bFBTEJTbl5MSJE2rbtq2OHj3q1BtRAK6AETFclmVZ2rVrl2O6OTU1Va1bt5bdbtdf\n/vIXhYeHc8vFCvLpp59q0KBBlDBQDhgRw6UcP35cq1atcpRvtWrVHNfz9unTR/Xq1TMd0SOEhIRo\n6tSp6tevn+kogMujiOHU8vPzlZqa6phuPnz4sHr37u2Ybm7dujWXFVWy3bt3q0+fPjp8+LCqVq1q\nOg7g8piahlMpLi7Wli1bHMWbmZmpzp07y263a/bs2QoODla1avyzNSkhIUGPPfYYJQyUE0bEMG7/\n/v2OqeaUlBQ1bNjQMd3cs2dP3XHHHaYj4oqSkhK1atVKixcv1n333Wc6DuAWGFqg0uXm5iolJcUx\n6s3Pz1ffvn01cOBAzZo1S/fcc4/piLiO9evXy9fXVx07djQdBXAbFDEq3I8//qgNGzY4inf37t0K\nDw+X3W7X888/r8DAQM7zuoiEhASNGjWKvy+gHDE1jXJnWZZ27NjhmG5OS0tTu3btHNPNYWFhqlmz\npumYuEWFhYVq1KiRtm3bxs1QgHLEiBjl4tixY46dipKTk+Xj4yO73a6nnnpKCQkJqlOnjumIKKMV\nK1aoY8eOlDBQzihi3JYLFy5o7dq1junm48ePq0+fPrLb7ZoyZYpatmxpOiLK2bx589hpCagATE3j\nphQVFWnTpk2OEe+WLVsUHBzsmG7u3Lkzl7O4sTNnzqhFixY6dOiQ/P39TccB3AojYhdw8uRJzY2P\nV05Wli6cO6c7/P0VEBSk0WPHqn79+hXynpZlae/evY7p5tWrV6tJkyay2+2Kjo5Wjx49uL2hB/n8\n88/1wAMPUMJABWBE7MQyMzM1KyZGyxMTNURSSGGh/CTlSfrW21uLLUsP9u+vCdHRCgkJKfP7nT59\n2nH7yKSkJF26dMkx4o2IiGC7Ow/WvXt3TZ48WQMHDjQdBXA7FLGTmh0XpzcjIzW5oECjLUu1Szkm\nV1K8zaZ3vL01ZcYMPTN+/C29R2FhodavX++Ybt6zZ4969OjhKN97772Xy1Sg/fv3q2vXrjp27Jiq\nV69uOg7gdpiadkKz4+I0LTJS6/Lz1foGx9WW9IplaWB+vu6PjJSkG5ZxSUmJsrKyHNPN6enpCgwM\nlN1u18yZM9W1a1fVqFGjfD8MXN78+fP16KOPUsJABWFE7GQyMzM1qFevn5XwRUl/kJSsy6PgVpLe\nlvTAVV+3V1IPHx8tW7tWwcHBjsePHDnimGpetWqV/P39HSPeXr166c4776ycDwaXZFmW2rVrp7lz\n56pr166m4wBuiRGxk5kVE6PJBQU/GwkXSWoqaZ2kJpKWSxomaceVxyWptaRJBQWa8ac/acS4cY7y\nPX36tCIiItS3b1/FxMSoWbNmlflx4OIyMzNlWZa6dOliOgrgthgRO5GTJ0+qbbNm2l9YWOo54at1\nlPSWpMFXPXZGUiNJIT166MEHH5Tdbtd9992nKlWqVFBiuLuXXnpJ9erV0x//+EfTUQC3xYjYicyN\nj9dg6VdL+ISkPZJ+c83jdSQN9/JS4MCBem3ixIqICA9y6dIlLVy4UBs2bDAdBXBrDJWcSE5WlroU\nFt7wmCJJj0saIymglOe7FBYqJzu7/MPB43zzzTdq06aNWrVqZToK4NYoYidy4dw5+d3geUuXS7im\npL9e5xg/SXm5ueUdDR6IW1oClYMidiJ3+Psr7wbPPyXpe0lfSrrezSTzJPnV/rXJbeDGzp8/r8TE\nRA0bNsx0FMDtUcROJCAoSN96eZX63HOSdktaKulGV/pmensroEOHCkgHT/Lll1+qd+/eqlu3ruko\ngNtj1bQTud6q6UOSmkvy0v8/ErZJ+rukx6467oykZtWqacu//602bdpURmS4qYiICI0fP16///3v\nTUcB3B4jYifSoEEDPdi/vz6+5raSTSWVSMrX5annPEnn9fMSli7f7rJJo0YKDQ3VxIkTdezYscqI\nDTdz5MgRbd26VQ899JDpKIBHoIidzIToaE3z9tbeW/y6vZKme3tr7hdfaNu2bSoqKlJgYKCefvpp\n5eTkVERUuKlPPvlEQ4cOldd1TpMAKF8UsZMJCQnRlBkzdL+Pz02X8V5J9/v4aMqMGQoODlaTJk00\nc+ZM7dmzR40bN1b37t31yCOPaNOmTRUZHW4iISFBo0aNMh0D8BgUsRN6Zvx4TZ4xQz18fDTTZtP1\nLkY6I+ldm009fHw0uZTdl+rWras333xTBw4cUPfu3TVkyBDZ7XatWrVKLA1AabZv365z586pe/fu\npqMAHoPFWk5s06ZNmhUTo69XrNBgm00hBQWO/Ygzr+xH/NCAAZoQHf2zjR6u5+LFi1qwYIGmTZsm\nX19fRUVF6Xe/+52qVr3exVDwNBMnTlSNGjU0depU01EAj0ERu4BTp05pbny8crKzlZebK7/atRXQ\noYOeGDNG9evXv+XXKykp0bJlyxQTE6Pc3FxNmjRJjz/+uGrWrFkB6eEqiouL1bRpUyUnJ+vee+81\nHQfwGBSxB7MsS6mpqYqNjVV2drZeeeUVPfPMM/Lzu9H9veCukpOTFRUVxVoCoJJxjtiD2Ww29ezZ\nU4mJiVq2bJk2bdqkli1b6o033tCpU6dMx0Ml45aWgBkUMSRJnTp10oIFC5SRkaHvv/9ebdu21Ysv\nvqiDBw+ajoZK8MMPP2jp0qV67LFrr04HUNEoYvxMq1atFBcXp507d8rX11edO3fWE088oR07dpiO\nhgq0dOlShYaG6q677jIdBfA4FDFKdffddys2Nlb79u1T+/btZbfbNWjQIKWnp5uOhgowb948rh0G\nDGGxFm5KQUGBPv74Y02fPl2NGjVSVFSU+vfvL9s1t+OE6zlx4oTatWunI0eOyNfX13QcwONQxLgl\nRUVF+uKLLxQbG6uSkhJFRUVp2LBhqlatmulouE2zZs3Sli1b9PHHH5uOAngkihi3xbIsrVy5UrGx\nsTp48KAmTpyosWPHytvb23Q03KKQkBC9/fbbstvtpqMAHolzxLgtNptNDzzwgNasWaNPPvlE33zz\njVq0aKG3335bZ8+eNR0PN2n37t06evSo+vTpYzoK4LEoYpRZWFiYlixZopSUFOXk5KhVq1aaNGkS\n2zC6gISEBI0YMYLbnAIGUcQoN+3bt1d8fLy2bt2qixcvKjAwUM8884z27NljOhpKUVJSooSEBG7i\nARhGEaPcNW3aVO+9955ycnJ0zz33qFu3bho2bJg2b95sOhqusn79evn5+aljx46mowAejSJGhalX\nr57eeustHThwQGFhYXr44YfVr18/rV69mm0YncBPt7TkEjTALFZNo9JcvHhR8+fP17Rp0+Tv76+o\nqCg9/PDDqlKFnwcrW2FhoRo1aqRt27apSZMmpuMAHo3vgKg0NWrU0NixY/Xvf/9bUVFRiomJUfv2\n7fXRRx/p4sWLpuN5lBUrVqhjx46UMOAEKGJUuipVqmjw4MHauHGj4uLitHDhQrVq1UozZ87UhQsX\nTMfzCNzSEnAeTE3DKWzZskXTpk1TSkqK/vCHP+jFF19UvXr1TMdyS2fOnFHLli116NAh1apVy3Qc\nwOMxIoZT6Ny5sz799FOlp6fr+PHjCggI0IQJE3To0CHT0dzOZ599pgceeIASBpwERQyn0qZNG/39\n73/Xzp075eXlpU6dOmn06NHauXOn6Whug2uHAedCEcMp3X333Zo2bZr27dundu3aKSIiQg8//LA2\nbNhgOppL279/v3JycnT//febjgLgCooYTu3OO+9UdHS0Dhw4oAceeEAjR45Uz549lZiYyLXIt2H+\n/Pl69NFHVb16ddNRAFzBYi24lKKiIn322WeKjY1VlSpVNHnyZD3yyCNsw3gTLMtS27ZtlZCQoC5d\nupiOA+AKRsRwKdWqVdOIESO0fft2vf3224qLi1Pbtm31t7/9TYWFhabjObXMzExJl7c9BOA8KGK4\nJJvNpgEDBig1NVVz587VihUr1KJFC8XGxurcuXOm4zklbmkJOCempuE2duzYoXfeeUfLly/X008/\nrZdfflkNGzY0HcspXLp0SY0aNVJGRoZatmxpOg6AqzAihtsIDAzU3LlztXnzZuXn56t9+/Z67rnn\ntHfvXtPRjFu5cqXatGlDCQNOiCKG22nevLnef/99fffdd2rQoIHCwsI0fPhwbd261XQ0YxISEril\nJeCkmJqG28vLy9OcOXP07rvvKjAwUFFRUerZs6fHnCs9f/68mjZtqn379qlu3bqm4wC4BiNiuD0/\nPz+9+uqr2rdvn4YNG6Znn31WYWFhWrJkiUpKSkzHq3CLFi1S7969KWHASTEihscpLi7WkiVLFBMT\nox9++EGTJ0/WiBEjVKNGDdPRKkRERIT+8Ic/aOjQoaajACgFRQyPZVmWUlJSFBsbq++++06vvvqq\nxo0bpzvuuMN0tHJz5MgRdezYUUePHpWXl5fpOABKwdQ0PJbNZlNERISSkpL05Zdfav369WrZsqXe\neustnT4x8lf9AAAGfklEQVR92nS8cvHJJ59o6NChlDDgxChiQFJwcLA+//xzpaWl6ejRo2rTpo1e\neeUVHT582HS022ZZlubNm8dqacDJUcTAVQICAjRnzhxlZ2erWrVquu+++zR27Fjt2rXLdLRblpWV\npby8PIWHh5uOAuAGKGKgFI0aNdL06dO1d+9etW7dWr169dLgwYO1ceNG09Fu2k+3tKxShf/NAWfG\nYi3gJuTn5+ujjz7S9OnT1aJFC0VFRalfv35Oey1ycXGxmjRpolWrVunee+81HQfADfCjMnATfHx8\n9Pzzz2vPnj0aN26cIiMj1blzZ3366acqLi42He8XUlJSdM8991DCgAtgRAzcBsuytGLFCsXExOj4\n8eOaOHGiRo8e7TSrk0ePHq3OnTtrwoQJpqMA+BUUMVBGaWlpio2N1ebNm/Xyyy/rueeek7+/v7E8\nP/zwgxo3bqzdu3frrrvuMpYDwM1hahooo+7du+vrr7/WypUrlZ2drZYtWyo6OlrHjx83kuerr75S\nWFgYJQy4CIoYKCdBQUFKSEjQpk2blJeXp/bt22v8+PHat29fpeZISEjQ448/XqnvCeD2UcRAOWvR\nooU++OAD7d69W3Xr1lXXrl01YsQIbd++vcLf+8SJE9qwYYN+97vfVfh7ASgfFDFQQRo0aKC//OUv\n2r9/vzp37qwBAwZowIABSk1NVUUtzVi4cKEGDRokHx+fCnl9AOWPIgYqWK1atRQZGan9+/dryJAh\nGjdunMLDw7V06dJy34aRW1oCrodV00AlKy4u1uLFixUTE6PCwkJNnjxZjz32mKpXr37Tr3Hy5EnN\njY9XTlaWLpw7pzv8/eXfsKHmJSTo6NGjqlq1agV+AgDliSIGDLEsS6tWrVJsbKz27Nmj1157TU89\n9ZR8fX2v+zWZmZmaFROj5YmJGiIppLBQfpLyJK2vVk1LLEsPDxqkCdHRCgkJqayPAqAMKGLACXz7\n7beaNm2a1q1bpxdeeEEvvPCC6tSp87NjZsfF6c3ISE0uKNBoy1LtUl4nV1K8zaZ3vL01ZcYMPTN+\nfKXkB3D7OEcMOIEuXbpo0aJFSk1N1cGDB9W6dWu9+uqrOnLkiKTLJTwtMlLr8vP18nVKWJJqS3rF\nsrQuP1/TIiM1Oy6u0j4DgNvDiBhwQkeOHNHMmTP10UcfKTw8XJnJyUorLFTrq475UFK8pGxJIyT9\n85rX2Cuph4+Plq1dq+Dg4MoJDuCWUcSAEztz5oz6de+ux3bt0mvXPLdEl6e0Vkoq0C+LWJJm2mza\nMniw5i1aVNFRAdwmihhwYidPnlTbZs20v7DwutPRb0g6qtKL+IykVl5eyjl0SPXr16+wnABuH+eI\nASc2Nz5eg6XrlvCvqSNpsM2mufHx5RcKQLmiiAEnlpOVpS6FhWV6jZCCAuVkZ5dTIgDljSIGnNiF\nc+fkV8bX8JOUl5tbHnEAVACKGHBid/j7K6+Mr5Enya/27U5uA6hoFDHgxAKCgvStl1epzxVLKrzy\ne5GkH6/897Uyvb0V0KFDhWUEUDasmgac2I1WTU+58st21WNvSvrjVX9m1TTg/BgRA06sQYMGerB/\nf31ss/3iuTcllejyKPinX3+85piPbTY9NGAAJQw4MUbEgJPLzMzUoF69tC4//2d31vo13FkLcA2M\niAEnFxISoikzZuh+Hx/tvcmv2Svpfh8fTZkxgxIGnBxFDLiAZ8aP1+QZM9TDx0czbTZd72KkM5Le\ntdnUw8dHk9l9CXAJTE0DLmTTpk2aFROjr1es0GCbTSEFBY79iDO9vbXYsvTQgAGaEB3NSBhwERQx\n4IJOnTqlufHxysnOVl5urvxq11ZAhw56YswYFmYBLoYiBgDAIM4RAwBgEEUMAIBBFDEAAAZRxAAA\nGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEA\nAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUM\nAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQR\nAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZR\nxAAAGEQRAwBgEEUMAIBBFDEAAAb9P603wxJf3z2wAAAAAElFTkSuQmCC\n",
"text/plain": [
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# CHOOSING A PROPER REPRESENTATION\n",
"\n",
"The choice of the proper network representation determines our ability to use network theory successfully.\n",
"\n",
"In some cases there is a unique, unambiguous representation. \n",
"In other cases, the representation is by no means unique.\n",
" \n",
"For example, the way we assign the links between a group of individuals will determine the nature of the question we can study.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"If you connect individuals that work with each other, you will explore the professional network.\n",
"\n",
"http://www.theyrule.net"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"If you connect those that have a romantic and sexual relationship, you will be exploring the sexual networks.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"If you connect individuals based on their first name (all Peters connected to each other), you will be exploring what? \n",
"\n",
"# It is a network, nevertheless.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# UNDIRECTED VS. DIRECTED NETWORKS\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"# Undirected\n",
"Links: undirected\n",
"- coauthorship \n",
"- actor network\n",
"- protein interactions"
]
},
{
"cell_type": "code",
"execution_count": 174,
"metadata": {
"collapsed": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeIAAAFBCAYAAACrYazjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8jWfi///3sWZppNZq7VuoiSifhEQYSxwtLR1MVami\n1cV00SVIPv11WjOjifKp6rSfzPCZaUqULkopGU0EERGNNWFobGN9WEoQTVKS3N8/6PmphiLLdZbX\n8/HwUOfcOed9HjTvXNd93fdlsyzLEgAAMKKK6QAAAHgyihgAAIMoYgAADKKIAQAwiCIGAMAgihgA\nAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIG\nAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKI\nAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKKIAQAwiCIGAMAgihgAAIMo\nYgAADKKIAQAwiCIGAMAgihgAAIMoYgAADKpmOgAAwDmdPHlSc+PjlZOVpQvnzukOf38FBAVp9Nix\nql+/vul4bsNmWZZlOgQAwHlkZmZqVkyMlicmaoikkMJC+UnKk/Stt7cWW5Ye7N9fE6KjFRISYjit\n66OIAQAOs+Pi9GZkpCYXFGi0Zal2KcfkSoq32fSOt7emzJihZ8aPr+yYboUiBgBIulzC0yIjtTI/\nX61v4vi9ku738dFkyrhMKGIAgDIzMzWoVy+tu6aER0lKlpQvqZ6kJyW9ftXzeyX18PHRsrVrFRwc\nXHmB3QirpgEAmhUTo8kFBb8YCUdLOiDpnKRESX+VtPKq51tLmlRQoFkxMZUT1A0xIgYAD3fy5Em1\nbdZM+wsLSz0n/JPvJPWV9JWkzlc9fkZSKy8v5Rw6xGrq28CIGAA83Nz4eA2WrlvCz0vylRSoy9PS\nna95vo6kwTab5sbHV1hGd0YRA4CHy8nKUpfCwus+/6GkC7p8rvj/k5RZyjEhBQXKyc6umIBujiIG\nAA934dw5+f3KMTZJPSU9ImlBKc/7ScrLzS3vaB6BIgYAD3eHv7/ybvLYIkk+pTyeJ8mv9o3OMON6\nKGIA8HABQUH61svrF4+fkvSppB8klejyaunPJT1cymtkensroEOHiozptlg1DQAe7nqrpr+X9HtJ\nWZIsSW0kvSFp4DVfz6rpsmFEDAAerkGDBnqwf3/F22w/e7yepDW6XLS5kr7VL0tYkj622fTQgAGU\n8G2iiAEACouI0BTL0t5b/Lq9kt7x9taE6OiKiOURKGIA8HBz5szRn//8Z417+WXd7+Nz02X8072m\np8yYwe0ty4D9iAHAQxUXF2vSpEn6+uuvtW7dOrVp00YBAQHqERmpSQUFGnOd3ZfO6PLuS9PZfalc\nsFgLADxQXl6eRowYofz8fH3xxReqfdWlR5s2bdKsmBh9vWKFBttsCikocOxHnHllP+KHBgzQhOho\nRsLlgCIGAA9z6NAhDRw4UKGhofrggw9UvXr1Uo87deqU5sbHKyc7W3m5ufKrXVsBHTroiTFjWJhV\njihiAPAgGzdu1JAhQxQZGamXX35ZtmtWSqPycY4YADzEp59+qhdeeEH//Oc/NXBgaRciwQSKGADc\nnGVZ+vOf/6x//OMfWrVqlYKCgkxHwlUoYgBwY4WFhXryySe1b98+bdy4UQ0bNjQdCdfgOmIAcFMn\nTpxQnz59VFJSojVr1lDCTooiBgA3tGPHDoWGhqpfv35asGCBvL29TUfCdTA1DQBuZsWKFRozZoze\ne+89jRgxwnQc/AqKGADchGVZev/99zVt2jR99dVXCgsLMx0JN4EiBgA3cOnSJb300ktKS0tTenq6\nmjdvbjoSbhJFDAAu7uzZs3rkkUdUvXp1rV+/XrVq1TIdCbeAxVoA4ML27dunsLAw/eY3v9HSpUsp\nYRdEEQOAi0pNTVV4eLgmTJig9957T9WqMcnpivhbAwAXFB8fr8mTJ2v+/Pnq27ev6TgoA4oYAFxI\nSUmJXn/9dX3++edau3at2rVrZzoSyogiBgAX8cMPP2jUqFH6/vvvlZGRoXr16pmOhHLAOWIAcAFH\njx5Vjx495O/vr6SkJErYjVDEAODkNm/erNDQUD366KP65z//qZo1a5qOhHLE1DQAOLEvv/xSzz77\nrGbPnq3BgwebjoMKQBEDgBOyLEvTpk3Thx9+qJUrV6pz586mI6GCUMQA4GR+/PFHPfvss8rOzlZG\nRoYaNWpkOhIqEOeIAcCJfP/997Lb7crLy1Nqaiol7AEoYgBwErt27VLXrl3VvXt3ff755/L19TUd\nCZWAqWkAcAJJSUkaOXKkpk+frtGjR5uOg0rEiBgADIuLi9OoUaO0aNEiStgDMSIGAEOKior02muv\n6ZtvvtH69evVqlUr05FgAEUMAAacP39ew4cPV1FRkTZs2KA777zTdCQYwtQ0AFSy//znP+rWrZua\nN2+uFStWUMIejiIGgEqUnp6ubt266dlnn9WHH37IHsJgahoAKsv8+fP1yiuv6OOPP1b//v1Nx4GT\noIgBoIKVlJTorbfe0rx585SSkqLAwEDTkeBEKGIAqEAFBQUaM2aMDh8+rI0bN6pBgwamI8HJcI4Y\nACrI8ePH1atXL1WrVk0pKSmUMEpFEQNABdi+fbu6du2qgQMHKiEhQV5eXqYjwUkxNQ0A5WzZsmV6\n6qmn9MEHH2jYsGGm48DJUcQAUE4sy9LMmTP1P//zP/r666/VpUsX05HgAihiACgHly5d0vPPP6+N\nGzdqw4YNatq0qelIcBEUMQCU0ZkzZ/TII4/I19dXaWlp8vPzMx0JLoTFWgBQBjk5OQoNDVWnTp20\nePFiShi3jCIGgNu0evVq9ejRQxMnTtSMGTNUtWpV05HggpiaBoDb8H//9396/fXXtXDhQvXu3dt0\nHLgwihgAbkFxcbGioqL01Vdfad26dQoICDAdCS6OIgaAm3ThwgWNHDlSeXl5ysjIUJ06dUxHghvg\nHDEA3ITDhw+re/fuql+/vv71r39Rwig3FDEA/IrMzEyFhYVp1KhRmjNnjmrUqGE6EtwIU9MAcAOf\nffaZnn/+ef3jH//QoEGDTMeBG6KIAaAUlmVp6tSpmj17tpKSknTfffeZjgQ3RREDwDUKCws1btw4\n5eTkaOPGjbr77rtNR4Ib4xwxAFzl5MmTioiI0MWLF7V27VpKGBWOIgaAK3bu3KnQ0FBFRERo4cKF\n8vb2Nh0JHoCpaQCQ9K9//UtPPPGEZs6cqZEjR5qOAw9CEQPweB988IGmTp2qxYsXKzw83HQceBiK\nGIDHKioq0oQJE7RmzRqlp6erRYsWpiPBA1HEADzS2bNn9eijj6pKlSpKT0+Xv7+/6UjwUCzWAuBx\n9u/fr27duqldu3ZatmwZJQyjKGIAHiUtLU3h4eF64YUXNGvWLFWrxsQgzOJfIACPMXfuXEVGRioh\nIUH9+vUzHQeQRBED8AAlJSV64403tHDhQq1Zs0bt27c3HQlwoIgBuLX8/Hw98cQTOnHihDIyMlS/\nfn3TkYCf4RwxALd17Ngx/fa3v5Wvr6+Sk5MpYTglihiAW9qyZYu6du2qoUOHKj4+XjVr1jQdCSgV\nU9MA3M6SJUv09NNP629/+5uGDh1qOg5wQxQxALdhWZamT5+u999/X4mJiQoODjYdCfhVFDEAt3Dx\n4kU999xz2rZtmzIyMtS4cWPTkYCbQhEDcHmnT5/WkCFDVKdOHa1bt06+vr6mIwE3jcVaAFza7t27\nFRoaqrCwMC1atIgShsuhiAG4rOTkZPXs2VP//d//rdjYWFWpwrc0uB7+1QJwSX//+9/1+OOP67PP\nPtPYsWNNxwFuG+eIAbiU4uJiRUZGKjExUWlpaWrdurXpSECZUMQAXEZeXp4ee+wxFRYWasOGDapd\nu7bpSECZMTUNwCUcPHhQ4eHhaty4sRITEylhuA2KGIDTy8jIUFhYmJ566inFxcWpevXqpiMB5Yap\naQBObeHChXrppZf00Ucf6cEHHzQdByh3FDEAp2RZlqZMmaL4+HitWrVKHTp0MB0JqBAUMQCnU1BQ\noCeffFL/+c9/tHHjRt11112mIwEVhnPEAJzK8ePH1bt3b0lSSkoKJQy3RxEDcBpZWVkKDQ1V//79\n9cknn8jb29t0JKDCMTUNwCksX75cY8eO1fvvv6/hw4ebjgNUGooYQLk7efKk5sbHKycrSxfOndMd\n/v4KCArS6LFjVb9+/Z8da1mWZs2apXfeeUdLly5VaGioodSAGTbLsizTIQC4h8zMTM2KidHyxEQN\nkRRSWCg/SXmSvvX21mLL0oP9+2tCdLRCQkJ06dIlvfjii0pPT9eyZcvUrFkzw58AqHwUMYByMTsu\nTm9GRmpyQYFGW5ZKu+9VrqR4m03veHtr0p/+pOWJifLy8tKCBQvk5+dX2ZEBp0ARAyiz2XFxmhYZ\nqZX5+bqZLRj2SvqtzabA3r2V+M03qlq1akVHBJwWq6YBlElmZqbevEEJ75HkLemJqx5rLSnVspSd\nkaGtW7dWSk7AWVHEAMpkVkyMJhcUXHck/IKkLqU83lrSpIICzYqJqbhwgAtgahrAbTt58qTaNmum\n/YWFpZ4TXihpiaT2ujwdPfea589IauXlpZxDh36xmhrwFIyIAdy2ufHxGiyVWsLnJb0p6V1J1/tp\nv46kwTab5sbHV0xAwAVQxABuW05WlroUFpb63B8lPS3pnl95jZCCAuVkZ5d3NMBlcEMPALftwrlz\nKu2io22Skq/8/mv8JOXl5pZrLsCVUMQAbpuPn5/ySnl8raSDkprq8rT0BUnFkv4tadM1x+ZJ8qtd\n2uQ24BkoYgA3zbIs7d69W0lJSUpKSlJyUpLybTY9d82az2clPXbVn6frcjH/rZTXzPT21m/Yaxge\njFXTAG7oxIkTSk5Ovly8ycmqWrWq7Ha77Ha7goKC1K1z5+uumv7JFEn7xKppoDQUMYCfyc/PV2pq\nqqN8Dx06pF69ejnKt3Xr1rLZbI7jHx8yRMFLlujl2/hWMtNm05bBgzVv0aLy/AiAS6GIAQ9XXFys\nrVu3OqabMzMz1alTJ0fxBgcHq1q165/FyszM1KBevbTuJm9v+ZO9knr4+GjZ2rUKDg4u8+cAXBVF\nDHigAwcOOIo3JSVFDRs2VN++fWW329WzZ89b3oDhdu41fb+PjybPmKFnxo+/rc8AuAuKGPAAubm5\nSklJcZznvXDhgqN4+/btq0aNGpX5PX7afWliQYHGXmf3pTO6vPvSdG9vTaGEAUkUMeCWLl68qPT0\ndMd53l27dik8PNwx3RwYGPiz87zlZdOmTXpy+HAdOHhQj1SvrpCCAsd+xJlX9iN+aMAATYiOZjoa\nuIIiBtyAZVnauXOnY7o5LS1N7dq1c4x4u3Xrppo1a1Z4jkuXLqlx48ZaunSp0lJTlZOdrbzcXPnV\nrq2ADh30xJgxrI4GrkERAy7q2LFjP7usyNvb2zHi7dOnj+rUqVPpmZYvX66pU6cqPT290t8bcFXc\n0ANwERcuXNDatWsd5Xvs2DH16dNHdrtdU6ZMUcuWLU1HVEJCgh5//HHTMQCXwogYcFJFRUXavHmz\nY7p5y5YtCg4Odkw3/9d//ZeqVq1qOqbD+fPn1aRJE+3fv19169Y1HQdwGYyIASdhWZb27dvnKN7V\nq1erSZMm6tu3r6KiovTb3/5Wvr6+pmNe15dffqlevXpRwsAtoogBg06fPq1Vq1Y5ppt//PFH2e12\nDRkyRP/7v/+rhg0bmo540+bNm6fxXI4E3DKmpoFKVFhYqPT0dMeod8+ePerRo4djkdW9995bIZcV\nVbQjR44oKChIx44dk5eXl+k4gEthRAxUoJKSEmVnZzuKNz09XYGBgbLb7Xr33XcVGhqqGjVqmI5Z\nZgsWLNDQoUMpYeA2MCIGytmRI0cclxQlJyerVq1ajhFv7969deedd5qOWO6CgoL017/+VT179jQd\nBXA5FDFQRufPn9fatWsdo95Tp04pIiLCsbq5efPmpiNWqKysLA0cOFAHDhxQlSpVTMcBXA5T08At\nKioq0rfffuso3u3bt6tr166y2+1KSEhQp06dPKqQ5s2bp5EjR3rUZwbKEyNi4FdYlqWcnBxH8a5d\nu1bNmzd3TDd3795dPj4+pmMaUVxcrKZNmyopKUnt27c3HQdwSYyIgVKcOnXKcY43KSlJlmXJbrdr\n+PDhmjNnjho0aGA6olNYvXq1GjZsSAkDZUARA5IKCgqUlpbmGPUeOHBAPXv2lN1u16RJkxQQEOCS\nlxVVNG5pCZQdU9PwSCUlJdq2bZujeDdu3KiOHTs69ujt0qWLqlevbjqmU8vPz1ejRo20a9cul7rx\nCOBsGBHDYxw8eNBxWdGqVatUt25d2e12vfTSS+rVq5dq1aplOqJL+eqrr9S1a1dKGCgjihhu6+zZ\ns1qzZo1j1Hv27Fn17dtX999/v6ZPn64mTZqYjujS5s2bp1GjRpmOAbg8pqbhNi5duqSMjAxH8e7Y\nsUPdunVzXM8bFBTEJTbl5MSJE2rbtq2OHj3q1BtRAK6AETFclmVZ2rVrl2O6OTU1Va1bt5bdbtdf\n/vIXhYeHc8vFCvLpp59q0KBBlDBQDhgRw6UcP35cq1atcpRvtWrVHNfz9unTR/Xq1TMd0SOEhIRo\n6tSp6tevn+kogMujiOHU8vPzlZqa6phuPnz4sHr37u2Ybm7dujWXFVWy3bt3q0+fPjp8+LCqVq1q\nOg7g8piahlMpLi7Wli1bHMWbmZmpzp07y263a/bs2QoODla1avyzNSkhIUGPPfYYJQyUE0bEMG7/\n/v2OqeaUlBQ1bNjQMd3cs2dP3XHHHaYj4oqSkhK1atVKixcv1n333Wc6DuAWGFqg0uXm5iolJcUx\n6s3Pz1ffvn01cOBAzZo1S/fcc4/piLiO9evXy9fXVx07djQdBXAbFDEq3I8//qgNGzY4inf37t0K\nDw+X3W7X888/r8DAQM7zuoiEhASNGjWKvy+gHDE1jXJnWZZ27NjhmG5OS0tTu3btHNPNYWFhqlmz\npumYuEWFhYVq1KiRtm3bxs1QgHLEiBjl4tixY46dipKTk+Xj4yO73a6nnnpKCQkJqlOnjumIKKMV\nK1aoY8eOlDBQzihi3JYLFy5o7dq1junm48ePq0+fPrLb7ZoyZYpatmxpOiLK2bx589hpCagATE3j\nphQVFWnTpk2OEe+WLVsUHBzsmG7u3Lkzl7O4sTNnzqhFixY6dOiQ/P39TccB3AojYhdw8uRJzY2P\nV05Wli6cO6c7/P0VEBSk0WPHqn79+hXynpZlae/evY7p5tWrV6tJkyay2+2Kjo5Wjx49uL2hB/n8\n88/1wAMPUMJABWBE7MQyMzM1KyZGyxMTNURSSGGh/CTlSfrW21uLLUsP9u+vCdHRCgkJKfP7nT59\n2nH7yKSkJF26dMkx4o2IiGC7Ow/WvXt3TZ48WQMHDjQdBXA7FLGTmh0XpzcjIzW5oECjLUu1Szkm\nV1K8zaZ3vL01ZcYMPTN+/C29R2FhodavX++Ybt6zZ4969OjhKN97772Xy1Sg/fv3q2vXrjp27Jiq\nV69uOg7gdpiadkKz4+I0LTJS6/Lz1foGx9WW9IplaWB+vu6PjJSkG5ZxSUmJsrKyHNPN6enpCgwM\nlN1u18yZM9W1a1fVqFGjfD8MXN78+fP16KOPUsJABWFE7GQyMzM1qFevn5XwRUl/kJSsy6PgVpLe\nlvTAVV+3V1IPHx8tW7tWwcHBjsePHDnimGpetWqV/P39HSPeXr166c4776ycDwaXZFmW2rVrp7lz\n56pr166m4wBuiRGxk5kVE6PJBQU/GwkXSWoqaZ2kJpKWSxomaceVxyWptaRJBQWa8ac/acS4cY7y\nPX36tCIiItS3b1/FxMSoWbNmlflx4OIyMzNlWZa6dOliOgrgthgRO5GTJ0+qbbNm2l9YWOo54at1\nlPSWpMFXPXZGUiNJIT166MEHH5Tdbtd9992nKlWqVFBiuLuXXnpJ9erV0x//+EfTUQC3xYjYicyN\nj9dg6VdL+ISkPZJ+c83jdSQN9/JS4MCBem3ixIqICA9y6dIlLVy4UBs2bDAdBXBrDJWcSE5WlroU\nFt7wmCJJj0saIymglOe7FBYqJzu7/MPB43zzzTdq06aNWrVqZToK4NYoYidy4dw5+d3geUuXS7im\npL9e5xg/SXm5ueUdDR6IW1oClYMidiJ3+Psr7wbPPyXpe0lfSrrezSTzJPnV/rXJbeDGzp8/r8TE\nRA0bNsx0FMDtUcROJCAoSN96eZX63HOSdktaKulGV/pmensroEOHCkgHT/Lll1+qd+/eqlu3ruko\ngNtj1bQTud6q6UOSmkvy0v8/ErZJ+rukx6467oykZtWqacu//602bdpURmS4qYiICI0fP16///3v\nTUcB3B4jYifSoEEDPdi/vz6+5raSTSWVSMrX5annPEnn9fMSli7f7rJJo0YKDQ3VxIkTdezYscqI\nDTdz5MgRbd26VQ899JDpKIBHoIidzIToaE3z9tbeW/y6vZKme3tr7hdfaNu2bSoqKlJgYKCefvpp\n5eTkVERUuKlPPvlEQ4cOldd1TpMAKF8UsZMJCQnRlBkzdL+Pz02X8V5J9/v4aMqMGQoODlaTJk00\nc+ZM7dmzR40bN1b37t31yCOPaNOmTRUZHW4iISFBo0aNMh0D8BgUsRN6Zvx4TZ4xQz18fDTTZtP1\nLkY6I+ldm009fHw0uZTdl+rWras333xTBw4cUPfu3TVkyBDZ7XatWrVKLA1AabZv365z586pe/fu\npqMAHoPFWk5s06ZNmhUTo69XrNBgm00hBQWO/Ygzr+xH/NCAAZoQHf2zjR6u5+LFi1qwYIGmTZsm\nX19fRUVF6Xe/+52qVr3exVDwNBMnTlSNGjU0depU01EAj0ERu4BTp05pbny8crKzlZebK7/atRXQ\noYOeGDNG9evXv+XXKykp0bJlyxQTE6Pc3FxNmjRJjz/+uGrWrFkB6eEqiouL1bRpUyUnJ+vee+81\nHQfwGBSxB7MsS6mpqYqNjVV2drZeeeUVPfPMM/Lzu9H9veCukpOTFRUVxVoCoJJxjtiD2Ww29ezZ\nU4mJiVq2bJk2bdqkli1b6o033tCpU6dMx0Ml45aWgBkUMSRJnTp10oIFC5SRkaHvv/9ebdu21Ysv\nvqiDBw+ajoZK8MMPP2jp0qV67LFrr04HUNEoYvxMq1atFBcXp507d8rX11edO3fWE088oR07dpiO\nhgq0dOlShYaG6q677jIdBfA4FDFKdffddys2Nlb79u1T+/btZbfbNWjQIKWnp5uOhgowb948rh0G\nDGGxFm5KQUGBPv74Y02fPl2NGjVSVFSU+vfvL9s1t+OE6zlx4oTatWunI0eOyNfX13QcwONQxLgl\nRUVF+uKLLxQbG6uSkhJFRUVp2LBhqlatmulouE2zZs3Sli1b9PHHH5uOAngkihi3xbIsrVy5UrGx\nsTp48KAmTpyosWPHytvb23Q03KKQkBC9/fbbstvtpqMAHolzxLgtNptNDzzwgNasWaNPPvlE33zz\njVq0aKG3335bZ8+eNR0PN2n37t06evSo+vTpYzoK4LEoYpRZWFiYlixZopSUFOXk5KhVq1aaNGkS\n2zC6gISEBI0YMYLbnAIGUcQoN+3bt1d8fLy2bt2qixcvKjAwUM8884z27NljOhpKUVJSooSEBG7i\nARhGEaPcNW3aVO+9955ycnJ0zz33qFu3bho2bJg2b95sOhqusn79evn5+aljx46mowAejSJGhalX\nr57eeustHThwQGFhYXr44YfVr18/rV69mm0YncBPt7TkEjTALFZNo9JcvHhR8+fP17Rp0+Tv76+o\nqCg9/PDDqlKFnwcrW2FhoRo1aqRt27apSZMmpuMAHo3vgKg0NWrU0NixY/Xvf/9bUVFRiomJUfv2\n7fXRRx/p4sWLpuN5lBUrVqhjx46UMOAEKGJUuipVqmjw4MHauHGj4uLitHDhQrVq1UozZ87UhQsX\nTMfzCNzSEnAeTE3DKWzZskXTpk1TSkqK/vCHP+jFF19UvXr1TMdyS2fOnFHLli116NAh1apVy3Qc\nwOMxIoZT6Ny5sz799FOlp6fr+PHjCggI0IQJE3To0CHT0dzOZ599pgceeIASBpwERQyn0qZNG/39\n73/Xzp075eXlpU6dOmn06NHauXOn6Whug2uHAedCEcMp3X333Zo2bZr27dundu3aKSIiQg8//LA2\nbNhgOppL279/v3JycnT//febjgLgCooYTu3OO+9UdHS0Dhw4oAceeEAjR45Uz549lZiYyLXIt2H+\n/Pl69NFHVb16ddNRAFzBYi24lKKiIn322WeKjY1VlSpVNHnyZD3yyCNsw3gTLMtS27ZtlZCQoC5d\nupiOA+AKRsRwKdWqVdOIESO0fft2vf3224qLi1Pbtm31t7/9TYWFhabjObXMzExJl7c9BOA8KGK4\nJJvNpgEDBig1NVVz587VihUr1KJFC8XGxurcuXOm4zklbmkJOCempuE2duzYoXfeeUfLly/X008/\nrZdfflkNGzY0HcspXLp0SY0aNVJGRoZatmxpOg6AqzAihtsIDAzU3LlztXnzZuXn56t9+/Z67rnn\ntHfvXtPRjFu5cqXatGlDCQNOiCKG22nevLnef/99fffdd2rQoIHCwsI0fPhwbd261XQ0YxISEril\nJeCkmJqG28vLy9OcOXP07rvvKjAwUFFRUerZs6fHnCs9f/68mjZtqn379qlu3bqm4wC4BiNiuD0/\nPz+9+uqr2rdvn4YNG6Znn31WYWFhWrJkiUpKSkzHq3CLFi1S7969KWHASTEihscpLi7WkiVLFBMT\nox9++EGTJ0/WiBEjVKNGDdPRKkRERIT+8Ic/aOjQoaajACgFRQyPZVmWUlJSFBsbq++++06vvvqq\nxo0bpzvuuMN0tHJz5MgRdezYUUePHpWXl5fpOABKwdQ0PJbNZlNERISSkpL05Zdfav369WrZsqXe\neustnT4x8lf9AAAGfklEQVR92nS8cvHJJ59o6NChlDDgxChiQFJwcLA+//xzpaWl6ejRo2rTpo1e\neeUVHT582HS022ZZlubNm8dqacDJUcTAVQICAjRnzhxlZ2erWrVquu+++zR27Fjt2rXLdLRblpWV\npby8PIWHh5uOAuAGKGKgFI0aNdL06dO1d+9etW7dWr169dLgwYO1ceNG09Fu2k+3tKxShf/NAWfG\nYi3gJuTn5+ujjz7S9OnT1aJFC0VFRalfv35Oey1ycXGxmjRpolWrVunee+81HQfADfCjMnATfHx8\n9Pzzz2vPnj0aN26cIiMj1blzZ3366acqLi42He8XUlJSdM8991DCgAtgRAzcBsuytGLFCsXExOj4\n8eOaOHGiRo8e7TSrk0ePHq3OnTtrwoQJpqMA+BUUMVBGaWlpio2N1ebNm/Xyyy/rueeek7+/v7E8\nP/zwgxo3bqzdu3frrrvuMpYDwM1hahooo+7du+vrr7/WypUrlZ2drZYtWyo6OlrHjx83kuerr75S\nWFgYJQy4CIoYKCdBQUFKSEjQpk2blJeXp/bt22v8+PHat29fpeZISEjQ448/XqnvCeD2UcRAOWvR\nooU++OAD7d69W3Xr1lXXrl01YsQIbd++vcLf+8SJE9qwYYN+97vfVfh7ASgfFDFQQRo0aKC//OUv\n2r9/vzp37qwBAwZowIABSk1NVUUtzVi4cKEGDRokHx+fCnl9AOWPIgYqWK1atRQZGan9+/dryJAh\nGjdunMLDw7V06dJy34aRW1oCrodV00AlKy4u1uLFixUTE6PCwkJNnjxZjz32mKpXr37Tr3Hy5EnN\njY9XTlaWLpw7pzv8/eXfsKHmJSTo6NGjqlq1agV+AgDliSIGDLEsS6tWrVJsbKz27Nmj1157TU89\n9ZR8fX2v+zWZmZmaFROj5YmJGiIppLBQfpLyJK2vVk1LLEsPDxqkCdHRCgkJqayPAqAMKGLACXz7\n7beaNm2a1q1bpxdeeEEvvPCC6tSp87NjZsfF6c3ISE0uKNBoy1LtUl4nV1K8zaZ3vL01ZcYMPTN+\nfKXkB3D7OEcMOIEuXbpo0aJFSk1N1cGDB9W6dWu9+uqrOnLkiKTLJTwtMlLr8vP18nVKWJJqS3rF\nsrQuP1/TIiM1Oy6u0j4DgNvDiBhwQkeOHNHMmTP10UcfKTw8XJnJyUorLFTrq475UFK8pGxJIyT9\n85rX2Cuph4+Plq1dq+Dg4MoJDuCWUcSAEztz5oz6de+ux3bt0mvXPLdEl6e0Vkoq0C+LWJJm2mza\nMniw5i1aVNFRAdwmihhwYidPnlTbZs20v7DwutPRb0g6qtKL+IykVl5eyjl0SPXr16+wnABuH+eI\nASc2Nz5eg6XrlvCvqSNpsM2mufHx5RcKQLmiiAEnlpOVpS6FhWV6jZCCAuVkZ5dTIgDljSIGnNiF\nc+fkV8bX8JOUl5tbHnEAVACKGHBid/j7K6+Mr5Enya/27U5uA6hoFDHgxAKCgvStl1epzxVLKrzy\ne5GkH6/897Uyvb0V0KFDhWUEUDasmgac2I1WTU+58st21WNvSvrjVX9m1TTg/BgRA06sQYMGerB/\nf31ss/3iuTcllejyKPinX3+85piPbTY9NGAAJQw4MUbEgJPLzMzUoF69tC4//2d31vo13FkLcA2M\niAEnFxISoikzZuh+Hx/tvcmv2Svpfh8fTZkxgxIGnBxFDLiAZ8aP1+QZM9TDx0czbTZd72KkM5Le\ntdnUw8dHk9l9CXAJTE0DLmTTpk2aFROjr1es0GCbTSEFBY79iDO9vbXYsvTQgAGaEB3NSBhwERQx\n4IJOnTqlufHxysnOVl5urvxq11ZAhw56YswYFmYBLoYiBgDAIM4RAwBgEEUMAIBBFDEAAAZRxAAA\nGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEA\nAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUM\nAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQR\nAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZRxAAAGEQRAwBgEEUMAIBBFDEAAAZR\nxAAAGEQRAwBgEEUMAIBBFDEAAAb9P603wxJf3z2wAAAAAElFTkSuQmCC\n",
"text/plain": [
"