Design and Analysis of Algorithms: Hash Tables *

Dictionaries

Dictionary ADT.

Operations associated with this data type allow:

the addition of a pair to the collection
the removal of a pair from the collection
the modification of an existing pair
the lookup of a value associated with a particular key

(Source)

Typical uses:

Symbol lookup in a programming language
Counting words in a book
Store colors by name as key and their numeric equivalent as the value. Then we can write set_text(colors["red"]).

(Ordered Dictionary ADT next time.)

Direct addressing and Hashing are two ways of implementing a dictionary. Are there others?

Direct addressing.

O(1) worst case time for lookup.
Uses:
- Memoization
- Bingo
- Sieve of Eratosthenes
- Mark zipcodes seen
Downside: wastes space. If you have no idea how many possible keys you need, direct addressing is not a good choice.
For instance, if your key is an arbitrary string!
Example code here.

Hashing

Basic Hashing:

O(1) average case time for lookup.
Universe of keys U mapped into slots of a hash table of size m by hash function h.
Because size(U) > m, collisions are always possible.
Imagine we hash by word length: 'mark' and 'beam' both hash to 4. (Stupid hash function, but it illustrates the idea.) We must resolve this collision somehow.
Resolve collisions by chaining:
Each slot holds a linked list of values.
Cryptographic hashing
Use large hash keys: SHA-1 uses 160 bit keys. SHA-2 uses keys of up to 512 bits.
Perceptual hashing

Introducing probability into an algorithm.

What happens to the usual assumptions?
Correctness: always, most of the time?
Termination: always, or almost always? What does "performance" mean if the running time/answer/even termination change from one run to the next?

Probability Basics

Reviewed in this document.

Simple uniform hashing

This employs chaining. Furthermore, we assume that the distribution of elements is uniform across hash table slots.

Hash table T with m slots storing n elements.
Load factor: α = n / m
α is the average number of elements stored in a chain.
Our analysis is in terms of α, which can be less than, equal to, or greater than one.
Worst case is very bad:
All n keys hash to the same slot.
Worst case for searching becomes Θ(n) plus time to compute hash function.
We could have just used a linked list directly!
Average case:
Assuming any given element is equally likely to hash into any slot...
We get average case Θ(1 + α) time.
See proofs in our textbook.

Hash functions

First, convert key to an integer.
E.g., we can interpret characters in a string by their ASCII values.
Then treat each value as a digit in a radix-128 integer.
( See this article for more on radices.)
Keys could be many other things besides strings.
E.g., genomes:
Division method:
h(k) = k mod P, where P is a suitably-chosen prime number.
Multiplication method:
h(k) = [m (k A mod 1)], where 0 < A < 1.

Universal hashing

Establish a family of hash functions.
Choose so that Prob[h(x) = h(y)] <= 1/m, where m is the size of our hash table.
In other words, the hash functions have no more chance of collision than simply randomly choosing to slots between 1 and m.
Choose one at random each execution.
Tricky: what if we store hash values?
Good average case behavior
If a "bad" function handles some data once, a "good" one will handle it another time.
So a "bad" set of programming variable names one run will turn into a good set the next run.

Open addressing

All elements are stored directly in the table; no chaining.
Linear probing
Easy: just move along array indices!
Prone to clustering
Quadratic probing
Double hashing
Uses two hash functions to search array for key.
Source code here.

Perfect hashing

Source Code

Java
Ruby
Go
Javascript
C++
Python
Clojure

Homework

Devise three possible hash functions. Analyze each for size of hash table necessary and possibility of collisions.
Let's say our hash function is h(k) = k mod 11 and we resolve conflicts with chaining. Analyze what happens if our data values are 23, 34, 12, 8, 19, 33, 2, 5, 15, 4, 31, 9, 3, 6, 18, 8, 19 and 22.
What will happen when we look up 19?
Write (pseudo) code to resolve collisions with chaining.
Consider the following hashing scheme:
h(k) = k mod m
m = 7
We convert a string into a hashable key by treating it as a base-8 number.
So 'abc', where a = 1, b = 2, and c = 3, is converted to a key as follows: 1 * 8² + 2 * 8 + 3 = 83.
In this hashing scheme, what do the strings 'cba' and 'bac' hash to?
Can you write a more general statement about a pattern we can detect here? Something along the lines of, "If the table size is 2^P - 1, and strings are interpreted in radix 2^P..."

Answer:

If h(k) = k mod m, where m = 2^P - 1, and k is a character string interpreted in radix 2^P, then all permutations of a given string will hash to the same value. So in the example above, 'abc', 'cba', and 'bac' all hash to the same value.

Proof:

Assumed (could be proven, but we won't do it here):
1. (x + y) mod z == (x mod z + y mod z) mod z
  Example: (10 + 12) mod 7 == (10 mod 7 + 12 mod 7) mod 7
2. (x * y) mod z == (x mod z) * (y mod z) mod z
  Example: (10 * 12) mod 7 == (10 mod 7) * (12 mod 7) mod 7
  (7 * 17 = 119)
3. if x mod z == 1, then xⁿ mod z == 1
  Example: 8 mod 7 == 1, and 8² mod 7 == 1
  This is a special case of 2!
So, we have:

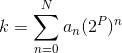
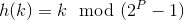
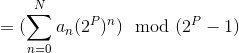
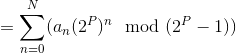  (By 1)

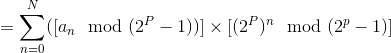  (By 2)

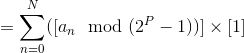  (By 3)

* Based on Prof. Boris Aronov's lecture notes.