
We assume that everyone is familiar with the basic concept of
probability (do not want to be very formal): what an EVENT is and what
Prob(EVENT) is. For example: We are using a fair die. The usual,
with six sides and numbers 1, 2, 3, 4, 5, 6 on its sides. We throw it
once. Then the probability of the event A:"4 came out" is 1/6. The
probability of the event B:"5 came out" is 1/6. The probability of the
event C:"an even number came out" is 1/2. Etc.
For any two events A, B:
Prob(A or B) = Prob(A) + Prob(B) - Prob(A and B)
["inclusion-exclusion"]
From this comes a crude way to estimate probabilities:
Prob(A or B) <= Prob(A) + Prob(B)
or more generally:
Prob(A1 or A2 or ... or An)
<= sum Prob (Ai)
Two events A, B are mutually exclusive if
Prob(A and B) = 0.
Two events are independent if
Prob(A and B) = Prob(A) * Prob(B).

Expected value of a real variable X is defined as
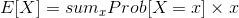
where the sum is taken over all values x that X can take.
In words:
the expected value of a variable is the weighted sum of
all its
values, weighted according to the probability that they
happen.
Example: You throw a die and get $10 if it comes out 1 and
$0 if not.
The expected value of your reward is $10 * 1/6 + $0
* 5/6 = $10/6.
You play the lottery. You pay $1 for the ticket and win
one million
dollars with probability 1/(1 billion). How much do you
expect to
win? What's the expected balance?
Expected outcome = -$1 + Expected win.
Expected win = $1,000,000 * 1/(1 billion) + $0 * (the
probability I do not win) = $1/1000 = 0.1cent.
So expected outcome = you lose 99.9 cents.
Linearity of expectation:
E[a X + b Y] = a E[X] + b E[Y]
for any two events X, Y
[there are some mild requirements on X and Y, but INDEPENDENCE IS NOT REQIURED!]
and constants a, b.

X is an indicator variable for an event A if
X = 1 if A happens
X = 0 if A does not happen
Useful properties of indicator variables:
If X is an indicator variable for A, then
Exp[X]=Prob[X=1]=Prob[A happens]
.
This easily follows from the definition:
Exp[X]=1 * Prob[X=1] + 0 * Prob[X=0]=Prob[X=1]=Prob[A happens]
Example:
We throw a fair die 100 times What is the expected number
of times we get 1 or 6?
Let Xi be the indicator variable of the event "in ith
throw we got 1 or 6".
Then notice that the number of times we get 1 or 6 is
exactly
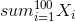
and we want the expectation of this. By linearity of expectations:
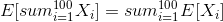
and by the indicator variable properties:
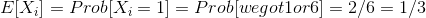
To summarize:
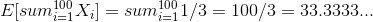
So we expect to get 1 or 6 about 33.33 times.
Finally, something that comes up very frequently:
Suppose you have a sequence of events, each of which
happens with
probability p, independent of the previous ones. What is
the expected
number of tries in the sequence you must observe until you
see an event you like.
Examples:
Flip a coin several times. How many tries until it comes
out heads.
Throw a pair of die. How many tries until they give you
{6,6}?
Play the lottery. How many tries until you win?
Probability event i happens is
(1 - p)i - 1p
In this case you need to
wait i steps. So the expected number of steps to wait is:
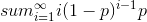
It's a standard summation that adds up to 1/p. [A cute or
painful algebra exercise, depending on how you do it, I guess...]
so:
Fact: If you have a sequence of independent events, each
succeeding
with probability p, the expected number of tries until the
first
success is 1/p.
Or slightly more generally:
Fact: If you have a sequence of independent events, each
succeeding
with probability at least p, the expected number of tries
until the
first success is at most 1/p.
[The last one is useful if you are doing sampling without
replacement, so the probabilities changes as you go along.]