Syllabus: Logistics, grading, exams, homeworks, cheating.
What's an algorithm?
A carefully written recipe.
We need to agree what steps are allowed in a recipe.
We need to agree what problem the recipe is solving, ahead of time.
Things to keep in mind about algorithms (when analyzing and/or designing them):
On any legal (meaning, consistent with algorithm specification) input, the procedure you are describing should always eventually stop, or terminate. (In this course we will not talk about algorithms that are intended to run "forever," such as the scheduler in an operating system.)
On any legal input, provided the procedure has terminated, the result that it produces has to be correct. Not sometimes correct, not mostly correct, but always correct.
You can measure performance in many different ways. The course will focus on the running time, but there are many others: space (memory use), disk use, amount of disk-memory communication, number of processors in a parallel program, total amount of work in a parallel program, number of cores in a multi-core program, total amount of communication in a distributed program, power consumed in an algorithm tuned to low-power devices and many many others. So in short, when you describe a recipe for doing something, make sure it always stops, make sure it always produces correct answers, and only after that worry about how efficient it is. (Depending on the algorithm, some or all of these are very easy, and some may not be obvious at all. We will see examples later.)
We surely do not want to talk about actual time in nanoseconds, as that depends on too many external things: what other processes are running, details of the hardware, compiler switches, etc, etc. So instead we come up with a very primitive abstract machine (RAM=the Random Access Machine: CPU + directly addressable memory) which we analyze instead of a real computer. Then primitive operations are memory reads/writes and operations in the CPU, such as address arithmetic, additions, multiplications, divisions, etc. Our idea of "running time" is then simply the number of operations performed when the program runs.
Even for inputs of a fixed size (saying, your favorite program sorting 10 numbers), different specific inputs will produce different performance. For example, a clever algorithm may notice that the input is already sorted and not try sorting it again. So, we distinguish between best- and worst-case performance (minimum and maximum number of operations performed by the algorithm, over all possible legal inputs of a given size). (There is also the concept of "average-case," but it is tricky, as it requires a definition of what average means: technically, you need to specify a distribution of the inputs. We will mostly stay away from average-case analysis and focus on the worst case; we will occasionally look at the best case too.)
In order to make life easier, we will not be focusing on the exact value of
such function, but on its asymptotic behavior.

In particular, we want to focus on the highest power of n in any function expressing the run time of an algorithm. That is because, as input size grows, that power will dwarf all others in significance. Consider the contribution of n2 and n in the runtime of the sorting algorithm mentioned above for various values of n:
| n | n2 |
|---|---|
| 10 | 100 |
| 100 | 10,000 |
| 1000 | 1,000,000 |
| 10,000 | 100,000,000 |
| 100,000 | 10,000,000,000 |
Now consider that Amazon is processing tens of millions of transactions per day: of what significance is the n factor in the performance of their servers, if they are using an algorithm with an n2 factor involved to sort them?
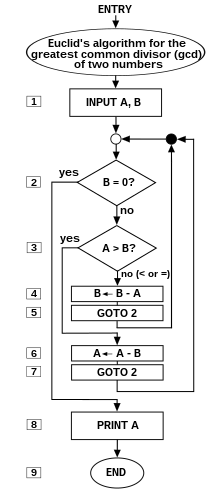
An example of a toy algorithmic problem and how to solve it, analyze it etc etc.
Who has the same birthday in class?
* Based on Prof. Boris Aronov's lecture notes.
** Material drawn from Khan Academy and
https://en.wikipedia.org/wiki/Big_O_notation.