{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"toc": "true"
},
"source": [
"# Table of Contents\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Texte d'oral de modélisation - Agrégation Option Informatique\n",
"## Préparation à l'agrégation - ENS de Rennes, 2016-17\n",
"- *Date* : 22 mai 2017\n",
"- *Auteur* : [Lilian Besson](https://GitHub.com/Naereen/notebooks/)\n",
"- *Texte*: Annale 2012, [\"Éclairage graphe\" (public2012-D1)](http://agreg.org/Textes/public2012-D1.pdf)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## À propos de ce document\n",
"- Ceci est une *proposition* de correction, partielle et probablement non-optimale, pour la partie implémentation d'un [texte d'annale de l'agrégation de mathématiques, option informatique](http://Agreg.org/Textes/).\n",
"- Ce document est un [notebook Jupyter](https://www.Jupyter.org/), et [est open-source sous Licence MIT sur GitHub](https://github.com/Naereen/notebooks/tree/master/agreg/), comme les autres solutions de textes de modélisation que [j](https://GitHub.com/Naereen)'ai écrite cette année.\n",
"- L'implémentation sera faite en OCaml, version 4+ :"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"The OCaml toplevel, version 4.04.2\n"
]
},
{
"data": {
"text/plain": [
"- : int = 0\n"
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Sys.command \"ocaml -version\";;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"----\n",
"## Question de programmation\n",
"La question de programmation pour ce texte était donnée au tout début, à la page 2 :\n",
"\n",
"### Exercice\n",
"\n",
"> Dans le langage de votre choix, implémenter un programme qui étant donnés un graphe et une proposition d’éclairage des lampadaires teste si celle-ci est correcte, *i.e.*, si toutes les rues sont bien éclairées.\n",
"\n",
"> Le tester sur différents exemples bien choisis (on pourra justifier la/les structures de données utilisée).\n",
"\n",
"### Besoin de plusieurs exemples\n",
"Pour une fois, on voit bien que le jury *exige* de tester la fonction sur *plusieurs* exemples."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"----\n",
"## Solution\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Représentation du graphe et de la proposition d'éclairage\n",
"\n",
"Les graphes ici seront constitués de *places* (= sommets), reliés entre elles par des *rues* (= arêtes).\n",
"\n",
"Pour vérifier un éclairage, donné sous forme d'une liste de places, on va devoir vérifier que chaque rue est connectée à une place éclairée.\n",
"\n",
"Une approche très simple, en trois étapes :\n",
"\n",
"1. compter le nombre de rues,\n",
"2. pour chaque place éclairée, compter le nombre de rues qui en partent (et qui sont donc éclairées),\n",
"3. s'il y a (au moins) une rue non éclairée, renvoyer `false`, sinon renvoyer `true`.\n",
"\n",
"Pour être efficace, il faut pouvoir accéder efficacement aux rues qui partent de chaque place (et il suffit de les compter, si on sait qu'elles sont uniques dans la représentation).\n",
"\n",
"$\\implies$ À partir de ce constat, on opte pour une représentation du graphe par **liste d'adjacence**.\n",
"\n",
"- Comme les graphes sont non orientés, chaque arête est présente deux fois dans la représentation du graphe : l'arête $u \\leftrightarrow v$ est présente comme $v \\in V[u]$ (les places voisines de $u$), et $u \\in V[v]$ (les places voisines de $v$).\n",
"\n",
"- Le fait que les graphes soient planaires n'apportent rien à la représentation.\n",
"\n",
"- Par simplicité, on va représenter les places par leur numéros (on pourra aussi prendre des chaînes de caractères, comme `\"Place de l'étoile\"`, `\"Nation\"`, `\"Champd de Mars\"` etc, mais c'est plus long à écrire)."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"text/plain": [
"type place = int\n"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"type rues = place list\n"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"type place = int;;\n",
"type rues = place list;;"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"type ville = rues list\n"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"type ville = rues list;;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
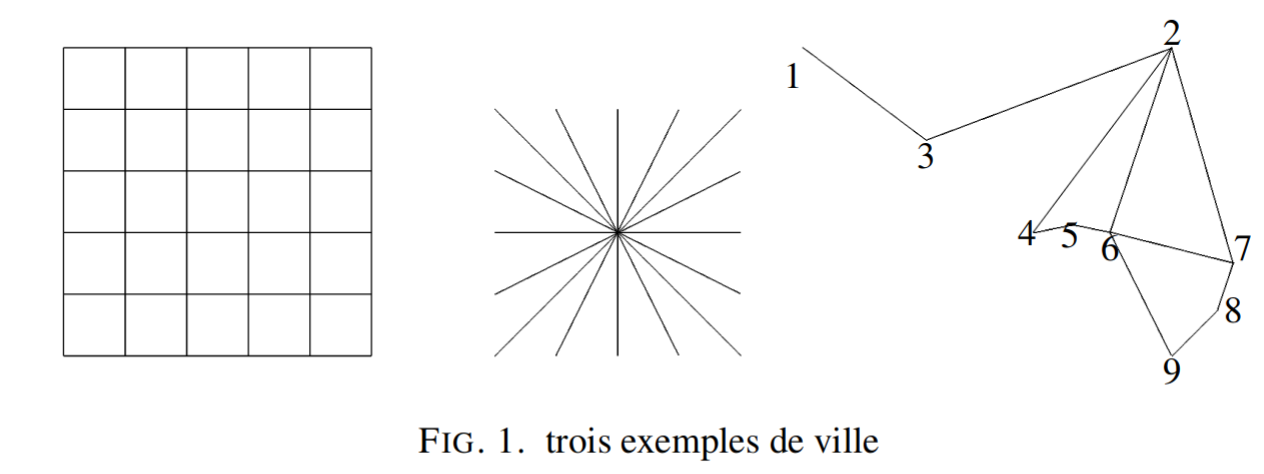
"On donne tout de suite un exemple de graphe, en prenant le 3ème exemple de la Figure 1 du texte.\n",
"\n",
""
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val graphe1 : ville =\n",
" [[2]; [2; 3; 6]; [0; 1]; [1; 4]; [3; 5]; [1; 4; 6; 8]; [1; 5; 7]; [6; 8];\n",
" [5; 7]]\n"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let graphe1 : ville = [\n",
" [2]; (* place 0 *)\n",
" [2; 3; 6]; (* place 1 *)\n",
" [0; 1]; (* place 2 *)\n",
" [1; 4]; (* place 3 *)\n",
" [3; 5]; (* place 4 *)\n",
" [1; 4; 6; 8]; (* place 5 *)\n",
" [1; 5; 7]; (* place 6 *)\n",
" [6; 8]; (* place 7 *)\n",
" [5; 7]; (* place 8 *)\n",
"];;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"On a besoin que les indices commence à $0$ et jusqu'à $n-1$ (où $n$ est le nombre de places), puisque la liste des rues utilisent implicitement la numérotation des places."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"type eclairage = place list\n"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"type eclairage = place list;;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Trois exemples d'éclairages, deux satisfaisant donc l'un trivialement, et l'autre non satisfaisant :"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val eclairage1_sat : eclairage = [0; 1; 2; 3; 4; 5; 6; 7; 8]\n"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"val eclairage2_sat : eclairage = [1; 2; 3; 5; 6; 8]\n"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let eclairage1_sat : eclairage = [\n",
" 0; 1; 2; 3; 4; 5; 6; 7; 8\n",
"];;\n",
"\n",
"let eclairage2_sat : eclairage = [\n",
" 1; 2; 3; 5; 6; 8\n",
"];;"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val eclairage1_nonsat : eclairage = [2; 4; 8]\n"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"val eclairage2_nonsat : eclairage = [1; 2; 3; 5; 6]\n"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let eclairage1_nonsat : eclairage = [\n",
" 2; 4; 8\n",
"];;\n",
"\n",
"let eclairage2_nonsat : eclairage = [\n",
" 1; 2; 3; 5; 6\n",
"];;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Vérification\n",
"\n",
"On pourrait écrire une première fonction pour vérifier que le graphe est bien valide, selon la représentation décrite ci-dessus, en vérifiant :\n",
"- que les places forment bien l'ensemble $\\{0,\\dots,n-1\\}$,\n",
"- que chaque rue n'est présente qu'une fois dans les listes d'adjacences $V[u]$,\n",
"- qu'aucune place inconnue n'est dans une liste $V[u]$,\n",
"- et que le graphe est bien symétrique non-orienté, i.e., que $u \\in V[u] \\Leftrightarrow v \\in V[u]$.\n",
"\n",
"... Mais le sujet n'exige rien de tout ça, donc on passe directement à la question demandée."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Quelques fonctions utiles :"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val somme : int list -> int = \n"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let somme =\n",
" List.fold_left (+) 0\n",
";;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"On met en place, facilement, l'algorithme décrit plus haut.\n",
"Une approche très simple, en trois étapes :\n",
"\n",
"1. compter le nombre de rues,\n",
"2. pour chaque place éclairée, compter le nombre de rues qui en partent (et qui sont donc éclairées),\n",
"3. s'il y a (au moins) une rue non éclairée, renvoyer `false`, sinon renvoyer `true`.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Il y a une finesse : en comptant une fois les rues dont les deux côtés sont éclairés, et deux fois les rues dont un seul côté est éclairé, on peut comparer au nombre de rues comptées doubles.\n",
"\n",
"C'est légérement sous-optimal, comme on va devoir vérifier (en temps linéaire en taille la de l'éclairage) si chaque rue a un ou deux côté éclairés.\n",
"Mais on gagne en mémoire puisqu'on n'a pas à construire une représentation de toutes les rues."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"File \"[9]\", line 1, characters 31-34:\n",
"Warning 27: unused variable ici.\n"
]
},
{
"data": {
"text/plain": [
"val compte_simple_ou_double_0 : place -> rues -> eclairage -> int = \n"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let compte_simple_ou_double_0 (ici : place) (voisines : rues) (proposition : eclairage) =\n",
" somme\n",
" (List.map (fun voisine -> \n",
" if List.mem voisine proposition\n",
" then 1\n",
" else 2\n",
" ) voisines)\n",
";;"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val verifie_eclairage_0 : ville -> eclairage -> bool = \n"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let verifie_eclairage_0 (graphe : ville) (proposition : eclairage) : bool =\n",
" (* 1. compter le nombre de rues *)\n",
" let nombre_rues =\n",
" List.fold_left (fun a b -> a + (List.length b)) 0 (graphe)\n",
" (* (List.length (List.flatten graphe)) *)\n",
" in\n",
" (* 2. pour chaque place *éclairée*, compter le nombre de rues qui en partent *)\n",
" let nombre_rues_eclairees =\n",
" somme\n",
" (List.map (fun place_eclairee ->\n",
" compte_simple_ou_double_0\n",
" place_eclairee\n",
" (List.nth graphe place_eclairee)\n",
" proposition\n",
" ) proposition)\n",
" in\n",
" (* 3. s'il y a (au moins) une rue non éclairée, renvoyer [false], sinon renvoyer [true] *)\n",
" nombre_rues <= nombre_rues_eclairees\n",
";;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Notez qu'on peut même faire mieux, puisque cet appel à `List.mem voisine proposition` est inefficace (au pire il est en $\\mathcal{O}(n)$, et on le fait au pire $n-1$ fois).\n",
"\n",
"En effet, on peut précalculer, dans la fonction `verifie_eclairage` un *tableau*, de taille $n$ fixée (et connue à l'avance), qui contient en indice $i$ le résultat de `List.mem i proposition` : sauf qu'au lieu d'appeler plusieurs fois la fonction `List.mem`, on a qu'à parcourir la liste `proposition` une fois, et remplir les cases du tableau."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val compte_simple_ou_double : place -> rues -> bool array -> int = \n"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let compte_simple_ou_double (_ : place) (voisines : rues) (est_eclairee : bool array) =\n",
" somme\n",
" (List.map (fun voisine -> \n",
" if est_eclairee.(voisine)\n",
" then 1\n",
" else 2\n",
" ) voisines)\n",
";;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Cette fonction précalcule, une seule fois, ce tableau."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val precalcule_places_eclairees : int -> eclairage -> bool array = \n"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let precalcule_places_eclairees (n : int) (proposition : eclairage) : bool array =\n",
" let resultat = Array.make n false in\n",
" List.iter (fun i -> \n",
" resultat.(i) <- true\n",
" ) proposition;\n",
" resultat\n",
";;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Et enfin, on s'en sert pour la fonction `verifie_eclairage` plus rapide."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val verifie_eclairage : ville -> eclairage -> bool = \n"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let verifie_eclairage (graphe : ville) (proposition : eclairage) : bool =\n",
" (* 0. précalcul *)\n",
" let n = List.length graphe in\n",
" let est_eclairee = precalcule_places_eclairees n proposition in\n",
" (* 1. compter le nombre de rues *)\n",
" let nombre_rues =\n",
" List.fold_left (fun a b -> a + (List.length b)) 0 (graphe)\n",
" (* (List.length (List.flatten graphe)) *)\n",
" in\n",
" (* 2. pour chaque place *éclairée*, compter le nombre de rues qui en partent *)\n",
" let nombre_rues_eclairees =\n",
" somme\n",
" (List.map (fun place_eclairee ->\n",
" compte_simple_ou_double\n",
" place_eclairee\n",
" (List.nth graphe place_eclairee)\n",
" est_eclairee\n",
" ) proposition)\n",
" in\n",
" (* 3. s'il y a (au moins) une rue non éclairée, renvoyer [false], sinon renvoyer [true] *)\n",
" nombre_rues <= nombre_rues_eclairees\n",
";;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Exemples\n",
"\n",
"Avec le graphe définit plus haut, et les deux propositions d'éclairages :"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : ville =\n",
"[[2]; [2; 3; 6]; [0; 1]; [1; 4]; [3; 5]; [1; 4; 6; 8]; [1; 5; 7]; [6; 8];\n",
" [5; 7]]\n"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"graphe1;;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Pour des éclairages valides.\n",
"\n",
"- Le premier est trivialement valide, on éclaire toutes les places donc toutes les rues sont bien éclairées."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : eclairage = [0; 1; 2; 3; 4; 5; 6; 7; 8]\n"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : rues list =\n",
"[[2]; [2; 3; 6]; [0; 1]; [1; 4]; [3; 5]; [1; 4; 6; 8]; [1; 5; 7]; [6; 8];\n",
" [5; 7]]\n"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : bool = true\n"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"eclairage1_sat;;\n",
"List.map (fun place_eclairee -> List.nth graphe1 place_eclairee) eclairage1_sat;;\n",
"\n",
"verifie_eclairage graphe1 eclairage1_sat;; (* true *)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- Le second est moins trivial, mais en vérifiant à la main sur le graphe on voit qu'il fonctionne.\n",
" + On a juste éteint la place $0$, mais l'arête $0-1$ reste éclairée par la place $1$,\n",
" + la place $4$ mais les arêtes $3-4$ et $4-5$ sont éclairées par les places $3$ et $5$,\n",
" + et la place $7$ mais les arêtes $6-7$ et $7-8$ sont éclairées par les places $6$ et $8$."
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : eclairage = [1; 2; 3; 5; 6; 8]\n"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : rues list = [[2; 3; 6]; [0; 1]; [1; 4]; [1; 4; 6; 8]; [1; 5; 7]; [5; 7]]\n"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : bool = true\n"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"eclairage2_sat;;\n",
"List.map (fun place_eclairee -> List.nth graphe1 place_eclairee) eclairage2_sat;;\n",
"\n",
"verifie_eclairage graphe1 eclairage2_sat;; (* true *)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- On peut essayer un éclairage de seulement 5 villes. Est-ce optimal ? (on répondra plus tard, mais oui)"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val eclairage3_sat : eclairage = [2; 3; 5; 6; 7]\n"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : rues list = [[0; 1]; [1; 4]; [1; 4; 6; 8]; [1; 5; 7]; [6; 8]]\n"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : bool = true\n"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let eclairage3_sat : eclairage = [\n",
" 2; 3; 5; 6; 7;\n",
"];;\n",
"\n",
"List.map (fun place_eclairee -> List.nth graphe1 place_eclairee) eclairage3_sat;;\n",
"\n",
"verifie_eclairage graphe1 eclairage3_sat;; (* true *)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Pour des éclairages non valides :\n",
"\n",
"- Clairement, le premier est trop gourmand et on a éteint trop de place."
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : eclairage = [2; 4; 8]\n"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : rues list = [[0; 1]; [3; 5]; [5; 7]]\n"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : bool = false\n"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"eclairage1_nonsat;;\n",
"List.map (fun place_eclairee -> List.nth graphe1 place_eclairee) eclairage1_nonsat;;\n",
"\n",
"verifie_eclairage graphe1 eclairage1_nonsat;; (* false *)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- Le second semble bon, mais la rue $8-9$ par exemple est éteinte."
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : eclairage = [1; 2; 3; 5; 6]\n"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : rues list = [[2; 3; 6]; [0; 1]; [1; 4]; [1; 4; 6; 8]; [1; 5; 7]]\n"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : bool = false\n"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"eclairage2_nonsat;;\n",
"List.map (fun place_eclairee -> List.nth graphe1 place_eclairee) eclairage2_nonsat;;\n",
"\n",
"verifie_eclairage graphe1 eclairage2_nonsat;; (* false *)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Bonus : vérifier que le graphe est valide\n",
"Bon... par acquis de conscience, on implémente l'étape de vérification évoquée plus haut.\n",
"\n",
"D'abord, quelques fonctions utiles :"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val max_liste : int list -> int = \n"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let max_liste (liste : int list) : int =\n",
" List.fold_left max (-max_int) liste\n",
";;"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : int = 123\n"
]
},
"execution_count": 24,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"max_liste [123; 12; 1];;"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val max_liste_liste : int list list -> int = \n"
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let max_liste_liste (listeliste : int list list) : int =\n",
" max_liste (List.map max_liste listeliste) \n",
";;"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : int = 1234\n"
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"max_liste_liste [[123; 12; 1]; [1234; 13]];;"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"text/plain": [
"- : bool = true\n"
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"List.for_all (fun x -> (0 <= x) && (x <= 1234)) (List.flatten [[123; 12; 1]; [1234; 13]])"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val compte_occurences : int list -> int -> int = \n"
]
},
"execution_count": 28,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let compte_occurences (liste : int list) (x : int) =\n",
" let rec aux xs x acc =\n",
" match xs with\n",
" | [] -> acc\n",
" | y :: ys when y = x -> aux ys x (acc + 1)\n",
" | _ :: ys -> aux ys x acc\n",
" in\n",
" aux liste x 0\n",
";;"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : int = 1\n"
]
},
"execution_count": 29,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int = 0\n"
]
},
"execution_count": 29,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int = 2\n"
]
},
"execution_count": 29,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"compte_occurences [1; 2; 3; 4; 5] 1;;\n",
"compte_occurences [1; 2; 3; 4; 5] 10;;\n",
"compte_occurences [1; 2; 3; 4; 5; 1; 6; 7] 1;;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Puis, la vérification annoncée :"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val graphe_valide : ville -> bool = \n"
]
},
"execution_count": 30,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let graphe_valide (graphe : ville) : bool =\n",
" let n = max_liste_liste graphe in\n",
" (* D'abord, on vérifie qu'il y a exactement n + 1 listes de places voisines *)\n",
" let test1 =\n",
" (List.length graphe) = (n + 1)\n",
" in\n",
" (* Ensuite, on vérifie que toutes les places voisines sont bien dans des places valides *)\n",
" let test2 =\n",
" List.for_all (\n",
" fun x -> (0 <= x) && (x <= n)\n",
" ) (List.flatten graphe)\n",
" in\n",
" (* Enfin, on vérifie qu'une place voisine v n'est présente qu'une fois dans V[u] *)\n",
" let test3 =\n",
" List.for_all (\n",
" fun voisines -> List.for_all (\n",
" fun place ->\n",
" (compte_occurences voisines place) = 1\n",
" ) voisines\n",
" ) graphe\n",
" in\n",
" (* test1, test2, test3 *)\n",
" test1 && test2 && test3\n",
";;"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : ville =\n",
"[[2]; [2; 3; 6]; [0; 1]; [1; 4]; [3; 5]; [1; 4; 6; 8]; [1; 5; 7]; [6; 8];\n",
" [5; 7]]\n"
]
},
"execution_count": 31,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"graphe1;;"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : bool = true\n"
]
},
"execution_count": 32,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"graphe_valide graphe1;;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"On doit aussi tester trois cas de graphes qui contredisent un de chaque test :"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- S'il manque une place dans la liste d'adjacence :"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val graphe2 : ville =\n",
" [[2]; [2; 3; 6]; [0; 1]; [1; 3]; [3; 5]; [1; 4; 6; 8]; [1; 5; 7]; [6; 8]]\n"
]
},
"execution_count": 33,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let graphe2 : ville = [\n",
" [2]; (* place 0 *)\n",
" [2; 3; 6]; (* place 1 *)\n",
" [0; 1]; (* place 2 *)\n",
" [1; 3]; (* place 3 *)\n",
" [3; 5]; (* place 4 *)\n",
" [1; 4; 6; 8]; (* place 5 *)\n",
" [1; 5; 7]; (* place 6 *)\n",
" [6; 8]; (* place 7 *)\n",
" (* place 8 absente ! *)\n",
"];;"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : bool = false\n"
]
},
"execution_count": 34,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"graphe_valide graphe2;;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- Si la liste d'adjacence est trop grande :"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val graphe3 : ville =\n",
" [[2]; [2; 3; 6]; [0; 1]; [1; 3]; [3; 5]; [1; 4; 6; 8]; [1; 5; 7]; [6; 8];\n",
" [5; 7]; [5; 7]]\n"
]
},
"execution_count": 35,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let graphe3 : ville = [\n",
" [2]; (* place 0 *)\n",
" [2; 3; 6]; (* place 1 *)\n",
" [0; 1]; (* place 2 *)\n",
" [1; 3]; (* place 3 *)\n",
" [3; 5]; (* place 4 *)\n",
" [1; 4; 6; 8]; (* place 5 *)\n",
" [1; 5; 7]; (* place 6 *)\n",
" [6; 8]; (* place 7 *)\n",
" [5; 7]; (* place 8 absente ! *)\n",
" [5; 7] (* place 9 ?! *)\n",
"];;"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : bool = false\n"
]
},
"execution_count": 36,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"graphe_valide graphe3;;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- Si une des places voisines n'est pas valide :"
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val graphe4 : ville =\n",
" [[2]; [2; 3; 6]; [0; 1]; [1; 3]; [3; 5]; [1; 4; 6; 8]; [1; 5; 7]; [6; 8];\n",
" [50]]\n"
]
},
"execution_count": 37,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let graphe4 : ville = [\n",
" [2]; (* place 0 *)\n",
" [2; 3; 6]; (* place 1 *)\n",
" [0; 1]; (* place 2 *)\n",
" [1; 3]; (* place 3 *)\n",
" [3; 5]; (* place 4 *)\n",
" [1; 4; 6; 8]; (* place 5 *)\n",
" [1; 5; 7]; (* place 6 *)\n",
" [6; 8]; (* place 7 *)\n",
" [50] (* place 8 -> 50 ?! *)\n",
"];;"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : bool = false\n"
]
},
"execution_count": 38,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"graphe_valide graphe4;;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- Et enfin, si une des listes d'adjacence contient deux fois la même place voisine :"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val graphe5 : ville =\n",
" [[2]; [2; 3; 6]; [0; 1]; [1; 3]; [3; 5]; [1; 4; 6; 8]; [1; 5; 7]; [6; 8];\n",
" [5; 7; 5]]\n"
]
},
"execution_count": 39,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let graphe5 : ville = [\n",
" [2]; (* place 0 *)\n",
" [2; 3; 6]; (* place 1 *)\n",
" [0; 1]; (* place 2 *)\n",
" [1; 3]; (* place 3 *)\n",
" [3; 5]; (* place 4 *)\n",
" [1; 4; 6; 8]; (* place 5 *)\n",
" [1; 5; 7]; (* place 6 *)\n",
" [6; 8]; (* place 7 *)\n",
" [5; 7; 5] (* place 8 -> 5 deux fois ! *)\n",
"];;"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : bool = false\n"
]
},
"execution_count": 40,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"graphe_valide graphe5;;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"----\n",
"## Bonus : énumération de tous les éclairages possibles\n",
"\n",
"Pour de tous petits graphes, on peut suivre l'approche naïve qui consiste à énumérer toutes les possibilités, et renvoyer celle de nombre de lampadaires minimal.\n",
"\n",
"On pourra ensuite vérifier avec la fonction précédente que l'éclairage donné est bien valide."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Énumération des éclairages possibles\n",
"\n",
"Un éclairage est un sous-ensemble, potentiellement vide, de $\\{0,\\dots,n-1\\}$.\n",
"Il y en a $2^n$ en tout.\n",
"\n",
"Comment les générer efficacement ? En fait, on s'en fiche, le reste du code sera déjà exponentiel en $n$...\n",
"\n",
"- La fonction suivante prend une liste de liste, `acc`, et la dédouble en ajoutant `x` aux listes qui ne le contiennent pas encore, et en gardant une copie des listes d'avant.\n",
"En travaillant avec des listes toutes distinctes, la liste `acc` est toujours dédoublée."
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val ajoute_ou_pas : 'a -> 'a list list -> 'a list list = \n"
]
},
"execution_count": 41,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let ajoute_ou_pas (x : 'a) (acc : 'a list list) =\n",
" (List.map (fun liste ->\n",
" if (List.mem x liste)\n",
" then liste\n",
" else x :: liste\n",
" ) acc\n",
" )\n",
" @\n",
" (List.filter (fun liste ->\n",
" not (List.mem x liste)\n",
" ) acc\n",
" )\n",
";;"
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : int list list = [[1]; []]\n"
]
},
"execution_count": 42,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int list list = [[2; 1]; [2]; [1]; []]\n"
]
},
"execution_count": 42,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"ajoute_ou_pas 1 [[]];;\n",
"ajoute_ou_pas 2 [[1]; []];;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- Maintenant, il suffit d'itérer cette fonction, depuis la liste `[[]]` contenant juste la liste vide."
]
},
{
"cell_type": "code",
"execution_count": 43,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val tous_sous_ensembles : 'a list -> 'a list list = \n"
]
},
"execution_count": 43,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let tous_sous_ensembles (liste : 'a list) : 'a list list =\n",
" let rec aux xs acc =\n",
" match xs with\n",
" | [] -> acc\n",
" | y :: ys ->\n",
" aux ys (ajoute_ou_pas y acc)\n",
" in\n",
" aux liste [ [] ]\n",
";;"
]
},
{
"cell_type": "code",
"execution_count": 44,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : 'a list list = [[]]\n"
]
},
"execution_count": 44,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int list list = [[1]; []]\n"
]
},
"execution_count": 44,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int list list = [[2; 1]; [2]; [1]; []]\n"
]
},
"execution_count": 44,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int list list = [[3; 2; 1]; [3; 2]; [3; 1]; [3]; [2; 1]; [2]; [1]; []]\n"
]
},
"execution_count": 44,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"tous_sous_ensembles [];;\n",
"tous_sous_ensembles [1];;\n",
"tous_sous_ensembles [1; 2];;\n",
"tous_sous_ensembles [1; 2; 3];; (* taille 2^3 = 8 *)"
]
},
{
"cell_type": "code",
"execution_count": 45,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : int list list =\n",
"[[3; 2; 1; 0]; [3; 2; 1]; [3; 2; 0]; [3; 2]; [3; 1; 0]; [3; 1]; [3; 0]; \n",
" [3]; [2; 1; 0]; [2; 1]; [2; 0]; [2]; [1; 0]; [1]; [0]; []]\n"
]
},
"execution_count": 45,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int list list =\n",
"[[4; 3; 2; 1; 0]; [4; 3; 2; 1]; [4; 3; 2; 0]; [4; 3; 2]; [4; 3; 1; 0];\n",
" [4; 3; 1]; [4; 3; 0]; [4; 3]; [4; 2; 1; 0]; [4; 2; 1]; [4; 2; 0]; [4; 2];\n",
" [4; 1; 0]; [4; 1]; [4; 0]; [4]; [3; 2; 1; 0]; [3; 2; 1]; [3; 2; 0]; \n",
" [3; 2]; [3; 1; 0]; [3; 1]; [3; 0]; [3]; [2; 1; 0]; [2; 1]; [2; 0]; [2];\n",
" [1; 0]; [1]; [0]; []]\n"
]
},
"execution_count": 45,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int list list =\n",
"[[5; 4; 3; 2; 1; 0]; [5; 4; 3; 2; 1]; [5; 4; 3; 2; 0]; [5; 4; 3; 2];\n",
" [5; 4; 3; 1; 0]; [5; 4; 3; 1]; [5; 4; 3; 0]; [5; 4; 3]; [5; 4; 2; 1; 0];\n",
" [5; 4; 2; 1]; [5; 4; 2; 0]; [5; 4; 2]; [5; 4; 1; 0]; [5; 4; 1]; [5; 4; 0];\n",
" [5; 4]; [5; 3; 2; 1; 0]; [5; 3; 2; 1]; [5; 3; 2; 0]; [5; 3; 2];\n",
" [5; 3; 1; 0]; [5; 3; 1]; [5; 3; 0]; [5; 3]; [5; 2; 1; 0]; [5; 2; 1];\n",
" [5; 2; 0]; [5; 2]; [5; 1; 0]; [5; 1]; [5; 0]; [5]; [4; 3; 2; 1; 0];\n",
" [4; 3; 2; 1]; [4; 3; 2; 0]; [4; 3; 2]; [4; 3; 1; 0]; [4; 3; 1]; [4; 3; 0];\n",
" [4; 3]; [4; 2; 1; 0]; [4; 2; 1]; [4; 2; 0]; [4; 2]; [4; 1; 0]; [4; 1];\n",
" [4; 0]; [4]; [3; 2; 1; 0]; [3; 2; 1]; [3; 2; 0]; [3; 2]; [3; 1; 0]; \n",
" [3; 1]; [3; 0]; [3]; [2; 1; 0]; [2; 1]; [2; 0]; [2]; [1; 0]; [1]; [0]; \n",
" []]\n"
]
},
"execution_count": 45,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int list list =\n",
"[[6; 5; 4; 3; 2; 1; 0]; [6; 5; 4; 3; 2; 1]; [6; 5; 4; 3; 2; 0];\n",
" [6; 5; 4; 3; 2]; [6; 5; 4; 3; 1; 0]; [6; 5; 4; 3; 1]; [6; 5; 4; 3; 0];\n",
" [6; 5; 4; 3]; [6; 5; 4; 2; 1; 0]; [6; 5; 4; 2; 1]; [6; 5; 4; 2; 0];\n",
" [6; 5; 4; 2]; [6; 5; 4; 1; 0]; [6; 5; 4; 1]; [6; 5; 4; 0]; [6; 5; 4];\n",
" [6; 5; 3; 2; 1; 0]; [6; 5; 3; 2; 1]; [6; 5; 3; 2; 0]; [6; 5; 3; 2];\n",
" [6; 5; 3; 1; 0]; [6; 5; 3; 1]; [6; 5; 3; 0]; [6; 5; 3]; [6; 5; 2; 1; 0];\n",
" [6; 5; 2; 1]; [6; 5; 2; 0]; [6; 5; 2]; [6; 5; 1; 0]; [6; 5; 1]; [6; 5; 0];\n",
" [6; 5]; [6; 4; 3; 2; 1; 0]; [6; 4; 3; 2; 1]; [6; 4; 3; 2; 0]; [6; 4; 3; 2];\n",
" [6; 4; 3; 1; 0]; [6; 4; 3; 1]; [6; 4; 3; 0]; [6; 4; 3]; [6; 4; 2; 1; 0];\n",
" [6; 4; 2; 1]; [6; 4; 2; 0]; [6; 4; 2]; [6; 4; 1; 0]; [6; 4; 1]; [6; 4; 0];\n",
" [6; 4]; [6; 3; 2; 1; 0]; [6; 3; 2; 1]; [6; 3; 2; 0]; [6; 3; 2];\n",
" [6; 3; 1; 0]; [6; 3; 1]; [6; 3; 0]; [6; 3]; [6; 2; 1; 0]; [6; ...]; ...]\n"
]
},
"execution_count": 45,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int list list =\n",
"[[7; 6; 5; 4; 3; 2; 1; 0]; [7; 6; 5; 4; 3; 2; 1]; [7; 6; 5; 4; 3; 2; 0];\n",
" [7; 6; 5; 4; 3; 2]; [7; 6; 5; 4; 3; 1; 0]; [7; 6; 5; 4; 3; 1];\n",
" [7; 6; 5; 4; 3; 0]; [7; 6; 5; 4; 3]; [7; 6; 5; 4; 2; 1; 0];\n",
" [7; 6; 5; 4; 2; 1]; [7; 6; 5; 4; 2; 0]; [7; 6; 5; 4; 2]; [7; 6; 5; 4; 1; 0];\n",
" [7; 6; 5; 4; 1]; [7; 6; 5; 4; 0]; [7; 6; 5; 4]; [7; 6; 5; 3; 2; 1; 0];\n",
" [7; 6; 5; 3; 2; 1]; [7; 6; 5; 3; 2; 0]; [7; 6; 5; 3; 2]; [7; 6; 5; 3; 1; 0];\n",
" [7; 6; 5; 3; 1]; [7; 6; 5; 3; 0]; [7; 6; 5; 3]; [7; 6; 5; 2; 1; 0];\n",
" [7; 6; 5; 2; 1]; [7; 6; 5; 2; 0]; [7; 6; 5; 2]; [7; 6; 5; 1; 0];\n",
" [7; 6; 5; 1]; [7; 6; 5; 0]; [7; 6; 5]; [7; 6; 4; 3; 2; 1; 0];\n",
" [7; 6; 4; 3; 2; 1]; [7; 6; 4; 3; 2; 0]; [7; 6; 4; 3; 2]; [7; 6; 4; 3; 1; 0];\n",
" [7; 6; 4; 3; 1]; [7; 6; 4; 3; 0]; [7; 6; 4; 3]; [7; 6; 4; 2; 1; 0];\n",
" [7; 6; 4; 2; 1]; [7; 6; 4; 2; 0]; [7; 6; 4; 2]; [7; 6; 4; 1; 0];\n",
" [7; 6; 4; 1]; [7; 6; 4; ...]; ...]\n"
]
},
"execution_count": 45,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int list list =\n",
"[[8; 7; 6; 5; 4; 3; 2; 1; 0]; [8; 7; 6; 5; 4; 3; 2; 1];\n",
" [8; 7; 6; 5; 4; 3; 2; 0]; [8; 7; 6; 5; 4; 3; 2]; [8; 7; 6; 5; 4; 3; 1; 0];\n",
" [8; 7; 6; 5; 4; 3; 1]; [8; 7; 6; 5; 4; 3; 0]; [8; 7; 6; 5; 4; 3];\n",
" [8; 7; 6; 5; 4; 2; 1; 0]; [8; 7; 6; 5; 4; 2; 1]; [8; 7; 6; 5; 4; 2; 0];\n",
" [8; 7; 6; 5; 4; 2]; [8; 7; 6; 5; 4; 1; 0]; [8; 7; 6; 5; 4; 1];\n",
" [8; 7; 6; 5; 4; 0]; [8; 7; 6; 5; 4]; [8; 7; 6; 5; 3; 2; 1; 0];\n",
" [8; 7; 6; 5; 3; 2; 1]; [8; 7; 6; 5; 3; 2; 0]; [8; 7; 6; 5; 3; 2];\n",
" [8; 7; 6; 5; 3; 1; 0]; [8; 7; 6; 5; 3; 1]; [8; 7; 6; 5; 3; 0];\n",
" [8; 7; 6; 5; 3]; [8; 7; 6; 5; 2; 1; 0]; [8; 7; 6; 5; 2; 1];\n",
" [8; 7; 6; 5; 2; 0]; [8; 7; 6; 5; 2]; [8; 7; 6; 5; 1; 0]; [8; 7; 6; 5; 1];\n",
" [8; 7; 6; 5; 0]; [8; 7; 6; 5]; [8; 7; 6; 4; 3; 2; 1; 0];\n",
" [8; 7; 6; 4; 3; 2; 1]; [8; 7; 6; 4; 3; 2; 0]; [8; 7; 6; 4; 3; 2];\n",
" [8; 7; 6; 4; 3; 1; 0]; [8; 7; 6; 4; 3; 1]; [8; 7; 6; 4; 3; 0];\n",
" [8; 7; 6; 4; ...]; ...]\n"
]
},
"execution_count": 45,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : unit = ()\n"
]
},
"execution_count": 45,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"tous_sous_ensembles [0; 1; 2; 3];; (* taille 2^4 = 16 *)\n",
"tous_sous_ensembles [0; 1; 2; 3; 4];; (* taille 2^5 = 32 *)\n",
"tous_sous_ensembles [0; 1; 2; 3; 4; 5];; (* taille 2^6 = 64 *)\n",
"tous_sous_ensembles [0; 1; 2; 3; 4; 5; 6];; (* taille 2^7 = 128 *)\n",
"tous_sous_ensembles [0; 1; 2; 3; 4; 5; 6; 7];; (* taille 2^8 = 256 *)\n",
"tous_sous_ensembles [0; 1; 2; 3; 4; 5; 6; 7; 8];; (* taille 2^9 = 512 *)\n",
"\n",
"assert ((List.length (tous_sous_ensembles [0; 1; 2; 3; 4; 5; 6; 7; 8])) = 512);;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"> C'est [tellement plus simple en Python](https://stackoverflow.com/questions/374626/how-can-i-find-all-the-subsets-of-a-set-with-exactly-n-elements)..."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Une autre fonction utile :"
]
},
{
"cell_type": "code",
"execution_count": 46,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val range : int -> int list = \n"
]
},
"execution_count": 46,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let range (n : int) : (int list) =\n",
" let rec range_x (n : int) : (int list) =\n",
" match n with\n",
" | n when n < 0 -> []\n",
" | 0 -> [0]\n",
" | n -> n :: (range_x (n - 1))\n",
" in\n",
" List.rev (range_x n)\n",
";;"
]
},
{
"cell_type": "code",
"execution_count": 47,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : int list = [0]\n"
]
},
"execution_count": 47,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int list = [0; 1]\n"
]
},
"execution_count": 47,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int list = [0; 1; 2; 3; 4; 5]\n"
]
},
"execution_count": 47,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int list = [0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10]\n"
]
},
"execution_count": 47,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"range 0;;\n",
"range 1;;\n",
"range 5;;\n",
"range 10;;"
]
},
{
"cell_type": "code",
"execution_count": 48,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val tous_les_eclairages_possibles : ville -> eclairage list = \n"
]
},
"execution_count": 48,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let tous_les_eclairages_possibles (graphe : ville) : (eclairage list) =\n",
" assert (graphe_valide graphe);\n",
" let n = (List.length graphe) - 1 in\n",
" let sommets = range n in\n",
" tous_sous_ensembles sommets \n",
";;"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : eclairage list =\n",
"[[8; 7; 6; 5; 4; 3; 2; 1; 0]; [8; 7; 6; 5; 4; 3; 2; 1];\n",
" [8; 7; 6; 5; 4; 3; 2; 0]; [8; 7; 6; 5; 4; 3; 2]; [8; 7; 6; 5; 4; 3; 1; 0];\n",
" [8; 7; 6; 5; 4; 3; 1]; [8; 7; 6; 5; 4; 3; 0]; [8; 7; 6; 5; 4; 3];\n",
" [8; 7; 6; 5; 4; 2; 1; 0]; [8; 7; 6; 5; 4; 2; 1]; [8; 7; 6; 5; 4; 2; 0];\n",
" [8; 7; 6; 5; 4; 2]; [8; 7; 6; 5; 4; 1; 0]; [8; 7; 6; 5; 4; 1];\n",
" [8; 7; 6; 5; 4; 0]; [8; 7; 6; 5; 4]; [8; 7; 6; 5; 3; 2; 1; 0];\n",
" [8; 7; 6; 5; 3; 2; 1]; [8; 7; 6; 5; 3; 2; 0]; [8; 7; 6; 5; 3; 2];\n",
" [8; 7; 6; 5; 3; 1; 0]; [8; 7; 6; 5; 3; 1]; [8; 7; 6; 5; 3; 0];\n",
" [8; 7; 6; 5; 3]; [8; 7; 6; 5; 2; 1; 0]; [8; 7; 6; 5; 2; 1];\n",
" [8; 7; 6; 5; 2; 0]; [8; 7; 6; 5; 2]; [8; 7; 6; 5; 1; 0]; [8; 7; 6; 5; 1];\n",
" [8; 7; 6; 5; 0]; [8; 7; 6; 5]; [8; 7; 6; 4; 3; 2; 1; 0];\n",
" [8; 7; 6; 4; 3; 2; 1]; [8; 7; 6; 4; 3; 2; ...]; ...]\n"
]
},
"execution_count": 49,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"tous_les_eclairages_possibles graphe1;;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Liste de taille minimale parmi une liste de listes"
]
},
{
"cell_type": "code",
"execution_count": 50,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val min_liste : int list -> int = \n"
]
},
"execution_count": 50,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let min_liste (liste : int list) : int =\n",
" List.fold_left min (max_int) liste\n",
";;"
]
},
{
"cell_type": "code",
"execution_count": 51,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : int = 1\n"
]
},
"execution_count": 51,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"min_liste [123; 12; 1];;"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val taille_min : int list list -> int = \n"
]
},
"execution_count": 52,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let taille_min (listes : int list list) : int =\n",
" min_liste (List.map List.length listes)\n",
";;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Trouver un éclairage optimal\n",
"\n",
"Ca va être assez naïf :\n",
"\n",
"1. on calcule tous les éclairages possibles,\n",
"2. on filtre les éclairages pour ne garder que ceux qui sont valides,\n",
"3. on calcule la longueur minimale,\n",
"4. tant qu'on y est, on filtre pour ne garder que ceux qui sont de longueur minimale (plutôt que d'en renvoyer un seul)."
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val eclairages_optimaux : ville -> eclairage list = \n"
]
},
"execution_count": 53,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let eclairages_optimaux (graphe : ville) : (eclairage list) =\n",
" let propositions =\n",
" tous_les_eclairages_possibles graphe\n",
" in\n",
" let propositions_valides =\n",
" List.filter (verifie_eclairage graphe) propositions\n",
" in\n",
" let taille_minimale = \n",
" taille_min propositions_valides\n",
" in\n",
" let propositions_minimales =\n",
" List.filter (fun li ->\n",
" (List.length li) = taille_minimale\n",
" ) propositions_valides\n",
" in\n",
" propositions_minimales\n",
";;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Exemples\n",
"\n",
"- On commence avec un tout petit graphe, pour vérifier rapidement avant de passer sur un plus gros graphe :"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"val graphe2 : ville = [[1; 2]; [0; 2]; [0; 1]]\n"
]
},
"execution_count": 54,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"let graphe2 : ville = [\n",
" [1; 2]; (* place 0 -> 1 2 *)\n",
" [0; 2]; (* place 1 -> 0 2 *)\n",
" [0; 1] (* place 2 -> 0 1 *)\n",
"] ;;"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : eclairage list = [[2; 1; 0]; [2; 1]; [2; 0]; [2]; [1; 0]; [1]; [0]; []]\n"
]
},
"execution_count": 55,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int = 8\n"
]
},
"execution_count": 55,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"tous_les_eclairages_possibles graphe2;;\n",
"\n",
"List.length (tous_les_eclairages_possibles graphe2);;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Il y a $8$ éclairages possibles ($2^3$) et les $3$ de taille $2$ sont optimaux : en effet sur un graphe complet à $n$ sommets, il faut et il suffit d'éclairer n'importe quel ensenble de $n-1$ places pour éclairer toutes les $n(n-1)$ arêtes."
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : eclairage list = [[2; 1]; [2; 0]; [1; 0]]\n"
]
},
"execution_count": 56,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"eclairages_optimaux graphe2;;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"- Et sur le graphe avec lequel on travaille depuis le début :"
]
},
{
"cell_type": "code",
"execution_count": 57,
"metadata": {
"scrolled": true
},
"outputs": [
{
"data": {
"text/plain": [
"- : ville =\n",
"[[2]; [2; 3; 6]; [0; 1]; [1; 4]; [3; 5]; [1; 4; 6; 8]; [1; 5; 7]; [6; 8];\n",
" [5; 7]]\n"
]
},
"execution_count": 57,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"graphe1;;"
]
},
{
"cell_type": "code",
"execution_count": 58,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : eclairage list =\n",
"[[8; 7; 6; 5; 4; 3; 2; 1; 0]; [8; 7; 6; 5; 4; 3; 2; 1];\n",
" [8; 7; 6; 5; 4; 3; 2; 0]; [8; 7; 6; 5; 4; 3; 2]; [8; 7; 6; 5; 4; 3; 1; 0];\n",
" [8; 7; 6; 5; 4; 3; 1]; [8; 7; 6; 5; 4; 3; 0]; [8; 7; 6; 5; 4; 3];\n",
" [8; 7; 6; 5; 4; 2; 1; 0]; [8; 7; 6; 5; 4; 2; 1]; [8; 7; 6; 5; 4; 2; 0];\n",
" [8; 7; 6; 5; 4; 2]; [8; 7; 6; 5; 4; 1; 0]; [8; 7; 6; 5; 4; 1];\n",
" [8; 7; 6; 5; 4; 0]; [8; 7; 6; 5; 4]; [8; 7; 6; 5; 3; 2; 1; 0];\n",
" [8; 7; 6; 5; 3; 2; 1]; [8; 7; 6; 5; 3; 2; 0]; [8; 7; 6; 5; 3; 2];\n",
" [8; 7; 6; 5; 3; 1; 0]; [8; 7; 6; 5; 3; 1]; [8; 7; 6; 5; 3; 0];\n",
" [8; 7; 6; 5; 3]; [8; 7; 6; 5; 2; 1; 0]; [8; 7; 6; 5; 2; 1];\n",
" [8; 7; 6; 5; 2; 0]; [8; 7; 6; 5; 2]; [8; 7; 6; 5; 1; 0]; [8; 7; 6; 5; 1];\n",
" [8; 7; 6; 5; 0]; [8; 7; 6; 5]; [8; 7; 6; 4; 3; 2; 1; 0];\n",
" [8; 7; 6; 4; 3; 2; 1]; [8; 7; 6; 4; 3; 2; ...]; ...]\n"
]
},
"execution_count": 58,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"text/plain": [
"- : int = 512\n"
]
},
"execution_count": 58,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"tous_les_eclairages_possibles graphe1;;\n",
"\n",
"List.length (tous_les_eclairages_possibles graphe1);;"
]
},
{
"cell_type": "code",
"execution_count": 59,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"- : eclairage list =\n",
"[[8; 6; 5; 3; 2]; [7; 6; 5; 3; 2]; [7; 5; 4; 2; 1]; [7; 5; 4; 1; 0];\n",
" [7; 5; 3; 2; 1]; [7; 5; 3; 1; 0]]\n"
]
},
"execution_count": 59,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"eclairages_optimaux graphe1;;"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"On vérifie ici que l'éclairage à $5$ places qu'on avait proposé plus haut est bien optimal."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"----\n",
"## Complexités en temps et espace (bonus)\n",
"\n",
"Il est toujours utile de préciser, rapidement à l'oral et/ou dans le code (un commentaire suffit) les complexité (ou ordre de grandeur) des fonctions exigées par l'énoncé.\n",
"\n",
"> Le*s* complexité*s* ? Oui, il ne faut pas oublier l'espace (trop souvent négligé !).\n",
"\n",
"Si vous n'êtes pas sûr ou ne savez pas comment le justifier, mieux vaut marquer :\n",
"\n",
"> « En $\\mathcal{O}(n^2)$ en temps et en espace. »\n",
"\n",
"que de marquer quelque chose de difficilement justifiable comme :\n",
"\n",
"> « Probablement en $\\mathcal{O}(n)$ en temps et en espace. »"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### En temps\n",
"\n",
"- La première fonction de vérification proposée `verifie_eclairage_0` est linéaire en temps, en $m$ le nombre de rues et $p$ le nombre de place éclairées, i.e., est en $\\mathcal{O}(m p)$. C'est sous-optimal pour vérifier que toutes les rues sont bien éclairées, on devrait réussir à faire mieux en $\\mathcal{O}(\\max(n, m))$ !\n",
"\n",
"- La deuxième fonction de vérification proposée `verifie_eclairage` est elle bien linéaire en temps, seulement en $m$ le nombre de rues, i.e., est en $\\mathcal{O}(\\max(n, m))$ (s'il y a moins de rues que de places, il faut quand même créer le tableau `est_eclairee` en $\\mathcal{O}(n)$). C'est optimal pour vérifier que toutes les rues sont bien éclairées ! Youpiiiiiii!!!!!!!!!!!\n",
"\n",
"- Les deux fonctions `tous_les_eclairages_possibles` et `eclairages_optimaux` sont en $\\mathcal{O}(2^n)$ en temps, et c'est *beaucoup* !"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### En espace (ou en mémoire)\n",
"- La première fonction de vérification proposée `verifie_eclairage` est aussi linéaire en espace en la taille du graphe.\n",
"- La deuxième fonction de vérification proposée `verifie_eclairage_0` est aussi linéaire en espace en la taille du graphe.\n",
"\n",
"- Les deux fonctions `tous_les_eclairages_possibles` et `eclairages_optimaux` sont aussi en $\\mathcal{O}(2^n)$ en mémoire, et c'est *beaucoup* ! A noter par contre que le résultat renvoyé par `eclairages_optimaux` est, lui, de taille bien plus raisonnables, mais toujours possiblement exponentielle (si le nombre minimal de places éclairées est $k$, alors ${n \\choose k}$)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"----\n",
"## Conclusion\n",
"\n",
"Voilà pour la question obligatoire de programmation, et un gros bonus.\n",
"\n",
"### Qualités\n",
"- On a décomposé le problème en sous-fonctions,\n",
"- on a fait des exemples et *on les garde* dans ce qu'on présente au jury,\n",
"- on a testé la fonction exigée sur différents exemples.\n",
"\n",
"### Défauts\n",
"- La première implémentation proposée de `verifie_eclairage_0` n'est pas optimale,\n",
"- La deuxième implémentation n'était pas immédiate,\n",
"- et on a pas testé sur des exemples très ambitieux.\n",
"\n",
"### Ouverture ?\n",
"> Bien-sûr, ce petit notebook ne se prétend pas être une solution optimale, ni exhaustive."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "OCaml 4.04.2",
"language": "OCaml",
"name": "ocaml-jupyter"
},
"language_info": {
"codemirror_mode": "text/x-ocaml",
"file_extension": ".ml",
"mimetype": "text/x-ocaml",
"name": "OCaml",
"nbconverter_exporter": null,
"pygments_lexer": "OCaml",
"version": "4.04.2"
},
"notify_time": "10",
"toc": {
"colors": {
"hover_highlight": "#DAA520",
"running_highlight": "#FF0000",
"selected_highlight": "#FFD700"
},
"moveMenuLeft": true,
"nav_menu": {
"height": "429px",
"width": "251px"
},
"navigate_menu": true,
"number_sections": true,
"sideBar": true,
"threshold": 4,
"toc_cell": true,
"toc_position": {
"height": "598px",
"left": "0px",
"right": "1258.47px",
"top": "117px",
"width": "212px"
},
"toc_section_display": "block",
"toc_window_display": true
}
},
"nbformat": 4,
"nbformat_minor": 2
}