#!/usr/bin/env python
# coding: utf-8
# # NAM 2019 pMuTT Workshop
#
# Instructions and materials for the "Theory, Applications, and Tools for Kinetic Modeling" workshop can be found on [our documentation page](https://vlachosgroup.github.io/pMuTT/nam_2019.html).
#
# # Table of Contents
#
# | **1\. [Virtual Kinetic Laboratory Ecosystem](#section_1)**
#
# | **2\. [Useful Links](#section_2)**
#
# | **3\. [Constants](#section_3)**
#
# |-- **3.1. [Access common constants in appropriate units](#section_3_1)**
#
# |-- **3.2. [Convert between units](#section_3_2)**
#
# |-- **3.3. [Convert between equivalent quantities](#section_3_3)**
#
# | **4\. [Exercise 1](#section_4)**
#
# | **5\. [Creating statistical mechanical objects using StatMech](#section_5)**
#
# |-- **5.1. [Supported StatMech models](#section_5_1)**
#
# |--|-- **5.1.1 [Translations](#section_5_1_1)**
#
# |--|-- **5.1.2. [Vibrations](#section_5_1_2)**
#
# |--|-- **5.1.3. [Rotations](#section_5_1_3)**
#
# |--|-- **5.1.4. [Electronic](#section_5_1_4)**
#
# |--|-- **5.1.5. [Miscellaneous](#section_5_1_5)**
#
# |-- **5.2. [Initializing StatMech modes individually](#section_5_2)**
#
# |-- **5.3. [Initializing StatMech modes using presets](#section_5_3)**
#
# | **6\. [Plot Thermodynamic Quantities](#section_6)**
#
# | **7\. [Exercise 2](#section_7)**
#
# | **8\. [Creating empirical objects](#section_8)**
#
# |-- **8.1. [Inputting a NASA polynomial directly](#section_8_1)**
#
# |-- **8.2. [Fitting an empirical object to a StatMech object](#section_8_2)**
#
# | **9\. [Input/Output](#section_9)**
#
# |-- **9.1. [Input via Excel](#section_9_1)**
#
# |-- **9.2. [Output via Thermdat](#section_9_2)**
#
# | **10\. [Reactions](#section_10)**
#
# | **11\. [Exercise 3](#section_11)**
#
# | **12\. [Solutions](#section_12)**
#
# |-- **12.1. [Solution 1](#section_12_1)**
#
# |-- **12.2. [Solution 2](#section_12_2)**
#
# |-- **12.3. [Solution 3](#section_12_3)**
#
# # 1. Virtual Kinetic Laboratory Ecosystem
#
#  #
#
#
#
#
#  #
# - Estimates thermochemical and kinetic parameters using statistical mechanics, transition state theory
# - Writes input files for kinetic models and eases thermodynamic analysis
# - Implemented in Python
# - Easy to learn
# - Heavily used in scientific community
# - Object-oriented approach is a natural analogy to chemical phenomenon
# - Library approach allows users to define the starting point and end point
#
#
#
# - Estimates thermochemical and kinetic parameters using statistical mechanics, transition state theory
# - Writes input files for kinetic models and eases thermodynamic analysis
# - Implemented in Python
# - Easy to learn
# - Heavily used in scientific community
# - Object-oriented approach is a natural analogy to chemical phenomenon
# - Library approach allows users to define the starting point and end point
#
#  #
#
# # 2. Useful Links
#
# - [Documentation](https://vlachosgroup.github.io/pMuTT/): find the most updated documentation
# - [Issues](https://github.com/VlachosGroup/pmutt/issues): report bugs, request features, receive help
# - [Examples](https://vlachosgroup.github.io/pMuTT/examples.html): see examples
#
# # 3. Constants
#
# The [constants module](https://vlachosgroup.github.io/pMuTT/constants.html) has a wide variety of functions for constants and unit conversion.
#
# ## 3.1. Access common constants in appropriate units
# Below, we access Planck's constant in J s.
# In[1]:
from pmutt import constants as c
h1 = c.h('eV s', bar=True)
print('h = {} eV s'.format(h1))
#
# ## 3.2. Convert between units
# Below, we convert 12 atm of pressure to psi.
# In[2]:
from pmutt import constants as c
P_atm = 12. # atm
P_psi = c.convert_unit(num=P_atm, initial='atm', final='psi')
print('{} atm = {} psi'.format(P_atm, P_psi))
#
# ## 3.3. Convert between equivalent quantities
# Below, we convert 1000 wavenumbers (cm-1) to frequency.
# In[3]:
from pmutt import constants as c
wave_num = 1000. # cm-1
freq = c.wavenumber_to_freq(wave_num) # Hz
print('{} cm-1 = {} Hz'.format(wave_num, freq))
#
# # 4. Exercise 1
#
# Using `pmutt.constants`, calculate the dimensionless enthalpy (H/RT) using the following information:
# - H = 0.5 eV
# - T = 77 F
# In[4]:
# Fill in your answer for Exercise 1 here
#
# # 5. Creating statistical mechanical objects using StatMech
#
# Molecules show translational, vibrational, rotational, electronic, and nuclear modes.
#
#
#
#
# # 2. Useful Links
#
# - [Documentation](https://vlachosgroup.github.io/pMuTT/): find the most updated documentation
# - [Issues](https://github.com/VlachosGroup/pmutt/issues): report bugs, request features, receive help
# - [Examples](https://vlachosgroup.github.io/pMuTT/examples.html): see examples
#
# # 3. Constants
#
# The [constants module](https://vlachosgroup.github.io/pMuTT/constants.html) has a wide variety of functions for constants and unit conversion.
#
# ## 3.1. Access common constants in appropriate units
# Below, we access Planck's constant in J s.
# In[1]:
from pmutt import constants as c
h1 = c.h('eV s', bar=True)
print('h = {} eV s'.format(h1))
#
# ## 3.2. Convert between units
# Below, we convert 12 atm of pressure to psi.
# In[2]:
from pmutt import constants as c
P_atm = 12. # atm
P_psi = c.convert_unit(num=P_atm, initial='atm', final='psi')
print('{} atm = {} psi'.format(P_atm, P_psi))
#
# ## 3.3. Convert between equivalent quantities
# Below, we convert 1000 wavenumbers (cm-1) to frequency.
# In[3]:
from pmutt import constants as c
wave_num = 1000. # cm-1
freq = c.wavenumber_to_freq(wave_num) # Hz
print('{} cm-1 = {} Hz'.format(wave_num, freq))
#
# # 4. Exercise 1
#
# Using `pmutt.constants`, calculate the dimensionless enthalpy (H/RT) using the following information:
# - H = 0.5 eV
# - T = 77 F
# In[4]:
# Fill in your answer for Exercise 1 here
#
# # 5. Creating statistical mechanical objects using StatMech
#
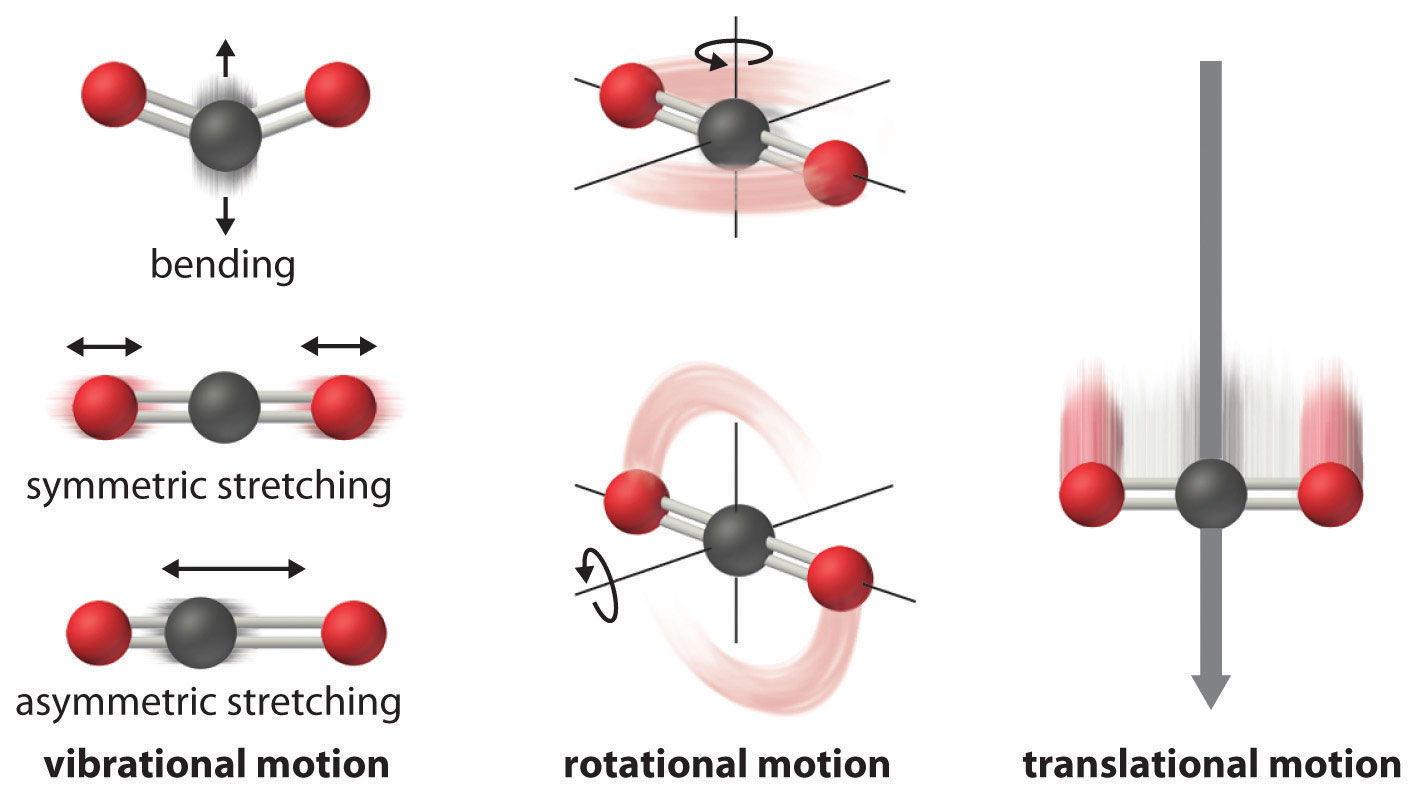
# Molecules show translational, vibrational, rotational, electronic, and nuclear modes.
#
#  #
# ## 5.1. Supported StatMech modes
#
#
#
# ## 5.1. Supported StatMech modes
#
#  #
# The StatMech object allows us to specify translational, vibrational, rotational, electronic and nuclear modes independently, which gives flexibility in what behavior you would like. Below are the available modes.
#
# ### 5.1.1. Translations
# - [``FreeTrans``](https://vlachosgroup.github.io/pMuTT/statmech.html#freetrans) - Translations assuming no intermolecular interactions
#
# ### 5.1.2. Vibrations
# - [``HarmonicVib``](https://vlachosgroup.github.io/pMuTT/statmech.html#harmonicvib) - Harmonic vibrations
# - [``QRRHOVib``](https://vlachosgroup.github.io/pMuTT/statmech.html#harmonicvib) - Quasi rigid rotor harmonic oscillator. Low frequency modes are treated as rigid rotations.
# - [``EinsteinVib``](https://vlachosgroup.github.io/pMuTT/statmech.html#einsteinvib) - Each atom in the crystal vibrates as independent 3D harmonic oscillators
# - [``DebyeVib``](https://vlachosgroup.github.io/pMuTT/statmech.html#debyevib) - Improves upon ``EinsteinVib`` by considering simultaneous vibrations. Improves accuracy at lower temperatures.
#
# ### 5.1.3. Rotations
# - [``RigidRotor``](https://vlachosgroup.github.io/pMuTT/statmech.html#rigidrotor) - Molecule can be rotated with no change in bond properties
#
# ### 5.1.4. Electronic
# - [``GroundStateElec``](https://vlachosgroup.github.io/pMuTT/statmech.html#groundstateelec) - Electronic ground state of the system
# - [``LSR``](https://vlachosgroup.github.io/pMuTT/statmech.html#linear-scaling-relationships-lsrs) - Linear Scaling Relationship to estimate binding energies using reference adsorbate
#
# ### 5.1.5. Miscellaneous
# - [``EmptyMode``](https://vlachosgroup.github.io/pMuTT/statmech.html#empty-mode) - Default mode if not specified. Does not contribute to any properties
# - [``ConstantMode``](https://vlachosgroup.github.io/pMuTT/statmech.html#constant-mode) - Specify arbitrary values to thermodynamic quantities
#
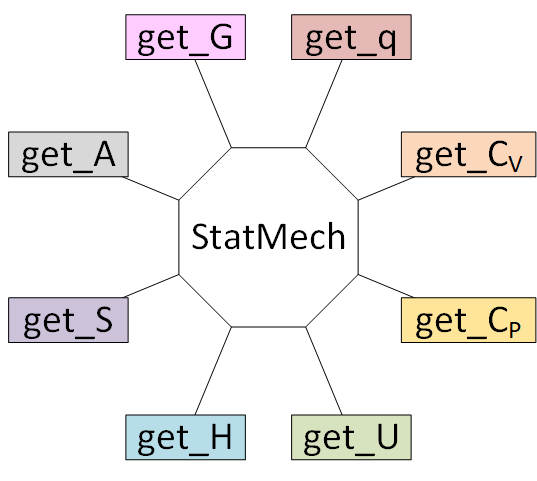
# Using a ``StatMech`` mode gives you access to all the common thermodynamic properties.
#
#
#
# The StatMech object allows us to specify translational, vibrational, rotational, electronic and nuclear modes independently, which gives flexibility in what behavior you would like. Below are the available modes.
#
# ### 5.1.1. Translations
# - [``FreeTrans``](https://vlachosgroup.github.io/pMuTT/statmech.html#freetrans) - Translations assuming no intermolecular interactions
#
# ### 5.1.2. Vibrations
# - [``HarmonicVib``](https://vlachosgroup.github.io/pMuTT/statmech.html#harmonicvib) - Harmonic vibrations
# - [``QRRHOVib``](https://vlachosgroup.github.io/pMuTT/statmech.html#harmonicvib) - Quasi rigid rotor harmonic oscillator. Low frequency modes are treated as rigid rotations.
# - [``EinsteinVib``](https://vlachosgroup.github.io/pMuTT/statmech.html#einsteinvib) - Each atom in the crystal vibrates as independent 3D harmonic oscillators
# - [``DebyeVib``](https://vlachosgroup.github.io/pMuTT/statmech.html#debyevib) - Improves upon ``EinsteinVib`` by considering simultaneous vibrations. Improves accuracy at lower temperatures.
#
# ### 5.1.3. Rotations
# - [``RigidRotor``](https://vlachosgroup.github.io/pMuTT/statmech.html#rigidrotor) - Molecule can be rotated with no change in bond properties
#
# ### 5.1.4. Electronic
# - [``GroundStateElec``](https://vlachosgroup.github.io/pMuTT/statmech.html#groundstateelec) - Electronic ground state of the system
# - [``LSR``](https://vlachosgroup.github.io/pMuTT/statmech.html#linear-scaling-relationships-lsrs) - Linear Scaling Relationship to estimate binding energies using reference adsorbate
#
# ### 5.1.5. Miscellaneous
# - [``EmptyMode``](https://vlachosgroup.github.io/pMuTT/statmech.html#empty-mode) - Default mode if not specified. Does not contribute to any properties
# - [``ConstantMode``](https://vlachosgroup.github.io/pMuTT/statmech.html#constant-mode) - Specify arbitrary values to thermodynamic quantities
#
# Using a ``StatMech`` mode gives you access to all the common thermodynamic properties.
#
#  #
# For this example, we will use a hydrogen molecule as an ideal gas:
# - translations with no interaction between molecules
# - harmonic vibrations
# - rigid rotor rotations
# - ground state electronic structure
# - no contribution from nuclear modes.
#
#
#
# For this example, we will use a hydrogen molecule as an ideal gas:
# - translations with no interaction between molecules
# - harmonic vibrations
# - rigid rotor rotations
# - ground state electronic structure
# - no contribution from nuclear modes.
#
#  #
# ## 5.2. Initializing StatMech modes individually
# In[5]:
from ase.build import molecule
from pmutt.statmech import StatMech, trans, vib, rot, elec
H2_atoms = molecule('H2')
'''Translational'''
H2_trans = trans.FreeTrans(n_degrees=3, atoms=H2_atoms)
'''Vibrational'''
H2_vib = vib.HarmonicVib(vib_wavenumbers=[4342.]) # vib_wavenumbers in cm-1
'''Rotational'''
H2_rot = rot.RigidRotor(symmetrynumber=2, atoms=H2_atoms)
'''Electronic'''
H2_elec = elec.GroundStateElec(potentialenergy=-6.77,spin=0) # potentialenergy in eV
'''StatMech Initialization'''
H2_statmech = StatMech(name='H2',
trans_model=H2_trans,
vib_model=H2_vib,
rot_model=H2_rot,
elec_model=H2_elec)
'''Calculate thermodynamic properties'''
H_statmech = H2_statmech.get_H(T=298., units='kJ/mol')
S_statmech = H2_statmech.get_S(T=298., units='J/mol/K')
print('H_H2(T=298 K) = {:.1f} kJ/mol'.format(H_statmech))
print('S_H2(T=298 K) = {:.2f} J/mol/K'.format(S_statmech))
#
# ## 5.3. Initializing StatMech modes using presets
#
# Commonly used models can be accessed via [``presets``](https://vlachosgroup.github.io/pMuTT/statmech.html#presets). The currently supported models are:
#
# - [``idealgas``](https://vlachosgroup.github.io/pMuTT/statmech.html#ideal-gas-idealgas) - Ideal gases
# - [``harmonic``](https://vlachosgroup.github.io/pMuTT/statmech.html#harmonic-approximation-harmonic) - Typical for surface species
# - [``electronic``](https://vlachosgroup.github.io/pMuTT/statmech.html#electronic-electronic) - Only has electronic modes
# - [``placeholder``](https://vlachosgroup.github.io/pMuTT/statmech.html#placeholder-placeholder) - No contribution to any property
# - [``constant``](https://vlachosgroup.github.io/pMuTT/statmech.html#constant-constant) - Use arbitrary constants to thermodynamic properties
#
# In[6]:
from ase.build import molecule
from pmutt.statmech import StatMech, presets
H2_statmech = StatMech(atoms=molecule('H2'),
vib_wavenumbers=[4342.], # cm-1
symmetrynumber=2,
potentialenergy=-6.77, # eV
spin=0.,
**presets['idealgas'])
'''Calculate thermodynamic properties'''
H_statmech = H2_statmech.get_H(T=298., units='kJ/mol')
S_statmech = H2_statmech.get_S(T=298., units='J/mol/K')
print('H_H2(T=298 K) = {:.1f} kJ/mol'.format(H_statmech))
print('S_H2(T=298 K) = {:.2f} J/mol/K'.format(S_statmech))
#
# # 6. Plot Thermodynamic Quantities
# Use [`pmutt.plot_1D`](https://vlachosgroup.github.io/pMuTT/visual.html#plot-1d) and [`pmutt.plot_2D`](https://vlachosgroup.github.io/pMuTT/visual.html#plot-2d) to plot any function with respect to 1 or 2 variables.
# In[7]:
import numpy as np
from matplotlib import pyplot as plt
from pmutt import plot_1D, plot_2D
T = np.linspace(300., 500.)
f1, ax1 = plot_1D(H2_statmech,
x_name='T', x_values=T,
methods=('get_H', 'get_S', 'get_G'),
get_H_kwargs={'units': 'kcal/mol'},
get_S_kwargs={'units': 'cal/mol/K'},
get_G_kwargs={'units': 'kcal/mol'})
f1.set_size_inches(6, 6)
f1.set_dpi(200)
plt.show()
#
# # 7. Exercise 2
#
# 1. Create a ``StatMech`` object for ideal gas-phase H2O. The necessary inputs are given below.
#
# | Parameter | Value |
# |--------------------------------|------------------------------|
# | atoms | `molecule('H2O')` |
# | Potential Energy (eV) | -6.7598 |
# | Symmetry number | 2 |
# | Spin | 0 |
# | Vibrational Wavenumbers (cm-1) | 3825.434, 3710.264, 1582.432 |
#
# 2. Calculate the Gibbs energy in eV for H2O at T = 500 K and P = 2 bar.
#
# 3. Create a ``StatMech`` object for a Cu crystal using the ``DebyeVib`` model for the vibration mode and ``GroundStateElec`` model for electronic mode. The necessary inputs are given below.
#
# | Parameter | Value |
# |------------------------|------------|
# | Debye Temperature (K) | 310 |
# | Interaction energy (eV)| 0 |
# | Potential energy (eV) | -14.922356 |
#
# 4. Plot the H (in eV) and S (in eV/K) for Cu between T = 300 - 700 K.
# In[8]:
# Fill in your answer for Exercise 2 here
# 1.
# 2.
# 3.
# 4.
#
# # 8. Creating empirical objects
# Currently, pMuTT supports [NASA polynomials](https://vlachosgroup.github.io/pMuTT/empirical.html#nasa) and [Shomate polynomials](https://vlachosgroup.github.io/pMuTT/empirical.html#shomate). They can be initialized in three ways:
# - passing in the polynomials directly
# - from a model (e.g. ``StatMech``, ``Shomate``) (``from_model``)
# - from heat capacity, enthalpy and entropy data (``from_data``)
#
#
#
# ## 5.2. Initializing StatMech modes individually
# In[5]:
from ase.build import molecule
from pmutt.statmech import StatMech, trans, vib, rot, elec
H2_atoms = molecule('H2')
'''Translational'''
H2_trans = trans.FreeTrans(n_degrees=3, atoms=H2_atoms)
'''Vibrational'''
H2_vib = vib.HarmonicVib(vib_wavenumbers=[4342.]) # vib_wavenumbers in cm-1
'''Rotational'''
H2_rot = rot.RigidRotor(symmetrynumber=2, atoms=H2_atoms)
'''Electronic'''
H2_elec = elec.GroundStateElec(potentialenergy=-6.77,spin=0) # potentialenergy in eV
'''StatMech Initialization'''
H2_statmech = StatMech(name='H2',
trans_model=H2_trans,
vib_model=H2_vib,
rot_model=H2_rot,
elec_model=H2_elec)
'''Calculate thermodynamic properties'''
H_statmech = H2_statmech.get_H(T=298., units='kJ/mol')
S_statmech = H2_statmech.get_S(T=298., units='J/mol/K')
print('H_H2(T=298 K) = {:.1f} kJ/mol'.format(H_statmech))
print('S_H2(T=298 K) = {:.2f} J/mol/K'.format(S_statmech))
#
# ## 5.3. Initializing StatMech modes using presets
#
# Commonly used models can be accessed via [``presets``](https://vlachosgroup.github.io/pMuTT/statmech.html#presets). The currently supported models are:
#
# - [``idealgas``](https://vlachosgroup.github.io/pMuTT/statmech.html#ideal-gas-idealgas) - Ideal gases
# - [``harmonic``](https://vlachosgroup.github.io/pMuTT/statmech.html#harmonic-approximation-harmonic) - Typical for surface species
# - [``electronic``](https://vlachosgroup.github.io/pMuTT/statmech.html#electronic-electronic) - Only has electronic modes
# - [``placeholder``](https://vlachosgroup.github.io/pMuTT/statmech.html#placeholder-placeholder) - No contribution to any property
# - [``constant``](https://vlachosgroup.github.io/pMuTT/statmech.html#constant-constant) - Use arbitrary constants to thermodynamic properties
#
# In[6]:
from ase.build import molecule
from pmutt.statmech import StatMech, presets
H2_statmech = StatMech(atoms=molecule('H2'),
vib_wavenumbers=[4342.], # cm-1
symmetrynumber=2,
potentialenergy=-6.77, # eV
spin=0.,
**presets['idealgas'])
'''Calculate thermodynamic properties'''
H_statmech = H2_statmech.get_H(T=298., units='kJ/mol')
S_statmech = H2_statmech.get_S(T=298., units='J/mol/K')
print('H_H2(T=298 K) = {:.1f} kJ/mol'.format(H_statmech))
print('S_H2(T=298 K) = {:.2f} J/mol/K'.format(S_statmech))
#
# # 6. Plot Thermodynamic Quantities
# Use [`pmutt.plot_1D`](https://vlachosgroup.github.io/pMuTT/visual.html#plot-1d) and [`pmutt.plot_2D`](https://vlachosgroup.github.io/pMuTT/visual.html#plot-2d) to plot any function with respect to 1 or 2 variables.
# In[7]:
import numpy as np
from matplotlib import pyplot as plt
from pmutt import plot_1D, plot_2D
T = np.linspace(300., 500.)
f1, ax1 = plot_1D(H2_statmech,
x_name='T', x_values=T,
methods=('get_H', 'get_S', 'get_G'),
get_H_kwargs={'units': 'kcal/mol'},
get_S_kwargs={'units': 'cal/mol/K'},
get_G_kwargs={'units': 'kcal/mol'})
f1.set_size_inches(6, 6)
f1.set_dpi(200)
plt.show()
#
# # 7. Exercise 2
#
# 1. Create a ``StatMech`` object for ideal gas-phase H2O. The necessary inputs are given below.
#
# | Parameter | Value |
# |--------------------------------|------------------------------|
# | atoms | `molecule('H2O')` |
# | Potential Energy (eV) | -6.7598 |
# | Symmetry number | 2 |
# | Spin | 0 |
# | Vibrational Wavenumbers (cm-1) | 3825.434, 3710.264, 1582.432 |
#
# 2. Calculate the Gibbs energy in eV for H2O at T = 500 K and P = 2 bar.
#
# 3. Create a ``StatMech`` object for a Cu crystal using the ``DebyeVib`` model for the vibration mode and ``GroundStateElec`` model for electronic mode. The necessary inputs are given below.
#
# | Parameter | Value |
# |------------------------|------------|
# | Debye Temperature (K) | 310 |
# | Interaction energy (eV)| 0 |
# | Potential energy (eV) | -14.922356 |
#
# 4. Plot the H (in eV) and S (in eV/K) for Cu between T = 300 - 700 K.
# In[8]:
# Fill in your answer for Exercise 2 here
# 1.
# 2.
# 3.
# 4.
#
# # 8. Creating empirical objects
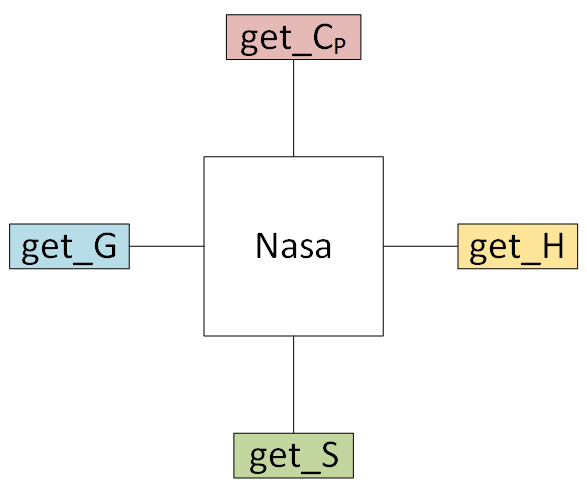
# Currently, pMuTT supports [NASA polynomials](https://vlachosgroup.github.io/pMuTT/empirical.html#nasa) and [Shomate polynomials](https://vlachosgroup.github.io/pMuTT/empirical.html#shomate). They can be initialized in three ways:
# - passing in the polynomials directly
# - from a model (e.g. ``StatMech``, ``Shomate``) (``from_model``)
# - from heat capacity, enthalpy and entropy data (``from_data``)
#
#  #
# ## 8.1. Inputting a NASA polynomial directly
#
# The H2 NASA polynomial from the [Burcat database](http://combustion.berkeley.edu/gri_mech/version30/files30/thermo30.dat) is represented as:
#
# ```
# H2 TPIS78H 2 G 200.000 3500.000 1000.000 1
# 3.33727920E+00-4.94024731E-05 4.99456778E-07-1.79566394E-10 2.00255376E-14 2
# -9.50158922E+02-3.20502331E+00 2.34433112E+00 7.98052075E-03-1.94781510E-05 3
# 2.01572094E-08-7.37611761E-12-9.17935173E+02 6.83010238E-01 4
# ```
#
# This can be translated to pMuTT syntax using:
# In[9]:
from pmutt.empirical.nasa import Nasa
# Initialize NASA polynomial
H2_nasa = Nasa(name='H2',
elements={'H': 2},
phase='G',
T_low=200., T_mid=1000., T_high=3500.,
a_low=[2.34433112E+00, 7.98052075E-03, -1.94781510E-05,
2.01572094E-08, -7.37611761E-12, -9.17935173E+02,
6.83010238E-01],
a_high=[3.33727920E+00, -4.94024731E-05, 4.99456778E-07,
-1.79566394E-10, 2.00255376E-14, -9.50158922E+02,
-3.20502331E+00])
# Calculate thermodynamic quantities using the same syntax as StatMech
H_H2 = H2_nasa.get_H(units='kcal/mol', T=298.)
print('H_H2(T=298 K) = {} kcal/mol'.format(H_H2))
# Show thermodynamic quantities vs. T
T = np.linspace(200., 3500.)
f2, ax2 = plot_1D(H2_nasa,
x_name='T', x_values=T,
methods=('get_H', 'get_S', 'get_G'),
get_H_kwargs={'units': 'kcal/mol'},
get_S_kwargs={'units': 'cal/mol/K'},
get_G_kwargs={'units': 'kcal/mol'})
f2.set_size_inches(6, 6)
f2.set_dpi(200)
plt.show()
#
# ## 8.2. Fitting an empirical object to a StatMech object
# Empirical objects can be made directly using ``StatMech`` objects and the ``from_model`` method.
# In[10]:
H2_nasa = Nasa.from_model(name='H2',
T_low=200.,
T_high=3500.,
model=H2_statmech)
# Compare the statistical mechanical model to the empirical model
f3, ax3 = H2_nasa.plot_statmech_and_empirical(Cp_units='J/mol/K',
H_units='kJ/mol',
S_units='J/mol/K',
G_units='kJ/mol')
f3.set_size_inches(6, 8)
f3.set_dpi(200)
plt.show()
#
# # 9. Input/Output
# pMuTT has more IO functionality than below. See this page for [supported IO functions](https://vlachosgroup.github.io/pMuTT/io.html).
#
# ## 9.1. Input via Excel
#
# Encoding each object in Python can be tedious. You can read several species from Excel spreadsheets using [``pmutt.io.excel.read_excel``](https://vlachosgroup.github.io/pmutt/io.html?highlight=read_excel#pmutt.io.excel.read_excel). Note that this function returns a list of dictionaries. This output allows you to initialize whichever object you want using kwargs syntax. There are also [special rules that depend on the header name](https://vlachosgroup.github.io/pMuTT/io.html#special-rules).
#
# Below, we show an example importing species data from a spreadsheet and creating a series of NASA polynomials.
# In[11]:
import os
from pprint import pprint
from pathlib import Path
from pmutt.io.excel import read_excel
from pmutt.empirical.nasa import Nasa
# Find the location of Jupyter notebook
# Note that normally Python scripts have a __file__ variable but Jupyter notebook doesn't.
# Using pathlib can overcome this limiation
try:
notebook_folder = os.path.dirname(__file__)
except NameError:
notebook_folder = Path().resolve()
os.chdir(notebook_folder)
# Read the data from Excel
ab_initio_data = read_excel(io='./input/NH3_Input_Data.xlsx', sheet_name='species')
pprint(ab_initio_data)
# In[12]:
# Create NASA polynomials using **kwargs syntax
nasa_species = []
for species_data in ab_initio_data:
single_nasa_species = Nasa.from_model(T_low=100.,
T_high=1500.,
**species_data)
nasa_species.append(single_nasa_species)
# Print out a table using enthalpy, entropy, Gibbs energy at 298 K for each species
print('Name Enthalpy (kcal/mol) Entropy (cal/mol/K) Gibbs energy (kcal/mol)')
print('--------------------------------------------------------------------------------')
for single_nasa_species in nasa_species:
name = single_nasa_species.name
H = single_nasa_species.get_H(units='kcal/mol', T=298.)
S = single_nasa_species.get_S(units='cal/mol/K', T=298.)
G = single_nasa_species.get_G(units='kcal/mol', T=298.)
print('{:12} {:10.1f} {:15.1f} {:15.1f}'.format(name, H, S, G))
#
# ## 9.2. Output via Thermdat
# The thermdat format uses NASA polynomials to represent several species. It has a very particular format so doing it manually is error-prone. You can write a list of ``Nasa`` objects to thermdat format using [``pmutt.io.thermdat.write_thermdat``](https://vlachosgroup.github.io/pmutt/io.html#pmutt.io.thermdat.write_thermdat).
#
# Below, we write a thermdat file using the species imported from the spreadsheet.
# In[13]:
from pmutt.io.thermdat import write_thermdat
write_thermdat(filename='./output/thermdat', nasa_species=nasa_species)
# Similarly, a list of ``Nasa`` objects can be read from a thermdat using [``pmutt.io.thermdat.read_thermdat``](https://vlachosgroup.github.io/pMuTT/io.html#pmutt.io.thermdat.read_thermdat).
# In[14]:
from pmutt.io.thermdat import read_thermdat
nasa_species = read_thermdat('./output/thermdat')
#
# # 10. Reactions
#
#
#
# ## 8.1. Inputting a NASA polynomial directly
#
# The H2 NASA polynomial from the [Burcat database](http://combustion.berkeley.edu/gri_mech/version30/files30/thermo30.dat) is represented as:
#
# ```
# H2 TPIS78H 2 G 200.000 3500.000 1000.000 1
# 3.33727920E+00-4.94024731E-05 4.99456778E-07-1.79566394E-10 2.00255376E-14 2
# -9.50158922E+02-3.20502331E+00 2.34433112E+00 7.98052075E-03-1.94781510E-05 3
# 2.01572094E-08-7.37611761E-12-9.17935173E+02 6.83010238E-01 4
# ```
#
# This can be translated to pMuTT syntax using:
# In[9]:
from pmutt.empirical.nasa import Nasa
# Initialize NASA polynomial
H2_nasa = Nasa(name='H2',
elements={'H': 2},
phase='G',
T_low=200., T_mid=1000., T_high=3500.,
a_low=[2.34433112E+00, 7.98052075E-03, -1.94781510E-05,
2.01572094E-08, -7.37611761E-12, -9.17935173E+02,
6.83010238E-01],
a_high=[3.33727920E+00, -4.94024731E-05, 4.99456778E-07,
-1.79566394E-10, 2.00255376E-14, -9.50158922E+02,
-3.20502331E+00])
# Calculate thermodynamic quantities using the same syntax as StatMech
H_H2 = H2_nasa.get_H(units='kcal/mol', T=298.)
print('H_H2(T=298 K) = {} kcal/mol'.format(H_H2))
# Show thermodynamic quantities vs. T
T = np.linspace(200., 3500.)
f2, ax2 = plot_1D(H2_nasa,
x_name='T', x_values=T,
methods=('get_H', 'get_S', 'get_G'),
get_H_kwargs={'units': 'kcal/mol'},
get_S_kwargs={'units': 'cal/mol/K'},
get_G_kwargs={'units': 'kcal/mol'})
f2.set_size_inches(6, 6)
f2.set_dpi(200)
plt.show()
#
# ## 8.2. Fitting an empirical object to a StatMech object
# Empirical objects can be made directly using ``StatMech`` objects and the ``from_model`` method.
# In[10]:
H2_nasa = Nasa.from_model(name='H2',
T_low=200.,
T_high=3500.,
model=H2_statmech)
# Compare the statistical mechanical model to the empirical model
f3, ax3 = H2_nasa.plot_statmech_and_empirical(Cp_units='J/mol/K',
H_units='kJ/mol',
S_units='J/mol/K',
G_units='kJ/mol')
f3.set_size_inches(6, 8)
f3.set_dpi(200)
plt.show()
#
# # 9. Input/Output
# pMuTT has more IO functionality than below. See this page for [supported IO functions](https://vlachosgroup.github.io/pMuTT/io.html).
#
# ## 9.1. Input via Excel
#
# Encoding each object in Python can be tedious. You can read several species from Excel spreadsheets using [``pmutt.io.excel.read_excel``](https://vlachosgroup.github.io/pmutt/io.html?highlight=read_excel#pmutt.io.excel.read_excel). Note that this function returns a list of dictionaries. This output allows you to initialize whichever object you want using kwargs syntax. There are also [special rules that depend on the header name](https://vlachosgroup.github.io/pMuTT/io.html#special-rules).
#
# Below, we show an example importing species data from a spreadsheet and creating a series of NASA polynomials.
# In[11]:
import os
from pprint import pprint
from pathlib import Path
from pmutt.io.excel import read_excel
from pmutt.empirical.nasa import Nasa
# Find the location of Jupyter notebook
# Note that normally Python scripts have a __file__ variable but Jupyter notebook doesn't.
# Using pathlib can overcome this limiation
try:
notebook_folder = os.path.dirname(__file__)
except NameError:
notebook_folder = Path().resolve()
os.chdir(notebook_folder)
# Read the data from Excel
ab_initio_data = read_excel(io='./input/NH3_Input_Data.xlsx', sheet_name='species')
pprint(ab_initio_data)
# In[12]:
# Create NASA polynomials using **kwargs syntax
nasa_species = []
for species_data in ab_initio_data:
single_nasa_species = Nasa.from_model(T_low=100.,
T_high=1500.,
**species_data)
nasa_species.append(single_nasa_species)
# Print out a table using enthalpy, entropy, Gibbs energy at 298 K for each species
print('Name Enthalpy (kcal/mol) Entropy (cal/mol/K) Gibbs energy (kcal/mol)')
print('--------------------------------------------------------------------------------')
for single_nasa_species in nasa_species:
name = single_nasa_species.name
H = single_nasa_species.get_H(units='kcal/mol', T=298.)
S = single_nasa_species.get_S(units='cal/mol/K', T=298.)
G = single_nasa_species.get_G(units='kcal/mol', T=298.)
print('{:12} {:10.1f} {:15.1f} {:15.1f}'.format(name, H, S, G))
#
# ## 9.2. Output via Thermdat
# The thermdat format uses NASA polynomials to represent several species. It has a very particular format so doing it manually is error-prone. You can write a list of ``Nasa`` objects to thermdat format using [``pmutt.io.thermdat.write_thermdat``](https://vlachosgroup.github.io/pmutt/io.html#pmutt.io.thermdat.write_thermdat).
#
# Below, we write a thermdat file using the species imported from the spreadsheet.
# In[13]:
from pmutt.io.thermdat import write_thermdat
write_thermdat(filename='./output/thermdat', nasa_species=nasa_species)
# Similarly, a list of ``Nasa`` objects can be read from a thermdat using [``pmutt.io.thermdat.read_thermdat``](https://vlachosgroup.github.io/pMuTT/io.html#pmutt.io.thermdat.read_thermdat).
# In[14]:
from pmutt.io.thermdat import read_thermdat
nasa_species = read_thermdat('./output/thermdat')
#
# # 10. Reactions
#
# 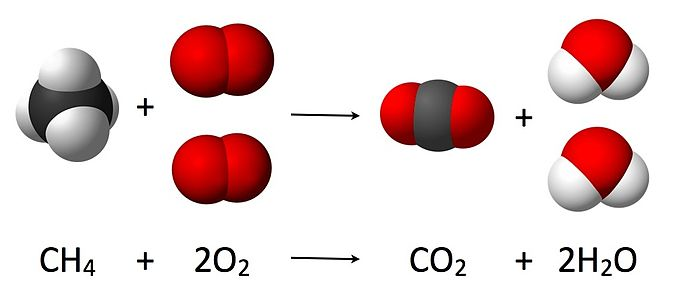 #
# ``Reaction`` objects can be created by putting together ``Nasa``, ``Shomate`` and ``StatMech`` objects.
#
#
#
# ``Reaction`` objects can be created by putting together ``Nasa``, ``Shomate`` and ``StatMech`` objects.
#
# 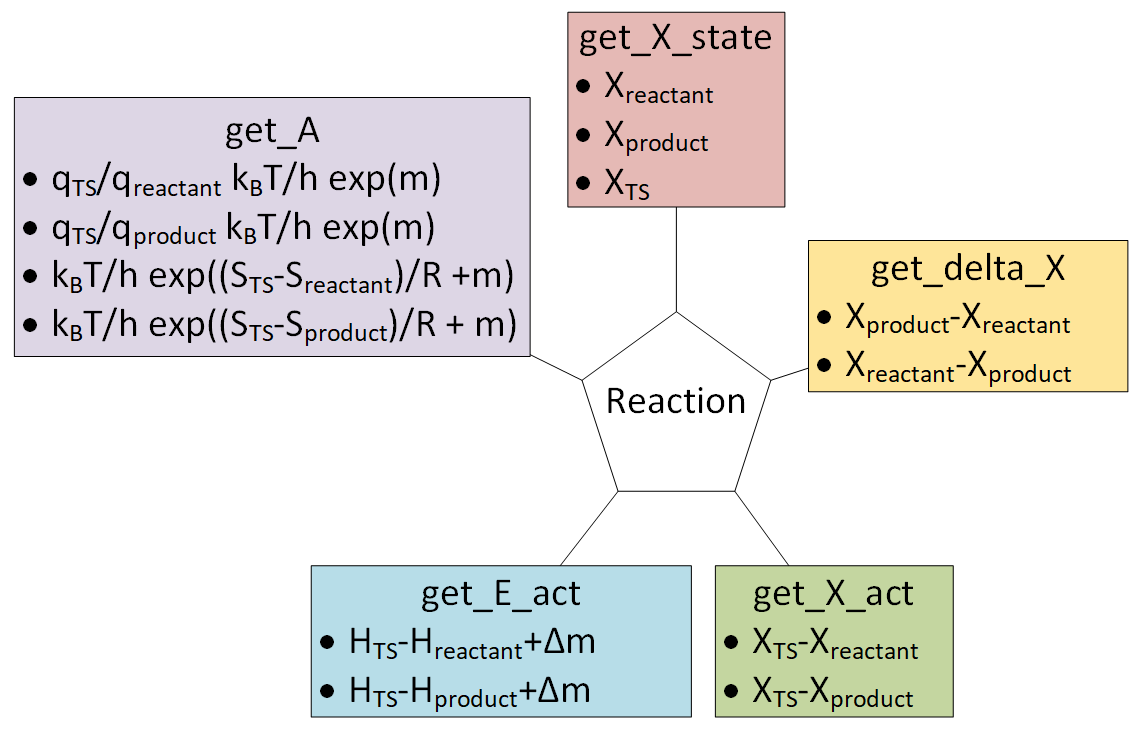 #
#
# The ``from_string`` method is the easiest way to create a ``Reaction`` object. It requires the relevant species to be in a dictionary and a string to describe the reaction.
#
#
#
#
# The ``from_string`` method is the easiest way to create a ``Reaction`` object. It requires the relevant species to be in a dictionary and a string to describe the reaction.
#
#  #
# We will demonstrate its use for the formation of NH3.
# In[15]:
from pmutt.empirical.nasa import Nasa
from pmutt.empirical.shomate import Shomate
from pmutt.reaction import Reaction
# Create species. Note that you can mix different types of species
species = {
'H2': StatMech(name='H2', atoms=molecule('H2'),
vib_wavenumbers=[4342.], # cm-1
symmetrynumber=2,
potentialenergy=-6.77, # eV
spin=0.,
**presets['idealgas']),
'N2': Nasa(name='N2', T_low=300., T_mid=643., T_high=1000.,
a_low=[3.3956319945669633, 0.001115707689025668,
-4.301993779374381e-06, 6.8071424019295535e-09,
-3.2903312791047058e-12, -191001.55648623788,
3.556111439828502],
a_high=[4.050329990684662, -0.0029677854067980108,
5.323485005316287e-06, -3.3518122405333548e-09,
7.58446718337381e-13, -191086.2004520406,
0.6858235504924011]),
'NH3': Shomate(name='NH3', T_low=300., T_high=1000.,
a=[18.792357134351683, 44.82725349479501,
-10.05898449447048, 0.3711633831565547,
0.2969942466370908, -1791.225746924463,
203.9035662274934, 1784.714638346206]),
}
# Define the formation of water reaction
rxn = Reaction.from_string('1.5H2 + 0.5N2 = NH3', species)
# Calculate forward change in enthalpy
H_rxn_fwd = rxn.get_delta_H(units='kcal/mol', T=300.)
print('Delta H_fwd(T = 300 K) = {:.1f} kcal/mol'.format(H_rxn_fwd))
# Calculate reverse change in enthalpy
H_rxn_rev = rxn.get_delta_H(units='kcal/mol', T=300., rev=True)
print('Delta H_rev(T = 300 K) = {:.1f} kcal/mol'.format(H_rxn_rev))
# Calculate enthalpy of reactants
H_react = rxn.get_H_state(units='kcal/mol', T=300., state='reactants')
print('H_reactants(T = 300 K) = {:.1f} kcal/mol'.format(H_react))
#
# ## 11. Exercise 3
#
# 1. Use [``pmutt.io.thermdat.read_thermdat``](https://vlachosgroup.github.io/pMuTT/io.html#pmutt.io.thermdat.read_thermdat) to read the thermdat from './output/thermdat'.
#
# 2. Convert the list of ``Nasa`` to a dictionary of ``Nasa`` using ``pmutt.pmutt_list_to_dict``. The syntax to use the function is shown below.
#
# ```
# from pmutt import pmutt_list_to_dict
#
# species_dict = pmutt_list_to_dict(species_list)
# ```
#
# 3. Create a ``Reaction`` from the string: ``NH3(S) + RU(S) = TS1_NH3(S) = NH2(S) + H(S)`` and the dictionary from step 2.
#
# 4. Calculate the forward reaction enthalpy in kcal/mol at 298 K using [``Reaction.get_delta_H``](https://vlachosgroup.github.io/pMuTT/reactions.html#pmutt.reaction.Reaction.get_E_act).
#
# 5. Calculate the forward activation energy in kcal/mol at 298 K using [``Reaction.get_E_act``](https://vlachosgroup.github.io/pMuTT/reactions.html#pmutt.reaction.Reaction.get_E_act).
# In[16]:
# Fill in your answer for Exercise 3
# 1.
# 2.
# 3.
# 4.
# 5.
#
# # 12. Solutions
#
# ## 12.1. Solution to Exercise 1
# [Link to Exercise 1](#section_4)
# In[17]:
from pmutt import constants as c
# Define information given
H = 0.5 # eV
T = 77 # F
# Calculate H/RT
HoRT = H/c.R('eV/K')/c.convert_unit(77, initial='F', final='K')
print('H/RT = {}'.format(HoRT))
#
# ## 12.2. Solution to Exercise 2
# [Link to Exercise 2](#section_7)
# In[18]:
from ase.build import molecule
from pmutt import plot_1D
from pmutt.statmech import StatMech, presets
from pmutt.statmech.vib import DebyeVib
from pmutt.statmech.elec import GroundStateElec
# 1. Create H2O molecule
H2O_statmech = StatMech(atoms=molecule('H2O'),
potentialenergy=-6.7598,
symmetrynumber=2,
spin=0,
vib_wavenumbers=[3825.434, 3710.264, 1582.432],
**presets['idealgas'])
# 2. Calculate Gibbs energy of H2O at T = 500 K and P = 2 bar
T = 500. # K
P = 2. # bar
G_H2O = H2O_statmech.get_G(units='eV', T=T, P=P)
print('G_H2O(T = 500 K, P = 2 bar) = {} eV'.format(G_H2O))
# 3. Create Cu crystal
Cu_vib = DebyeVib(debye_temperature=310., interaction_energy=0.)
Cu_elec = GroundStateElec(potentialenergy=-14.922356)
Cu_statmech = StatMech(vib_model=Cu_vib, elec_model=Cu_elec)
# 4. Plot the 1D profile for H and S between 300 K and 700 K
T = np.linspace(300., 700.) # K
f2, ax2 = plot_1D(Cu_statmech,
x_name='T', x_values=T,
methods=('get_H', 'get_S'),
get_H_kwargs={'units': 'eV'},
get_S_kwargs={'units': 'eV/K'})
f2.set_size_inches(6, 6)
f2.set_dpi(200)
plt.show()
#
# ## 12.3. Solution to Exercise 3
# [Link to Exercise 3](#section_11)
# In[19]:
from pmutt.io.thermdat import read_thermdat
from pmutt import pmutt_list_to_dict
from pmutt.reaction import Reaction
# 1. Read the thermdat file
species_list = read_thermdat('./output/thermdat')
# 2. Convert the list of Nasa to a dictionary of Nasa
species_dict = pmutt_list_to_dict(species_list)
# 3. Create a Reaction from the specified string
rxn = Reaction.from_string('NH3(S) + RU(S) = TS1_NH3(S) = NH2(S) + H(S)', species_dict)
# 4. Calculate the reaction enthalpy
H_rxn = rxn.get_delta_H(units='kcal/mol', T=298.)
print('H_rxn = {:.1f} kcal/mol'.format(H_rxn))
# 5. Calculate the forward activation energy
Ea = rxn.get_E_act(units='kcal/mol', T=298.)
print('Ea_fwd = {:.1f} kcal/mol'.format(Ea))
#
# We will demonstrate its use for the formation of NH3.
# In[15]:
from pmutt.empirical.nasa import Nasa
from pmutt.empirical.shomate import Shomate
from pmutt.reaction import Reaction
# Create species. Note that you can mix different types of species
species = {
'H2': StatMech(name='H2', atoms=molecule('H2'),
vib_wavenumbers=[4342.], # cm-1
symmetrynumber=2,
potentialenergy=-6.77, # eV
spin=0.,
**presets['idealgas']),
'N2': Nasa(name='N2', T_low=300., T_mid=643., T_high=1000.,
a_low=[3.3956319945669633, 0.001115707689025668,
-4.301993779374381e-06, 6.8071424019295535e-09,
-3.2903312791047058e-12, -191001.55648623788,
3.556111439828502],
a_high=[4.050329990684662, -0.0029677854067980108,
5.323485005316287e-06, -3.3518122405333548e-09,
7.58446718337381e-13, -191086.2004520406,
0.6858235504924011]),
'NH3': Shomate(name='NH3', T_low=300., T_high=1000.,
a=[18.792357134351683, 44.82725349479501,
-10.05898449447048, 0.3711633831565547,
0.2969942466370908, -1791.225746924463,
203.9035662274934, 1784.714638346206]),
}
# Define the formation of water reaction
rxn = Reaction.from_string('1.5H2 + 0.5N2 = NH3', species)
# Calculate forward change in enthalpy
H_rxn_fwd = rxn.get_delta_H(units='kcal/mol', T=300.)
print('Delta H_fwd(T = 300 K) = {:.1f} kcal/mol'.format(H_rxn_fwd))
# Calculate reverse change in enthalpy
H_rxn_rev = rxn.get_delta_H(units='kcal/mol', T=300., rev=True)
print('Delta H_rev(T = 300 K) = {:.1f} kcal/mol'.format(H_rxn_rev))
# Calculate enthalpy of reactants
H_react = rxn.get_H_state(units='kcal/mol', T=300., state='reactants')
print('H_reactants(T = 300 K) = {:.1f} kcal/mol'.format(H_react))
#
# ## 11. Exercise 3
#
# 1. Use [``pmutt.io.thermdat.read_thermdat``](https://vlachosgroup.github.io/pMuTT/io.html#pmutt.io.thermdat.read_thermdat) to read the thermdat from './output/thermdat'.
#
# 2. Convert the list of ``Nasa`` to a dictionary of ``Nasa`` using ``pmutt.pmutt_list_to_dict``. The syntax to use the function is shown below.
#
# ```
# from pmutt import pmutt_list_to_dict
#
# species_dict = pmutt_list_to_dict(species_list)
# ```
#
# 3. Create a ``Reaction`` from the string: ``NH3(S) + RU(S) = TS1_NH3(S) = NH2(S) + H(S)`` and the dictionary from step 2.
#
# 4. Calculate the forward reaction enthalpy in kcal/mol at 298 K using [``Reaction.get_delta_H``](https://vlachosgroup.github.io/pMuTT/reactions.html#pmutt.reaction.Reaction.get_E_act).
#
# 5. Calculate the forward activation energy in kcal/mol at 298 K using [``Reaction.get_E_act``](https://vlachosgroup.github.io/pMuTT/reactions.html#pmutt.reaction.Reaction.get_E_act).
# In[16]:
# Fill in your answer for Exercise 3
# 1.
# 2.
# 3.
# 4.
# 5.
#
# # 12. Solutions
#
# ## 12.1. Solution to Exercise 1
# [Link to Exercise 1](#section_4)
# In[17]:
from pmutt import constants as c
# Define information given
H = 0.5 # eV
T = 77 # F
# Calculate H/RT
HoRT = H/c.R('eV/K')/c.convert_unit(77, initial='F', final='K')
print('H/RT = {}'.format(HoRT))
#
# ## 12.2. Solution to Exercise 2
# [Link to Exercise 2](#section_7)
# In[18]:
from ase.build import molecule
from pmutt import plot_1D
from pmutt.statmech import StatMech, presets
from pmutt.statmech.vib import DebyeVib
from pmutt.statmech.elec import GroundStateElec
# 1. Create H2O molecule
H2O_statmech = StatMech(atoms=molecule('H2O'),
potentialenergy=-6.7598,
symmetrynumber=2,
spin=0,
vib_wavenumbers=[3825.434, 3710.264, 1582.432],
**presets['idealgas'])
# 2. Calculate Gibbs energy of H2O at T = 500 K and P = 2 bar
T = 500. # K
P = 2. # bar
G_H2O = H2O_statmech.get_G(units='eV', T=T, P=P)
print('G_H2O(T = 500 K, P = 2 bar) = {} eV'.format(G_H2O))
# 3. Create Cu crystal
Cu_vib = DebyeVib(debye_temperature=310., interaction_energy=0.)
Cu_elec = GroundStateElec(potentialenergy=-14.922356)
Cu_statmech = StatMech(vib_model=Cu_vib, elec_model=Cu_elec)
# 4. Plot the 1D profile for H and S between 300 K and 700 K
T = np.linspace(300., 700.) # K
f2, ax2 = plot_1D(Cu_statmech,
x_name='T', x_values=T,
methods=('get_H', 'get_S'),
get_H_kwargs={'units': 'eV'},
get_S_kwargs={'units': 'eV/K'})
f2.set_size_inches(6, 6)
f2.set_dpi(200)
plt.show()
#
# ## 12.3. Solution to Exercise 3
# [Link to Exercise 3](#section_11)
# In[19]:
from pmutt.io.thermdat import read_thermdat
from pmutt import pmutt_list_to_dict
from pmutt.reaction import Reaction
# 1. Read the thermdat file
species_list = read_thermdat('./output/thermdat')
# 2. Convert the list of Nasa to a dictionary of Nasa
species_dict = pmutt_list_to_dict(species_list)
# 3. Create a Reaction from the specified string
rxn = Reaction.from_string('NH3(S) + RU(S) = TS1_NH3(S) = NH2(S) + H(S)', species_dict)
# 4. Calculate the reaction enthalpy
H_rxn = rxn.get_delta_H(units='kcal/mol', T=298.)
print('H_rxn = {:.1f} kcal/mol'.format(H_rxn))
# 5. Calculate the forward activation energy
Ea = rxn.get_E_act(units='kcal/mol', T=298.)
print('Ea_fwd = {:.1f} kcal/mol'.format(Ea))
 #
# - Estimates thermochemical and kinetic parameters using statistical mechanics, transition state theory
# - Writes input files for kinetic models and eases thermodynamic analysis
# - Implemented in Python
# - Easy to learn
# - Heavily used in scientific community
# - Object-oriented approach is a natural analogy to chemical phenomenon
# - Library approach allows users to define the starting point and end point
#
#
#
# - Estimates thermochemical and kinetic parameters using statistical mechanics, transition state theory
# - Writes input files for kinetic models and eases thermodynamic analysis
# - Implemented in Python
# - Easy to learn
# - Heavily used in scientific community
# - Object-oriented approach is a natural analogy to chemical phenomenon
# - Library approach allows users to define the starting point and end point
#
#  #
#
# # 2. Useful Links
#
# - [Documentation](https://vlachosgroup.github.io/pMuTT/): find the most updated documentation
# - [Issues](https://github.com/VlachosGroup/pmutt/issues): report bugs, request features, receive help
# - [Examples](https://vlachosgroup.github.io/pMuTT/examples.html): see examples
#
# # 3. Constants
#
# The [constants module](https://vlachosgroup.github.io/pMuTT/constants.html) has a wide variety of functions for constants and unit conversion.
#
# ## 3.1. Access common constants in appropriate units
# Below, we access Planck's constant in J s.
# In[1]:
from pmutt import constants as c
h1 = c.h('eV s', bar=True)
print('h = {} eV s'.format(h1))
#
# ## 3.2. Convert between units
# Below, we convert 12 atm of pressure to psi.
# In[2]:
from pmutt import constants as c
P_atm = 12. # atm
P_psi = c.convert_unit(num=P_atm, initial='atm', final='psi')
print('{} atm = {} psi'.format(P_atm, P_psi))
#
# ## 3.3. Convert between equivalent quantities
# Below, we convert 1000 wavenumbers (cm-1) to frequency.
# In[3]:
from pmutt import constants as c
wave_num = 1000. # cm-1
freq = c.wavenumber_to_freq(wave_num) # Hz
print('{} cm-1 = {} Hz'.format(wave_num, freq))
#
# # 4. Exercise 1
#
# Using `pmutt.constants`, calculate the dimensionless enthalpy (H/RT) using the following information:
# - H = 0.5 eV
# - T = 77 F
# In[4]:
# Fill in your answer for Exercise 1 here
#
# # 5. Creating statistical mechanical objects using StatMech
#
# Molecules show translational, vibrational, rotational, electronic, and nuclear modes.
#
#
#
#
# # 2. Useful Links
#
# - [Documentation](https://vlachosgroup.github.io/pMuTT/): find the most updated documentation
# - [Issues](https://github.com/VlachosGroup/pmutt/issues): report bugs, request features, receive help
# - [Examples](https://vlachosgroup.github.io/pMuTT/examples.html): see examples
#
# # 3. Constants
#
# The [constants module](https://vlachosgroup.github.io/pMuTT/constants.html) has a wide variety of functions for constants and unit conversion.
#
# ## 3.1. Access common constants in appropriate units
# Below, we access Planck's constant in J s.
# In[1]:
from pmutt import constants as c
h1 = c.h('eV s', bar=True)
print('h = {} eV s'.format(h1))
#
# ## 3.2. Convert between units
# Below, we convert 12 atm of pressure to psi.
# In[2]:
from pmutt import constants as c
P_atm = 12. # atm
P_psi = c.convert_unit(num=P_atm, initial='atm', final='psi')
print('{} atm = {} psi'.format(P_atm, P_psi))
#
# ## 3.3. Convert between equivalent quantities
# Below, we convert 1000 wavenumbers (cm-1) to frequency.
# In[3]:
from pmutt import constants as c
wave_num = 1000. # cm-1
freq = c.wavenumber_to_freq(wave_num) # Hz
print('{} cm-1 = {} Hz'.format(wave_num, freq))
#
# # 4. Exercise 1
#
# Using `pmutt.constants`, calculate the dimensionless enthalpy (H/RT) using the following information:
# - H = 0.5 eV
# - T = 77 F
# In[4]:
# Fill in your answer for Exercise 1 here
#
# # 5. Creating statistical mechanical objects using StatMech
#
# Molecules show translational, vibrational, rotational, electronic, and nuclear modes.
#
#  #
# ## 5.1. Supported StatMech modes
#
#
#
# ## 5.1. Supported StatMech modes
#
#  #
# For this example, we will use a hydrogen molecule as an ideal gas:
# - translations with no interaction between molecules
# - harmonic vibrations
# - rigid rotor rotations
# - ground state electronic structure
# - no contribution from nuclear modes.
#
#
#
# For this example, we will use a hydrogen molecule as an ideal gas:
# - translations with no interaction between molecules
# - harmonic vibrations
# - rigid rotor rotations
# - ground state electronic structure
# - no contribution from nuclear modes.
#
#  #
# ## 5.2. Initializing StatMech modes individually
# In[5]:
from ase.build import molecule
from pmutt.statmech import StatMech, trans, vib, rot, elec
H2_atoms = molecule('H2')
'''Translational'''
H2_trans = trans.FreeTrans(n_degrees=3, atoms=H2_atoms)
'''Vibrational'''
H2_vib = vib.HarmonicVib(vib_wavenumbers=[4342.]) # vib_wavenumbers in cm-1
'''Rotational'''
H2_rot = rot.RigidRotor(symmetrynumber=2, atoms=H2_atoms)
'''Electronic'''
H2_elec = elec.GroundStateElec(potentialenergy=-6.77,spin=0) # potentialenergy in eV
'''StatMech Initialization'''
H2_statmech = StatMech(name='H2',
trans_model=H2_trans,
vib_model=H2_vib,
rot_model=H2_rot,
elec_model=H2_elec)
'''Calculate thermodynamic properties'''
H_statmech = H2_statmech.get_H(T=298., units='kJ/mol')
S_statmech = H2_statmech.get_S(T=298., units='J/mol/K')
print('H_H2(T=298 K) = {:.1f} kJ/mol'.format(H_statmech))
print('S_H2(T=298 K) = {:.2f} J/mol/K'.format(S_statmech))
#
# ## 5.3. Initializing StatMech modes using presets
#
# Commonly used models can be accessed via [``presets``](https://vlachosgroup.github.io/pMuTT/statmech.html#presets). The currently supported models are:
#
# - [``idealgas``](https://vlachosgroup.github.io/pMuTT/statmech.html#ideal-gas-idealgas) - Ideal gases
# - [``harmonic``](https://vlachosgroup.github.io/pMuTT/statmech.html#harmonic-approximation-harmonic) - Typical for surface species
# - [``electronic``](https://vlachosgroup.github.io/pMuTT/statmech.html#electronic-electronic) - Only has electronic modes
# - [``placeholder``](https://vlachosgroup.github.io/pMuTT/statmech.html#placeholder-placeholder) - No contribution to any property
# - [``constant``](https://vlachosgroup.github.io/pMuTT/statmech.html#constant-constant) - Use arbitrary constants to thermodynamic properties
#
# In[6]:
from ase.build import molecule
from pmutt.statmech import StatMech, presets
H2_statmech = StatMech(atoms=molecule('H2'),
vib_wavenumbers=[4342.], # cm-1
symmetrynumber=2,
potentialenergy=-6.77, # eV
spin=0.,
**presets['idealgas'])
'''Calculate thermodynamic properties'''
H_statmech = H2_statmech.get_H(T=298., units='kJ/mol')
S_statmech = H2_statmech.get_S(T=298., units='J/mol/K')
print('H_H2(T=298 K) = {:.1f} kJ/mol'.format(H_statmech))
print('S_H2(T=298 K) = {:.2f} J/mol/K'.format(S_statmech))
#
# # 6. Plot Thermodynamic Quantities
# Use [`pmutt.plot_1D`](https://vlachosgroup.github.io/pMuTT/visual.html#plot-1d) and [`pmutt.plot_2D`](https://vlachosgroup.github.io/pMuTT/visual.html#plot-2d) to plot any function with respect to 1 or 2 variables.
# In[7]:
import numpy as np
from matplotlib import pyplot as plt
from pmutt import plot_1D, plot_2D
T = np.linspace(300., 500.)
f1, ax1 = plot_1D(H2_statmech,
x_name='T', x_values=T,
methods=('get_H', 'get_S', 'get_G'),
get_H_kwargs={'units': 'kcal/mol'},
get_S_kwargs={'units': 'cal/mol/K'},
get_G_kwargs={'units': 'kcal/mol'})
f1.set_size_inches(6, 6)
f1.set_dpi(200)
plt.show()
#
# # 7. Exercise 2
#
# 1. Create a ``StatMech`` object for ideal gas-phase H2O. The necessary inputs are given below.
#
# | Parameter | Value |
# |--------------------------------|------------------------------|
# | atoms | `molecule('H2O')` |
# | Potential Energy (eV) | -6.7598 |
# | Symmetry number | 2 |
# | Spin | 0 |
# | Vibrational Wavenumbers (cm-1) | 3825.434, 3710.264, 1582.432 |
#
# 2. Calculate the Gibbs energy in eV for H2O at T = 500 K and P = 2 bar.
#
# 3. Create a ``StatMech`` object for a Cu crystal using the ``DebyeVib`` model for the vibration mode and ``GroundStateElec`` model for electronic mode. The necessary inputs are given below.
#
# | Parameter | Value |
# |------------------------|------------|
# | Debye Temperature (K) | 310 |
# | Interaction energy (eV)| 0 |
# | Potential energy (eV) | -14.922356 |
#
# 4. Plot the H (in eV) and S (in eV/K) for Cu between T = 300 - 700 K.
# In[8]:
# Fill in your answer for Exercise 2 here
# 1.
# 2.
# 3.
# 4.
#
# # 8. Creating empirical objects
# Currently, pMuTT supports [NASA polynomials](https://vlachosgroup.github.io/pMuTT/empirical.html#nasa) and [Shomate polynomials](https://vlachosgroup.github.io/pMuTT/empirical.html#shomate). They can be initialized in three ways:
# - passing in the polynomials directly
# - from a model (e.g. ``StatMech``, ``Shomate``) (``from_model``)
# - from heat capacity, enthalpy and entropy data (``from_data``)
#
#
#
# ## 5.2. Initializing StatMech modes individually
# In[5]:
from ase.build import molecule
from pmutt.statmech import StatMech, trans, vib, rot, elec
H2_atoms = molecule('H2')
'''Translational'''
H2_trans = trans.FreeTrans(n_degrees=3, atoms=H2_atoms)
'''Vibrational'''
H2_vib = vib.HarmonicVib(vib_wavenumbers=[4342.]) # vib_wavenumbers in cm-1
'''Rotational'''
H2_rot = rot.RigidRotor(symmetrynumber=2, atoms=H2_atoms)
'''Electronic'''
H2_elec = elec.GroundStateElec(potentialenergy=-6.77,spin=0) # potentialenergy in eV
'''StatMech Initialization'''
H2_statmech = StatMech(name='H2',
trans_model=H2_trans,
vib_model=H2_vib,
rot_model=H2_rot,
elec_model=H2_elec)
'''Calculate thermodynamic properties'''
H_statmech = H2_statmech.get_H(T=298., units='kJ/mol')
S_statmech = H2_statmech.get_S(T=298., units='J/mol/K')
print('H_H2(T=298 K) = {:.1f} kJ/mol'.format(H_statmech))
print('S_H2(T=298 K) = {:.2f} J/mol/K'.format(S_statmech))
#
# ## 5.3. Initializing StatMech modes using presets
#
# Commonly used models can be accessed via [``presets``](https://vlachosgroup.github.io/pMuTT/statmech.html#presets). The currently supported models are:
#
# - [``idealgas``](https://vlachosgroup.github.io/pMuTT/statmech.html#ideal-gas-idealgas) - Ideal gases
# - [``harmonic``](https://vlachosgroup.github.io/pMuTT/statmech.html#harmonic-approximation-harmonic) - Typical for surface species
# - [``electronic``](https://vlachosgroup.github.io/pMuTT/statmech.html#electronic-electronic) - Only has electronic modes
# - [``placeholder``](https://vlachosgroup.github.io/pMuTT/statmech.html#placeholder-placeholder) - No contribution to any property
# - [``constant``](https://vlachosgroup.github.io/pMuTT/statmech.html#constant-constant) - Use arbitrary constants to thermodynamic properties
#
# In[6]:
from ase.build import molecule
from pmutt.statmech import StatMech, presets
H2_statmech = StatMech(atoms=molecule('H2'),
vib_wavenumbers=[4342.], # cm-1
symmetrynumber=2,
potentialenergy=-6.77, # eV
spin=0.,
**presets['idealgas'])
'''Calculate thermodynamic properties'''
H_statmech = H2_statmech.get_H(T=298., units='kJ/mol')
S_statmech = H2_statmech.get_S(T=298., units='J/mol/K')
print('H_H2(T=298 K) = {:.1f} kJ/mol'.format(H_statmech))
print('S_H2(T=298 K) = {:.2f} J/mol/K'.format(S_statmech))
#
# # 6. Plot Thermodynamic Quantities
# Use [`pmutt.plot_1D`](https://vlachosgroup.github.io/pMuTT/visual.html#plot-1d) and [`pmutt.plot_2D`](https://vlachosgroup.github.io/pMuTT/visual.html#plot-2d) to plot any function with respect to 1 or 2 variables.
# In[7]:
import numpy as np
from matplotlib import pyplot as plt
from pmutt import plot_1D, plot_2D
T = np.linspace(300., 500.)
f1, ax1 = plot_1D(H2_statmech,
x_name='T', x_values=T,
methods=('get_H', 'get_S', 'get_G'),
get_H_kwargs={'units': 'kcal/mol'},
get_S_kwargs={'units': 'cal/mol/K'},
get_G_kwargs={'units': 'kcal/mol'})
f1.set_size_inches(6, 6)
f1.set_dpi(200)
plt.show()
#
# # 7. Exercise 2
#
# 1. Create a ``StatMech`` object for ideal gas-phase H2O. The necessary inputs are given below.
#
# | Parameter | Value |
# |--------------------------------|------------------------------|
# | atoms | `molecule('H2O')` |
# | Potential Energy (eV) | -6.7598 |
# | Symmetry number | 2 |
# | Spin | 0 |
# | Vibrational Wavenumbers (cm-1) | 3825.434, 3710.264, 1582.432 |
#
# 2. Calculate the Gibbs energy in eV for H2O at T = 500 K and P = 2 bar.
#
# 3. Create a ``StatMech`` object for a Cu crystal using the ``DebyeVib`` model for the vibration mode and ``GroundStateElec`` model for electronic mode. The necessary inputs are given below.
#
# | Parameter | Value |
# |------------------------|------------|
# | Debye Temperature (K) | 310 |
# | Interaction energy (eV)| 0 |
# | Potential energy (eV) | -14.922356 |
#
# 4. Plot the H (in eV) and S (in eV/K) for Cu between T = 300 - 700 K.
# In[8]:
# Fill in your answer for Exercise 2 here
# 1.
# 2.
# 3.
# 4.
#
# # 8. Creating empirical objects
# Currently, pMuTT supports [NASA polynomials](https://vlachosgroup.github.io/pMuTT/empirical.html#nasa) and [Shomate polynomials](https://vlachosgroup.github.io/pMuTT/empirical.html#shomate). They can be initialized in three ways:
# - passing in the polynomials directly
# - from a model (e.g. ``StatMech``, ``Shomate``) (``from_model``)
# - from heat capacity, enthalpy and entropy data (``from_data``)
#
#  #
# ## 8.1. Inputting a NASA polynomial directly
#
# The H2 NASA polynomial from the [Burcat database](http://combustion.berkeley.edu/gri_mech/version30/files30/thermo30.dat) is represented as:
#
# ```
# H2 TPIS78H 2 G 200.000 3500.000 1000.000 1
# 3.33727920E+00-4.94024731E-05 4.99456778E-07-1.79566394E-10 2.00255376E-14 2
# -9.50158922E+02-3.20502331E+00 2.34433112E+00 7.98052075E-03-1.94781510E-05 3
# 2.01572094E-08-7.37611761E-12-9.17935173E+02 6.83010238E-01 4
# ```
#
# This can be translated to pMuTT syntax using:
# In[9]:
from pmutt.empirical.nasa import Nasa
# Initialize NASA polynomial
H2_nasa = Nasa(name='H2',
elements={'H': 2},
phase='G',
T_low=200., T_mid=1000., T_high=3500.,
a_low=[2.34433112E+00, 7.98052075E-03, -1.94781510E-05,
2.01572094E-08, -7.37611761E-12, -9.17935173E+02,
6.83010238E-01],
a_high=[3.33727920E+00, -4.94024731E-05, 4.99456778E-07,
-1.79566394E-10, 2.00255376E-14, -9.50158922E+02,
-3.20502331E+00])
# Calculate thermodynamic quantities using the same syntax as StatMech
H_H2 = H2_nasa.get_H(units='kcal/mol', T=298.)
print('H_H2(T=298 K) = {} kcal/mol'.format(H_H2))
# Show thermodynamic quantities vs. T
T = np.linspace(200., 3500.)
f2, ax2 = plot_1D(H2_nasa,
x_name='T', x_values=T,
methods=('get_H', 'get_S', 'get_G'),
get_H_kwargs={'units': 'kcal/mol'},
get_S_kwargs={'units': 'cal/mol/K'},
get_G_kwargs={'units': 'kcal/mol'})
f2.set_size_inches(6, 6)
f2.set_dpi(200)
plt.show()
#
# ## 8.2. Fitting an empirical object to a StatMech object
# Empirical objects can be made directly using ``StatMech`` objects and the ``from_model`` method.
# In[10]:
H2_nasa = Nasa.from_model(name='H2',
T_low=200.,
T_high=3500.,
model=H2_statmech)
# Compare the statistical mechanical model to the empirical model
f3, ax3 = H2_nasa.plot_statmech_and_empirical(Cp_units='J/mol/K',
H_units='kJ/mol',
S_units='J/mol/K',
G_units='kJ/mol')
f3.set_size_inches(6, 8)
f3.set_dpi(200)
plt.show()
#
# # 9. Input/Output
# pMuTT has more IO functionality than below. See this page for [supported IO functions](https://vlachosgroup.github.io/pMuTT/io.html).
#
# ## 9.1. Input via Excel
#
# Encoding each object in Python can be tedious. You can read several species from Excel spreadsheets using [``pmutt.io.excel.read_excel``](https://vlachosgroup.github.io/pmutt/io.html?highlight=read_excel#pmutt.io.excel.read_excel). Note that this function returns a list of dictionaries. This output allows you to initialize whichever object you want using kwargs syntax. There are also [special rules that depend on the header name](https://vlachosgroup.github.io/pMuTT/io.html#special-rules).
#
# Below, we show an example importing species data from a spreadsheet and creating a series of NASA polynomials.
# In[11]:
import os
from pprint import pprint
from pathlib import Path
from pmutt.io.excel import read_excel
from pmutt.empirical.nasa import Nasa
# Find the location of Jupyter notebook
# Note that normally Python scripts have a __file__ variable but Jupyter notebook doesn't.
# Using pathlib can overcome this limiation
try:
notebook_folder = os.path.dirname(__file__)
except NameError:
notebook_folder = Path().resolve()
os.chdir(notebook_folder)
# Read the data from Excel
ab_initio_data = read_excel(io='./input/NH3_Input_Data.xlsx', sheet_name='species')
pprint(ab_initio_data)
# In[12]:
# Create NASA polynomials using **kwargs syntax
nasa_species = []
for species_data in ab_initio_data:
single_nasa_species = Nasa.from_model(T_low=100.,
T_high=1500.,
**species_data)
nasa_species.append(single_nasa_species)
# Print out a table using enthalpy, entropy, Gibbs energy at 298 K for each species
print('Name Enthalpy (kcal/mol) Entropy (cal/mol/K) Gibbs energy (kcal/mol)')
print('--------------------------------------------------------------------------------')
for single_nasa_species in nasa_species:
name = single_nasa_species.name
H = single_nasa_species.get_H(units='kcal/mol', T=298.)
S = single_nasa_species.get_S(units='cal/mol/K', T=298.)
G = single_nasa_species.get_G(units='kcal/mol', T=298.)
print('{:12} {:10.1f} {:15.1f} {:15.1f}'.format(name, H, S, G))
#
# ## 9.2. Output via Thermdat
# The thermdat format uses NASA polynomials to represent several species. It has a very particular format so doing it manually is error-prone. You can write a list of ``Nasa`` objects to thermdat format using [``pmutt.io.thermdat.write_thermdat``](https://vlachosgroup.github.io/pmutt/io.html#pmutt.io.thermdat.write_thermdat).
#
# Below, we write a thermdat file using the species imported from the spreadsheet.
# In[13]:
from pmutt.io.thermdat import write_thermdat
write_thermdat(filename='./output/thermdat', nasa_species=nasa_species)
# Similarly, a list of ``Nasa`` objects can be read from a thermdat using [``pmutt.io.thermdat.read_thermdat``](https://vlachosgroup.github.io/pMuTT/io.html#pmutt.io.thermdat.read_thermdat).
# In[14]:
from pmutt.io.thermdat import read_thermdat
nasa_species = read_thermdat('./output/thermdat')
#
# # 10. Reactions
#
#
#
# ## 8.1. Inputting a NASA polynomial directly
#
# The H2 NASA polynomial from the [Burcat database](http://combustion.berkeley.edu/gri_mech/version30/files30/thermo30.dat) is represented as:
#
# ```
# H2 TPIS78H 2 G 200.000 3500.000 1000.000 1
# 3.33727920E+00-4.94024731E-05 4.99456778E-07-1.79566394E-10 2.00255376E-14 2
# -9.50158922E+02-3.20502331E+00 2.34433112E+00 7.98052075E-03-1.94781510E-05 3
# 2.01572094E-08-7.37611761E-12-9.17935173E+02 6.83010238E-01 4
# ```
#
# This can be translated to pMuTT syntax using:
# In[9]:
from pmutt.empirical.nasa import Nasa
# Initialize NASA polynomial
H2_nasa = Nasa(name='H2',
elements={'H': 2},
phase='G',
T_low=200., T_mid=1000., T_high=3500.,
a_low=[2.34433112E+00, 7.98052075E-03, -1.94781510E-05,
2.01572094E-08, -7.37611761E-12, -9.17935173E+02,
6.83010238E-01],
a_high=[3.33727920E+00, -4.94024731E-05, 4.99456778E-07,
-1.79566394E-10, 2.00255376E-14, -9.50158922E+02,
-3.20502331E+00])
# Calculate thermodynamic quantities using the same syntax as StatMech
H_H2 = H2_nasa.get_H(units='kcal/mol', T=298.)
print('H_H2(T=298 K) = {} kcal/mol'.format(H_H2))
# Show thermodynamic quantities vs. T
T = np.linspace(200., 3500.)
f2, ax2 = plot_1D(H2_nasa,
x_name='T', x_values=T,
methods=('get_H', 'get_S', 'get_G'),
get_H_kwargs={'units': 'kcal/mol'},
get_S_kwargs={'units': 'cal/mol/K'},
get_G_kwargs={'units': 'kcal/mol'})
f2.set_size_inches(6, 6)
f2.set_dpi(200)
plt.show()
#
# ## 8.2. Fitting an empirical object to a StatMech object
# Empirical objects can be made directly using ``StatMech`` objects and the ``from_model`` method.
# In[10]:
H2_nasa = Nasa.from_model(name='H2',
T_low=200.,
T_high=3500.,
model=H2_statmech)
# Compare the statistical mechanical model to the empirical model
f3, ax3 = H2_nasa.plot_statmech_and_empirical(Cp_units='J/mol/K',
H_units='kJ/mol',
S_units='J/mol/K',
G_units='kJ/mol')
f3.set_size_inches(6, 8)
f3.set_dpi(200)
plt.show()
#
# # 9. Input/Output
# pMuTT has more IO functionality than below. See this page for [supported IO functions](https://vlachosgroup.github.io/pMuTT/io.html).
#
# ## 9.1. Input via Excel
#
# Encoding each object in Python can be tedious. You can read several species from Excel spreadsheets using [``pmutt.io.excel.read_excel``](https://vlachosgroup.github.io/pmutt/io.html?highlight=read_excel#pmutt.io.excel.read_excel). Note that this function returns a list of dictionaries. This output allows you to initialize whichever object you want using kwargs syntax. There are also [special rules that depend on the header name](https://vlachosgroup.github.io/pMuTT/io.html#special-rules).
#
# Below, we show an example importing species data from a spreadsheet and creating a series of NASA polynomials.
# In[11]:
import os
from pprint import pprint
from pathlib import Path
from pmutt.io.excel import read_excel
from pmutt.empirical.nasa import Nasa
# Find the location of Jupyter notebook
# Note that normally Python scripts have a __file__ variable but Jupyter notebook doesn't.
# Using pathlib can overcome this limiation
try:
notebook_folder = os.path.dirname(__file__)
except NameError:
notebook_folder = Path().resolve()
os.chdir(notebook_folder)
# Read the data from Excel
ab_initio_data = read_excel(io='./input/NH3_Input_Data.xlsx', sheet_name='species')
pprint(ab_initio_data)
# In[12]:
# Create NASA polynomials using **kwargs syntax
nasa_species = []
for species_data in ab_initio_data:
single_nasa_species = Nasa.from_model(T_low=100.,
T_high=1500.,
**species_data)
nasa_species.append(single_nasa_species)
# Print out a table using enthalpy, entropy, Gibbs energy at 298 K for each species
print('Name Enthalpy (kcal/mol) Entropy (cal/mol/K) Gibbs energy (kcal/mol)')
print('--------------------------------------------------------------------------------')
for single_nasa_species in nasa_species:
name = single_nasa_species.name
H = single_nasa_species.get_H(units='kcal/mol', T=298.)
S = single_nasa_species.get_S(units='cal/mol/K', T=298.)
G = single_nasa_species.get_G(units='kcal/mol', T=298.)
print('{:12} {:10.1f} {:15.1f} {:15.1f}'.format(name, H, S, G))
#
# ## 9.2. Output via Thermdat
# The thermdat format uses NASA polynomials to represent several species. It has a very particular format so doing it manually is error-prone. You can write a list of ``Nasa`` objects to thermdat format using [``pmutt.io.thermdat.write_thermdat``](https://vlachosgroup.github.io/pmutt/io.html#pmutt.io.thermdat.write_thermdat).
#
# Below, we write a thermdat file using the species imported from the spreadsheet.
# In[13]:
from pmutt.io.thermdat import write_thermdat
write_thermdat(filename='./output/thermdat', nasa_species=nasa_species)
# Similarly, a list of ``Nasa`` objects can be read from a thermdat using [``pmutt.io.thermdat.read_thermdat``](https://vlachosgroup.github.io/pMuTT/io.html#pmutt.io.thermdat.read_thermdat).
# In[14]:
from pmutt.io.thermdat import read_thermdat
nasa_species = read_thermdat('./output/thermdat')
#
# # 10. Reactions
#
#  #
# ``Reaction`` objects can be created by putting together ``Nasa``, ``Shomate`` and ``StatMech`` objects.
#
#
#
# ``Reaction`` objects can be created by putting together ``Nasa``, ``Shomate`` and ``StatMech`` objects.
#
#  #
#
# The ``from_string`` method is the easiest way to create a ``Reaction`` object. It requires the relevant species to be in a dictionary and a string to describe the reaction.
#
#
#
#
# The ``from_string`` method is the easiest way to create a ``Reaction`` object. It requires the relevant species to be in a dictionary and a string to describe the reaction.
#
#