{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# How does the SFF method work?"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Vanderburg and Johnson (2014) introduced a method for \"Self Flat Fielding\" by tracking how the lightcurve changes with motion of the spacecraft:\n",
"\n",
"[A Technique for Extracting Highly Precise Photometry for the Two-Wheeled Kepler Mission](http://adsabs.harvard.edu/abs/2014PASP..126..948V)\n",
"\n",
"In this notebook we replicate the K2SFF method following the same example source, #60021426, as that in the publication. We aim to demystify the technique, which is extremely popular within the K2 community. We have focused on reproducibility, so that we achieve the same result at the publication.\n",
"\n",
"The Vanderburg & Johnson 2014 paper uses data from the Kepler two-wheel \"Concept Engineering Test\", predating campaign 0, and sometimes called campaign *\"eng\"* or abbreviated CET. This vestigal \"campaign\" lacks some of the standardization of later K2 campaigns--- it was much shorter, only about 9 days long, it lacks some of the standard quality flags, targets have non-traditional EPIC IDs, and other quirks."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from astropy.io import fits\n",
"import pandas as pd"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Retrieve the K2SFF data for ENG test source `60021426`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"First we will retrieve data and inspect the mask used in the paper."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"path = 'http://archive.stsci.edu/hlsps/k2sff/cet/060000000/21426/hlsp_k2sff_k2_lightcurve_060021426-cet_kepler_v1_llc.fits'\n",
"vdb_fits = fits.open(path)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The `BESTAPER` keyword explains which aperture was chosen as the \"best\" by Vanderburg & Johnson 2014. The FITS header for that slice contains the metadata needed to reproduce the mask."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"MASKTYPE : PRF FIT\n",
"MASKINDE : 4\n",
"NPIXSAP : 29.0\n"
]
}
],
"source": [
"keys = ['MASKTYPE', 'MASKINDE', 'NPIXSAP']\n",
"_ = [print(key, ' : ', vdb_fits['BESTAPER'].header[key]) for key in keys]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We want the *exact same* mask as Vanderburg & Johnson 2014, but the publication version and MAST version differ!\n",
"\n",
"Publication version:\n",
"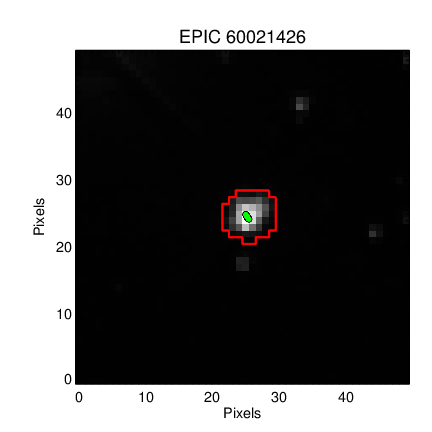"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"MAST Version:\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Aperture 7 should yield a bigger mask, more similar to what was used in the paper."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"53"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"VDB_J_mask = vdb_fits['PRF_APER_TBL'].data[7,:, :] == True\n",
"VDB_J_mask.sum()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Save the mask for easy use in our next notebook."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"np.save('VDB_J_2014_mask.npy', VDB_J_mask)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Manually reproduce with the Vanderburg-provided diagnostic data\n",
"Retrieve the Vanderburg-provided diagnostic data for the Kepler ENG testing. \n",
"Uncomment the line below to retrieve the data programmatically, or manually get the linked file in a browser and save it to this directory."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"#! wget https://www.cfa.harvard.edu/~avanderb/k2/ep60021426alldiagnostics.csv"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"\n",
"\n",
"
\n",
" \n",
" \n",
" | \n",
" BJD - 2454833 | \n",
" Raw Flux | \n",
" Corrected Flux | \n",
" X-centroid | \n",
" Y-centroid | \n",
" arclength | \n",
" Correction | \n",
" Thrusters On | \n",
"
\n",
" \n",
" \n",
" \n",
" | 0 | \n",
" 1862.502368 | \n",
" 0.995119 | \n",
" 0.995985 | \n",
" 25.135097 | \n",
" 24.661074 | \n",
" 2.327480 | \n",
" 0.999130 | \n",
" 1.0 | \n",
"
\n",
" \n",
" | 1 | \n",
" 1862.522801 | \n",
" 0.997313 | \n",
" 0.996767 | \n",
" 25.289752 | \n",
" 24.418689 | \n",
" 1.175322 | \n",
" 1.000548 | \n",
" 1.0 | \n",
"
\n",
" \n",
" | 2 | \n",
" 1862.543235 | \n",
" 0.996713 | \n",
" 0.996136 | \n",
" 25.288052 | \n",
" 24.429406 | \n",
" 1.214627 | \n",
" 1.000580 | \n",
" 0.0 | \n",
"
\n",
" \n",
" | 3 | \n",
" 1862.563668 | \n",
" 0.996930 | \n",
" 0.996277 | \n",
" 25.275216 | \n",
" 24.448405 | \n",
" 1.306617 | \n",
" 1.000656 | \n",
" 0.0 | \n",
"
\n",
" \n",
" | 4 | \n",
" 1862.584102 | \n",
" 0.996862 | \n",
" 0.996228 | \n",
" 25.253864 | \n",
" 24.480184 | \n",
" 1.460259 | \n",
" 1.000636 | \n",
" 0.0 | \n",
"
\n",
" \n",
"
\n",
"