| ⚠️ |
The answers here are given by the community. Be careful and double check the answers before using them. If you see an error, please create a PR with a fix |
 Write SQL queries to extract the following information:
**1)** The number of active ads.
```sql
SELECT count(*) FROM Ads WHERE status = 'active';
```
Write SQL queries to extract the following information:
**1)** The number of active ads.
```sql
SELECT count(*) FROM Ads WHERE status = 'active';
```
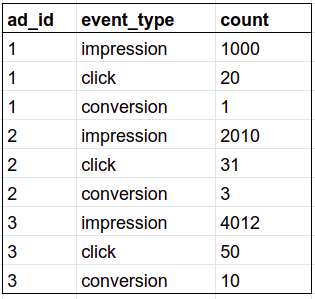 ```sql
SELECT e.ad_id, e.event_type, count(*) as "count"
FROM Events AS e
GROUP BY e.ad_id, e.event_type
ORDER BY e.ad_id, "count" DESC;
```
```sql
SELECT e.ad_id, e.event_type, count(*) as "count"
FROM Events AS e
GROUP BY e.ad_id, e.event_type
ORDER BY e.ad_id, "count" DESC;
```
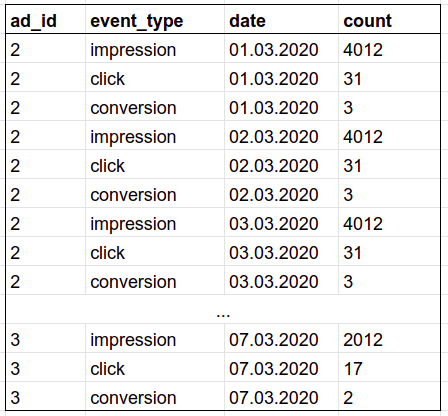 ```sql
SELECT a.ad_id, e.event_type, e.date, count(*) as "count"
FROM Ads AS a
JOIN Events AS e
ON a.ad_id = e.ad_id
WHERE a.status = 'active'
AND e.date >= DATEADD(week, -1, GETDATE())
GROUP BY a.ad_id, e.event_type, e.date
ORDER BY e.date ASC, "count" DESC;
```
```sql
SELECT a.ad_id, e.event_type, e.date, count(*) as "count"
FROM Ads AS a
JOIN Events AS e
ON a.ad_id = e.ad_id
WHERE a.status = 'active'
AND e.date >= DATEADD(week, -1, GETDATE())
GROUP BY a.ad_id, e.event_type, e.date
ORDER BY e.date ASC, "count" DESC;
```
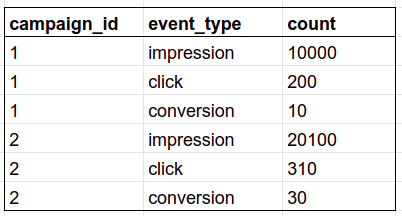 ```sql
SELECT a.campaign_id, e.event_type, count(*) as count
FROM Ads AS a
INNER JOIN Events AS e
ON a.ad_id = e.ad_id
GROUP BY a.campaign_id, e.event_type
ORDER BY a.campaign_id, "count" DESC
```
```sql
SELECT a.campaign_id, e.event_type, count(*) as count
FROM Ads AS a
INNER JOIN Events AS e
ON a.ad_id = e.ad_id
GROUP BY a.campaign_id, e.event_type
ORDER BY a.campaign_id, "count" DESC
```
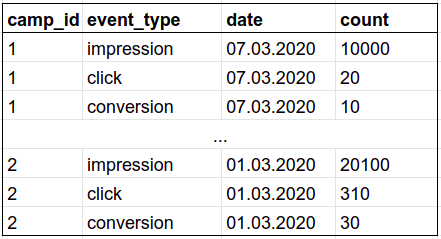 ```sql
-- for Postgres
SELECT a.campaign_id AS camp_id, e.event_type, e.date, count(*)
FROM Ads AS a
INNER JOIN Events AS e
ON a.ad_id = e.ad_id
WHERE e.date >= DATEADD(week, -1, GETDATE())
GROUP BY a.campaign_id, e.event_type, e.date
ORDER BY a.campaign_id, e.date DESC, "count" DESC;
```
```sql
-- for Postgres
SELECT a.campaign_id AS camp_id, e.event_type, e.date, count(*)
FROM Ads AS a
INNER JOIN Events AS e
ON a.ad_id = e.ad_id
WHERE e.date >= DATEADD(week, -1, GETDATE())
GROUP BY a.campaign_id, e.event_type, e.date
ORDER BY a.campaign_id, e.date DESC, "count" DESC;
```
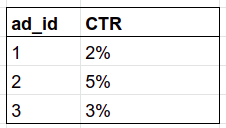 ```sql
-- for Postgres
SELECT impressions_clicks_table.ad_id,
(impressions_clicks_table.clicks * 100 / impressions_clicks_table.impressions)::FLOAT || '%' AS CTR
FROM
(
SELECT e.ad_id,
SUM(CASE e.event_type WHEN 'impression' THEN 1 ELSE 0 END) impressions,
SUM(CASE e.event_type WHEN 'click' THEN 1 ELSE 0 END) clicks
FROM Events AS e
GROUP BY e.ad_id
) AS impressions_clicks_table
ORDER BY impressions_clicks_table.ad_id;
```
```sql
-- for Postgres
SELECT impressions_clicks_table.ad_id,
(impressions_clicks_table.clicks * 100 / impressions_clicks_table.impressions)::FLOAT || '%' AS CTR
FROM
(
SELECT e.ad_id,
SUM(CASE e.event_type WHEN 'impression' THEN 1 ELSE 0 END) impressions,
SUM(CASE e.event_type WHEN 'click' THEN 1 ELSE 0 END) clicks
FROM Events AS e
GROUP BY e.ad_id
) AS impressions_clicks_table
ORDER BY impressions_clicks_table.ad_id;
```
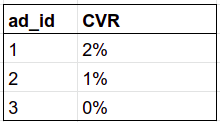 ```sql
-- for Postgres
SELECT conversions_clicks_table.ad_id,
(conversions_clicks_table.conversions * 100 / conversions_clicks_table.clicks)::FLOAT || '%' AS CVR
FROM
(
SELECT e.ad_id,
SUM(CASE e.event_type WHEN 'conversion' THEN 1 ELSE 0 END) conversions,
SUM(CASE e.event_type WHEN 'click' THEN 1 ELSE 0 END) clicks
FROM Events AS e
GROUP BY e.ad_id
) AS conversions_clicks_table
ORDER BY conversions_clicks_table.ad_id;
```
```sql
-- for Postgres
SELECT conversions_clicks_table.ad_id,
(conversions_clicks_table.conversions * 100 / conversions_clicks_table.clicks)::FLOAT || '%' AS CVR
FROM
(
SELECT e.ad_id,
SUM(CASE e.event_type WHEN 'conversion' THEN 1 ELSE 0 END) conversions,
SUM(CASE e.event_type WHEN 'click' THEN 1 ELSE 0 END) clicks
FROM Events AS e
GROUP BY e.ad_id
) AS conversions_clicks_table
ORDER BY conversions_clicks_table.ad_id;
```
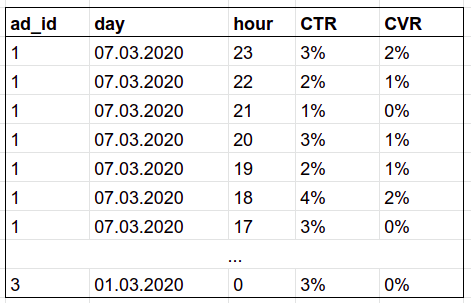 ```sql
-- for Postgres
SELECT conversions_clicks_table.ad_id,
conversions_clicks_table.date,
conversions_clicks_table.hour,
(impressions_clicks_table.clicks * 100 / impressions_clicks_table.impressions)::FLOAT || '%' AS CTR,
(conversions_clicks_table.conversions * 100 / conversions_clicks_table.clicks)::FLOAT || '%' AS CVR
FROM
(
SELECT e.ad_id, e.date, e.hour,
SUM(CASE e.event_type WHEN 'conversion' THEN 1 ELSE 0 END) conversions,
SUM(CASE e.event_type WHEN 'click' THEN 1 ELSE 0 END) clicks,
SUM(CASE e.event_type WHEN 'impression' THEN 1 ELSE 0 END) impressions
FROM Events AS e
GROUP BY e.ad_id, e.date, e.hour
) AS conversions_clicks_table
ORDER BY conversions_clicks_table.ad_id, conversions_clicks_table.date DESC, conversions_clicks_table.hour DESC, "CTR" DESC, "CVR" DESC;
```
```sql
-- for Postgres
SELECT conversions_clicks_table.ad_id,
conversions_clicks_table.date,
conversions_clicks_table.hour,
(impressions_clicks_table.clicks * 100 / impressions_clicks_table.impressions)::FLOAT || '%' AS CTR,
(conversions_clicks_table.conversions * 100 / conversions_clicks_table.clicks)::FLOAT || '%' AS CVR
FROM
(
SELECT e.ad_id, e.date, e.hour,
SUM(CASE e.event_type WHEN 'conversion' THEN 1 ELSE 0 END) conversions,
SUM(CASE e.event_type WHEN 'click' THEN 1 ELSE 0 END) clicks,
SUM(CASE e.event_type WHEN 'impression' THEN 1 ELSE 0 END) impressions
FROM Events AS e
GROUP BY e.ad_id, e.date, e.hour
) AS conversions_clicks_table
ORDER BY conversions_clicks_table.ad_id, conversions_clicks_table.date DESC, conversions_clicks_table.hour DESC, "CTR" DESC, "CVR" DESC;
```
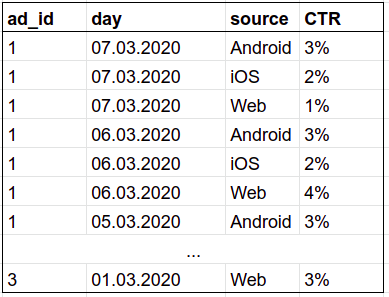 ```sql
-- for Postgres
SELECT conversions_clicks_table.ad_id,
conversions_clicks_table.date,
conversions_clicks_table.source,
(impressions_clicks_table.clicks * 100 / impressions_clicks_table.impressions)::FLOAT || '%' AS CTR
FROM
(
SELECT e.ad_id, e.date, e.source,
SUM(CASE e.event_type WHEN 'click' THEN 1 ELSE 0 END) clicks,
SUM(CASE e.event_type WHEN 'impression' THEN 1 ELSE 0 END) impressions
FROM Events AS e
GROUP BY e.ad_id, e.date, e.source
) AS conversions_clicks_table
ORDER BY conversions_clicks_table.ad_id, conversions_clicks_table.date DESC, conversions_clicks_table.source, "CTR" DESC;
```
```sql
-- for Postgres
SELECT conversions_clicks_table.ad_id,
conversions_clicks_table.date,
conversions_clicks_table.source,
(impressions_clicks_table.clicks * 100 / impressions_clicks_table.impressions)::FLOAT || '%' AS CTR
FROM
(
SELECT e.ad_id, e.date, e.source,
SUM(CASE e.event_type WHEN 'click' THEN 1 ELSE 0 END) clicks,
SUM(CASE e.event_type WHEN 'impression' THEN 1 ELSE 0 END) impressions
FROM Events AS e
GROUP BY e.ad_id, e.date, e.source
) AS conversions_clicks_table
ORDER BY conversions_clicks_table.ad_id, conversions_clicks_table.date DESC, conversions_clicks_table.source, "CTR" DESC;
```
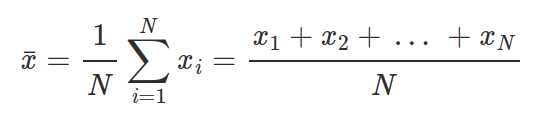 ```python
def mean(numbers):
if len(numbers) > 0:
return sum(numbers) / len(numbers)
return float('NaN')
```
```python
def mean(numbers):
if len(numbers) > 0:
return sum(numbers) / len(numbers)
return float('NaN')
```
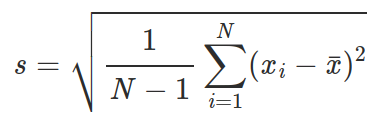 ```python
from math import sqrt
from statistics import mean
def std_dev(numbers):
if len(numbers) > 1:
avg = mean(numbers)
var = sum((i - avg) ** 2 for i in numbers) / (len(numbers) - 1)
std = sqrt(var)
return std
return float('NaN')
```
```python
from math import sqrt
from statistics import mean
def std_dev(numbers):
if len(numbers) > 1:
avg = mean(numbers)
var = sum((i - avg) ** 2 for i in numbers) / (len(numbers) - 1)
std = sqrt(var)
return std
return float('NaN')
```
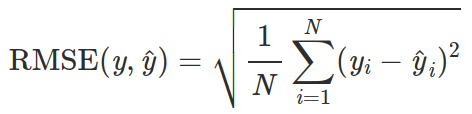 ```python
import math
def rmse(y_true, y_pred):
assert len(y_true) == len(y_pred), 'different sizes of the arguments'
squares = sum((x - y)**2 for x, y in zip(y_true, y_pred))
return math.sqrt(squares / len(y_true))
```
```python
import math
def rmse(y_true, y_pred):
assert len(y_true) == len(y_pred), 'different sizes of the arguments'
squares = sum((x - y)**2 for x, y in zip(y_true, y_pred))
return math.sqrt(squares / len(y_true))
```
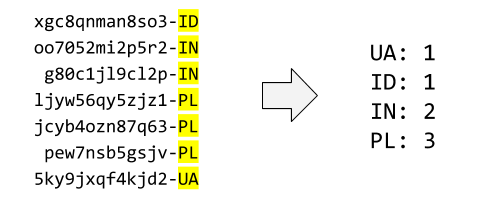 ```python
def counter(lst):
ans = {}
for i in lst:
site = i[-2:]
ans[site] = ans.get(site, 0) + 1
return ans
```
```python
def counter(lst):
ans = {}
for i in lst:
site = i[-2:]
ans[site] = ans.get(site, 0) + 1
return ans
```
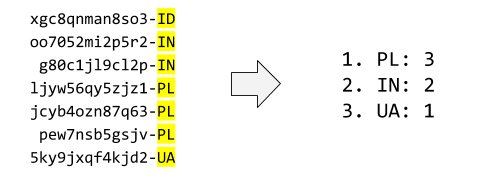 ```python
def top_counter(lst):
site_dict = counter(lst) # using last problem's solution
top_keys = sorted(site_dict, reverse=True, key=site_dict.get)[:3]
return {key: site_dict[key] for key in top_keys}
```
```python
def top_counter(lst):
site_dict = counter(lst) # using last problem's solution
top_keys = sorted(site_dict, reverse=True, key=site_dict.get)[:3]
return {key: site_dict[key] for key in top_keys}
```
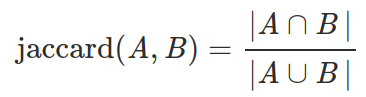 ```python
def jaccard(a, b):
return len(a & b) / len(a | b)
```
```python
def jaccard(a, b):
return len(a & b) / len(a | b)
```
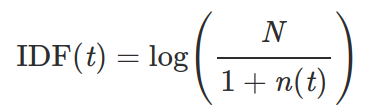 Where:
* t is the token,
* n(t) is the number of documents that t occurs in,
* N is the total number of documents
```python
from math import log10
def idf1(docs):
docs = [set(doc) for doc in docs]
n_tokens = {}
for doc in docs:
for token in doc:
n_tokens[token] = n_tokens.get(token, 0) + 1
ans = {}
for token in n_tokens:
ans[token] = log10(len(docs) / (1 + n_tokens[token]))
return ans
```
```python
import math
def idf2(docs):
n_docs = len(docs)
docs = [set(doc) for doc in docs]
all_tokens = set.union(*docs)
idf_coefficients = {}
for token in all_tokens:
n_docs_w_token = sum(token in doc for doc in docs)
idf_c = math.log10(n_docs / (1 + n_docs_w_token))
idf_coefficients[token] = idf_c
return idf_coefficients
```
Where:
* t is the token,
* n(t) is the number of documents that t occurs in,
* N is the total number of documents
```python
from math import log10
def idf1(docs):
docs = [set(doc) for doc in docs]
n_tokens = {}
for doc in docs:
for token in doc:
n_tokens[token] = n_tokens.get(token, 0) + 1
ans = {}
for token in n_tokens:
ans[token] = log10(len(docs) / (1 + n_tokens[token]))
return ans
```
```python
import math
def idf2(docs):
n_docs = len(docs)
docs = [set(doc) for doc in docs]
all_tokens = set.union(*docs)
idf_coefficients = {}
for token in all_tokens:
n_docs_w_token = sum(token in doc for doc in docs)
idf_c = math.log10(n_docs / (1 + n_docs_w_token))
idf_coefficients[token] = idf_c
return idf_coefficients
```
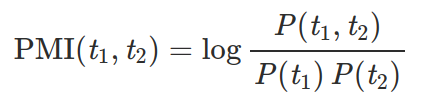 The higher the PMI, the more likely these two tokens form a collection. We can estimate PMI by counting:
The higher the PMI, the more likely these two tokens form a collection. We can estimate PMI by counting:
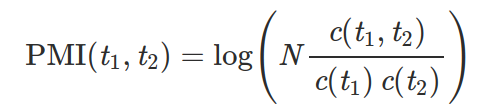 Where:
* N is the total number of tokens in the text,
* c(t1, t2) is the number of times t1 and t2 appear together,
* c(t1) and c(t2) — the number of times they appear separately.
```python
import math
def pmi(docs):
n_pairs = {}
n_tokens = {}
docs = [tuple(doc) for doc in docs]
for doc in docs:
for token in doc:
n_tokens[token] = n_tokens.get(token, 0) + 1
n_pairs[doc] = n_pairs.get(doc, 0) + 1
ans = {}
for pair in n_pairs:
ans[pair] = math.log2(n_pairs[pair] * (sum(n_tokens.values())) / (n_tokens[pair[0]] * n_tokens[pair[1]]))
srt = sorted(ans.items(), key=lambda x: x[1], reverse=True)[:10]
return srt
```
Where:
* N is the total number of tokens in the text,
* c(t1, t2) is the number of times t1 and t2 appear together,
* c(t1) and c(t2) — the number of times they appear separately.
```python
import math
def pmi(docs):
n_pairs = {}
n_tokens = {}
docs = [tuple(doc) for doc in docs]
for doc in docs:
for token in doc:
n_tokens[token] = n_tokens.get(token, 0) + 1
n_pairs[doc] = n_pairs.get(doc, 0) + 1
ans = {}
for pair in n_pairs:
ans[pair] = math.log2(n_pairs[pair] * (sum(n_tokens.values())) / (n_tokens[pair[0]] * n_tokens[pair[1]]))
srt = sorted(ans.items(), key=lambda x: x[1], reverse=True)[:10]
return srt
```
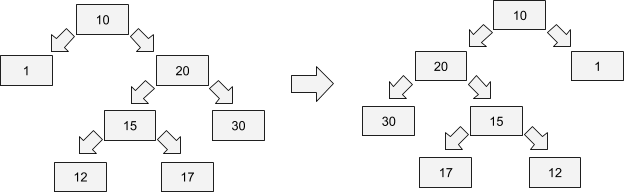 ```python
def flip_bt(head):
if head is not None:
head.left, head.right = head.right, head.left
flip_bt(head.left)
flip_bt(head.right)
```
```python
def flip_bt(head):
if head is not None:
head.left, head.right = head.right, head.left
flip_bt(head.left)
flip_bt(head.right)
```