Els grafs: xarxes, camins i connexions.
De la matemàtica discreta a la realitat.
Aniol Garcia i Serrano
El meu primer graf
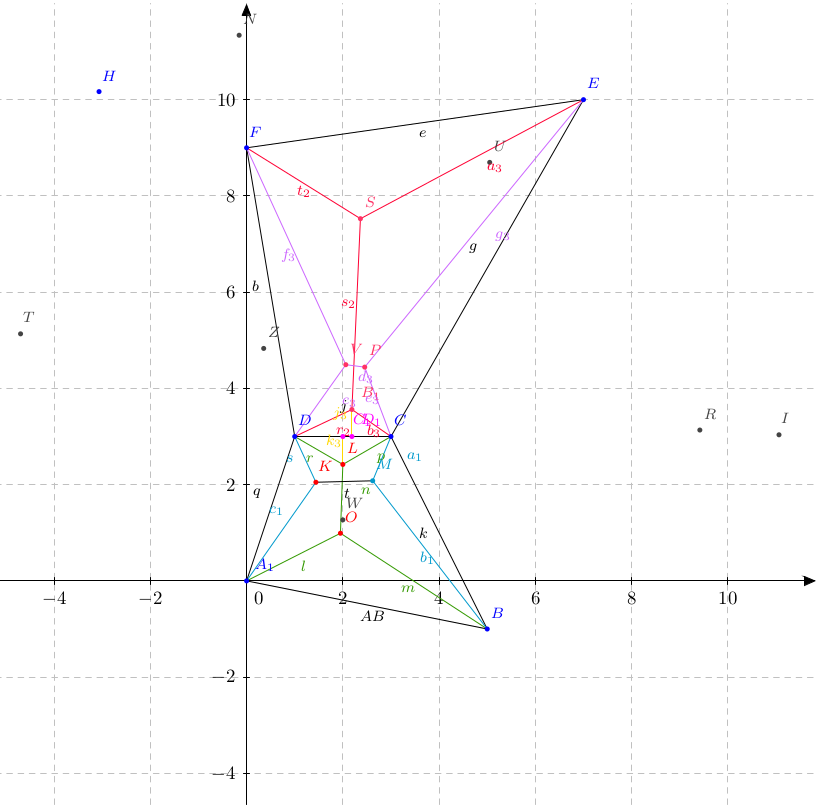
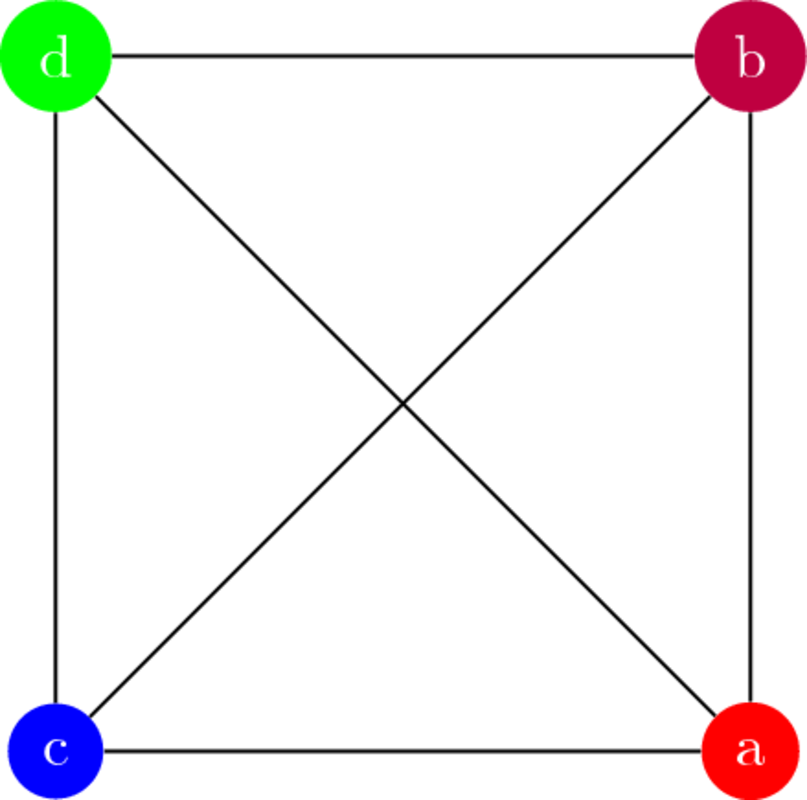
El primer graf
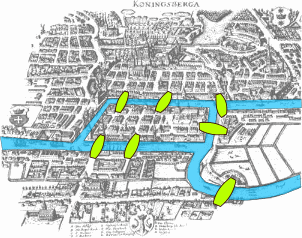
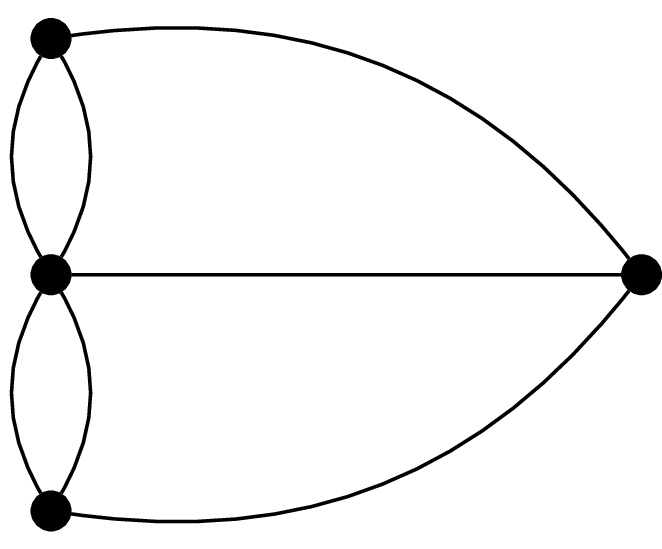
node
aresta
Breu història

Leonhard Euler
Gottfried W. Leibniz
Geometria de la posició
Els grafs: xarxes, camins i connexions.
De la matemàtica discreta a la realitat.
Aniol Garcia i Serrano
Objectius
- Conèixer la teoria de grafs
- Estudiar i implementar algorismes
- Mostrar-ne algunes de les aplicacions
Hipòtesi
La teoria de grafs, com a branca de la matemàtica discreta, ens proporciona eines per modelitzar estructures i processos i ens permet crear aplicacions pràctiques mitjançant procediments algorísmics.
Tipus de grafs
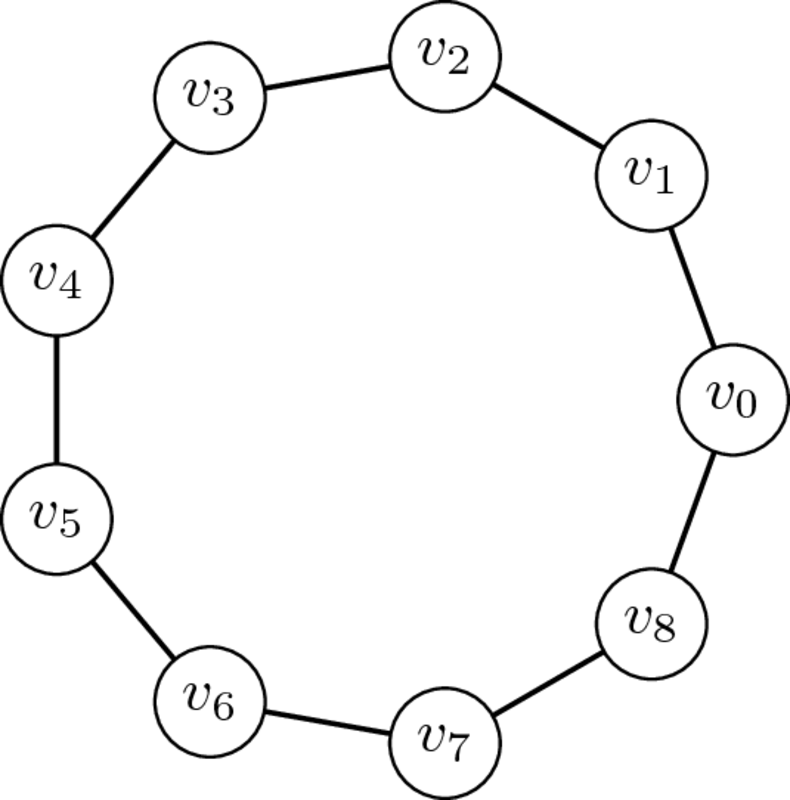
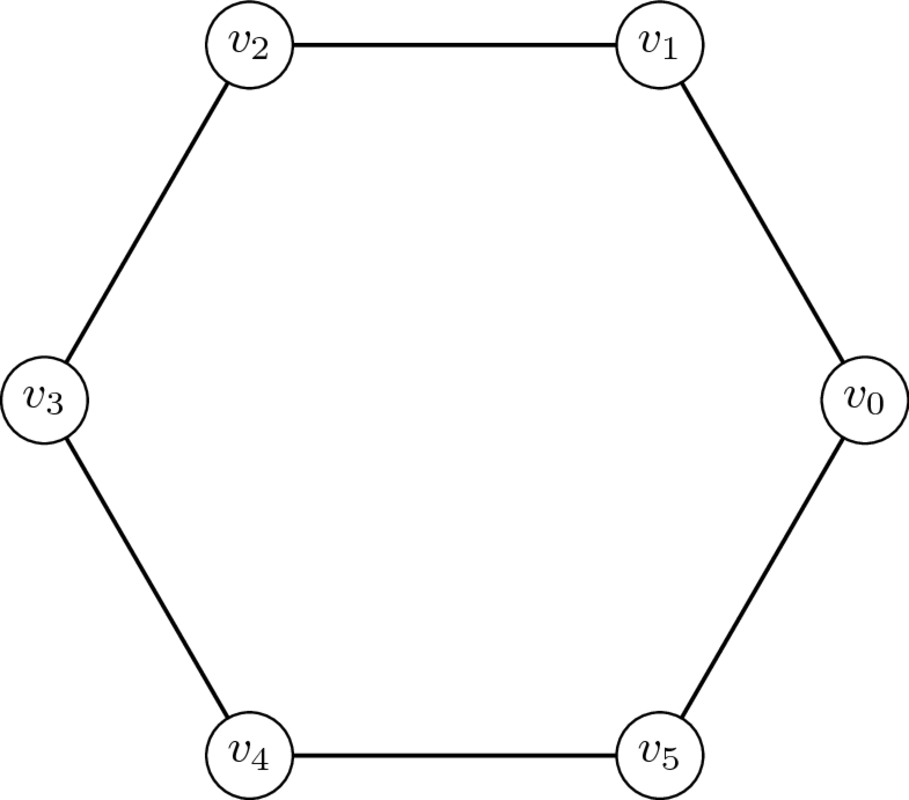
Cicle
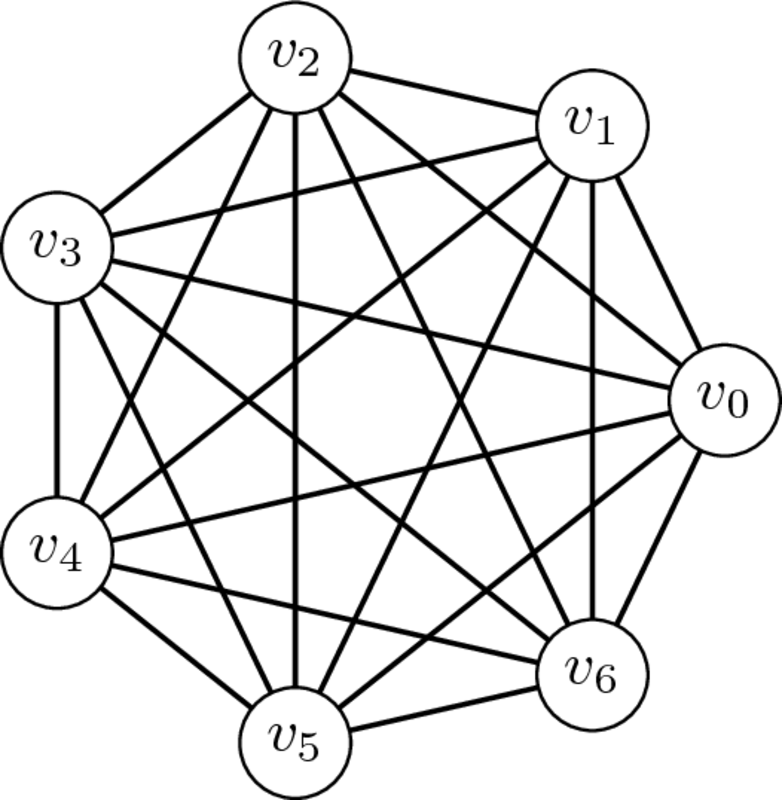
Complet
Estrella
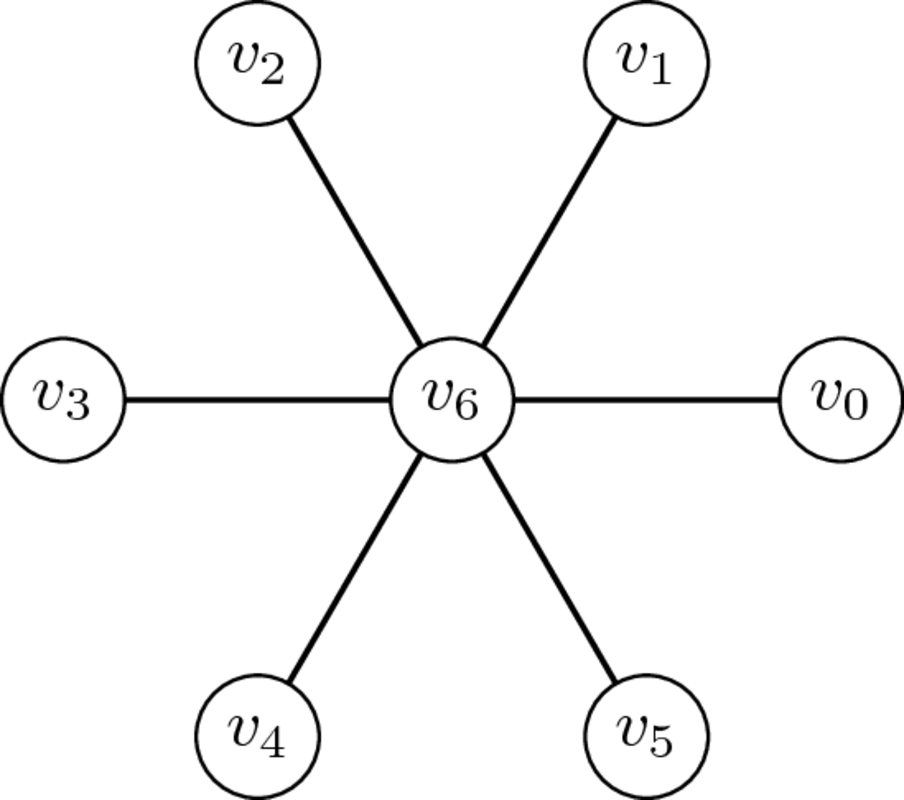
Roda
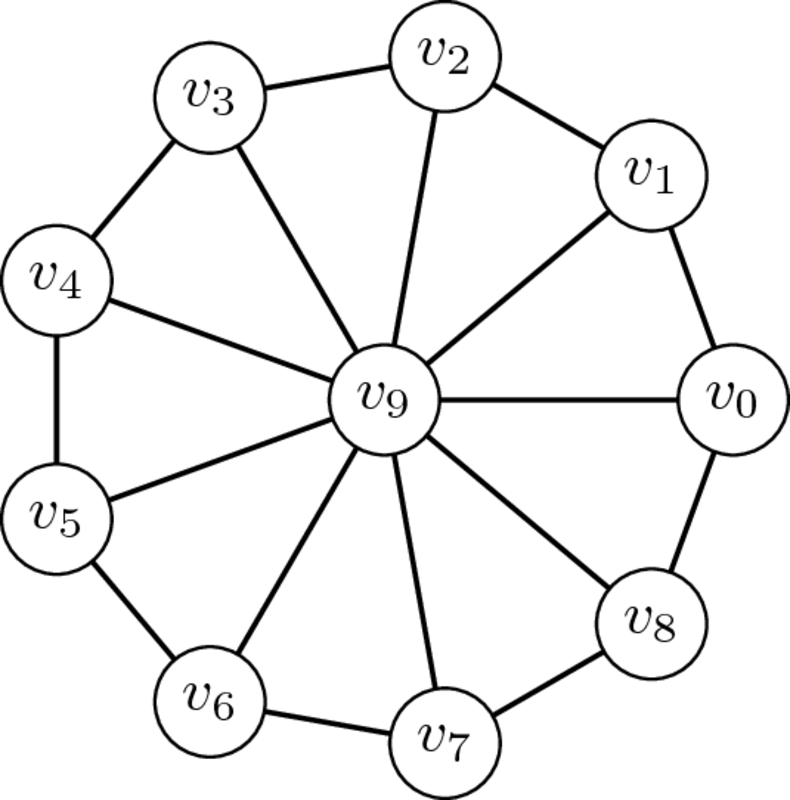
Xarxa
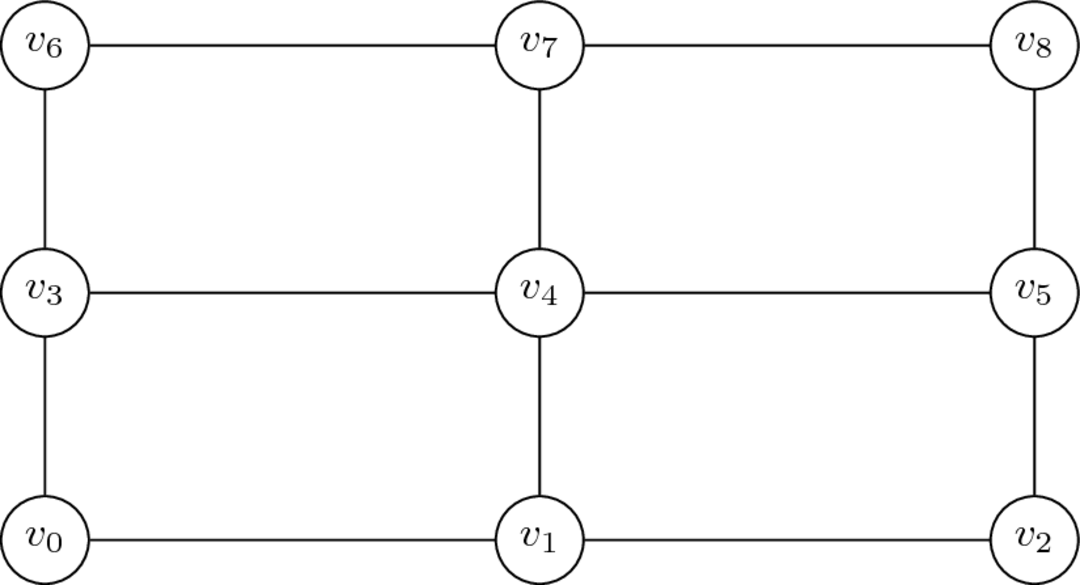
Complementaris
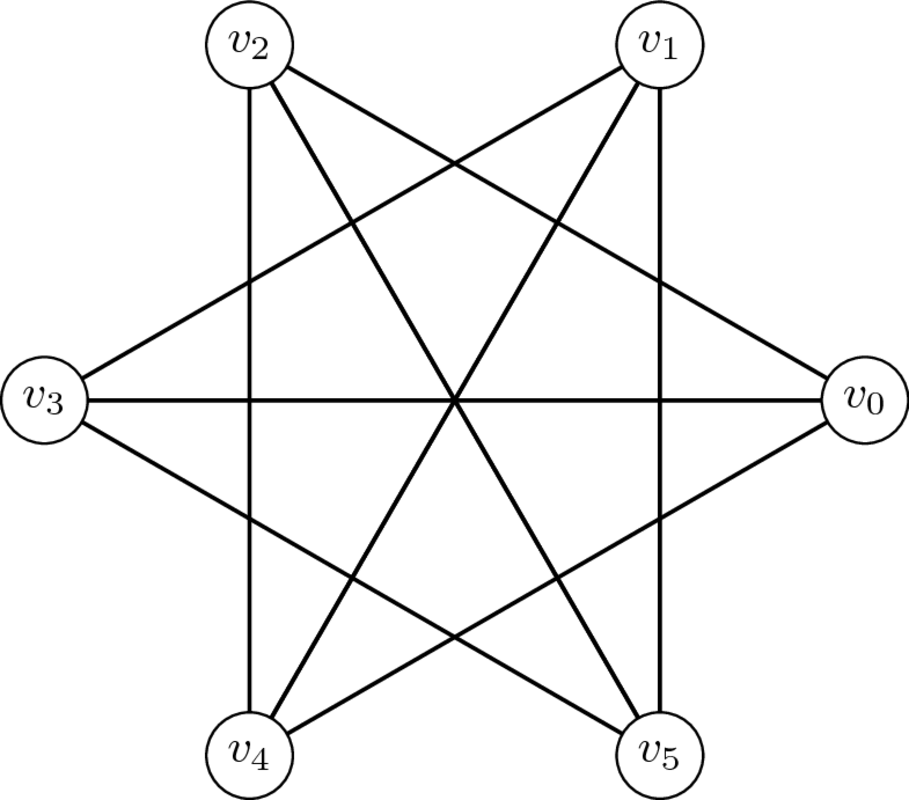
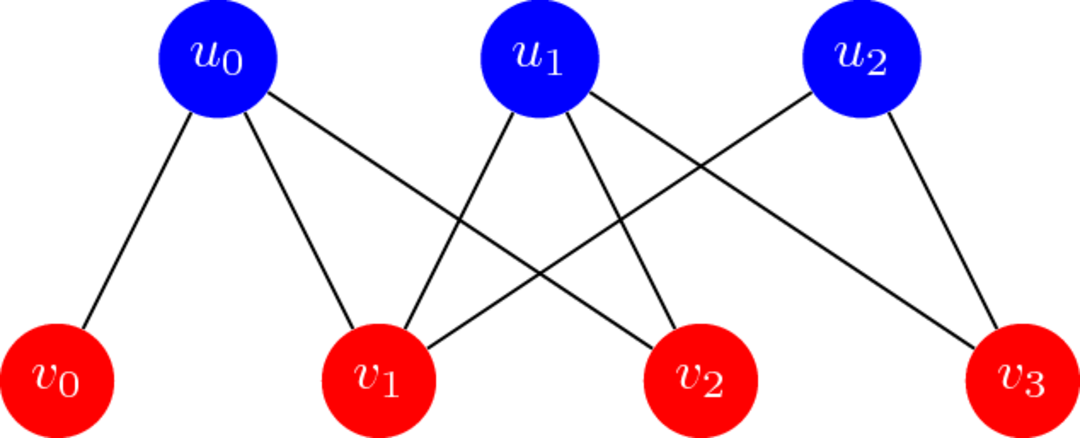
Bipartits
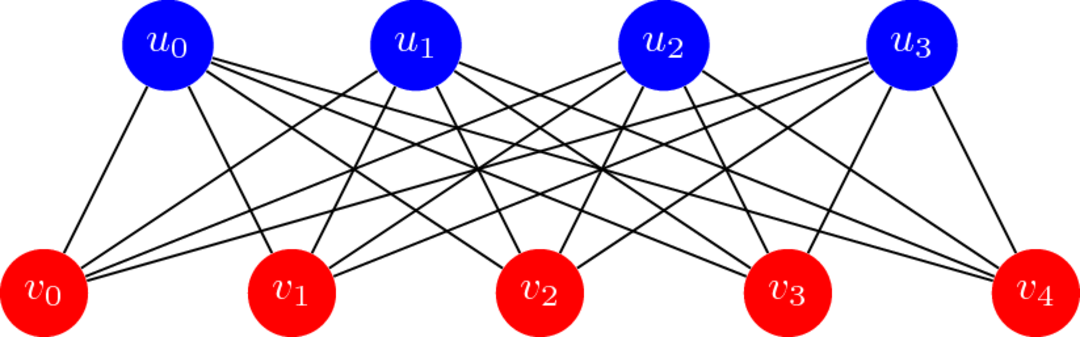
Buit
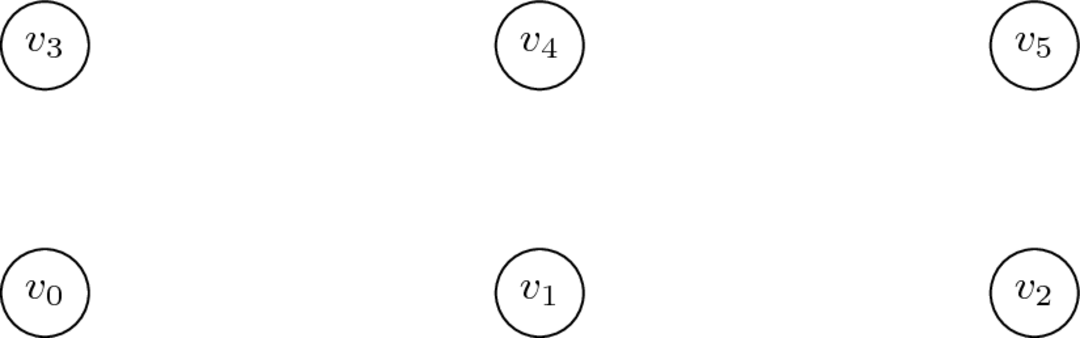
Nul
Arbres
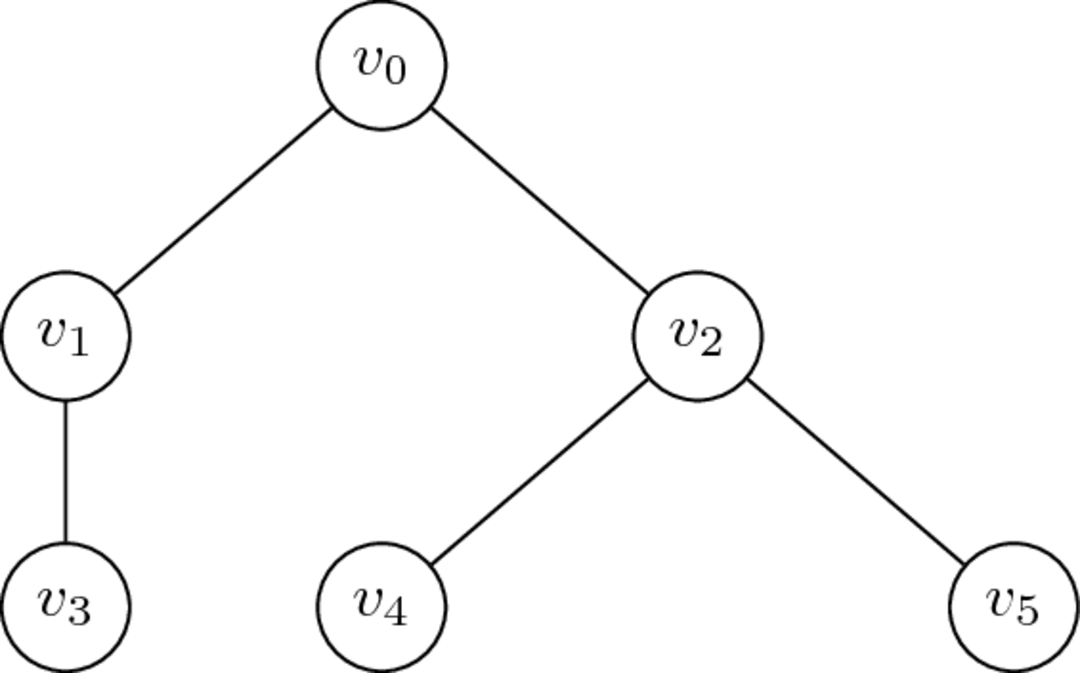
Lineals
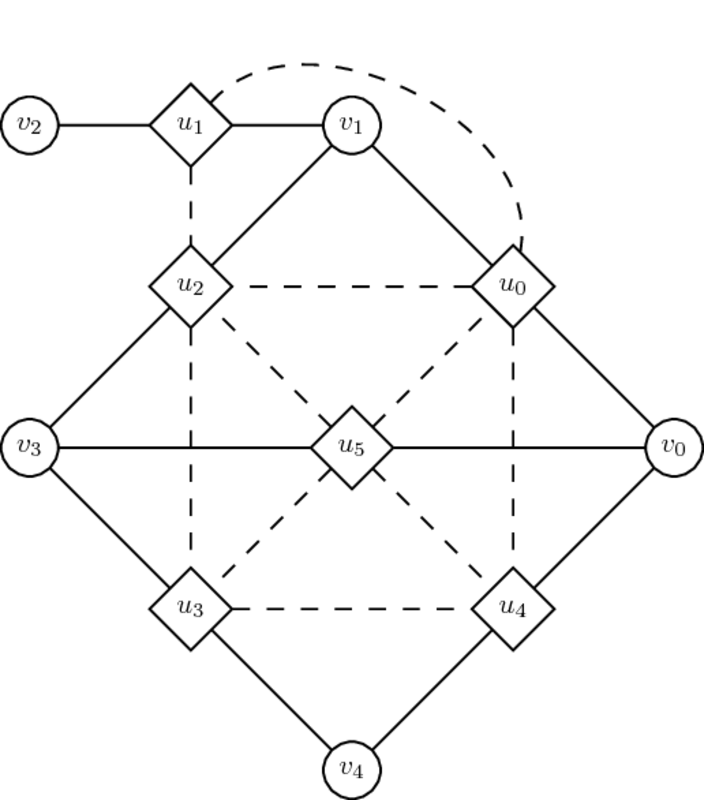
Propietats i demostracions

A tall d'exemple:
Altres classificacions
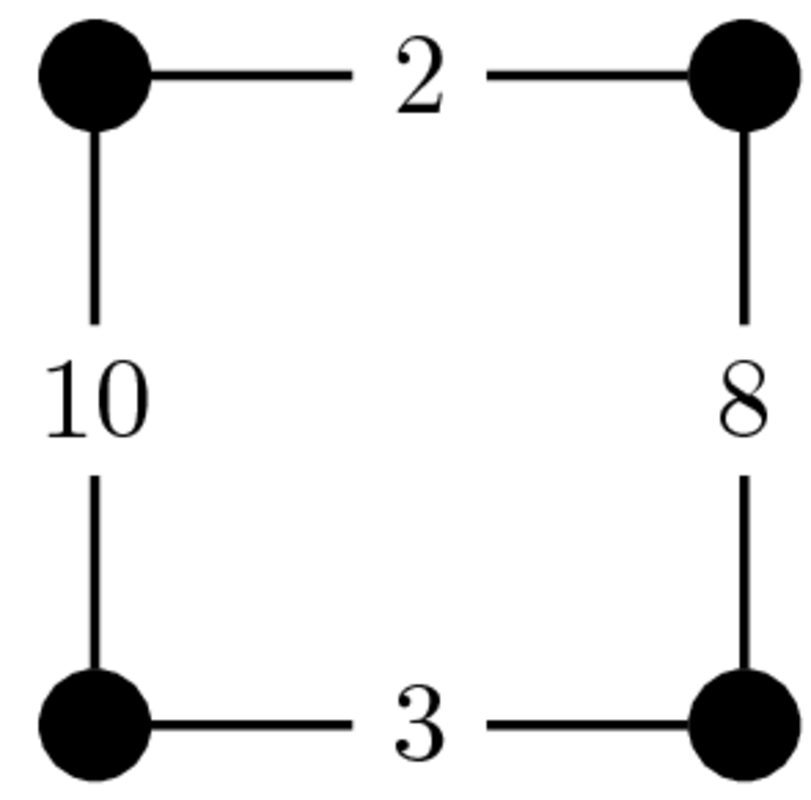
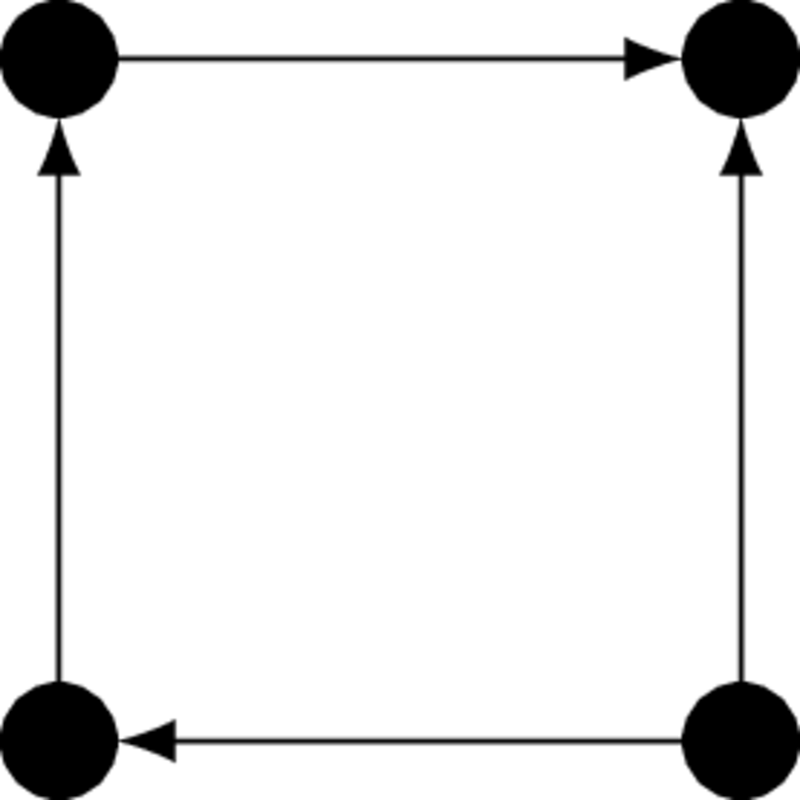
Dirigits
Ponderats
Algorismes
MST
Camins
Coloració
Exploració
DFS
Aniol
BFS
Dijkstra
Bellman-Ford
Kruskal
Prim
Floyd-Warshall
Euler
Hamilton
Xarxa de metro
Plantejament
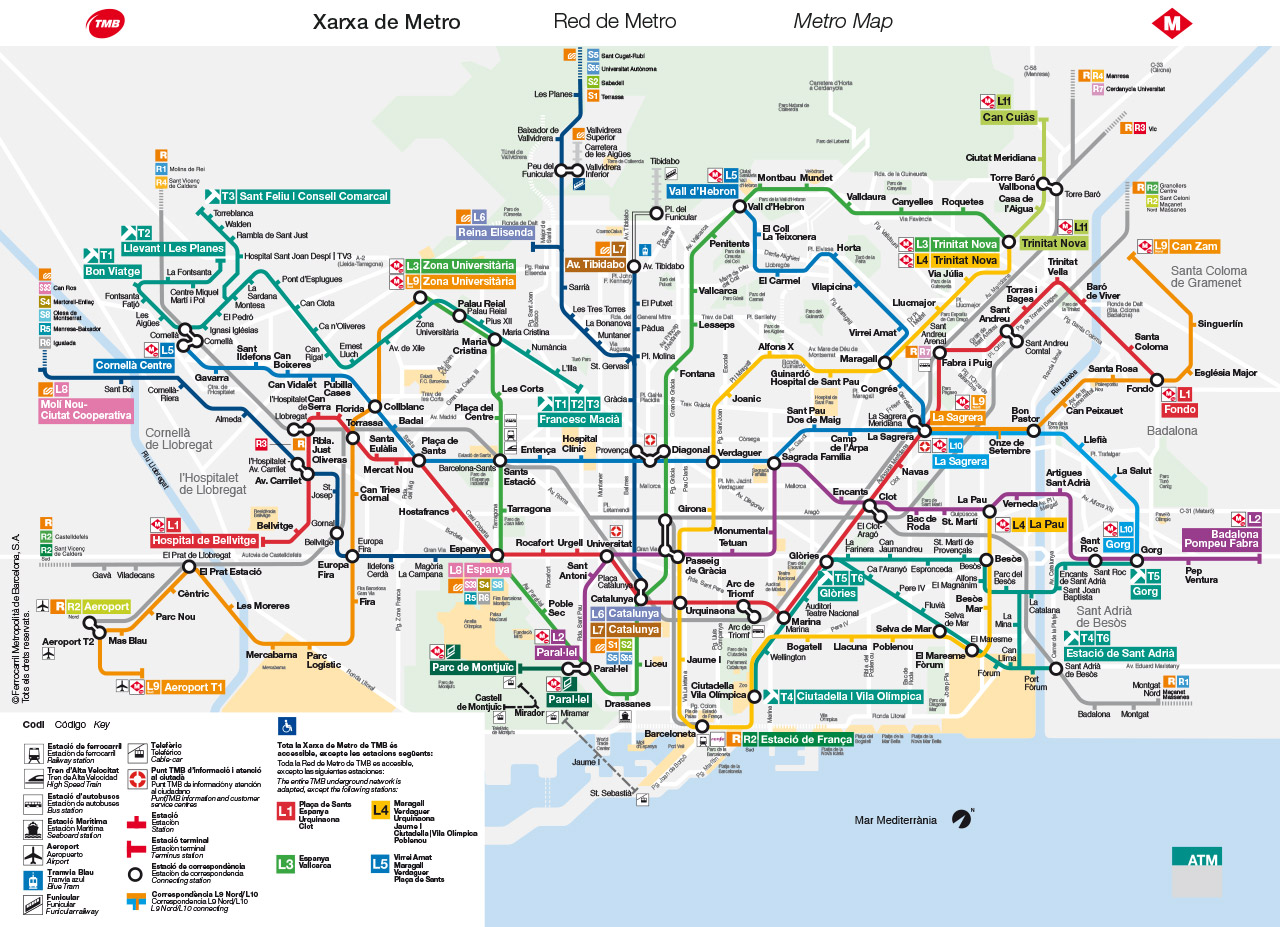
Organització
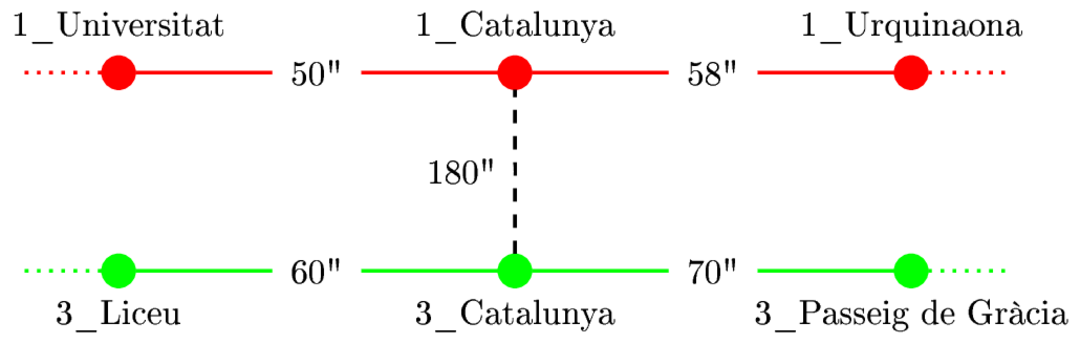
def metro(Adj, inici, final, k):
recorregut=[]
print "Punt inicial:", inici.decode("ISO-8859-15")
print "Punt final:", final.decode("ISO-8859-15")
for i in Adj:
for j in Adj[i]:
Adj[i][j] = Adj[i][j] + 25
dist, tree = OrderedDijkstra(Adj, inici, k)
i = final
while tree[i] != inici:
recorregut.append(tree[i])
i = tree[i]
recorregut.append(inici)
recorregut.reverse()
total= dist[final]-k -25
print "Temps amb estacions del recorregut:", dist[final], "Temps real:", total
if total < 60:
print "Temps total del recorregut:",int(total), "segons"
else:
minuts = total/60
segons = (total%60)
print "Temps total del recorregut:", int(minuts),"minuts i", int(segons), "segons"
print "Recorregut:",
print "[",
for i in range(0,len(recorregut)):
print recorregut[i].decode("ISO-8859-15")+",",
print final.decode("ISO-8859-15"),"]" def OrderedDijkstra(Adj, s, k):
Q = dict.fromkeys(Adj.keys(), float("inf"))
dist = dict.fromkeys(Adj.keys(), float("inf"))
tree = {}
Q[s] = 0
while Q:
u = min(Q, key=Q.get)
dist[u] = Q[u]
for v in Adj[u]:
if v in Q:
if Q[v] > Q[u] + Adj[u][v]:
Q[v] = Q[u] + Adj[u][v] + k
tree[v] = u
Q.pop(u)
return dist, tree

metro(metro_barcelona, "4_Llucmajor", "9S_Aeroport T1", 25)Punt inicial: 4_Llucmajor
Punt final: 9S_Aeroport T1
Temps net del recorregut: 3565
Temps total del recorregut: 59 minuts i 25 segons
Recorregut: [ 4_Llucmajor, 4_Maragall, 4_Guinardó Hospital de Sant Pau, 4_Alfons X, 4_Joanic,
4_Verdaguer, 5_Verdaguer, 5_Diagonal, 5_Hospital Clínic, 5_Entença, 5_Sants Estació,
5_Plaça de Sants, 5_Badal, 5_Collblanc, 9S_Collblanc, 9S_Torrassa, 9S_Can Tries Gornal,
9S_Europa Fira, 9S_Fira, 9S_Parc Logístic, 9S_Mercabarna, 9S_Les Moreres,
9S_El Prat Estació,9S_Cèntric, 9S_Parc Nou, 9S_Mas Blau, 9S_Aeroport T2, 9S_Aeroport T1 ]Conclusions
- Objectius assolits.
- Podem trobar grafs a una gran quantitat d'àmbits i amb moltes aplicacions diferents.
- Importància de la computació en procediments matemàtics.
- Queda molta feina per fer.
Programari lliure
- Ubuntu i Debian com a S.O.
- Python com a llenguatge de programació
- LaTeX i els seus paquets per a la redacció de la memòria
- Git com a sistema de control de versions
- Geogebra, Spyder, Scilab, Vim, Meld... i molts d'altres
Moltes gràcies!
Aniol Garcia i Serrano
aniolgarcia@gmail.com
Més informació del treball a