GEOG 172: INTERMEDIATE GEOGRAPHICAL ANALYSIS
Evgeny Noi
Lecture 13: Clustering and Regionalization
Review¶
- Many of the techniques we covered had to do with either one variable (autocorrelation) or pairs of variables (correlation). Today from univariate to multivariate.
Clustering¶
- Part of unsupervised learning.
- Latent patterns in our data
- NO LABELS!
- Groups are not pre-determined (classification)
- DBSCAN - example of density-based clustering
Classical clustering tasks¶
- Online shoppers (segmentation)
- Spotify users who like similar music
- Hospital Patients
Clustering¶
Partition the observations into groups, where each observation is similar to another member of the group.
- Partitioning (pre-define number of clusters, pre-defined number of members in a group, pre-define radius)
- Similarity can be measured differently (attribute space - multidimensional, we can also add geography or spaital similarity to the clustering)
Regionalization¶
We can think of clusters as regions (similar groups of observations that have common attributes and spatial proximity)
Types of Clustering Algorithms¶
- Connectivity-based (hierarchical)
- Centroid-based (k-means, k-medoid, c-means, etc.)
- Distribution-based (clusters are groups most likely belonging to the same distribution)
- Density-based (DBSCAN)
- Grid-based
In [1]:
import pandas as pd
import geopandas as gpd
from esda.moran import Moran
from libpysal.weights import Queen, KNN
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pingouin as pg
C:\Users\barguzin\Anaconda3\envs\geo_env\lib\site-packages\outdated\utils.py:14: OutdatedPackageWarning: The package outdated is out of date. Your version is 0.2.1, the latest is 0.2.2. Set the environment variable OUTDATED_IGNORE=1 to disable these warnings. return warn(
Using PySAL example data¶
In [2]:
from libpysal.examples import load_example, available
#[_ for _ in available().Name]
cin = load_example('Cincinnati')
cin.get_file_list()
Example not available: Cincinnati Example not downloaded: Chicago parcels Example not downloaded: Chile Migration Example not downloaded: Spirals
Out[2]:
['C:\\Users\\barguzin\\pysal_data\\Cincinnati\\walnuthills_updated\\.DS_Store', 'C:\\Users\\barguzin\\pysal_data\\Cincinnati\\walnuthills_updated\\cincinnati.dbf', 'C:\\Users\\barguzin\\pysal_data\\Cincinnati\\walnuthills_updated\\cincinnati.prj', 'C:\\Users\\barguzin\\pysal_data\\Cincinnati\\walnuthills_updated\\cincinnati.shp', 'C:\\Users\\barguzin\\pysal_data\\Cincinnati\\walnuthills_updated\\cincinnati.shx', 'C:\\Users\\barguzin\\pysal_data\\Cincinnati\\__MACOSX\\walnuthills_updated\\._.DS_Store']
In [3]:
cin_df = gpd.read_file(cin.get_path('cincinnati.shp'))
print(cin_df.shape)
cin_df.head()
(457, 73)
Out[3]:
| ID | AREA | BLOCK | BG | TRACT | COUNTY | MSA | POPULATION | MALE | FEMALE | ... | OWNER_SIZE | RENTER_SIZ | DENSITY | BURGLARY | ASSAULT | THEFT | BURG_D | ASSALT_D | THEFT_D | geometry | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 726907.0 | 0.09 | 390610042002001 | 390610042002 | 39061004200 | 39061 | 1640 | 479.0 | 221.0 | 258.0 | ... | 1.46 | 1.42 | 5384.7901 | 1 | 0 | 4 | 1.0 | 0.0 | 1.0 | POLYGON ((1407302.966 415693.734, 1407473.141 ... |
| 1 | 695744.0 | 0.01 | 390610022004003 | 390610022004 | 39061002200 | 39061 | 1640 | 85.0 | 39.0 | 46.0 | ... | 3.22 | 2.15 | 6643.1423 | 0 | 2 | 2 | 0.0 | 1.0 | 1.0 | POLYGON ((1398841.243 416718.444, 1399605.382 ... |
| 2 | 695762.0 | 0.01 | 390610033002017 | 390610033002 | 39061003300 | 39061 | 1640 | 29.0 | 18.0 | 11.0 | ... | 1.00 | 1.33 | 4326.5018 | 0 | 0 | 0 | 0.0 | 0.0 | 0.0 | POLYGON ((1398733.468 416975.853, 1398794.240 ... |
| 3 | 695780.0 | 0.01 | 390610022004002 | 390610022004 | 39061002200 | 39061 | 1640 | 117.0 | 59.0 | 58.0 | ... | 2.57 | 2.25 | 20784.6991 | 2 | 3 | 4 | 1.0 | 1.0 | 1.0 | POLYGON ((1399564.078 416046.633, 1399605.382 ... |
| 4 | 695798.0 | 0.02 | 390610033001009 | 390610033001 | 39061003300 | 39061 | 1640 | 96.0 | 51.0 | 45.0 | ... | 1.00 | 1.42 | 4019.0506 | 0 | 0 | 2 | 0.0 | 0.0 | 1.0 | POLYGON ((1398841.243 416718.444, 1398733.468 ... |
5 rows × 73 columns
In [4]:
cin_df[['WHITE', 'AP_WHITE']].describe()
Out[4]:
| WHITE | AP_WHITE | |
|---|---|---|
| count | 457.000000 | 457.000000 |
| mean | 23.954048 | 24.870897 |
| std | 65.200837 | 66.990628 |
| min | 0.000000 | 0.000000 |
| 25% | 0.000000 | 0.000000 |
| 50% | 3.000000 | 4.000000 |
| 75% | 19.000000 | 21.000000 |
| max | 634.000000 | 657.000000 |
In [5]:
cin_df[['OCCHU_OWNE', 'OCCHU_RENT']].describe()
Out[5]:
| OCCHU_OWNE | OCCHU_RENT | |
|---|---|---|
| count | 457.000000 | 457.000000 |
| mean | 8.617068 | 28.070022 |
| std | 18.680250 | 46.020203 |
| min | 0.000000 | 0.000000 |
| 25% | 0.000000 | 1.000000 |
| 50% | 4.000000 | 14.000000 |
| 75% | 10.000000 | 35.000000 |
| max | 245.000000 | 543.000000 |
In [6]:
cin_df.plot()
Out[6]:
<AxesSubplot:>
In [7]:
cin_df.info()
<class 'geopandas.geodataframe.GeoDataFrame'> RangeIndex: 457 entries, 0 to 456 Data columns (total 73 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 ID 457 non-null float64 1 AREA 457 non-null float64 2 BLOCK 457 non-null object 3 BG 457 non-null object 4 TRACT 457 non-null object 5 COUNTY 457 non-null object 6 MSA 457 non-null object 7 POPULATION 457 non-null float64 8 MALE 457 non-null float64 9 FEMALE 457 non-null float64 10 AGE_0_5 457 non-null float64 11 AGE_5_9 457 non-null float64 12 AGE_10_14 457 non-null float64 13 AGE_15_19 457 non-null float64 14 AGE_20_24 457 non-null float64 15 AGE_25_34 457 non-null float64 16 AGE_35_44 457 non-null float64 17 AGE_45_54 457 non-null float64 18 AGE_55_59 457 non-null float64 19 AGE_60_64 457 non-null float64 20 AGE_65_74 457 non-null float64 21 AGE_75_84 457 non-null float64 22 AGE_85 457 non-null float64 23 MEDIAN_AGE 457 non-null float64 24 AGE_18 457 non-null float64 25 MALE_18 457 non-null float64 26 FEMALE_18 457 non-null float64 27 AGE_21 457 non-null float64 28 AGE_62 457 non-null float64 29 AGE_65 457 non-null float64 30 MALE_65 457 non-null float64 31 FEMALE_65 457 non-null float64 32 F1_RACE 457 non-null float64 33 WHITE 457 non-null float64 34 BLACK 457 non-null float64 35 AMINDIAN 457 non-null float64 36 ASIAN 457 non-null float64 37 HAWAIIAN 457 non-null float64 38 OTHER_RACE 457 non-null float64 39 F2_RACES 457 non-null float64 40 AP_WHITE 457 non-null float64 41 AP_BLACK 457 non-null float64 42 AP_AMINDIA 457 non-null float64 43 AP_ASIAN 457 non-null float64 44 AP_HAWAIIA 457 non-null float64 45 AP_OTHER 457 non-null float64 46 AP_HISPANI 457 non-null float64 47 NOT_HISPAN 457 non-null float64 48 NH_WHITE 457 non-null float64 49 IN_HOUSEHO 457 non-null float64 50 GROUP_QUAR 457 non-null float64 51 GQ_INSTITU 457 non-null float64 52 GQ_NONINST 457 non-null float64 53 HOUSEHOLDS 457 non-null float64 54 HH_FAMILY 457 non-null float64 55 HH_NONFAMI 457 non-null float64 56 AVG_HHSIZE 457 non-null float64 57 AVG_FAMSIZ 457 non-null float64 58 HSNG_UNITS 457 non-null float64 59 HU_OCCUPIE 457 non-null float64 60 HU_VACANT 457 non-null float64 61 OCCHU_OWNE 457 non-null float64 62 OCCHU_RENT 457 non-null float64 63 OWNER_SIZE 457 non-null float64 64 RENTER_SIZ 457 non-null float64 65 DENSITY 457 non-null float64 66 BURGLARY 457 non-null int64 67 ASSAULT 457 non-null int64 68 THEFT 457 non-null int64 69 BURG_D 457 non-null float64 70 ASSALT_D 457 non-null float64 71 THEFT_D 457 non-null float64 72 geometry 457 non-null geometry dtypes: float64(64), geometry(1), int64(3), object(5) memory usage: 260.8+ KB
In [8]:
# consider only specific variables for clustering
# see variable description at GEODA lab
# https://geodacenter.github.io/data-and-lab/walnut_hills/
predictors = ['POPULATION', 'MEDIAN_AGE', 'AGE_65', 'WHITE', 'BLACK', 'ASIAN',
'NH_WHITE', 'HOUSEHOLDS', 'AVG_HHSIZE', 'HU_VACANT', 'OCCHU_OWNE', 'OCCHU_RENT']
crime_vars = ['BURGLARY', 'ASSAULT', 'THEFT']
# more examples with plotting available from
# https://geographicdata.science/book/notebooks/10_clustering_and_regionalization.html
In [9]:
f, axs = plt.subplots(nrows=3, ncols=4, figsize=(16, 12))
# Make the axes accessible with single indexing
axs = axs.flatten()
# Start a loop over all the variables of interest
for i, col in enumerate(predictors):
# select the axis where the map will go
ax = axs[i]
# Plot the map
cin_df.plot(
column=col,
ax=ax,
scheme="Quantiles",
linewidth=0,
cmap="BuPu",
)
# Remove axis clutter
ax.set_axis_off()
# Set the axis title to the name of variable being plotted
ax.set_title(col)
f.savefig('crime_predictors.png')
plt.close()
C:\Users\barguzin\Anaconda3\envs\geo_env\lib\site-packages\mapclassify\classifiers.py:238: UserWarning: Warning: Not enough unique values in array to form k classes
Warn(
C:\Users\barguzin\Anaconda3\envs\geo_env\lib\site-packages\mapclassify\classifiers.py:241: UserWarning: Warning: setting k to 3
Warn("Warning: setting k to %d" % k_q, UserWarning)
In [10]:
from IPython.display import Image
Image(filename='crime_predictors.png')
Out[10]:
In [11]:
f, axs = plt.subplots(nrows=1, ncols=3, figsize=(16, 4))
# Make the axes accessible with single indexing
axs = axs.flatten()
# Start a loop over all the variables of interest
for i, col in enumerate(crime_vars):
# select the axis where the map will go
ax = axs[i]
# Plot the map
cin_df.plot(
column=col,
ax=ax,
scheme="Quantiles",
linewidth=0,
cmap="BuPu",
)
# Remove axis clutter
ax.set_axis_off()
# Set the axis title to the name of variable being plotted
ax.set_title(col)
f.savefig('crime_types.png')
plt.close()
C:\Users\barguzin\Anaconda3\envs\geo_env\lib\site-packages\mapclassify\classifiers.py:238: UserWarning: Warning: Not enough unique values in array to form k classes
Warn(
C:\Users\barguzin\Anaconda3\envs\geo_env\lib\site-packages\mapclassify\classifiers.py:241: UserWarning: Warning: setting k to 3
Warn("Warning: setting k to %d" % k_q, UserWarning)
C:\Users\barguzin\Anaconda3\envs\geo_env\lib\site-packages\mapclassify\classifiers.py:238: UserWarning: Warning: Not enough unique values in array to form k classes
Warn(
C:\Users\barguzin\Anaconda3\envs\geo_env\lib\site-packages\mapclassify\classifiers.py:241: UserWarning: Warning: setting k to 3
Warn("Warning: setting k to %d" % k_q, UserWarning)
C:\Users\barguzin\Anaconda3\envs\geo_env\lib\site-packages\mapclassify\classifiers.py:238: UserWarning: Warning: Not enough unique values in array to form k classes
Warn(
C:\Users\barguzin\Anaconda3\envs\geo_env\lib\site-packages\mapclassify\classifiers.py:241: UserWarning: Warning: setting k to 4
Warn("Warning: setting k to %d" % k_q, UserWarning)
In [12]:
from IPython.display import Image
Image(filename='crime_types.png')
Out[12]:
In [13]:
w = Queen.from_dataframe(cin_df)
# Calculate Moran's I for each variable
mi_results = [
Moran(cin_df[variable], w) for variable in predictors
]
# Structure results as a list of tuples
mi_results = [
(variable, res.I, res.p_sim)
for variable, res in zip(predictors, mi_results)
]
# Display on table
table = pd.DataFrame(
mi_results, columns=["Variable", "Moran's I", "P-value"]
).set_index("Variable")
table
C:\Users\barguzin\Anaconda3\envs\geo_env\lib\site-packages\libpysal\weights\_contW_lists.py:29: ShapelyDeprecationWarning: Iteration over multi-part geometries is deprecated and will be removed in Shapely 2.0. Use the `geoms` property to access the constituent parts of a multi-part geometry. return list(it.chain(*(list(zip(*shape.coords.xy)) for shape in shape)))
Out[13]:
| Moran's I | P-value | |
|---|---|---|
| Variable | ||
| POPULATION | 0.162529 | 0.001 |
| MEDIAN_AGE | 0.175654 | 0.001 |
| AGE_65 | 0.127756 | 0.002 |
| WHITE | 0.264340 | 0.001 |
| BLACK | 0.285679 | 0.001 |
| ASIAN | 0.057050 | 0.011 |
| NH_WHITE | 0.263554 | 0.001 |
| HOUSEHOLDS | 0.165267 | 0.001 |
| AVG_HHSIZE | 0.284141 | 0.001 |
| HU_VACANT | 0.198203 | 0.001 |
| OCCHU_OWNE | 0.245055 | 0.001 |
| OCCHU_RENT | 0.133238 | 0.001 |
Each of the variables displays significant positive spatial autocorrelation, suggesting clear spatial structure in the socioeconomic geography of San Diego. This means it is likely the clusters we find will have a non random spatial distribution.
In [14]:
xy_vars = predictors + ['BURGLARY']
corr_df = pg.pairwise_corr(cin_df[xy_vars], method='pearson')
corr_df.loc[corr_df.Y == 'BURGLARY'].sort_values(by='r', ascending=False)
Out[14]:
| X | Y | method | alternative | n | r | CI95% | p-unc | BF10 | power | |
|---|---|---|---|---|---|---|---|---|---|---|
| 67 | HOUSEHOLDS | BURGLARY | pearson | two-sided | 457 | 0.550126 | [0.48, 0.61] | 1.647029e-37 | 1.683e+34 | 1.000000 |
| 77 | OCCHU_RENT | BURGLARY | pearson | two-sided | 457 | 0.541269 | [0.47, 0.6] | 3.835054e-36 | 7.444e+32 | 1.000000 |
| 11 | POPULATION | BURGLARY | pearson | two-sided | 457 | 0.499936 | [0.43, 0.57] | 2.856307e-30 | 1.146e+27 | 1.000000 |
| 74 | HU_VACANT | BURGLARY | pearson | two-sided | 457 | 0.499887 | [0.43, 0.57] | 2.899383e-30 | 1.129e+27 | 1.000000 |
| 49 | BLACK | BURGLARY | pearson | two-sided | 457 | 0.492950 | [0.42, 0.56] | 2.351419e-29 | 1.424e+26 | 1.000000 |
| 76 | OCCHU_OWNE | BURGLARY | pearson | two-sided | 457 | 0.385024 | [0.3, 0.46] | 1.344824e-17 | 3.565e+14 | 1.000000 |
| 32 | AGE_65 | BURGLARY | pearson | two-sided | 457 | 0.377739 | [0.3, 0.45] | 6.014186e-17 | 8.173e+13 | 1.000000 |
| 62 | NH_WHITE | BURGLARY | pearson | two-sided | 457 | 0.240948 | [0.15, 0.33] | 1.850323e-07 | 4.481e+04 | 0.999485 |
| 41 | WHITE | BURGLARY | pearson | two-sided | 457 | 0.239724 | [0.15, 0.32] | 2.142888e-07 | 3.89e+04 | 0.999432 |
| 71 | AVG_HHSIZE | BURGLARY | pearson | two-sided | 457 | 0.144546 | [0.05, 0.23] | 1.949163e-03 | 6.998 | 0.873839 |
| 22 | MEDIAN_AGE | BURGLARY | pearson | two-sided | 457 | 0.115112 | [0.02, 0.2] | 1.380667e-02 | 1.202 | 0.693597 |
| 56 | ASIAN | BURGLARY | pearson | two-sided | 457 | 0.035869 | [-0.06, 0.13] | 4.443094e-01 | 0.078 | 0.119285 |
Similarity¶
- Absolute values will drown variables which have higher range of values (0-1 Vs 0-1000)
- Standardize values by mean and stdev
- For non-normal, skewed and bimodal distributions robust scaling may be required!
- Use sklearn package
Standardizing Variables¶
- scale(): $z = \frac{x_i - \bar{x}}{\sigma_x}$
- robust_scale(): $z = \frac{x_i - \tilde{x}}{\lceil x \rceil_{75} - \lceil x \rceil_{25}}$ (median and IQR)
- minmax_scale(): $z = \frac{x - min(x)}{max(x-min(x))}$
In [15]:
from sklearn.preprocessing import robust_scale
db_scaled = robust_scale(cin_df[predictors])
K-means Clustering¶
- Pre-specified number of clusters (groups)
- Each observation is closer to the mean of its own group than it is to the mean of any other group
K-means Clustering Algorithm¶
- Assign all observations to one of the $k$ labels
- Calculate multivariate mean over all covaraites for each cluster
- Reassign observations to the cluster with closest mean
- Repeat and update until there are no more changes
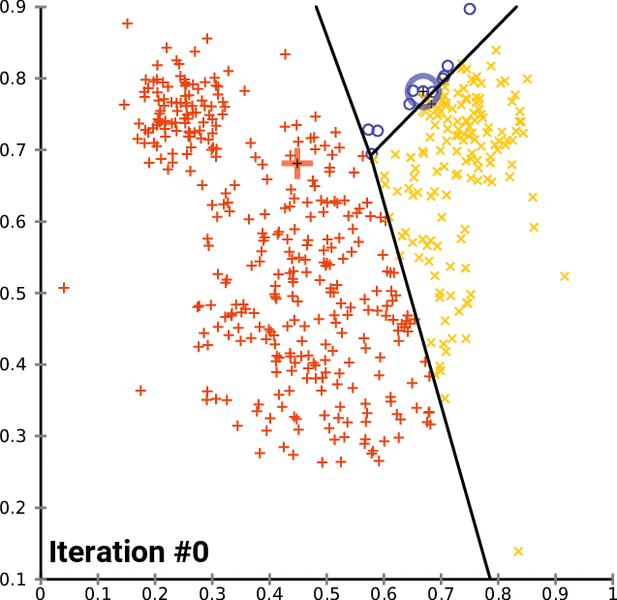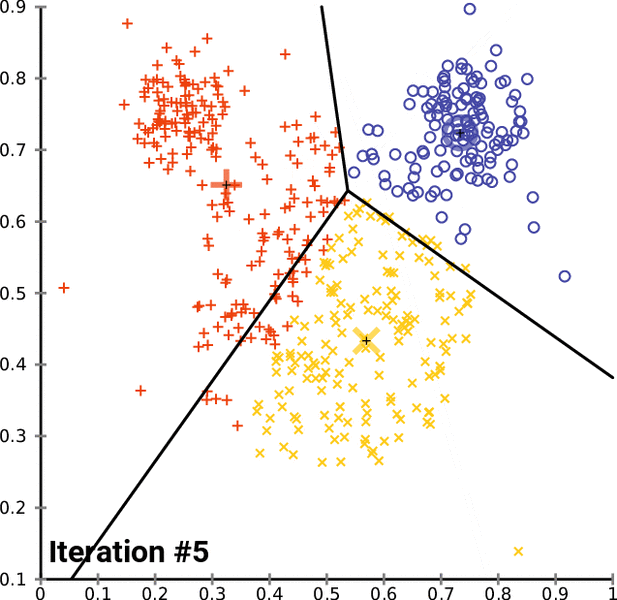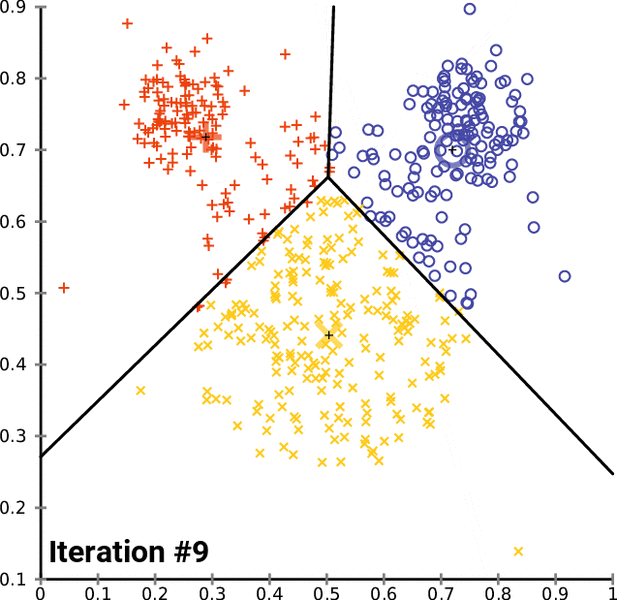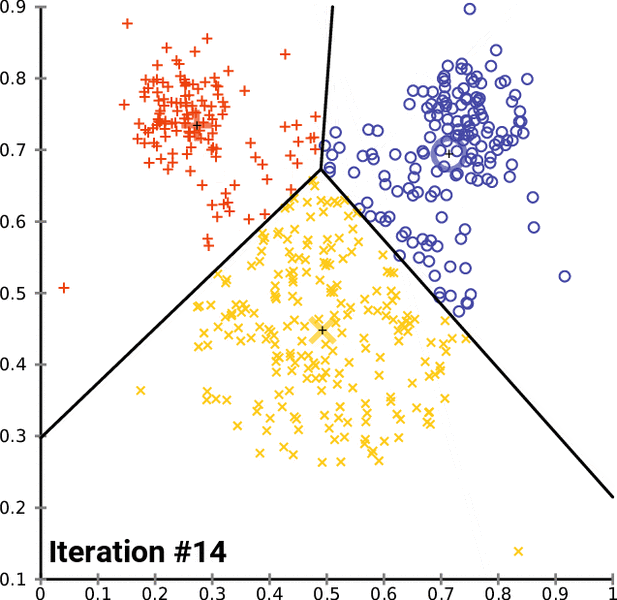
In [16]:
# Initialise KMeans instance
from sklearn.cluster import KMeans
# Initialise KMeans instance
kmeans = KMeans(n_clusters=5)
# Set the seed for reproducibility
np.random.seed(1234)
# Run K-Means algorithm
k5cls = kmeans.fit(db_scaled)
# Print first five labels
k5cls.labels_[:5]
C:\Users\barguzin\Anaconda3\envs\geo_env\lib\site-packages\sklearn\cluster\_kmeans.py:1334: UserWarning: KMeans is known to have a memory leak on Windows with MKL, when there are less chunks than available threads. You can avoid it by setting the environment variable OMP_NUM_THREADS=2. warnings.warn(
Out[16]:
array([3, 0, 0, 0, 0])
In [17]:
# Assign labels into a column
cin_df["k5cls"] = k5cls.labels_
# Setup figure and ax
f, ax = plt.subplots(1, figsize=(9, 9))
# Plot unique values choropleth including
# a legend and with no boundary lines
cin_df.plot(
column="k5cls", categorical=True, legend=True, linewidth=0, ax=ax
)
# Remove axis
ax.set_axis_off()
f.savefig('kmeans.png')
plt.close()
In [18]:
Image(filename='kmeans.png')
Out[18]:
Characterizing Clusters¶
- Very imbalanced partitioning
- Some contiguity is noticeable, but the arrangement is patchy
In [19]:
# Group data table by cluster label and count observations
k5sizes = cin_df.groupby("k5cls").size()
k5sizes
Out[19]:
k5cls 0 417 1 1 2 1 3 10 4 28 dtype: int64
In [20]:
# Dissolve areas by Cluster, aggregate by summing,
# and keep column for area
areas = cin_df.dissolve(by="k5cls", aggfunc="sum")['geometry'].area
areas
Out[20]:
k5cls 0 9.993732e+07 1 1.116340e+06 2 6.673713e+05 3 1.572282e+07 4 3.126180e+07 dtype: float64
In [21]:
# Group table by cluster label, keep the variables used
# for clustering, and obtain their mean
k5means = cin_df.groupby("k5cls")[predictors].mean()
# Transpose the table and print it rounding each value
# to three decimals
k5means.T.round(3)
Out[21]:
| k5cls | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| POPULATION | 56.942 | 1108.00 | 361.00 | 420.400 | 331.893 |
| MEDIAN_AGE | 26.170 | 21.80 | 25.00 | 29.310 | 41.879 |
| AGE_65 | 4.851 | 6.00 | 16.00 | 35.400 | 72.179 |
| WHITE | 13.084 | 435.00 | 259.00 | 325.000 | 55.250 |
| BLACK | 41.806 | 244.00 | 5.00 | 61.300 | 268.821 |
| ASIAN | 0.518 | 372.00 | 85.00 | 21.900 | 1.250 |
| NH_WHITE | 12.926 | 422.00 | 258.00 | 322.300 | 54.464 |
| HOUSEHOLDS | 24.890 | 356.00 | 180.00 | 139.500 | 159.143 |
| AVG_HHSIZE | 1.830 | 1.92 | 1.87 | 1.548 | 1.915 |
| HU_VACANT | 5.309 | 6.00 | 13.00 | 17.900 | 22.393 |
| OCCHU_OWNE | 5.746 | 2.00 | 29.00 | 45.000 | 37.893 |
| OCCHU_RENT | 19.144 | 354.00 | 151.00 | 94.500 | 121.250 |
In [22]:
# Index db on cluster ID
tidy_db = cin_df.set_index("k5cls")
# Keep only variables used for clustering
tidy_db = tidy_db[predictors]
# Stack column names into a column, obtaining
# a "long" version of the dataset
tidy_db = tidy_db.stack()
# Take indices into proper columns
tidy_db = tidy_db.reset_index()
# Rename column names
tidy_db = tidy_db.rename(
columns={"level_1": "Attribute", 0: "Values"}
)
# Check out result
tidy_db.head()
Out[22]:
| k5cls | Attribute | Values | |
|---|---|---|---|
| 0 | 3 | POPULATION | 479.0 |
| 1 | 3 | MEDIAN_AGE | 55.7 |
| 2 | 3 | AGE_65 | 174.0 |
| 3 | 3 | WHITE | 433.0 |
| 4 | 3 | BLACK | 32.0 |
In [23]:
# Scale fonts to make them more readable
sns.set(font_scale=1.5)
# Setup the facets
facets = sns.FacetGrid(
data=tidy_db,
col="Attribute",
hue="k5cls",
sharey=False,
sharex=False,
aspect=2,
col_wrap=3
)
# Build the plot from `sns.kdeplot`
_ = facets.map(sns.kdeplot, "Values", fill=True, warn_singular=False).add_legend()
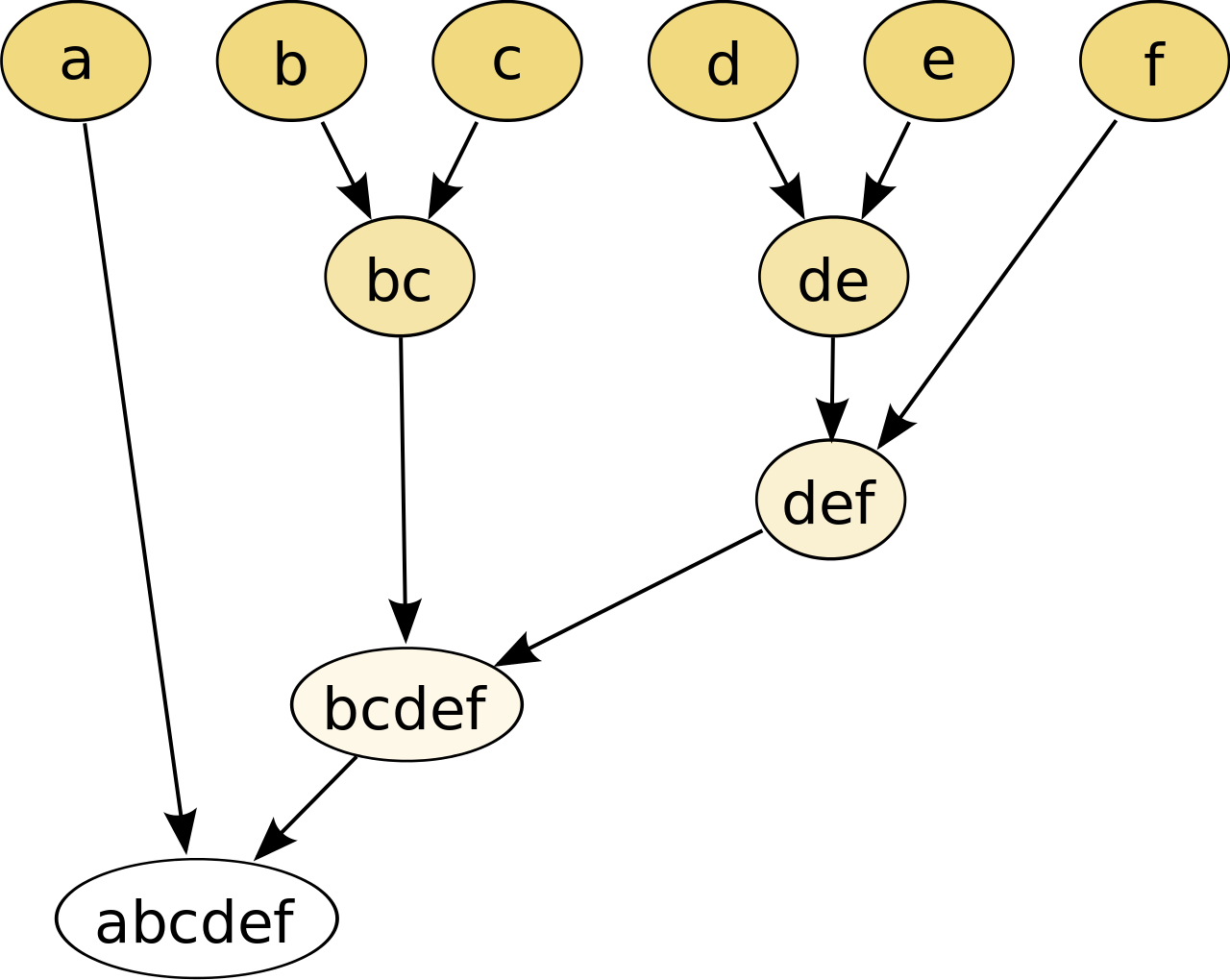
Hierarchical Clustering¶
- Agglomerative Hierarchical Clustering (AHC)
- Hierarchy of solutions (starts at singletons) and assign all observations into same cluster
- We are looking for in-between clustering solutions
AHC Algorithm¶
- Every observation is its own cluster
- Find two closest observations based on distance metric (Euclidean Distance)
- Join the closest into a new cluster
- Repeat 2 and 3 until reaching the desired degree of aggregation
In [24]:
from sklearn.cluster import AgglomerativeClustering
# Set seed for reproducibility
np.random.seed(0)
# Iniciate the algorithm
model = AgglomerativeClustering(linkage="ward", n_clusters=5)
# Run clustering
model.fit(db_scaled)
# Assign labels to main data table
cin_df["ward5"] = model.labels_
In [25]:
ward5sizes = cin_df.groupby("ward5").size()
ward5sizes
Out[25]:
ward5 0 442 1 5 2 8 3 1 4 1 dtype: int64
In [26]:
ward5means = cin_df.groupby("ward5")[predictors].mean()
ward5means.T.round(3)
Out[26]:
| ward5 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| POPULATION | 70.152 | 583.600 | 414.625 | 1108.00 | 361.00 |
| MEDIAN_AGE | 26.969 | 52.520 | 24.462 | 21.80 | 25.00 |
| AGE_65 | 7.964 | 154.600 | 13.125 | 6.00 | 16.00 |
| WHITE | 14.760 | 244.400 | 313.375 | 435.00 | 259.00 |
| BLACK | 53.041 | 324.200 | 63.500 | 244.00 | 5.00 |
| ASIAN | 0.550 | 5.000 | 25.250 | 372.00 | 85.00 |
| NH_WHITE | 14.566 | 242.200 | 311.125 | 422.00 | 258.00 |
| HOUSEHOLDS | 31.260 | 317.200 | 103.375 | 356.00 | 180.00 |
| AVG_HHSIZE | 1.835 | 1.688 | 1.557 | 1.92 | 1.87 |
| HU_VACANT | 6.163 | 38.400 | 13.000 | 6.00 | 13.00 |
| OCCHU_OWNE | 7.165 | 125.000 | 14.375 | 2.00 | 29.00 |
| OCCHU_RENT | 24.095 | 192.200 | 89.000 | 354.00 | 151.00 |
In [27]:
# Index db on cluster ID
tidy_db = cin_df.set_index("ward5")
# Keep only variables used for clustering
tidy_db = tidy_db[predictors]
# Stack column names into a column, obtaining
# a "long" version of the dataset
tidy_db = tidy_db.stack()
# Take indices into proper columns
tidy_db = tidy_db.reset_index()
# Rename column names
tidy_db = tidy_db.rename(
columns={"level_1": "Attribute", 0: "Values"}
)
# Check out result
tidy_db.head()
Out[27]:
| ward5 | Attribute | Values | |
|---|---|---|---|
| 0 | 1 | POPULATION | 479.0 |
| 1 | 1 | MEDIAN_AGE | 55.7 |
| 2 | 1 | AGE_65 | 174.0 |
| 3 | 1 | WHITE | 433.0 |
| 4 | 1 | BLACK | 32.0 |
In [28]:
# Setup the facets
facets = sns.FacetGrid(
data=tidy_db,
col="Attribute",
hue="ward5",
sharey=False,
sharex=False,
aspect=2,
col_wrap=3,
)
# Build the plot as a `sns.kdeplot`
facets.map(sns.kdeplot, "Values", fill=True, warn_singular=False).add_legend()
Out[28]:
<seaborn.axisgrid.FacetGrid at 0x212a852c7f0>
In [29]:
# Setup figure and ax
f, axs = plt.subplots(1, 2, figsize=(12, 6))
### K-Means ###
ax = axs[0]
# Plot unique values choropleth including
# a legend and with no boundary lines
cin_df.plot(
column="k5cls",
categorical=True,
cmap="Set2",
legend=True,
linewidth=0,
ax=ax,
)
# Remove axis
ax.set_axis_off()
# Add title
ax.set_title("K-Means solution ($k=5$)")
### AHC ###
ax = axs[1]
# Plot unique values choropleth including
# a legend and with no boundary lines
cin_df.plot(
column="ward5",
categorical=True,
cmap="Set3",
legend=True,
linewidth=0,
ax=ax,
)
# Remove axis
ax.set_axis_off()
# Add title
ax.set_title("AHC solution ($k=5$)")
# Display the map
f.savefig('two_clust.png')
plt.close()
In [30]:
Image(filename='two_clust.png')
Out[30]:
Why Regionalization¶
- Clustering helps us investigate the structure of our data (spatial contiguity is not always a requirement)
- We impose spatial constraint on clusters (geographically coherent areas + coherent data profiles)
- Counties within states (administrative principles), clusters within out data (statistical similarity)
- Spatial weights matrix can be used as a measure of spatial similarity
In [31]:
# Set the seed for reproducibility
np.random.seed(123456)
# Specify cluster model with spatial constraint
regi = AgglomerativeClustering(
linkage="ward", connectivity=w.sparse, n_clusters=5
)
# Fit algorithm to the data
regi.fit(db_scaled)
Out[31]:
AgglomerativeClustering(connectivity=<457x457 sparse matrix of type '<class 'numpy.float64'>'
with 2970 stored elements in Compressed Sparse Row format>,
n_clusters=5)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
AgglomerativeClustering(connectivity=<457x457 sparse matrix of type '<class 'numpy.float64'>'
with 2970 stored elements in Compressed Sparse Row format>,
n_clusters=5)In [32]:
cin_df["ward5wq"] = regi.labels_
# Setup figure and ax
f, ax = plt.subplots(1, figsize=(5, 5))
# Plot unique values choropleth including a legend and with no boundary lines
cin_df.plot(
column="ward5wq",
categorical=True,
legend=True,
linewidth=0,
ax=ax,
)
# Remove axis
ax.set_axis_off()
# Display the map
plt.show()
Why are we getting imbalanced clusters?¶
- Data is not normal
- Methods are not robust to outliers
In [33]:
cin_df[predictors].plot.hist(subplots=True, legend=True, layout=(4,3), figsize=(16,12), sharex=False);
K-Medoids Clustering (PAM)¶
- Partitioning around medoid (instead of 'mean', select most central actual observation).
- The medoid of a cluster is defined as the object in the cluster whose average dissimilarity to all the objects in the cluster is minimal, that is, it is a most centrally located point in the cluster.
- $k$-medoids minimizes a sum of pairwise dissimilarities instead of a sum of squared Euclidean distances (depends on implementation), it is more robust to noise and outliers than k-means
In [34]:
from sklearn_extra.cluster import KMedoids
kmedoids = KMedoids(n_clusters=5, random_state=0)
medo = kmedoids.fit(db_scaled)
In [35]:
cin_df["medo_k5"] = medo.labels_
# Setup figure and ax
f, ax = plt.subplots(1, figsize=(5, 5))
# Plot unique values choropleth including a legend and with no boundary lines
cin_df.plot(
column="medo_k5",
categorical=True,
legend=True,
linewidth=0,
ax=ax,
)
# Remove axis
ax.set_axis_off()
# Display the map
plt.show()
Feature Engineering¶
- Get $X$ and $Y$ coordinates from block centroids
- Normalize absolute values into percentage points
- pct_elder
- pct_white
- pct_black
- pct_own
- pct_rent
- pct_vac
- fill missing values with zeroes (for any gaps in our data)
In [36]:
# add xy to clustering
cin_df2 = cin_df.copy()
# calculate centroid locs
cin_df2['lng'] = cin_df2.centroid.x
cin_df2['lat'] = cin_df2.centroid.y
# pct vars
cin_df2['pct_elder'] = cin_df2.AGE_65 / cin_df2.POPULATION
cin_df2['pct_white'] = cin_df2.WHITE / cin_df2.POPULATION
cin_df2['pct_black'] = cin_df2.BLACK / cin_df2.POPULATION
cin_df2['pct_own'] = cin_df2.OCCHU_OWNE / cin_df2.HSNG_UNITS
cin_df2['pct_rent'] = cin_df2.OCCHU_RENT / cin_df2.HSNG_UNITS
cin_df2['pct_vac'] = cin_df2.HU_VACANT / cin_df2.HSNG_UNITS
cin_df2 = cin_df2.fillna(0)
new_predictors = ['POPULATION', 'MEDIAN_AGE', 'lng', 'lat', 'pct_elder', 'pct_white', 'pct_black',
'pct_own', 'pct_rent', 'pct_vac']
In [37]:
db_scaled2 = robust_scale(cin_df2[new_predictors])
In [38]:
# Set the seed for reproducibility
np.random.seed(123456)
# Specify cluster model with spatial constraint
xy_norm_model = AgglomerativeClustering(
linkage="ward",
#connectivity=w.sparse,
n_clusters=5
)
# Fit algorithm to the data
xy_norm_model.fit(db_scaled2)
Out[38]:
AgglomerativeClustering(n_clusters=5)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
AgglomerativeClustering(n_clusters=5)
In [39]:
cin_df2["xy_norm_model"] = xy_norm_model.labels_
# Setup figure and ax
f, ax = plt.subplots(1, figsize=(5, 5))
# Plot unique values choropleth including a legend and with no boundary lines
cin_df2.plot(
column="xy_norm_model",
categorical=True,
legend=True,
linewidth=0,
ax=ax,
)
# Remove axis
ax.set_axis_off()
# Display the map
plt.show()
In [40]:
# Set the seed for reproducibility
np.random.seed(123456)
# Specify cluster model with spatial constraint
xy_norm_geo_model = AgglomerativeClustering(
linkage="ward",
connectivity=w.sparse,
n_clusters=5
)
# Fit algorithm to the data
xy_norm_geo_model.fit(db_scaled2)
Out[40]:
AgglomerativeClustering(connectivity=<457x457 sparse matrix of type '<class 'numpy.float64'>'
with 2970 stored elements in Compressed Sparse Row format>,
n_clusters=5)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
AgglomerativeClustering(connectivity=<457x457 sparse matrix of type '<class 'numpy.float64'>'
with 2970 stored elements in Compressed Sparse Row format>,
n_clusters=5)In [41]:
cin_df2["xy_norm_geo5"] = xy_norm_geo_model.labels_
# Setup figure and ax
f, ax = plt.subplots(1, figsize=(5, 5))
# Plot unique values choropleth including a legend and with no boundary lines
cin_df2.plot(
column="xy_norm_geo5",
categorical=True,
legend=True,
linewidth=0,
ax=ax,
)
# Remove axis
ax.set_axis_off()
# Display the map
plt.show()
The Final View of Partitioning for Data¶
In [42]:
sns.set(font_scale=1)
fig, axs = plt.subplots(3, 2, figsize=(10, 16))
axs = axs.flatten();
cin_df2.plot(column="k5cls", categorical=True, legend=True, linewidth=0, ax=axs[0]);
axs[0].set_title('k-Means Clustering (k=5)', fontsize=14);
cin_df2.plot(column="ward5", categorical=True, legend=True, linewidth=0, ax=axs[1]);
axs[1].set_title('AHC Clustering (k=5)', fontsize=14);
cin_df2.plot(column="ward5wq", categorical=True, legend=True, linewidth=0, ax=axs[2]);
axs[2].set_title('Regionalized AHC Clustering (k=5)', fontsize=14);
cin_df2.plot(column="medo_k5", categorical=True, legend=True, linewidth=0, ax=axs[3]);
axs[3].set_title('k-Medoids Clustering (k=5)', fontsize=14);
cin_df2.plot(column="xy_norm_model", categorical=True, legend=True, linewidth=0, ax=axs[4]);
axs[4].set_title('AHC Clustering with Normalized Variables \n and Geographic Coordinates (k=5)', fontsize=14);
cin_df2.plot(column="xy_norm_geo5", categorical=True, legend=True, linewidth=0, ax=axs[5]);
axs[5].set_title('AHC Clustering with Normalized Variables \n and Geographic Coordinates and Contiguity (k=5)', fontsize=14);
[i.set_axis_off() for i in axs]
plt.subplots_adjust(hspace=-0.45)
fig.savefig('all_clust.png', bbox_inches='tight')
plt.close()
In [43]:
Image(filename='all_clust.png')
Out[43]: