GEOG 172: INTERMEDIATE GEOGRAPHICAL ANALYSIS
Evgeny Noi
Lecture 18: Multi-scale Geographically Weighted Regression
Regression Modeling for Spatial Relations¶
- Spatial heterogeneity
- Fixed-effect model
- Spatial regimes
- Spatial Dependence
- SLX (spatial feature engineering)
- Spatial error model
- Spatial lag model
- Local Modeling Frameworks (GWR and MGWR)
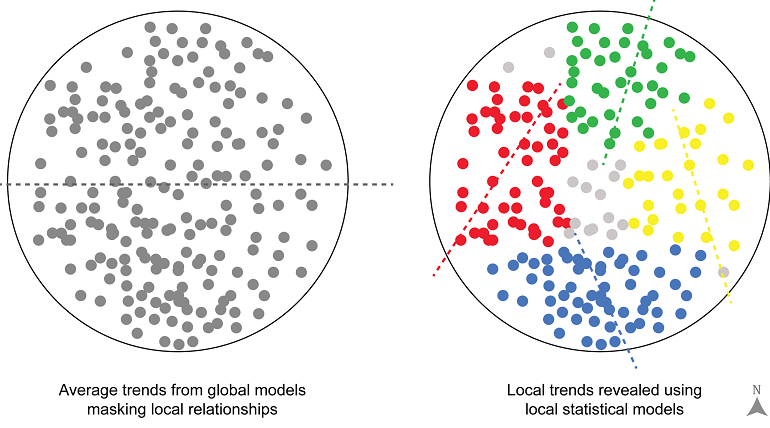
(M)GWR¶
- estimate location-dependent relationship between dependent and independent variables
- place-based analytic technique
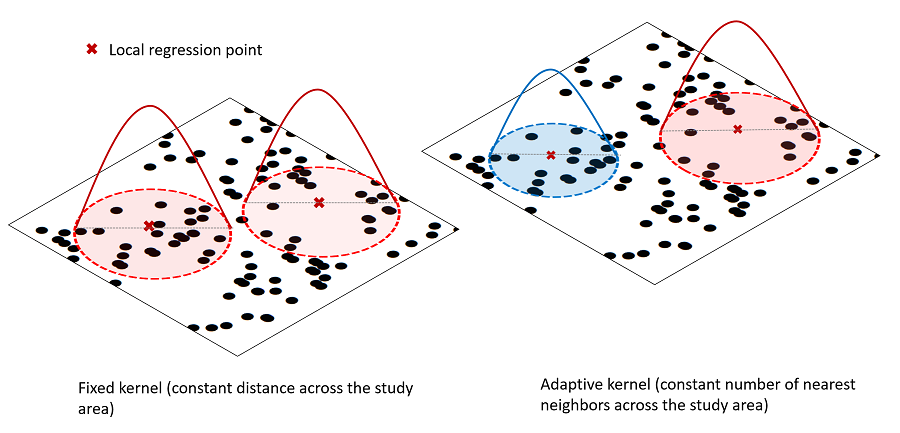
- GWR models borrow data from neighboring observations and weight these data according to a smooth decay function based on either a physical distance or the number of nearest neighbors (higher weight for nearby locations)
(M)GWR¶
- Small bandwidths denote more local processes; large bandwidths indicate regional or global processes.
- As long as an optimal bandwidth is determined in the calibration of the GWR model and some continuous smooth function of distance is used, the specific kernel function chosen is not critical.
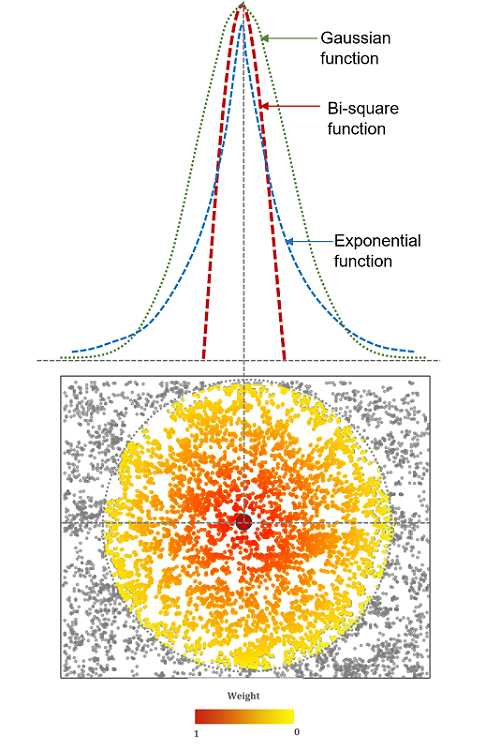
Selecting Optimal Bandwidth¶
- Trade-off between bias and variance.
- As bw increases, the bias increases, because we are borrowing from locations that could have been generated by increasingly different processes
- As bw decreases, the local parameter estimation uncertainty rises (fewer data points)
- Statistical optimization: trade-off between model fit and model complexity (e.g. AIC)
GWR Model Specification¶
$$ Y_i = \beta_0(u_i, v_i) + \sum_{j}\beta_j(u_i, v_i)X_{ji} + \epsilon_i $$where $j$ is the number of dependent variables and $\beta$ vary across space (surface estimation)
- overlapping sets of points are used, classical t-tests are not appropriate, thus $\alpha$ needs to be corrected and MC appliedd
MGWR Model Specification¶
$$ Y_i = \beta_0(u_i, v_i) + \sum_{j}\beta_{bwj}(u_i, v_i)X_{ji} + \epsilon_i $$where $\beta_{bwj}$ indicates the bandwidth used for calibration of the $j$th relationship.
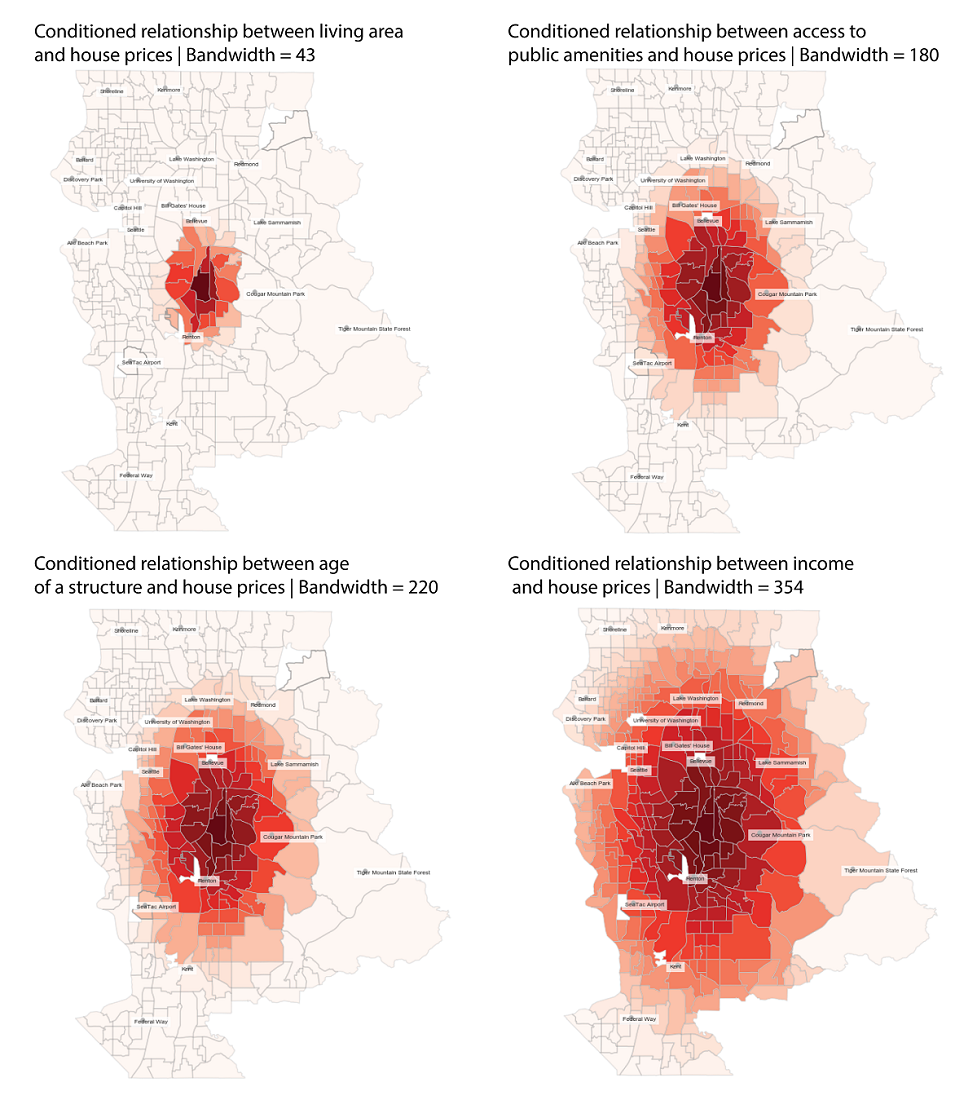
(M)GWR Limitations¶
- More computationally intensive (if you have >500 observations might take too long on desktop computers)
- Limited interpretation
In [5]:
db = gpd.read_file("regression_db.geojson")
print(db.shape)
db.head()
(6110, 20)
Out[5]:
| accommodates | bathrooms | bedrooms | beds | neighborhood | pool | d2balboa | coastal | price | log_price | id | pg_Apartment | pg_Condominium | pg_House | pg_Other | pg_Townhouse | rt_Entire_home/apt | rt_Private_room | rt_Shared_room | geometry | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 5 | 2.0 | 2.0 | 2.0 | North Hills | 0 | 2.972077 | 0 | 425.0 | 6.052089 | 6 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | POINT (-117.12971 32.75399) |
| 1 | 6 | 1.0 | 2.0 | 4.0 | Mission Bay | 0 | 11.501385 | 1 | 205.0 | 5.323010 | 5570 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | POINT (-117.25253 32.78421) |
| 2 | 2 | 1.0 | 1.0 | 1.0 | North Hills | 0 | 2.493893 | 0 | 99.0 | 4.595120 | 9553 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | POINT (-117.14121 32.75327) |
| 3 | 2 | 1.0 | 1.0 | 1.0 | Mira Mesa | 0 | 22.293757 | 0 | 72.0 | 4.276666 | 14668 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | POINT (-117.15269 32.93110) |
| 4 | 2 | 1.0 | 1.0 | 1.0 | Roseville | 0 | 6.829451 | 0 | 55.0 | 4.007333 | 38245 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | POINT (-117.21870 32.74202) |
In [7]:
variable_names = [
"accommodates", # Number of people it accommodates
"bathrooms", # Number of bathrooms
"bedrooms", # Number of bedrooms
"beds", # Number of beds
# Below are binary variables, 1 True, 0 False
"rt_Private_room", # Room type: private room
"rt_Shared_room", # Room type: shared room
"pg_Condominium", # Property group: condo
"pg_House", # Property group: house
"pg_Other", # Property group: other
"pg_Townhouse", # Property group: townhouse
]
In [13]:
f,ax = plt.subplots(figsize=(5,5))
db.plot(column='log_price', ax=ax, legend=True, markersize=5, alpha=.5);
ax.set_title('AirBnb listing price in San Diego \n log(price)')
Out[13]:
Text(0.5, 1.0, 'AirBnb listing price in San Diego \n log(price)')
In [8]:
# Fit OLS model
m1 = spreg.OLS(
# Dependent variable
db[["log_price"]].values,
# Independent variables
db[variable_names].values,
# Dependent variable name
name_y="log_price",
# Independent variable name
name_x=variable_names,
)
In [9]:
print(m1.summary)
REGRESSION
----------
SUMMARY OF OUTPUT: ORDINARY LEAST SQUARES
-----------------------------------------
Data set : unknown
Weights matrix : None
Dependent Variable : log_price Number of Observations: 6110
Mean dependent var : 4.9958 Number of Variables : 11
S.D. dependent var : 0.8072 Degrees of Freedom : 6099
R-squared : 0.6683
Adjusted R-squared : 0.6678
Sum squared residual: 1320.148 F-statistic : 1229.0564
Sigma-square : 0.216 Prob(F-statistic) : 0
S.E. of regression : 0.465 Log likelihood : -3988.895
Sigma-square ML : 0.216 Akaike info criterion : 7999.790
S.E of regression ML: 0.4648 Schwarz criterion : 8073.685
------------------------------------------------------------------------------------
Variable Coefficient Std.Error t-Statistic Probability
------------------------------------------------------------------------------------
CONSTANT 4.3883830 0.0161147 272.3217773 0.0000000
accommodates 0.0834523 0.0050781 16.4336318 0.0000000
bathrooms 0.1923790 0.0109668 17.5419773 0.0000000
bedrooms 0.1525221 0.0111323 13.7009195 0.0000000
beds -0.0417231 0.0069383 -6.0134430 0.0000000
rt_Private_room -0.5506868 0.0159046 -34.6244758 0.0000000
rt_Shared_room -1.2383055 0.0384329 -32.2198992 0.0000000
pg_Condominium 0.1436347 0.0221499 6.4846529 0.0000000
pg_House -0.0104894 0.0145315 -0.7218393 0.4704209
pg_Other 0.1411546 0.0228016 6.1905633 0.0000000
pg_Townhouse -0.0416702 0.0342758 -1.2157316 0.2241342
------------------------------------------------------------------------------------
REGRESSION DIAGNOSTICS
MULTICOLLINEARITY CONDITION NUMBER 11.964
TEST ON NORMALITY OF ERRORS
TEST DF VALUE PROB
Jarque-Bera 2 2671.611 0.0000
DIAGNOSTICS FOR HETEROSKEDASTICITY
RANDOM COEFFICIENTS
TEST DF VALUE PROB
Breusch-Pagan test 10 322.532 0.0000
Koenker-Bassett test 10 135.581 0.0000
================================ END OF REPORT =====================================
In [15]:
db.head()
Out[15]:
| accommodates | bathrooms | bedrooms | beds | neighborhood | pool | d2balboa | coastal | price | log_price | id | pg_Apartment | pg_Condominium | pg_House | pg_Other | pg_Townhouse | rt_Entire_home/apt | rt_Private_room | rt_Shared_room | geometry | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 5 | 2.0 | 2.0 | 2.0 | North Hills | 0 | 2.972077 | 0 | 425.0 | 6.052089 | 6 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | POINT (-117.12971 32.75399) |
| 1 | 6 | 1.0 | 2.0 | 4.0 | Mission Bay | 0 | 11.501385 | 1 | 205.0 | 5.323010 | 5570 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | POINT (-117.25253 32.78421) |
| 2 | 2 | 1.0 | 1.0 | 1.0 | North Hills | 0 | 2.493893 | 0 | 99.0 | 4.595120 | 9553 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | POINT (-117.14121 32.75327) |
| 3 | 2 | 1.0 | 1.0 | 1.0 | Mira Mesa | 0 | 22.293757 | 0 | 72.0 | 4.276666 | 14668 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | POINT (-117.15269 32.93110) |
| 4 | 2 | 1.0 | 1.0 | 1.0 | Roseville | 0 | 6.829451 | 0 | 55.0 | 4.007333 | 38245 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | POINT (-117.21870 32.74202) |
In [19]:
#Prepare Georgia dataset inputs
g_y = db['log_price'].values.reshape((-1,1))
g_X = db[variable_names].values
# reproject to get meters
db = db.to_crs('EPSG:32611')
u = db.geometry.centroid.x
v = db.geometry.centroid.y
g_coords = list(zip(u,v))
g_X = (g_X - g_X.mean(axis=0)) / g_X.std(axis=0)
# this rescales variables
g_y = g_y.reshape((-1,1))
g_y = (g_y - g_y.mean(axis=0)) / g_y.std(axis=0)
In [32]:
#This might be needed to turn off the OpenMP multi-threading
# %env OMP_NUM_THREADS = 1
import multiprocessing as mp
# here is how to use parallalization (works better on local machine)
n_proc = 4 #two processors
pool = mp.Pool(n_proc)
In [33]:
from mgwr.gwr import GWR, MGWR
from mgwr.sel_bw import Sel_BW
#Calibrate GWR model
gwr_selector = Sel_BW(g_coords, g_y, g_X)
gwr_bw = gwr_selector.search()
print(gwr_bw)
gwr_results = GWR(g_coords, g_y, g_X, gwr_bw).fit() #bw=384
384.0
In [34]:
gwr_results.localR2[0:10]
Out[34]:
array([[0.64594203],
[0.69396307],
[0.59707561],
[0.76902883],
[0.68488587],
[0.57839382],
[0.65114373],
[0.84073123],
[0.7878669 ],
[0.75561498]])
In [35]:
gwr_results.summary()
=========================================================================== Model type Gaussian Number of observations: 6110 Number of covariates: 11 Global Regression Results --------------------------------------------------------------------------- Residual sum of squares: 2026.415 Log-likelihood: -5298.038 AIC: 10618.075 AICc: 10620.127 BIC: -51142.728 R2: 0.668 Adj. R2: 0.668 Variable Est. SE t(Est/SE) p-value ------------------------------- ---------- ---------- ---------- ---------- X0 -0.000 0.007 -0.000 1.000 X1 0.294 0.018 16.434 0.000 X2 0.206 0.012 17.542 0.000 X3 0.215 0.016 13.701 0.000 X4 -0.089 0.015 -6.013 0.000 X5 -0.312 0.009 -34.624 0.000 X6 -0.253 0.008 -32.220 0.000 X7 0.051 0.008 6.485 0.000 X8 -0.006 0.009 -0.722 0.470 X9 0.049 0.008 6.191 0.000 X10 -0.009 0.008 -1.216 0.224 Geographically Weighted Regression (GWR) Results --------------------------------------------------------------------------- Spatial kernel: Adaptive bisquare Bandwidth used: 384.000 Diagnostic information --------------------------------------------------------------------------- Residual sum of squares: 1452.044 Effective number of parameters (trace(S)): 428.246 Degree of freedom (n - trace(S)): 5681.754 Sigma estimate: 0.506 Log-likelihood: -4279.817 AIC: 9418.126 AICc: 9483.157 BIC: 12301.661 R2: 0.762 Adjusted R2: 0.744 Adj. alpha (95%): 0.001 Adj. critical t value (95%): 3.221 Summary Statistics For GWR Parameter Estimates --------------------------------------------------------------------------- Variable Mean STD Min Median Max -------------------- ---------- ---------- ---------- ---------- ---------- X0 225137641741.179 9249623383133.199 -2753748900385.411 0.004 624978556242947.625 X1 0.221 0.129 -0.259 0.215 0.654 X2 0.184 0.118 -0.396 0.186 0.569 X3 0.228 0.136 -0.156 0.255 0.745 X4 -0.048 0.117 -0.415 -0.063 0.356 X5 -0.274 0.054 -0.440 -0.282 -0.089 X6 1326803840988.813 54510812752279.562 -16228670558569.268 -0.198 3683186616621919.500 X7 0.048 0.061 -0.301 0.051 0.179 X8 0.044 0.079 -0.190 0.040 0.438 X9 0.037 0.076 -0.179 0.030 0.263 X10 0.001 0.042 -0.171 -0.000 0.198 ===========================================================================
In [37]:
# # THIS CODE TAKES TOO LONG TO RUN ON MY LAPTOP
# #Calibrate MGWR model
# mgwr_selector = Sel_BW(g_coords, g_y, g_X, multi=True)
# mgwr_bw = mgwr_selector.search(multi_bw_min=[2])
# print(mgwr_bw)
# mgwr_results = MGWR(g_coords, g_y, g_X, mgwr_selector).fit()
In [38]:
pool.close() # Close the pool when you finish
pool.join()
In [42]:
# Add R2 to GeoDataframe
db['gwr_R2'] = gwr_results.localR2
fig, ax = plt.subplots(figsize=(6, 6))
db.plot(column='gwr_R2', cmap = 'coolwarm', linewidth=0.01, scheme = 'FisherJenks', k=5, legend=True, legend_kwds={'bbox_to_anchor':(1.10, 0.96)}, ax=ax)
ax.set_title('Local R2', fontsize=12)
ax.axis("off")
#plt.savefig('myMap.png',dpi=150, bbox_inches='tight')
plt.show()
In [44]:
#Add GWR parameters to GeoDataframe
db['gwr_intercept'] = gwr_results.params[:,0]
db['gwr_accom'] = gwr_results.params[:,1]
db['gwr_bathroom'] = gwr_results.params[:,2]
db['gwr_beddroom'] = gwr_results.params[:,3]
#Obtain t-vals filtered based on multiple testing correction
gwr_filtered_t = gwr_results.filter_tvals()
In [49]:
f, ax = plt.subplots()
db.plot('gwr_accom',ax=ax, cmap='coolwarm', legend=True);
ax.set_title('Coefficients for Accommodation');
Out[49]:
Text(0.5, 1.0, 'Coefficients for Accommodation')