{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Introduction to Bioinformatics**
\n",
"A masters course by Blaž Zupan and Tomaž Curk
\n",
"University of Ljubljana (C) 2016-2018\n",
"\n",
"Disclaimer: this work is a first draft of our working notes. The images were obtained from various web sites, but mainly from the wikipedia entries with explanations of different biological entities. Material is intended for our bioinformatics class and is not meant for distribution.\n",
"\n",
"## Lecture Notes Part 6\n",
"\n",
"# Sequence Alignment: Few More Tricks"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The last lecture was about sequence alignment and dynamic\n",
"programming. We have learned that the type of problems that includes\n",
"sequence alignment can be solved with algorithms whose complexity only\n",
"linearly depend on the sequence length. This was due to a class of\n",
"scoring function used, where the value of the scoring function depends\n",
"only on the pair of symbols of the align sequences, and not on any of\n",
"its neighbors. Hence, it is possible to find optimal alignments by\n",
"first finding (scoring) optimal alignments of sequence heads, that is,\n",
"subsequences from the start to some position of the sequence, and the\n",
"scoring the alignment of the rest of the sequence.\n",
"\n",
"We have introduced Needleman-Wunsch algorithm that perform global\n",
"alignment and aligns all the symbols of the two sequences. Just like\n",
"any other dynamic programming algorithm, it uses dynamic programming\n",
"table and the steps that include table initialization, table\n",
"computation and trace-back. Let us illustrate this approach on a\n",
"related problem of longest common subsequence."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Longest common subsequence (LCS)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For a start, consider a sequence $s$. A subsequence of $s$ is a\n",
"sequence that can be derived from $s$ by deleting some elements\n",
"without changing the order of the remaining elements. Say, ATACG is a\n",
"subsequence of ATTATCTG, and so is ATTA, and ACG, and TTG. With\n",
"$n=|s|$ being the length of $s$, thera are $2^n$ subsequences of $s$,\n",
"counting also an empty subsequence.\n",
"\n",
"We will design the algorithm to solve LCS for a pair of\n",
"sequences. Given two sequences, $s$ and $t$, our aim is to find a\n",
"sequence $p$ that is a subsequence of $s$ and subsequence of $t$, such\n",
"that there is no $p'$ that is a subsequence of $s$ and $t$ and\n",
"that is longer than $p$.\n",
"\n",
"For a start, we will consider a simpler problem of finding the length\n",
"of such subsequence. We will use dynamic programming. The scoring\n",
"function for our problem is simple: we can take a symbol from either\n",
"$s$ or $t$, and the score will not change. But if we take a symbol\n",
"from both sequences, the alignment score would increase by $1$ if the\n",
"two symbols are equal and would not change if the symbols are\n",
"different. Increasing the score also means that we have, locally,\n",
"increased the common subsequence with that particular symbol.\n",
"\n",
"Our recursive definition of the entries of dynamic programming table\n",
"are is thus:\n",
"\n",
"$$M_{i,j}= \\max\n",
"\\begin{cases}\n",
"M_{i-1,j}\\\\\n",
"M_{i,j-1}\\\\\n",
"M_{i-1,j-1}+{\\bf 1}(s_i\\equiv t_i)\n",
"\\end{cases}$$\n",
"\n",
"Here, ${\\bf 1}(x)$ is an indicator function that has a value of 1 when $x$ is true and 0 otherwise. \n",
"\n",
"For initialization, we assume that subsequences where no symbol has been taken from $s$ (or from $t$) have all zero length. So, $M_{i, 1}=0$ for $i\\in\\{1,\\ldots,|s|\\}$ and $M_{1, j}=0$ for $j\\in\\{1,\\ldots,|t|\\}$.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This looks so easy. In our implementation, we will also use a trick and define the dynamic programming table as a dictionary whose default values are 0. So, no need for explicit initialization. The function that computes the length of longest common subsequence for two sequences is therefore as follows."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from collections import defaultdict\n",
"\n",
"def lcs_length(s, t):\n",
" \"\"\"Length of longest common subsequence.\"\"\"\n",
" table = defaultdict(int)\n",
" for i, si in enumerate(s):\n",
" for j, tj in enumerate(t):\n",
" table[i, j] = max(\n",
" table[i-1, j],\n",
" table[i, j-1],\n",
" table[i-1, j-1] + (si == tj)\n",
" )\n",
" return table[len(s)-1, len(t)-1]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now for a few tests."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"3"
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"s = \"AACC\"\n",
"t = \"ATAGCG\"\n",
"lcs_length(s, t)"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"4"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"s = \"AAAAAGGGG\"\n",
"t = \"GGGGAA\"\n",
"lcs_length(s, t)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"11"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"s = \"ATGTATCTATA\"\n",
"t = \"ACTCGTCACTCCTCATCA\"\n",
"lcs_length(s, t)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Seems to work. Though, at least for the last example, it is hard to\n",
"tell. It would be easier if we would print out the subsequence. The\n",
"code for this is a bit more complicated. For each cell in dynamic\n",
"programming table, we need to remember which was the optimal path,\n",
"that is the longest subsequence that led us to the state represented\n",
"with the cell in the table. We will store this in a separate\n",
"dictionary we will call *prev* (as for the *previous* best cell). "
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def lcs_table(s, t):\n",
" \"\"\"Construction of dynamic programming table.\"\"\"\n",
" table = defaultdict(int)\n",
" prev = {}\n",
" for i, si in enumerate(s):\n",
" for j, tj in enumerate(t):\n",
" table[i, j], prev[i, j] = max(\n",
" (table[i-1, j], (i-1, j)),\n",
" (table[i, j-1], (i, j-1)),\n",
" (table[i-1, j-1] + (si == tj), (i-1, j-1))\n",
" )\n",
" return table, prev"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The above function constructs the dynamic programming table, and a\n",
"table with an entry for the *best* previous cell. To obtain the\n",
"longest common subsequence, we have to traverse the table: any time we\n",
"find that the move that we have made was diagonal and the symbols we\n",
"took from $s$ and $t$ were the same, that symbol is a part of the\n",
"common subsequence."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def trace_back(s, t, table, prev):\n",
" \"\"\"Trace-back and return the longest common subsequence.\"\"\"\n",
" i, j = len(s)-1, len(t)-1\n",
" lcs = \"\"\n",
" while table[i, j] != 0:\n",
" if prev[i, j] == (i-1, j-1) and (s[i]==t[j]):\n",
" lcs = s[i] + lcs\n",
" i, j = prev[i, j]\n",
" return lcs\n",
"\n",
"def lcs(s, t):\n",
" table, prev = lcs_table(s, t)\n",
" return trace_back(s, t, table, prev)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let us try this out."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"'GGGG'"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"s = \"AAAAAGGGG\"\n",
"t = \"GGGGAA\"\n",
"lcs(s, t)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"'ATGTATCTATA'"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"s = \"ATGTATCTATA\"\n",
"t = \"ACTCGTCACTCCTCATCA\"\n",
"lcs(s, t)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Wow, works! But this was a simple example of dynamic programming. Now for some more complex ones."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Local Alignment"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Needleman-Wunsch globally aligns two sequences. But what we are\n",
"actually after optimal local alignment. That is, we are looking for\n",
"alignment of two subsequences from $s$ and $t$ with the highest\n",
"alignment score. At first, this algorithm looks so much different from\n",
"Needleman-Wunsch algorithm that it requires another name: a\n",
"Smith-Waterman algorithm. Turns out Needleman-Wunsch algorithm was proposed in\n",
"1970, and Smith-Waterman somehow later, in 1981. The difference\n",
"between these two approaches is, though, surprisingly small. For a\n",
"taste, here is the recursive definition of entries of dynamic\n",
"programming table for Needleman-Wunsch:\n",
"\n",
"$$M_{i,j}= \\max\n",
"\\begin{cases}\n",
"M_{i-1,j}+\\sigma(s_i,-)\\\\\n",
"M_{i,j-1}+\\sigma(-,t_i)\\\\\n",
"M_{i-1,j-1}+\\sigma(s_i,t_i)\n",
"\\end{cases}$$\n",
"\n",
"And here goes the definition for Smith-Waterman:\n",
"\n",
"$$M_{i,j}= \\max\n",
"\\begin{cases}\n",
"M_{i-1,j}+\\sigma(s_i,-)\\\\\n",
"M_{i,j-1}+\\sigma(-,t_i)\\\\\n",
"M_{i-1,j-1}+\\sigma(s_i,t_i) \\\\\n",
"0\n",
"\\end{cases}$$\n",
"\n",
"That's it. Crazy, right? That is the only difference between global\n",
"and local alignment. Of course we have assumed we are not interested\n",
"in alignments which are scored below $0$, and are only looking for\n",
"subsequences whose alignment scores are positive. Therefore, we have\n",
"to set the scoring function $\\sigma$ accordingly. For DNA alignment, the\n",
"scoring functions we have introduced in our last lecture would do just fine.\n",
"\n",
"Here is an example of optimal local alignment of two sequences:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"`\n",
"------------------TCCCAGTTATGTCAGGGGACACGAGCATGCAGAGAC\n",
" ||||||||||||\n",
"AATTGCCGCCGTCGTTTTCAGCAGTTATGTCAGATC------------------\n",
"`"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Do not be misguided by this example, the optimal local alignment may contain also indels, or can include conflicting pairs of symbols (our example does not). The idea of Smith-Waterman is now the following: find the cell with the maximum alignment score in the dynamic programming table, and from this cell trace-back to the last cell with a positive score. The traced path reveals an optimal local alignment. For the two sequences above, the dynamic programming table and the traced path (the uderlined scores) are shown below."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Local alignment is therefore just like global alignment where history does not matter and restarts from 0 are allowed."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Local Alignment and Permutation Tests\n",
"\n",
"We can find local alignments with some positive scores in virtually\n",
"any pair of sequences. But how likely is it that are our finding is\n",
"not due to chance? Permutation analysis comes to the rescue. We could\n",
"take two sequences, $s$ and $t$, compute the local alignment score $M$,\n",
"and then ask what is the probability that this score could not be\n",
"obtained on a set of arbitrary sequence. For this purpose, we take\n",
"$s$, randomly permute its symbols, compute the maximal alignment\n",
"score, and repeat the procedure, say, 10.000 times. We then compute\n",
"how many times we obtain the score that is equal to or greater than\n",
"$M$. The proportion of such scores is our $p$ value, and tells us\n",
"about probability we could achieve this score in unstructured\n",
"sequences. We would like the $p$-value to be small, say, below\n",
"$0.0001$ and report on local alignment only if it is not due by\n",
"chance, or better, when this chance is very very small."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Alignment with Affine Gap Scores"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So far, we have brutally penalized gaps, that is, the parts of the\n",
"alignments where we took a symbol from one sequence but retained the\n",
"position in the other sequence. In nature, insertions would often\n",
"involve a series of nucleotides. We should penalize the start of the\n",
"insertion, but then the penalty should less depend on the length of\n",
"the inserted sequence. The total penalty for the insertion should\n",
"therefore be something like:\n",
"\n",
"$$\\gamma(x)=-(\\rho+\\eta x)$$\n",
"\n",
"where $\\rho$ is the penalty for the introduction of the gap, $\\eta$\n",
"the cost of each gap symbol, and $x$ the length of the gap. Normally,\n",
"$\\rho\\gg\\eta$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We now need to design the algorithm that can consider affine gap\n",
"penalties, that is the algorithm that assigns different penalties for\n",
"the opening and extending the gap. Notice that the gap may span\n",
"across one or the other sequence. The solution for the problem is\n",
"decomposition of the dynamic programming table to three tables. We\n",
"will use the table $M$ for scoring the alignments when we consume both\n",
"symbols, one from $s$ and the other from $t$. For consuming symbols\n",
"from $s$ only (gaps in sequence $t$) we will consult the table\n",
"$M^{\\downarrow}$, and for consuming symbols from $t$ (skipping the\n",
"sequence from $s$) we will consult $M^{\\rightarrow}$. This is like\n",
"traversing the three-layered transit system. In the world of $M$, we\n",
"can only go diagonally, south-east. But then we can jump to the layer\n",
"$M^{\\downarrow}$, where we can only go south, or can jump to\n",
"$M^{\\rightarrow}$, where we can only go east. Direct jumps from\n",
"$M^{\\downarrow}$ to $M^{\\rightarrow}$ are not allowed, and can only go\n",
"through $M$. Let us write this in equations:\n",
"\n",
"$$M^{\\downarrow}_{i,j}= \\max\n",
"\\begin{cases}\n",
"M^{\\downarrow}_{i-1,j}-\\eta\\\\\n",
"M_{i-1,j}-(\\eta+\\rho)\n",
"\\end{cases}$$\n",
"\n",
"$$M^{\\rightarrow}_{i,j}= \\max\n",
"\\begin{cases}\n",
"M^{\\rightarrow}_{i,j-1}-\\eta\\\\\n",
"M_{i,j-1}-(\\eta+\\rho)\n",
"\\end{cases}$$\n",
"\n",
"$$M_{i,j}= \\max\n",
"\\begin{cases}\n",
"M_{i-1,j-1}+\\sigma(s_i,t_j)\\\\\n",
"M^{\\downarrow}_{i,j}\\\\\n",
"M^{\\rightarrow}_{i,j}\n",
"\\end{cases}$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Multiple Sequence Alignment"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Consider an example of a global alignment of three sequences:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"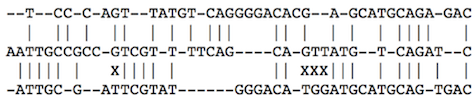"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We can extend the basic Needleman-Wunsch to consider any number of\n",
"sequences. For three sequences, the table $M$ is three dimensional,\n",
"and any of its cells can be reached from seven different neighboring\n",
"cells: from 1 taking symbols from all three sequences, from 3 taking\n",
"symbols from two but not from one sequence (there are three such\n",
"combinations), and from 3 taking a symbol just from one of the three\n",
"sequences. Also, the scoring function has now to consider three\n",
"symbols, that is $\\sigma(s_i, t_j, u_k)$.\n",
"\n",
"The complexity of multiple sequence alignment grows with the number of\n",
"sequences. For $q$ sequences, assuming they are of the equal length of\n",
"$n$, the complexity of the algorithm is now\n",
"$\\mathcal{O}(n^q)$. Despite using dynamic programming, simultaneously\n",
"aligning many sequences is not feasible, and other heuristics come\n",
"into play, like those used in [Clustal](https://en.wikipedia.org/wiki/Clustal) series of algorithms.\n",
"\n",
"We could, intuitively, immediately think of some tricks that we could\n",
"use in such situations. Say, we are looking for the alignment of $q$\n",
"sequences. We will start with two most similar sequences, align them\n",
"and then, by fixing the alignment align a third sequences. We will\n",
"repeat the procedure, each time aligning another non-align sequence\n",
"that will be most similar to the current alignment. We could also\n",
"replace an aligned sequence with consensus sequence, represented with\n",
"symbols that are most frequent at some alignment position. Or\n",
"represent each alignment position with probability of the symbols, and\n",
"then change the scoring function so that it would consider these\n",
"probabilities instead of crisp symbols. The scoring function could\n",
"then be entropy-based, say using $\\sum_{x\\in {\\mathcal A}}p_x\\log p_x$,\n",
"where ${\\mathcal A}$ is an alphabet and $p_x$ is probability of the\n",
"symbol $x$ at a given position of the alignment. Those of you already\n",
"introduced in data science would remember this formula from several\n",
"machine learning algorithms.\n",
"\n",
"Oh, so many ideas. But in fact these above, although looking quite\n",
"simple, are not far from what constitutes industrial-level alignment\n",
"algorithms, like [Clustal](https://en.wikipedia.org/wiki/Clustal). The\n",
"guiding principle for these algorithms is that they have to work\n",
"reasonably well and they have to be very fast, as --- what we know by\n",
"now --- biological sequences are long and they come in plenty."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Substitution Matrices"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"So far we have assumed that the penalty of substituting one nucleotide\n",
"with another does not depend on the nucleotides. That is, substituting\n",
"A with T would receive the same penalty as substituting A with G. But\n",
"in nature, substitutions, even on the nucleotide level, are not\n",
"equally likely and because of redundancy of genetic code have\n",
"different implications. This is even more true if we consider\n",
"sequences of aminoacids. Say, some aminoacids are polar, so replacing\n",
"a polar aminoacid Glutamine (Q) with another polar aminoacid\n",
"Asparagine (N) may have a lesser effect then replacement with hydrophobic amino acid\n",
"Alanine (A). The evolution would be more prone to replacements which cause\n",
"lesser harm, so in theory we could derive a scoring (substitution)\n",
"matrix from sequence comparison of homologous genes. This has indeed\n",
"been done and has resulted in a series of [substitution matrices](https://en.wikipedia.org/wiki/Substitution_matrix) called\n",
"PAM and BLOSUM. Here is an example of BLOSUM50 substitution matrix:"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.5"
}
},
"nbformat": 4,
"nbformat_minor": 1
}